和
。摘要 基于印制电路板（PCB）绕组及平面变压器技术，提出一种仅包含单一磁件的磁集成设计方案，可有效解决多谐振变换器中磁性元件数量过多的问题，并将其成功应用到CLTLC多谐振变换器中。该变换器的所有磁性元件，包括两个谐振电感和两个高频变压器，都可集成到EIE型磁心结构中。为实现变压器励磁电感和漏感的解耦控制，利用矩阵变压器思想和绕组不均匀分布设计，在磁心的中柱引入一定气隙，可得到一种新型E型磁心结构。另外，基于该结构，建立变压器的磁阻模型，从数学角度对所提磁集成方案进行论证。同时，给出最终的磁集成设计方案。最后，建立一台额定功率为1kW的CLTLC多谐振变换器样机，并进行了相关实验。实验结果验证了所提磁集成设计方案的可行性和有效性，变换器的最大效率可达96.45%。
关键词：PCB绕组 平面变压器 不均匀分布绕组 谐振型直流变换器 高转换效率
谐振型直流变换器因其具有高效率、高频率、高功率密度和低电磁干扰的优点，得到了学术界的广泛关注。三元件LLC谐振变换器是其中的典型代表，它结构简单，且可以在全负载范围内实现零电压软开关（Zero Voltage Switching, ZVS）开通。虽然具备上述优点，但受限于谐振元件的数量，在轻载条件下，LLC的转换效率和电压增益特性互相限制，彼此矛盾[1-2]。为了满足某一方面的性能需求，往往需要牺牲另一方面的性能。相较而言，多谐振变换器的出现可有效解决该问题[3-4]。由于其谐振腔内无源器件（包括电容、电感和变压器）的数量和连接方式迥异，可以表现出更为灵活的谐振特性，如较宽的电压增益范围和内在的过电流保护功能等，针对此类变换器的研究层出不穷[3-6]。本文将以多谐振变换器作为研究对象，并对其相关技术进行深入研究。
谐振腔单元是多谐振变换器的核心结构，而包括电感和变压器在内的磁性元件又是谐振腔单元的关键元器件。它们一般占变换器总体的较大比例，对变换器的总体性能，有重要的影响。随着直流变换器朝着高频化、轻量化和小型化的趋势不断发展，相应地，对磁性元件也提出了更高的发展要求。采用利兹线和铜箔作为绕组的传统磁件的体积和其产生的损耗较大。相较而言，采用印制电路板（Printed Circuit Board, PCB）绕组制成的平面磁件成为了新的替代品[7-10]。不同于传统磁件，平面磁件多采用平面磁心，省去了磁心骨架，其面积与体积的比值较大，增大了磁件的散热面积，可有效改善热耗散问题。同时，该技术比传统变压器更容易实现机械加工，保证了制作过程和产品外观良好的一致性。另外，磁件的平面化设计也推动了绕组结构的平面化研究，一次绕组和二次绕组可实现紧密耦合，从而有效减小涡流损耗。采用PCB作为绕组的平面磁件有助于磁件向“轻”、“小”、“薄”方向发展，利于变换器实现高效率和自动化生产。
磁性元件的设计除了电感和变压器的优化设计之外，还包括多个磁件的集成设计。磁集成技术通过将两个或多个分立磁件集成到一个磁心内，以单一集成磁件实现多个分立磁件的功能，更有利于实现变换器的高功率密度、高频化和模块化设计，具有重要的现实意义[11-19]。按照磁集成对象的不同，主要有三种集成应用，分别是电感之间的集成[11-12]、变压器之间的集成[13]以及电感和变压器的集成[14-18]。文献[12]提出了一种适用于多模块交错准方波（Quasi Square Wave, QSW）变换器的电感集成方案，通过合理利用模块之间的电流相位关系，将各模块的所有独立电感集成到一个磁心中，大幅减小了电感的体积和损耗。文献[13]提出一种解耦集成方法，通过完全抵消绕组间的耦合作用来实现两个变压器的集成。电感与变压器的集成多应用于隔离型直流变换器中。文献[15]提出一种EIE型磁心结构。其中，变压器绕组对称分布在E型磁心的外侧柱，电感绕组则缠绕在磁心中柱，由此实现电感和变压器的独立灵活控制，同时变换器的体积和效率均得到了一定优化。得益于谐振型直流变换器展现出来的优势，不少学者考虑将磁集成技术应用到该类变换器中。特别地，将变压器的漏感作为谐振电感加以利用从而简化磁集成设计。因此，一些文献通过选择低磁导率材料构造磁分路器来获得理想的漏感值[16-17]。但引入磁分路器也会增加变换器结构的复杂程度。为此，有学者提出将变压器一次绕组和二次绕组完全分开以对漏感进行独立控制[18]。尽管如此，上述研究都对磁集成方案进行了详细的分析并取得了较好的效果。
本文以文献[6]提出的CLTLC多谐振变换器作为研究对象，目的在于解决其谐振腔内磁性元件数量多、体积大的问题。本文提出了一种仅包含单一磁件的磁集成设计方案，可以将谐振腔内的两个谐振电感和两个变压器进行有效集成。同时，基于矩阵变压器概念和绕组不均分设计，在磁心的中柱引入一定气隙，可得到一种新型E型磁心，该结构能实现对变压器励磁电感和漏感的解耦控制。此外，依据该磁心结构建立其磁阻模型，从数学角度进行论证。最后，本文针对一台1kW的实验样机进行实验验证，由此来证明所提方案的可行性。
首先，对CLTLC多谐振变换器进行简要介绍；其次，对矩阵变压器进行了详细讨论，并指出变换器采用该设计后造成的磁集成方案的局限性；最后，基于矩阵变压器及绕组不均分设计，提出了漏感可控的新型磁心结构，并搭建了相应的仿真平台。
文献[6]提出了一种采用双变压器结构的多谐振软开关CLTLC直流变换器，其谐振腔如图1所示。该谐振腔单元共有6个谐振元件，包括两个谐振电感L1、L2，两个谐振电容C1、C2以及两个高频变压器T1、T2，它们的匝比分别为和。
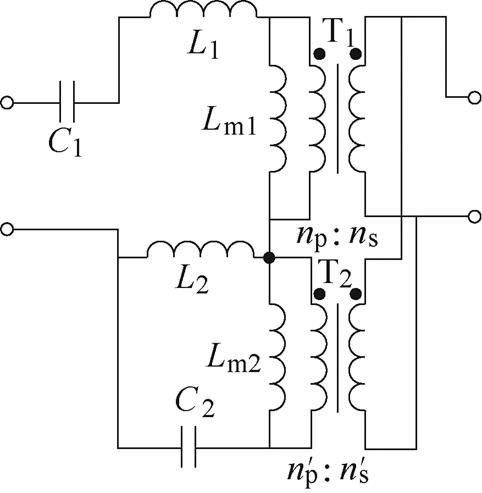
图1 CLTLC变换器拓扑的谐振腔
Fig.1 The resonant unit of CLTLC converter
根据文献[6]，该变换器可取得良好的变换效果，如有效传递基波和3次谐波有功功率，同时功率器件均能实现优异的软开关性能，降低开关损耗。但其谐振腔内，磁性元件（电感和变压器）均是分立磁件，数量多、体积大，影响变换器的效率和功率密度等。另外，相关磁件均为手工缠绕，制作过程复杂，进一步限制了该变换器的应用和推广。
针对这一问题，本文提出将谐振腔内的4个磁件（两个电感和两个变压器）进行集成设计。在设计之前，为更好地满足低压大电流场合的应用需求，本文将变换器的额定功率提升至1kW，并依照文献[6]给出的参数设计方法对谐振参数进行重新设计。但该过程不是本文重点内容，这里不再赘述。下面将详细叙述所提磁集成方案的设计过程。
变压器的设计对于直流变换器，特别是对应用于低电压大电流场合下的变换器至关重要。当采用PCB绕组取代传统的利兹线和铜箔时，可较易实现磁件的自动化生产，同时保证寄生参数良好的一致性等[19]。进一步地，利用矩阵变压器的概念[20-21]，将单一变压器拆分成多个子变压器，通过串联或并联多个子变压器的一次和二次绕组，以满足所需的匝比要求。其显著优点为能够减少PCB绕组的层数以及变压器的绕组损耗。
这里以变压器T1为例简述该设计方法。首先，将匝比为6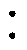
1的T1拆分成两个匝比均为3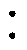1的子变压器，图2a给出了各自的UI磁心结构及对应的磁通方向。接着，采用一次侧串联、二次侧并联的连接方式，如图2b所示，将上述的两个UI磁心集成到一个EI磁心。此时，根据矩阵变压器设计，图2b中E型磁心中柱内的磁通大小完全相同且方向相反，可以相消。进一步地，根据磁通抵消原理，可将该中柱移除，由此形成了图2c所示的集成后的简化UI磁心结构，同时绕组的具体布置方案以及磁动势大小也示于图中。此时，一次和二次绕组间的磁动势为流过一次电流ipri的3倍，而较低的磁动势也代表着更小的绕组交流电阻及更低的绕组损耗[19]。根据上述分析，包含两个分立UI磁心的矩阵变压器结构，通过优化设计，可以合并为仅包含单一UI磁心的集成结构。
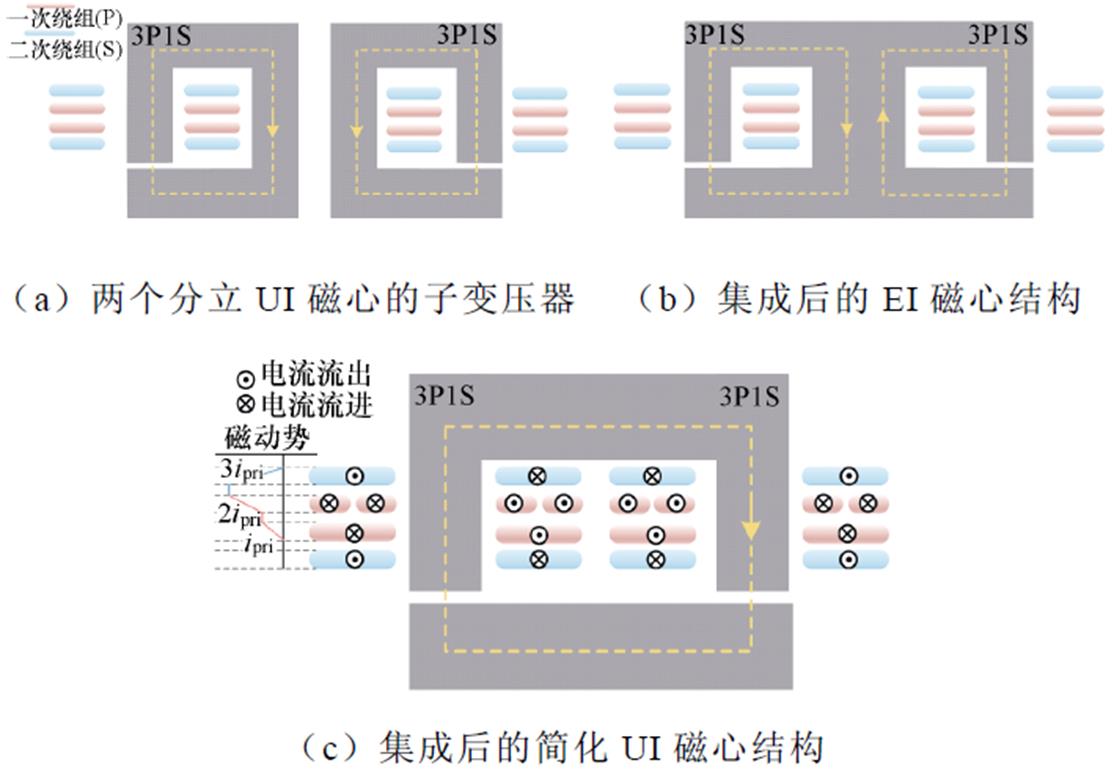
图2 矩阵变压器T1的设计过程
Fig.2 The design process of matrix transformer T1
以上设计有利于提升变换器的性能，但其仅针对谐振腔中的变压器进行了相关优化。各子变压器的绕组分布完全相同，且采用了相对较好的交错结构，消除了磁心中柱的磁通，由该设计产生的漏感值很小。对CLTLC多谐振变换器来说，虽然变压器的漏感可作为谐振电感的一部分并参与谐振过程，但该漏感值较小，此时仍需外接电感元件来构成谐振腔中的电感，磁性元件的集成设计仍待进一步的研究。
为获得期望的漏感值，应创造不与一次绕组和二次绕组耦合的磁通，即漏磁通。相比于矩阵变压器中均匀分布的绕组，这里考虑对绕组布置方案进行调整以达到更好的集成效果，即采用绕组不均分设计。
仍以变压器T1为例对该方法进行简要说明。将T1拆分为两个匝比分别为4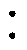1和2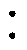1的子变压器T11和T12，并将它们按照图3所示的一次侧串联、二次侧并联的方式进行连接，同样满足匝比为6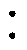1的设计需求。
T1的等效连接如图3所示。图中，vp、vs和ip、is分别为变压器T1的一次、二次电压和电流。vp1、vp2和vs1、vs2分别为T11和T12的一次电压和二次电压，ip1、ip2和is1、is2则为其对应的电流。
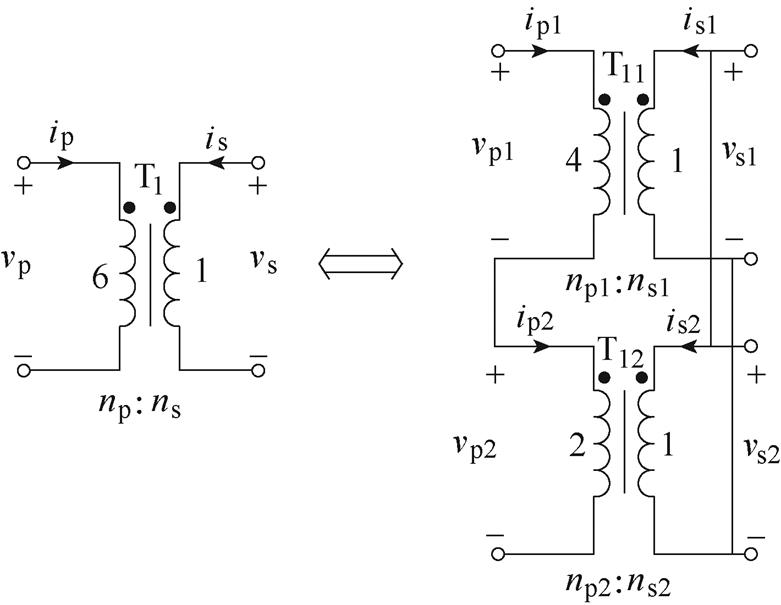
图3 T1的等效连接
Fig.3 Equivalent connection way of transformer T1
根据图3所示的连接方式，由电路定律得
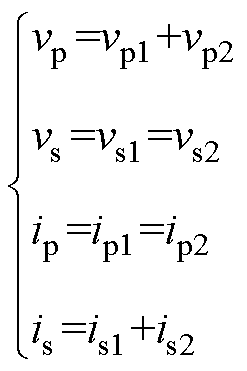（1）进一步地，将上述两个UI磁心进行集成设计，可得到如图4所示的T1的新型EI磁心结构。与图2不同的是，此时各子变压器的绕组采用不均匀分布设计，因此，该磁心中柱内的磁通不能实现完全抵消，即该中柱不能被移除，必须保留。在增加漏磁通的同时，各子变压器的绕组间也保持了相对较好的交错结构，有利于降低绕组的损耗。值得注意的是，此时流经中柱的磁通是不与一次、二次绕组耦合的漏磁通。另外，虽然中柱内的磁通不能实现完全抵消，但仍可以实现部分抵消。因此，在该磁心内，中柱的长度会比其他两个侧柱短，这也是该新型EI磁心与传统EI磁心在结构上的主要区别。
图5分别给出了基于图2c和图4设计方案的仿真结果。相比在UI磁心结构下绕组均分的设计，在新型EI磁心结构中，大量磁通集中在磁心中柱，这部分磁通即为由绕组不均分设计所产生的漏磁通。第2节将从数学角度进行论证。
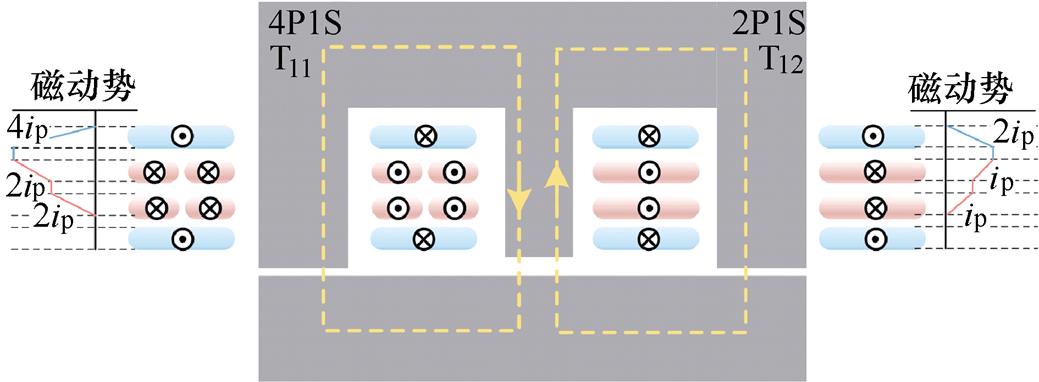
图4 T1的新型EI磁心结构
Fig.4 The novel EI core structure of transformer T1
图5 两种不同磁心结构下的仿真对比
Fig.5 Simulation comparison of two different cores
根据所提的新型EI磁心结构，建立其对应的磁阻模型，新型EI磁心结构的磁阻模型如图6所示。为简化分析，这里作出以下三点假设：
（1）磁心的磁导率远远大于空气的磁导率，忽略磁心磁阻。
（2）空气中的漏磁很小，可以忽略不计。
（3）忽略气隙磁阻的磁场边缘效应。
图6 新型EI磁心结构的磁阻模型
Fig.6 The equivalent reluctance model of the novel EI core structure
np1、np2分别为T1的一次绕组在左、右磁柱上的匝数，类似地，ns1、ns2为对应的二次绕组的匝数。F1、F3和F2分别为左、右磁柱和中柱的磁通，方向如图中箭头标注。根据磁动势平衡方程并利用叠加定理，结合式（1），可求解出流经每根磁柱的磁通为
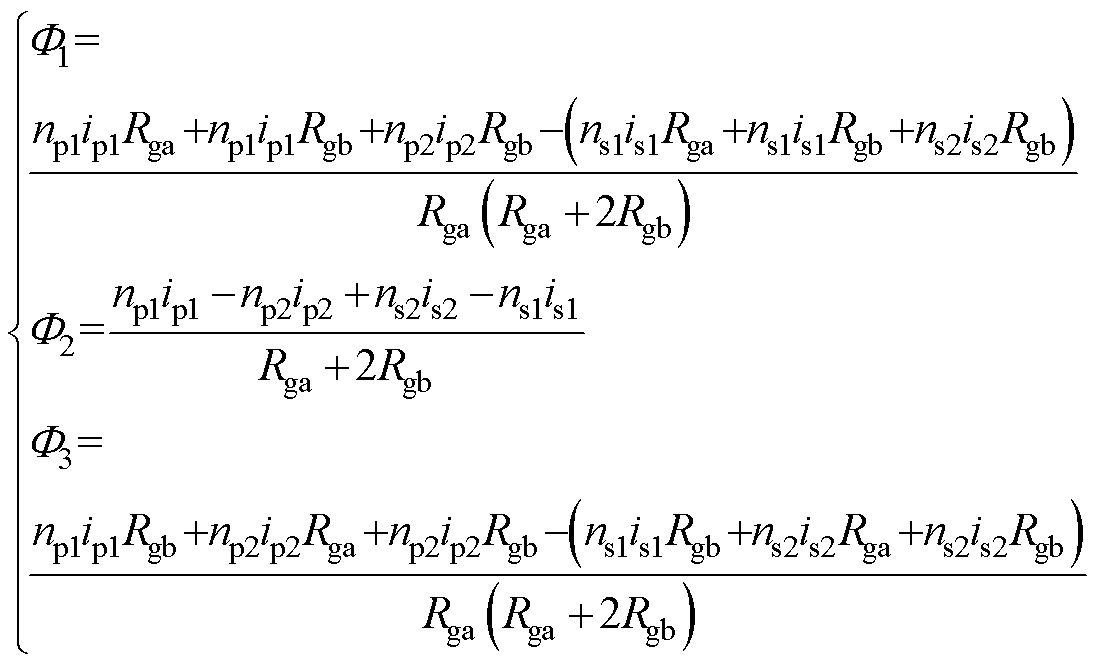（2）式中，Rga、Rgb分别为外侧柱和中柱的气隙磁阻；lga和lgb分别为其对应的气隙长度；Ac和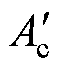
分别为磁心外侧柱和中柱的截面积。根据磁阻的定义，可以列写出气隙磁阻的计算公式为
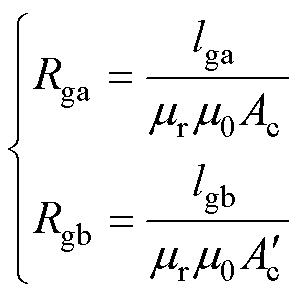（3）
考虑各子变压器的实际匝比，式（2）可以进一步化简为
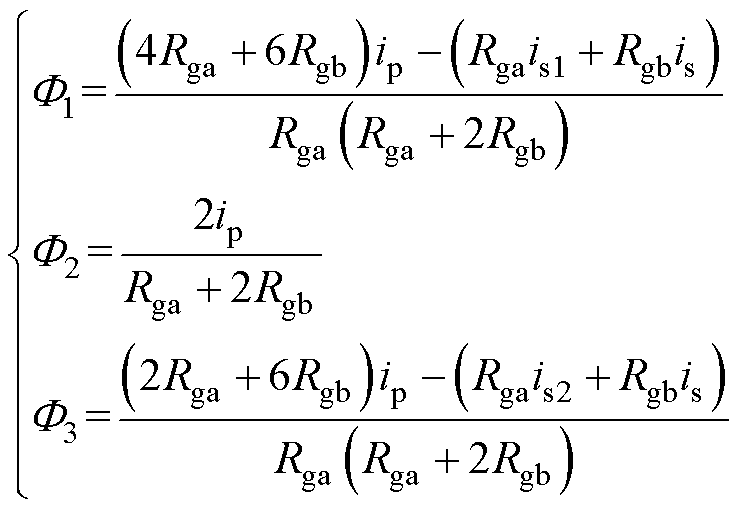（4）为了得到励磁电感和漏感值，建立如图7所示的变压器T型等效模型。变压器T1的励磁电感为Lm1，一次侧和二次侧的漏感分别为Lk11和Lk12。由图1可知，谐振电感L1与变压器T1为串联连接，因此，其一次侧漏感Lk11可用来代替L1。
根据图7，列写基尔霍夫电压定律（KVL），得
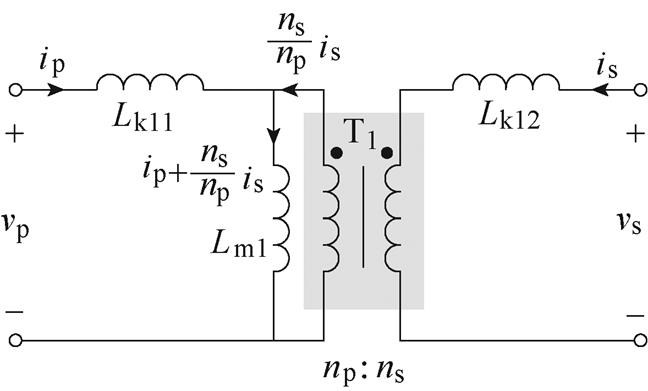
图7 T1的T型等效模型
Fig.7 T-type of the transformer T1
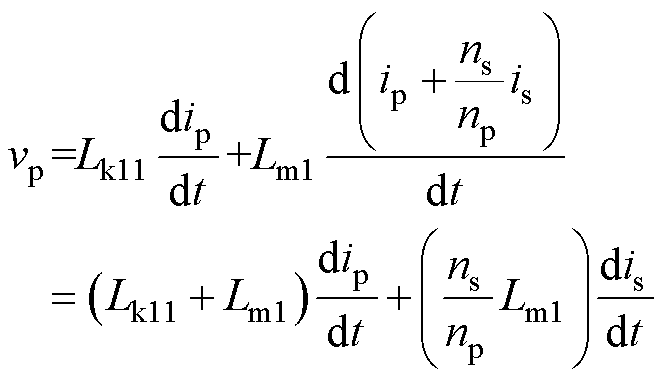（5）结合法拉第电磁感应定律，T1的一次电压vp、二次电压vs还可以表示为
（6）
式中，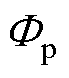
、
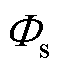分别为一次或二次绕组对应的总磁通。结合式（5）、式（6），在二次侧开路时（is=0），
可以得到Lk11以及Lm1的表达式为
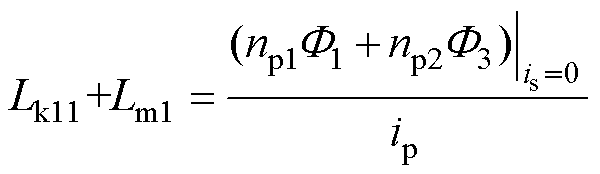（7）
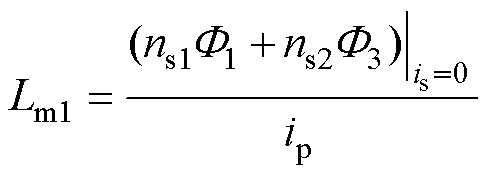（8）
联立式（1）～式（8），计算得到在该新型EI结构下，变压器T1的Lm1和Lk11分别为
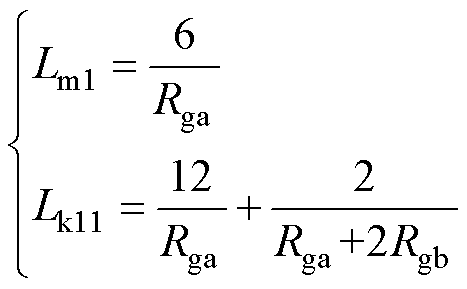（9）由式（9）可知，对于图4所示的结构，变压器的励磁电感和漏感都与气隙磁阻Rga和Rgb有关。因此，Rga和Rgb可根据所需要的励磁电感值和漏感值来确定。此外，从式（3）可知，气隙磁阻是气隙长度和磁柱截面积的函数，因此，通过改变这两个变量，就可以灵活地控制励磁电感和漏感值的大小。根据上述分析，谐振腔内的电感L1可由变压器T1的漏感来代替，由此实现了变压器和谐振电感的集成设计。
采用相同的分析方法，将变压器T2分为两个匝比分别为3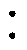3和1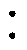5的子变压器T21和T22。与T1不同的是，T2的一次绕组和二次绕组均是串联连接的，以满足匝比为4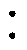8的设计目标。此外，T2的相关变量均用上标“'”进行标记，以与T1的相关变量进行区分。
变压器T2绕组连接方式及磁心结构如图8所示。图8a给出了T2详细的绕组连接方式，其绕组分布方式及对应的磁心结构示于图8b中，其电压和电流之间的关系可以表示为
（10）
图8 变压器T2绕组连接方式及磁心结构
Fig.8 Equivalent winding connection way and core structure of T2
类似地，通过建立变压器T2的T型等效模型和磁阻模型，可推得其励磁电感Lm2和一次侧漏感Lk21的表达式，如式（11）所示。其中，Lk21仍可以完全代替谐振电感L2。
（11）从式（13）可知，通过调整变压器T2的气隙磁阻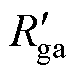
和
的大小，可以确定T2的Lm2和Lk21。
综上所述，新型EI型磁心结构具有突出的优势。具体来说，通过调整不同磁柱的气隙磁阻，实现改变变压器励磁电感值和漏感值的目的。在该磁心结构中，漏感是由中心磁柱来控制。如果中柱的气隙磁阻比侧柱的气隙磁阻小，则通过中柱的漏磁通会增多，相应地，漏感值就会升高，反之亦然。变压器的漏感是可控的，且在所提CLTLC变换器中能够作为谐振电感以实现充分利用。
根据1.2节分析，本文采用PCB绕组形式来制作变压器。采用多层绕组并联可显著提高变压器绕组的载流能力。但是，随着PCB层数的增加，相应的制造成本也会越高，综合考虑成本和制作的难易程度，本文选用4层PCB。此外，为进一步优化集成方案，将两个分立的新型EI磁心集成为一个EIE型磁心结构。
第2节内容已经通过所提新型EI磁心结构把变压器与其各自串联连接的电感有效集成在一起，但该设计还可做进一步的优化。新型EIE磁心的磁集成结构如图9所示，本文采用EIE型磁心结构将变换器中所有磁件集成到一起。
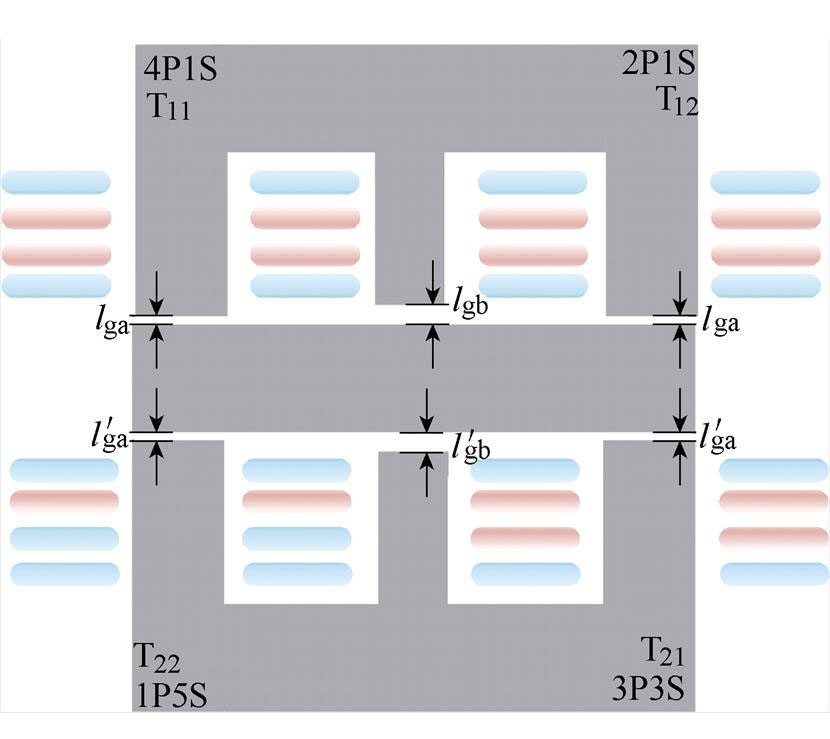
图9 新型EIE磁心的磁集成结构
Fig.9 Magnetic integrated structure of novel EIE core
由图9可知，变压器T1和T2分别分布在I型磁心的上方和下方。中间I型磁心为两个变压器共用，且该磁心为这两个变压器提供了一条低磁阻磁路，由此实现两个变压器间的解耦。由于T1和T2分担的功率不同，所以在该共用I型磁心中产生的磁通大小不同，磁通可以被部分抵消，因此I型磁心的高度可以适当减小，但不能省去。
相比于两个分立的EI结构，该EIE型磁心结构可以省去一条I型磁心，同时保留的I型磁心的体积也可以适当减小，这更利于减小磁心的总体积和降低损耗。至此，CLTLC变换器的最终集成方案得以确定。
基于所提的新型EIE磁心结构，利用Maxwell软件搭建仿真模型来验证上述理论分析过程，仿真结果如图10所示。
图10中给出了所提磁心结构的磁感应强度B和空气中的磁场强度H的分布情况。可以看到，大量的磁通都流经磁心中柱，且这部分磁通主要为变压器的漏磁通。相比磁心内部，空气中的漏磁较少，这种将磁通限制在磁心中的设计有助于降低电磁干扰、减小周围导体的损耗。另外，虽然中柱的磁通密度较高，但磁通密度的最大值仍被限制在合理的范围内，能够很好地满足变换器的设计目标。
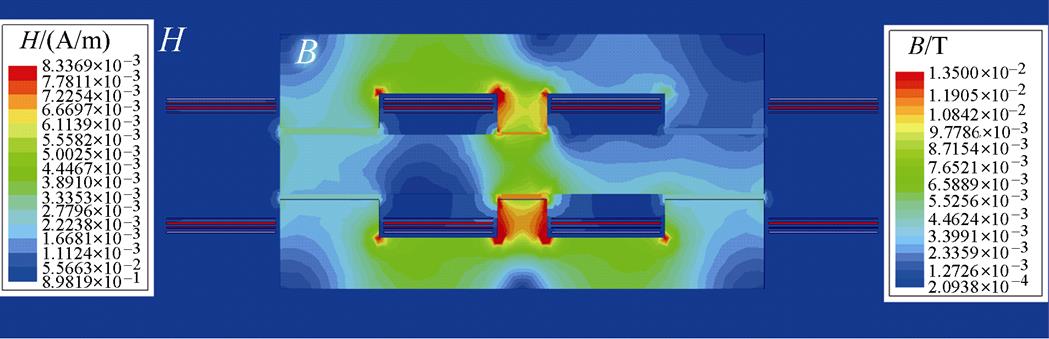
图10 新型EIE磁心结构的仿真结果
Fig.10 Simulation results of the novel EIE core structure
为了验证上述理论分析的正确性，搭建了一台1kW的实验样机，实验样机如图11所示。相应的参数见表1。
图11 所提变换器的实验样机
Fig.11 Experimental prototype of the proposed converter
表1 变换器的主要参数
Tab.1 Parameters of the proposed converter
参 数数 值 额定功率P/kW1 额定负载R/W0.9 额定开关频率fs/kHz300 电感L1/mH25 电感L2/mH24 电容C1/nF5 电容C2/nF3 匝比 匝比
图12为额定负载下的实验波形。此时的开关频率为300kHz。图中，vGS为驱动信号，vS1、iS1和vD1、iD1分别为开关管S1和二极管VD1两端的电压和流经电流。从图中可以看出，开关管和二极管的电流均呈现马鞍波形状，这是由于基波和3次谐波分量的叠加造成的。此时，变换器的输入电压固定为400V，输出电压实测为29.58V，与设计值保持一致。此外，开关管实现了ZVS开通，二极管实现了零电流（Zero Current Soft-Switching, ZCS）关断，良好的软开关特性保证了变换器在额定条件下的转换效率为95.72%。
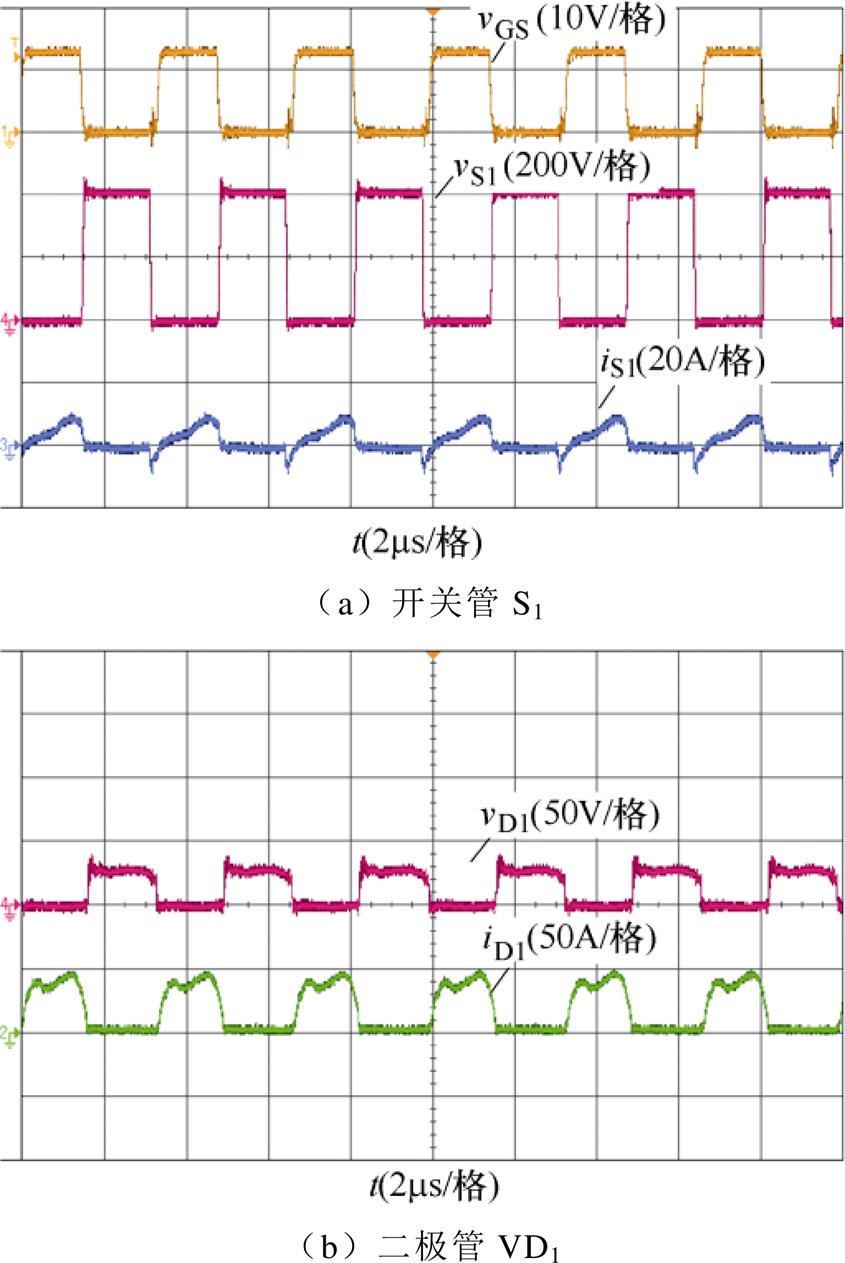
图12 额定条件下的实验波形
Fig.12 Experimental waveforms at rated condition
图13和图14分别给出了在额定负载下频率为350kHz和400kHz的实验波形。由图可知，开关管和二极管电流均呈现马鞍波，代表着变换器可以在较宽的频率范围内有效传递3次谐波，谐振电流的利用率得到提升。此外，开关管仍可以实现ZVS开通，二极管在开通和关断时刻的电流接近为零，保证了它的ZCS特性。
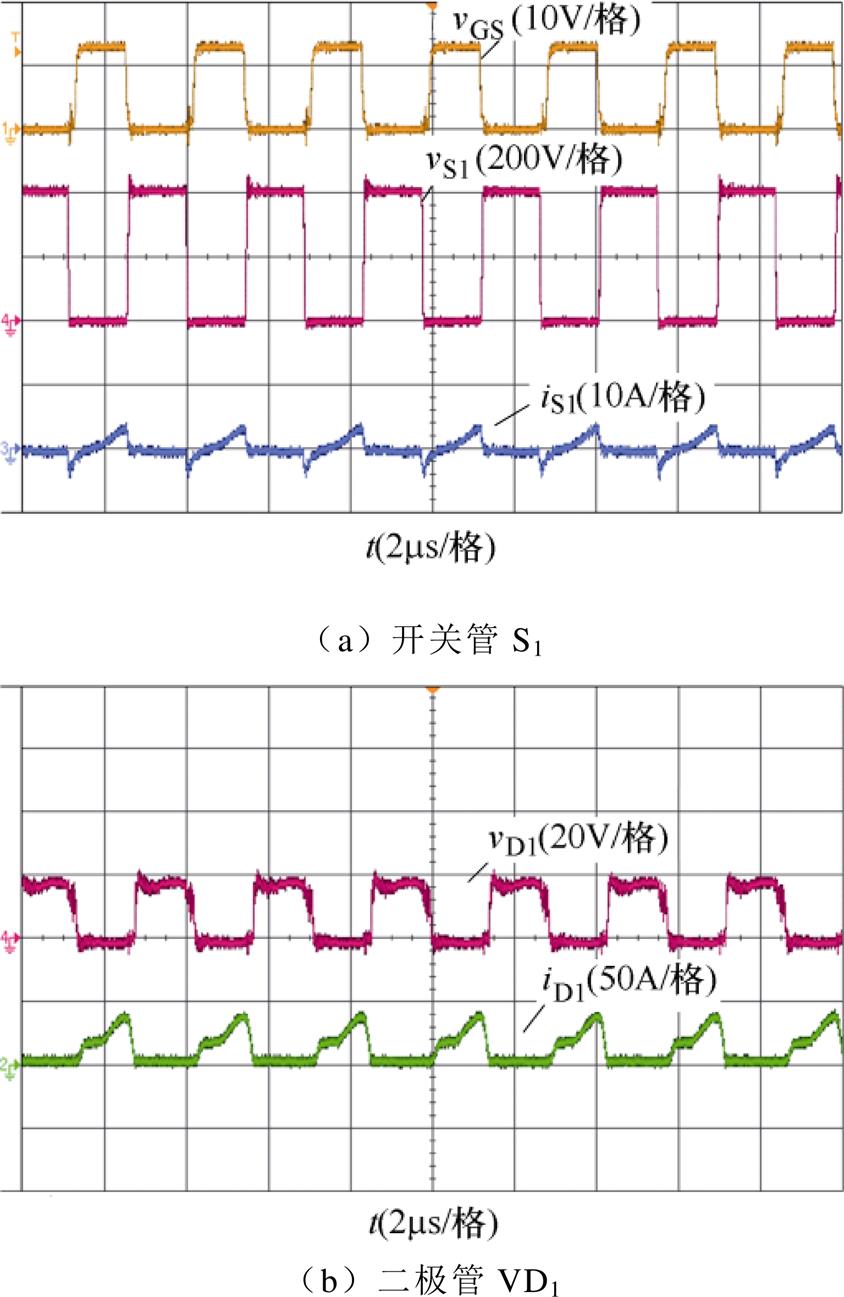
图13 额定负载下350kHz时的实验波形
Fig.13 Experimental waveforms of rated load at 350kHz
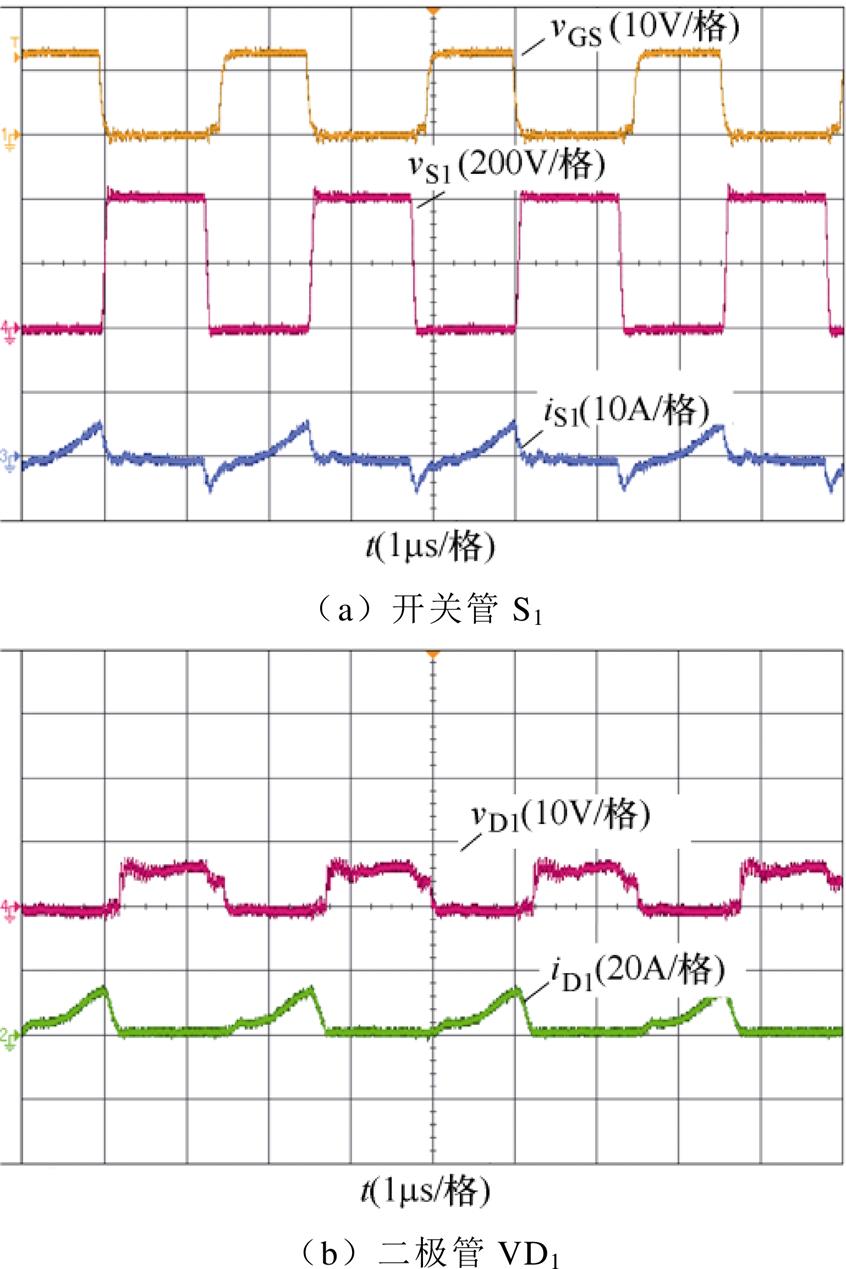
图14 额定负载下400kHz时的实验波形
Fig.14 Experimental waveforms of rated load at 400kHz
进一步地，图15给出了CLTLC变换器在不同负载下的效率曲线。采用所提磁集成结构的变换器可以在全负载范围内保持较高的转换效率，其效率优势主要体现在以下几个方面：首先，变换器在全负载范围内实现了优异的软开关特性，额定工况下开关损耗进一步减小；其次，谐振腔内的所有分立磁件都被集成到所提新型EIE磁心结构中，与谐振电感相关的损耗被完全消除，有助于降低磁件损耗；最后，得益于谐振腔内高次谐波有功功率的传输，谐振腔内的电流利用率得到提高，无功环流减少。因此，变换器可以实现较高的转换效率，最高可达96.45%。
图15 不同负载下的效率曲线
Fig.15 Efficiency curve under different output power
针对CLTLC多谐振变换器中存在的磁性元件数量多、体积大等问题，本文设计了一种新型EIE磁心结构的磁集成方法，可以将两个高频变压器和两个谐振电感全部集成到该磁心中。基于矩阵变压器的概念和绕组不均匀分布的思想，通过在磁心中柱引入气隙，实现了对变压器的励磁电感和漏感的灵活控制。同时，依据该结构建立了相关磁阻模型，从数学角度验证了所提方案的可行性。本文还给出了最终的集成方案，并在Maxwell软件中搭建了相应的仿真模型。最后，建立了一台1kW的实验样机。实验结果证明，采用所提磁集成结构的变换器能够在全负载范围内保持较高的效率，其最高效率达96.45%。
参考文献
[1] 胡海兵, 王万宝, 孙文进, 等. LLC谐振变换器效率优化设计[J]. 中国电机工程学报, 2013, 33(18): 48-56, 16.
Hu Haibing, Wang Wanbao, Sun Wenjin, et al. Optimal efficiency design of LLC resonant converters[J]. Proceedings of the CSEE, 2013, 33(18): 48-56, 16.
[2] 王泽景, 王颖, 龚春英. 高降压比LLC谐振型直流变压器[J]. 电工技术学报, 2015, 30(14): 193-200.
Wang Zejing, Wang Ying, Gong Chunying. High step-down LLC resonant DC-DC transformer[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(14): 193-200.
[3] 李舒成, 刘邦银, 姜庆, 等. 基于同步PWM控制的双向CLLLC谐振型直流变换器运行特性分析[J]. 电工技术学报, 2019, 34(增刊2): 543-552.
Li Shucheng, Liu Bangyin, Jiang Qing, et al. Perfor- mance analysis of bidirectional CLLLC resonant converter with synchronous PWM control strategy[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 543-552.
[4] Wu Hongfei, Xiang Jin, Hu Haibing, et al. Multiele- ment resonant converters with a notch filter on secondary side[J]. IEEE Transactions on Power Elec- tronics, 2016, 31(6): 3999-4004.
[5] Lu Jie, Perreault D J, David M Otten, et al. Impedance control network resonant DC-DC converter for wide- range high-efficiency operation[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 5040-5056.
[6] 王议锋, 韩富强, 杨良, 等. 一种双变压器结构的多谐振型软开关直流变换器[J]. 电工技术学报, 2019, 34(4): 738-746.
Wang Yifeng, Han Fuqiang, Yang Liang, et al. A dual transformer-structured multi-resonant soft-switching DC-DC converter[J]. Transactions of China Electro- technical Society, 2019, 34(4): 738-746.
[7] Ouyang Ziwei, Michael A E Andersen. Overview of planar magnetic technology-fundamental properties[J]. IEEE Transactions on Power Electronics, 2014, 29(9): 4888-4900.
[8] 舒畅. 开关变换器中平面集成磁件设计的研究[D]. 重庆: 重庆大学, 2007.
[9] 杨玉岗, 吴瑶, 黄伟义. 旋转式松耦合变压器的绕组优化设计[J]. 电工技术学报, 2019, 34(13): 2782- 2792.
Yang Yugang, Wu Yao, Huang Weiyi. The optimized design of winding for rotary loosely coupled trans- former[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2782-2792.
[10] 旷建军. 平面变压器PCB 板绕组的损耗分析、计算与设计优化[D]. 福州: 福州大学, 2002.
[11] 陈乾宏. 开关电源中磁集成技术的应用研究[D]. 南京: 南京航空航天大学, 2002.
[12] Chen Wei, Lee F C, Zhou Xunwei, et al. Integrated planar inductor scheme for multi-module interleaved quasi- square-wave (QSW) DC/DC converter[C]//IEEE Power Electron, Specialists Conference, Charleston, SC, USA, 1999: 759-762.
[13] Cheng D K W, Leung-Pong Wong, Yim-Shu Lee. Design, modeling, and analysis of integrated mag- netics for power converters[C]//Proceedings of Power Electronics Specialists, Galway, Ireland, 2000: 320- 325.
[14] Chen Wei, Hua Guichao, Sable D, et al. Design of high efficiency, low profile, low voltage converter with integrated magnetics[C]//Proceedings of Applied Power Electronics Conference, Atlanta, GA, USA, 1997: 911-917.
[15] Ouyang Ziwei, Gokhan Sen, Ole C Thomsen, et al. Analysis and design of fully integrated planar magnetics for primary-parallel isolated boost con- verter[J]. IEEE Transactions on Industrial Electronics, 2013, 60(2): 494-508.
[16] Zhang Jun, Ouyang Ziwei, Duffy M C, et al. Leakage inductance calculation for planar transformers with a magnetic shunts[J]. IEEE Transactions on Industrial Electronics, 2014, 50(6): 4107-4112.
[17] Li Mingxiao, Ouyang Ziwei, Andersen M. High- frequency LLC resonant converter with magnetic shunt integrated planar transformer[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(3): 2405-2415.
[18] He Peiwen, Ayan Mallik, Arun Sankar, et al. Design of a 1MHz high-efficiency high-power-density bidire- ctional GaN-based CLLC converter for electric vehicles[J]. IEEE Transactions on Vehicular Tech- nology, 2019, 68(1): 213-223.
[19] Huang Daocheng, Ji Shu, Fred C Lee. LLC resonant converter with matrix transformer[J]. IEEE Transa- ctions on Power Electronics, 2014, 29(8): 4339-4347.
[20] 肖龙, 伍梁, 李新, 等. 高频LLC变换器平面磁集成矩阵变压器的优化设计[J]. 电工技术学报, 2020, 35(4): 758-766.
Xiao Long, Wu Liang, Li Xin, et al. Optimal design of planar magnetic integrated matrix transformer for high frequency LLC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 758-766.
[21] Mohamed Ahmed, Chao Fei, Lee F C, et al. 48V voltage regulator module with PCB winding matrix transformer for future data centers[J]. IEEE Transactions on Industrial Electronics, 2017, 64(12): 9302-9310.
Magnetic Integration Method for CLTLC Multi-Resonant Converter
Abstract On the basis of the printed circuit board (PCB) winding and planar transformer technology, a magnetic integration design scheme is proposed with only a single magnetic component. It solves the problem of the excessive number of magnetic components in the multi-resonant converter, and is successfully applied to the CLTLC multi-resonant converter. All the magnetic components of the converter, including two resonant inductors and two high-frequency transformers, can be integrated into the EIE core structure. In this regard, with the matrix transformer concept and uneven winding distribution, a novel E-type core can be obtained by introducing an air gap to the center core leg. Thus, the decoupling control of magnetizing inductance and leakage inductance of the transformer can be realized. In addition, according to the proposed structure, the reluctance model of the transformer is established. Then the magnetic integration scheme is further demonstrated from the mathematical aspect. The final magnetic integration design is also discussed. In the end, a 1kW CLTLC prototype is built and relevant experiments are carried out. The experimental results verify the feasibility and effectiveness of the proposed scheme. The peak efficiency of the converter can reach 96.45%.
Keywords：PCB winding, planar transformer, uneven winding distribution, resonant DC-DC converter, high conversion efficiency
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.L90052
国家重点研发计划“智能电网技术与装备”重点专项“中低压直流配用电系统关键技术及应用（2018YFB0904700）”资助项目。
收稿日期 2020-06-10
改稿日期 2020-10-24
E-mail: wayif@tju.edu.cn
刘瑞欣 女，1995年生，硕士研究生，研究方向为谐振型软开关直流变换器。
E-mail: rxliu1210@tju.edu.cn（通信作者）
（编辑 陈 诚）