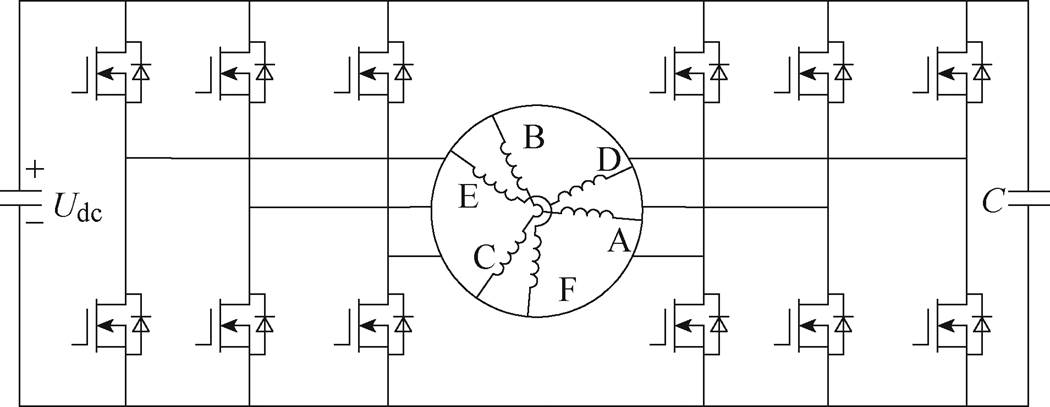
图1 双三相永磁电机电压型驱动器结构
Fig.1 Structure of dual three-phase permanent-magnet machine voltage source drive
摘要 传统直接转矩控制的双三相永磁电机存在电流谐波含量高、磁链脉动和转矩脉动大的缺点。为改善双三相永磁电机稳态性能,该文提出虚拟电压矢量集的新型占空比调制直接转矩控制。首先,电压矢量集由传统的12个基本电压矢量拓展到24个虚拟电压矢量,通过虚拟电压矢量实现对谐波平面的控制,减小谐波电流;再通过增加矢量个数减小磁链的控制误差,达到降低磁链脉动的目的。其次,分别定义用于动态工况和稳态工况的开关表及占空比的计算方法,稳态工况的开关表和占空比计算可减小稳态时的转矩脉动,动态工况的开关表和占空比计算用于保证系统的动态响应。最后,通过实验验证所提控制算法的可行性。
关键词:直接转矩控制 双三相永磁电机 占空比调制 虚拟电压矢量 转矩脉动 电流谐波
双三相永磁电机具有功率密度高、效率高、转矩脉动小、可靠性高等优点,在电动汽车和舰船推进等领域具有广泛的应用前景[1]。如其他多相电机,双三相永磁电机存在着低阻抗的谐波平面,较小的谐波电压就能产生较大的谐波电流。因此,除了需要控制电机的电磁转矩外,还需对谐波平面进行控制,以获得更好的运行性能[2-8]。
已有研究表明,磁场定向的解耦控制结合空间矢量调制技术,可以获得优异的稳态性能。然而,为控制双三相永磁电机电磁转矩和谐波电流,需要多个PI控制器,其参数设置异常复杂。另外,需要在线求解多元线性方程,以便于通过空间电压矢量调制获得目标电压矢量,但这会消耗控制器大量的计算时间[3-5]。直接转矩控制(Direct Torque Control, DTC)策略兼具结构简单、转矩响应速度快、鲁棒性强等优点,在电机驱动领域受到广泛关注。然而,传统DTC仅对ab 平面分量进行控制,忽略了多相电机的谐波平面,导致多相电机的定子电流中含有大量谐波,降低了电机系统的运行效率。另外,传统DTC在一个控制周期内只作用一个电压矢量,不可避免地存在着磁链脉动大、转矩脉动大的缺点[9-12]。
针对多相电机采用传统DTC策略存在谐波电流大的缺点,文献[13-16]提出合成谐波平面等效幅值为零的虚拟电压矢量方法,抑制了谐波电流。但该方法旨在减小电流谐波,未能很好地解决电机转矩和磁链的脉动问题。文献[17-19]通过拓展电压矢量集方法,减小转矩脉动和磁链脉动。该方法为获得较好的控制效果,需要预先合成足够多的幅值和方向不同的电压矢量,并且需要设计多维的开关表。随着合成电压矢量个数和开关表维数的增加,算法的复杂性也随之增加。文献[20-26]研究了占空比调制的直接转矩控制(Duty Ratio Modulation Direct Torque Control, DRM-DTC)方法。在传统查表法DTC的基础上增加了零矢量,通过优化非零电压矢量和零矢量的作用时间,达到减小转矩脉动的目的。单周期单个有效矢量的DRM-DTC通常以减小转矩脉动为优化目标,不能很好地减小磁链脉动。文献[27-29]提出矢量多选取的方法,在一个控制周期内选取多个非零电压矢量,可同时实现对转矩磁链的优化控制。但是,该方法需要求解多个矢量的占空比,以及考虑脉冲宽度调制(Pulse Width Modulation, PWM)生成的问题,因而工程实现较复杂,且计算量较大。
针对上述传统DRM-DTC存在的问题,本文以双三相表贴式永磁电机为控制对象,研究一种新型DRM-DTC策略。根据空间电压矢量调制原理合成24个虚拟电压矢量集,在虚拟电压矢量集的基础上,分别设计用于稳态和动态的新型开关表和占空比计算方法,从而达到减小稳态转矩脉动和抑制谐波电流的目的,同时保证系统的动态响应。实验结果验证了提出的新型DRM-DTC策略应用于双三相永磁电机的可行性与有效性。
双三相永磁电机电压型驱动器结构如图1所示。图中,Udc为直流母线电压,C为直流母线电容。根据开关状态不同可得到64个基本电压矢量,其中包含60个非零电压矢量和4个零电压矢量。基本电压矢量的编号按照ABC和DEF的桥臂顺序,分别转换为八进制数。图2为非零电压矢量在ab 平面和z1z2平面的分布情况。

图1 双三相永磁电机电压型驱动器结构
Fig.1 Structure of dual three-phase permanent-magnet machine voltage source drive
通过坐标变换的方法,可将双三相永磁电机的电压、电流、磁链变换到ab 、z1z2和o1o2相互正交的3个平面。其中,ab 平面包含基波和12k±1 (k=1, 2, 3,…)次谐波。z1z2平面包含6k±1(k= 1, 3, 5,…)次谐波。o1o2平包含3k(k=1, 3, 5,…)次谐波[4]。

图2 双三相逆变器空间电压矢量分布
Fig.2 Space voltage vectors distribution of dual three-phase permanent-magnet machine drive
图3为常用坐标系的空间位置示意图。图中,a 轴和电机A相重合,d轴和转子永磁体基波磁链方向重合,x轴和定子磁链ys方向重合。图中,Is为定子电流,ia、ib、id、iq、ix、iy分别为定子电流Is在a 轴、b 轴、d轴、q轴、x轴、y轴的分量;ψf为转子永磁体磁链幅值;d 为定子磁链ys和d轴的夹角;qr为d轴和a 轴的夹角。
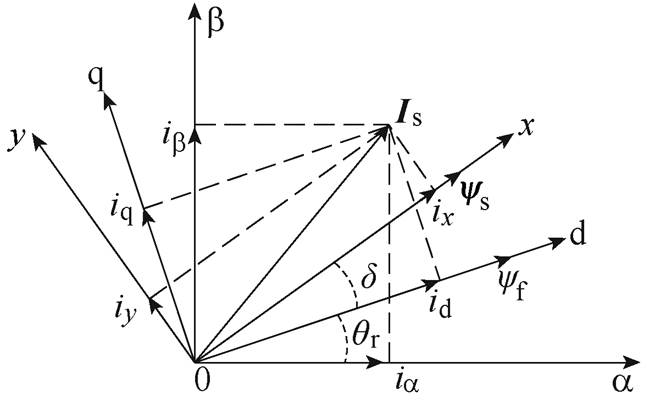
图3 常用坐标系关系示意图
Fig.3 Schematic diagram of each coordinate system
在转子磁场定向的dq旋转坐标系中,双三相永磁电机的电压方程表示为
 (1)
(1)式中,ud、uq分别为基本电压矢量Us在d轴和q轴的分量;yd、yq分别为定子磁链ys在d轴和q轴的分量;Ld、Lq分别为d轴和q轴电感;Rs为定子电阻;w 为电角速度。dq坐标系下,双三相永磁电机磁链方程可表示为
 (2)
(2)
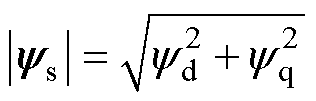 (3)
(3) (4)
(4)
式中,qs为定子磁链ys和a 轴的夹角。dq坐标系下,双三相永磁电机转矩可表示为
 (5)
(5)式中,Te为电磁转矩;np为极对数。双三相永磁电机的机械方程可表示为
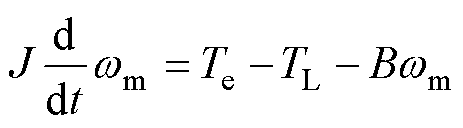 (6)
(6)
式中,J为转动惯量;TL为负载转矩;B为黏滞系数;wm为机械角速度。
DRM-DTC通过分配非零电压矢量和零电压矢量作用时间,调节转矩在一个周期内变化量。当d轴电流为0时,根据式(1)、式(2)、式(5)可知,双三相永磁电机转矩变化斜率可近似表示为
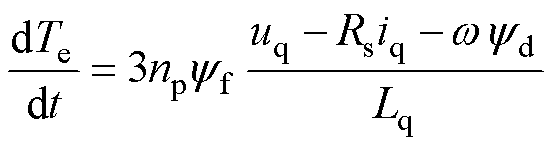 (7)
(7)将非零电压矢量uact和零电压矢量u0代入式(7),得到uact作用下转矩变化斜率f1,以及u0作用下转矩变化斜率f0,f1和f0分别表示为
 (8)
(8)
由式(8)可知,uact在一个控制周期的转矩变化量TeN和u0在一个控制周期的转矩变化量TeZ分别为
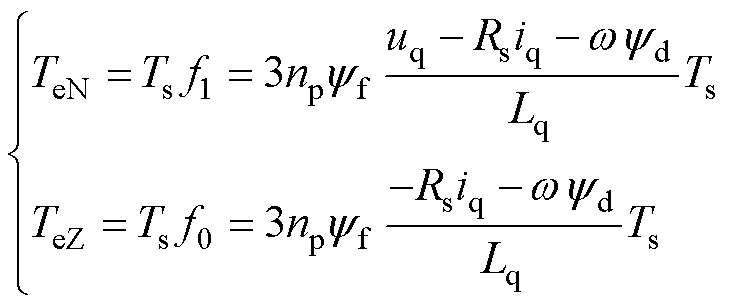 (9)
(9)式中,Ts为系统控制周期。可知,DRM-DTC在一个控制周期Ts内,转矩变化量在TeN和TeZ之间可控,从而达到减小转矩脉动的目的。
负载脉动、电压矢量选取等因素常导致传统DRM-DTC稳态控制效果不理想。为提高传统DRM- DTC的稳态性能,提出的新型DRM-DTC将从电压矢量集、开关表和占空比计算三个方面进行优化,以达到减小谐波电流、减小稳态转矩脉动和磁链脉动的目的。
理想状态下,z1z2平面电压方程可表示为
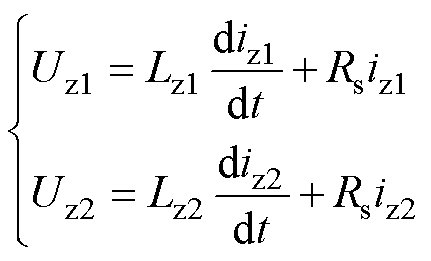 (10)
(10)式中,Uz1和Uz2为基本电压矢量Us在z1z2平面的分量;iz1和iz2为电流矢量Is在z1z2平面的分量;Lz1和Lz2为z1z2平面的等效电感。可知,当Uz1和Uz2的幅值不为零时,Uz1和Uz2会在Lz1和Lz2中产生谐波电流。由图2可知,非零电压矢量在z1z2平面分量不为零,直接使用基本电压作为DRM-DTC待选矢量集会导致谐波电流问题,进而影响电机稳态性能。
虚拟电压矢量的基本原理为通过选取若干个基本电压矢量,并按一定比例分配各矢量作用时间,使得一个周期内Uz1和Uz2的等效幅值为0,达到抑制谐波电流为目的。以基本电压矢量u44和u65为例,在一个周期Ts内,u44作用0.732Ts,u65作用0.268Ts时,合成的虚拟电压矢量在一个周期内z1z2平面等效幅值为0,ab 平面等效幅值约为0.6Udc。图4为基本电压矢量u44和u65合成虚拟电压矢量的示意图。
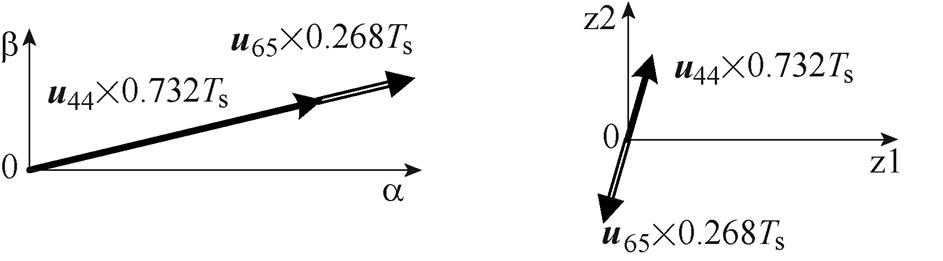
图4 虚拟电压矢量合成示意图
Fig.4 Demonstration of virtual voltage vector synthesis
为抑制谐波电流和减小磁链脉动,采用空间电压矢量调制的方法合成24个虚拟电压矢量,合成的虚拟电压矢量在ab 平面分布如图5所示。图中,V1~V24为合成的虚拟电压矢量,S1~S24为根据虚拟矢量划分的扇区。
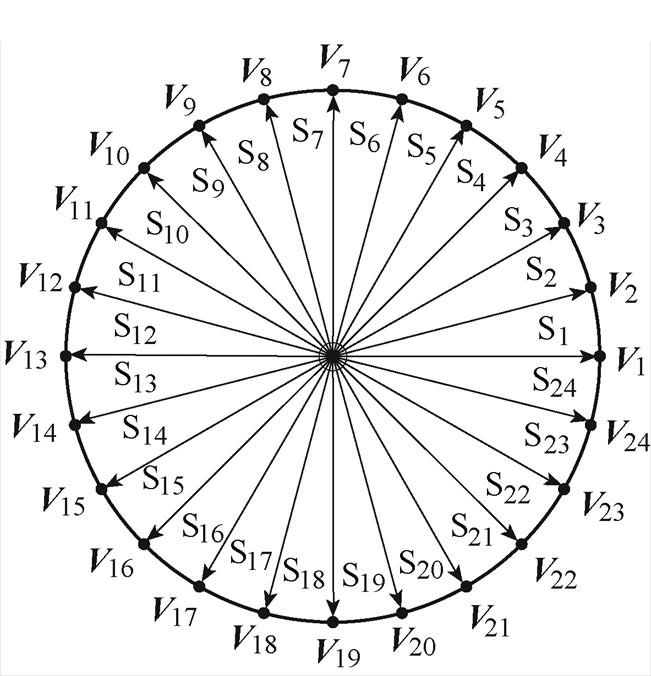
图5 24个虚拟电压矢量在ab 平面分布
Fig.5 Distribution diagram of 24 virtual voltage vectors in ab plane
合成的虚拟电压矢量在ab 平面等效幅值为0.5Udc,谐波平面等效幅值为0。为了使合成的虚拟电压矢量满足标准开关序列的要求,即一个PWM周期内每个功率器件只开关一次,且各桥臂开通时序能够中心化。合成的24个虚拟电压矢量采用两种基本电压矢量选取方式。第一种选取方式采用ab 平面最外层相邻的3个基本电压矢量合成虚拟电压矢量,例如,采用u55、u45、u44合成虚拟电压矢量V1。当虚拟电压矢量V2采用相同的方法选取u45、u44、u64合成时,桥臂F在一个周期内需要动作两次,不满足标准开关序列要求。为使V2的开关序列标准化,V2采用了第二种基本电压矢量选取方式,采用ab 平面同一方向的最外层和次外层的两个基本电压矢量u44和u65合成,当采用第二种基本电压矢量选取方式时,V2的开关序列为标准开关序列。图6为虚拟电压矢量V2的两种合成方式。图6a为V2采用第一种合成方式对应的开关序列,图6b为V2采用第二种合成方式对应开关序列,该开关序列为标准开关序列。图中,Sx为各桥臂的驱动信号,x取A、B、C、D、E、F代表相应的桥臂。
根据空间电压矢量调制的原理可以求得各基本电压矢量作用比例。以采用最外层相邻的3个电压矢量合成虚拟电压矢量为例,虚拟电压矢量和基本电压矢量的关系可表示为
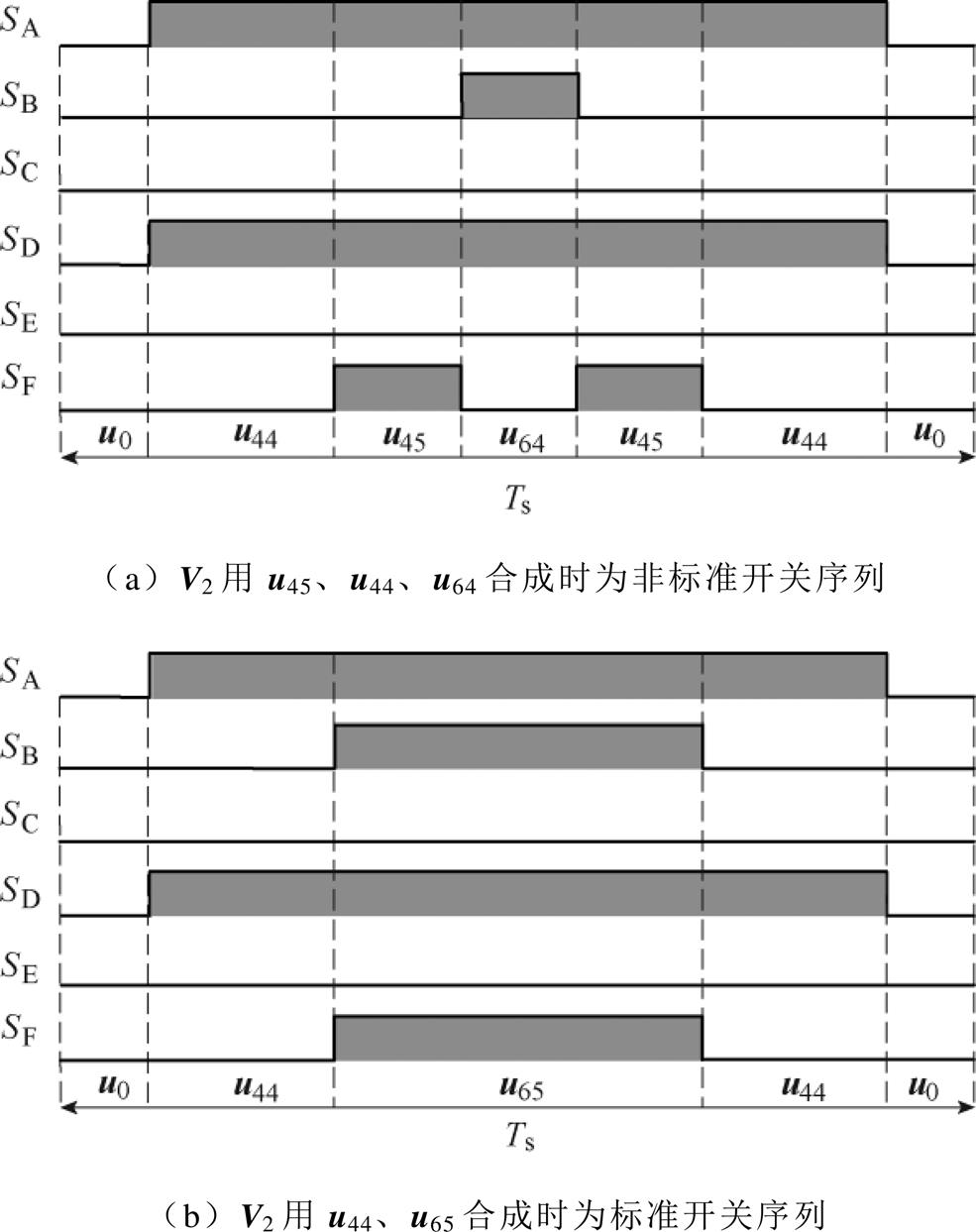
图6 虚拟电压矢量V2的两种合成方式
Fig.6 Two ways of synthesizing virtual voltage vectors V2
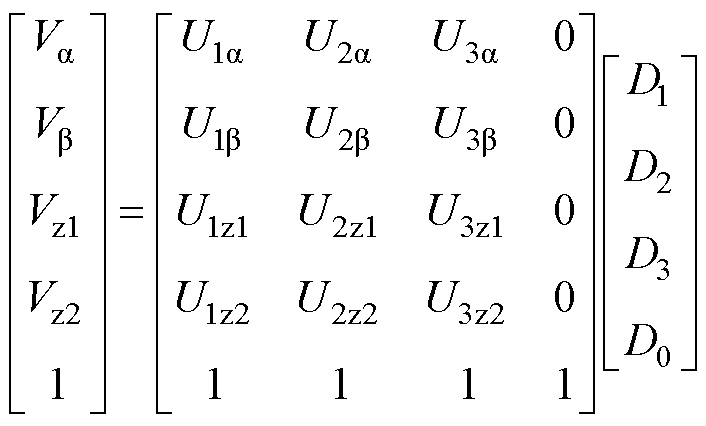 (11)
(11)式中,Va、Vb、Vz1、Vz2分别为虚拟电压矢量V在a 轴、b 轴、z1轴、z2轴的分量;U1a、U1b、U1z1、U1z2分别为选取的基本电压矢量U1在a 轴、b 轴、z1轴、z2轴的分量;U2a、U2b、U2z1、U2z2分别为选取的基本电压矢量U2在a 轴、b 轴、z1轴、z2轴的分量;U3a、U3b、U3z1、U3z2分别为选取的基本电压矢量U3在a 轴、b 轴、z1轴、z2轴的分量;D0、D1、D2、D3分别为U0、U2、U1、U3对应作用时间比例。各基本电压矢量的作用时间比例为
 (12)
(12)
根据空间电压矢量调制的原理,可离线计算得到各基本电压矢量作用比例,计算结果见表1。
各桥臂导通占空比Dx可由式(13)求得,按照中心对称方式生成所需的PWM。
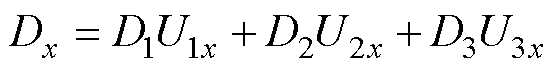 (13)
(13)式中,Dx为各桥臂的占空比,下标x取A、B、C、D、E、F,代表相应的桥臂;各虚拟电压矢量对应的作用时间比例D1、D2、D3由表1得到;U1x、U2x、U3x分别为基本电压矢量U1、U1、U3的各桥臂开关状态;U1x、U2x、U3x对应的桥臂导通则取值1,关断则取值0。
表1 虚拟电压矢量合成方法
Tab.1 Virtual voltage vector synthesis method

虚拟电压矢量基本电压矢量各电压矢量作用比例 VU1U2U3U0D1D2D3D0 V1u55u45u44u00.0290.3750.4040.192 V2u44u65—u00.6120.22400.163 V3u44u64u66u00.4040.3750.0290.192 V4u44u64u66u00.2240.3880.2240.163 V5u44u64u66u00.0290.3750.4040.192 V6u66u24—u00.6120.22400.163 V7u66u26u22u00.4040.3750.0290.192 V8u66u26u22u00.2240.3880.2240.163 V9u66u26u22u00.0290.3750.4040.192 V10u22u36—u00.6120.22400.163 V11u22u32u33u00.4040.3750.0290.192 V12u22u32u33u00.2240.3880.2240.163 V13u22u32u33u00.0290.3750.4040.192 V14u33u12—u00.6120.22400.163 V15u33u13u11u00.4040.3750.0290.192 V16u33u13u11u00.2240.3880.2240.163 V17u33u13u11u00.0290.3750.4040.192 V18u11u53—u00.6120.22400.163 V19u11u51u55u00.4040.3750.0290.192 V20u11u51u55u00.2240.3880.2240.163 V21u11u51u55u00.0290.3750.4040.192 V22u55u41—u00.6120.22400.163 V23u55u45u44u00.4040.3750.0290.192 V24u55u45u44u00.2240.3880.2240.163
传统DRM-DTC从超前定子磁链90°和滞后定子磁链90°方向相邻的4个电压矢量中,根据转矩和磁链的控制要求,选择满足控制要求的电压矢量,然后通过加入零矢量调整电压矢量的幅值。定义逆时针旋转为正,当定子磁链位于第1扇区时,基于虚拟电压矢量集DRM-DTC的待选电压矢量如图7所示。开关表见表2,表中,符号+表示增加,符号-表示减小。k为定子磁链所在扇区,表中若矢量下标大于24则减24。
当定子磁链位于第1扇区时,传统DRM-DTC在一个PWM周期内可实现的转矩调节区间如图8所示。控制转矩增加时选取矢量V7或V8,此时转矩调节范围在TeZ(u0)~TeN(V7V8)之间,其中,0~TeN(V7V8)的Z3区间可增加输出转矩。控制转矩减小时选择矢量V19和V20,此时转矩调节范围在TeZ(u0)~TeN(V19V20)之间。
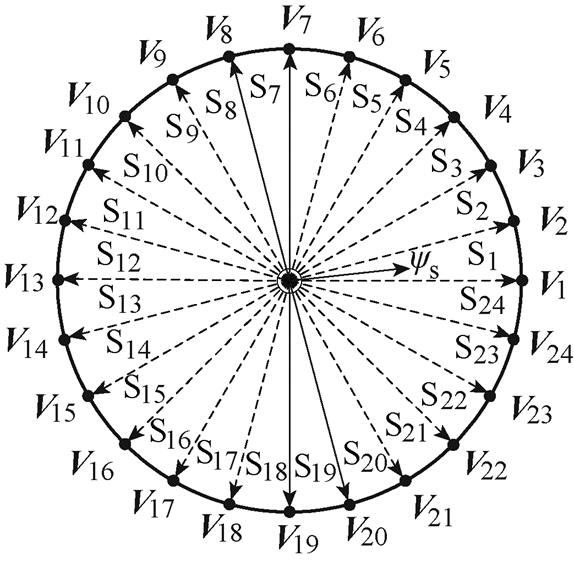
图7 传统DRM-DTC电压矢量选取方法
Fig.7 Classical DRM-DTC voltage vector selection method
表2 传统DRM-DTC开关表
Tab.2 Switching table of classical DRM-DTC
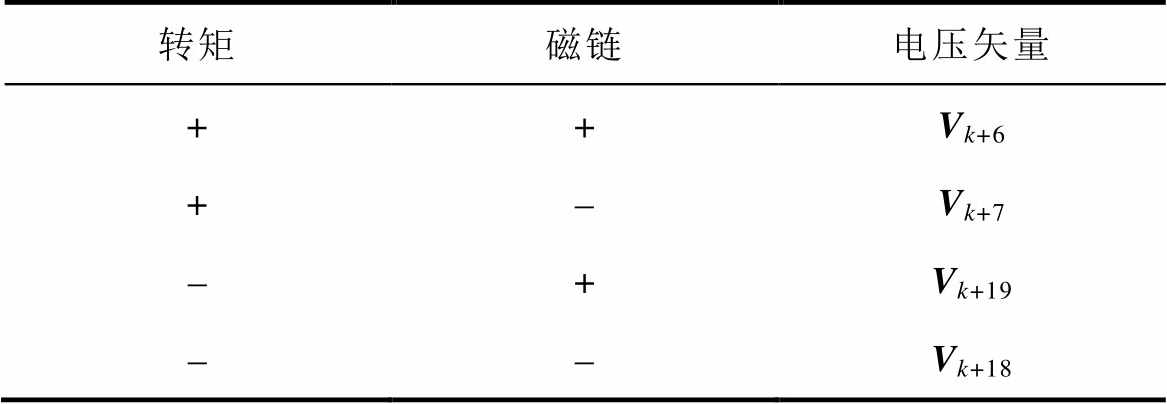
转矩磁链电压矢量 ++Vk+6 +-Vk+7 -+Vk+19 --Vk+18
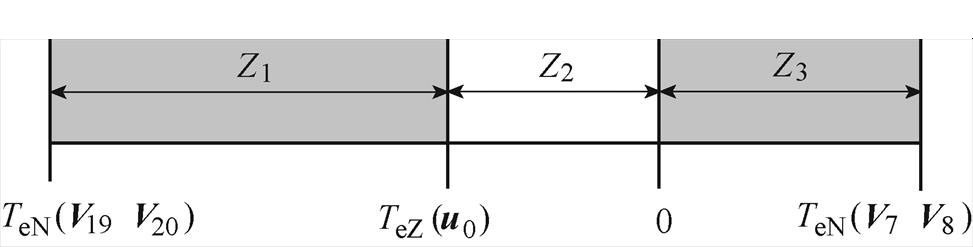
图8 传统DRM-DTC转矩调节区间
Fig.8 Region of traditional DRM-DTC torque regulation
由图8可知,传统电压矢量选取方式能够实现单周期转矩最大变化量TeN,从而保证电压矢量的利用率和转矩响应速度,但0~TeZ(u0)的Z2区间没有被合理利用。尤其当电机运行于稳态时,单周期的转矩调节量在0附近波动,若单周期转矩调节范围在Z2区间时,传统DRM-DTC受限于电压矢量选取方式无法满足控制要求,使得稳态转矩脉动变大。
针对传统DRM-DTC电压矢量选择方式的不足,提出一种用于稳态的电压矢量选取方法。当系统运行在稳态时,仅从超前定子磁链90°方向相邻的2个电压矢量中选取所需电压矢量,此时,转矩调节范围为图8中Z2和Z3区间,Z3用于增加输出转矩,Z2用于减小输出转矩,控制稳态时转矩变换量在0附近波动,有利于减小稳态转矩脉动。
图9为定子磁链位于第1扇区时用于稳态的电压矢量选取示意图。提出的开关表见表3,表中,若矢量下标大于24则减24。当系统处于动态时,采用表2所示的开关表,当系统处于稳态时,采用表3所示的开关表。
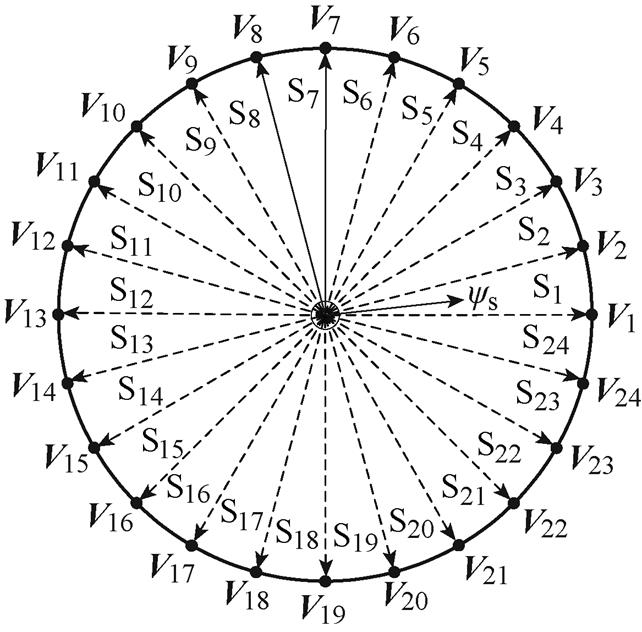
图9 提出的用于稳态的电压矢量选取方法
Fig.9 Voltage vector selection method for steady state
表3 新型DRM-DTC稳态开关表
Tab.3 Switching table of proposed DRM-DTC in steady state
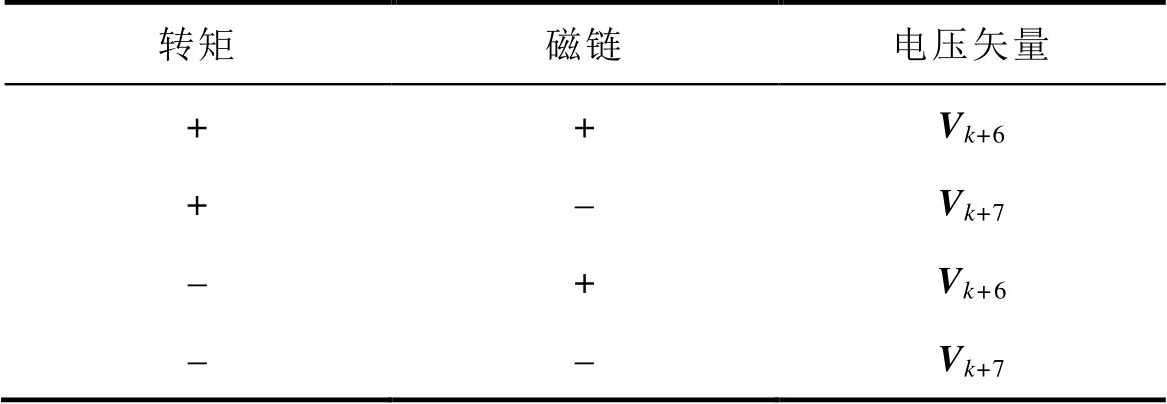
转矩磁链电压矢量 ++Vk+6 +-Vk+7 -+Vk+6 --Vk+7
DRM-DTC占空比的计算有终值法、平均值法、有效值法等[21]。图10为终值法占空比计算方法。根据转矩变化斜率f1、f0以及当前转矩Te和给定转矩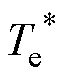 可求得非零电压矢量占空比Dset为
可求得非零电压矢量占空比Dset为
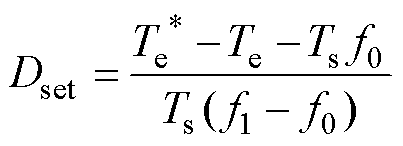 (14)
(14)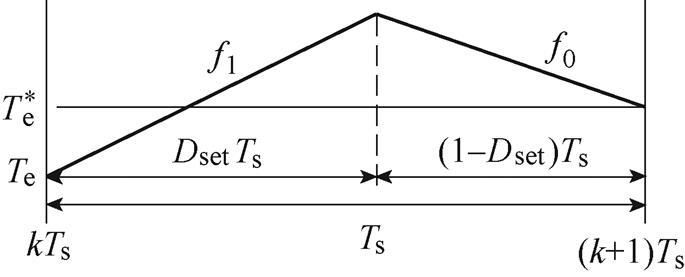
图10 终值法占空比计算方法
Fig.10 Terminal value duty cycle calculation method
由于负载的脉动、系统惯性的存在,传统占空比计算方法会出现占空比饱和的情况,导致占空比在0~1之间波动,影响系统的稳态性能。为降低稳态时转矩脉动,通过设定一个周期转矩变化量,达到降低稳态转矩脉动的目的。图11为提出的新型DRM- DTC占空比计算方法示意图,Tripple1和Tripple2为转矩脉动。虚线部分为用于稳态时的占空比计算示意图,当设定的单周期转矩变化量DTedef值比控制系统转矩误差小时,可有效减小单周期的转矩脉动。稳态时的占空比计算如式(15)所示。控制转矩增加时DTedef给定正值,控制转矩减小时DTedef给定负值。
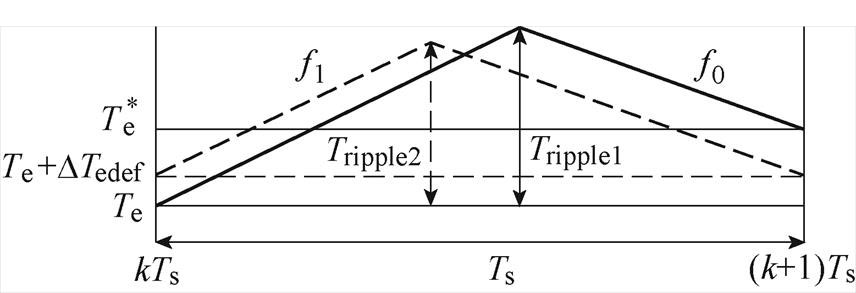
图11 新型DRM-DTC占空比计算方法示意图
Fig.11 Schematic diagram of proposed DRM-DTC duty cycle calculation method
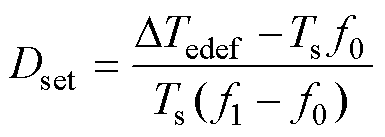 (15)
(15)限制单周期转矩变化量有利于减小稳态转矩脉动,但这会影响系统的动态响应。为此,提出的占空比计算方法仅用于稳态工况,保留传统占空比计算方法用于动态工况。当系统处于动态时,占空比的计算采用式(14),当系统处于稳态时,采用式(15)。
图12为提出的新型DRM-DTC的系统结构框图。观测器模块根据电机参数、电流以及位置信号得到转矩、定子磁链幅值、定子磁链扇区和转速。运行工况判断模块根据转速误差判断系统处于稳态或者动态,Cs用来表示系统的运行状态。为防止判断出现边沿抖动,采用了滞环判断的方法。当转速误差小于等于3%时系统设置为稳态,此时Cs=0;当转速误差大于或等于6%时,系统设置为动态,此时Cs=1;当误差在3%~6%之间时,Cs维持当前值。Mst模块由稳态开关表(见表3)和稳态占空比计算式(15)构成。Mdy模块由动态开关表(见表2)和动态占空比计算式(14)构成。当系统工作在稳态时,运行Mst模块得到虚拟电压矢量和占空比。当系统工作在动态时,运行Mdy模块得到虚拟电压矢量和占空比。最后,PWM生成模块根据选取的虚拟电压矢量和占空比得到各桥臂的开关信号,实现对双三相永磁电机的控制。图12中,n为
电机转速,n*为给定转速,Dn为转速误差;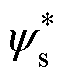 为给定定子磁链幅值,Dys为磁链误差;
为给定定子磁链幅值,Dys为磁链误差;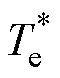 为转速外环PI控制输出的转矩,
为转速外环PI控制输出的转矩,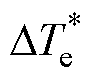 转矩误差;Sk为定子磁链扇区;Cy为磁链控制状态,CTe为转矩控制状态。
转矩误差;Sk为定子磁链扇区;Cy为磁链控制状态,CTe为转矩控制状态。
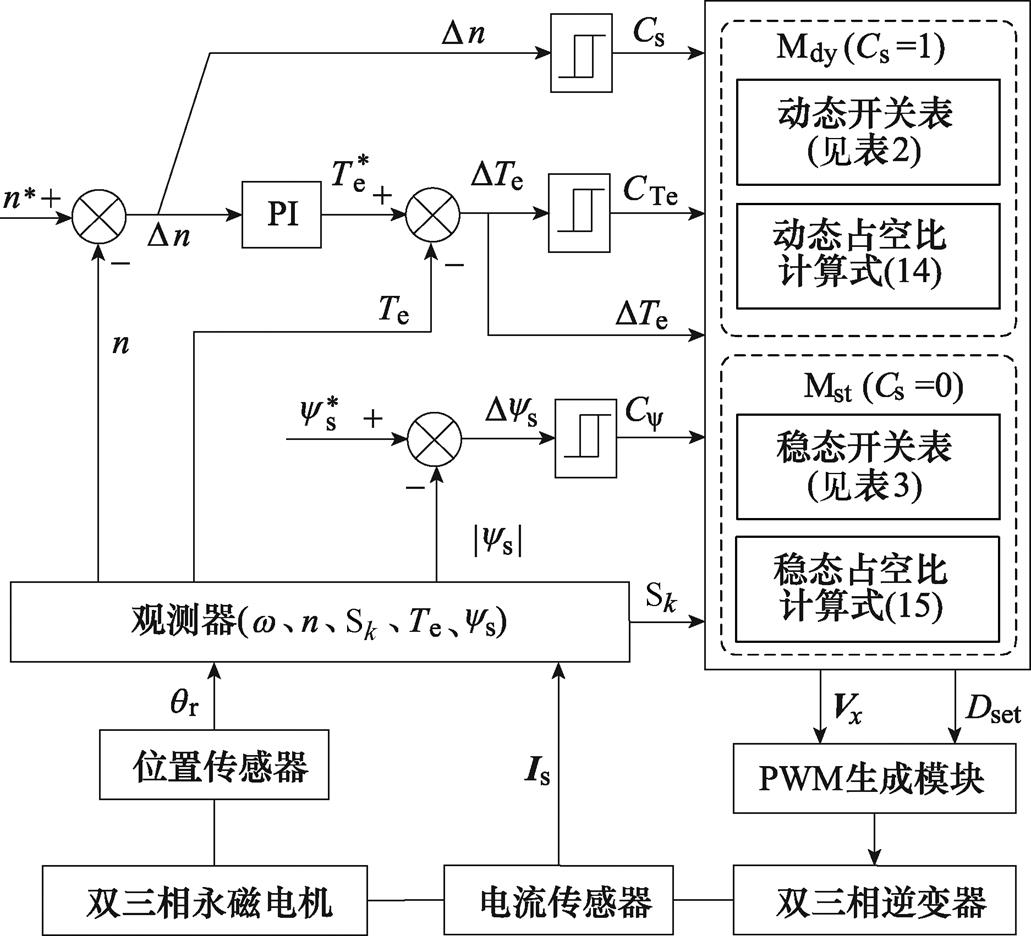
图12 新型DRM-DTC结构框图
Fig.12 Diagram of proposed DRM-DTC
为验证新型DRM-DTC策略的有效性和可行性,在双三相永磁电机实验平台开展实验研究。实验平台主要由直流电源、双三相永磁电机、双三相驱动器、转矩传感器、磁粉制动器、磁粉控制器组成,构建的实验平台如图13所示。

图13 实验平台
Fig.13 Experiment platform
实验的表贴式双三相永磁电机的d轴电感和q轴电感为15.2mH,永磁体磁链为0.88Wb,极对数为11。控制周期Ts=100ms,磁链给定为0.88Wb,PWM载波频率为10kHz,死区时间设定为2ms。
实验中,母线电压设置为150V,转速给定为40r/min,负载给定为100N·m。实验研究了四种DTC算法。算法1为传统查表法DTC,采用传统基本电压矢量集,矢量个数为12。算法2为传统DRM-DTC,在传统基本电压矢量集的基础上增加了占空比调制。算法3为基于虚拟电压矢量集的DRM-DTC,该算法采用了提出的虚拟电压矢量集和传统占空比计算方法、矢量个数为24。算法4为提出的新型DRM-DTC,采用提出的区分稳态和动态的开关表和占空比计算方法。四种实验算法对比见表4。新型DRM-DTC的DTedef参数,控制转矩增加时给定1N·m,控制转矩减小时给定-1N·m。
表4 实验算法对比
Tab.4 Comparison of experimental algorithms

实验算法矢量集开关表占空比计算 算法1基本电压矢量传统开关表无 算法2基本电压矢量传统开关表式(14) 算法3虚拟电压矢量表(2)式(14) 提出的DRM-DTC虚拟电压矢量 表(2),表(3) 式(14),式(15)
图14为四种控制算法对应的稳态实验结果。四种控制算法的稳态转矩脉动量分别为100N·m、70N·m、45N·m、23N·m。四种算法A相对应的电流谐波含量分别为69.19%、63.51%、24.15%、23.15%。磁链脉动分别为0.08Wb、0.07Wb、0.04Wb、0.04Wb。转速脉动分别为1.4r/min、1.2r/min、1r/min、1r/min。从稳态实验结果可知,采用虚拟电压矢量集的算法3和算法4相比于采用基本电压矢量集的算法1和算法2,电流的谐波含量和磁链脉动均有显著的下降。另外,新型DRM-DTC的转矩脉动相比于传统DRM- DTC也有明显的改善。说明新型DRM-DTC能有效降低稳态时的转矩脉动、磁链脉动和电流谐波。
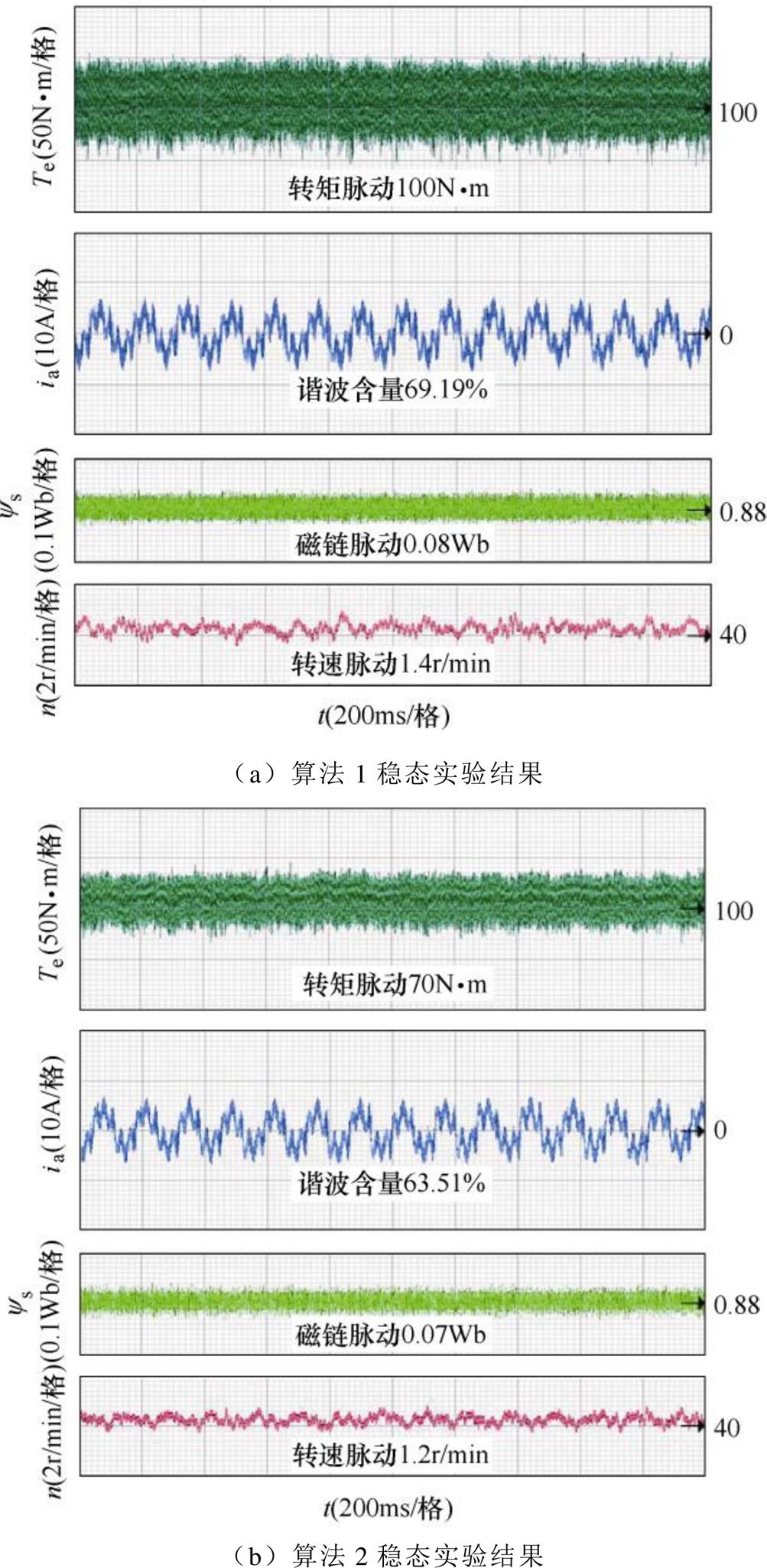
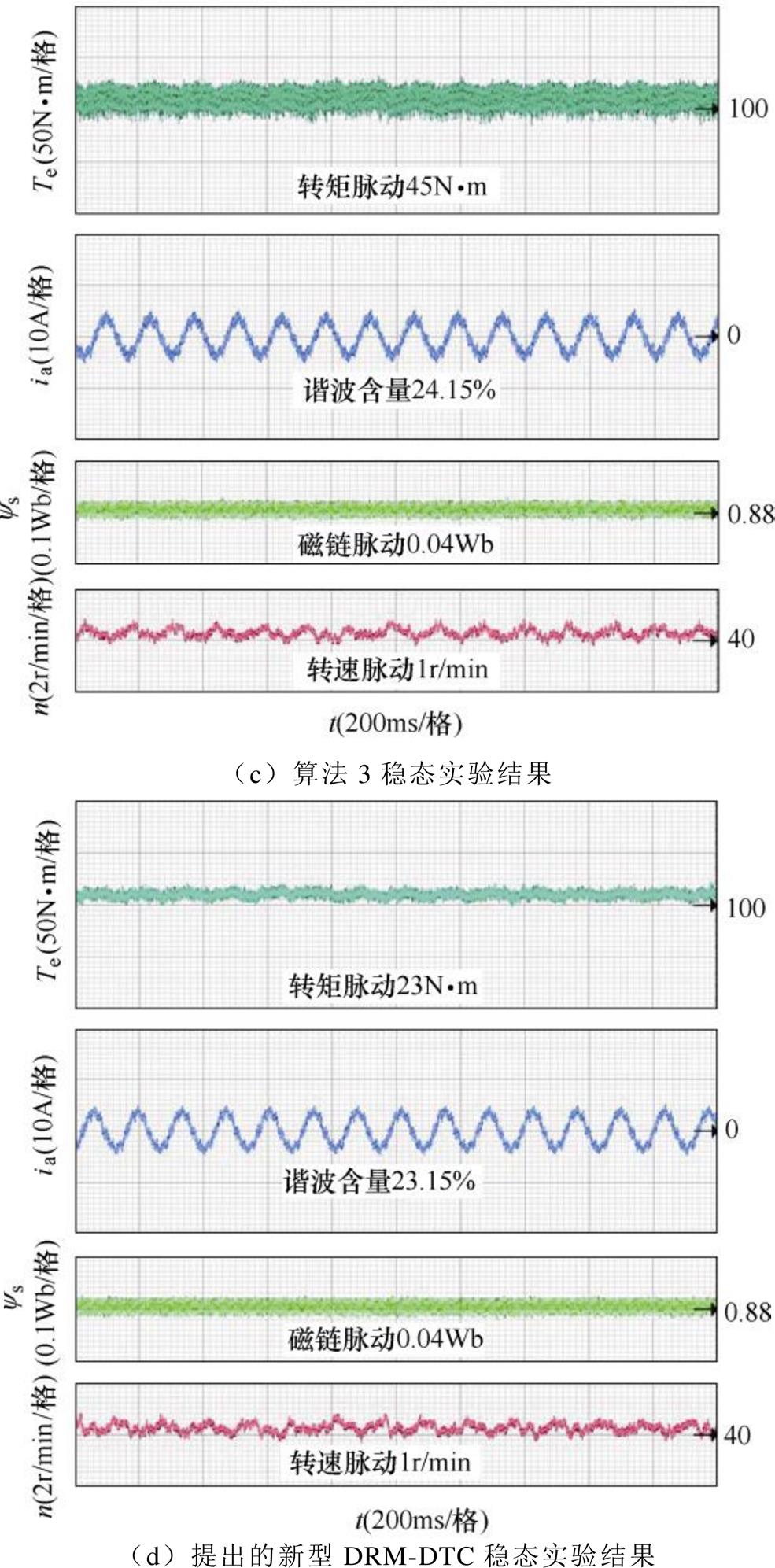
图14 四种控制算法稳态实验结果
Fig.14 Steady state experimental results of four algorithms
四种控制策略的转矩脉动主要由单周期内矢量的作用方式不同造成的,单周期内四种算法的电压矢量作用方式差异较大,转矩脉动在单个周期内变化明显,提出的新型DRM-DTC可以有效改善稳态的转矩脉动,因此,四种控制策略的转矩脉动差异较大。但由于系统转动惯量的存在,转速的脉动频率低,是转矩在一定时间内的作用结果,由于这四种控制策略采用了相同参数转速PI控制器,即转矩的给定相似,因此,在稳态时转速脉动差异较小。
图15和图16分别为算法3和算法4稳态实验占空比波形。从实验结果可以得到,算法3稳态时占空比变化为0~1之间,算法4稳态时占空比变化为0.5~0.8之间,提出的DRM-DTC占空比变化范围小,更有利于稳态运行。
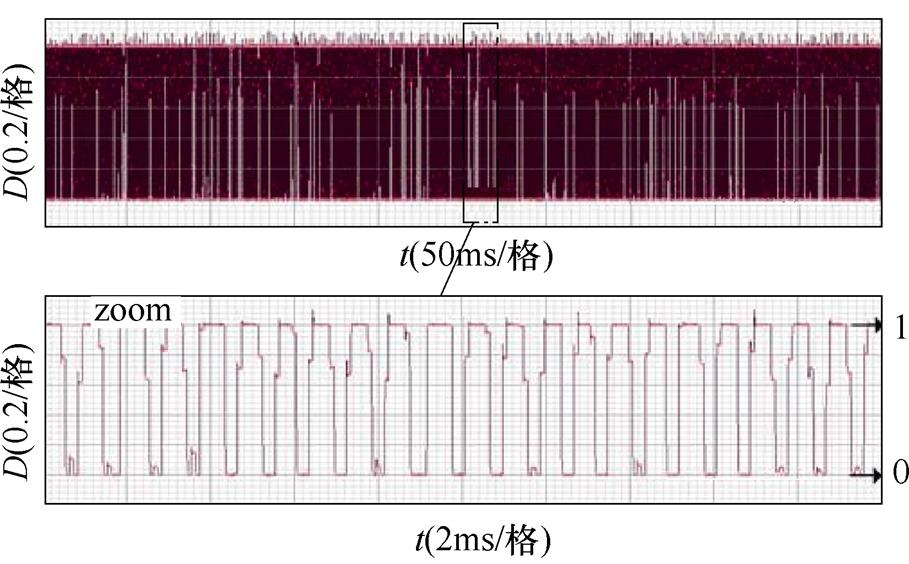
图15 算法3稳态实验占空比波形
Fig.15 Duty cycle waveform of algorithm 3 in experimental steady state
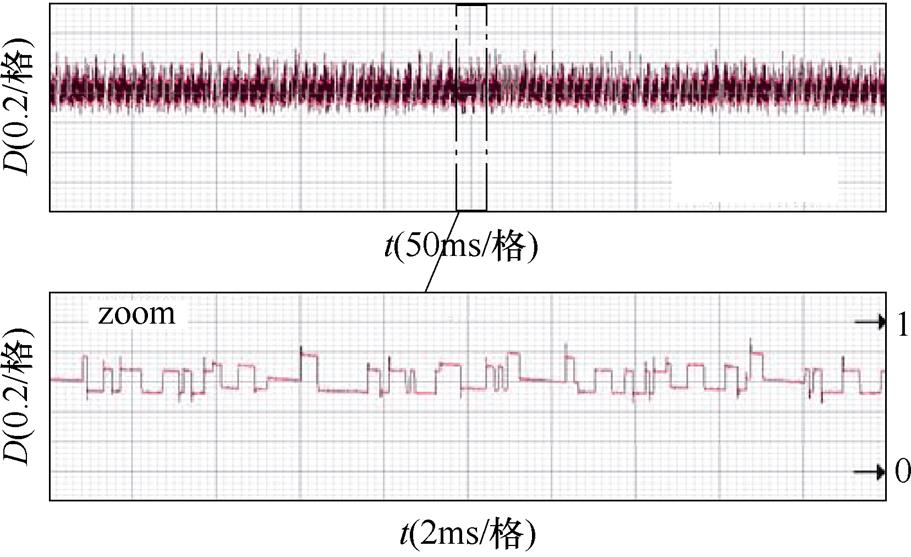
图16 算法4稳态实验占空比波形
Fig.16 Duty cycle waveforms of algorithm 4 in experimental steady state
为进一步验证新型DRM-DTC对转矩脉动的抑制效果,对比了算法3的DRM-DTC和提出的新型DRM-DTC在转速为40r/min,不同负载转矩下的稳态转矩脉动,实验结果如图17所示。可以看出,在实验的不同负载条件下,提出的新型DRM-DTC的转矩脉动均小于算法3的转矩脉动。
为验证新型DRM-DTC动态性能,实验研究了新型DRM-DTC仅运行Mst模块(稳态开关表和稳态占空比计算方法)、新型DRM-DTC仅运行Mdy模块(动态开关表和动态占空计算方法)、新型DRM-DTC(Mst和Mdy根据系统工况运行)的转速动态和负载动态性能。为满足负载动态要求,动态实验将磁粉制动器换成了永磁同步发电机,通过改变整流后电阻实现对负载转矩的调节。
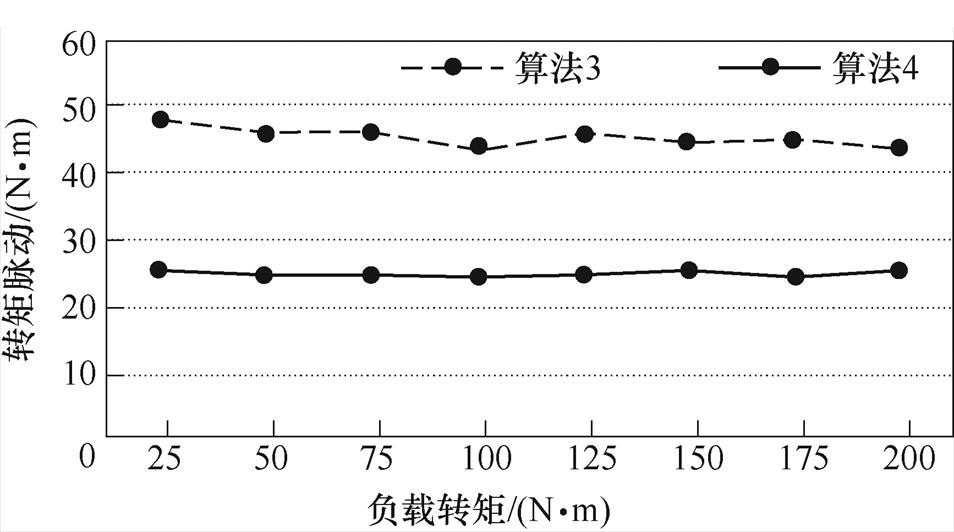
图17 不同负载条件下的转矩脉动对比结果
Fig.17 Comparison of torque ripple under different load conditions
转速动态实验中,直流母线电压为200V,转速给定为80r/min和20r/min之间动态阶跃变化,保持负载电阻值不变,80r/min时对应负载转矩为100N·m。图18为实验的三种控制方式的动态实验结果。从实验结果中可知,在20r/min到80r/min加速过程中,三种控制方式对应的上升时间分别为108ms、52ms、52ms。在80r/min到20r/min减速过程中,三种控制方式对应的下降时间分别为660ms、56ms、56ms。图中,Cs=0表示系统运行Mst模块,Cs=1表示系统运行Mdy模块。对比图18a和图18b实验结果可知,当提出的控制策略仅运行Mst模块时,系统的动态响应速度要比仅采用Mdy模块慢。图18a由于转矩变化速度慢,在80r/min突变到20r/min过程中还出现了转速为0的情况,这是由于Mst模块限制了系统的增益导致。由图18c可知,新型DRM-DTC在稳态时,Cs=0系统运行Mst模块,在转速给定突变时,系统统检测到转速误差大于6%时系统识别为动态工况,此时Cs=1,系统运行Mdy模块。新型DRM-DTC系统的动态响应和采用传统开关表和占空比计算时的动态响应速度基本一致,说明通过分别定义动态和稳态的开关表和占空比计算方法的策略可以有效保证动态响应。
由式(6)可知,电机的加速时间主要由电机转动惯量、电磁转矩、负载转矩、转速以及转速的变化量决定,通过控制电磁转矩实现对转速的控制。当电机及工况一定时,加速时间主要取决于转矩的变化斜率,即转矩变化越快,速度变化越快。从式(7)可以看到,转矩的变化斜率和q轴电压分量uq、q轴电流以及转速相关,当f1<0且uq<0,减速时转矩变化斜率的绝对值大于加速时刻的绝对值,即由于负载作用电机的加速时间长于减速时间。电机实际运行过程中,加速时的转矩变化斜率和减速时的转矩变化斜率由控制算法决定,即在确定条件下加速和减速时间由控制策略决定。

图18 不同条件下新型DRM-DTC转速动态实验结果
Fig.18 Speed dynamic experimental results of proposed DRM-DTC under three conditions
负载动态实验中,转速给定为80r/min,转矩为100N·m。通过断路器切除或切入电阻负载实现负载转矩的突变。图19为三种控制方式下的负载动态实验结果。从实验结果中可知,在负载由100N·m突变到40N·m过程中,三种控制方式对应的调节时间分别为241ms、234ms、252ms。在负载由40N·m突变到100N·m过程中,三种控制方式对应的调节时间分别为120ms、123ms、121ms。从图19的实验结果可以看出,三种控制方式突加和突卸负载的系统调节时间没有明显的差异,这主要是由于负载的惯量较大,实验中负载变化60N·m,提出的控制策略单周期转矩的变换量限幅为1N·m,对系统的影响至多需要60个控制周期即6ms可以跟随给定,而惯量对系统的影响较大,需要较长的加速时间,因此,在实验条件下三种控制方式对负载动态控制结果没有明显差异。

图19 三种条件下新型DRM-DTC负载动态实验结果
Fig.19 Load dynamic experimental results of proposed DRM-DTC under three conditions
为提高传统DRM-DTC稳态性能,本文提出一种新型DRM-DTC策略,构造了虚拟电压矢量集,提出了区分系统运行状态的开关表以及占空比计算方式。构建了实验平台,开展了实验验证。研究结果表明,采用提出的新型DRM-DTC策略,可以有效地减小传统DRM-DTC稳态转矩脉动和稳态磁链脉动,并且能显著减小稳态谐波电流。所提控制策略在改善稳态性能的同时,保证了系统的动态性能,具有较好的理论意义和工程价值。
参考文献
[1] 赵勇, 黄文新, 林晓刚, 等. 基于权重系数消除和有限控制集优化的双三相永磁容错电机快速预测直接转矩控制[J]. 电工技术学报, 2020, 36(1): 3-14.
Zhao Yong, Huang Wenxin, Lin Xiaogang, et al. Fast predictive direct torque control of dual three-phase permanent magnet fault tolerant machine based on weighting factor elimination and finite control set optimization[J]. Transactions of China Electro- technical Society, 2020, 36(1): 3-14.
[2] 陈前, 夏雨航, 赵文祥, 等. 采用无差拍电流跟踪的五相梯形反电势永磁电机开路容错控制[J]. 电工技术学报, DOI: 10.19595/j.cnki.1000-6753.tces. 200897.
Chen Qian, Xia Yuhang, Zhao Wenxiang, et al. Open-circuit fault-tolerant control for five-phase permanent magnet motors with trapezoidal back-EMF by deadbeat current tracking[J]. Transactions of China Electrotechnical Society, DOI: 10.19595/j.cnki. 1000-6753.tces.200897.
[3] 黄守道, 赵礼, 郑剑, 等. 基于扇区细分六相电压源逆变器全调制范围的空间矢量脉宽调制方法[J]. 电工技术学报, 2019, 34(24): 5070-5083.
Huang Shoudao, Zhao Li, Zheng Jian, et al. Space vector pulse width modulation strategy for six-phase voltage source inverter in full modulation range based on sector subdivision method[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5070-5083.
[4] 麦志勤, 肖飞, 刘计龙, 等. 基于准比例谐振级联PI的双三相永磁同步电机谐波电流抑制策略[J]. 电工技术学报, 2018, 33(24): 5751-5759.
Mai Zhiqin, Xiao Fei, Liu Jilong, et al. Harmonic current suppression strategy of dual three-phase permanent magnet synchronous motor based on quasi proportional resonant cascading PI[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5751-5759.
[5] 张建亚, 王凯, 朱姝姝, 等. 双三相永磁同步电机多谐波电流协同控制策略[J]. 中国电机工程学报, 2020, 40(2): 644-651.
Zhang Jianya, Wang Kai, Zhu Shushu, et al. Control strategies of dual three-phase permanent magnet machines with multi-harmonics[J]. Proceedings of the CSEE, 2020, 40(2): 644-651.
[6] 高闯, 赵文祥, 吉敬华, 等. 低谐波双三相永磁同步电机及其容错控制[J]. 电工技术学报, 2017, 32(增刊1): 124-130.
Gao Chuang, Zhao Wenxiang, Ji Jinghua, et al. Low harmonic dual three-phase permanent magnet syn- chronous motor and fault-tolerant control[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(S1): 124-130.
[7] Ma Xiaojun, Bi Chao. A technology for online parameter identification of permanent magnet syn- chronous motor[J]. China Electrotechnical Society Transactions on Electrical Machines and Systems, 2020, 4(3): 237-242.
[8] Akay A, Lefley P. Research on torque ripple under healthy and open-circuit fault-tolerant con- ditions in a PM multiphase machine[J]. China Electrotechnical Society Transactions on Electrical Machines and Systems, 2020, 4(4): 349-359.
[9] 林晓刚, 黄文新, 姜文, 等. 共母线开绕组永磁同步电机缺相容错型直接转矩控制[J]. 电工技术学报, 2020, 35(24): 5064-5074.
Lin Xiaogang, Huang Wenxin, Jiang Wen. Fault- tolerant direct torque control for open-end winding permanent magnet synchronous motor with common DC bus under open phase circuit[J]. Transactions of China Electrotechnical Society, 2020, 35(24): 5064- 5074.
[10] 徐心愿, 王云冲, 沈建新. 基于最大转矩电流比的同步磁阻电机DTC-SVM控制策略[J]. 电工技术学报, 2020, 35(2): 246-254.
Xu Xinyuan, Wang Yunchong, Shen Jianxin. Direct torque control-space vector modulation control strategy of synchronous reluctance motor based on maximum torque per-ampere[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 246- 254.
[11] Zheng Junqiang, Zhao Wenxiang, Christopher H T L, et al. Improvement torque performances of interior permanent-magnet machines[J]. China Electrotechnical Society Transactions on Electrical Machines and Systems, 2019, 3(1): 12-18.
[12] Wang Shuai, Li Chushan, Che Chen, et al. Direct torque control for 2L-VSI PMSM using switching instant table[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9410-9420.
[13] Levi E, Aware M, Pandit J, et al. Direct torque control scheme for a six-phase induction motor with reduced torque ripple[J]. IEEE Transactions on Power Electronics, 2017, 32(9): 7118-7129.
[14] Ren Yuan, Zhu Ziqiang. Reduction of both harmonic current and torque ripple for dual three-phase permanent magnet synchronous machine using modified switching-table-based direct torque control[J]. IEEE Transactions on Industrial Electronics, 2015, 62(11): 6671-6683.
[15] 余彬, 宋文胜, 冯加旭, 等. 基于虚拟电压矢量的五相电压源逆变器空间矢量调制算法[J]. 中国电机工程学报, 2020, 40(1): 212-221.
Yu Bin, Song Wensheng, Feng Jiaxu, et al. Virtual voltage vectors based space vector PWM method for five phase voltage source inverters[J]. Proceedings of the CSEE, 2020, 40(1): 212-221.
[16] Garcia-Entrambasaguas P, Zoric I, González-Prieto I, et al. Direct torque and predictive control strategies in nine-phase electric drives using virtual voltage vectors[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 12106-12119.
[17] 曹鑫, 户红艳, 颜宁, 等. 扇区实时优化的开关磁阻电机直接转矩控制方法[J]. 电工技术学报, 2018, 33(19): 4526-4534.
Cao Xin, Hu Hongyan, Yan Ning, et al. Direct torque control of switched reluctance motor with real-time optimization of sectors[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4526-4534.
[18] Xia Changliang, Wang Shuai, Wang Zhiqiang, et al. Direct torque control for VSI-PMSMs using four- dimensional switching-table[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 5774-5785.
[19] Wang Wusen, Fan Ying, Chen Siyu, et al. Finite control set model predictive current control of a five-phase PMSM with virtual voltage vectors and adaptive control set[J]. China Electrotechnical Society Transactions on Electrical Machines and Systems, 2018, 2(1): 136-141.
[20] 吕帅帅, 林辉, 李兵强. 开关频率恒定与占空比调制相结合的PMSM-DTC控制[J]. 电工技术学报, 2016, 31(3): 72-80.
Lü Shuaishuai, Lin Hui, Li Bingqiang. Direct torque control based on simple duty ratio and fixed switching frequency for PMSM[J]. Transactions of China Electrotechnical Society, 2016, 31(3): 72-80.
[21] 牛峰, 李奎, 王尧. 基于占空比调制的永磁同步电机直接转矩控制[J]. 电工技术学报, 2014, 29(11): 20-29.
Niu Feng, Li Kui, Wang Yao. Model predictive direct torque control for permanent magnet synchronous machines based on duty ratio modulation[J]. Transa- ctions of China Electrotechnical Society, 2014, 29(11): 20-29.
[22] Ibrahim Mohd Alsofyani, Nik Rumzi Nik Idris, Kyo-Beum Lee. Dynamic hysteresis torque band for improving the performance of lookup-table-based DTC of induction machines[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7959-7970.
[23] 武雪松, 宋文胜, 薛诚. 基于虚拟电压矢量集占空比优化的五相永磁同步电机直接转矩控制算法[J]. 中国电机工程学报, 2019, 39(3): 857-867.
Wu Xuesong, Song Wensheng, Xue Cheng. Direct torque control schemes for five-phase permanent- magnet synchronous machines based on duty ratio optimization of virtual voltage vector sets[J]. Pro- ceedings of the CSEE, 2019, 39(3): 857-867.
[24] 余彬, 宋文胜, 薛诚, 等. 一种基于优化占空比的五相永磁同步电机直接转矩控制算法[J]. 中国电机工程学报, 2019, 39(19): 5857-5866.
Yu Bin, Song Wensheng, Xue Cheng, et al. A direct torque control scheme of five-phase permanent magnet synchronous machine based on optimized duty ratio[J]. Proceedings of the CSEE, 2019, 39(19): 5857-5866.
[25] 陈浩, 和阳, 赵文祥, 等. 基于占空比调制的五相容错永磁游标电机直接转矩控制[J]. 电工技术学报, 2020, 33(5): 1055-1064.
Chen Hao, He Yang, Zhao Wenxiang, et al. Direct torque control of five-phase fault-tolerant permanent magnet vernier motor based on duty cycle modu- lation[J]. Transactions of China Electrotechnical Society, 2020, 33(5): 1055-1064.
[26] Yuan Ren, Zhu Ziqiang, Green J E, et al. Improved duty-ratio-based direct torque control for dual three-phase permanent magnet synchronous machine drives[J]. IEEE Transactions on Industry Appli- cations, 2019, 55(6): 5843-5853.
[27] 於锋, 朱晨光, 吴晓新, 等. 基于矢量分区的永磁同步电机三电平双矢量模型预测磁链控制[J]. 电工技术学报, 2020, 35(10): 2130-2140.
Yu Feng, Zhu Chenguang, Wu Xiaoxin, et al. Two- vector-based model predictive flux control of three- level based permanent magnet synchronous motor with sector subregion[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2130-2140.
[28] 徐艳平, 李园园, 周钦, 等. 矢量双选取的永磁同步电动机直接转矩控制策略[J]. 中国电机工程学报, 2018, 38(17): 5211-5218.
Xu Yanping, Li Yuanyuan, Zhou Qin, et al. A double vectors selection direct torque control strategy of permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2018, 38(17): 5211-5218.
[29] 徐艳平, 王极兵, 张保程, 等. 永磁同步电机三矢量模型预测电流控制[J]. 电工技术学报, 2017, 32(20): 222-230.
Xu Yanping, Wang Jibing, Zhang Baocheng, et al. Three-vector-based model predictive current control for permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(20): 222-230.
Direct Torque Control for Dual Three-Phase Permanent-Magnet Machine with Improved Steady-State Performance
Abstract The classical direct torque control (DTC) strategy-controlled dual three-phase permanent-magnet machine usually suffers from high harmonic current, flux ripple and torque ripple. To improve the steady state performance of DTC, a duty ratio modulation direct torque control (DRM-DTC) strategy based on virtual voltage vector set is proposed in this paper. Firstly, the voltage vector set is extended from 12 basic voltage vectors to 24 virtual voltage vectors. The harmonic plane is controlled by the virtual voltage vector, and the harmonic current is suppressed. By increasing the number of voltage vectors, the control of the flux is more accurate and the flux ripple can be reduced. Moreover, the switching table and duty cycle calculation method for dynamic and steady state conditions are defined. Subsequently, the torque ripple in steady state can be reduced, and the dynamic performance can be ensured, respectively. Experiments on the prototype machine are carried out to verify the feasibility of the proposed DRM-DTC strategy.
Keywords:Direct torque control, dual three-phase permanent-magnet machine, duty ratio modulation, virtual voltage vectors, torque ripple, harmonic current
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.200839
国家杰出青年科学基金(52025073)和江苏省重点研发计划(BE2018107)资助项目。
收稿日期 2020-07-10
改稿日期 2020-10-27
E-mail: linsen.huang@qq.com
赵文祥 男,1976年生,教授,博士生导师,研究方向为电机设计与控制。
E-mail: zwx@ujs.edu.cn(通信作者)
(编辑 崔文静)