 (1)
(1)摘要 传统损耗统计理论对铁磁材料的高频损耗预测误差较大且存在过高估算的问题。为此,该文首先考虑高频条件下磁通密度不均匀分布对磁滞损耗的影响,提出基于有限单元剖分法的磁滞损耗计算方法。然后基于R-L型分数阶导数对传统损耗统计理论中的涡流场和涡流损耗计算式进行改进,并引入量子遗传算法对分数阶导数模型中阻尼系数和导数阶次进行全局寻优。在上述磁滞损耗、涡流损耗模型以及参数提取方法的基础上,提出适用于宽频率、宽磁通密度范围的改进型损耗统计方法。最后采用爱泼斯坦方圈测量了3% Si-Fe超薄取向硅钢片在10Hz~10kHz频率范围的损耗,将理论计算值与实验测量值进行对比,结果表明,所提方法在整个频段内的最大平均相对误差为9.14%,最小平均相对误差为2.13%,相比于传统损耗理论,损耗预测精度大大提高,验证了该文方法的有效性。
关键词:损耗统计理论 磁滞损耗 涡流损耗 分数阶导数 量子遗传算法
在中高频应用工况下,非晶合金、纳米晶合金、超薄硅钢等铁磁材料具有优异的软磁性能,是电力电子、航空航天、国防军工等领域不可缺少的关键材料[1-2]。随着工作频率的提高,铁磁材料的能量损耗将显著增加。为了提高设备的运行效率、能源利用率,需要在了解铁磁材料损耗机理的基础上,掌握铁磁材料在高频磁化条件下的损耗求解方法。
1892年,C. P. Steinmetz首次提出基于实验数据拟合的经验公式法求解铁心损耗并认为铁心损耗仅决定于铁心材料、频率与峰值磁通密度[3]。Steinmetz经验公式法虽然具有计算参数少、形式简便等优点,但本质上属于现象学模型,缺乏对损耗产生机理的解释且计算精度较低[4]。为解决上述问题,G. Bertotti基于对巴克豪森跳跃现象描述,提出经典损耗统计理论(Statistical Theory of Loss, STL),将总损耗分离为磁滞损耗、涡流损耗与剩余损耗分量[5]。损耗统计理论具有物理概念清晰,适用于任意波形损耗计算的优点,但铁磁材料内部磁通密度均匀分布、趋肤效应可忽略的假设条件使得损耗统计理论仅在低频段适用[6]。文献[7-8]在损耗统计理论框架下,基于复磁导率与线性磁化法则从麦克斯韦方程中推导出了高频涡流损耗计算表达式,但这种改进方法仅适用于较低磁通密度下的损耗计算。一些学者将磁滞模型如Preisach模型[9]、Energetic模型[10]与电磁场扩散方程进行耦合[11],采用有限元法或有限差分法等数值计算方法,获取了高精度的高频损耗计算结果。然而,这些数值计算方法在实现过程中会耗费大量的计算时间和存储空间,磁滞的高度非线性特性也会导致计算结果收敛的不确定性[12]。
近年来,B. Ducharne等将分数阶导数引入铁磁材料的涡流场计算中,实现了铁磁材料在高频条件下动态磁滞回线的精确模拟[13]。分数阶导数具有时间记忆性与全局相关性的特点,其阶数提供了全新的自由度,避免了数值计算方法进行空间离散造成的所需计算时间较长、所需存储空间较大的问题,保证了高频动态磁滞回线模拟的准确性,因而被广泛应用于电磁理论领域。比如:D. Guyomar基于机械干摩擦概念的准静态磁滞模型与分数阶导数结合构造的动态模型用于铁电材料的动态磁滞行为模拟,取得了良好的效果[14];Zhang Bin等分别将J-A磁滞模型和Preisach模型与分数阶导数组合应用于铁磁材料的动态磁滞模拟,针对取向晶粒硅钢铁磁材料的动态磁滞回线与损耗计算取得了良好的模拟效果[15-16]。然而,上述基于分数阶导数的动态磁滞模拟与损耗计算存在如下几个问题:①在高频条件下磁通密度呈不均匀分布,磁滞损耗将随磁化频率与峰值磁通密度发生变化[17],基于静态磁滞模型获得的单位周期内磁滞损耗与频率无关,这与实际情况不相符。同时,磁滞模型实现起来较为复杂且需要较大的数据量与计算量[4]。②分数阶导数的参数提取(包括分数阶导数的阶数与阻尼系数)是根据低频和高频条件下的磁滞回线数据通过试凑得到,得到的参数值并不能保证为全局最优值。
在传统损耗统计理论基础上,本文考虑了高频条件下磁通密度不均匀分布对磁滞损耗的影响,提出了基于有限单元剖分法的磁滞损耗计算方法。在对R-L型和G-L型分数阶导数特点进行分析的基础上,利用R-L型分数阶导数对传统损耗统计理论中的涡流场和涡流损耗计算式进行改进。引入量子遗传算法,以涡流损耗计算值与测量值之间误差最小为目标函数,实现对分数阶导数模型中的阻尼系数和导数阶次的全局寻优。以3%Si-Fe超薄取向硅钢片为例,通过爱泼斯坦方圈测量了超薄取向硅钢叠片的损耗,比较了不同频率、不同磁通密度下传统损耗统计模型、基于线性磁化法则的损耗统计模型与基于分数阶导数的损耗统计模型的预测精度。近年来,多相电机及其调速传动系统已成为国内外研究的焦点。
基于损耗统计理论,G. Bertotti提出了铁磁材料损耗统计模型,将单个周期内的铁磁材料总损耗Wt分解为静态磁滞损耗Wh、涡流损耗Wcl和剩余损耗Wex,总损耗的表达式为
 (1)
(1)在损耗统计理论框架下,静态磁滞损耗仅与峰值磁通密度Bp有关,文献[18]提出了适用于计算高磁通密度下的磁滞损耗计算式为
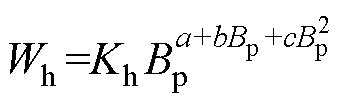 (2)
(2)
式中,Kh、a、b、c为参数,可以根据静态磁滞损耗测量值拟合得到。
在低频条件下,传统损耗统计理论基于铁磁材料内部磁通密度均匀分布的假设条件,根据Maxwell方程推导出涡流损耗的计算式为
 (3)
(3)式中, 为铁磁材料电导率;d为铁磁材料叠片的厚度;f为磁化频率;B(t)为瞬时磁通密度。
为铁磁材料电导率;d为铁磁材料叠片的厚度;f为磁化频率;B(t)为瞬时磁通密度。
在高频条件下,趋肤效应显著,铁磁材料内部的磁通密密度不再均匀分布。文献[7-8]基于线性磁化法则,考虑趋肤效应的影响,提出正弦波激励下的涡流损耗表达式为
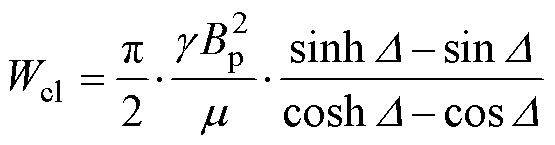 (4)
(4)其中

式中,D为归一化叠片厚度;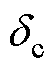 为趋肤深度;m为铁磁材料的磁导率。
为趋肤深度;m为铁磁材料的磁导率。
G. Bertotti基于材料内部微观结构和磁畴结构的随机统计分布特性推导了剩余损耗计算解析式为
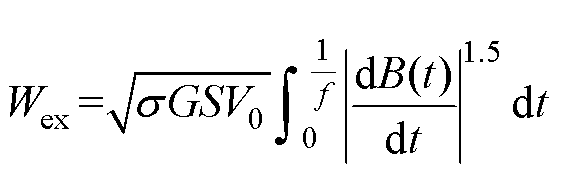 (5)
(5)式中,G为无量纲数,G=0.135 6;S为铁磁材料横截面积;V0为表征磁体局部磁场分布的统计参数。
式(2)、式(3)和式(5)所组成的传统损耗统计理论在低频条件下对铁磁材料的损耗预测精度较好,但随着频率的升高,趋肤效应显著,此时铁磁材料内部磁通密度均匀分布的假设条件将不再适用,进而使得传统损耗统计理论的损耗预测值与实验测量值的误差逐渐增加。为了说明传统损耗理论所存在的这一固有缺陷,本文基于式(2)、式(3)和式(5)计算了厚度为0.071 9mm的超薄取向硅钢在磁通密度为0.4T、1T和1.5T下10Hz~10kHz频率范围内的损耗,并与测量值进行比较,如图1a~图1c所示。由图1可知,随着频率的增加,传统损耗统计理论的预测值与测量值的误差逐渐增大,并且预测值明显高于测量值。
为了将损耗统计理论的应用范围扩展至宽频率、宽磁通密度范围,必须对传统损耗统计理论进行改进。需要注意的是,文献[7-8]研究表明,趋肤效应对剩余损耗分量的影响较小,式(5)仍然适用于高频条件下剩余损耗的预测。
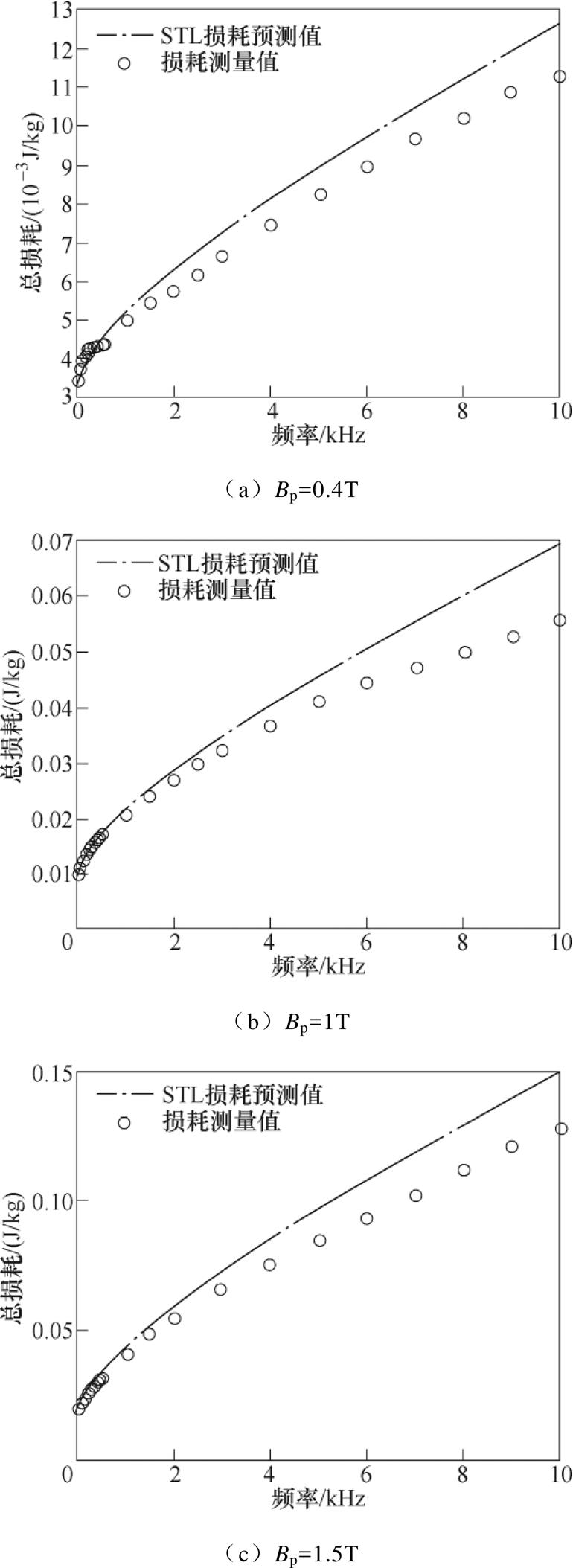
图1 传统损耗统计理论的损耗计算值与测量值对比
Fig.1 Comparison of the predictive losses based on traditional STL and measured losses
在低频率下,铁磁材料内部涡流较小,趋肤效应可以忽略。随着频率的增加,趋肤效应逐渐明显,趋肤深度的表达式为
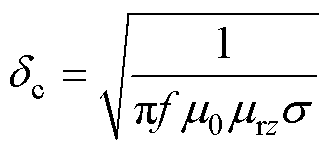 (6)
(6)式中,m0为真空中磁导率,m0=4p×10-7;s 为硅钢片的电导率;mrz为沿轧制方向的常数相对磁导率。
计及峰值磁通密度对相对磁导率的影响,可以表示为以mrz为自变量的多项式,有
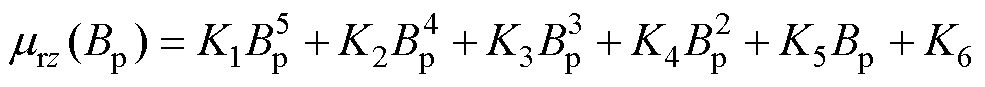 (7)
(7)式中,K1~K6为拟合系数,可以采用沿轧制方向的铁磁材料磁导率测量值拟合得到。
铁磁材料处于高频交变磁场中,其磁通密度和磁场强度之间将存在相位差,因此高频条件下磁导率为复数。铁磁材料的串联复数磁导率可以表示为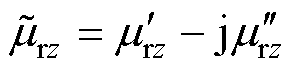 ,轧制方向的相对复数磁导率表达式可以由平均峰值磁通密度Bp与表面磁场强度Hs的比值得到[19],有
,轧制方向的相对复数磁导率表达式可以由平均峰值磁通密度Bp与表面磁场强度Hs的比值得到[19],有
 (8)
(8)式中,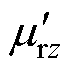 和
和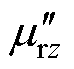 分别为相对复数磁导率的实部和虚部;j为虚数单位;
分别为相对复数磁导率的实部和虚部;j为虚数单位;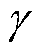 为传播常数,
为传播常数,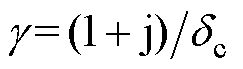 。
。
高频条件下,铁磁材料内部磁通密度受趋肤效应、复数磁导率、非线性磁化特性等因素的共同影响,沿铁磁材料厚度方向上各个部分的磁滞回线不同[19],硅钢片截面划分示意图如图2所示。假设硅钢片被划分为5层区域,从外至内的区域分别编号为1、2、3(即表层为区域1,中心为区域3),记硅钢片截面上磁通密度为Bpk(k=1, 2, 3),对应区域内产生的涡流为ie1、ie2。图2中,w为硅钢片截面宽度,d为硅钢片的厚度,dk(k=1, 2, 3)为硅钢片划分后各层区域的厚度。硅钢片外表面上的交变磁通密度Bscos(w t)的方向平行于z轴方向,即轧制方向。上述变化影响了单位周期的总磁滞损耗,一个周期内磁滞损耗不再等于一个周期内、相同磁峰密度下的静态磁滞损耗。精确获取高频下磁滞损耗必须考虑铁磁材料厚度方向的磁通密度分布。
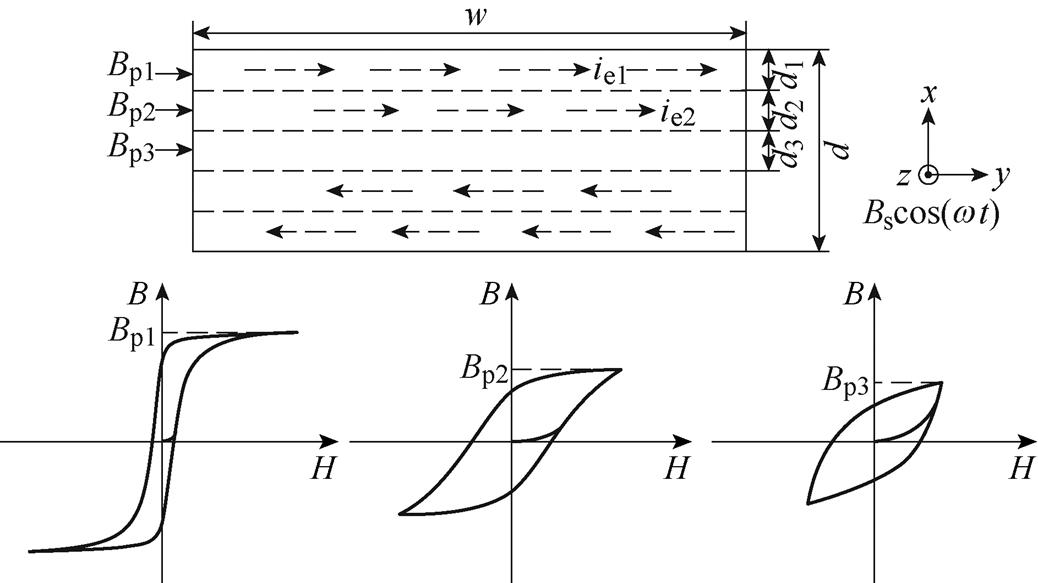
图2 硅钢片截面划分示意图
Fig.2 Schematic diagram of dividing a single steel sheet
硅钢片厚度方向任意位置处的瞬时磁通密度表达式[19]为
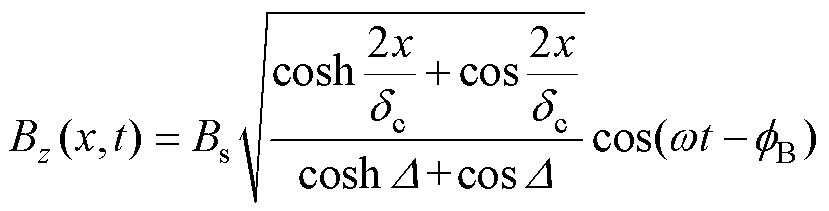 (9)
(9)式中,Bs为硅钢片外表面的磁通密度; 为磁通密度相位;w 为角频率。
为磁通密度相位;w 为角频率。
平均峰值磁通密度Bp与表面磁通密度Bs的关系为
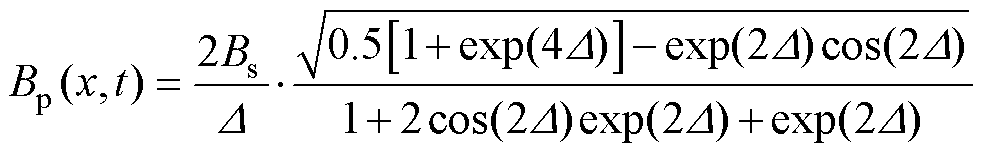 (10)
(10)考虑到高频条件下磁通密度不均匀分布的情况,对磁滞损耗计算式(2)进行了改进,使其能够适用于高频条件下磁滞损耗计算。改进步骤为:利用式(8)~式(10)得到给定频率与表面峰值磁通密度下的磁通密度分布;沿厚度方向上将铁磁材料划分为N个单元,计算各个单元内部磁通密度Bpn (n=1, 2,…, N)。采用式(2)计算各个单元磁滞损耗,总磁滞损耗为各剖分单元磁滞损耗的叠加,有
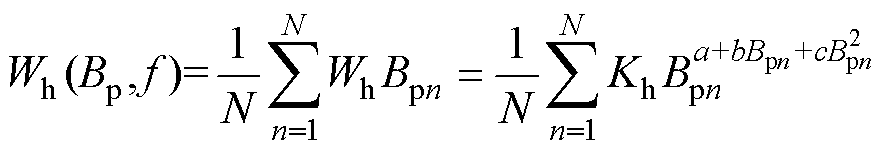 (11)
(11)
传统涡流损耗表达式中含有瞬时磁通密度对时间的整数阶导数。整数阶导数的局部极限定义不适用于描述非局部、频率、历史等依赖性过程[20]。为了避免数值计算方法进行空间离散造成的所需计算时间较长、存储空间较大的问题,同时能够考虑涡流损耗对频率的依赖特性,本文引入分数阶导数,实现对高频涡流损耗的解析建模和计算。
分数阶导数将传统导数的阶数n由整数推广至非整数和复数[21]。Grünwald-Letnikov(G-L)型与Riemann-Liouville(R-L)型分数阶作为分数阶算子的特例,前者表示n阶导数,后者表示n阶积分。R-L型分数阶是对G-L型分数阶的改进与扩展[21],R-L型分数阶所能描述的函数类别比G-L型分数阶更加广泛,G-L型仅能用于描述可积的函数。然而,对于本文所研究的正弦磁通密度函数,两类分数阶导数算子是等价的。因此,本文将依据R-L型分数阶导数对传统损耗统计理论中的涡流场和涡流损耗计算式进行改进,R-L型分数阶导数的具体形式[20]为
 (12)
(12)式中,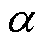 为非整数阶,该系数的取值范围为
为非整数阶,该系数的取值范围为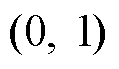 [20];
[20];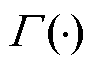 为欧拉伽马函数。
为欧拉伽马函数。
上述R-L型分数阶定义式为分数阶微分算子形式,可以考虑变量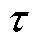 从初始时刻0到当前时刻t的整个过程的影响,体现了分数阶的时间记忆性与全局相关性的特点。这些特点使得分数阶相对于整数阶能够更加精确地描述具有幂律性、非局部、频率、路径或历史依赖特性的反常复杂物理现象[20]。此外,
从初始时刻0到当前时刻t的整个过程的影响,体现了分数阶的时间记忆性与全局相关性的特点。这些特点使得分数阶相对于整数阶能够更加精确地描述具有幂律性、非局部、频率、路径或历史依赖特性的反常复杂物理现象[20]。此外,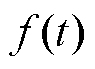 在R-L型分数阶导数的傅里叶变换中的表达式为
在R-L型分数阶导数的傅里叶变换中的表达式为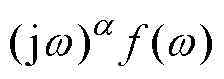 ,由于
,由于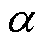 可为任意非负实数,因而分数阶微分算子可以描述对任意阶频率的依赖性,这为低频段与高频段涡流损耗计算精度的整体平衡性提供了可能。
可为任意非负实数,因而分数阶微分算子可以描述对任意阶频率的依赖性,这为低频段与高频段涡流损耗计算精度的整体平衡性提供了可能。
根据场分离假设[22],涡流场Hcl与传统损耗统计理论的涡流损耗Wcl计算式满足
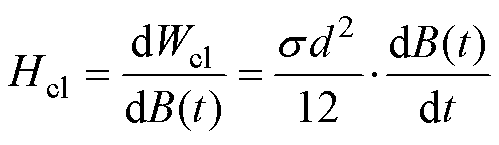 (13)
(13)将式(12)引入式(13),可以实现对传统损耗统计理论中的涡流场的改进,有
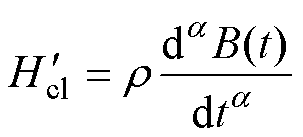 (14)
(14)
式中, 为改进后的涡流场阻尼系数。在正弦磁通密度激励下,基于分数阶导数改进的涡流场计算式可进一步表示[23]为
为改进后的涡流场阻尼系数。在正弦磁通密度激励下,基于分数阶导数改进的涡流场计算式可进一步表示[23]为
进而得到的基于分数阶导数的改进涡流损耗解析计算式,有
 (16)
(16)
需要说明的是,文献[24]基于电磁场扩散方程与分数阶导数项的等价证明了式(14)中阻尼系数 与铁磁材料厚度、磁导率、电导率等物理参数有关,而分数阶导数阶数
与铁磁材料厚度、磁导率、电导率等物理参数有关,而分数阶导数阶数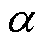 与频率-损耗(f-W)曲线的形状有关,并通过实验得到了验证,这为分数阶导数在损耗统计理论中的改进应用提供了具体物理意义。
与频率-损耗(f-W)曲线的形状有关,并通过实验得到了验证,这为分数阶导数在损耗统计理论中的改进应用提供了具体物理意义。
基于分数阶导数的改进涡流损耗计算模型面临的一个关键问题,即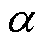 和
和 参数的确定。文献[14-16]通过对比低频和高频条件下两个模拟磁滞回线与测量磁滞回线对应的面积和矫顽力,确定
参数的确定。文献[14-16]通过对比低频和高频条件下两个模拟磁滞回线与测量磁滞回线对应的面积和矫顽力,确定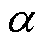 和
和 的大概取值。然而,这种方法需要大量的磁滞回线测量数据,而且不能保证获得的
的大概取值。然而,这种方法需要大量的磁滞回线测量数据,而且不能保证获得的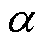 和
和 值为全局最优。为了更加精确、快速地提取
值为全局最优。为了更加精确、快速地提取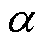 和
和 的最优值,本文引入量子遗传算法,将含待优化参数
的最优值,本文引入量子遗传算法,将含待优化参数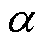 、
、 的改进涡流损耗表达式的计算值与涡流损耗测量值之间的方均根误差作为优化算法的目标函数,进而将分数阶参数
的改进涡流损耗表达式的计算值与涡流损耗测量值之间的方均根误差作为优化算法的目标函数,进而将分数阶参数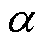 和
和 的最优值提取问题转化为目标函数最小化问题。目标函数为
的最优值提取问题转化为目标函数最小化问题。目标函数为
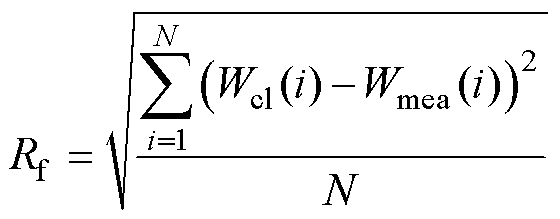 (17)
(17)式中,Rf为方均根误差;Wcl为基于式(16)的理论计算值;Wmea为损耗测量值。
值得注意的是,本文选用不同磁通密度下低频段与高频段中几个典型频点的损耗测量值作为算法的拟合数据点,这样保证了所获取的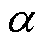 和
和 最优值对任意磁通密度内的不同频率的损耗预测均适用。
最优值对任意磁通密度内的不同频率的损耗预测均适用。
传统遗传算法易受交叉、变异概率取值不当影响而产生过早收敛于局部最优解、局部搜索能力弱等问题[25]。量子遗传算法是量子计算与遗传算法相结合新兴发展起来的概率进化算法。利用量子态的叠加、纠缠和干涉特性,将量子的态矢量引入遗传编码,使一条染色体可以表达多个态的叠加,并利用量子逻辑门实现染色体的更新操作,进而实现目标函数的优化与求解。量子遗传算法既克服了传统遗传算法的固有缺陷,同时也保留了其高鲁棒性与广泛适用性等优点。
基于量子遗传算法提取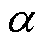 和
和 最优值的基本步骤如下:
最优值的基本步骤如下:
(1)种群初始化:将不同磁通密度不同频点的损耗测量值数据点归为一个种群集合,利用量子遗传算法函数IntPop产生初始化种群下量子比特应用于染色体的编码矩阵chrom,有
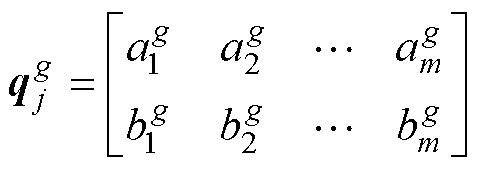 (18)
(18)式中,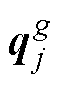 为种群进化至第g代第j个染色体;m为染色体中基因总量;
为种群进化至第g代第j个染色体;m为染色体中基因总量;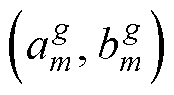 为第g代染色体第m个基因中的量子比特,满足归一化条件
为第g代染色体第m个基因中的量子比特,满足归一化条件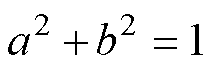 。
。
(2)采用collapse函数对种群进行一次测量,获得确定解集。
(3)基于目标函数(式(17))对P(g)中每个个体进行适应度评估,并作为下一步进化目标值。
(4)对步骤(3)进行循环迭代,并保留P(g)中适应度最优个体及适应度值。
(5)种群迭代次数是否大于最大迭代数,满足条件计算结束;否则,继续下一步运算。
(6)实行量子门操作,实现染色体基因的变异进化,从而形成新的种群。量子旋转门的更新式[26]为
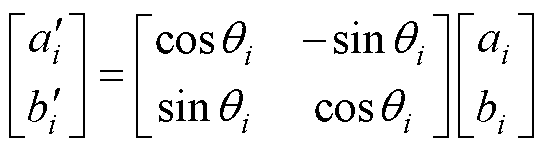 (19)
(19)其中
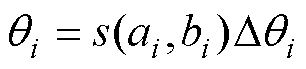
式中,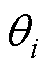 为旋转角;
为旋转角;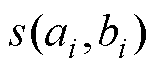 和
和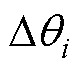 分别为旋转方向与大小,其值会根据某一策略具体确定。
分别为旋转方向与大小,其值会根据某一策略具体确定。
(7)迭代次数g加1,返回步骤(3)。
基于量子遗传算法的分数阶导数参数提取流程如图3所示。
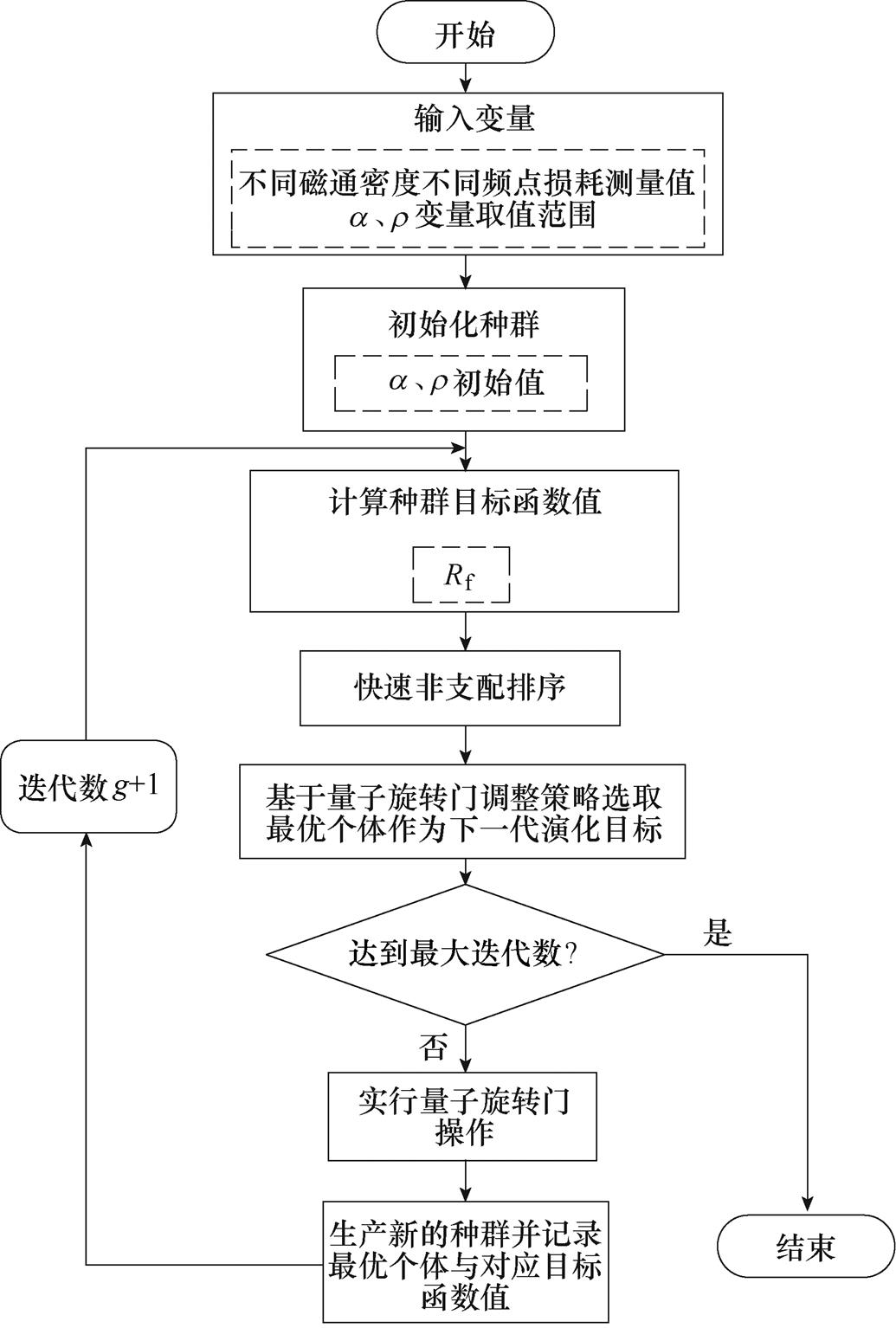
图3 基于量子遗传算法的分数阶导数参数提取流程
Fig.3 Flow chart of parameter extraction of fractional derivative model based on quantum genetic algorithm
将改进磁滞损耗表达式与改进涡流损耗表达式引入损耗统计理论框架实现对高频损耗的精确计算。基于有限单元剖分法与分数阶导数的改进损耗统计理论计算流程如图4所示。
采用爱泼斯坦方圈对超薄取向硅钢片的磁性能进行测试,激励信号的波形、幅值控制通过二维磁性能测量系统BROCKHAUS-MPG-200D实现[27],超薄取向硅钢片磁特性测量系统如图5所示。磁场强度由直接电流法获得,磁通密度由电磁感应定律获得。超薄取向硅钢单片的基本参数见表1,其损耗测量值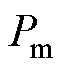 可以表示为
可以表示为
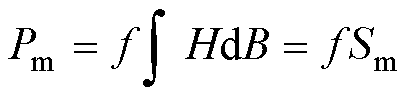 (20)
(20)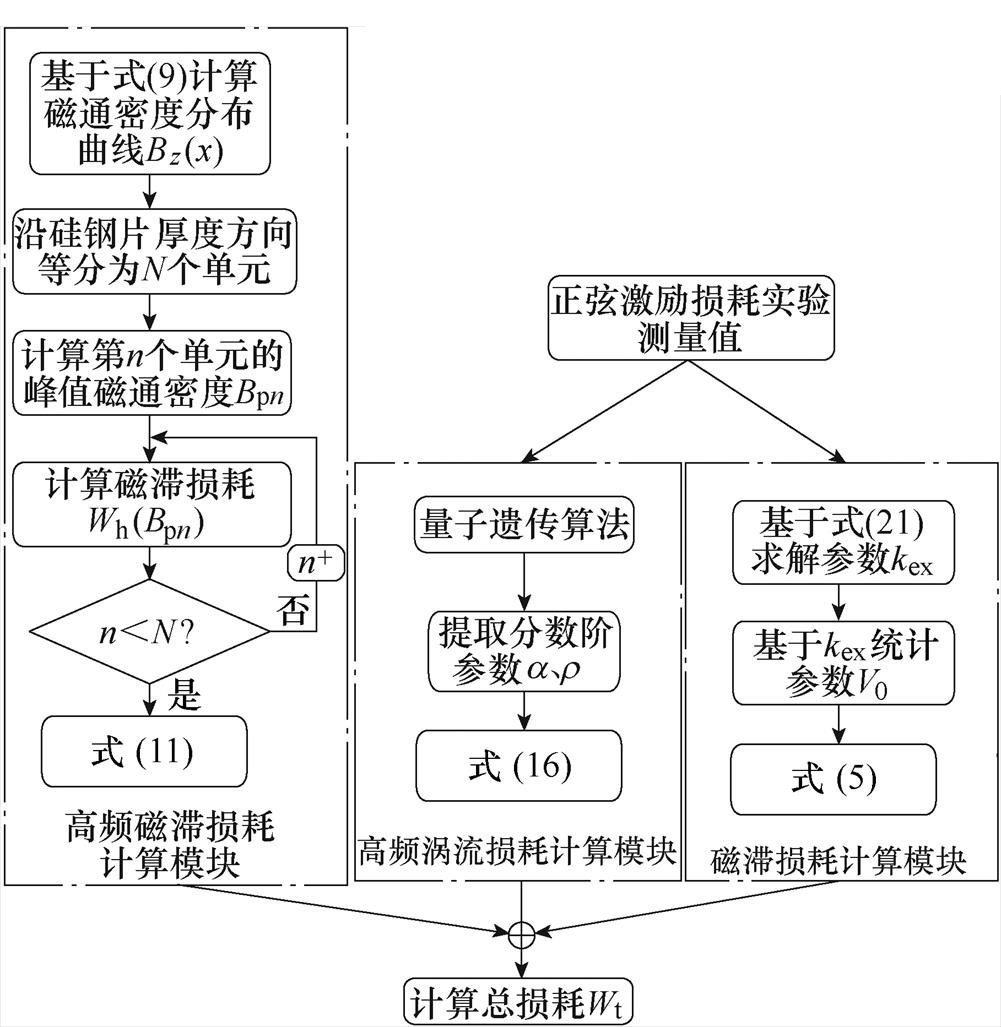
图4 基于有限单元剖分法与分数阶导数的改进损耗统计理论计算流程
Fig.4 Flow chart of loss calculation based on finite section method and fractional derivative
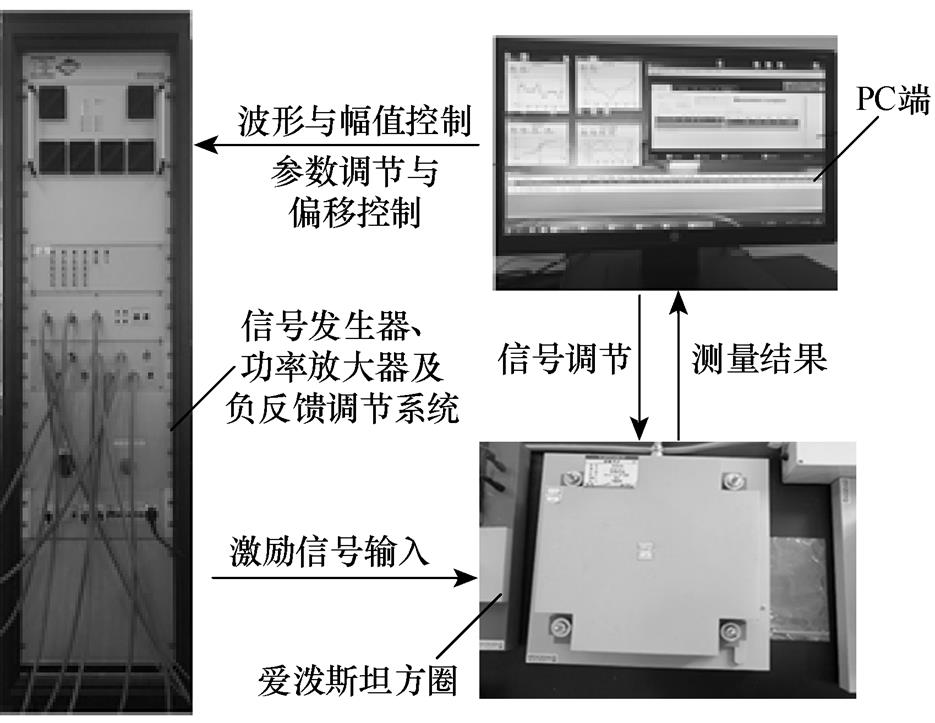
图5 超薄取向硅钢片磁特性测量系统
Fig.5 Ultra thingrain oriented silicon steel sheet measuring device for magnetizing feature
表1 超薄取向硅钢片样品参数
Tab.1 Sample parameters of ultra thingrain oriented silicon steel sheet
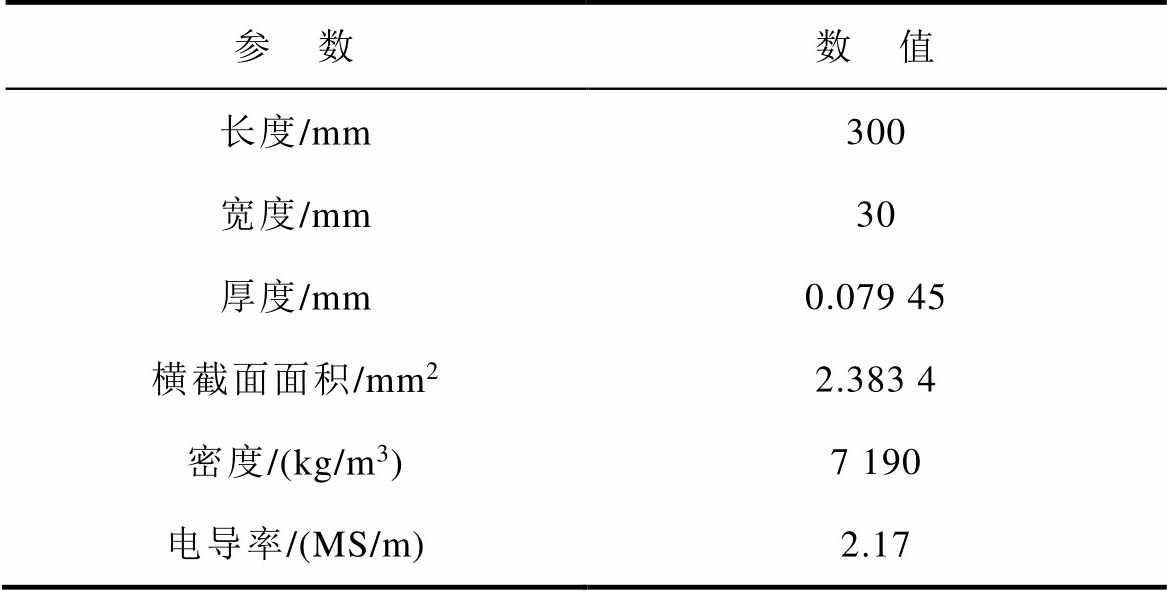
参 数数 值 长度/mm300 宽度/mm30 厚度/mm0.079 45 横截面面积/mm22.383 4 密度/(kg/m3)7 190 电导率/(MS/m)2.17
式中,Sm为频率f下动态磁滞回线面积。
单个周期内的磁滞损耗Wh(Bp)和剩余损耗中的V0可以通过低频条件下的总损耗测量值Wt,m(Bp, f)来确定,此时趋肤效应可以忽略。将总损耗测量值Wt,m(Bp, f)减去式(3)得到的涡流损耗计算值Wcl(Bp, f),可以得一个频率区间内不同峰值磁通密度对应的Wh+Wex随f 0.5的变化曲线[28],有
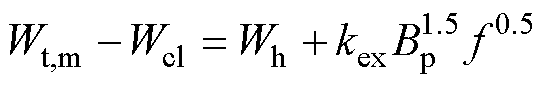 (21)
(21)其中
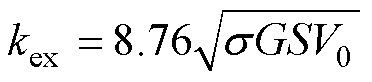
式中,kex为剩余损耗拟合系数。
由式(21)可知,该曲线的节距对应于静态磁滞损耗,V0可以通过曲线的斜率得到。本文基于实验测量的不同磁通密度下的低频损耗(10Hz、50Hz、100Hz和150Hz),提取了超薄取向硅钢片的静态磁滞损耗Wh(Bp)和V0(Bp)值,结果如图6所示。
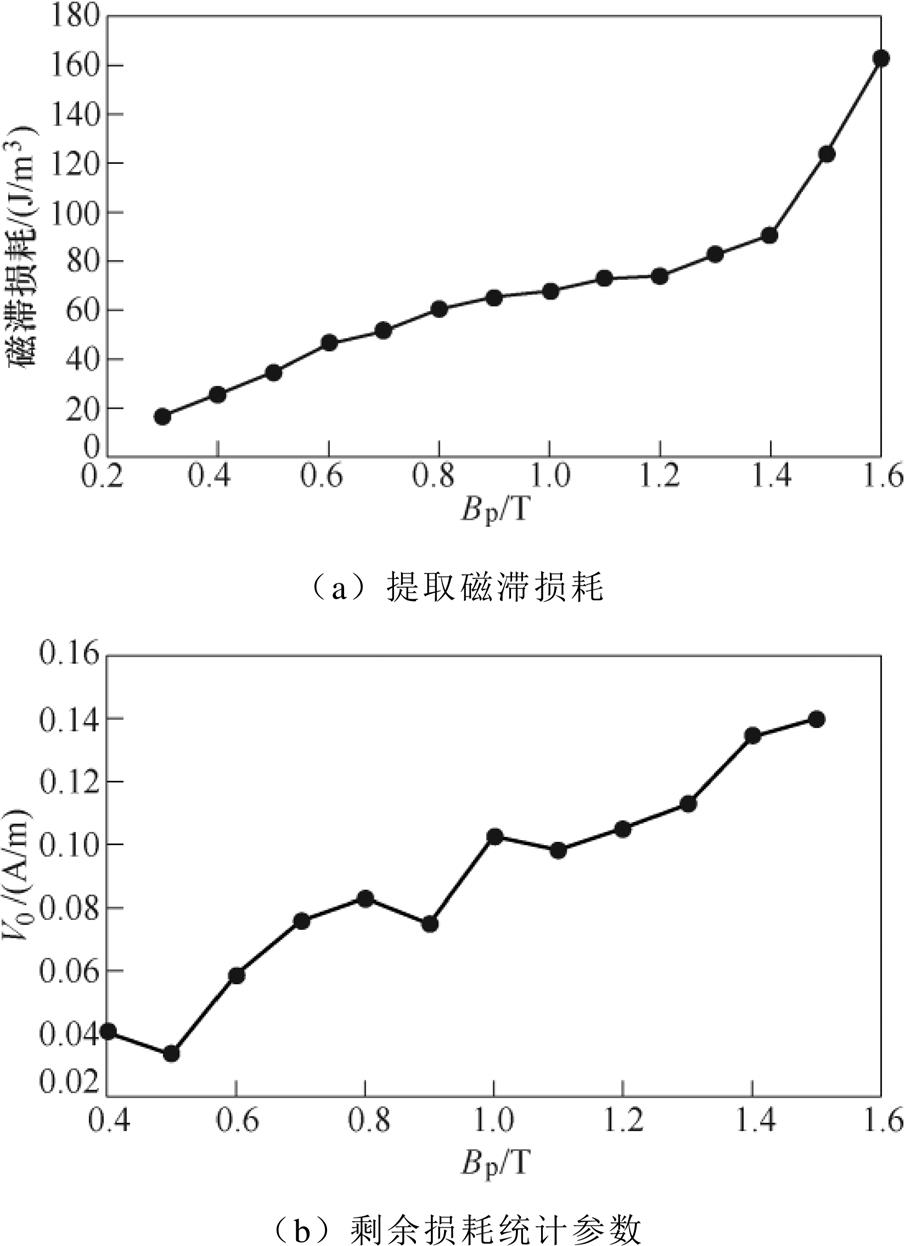
图6 由测量值拟合获得的Wh和V0随Bp的变化曲线
Fig. 6 Wh and V0 fitted from measurements as a function of peak flux density Bp
基于不同磁通密度下的相对磁导率测量值,利用最小二乘法对式(7)进行拟合,得到超薄取向硅钢片10Hz下(准静态情况)相对磁导率随峰值磁通密度变化曲线,如图7所示。曲线系数K1~K6对应为11 014.86、-84 140.82、150 670.69、-105 271.87、60 410.24和-2 035.49。进一步将式(7)拟合曲线值代入式(8)可得到不同磁通密度的复数磁导率。
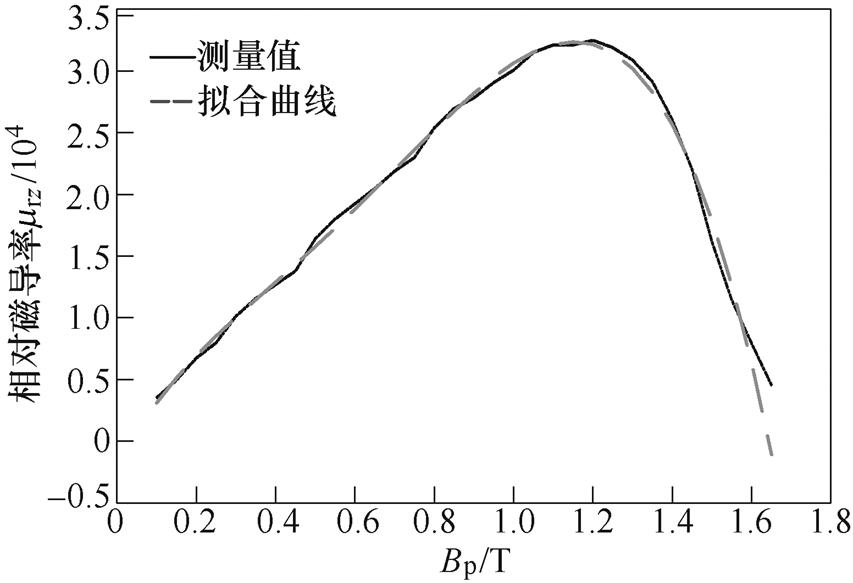
图7 超薄取向硅钢片10Hz相对磁导率随磁通密度峰值变化
Fig.7 Variation of the relative permeability of ultra-thin grain-oriented steel sheet with peak flux density at magnetizing frequency 10Hz
图8为超薄硅钢片在磁通密度为1T下的复数磁导率实部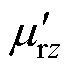 与虚部
与虚部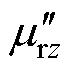 随频率变化曲线。
随频率变化曲线。
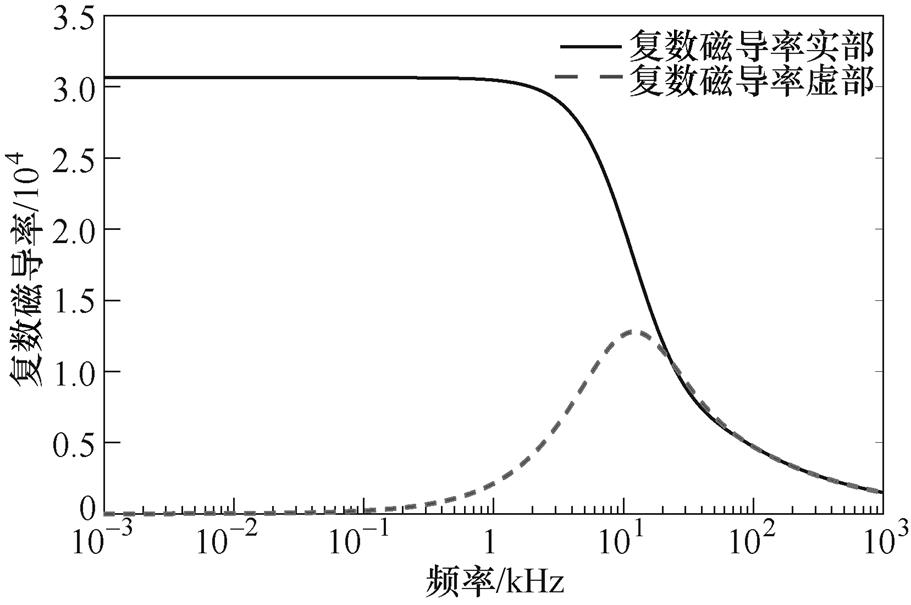
图8 超薄取向硅钢片1T下复数磁导率
Fig.8 Complex relative permeability of a single-strip ultrathin grain-oriented steel sheet at 1T
本文选用超薄取向硅钢在0.5T、1T、1.3T和1.5T磁通密度下频率为100Hz、500Hz、1 000Hz和2 000Hz共16个损耗测量数据作为优化算法的拟合对象。根据文献[29]推导证明的分数阶导数阶次大于0.5,阻尼系数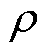 >sd2/12的结论,利用2.3节 给出的量子遗传算法提取了
>sd2/12的结论,利用2.3节 给出的量子遗传算法提取了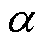 和
和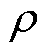 的最优值,分别为0.812和0.005 2,优化过程中的迭代曲线如图9所示。
的最优值,分别为0.812和0.005 2,优化过程中的迭代曲线如图9所示。
本文将采用传统STL模型(式(2)、式(3)、式(5)组成传统STL模型)、基于线性磁化法则的改进损耗统计模型(式(2)、式(4)、式(5)组成模型一)、基于分数阶导数的改进损耗统计模型(式(5)、式(10)、式(16)组成模型二),对10Hz~10kHz频率范围,0.4~1.5T磁通密度范围内超薄取向硅钢片的损耗进行计算,将上述三种模型的预测值与损耗测量值进行比较,结果如图10~图16所示。
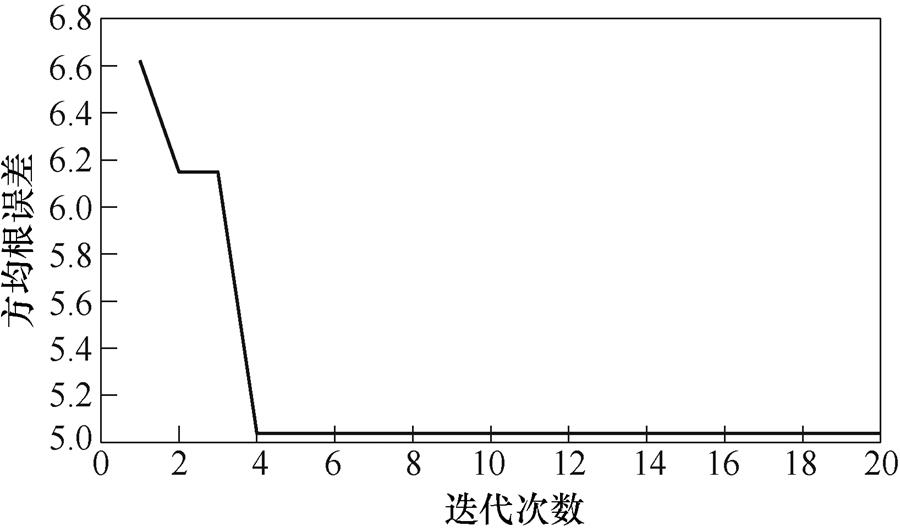
图9 量子遗传算法方均根误差随迭代次数变化
Fig.9 Result of RMSE variation with the iterative number based on quantum genetic algorithm
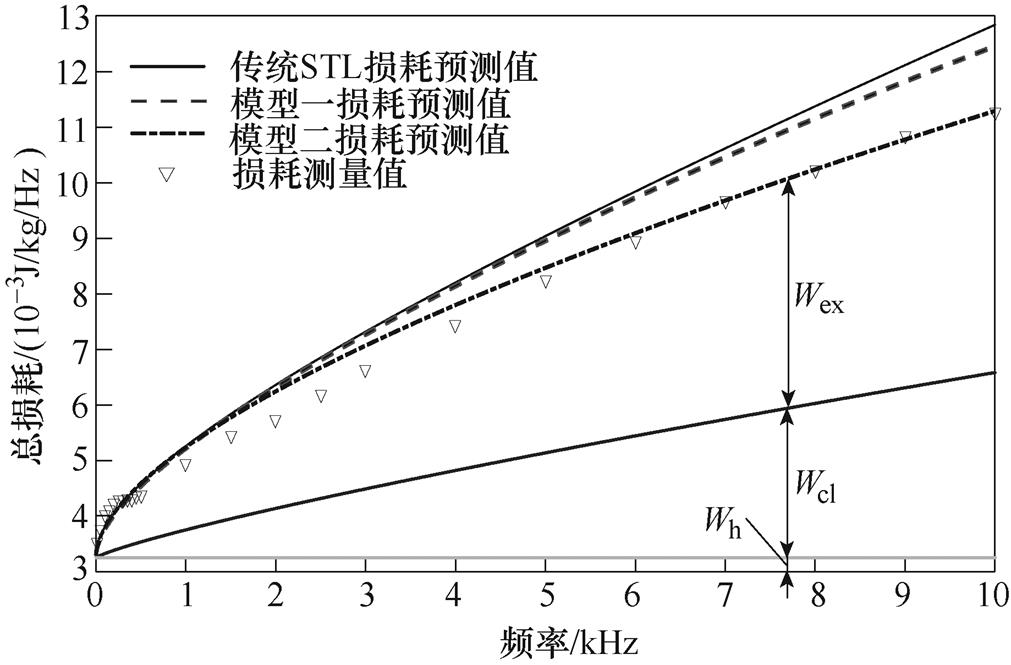
图10 Bp=0.4T损耗预测与测量值对比
Fig.10 Estimated and measured core losses at Bp=0.4T
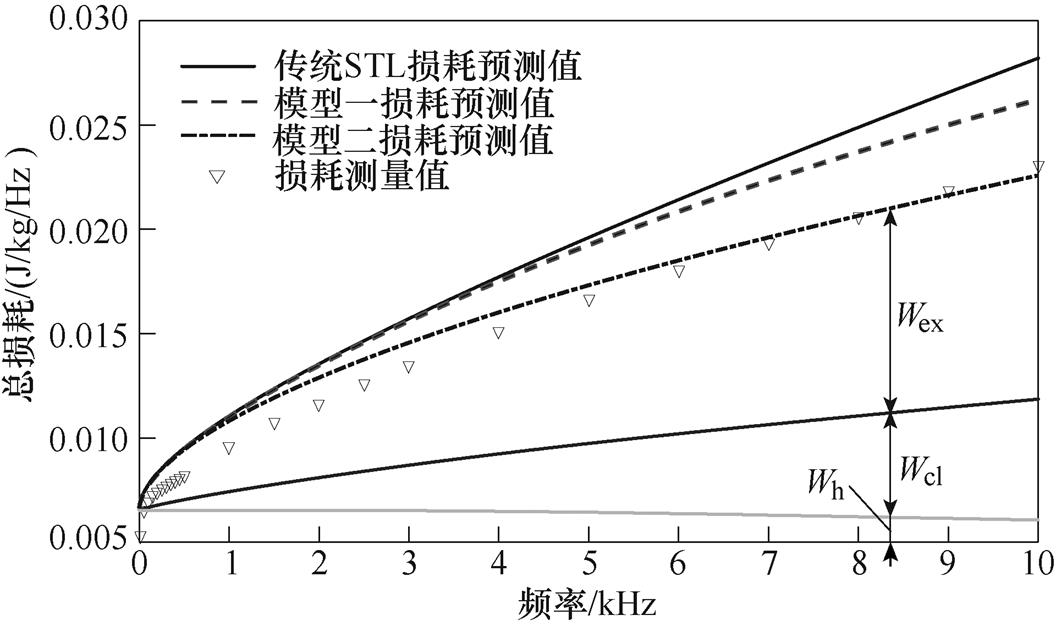
图11 Bp=0.5T损耗预测与测量值对比
Fig.11 Estimated and measured core losses at Bp=0.5T
为了定量比较三种损耗计算模型的预测效果,本文引入平均相对误差用于描述损耗计算模型的整体预测效果,平均相对误差的表达式为
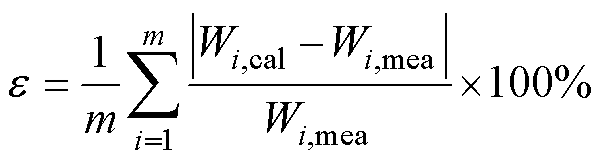 (22)
(22)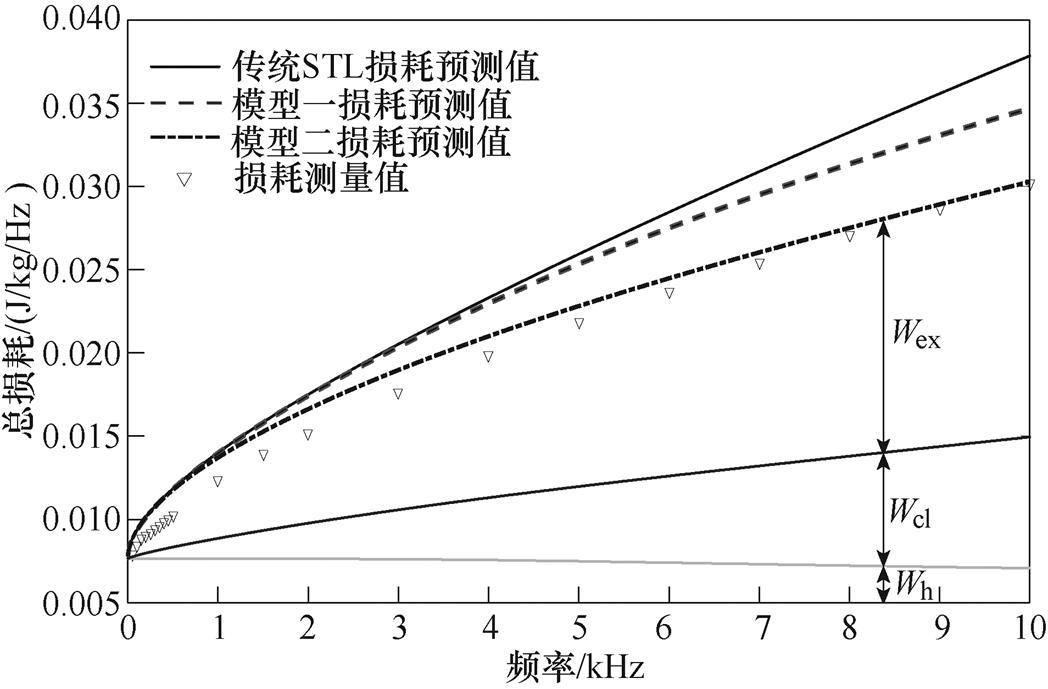
图12 Bp=0.7T损耗预测与测量值对比
Fig.12 Estimated and measured core losses at Bp=0.7T
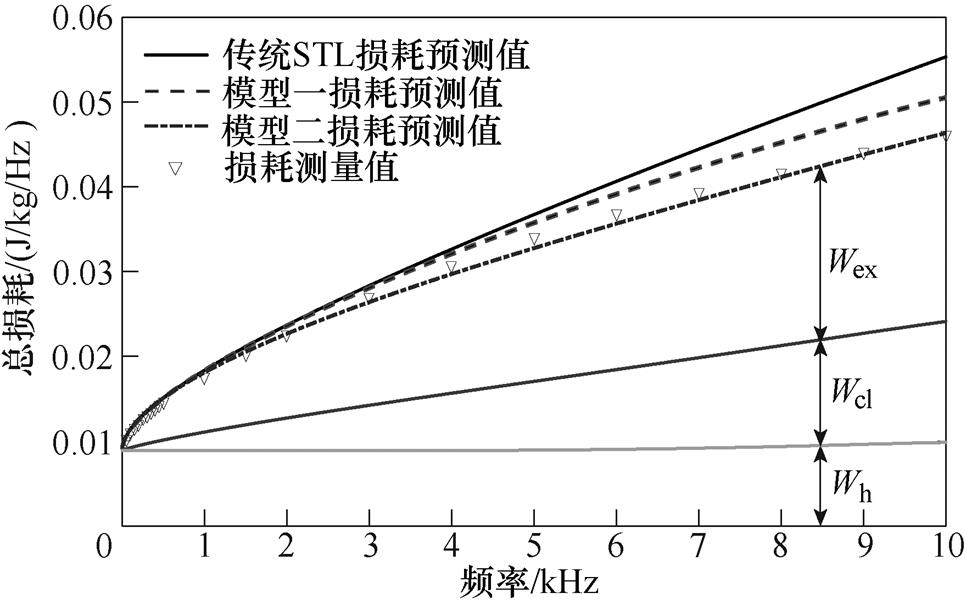
图13 Bp=0.9T损耗预测与测量值对比
Fig.13 Estimated and measured core losses at Bp=0.9T
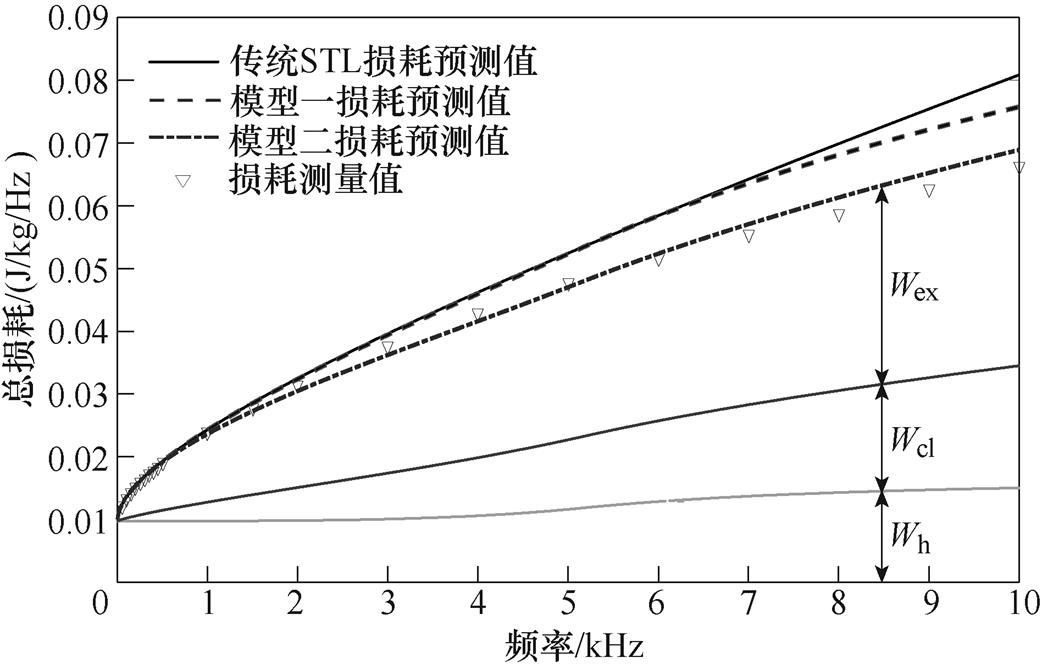
图14 Bp=1.1T损耗预测与测量值对比
Fig.14 Estimated and measured core losses at Bp=1.1T
式中,m为不同磁通密度下10Hz~10kHz范围内的测量频点数目,每个磁通密度下取22个测量频点;Wi,cal为三类损耗计算模型不同磁通密度下计算值;Wi,mea为不同磁通密度实验测量值。
表2对比了三种损耗计算模型在0.4~1.5T磁通密度范围内的平均相对误差。
三种损耗计算模型的平均相对误差与峰值磁通密度变化曲线如图17所示。可知,基于分数阶的改进损耗统计模型(模型二)的平均相对误差远低于传统STL和基于线性磁化准则的改进损耗统计模型(模型一),而模型一在低磁通密度下对损耗预测的精度较传统STL有所改进,但在高磁通密度下预测精度的改善效果将不再明显,这是由于线性磁化法仅适用于低磁通密度,这也进一步说明了模型一具有高磁通密度高频损耗预测精度差的缺点,这与文献[8-9]结论一致。
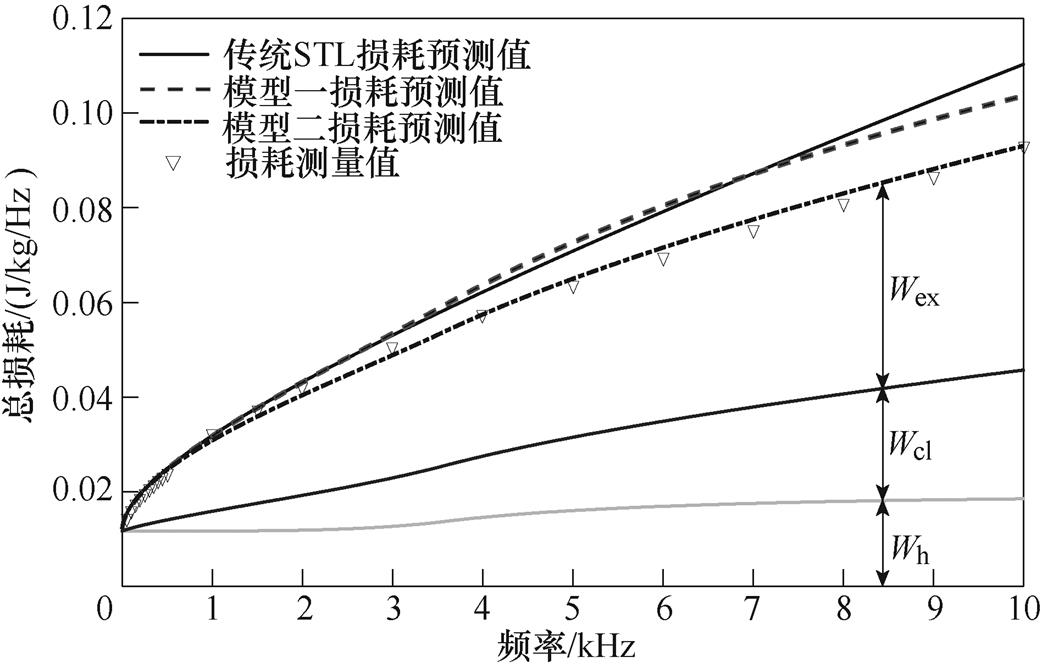
图15 Bp=1.3T损耗预测与测量值对比
Fig.15 Estimated and measured core losses at Bp=1.3T
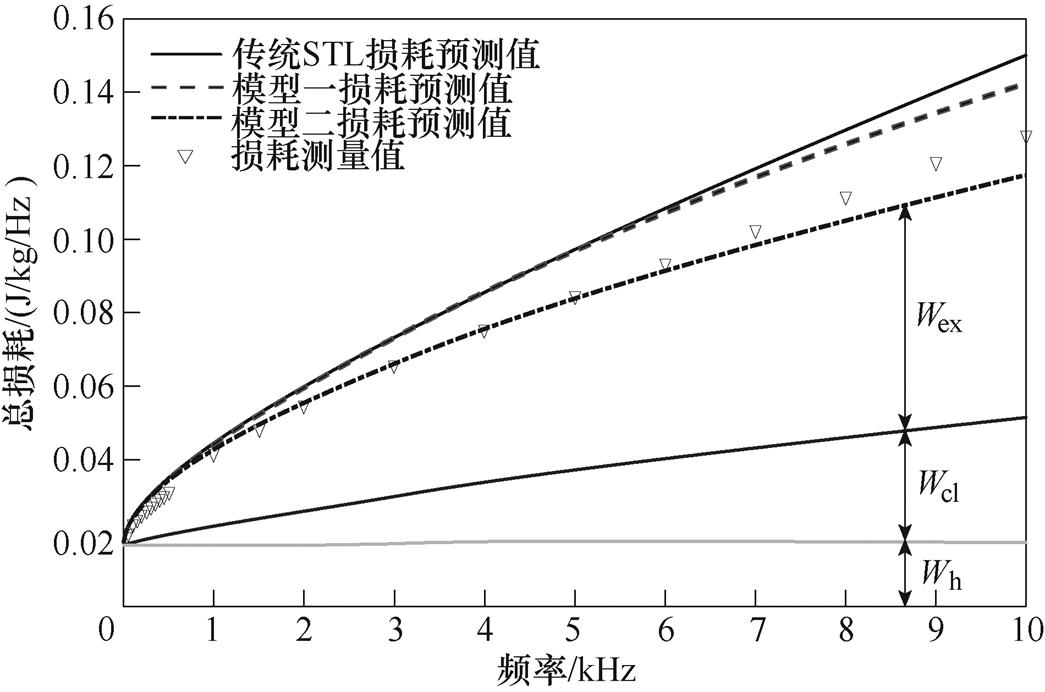
图16 Bp=1.5T损耗预测与测量值对比
Fig.16 Estimated and measured core losses at Bp=1.5T
表2 三种损耗计算模型平均相对误差e 对比
Tab.2 Comparison of average relative error e of three loss calculation models
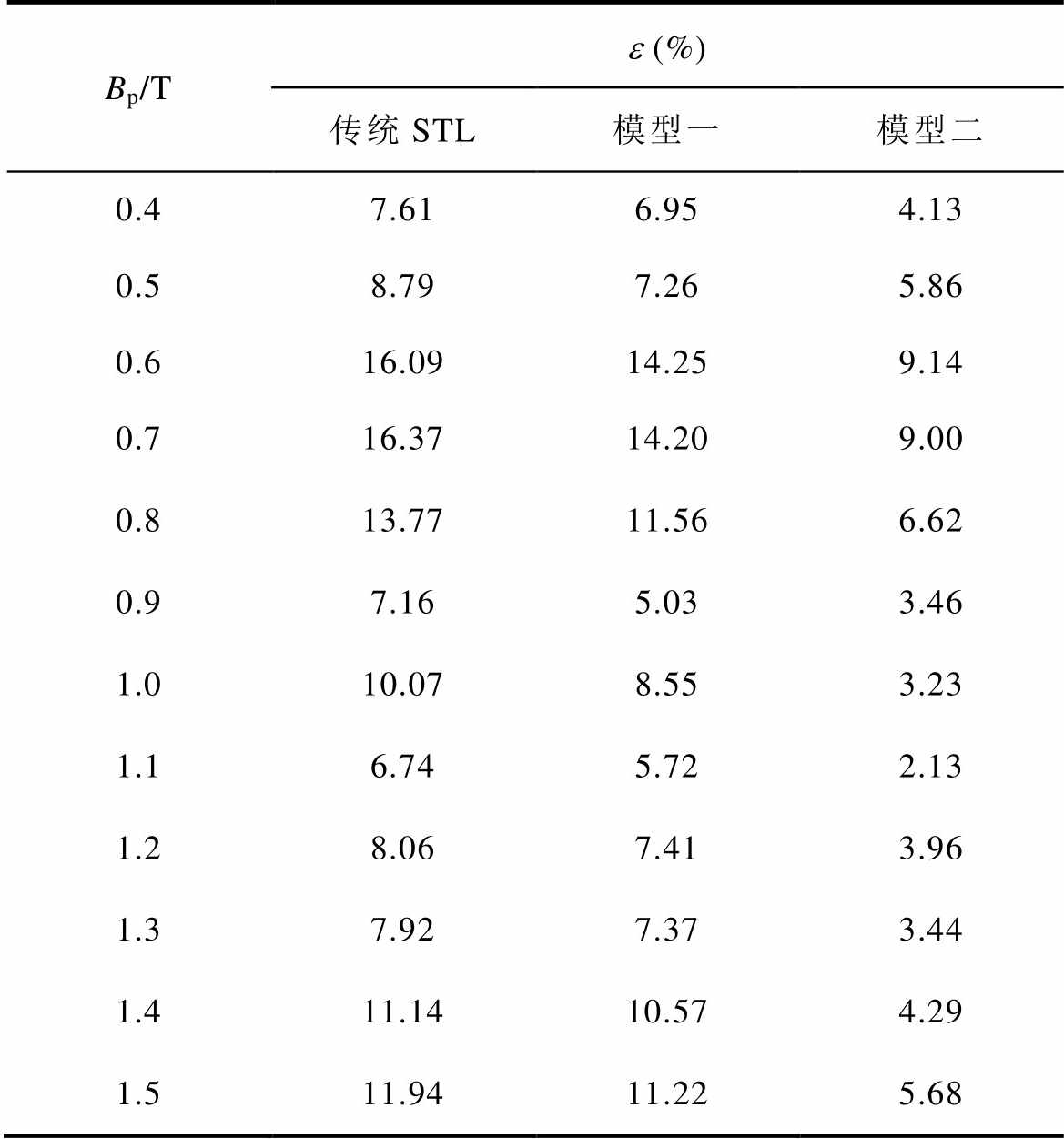
Bp/Te(%) 传统STL模型一模型二 0.47.616.954.13 0.58.797.265.86 0.616.0914.259.14 0.716.3714.209.00 0.813.7711.566.62 0.97.165.033.46 1.010.078.553.23 1.16.745.722.13 1.28.067.413.96 1.37.927.373.44 1.411.1410.574.29 1.511.9411.225.68
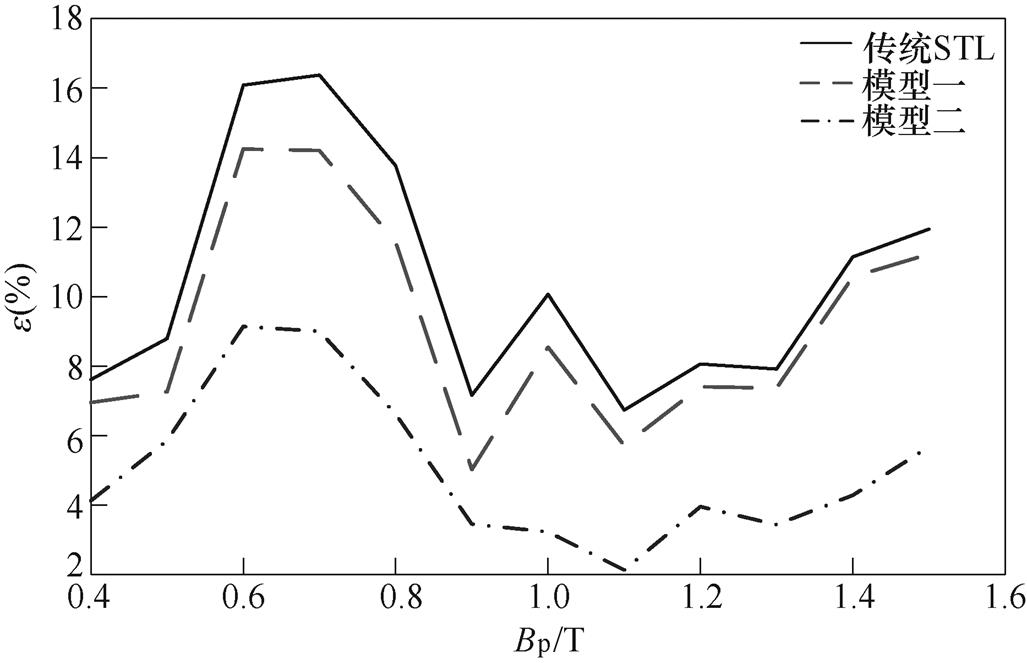
图17 平均相对误差随峰值磁通密度变化曲线
Fig.17 Mean relative error versus peak flux density
针对传统损耗统计理论对高频段损耗预测精度低的问题,本文考虑了高频段铁磁材料内部磁通密度不均匀分布的特点,计及复数磁导率、非线性磁化特性的影响,提出了基于有限单元剖分法的磁滞损耗计算方法。基于场分离假设和分数阶导数理论,推导出高频涡流损耗计算方法。引入量子遗传算法实现对分数阶参数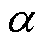 和
和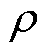 最优值的提取,将磁滞损耗、涡流损耗分量解析式与传统损耗分离框架下的剩余损耗表达式相结合,实现对高频条件下铁磁材料损耗的准确预测。结果表明,所提方法在整个频段内的最大平均相对误差为9.14%,最小平均相对误差为2.13%,相比于传统损耗理论和基于线性磁化法则的改进损耗统计模型,损耗预测精度大大提高,验证了该方法的有效性。
最优值的提取,将磁滞损耗、涡流损耗分量解析式与传统损耗分离框架下的剩余损耗表达式相结合,实现对高频条件下铁磁材料损耗的准确预测。结果表明,所提方法在整个频段内的最大平均相对误差为9.14%,最小平均相对误差为2.13%,相比于传统损耗理论和基于线性磁化法则的改进损耗统计模型,损耗预测精度大大提高,验证了该方法的有效性。
参考文献
[1] 杨庆新, 李永建. 先进电工铁磁材料特性与应用发展研究综述[J]. 电工技术学报, 2016, 31(20): 1-11.
Yang Qingxin, Li Yongjian. Characteristics and developments of advanced magnetic materials in electrical engineering: a review[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 1- 11.
[2] 刘任, 李琳, 王亚琦, 等. 基于随机性与确定性混合优化算法的Jiles-Atherton磁滞模型参数提取[J]. 电工技术学报, 2019, 34(11): 2260-2268.
Liu Ren, Li Lin, Wang Yaqi, et al. Parameter extraction for Jiles-Atherton hysteresis model based on the hybrid technique of stochastic and deter- ministic optimization algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2260- 2268.
[3] Steinmetz C P. On the law of hysteresis[J]. Pro- ceedings of the IEEE, 1984, 72(2): 197-221.
[4] 刘刚, 孙立鹏, 王雪刚, 等. 正弦及谐波激励下的铁心损耗计算方法改进及仿真应用[J]. 电工技术学报, 2018, 33(21): 4909-4918.
Liu Gang, Sun Lipeng, Wang Xuegang, et al. Improvement of core loss calculation method and simulation application under sinusoidal and harmonic excitations[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4909-4918.
[5] Bertotti G. General properties of power losses in soft ferromagnetic materials[J]. IEEE Transactions on Magnetics, 1988, 24(1): 621-630.
[6] Kowal D, Sergeant P, Dupré L, et al. Comparison of iron loss models for electrical machines with different frequency domain and time domain methods for excess loss prediction[J]. IEEE Transactions on Magnetics, 2015, 51(1): 6300110.
[7] Zhao Hanyu, Ragusa C, Appino C, et al. Energy losses in soft magnetic materials under symmetric and asymmetric induction waveforms[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(3): 2655- 2665.
[8] Zhao Hanyu, Ragusa C, de la Barrière O, et al. Magnetic loss versus frequency in non-oriented steel sheets and its prediction: minor loops, PWM, and the limits of the analytical approach[J]. IEEE Transa- ctions on Magnetics, 2017, 53(11): 1-4.
[9] 段娜娜, 徐伟杰, 李永建, 等. 基于极限磁滞回线法的软磁复合材料磁特性模拟[J]. 电工技术学报, 2018, 33(20): 4739-4745.
Duan Nana, Xu Weijie, Li Yongjian, et al. Electro- magnetic property modeling of the soft magnetic composite material based on the limiting loop method[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4739-4745.
[10] Zhang Yu, Pillay P, Ibrahim M, et al. Magnetic characteristics and core losses in machine laminations: high-frequency loss prediction from low-frequency measurements[J]. IEEE Transactions on Industry Applications, 2012, 48(2): 623-629.
[11] Steentjes S, Hameyer K, Dolinar D, et al. Iron-loss and magnetic hysteresis under arbitrary waveforms in NO electrical steel: a comparative study of hysteresis models[J]. IEEE Transactions on Industrial Elec- tronics, 2017, 64(3): 2511-2521.
[12] Raulet M A, Ducharne B, Masson J P, et al. The magnetic field diffusion equation including dynamic hysteresis: a linear formulation of the problem[J]. IEEE Transactions on Magnetics, 2004, 40(2): 872- 875.
[13] Ducharne B, Sebald G, Guyomar D, et al. Fractional model of magnetic field penetration into a toroidal soft ferromagnetic sample[J]. International Journal of Dynamics and Control, 2017, 6(1): 89-96.
[14] Guyomar D, Ducharne B, Sebald G, et al. Fractional derivative operators for modeling the dynamic polarization behavior as a function of frequency and electric field amplitude[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 2009, 56(3): 437-443.
[15] Zhang Bin, Gupta B, Ducharne B, et al. Dynamic magnetic scalar hysteresis lump model based on Jiles-Atherton quasi-static hysteresis model extended with dynamic fractional derivative contribution[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.
[16] Zhang Bin, Gupta B, Ducharne B, et al. Preisach's model extended with dynamic fractional derivation contribution[J]. IEEE Transactions on Magnetics, 2018, 54(3): 1-4.
[17] Ibrahim M, Pillay P. Advanced testing and modeling of magnetic materials including a new method of core loss separation for electrical machines[J]. IEEE Transactions on Industry Applications, 2012, 48(5): 1507-1515.
[18] Mthombeni T L, Pillay P. Physical basis for the variation of lamination core loss coefficients as a function of frequency and flux density[C]//IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, 2006: 1381-1387.
[19] Hamzehbahmani H, Anderson P, Hall J, et al. Eddy current loss estimation of edge burr-affected magnetic laminations based on equivalent electrical network- part II: analytical modeling and experimental results[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 651-659.
[20] 陈文, 孙洪广, 李西成. 力学与工程问题的分数阶导数建模[M]. 北京: 科学出版社, 2010.
[21] 吴强, 黄建华. 分数阶微积分[M]. 北京: 清华大学出版社, 2016.
[22] Chandrasena W, McLaren P G, Annakkage U D, et al. An improved low-frequency transformer model for use in GIC studies[J]. IEEE Transactions on Power Delivery, 2004, 19(2): 643-651.
[23] Zhang Bin, Ducharne B, Sebald G, et al. Characteri- zation of fractional order for high-frequency band- width model of dielectric ferroelectrics[J]. Journal of Intelligent Material Systems and Structures, 2014, 27(4): 437-443.
[24] Ducharne B, Sebald G, Guyomar D, et al. Dynamics of magnetic field penetration into soft ferromagnets[J]. Journal of Applied Physics, 2005, 117(24): 243907.
[25] 苏玉刚, 吴学颖, 赵鱼名, 等. 互补对称式LCC谐振网络的电场耦合式无线电能传输系统参数优化[J]. 电工技术学报, 2019, 34(14): 2874-2883.
Su Yugang, Wu Xueying, Zhao Yuming, et al. Parameter optimization of electric-field coupled wireless power transfer system with complementary symmetric LCC resonant network[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2874- 2883.
[26] 马书民, 戎子睿, 林湘宁, 等. 计及多类装置协同的直流偏磁治理设备全局优化配置研究[J]. 中国电机工程学报, 2020, 40(14): 4387-4399, 4720.
Ma Shumin, Rong Zirui, Lin Xiangning, et al. Study on the global optimal configuration of DC bias equipment considering the cooperation of multiple devices[J]. Proceedings of the CSEE, 2020, 40(14): 4387-4399, 4720.
[27] 赵小军, 刘小娜, 肖帆, 等. 基于Preisach模型的取向硅钢片直流偏磁磁滞及损耗特性模拟[J]. 电工技术学报, 2020, 35(9): 1849-1857.
Zhao Xiaojun, Liu Xiaona, Xiao Fan, et al. Hysteretic and loss modeling of silicon steel sheet under the DC biased magnetization based on the Preisach model[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1849-1857.
[28] Barbisio E, Fiorillo F, Ragusa C. Predicting loss in magnetic steels under arbitrary induction waveform and with minor hysteresis loops[J]. IEEE Transa- ctions on Magnetics, 2004, 40(4): 1810-1819.
[29] Liu Ren, Li Lin. Analytical prediction model of energy losses in soft magnetic materials over broad- band frequency range[J]. IEEE Transactions on Power Electronics, 2020, 36(2): 2009-2017.
Calculation Method of High-Frequency Loss of Ferromagnetic Materials Based on R-L Type Fractional Derivative and Loss Statistical Theory
Abstract The traditional statistical theory of loss (STL) has a large prediction error of high-frequency loss of ferromagnetic materials and the estimation is too high. For this reason, this paper firstly considers the influence of the uneven distribution of magnetic flux density on hysteresis loss under high-frequency conditions, and proposes a calculation method for hysteresis loss based on the finite element method. Then based on the R-L type fractional derivative, the eddy current field and eddy current loss calculation formulae in the traditional STL are improved, and the quantum genetic algorithm is introduced to optimize the damping coefficient and the order of the derivative in the fractional derivative model. Subsequently, an improved STL method suitable for wide frequency and wide magnetic density range is proposed. Finally, the Epstein frame is used to measure the loss of 3% Si-Fe ultra-thin oriented silicon steel sheet in the frequency range of 10Hz to 10kHz. Comparing the theoretical calculation value with the experimental measurement value, the result shows that the maximum average relative error of the proposed method in the entire frequency band is 9.14%, the minimum average relative error is 2.13%. Compared with the traditional loss theory, the loss prediction accuracy is greatly improved, which verifies the effectiveness of this method.
Keywords:Loss statistical theory, hysteresis loss, eddy current loss, fractional derivative, quantum genetic algorithm
中图分类号:TM153; TM275
DOI: 10.19595/j.cnki.1000-6753.tces.201462
国家自然科学基金青年科学基金项目(52107006)和湖北省自然科学基金面上项目(2021CFB149)资助。
收稿日期 2020-11-01
改稿日期 2020-12-06
E-mail: chenbin@ctgu.edu.cn(通信作者)
秦小彬 男,1994年生,硕士研究生,研究方向为新型磁性材料损耗与磁滞特性模拟。
E-mail: 2902915609@qq.com
(编辑 崔文静)