

图1 脉冲磁体结构和受力分析
Fig.1 Structure and force analysis of a pulse magnet
摘要 结构力学表明,磁体失效包含材料强度失效和结构整体失效两个方面。现有磁体失效模型是基于材料强度模型,忽略结构失稳问题,难以解释超高场脉冲磁体经常在低于其设计值就发生破坏的现象。且已有研究显示,屈曲是导致超高场脉冲磁体失效的主要原因之一,但脉冲磁体屈曲的形成机理和演变规律尚不明确。该文从结构稳定性的角度出发,分析指出脉冲磁体自由分离层可等效为薄壁圆柱壳,具有高屈曲风险,并提出基于圆柱壳体结构屈曲的超高场脉冲磁体力学失效分析方法,建立脉冲磁体静态电磁屈曲Ansys有限元模型,进行了屈曲行为研究分析,仿真结果与实际结果吻合。屈曲分析结果表明:在电磁载荷方面,轴向电磁力是产生屈曲的决定性因素,径向电磁力对于外层绕组轴向屈曲的影响不明显,可在一定程度上抑制内层绕组的轴向屈曲;在绕组结构方面,外层绕组对螺旋绕组缝隙较为敏感,需重点关注。
关键词:脉冲强磁场 脉冲磁体 自由分离层 屈曲
强磁场对核磁矩、电子自旋和电子轨道磁矩都有强烈作用,是现代基础科学研究最为重要的极端条件之一,相关研究产生了整数量子霍尔效应、分数量子霍尔效应等十余项诺贝尔奖[1]。磁场强度越高,对物质作用的效果越明显,发现新现象和新原理的可能性也越大,会催生更多重大成果。为促进基础科学的发展,我国已经建成了脉冲强磁场国家重大科技基础设施。
脉冲强磁场技术是目前产生50T以上非破坏性强磁场的最有效技术途径,而脉冲磁体是其中关键核心技术。脉冲磁体结构及受力方向如图1a所示,脉冲磁体由多层特殊加固的空心螺线管组成,工作在瞬变超高磁场、大电流、高电压等条件下,承受着巨大的电磁力,如100T时达到4GPa(最强合金金属强度的2倍)[1-2]。强大电磁力下脉冲磁体寿命短、易失效,其中力学破坏是脉冲磁体的首要矛盾,力学失效机制研究是重中之重,对于提升脉冲磁体技术水平十分关键[3]。同时,脉冲磁体也是一种典型的极端电磁能装置,其力学失效机制的精准阐释对发展线圈炮、电磁轨道炮等极端电磁能装备也有潜在的借鉴意义。


图1 脉冲磁体结构和受力分析
Fig.1 Structure and force analysis of a pulse magnet
脉冲磁体的失效分析建立在力学模型基础之上,脉冲磁体力学理论主要经历了三个发展阶段:一维弹性模型[4-5]、一维弹塑性模型[4,6]以及二维轴对称弹塑性模型[7]。脉冲磁体的结构和电磁特性具有上下和轴对称性,早期研究对轴向电磁力Fz做了简化等效,重点研究径向电磁力Fr的作用,建立磁体中平面的一维弹性力学模型,随后发展出了一维弹塑性力学模型,脉冲磁体中自由分离层如图1b所示。一维模型的提出有力推动了磁体失效机制研究和磁体技术发展。研究人员据此发现了应力向内层集中的磁体失效机理[4,8],并发展了自由分离和分层加固技术[1,9-10],磁场强度从40T提升至70T以上[1,9]。
随着磁场强度提高到70T以上,轴向压缩变形不可忽略,一维模型中轴向电磁力Fz的简化等效会造成较大误差,已不再适用。考虑了轴向变形的二维轴对称模型(见图1c)逐渐成为主流,并取得丰硕研究成果:德国S. Zherlitsyn指出层间过渡处绕组的明显轴向移动可能会触发磁体失效[11];美国D. N. Nguyen[12]指出冷却通道造成的应力集中会缩短磁体寿命;法国P. Frings[13]发现了磁体中导体累计塑性软化效应会影响磁体寿命。
2010年以来,世界各国都在不断追求100T极限磁场,但成少败多,基于经典理论设计的高场磁体常常显著低于理论值就发生破坏,而且无法合理解释失效机制,其存在的缺陷和不足愈发突出。例如,国家脉冲强磁场科学中心(WHMFC)于2017~ 2021年间多次冲击100T,但磁体都在低应力水平下发生破坏(2.5GPa, 83T),远低于设计限值(4GPa)。美国国家强磁场实验室(NHMFL)[14]、德国强磁场实验室(HLD)[15]等世界顶尖脉冲强磁场实验室的100T磁体也是如此,美国的100T超高场脉冲磁体更是失败了8次之多。
超高场磁体理论设计严重偏差现象已成为当前脉冲磁体技术发展中的难题。究其原因,现有磁体失效模型都是在弹塑性小变形假设下计算应力分布,然后通过von Mises或其他等效应力进行强度判断,从本质上看都属于材料强度模型[16]。该模型在以往80T以下脉冲磁体分析设计中得到了验证,理论计算结果与实验结果吻合较好,这主要归因于该类磁体体积和所受到的电磁力都相对较小,结构失稳风险低,材料强度破坏是磁体失效的主因。但是,依据结构力学理论可知,随着磁场强度的提高和磁体结构的增大,脉冲磁体中主要力学矛盾从局部的材料强度问题逐渐转化为全局的结构稳定性问题,特别是具有薄壁特征自由分离层的失稳,而相关理论研究尚在起步阶段。
综上所述,超高场脉冲磁体在材料强度破坏之前可能发生薄壁绕组层整体结构失稳,现有强度失效模型无法准确描述,亟需开展结构失稳理论和方法等方面的研究。本文将从结构稳定性角度出发,分析超高场、大电流、高机械应力等极端条件下脉冲磁体自由分离层所形成薄壁结构的电磁屈曲行为。
如图1a,脉冲磁体由多层特殊加固的空心螺线管组成,承受着“径向膨胀、轴向压缩”的电磁力。为抵抗强大的电磁力,每层绕组外都有高强度纤维加固层,同时通过设置多个自由分离层避免应力集中,在径向电磁作用下自由分离层会形成薄壁层(如图1b中前五层,此图为1/2轴对称模型)。
依据结构力学屈曲理论可知,脉冲磁体中自由分离层具有薄壁特征,在轴向电磁压力下,易发生轴向屈曲变形。自由分离层可等效为圆柱壳体,其屈曲变形行为属于圆柱壳体屈曲范畴,本文将围绕结构力学中圆柱壳体展开阐述。依据载荷类型,可分为静态和动态屈曲分析两类;依据材料特性,又可分为线性和非线性屈曲两类,其中线性屈曲相对简单,已经有成熟解析模型。
轴向压力下的薄壁圆柱壳模型如图2所示。图2中,R为壳体平均半径,t为厚度,L为长度。依据线性屈曲理论可得到对应屈曲轴向压应力(也称为屈曲强度)为[17-18]
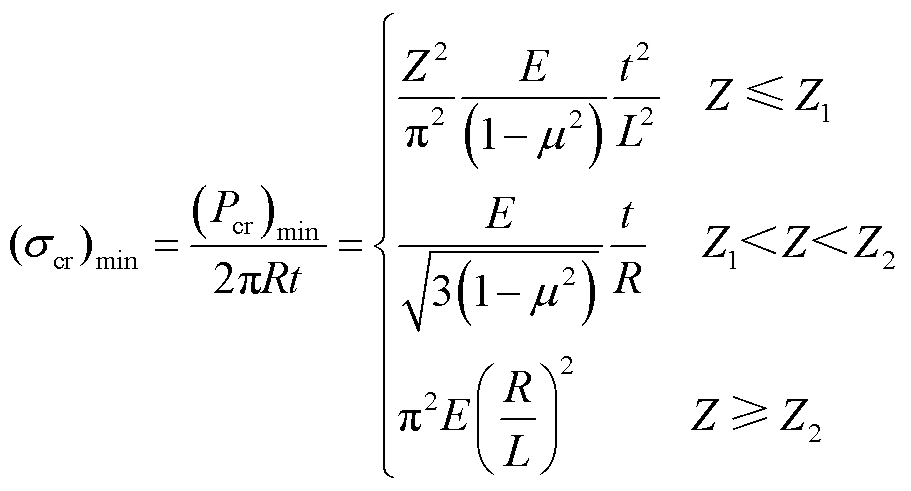 (1)
(1)

式中,E为杨氏模量;Z为Batdorf参数[17],取决于圆柱壳的几何参数和材料属性(泊松比μ),其表达式为
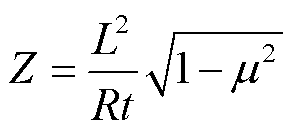 (2)
(2)
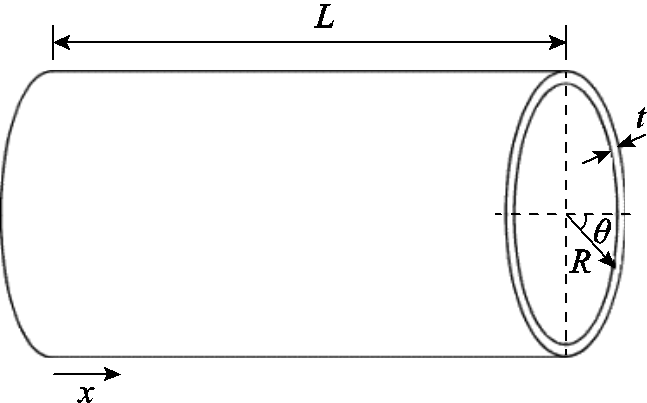
图2 轴向压力下的薄壁圆柱壳模型
Fig.2 Thin walled cylindrical shell model
为研究几何尺寸对屈曲行为的影响,对多种实际磁体尺寸的金属结构圆柱壳(铜筒)进行解析解和有限元分析,如图3所示。圆柱壳高度为100~500mm,圆柱壳半径为10~100mm,圆柱壳厚度为2~10mm,对应的Batdorf参数Z范围在10~11 800。图3中m和n为屈曲模数,反映了屈曲的变形特征。
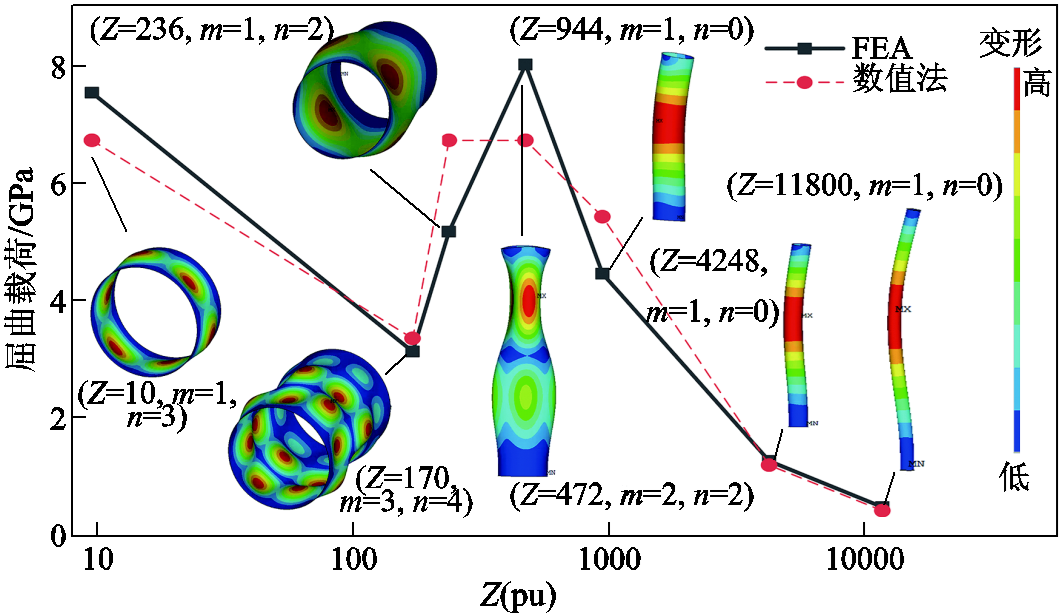
图3 不同几何结构圆柱壳的屈曲行为
Fig.3 Buckling performance of cylindrical shells with different geometric structures
可以得到以下结论:①随着Z参数的增加,屈曲模式逐渐从短筒向中筒、长筒特征转变,轴向径向屈曲模数先增大后减少,最后表现为欧拉屈曲模式(细长杆, m=1, n=1);②与此对应的屈曲载荷,也呈现先降低,后增加,再减少的趋势;③任何类型圆柱壳屈曲时的m都大于0,而n是可以等于0的(以短型圆柱壳为主)。需要指出的是,常规脉冲磁体的Batdorf参数Z一般在100以上,对应图3中的右半部分,即脉冲磁体中不会存在短型圆柱壳情况,主要以中长型圆柱壳为主。磁体的最内层自由分离绕组属于细长筒结构,而中部自由分离层属于中长筒。单从结构上看,长筒屈曲载荷将比中筒屈曲载荷低一些,即磁体的内层比中层对轴向载荷更敏感。但实际中,还需要考虑电磁力的分布情况,会造成不同结果。
圆柱壳在集中载荷作用下的线性屈曲分析可以在一定程度上反映脉冲磁体的结构特点,但与实际中脉冲磁体屈曲行为还有很大差距:①脉冲磁体中是体分布的电磁载荷,这会使得脉冲磁体的屈曲行为有很大不同;②同时脉冲磁体导体进入了深度塑性阶段,也需要考虑材料非线性;③最后径向外压对脉冲磁体屈曲行为的影响也不可忽视。因此,分析相关问题的难点在于:在超高场条件下,线性屈曲理论关于轴向集中载荷、材料小变形(处于弹性阶段)的假设已经失效,磁体的屈曲临界载荷不能通过经典解析公式获得,需要综合考虑电磁-结构多场耦合、电磁力分布、材料非线性、几何大变形等因素的影响。
本文利用Ansys有限元软件进行电磁场-结构场多场耦合分析,基于节点法求解电磁场,建立考虑了材料非线性、几何大变形的非线性屈曲有限元模型。流程如图4所示,包括有限元建模、电磁场分析、预应力分析、线性/非线性屈曲等四个步骤。为分析绕组中电磁力载荷,需要先使用SOLID97单元求解单绕组层产生的磁场和电磁载荷,然后,删除空气单元,完善材料属性,进入力学求解环节。采用SOLID185单元和Lanczos法分别先进行预应力求解和线性屈曲求解,接着将线性屈曲的模态作为初始微扰(通常取0.1%)并打开大变形开关,采用弧长法进行非线性屈曲求解。超高场工况下脉冲磁体中导体材料处于塑性、非线性状态,非线性屈曲方法可以更为准确地计算脉冲磁体屈曲行为。
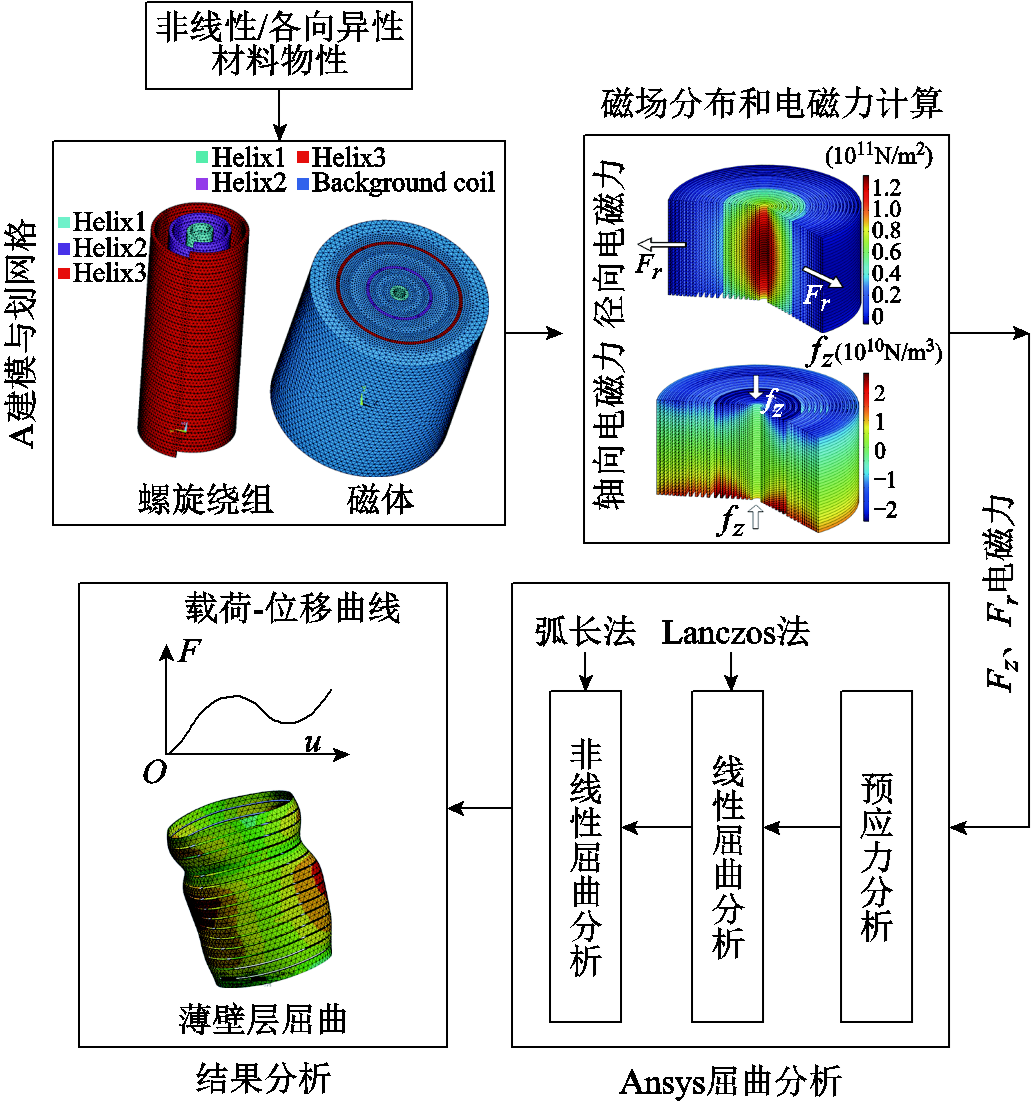
图4 Ansys模型分析过程
Fig.4 The process of analyzing Ansys models
下面将仿照实际80T脉冲磁体内线圈的最内层和最外层绕组参数,进行单层绕组的电磁屈曲行为分析。两层磁体绕组具体参数见表1。两层绕组均为40匝,铜导线为2.4mm×4.4mm,加固纤维为1mm厚的柴龙纤维(Zylon),8kA电流驱动下分别在中心产生2.33T和2.15T磁场,它们分别属于长型圆柱壳和中型圆柱壳。在进行电磁分析后,其中中长筒电磁场和电磁力分布结果如图5所示。
表1 两层绕组主要参数
Tab.1 Main parameters of two winding layers

绕组材料尺寸/mm磁感应强度B/T电流I/kA LRt 内层铜+柴龙1806.532.338 外层铜+柴龙18061.532.158
在非线性屈曲求解过程中,两个绕组的轴向缩短位移-载荷曲线如图6所示。对于给定结构的线圈,电磁力载荷与磁感应强度密切相关(F∝B2),采用磁场标定线圈载荷使得磁体分析设计更为方便,将以磁感应强度代表电磁力载荷。当磁场随轴向缩短量的增长斜率为0时,这表明已经达到了结构所能承受的最大载荷,即为屈曲点。内外层绕组对应的屈曲磁场分别为19.67T和7.2T,内层绕组屈曲磁场高于外层,主要由于内层线圈内部磁场较为均匀,径向磁场(轴向电磁力)分量较低,而外层绕组则反之,所以内层绕组屈曲磁场较高。这说明轴向电磁载荷在脉冲磁体屈曲过程占主导作用。由图6可知,基于非线性屈曲的计算结果表明内层线圈应呈现出轴向弯曲破坏,而外层线圈呈现为中部破坏。
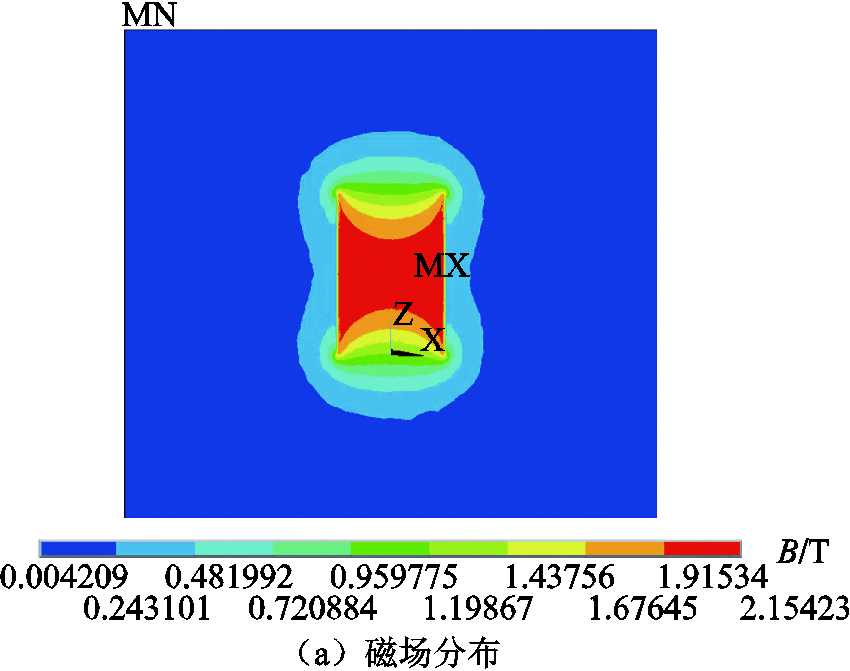
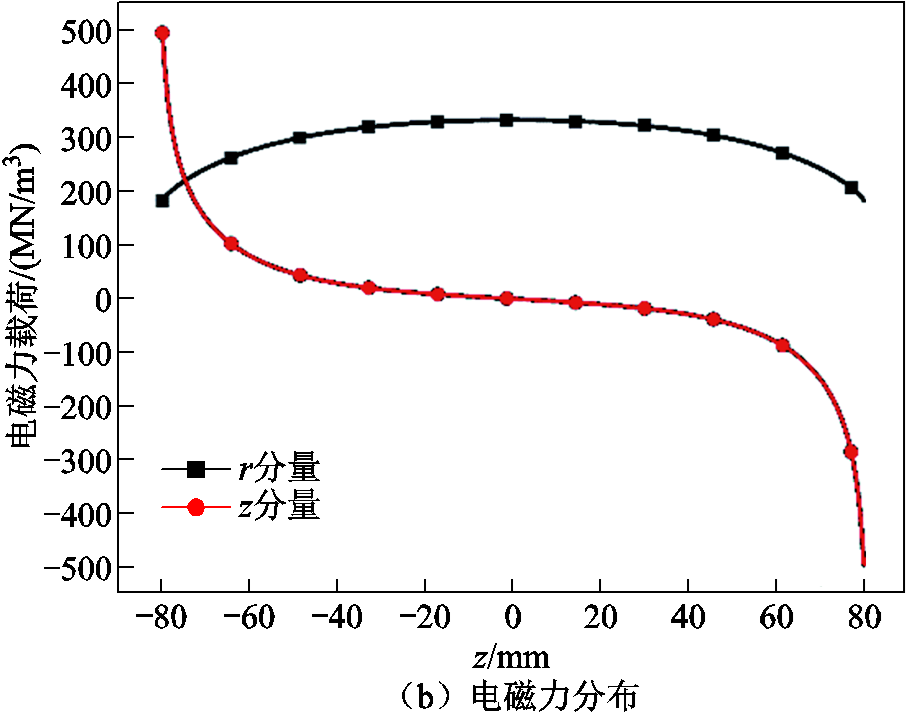
图5 线圈电磁分析结果
Fig.5 Results of electromagnetic analysis
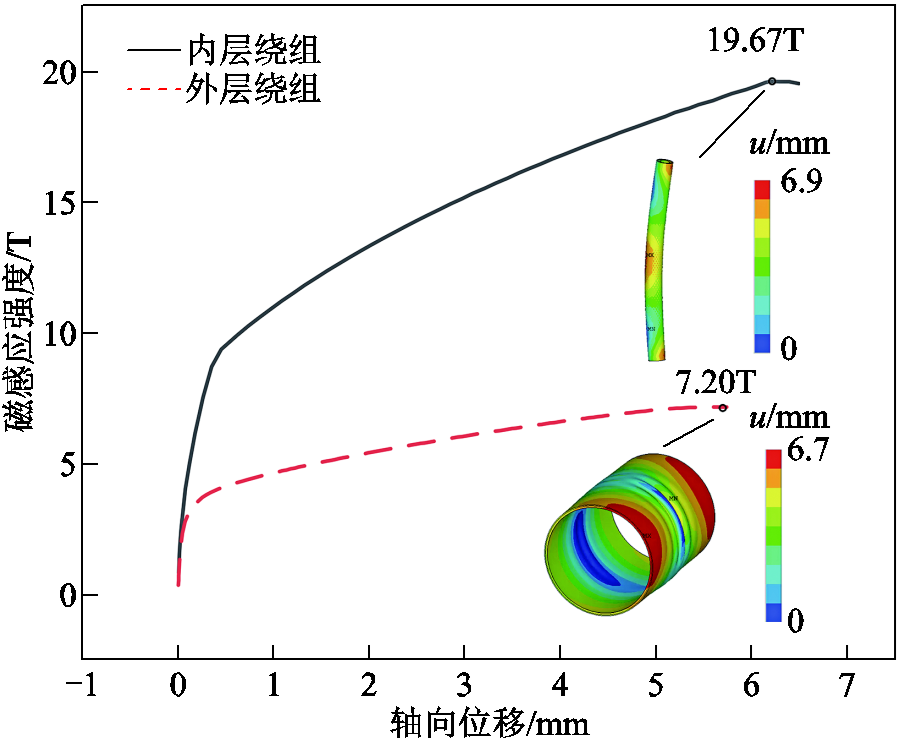
图6 非线性屈曲求解中位移-载荷曲线
Fig.6 Displacement-load curves of non-liner electromagnetic buckling
图7a给出了基于非线性屈曲计算得到的外线圈结果,而图7b则为美国NHMFL强磁场实验室80 T磁体破坏前后[19]的图片。衡量屈曲行为主要指标是屈曲破坏形式和屈曲强度。从仿真结果与实际结果对比可以看出,二者都是在磁体中部发生破坏,而且均有明显的轴向弯曲。实际磁体的破坏形式和破坏时磁场与经典材料强度破坏不同,而与屈曲模型理论预测接近,表明了本文所采取的研究方法和建立模型的正确性。

图7 中长型绕组屈曲仿真和实验结果对比
Fig.7 Simulation and experimental results of mediumcylinder layer in pulsed magnets
径向电磁力对轴向屈曲行为的影响如图8所示,横坐标Fr(r,z) /Fr0(r,z)表示径向电磁载荷的放大倍数,纵坐标B/B0为其相应屈曲磁场与1倍径向电磁载荷的比值。对于内层绕组,其屈曲磁场强度随着径向电磁载荷的增大先上升后减小,在这变化的过程中经历了屈曲的转变,从欧拉杆状屈曲(m=1, n=1)变成了盘状屈曲(m=1,n=0)。而且,径向电磁载荷的存在一定程度上提高了其轴向稳定性。而外层绕组的屈曲磁场随着径向电磁载荷比例的增大而出现了小幅度降低,影响不显著。
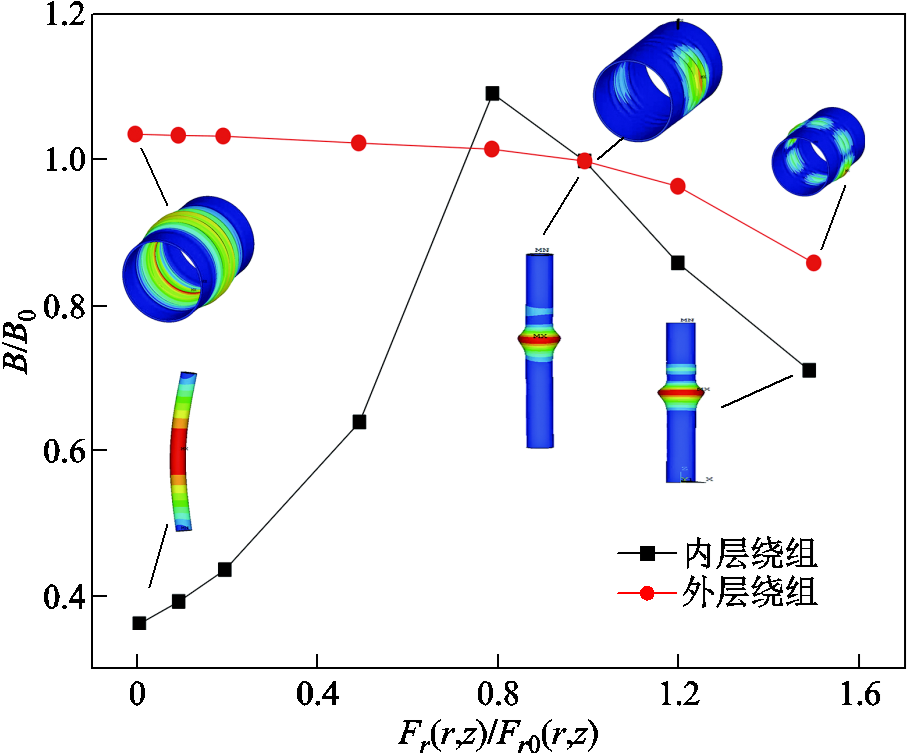
图8 径向电磁力对轴向屈曲强度的影响
Fig.8 Effect of radial electromagnetic force on axial buckling strength
实际中磁体导体层并不是一个完整的圆柱壳,是由螺旋绕组与加固层组成的,可等效为加筋圆柱壳,只不过这个“筋”占比较大,需要研究螺旋绕组缝隙对屈曲强度和模态的影响。在电磁载荷下,内层和外层绕组中导线占空比对屈曲强度的影响如图9所示,导线所占比例从50%到100%,屈曲强度归一化值相应从0.45提高到了1,表明螺旋绕组缝隙对屈曲强度有很大影响,缝隙越大,屈曲强度越低。在占空比较大时,外层圆柱壳结构比长型线圈更为敏感,当缝隙宽度超过一定限度时,结构稳定性都将出现大幅下降。而实际中脉冲磁体是密绕螺线管,导线占空比往往很大(80%以上),缝隙极小,缝隙影响是有限的。
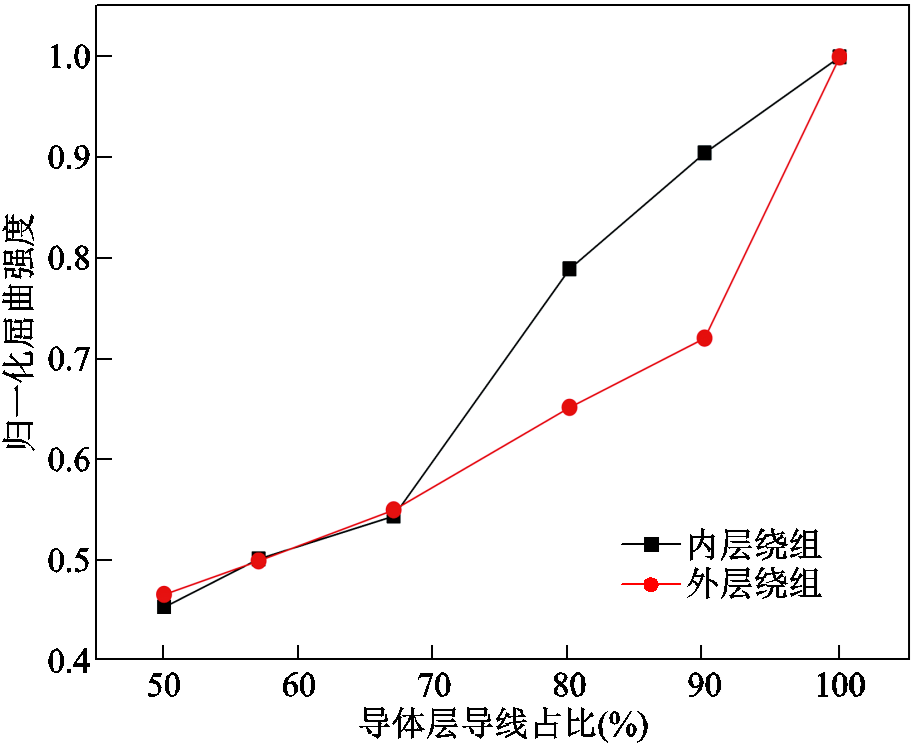
图9 螺旋绕组对屈曲强度的影响
Fig.9 Effect of helical winding on buckling strength
结构力学表明,磁体失效包含材料强度失效和结构整体失效两个方面。然而,现有磁体失效模型是基于材料强度模型,忽略了结构失稳问题,难以解释超高场脉冲磁体经常低于其设计值就发生破坏的现象。因此,本文从结构稳定性的角度出发,重点研究脉冲磁体自由分离的薄壁层,提出了基于圆柱壳体结构屈曲的超高场脉冲磁体力学失效分析方法,建立并计算了脉冲磁体静态电磁屈曲Ansys有限元模型,仿真结果与实际结果吻合,表明本文方法的可靠性。通过仿真对比,可以得出以下结论:
1)与经典材料强度模型相比,考虑磁体整体结构屈曲的方法可以更为准确地模拟与预测超高场脉冲磁体的力学失效行为。
2)轴向电磁载荷在脉冲磁体屈曲过程占主导作用。径向电磁力的对于外层绕组轴向屈曲影响不明显,但对内层绕组的轴向稳定有一定帮助。
3)在绕组结构方面,外层绕组对螺旋绕组缝隙较为敏感,需重点关注。
目前,本文的相关研究聚焦于磁体中单层绕组在磁场峰值处的静态屈曲行为,下一步将开展动态载荷对于磁体屈曲行为的研究。
参考文献
[1] Herlach F. High magnetic fields: science and technology - volume 2: theory and experiments I[M]. Singapore: World Scientific Publishing, 2006.
[2] Peng T, Jiang F, Sun Q Q, et al. Concept design of 100-T pulsed magnet at the Wuhan national high magnetic field center[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4): 1-4.
[3] Boebinger G. High magnetic field science and technology[R]. 25th International Conference on Magnet Technology (MT25), Amsterdam, Netherlands, 2017.
[4] 王秋良. 高磁场超导磁体科学[M]. 北京: 科学出版社, 2008.
[5] Arp V. Stresses in superconducting solenoids[J]. Journal of Applied Physics, 1977, 48(5): 2026-2036.
[6] Eyssa Y M, Denis Markiewicz W, Pernambuco-Wise P. Plastic stress analysis of pulse and resistive magnets[J]. IEEE Transactions on Magnetics, 1996, 32(4): 2526-2529.
[7] Peng T, Gu C L, Rosseel K, et al. Advanced numerical simulation of pulsed magnets with a finite element method[J]. Measurement Science and Technology, 2005, 16(2): 562-568.
[8] Witters J, Herlach F. Analytical stress calculations for magnetic field coils with anisotropic modulus of elasticity[J]. Journal of Physics D: Applied Physics, 1983, 16(3): 255-260.
[9] Van Bockstal L, Heremans G, Herlach F. Coils with fibre composite reinforcement for pulsed magnetic fields in the 50-70 T range[J]. Measurement Science and Technology, 1991, 2(12): 1159-1164.
[10] Li H, Herlach F. Deformation analysis of pulsed magnets with internal and external reinforcement[J]. Measurement Science and Technology, 1995, 6(7): 1035-1042.
[11] Zherlitsyn S, Wustmann B, Herrmannsdorfer T, et al. Status of the pulsed-magnet-development program at the Dresden high magnetic field laboratory[J]. IEEE Transactions on Applied Superconductivity, 2012, 22(3): 4300603.
[12] Nguyen D N, Michel J, Mielke C H. Status and development of pulsed magnets at the NHMFL pulsed field facility[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4): 1-5.
[13] Frings P, Billette J, Beard J, et al. New developments at the national pulsed field laboratory in Toulouse[J]. IEEE Transactions on Applied Superconductivity, 2008, 18(2): 592-595.
[14] Mielke C. The NHMFL pulsed field facility at los alamos national lab[C]//Workshop on Frontier Science Research of Pulsed High Magnetic Field, Wuhan, China, 2010: 1-26.
[15] Zherlitsyn S. Pulsed-magnet developments at the Dresden high magnetic field laboratory[C]//26th International Conference on Magnet Technology (MT26), Vancouver, Canada, 2019: 1-5.
[16] 卓卫东. 应用弹塑性力学[M]. 北京: 科学出版社, 2005.
[17] Ziemian R D. Guide to stability design criteria for metal structures[M]. 6th ed. Hoboken, NJ: John Wiley & Sons, 2010
[18] Özgen C. Buckling analysis of circular cylinder shells under axial compression loading[D]. Istanbul: Istanbul Technical University, 2017.
[19] Swenson C A, Rickel D G, Sims J R. 80 T magnet operational performance and design implications[J]. IEEE Transactions on Applied Superconductivity, 2008, 18(2): 604-607.
Study on Failure and Structural Buckling of Ultra-High Field Pulsed Magnets
Abstract The theory of structural mechanics shows that magnet failure can be attributed to over-stress failure or windings buckling. The present magnet failure model is based on the stress model and ignores the problem of structural instability, which makes it impossible to explain why ultra-high fieldmagnets frequently sustain damage at low stress levels. However, the mechanism and criterion of buckling in pulsed magnets are still unclear. Previous study has indicated that buckling is another significant cause of ultra-high field pulsed magnet failure. In this paper, the free-standing layer of the pulsed magnet can be equivalent to a thin-walled cylindrical shell with a high risk of buckling. A failure analysis method of ultra-high-field pulsed magnets based on the buckling of the cylindrical shell structure, along with an Ansys finite element model of the static electromagnetic buckling, is proposed. The simulation results match well with the experimental results. The buckling analysis shows that: the axial electromagnetic force is the key factor for buckling, while the radial electromagnetic force has no significant effect on the axial buckling of the outer winding, and itcan suppress the axial buckling of the inner winding to some extent; in terms of winding structure, the outer winding is more sensitive to the spiral winding gap and needs to be focused on.
keywords:High magnetic field, pulsed magnets, free-standing layers, buckling
DOI: 10.19595/j.cnki.1000-6753.tces.211714
中图分类号:TM551; O342
国家重点研发计划(2021YFA1600303)和湖北省重点研发计划(2021BAA167)资助项目。
收稿日期 2021-10-26
改稿日期 2022-04-12
肖后秀 男,1981年生,副教授,研究方向为脉冲强磁场技术及其应用。E-mail:xiaohouxiu@mail.hust.edu.cn(通信作者)
黄 煜 男,1999年生,硕士研究生,研究方向大功率脉冲磁体回旋管及其应用。E-mail:m202172077@hust.edu.cn
(编辑 郭丽军)