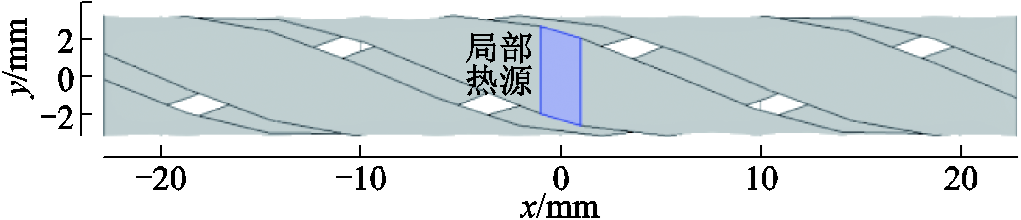
图1 三根并绕CORC电缆局部失超几何模型
Fig.1 Geometric model of CORC cable with three tapes for local quench
摘要 高温超导CORC（conductor on round core）电缆失超时的热负荷严重威胁了低温系统和电缆本体的安全稳定运行。受微米级超导薄膜制备工艺等的影响，CORC电缆并绕的多根高温超导带材不均匀。为分析不均匀临界电流对CORC电缆失超特性的影响，该文搭建了基于三维T-A方程的有限元模型。以降维的带材曲面为求解区域，以等效的电流密度为求解变量，失超模型在同一几何中表达超导和常导两种属性，构建电流和电势两种约束。在导体域建立降维的热模型，用以考虑损耗和传热的影响；在全局建立等效的电路模型，用以控制并联导体的分流。进一步地，耦合模型考虑温度依赖的接头电阻以模拟CORC电缆带材的烧断和电流的突变。结果表明，非均匀高温超导带材影响了电流重分配的动态响应，加快了局部失超的发展过程。
关键词：高温超导CORC电缆 局部失超 不均匀性 临界电流 有限元法
面对我国电力资源和负荷资源分布不均的矛盾，超导输电技术是实现大规模远距离输电的潜在解决方案之一[1-2]。随着第二代高温超导带材的发展，为了满足高载流量需求，目前主要发展了三种主流的电缆拓扑结构：罗贝尔（Roebel）电缆[3]、TSTC电缆（twisted stacked-tape cable）[4]和CORC（conductor on round core）电缆[5]。其中，由高温超导带材螺旋绕制的CORC电缆，具有损耗小、容量大、柔韧性高、机械性能强和电磁环境友好等优点，因此被广泛应用于电力输送[6]、高场磁体[7]和军工国防[8]等领域。
虽然超导带材在正常通流情况下几乎没有损耗，但局部缺陷、热设计和外部环境变化等因素，都可能加重制冷系统的负担，从而引起带材温升、临界电流（Ic）下降，最终导致超导设备失超甚至烧毁[9]。因此，为了保障超导电缆的安全稳定运行，对于其局部失超特性的研究十分关键。目前，虽然已对单根超导带材的失超行为开展了大量的实验研究和基于H方程的仿真分析[10-12]，但CORC电缆并联导体的失超行为与单根带材有所不同。在实验研究方面，测量了超导带材并联结构的失超传播特性[13]，研究了CORC电缆的稳定性和正常区传播[14]；在仿真分析方面，模拟了不均匀接头电阻对CORC电缆失超的影响[15-16]；在解析计算方面，通过电热耦合对高温超导电缆的失超恢复特性进行了一维模型基础研究[17]。
实际上，受高温超导薄膜制备工艺的影响，带材不同批次甚至不同长度处的载流能力有差异，在CORC电缆中即表征为整体不均匀的临界电流[18]；而受机械损伤、冷却工况和电磁环境等的影响，带材难免产生外源性的局部弱点[19]，在电缆中即可视为引起失超的局部热点。因此，研究不均匀临界电流下的失超特性，对超导电缆的监控与保护具有重要应用意义。
本文在T-A方程的基础上，以超导层和常导层厚度相等为假设，耦合失超模型以考虑带材各层间分流；利用均质化等效降维的材料物性参数，耦合热模型以引入温度和热效应；基于电缆的等效电路和阻抗特性，耦合分流模型以计算动态响应中电缆各带材间电流的转移。对于临界电流不均匀的单层CORC电缆，模型分析了带材单个局部热点引起的电流重分配，以及对电缆整体失超速度的恶化。
CORC电缆一般由多根高温超导带材螺旋并绕而成，为便于分析，本文选取了最典型的单层三根并绕结构，如图1所示。其中，三根带材在空间中的相对位置完全对称，使得各带材的自感和互感分别相等，从而减少了模型中的变量。
图1 三根并绕CORC电缆局部失超几何模型
Fig.1 Geometric model of CORC cable with three tapes for local quench
电缆模型的参数见表1。其中，带材参数取自上海上创超导的商业化带材，经测试其既具有较好的抗弯性能，又满足电缆对过电流能力和热稳定性的需求。根据对带材和电缆应力应变的计算[20]，CORC电缆的绕制角度设计为25°。此外，在77K自场环境下，假设电缆受损后各带材的平均临界电流由标称值146A衰退至136A。
表1 电缆模型参数
Tab.1 The parameters of cable model
参数数值 电缆骨架半径/mm3 绕制角度/(°)25 节距/mm约40 带材数量3 接头电阻/μΩ50 带材宽度/mm4 超导层厚度/μm1 哈氏合金基底层厚度/μm60 铜稳定层厚度/(μm/面)80 77 K自场临界电流/A146/136（受损） 工况初始温度/K77 电缆升流时间/ms0～6 热源发热时间/ms10～100
在超导域求解的T方程的状态变量为电流矢量势T。参考磁矢势A，它的旋度定义为[21]
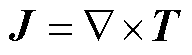（1）
由于电流密度J主要沿导体的长度方向流动，电流矢量势为导体面的法线方向。若T为电流矢量势的幅值，则电流密度可以表示为
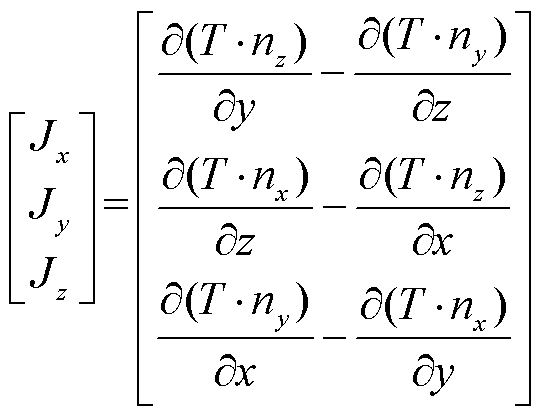（2）
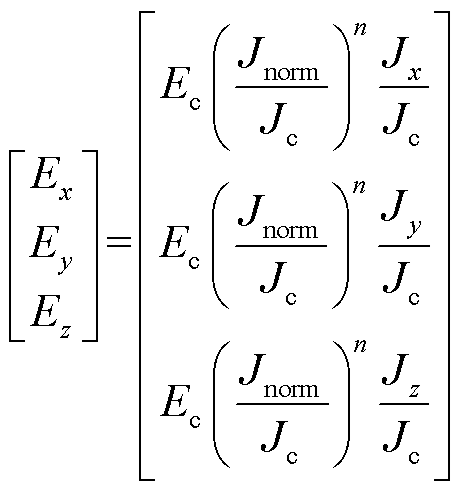
对于第二代高温超导带材，可以通过E-J power law描述电场和电流密度的关系为
（3）
式中，Ec为临界判据，1×10-4V/m；Jnorm为电流密度模；Jc为临界电流密度；n为常数，本文取为30。
超导域内的法拉第定律为
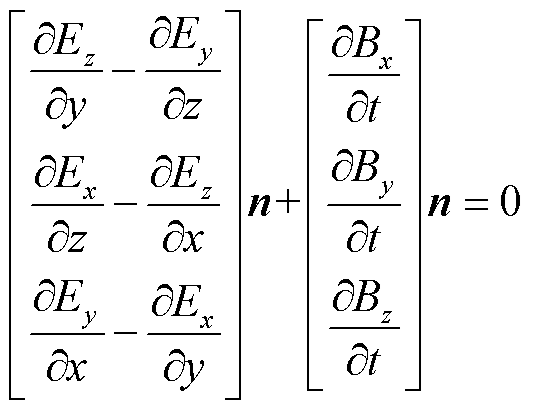（4）
式中，n为法向量，n=[nx ny nz]T。
超导带材的电流等于带材截面电流密度的积分。根据式（1）对电流矢量势的定义，利用斯托克斯定理，可以得到电流I与电流矢量势T的关系为
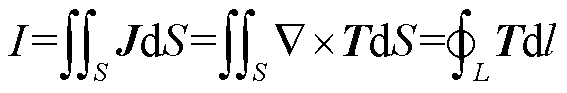（5）
式中，S为带材截面积；L为带材截面的周长。
如前所述，电流矢量势为导体面的法线方向，即平行于带材表面的T分量为0。因此
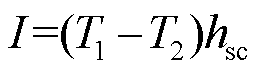（6）
式中，T1和T2分别为带材两侧T的值；hsc为超导层的厚度。
在空气域求解A方程计算磁场，其控制方程由安培定理推导得到
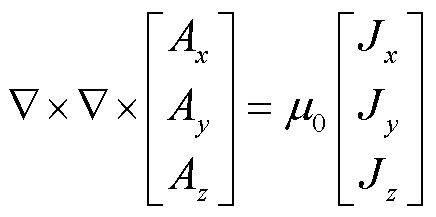（7）
此外，可以通过对空气域外边界施加狄利克雷-纽曼边界条件[22]，以分析外加磁场下的电缆特性。
由磁场方程计算的磁通密度反馈至式（4），影响了带材表面的电流密度分布，从而实现了T方程和A方程的耦合。
当超导带材发生过电流失超或者过热失超时，带材总电流超过超导层的临界电流，从而向常导层分流。由于T-A方程不仅将涂层导体超导层视为无限薄的曲面，还忽略了基带、镀铜和银等构成层，因此常规的T-A方程只能用于超导态的分析。例如，超导层损耗与其电流密度紧密相关，常用的均质化方法不适用于不完全失超状态；超导层在带材宽度方向上的电阻率具有非线性，无法用并联电阻公式进行等效。此外，当超导带材发生失超时，受阻抗特性影响的电流会在电缆导体间发生转移，常规的T-A方程预设了各带材的电流，无法表征这一场路综合作用下的动态过程。因此，为了准确描述超导带材的失超过程，研究超导电缆的过电流特性，构建高效普适的电磁热模型，需要在T-A方程的基础上搭建失超分流模型。
基于T-A方程的失超模型，需在一个导体面内表达超导和常导两种属性，考虑电流和电势的约束关系。此时，T方程的源项为带材受控的总电流，因变量为带材的工程电流密度。由式（6）可得
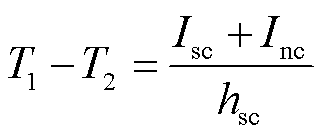（8）
式中，Isc和Inc分别为带材超导层和常导层的电流。
假设常导层厚度与超导层厚度相等，则有限元模型中式（9）所示的电流的积分约束[12]转换为式（10）所示的电流密度的逐点约束[15-16]。
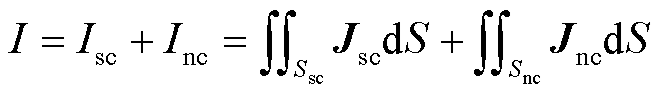（9）
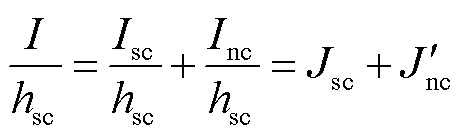（10）
式中，Jsc和Jnc分别为超导层和常导层电流密度；Ssc和Snc分别为超导层和常导层截面积；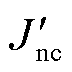
为常导层的等效电流密度。
进一步地，考虑电势的约束关系[23]，假设带材宽度方向上常导层电势与超导层电势处处相等。由式（3）可得
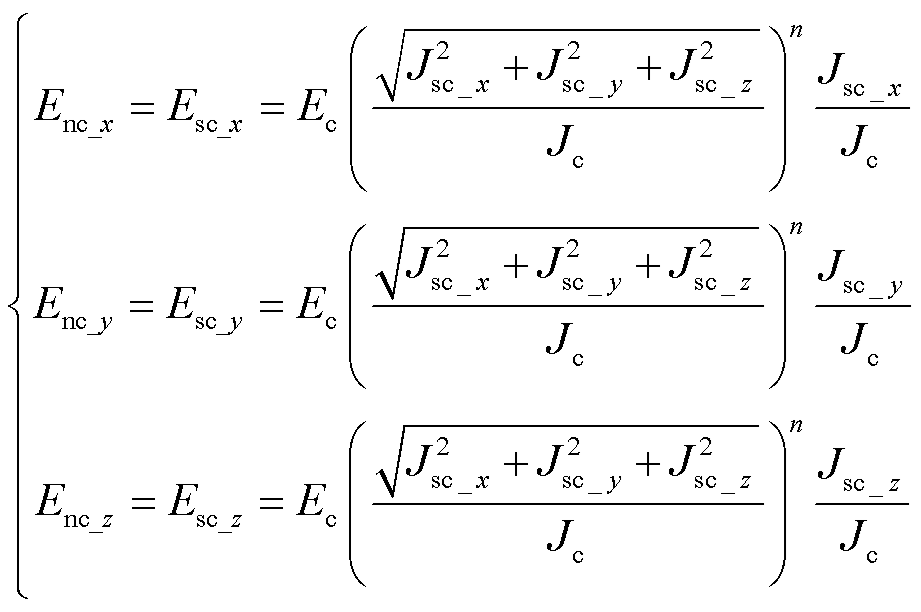（11）
式中，Enc_x、Enc_y和Enc_z分别为常导层x、y和z三个方向的电势；Esc_x、Esc_y和Esc_z分别为超导层x、y和z三个方向的电势；Jsc_x、Jsc_y和Jsc_z分别为超导层x、y和z三个方向的电流密度。
此外，常导层电阻率由并联电阻公式计算。考虑常导层厚度与超导层厚度相等的假设，常导层的等效电阻率为
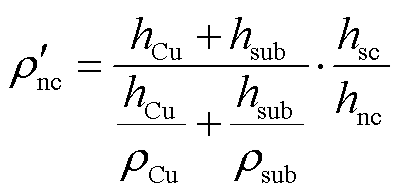（12）
式中，hCu和hsub分别为铜层和基底层的厚度；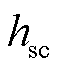
为常导层厚度；
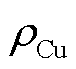和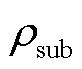
分别为铜层和基底层的电阻率。由于相对厚度太小，模型忽略了缓冲层和银层。
将式（11）和式（12）代入式（10），即可得到带材表面任意点超导层和常导层的分流比。
与超导层相比，主要由哈氏合金和铜构成的常导层具有良好的导热性，带材厚度方向的温度梯度可以忽略不计。基于该温度均匀分布假设，导体域热模型既表征超导层温度，也表征常导层温度。根据热平衡方程，热模型的控制方程为
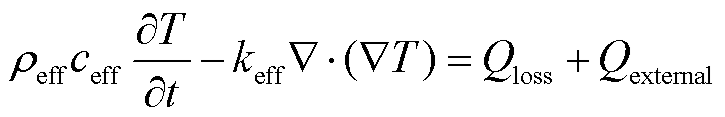（13）
式中，ρeff、
和keff分别为等效密度、等效比热容和等效热导率；Qloss和Qexternal分别为带材损耗和外部热源功率。需要说明的是，由于电缆和带材的失超发展速度较快，与环境的换热不充分，模型只考虑了传导热而忽略了对流换热[15-16,24]，同时以留有更大的安全裕度。
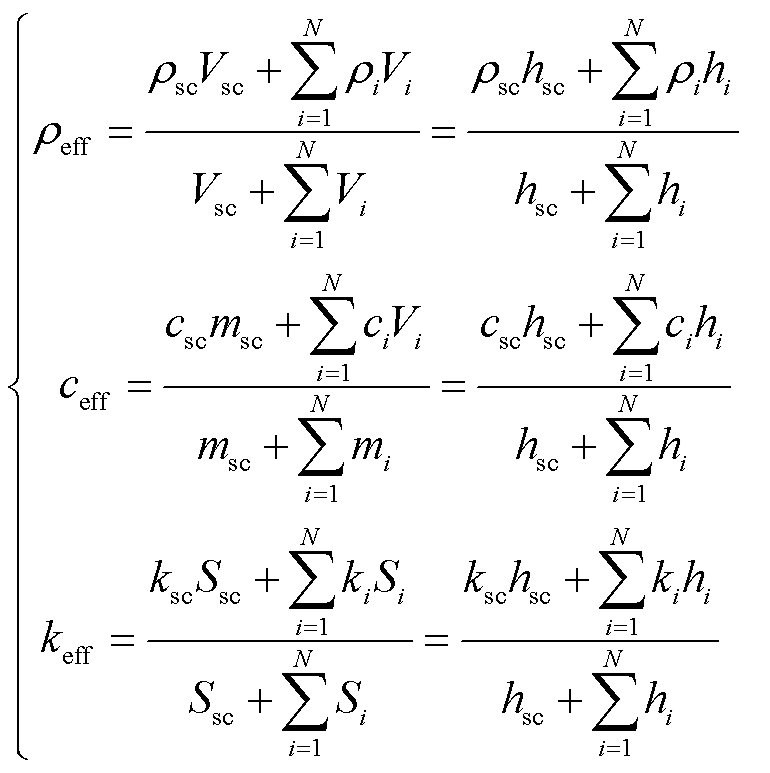
利用体积平均法，带材的等效密度、等效比热容和等效热导率分别为
（14）
式中，ρsc和ρi分别为超导层和各常导构成层的密度；N为常导构成层的层数；Vsc和Vi分别为超导层和各常导构成层的体积；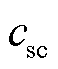
和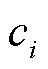
分别为超导层和各常导构成层的比热容；msc和mi分别为超导层和各常导构成层的质量；ksc和ki分别为超导层和各常导构成层的热导率；Si为各常导构成层的截面积；hi为各常导构成层的厚度。忽略超导带材侧边铜封装的影响，带材各层的体积比、质量比和面积比都等于厚度比。
最重要的是，热模型引入了温度变量。根据超导基本原理，超导体的临界电流与温度有关。T-A方程、失超模型和热模型中的临界电流密度Jc均需表示为温度依赖的函数，即
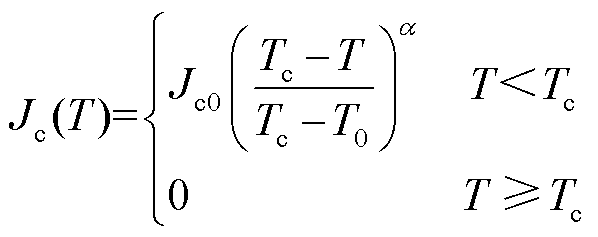（15）
式中，Tc为高温超导带材的临界温度，一般为92K；T0为带材的初始温度，77K；α表征温度对临界电流的影响，一般为1～2；Jc0为带材在77K自场下的临界电流密度。
对于CORC电缆，当超导带材发生失超时，受电阻和电感影响的电流会在电缆导体间发生转移。由T方程模型已知，各导体域的电流通过式（6）所示狄利克雷边界条件逐个给定。为了表征这一过程，需要构建电缆分流模型，使其根据场路耦合关系实时更新电流矩阵，并自动分配给各带材。
单层三根带材并绕的CORC电缆等效电路模型如图2所示。其中，Isum为电缆运行电流；Ii为各支路电流；Rteri为终端接头电阻；Rnci为带材常导层电阻；Rsci为带材超导层电阻；Li为带材自感；Mi,j为带材间互感；i=1,2,3。
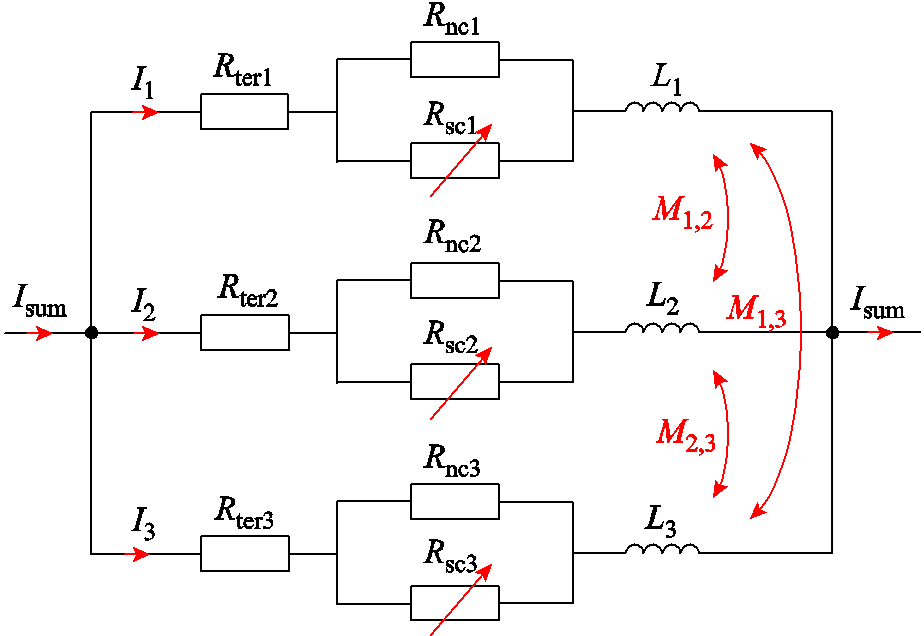
图2 CORC电缆等效电路模型
Fig.2 Equivalent circuit model of CORC cable
根据图2所示的等效电路，其支路电压的数学模型为
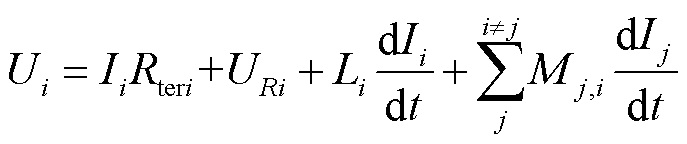（16）
式中，Ui和Ii分别为各支路的电压和电流，也是分流模型的状态变量，其对应的控制方程为
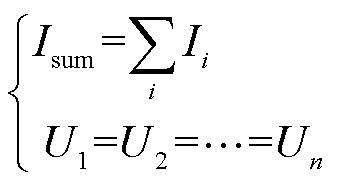（17）
此外，根据表1中的电缆模型参数，利用磁场能量法，计算可得带材自感Li为6.48×10-7μH/m，带材间互感Mi,j为3.24×10-7μH/m。
失超作为一种局部过热现象，是超导装置运行过程中可能发生的最严重的故障之一。失超时超导带材向阻性状态的转变，伴随着温度和电压的升高，产生的焦耳热引起低温环境的失稳，从而可能导致超导磁体的烧毁[25-26]。因此，失超监控与保护系统是超导电力装置的重要组成部分。
由式（3）和式（16）可知，带材的临界电流会影响其阻性电压，从而影响失超过程中电缆的分流。因此，本节首先分析了临界电流不均匀程度对失超过程中电流重分配动态过程的影响；接着，分析了响应末态，即并联导体的失超速度；最后，考虑长电缆电感和带材烧断的影响，比较了CORC电缆的失超时间，以指导失超监控与保护系统的研制。
电缆在0～6ms内线性升流至运行电流321A并保持不变，2mm长的局部热源区域在10～100ms内以恒定功率产生约414.3mJ的热量。之后，电缆进入局部失超的动态变化过程。为便于区分，本文假设局部热源所在的带材为1号，另外两根带材分别为2号和3号。
当2号带材临界电流Ic2最大，3号带材临界电流Ic3最小，即Ic2＞Ic1＞Ic3时，临界电流不均匀程度（ΔIc=2%，5%和8%）对2号和3号带材的影响如图3所示。图3中URi为带材阻性电压；ULii为带材自感电压；UMij为带材互感电压；Uteri为终端接头电阻电压；i, j=2, 3且i≠j。模型虽然考虑了失超时常导层的分流，但受传热的影响，带材轴向和径向各点的温度并不相等。因此，带材失超模型计算的超导层和常导层的分流比不相等，即带材表面各点的电流密度不相等。同样地，超导层损耗与其温度和电流有关，常导层损耗与其电流几乎成正比，则带材表面各点的损耗功率也不相等。综上所述，与细化的各构成层局部分流情况相比，各带材整体的分流情况能更加直观地反映其电磁热特性，如图3a所示。
图3 不均匀临界电流对CORC电缆失超特性的影响（Ic2＞Ic1＞Ic3）
Fig.3 Influence of non-uniform critical current on quench characteristics of CORC cable（Ic2＞Ic1＞Ic3）
在t＜10ms的稳态，各带材电流与临界电流几乎成正比。在10～100ms的局部热源发热过程中，1号带材向2号和3号带材分流。此时，受临界电流大小的影响，1号带材向2号和3号带材转移的电流并不相等。
为了分析临界电流大小对电流增量的影响，首先假设两根带材的电流增量ΔI相等。因为ΔI为一个极小值，其对带材宽度方向上电流密度的分布没有影响，即ΔJ∝ΔI。根据式（3），超导层电阻率正比于电流密度与临界电流密度比值的n次方。由于超导带材载流量小于临界电流，且带材的n指数为30，利用不等式关系易知，临界电流越大，电阻率增量越小，阻性电压增量也就越小。因此，根据式（16），临界电流较大的带材需分得更多的电流，以满足电路模型的控制方程。
图3a所示的仿真结果与上述分析一致，电流峰值时刻临界电流最大的2号带材的分流更多。当临界电流不均匀程度ΔIc从2%增大到8%，电流峰值时刻2号和3号带材的电流差值从0.59A增大到2.35A。此后，2号和3号带材的电流逐渐恢复至相等。
进一步分析临界电流不均匀程度为8%时2号和3号支路各组分电压，如图3b所示。值得注意的是，由于带材超导态电阻几乎为0，且失超时电阻会被常导层钳制，因此除接头电阻电压外，带材自感电压大于互感电压大于阻性电压。其中，根据2号和3号带材自感和互感的大小，自感电压约为互感电压的2倍。而2号和3号带材阻性电压间的显著差异也验证了不均匀的电流分配是由阻性电压引起的。
当1号带材临界电流最大，3号带材临界电流最小，即Ic1＞Ic2＞Ic3时，临界电流不均匀程度（ΔIc=2%，5%和8%）对1号、2号和3号带材电流的影响如图4所示。随着临界电流不均匀程度的增大，临界电流较大的1号和2号带材的峰值电流几乎不变，临界电流最小的3号带材的峰值电流从142.46A减小至141.48A。然而，不均匀的临界电流主要影响了t＞200ms时电流的分配。在t=800ms的末态，当临界电流不均匀程度为2%时，1号带材电流为96.21A，2号和3号带材电流为112.61A；当临界电流不均匀程度为5%时，1号带材电流为99.72A，2号和3号带材电流为110.86A；当临界电流不均匀程度为8%时，1号带材电流为102.69A，2号和3号带材电流为109.37A。
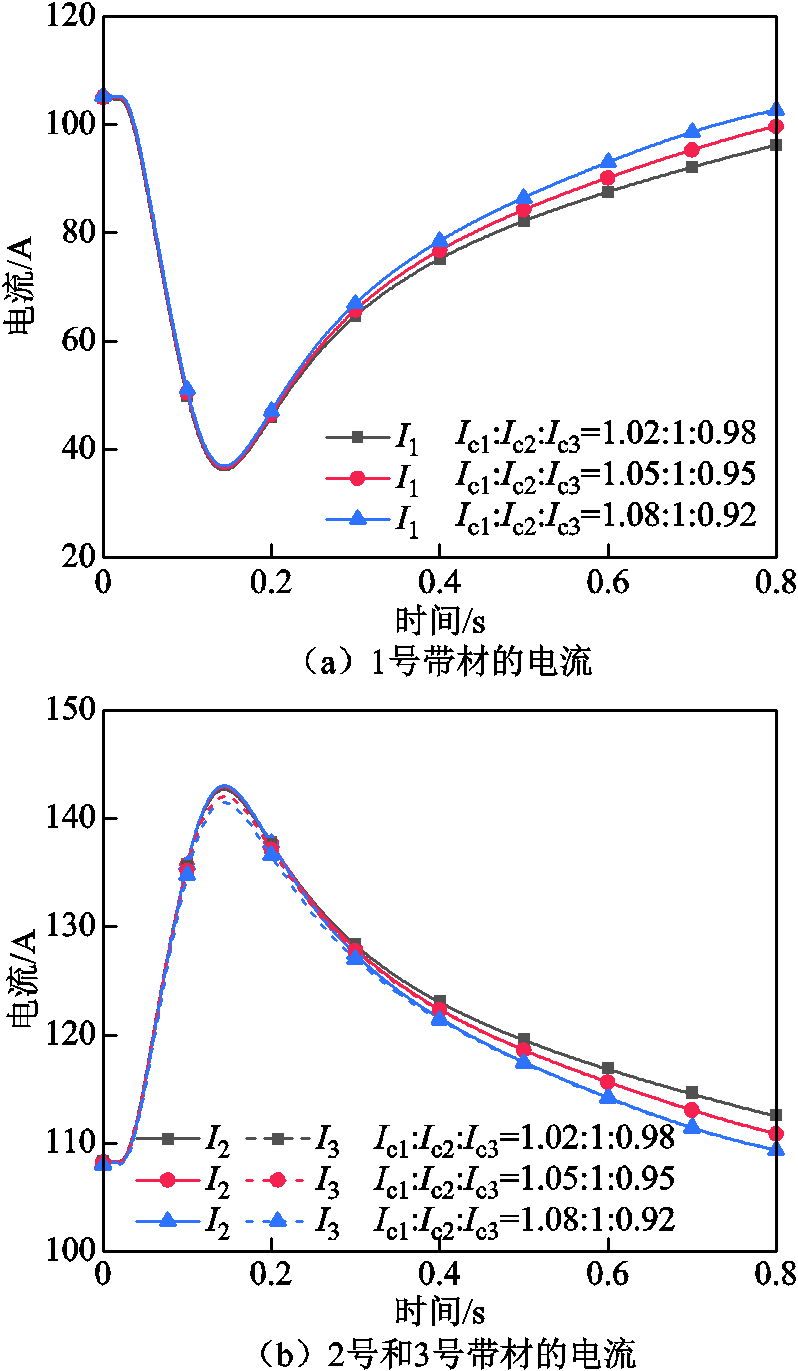
图4 不均匀临界电流对CORC电缆失超特性的影响（Ic1＞Ic2＞Ic3）
Fig.4 Influence of non-uniform critical current on quench characteristics of CORC cable（Ic1＞Ic2＞Ic3）
当3号带材临界电流最大，1号带材临界电流最小，即Ic3＞Ic2＞Ic1时，临界电流不均匀程度（ΔIc=2%，5%和8%）对1号、2号和3号带材电流的影响如图5所示。此时，随着临界电流不均匀程度的增大，临界电流较小的1号和2号带材的峰值电流几乎不变，临界电流最大的3号带材的峰值电流从143.07A增大至143.74A。同样地，不均匀的临界电流主要影响了t＞0.2s时电流的分配。在t=0.8s的末态，当临界电流不均匀程度为2%时，1号带材电流为90.99A，2号和3号带材电流为115.22A；当临界电流不均匀程度为5%时，1号带材电流为87.46A，2号和3号带材电流为116.98A；当临界电流不均匀程度为8%时，1号带材电流为84.2A，2号和3号带材电流为118.62A。
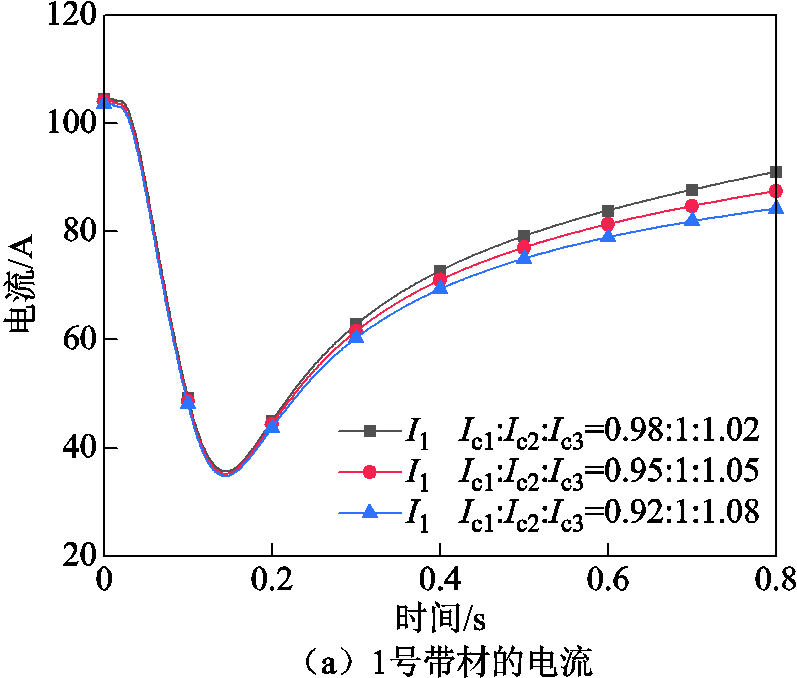
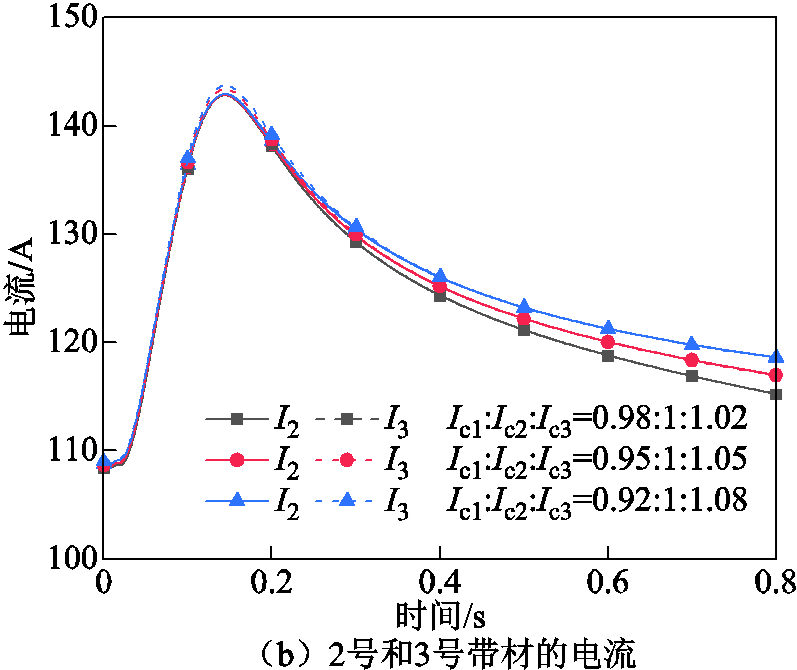
图5 不均匀临界电流对CORC电缆失超特性的影响（Ic3＞Ic2＞Ic1）
Fig.5 Influence of non-uniform critical current on quench characteristics of CORC cable（Ic3＞Ic2＞Ic1）
综上所述，电缆失超的动态响应过程中，重分配电流的差异主要是由不均匀带材的阻性电压引起的。不同工况下，电缆各带材的电流重分配情况见表2。局部发热的1号带材临界电流越小，其向2号和3号带材转移的电流越多，且2号和3号带材电流增量的不均匀性与临界电流的不均匀程度一致。另一方面，以仿真末态t=0.8s时刻的1号带材电流和相对电流作为评价指标，其中I0为失超前初始稳态电流，局部发热带材的临界电流越大，其动态响应后的电流恢复速度越快，且当局部发热带材的临界电流为中间值时，临界电流不均匀程度对电流恢复速度的影响较小。因此，临界电流较大的带材或线圈，在超导装置中应承担更严苛的电磁和力学工况，以降低失超的风险。
表2 电流重分配
Tab.2 Current redistribution
临界电流相对大小时刻电流临界电流不均匀程度 ΔIc=2 %ΔIc=5 %ΔIc=8 % Ic2＞Ic1＞Ic3峰值时刻I1/A35.80135.84535.986 |I2-I3|/A 0.591.432.35 t=0.8sI1/A93.42293.43393.543 (I0-I1)/I0(%)10.7510.7410.63 Ic1＞Ic2＞Ic3峰值时刻I1/A36.17936.51836.945 |I2-I3|/A0.330.851.52 t=0.8sI1/A96.20999.716102.69 (I0-I1)/I0(%)8.825.52.68 Ic3＞Ic2＞Ic1峰值时刻I1/A35.54635.14834.762 |I2-I3|/A0.260.580.81 t=0.8sI1/A90.98587.46184.203 (I0-I1)/I0(%)12.5816.0119.1
除了局部失超过程中的电流重分配，不均匀的临界电流还会影响电缆的失超时间。假设在各种因素的影响下，CORC电缆受损后三根带材的平均临界电流减小为136A，而临界电流的不均匀程度仍选取为8%，以保证临界电流较小的带材在稳态通流情况下不失超。为了缩短模型的计算时间，电缆的运行电流提高到360A。对于8cm长的电缆模型，CORC电缆各带材的最高温度和电流如图6所示。
当Ic2＞Ic1＞Ic3时，随着1号带材温度的持续上升，1号带材的电流不断减小，并转移至2号和3号带材。当t=1.4s时，临界电流最小的3号带材的温度开始上升，此时其电流约为160.19A，1号带材的电流几乎全部向临界电流最大的2号带材转移。此后，随着3号带材温度的升高，其临界电流逐渐下降，更多的电流向2号带材转移。当t=2.15s时，2号带材的电流达到峰值200.06A，此时其温度开始迅速升高，大部分电流向即将失超的1号带材转移。此后，1号带材、3号带材和2号带材依次失超。
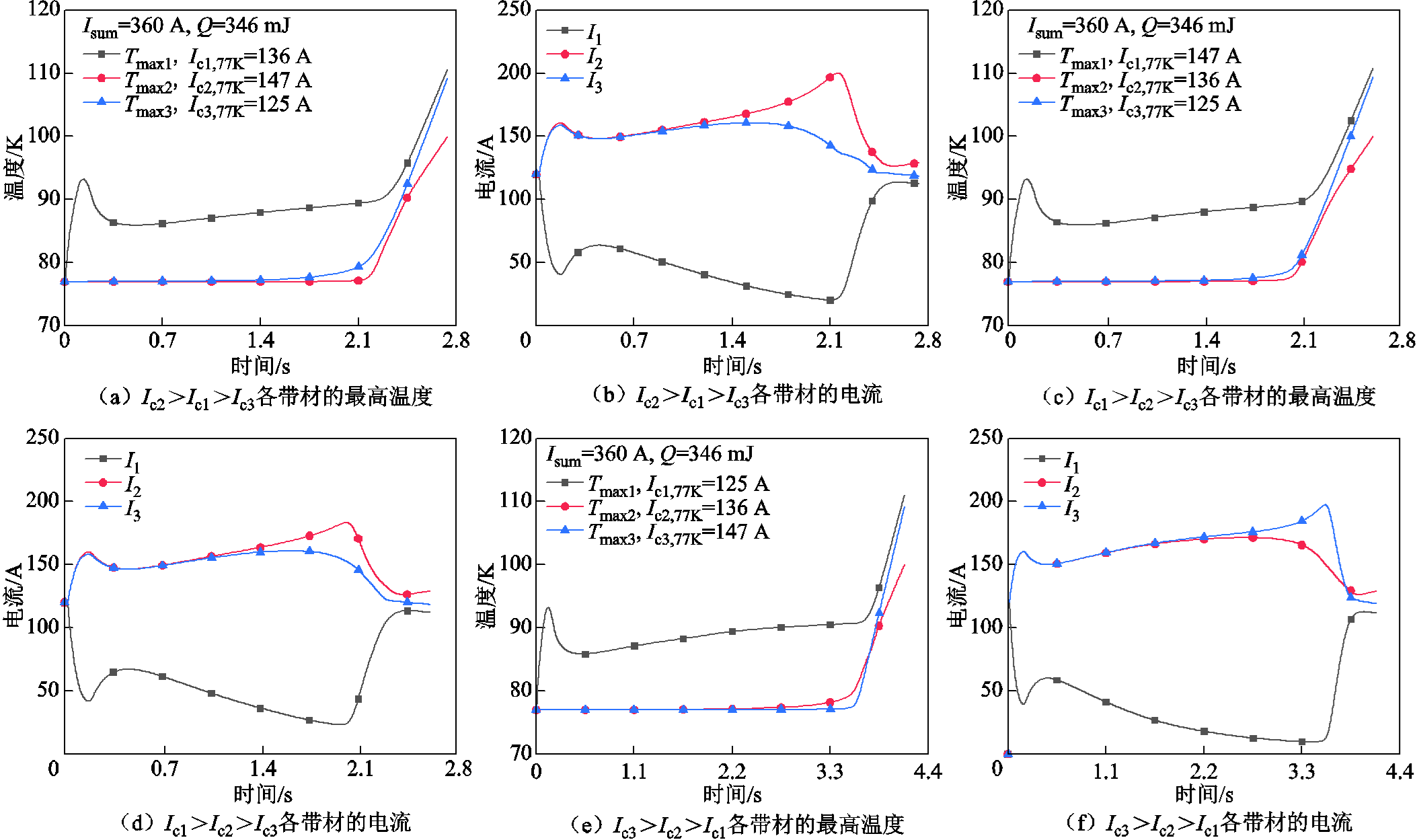
图6 不均匀临界电流对8cm长的CORC电缆失超时间的影响
Fig.6 Influence of non-uniform critical current on quench time of 8cm long CORC cable
当Ic1＞Ic2＞Ic3时，各带材温度和电流的转移过程与Ic2＞Ic1＞Ic3时类似。由于2号带材的临界电流为136A，在t=2.01s时，临界电流相对更大的2号带材的电流达到峰值183.2A，在超导层损耗和常导层损耗的作用下，此时其最大温度为77.6K并开始迅速升高。此后，1号带材、3号带材和2号带材依次失超。
当Ic3＞Ic2＞Ic1时，由于1号带材的临界电流最小，当t=2.2s时，2号带材的温度开始上升，此时其电流已超过170A，1号带材的电流几乎全部向临界电流最大的3号带材转移。此后，随着2号带材温度的升高，其临界电流逐渐下降，更多的电流向3号带材转移。当t=3.56s时，2号带材的电流达到峰值197.46A，此时其温度开始迅速升高，大部分电流向即将失超的1号带材转移。然而，由于2号带材临界电流也较大，其在3号带材电流转移过程中的发热功率较小。在t=3.74s时，3号带材的最大温度反超2号带材，同样使得1号带材最先失超，3号带材先于2号带材失超。
受带材电感续流作用的影响，长电缆可以抑制电缆的失超过程。然而，基于上述失超模型，当带材完全失超时其电压会被失超电阻钳制，从而使得局部发热带材的电流和温度持续上升，其他并联导体受到的影响较小。实际上，当温度或瞬时温升到达一定程度时，带材会被烧断且电流骤降为0，带材原有的电流会全部转移至其他并联导体[27]。对于这一过程和现象，在有限元软件中一般是无法直接模拟的，这主要是因为模型参数，尤其是自变量的突变极易造成求解器的不收敛。
为了解决这一问题，根据式（16）所描述的CORC电缆支路电压方程，本节提出了基于温度依赖的接触电阻定义方法，以模拟并联结构中带材的烧断。该电阻定义为
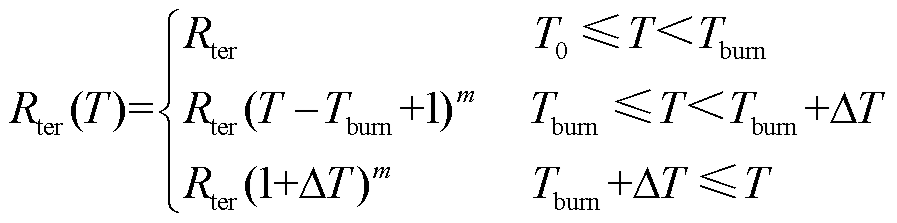（18）
式中，Tburn为带材烧毁温度；ΔT为带材烧毁的温度判据区域；m为常数。
该方法的主要思想为：当带材温度小于烧毁温度时，接头电阻阻值为正常值；当带材温度大于烧毁温度时，接头电阻阻值按指数幂迅速升高。假定m为与式（3）中n相同的常数，则当带材温度略大于烧毁温度时，接头电阻阻值趋向于无穷大，电压一定的情况下电流骤降为0，等效为支路开路。在该模型中，Tburn为150K，ΔT为0.2K，m为100。该定义保证了电流截断处的平滑过渡。
因此，在不影响场特性的情况下修改电路模型中电阻和电感项的长度，结合模拟带材烧毁的接头电阻定义方法，10m长的CORC电缆各带材的最高温度和电流如图7所示。由图6的分析可知，失超对电缆的影响本质上是温度对超导带材临界特性的影响，因此局部失超时的温升会引起并联导体电流重分配，而热源、热传导和换热的共同作用会使得系统处于一个动态的变化中。当2号和3号带材的电流上升到一定程度时，过电流引起的整体损耗超过了冷却效率，局部温升及热量扩散使得其阻性电压迅速增大。在支路电压相等的电路模型控制方程中，此时即将失超的1号带材电流反而升高，加剧了其失超发展速度。当1号带材的最高温度达到150K时，由图7b可见，1号带材的电流迅速骤降至0，2号和3号带材的电流阶跃上升。对应图7a中，1号带材的最高温度维持在150K，2号和3号带材的最高温度迅速上升。
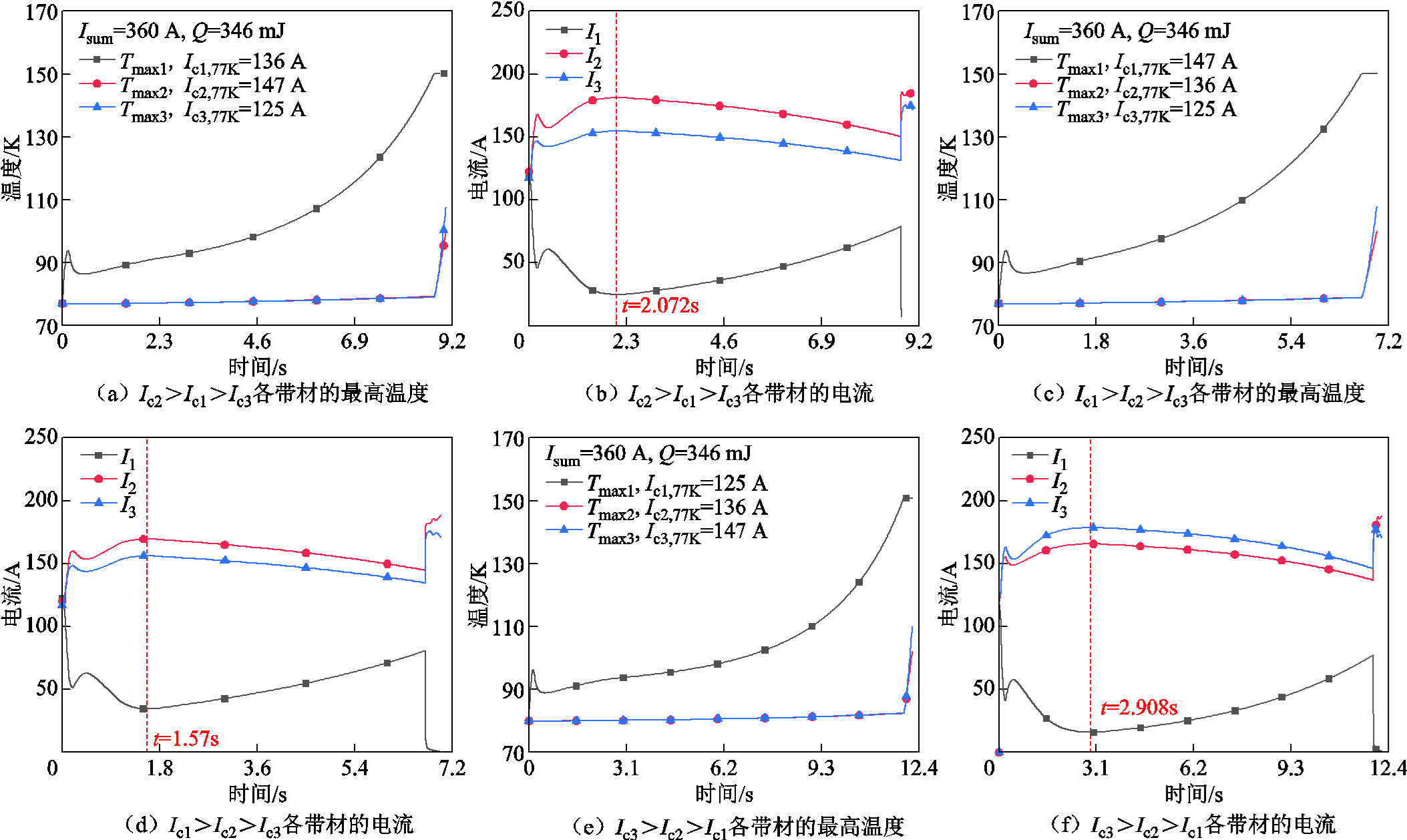
图7 不均匀临界电流对10m长的CORC电缆失超时间的影响
Fig.7 Influence of non-uniform critical current on quench time of 10m long CORC cable
当Ic2＞Ic1＞Ic3时，2号和3号带材的电流在t=2.072s前后的50ms区间内分别达到峰值180.93A和154.48A，此时1号带材的电流几乎达到最小值24.59A，此后1号带材约在t=8.79s烧断；当Ic1＞Ic2＞Ic3时，2号和3号带材的电流在t=1.57s前后的10ms区间内分别达到峰值169.37A和155.99A，此时1号带材的电流几乎达到最小值34.642A，此后1号带材约在t=6.715s烧断；当Ic3＞Ic2＞Ic1时，2号和3号带材的电流在t=2.908s前后的80ms区间分别达到峰值165.52A和178.51A，此时1号带材的电流几乎达到最小值15.97A，此后1号带材约在t=11.93s烧断。此外，与8cm长的电缆相同，在这三种不均匀临界电流情况下，总是1号带材最先失超，3号带材其次失超，2号带材最后失超。
以临界温度Tc为92K作为失超判据，不均匀临界电流对失超时间的影响见表3。
对于8cm长的电缆，当CORC电缆各带材临界电流相等时，1号带材的失超时间为3.132s，2号和3号带材的失超时间平均滞后0.136s。当1号带材的临界电流不变，2号和3号带材的临界电流不均匀，则1号带材的失超时间缩短为2.355s，缩短了0.777s，3号带材的失超时间仅滞后0.019s，2号带材的失超时间最多滞后0.088s。当1号带材的临界电流最大时，其失超时间进一步缩短至2.222s；当1号带材的临界电流最小时，电缆耐局部失超的能力有所提高。
对于10m长的电缆，受电感续流作用的影响，整体上1号带材的失超时间略有缩短，但2号和3号带材的失超时间显著增长。当1号带材的临界电流为中间值时，2号和3号带材的失超时间平均滞后6.273s；当1号带材的临界电流最大时，2号和3号带材的失超时间平均滞后4.887s；当1号带材的临界电流最小时，2号和3号带材的失超时间平均滞后8.259s。
表3 失超时间
Tab.3 Quench time
模型参数1号带材2号带材3号带材 Ic/A失超时间/sIc/A失超时间/sIc/A失超时间/s 8 cmIc1:Ic2:Ic3=1:1:11363.1321363.2941363.241 Ic1:Ic2:Ic3=1:1.08:0.921362.3551472.4421252.374 Ic1:Ic2:Ic3=1.08:1:0.921472.2221362.3661252.311 Ic1:Ic2:Ic3=0.92:1:1.081253.731363.8951473.846 10 mIc1:Ic2:Ic3=1:1.08:0.921362.4771478.7621258.738 Ic1:Ic2:Ic3=1.08:1:0.921471.7891366.691256.662 Ic1:Ic2:Ic3=0.92:1:1.081253.62713611.90214711.87
综上所述，非均匀高温超导带材会加快CORC电缆的失超发展过程，且局部发热带材的临界电流越大，失超速度越快。当ΔIc为8%时，对于局部发热带材临界电流非最小的短电缆，其失超时间缩短超过25%；对于局部发热带材临界电流最大的长电缆，其失超时间进一步缩短约20%。因此，高温超导带材的非均匀性，对基于分布式光纤测温的超导电缆失超保护方法研究和监测系统研制提出了更高的要求[28-29]。
本文基于三维T-A方程，搭建了CORC电缆的失超分流模型，进一步提出了并联导体带材烧断的模拟方法，从而分析了非均匀高温超导带材对CORC电缆失超特性的影响，得出如下结论。
1）对于局部失超的电流重分配过程，重分配电流的差异主要是由不均匀带材的阻性电压引起的，且随临界电流不均匀程度的增大而增大。局部发热带材的临界电流越大，其向外转移的电流越小，不完全失超状态下的恢复速度越快。
2）对于短电缆，非均匀高温超导带材显著加快了并联导体的失超速度。当ΔIc为8%且局部发热带材的临界电流非最小时，失超时间缩短超过25%。
3）对于长电缆，非均匀高温超导带材进一步加快了CORC电缆的失超速度。当ΔIc为8%且局部发热带材的临界电流最大时，失超时间较短电缆缩短约20%。
参考文献
[1] 肖立业, 林良真. 超导输电技术发展现状与趋势[J]. 电工技术学报, 2015, 30(7): 1-9.
Xiao Liye, Lin Liangzhen. Status quo and trends of superconducting power transmission technology[J]. Transactions of China Electrotechnical Society, 2015, 30(7): 1-9.
[2] 张国民, 陈建辉, 邱清泉, 等. 超导直流能源管道的研究进展[J]. 电工技术学报, 2021, 36(21): 4389-4398, 4428.
Zhang Guomin, Chen Jianhui, Qiu Qingquan, et al. Research progress on the superconducting DC energy pipeline[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4389-4398, 4428.
[3] Goldacker W, Frank A, Heller R, et al. ROEBEL assembled coated conductors (RACC): preparation, properties and progress[J]. IEEE Transactions on Applied Superconductivity, 2007, 17(2): 3398-3401.
[4] Takayasu M, Chiesa L, Noyes P D, et al. Investigation of HTS twisted stacked-tape cable (TSTC) conductor for high-field, high-current fusion magnets[J]. IEEE Transactions on Applied Superconductivity, 2017, 27(4): 1-5.
[5] Weiss J D, Mulder T, ten Kate H J, et al. Introduction of CORC®wires: highly flexible, round high-temperature superconducting wires for magnet and power transmission applications[J]. Superconductor Science and Technology, 2017, 30(1): 014002.
[6] 张喜泽, 宗曦华, 黄逸佳. 上海公里级超导电缆的设计研究[J]. 低温与超导, 2022, 50(6): 35-41.
Zhang Xize, Zong Xihua, Huang Yijia. Investigation on design of the kilometer superconducting cable in Shanghai[J]. Cryogenics ＆ Superconductivity, 2022, 50(6): 35-41.
[7] Jin Huan, Qin Jinggang, Liu H, et al. The performance of first CORC cable insert solenoid for development of CFETR high field magnet[J]. Nuclear Fusion, 2020, 60(9): 096028.
[8] Fitzpatrick B K, Kephartl J T, Golda E M. Characterization of gaseous helium flow cryogen in a flexible cryostat for naval applications of high temperature superconductors[J]. IEEE Transactions on Applied Superconductivity, 2007, 17(2): 1752-1755.
[9] Guo Shuqiang, Ren Li, Xu Ying, et al. Study on energy storage magnet state assessment method considering temperature rise[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(2): 1-11.
[10] Song Honghai, Schwartz J. Stability and quench behavior of - coated conductor at 4.2 K, self-field[J]. IEEE Transactions on Applied Superconductivity, 2009, 19(5): 3735-3743.
[11] Chan W K, Schwartz J. Three-dimensional micrometer-scale modeling of quenching in high-aspect-ratio YBa2Cu3O7-δ coated conductor tapes—part II: influence of geometric and material properties and implications for conductor engineering and magnet design[J]. IEEE Transactions on Applied Superconductivity, 2011, 21(6): 3628-3634.
[12] Ma Jun, Geng Jianzhao, Chan W K, et al. A temperature-dependent multilayer model for direct current carrying HTS coated-conductors under perpendicular AC magnetic fields[J]. Superconductor Science and Technology, 2020, 33(4): 045007.
[13] 蒲东昇, 任丽, 胡子珩, 等. 超导带材并联结构的失超传播特性研究[J]. 低温与超导, 2020, 48(6): 36-42.
Pu Dongsheng, Ren Li, Hu Ziheng, et al. Experimental study on the quench characteristic of YBCO tapes with different arranggements[J]. Cryogenics ＆ Superconductivity, 2020, 48(6): 36-42.
[14] Majoros M, Sumption M D, Collings E W, et al. Stability and normal zone propagation in YBCO CORC cables[J]. Superconductor Science and Technology, 2016, 29(4): 044006.
[15] Zhu Zixuan, Wang Yawei, Xing Dong, et al. Quench of a single-layer ReBCO CORC cable with non-uniform terminal contact resistance[J]. IEEE Transactions on Applied Superconductivity, 2019, 29(5): 1-5.
[16] Wang Yawei, Zheng Jinxing, Zhu Zixuan, et al. Quench behavior of high-temperature superconductor (RE)Ba2Cu3Ox CORC cable[J]. Journal of Physics D: Applied Physics, 2019, 52(34): 345303.
[17] 祝乘风, 厉彦忠, 谭宏博, 等. 热扰动冲击下的高温超导电缆失超恢复特性[J]. 电工技术学报, 2021, 36(18): 3884-3890.
Zhu Chengfeng, Li Yanzhong, Tan Hongbo, et al. Numerical analysis on the quench and recovery of the high temperature superconducting cable subjected to thermal disturbance[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3884-3890.
[18] 谭亚雄, 文明乾, 周湶, 等. 超导电力设备中YBCO超导带材不均匀性对载流特性的影响[J]. 电网技术, 2021, 45(3): 1150-1157.
Tan Yaxiong, Wen Mingqian, Zhou Quan, et al. Influence of inhomogeneity of YBCO superconducting tape on current carrying characteristics in superconductive electrical equipment[J]. Power System Technology, 2021, 45(3): 1150-1157.
[19] 陈炜. 高温超导线缆局部特性对交流损耗的影响研究[D]. 成都: 西南交通大学, 2021.
[20] Anvar V A, Ilin K, Yagotintsev K A, et al. Bending of CORC® cables and wires: finite element parametric study and experimental validation[J]. Superconductor Science and Technology, 2018, 31(11): 115006.
[21] Zhang Huiming, Zhang Min, Yuan Weijia. An efficient 3D finite element method model based on the T-A formulation for superconducting coated conductors[J]. Superconductor Science and Technology, 2017, 30(2): 024005.
[22] Wang Yawei, Zhang Min, Grilli F, et al. Study of the magnetization loss of CORC® cables using a 3D T-a formulation[J]. Superconductor Science and Technology, 2019, 32(2): 025003.
[23] Li Xianhao, Ren Li, Xu Ying, et al. Calculation of CORC cable loss using a coupled electromagnetic-thermal T-a formulation model[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(4): 1-7.
[24] Liang Siyuan, Ren Li, Ma Tao, et al. Study on quenching characteristics and resistance equivalent estimation method of second-generation high temperature superconducting tape under different overcurrent[J]. Materials (Basel, Switzerland), 2019, 12(15): 2374.
[25] 杨平, 王亚伟, 盛杰, 等. 非均匀ReBCO超导带材失超传播特性的建模与实验研究[J]. 中国电机工程学报, 2017, 37(16): 4842-4849, 4910.
Yang Ping, Wang Yawei, Sheng Jie, et al. Modeling and experimental study on the quench characteristics of non-uniform REBCO coated conductors[J]. Proceedings of the CSEE, 2017, 37(16): 4842-4849, 4910.
[26] 张正硕, 郑金星, 宋云涛, 等. 中国聚变工程实验堆纵场超导磁体高性能Nb3Sn CICC导体稳定性分析[J]. 电工技术学报, 2020, 35(24): 5031-5040.
Zhang Zhengshuo, Zheng Jinxing, Song Yuntao, et al. Stability analysis of high-performance Nb3Sn CICC conductor in China fusion engineering testing reactor toroidal field superconducting magnets[J]. Transactions of China Electrotechnical Society, 2020, 35(24): 5031-5040.
[27] Chen Lei, Li Guocheng, Chen Hongkun, et al. Combinatorial multi-objective optimization of resistive SFCL and DC circuit breaker in hybrid HVDC transmission system[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(8): 1-6.
[28] 黄金朋, 张哲, 汪伟, 等. 基于分布式光纤测温技术的超导电缆局部失超检测和保护方法[J]. 电力系统保护与控制, 2020, 48(14): 76-84.
Huang Jinpeng, Zhang Zhe, Wang Wei, et al. A local quench detection and protection method for a superconducting cable based on distributed optical fiber temperature measurement technology[J]. Power System Protection and Control, 2020, 48(14): 76-84.
[29] 王鹤, 李兴宝, 路俊海, 等. 基于叠加原理的光纤复合低压电缆热路模型建模[J]. 电工技术学报, 2019, 34(7): 1381-1391.
Wang He, Li Xingbao, Lu Junhai, et al. Modeling method of OPLC thermal circuit model based on superposition principle[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1381-1391.
Influence of Non-Uniform High Temperature Superconducting Tapes on Quench Characteristics of CORC Cable
Abstract The thermal load of the high temperature superconducting (HTS) CORC cable during quenching threatens the safe and stable operation of the cryogenic system and the cable body. Affected by the preparation process of micron-scale superconducting thin films, multiple HTS tapes wound in parallel with the CORC cable are not uniform. To analyze the influence of non-uniform critical current on quench characteristics of CORC cables, a finite element model based on the three-dimensional T-A formulation was built. Taking the reduced-dimensional tape surface as the solution area and the equivalent current density as the solution variable, the quench model expressed two properties of superconductivity and normal-conductivity, and constructed two constraints of current and potential in the same geometry. A reduced-dimensional thermal model was established in the conductor domain to consider the effects of loss and heat transfer; an equivalent circuit model was established globally to control the current redistribution. Further, the coupled model considered the temperature-dependent terminal resistance to simulate the burnout of tape and abrupt changes in current. The simulation results show that non-uniform HTS tapes affect the dynamic response of current redistribution and accelerate the development of local quench.
keywords：High temperature superconducting CORC cable, local quench, non-uniformity, critical current, finite element method
DOI:10.19595/j.cnki.1000-6753.tces.221256
中图分类号：TM26
GF科技重点实验室基金资助项目（6142217210207）。
收稿日期 2022-06-30
改稿日期 2022-07-28
李显皓 男，1997年生，博士研究生，研究方向为超导电缆多场分析。E-mail：lixh@hust.edu.cn
任 丽 女，1968年生，教授，博士生导师，研究方向为超导电力。E-mail：renli@mail.hust.edu.cn（通信作者）
（编辑 赫蕾）