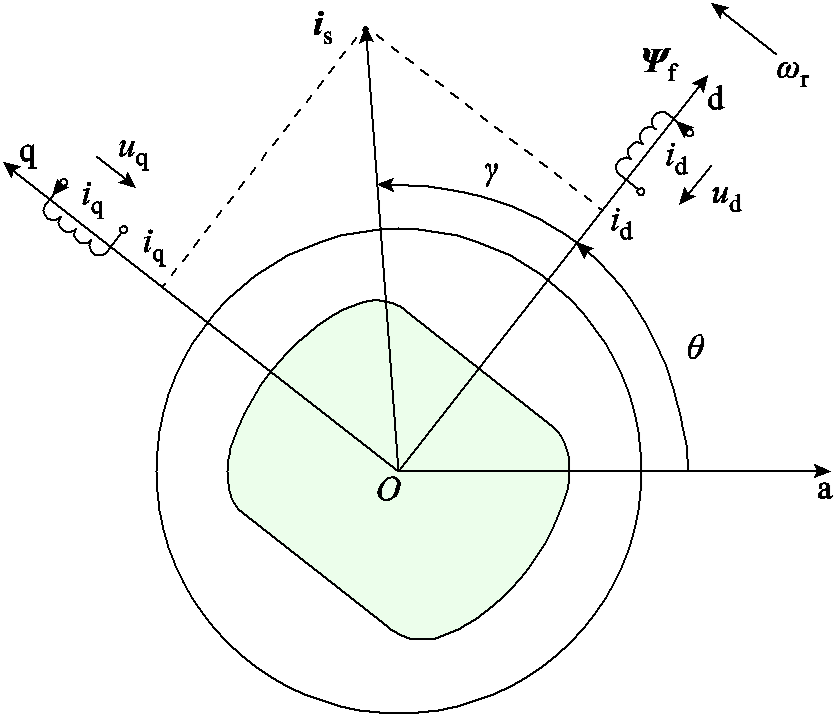
图1 同步旋转轴系
Fig.1 Synchronous reference frame
摘要 在永磁同步电机长线缆驱动系统安装LC滤波器可能会引起谐振，导致转子初始位置辨识失败。主动阻尼控制能够抑制LC滤波器引起的谐振，从而保障转子初始位置辨识的成功。在估计的同步旋转轴系上注入高频电压信号，对高频电流响应解调后得到两种可能的结果，对应不同的极性。根据电机磁路的饱和效应，施加不同的直流电流激励并对比每种激励下的实验结果，可以完成极性辨别。在注入高频电压信号和施加直流电流激励的过程中，LC滤波器将引起系统谐振。针对这一问题，提出一种基于高通滤波器的主动阻尼控制方法，在传统电流环的基础上增加一个反馈通路，等效地增大谐振频率处的系统阻尼；然后进行主动阻尼控制方法的参数设计和稳定性证明；最后开展实验，得到成功抑制谐振后的实验结果，证明所提考虑谐振抑制的永磁同步电机长线缆驱动系统转子初始位置辨识技术的有效性。
关键词：永磁同步电机 初始位置辨识 主动阻尼 谐振抑制
与传统的感应电机相比，永磁同步电机具有转矩密度高、调速性能好、效率高等显著优势，在石油钻探和开采等领域具有广泛的应用前景[1]。在潜油电机长线缆驱动系统中，常使用脉宽调制（Pulse Width Modulation, PWM）技术输出高频方波电压，可能引起很高的反射过电压，威胁电缆和电机绕组的绝缘[2]。在逆变器输出侧装备LC滤波器可以滤除高频信号，进而有效地避免上述危害。
装备LC滤波器的潜油电机长线缆驱动系统常使用转子磁场定向控制（Field-Oriented Control, FOC）技术，该技术需要精确的转子位置。通常，转子位置由安装在电机端部的位置传感器来测量[3]。但在潜油电机等应用场合，位置传感器的安装和长距离信号传输比较困难、可靠性差[4]。因此，作为一种替代方案，无位置传感器控制得到了广泛的关注和研究。
目前的研究可分为两个方面：中高速运行和零低速运行[5]。在中高速运行时，可利用电机基波模型计算磁链或反电动势，进而得到转子位置[6]。在零低速运行时，可利用电机凸极模型，向定子绕组注入高频信号来实现转子位置辨识，主要有高频旋转电压注入法、高频脉振电压注入法等[7]。与高频旋转电压注入法相比，高频脉振电压注入法更适合应用于凸极率较低的永磁电机中[8]。凸极模型不含转子永磁体的极性信息，所以还需进一步辨别永磁体极性[9]。
永磁体极性的辨别依赖电机磁路的饱和效应，即电感的大小与磁路的饱和程度有关。基于饱和效应的辨别方法有二次谐波法、电压脉冲法、单向电流激励法和双向电流激励法等[10]。二次谐波法通过比较高频响应电流正负向振幅的大小来辨别极性。这种方法的可靠性较差[11]。电压脉冲法通过注入两个相反的电压脉冲信号并比较电流响应来辨别极性。在逆变器输出侧装备LC滤波器后，电流响应的特性发生了很大变化。电流响应中的谐波将会影响位置辨识的精度，尤其是在LC滤波器截止频率较低时[12]。单向电流激励法与双向电流激励法的原理相同，都是施加两个直流电流激励并比较高频电流响应幅值的大小，以此作为极性辨别的依据。双向电流激励法施加的直流电流激励差异更大，因此可靠性更高，可以实现永磁体极性的准确辨别[13]。装备LC滤波器后，这种方法将受到系统谐振的限制。在电机绕组中注入高频电压并施加直流电流激励时，滤波器电感与电机定子的磁路都会受到饱和及磁滞涡流的影响，使电流中含有较大的谐波。由于LC滤波器引入了谐振峰，这些谐波将使系统发生谐振。因此，注入电压的频率和施加直流电流激励的大小都不能太大，这将降低位置观测的带宽和极性辨别的准确性。
针对LC滤波器引起的谐振问题，主要有被动阻尼法[14-15]和主动阻尼法[16-18]两种抑制方法。被动阻尼法通过在滤波器的电容支路串联阻尼电阻来抑制谐振。被动阻尼法简单可靠，不需要改变控制器的结构，但是阻尼电阻的损耗会降低系统效率。主动阻尼法无需阻尼电阻，而是通过改变控制器结构来抑制谐振，受到越来越多的关注。有的主动阻尼法需要在电容支路安装传感器，增加了系统成本、提高了装配难度[19]。
本文在使用高频电压注入法辨识永磁电机转子初始位置的基础上，增加了基于高通滤波器的主动阻尼控制，以此抑制LC滤波器引起的谐振，不会增加系统损耗，也不需要在电容支路安装传感器。首先在估算出的同步旋转轴系上注入一个高频电压信号，获得高频电流响应，解调之后得到位置误差信息。进一步利用电机磁路的饱和效应，施加不同的直流电流激励，根据直流电流激励的大小辨别转子永磁体的极性。然后针对这一过程中LC滤波器引起的系统谐振，在电流环加入基于高通滤波器的主动阻尼控制，增加谐振频率处的阻尼，有效地抑制谐振，保障转子初始位置辨识的成功。
如图1所示的同步旋转轴系可用来构建永磁电机的数学模型。将永磁体磁场轴线定义为d轴，q轴沿旋转方向超前d轴90°电角度。对于内置式永磁电机，d轴方向的气隙磁阻大于q轴方向的气隙磁阻。永磁电机的初始位置辨识亦即计算出d轴相对于a相绕组轴线的位置。
图1 同步旋转轴系
Fig.1 Synchronous reference frame
在上述同步旋转轴系下，永磁电机的数学模型可表示为
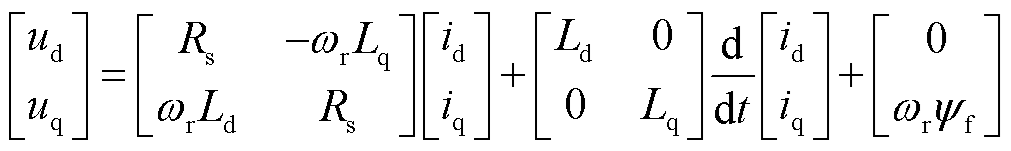（1）
式中，ud和uq分别为d轴和q轴电压；id和iq分别为d轴和q轴电流；Rs为定子电阻；Ld和Lq分别为d轴和q轴电感；ωr为电角速度；ψf为永磁体磁链。
在高频注入法中，注入电压的频率远高于基波频率，定子电阻压降、反电动势及旋转电压都可以忽略不计。只考虑高频响应，式（1）可简化为
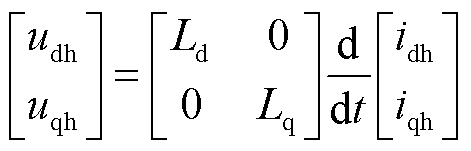（2）
式中，udh和uqh分别为d轴和q轴电压的高频分量；idh和iqh分别为d轴和q轴电流的高频分量。
在估计的同步旋转轴系上注入一个高频电压信号，可实现转子位置观测。该信号可表示为
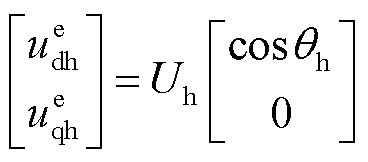
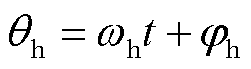（3）
式中，Uh、ωh和φh分别为注入电压信号的幅值、角频率和相位；上标e表示估计的同步旋转轴系。
定义实际的与估计的同步旋转轴系之间的误差角度为Δθ，可求得注入高频电压的电流响应为
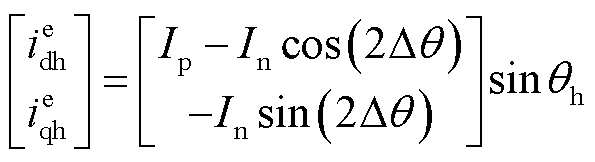（4）
其中
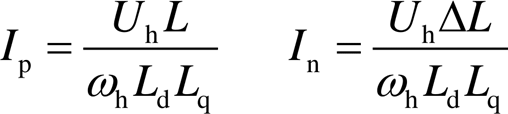（5）
式中，L和ΔL分别为平均电感和差值电感，可表示为
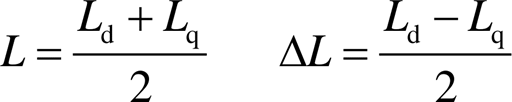（6）
由式（4），电流响应的qe轴分量是一个幅值被低频分量调制的高频信号，其幅值中含有位置误差信息。对电流响应进行解调，可以得到位置误差信息。解调过程如图2所示。在锁相环的作用下，电流响应的qe轴分量调整至零，转子位置误差为0°或180°，表明需要进一步辨别转子极性。
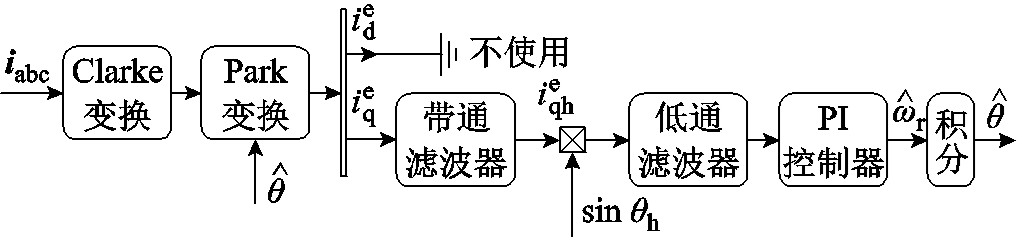
图2 解调过程
Fig.2 Demodulation process
当d轴电流为正时，电机磁路饱和程度增加；当d轴电流为负时，磁路饱和程度降低。这种现象称为磁路的饱和效应。
在估计的de轴上施加一个正的直流电流激励，若此前转子位置误差为0°，即de轴与d轴（N极）重合时，d轴电流为正，磁路饱和程度高；若此前转子位置误差为180°，即de轴与-d轴（S极）重合时，d轴电流为负，磁路饱和程度低。磁路饱和程度越高，d轴电感越小，注入高频电压的电流响应的幅值越大。根据这一原理，可以实现永磁体的极性辨别。首先，保持高频注入电压的频率和幅值不变，意味着高频磁链的频率和幅值基本不变。然后，在估计的de轴上分别施加一正一负两个直流电流激励，得到两个高频注入电压的电流响应，基于饱和效应的极性辨别如图3所示。最后，比较两种情况下高频注入电压的电流响应的幅值大小。若施加正直流激励时，高频电流响应的幅值更大，则表明de轴与d轴（N极）重合；反之表明de轴与-d轴（S极）重合。
高频电流响应的幅值可由锁相环求得，锁相环的结构如图4所示。在PI控制器的作用下，锁相环能够实时地计算出高频电流响应的幅值，用来辨别永磁体的极性。
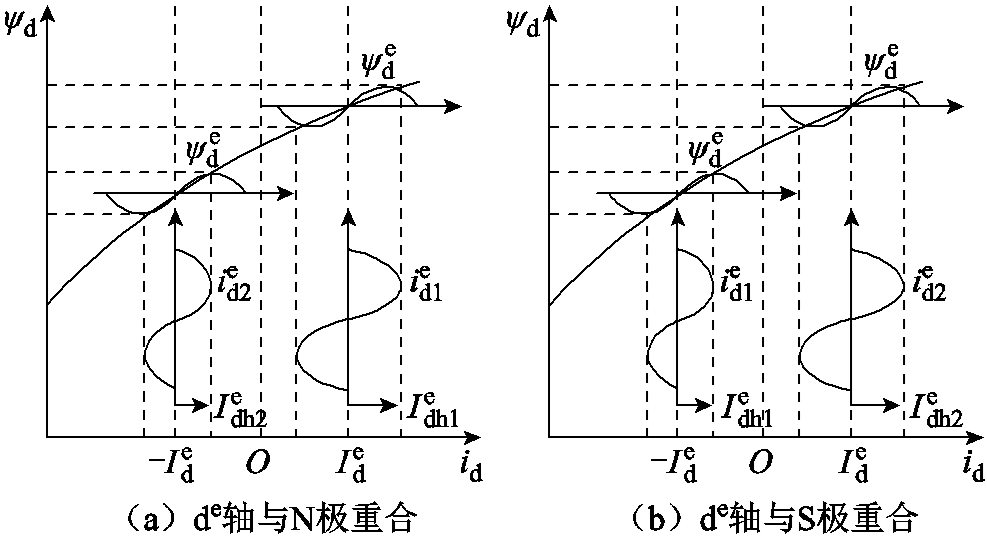
图3 基于饱和效应的极性辨别
Fig.3 Identification of rotor polarity based on saturation effects
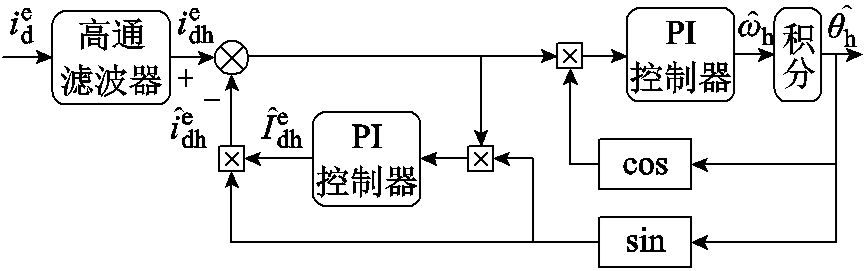
图4 锁相环结构
Fig.4 Structure of PLL
由前面的分析可知，永磁电机的初始位置辨识依赖于高频电压注入与直流电流激励。在常规的电机系统中，这两种方法的实现主要受限于开关频率和电机磁路的饱和程度。随着LC滤波器的使用越来越广泛，高频电压注入与直流电流激励的实现还将受限于LC滤波器引起的系统谐振。
在逆变器输出侧装备LC滤波器的系统如图5所示。滤波器可以滤除输出电压中的高频分量，因此注入高频电压的频率将受到限制。与此同时，注入高频电压并施加直流电流激励时，滤波器电感与电机定子的磁路都容易受到饱和及磁滞涡流的影响，从而使电流中含有较大的谐波。由于LC滤波器的存在，这些谐波容易使系统发生谐振。
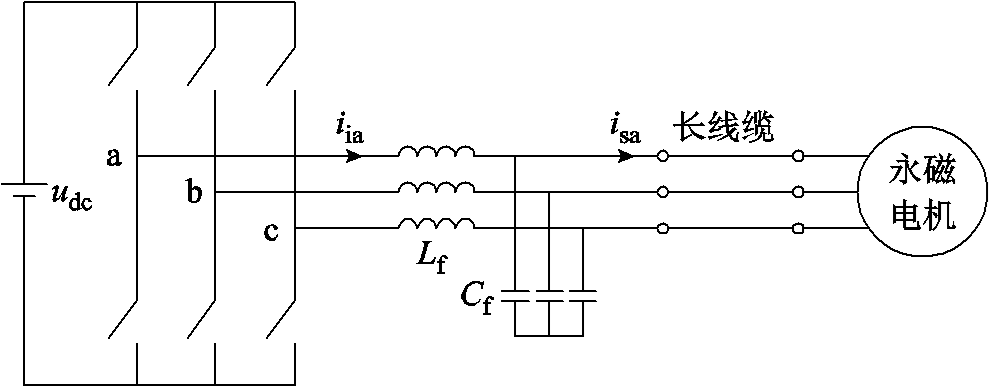
图5 装备输出滤波器的长线缆驱动系统
Fig.5 System equipped with output filter
同步旋转轴下的传统电流环如图6所示。文献[20]推导了负载电阻为零时逆变器输出电压到负载电流的传递函数。本文中的负载为电机，电机电阻不为零。此时以q轴分量为例，逆变器输出电压
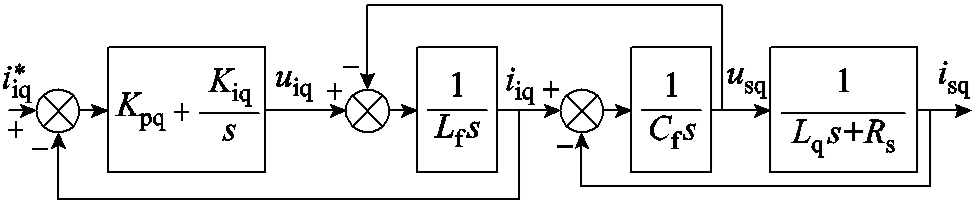
图6 传统的电流环
Fig.6 Conventional current loop
到电机电流的传递函数为
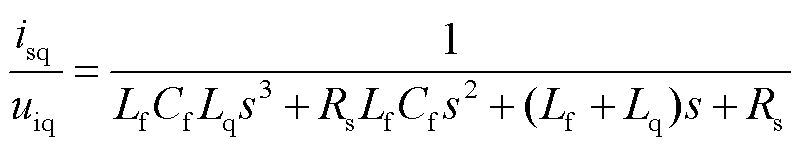（7）
式中，s为微分算子；Lf、Cf分别为LC滤波器的电感、电容；isq为电机定子电流的q轴分量；uiq为逆变器输出电压的q轴分量。
由式（7）可算出谐振频率（阻尼最小之处）为
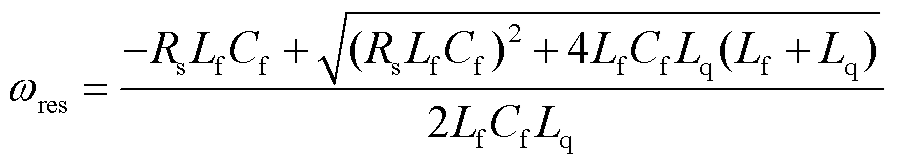（8）
式（7）表示的传递函数的伯德图如图7所示。由幅频特性可知，由于在逆变器后端加入了LC滤波器，低频时的等效阻抗增大；幅频响应在谐振频率处存在一个约20dB大小的尖峰，意味着谐振频率处的系统阻尼非常小。如果不抑制这个尖峰，一个较小的电压将产生非常大的电流，使系统发生故障，无法实现永磁电机的初始位置辨识。由相频特性可知，加入LC滤波器后，系统的稳定裕度下降。
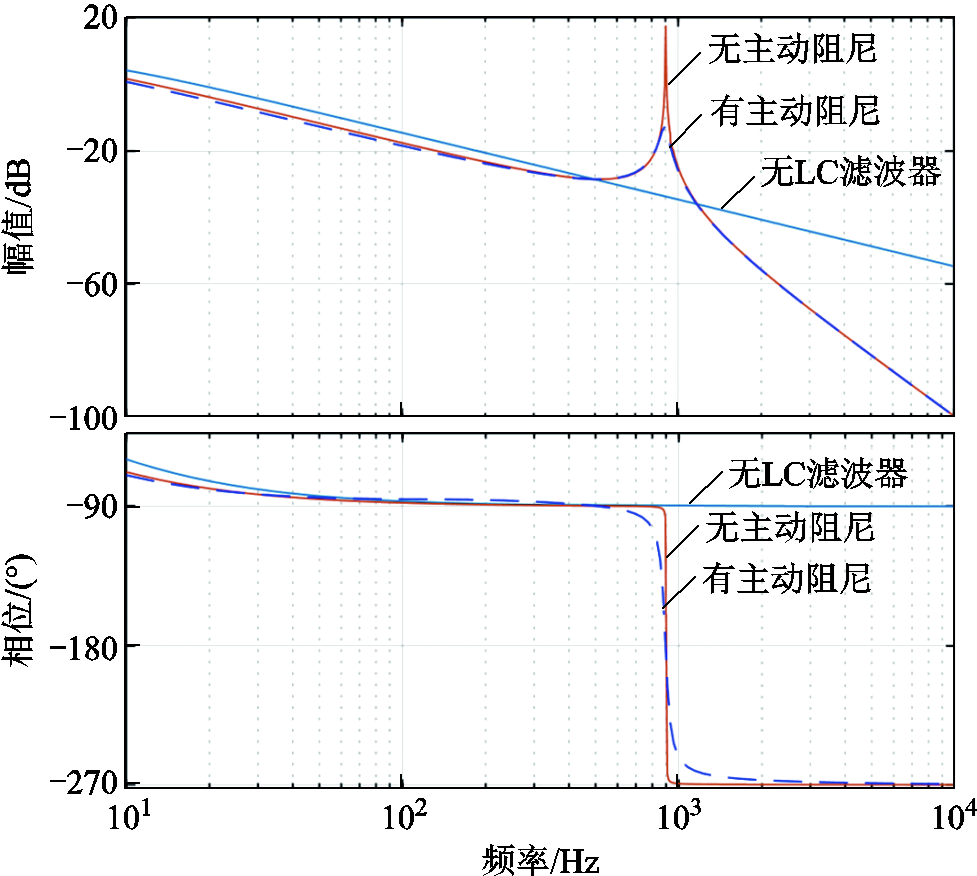
图7 开环传递函数的伯德图
Fig.7 Bode diagram of the open-loop transfer function
电流环闭环传递函数的伯德图如图8所示。由幅频特性可知，加入LC滤波器后，电流环带宽下降约四分之一；谐振频率处出现尖峰，表明此处阻尼较小。
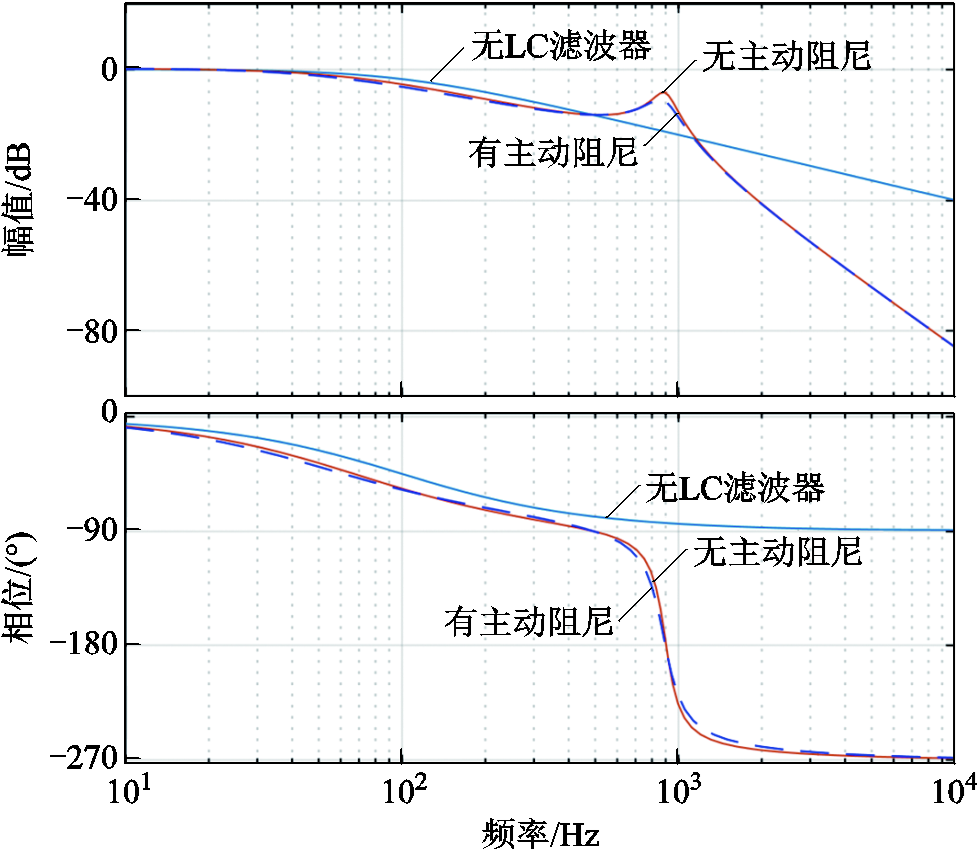
图8 电流环闭环传递函数的伯德图
Fig.8 Bode diagram of the closed-loop transfer function of the current loop
本文通过主动阻尼控制来抑制谐振，其控制框图如图9所示，在传统电流环的基础上增加一个反馈通路，这个通路可以等效为一个增益为K、时间常数为τ的高通滤波器[18]。
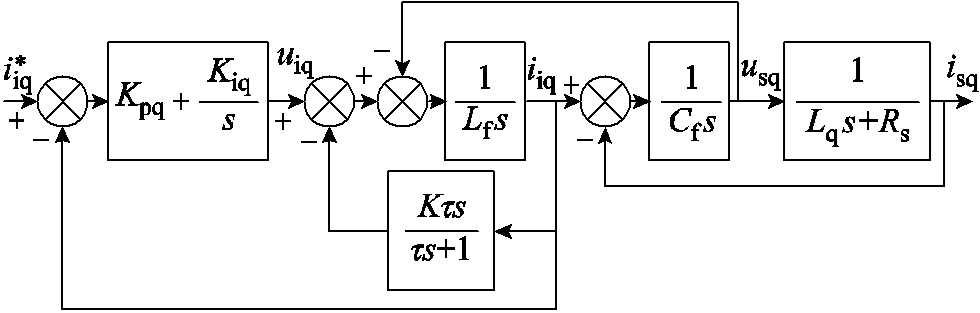
图9 主动阻尼控制框图
Fig.9 Active damping control
τ不变，K逐渐增大时，电流环闭环传递函数的零极点分布如图10所示。K不变，τ逐渐增大时，电流环闭环传递函数的零极点分布如图11所示。
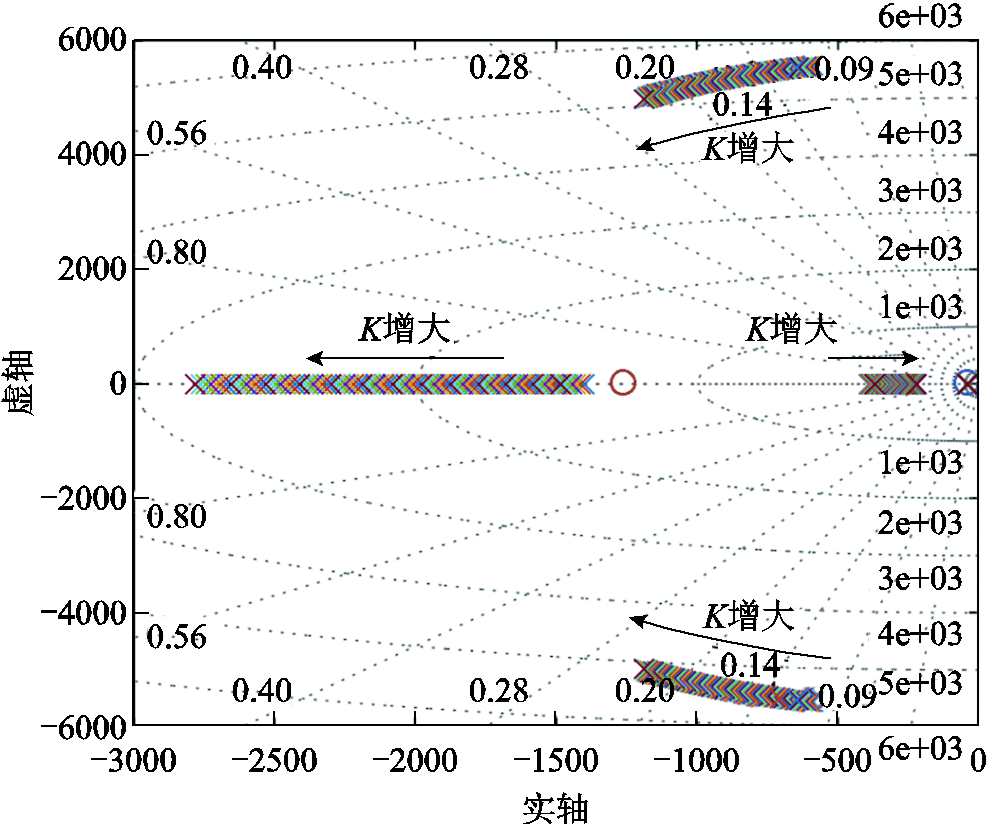
图10 K变化过程中电流环闭环传递函数的零极点分布
Fig.10 Zero pole distribution of the closed-loop transfer function of the current loop when K changes
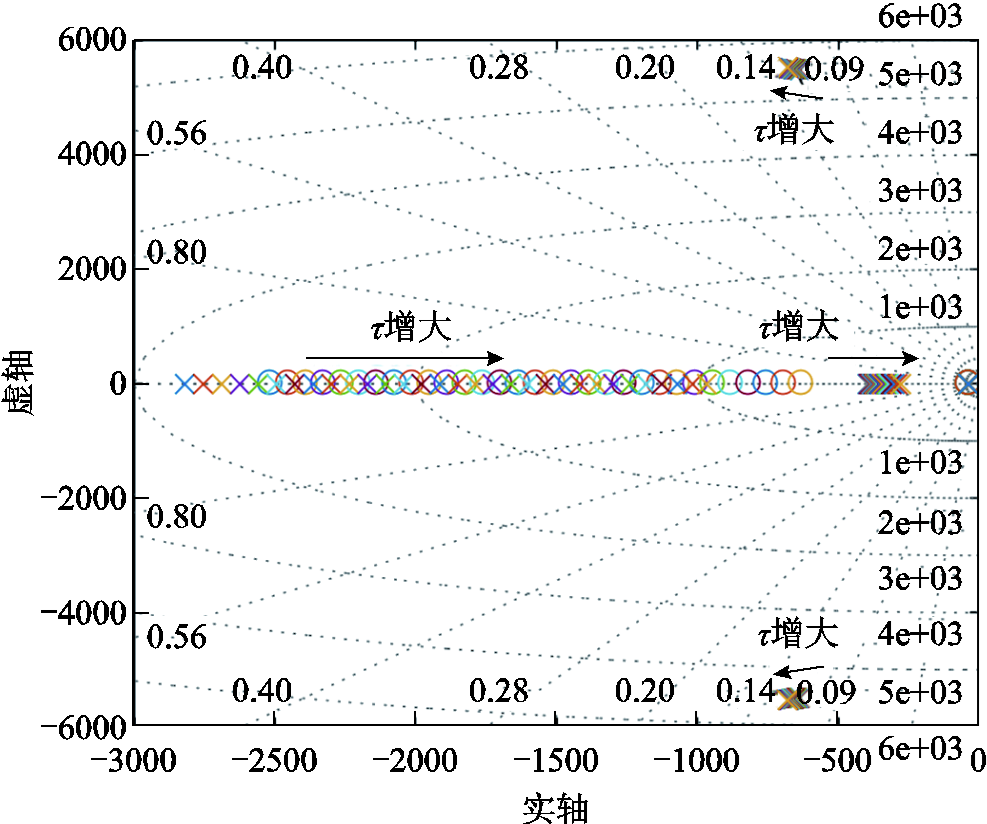
图11 τ变化过程中电流环闭环传递函数的零极点分布
Fig.11 Zero pole distribution of the closed-loop transfer function of the current loop when τ changes
在K和τ变化的过程中，所有闭环极点均具有负实部，控制系统稳定；增大K或τ使主导极点的位置更靠近虚轴，降低了电流环的响应速度；增大K或τ使非主导共轭极点的阻尼比增加，有利于谐振抑制。因此，主动阻尼控制的参数选取需要兼顾电流环的响应速度和谐振抑制能力。
增加主动阻尼控制后，逆变器输出电压到电机电流的传递函数为
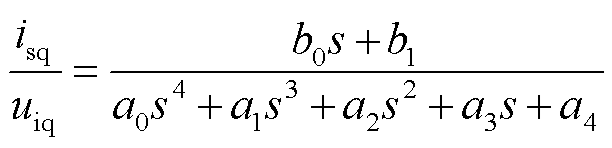（9）
其中
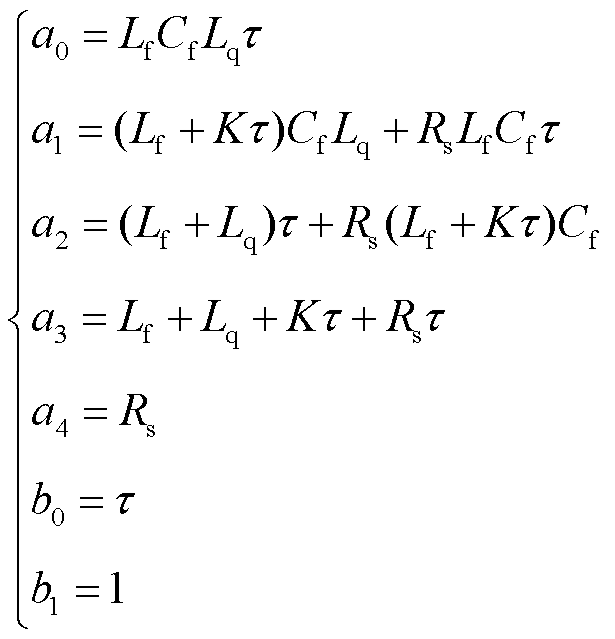（10）
对于不同的K与τ的组合，分别绘制出式（9）表示的传递函数的伯德图，如图12所示。若K或τ太小，则对谐振频率处尖峰的抑制作用不明显；若K或τ太大，则低频段的增益下降严重。
电流环闭环传递函数的伯德图如图13所示。若K或τ太小，则对谐振频率处尖峰的抑制作用不明显；若K或τ太大，则电流环带宽下降严重。因此，综合考虑之后，本文选取K为2.00、τ为10-3。
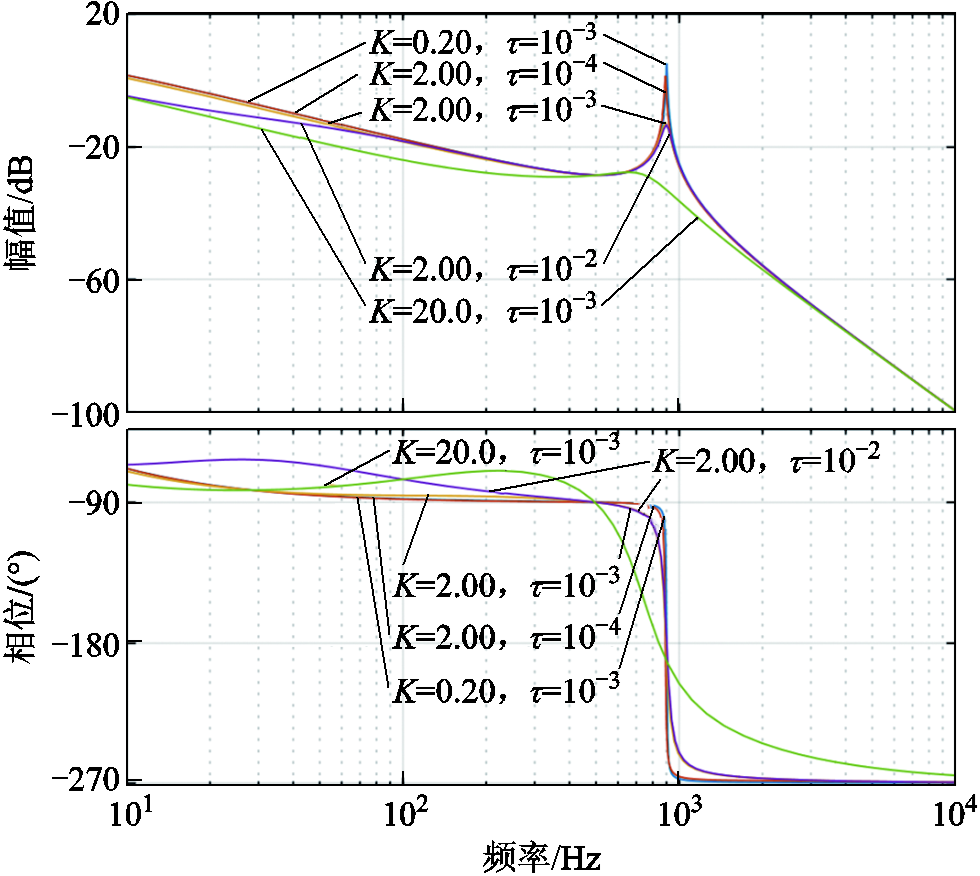
图12 不同参数下开环传递函数的伯德图
Fig.12 Bode diagram of the open-loop transfer function with different parameters
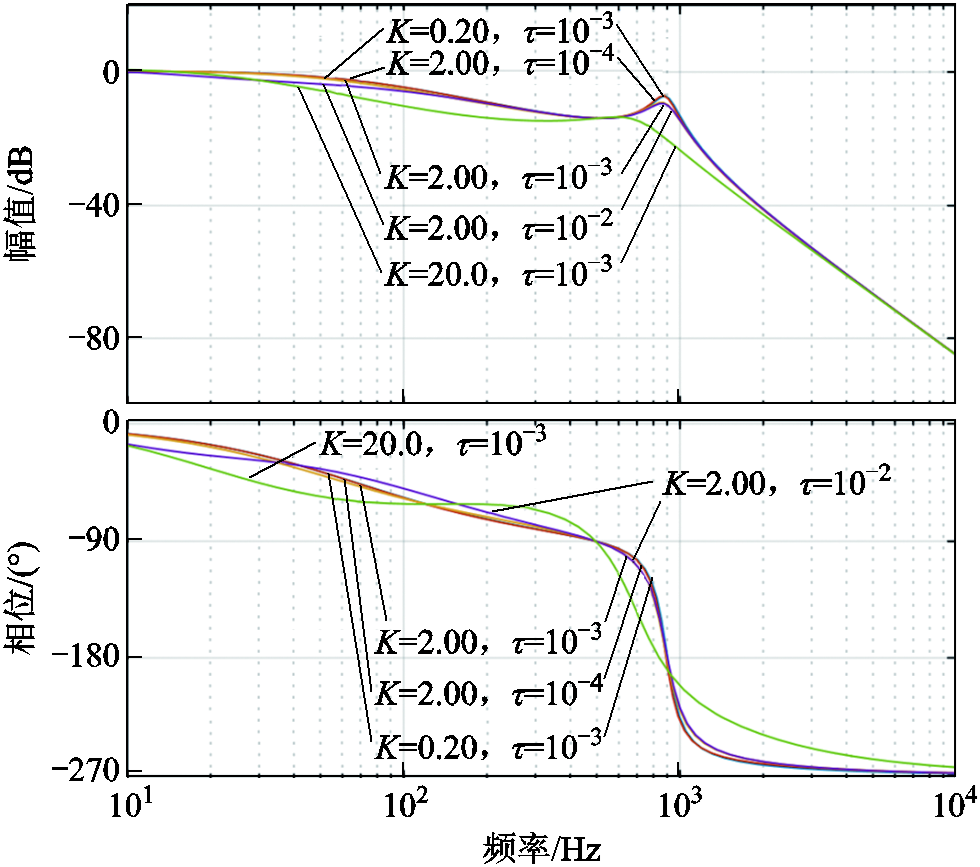
图13 不同参数下电流环闭环传递函数的伯德图
Fig.13 Bode diagram of the closed-loop transfer function of the current loop with different parameters
当K为2.00、τ为10-3时，开环传递函数的伯德图如图7中虚线所示。谐振频率处的尖峰由20dB下降为-13dB，意味着谐振频率处的系统阻尼增加。施加合理的电压将不会使系统发生故障，保障永磁电机的初始位置辨识得以成功实施。系统的稳定裕度没有明显改变。电流环闭环传递函数的伯德图如图8中虚线所示。电流环带宽没有明显变化；谐振频率处的尖峰降低，表明此处阻尼增加。
本文的实验平台如图14所示。LC滤波器安装在逆变器与永磁电机之间。永磁电机转子永磁体的位置由编码器测得，用于与观测得到的位置进行对比，验证所提方法的效果。主动阻尼控制的增益和时间常数分别为2.00和10-3，永磁同步电机长线缆驱动系统各部分参数见表1。
图14 实验平台
Fig.14 Experimental platform
表1 装备输出滤波器的永磁电机驱动系统参数
Tab.1 The parameters of the PMSM drive system equipped with output filter
参数数值 永磁体磁链ψf/Wb0.223 定子电阻Rs/Ω0.316 直轴电感Ld/mH4.1 交轴电感Lq/mH8.5 额定功率PN/kW1.5 额定电流IN/A10 额定转矩TN/(N·m)10 额定转速nN/(r/min)1 500 直流母线电压udc/V200 滤波器电感Lf/mH3.73 滤波器电容Cf/μF12
由于装备了输出滤波器，注入高频电压的频率受到限制，不能过高；另一方面，考虑到位置观测带宽，注入频率也不能过低。综合考虑，本文选取注入电压频率为200Hz。实验结果如图15所示。
图15中波形分别为de轴电流、qe轴电流和位置观测误差。位置观测误差由实际位置θ与观测位置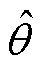
相减得到，实际位置由光电编码器测得。
算法启动后，经过一段时间的振荡，观测误差逐渐收敛，出现两种可能的结果：当初始辨识结果为N极时，最终的观测误差为0°；当初始辨识结果为S极时，最终的观测误差为180°。以上实验结果表明，注入合适的高频电压可以辨识出转子的初始位置，但辨识结果有两种可能，这与理论分析是一致的。为了进一步分辨N极或S极，需要在高频电压注入的基础上施加直流电流激励，利用电机磁路的饱和效应完成辨识。
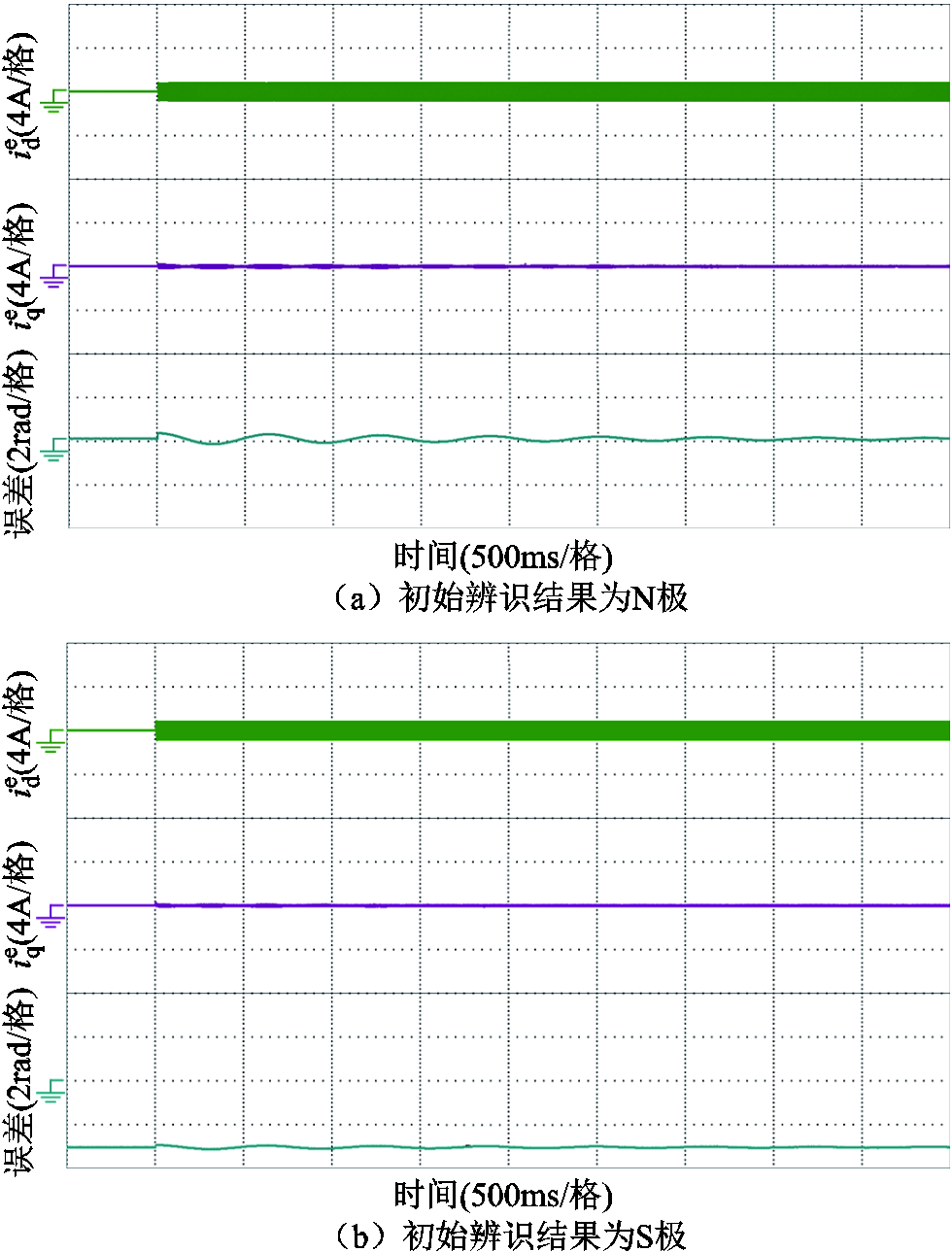
图15 两种可能的辨识结果
Fig.15 Two possible identification results
如图15所示，由于此时没有施加直流电流激励，电流较小，滤波器电感与电机定子的磁路都处于线性区，饱和及磁滞涡流现象不明显，电流中谐波含量低，因此尚未发生谐振。
为了辨别极性，需要施加直流电流激励，这将使滤波器电感与电机定子的磁路受到饱和及磁滞涡流的影响，从而使电流中的谐波含量增加，系统在谐振频率处发生谐振，如图16所示。在观测误差逐渐收敛后，施加一个正的直流电流激励，电流中的谐波将逐渐增加、直至发生过电流故障，系统保护。
发生谐振前后的局部情形如图17所示。de轴电流频率为200Hz，与注入电压频率一致；qe轴电流频率较高，逐渐失控。这表明谐振主要是qe轴电流失控引起的。因为q轴电感比d轴电感大，根据式（8），谐振频率与电感大小成反比，所以q轴电流更容易发生谐振。为了保障初始位置辨识的成功实施，需要在辨识过程中抑制谐振。
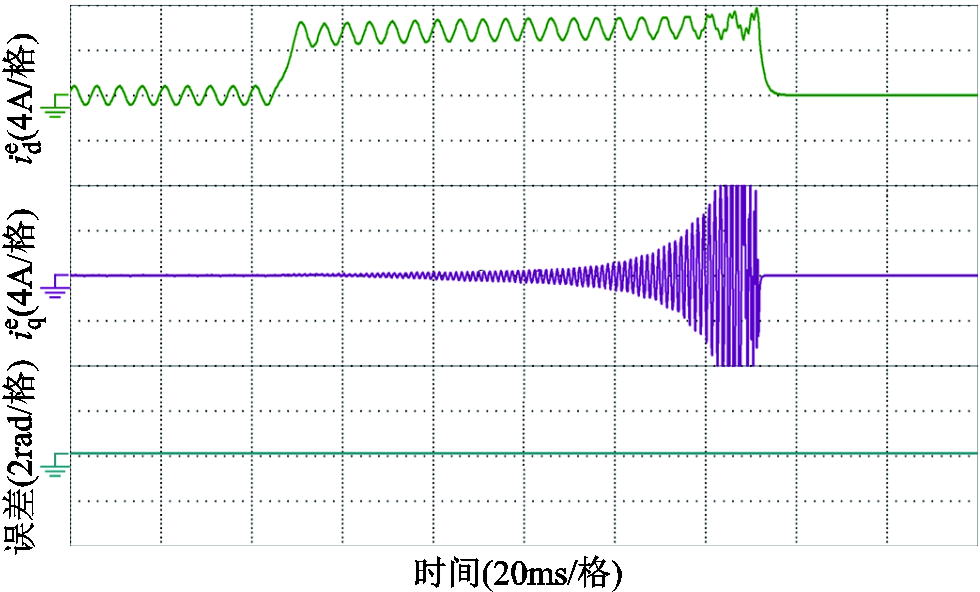
图16 直流电流激励导致的谐振
Fig.16 Resonance caused by DC current excitation
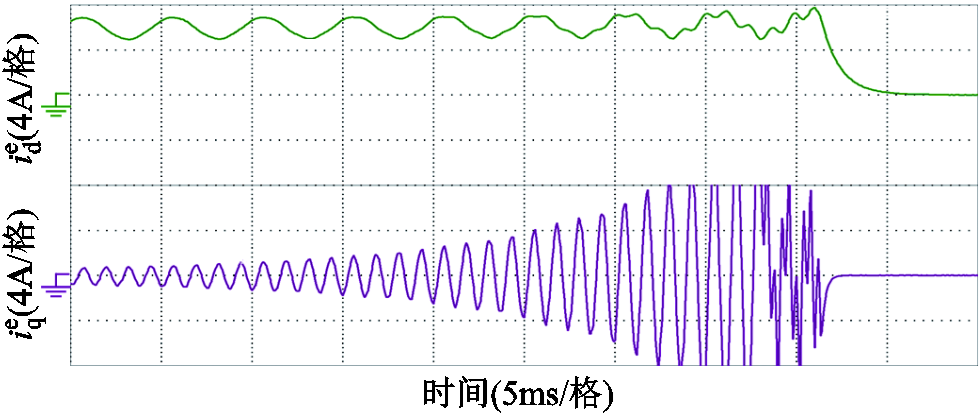
图17 谐振的局部放大图
Fig.17 Zoomed view of resonance
采用前述主动阻尼控制策略可以有效地抑制谐振，实验结果如图18所示。
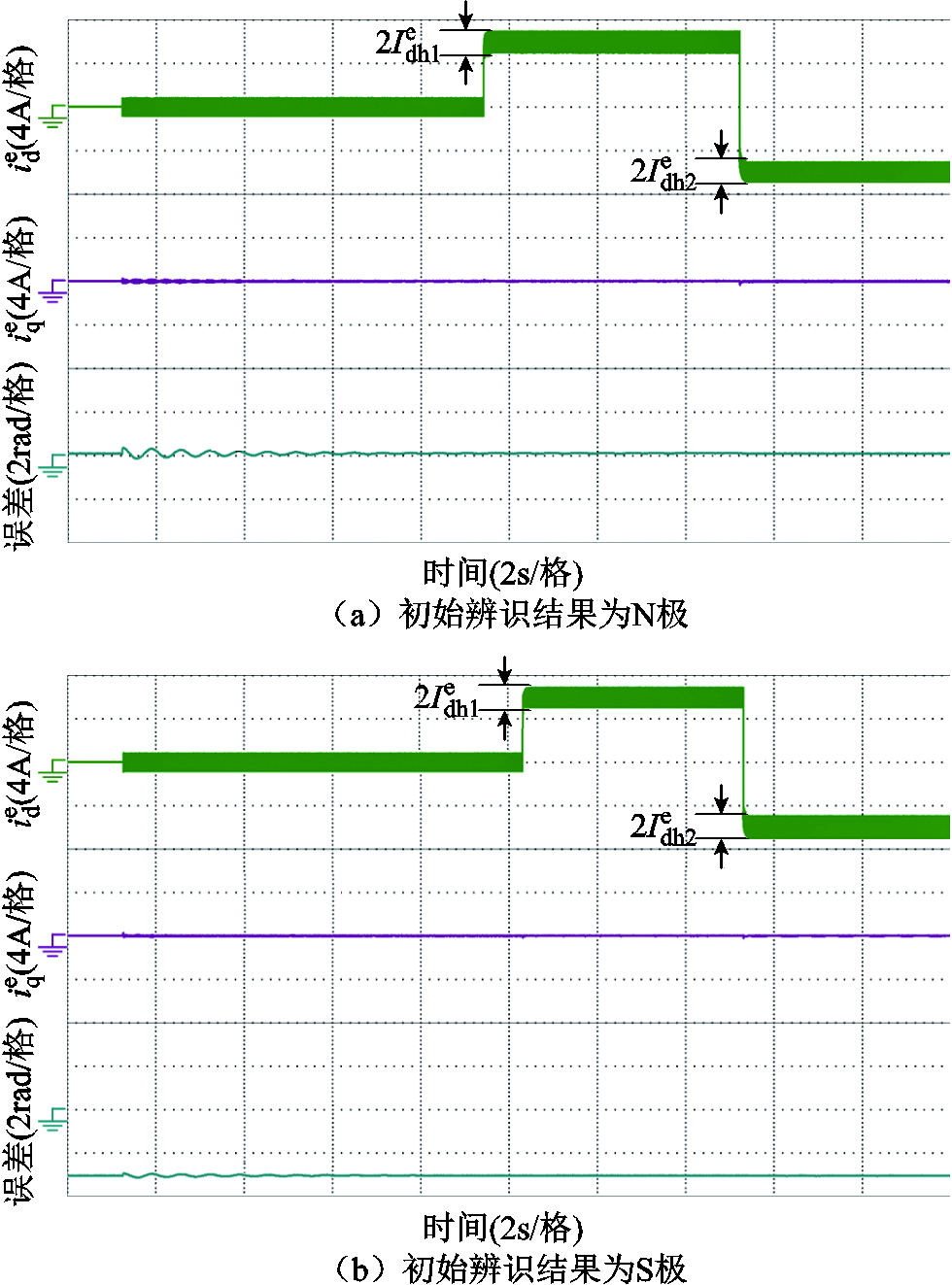
图18 抑制谐振后的辨识结果
Fig.18 Identification results after resonance suppression
首先不施加直流电流激励，仅注入高频电压，一段时间后辨识得到初始位置。这时出现两种结果：N极或S极。然后保持注入高频电压不变，在de轴上额外施加一个正的直流电流激励，稳定后算出高频电流响应的幅值。接着在de轴上施加一个负的直流电流激励，稳定后算出高频电流响应的幅值。这两个直流电流激励大小相等、符号相反。最后比较两个高频电流响应幅值的大小。若前者大于后者，则说明初始辨识结果为N极；若前者小于后者，则说明初始辨识结果为S极。使用主动阻尼控制，系统在谐振频率处的阻尼增大，在施加直流电流激励时，谐振得到了有效抑制。并且，由于参数选取合理，电流环的动态响应也没有受到明显的影响。
本文提出一种基于高通滤波器的主动阻尼控制方法，抑制永磁电机长线缆驱动系统LC滤波器引起的系统谐振，解决谐振导致的转子初始位置辨识失败的问题。分析表明，应用该方法后，系统仍然稳定。该方法的参数会影响谐振抑制的效果和电流环的响应速度。综合考虑二者的影响，通过参数扫描可以选取出合适的参数。实验结果表明，该方法在没有显著降低电流环响应速度的条件下，有效地抑制了系统谐振，保障了转子初始位置辨识的成功。该方法使装备LC滤波器的永磁电机长线缆驱动系统仍然可以通过高频信号注入方法精确地辨识转子初始位置，从而实现可靠的转子磁场定向控制。
参考文献
[1] 刘计龙, 肖飞, 沈洋, 等. 永磁同步电机无位置传感器控制技术研究综述[J]. 电工技术学报, 2017, 32(16): 76-88.
Liu Jilong, Xiao Fei, Shen Yang, et al. Position-sensorless control technology of permanent-magnet synchronous motor-a review[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 76-88.
[2] SalomÄki J, Hinkkanen M, Luomi J. Influence of inverter output filter on maximum torque and speed of PMSM drives[J]. IEEE Transactions on Industry Applications, 2008, 44(1): 153-160.
[3] Wang Yangrui, Xu Yongxiang, Zou Jibin. Online multiparameter identification method for sensorless control of SPMSM[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 10601-10613.
[4] Liu Jingbo, Nondahl T, Dai Jingya, et al. A seamless transition scheme of position sensorless control in industrial permanent magnet motor drives with output filter and transformer for oil pump applications[J]. IEEE Transactions on Industry Applications, 2020, 56(3): 2180-2189.
[5] 赵文祥, 刘桓, 陶涛, 等. 基于虚拟信号和高频脉振信号注入的无位置传感器内置式永磁同步电机MTPA控制[J]. 电工技术学报, 2021, 36(24): 5092-5100.
Zhao Wenxiang, Liu Huan, Tao Tao, et al. MTPA control of sensorless IPMSM based on virtual signal and high-frequency pulsating signal injection[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5092-5100.
[6] 姜燕, 李博文, 吴轩, 等. 基于比例谐振滤波的改进永磁同步电机转子位置观测器[J]. 电工技术学报, 2020, 35(17): 3619-3630.
Jiang Yan, Li Bowen, Wu Xuan, et al. An improved rotor position observer for permanent magnet synchronous motors based on proportional resonant filtering[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3619-3630.
[7] 王高林, 杨荣峰, 李刚, 等. 基于高频信号注入的IPMSM无位置传感器控制策略[J]. 电工技术学报, 2012, 27(11): 62-68.
Wang Gaolin, Yang Rongfeng, Li Gang, et al. Position sensorless control strategy of IPMSM based on high frequency signal injection[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 62-68.
[8] 阙鸿杰, 全力, 张丽, 等. 基于自适应滤波器在线解耦的磁场增强型永磁电机无位置传感器控制[J]. 电工技术学报, 2022, 37(2): 344-354.
Que Hongjie, Quan Li, Zhang Li, et al. Sensorless control of flux-intensifying permanent magnet synchronous motor based on adaptive Notch filter online decoupling[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 344-354.
[9] 田兵, 安群涛, 孙东阳, 等. 基于磁饱和效应的表贴式永磁同步电机初始位置检测方法[J]. 电工技术学报, 2016, 31(1): 155-164.
Tian Bing, An Quntao, Sun Dongyang, et al. Initial position estimation for surface permanent magnet synchronous motors based on magnetic saturation effect[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 155-164.
[10] 王子辉, 陆凯元, 叶云岳. 基于改进的脉冲电压注入永磁同步电机转子初始位置检测方法[J]. 中国电机工程学报, 2011, 31(36): 95-101.
Wang Zihui, Lu Kaiyuan, Ye Yunyue. Initial position estimation method for permanent magnet synchronous motor based on improved pulse voltage injection[J]. Proceedings of the CSEE, 2011, 31(36): 95-101.
[11] 孙伟. 永磁同步电动机无位置传感器控制与高性能运行策略的研究[D]. 杭州: 浙江大学, 2017.
[12] 王明辉. 带LC滤波器永磁同步电机控制关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2021.
[13] Sun Wei, Shen Jianxin, Jin Mengjia, et al. A robust magnetic polarity self-sensing method for start up of PM synchronous machine in fanlike system[J]. IEEE Transactions on Industry Applications, 2017, 53(3): 2169-2177.
[14] 徐志英, 许爱国, 谢少军. 采用LCL滤波器的并网逆变器双闭环入网电流控制技术[J]. 中国电机工程学报, 2009, 29(27): 36-41.
Xu Zhiying, Xu Aiguo, Xie Shaojun. Dual-loop grid current control technique for grid-connected inverter using an LCL filter[J]. Proceedings of the CSEE, 2009, 29(27): 36-41.
[15] Liserre M, Blaabjerg F, Hansen S. Design and control of an LCL-filter-based three-phase active rectifier[J]. IEEE Transactions on Industry Applications, 2005, 41(5): 1281-1291.
[16] 黄宇淇, 姜新建, 邱阿瑞. LCL滤波的电压型有源整流器新型主动阻尼控制[J]. 电工技术学报, 2008, 23(9): 86-91.
Huang Yuqi, Jiang Xinjian, Qiu Arui. A novel active damping control scheme for a three-phase active rectifier with LCL-filter[J]. Transactions of China Electrotechnical Society, 2008, 23(9): 86-91.
[17] Malinowski M, Bernet S. A simple voltage sensorless active damping scheme for three-phase PWM converters with an LCL filter[J]. IEEE Transactions on Industrial Electronics, 2008, 55(4): 1876-1880.
[18] 王颖杰, 伍小杰, 戴鹏, 等. 采用参数辨识及新型主动阻尼控制的LCL滤波脉宽调制整流器[J]. 中国电机工程学报, 2012, 32(15): 31-39, 17.
Wang Yingjie, Wu Xiaojie, Dai Peng, et al. PWM rectifier with LCL filter based on parameter identification and a new active damping control[J]. Proceedings of the CSEE, 2012, 32(15): 31-39, 17.
[19] Dahono P A. A control method to damp oscillation in the input LC filter[C]//2002 IEEE 33rd Annual IEEE Power Electronics Specialists Conference Proceedings (Cat. No.02CH37289), Cairns, QLD, Australia, 2002: 1630-1635.
[20] Parker S G, McGrath B P, Holmes D G. Regions of active damping control for LCL filters[J]. IEEE Transactions on Industry Applications, 2014, 50(1): 424-432.
Rotor Initial Position Identification Technology for Long Cable Drive System of Permanent Magnet Synchronous Motor Considering Resonance Suppression
Abstract Installing LC filter in the long cable drive system of permanent magnet synchronous motor may cause resonance, resulting in the failure of rotor initial position identification. Active damping control can suppress the resonance caused by LC filter, so as to ensure the success of rotor initial position identification. After injecting high-frequency voltage signal into the estimated synchronous rotating shafting and demodulating the high-frequency current response, two possible results are obtained, corresponding to different polarities. According to the saturation effect of the magnetic circuit of the motor, applying different DC current excitation and comparing the experimental results under each excitation can complete the polarity discrimination. In the process of injecting high-frequency voltage signal and applying DC current excitation, LC filter will cause system resonance. To solve this problem, an active damping control method based on high pass filter is proposed. A feedback path is added to the traditional current loop to increase the system damping at the resonant frequency equivalently, and then the parameter design and stability verification of the active damping control method are carried out. Finally, experiments are carried out to obtain the experimental results after successfully suppressing resonance, which proves the effectiveness of the proposed rotor initial position identification technology of permanent magnet synchronous motor long cable drive system considering resonance suppression.
keywords：Permanent magnet synchronous motor, initial position identification, active damping, resonance suppression
DOI:10.19595/j.cnki.1000-6753.tces.221274
中图分类号：TM351
收稿日期 2022-06-30
改稿日期 2022-08-06
陈东东 男，1995年生，博士研究生，研究方向为永磁电机无位置传感器控制。E-mail：ddchen@hust.edu.cn
王 晋 男，1979年生，副教授，硕士生导师，研究方向为大型与特种电机设计及其控制。E-mail：jinwang@hust.edu.cn（通信作者）
（编辑 赫蕾）