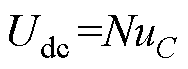（1）
为保持直流侧电压不变，每相处于投入和旁路状态的子模块均为N，使得
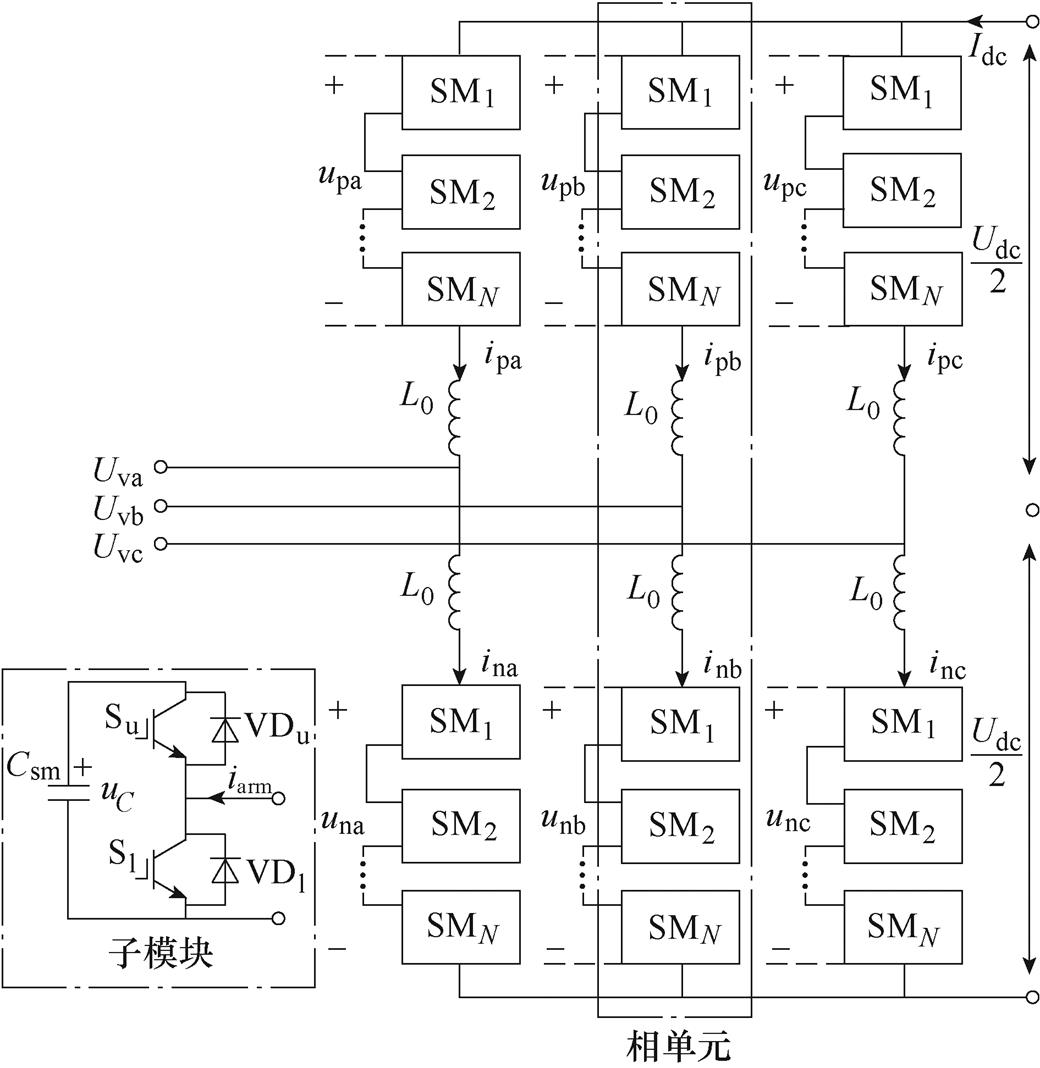
图1 三相MMC拓扑结构
Fig.1 Topology of three-phase MMC
摘要 基于模块化多电平换流器（MMC）子模块（SM）开关器件故障引起的电容电压异常变化问题，该文提出一种故障快速检测与诊断方法。首先通过局部离群因子（LOF）算法分析桥臂中所有子模块对应的电容电压逐段求和值，从而同时实现对故障子模块的快速检测与定位；之后通过判断故障子模块所在桥臂中正常子模块电容电压的变化趋势快速识别故障开关器件，完成故障分类。由于所提方法具有局部异常特征分析的特性，可适用于单一故障、同桥臂多故障及不同桥臂多故障发生的全部故障类型。同时，该方法不受系统参数不确定性的影响，适用性强，且相较于传统方法具有更快的诊断速率。仿真与实验结果验证了所提方法的有效性。
关键词：模块化多电平换流器 故障检测 故障诊断 局部离群因子
模块化多电平换流器（Modular Multilevel Converter, MMC）因其子模块（Sub-Module, SM）串联结构所带来的优势而在柔性直流输电系统中受到广泛的关注并得到应用[1-7]。但是由于大量的子模块串联，MMC的可靠性问题成了一个无法忽视的问题，其中开关器件故障是MMC子模块故障的主要形式[8-10]。子模块开关器件故障分为开路故障与短路故障，由于短路故障特征明显，因此通常在驱动中集成了短路故障的处理方案[11]，但开路故障现象并不明显，若不能被快速诊断会严重危害系统运行。
目前的研究主要集中于如何在不添加额外硬件的情况下，完成对开路故障的检测与诊断。文献[12]提出基于人工神经网络的故障诊断方法，算法复杂程度高且依赖于大量的数据训练，同时鲁棒性较差且诊断时间长。通过滑模观测器[13]和卡尔曼滤波 器[14-15]诊断故障，需要建立精确的数学模型，同时不同系统参数下的故障检测阈值难以确定且故障诊断时间长。文献[16-19]通过分析桥臂电流或者相电流检测故障，只能定位故障桥臂，而故障子模块的定位则需要额外的步骤，因此需要较长的故障诊断时间。文献[20]通过分析桥臂电压检测故障，可以做到快速检测，但不适用于多故障场合。
上述方法均将故障检测与定位分开，增加了复杂程度和诊断时间，同时也无法完成故障分类以及对多故障的检测与诊断。由于多故障尤其是同桥臂多故障会对系统造成更加严重的危害，因此需要被有效诊断[21]。文献[22-23]中的方法虽然可以对发生在不同桥臂的多个故障进行诊断，但不适用于同桥臂多故障发生的情况。在可以完成全部故障类型检测与诊断的方法中，文献[24]通过比较桥臂电压的测量值和预测值检测故障，但预测值的准确性会受到系统参数的影响，需要在线估计器件参数，当子模块数量较多时，需要提高传感器的精度以保证鲁棒性，适用性较差。文献[25]提出的方法需要较长的时间使电容电压增加到阈值而导致快速性差，同时在不同系统输出功率下难以进行阈值选取。
综合上述调研可知，目前已提出的方法无法同时做到以下几点：①单步骤同时对故障快速检测与定位；②对故障进行快速分类；③对全部故障类型进行有效的检测与诊断。
针对现有方法存在的问题，本文一种提出基于局部离群因子（Local Outlier Factor, LOF）算法的故障检测与诊断方法。故障SM的电容电压由于与正常SM的电容电压存在明显的差异性而被视为离群数据，本文所提方法通过LOF算法判断SM电容电压中的离群值，从而完成对故障SM的检测与定位。LOF算法是基于数据局部分布密度进行离群值检测的算法，鲁棒性强且算法简单，常用于数据挖掘领域中离群值的检测[26]。但通过LOF算法直接对电容电压进行离群值判断不仅速度较慢，同时准确性也会受到影响，为了解决这些问题，本文首先对子模块电容电压以基波周期为段逐段求和，计算逐段求和值（Stepwise Summation Value, SSV）后进行分析。可以将故障SM与正常SM电容电压之间的差异进行放大，在此基础上逐段求和值也可以减小正常SM电容电压之间的差异，有利于离群值的判断，增强诊断方法的鲁棒性和快速性。通过LOF算法计算同桥臂中所有SM电容电压SSV的局部离群因子并与阈值进行比较，从而同时检测并定位故障SM，之后判断故障发生后桥臂中正常SM电容电压SSV的变化趋势，完成对故障开关器件的快速分类。该方法适用于全部故障类型，同时不受系统参数以及控制策略的影响，算法复杂度低且适用性和快速性较强。
本文首先介绍了MMC的基本运行原理和子模块开关器件的开路故障特征，根据故障特征，提出一种基于LOF算法的子模块开关器件开路故障的检测与诊断方法；然后将其与现有的方法进行了分析比对；最后通过仿真和实验验证了所提方法的快速性与有效性。
三相MMC拓扑结构如图1所示[4]。abc三相结构相同，每相包含上下两个桥臂。不考虑冗余子模块，每个桥臂中有N个串联半桥子模块。图中，Udc为直流侧电压；upx、unx（x=a, b, c）为各相上、下桥臂电压；ipx、inx为各相上、下桥臂电流。SMi（i=1, 2, …, N）为半桥子模块；Su、Sl为子模块的上、下开关器件；VDu、VDl为Su、Sl的反并联二极管；uC为子模块电容电压。MMC正常运行时，每相直流侧电压恒定，可以表示为
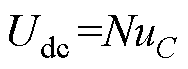（1）
为保持直流侧电压不变，每相处于投入和旁路状态的子模块均为N，使得
图1 三相MMC拓扑结构
Fig.1 Topology of three-phase MMC
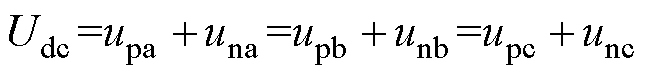（2）
半桥子模块在正常工作情况下，子模块电容电压在每个开关周期的变化量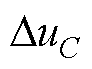
表示为
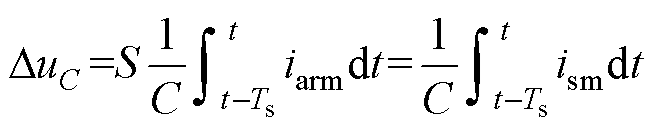（3）
式中，S为SM的开关函数，S=1时SM被投入，S=0时SM被切除；C为子模块电容器Csm的电容值；iarm为桥臂电流；ism为流过Csm的电流；Ts为控制周期。
当iarm＞0时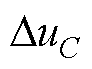，＞0；当iarm＜0时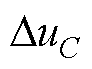，＜0。子模块开关器件开路故障示意图如图2所示，子模块开关器件开路故障分为下开关器件Sl开路故障、上开关器件Su开路故障和Su与Sl同时发生开路故障三类。
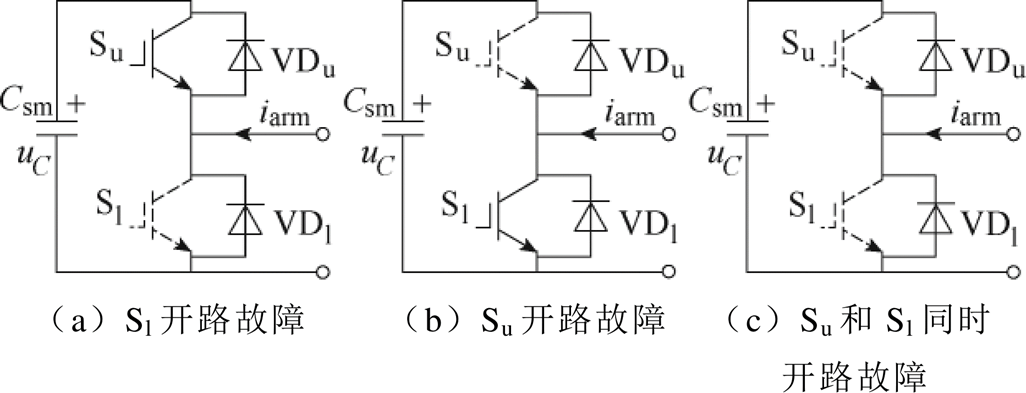
图2 子模块开关器件开路故障示意图
Fig.2 Diagram of SM switching device open-circuit fault
1.2.1 Sl开路故障
SM在正常和Sl开路故障情况下的电流路径和电容电压变化见表1。Sl发生开路故障后，当流过SM的桥臂电流iarm＜0时，Sl开路故障对子模块不会产生影响；当iarm＞0时，虽然S=0，但iarm无法流过Sl将SM旁路，正的iarm流过VDu对Csm充电。因此当iarm＞0时，Csm一直被充电。Sl开路故障会导致故障SM电容电压高于正常SM电容电压。每个开关周期内，发生Sl开路故障的SM与正常SM电容电压的差值增量Dusl表示为
（4）
式中，Snor为正常SM的开关函数。当Snor=1时，Dusl=0；当Snor=0时，Dusl=DuC。
表1 正常情况与Sl开路故障情况的对比
Tab.1 Comparison between normal condition and Sl open-circuit fault condition
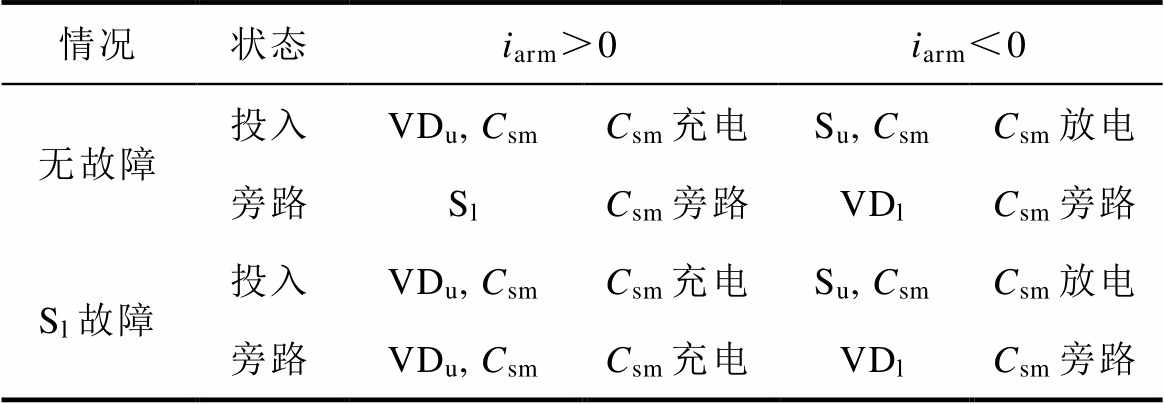
情况状态iarm＞0iarm＜0 无故障投入VDu, CsmCsm充电Su, CsmCsm放电 旁路SlCsm旁路VDlCsm旁路 Sl故障投入VDu, CsmCsm充电Su, CsmCsm放电 旁路VDu, CsmCsm充电VDlCsm旁路
1.2.2 Su开路故障
SM在正常和Su开路故障情况下的电流路径和电容电压变化见表2。Su发生开路故障后，当iarm＞0时，Su开路故障对SM不会产生影响；当iarm＜0时，虽然S=1，但iarm无法流过Su使Csm放电，故障SM被旁路。因此，当iarm＜0时，Csm不能放电，Su开路故障同样会导致故障SM电容电压高于正常SM电容电压。发生Su开路故障的SM与正常SM电容电压的差值增量Dusu表示为
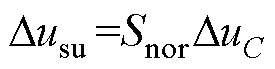（5）
表2 正常情况与Su开路故障情况的对比
Tab.2 Comparison between normal condition and Su open-circuit fault condition
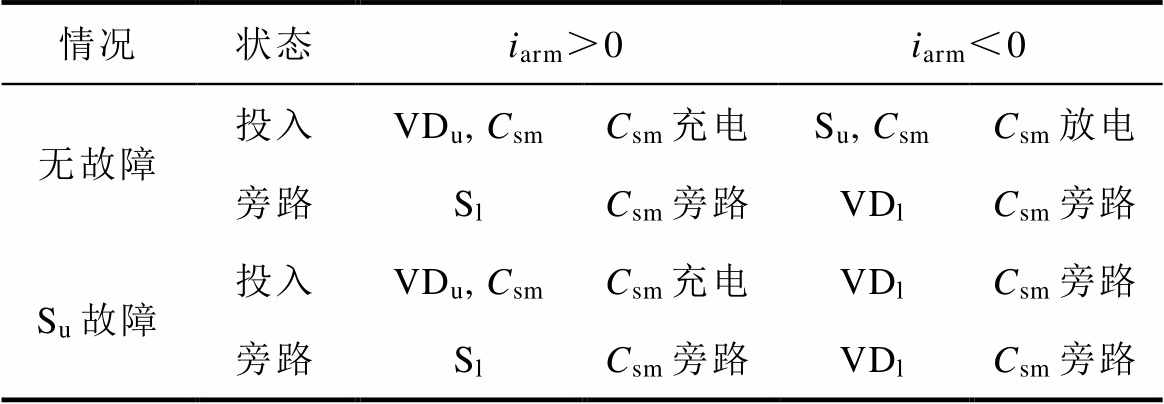
情况状态iarm＞0iarm＜0 无故障投入VDu, CsmCsm充电Su, CsmCsm放电 旁路SlCsm旁路VDlCsm旁路 Su故障投入VDu, CsmCsm充电VDlCsm旁路 旁路SlCsm旁路VDlCsm旁路
当Snor=1时，Dusu=DuC；当Snor=0时，Dusu=0。由式（4）和式（5）可以看出，故障发生后，故障SM和正常SM电容电压之间的差值变化与正常SM的运行状态有关，并不是始终保持增大的。
1.2.3 Su与Sl同时发生开路故障
SM在Su与Sl同时发生开路故障的情况下，电流路径和电容电压变化见表3。Su与Sl同时发生开路故障后的故障特征同时具有Su开路故障和Sl开路故障的故障特征，即iarm＞0时，Csm一直被充电；iarm＜0时，一直被旁路，因此故障SM与正常SM的电容电压同样表现出明显的差异。
表3 正常情况与Su和Sl同时发生开路故障情况的对比
Tab.3 Comparison between normal condition and Su & Sl open-circuit fault condition
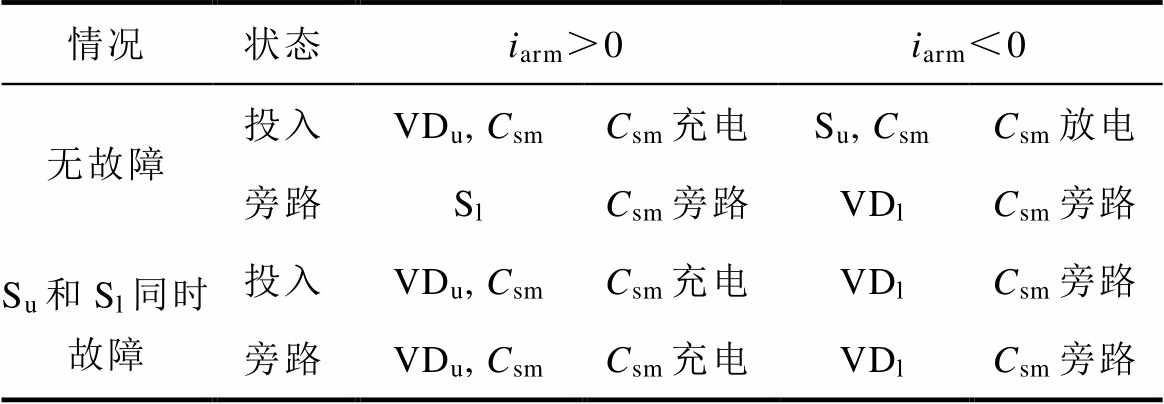
情况状态iarm＞0iarm＜0 无故障投入VDu, CsmCsm充电Su, CsmCsm放电 旁路SlCsm旁路VDlCsm旁路 Su和Sl同时故障投入VDu, CsmCsm充电VDlCsm旁路 旁路VDu, CsmCsm充电VDlCsm旁路
综上所述，无论故障是否发生，正常SM的电容电压的高一致性不会受到影响。而在不同故障情况下，故障SM由于开关器件开路导致流过SM的电流路径发生改变，因此电容电压产生了异常变化，相比于桥臂中其他正常SM的电容电压，表现出明显的差异性。
由故障特征分析可知，故障SM电容电压为异常数据，因此可以采用LOF算法判断离群值完成对故障SM的检测与诊断。LOF算法判断离群值的核心思想是：通过局部比较而非全局比较判断某数据是否为离群值。因此该算法不受已经发生故障的SM的影响，适用于同桥臂多故障发生的情况，可以实现全部故障类型的诊断。同时，由于LOF算法具有高敏感度，进行离群值检测时可以在满足快速性的同时保证鲁棒性。此外，LOF算法离群值的判断阈值由算法自身的特性决定，不受系统输出功率和系统参数的影响，易于选取，具有较强的适用性。
LOF算法给每个数据点分配一个表征其离群程度的因子，而不是将其硬性划分为正常或离群点。LOF算法说明如图3所示。LOF算法的基本思想是比较所有数据中某个点和其近邻点的局部密度，由图3a可见，点O的局部密度明显小于其近邻点。
如图3b所示，数据组D中任意一点O的第k距离kdist(O)为离O点距离最近的第k个点Pk到点O的绝对距离d(O, Pk)，即
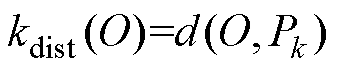（6）
Nkd(O)为点O的第k距离邻域，如图3a所示，满足
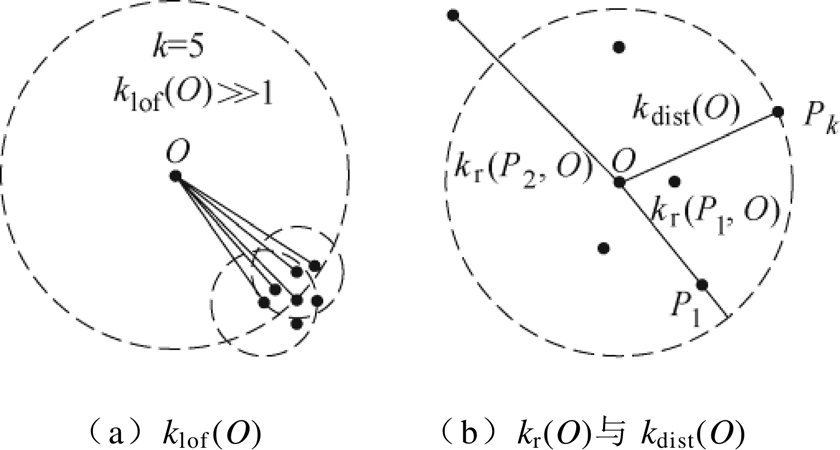
图3 LOF算法说明
Fig.3 Description of local outlier factor algorithm
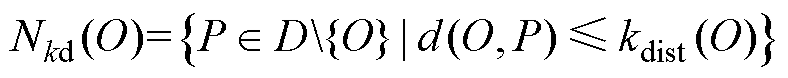（7）
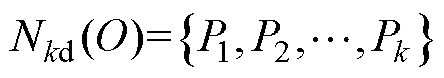（8）
式中，P为数组D中任意一点。以O为中心，定义kr(O, P)为O到P的第k可达距离，表示为
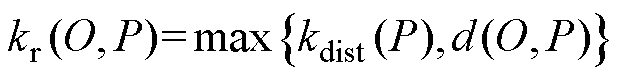（9）
由式（9）可知，图3b中点P1到点O的第k可达距离等于kdist(O)，点P2到点O的第k可达距离等于d(O, P2)。点O的局部可达密度klrd(O) 指点O到Nkd(O)内的所有点的平均可达距离的倒数，即
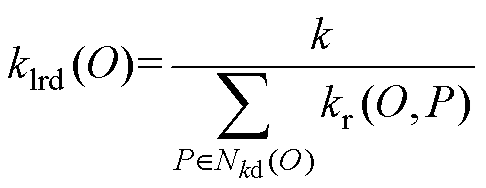（10）
如果点O的离群程度很高，周围近邻点很少，则它的邻域Nkd(O)覆盖范围很广，对于点O的Nkd(O)内的点P，点O在点P的邻域Nkd(P)内的概率很小，kr(O, P)取较大值d(O, P)的可能性较大；反之，若点O为非离群值，点O在点P的邻域Nkd(P)内的概率很大，kr(O, P)取较小值kdist(P)的可能性较大。由以上分析可知，离群点的局部可达密度较小，同一簇中的点的局部可达密度接近且较大，即局部可达密度反映了数据局部范围内的密度情况。
点O的局部离群因子klof(O)表示为
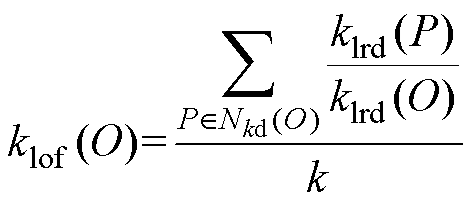（11）
klof(O)表示点O的Nkd(O)内的每个点的局部可达密度与点O局部可达密度之比的平均数。如果点O与其邻域内的点的局部可达密度相近，则与其邻域内的点同属一簇，klof(O)接近1；若klof(O)明显大于1，点O即为离群值，klof(O)越大于1，则表明点O的离群程度越大，局部离群因子的大小可以表征数据点的离群程度。
在正常和故障发生的情况下，正常SM电容电压差异小、分布密集，局部可达密度始终接近且较大，局部离群因子均接近1。而在三种故障类型下，故障SM与正常SM的电容电压均具有较大的差异，远大于正常SM电容电压之间的差异，因此故障SM的电容电压为离群值，其局部可达密度远小于正常SM电容电压的局部可达密度，计算出的局部离群因子会远大于1，从而超过阈值。
当同一桥臂存在多个故障SM时，它们的电容电压均为离群值，LOF算法通过对数据点与其近邻点进行局部比较而非全局比较判断离群值，在判断离群值时不受其他离群值的影响，可以对多个离群值进行判断，因此可以完成同桥臂中多个故障的检测与诊断。
通过上述分析可知，LOF算法可以有效地判断出同桥臂中SM电容电压中的离群值，从而完成对故障SM的检测与定位。但并不能通过LOF算法直接对SM电容电压进行离群值判断，因为实际中电容电压的采样值不仅存在采样误差，并且采样误差会进一步造成均压算法产生错误的脉冲信号，从而导致电容电压会在短时间内出现较大的偏差。同时，由式（4）和式（5）可知，由于正常SM的运行状态是在投入和旁路之间不断切换的，发生Sl开路故障的SM只有在正常SM处于切除状态时，与正常SM电容电压的差值才会变化；发生Su开路故障的SM只有在正常SM处于投入状态时，与正常SM电容电压的差值才会变化，所以故障SM与正常SM电容电压之间的差异并不是保持连续增大的，因此通过LOF算法直接分析电容电压的采样值构成的数据集合，会导致诊断速度较慢并且会对准确性产生影响。为了避免上述问题，加快诊断速度并提高鲁棒性，首先对SM的电容电压进行周期内的逐段求和，利用电容电压的逐段求和值构建数据集合后再通过LOF算法进行分析。
MMC桥臂中SMi的电容电压为uCi，uCi( j)表示uCi在第j采样时刻的采样值，以L个连续的电容电压采样值为段逐段求和，得到SMi对应的电容电压逐段求和值usumi，对电容电压每采样一次，usumi的值更新一次，加上最新时刻的采样值，减去最早时刻的采样值，usumi表示为
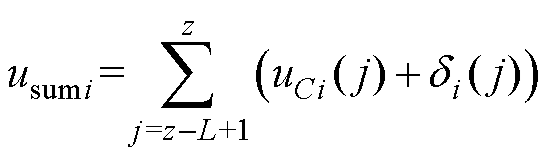（12）
式中，
为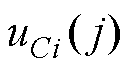
的采样随机误差；L为采样频率fs与基波频率fo的比值；z为最新的采样时刻。
随机误差满足均值m =0的标准正态分布，因此有如下推导
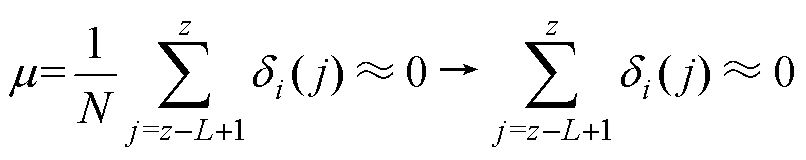（13）
在第j-1采样时刻到第j采样时刻之间，将发生Sl开路故障和Su开路故障的SM与正常SM电容电压的差值增量，分别定义为Dusl( j)和Dusu( j)；将发生Sl开路故障和Su开路故障的SM与正常SM电容电压逐段求和值的差值增量，分别定义为Dusumsl( j)和Dusumsu( j)，由式（12）可以得出
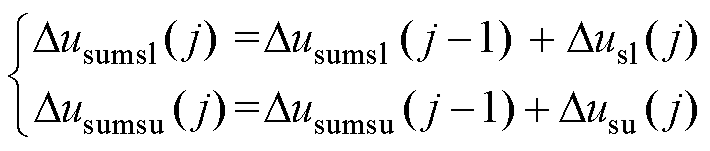（14）
可以看出，在故障发生后的采样时刻，即使Dusl( j)=0或Dusu( j)=0，故障SM和正常SM电容电压逐段求和值之间的差值不仅仍会增大，同时累加了上一采样时刻电容电压逐段求和值的差值增量，因此增大的速度会更快。同时，正常SM电容电压的采样值经过逐段求和之后，减小了实际中电压传感器采样误差的影响，一致性和分布密度会更高，因此用SM电容电压的逐段求和值构建数据集合后，再通过LOF算法判断离群值，有利于增强诊断方法的快速性和鲁棒性。
故障子模块检测、定位与分类方法流程如图4所示。将usumi存入长度为N的数组X中，每采样一次，数组X中所存的数据值同样更新一次。通过LOF算法分析每次更新后的数组X中的数据值，计算出每个usumi对应的局部离群因子klofi，设定离群值判断阈值Lth，如果所有的klofi均没有超过阈值，则表明无故障发生。如果某个SM电容电压的逐段求和值对应的klofi＞Lth，则表明该SM发生开路故障，此时检测并定位故障子模块。由于计算出的正常SM电容电压的逐段求和值一致性和分布密度非常高，因此对应的klofi均接近1；而故障SM电容电压的逐段求和值为强离群数据，分布密度远低于正常SM电容电压逐段求和值的分布密度，对应的klofi在故障发生后会快速增大并远大于1。在LOF算法中，将局部离群因子大于6的数据即判断为强离群数据[26]，为了保证本文所提方法的鲁棒性，在此基础上保留充分裕度，将阈值Lth设置为20。因为故障SM对应的klofi在故障发生后会快速增大并远大于1，因此在本文使用阈值的小范围内选取其他阈值同样具有较强的鲁棒性，且对快速性基本不产生影响。
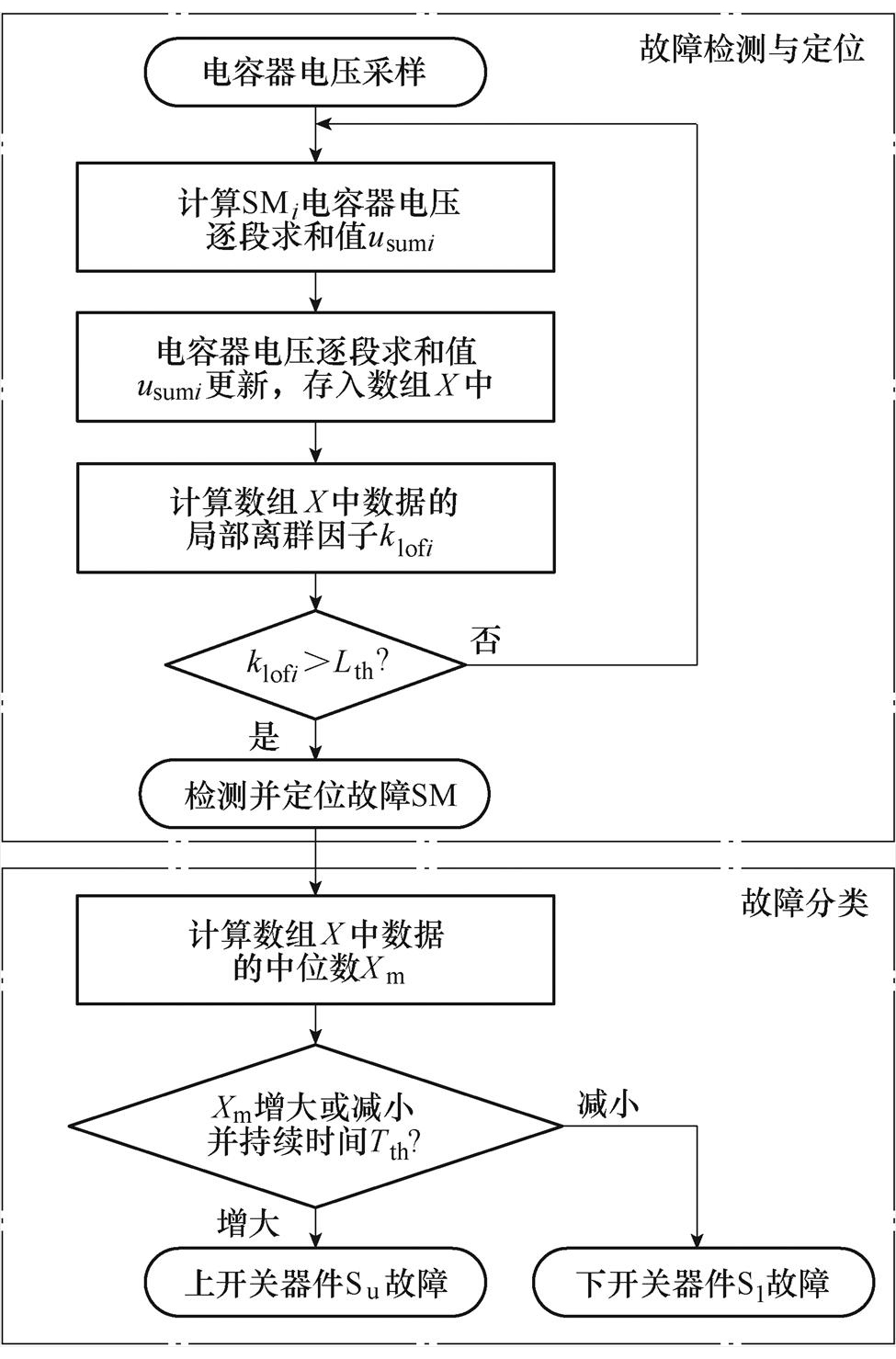
图4 故障检测与定位及分类方法流程
Fig.4 Flowchart of the fault detection, location and classification method
根据故障特征分析，当Su发生开路故障后，故障SM在iarm＜0时一直被旁路，此时桥臂中等效SM数量为N-1，在整个基波周期内，串联SM的等效平均数量减少，根据式（1）和式（2），该故障SM所在桥臂中正常的SM电容电压将会呈上升趋势；当Sl发生开路故障后，故障SM在iarm＞0时一直被投入，此时桥臂中等效SM数量为N+1，在整个基波周期内，串联SM的等效平均数量增加，故障SM所在桥臂中的正常SM电容电压将会呈下降趋势。因为在故障SM检测与定位步骤中，已经对电容电压的采样值进行了基波周期内的求和运算，与对连续的电容电压进行基波周期内的积分运算效果相同，分析如下。
稳态时，连续的电容电压uC(t)表示[4]为
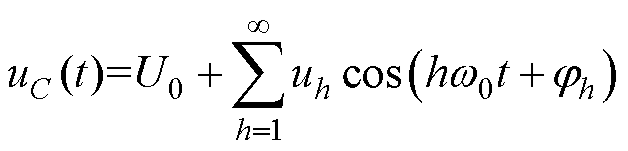（15）
式中，w0为基波角频率；U0为uC(t)的直流分量；h为基波频率的倍数；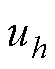
和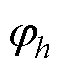
分别为h次交流分量的幅值和相位。
积分后的uC(t)表示为
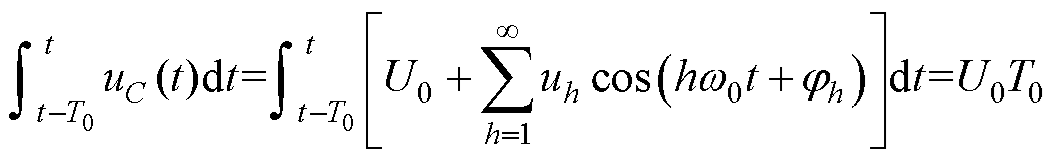（16）
式中，T0为基波周期。
可以看出，在基波周期时间内积分后的uC(t)变为直流量，避免了电容电压瞬时值的波动，因此可以清晰地判断出故障发生后正常SM电容电压的变化趋势，进而完成故障开关器件的分类。中位数可以反应数组X中数据的整体变化情况，且不会受到离群值的影响，因此对故障发生后每个采样时刻的X中的数据，计算中位数Xm为
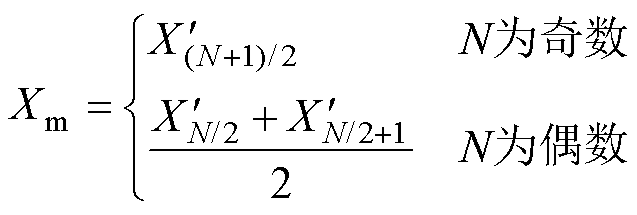（17）
式中，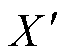
为对X升序排列后得到。
比较每次电容电压采样后计算得到的Xm和上一个采样时刻计算得到的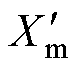
，如果Xm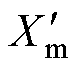＞并持续Tth时间，则判断出Su开路故障；如果Xm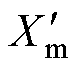＜并持续Tth时间，则判断出Sl开路故障，故障开关器件分类方法的流程如图4所示。故障分类时间阈值Tth设置为1ms，在检测与定位故障后进行故障分类，电容电压SSV上升或下降的变化趋势已经建立，因此只需要判断较少采样时刻Xm的变化趋势，则Tth可以表示为
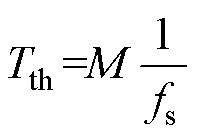（18）
式中，M为检测并定位故障SM后采样时刻的个数，本文选取M=5。
本文所提故障检测与诊断方法首先通过计算SM电容电压的SSV表征电容电压的异常变化，提高了故障SM和正常SM电容电压之间差异的增大速度，同时减小了实际中电容电压采样值的随机误差对故障检测与诊断所带来的影响，加快了诊断速度的同时防止误诊断。其次，利用LOF算法判断故障SM电容电压的逐段求和值是否为离群值完成对故障SM的检测与定位，判断阈值不受系统参数影响，并且可以完成全部故障类型的检测与定位。最后，通过判断正常SM电容电压在故障发生后不同的变化趋势，完成对故障开关器件的快速分类，从而降低后续设备的维修成本。本文所提故障诊断方法不受系统参数的影响，快速性和适用性强。
为了与现有方法进行对比，表4总结了主要的MMC子模块开关器件开路故障的检测与诊断方法。文献[12]中基于人工智能的方法依赖于大量的数据训练从而提高检测的准确性，复杂程度较高容易受到系统参数变化的影响，同时随着子模块数量增多，鲁棒性无法得到保证。文献[13-15, 17-18]中基于模型的方法需要准确的系统参数建立数学模型，对系统参数较为敏感，同时诊断时间较长且无法完成对同桥臂多故障的诊断。文献[20]通过分析桥臂电压检测故障，进而分析电容电压进行故障定位，可以在20ms内完成故障诊断，但不适用于同一桥臂中发生多个故障的情况。文献[23]中的方法检测与诊断故障时虽然不受系统参数的影响，但是无法判断出同一桥臂中是否发生多个开路故障且无法做到故障分类。文献[24]中的方法通过比较桥臂电压的测量值与预测值检测故障，需要在线估计系统参数以保证预测值的准确性，当子模块数量增多时需要提高传感器精度，适用性较差。文献[25]中的诊断故障方法需要电容电压增大到一定阈值，因此诊断故障的时间较长，快速性较差。
表4 现有故障检测与诊断方法的对比
Tab.4 Summary of existing fault detection and diagnosis methods
参考文献故障分类同桥臂多故障诊断诊断时间/ms参数不确定性影响 [12]否否≈100是 [13]否否≥90是 [14]否否≈100是 [15]否否≈80是 [17]否否≤150是 [18]否否≈240是 [20]否否≤20是 [23]否否≤40否 [24]能能≤20是 [25]能能≈60否 本文方法能能≤10否
与现有故障检测与诊断方法相比，本文所提出的故障检测与诊断方法可以完成对全部故障类型的检测与定位，并且可以完成对故障的快速分类，同时该方法不受系统参数的影响，具有较强的适用性，可以在10ms内完成故障诊断，诊断速度更快。
为了验证本文所提出的故障检测与诊断方法，在Matlab/Simulink软件中对三相MMC在额定负载下不同故障类型的检测与诊断进行了仿真证明。仿真时采用的系统参数均与实际的MMC实验平台系统参数相同，见表5。
表5 系统参数
Tab.5 System parameters
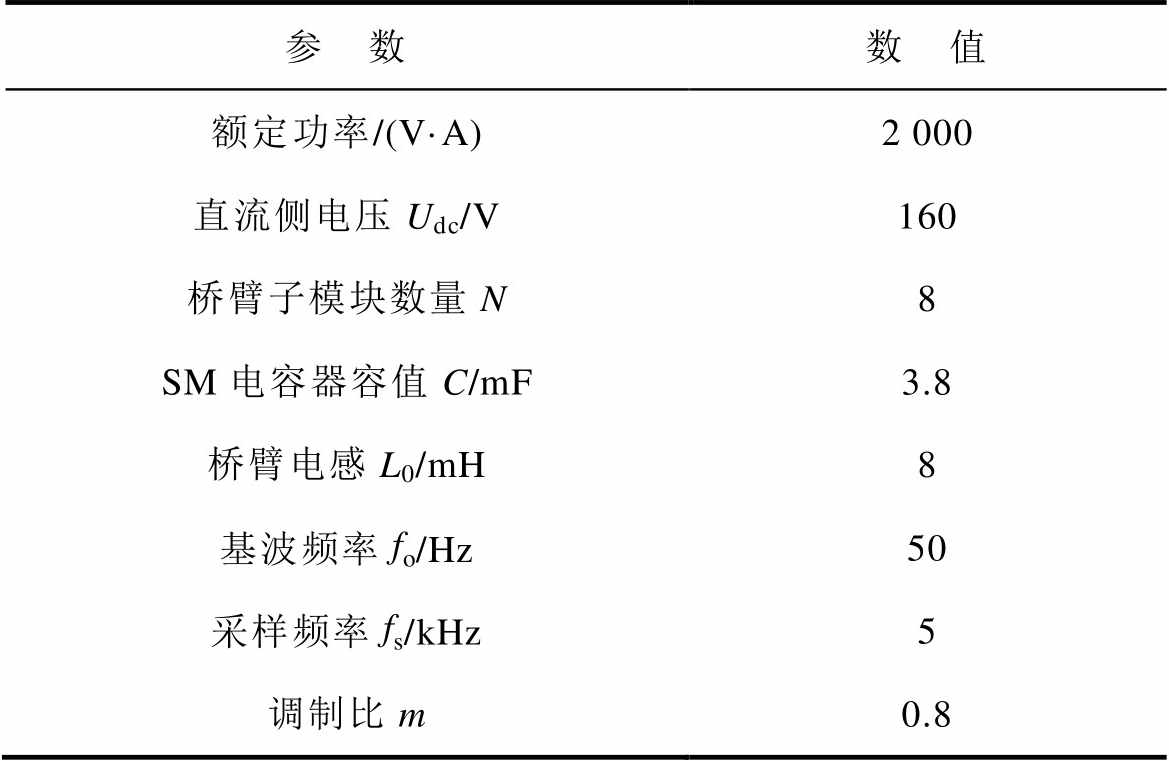
参 数数 值 额定功率/(V·A)2 000 直流侧电压Udc/V160 桥臂子模块数量N8 SM电容器容值C/mF3.8 桥臂电感L0/mH8 基波频率fo/Hz50 采样频率fs/kHz5 调制比m0.8
由于Su与Sl同时发生开路故障的故障特征是对Su和Sl分别发生开路故障的故障特征的结合，因此对发生Su和Sl开路故障的子模块均能够进行检测与定位的方法，同样也适用于Su与Sl同时发生开路故障的情况。因篇幅有限，本文仅对Su和Sl发生开路故障时的故障检测与诊断进行仿真和实验验证。
上桥臂SM1 Su开路故障，仿真结果如图5所示，图中，Foc为故障发生时刻；Fdl为检测并定位故障时刻；Fc为完成故障分类时刻。SM1 Su开路故障发生在3.203s。故障发生后，正常SM的klofi均接近1，klof1快速增大并超过阈值Lth，Xm的变化趋势为上升且持续时间超过Tth，在3.205s完成SM1 Su故障检测与诊断，用时2ms。
上桥臂SM2Sl开路故障，仿真结果如图6所示。SM2 Sl开路故障发生在3.29s。故障发生后，klof2快速增大超过阈值Lth，Xm的变化趋势为下降且持续时间超过Tth，在3.292s完成SM2 Sl故障检测与诊断，用时2ms。
上桥臂SM1 Su与SM2 Sl开路故障，仿真结果如图7所示。SM1 Su开路故障发生在3.204s；SM2 Sl开路故障发生在3.29s。在3.206s完成SM1 Su故障检测与诊断，用时2ms；在3.293s完成SM2 Sl故障检测与诊断，用时3ms。
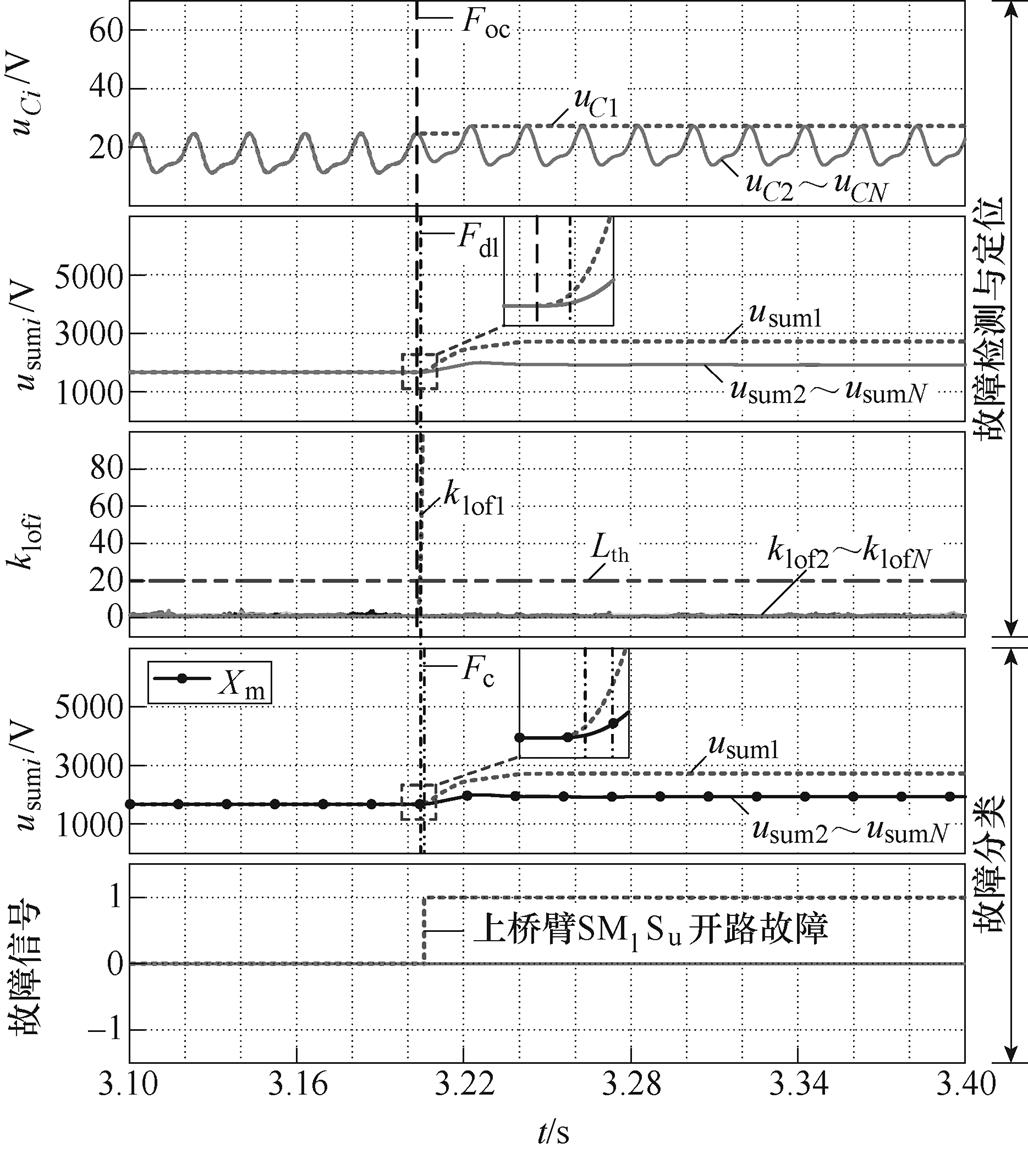
图5 SM1 Su故障检测与诊断仿真波形
Fig.5 Simulation waveforms of SM1 Su fault detection and diagnosis
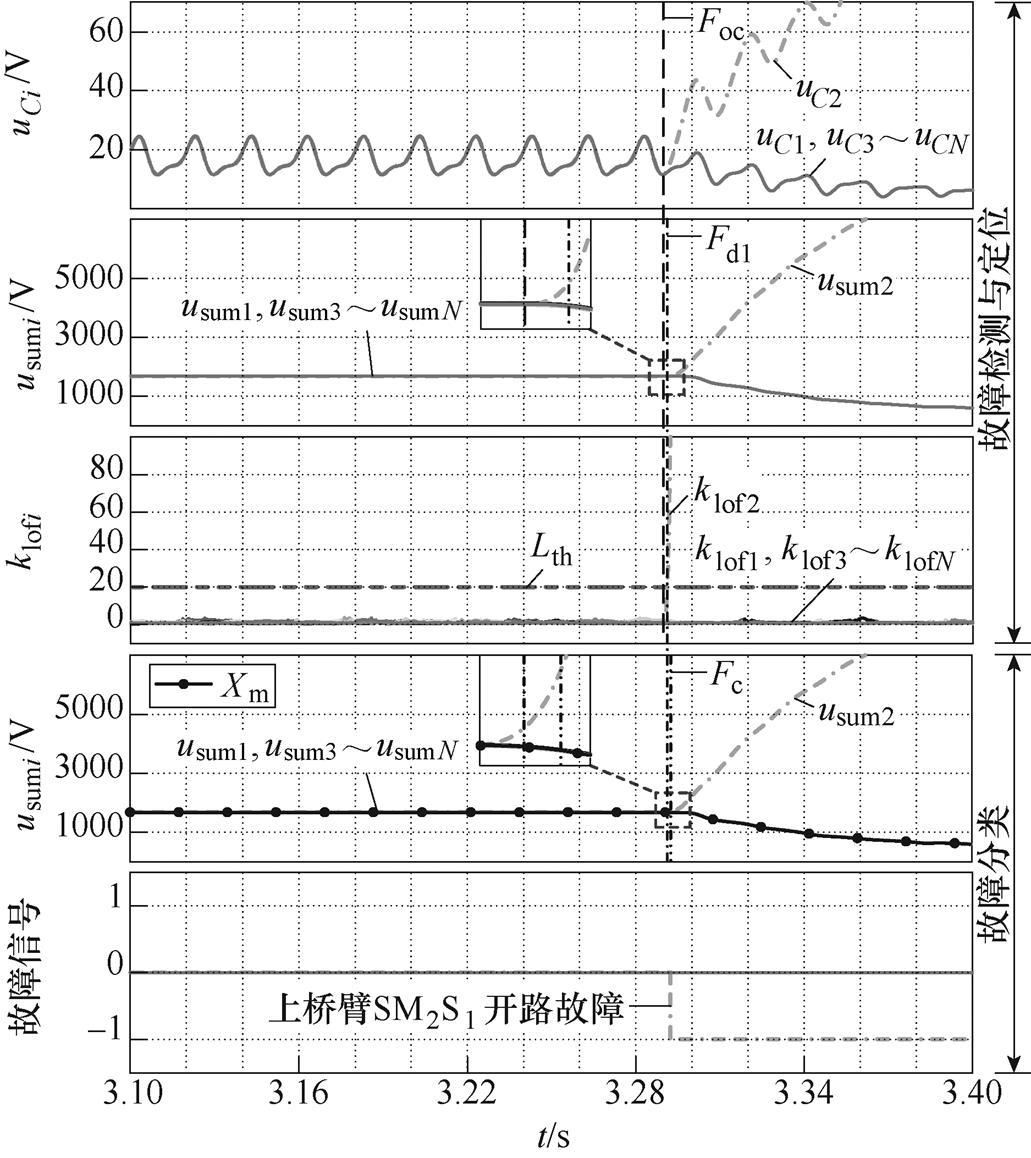
图6 SM2 Sl故障检测与诊断仿真波形
Fig.6 Simulation waveforms of SM2 Sl fault detection and diagnosis
从仿真结果可以看出，所提故障检测与诊断方法具有鲁棒性。此外，虽然仿真中使用的系统功率较小，但所有故障类型的诊断时间均不超过3ms，验证了所提方法的快速性。
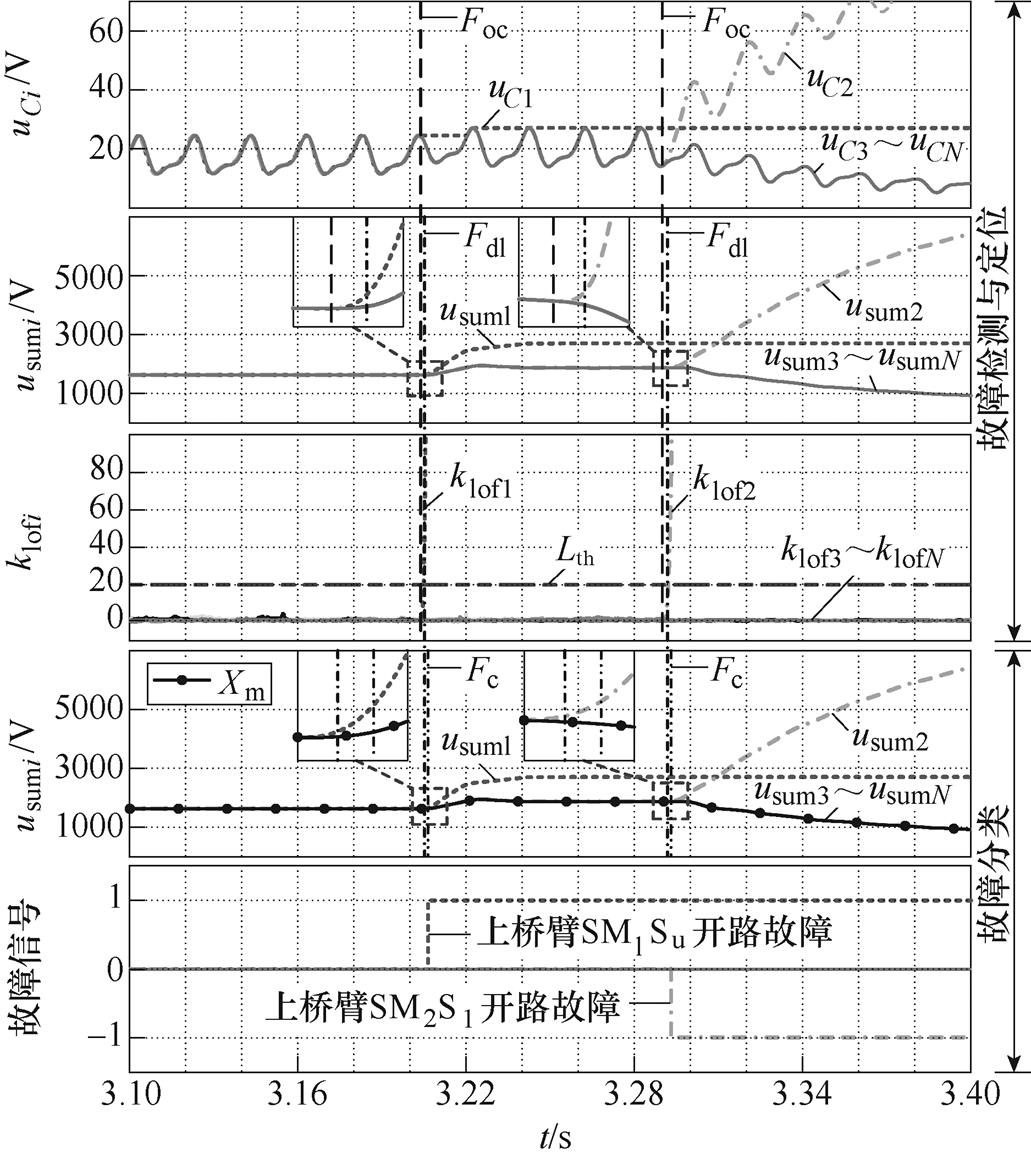
图7 SM1 Su与SM2 Sl故障检测与诊断仿真波形
Fig.7 Simulation waveforms of SM1 Su and SM2 Sl fault detection and diagnosis
为了进一步验证本文所提方法的有效性和快速性，在单相包含16个半桥子模块的MMC实验平台进行了实验，实验平台如图8所示。其中控制系统由数字信号处理芯片DSP（型号TMS320F28335）和FPGA（型号EP3C25Q240C8N）组成，由DSP计算产生调制信号，由FPGA实现电容电压排序及驱动脉冲生成，驱动信号和测量值通过光纤传输，系统的主要参数见表5。实验过程分别在额定功率（满载）以及半额定功率（半载）下进行。
（1）满载下上桥臂SM1Su故障，实验结果如图9所示。SM1 Su开路故障发生在3.207s，在3.212s时被成功诊断，用时5ms，没有发生误诊断。
图8 单相MMC实验平台
Fig.8 The experimental platform of single-phase MMC
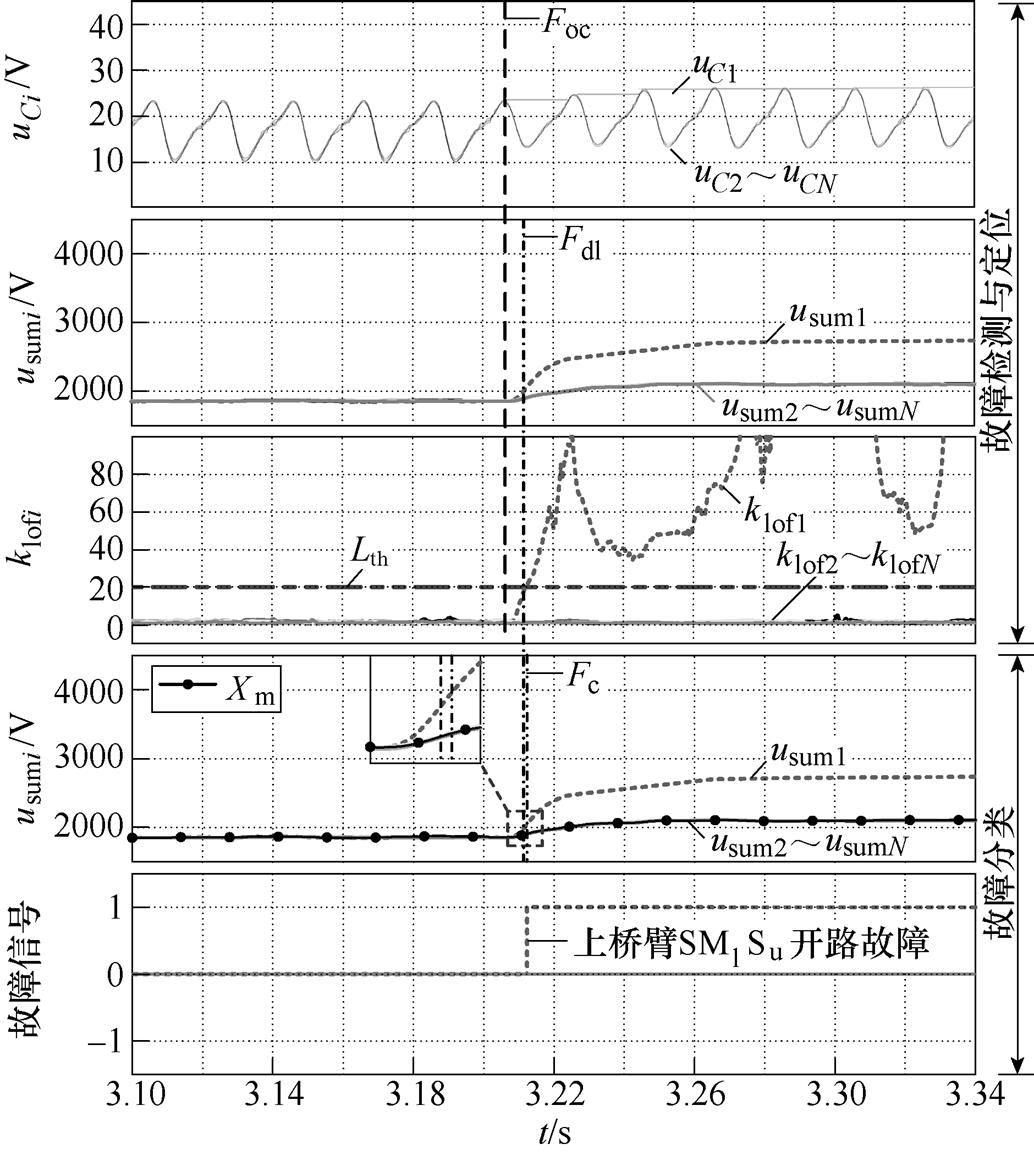
图9 满载下SM1 Su故障检测与诊断实验波形
Fig.9 Experimental waveforms of SM1 Su fault detection and diagnosis under rated load
（2）满载下上桥臂SM2Sl故障，实验结果如图10所示。SM2 Sl在3.237s时发生开路故障，在3.242s时被成功诊断，用时5ms。
图10 满载下SM2 Sl故障检测与诊断实验波形
Fig.10 Experimental waveforms of SM2 Sl fault detection and diagnosis under rated load
（3）满载下上桥臂SM1Su和SM2Sl故障，实验结果如图11所示。SM1 Su和SM2 Sl分别在3.165s和3.274s发生开路故障，在3.171s时SM1 Su故障检测与诊断完成，用时6ms；3.281s时SM2 Sl故障检测与诊断完成，用时7ms。
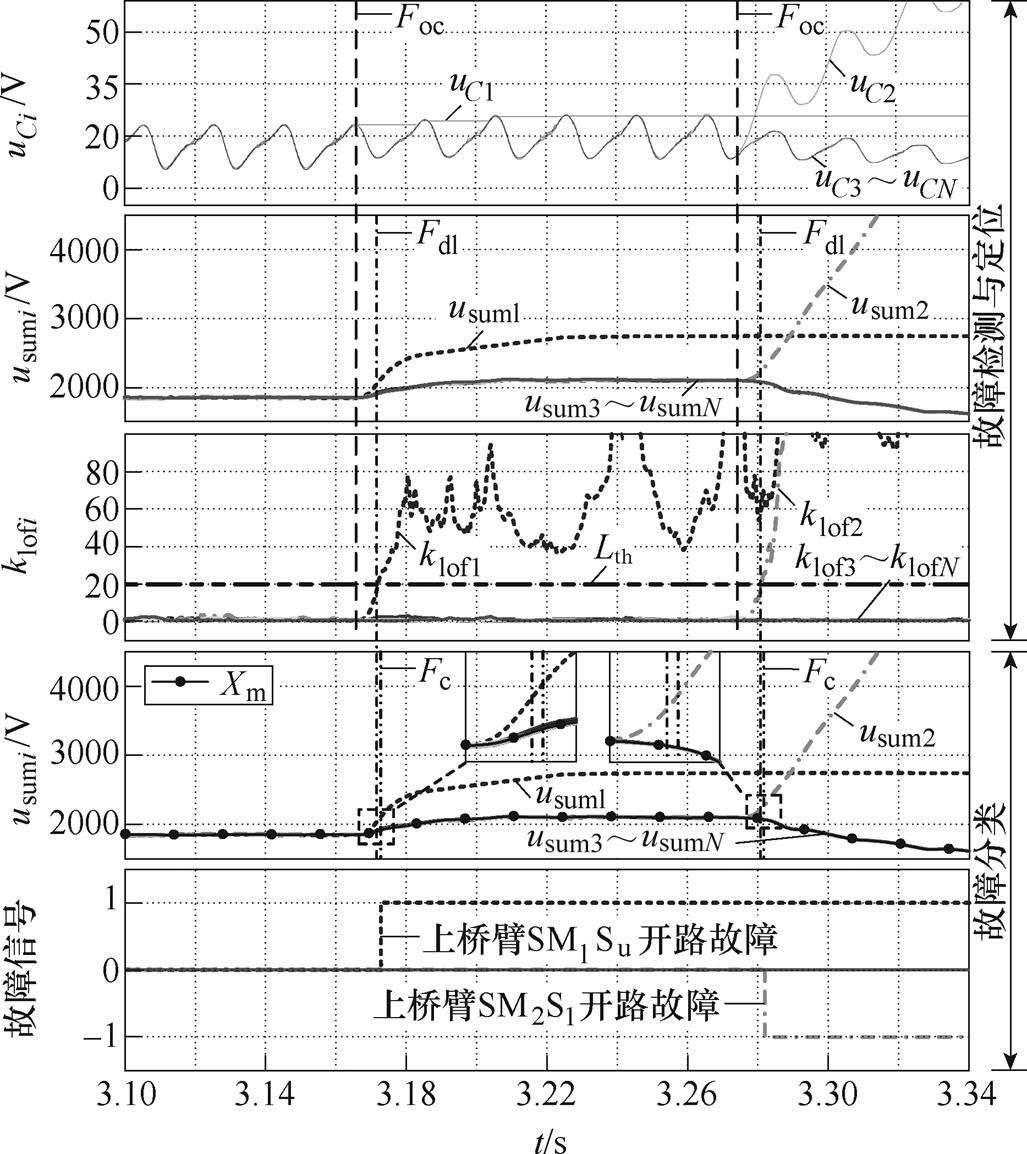
图11 满载下SM1 Su与SM2 Sl故障检测与诊断实验波形
Fig.11 Experimental waveforms of SM1 Su and SM2 Sl fault detection and diagnosis under rated load
（4）半载下上桥臂SM1Su故障，实验结果如图12所示。SM1Su开路故障发生在3.198s，在3.204s时被成功诊断，用时6ms。
（5）半载下上桥臂SM2Sl故障，实验结果如图13所示。SM2 Sl在3.240s时发生开路故障，在3.247s时被成功诊断，用时7ms。
（6）半载下上桥臂SM1Su和SM2Sl故障，实验结果如图14所示。SM1 Su和SM2 Sl分别在3.139s和3.286s发生开路故障。在3.147s时SM1 Su故障检测与诊断完成，用时8ms；3.296s时SM2 Sl故障检测与诊断完成，用时10ms。
仿真及实验结果见表6，实验中在使用额定负载的情况下，由于受到采样误差、干扰等因素的影响，故障检测与诊断的时间相比仿真中变长，但对各种故障类型的诊断时间均不超过7ms。此时系统功率已经足够小，实验中使系统功率进一步减小即使用半额定负载时，由于系统功率减小，电容电压差异形成的速度变慢，因此诊断时间略有增大，但也均不超过10ms。同时可以看出，本文所提方法的有效性并不受系统参数及输出功率的影响。
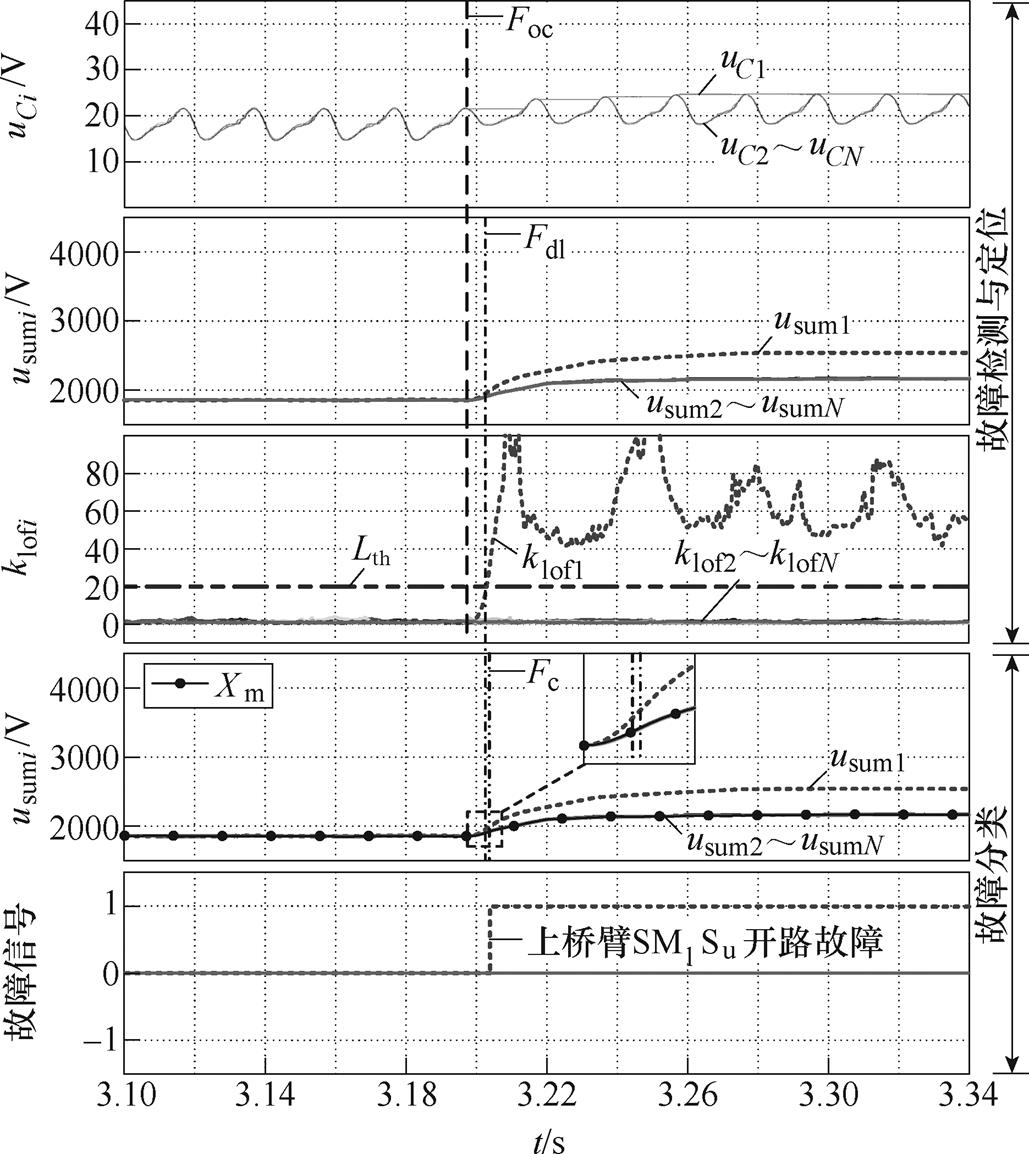
图12 半载下SM1 Su故障检测与诊断实验波形
Fig.12 Experimental waveforms of SM1 Su fault detection and diagnosis under half-load
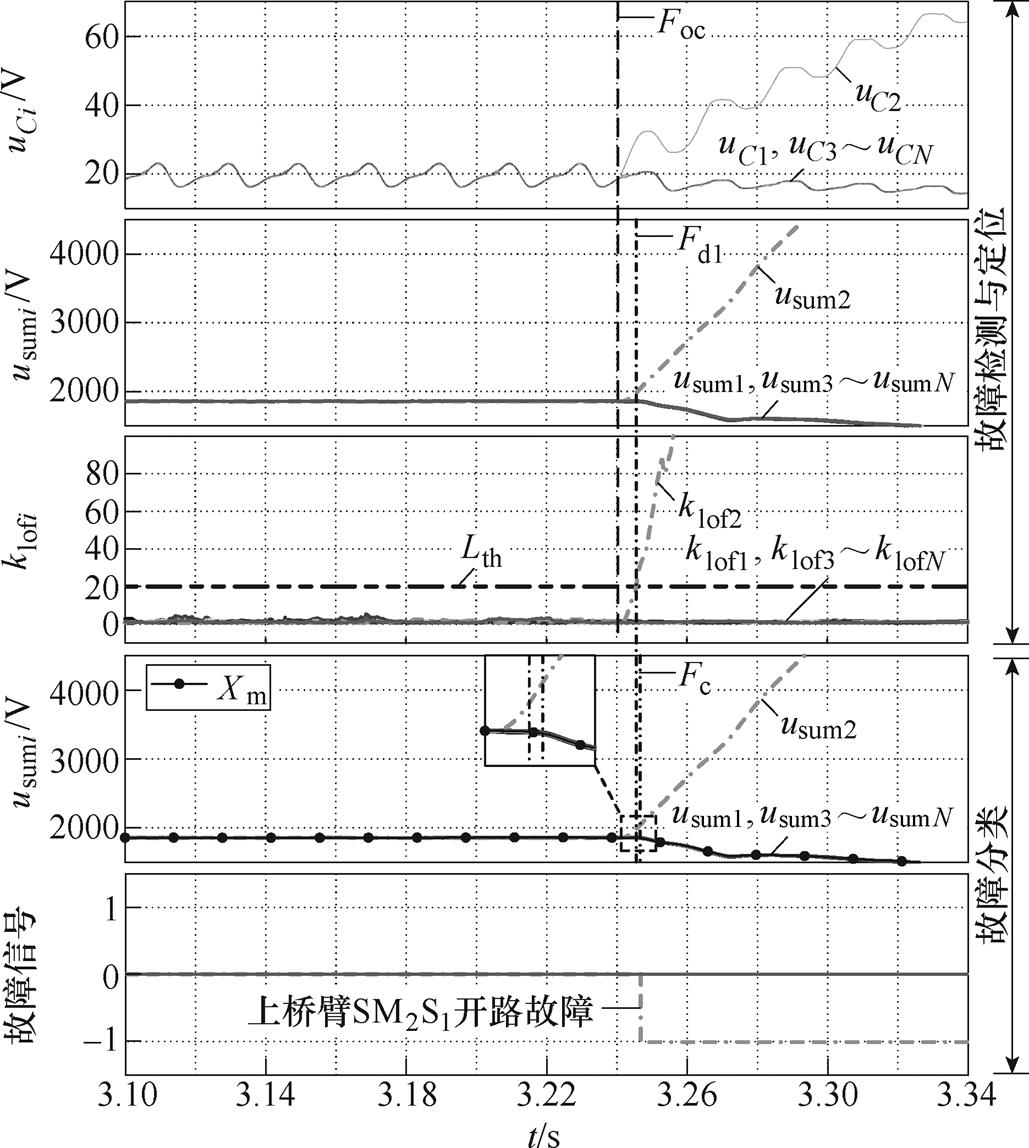
图13 半载下SM2 Sl故障检测与诊断实验波形
Fig.13 Experimental waveforms of SM2 Sl fault detection and diagnosis under half-load
仿真及实验结果表明，一方面，故障SM与正常SM电容电压逐段求和值之间的差值在系统输出功率增大时会增加得更快，有助于提高故障检测与诊断速度；另一方面，fs增大（即L增大）也可以进一步加快诊断速度。同时，当子模块数量增多时，SM电容电压的分布密度增大，基于密度的LOF算法可以更加快速准确地判断离群值。
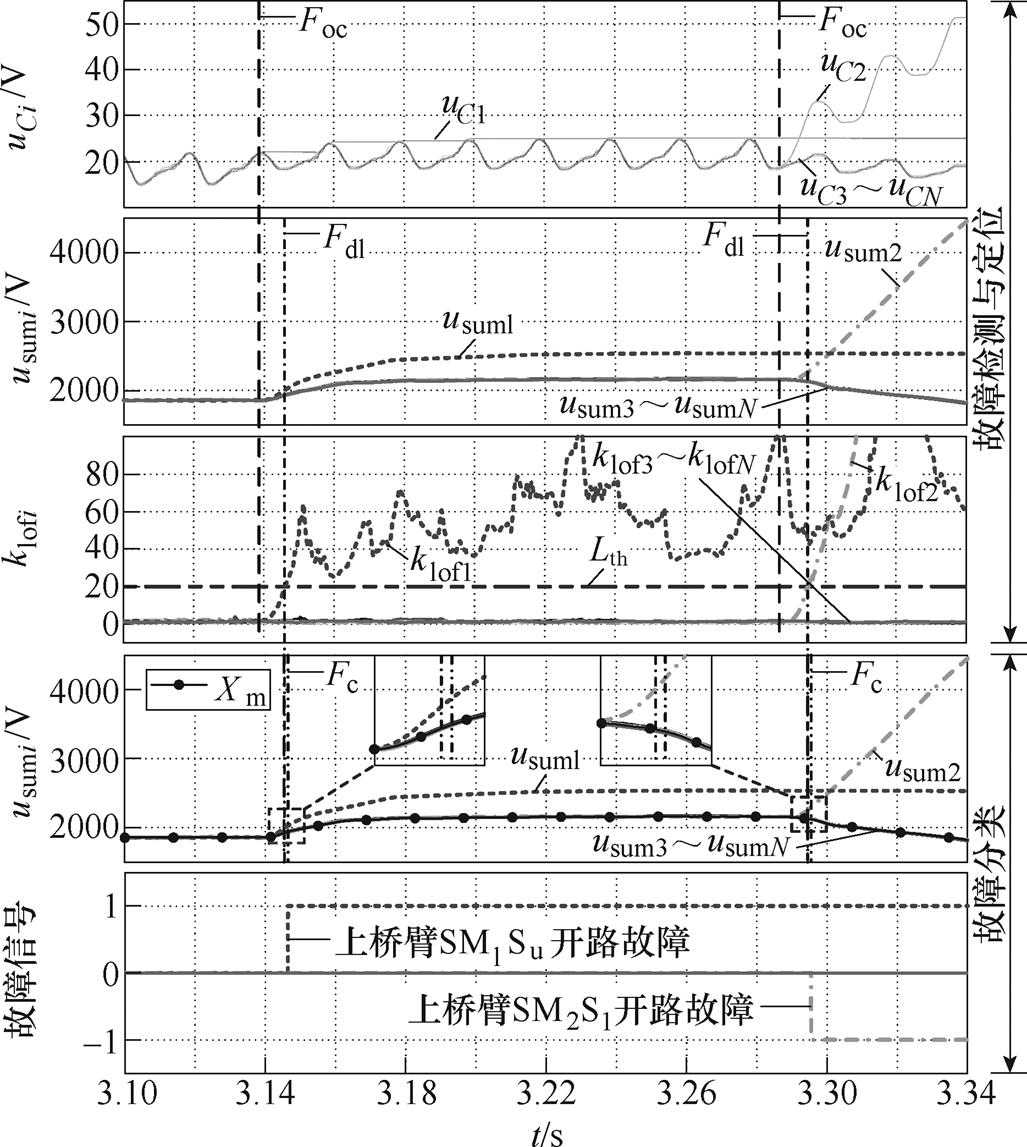
图14 半载下SM1 Su与SM2 Sl故障检测与诊断实验波形
Fig.14 Experimental waveforms of SM1 Su and SM2 Sl fault detection and diagnosis under half-load
表6 仿真与实验结果
Tab.6 The results of simulation and experimental
系统负载验证方式故障类型诊断时间/ms 满载仿真单一故障≤2 同桥臂多故障≤3 实验单一故障≤5 同桥臂多故障≤7 半载实验单一故障≤7 同桥臂多故障≤10
由于MMC三相各桥臂的对称性，所提故障检测与诊断方法对发生在不同桥臂及同桥臂中的单故障或多故障情况同样有效。并且所提方法的检测与诊断速度快，即使在低输出功率下的故障诊断用时也不超过10ms。
本文首先分析了子模块电容电压在发生开关器件开路故障后的异常变化，并通过计算电容电压逐段求和值对其进行表征。在此基础上，首次提出一种基于LOF算法的故障快速检测与诊断方法，通过计算子模块电容电压逐段求和值的局部离群因子并与阈值比较判断离群值，可以同时完成对故障子模块的检测与定位；之后通过判断故障SM所在桥臂中正常SM电容电压的变化趋势，快速识别故障开关器件，不仅适用于单故障和不同桥臂多故障发生情况，对同桥臂发生多个故障的情况同样有效。所提方法中阈值选取不受系统输出功率和系统参数的影响，可以在半个基波周期内同时对故障子模块进行检测与定位，并识别故障开关器件，具有较强的快速性和适用性。
参考文献
[1] 王浩翔, 赵冬梅, 陶然, 等. 基于分解的多目标进化算法的含MMC-HVDC交直流混合系统最优潮流研究[J]. 电工技术学报, 2020, 35(17): 3691-3702.
Wang Haoxiang, Zhao Dongmei, Tao Ran, et al. Study on optimal power flow for AC/DC hybrid system incorporating MMC-HVDC based on MOEA/D[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3691-3702.
[2] 易灵芝, 黄晓辉, 黄守道, 等. 基于最近电平逼近调制的模块化多电平变换器中高压变频调速系统运行控制[J]. 电工技术学报, 2020, 35(6): 1303- 1315.
Yi Lingzhi, Huang Xiaohui, Huang Shoudao, et al. A medium-voltage motor drive with modular multilevel converter based on nearest level modulation[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1303-1315.
[3] 徐殿国, 李彬彬, 周少泽. 模块化多电平高压变频技术研究综述[J]. 电工技术学报, 2017, 32(20): 104-116.
Xu Dianguo, Li Binbin, Zhou Shaoze. Overview of the modular multilevel converter based high voltage motor drive[J]. Transactions of China Electrotech- nical Society, 2017, 32(20): 104-116.
[4] 徐政. 柔性直流输电系统[M]. 北京: 机械工业出版社, 2012.
[5] 贾科, 冯涛, 陈淼, 等. LCC-MMC型混合直流配电系统线路保护方案[J]. 电工技术学报, 2021, 36(3): 656-665.
Jia Ke, Feng Tao, Chen Miao, et al. Line protection scheme for hybrid LCC-MMC type DC distribution system[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 656-665.
[6] 王婷, 杨明发. 基于改进型模块化嵌入式多电平换流器拓扑的HVDC直流故障清除策略[J]. 电气技术, 2020, 21(12): 17-22, 35.
Wang Ting, Yang Mingfa. HVDC DC fault clearing strategy based on improved MEMC topology[J]. Electrical Engineering, 2020, 21(12): 17-22, 35.
[7] Chen Yongyang, Pan Shangzhi, Huang Meng, et al. MMC-MTDC transmission system with partially hybrid branches[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(2): 124-132.
[8] Lu Bin, Sharma S K. A literature review of IGBT fault diagnostic and protection methods for power inverters[J]. IEEE Transactions on Industry Appli- cations, 2009, 45(5): 1770-1777.
[9] 汪涛, 虞晓阳, 文继锋, 等. 模块化多电平柔性直流输电换流器子模块过电压保护[J]. 电力系统自动化, 2020, 44(21): 107-115.
Wang Tao, Yu Xiaoyang, Wen Jifeng, et al. Sub- module overvoltage protection of modular multilevel converter for flexible DC transmission[J]. Automation of Electric Power Systems, 2020, 44(21): 107-115.
[10] Wu Rui, Blaabjerg F, Wang Huai, et al. Catastrophic failure and fault-tolerant design of IGBT power electronic converters-an overview[C]//IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 2013: 507-513.
[11] 敬华兵, 年晓红, 龚芬. MMC子模块元件短路故障机理及其新型保护策略[J]. 电工技术学报, 2015, 30(3): 21-27.
Jing Huabing, Nian Xiaohong, Gong Fen. Fault mechanism and novel protection strategy of MMC sub-module component short-circuit[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 21-27.
[12] Kiranyaz S, Gastli A, Ben-Brahim L, et al. Real-time fault detection and identification for MMC using 1-D convolutional neural networks[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8760-8771.
[13] Shao Shuai, Wheeler P W, Clare J C, et al. Fault detection for modular multilevel converters based on sliding mode observer[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 4867-4872.
[14] Deng Fujin, Chen Zhe, Khan M R, et al. Fault detection and localization method for modular multi- level converters[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2721-2732.
[15] 殷实, 谭国俊. 一种基于扩展卡尔曼滤波算法的MMC系统故障诊断策略[J]. 电工技术学报, 2016, 31(19): 74-84.
Yin Shi, Tan Guojun. A novel fault diagnosis strategy of MMC system based on EKFA[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 74-84.
[16] 李探, 赵成勇, 李路遥, 等. MMC-HVDC子模块故障诊断与就地保护策略[J]. 中国电机工程学报, 2014, 34(10): 1641-1649.
Li Tan, Zhao Chengyong, Li Luyao, et al. Sub-module fault diagnosis and the local protection scheme for MMC-HVDC system[J]. Proceedings of the CSEE, 2014, 34(10): 1641-1649.
[17] 徐坤山, 谢少军, 袁小峰, 等. 模块化多电平换流器子模块故障快速诊断方法[J]. 电力系统自动化, 2017, 41(18): 103-110.
Xu Kunshan, Xie Shaojun, Yuan Xiaofeng, et al. Rapid diagnostic method for submodule failure in modular multilevel converter[J]. Automation of Elec- tric Power Systems, 2017, 41(18): 103-110.
[18] Li Binbin, Shi Shaolei, Wang Bo, et al. Fault diagnosis and tolerant control of single IGBT open- circuit failure in modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2016, 31(4): 3165-3176.
[19] 李翠, 刘振兴, 柴利, 等. 模块化多电平换流器的子模块开路故障检测方法[J]. 中国电机工程学报, 2017, 37(23): 6995-7003, 7091.
Li Cui, Liu Zhenxing, Chai Li, et al. An open circuit fault detection method for sub-modules in modular multi-level converters[J]. Proceedings of the CSEE, 2017, 37(23): 6995-7003, 7091.
[20] Zhou Dehong, Qiu Huan, Yang Shunfeng, et al. Submodule voltage similarity-based open-circuit fault diagnosis for modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2019, 34(8): 8008- 8016.
[21] Wang Chao, Wang Kui, Zheng Zedong, et al. Analysis and control of three-phase modular multilevel con- verters under the single arm fault condition[J]. IEEE Transactions on Power Electronics, 2019, 34(9): 8293-8298.
[22] Yang Qichen, Qin Jiangchao, Saeedifard M. Analysis, detection, and location of open-switch submodule failures in a modular multilevel converter[J]. IEEE Transactions on Power Delivery, 2016, 31(1): 155- 164.
[23] Zhou Weihao, Sheng Jing, Luo Haoze, et al. Dete- ction and localization of submodule open-circuit failures for modular multilevel converters with single ring theorem[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(4): 3729-3739.
[24] Chen Xingxing, Liu Jinjun, Deng Zhifeng, et al. A diagnosis strategy for multiple IGBT open-circuit faults of modular multilevel converters[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(1): 191-203.
[25] Yang Heya, Zhou Weihao, Sheng Jing, et al. A statistical submodule open-circuit failure diagnosis method for modular multilevel converters (MMCs) with variance measurement[J]. IEEE Open Journal of Power Electronics, 2020, 1(1): 180-189.
[26] Breunig M M, Kriegel H P, Ng R T, et al. LOF: identifying density-based local outliers[C]//Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, USA, 2000: 93-104.
A Fast Open-Circuit Fault Detection and Diagnosis Method for Sub-Modules of Modular Multilevel Converters
Abstract Based on the abnormal change of capacitor voltage caused by the fault of the modular multilevel converter (MMC) sub-module (SM) switching device, a fast fault detection and diagnosis method was proposed in this paper. The local outlier factor (LOF) algorithm was used to analyze the stepwise summation value of capacitor voltages of all sub-modules in one arm, so as to detect and locate the faulty SM(s) rapidly and simultaneously. Then, from the capacitor voltage variation of the healthy SM in the same arm, the faulty switching device can be quickly identified and the fault classification can be completed. Because the proposed method can analyze local abnormal characteristics, it can be applied to any fault types including single fault, multiple faults in the same arm and multiple faults in different arms. The proposed method is not affected by the uncertainty of system parameters, and has strong applicability and fast diagnostic speed. Simulation and experimental results verify the effectiveness of the proposed method.
keywords：Modular multilevel converter (MMC), fault detection, fault diagnosis, local outlier factor (LOF)
DOI: 10.19595/j.cnki.1000-6753.tces.211418
中图分类号：TM46
国家自然科学基金项目（51977093）和湖北省自然科学基金重点项目（2019CFA049）资助。
收稿日期 2021-09-08
改稿日期 2022-01-12
刘座辰 男，1997年生，硕士研究生，研究方向为柔性直流输电技术。E-mail: liuzuochen@hust.edu.cn
林 磊 男，1980年生，教授，博士生导师，研究方向为高压大功率特种电源、高压柔性直流输电控制技术、模块化多电平功率变换技术、基于新一代宽禁带半导体器件的功率变换器等。E-mail: linlei@hust.edu.cn（通信作者）
（编辑 陈诚）