
图1 锂离子电池老化路径示意图
Fig.1 Schematic diagram of aging path of lithium-ion batteries
摘要 为了验证锂离子电池在长期使用中的性能,需要对锂离子电池进行寿命测试。现阶段锂离子电池寿命一般长达数千循环,进行常规寿命测试十分耗时,需要开发加速寿命的实验方法。由于锂离子电池寿命衰减具有对使用路径的依赖性,因此设计该加速寿命实验方法的约束是:既要保证加速前后总容量衰减的等价性,还要保证内部衰减机理即老化路径的不变性。该文提出一套基于模型的可保证上述约束的加速寿命工况自动生成方法。方法设计了综合考虑加速因子(加速时间倍率)和老化路径相对误差两个指标的目标函数,并采用双闭环构架求取符合该目标函数的加速工况最优解。双闭环的外环为加速因子优化算法,旨在寻找最优的加速时间倍率;内环为加速工况搜索算法,旨在搜索对应于加速因子和上述约束的最优加速工况。针对中国轻型汽车行驶工况中的乘用车行驶工况,该文方法基于作者研发的考虑锂离子电池主导衰减机理的半经验分数阶模型进行仿真,仿真结果证明了方法的有效性。
关键词:锂离子电池 老化路径 双闭环构架 加速因子 禁忌搜索
锂离子电池具有能量密度高、功率密度高和寿命长等优点,使其在储能系统和新能源汽车等领域得到广泛应用[1-3]。锂离子电池在使用过程中会发生老化,体现为容量的衰减和内部阻抗的增加[4-5]。因此,为保证锂离子电池在长期使用过程中的可靠性,需要对其进行寿命测试[6-7]。现阶段,锂离子电池寿命一般长达数千循环,这导致传统的寿命测试非常耗时。于是,需要考虑锂离子电池老化机理并针对性地开发加速寿命测试方法。考虑到锂离子电池具有路径依赖特性,这类加速方法不仅要保证锂离子电池外特性(容量)的等价性,还要保证其内部老化机理的不变性[8-9]。
锂离子电池的主导老化机理包括:可用锂离子损失、可用活性材料损失和内部阻抗增加,其中阻抗增加又以欧姆内阻和扩散阻抗占主导地位[10-11]。影响锂离子电池寿命的主要因素包括:时间(循环次数)、温度、电流倍率(Current rate, C-rate)、荷电状态(State of Charge, SOC)和放电深度(Depth of Discharge, DOD)[12-14]。
老化路径是指锂离子电池内部主导老化机理在电池衰减中经过的某条路径[15]。锂离子电池老化路径示意图如图1所示。具体地,如果能够采用一组机理参数反映电池内部主导老化机理,则可以用图1来阐释电池的老化路径及路径依赖特性。图1中,不同的坐标轴代表不同的机理参数;圆点表示电池初始时处于的新鲜状态;菱形表示电池老化后处于的老化状态;实线和虚线表示电池从新鲜状态到老化状态可能经过的两条老化路径。由于锂离子电池的老化受多种因素耦合影响,不同影响因素的组合会导致各机理参数不同的衰减规律[16-18],这体现为图1中不同的老化路径。即使从相同的新鲜状态衰减到相同的老化状态,不同影响因素的组合也会造成老化路径的不同,这是由锂离子电池的路径依赖特性导致的。

图1 锂离子电池老化路径示意图
Fig.1 Schematic diagram of aging path of lithium-ion batteries
在锂离子电池的实际使用中,其老化过程受到的正是不同影响因素的组合。以新能源汽车为例,由于其速度工况复杂,导致为其提供驱动能量的锂离子电池的电流工况变化剧烈[19]。与复杂电流工况相对应的是较低的电流倍率,以中国轻型汽车行驶工况中的乘用车行驶工况(China Light-duty vehicle Test Cycle-Passenger car, CLTC-P)为例,图2为其工况曲线[20]。根据工况曲线和统计结果,CLTC-P工况的最高速度接近120km/h,最大加速度为1.47m/s2,而平均速度为28.96km/h。以当前市场上主流的续航里程在300~500km的新能源汽车为例,为其供能的锂离子电池系统最大倍率约1C,而平均倍率仅有约1/10C[21]。因此,若按照锂离子电池实际所经历的工况对其进行寿命测试将十分耗时,需要针对性地设计加速寿命工况,以有效节约测试时间。
考虑锂离子电池老化的路径依赖性,加速寿命工况的设计需要以锂离子电池的实际工况和锂离子电池在实际工况下的实际老化路径为基准。在实际老化路径的误差允许范围内,按照一定的设计原则对实际工况进行化繁为简、化曲为直的简化或优化,以达到加速寿命测试的目的。
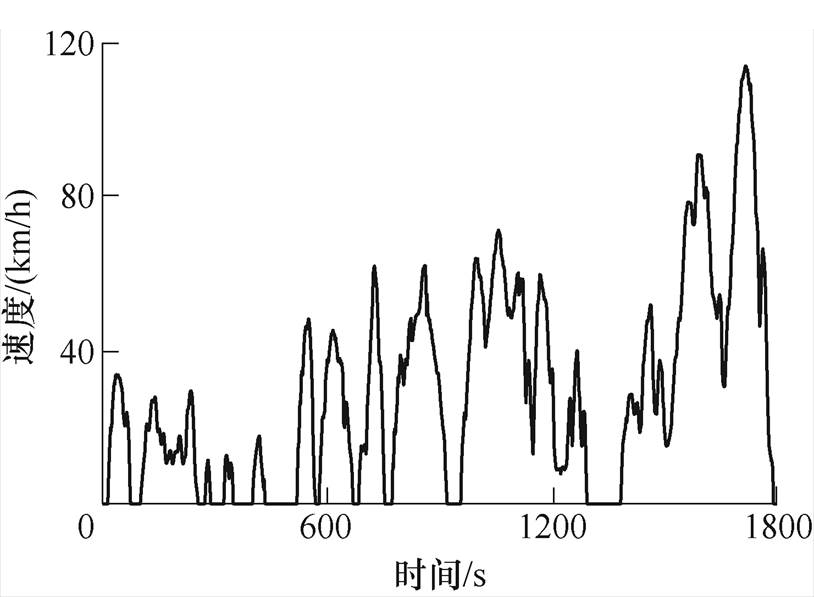
图2 CLTC-P行驶工况
Fig.2 CLTC-P driving cycle
现有研究中关于加速寿命工况的相关研究并不多。同时,迄今的加速寿命测试对“路径依赖”问题关注不够。现有研究主要侧重于对锂离子电池外特性衰减的加速。具体来说,相关研究考虑的加速应力主要有温度和电流倍率[22-24],而评价加速寿命测试效果的一般为容量衰减和内阻增加[25-26]。
本文提出计及锂离子动力电池老化路径,且基于双闭环构架并采用禁忌搜索算法求取加速工况最优解的加速寿命工况自动生成方法。首先,通过综合考虑加速因子和加速寿命工况与原始工况造成的电池老化路径的误差这两个因素,提出基于双闭环构架的加速寿命工况生成方法。这里加速因子是反映加速测试中某一加速应力的加速效果的量,其一般定义为元件或设备在正常工作应力下的寿命与在加速应力下的寿命之比[27-28]。其次,给出基于电池实际工况(这里以乘用车行驶工况CLTC-P为例)的加速寿命工况生成结果,以及在考虑电池主导衰减机理的半经验寿命模型下,加速寿命工况与原始工况造成的锂离子动力电池老化路径的误差情况。最后,对全文进行总结。
对于动力电池,工况一般指其经历的电流大小,然而对于不同容量等级的电池,其电流大小不具有可比性。本研究为了通用性考虑,以电流倍率这一归一化的无量纲数而非电流大小这一物理量来描述工况。基于上述对工况的描述,将原始工况记为一组随时间变化的电流倍率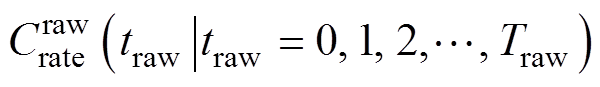 ,并将所求加速寿命工况记为
,并将所求加速寿命工况记为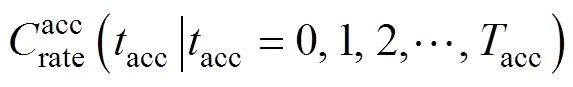 。
。
本文提出加速寿命工况设计原则如下:
(1)电荷量相等原则。原始工况和加速寿命工况对电池进行充/放电的电荷量相等,目的是控制电荷量这个影响因素不变从而仅研究工况的影响。
(2)加速原则。将加速因子定义为原始工况耗时Traw与加速寿命工况耗时Tacc之比,其值应大于1,这样生成的加速寿命工况才具有加速的意义。
(3)最小误差原则。加速寿命工况导致的电池老化路径和原始工况导致的电池老化路径之间的误差应尽可能小。
基于以上原则中的(2)和(3),可以定性分析得到:加速因子越大,加速寿命工况相比原始工况耗时就越短;然而,加速因子越大,加速寿命工况越难完全表征原始工况的关键特征,加速寿命工况与原始工况造成的电池老化路径的误差也越大。加速寿命工况耗时与原始工况耗时百分比和加速寿命工况与原始工况造成的电池老化路径的误差如图3所示。
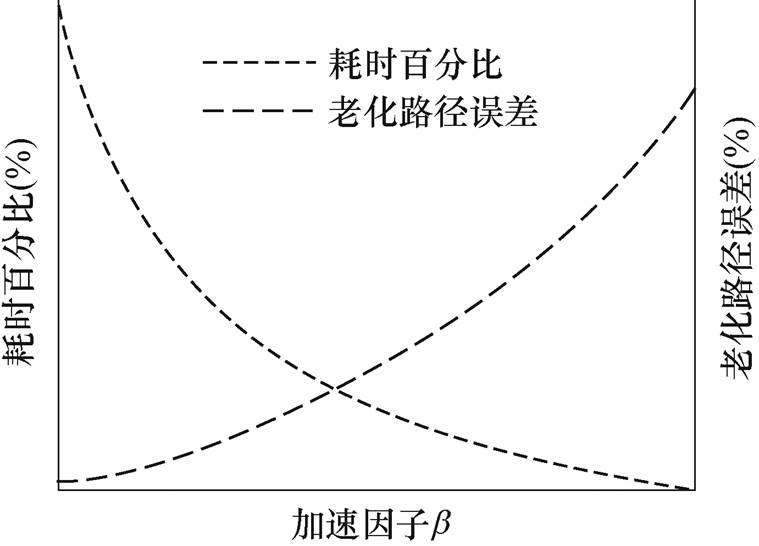
图3 耗时百分比和老化路径误差示意图
Fig.3 Schematic diagram of time consumption percentage and aging path error
于是,需要一个量化的方法,综合考虑加速因子和老化路径误差这两个指标。为此,首先给出二者的表达式。根据定义,加速因子b 表示为
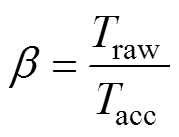 (1)
(1)
式中,Traw为原始工况 的时长;Tacc为加速寿命工况
的时长;Tacc为加速寿命工况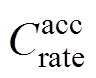 的时长。老化路径误差可以记为
的时长。老化路径误差可以记为
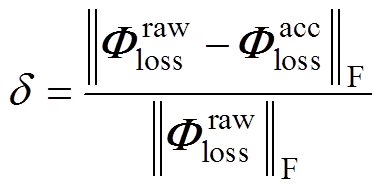 (2)
(2)
式中,d 为原始工况导致的电池老化路径与加速寿命工况导致的电池老化路径的相对误差;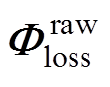 为原始工况下的动力电池老化路径;
为原始工况下的动力电池老化路径;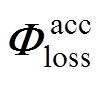 为加速寿命工况下的动力电池老化路径。动力电池老化路径
为加速寿命工况下的动力电池老化路径。动力电池老化路径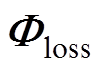 由动力电池所经历的工况
由动力电池所经历的工况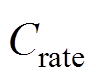 决定,经历不同的工况会导致不同的电池老化路径。
决定,经历不同的工况会导致不同的电池老化路径。
由于Traw与Tacc不同,也即 与
与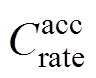 序列长度不同,这导致无法直接在时间t坐标下求
序列长度不同,这导致无法直接在时间t坐标下求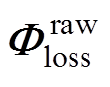 与
与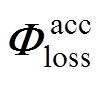 误差的F范数。根据电荷量相等原则,本研究将二者转换到安时(A·h)坐标下求误差的F范数,具体推导过程见附录。F范数的作用是衡量一个矩阵的大小,即衡量这个矩阵和零矩阵的距离,在本研究中用来衡量整体误差的大小。
误差的F范数。根据电荷量相等原则,本研究将二者转换到安时(A·h)坐标下求误差的F范数,具体推导过程见附录。F范数的作用是衡量一个矩阵的大小,即衡量这个矩阵和零矩阵的距离,在本研究中用来衡量整体误差的大小。
基于前述加速寿命工况设计三原则及式(1)和式(2)给出的加速因子和老化路径误差的表达式,提出综合考虑二者的目标函数为
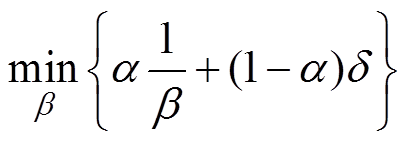 (3)
(3)
s.t.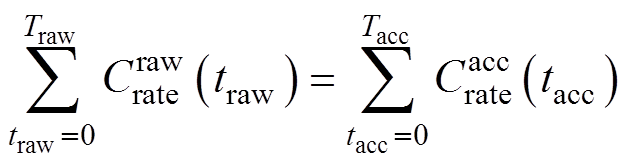 (4)
(4)
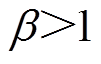 (5)
(5)
式中,a 为权重系数。式(3)~式(5)反映了加速寿命工况设计三原则。具体地,式(3)第二项反映了原则(3)——最小误差原则;式(4)反映了原则(1)——电荷量相等原则;式(5)反映了原则(2)——加速原则。
式(3)所述目标函数中,第一项为加速因子b的倒数,其含义是加速寿命工况耗时与原始工况耗时之比;第二项为老化路径的误差,其中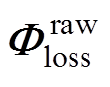 为已知原始工况造成的老化路径,
为已知原始工况造成的老化路径,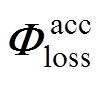 为加速因子b 的函数,因此第二项也为加速因子b 的函数。于是,目标函数的优化可通过对加速因子b 的搜索实现。然而,由于目标函数中的第二项,即老化路径误差的计算依赖加速寿命工况,而加速寿命工况并不能由加速因子b 唯一确定,需要通过搜索的方式得到给定加速因子b 下的最优加速寿命工况
为加速因子b 的函数,因此第二项也为加速因子b 的函数。于是,目标函数的优化可通过对加速因子b 的搜索实现。然而,由于目标函数中的第二项,即老化路径误差的计算依赖加速寿命工况,而加速寿命工况并不能由加速因子b 唯一确定,需要通过搜索的方式得到给定加速因子b 下的最优加速寿命工况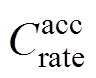 。因此,本研究提出了双闭环构架以实现对目标函数的求解。双闭环中,外环为加速因子优化算法,如图4所示,旨在寻找最优的加速因子;内环为加速工况搜索算法,如图5所示,旨在基于给定的加速因子搜索最优的加速寿命工况。
。因此,本研究提出了双闭环构架以实现对目标函数的求解。双闭环中,外环为加速因子优化算法,如图4所示,旨在寻找最优的加速因子;内环为加速工况搜索算法,如图5所示,旨在基于给定的加速因子搜索最优的加速寿命工况。
外环以一个随机的初始加速因子b0为初值,通过加速工况搜索算法(内环)搜索出该加速因子b0下的最优加速寿命工况,并基于老化路径误差和加速因子b0计算目标函数值。根据目标函数值的变化情况,外环通过对加速因子进行不断修正,得到使目标函数达到最小值的最优加速因子。
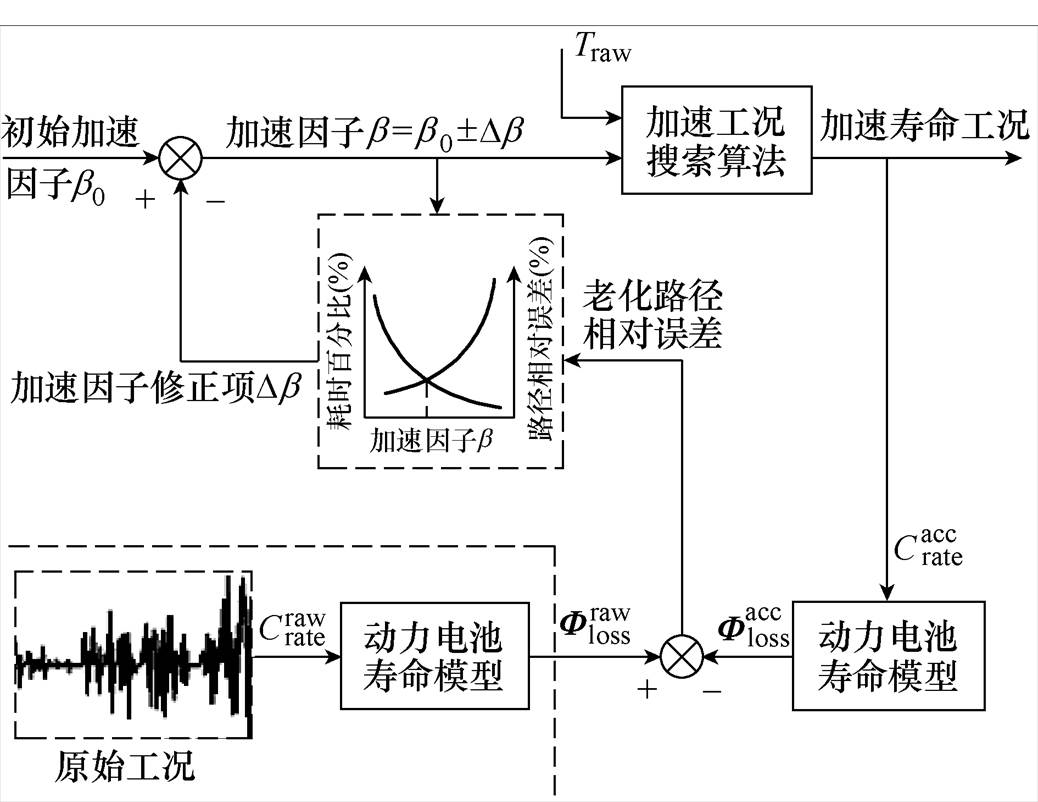
图4 双闭环构架的外环——加速因子优化算法
Fig.4 Outer loop of the double closed-loop architecture–optimization algorithm of acceleration factor
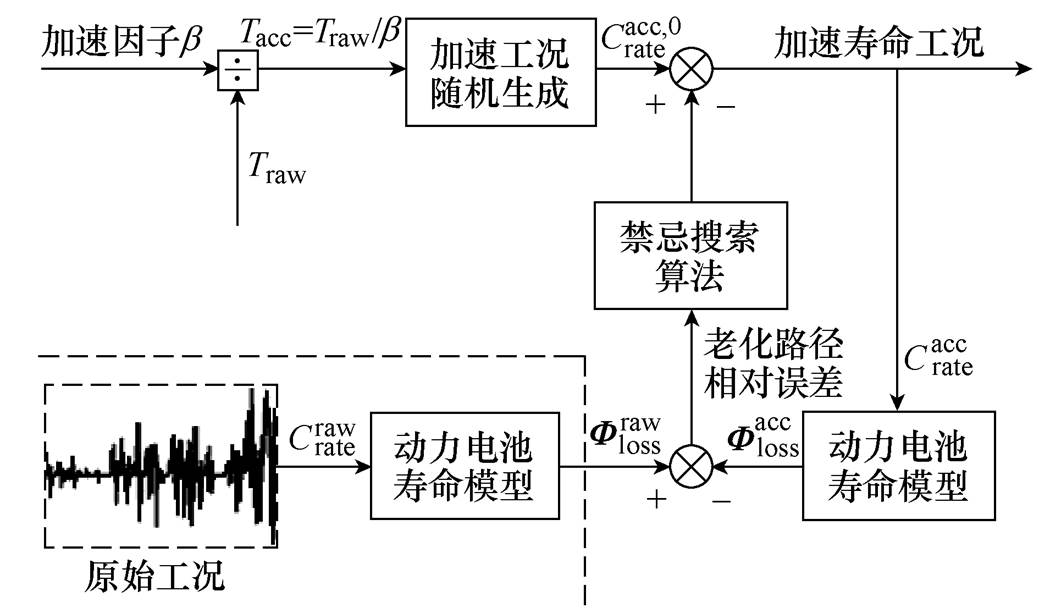
图5 双闭环构架的内环(外环中加速工况搜索算法部分)
Fig.5 Inner loop of the double closed-loop architecture (search algorithm for acceleration condition of the outer loop)
内环为加速工况搜索算法。其与外环的联系为,内环根据外环给定的加速因子和式(4)的电荷量相等约束,随机生成一个初始的加速工况。基于动力电池寿命模型对此初始工况加速工况计算其与原始工况的老化路径相对误差,以老化路径相对误差作为目标函数,使用禁忌搜索算法对工况进行搜索,直至搜索到给定加速因子下的最优加速寿命工况并返回至外环。值得注意的是,外环和内环虽然均会计算老化路径误差,但二者的时间尺度是不一样的,内环在每次禁忌搜索算法迭代得到新的加速工况后均会计算老化路径误差,并以此误差为参考继续迭代禁忌搜索算法;而外环仅在内环搜索到给定加速因子下的最优加速工况后,基于此最优加速工况计算老化路径误差。
为了避免局部搜索可能带来的局部最优解问题,本研究采用禁忌搜索算法进行全局寻优以期尽可能找到“全局最优解”[29]。禁忌搜索算法是对局部邻域搜索的一种扩展,它是一种全局逐步寻优算法[30]。禁忌搜索算法通过引入一个存储结构和相应的禁忌准则(Tabu表)来避免迂回搜索及陷入局部最优等问题,并通过特赦准则来赦免一些优良状态,进而保证充分有效探索以最终达到全局优化的目的。
具体在本研究中,需要搜索的工况可以被视为一个由一组Crate组成的时间序列。于是,将禁忌搜索算法中的关键参数:邻域、邻域动作和评价函数定义如下。
(1)邻域。对于一个给定的Crate序列,交换其中任意两位置的Crate值,得到所有解的集合。
(2)邻域动作。交换Crate序列中任意两位置的Crate值这个操作构成的函数。
(3)评价函数。老化路径的相对误差d。
基于上述参数,使用禁忌搜索算法实现对给定加速因子下加速寿命工况的全局最优搜索。
如1.1~1.3节所述,已经提出了基于双闭环构架求取最优加速因子并自动生成加速工况的方法。然而,算法实际运行时,仍需对式(4)进行离散化以解决下述两点问题:
(1)原始工况 的时长Traw可能会非常长,若将原始工况作为整体求其加速工况,与实际工程应用背景不符且难以实现。
的时长Traw可能会非常长,若将原始工况作为整体求其加速工况,与实际工程应用背景不符且难以实现。
(2)电流倍率Crate的取值是连续的,这会导致加速工况的搜索空间过大。
针对问题(1),本研究对加速工况的搜索过程进行离散化,即分段对原始工况对应的加速工况进行搜索。具体地,认为原始工况由很多段构成,每段时长为DTraw,在给定的加速因子b 下,其对应的加速工况每段时长为DTacc,据此可将式(4)修改为针对每一段原始工况和待求加速工况的约束,以其中第m段为例,其约束可表示为
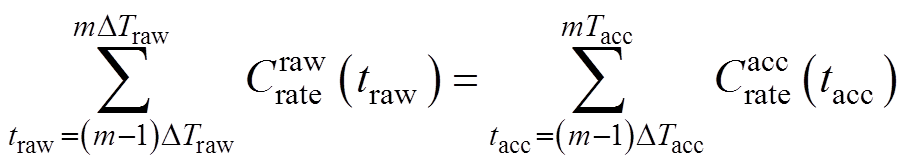 (6)
(6)
将约束修改为式(6)后,可基于上述双闭环构架实现对加速工况的逐段求取。
针对问题(2),本研究采用对Crate取值进行离散化的方式减小搜索空间,其离散取值为
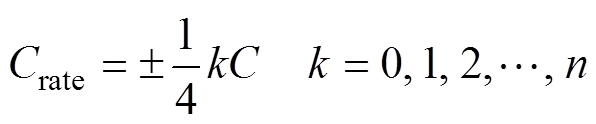 (7)
(7)
将Crate的取值限制为式(7)后,可有效缩减加速工况需要搜索的空间。
具体在本文中,选取DTraw=300s。进行上述离散后,可基于1.2节双闭环构架实现对加速工况的逐段优化和自动生成。
本研究采用考虑电池主导衰减机理的半经验寿命模型评估动力电池老化路径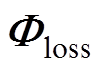 以及计算老化路径误差d,本节对此模型进行介绍。
以及计算老化路径误差d,本节对此模型进行介绍。
本研究采用如图6所示的考虑固相扩散的半经验分数阶模型表征电池主导机理,并通过建模主导机理的衰减来得到考虑主导衰减机理的半经验寿命模型。具体地,图6所示的半经验分数阶模型包含7个与电池机理相关的物理参数[31],各物理参数见表1。
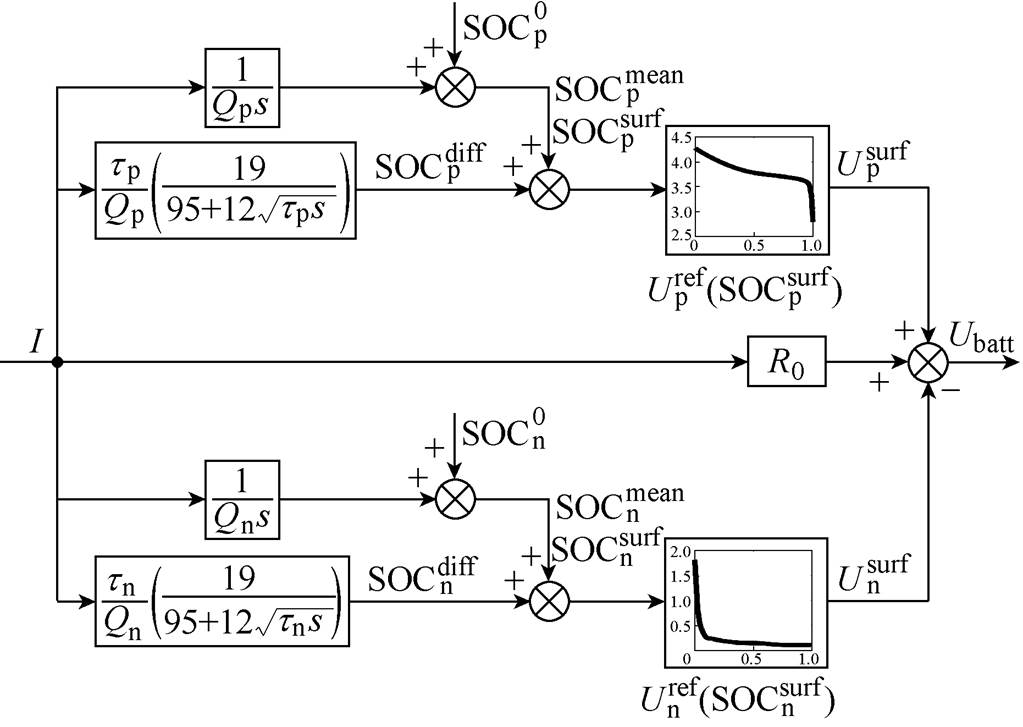
图6 考虑固相扩散的半经验分数阶模型
Fig.6 Semi empirical fractional-order model considering solid phase diffusion
表1 与电池机理相关的物理参数
Tab.1 Physical parameters related to battery mechanism
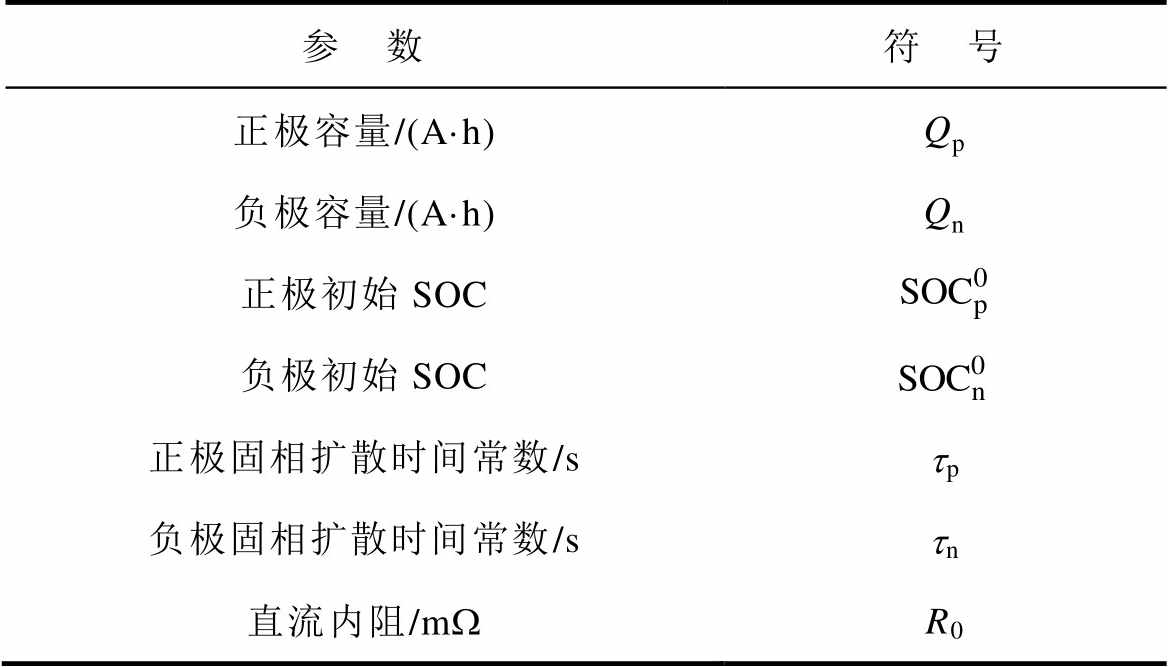
参 数符 号 正极容量/(A·h)Qp 负极容量/(A·h)Qn 正极初始SOC 负极初始SOC 正极固相扩散时间常数/stp 负极固相扩散时间常数/stn 直流内阻/mWR0
对于电池主导机理衰减规律的建模,帕里斯定律(Paris’s law)虽然能从微观层面描述电流冲击对电极材料颗粒疲劳损伤的影响[32-33],但据此建立和宏观锂离子电池寿命的联系仍需要引入复杂的偏微分方程[34-35],这导致需要辨识过多参数并增加工程应用的难度。Ouyang Minggao等在帕里斯定律积分式的基础上,结合J. Wang等基于大量电池实验结果建立的容量衰减经验模型[12],提出改进的阿伦尼乌斯公式并建立考虑电流冲击的电池寿命模型,同时验证了电池的主导衰减机理均可通过此模型描 述[10]。据此,本研究采用式(8)所示改进的阿伦尼乌斯公式描述半经验分数阶模型中7个物理参数的衰减规律。
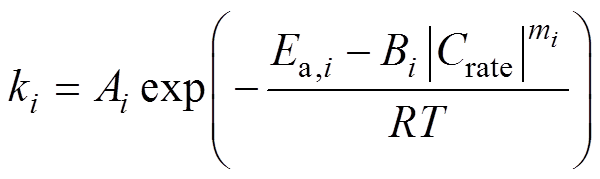 (8)
(8)
式中,ki为物理参数i的衰减速率;i为表1中的物理参数;Ai为阿伦尼乌斯公式指前因子[36],也称为阿伦尼乌斯常数;Ea,i为活化能;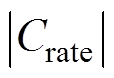 为电流倍率的绝对值;Bi为倍率因子系数,根据帕里斯定律,其为与锂离子电池材料有关的常数;mi为倍率因子指数,也是与锂离子电池材料有关的常数;R为理想气体常数;T为绝对温度。
为电流倍率的绝对值;Bi为倍率因子系数,根据帕里斯定律,其为与锂离子电池材料有关的常数;mi为倍率因子指数,也是与锂离子电池材料有关的常数;R为理想气体常数;T为绝对温度。
本研究采用一款商用锂离子电池进行老化实验以辨识上述半经验分数阶模型中各物理参数的变化规律。实验所使用的电池参数见表2。实验采用深圳新威尔的电池充放电测试设备(Neware BTS4000- 5V100A)进行,实验电池在不同老化路径下的寿命衰减如图7所示。
表2 电池参数
Tab.2 Specifications of the battery
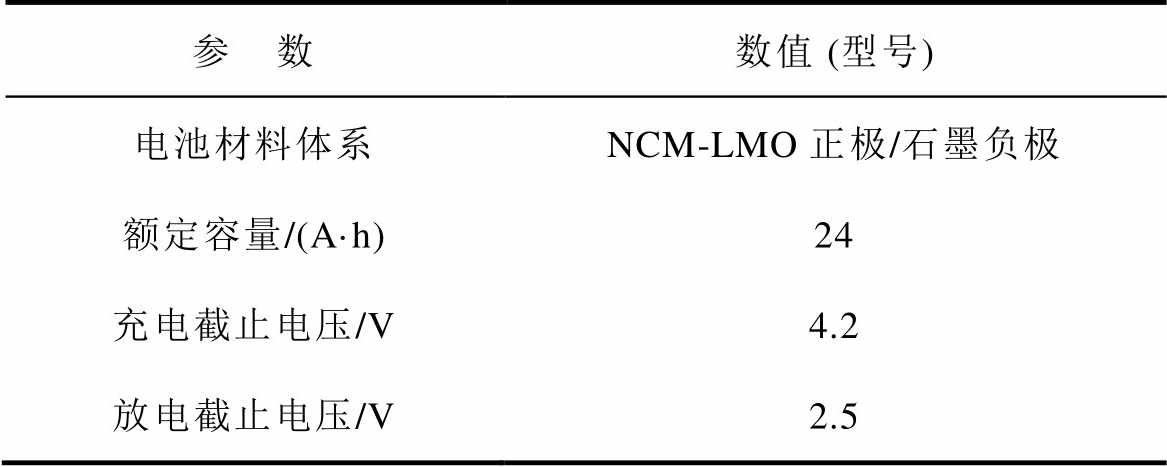
参 数数值 (型号) 电池材料体系NCM-LMO正极/石墨负极 额定容量/(A·h)24 充电截止电压/V4.2 放电截止电压/V2.5
基于上述不同老化路径下锂离子电池寿命衰减数据,对分数阶模型中各物理量的衰减规律进行辨识,得到辨识结果见表3。基于表3所示参数构建考虑主导衰减机理的半经验寿命模型,建模结果如图7中实线所示,该模型作为本研究评价动力电池老化路径误差的模型基础。

图7 不同老化路径下电池容量衰减
Fig.7 Capacity degradation under different aging paths
表3 式(8)中不同物理量的衰减参数
Tab.3 Correlated parameters in Eq.(8) for different physical quantities
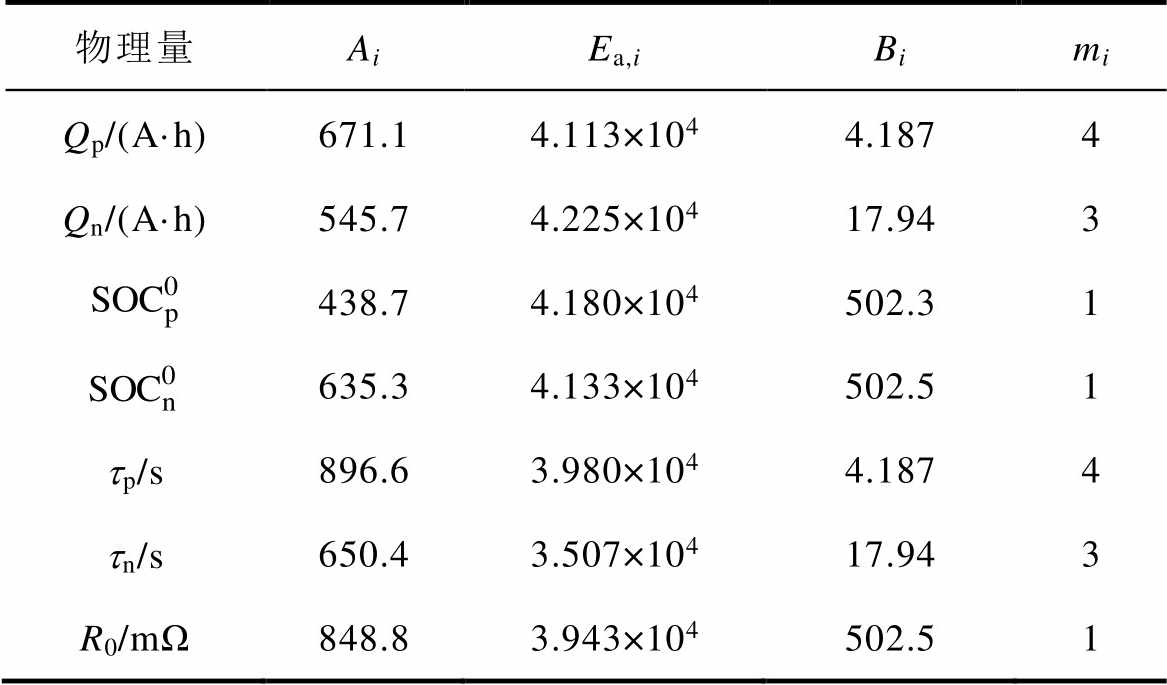
物理量AiEa,iBimi Qp/(A·h)671.14.113×1044.1874 Qn/(A·h)545.74.225×10417.943 438.74.180×104502.31 635.34.133×104502.51 tp/s896.63.980×1044.1874 tn/s650.43.507×10417.943 R0/mΩ848.83.943×104502.51
本研究的重点在于基于动力电池的典型运行工况,自动生成其对应的加速寿命工况。关于动力电池典型工况的获取已有很多研究[19, 37],且工信部也已发布了由中国汽车技术研究中心主要起草的中国汽车行驶工况[20, 38]。因此,本研究直接基于中国轻型汽车行驶工况中的乘用车行驶工况CLTC-P作为典型工况,自动生成其对应的加速寿命工况,并进行相应的结果分析和讨论。
乘用车行驶工况CLTC-P为车速工况,本研究采用中国汽车技术研究中心推出的EV-TEST电动汽车测试评价规程中的测试和计算方法将其转化为对应的电流倍率工况[39]。转化后的电流倍率工况如图8所示,其将作为生成加速寿命工况的原始工况。
在本研究中,认为加速寿命工况应尽可能与原始工况对锂离子电池造成的老化路径一致,因此老化路径误差应在目标函数中占据较大权重。基于此,本研究将权重系数a 设定为1/6(即认为老化路径误差的重要性5倍于加速因子)。在此权重系数条件下,针对原始工况CLTC-P的优化目标函数结果如图9所示。从图9中可以看出,当加速因子b 为2.5时目标函数取得最小值。
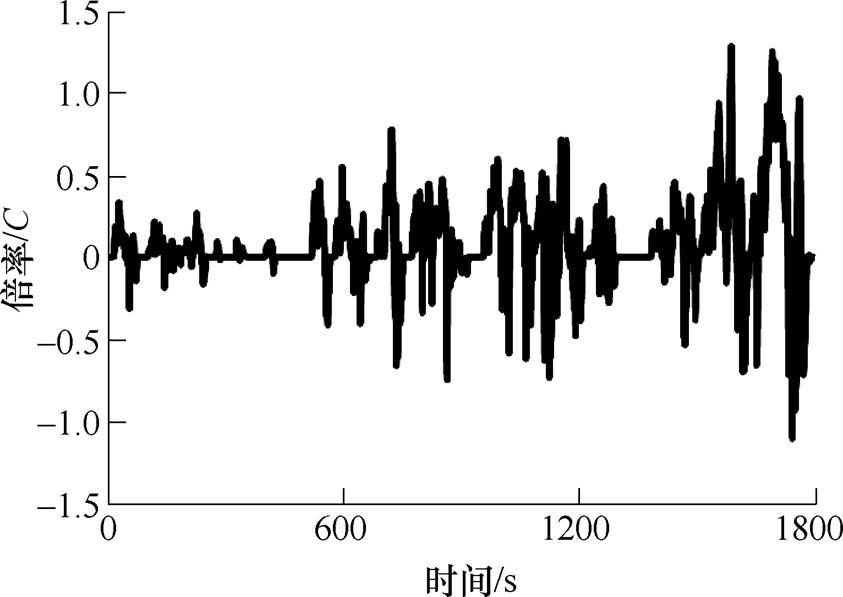
图8 CLTC-P电流倍率工况
Fig.8 CLTC-P current rate profile
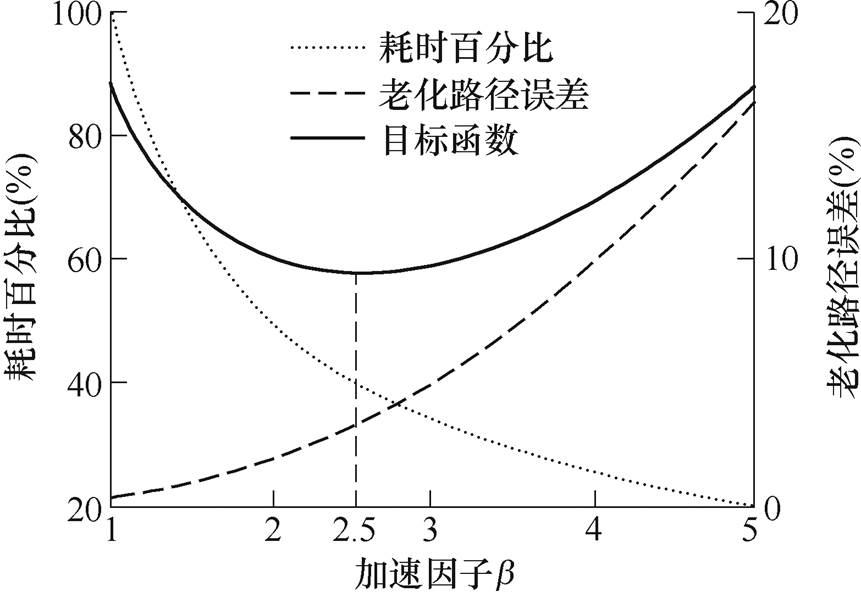
图9 权重系数a 为1/6时的目标函数曲线
Fig.9 Objective function curve when a is 1/6
当目标函数取得最小值时,基于原始工况CLTC-P生成的加速寿命工况如图10所示。相比原始工况的时长1 800s,生成的加速寿命工况时长仅为720s,这意味着使用加速寿命工况可节约60%的寿命测试时间。
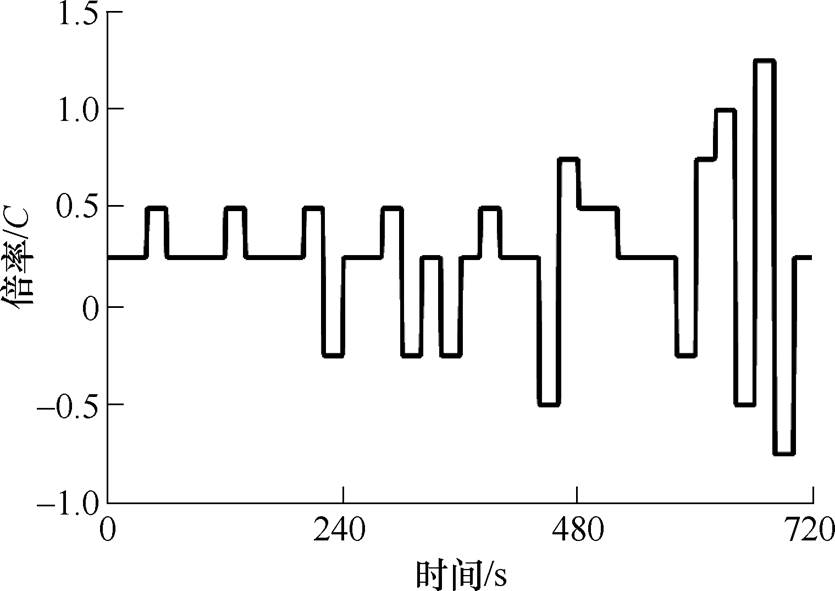
图10 生成的加速寿命工况
Fig.10 The accelerated aging profile
如第2节所述,本研究采用反映电池主导衰减机理的半经验寿命模型评估动力电池老化路径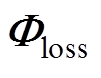 以及计算老化路径误差d。具体为,采用模型中7个物理参数的变化规律来评估电池老化路径
以及计算老化路径误差d。具体为,采用模型中7个物理参数的变化规律来评估电池老化路径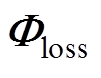 。关于动态工况导致的Qp、Qn、
。关于动态工况导致的Qp、Qn、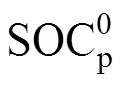 、
、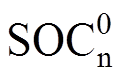 和R0的参数演变规律,Ouyang Minggao等的工作中已给出初步结果和分析[10]。出于篇幅考虑,本节只对比原始工况和加速寿命工况导致的固相扩散时间常数(tp和tn)变化差异,如图11所示。从图11中可以看出,基于本研究加速工况生成算法生成的加速寿命工况造成的动力电池老化路径与原始工况造成的动力电池老化路径基本一致。
和R0的参数演变规律,Ouyang Minggao等的工作中已给出初步结果和分析[10]。出于篇幅考虑,本节只对比原始工况和加速寿命工况导致的固相扩散时间常数(tp和tn)变化差异,如图11所示。从图11中可以看出,基于本研究加速工况生成算法生成的加速寿命工况造成的动力电池老化路径与原始工况造成的动力电池老化路径基本一致。
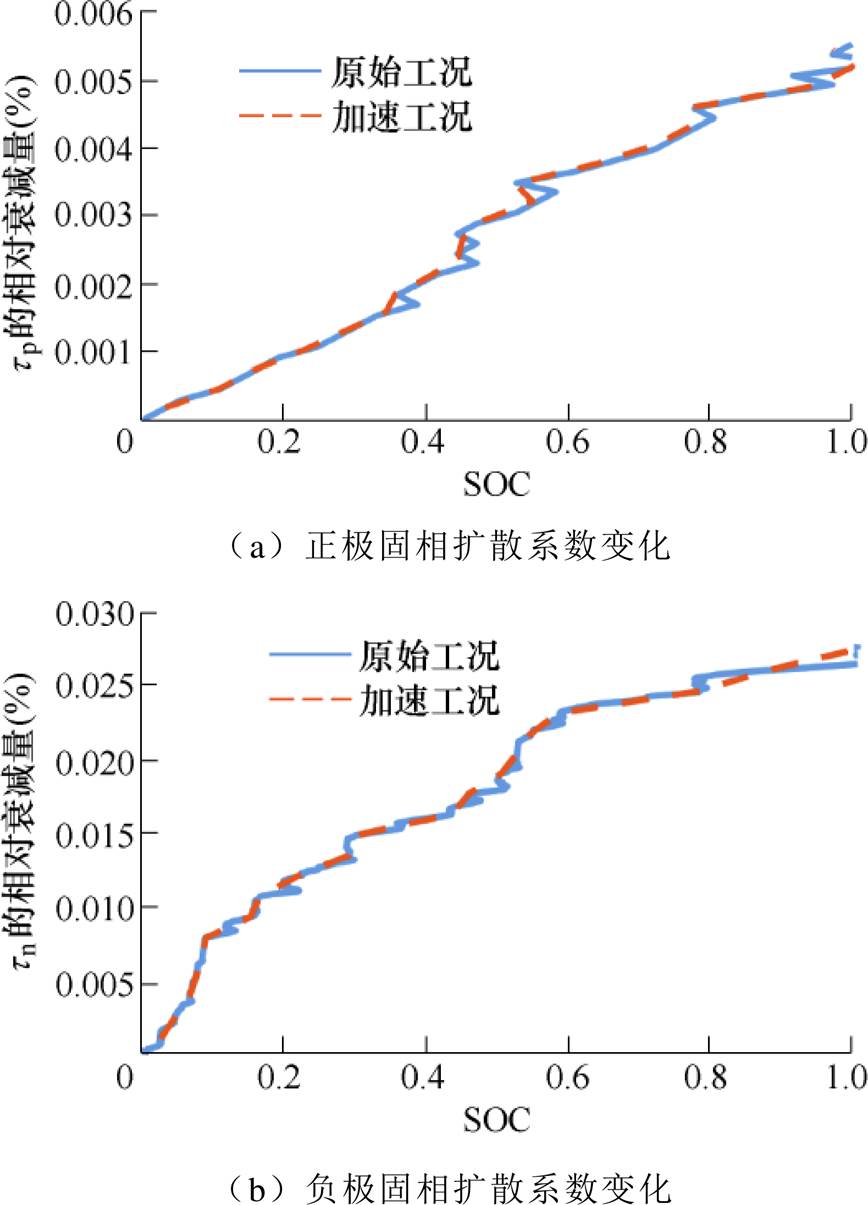
图11 原始工况和加速寿命工况导致的关键参数变化
Fig.11 Comparison of the key parametes change caused by the original profile and the accelerated aging profile
本研究考虑锂离子电池寿命对使用路径的依赖性,提出了计及老化路径的锂离子电池寿命工况自动生成方法。方法基于电荷量相等、加速和最小误差三个原则,设计了目标函数最优化加速因子和老化路径误差这两个指标。进一步地,考虑加速寿命工况的搜索过程,方法采用双闭环自动实现对目标函数的求解和最优工况的生成。
方法采用反映电池主导衰减机理的半经验寿命模型进行验证。该模型以锂离子电池工况为输入,以表征锂离子电池内部主导衰减机理的物理量为输出。加速寿命工况和原始工况造成的寿命衰减路径的误差通过模型中的7个物理参数构成的误差矩阵的F范数进行衡量。模型验证结果表明,所提方法生成的加速寿命工况可在保证电池老化路径基本不变的情况下有效实现对原始工况的加速。
将动力电池在原始工况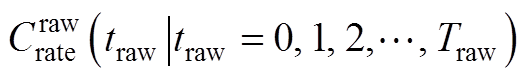 下的老化路径记为
下的老化路径记为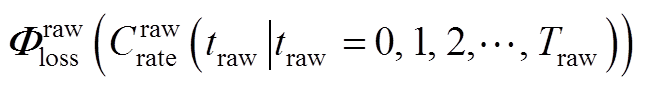 ,在加速寿命工况
,在加速寿命工况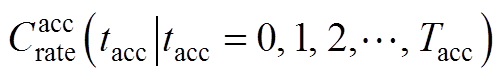 下的老化路径记为
下的老化路径记为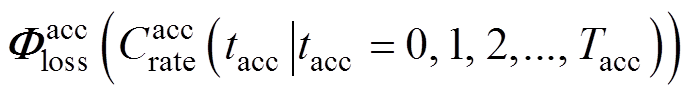 。其中
。其中
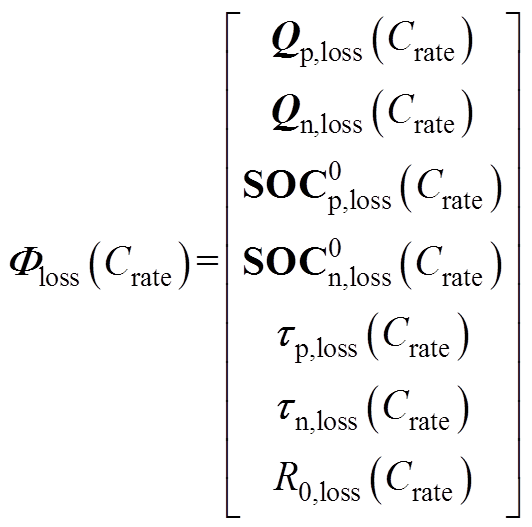 (A1)
(A1)
式中,各物理量的定义见表1。式(A1)中各物理量的衰减均采用相对值,即衰减量与该物理量初值的比例。同时,式(A1)中,各物理量均为一时间序列,在原始工况导致的老化路径下,该时间序列长度为Traw;在加速寿命工况导致的老化路径下,该时间序列长度为Tacc。首先,分别根据原始工况和加速寿命工况求其时间序列对应的安时积分序列。记原始工况安时积分序列的第j项为
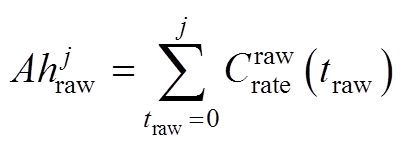 (A2)
(A2)
记加速寿命工况安时积分序列的第k项为
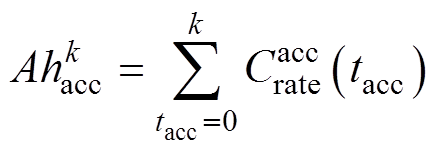 (A3)
(A3)
根据电荷量相等约束,有
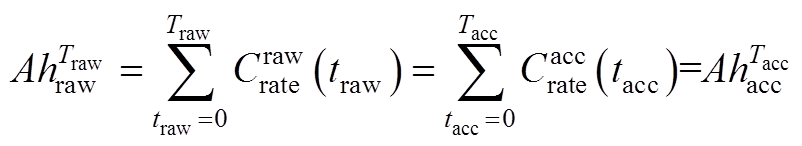 (A4)
(A4)
将此电荷量记为
 (A5)
(A5)
则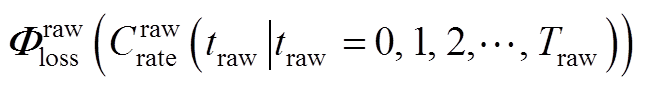 在安时坐标系下可以表示为
在安时坐标系下可以表示为
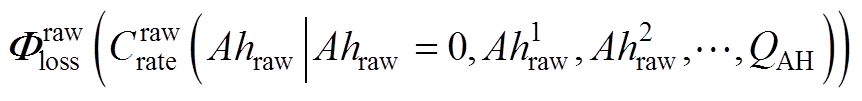 (A6)
(A6)
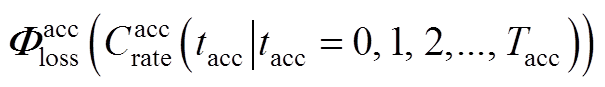 在安时坐标系下可以表示为
在安时坐标系下可以表示为
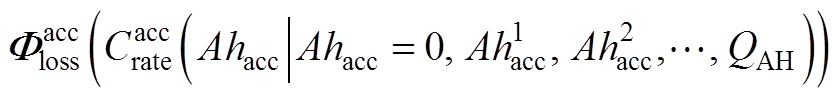 (A7)
(A7)
对比式(A6)和式(A7)的安时积分序列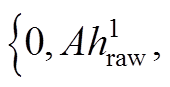
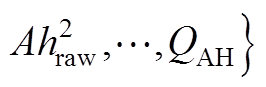 和
和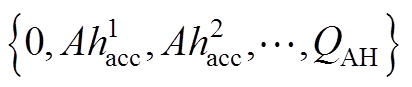 ,二者具有相同的初值和终值,但序列长度不同。这使得式(A6)和式(A7)由于序列长度不同无法直接做差比较,但可以通过对式(A6)进行降采样的方式,使其与式(A7)序列长度相同。对式(A6)在
,二者具有相同的初值和终值,但序列长度不同。这使得式(A6)和式(A7)由于序列长度不同无法直接做差比较,但可以通过对式(A6)进行降采样的方式,使其与式(A7)序列长度相同。对式(A6)在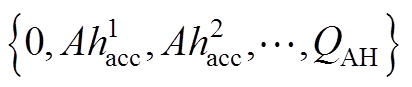 处进行采样,得到
处进行采样,得到
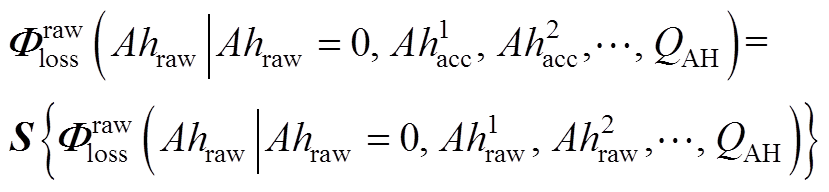 (A8)
(A8)
式中,S为采样函数。于是原始工况导致的电池老化路径与加速寿命工况导致的电池老化路径的相对误差可以表示为
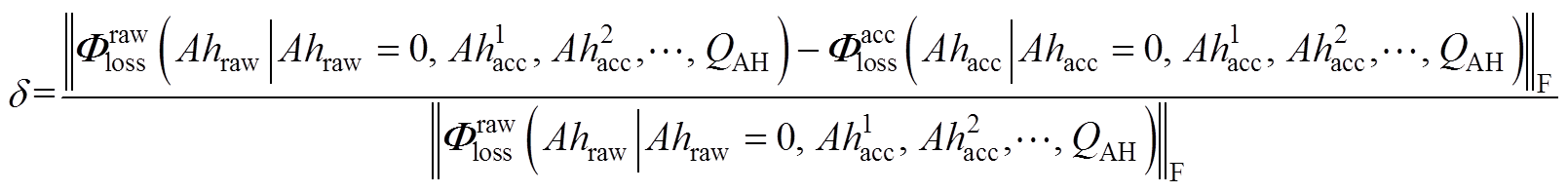 (A9)
(A9)
简记为
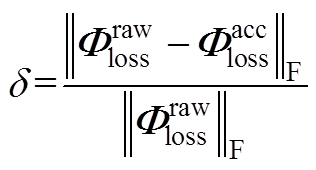 (A10)
(A10)
式(A10)即正文式(2)。
参考文献
[1] Lu Languang, Han Xuebing, Li Jianqiu, et al. A review on the key issues for lithium-ion battery management in electric vehicles[J]. Journal of Power Sources, 2013, 226: 272-288.
[2] 严康为, 龙鑫林, 鲁军勇, 等. 高倍率磷酸铁锂电池简化机理建模与放电特性分析[J]. 电工技术学报, 2022, 37(3): 599-609.
Yan Kangwei, Long Xinlin, Lu Junyong, et al. Simplified mechanism modeling and discharge characteristic analysis of high C-rate LiFePO4 battery[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 599-609.
[3] 肖迁, 焦志鹏, 穆云飞, 等. 基于LightGBM的电动汽车行驶工况下电池剩余使用寿命预测[J]. 电工技术学报, 2021, 36 (24): 5176-5185.
Xiao Qian, Jiao Zhipeng, Mu Yunfei, et al. LightGBM based remaining useful life prediction of electric vehicle lithium-ion battery under driving con- ditions[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5176-5185.
[4] Han Xuebing, Lu Languang, Zheng Yuejiu, et al. A review on the key issues of the lithium ion battery degradation among the whole life cycle[J]. eTransportation, 2019, 1: 100005.
[5] 王萍, 弓清瑞, 张吉昂, 等. 一种基于数据驱动与经验模型组合的锂电池在线健康状态预测方法[J]. 电工技术学报, 2021, 36(24): 5201-5212.
Wang Ping, Gong Qingrui, Zhang Ji’ang, et al. An online state of health prediction method for lithium batteries based on combination of data-driven and empirical model[J]. Transactions of China Electro- technical Society, 2021, 36(24): 5201-5212.
[6] 柴炜, 李征, 蔡旭, 等. 基于使用寿命模型的大容量电池储能系统变步长优化控制方法[J]. 电工技术学报, 2016, 31(14): 58-66.
Chai Wei, Li Zheng, Cai Xu, et al. Variable step-size control method of large capacity battery energy storage system based on the life model[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(14): 58-66.
[7] 刘伟, 杨耕, 孟德越, 等.计及常用恒流工况的锂离子电池建模方法[J].电工技术学报, 2021, 36(24): 5186-5200.
Liu Wei, Yang Geng, Meng Deyue, et al. Modeling method of lithium-ion battery considering commonly used constant current conditions[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5186- 5200.
[8] Ma Zeyu, Jiang Jiuchun, Shi Wei, et al. Investigation of path dependence in commercial lithium-ion cells for pure electric bus applications: aging mechanism identification[J]. Journal of Power Sources, 2015, 274: 29-40.
[9] Su Laisuo, Zhang Jianbo, Huang Jun, et al. Path dependence of lithium ion cells aging under storage conditions[J]. Journal of Power Sources, 2016, 315: 35-46.
[10] Ouyang Minggao, Feng Xuning, Han Xuebing, et al. A dynamic capacity degradation model and its applications considering varying load for a large format li-ion battery[J]. Applied Energy, 2016, 165: 48-59.
[11] Li S E, Wang Baojin, Peng H, et al. An electrochemistry- based impedance model for lithium-ion batteries[J]. Journal of Power Sources, 2014, 258: 9-18.
[12] Wang J, Liu Ping, Hicks-Garner J, et al. Cycle-life model for graphite-LiFePO4 cells[J]. Journal of Power Sources, 2011, 196(8): 3942-3948.
[13] Simolka M, Heger J-F, Kaess H, et al. Influence of cycling profile, depth of discharge and temperature on commercial LFP/C cell ageing: post-mortem material analysis of structure, morphology and chemical composition[J]. Journal of Applied Electrochemistry, 2020, 50(11): 1101-1117.
[14] Preger Y, Barkholtz H M, Fresquez A, et al. Degra- dation of commercial lithium-ion cells as a function of chemistry and cycling conditions[J]. Journal of the Electrochemical Society, 2020, 167(12): 120532.
[15] Gering K L, Sazhin S V, Jamison D K, et al. Investigation of path dependence in commercial lithium-ion cells chosen for plug-in hybrid vehicle duty cycle protocols[J]. Journal of Power Sources, 2011, 196(7): 3395-3403.
[16] 孙丙香, 刘佳, 韩智强, 等. 不同区间衰退路径下锂离子电池的性能相关性及温度适用性分析[J]. 电工技术学报, 2020, 35(9): 2063-2073.
Sun Bingxiang, Liu Jia, Han Zhiqiang, et al. Per- formance correlation and temperature applicability of Li-ion batteries under different range degradation paths[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2063-2073.
[17] 孙丙香, 任鹏博, 陈育哲, 等. 锂离子电池在不同区间下的衰退影响因素分析及任意区间的老化趋势预测[J]. 电工技术学报, 2021, 36(3): 666-674.
Sun Bingxiang, Ren Pengbo, Chen Yuzhe, et al. Analysis of influencing factors of degradation under different interval stress and prediction of aging trend in any interval for lithium-ion battery[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 666- 674.
[18] 张谦, 邓小松, 岳焕展, 等. 计及电池寿命损耗的电动汽车参与能量-调频市场协同优化策略[J]. 电工技术学报, 2022, 37(1): 72-81.
Zhang Qian, Deng Xiaosong, Yue Huanzhan, et al. Coordinated optimization strategy of electric vehicle cluster participating in energy and frequency regu- lation markets considering battery lifetime degra- dation[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 72-81.
[19] 孙逢春, 孟祥峰, 林程, 等. 电动汽车动力电池动态测试工况研究[J]. 北京理工大学学报, 2010, 30(3): 297-301.
Sun Fengchun, Meng Xiangfeng, Lin Cheng, et al. Dynamic stress test profile of power battery for electric vehicle[J]. Transactions of Beijing Institute of Technology, 2010, 30(3): 297-301.
[20] 中国汽车技术研究中心有限公司. 中国汽车行驶工况 第1部分: 轻型汽车[S]. 国家市场监督管理总局;中国国家标准化管理委员会, 2019.
[21] 霍云龙, 杨钫, 王燕, 等. 新能源汽车能耗测试评价规程比较研究[J]. 汽车文摘, 2020(8): 11-14.
Huo Yunlong, Yang Fang, Wang Yan, et al. Com- parison and study of NEV energy consumption test and evaluation procedures[J]. Automotive Digest, 2020(8): 11-14.
[22] Takei K, Kumai K, Kobayashi Y, et al. Cycle life estimation of lithium secondary battery by extrapo- lation method and accelerated aging test[J]. Journal of Power Sources, 2001, 97: 697-701.
[23] Saxena S, Xing Yinjiao, Kwon D, et al. Accelerated degradation model for C-rate loading of lithium-ion batteries[J]. International Journal of Electrical Power & Energy Systems, 2019, 107: 438-445.
[24] Saxena S, Roman D, Robu V, et al. Battery stress factor ranking for accelerated degradation test planning using machine learning[J]. Energies, 2021, 14(3): 723.
[25] Jiang Jiuchun, Gao Yang, Zhang Caiping, et al. Lifetime rapid evaluation method for lithium-ion battery with Li(NiMnCo)O2 cathode[J]. Journal of the Electrochemical Society, 2019, 166(6): 1070-1081.
[26] Stroe D I, Swierczynski M, Laserna E M, et al. Accelerated aging of lithium-ion batteries based on electric vehicle mission profile[C]//IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, 2017: 5631-5637.
[27] Yurkowsky W, Schafer R, Finkelstein J M. Accelerated testing technology[R]. Hughes Aircraft CO Fullerton CA Ground Systems Group, 1967.
[28] 陈志军, 王前程, 陈云霞. 基于寿命分布和贝叶斯的加速因子确定方法[J]. 系统工程与电子技术, 2015, 37(5): 1224-1228.
Chen Zhijun, Wang Qiancheng, Chen Yunxia. Deter- mination method of acceleration factor based on life distribution and bayes[J]. Systems Engineering and Electronics, 2015, 37(5): 1224-1228.
[29] 张栋, 张刘春, 傅正财. 基于改进禁忌算法的配电网络重构[J]. 电工技术学报, 2005, 20(11): 60-64.
Zhang Dong, Zhang Liuchun, Fu Zhengcai. Network reconfiguration in distribution systems using a modified TS algorithm[J]. Transactions of China Electrotechnical Society, 2005, 20(11): 60-64.
[30] 王凌. 智能优化算法及其应用[M]. 北京: 清华大学出版社, 2001.
[31] Guo Dongxu, Yang Geng, Feng Xuning, et al. Physics- based fractional-order model with simplified solid phase diffusion of lithium-ion battery[J]. Journal of Energy Storage, 2020, 30: 101404.
[32] Paris P, Erdogan F. A critical analysis of crack propagation laws[J]. Journal of Basic Engineering, 1963, 85(4): 528-533.
[33] Deshpande R, Verbrugge M, Cheng Yang-Tse, et al. Battery cycle life prediction with coupled chemical degradation and fatigue mechanics[J]. Journal of the Electrochemical Society, 2012, 159(10): 1730-1738.
[34] Safari M, Morcrette M, Teyssot A, et al. Life- prediction methods for lithium-ion batteries derived from a fatigue approach I. introduction: capacity-loss prediction based on damage accumulation[J]. Journal of the Electrochemical Society, 2010, 157(6): 713- 720.
[35] Safari M, Morcrette M, Teyssot A, et al. Life prediction methods for lithium-ion batteries derived from a fatigue approach II. capacity-loss prediction of batteries subjected to complex current profiles[J]. Journal of the Electrochemical Society, 2010, 157(7): 892-898.
[36] Laidler K J. The development of the Arrhenius equation[J]. Journal of Chemical Education, 1984, 61(6): 494.
[37] 张曼, 施树明. 面向汽车运行工况设计的马氏链非等长交叉进化算法[J]. 浙江大学学报(工学版), 2018, 52(9): 1658-1666.
Zhang Man, Shi Shuming. Non-isometric crossover evolution algorithm of Markov chain for designing vehicle driving cycles[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(9): 1658-1666.
[38] 中国汽车技术研究中心有限公司. 中国汽车行驶工况 第2部分: 重型商用车辆[S]. 国家市场监督管理总局; 中国国家标准化管理委员会, 2019.
[39] 陈光, 张妍懿, 郝冬, 等. EV-TEST评价体系中性能指标的确定分析[J]. 汽车工程师, 2017(11): 14-17.
Chen Guang, Zhang Yanyi, Hao Dong, et al. Defini- tion and analysis on performance items of EV-TEST evaluation system[J]. Auto Engineer, 2017(11): 14-17.
Accelerated Aging Profile Generation Method for Lithium-Ion Batteries Considering Aging Path
Abstract The lithium-ion battery (LiB) requires an aging test to ensure its reliability during long-term use. The conventional aging test is very time-consuming because the current LiB life span is thousands of cycles. Therefore, an accelerated aging test method for LiB is needed. The degradation of the LiB is path-dependent. Therefore, the constraints of designing this accelerated aging test method are: to ensure both the equivalence of LiB capacity and the invariance of its internal degradation mechanism. This paper proposes a model-based method for generating an accelerated aging profile. The objective function considering the acceleration factor and the relative error of the aging path is constructed, and the optimal solution of the objective function is obtained by a double closed-loop architecture. In the double closed-loop architecture, the outer loop is an acceleration factor optimization algorithm that aims to find the optimal acceleration factor; the inner loop is an acceleration profile search algorithm, aiming to search the optimal acceleration profile under a given acceleration factor. The accelerated aging profile of the China light-duty vehicle test cycle-passenger car (CLTC-P) is generated under the given objective function based on the proposed method. The simulation is carried out based on the semi-empirical fractional-order model considering the dominant degradation mechanism of the LiB developed by the authors, which verifies the effectiveness of the method.
keywords:Lithium-ion battery, aging path, double closed-loop architecture, acceleration factor, tabu search
DOI: 10.19595/j.cnki.1000-6753.tces.210336
中图分类号:TM912
科技部国际科技合作专项项目(2019YFE0102200)、科技部重点研发计划新能源汽车重点专项(2018YFB0104404)和台达电力电子科教发展计划项目(DREK2020001)资助。
收稿日期 2021-03-12
改稿日期 2021-07-24
郭东旭 男,1993年生,博士,研究方向为锂离子动力电池寿命建模。E-mail: guodongxu@tsinghua.edu.cn
杨 耕 男,1957年生,教授,博士生导师,研究方向为电机拖动系统与电力电子系统控制技术、风电和光伏系统的控制和优化、动力电池系统建模。E-mail: yanggeng@tsinghua.edu.cn(通信作者)
(编辑 崔文静)