（1）
摘要 为分析干式变压器在典型过载情况下绕组的轴向温度分布和热点温度，该文提出一种考虑流体动力学的热网络模型。首先，在考虑了温度对材料损耗特性的影响下，建立了干式变压器三维磁-热-流耦合仿真模型，精确模拟了干式变压器强迫散热过程，实现了不同负载系数下干式变压器绕组的温升计算和热点温度预测，高压绕组、低压绕组最热点温度的仿真结果与出厂温升试验数据的误差分别为4.1%和9.0%。在此基础上，结合有限元模型的流体场仿真结果，对热网络模型中的对流传热热阻进行修正。结果表明，热网络模型在进行对流传热热阻修正后，高压绕组、低压绕组的最热点温度的仿真结果与出厂温升试验数据的误差分别为2.9%和10.7%，轴向温度分布规律吻合度较高。该文提出的考虑流体动力学的干式变压器热网络模型克服了传统热路模型计算精度较低的问题和有限元模型计算时间长的缺点，对干式变压器的设计和运行评估具有较好的指导作用。
关键词：干式变压器 热网络模型 流体动力学 多物理场耦合 温升计算
干式变压器以阻燃性固体绝缘材料和空气为绝缘介质，主要应用在对安全环保要求较高的配电系统中。但由于其绕组一般由环氧树脂浇注而成，导热性能差，容易导致绕组内部热点温度过高，加速绝缘老化甚至引发烧毁事故[1-3]。因此，对干式变压器温度分布情况和热点温度的预测在设计和运行阶段都是至关重要的。
目前，对干式变压器温度场的计算有两类方法：一类是数值分析方法；另一类是热网络模型。数值分析方法注重求解偏微分方程的近似解。文献[4]通过分析干式变压器的温度场和流体场之间的关系，进行流固耦合建模仿真，得到了干式变压器内部温度场的分布情况。电与热在时间尺度上的差异为电热耦合仿真带来了不便[5]。文献[6]首先对电磁场进行三维建模分析，将得到的损耗作为热源代入二维热-流场模型中，实现了电-热流的单向耦合。文献[7]提出在Simulink和COMSOL中分别构建基于物理模型的电路模型和基于有限元的热模型，通过Matlab控制脚本实现了电热联合仿真，为电热耦合仿真提供了新的思路。文献[8-9]提出了完整的电磁-热流分析，在充分考虑温度对电磁损耗计算的影响后，通过迭代计算实现了电磁-热流的双向耦合。然而，有限元法对网格质量要求过高[10]，为提高计算效率，文献[11-12]在计算流体场时使用了有限体积法，但面临计算精度受限的问题。数值分析方法已经成为国内外学者的重要研究手段，但是该方法要进行密集的计算，通常需要较长的执行时间和较大的计算机内存，并且一般只用于稳态计算，不同时间尺度下的多物理场耦合仿真也存在收敛困难的问题。
基于热电类比的热路模型具有计算量小、计算时间短以及所需资源少等优点，已广泛应用于干式变压器的热点温度预测[13-14]。但是热路模型由于大量简化干式变压器的实际结构，其计算精度较低。进一步地，为了得到温度分布情况，需要同时考虑径向传热和轴向传热，此时根据径向热阻和轴向热阻的划分可将热路模型扩展为热网络模型[15-17]，热网络模型更加符合干式变压器的实际传热过程。但是，热网络模型不能反映出干式变压器空气域的流体动力学特征，使得难以准确计算对流传热热阻，温度分布和热点温度的计算误差也将随之增大。根据国际大电网会议关于变压器热建模的报告，计算流体动力学是提高热网络模型精度的最佳途径[17]，但是目前尚无用流体动力学去修正干式变压器热网络模型的先例。
基于上述问题，本文提出了一种考虑流体动力学的干式变压器热网络模型。首先，利用热电类比关系建立了热网络模型。然后，针对不同负载系数下干式变压器强迫对流散热问题建立了基于磁-热-流耦合的三维有限元模型，得到了相应的温度场和流体场的分布情况。结合流体场流速计算结果对热网络模型进行了修正，提高了热网络模型的计算精度。最后，将所提出的热网络模型应用于型号为SCB10-400kV·A/10kV的干式变压器，修正后的热网络模型的仿真结果与有限元仿真结果、温升试验数据对比，结果表明，本文提出的热网络模型具有较高的合理性与准确性。
干式变压器在运行时会产生不同形式的能量损耗，这种损耗不但会降低变压器的运行效率，还会产生热量。产热和散热共同决定着干式变压器的温升，尤其是散热能力的强弱直接影响变压器的平均温升值和热点温升值。若干式变压器长期运行在较高温度下，会加速绝缘系统的热老化，进而影响其可靠性和使用寿命。
干式变压器的内部热源包括绕组的负载损耗和铁心的空载损耗。变压器的负载损耗由电阻损耗、涡流损耗和杂散损耗组成，但由于干式变压器产生的热量是通过冷空气散发的，因此不用考虑杂散损耗[18]，所以负载损耗PCu[4]可表示为
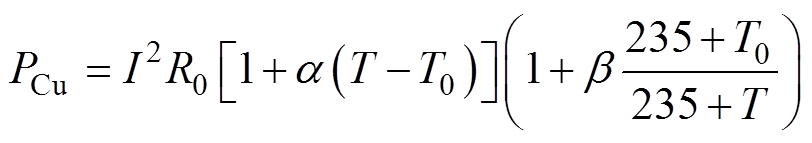（1）
式中，I为绕组电流；T为绕组温度；T0为空气温度；R0为T0时绕组的电阻；a 为电阻温度系数；b 为涡流损耗百分数。干式变压器铁心空载损耗PFe主要包括磁滞损耗和涡流损耗[19]，计算公式[4]为
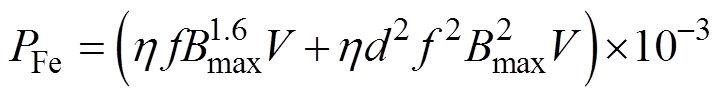（2）
式中，h 为铁心的磁滞系数；f为频率；Bmax为最大磁通密度；V为铁心体积；d为硅钢片的厚度。
上述能量损耗产生的热量将通过热传导、热对流和热辐射三种方式进行传导，干式变压器传热示意图如图1所示，具体传热路径有以下几种：①铁心、低压绕组和高压绕组通过热传导方式将热量在各自内部和表面之间传递；②铁心心柱表面、低压绕组和高压绕组的内侧及外侧表面主要通过散热气道中的空气以热对流方式进行热交换，但也有少部分热量在经过流体薄层时以热辐射方式传递到空气中；③铁心心柱表面和低压绕组内侧表面之间、低压绕组外侧表面和高压绕组内侧表面之间以及高压绕组外侧表面与外部空气之间主要以热辐射方式进行热交换，但也通过气道撑条以热传导方式进行微量的热交换，通常这部分传热可以忽略不计。
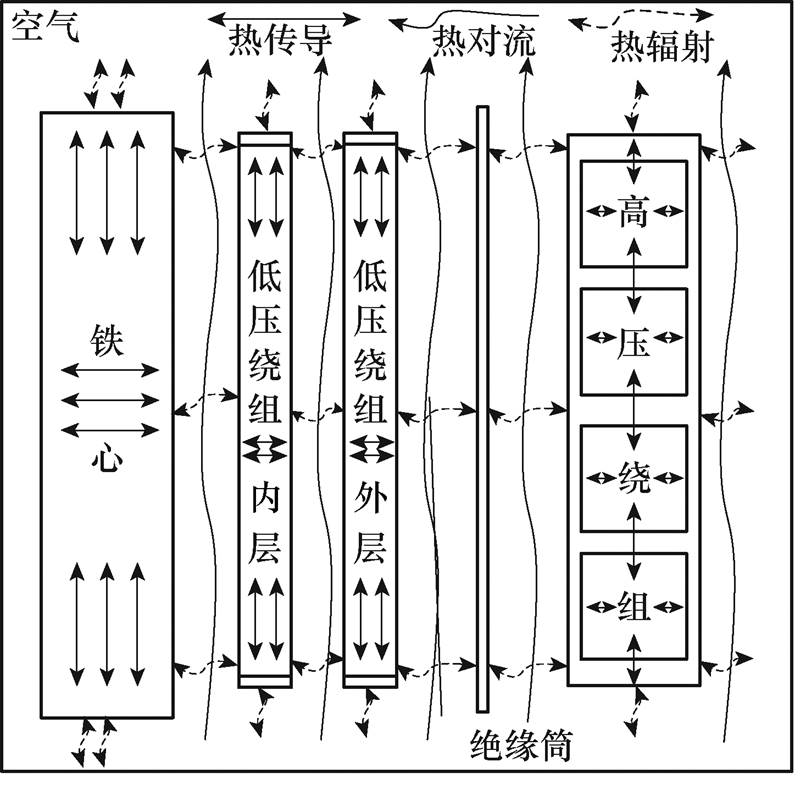
图1 干式变压器传热示意图
Fig.1 Diagram of heat transfer of dry-type transformer
热网络模型能够用于干式变压器温度场分析是因为热网络与电路的相似性。热电类比关系见表1，将热学参变量类比于电学参变量，就可以构建干式变压器的等效热网络模型。
表1 热电类比关系
Tab.1 Analogy between thermal and electric parameters
热网络参变量电路参变量 热流量Q/W电流I/A 温差DT/℃电压U/V 热阻Rth/(℃/W)电阻R/W 热容Cth/(J/℃)电容C/F
干式变压器为平面中心轴对称结构，取其中一相进行分析，其局部热网络模型如图2所示。干式变压器的热网络模型中的内部热源用电流源表示。环境温度是能够轻易获得的唯一的外部边界条件，用电压源表示。通常建立的热网络模型没有考虑实际变压器的温度分布情况，仅注重于求解平均温升，与实际情况不符。为了表征干式变压器在轴向上存在温度差而引起的热量流动，在轴向上将干式变压器划分为N部分，用轴向热阻来模拟沿轴向方向的传热，轴向传热热阻[16]为
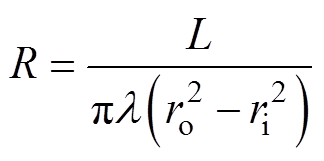（3）
图2 考虑轴向和径向热流的干式变压器热网络模型
Fig.2 Thermal network of dry-type transformer with axial and radial thermal flow
式中，l 为介质导热系数；L为圆筒长度；ro和ri分别为圆筒的外半径和内半径。一般来说，N值越大，热网络模型精度越高，计算模型的复杂性增大[16]。
干式变压器绕组绝缘层的径向传热过程可认为是圆筒壁导热和平壁导热相并联，其传导热阻Rcond可通过式（4）和式（5）计算[16]，有
（4）
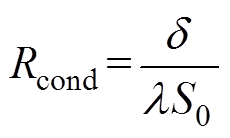（5）
式中，d 为平壁的厚度；S0为平壁的表面积。
干式变压器中的热辐射存在于铁心和低压绕组之间、低压绕组和高压绕组之间、高压绕组和空气域之间，可以看作是两个漫灰表面组成的封闭腔的辐射传热，径向传热过程中的辐射传热热阻可计 算[20]为
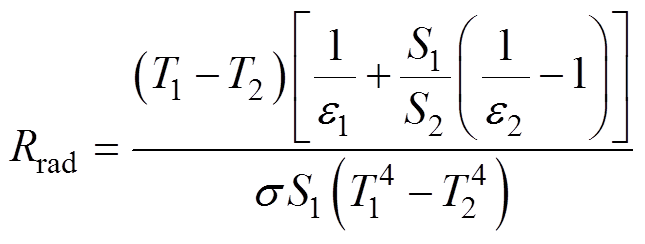（6）
式中，s 为斯蒂芬-玻耳兹曼常数；S1和S2分别为两个表面的面积；e1和e2分别为两个表面的发射率；T1和T2分别为两个表面的温度。
干式变压器的对流传热与流体的物理性质、流动状态以及换热界面的几何因素、温差等有关，因而对流传热的过程是非线性的，径向传热过程中的对流传热热阻可计算为
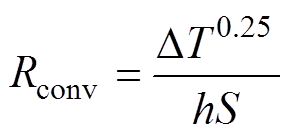（7）
式中，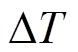
为换热界面处固体表面温度与流体温度的差值；h为对流传热系数；S为对流传热有效面积。然而，对流传热系数h的计算较为复杂，为了解决这一问题，使用基于磁-热-流耦合的有限元模型对热网络模型进行修正，计算了对流传热热阻。
图3为干式变压器热网络温升计算非线性迭代流程。首先需确定热网络的热阻和热容的初始值，然后确定干式变压器的负载损耗和空载损耗，此时导体电阻率取20℃时的值，施加温度边界条件，在Matlab中求取干式变压器热网络模型的各节点温度值，根据节点初始温度值计算对流热阻Rconv、辐射热阻Rrad，提取线圈节点处的温度值并修正线圈损耗值。在Matlab中计算修正过热阻和线圈损耗后的热网络各节点温度值，如此迭代计算直至两次温度值之差小于0.01K为止。可将上述计算结果作为初始值进行暂态温度场计算，绘制温升曲线。
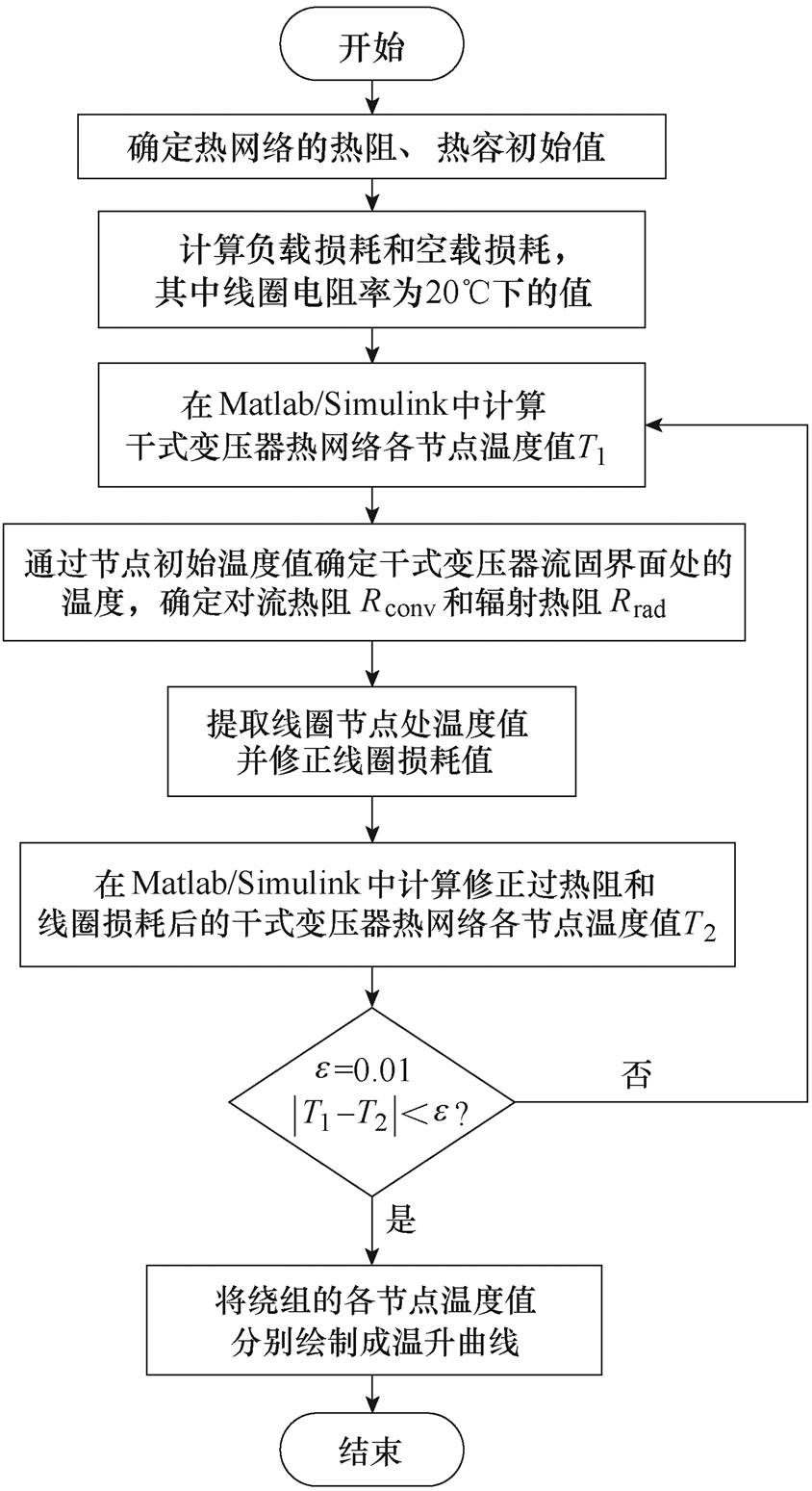
图3 干式变压器热网络温升计算非线性迭代流程
Fig.3 Non-linear iterative process of dry-type transformer thermal network temperature rise calculation
干式变压器中的固体材料通过热传导方式将热量传递到变压器表面，其中固体材料的导热微分方程是根据傅里叶导热定律和能量守恒定律确定的。对于绕组、铁心等有内热源的固体材料，其常物性的三维稳态导热微分方程如式（8）所示，对于固体绝缘材料，其介质损耗很小，可认为是无内热源的固体材料，其常物性的三维稳态导热微分方程如式（9）所示[21]。
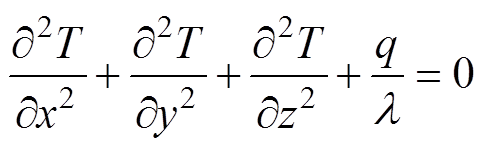（8）
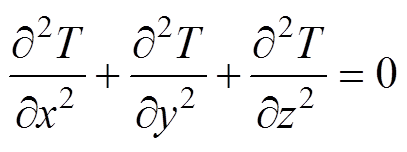（9）
式中，q为单位体积热流密度。
干式变压器周围的冷空气是对流传热的关键介质，作为一种不可压缩的牛顿型流体，它的流动和传热遵循质量守恒定律、动量守恒定律及能量守恒定律。变物性、无内热源的三维稳态控制方程[21]为
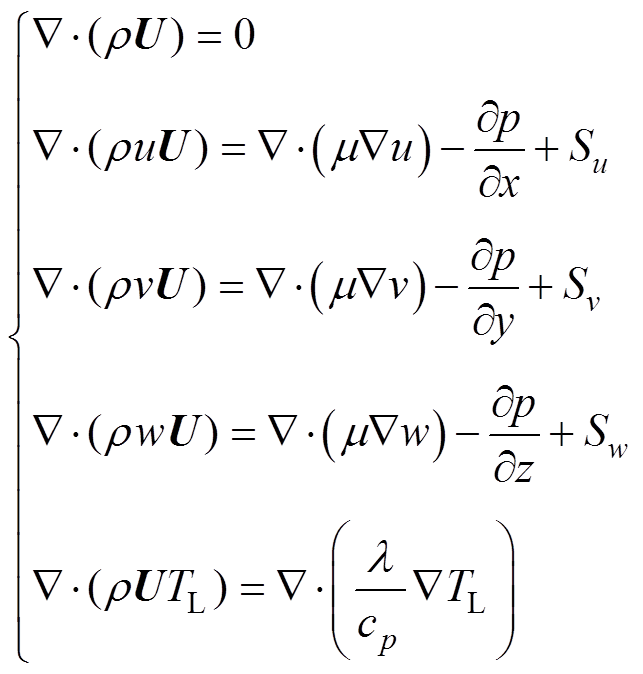（10）
式中，r 为流体密度，与温度和压力有关，与时间无关；U为速度矢量；u、v、w分别为速度矢量U在x、y、z方向的分量；m 为流体运动黏性系数；p为流体压力，p=rRT；Su、Sv、Sw为动量守恒广义源项在各个方向的分量；TL为流体温度；cp为流体比热容。
建立以干式变压器固体部分的几何中心为坐标原点的三维坐标系，如图4所示为干式变压器三维结构模型（部分结构已隐藏），固体部分遵循型号为SCB10-400kV·A/10kV的干式变压器的实际尺寸，具体样机参数见表2。流体区域根据强迫风冷散热时的实际情况去设置，即流体区域的下半部分要遵循绕组和铁心的下端面距离地面的高度以及侧吹式散热风机的位置，流体区域的上半部分取适当高度，可在流体边界设置时将流体区域的上表面设置为出口来模拟实际情况中的无穷远边界条件。
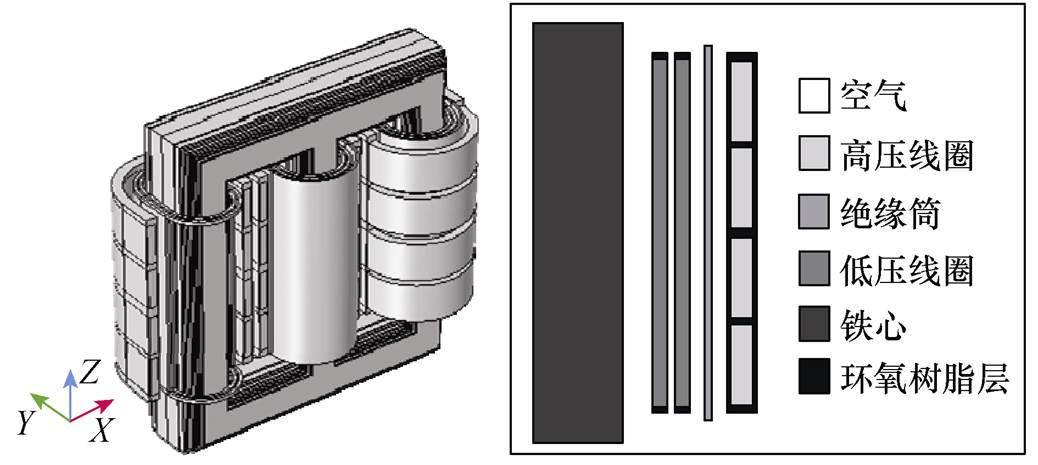
图4 干式变压器的结构模型
Fig.4 Structural model of dry-type transformer
为了能够得到可以满足工程实际需求的干式变压器温度场分布特性，且不至于消耗太大的计算成本，在建立干式变压器三维模型时还作出了以下假设：模型中主要结构有铁心、三相绕组、绝缘筒、散热气道和空气域，保留了绕组端部绝缘、高压绕组的段间绝缘以及包封绝缘，忽略了匝间绝缘、夹件、气道撑条等结构。
表2 样机参数
Tab.2 Parameters of prototype model
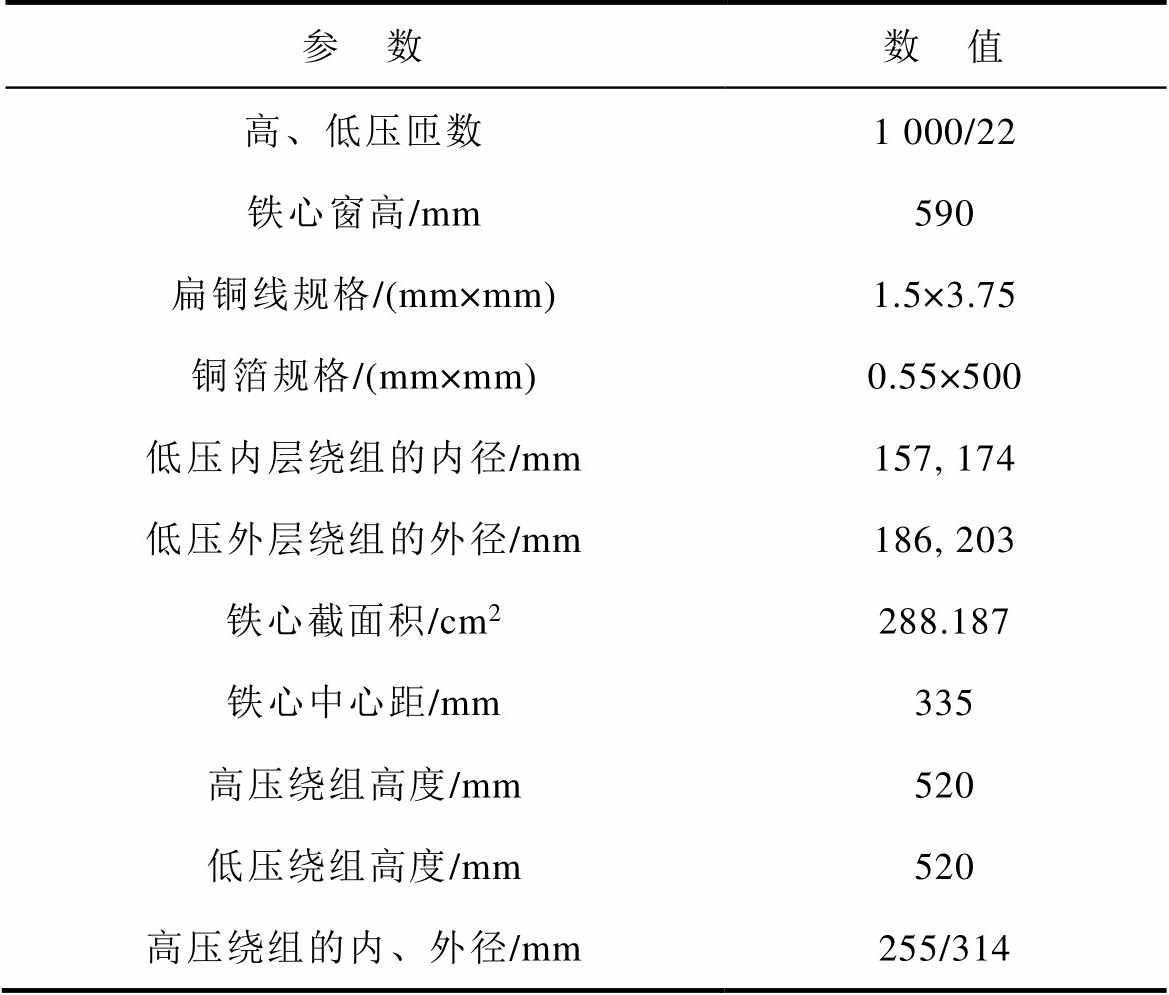
参 数数 值 高、低压匝数1 000/22 铁心窗高/mm590 扁铜线规格/(mm×mm)1.5×3.75 铜箔规格/(mm×mm)0.55×500 低压内层绕组的内径/mm157, 174 低压外层绕组的外径/mm186, 203 铁心截面积/cm2288.187 铁心中心距/mm335 高压绕组高度/mm520 低压绕组高度/mm520 高压绕组的内、外径/mm255/314
干式变压器在运行过程中，流体与固体表面间的热交换是由流体的宏观位移所致的，根据边界层理论中的流动边界层和热边界层，流体与固体之间的热交换同时也是通过固体壁面附近的流体薄层的导热进行的。在流固交界面处，由于流体的黏性作用，在靠近壁面的地方流速逐渐减小至相对于壁面静止不动，即将壁面设为无滑移边界条件。
除此之外，在几何中添加空气域，设置不同的空气流速，来精确模拟强迫空气流动冷却效果，从而减小使用近似传热系数所带来的误差。
建立物理模型时忽略了匝间绝缘的几何结构，但不能忽略匝间绝缘对绕组整体导热系数的影响。以干式变压器的低压绕组为例，其导体为铜箔，铜箔间用聚酯薄膜材料浸渍环氧固化后（DMD预浸布）作为层间绝缘，即匝间绝缘，因此径向方向的导热可以看作是多层平壁导热。根据傅里叶导热定律可推得径向等效导热系数的计算公式如式（11）所示[20, 22]。据此可将多层材料径向等效导热系数的计算扩展到低压绕组的径向等效导热系数计算中。
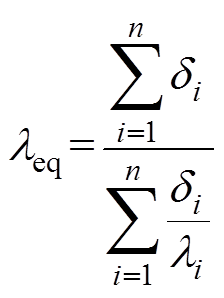（11）
式中，leq为等效绝缘的导热系数[W/(m·K)]；di为各绝缘材料的等效厚度（m）；li为相应绝缘材料的导热系数[W/(m·K)]。
干式变压器固体部分的材料物性参数见表3。铁心材料为武钢生产的公称厚度0.3mm的普通取向硅钢30Q140，铁损P1.7/50低于1.4W/kg，外层涂有绝缘漆；高压绕组的包封绝缘为环氧树脂，低压绕组的外部绝缘为DMD预浸纸，所以其固体表面辐射系数均可设定为0.9W/(m2·sr)。干式变压器周围的冷却空气的物性参数均与温度相关，其中密度还与压力有关，空气物性参数见表4。
表3 固体材料物性参数
Tab.3 The parameters of material
结构材料导热系数/ [W/(m·K)]比热容/ [J/(kg·K)]密度/ (kg/m3) 铁心30Q140204457 650 低压线圈铜箔径向0.88轴向3863858 940 高压线圈扁铜线3863858 940 绝缘环氧树脂0.262 0001 800 绝缘筒复合膜0.0351 23050
表4 空气物性参数
Tab.4 The parameters of air
物性参数表达式 密度/(kg/m3)1.263×10-0.003(T-273) 动力黏度/[kg/(m·K)]1.755×10-5+(T-273)×4.1×10-8 导热系数/[W/(m·K)]0.023 7-(T-273)×7×10-5 比热容/[J/(kg·K)]1.011+1.103×(T-273)
3.1.1 电磁损耗仿真分析
为模拟干式变压器运行在空载状态下，对高压线圈施加额定电压激励，同时使低压线圈断路。图5为稳态下的铁心磁通密度模分布，左边为ZX截面，右边为铁心外表面，铁心柱磁通密度模的仿真结果为1.54T，其理论计算值为1.56T，误差控制在1.28%，仿真计算精度满足要求。
图6为变压器空载电流，仿真结果满足设计时的裕度要求，但空载电流三相不对称，主要原因是变压器的空载电流由铁耗电流和励磁电流合成：一方面铁耗电流占比较小；另一方面对于平面叠铁心式的三相变压器，中间心柱的磁路短，两边心柱的磁路长，所以在三相心柱磁通密度模相等的情况下，中间相的励磁电流要小于另外两相的励磁电流。
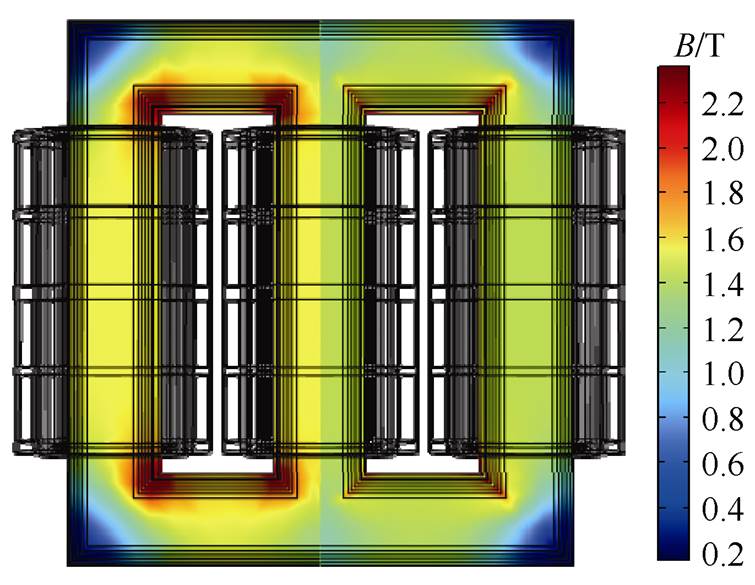
图5 铁心磁通密度模
Fig.5 Iron core flux density mode
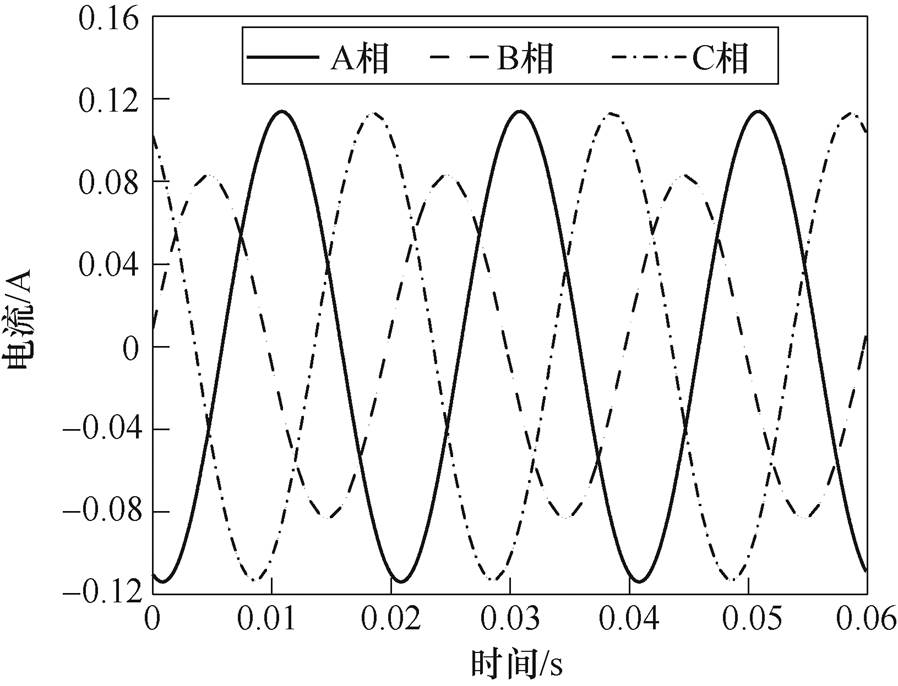
图6 空载电流
Fig.6 No-load current
为模拟干式变压器运行在额定负载状态下，对高压线圈和低压线圈分别施加其额定电流激励，线圈电导率设置为随温度变化函数。图7为干式变压器B相绕组的空间漏磁场分布，基本呈上下对称，高、低压绕组之间的漏磁场强度最强，轴向漏磁场在每一段高压绕组的中部与低压绕组之间出现最大值，并逐渐向两端递减，而在绕组端部辐向漏磁场出现最大值。根据文献[9]中提到的绕组主空道最大漏磁感应强度计算经验公式，代入相应的参数计算，得到该变压器的最大漏磁通密度模为0.054T。
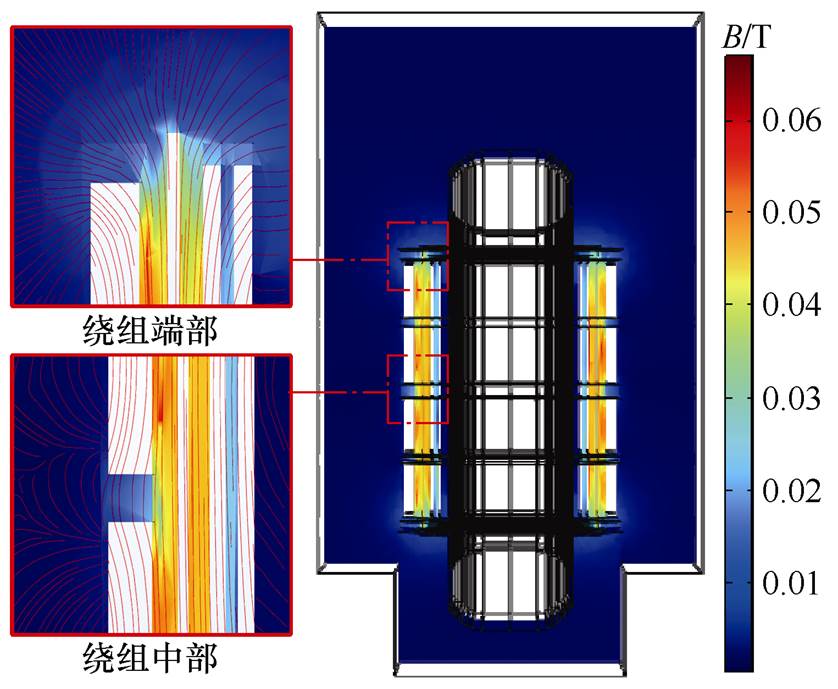
图7 变压器漏磁场分布
Fig.7 Transformer leakage magnetic field distribution
将该干式变压器的空载损耗、负载损耗的仿真值和出厂试验值进行比对分析，见表5，误差均小于5%，故该仿真模型较为可靠准确。
表5 电磁损耗参数对比
Tab.5 Comparison of electromagnetic loss parameters（单位: W）
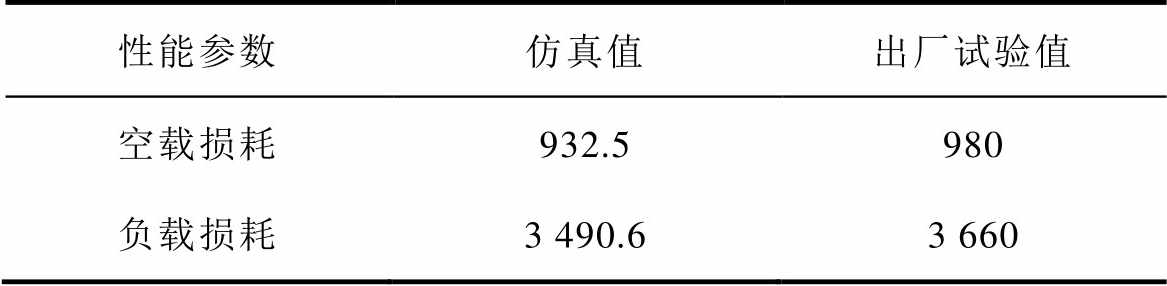
性能参数仿真值出厂试验值 空载损耗932.5980 负载损耗3 490.63 660
3.1.2 流体场仿真分析
该干式变压器采用强迫对流散热，将模型上边界设置为压力出口，表压设为0；下边界设置为速度入口。该干式变压器所用的散热风机为GFDD560- 90，每侧2台，总共4台。风速与风量换算公式：Q=3600Fv，其中，Q为风量（m3/h），F为风口通风面积（m2），v为测得的风口平均风速（m/s）。该散热风机的风量要大于750m3/h，风速则要大于2.66m/s，考虑到实际效率，速度设为3m/s。
图8为干式变压器空气域流体速度分布的正视图和侧视图，散热风机从变压器铁心两侧的下表面与水平方向呈45°向上吹风，在变压器的不同轴向位置和径向位置的空气流速都不相同。其中高压绕组外表面空气流速较大，增强了高压绕组表面的对流散热能力，但内部散热气道较窄，空气流速较小，尤其在铁心窗上部气流通道受到铁轭的阻挡，空气流速迅速下降，这会导致低压绕组表面的对流散热能力减弱，同时高、低压绕组之间的温差增大会增强两者之间的辐射传热能力。
图8 干式变压器内部流体速度分布
Fig.8 Velocity distribution inside dry-type transformer
3.1.3 温度场仿真分析
图9为强迫散热方式下干式变压器在额定工作状态时的温度分布，铁心中间心柱的温度明显高于两侧的心柱，绕组温度高于铁心温度，并且绕组温度分布与轴向高度相关。这是由于绕组和铁心将其内部损耗产生的热量通过热传导方式传递至外表面，根据2.3节的传热学理论和边界层理论，散热气道内的空气因受热而温度升高，一方面热空气沿气流方向不断向顶部积聚；另一方面空气黏度随温度的升高而增大，最终导致顶部流固交界面处的流体换热薄层的厚度增加，不利于顶部对流散热，因此变压器温升随轴向高度的增加呈上升趋势。
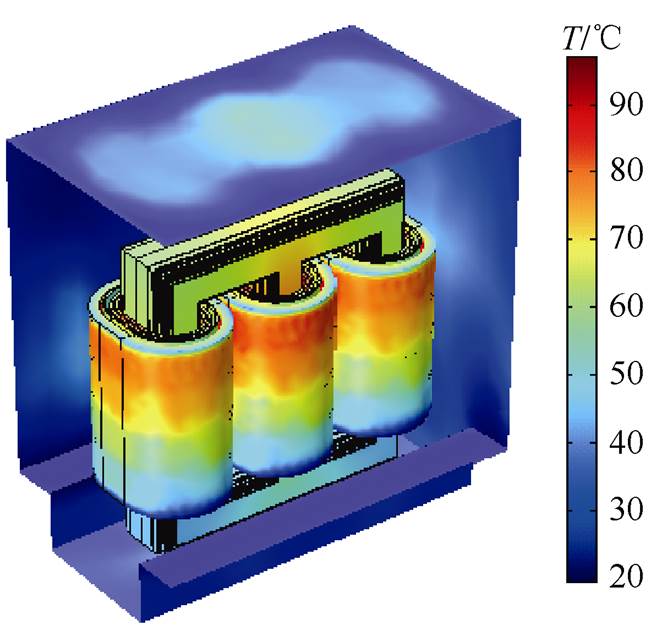
图9 干式变压器温度分布
Fig.9 Temperature distribution of dry-type transformer
图10为强迫散热方式下干式变压器在额定工作状态时绕组沿轴向的温度分布曲线，高压绕组和低压绕组的最热点温度分别为91.64℃和97.32℃，其位置坐标分别为（15.40, -2.70, 17.75）和（8.70, -0.61, 25.00）（cm）。对比变压器高、低压绕组的出厂温升试验数据88℃、107℃，低压绕组的热点温度与试验数据相比略小，是因为气道撑条、夹件等结构件以及强迫对流散热风速的误差对散热能力有一定的影响，高压绕组的热点温度与试验数据基本吻合，验证了有限元模型的准确性。
图10 强迫散热方式下绕组沿轴向的温度分布曲线
Fig.10 The temperature distribution curves of the winding under the forced heat dissipation mode
从图10中还可以看出，高压绕组的轴向温度分布出现明显的分段梯度现象，每段内轴向温差在1K左右，每段之间的温差在6～10K左右，而低压绕组内部的轴向温差较小，在6K左右。这是因为高压绕组在轴向方向分为4段，段间绝缘的导热系数要远低于绕组导体部分的导热系数，每段绕组之间不能进行很好的热量传导，且高压绕组为环氧浇注式，外包封绝缘使得强迫散热方式对每段绕组的散热效果也不同。除此之外，绕组两端的端部绝缘温度要低于绕组导体部分的温度，且上端部绝缘温度大于下端部绝缘的温度。
3.2.1 热网络模型的修正
由于热网络模型自身不能表示出干式变压器绕组的结构特征，并且在散热气道内同一轴向高度但不同径向位置的空气流速也不同，所以在修正前，只用一个固定的空气流速值难以准确计算热网络模型中不同位置处的对流传热系数及对流传热热阻。
根据图2可将干式变压器的散热气道铁心-低压绕组内层、低压绕组内层-低压绕组外层、低压绕组外层-高压绕组和高压绕组外表面分别表示为Ⅰ、Ⅱ、Ⅲ和Ⅳ。在计算各个散热气道内不同轴向高度的空气流速时，要考虑在该轴向高度下不同径向位置空气流速的加权结果。根据图8所示的基于有限元模型的干式变压器空气域流体速度分布，对不同轴向高度空气流速的加权计算结果见表6。
表6 不同轴向高度的空气流速
Tab.6 Air velocity at different axial heights
轴向高度/mm散热气道内空气流速/(m/s) ⅠⅡⅢⅣ 188.250.9770.4210.6811.860 65.750.9730.3740.7022.110 -65.750.9250.3980.7002.250 -188.250.8750.3720.4202.170
按照式（3）～式（6）计算传热热阻和辐射热阻，同时计算出表6所示不同空间位置的空气流速与散热风机风速（3m/s）的比值系数Ki,j,将其代入式（7），计算得到修正后的不同空间位置处的对流传热热阻Ri,j=Ki,jRconv（i=1, 2, 3, 4；j=1, 2, 3, 4），并结合图3所示的迭代计算流程，得到了修正后的基于热网络模型的干式变压器绕组温度分布和绕组温升曲线，分别如图11和图12所示，其中高压绕组和低压绕组的最热点温度分别为85.46℃和95.58℃，与出厂温升试验数据的误差分别为2.9%和10.7%，仿真结果与试验数据基本吻合。
图11 热网络模型和有限元模型的绕组轴向温度对比
Fig.11 Comparison of the modified thermal network model and the finite element method values on winding temperature
与未修正前的热网络模型温升仿真结果相比，低压绕组的平均温度更接近于基于有限元模型的绕组温升仿真结果，但低压绕组温度随轴向高度的增大而增加并不明显；高压绕组温度随轴向高度的增大而增加，同时各段之间轴向温差偏大的问题得到显著改善。这是因为热网络模型在轴向的分层数过少，并没有很好地分辨出绕组轴向温差；另一方面热网络模型忽略了高、低压绕组之间的绝缘筒结构，增强了高、低压绕组之间的辐射传热能力，导致高压绕组各段之间的温差变小。
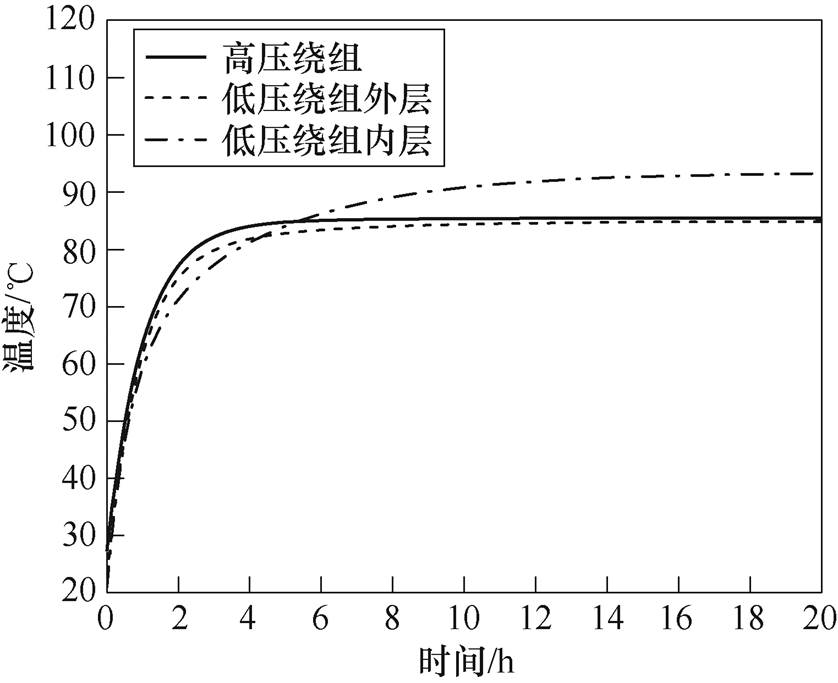
图12 干式变压器绕组温升曲线
Fig.12 Dry-type transformer winding temperature curves
图12为基于热网络模型的干式变压器绕组的温升曲线，经过5h的运行，高压绕组和低压绕组外层的最热点温度在1h周期内的温升变化小于1K，而经过8h的运行，低压绕组内层的热点温度在1h周期内的温升变化小于1K，此时变压器处于稳态运行。
3.2.2 典型过负载下温度场仿真分析
为研究干式变压器在典型过负载情况下的温度分布，设置干式变压器的负载系数分别为1.0、1.1、1.2、1.3和1.4，强迫散热风速仍然为3m/s，绕组沿轴向的温度分布曲线如图13所示，绕组最热点温度的变化曲线如图14所示。当过负载40%时，高压绕组、低压绕组外层和低压绕组内层的最热点温度分别为148.45℃、150.62℃和152.02℃。环氧浇注式干式变压器的绝缘耐热等级为F级，最高允许温度为155℃，绕组额定最热点温度145℃，因此尽量避免该干式变压器在过负载40%及以上的状态下运行。
将该干式变压器的有限元模型和热网络模型的占用内存、迭代次数、仿真时长以及高、低压绕组的温升仿真误差等参数进行对比分析，见表7，与出厂温升试验数据相比，经过修正后的热网络模型仿真误差大幅减小，同时热网络模型占用内存小、迭代次数少、计算时间短，与有限元模型相比具有显著的优势。
图13 不同负载系数下绕组沿轴向的温度分布曲线
Fig.13 The temperature distribution curves of the winding under different load factors
图14 不同负载系数下绕组最热点温度变化曲线
Fig.14 Winding temperature curves under different load factors
表7 仿真模型关键参数对比
Tab.7 Comparison of key parameters of models
模型占用内存/GB迭代次数仿真时长/min仿真误差(%) 有限元96.0301 920.64.1/9.0 热网络1.890.72.9/10.7
本文提出了一种基于热网络模型的干式变压器绕组温度分布仿真模型，利用有限元模型的流体场仿真结果对热网络模型的对流传热热阻进行修正，分析其典型过载情况下绕组轴向温度分布和最热点温度，得到以下结论：
1）考虑磁-热-流多物理场耦合下的损耗计算和温度分布更加符合干式变压器的实际运行状态。有限元模型仿真结果显示在额定状态下，最热点温度位于低压绕组内层的导体上，低压绕组沿轴向温度逐渐增大，温差小于6K；高压绕组温度出现分段梯度现象，各段之内温差小于1K，各段之间温差在6～10K。通过与出厂温升试验数据对比，验证了有限元模型的合理性和准确性。
2）热网络模型可将干式变压器的传导、对流和辐射三种传热方式考虑到热网络参数中，但通过研究变压器内部空气流速对对流传热热阻的影响，发现需要利用有限元模型的内部流体场仿真结果对热网络模型进行修正。
3）将修正前、后的热网络模型得到的绕组最热点温度与有限元模型仿真结果相比，高压绕组、低压绕组外层、低压绕组内层的误差分别从7.35K、21.06K、17.29K减小为6.16K、4.59K、2.92K，计算精度大幅提高。
4）将修正后的热网络模型得到的绕组温度分布曲线与有限元模型仿真结果相比，总体变化趋势接近，但难以表征一些温度变化细节，具有一定的有效性。下一步将通过增加热网络模型的轴向方向的分层数，进一步优化改进热网络计算模型。
参考文献
[1] 蔡定国, 唐金权. 干式变压器用绝缘材料、绝缘结构与系统综述[J]. 绝缘材料, 2019, 52(11): 1-8.
Cai Dingguo, Tang Jinquan. Summary of insulating material, insulation structure and system for dry-type transformer[J]. Insulating Materials, 2019, 52(11): 1-8.
[2] 王有元, 王施又, 黄炎光, 等. 干式变压器环氧树脂热老化特性研究[J]. 高电压技术, 2018, 44(1): 187-194.
Wang Youyuan, Wang Shiyou, Huang Yanguang, et al. Study on thermal aging characteristics of epoxy resin of dry-type transformer[J]. High Voltage Engin- eering, 2018, 44(1): 187-194.
[3] 张鑫, 王伟, 马昊, 等. 干式变压器绝缘试样活化能与热老化程度的关联特性[J]. 电工电能新技术, 2020, 39(3): 9-16.
Zhang Xin, Wang Wei, Ma Hao, et al. Correlation between activation energy and thermal aging degree of insulating samples from dry-type transformer[J]. Advanced Technology of Electrical Engineering and Energy, 2020, 39(3): 9-16.
[4] 田慕琴, 朱晶晶, 宋建成, 等. 基于流固耦合分析的矿用干式变压器温度场仿真[J]. 高电压技术, 2016, 42(12): 3972-3981.
Tian Muqin, Zhu Jingjing, Song Jiancheng, et al. Temperature field simulation of coal dry-type trans- former based on fluid-solid coupling analysis[J]. High Voltage Engineering, 2016, 42(12): 3972-3981.
[5] 曾非同, 关向雨, 黄以政, 等. 基于多尺度多物理场的油浸式变压器流动-传热数值研究[J]. 电工技术学报, 2020, 35(16): 3436-3444.
Zeng Feitong, Guan Xiangyu, Huang Yizheng, et al. Numerical study on flow-heat transfer of oil- immersed transformer based on multiple-scale and multiple-physical fields[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3436-3444.
[6] Liu Chao, Ruan Jiangjun, Wen Wu, et al. Temperature rise of a dry-type transformer with quasi-3D coupled- field method[J]. IET Electric Power Applications, 2016, 10(7): 598-603.
[7] 贾英杰, 肖飞, 罗毅飞, 等. 基于场路耦合的大功率IGBT多速率电热联合仿真方法[J]. 电工技术学报, 2020, 35(9): 1952-1961.
Jia Yingjie, Xiao Fei, Luo Yifei, et al. Multi-rate electro-thermal simulation method for high power IGBT based on field-circuit coupling[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1952-1961.
[8] Wang Qingyu, Wang Haoran, Peng Zongren, et al. 3-D coupled electromagnetic-fluid-thermal analysis of epoxy impregnated paper converter transformer bushings[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(1): 630-638.
[9] 李永建, 闫鑫笑, 张长庚, 等. 基于磁-热-流耦合模型的变压器损耗计算和热点预测[J]. 电工技术学报, 2020, 35(21): 4483-4491.
Li Yongjian, Yan Xinxiao, Zhang Changgeng, et al. Numerical prediction of losses and local overheating in transformer windings based on magnetic-thermal- fluid model[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4483-4491.
[10] 王泽忠, 李明洋, 宣梦真, 等. 单相四柱式变压器直流偏磁下的温升试验及仿真分析[J]. 电工技术学报, 2021, 36(5): 1006-1013.
Wang Zezhong, Li Mingyang, Xuan Mengzhen, et al. Temperature rise test and simulation of single-phase four-column transformer under DC-bias[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(5): 1006-1013.
[11] Liao Caibo, Ruan Jiangjun, Liu Chao, et al. 3-D coupled electromagnetic-fluid-thermal analysis of oil- immersed triangular wound core transformer[J]. IEEE Transactions on Magnetics, 2014, 50(11): 1-4.
[12] 王永强, 马伦, 律方成, 等. 基于有限差分和有限体积法相结合的油浸式变压器三维温度场计算[J]. 高电压技术, 2014, 40(10): 3179-3185.
Wang Yongqiang, Ma Lun, Lü Fangcheng, et al. Calculation of 3D temperature field of oil immersed transformer by the combination of the finite element and finite volume method[J]. High Voltage Engin- eering, 2014, 40(10): 3179-3185.
[13] 冯建勤, 康国平, 赵楠, 等. 干式变压器热等效电路研究[J]. 变压器, 2012, 49(12): 17-20.
Feng Jianqin, Kang Guoping, Zhao Nan, et al. Research on thermal equivalent circuit for dry-type transformer[J]. Transformer, 2012, 49(12): 17-20.
[14] 罗汉武, 陈连凯, 姜国义, 等. 计及环境条件的电力变压器热路模型及其应用[J]. 高电压技术, 2018, 44(11): 3561-3568.
Luo Hanwu, Chen Liankai, Jiang Guoyi, et al. Thermal circuit model of the transformer considering environment factors and its application[J]. High Voltage Engineering, 2018, 44(11): 3561-3568.
[15] Zhang Shibao. Evaluation of thermal transient and overload capability of high-voltage bushings with ATP[J]. IEEE Transactions on Power Delivery, 2009, 24(3): 1295-1301.
[16] 张施令, 彭宗仁, 邓志祥, 等. 集总RC热网络方法应用于油气套管暂态温度计算[J]. 高电压技术, 2015, 41(7): 2294-2301.
Zhang Shiling, Peng Zongren, Deng Zhixiang, et al. Application of lumped RC thermal network method in transient temperature calculation of oil/SF6 bushing[J]. High Voltage Engineering, 2015, 41(7): 2294-2301.
[17] Akbari M, Rezaei-Zare A. Transformer bushing thermal model for calculation of hot-spot temperature considering oil flow dynamics[J]. IEEE Transactions on Power Delivery, 2021, 36(3): 1726-1734.
[18] IEEE C57.110-2018. IEEE recommended practice for establishing liquid-immersed and dry-type power and distribution transformer capability when supplying nonsinusoidal load currents[S]. America: IEEE Power and Energy Society, 2018.
[19] 赵志刚, 徐曼, 胡鑫剑. 基于改进损耗分离模型的铁磁材料损耗特性研究[J]. 电工技术学报, 2021, 36(13): 2782-2790.
Zhao Zhigang, Xu Man, Hu Xinjian. Research on magnetic losses characteristics of ferromagnetic materials based on improvement loss separation model[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2782-2790.
[20] 杨世铭, 陶文铨. 传热学[M]. 4版. 北京: 高等教育出版社, 2006.
[21] 陶文铨. 数值传热学[M]. 2版. 西安: 西安交通大学出版社, 2001.
[22] 王小飞, 代颖, 罗建. 基于流固耦合的车用永磁同步电机水道设计与温度场分析[J]. 电工技术学报, 2019, 34(增刊1): 22-29.
Wang Xiaofei, Dai Ying, Luo Jian. Waterway design and temperature field analysis of vehicle permanent magnet synchronous motor based on fluid-solid coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 22-29.
Simulation Analysis of Dry-Type Transformer Thermal Network Model Considering Fluid Dynamics
Abstract In order to analyze the axial temperature distribution and hot spot temperature of the windings of dry-type transformers under typical overload conditions, this paper proposes a thermal network model that considers fluid dynamics. First of all, considering the influence of temperature on material loss characteristics, a dry-type transformer three-dimensional magnetic-heat-fluid coupling simulation model was established. Accordingly, the forced heat dissipation process of dry-type transformers was accurately simulated, the temperature rise of transformer windings was calculated and the hot spot temperature under different load factors was predicted. The errors between the simulation and the factory temperature rise test data of the hottest temperature of the high-voltage winding and the low-voltage winding were 4.1% and 9.0%. According to the fluid field simulation results of the finite element model, the convective heat transfer resistance in the thermal network model was corrected. It is shown that after the thermal network model is corrected for the convective heat transfer resistance, the errors between the hottest temperature simulation results of the high-voltage winding and low-voltage winding and the factory temperature rise test data are 2.9% and 10.7%, respectively, and the axial temperature distribution has a good agreement. The proposed thermal network model of dry-type transformers considering fluid dynamics overcomes the shortcomings of low calculation accuracy of traditional thermal circuit models and long calculation time of finite element models, which has good guidance for dry-type transformer design and operation evaluation effect.
keywords：Dry-type transformer, thermal network model, fluid dynamics, multiphysics coupling, temperature rise calculation
DOI: 10.19595/j.cnki.1000-6753.tces.210675
中图分类号：TM412
国家电网有限公司科技项目“关键电力装备状态复合感知技术研究”（5500-201999543A-0-0-00）资助。
收稿日期 2021-05-13
改稿日期 2021-07-19
唐 钊 男，1997年生，硕士研究生，研究方向为干式变压器多物理场耦合仿真技术。E-mail: tangzhao@stu.xjtu.edu.cn
刘轩东 男，1981年生，副教授，博士生导师，研究方向为直流电力设备设计、气体绝缘与放电等离子体、高功率脉冲源、气体开关及应用。E-mail: liuxuand@mail.xjtu.edu.cn（通信作者）
（编辑 崔文静）