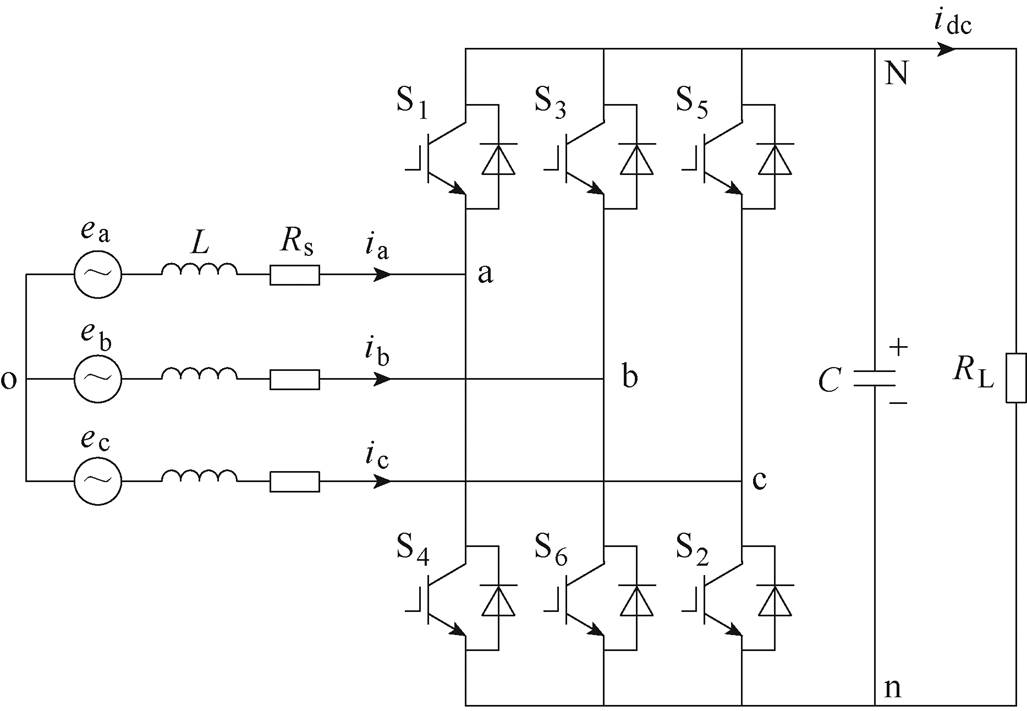
图1 PWM整流器拓扑
Fig.1 Topology of the PWM rectifier
摘要 模型预测功率控制(MPPC)基于代价函数最小化原则,选取下一时刻最优开关状态作用于系统。然而当电网电压处于不平衡状态时,MPPC网侧电流将发生严重畸变进而对PWM整流器输出性能产生危害。针对此问题,该文将扩展无功功率新定义应用于MPPC,无需复杂的正负序提取和功率补偿算法,获得恒定有功功率和网侧正弦电流。此外,针对传统模型预测功率控制(C-MPPC)存在的开关频率不固定、系统计算量大的问题,提出一种优化模型预测功率控制(O-MPPC)策略。通过对有限控制集优化,减小系统计算量;同时采用多矢量合成方法取代单一矢量作用,将所选矢量开关序列重组优化并计算每个矢量作用时间,解决C-MPPC开关频率不固定的问题,提高系统控制性能。通过与C-MPPC进行对比实验,验证了所提优化控制策略的可行性与优越性。
关键词:预测功率控制 不平衡电网电压 PWM整流器 扩展无功功率 开关序列优化
PWM整流器是一种高性能的功率转换器,广泛应用于有源电力滤波[1]、混合微电网[2]、光伏发电[3]等电力变换器系统,其具有电能质量可控、功率可双向流动和网侧电流正弦化等优点。
与目前广泛应用的电压定向控制(Voltage- Oriented Control, VOC)相比,直接功率控制(Direct Power Control, DPC)对有功功率和无功功率进行直接调节,无需内部电流回路[4],因而控制结构简单且动态响应快[5],是一种直接有效的控制方案,然而其性能往往依赖于系统采样频率和预定义的开 关表[6]。
模型预测功率控制(Model Predictive Power Control, MPPC)因其概念直观且无需复杂控制参数设计,而受到广泛关注[7-10]。MPPC将预测下一时刻有功功率、无功功率与当前时刻有功功率、无功功率误差二次方和设定为代价函数,将整流器控制模型离散化后,选取最优开关状态作用于系统[11]。传统MPPC(Conventional MPPC, C-MPPC)由于每个控制周期的开关矢量特性不同而导致控制开关频率不固定,网侧电流总谐波畸变率(Total Harmonic Distortion,THD)较高。虽然可以通过提高系统开关频率来降低电流失真和功率纹波,改善C-MPPC的稳态控制性能,但会导致更高的硬件成本和计算负担。为了在不增加开关频率的情况下进一步提高C-MPPC的性能,文献[12]提出一种改进型双矢量控制策略,通过在单个有效矢量作用的基础上搭配一个零矢量来最小化跟踪误差。文献[13]采用无差拍预测控制策略,以减小系统功率脉动与电流谐波,但由于引入调制模块,动态性能有所降低。
上述方案考虑电网为平衡条件,然而电网电压由于电网故障以及三相负载不平衡等因素而常常处于不平衡状态[14-15]。在弱电网中,常存在单相15%的电压骤降[16]。在该情况下,若沿用电网处于平衡状态时的控制策略,网侧电流会发生畸变,从而影响整流器的控制性能,并对负载侧的电容器及负载产生隐患。
近年来,有文献将扩展无功功率新定义应用于MPPC,与传统无功功率相比,其在电网不平衡情况下表现出了较为优越的性能[17]。文献[18]提出的MPPC通过在预定义的代价函数中使用扩展无功功率新定义,使得电压源型逆变器在不平衡电网下获得了良好的控制性能。文献[19]提出了一种无网压传感器模型预测控制,但由于最佳电压矢量的选择缺乏灵活性,其MPPC性能尚未达到理想效果。
本文为提高PWM整流器在不平衡电网下的控制性能,将扩展无功功率新定义应用于MPPC,无需复杂的正负序分解和功率补偿算法就可同时实现恒定有功功率和网侧正弦电流。此外,为改善C-MPPC存在的控制问题,提出了一种优化模型预测功率控制(Optimized MPPC, O-MPPC)策略。首先对控制集优化,减小系统计算量;通过多矢量合成的方法取代单一矢量作用,将所选矢量开关序列重组优化,解决了C-MPPC开关频率不固定的问题。当电网电压处于不平衡状态时,该方法对网侧电流谐波频谱分布和系统功率纹波具有明显改善作用。
如图1所示为PWM整流器的拓扑。图中,ea、eb、ec和ia、ib、ic分别为网侧三相电压和电流;L、Rs分别为滤波电感及其等效串联电阻,C为滤波电容。

图1 PWM整流器拓扑
Fig.1 Topology of the PWM rectifier
两相静止ab 坐标系下的整流器数学模型为
 (1)
(1)
式中,ea、eb和ia、ib分别为网侧电压和电流在ab坐标系下的分量;ua、ub为整流器交流侧输入电压在ab坐标系下的分量。
当电网电压处于不平衡状态时,网侧电压及电流表示为正负序矢量之和形式,即
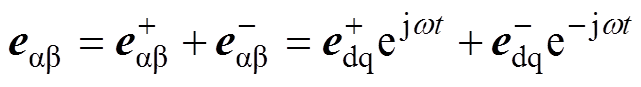 (2)
(2)
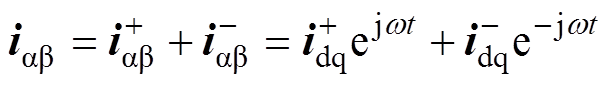 (3)
(3)
式中,w 为电网频率;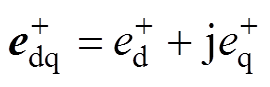 ;
; ;
;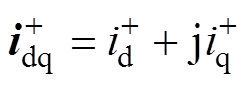 ;
;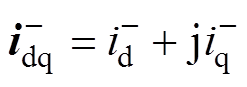 。
。
延迟电网电压1/4周期的正交延迟信号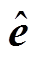 为
为
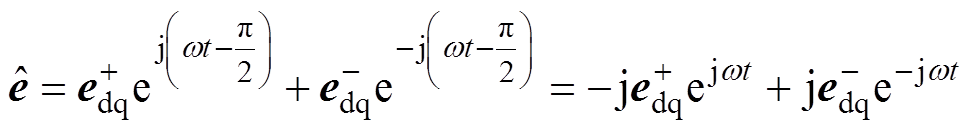 (4)
(4)
三相系统复功率S可表示为
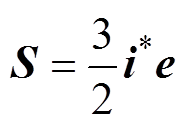 (5)
(5)
式中,e为网侧电压矢量;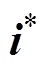 为网侧电流矢量的共轭。
为网侧电流矢量的共轭。
瞬时有功功率和无功功率分别为
 (6)
(6)
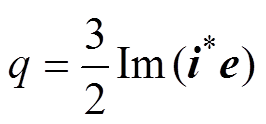 (7)
(7)
当电网电压不平衡时,系统功率存在二倍频振荡分量。如果应用经典瞬时功率理论,即采用传统有功和无功功率作为控制参数,有功和无功功率振荡分量无法同时去除。此时,如果仍然控制系统有功功率恒定,网侧电流会发生严重畸变。针对此问题,本文引入扩展无功功率为
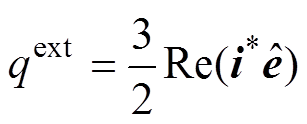 (8)
(8)
此扩展无功功率与有功功率共同作用时,在消除振荡功率方面比传统瞬时功率理论更有效[20]。
将式(2)~式(4)代入式(6)和式(8)中可得
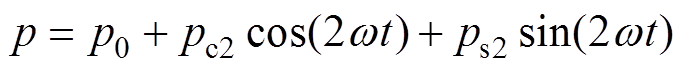 (9)
(9)
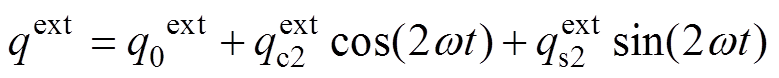 (10)
(10)
其中
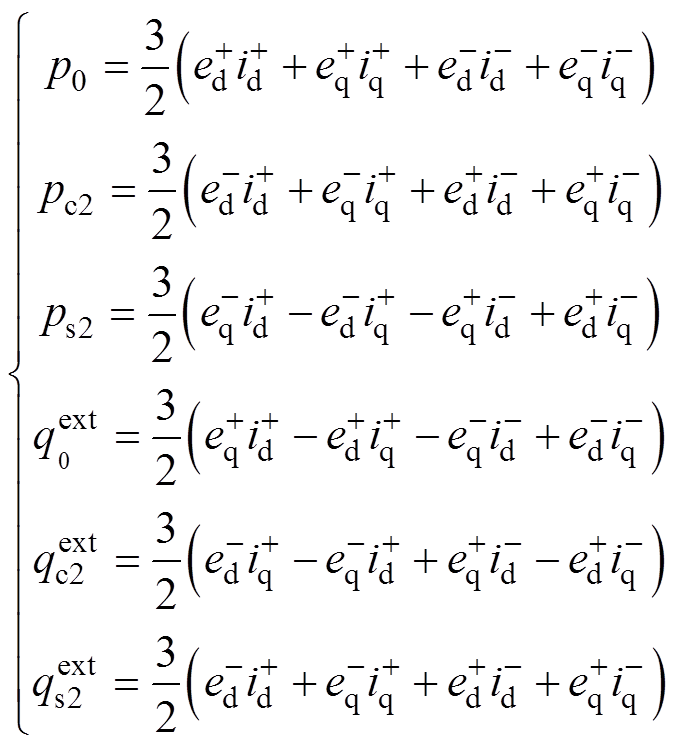 (11)
(11)
瞬时有功功率和扩展无功功率在ab 坐标系下的表达式可推导为
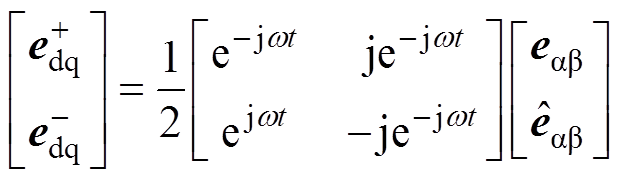 (12)
(12)
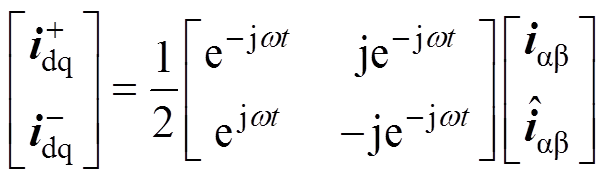 (13)
(13)
式中,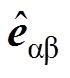 为网侧电压
为网侧电压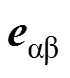 的90°正交延迟信号;
的90°正交延迟信号;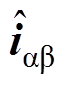 为网侧电流
为网侧电流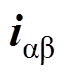 的90°正交延迟信号。
的90°正交延迟信号。
将式(12)、式(13)代入式(11)后可得
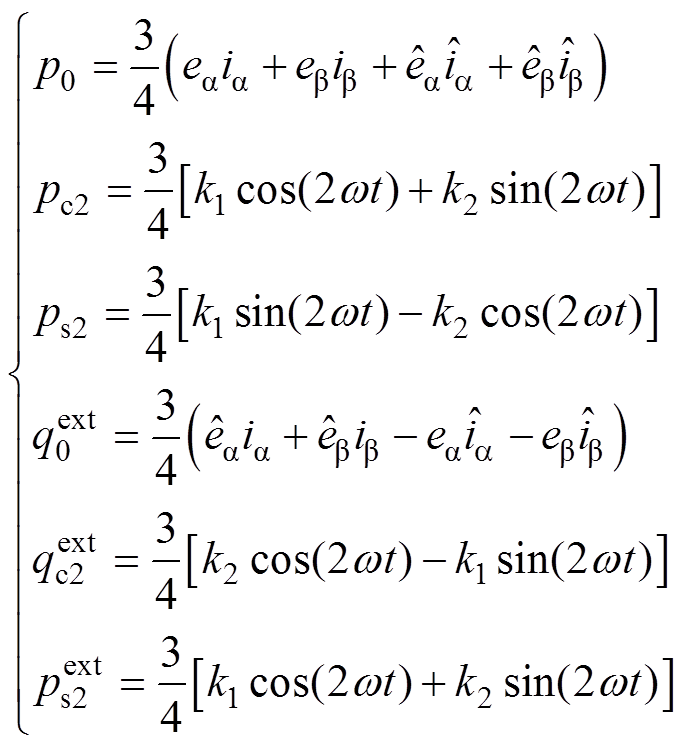 (14)
(14)
其中
 (15)
(15)
由式(14)可以得出, ,由此表明,当消除有功功率脉动的同时也会消除无功功率脉动,此特性是经典瞬时功率理论无法实现的。
,由此表明,当消除有功功率脉动的同时也会消除无功功率脉动,此特性是经典瞬时功率理论无法实现的。
网侧电流变化率可表示为
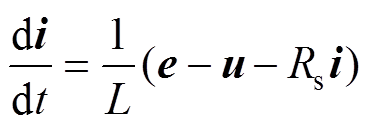 (16)
(16)
式中,u为整流器交流侧电压矢量;i为网侧电流 矢量。
对电网电压e及其延迟电压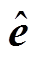 求导可得
求导可得
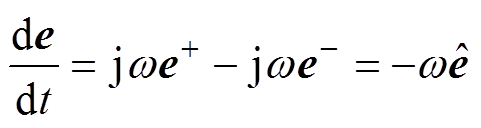 (17)
(17)
 (18)
(18)
对有功功率和扩展无功功率求导可得
 (19)
(19)
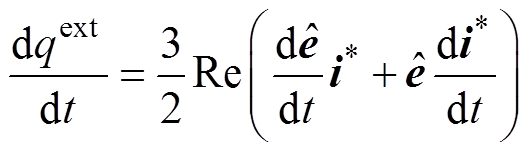 (20)
(20)
将式(16)~式(18)代入式(19)、式(20)可得
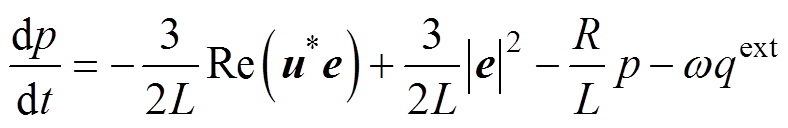 (21)
(21)
 (22)
(22)
式中,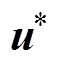 为整流器交流侧电压矢量的共轭。
为整流器交流侧电压矢量的共轭。
有限集模型预测控制首先通过构建整流器离散数学模型,根据系统有限开关工作状态,分别计算不同开关状态下系统的输出情况,然后选择最优开关状态作用于系统[21]。在下一个周期重复上述过程,以实现每个采样周期的持续预测能力。对于MPPC,通过将所预测下一时刻的有功功率、无功功率与当前时刻有功功率、无功功率误差二次方和设定为代价函数J来提高系统的控制精度。
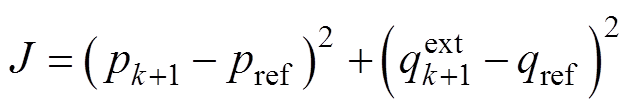 (23)
(23)
整流桥开关函数为
 (24)
(24)
不同开关状态的整流器输入电压可由式(25)表示,其对应关系见表1。
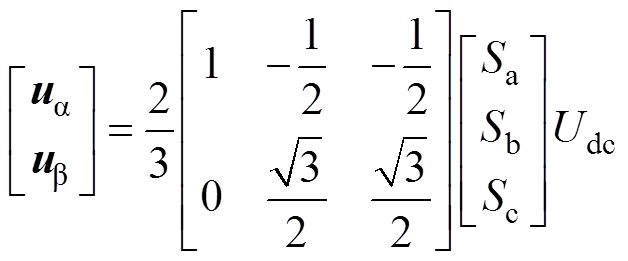 (25)
(25)
式中,Udc为直流侧输出电压。
传统C-MPPC采用单矢量作用,通过遍历寻优选取最优开关状态作用于系统[22]。随着拓扑结构的改变,当变换器电平数增加时,系统开关状态将呈指数增长,此时会极大地增加处理器的运算负担[23]。电压矢量选择示意图如图2所示,由图2a可以看出,该方法所选取的最优矢量的幅值和相位固定,即该最优矢量仅限于在8个基本电压矢量中为最优,而在整个电压矢量复平面内不一定为最优电压矢量。
表1 不同开关状态对应的电压矢量
Tab.1 Voltage vectors corresponding to different switching states

x开关状态Sx电压矢量ux Sa,xSb,xSc,xua,xub,x 0{000}00 1{100}0 2{110} 3{010} 4{011}0 5{001} 6{101} 7{111}00
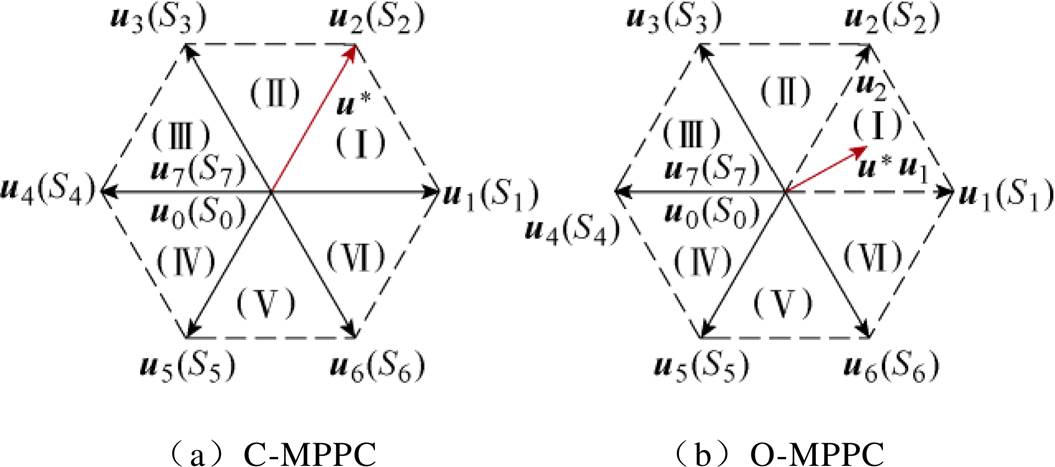
图2 电压矢量选择示意图
Fig.2 Diagram of voltage vector selection
针对上述问题,本文将传统的C-MPPC策略与空间矢量脉宽调制思想相结合,系统根据网侧电压所处扇区不同,选取与其相邻的电压矢量与零矢量进行矢量合成。图2b中,矢量u*为当前时刻电压矢量,矢量u1、u2为优化后备选电压矢量。与图2a进行对比可以看出,通过采用多矢量合成的方法取代单一矢量作用后,最优矢量的调节范围从固定相位和幅值扩展到任意相位和幅值。此时最优电压矢量的选择具有高度灵活性,且该最优矢量为整个复平面内最优电压矢量。
通过此方法实现控制集优化见表2,每次预测八种不同开关状态的系统输出,减少为每次仅计算四种不同开关状态,在降低系统运算负担的同时还提高了响应速度。
传统的C-MPPC策略在每个采样周期内最优代价函数的计算结果相互独立,造成了开关频率不固定。
表2 有限控制集优化
Tab.2 Optimization of finite control set

扇区有效矢量零矢量 Ⅰu1, u2u0, u7 Ⅱu2, u3u0, u7 Ⅲu3, u4u0, u7 Ⅳu4, u5u0, u7 Ⅴu5, u6u0, u7 Ⅵu6, u1u0, u7
本文采用多矢量合成的方法取代单一矢量作用,并将所选矢量的开关序列顺序进行重组优化,解决了C-MPPC策略系统开关频率不固定的问题。所选取的三个矢量在协调作用下将影响有功功率和扩展无功功率的变化速率。基于功率误差最小化原则计算每个矢量的作用时间,以实现对功率参考值的精确跟踪。即
 (26)
(26)
式中,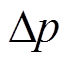 、
、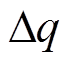 分别为有功功率和无功功率误差;
分别为有功功率和无功功率误差;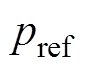 、
、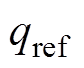 分别为有功、无功功率参考值;
分别为有功、无功功率参考值;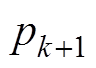 、
、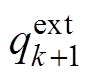 分别为有功功率、扩展无功功率在k+1时刻的预测值。
分别为有功功率、扩展无功功率在k+1时刻的预测值。
在数字控制中,对有功功率和扩展无功功率的变化率以选定的变换器电压矢量进行数学定义为
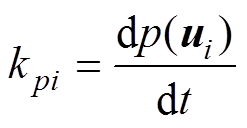 (27)
(27)
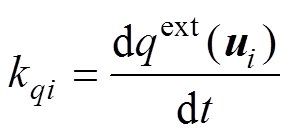 (28)
(28)
式中,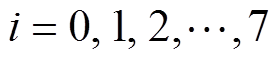 。
。
因此,在k+1时刻系统预测有功功率、扩展无功功率可表示为
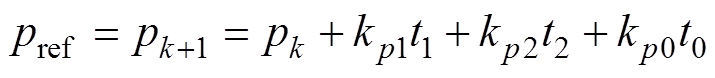 (29)
(29)
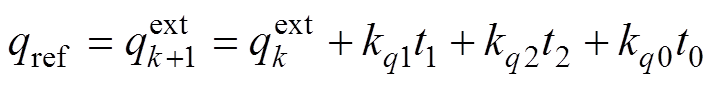 (30)
(30)
式中,pk、 分别为当前时刻系统的有功功率和扩展无功功率;kp1、kp2、kp0、kq1、kq2、kq0分别为两个基本矢量和零矢量的有功功率、扩展无功功率导数。
分别为当前时刻系统的有功功率和扩展无功功率;kp1、kp2、kp0、kq1、kq2、kq0分别为两个基本矢量和零矢量的有功功率、扩展无功功率导数。
基于功率误差最小化原则,联立式(21)、式(22)和式(26)~式(30)可得
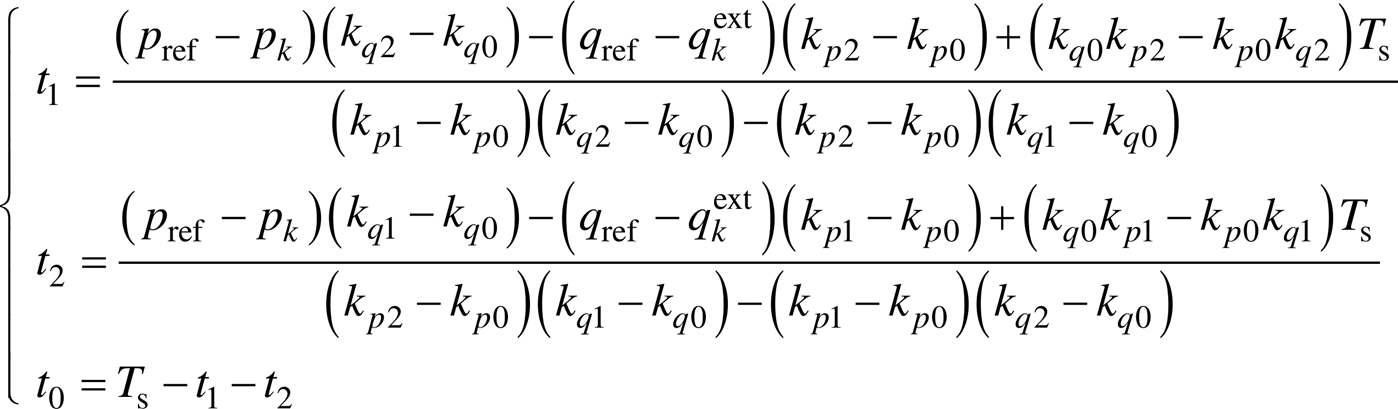 (31)
(31)
在系统动态调节过程中,当出现在一个周期内动态跟踪能力与系统实际偏差不匹配情况时,有功或扩展无功功率的给定值与实际值之间可能存在较大偏差,此时需对矢量作用时间重新分配
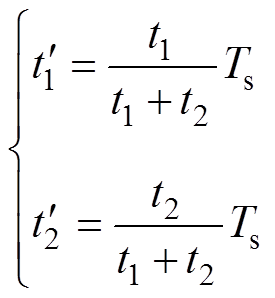 (32)
(32)
对于三相PWM整流器,由三矢量合成作用原理可知,根据选取零矢量不同和矢量作用顺序不同,每个扇区共对应八种不同开关序列。在一个控制周期内,开关序列的选择直接决定桥臂开关器件的动作次数。开关次数过多不仅会增加功率器件的损耗,还会进一步增加系统谐波分量。因此,本文对开关序列的优化在于通过选择适当的开关序列,减小开关动作次数。
在确定好两个有效电压矢量及其最佳作用时间后,在每个控制周期插入零矢量,以第Ⅰ扇区为例,选取优化开关序列见表3。
表3 以第Ⅰ扇区为例所选优化开关序列
Tab.3 Optimized switch sequences take sector Ⅰ as an example
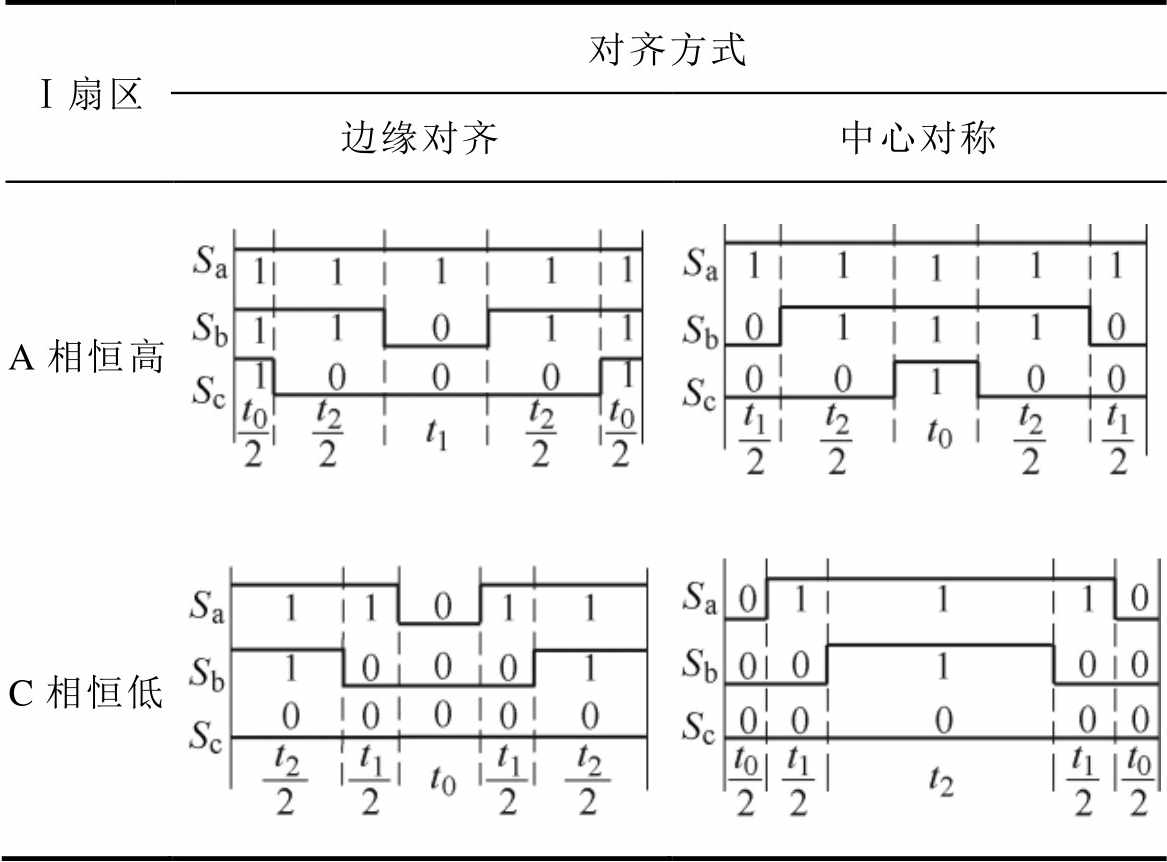
Ⅰ扇区对齐方式 边缘对齐中心对称 A相恒高 C相恒低
为充分利用模型预测控制解决多约束问题的特性,在代价函数中增加最小开关切换次数作为约束条件。在当前采样周期,通过分析存储的上一个周期的开关序列,对预测的下一个周期开关序列进行优化,得到新的代价函数 为
为
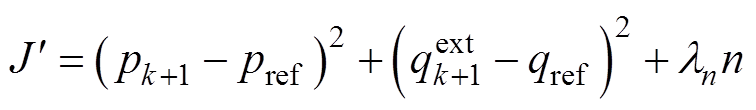 (33)
(33)
式中,ln为权重系数;n为相邻两个控制周期切换点处开关切换次数。
在MPPC的数字控制实现过程中,指令电压矢量和施加电压矢量之间存在由计算引起的一步延迟问题[24],即通过计算得到在当前k时刻满足控制目标的电压矢量,在k+1时刻才会真正作用于系统。为了消除由于一步延迟对控制系统产生的不良影响,需进行延迟补偿。首先合成等效电压矢量,如式(34)所示,然后在式(33)的代价函数中将k+2时刻而不是k+1时刻的电压矢量作用于转换器。
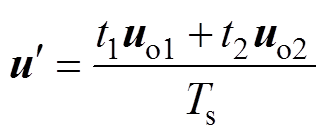 (34)
(34)
式中,uo1和uo2为所选非零有效矢量。
将式(34)代入式(16),可得到k+1时刻的网侧电流。k+1时刻的网侧电压为
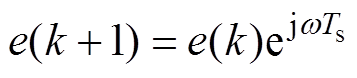 (35)
(35)
在得到k+1时刻的网侧电流和网侧电压之后,可通过计算得到k+1时刻的有功功率和扩展无功功率,最后将这些k+1时刻的电信号作为初始值用于本文所提出的控制策略。
优化预测功率控制系统框图如图3所示。
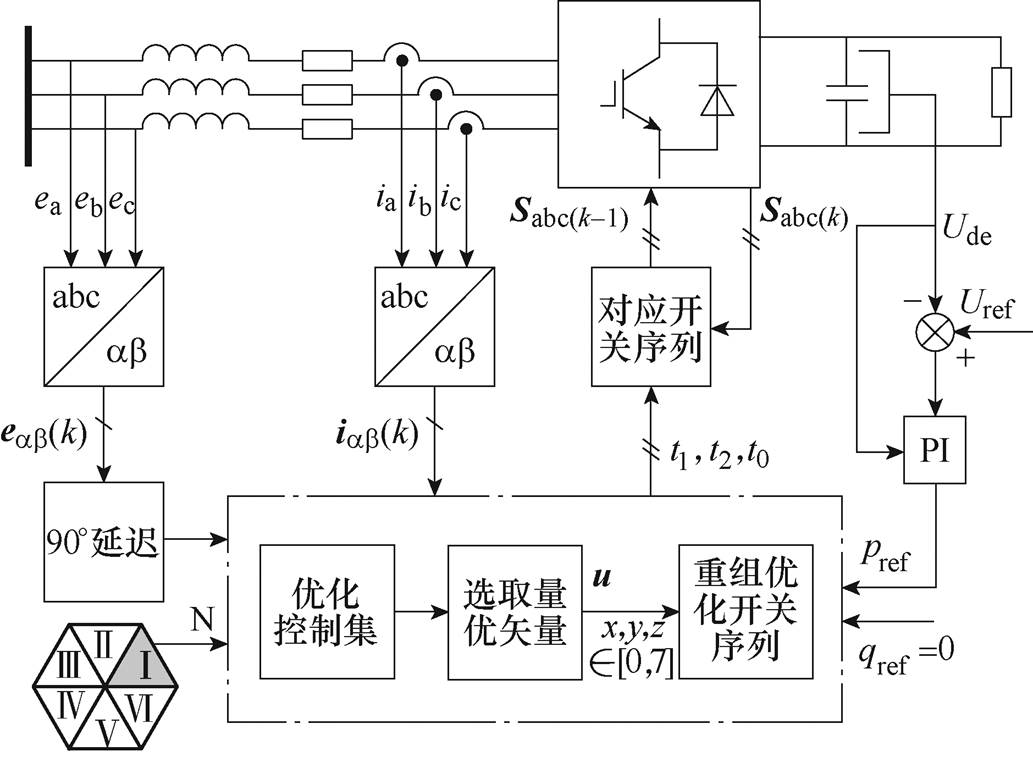
图3 优化预测功率控制系统框图
Fig.3 Block diagram of optimised control strategy
在Matlab/Simulink中搭建预测功率控制模型来验证所提控制策略的有效性。主要参数见表4。
表4 主要参数
Tab.4 Main parameters

参 数数 值 电网相电压有效值E/V110 电网频率f/Hz50 网侧滤波电感L/mH3 等效电阻Rs/W0.2 直流侧电压Udc/V350 直流侧电容C/mF2 000 开关频率fs/kHz10
图4为MPPC采用传统瞬时功率作为控制参数的仿真结果,首先系统输出功率稳定运行在5kW,在t =0.14s时刻,a相电网电压跌落20%,网侧三相电压如图4a所示,其中ea幅值为124V,eb、ec幅值均为156V。
对比图4b、图4c可知,电网电压处于平衡状态时,两种控制策略下网侧电流波形均可实现正弦化,但C-MPPC策略由于相邻周期开关状态变化无规律,导致网侧电流谐波含量较高,THD值为5.89%。而在O-MPPC策略作用下,网侧电流THD值仅为1.96%。当电网电压进入不平衡状态后,如果仍控制有功功率恒定,两种控制策略作用下的网侧电流均存在明显畸变。由此验证,采用传统瞬时功率作为控制参数的MPPC不适用于不平衡电网。
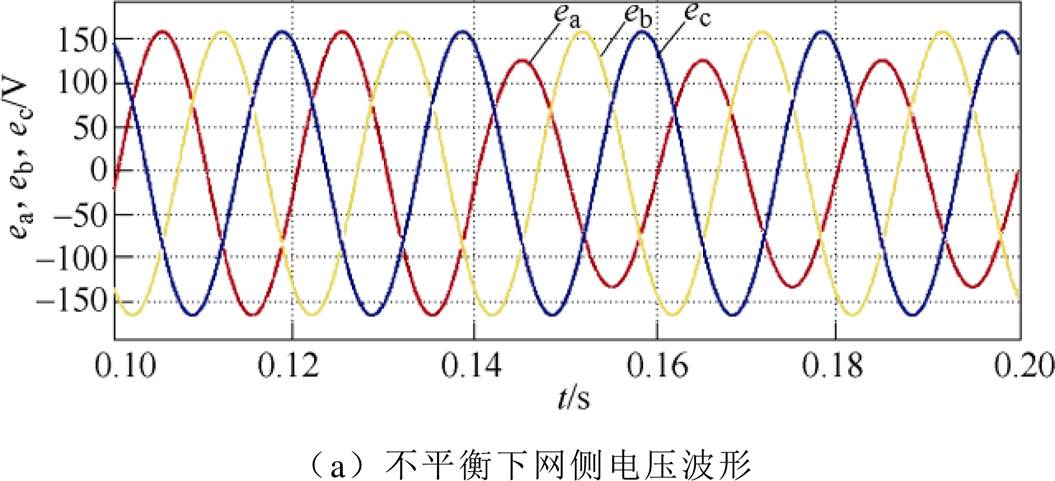

图4 以p、q为控制参数时不平衡下网侧仿真结果
Fig.4 Grid-side simulation results under unbalanced state that take p, q as the control parameters
对比图4d、图4e可知,C-MPPC和O-MPPC两种控制策略在平衡和不平衡电网下都能实现给定功率的跟踪。相比之下,O-MPPC策略能显著降低有功功率和无功功率脉动。
图5、图6为C-MPPC和O-MPPC策略采用有功功率p和扩展无功功率qext作为控制参数仿真结果,首先系统输出功率稳定运行在5kW,在t =0.14s时刻,a相电网电压跌落20%,网侧三相电压如图5a所示,其中ea幅值为124V,eb、ec幅值均为156V。
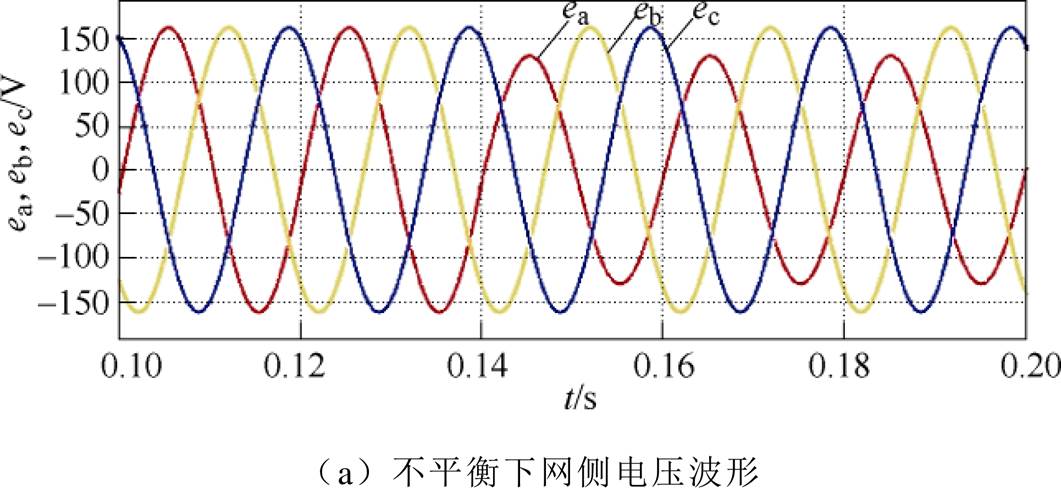
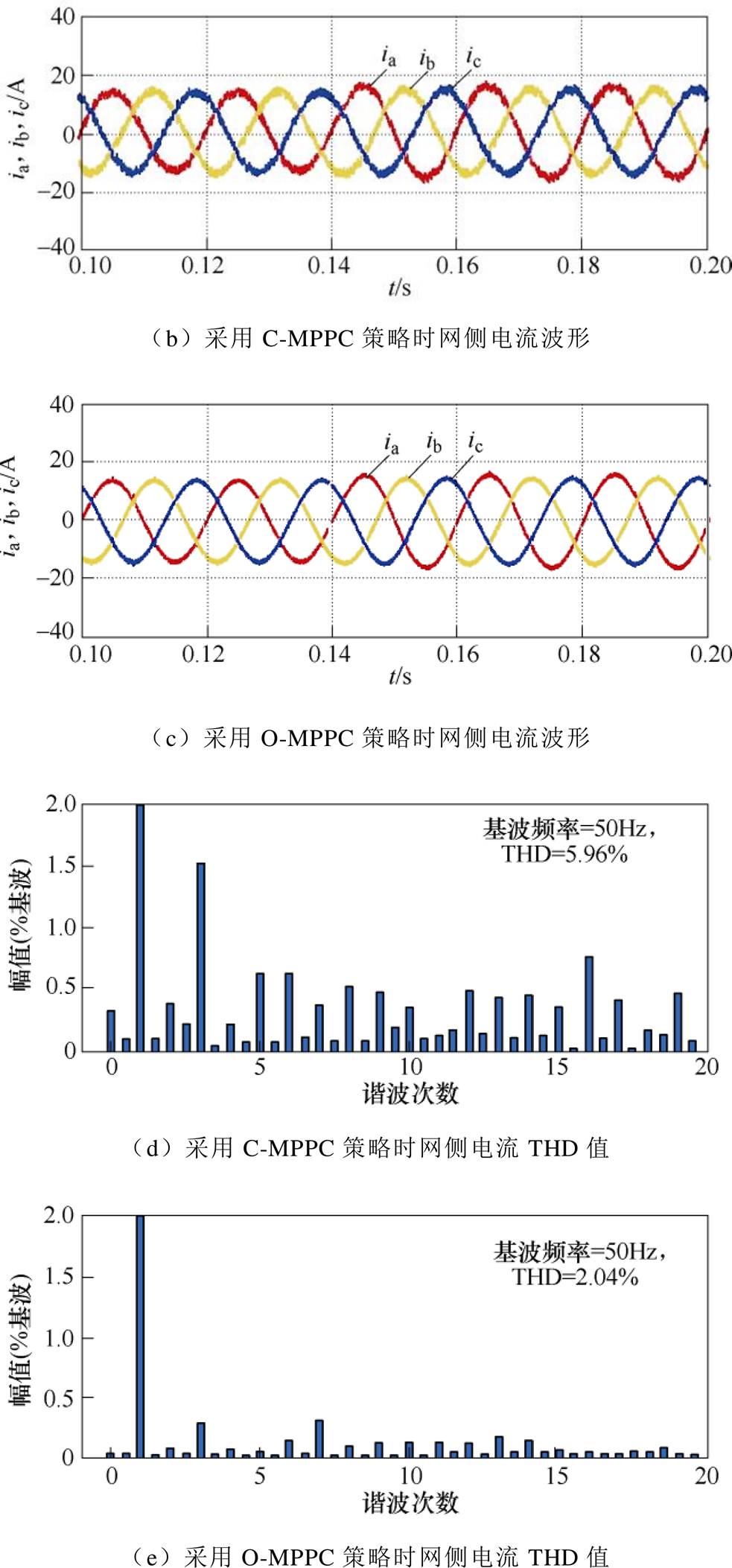
图5 以p、qext为控制参数时不平衡下网侧电流波形及其频谱分析
Fig.5 Network current waveformsandspectrum under unbalanced state with p and qext as the control parameters

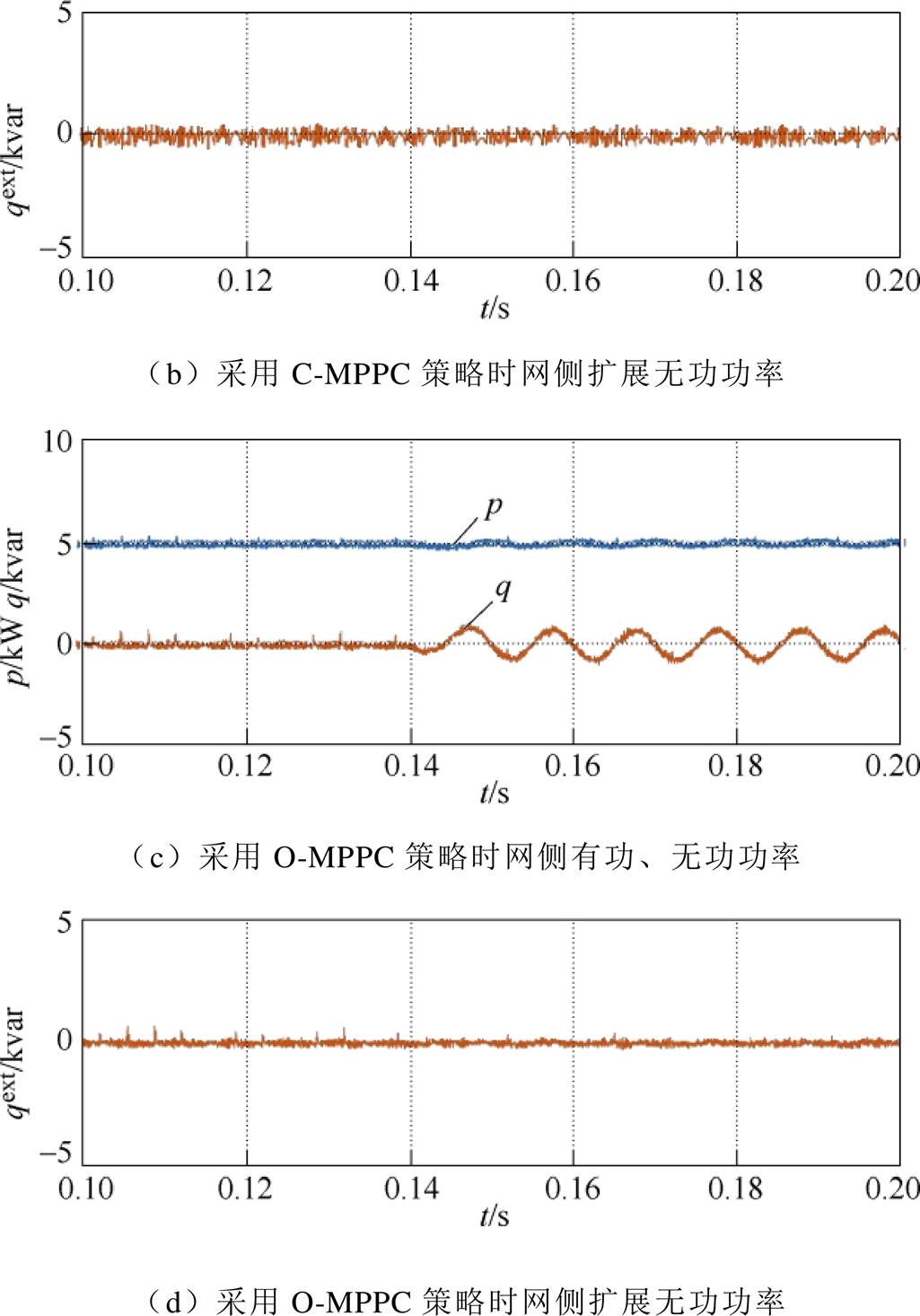
图6 以p、qext为控制参数时不平衡下网侧功率仿真结果
Fig.6 Grid-side power simulation results under unbalanced statethattake p and qext as the control parameters
对比图5b、图5c可知,电网电压处于平衡和不平衡状态时,两种控制策略下网侧电流波形均可实现正弦化。而本文所提O-MPPC策略网侧电流谐波含量少,且改善了C-MPPC策略频谱分散的问题。当电网电压处于不平衡状态时,采用C-MPPC策略网侧THD为5.96%,而在O-MPPC策略作用下仅为2.04%,电流质量有较为明显的改善。
系统功率网侧输入如图6所示。C-MPPC和O-MPPC策略在平衡和不平衡电网下都能实现给定功率的跟踪。无功功率q在平衡电网下保持恒定,在不平衡电网下出现二倍频振荡,而有功功率和扩展无功功率在两种情况下始终保持恒定。相比之下,O-MPPC策略能够显著降低有功和无功功率脉动,实现功率的精确控制。
除稳态性能评估外,还在电网电压不平衡状态下进行了动态性能评估,在0.14s时刻通过改变直流侧负载来改变系统有功功率参考。
以p、qext为控制参数时不平衡下功率突变网侧电流波形如图7所示。对比图7的仿真结果可以看出,C-MPPC与O-MPPC策略均能快速跟踪负载波动引起的功率变化。当系统功率稳定运行在10kW时,采用C-MPPC策略的网侧电流THD值为4.85%,而在本文所提出的O-MPPC策略作用下,网侧THD值仅为1.38%,显著降低了电流谐波含量,从而验证了该优化策略较为优越的动态性能。
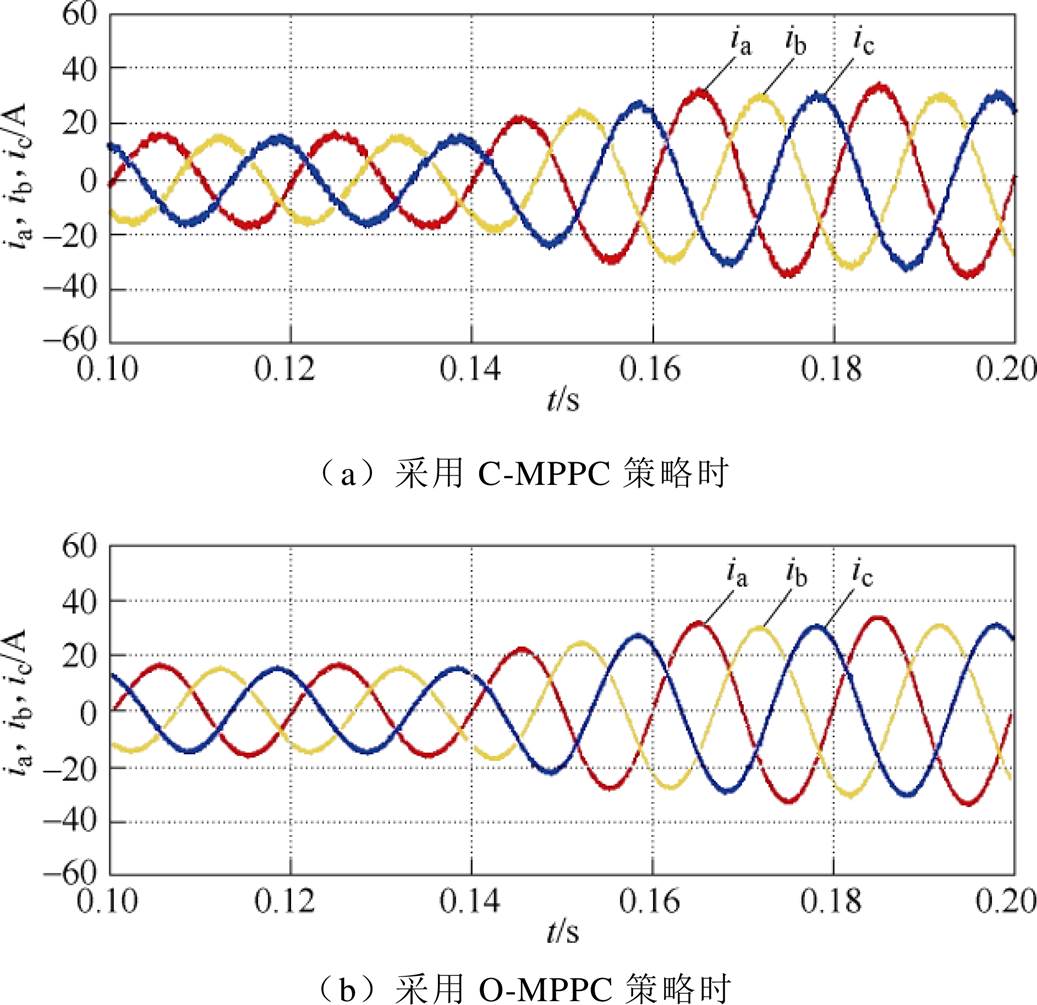
图7 以p、qext为控制参数时不平衡下功率突变网侧电流波形
Fig.7 Grid side current waveforms of power change under unbalanced state that take p and qext as the control parameters
本文采用TI公司TMS320F28335为主控芯片,三菱PM75DSA120模块为功率器件来搭建PWM整流器实验平台,进一步验证所提控制方法的有效性。输入接三相可编程交流电源(CHROMA 61830),输出端接交直流电子负载(ITECH IT 8918A),通过改变负载参数进行系统动态响应实验。实验参数与仿真参数一致。整流器实验平台如图8所示。

图8 整流器实验平台
Fig.8 Experimental platform ofrectifier
网侧电压、电流波形及THD分布如图9所示。网侧三相电压如图9a所示。其中,a相电网电压跌落20%,ea幅值为124V,eb、ec幅值均为156V。如图9b~图9e所示,采用C-MPPC策略时网侧电流发生了较为明显的畸变,其THD值为8.21%,谐波含量分散;而当采用有功功率p和扩展无功功率qext作为控制参数,在O-MPPC策略作用下时,网侧THD降低为2.42%,且谐波分布明显改善。
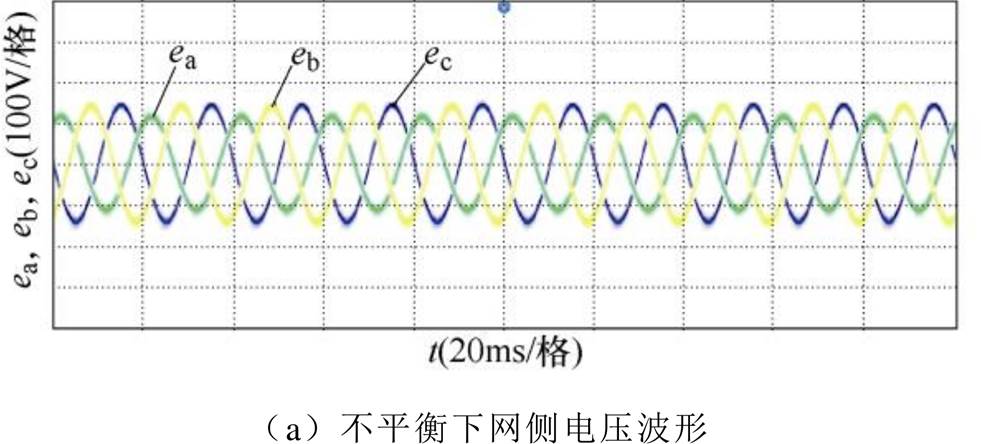
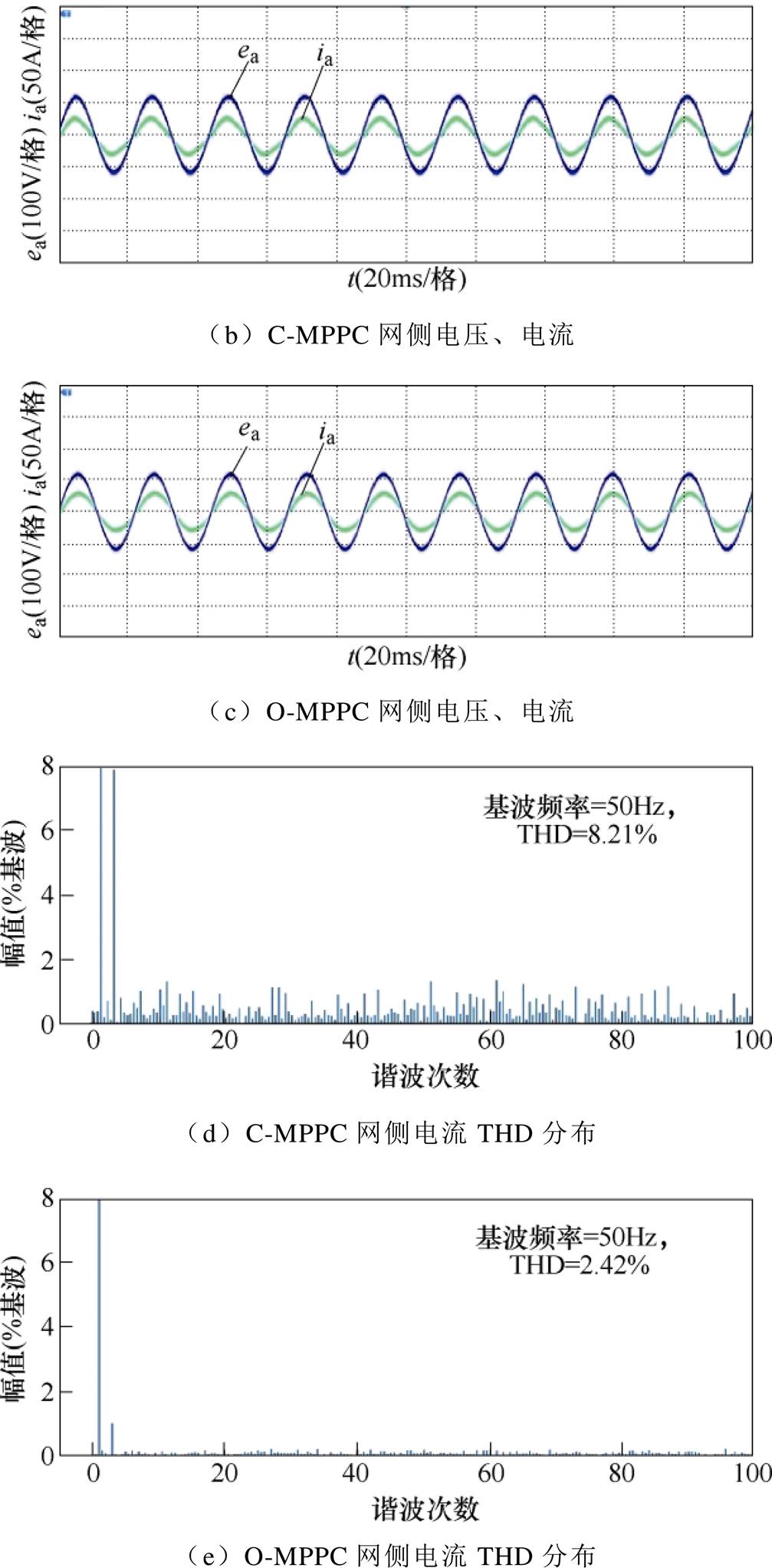
图9 网侧电压、电流波形及THD分布
Fig.9 Grid side voltage and current waveforms and THD distribution
图10所示为在不平衡状态下,系统额定功率从5kW突变至10kW,两种控制策略作用下的网侧电流波形。C-MPPC网侧电流在波峰和波谷处都出现了一定程度的畸变,而在O-MPPC作用下网侧电流正弦度较高,电流波形较为平滑。
图11所示为系统功率由5kW突变至10kW以及由10kW突变至5kW的动态实验结果。通过测量网侧电压和电流的变化,两种不同控制策略作用下系统均能较快地跟踪负载波动引起的变化,且在整个动态过程中均实现了网侧电压电流同相位。但本文所提出的优化O-MPPC策略通过将扩展无功功率新定义应用于MPPC,且对控制集和开关序列进行优化,在动态调节过程中具有较强的稳定性,网侧电流正弦度较高。可见当电网电压处于不平衡状态时,本文所提出的优化控制策略对系统稳态性能和动态性能都具有显著的改善作用。

图10 功率由5kW变至10kW网侧电流波形
Fig.10 The power changes from 5kW to 10kW current waveforms on grid side

图11 功率变化动态实验结果
Fig.11 Dynamic experimental results of power changed
本文在电网电压不平衡工况下推导PWM整流器和系统功率数学模型,提出一种优化预测功率控制方案。在MPPC中通过将扩展无功功率取代传统无功功率作用,实现了在不平衡电网电压下的控制性能优化。与现有方法相比,该方法具有以下优点:
1)无需复杂的正负序提取和功率补偿算法,通过优化有限控制集,减小了系统计算量。
2)通过选取与所在扇区相邻电压矢量与零矢量进行矢量合成,实现网侧电压电流同相位;基于代价函数最小化原则计算所选矢量的作用时间,实现跟踪误差最小化。
3)每个采样周期内将三个矢量开关序列顺序重组优化,解决了C-MPPC策略开关频率不固定的问题,改善了网侧电流频谱分布并有效降低系统功率脉动。
参考文献
[1] 朱进权, 葛琼璇, 王晓新, 等. 基于自抗扰和负载功率前馈的高速磁悬浮系统PWM整流器控制策略[J]. 电工技术学报, 2021, 36(2): 320-329.
Zhu Jinquan, Ge Qiongxuan, Wang Xiaoxin, et al. Control strategy for PWM rectifier of high-speed maglev based on active disturbance rejection control and load power feed-forward[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 320- 329.
[2] Kulikowski K,Sikorski A. New DPC look-up table methods for three-level AC/DC converter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7930-7938.
[3] 李景灏, 吴爱国. 基于离散趋近律与无差拍双闭环结构的单相LCL型PWM整流器控制策略[J]. 电工技术学报, 2021, 36(6): 1290-1303.
Li Jinghao, Wu Aiguo.A double closed-loop control method for single-phase PWM rectifiers with LCL filter based on discrete reaching law and dead- beat algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1290-1303.
[4] 范必双, 谭冠政, 樊绍胜, 等. 一种具有双非零电压矢量输出的三电平PWM整流器直接功率控制方法[J]. 中国电机工程学报, 2015, 35(22): 5832- 5841.
Fan Bishuang, Tan Guanzheng, Fan Shaosheng, et al. A direct power control method for three-level PWM rectifier[J]. Proceedings of the CSEE, 2015, 35(22): 5832-5841.
[5] 张辉, 李志新, 王涛, 等. 基于三矢量的三相PWM整流器低复杂性模型预测直接功率控制[J]. 电网技术, 2018, 42(3): 957-965.
Zhang Hui, Li Zhixin, Wang Tao, et al. Three vectors based low complexity model predictive direct power control for three-phase PWM rectifier with output of double non-zero voltage vectors[J]. Power System Technology, 2018, 42(3): 957-965.
[6] Zhang Yongchang, Jiao Jian, Liu Jie. Direct power control of PWM rectifiers with online inductance identification under unbalanced and distorted network conditions[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(12): 12524-12537.
[7] Vazquez S, Marquez A, Aguilera R, et al. Predictive optimal switching sequence direct power control for grid- connected power converters[J]. IEEE Transa- ctions on Industrial Electronics, 2015, 62(4): 2010- 2020.
[8] Zhang Yongchang, Xie Wei. Low complexity model predictive control-single vector-based approach[J]. IEEE Transactions on Power Electronics, 2014, 29(10): 5532-5541.
[9] 魏新迟, 许利通, 骆仁松, 等. 考虑饱和效应的无刷双馈发电机功率模型预测控制[J]. 电工技术学报, 2021, 36(17): 3721-3729.
Wei Xinchi, Xu Litong, Luo Rensong, et al. Model predictive power control of brushless doubly-fed induction generator considering saturation effect[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3721-3729.
[10] 夏文婧, 刘碧, 王嵩, 等. 基于输入端电压动态分量优化的PWM整流器模型预测控制[J]. 电力系统自动化, 2020, 44(1): 200-207.
Xia Wenjing, Liu Bi, Wang Song, et al. Model predictive control of PWM rectifiers based on dynamic component optimization of input-port voltage[J]. Auto- mation of Electric Power Systems, 2020, 44(1): 200-207.
[11] Tao Yukun, Wu Qinghua, Wang Lei, et al. Voltage sensorless predictive direct power control of three- phase PWM converters[J]. IET Power Electronics, 2016, 9(5): 1009-1018.
[12] Choi D K, Lee K B. Dynamic performance improve- ment of AC/DC converter using model predictive direct power control with finite control set[J]. IEEE Transactions on Industrial Electronics, 2015, 62(2): 757-767.
[13] 叶虹志, 姜燕, 黄守道, 等. 电压型PWM整流器无差拍预测直接功率控制[J]. 电工技术学报, 2015, 30(4): 121-128.
Ye Hongzhi, Jiang Yan, Huang Shoudao, et al. Deadbeat predictive direct power control for three phase voltage source PWM rectifiers[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 121- 128.
[14] 杨美辉,周念成, 王强钢, 等. 基于分布式协同的双极直流微电网不平衡电压控制策略[J]. 电工技术学报, 2021, 36(3): 634-645.
Yang Meihui, Zhou Niancheng, Wang Qianggang, et al. Unbalanced voltage control strategy of bipolar DC microgrid based on distributed cooperation[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(3): 634-645.
[15] Cheng Chenwen, Nian Heng. Low-complexity model predictive stator current control of DFIG under harmonic grid voltages[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1072-1080.
[16] Suh Y, Lipo T A. Control scheme in hybrid syn- chronous stationary frame for PWM AC/DC converter under generalized unbalanced operating conditions[J]. IEEE Transactions on Industry Applications, 2006, 42(3): 825-835.
[17] 张永昌, 彭玉宾, 曲昌琦. 不平衡电网电压下的PWM整流器预测电流控制[J]. 电工技术学报, 2016, 31(4): 88-94, 103.
Zhang Yongchang, Peng Yubin, Qu Changqi. Predi- ctive current control of PWM rectifier under unbalanced grid voltage condition[J]. Transactions of China Electrotechnical Society, 2016, 31(4): 88-94, 103.
[18] Eloy-García J, Arnaltes S, Rodríguez-Amenedo J L. Direct power control of voltage source inverters with unbalanced grid voltages[J]. IET Power Electronics, 2008, 1(3): 395-407.
[19] Yang Haitao, Zhang Yongchang, Liang Jiejunyi, et al. Robust deadbeat predictive power control with a discrete-time disturbance observer for PWM rectifiers under unbalanced grid conditions[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(1): 287-300.
[20] Yan Shuo, Chen Jie, Yang Tianbo, et al. Improving the performance of direct power control using duty cycle optimization[J]. IEEE Transactions on Power Electronics, 2019, 34(9): 9213-9223.
[21] 肖蕙蕙, 苏新柱, 郭强, 等. 三相Vienna整流器无网压传感器预测电流控制策略[J]. 电工技术学报, 2021, 36(6): 1304-1312.
Xiao Huihui, Su Xinzhu, Guo Qiang, et al. Predictive current control of three-phase Vienna rectifier without grid voltage sensors[J]. Transactions of China Elec- trotechnical Society, 2021, 36(6): 1304-1312.
[22] 柳志飞, 杜贵平, 杜发达. 有限集模型预测控制在电力电子系统中的研究现状和发展趋势[J]. 电工技术学报, 2017, 32(22): 58-69.
Liu Zhifei, Du Guiping, Du Fada. Research status and development trend of finite control set model predictive control in power electronics[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(22): 58-69.
[23] Yan Shuo, Chen Jie, Tan S C, et al. A new geometric vector optimization of predictive direct power control[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 5427-5436.
[24] Cortes P, Rodriguez J, Silva C, et al. Delay com- pensation in model predictive current control of a three-phase inverter[J]. IEEE Transactions on Indu- strial Electronics, 2012, 59(2): 1323-1325.
Optimal Predictive Power Control of PWM Rectifier under Nonideal Grid Conditions
Abstract Model predictive power control (MPPC) is based on the minimization principle of the cost function, which selects the optimal switching state to act on the system. However, the grid side current of the MPPC will be distorted seriously under unbalanced grid voltage conditions, which affects the output performance of PWM rectifier. To address this problem, the paper applies the new definition of extended reactive power to MPPC to obtain constant active power and grid-side sinusoidal current without power compensation algorithms. In addition, aiming at the problems of conventional MPPC (C-MPPC), such as variable switching frequency and large system computation, an optimized MPPC (O-MPPC) is proposed. By optimizing the finite control set, the system computation is reduced, and the selected vector switching sequence is reorganized for optimization and the action time of each vector is calculated by the multi-vector synthesis method. As a result, the problem of the unstable switching frequency of C-MPPC is solved, and the system control performance is enhanced. The feasibility and superiority of the proposed optimized control method are verified through comparative experiments with C-MPPC.
keywords:Predictive power control, unbalanced grid voltage, PWM rectifier, extended reactive power, switching sequence optimization
DOI: 10.19595/j.cnki.1000-6753.tces.211924
中图分类号:TM461
重庆市教育委员会科学技术研究计划重点项目(KJZD-K201901102)和重庆市教育委员会科学技术研究项目(KJQN201801142)资助。
收稿日期 2021-11-25
改稿日期 2021-12-21
李 山 男,1965年生,博士,教授,主要从事电力电子与电力传动方面研究。E-mail: Lishan@cqut.edu.cn
郭 强 男,1984年生,博士,研究方向为大功率变换器及其控制技术。E-mail: guoqiang@cqut.edu.cn(通信作者)
(编辑 陈 诚)