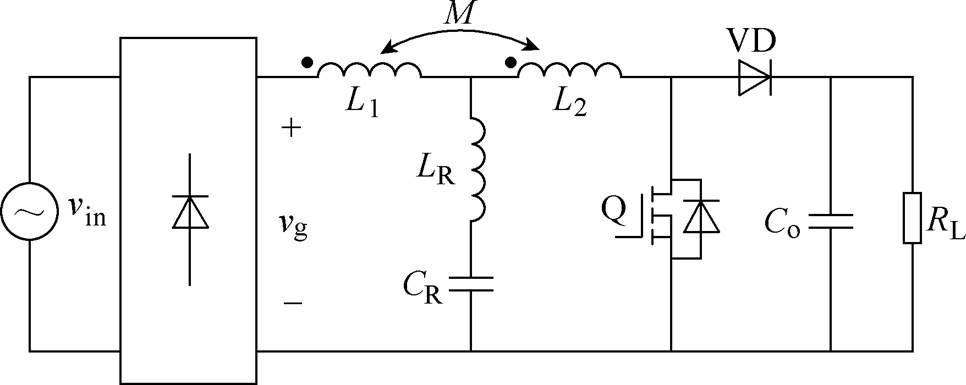
图1 基于耦合电感的零电流纹波PFC变换器
Fig.1 Zero current ripple tapped inductor PFC converter
摘要 为了降低传统Boost功率因数校正(PFC)变换器的输入电流纹波,改善输入电流的总谐波畸变率(THD),提升PFC效果,该文提出一种基于耦合电感的零电流纹波PFC变换器。首先,基于零电流纹波工作原理分析并推导PFC工况下的电路参数设计方法。分析表明,由于所增加的辅助电感仅用于消除电流纹波而不参与主功率传输,因此其体积远小于传统Boost PFC的输入滤波器。其次,在拓扑研究基础上结合零电流纹波特性,提出采用数字单周期控制策略,给出数字控制器的设计及实现方法。最后,通过实验将所提出拓扑的性能与传统Boost PFC进行对比。实验结果表明,该文所提出的基于耦合电感的零电流纹波PFC变换器输入电感电流纹波近似为零,THD明显低于传统Boost PFC变换器,且功率因数(PF)显著提升。
关键词:数字单周期控制 零电流纹波 耦合电感 功率因数校正
传统Boost变换器因其拓扑结构简单、成本较低等优点被广泛应用于功率因数校正(Power Factor Correction, PFC)[1-3]变换器中。根据电感电流状态,Boost变换器可以工作于电流连续导通模式(Continous Conduction Mode, CCM)、临界导通模式(Boundary Conduction Mode, BCM)和断续导通模式(Discon- tinous Conduction Mode, DCM),当变换器运行在CCM时,其输入滤波电感的体积与功率成正比,与输入电流纹波成反比,降低了变换器的功率密度;当变换器运行在BCM和DCM时,续流二极管无反向恢复问题,但是输入电流纹波较大,引起较大的功率损耗且功率因数较低。即对于传统Boost PFC变换器而言,以上三种工作模式均存在输入电流纹波较大、容易产生电磁干扰(Electromagnetic Inter- ference, EMI)等问题[4]。为了满足各类谐波标准,如IEC 61000-3-2,其需要在前级添加尺寸较大的EMI滤波器,而这将进一步增加变换器的体积和质量。因此,研究具有低输入电感电流纹波、低EMI的PFC变换器具有重要意义。
文献[5-7]利用交错并联技术来降低输入电感电流纹波,同时交错并联技术带来的占空比倍增效应也可以有效降低滤波器的体积和质量,但是该类拓扑开关器件较多,对于小功率应用,成本上升,控制复杂度增加。文献[8]在输入侧滤波电容基础上并联了阻容纹波抑制支路,搭配使用功率半导体滤波器(Power Semiconductor Filter, PSF),从而改善了输入电感电流纹波,但其主电路拓扑引入了大量全控型器件,导致控制电路复杂、成本上升。文献[9]利用二次型Boost变换器实现降低PFC变换器的输入电感电流纹波,该拓扑采用一个开关管即可实现与占空比成二次方关系的直流传输比,具有直流增益大的优点,但相比Boost变换器其多了两个二极管,电路子工作模态增多、系统效率降低。文献[10]采用双独立电感降低输入电感电流纹波,该拓扑具有控制相对简单、元器件少的优点,但仅适用于DCM。文献[11]利用耦合电感和隔直电容将高频电流旁路,从而在一定程度上降低PFC变换器输入电感电流纹波,但仍需要前置较大的共模EMI滤波器,且开关管的电流应力增大,影响系统整体效率。零电流纹波拓扑技术最早出现于直流变换器的设计中[12-15],例如,可使用耦合电感实现直流变换器的输入或输出电流零纹波。但将该类拓扑应用于PFC
场合时,与直流变换器设计时相比新的挑战主要在以下两个方面:一方面,在电感、电容等电路参数设计上,由于其输入电压为二倍工频的正弦半波,电压波动大,且PFC变换器的占空比将随输入电压的变化呈周期性变化;同时,由于输入电压和占空比的正弦波动导致电路中电感和电容对应的电流和电压纹波大小也在不断的变化,因此,在PFC变换器的电感和电容参数设计时,需要考虑其电流和电压纹波大小最恶劣时的工作状态。另一方面,在变换器的控制上,直流变换器主要对输出电压进行控制,但是在PFC变换器设计中,不仅需要控制变换器输出稳定的直流电压,而且更重要的是需要控制输入电流使其跟随输入电压呈正弦规律变化,即需要保持二者相位一致且输入电流无明显畸变。
常见的PFC控制策略包括峰值电流控制[16]、平均电流控制[17]、滞环电流控制[18]及单周期控制[19-22]等。峰值电流控制和滞环电流控制是基于输入电流纹波的控制方法,响应速度快但对电流纹波十分敏感,且峰值电流控制在占空比大于0.5时存在次谐波振荡问题,需要引入斜坡补偿,滞环电流控制存在滞环宽度对系统性能和开关频率有较大影响,导致开关频率在一个工频周期内不恒定。平均电流控制因其控制器中含有电流误差放大器而具备高频开关噪声滤除能力,同时也导致其响应速度较慢。除此之外,上述三类控制策略除了需要采样输出电压和电感电流之外,仍需要采样输入电压,且控制器需要乘法器,这使得控制电路较为复杂。
相比之下,单周期控制技术具有无需采样输入电压、响应速度快且控制电路无需乘法器等优点,被越来越多地应用在PFC场合[19-22],但单周期控制算法本身无滤波效果,导致该控制算法对于被采样电流信号的开关周期纹波及噪声较为敏感[19-20]。因此,在单周期控制器设计过程中往往需要设置较低的电流环路带宽和电流采样滤波器截止频率用于抑制开关周期的电流纹波,此举增加了变换器的整体设计难度,同时也将影响单周期控制器的响应速度。此外,电路中电感电流的纹波过大将影响单周期控制中对于当前开关周期的电感电流均值的判断,尤其在数字化实现时,由于数字控制系统的固有延时,容易引起系统的振荡和不稳定[22]。
综上所述,若可以将具有低输入电流纹波的PFC变换器与数字单周期控制策略进行结合,则不仅有利于提高数字单周期控制中输入电感电流均值采样精度,降低滤波器的设计难度,提高电流环路带宽,从而充分发挥单周期控制的优点,同时可以实现低输入电流纹波、减小滤波电感体积、提高变换器的功率因数校正性能。但是,关于如何将低输入电流纹波PFC变换器与单周期控制算法相结合,尚未见相关研究。
根据以上思路,本文将基于耦合电感的零纹波拓扑技术应用于PFC变换器,对传统Boost PFC变换器进行改进,并采用数字单周期控制方案,主电路拓扑如图1所示。

图1 基于耦合电感的零电流纹波PFC变换器
Fig.1 Zero current ripple tapped inductor PFC converter
本文首先介绍了零电流纹波PFC电路的基本工作原理,推导了零电流纹波实现的条件,给出了电路主要元件参数的设计和选取标准。然后给出了基于数字单周期控制零电流纹波PFC电路闭环控制器的设计方法。最后,根据文中的设计方法进行仿真和实验验证,设计了两台输出400V、功率200W的实验样机,通过与传统Boost PFC进行实验对比,验证了仿真和理论分析的正确性。
零电流纹波PFC等效电感电路如图1所示。图中,L1、L2分别为耦合电感两个绕组的自感,n为耦合电感的匝数比, ,M为耦合电感的互感,
,M为耦合电感的互感,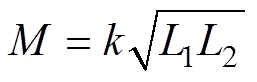 ,k为耦合系数(0<k<1
,k为耦合系数(0<k<1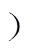 ,LR、CR分别为纹波抵消支路的电感和电容,Q、VD分别为开关管和输出二极管,Co和RL分别为输出滤波电容和负载。
,LR、CR分别为纹波抵消支路的电感和电容,Q、VD分别为开关管和输出二极管,Co和RL分别为输出滤波电容和负载。
在工作原理分析之前,首先做如下合理假设:
(1)输入电压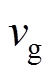 为整流后理想的正弦半波,即
为整流后理想的正弦半波,即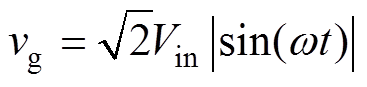 ,其中Vin、w 分别为交流输入电压有效值和角频率。
,其中Vin、w 分别为交流输入电压有效值和角频率。
(2)电路中所有元器件均为理想元器件。
(3)开关频率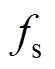 远大于交流输入电压频率
远大于交流输入电压频率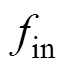 ,开关周期内输入电压可视为定值。
,开关周期内输入电压可视为定值。
(4)电容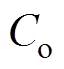 、
、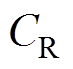 视为足够大,其两端电压纹波相对于直流量很小,在开关周期内可以忽略不计。
视为足够大,其两端电压纹波相对于直流量很小,在开关周期内可以忽略不计。
根据电路分析原理,图1所示的变换器可以等效为如图2所示由三个普通电感LA、LB及LC组成的变换器[13],等效电感LA、LB及LC与互感M的关系为
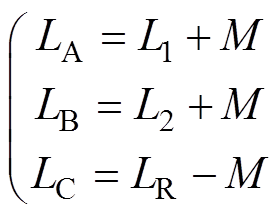 (1)
(1)
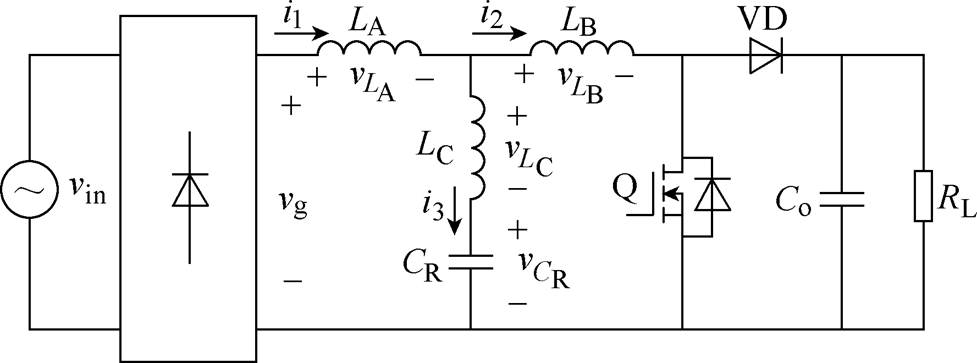
图2 零电流纹波PFC等效电感电路
Fig.2 Equivalent circuit of the zero current ripple tapped PDF converter
当变换器工作于CCM时,在每个开关周期内可分为两种工作模态如图3所示,其主要电压电流波形如图4所示。
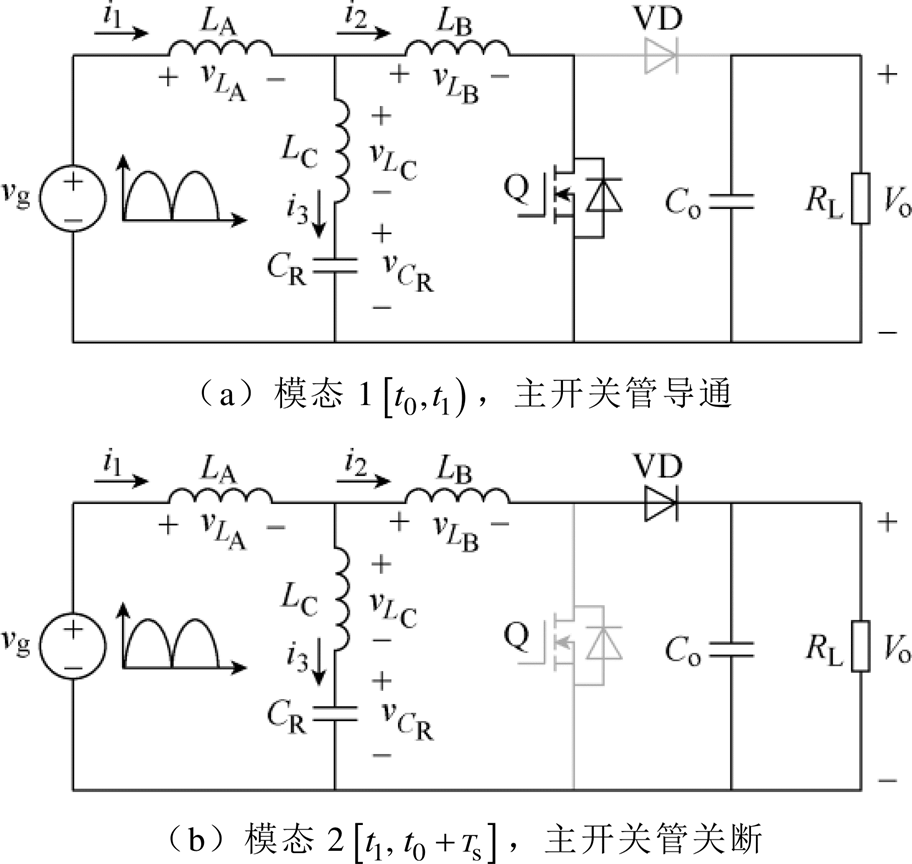
图3 零电流纹波PFC变换器工作模态
Fig.3 Operation stages of the proposed converter
模态1[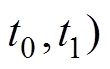 下变换器的等效电路如图3a所示。在t0时刻变换器开关管Q导通、输出二极管关断,由基尔霍夫电流、电压定律可得,此期间的电感电流和电压的关系为
下变换器的等效电路如图3a所示。在t0时刻变换器开关管Q导通、输出二极管关断,由基尔霍夫电流、电压定律可得,此期间的电感电流和电压的关系为
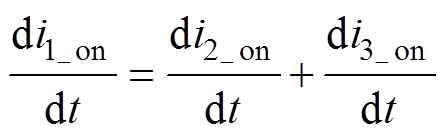 (2)
(2)
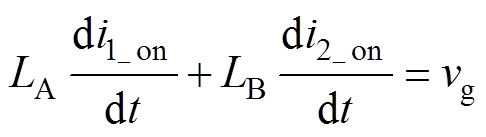 (3)
(3)
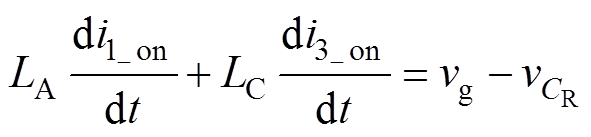 (4)
(4)
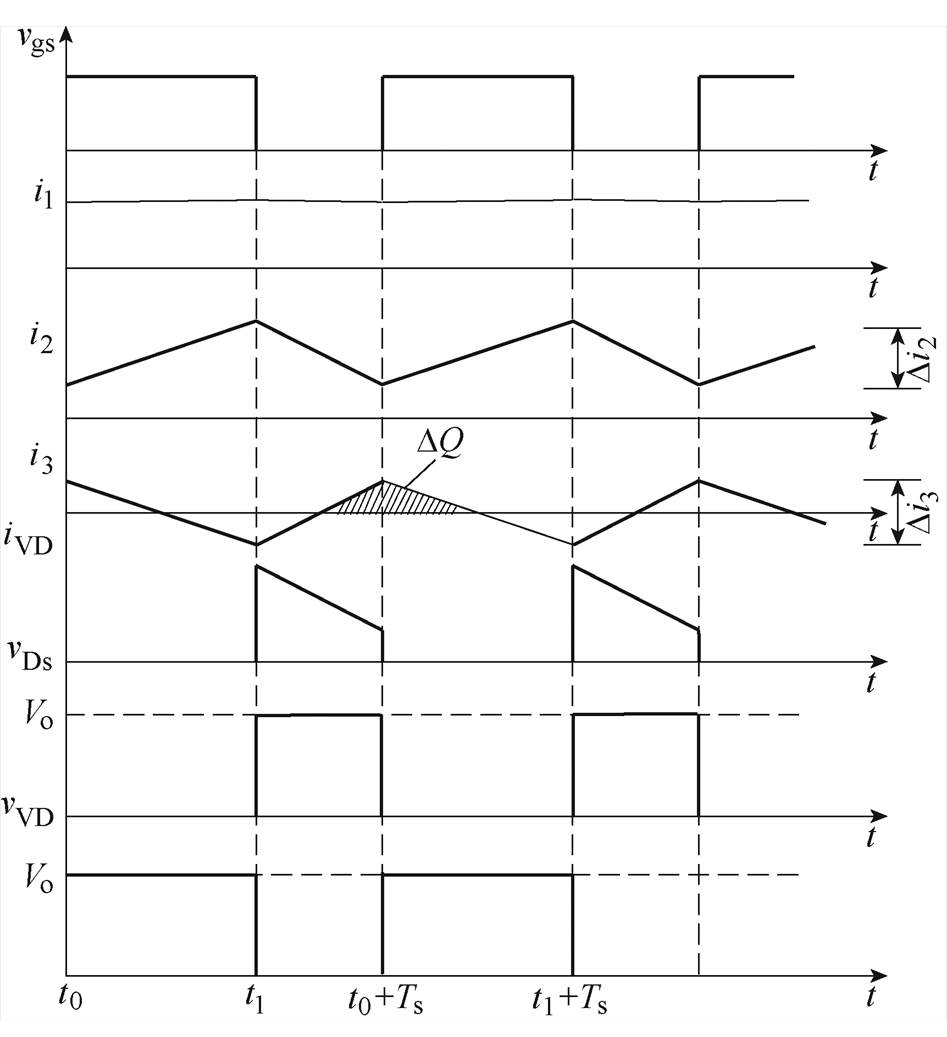
图4 变换器稳态工作时主要波形
Fig.4 Key waveforms of the proposed converter during steady-state operation
考虑到开关频率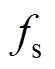 远大于交流输入电压频率
远大于交流输入电压频率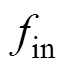 ,且电容
,且电容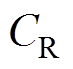 视为足够大。因此,输入电压以及电容电压在开关周期内的纹波可以忽略。即
视为足够大。因此,输入电压以及电容电压在开关周期内的纹波可以忽略。即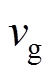 、
、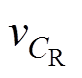 分别为忽略开关周期内纹波时的输入电压和电容
分别为忽略开关周期内纹波时的输入电压和电容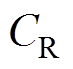 电压。结合图3,根据伏秒平衡原理,在一个开关周期中电感
电压。结合图3,根据伏秒平衡原理,在一个开关周期中电感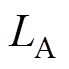 、
、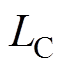 两端电压为零,此时有
两端电压为零,此时有
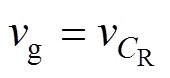 (5)
(5)
将式(5)代入式(4)并结合式(2)、式(3)可得,等效电感LA、LB和LC在开关导通期间的电流变化率为
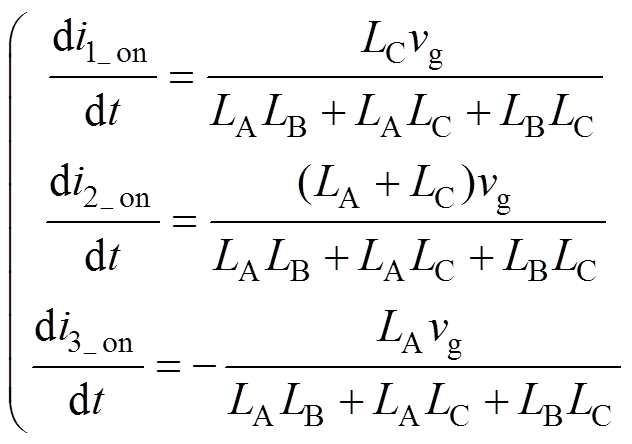 (6)
(6)
由式(6)可知,电流i2、i3变化率方向相反,有电流纹波抵消效果。由于输入电流i1=i2+i3,当电流i2、i3变化率相反且数值完全相等时,输入电流i1接近零电流纹波。根据式(6)可推导零电流纹波实现条件为等效电感LC=0,考虑式(1),可知实现零电流纹波的条件为纹波抵消支路电感LR等于耦合电感的互感M,即
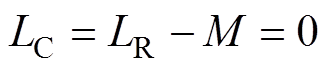 (7)
(7)
将式(7)代入式(6)可知,此时电流i2和i3的纹波绝对值相等,即
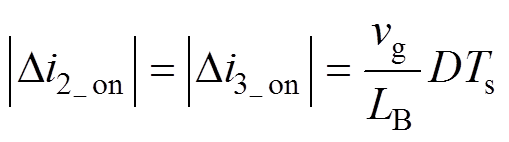 (8)
(8)
式中,D为开关管Q的占空比;Ts为开关周期。
模态2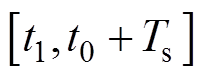 下变换器的等效电路如图3b所示。在t1时刻变换器开关管Q关断,输出二极管导通,由基尔霍夫电流、电压定律可得此期间的电感电流和电压的关系为
下变换器的等效电路如图3b所示。在t1时刻变换器开关管Q关断,输出二极管导通,由基尔霍夫电流、电压定律可得此期间的电感电流和电压的关系为
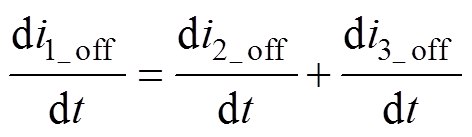 (9)
(9)
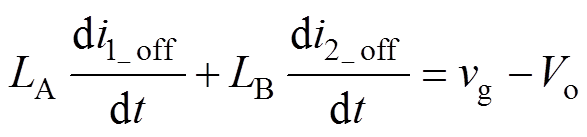 (10)
(10)
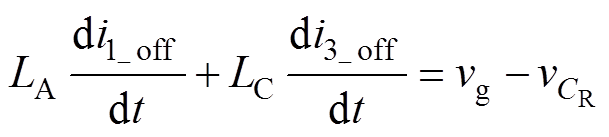 (11)
(11)
将式(5)代入式(11)并结合式(9)、式(10)可得,等效电感LA、LB和LC在开关关断期间的电流变化率为
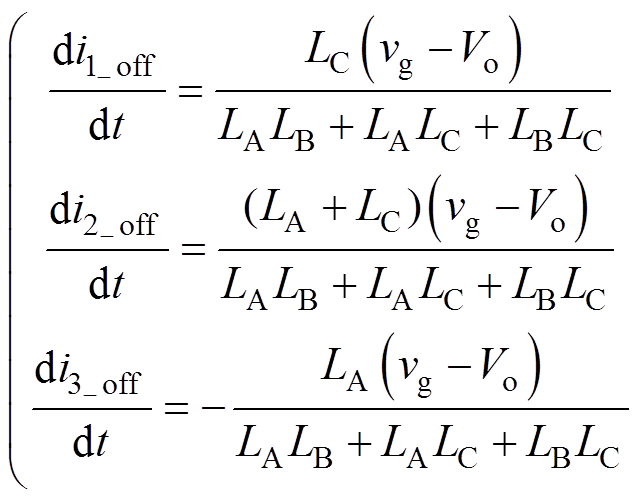 (12)
(12)
将式(7)代入式(12)可知,在开关断开时,电流i2、i3变化率相反且数值完全相等,即输入电流i1仍然接近零电流纹波,即
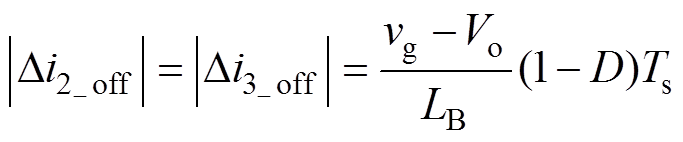 (13)
(13)
对式(3)和式(10)应用伏秒平衡原理,可得变换器的输出电压稳态增益为
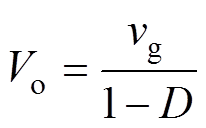 (14)
(14)
根据图4,并结合式(8),可知电路运行在CCM的边界条件为电感LB≥LB_min,即
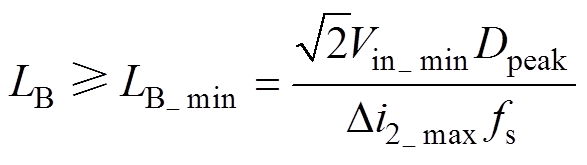 (15)
(15)
式中,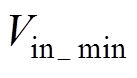 为输入电压最小有效值;
为输入电压最小有效值;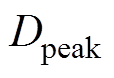 为输入电压为
为输入电压为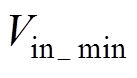 时正弦波幅值处对应的占空比;
时正弦波幅值处对应的占空比;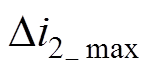 为电流纹波
为电流纹波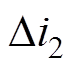 的最大值。
的最大值。
由输入、输出功率的关系可知,输出功率满载时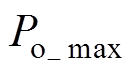 电路的最大输入功率为
电路的最大输入功率为
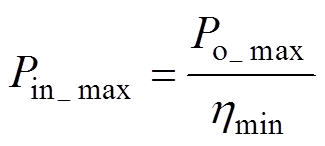 (16)
(16)
当输入电压有效值最小时,输入电流最大有效值为
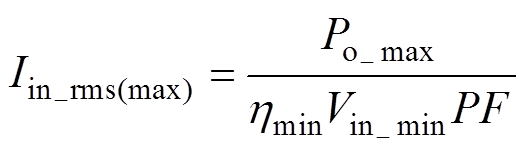 (17)
(17)
式中,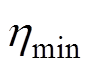 、PF分别为变换器的效率最小值和功率因数。
、PF分别为变换器的效率最小值和功率因数。
则输入电流最大幅值为
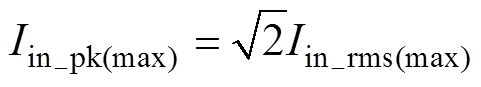 (18)
(18)
工程设计中电流纹波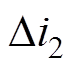 的最大值一般不大于20%
的最大值一般不大于20%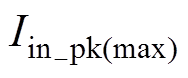 [6]。即
[6]。即
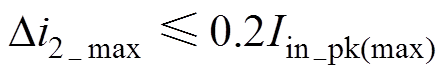 (19)
(19)
由式(14)可知,输出电压Vo一定时,PFC变换器的占空比D随着vg的变化而发生周期性变化。因此,由式(14)可得变换器在输入电压最小有效值正弦波幅值处的占空比Dpeak为
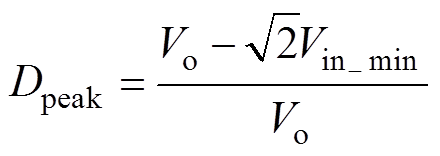 (20)
(20)
因此,将式(19)、式(20)代入式(15),可得电感电路运行于CCM时,LB的最小值为
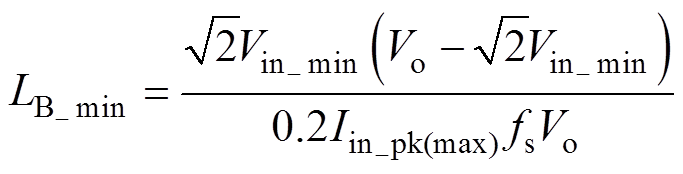 (21)
(21)
电容CR的参数选取与其电压纹波的大小相关,电容CR的电压纹波为
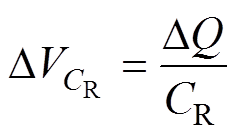 (22)
(22)
由图4可知,电荷变化量DQ为
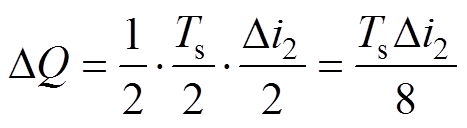 (23)
(23)
则将式(23)代入式(22)可以化简为
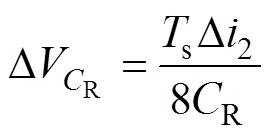 (24)
(24)
将式(8)代入式(24)可得
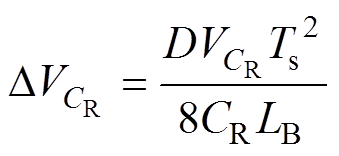 (25)
(25)
由式(17)、式(18)可知,在输入电压最小有效值时变换器对应输入电流最大幅值,且此时对应占空比为Dpeak。结合图4可以发现,此时为对应电容CR电流纹波的最恶劣情况,因此,将式(20)代入式(25)可得电容CR的表达式为
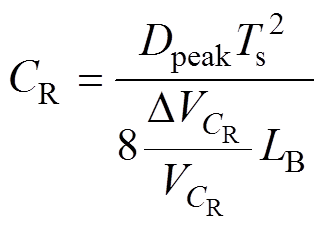 (26)
(26)
故电容CR的参数选取只需保持其电压纹波小于一定值即可,一般取纹波系数小于5%[13]。
输出电容Co的参数选取有两种方法输出电压的维持时间Dt约束法和输出电压纹波DVo约束 法[17]。本文采用维持时间Dt约束法,即输出电容Co由式(27)决定。维持时间是指切断变换器输入电源后,输出电压值维持在Vo_min~Vo范围内的时间长度。维持时间一般为15~50ms,在这里取维持时间为20ms,Vo_min取输出电压Vo的80%[22]。
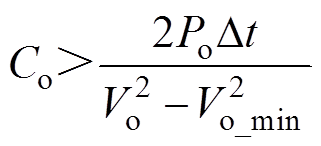 (27)
(27)
单周期控制作为一种非线性控制,其基本思想是在每个开关周期内令开关变量的平均值与控制参考量相等或呈比例,从而达到控制目标[21]。本文将数字单周期控制方法应用于零电流纹波PFC电路中,图5为数字单周期控制零电流纹波PFC电路及其控制电路原理。
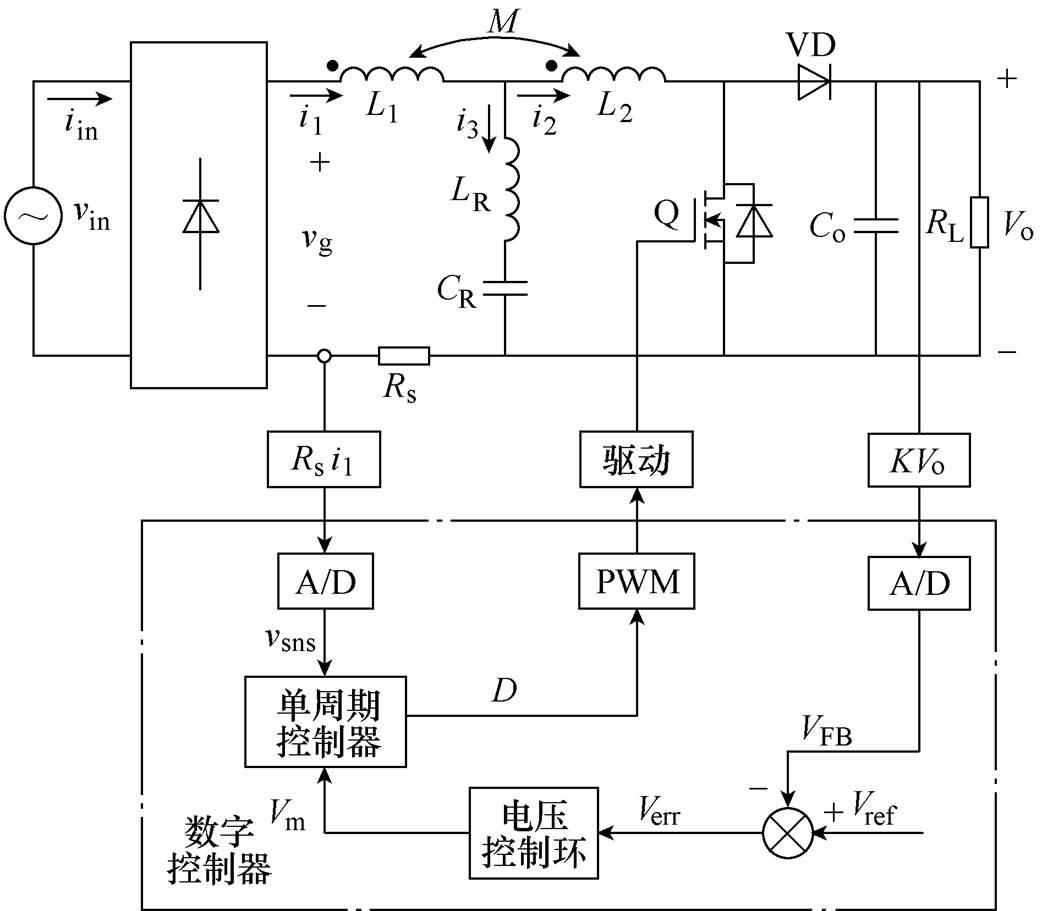
图5 数字单周期控制零电流纹波PFC变换器
Fig.5 Zero current ripple PFC converter with digital OCC
根据单周期控制原理[20],结合式(14)可以推出图5所示变换器的单周期控制平衡方程为
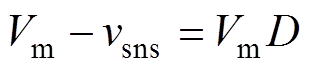 (28)
(28)
式中,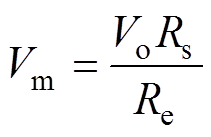 ;
;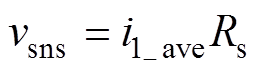 ;i1_ave为一个开关周期Ts内的输入电感电流平均值;Re为变换器的等效电阻;Rs为电流采样电阻。
;i1_ave为一个开关周期Ts内的输入电感电流平均值;Re为变换器的等效电阻;Rs为电流采样电阻。
在单周期控制的PFC电路中,变换器的控制回路由电流内环和电压外环构成。电压外环的输出Vm作为电流内环的控制参数参与对变换器输入电流的控制,电压外环的补偿控制目标是得到稳定的输出电压。图6所示为零电流纹波PFC变换器闭环控制传递函数框图,环路增益为
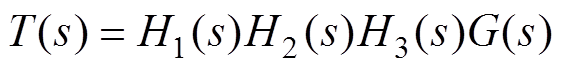 (29)
(29)
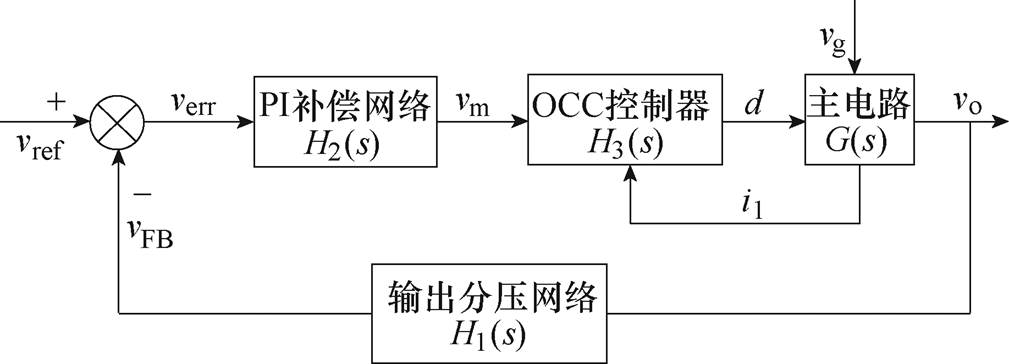
图6 零电流纹波PFC变换器闭环控制传递函数框图
Fig.6 Block diagram of the closed-loop control system
输出分压网络H1(s)为参考电压与输出电压目标值之比,即
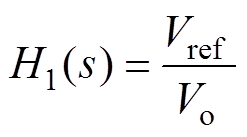 (30)
(30)
根据输入电压有效值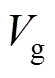 与输入功率
与输入功率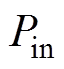 的关系,并结合式(28)可得
的关系,并结合式(28)可得
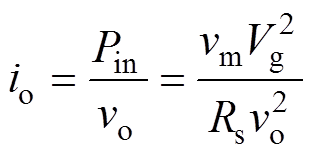 (31)
(31)
根据小信号模型分析原理[23],由式(31)可得输出电流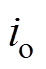 的低频小信号扰动表达式为
的低频小信号扰动表达式为
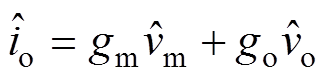 (32)
(32)
其中
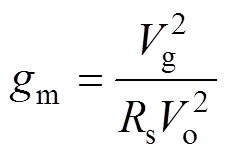
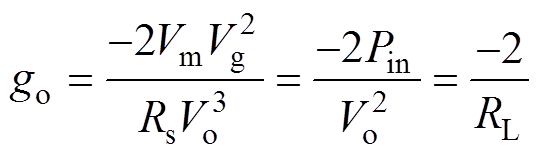
结合式(32)以及图6可得闭环控制环路小信号流如图7所示。
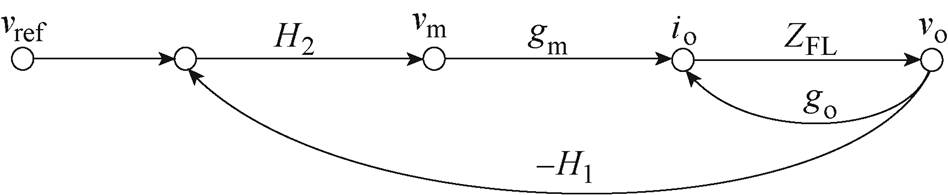
图7 闭环控制环路小信号流
Fig.7 Small-signal model of the closed-loop control system
图7中,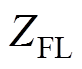 为变换器输出电容
为变换器输出电容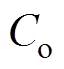 和负载电阻
和负载电阻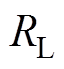 并联的阻抗表达式,即
并联的阻抗表达式,即
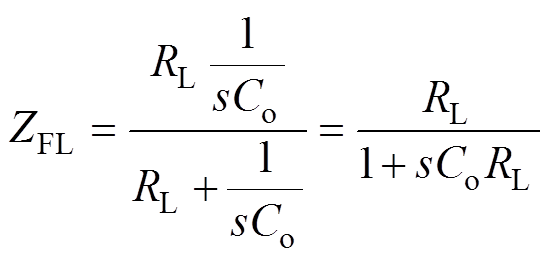 (33)
(33)
因此,由图7可得传递函数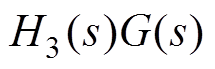 为
为
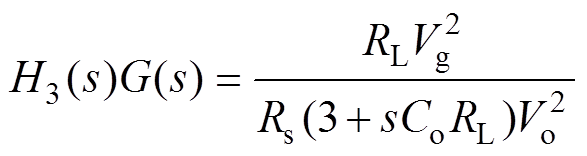 (34)
(34)
本文采用比例积分(PI)补偿网络对电压外环进行补偿[6],即电压误差补偿网络H2(s)为
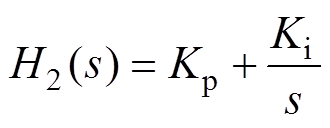 (35)
(35)
因此,整体环路传递函数T(s)为
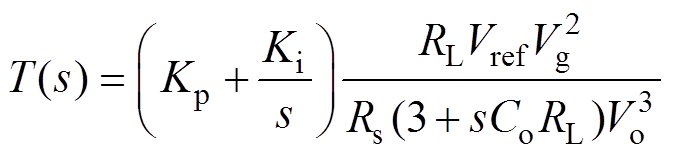 (36)
(36)
式中,Kp=1.22, Ki=124.52, Vref =2V, Rs=0.185W,其他参数见表1。对于电压外环的补偿,是为了避免输出电压中二倍工频(100Hz)对于控制的影响。电压外环在保证环路稳定的情况下,带宽应小于二倍工频,同时考虑到数字控制器的相位滞后效应,其相位稳定裕度可选择60°以上。利用Matlab/ Simulink中的线性系统分析工具(sisotool)对H2(s)中的参数进行优化设计,补偿前环路传递函数T(s)的Bode图如图8中的实线所示,其穿越频率fc= 21Hz,相位裕度g =63°。
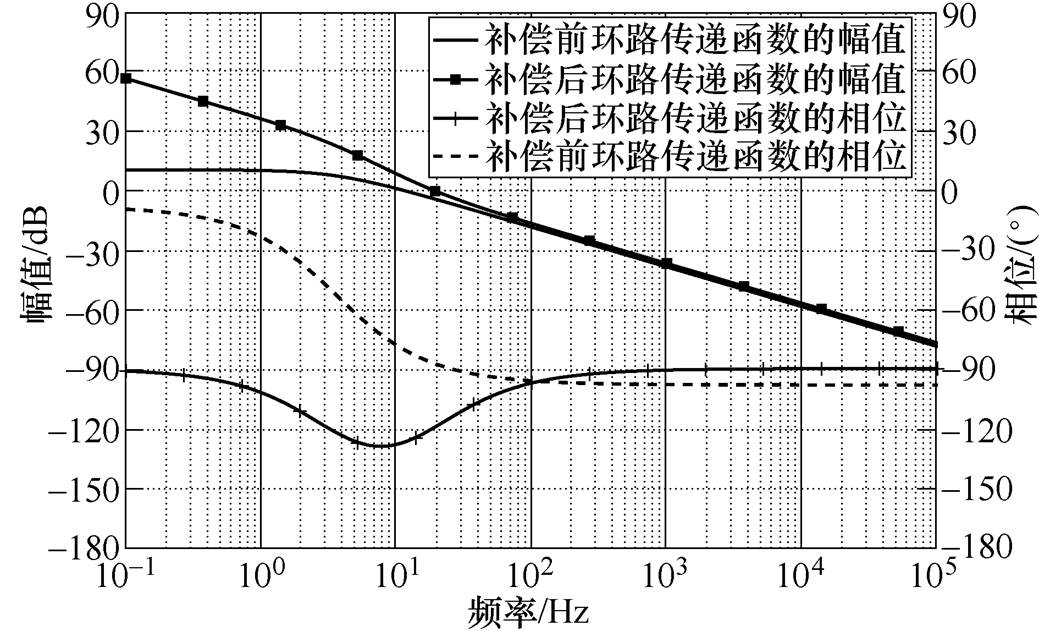
图8 环路传递函数的伯德图
Fig.8 Bode diagram of closed-loop transfer function
传统的模拟单周期控制器电压、电流连续采样,系统实时性高。而数字控制系统具有固有的采样延时和失真问题,无法实现类似模拟系统的实时采样和控制[22]。因此,在数字控制器的实现中首先要解决采样问题,尽量减少系统延时和采样误差。
对于电压采样,由于电压外环的速度较慢,采样频率一般设置为电压外环截止频率的10~20倍以上;对于电流采样,为实现电流快速跟踪,同时避免开关频率噪声干扰,电流内环带宽一般为开关频率的1/10[22]。因此本设计中数字控制系统采样频率为开关频率,即采用单周期单点采样法[20]。该采样法的采样时刻对控制精度有重要影响,由式(28)可知,单周期控制需要获知输入电流均值i1_ave,从而计算当前开关周期内的占空比D为
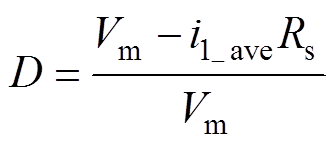 (37)
(37)
本文采用的电流采样触发时序如图9所示。设置数字信号处理器(DSP),令数字PWM模块载波信号为对称三角形,并在峰值处触发电流采样,该点为开关导通时间中点,因此采样电流值接近电流均值。占空比更新时刻为下一个三角载波的起始时刻。数字信号延时为开关周期的1/2,既给予系统足够的控制算法实现时间,又尽可能减小数字系统延时。从后面的实验结果来看,该数字PWM策略实现简单且效果良好。
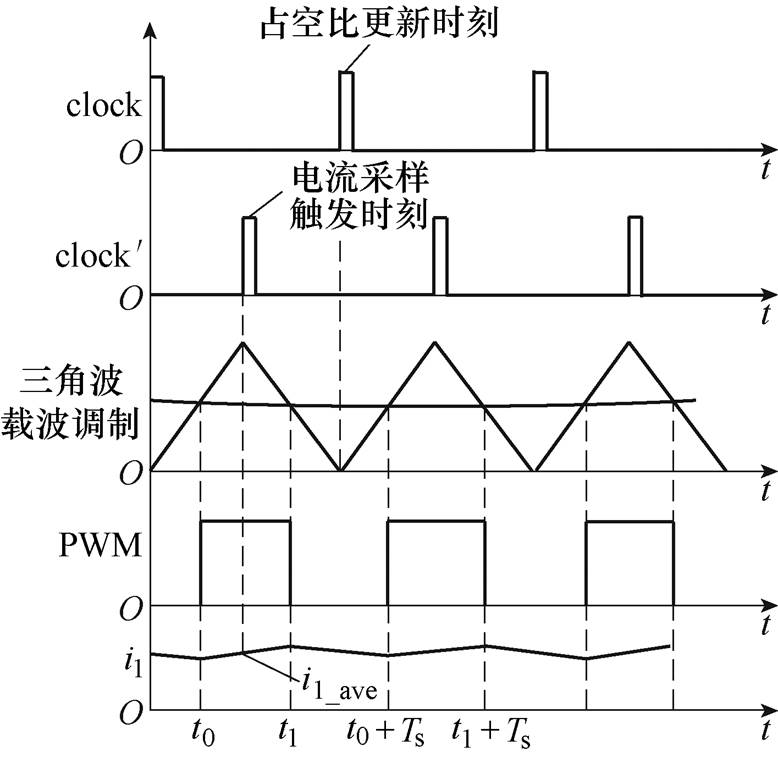
图9 电流采样示意图
Fig.9 Sampling of input current
本文在仿真平台PSIM上搭建了如图5所示的数字单周期控制零电流纹波PFC电路,实验样机参数见表1,输出满载、输入Vin=220Vrms的仿真结果如图10所示。根据图10a可知,输入电流与输入电压同相位,且输入电流无畸变,PF>0.999,THD= 2.43%,输出电压稳定在400V左右。图10b为电感电流i1、i2、i3波形,图10c为对应电感电流在开关频率内的仿真波形,结合图10b、图10c可以看出,电流i2、i3的变化率相反,且两者的峰-峰值基本相同,图10d为整流后输入电压vg、电容电压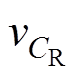 在工频周期及开关周期的仿真波形,由此可知,仿真验证了前文理论分析的正确性(见式(5))以及电容CR参数设计的正确性。综上所述,由图10可知,变换器输入电流i1纹波几乎为零,实现了零电流纹波功能,且功率因数较高,输出电压稳定在400V。
在工频周期及开关周期的仿真波形,由此可知,仿真验证了前文理论分析的正确性(见式(5))以及电容CR参数设计的正确性。综上所述,由图10可知,变换器输入电流i1纹波几乎为零,实现了零电流纹波功能,且功率因数较高,输出电压稳定在400V。
表1 实验样机参数
Tab.1 The specifications of prototypes

参 数传统Boost PFC变换器零电流纹波 PFC变换器 传统Boost电感L/mH1 100 (83匝)— 输入滤波电感Lin/mH1 100 (83匝)— 输入滤波电容Cin/mF0.62— 耦合电感匝比n—1 耦合系数k—0.83 自感值L1/mH—600 (62匝) 自感值L2/mH—600 (62匝) 互感值M/mH—500 纹波抵消电感LR/mH—500 (100匝) 纹波抵消电容CR/nF—68 输出电容Co/mF165— 开关管QSPP21N50C3— 输出二极管VDC3D04065A—
为验证以上分析的正确性,本文对传统Boost PFC变换器和所提出的基于耦合电感的零电流纹波PFC变换器进行了实验对比,均采用数字单周期控制方法。实验样机对比如图11所示,图中左侧为零电流纹波PFC变换器,右侧为传统Boost PFC变换器。通过对比可知,零电流纹波PFC变换器通过磁集成的方式提高了磁心的利用率,虽然与传统Boost PFC变换器相比磁心数量没有减少,但磁心体积和质量均显著降低(其中耦合电感、输入滤波电感Lin以及输入电感L的磁心材料为铁硅铝磁粉心BS157125A,尺寸为40.0mm×24.1mm×14.5mm;电感LR磁心材料为铁硅铝磁粉心77210A7,尺寸为20.3mm×12.7mm×6.3mm)。
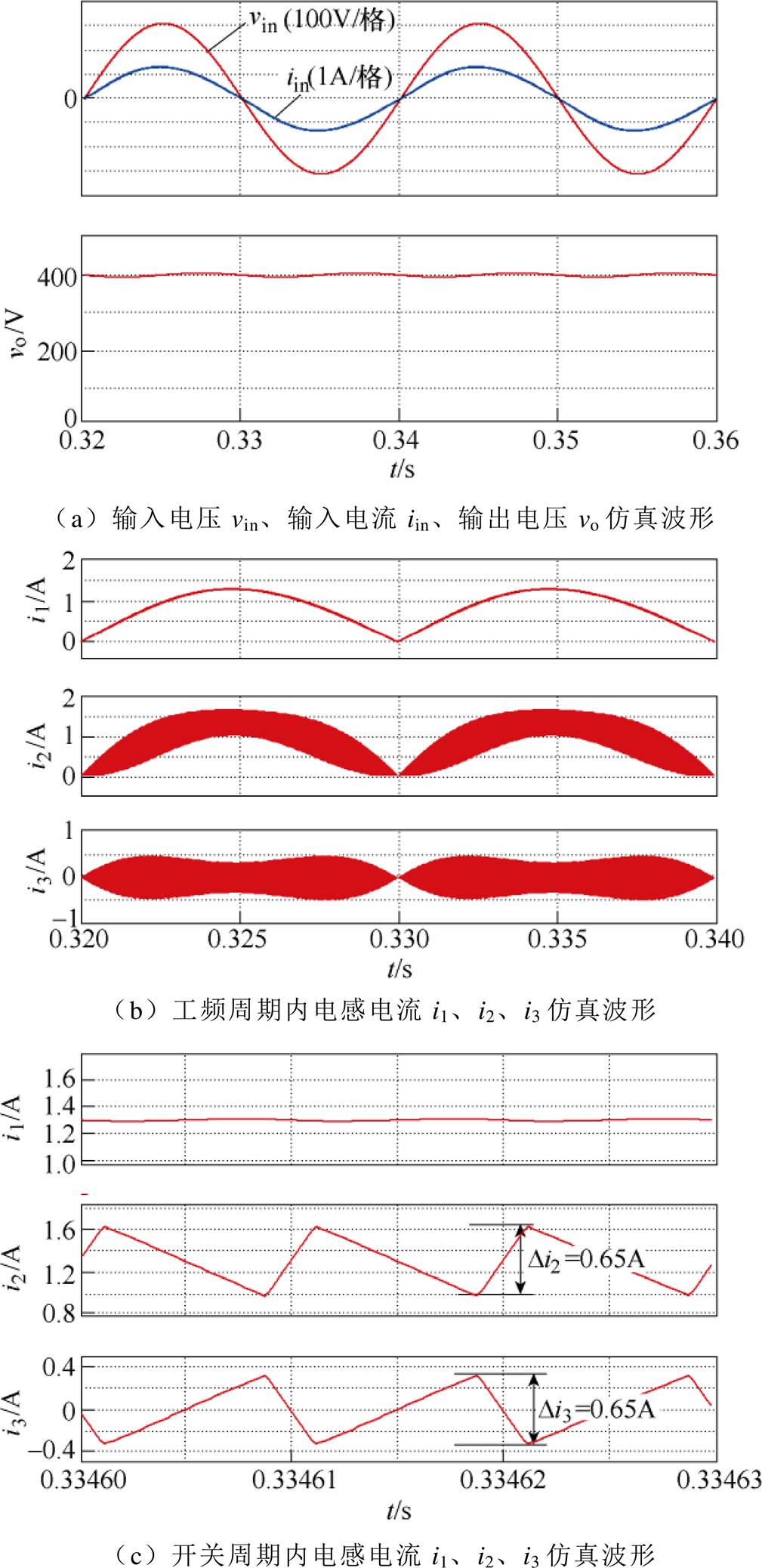
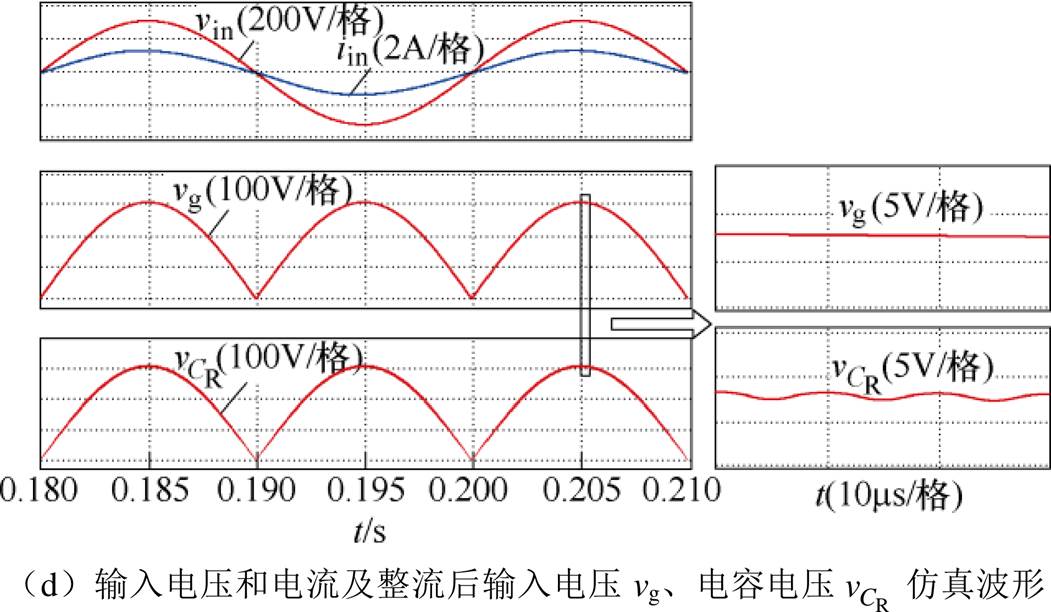
图10 Po=200W、Vin=220Vrms时零电流纹波PFC变换器的仿真波形
Fig.10 Simulation waveforms of the proposed converter when Po=200W and Vin=220Vrms

图11 实验样机对比
Fig.11 Comparison of experimental prototypes
此外,所搭建的两台实验样机基本实验参数为:输入电压vin=85~265Vrms、输入电压频率fin=50Hz、开关频率fs=100kHz、输出电压vo=400V、输出功率Po=200W,其他实验参数见表1。
为了体现所提出的变换器的纹波抵消效果以及对于功率因数校正效果的改善,首先通过实验对比展示如下:图12和图13为不同交流输入电压时,零电流纹波PFC变换器和传统Boost PFC变换器在输出满载状态下输入电压vin、输入电流iin以及输入电感电流i1、iL的实验波形。
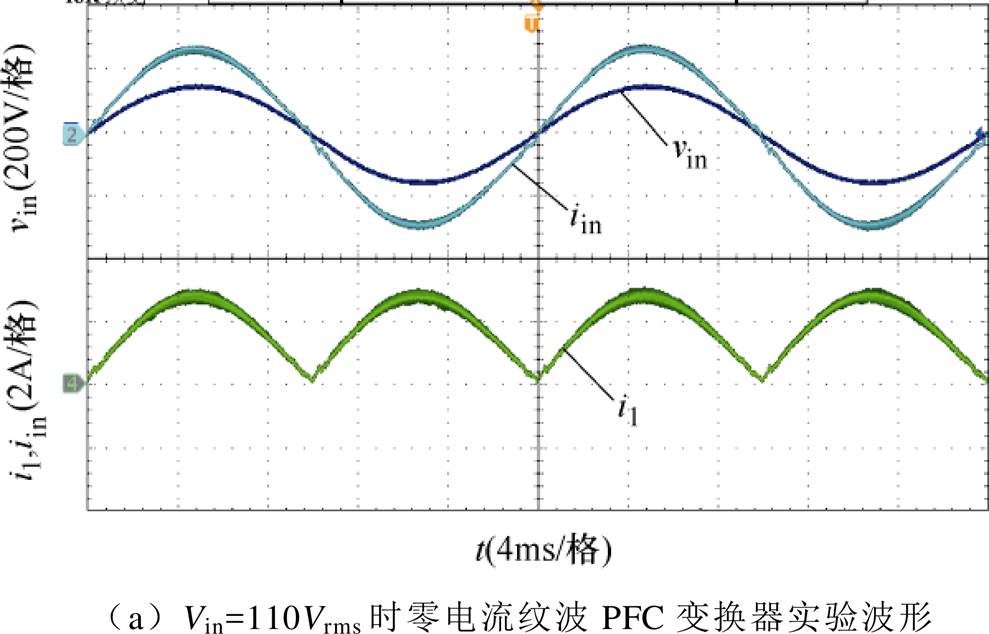
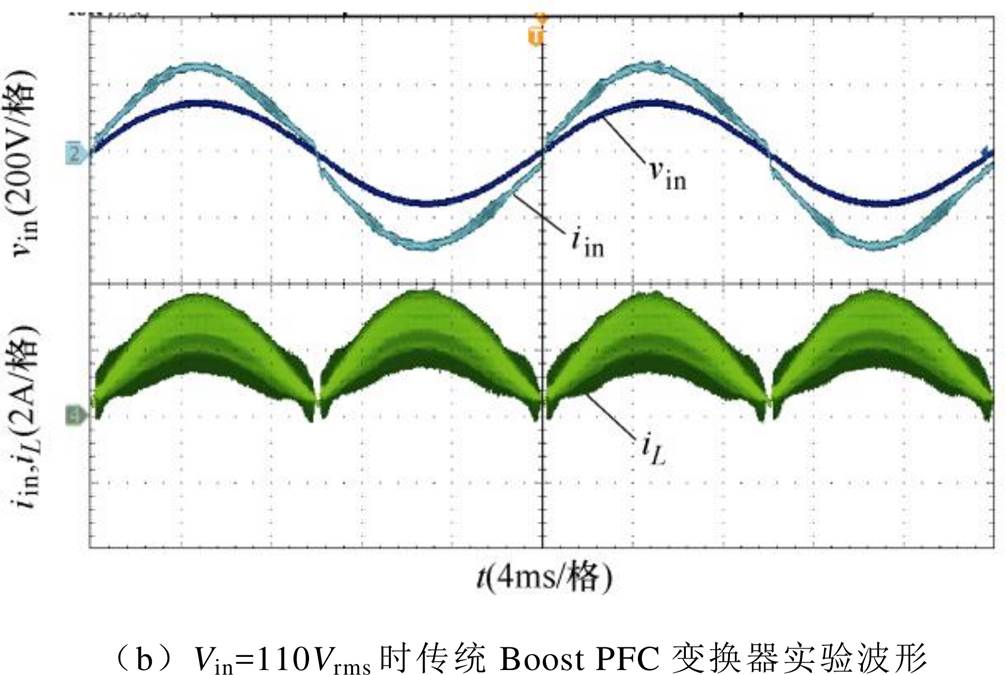
图12 Vin=110Vrms时不同PFC变换器输入电压、输入电流、输入电感的电流波形
Fig.12 Waveforms of voltage vin and currents iin, i1, iL with different PFC converters at Vin=110Vrms
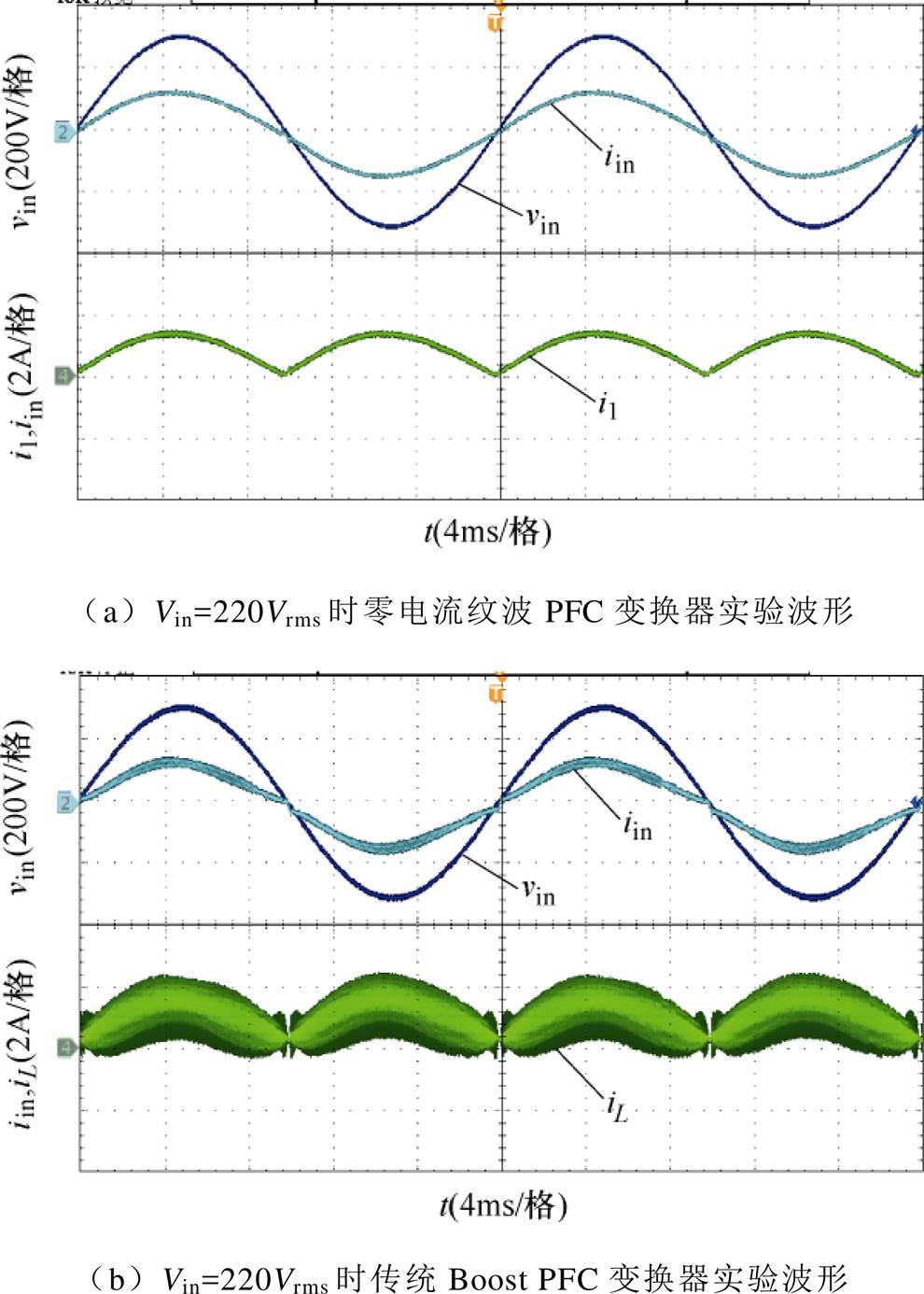
图13 Vin=220Vrms时不同PFC变换器输入电压、输入电流、输入电感的电流波形
Fig.13 Waveforms of voltage vin and currents iin, i1, iL with different PFC converters at Vin=220Vrms
由图12a、图12b和图13a、图13b可以发现,相同的输入电压等级下,零电流纹波PFC变换器的输入电流iin的畸变率显著低于传统Boost PFC变换器,输入电感电流的纹波值也显著降低。
图14为零电流纹波PFC变换器和传统Boost PFC变换器在满载时其PF和THD随输入电压的对比曲线。由图可知,在输入电压范围内,零电流纹波PFC变换器均比传统Boost PFC变换器的PF值高且输入电流的THD更低。其中,零电流纹波PFC变换器在输入电压范围内,其PF值均大于0.993 5、THD均小于3.85%。
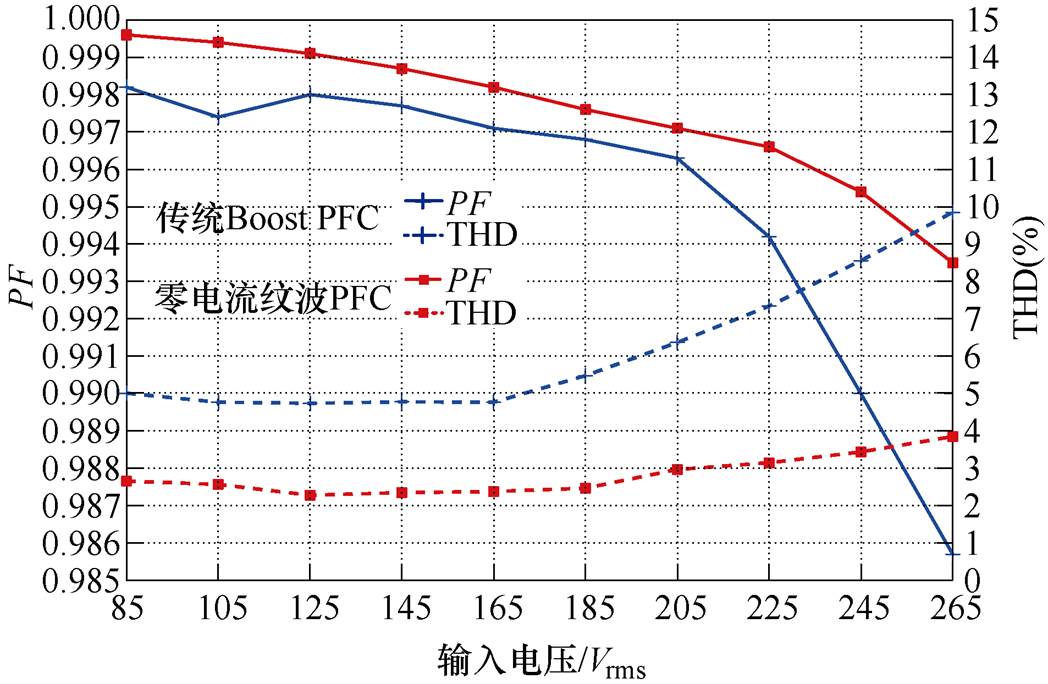
图14 满载时PF、THD随输入电压变化的对比曲线
Fig.14 PF and THD with the variation of input voltage at full load
图15所示为不同输入电压时,零电流纹波PFC变换器和传统Boost PFC变换器的效率曲线。由图可以看出,二者效率几乎一致,且随着输入电压升高,零电流纹波PFC变换器效率略高于传统Boost PFC变换器。

图15 零电流纹波PFC变换器和传统Boost PFC变换器的效率与输入电压的关系
Fig.15 Efficiency of the proposed converter and traditional Boost PFC with the variation of input voltage
图16所示为零电流纹波PFC变换器在输入电压为85Vrms和265Vrms,输出功率200W时,输入电压vin、输入电流iin和输出电压vo的实验波形。由图可知,输入电压和输入电流均为正弦波,电流与电压保持同相位且无明显畸变,输出电压稳定在400V。
图17及图18分别为零电流纹波PFC变换器满载情况下在输入电压Vin=110Vrms、220Vrms时工频周期内及其在开关周期内的电感电流i1、i2、i3实验波形。与图4、图10对比可知,实验与理论分析和仿真一致,电感电流i2的变化率与电感电流i3的变化率相反且幅值几乎一致,从而验证了理论分析和仿真的正确性。但是,通过对比仿真和实验波形可以发现,实验中并未完全实现与仿真一致的零电流纹波效果,原因在于实际电路中电感电流i1、i2中直流分量对于耦合电感B-H曲线的影响,导致互感随直流分量的增加而减小;而电感LR流过的电流i3呈现交流特性,即其感值大小基本不变。因此,结合式(6)、式(7)及式(12)可知,此时电流i2的纹波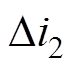 将大于电流i3的纹波
将大于电流i3的纹波 。但是,整体而言本文所提零电流纹波PFC变换器仍具有较好的纹波抵消效果。
。但是,整体而言本文所提零电流纹波PFC变换器仍具有较好的纹波抵消效果。
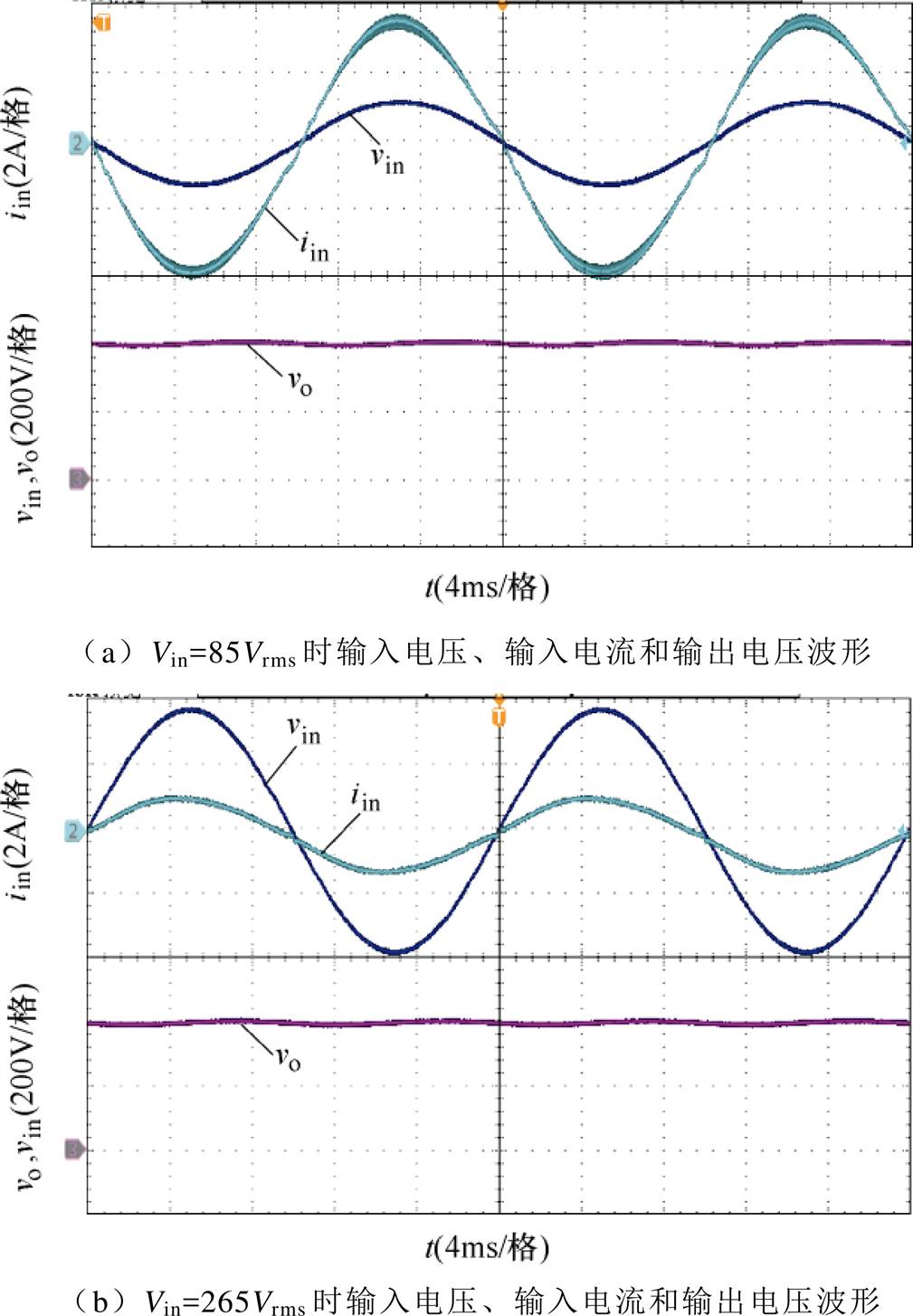
图16 零电流纹波PFC变换器输入电压、输出电压与输入电流波形
Fig.16 Waveforms of voltage vin, vo and current iin of the proposed converter
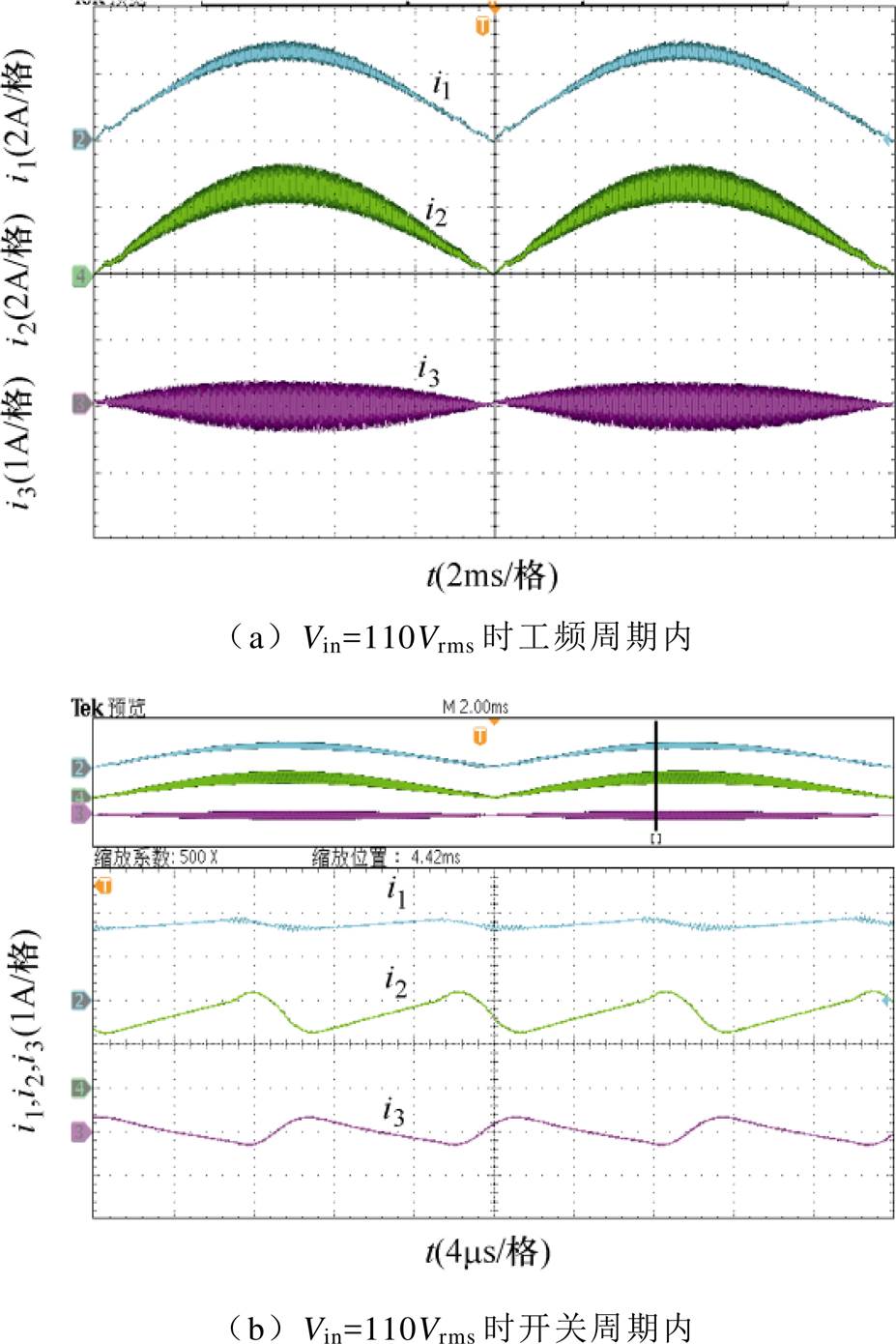
图17 Po=200W、Vin=110Vrms时零电流纹波PFC变换器电感电流波形
Fig.17 Waveforms of inductor currents i1, i2 and i3 of the proposed converter when Po=200W and Vin=110Vrms
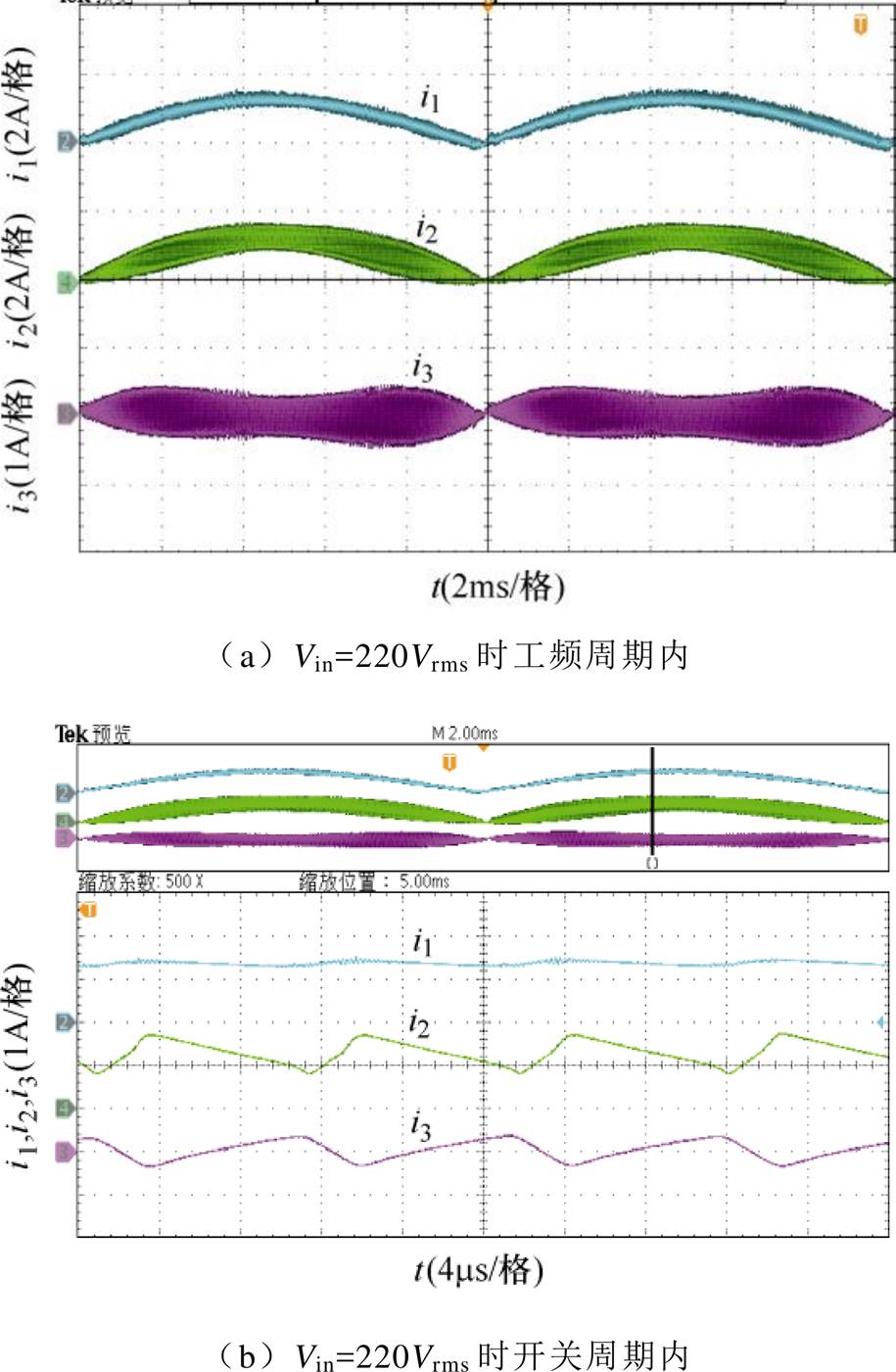
图18 Po=200W、Vin=220Vrms时零电流纹波PFC变换器电感电流波形
Fig.18 Waveforms of inductor currents i1, i2 and i3 of the proposed converter when Po=200W and Vin=220Vrms
图19为零电流纹波PFC变换器整流后输入电压vg、电容电压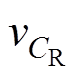 在工频周期及开关周期内的实验波形。实验波形证明了前文理论分析(见式(5))和仿真波形(见图10)的正确性,即电容CR电压纹波大小相对直流量较小,可以忽略。故无论工频周期还是开关周期内,电容CR两端电压均等于整流后输入电压。
在工频周期及开关周期内的实验波形。实验波形证明了前文理论分析(见式(5))和仿真波形(见图10)的正确性,即电容CR电压纹波大小相对直流量较小,可以忽略。故无论工频周期还是开关周期内,电容CR两端电压均等于整流后输入电压。
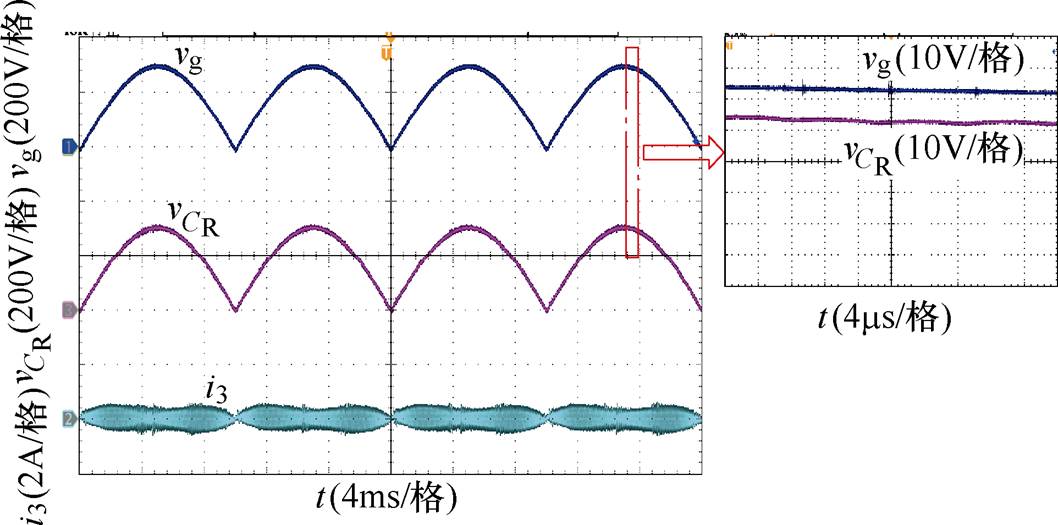
图19 Po=200W、Vin=220Vrms时零电流纹波PFC变换器整流后输入电压vg、电容电压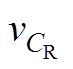 、电感电流i3波形
、电感电流i3波形
Fig.19 Waveforms of voltages vg, 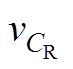 and inductor current i3 of the proposed converter when Po=200W and Vin=220Vrms
and inductor current i3 of the proposed converter when Po=200W and Vin=220Vrms
图20为零电流纹波PFC变换器满载情况下开关管Q和输出二极管VD两端的电压应力,可以看出,两者的电压应力均等于输出电压且无明显电压尖峰。
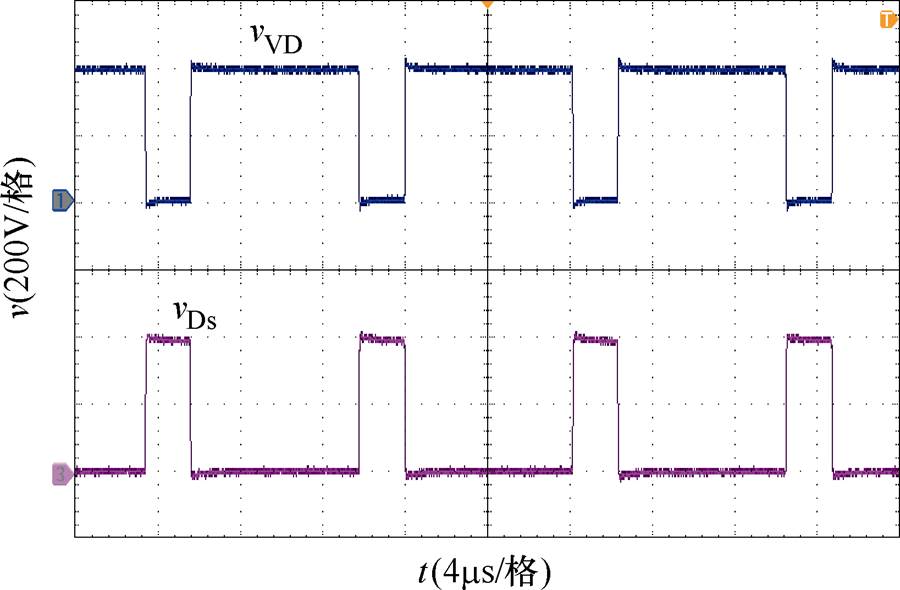
图20 零电流纹波PFC变换器开关管Q和输出二极管VD的电压应力波形
Fig.20 Waveforms of voltages of the main switch and output diode of the proposed converter
图21给出了零电流纹波PFC变换器负载跳变时(200W→100W)的输入电压vin、输入电流iin以及输出电压vo的波形。由图可以看出,动态切换前后输入电压和输入电流均保持同相位,无明显畸变,且动态过程中输出电压波动较小,能够平稳过渡至稳定状态。即通过实验验证了变换器闭环控制器设计的正确性和有效性。
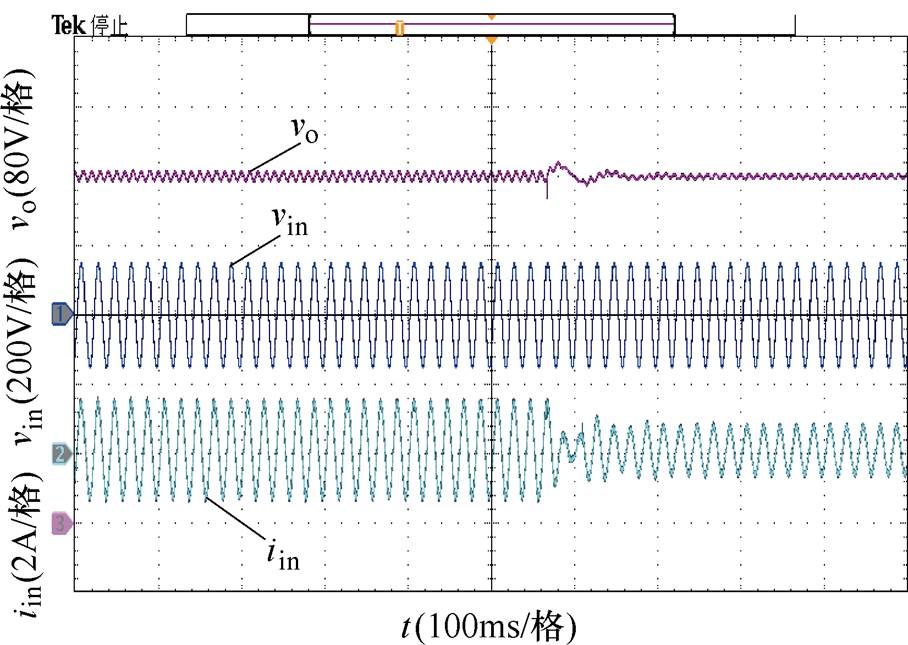
图21 零电流纹波PFC变换器负载跳变实验波形(200W→100W)
Fig.21 Experimental waveforms of the proposed converter with load transient (200W→100W)
为了提高传统Boost PFC变换器的性能,本文采用耦合电感的零电流纹波技术与PFC应用相结合,针对零电流纹波电路在PFC应用场合时面临的参数设计、控制等方面的挑战开展了以下研究:首先,基于零电流纹波电路的工作原理,给出了PFC应用场景下的电路参数设计方法;其次,根据输入电流纹波特点,对功率因数校正控制方法进行了筛选,提出了单周期控制器的解决方案和实现方法;最后,搭建了两台输出功率为200W,输入电压为85~265Vrms的PFC实验样机。通过将所提出的零电流纹波PFC变换器与传统Boost PFC性能进行对比,验证了理论分析的正确性。实验结果表明,所提出的零电流纹波PFC变换器,电路体积和质量明显降低,且输入电感电流纹波几乎为零,输出直流电压稳定在400V,功率因数PF>0.99,THD<3.85%,最高效率近97%,均显著优于传统Boost PFC变换器。
参考文献
[1] 周玉婷, 吴羽, 任小永, 等. 基于改进恒导通时间控制的临界连续导通模式Boost功率因数校正变换器[J]. 电工技术学报, 2021, 36(20): 4329-4338.
Zhou Yuting, Wu Yu, Ren Xiaoyong, et al. Improved constant on-time control of boundary conduction mode Boost power factor correction converter[J]. Transactions of China Electrotechnical Society, 2021, 36(20): 4329-4338.
[2] 吕寻斋, 刘雪山, 周群, 等. 谐振式单开关多路低纹波输出LED驱动器[J]. 电工技术学报, 2021, 36(10): 2081-2091.
Lü Xunzhai, Liu Xueshan, Zhou Qun, et al. Resonant single-switch multi-channel low-ripple LED driver[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2081-2091.
[3] 姚凯, 李强, 薄煜明, 等. 采用开关周期最优利用率控制的电流断续模式升压功率因数校正变换器[J]. 电工技术学报, 2015, 30(17): 13-25.
Yao Kai, Li Qiang, Bo Yuming, et al. DCM Boost PFC converter with optimum utilization control of switching cycles[J]. Transactions of China Electro- technical Society, 2015, 30(17): 13-25.
[4] 贾圣钰, 赵争鸣, 施博辰, 等. 电力电子系统电磁干扰数值建模分析[J]. 电工技术学报, 2021, 36(11): 2383-2393, 2423.
Jia Shengyu, Zhao Zhengming, Shi Bochen, et al. Numerical modeling and analysis of electromagnetic interference in power electronics systems[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(11): 2383-2393, 2423.
[5] 任小永, 白雷, 惠琦, 等. 一种快速动态响应低电压纹波功率因数校正变换器的控制策略[J]. 电工技术学报, 2019, 34(14): 2936-2945.
Ren Xiaoyong, Bai Lei, Hui Qi, et al. Control strategy of power factor correction converter for fast dynamic response and low output voltage ripple[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(14): 2936-2945.
[6] 曹勇, 杨飞, 李春晖, 等. 不同耦合系数下的交错并联电流连续模式Boost功率因数校正变换器的传导电磁干扰[J]. 电工技术学报, 2019, 34(10): 2176- 2186.
Cao Yong, Yang Fei, Li Chunhui, et al. Conducted electromagnetic interference of interleaved con- tinuous current mode Boost power factor correction converter with different coupling coefficients[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2176-2186.
[7] Yang Fei, Ruan Xinbo, Yang Yang, et al. Interleaved critical current mode Boost PFC converter with coupled inductor[J]. IEEE Transactions on Power Electronics, 2011, 26(9): 2404-2413.
[8] Tung C P, Fan J W T, Chow J P W, et al. 1kW Boost-type PFC using a low-voltage series pass module for input current shaping[J]. IEEE Transa- ctions on Power Electronics, 2020, 35(7): 7596- 7611.
[9] 杨平, 许建平, 董政, 等. 低输入电感电流纹波二次型Boost PFC变换器[J]. 中国电机工程学报, 2013, 33(12): 32-38, 183.
Yang Ping, Xu Jianping, Dong Zheng, et al. Quadratic Boost power factor correction converters with small input inductor current ripple[J]. Proceedings of the CSEE, 2013, 33(12): 32-38, 183.
[10] Garinto D. A new zero-ripple Boost converter with separate inductors for power factor correction[C]// IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 2007: 1309-1313.
[11] Chou E, Chen F, Adragna C, et al. Ripple steering AC-DC converters to minimize input filter[C]//IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 2009: 1325-1330.
[12] Zhang Neng, Zhang Guidong, See K W. A D-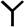 hybrid impedance network Boost converter with reduced input current ripple[J]. IEEE Transactions on Power Electronics, 2018, 33(4): 2803-2808.
hybrid impedance network Boost converter with reduced input current ripple[J]. IEEE Transactions on Power Electronics, 2018, 33(4): 2803-2808.
[13] Gu Yu, Zhang Donglai, Zhao Zhongyang. Input current ripple cancellation technique for Boost converter using tapped inductor[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5323-5333.
[14] 郭小强, 魏玉鹏, 万燕鸣, 等. 新能源制氢电力电子变换器综述[J]. 电力系统自动化, 2021, 45(20): 185-199.
Guo Xiaoqiang, Wei Yupeng, Wan Yanming, et al. Review on power electronic converters for producing hydrogen from renewable energy sources[J]. Auto- mation of Electric Power Systems, 2021, 45(20): 185-199.
[15] Shamsi P, Shen A. Design and analysis of a class of zero fundamental ripple converters[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(6): 4543- 4552.
[16] Cheng Weibin, Song Jiuxu, Li Hong, et al. Time- varying compensation for peak current-controlled PFC Boost converter[J]. IEEE Transactions on Power Electronics, 2015, 30(6):3431-3437.
[17] 杨潮晖. Boost-PFC电路拓扑和数字控制的研究[D].哈尔滨: 哈尔滨工业大学, 2010.
[18] Jappe T K, Mussa S A. Current control techniques applied in PFC Boost converter at instantaneous power interruption[C]//Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 2009: 346- 351.
[19] de Melo Bento A, Cabral de Silva E R. Hybrid one-cycle controller for Boost PFC rectifier[J]. IEEE Transactions on Industy Applications, 2009, 45(1): 268-277.
[20] 江涛, 毛鹏, 谢少军. 单周期控制PFC变换器的输入电流畸变研究[J]. 中国电机工程学报, 2011, 31(12): 51-56.
Jiang Tao, Mao Peng, Xie Shaojun. Distortion issue on input current of OCC-PFC converter and its solution[J]. Proceedings of the CSEE, 2011, 31(12): 51-56.
[21] Fischer G d S, Rech C, de Novaes Y R. Extensions of leading-edge modulated one-cycle control for totem- pole bridgeless rectifiers[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 5447-5460.
[22] 赖力. 数字式单相功率因数校正控制方法研究[D]. 成都: 电子科技大学, 2016.
[23] Abramovitz A, Yao Jia, Smedley K. Unified modeling of PWM converters with regular or tapped inductors using TIS-SFG approach[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1702-1716.
A Zero Current Ripple Tapped Inductor Power Factor Correction Converter
Abstract In order to reduce the input current ripple and improve the EMI performance of traditional Boost power factor correction (PFC) converter, a zero current ripple tapped inductor (TI) PFC converter was proposed. First, the operation principle of the proposed PFC converter was studied. The current ripple cancellation network employed a tapped inductor and a series-connected LC filter. Since the inductance does not participate in the main power transmission, the LC filter in the proposed topology is much smaller than the conventional Boost PFC input LC filter. Detailed design consideration of the proposed converter for PFC purpose is presented. Secondly, considering the feature of the extreme low input current ripple, the one-cycle control (OCC) strategy is realized by a digital controller. Finally, the prototype of the proposed zero current ripple PFC converter and the conventional Boost PFC converter were compared. It is shown that the proposed converter has approximately “zero” input current ripple, smaller size, much lower THD, and significantly improved power factor (PF).
keywords:Digital one-cycle control, zero current ripple, tapped inductor, power factor correction
DOI: 10.19595/j.cnki.1000-6753.tces.211798
中图分类号:TM461
国家自然科学基金资助项目(51707096)。
收稿日期 2021-11-05
改稿日期 2021-12-07
林 通 男,1995年生,硕士研究生,研究方向为功率因数校正变换器及其控制技术。E-mail: lintong@njust.edu.cn
姚 佳 女,1980年生,博士,硕士生导师,研究方向为高增益DC/DC变换器、电力电子变换器建模和光伏/电池应用。E-mail: yaojia@njust.edu.cn(通信作者)
(编辑 陈 诚)