 1,fs和Ts分别为开关频率和周期。分析时假设各类元器件均是理想的。
1,fs和Ts分别为开关频率和周期。分析时假设各类元器件均是理想的。摘要 为减小双有源桥(DAB)变换器的电流应力和导通损耗,提升变换器效率,该文提出一种三重移相(TPS)调制模式下的电感电流优化控制方法。针对TPS调制模式下DAB多工作模式产生的复杂优化问题,该文在交流模型的基础上,借鉴对称变换和空间投影思想对变换器可行域进行化简,并以减小电感电流为优化目标,采用最优性条件进行求解得到优化结果。此外,为进一步提高动态性能,提出一种基于最小电感电流有效值模型的直接功率控制(DPC)算法,在输入电压波动和负载突变的情况下,变换器能实现电压快速无超调稳定输出。最后,在SiC器件的小功率实验平台上进行实验,验证了该控制策略的优越性。
关键词:双有源桥(DAB)变换器 三重移相(TPS)调制 最优性条件求解法 直接功率控制
环境污染、能源紧缺问题的日益严重,促使着新能源发电技术不断完善、发展。直流微电网作为连接分布式电源的局域化智能电网,受到了广泛的关注和研究。直流微电网由分布式电源、直流母线、储能系统和双向变换器组成,其中双向DC-DC变换器是稳定直流母线电压,确保分布式可再生能源发电设备灵活接入的有效解决方法[1]。双有源桥(Dual Active Bridge, DAB)变换器因其输入输出隔离、高功率密度和能量双向传输等特点在直流微电网中得到广泛应用[2]。
单移相(Single Phase Shift, SPS)调制是DAB变换器最基础的调制方式,其中移相发生在两个桥之间,该调制方法只有一个控制量,仅能满足传输功率要求,无额外的优化空间。因此在输入输出电压不匹配或轻载情况下,SPS调制会造成软开关丢失,回流功率和电流应力增加,变换器传输效率[3]降低。为提高DAB变换器控制灵活度,文献[4-5]分别引入双重移相(Dual Phase Shift, DPS)调制与扩展移相(Extended Phase Shift, EPS)调制方式,通过优化2个控制变量来减小回流功率和电流有效值,从而提高变换器效率。然而,三重移相(Tripple Phase Shift, TPS)调制具有3个控制变量,DPS和EPS调制均被视为TPS调制的特例,优化所得解仅为局部最优解[6]。为获得真正严格的全局最优解,需在TPS调制模式下对变换器优化问题进行求解。
TPS调制模式下,DAB变换器工作模式种类划分众多,因此通过列举工作模式变量组合来获得最优解是一个复杂的难题。传统方案通常使用交流端口电压和变压器电流的基波分量近似求解,通过最大化基波功率因数[7]、最小化基波变压器电流幅值[8]或最小化基波无功功率[9]的方法得到最优的3个移相角。然而,基波近似法会引入一定的计算误差,尤其在两侧电压占空比接近零时,端口电压的基波分量不再是主要频率分量[10]。因此,对于TPS调制,基波近似不再是一个精确的方法,所得最优移相角也并不准确。此外,对于宽输入、输出电压和全功率范围的工况,更需要一组精确的闭式解去进行调制,从而在整个宽电压和功率区间内取得最优的控制效果。
工业应用中对变换器快速性与稳定性要求较高,传统的电压闭环控制方式无法有效应对负载与直流母线电压波动问题,导致缓慢的响应速度和较大的功率纹波[11],为此,亟待探寻优化DAB变换器动态性能的方法。文献[12-14]通过推导变换器的离散时间平均模型,对变换器的动态特性进行了初步分析。文献[15]基于该模型,提出负载电流前馈(Load Current Feed-Forward, LCFF)控制法,通过将负载电流引入电压控制环中,可以提高简单反馈控制的性能。然而,该控制方式将输入电压视为常数,因此在输入电压跳变时产生的功率变化大部分仍需PI控制器进行补偿,动态性能变得与电压环PI控制无异。为改进该问题,文献[16]基于SPS调制模式提出了针对DAB变换器的直接功率控制方法(Direct Power Control strategy, DPC),给出包含输入电压的移相占空比表达式,可有效应对负载和输入电压扰动,实现快速无超调响应。但该文献没有涉及基于TPS调制框架下的优化占空比表达式。
本文首先借鉴对称变换和空间投影的思想,在交流等效模型的基础上对TPS调制模式下DAB变换器的可行域进行分类、分析,消除冗余可行域,减小电感电流有效值优化过程的复杂度。对于约束优化问题,使用最优性条件求解得到严格的闭式解。此外,为提升变换器的动态响应速度,提出基于最小电感电流有效值控制模型的直接功率控制策略。最后在小功率实验平台上验证该控制策略的优越性。
双向半桥三电平DC-DC变换器拓扑结构如图1所示,图中,等效电感L为变压器漏感Ls与辅助电感Laux之和,C1~C4为一次、二次侧直流侧支撑电容,uab和ucd分别为一次侧和二次侧桥臂端口电压,uL和iL分别为电感L的电压和电流,变压器的电压比为n 1,fs和Ts分别为开关频率和周期。分析时假设各类元器件均是理想的。
1,fs和Ts分别为开关频率和周期。分析时假设各类元器件均是理想的。

图1 双向半桥三电平DC-DC变换器拓扑结构
Fig.1 Three level half bridge isolated bidirectional DC-DC converter
工作波形和等效电路如图2所示。在TPS调制框架下,以功率从端口1传输到端口2为例,交流端口处输出电压uab和ucd波形如图2a所示,幅值分别为直流侧电压U1和U2的一半,变换器由3个变量来控制能量在一次、二次侧的流动,其中D1、D2分别为一次和二次电压占空比,Dj为移相占空比,三者取值范围均为[0, 1]。为便于进一步建模分析,定义变换器的电压增益比为k=nU2/U1,当0< k<1时,认为变换器工作在Buck模式;当k>1时为Boost模式;当k=1时为匹配模式。

图2 工作波形和等效电路
Fig.2 Key waveforms and Equivalent circuit of DAB
TPS调制下DAB变换器的等效拓扑如图2b所示,由两个等效的方波电压源uab、ucd和线路总电感L构成。将uab、ucd波形展开为Fourier级数,并通过计算得到第m次电感电流有效值二次方为

 (1)
(1)
则第m次有功功率为
 (2)
(2)
式中, 。
。
因此,传输功率和电感电流有效值二次方表达式为
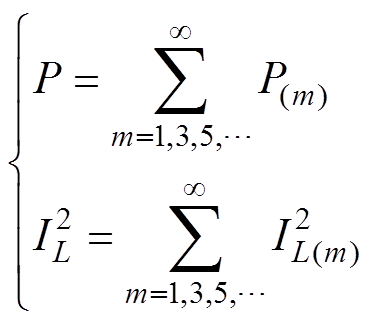 (3)
(3)
实际工作时,输入和输出电压固定,变换器参数L、n、Ts为常数,通过以上函数可知,传输功率和电流有效值仅由D1、D2和Dj决定,即当前电路工作点D=(D1, D2, Dj)对应电感电流有效值为 ,传输功率为P(D)。
,传输功率为P(D)。
正向功率传输(Dj>0)的情况下,为分析可行域中变换器传输功率、电感电流的对称性,对占空比的可行域进行划分,如图3所示。

图3 可行域划分
Fig.3 Feasible region division
这里列举两种可行域划分,式(4)分别对应图3a和图3b。分析比较各区域间传输功率与电流有效值特性,即
 (4)
(4)
(1)针对Dj=1/2镜面对称点Y与 ,有
,有 =
=  ,对比电流有效值二次方为
,对比电流有效值二次方为
 (5)
(5)
当D1、D2 (0, 1
(0, 1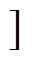 ,且Dj
,且Dj (0, 1/2
(0, 1/2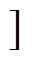 时,
时, ≤
≤ 恒成立,因此传输相同功率时,工作在W 1区域内电流有效值更小。
恒成立,因此传输相同功率时,工作在W 1区域内电流有效值更小。
(2)针对D1=D2平面镜像对称点Z与 ,有
,有 =
= ,对比电流有效值二次方为
,对比电流有效值二次方为
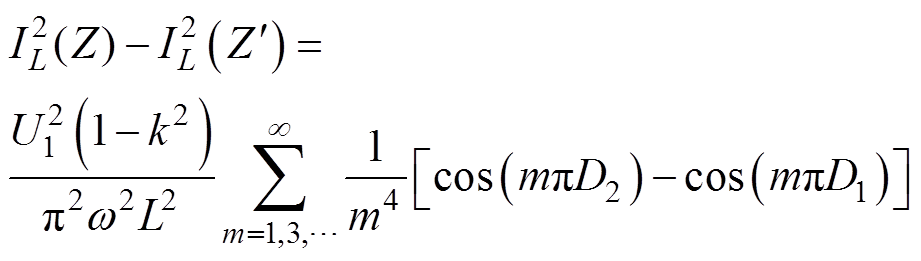 (6)
(6)
根据电压增益比k范围不同,有
 (7)
(7)
即变换器工作在Buck模式下传输相同功率时,电流有效值最优解只存在于W 3区域;同理,Boost模式下只需考虑W 4区域的解。
综上所述,如图3c所示,对于Buck模式,最优解存在于W 5=W 1∩W 3;对于Boost模式,最优解存在于W 6=W 1∩W 4;对于匹配模式,需在W 1内考虑最优解。
对于工作在Buck模式的变换器,在uab和ucd的不同边沿关系下,其电感电流有效值二次方 和传输功率P有不同的分段表达式,以图2a的边沿标注为参照,在满足可行域W 5的前提下,调制模式边界有三种:①边沿1和边沿5对齐,Dj=(D2-D1)/2;②边沿2和边沿5对齐,Dj=(D1+D2)/2;③边沿3和边沿6对齐,Dj=(2-D1-D2)/2。根据以上边界,将可行域W 5进一步划分为四种,调制模式划分及对应全局极小值轨迹如图4所示。
和传输功率P有不同的分段表达式,以图2a的边沿标注为参照,在满足可行域W 5的前提下,调制模式边界有三种:①边沿1和边沿5对齐,Dj=(D2-D1)/2;②边沿2和边沿5对齐,Dj=(D1+D2)/2;③边沿3和边沿6对齐,Dj=(2-D1-D2)/2。根据以上边界,将可行域W 5进一步划分为四种,调制模式划分及对应全局极小值轨迹如图4所示。
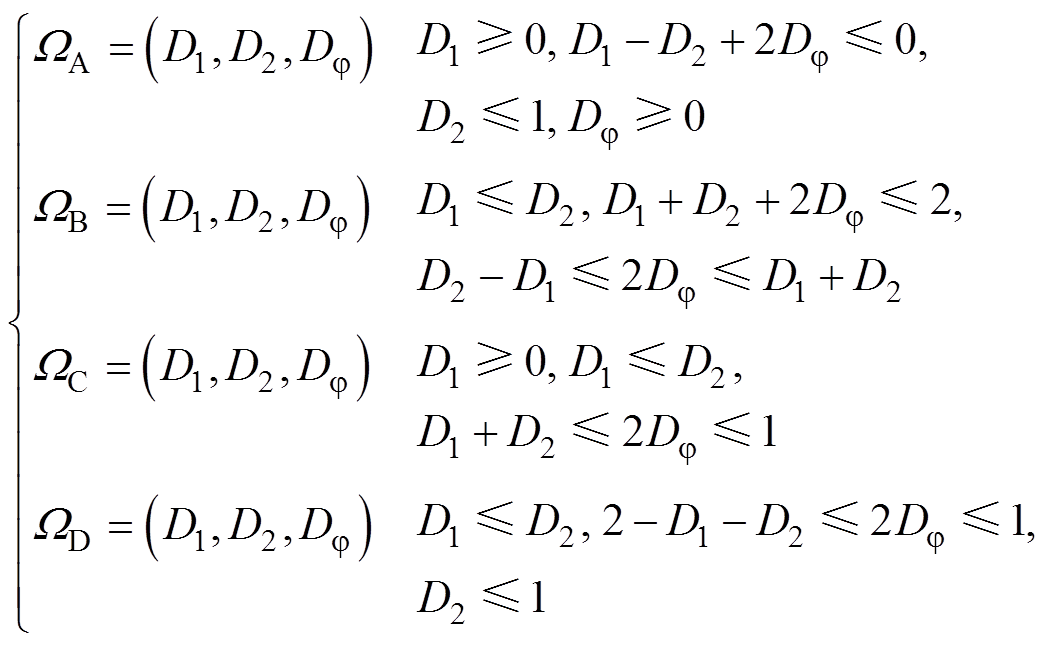 (8)
(8)
图4中,调制模式C为间接传能(即一次侧的能量先全部存储到电感中,然后再传输到二次侧),这种传输方式会导致电感电流有效值的增加[3],因此只保留其他三种调制模式。

图4 调制模式划分及对应全局极小值轨迹
Fig.4 Divisions of operating mode and global minimum trajectory
进一步对其他三种调制模式A、B、D进行分析。不同调制模式下各个区间的电感电流上升斜率diL/dt见表1。
 (9)
(9)
Buck模式的最优工作波形如图5所示,根据伏秒平衡原则,电路稳态工作时电感电流平均值为0,因此iL具有半周期对称特性,即iL(t0)=-iL(t0+Ts/2),从而可以求得周期开始时刻的电感电流值iL(t0),根据表1和初始值可计算出其他任意时刻电流值。传输功率P和电感电流有效值二次方 只需按半周期计算如下
只需按半周期计算如下
 (10)
(10)
为简化推导过程,定义k =1时SPS调制下传输功率最大值为基准功率,即Pbase=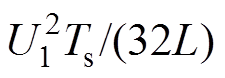 ,故基准电流Ibase=Pbase/U1=U1Ts/(16L)。得到各调制模式下的电感电流有效值和传输功率标幺值如下模式A
,故基准电流Ibase=Pbase/U1=U1Ts/(16L)。得到各调制模式下的电感电流有效值和传输功率标幺值如下模式A
表1 时间间隔内电感电流变化率diL/dt
Tab.1 Rise slope of inductive current in time interval diL/dt

区域区间[t0, t1区间[t1, t2区间[t2, t3区间[t3, t4] A0 B0 D

图5 Buck模式的最优工作波形
Fig.5 Optimal operating waveforms of Buck mode
 (11)
(11)
模式B
 (12)
(12)
模式D
 (13)
(13)
以电感电流有效值二次方最小为控制目标,进行约束优化问题求解,构造Lagrange函数如式(14)所示,其可行域为W。
 (14)
(14)
式中,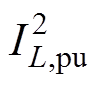 为目标变量;控制变量D=[ D1D2Dj];
为目标变量;控制变量D=[ D1D2Dj];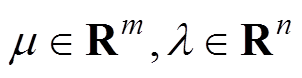 为Lagrange乘子;等式约束条件gi(D)(i=1)为给定功率;不等式约束条件hj(D),(j=1, 2, 3, 4)为可行域A、B、D的边界范围,各模式四面体存在4个边界。
为Lagrange乘子;等式约束条件gi(D)(i=1)为给定功率;不等式约束条件hj(D),(j=1, 2, 3, 4)为可行域A、B、D的边界范围,各模式四面体存在4个边界。
根据给定调制模式的约束问题,工作点有位于边界上或区域内的两种情况,那么图4的空间四面体共存在最多16种情况,对于每一种情况,使用最优性条件进行严格求解:首先,判断是否满足线性独立约束规范(Linear Independence Constraint Qualification, LICQ),若不满足,那么问题无法使用最优性条件求解,这种情况得到非正则解。反之,可使用KKT条件(一阶必要条件)和二阶充分条件进行求解,不满足必要条件则无解;不满足充分条件的解,后续需要特殊讨论。在得到非正则解、严格局部极小解和可能的局部极小解后,通过对比相同传输功率Ppu下电感电流有效值二次方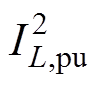 即可得出各模式下的全局极小值解。最后,将调制模式A、B、D的全局极小值解进行综合,得到整个可行域的全局最小值解。
即可得出各模式下的全局极小值解。最后,将调制模式A、B、D的全局极小值解进行综合,得到整个可行域的全局最小值解。
针对模式A,优化目标和约束条件如式(15)所示。按照最优性条件求解,得到调制模式A的全局极小值解如式(16)、式(17)所示。在功率传输范围[0, k/2]内,整条最优解轨迹(APQ)被分为AP、PQ两段且在分界线处全局极小值解连续。
 (15)
(15)
式中,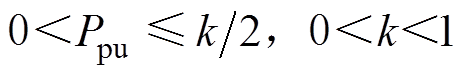 。
。
(1)曲线AP,Ppu (0, 2k2(1-k)
(0, 2k2(1-k)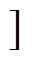
 (16)
(16)
式中, ;电感电流表达式
;电感电流表达式 。
。
(2)曲线PQ,Ppu (2k2(1-k), k/2
(2k2(1-k), k/2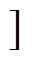
 (17)
(17)
其中

电感电流表达式为

同理可得,B、D模式下最优解轨迹APR、HPSG。绘制A、B、D模式下全局极小值解轨迹如图4所示。随着功率增加,工作点在调制模式A下的运动轨迹为A→P→Q。在模式B下的轨迹为A→P→R,其中直线AP与模式A的轨迹相同。对于模式D,轨迹在k>0.5时为C→P→S→G;k<0.5时为H→ P→S→G。特别地,k=0.5时,调制模式A的P工作点与Q工作点重合;调制模式D同时存在曲线HP与CP两个对称分支,随着功率增加,模式D工作点的变化轨迹为H(C)→P→S→G。
结合A、B、D三种调制模式,选择不同功率区间下的电感电流全局最小值解轨迹如下:
(1)当Ppu (0, 2k2(1-k)
(0, 2k2(1-k)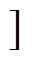 时,min[
时,min[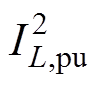 ]=
]=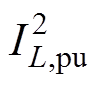 (D|D
(D|D A),曲线AP为此功率段的电感电流最小值解。
A),曲线AP为此功率段的电感电流最小值解。
(2)当Ppu [2k2(1-k), k(1-k4)]时,min[
[2k2(1-k), k(1-k4)]时,min[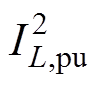 ]=
]= 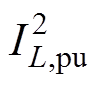 (D|D
(D|D D),因此曲线PS为最小值解。
D),因此曲线PS为最小值解。
(3)当Ppu [k(1-k4), k]时,调制模式A、B无解,故曲线PSG为最小值解。
[k(1-k4), k]时,调制模式A、B无解,故曲线PSG为最小值解。
综合可得,Buck工作模式(k<1 下全局极小值最优轨迹为APSG,对应解析表达式如式(18)所示。占空比表达式在分段点处光滑连续,因此可以保证平滑切换。以k=2/3为例,有
下全局极小值最优轨迹为APSG,对应解析表达式如式(18)所示。占空比表达式在分段点处光滑连续,因此可以保证平滑切换。以k=2/3为例,有
 (18)
(18)
全功率范围内,Buck模式下DAB变换器工作波形如图5所示,最优控制轨迹如图5a所示。根据式(18)分段点,工作区间被划分为低功率段、中功率段和高功率段,分别对应TPS、EPS、SPS调制模式。
传统电压环控制下变换器的动态性能与PI控制器相关,对于变换器不同的工作状态,同一PI控制器参数并不适用,尤其在输入电压波动、负载跳变时,输出电压需要较长时间才能重新稳定,在此过程中会伴随一定的电压跌落或超调[15]。而变换器的输出电压之所以产生跌落和超调,其根本原因是输出电容的充电功率P(即变换器传输功率)和放电功率PR(即负载功率)不一致,导致电荷累积或释放,因此,实现快速的功率平衡P=PR,是保证快速动态响应核心所在,这种方法被称为直接功率控制[16]。
针对变换器的直接功率传输控制方式,下面以Buck模式下低功率段为例进行分析。
首先对实际负载功率PR=U2I2标幺化得
 (19)
(19)
在直接功率控制中,如果可以立刻实现预期的输出功率,通过输出相应的移相占空比D使得Ppu=  ,那么变换器将拥有卓越的动态性能。但由于变换器损耗、模型的非理想性、死区等因素的影响[14-16],导致模型准确度下降,因此变换器传输功率和负载功率会存在误差,实际的输出功率不能简单的用输出电压U2和输出电流I2的数学函数表示,需要额外提供补偿功率DP来抵消变换器损耗导致的电压跌落,使得预测器的输出占空比精准跟随实际占空比,合成的给定功率为
,那么变换器将拥有卓越的动态性能。但由于变换器损耗、模型的非理想性、死区等因素的影响[14-16],导致模型准确度下降,因此变换器传输功率和负载功率会存在误差,实际的输出功率不能简单的用输出电压U2和输出电流I2的数学函数表示,需要额外提供补偿功率DP来抵消变换器损耗导致的电压跌落,使得预测器的输出占空比精准跟随实际占空比,合成的给定功率为
 (20)
(20)
式中,补偿功率DPpu可由PI控制器产生,当输出到达稳态时U2≈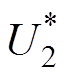 ,实际占空比D将和给定占空比D*保持一致,即
,实际占空比D将和给定占空比D*保持一致,即
 (21)
(21)
式中,为了保证变换器电流有效值实时最小,电压增益k需要使用实时的电压进行计算。
以上步骤对应的直接功率控制框图如图6所示。

图6 直接功率控制框图
Fig.6 Block diagram of the direct power control
直接功率控制可以估算维持输出电压的功率所需的占空比D,当负载和输出电压发生变化时,预测器根据输出电压和负载电流的反馈计算出负载功率,从而估算D*,因此其动态性能优于传统的电压环PI控制。
在占空比关于功率的表达式(21)中,存在复杂的乘除法、高次乘方、开二次方计算,并且除法和开二次方会导致精度降低,调制产生的占空比分辨率直接决定了控制的精度[17],而精确检测功率是实现占空比准确切换的前提。因此,功率检测与占空比计算是决定本控制方法快速性的重要环节。
在变换器参数L、fs、n确定的情况下,直接功率控制的一个计算周期控制流程可以描述如下:

图7 功率检测与占空比切换实现流程
Fig.7 Flow chart of power detection and duty cycle switching
(1)首先,通过高速AD芯片采样得到输出电压U2和输出电流I2,计算出实际功率PR=U2I2,进一步得到实际输出功率标幺值PR,pu。为保证采样的准确性,在实验20kHz的开关频率下,利用单通道最高采样速度166.67kHz的ADS7864进行8倍过采样(即每采样8次取平均值)确保采样的准确性。
(2)电压误差DU2=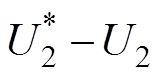 经过PI控制器,输出补偿功率标幺值DPpu以修正输出电压,最终合成给定功率标幺值
经过PI控制器,输出补偿功率标幺值DPpu以修正输出电压,最终合成给定功率标幺值 。
。
(3)实时计算电压增益k=nU2/U1值,并计算低中高功率分界点P1、P2、P3。
(4)比较确定给定功率所属范围,从而确定输出占空比计算式;由于式(18)过于复杂,因此使用流水线设计计算给定占空比D*,提高数据吞吐量,保证速度。为方便流水线计算,将复杂的式(18)拆分为多个子表达式分步骤计算,同时规定每个时钟周期,至多进行一次除法、开二次方或乘法运算,加减法不设限来确保一定的占空比分辨率。
(5)最后,通过调制模块输出8路开关信号。
为了验证本文所提控制策略的优越性,在Matlab/ Simulink软件中根据图1和表2所示的实验平台参数,搭建仿真模型。在负载阶跃与输入电压阶跃两种情况下,对本文所提直接功率控制(TPS+DPC)、负载电流前馈控制(SPS+LCFF)[15]和传统PI稳压控制(TPS+PI)方法动态特性进行对比、分析。
表2 实验平台参数
Tab.2 DAB converter prototype parameters
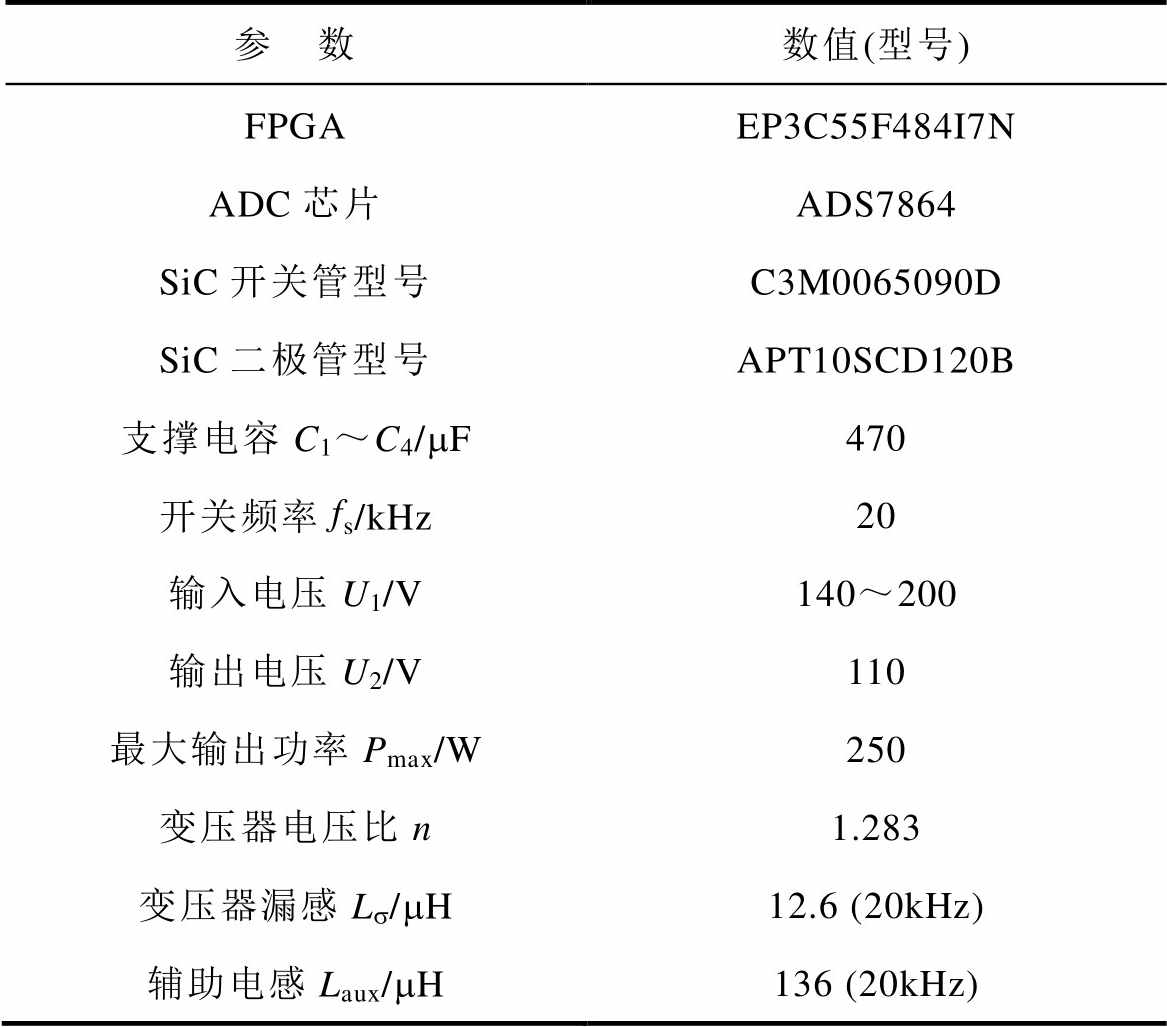
参 数数值(型号) FPGAEP3C55F484I7N ADC芯片ADS7864 SiC开关管型号C3M0065090D SiC二极管型号APT10SCD120B 支撑电容C1~C4/mF470 开关频率fs/kHz20 输入电压U1/V140~200 输出电压U2/V110 最大输出功率Pmax/W250 变压器电压比n1.283 变压器漏感Ls/mH12.6 (20kHz) 辅助电感Laux/mH136 (20kHz)
在输入200V、输出稳压110V条件下三种控制方式由0.1W到满载(250W)动态仿真波形如图8所示,直接功率控制与负载电流前馈控制都能快速反应负载变化并提供所需功率,因此相比传统PI,稳压控制响应速度更快并且输出电压几乎没有跌落。
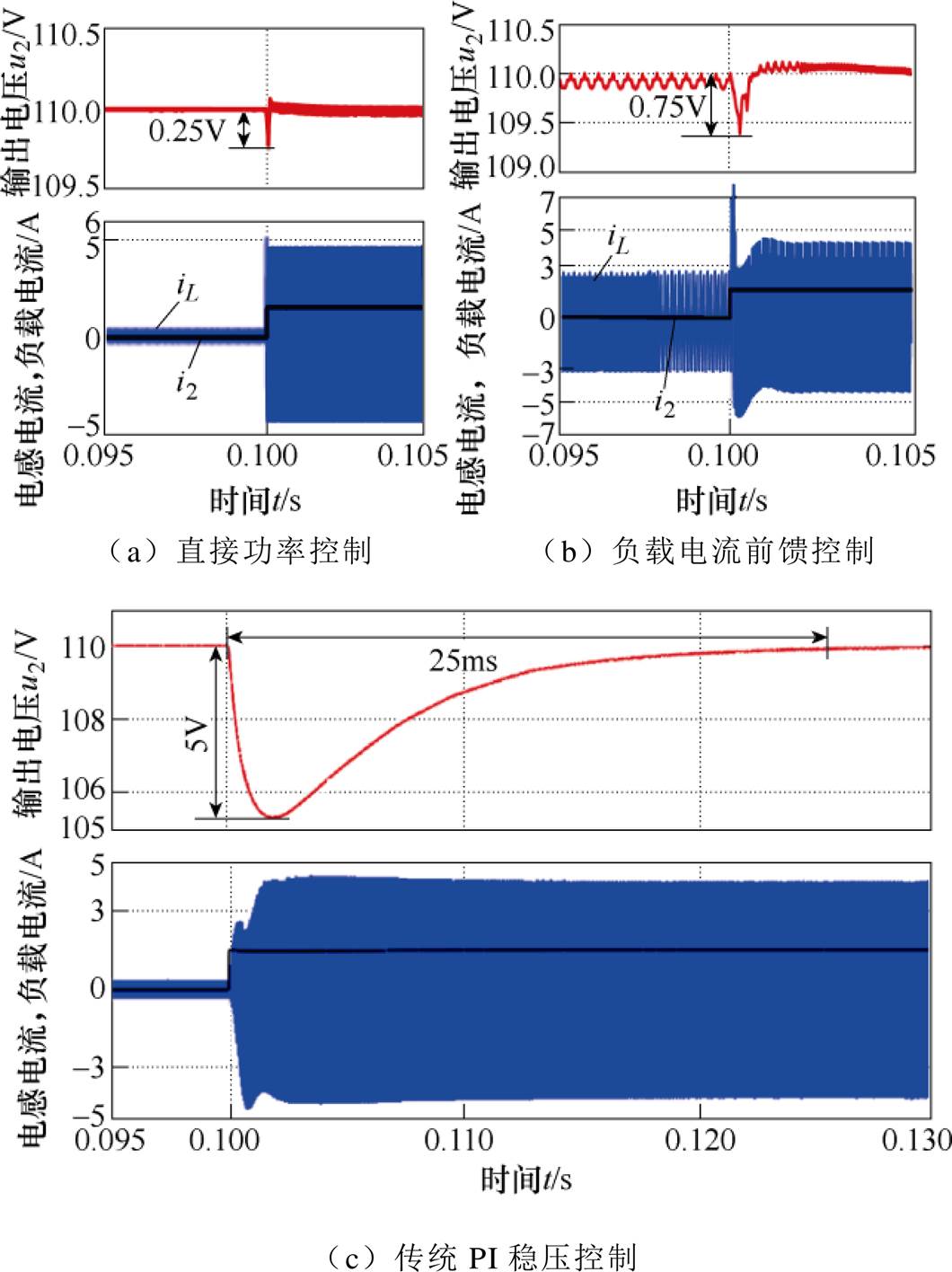
图8 负载从0.1W加载到250W(200V)仿真波形
Fig.8 Simulation waveforms of load steps (0.1W to 250W) (200V)
当输出负载为200W时,图9为DAB变换器输入电压阶跃波形。从图9b中可以看出,当输入电压变化时,由于输入电压没有直接参与控制环路响应变化,负载电流前馈控制会依靠PI控制器补偿大部分功率来稳定输出电压,因此动态响应与传统PI稳压控制方法一致,输出电压都存在2V左右的跌落。而本文所提出的直接功率控制在输入电压变化瞬间从新计算期望功率并调整输出对应占空比,因此响应速度更快并且输出电压几乎没有变化。

图9 输入电压从200V跌落到140V(170W)仿真波形
Fig.9 Simulation waveforms of Input steps (200V to 140V) (170W)
为验证本文所提控制策略的正确性,搭建基于FPGA控制器的小功率SiC实验平台,实验平台参数见表2。
在输入200V、输出110V条件下,电压增益k= 0.706,此时变换器工作在Buck模式,同时计算得到功率分界点为123W、223W。选取工作点在50W、170W和250W,分别位于低功率段、中功率段和高功率段,工作波形如图10所示。
从图10a、图10b中可以看出,轻载时变换器的调制模式为TPS,空载时,iL几乎为0。随着功率增加进入中功率段,低压侧占空比D2达到满占空比,调制模式进入EPS,工作波形如图10c所示。进一步增加功率至高功率段,高压侧占空比D1也达到1,此时为SPS调制模式,如图10d所示。全程输出电压稳定在110V左右。
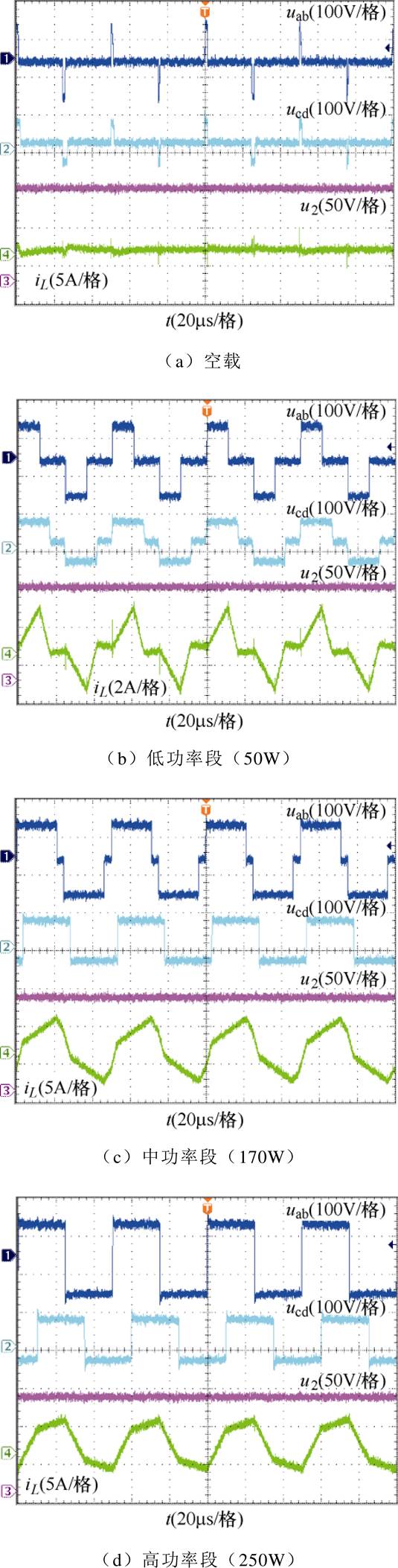
图10 稳态工作波形
Fig.10 Steady state working waveforms
基于本文所提出直接功率控制策略,在输入200V、输出110V电压等级下进行了不同功率段之间的切载实验,波形如图11所示。由图可知,空载与重载之间切换所需稳定时间最长只需230ms。
为了进一步体现直接功率控制的动态性能,图12分别给出了直接功率控制和传统电压环PI控制下空载与满载(250W)切换实验波形。
在带载过程中,直接功率控制下U2几乎没有电压跌落,通过图11d的细节波形可知,调制时间只有10个开关周期,而传统PI控制在加载瞬间会有5V的电压跌落,再经过约72ms的调节时间才达到新的稳态。同样地,减载过程中,PI控制下输出电压会有7V的超调量且调节时间为80ms,而直接功率控制下输出电压几乎没有变化。


图11 不同功率段之间负载阶跃实验
Fig.11 Load steps experiments between different powers


图12 切载实验不同控制方法对比
Fig.12 Comparison of different control strategies in load steps experiment
110V稳压输出时,为满足170W的功率输出,输入电压最低值设定为140V。输入200V与140V的阶跃过程会出现k>1和k=1两种情况,分别对应EPS调制模式和SPS调制模式。图13a、图13c所示,输入电压跳变时直接功率控制下输出电压U2几乎没有变化;图13b为电压环PI控制,输入电压跳变时输出电压有5V超调量,经过132ms后进入稳态;图13d输入电压下降时,输出电压跌落3V,调节时间为150ms。
对本文所提出的调制方法,在200V(k=0.71)输入电压等级下,与传统SPS调制方法进行比较。变换器效率h、电感电流有效值IL关于输出功率P2的曲线如图14所示。从图中可以看出,对于Buck模式来说,中低功率段TPS调制电流有效值明显小于SPS调制模式,重载情况下,TPS调制退化为SPS调制,因此曲线重合。另外,根据传输效率曲线,本文所提调制方式的最高效率可达到96.1%。

图13 输入阶跃实验不同控制方式对比
Fig.13 Comparison of different control strategies in input steps experiment

图14 不同调制模式下电流有效值、效率对比
Fig.14 The comparison of RMS value and efficiency
本文提出了一种DAB变换器TPS调制的优化问题分析方法,借鉴对称变换和空间投影思想,减小了电感电流优化过程的复杂度;并利用最优条件对带有等式和不等式约束条件的优化问题进行严格求解,分类讨论并得到了所有可行域情况下的全局极小值解析式。为进一步改善变换器的动态特性,基于最小电感电流有效值的TPS调制模型,提出了直接功率控制策略。实验结果表明,相比于SPS调制方式,TPS调制在中低功率段电感电流有效值更小,效率更高。此外,本文所提出基于电感电流有效值最小的直接功率控制无论在负载或是输入电压变换时都比传统电压环PI控制有更好的动态特性。
参考文献
[1] 贺悝, 李勇, 曹一家, 等. 考虑分布式储能参与的直流配电网电压柔性控制策略[J]. 电工技术学报, 2017, 32(10): 101-110.
He Li, Li Yong, Cao Yijia, et al. Flexible voltage control strategy of DC distribution network con- sidering distributed energy storage[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 101- 110.
[2] 张辉, 梁誉馨, 孙凯, 等. 直流微电网中多端口隔离型DC-DC变换器的改进虚拟电容控制策略[J]. 电工技术学报, 2021, 36(2): 292-304.
Zhang Hui, Liang Yuxin, Sun Kai, et al. Improved virtual capacitor control strategy of multi-port isolated DC-DC converter in DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 292-304.
[3] 童安平, 杭丽君, 李国杰. 三重移相控制下DAB变换器全局优化控制策略及分析[J]. 中国电机工程学报, 2017, 37(20): 6037-6049.
Tong Anping, Hang Lijun, Li Guojie. Global optimized control strategy of dual active bridge converter controlled by triple-phase-shift modulation scheme and its analysis[J]. Proceedings of the CSEE, 2017, 37(20): 6037-6049.
[4] 曾进辉, 孙志峰, 雷敏, 等. 双重移相控制的双主动全桥变换器全局电流应力分析及优化控制策略[J]. 电工技术学报, 2019, 34(12): 2507-2518.
Zeng Jinhui, Sun Zhifeng, Lei Min, et al. Global current stress analysis and optimal control strategy of dual-active full bridge converter based on dual phase shift control[J]. Transactions of China Electro- technical Society, 2019, 34(12): 2507-2518.
[5] 涂春鸣, 管亮, 肖凡, 等. 基于扩展移相控制下双有源桥移相角优化选取与分析[J]. 电工技术学报, 2020, 35(4): 850-861.
Tu Chunming, Guan Liang, Xiao Fan, et al. Parameter optimization selection and analysis of dual active bridge based on extended phase shift control[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 850-861.
[6] 谷庆, 袁立强, 聂金铜, 等. 基于开关组合规律的双有源桥DC-DC变换器传输功率特性[J]. 电工技术学报, 2017, 32(13): 69-79.
Gu Qing, Yuan Liqiang, Nie Jintong, et al. Transmi- ssion power characteristics of dual-active-bridge DC-DC converter based on the switching combination rules[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 69-79.
[7] Zhao Biao, Song Qiang, Liu Wenhua, et al. Universal high-frequency-link characterization and practical fundamental-optimal strategy for dual-active-bridge DC-DC converter under PWM plus phase-shift control[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 6488-6494.
[8] Choi W, Rho K M, Cho B H. Fundamental duty modulation of dual-active-bridge converter for wide- range operation[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 4048-4064.
[9] Shi Haochen, Wen Huiqing, Chen Jie, et al. Minimum- reactive-power scheme of dual-active bridge DC-DC converter with three-level modulated phase-shift control[J]. IEEE Transactions on Industry Appli- cations, 2017, 53(6): 5573-5586.
[10] Shao Shuai, Jiang Minging, Ye Weiwen, et al. Optimal phase-shift control to minimize reactive power for a dual active bridge DC-DC converter[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 10193-10205.
[11] 年珩, 叶余桦. 三端口隔离双向DC-DC变换器模型预测控制技术[J]. 电工技术学报, 2020, 35(16): 3478-3488.
Nian Heng, Ye Yuhua. Model predictive control of three-port isolated bidirectional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3478-3488.
[12] Zhao C, Round S D, Kolar J W. Full-order averaging modelling of zero-voltage-switching phase-shift bidire- ctional DC-DC converters[J]. IET Power Electronics, 2010, 3(3): 400-410.
[13] Qin Hongsi, Kimball J W. Generalized average modeling of dual active bridge DC-DC converter[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 2078-2084.
[14] Krismer F, Kolar J W. Accurate small-signal model for the digital control of an automotive bidirectional dual active bridge[J]. IEEE Transactions on Power Electronics, 2009, 24(12): 2756-2768.
[15] 侯聂, 宋文胜, 武明义. 双向全桥DC-DC变换器的负载电流前馈控制方法[J]. 中国电机工程学报, 2016, 36(9): 2478-2485.
Hou Nie, Song Wensheng, Wu Mingyi. A load current feedforward control scheme of dual active bridge DC-DC converters[J]. Proceedings of the CSEE, 2016, 36(9): 2478-2485.
[16] Song Wensheng, Hou Nie, Wu Mingyi. Virtual direct power control scheme of dual active bridge DC-DC converters for fast dynamic response[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(2): 1750-1759.
[17] 王江宏, 蔡海宁, 颜远. Inter FPGA/CPLD设计(高级篇)[M]. 北京: 人民邮电出版社, 2017.
Triple Phase Shift Modulation-Based Direct Power Control Strategy for a Dual Active Bridge Converter
Abstract In order to reduce the current stress and conduction loss of dual active bridge converter (DAB) and improve the efficiency of the converter, this paper proposes an optimal control method based on the inductor current under the mode of triple phase shift (TPS) modulation. Considering the complex optimization issue caused by DAB multi-mode operations in TPS modulation, a symmetric transformation and a space projection method based on an AC equivalent model are used to eliminate redundant feasible regions. Taking the minimum inductive current as the optimization object, this strategy uses the optimality conditions to resolve it. In addition, to improve the dynamic performance, a direct power control strategy (DPC) incorporated with a minimum inductor RMS current model is explored. In the case of input voltage fluctuation and load mutation, the converter can achieve accurate control output without overshoot within a few of duty cycles. Finally, the proposed strategy is verified on a low-power prototype using SiC devices.
keywords:Dual active bridge (DAB) converter, triple phase shift (TPS) modulation, optimality conditions solving, direct power control
DOI: 10.19595/j.cnki.1000-6753.tces.211940
中图分类号:TM46
国家自然科学基金项目(52077183)和广西高等学校高水平创新团队及卓越学者计划项目(桂教人才〔2020〕6号)资助。
收稿日期 2021-11-29
改稿日期 2022-01-28
高 宇 男,1997年生,硕士研究生,研究方向为隔离DC-DC变换器拓扑及控制策略。E-mail: mer_swjtu@163.com
舒泽亮 男,1979年生,教授,博士生导师,研究方向为电力电子技术及应用、多电平变换装置和同相供电系统等。E-mail: shuzeliang@swjtu.edu.cn(通信作者)
(编辑 陈 诚)