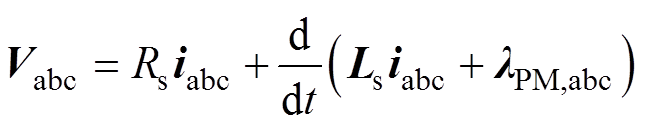 (1)
(1)
摘要 永磁同步电机定子绕组相邻线圈之间绝缘的退化会导致匝间短路故障,而目前的研究较多集中于短路匝数辨识,较难在故障初期检测到绝缘电阻的退化过程。该文基于匝间短路故障电机有限元联合仿真模型分析了剩余绝缘电阻对定子电流的影响,提出一种基于电流9次谐波的故障检测方法。这种方法在时频域内可有效提取故障特征,并可解耦转速波动对故障检测结果的影响,因而能在稳态和瞬态运行工况下对剩余绝缘电阻从故障初期到晚期的退化趋势进行有效追踪。所提方法在一台24槽4极分布式绕组的三相永磁同步电机上进行了实验验证,结果显示,该方法对绕组剩余绝缘电阻衰减变化具有较高的监测精度,并且对于转速突变扰动具有优异的鲁棒性。
关键词:三相永磁同步电机 匝间短路 故障检测 时频分析
永磁同步电机(Permanent Magnet Synchronous Machine, PMSM)由于其高效率、高功率和高转矩密度的特点被广泛使用[1-2]。当电机频繁工作在过热、过电压、冲击环境下,可能会导致定子绕组匝间短路(Inter-Turn Short Circuit, ITSC)、永磁体永久性退磁、绕组开路、接地短路等多种电气故障。其中ITSC故障占比最高且往往是其他故障的起 因[3-4]。
ITSC故障的最初形态为定子绕组内相邻线圈之间绝缘的轻微退化,但短路电流产生的热量会加快此进程,进一步导致更严重的绝缘下降。然而,目前关于ITSC初期故障的研究较多集中于短路匝数的评估,但匝间剩余绝缘电阻通常设置为接近于零,即绝缘几乎完全失效[5-8]。在此实验条件下,尽管短路匝数较少,短路支路中仍会产生远超相电流幅值的短路电流,导致明显的转矩脉动和温升。初期ITSC故障形成后,只有绝缘退化到一定程度才会产生足够的热量导致附近线圈的大面积短路。因此,能够检测出绝缘电阻的退化情况具有重要的学术意义和工程价值。
现有ITSC故障检测主要可以分为三种类型,分别为基于模型、信号处理和数据驱动的方法[9]。其中,基于模型的方法从故障机理出发,依据电磁场理论推导出故障模型,通过比较模型输出和故障阈值得到诊断结果[10-13]。该方法通常需要设置一个较高的阈值以防止错误诊断,但ITSC初期故障特征微弱,难以触发故障预警。此外,该方法高度依赖模型和电机参数的精度。基于数据驱动的方法利用大量实验数据和深度学习算法识别出故障特征相关的信息[14-16]。该方法要求数据服从独立同分布的要求,而获取所需不同故障程度和不同工况下的实验数据存在一定难度,使得其难以应用于工程实际中。考虑到电机内部的异常往往会在电流、电压、转矩、振动等信号中体现,本文采用基于信号的处理方法,通过在时频联合域内提取信号中和故障相关的特定谐波分量进行故障判定[17-21]。
对于特定谐波分量的提取,基于科恩克莱斯分布的双线性时频能够实现较高的时频分辨率[17],但交叉项干扰会对特定频带的提取造成一定影响。而其改进方法,如平滑伪Wigner-Ville、Choi-Williams分布,虽抑制了大多数交叉项,但不仅降低了时频分辨率,引入新的干扰,还增加了计算负担。线性时频方法从本质上避免了交叉项干扰的问题[3, 18],但受限于海森堡不确定性原理,无法同时实现时、频域的高分辨率。为提高时频聚集性,I. Daubechies等提出的同步压缩变换(Synchrosqueezing Trans- form, SST)被广泛应用于不同研究领域中[19-21]。然而,该方法由于忽略了原始信号泰勒展开后瞬时幅值一阶、瞬时相位二阶及以上分量,导致其瞬时频率估计产生偏差,对于处理时变信号存在一定局限性。因此,二阶、高阶、多重SST等算法被相继提出[22-24]。其中,多重SST能够较好地处理多分量时变信号,且计算量基本不受迭代次数影响,但无法通过其变换结果直观获取各频带幅值变化信息。
本文建立了ITSC故障电机的有限元联合仿真模型,分析了不同短路匝数和不同剩余绝缘电阻对于定子电流的影响,并在此基础上提出了基于定子电流9次谐波的故障诊断方法。相比于3次谐波,9次谐波对于故障初期微弱特征更敏感。同时,针对目前研究中匝间绝缘电阻往往设置为接近于0的实验方法而无法体现故障初期微弱特征的情况,提出了对于匝间剩余绝缘电阻的检测方法。通过多重SST算法对其进行精确提取,并提出将多重SST三维时频矩阵重新映射到时域平面,得到特定阶次谐波幅值的时变特性,最终建立不受转速影响的故障指示器。最后,所提方法在一台24槽4极三相PMSM上进行了ITSC故障模拟检测,结果显示,该方法能够有效检测出故障程度由初期到晚期的变化过程,且在瞬态运行工况下对转速具有较好的鲁棒性,实现了对剩余绝缘电阻退化趋势的有效追踪。
正常PMSM在abc坐标系下的电气方程为
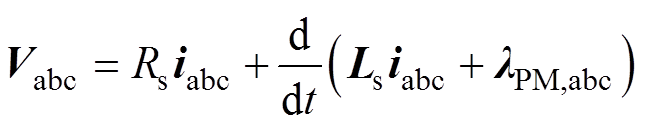 (1)
(1)
其中
Vabc=[Va Vb Vc]T
iabc=[ia ib ic]T
Ls=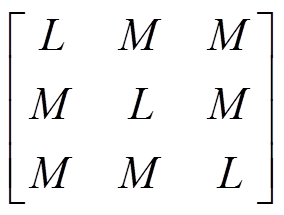
lPM,abc=[lPM,a lPM,b lPM,c]
式中,Vabc为三相电压;Rs为相电阻;iabc为三相电流;Ls为相电感;L为每相绕组的自感;M为两相绕组间的互感;lPM,abc为三相永磁磁链。
当某一相发生ITSC故障时,绕组内部连接关系如图1所示。Rf为被短路两匝之间的剩余绝缘电阻:当Rf足够大时电机无故障;当Rf =0时匝间彻底短路。if为短路支路电流。忽略铁心磁饱和及其他非线性因素影响,其电气方程[13]为
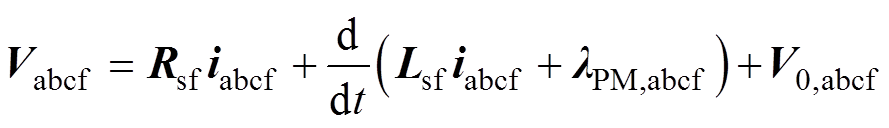 (2)
(2)
其中
Vabcf =[Va Vb Vc 0]T
iabcf=[ia ib ic if]T
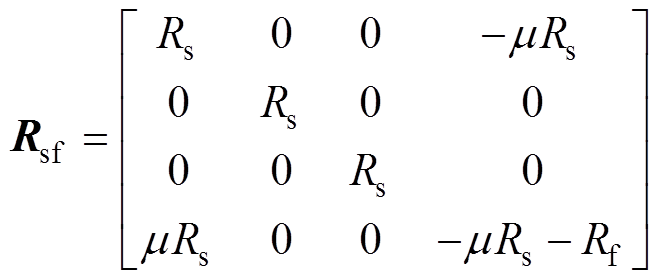
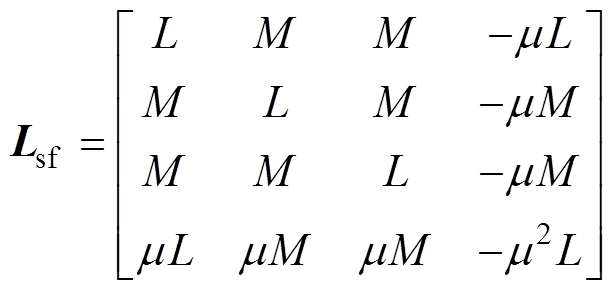
lPM,abcf =[lPM,a lPM,b lPM,c lPM,f]
V0,abcf =[V0 V0 V0 0]
式中,f下标代表故障后;lPM,abcf为三相和故障支路的永磁磁链,lPM,a、lPM,b、lPM,c、lPM,f 分别为A、B、C三相和故障支路永磁磁链;V0,abcf 为三相和故障相的零序电压矩阵;V0为三相每相的零序电压分量;m 为被短路线圈匝数占该相线圈总匝数的比例。
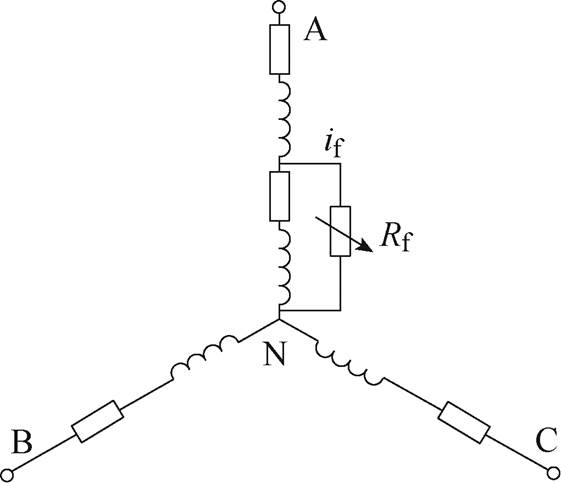
图1 PMSM匝间短路故障等效示意图
Fig.1 Equivalent diagram of PMSM with ITSC fault
对于三相星形联结绕组,ia+ib+ic=0。因此,将式(2)中的三相相加[13]可得
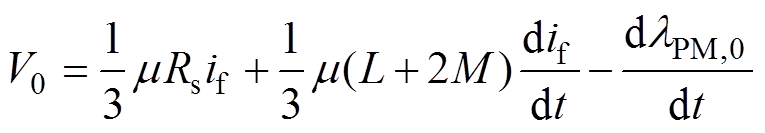 (3)
(3)
式中,lPM,0为三相合成永磁磁链的均值;t为时间。
对于正常电机,故障电流if =0,故V0仅取决于式(3)的最后一项,即
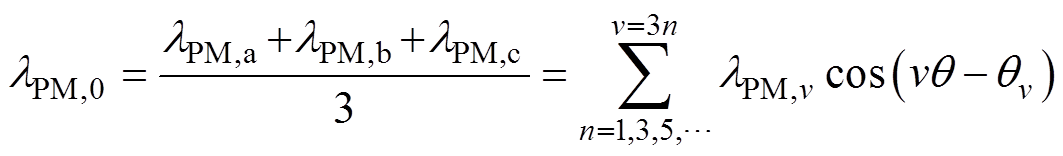 (4)
(4)
式中,n为每相磁链的谐波阶数;v为lPM,0的谐波阶数;q 为电角度;qv为第v阶谐波和基波的相位差。
由式(4)可见,在正常三相PMSM中,三相信号中的3次及其奇数倍谐波由于幅值相同、相位一致,在中性线无通路情况下无法闭合,因而零序分量为零。当定子绕组中某一相发生ITSC故障时会破坏电机的三相平衡关系,在短路支路中产生回流,进而引起零序分量的异常变化。由于通常认为高次谐波幅值相对较小,因此会选取3次谐波用于诊断。电机的反电动势谐波幅值越大,在相同故障程度下,其零序分量的变化量越大,用于故障诊断时受噪声及信号处理算法的影响越小,因此更适用于故障判定。然而,各谐波的反电动势幅值取决于电机本身的设计参数,因此需要根据电机本体的故障谐波特性选择合适的特征谐波用于诊断。
对于故障电机,在故障初期,由于剩余绝缘电阻Rf较大,短路支路的故障电流if幅值很小,因此式(3)中前两项的影响可以忽略。而短路支路的存在会改变故障所在相磁链,破坏原本的三相平衡关系,导致3次及其奇数倍谐波幅值的改变。
由于等效电路模型忽略了故障导致的铁心磁饱和及其他非线性因素的影响,且部分参数难以准确获取,因此本文通过Ansys Maxwell建立了基于2D有限元方法(Finite Element Method, FEM)的故障模型[25]。为验证模型的有效性,首先建立正常电机模型,PMSM样机参数见表1。仿真和示波器测量的反电动势波形及其谐波特性基本一致,如图2所示。此外,在3、9和15次谐波中,9次谐波幅值明显较高。
在正常电机模型的基础上,通过重新分配故障后绕组在定子槽内的分布建立了ITSC故障电机2D模型。此外,通过Ansys Twinbuilder搭建了外电路以模拟相绕组、短路支路和剩余绝缘电阻的连接关系,实现了如图3所示的ITSC故障联合仿真模型。其中,RsA~RsC为相电阻,R1~R3为阻性负载,L1~L3为端部漏感,Rf为剩余绝缘电阻,RsF=(1-m)RsA为被短路绕组电阻。
表1 PMSM样机参数
Tab.1 The parameters of prototype PMSM

参 数数 值 额定功率/kW2.2 额定转速/(r/min)3 000 额定电压/V380 定子绕组电阻/W2.3 每相线圈匝数200
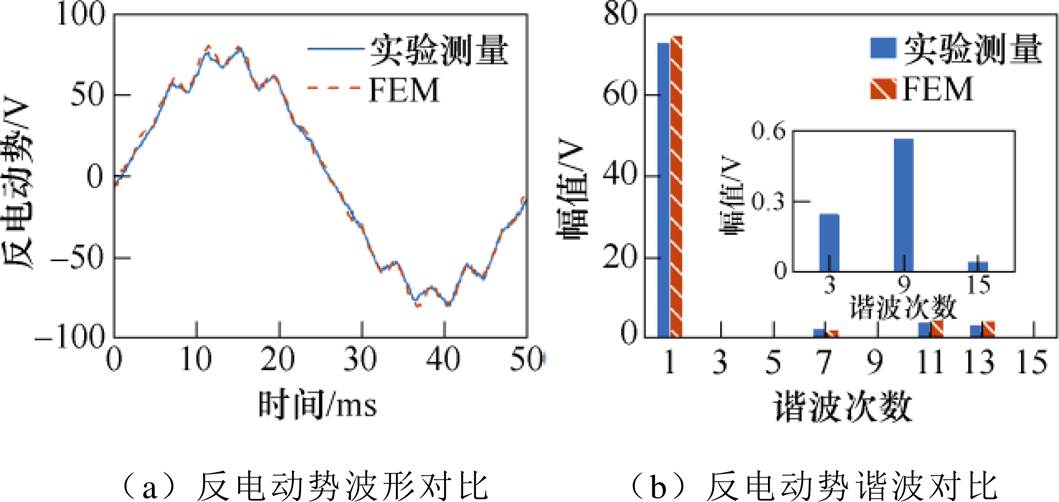
图2 有限元仿真与实验测量反电动势对比
Fig.2 Comparation of the back electromotive force between a healthy prototype PMSM and the FEM model
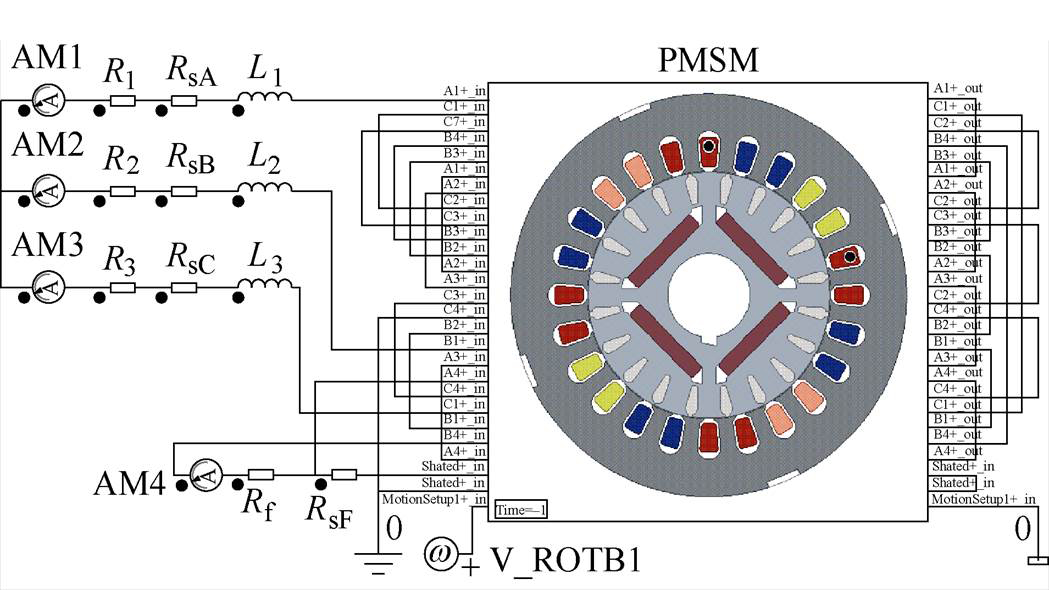
图3 基于TwinBuilder软件搭建的ITSC故障联合仿真模型
Fig.3 The co-simulation model of the ITSC fault built by TwinBuilder
ITSC故障模型定子电流谐波如图4所示,仿真数据基于基波进行了标幺处理,在600r/min的转速下,随着Rf的减小,即故障程度的增加,如图4b所示,1、5、7、11和13次谐波中的幅值最大变化量仅达到0.63dB。在相对较低的转速下,各谐波幅值变化量较小,同时在剩余绝缘电阻并非接近于0的情况下,短路故障产生的影响不明显,因此对除零序分量之外的主要谐波的作用可忽略。而3、9次谐波基本呈现出与故障程度一样的变化趋势,且9次谐波幅值整体高于3次谐波,但15次谐波幅值变化无规律性,无法作为故障判定依据,如图4c所示。
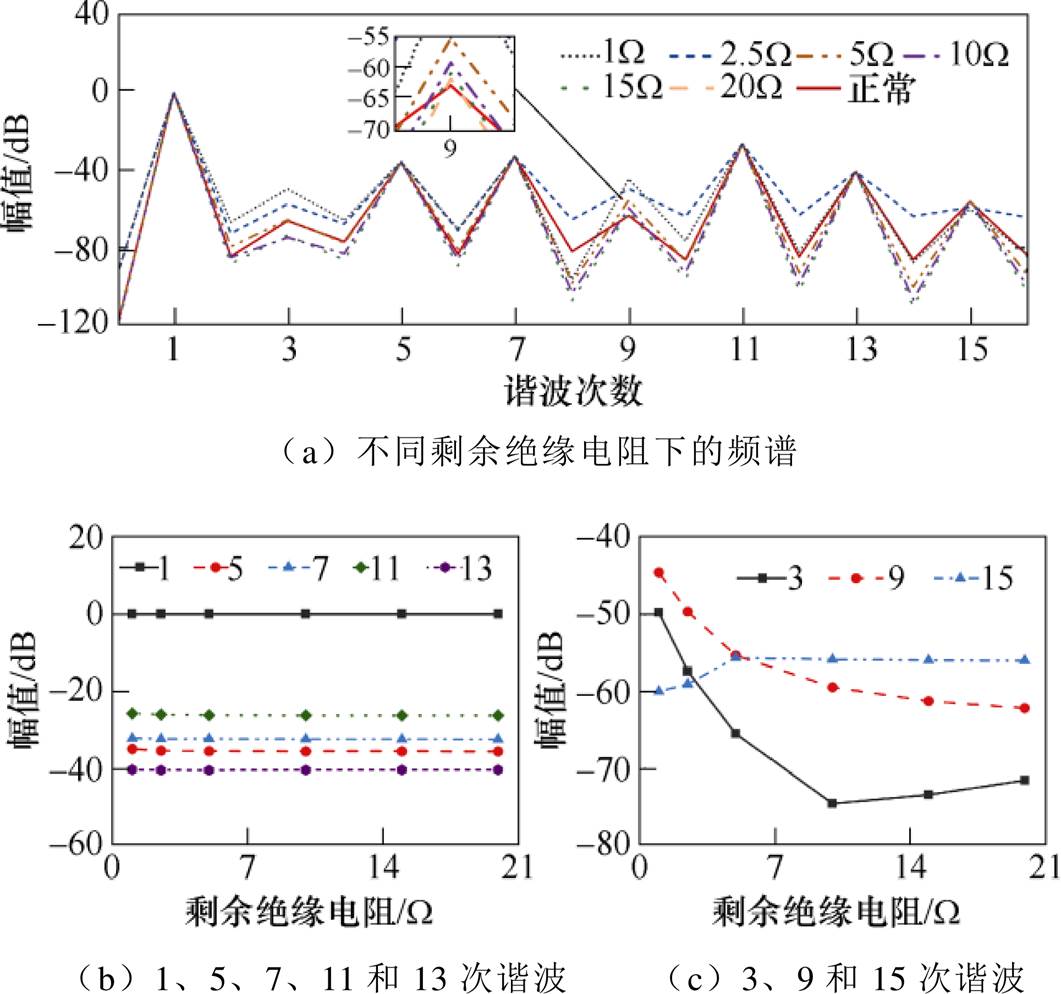
图4 ITSC故障模型定子电流谐波(600r/min)
Fig.4 Stator current harmonics of the fault model with ITSC fault at 600r/min
此外,短路匝数仅为1且接近于完全短路(Rf ≈0)的故障情况被普遍视作为初期故障。然而,尽管短路支路中仅存在1匝线圈产生反电动势,而在绝缘电阻接近于0的情况下,尽管转速较低、短路匝数较少、短路支路的反电动势较小,过低的支路电阻仍会导致巨大的短路电流,如图5a所示。因而故障会引起相电流波形发生明显的畸变,同时谐波也产生了明显变化,故障后A相电流和故障前后相电流9次谐波如图5b和图5c所示。因此,目前较多研究使用接近于0的剩余绝缘电阻作为初期故障的评价方式并不准确,该实验条件下故障特征较为明显,对于诊断方法的要求不高。
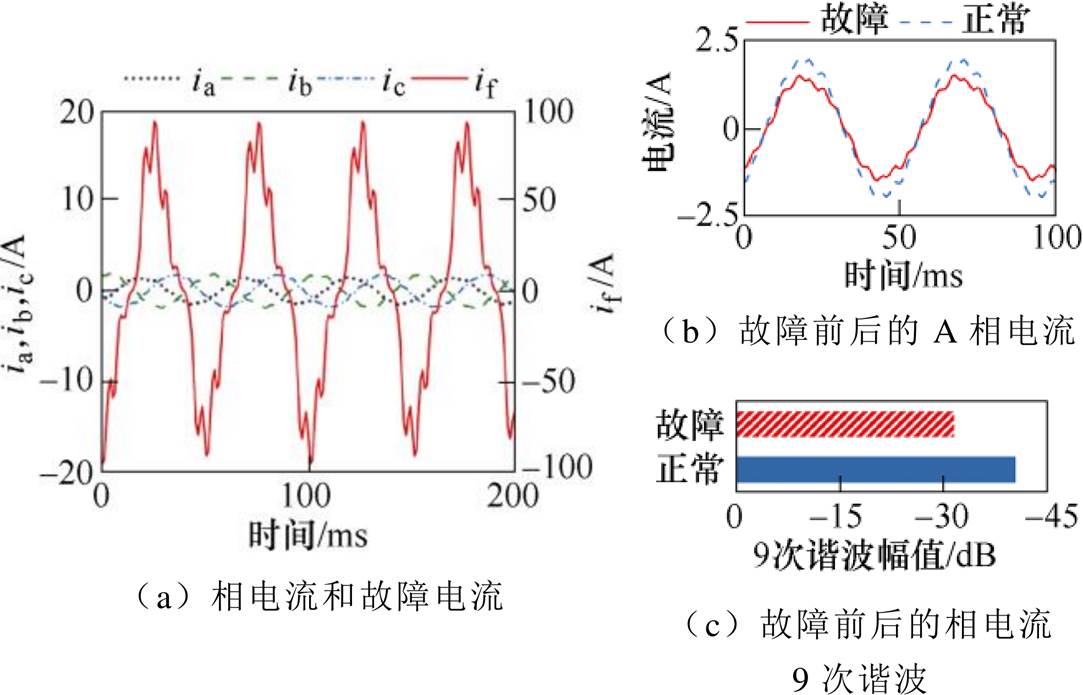
图5 单匝完全短路情况下的仿真结果(600r/min)
Fig.5 One turn shorted and complete loss of insulation capacity at 600r/min
在故障初期匝间剩余绝缘损坏程度较低的情况下,所产生的短路支路电流较小,对于驱动系统的影响并不显著,故障特征相对微弱,因此需要选择合适的时频算法提取出ITSC故障相关的特征分量作为判定依据。本文中所选用的4极24槽测试电机由于本体谐波特性,其相反电动势的3、9次谐波幅值均较小。但相比之下,9次谐波幅值远大于3次谐波,且考虑到3次谐波在转子偏心、退磁等故障中也会作为故障特征分量[26-27],因此本文选择9次谐波用于ITSC故障的检测。
为在时频联合域中提取出电流信号中的故障特征,本文提出基于多重SST的匝间剩余绝缘电阻退化趋势检测方法。该方法主要包含两部分:对电流信号进行多重SST处理,以获取聚集性良好的时频表示;根据电机转速提取出时频分布中的基波和9次谐波,将时频三维矩阵重新映射到二维时域-幅值平面中,得到基波和9次谐波幅值的时变特性,建立不受转速影响的故障指示,匝间剩余绝缘电阻退化趋势检测方法流程如图6所示。
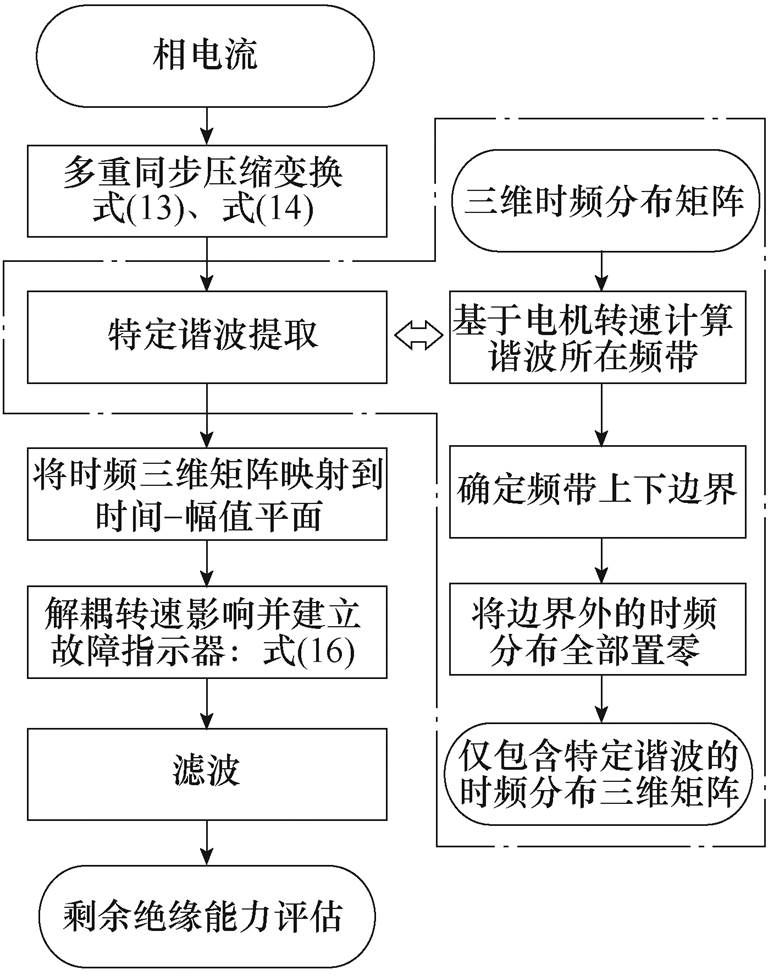
图6 匝间剩余绝缘电阻退化趋势检测方法流程
Fig.6 Flow chart of the proposed fault detection algorithm
在图2b中,稳态运行工况下的9次谐波幅值占比非常小,而在变转速工况下其信噪比会进一步降低。连续小波变换处理后的时频表示如图7所示,不仅各频带的频率成分随转速改变,其宽度也会发生变化。使用传统的线性时频方法会不可避免地造成时频分布模糊现象,导致特定谐波成分难以提取。
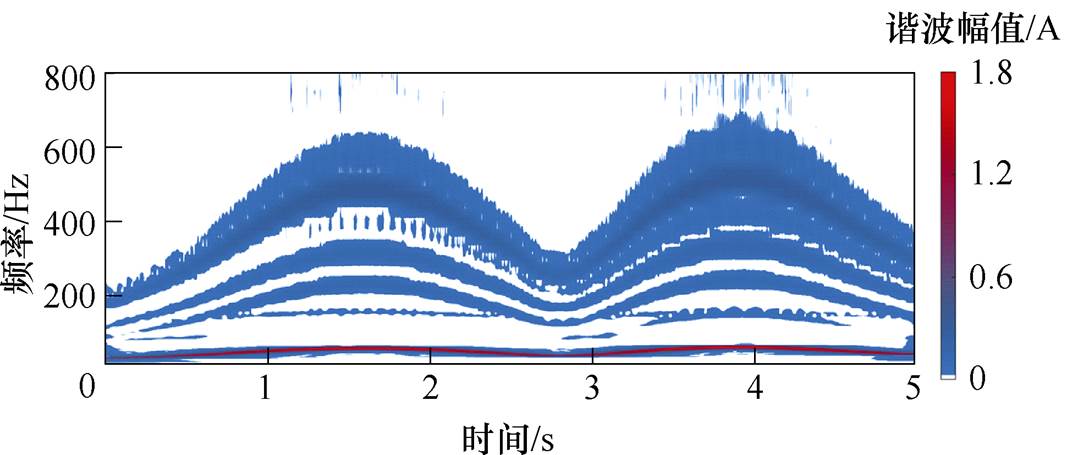
图7 连续小波变换处理后的时频表示
Fig.7 TF representation using continuous wavelet transform
为从多分量信号中准确分离出目标谐波分量,减少信号失真,本文采用多重SST对电流信号进行处理。对于包含K个分量的多分量非稳态信号x(t),有
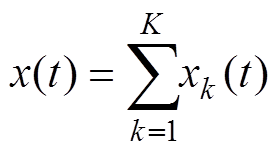 (5)
(5)
式中,t为时间。第k个分量可以表示为
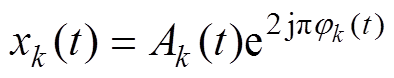 (6)
(6)
式中,Ak(t)为瞬时幅值;jk(t)为瞬时相位。SST的原理是基于线性时频方法通过时频重排运算抑制模糊现象。以短时傅里叶变换为例,变化结果[24]为
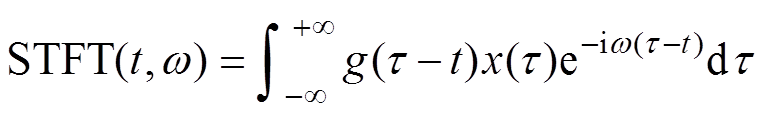 (7)
(7)
式中,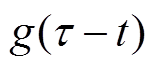 为中心时刻为t的窗函数;t 为时间变量;w 为角速度。对于缓变信号,忽略瞬时幅值泰勒展开的一阶、瞬时相位的二阶及其高次项,即
为中心时刻为t的窗函数;t 为时间变量;w 为角速度。对于缓变信号,忽略瞬时幅值泰勒展开的一阶、瞬时相位的二阶及其高次项,即
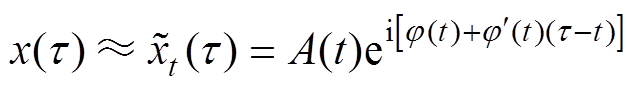 (8)
(8)
式中,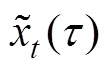 为
为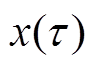 估计值;
估计值;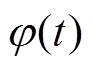 为瞬时相位;
为瞬时相位;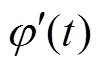 为瞬时频率。
为瞬时频率。
因此,短时傅里叶变换可以表示为
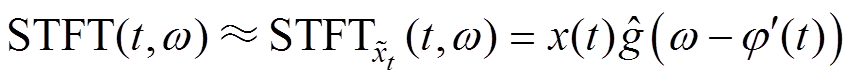 (9)
(9)
式中,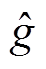 为窗函数的傅里叶变换;
为窗函数的傅里叶变换;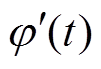 为瞬时频率估计值。STFT(t, w)对时间的偏微分为
为瞬时频率估计值。STFT(t, w)对时间的偏微分为
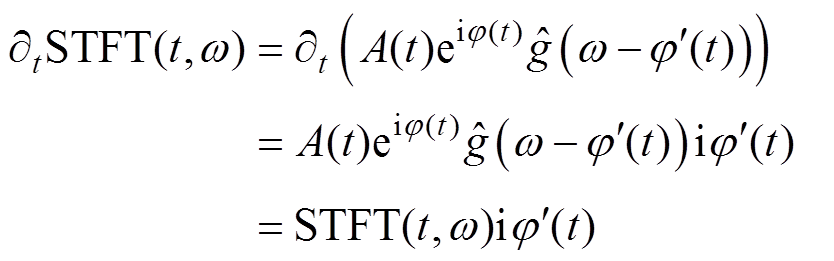 (10)
(10)
因此,可以得到瞬时频率估计值为
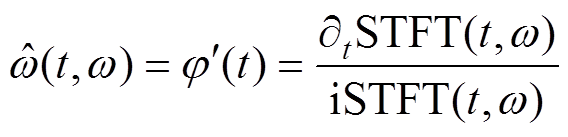 (11)
(11)
在获取信号瞬时频率的基础上,通过时频重排运算将分散的能量压缩到瞬时频率轨线中,得到新的时频分布[24]为
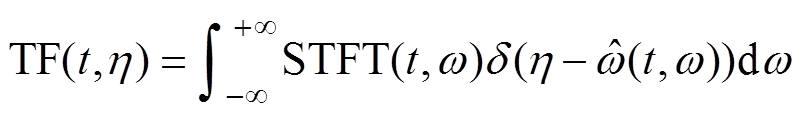 (12)
(12)
式中,h 为频率;d 为狄拉克函数。
然而,定子电流信号为时变多分量信号,忽略式(8)中泰勒展开的高阶分量会导致时频分布中时变信息的丢失。因此,多重SST考虑了瞬时幅值的一阶分量及瞬时相位的二阶分量,并通过多重的瞬时频率估计运算进一步提高时频分辨率[24],有
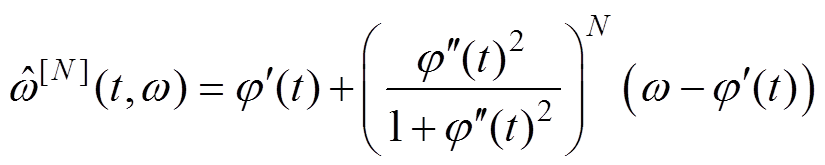 (13)
(13)
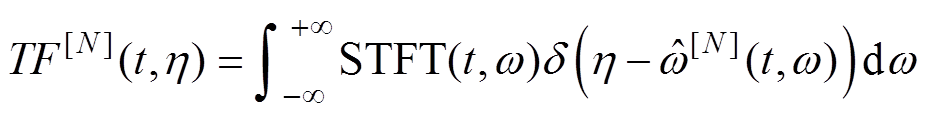 (14)
(14)
式中,N为迭代次数,迭代次数越多,信号能量分布就越集中。
为增强剩余绝缘电阻退化趋势监测结果的可读性,本文提出了一种基于多重SST结果的故障指示,具体如下:
(1)当电流信号转化为能量聚集的时频三维矩阵后,根据电流基频能够获得各谐波中心频率,通过设置合理的频带边界提取出目标谐波分量。根据电机转速,各谐波分量的中心频率为
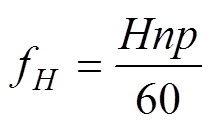 (15)
(15)
式中,H为谐波次数;n为电机转速;p为磁极对数。基于频带中心频率和相邻频带的间距设置目标谐波分量的上下边界,通过将边界之外的时频点全部置零以过滤噪声成分,进而得到仅包含特定谐波分量的时频分布。
(2)对于所提取的特定谐波分量,其形式为时间-频率-幅值所构成的三维矩阵,无法直接量化其谐波幅值信息并建立数学解析故障指示。由于经过多次迭代后,单分量时频分布会被压缩到一条时频轨线内,因此通过选择每个时间点对应的向量中的最大值,可以将时间-频率-幅值三维矩阵映射到时间-幅值平面上以解耦频率维度的影响。
(3)由于匝间剩余绝缘电阻和转速均作用于9次谐波幅值,为解耦转速的影响,对9次谐波A9的二维矩阵基于基波A1矩阵进行标幺处理,经进行平滑滤波后,得到故障指示FI为
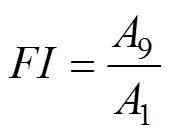 (16)
(16)
该故障指示FI能够反映ITSC剩余绝缘电阻的失效情况,FI幅值越大表示剩余绝缘电阻越小,即故障程度越严重。
本文所搭建的实验平台及示意图如图8所示,其参照了该领域权威学者B. Akin教授[6],S. W. Kim教授[10]等针对ITSC故障提出的实验模拟方案并在此基础上加以改进。
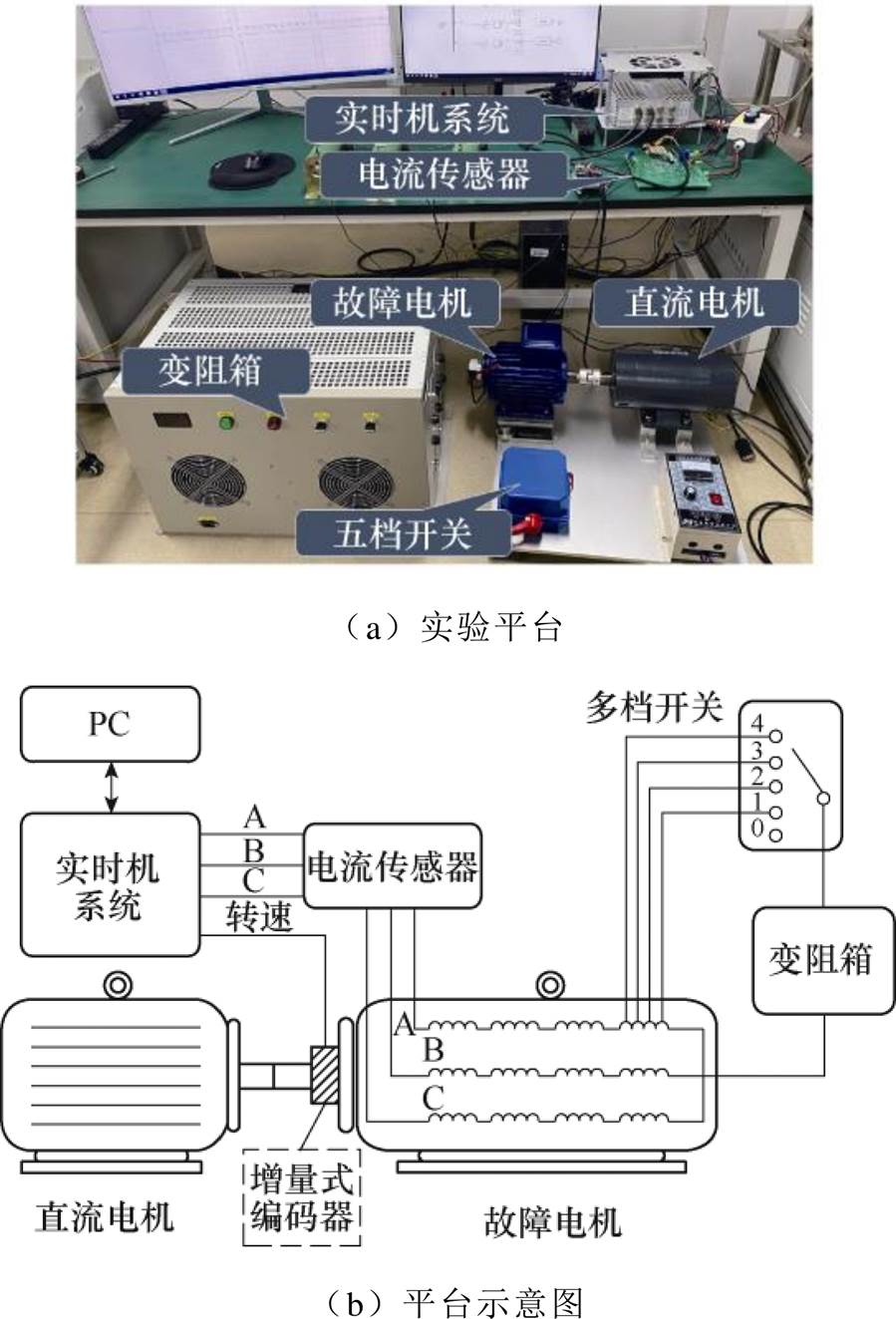
图8 实验平台及示意图
Fig.8 Experimental platform and schematic diagram
该平台包括一台特制三相PMSM(可选择ITSC故障模式和正常模式)、一台直流牵引电机、电流传感器、增量式编码器、可变电阻箱(用于模拟匝间剩余绝缘电阻由故障初期到晚期的退化过程)、多档开关(用于选择不同短路匝数)、Speedgoat实时机系统(10kHz采样频率)和计算机等。
实验样机经过改制,从A相定子绕组中引出不同比例的匝数抽头,能够实现8%、12%、16%和20%四种短路匝数情况。这些抽头通过五档开关、可变电阻箱与中性线相连。电阻箱既可以设定为固定阻值,也能够连续调节以模拟绝缘变化过程。对于特定匝数的短路故障,通过调节变阻箱的阻值模拟剩余绝缘电阻的变化,当阻值逐渐降低并趋近于0时,代表剩余绝缘电阻不断退化直至完全失效。
不同转速下正常电机和故障电机定子电流的频谱对比如图9所示。
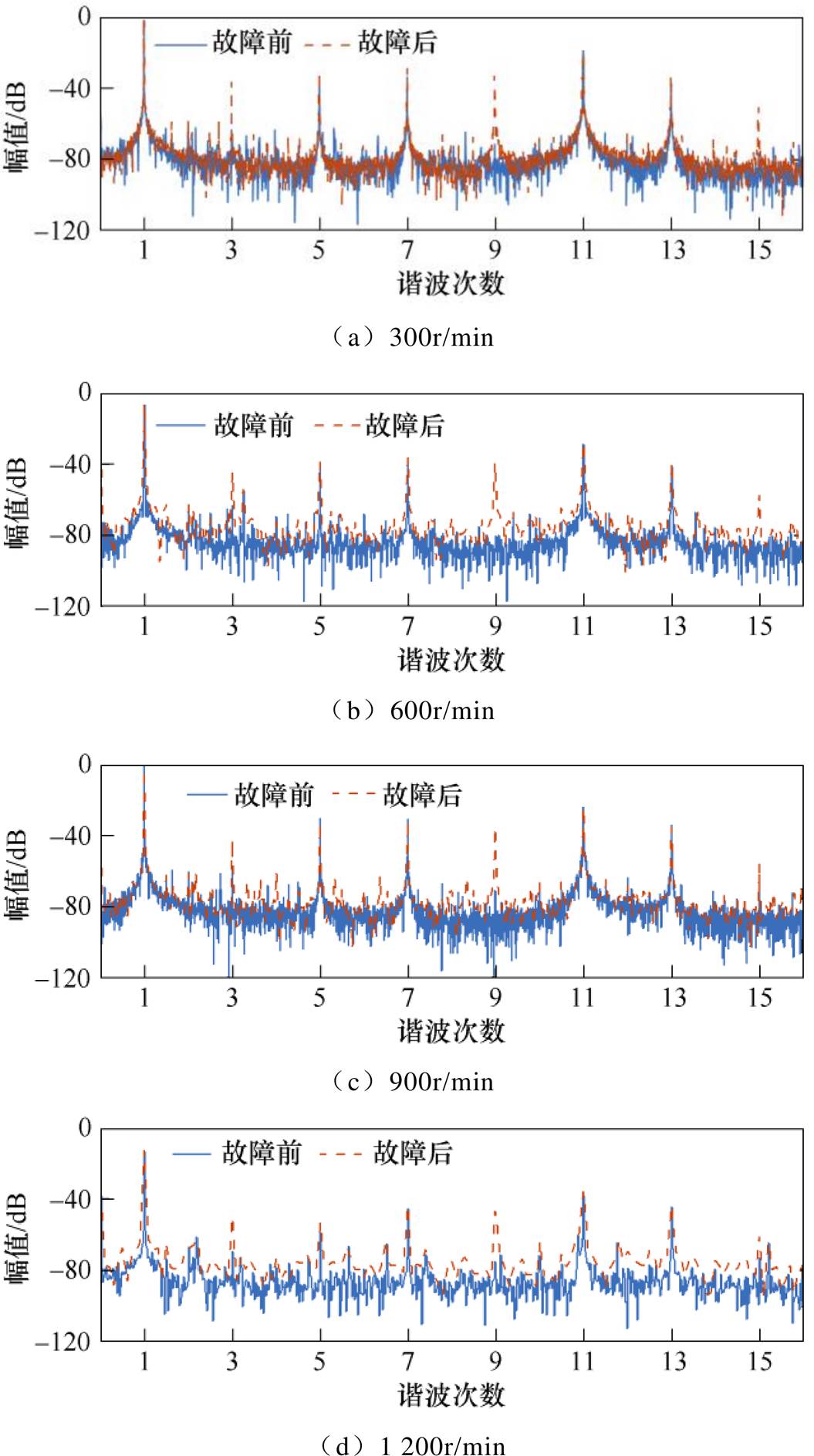
图9 不同转速下电机故障前后定子电流频谱
Fig.9 Stator current spectrum at various speed for healthy and faulty machine
正常情况下,电机的主要谐波包含1、5、7、11和13次谐波,其中5、7、11和13次谐波是由于电机本体结构特性所产生的。故障情况下,定子电流中出现明显的零序分量3、9和15次谐波,而其他分量幅值基本不变。
此外,不同剩余绝缘电阻Rf和短路匝数占比m 的改变对于9次谐波幅值的影响如图10~图12所示。随着转速的升高,9次谐波幅值整体增长且均呈现出和Rf及m 近似线性的关系。3次谐波幅值的变化仅在高转速下符合故障情况,而15次谐波无明显的变化规律。这是由于3次谐波幅值相对较小,信噪比相对较差,在高速情况下由于幅值增加,逐渐表现出和故障程度的正相关,而15次谐波幅值更小,因此故障指示能力较差。
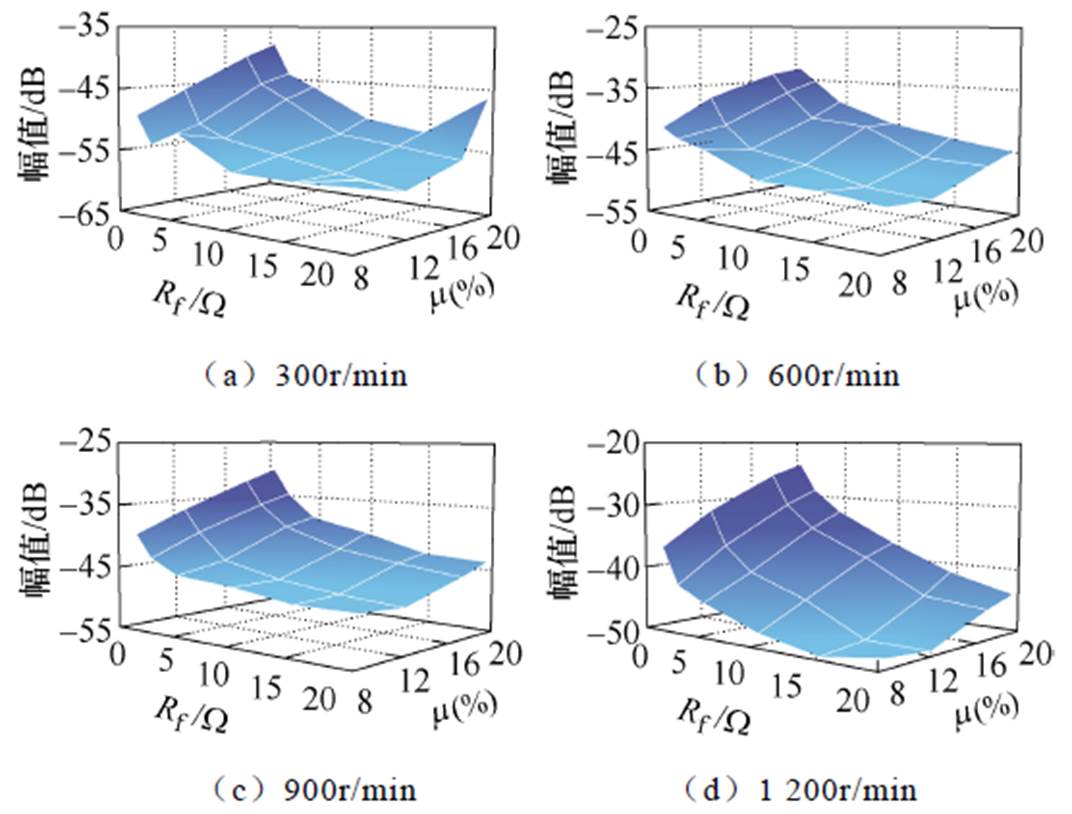
图10 剩余绝缘电阻和短路匝数对于3次谐波的影响
Fig.10 The impact of Rfand m on the 3rd harmonic
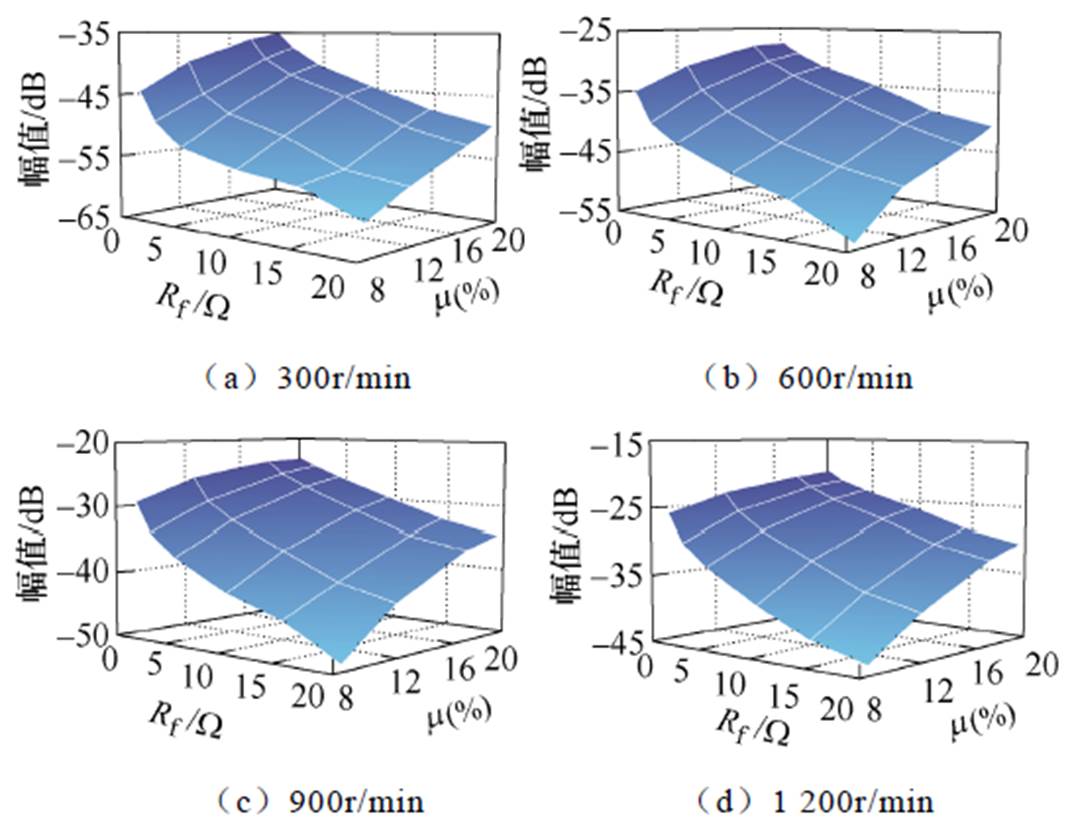
图11 剩余绝缘电阻和短路匝数对于9次谐波的影响
Fig.11 The impact of Rfand m on the 9th harmonic
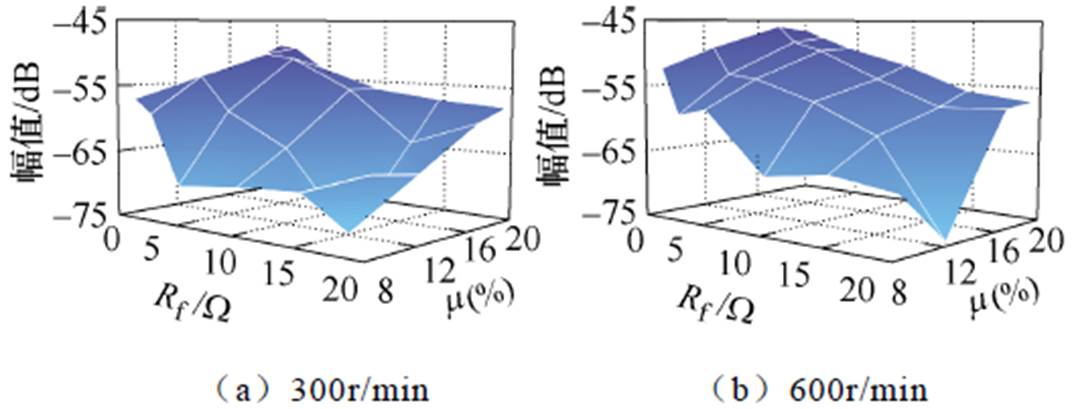
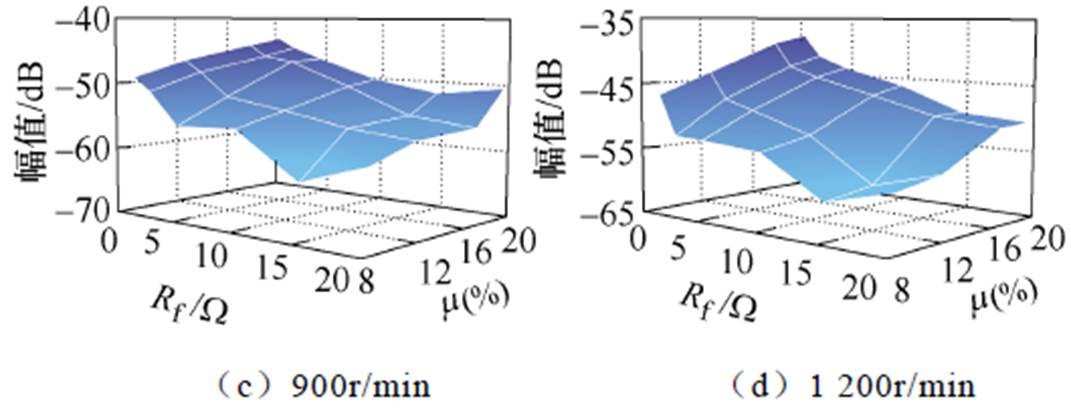
图12 剩余绝缘电阻和短路匝数对于15次谐波的影响
Fig.12 The impact of Rf and m on the 15th harmonic
基于上述9次谐波的故障指示能力,在稳态和瞬态工况下验证了所提出的ITSC故障剩余绝缘电阻退化趋势检测的方法。
首先,对定子电流信号进行多重SST处理,并通过时变频带边界提取出基波和9次谐波,多重压缩变换时频分布及频带边界如图13所示。根据局部放大图可以看出,相比图7,对于相同的信号使用多重SST能够在很大程度上抑制能量分布的模糊现象。然后基于转速计算出谐波中心频率并设定其上下边界提取出目标谐波,即图中的深色区域。再根据时间向量提取出基波和9次谐波两个三维矩阵在每个时间点对应的最大幅值,进而转化为时间-幅值二维矩阵并建立式(16)所示的故障指示。
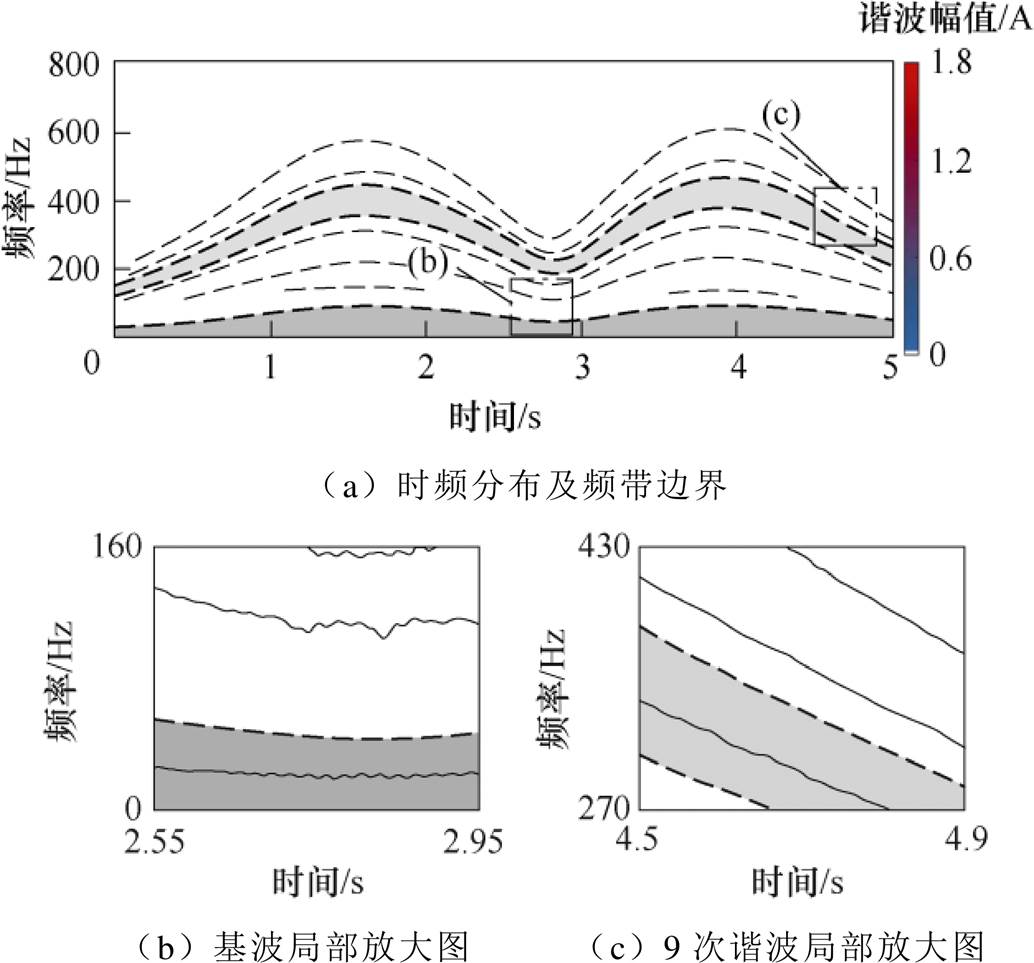
图13 多重压缩变换时频分布及频带边界
Fig.13 TF representation using multi-synchrosqueezing transform and edges of the frequency bands
为充分验证该故障指示的有效性,开展了不同转速和故障程度下的实验。其中,变故障程度是将可变电阻箱从30W 连续调节至0W 以模拟故障初期到晚期绝缘电阻退化过程,短路匝数比例选取为8%。
(1)恒转速-恒故障程度。该实验用于验证所提方法对于检测故障发生的有效性。恒转速-恒故障程度下的故障指示如图14所示。如图14a所示,电机运行转速为900r/min,对应的短路支路电流如图14b所示,在电机正常状态下为0,而在0.6s短路故障发生时,短路电流出现并迅速增长到3.47A。滤波后的9次谐波和基波幅值分别为0.035A、3.38A,如图14c和图14d所示。故障指示器如图14e所示,在短路电流出现的时刻,由于短路支路导通,而故障指示是基于特征谐波9次谐波建立的,因此在故障发生时原本接近于0的故障指示会突然增大,因而能够准确检测到故障的发生。
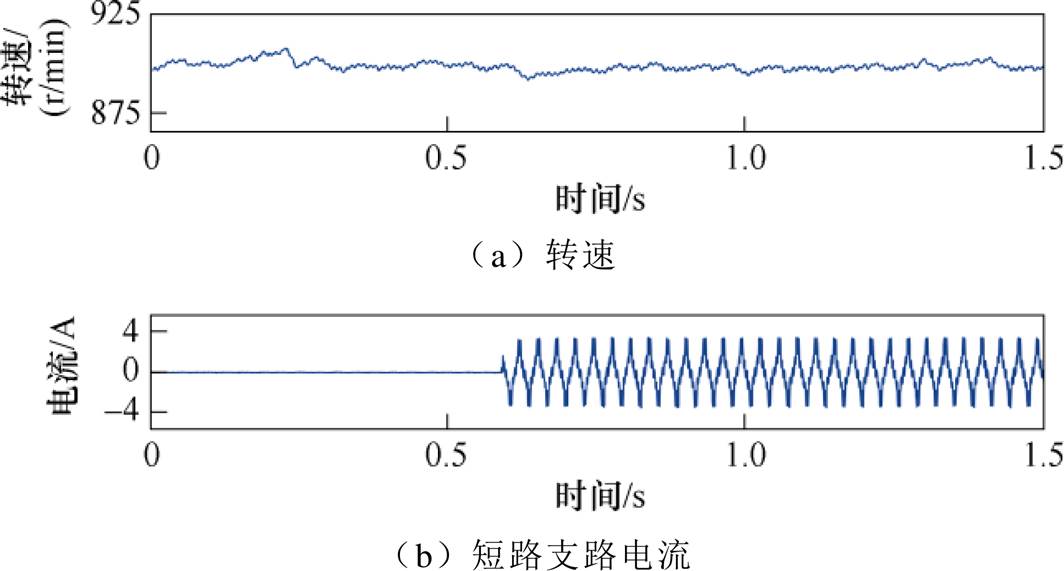
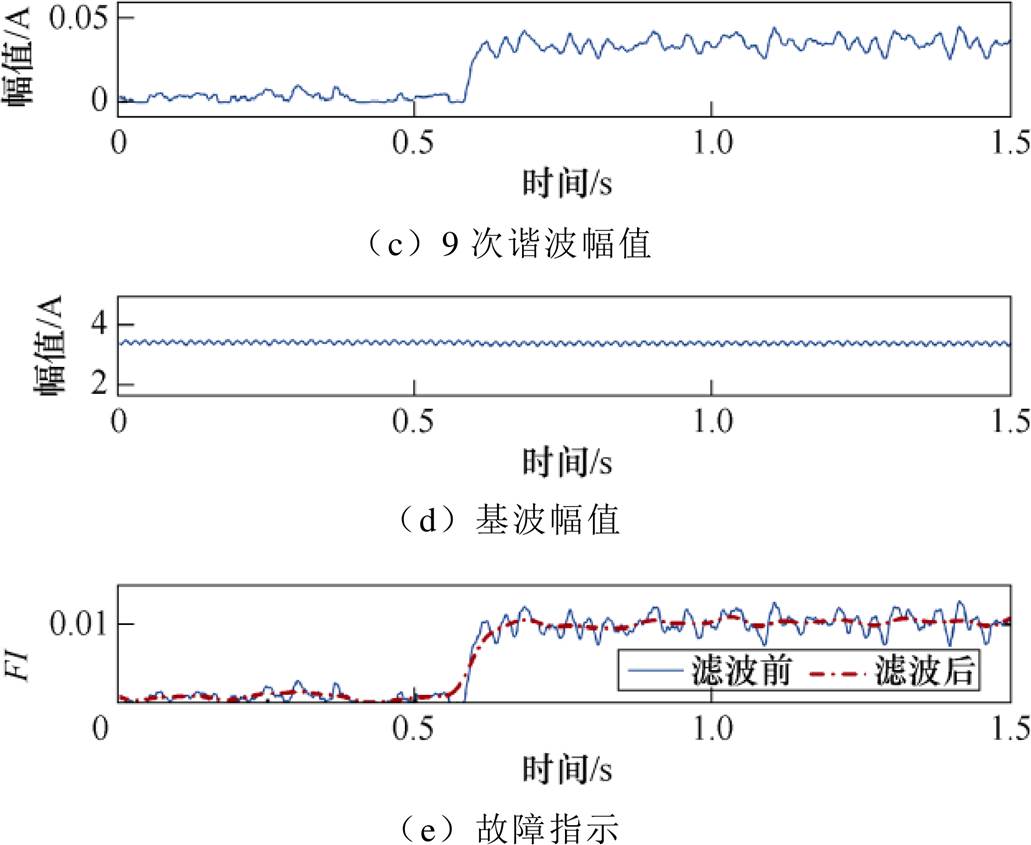
图14 恒转速-恒故障程度下的故障指示
Fig.14 Fault indicator under constant speed and fault
(2)恒转速-变故障程度。该实验用于验证所提方法对于故障初期到晚期绝缘电阻退化动态过程的检测能力。恒转速-变故障程度下的故障指示如图15所示。如图15a所示,电机运行转速为900r/min,故障电阻由30W 逐渐调节至0W。由图15b可以看出,随着剩余绝缘电阻的降低故障电流从0逐渐增大,最终在2.2s处维持不变,此时在绝缘完全失效情况下故障电流峰值达到14.6A,远超相电流基波幅值(3.2A)。在图15e中,由于匝间剩余绝缘不断恶化,短路支路中的电阻不断降低,短路支路产生的短路电流逐渐变大,三相不平衡度逐渐提高,零序分量幅值也逐渐增加,因此故障指示跟随故障程度而增加,能够反映匝间剩余绝缘电阻的退化趋势。
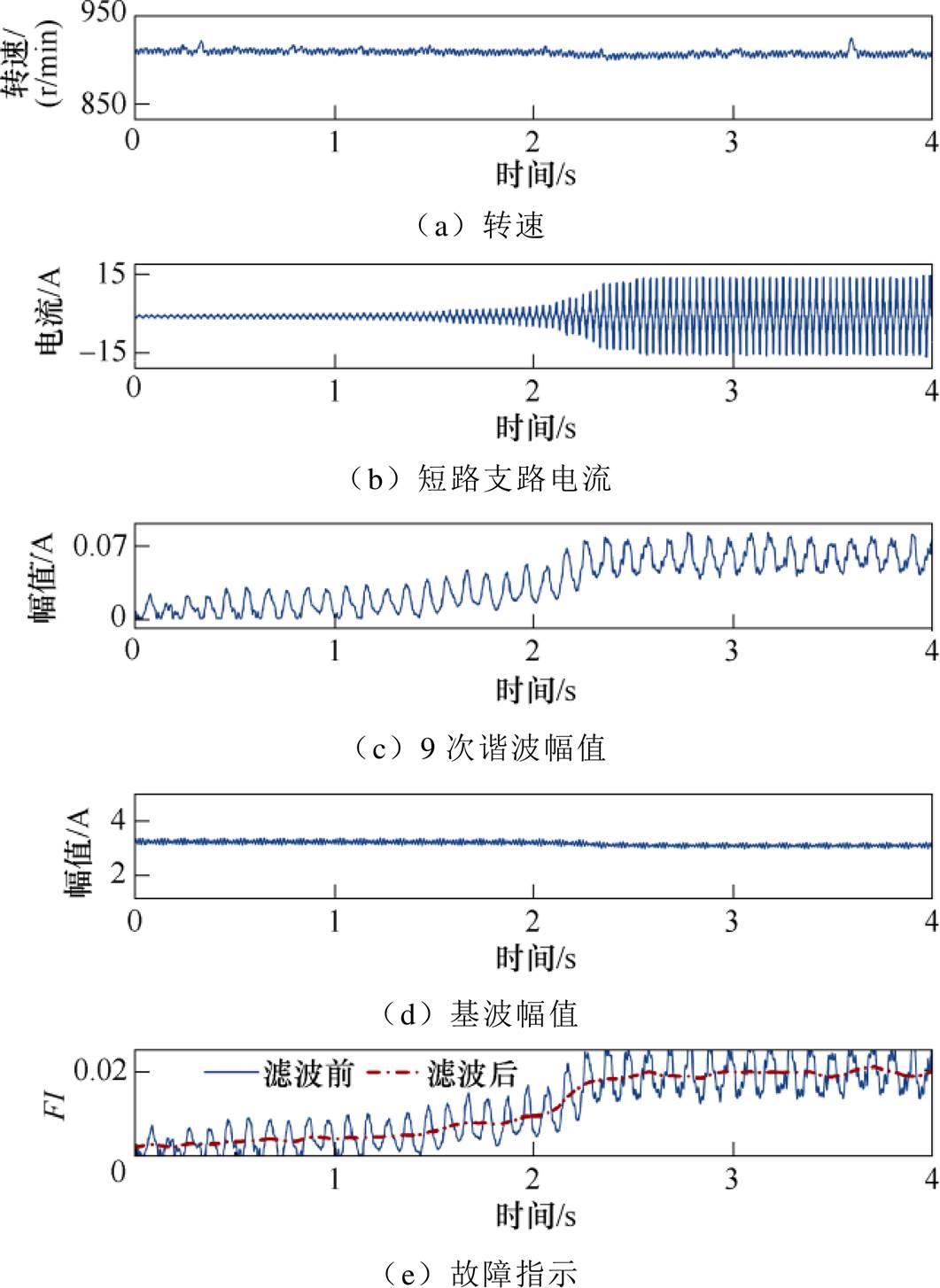
图15 恒转速-变故障程度下的故障指示
Fig.15 Fault indicator under constant speed and varying fault condition
(3)变转速-变故障程度。该实验用于验证所提出方法能够解耦转速产生的影响。减速-变故障程度下的故障指示如图16所示。图16a中,电机转速由1 700r/min下降至1 400r/min。同时,匝间绝缘由故障初期30W 降低至晚期0W 彻底断路,并在第3s之后维持0W。连续变转速-变故障程度下的故障指示如图17所示。图17a中,电机转速在1 700r/min至1 400r/min范围内连续波动。同时,匝间绝缘也由30W 降低至0W,并于第4s后维持在0W。该实验中,各谐波幅值会根据转速变化而变化,导致故障特征谐波同时受到转速和ITSC故障的影响。根据图16b和图17b可以看出,该故障指示能够反映故障变化趋势而基本不受转速影响。
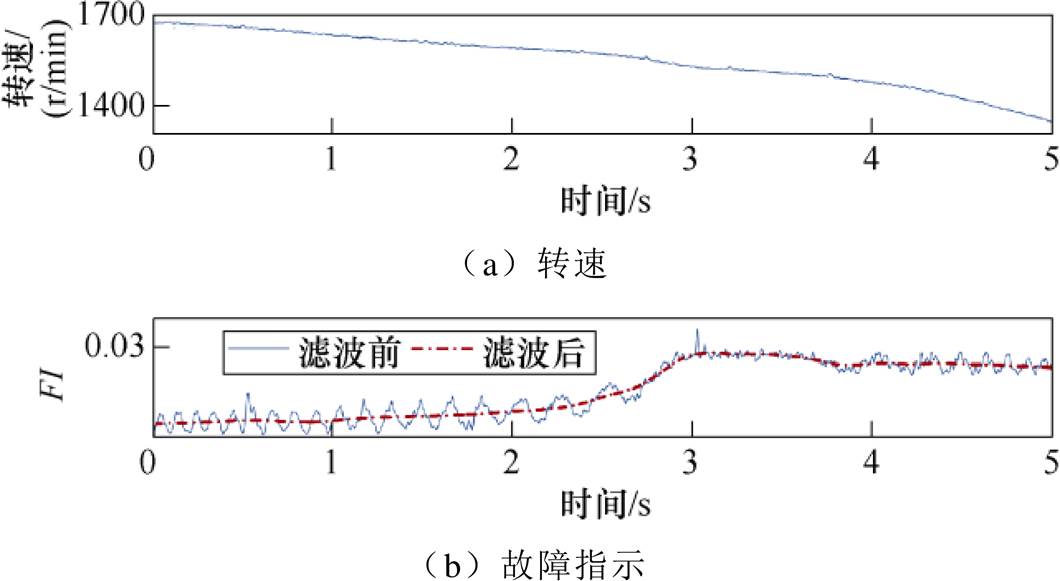
图16 减速-变故障程度下的故障指示
Fig.16 Fault indicator under speed reduction and varying fault condition
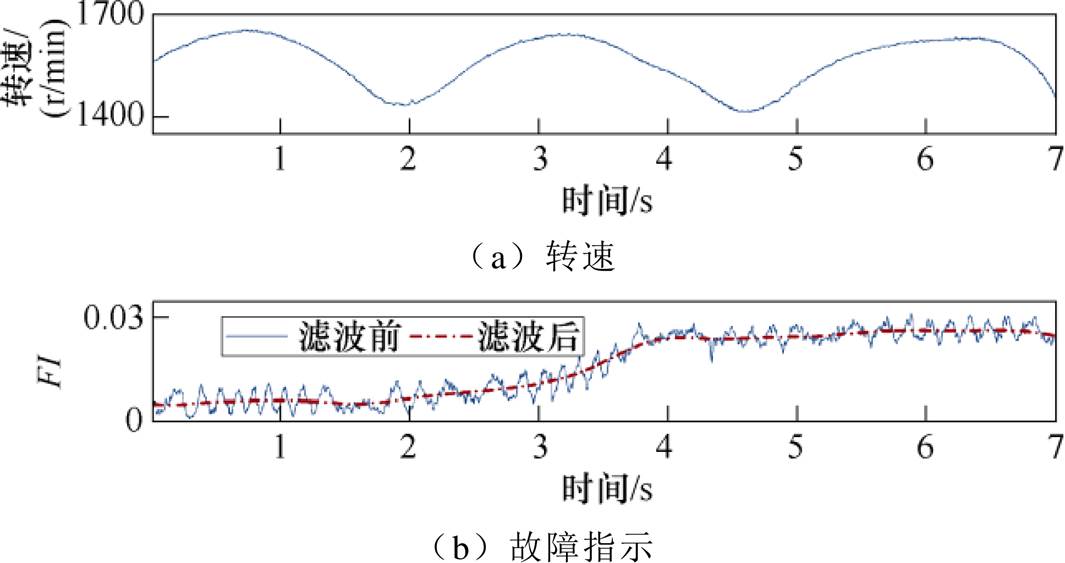
图17 连续变转速-变故障程度下的故障指示
Fig.17 Fault indicator under varying speed and varying fault condition
为验证所提出方法对于ITSC从故障初期到晚期彻底断路变化过程的指示能力,本文对比了基于线性时频的离散小波变换(Discrete Wavelet Trans- form, DWT)算法[28-29]和基于自适应模式分解的变分模式分解(Variational Mode Decomposition, VMD)算法[30-31]。针对图15恒转速-变故障程度运行工况使用上述方法对相同的运行数据进行处理。
(1)离散小波变换。对于图15所示工况,电机运行转速为900r/min,电流基频为30Hz,9次谐波为270Hz,根据表2的离散小波分解频带,基波和9次谐波分别在高频细节信号D9和D6中。信号总能量可以通过累加各细节信号(D1~D6)和逼近信号(A6)的能量计算得到。
表2 离散小波分解频带
Tab.2 DWT frequency bandwiths
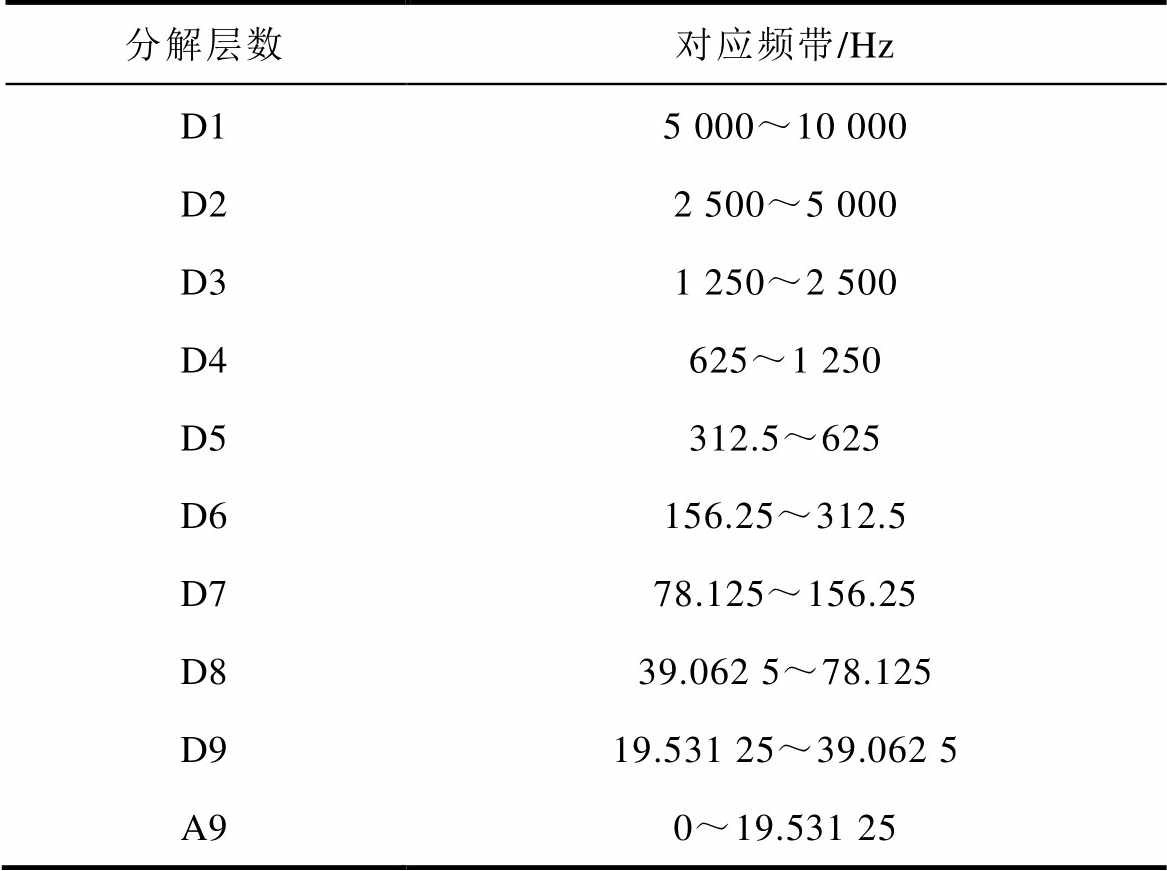
分解层数对应频带/Hz D15 000~10 000 D22 500~5 000 D31 250~2 500 D4625~1 250 D5312.5~625 D6156.25~312.5 D778.125~156.25 D839.062 5~78.125 D919.531 25~39.062 5 A90~19.531 25
第n层能量为
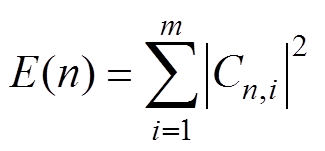 (17)
(17)
式中,m为小波系数个数;n为分解层数;Cn,i为第n层的第i个小波系数。总能量为
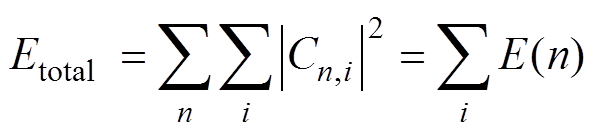 (18)
(18)
因此,基于DWT的故障指示可以定义为
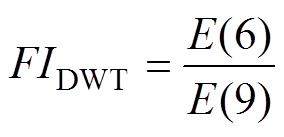 (19)
(19)
恒转速-变故障程度下的方法对比如图18所示。为指示故障的时变特性,将实验数据通过滑动窗口的方式分割为3 000个长度0.1s的数据,结果如图18a所示。
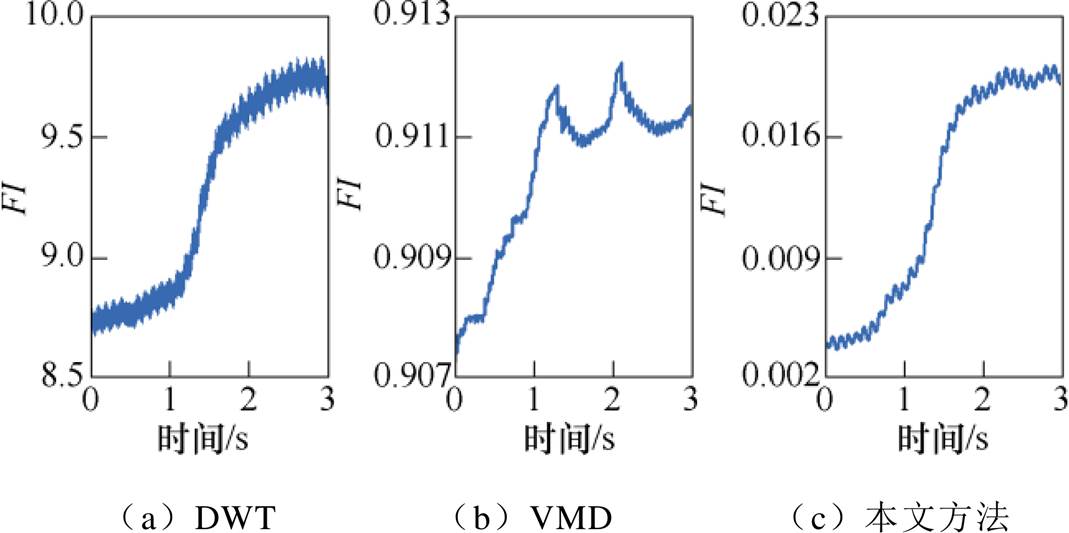
图18 恒转速-变故障程度下的方法对比
Fig.18 Comparation of the fault indicators under constant speed and varying fault condition
(2)变分模态分解。VMD是一种非递归分解方法,能够自适应同步提取复杂多分量信号中的调幅-调频分量。本文中模态分解个数K设置为4,误差精度为10-5,平衡参数为1 000,并将实验数据通过滑动窗口的方式分割为3 000个长度0.2s的数据。此外,为降低VMD的计算量,对实验信号进行重采样至2kHz,有效频带范围为[0, 1 000]Hz,能够覆盖故障特征所在的九倍频。基于VMD的故障检测方法同样使用式(17)~式(19)的标准,通过本征模态分量IMF4和IMF1建立故障指示,结果如图18b所示。
根据图18的对比结果可以看出,在剩余匝间绝缘电阻由故障初期30W 降低至晚期0W 的过程中,三种方法都可以有效地检测出故障情况。在图18a中,从初期轻微故障到最后彻底短路,FI由8.7上升至9.7,增加了11.5%。对于相同的数据,图18b中基于VMD的故障指示由0.894 6上升至0.911 4,增加了1.9%。而图18c中基于本文所提出的故障指示由0.004上升至0.02,对于剩余绝缘电阻退化趋势的检测灵敏度更高。
上述方法的处理结果是包含了故障特征所在的频带,该频带内不仅包含了所需频率成分,还有其他与故障无关的成分,因此会大大降低信噪比,进而降低了对于故障的灵敏程度。同时,受限于频带宽度及变转速情况下故障特征所在频带位置不固定,基于DWT的方法无法有效处理变转速工况下的运行数据。而对于变分模态分解也存在相同问题,除此之外,由于测试信号的频率成分随时间改变,对于固定的平衡参数和分解层数,故障特征所在本征模态分量中的成分也会相应发生改变,导致FI出现异常波动。而本文使用多重同步压缩变换将各频率分量压缩到较窄的频带内,从而能提取出对应频率的幅值。该方法直接提取了故障指示所需要的谐波分量,其他频率分量对结果的影响极小。
本文提出了基于定子电流9次谐波的PMSM定子绕组匝间剩余绝缘电阻退化趋势的检测方法,验证了故障特征谐波的选择并不仅仅局限于零序分量中的3次谐波,而是需要综合考虑特定电机本体的故障谐波特性。通过实验和建模证明,本文中所使用PMSM的9次谐波相比3次谐波对微弱故障特征更敏感。在此基础上,针对剩余绝缘电阻接近于0这一目前较多研究所使用的故障评价方式,提出了基于匝间剩余绝缘电阻的初期故障检测方法,并通过多重同步压缩变换算法对剩余绝缘电阻退化程度进行精确提取。该方法能够在电机稳态和瞬态运行工况下检测出故障发生的初期、晚期和故障程度的变化过程,相比基于3次谐波的方法具有更高的信噪比。
与以往的研究相比,所提出方法大幅降低了频谱混叠现象,可以更加精确地提取出故障特征相关谐波分量并构建故障指示。其中,稳态实验结果表明,该方法能够有效检测到故障的发生,而瞬态实验证明该方法可以较好地追踪剩余绝缘电阻由故障初期到晚期彻底断路的退化过程而不受运行转速的影响。
除此之外,对比了基于离散小波变换和变分模态分解的故障检测方法,进一步证明了本文所提出方法的有效性和优越性。虽然本方法可通过比较三相的故障指示幅值大小来判定故障所在相,但是如何确定短路匝的空间位置(如故障所在槽、线圈等),依然是当前工作难点和未来努力方向。
参考文献
[1] 黄科元, 周佳新, 刘思美, 等. 考虑逆变器非线性永磁同步电机高频注入电感辨识方法[J]. 电工技术学报, 2021, 36(8): 1607-1616.
Huang Keyuan, Zhou Jiaxin, Liu Simei, et al. Indu- ctance identification method of permanent magnet synchronous motor considering inverter nonlinearity based on high-frequency injection[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1607- 1616.
[2] 于安博, 刘利, 阚志忠, 等. 高频脉振信号注入永磁同步电机无滤波器初始位置辨识方法[J]. 电工技术学报, 2021, 36(4): 801-809.
Yu Anbo, Liu Li, Kan Zhizhong, et al. Initial position identification of PMSM with filterless high frequency pulse signal injection method[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 801- 809.
[3] 张业成, 刘国海, 陈前. 基于电流波动特征的永磁同步电机匝间短路与局部退磁故障分类诊断研究[J]. 电工技术学报, 2022, 37(7): 1634-1643, 1653.
Zhang Yecheng, Liu Guohai, Chen Qian. Dis- crimination of interturn short-circuit and local demagnetization in permanent magnet synchronous motor based on current fluctuation characteristics[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1634-1643, 1653.
[4] 谢颖, 胡圣明, 陈鹏, 等. 永磁同步电机匝间短路故障温度场分析[J]. 电工技术学报, 2022, 37(2): 322-331.
Xie Ying, Hu Shengming, Chen Peng, et al. Thermal field analysis on inter-turn short circuit fault of permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(2): 322-331.
[5] Romeral L, Urresty J C, Riba Ruiz J R, et al. Modeling of surface-mounted permanent magnet synchronous motors with stator winding interturn faults[J]. IEEE Transactions on Industrial Electronics, 2011, 58(5): 1576-1585.
[6] Qi Yuan, Zafarani M, Gurusamy V, et al. Advanced severity monitoring of interturn short circuit faults in PMSMs[J]. IEEE Transactions on Transportation Electrification, 2019, 5(2): 395-404.
[7] Mahmoud H, Abou-Elyazied Abdallh A, Bianchi N, et al. An inverse approach for interturn fault detection in asynchronous machines using magnetic pendulous oscillation technique[J]. IEEE Transactions on Indu- stry Applications, 2016, 52(1): 226-233.
[8] van der Geest M, Polinder H, Ferreira J A, et al. Analysis and neutral voltage-based detection of interturn faults in high-speed permanent-magnet machines with parallel strands[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3862-3873.
[9] 孙宇光, 余锡文, 魏锟, 等. 发电机绕组匝间故障检测的新型探测线圈[J]. 中国电机工程学报, 2014, 34(6): 917-924.
Sun Yuguang, Yu Xiwen, Wei Kun, et al. A new type of search coil for detecting inter-turn faults in synchronous machines[J]. Proceedings of the CSEE, 2014, 34(6): 917-924.
[10] Jeong H, Moon S, Kim S W. An early stage interturn fault diagnosis of PMSMs by using negative-sequence components[J]. IEEE Transactions on Industrial Elec- tronics, 2017, 64(7): 5701-5708.
[11] Urresty J C, Riba J R, Romeral L. Diagnosis of interturn faults in PMSMs operating under nonsta- tionary conditions by applying order tracking filtering[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 507-515.
[12] 丁石川, 王清明, 杭俊, 等. 计及模型预测控制的永磁同步电机匝间短路故障诊断[J]. 中国电机工程学报, 2019, 39(12): 3697-3707.
Ding Shichuan, Wang Qingming, Hang Jun, et al. Inter-turn fault diagnosis of permanent magnet synchronous machine considering model predictive control[J]. Proceedings of the CSEE, 2019, 39(12): 3697-3707.
[13] Hang Jun, Zhang Jianzhong, Cheng Ming, et al. Online interturn fault diagnosis of permanent magnet synchronous machine using zero-sequence com- ponents[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 6731-6741.
[14] 李俊卿, 陈雅婷, 李斯璇. 基于深度置信网络的同步发电机励磁绕组匝间短路故障预警[J]. 电力自动化设备, 2021, 41(2): 153-158.
Li Junqing, Chen Yating, Li Sixuan. Early warning of inter-turn short circuit fault in excitation windings of synchronous generator based on deep belief net- work[J]. Electric Power Automation Equipment, 2021, 41(2): 153-158.
[15] 丁石川, 厉雪衣, 杭俊, 等. 深度学习理论及其在电机故障诊断中的研究现状与展望[J]. 电力系统保护与控制, 2020, 48(8): 172-187.
Ding Shichuan, Li Xueyi, Hang Jun, et al. Deep learning theory and its application to fault diagnosis of an electric machine[J]. Power System Protection and Control, 2020, 48(8): 172-187.
[16] 李垣江, 张周磊, 李梦含, 等. 采用深度学习的永磁同步电机匝间短路故障诊断方法[J]. 电机与控制学报, 2020, 24(9): 173-180.
Li Yuanjiang, Zhang Zhoulei, Li Menghan, et al. Fault diagnosis of inter-turn short circuit of per- manent magnet synchronous motor based on deep learning[J]. Electric Machines and Control, 2020, 24(9): 173-180.
[17] 曾发林, 孙苏民. 基于RNR-WVD与GA-小波的非稳态排气噪声声品质研究[J]. 振动与冲击, 2019, 38(12): 74-80, 104.
Zeng Falin, Sun Sumin. Study on the sound quality of unsteady exhaust noise based on RNR-WVD calcu- lation and GA-wavelet network[J]. Journal of Vibration and Shock, 2019, 38(12): 74-80, 104.
[18] 夏长亮, 金雪峰, 方红伟, 等. 基于R/S分析和小波变换的同步发电机定子绕组匝间短路故障分析[J]. 电工技术学报, 2006, 21(6): 101-105.
Xia Changliang, Jin Xuefeng, Fang Hongwei, et al. Fault analysis of internal stator windings in synchronous generators based on R/S and wavelet transform[J]. Transactions of China Electrotechnical Society, 2006, 21(6): 101-105.
[19] Daubechies I, Lu Jianfeng, Wu Hau-Tieng. Syn- chrosqueezed wavelet transforms: an empirical mode decomposition-like tool[J]. Applied and Computa- tional Harmonic Analysis, 2011, 30(2): 243-261.
[20] 吴龙文, 牛金鹏, 王昭, 等. 基于同步压缩小波变换的主信号抑制技术[J]. 电子与信息学报, 2020, 42(8): 2045-2052.
Wu Longwen, Niu Jinpeng, Wang Zhao, et al. Primary signal suppression based on synchrosqueezed wavelet transform[J]. Journal of Electronics & Information Technology, 2020, 42(8): 2045-2052.
[21] 张郑武, 冯志鹏, 陈小旺. 基于高阶同步压缩变换的行星齿轮箱声音信号共振频带特征提取[J]. 工程科学学报, 2020, 42(8): 1048-1054.
Zhang Zhengwu, Feng Zhipeng, Chen Xiaowang. Acoustic signal analysis of the resonance frequency region for planetary gearbox fault diagnosis based on high-order synchrosqueezing transform[J]. Chinese Journal of Engineering, 2020, 42(8): 1048-1054.
[22] Oberlin T, Meignen S, Perrier V. Second-order syn- chrosqueezing transform or invertible reassignment? towards ideal time-frequency representations[J]. IEEE Transactions on Signal Processing, 2015, 63(5): 1335- 1344.
[23] Pham D H, Meignen S. High-order synchrosqueezing transform for multicomponent signals analysis-with an application to gravitational-wave signal[J]. IEEE Transactions on Signal Processing, 2017, 65(12): 3168-3178.
[24] Yu Gang, Wang Zhonghua, Zhao Ping. Multi- synchrosqueezing transform[J]. IEEE Transactions on Industrial Electronics, 2019, 66(7): 5441-5455.
[25] Kumar N P, Isha T B. FEM based electromagnetic signature analysis of winding inter-turn short-circuit fault in inverter fed induction motor[J]. CES Transa- ctions on Electrical Machines and Systems, 2019, 3(3): 309-315.
[26] Rosero J A, Cusido J, Garcia A, et al. Broken bearings and eccentricity fault detection for a permanent magnet synchronous motor[C]//IECON 2006-32nd Annual Conference on IEEE Industrial Electronics. Paris, France, 2006: 964-969.
[27] Ding Shichuan, Hang Jun, Li Hao, et al. Demagneti- sation fault detection in PMSM using zero sequence current components[J]. Electronics Letters, 2017, 53(3): 148-150.
[28] Fang Jie, Sun Yining, Wang Yibing, et al. Improved ZSVC-based fault detection technique for incipient stage inter-turn fault in PMSM[J]. IET Electric Power Applications, 2019, 13(12): 2015-2026.
[29] Hang Jun, Zhang Jibo, Xia Mengjie, et al. Interturn fault diagnosis for model-predictive-controlled-PMSM based on cost function and wavelet transform[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 6405-6418.
[30] 张民谣, 高云鹏, 吴聪, 等. 基于自适应变分模式分解的非稳态电压闪变包络参数检测[J]. 电工技术学报, 2021, 36(3): 599-608.
Zhang Minyao, Gao Yunpeng, Wu Cong, et al. Non- stationary voltage flicker envelope parameters detection based on adaptive variational mode decom- position[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 599-608.
[31] 何玉灵, 孙凯, 王涛, 等. 基于变分模态分解与精细复合多尺度散布熵的发电机匝间短路故障诊断[J]. 电力自动化设备, 2021, 41(3): 164-172.
He Yuling, Sun Kai, Wang Tao, et al. Fault diagnosis of generator interturn short circuit fault based on variational mode decomposition and refined com- posite multiscale dispersion entropy[J]. Electric Power Automation Equipment, 2021, 41(3): 164-172.
A Multi-Synchrosqueezing Transformation Based Early Stage Detection of Inter-Turn Short Circuit Fault in Permanent Magnet Synchronous Machine
Abstract The degradation of insulation capacity between adjacent coils of permanent magnet synchronous machine (PMSM) stator winding will lead to inter-turn short circuit (ITSC) fault. The current mainstream research mainly focuses on the estimation of the number of short-circuit turns, and it is difficult to detect the failure process of insulation resistance at the early stage. In this paper, the influence of residual insulation resistance on stator current is analyzed based on the finite element co-simulation model of PMSM with ITSC fault, and a fault detection method based on 9th harmonic of the current is proposed. This method is able to extract fault features effectively in time-frequency domain, and decouple the influence of speed fluctuation on fault detection results. Hence, it can effectively track the degradation trend of residual insulation resistance from the initial stage to the late stage of the fault under steady and transient operating conditions. The proposed method is verified on a 24-slot-4-pole three-phase PMSM with the distributed winding, and the results show that the proposed method has a good accuracy in monitoring the degradation of residual insulation resistance and is robust against the abrupt disturbance in rotor speed.
keywords:Three-phase permanent magnet synchronous machine, inter-turn short circuit, fault detection, time-frequency analysis
DOI: 10.19595/j.cnki.1000-6753.tces.210464
中图分类号:TM341
国家自然科学基金项目(51877075)和湖湘高层次人才聚集工程-创新人才项目(S2019RSCXRC0094)资助。
收稿日期 2021-04-06
改稿日期 2021-08-12
魏 东 男,1993年生,博士研究生,研究方向为永磁同步电机故障诊断。E-mail: dongwei@hnu.edu.cn
刘 侃 男,1982年生,教授,博士生导师,研究方向为轨道交通/新能源车电驱技术、精密伺服控制等。E-mail: lkan@hnu.edu.cn(通信作者)
(编辑 崔文静)