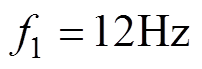 ,在线测得原电机三相电流及对其提取出的直流分量、基波和各倍频谐波电流时域图如图1所示,可以看出,三相电流中除了含有奇数倍频谐波电流,还存在偶数倍频谐波电流和直流分量,这些倍频谐波电流有对称的或不对称的。
,在线测得原电机三相电流及对其提取出的直流分量、基波和各倍频谐波电流时域图如图1所示,可以看出,三相电流中除了含有奇数倍频谐波电流,还存在偶数倍频谐波电流和直流分量,这些倍频谐波电流有对称的或不对称的。摘要 变频驱动三相永磁电机绕组中含有各频次对称电流和非对称电流,甚至还有直流分量,在电机极槽磁导调制作用下,这些电流磁场与永磁磁场相互作用都会引起电机的径向振动。该文对样机的三相电流进行分析,分别推导出基波、直流分量、对称倍频电流和非对称倍频电流的径向磁动势,根据麦克斯韦磁力公式推导出各成分电流引起的径向振动模型,通过样机验证模型的正确性。最后推导出一种多倍频电流注入法的径向振动抑制模型,并设计出一种基于多目标RMSProp优化算法的永磁电机径向振动综合抑振控制策略,通过样机实验验证了该方法的正确性和有效性。
关键词:三相永磁同步电机 谐波注入 径向振动 多目标RMSProp优化
永磁同步电机在水下航行器驱动中应用越来越广泛,电机通过机座向航行器壳体传递结构振 动[1-2],影响水下航行器隐蔽性,其中,低频振动不容易被减振器吸收,能通过航行器壳体传递到水中,是影响水下航行器隐蔽性的主要原因。永磁电机在卧式安装时,气隙磁场作用在定子上的径向电磁力波形成的振动是对外传播的主要成分。有些径向振动经过对电机的材料和结构优化后依然存在,这就需要用控制方法来抑制,径向电磁振动频率通常是电频率的倍数,其中三相永磁电机在基波电流下引起的极槽径向振动是偶次振动[3],但是绕组中除了基波电流,还有很多其他倍频电流,如果电机系统是对称系统,则三相绕组电流中只含有奇次倍频电流,但是实际电机系统在结构和控制电路方面存在很多不对称因素,反馈通道中的不对称因素较多,所以三相绕组中除了含有奇数倍频电流外,还有偶数倍频电流,甚至还有直流分量,其中的各倍频电流可能是对称电流,也可能是不对称电流,在极槽磁导调制作用下,这些电流形成的磁场与永磁磁场作用都会引起电机的径向振动,都需要对其进行研究和抑制。
目前,抑制谐波振动的方法有滤波器[4-5]、脉宽调制[6-7]、混合空间调制策略[8]、谐振控制器[9-10]、谐波电流注入法[11-14]等,这些方法都是抑制转矩脉动的,是通过抑制励磁电流中的谐波分量来抑制转矩脉动,没有建立谐波电流与振动之间的关系;在径向振动抑制中,文献[15-16]也是通过抑制谐波电流来抑制径向振动的,没有建立谐波电流与振动之间的关系。目前,关于绕组中的直流分量、对称倍频电流和不对称倍频电流引起的电机径向振动机理分析的文章未见发表。本文推导出绕组中直流分量、基波、对称倍频电流和不对称倍频电流的径向振动模型,用样机验证模型的正确性,推导出一种基于多倍频谐波电流注入法的径向振动抑制模型,并设计一种基于多目标RMSProp优化算法的综合抑振控制策略,实现对电机的200Hz以下各低频倍频径向振动的综合抑制控制,通过样机实验验证本文方法的正确性和有效性。
三相三线制的对称(电源对称、负载对称)系统中,三相电流中不含偶次谐波及3的整数倍频谐波,但是对于实际电机系统,在机械和控制方面都存在很多不对称因素,所以实际电机三相电流中另外会出现偶次谐波分量,甚至是直流分量,原因如下:
(1)电源质量不高,电流中会产生谐波[17-18]。
(2)闭环电机控制系统中的三相电流采样模块,在采样过程中加入的偏置电流很难准确的在被测电流零点处,这样就会在相电流中出现直流量[19]。
(3)三相逆变器通道不对称,会产生各倍频不对称谐波电流[20]。
(4)空间矢量调制过程中产生电流谐波[21]。
以750W三相永磁同步电机样机为例,采用空间矢量控制法,基波频率为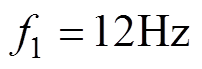 ,在线测得原电机三相电流及对其提取出的直流分量、基波和各倍频谐波电流时域图如图1所示,可以看出,三相电流中除了含有奇数倍频谐波电流,还存在偶数倍频谐波电流和直流分量,这些倍频谐波电流有对称的或不对称的。
,在线测得原电机三相电流及对其提取出的直流分量、基波和各倍频谐波电流时域图如图1所示,可以看出,三相电流中除了含有奇数倍频谐波电流,还存在偶数倍频谐波电流和直流分量,这些倍频谐波电流有对称的或不对称的。
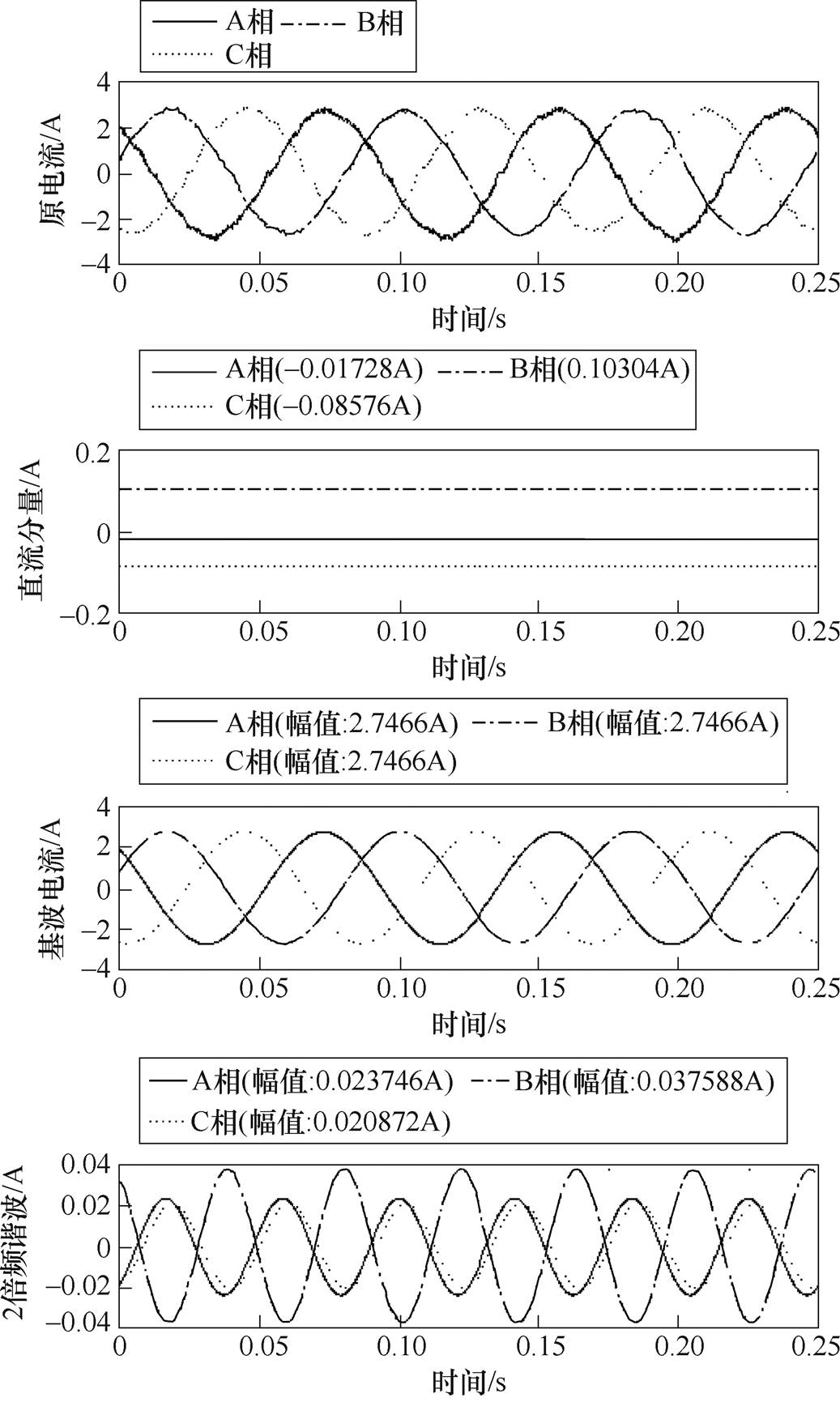

图1 原电机电流和各电流成分的时域图
Fig.1 Time-domain diagram of original current and current components
虽然定子为星形联结,三相电流值相加为零,但是三相电流空间合成矢量不一定为零,其沿各空间机械角方向上的径向矢量也不一定为零,其产生的径向磁动势与永磁磁动势作用会产生电机的径向振动。所以需要分析直流、基波及各对称与不对称倍频谐波电流引起的径向振动。
图1中的电流波形可以分为四类,有直流、基波、相位相差120°等幅的三相谐波(7倍频谐波)、相位不相差120°不等幅的三相谐波(2、3、4、5、6倍频谐波)。其中,直流产生的原因主要是闭环电机控制系统中的三相电流采样模块,在采样过程中加入的偏置电流很难准确的在被测电流零点处;第四类电流产生的原因主要是电源质量不高和三相逆变器通道不完全对称;还有一些谐波是在空间矢量调制过程中产生的。
本文假设三相绕组空间对称,因为定子是星形联结,三相电流值相加为零,对于直流量来说,即使三相直流相加为零,各相也可能存在直流,则A、B、C三相直流产生的合成磁动势是一个不随时间变化的空间向量。
假设气隙均匀,如果三相k倍频(包括基波k=1)电流是对称的,则A、B、C三相绕组产生的合成磁动势是圆形旋转磁动势。
如果三相k倍频(包括基波k=1)电流是不对称的,设三相k倍频电流为
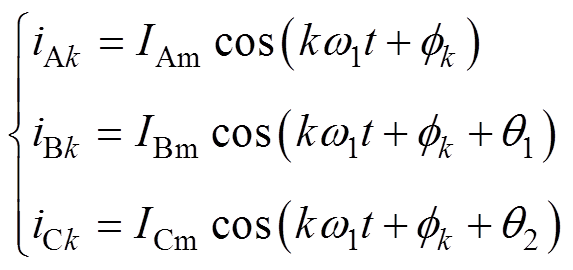 (1)
(1)
式中, 和
和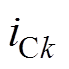 为三相k倍频电流;
为三相k倍频电流;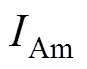 、
、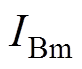 和
和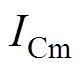 为三相k倍频电流幅值;
为三相k倍频电流幅值;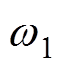 为基波角频率;
为基波角频率;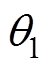 和
和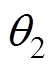 分别为B和C相与A相的k倍频电流的相位差;
分别为B和C相与A相的k倍频电流的相位差;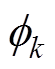 为三相k倍频电流的初始相位。
为三相k倍频电流的初始相位。
对于式(1)的k倍频电流,有
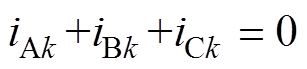 (2)
(2)
解得
 (3)
(3)
从式(3)可以看出,定子星形联结时,三相相位不对称的k倍频电流,其幅值也一定不相等,三相相位对称的k倍频电流,其幅值一定相等。
式(1)的k倍频电流产生的三相绕组磁动势沿空间角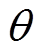 的径向磁动势[22-23]为
的径向磁动势[22-23]为
 (4)
(4)
式中,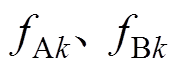 和
和 分别为A相、B相和C相的k倍频电流引起的径向磁动势;
分别为A相、B相和C相的k倍频电流引起的径向磁动势;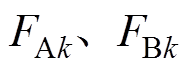 和
和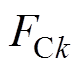 分别为A相、B相和C相的k倍频电流引起的径向磁动势幅值;
分别为A相、B相和C相的k倍频电流引起的径向磁动势幅值;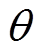 为空间机械角。
为空间机械角。
整理得到
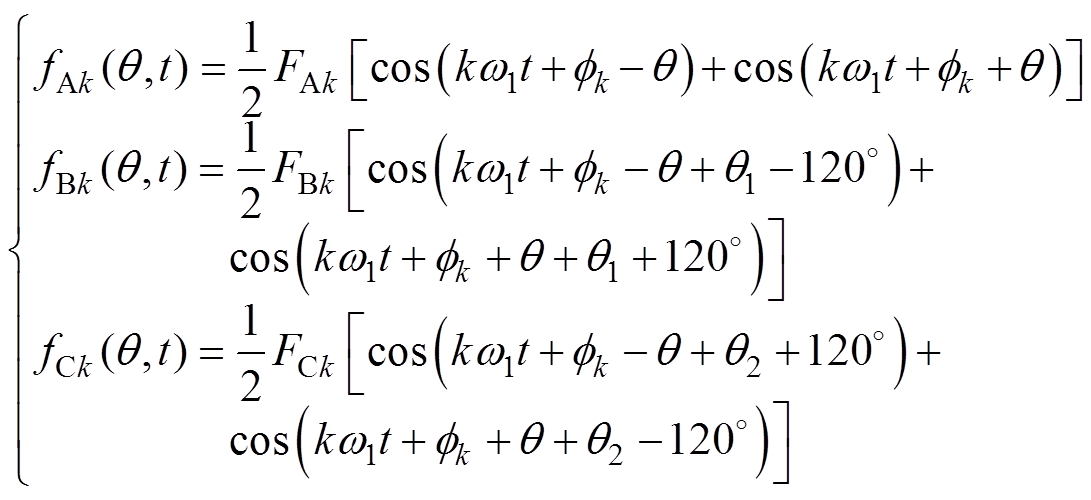 (5)
(5)
则合成径向磁动势为
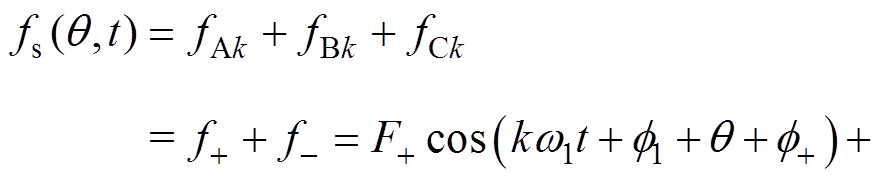
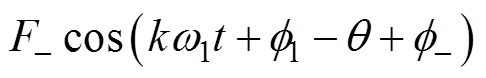 (6)
(6)
其中
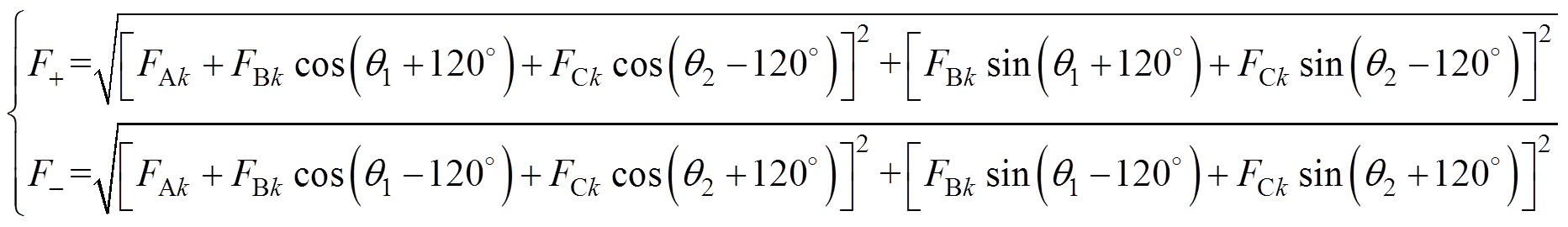
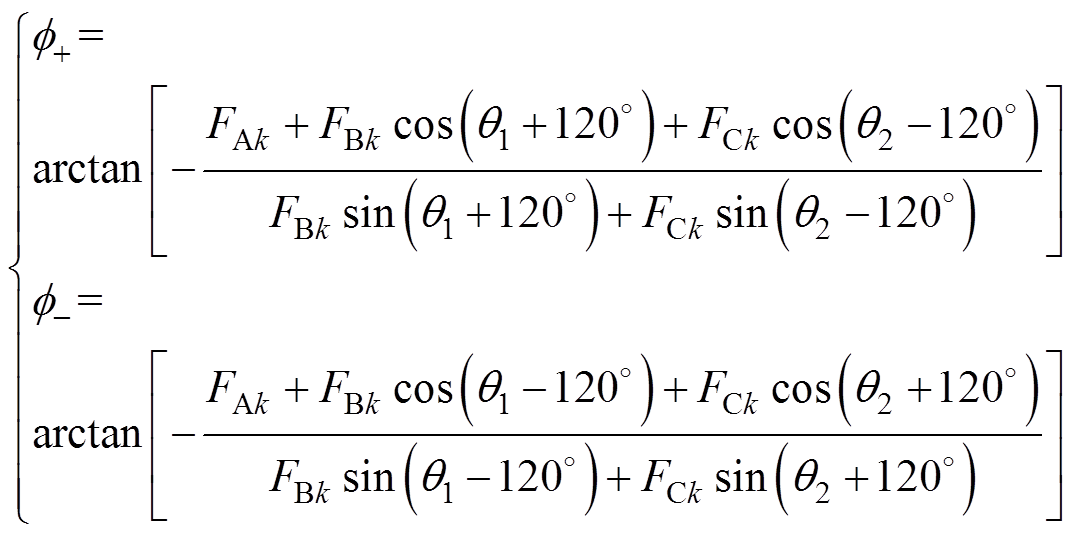
式中,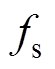 为k倍频电流引起的三相合成径向磁动势;
为k倍频电流引起的三相合成径向磁动势;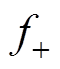 和
和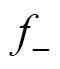 分别为正、反方向磁动势;
分别为正、反方向磁动势;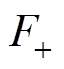 和
和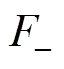 分别为正、反方向磁动势幅值;
分别为正、反方向磁动势幅值;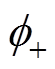 和
和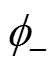 分别为正、反方向磁动势与A相磁动势的相位差,
分别为正、反方向磁动势与A相磁动势的相位差,
从式(6)可以看出,k倍频不对称三相电流产生的合成径向磁动势可以分解成k倍频幅值不同、正负方向旋转的两个圆形磁动势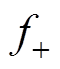 和
和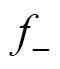 ,其合成的轨迹为椭圆形。
,其合成的轨迹为椭圆形。
根据现代电机控制技术[24],设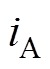 、
、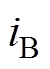 和
和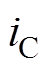 三相电流方向为相电流正方向,当相电流为正时,产生的磁动势矢量与绕组轴线一致;否则相反,则三相合成磁动势
三相电流方向为相电流正方向,当相电流为正时,产生的磁动势矢量与绕组轴线一致;否则相反,则三相合成磁动势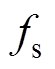 可以用三相合成电流
可以用三相合成电流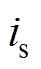 表示,即
表示,即
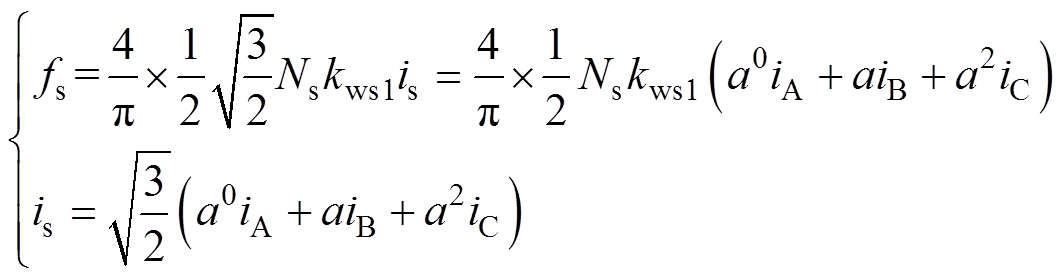 (7)
(7)
式中,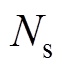 为A、B、C相绕组匝数;
为A、B、C相绕组匝数;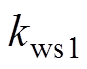 为基波磁动势的绕组因数;
为基波磁动势的绕组因数;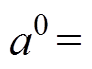
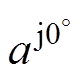 ,
,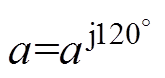 ,
,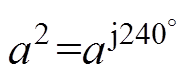 ,为空间算子。
,为空间算子。
根据式(7)对实时测得的电机样机的三相电流进行计算得到直流、基波及各倍频谐波电流合成矢量空间运行轨迹如图2所示,如果气隙均匀,合成电流轨迹形状与合成径向磁动势轨迹形状一致。
通过图2分析可以得出,对称k倍频电流产生的合成径向磁动势(参考基波电流和7倍频谐波电流)是圆形旋转磁动势,不对称k倍频电流产生的合成径向磁动势(参考2、3、4、5和6倍频谐波电流)是椭圆形旋转磁动势。


图2 三相直流、基波及各倍频谐波电流合成矢量空间运行轨迹
Fig.2 The space trajectories of the resultant vectors of three-phase DC, fundamental and each harmonic current
对于整数槽绕组的永磁电机,受到极槽的影响,基波电流产生的径向磁动势波实际上是矩形波,除了基波磁动势外,还存在着基波的奇数倍频的谐波磁动势。同理,绕组中谐波电流产生的径向磁动势也是矩形波,也存在着其奇数倍频的谐波磁动势,则k倍频电流产生的三相绕组径向磁动势傅里叶分解为
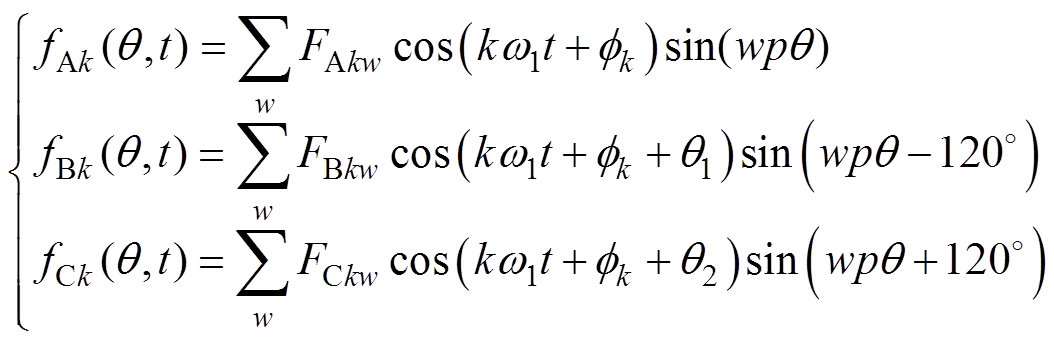 (8)
(8)
式中,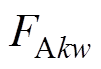 、
、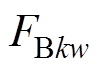 和
和 分别为A相、B相和C相的k倍频电流引起的空间w次谐波径向磁动势幅值;w为空间谐波次数;p为极对数。
分别为A相、B相和C相的k倍频电流引起的空间w次谐波径向磁动势幅值;w为空间谐波次数;p为极对数。
如果是三相对称的k倍频电流,可以推导出合成径向磁动势为
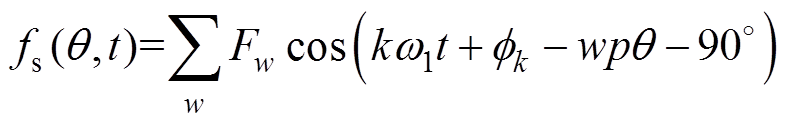 (9)
(9)
式中,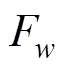 为合成的k倍频电流引起的空间w次谐波径向磁动势幅值。
为合成的k倍频电流引起的空间w次谐波径向磁动势幅值。
如果是三相不对称的k倍频电流,可以推导出合成径向磁动势为
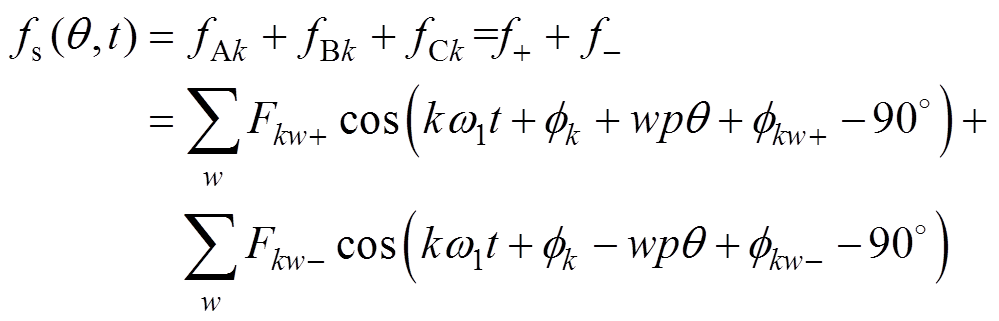 (10)
(10)
式中,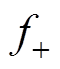 和
和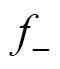 分别为正、反方向磁动势;
分别为正、反方向磁动势;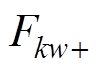 和
和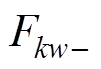 分别为k倍频电流引起的正、反方向的空间w次谐波合成径向磁动势幅值;
分别为k倍频电流引起的正、反方向的空间w次谐波合成径向磁动势幅值;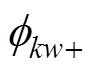 和
和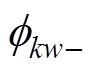 分别为正、反方向磁动势与A相磁动势的相位差。
分别为正、反方向磁动势与A相磁动势的相位差。
如果是三相直流,可以推导出合成径向磁动势为
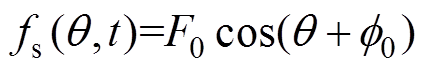 (11)
(11)
其中
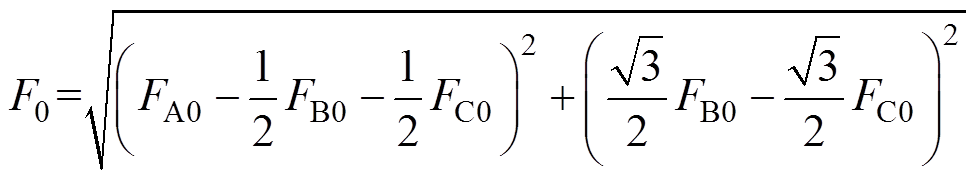
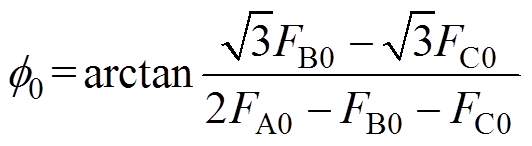
式中,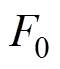 为磁动势幅值;FA0、FB0、FC0、分别为A、B、C三相绕组径向磁动势幅值;
为磁动势幅值;FA0、FB0、FC0、分别为A、B、C三相绕组径向磁动势幅值;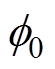 为合成磁动势方向与A相方向的夹角。
为合成磁动势方向与A相方向的夹角。
下面对绕组中的直流、基波、对称谐波电流和不对称谐波电流引起的径向振动进行分析。
永磁同步电机的气隙磁场由永磁磁场和电枢反应磁场两部分组成。忽略磁路饱和,根据麦克斯韦应力张量法得到永磁电机径向力公式[3]为
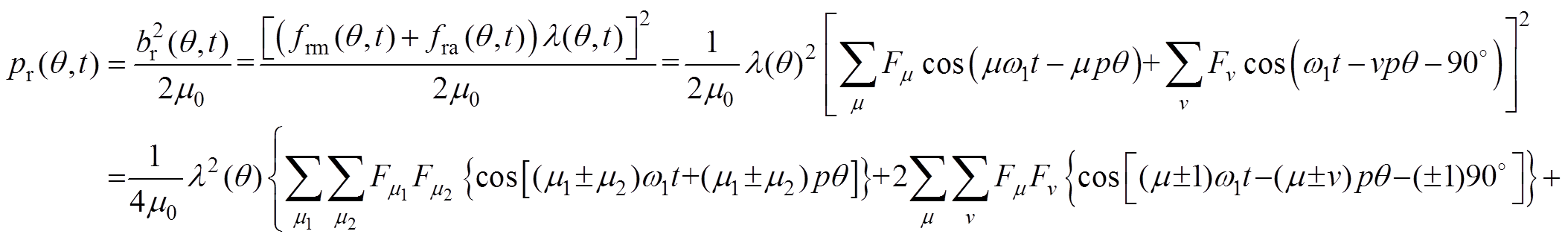
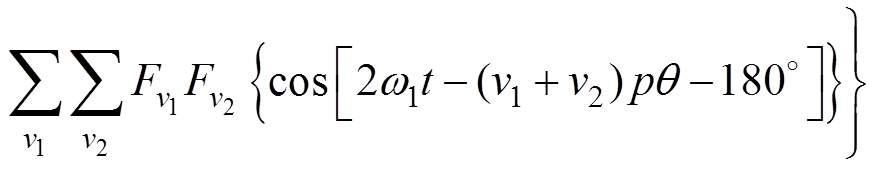 (12)
(12)
式中,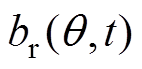 为径向气隙磁通密度;
为径向气隙磁通密度;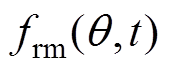 和
和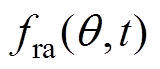 分别为永磁磁动势和电枢磁动势的径向分量;
分别为永磁磁动势和电枢磁动势的径向分量;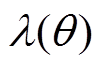 为只考虑定子开槽,转子表面平滑时的气隙磁导,所以磁导只随空间角度变化,不随时间变化;m、m1、m2为磁动势谐波的次数,m、m1、m2=2r+1(r=1, 2, 3,…);
为只考虑定子开槽,转子表面平滑时的气隙磁导,所以磁导只随空间角度变化,不随时间变化;m、m1、m2为磁动势谐波的次数,m、m1、m2=2r+1(r=1, 2, 3,…);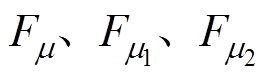 分别为m、m1、m2次径向永磁磁动势谐波幅值;v、v1、v2为电枢反应磁场谐波次数;
分别为m、m1、m2次径向永磁磁动势谐波幅值;v、v1、v2为电枢反应磁场谐波次数; 分别为v、v1、v2次径向电枢磁动势谐波幅值;m0为真空或空气中的磁导率。
分别为v、v1、v2次径向电枢磁动势谐波幅值;m0为真空或空气中的磁导率。
因为m 为奇数,所以在三相基波电流下,电机的振动是基频的偶数倍频。
当三相电流中含有k(k=2, 3, 4,…)倍频对称谐波时,气隙磁场除了永磁磁场和基波磁场外,还有k倍频对称谐波电流产生的谐波磁场,将式(9)代入式(12),得到径向力为
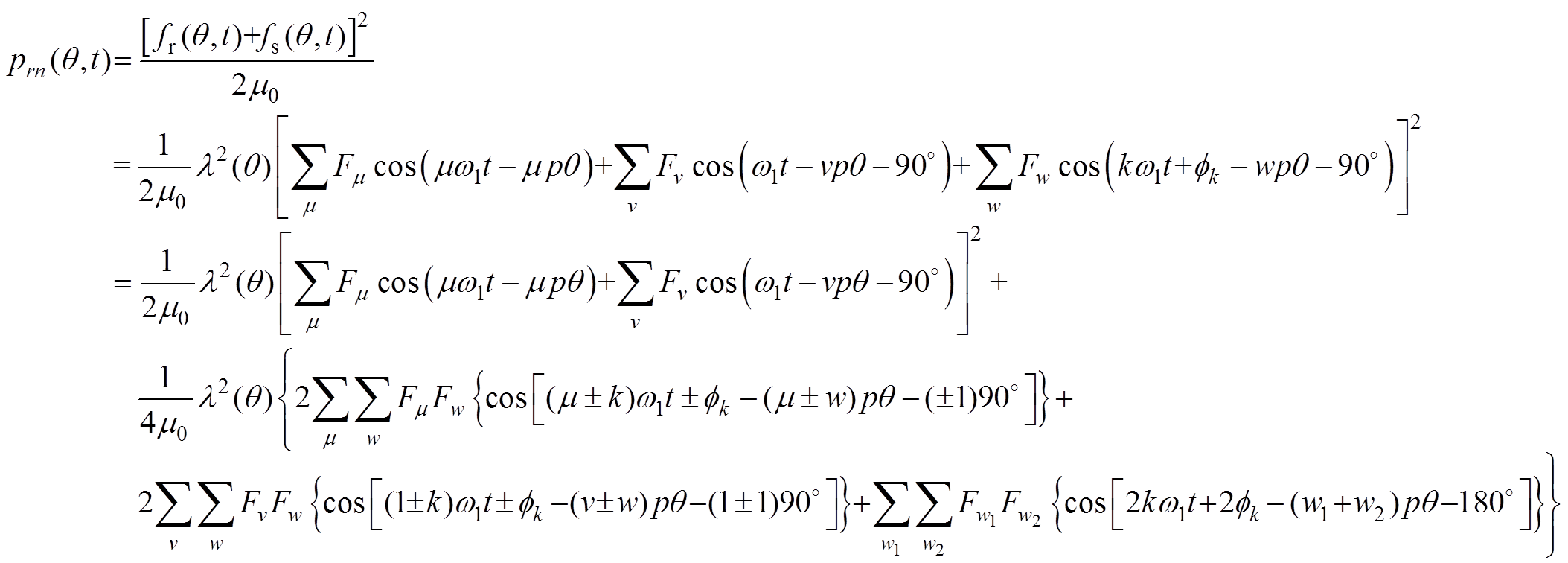 (13)
(13)
式中,w、w1、w2分别为电枢中的k倍频谐波电流的反应磁场谐波次数;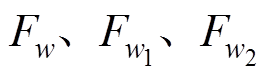 分别为k倍频谐波的w、w1、w2次径向磁动势的幅值。式(13)中的最后一项是只由k倍谐波电流所引起的径向振动,其主要成分是第一项,是谐波磁场与永磁磁场之间相互作用产生的振动,可以看出,奇数倍频谐波电流引起的径向振动是偶数倍频谐波振动,偶数倍频谐波电流引起的径向振动是奇数倍频谐波振动,磁动势谐波次数
分别为k倍频谐波的w、w1、w2次径向磁动势的幅值。式(13)中的最后一项是只由k倍谐波电流所引起的径向振动,其主要成分是第一项,是谐波磁场与永磁磁场之间相互作用产生的振动,可以看出,奇数倍频谐波电流引起的径向振动是偶数倍频谐波振动,偶数倍频谐波电流引起的径向振动是奇数倍频谐波振动,磁动势谐波次数 =1的时候谐波电流引起的径向振动幅值最大,随着磁动势谐波次数的增大,径向振动幅值急剧下降,即
=1的时候谐波电流引起的径向振动幅值最大,随着磁动势谐波次数的增大,径向振动幅值急剧下降,即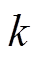 倍频谐波电流对
倍频谐波电流对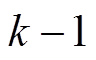 和
和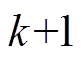 倍频径向振动影响较大,其余倍频径向振动几乎不变。因为相位中的
倍频径向振动影响较大,其余倍频径向振动几乎不变。因为相位中的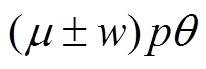 对于
对于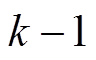 和
和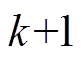 倍频径向振动得到的值不同,所以两个振动幅值的增大或减小的程度可能不同。
倍频径向振动得到的值不同,所以两个振动幅值的增大或减小的程度可能不同。
为了分析绕组中对称的k倍谐波电流引起的径向振动,以750W三相永磁同步电机为例,基波频率为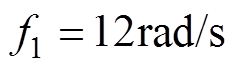 ,原电机径向振动幅值频谱如图3所示。三相注入顺序相差120°的4倍频谐波电流,幅值为基波幅值的1/20,相位为0°,得到的电机径向振动幅值频谱如图4所示。同样注入5倍频谐波电流得到的电机径向振动幅值频谱如图5所示。同样注入6倍频谐波电流得到的电机径向振动幅值频谱如图6所示。
,原电机径向振动幅值频谱如图3所示。三相注入顺序相差120°的4倍频谐波电流,幅值为基波幅值的1/20,相位为0°,得到的电机径向振动幅值频谱如图4所示。同样注入5倍频谐波电流得到的电机径向振动幅值频谱如图5所示。同样注入6倍频谐波电流得到的电机径向振动幅值频谱如图6所示。
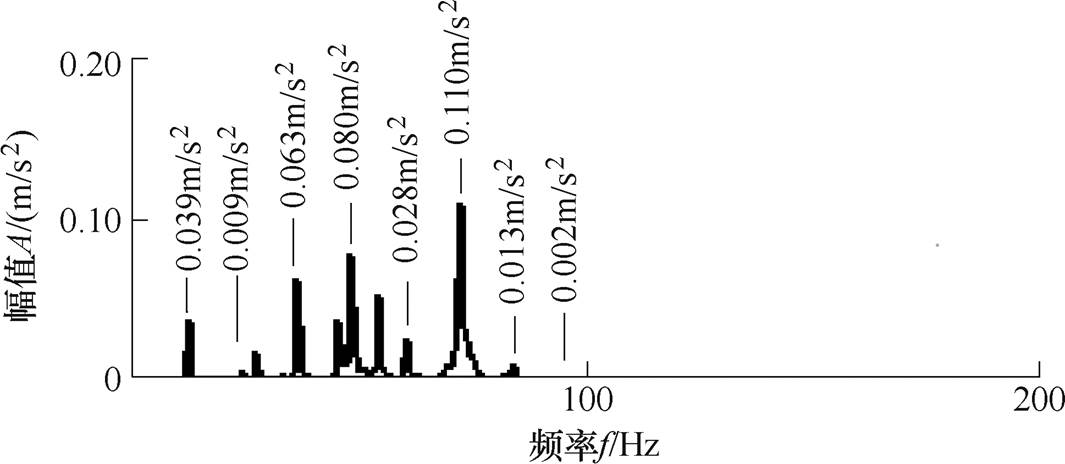
图3 原电机径向振动幅值频谱
Fig.3 Radial vibration amplitude spectrum of the original motor
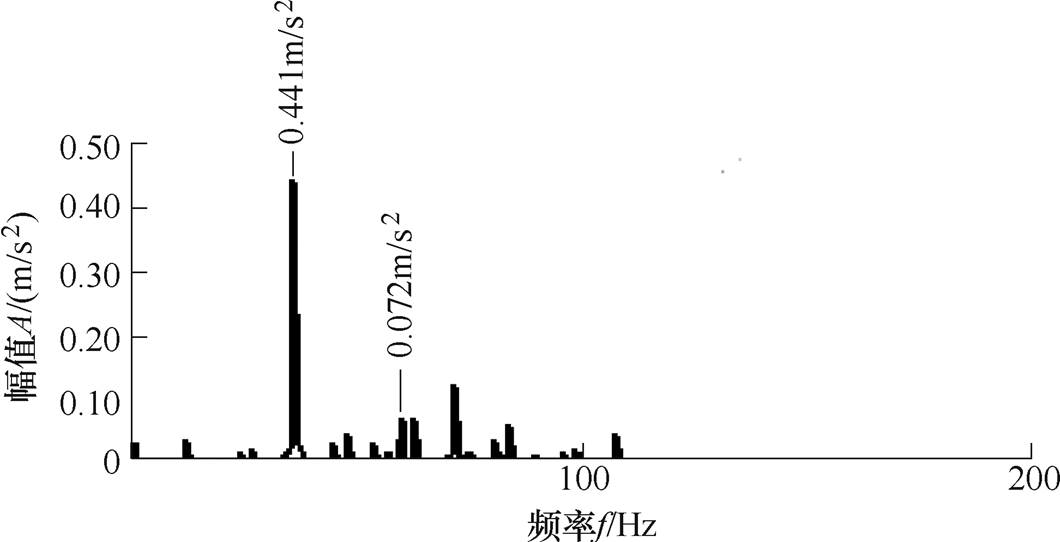
图4 注入4次谐波电流的径向振动幅值频谱
Fig.4 Radial vibration amplitude spectrum of 4th harmonic current injection
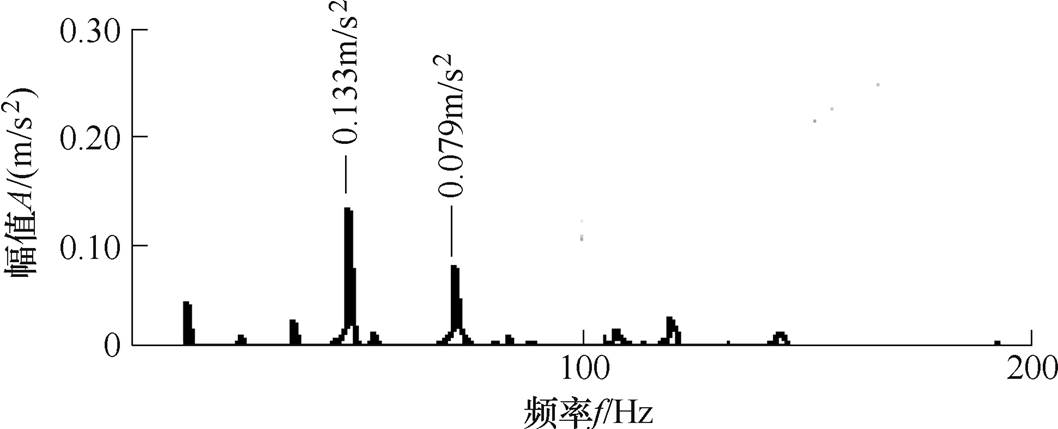
图5 注入5次谐波电流的径向振动幅值频谱
Fig.5 Radial vibration amplitude spectrum of 5th harmonic current injection

图6 注入6次谐波电流的径向振动幅值频谱
Fig.6 Radial vibration amplitude spectrum of 6th harmonic current injection
从图4~图6可以看出,注入k倍谐波电流对k-1倍径向振动影响最大,其次是对k+1倍谐波径向振动的影响,其余倍频径向振动几乎没有 变化。
当三相电流中含有k(k=2, 3, 4,…)倍频不对称谐波时,气隙磁场除了永磁磁场和基波磁场外,还有k倍频不对称谐波电流产生的谐波磁场,将式(10)代入式(12),得到径向力为
 (14)
(14)
式中,w、w1、w2分别为电枢中的k倍频不对称谐波电流的反应磁场谐波次数;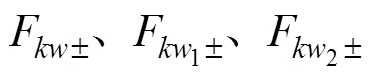 分别为k倍频不对称谐波电流的w、w1、w2次正反向径向磁动势的幅值。
分别为k倍频不对称谐波电流的w、w1、w2次正反向径向磁动势的幅值。
同理,从式(14)中可以看出,奇数倍频不对称谐波电流引起偶数倍频谐波径向振动,偶数倍频不对称谐波电流引起奇数倍频谐波径向振动,k倍频不对称谐波电流对k-1和k+1倍频谐波径向振动影响最大,其余倍频径向振动几乎不变。以750W三相永磁同步电机样机为例,基波频率为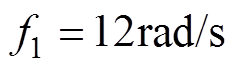 ,在A和B相分别注入幅值为基波幅值的1/20的正反向的4倍频不对称谐波电流和5倍频不对称谐波电流,即构造符合定子星形联结的4倍频不对称谐波电流和5倍频不对称谐波电流,图7为注入4倍频不对称谐波电流的径向振动幅值频谱,图8为注入5倍频不对称谐波电流的径向振动幅值频谱,图中带方框的谐波径向振动是变化最大的振动,即k-1和k+1次谐波径向振动,其余倍频径向振动几乎没有变化。
,在A和B相分别注入幅值为基波幅值的1/20的正反向的4倍频不对称谐波电流和5倍频不对称谐波电流,即构造符合定子星形联结的4倍频不对称谐波电流和5倍频不对称谐波电流,图7为注入4倍频不对称谐波电流的径向振动幅值频谱,图8为注入5倍频不对称谐波电流的径向振动幅值频谱,图中带方框的谐波径向振动是变化最大的振动,即k-1和k+1次谐波径向振动,其余倍频径向振动几乎没有变化。
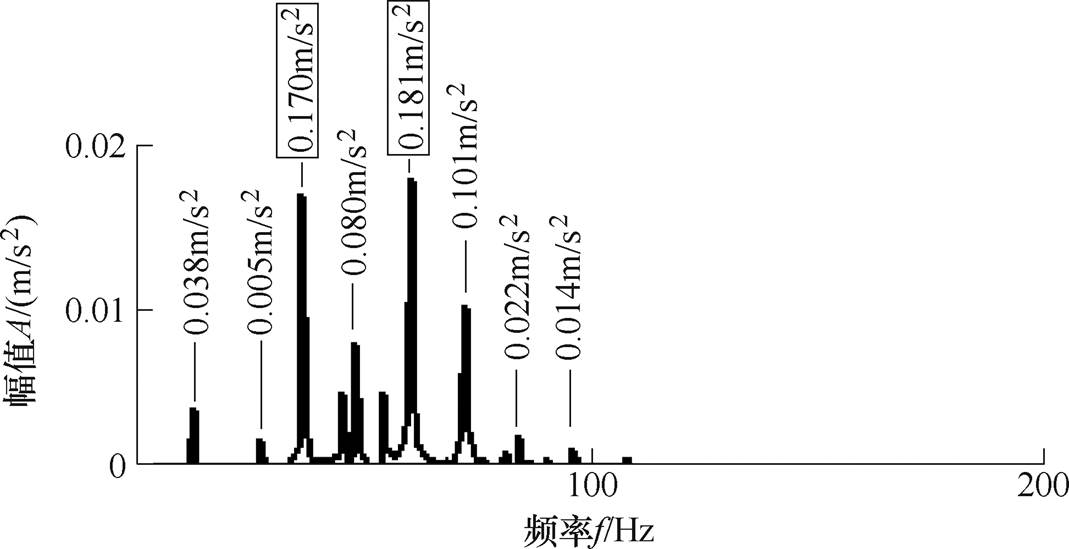
图7 注入4倍频谐波电流的径向振动幅值频谱
Fig.7 Radial vibration amplitude spectrum of 4th harmonic current injection
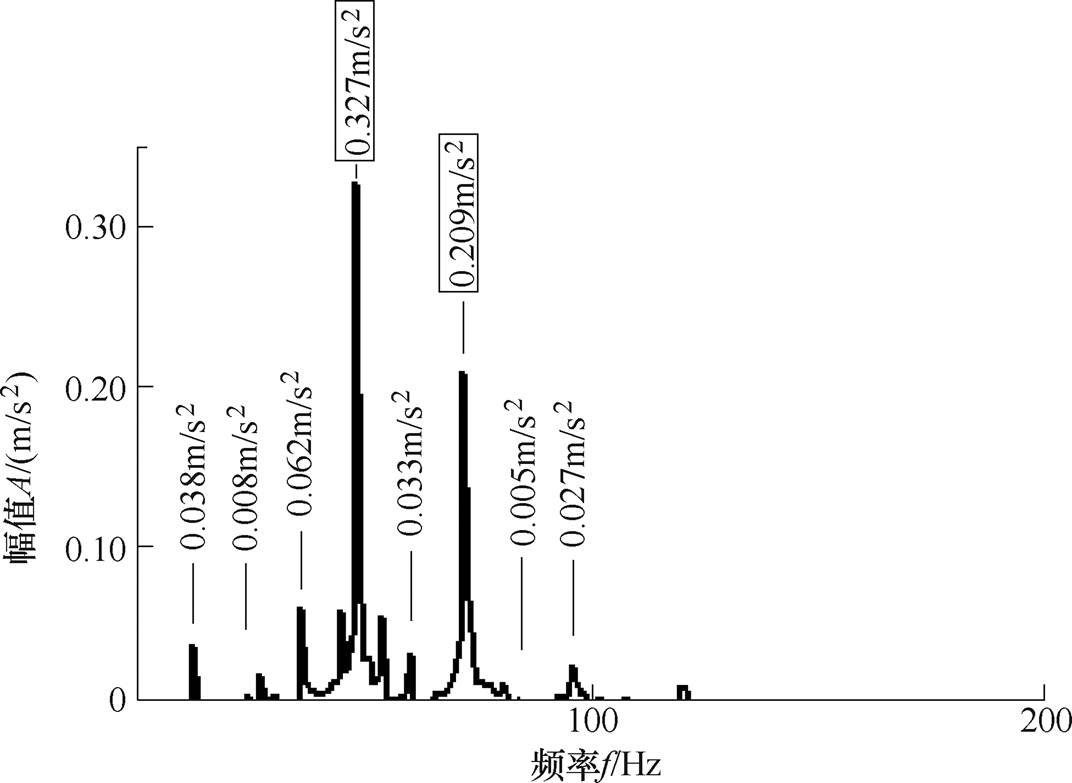
图8 注入5倍频谐波电流的径向振动幅值频谱
Fig.8 Radial vibration amplitude spectrum of 5th harmonic current injection
当三相电流中含有直流分量时,气隙磁场除了永磁磁场和基波磁场外,还有直流电流分量产生的磁场,将式(11)代入式(12),得到径向力为
 (15)
(15)
式(15)中的最后一项是只由直流电流分量引起的径向振动,可以看出,直流电流分量对各个谐波径向振动的幅值都有影响。以750W三相永磁同步电机样机为例,基波频率为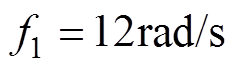 ,在A相和B相分别注入基波幅值的1/20正反方向的直流,即构造一个符合星形联结的直流电流分量,图9和图10分别为原电机径向振动和注入直流电流分量的径向振动幅值频谱,从图中可以看出,每个倍频径向振动幅值都有变化,在这里是大部分倍频径向振动幅值都变大了。
,在A相和B相分别注入基波幅值的1/20正反方向的直流,即构造一个符合星形联结的直流电流分量,图9和图10分别为原电机径向振动和注入直流电流分量的径向振动幅值频谱,从图中可以看出,每个倍频径向振动幅值都有变化,在这里是大部分倍频径向振动幅值都变大了。

图9 原电机径向振动幅值频谱
Fig.9 Radial vibration amplitude spectrum of the original motor
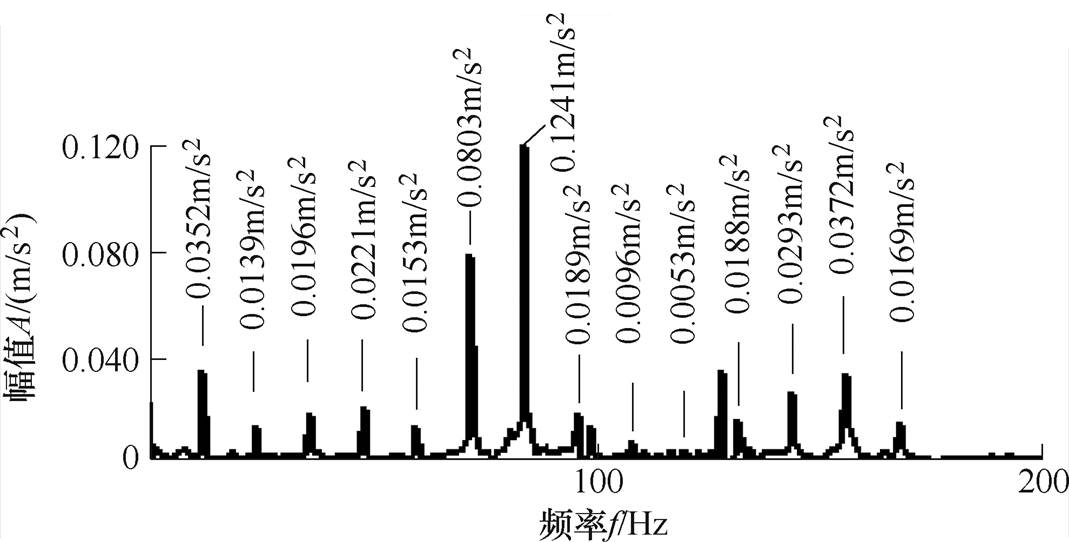
图10 注入直流电流分量的径向振动幅值频谱
Fig.10 Radial vibration amplitude spectrum of DC current injection
虽然绕组中有各倍频的对称和不对称电流,但是它们所引起的径向振动都是电频率的倍频振动,都可以根据式(13)的k倍对称谐波电流的径向振动模型,注入k倍对称谐波电流来抑制k-1次谐波径向振动,可以保证在空间上对振动的均匀抑制。
从式(13)的最后一项k次谐波引起的振动分析得出,起主要作用的是谐波磁场与永磁磁场作用引起的径向力,有
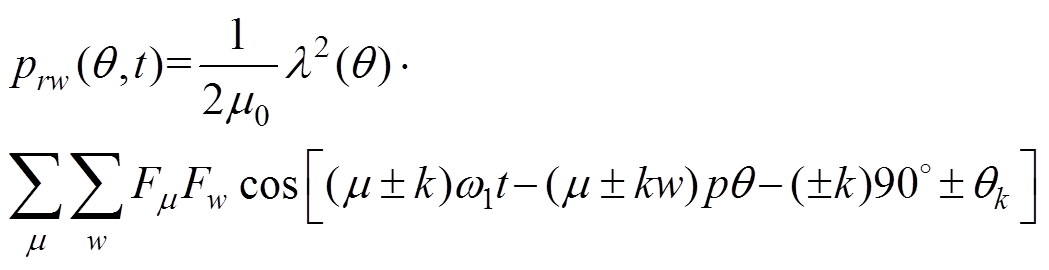 (16)
(16)
式中,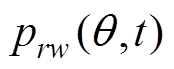 为由k倍频对称谐波电流引起的k-1次径向力。
为由k倍频对称谐波电流引起的k-1次径向力。
根据文献[3]可知,因为谐波电流幅值与谐波磁动势幅值是线性关系,所以谐波电流引起的谐波径向振动幅值与谐波电流幅值也是线性关系,并且与谐波电流的相位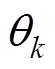 也存在着周期关系。
也存在着周期关系。
以750W三相永磁同步电机样机为例,基波频率为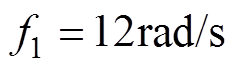 ,分别注入4、5、6、7次谐波,谐波幅值基波幅值比(简称为谐波基波幅值比)从0~0.05变化,相位从0°~360°变化,得到的3、4、5、6倍频径向振动幅值变化如图11~图14所示。
,分别注入4、5、6、7次谐波,谐波幅值基波幅值比(简称为谐波基波幅值比)从0~0.05变化,相位从0°~360°变化,得到的3、4、5、6倍频径向振动幅值变化如图11~图14所示。
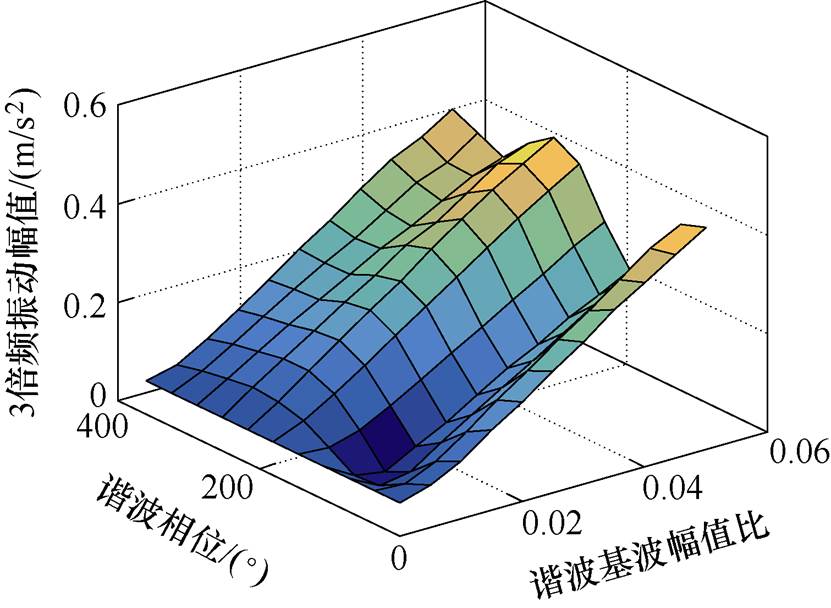
图11 3倍频径向振动幅值随4倍频谐波电流幅值和相位变化
Fig.11 The 3th harmonic radial vibration amplitude variation with the amplitude and phase of the 4th harmonic current
从图11~图14可以看出,谐波电流的幅值和相位变化会影响径向振动的幅值变化,所以,需要选择使径向振动幅值最小的谐波电流幅值和相位。
要实现低频各倍频径向振动的综合抑制,设计一种控制算法,使其实现:
(1)通过调节k倍频电流的幅值和相位两个变量来抑制k-1倍频谐波径向振动。
(2)由于k倍频电流也会对k-1倍频以外的谐波径向振动有影响,而且各倍频电流之间会产生耦
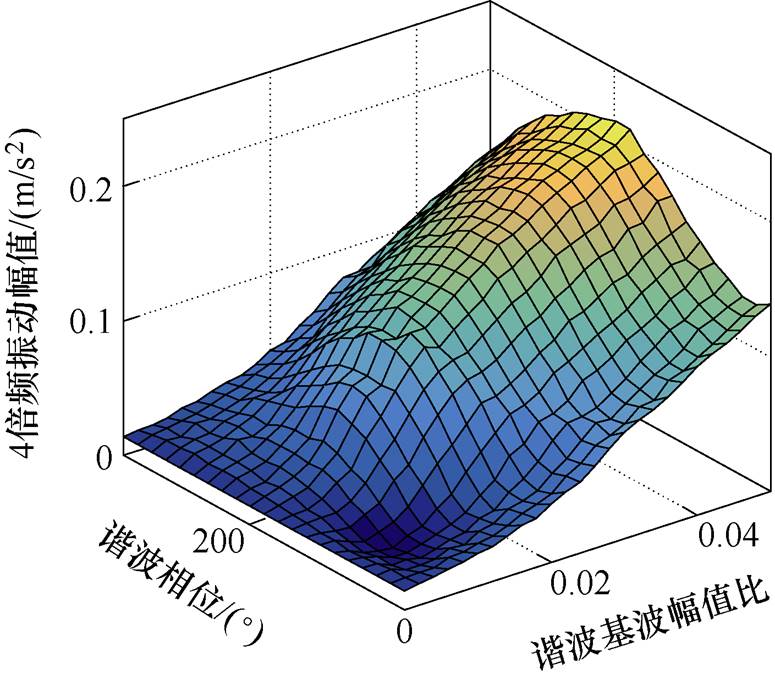
图12 4倍频径向振动幅值随5倍频谐波电流幅值和相位变化
Fig.12 The 4th harmonic radial vibration amplitude variation with the amplitude and phase of the 5th harmonic current
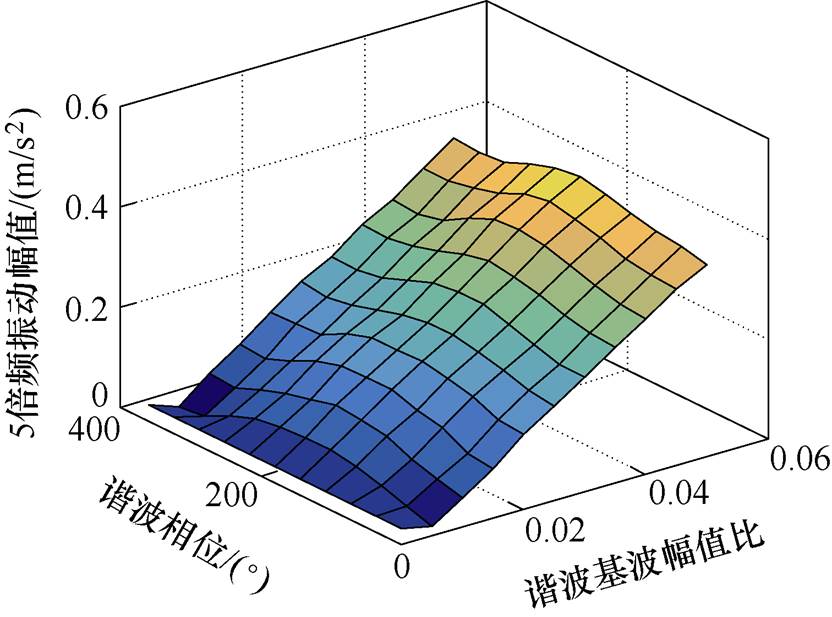
图13 5倍频径向振动幅值随6倍频谐波电流幅值和相位变化
Fig.13 The 5th harmonic radial vibration amplitude variation with the amplitude and phase of the 6th harmonic current
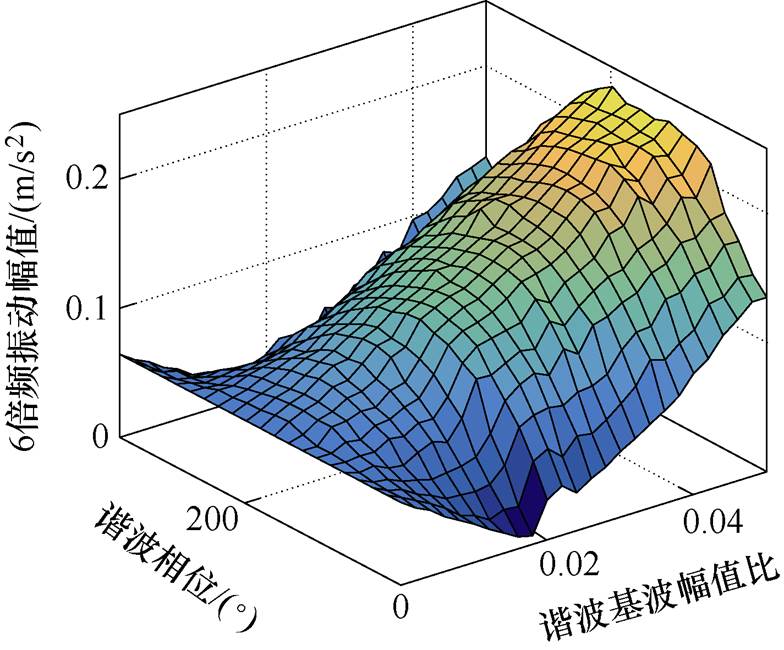
图14 6倍频径向振动幅值随7倍频谐波电流幅值和相位变化
Fig.14 The 6th harmonic radial vibration amplitude variation with the amplitude and phase of the 7th harmonic current
合振动,虽然耦合振动幅值很小,但是依然存在,会随着注入电流谐波数量的增加而产生叠加,需要一种多目标优化控制,来实现各低频次径向振动的综合抑制。
本文为了使各低频次谐波径向振动幅值最小,设计了一个多目标优化模型为
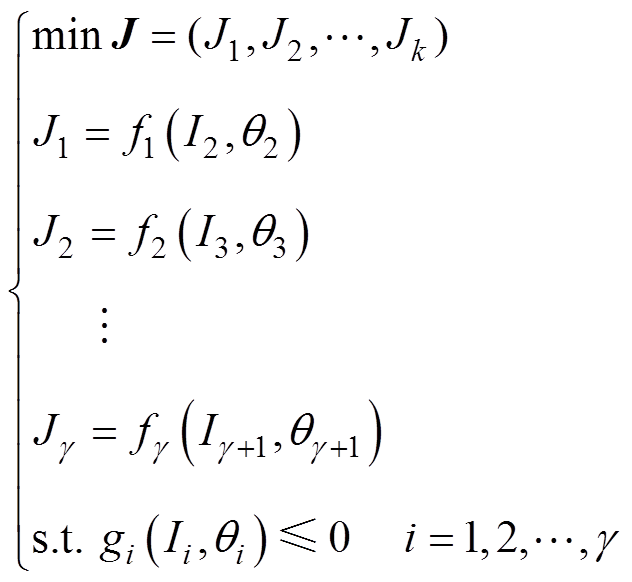 (17)
(17)
式中,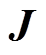 为目标函数向量,即各谐波径向振动幅值向量;
为目标函数向量,即各谐波径向振动幅值向量;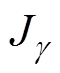 为
为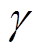 倍谐波径向振动;
倍谐波径向振动;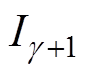 、
、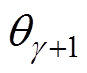 分别为注入的
分别为注入的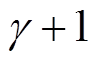 倍频谐波电流的幅值和初始相位;
倍频谐波电流的幅值和初始相位;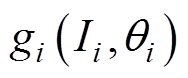 为第i个约束条件。
为第i个约束条件。
此多目标优化模型中的各个目标虽然不在同一个论域里,但是内部有一定的耦合,可以采用自适应优化方法实现解耦。
本文采用RMSProp深度学习算法同时对所有单目标函数寻找最小值。此算法可以自动调整学习率,收敛速度快,算法稳定,第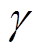 个单目标函数具体步骤如下:
个单目标函数具体步骤如下:
设:衰减速率r,初始学习率h,初始参数q。
设:梯度累积量ν初始化为0,初始常数d =10-7。
循环体如下:
同时采集l个样本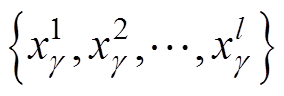 ,其中
,其中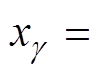
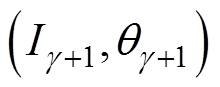 ,
,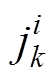 为样本
为样本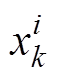 的真实值。计算l个样本的平均梯度为
的真实值。计算l个样本的平均梯度为
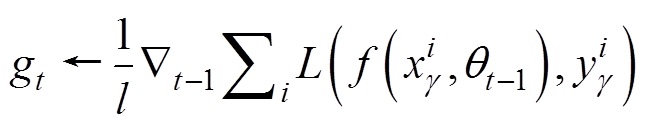
累积历史梯度的二次方,有
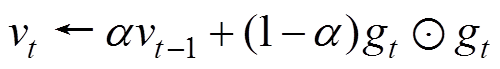
计算更新量(元素级别的运算)为
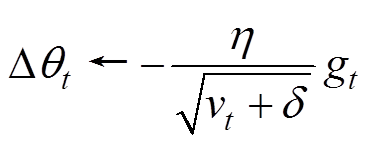
参数更新为
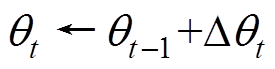
循环体结束。
循环结束条件为
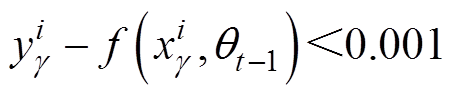
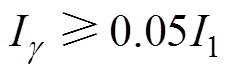
式中,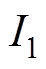 为基波电流幅值。
为基波电流幅值。
同时对多个单目标函数寻找最小值的方法可以实现自适应解耦,使得抑制效果更好。
本文只对200Hz内的低频次振动噪声进行研究,所以,处理的谐波信号都是周期超过1ms的信号,对于DSP28335来说,本文设计的整个系统在可控时间范围内。
样机为750W三相永磁同步电机,对拖一台同型号的电机,三相负载电阻分别为1W,参数见表1,实验装置如图15所示。
表1 750W表贴式永磁电机参数
Tab.1 750W surface type PMSM parameters
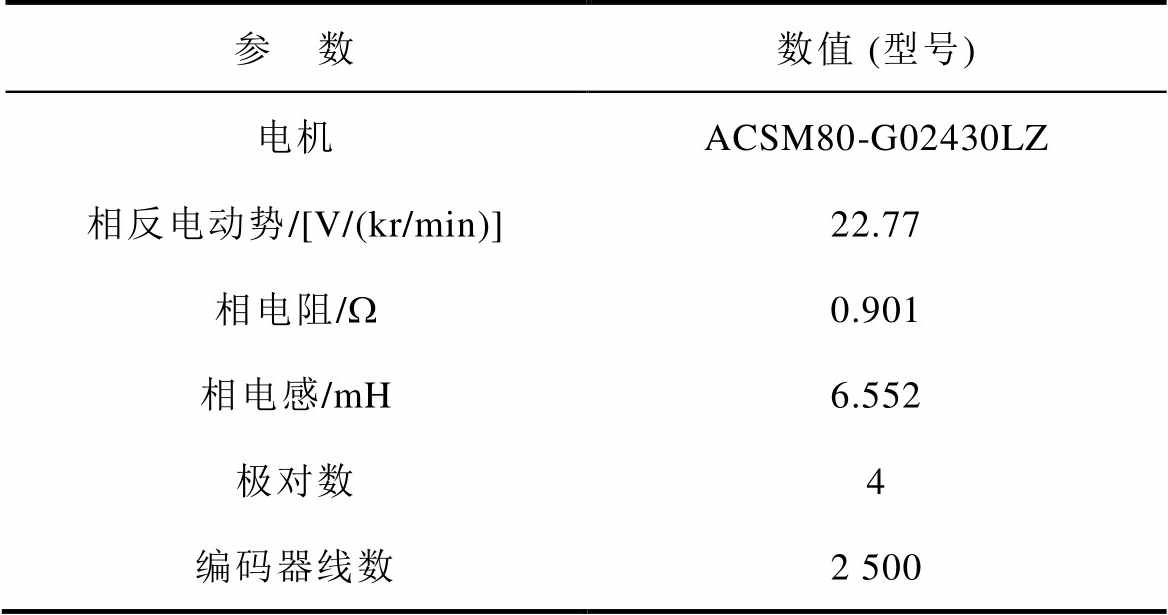
参 数数值 (型号) 电机ACSM80-G02430LZ 相反电动势/[V/(kr/min)]22.77 相电阻/W0.901 相电感/mH6.552 极对数4 编码器线数2 500

图15 实验装置
Fig.15 Experimental apparatus diagram
电机在180r/min转速下,原三相电流和使径向振动最小时的三相电流分别如图16所示。图17为无谐波注入的径向振动幅值频谱。同时注入2~17倍频谐波电流,用多目标RMSProp算法得到200Hz内的各低频倍频径向振动幅值最小时的变量值见表2,振动幅值频谱如图18所示。
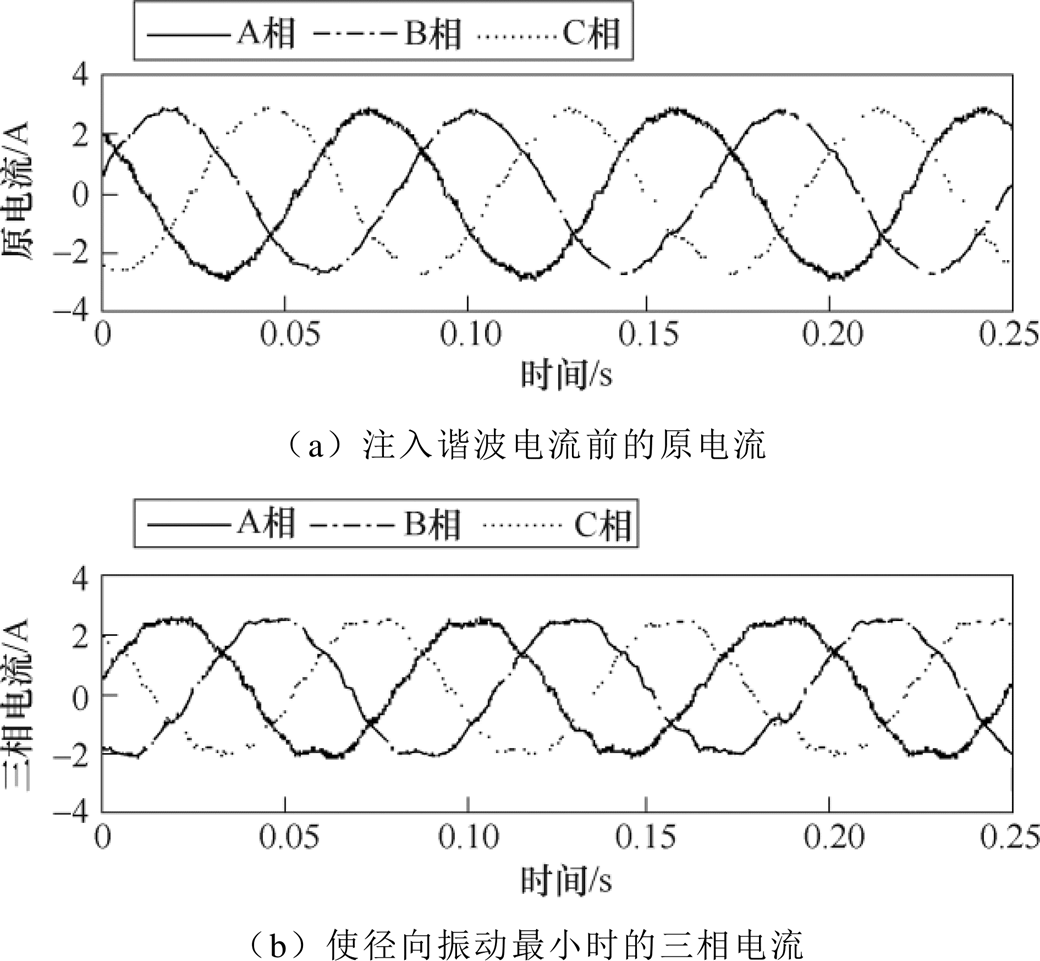
图16 没有注入谐波的三相电流和使径向振动最小时的三相电流
Fig.16 Three-phase current with no injection and three-phase current with minimized radial vibration
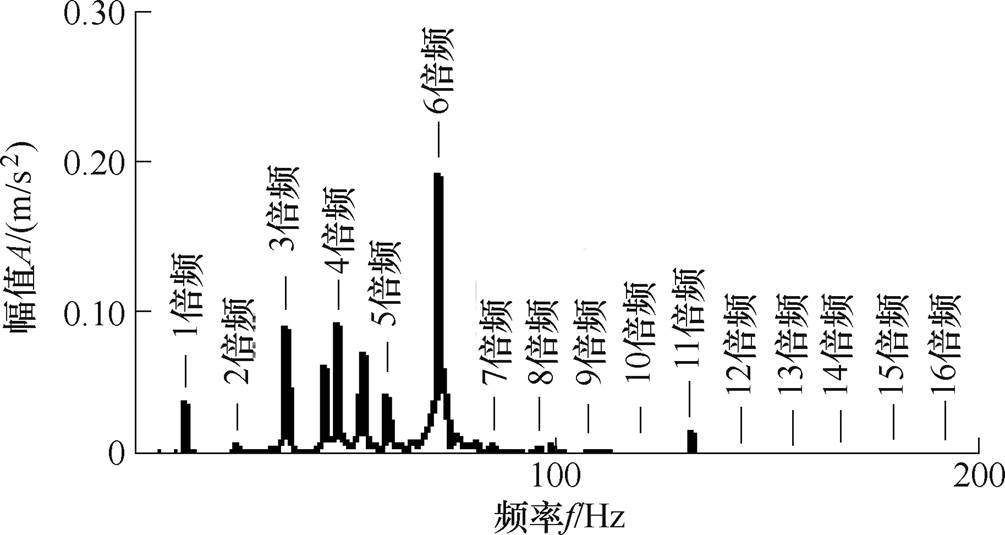
图17 没有注入谐波电流前的径向振动幅值频谱
Fig.17 Radial vibration amplitude spectrum with no injection
表2 低频段各倍频径向振动最小时各变量的值
Tab.2 The value of each variable of the minimum harmonic radial vibration in the low frequency band

电流谐波倍频数幅值比相位/(°)振动谐波倍数未注入前振动幅值/ (m/s2)算法得到最小振动幅值/ (m/s2) 20.00125210.0390.038 30.001020.0090.004 40.00610830.0880.014 50.0023640.0900.010
(续)

电流谐波倍数幅值比相位/(°)振动谐波倍数未注入前振动幅值/ (m/s2)算法得到最小振动幅值/ (m/s2) 60.006050.0420.003 70.02334260.1910.010 80.001070.0070.002 90.0011880.0080.005 100.001090.0060.001 1100100.0030.003 120.002324110.0190.002 1300120.0020.002 1400130.0010.001 1500140.0020.002 1600150.0010.001 1700160.0010.001

图18 同时注入2~17倍频谐波电流,用多目标 RMSProp算法得到的振动频谱
Fig.18 At the same time, 2~17th harmonic current is injected, the vibration spectrum is obtained by the multi-objective RMSProp algorithm
从图16可以看出,注入电流谐波使径向振动最小时,三相电流仍然存在电流谐波,即本文抑制振动的方法不是通过抵消电流谐波来抑制振动,而是通过调节电流谐波使径向振动幅值达到最小值,通过图18和表2可以看出,本文的控制方法对电机低频次径向振动抑制效果显著。
本文推导出绕组中的直流分量、基波、对称谐波电流和不对称谐波电流的径向振动模型和一种可以抑制电机各频次径向振动的模型;并设计一种基于多目标RMSProp算法的永磁电机径向振动抑制策略;实验结果说明,本文方法抑制低频径向振动效果显著。
1)本文注入谐波电流不是为了抵消原电流中的谐波电流,而是通过注入谐波电流来直接抑制径向振动的,所以控制后的电流非正弦是正常的。
2)本文无需求出补偿振动,直接通过调节各倍频电流的幅值和相位寻找径向振动幅值最小值,算法简单,适合在线检测。
3)在实际应用中,高频振动可以用减振器吸收掉,所以本文无需考虑高频振动的抑制。
参考文献
[1] 李清, 杨德庆, 郁扬. 舰船低频水下辐射噪声数值计算方法对比研究[J]. 中国造船, 2017, 58(3): 114- 127.
Li Qing, Yang Deqing, Yu Yang. Comparative study on numerical methods for underwater low-frequency radiation noise of ship[J]. Shipbuilding of China, 2017, 58(3): 114-127.
[2] 向万龙. 基于统计能量法的水下航行器振动分析[D]. 北京: 中国舰船研究院, 2017.
[3] 夏加宽, 康乐, 詹宇声, 等. 表贴式三相永磁同步电机极槽径向力波补偿模型及参数辨识[J]. 电工技术学报, 2021, 36(8): 1596-1606.
Xia Jiakuan, Kang Le, Zhan Yusheng, et al. The model of pole slot radial force wave compensation for surface-mounted three-phase permanent magnet syn- chronous motor and parameter identification[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1596-1606.
[4] Xie Fang, Liang Kangkang, Wu Wenming, et al. Multiple harmonic suppression method for induction motor based on hybrid morphological filters[J]. IEEE Access, 2019, 7: 151618-151627.
[5] 赵强松, 陈莎莎, 周晓宇, 等. 用于并网逆变器谐波抑制的重复-比例复合控制器分析与设计[J]. 电工技术学报, 2019, 34(24): 5189-5198.
Zhao Qiangsong, Chen Shasha, Zhou Xiaoyu, et al. Analysis and design of combination controller based on repetitive control and proportional control for harmonics suppression of grid-tied inverters[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5189-5198.
[6] Han Xun, Jiang Dong, Zou Tianjie, et al. Two- segment three-phase PMSM drive with carrier phase- shift PWM for torque ripple and vibration redu- ction[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 588-599.
[7] Pindoriya R M, Rajpurohit B S, Kumar R. A novel application of harmonics spread spectrum technique for acoustic noise and vibration reduction of PMSM drive[J]. IEEE Access, 2020, 8: 103273-103284.
[8] Zhu Chong, Zeng Zhiyong, Zhao Rongxiang. Com- prehensive analysis and reduction of torque ripples in
three-phase four-switch inverter-fed PMSM drives using space vector pulse-width modulation[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5411-5424.
[9] Yang Ming, Lü Zekai, Xu Donglin, et al. Resonance suppression and EMI reduction of GaN-based motor drive with sine wave filter[J]. IEEE Transactions on Industry Applications, 2020, 56(3): 2741-2751.
[10] 姜燕, 李博文, 吴轩, 等. 基于比例谐振滤波的改进永磁同步电机转子位置观测器[J]. 电工技术学报, 2020, 35(17): 3619-3630.
Jiang Yan, Li Bowen, Wu Xuan, et al. An improved rotor position observer for permanent magnet syn- chronous motors based on proportional resonant filtering[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3619-3630.
[11] Lyra R O C, Lipo T A. Torque density improvement in a six-phase induction motor with third harmonic current injection[J]. IEEE Transactions on Industry Applications, 2002, 38(5): 1351-1360.
[12] Liu Gang, Chen Baodong, Wang Kun, et al. Selective current harmonic suppression for high-speed PMSM based on high-precision harmonic detection method[J]. IEEE Transactions on Industrial Informatics, 2019, 15(6): 3457-3468.
[13] Wu Zhaoqian, Yang Zhijian, Ding Kang, et al. Order- domain-based harmonic injection method for multiple speed harmonics suppression of PMSM[J]. IEEE Transactions on Power Electronics, 2021, 36(4): 4478-4487.
[14] 武永燎, 李红, 宋欣达, 等. 基于改进型重复控制器的永磁同步电机电流谐波抑制方法研究[J]. 电工技术学报, 2019, 34(11): 2277-2286.
Wu Yongliao, Li Hong, Song Xinda, et al. Suppre- ssion of harmonic current in permanent magnet synchronous motors using improved repetitive con- troller[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2277-2286.
[15] Pramanick S, Karthik R S, Azeez N A, et al. A harmonic suppression scheme for full speed range of a two-level inverter fed induction motor drive using switched capacitive filter[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2064-2071.
[16] Li Lei, Lee K M, Bai Kun, et al. Inverse models and harmonics compensation for suppressing torque ripples of multiphase permanent magnet motor[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 8730-8739.
[17] 梁倍华, 何晋伟, 金子开, 等. 基于谐波阻抗匹配的微电网互联线路谐振分析及抑制措施[J]. 电力系统自动化, 2021, 45(14): 123-131.
Liang Beihua, He Jinwei, Jin Zikai, et al. Analysis and suppression measures for resonance on inter- connection line between mircogrids based on harmonic impedance matching[J]. Automation of Electric Power Systems, 2021, 45(14): 123-131.
[18] 林丽娟, 贾清泉, 田书娅, 等. 基于一致性算法的配电网谐波分布式治理策略[J]. 电力系统自动化, 2022, 46(2): 109-117.
Lin Lijuan, Jia Qingquan, Tian Shuya, et al. Dis- tributed harmonic mitigation strategy of distribution network based on consensus algorithm[J]. Automation of Electric Power Systems, 2022, 46(2): 109-117.
[19] Jung H S, Kim J M, Kim C U, et al. Diminution of current measurement error for vector controlled AC motor drives[C]//IEEE International Conference on Electric Machines and Drives, San Antonio, TX, USA, 2005: 551-557.
[20] Boys J T, Handley P G. Harmonic analysis of space vector modulated PWM waveforms[J]. IEE Proceedings B Electric Power Applications, 1990, 137(4): 197.
[21] Liang Wenyi, Wang Jianfeng, Luk P C K, et al. Analytical modeling of current harmonic components in PMSM drive with voltage-source inverter by SVPWM technique[J]. IEEE Transactions on Energy Conversion, 2014, 29(3): 673-680.
[22] 谢宝昌. 电机学[M]. 北京: 机械工业出版社, 2017.
[23] 沈启平, 韩雪岩. 变频器供电下定子磁动势引起的永磁同步电机转子损耗分析[J]. 电工技术学报, 2016, 31(4): 51-57.
Shen Qiping, Han Xueyan. Rotor loss analysis of the permanent magnet synchronous machine caused by stator magnetomotive force with converter powering[J]. Transactions of China Electrotechnical Society, 2016, 31(4): 51-57.
[24] 王成元, 夏加宽, 孙宜标. 现代电机控制技术[M]. 2版. 北京: 机械工业出版社, 2014.
Mechanism Analysis and Comprehensive Suppression Strategy of Radial Vibration Induced by Each Current of Surface Magnet Motor
Abstract The three-phase permanent magnet motor is driven by frequency conversion. The windings contain symmetrical current and asymmetric current of various frequencies, and even DC components. Under the modulation of the pole slot of the motor, the interaction between the current magnetic field and the permanent magnet magnetic field will cause the radial vibration of the motor. In this paper, the three-phase current of the prototype is analyzed, and the radial magnetomotive force of fundamental wave, DC component, symmetrical harmonic current and asymmetric harmonic current are deduced respectively. The radial vibration model caused by the current of each component is deduced according to Maxwell's magnetic force formula, and the correctness of the model is verified by the prototype. Finally, a radial vibration suppression model of multi-harmonic current injection method is derived, and a comprehensive radial vibration suppression control strategy of permanent magnet motor is designed based on the multi-objective RMSProp optimization algorithm. The correctness and effectiveness of the proposed method are verified by the prototype experiment.
keywords:Three phase permanent magnet synchronous motor, harmonic current injection, radial vibration, multi-objective RMSProp optimization
DOI: 10.19595/j.cnki.1000-6753.tces.210380
中图分类号:TM351
国家自然科学基金资助项目(52077142)。
收稿日期 2021-03-19
改稿日期 2021-09-14
康 乐 女,1983年生,博士研究生,讲师,研究方向为永磁电机振动分析与抑制。E-mail: kangle_mail@163.com
夏加宽 男,1962年生,教授,博士生导师,研究方向为永磁电机振动分析与抑制。E-mail: xiajk@sut.edu.cn(通信作者)
(编辑 崔文静)