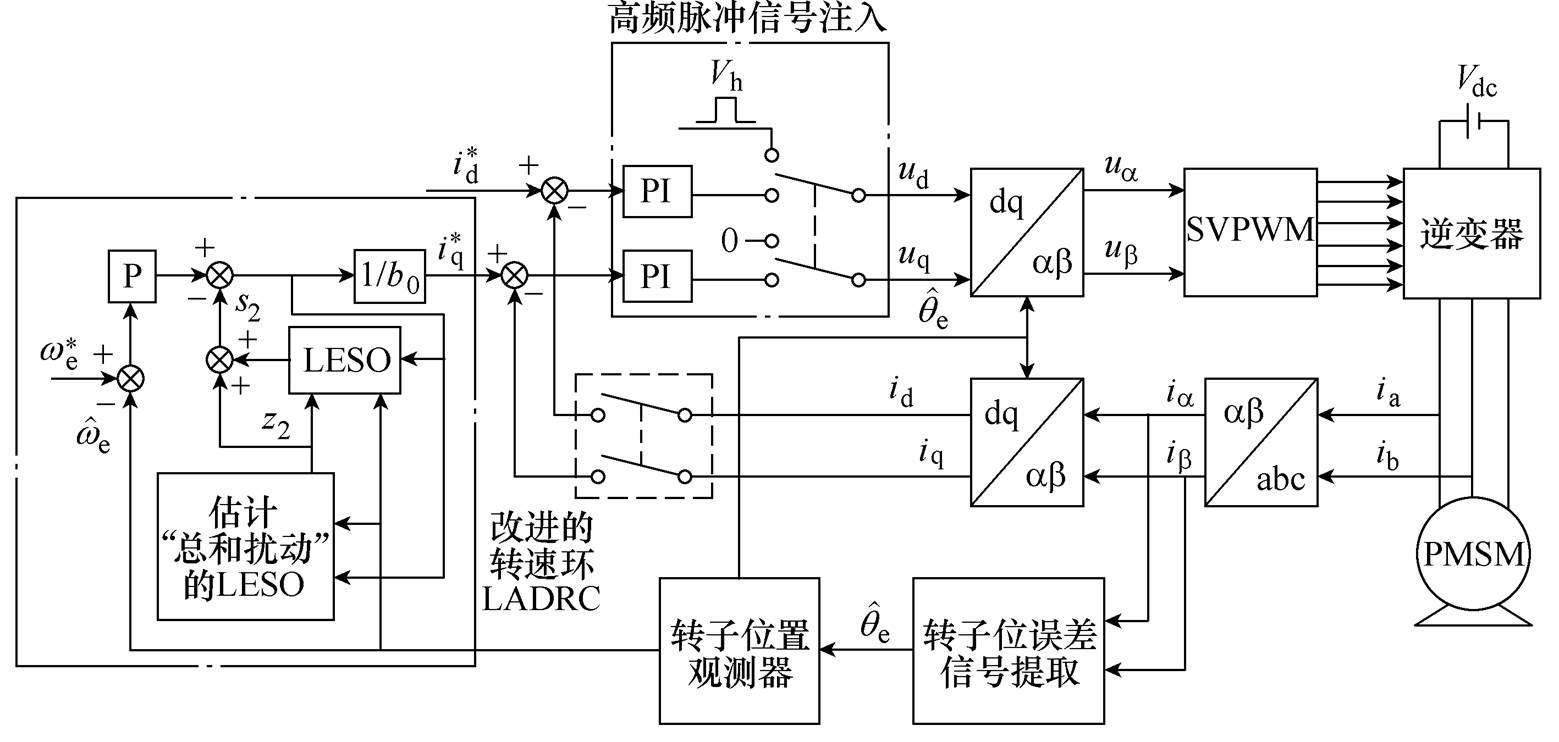
图1 基于改进自抗扰算法的PMSM无传感器控制框图
Fig.1 Sensorless control block diagram of PMSM based on improved active disturbance rejection algorithm
摘要 针对永磁电机矢量控制系统安装位置传感器导致可靠性降低、抗干扰能力下降等问题，采用高频脉冲电压信号注入法实现电机在零低速无传感器控制运行。在此基础上，为了改善无传感器系统采用传统控制方法导致系统刚度下降的问题，该文提出一种改进的转速环线性自抗扰控制策略，利用级联的扩张状态观测器估计系统所受的集总扰动，减小传统线性扩张状态观测器对于斜坡型扰动的估计误差，以提高系统对扰动的估计精度，增强鲁棒性。最后，在7.5kW永磁电机对拖加载实验平台进行实验，验证了控制策略的有效性。
关键词：永磁同步电机 无传感器 自抗扰控制器 级联扩张状态观测器
永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）因高效率、高转矩密度和高功率密度等优势被广泛应用于工业传动及家用电器等场 合[1-2]。在永磁电机矢量控制系统中，准确获取转子位置信息是实现高性能控制的关键环节[3]。传统方法通常需要在电机轴端部安装位置传感器。然而，位置传感器的使用导致系统体积变大、成本增加，而且位置传感器信号易受到外界环境的影响，给系统带来可靠性降低、鲁棒性下降等诸多问题。为了进一步提升永磁电机系统应用适应性，无传感器控制成为电力传动领域的热门课题[4]。当电机零低速运行时，由于反电动势较低，模型法不再适用[5-8]，通常需要注入额外信号获取转子位置及转速信息[9-20]。
此外，随着对永磁电机系统控制性能要求的不断提升，传统控制器的缺陷日益显露，为了进一步满足无位置传感器控制系统低速运行需求，研究性能更加优越的控制器具有重要理论意义和应用价 值[21-22]。自抗扰控制策略对扰动具有强鲁棒性的优点，在永磁电机系统中得到了广泛应用。文献[23]采用一阶自抗扰控制器实现转速闭环控制，为了简化结构，取消了跟踪微分器，并将扩张状态观测器（Extended State Observer, ESO）和状态误差反馈环节线性化，与传统PI控制器相比，动态性能和抗扰性能都得到了明显改善。文献[24]考虑转速反馈环节滤波时间常数的影响，将转速环扩张为二阶系统，并针对其设计三阶ESO，对滤波前的转速进行观测，从而消除滤波器对系统动态性能的影响。文献[25]采用正负脉冲电压信号注入法获取位置信息，提出了一种改进的线性自抗扰控制（Linear Active Disturbance Rejection Control, LADRC）策略，提高了内置式永磁同步电机无位置传感器控制系统的抗扰性能。文献[26]针对二阶自抗扰控制器存在建模误差，且对时变输入跟踪精度较差的问题，提出了一种改进的模型补偿自抗扰控制器，通过模型补偿改善系统对扰动的观测精度，并引入输入微分前馈消除建模误差，进一步提高了系统对时变输入的跟踪能力。文献[27]通过辨识转动惯量和粘滞摩擦因数，减轻了ESO对扰动的估计负担，提高了扰动估计精度，但增加了算法的复杂性，同时控制器的参数设计较为复杂。文献[28]提出了一种将高频电流注入法和线性扩张状态观测器（Linear ESO, LESO）相结合的无位置传感器控制策略，减小了观测器相位延迟和速度抖动，提高了系统对阶跃型负载的抗扰能力。文献[29]提出了一种线性-非线性切换的自抗扰控制策略，改进了无位置传感器控制系统的反馈功能。该方法结合了LESO对扰动的良好耐受性和非线性ESO的高估计精度，而且降低了非线性ESO对参数的敏感性，然而该控制系统参数较多，非线性自抗扰控制系统在参数整定和稳定性方面存在困难。
为此，本文提出一种基于级联扩张观测器自抗扰理论的永磁电机无位置传感器控制策略，以提高系统对扰动的鲁棒性。利用级联的ESO估计系统所受的集总扰动，对其进行补偿，并通过极点配置方法整定参数。所研究的改进LESO可以准确估计斜坡变化的扰动，且无稳态误差。最后，通过7.5kW永磁电机对拖加载平台进行实验验证。
图1为基于改进自抗扰算法的永磁同步电机无传感器控制策略框图。在dq坐标系中注入高频脉冲电压信号，在ab 坐标系中提取高频响应电流，并估计转子位置和转速信息，分别用于坐标变换和转速反馈。其中采用级联ESO估计系统所受的集总扰动，并结合自抗扰控制器实现转速闭环控制。
图1 基于改进自抗扰算法的PMSM无传感器控制框图
Fig.1 Sensorless control block diagram of PMSM based on improved active disturbance rejection algorithm
高频脉冲电压信号注入过程相当于在定子电压ud、uq处设置一个“高频开关”，当处于磁场定向控制周期时，开关切换到电流环PI控制器的输出端，形成双闭环矢量控制，由于没有高频信号注入，因此可以避免高频分量对电流环的影响；当处于注入周期时，切断正常的磁场定向控制，包括电流调节器输出通道和电流反馈通道，从而避免电流环调节量对高频电流的影响，注入时序如图2所示，通过向估计的直轴注入幅值为Vh的电压分量，估计的交轴注入零电压分量，对实时检测到的电流信号（不含基频分量）进行处理，实现对转子位置及转速信息的有效获取。该高频脉冲电压注入形式与传统叠加注入方法均可以准确估计转子位置，该形式可以保证控制周期的采样电流中没有附加高频分量，而注入周期的采样电流没有基频分量的影响，从而无需使用数字滤波器，有利于减小相位滞后和系统延时[30]。
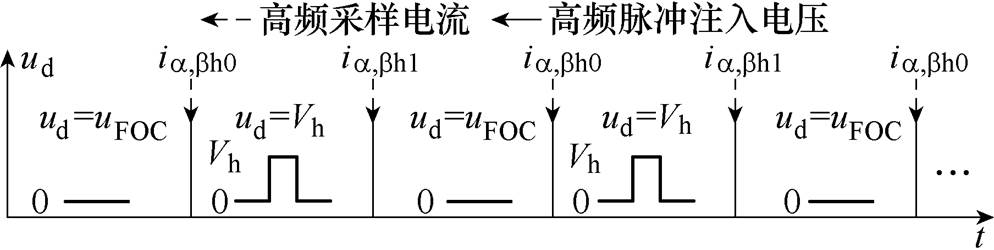
图2 高频脉冲电压信号注入时序
Fig.2 Sequence of high frequency pulse voltage signal injection
采用单向脉冲信号注入代替正负脉冲信号注入可以进一步提高注入频率和控制频率，减少电流采样点个数，使算法和程序设计得到简化。对于电感较小的电机驱动系统，采用单向脉冲信号注入时电感续流时间很短，高频脉冲响应电流快速衰减，对磁场定向控制周期采集的基波电流影响较小。
当电机低速运行时，注入的高频信号频率远高于运行频率，可以忽略定子电阻压降及反电动势相关项，则静止坐标系下永磁电机高频数学模型可表示为
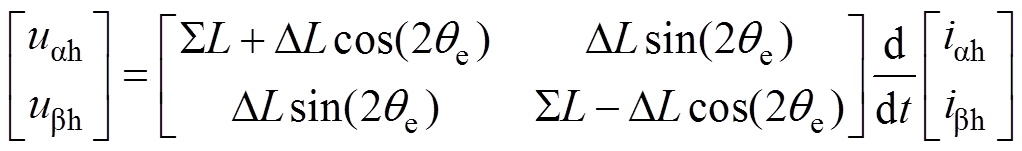（1）
其中
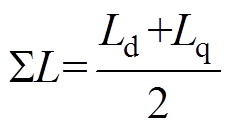
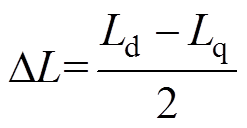
式中，uah、ubh和iah、ibh分别为静止坐标系下高频电压和电流分量；Ld和Lq分别为d、q轴电感；
和DL分别为均值电感和差值电感；qe为实际转子 位置。
由于在估计的直轴注入电压分量，可以得到
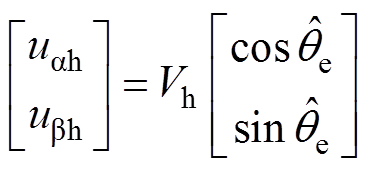（2）
式中，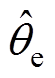
为估计的转子位置。将式（2）代入式（1）的永磁电机高频数学模型，可以得到
（3）
其中
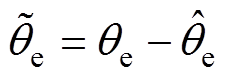
式中，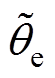
为转子位置误差。当转子位置误差趋近于0时，式（3）可以进一步简化为
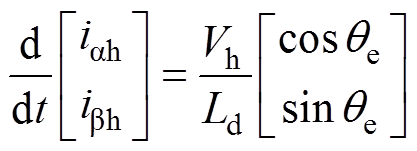（4）
利用电流差分信号代替微分信号，Dt为电流两次采样时间间隔，便可进一步得到
（5）
式中，Diah和Dibh分别为a、b 轴定子高频电流变化量；iah1、ibh1和iah0、ibh0分别为两个连续采样周期内的a、b 轴定子高频电流。
通过注入周期内两次电流采样值作差，可以获得一组包含转子位置信息的正交信号。为了使估计的转子位置更为平滑，采用正交锁相环（Phase Locked Loop, PLL）获取转子位置信息。首先将Diah与Dibh进行幅值归一化处理得到icos与isin，从而减小直轴电感参数以及注入信号幅值变化对转子位置估计精度的影响，再通过外差法获取转子位置误差，最后将其作为转子位置观测器的输入，便可实现对转子位置的观测[7]，转子位置估计信号处理框图如图3所示，外差法的表达式为
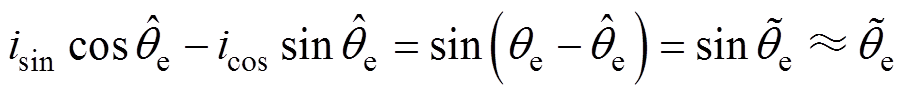（6）
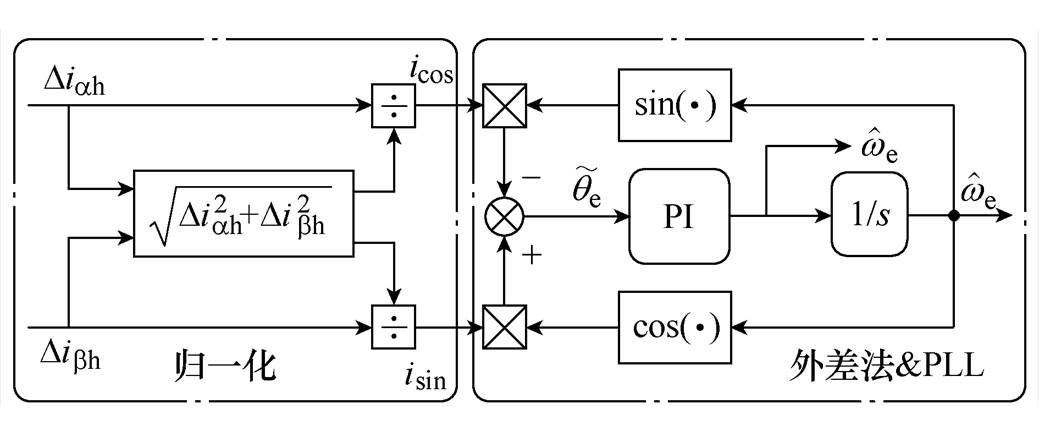
图3 转子位置估计信号处理框图
Fig.3 Block diagram of signal processing for rotor position estimation
线性自抗扰控制器主要包含四部分：线性跟踪微分器、LESO、线性状态误差反馈以及扰动补偿，其结构如图4所示。图中，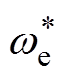
、
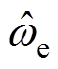和ωeLTD分别为给定角速度、反馈角速度和时序差分（Temporal Difference, TD）环节输出角速度；iq0和
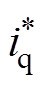分别为线性状态误差反馈（State Error Feedback, SEF）环节输出电流和q轴电流给定值。
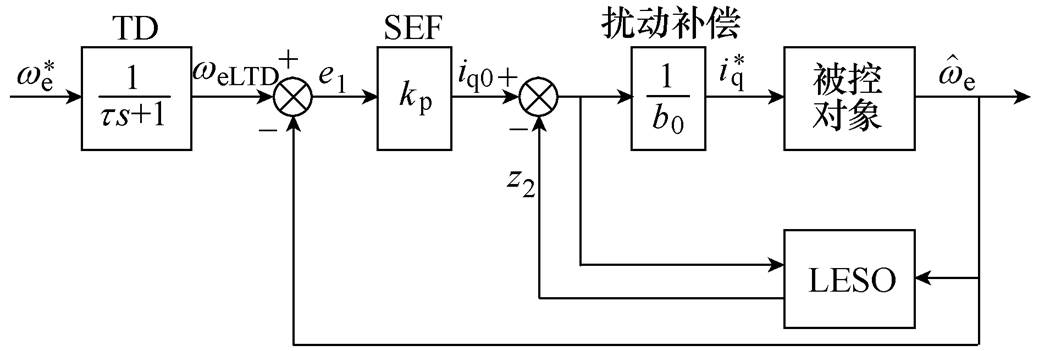
图4 传统线性自抗扰控制器结构
Fig.4 Structure diagram of traditional LADRC
由于转速环带宽相对较低，因此使用LADRC便可以达到较好的抗扰效果，且其算法简单，参数整定和稳定性分析较为容易。在PMSM调速系统中，经常采用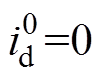
矢量控制方法，由机械运动方程和转矩方程可以得到PMSM速度输出方程为
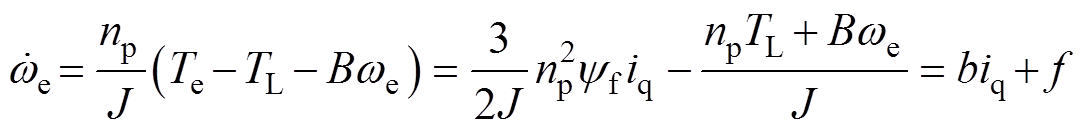（7）
式中，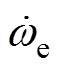
、Te和TL分别为角速度的导数、电磁转矩和负载转矩；Te、TL分别为电磁转矩与负载转矩；J、B分别为电机转动惯量与阻尼系数；np为电机极对数；yf为永磁体磁链；f为扰动总集。在永磁电机无位置传感器矢量控制系统中，转速信息可以通过观测器进行观测，可得
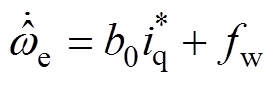（8）
其中
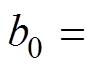
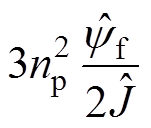
式中，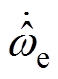
为估计角速度的导数；b0为可调参数，是参数b的估计值；
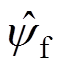和
分别为估计磁链和估计转动惯量；fw为转速环集总扰动作用，包括负载转矩扰动、粘滞摩擦以及q轴电流扰动作用等。令
，
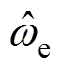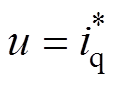，并将fw扩张为状态变量x2，假定x2有界且可微。
LESO可以根据被控对象的输入和输出信号，观测出包含扩张状态在内的所有状态变量。因此，二阶LESO的数学模型为
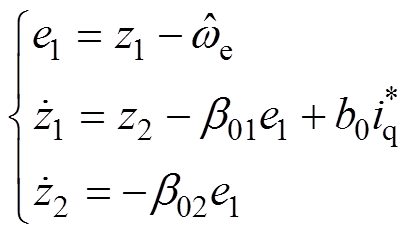（9）
式中，z1、z2分别为转速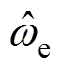、系统所受集总扰动x2的观测值；b01、b02为LESO的控制增益；e1为观测误差。
当采用比例环节对其进行线性状态误差反馈时，可以得到
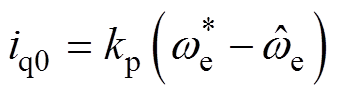（10）
式中，kp为线性自抗扰控制器比例环节比例系数。
扰动补偿是用集总扰动的估计值z2对线性状态误差反馈的输出量进行补偿，从而获得最终的控制量为
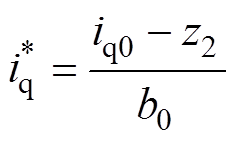（11）
扰动补偿的过程将多阶系统补偿成积分器串联型系统，将一阶系统补偿成积分型系统，使其不再受不确定扰动的影响，即为
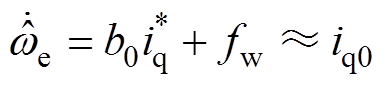（12）
由式（9）可知，在传统线性自抗扰控制器中，系统所受“集总扰动”作用x2和其估计值z2在频域的传递函数为
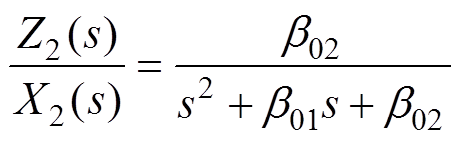（13）
当“集总扰动”作用x2以k为斜率的斜坡变化时，将LESO的极点配置在带宽w 0处，可以得到对扰动的估计量为
（14）
将其变换到时域，则z2的响应可表示为
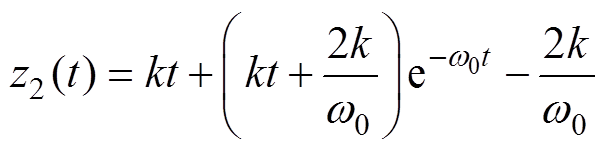（15）
可以看出，当“集总扰动”作用x2以k为斜率的斜坡变化时，传统线性自抗扰控制器对扰动的估计值z2存在稳态误差-2k/w 0。因此，本文提出一种改进的转速环线性自抗扰控制策略。
首先，取消跟踪微分器环节，一阶线性跟踪微分器相当于滤波器。为了简化系统的结构，减小相位滞后和系统延时，改善系统动态性能，在转速环LADRC的设计中，省去跟踪微分器环节；其次，采用两个二阶ESO级联的方式，其中一个二阶ESO用于估计系统所受“集总扰动”的作用，并将估计值z2作为另一个二阶ESO的“已知扰动”作用部分，因此其只需估计除了“已知扰动”作用外的“未知扰动”作用即可，从而减轻对扰动的估计负担，有利于估计精度的提高。基于级联ESO的改进线性自抗扰控制框图如图5所示。
图5 基于级联ESO的改进线性自抗扰控制框图
Fig.5 Structure diagram of improved LADRC based on cascade ESO
类似于式（9），将z2作为另一个LESO的“已知扰动”作用部分，可以得到第二个LESO数学模型的表达式为
（16）
式中，s1、s2分别为估计转速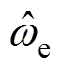、除z2外的扰动观测值；b03、b04为第二个LESO的控制增益。
基于级联ESO的改进LADRC仍采用比例控制作为状态误差反馈环节，相比于传统线性自抗扰控制器，采用LESO对扰动的估计值z2进行补偿，改进线性自抗扰控制器利用两个LESO级联提高扰动估计精度。通过两个LESO对扰动的估计值z2和s2之和进行补偿，补偿过程为
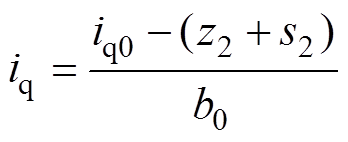（17）
改进后系统所受“集总扰动”作用x2和其估计值z2+s2在频域下的传递函数为
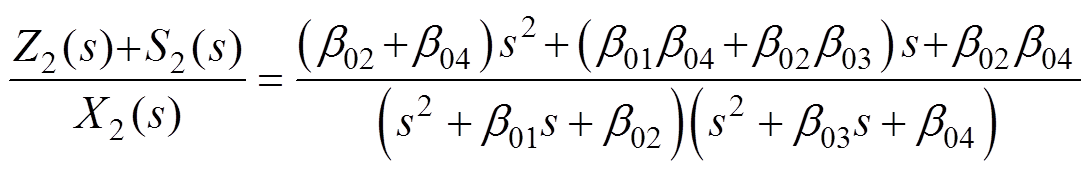（18）
当系统所受“集总扰动”作用x2以k为斜率的斜坡变化时，将两个LESO的极点均配置在w 0处，可以得到两次扰动估计值的集总，其时域响应为
（19）
因此，当“集总扰动”作用发生斜坡变化时，改进线性自抗扰控制器对扰动的估计无稳态误差。相比于传统线性自抗扰控制器，提高了对扰动的估计精度，增强了系统对扰动的鲁棒性。
图6为传统LADRC与改进LADRC对扰动的估计误差对比结果，箭头方向表示LESO带宽增加的方向。其中，改变LESO的带宽w 0，使其从50rad/s开始以10rad/s为步进增大到100rad/s，“集总扰动”作用以10为斜率发生斜坡变化。由图6可见，随着LESO带宽的增加，无论是传统LADRC还是改进LADRC，对扰动的估计速度有所增大，估计误差不断减小。当“集总扰动”作用发生斜坡变化时，传统LADRC对扰动的估计值存在稳态误差，带宽越高，稳态误差的绝对值越小；而对于改进LADRC，扰动估计值稳态误差为零，提高了对扰动的估计精度。
图6 ESO带宽对扰动观测性能的影响
Fig.6 Influence of bandwidth of the ESO on the disturbance observation
当LESO的带宽w 0=50rad/s时，改变“集总扰动”作用的斜率，使其从10开始以2为步长增大到20。图7为传统LADRC与改进LADRC对扰动的估计误差，箭头方向表示k增加的方向。随着“集总扰动”斜率的增大，无论是传统LADRC还是改进LADRC，对扰动的估计速度不变，但是估计误差不断增大。当“集总扰动”作用发生斜坡变化时，传统LADRC对扰动的估计值存在稳态误差，“总和扰动”的斜率越大，稳态误差的绝对值越大。对于改进LADRC，使用两个LESO级联对扰动进行二次估计，因此扰动估计值的稳态误差为零，减轻了每个LESO的估计负担，提高了对扰动的估计精度，改善了系统刚度。
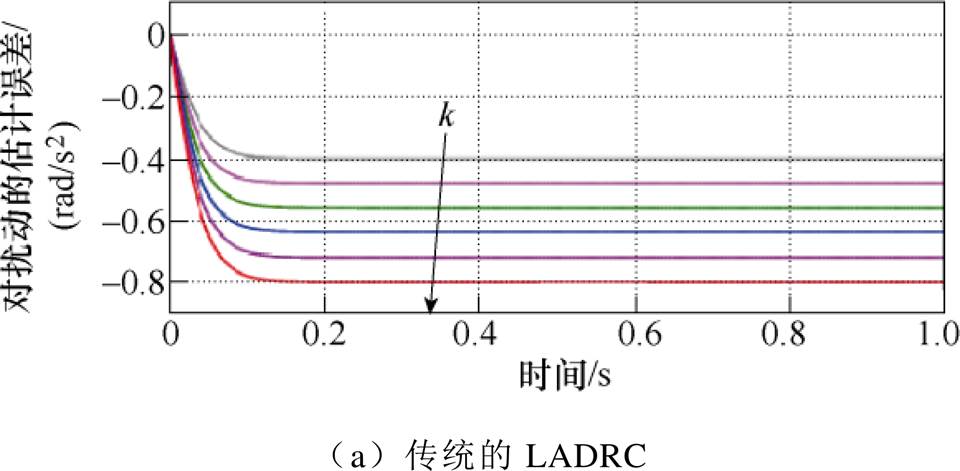
图7 扰动变化率对ESO性能的影响
Fig.7 Influence of the disturbance rate on the performance of the ESO
理论上，二阶LESO的带宽w 0越高，其响应速度越快，对扰动的估计和补偿越及时。但是在实际系统中，w 0受采样频率与系统噪声的影响。由式（9）和式（16）可以得到估计“集总扰动”作用的LESO误差状态方程矩阵
，由李雅普诺夫第一判据可知，当Ae所有特征值均位于s平面左半平面时，LESO的误差必收敛于零。根据矩阵Ae的特征多项式，将极点配置在w 0处，可以得到LESO的控制增益b01=b03=2w0、b02=b04=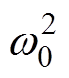
。在实际系统中，LESO的带宽取值一般选择小于100rad/s。
经过LESO以及扰动补偿后，转速环可以等效成一个一阶惯性环节，比例环节的增益为转速环带宽，可以根据选定的转速环带宽来确定线性状态误差反馈的比例增益。
采用图1所示的PMSM无传感器自抗扰控制策略，在如图8所示的7.5kW表贴式永磁电机对拖加载实验平台上进行验证。为改善高频信号注入法应用效果，采用注入d轴偏置电流的方式激发表贴式永磁电机产生饱和凸极效应，提高零低速区间无位置传感器控制性能。采用线性拟合的方法调整d轴偏置电流注入值，空载时注入值为5% 额定电流，额定负载时注入值为20% 额定电流。将两台同型号永磁电机同轴连接，其中一台用来模拟负载。电机轴端部安装位置传感器，用于实时检测转子位置信息，验证所研究方法的有效性。本文主要针对所研究的改进转速环线性自抗扰控制策略的实验效果进行验证，因此在实验过程中未考虑由d轴和q轴电流在重载条件下引起的磁场交叉饱和效应对无位置传感器控制性能的影响，后续将针对此问题进一步展开研究。逆变器开关频率为8kHz，主控制芯片为数字信号处理（Digital Signal Processing, DSP）芯片，型号为TMS320F28075。永磁同步电机参数见表1。实验过程中高频电压注入幅值选取为62V，由于所用电机电感值较小，因此高频响应电流较大，有助于进一步激发饱和凸极效应，实现电机无位置传感器稳定运行，为验证所研究的改进自抗扰控制策略的有效性提供保障。
图8 实验平台
Fig.8 Experimental platform
表1 永磁同步电机参数
Tab.1 Parameters of permanent magnet synchronous motor
参 数数 值 额定功率/kW7.5 额定转矩/(N·m)48 额定电流/A20 额定电压/V380 额定转速/(r/min)1 500 定子相电阻/W0.273 d、q轴电感/mΗ1.05 极对数4
为了保证系统稳定性，同时获得较快的响应速度，ESO的极点选为p=60。为了与PI控制进行对比，速度环的PI参数经过整定，取得最优化的控制参数，转速环比例系数和积分系数分别为Kp=15, Ki=0.2。经计算与实验调试，线性自抗扰控制器中kp=200，b0=7.06。为了减小级联ESO产生的超调，二级ESO极点选取应略小于一级ESO，故ESO的极点分别设置在20和40。
图9为电机运行在给定频率3Hz条件下，突加100%额定负载转矩，速度环采用PI调节器的无位置传感器控制实验结果。图9中分别给出利用高频信号注入法得到的观测转速、转子位置及a相电流波形。从实验结果中可见，当速度环采用PI控制时，系统的刚度较差。在突加100%额定负载转矩时转速跌落与恢复时间分别为11.2Hz和600ms。
图9 PI控制下的实验结果
Fig.9 Experimental results by PI control
图10和图11分别为电机无位置传感器运行在给定频率3Hz条件下，突加100%额定负载转矩时，速度环采用传统LADRC和改进LADRC调节器时对扰动估计的实验结果。从扰动估计误差对比可以看出，采用传统自抗扰控制器完全跟踪阶跃负载的时间为450ms，而采用改进自抗扰控制器跟踪时间为350ms，相较传统控制器减少22.2%。因此，改进LADRC控制器具有更快的扰动估计速度。
图10 LADRC扰动观测实验结果
Fig.10 Experimental results of disturbance estimation by LADRC
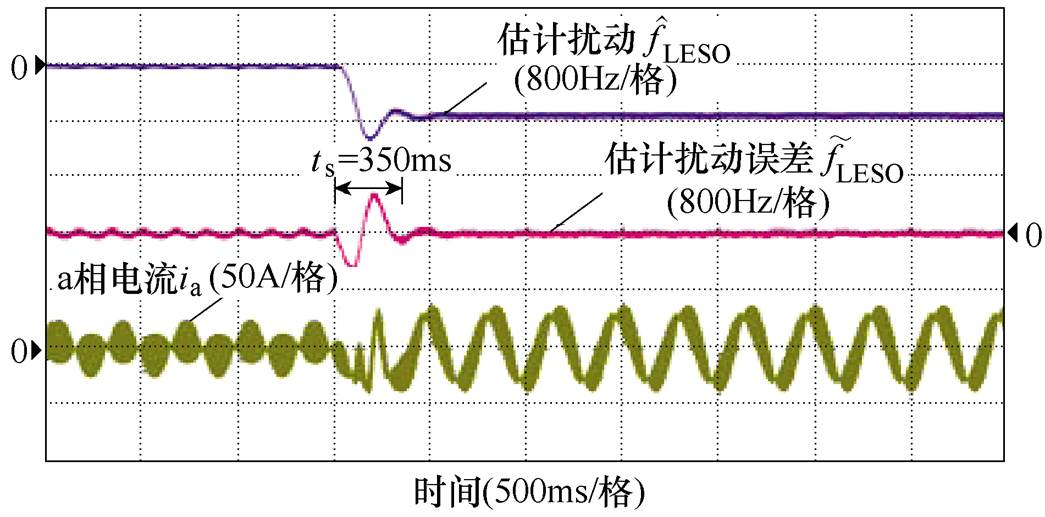
图11 改进LADRC扰动观测实验结果
Fig.11 Experimental results of disturbance estimation by improved LADRC
图12和图13分别为相同运行环境下速度环采用传统LADRC和改进LADRC调节器时的无位置传感器实验结果。由于ADRC中的ESO可以估计并补偿电机加载过程所受的扰动，因此当速度环采用传统LADRC时，在突加100%额定负载时，转速跌落与恢复时间分别减小至7.9Hz和390ms。由于级联ESO可以进一步估计系统所受扰动，提高对于扰动的估计速度。因此，当速度环采用改进LADRC时，电机在突加100%额定负载时转速跌落为5.6Hz，恢复时间进一步减小至270ms。根据实验对比，由于系统所加负载是阶跃型负载，阶跃后负载大小不再变化，此时斜率k=0。因此，在稳态条件下，传统和改进方法都无稳态误差。但是，在暂态调整过程中，由于扰动估计误差的存在，传统自抗扰控制器的转速跌落更为明显，恢复时间更长，改进自抗扰控制器具有更快的响应速度，增强了系统对扰动的刚度。虽然当电机突加负载时，相比于PI控制器，转速跌落明显减小，但由于级联的ESO增加了系统的阶数，因此在调整过程中系统的超调量变大，可以通过调整级联ESO的极点配置来调节。
图12 LADRC实验结果
Fig.12 Experimental results by LADRC
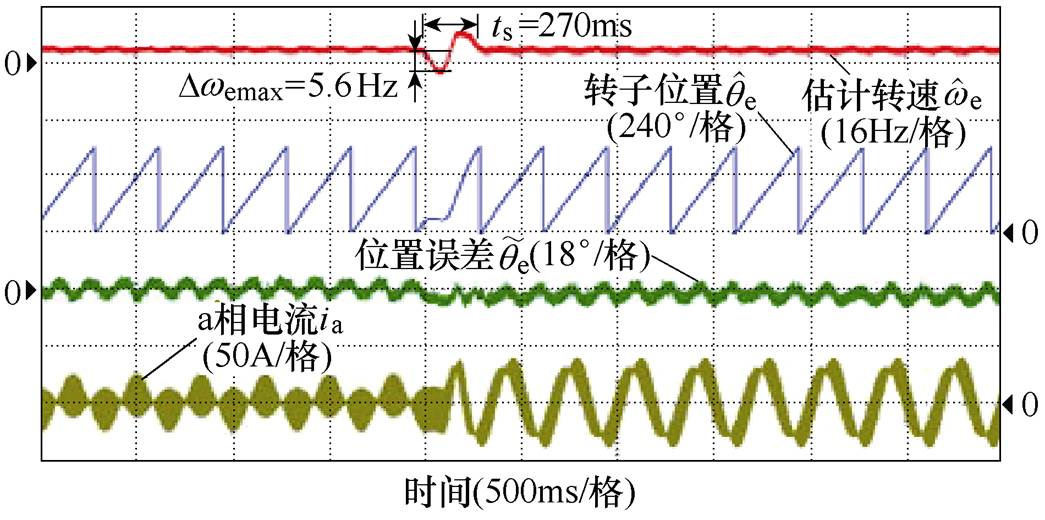
图13 改进LADRC实验结果
Fig.13 Experimental results by improved LADRC
图14和图15分别为零速运行条件下，速度环采用传统LADRC和改进LADRC调节器时无位置传感器控制实验结果。实验过程中转速参考值为零，对转子位置未施加控制，因此加载前后转子位置随机分布。可以看出，在突加额定负载扰动时，电机可以在零转速条件下保持无位置传感器稳定运行。与传统LADRC相比，改进自抗扰调节器可以有效降低转速跌落和恢复时间，验证了该方法的有效性。
图14 零速运行条件下LADRC实验结果
Fig.14 Experimental results by LADRC at zero speed operation
图15 零速运行条件下改进LADRC实验结果
Fig.15 Experimental results by improved LADRC at zero speed operation
为进一步验证所研究方法的有效性，图16和图17分别为电机给定运行频率在4～10Hz范围内，突加25%～100%额定负载时，速度环采用PI控制器、传统LADRC和改进LADRC时的最大转速跌落和恢复时间对比。从图16a和图17a中可以看出，转速跌落与恢复时间随着给定频率的降低而增大，故系统刚度随着给定频率的降低而降低。因此，如何提高永磁电机在低速运行条件下的刚度尤为重要。根据图16和图17a～图17c的对比可知，在4Hz运行频率、100%额定负载扰动条件下，相比于PI控制器，改进线性自抗扰控制器在受到扰动时，转速跌落减小了66.7%。相同运行条件下，相较于PI控制器和传统LADRC控制器，采用改进线性自抗扰控制器后，系统恢复时间分别降低了70%和51%。因此，改进自抗扰控制器可以有效抑制转速跌落和恢复时间，提高系统刚度。此外，根据实验对比可知，当使用改进LADRC时，给定转速越低、突加负载越大，系统超调越明显，转速恢复至给定的时间也就越长，但效果均优于PI控制器和传统LADRC控制器。因此，改进线性自抗扰控制器可以有效地改善永磁电机在零、低速条件下无传感器运行的动态性能。
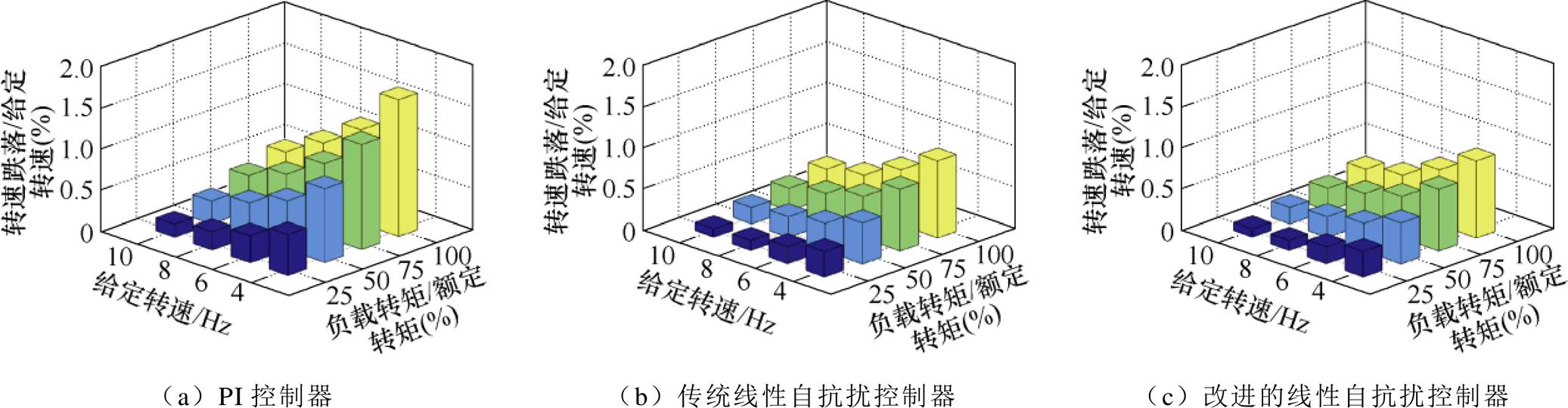
图16 最大转速跌落的实验对比
Fig.16 Experimental comparison of maximum speed drop
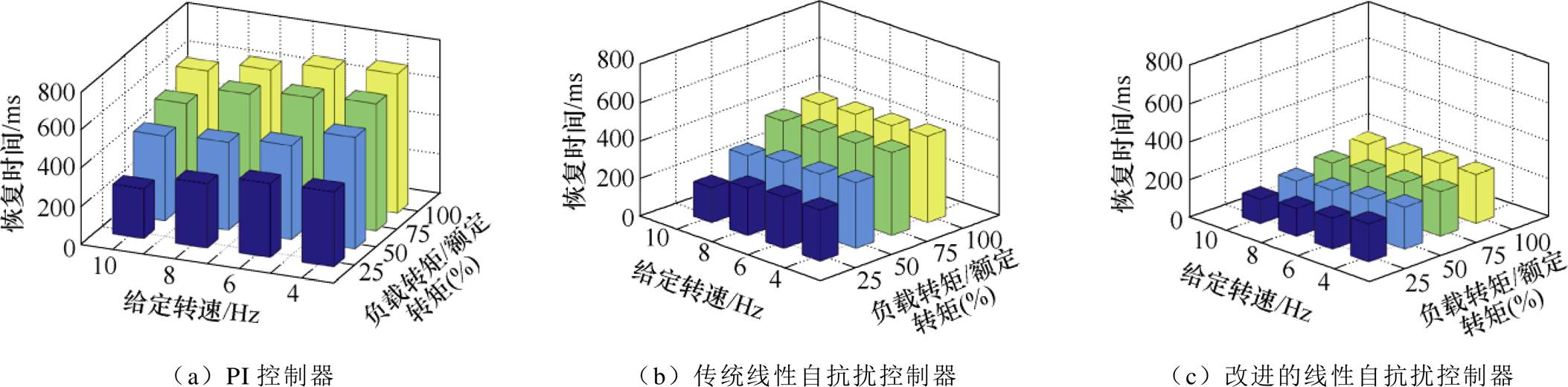
图17 恢复时间的实验对比
Fig.17 Experimental comparison of recovery time
本文通过高频脉冲电压信号注入法实现永磁电机在零/低速条件下的无位置传感器运行，并提出了一种基于级联扩张状态观测器的线性自抗扰控制策略。利用级联的ESO对系统所受的集总扰动进行观测与补偿，消除了传统LESO对斜坡扰动的估计误差，提高了估计速度，改善了系统动态性能，增强了系统鲁棒性。实验结果表明，当电机稳定运行于零/低速给定频率且受到额定负载扰动时，相较于PI控制器，采用改进线性自抗扰控制器后，电机最大转速跌落和恢复时间分别减小66.7%和70%，有效提高了系统的抗扰性能。
参考文献
[1] Wang Zihui, Cao Zewei, He Zhiyuan. Improved fast method of initial rotor position estimation for interior permanent magnet synchronous motor by symmetric pulse voltage injection[J]. IEEE Access, 8: 59998- 60007.
[2] Chen Zhe, Zhang Hang, Tu Wencong, et al. Sensor- less control for permanent magnet synchronous motor in rail transit application using segmented syn- chronous modulation[J]. IEEE Access, 2019, 7: 76669- 76679.
[3] Verrelli C M, Bifaretti S, Carfagna E, et al. Speed sensor fault tolerant PMSM machines: from position- sensorless to sensorless control[J]. IEEE Transactions on Industry Applications, 2019, 55(4): 3946-3954.
[4] 李垣江, 董鑫, 魏海峰, 等. 表贴式永磁同步电机转速环复合PI无位置传感器控制[J]. 电工技术学报, 2020, 35(10): 2119-2129.
Li Yuanjiang, Dong Xin, Wei Haifeng, et al. Sensor- less compound PI control for surface permanent magnet synchronous motor speed regulation system[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2119-2129.
[5] Wang Yaoqiang, Feng Yutao, Zhang Xiaoguang, et al. A new reaching law for antidisturbance sliding-mode control of PMSM speed regulation system[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4117-4126.
[6] 何延昭, 王贞艳, 王金霞, 等. 高速永磁同步电机模型参考自适应转速观测[J]. 电气传动, 2020, 50(10): 16-22.
He Yanzhao, Wang Zhenyan, Wang Jinxia, et al. Speed observation for high-speed permanent magnet synchronous motor with model reference adaptive system[J]. Electric Drive, 2020, 50(10): 16-22.
[7] 赵亚辉, 冯明, 李卫文. 基于SMO的改进型转子位置检测方法[J]. 北京航空航天大学学报, 2020, 46(12): 2329-2338.
Zhao Yahui, Feng Ming, Li Weiwen. Improved rotor position detection method based on SMO[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(12): 2329-2338.
[8] Ni Ronggang, Xu Dianguo, Blaabjerg F, et al. Square-wave voltage injection algorithm for PMSM position sensorless control with high robustness to voltage errors[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5425-5437.
[9] 王爽, 曹栋逸, 杨影, 等. 正负高频脉冲电压注入的永磁同步电机无位置传感器控制[J]. 电工技术学报, 2020, 35(增刊1): 164-171.
Wang Shuang, Cao Dongyi, Yang Ying, et al. Sensorless control of PMSM with positive and negative high frequency pulse voltage signal injection[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 164-171.
[10] 王高林, 杨荣峰, 李刚, 等. 基于高频信号注入的IPMSM无位置传感器控制策略[J]. 电工技术学报, 2012, 27(11): 62-68.
Wang Gaolin, Yang Rongfeng, Li Gang, et al. Position sensorless control strategy of IPMSM based on high frequency signal injection[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 62-68.
[11] Li Haoyuan, Zhang Xing, Yang Shuying, et al. Unified graphical model of high-frequency signal injection methods for PMSM sensorless control[J]. IEEE Transactions on Industrial Electronics, 2020, 67(6): 4411-4421.
[12] Wang Shuang, Yang Kang, Chen Kang. An improved position-sensorless control method at low speed for PMSM based on high-frequency signal injection into a rotating reference frame[J]. IEEE Access, 7: 86510- 86521.
[13] 杜博超, 崔淑梅, 宋立伟, 等. 一种基于变频电流信号的IPMSM无位置传感器高频注入电流噪声抑制方法[J]. 电工技术学报, 2020, 35(18): 3830-3837.
Du Bochao, Cui Shumei, Song Liwei, et al. A variable frequency current injection sensorless control strategy of IPMSM for audible noise reduction[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(18): 3830-3837.
[14] Wang Gaolin, Valla M, Solsona J. Position sensorless permanent magnet synchronous machine drives-a review[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 67(7): 5830-5842.
[15] 赵文祥, 刘桓, 陶涛, 等. 基于虚拟信号和高频脉振信号注入的无位置传感器内置式永磁同步电机MTPA控制[J]. 电工技术学报, 2021, 36(24): 5092- 5100.
Zhao Wenxiang, Liu Huan, Tao Tao, et al. MTPA control of sensorless IPMSM based on virtual signal and high-frequency pulsating signal injection[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5092-5100.
[16] 阙鸿杰, 全力, 张丽, 等. 基于自适应滤波器在线解耦的磁场增强型永磁电机无位置传感器控制[J].电工技术学报, 2022, 37(2): 344-354.
Que Hongjie, Quan Li, Zhang Li, et al. Sensorless control of flux-intensifying permanent magnet syn- chronous motor based on adaptive notch filter online decoupling[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 344-354.
[17] 麦志勤, 刘计龙, 肖飞, 等. 基于估计位置反馈电流解调算法的改进型高频旋转电压注入无位置传感器控制策略[J]. 电工技术学报, 2022, 37(4): 870- 881, 891.
Mai Zhiqin, Liu Jilong, Xiao Fei, et al. Sensorless control strategy of improved HF rotating voltage injection based on estimated position feedback current demodulation algorithm[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 870-881, 891.
[18] 麦志勤, 肖飞, 刘计龙, 等. 基于改进型自调整轴系幅值收敛电流解调算法的旋转高频电压注入法[J]. 电工技术学报, 2021, 36(10): 2049-2060.
Mai Zhiqin, Xiao Fei, Liu Jilong, et al. Rotating high- frequency voltage injection method based on improved self-adjusting frame amplitude convergence current demodulation algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2049- 2060.
[19] 于安博, 刘利, 阚志忠, 等. 高频脉振信号注入永磁同步电机无滤波器初始位置辨识方法[J]. 电工技术学报, 2021, 36(4): 801-809.
Yu Anbo, Liu Li, Kan Zhizhong, et al. Initial position identification of PMSM with filterless high frequency pulse signal injection method[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 801-809.
[20] Zhang Guoqiang, Xiang Runhua, Wang Gaolin, et al. Hybrid pseudorandom signal injection for position sensorless synrm drives with acoustic noise redu- ction[J]. IEEE Transaction on Transport Electrific, 2022, 8(1): 1313-1325.
[21] 朱进权, 葛琼璇, 孙鹏琨, 等. 基于自抗扰的高速磁浮列车牵引控制策略[J]. 电工技术学报, 2020, 35(5): 1065-1074.
Zhu Jinquan, Ge Qiongxuan, Sun Pengkun, et al. Traction-system research of high-speed maglev based on active disturbance rejection control[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(5): 1065-1074.
[22] 吴春, 傅子俊, 孙明轩, 等. 基于扩张状态观测器负载转矩补偿的永磁同步电机全速范围无位置传感器控制[J]. 电工技术学报, 2020, 35(增刊1): 172- 181.
Wu Chun, Fu Zijun, Sun Mingxuan, et al. Sensorless control of PMSM in all speed range based on extended state observer for load toque com- pensation[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 172-181.
[23] Luan Tianrui, Yang Ming, Lang Xiaoyu, et al. A novel active disturbance rejection control speed controller for PMSM drive[C]//2016 IEEE 8th International Power Electronics and Motion Control Conference, Hefei, China, 2016: 116-120.
[24] 左月飞, 符慧, 刘闯, 等. 考虑转速滤波的永磁同步电动机转速伺服系统改进型自抗扰控制器[J]. 电工技术学报, 2016, 31(9): 137-145.
Zuo Yuefei, Fu Hui, Liu Chuang, et al. A modified active disturbance rejection controller concerning speed filter for PMSM speed servo system[J]. Transactions of China Electrotechnical Society, 2016, 31(9): 137-145.
[25] Wang Gaolin, Liu Ran, Zhao Nannan, et al. Enhanced linear ADRC strategy for HF pulse voltage signal injection-based sensorless IPMSM drives[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 514-525.
[26] 左月飞, 张捷, 刘闯, 等. 针对时变输入的永磁同步电机改进型自抗扰控制器[J]. 电工技术学报, 2017, 32(2): 161-170.
Zuo Yuefei, Zhang Jie, Liu Chuang, et al. A modified adaptive disturbance rejection controller for per- manent magnetic synchronous motor speed-regulation system with time-varying input[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 161-170.
[27] 盖江涛, 黄庆, 黄守道, 等. 基于模型补偿的永磁同步电机自抗扰控制[J]. 浙江大学学报(工学版), 2014, 48(4): 581-588.
Gai Jiangtao, Huang Qing, Huang Shoudao, et al. Active-disturbance rejection controller for permanent magnet synchronous motor based on model com- pensation[J]. Journal of Zhejiang University (Engineering Science), 2014, 48(4): 581-588.
[28] Du Bochao, Wu Shaopeng, Han Shouliang, et al. Application of linear active disturbance rejection controller for sensorless control of internal permanent- magnet synchronous motor[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3019-3027.
[29] Jiang Feng, Yang Kai, Sun Songjun, et al. An improved extended state observer based on linear- nonlinear switching strategy for PMSM sensorless control[C]//2018 IEEE 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea (South), 2018: 1696-1702.
[30] Wang Gaolin, Xiao Dianxun, Zhao Nannan, et al. Low-frequency pulse voltage injection scheme-based sensorless control of IPMSM drives for audible noise reduction[J]. IEEE Transactions on Industrial Elec- tronics, 2017, 64(11): 8415-8426.
Active Disturbance Rejection Control for Position Sensorless Permanent Magnet Synchronous Motor Drives Based on Cascade Extended State Observer
Abstract In order to solve the problem that the installation of the position sensor decreases reliability and impairs anti-disturbance ability in permanent magnet synchronous motor (PMSM) drives, the high frequency pulse voltage signal injection method is adopted to realize PMSM sensorless drives at zero and low speed. When the traditional control method is used in PMSM sensorless drives, the stiffness of the drive system will be decreased. Therefore, this paper proposes an improved linear active disturbance rejection control (LADRC) strategy. A cascade of extended state observer (ESO) is used to estimate the total disturbance imposed on the system. The estimation error for the slope load disturbance can be eliminated, which improves the estimation precision against disturbance and enhances the robustness of the system. Finally, the feasibility of the proposed strategy is verified by the experimental results on a 7.5kW PMSM platform.
keywords：Permanent magnet synchronous motor, sensorless, active disturbance rejection control, cascade extended state observer
DOI: 10.19595/j.cnki.1000-6753.tces.210615
中图分类号：TM346
国家自然科学基金资助项目（52177034, 52125701）。
收稿日期 2021-05-05
改稿日期 2021-09-14
朱良红 男，1977年生，硕士研究生，教授级高工，研究方向为空调永磁压缩机小电容驱动系统关键控制技术。E-mail: zhulh@midea.com
张国强 男，1987年生，博士，副教授，研究方向为交流电机控制理论与应用技术。E-mail: ZhGQ@hit.edu.cn（通信作者）
（编辑 崔文静）