
图1 模块电机定子
Fig.1 Geometric diagram of modular stator
摘要 为准确计算模块组合式永磁电机的电磁性能,该文建立了一种子域法和等效磁网络法相结合的非线性混合磁场解析模型。通过在子域模型定子槽边界施加等效电流片,非线性磁场解析模型可等效成为考虑了饱和效应的线性磁场解析模型。改进子域解析模型边界上的等效电流密度在等效磁网络模型中计算,等效磁网络中的磁通源需要在子域法中计算,因此需采用迭代算法进行求解。等效磁网络模型中考虑了相邻定子模块之间的装配气隙。基于该非线性混合磁场解析模型计算了电机的气隙磁通密度、空载反电动势和电磁转矩,并重点分析模块组合式永磁电机在不对称运行状态下的电磁特性。最后通过有限元仿真结果和样机实验数据验证了该非线性混合磁场解析模型的正确性。
关键词:解析计算 磁场 模块组合式永磁电机 混合模型
模块组合式永磁电机定子由多个相互独立的扇形定子模块组成,扇形定子模块分别独立生产加工,最后拼接成一个完整的环形定子。定子绕组采用大跨距和小跨距线圈相结合的方式,实现了各个扇形定子模块机械上和电气控制上互相独立[1]。这种新型模块定子结构能够降低生产制造难度,提高冲片利用率,方便运输和简化维修拆卸过程。球磨机用直驱永磁电机体积巨大,采用模块组合式永磁电机解决了大型电机制造以及维修的难题[2]。此外,当某个模块定子出现故障无法正常运行时,可以停止给该模块定子供电,其他定子模块继续正常运行,同时可增加非故障定子模块的电流,用来维持额定输出转矩不变,保证电机能够正常可靠地工作。模块组合式永磁电机由于具有较好的容错性,适合风力发电、船舶推进以及其他特殊工况[3]。
加大非故障定子模块绕组电流用来弥补故障定子模块转矩的缺失时,非故障模块定子铁心饱和现象会更为突出,因此准确地计算模块组合式永磁电机的磁场分布十分重要。电机的磁场计算方法主要分为有限元法和解析法。有限元法能够考虑电机复杂的模型和非线性的铁磁材料,计算结果准确,但耗时较长;解析法计算速度快,物理概念清晰,能够体现电机设计参数和性能之间关联,适用于电机初步方案设计和优化。近些年,国内外学者在电机的磁场解析法的研究上做了大量工作,其中主要包括等效磁路法[4-5]、保角变换法[6-7]和精确子域法[8-10]。
文献[2]采用去线圈法实现定子模块独立,对电机磁动势进行了分析,有限元法计算了不同模块运行时的转矩特性。文献[3]建立了模块组合式永磁电机的数学模型,对电机不平衡磁拉力解析表达式进行了推导。文献[4-5]建立了电机非线性等效磁网络模型,计算了电机的磁场分布。等效磁网络法能够考虑铁心材料的饱和效应,等效磁网络模型中等效磁导单元的数量可根据计算精度的要求进行合理的划分,但等效磁导单元数量过多会导致计算时间增加,因此等效磁导数量的划分需要综合考虑计算精度与计算时间。文献[6-7]采用保角变换法对永磁电机的气隙磁场和转矩特性进行了分析,能够准确计及齿槽效应对电机气隙磁场分布的影响,但无法明确体现设计参数与电磁性能之间的联系。文献[8-10]建立了永磁电机的精确子域模型,但都假设相对铁心磁导率无穷大,忽略了饱和效应。文献[11]利用谐波建模法建立了考虑饱和的永磁同步电机解析模型,将铁心材料的相对磁导率考虑进去,但是没有考虑相对磁导率的实时变化。文献[12]建立了开关磁阻电机的谐波模型,考虑了定转子齿部的非线性磁导率,但是模型中没有涉及永磁体。文献[13]建立了混合磁场解析模型,计算了永磁电机的气隙磁场,考虑了非线性的磁导率,但都是基于保角变换法。文献[14]建立子域法和等效磁网络法的混合磁场解析模型,并分析了磁极偏心对电机性能的影响,但是只能分析电机的空载磁场。文献[15]基于子域法和等效磁路法,建立了表贴式永磁电机的非线性混合解析模型,介绍了解析模型的等效原理,并分析了永磁电机的空载磁场。文献[16]在文献[15]的基础上,计算了永磁电机的负载磁场,并在等效磁路法中考虑了定子平行齿结构。
在前人研究的基础上,本文以一台三定子模块的30极72槽的模块组合式永磁同步电机为研究对象,将子域法和等效磁网络法相结合,建立一种考虑铁心非线性磁导率的混合磁场解析模型。非线性铁心磁阻上的磁压降可用等效电流产生的磁动势来代替。因此,非线性磁场解析模型可通过在线性磁场解析模型边界施加等效电流来实现。首先采用子域法计算出不考虑铁心磁导率的磁场解析结果,得到气隙磁通后在等效磁网络法中计算出等效电流密度,然后将等效电流密度作为子域模型中的边界条件重新进行磁场解析计算。等效磁网络中考虑了模块之间的装配气隙。根据铁磁材料的磁化曲线,通过插值计算得到非线性铁心的磁导率,采用迭代算法,直到误差满足计算精度为止。利用该非线性混合磁场解析模型对模块组合式永磁电机的气隙磁感应强度、空载反电动势(back Electromotive Force, back EMF)和电磁转矩进行了计算。在此基础上,重点分析了模块组合式永磁电机在不对称运行状态下的电磁特性,并给出了不同数量定子模块运行时电流值预测方法。最后将非线性混合磁场模型解析结果与有限元仿真结果和实验结果进行比较,验证了该文建立模型的正确性。
模块组合式永磁电机定子由多个扇形的定子单元模块构成,每个扇形的定子模块都是分别加工,然后进行绕组下线,最后各个定子模块再安装连接在一起。维修时仅需拆掉故障定子模块,安装上新的模块单元,不需拆卸和安装完整的电机,简化了安装、拆卸和后期维护工作。模块电机定子如图1所示。模块定子结构如图1a所示。模块组合式永磁电机的绕组与常规电机定子绕组的区别在于,定子模块中的绕组跨距不是一种,而是采用大小两种跨距相结合的不等跨距绕组,如图1b所示。不等跨距绕组中的小跨距线圈与普通绕组一致,而在一个单元电机末端的线圈不再继续顺着原方向继续下线,而是反方向与单元电机的另一端进行连接,与常规双层绕组线圈相比,大跨距绕组只是改变了绕组端部的连接方式,而绕组在槽中有效部分的排布情况与常规双层绕组是一致的,不会改变电机内部的机电能量转换。因此,一个单元电机内的三相绕组不会跨在其他单元定子的铁心上,使得各个定子单元模块可相互独立。

图1 模块电机定子
Fig.1 Geometric diagram of modular stator
每个定子模块都有一套三相绕组,整台电机有多套三相绕组,各个定子模块的三相绕组不与其他模块的三相绕组相连。采用不等跨距绕组相结合的方式,通过大跨距线圈反向嵌放实现每个定子模块中的三相绕组结构上完全独立,绕组在控制上也是相互独立的,每个定子模块都有独立的变频器控制,实现了各定子模块机械与电气互相解耦,控制系统如图2所示。当某定子模块发生故障时,切除故障模块,其余定子模块可以继续工作,同时可增加非故障定子模块绕组中的电流,来维持总输出转矩不变,保证了系统的可靠性,因此模块组合式永磁电机有着良好的容错性。模块组合式永磁电机在容错状态下运行时,磁场会出现不对称分布和严重的饱和现象,因此需要准确地计算电机的磁场。

图2 模块组合式永磁电机控制系统
Fig.2 Control system of modular combined permanent magnet motor
解析模型能够考虑铁心材料非线性的原理是线性铁心槽边界上的等效电流产生的磁动势等于非线性铁心上的磁压降。解析模型的等效变换如图3所示。通常电机设计时,定子饱和程度明显,转子饱和程度不严重,因此只在定子槽边界上施加等效电流片。因此,图3a中的非线性定子铁心等效成图3b中定子槽边界带有等效电流片的线性铁心。

图3 解析模型的等效变换
Fig.3 Equivalent transformation of analytical model
如图3中所示,解析模型在二维极坐标系下,Rsb、Rs、Rm、Rr分别为定子槽底半径、定子内表面半径、永磁体外表面半径、永磁体内表面半径,Ji1、Ji2、和Ji3分别为第i个槽两边和底边的等效电流片密度。绕组排布如图4所示。图中,Jami1和Jami2为电枢绕组两侧的电流密度,bsa为槽宽角,d为绕组线圈角度。

图4 绕组排布
Fig.4 Winding layout
改进子域模型与传统解析模型的区别在于,改进子域模型定子槽的边界条件径向或切向磁场强度不为零,而是用等效电流密度代替,用来等效定子齿部和轭部非线性铁心上的磁压降。改进子域解析模型的铁心变为线性,这与传统解析模型中假设铁心磁导率无穷大是一致的。改进子域模型的其他基本假设与传统解析模型的基本假设相同,这里不再赘述。由于定子槽边界条件发生变化,矢量磁位解析表达式需要重新推导。改进子域模型各个子域矢量磁位和磁通密度的解析表达式如下。
1)定子槽子域通解
改进定子槽子域的边界条件用等效电流密度表示为
 (1)
(1)
 (2)
(2)
 (3)
(3)
式中,ai为第i个槽中心位置。
通过求解在定子槽子域建立的泊松方程,可以得到该子域矢量磁位的通解为
 (4)
(4)
其中

 (5)
(5)
 (6)
(6)
其中
 (7)
(7)
 (8)
(8)
 (9)
(9)
 (10)
(10)
 (11)
(11)
 (12)
(12)
式中,Q3i和B3n为待定求解系数;m0为真空磁导率。
得到矢量磁位解析解后,该子域的径向和切向磁通密度表达式分别为
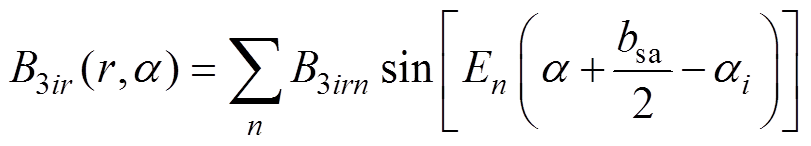 (13)
(13)
 (14)
(14)
其中
 (15)
(15)

 (16)
(16)
 (17)
(17)
2)永磁体子域和气隙子域通解
改进子域模型的永磁体子域和气隙子域与传统子域模型矢量磁位表达式相同,通解表达式分别为
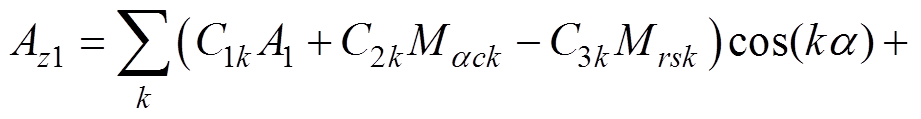
 (18)
(18)
 (19)
(19)
永磁体子域和气隙子域径向磁通密度表达式分别为
 (20)
(20)

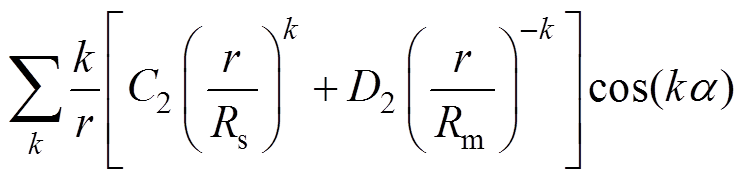 (21)
(21)
切向磁通密度表达式分别为
 (22)
(22)

 (23)
(23)
式中,A1、C1、A2、B2、C2和D2为谐波系数,可由各子域相连处的边界条件确定;C1k、C2k、C3k、C4k、C5k、C6k、Mask、Mack、Mrsk和Mrck为已知参数,详细推导过程本文不再详述。
3)边界条件联立
为求解各子域通解表达式中的未知系数,需要联立相邻子域的边界条件。根据磁场中径向磁通密度连续性和切向磁场强度连续性,有
 (24)
(24)
 (25)
(25)
 (26)
(26)
 (27)
(27)
 (28)
(28)
通过联立以上方程组,便可得到各个子域矢量磁位表达式中的谐波系数[15-16]。
铁心的非线性磁阻需要在等效磁网络模型中计算。改进子域模型中的磁场解析表达式已经得到,而定子槽边界条件等效电流密度,可由等效磁网络法中各个节点的磁动势计算。在等效磁网络模型中,根据饱和程度以及计算精度的要求,定子齿部和轭部可以分别划分成任意数量的等效磁导。本文将周向上每个定子齿部和轭部都划分为两个等效磁导。由于模块组合式永磁电机相邻的定子模块之间存在装配气隙,与传统永磁电机的定子磁网络模型发生改变,考虑定子模块间气隙的第i个槽的定子等效磁路模型如图5所示,图中,Gt为常规齿磁导,Gtm为装配齿磁导,Gy为常规轭磁导,Gym为装配轭磁导,Gat为装配气隙切向磁导,Gar为装配气隙径向磁导。

图5 定子等效磁路模型
Fig.5 Equivalent magnetic circuit of stator
改进子域解析法求解完成后,可得到各个子域的径向磁通密度和切向磁通密度。通过积分运算,得到等效磁网络模型中各个磁通源的数值。再根据基尔霍夫电流定律,便可计算出等效磁网络模型中每个定子铁心支路的磁通,根据铁磁材料B-H曲线,进行插值迭代运算得到每个定子铁心支路的相对磁导率,再由电机的几何尺寸,就可得到等效磁网络模型的磁导矩阵。各个节点的磁动势计算公式为
 (29)
(29)
式中,V为矢量磁位矩阵; 为磁通源矩阵;G为磁导矩阵。
为磁通源矩阵;G为磁导矩阵。
得到等效磁网络模型中各个节点的磁动势后,第i个槽边界上的等效电流密度分别为
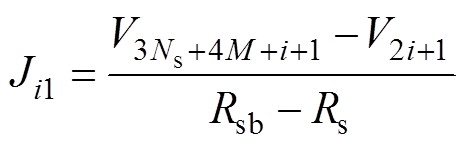 (30)
(30)
 (31)
(31)
 (32)
(32)
式中,Rsb-Rs和Rsbbsa分别为定子单个齿部和轭部的长度。
在非线性混合磁场解析模型中,等效电流密度作为改进子域模型中槽的边界条件,其数值大小需要在等效磁网络法中求得,而等效磁网络模型中的磁通源是通过改进子域解析法计算得到,因此将两种磁场解析法相结合,需要迭代算法来计算非线性混合模型的收敛解。非线性混合模型磁场计算流程如图6所示。

图6 非线性混合模型计算流程
Fig.6 Flow chart of hybrid model for calculation
本文以一台30极72槽三定子模块内转子表贴式永磁电机为例,采用本文建立的非线性混合解析模型进行磁场计算,表1给出了永磁电机的主要设计参数。
表1 模块组合式永磁电机主要设计参数
Tab.1 The main design parameters of modular combined permanent-magnet motor
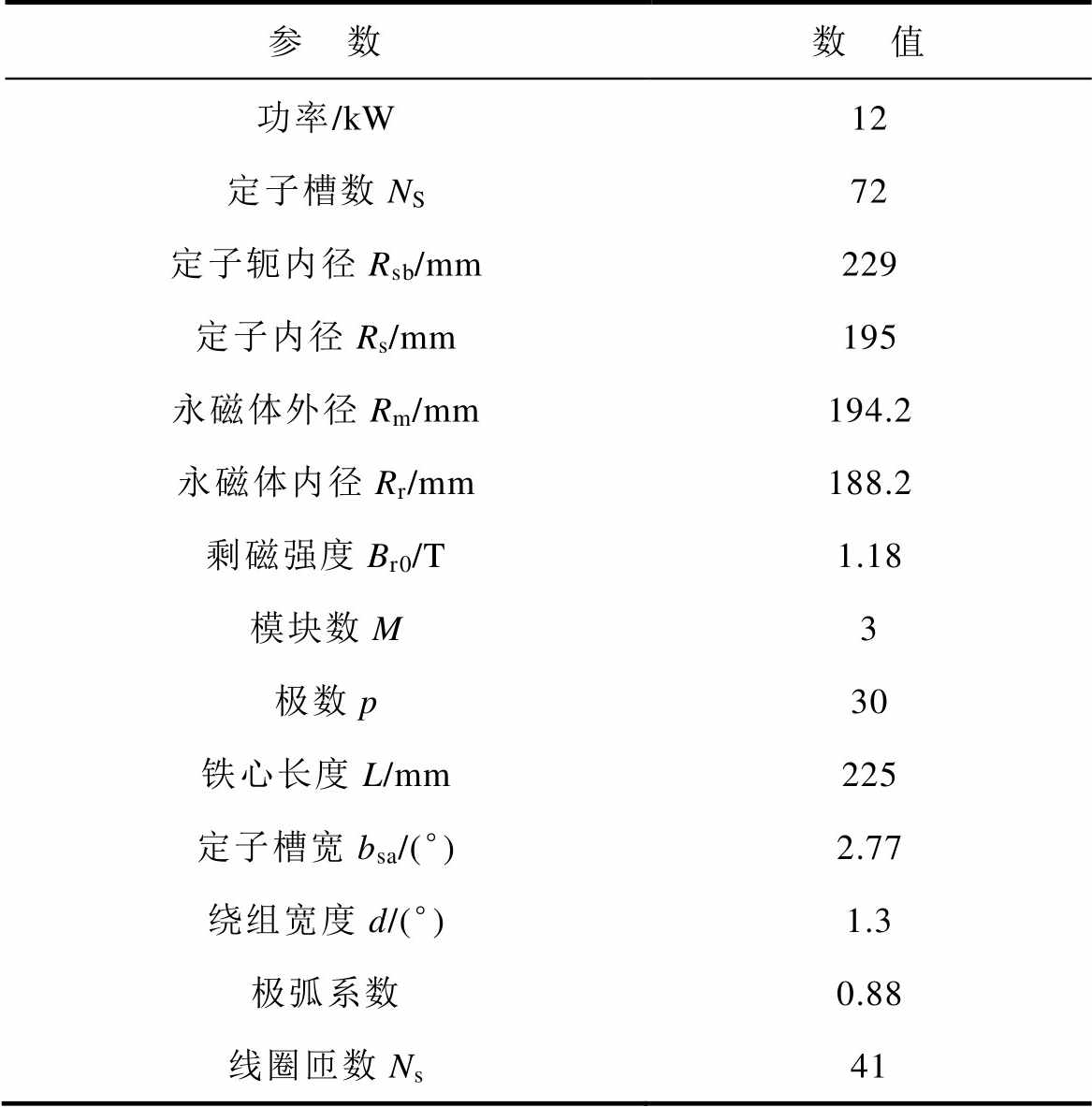
参 数数 值 功率/kW12 定子槽数NS72 定子轭内径Rsb/mm229 定子内径Rs/mm195 永磁体外径Rm/mm194.2 永磁体内径Rr/mm188.2 剩磁强度Br0/T1.18 模块数M3 极数p30 铁心长度L/mm225 定子槽宽bsa/(°)2.77 绕组宽度d/(°)1.3 极弧系数0.88 线圈匝数Ns41
为验证本文建立的考虑非线性效应的混合磁场解析模型的正确性,利用有限元计算结果进行比较。有限元仿真磁通密度云图如图7所示,其中Ⅰ区、Ⅱ区和Ⅲ区分别代表定子3个单元模块,Ⅰ区通入额定电流、Ⅱ区通入1.5倍额定电流和Ⅲ区通入3倍额定电流。由于故障定子模块造成转矩缺失,可加大非故障定子模块电流维持额定输出转矩恒定,不同数量定子模块投入运行时电流需要加大相应的倍数,图7反映出三种情况下模块定子的磁场分布情况。
图8给出传统子域法、非线性混合磁场解析法和有限元法这三种计算方法下,气隙平均半径处的负载磁场气隙磁感应强度径向分量和切向分量的波形。从图8中可以看出,非线性混合磁场解析结果和有限元结果吻合度较好,传统子域法由于没有考虑铁心非线性磁阻,所以计算结果相比其他两种方法的计算结果偏高。三种计算方法下的径向磁通密度有效值分别为0.865T、0.84T和0.83T,切向磁通密度有效值分别为0.268T、0.256T和0.252T。和有限元仿真结果相比,传统解析法计算的径向和切向磁通密度有效值误差分别为3.0%和4.7%,本文建立的非线性混合磁场解析模型计算的径向和切向磁通密度有效值的误差仅为1.2%和1.6%。

图7 负载磁通密度云图
Fig.7 Flux density distribution under load conditions

图8 负载径向和切向气隙磁通密度
Fig.8 Radial and tangential components of air-gap on-load magnetic flux density
空载反电动势是永磁电机设计过程中非常重要的一个参数指标,需要合理地设计其值大小,所以准确地计算十分关键。由于本文采用的非线性混合磁场解析模型和有限元仿真模型都是基于2D模型,没有考虑端部漏磁对模块组合式永磁电机三相空载反电动势的影响差异。图9给出了传统子域法、非线性混合磁场解析法和有限元法这三种计算方法下,模块组合式永磁电机相空载反电动势波形。三种计算方法的空载反电动势有效值分别为225.1V、218V和219.5V。传统子域法和混合磁场解析法的计算结果与有限元仿真结果相比,有效值误差分别为2.55%和0.68%,进一步验证了混合磁场解析模型的准确性。

图9 相空载反电动势
Fig.9 Phase no-load back EMF
电磁转矩是衡量电机性能的重要指标。在磁场解析计算完成后,得到电机气隙的径向磁通密度和切向磁通密度分布,积分路径选择气隙平均半径位置,然后采用麦克斯韦张量法对电磁转矩进行计算。图10为电磁转矩。传统解析法、混合磁场解析法和有限元计算结果的平均转矩分别1 231N·m、1 157.9N·m和1 170.5N·m。混合磁场解析计算结果与有限元仿真结果曲线吻合度较高,进一步验证了该方法的正确性。传统解析法假设磁导率为无穷大,由于高磁导率低磁阻特性,解析结果整体偏大,同时转矩波动更平稳。

图10 电磁转矩
Fig.10 Electromagnetic torque
当3个模块运行时,每个定子模块通入额定电流为额定运行状态。当一个定子模块出现故障时,只有两个定子模块运行,如果这个两个定子模块继续额定运行,此时输出转矩为额定转矩的2/3,为了正常输出额定转矩,运行的两个定子模块需要输入1.5倍额定电流。当两个定子模块出现故障时,只有一个定子模块运行,如果此定子模块继续额定运行,此时输出转矩为额定转矩的1/3,为了正常输出额定转矩,运行的一个定子模块需要输入3倍额定电流。但由于饱和效应,这两种故障运行状态的电磁特性会发生变化。本节根据模块组合式永磁电机的结构与运行特点,将重点分析模块组合式永磁电机在不对称运行状态下的电磁特性。
图11给出了传统子域法、非线性混合磁场解析法和有限元法这三种计算方法下,一个定子模块的电枢绕组分别通入额定电流、1.5倍额定电流和3倍额定电流时,气隙平均半径处的负载磁场气隙磁通密度径向分量和切向分量的有效值。

图11 不同电流时径向和切向负载气隙磁通密度
Fig.11 Radial and tangential components of air-gap on-load magnetic flux density varied with current
从图11中可以看出,相比于电枢绕组通入额定电流时的负载磁场,电枢绕组通入1.5倍额定电流时,在三种计算方法下,径向磁通密度有效值分别增加1.62%、1.33%和1.2%,切向磁通密度有效值分别增加1.5%、0.79%和1.1%。电枢绕组通入3倍额定电流时,在三种计算方法下,径向磁通密度有效值分别增加3.93%、1.81%和1.67%,切向磁通密度有效值分别增加11.9%、6.35%和7%。随着电枢电流的增加,径向磁通密度有效值增加不明显,切向磁通密度有效值显著增加。这是由于表贴式永磁电机采用Id=0的控制方式,电枢电流都是交轴分量。
电枢绕组中通入1.5倍额定电流时,传统子域法和混合磁场解析法与有限元法计算的径向磁通密度有效值误差分别为3.4%和1.3%,切向磁通密度有效值误差分别为5%和1.9%。电枢绕组中通入3倍额定电流时,传统子域法和混合磁场解析法与有限元法计算的径向磁通密度有效值误差分别为5.3%和1.1%,切向磁通密度有效值误差分别为9.4%和2.2%。传统子域解析模型假设铁心磁导率无穷大,忽略铁心的非线性磁阻,因此传统子域法与有限元法的计算结果相比,随着磁场饱和度的增加,计算结果误差会越来越大。混合磁场解析计算结果与有限元仿真结果的误差并不会随着饱和程度的增加而变大,验证了混合磁场解析模型能够充分考虑电机严重饱和时铁心的非线性效应。
由于模块组合式永磁电机的各个定子可以独立控制,当某个定子模块发生故障时,可以切除故障定子模块,其他定子模块可继续正常运行,并且非故障定子模块可以加大电流运行,来补偿故障定子模块造成的转矩缺失,维持输出转矩恒定,保证系统稳定可靠的运行。非故障定子模块绕组电流的增加会导致电机饱和程度更为严重,因此需要研究不同运行状态下的转矩特性。
图12给出模块组合式永磁电机在两种故障状态运行时的转矩波形,分别为两个定子模块绕组通入1.5倍额定电流运行和一个定子模块绕组通入3倍额定电流运行,采用传统磁场解析法、非线性混合磁场解析法和有限元法三种计算方法进行转矩波形对比。采用传统解析法计算这两种运行状态下的平均转矩都是1 231N·m,这与3.4节计算额定状态运行下的结果是一致的,传统子域法由于忽略铁心磁阻的影响,计算结果偏高,并且三种工况下的传统子域解析计算的转矩波形完全一致,也证明了传统解析法无法考虑饱和对电磁转矩的影响。从图12中可以看出,非线性解析结果与有限元结果吻合度较高。混合磁场解析法计算的电机两种故障状态运行时的平均转矩分别为1 145.2N·m和1 090.7N·m,相比于额定转矩,平均转矩分别下降了1.1%和5.8%。转矩下降是由于电流增加引起饱和程度更严重。当不同数量定子模块投入运行时,为维持额定输出转矩恒定,投入运行的定子模块数量越少,需要的电流就会越大,随着饱和程度的增加,平均电磁转矩下降的就会越多。
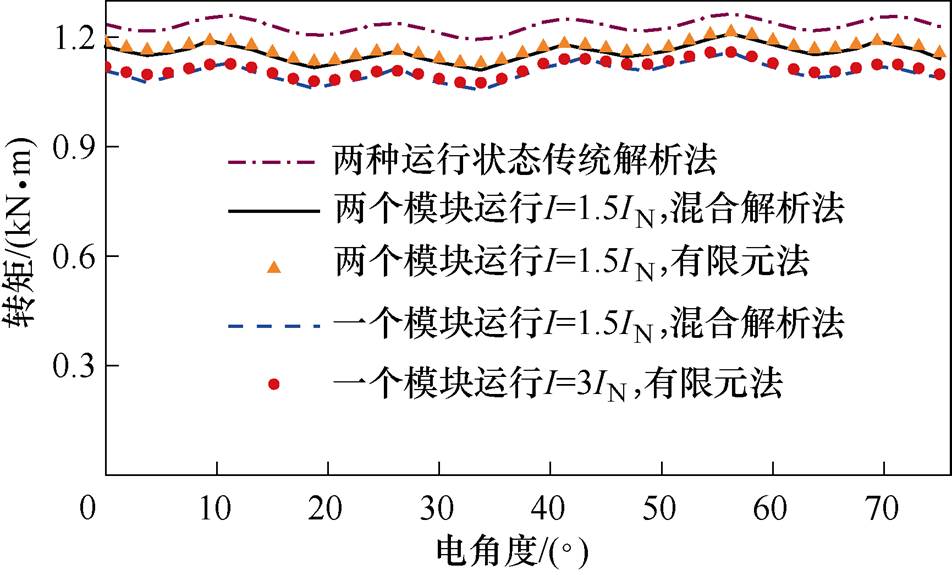
图12 电磁转矩
Fig.12 Electromagnetic torque
考虑到磁场饱和的影响,为了保证额定输出转矩不变,根据投入运行定子模块的数量,仅线性地增加输入电流是无法满足输出转矩恒定的,因此需要准确地计算出不同数量定子模块投入运行输出额定转矩时,需要的电流值大小。基于非线性混合磁场解析模型,利用迭代算法,可计算不同数量定子模块运行输出额定转矩时,定子需要电流值的大小。图13给出了电流预测流程。

图13 不同数量定子模块运行时电流预测流程
Fig.13 Flow chart for current prediction of different number modular stators in operation
为了验证本文建立的非线性混合磁场解析模型的正确性,设计并制作了一台30极72槽三定子模块组合式表贴永磁同步电机,定子结构如图14所示。搭建了实验平台,对样机的空载反电动势进行了测试,实验测试平台如图15所示。
由于模块组合式永磁电机多个定子模块中的绕组相互独立的特点,当测试电机的相空载反电动势时,无需采用反拖法,可以给一个或者两个定子模块通电在额定转速下空载运行,在未通电的定子模块绕组测试即可,样机空载反电动势测试如图16所示,功率分析仪测试的相空载反电动势波形与非线性混合磁场解析计算结果吻合度很好,解析法计算结果有效值为218V,实验测试的空载反电动势有效值的三相平均值为215.7V,误差仅为1.1%。由于二维磁场解析模型没有考虑电机的端部效应,所以计算结果会比实验结果偏大一点。

图14 样机定子结构
Fig.14 Stator of prototype machine

图15 实验测试平台
Fig.15 Experimental platform

图16 样机空载反电动势测试
Fig.16 No-load back measurement of prototype machine
图17给出混合解析法和实验测试在不同数量定子模块投入运行时,转矩随电流的变化曲线。混合解析法计算结果和实验数据吻合度较好,验证了该文提出混合解析模型的正确性。

图17 转矩随电流变化
Fig.17 Torque varied with current
本文基于子域法和等效磁网络法,建立了一种模块组合式永磁电机非线性混合磁场解析模型,解决了传统解析法无法考虑铁心磁导率的问题。通过在线性子域模型中施加等效电流密度边界条件,考虑了铁心非线性磁导。等效电流密度的大小在等效磁网络法中计算,等效磁网络法中的磁通源在子域法中获取。等效磁网络模型中考虑了模块间的装配气隙。根据铁心材料非线性的B-H曲线,通过插值计算得到每个定子模块不同位置处的相对磁导率。基于混合解析模型计算了电机的电磁特性,有限元仿真和实验验证了混合解析法比传统子域法有更好的准确性。在此基础上,重点分析了模块组合式永磁电机在不对称运行状态下的电磁特性,给出不同数量定子模块运行时需要的电流预测方法,电机在严重饱和时,非线性混合磁场解析解结果与有限元结果十分吻合。本文为永磁电机磁场的准确计算提供了一种精确而快速的计算方法。
参考文献
[1] 张炳义, 贾宇琪, 冯桂宏. 新型模块组合式定子永磁电机[J]. 电工技术学报, 2015, 30(12): 243-252.
Zhang Bingyi, Jia Yuqi, Feng Guihong. Novel permanent magnet synchronous machines with modules combination stator[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 243-252.
[2] Xu Yingying, Zhang Bingyi, Feng Guihong. Analysis of unwinding stator module combined permanent magnet synchronous machine[J]. IEEE Access, 8: 191901-191909.
[3] Zhang Bingyi, Gan Baoping, Li Qiaoshan. Analysis of a fault-tolerant module-combined stator permanent magnet synchronous machine[J]. IEEE Access, 8: 70438-70452.
[4] 郭凯凯, 郭有光. 磁通反向直线旋转永磁电机三维非线性等效磁路模型分析[J]. 电工技术学报, 2020, 35(20): 4278-4286.
Guo Kaikai, Guo Youguang. 3D nonlinear equivalent magnetic circuit model analysis of a flux reversal linear rotary permanent magnet machine[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(20): 4278-4286.
[5] 张淦, 花为, 程明, 等. 磁通切换型永磁电机非线性磁网络分析[J]. 电工技术学报, 2015, 30(2): 34-42.
Zhang Gan, Hua Wei, Cheng Ming, et al. Analysis of nonlinear magnetic network models for flux- switching permanent magnet machines[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(2): 34-42.
[6] Hafner M, Franck D, Hameyer K. Static electro- magnetic field computation by conformal mapping in permanent magnet synchronous machines[J]. IEEE Transactions on Magnetics, 2010, 46(8): 3105-3108.
[7] Ko Y Y, Song J Y, Seo M K, et al. Analytical method for overhang effect of surface-mounted permanent- magnet motor using conformal mapping[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.
[8] 王明杰, 徐伟, 杨存祥, 等. 基于精确子域模型的永磁直线同步电机空载磁场解析计算[J]. 电工技术学报, 2020, 35(5): 942-953.
Wang Mingjie, Xu Wei, Yang Cunxiang, et al. Analytical calculation of no-load magnetic field in permanent magnet linear synchronous motors based on an accurate subdomain model[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 942- 953.
[9] 张守首, 郭思源. 考虑分段斜极和磁性槽楔的永磁同步电机磁场解析方法[J]. 电工技术学报, 2019, 34(1): 11-22.
Zhang Shoushou, Guo Siyuan. Analytical magnetic field method of permanent magnet synchronous machine considering step-skewed magnets and magnetic slot wedge[J]. Transactions of China Elec- trotechnical Society, 2019, 34(1): 11-22.
[10] Zhu Minchen, Wu Lijian, Fang Youtong, et al. Subdomain model for predicting armature reaction field of dual-stator consequent-pole PM machines accounting for tooth-tips[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(2): 143- 150.
[11] 杨定伟, 邓兆祥, 张河山, 等. 永磁轮毂电机磁场解析建模[J]. 电工技术学报, 2019, 34(7): 1423- 1433.
Yang Dingwei, Deng Zhaoxiang, Zhang Heshan, et al. Exact analytical solution of magnetic field in permanent magnet in-wheel motor[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1423- 1433.
[12] Djelloul-Khedda Z, Boughrara K, Dubas F, et al. Nonlinear analytical prediction of magnetic field and electromagnetic performances in switched reluctance machines[J]. IEEE Transactions on Magnetics, 2017, 53(7): 1-11.
[13] Hanic A, Zarko D, Kuhinek D, et al. On-load analysis of saturated surface permanent magnet machines using conformal mapping and magnetic equivalent circuits[J]. IEEE Transactions on Energy Conversion, 2018, 33(3): 915-924.
[14] 于占洋, 李岩, 井永腾, 等. 基于混合磁场解析法的磁极偏心型表贴式永磁同步电机空载特性分析[J]. 电工技术学报, 2020, 35(18): 3811-3820.
Yu Zhanyang, Li Yan, Jing Yongteng, et al. No-load characteristic analysis of surface-mounted permanent magnet synchronous motor with non-concentric pole based on hybrid magnetic field analysis method[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3811-3820.
[15] Wu Lijian, Yin Hao, Wang Dong, et al. A nonlinear subdomain and magnetic circuit hybrid model for open-circuit field prediction in surface-mounted PM machines[J]. IEEE Transactions on Energy Con- version, 2019, 34(3): 1485-1495.
[16] Wu Lijian, Yin Hao, Wang Dong, et al. On-load field prediction in SPM machines by a subdomain and magnetic circuit hybrid model[J]. IEEE Transactions on Industrial Electronics, 2020, 67(9): 7190-7201.
Analytical Prediction of Magnetic Field in Modular Combined Permanent Magnet Motor by a Nonlinear Hybrid Model
Abstract This paper proposes a nonlinear subdomain and equivalent magnetic network hybrid analytical model for electromagnetic performance calculation in modular combined permanent-magnet machines (MCPMM). The nonlinear analytical model can be transformed into a linear subdomain model considering saturation effect with equivalent current densities on the boundary of the slots. The values of equivalent current densities are obtained by the equivalent magnetic network and used as boundary conditions in subdomain model, and the flux sources flowing to the equivalent magnetic network are calculated by the subdomain model. An iteration process is needed between the two analytical models. The air gap between adjacent modules is considered in the equivalent magnetic network model. The nonlinear hybrid model can accurately calculate the air gap flux density, no-load back EMF and torque. The electromagnetic characteristics of modular permanent magnet motor under asymmetric conditions are analyzed. The finite element results and experimental test verify the proposed nonlinear analytical method.
keywords:Analytical prediction, magnetic field, modular combined permanent magnet motor (MCPMM), hybrid model
DOI: 10.19595/j.cnki.1000-6753.tces.210691
中图分类号:TM351
收稿日期 2021-05-18
改稿日期 2021-06-16
刘云飞 男,1991年生,博士研究生,研究方向为特种电机设计及其控制。E-mail: 441514626@qq.com
张炳义 男,1954年生,教授,博士生导师,研究方向为电子-电气-机械一体化低速大转矩无齿轮传动系统的理论与技术。E-mail: 1392326904@qq.com(通信作者)
(编辑 崔文静)