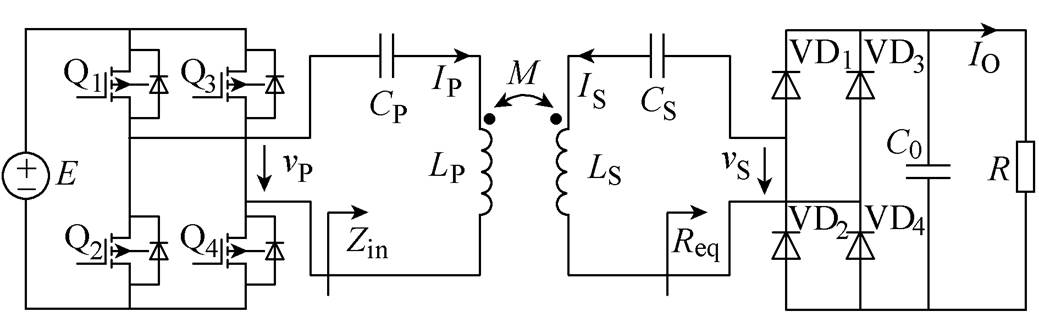
图1 采用SS补偿拓扑的DWPT系统电路
Fig.1 The SS compensated topology for DWPT
摘要 在自动导引车的动态无线电能传输(DWPT)系统中,由于载重变化导致的接收端高度变化是不可避免的。这会造成系统线圈参数(自感和互感)改变,进而影响系统增益平稳。为了在DWPT系统接收端发生垂直偏移时保证系统增益平稳,该文基于串联串联(SS)拓扑提出一种考虑线圈参数变化的补偿拓扑参数设计方法。通过建立考虑线圈参数变化的SS拓扑等效环路模型,分析系统增益与补偿参数的关系,确定补偿拓扑参数设计的约束条件与解空间范围。设计以输出电流增益平稳性与效率为目标的优化函数,基于粒子群优化算法提出一种SS拓扑补偿参数设计方法。所提方法在系统线圈参数变化的条件下,实现输出电流的稳定,且保有较高的效率。最后,搭建一套1kW的原理样机用于验证所提方法的有效性。实验结果表明:在设定的高度变化范围(20~80mm)内,耦合机构自感增加19.1mH、45.22mH,互感增加至2.4倍,系统输出电流最大波动率仅为3.55%,最高效率达96.52%。
关键词:动态无线电能传输 线圈参数变化 参数设计 平稳输出 粒子群优化算法
动态无线电能传输(Dynamic Wireless Power Transfer, DWPT)技术能够将电能以非接触的方式通过电磁耦合传输给用电设备[1-2],与传统有线插拔系统相比,DWPT系统供电灵活,能减轻用电设备的电池质量,增加移动用电设备运行里程[3]。近年来,DWPT技术已广泛应用在自动导航牵引车(Auto- matic Guided Vehicles, AGVs)[4-5]、电动汽车[6]以及轨道交通[7]等领域。
AGVs具有高精度循迹跟踪能力[8],但当车辆装载不同质量的货物时,由于轮胎与减振弹簧形变等原因,车身的垂直振动是不可避免的。当使用DWPT系统为AGVs供电时,由于安装在车身底盘的接收线圈垂直振动,易引起DWPT系统的传输增益波动,存在过电流/过电压等风险。
为了保证DWPT系统在一定耦合系数范围内输出相对平稳,现有方法主要集中于控制策略[9-11]、耦合机构设计[12-13]和补偿拓扑参数设计[14-15]三个方面。
常见的控制策略主要在系统发射端或接收端级联DC-DC变换器[9-10],或者通过移相控制调节逆变器输出电压[11]等。但控制系统对接收端反馈信号的检测精度及实时性都有较高要求,且对控制裕度要求较高[16]。为了减缓控制压力,简化DWPT系统控制复杂度,有学者提出耦合机构设计方法[12-13],分别从优化发射、接收线圈结构两个方面着手,以降低系统偏移过程中的互感变化。如韩国科学技术院提出了I型[12]、S型[13]两种发射线圈阵列结构,有效地增大了耦合机构互感及抗偏移能力。但耦合机构设计方法通常仅对接收线圈水平偏移导致的互感变化具有较好的抑制效果,且会增加耦合机构成本。进一步地,有学者提出补偿拓扑参数设计方法。如华中科技大学通过设计耦合系数不敏感(Coupling- Insensitive, CI)拓扑提出了基于X型拓扑[17]、T型拓扑[18]、LCC[14]拓扑和SS[15,19]拓扑的参数设计方法,在耦合系数变化200%的范围内,输出功率仅下降不超过20%。哈尔滨工业大学基于粒子群优化(Particle Swarm Optimization, PSO)算法提出了一种S/CLC拓扑参数设计方法,在耦合系数变化200%的条件下,输出电压变化率仅为6.21%[20]。目前,已有的补偿拓扑参数设计方法更加适用于线圈自感不变或者微小变化的情况,若线圈自感存在较大变化,已有的设计方法可能不再适用。
在DWPT系统的实际应用中,常使用铁氧体磁心增强耦合系数,同时减少漏磁,但这也使得线圈自感、互感变得更为敏感,尤其是当系统接收线圈高度发生变化时[21]。而目前已有的补偿拓扑参数设计方法缺乏对线圈自感、互感同时变化问题的讨论,因此研究考虑线圈参数(自感、互感)变化的补偿拓扑参数设计方法具有重要意义。
本文分析了考虑线圈参数变化的SS拓扑电路,得出了DWPT系统线圈参数变化过程中线圈自感、互感和接收线圈高度的关系,并建立系统传输增益模型。在此基础上,通过建立等效环路模型,分析系统传输增益与补偿参数的关系,确定了补偿拓扑参数设计的约束条件与解空间范围。最后,设计了以传输增益平稳性与效率为目标的优化函数,基于PSO算法提出了一种考虑线圈参数变化的SS型DWPT系统补偿拓扑参数优化设计方法。在接收线圈高度变化过程中,互感与自感发生变化时,系统输出电流增益仍然保持平稳,且保有较高的系统效率。所提方法简化了系统的控制复杂度,降低了系统输出对线圈参数的敏感性。最后,设计并搭建了1kW实验原理样机,验证了理论分析的正确性和可行性。
采用SS补偿拓扑的DWPT系统电路如图1所示。图1中,E为输入直流电压,vP为逆变器输出电压,vS为整流器输入电压,IP为发射线圈电流,IS为接收线圈电流,IO为流经负载R的电流。Req为系统交流侧等效负载,Zin为系统输入阻抗。LP、LS分别为发射线圈、接收线圈自感,M为发射线圈与接收线圈之间的互感,CP、CS分别为原、副边补偿电容。

图1 采用SS补偿拓扑的DWPT系统电路
Fig.1 The SS compensated topology for DWPT
使用基波等效分析法对电路进行简化,等效电路如图2所示,ZP、ZS分别为原、副边补偿电容等效阻抗,即
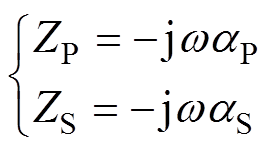 (1)
(1)
其中
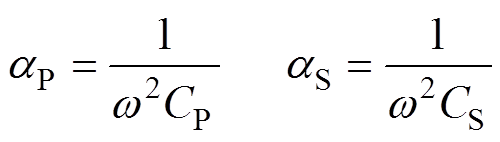
式中,w 为逆变器的工作角频率。
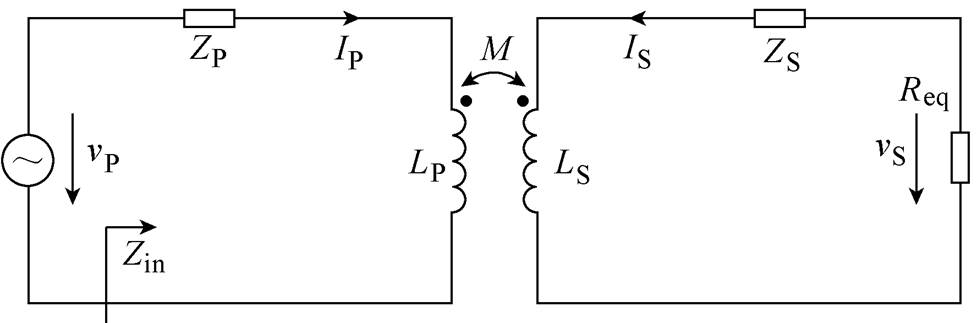
图2 SS拓扑等效电路
Fig.2 The equivalent circuit of SS compensated topology
图2中
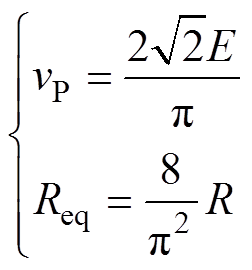 (2)
(2)
根据基尔霍夫电压定律,解得发射线圈电流IP、接收线圈电流IS分别为
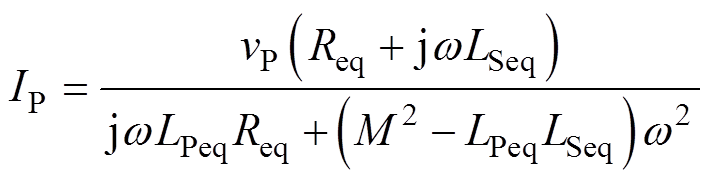 (3)
(3)
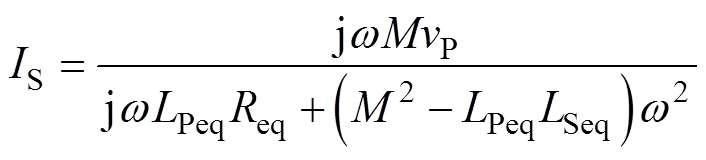 (4)
(4)
其中
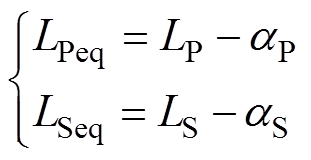 (5)
(5)
系统的输入阻抗Zin为
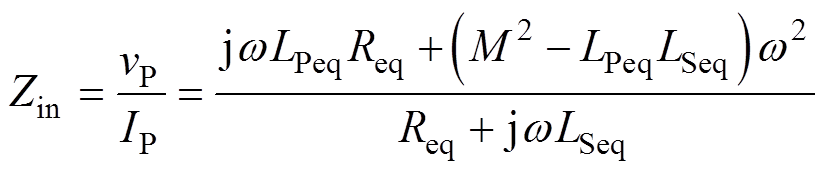 (6)
(6)
根据式(6),系统的输入阻抗角q 为
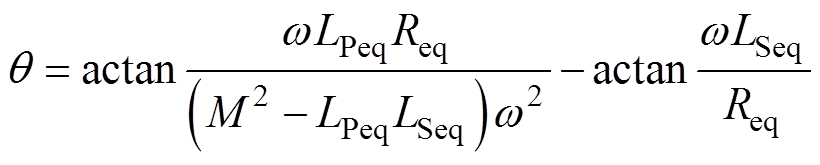 (7)
(7)
系统的输出电流增益G为
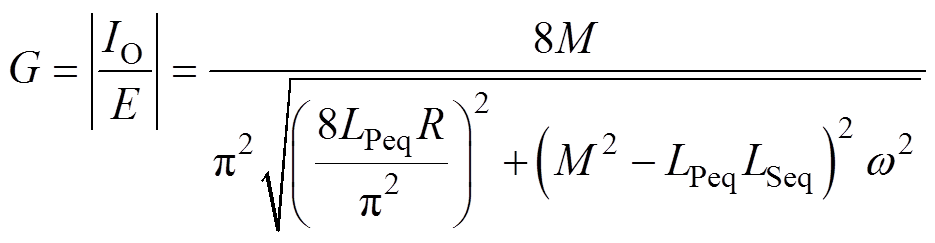 (8)
(8)
1.2.1 线圈参数变化下稳定电流增益约束条件
DWPT系统耦合机构示意图与线圈参数变化趋势如图3所示,本文采用长导轨结构。磁心厚度d= 10mm,发射线圈长lP=1 500mm,宽wP=300mm;接收线圈长lS、宽wS均为300mm。对于DWPT系统的长导轨耦合机构,其发射线圈通常长达几米甚至几十米[22]。当接收线圈在工作区域内(未包含导轨边缘)相同高度下沿轨道方向移动时,线圈参数几乎是恒定的[23]。然而当接收线圈高度h(气隙)发生变化时,因为耦合机构中铁氧体磁心的存在,系统发射线圈自感LP、接收线圈自感LS与互感M均会发生变化[21],其中,互感M的变化更为显著。本文将接收线圈工作区域定义为长lwork=1 000mm,宽wwork=300mm,高hwork=80mm的矩形空间,线圈参数变化范围分别定义为[LPmin, LPmax]、[LSmin,LSmax]和[Mmin, Mmax]。
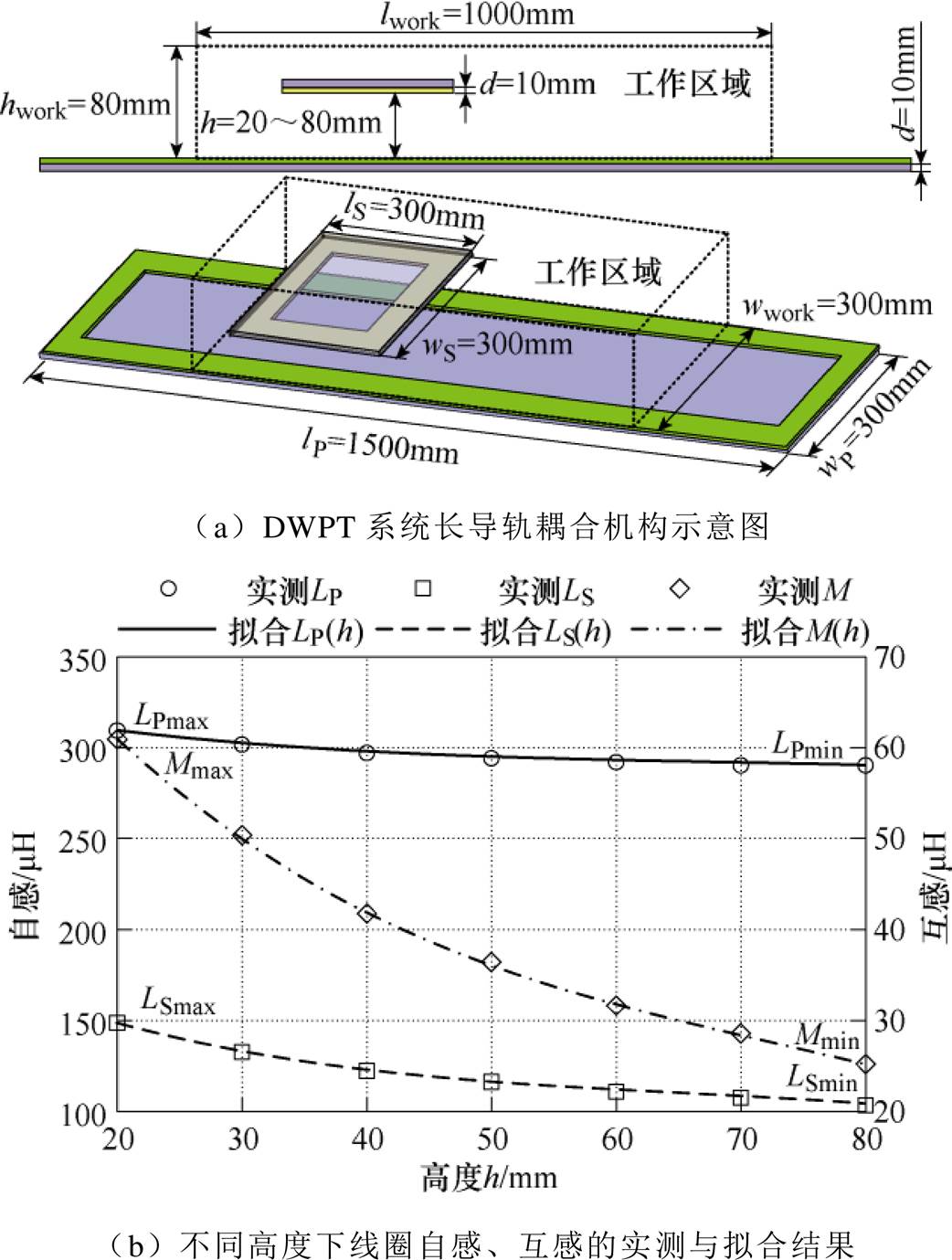
图3 DWPT系统耦合机构示意图与线圈参数
Fig.3 The coupling mechanism diagram and coils’ parameters of DWPT system
在任意确定高度范围内,接收线圈高度h、发射线圈自感LP、接收线圈自感LS和互感M可借助数学工具进行多项式拟合,实现多变量的归一化处理,简化分析过程。其中,多项式次数n小于采样样本数m,其取值主要取决于拟合优度R2与计算复杂度。多项式拟合公式与拟合优度R2分别为
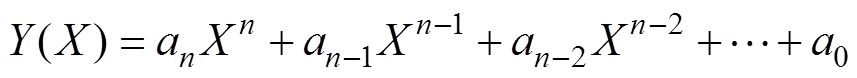 (9)
(9)
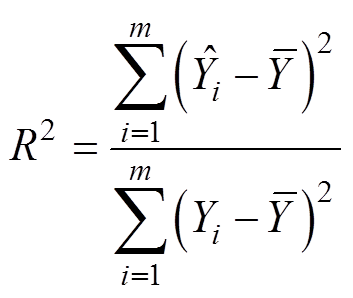 (10)
(10)
式中, 为拟合值;
为拟合值;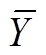 为均值;
为均值;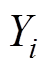 为实际值。对于任意拟合函数Y(X),其拟合优度R2的值越接近1,则其函数拟合度越好。以如图3a所示原、副边均为10匝利兹线圈(线径4.2mm)的DWPT系统长导轨耦合机构为例,其线圈实测参数与拟合结果如图3b所示。拟合函数LP(h)、LS(h)、M(h)的拟合优度分别为0.999 3、0.999 7、0.999 7,拟合度良好。
为实际值。对于任意拟合函数Y(X),其拟合优度R2的值越接近1,则其函数拟合度越好。以如图3a所示原、副边均为10匝利兹线圈(线径4.2mm)的DWPT系统长导轨耦合机构为例,其线圈实测参数与拟合结果如图3b所示。拟合函数LP(h)、LS(h)、M(h)的拟合优度分别为0.999 3、0.999 7、0.999 7,拟合度良好。
当原边完全谐振,即LPeq=0时,对于式(8),有
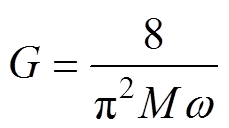 (11)
(11)
此时系统增益仅与互感M有关,系统设计自由度不足且不具备稳定传输能力。则aP的取值应满足
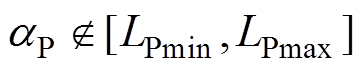 (12)
(12)
为进一步简化分析,根据戴维南定理,图2所示电路可以简化为图4所示等效环路模型。其中
 (13)
(13)
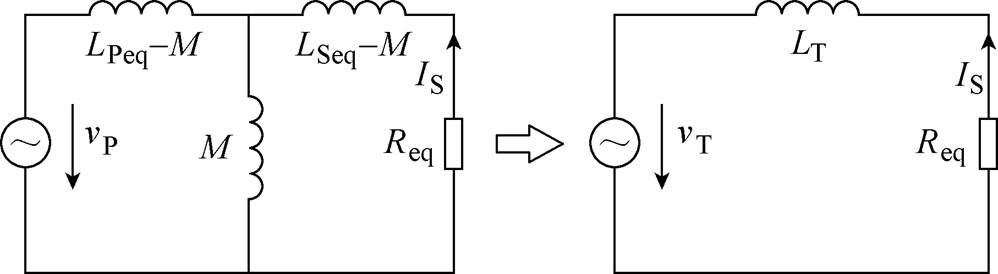
图4 等效环路模型
Fig.4 The equivalent circuit model
式(13)所示等效电压源vT,对于其分母LP-aP,因式(12)约束(即aP<LPmin或aP>LPmax),在系统接收线圈高度变化范围内,必存在一段区间令|LP(h)-aP|>LPmax-LPmin。在这段区间内,其等效电压源vT满足
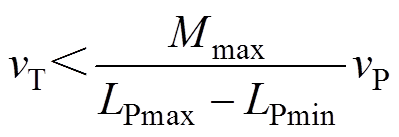 (14)
(14)
给定系统设定最小增益GNmin,若
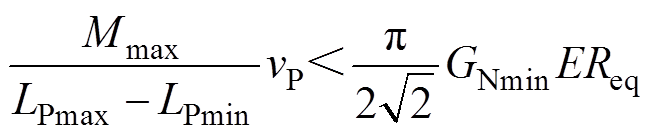 (15)
(15)
则系统在这段区间内无法满足最小增益要求。联立式(2),系统设定的最小增益应满足
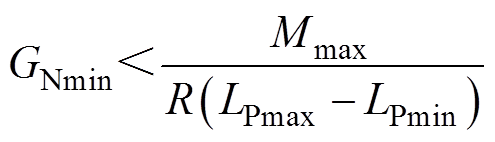 (16)
(16)
同时,为保证系统最低增益约束条件,aP的取值应令等效电压源vT满足
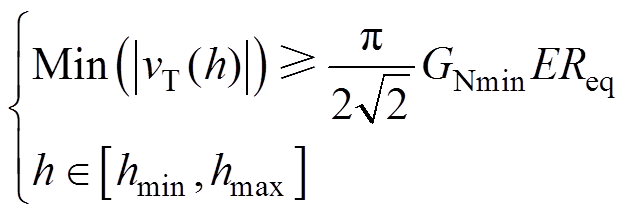 (17)
(17)
对式(17)求解,联立式(12),得到aP取值范围为
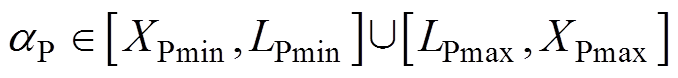 (18)
(18)
由图4可知,当vT与等效阻抗LT在给定高度范围[hmin, hmax]内具有趋近的变化趋势时,输出电流增益G可保持稳定。对于LT,等效阻抗aS仅与LT值的大小有关,与LT的变化趋势无关。即vT与LT的变化趋势仅与等效阻抗aP有关。
以图3所示耦合机构为例,给定任意aS值(以aS=120mH为例),在aP不同取值下,vT/vP与LT随高度h变化如图5所示。图中,vT2/vP呈单调递增趋势,LT2呈非单调趋势,输出电流增益G无法保持稳定;vT1/vP与LT1、vT3/vP与LT3均呈相同变化趋势,相较vT2/vP与LT2的情况,输出电流增益G具有相对稳定的变化趋势。然而,在考虑线圈参数变化的DWPT系统中,由于变化的参数数量繁多(LP、LS与M),且不同耦合机构的参数变化不具有一般规律,给出两个补偿参数最优解的解析解是困难的。因此,本文1.3节基于PSO算法,通过设计以传输增益平稳性与效率为目标的目标函数,给出了一种考虑线圈参数变化的DWPT系统参数设计方法。
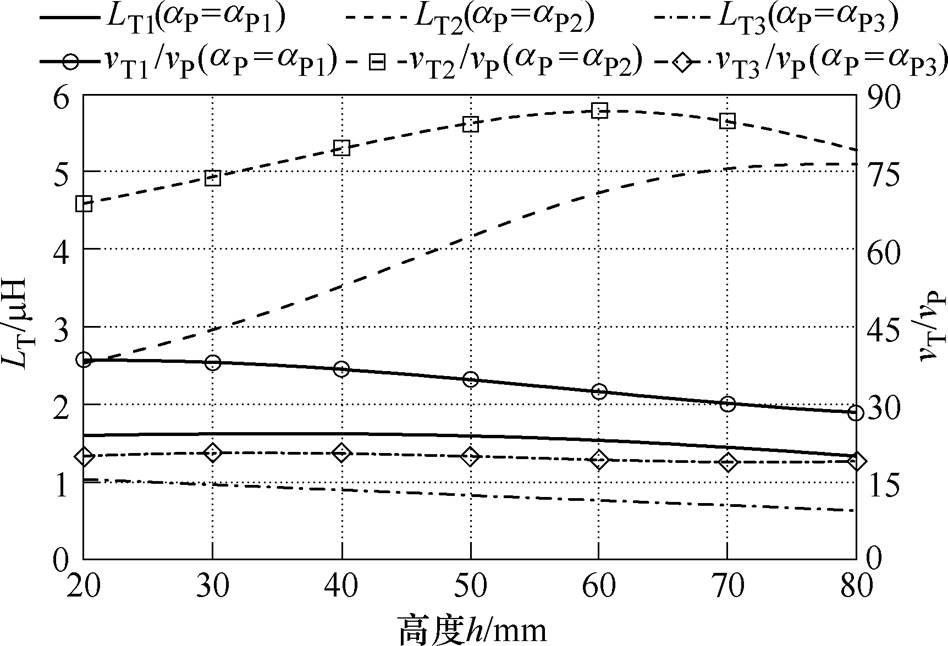
图5 不同aP取值下vT/vP与LT与高度h的关系
Fig.5 The vT/vP and LT along the h with different aP
1.2.2 不谐振系统效率保持约束条件
因为系统工作于不谐振状态,系统的功率损耗将增加。系统功率损耗Ploss为
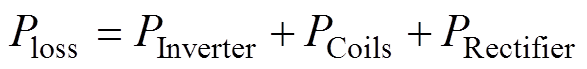 (19)
(19)
式中,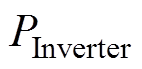 为逆变器功率损耗;
为逆变器功率损耗;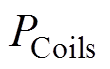 为线圈损耗;
为线圈损耗;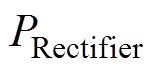 为整流器功率损耗。
为整流器功率损耗。
对于逆变器功率损耗PInverter,其由MOSFET的开通损耗PSW_on、导通损耗PCond与关断损耗PSW_off
构成。对于开通损耗PSW_on,MOSFET的零电压软开关(Zero Voltage Switching, ZVS)可以降低甚至消除MOSFET的开通损耗[24]。因此,为了降低逆变器功率损耗,在系统的工作范围内,aP与aS的取值应使系统的输入阻抗呈感性。即
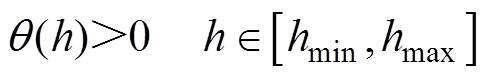 (20)
(20)
然而,若系统输入阻抗感性过强,虽能实现ZVS,但过大的输入电流也会使MOSFET产生额外的导通损耗与关断损耗。对于导通损耗PCond与关断损耗PSW_off,其可以表示[25-27]为
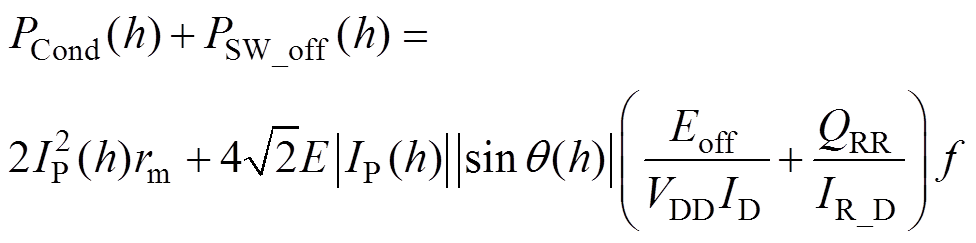 (21)
(21)
式中,rm为MOSFET的正向导通电阻;Poff为测试条件“MOSFET两端承压为VDD、关断电流为ID”时测得的MOSFET关断损耗;QRR为二极管的反向恢复电荷;IR_D为二极管的反向恢复电流。以上参数均可从器件厂商所提供的数据手册中获取[25-27]。
因本文以稳定的输出电流增益为目标,当系统输出电流增益稳定时,可以近似认为副边线圈电流IS恒定。对于线圈损耗Ploss与整流器损耗PRectifier,当副边线圈电流IS恒定且系统结构与元器件选型固定时,副边线圈损耗PCoils_S与整流器损耗PRectifier无法降低,因此副边线圈损耗与整流器损耗不作为本文功率损耗的优化目标。而原边线圈损耗PCoils_P与发射线圈电流IP、发射线圈交流等效内阻rP有关,即
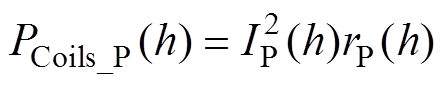 (22)
(22)
式中,受磁阻变化影响,发射线圈交流等效内阻rP随接收线圈高度h变化而变化。以图3a所示耦合机构为例,在确定的高度变化范围内,发射线圈交流等效内阻rP与接收线圈高度h可通过式(9)进行多项式拟合,拟合结果如图6所示。拟合函数rP(h)的拟合优度R2=0.996,拟合效果良好。
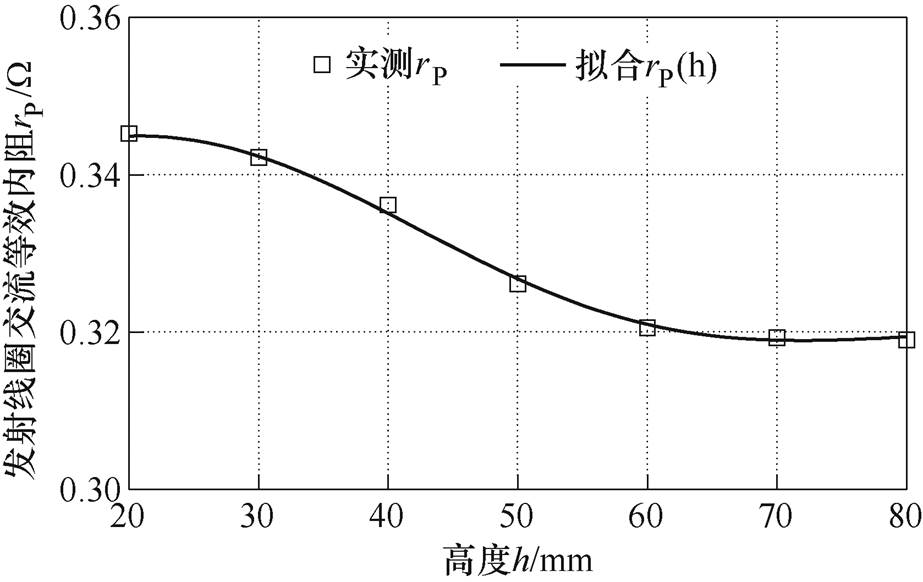
图6 发射线圈交流等效内阻rP与高度h的关系
Fig.6 The AC equivalent resistance rP versus h
为使系统在工作范围内保持较高效率,在满足系统增益要求的前提下,应令A最小,即
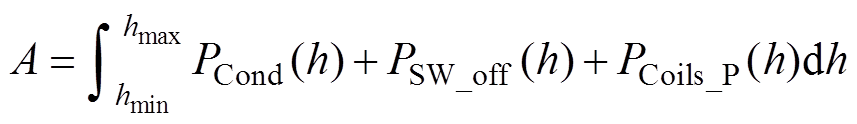 (23)
(23)
式中,A为系统工作范围内逆变器功率损耗与原边线圈功率损耗大小。
1.3.1 目标函数
考虑线圈参数变化的SS拓扑DWPT系统需要确定两个参数(aP与aS)。则参数的确定可以抽象为一个二维优化问题。目标函数为
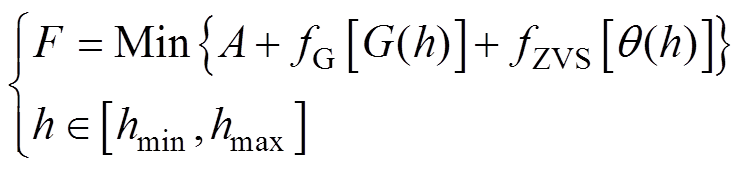 (24)
(24)
其中
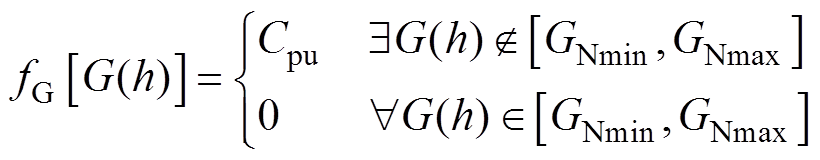 (25)
(25)
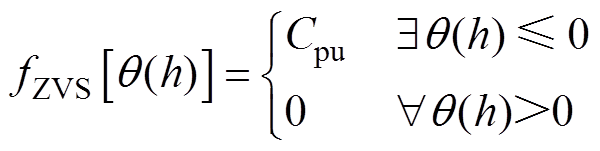 (26)
(26)
式中,Cpu为一足够大的惩罚常数,这保证了系统在[hmin, hmax]范围内的增益符合设计要求且逆变器工作于ZVS状态。
目标函数包含三个目标:①符合设计要求的系统增益;②较小的逆变器与原边线圈功率损耗; ③逆变器实现ZVS。
1.3.2 解空间与粒子速度限制
解空间的确定非常重要,若解空间太小,可能无法包含最优解;若解空间太大,寻找最优解将变得困难,甚至陷入局部最优解。对于参数aP,其范围可根据式(18)得到;对于参数aS,其值应在合理范围内,不能为负数,且由于系统增益的限制,其值不能特别大。
粒子最大速度Vmax与最小速度Vmin被设置为相反数。最大速度Vmax的大小与收敛速度、搜索能力有关。最大速度Vmax越小,搜索精度越高,但算法收敛速度越慢,且最大速度Vmax的取值也受到补偿元件参数精度的限制。因此,本文粒子速度限制被设定为[-5, 5]mH。
1.3.3 基于PSO算法的参数设计流程
PSO算法中粒子的速度与位置的迭代公式为
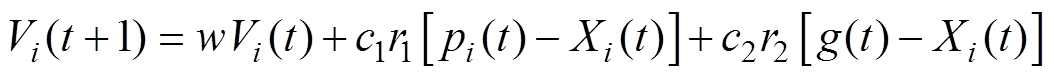 (27)
(27)
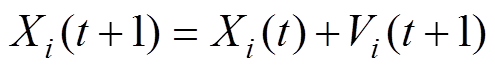 (28)
(28)
式中, ,N为粒子群体数量;t为当前迭代次数;w为惯性权重参数;r1、r2为[0, 1]范围内的随机数;c1、c2分别为认知加速系数与社会加速系数;pi(t)为粒子i在第t次迭代中的个体历史最优位置;g(t)为第t次迭代中的全局历史最优位置。式(27)等式右面的第一部分为惯性部分,由惯性权重和例子自身速度构成;第二部分为认知部分,代表粒子当前位置与自身局部历史最优位置之间的距离与方向;第三部分为社会部分,代表粒子当前位置与粒子全局历史最优位置之间的距离与方向。根据如图7所示参数设计流程编写程序并得到最优解。
,N为粒子群体数量;t为当前迭代次数;w为惯性权重参数;r1、r2为[0, 1]范围内的随机数;c1、c2分别为认知加速系数与社会加速系数;pi(t)为粒子i在第t次迭代中的个体历史最优位置;g(t)为第t次迭代中的全局历史最优位置。式(27)等式右面的第一部分为惯性部分,由惯性权重和例子自身速度构成;第二部分为认知部分,代表粒子当前位置与自身局部历史最优位置之间的距离与方向;第三部分为社会部分,代表粒子当前位置与粒子全局历史最优位置之间的距离与方向。根据如图7所示参数设计流程编写程序并得到最优解。
以图3所示耦合机构为例,给出考虑线圈参数变化的DWPT系统参数设计实例。选用MOSFET型号为C2M0080120D,DWPT系统设计有关的参数见表1。本文中使用的PSO算法相关参数见表2。对于每一组参数,可通过式(3)、式(7)与式(8)计算出其对应的输入电流IP、输入阻抗角q 与增益G,代入式(24)得到其对应的目标函数值。全局最优位置的目标函数值与迭代次数的关系如图8所示。图中,初始目标函数值为10 209,迭代后目标函数值逐渐收敛至1 810。此时,aP=269mH,aS= 123mH。
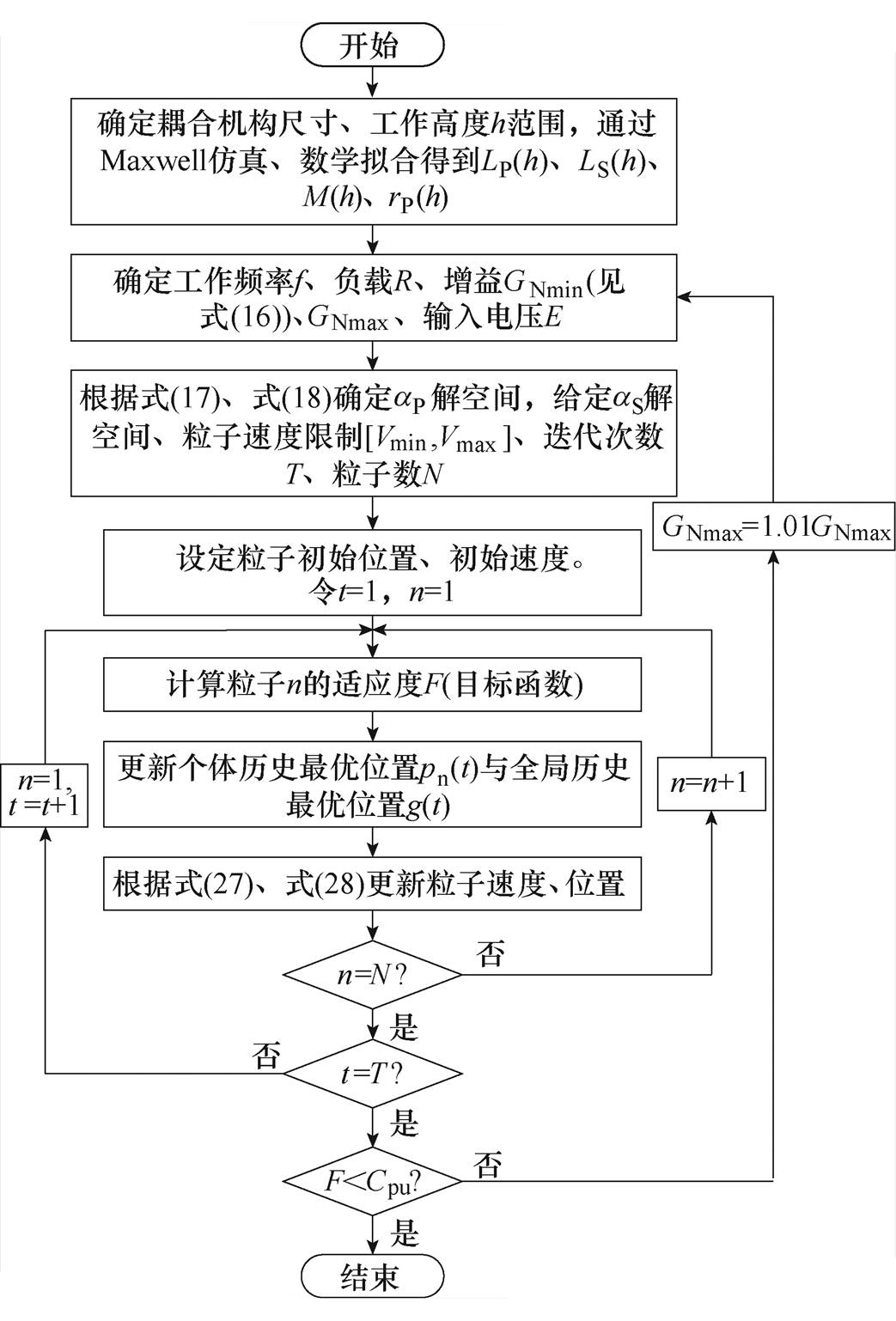
图7 参数设计流程
Fig.7 The flow chart of parameter design
表1 DWPT系统设计有关的参数
Tab.1 The parameters related to DWPT system design

参 数数 值 直流源电压E/V200 工作频率f/kHz85 负载电阻R/W40 设计增益范围[GNmin, GNmax][5A/200V, 5.5A/200V] 互感范围[Mmin, Mmax]/mH[25.2, 60.9] 发射线圈电感范围[LPmin, LPmax]/mH[290.2, 309.3] 接收线圈电感范围[LSmin, LSmax]/mH[103.4, 148.6] 发射线圈交流等效内阻范围[rPmin, rPmax]/W[0.319, 0.345]
表2 PSO算法相关参数
Tab.2 The parameters related to PSO algorithm
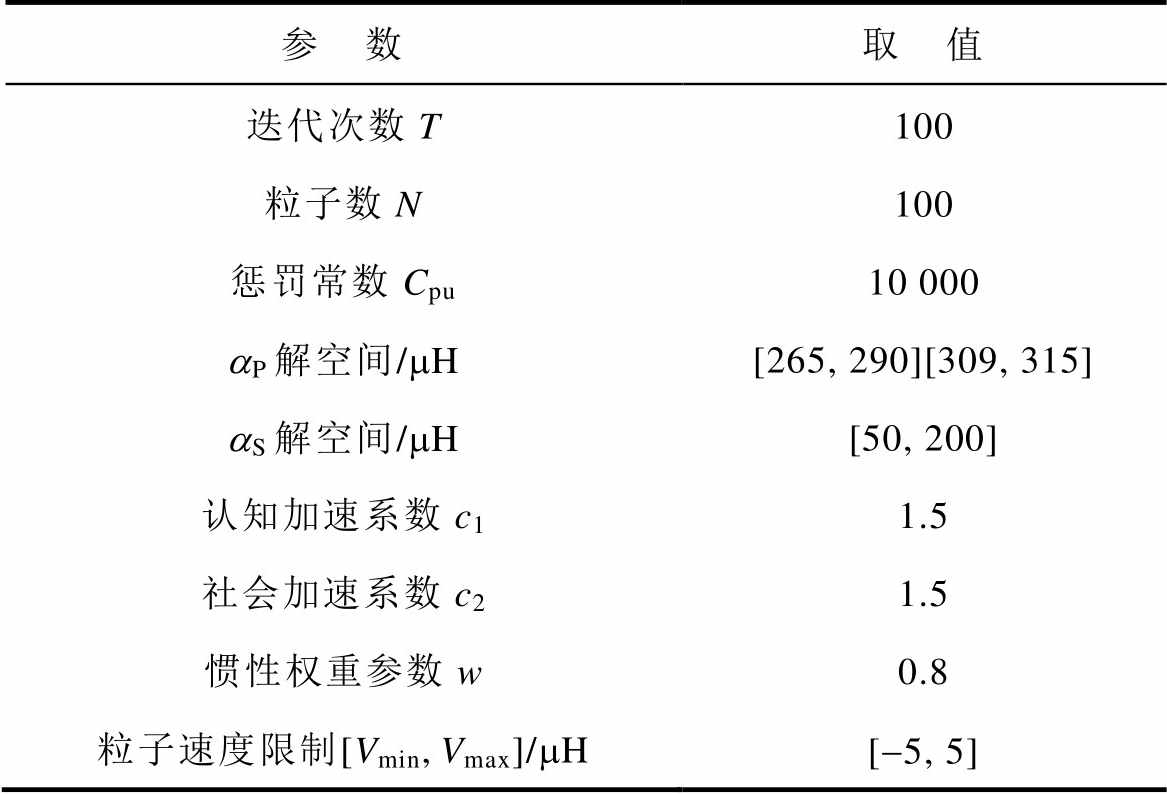
参 数取 值 迭代次数T100 粒子数N100 惩罚常数Cpu10 000 aP解空间/mH[265, 290][309, 315] aS解空间/mH[50, 200] 认知加速系数c11.5 社会加速系数c21.5 惯性权重参数w0.8 粒子速度限制[Vmin,Vmax]/mH[-5, 5]
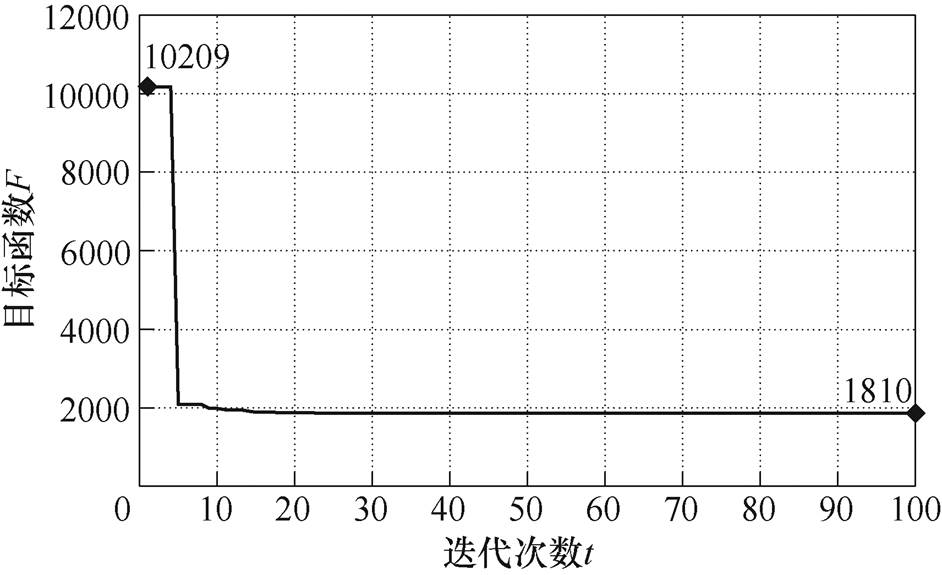
图8 目标函数值F与迭代次数t的关系
Fig.8 The value of F versus t
为了验证所提方法的有效性,规定接收线圈沿导轨运动方向为X方向,当发射线圈与接收线圈左端对齐时,X=0cm。线圈参数与高度h、X方向位移关系如图9所示。本文设计并搭建了一套如图10所示的1kW实验原理样机。
实验原理样机参数见表2,表中,aP、aS对应的补偿电容容值由式(1)求得CP=13nF、CS=28.5nF。改变接收线圈高度h,令其在20~80mm范围内运动。同时,令系统接收线圈沿导轨方向运动,从X=0cm(发射线圈与接收线圈左对齐)运动至X=120cm(发射线圈与接收线圈右对齐)。在长导轨耦合机构工作区域(20cm<X<100cm 内,线圈参数基本不随接收线圈X方向位移而发生变化。图11所示为系统接收线圈移动过程中的输出电流IO与高度h、X方向位移关系。接收线圈移动过程中的系统效率与高度h、X方向位移关系如图12所示。
内,线圈参数基本不随接收线圈X方向位移而发生变化。图11所示为系统接收线圈移动过程中的输出电流IO与高度h、X方向位移关系。接收线圈移动过程中的系统效率与高度h、X方向位移关系如图12所示。
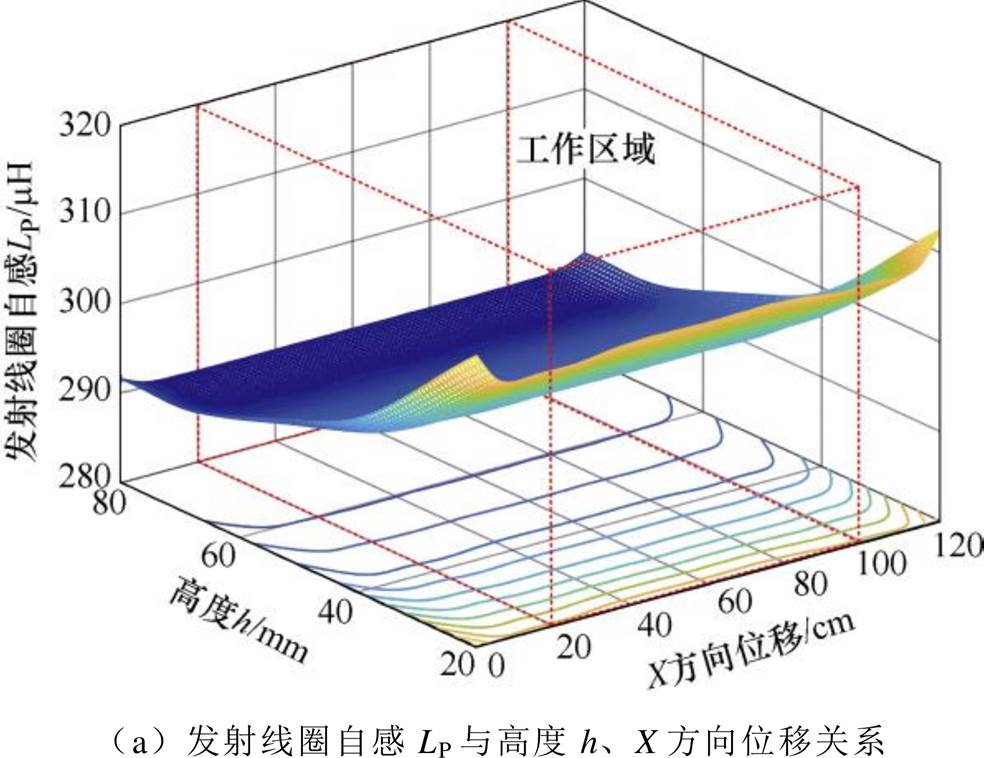
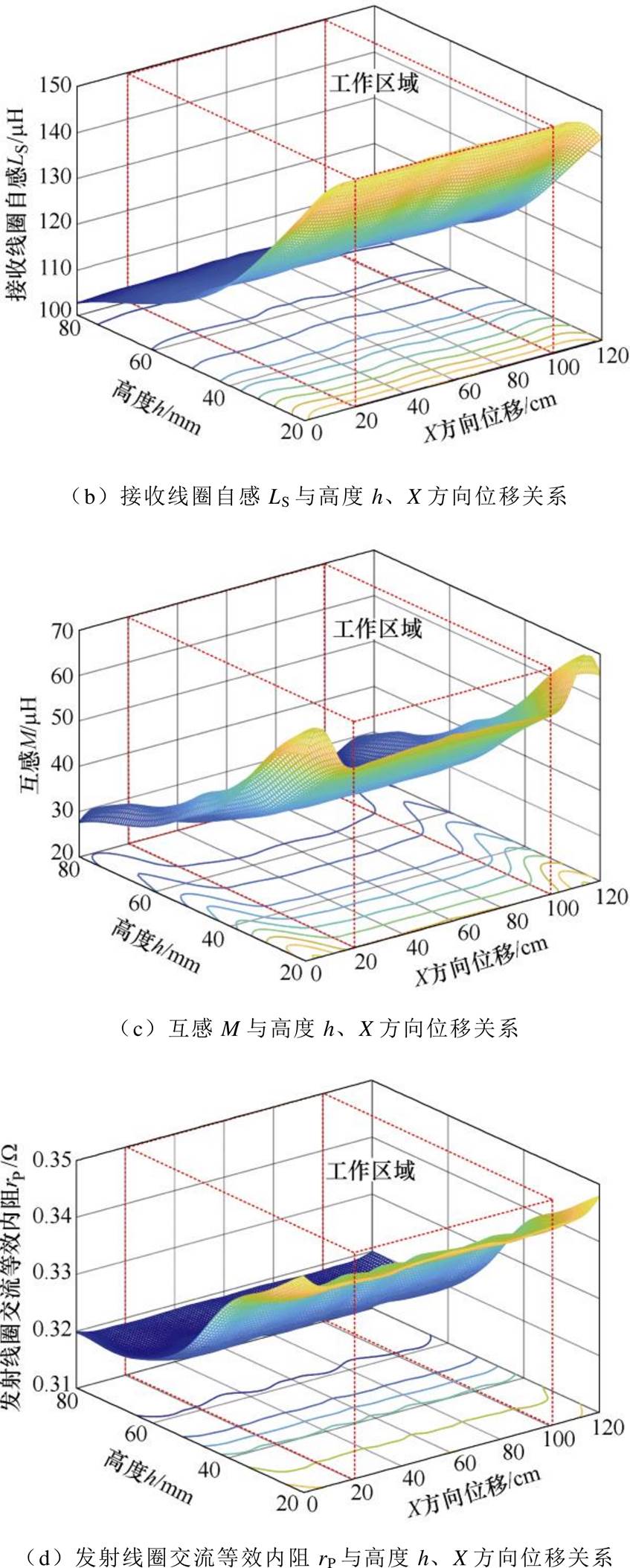
图9 线圈参数与高度h、X方向位移关系
Fig.9 The coils’ parameters versus h and X

图10 实验原理样机
Fig.10 The experimental prototype
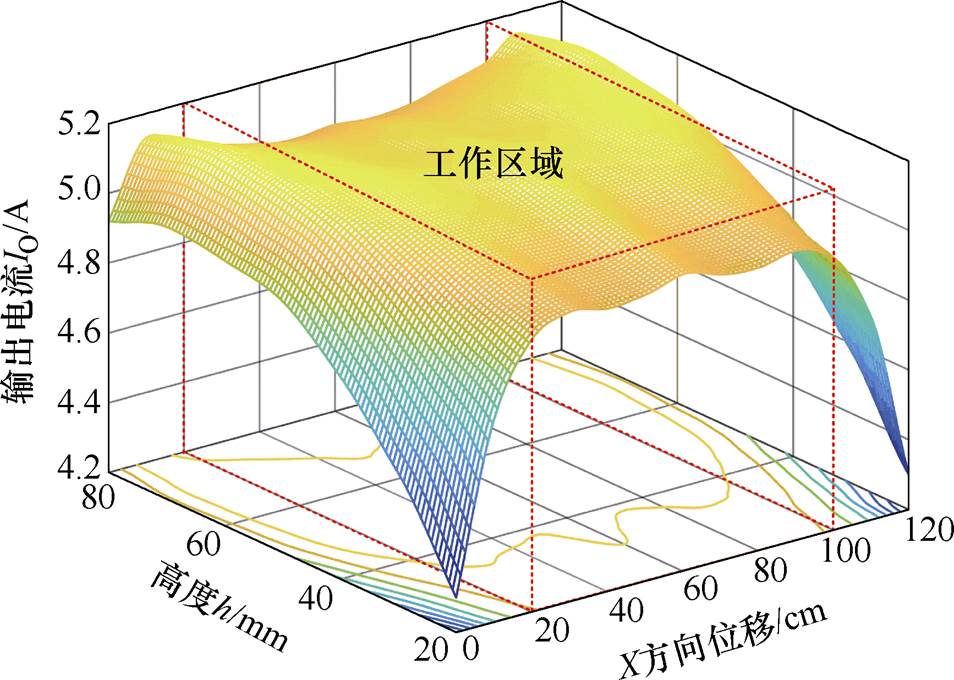
图11 输出电流IO与高度h、X方向位移关系
Fig.11 The output current versus h and X
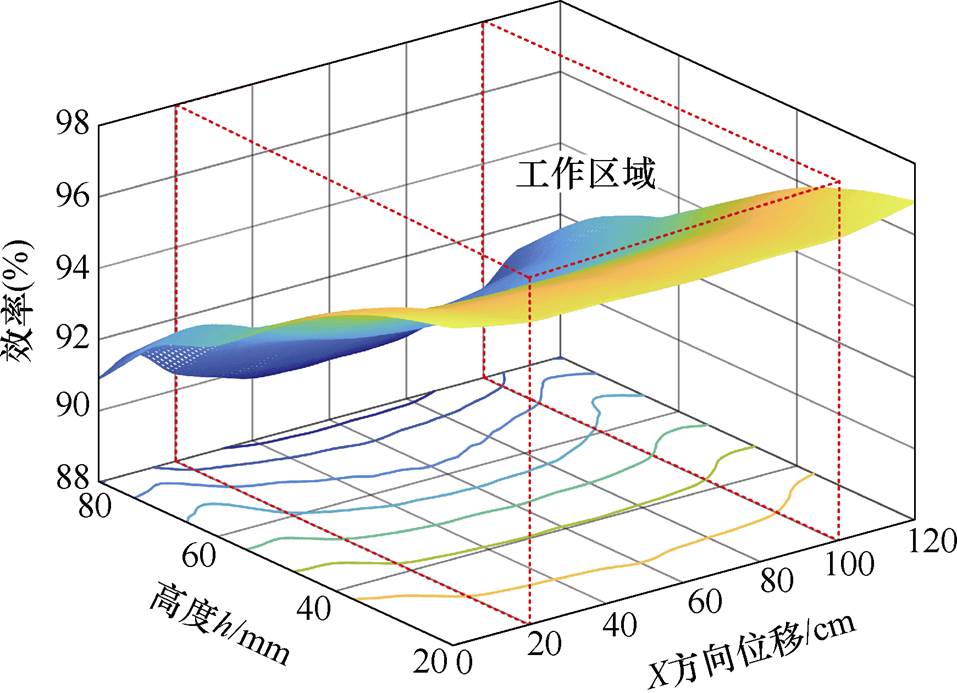
图12 系统效率与高度h、X方向位移关系
Fig.12 The efficiency versus h and X
实验结果显示:在系统工作区域(20cm<X<100cm 内,耦合机构自感增加19.1mH、45.2mH,互感增加至2.4倍,系统的输出电流波动率D =3.55%,最高效率为96.52%,最低效率为89.69%。当接收线圈离开工作区域、接近长导轨边缘(0cm<X<20cm、100cm<X<120cm)时,系统输出电流IO出现较大波动。这是由于线圈参数在接收线圈接近长导轨耦合机构边缘时,受接收线圈X方向所处位置影响剧烈造成的。在实际应用中,可以通过增加导轨长度、划分工作区域、设置路障等方法避免这种情况。
内,耦合机构自感增加19.1mH、45.2mH,互感增加至2.4倍,系统的输出电流波动率D =3.55%,最高效率为96.52%,最低效率为89.69%。当接收线圈离开工作区域、接近长导轨边缘(0cm<X<20cm、100cm<X<120cm)时,系统输出电流IO出现较大波动。这是由于线圈参数在接收线圈接近长导轨耦合机构边缘时,受接收线圈X方向所处位置影响剧烈造成的。在实际应用中,可以通过增加导轨长度、划分工作区域、设置路障等方法避免这种情况。
如图13所示为接收线圈高度h分别为20mm、40mm、60mm与80mm时的逆变器输出电压vP、逆变器输出电流IP、整流桥输入电压vS和整流桥输入电流IS的波形。从实验波形可以看出,系统输入阻抗呈感性,且随接收线圈高度h增加输入阻抗角q 逐渐增大,逆变器工作于ZVS状态。
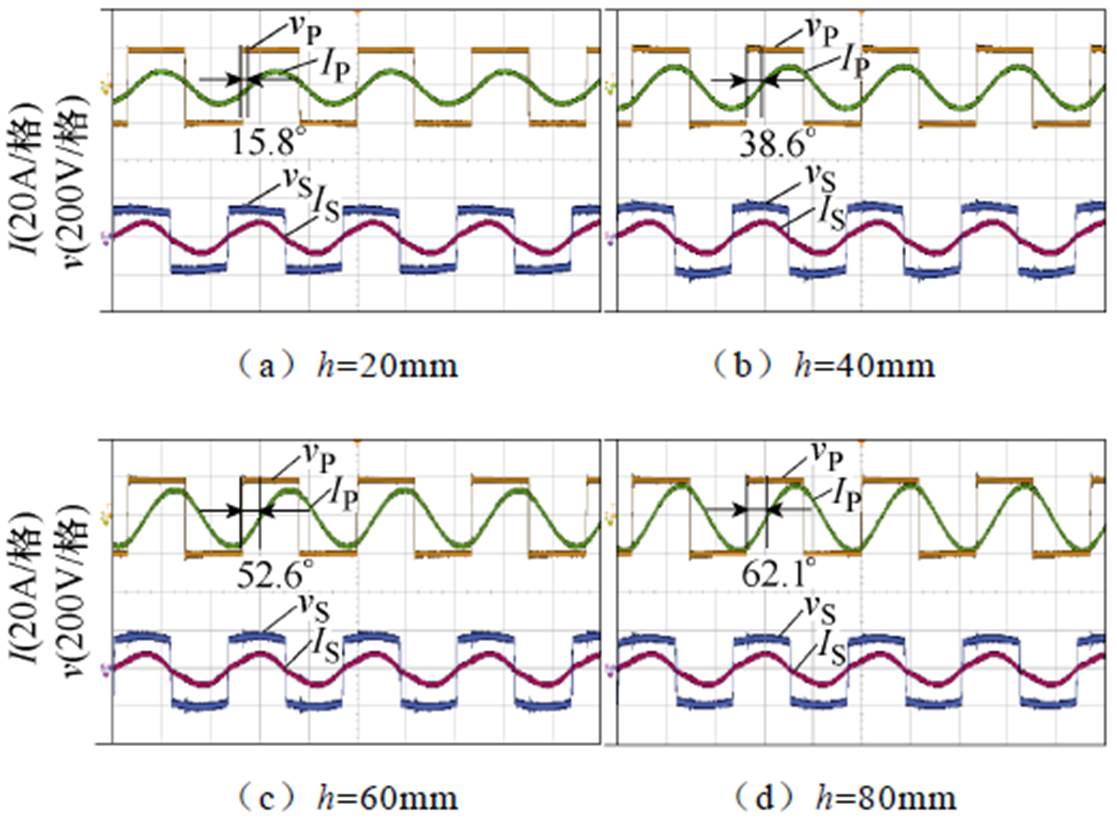
图13 h=20mm、40mm、60mm、80mm时逆变器输出电压vP、逆变器输出电流IP、整流桥输入电压vS与整流桥输入电流IS波形
Fig.13 Experimental waveforms of vP, IP, vS and IS at h=20mm, 40mm, 60mm, 80mm
系统接收线圈移动过程中的原边线圈功率损耗与逆变器功率损耗分别如图14、图15所示。实验结果显示:在系统工作区域内,原边线圈最大功率损耗为63.8W,最小功率损耗为15.5W;逆变器最大功率损耗为40.7W,最小功率损耗为7.8W。随着接收线圈高度增加,输入阻抗角q 与原边线圈电流IP增加,导致原边线圈功率损耗PCoils_P与逆变器损耗PInverter逐渐增大,与前文损耗分析、实验结果吻合。
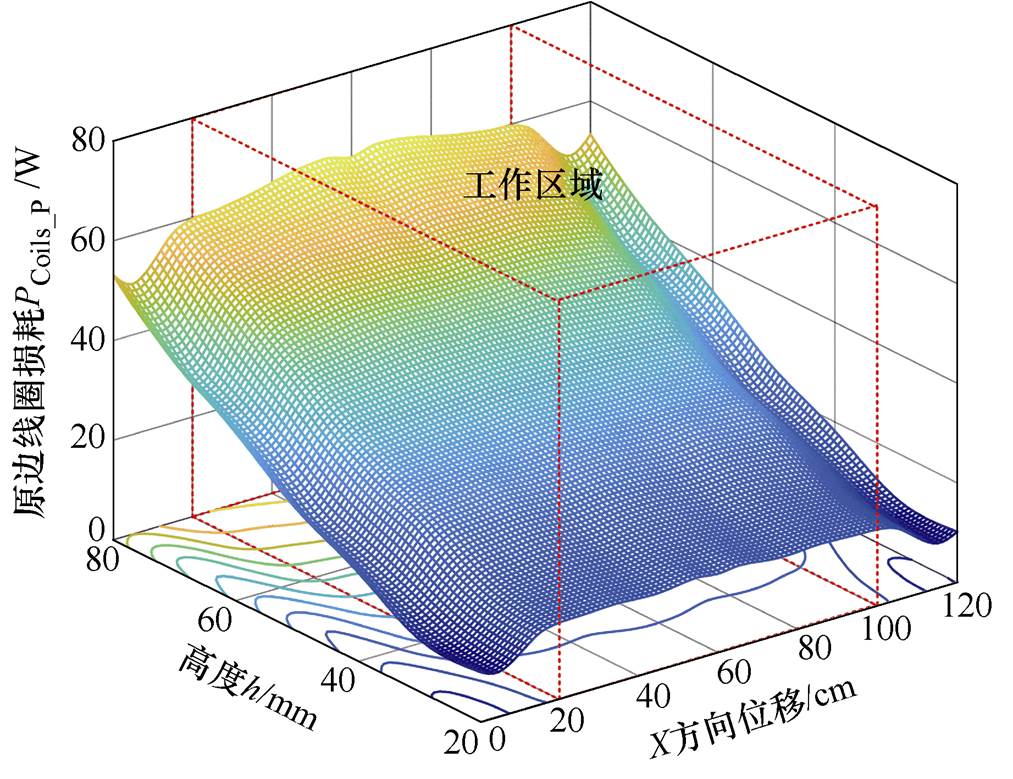
图14 原边线圈损耗PCoils_P与高度h、X方向位移关系
Fig.14 The PCoils_P versus h and X
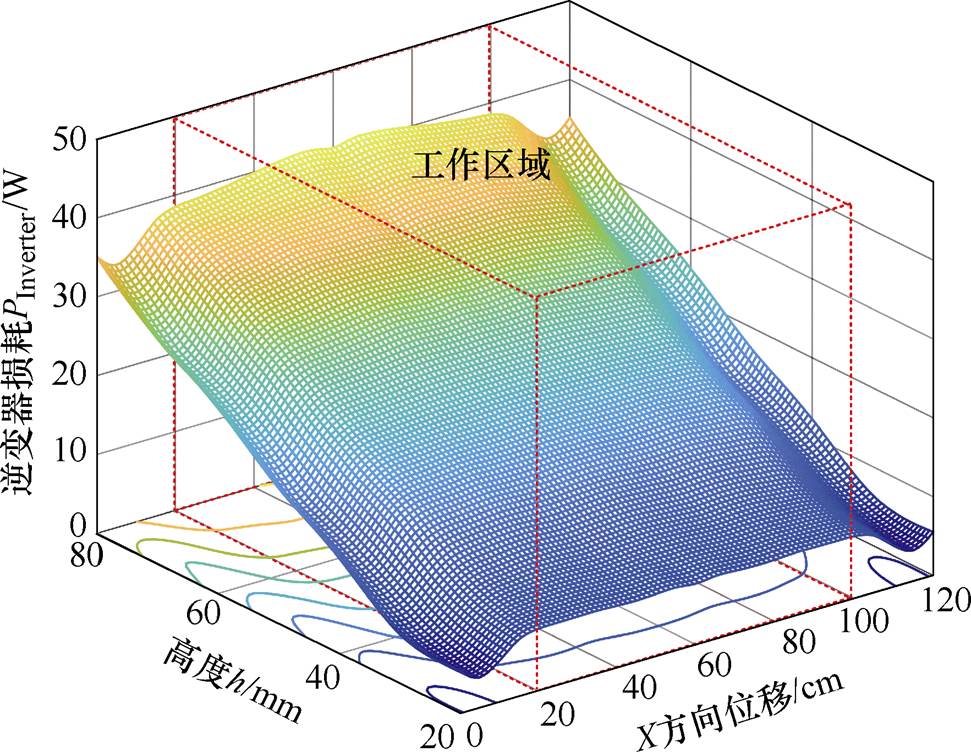
图15 逆变器损耗PInverter与高度h、X方向位移关系
Fig.15 The PInverter versus h and X
本文与已有补偿拓扑设计方案对比见表3,本文所提方法系统简单、成本较低。且本文所提方法考虑了接收线圈垂直偏移过程中导致的线圈自感变化,具有良好的抗垂直偏移稳定传输效果。
表3 本文与已有研究方法对比结果
Tab.3 Comparison results between this paper and other methods
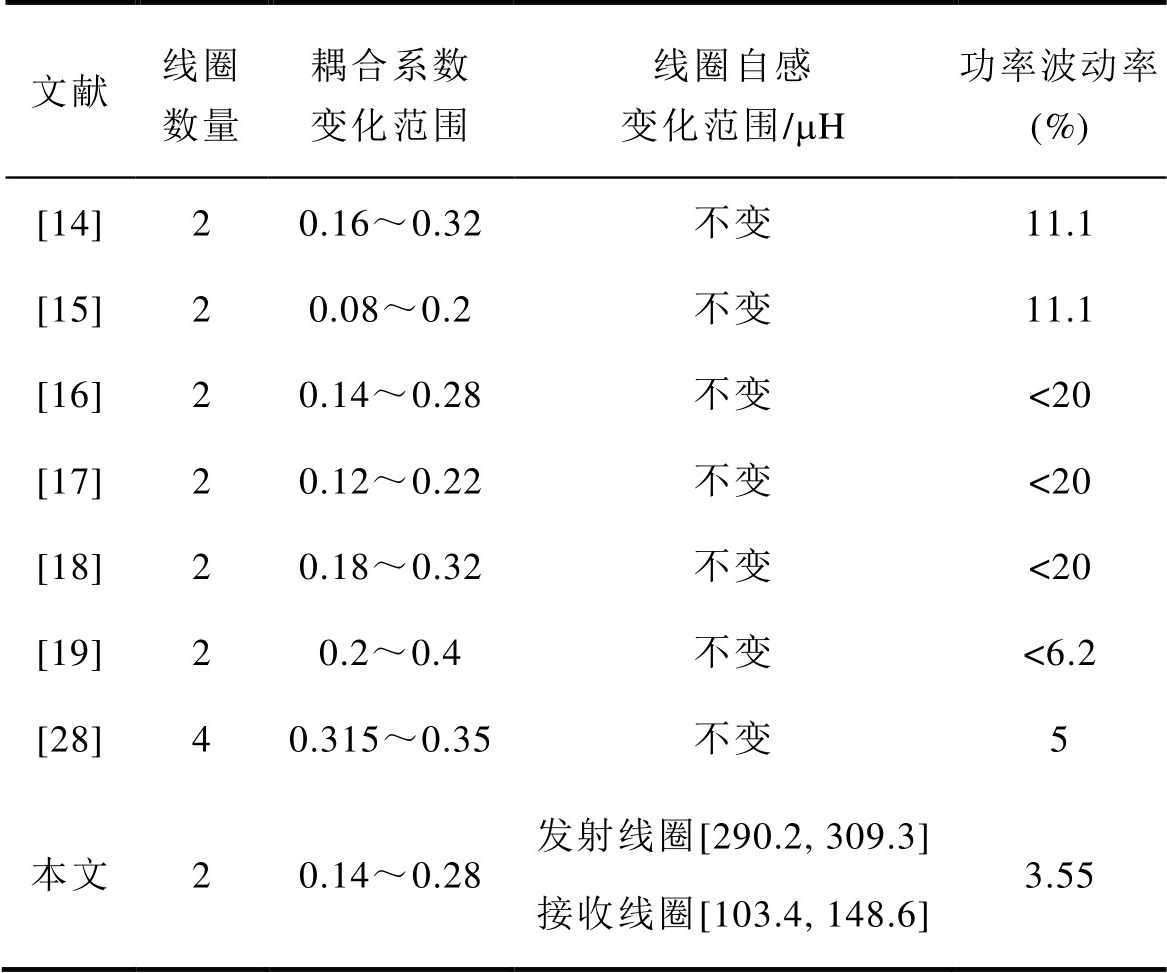
文献线圈数量耦合系数变化范围线圈自感变化范围/mH功率波动率 (%) [14]20.16~0.32不变11.1 [15]20.08~0.2不变11.1 [16]20.14~0.28不变<20 [17]20.12~0.22不变<20 [18]20.18~0.32不变<20 [19]20.2~0.4不变<6.2 [28]40.315~0.35不变5 本文20.14~0.28发射线圈[290.2, 309.3]接收线圈[103.4, 148.6]3.55
为了使系统在互感与自感发生剧烈变化时保持稳定的输出电流增益,本文基于PSO算法提出了一种考虑线圈参数变化的SS型拓扑的DWPT系统参数设计方法。搭建了一套1kW的原理样机,在接收线圈高度h在[20, 80]mm之间变化时,线圈自感增加19.1mH、45.22mH,互感增加至2.4倍情况下,系统输出电流增益波动率仅为3.55%,MOSFET全范围工作于ZVS状态,系统最低效率为89.69%,最高效率为96.52%。实验结果表明,该系统可以在接收线圈发生垂直偏移时,自感、互感剧烈变化的条件下实现稳定输出,且保有了较高的效率。本文所提设计方法适用于负载固定的情况,后续将研究负载可变化的情况。
参考文献
[1] 赵进国, 赵晋斌, 张俊伟, 等. 无线电能传输系统中有源阻抗匹配网络断续电流模式最大效率跟踪研究[J]. 电工技术学报, 2022, 37(1): 24-35.
Zhao Jinguo, Zhao Jinbin, Zhang Junwei, et al. Maximum efficiency tracking study of active impedance matching network discontinous current mode in wireless power transfer system[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(1): 24-35.
[2] 王奉献, 张献, 杨庆新, 等. 基于相差调控的无线电能传输系统耦合机构结构电磁力的平抑[J]. 电工技术学报, 2022, 37(1): 141-151.
Wang Fengxian, Zhang Xian, Yang Qingxin, et al. Electromagnetic force suppression of the coupling mechanism structure of WPT system based on phase difference control[J]. Transactions of China Electro- technical Society, 2022, 37(1): 141-151.
[3] 崔淑梅, 宋贝贝, 王志远. 电动汽车动态无线供电磁耦合机构研究综述[J]. 电工技术学报, 2022, 37(3): 537-554.
Cui Shumei, Song Beibei, Wang Zhiyuan. Overview of magnetic coupler for electric vehicles dynamic wireless charging[J]. Transactions of China Electro- technical Society, 2022, 37(3): 537-554.
[4] Lu Fei, Zhang Hua, Zhu Chong, et al. A tightly coupled inductive power transfer system for low- voltage and high-current charging of automatic guided vehicles[J]. IEEE Transactions on Industrial Electronics, 2019, 66(9): 6867-6875.
[5] 潘帅帅, 麦瑞坤, 徐叶飞, 等. 自动导引车感应充电系统目标三维空间漏磁屏蔽[J]. 电工技术学报, 2022, 37(5): 1078-1087.
Pan Shuaishuai, Mai Ruikun, Xu Yefei, et al. Three- dimensional target space magnetic leakage shielding for AGV inductive charging system[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1078- 1087.
[6] 周玮, 蓝嘉豪, 麦瑞坤, 等. 无线充电电动汽车V2G模式下光储直流微电网能量管理策略[J]. 电工技术学报, 2022, 37(1): 82-91.
Zhou Wei, Lan Jiahao, Mai Ruikun, et al. Research on power management strategy of DC microgrid with photovoltaic, energy storage and EV-wireless power transfer in V2G mode[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 82-91.
[7] 戴卫力, 费峻涛, 肖建康, 等. 无线电能传输技术综述及应用前景[J]. 电气技术, 2010, 11(7): 1-6.
Dai Weili, Fei Juntao, Xiao Jiankang, et al. An overview and application prospect of wireless power transmission technology[J]. Electrical Engineering, 2010, 11(7): 1-6.
[8] Li Shuaijun, Zhang Guilin, Lei Xiangyu, et al. Trajectory tracking control of a unicycle-type mobile robot with a new planning algorithm[C]//2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 2017: 780-786.
[9] Li Zhenjie, Zhu Chunbo, Jiang Jinhai, et al. A 3kW wireless power transfer system for sightseeing car supercapacitor charge[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3301-3316.
[10] Li Hongchang, Li Jie, Wang Kangping, et al. A maximum efficiency point tracking control scheme for wireless power transfer systems using magnetic resonant coupling[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3998-4008.
[11] Berger A, Agostinelli M, Vesti S, et al. A wireless charging system applying phase-shift and amplitude control to maximize efficiency and extractable power[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6338-6348.
[12] Huh J, Lee S W, Cho G H, et al. Narrow-width inductive power transfer system for online electrical vehicles[J]. IEEE Transactions on Power Electronics, 2011, 26(12): 3666-3679.
[13] Choi S Y, Jeong S Y, Gu B W, et al. Ultraslim S-type power supply rails for roadway-powered electric vehicles[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6456-6468.
[14] Feng Hao, Cai Tao, Duan Shanxu, et al. An LCC- compensated resonant converter optimized for robust reaction to large coupling variation in dynamic wireless power transfer[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6591-6601.
[15] Feng Hao, Cai Tao, Duan Shanxu, et al. A dual- side-detuned series-series compensated resonant con- verter for wide charging region in a wireless power transfer system[J]. IEEE Transactions on Industrial Electronics, 2018, 65(3): 2177-2188.
[16] Hao H, Covic G A, Boys J T. A parallel topology for inductive power transfer power supplies[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1140-1151.
[17] Feng Hao, Dayerizadeh A, Lukic S. A coupling- insensitive X-type IPT system for high position tolerance[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 68(8): 6917-6926.
[18] 丰昊, 蔡涛, 段善旭, 等. 一种抗宽范围耦合系数波动的三元件补偿型感应式能量传输系统[J]. 电工技术学报, 2017, 32(增刊2): 10-17.
Feng Hao, Cai Tao, Duan Shanxu, et al. A three- element inductive power transfer system with high misalignment tolerance[J]. Transactions of China Electrotechnical Society, 2017, 32(S2): 10-17.
[19] 胡宏晟, 蔡涛, 段善旭, 等. 用于WPT系统的一次侧失谐SS型补偿拓扑及其参数设计方法[J]. 电工技术学报, 2017, 32(18): 73-82.
Hu Hongsheng, Cai Tao, Duan Shanxu, et al. Study of the primary side detuned series-series compensated topology and parameter design for WPT system[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 73-82.
[20] Yao Yousu, Wang Yijie, Liu Xiaosheng, et al. Particle swarm optimization-based parameter design method for S/CLC-compensated IPT systems featuring high tolerance to misalignment and load variation[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5268-5282.
[21] Jeong S Y, Park J H, Hong G P, et al. Autotuning control system by variation of self-inductance for dynamic wireless EV charging with small air gap[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5165-5174.
[22] Grant A C, John T B, Michael L G K, et al. A three-phase inductive power transfer system for roadway-powered vehicles[J]. IEEE Transactions on Industrial Electronics, 2007, 54(6): 3370-3378.
[23] Sampath J P K, Vilathgamuwa D M, Alphones A. Efficiency enhancement for dynamic wireless power transfer system with segmented transmitter array[J]. IEEE Transactions on Transportation Electrification, 2016, 2(1): 76-85.
[24] Erickson R W, Maksimovic D. Fundamentals of power electronics[M]. New York: Springer, 2001.
[25] 刘方, 陈凯楠, 蒋烨, 等. 双向无线电能传输系统效率优化控制策略研究[J]. 电工技术学报, 2019, 34(5): 891-901.
Liu Fang, Chen Kainan, Jiang Ye, et al. Research on the overall efficiency optimization of the bidirectional wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 891- 901.
[26] Li Yong, Liu Shunpan, Zhu Xiao, et al. Extension of ZVS region of series-series WPT systems by an auxiliary variable inductor for improving efficiency[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 7513-7525.
[27] Nguyen B X, Vilathgamuwa D M, Foo G H B, et al. An efficiency optimization scheme for bidirectional inductive power transfer systems[J]. IEEE Transa- ctions on Power Electronics, 2015, 30(11): 6310- 6319.
[28] Zhao Lei, Thrimawithana D J, Madawala U K, et al. A misalignment-tolerant series-hybrid wireless EV charging system with integrated magnetics[J]. IEEE Transactions on Power Electronics, 2019, 34(2): 1276-1285.
Parameter Design Method for SS Compensated Dynamic Wireless Power Transfer System Considering Coils’ Parameters Variations
Abstract For automatic guided vehicles with dynamic wireless power transfer (DWPT), the gap of the receiver is inevitable due to the variation of load. It can cause the system coils’ parameters (self-inductances and mutual inductance) to change, further affecting the stability of the system output. In order to realize a stable output of the DWPT system when the gap of the receiver is variable, a parameter design method based on a series-series (SS) topology is proposed in this paper. An equivalent circuit model of the SS topology considering the change of coil parameters is established to analyze the influence of the compensation parameters on system output. Thus, the constraints and solution space of compensation topology parameters are determined. A parameter design method for SS topology is proposed based on particle swarm optimization algorithm to maintain stable output current and high efficiency. Finally, a 1kW prototype was built to verify the effectiveness of the proposed approach. Experimental results indicate that within the gap range (20mm~80mm), the maximum fluctuation of the designed system output current is only 3.55% when the self-inductances increase by 19.1mH and 45.22mH, respectively, and the mutual inductance increase to 2.4 times. Furthermore, the highest efficiency of the system reaches 96.52%.
keywords:Dynamic wireless power transfer, variable coils’ parameters, parameter design, stable output, particle swarm optimization algorithm
DOI: 10.19595/j.cnki.1000-6753.tces.220014
中图分类号:TM724
国家自然科学基金面上项目(51977184)、中国博士后科学基金项目(2020M683352)和深圳市中央引导地方科技发展专项资金项目(2021Szvup122)资助。
收稿日期 2022-01-04
改稿日期 2022-03-25
陆远方 男,1997年生,硕士研究生,研究方向为感应式无线电能传输系统补偿拓扑设计。E-mail: luyuanfang1997@163.com
陈 阳 男,1992年生,博士,助理研究员,研究方向为无线电能传输技术。E-mail: yangchen@swjtu.edu.cn(通信作者)
(编辑 陈 诚)