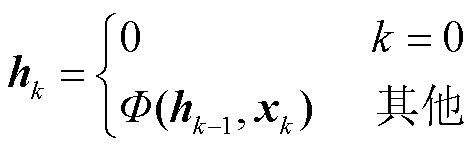 (1)
(1)
式中,xk为第k个输入向量; F (·)为非线性函数。实际上,式(1)中的隐藏状态的更新被实现为
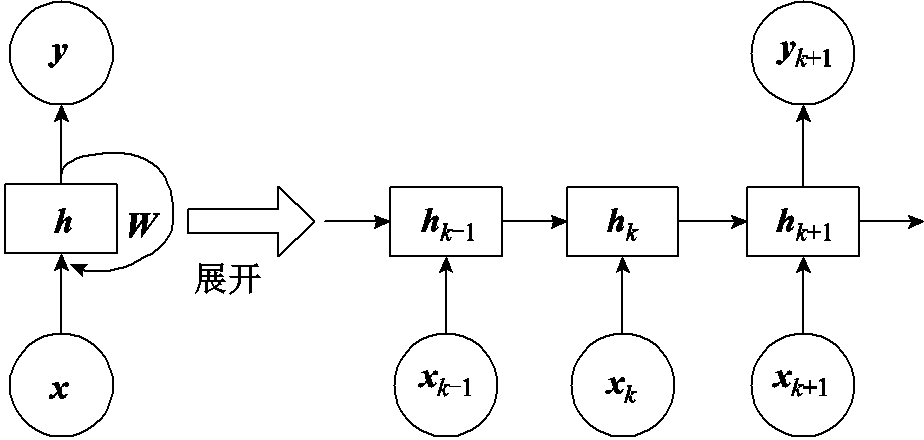
图1 RNN结构
Fig.1 Structure of the RNN
摘要 锂离子电池荷电状态(SOC)估计技术是电动汽车电池监测系统(BMS)设计的重要组成部分。该文提出一种基于经验模态分解(EMD)的门控循环单元(GRU)神经网络的锂离子电池荷电状态估计方法,在GRU估计SOC的基础上,引入EMD算法分解放电电流,不仅提高GRU模型对长时间电流信号保持长期信息的能力,而且提高锂离子电池荷电状态估计精度。仿真实验表明,与传统的循环神经网络和长短期记忆网络相比,该文所提基于EMD-GRU方法的锂离子电池SOC估计平均绝对误差为1.5093%,同比降低了20.7924%。
关键词:锂离子电池 荷电状态估计 门控循环单元 经验模态分解
石油能源的枯竭推动了新能源电动汽车的蓬勃发展。2021年,百度、小米和华为也开始进军电动汽车产业,锂离子电池作为电动汽车动力电池的需求将会越来越大。然而安全性和续航里程问题制约了电动汽车的发展,许多车企研发了锂离子电池管理系统(Battery Management System, BMS),以检测电池温度并保护汽车安全稳定运行[1]。
锂离子电池荷电状态(State of Charge, SOC)的准确评估和预测是BMS的关键功能之一。一般来说,SOC定义为剩余容量与当前最大可用容量的百分比,主要为BMS系统提供充放电测量参考,防止电池过充和过放[2]。由于单体电池的制造工艺和使用环境不同,导致电池性能存在差异,会影响到整个电池组的效率,因此BMS主要通过监控每个单体电池SOC,合理地对每个单体电池充放电,补偿电池之间的差异。然而,由于复杂多变的负载和环境,电池SOC往往不能通过直接测量其内部状态参数求得,需要采用外部参数构建的模型对SOC进行估计,这种采用外部参数构建的模型成为了SOC估计的研究热点[3]。
现有的SOC估计方法主要有安时积分法[4]、开路电压法[5]、内阻法[6]、滤波法[7-9]和神经网络法[10-12]等。随着计算机硬件及信息技术的发展,滤波法和神经网络法成为锂离子电池的研究热点。神经网络法相比于其他方法具有如下优点:①电池测量数据直接映射到SOC值,而无需依赖运行参数的其他电池模型;②通过梯度下降算法学习权重和偏差,这与需要大量努力进行人工设计和参数化的数学模型大不相同;③具有一组网络参数,可以在各种环境温度下实现SOC估计,而其他传统方法则需要针对不同的工作条件具有不同参数的模型。因此,本文采用基于神经网络法进行锂离子电池SOC估计。
常见的应用于SOC估计的神经网络法有支持向量机法和前馈式神经网络法[11-12]。但是,这两种方法在SOC估计中也有一些缺陷:①输入数据及特征需要人为进行设计和提取,花费大量的时间;②模型结构采用浅层学习架构,这些架构的分析能力不足并且难以处理高维数据。
深度神经网络可用于解决上述问题,通过使用多次非线性变换构建深度神经网络(Deep Neural Network, DNN),从输入数据中分层提取复杂的特征信息。近年来,已经提出了几种基于DNN的SOC估计方法。文献[13]使用多层感知器(Multi-Layered Perceptron, MLP)网络构造了SOC估计器,并使用不同环境温度下测得的信号训练了该估计器。结果表明训练后的模型可以减小SOC的估计误差。在这项研究的基础上,考虑到长短期记忆网络(Long Short-Term Memory, LSTM)在时间序列数据中捕获时间信息方面的优势,文献[14-15]开发了一种基于LSTM的SOC估计器,以进一步提高估计精度,并取得了良好的效果。作为循环神经网络(Recurrent Neural Network, RNN)的另一个变体,门控循环单元(GatedRecurrent Unit, GRU)神经网络也已应用于SOC估计。文献[16-17]将GRU结构引入RNN网络,以提高锂离子电池非线性行为的建模能力,并分别构建了两个使用电流和电压信号作为输入的模型来进行SOC估计。然而上述文献未考虑变工况条件下的锂离子电池SOC估计,并且在长时间序列信号下会降低SOC的估计精度。
为解决上述问题,本文首先对比分析了RNN、LSTM和GRU在锂离子电池SOC估计中的应用,证明GRU模型相比其他两种方法更适用于SOC估计;其次研究了变温度工况条件下GRU锂离子电池SOC估计模型;最后提出一种EMD-GRU锂离子电池SOC估计方法,将电流信号分为趋势电流、周期电流和波动电流信号,提高了GRU面临长时间序列信号的能力,进而提高锂离子电池SOC估计精度。
传统的前馈神经网络缺乏使用历史信息的能力,然而这些历史信息在序列问题中显得至关重要,例如短语或句子的翻译,以及视频输入生成标题等。此外,传统的前馈神经网络无法处理具有可变输入和输出大小的时序信号。与前馈神经网络不同,门控循环单元神经网络使用循环单元来存储和处理历史信息,能有效克服前馈神经网络缺记忆能力的问题[18]。
RNN结构如图1所示,循环单元有一个反馈回路,隐藏状态hk更新为
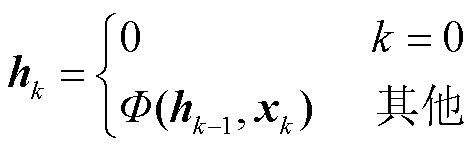 (1)
(1)
式中,xk为第k个输入向量; F (·)为非线性函数。实际上,式(1)中的隐藏状态的更新被实现为

图1 RNN结构
Fig.1 Structure of the RNN
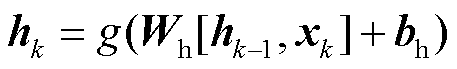 (2)
(2)
式中,g(·)为平滑有界的激活函数,例如Sigmoid函数或tanh函数;Wh为隐藏层和输入层之间的权重矩阵;bh为表示每个节点的偏移量的偏差参数。然后可以获得相应的输出yk,即
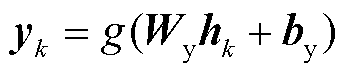 (3)
(3)
式中, 为隐藏层和输出层之间的权重矩阵;
为隐藏层和输出层之间的权重矩阵;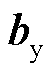 为每个节点的偏置参数。
为每个节点的偏置参数。
时间步长的递归边缘使RNN在处理诸如连接文字或语音识别的任务方面表现出色。然而当序列变长时,会出现梯度消失或梯度爆炸的问题,难以训练RNN。为了解决这一问题,可以设计一种新的激活函数如LSTM和GRU[16-17,19]。GRU相比于LSTM参数和结构更为简单,在较小的数据集上性能优于LSTM,因此本文采用GRU进行锂离子电池SOC估计。
GRU先前的隐藏状态hk-1和当前输入xk不会直接影响标准RNN中的当前隐藏状态hk。取而代之的是,GRU使用更新门来确定应该传递多少过去的信息,并使用重置门来确定要丢弃多少信息。
图2表示GRU的一般结构,其中,GRU的激活是先前状态hk-1和候选状态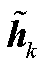 的线性组合
的线性组合
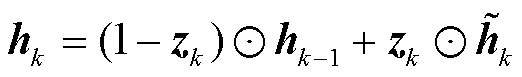 (4)
(4)
式中,zk称为更新门,由Sigmoid函数激活;“ ”是Hadamard乘积符号。
”是Hadamard乘积符号。
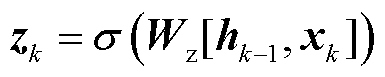 (5)
(5)
如果zk数值接近于1,则当前状态更多地取决于候选状态;而如果zk数值接近0,则当前状态更依赖先前状态。直观地,zk确定应接受多少比例的候选状态。
GRU的候选状态计算为
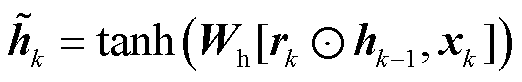 (6)
(6)
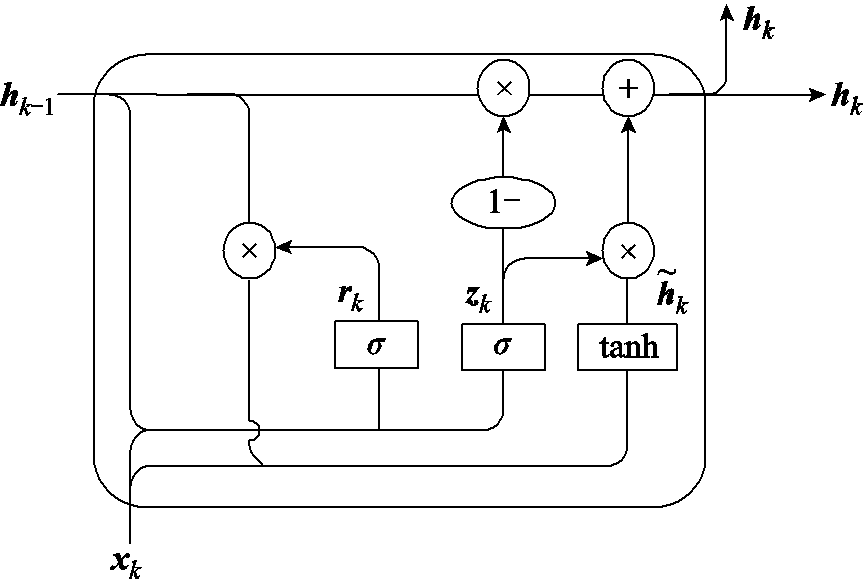
图2 GRU结构
Fig.2 Structure of the GRU
式中,rk称为重置门,由Sigmoid函数激活,即
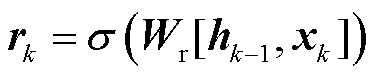 (7)
(7)
与更新门类似,重置门可以限制先前的隐藏状态对候选状态的影响。
虽然标准RNN循环单元以指数移动平均方式更新,但GRU可以决定更新什么,重置什么。此外,如果门控因子接近1,隐藏单元的输出会沿着扩展链流动很长的距离。同时,也可以大大避免梯度消失现象,因为误差也可以反向传播许多时间步骤。随后,捕获长期依赖关系成为可能。
标准RNN循环单元以指数移动平均方式进行更新,而GRU可以决定要更新的内容和重置的内容。此外,如果门控因子接近1,则隐藏的单元输出将沿着扩展链流动很长的距离。同时,由于误差还可以反向传播许多时间步骤,因此也可以有效避免梯度消失现象。随后,捕获长期依赖性成为可能。
传统的GRU网络进行锂离子电池SOC估计时采用电流、电压、温度作为网络输入,SOC作为网络输出。然而在面临较长时间序列时,会出现丢失部分中长期序列信息的情况,影响模型预测精度。因此本文为了提高GRU网络面对较长时间序列时保存趋势信号的能力,采用经验模态分解(Empirical Mode Decomposition, EMD)[20]算法进行电流信号的预处理。将电流信号分解为若干个电流子序列,提取出长时低频电流信号,剔除了电流中的噪声数据,并结合电压和温度组成网络模型的输入,提高GRU模型估计精度。
EMD是一种信号处理方法,主要应用于非平稳信号的预处理。该方法相比于小波分解,不需要提前设定任何基函数,具有自适应特性。分解得到的子序列集被称作固有模态函数(Intrinsic Mode Function, IMF)。
锂离子电池实际运行中电压和温度变化相对缓慢,是一个平稳信号,充电时电压上升,放电时电压下降,温度在充放电过程都会上升。然而其电流随着速度的变化而变化,是一个不平稳信号,因此只需要对电流进行EMD分解。EMD分解的流程如图3所示。
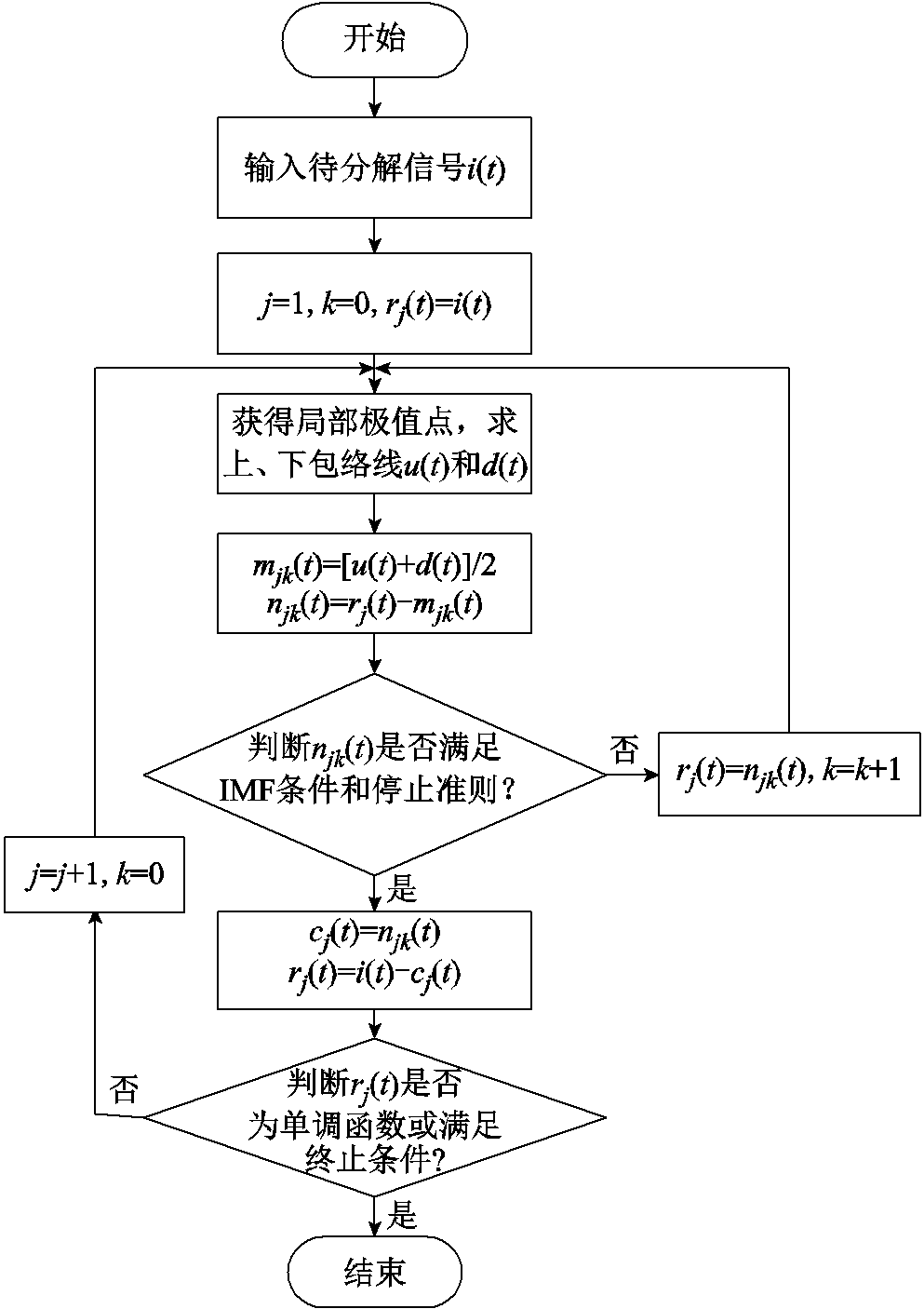
图3 EMD算法流程
Fig.3 Flow chart of EMD algorithm
具体分解的步骤如下:
首先,确定原始电流时间序列i(t)的所有极值点,采用三次样条插值法进行上包络线u(t)和下包络线d(t)拟合。并计算出上下包络线均值曲线m10(t),即
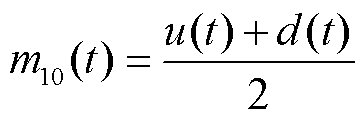 (8)
(8)
将m10(t)从原始电流时间序列i(t)移除,得到一个新的时间序列n10(t),即
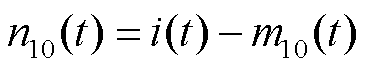 (9)
(9)
判断新的时间序列n10(t)是否满足IMF两个基本条件,如果满足,那么它就是所求的IMF分量;如果不满足条件,重复以上步骤,将均值曲线m1k(t)从n1(k-1)(t)中移除,即
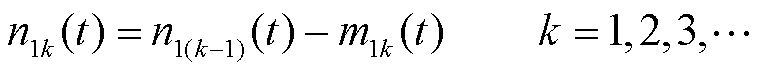 (10)
(10)
直到移除均值曲线后的分量n1k(t)满足IMF的基本条件,且满足停止准则
 (11)
(11)
式中,T为时间序列的长度;e设置在0.2~0.3;SD为两个连续筛选结果计算的标准偏差。那么n1k(t)即为最小时间尺度的IMF分量,记为c1(t),即
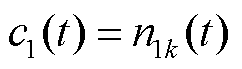 (12)
(12)
将c1(t)从原始时间序列i(t)中去除,得到残余序列r1(t),为
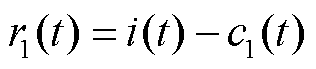 (13)
(13)
再把r1(t)作为新的时间序列重复以上步骤,获得新的IMF分量,直到残余序列rn(t)为恒定值或者单调函数时,分解结束。
综上,原始时间序列i(t)被分解成n个IMF和一个残余序列rn(t),可表示为
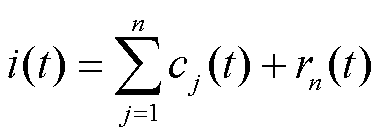 (14)
(14)
基于前文对EMD和GRU算法的介绍,提出一种基于EMD-GRU锂离子电池SOC估计方法,如图4所示。该方法采用EMD算法对电池电流信号进行分解,把电流分解为若干个电流子序列,然后结合电池电压和电池温度波动作为GRU神经网络输入,经过全连接层网络后,电池SOC作为输出。已有的数据进行模型训练,得到模型参数,引入新的电流子序列、电压和温度作为网络输入,预测网络的SOC。
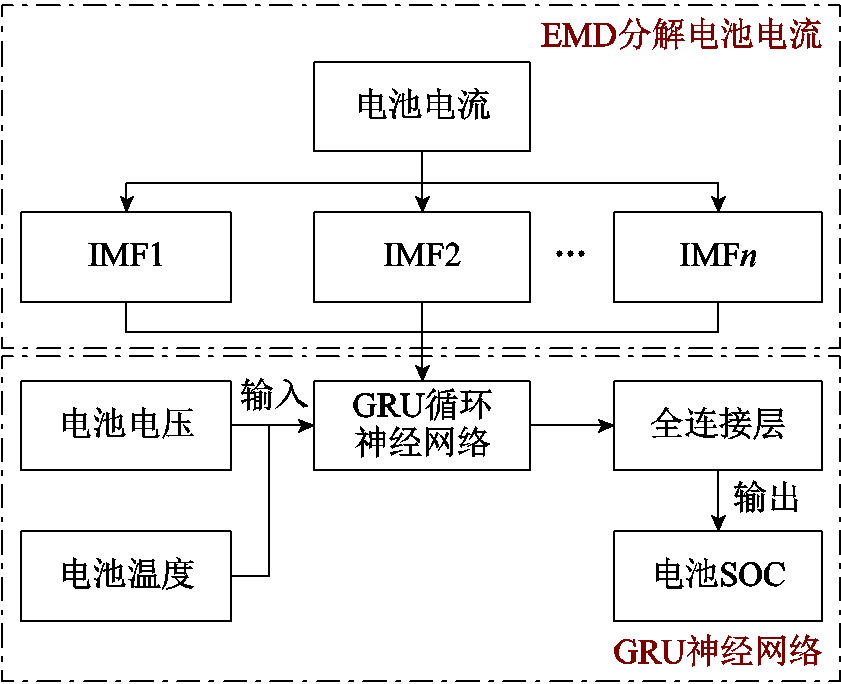
图4 EMD-GRU锂离子电池SOC估计方法
Fig.4 EMD-GRU lithium-ion battery SOC estimation method
EMD-GRU锂离子电池SOC估计具体步骤如下:
(1)数据预处理。数据的准确性决定着网络模型的准确性,收集电流、电压、温度xk=[Ik Vk Tk]和SOC数据yk={SOCk},完成错误及缺失数据的修正,划分训练集和测试集。
(2)经验模态分解。采用EMD将电流信号Ik分为子电流序列集合{I1k, I2k,…, Ijk}。考虑到分解后的电流序列数值单位相差较大,采用min-max归一化电流子序列集,将数值缩放到0~1之间。
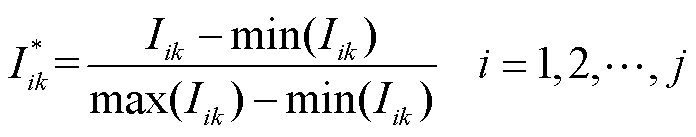 (15)
(15)
式中,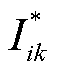 为归一化后的电流子序列集。
为归一化后的电流子序列集。
(3)GRU模型时序预测。采用训练集数据建立基于GRU的锂离子电池SOC估计模型,通过设定网络结构及参数,Adam作为网络的训练优化算法,ReLU作为网络激活函数,方均误差函数作为优化目标函数,进而训练得到最优的SOC估计模型参数。
(4)模型评价。测试集作为GRU模型的输入,得到估计的SOC值,进而通过预测值和实际值的误差度量模型准确性,选用平均绝对误差(Mean Absolute Error, MAE)、方均误差(Mean Square Error, MSE)、方均根误差(Root Mean Square Error, RMSE)。计算公式分别为
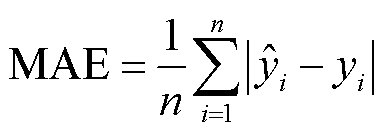 (16)
(16)
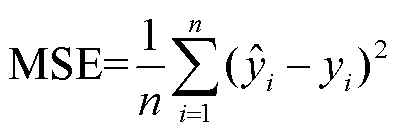 (17)
(17)
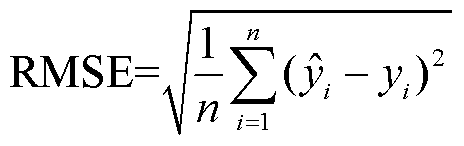 (18)
(18)
式中, 为第i个预测值;yi为第i个实际值;n为预测数量。
为第i个预测值;yi为第i个实际值;n为预测数量。
电动汽车的实际行驶条件是复杂而不确定的。为了尽可能地模拟电动汽车的真实驾驶条件,训练数据需要推广到其他驾驶条件。本文使用了来自美国马里兰大学高级生命周期工程中心(Center for Advanced Life Cycle Engineering, CALCE)的数据仓库的公共数据集[21]。
实验中,将A123型号的电池放置在温度室中,进行充放电,A123型号电池详细参数见表1,测量电流和测量电压如图5所示,图5a、图5c和图5e为测量电流,图5b、图5d和图5f为测量电压。动态应力测试(Dynamic Stress Test, DST)数据集(图5a和图5b)与联邦城市驾驶工况(Federal Urban Driving Schedule, FUDS)数据集(图5c和图5d)和US06数据集(图5e和图5f)都有不同的测量结果,DST和FUDS与US06在放电电流和电压上有明显的差异。由于训练数据往往多于测试数据,因此本文以DST和FUDS数据集作为训练数据集,US06作为测试数据集,温度为10℃、20℃、30℃和40℃。
表1 A123型号电池参数
Tab.1 Detailed parameters of A123 battery

参数数值(成分) 额定容量/(A·h)2.230 化学成分LiFePO4 重量/g76 尺寸/mm25.4 长度/mm65
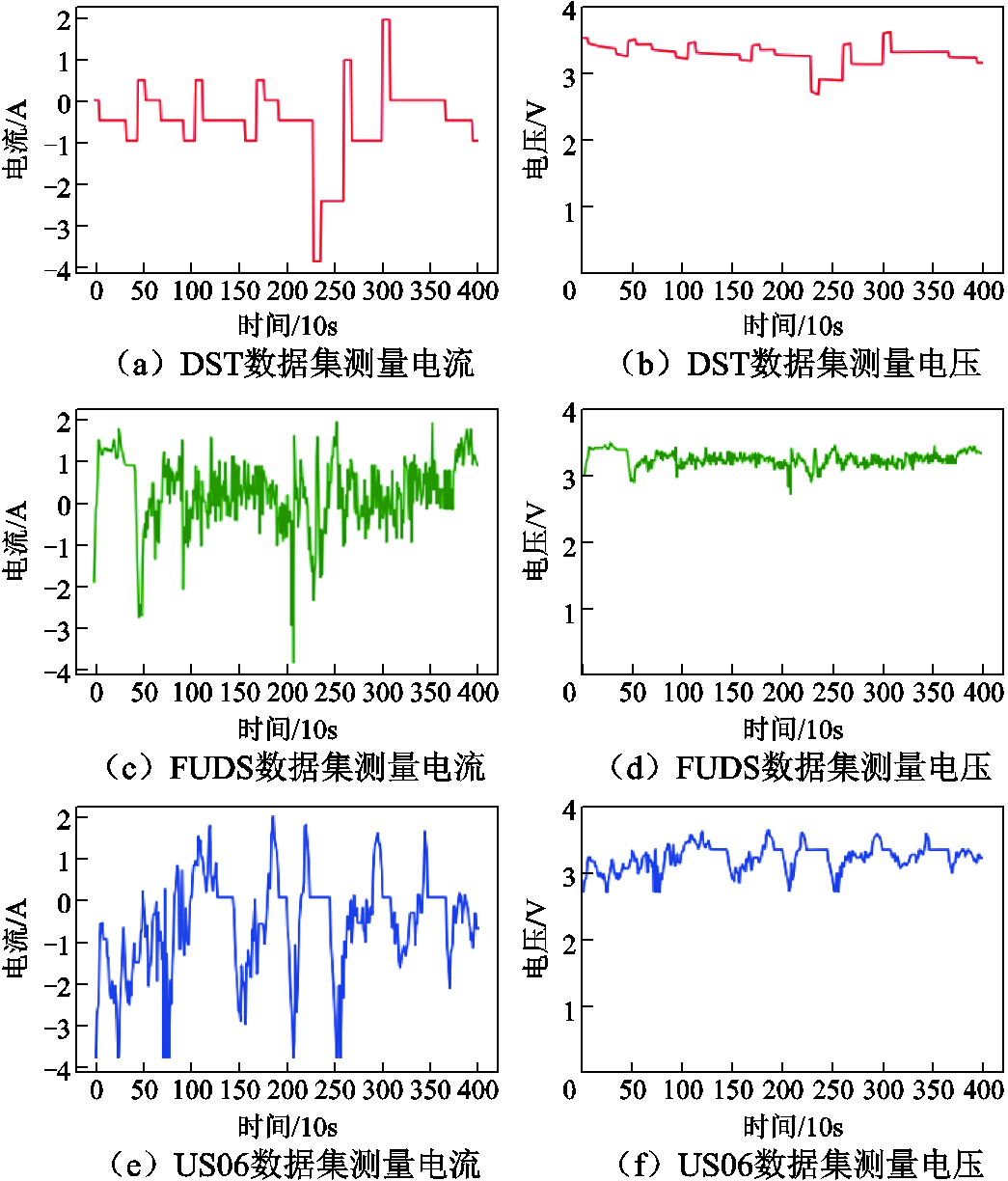
图5 测量电流和测量电压波形
Fig.5 Measurement current and measurement voltage waveforms
为了验证GRU模型是否适用于锂离子电池SOC估计,对比分析了RNN模型和LSTM模型仿真结果。网络模型结构和参数统一为表2给出的数据。首先需要确定迭代次数,本文采用常温20℃下进行迭代次数的选择,表3和图6分别为三种循环神经网络锂离子电池SOC估计迭代次数和误差之间的关系。
表2 网络模型结构及参数
Tab.2 Network model structure and parameters

结构和参数数值及名称 采样时间/s5 时间步长30 训练批量大小3 000 隐含层层数2 隐含层节点个数32 激活函数ReLU 训练优化算法Adam 初始学习率0.01 优化目标函数MSE
表3 迭代次数与误差关系表
Tab.3 The relationship between the number of iterations and the error
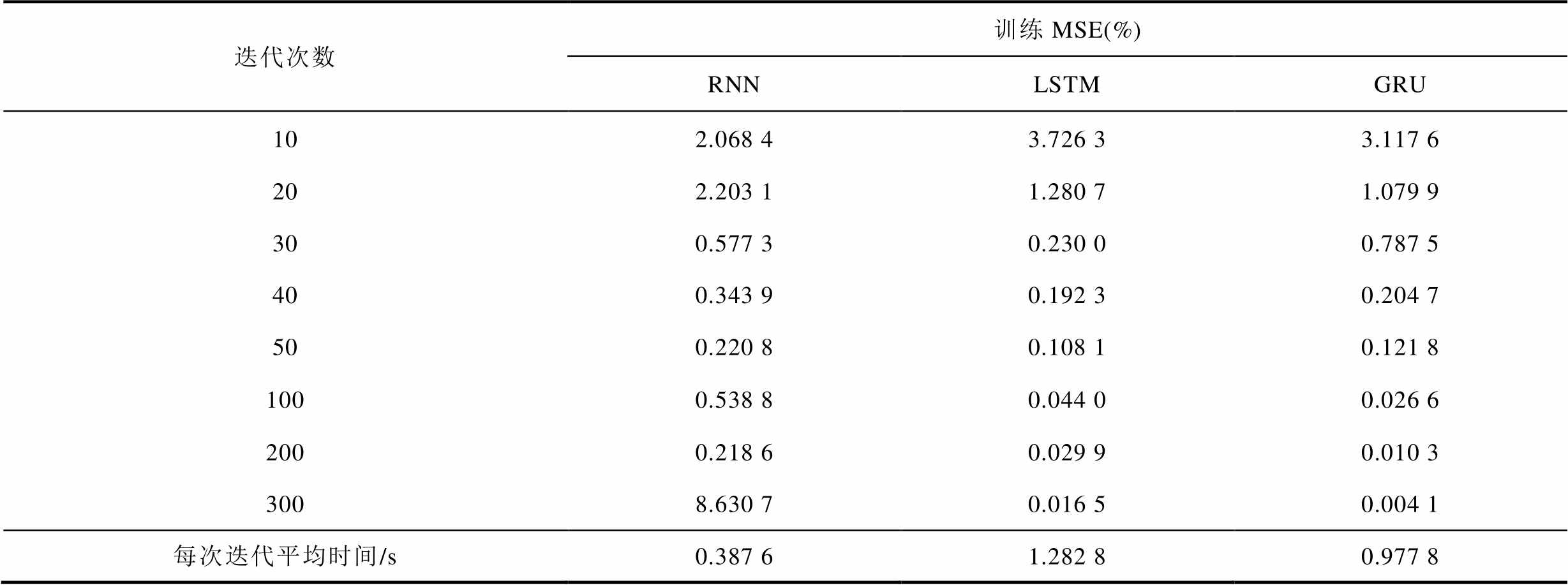
迭代次数训练MSE(%) RNNLSTMGRU 102.068 43.726 33.117 6 202.203 11.280 71.079 9 300.577 30.230 00.787 5 400.343 90.192 30.204 7 500.220 80.108 10.121 8 1000.538 80.044 00.026 6 2000.218 60.029 90.010 3 3008.630 70.016 50.004 1 每次迭代平均时间/s0.387 61.282 80.977 8
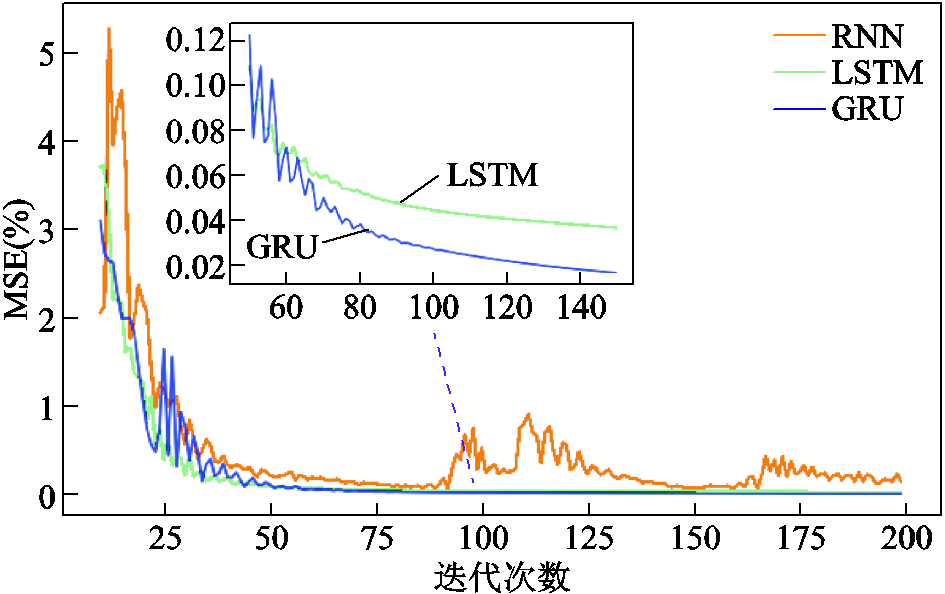
图6 迭代次数与误差关系
Fig.6 The relationship between the number of iterations and MSE
从表3可以看出刚开始10次迭代阶段,RNN的精度较高,LSTM和GRU相对误差较大,这与网络随机初始化参数有关联,RNN初始化的参数更加接近于最优参数。当迭代次数达到20次,LSTM和GRU这两个变种循环网络的精度已经高于传统的RNN。RNN在迭代次数50附近达到最优,然而随着迭代次数增加,由于过拟合导致模型误差升高,因此RNN模型实验迭代次数不宜过多。LSTM和GRU随着迭代次数的增加,误差持续降低,然而所求误差是训练误差,不能反映实际测试误差,当训练误差远远小于电池测试仪器的测试精度0.05%时,将会过度拟合电池测量仪器噪声。
由图6可以明显地看出,三种算法迭代次数在50次时收敛在较高的精度;迭代的MSE关系为GRU<LSTM<RNN;迭代次数在100次时的误差在0.05%附近,因此为了防止过拟合,本文后续实验部分迭代次数固定为100。
表4为GRU模型锂离子电池不同温度下SOC估计误差,MAE为1.905 5%,MSE为0.065 5%,RMSE为2.508 5%。MAE满足在2%以内,已经满足诸多SOC估计的需求。GRU模型锂离子电池不同温度SOC估计结果如图7所示,其估计误差值波动幅值较小,波动的频率平缓,估计波动趋势和图5电流波动趋势相近。
表4 GRU模型锂离子电池不同温度下SOC估计误差
Tab.4 GRU model lithium-ion battery SOC estimation error at different temperatures

温度MAE(%)MSE(%)RMSE(%) 10℃1.738 80.048 72.207 2 20℃1.608 20.049 82.232 2 30℃1.719 60.048 32.197 8 40℃2.555 30.115 33.396 6 平均1.905 50.065 52.508 5
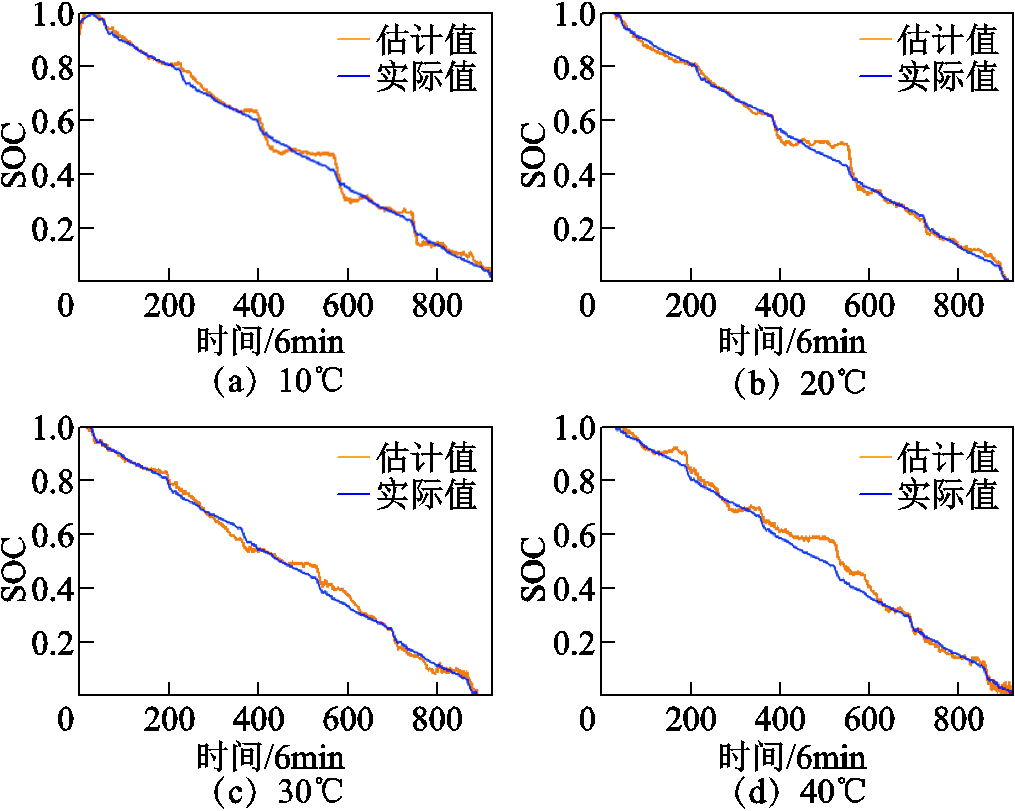
图7 GRU模型锂离子电池不同温度SOC估计结果
Fig.7 GRU model lithium-ion battery SOC estimation results at different temperatures
由4.2节实验可以得出,SOC估计趋势和充放电电流信号是最为相关的。为了更深入地研究电流对SOC的影响,提高其估计精度,本文对充放电电流进行EMD分解,这里采用20℃数据。图8所示为基于EMD算法分解锂离子电池充放电电流过程图,图8a~图8h分别代表第1~8个IMF分量。其中IMF1~IMF3频率较高,表现出非常强的随机性与波动性,因此可以体现电流的波动性;IMF4~IMF6随机性降低,呈现出一定的周期性;IMF7和IMF8基本平稳,故可体现电流的长期趋势。图9为EMD分解后锂离子电池充放电电流残差,可以看出残差电流单位与正常电流信号差异已经小于1%,因此可以不用作为GRU网络的输入。
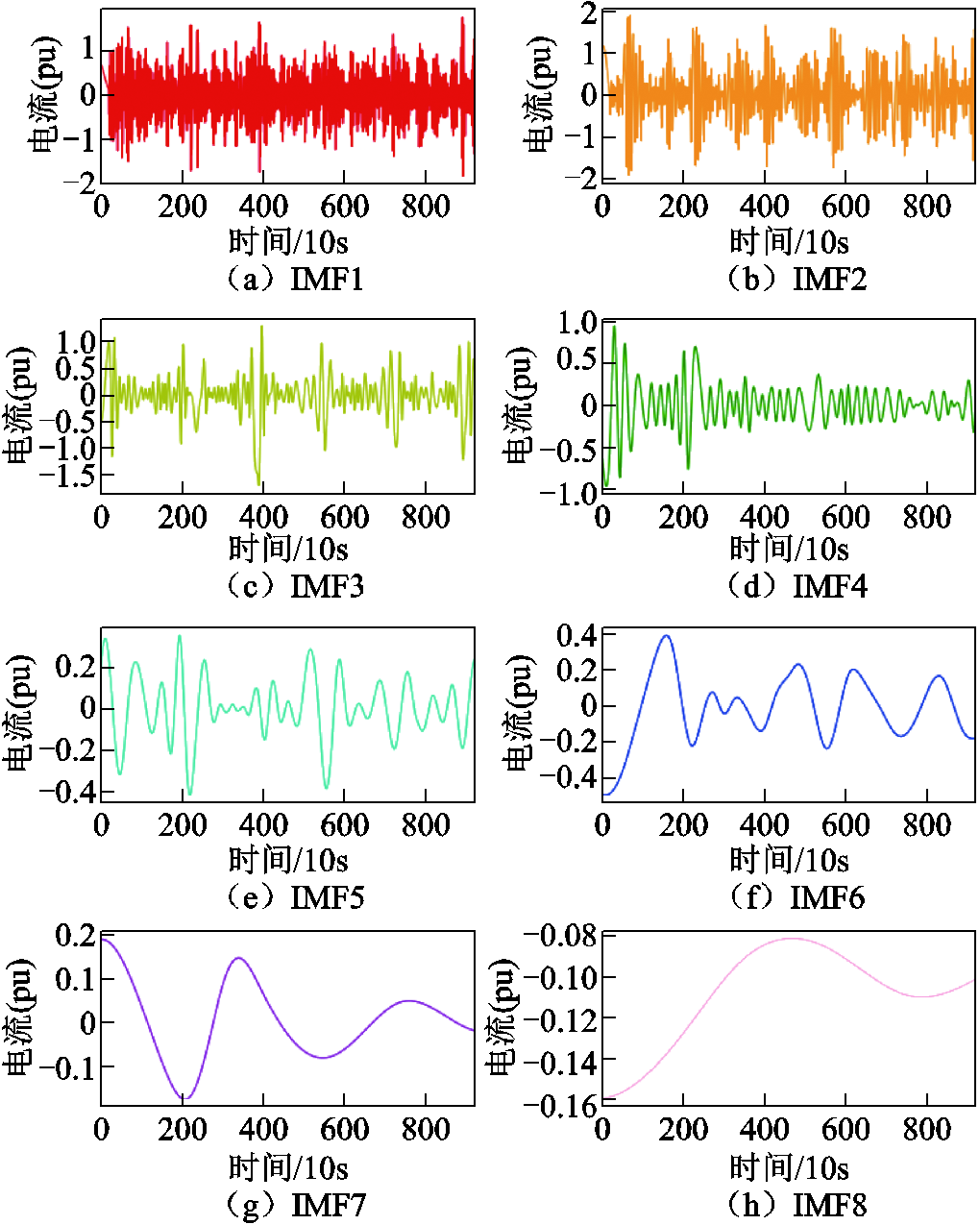
图8 EMD分解的锂离子电池充放电电流
Fig.8 Charge and discharge current of lithium-ion battery decomposed by EMD
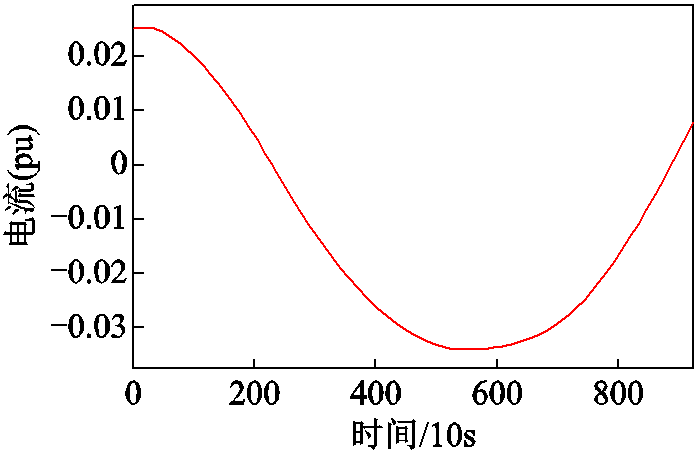
图9 EMD分解的锂离子电池充放电电流残差
Fig.9 The residual charge and discharge current of lithium-ion battery decomposed by EMD
表5所示为EMD-GRU模型锂离子电池SOC估计误差,相比于RNN、LSTM和GRU在三种误差指标都有一定的提升。MAE为1.509 3%,同比于GRU模型误差降低了20.792 4%;MSE为0.037 5%,同比于GRU模型误差降低了42.813 5%;RMSE为1.930 3%,同比于GRU模型误差降低了23.049 6%。为了验证本文在不同温度下EMD-GRU模型的有效性,EMD-GRU模型锂离子电池不同温度下SOC估计误差见表6,可以看出所有温度条件下的MAE均在1.7%以内,满足SOC估计的需求。
表5 EMD-GRU模型锂离子电池SOC估计误差
Tab.5 EMD-GRU model lithium-ion battery SOC estimation error

方法MAE(%)MSE(%)RMSE(%) RNN3.046 70.148 33.838 7 LSTM2.253 70.091 33.011 1 GRU1.9055 0.065 52.508 5 EMD-GRU1.509 30.037 51.930 3
表6 EMD-GRU模型锂离子电池不同温度下SOC估计误差
Tab.6 EMD-GRU model lithium-ion battery SOC estimation error at different temperatures

温度MAE(%)MSE(%)RMSE(%) 10℃1.546 10.040 02.000 8 20℃1.298 30.028 11.675 9 30℃1.617 20.042 22.054 8 40℃1.575 60.039 61.989 6 平均1.509 30.037 51.930 3
图10为EMD-GRU模型锂离子电池不同温度SOC估计结果,可以得到不同时刻的SOC估计情况。当SOC在50%时,图形的斜率变缓,导致误差增加,经过分析得出,10℃温度下这部分误差主要是因为训练数据和测试数据之间差异较大,训练数据的放电电流时间积分与充电电流时间积分的差值要大于测试数据,当满足训练数据的模型参数应用于测试数据时,导致在中间部分下降较为缓慢,符合实际理论。
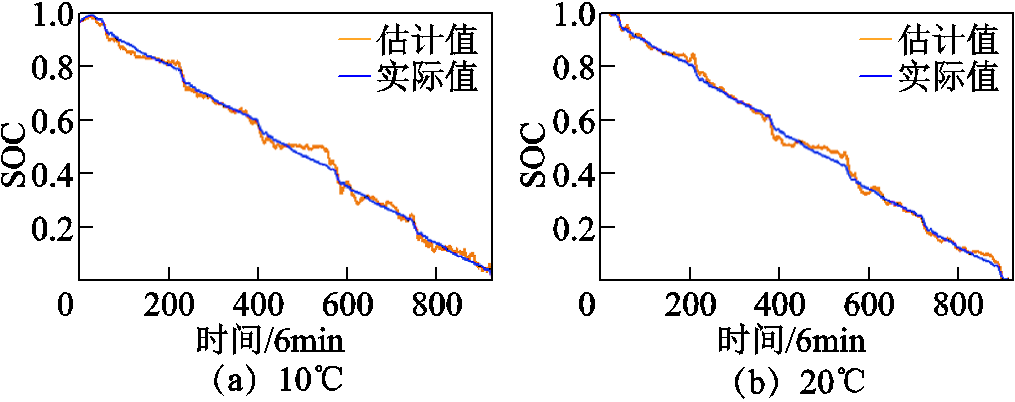
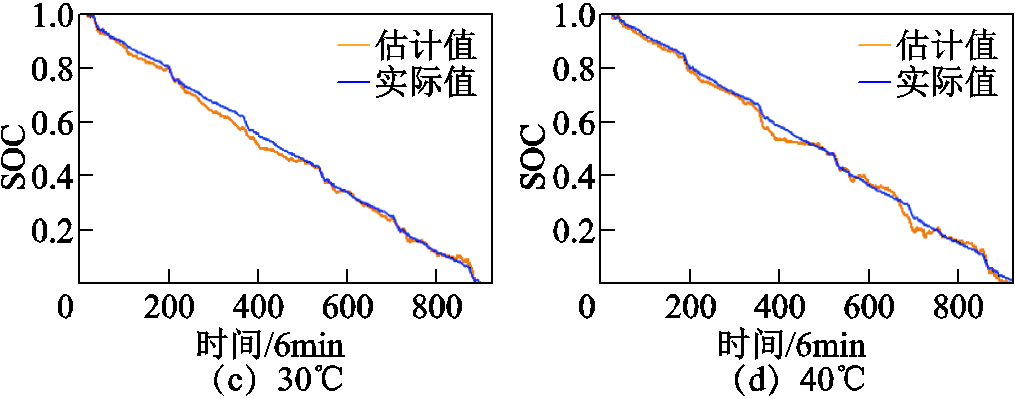
图10 EMD-GRU模型锂离子电池不同温度SOC估计结果
Fig.10 EMD-GRU model lithium-ion battery SOC estimation results at different temperatures
本文介绍了循环神经网络算法优缺点,进而引入一种循环神经网络的变种GRU。为了提高GRU模型锂离子电池SOC估计精度,提出用EMD算法分解电流,将电流分为若干个电流子序列,加上电压和温度信号作为GRU网络输入,SOC值作为GRU网络输出来训练网络参数,提高了SOC的估计精度。在不同温度和不同工况下仿真分析得出,GRU网络的锂离子电池SOC估计精度优于RNN和LSTM,所提EMD-GRU在SOC估计中,MAE为1.509 3%,MSE为0.037 5%,RMSE为1.930 3%,均小于2%,验证了本文方法的有效性。
本文方法是在不同温度下进行SOC估计,在实际应用场景中,电池的温度是动态变化的,因此缺乏系统温度变化和老化适应性的讨论,测量电流信号分解过程是经验过程,也不易于快速估计电池的SOC。
参考文献
[1] 温法政. 锂离子动力电池高精度建模与多状态智能估计[D]. 济南: 山东大学, 2020.
[2] 孙国强, 任佳琦, 成乐祥, 等. 基于分数阶阻抗模型的磷酸铁锂电池荷电状态估计[J]. 电力系统自动化, 2018, 42(23): 57-63.
Sun Guoqiang, Ren Jiaqi, Cheng Lexiang, et al. State of charge estimation of LiFePO4 battery based on fractional-order impedance model[J]. Automation of Electric Power Systems, 2018, 42(23): 57-63.
[3] 费亚龙, 谢长君, 汤泽波, 等. 基于平方根无迹卡尔曼滤波的锂电池状态估计[J]. 中国电机工程学报, 2017, 37(15): 4514-4520, 4593.
Fei Yalong, Xie Changjun, Tang Zebo, et al. State-of-charge estimation based on square root unscented Kalman filter algorithm for Li-ion batteries[J]. Proceedings of the CSEE, 2017, 37(15): 4514-4520, 4593.
[4] Chen Lin, Wang Zhengzheng, Lü Zhiqiang, et al. A novel state-of-charge estimation method of lithium-ion batteries combining the grey model and genetic algorithms[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8797-8807.
[5] Meng Jinhao, Stroe D I, Ricco M, et al. A simplified model-based state-of-charge estimation approach for lithium-ion battery with dynamic linear model[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 7717-7727.
[6] 杨亚丽, 李匡成, 陈涛, 等. 采用电动势-内阻模型在线估计蓄电池荷电状态[J]. 电测与仪表, 2010, 47(3): 16-19, 37.
Yang Yali, Li Kuangcheng, Chen Tao, et al. Introducing the model of electromotive force-impedance estimating the SOC of battery on line[J]. Electrical Measurement & Instrumentation, 2010, 47(3): 16-19, 37.
[7] 刘芳, 马杰, 苏卫星, 等. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工技术学报, 2020, 35(4): 698-707.
Liu Fang, Ma Jie, Su Weixing, et al. State of charge estimation method of electric vehicle power battery life cycle based on auto regression extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 698-707.
[8] 王榘, 熊瑞, 穆浩. 温度和老化意识融合驱动的电动车辆锂离子动力电池电量和容量协同估计[J]. 电工技术学报, 2020, 35(23): 4980-4987.
Wang Ju, Xiong Rui, Mu Hao. Co-estimation of lithium-ion battery state-of-charge and capacity through the temperature and aging awareness model for electric vehicles[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4980-4987.
[9] 魏克新, 陈峭岩. 基于自适应无迹卡尔曼滤波算法的锂离子动力电池状态估计[J]. 中国电机工程学报, 2014, 34(3): 445-452.
Wei Kexin, Chen Qiaoyan. States estimation of Li-ion power batteries based on adaptive unscented Kalman filters[J]. Proceedings of the CSEE, 2014, 34(3): 445-452.
[10] Ragone M, Yurkiv V, Ramasubramanian A, et al. Data driven estimation of electric vehicle battery state-of-charge informed by automotive simulations and multi-physics modeling[J]. Journal of Power Sources, 2021, 483: 229108.
[11] 刘兴涛, 李坤, 武骥, 等. 基于EKF-SVM算法的动力电池SOC估计[J]. 汽车工程, 2020, 42(11): 1522-1528, 1544.
Liu Xingtao, Li Kun, Wu Ji, et al. State of charge estimation for traction battery based on EKF-SVM algorithm[J]. Automotive Engineering, 2020, 42(11): 1522-1528, 1544.
[12] 孔祥创, 赵万忠, 王春燕. 基于BP-EKF算法的锂电池SOC联合估计[J]. 汽车工程, 2017, 39(6): 648-652.
Kong Xiangchuang, Zhao Wanzhong, Wang Chunyan. Co-estimation of lithium battery SOC based on BP-EKF algorithm[J]. Automotive Engineering, 2017, 39(6): 648-652.
[13] Hu Xiaosong, Li Shengbo, Peng Huei, et al. Robustness analysis of state-of-charge estimation methods for two types of Li-ion batteries[J]. Journal of Power Sources, 2012, 217: 209-219.
[14] Tian Yong, Lai Rucong, Li Xiaoyu, et al. A combined method for state-of-charge estimation for lithium-ion batteries using a long short-term memory network and an adaptive cubature Kalman filter[J]. Applied Energy, 2020, 265: 114789.
[15] Yang Fangfang, Zhang Shaohui, Li Weihua, et al. State-of-charge estimation of lithium-ion batteries using LSTM and UKF[J]. Energy, 2020, 201: 117664.
[16] Yang Fangfang, Li Weihua, Li Chuan, et al. State-of-charge estimation of lithium-ion batteries based on gated recurrent neural network[J]. Energy, 2019, 175: 66-75.
[17] 李超然, 肖飞, 樊亚翔, 等. 基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法[J]. 电工技术学报, 2020, 35(9): 2051-2062.
Li Chaoran, Xiao Fei, Fan Yaxiang, et al. A hybrid approach to lithium-ion battery SOC estimation based on recurrent neural network with gated recurrent unit and Huber-M robust Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2051-2062.
[18] 李超然, 肖飞, 樊亚翔, 等. 基于深度学习的锂离子电池SOC和SOH联合估算[J]. 中国电机工程学报, 2021, 41(2): 681-692.
Li Chaoran, Xiao Fei, Fan Yaxiang, et al. Joint estimation of the state of charge and the state of health based on deep learning for lithium-ion batteries[J]. Proceedings of the CSEE, 2021, 41(2): 681-692.
[19] 刘昊天, 王萍, 程泽. 一种编解码器模型的锂离子电池健康状态估算[J]. 中国电机工程学报, 2021, 41(5): 1851-1860.
Liu Haotian, Wang Ping, Cheng Ze. A novel method based on encoder-decoder framework for Li-ion battery state of health estimation[J]. Proceedings of the CSEE, 2021, 41(5): 1851-1860.
[20] 金秀章, 刘岳, 于静, 等. 基于变量选择和EMD-LSTM网络的出口SO2浓度预测[J]. 中国电机工程学报, 2021, 41(24): 8475-8484.
Jin Xiuzhang, Liu Yue, Yu Jing, et al. Prediction of outlet SO2 concentration based on variable selection and EMD-LSTM network[J]. Proceedings of the CSEE, 2021, 41(24): 8475-8484.
[21] 庞辉, 郭龙, 武龙星, 等. 考虑环境温度影响的锂离子电池改进双极化模型及其荷电状态估算[J]. 电工技术学报, 2021, 36(10): 2178-2189.
Pang Hui, Guo Long, Wu Longxing, et al. An improved dual polarization model of Li-ion battery and its state of charge estimation considering ambient temperature[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2178-2189.
Abstract State of charge (SOC) estimation technology of lithium-ion battery is an important part of the battery management system (BMS) design of electric vehicles. In this paper, an SOC estimation method for lithium-ion batteries based on gated recurrent unit (GRU) using empirical mode decomposition (EMD) is proposed. The EMD algorithm is introduced to decompose the discharge current, based on the GRU estimation of the SOC, which not only improves the ability of the GRU model to maintain long-term information for long-term current signals, but also betters the accuracy of SOC estimation of lithium-ion battery. Simulation experiments show that, compared with the traditional recurrent neural network and long-term and short-term memory network, the EMD-GRU method proposed in this paper displays the average absolute error of the lithium-ion battery SOC estimation is 1.509 3%, a year-on-year decrease of 20.792 4%.
keywords:Lithium-ion battery, state-of-charge estimation, gated recurrent unit, empirical mode decomposition
DOI: 10.19595/j.cnki.1000-6753.tces.211069
中图分类号:TM912
国家自然科学基金(51507140)、国家留学基金委国际清洁能源拔尖人才项目([2018]5046, [2019]157)、江苏省配电网智能技术与装备协同创新中心开放基金项目(XTCX202007)资助。
收稿日期 2021-06-19
改稿日期 2021-12-07
李 宁 男,1983年生,博士,副教授,研究方向为电力电子化的电力系统及其控制。E-mail:lining83@xaut.edu.cn(通信作者)
何复兴 男,1995年生,硕士研究生,研究方向为锂离子电池SOC估计。E-mail:2180320030@stu.xaut.edu.cn
(编辑 李冰)