
图1 行驶工况下电池全生命周期容量测试系统
Fig.1 Experimental bench of battery life cycle capacity under driving conditions
摘要 为实现电池剩余使用寿命(RUL)在线预测和降低数据离群值对预测精度影响,提出基于改进轻量型梯度提升机(LightGBM)的RUL在线预测方法。首先,为实现RUL在线预测,通过等压降时间与容量衰减的关系,选取等压降时间为健康因子;然后,为降低数据离群值对预测精度的影响,构建基于LightGBM的预测模型,采用Bagging的学习方式,忽略离群值权重;接着,为进一步降低离群值影响,基于一种兼具自适应性和鲁棒性的损失函数(ARLF)对LightGBM进行改进,通过超参数α限制损失函数一阶导数幅值的饱和值,在残差增长时,限制离群值对梯度的影响;最后,通过行驶工况下电池全生命周期容量测试实验数据,对比基于不同损失函数的RUL在线预测效果,验证所构建健康因子和所提预测方法的有效性。
关键词:锂离子电池 剩余使用寿命 在线预测 离群值 改进轻量型梯度提升机
根据中关村储能产业技术联盟发布的《储能产业研究白皮书2020》[1],锂离子电池累计装机规模在电化学储能中占比最大,为88.8%。锂离子电池凭借其高能量密度、长使用寿命、低自放电率、宽工作温度范围等优点,在电动交通工具、储能系统、移动穿戴等领域得到广泛应用[2-3]。
随着锂离子电池循环充放电次数的增加,电池内副反应导致电池容量衰减。当电池容量衰减至标称容量的70%~80%[4],其充放电性能会受到严重影响,甚至无法正常工作,严重时会导致交通事故,应及时更换电池。作为电池故障预测与健康管理(Prognostics and Health Management, PHM)的重要功能,剩余使用寿命(Remaining Useful Life, RUL)预测可为电池定期维护和安全稳定运行提供参考,降低高昂的维修成本,降低灾难性后果发生概率[5]。
为了实现RUL在线预测,许多研究人员开展了基于健康因子(Health Indicator, HI)的RUL间接/在线预测相关研究。文献[6]采用Box-Cox变换方法,从增量容量曲线峰值面积和充放电时间周期中,提取多个HI,构建电池健康状态估计框架。文献[7]考虑容量衰退和内阻增长(将两者作为HI),对电池健康状态进行估计。文献[8-10]均以等压降时间作为HI,分别采用卷积神经网络-长短期记忆神经网络[8]、极限学习机[9]和反向传播神经网络[10]对电池RUL进行预测。文献[11]提取电压、电流和阻抗等参数作为HI,采用循环神经网络对电池健康状态进行估计。基于现有研究,本文选取等压降时间作为HI,进行电池RUL的在线预测。
基于模型的RUL预测方法通常利用先验知识对电池退化机理[12]进行建模,通过电池全生命周期测试数据[3]和电化学交流阻抗谱[13],借助最小二乘法[14]或观测器[9]对模型内参数进行辨识。上述方法中的RUL退化模型虽然可以考虑不同温度应力[16]和不可观测状态量[17]对电池容量衰退的影响,具有明确的物理意义,但往往忽略电池工作所处环境条件,如振动应力[18]等。电池模型参数会随服役环境的改变而不同,导致固定参数的模型精度会随着电池老化而降低。为了提升预测精度,需根据不同电池型号和工作状态对模型进行修正,由此带来庞大的参数辨识计算量和复杂的物理模型,使得其难以实现扩展应用。同时,其属于开环方法,难以兼顾鲁棒性。随着机器学习方法的发展,支持向量机(Support Vector Machine, SVM)[19]、神经网络[20]、高斯回归[21]、蒙特卡洛模拟[22]和极限梯度提升(eXtreme Gradient Boosting, XGBoost)[23]等机器学习方法逐渐广泛应用于电池的RUL预测。
文献[19]采用改进鸡群算法对SVM进行参数调优,解决RUL预测过程中的非线性数据和收敛精度问题;文献[20]利用卷积神经网络建立RUL预测模型,输入恒流-恒压充电过程中的电压、电流、温度曲线,实现RUL预测。但上述两者未能考虑充放电应力和电池所处工作环境。文献[21]采用模糊理论对高斯回归模型进行优化,以解决RUL预测中的不确定性问题;文献[22]利用蒙特卡洛模拟算法对RUL进行预测,以解决老化实验设计困难和不确定性问题。但上述两者需要庞大的计算量。文献[23]利用XGBoost算法构建电池RUL预测模型,以解决预测精度和速度的问题,但XGBoost采用的是传统的Boosting集成学习方式,即需要在预测时多次遍历整个训练集,选取最佳的分割点,效率较低。轻量型梯度提升机(Light Gradient Boosting Machine, LightGBM)[18]和随机森林(Random Forest, RF)采用Bagging集成学习方式,能够提升训练效率,节省预测时间。LightGBM通过直方图优化、单边梯度采样(Gradient-based One-side Sampling, GOSS)、互斥稀疏特征绑定(Exclusive Feature Bundling, EFB),以及深度限制的按叶子生长(Leaf-wise)方式等,降低样本和特征维度,减小内存使用率,进一步提升训练效率和预测精度。
针对数据存在离群值的问题[19],机器学习中常用的损失函数,对大误差的灵敏度比小误差高,即模型偏向于减少最大的误差,难以有效降低离群值对预测效果的影响,且常用的损失函数无法根据样本特征自适应调整[20]。为解决该问题,本文基于自适应鲁棒损失函数(Adaptive Robust Loss Function, ARLF)对LightGBM进行改进,通过其超参数α控制ARLF表现出不同形式,提升行驶工况下的RUL预测鲁棒性。为模拟行驶工况下电池所受振动应力、充放电应力环境,搭建行驶工况下电池全生命周期容量测试系统,获取电池容量衰退情况。通过行驶工况下电池全生命周期容量实验数据,验证所提RUL预测方法的有效性。对比分析基于不同损失函数的RUL预测效果,表明所提预测方法有较高的预测精度和较好的鲁棒性。
为模拟行驶工况下电动汽车电池所受振动应力和充放电应力,本文搭建行驶工况下电池全生命周期容量测试系统,如图1所示。

图1 行驶工况下电池全生命周期容量测试系统
Fig.1 Experimental bench of battery life cycle capacity under driving conditions
测试系统的组成及功能如下:
(1)振动环境试验系统:提供200~18 000kgf(1kgf= 9.806 65N)的激振力,用以模拟行驶工况下电池所受振动应力。该系统还包含功率放大器、鼓风机、振动台等部件,其目标谱设置见1.2节。
(2)电池充放电系统:配有电压辅助采集通道,测量量程为30V100A,用以模拟行驶工况下电池所受充放电应力,测试曲线见1.2节。
(3)动力电池:以磷酸铁锂电池为研究对象,正极材料为LiFePO4,负极材料为石墨,其特征参数见表1。
表1 磷酸铁锂电池特征参数
Tab.1 Nominal specifications of lithium-ion battery

参数数值 额定容量/(A∙h)1.35 标称电压/V3.3 充电截止电压/V3.65
在放电过程中,锂离子电池内部的主要反应如下:①基本的嵌入/脱嵌:锂离子从阳极活性粒子传输到表面;②化学反应:活性粒子表面发生氧化反应,产生电子和锂离子;③液相扩散:电子被输送到集电极,锂离子通过隔膜从阳极流到阴极;④固相扩散:锂离子从活性粒子表面转移到粒子中心。这些反应不仅伴随着氧化还原,还会诱发其他副反应,如电解液分解、活性物质溶解、金属锂沉积等。这些反应或副反应,使得锂离子在正极电解质中的移动速度变缓,造成电解质液相电流密度减小,同时锂离子不能及时通过隔膜移动到负极,最终表现为电池内阻增加,相同电流倍率下,电压下降速度变快,同时伴随主要反应的内阻增加、锂损失、析锂、枝晶等副反应,会导致电池容量衰减[24]。
根据城市行驶工况(Urban Driving Condition, UDC)[18],振动台功率密度谱设置如图2所示。
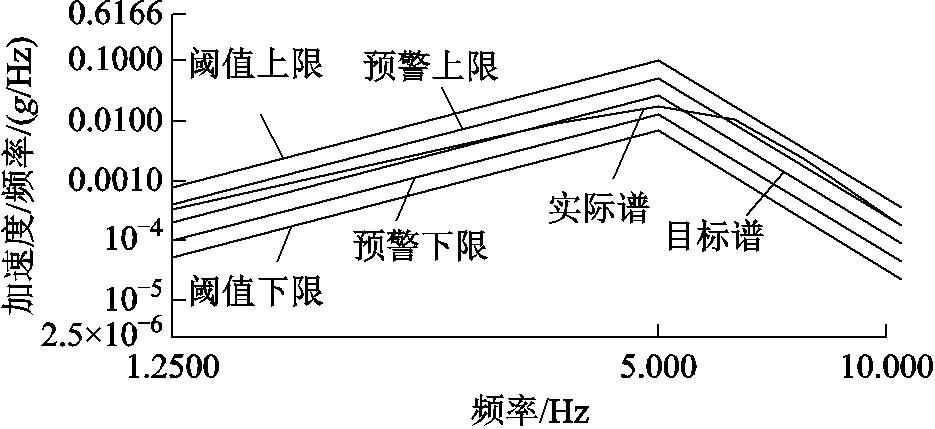
图2 振动台功率密度谱
Fig.2 Power density spectrum of vibration platform
振动台的其他参数设置:平均加速度为0.238 031g,平均速度为8.684 691cm/s,平均位移为4.253 971mm,最大加速度为0.714 093g,最大速度为26.054 1cm/s,最大位移为25.523 8mm。
行驶工况对电动汽车最直观的体现是车辆行驶速度,具体表现为匀速、加速、怠速和减速等。设置行驶工况下电池充放电测试曲线,如图3所示。电池测试工步设置情况见表2。
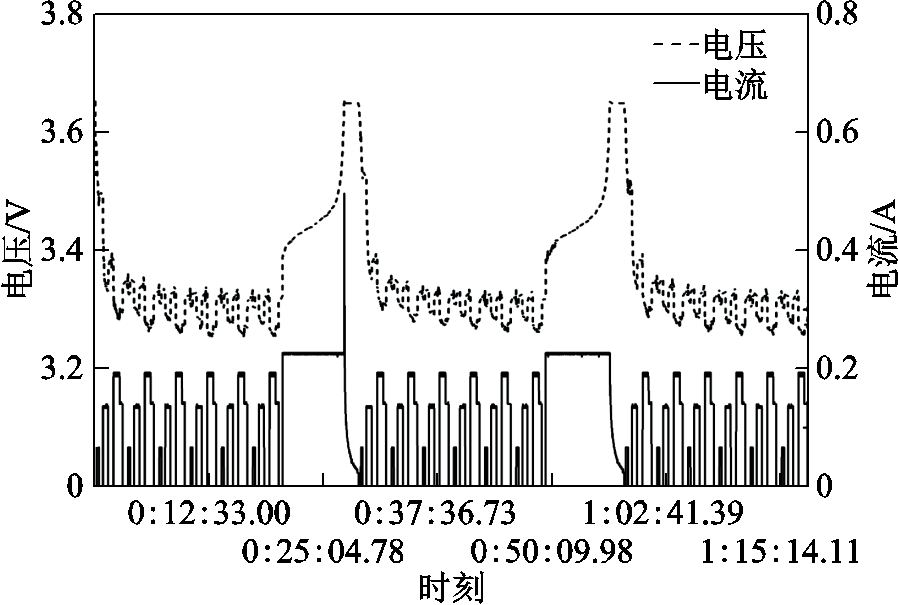
图3 行驶工况下电池充放电测试曲线
Fig.3 Testing curves of battery under driving conditions
表2 电池测试工步设置
Tab.2 Experimental steps of battery test

步骤充放电工步结束条件 1恒流充电达到截止电压 2恒压充电小于截止电流 3静置持续10s 40.07A恒流放电持续15s 5静置持续25s 60.14A恒流放电持续35s 7静置持续35s 80.2A恒流放电持续40s 9静置持续25s 103~9工步循环6次 111~10工步循环1次进行容量测试循环1次 12循环1~11工步容量达到EOL
根据1.2节中的实验设计,测得行驶工况下电池全生命周期容量衰退情况如图4所示。当行驶工况(实验组)和静置工况(对照组)下电池循环充放电至剩余容量为标称容量的80%,即寿命终止(End ofLife, EOL)时,认定电池服役结束。行驶工况下的电池在2 414次循环充放电后到达EOL,而静置工况下的电池尚未到达EOL。
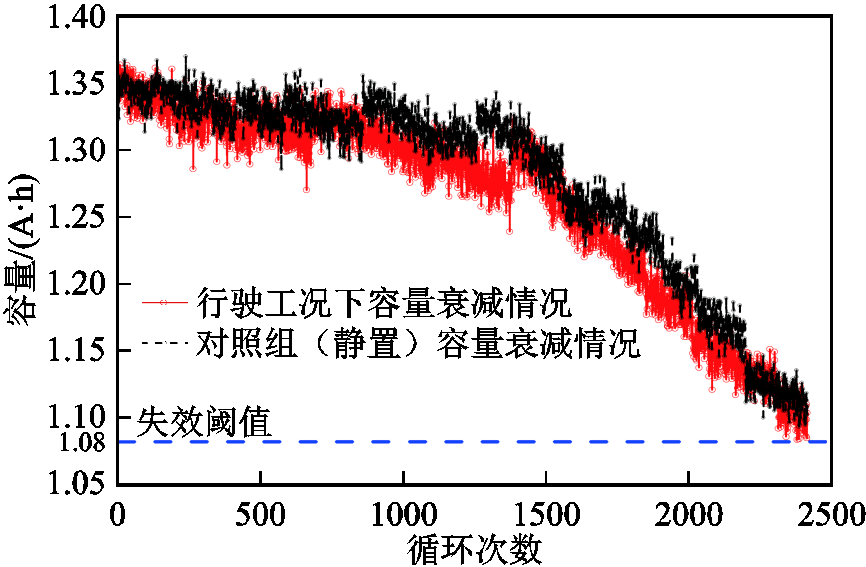
图4 行驶工况下锂离子电池容量衰退情况
Fig.4 Degradation of lithium-ion battery
在1 300~1 600次循环间电池容量出现了突然上升,原因是试验过程中锂离子电池出现了自充电现象[16]。之后,容量衰退速率明显加剧,造成该现象的主要原因是随着充放电循环次数增加,导致电池电解质界面膜增厚和负极锂沉积[24]。
根据文献[25],相较于利用电化学分析、安时积分等特征间接表征电池容量,以等压降时间(从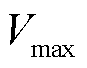 到
到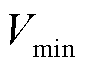 的区间)作为健康因子[8-10],不仅相关数据易采集,而且精度满足需求。
的区间)作为健康因子[8-10],不仅相关数据易采集,而且精度满足需求。
等压降时间示意图如图5所示,在每次放电过程中,取电压第一次到达3.6V(即电压值到达等压降的电压上限值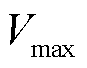 )的时刻
)的时刻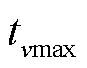 ,放电结束(即电压值到达等压降的电压下限值
,放电结束(即电压值到达等压降的电压下限值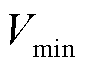 )时刻
)时刻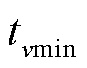 ,根据式(1),计算出等压降时间,并将其作为健康因子。
,根据式(1),计算出等压降时间,并将其作为健康因子。
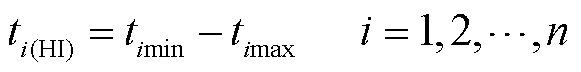 (1)
(1)
式中,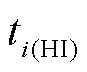 为第i次循环对应的等压降时间;
为第i次循环对应的等压降时间;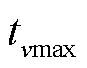 和
和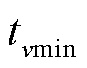 分别为等压降区间电压上、下限值对应的时刻。
分别为等压降区间电压上、下限值对应的时刻。
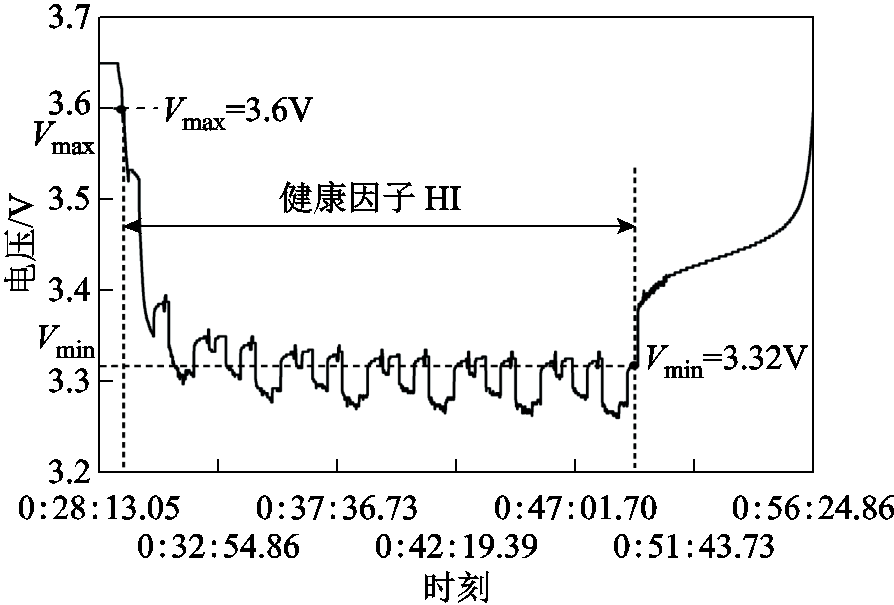
图5 等压降时间示意图
Fig.5 Schematic of isobaric time series
等压降时间和容量随循环次数的变化关系如图6所示。从图6可以看出,等压降时间与容量衰减呈相关关系,定性反映出将等压降时间作为健康因子的合理性。本文采用灰色关联分析法对两者的关联度进行计算分析,进一步定量说明将等压降时间作为健康因子的合理性。

图6 等压降时间和容量随循环次数的变化关系
Fig.6 Relationship between isobaric time series and capacity degradation with cycle
容量序列定义为
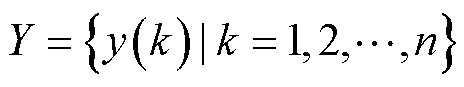 (2)
(2)
HI序列定义为
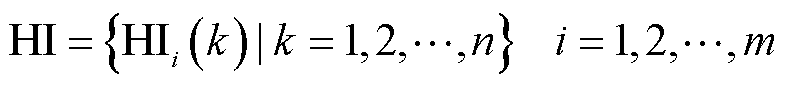 (3)
(3)
式中,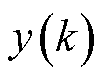 为第k次循环的电池容量;n为序列长度(即全生命周期循环次数);m为序列个数。
为第k次循环的电池容量;n为序列长度(即全生命周期循环次数);m为序列个数。
根据灰色关联分析理论[26],等压降时间(HI)和容量间的关联度为
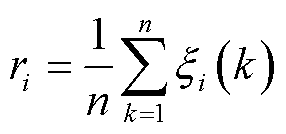 (4)
(4)
关联度系数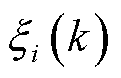 为
为
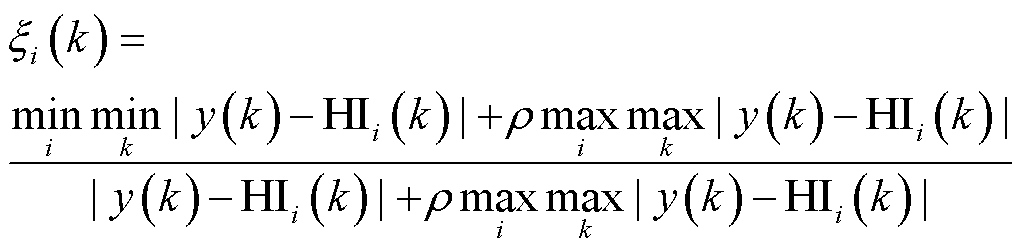 (5)
(5)
式中,分辨系数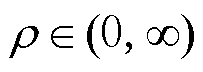 ,通常取
,通常取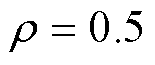 。
。
通过计算,当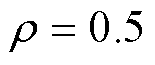 时,
时,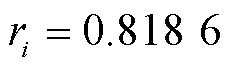 ;当
;当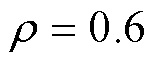 时,
时,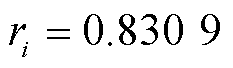 。关联度越接近1,说明序列越相关。由此,从理论上证明了所选等压降时间作为健康因子的合理性。后续章节将讨论通过RUL预测模型,利用行驶工况下电池容量测试实验数据,验证所构建健康因子的有效性。
。关联度越接近1,说明序列越相关。由此,从理论上证明了所选等压降时间作为健康因子的合理性。后续章节将讨论通过RUL预测模型,利用行驶工况下电池容量测试实验数据,验证所构建健康因子的有效性。
LightGBM是基于分布式梯度提升树(Gradient Boosting Decision Tree, GBDT)的集成强学习器模型,凭借其快速、低内耗、高准确性等优势被应用于回归问题。LightGBM将决策树作为基学习器,其可表示为[27]
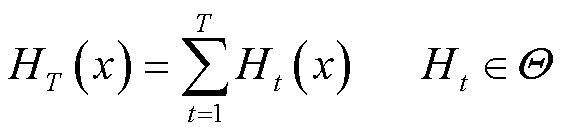 (6)
(6)
式中,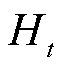 为第t个学习器;
为第t个学习器; 为所有学习器的集合空间。
为所有学习器的集合空间。
LightGBM通过多次迭代不断地提升学习器的性能,使用学习器来获取从输入空间Xs到梯度空间G的映射函数。假设有一个数据量为n的训练集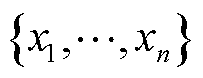 ,其中,xi是空间Xs中第i个维度为s的向量。若前一轮迭代获得的学习器为
,其中,xi是空间Xs中第i个维度为s的向量。若前一轮迭代获得的学习器为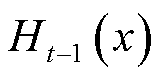 ,损失函数为
,损失函数为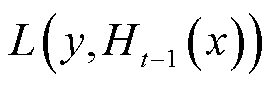 ,则本轮迭代的目标为寻找弱学习器
,则本轮迭代的目标为寻找弱学习器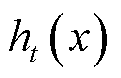 ,使得本轮的损失函数最小,即
,使得本轮的损失函数最小,即
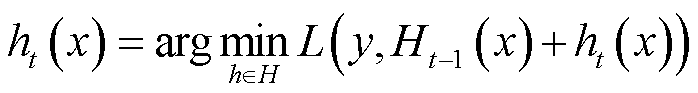 (7)
(7)
计算该损失函数的负梯度,用于获取本轮损失函数的近似值,可表示为
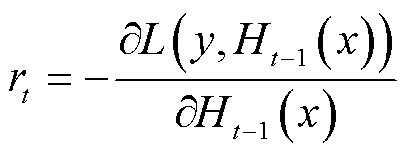 (8)
(8)
目标函数通常为二次方差,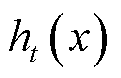 可近似表示为
可近似表示为
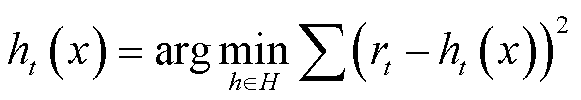 (9)
(9)
最终获得本轮迭代的强学习器为
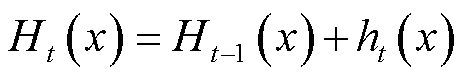 (10)
(10)
传统的损失函数主要有以下几种:柯西损失(Cauchy Loss)、L1 范数损失、L2范数损失、Welsch 损失(Welsch Loss)、Geman-McClure 损失(Geman-McClure Loss),各损失函数的表达式如下。
柯西损失函数
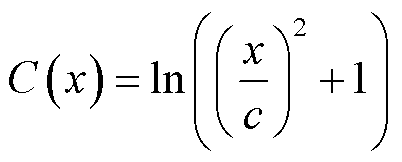 (11)
(11)
L1范数损失函数
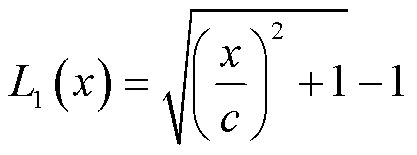 (12)
(12)
L2范数损失函数
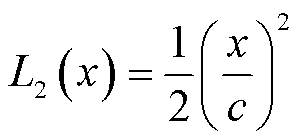 (13)
(13)
Welsch损失函数
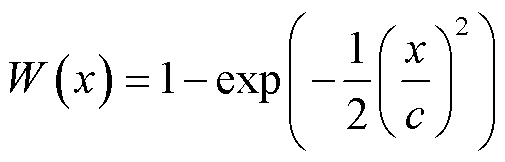 (14)
(14)
Geman-McClure损失函数
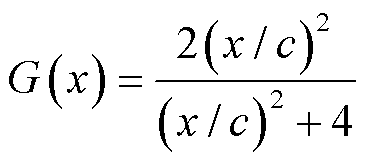 (15)
(15)
针对数据存在离群值的问题[28-30],上述机器学习中常用的损失函数,对大误差的灵敏度比小误差的低,即模型偏向于减少最大的误差,难以有效降低离群值对预测效果的影响,且常用的损失函数无法根据样本特征自适应调整。LightGBM采用Bagging的学习方式,在一定程度上可以应对含有离群值的样本,为进一步降低离群值的影响,本文引入自适应鲁棒损失函数[29]为
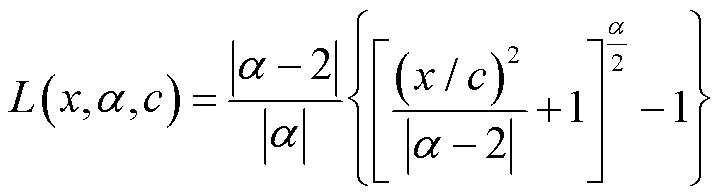 (16)
(16)
式中,c为协调参数,用以调整损失函数在x=0处曲线弯曲的尺度。
虽然α在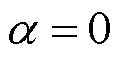 (Cauchy Loss)、
(Cauchy Loss)、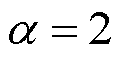 (L2 Loss)、
(L2 Loss)、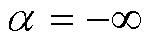 (Welsch Loss)处没有定义,但可通过取极限进行近似。因此,最终的自适应鲁棒损失函数可表示为
(Welsch Loss)处没有定义,但可通过取极限进行近似。因此,最终的自适应鲁棒损失函数可表示为
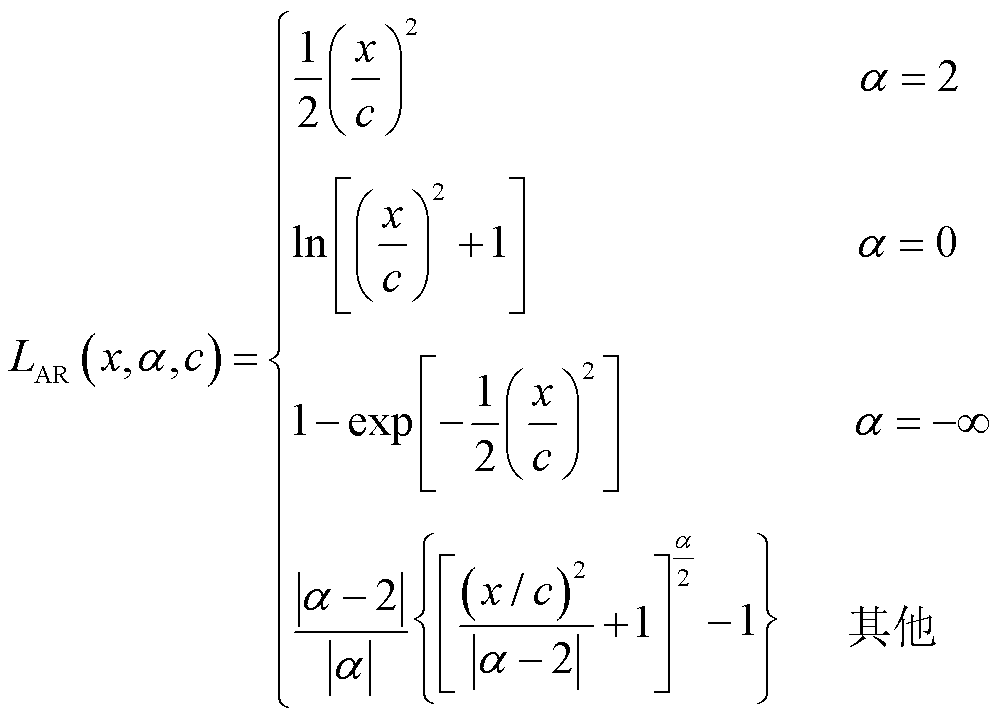 (17)
(17)
由式(11)~式(17)可知,该自适应鲁棒损失函数主要通过超参数α控制损失函数的鲁棒性,即α为不同值时可表示其他损失函数,即根据数据特征表示为合适的损失函数,即
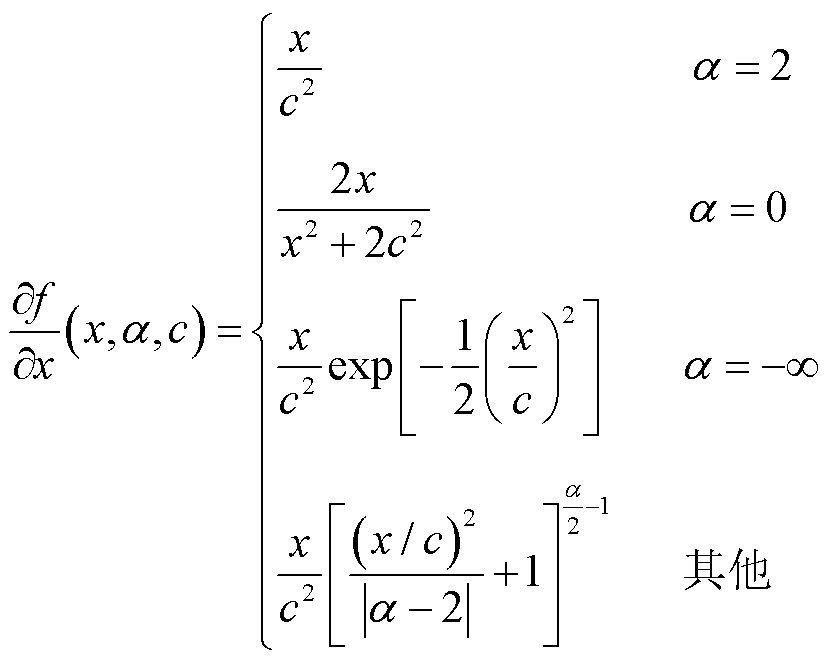 (18)
(18)
由此,为降低离群值对预测精度影响,通过自适应鲁棒损失函数对LightGBM原损失函数进行改进。
基于改进LightGBM的电池RUL在线预测流程如图7所示,具体步骤阐述如下。
1)离线训练
步骤1:基于多线程并行直方图处理数据和获取自适应损失函数参数。针对每一维特征,将连续的浮点型数据划分进离散的k个范围内,得到k个“桶”(bin),构造一个宽度为k的直方图,如图7中直方图优化伪代码所示。与传统的Boosting方式相比,仅需遍历k个bin,减少运算量,提高训练速度。此外,考虑到决策树为弱模型,k决定了正则化的程度,从而避免过拟合。获取行驶工况下电池全生命周期容量数据后,通过自适应鲁棒损失函数得到超参数α和协调参数c,用于配置LightGBM的损失函数。
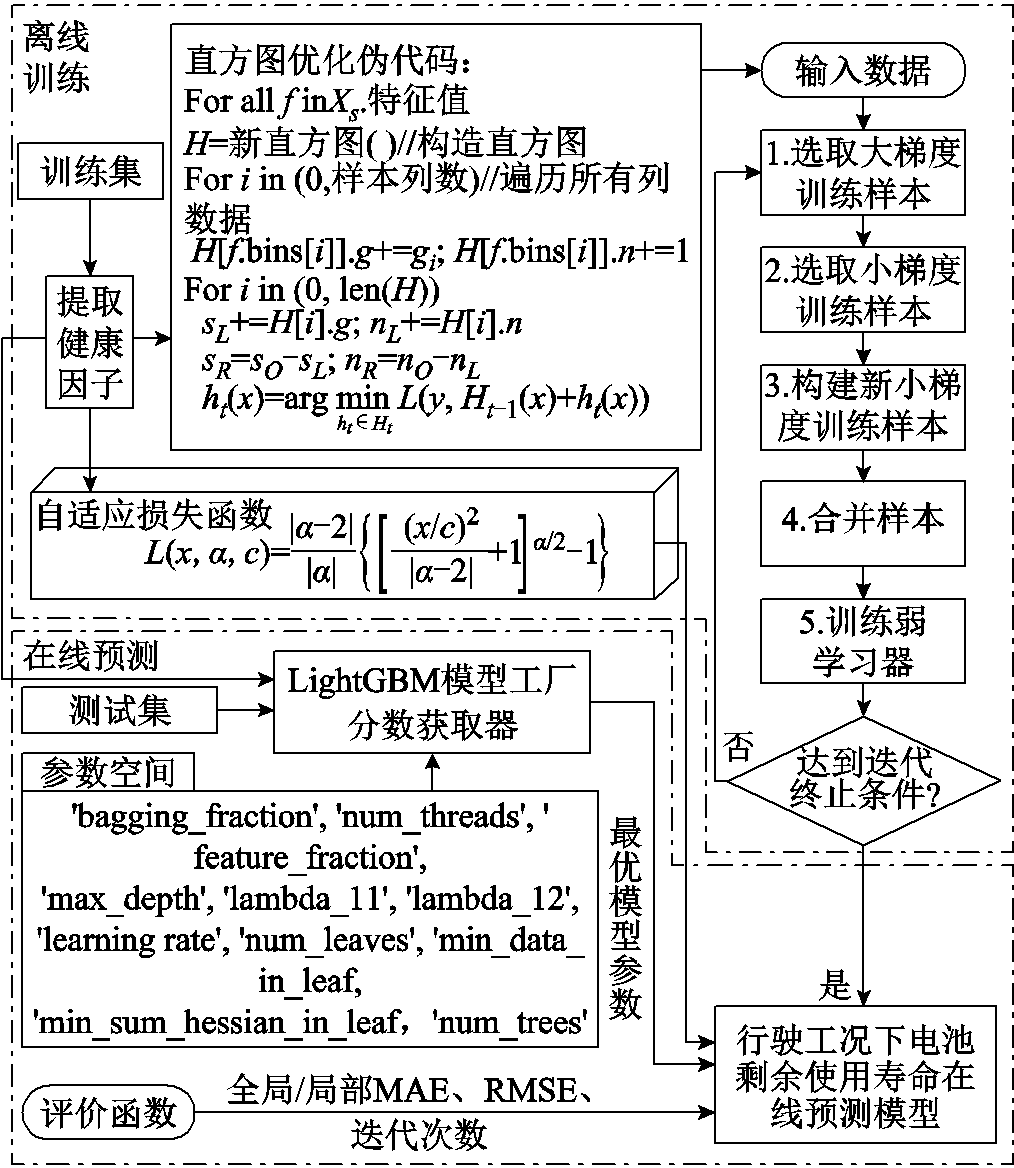
图7 电池RUL预测流程
Fig.7 Flow chart of battery RUL prediction
步骤2:梯度单边采样。将训练集按照梯度降序排列,选取前m×100%较大梯度的样本作为大梯度训练样本;将剩下的样本,选取n×100%较小梯度的样本作为小梯度训练样本;然后将其放大(1-m)/n×100%,作为新小梯度训练样本;合并大梯度和新小梯度训练样本;训练弱学习器。
2)在线预测
步骤3:基于元学习超参数自动调优(Hyper- parameter Optimization, Hyperopt)获取模型最优参数,并设置性能评价函数。根据Hyperopt超参数优化框架,构建模型参数空间、LightGBM模型工厂和分数获取器。其中,模型工厂用于“生产”所需模型,分数获取器则是用于解耦。通过多轮迭代,获得模型超参数见表3。
表3 RUL预测模型超参数
Tab.3 Parameters of different RUL prediction models
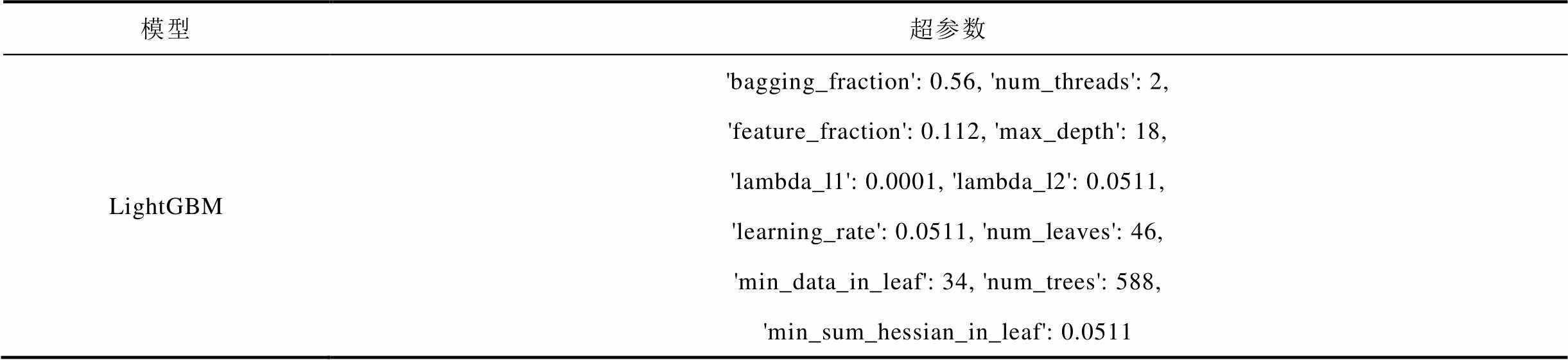
模型超参数 LightGBM'bagging_fraction': 0.56, 'num_threads': 2, 'feature_fraction': 0.112, 'max_depth': 18, 'lambda_l1': 0.0001, 'lambda_l2': 0.0511, 'learning_rate': 0.0511, 'num_leaves': 46, 'min_data_in_leaf': 34, 'num_trees': 588, 'min_sum_hessian_in_leaf': 0.0511
设置评价标准:使用实际容量和预测容量之间的全局方均根误差(Root Mean Square Error, RMSE)、局部RMSE、全局平均绝对误差(Mean Absolute Error, MAE)、局部MAE和迭代次数作为评价标准。其中,全局为全生命周期循环次数,局部为容量回弹处循环次数(即为1 300~1 600次循环)。迭代次数为损失值(Loss值)达到最小前的迭代轮数。
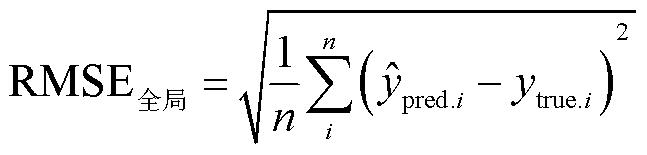 (19)
(19)
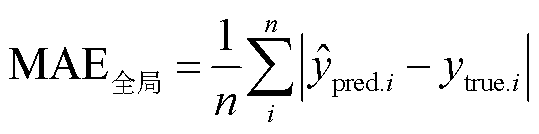 (20)
(20)
式中,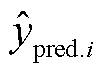 为第i次循环的预测容量;
为第i次循环的预测容量;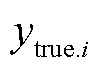 为第i次循环的实际容量;n为全生命周期循环次数。
为第i次循环的实际容量;n为全生命周期循环次数。
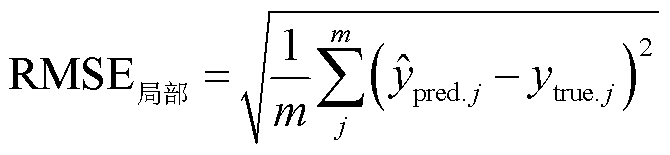 (21)
(21)
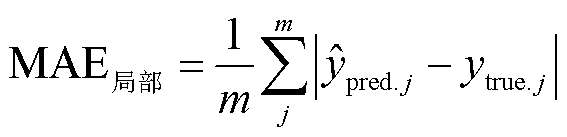 (22)
(22)
式中,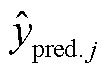 为第j次循环的预测容量;
为第j次循环的预测容量;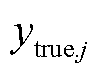 为第j次循环的实际容量;m为容量回弹处循环次数。
为第j次循环的实际容量;m为容量回弹处循环次数。
步骤4:完成RUL预测。RUL是电池可用容量衰减至标准容量的70%~80%(电池服役结束)前所经历的充放电循环次数,将行驶工况下电池全生命周期容量数据分成训练集和测试集,训练集用于训练模型和获取相关参数,测试集用于验证模型的有效性。
以总循环次数的40%作为预测起点,以等压降时间为健康因子作为输入,以对比LightGBM、XGBoost、GBDT和一维卷积神经网络(1D-CNN)的预测效果(方均根误差分别为1.03%、1.05%、3.66%和1.11%),结果如图8所示。从图8可以看出,所提方法可以实现RUL的在线预测,从而验证HI的有效性。另一方面,采用Bagging学习方式的LightGBM较其他预测模型在应对含有离群值的样本时,有良好的预测效果。
将行驶工况下电动汽车电池全生命周期实验样本作为数据集,验证所提RUL预测方法。将数据集的40%作为训练集,其余作为测试集,通过自适应鲁棒损失函数,获得超参数α=0.809 609,协调参数c=1.268 496。根据式(13),可得α不同值对应的损失函数和其一阶导数,除传统常规损失函数以外,本文增加了α=0.5和α=1.5,其分别为所得α与L1 Loss和L2 Loss损失的中间值,如图9和图10所示。
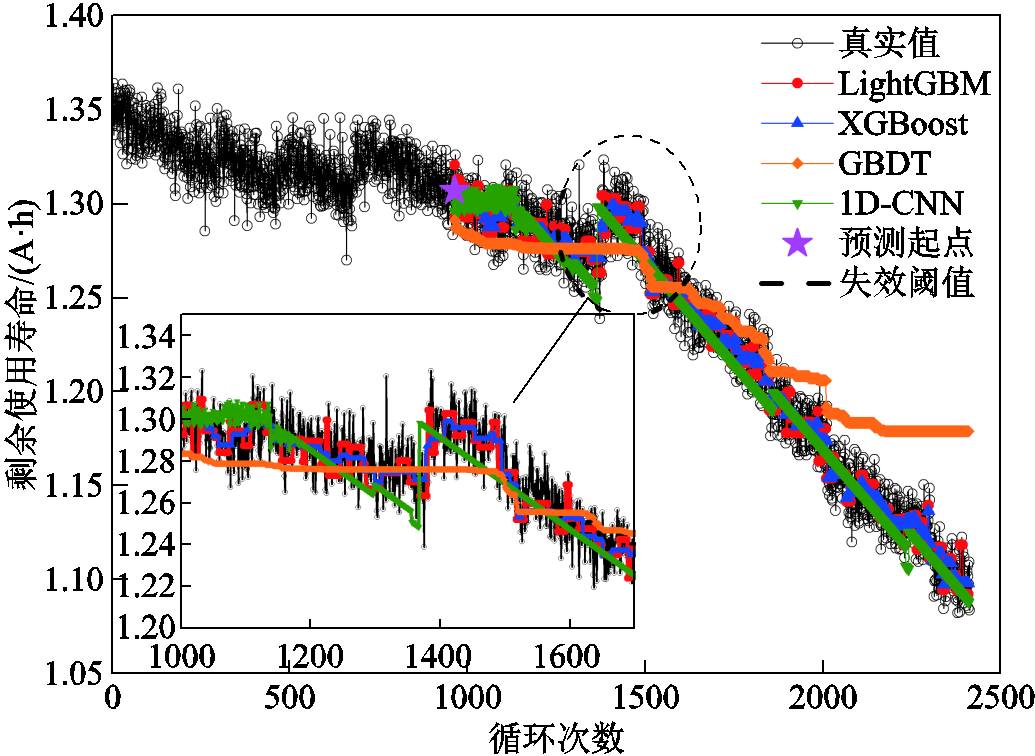
图8 不同预测模型的预测结果
Fig.8 RUL prediction based different models
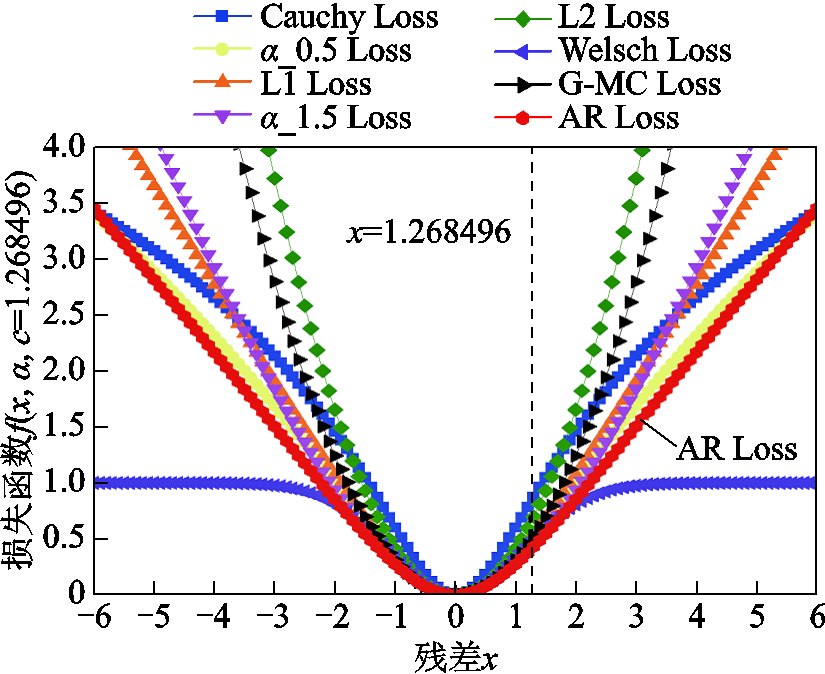
图9 损失函数
Fig.9 Loss function

图10 损失函数一阶导数
Fig.10 First-order derivative of loss function
从图9中可以看出,损失函数为平滑曲线(可微),适用于基于梯度的算法优化。在|x|>0的区间,损失函数为单调递增。对于超参数α而言,也是单调递增的,这一特性决定损失函数具有较好的鲁棒性。原因是在优化过程中,损失函数可以从较大的α值开始逐渐减小,从而使得鲁棒性预测避免局部极小值。从图9可以看出,自适应鲁棒损失函数可以完成不同损失函数的平滑转换。
从图10中可以看出,随着α值的减小,损失函数一阶导数的幅度饱和值也随之减小,其幅值不会超过1/c。也就是说,随残差x(>|c|)的增大,其对梯度的影响降低,因此,在梯度下降的过程中,离群值对RUL预测的影响也随之降低。
为了进一步验证自适应损失函数具有较好的鲁棒性,分析RUL预测过程的每轮迭代中不同损失函数的Loss值情况,如图11所示。
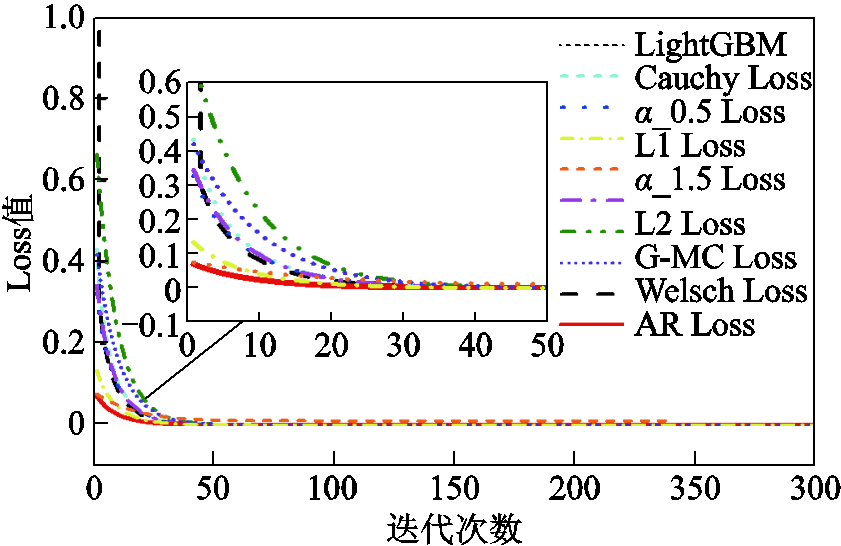
图11 Loss值
Fig.11 Loss value
根据图11所示,自适应损失函数的Loss值的起始值较小,在27轮迭代后达到稳定,其余损失函数分别为:44轮迭代(Cauchy Loss),32轮迭代(α_0.5 Loss),40轮迭代(L1 Loss),38轮迭代(α_1.5 Loss),49轮迭代(L2 Loss),40(G-MC Loss),36轮迭代(Welsch Loss),77轮迭代(LightGBM)。表明自适应鲁棒损失函数具有较好的鲁棒性。
为了验证所改进的RUL预测方法的有效性,将所提RUL预测方法应用于行驶工况下电池全生命周期容量数据,其中,按照表2对LightGBM预测模型的超参数进行设置,所用数据的容量衰减情况如图4所示,相应的实验条件如1.2节中所述。
RUL预测结果如图12所示。从图12可以看出,所提改进LightGBM的RUL预测方法能够实现1.02%的RUL预测方均根误差值(原LightGBM的RUL预测方均根误差值为1.03%)。同时,在局部处,所提RUL预测方法的预测效果(1.195%)要优于LightGBM预测方法(1.225%)。
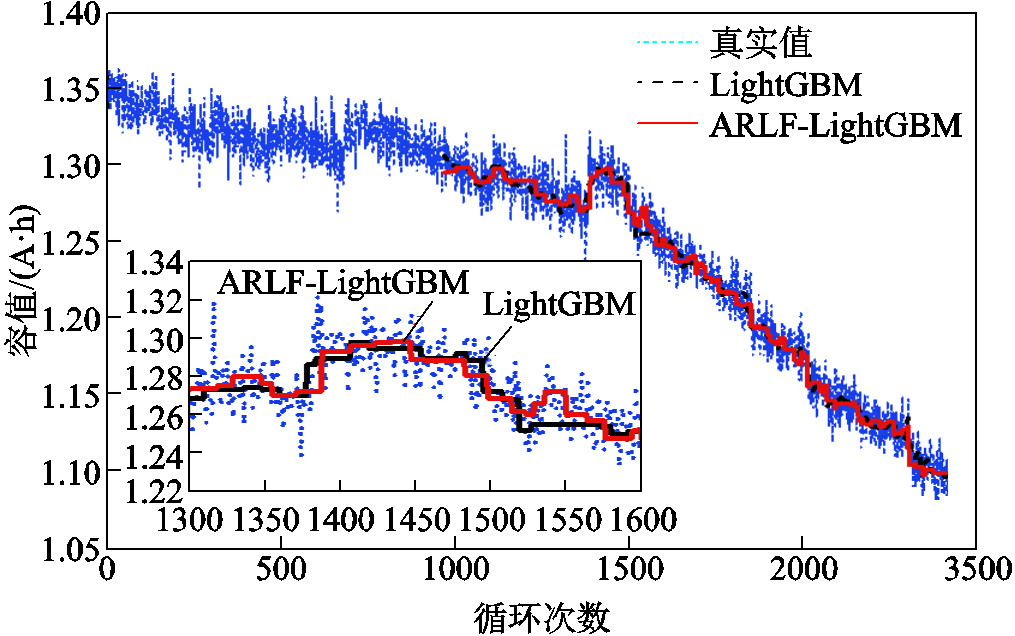
图12 RUL预测结果
Fig.12 RUL prediction results
按照第3节中步骤3所述,从全局MAE、局部MAE、全局RMSE、局部RMSE和迭代次数五个方面,综合评价基于不同损失函数(包括Cauchy Loss、α_0.5 Loss、L1 Loss、α_1.5 Loss、L2 Loss、Welsch Loss、G-MC Loss和AR Loss)的RUL预测效果,对比结果如图13所示。
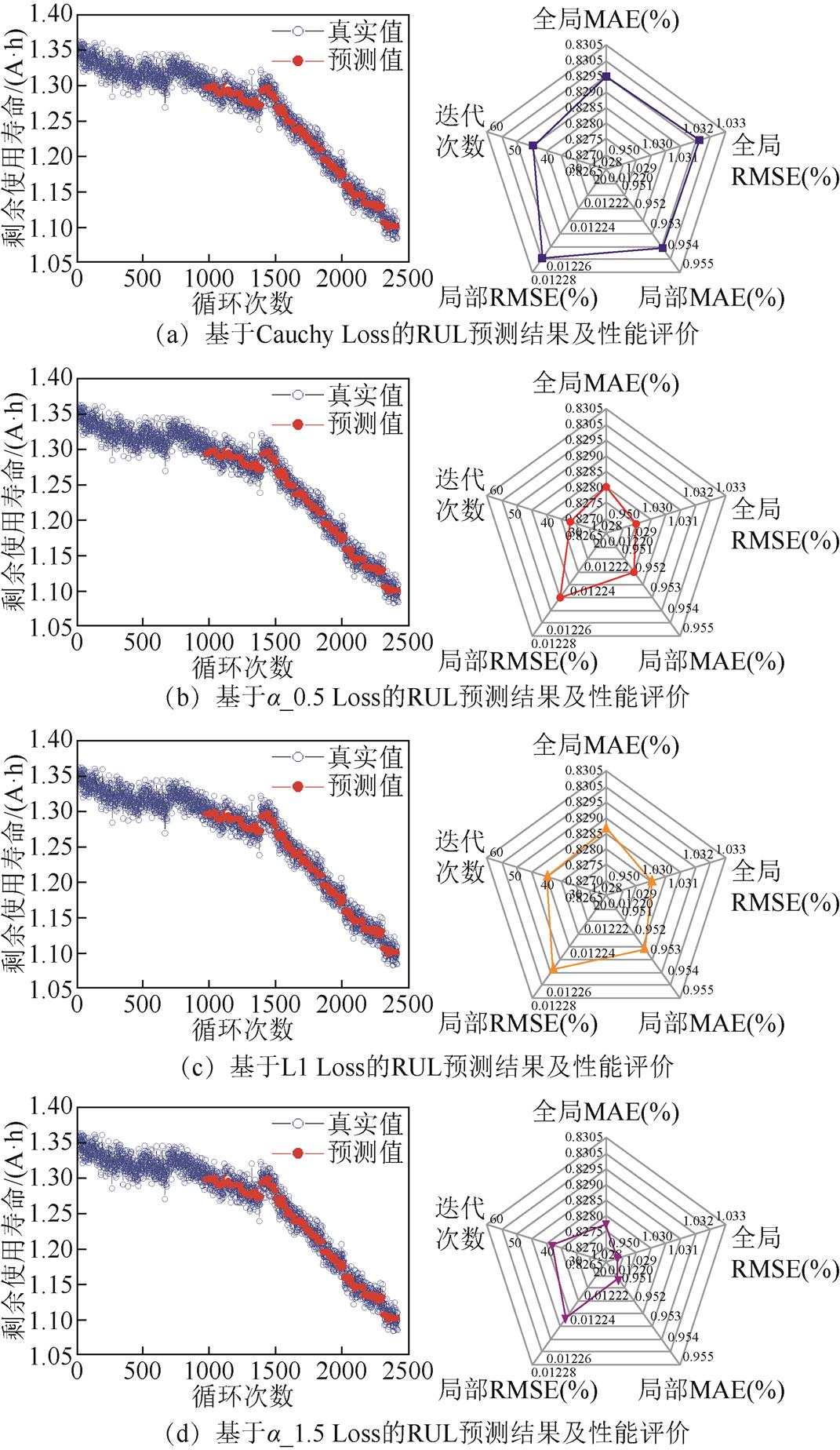
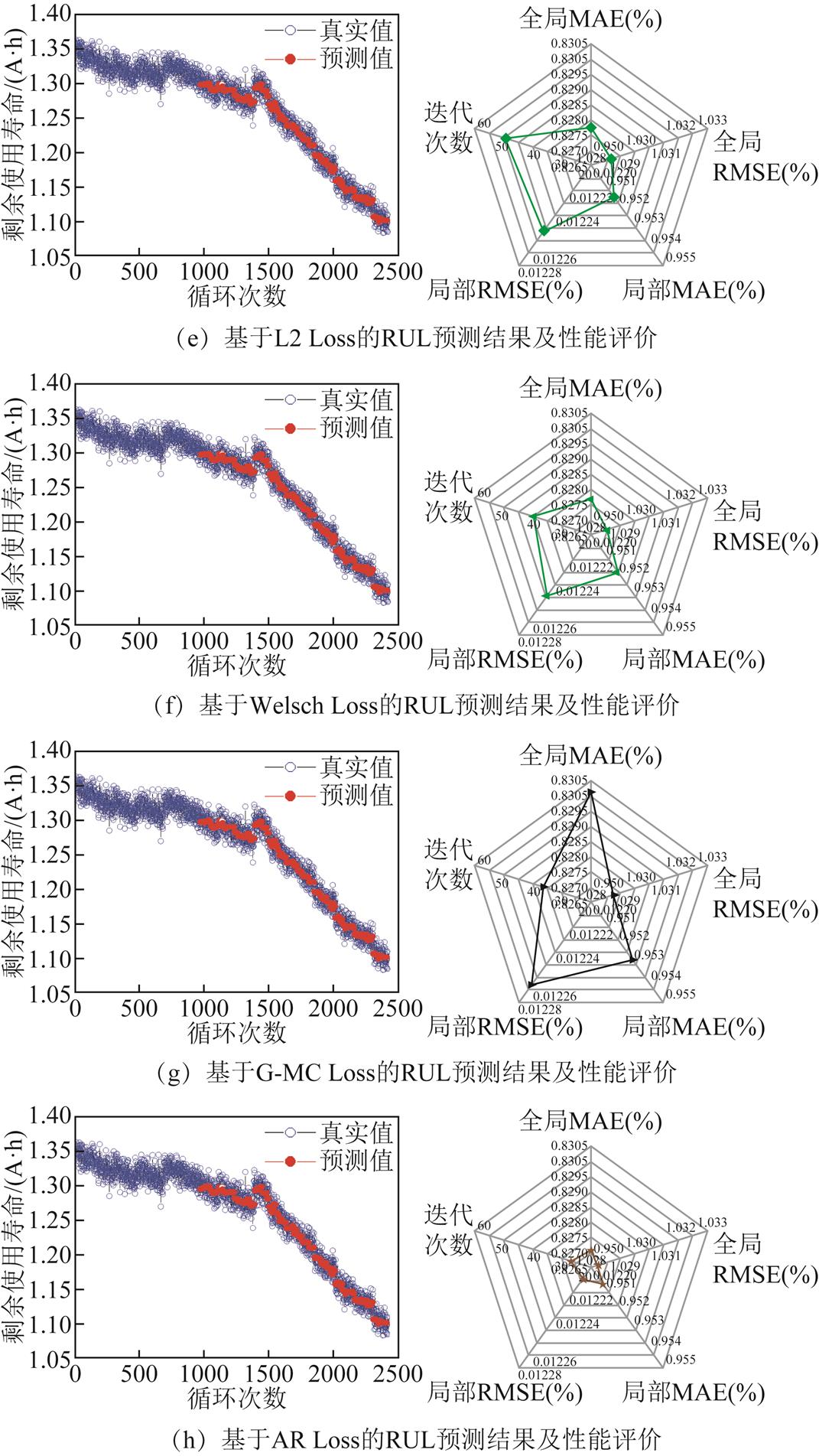
图13 基于不同损失函数的RUL预测效果对比
Fig.13 Comparison of RUL prediction performance based on different loss functions
根据图13所示,基于AR Loss的RUL预测效果在预测精度、鲁棒性方面均较好表现,而基于Cauchy Loss的RUL预测效果较其他有较差的表现。对比结果表明,较之传统损失函数,ARLF具有较好的自适应性,可以根据所需产生不同的表现形式,更好地满足实际需求,有助于提升模型的泛化能力,说明ARLF对LightGBM的RUL预测性能具有提升作用。
为实现RUL在线预测和降低数据离群值对预测精度的影响,本文提出一种基于ARLF-LightGBM的电池RUL在线预测方法。采用行驶工况下电池全生命周期容量测试数据验证所提RUL预测方法的有效性,对比分析基于不同损失函数的RUL预测效果,得出以下结论:
1)以等压降时间作为健康因子,具有易采集和方便计算的特点,有助于实现行驶工况下电池剩余使用寿命的在线预测。
2)相较于传统常规损失函数,ARLF可以根据所需产生不同的表现形式,使得ARLF-LightGBM不仅可以降低离群值对预测精度的影响,而且具有较好的自适应性,有助于提升LightGBM预测模型的泛化能力。
3)本文所提的ARLF-LightGBM方法,通过与原LightGBM方法对比,全局预测误差降低了0.970%,局部预测误差降低了2.45%,迭代轮数降低了50轮。
基于现有实验平台和数据,本文仅考虑电压降单一健康因子,随着平台完善,将探究其他健康因子或多健康因子,实现快速、精确、实时预测电池剩余使用寿命。
参考文献
[1] 中关村储能产业技术联盟. 储能产业研究白皮书2019[R]. 2019.
[2] Krein P T, Fasugba M A, Vehicle-to-grid power system services with electric and plug-in vehicles based on flexibility in unidirectional charging[J]. CES Transactions on Electrical Machines and Systems, 2017, 1(1): 26-36.
[3] Ng M F, Zhao Jin, Yan Qingyu, et al. Predicting the state of charge and health of batteries using data-driven machine learning[J]. Nature Machine Intelligence, 2020, 2: 161-170.
[4] 王瀛洲, 倪裕隆, 郑宇清, 等. 基于ALO-SVR的锂离子电池剩余使用寿命预测[J]. 中国电机工程学报, 2021, 41(4): 1445-1457, 1550.
Wang Yingzhou, Ni Yulong, Zheng Yuqing, et al. Remaining useful life prediction of lithium-ion batteries based on support vector regression optimized and ant lion optimizations[J]. Proceedings of the CSEE, 2021, 41(4): 1445-1457, 1550.
[5] 李超然, 肖飞, 樊亚翔, 等. 基于卷积神经网络的离子电池SOH估算[J]. 电工技术学报, 2020, 35(19): 4106-4119.
Li Chaoran, Xiao Fei, Fan Yaxiang, et al. An approach to lithium-ion battery SOH estimation based on convolutional neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4106- 4119.
[6] Wang Junhua, Liu Shiqi, Wang Shuxiao, et al. Multiple indicators-based health diagnostics and prognostics for energy storage technologies using fuzzy comprehensive evaluation and improved multivariate grey model[J]. IEEE Transactions on Power Electronics, 2021, 36(11): 12309-12320.
[7] Adib K M, Caliwag A C, Lim W. Novel SOH estimation of lithium-ion batteries for real-time embedded applications[J]. IEEE Embedded Systems Letters, 2021, 13(4): 206-209.
[8] 陈赐阳, 陈德旺. 基于CNN-LSTM的锂电池剩余寿命(RUL)间接预测研究[J]. 电源技术, 2021, 45(5): 589-594.
Chen Ciyang, Chen Dewang. Research on indirect prediction of lithium battery RUL based on CNN-LSTM[J]. Chinese Journal of Power Sources, 2021, 45(5): 589-594.
[9] Liu Wei, Xu Yan. Data-driven online health estimation of Li-ion batteries using a novel energy-based health indicator[J]. IEEE Transactions on Energy Conversion, 2020, 35(3): 1715-1718.
[10] 郭永芳, 黄凯, 李志刚. 基于短时搁置端电压压降的快速锂离子电池健康状态预测[J]. 电工技术学报, 2019, 34(19): 3968-3978.
Guo Yongfang, Huang Kai, Li Zhigang. Fast state of health prediction of lithium-ion battery based on terminal voltage drop during rest for short time[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 3968-3978.
[11] 史永胜, 王凡, 刘博亲, 等. 基于注意力改进BiGRU的锂离子电池健康状态估计[J/OL]. 储能科学与技术, DOI: 10.19799/j.cnki.2095-4239.2021. 0099.
Shi Yongsheng, Wang Fan, Liu Boqin, et al. Health state estimation of lithium-ion batteries based on attention augmented BiGRU[J]. Science and Technology of Energy Storage, DOI: 10.19799/j.cnki. 2095-4239.2021.0099.
[12] Cong Xinwei, Zhang Caiping, Jiang Jiuchun, et al. A hybrid method for the prediction of the remaining useful life of lithium-ion batteries with accelerated capacity degradation[J]. IEEE Transactions on Vehicular Technology, 2020, 69(11): 12775-12785.
[13] Sadabadi K K, Jin Xin, Rizzoni G. Prediction of remaining useful life for a composite electrode lithium ion battery cell using an electrochemical model to estimate the state of health[J]. Journal of Power Sources, 2021, 481: 228861.
[14] 卫志农, 原康康, 成乐祥, 等. 基于多新息最小二乘算法的锂电池参数辨识[J]. 电力系统自动化, 2019, 43(15): 139-145.
Wei Zhinong, Yuan Kangkang, Cheng Lexiang, et al. Parameter identification of lithium-ion battery based on multi-innovation least squares algorithm[J]. Automation of Electric Power Systems, 2019, 43(15): 139-145.
[15] 刘芳, 马杰, 苏卫星, 等. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工技术学报, 2020, 35(4): 698-707.
Liu Fang, Ma Jie, Su Weixing, et al. State of charge estimation method of electric vehicle power battery life cycle based on auto regression extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 698-707.
[16] Feng Hailin, Song Dandan. A health indicator extraction based on surface temperature for lithium-ion batteries remaining useful life prediction[J]. Journal of Energy Storage, 2021, 34: 102118.
[17] 刘昊天, 王萍, 程泽. 一种编解码器模型的锂离子电池健康状态估算[J]. 中国电机工程学报, 2021, 41(5): 1851-1860.
Liu Haotian, Wang Ping, Cheng Ze. A novel method based on encoder-decoder framework for Li-ion battery state of health estimation[J]. Proceedings of the CSEE, 2021, 41(5): 1851-1860.
[18] Li Wenhua, Jiao Zhipeng, Du Le, et al. An indirect RUL prognosis for lithium-ion battery under vibration stress using Elman neural network[J]. International Journal of Hydrogen Energy, 2019, 44(23): 12270- 12276.
[19] 张婷婷, 于明, 李宾, 等. 基于Wavelet降噪和支持向量机的锂离子电池容量预测研究[J]. 电工技术学报, 2020, 35(14): 3126-3136.
Zhang Tingting, Yu Ming, Li Bin, et al. Capacity prediction of lithium-ion batteries based on Wavelet noise reduction and support vector machine[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 3126-3136.
[20] Bai Lu, Cui Lixin, Zhang Zhihong, et al. Entropic dynamic time warping kernels for co-evolving financial time series analysis[J/OL]. IEEE Transactions on Neural Networks and Learning Systems, 2020, DOI: 10.1109/TNNLS.2020.3006738.
[21] Kang Weijie, Xiao Jiyang, Xiao Mingqing, et al. Research on remaining useful life prognostics based on fuzzy evaluation-Gaussian process regression method[J]. IEEE Access, 2020, 8: 71965-71973.
[22] Zhang Yongzhi, Xiong Rui, He Hongwen, et al. Lithium-ion battery remaining useful life prediction with Box-Cox transformation and monte carlo simulation[J]. IEEE Transactions on Industrial Electronics, 2018, 66(2): 1585-1597.
[23] 李奇, 刘嘉蔚, 陈维荣. 质子交换膜燃料电池剩余使用寿命预测方法综述及展望[J]. 中国电机工程学报, 2019, 39(8): 2365-2375.
Li Qi, Liu Jiawei, Chen Weirong. Review and prospect of remaining useful life prediction methods for proton exchange membrane fuel cell[J]. Proceedings of the CSEE, 2019, 39(8): 2365-2375.
[24] Liang Jialin, Gan Yunhua, Song Weifeng, et al. Thermal-electrochemical simulation of electro- chemical characteristics and temperature difference for a battery module under two-stage fast charging[J]. Journal of Energy Storage, 2020, 29: 101307.
[25] Li Xiaoyu, Zhang Lei, Wang Zhenpo, et al. Remaining useful life prognosis for lithium-ion batteries based on a hybrid model combining the long short-term memory and Elman neural networks[J]. Journal of Energy Storage, 2019, 21: 510-518.
[26] 魏子茹, 卢延辉, 王鹏宇, 等. 基于CRITIC法的灰色关联理论在无人驾驶车辆测试评价中的应用[J]. 机械工程学报, 2021, 51(12): 99-108.
Wei Ziru, Lu Yanhui, Wang Pengyu, et al. Application of grey correlation theory based on CRITIC method in autonomous vehicles test and evaluation[J]. Journal of Mechanical Engineering, 2021, 51(12): 99-108.
[27] 肖迁, 焦志鹏, 穆云飞, 等. 基于LightGBM的电动汽车行驶工况下电池剩余使用寿命预测[J/OL]. 电工技术学报, 1-10[2021-12-27]. DOI: 10.19595/ j.cnki.1000-6753.tces.201653.
Xiao Qian, Jiao Zhipeng, Mu Yunfei, et al. LightGBM based remaining useful life prediction of electric vehicle lithium-ion battery under driving conditions[J/OL]. Transactions of China Electrotechnical Society, 1-10[2021-12-27]. DOI: 10.19595/j.cnki.1000-6753.tces.201653.
[28] 颜诗旋, 朱平, 刘钊. 基于改进LightGBM模型的汽车故障预测方法研究[J]. 汽车工程, 2020, 42(6): 815-819, 825.
Yan Shixuan, Zhu Ping, Liu Zhao. Research on vehicle fault prediction scheme based on improved LightGBM model[J]. Automotive Engineering, 2020, 42(6): 815-819, 825.
[29] Jonathan T Barron. A general and adaptive robust loss function[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 2019: 4326-4334.
[30] 韦海燕, 陈静, 王惠民, 等. 新陈代谢灰色粒子滤波实现电池剩余寿命预测[J]. 电工技术学报, 2020, 35(6): 1181-1188.
Wei Haiyan, Chen Jing, Wang Huimin, et al. Remaining useful life prediction of battery using metabolic grey particle filter[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1181-1188.
Abstract In order to achieve the remaining useful life (RUL) on-line prediction and reduce the impact of outlier value on prediction accuracy, this paper proposes an on-line prediction method based on the improved light gradient boosting machine (LightGBM). Firstly, in order to accomplish RUL on-line prediction, the health indicator is selected according to the relationship between isobaric time series and capacity. Then, in order to reduce the impact of outliers on the prediction accuracy, the prediction model based on LightGBM is built, and Bagging learning method is adopted, which ignores the weights of outliers. The improved LigthGBM based on adaptive robust loss function is established to reduce the impact further. Parameter α is utilized to limit the saturation value for first-order derivative of loss function, so that the influence of residual error on the gradient is reduced. Finally, the effectiveness of the established health indicator and the proposed RUL prediction method is verified by experimental data, and the RUL prediction performance based on different loss functions are compared. The results demonstrate that the proposed method has higher prediction accuracy and better robustness.
keywords:Lithium-ion battery, remaining useful life, on-line prediction, outlier value, improved light gradient boosting machine
DOI:10.19595/j.cnki.1000-6753.tces.211075
中图分类号:TM911
国家自然科学基金(52107121, U2066213)和中国博士后科学基金(2020M680880)资助项目。
收稿日期 2021-07-15
改稿日期 2021-10-24
肖 迁 男,1988年生,博士,讲师,博士生导师,研究方向为分布式能源与微电网、直流配电网、电力电子技术及其在智能电网和综合能源系统中的应用、电池储能系统。E-mail:xiaoqian@tju.edu.cn
穆云飞 男,1984年生,博士,教授,博士生导师,研究方向为电力系统安全性与稳定性、综合能源集成与应用、电动汽车并网规划与运行控制。E-mail:yunfeimu@tju.edu.cn(通信作者)
(编辑 赫蕾)