
图1 混合时间尺度的无功/电压优化控制框架
Fig.1 Hybrid timescale voltage/var control framework
摘要 针对大量光伏接入配电网造成的诸如网损增加、电压波动和越限等调压方面的问题,该文提出一种日前无功/电压优化控制与实时自治控制相结合的混合时间尺度无功/电压控制方法。在日前时间尺度上,构建了以期望网损、电压偏移以及电压越限风险为目标,综合考虑变压器有载分接头和电容器组动作,以及光伏逆变器无功发生能力约束的不确定优化模型,为高效求解无功动态优化这一高维度的混合整数非线性规划问题,提出一种基于概率潮流的松弛-聚类-校正动态无功优化解耦求解方法;在实时时间尺度上,以日前优化控制结果为运行基准点,推导出逆变器无功出力调节增量与光伏实时出力预测误差之间的近似关系,融合日前时间尺度的电压灵敏度信息构建了仅依赖本地实时信息的实时自治控制策略。通过改进的IEEE 33系统进行仿真分析,验证了所提无功/电压控制策略的有效性。
关键词:配电网 光伏发电 无功/电压控制 混合时间尺度 电压越限风险
光伏发电功率具有间歇性和随机性,其接入配电网后,配电网无功/电压控制面临严重挑战[1-2]。主要表现在两个方面:光伏发电大量接入中低压配电网,配电网潮流及电压分布变得复杂,存在网损增加、电压越限风险;以有载调压变压器分接头(On-Load Tap Changer, OLTC)和电容器组等为代表的传统调压装置无法频繁响应电压快速变化,平抑电压波动效果欠佳[3-4]。光伏并网逆变器具有一定的无功发生能力[5],如何发挥其无功发生能力,使其与传统调压装置实现协调控制,以应对大量光伏接入配电网带来的电压波动问题,对配电网安全经济运行具有重要意义。
按照控制时间尺度不同,无功/电压优化控制可分为日前无功/电压优化控制、实时自治控制以及多时间尺度协调控制[6]。日前无功/电压优化控制,基于日前分布式电源有功功率和负荷预测数据,制定配电网可控设备的调节计划,以实现电网安全经济运行,既涉及调控OLTC和电容器组等离散控制设备,也涉及光伏逆变器等连续控制设备。离散控制设备多时段耦合关系,使得该无功/电压优化控制问题在数学呈现为时空耦合的混合整数非线性规划问题,为提高其求解速度通常需要在保障解的趋优性同时进行简化处理。文献[7]为避免控制设备的频繁动作,将相关设备动作成本纳入目标函数,采用改进遗传算法进行求解,因动作成本直接影响动作次数且其较难确定,应用中存在动作次数过多或过少的问题。文献[8]将动态无功优化问题分解为非线性规划与混合整数规划两个子问题进行求解,降低了求解难度,提高了求解速度,但需要目标函数对控制变量的灵敏度信息。文献[9]利用聚类方法对各时段静态优化的电容器投切组进行时序分段融合,先制定电容器的日前投切计划,再对分布式电源无功功率进行优化,该方法将动态优化转换为静态优化,降低了求解维数,但该方法并未考虑分布式电源发电功率和负荷的不确定[10]。由于日前光伏出力具有预测精度低和实时波动性的特点,实时运行时并网点电压存在波动剧烈及越限风险。实时自治控制基于本地测量信息[11],以安全性为首要目标,实时修正控制。其对通信要求低,不受通信网故障的影响[12],同时可快速响应分布式电源出力变化,可靠性较高,但缺乏整体协调性[13],可能导致全局控制方案并非最佳。
多时间尺度协调控制,借鉴模型预测控制理论,基于“多级协调,逐级细化,反馈校正”的思想,通过日前优化、日内滚动优化和实时反馈校正实现闭环控制,并削弱分布式电源出力和负荷误差对其优化控制方案的影响[14]。但该方法的实施需要配电网具备高质量的通信条件,对于中低压配电系统较难达到其所需的通信水平[15-16]。文献[17-18]日前长时间尺度集中优化慢速设备挡位,日内进行滚动修正,以减少预测误差的影响,但日内优化仍需要全局信息,对通信水平要求较高。文献[19]日前长时间尺度提出两阶段动态随机优化模型,短时间尺度提出并网点PV-PQ-QV节点类型转换的自适应趋优控制,提高了电网运行的安全性和经济性,但所提最优潮流解耦法无法保证解的最优性。文献[20]日前集中优化整定逆变器P-V及Q-V曲线控制参数,实时自治控制阶段各逆变器采用本地下垂控制,但下垂曲线参数受分布式电源出力预测精度影响较大。
本文提出一种日前无功/电压优化控制与实时自治控制相结合的混合时间尺度无功/电压控制方法。在日前时间尺度上,采用基于半不变量法的概率潮流,构建了以期望网损、电压偏移及电压越限风险为目标,综合考虑OLTC和电容器组动作次数,以及光伏逆变器无功发生约束的不确定优化模型,提出一种基于Word系统聚类的松弛-聚类-校正动态无功优化解耦求解方法。首先将OLTC挡位及电容器组投切容量松弛为连续变量,采用改进粒子群方法求解各时段静态优化解,得到OLTC挡位和电容器组投切计划,以及光伏逆变器无功补偿量;其次运用Word系统聚类方法划分时段并确定各时段离散变量解;最后再修正光伏逆变器无功出力。在实时时间尺度上,以日前无功/电压优化控制结果为运行基准点,推导出光伏逆变器无功出力增量与光伏实时出力预测误差之间的近似关系。在此基础上综合考虑光伏逆变器无功响应能力与其有功出力的关系,构建了仅依赖本地实时信息的实时无功/电压控制策略,利用光伏逆变器无功动态响应能力平抑电压波动并规避节点电压越限风险。
本文所提出的混合时间尺度无功/电压控制整体框架如图1所示。在日前时间尺度上,根据光伏出力和负荷日前预测,以及其历史统计数据,构建各时段光伏出力与负荷的概率模型,通过求解一个不确定优化模型来确定OLTC、电容器组和光伏逆变器无功出力的日前调节计划。日前无功/电压优化控制在兼顾网络损耗及电压偏移的情况下,使电压越限风险最小化,将优化结果、各时段电压灵敏度矩阵及光伏并网点上游节点电压信息传递至光伏并网的实时控制厂站。在光伏并网点实时自治控制环节,采用一种分散电压控制逻辑,利用光伏逆变器无功动态响应能力实现对并网点电压波动和越限的抑制,尽可能使并网点和上游节点电压趋向日前优化值。

图1 混合时间尺度的无功/电压优化控制框架
Fig.1 Hybrid timescale voltage/var control framework
2.1.1 源荷不确定性建模及概率潮流
1)光伏出力不确定性建模
光强随时间波动的特性造成了光伏出力的不确定性,光伏出力服从Beta分布,可得到光强的概率密度函数为
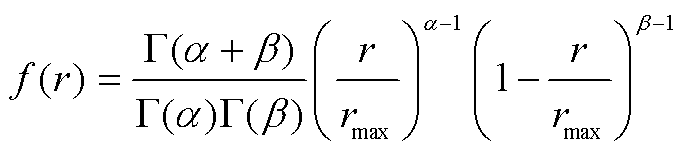 (1)
(1)
式中,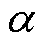 和
和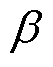 为Beta分布的形状参数;r和
为Beta分布的形状参数;r和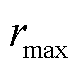 分别为确定时段内的实际光强和最大光强;
分别为确定时段内的实际光强和最大光强;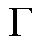 为Gamma函数。
为Gamma函数。
通过光强的平均值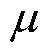 和标准差
和标准差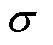 可以得到Beta分布的形状参数,可表示为
可以得到Beta分布的形状参数,可表示为
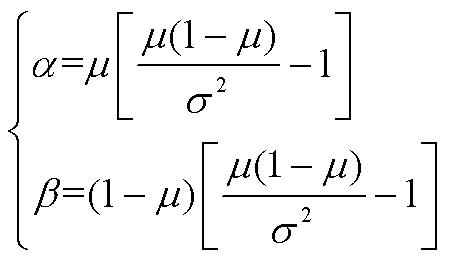 (2)
(2)
结合式(1)和式(2)可得到光伏出力的概率密度函数为
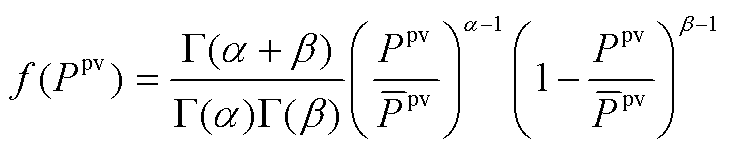 (3)
(3)
式中,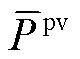 为光伏最大有功出力,
为光伏最大有功出力,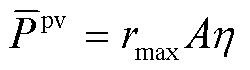 ,A为太阳能电池阵列的总面积,
,A为太阳能电池阵列的总面积,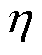 为太阳能电池阵列的光电装换效率。
为太阳能电池阵列的光电装换效率。
2)负荷不确定性建模
一般假设负荷的预测误差服从正态分布,则负荷有功和无功功率的概率密度函数为
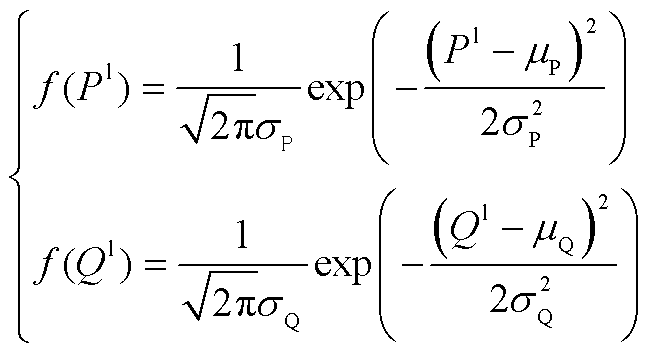 (4)
(4)
式中,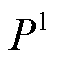 和
和 分别为有功负荷和无功负荷;
分别为有功负荷和无功负荷; 、
、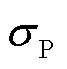 和
和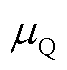 、
、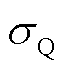 分别为有功负荷和无功负荷的均值和标准差。
分别为有功负荷和无功负荷的均值和标准差。
3)半不变量概率潮流法
配电网中半不变量法计算概率潮流的步骤如下:
(1)根据负荷和光伏预测数据进行确定性潮流得到基准运行点上的状态变量 、支路功率变量
、支路功率变量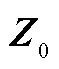 和雅可比矩阵
和雅可比矩阵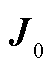 ,求出灵敏度矩阵
,求出灵敏度矩阵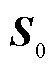 。
。
(2)针对光伏、负荷的随机特性进行概率建模,根据其概率分布求得各阶半不变量。
(3)根据式(5)计算出各节点电压和各支路功率等的半不变量。
 (5)
(5)
式中,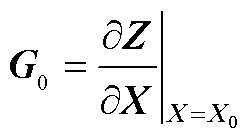 ;
;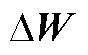 为节点注入功率的扰动量。
为节点注入功率的扰动量。
(4)通过Gram-Charlier级数展开得到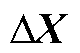 和
和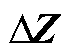 的概率密度函数和累积分布函数,进而得到系统状态变量的概率分布及其越限概率。
的概率密度函数和累积分布函数,进而得到系统状态变量的概率分布及其越限概率。
2.1.2 目标函数
传统日前无功优化通常以网损和电压偏差最小为目标函数,由于光伏有功出力日前预测误差较大,并且随着光伏渗透率的提高,电网电压存在较大的越限可能性,为反映由光伏出力不确定性给电网电压带来的不利影响,减少电压越限概率,本文将电网电压越限风险加入到目标函数。
1)电压越限风险指标
本文采用风险偏好型效用函数[21]作为定量评价电压越限严重度,其表达式为
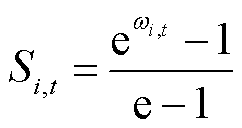 (6)
(6)
式中,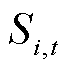 为电压越限的严重度;
为电压越限的严重度;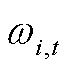 为t时刻节点i电压越限严重度指标。电压越限严重度指标
为t时刻节点i电压越限严重度指标。电压越限严重度指标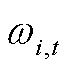 为
为
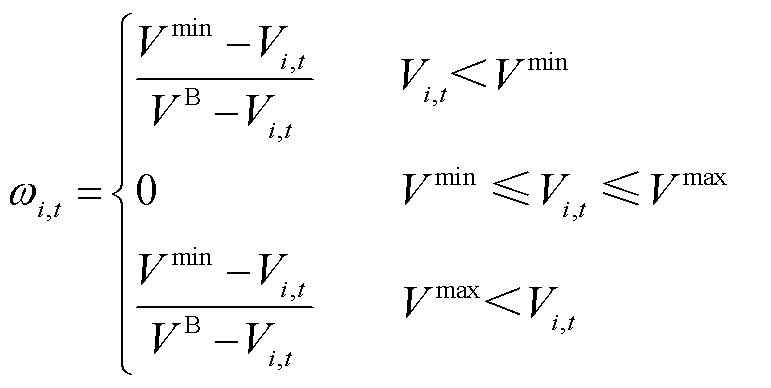 (7)
(7)
式中,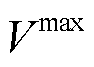 、
、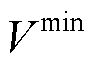 和
和 分别为最大允许电压、最小允许电压和基准电压;
分别为最大允许电压、最小允许电压和基准电压;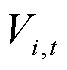 为t时刻节点i的电压。
为t时刻节点i的电压。
将配电网中i节点t时刻的电压越限概率与其严重度的乘积定义为i节点t时刻的节点电压越限风险指标,具体表达式为
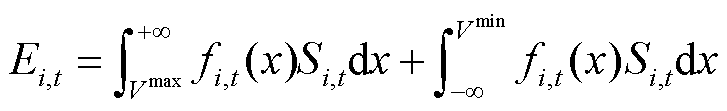 (8)
(8)
式中,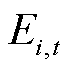 为i节点在t时刻的电压越限风险指标;
为i节点在t时刻的电压越限风险指标;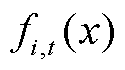 为i节点在t时刻的电压概率分布。该风险指标的含义为,节点电压越限严重度的条件期望值。
为i节点在t时刻的电压概率分布。该风险指标的含义为,节点电压越限严重度的条件期望值。
日前时间尺度下配电网整体的电压越限风险指标为每时刻所有节点电压越限风险的累积,即
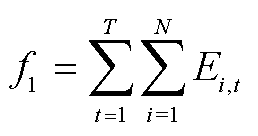 (9)
(9)
式中,T为时段数;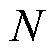 为节点数。
为节点数。
2)期望网损指标
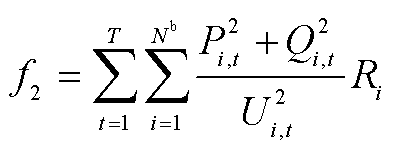 (10)
(10)
式中,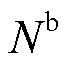 为支路数;
为支路数;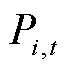 和
和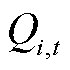 分别为t时刻i支路有功功率和无功功率;
分别为t时刻i支路有功功率和无功功率;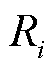 和
和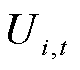 分别为t时刻i支路电阻和首端电压。
分别为t时刻i支路电阻和首端电压。
3)电压偏差指标
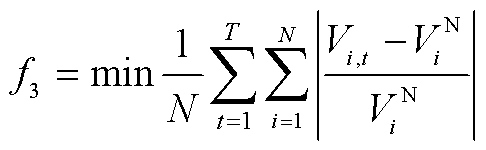 (11)
(11)
式中,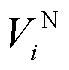 为节点i额定电压。
为节点i额定电压。
参照模糊集理论,采用隶属度函数F来描述各目标函数的优化结果[22],其取值范围为0~1之间,F越小表示离最优值越近,说明优化结果越理想。
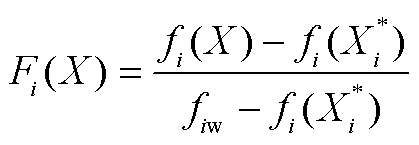 (12)
(12)
式中,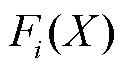 为目标函数
为目标函数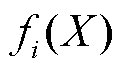 的隶属度函数;
的隶属度函数;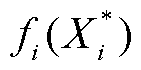 为单独以
为单独以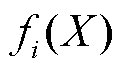 为目标函数优化的策略;
为目标函数优化的策略;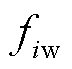 为目标
为目标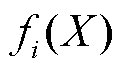 在各单目标最优策略
在各单目标最优策略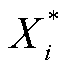 中的最劣取值。
中的最劣取值。
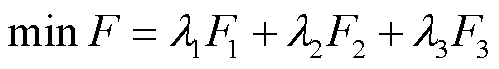 (13)
(13)
式中,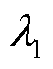 、
、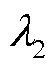 和
和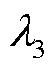 为反映各子目标重要程度的权重,其确定方法可参照文献[23]。
为反映各子目标重要程度的权重,其确定方法可参照文献[23]。
2.1.3 约束条件
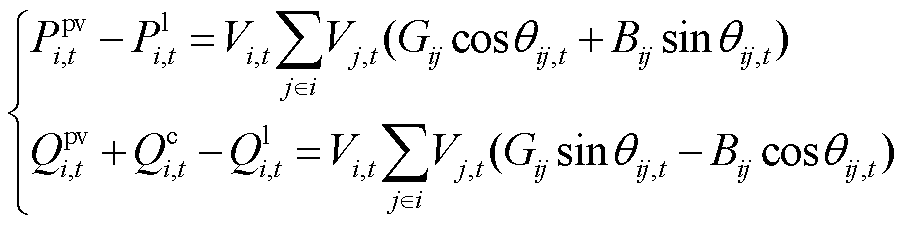 (14)
(14)
式中,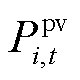 和
和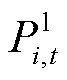 分别为t时刻节点i的光伏有功出力及有功负荷;
分别为t时刻节点i的光伏有功出力及有功负荷;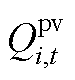 、
、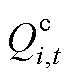 和
和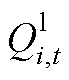 分别为节点i在t时刻光伏无功出力、电容器无功出力及无功负荷。
分别为节点i在t时刻光伏无功出力、电容器无功出力及无功负荷。
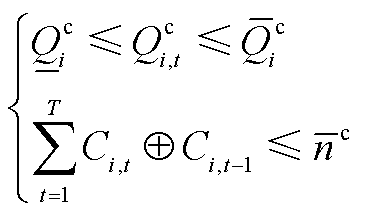 (15)
(15)
式中,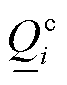 和
和 分别为接入节点i的电容器组无功出力下限和上限;
分别为接入节点i的电容器组无功出力下限和上限;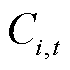 为接入节点i的电容器组在t时刻的投切容量;
为接入节点i的电容器组在t时刻的投切容量; 为异或运算符,当两变量相同时为1,不相同时为0。
为异或运算符,当两变量相同时为1,不相同时为0。
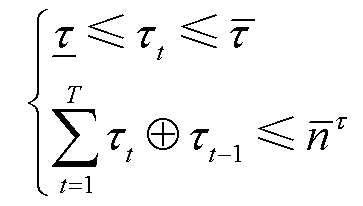 (16)
(16)
式中, 、
、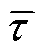 和
和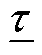 分别为变压器的挡位及其上、下限;
分别为变压器的挡位及其上、下限;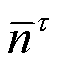 为变压器允许最大投切次数。
为变压器允许最大投切次数。
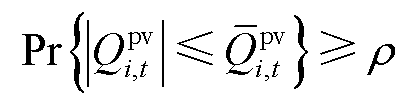 (17)
(17)
式中,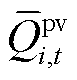 为光伏无功出力上限;
为光伏无功出力上限;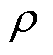 为无功置信水平。光伏逆变器无功出力上限为
为无功置信水平。光伏逆变器无功出力上限为
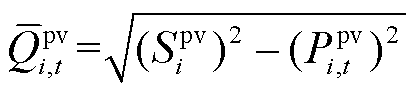 (18)
(18)
式中,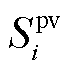 和
和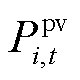 分别为光伏并网节点i的光伏逆变器视在容量和t时刻有功出力。
分别为光伏并网节点i的光伏逆变器视在容量和t时刻有功出力。
日前无功/电压优化控制问题属于大规模、多时段、强耦合的混合整数非线性规划问题,直接求解难度较大。为提高求解精度,采用基于Word系统聚类的时段解耦策略,首先将离散变量松弛为连续变量,利用改进粒子群算法进行24h静态优化得到24h各电容器组及OLTC最优调节计划的连续值,通过基于Word系统聚类完成对各电容器组容量曲线及OLTC分接头挡位曲线的时序分段,并计算各分段内的容量或挡位,然后固定离散设备调节计划,利用改进粒子群优化求解光伏逆变器无功出力,最终完成日前无功调度计划。求解整体流程如图2所示。
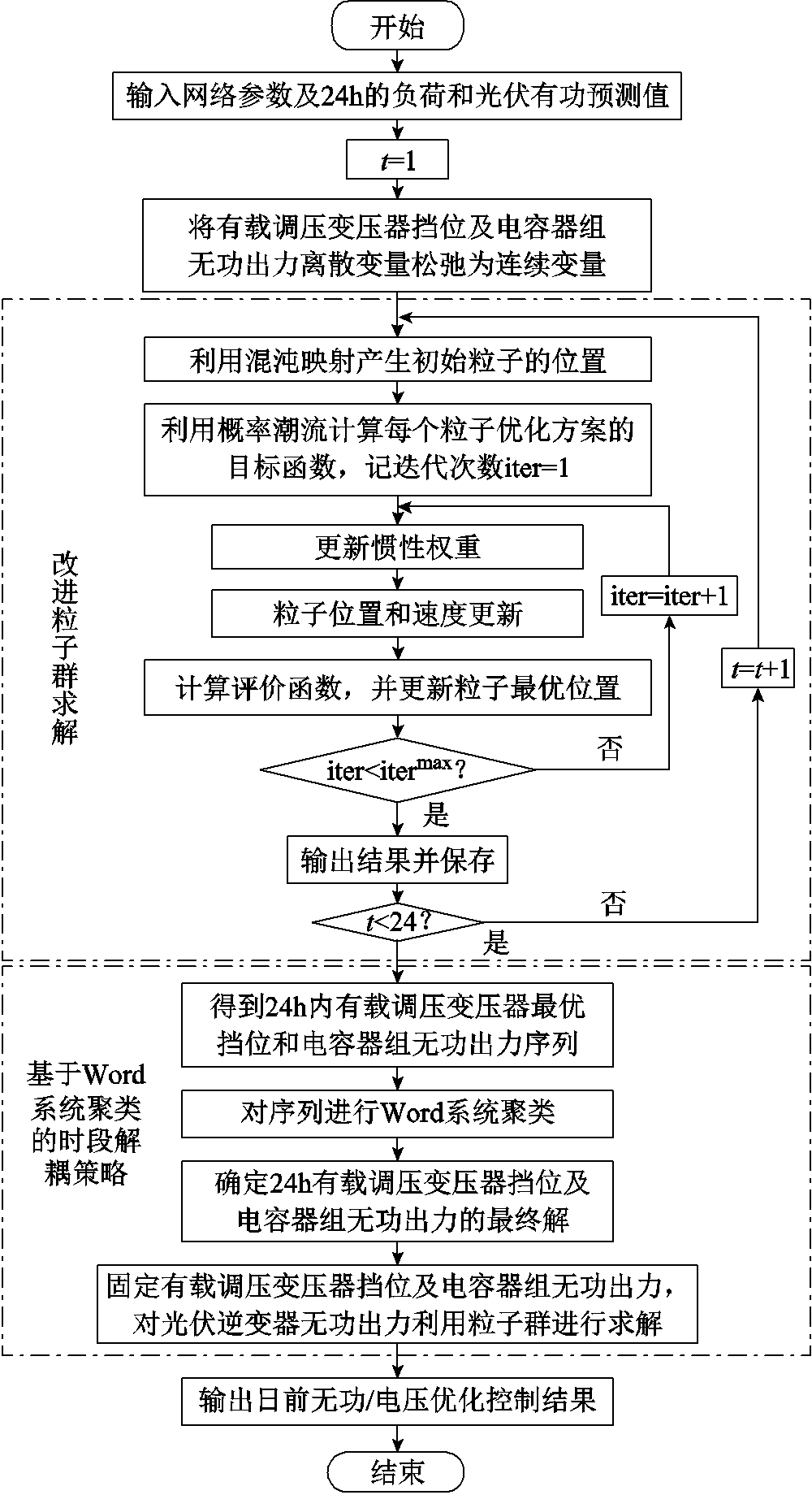
图2 日前无功/电压优化控制求解流程
Fig.2 Flow chart of voltage/var optimal control solution under the day-ahead time scale
2.2.1 模型求解算法
粒子群算法具有操作简单、控制变量少、计算效率高等特点,被广泛用于解决配电网无功优化问题。但针对本文多约束、多维度、多峰值的非线性规划问题存在收敛精度低,随机产生并不均匀的初始种群,会使粒子群无法全面搜索解空间,可能陷入局部最优而出现“早熟”现象[24]。本文采用混沌映射进行初始化。相比典型Logistic混沌系统,Bernoulli shift混沌系统在[0,1]上的分布更均匀[25]。Bernoulli shift混沌方程为
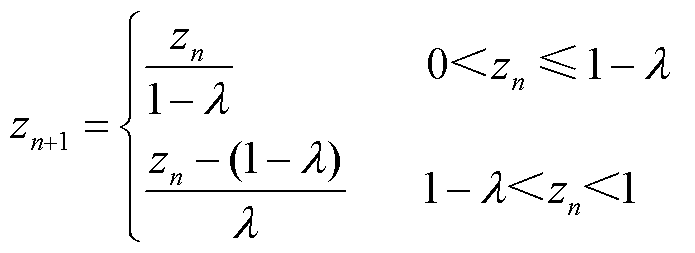 (19)
(19)
式中,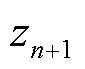 为混沌序列;
为混沌序列; 为常数。
为常数。
设某个变量的取值范围为[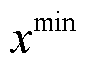 ,
, 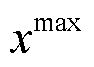 ],则通过式(20)产生初始值。
],则通过式(20)产生初始值。
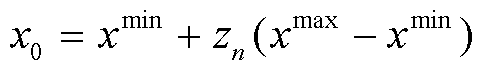 (20)
(20)
式中,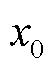 为某变量的初始值;
为某变量的初始值;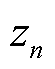 为由式(19)产生的0~1之间的混沌序列。
为由式(19)产生的0~1之间的混沌序列。
在粒子群优化算法中,惯性权重不仅对其收敛性有着至关重要的影响,而且在进化过程中对平衡探索起着重要的作用。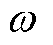 较大时有利于全局搜索,收敛精度低;而
较大时有利于全局搜索,收敛精度低;而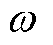 较小时有利于收敛精度提高,但亦陷入局部最优。本文的改进算法对惯性权重采用对称的Sigmoid曲线进行动态调整,第
较小时有利于收敛精度提高,但亦陷入局部最优。本文的改进算法对惯性权重采用对称的Sigmoid曲线进行动态调整,第 次迭代惯性权重为
次迭代惯性权重为
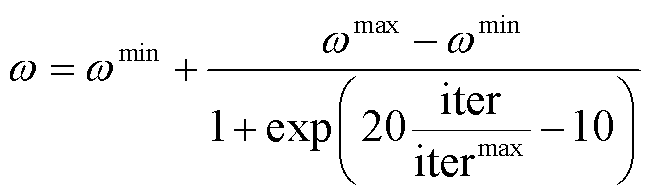 (21)
(21)
式中, 和
和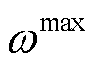 分别为最小权重和最大权重;
分别为最小权重和最大权重; 和
和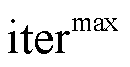 分别为当前迭代次数和最大迭代次数。
分别为当前迭代次数和最大迭代次数。
2.2.2 基于Word系统聚类的时段解耦策略
Word系统聚类又称为离差平方和法,是一种可以用来处理有序样本的聚类方法[26-27],其基本思想源于方差分析,如果类分得好,则同类样品的离差平方和较小,类之间的离差平方和较大。基本思路为:先将集合中每个样本各自看成一类,以平方欧式距离作为两类之间的距离,在进行类别合并时,计算类重心间方差,将离差平方和增加幅度最小的两类首先合并,再依次将所有类别逐级合并[28]。
考虑到OLTC和电容器组不能频繁动作,需对静态优化的相邻时刻最优动作挡位进行融合。为减少融合前后差值,本文采用基于Word系统类聚方法将24h动作序列进行聚类合并,得到满足日动作次数的聚类数,使同一类归为同一时间段,该时间段内离散装置不动作。投切挡位为各最优投切挡位的平均值。其具体步骤如下:
(1)首先将离散装置的24h动作挡位按时间顺序排列,将其看作一组有顺序的样本集。
(2)由式(22)计算两两相邻样本合并后的离差二次方和。
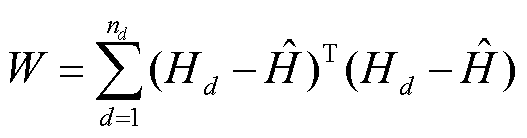 (22)
(22)
式中,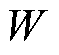 为离差平方和;
为离差平方和;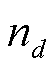 为相邻样本合并后组成新样本的个数;
为相邻样本合并后组成新样本的个数;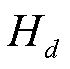 为新样本中第d个样本;
为新样本中第d个样本;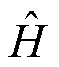 为新样本的平均值,即
为新样本的平均值,即
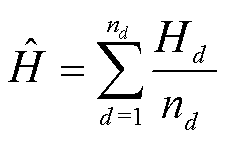 (23)
(23)
(3)选出离差平方和最小的两个样本进行合并,若存在相邻的两个以上样本离差平方和相同并且最小,将其合并为一类。
(4)将经过合并后的多个样本视为一个新样本,并且保持时段顺序不变,进行样本集更新。
(5)返回步骤(2),直到聚类数与离散装置动作约束次数相同。
(6)将每一类中各动作挡位的平均值规整,得到离散设备的调节挡位。
对于自动化和通信水平较低的配电网,无法满足基于模型预测控制的多时间尺度协调控制的要求。本文以日前无功/电压优化控制的结果为基础,充分利用光伏逆变器动态无功响应能力,采用基于本地信息的实时自治控制策略,通过调节逆变器无功调整量和光伏有功功率实现对电压越限和波动的抑制。
实时自治控制的时间粒度为1min,在日前时段t内,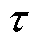 时刻的光伏逆变器无功功率和光伏有功功率分别为
时刻的光伏逆变器无功功率和光伏有功功率分别为
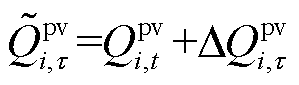 (24)
(24)
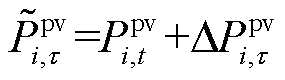 (25)
(25)
式中,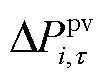 和
和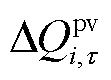 分别为实时时间尺度下
分别为实时时间尺度下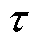 时刻的光伏有功功率和无功功率调整量。t时段
时刻的光伏有功功率和无功功率调整量。t时段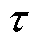 时刻并网点有功负荷和无功负荷也可以式(24)和式(25)的形式进行表达。
时刻并网点有功负荷和无功负荷也可以式(24)和式(25)的形式进行表达。
设光伏并网节点i在t时段内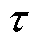 时刻实时有功注入与日前有功注入预测功率的偏差为
时刻实时有功注入与日前有功注入预测功率的偏差为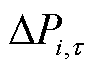 ,则为使
,则为使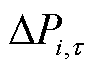 对节点电压影响最小[29],并网点无功出力所需的总无功注入变化量设为
对节点电压影响最小[29],并网点无功出力所需的总无功注入变化量设为 。并网点及其上游节点形成的部分配电网接线图如图3所示。
。并网点及其上游节点形成的部分配电网接线图如图3所示。
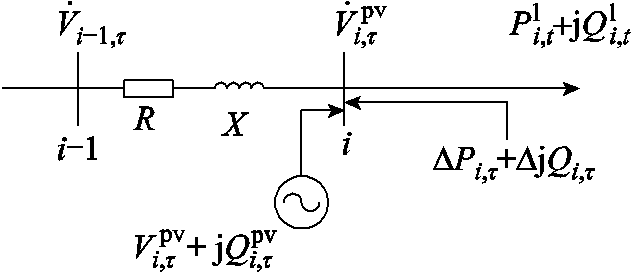
图3 光伏并网点部分配电网等效接线图
Fig.3 Single-line model of the PV’s localized upstream network
图3中,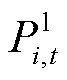 和
和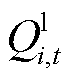 分别为t时段内节点i下游等效有功和无功负荷期望值;
分别为t时段内节点i下游等效有功和无功负荷期望值;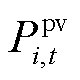 和
和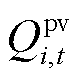 分别为t时段内节点i的光伏期望有功功率和逆变器无功计划功率;
分别为t时段内节点i的光伏期望有功功率和逆变器无功计划功率;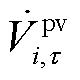 和
和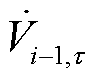 分别为光伏并网节点i以及上游节点i-1在
分别为光伏并网节点i以及上游节点i-1在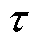 时刻的电压相量;
时刻的电压相量;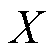 和
和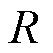 分别为光伏并网点上游馈线电抗和电阻。
分别为光伏并网点上游馈线电抗和电阻。
由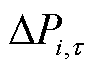 和
和 引起的节点注入电流为
引起的节点注入电流为
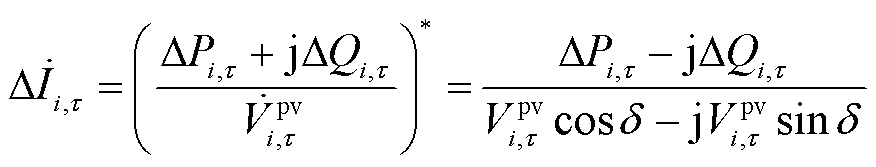 (26)
(26)
式中,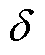 为
为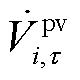 和
和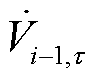 的相位差。由注入电流变化量
的相位差。由注入电流变化量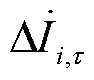 引起的线路压降为零时表示为
引起的线路压降为零时表示为
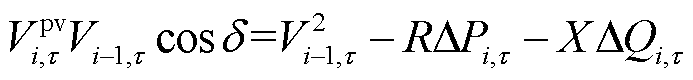 (27)
(27)
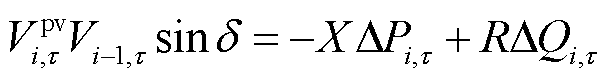 (28)
(28)
将式(27)和式(28)联立可得
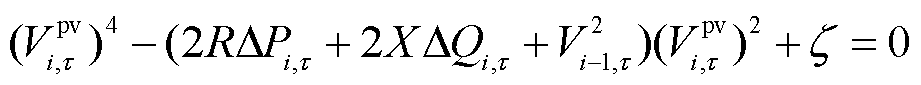 (29)
(29)
其中
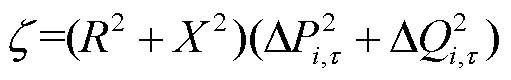 (30)
(30)
为尽量降低光伏并网点上游馈线压降,且降低并网点电压波动,令 ,可求得满足上述要求的光伏并网点无功功率变化量为
,可求得满足上述要求的光伏并网点无功功率变化量为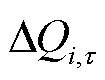 为
为
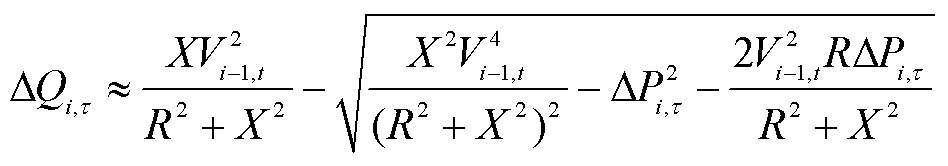 (31)
(31)
光伏逆变器无功出力增量为
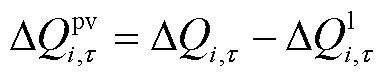 (32)
(32)
式中,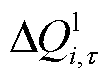 为并网点i在
为并网点i在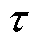 时刻下游等效负荷无功功率与日前无功负荷的偏差值。此时光伏逆变器无功功率仍需满足约束关系式(18)。
时刻下游等效负荷无功功率与日前无功负荷的偏差值。此时光伏逆变器无功功率仍需满足约束关系式(18)。
本文实时自治电压控制以日前无功/电压优化控制得到的OLTC、电容器投切计划以及光伏逆变器无功出力为基础,根据光伏有功出力预测误差与其光伏逆变器无功出力的函数关系计算光伏逆变器无功出力增量,将增量与该时段的日前计划值叠加得到逆变器无功出力,经过动态调整光伏逆变器无功出力后,当检测到光伏并网点电压越限时,通过式(33)计算出光伏逆变器调压所需要的无功功率。
若逆变器容量不足时,因配电网具有较高的R/X值,节点电压亦受有功影响,则根据式(33)和式(34)确定光伏逆变器需消减的有功功率。
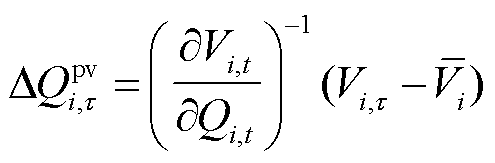 (33)
(33)
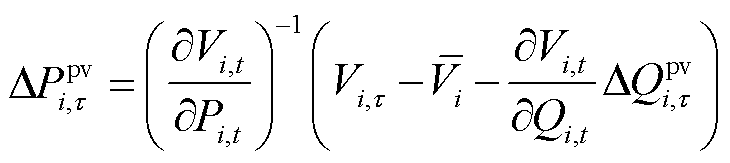 (34)
(34)
式中,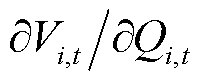 和
和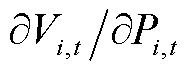 分别为节点i的在时段t的电压无功灵敏度和电压有功灵敏度系数,由日前计算给定工作点雅克比矩阵求逆获得;
分别为节点i的在时段t的电压无功灵敏度和电压有功灵敏度系数,由日前计算给定工作点雅克比矩阵求逆获得; 为节点i的电压限值。
为节点i的电压限值。
实时自治控制流程如图4所示。
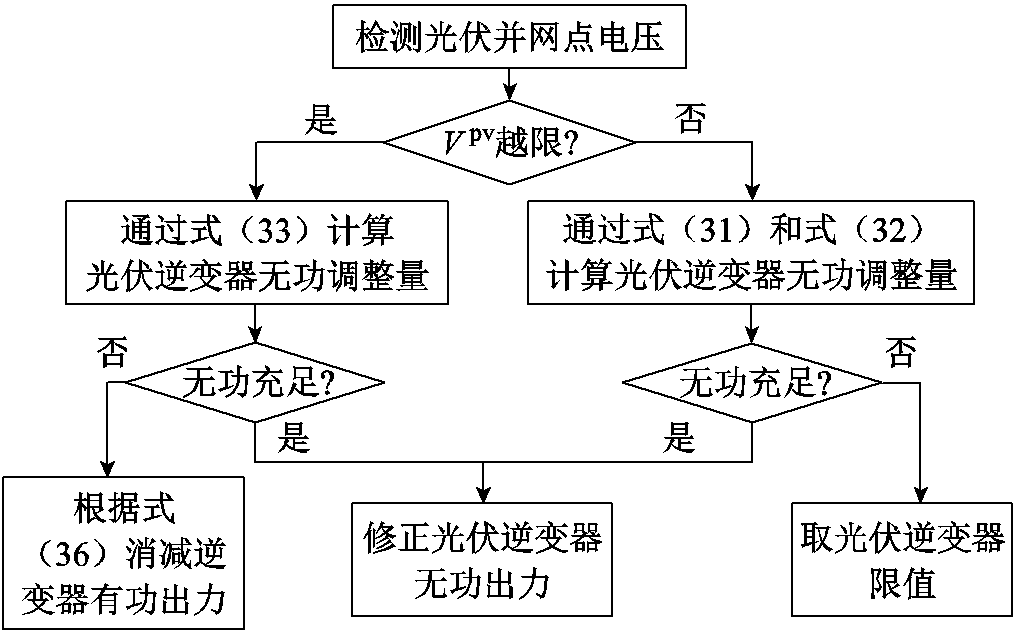
图4 实时自治控制流程
Fig.4 Real-time voltage/var control flow chart
以附图1所示接线的改进IEEE 33节点系统为例,其线路参数可参见文献[30]。在节点15、25和28分别接入光伏电源,光伏阵列面积分别为9 000m2、5 000m2和9 000m2,光电转换效率为0.2,光强数据见文献[31],各节点光伏并网逆变器容量分别为2.1MV·A、1.2MV·A和2.1MV·A;在节点18和32分别接入1号和2号电容器组,单组电容器为50kvar,各节点分别安装10组和20组,单日最大投切次数均为5次;有载调压变压器的电压比范围为0.9~1.1,上下挡位数为±4;各节点电压上下限分别设置为1.07(pu)和0.93(pu)。
在改进IEEE 33节点系统中,各节点日前负荷预测值由IEEE 33节点系统各节点负荷数据乘以该负荷变化系数得到,日前光伏有功出力预测值和负荷变化系数如附图2所示。求解算法采用改进粒子群,种群规模为20,学习因子为2.05,最大惯性权重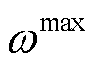 =0.9,最小惯性权重
=0.9,最小惯性权重 =0.4。各子目标对应的权重分别设为
=0.4。各子目标对应的权重分别设为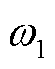 =0.258,
=0.258,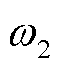 =0.637,
=0.637, =0.105,无功置信水平
=0.105,无功置信水平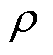 =0.9。
=0.9。
用本文方法计算出的日前无功计划见表1,OLTC及电容器组动作次数均为5次,均满足一天当中动作次数约束。OLTC分别在1、8、10、16、18时刻进行调节挡位,电容器组1分别在1、7、17、20、23时刻投切,电容器组2在1、11、16、19、21时刻投切。
表1 配电网日前无功计划
Tab.1 Day ahead reactive power plan of distribution network
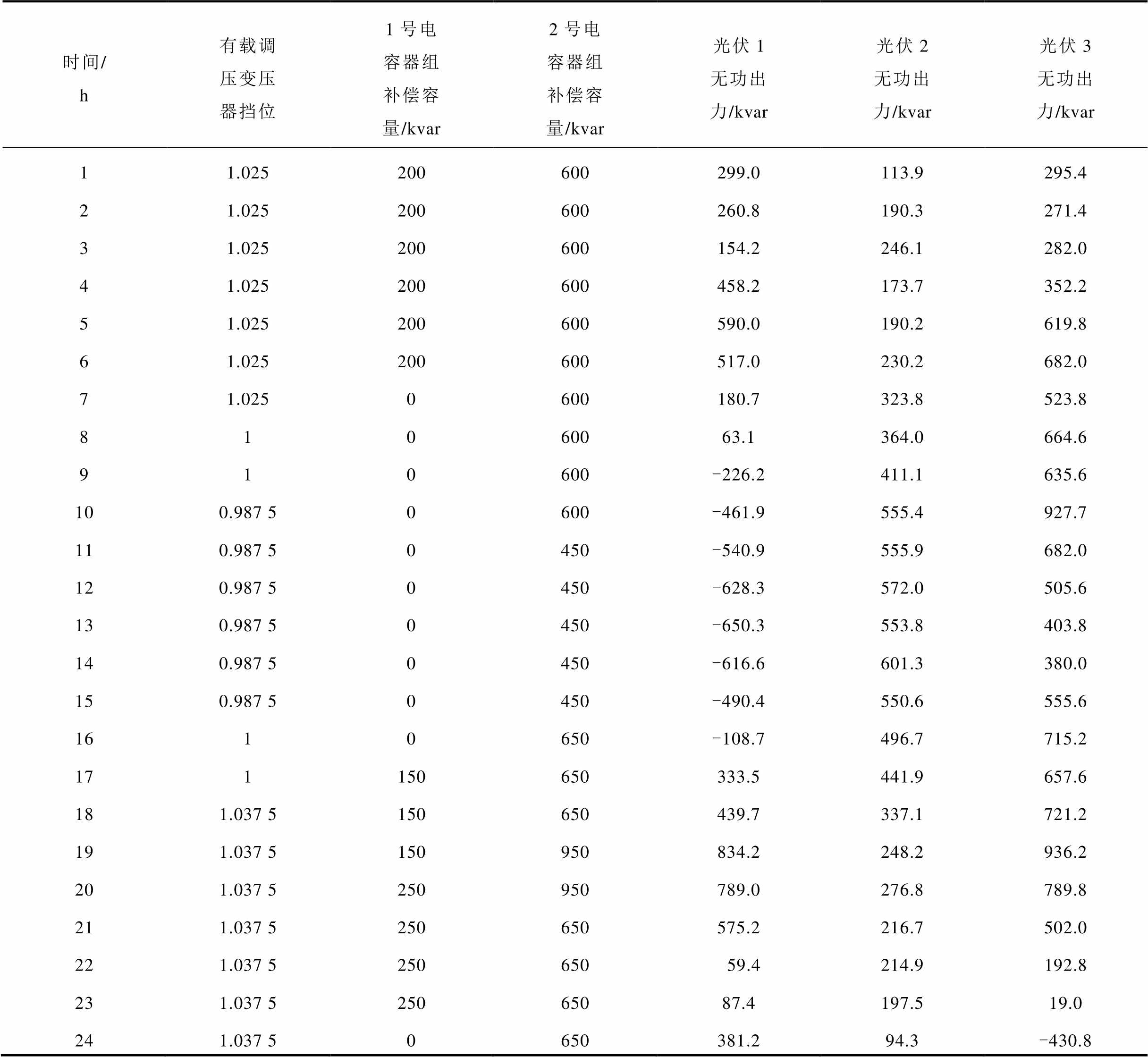
时间/h有载调压变压器挡位1号电容器组补偿容量/kvar2号电容器组补偿容量/kvar光伏1无功出力/kvar光伏2无功出力/kvar光伏3无功出力/kvar 11.025200600299.0113.9295.4 21.025200600260.8190.3271.4 31.025200600154.2246.1282.0 41.025200600458.2173.7352.2 51.025200600590.0190.2619.8 61.025200600517.0230.2682.0 71.0250600180.7323.8523.8 81060063.1364.0664.6 910600-226.2411.1635.6 100.987 50600-461.9555.4927.7 110.987 50450-540.9555.9682.0 120.987 50450-628.3572.0505.6 130.987 50450-650.3553.8403.8 140.987 50450-616.6601.3380.0 150.987 50450-490.4550.6555.6 1610650-108.7496.7715.2 171150650333.5441.9657.6 181.037 5150650439.7337.1721.2 191.037 5150950834.2248.2936.2 201.037 5250950789.0276.8789.8 211.037 5250650575.2216.7502.0 221.037 5250650 59.4214.9192.8 231.037 525065087.4197.519.0 241.037 50650381.294.3-430.8
光伏逆变器无功出力占最大容量比如图5所示,由此可见,各光伏逆变器无功出力均在最大出力范围内,在光伏有功出力较大的10:00~15:00时,由于无功容量较小,实际无功出力占比较大。在5:00和20:00,因该时段负荷较大而光伏有功出力为零,为支撑电网电压,光伏逆变器无功实际出力较大,所以占比较大。光伏2所接支路负荷较少,5时和20时负荷增加对光伏2无功出力影响较小。
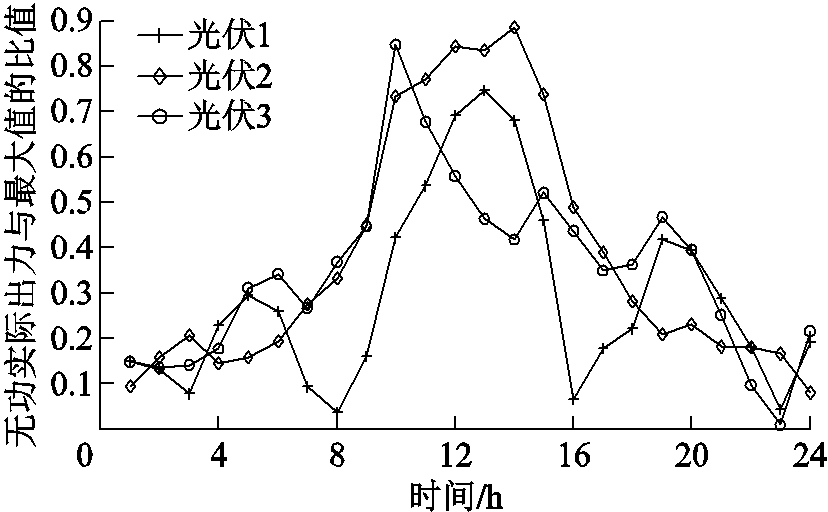
图5 光伏逆变器无功出力占最大容量比
Fig.5 Photovoltaic inverter reactive power output to maximum capacity ratio
各时段各节点电压越限风险指标如图6所示,在光伏有功出力较大的10时~13时,节点12~节点17存在一定的电压越限风险,除15节点外其他光伏并网点经过日前优化后并无电压越限风险,这说明光伏并网点越靠近网络末端对配电网电压影响越大,易造成电压剧烈波动,存在越限风险。

图6 各节点各时段电压越限风险指标
Fig.6 Voltage over-limit risk index of each node at each time period
为验证本文解耦方法的有效性,比较本文所提的松弛-聚类-校正的解耦算法与文献[32]所提出的预动作时间表法。给出静态优化、本文方法和文献[32]方法的1号电容器组与2号电容器组日前投切计划如图7和图8所示;相应方法计算得到的OLTC日前挡位调节计划如图9所示。从图7~图9可知,本文方法和文献[32]方法优化结果不同,但均能满足日内设备动作次数约束。
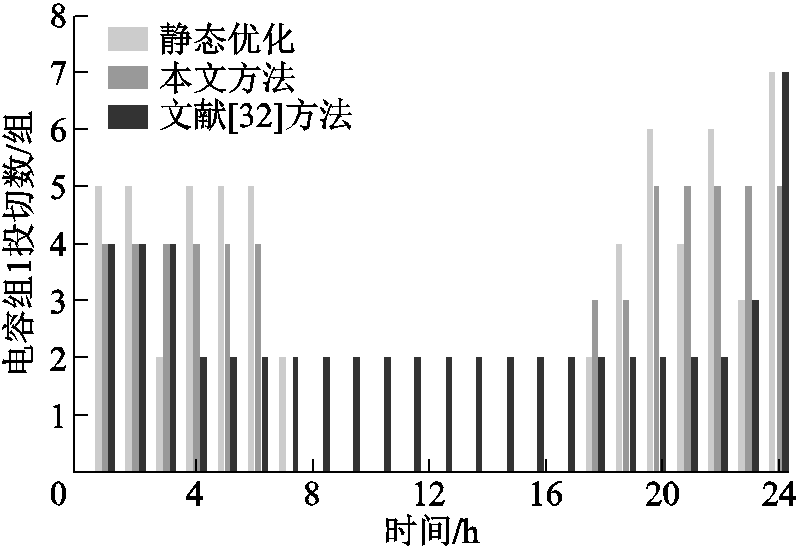
图7 1号电容器投切计划
Fig.7 No. 1 capacitor switching plan
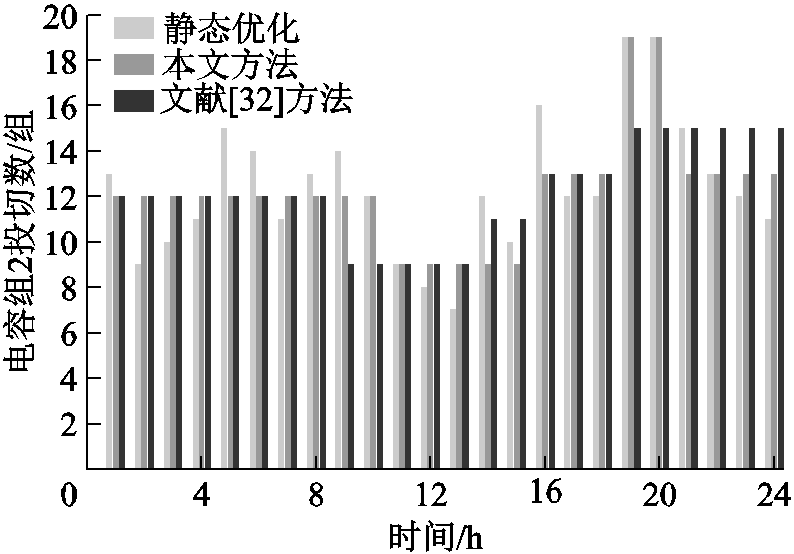
图8 2号电容器投切计划
Fig.8 No. 2 capacitor switching plan

图9 OLTC挡位
Fig.9 OLTC transfer plan
为进一步比较各方案的优劣,引入偏差均方值,用来反映各种日前时间尺度下无功/电压控制方案中离散控制设备调节计划与静态无功优化下的最优调节计划的偏差。偏差均方值指标的计算公式为
 (35)
(35)
式中,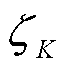 为考察时段内的偏差方均值;K为所考察的时段数;
为考察时段内的偏差方均值;K为所考察的时段数;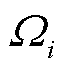 和
和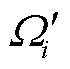 分别为静态优化和相应待比较的日前无功/电压控制方案的电容器组投切组数或OLTC分接头挡位。偏差方均值越小,说明待比较方案的离散装置调节计划越接近无时间耦合约束静态优化下的最优状态,能有效地反映各动态方案的合理性。
分别为静态优化和相应待比较的日前无功/电压控制方案的电容器组投切组数或OLTC分接头挡位。偏差方均值越小,说明待比较方案的离散装置调节计划越接近无时间耦合约束静态优化下的最优状态,能有效地反映各动态方案的合理性。
不同方案结果比较见表2。对比静态无功优化与本文提出的方法,本文方法总目标函数、有功网损、运行风险及电压偏差均高于静态优化,但是1号、2号电容器组及OLTC动作次数分别为13次、22次和8次,不满足要求,本文方法各设备动作次数均为5次,降幅分别为53.85%、77.27%和37.5%。
表2 不同方案结果比较
Tab.2 Comparison of the results of different schemes
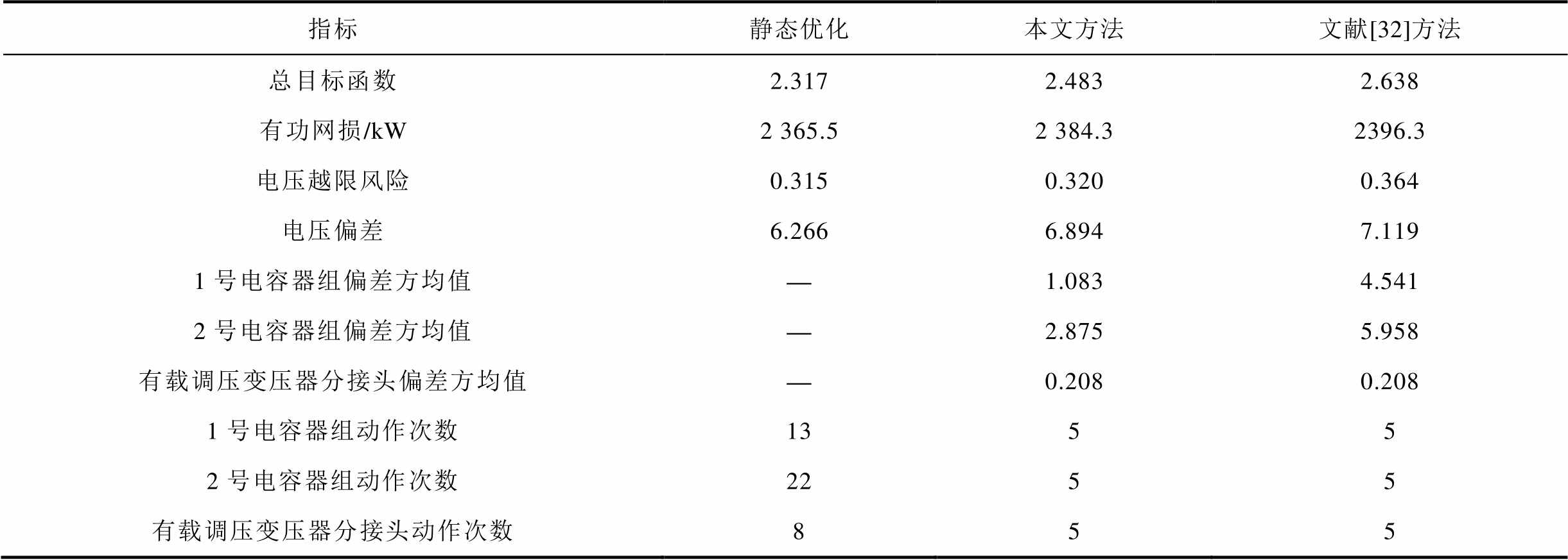
指标静态优化本文方法文献[32]方法 总目标函数2.3172.4832.638 有功网损/kW2 365.52 384.32396.3 电压越限风险0.3150.3200.364 电压偏差6.2666.8947.119 1号电容器组偏差方均值—1.0834.541 2号电容器组偏差方均值—2.8755.958 有载调压变压器分接头偏差方均值—0.2080.208 1号电容器组动作次数1355 2号电容器组动作次数2255 有载调压变压器分接头动作次数855
对比本文方法和文献[32]方法,文献[32]方法比静态优化总目标函数、有功网损、电压越限风险及电压偏差分别高出0.320、30.8kW、0.048和0.853,而采用本文方法分别高出0.165、18.8kW、0.004和0.627。降幅分别为48.41%、38.96%、90.39%和26.4%。可见通过本文方法,无功优化效果明显优于文献[32]方法。从偏差方均值角度看,本文方法的电容器的方均值明显低于文献[32]方法的值,说明本文方法通过Word系统聚类法的时序合并能使聚类前后差值最小,使电容器投切计划更接近于静态优化的最优值。OLTC分接头因静态优化动作次数较少,本文方法和文献[32]方法的均方值相同。
本文根据光伏有功出力和负荷的概率密度函数,以1min为抽样周期产生1440min的光伏和负荷功率变化值,以日前调度计划值为已知量,模拟电网实时运行情况。通过设置两种方案,以光伏并网点15节点为例,验证本文短时间电压控制的有效性,15节点光伏全天有功出力模拟曲线如附图3所示。方案1为光伏逆变器无功出力保持日前计划不变,方案2为根据并网点注入有功预测误差,动态调整光伏逆变器无功出力抑制电压波动,当电压越限时根据电压灵敏度进行控制。
图10为方案1和方案2下15节点电压时序模拟图。由图10可见,光伏逆变器无功出力保持不变时,光伏并网点电压会随着光伏有功出力的波动而发生剧烈波动,日中时段1h内电压波动相差甚至超出0.03(pu),严重影响电压质量,不满足《分布式光伏接入电网技术规范》(Q/CSG1211001—2014)的要求。在光伏有功出力较高且波动幅度较大时,部分时刻电压越上限,通过本文控制策略能将电压限制在1.07(pu)以下,在光伏逆变器剩余无功充足时可以通过动态调整其无功出力使并网点电压波动幅度明显减小,电压质量明显提高。在720min附近负荷有功需求较少,光伏有功出力较大,电压越上限,而光伏逆变器剩余无功功率不足,采用消减光伏有功的策略,为充分消纳光伏有功,将电压限制在1.07(pu)。有功消减量如图11所示,在840~960min时间段内部分时刻电压越上限,通过调节光伏逆变器剩余无功可防止电压越限,但不足以抑制电压剧烈波动,节点电压出现小幅度升高。15节点光伏逆变器无功出力时序模拟曲线如图12所示。
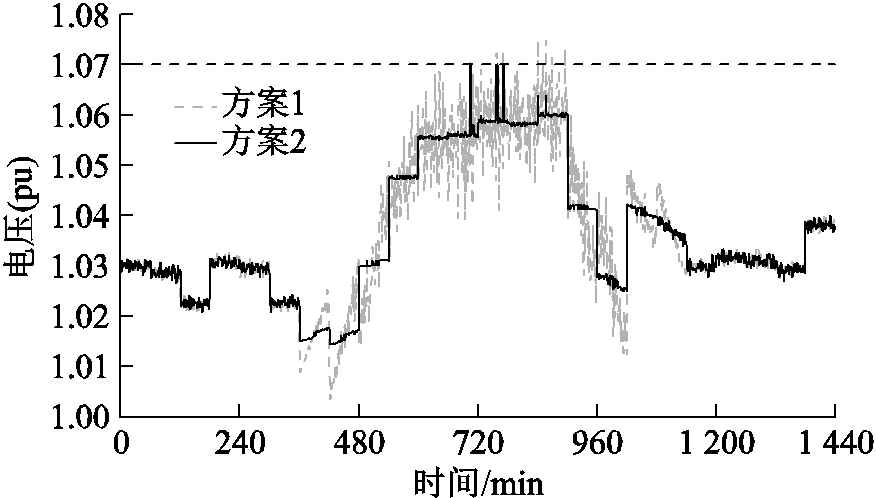
图10 15节点电压时序模拟图
Fig.10 15-node voltage timing simulation diagram
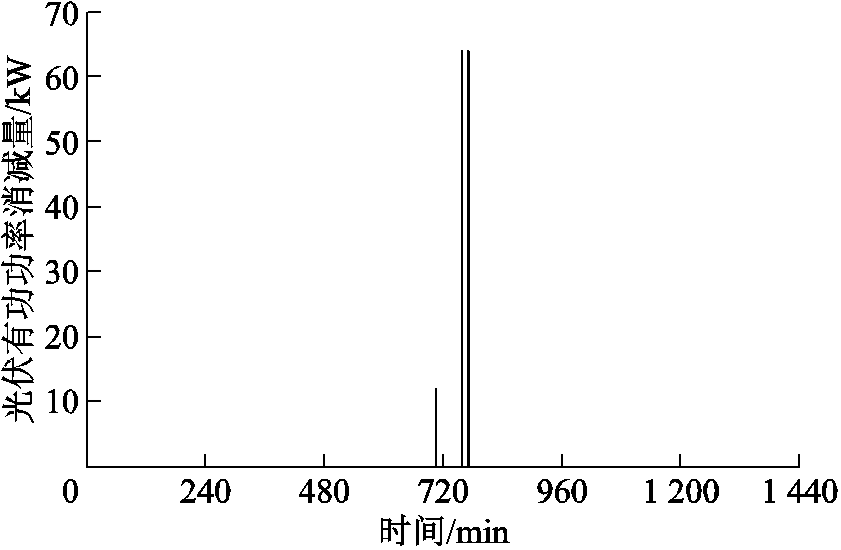
图11 15节点光伏逆变器有功功率消减量
Fig.11 15-node PV inverter active power dissipation
图13为方案2下节点14、15和16电压时序模拟图,相比于相邻节点光伏并网点电压最高。图14为在方案1和方案2下配电网最大最小电压。在8~12h及13~18h,动态调整光伏无功,使电网电压最大值降低,在12h因光伏剩余无功不足,电网电压较高但仍在电压上限下方。
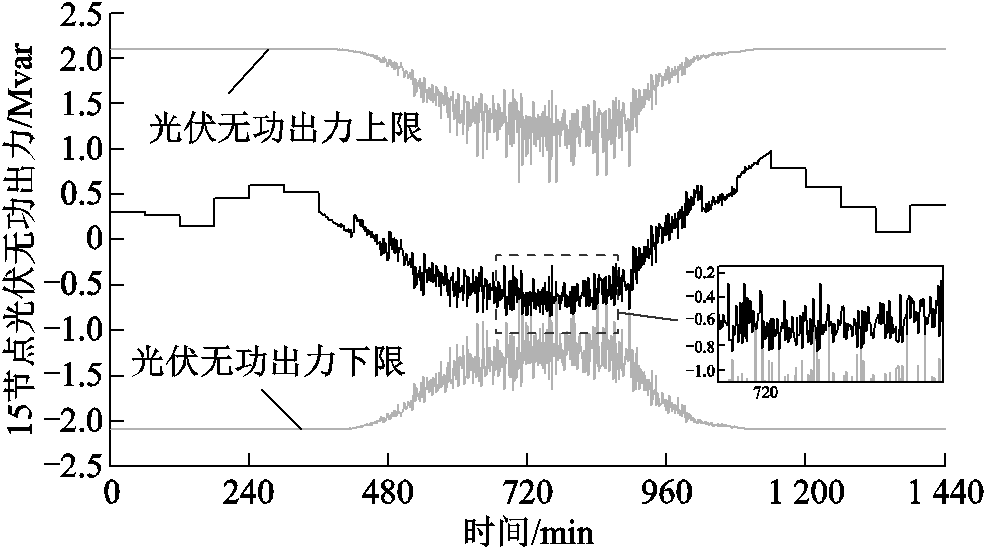
图12 15节点光伏逆变器无功出力时序模拟曲线
Fig.12 15-node PV inverter reactive power output timing simulation curve
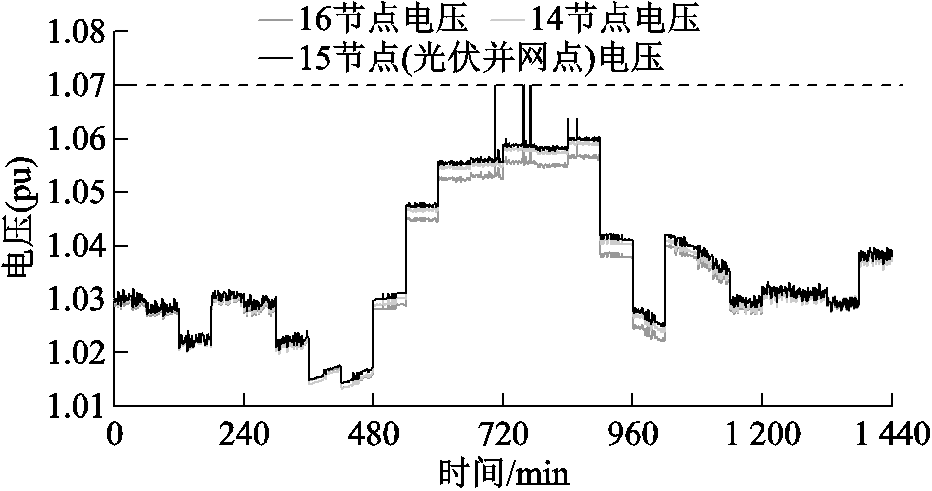
图13 方案2下节点14、15和16电压时序模拟曲线
Fig.13 Simulation curve of voltage timing of nodes 14, 15 and 16 under scheme 2
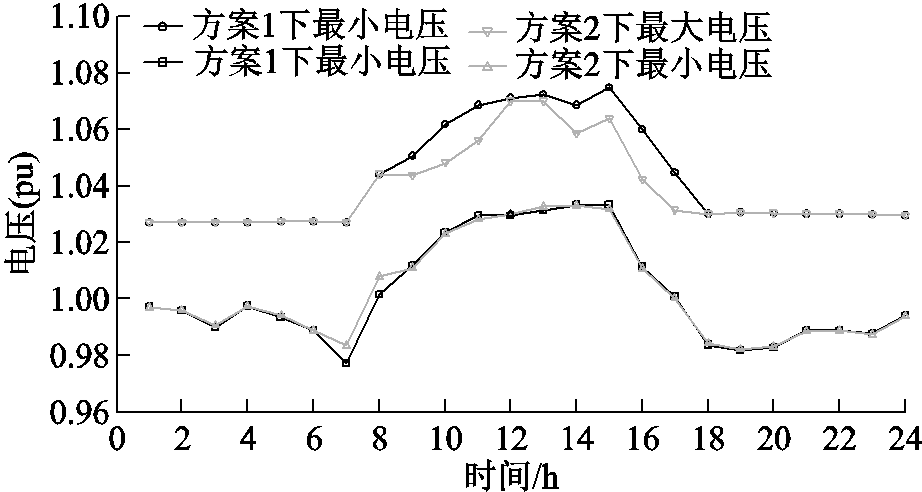
图14 方案1及方案2下配电网中最大最小电压
Fig.14 Maximum and minimum voltage in the distribution network under scheme 1 and scheme 2
针对大量光伏接入配电网引起的离散调压装置动作频繁、网损增加及并网点电压波动等问题,对于自动化和通信水平无法满足多时间尺度无功/电压协调控制的配电网,本文提出一种日前无功/电压优化控制与实时自治控制相结合的混合时间尺度无功/电压控制方法,算例验证结果表明:
1)针对光伏出力和负荷的不确定性,构建了以期望网损、电压偏移及电压越限风险为目标,综合考虑OLTC和电容器组动作,以及光伏逆变器无功发生能力约束的不确定优化模型,该模型可实现日前无功/电压控制在兼顾网损指标的同时有效降低电压越限风险;所提出的基于概率潮流的松弛-聚类-校正动态无功优化解耦求解方法,将动态优化问题转换为静态优化问题,在满足求解精度的前提下降低了优化问题的求解难度;日前无功/电压优化控制策略在降低离散调压装置动作次数的同时,能够实现OLTC、电容器组和光伏逆变器协调优化。
2)针对因日前光伏出力预测误差及光伏有功出力波动剧烈造成光伏并网点电压波动剧烈的问题,提出了以日前光伏逆变器无功调节计划为运行基准点的实时自治控制策略,充分利用光伏逆变器无功剩余容量并发挥其无功动态响应能力,推导出逆变器无功出力增量与光伏实时出力预测误差之间的近似关系。通过动态调整逆变器无功出力能够有效抑制因光伏并网点有功功率注入波动造成的电压剧烈波动,提高的电压质量。
本文采用贝塔分布和正态分布分别刻画日前光伏有功出力和有功负荷的随机性,与真实概率分布存在一定的差别。实时自治控制尽管能有效地抑制因光伏有功预测误差造成的电压波动,但当光伏电站接入数量较多时可能因缺乏协调性影响控制效果。下一阶段将采用更为准确的光伏有功出力和有功负荷的不确定性建模方法,研究多个光伏电站在通信受限的情况下相互协调的控制策略。
附 录
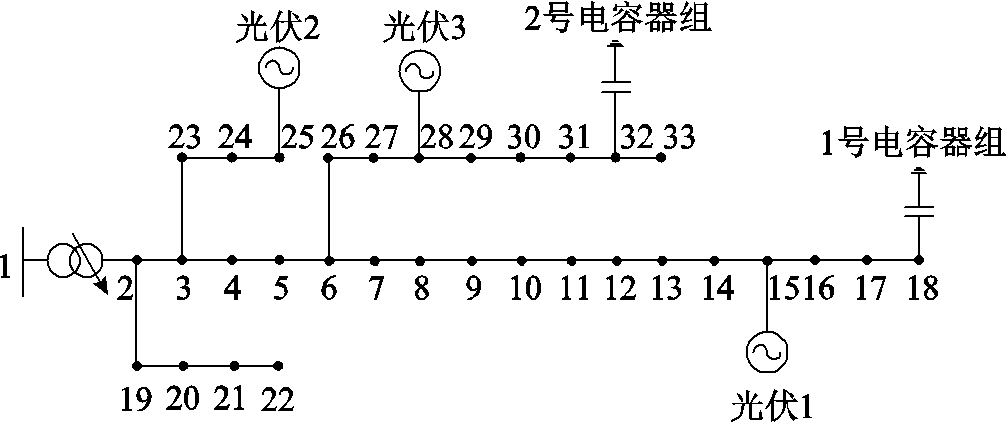
附图1 改进的IEEE 33配电系统接线图
App.Fig.1 Modified IEEE 33 power distribution system wiring diagram
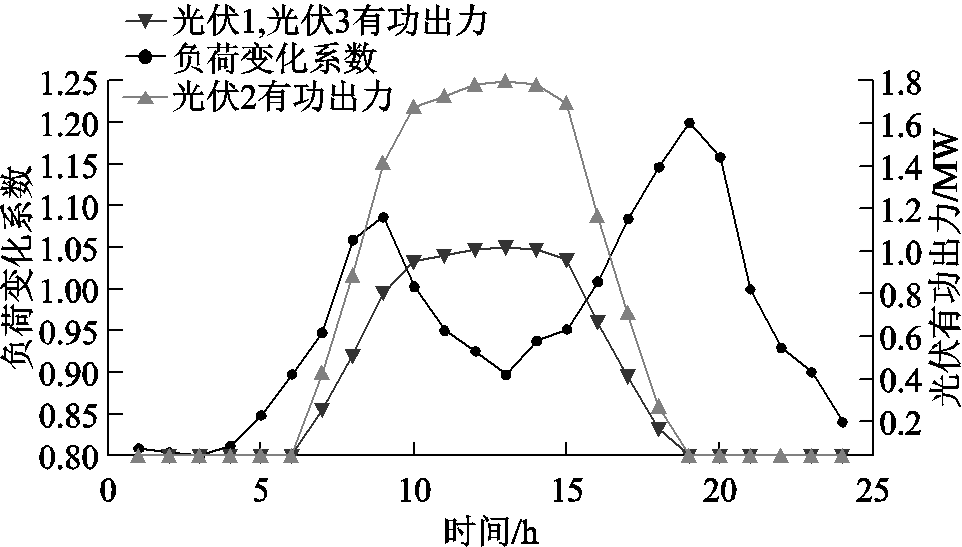
附图2 日前光伏有功出力预测及负荷变化系数
App.Fig.2 PV active power output and load variation coefficient
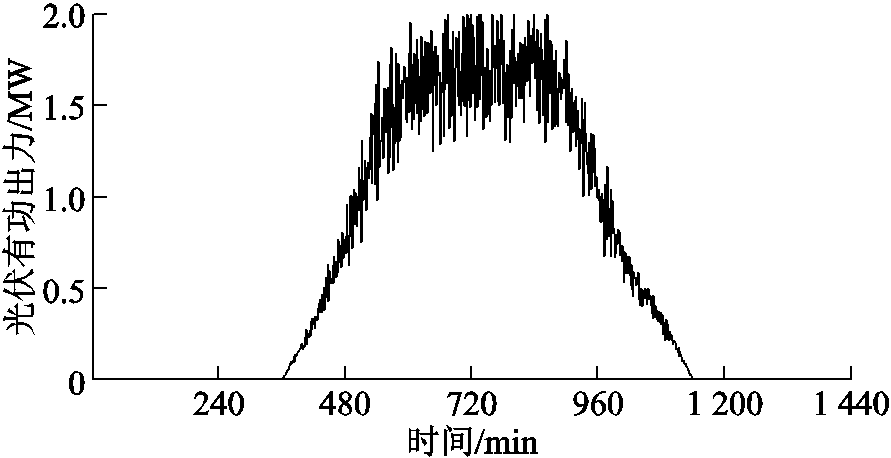
附图3 15节点光伏全天有功出力模拟曲线
App.Fig.3 15-node photovoltaic full-day active output simulation curve
参考文献
[1] 周念成, 谷飞强, 雷超, 等. 考虑合环电流约束的主动配电网转供优化模型[J]. 电工技术学报, 2020, 35(15): 3281-3291.
Zhou Niancheng, Gu Feiqiang, Lei Chao, et al. A power transfer optimization model of active distribution networks in consideration of loop closing current constraints[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3281-3291.
[2] 曲正伟, 张嘉曦, 王云静, 等. 考虑分布式电源不确定性的配电网改进仿射状态估计[J/OL]. 电力系统自动化: 1-13[2021-10-01]. http://kns.cnki.net/ kcms/detail/32.1180.TP.20210811.0903.004.html.
Qu Zhengwei, Zhang Jiaxin, Wang Yunjing, et al. Improved affine state estimation for distribution networks considering uncertainty of distributed power sources[J/OL]. Automation of Electric Power Systems: 1-13 [2021-10-01]. http://kns.cnki.net/kcms/detail/ 32.1180.TP.20210811.0903.004.html.
[3] Giacomuzzi S, Langwasser M. Smart transformer-based medium voltage grid support by means of active power control[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 285-293.
[4] 赵平, 赵期期, 艾小猛. 考虑极限场景的主动配电网重构与无功电压调整联合鲁棒优化[J/OL]. 电工技术学报: 1-11[2021-08-20]. https://doi.org/10. 19595/j.cnki.1000-6753.tces.L90356
Zhao Ping, Zhao Qiqi, Ai Xiaomeng. Combined robust optimization of active distribution network reconfiguration and reactive voltage adjustment considering extreme scenarios[J/OL]. Transactions of China Electrotechnical Society: 1-11[2021-08-20]. https://doi.org/10.19595/j.cnki.1000-6753.tces. L90356
[5] 李培帅, 吴在军, 张错, 等. 主动配电网分布式混合时间尺度无功/电压控制[J]. 电力系统自动化, 2021, 45(16): 160-168.
Li Peishuai, Wu Zaijun, Zhang Cuo, et al. Distributed hybrid time-scale reactive power/voltage control for active distribution networks[J]. Automation of Electric Power Systems, 2021, 45(16): 160-168.
[6] 尤毅, 刘东, 钟清, 等. 多时间尺度下基于主动配电网的分布式电源协调控制[J]. 电力系统自动化, 2014, 38(9): 192-198.
You Yi, Liu Dong, Zhong Qing, et al. Coordinated control of distributed power sources based on active distribution network under multiple time scales[J]. Automation of Electric Power Systems, 2014, 38(9): 192-198.
[7] Iriaab J, Helenoa M, Cardoso G. Optimal sizing and placement of energy storage systems and on-load tap changer transformers in distribution networks[J]. Applied Energy, 2019, 250: 1147-1157.
[8] 孙田, 邹鹏, 杨知方, 等. 动态无功优化的多阶段求解方法[J]. 电网技术, 2016, 40(6): 1804-1810.
Sun Tian, Zou Peng, Yang Zhifang, et al. Multi-stage solution method for dynamic reactive power optimization[J]. Power System Technology, 2016, 40(6): 1804-1810.
[9] 罗培, 孙吉浩. 有源配电网动态无功优化解耦方法研究[J]. 高电压技术, 2021, 47(4): 1323-1333.
Luo Pei, Sun Jihao. Research on decoupling method of active distribution network dynamic reactive power optimization[J]. High Voltage Engineering, 2021, 47(4): 1323-1333.
[10] 金国彬, 潘狄, 陈庆, 等. 考虑源荷不确定性的直流配电网模糊随机日前优化调度[J]. 电工技术学报, 2021, 36(21): 4517-4528.
Jin Guobin, Pan Di, Chen Qing, et al. Fuzzy random day-ahead optimal scheduling of DC distribution network considering the uncertainty of source and load[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4517-4528.
[11] 石宪, 薛毓强, 曾静岚. 基于有功-无功控制的光伏并网点电压调节方案[J]. 电气技术, 2019, 20(3): 50-61.
Shi Xian, Xue Yuqiang, Zeng Jinglan. Voltage regulation strategies based on power control for grid-connected photovoltaic at point of common coupling[J]. Electrical Engineering, 2019, 20(3): 50-61.
[12] 刘文霞, 富梦迪, 李涵深, 等. 计及信息失效的柔性配电系统集中-分散协调控制策略优化[J]. 电工技术学报, 2021, 36(22): 4749-4759.
Liu Wenxia, Fu Mengdi, Li Hanshen, et al. Optimization of centralized-decentralized coordinated control strategy for flexible distribution system considering information failure[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4749-4759.
[13] 倪萌, 王蓓蓓, 朱红, 等. 能源互联背景下面向高弹性的多元融合配电网双层分布式优化调度方法研究[J/OL]. 电工技术学报: 1-13[2021-08-20]. https://doi.org/10.19595/j.cnki.1000-6753.tces.201390.
Ni Meng, Wang Beibei, Zhu Hong, et al. Under the background of energy interconnection, the research on the two-layer distributed optimal dispatching method for the highly flexible multi-converged distribution network[J/OL]. Transactions of China Electrotechnical Society: 1-13[2021-08-20]. https://doi.org/ 10.19595/ j.cnki.1000-6753.tces.201390.
[14] 颜湘武, 徐韵, 李若瑾, 等. 基于模型预测控制含可再生分布式电源参与调控的配电网多时间尺度无功动态优化[J]. 电工技术学报, 2019, 34(10): 2022-2037.
Yan Xiangwu, Xu Yun, Li Ruojin, et al. Multi-time scale reactive power dynamic optimization of distribution network based on model predictive control with renewable distributed power sources participating in regulation[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2022-2037.
[15] 杨珺, 侯俊浩, 刘亚威, 等. 分布式协同控制方法及在电力系统中的应用综述[J]. 电工技术学报, 2021, 36(19): 4035-4049.
Yang Jun, Hou Junhao, Liu Yawei, et al. Distributed cooperative control method and its application in power system[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4035-4049.
[16] 乐健, 王曹, 李星锐, 等. 中压配电网多目标分布式优化控制策略[J]. 电工技术学报, 2019, 34(23): 4972-4981.
Le Jian, Wang Cao, Li Xingrui, et al. Multi-objective distributed optimization control strategy for medium voltage distribution network[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4972-4981.
[17] 丛鹏伟, 唐巍, 娄铖伟, 等. 含高渗透率可再生能源的主动配电网两阶段柔性软开关与联络开关协调优化控制[J]. 电工技术学报, 2019, 34(6): 1263-1272.
Cong Pengwei, Tang Wei, Lou Chengwei, et al. Coordinated and optimized control of two-stage flexible soft switch and tie switch in active distribution network with high-permeability renewable energy[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1263-1272.
[18] 褚国伟, 张友旺, 葛乐, 等. 自储能柔性互联配电网多时间尺度电压优化[J]. 电力系统自动化, 2021, 45(9): 71-79.
Chu Guowei, Zhang Youwang, Ge Le, et al. Multi-time-scale voltage optimization of flexible interconnected distribution network with self-energy storage[J]. Automation of Electric Power Systems, 2021, 45(9): 71-79.
[19] 黄伟, 刘斯亮, 羿应棋, 等. 基于光伏并网点电压优化的配电网多时间尺度趋优控制[J]. 电力系统自动化, 2019, 43(3): 92-100.
Huang Wei, Liu Siliang, Yi Yingqi, et al. Multi-time scale optimization control of distribution network based on photovoltaic grid-connected point voltage optimization[J]. Automation of Electric Power Systems, 2019, 43(3): 92-100.
[20] Jia Haoran, Chengshan Wanga, Peng Lia. A centralized-based method to determine the local voltage control strategies of distributed generator operation in active distribution networks[J]. Applied Energy, 2018, 228: 2024-2036.
[21] 姬广龙, 袁越, 范绚然, 等. 基于Cornish-Fisher展开的配电网电压越限风险评估[J]. 太阳能学报, 2020, 41(1): 358-366.
Ji Guanglong, Yuan Yue, Fan Xuanran, et al. Risk assessment of voltage over-limit of distribution network based on Cornish-Fisher[J]. Acta Energiae Solaris Sinica, 2020, 41(1): 358-366.
[22] 孙辉, 刘鑫, 贲驰, 等. 含风储一体化电站的电力系统多目标风险调度模型[J]. 电力系统自动化, 2018, 42(5): 94-101.
Sun Hui, Liu Xin, Ben Chi, et al. Multi-objective risk dispatch model of power system with integrated wind-storage power station[J]. Automation of Electric Power Systems, 2018, 42(5): 94-101.
[23] 李国庆, 翟晓娟. 基于层次分析法的孤立微电网多目标优化运行[J]. 电力系统保护与控制, 2018, 46(10): 17-23.
Li Guoqing, Zhai Xiaojuan. Multi-objective optimization operation of isolated microgrid based on analytic hierarchy process[J]. Power System Protection and Control, 2018, 46(10): 17-23.
[24] Ahmed G, Sheltami T, Mahmoud A. IoD swarms collision avoidance via improved particle swarm optimization[J]. Transportation Research Part A, 2020, 142: 260-278.
[25] Yang Dixiong, Li Gang, Cheng Gengdong. On the efficiency of chaos optimization algorithms for global optimization[J]. Chaos, Solitons and Fractals, 2007, 34: 1366-1375.
[26] Jr J H W. Hierarchical grouping to optimize an objective function[J]. Journal of the American Statistical Association, 1963, 58(301): 236-244.
[27] 方开泰. 有序样品的一些聚类方法[J]. 应用数学学报, 1982, 5(1): 94-101.
Fang Kaitai. Some clustering methods for ordered samples[J]. Acta Mathematicae Applicatae Sinica, 1982, 5(1): 94-101.
[28] 李亚杰. 多元统计分析[M]. 北京: 北京邮电大学出版社, 2018.
[29] Carvalho P M S, Correia P F. Distributed reactive power generation control for voltage rise mitigation in distribution networks[J]. IEEE Transactions on Power Systems, 2009, 23(2): 766-771.
[30] Baran M E, Wu F F. Network reconfiguration in distribution systems for loss reduction and load balancing[J]. IEEE Power Engineering Review, 1989, 9(4): 101-102.
[31] 易海川, 张彼德, 王海颖, 等. 提高DG接纳能力的配电网动态重构方法[J]. 电网技术, 2016, 40(5): 1431-1436.
Yi Haichuan, Zhang Bide, Wang Haiying, et al. Dynamic reconfiguration method of distribution network to improve DG acceptance ability[J]. Power System Technology, 2016, 40(5): 1431-1436.
[32] 蔡昌春, 丁晓群, 王宽, 等. 动态无功优化的简化方法及实现[J]. 电力系统自动化, 2008, 32(5): 43-46.
Cai Changchun, Ding Xiaoqun, Wang Kuan, at el. Simplified method and realization of dynamic reactive power optimization[J]. Automation of Electric Power Systems, 2008, 32(5): 43-46.
Abstract A hybrid time-scale voltage/var control method combining day-ahead optimization and real-time local control is proposed to resolve voltage regulation problems such as network loss increase, voltage fluctuation and voltage crossing caused by large number of photovoltaic (PV) connections to the distribution network. On the day-ahead scale, an uncertain optimization model is constructed with the expected network loss, voltage drift and voltage overrun risk as the objectives, the on-load tap changer (OLTC) and capacitor bank actions is taken into account as well as the PV inverter reactive power generation constraints. On the real-time time scale, the approximate relationship between the inverter reactive power output increment and the PV real-time power output prediction error is derived using the day-ahead optimization results as the operational reference point, and a real-time autonomous voltage/var control strategy relying only on local real-time information is constructed. The effectiveness of the proposed hybrid time-scale voltage/var control strategy is proved by the simulation of the modified IEEE 33 system.
Keywords:Distribution network, photovoltaic power generation, voltage/var control, hybrid time scale, voltage over-limit risk
DOI:10.19595/j.cnki.1000-6753.tces.211188
中图分类号:TM73
国家科技重大专项(2017YFB0903402)和吉林省发改委科技项目(2018C034-7)资助。
收稿日期 2021-08-04
改稿日期 2021-10-12
黄大为 男,1976年生, 博士,副教授,研究方向为电力系统运行与控制、综合能源系统运行与规划。E-mail:hdw76@163.com(通信作者)
王孝泉 男,1996年生,硕士研究生,研究方向为配电网优化运行。E-mail:15604329200@163.com
(编辑 赫蕾)