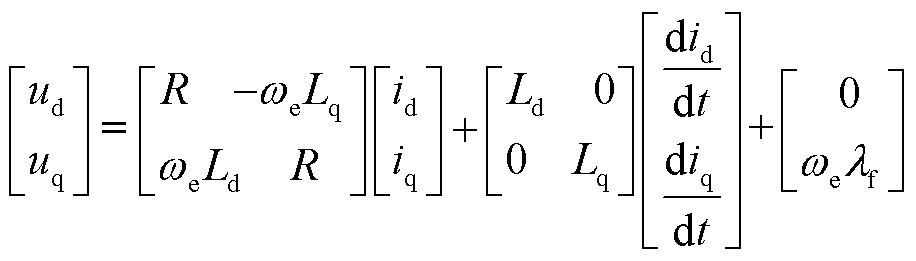（1）
摘要 高性能永磁同步电机控制系统对电流环的动态性能要求很高，传统的PI控制带宽有限，且易出现超调等现象，基于电流预测的无差拍控制具有较好的动态响应。为此，提出了一种在同步旋转轴系下改进时序的电流预测无差拍控制算法。通过对传统电流预测无差拍控制的时序分析，电流控制器对电流指令进行分段采样，基于永磁同步电机交直轴电压方程模型得到电压指令的补偿值，消除了原有电流指令滞后一拍的计算延时。同时，分析功率器件非理想因素与延时效应对电压状态量产生的偏差，引入电压重构算法，减小状态量误差对电流跟踪精度的影响。仿真和实验结果表明，与传统无差拍电流预测控制相比，改进后的电流预测控制算法有效地提高了电流环的动态性能和稳态精度。
关键词：永磁同步电机 电流预测 无差拍控制 时序优化 电压重构
由于功率密度高、效率高等特性，永磁同步电机（Permanent Magnetic Synchronous Motor, PMSM）在工业领域得到了广泛的应用[1-4]。电流环作为永磁同步电机控制的最内环，其响应速度是控制系统动态性能的关键。
永磁同步电机电流环传统的控制方法为PI调节器控制，PI调节器结构简单，且鲁棒性较好。通过增大PI调节器的增益可以提高系统响应速度，但过大的增益会造成超调，严重时会影响系统稳定性，实际控制中需要同时兼顾控制系统的动态性能和稳态性能，在高性能应用场合会受到限制[5-6]。相较于PI调节器控制，预测控制在保证系统稳态性能的条件下，能够获得更好的动态性能，在电机控制领域有很好的应用潜力。
预测控制的思想是根据现有时刻的输入和历史输入输出信息，预测过程未来的输出状态，并以此指导控制量设计[7-14]。文献[7]中运用有限控制集模型电流预测控制的思想，分析八种空间矢量对系统输出的影响，制定相应的评价准则，选出最合适的空间矢量并输出，但这种控制方案电流纹波比较大。文献[8]提出一种预测转矩控制策略，通过建立转矩预测模型，以保证在参数失配的情况下仍能获得较为精确的转矩和磁链预测值，克服电机参数失配带来的性能降低问题，从而提升预测算法的整体控制性能。文献[9]在转矩电流环控制中采用并联积分器的预测控制方法，通过改进占空比更新策略使电流控制延时缩短至1.5个控制周期，并有效降低对参数准确性的依赖。文献[10-14]均采用无差拍预测控制思想，基于同步旋转坐标系下的永磁同步电机数学模型，预测下一拍的输出状态，从而找到一个控制量使得下一时刻的系统误差为零。无差拍预测控制算法动态响应速度快，稳态谐波含量小，是永磁同步电机电流预测控制的理想方式。其中，文献[10]提出了一种三矢量预测电流控制策略，在每个扇区用三个基本电压矢量合成期望电压矢量，在旋转坐标系下利用无差拍方法计算矢量作用时间，减小了电流脉动，并提高了系统稳态性能。文献[11]在无差拍控制中引入了鲁棒电流预测算法，减小了预测模型参数误差对系统稳定性的影响，提升了电流环的动态性能和稳态精度。文献[12]提出一种改进无差拍预测控制算法，修改了电流偏差约束条件和输出电压预测方法，解决了电感参数失配引起的控制不稳定的问题。文献[13]提出了一种基于虚拟矢量的预测电流控制策略，采用无差拍控制思想，计算虚拟矢量所在扇区位置，并设计带有预测误差反馈校正的评价函数，提升了电流控制精度，优化了永磁同步电机运行过程中性能受参数变化的问题。
无差拍控制的性能依赖状态量的获取精度，针对无差拍控制中数字延时和逆变器非理想因素等对控制性能造成影响的问题，文献[15-20]提出了相应的补偿策略。其中，文献[15-16]通过扰动观测器的形式解决了电压扰动引起的控制性能下降问题。文献[15]将内模干扰观测器估计的系统扰动引入含参数扰动的电压方程，保证观测的状态变量不断逼近准确的系统状态变量，达到实时补偿的效果。文献[16]通过设计两个并行的扰动观测器，达到对模型不确定项及由逆变器非线性所引起的扰动电压补偿的目的，从而减小了电压扰动对电流控制精度的影响。文献[17]提出一种基于神经网络带通滤波器和扩展卡尔曼滤波器相结合的补偿方法。传统无差拍控制具有两拍跟随效应，这是由于固有数字延时导致的。针对电流环时序延时问题，文献[21]提出一种基于现场可编程逻辑阵列（Field Programmable Gate Array, FPGA）的电流过采样的方案，提升电流环控制中的数据精度，达到提升控制性能的目的。文献[22]提出一种在一个载波周期内实现两次电流采样占空比更新的控制策略，扩展了电流环带宽，提高了系统的动态响应。这种方案虽然不以提高脉冲宽度调制（Pulse Width Modulation, PWM）开关频率为前提，但是要求主程序在半个开关周期内执行完毕。文献[9]在一个开关周期内单次采样单次更新占空比的前提下，将占空比更新与采样错开半个周期进行，从而缩短了半个周期延时。
本文以永磁同步电机数学模型为基础，通过分析传统无差拍电流预测控制时序，提出一种改进时序的电流预测算法，消除电流指令计算的一拍延时，进一步提升电流的响应速度。同时，考虑功率器件非理想因素及数字延迟对电压状态量的影响，提出一种电压重构算法，解决了参考电压不准引起的电流预测偏差问题，并减小了永磁同步电机的电流谐波。
永磁同步电机是一个非线性、强耦合的系统，为了方便研究，作如下假设：①忽略电机铁心饱和，不计涡流和磁滞损耗；②三相绕组对称分布；③相绕组感应电动势为正弦波。
在同步旋转坐标系下，PMSM的电压方程为
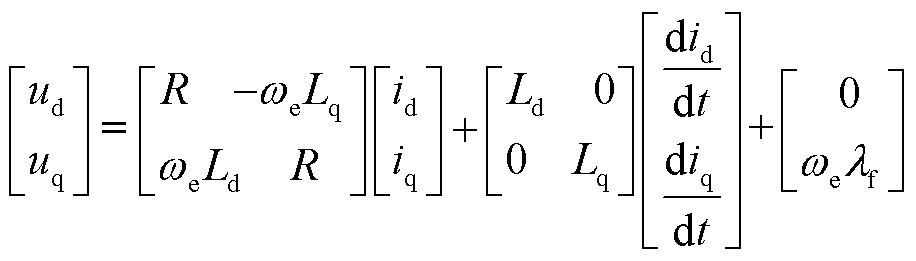（1）
式中，ud、uq和id、iq分别为定子直、交轴电压和电流；R为定子电阻；Ld、Lq分别为定子直、交轴电感；λf为永磁磁链；ωe为转子电角频率。
永磁同步电机电流环控制系统框图如图1所示。数字控制器在每个控制周期，通过采样得到母线电压、三相电流和转子位置信号，计算得出参考电压值，并调制获得三相逆变器的PWM信号，达到对电机定子电流控制的目的。图中，i*d、i*q, u*d、u*q和u*α、u*β分别为定子直、交轴电流、电压指令值及静止坐标系α、β轴电压指令值；ia、ib、ic为定子三相电流；θ为转子位置角。
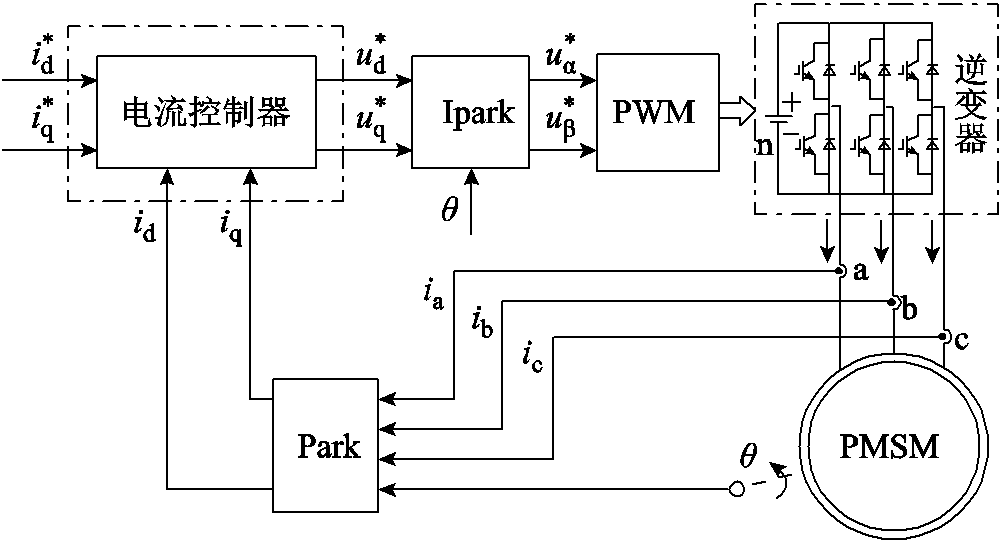
图1 永磁同步电机电流环控制系统框图
Fig.1 Block diagram of PMSM control system
电流环传统的PI调节器控制思想为，利用当前指令值Iref与实际值I的差值调节生成参考电压矢量，从而改变电流输出，达到跟随指令值的目的。与该方式不同，基于电流预测的控制方式，是利用永磁同步电机的数学模型，建立参考电压矢量和电流输出的关系，提前一拍计算得到电流预测值，并以此来指导生成最优的参考电压矢量。实际系统中，电流环控制的时序如图2所示。
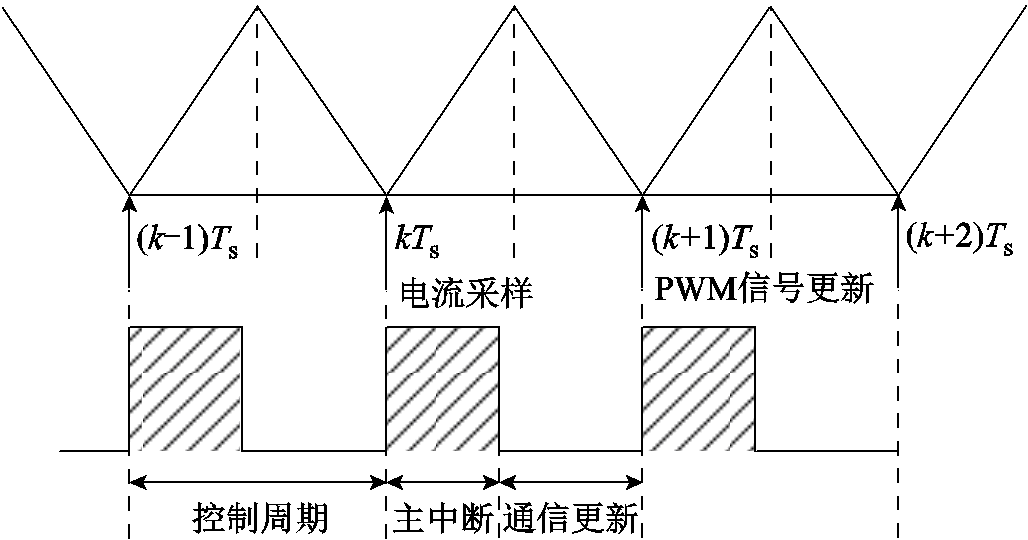
图2 传统电流环数字控制时序
Fig.2 Timing of traditional control strategy
Ts为载波周期时长，则在第k个载波周期[kTs, (k+1)Ts]内，对式（1）进行离散化，得到永磁同步电机的离散化数学模型如式（2）所示。由于转速环带宽远小于电流环带宽，在一个控制周期内可忽略转速变化带来的影响。
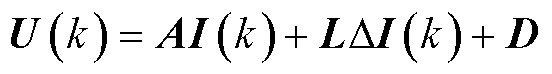（2）
其中
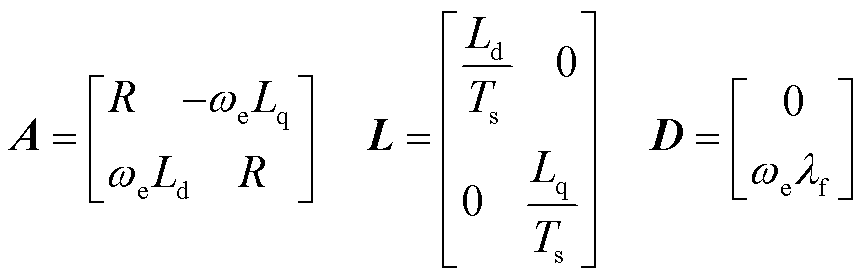
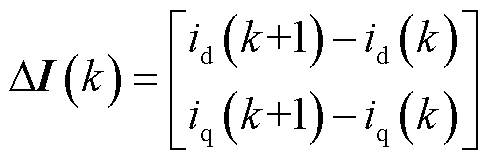
控制器在kTs时刻采样得到实际电流矢量I(k)，并根据上一拍计算得到的当前拍参考电压矢量U(k)，可以得到下一拍的电流矢量预测Ip(k+1)，预测方程为
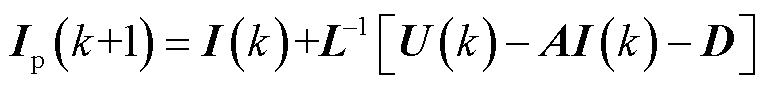（3）
根据预测电流矢量和参考电流矢量，可计算得到使电流误差为0的最优参考电压矢量Up(k+1)，即
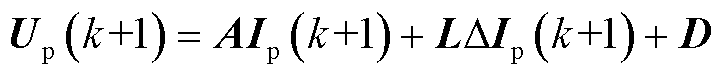（4）
其中
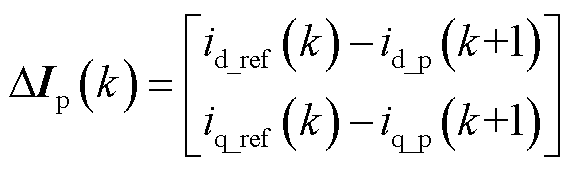
式中，id_ref(k)、iq_ref(k)为第k拍直、交轴电流参考值；id_p(k+1)、iq_p(k+1)为第k拍预测得到的k+1拍直、交轴电流值。
又因为
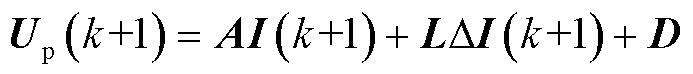（5）
结合式（2）～式（5），可以得到
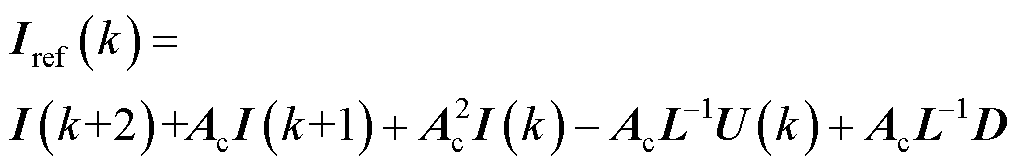（6）
其中
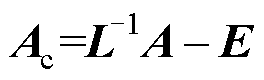
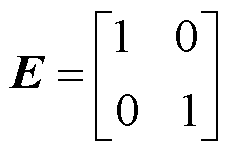
展开式（6）并将式（2）代入，可得
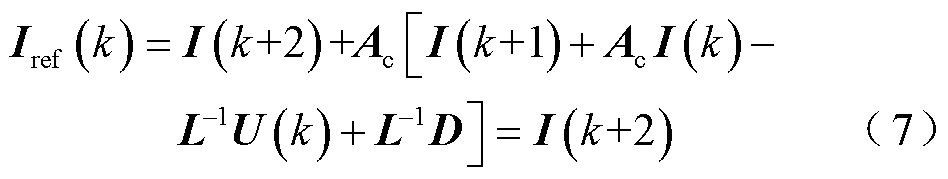
根据上述分析绘制传统无差拍电流预测控制结构如图3所示，并且由式（7）可知，该控制系统具有两拍跟随特性。
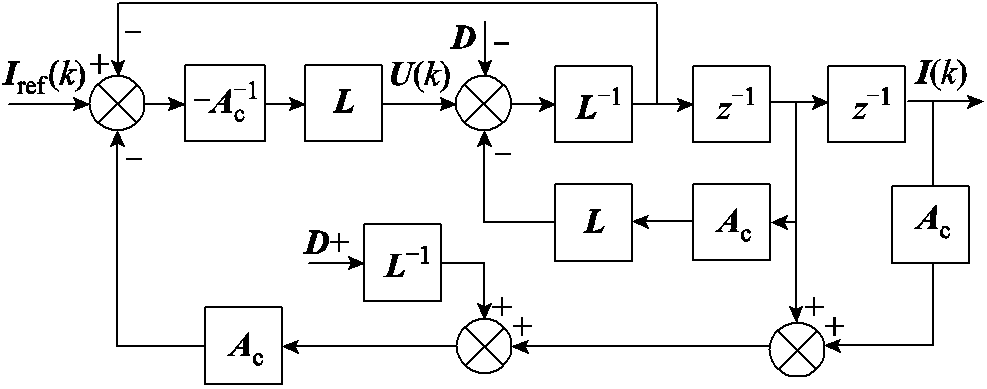
图3 传统无差拍电流预测控制结构
Fig.3 Block diagram of traditional deadbeat predictive current control
传统无差拍电流预测控制沿用了控制器下溢点采样延迟一拍更新的策略，上位机指令下发与实际接收的时间差使得电流指令已滞后一个控制周期。为了对传统更新时序的这种弊端进行优化，针对电流环时序进行了改进，改进后的时序如图4所示。
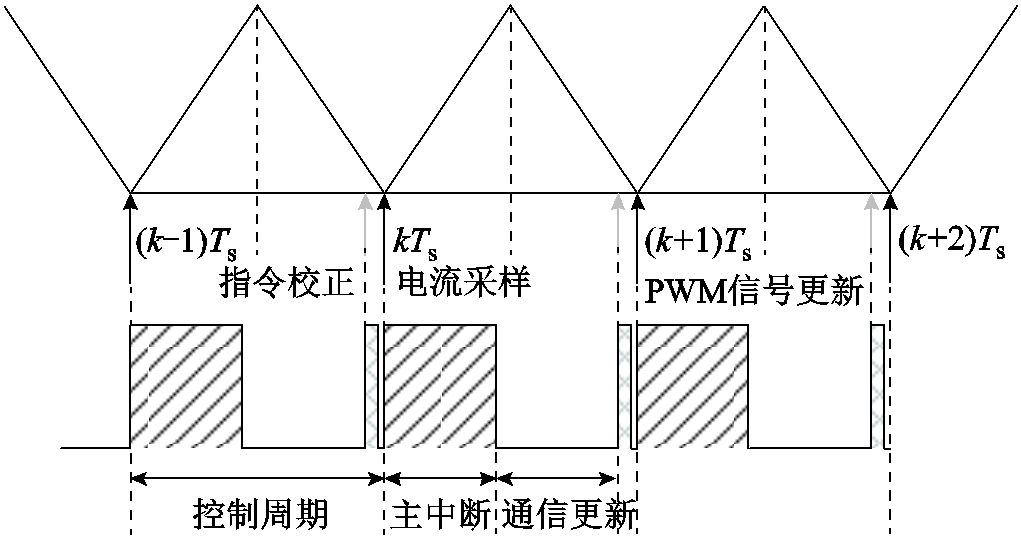
图4 改进的电流环数字控制时序
Fig.4 Timing of improved deadbeat predictive current control
改进时序下，电流环执行程序包含原有主中断和指令校正两个中断程序。主中断程序执行原有电流环采样、坐标变换和发波等各环节；指令校正中断负责对由于电流指令变化造成的电压指令偏差进行校正，上位机与下位机在两个中断之间进行信息交互。图5所示为时序优化的无差拍电流预测控制具体实现流程，图中Ta、Tb、Tc分别为三相桥臂上管的实际导通时间。
指令校正中断程序在下溢点占空比更新前对电流环参考值的变化进行判断，若指令发生变化，则将变化指令部分对应的参考电压进行补偿，补偿电压如式（8）所示，并更新占空比；若指令没有变化，则直接跳出。电流指令为常值时，电流环更新时序与传统无差拍预测控制相同，对电机的稳态性能不会造成影响；当电流指令值变化时，指令变化直接
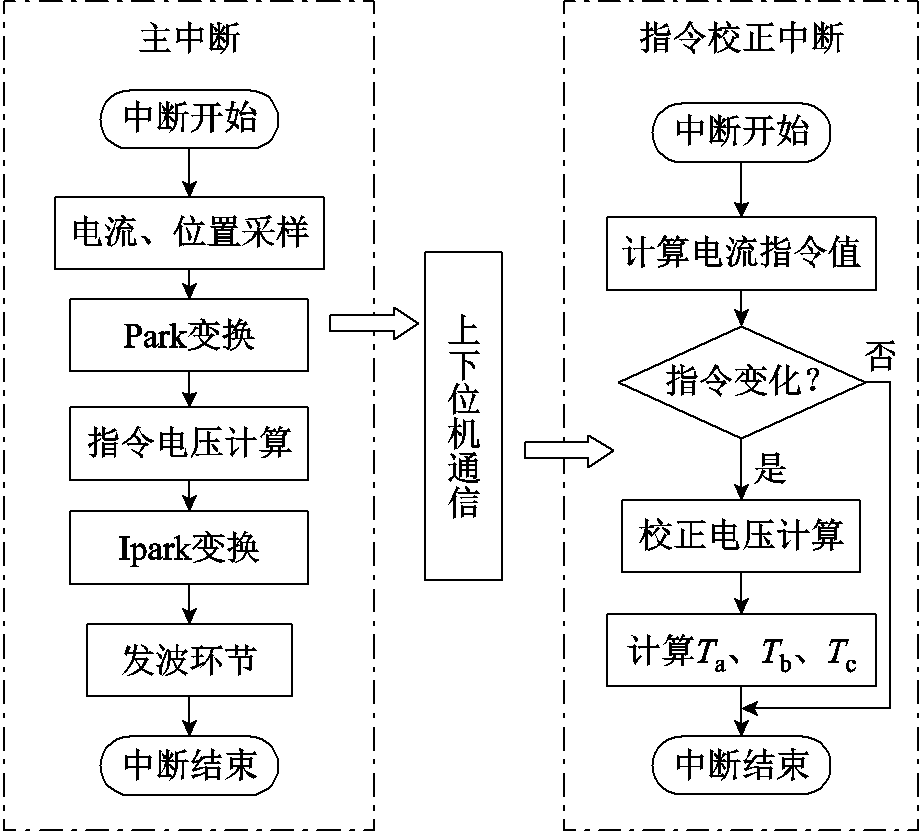
图5 新时序中断执行流程
Fig.5 Flow chart of interrupt based on improved algorithm
体现在参考电压上，从而减小指令响应时间，提升系统带宽。由于电压指令优化部分代码量小，对数字控制系统基本不产生影响。
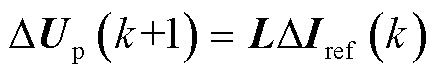（8）
其中
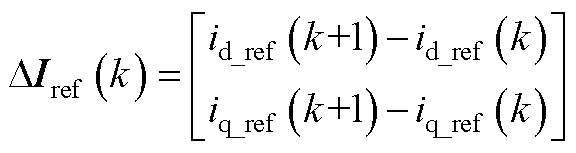
将式（8）代入式（4），可得
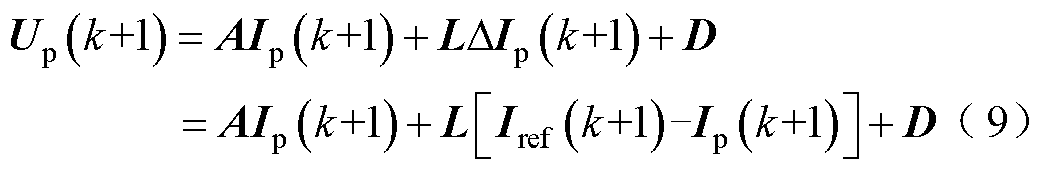
式（9）为新时序下的预测电压方程，将式（2）、式（3）和式（5）分别代入式（9）中，可以得到
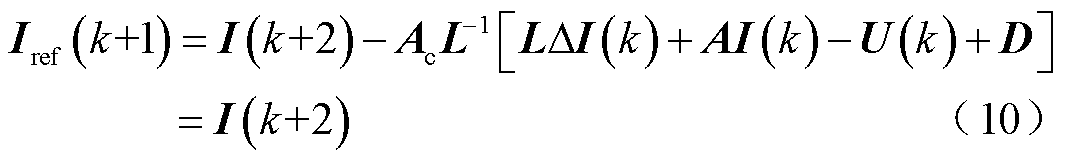
根据上述分析绘制时序优化后的无差拍电流预测控制结构如图6所示。由式（10）可以看出，优化后的电流控制系统实现了“准一拍”跟随。
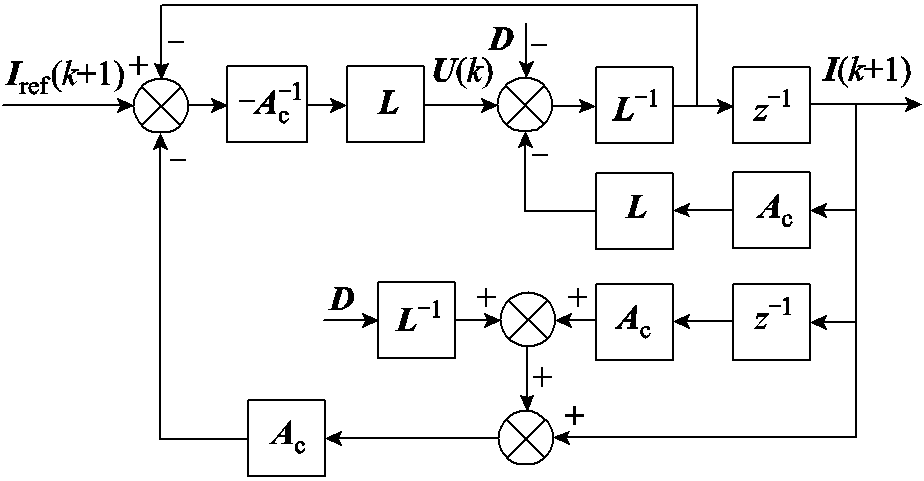
图6 改进时序的无差拍电流预测控制结构
Fig.6 Block diagram of improved deadbeat predictive current control based on new timing
传统理想无差拍电流预测控制算法能够实现指令电流的两拍跟随，但由于状态量精度及控制延时等各种因素，实际电流跟踪速度往往会受到影响。
功率器件在开关过程中的压降和导通关断时间、防止逆变器桥臂直通设置的死区时间以及功率器件本身的压降，导致逆变器输出电压畸变。畸变电压会导致电流预测值出现偏差，从而影响无差拍电流预测控制的精度和响应速度。
以逆变器A相为例，功率器件非理想因素对三相逆变器输出电压的影响如图7所示。图中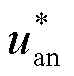
、
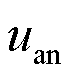分别为图1中a点与n点之间输出电压的理想值与实际值；usw为功率器件的正向导通压降；ud为二极管压降；Udc为母线电压；Ton为开通延时；Toff为关断延时；Td为死区时间。
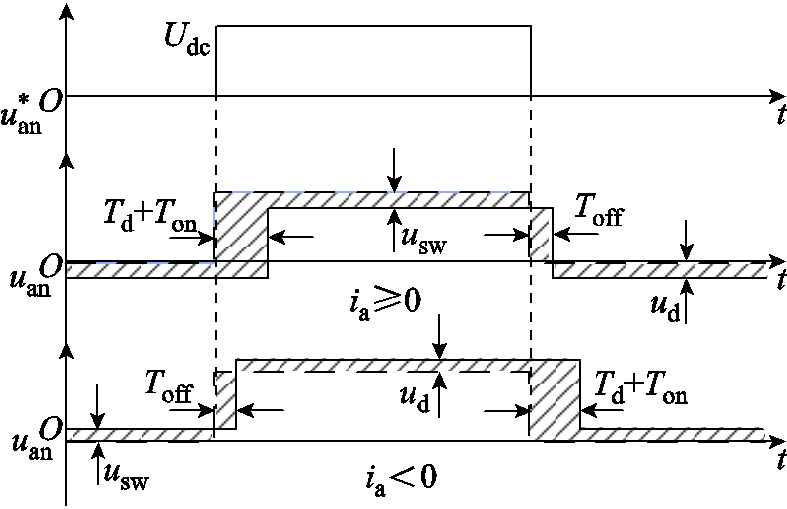
图7 逆变器非理想因素影响示意图
Fig.7 The influence of non-ideal factors of inverter
假设电流方向在一个开关周期内不发生变化，三相逆变器输出相电压表达式可归纳为
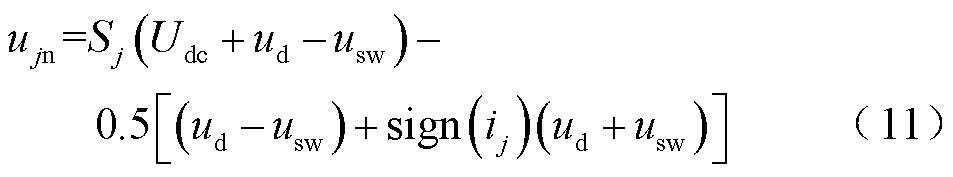
式中，Sj=1表示上桥臂导通；Sj=0表示下桥臂导通；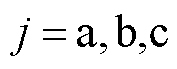
。
在三相对称负载中，相电压满足
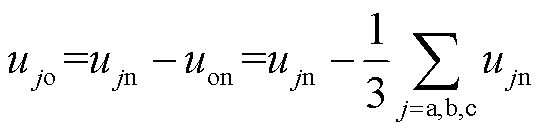（12）
式中，ujo为三相绕组与电机中性点间的电压；ujn为三相绕组与直流母线负端的电压；uon为电机中性点与直流母线负端的电压。
从而得出A相电压误差值uao_err的表达式为
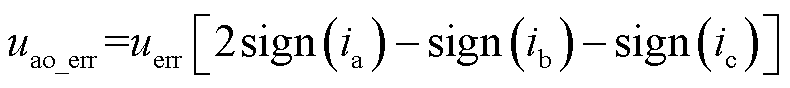（13）
其中
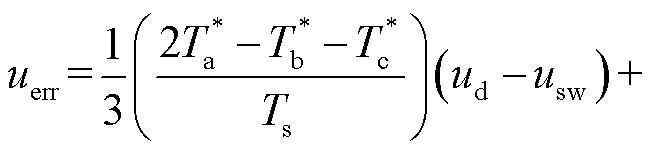
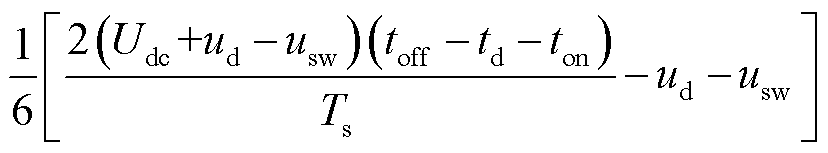（14）
式中，T* a、T*b、T*c分别为三相桥臂上管的理想导通时间。
根据式（14）可知误差电压与开关管的通断延时、功率器件管压降、死区时间及母线电压的关系，根据这种关系可以直接计算误差电压的数值，对三相电压误差进行坐标变换便可以获得在两相旋转坐标系下的误差电压为
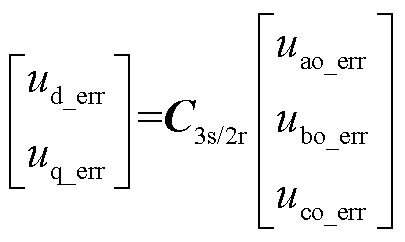（15）
式中，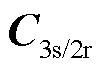
为变换矩阵。
由于死区导致的零电流钳位效应，使电流过零时电流方向的判断会出现偏差，导致重构电压的不准确，为此可以用三相电流的参考值作为电流方向的判断条件，从而避免这种现象。
同时，由于数字控制延时和PWM固有延时的存在，电机控制中Ipark变换时采用的电角度信号与真实电角度存在滞后角度qd，导致指令电压与实际电压存在误差，实际控制中需要对角度进行补偿。考虑逆变器非理想因素和控制延时的电压重构算法如图8所示。图中，i*a、i*b、i*c分别为三相定子电流给定值；udcom、uqcom为电流控制器输出电压。
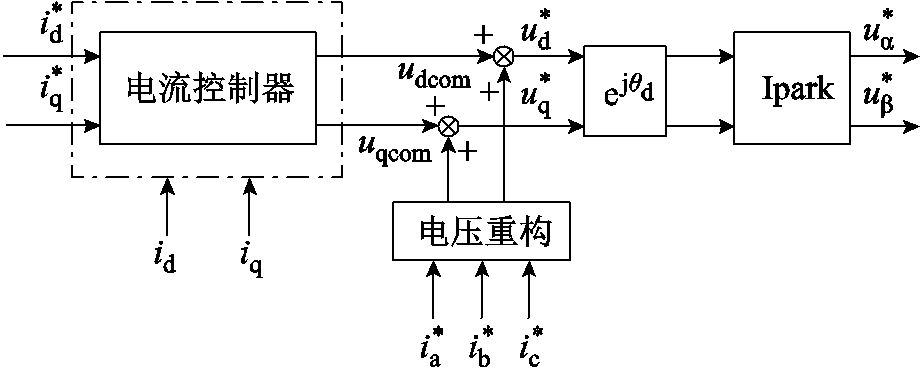
图8 电压重构结构框图
Fig.8 Block diagram of voltage reconstruction
为了验证改进无差拍电流预测算法的有效性，基于Simulink仿真平台搭建了本算法的仿真模型。同时，搭建了基于TI公司的TMS320F28335DSP作为主控芯片的实验平台。仿真与实验中直流母线电压均为200V，逆变器开关频率fs=5kHz，功率器件死区为3μs。仿真用永磁同步电机采用实际永磁同步电机的参数模型，详细参数见表1。
表1 永磁同步电机参数
Tab.1 Parameters of PMSM
参数数值 永磁体极对数p4 永磁磁链yf/Wb0.085 4 相电阻Rs/mW24 直轴电感Ld/μH258 交轴电感Lq/μH770 额定电流/A200 额定电压/V220 额定功率/kW40 额定转矩/(N×m)125 额定转速/(r/min)3 000
仿真的目的在于对比改进时序后电流预测控制方法的性能以及电压重构算法的有效性。仿真时，参照图1搭建Simulink仿真平台，被测电机设置为转速输入模式，让电机仅运行电流环，电流指令按照预设方式给定。电机运行工况为300r/min，采用id=0的控制策略。
图9给出了传统无差拍电流预测控制的电流响应波形及相电流快速傅里叶变换（Fast Fourier Transform, FFT）分析，q轴电流指令在t=0.05s时从0阶跃至20A。可以看出，由于控制延时和逆变器死区等非理想因素的存在，导致电流跟踪存在静态偏差，且相电流波形中5、7次谐波含量很重，占基频百分比分别为6.8%和4.1%。
图10为电压重构后无差拍电流预测控制电流响应波形，在原有控制基础上，增加了电压重构算法，其余仿真工况与图9相同。对比图9和图10可知，电压重构算法能有效消除逆变器非理想因素和控制延时引起的状态量偏差，无静差跟随电流指令。传统的无差拍电流预测控制具有两拍的跟随效果，与理论分析结论一致。
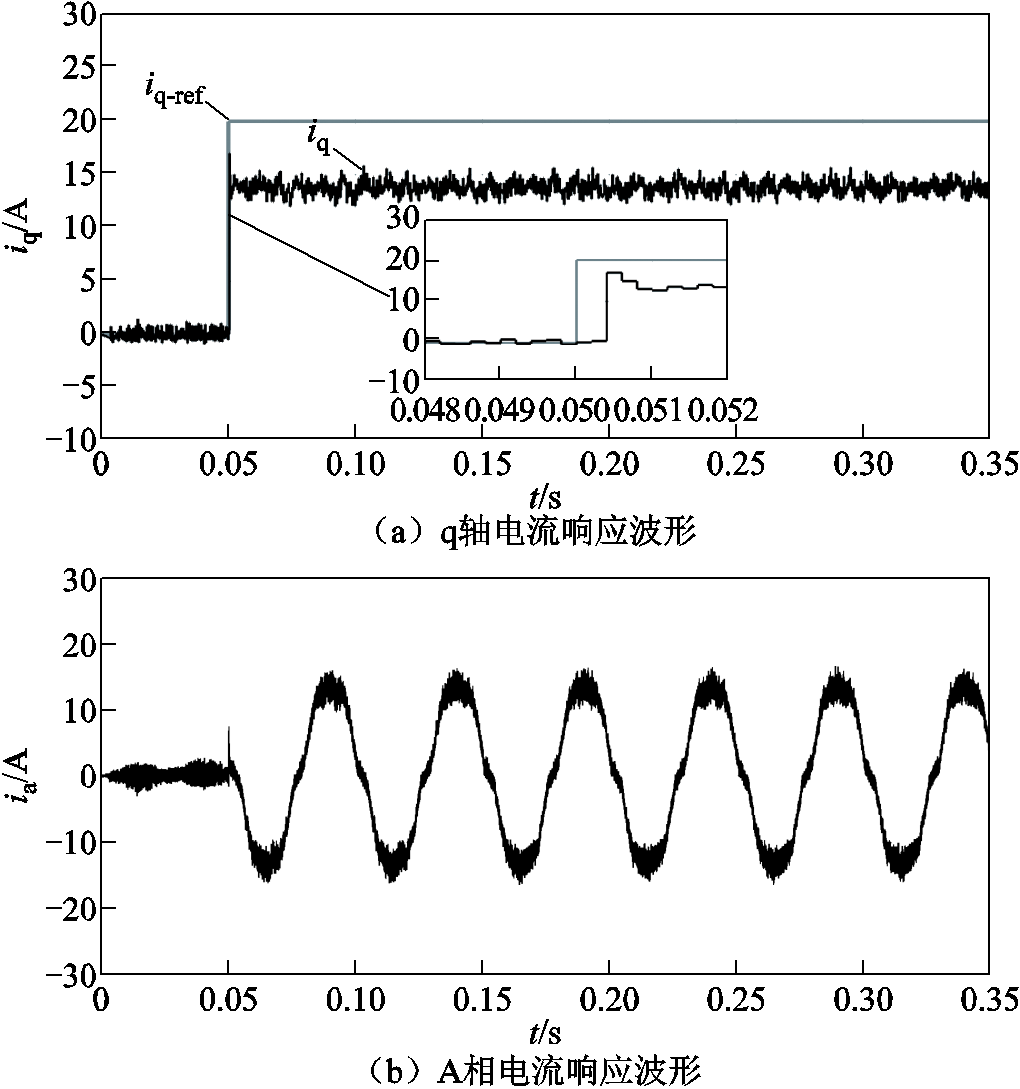
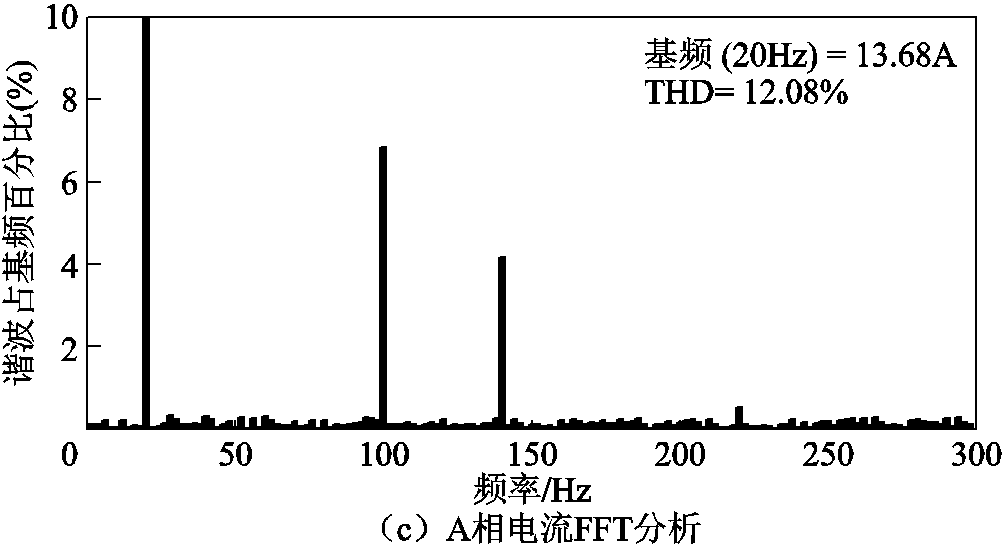
图9 传统无差拍电流预测控制电流响应仿真波形
Fig.9 Simulation results of current response of traditional deadbeat predictive current control
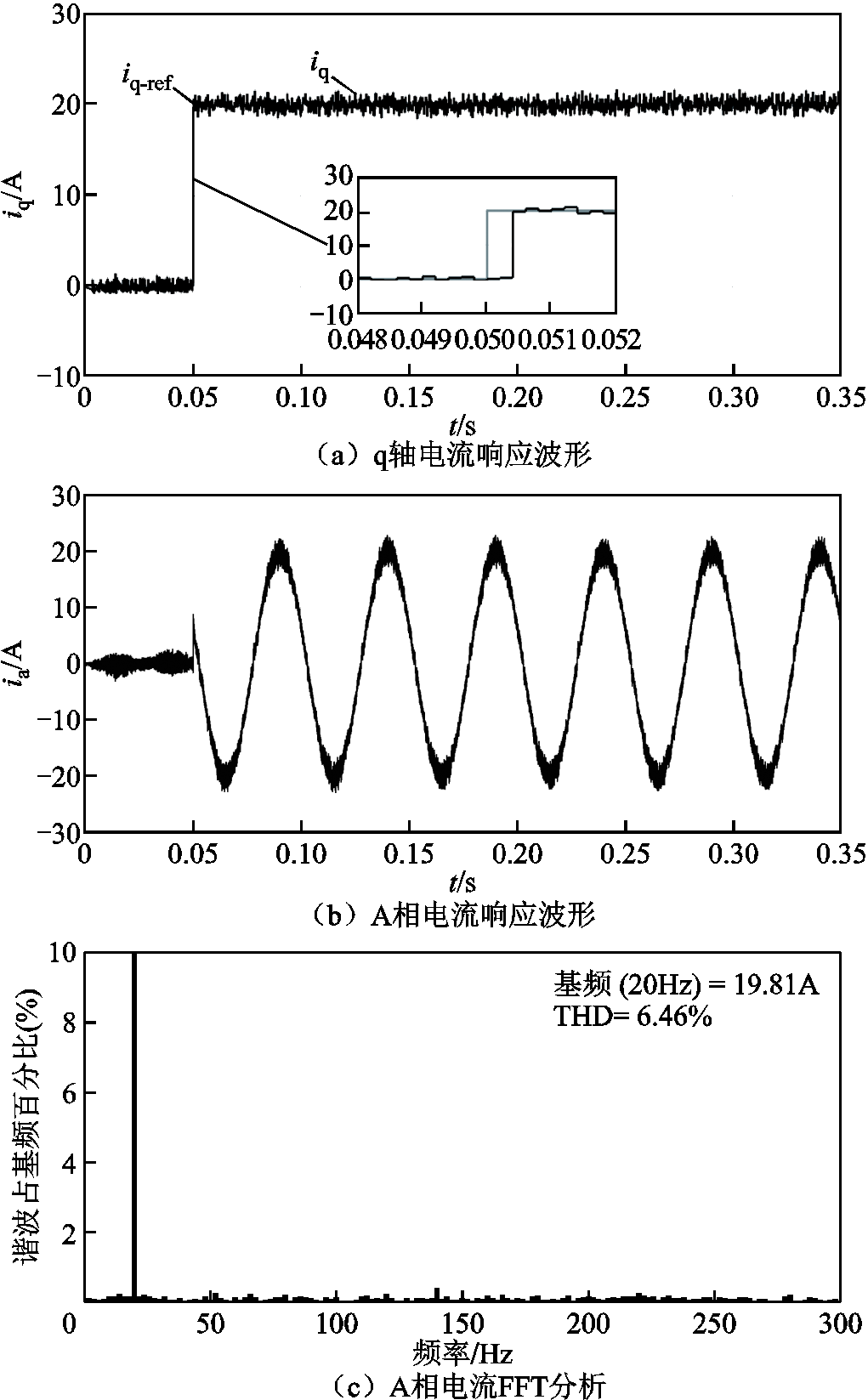
图10 电压重构后无差拍电流预测控制电流响应仿真波形
Fig.10 Simulation results of current response of deadbeat predictive current control with voltage reconstruction
图11为在新时序控制条件下，其他工况与图9相同的无差拍电流预测控制响应仿真波形。对比图9和图11可以看出，新时序下电流环输出对指令响应时间为1个控制周期，但是电流输出有稳态偏差，且其谐波含量和稳态值与传统无差拍电流预测控制基本相同，说明改进时序基本不影响电流环的稳态响应。
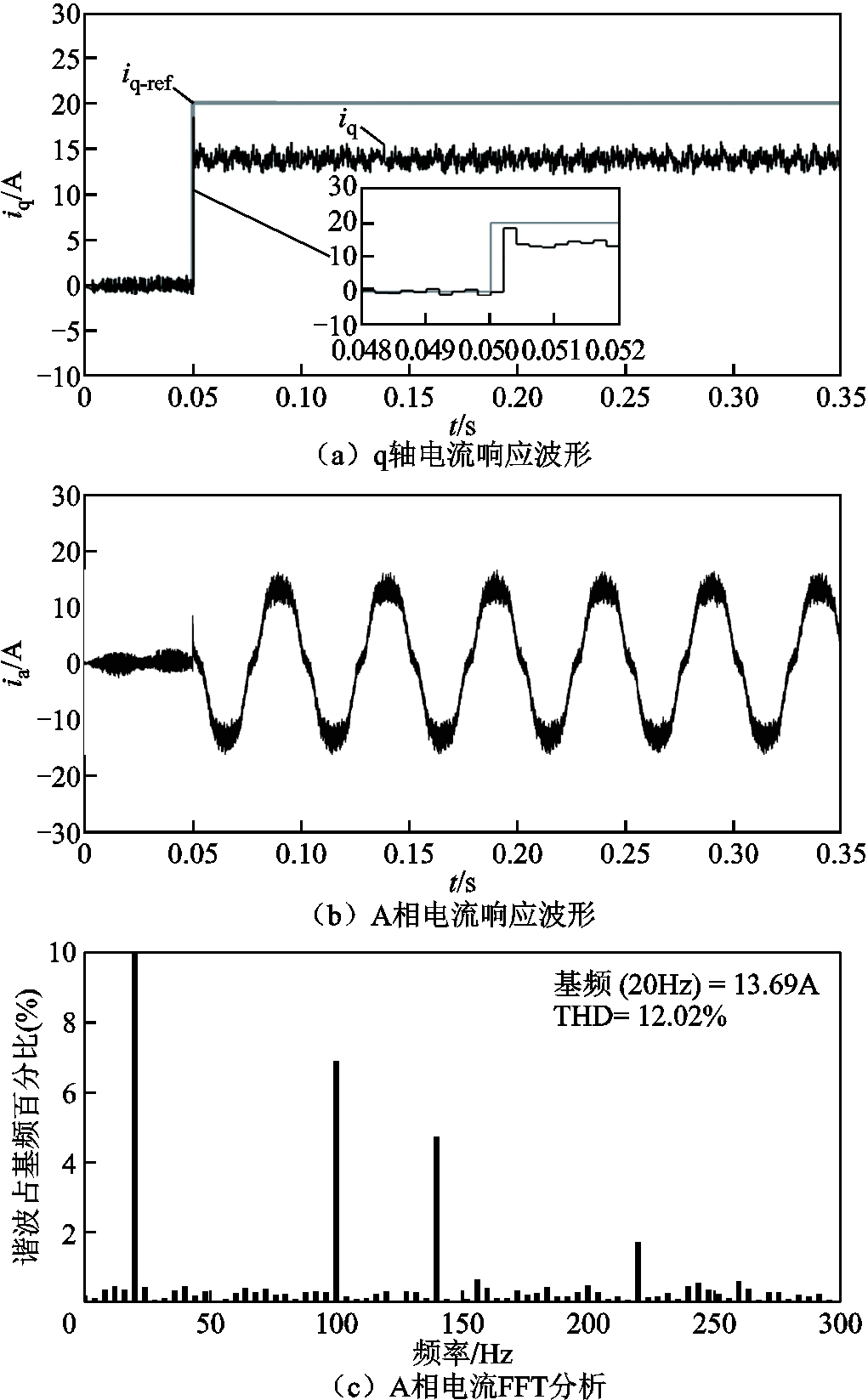
图11 改进时序的无差拍电流预测控制响应仿真波形
Fig.11 Simulation results of current response of deadbeat predictive current control based on new timing
图12给出了加入电压重构算法的改进时序无差拍电流预测控制的电流响应波形及相电流FFT分析。可以看出，改进时序后的控制方法对指令信号的响应时间为1个控制周期，与理论分析的结果吻合。相对于传统无差拍电流预测控制两拍跟随的控制效果，改进后的预测控制方法对电流指令信号的响应速度更快。同时，对比图10和图12可知，改进后的算法并不会影响电机的稳态性能。
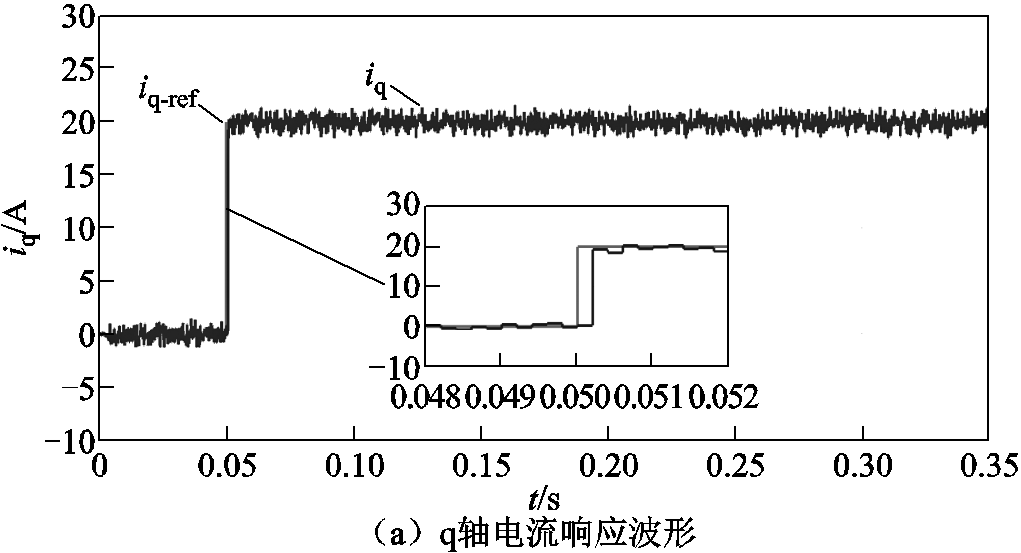
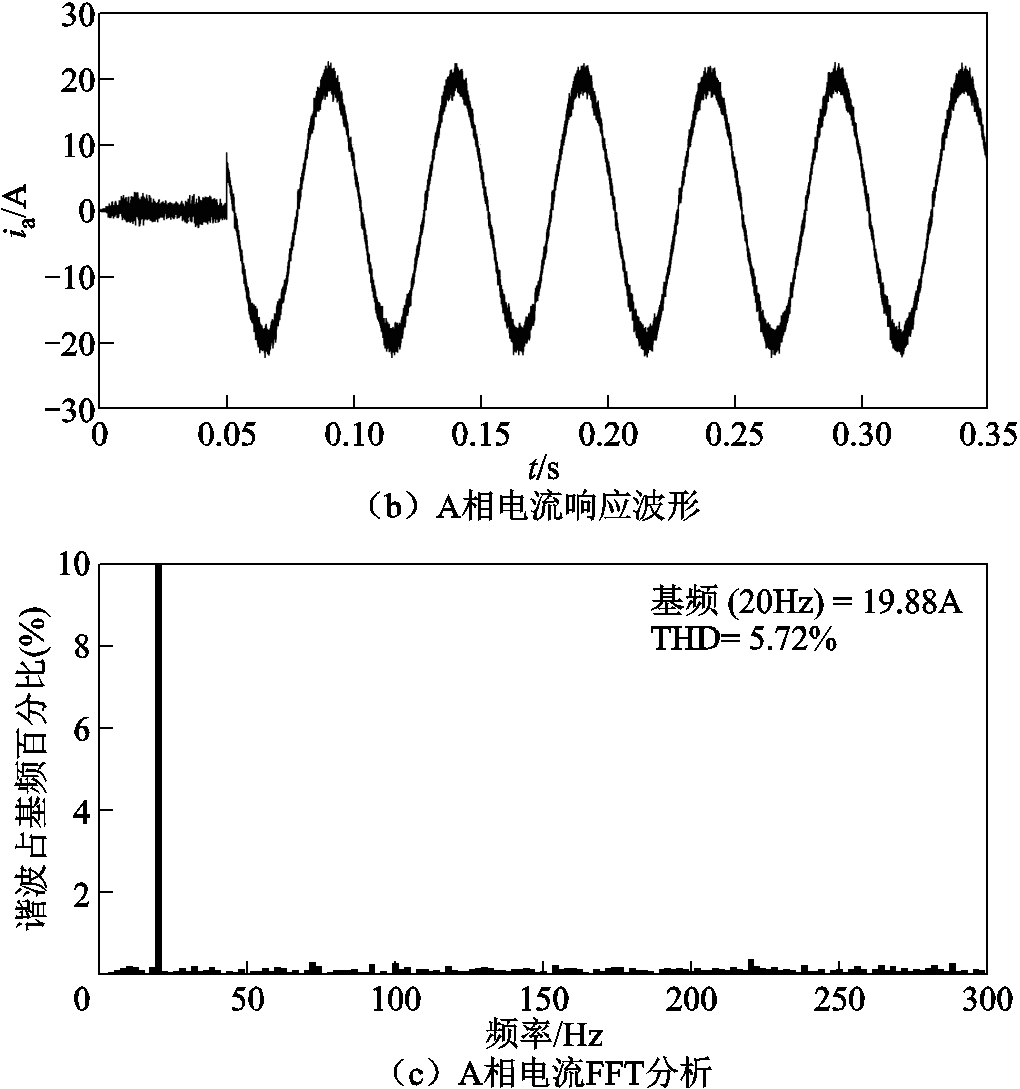
图12 电压重构后的改进时序无差拍电流预测控制响应仿真波形
Fig.12 Simulation results of current response of improved deadbeat predictive current control
实验平台如图13所示，逆变桥由英飞凌公司型号为FS800R07A2E3的IGBT组成，两台永磁同步电机同轴旋转，构成了对拖系统，其中被测电机工作在电流环模式，另一台电机工作在转速环模式，以达到稳速的目的。电机运行工况为300r/min，采用id=0的控制策略。
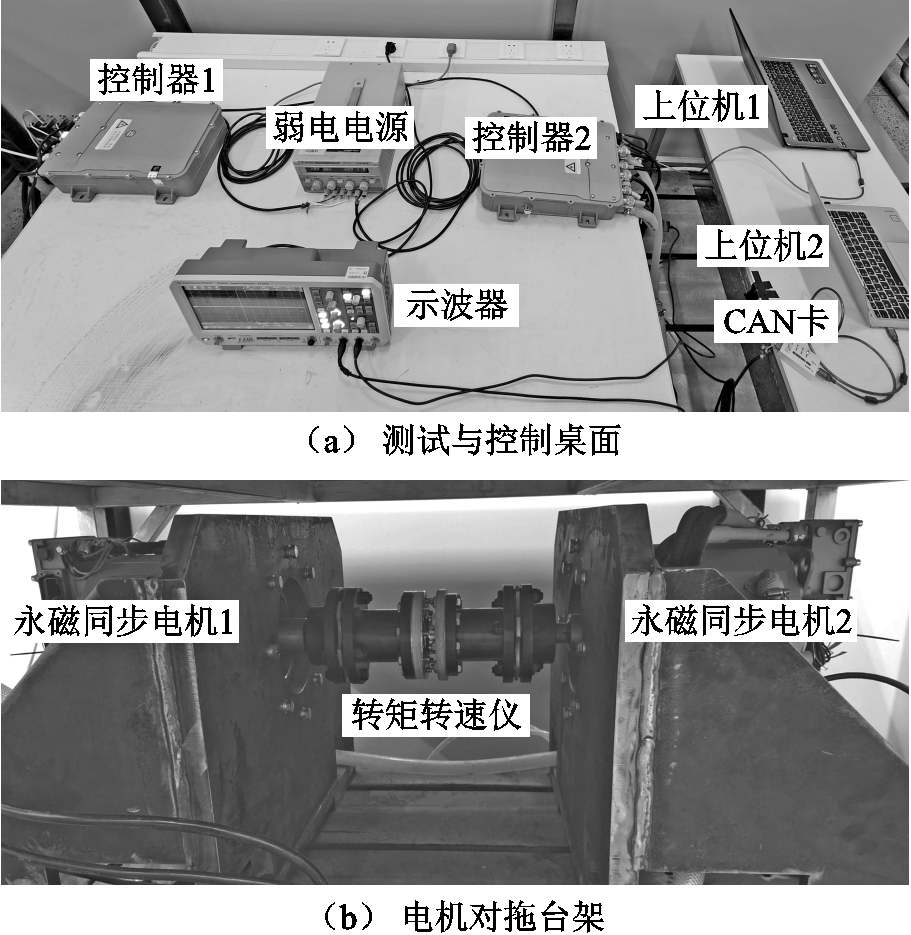
图13 对拖实验平台
Fig.13 Back-to-back testing platform
图14给出了传统无差拍电流预测控制的电流响应波形，q轴电流指令在某一时刻从0阶跃至20A。可以看出，由于控制延时和逆变器死区等非理想因素的存在，导致电流跟踪存在静态偏差。其中，A相电流波形由交流电流钳在示波器上得到，q轴电流由CAN通信以5kHz的速率传至上位机获得。
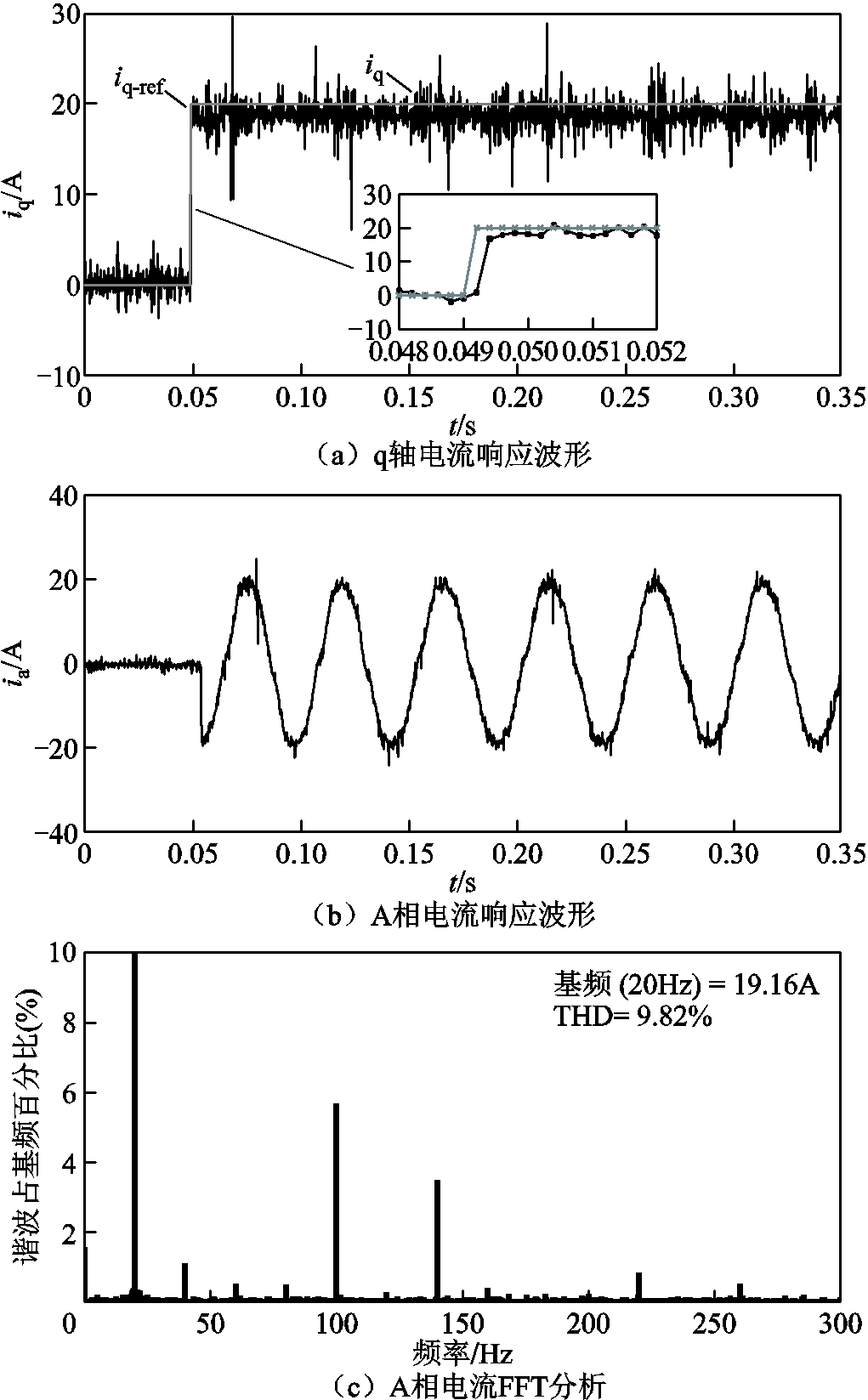
图14 传统无差拍电流预测控制电流响应实验波形
Fig.14 Experimental results of traditional deadbeat predictive current control
图15给出了增加电压重构算法后的电流响应波形，其余实验工况与图14相同。对比图14和图15可知，电压重构算法能有效消除逆变器非理想因素和控制延时引起的状态量偏差，无静差跟随电流指令。通过相电流FFT分析可知，电机电流中的5、7次谐波大大降低。
实验中，由于电流采样存在噪声问题，导致实际电流波形存在比较大的“毛刺”，但是并不会影响算法的执行效果。考虑电流纹波效应，以q轴电流第一次达到指令值的90%作为响应时间。
图14a中未经电压重构的系统q轴电流响应时间为4个控制周期，且电流跟随存在稳态偏差。图15a中电压重构后q轴电流的响应时间为2个控制周期，与传统无差拍控制的两拍跟随效应相符。同时，通过对q轴电流的动态响应可知，在电流指令发生变化一拍后，实际电流才开始响应，这也印证了在传统更新时序中电流指令下发与控制指令更新存在一拍天然的延时效应。对比图14b、图14c和图15b、图15c可知，电压重构后相电流中的5、7次谐波显著减小，相电流的总谐波畸变率（Total Harmonic Distortion, THD）也相应降低。
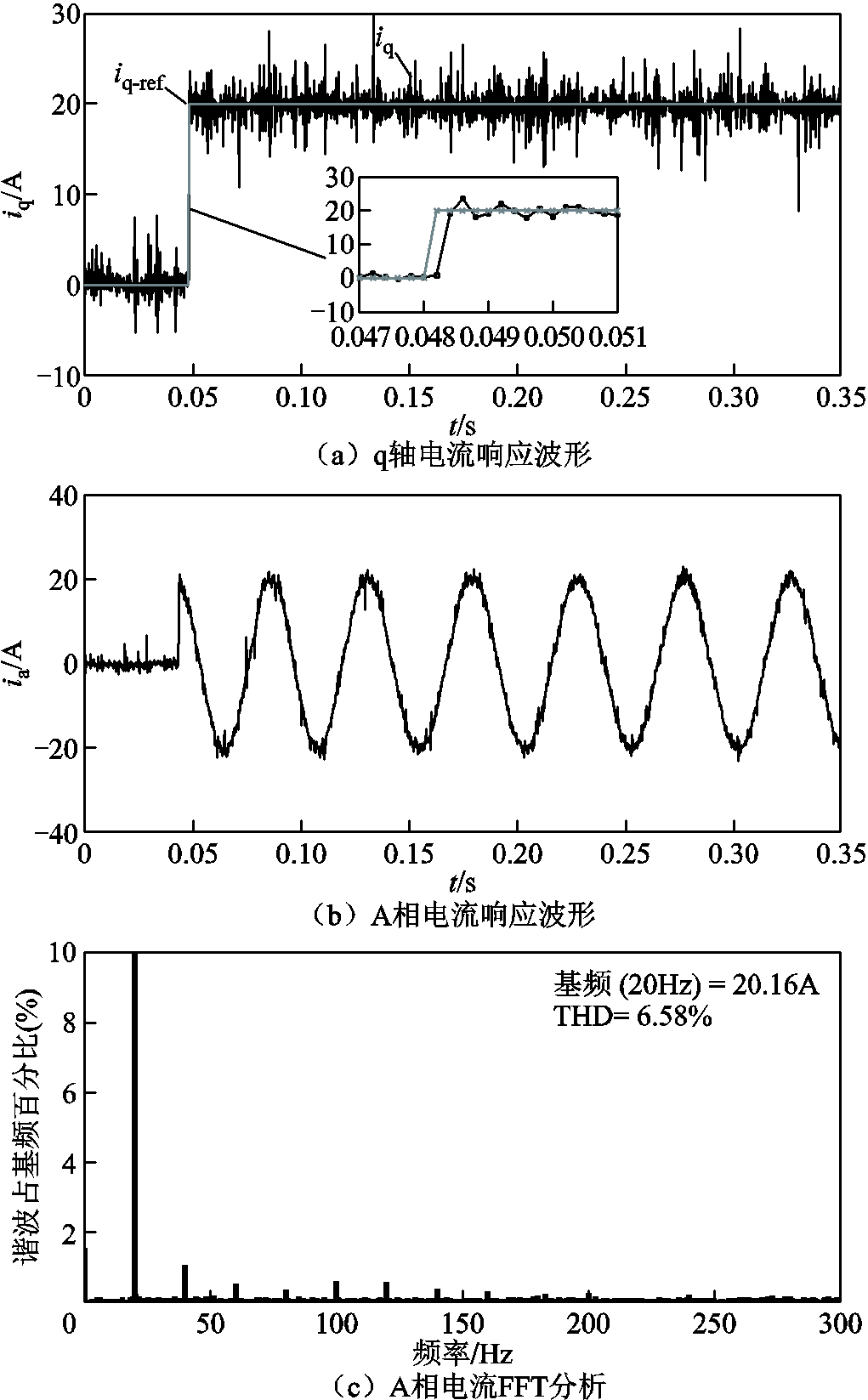
图15 电压重构后无差拍电流预测控制电流实验波形
Fig.15 Experimental results of deadbeat predictive current control with voltage reconstruction
图16给出了改进时序后的电流响应波形，其余实验工况与图14相同。可以看出，改进了电流环控制时序后，q轴电流响应时间为一个控制周期。在传统的电流环时序下，当前拍的电流指令需要在下个周期才能被控制算法采样到，导致电流指令本身存在一个控制周期的滞后。改进时序后的电流预测控制方法避免了这种问题的出现，实现了对电流指令更快速的跟踪。但是电流输出有稳态偏差，对比图14b、图14c和图16b、图16c可知，改进时序后的无差拍电流预测控制谐波含量和稳态值与传统无差拍电流预测控制基本相同，说明改进时序基本不影响电流环的稳态响应。
图17给出了加入电压重构算法的改进时序无差拍电流预测控制的电流响应波形，对比图14～图17可知，改进时序的算法能有效提升电流环响应速度，同时基本不会影响电机的稳态性能，电压重构算法能有效降低电压偏差对电流环控制的影响。
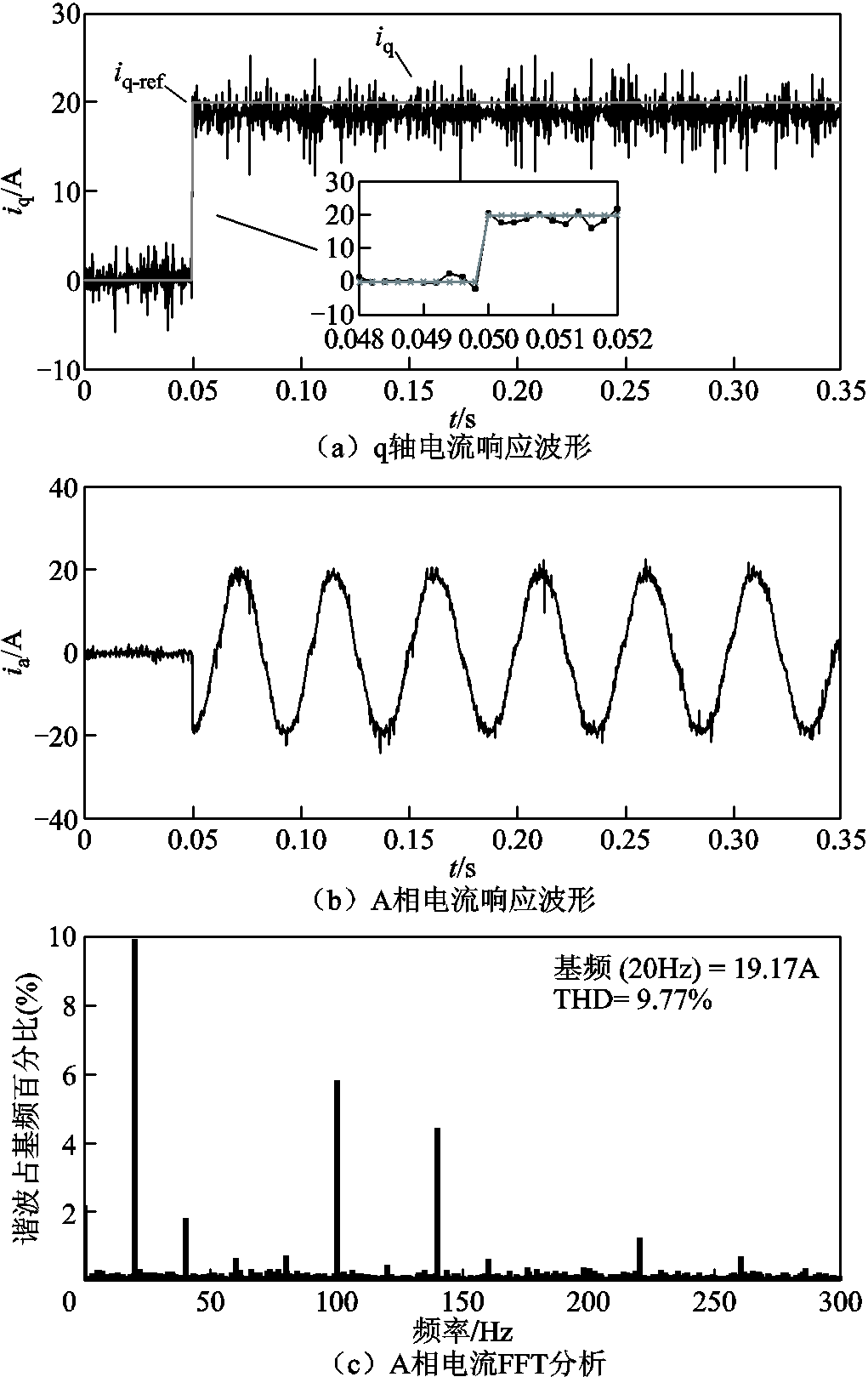
图16 改进时序的无差拍电流预测控制电流实验波形
Fig.16 Experimental results of deadbeat predictive current control with voltage reconstruction
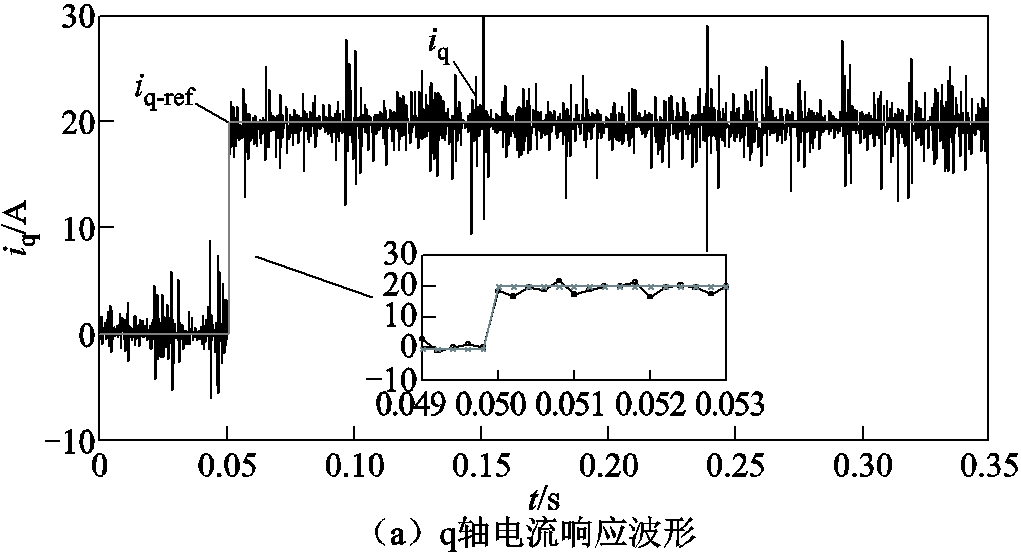
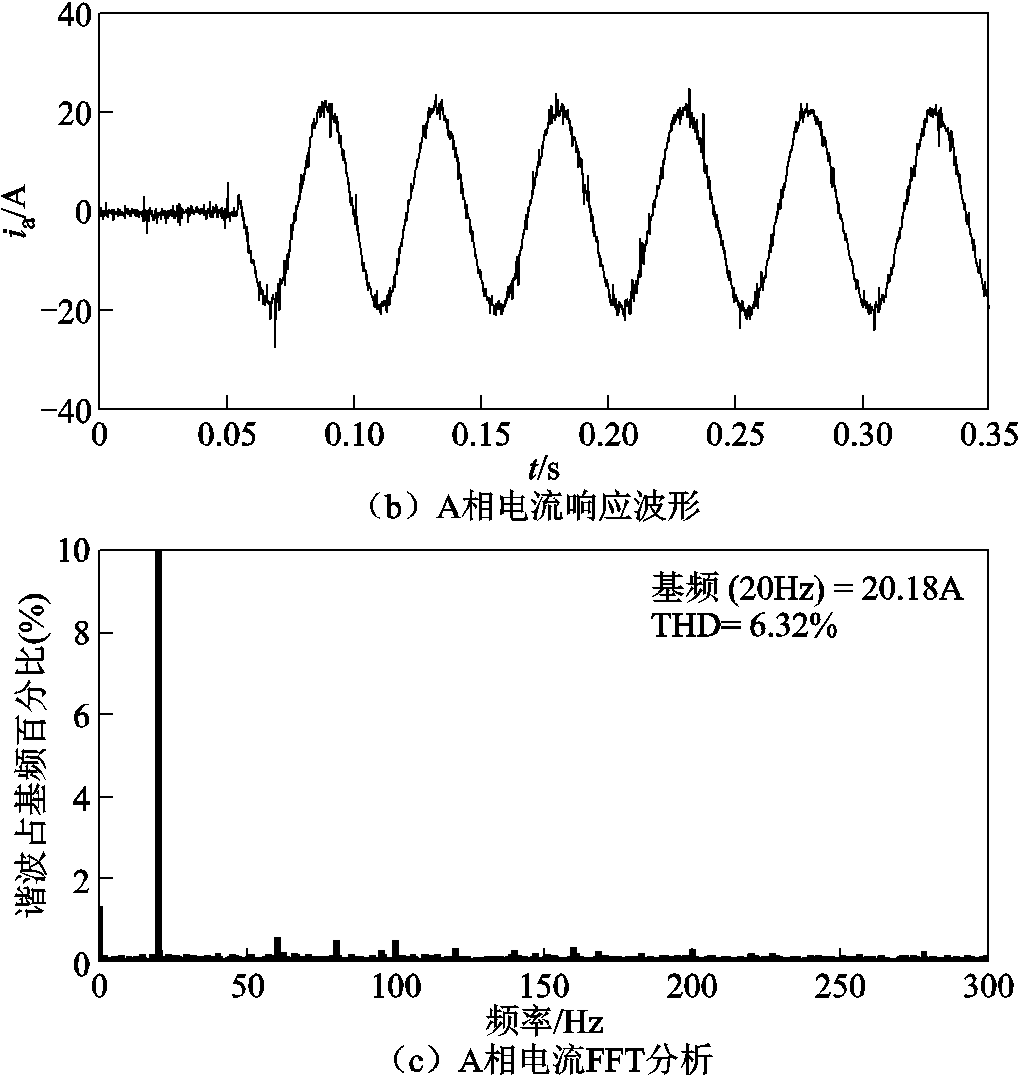
图17 电压重构后的改进时序无差拍电流预测控制实验波形
Fig.17 Experimental results of improved deadbeat predictive current control
本文针对永磁同步电机控制系统提出一种高动态响应性能的电流环控制方案，在传统无差拍电流预测控制方案的基础上，优化控制时序，进一步提高系统响应速度，得出以下结论：
1）改进时序后的电流环控制消除了电流指令滞后一拍的计算延时，相对于传统无差拍电流预测控制算法，本方案电流的响应速度更快。
2）功率器件非理想因素和控制延时带来的状态量偏差不可避免地造成电流跟随的静态偏差，本方案所提出的电压重构策略能够有效避免这种问题的出现，实现电流的无静差跟随。
参考文献
[1] 陈卓易, 屈稳太. 基于PID型代价函数的永磁同步电机模型预测电流控制[J]. 电工技术学报, 2021, 36(14): 2971-2978.
Chen Zhuoyi, Qu Wentai. Model predictive current control for permanent magnet synchronous motors based on PID-type cost function[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2971-2978.
[2] Ma Xiaojun, Bi Chao. A technology for online parameter identification of permanent magnet synchronous motor[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(3): 237-242.
[3] 姚绪梁, 黄乘齐, 王景芳, 等. 两相静止坐标系下的永磁同步电动机模型预测功率控制[J]. 电工技术学报, 2021, 36(1): 60-67.
Yao Xuliang, Huang Shengqi, Wang Jingfang, et al. Model predictive power control of permanent magnet synchronous motor in two-phase static coordinate system[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 60-67.
[4] 谭继鑫, 井永腾, 郭昊, 等. 基于Boost变换的永磁同步电机变频电源电压谐波优化控制[J]. 电工技术学报, 2020, 35(21): 4475-4482.
Tan Jixin, Jing Yongteng, Guo Hao, et al. Optimization control voltage harmonics of PMSM variable frequency power supply based on boost transform[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4475-4482.
[5] Zhang Xiaoguang, Hou Benshuai, Mei Yang. Deadbeat predictive current control of permanent-magnet synchronous motors with stator current and disturbance observer[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3818-3834.
[6] Tang Mi, Gaeta A, Formentini A, et al. A fractional delay variable frequency repetitive control for torque ripple reduction in PMSMs[J]. IEEE Transactions on Industry Applications, 2017, 53(6): 5553-5562.
[7] Morel F, Linshi X, Retif J M, et al. A comparative study of predictive current control schemes for a permanent-magnet synchronous machine drive[J]. IEEE Transactions on Industrial Electronics, 2009, 56(7): 2715-2728.
[8] 周湛清, 夏长亮, 陈炜, 等. 具有参数鲁棒性的永磁同步电机改进型预测转矩控制[J]. 电工技术学报, 2018, 33(5): 965-972.
Zhou Zhanqing, Xia Changliang, Chen Wei, et al. Modified predictive torque control for PMSM drives with parameter robustness[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 965-972.
[9] 王伟华, 肖曦. 永磁同步电机高动态响应电流控制方法研究[J]. 中国电机工程学报, 2013, 33(21): 117-123, 200.
Wang Weihua, Xiao Xi. A current control method for permanent magnet synchronous motors with high dynamic performance[J]. Proceedings of the CSEE, 2013, 33(21): 117-123, 200.
[10] 徐艳平, 王极兵, 张保程, 等. 永磁同步电机三矢量模型预测电流控制[J]. 电工技术学报, 2018, 33(5): 980-988.
Xu Yanping, Wang Jibing, Zhang Baocheng, et al. Three-vector-based model predictive current control for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 980-988.
[11] 牛里, 杨明, 王庚, 等. 基于无差拍控制的永磁同步电机鲁棒电流控制算法研究[J]. 中国电机工程学报, 2013, 33(15): 78-85, 13.
Niu Li, Yang Ming, Wang Geng, et al. Research on the robust current control algorithm of permanent magnet synchronous motor based on deadbeat control principle[J]. Proceedings of the CSEE, 2013, 33(15): 78-85, 13.
[12] 王宏佳, 徐殿国, 杨明. 永磁同步电机改进无差拍电流预测控制[J]. 电工技术学报, 2011, 26(6): 39-45.
Wang Hongjia, Xu Dianguo, Yang Ming. Improved deadbeat predictive current control strategy of permanent magnet motor drives[J]. Transactions of China Electrotechnical Society, 2011, 26(6): 39-45.
[13] 康劲松, 李旭东, 王硕. 计及参数误差的永磁同步电机最优虚拟矢量预测电流控制[J]. 电工技术学报, 2018, 33(24): 5731-5740.
Kang Jinsong, Li Xudong, Wang Shuo. Optimal virtual vector predictive current control for permanent magnet synchronous motor considering parameter errors[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5731-5740.
[14] 贾成禹, 王旭东, 周凯. 基于线性变参数模型预测控制的内置式永磁同步电机转速控制器设计[J]. 电工技术学报, 2020, 35(22): 4666-4677.
Jia Chengyu, Wang Xudong, Zhou Kai. Design of interior permanent magnet synchronous motor speed controller based on linear parameter-varying model predictive control[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4666-4677.
[15] 尹忠刚, 白聪, 杜超, 等. 基于内模干扰观测器的永磁同步直线电机无差拍电流预测控制方法[J]. 电工技术学报, 2018, 33(24): 5741-5750.
Yin Zhonggang, Bai Cong, Du Chao, et al. Deadbeat predictive current control for permanent magnet linear synchronous motor based on internal model disturbance observer[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5741-5750.
[16] 易伯瑜, 康龙云, 冯自成, 等. 基于扰动观测器的永磁同步电机预测电流控制[J]. 电工技术学报, 2016, 31(18): 37-45.
Yi Boyu, Kang Longyun, Feng Zicheng, et al. Predictive current control for permanent magnet synchronous motor based on disturbance observer[J]. Transactions of China Electrotechnical Society, 2016, 31(18): 37-45.
[17] 朱利东, 王鑫, 朱熀秋. 基于NNBPF-EKF的内置式永磁同步电机死区补偿方法[J]. 中国电机工程学报, 2020, 40(15): 5011-5020.
Zhu Lidong, Wang Xin, Zhu Huangqiu. IPMSM dead time compensation method based on NNBPF-EKF[J]. Proceedings of the CSEE, 2020, 40(15): 5011-5020.
[18] 陈杰, 章新颖, 闫震宇, 等. 基于虚拟阻抗的逆变器死区补偿及谐波电流抑制分析[J]. 电工技术学报, 2021, 36(8): 1671-1680.
Chen Jie, Zhang Xinying, Yan Zhenyu, et al. Dead-time effect and background grid-voltage harmonic suppression methods for inverters with virtual impedance control[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1671-1680.
[19] 吴春, 齐蓉.PWM电压源逆变器非线性因素迭代学习补偿[J]. 中国电机工程学报, 2015, 35(3): 702-709.
Wu Chun, Qi Rong. An iterative-learning-based compensation for PWM VSI nonlinearities[J]. Proceedings of the CSEE, 2015, 35(3): 702-709.
[20] 李红梅, 候书寒, 姚宏洋. 基于纹波电流计算的面装式永磁同步电机驱动系统逆变器死区补偿[J]. 电工技术学报, 2017, 32(增刊2): 34-41.
Li Hongmei, Hou Shuhan, Yao Hongyang. The inverter dead-time compensation of surface mounted permanent magnet synchronous motor drive system based on ripple current calculation[J]. Transactions of China Electrotechnical Society, 2017, 32(S2): 34-41.
[21] Rovere L, Formentini A, Zanchetta P. FPGA implementation of a novel oversampling deadbeat controller for PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5): 3731-3741.
[22] 王宏佳, 杨明, 牛里, 等. 永磁交流伺服系统电流环带宽扩展研究[J]. 中国电机工程学报, 2010, 30(12): 56-62.
Wang Hongjia, Yang Ming, Niu Li, et al. Current loop bandwidth expansion for permanent magnet AC servo system[J]. Proceedings of the CSEE, 2010, 30(12): 56-62.
Predictive Current Control Strategy of Permanent Magnet Synchronous Motors with High Performance
Abstract High performance control system of permanent magnet synchronous motor (PMSM) requires high dynamic performance of current loop. Traditional PI control method has limited bandwidth and is prone to overshoot. The deadbeat control algorithm based on current prediction has a good dynamic performance. Therefore, an improved deadbeat control algorithm based on timing optimization is proposed. The current controller samples the current instruction piecewise, then calculates the compensation value of the voltage instruction, thus eliminating the one beat lagging of the original current instruction. Meanwhile, the deviation of voltage caused by non-ideal factors of power devices and time delay effect is analyzed, and a voltage reconstruction algorithm is introduced to reduce the influence of instruction error on current tracking precision. Simulation and experimental results showed that the improved current prediction algorithm can effectively improve both the dynamic performance and steady-state precision of the current loop.
keywords：Permanent magnet synchronous motor, current prediction, deadbeat control, timing optimization, voltage reconstruction
DOI:10.19595/j.cnki.1000-6753.tces.211054
中图分类号：TM341
国家重点研发计划资助项目（2019YFE0100200）。
收稿日期 2021-07-15
改稿日期 2021-09-27
章回炫 男，1994年生，博士研究生，研究方向为永磁同步电机驱动控制技术。E-mail：zhanghuixuan@mail.iee.ac.cn
范 涛 男，1981年生，研究员，博士生导师，研究方向为永磁电机分析与优化设计、先进电机控制、高性能电力电子装备电子系统设计开发。E-mail：fantao@mail.iee.ac.cn（通信作者）
（编辑 李冰）