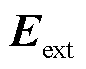和加入时间t时，可得到描述空间中任意一点
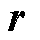处电场强度的表达式为摘要 印制电路板（PCB）射频线圈具有性能优良、占用空间少且制作工艺简单的特点，常用于无线电能传输以及单边核磁测井等领域。为分析线圈性能，需计算交流电阻、电感以及射频磁场分布。由于PCB线圈铜线厚度与外围尺寸跨度大，尤其在考虑金属涡流时，常规有限元软件与解析法在处理这种多尺度电磁场问题时的计算速度与精度无法达到要求。在0.5～15MHz频率范围内，该文采用部分元等效电路（PEEC）法计算金属涡流下PCB线圈（铜厚为35μm）的阻抗与射频磁场分布。建立平面矩形螺旋PCB线圈的PEEC模型；通过计算结果与实测结果对比，总结给出PEEC剖分参数选取方法；分析PEEC模型下线圈的磁场分布；最终实现金属涡流下PCB线圈的阻抗与射频磁场的准确且快速计算。该文工作可为应用于无线电能传输以及单边核磁测井等领域的PCB线圈分析提供参考。
关键词：部分元等效电路 PCB线圈 多尺度 交流电阻 涡流
平面印制电路板（Printed Circuit Boards, PCB）射频线圈采用印制电路板技术，占用空间少且质量稳定可靠，常应用于无线电能传输以及单边核磁测井等领域[1-6]。例如，用于核磁测井的PCB线圈的铜线厚度通常为几十μm，横截面宽度在mm级别，而整个线圈外围尺寸则能达到cm甚至m的级别。尤其当考虑金属涡流时，整个线圈模型是一个明显的多尺度电磁场问题。分析PCB线圈性能与设计线圈结构，首先需要准确且快速地计算其交流电阻、电感以及射频磁场分布。
高频下，PCB线圈铜线横截面的电流密度分布不均匀，影响PCB线圈电磁参数的因素主要包括趋肤效应、邻近效应以及金属的涡流效应。例如，在频率为8MHz下，趋肤效应使得铜线的趋肤深度仅为23.6μm，且频率越高，铜线由表及里的电流密度衰减越快，要准确且快速计算多尺度PCB线圈电磁参数十分困难[7-8]。
高频下PCB线圈电磁参数的计算方法主要有三种：①解析法[9-10]，目前只针对一些简单的线圈结构有解析解表达式，尤其针对涡流场的求解是所有电磁场解析求解中最困难的；②有限元法[6, 11-12]，在求解过程中，除了模拟目标区域之外，还需要对背景区域一起模拟，很大程度上降低了求解效率；③细丝法[13]，是一种忽略时间延迟效应，且由电阻和电感效应为主导的简化计算方法。高频下，由于平面线圈自身的电容效应，以及介质基片所带来的耦合电容等影响，导致细丝法计算电阻的误差越来越大。
部分元等效电路（Partial Element Equivalent Circuit, PEEC）法由于无需对背景空气域进行剖分，且能将电磁问题自然地解释为一个纯电路问题，便于分析局部元件的特性，已被证明非常适用于互连线[14]和天线[15]等电磁装置的分析。但是，目前PEEC法在分析矩形PCB线圈这种特定对象时，缺少系统的剖分策略，且剖分参数的选取主要依赖经验。同时，进一步考虑金属涡流的PEEC建模仍有待于研究。
本文基于PEEC法，在0.5～15MHz频率范围内，建立了矩形螺旋PCB线圈的PEEC模型，包括铜线、介质基片、引接线，重点分析并建立了线圈下方金属涡流的PEEC模型，并分析了各个PEEC剖分参数对计算阻抗的影响。通过分析总结给出了金属涡流下平面矩形螺旋PCB线圈PEEC剖分参数的通用选取方法，计算分析了涡流影响下的线圈射频磁场分布，最终实现了考虑金属涡流下PCB线圈阻抗和射频磁场分布的快速且准确的计算。
考虑外加激励电场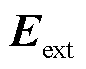和加入时间t时，可得到描述空间中任意一点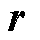处电场强度的表达式为
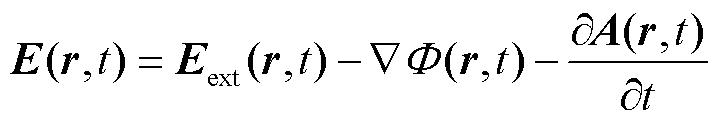（1）
式中，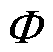
为标量电位；A为矢量磁位；且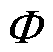和A分别是关于自由电荷密度
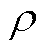和电流密度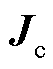
的积分函数。本文所研究的PCB线圈工作频率为0.5～15MHz，外围尺寸在cm级别的射频线圈为电小尺寸，可忽略场点与源点之间的时间延迟。
利用式（1）可推导PEEC模型的电阻、电感与电容模型[16]。图1为一电流密度
的导体PEEC剖分，黑色长方体代表PEEC剖分后的一个体单元，其等效串联电阻可根据欧姆定律给出。文献[17]给出了考虑体单元横截面尺寸下串联部分自感的计算公式。在计算两个体单元m和k之间的部分互感时，若其长度远大于截面的线尺寸，可将长方体轴向元素线近似为其几何中心线，即等效为线段m和线段k，平行体单元之间部分互感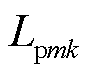
的计算模型如图2所示。此时[18]
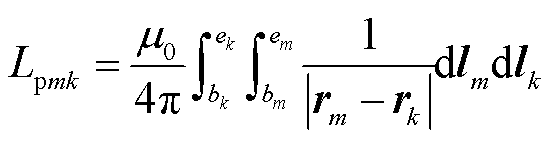（2）
式中，rk和rm对应m和k上的坐标点。线段m的起点和终点分别为bm和em，长度为lm；线段k的起点和终点分别为bk和ek，长度为lk。
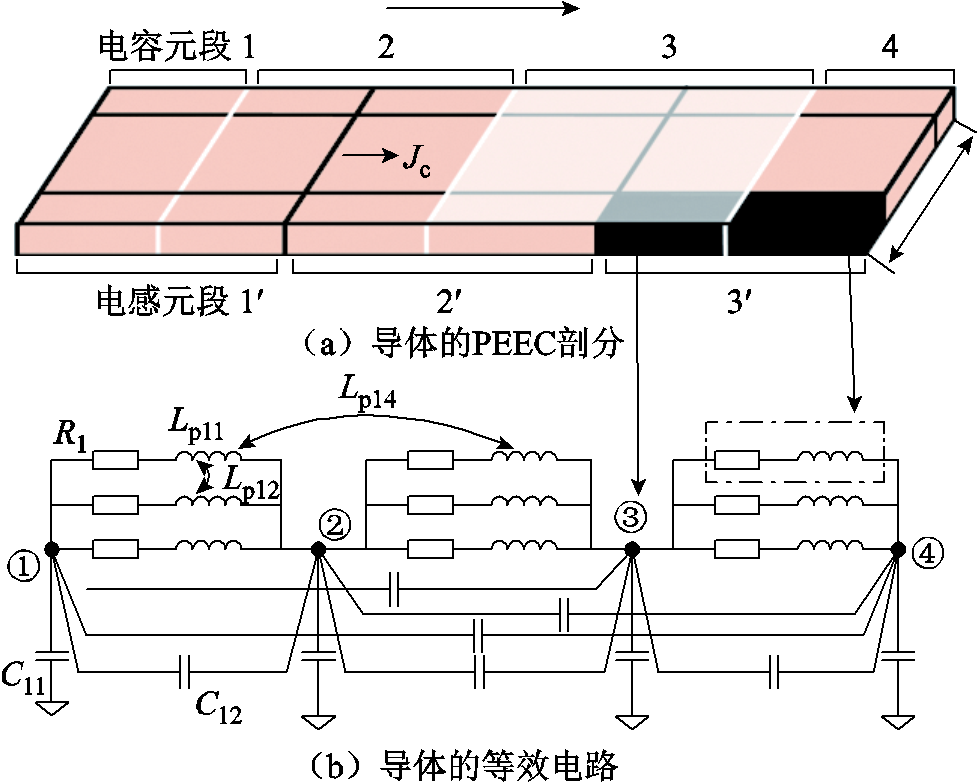
图1 导体的PEEC模型
Fig.1 PEEC model of conductor
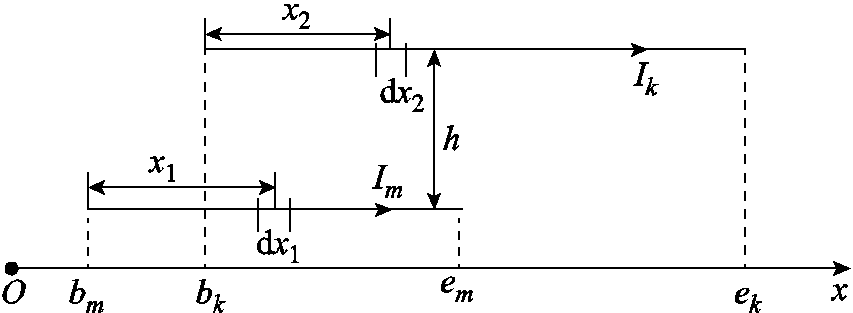
图2 平行体单元的部分互感计算模型
Fig.2 Partial mutual inductance calculation model of parallel volume elements
导体表面存在自由电荷，还需考虑自由电荷带来的电容效应。PEEC模型中，电容单元偏移半个电感单元长度。将导体单元表面剖分后，图1中白色矩形i表示电容单元，其表面积为Si。PEEC法中采用电位系数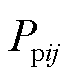
描述电容单元i和j之间的耦合关系[19]，电位系数只与电容单元的几何形状有关，且通过计算电位系数，即可反推得到电容单元间的部分电容。
PEEC建模是将电磁场问题转化为纯电路问题分析。导体剖分后，按电容单元中心为电位节点，相邻两电位节点之间为串联电阻电感单元的原则，可得到图1b所示电阻、电感与电容单元构成的等效电路。最后采用电路中的改进节点分析（Modified Nodal Analysis, MNA）法，即可求解得到导体等效阻抗。
平面矩形螺旋PCB线圈的几何结构如图3所示，采用PCB工艺，包括走线、基片以及引接线。其中矩形螺旋走线在x轴方向的内径为dx，在y轴方向的内径为dy，线宽为w，匝间距为p，线厚为t，匝数为N，电导率为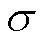
。本文研究的线圈铜线厚度t=35μm。在走线的两端各连接一段引接线，可用于线圈与外部电路的连接；基片的相对介电常数εr=3.5，厚度h=1.6mm。
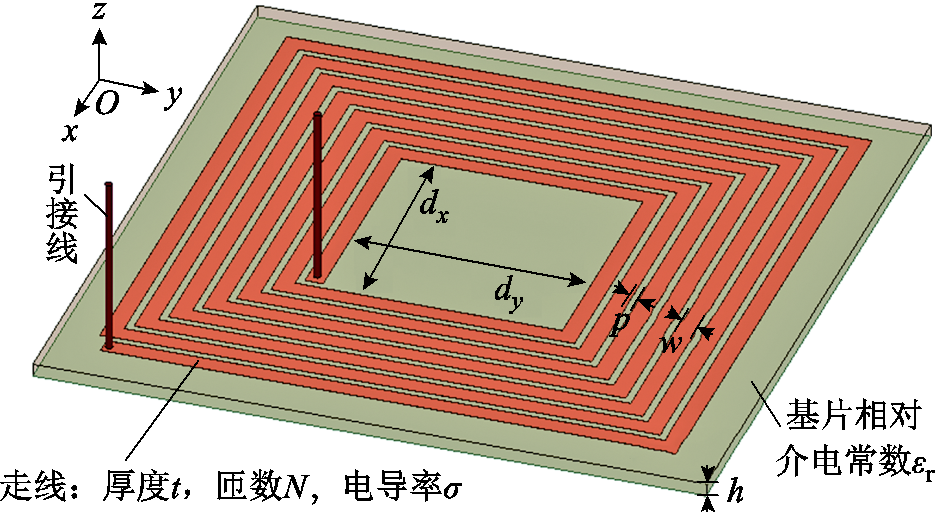
图3 矩形螺旋PCB线圈几何结构
Fig.3 Geometric structure of rectangular spiral PCB coil
2.2.1 直导线剖分策略
首先考虑铜线的电阻和电感效应。趋肤效应和邻近效应使得有效电流密度集中分布在铜线表面薄层。在铜线截面剖分时，需将最外层进行细密剖分。同时，由于截面中心处的电流密度差别不大，为节约计算资源，在截面中心处采用相对粗糙的剖分。对于图3中矩形线圈的一条边，设长度为l（电流密度方向），横截面宽度为w，厚度为t（l
w且lt），本文采用的铜线横截面体剖分策略如图4所示。
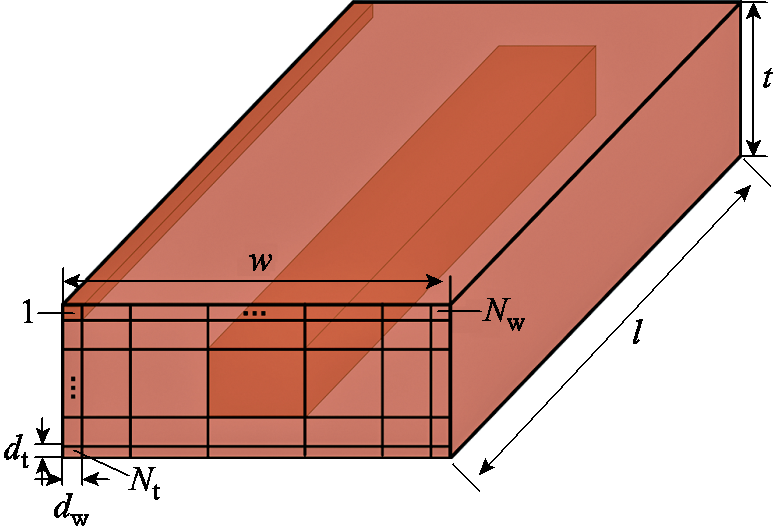
图4 铜线横截面的体剖分
Fig.4 Volume meshing of the cross section of copper wire
在满足精度的前提下，为尽量减少剖分单元数，剖分单元的宽度由表及里呈等比数列关系递增，设等比数列的公比即趋肤因子为β，且在整个宽度方向采用左右对称剖分。铜线厚度方向可按照同样的剖分策略。
考虑铜线表面的电容效应时，由于线宽在mm级别，而厚度只有35μm，可采用无限薄的矩形平板进行表面电容单元等效，避免对铜线侧面和下底面剖分[20]。对铜线表面的电容单元剖分策略如图5所示，首先将铜线的每一边分割为两段大电容单元，拐角ni(i=1,2,…)代表电容单元的电位节点。为体现铜线表面自由电荷分布的不均匀性，需对大电容单元进一步剖分。对每一个大电容单元，采用降低最外层单元宽度，且内层单元宽度均分的剖分方案。设内层小电容单元的宽度为win，外层小单元和内层小单元宽度之比为k，且每边剖分为M个小电容单元。通过对一边长为1m的无限薄正方形平板自电容计算得知，当k=0.1，即最外层单元宽度为内层单元宽度的0.1倍，M=4，即每边分为4段小电容单元时，电容计算值即趋于稳定。
2.2.2 拐角剖分策略
平面矩形线圈拐角剖分策略如图6所示，电流密度集中分布在矩形PCB线圈拐角的相对内侧。为体现拐角电流密度分布的差异性，本文对平面矩形螺旋线圈拐角剖分采用一维非重叠剖分。
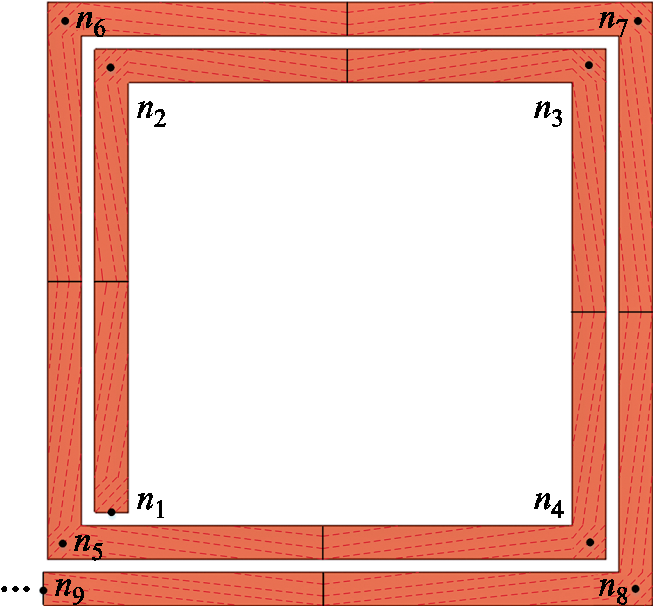
图5 铜线表面电容单元剖分
Fig.5 Capacitance meshing of copper wire surface
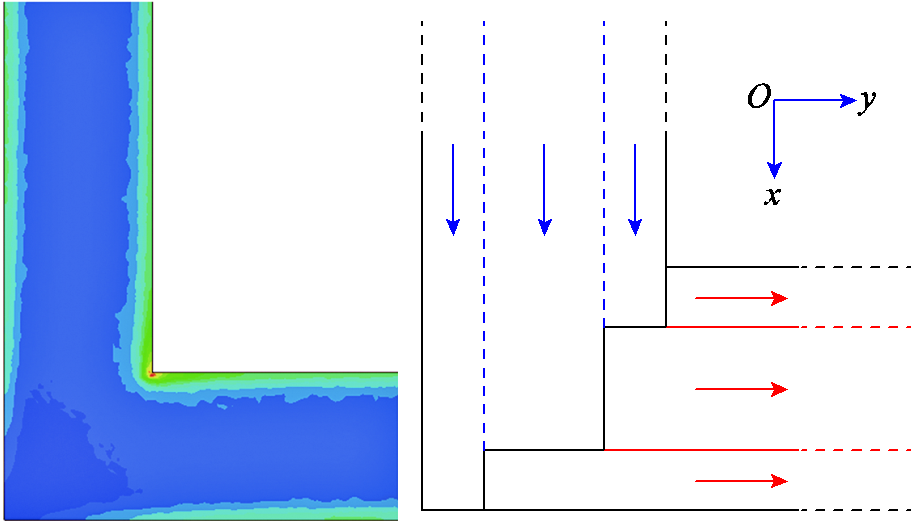
图6 平面矩形线圈拐角剖分
Fig.6 Meshing of the corner of planar rectangular coil
2.2.3 引接线剖分策略
PCB线圈需通过引接线连接至外部电路，引接线采用横截面为圆形的漆包线，长度为l1，横截面半径为Rs。引接线剖分策略如图7所示。
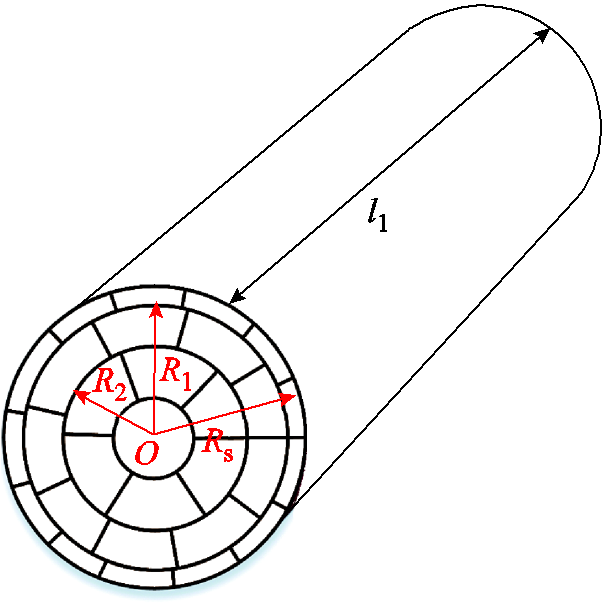
图7 引接线剖分
Fig.7 Meshing of lead wire
引接线表面的电流密度为Js，设电流密度从表面向圆心按指数规律衰减，则引接线横截面上半径为Rl处的电流密度表达式为
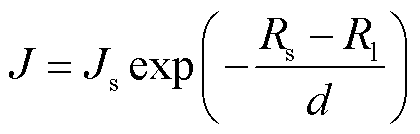（3）
式中，d为趋肤深度。在径向方向上，将横截面分为llayer层同心圆环，且由表及里的每层圆环电流密度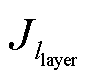
按10%衰减，并设总的剖分层数为10，第十层再往里的电流密度约为表面电流密度的0.1%，再进行更精细的剖分已没有意义[21]。每层圆环的外半径为
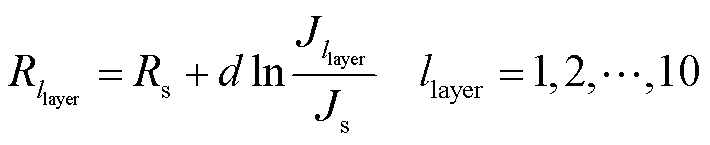（4）
在引接线周向方向上，按照经验公式对每一层圆环在周向方向上进行剖分[22]，为在保证计算精度的前提下减少剖分单元数，每层圆环的剖分扇形数均少于20个。每层圆环的扇形单元剖分数表达式为
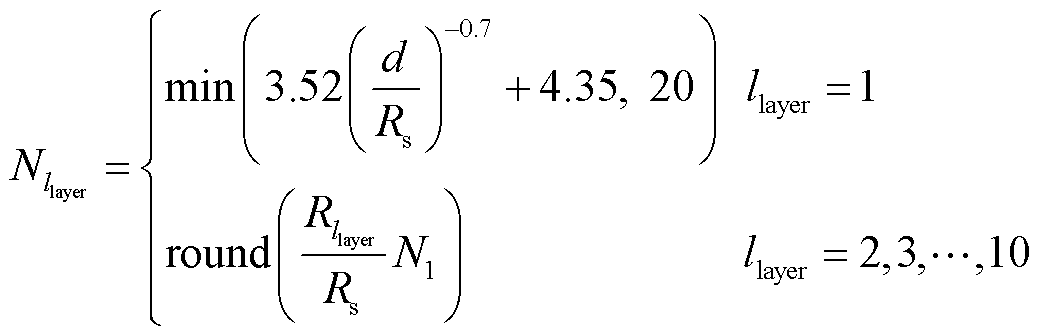（5）
式中，round(x)表示对x四舍五入取整。
2.2.4 基片剖分
为分析全面，还需考虑铜线下方FR4基片的电容效应。介质基片建模如图8所示。对于图8a所示的介质基片模型，长为ldi，宽为Wdi，厚度为Tdi，在对介质基片的表面单元剖分时，只考虑上下表面的影响，将介质基片的上下两表面视为电容单元，且定义电位节点之间的附加电容C+为[23]
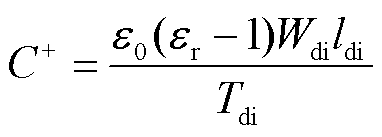（6）
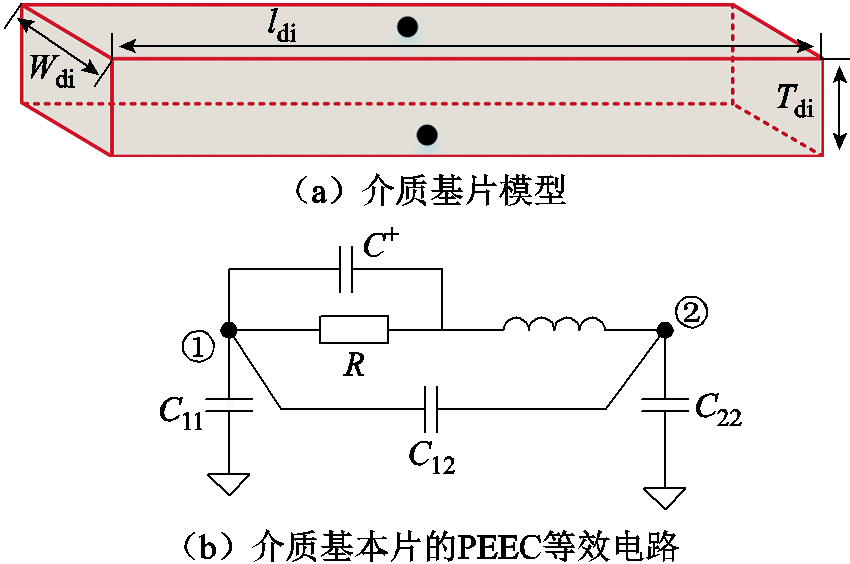
图 8 介质基片建模
Fig.8 Dielectric substrate modeling
对比导体的等效电路，介质的等效电路需要在导体的基础上增加附加电容，介质基片的PEEC等效电路如图8b所示。
计算时忽略介质基片的功率损耗和极化电流的影响，即节点1和节点2只通过束缚电荷为源的表面等效部分电容关联[19]，只考虑基片上表面和下表面的电容效应，并采用与线圈电容单元对应的映射剖分方法[16]。例如，对于基片的上表面剖分，首先将线圈正对的基片上表面分为线圈铜线正下方区域和线圈匝间空隙正下方区域，对应基片电容单元的宽度分别为铜线线宽和匝间距。对于基片表面其余区域的电容单元的宽度均设置为铜线匝间距宽度。令拐角的电位节点为电容单元的中心，介质基片的剖分策略以及基片表面与铜线表面之间的耦合电容C如图9所示。
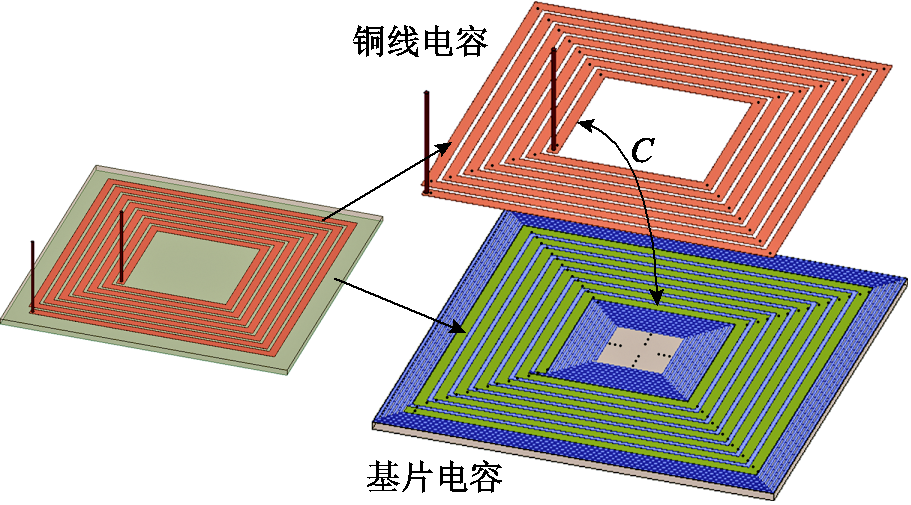
图9 PCB线圈的介质基片剖分策略
Fig.9 Dielectric substrate meshing strategy of PCB coil
综合考虑线圈铜线、引接线与介质基片的PEEC模型后，单匝PCB线圈的等效电路如图10所示。为了清楚起见，图10中只画出了部分电感和电容。
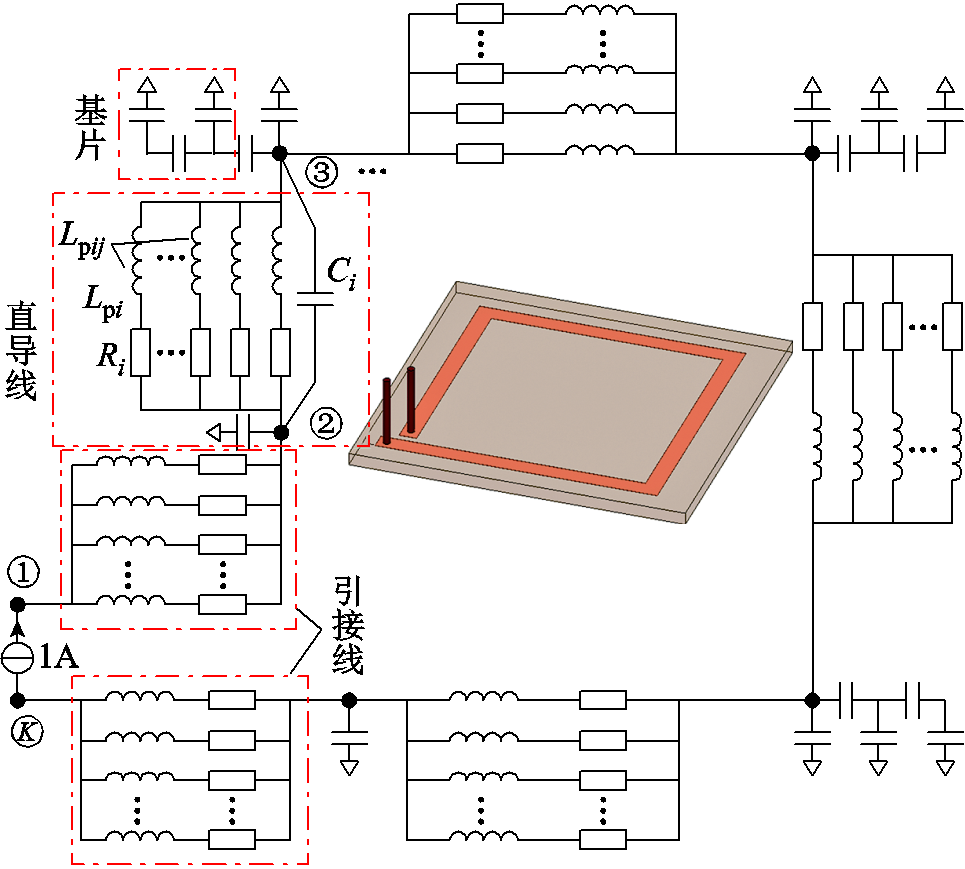
图10 单匝线圈完整的等效电路
Fig.10 Complete equivalent circuit of single-turn coil
在图10所示等效电路的引接线节点1和节点K两端施加单位电流，并采用式（7）的MNA方程对等效电路求解。
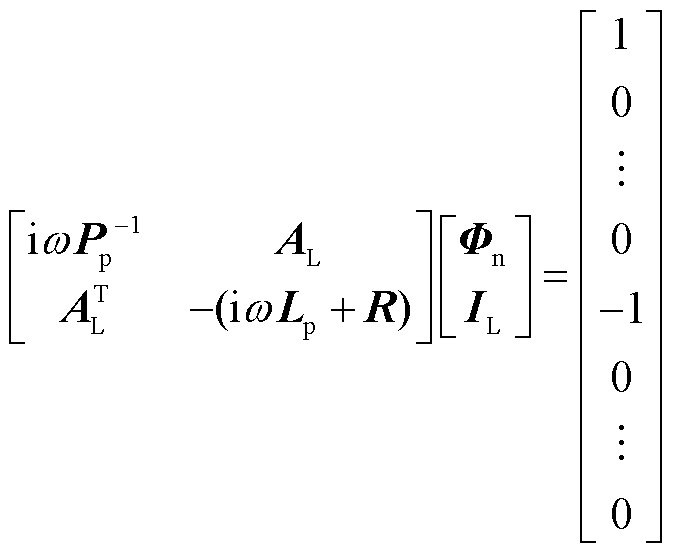（7）
式中，等式右端向量中，第一个元素为1，第N个元素为-1，其余元素全为0；ω为电路工作的角频率；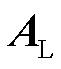
为支路的KCL矩阵；
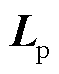为部分电感矩阵；
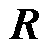为等效电阻矩阵；
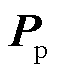为电位系数矩阵；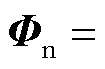
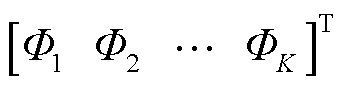，其中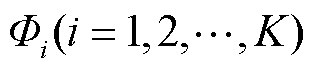
为节点i的电位；
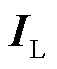为各支路电流。等效电阻R和等效电抗X为
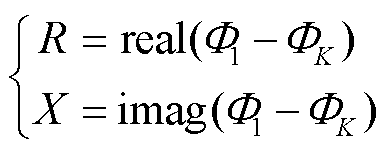（8）
式中，real表示取实部；imag表示取虚部。
本文在0.5～15MHz频率范围内采用PEEC法计算平面矩形螺旋PCB线圈的阻抗。为分析铜线横截面的电流密度分布，需在电流密度大且变化剧烈的表面加密剖分，同时，为保证计算速度，在电流密度小且变化缓慢的截面中心，采用较为粗糙的剖分策略。因此，需要确定最优的PEEC剖分参数。
对于最外层的剖分单元宽度，一般取横截面宽度方向上最外层剖分单元宽度dw与厚度方向上最外层剖分单元宽度dt相同。需要确定的剖分参数有：①最外层单元宽度dw（dw=dt）；②趋肤因子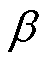
。本文通过与实测对比来确定剖分参数。加工PCB线圈1，如图11所示。铜线的电导率取为5.7×107S/m，FR4介质基片的厚度为1.6mm，线圈两端引接线采用线径为0.5mm的漆包线，长度均为25mm，矩形线圈1的剩余参数见表1。首先在8MHz下，利用阻抗分析仪，测得矩形线圈1的电阻为668.63mΩ，电抗为83.17Ω。
图11 矩形线圈1
Fig.11 Rectangular coil 1
表1 矩形线圈1结构参数
Tab.1 Structural parameters of the rectangular coil 1
参数数值 x方向内径dx/mm29 y方向内径dy/mm29 线宽w/mm1.5 线厚t/mm0.035 匝间距p/mm2 匝数N5
首先分析最外层单元宽度dw对线圈阻抗计算结果的影响。此时，将趋肤因子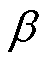固定为2。在8MHz下，线圈的趋肤深度d=23.5μm。为体现趋肤效应和邻近效应，以趋肤深度为参考量，设置最外层剖分单元宽度dw的扫描范围为0.1d～d（即2.35～23.5μm），得到不同dw下线圈1的电阻和电抗值，如图12所示。
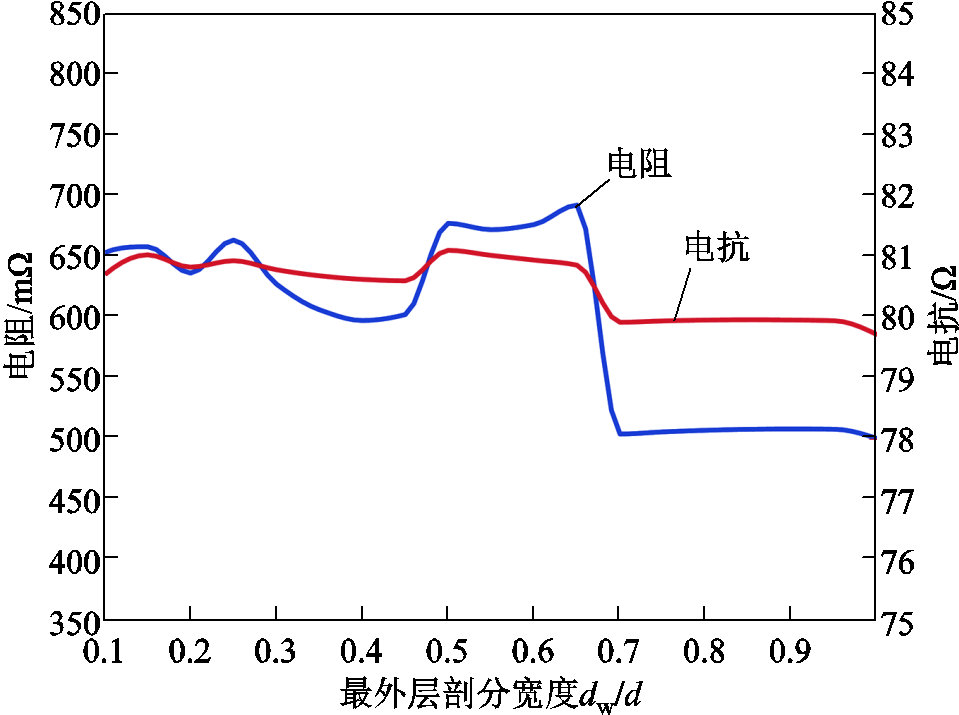
图12 最外层剖分宽度dw对应阻抗计算值
Fig.12 Calculated impedance corresponding to the width dw of the outermost layer
最外层单元的剖分宽度dw从0.1d到d变化，电抗从79.7Ω到81.1Ω，误差范围从4.17%到2.5%，说明PEEC剖分时，当dw在趋肤深度范围内，dw的变化对电抗计算结果的影响很小。
当dw＞0.3d时，计算电阻值变化很大。当dw在0.1d～0.3d之间时，电阻计算值的变化稳定，且在实测值650mΩ附近，这说明dw在此范围内时，选择合适的趋肤因子β可使电阻计算值接近实测值。本文考虑的频率范围为0.5～15MHz，在15MHz下，趋肤深度为17.2μm，因此，剖分计算时，将最外层剖分宽度设置为dw＝4μm，即满足所计算频率范围内dw小于0.3倍趋肤深度的要求。
固定dw＝4μm，设置趋肤因子β的扫描范围为1.1～4，得到不同β下线圈1的电阻和电抗值，如图13所示。当β从4减小到1.1的过程中，计算电抗值在80～82Ω之间，且与实测电抗值的偏差始终小于4%，这是一个可接受的误差范围。计算电阻值受β的影响较大，随着β的降低，整体呈现出减小的趋势，且当β在2.2～2.5范围内，电阻计算值在实测值668.63mΩ附近。总体而言，计算电抗值受趋肤因子β的影响较小，而计算电阻值受β的影响较大。
根据图13，在0.5～15MHz下，取dw＝4μm，β＝2.4，对应线圈横截面宽度方向剖分单元数为13，最中心单元的宽度为413μm，厚度方向的剖分层数为5层。画出PEEC法计算得到的矩形PCB线圈1的阻抗值，并与实测值对比，如图14所示。随着频率的增加，计算阻抗与实测值保持了相同的变化趋势，其中，计算电抗误差始终小于2%，计算电阻误差小于4%。
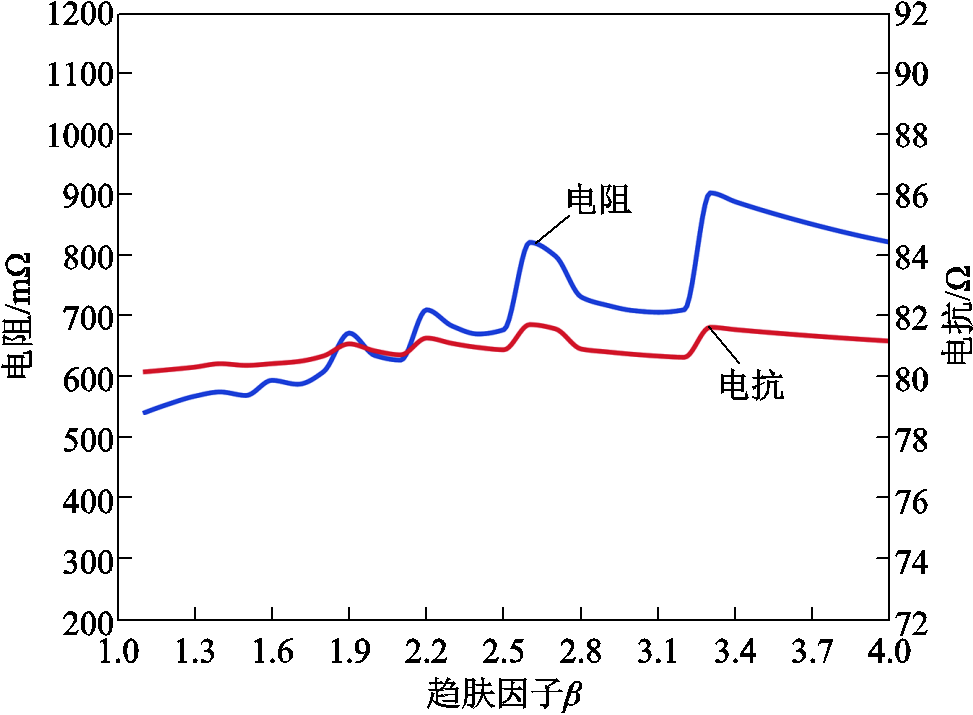
图13 趋肤因子β对应阻抗计算值
Fig.13 Calculated impedance corresponding to the skin factor β
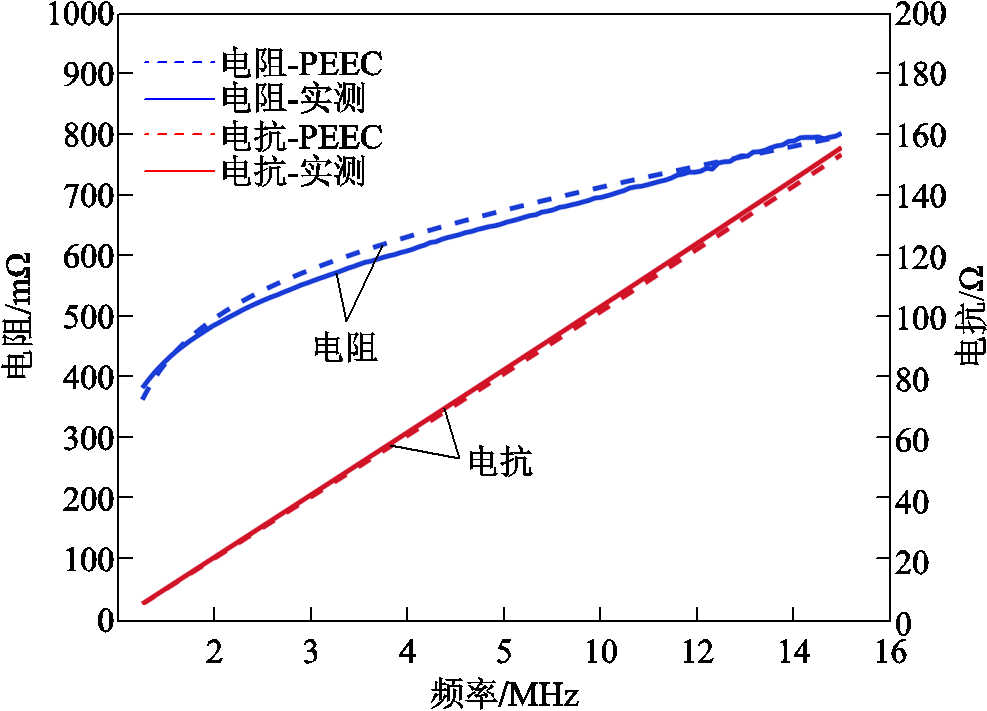
图14 矩形线圈1的PEEC计算阻抗与实测对比（dw=4μm，β=2.4）
Fig.14 Impedance of rectangular coil 1 acquired by PEEC and measurement (dw=4μm，β=2.4)
在采用上述剖分策略及剖分参数下，图15显示了PCB线圈相邻两直导线横截面的相对电流密度分布。可以明显看出，趋肤效应和邻近效应使得有效电流密度集中分布于线圈表面。
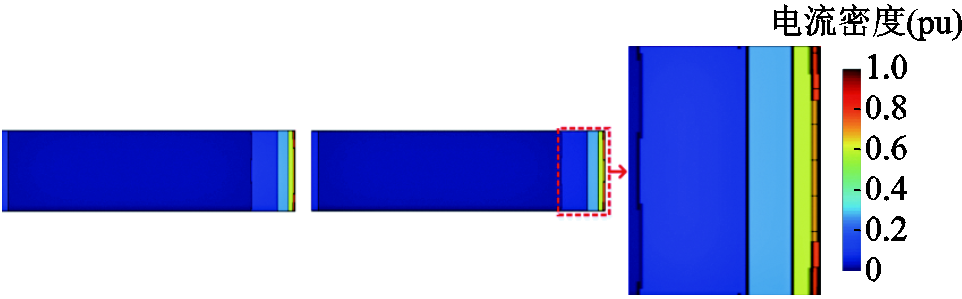
图15 导线横截面电流密度分布
Fig.15 Current density distribution of conductor cross section
在线圈1剖分时，dw＝4μm，β＝2.4，对应剖分后小长方体单元的最大宽度为413μm。由于矩形线圈1的内径为29mm，可以得出直导线剖分后的小长方体单元的轴长与横截面宽度构成的最小轴宽比约为70.1。在0.5～15MHz频率范围内，为给出平面矩形螺旋PCB线圈的一般性剖分参数选取原则，计算不同尺寸线圈的阻抗值，并与阻抗分析仪实测对比分析。结果表明，固定最外层单元宽度dw＝4μm，同时为保证部分互感计算时长方体单元到线段模型的有效性，趋肤因子β的选取应考虑线圈内径，并使得剖分小长方体单元的最小轴宽比大于90即可。最终不同尺寸的矩形螺旋PCB线圈计算电阻误差保持在20%以内，计算电抗误差保持在2%以内。考虑到不同线圈铜线本身的电导率存在偏差，计算结果在可接受范围内。
本文采用的PEEC法完整地考虑了矩形PCB线圈的电阻、电感和电容效应，为说明完整的PEEC法（PEEC/R+L+C）与只考虑电阻和电感的PEEC法（PEEC/R+L）在计算精度上的差异，图16给出了阻抗分析仪实测、PEEC/R+L+C和PEEC/R+L得到的矩形PCB线圈1的阻抗对比。考虑电容效应虽对电抗影响较小，但是能明显提高电阻值的计算精度，且随着频率的增加，电容效应越明显。
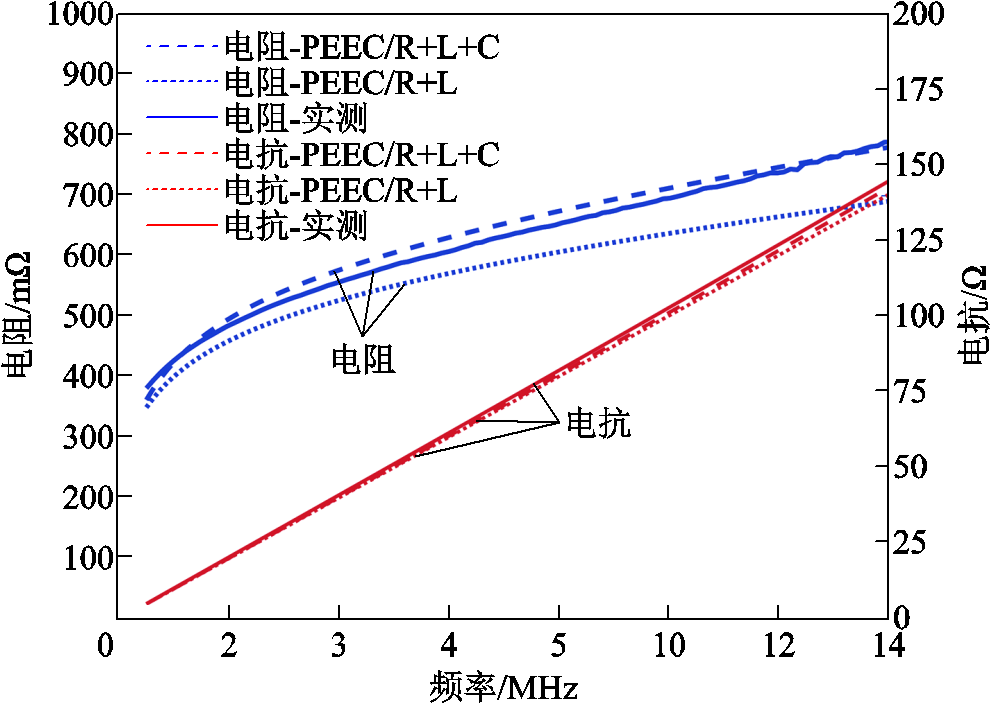
图16 不同方式得到的矩形线圈1阻抗对比
Fig.16 Impedance comparison of rectangular coil 1 acquired by different ways
在计算时间方面，在同一台个人计算机上（16G内存，3.50GHz的四核AMD Ryzen 3 2200G处理器），在单一频点下计算线圈1的阻抗，在达到相同计算精度的前提下（计算阻抗相对实测的误差＜5%），本文PEEC/R+L+C法使用Matlab语言与基于有限元的商用软件HFSS的计算效率对比见表2，可以看出，PEEC法极大地提高了PCB线圈的计算效率。
表2 PEEC法与有限元法计算效率对比
Tab.2 Comparison of calculation efficiency between PEEC and finite element method
效率参数PEEC法有限元法 剖分单元数铜线1 506653 737 介质基片288112 972 空气域0260 990 总计1 7941 027 699 计算时间/s1.922 160
核磁测井中的射频线圈周围存在金属，金属中会产生感应涡流。由于涡流具有热效应和去磁效应，会影响整个线圈系统的阻抗和目标区域射频磁场的大小和分布。在考虑涡流的影响下准确计算线圈的阻抗至关重要。不失一般性，在矩形PCB线圈1正下方1cm处放置一厚度为2mm的金属铝板，且铝板能完全覆盖矩形线圈铜线的正下方区域，如图17所示。PCB线圈与铝板之间用载玻片隔开，铝板参数见表3。
图17 铝板位于矩形线圈1下方
Fig.17 An aluminum plate under rectangular coil 1
表3 铝板参数
Tab.3 Parameters of aluminum plate
参数数值 长/mm67 宽/mm67 厚度/mm2 电导率/(S/m)34.2×106
在8MHz下，利用阻抗分析仪实测，在铝板存在的情况下，由于铝板中感应出金属涡流，涡流的热效应导致整个线圈两端等效电阻增加，即电阻从641mΩ增加到699mΩ；涡流的去磁效应导致线圈的磁链减小，从而引起电抗的降低，即线圈的电抗从83.22Ω降低到70.54Ω。线圈阻抗参数直接关系到线圈的性能，因此有必要对金属存在下的PCB线圈阻抗变化进行分析。
由于线圈1具有平面矩形螺旋的特点，在下方金属铝板感应的涡流可以看作线圈中的等效电感与铝板中的等效电感之间相互耦合而成的，因此，铝板中感应涡流的分布应具有类似线圈中电流沿矩形螺旋流向的特点。为此，铝板水平方向的剖分，可以看作是等宽的同轴孤立矩形涡流线圈，且铝板中等效孤立矩形线圈的外围长宽比与矩形PCB铜线的外围长宽比相同，如图18所示（图中未画出基片），其中每匝等效涡流线圈的宽度均为Pe。金属板竖直方向则同样按照等比数列增长的剖分方式，设置铝板的剖分总深度为趋肤深度d的n倍，深度方向第一层的高度dt为4μm，同时，再往下的每一层按照公比（趋肤因子）为β1的等比数列增长。
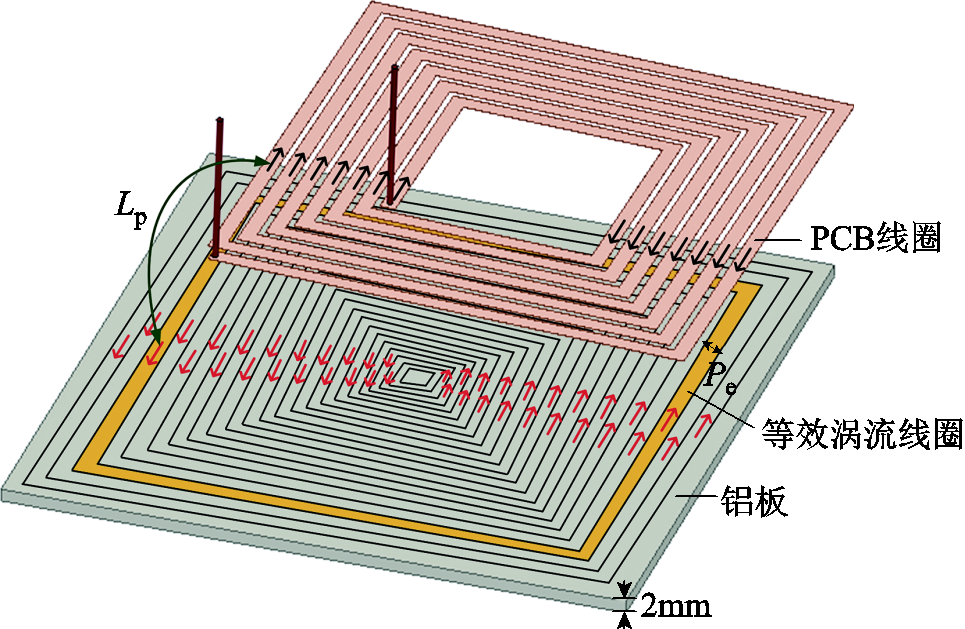
图18 铝板水平方向剖分
Fig.18 Horizontal meshing of aluminum plate
按照铜线剖分参数同样的寻优方法，最终得到铝板的剖分参数见表4。
表4 铝板剖分参数
Tab.4 Meshing parameters of aluminum plate
参数数值 Pe/μm240 β13.6 n3 dt/μm4
根据表4的剖分参数，可以画出矩形线圈1下方存在铝板时，PEEC计算阻抗与阻抗分析仪实测阻抗随频率变化规律，如图19所示，计算阻抗与实测基本吻合。由于本文主要考虑金属铝板与PCB线圈之间的耦合电感效应，若要使得计算结果更加精确，应更进一步考虑铝板的表面电容效应，此时按照2.2节中基片表面电容单元的剖分方法对铝板表面的电容单元进行剖分即可。
当在射频线圈两端施加激励时，线圈会在目标区域产生射频磁场，通过PEEC等效，将线圈剖分为若干等效电阻和等效电感串联的传导电流支路，通过MNA法求得每条支路的电流幅值，再利用毕奥-萨伐尔定律即可求解得到目标区域的射频磁场分布。
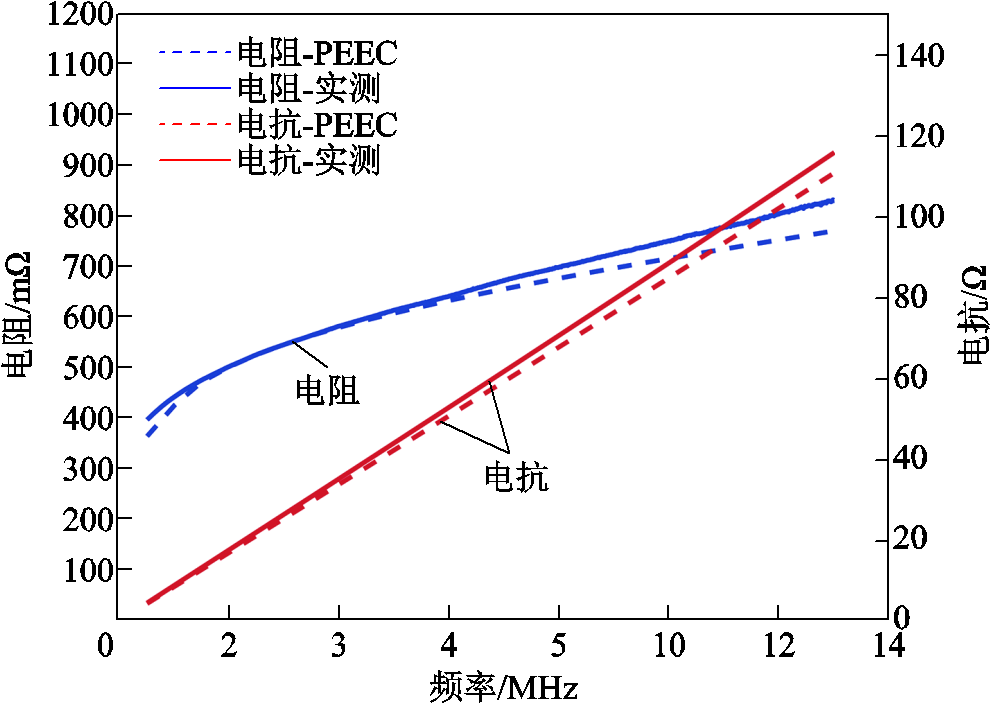
图19 铝板存在下线圈1阻抗计算值与实测对比
Fig.19 Comparison of calculated and measured impedance of coil 1 in the presence of aluminum plate
以矩形线圈1为例，当在线圈端口注入频率为8MHz的单位电流时，对比得到了在线圈正下方有无铝板时，线圈上方1mm处目标层面的射频磁场分布，如图20所示。PCB线圈下方存在铝板时，目标层面上的射频磁场与没有铝板时的射频磁场等值线分布形状基本一致，但是由于金属铝板感应涡流的去磁效应，使得目标层面射频磁场整体强度明显降低。在无线电能传输和单边核磁测井传感器的PCB线圈射频磁场分析中，必须考虑金属涡流的影响。
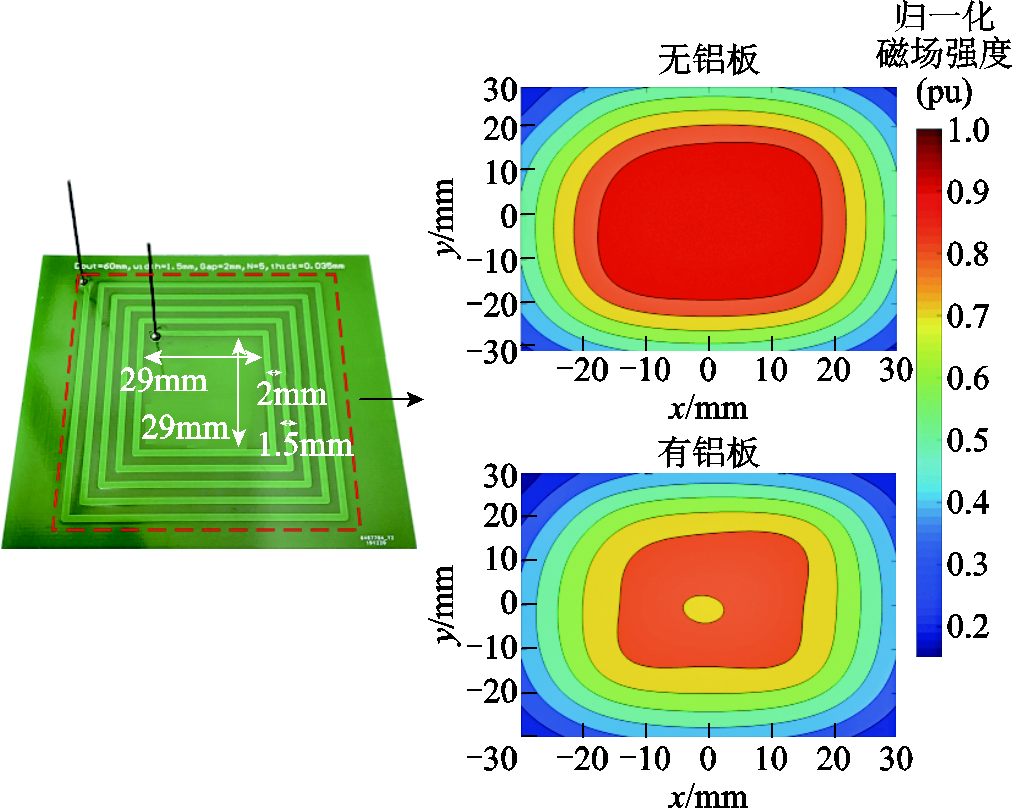
图20 目标层面上射频磁场强度归一化分布
Fig.20 Normalized distribution of RF magnetic field intensity on target slice
本文采用PEEC法对考虑金属涡流的PCB线圈进行电磁场求解，确定了适合0.5～15MHz频率范围内平面矩形螺旋PCB线圈以及金属板的PEEC模型及剖分参数，并提出了以剖分体单元的轴长与横截面宽度之比大于90作为趋肤因子取值上限，从而建立了不同尺寸的平面矩形螺旋PCB线圈PEEC剖分参数选取方法。本文建立的PCB线圈PEEC模型综合考虑了电阻、电感和电容效应，实现了PCB线圈阻抗及射频场分布的准确且快速求解。可进一步用于无线电能传输以及单边核磁测井中的PCB线圈分析，同时对更高频下的PCB线圈建模分析同样具有借鉴意义。
参考文献
[1] 卿晓东, 苏玉刚. 电场耦合无线电能传输技术综述[J]. 电工技术学报, 2021, 36(17): 3649-3663.
Qing Xiaodong, Su Yugang. An overview of electric-filed coupling wireless power transfer technology[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3649-3663.
[2] Xu Xianneng, Guo Pan, Lu Ming, et al. Optimized portable unilateral magnetic resonance sensor for assessing the aging status of silicon rubber insulators[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-11.
[3] 肖立志. 井下极端环境核磁共振科学仪器[M]. 北京: 科学出版社, 2016.
[4] 罗成鑫, 丘东元, 张波, 等. 多负载无线电能传输系统[J]. 电工技术学报, 2020, 35(12): 2499-2516.
Luo Chengxin, Qiu Dongyuan, Zhang Bo, et al. Wireless power transfer system for multiple loads[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2499-2516.
[5] 薛明, 杨庆新, 章鹏程, 等. 无线电能传输技术应用研究现状与关键问题[J]. 电工技术学报, 2021, 36(8): 1547-1568.
Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.
[6] 肖思宇, 马殿光, 张汉花, 等. 耦合谐振式无线电能传输系统的线圈优化[J]. 电工技术学报, 2015, 30(增刊1): 221-225.
Xiao Siyu, Ma Dianguang, Zhang Hanhua, et al. The coil model of coupled magnetic resonance wireless power transmission system[J]. Transactions of China Electrotechnical Society, 2015, 30(S1): 221-225.
[7] 陈垣, 张波, 谢帆, 等. 电力电子化电力系统多时间尺度建模与算法相关性研究进展[J]. 电力系统自动化, 2021, 45(15): 172-183.
Chen Yuan, Zhang Bo, Xie Fan, et al. Research progress of interrelationship between multi-time-scale modeling and algorithm of power-electronized power system[J]. Automation of Electric Power Systems, 2021, 45(15): 172-183.
[8] 曾非同, 关向雨, 黄以政, 等. 基于多尺度多物理场的油浸式变压器流动-传热数值研究[J]. 电工技术学报, 2020, 35(16): 3436-3444.
Zeng Feitong, Guan Xiangyu, Huang Yizheng, et al. Numerical study on flow-heat transfer of oil-immersed transformer based on multiple-scale and multiple-physical fields[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3436-3444.
[9] 雷银照. 关于电磁场解析方法的一些认识[J]. 电工技术学报, 2016, 31(19): 11-25.
Lei Yinzhao. Reviews of analytical methods for electromagnetic fields[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 11-25.
[10] 吴晓鹏. 车用表贴式永磁同步电机全域损耗高效计算方法研究[D]. 北京: 北京理工大学, 2016.
[11] Acero J, Hernandez P J, Burdio J M, et al. Simple resistance calculation in litz-wire planar windings for induction cooking appliances[J]. IEEE Transactions on Magnetics, 2005, 41(4): 1280-1288.
[12] 吴嘉敏. 土壤水分的磁共振测量方法基础研究[D]. 重庆: 重庆大学, 2019.
[13] Kim D H, Park Y J. Calculation of the inductance and AC resistance of planar rectangular coils[J]. Electronics Letters, 2016, 52(15): 1321-1323.
[14] Romano D, Kovačević-Badstübner I, Parise M, et al. Rigorous dc solution of partial element equivalent circuit models including conductive, dielectric, and magnetic materials[J]. IEEE Transactions on Electromagnetic Compatibility, 2020, 62(3): 870-879.
[15] Baumgartner P, Bauernfeind T, Bíró O, et al. Multi-objective optimization of Yagi-Uda antenna applying enhanced firefly algorithm with adaptive cost function[J]. IEEE Transactions on Magnetics, 2018, 54(3): 1-4.
[16] Ruehli A E, Antonini G, Jiang Lijun. Circuit oriented electromagnetic modeling using the PEEC techniques[M]. Hoboken: Wiley, 2017.
[17] (苏)卡兰塔罗夫, (苏)采依特林. 电感计算手册[M].陈汤铭, 刘保安, 罗应立, 等译. 北京: 机械工业出版社, 1992.
[18] 高飞, 陈维江, 李国富, 等. 基于完备集合思想的多导体部分电感计算方法[J]. 中国电机工程学报, 2011, 31(34): 127-134.
Gao Fei, Chen Weijiang, Li Guofu, et al. Calculating method of multi-conductor partial inductance based on complete set[J]. Proceedings of the CSEE, 2011, 31(34): 127-134.
[19] 钟玉林, 咸哲龙, 孙旭东, 等. 计及部分电容的接地回路高频电路模型[J]. 中国电机工程学报, 2005, 25(17): 37-41, 149.
Zhong Yulin, Xian Zhelong, Sun Xudong, et al. HF circuit model of conducted EMI of ground net based on PEEC[J]. Proceedings of the CSEE, 2005, 25(17): 37-41, 149.
[20] Scholz P, Ackermann W, Weiland T. PEEC antenna modeling of rectangular spiral inductors for RFID systems[J]. COMPEL-the International journal for computation and mathematics in electrical and electronic engineering, 2010, 29(6): 1453-1463.
[21] Lyu Jiahua, Chen Hongcai, Zhang Yang, et al. Fast simulation of Litz wire using multilevel PEEC method[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 12612-12616.
[22] Chen Hongcai, Du Yaping. Proximity effect modelling for cables of finite length using the hybrid partial element equivalent circuit and artificial neural network method[J]. IET Generation, Transmission & Distribution, 2018, 12(16): 3876-3882.
[23] He Junping, Tao Sili, Wu Huazhao. A PEEC-based concise broadband physical circuit modeling method with parameter extraction for PCB inductive components[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 10852-10862.
Research on the Partial Element Equivalent Circuit of Radio Frequency Coil on the Printed Circuit Board
Abstract PCB coils have the features of excellent performance, less space and easy manufacture artwork, and they are often used in fields of wireless power transmission and unilateral nuclear magnetic logging. In order to analyze the performance of PCB coil, it is necessary to calculate AC resistance, inductance and radio frequency magnetic field distribution. Due to the large span of copper wire thickness and outer dimensions, the calculation speed and accuracy of conventional finite element software and analytical methods cannot meet requirements, particularly when considering the metal eddy currents. In the frequency range of 0.5～15MHz, this paper adopted the partial element equivalent circuit (PEEC) method to calculate the impedance and radio frequency magnetic field distribution of PCB coil (copper thickness of 35μm) under metal eddy current. The PEEC model of the planar rectangular spiral PCB coil was established, the method for selecting the PEEC meshing parameters was summarized by making a comparison between calculation and the measurement results and the magnetic field distribution of the coil under PEEC model was analyzed. Finally, the accurate and fast calculation of the impedance and the radio frequency magnetic field of PCB coil under metal eddy current was realized. The work in this paper can provide references for PCB coil analysis in the fields of wireless power transmission and unilateral nuclear magnetic logging.
keywords：Partial element equivalent circuit, printed circuit board (PCB) coil, multiscale, AC resistance, eddy current
DOI:10.19595/j.cnki.1000-6753.tces.211013
中图分类号：TM13；TH89
国家自然科学基金资助项目（52077023）。
收稿日期 2021-07-04
改稿日期 2021-10-18
徐显能 男，1994年生，博士研究生，研究方向为电磁场数值计算。E-mail：xuxianneng@cqu.edu.cn
徐 征 男，1980年生，博士，教授，研究方向为电磁场数值计算。E-mail：xuzheng@cqu.edu.cn（通信作者）
（编辑 李冰）