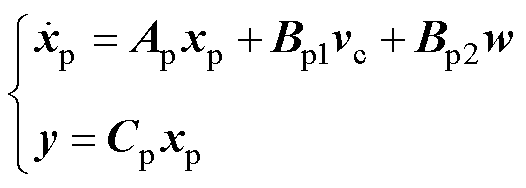（1）
采用复状态空间变量xp=[iLdq uCdq]T=[iLd+jiLq uCd+juCq]T为dq轴坐标系下的电感电流和电容电压；w=iwdq=iwd+jiwq为负载电流扰动；vc为逆变器桥臂中点电压矢量，并定义其为功率控制输入，与后文中提出的信号控制输入相区分。定义a1=1/L，a2=1/C，由基尔霍夫电压和电流定律可得到状态空间模型中的矩阵为
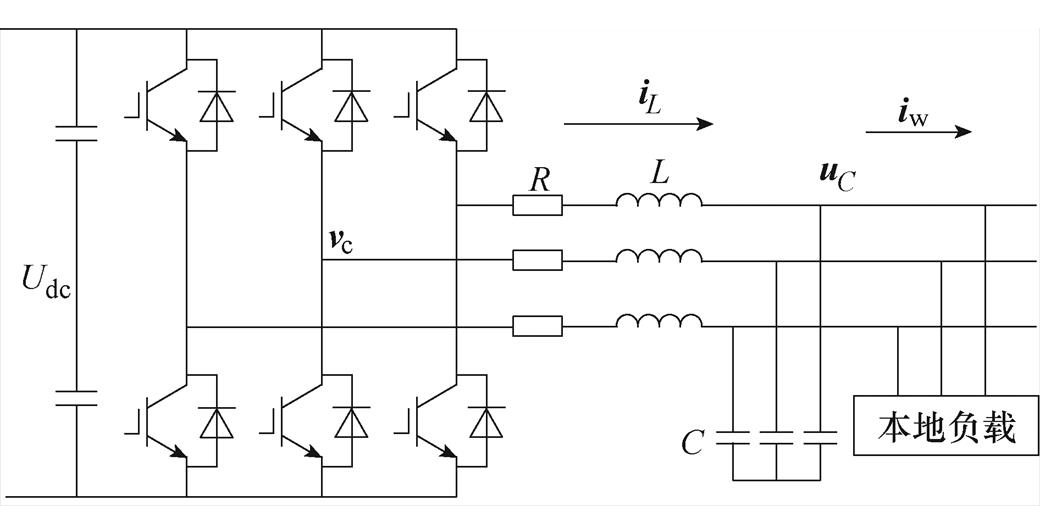
图1 三相逆变器拓扑
Fig.1 Topology of three-phase inverter
摘要 针对三相逆变器控制，该文提出一种基于多重谐振控制器的参考值前馈自适应控制。首先，基于复变量建立状态空间模型，并设计状态反馈控制，作为功率控制输入，用以改善系统动态响应。同时，设计参考值动态前馈控制，定义动态前馈增益为信号控制输入，创新性地利用积分谐振控制器，自适应调节动态前馈增益，即信号控制输入，从而达到无静差控制。基于根轨迹方法分析整定多重谐振控制参数。该文提出的控制方法是一种新型的多重谐振控制结构，给出一种新的自适应控制思路，且所提控制方法具有良好的电压调节能力，如快速暂态响应、稳态误差小及总谐波畸变率低等。最后，通过实验验证了所提多谐振自适应控制的有效性。
关键词：逆变器控制 自适应控制 多重谐振控制 复变量
输出电压控制为一种常见的逆变器控制方式，其在分布式电源并离网和不间断供电（Uninterruptible Power Supply, UPS）应用中具有重要作用。近年来，随着电网构成型并网逆变器的应用研究，逆变器电压控制又重新受到关注[1-2]。
针对逆变器电压控制，国内外众多学者已经做了大量工作，并提出了相应的控制方法。逆变器电压控制包括线性控制和非线性控制两种。对于线性控制方法，常采用dq坐标系下比例积分（Pro- portional Integral, PI）控制器[3]或ab 坐标系下比例谐振（Proportional Resonant, PR）控制器[4]。早期的控制算法一般基于传递函数的频域设计方法，如单环控制[5]、多环控制[6]等，已在工业界得到广泛应用。此外，输出电压质量是逆变器控制的重要性能指标，因此逆变器输出电压谐波控制的研究同样受到较大关注，以满足非线性负载下的电能质量要求[7]。输出电压谐波控制一般可采用重复控制器或者多重谐振控制器。重复控制器利用内模原理，通过记录一个基波周期的采样数据，从而抑制周期性扰动，进而减少电压谐波，由于重复控制固有的延时特性，使得其动态性能较差[8-9]。相比于重复控制器，多重谐振控制器如PR、复变量谐振控制器（Complex Variables Resonant Controller, CVRC）的使用则一般可实现较好的动态性能，而CVRC可实现正负序分离控制，可以对指定负序谐波次数进行补偿，可显著减少控制器的计算负担[10]。然而多个谐振控制器的使用大大增加了系统的阶数，使得控制器参数的整定变得非常复杂，因此多重谐振控制参数的整定尤为关键。
线性控制系统参数设计方法较为成熟，且应用广泛，从经典控制理论的角度，包括闭环传递函数根轨迹法[11-12]、开环Bode图法[12-14]、闭环Bode图法[15]和Nyquist图法[16]等。现代控制理论则一般采用状态空间模型，其将控制器参数整定转换为状态反馈控制律的设计，进而通过极点配置法、线性最优二次调节[10, 17]、H∞鲁棒控制[18]等方法进行设计。另外，基于现代控制理论的时域优化控制方法也可用于控制器参数整定，一般可通过设计不同的优化目标实现控制参数整定，如最小化线性二次型[17]、最小化无穷范数[18]和最大收敛速率[19]，以获得优良的动态控制性能，目前已成功应用在逆变器电压控制上[17-19]。
近年来，非线性控制技术同样在逆变器电压控制中得到广泛应用。文献[20-21]将模型预测控制（Model Predictive Control, MPC）技术成功应用于不间断电源控制，然而MPC过度依赖电路模型参数，因此延时问题和参数失配问题将严重影响MPC的控制性能和稳定性。无差拍控制（Dead-Beat Control, DBC）[22]同样是基于电路模型进行预测的数字控制，亦存在过于依赖模型的问题。文献[23]提出了一种基于扩展李雅普诺夫（Lyapunov）函数的控制方法，从而实现了闭环系统的全局稳定性。对于非线性控制器参数设计[20-26]，由于缺少如积分器或者谐振控制器等内模控制器，因此其控制律需要精心设计以实现零稳态误差控制。此外非线性控制方法[20-26]一般采用李雅普诺夫函数证明其稳定性，然而找寻有效的李雅普诺夫函数缺乏系统性方法，因此使用李雅普诺夫方法较为困难。
作为非线性控制器的一种，自适应控制具有高鲁棒性、动态性能良好的特点，其成功的应用，大大提高了逆变器应对参数变化、扰动变化的能力，使得控制系统兼顾动态性能和鲁棒性，表现出良好的控制特性[24-26]。然而常规自适应控制方法一般从数学模型的角度设计，寻求Lyapunov稳定，使得系统误差状态量最终收敛到稳态工作点（零点），从而实现系统稳定的同时，达到零稳态误差，此过程往往伴随着高度非线性，控制增益的设计较为复杂，且需要较多的数学知识，一般缺乏物理意义。而这类自适应控制由于设计较为复杂，难以配置多重控制器，谐波抑制能力较差，在非线性负载下输出电压往往畸变严重。
本文提出了一种基于复变量多重谐振控制器的参考值前馈自适应控制方法，从系统传递函数物理意义出发，设计一种参考值动态前馈控制，从而引入信号控制输入的概念，设计系统参考值-输出传递函数在指定频率处始终为单位增益，实现零稳态误差控制，且便于采用线性控制理论分析所提出的自适应控制。同时方便将多重谐振控制器纳入本文参考值前馈自适应控制系统中，实现与传统多重谐振控制器截然不同的多重谐振自适应控制器。通过分析复系数参数的幅值、相位及各参数之间对系统极点位置的影响，实现多重谐振自适应控制器的优化整定，在系统稳定的同时保证了系统的动态性能。最后，通过实验结果证明了所提控制策略的有效性。
三相LC型逆变器拓扑如图1所示，图中，Udc为直流侧电压。在dq坐标系下建立其状态空间模型为
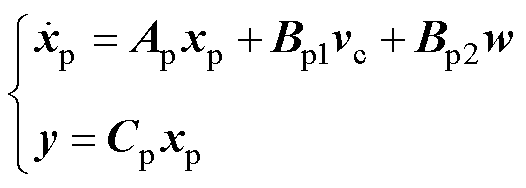（1）
采用复状态空间变量xp=[iLdq uCdq]T=[iLd+jiLq uCd+juCq]T为dq轴坐标系下的电感电流和电容电压；w=iwdq=iwd+jiwq为负载电流扰动；vc为逆变器桥臂中点电压矢量，并定义其为功率控制输入，与后文中提出的信号控制输入相区分。定义a1=1/L，a2=1/C，由基尔霍夫电压和电流定律可得到状态空间模型中的矩阵为
图1 三相逆变器拓扑
Fig.1 Topology of three-phase inverter
（2）
同步旋转dq轴坐标系下，比例多重谐振（Pro- portional Multi Resonant, PMR）电压控制一般采用双环控制，其控制结构如图2所示，其中电压外环控制器为
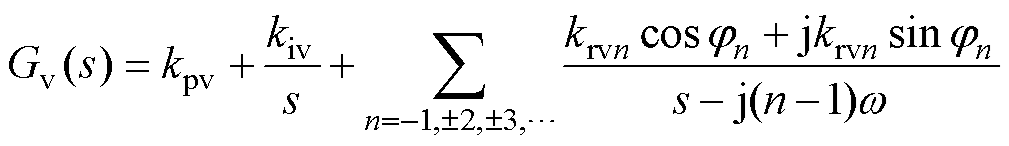（3）
式中，w 为谐振频率，同时为系统电压参考频率；(n-1)w 为各次谐波在dq轴坐标系下的角频率；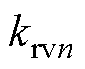
为谐振控制器控制增益；
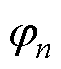用于相位补偿。电流内环则采用比例控制器GP=kpc，电容电压前馈解耦用于解耦电容电压对电感电流的影响[27]。传统双环PMR控制为基于经典控制理论的串联补偿控制方法，在设计内外环时需带宽解耦。另外，为实现传统双环PMR控制的d轴与q轴独立控制，常采用前馈解耦从而避免相互影响。然而由于电流内环的存在，使得该解耦策略并不能做到完全消除耦合。
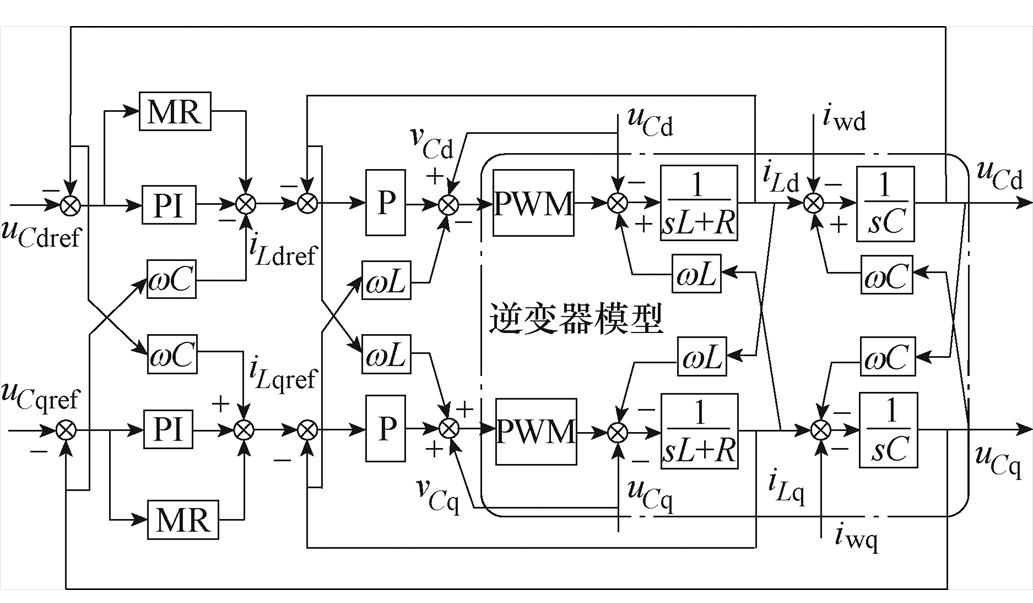
图2 传统串联PMR控制框图
Fig.2 Traditional series PMR control block diagram
与传统控制方法不同，本文采用复变量，设计了一种新型基于线性积分谐振控制的自适应控制器。自适应控制策略示意图如图3所示，图中所有运算均为复变量运算，首先设计状态反馈单独作用于功率控制输入vc，以改善系统状态变量的动态响应；然而状态反馈无法保证输入输出传递函数为单位增益，因此利用前馈复增益kr调节系统输入输出传递函数为单位增益。考虑到系统模型参数不确定性及负载变化，静态前馈增益kr往往无法达到实时运行时的单位增益效果，因此设计复增益kr分为静态与动态两部分，即kr=kr0+kra。静态增益kr0使得系统输入输出传递函数在指定频率处（采用dq轴控制时，由于dq轴电压为直流量，因此该频率为0Hz）的理论增益为单位1；动态自适应复增益kra则通过输出反馈自适应调节，以提高系统抗干扰能力，此时kra可以视为一个实时信号，本文定义为信号控制输入，通过设计输出电压反馈，动态改变该信号，从而使得参考值到输出传递函数在指定频率处实时精确为1（反馈的作用）。
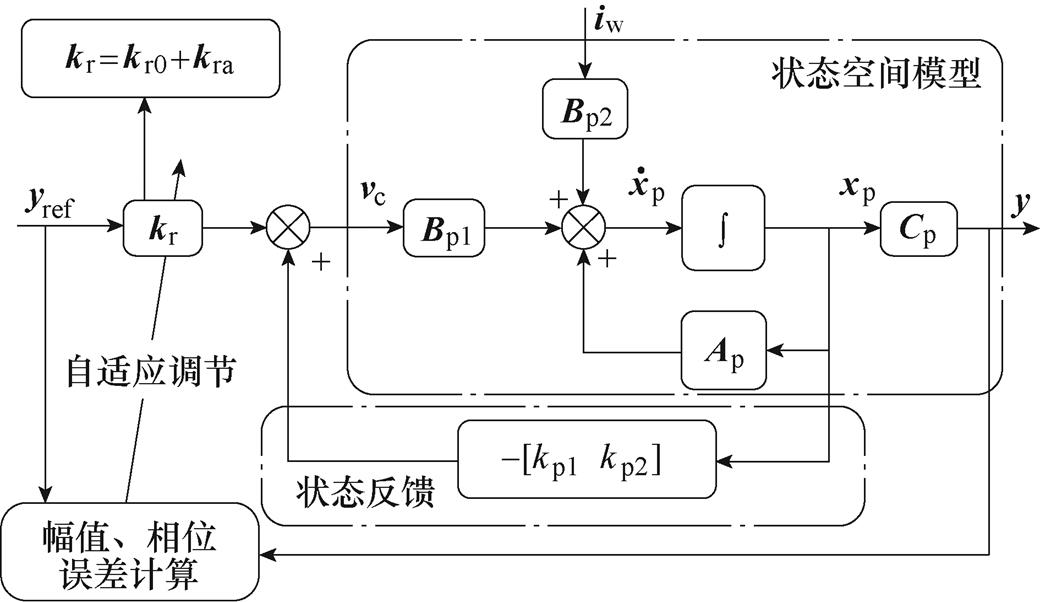
图3 本文所提自适应控制策略示意图
Fig.3 Schematic diagram of adaptive control strategy
1.3.1 静态前馈增益与状态反馈
首先忽略动态自适应前馈增益，在dq坐标系下的功率控制输入为vc=-Kxp+kr0yref，K=[kp1 kp2]，将此控制律代入原系统方程，可得输出电压为
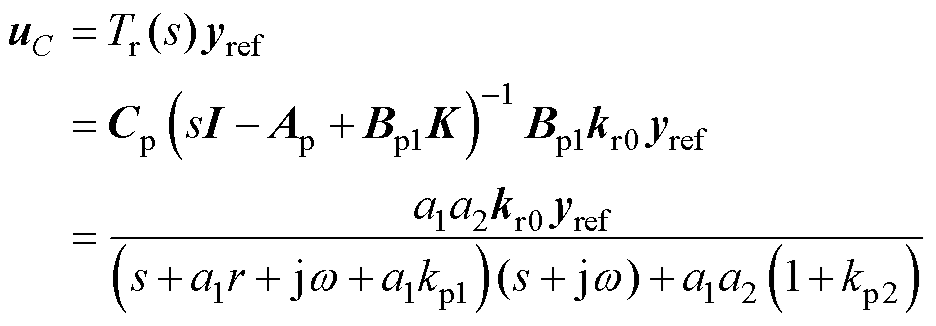（4）
式中，Tr(s)为系统参考值到输出闭环传递函数。由式（4）可知，状态反馈可调节系统极点分布，因此可改善系统自然极点，从而提高系统的动态性能。
为了保证传递函数在dq坐标系下0Hz处取得单位增益，即输出能够完全跟踪输入，实现无稳态误差跟踪控制，复系数kr0可确定为
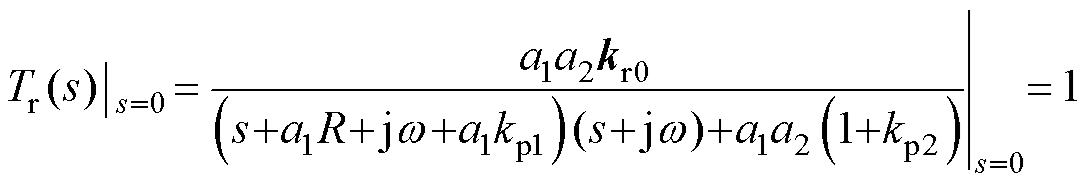（5）
根据式（5）可得
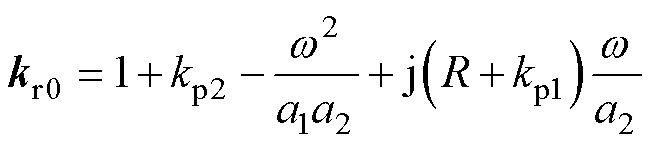（6）
1.3.2 动态前馈增益
理论上，式（6）可使得输入输出传递函数在直流处为单位增益，从而使得输出电压幅值与输入电压相等，且无相位差。然而，实际上，由于系统参数的不确定性和负载的变化，kr0并不能完全确保传递函数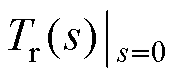
=1。为了补偿不确定性，本文利用动态自适应复增益kra来响应逆变器电压信号的幅值偏差和相位偏差。
考虑动态部分后，复变量前馈增益kr可表示为幅值、相位形式，即
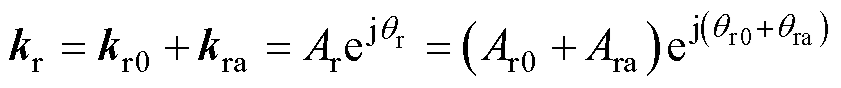（7）
由于传递函数Tr的幅值与Ar相关，与qr无关；相反，Tr的相位与qr相关，与Ar无关，因此，可通过输出电压的幅值反馈调节Tr的幅值，输出电压的相位反馈调节Tr的相位，即
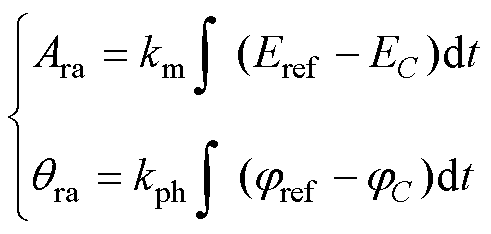（8）
式中，Eref、jref分别为参考电压的幅值和相位；EC、jC分别为输出电容电压的幅值和相位。需要说明的是，式（8）中的积分控制器并不同于传统dq控制中的积分控制器，因为此处的积分控制器用于调节前馈控制增益，而传统dq控制中的积分器则用于调节内环电流参考值。
然而，如果采用式（8）所示的控制率，式（7）为非线性计算，且输出电压的相位无法获得，这给自适应控制增益系数km和kph的整定带来困难。考虑复变量前馈增益kr的直角坐标形式为
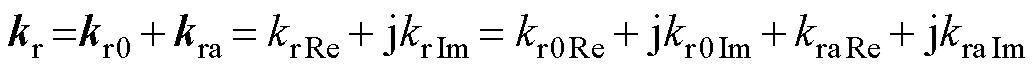（9）
根据式（6），在实际的三相逆变器系统中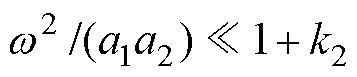
，可忽略不计，且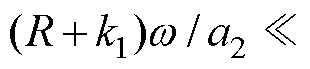
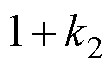，即kr0Im
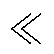kr0Re，因此qr0→0，又由于动态自适应复系数kra较小，同理可得qr→0，因此
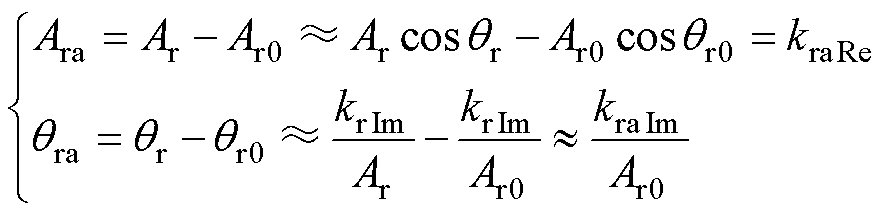（10）
因此Ara可由kraRe代替，qra可由kraIm代替。此外，以参考值相位为基准，变换到dq坐标系下后，输出电压变为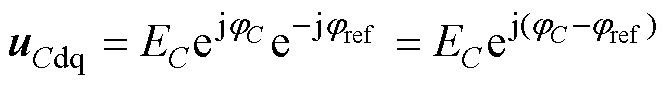
，因此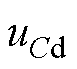
、
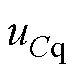分别包含了输出电压的幅值信息和相位差信息，则自适应控制律式（7）可线性化表示为
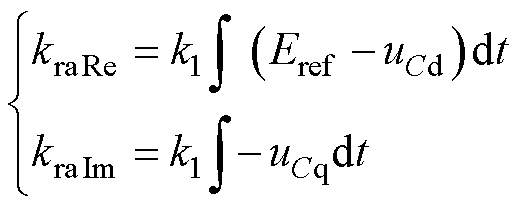（11）
线性化后的自适应控制律可统一为
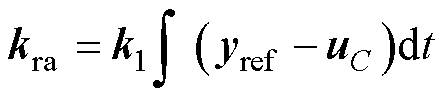（12）
式中，yref=Eref ej0=Eref，uC=uCdq；k1扩展为复系数（详细设计于第2节中说明）。最终，基于所提线性化条件1：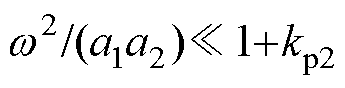
和线性化条件2：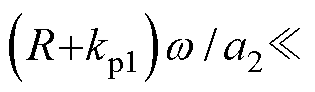
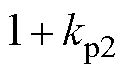，本文自适应控制实现机制如图4所示。同样，图4中的积分控制器并不同于传统dq控制中的积分控制器，因为此处的积分控制器用于调节前馈控制增益。
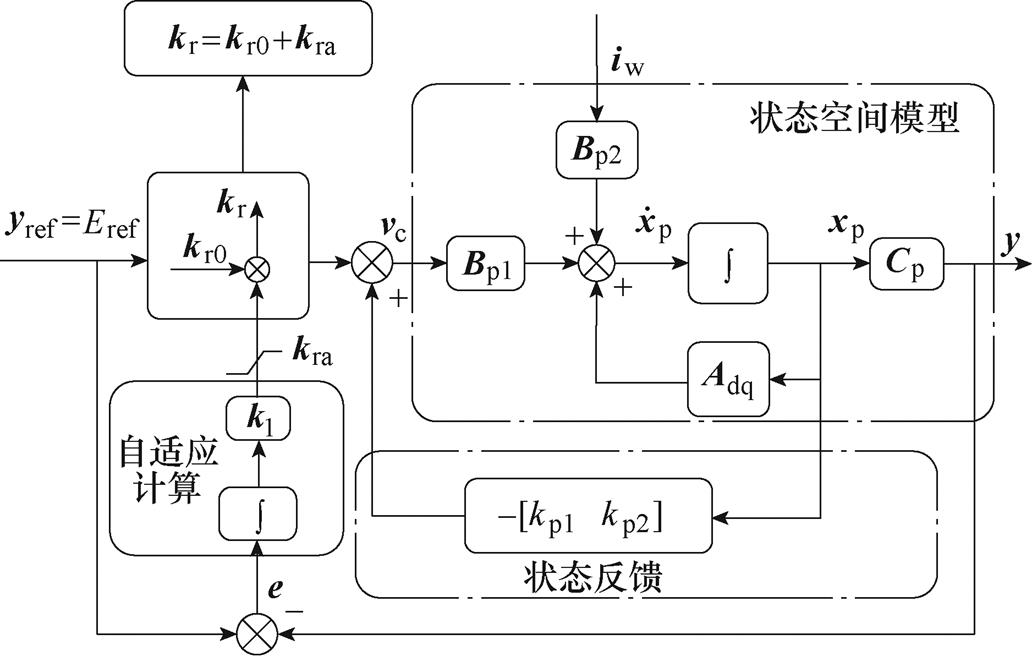
图4 自适应控制策略控制基本框图
Fig.4 Basic block diagram of adaptive control strategy
为提高非线性负载带载能力，借鉴传统多重谐振控制器思想，本文在自适应计算环路中引入多重谐振控制器，用于动态调节前馈增益，进行谐波补偿，从而使信号控制输入kra具备较强的谐波补偿能力，自适应非线性负载的变化，提升电压质量。考虑传递函数的CVRC[10]为
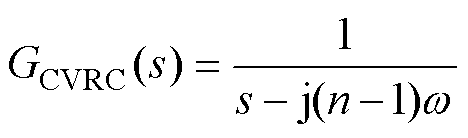（13）
多重CVRC（Multiple CVRC, M-CVRC）自适应控制算法控制框图如图5所示，可配置M-CVRC；kn为各次谐波控制器的复增益。此外，由于本文所采用的谐振控制器属于理想型振控制器，当系统频率发生变化时，DSP实时计算过程中的谐振频率亦将发生变化，使得控制器谐振频率跟随系统频率变化。
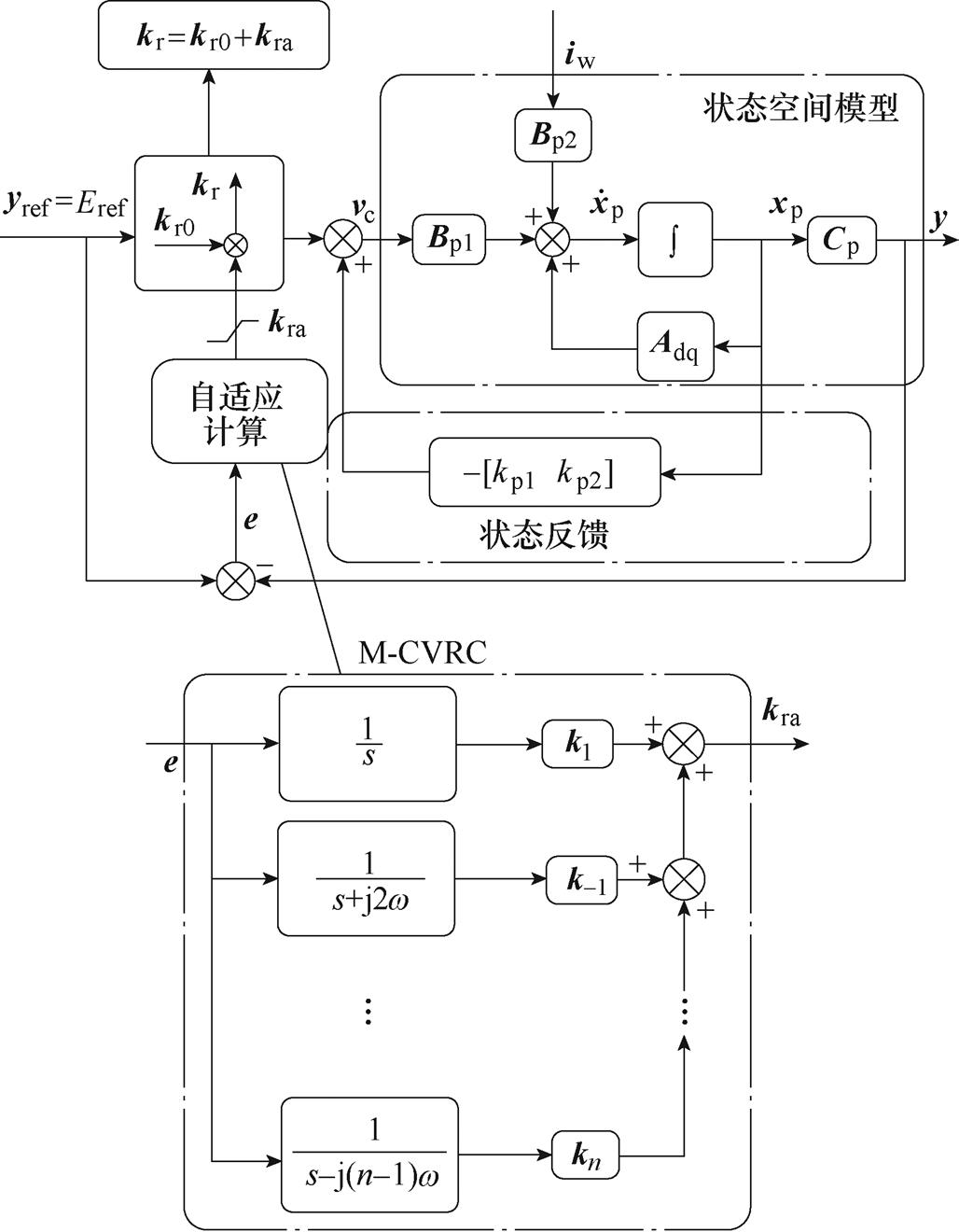
图5 M-CVRC自适应控制算法控制框图
Fig.5 Block diagram of adaptive control strategy based on M-CVRC
本文所述自适应控制器需要确定的参数为kr0、kp1、kp2以及多重谐振控制系数kn。
参考值前馈kr0可由式（4）计算，kp1和kp2的设计可采用极点配置法或者最优线性二次调节（Linear Quadratic Regulation, LQR）法，不仅能使控制系统在二次型性能指标意义下达到最优，同时还保证了闭环系统的渐近稳定性，具有较大的增益裕度，相位裕度不小于60°[28]，因此本文状态反馈采用LQR设计。
信号控制输入多重控制器参数kn的整定为本文所提控制器的关键。为分析设计kn，暂时忽略Eref变化（实际运行时，Eref变化较小），由图4可推导kra到输出的传递函数为
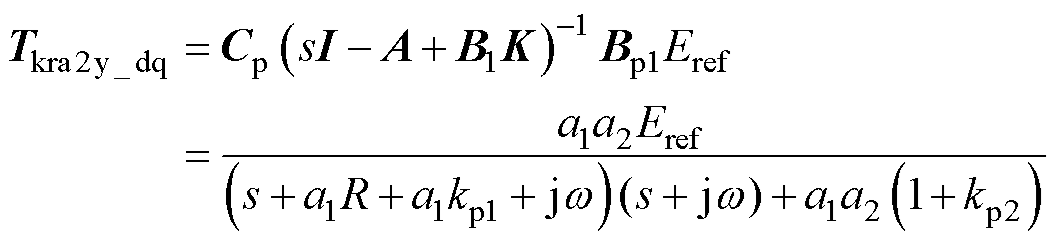（14）
由此可得如图6所示的小信号框图，式（13）为控制信号输入kra的控制对象，因此图6可用于设计kra中的多重谐振系数，其参考值到输出动态闭环传递函数Nv(s)表示为
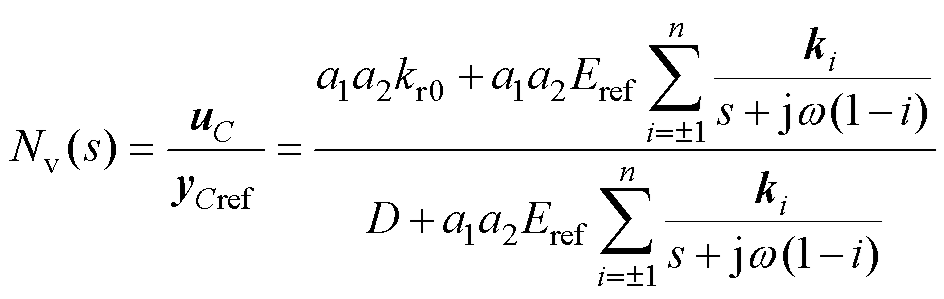（15）
其中
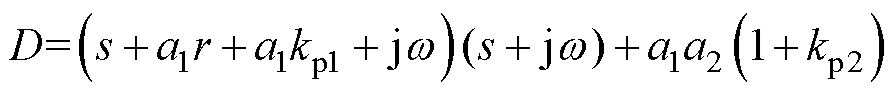
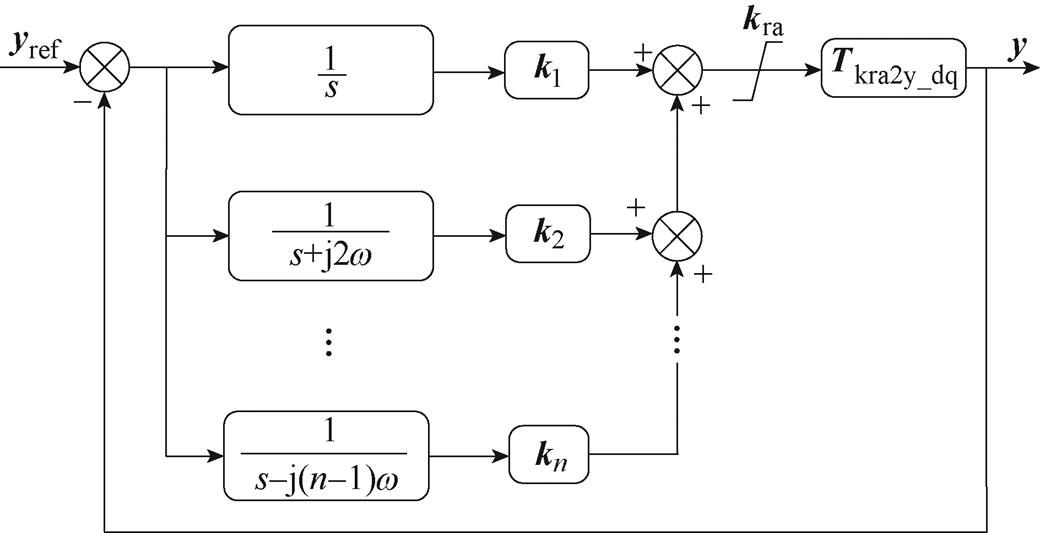
图6 M-CVRC控制器参数设计等效控制框图
Fig.6 Equivalent block diagram of M-CVRC control to design parameters
同理推导系统扰动（负载电流）到输出闭环传递函数Nw(s)为
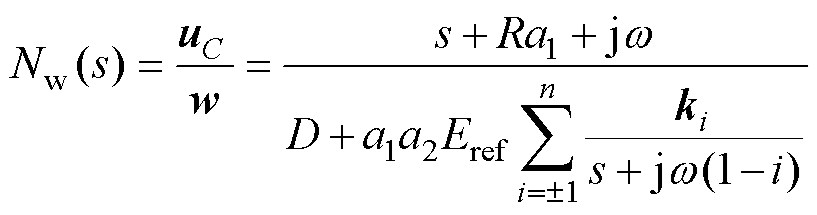（16）
本文利用参数根轨迹方法，分析设计参数kn，考虑典型谐波次数为-5、7、-11、13次谐波（负号表示负序谐波分量）。本文以上述谐波次数的CVRC为例说明相应kn设计方法，具体包括积分复增益k1，各谐波复增益k-5、k7、k-11、k-13。为方便后文讨论分析，定义系统对应LC滤波器的自然极点分别为p1、p2，由k1、k-5、k7、k-11、k-13引入的极点分别为p3、p4、p5、p6、p7。当分别单独配置基波与负序11次谐波CVRC时，以k1、k-11为例讨论参数幅值相位设计方法；当配置多个CVRC时，以k1、k-5、k7为例，分析多个kn幅值、相位及不同kn之间的相互影响。
当kra的自适应计算只存在基波控制器时，需确定复系数k1的幅值|k1|和相位q1。图7所示为|k1|变化（0～20）参数根轨迹，随着幅值的增加，系统极点p3左移，自然极点右移，系统调节时间加快；随着幅值继续增大，自然极点的右移导致阻尼大大减少，系统振荡，当|k1|过大时，系统失稳，因此|k1|的选取需要在系统动态调节时间与系统阻尼、稳定性之间权衡，其余|kn|选取与此类似。
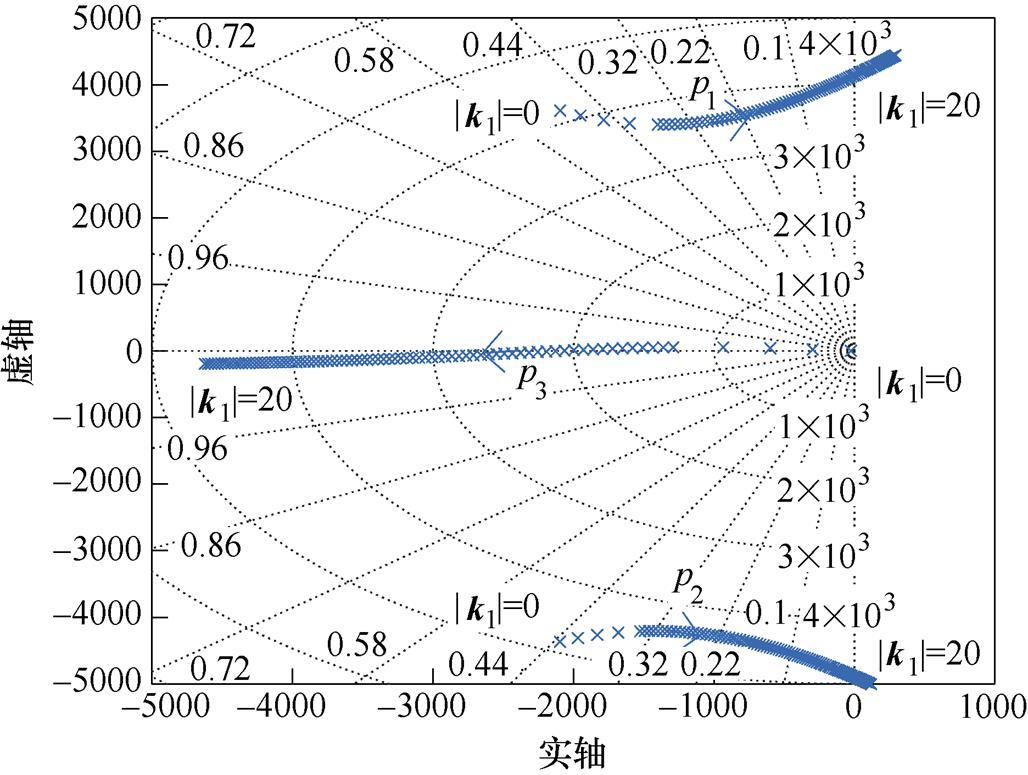
图7 |k1|变化（0～20）参数根轨迹
Fig.7 Root locus of |k1| variation (0～20)
图8所示为q1变化（-90°～90°）参数根轨迹，当q1从0°逐渐增大或减小时，极点p3阻尼均逐渐减小，极点p1、p2阻尼发生不同程度的变化，当q1变化较大时，p3不断右移，系统发生振荡甚至失稳，因此k1相位q1的选取应在0°附近。
图9所示为k-11变化（|k-11|=1, 2, 3，q-11=0°～-90°）参数根轨迹，此时相位q-11的选取应小于0°，否则p6将移动到平面右侧造成系统失稳；另一方面，当相位q-11过小时，系统自然极点p2不断右移，亦将弱化系统的动态性能，因此综合考虑下，k-11相位q-11选取为-40°附近。同理可分析k13根轨迹运动规律，与k-11相反，k13相位q13选取为40°附近。
图8 q1变化（-90°～90°）参数根轨迹
Fig.8 Root locus of q1 variation (-90°～90°)
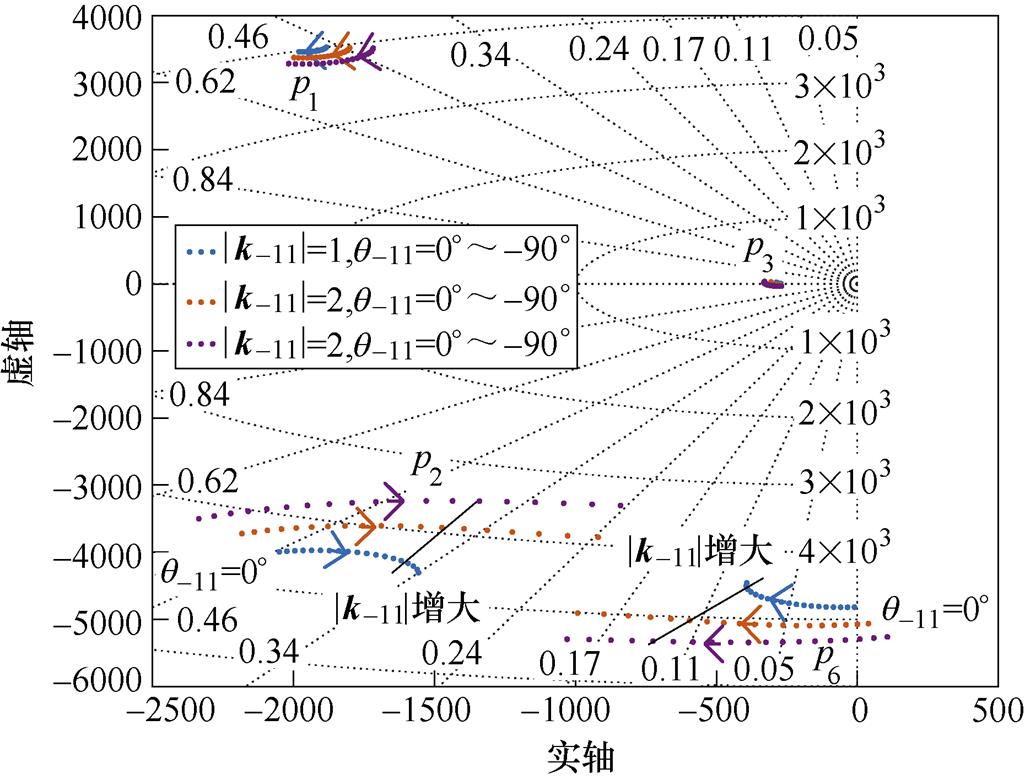
图9 k-11变化（|k-11|=1, 2, 3，q-11=0°～-90°）参数根轨迹
Fig.9 Root locus of k-11 variation (|k-11|=1, 2, 3,q-11=0°～-90°)
当kra中配置多个CVRC时，以k1、k-5、k7为例，分析kn变化对系统根轨迹的影响。
如图10所示为当|k1|变化（0～20）参数根轨迹，此时取|k-5|=1.5、|k7|=1.5。当|k1|从0开始增加时，极点p3迅速左移，p4、p5也有一定程度左移，自然极点p1、p2逐步右移，阻尼逐渐减小；随着幅值继续增大，极点p3左移，系统调节时间加快，其余极点均向平面右边移动，系统阻尼大大减少，造成系统振荡直至失稳，因此|k1|的选取同样需要在系统动态调节时间与系统阻尼、稳定性之间权衡。其余|kn|分析设计同理。
图11为当k1变化（|k1|=1, 2, 3，q1=-90°～90°）参数根轨迹，此时取|k-5|=1.5、|k7|=1.5。当q1在0°附近变化时，自身极点p3阻尼降低，q1变化对其他极点也有一定程度的影响，且影响程度与其幅值大小呈正相关。当q1从0°增加时，降低了极点p5的阻尼，增加了极点p2、p4的阻尼，提高了极点p1的自然频率；当q1变化较大时，从极点p3的根轨迹变化可以看出，系统将振荡甚至失稳，因此q1依然在0°附近选取。其余kn相位分析同理，仅是不同kn相位合理选取范围有所不同。
图10 多CVRC下|k1|变化（0～20）根轨迹
Fig.10 Root locus of |k1| variation (0～20) under M-CVRC
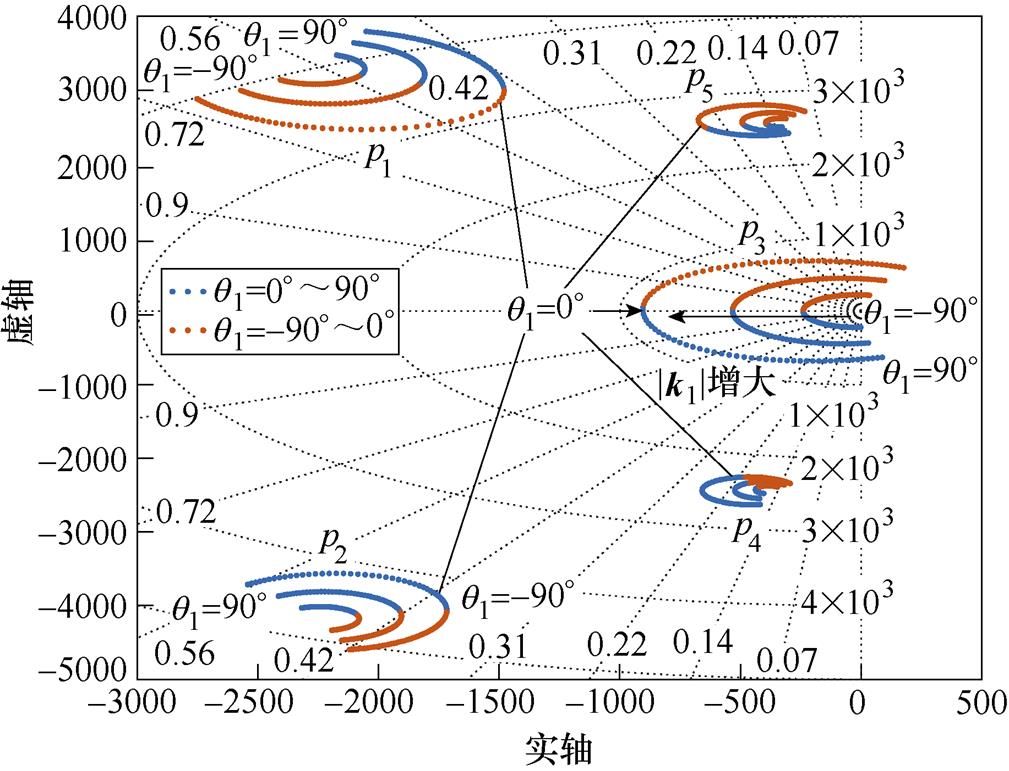
图11 多重CVRC下k1变化（|k1|=1, 2, 3，q =-90°～90°）参数根轨迹
Fig.11 Root locus of k1 variation (|k1|=1, 2, 3, q =-90°～90°) under M-CVRC
本文状态反馈系数根据LQR计算得：kp1= 6.780 8，kp2=0.107 5。需要注意的是，kp1的设计值不宜过大：一方面为了满足1.2节中自适应控制的线性化条件；另一方面过大的kp1也会由于硬件控制饱和而导致系统崩溃。静态前馈增益根据式（6）计算得kr0=1.103 6+j0.042 9。此外，根据2.2节分析，总结kn根轨迹参数分析结论如下：
（1）kn幅值选取需要在系统动态调节时间与系统阻尼、稳定性之间权衡。
（2）kn相位的合理选取对系统的稳定性影响较大，且不同kn合理选取范围有所不同。
（3）不同kn之间的影响与其幅值呈正相关，当kn选取的幅值较小时，可近似忽略不同kn之间的影响，从而给系统参数设计带来便利。
根据上述根轨迹设计思路，最终选定kra自适应计算的参数分别为k1=1.95、k-5=0.909ej(-5.7)、k7= 0.909ej5.7、k-11=0.909ej(-40.1)、k13=0.909ej40.1。所得系统自然极点为：p1=-1 857+j4 482；p2=-1 857- j4 482；M-CVRC极点为：p3=-839.4；p4=-462.3- j1 773；p5=-462.3+j1 773；p6=-269.7-j4 343；p7= -269.7+j4 343。
另外，根据式（15）即可得到系统闭环扰动传递函数Bode图如图12所示，从图中可以看出，在dq坐标系下系统对0Hz、±300Hz、±600Hz频率下扰动均具有无穷小增益（转换到ab 坐标系下，该频率相应转换为+1、-5、+7、-11、+13次谐波频率），系统对这些频率下的扰动具有较强的抑制作用，表明本文所提自适应控制系统具备较强的带非线性负载能力。
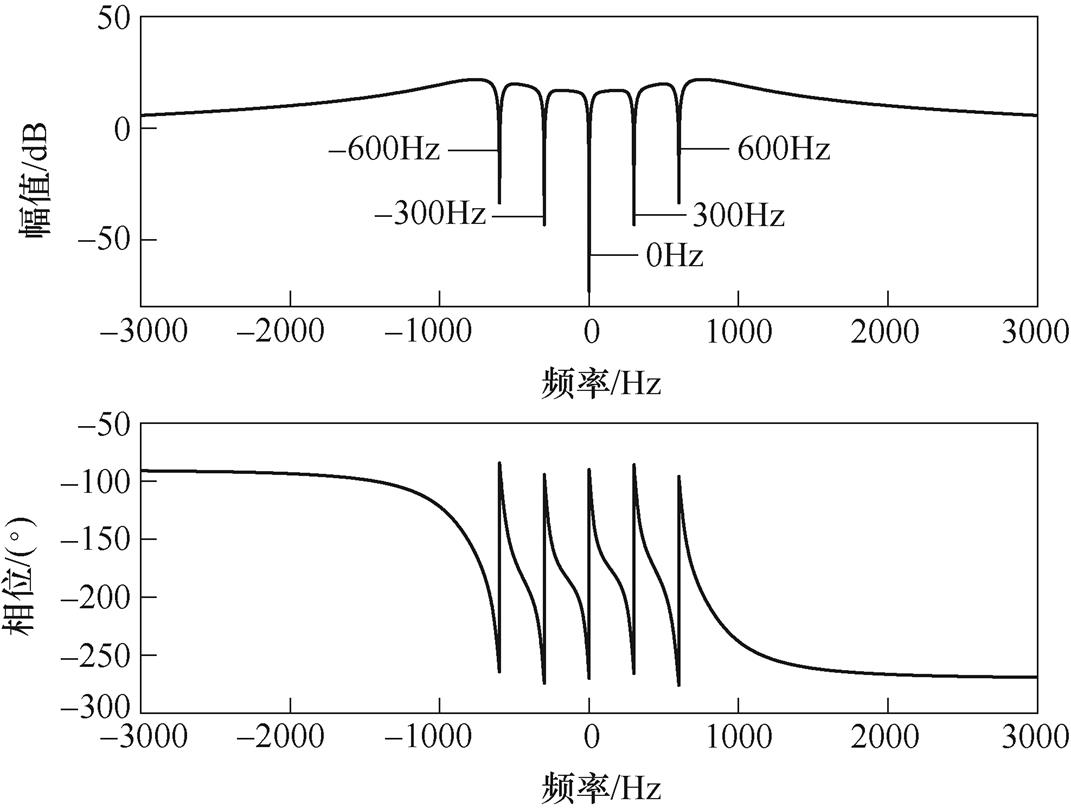
图12 系统闭环扰动传递函数Bode图
Fig.12 Bode diagram of system closed-loop disturbance transfer function
由于电感磁心饱和的影响，随着电流的增加，电感值大小会出现变化，因此当模型参数变化时，本文以电感参数变化为例，对电感变化下系统参数根轨迹进行分析。电感L变化（1.5～2.5mL）下系统参数根轨迹如图13所示，当电感变化（1.5～2.5mL）时对LC滤波器引入的极点影响较大，对控制器引入的极点影响较小，kn参数主要用于调节控制器引入的极点，且系统极点均处于左半平面，即能够保持系统的稳定性，说明本文设计控制参数对系统参数变化具有一定的鲁棒性，即当模型参数不确定时，所设计出的kn参数仍然具备一定的准确性。
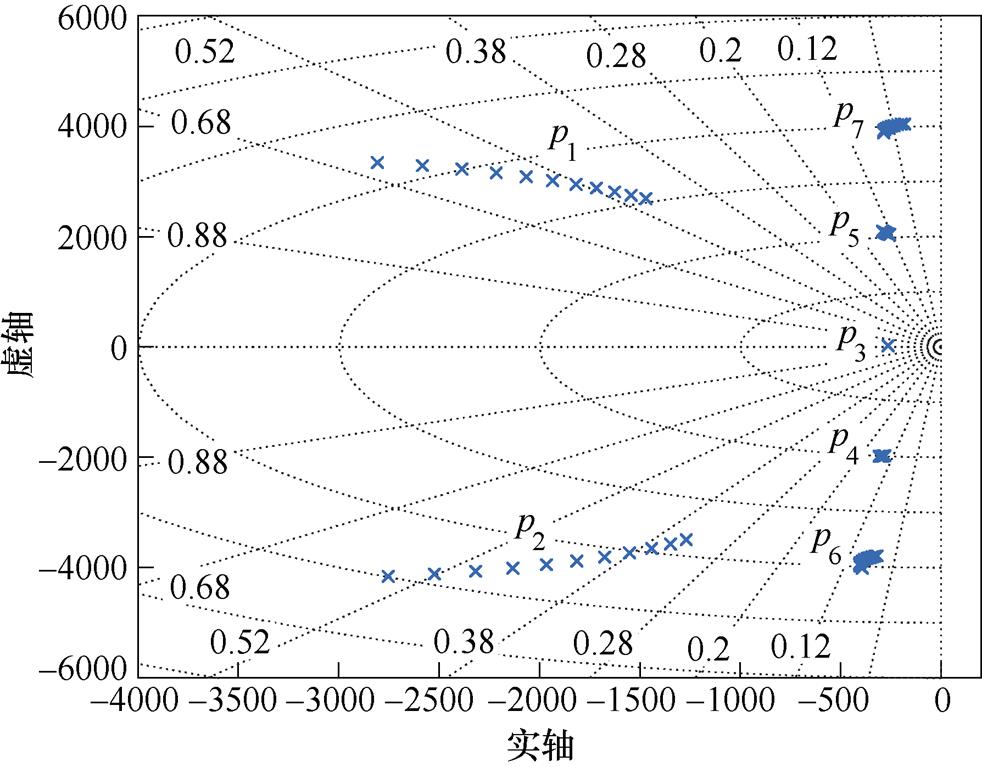
图13 电感L变化（1.5～2.5mL）下系统参数根轨迹
Fig.13 Root locus of L variation (1.5～2.5mL)
为验证所提控制策略的有效性，本文搭建了基于IGBT的逆变器实验平台，滤波器采用LC滤波电路，基于TMS320F28335控制板采集电压电流信号并实现了本文所提控制策略。实验结果中的电压偏差数据和信号控制输入数据均通过DSP缓存数组导出得到。逆变器参数见表1，结合2.3节中控制参数选取结果，并计算控制参数和逆变器参数满足1.3节中自适应控制的线性化条件。此外，在滤波电容较大的应用场合，为满足1.3节中的线性化条件，可适当减少控制器参数kp1，以增加滤波电容的选取裕度。
表1 逆变器参数
Tab.1 Parameters of the inverter
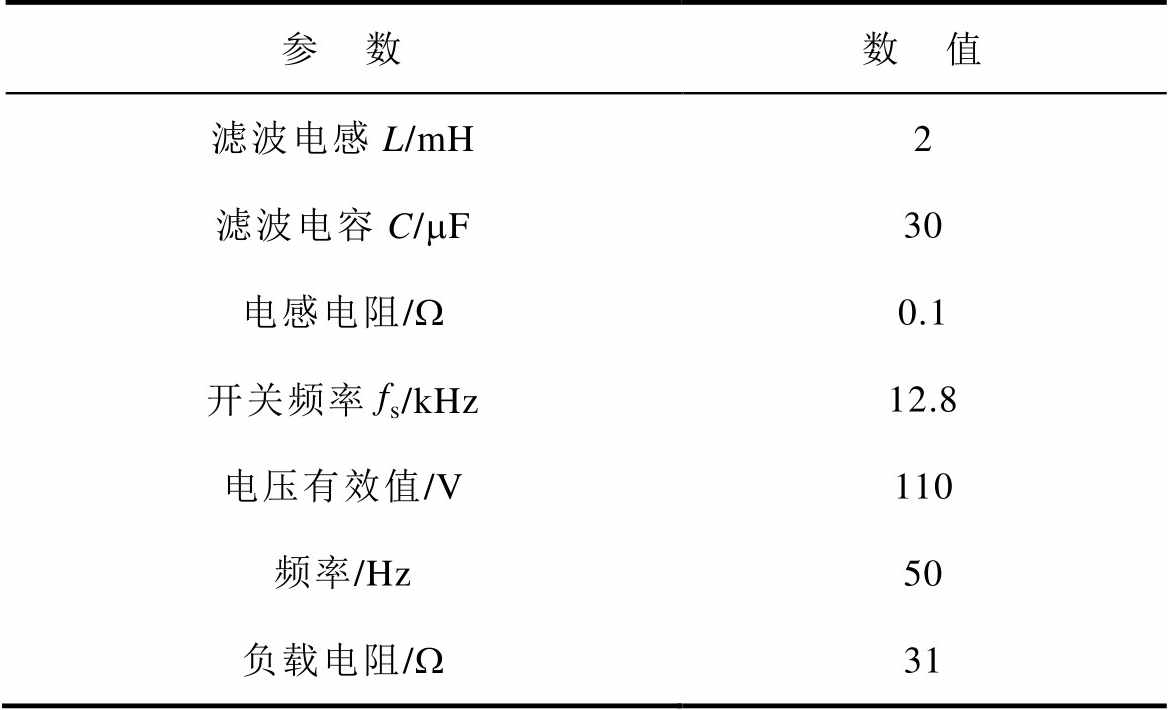
参 数数 值 滤波电感L/mH2 滤波电容C/mF30 电感电阻/W0.1 开关频率fs/kHz12.8 电压有效值/V110 频率/Hz50 负载电阻/W31
自适应控制电压参考值阶跃实验如图14所示，由图可知，当逆变器参考电压Eref由155.5V突增至205.5V时，瞬态过程非常短，输出电压仅需1.5ms即可快速跟踪。输出电压的快速跟踪对电压控制型逆变器并网功率控制具有重要意义，直接关系到电网构成型逆变器并网时的动态性能[29]。
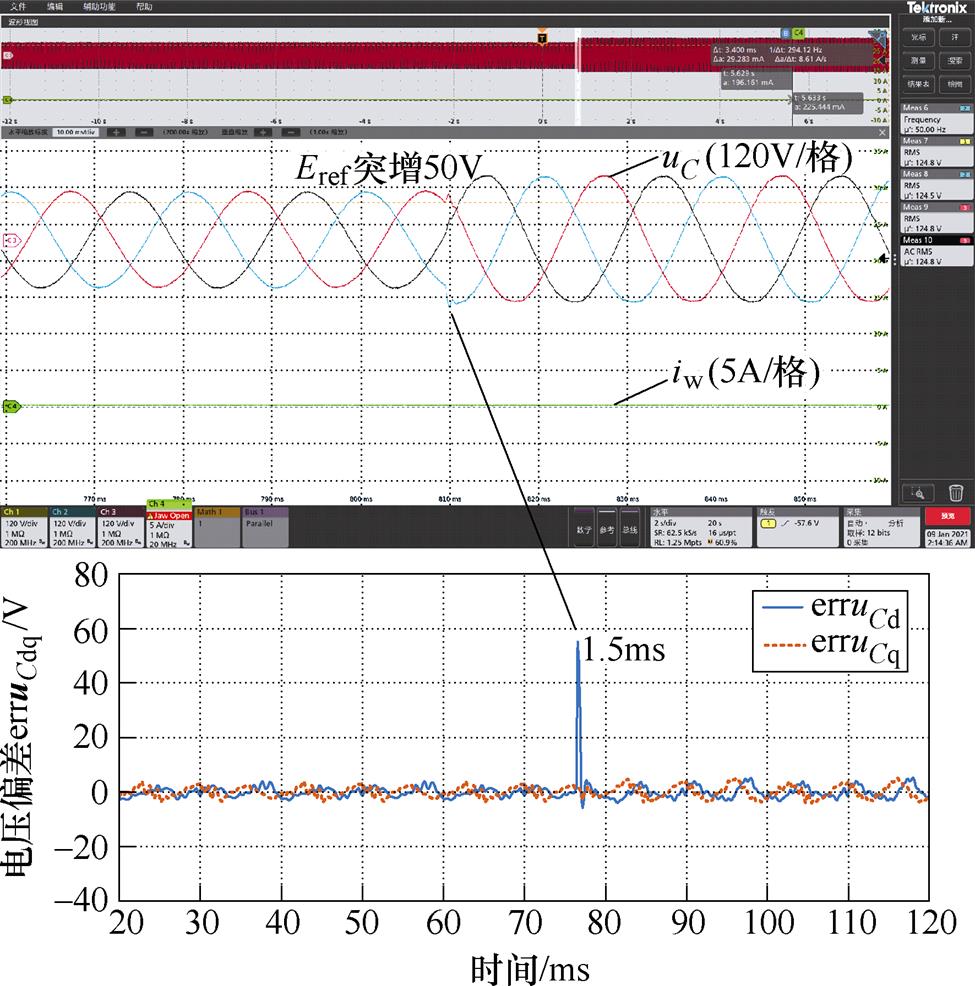
图14 自适应控制电压阶跃实验
Fig.14 Voltage step experiment of adaptive control
Udc变化实验波形如图15所示，从图中可以看出，当直流母线电压Udc发生变化时，逆变器输出电压、输出电流无明显变化，表明本文所提控制策略对Udc变化具备一定的抗扰能力。
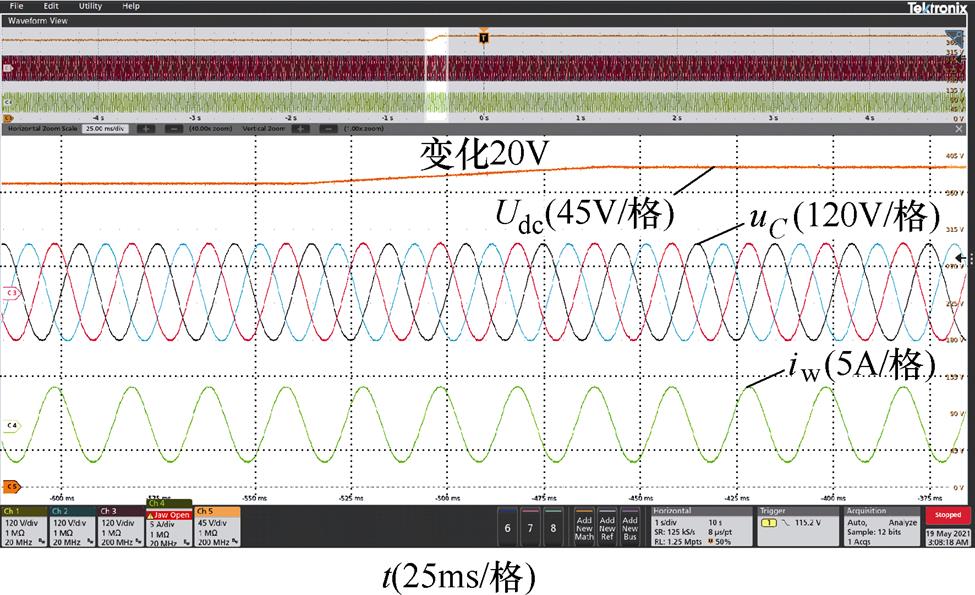
图15 Udc变化实验波形
Fig.15 Udc variation experimental waveforms
本文所提控制策略投入线性负载时的电压电流波形如图16所示，负载投入时信号控制输入主要通过d轴分量krad产生作用，krad在空载时近乎为0，在投载时发生变化以补偿负载扰动。虽然此时kra的实部和虚部很小，但是准确消除了稳态误差，且具备较快的动态响应时间，在无负载电流前馈的情况下，5ms内输出电压恢复稳定。
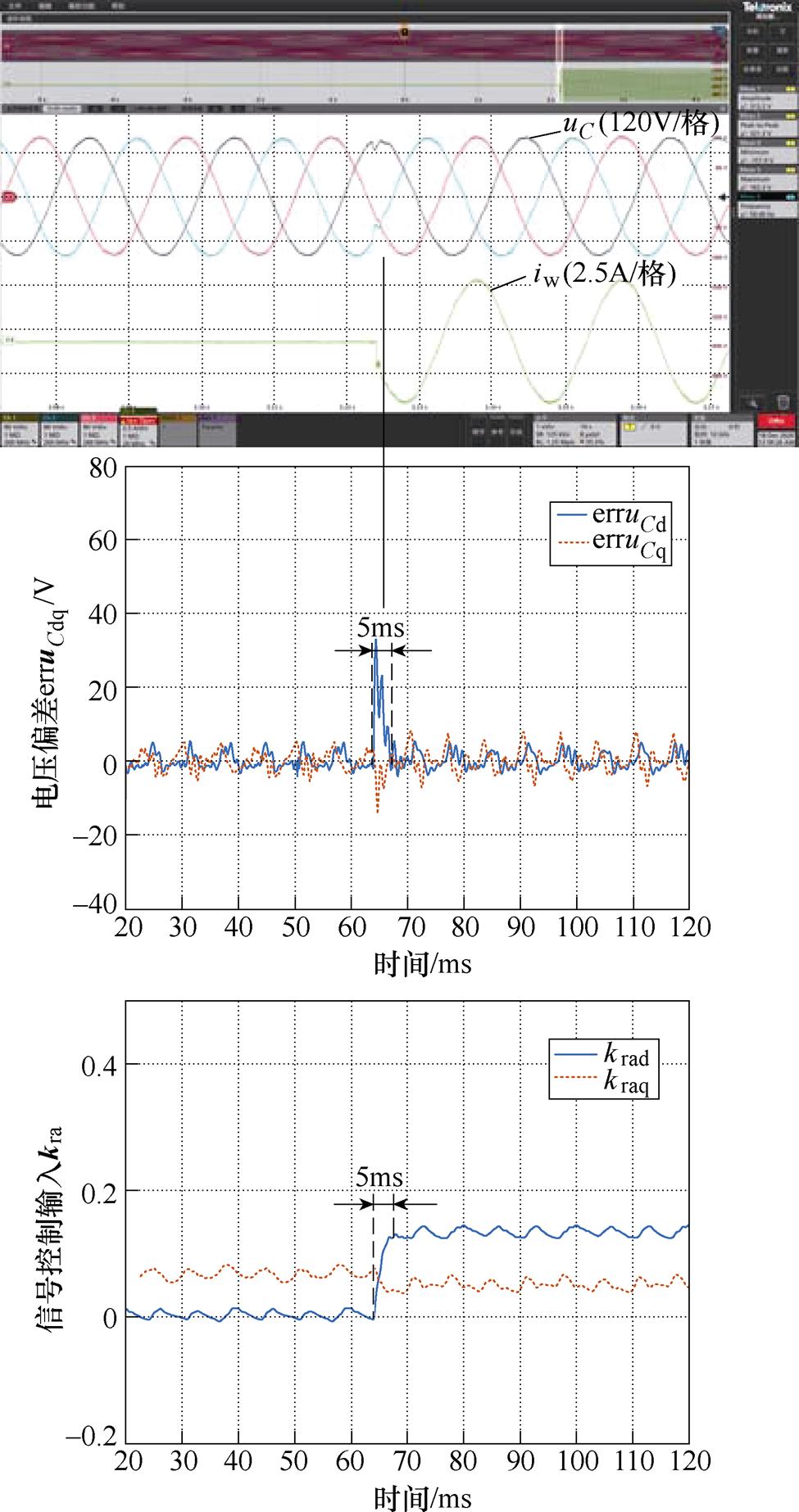
图16 自适应控制线性负载实验波形
Fig.16 Linear load variation experimental waveforms of adaptive control
为证明2.2节分析kn幅值选取对系统动态性能的影响结论，实验中以k1为例，进行了当k1分别为0.5, 2.5, 4时系统的投载实验。
不同k1值系统动态性能对比如图17所示，不同k1下系统理论值与实验值对应见表2，当k1由0.5增加到2时，系统极点p3逐渐左移，电压恢复时间由30ms加快到5ms，但是当k1继续增加时，其根轨迹分析如图7所示，极点p3由主导极点变为非主导极点，此时在3.5ms内kra虽已经完全作用，但系统此时仍有振荡，这是由于系统自然极点p1、p2右移，其动态过程逐渐显现，且系统阻尼比减低，弱化了系统的动态性能，导致系统最终在17ms才完全稳定。
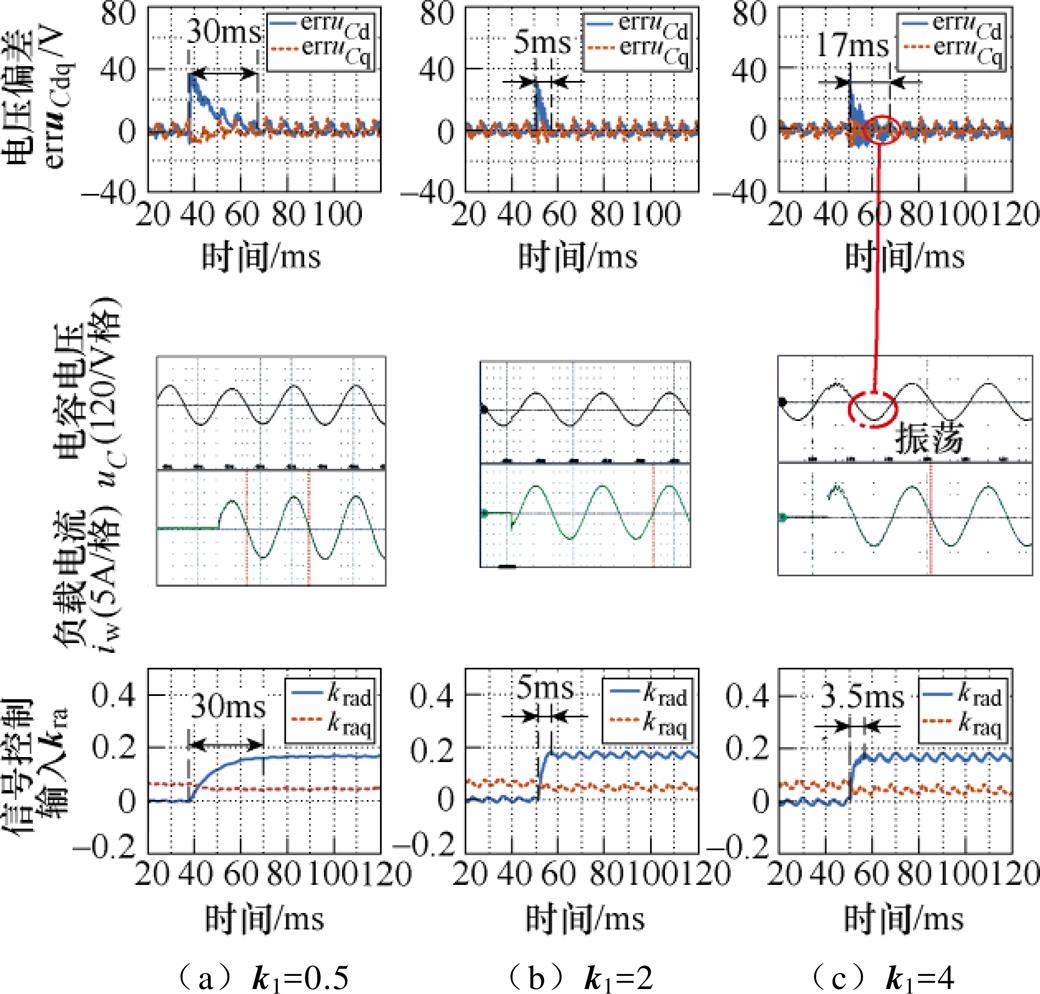
图17 不同k1值系统动态性能对比
Fig.17 Dynamic performance comparison experiment under different k1
表2 不同k1下系统理论值与实验值对应表
Tab.2 Correspondence table between theoretical and experimental values of system under different k1
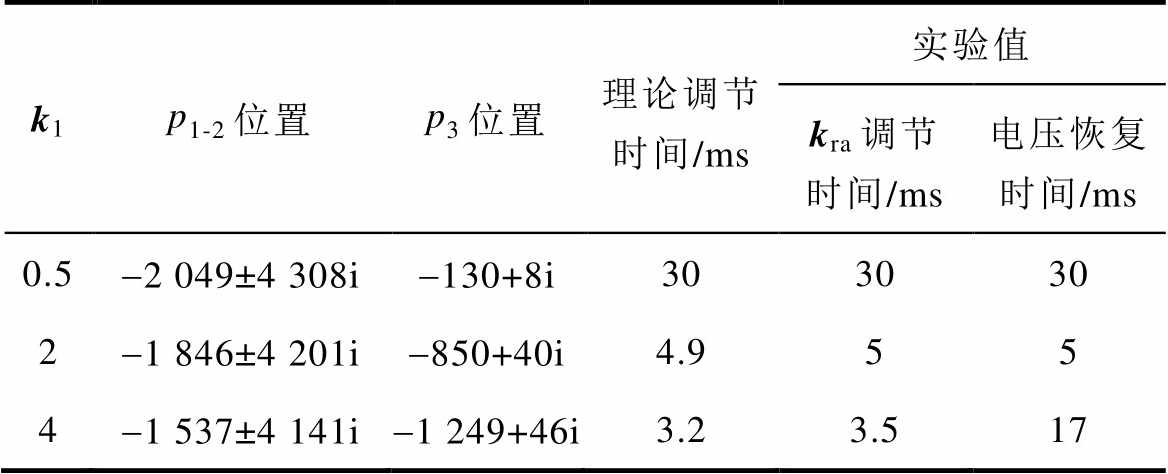
k1p1-2位置p3位置理论调节时间/ms实验值 kra调节时间/ms电压恢复时间/ms 0.5-2 049±4 308i-130+8i303030 2-1 846±4 201i-850+40i4.955 4-1 537±4 141i-1 249+46i3.23.517
本文采用如图18所示的三相不控整流电路作为非线性负载，电容C=3 400mF，电阻R=50W，采用最恶劣的无平波电感工况[7]。
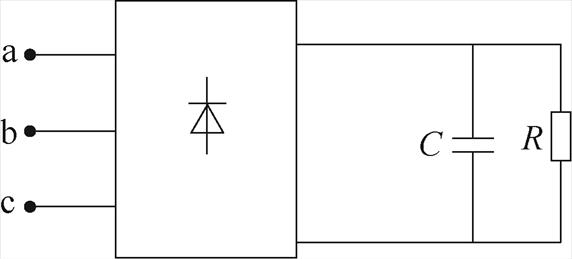
图18 三相不控整流电路
Fig.18 Topology of three-phase uncontrolled rectifier
图19所示为系统在非线性负载下的输出电压波形，当非线性负载投入时，由图21中的kra稳态波形可知，信号控制输入kra产生作用，进而抵抗非线性负载扰动，成功补偿非线性负载下的各次谐波，大大降低了电压总谐波畸变率（Total Harmonic Distortion, THD），在无负载电流前馈的工况下，输出电压THD为2.6%，配置有相应CVRC的-5、7、-11、13次谐波得到较大的衰减，2.6%的THD主要来自于未配置CVRC控制器的谐波含量。
图19 自适应控制非线性负载实验
Fig.19 Nonlinear load experiment of adaptive control
图20～图22分别为传统PMR控制电压阶跃、线性负载、非线性负载实验波形。PMR中PI参数按照经典控制理论带宽设计，电流环1 400Hz，电压环160Hz。多重谐振控制器参数基于传递函数开环Bode图方法设计，各谐振控制器之间独立设计，通过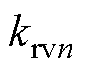
对多重谐振控制器的响应速度及系统稳定裕度进行权衡，并通过
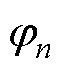对系统相位滞后进行补偿，最终使得系统相位裕度在30°～60°之间[13]。
对比图14和图20可知，当电压参考值由155.5V突增至205.5V时，传统PMR控制需要4ms才可跟踪电压参考值，而本文所提自适应控制仅需1.5ms，快速性优于传统PMR控制。
对比图16、图17和图21，传统PMR控制需要内外环解耦，因此线性负载投载时需要较长的电压恢复时间（10ms）。而本文所提自适应控制方法动态恢复时间快，仅需要较小的控制增益即可实现良好的动态性能，且理论设计值与实验值基本一致，无须频繁试凑设计参数。
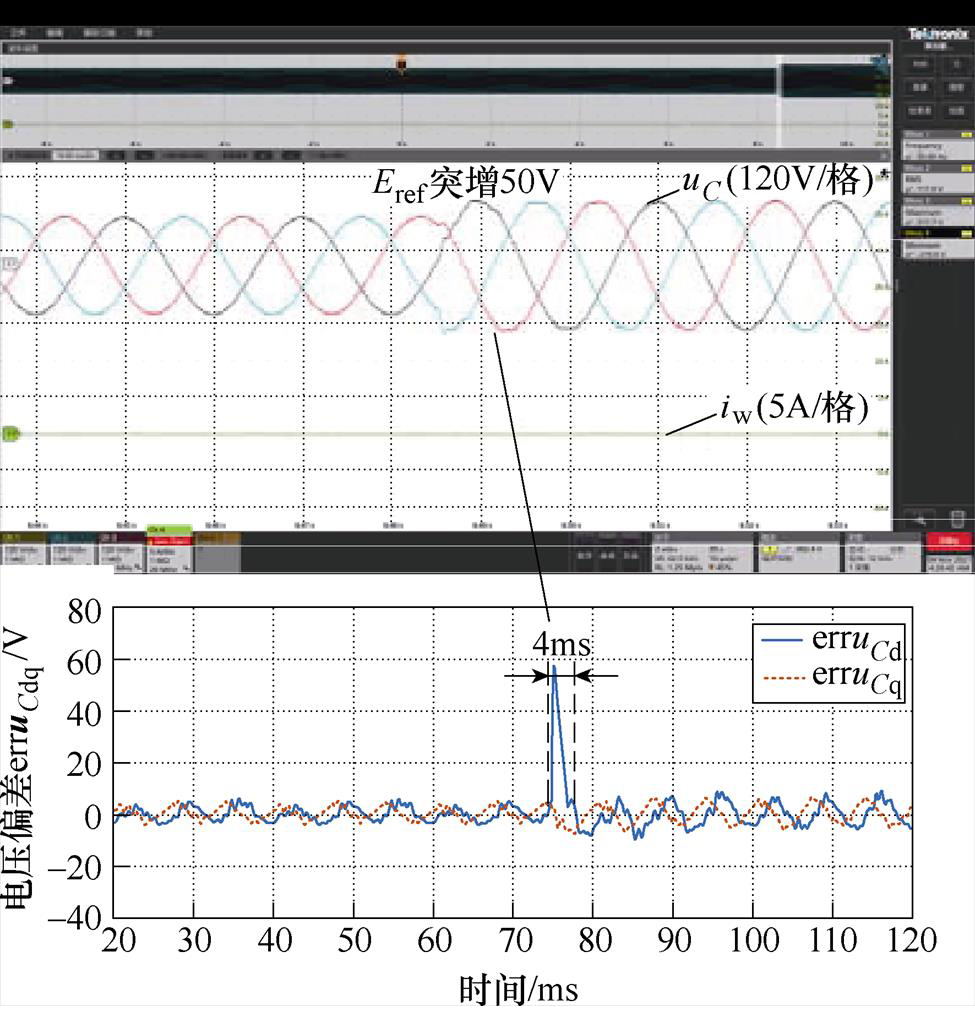
图20 传统PMR控制电压阶跃实验
Fig.20 Voltage step experiment of traditional PMR control
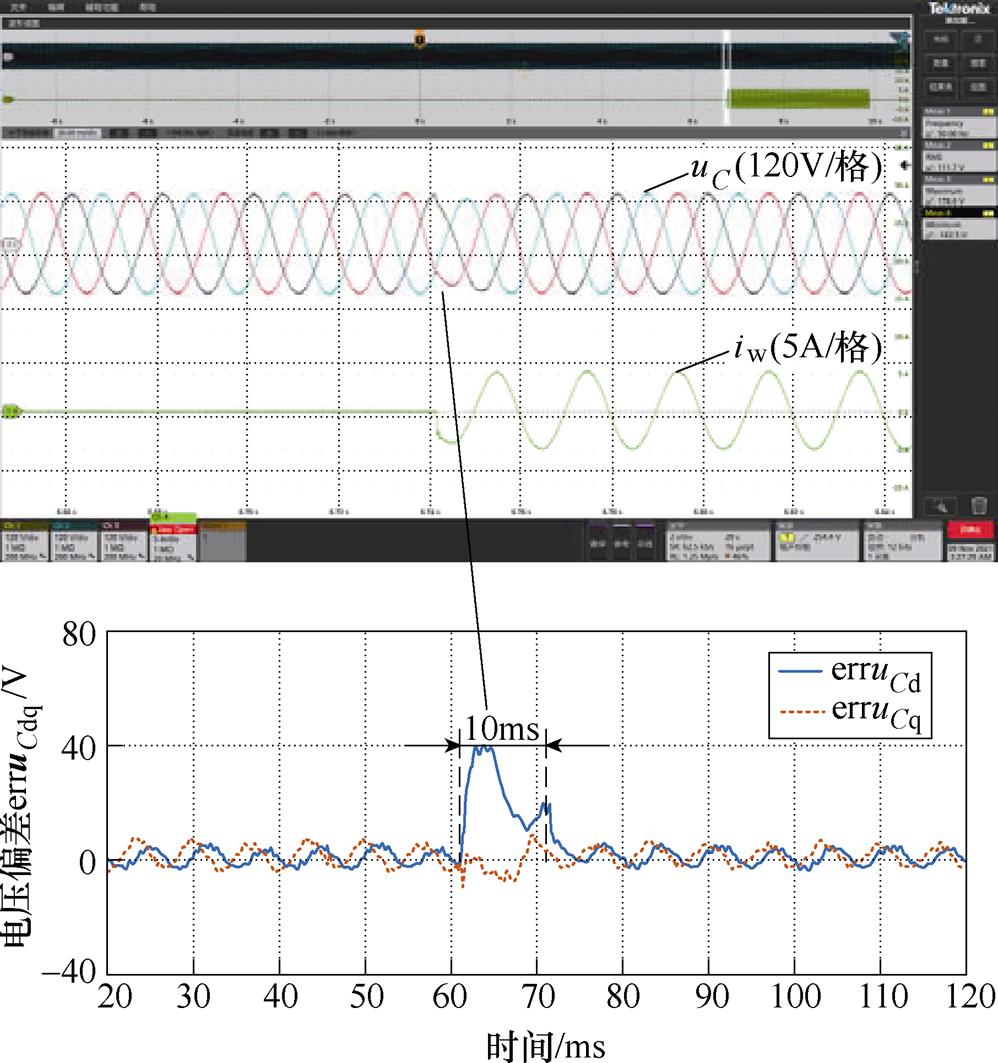
图21 传统PMR控制线性负载波形
Fig.21 Linear load variation waveforms of traditional PMR control
传统PMR控制非线性负载实验如图22所示。对比图19和图22，在非线性负载投载实验中，两种控制方式的稳态THD相差不大，但本文所提多重谐振控制自适应控制动态恢复时间更快（100ms），优于传统PMR控制（160ms），且本文所提控制物理意义明确，对非线性负载扰动的补偿作用在信号控制输入kra得到体现。
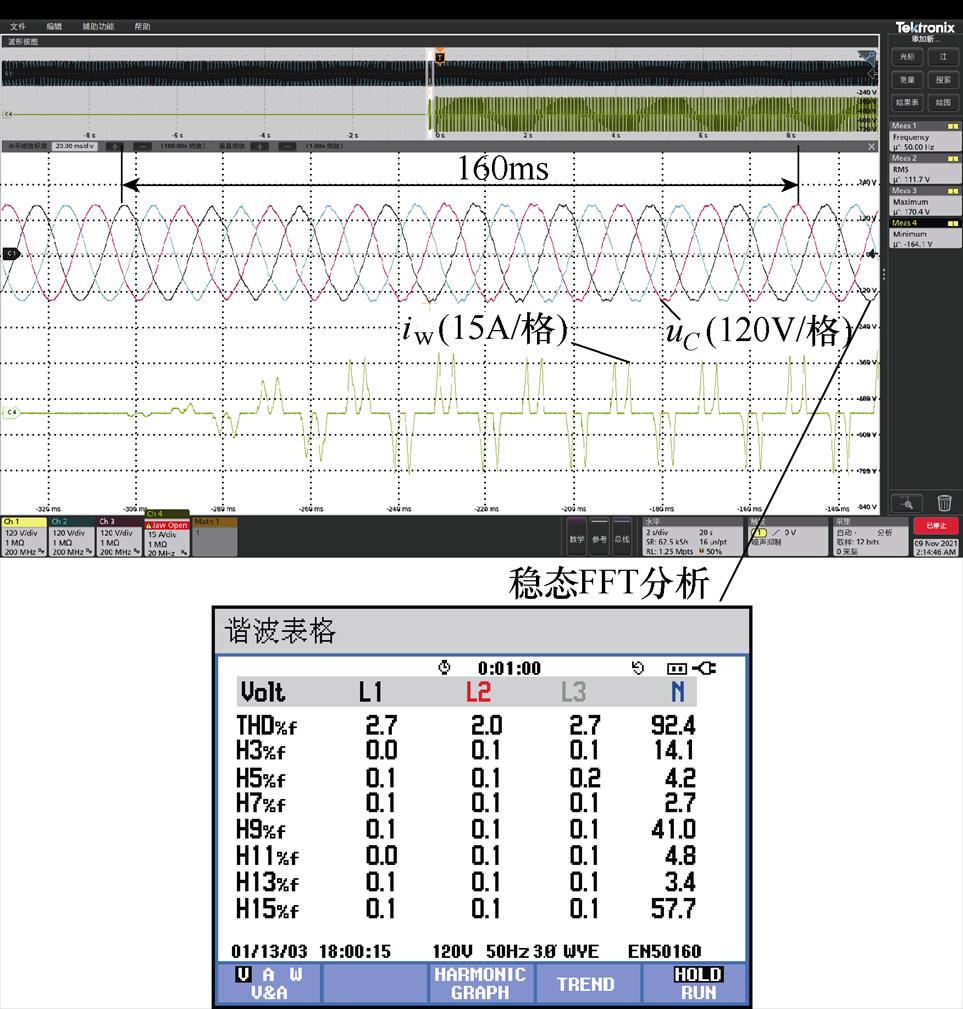
图22 传统PMR控制非线性负载实验
Fig.22 Nonlinear load experiment of traditional PMR control
本文基于复变量模型，提出了一种逆变器参考值前馈自适应电压控制策略，设计了功率控制输入和信号控制输入两种不同的控制输入变量。功率控制输入改善系统自然状态变量动态性能。因信号控制输入的引入，而设计出一种新型多重谐振自适应控制器。
所提多重谐振自适应控制器可通过较小的控制增益，获得较好的动稳态控制性能，动态响应速度快，非线性负载下的稳态THD低。最后实验结果验证了本文所提自适应控制策略的有效性和可行性。
参考文献
[1] 颜湘武, 张伟超, 崔森, 等. 基于虚拟同步机的电压源逆变器频率响应时域特性和自适应参数设计[J]. 电工技术学报, 2021, 36(增刊1): 241-254.
Yan Xiangwu, Zhang Weichao, Cui Sen, et al. Frequency response characteristics and adaptive parameter tuning of voltage-sourced converters under VSG control[J]. Transactions of China Electro- technical Society, 2021, 36(S1): 241-254.
[2] Quan Xiangjun, Yu Ruiyang, Zhao Xin, et al. Photo- voltaic synchronous generator: architecture and control strategy for a grid-forming PV energy system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 936-948.
[3] 唐诗颖, 彭力, 康勇. 脉宽调制逆变电源数字双环控制技术研究[J]. 中国电机工程学报, 2009, 29(15): 55-60.
Tang Shiying, Peng Li, Kang Yong. Research on dual-loop digital control technique for pulse width modulation inverters[J]. Proceedings of the CSEE, 2009, 29(15): 55-60.
[4] 黄如海, 谢少军. 基于比例谐振调节器的逆变器双环控制策略研究[J]. 电工技术学报, 2012, 27(2): 77-81.
Huang Ruhai, Xie Shaojun. Double-loop digital control strategy based on proportional-resonant con- troller[J]. Transactions of China Electrotechnical Society, 2012, 27(2): 77-81.
[5] 孙孝峰, 孟令杰, 杨超. 三相逆变器采样模型重复控制研究[J]. 中国电机工程学报, 2009, 29(15): 36-42.
Sun Xiaofeng, Meng Lingjie, Yang Chao. Repetitive control of three-phase inverter based on sampling model[J]. Proceedings of the CSEE, 2009, 29(15): 36-42.
[6] 曹文远, 韩民晓, 谢文强, 等. 基于扰动观测器的电压源型逆变器负载电流前馈控制及参数设计方法[J]. 电工技术学报, 2020, 35(4): 862-873.
Cao Wenyuan, Han Minxiao, Xie Wenqiang, et al. A disturbance-observer-based load current feedforward control and parameter design method for voltage- sourced inverter[J]. Transactions of China Electro- technical Society, 2020, 35(4): 862-873.
[7] IEC 62040-3. Uninterruptible power systems (UPS)-part 3: method of specifying the performance and test requirements[S]. Switzerland: IEC, 2011.
[8] 赵强松, 叶永强, 徐国峰, 等. 改进重复控制在低采样频率逆变器中的应用[J]. 电工技术学报, 2015, 30(19): 120-127.
Zhao Qiangsong, Ye Yongqiang, Xu Guofeng, et al. Application of improved repetitive control scheme to inverter with low sampling frequency[J]. Transactions of China Electrotechnical Society, 2015, 30(19): 120-127.
[9] 赵强松, 陈莎莎, 周晓宇, 等. 用于并网逆变器谐波抑制的重复-比例复合控制器分析与设计[J]. 电工技术学报, 2019, 34(24): 5189-5198.
Zhao Qiangsong, Chen Shasha, Zhou Xiaoyu, et al. Analysis and design of combination controller based on repetitive control and proportional control for harmonics suppression of grid-tied inverters[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5189-5198.
[10] 全相军, 窦晓波, 龙昌明, 等. 逆变器电压复变量谐振优化控制[J]. 中国电机工程学报, 2016, 36(15): 4214-4223.
Quan Xiangjun, Dou Xiaobo, Long Changming, et al. Optimal design for inverters based on complex variable resonant controllers[J]. Proceedings of the CSEE, 2016, 36(15): 4214-4223.
[11] 杭丽君, 李宾, 黄龙, 等. 一种可再生能源并网逆变器的多谐振PR电流控制技术[J]. 中国电机工程学报, 2012, 32(12): 51-58.
Hang Lijun, Li Bin, Huang Long, et al. A multi- resonant PR current controller for grid-connected inverters in renewable energy systems[J]. Proceedings of the CSEE, 2012, 32(12): 51-58.
[12] Carballo R E, Botterón F, Oggier G G, et al. Design approach of discrete-time resonant controllers for uninterruptible power supply applications through frequency response analysis[J]. IET Power Electro- nics, 2016, 9(15): 2871-2879.
[13] 慕玫君, 林飞, 杨中平, 等. 基于多重化电流跟踪控制的电力机车辅助变流器抑制车网谐振的方法[J]. 电工技术学报, 2018, 33(增刊1):139-148.
Mu Meijun, Lin Fei, Yang Zhongping, et al. Scheme for suppressing resonance oscillation by auxiliary converter of electric locomotive based on multiple- current command tracking[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 139-148.
[14] Hans F, Schumacher W, Chou S F, et al. Design of multifrequency proportional-resonant current controllers for voltage-source converters[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 13573-13589.
[15] 盖阔, 安群涛, 孙力. 基于多重比例谐振的动态电压恢复器谐波补偿策略[J]. 电力自动化设备, 2018, 38(1): 156-161.
Gai Kuo, An Quntao, Sun Li. Harmonic compensation strategy of dynamic voltage restorer based on multiple proportional resonant[J]. Electric Power Automation Equipment, 2018, 38(1): 156-161.
[16] Yepes A G, Freijedo F D, Lopez Ó, et al. Analysis and design of resonant current controllers for voltage- source converters by means of Nyquist diagrams and sensitivity function[J]. IEEE Transactions on Industrial Electronics, 2011, 58(11): 5231-5250.
[17] de Almeida P M, Ribeiro A S B, Souza I D N, et al. Systematic design of a DLQR applied to grid-forming converters[J]. IEEE Journal of Emerging and Selected Topics in Industrial Electronics, 2020, 1(2): 200- 210.
[18] Ribas S P, Maccari Jr L A, Pinheiro H, et al. Design and implementation of a discrete-time H-infinity con- troller for uninterruptible power supply systems[J]. IET Power Electronics, 2014, 7(9): 2233-2241.
[19] Lim J S, Park C, Han J, et al. Robust tracking control of a three-phase DC-AC inverter for UPS appli- cations[J]. IEEE Transactions on Industrial Elec- tronics, 2014, 61(8): 4142-4151.
[20] Cortes P, Ortiz G, Yuz J I, et al. Model predictive control of an inverter with output LC filter for UPS applications[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 1875-1883.
[21] Yaramasu V, Rivera M, Narimani M, et al. Model predictive approach for a simple and effective load voltage control of four-leg inverter with an output LC filter[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5259-5270.
[22] 李景灏, 吴爱国. 基于离散趋近律与无差拍双闭环结构的单相LCL型PWM整流器控制策略[J]. 电工技术学报, 2021, 36(6): 1290-1303.
Li Jinghao, Wu Aiguo. A double closed-loop control method for single-phase PWM rectifiers with LCL filter based on discrete reaching law and deadbeat algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1290-1303.
[23] Komurcugil H, Altin N, Ozdemir S, et al. An extended Lyapunov-function-based control strategy for single-phase UPS inverters[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3976-3983.
[24] Do T D, Leu V Q, Choi Y S, et al. An adaptive voltage control strategy of three-phase inverter for stand-alone distributed generation systems[J]. IEEE Transactions on industrial Electronics, 2013, 60(12): 5660-5672.
[25] Jung J W, Vu N T T, Dang D Q, et al. A three-phase inverter for a standalone distributed generation system: adaptive voltage control design and stability analysis[J]. IEEE Transactions on Energy Conversion, 2014, 29(1): 46-56.
[26] Dang D Q, Choi Y S, Choi H H, et al. Experimental validation of a fuzzy adaptive voltage controller for three-phase PWM inverter of a standalone DG unit[J]. IEEE Transactions on Industrial Informatics, 2015, 11(3): 632-641.
[27] de Bosio F, de Souza Ribeiro L A, Freijedo F D, et al. Effect of state feedback coupling and system delays on the transient performance of stand-alone VSI with LC output filter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(8): 4909-4918.
[28] 解学书. 最优控制理论与应用[M]. 北京: 清华大学出版社, 1986.
[29] Quan Xiangjun, Dou Xiaobo, Wu Zaijun, et al. A novel dominant dynamic elimination (DDE) control for voltage-controlled inverter[J]. IEEE Transactions on Industrial Electronics, 2018, 65(8): 6800-6812.
A Multiple Resonant Based on Reference Feedforward Adaptive Voltage Control of Three-Phase Inverter
Abstract This paper proposes a multiple resonant based reference feedforward adaptive voltage control for three-phase inverters. The state-space model is established based on complex variables. Then, the proposed voltage controller includes two control parts: power control input and signal control input. The former improvesdynamic performance using state feedback and reference feedforward. A dynamic adaptive gain of the reference feedforward is defined as the signal control input, and the integral resonant controller is used to achieve no static error control. The rule of parameter variation is discussed by the root locus method to improve the dynamic performance. The proposed control strategy is a new type of multiple resonance control structure, and a new adaptive control idea is given. Besides, the proposed control method has excellent voltage regulation performance, including fast transient response, zero steady-state error, and low total harmonic distortion. The experimental results verify the proposed control scheme.
keywords：Inverter control, adaptive control, multiple resonant controller, complex variable
DOI: 10.19595/j.cnki.1000-6753.tces.211457
中图分类号：TM464
国家电网有限公司总部科技资助项目（SGMD0000YXJS1900502）。
收稿日期 2021-09-13
改稿日期 2021-12-23
黄仁志 男，1994年生，博士研究生，研究方向为逆变器运行控制。E-mail: 230189233@seu.edu.cn
全相军 男，1985年生，博士，讲师，研究方向为电力电子控制、储能变流器、分布式电源控制技术。E-mail: xquan@seu.edu.cn（通信作者）
（编辑 陈 诚）