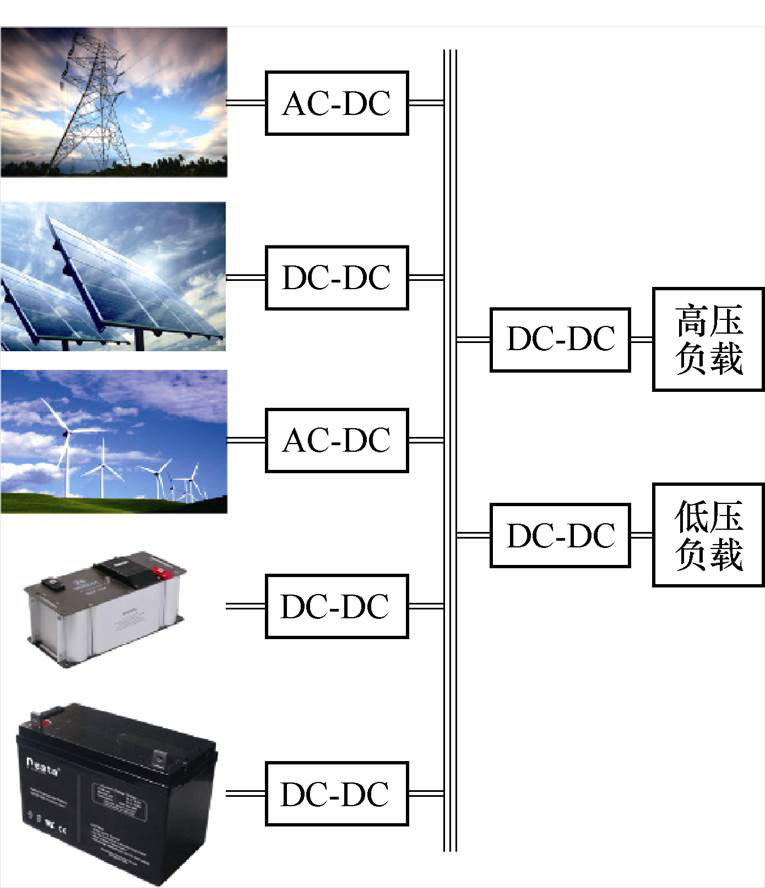
图1 混合储能微电网
Fig.1 Hybrid energy storage microgrid
摘要 混合储能微电网的并、离网模式灵活切换可较好地容纳分布式能源,但在复杂的工况下,其用电端降压接口的电能质量会受到影响。为此,该文提出一种带有参数自寻优的模糊自抗扰控制(FLADRC)策略对传统双闭环PI控制方式的外环进行改造。首先,根据需求对变换器模型进行分析与化简,并通过状态空间平均法进行建模;然后,依据状态方程包含的模型信息设计了FLADRC的线性扩张状态观测器(LESO)矩阵;之后,在频域分析部分,探究应用FLADRC时的系统性能,从理论上分析FLADRC的跟踪性、收敛性和抗扰性,并基于分析结果给出参数自寻优的模糊逻辑规则;此外,运用李雅普诺夫稳定性理论证明了应用FLADRC时微电网接口变换器的稳定性;最后,在40kW的实验平台上进行实验测试,得到了在多种工况下不同控制策略的动态曲线。实验结果验证了该文所提FLADRC方法的可行性和有效性。
关键词:微电网 状态空间平均法 自抗扰控制 模糊逻辑 李雅普诺夫稳定性理论
能源短缺和环境污染推动着能源结构的变革,使分布式能源得到了快速发展,并在社会的发展中扮演愈发重要的角色[1-2]。微电网技术代表了未来分布式能源供应系统的发展趋势,而其中传统的电能变换技术已经不能满足未来智能配用电系统对电能变换特性的需求。随着碳化硅、氮化镓等宽禁带电力电子器件的快速发展和应用,微电网系统的接口变换器正朝着小型化、高频化的方向发展[3-4]。在微电网的运行中,宽禁带器件具有超高频、可靠性强和功率密度大等优良特性,这不仅降低了功率器件损耗,同时能够大幅提高微电网接口变换器的工作频率和效率[5-6]。
目前,主要通过对微电网接口变换器控制环节进行优化和改造来实现对扰动型输出电压波动的抑制。根据目前研究中的建模分析得知,蓄电池和超级电容储能系统均具有典型的非线性特性,与此同时,接口变换器也是一个非线性结构[7-8]。特别是在基于宽禁带器件的背景下,微电网系统中非线性、时变性将更加明显,这就更加恶化了经典PI控制的动态响应[9]。为此,很多学者将一些先进的算法(如粒子群、神经网络算法等)应用到变换器的控制中[10-11]。然而,由于这些算法的过程复杂,难以获得准确的数学模型,进而难以推广。
自抗扰控制技术[12]由韩京清提出的,是一种在传统PID控制基础上发展起来的新型非线性控制策略。它通过跟踪-微分器安排闭环系统的过渡过程,在几乎无超调的前提下实现指令的快速跟踪;再通过扩张状态观测器(Extended State Observer, ESO)将含有未知扰动的非线性不确定对象用非线性状态反馈转化为“积分器串联型”;非线性状态误差反馈控制律组合出理想的控制器。该控制方式核心是基于扰动消除扰动,具备鲁棒性、抗干扰能力强的特点[13-14]。目前自抗扰控制器已初步应用于有源电力滤波器控制[15]、电机控制[16]和静止无功发生器控制[17]。但是传统的自抗扰控制器主要由非线性函数构成,其参数众多、分析困难,难以在工程中推广应用。因此高志强教授和他的团队开发出线性自抗扰控制(Linear Active Disturbance Rejection Control, LADRC)策略,此方法继承了传统非线性自抗扰的核心功能,并将大多数参数整合,使其与带宽线性相关,简化了调参过程,促进了自抗扰控制的工程化应用[18-19]。
微电网的非线性、强耦合、负载扰动强等特性决定了负载侧变换器需要很轻的抗扰性才能满足用户端对电能质量的需求。为此本文将模糊逻辑与自抗扰控制技术相结合,构造一种在运行时自动寻优的模糊自抗扰控制策略来提高微电网接口变换器的鲁棒性。首先,分析了交错并联Buck变换器的数学模型。然后,本文基于状态空间表达式将已知的部分模型信息集成到LESO的系数矩阵中,同时介绍了结合模糊逻辑规则的控制律,给出了模糊自抗扰控制策略的具体结构。再者,应用频域分析法和李雅普诺夫(Lyapunov)稳定性理论分析了系统的跟踪性、抗扰性、收敛性和稳定性,并基于动态特性与控制增益的关系给出了参数自寻优的模糊逻辑规则表。最后,在40kW实验平台上进行了性能测试,验证了所提控制策略的正确性、有效性和可行性。
混合储能微电网的结构如图1所示,在其运行中,由于分布式能源的不稳定性导致各接口变换器都需要很强的鲁棒性才能维持较好的电能质量。本文以负载侧低压接口变换器的控制策略为研究目标,提高低压负载接口变换器的鲁棒性。

图1 混合储能微电网
Fig.1 Hybrid energy storage microgrid
降压接口处采用的是6路交错并联型变换器拓扑结构,如图2所示。由于动态过程相似,接下来仅对单路进行分析。假设电路元器件均为理想元器件。针对一个周期内,S1的开通与关断,将电路的工作状态在每个周期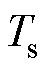 内分成
内分成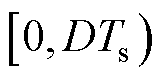 与
与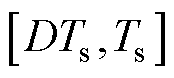 两部分,即工作状态1和工作状态2,其中
两部分,即工作状态1和工作状态2,其中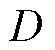 为占空比。在工作状态1即
为占空比。在工作状态1即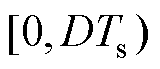 时段内,S1导通,VD1截止。电感电压
时段内,S1导通,VD1截止。电感电压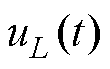 与电容电流
与电容电流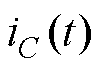 分别为
分别为
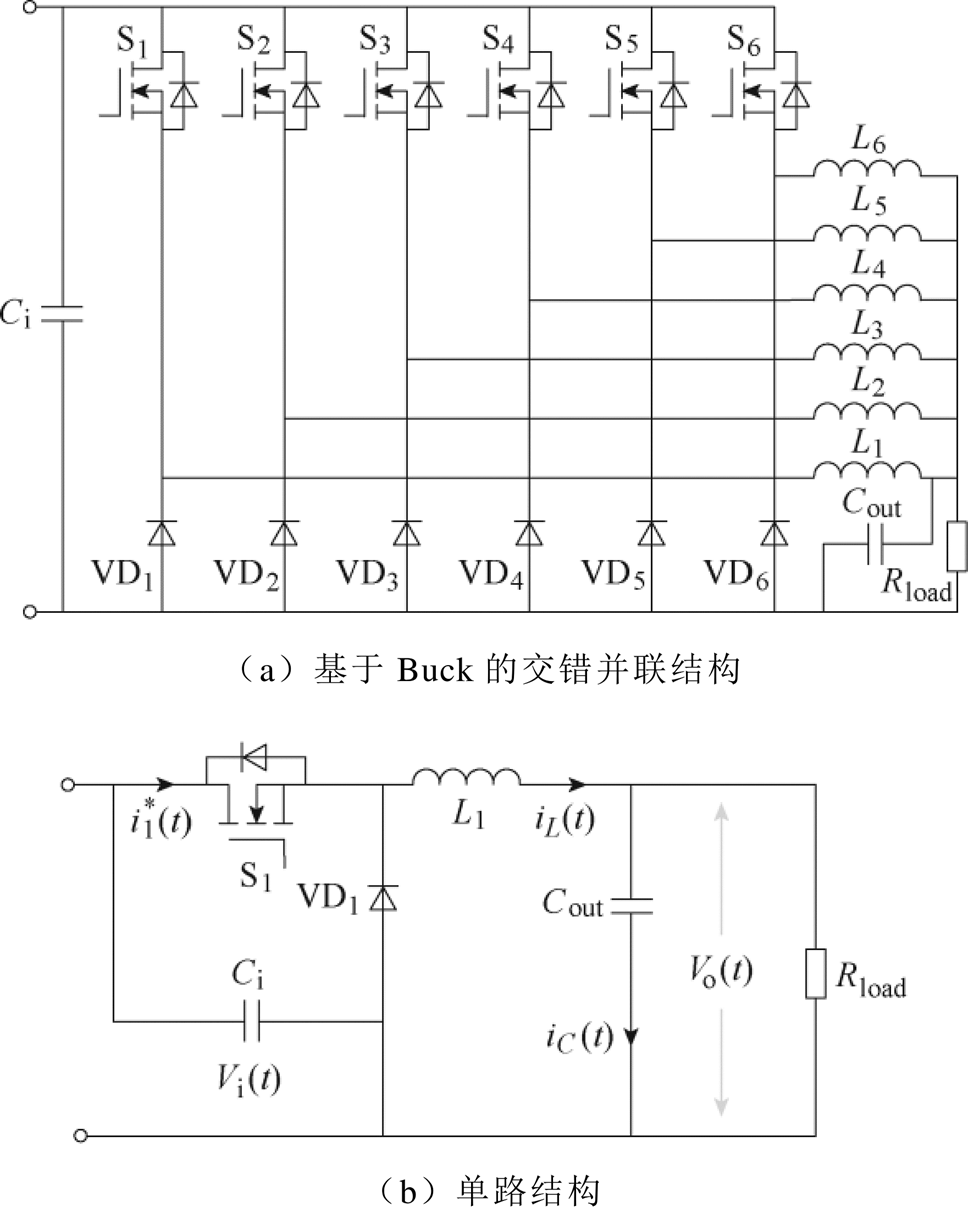
图2 变换器拓扑
Fig.2 Converter topology
 (1)
(1)
式中,L1为电感;Vi(t)为输入电压;Vo(t)为输出电压;Cout为输出电容;Rload为负载电阻。
输入电流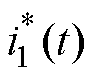 即为电感电流
即为电感电流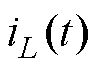 ,输出电压
,输出电压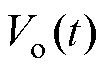 即为电容电压。将式(1)写成状态方程与输出方程的形式,分别为
即为电容电压。将式(1)写成状态方程与输出方程的形式,分别为
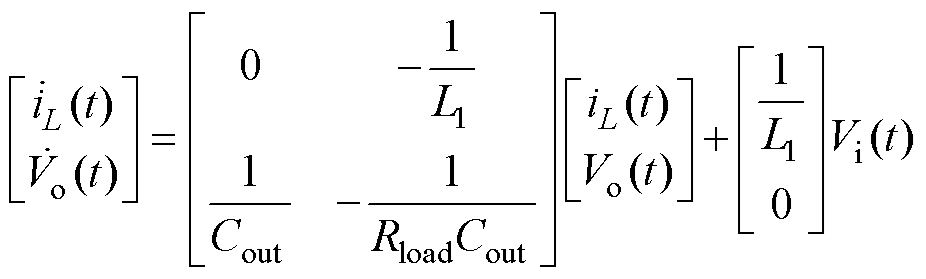 (2)
(2)
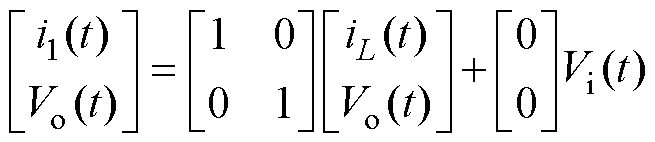 (3)
(3)
为了方便表示,令
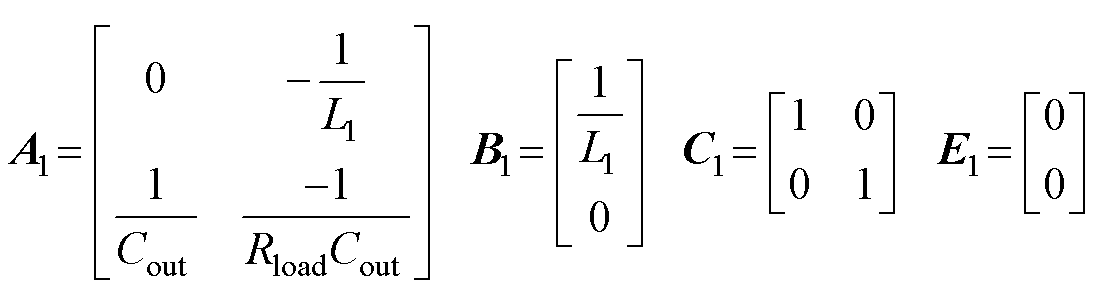
在工作状态2即 时段内,S1截止,VD1导通。在此工作状态下,状态方程与输出方程的形式分别为
时段内,S1截止,VD1导通。在此工作状态下,状态方程与输出方程的形式分别为
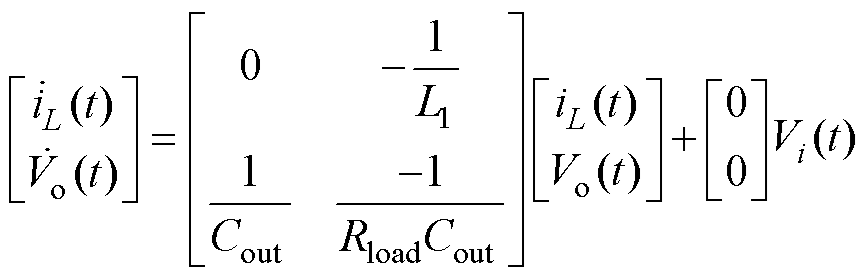 (4)
(4)
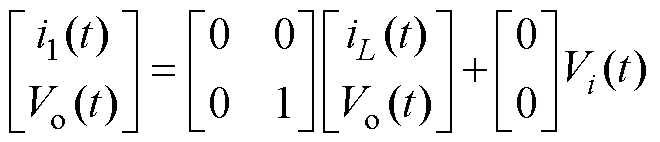 (5)
(5)
同理,令
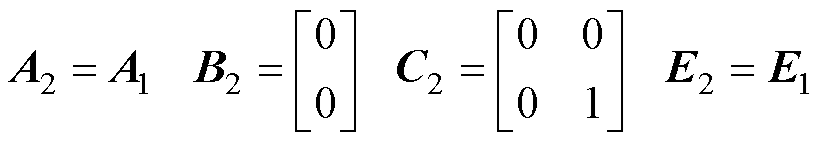
当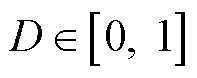 时,可得到状态方程的通用表达式为
时,可得到状态方程的通用表达式为
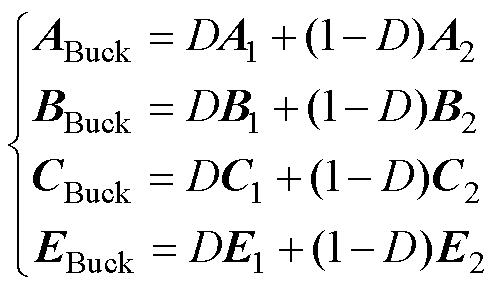 (6)
(6)
算得
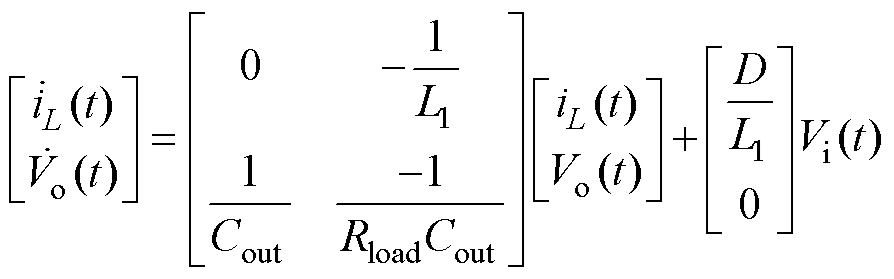 (7)
(7)
实际应用中变换器每次动作都存在一定的损耗,随着微电网变换器逐渐高频化,基于SiC的变换器损耗会比较严重。所以对变换器建模时,应该考虑器件的寄生元件。显然,式(7)没有考虑寄生元件对动态过程的影响。为了达到较为理想的控制目标,本文将这些寄生参数视为内扰,同时将直流母线电压的波动视为外扰,利用强鲁棒性的一阶线性自抗扰控制器对其进行控制。
根据状态方程的数学意义可知,输入输出满足一阶齐次微分方程的对应关系。为了达到较好的控制性能,应选用一阶自抗扰控制器。经典的一阶自抗扰控制器结构如图3所示。
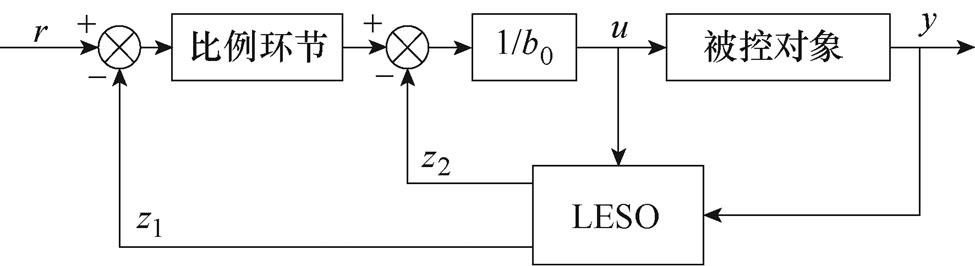
图3 1st-LADRC控制器
Fig.3 1st-LADRC controller
图3中,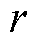 为负载所需电压的参考值;
为负载所需电压的参考值;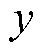 为负载所需电压的实际值;
为负载所需电压的实际值;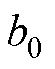 为控制增益;
为控制增益; 为
为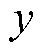 的观测值;
的观测值;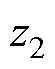 为总扰动的观测值;
为总扰动的观测值;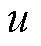 为含有控制信息信号流,其物理含义为SiC的触发信号。
为含有控制信息信号流,其物理含义为SiC的触发信号。
以LESO为核心的常规LADRC是一种基于扰动消除扰动的控制策略。区别于基于误差消除的传统控制方式,它通过对图2所示变换器所有信息的观测和补偿来实现对建模误差的估计。器件的寄生元件被视为建模偏差即内扰,与外部扰动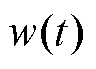 一起记为未知扰动总和
一起记为未知扰动总和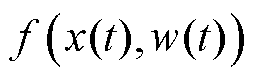 ,其包含了所有的外扰与模型信息、控制增益以及它们受参数飘动等不确定性因素影响的变化量。由LESO和扰动补偿环节进行计算和处理。为简化推导过程,后文中将
,其包含了所有的外扰与模型信息、控制增益以及它们受参数飘动等不确定性因素影响的变化量。由LESO和扰动补偿环节进行计算和处理。为简化推导过程,后文中将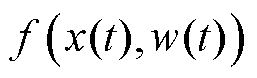 简化为
简化为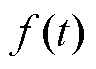 。为了降低LESO的观测负担,将部分已知的参数写入系统矩阵
。为了降低LESO的观测负担,将部分已知的参数写入系统矩阵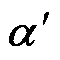 ,使其不再依赖扰动环节的观测和补偿。为了方便结合模型信息LESO矩阵的推导,基于本文第1节对接口变换器的模型分析,将式(7)重写为
,使其不再依赖扰动环节的观测和补偿。为了方便结合模型信息LESO矩阵的推导,基于本文第1节对接口变换器的模型分析,将式(7)重写为
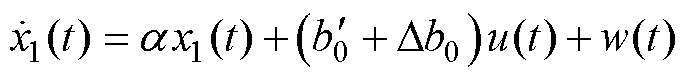 (8)
(8)
式中,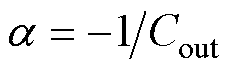 ;
;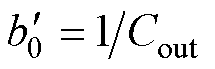 ;
;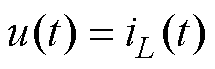 。
。
根据模型分析,选取相同的状态变量,则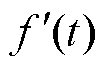 为实际的未知扰动总和,即
为实际的未知扰动总和,即
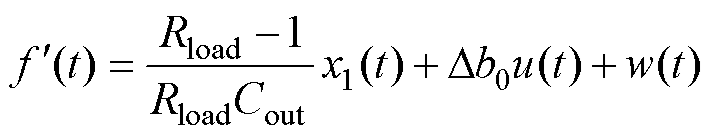 (9)
(9)
则式(8)又可写为
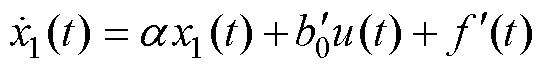 (10)
(10)
写成状态空间形式为
 (11)
(11)
其中
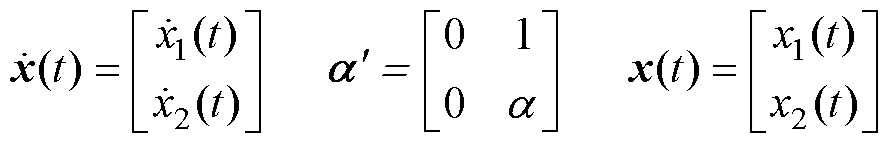
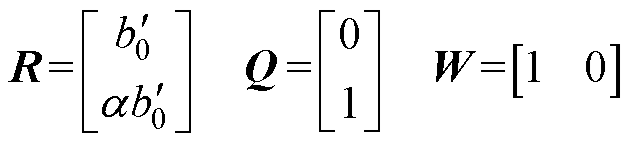
对应的连续LESO为
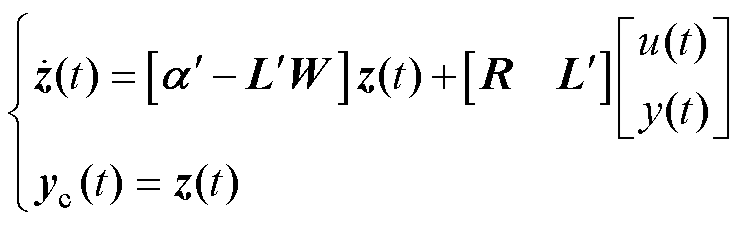 (12)
(12)
式中, ,
,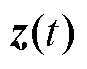 为扩张状态观测器的状态变量矩阵;
为扩张状态观测器的状态变量矩阵;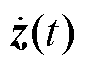 为状态变量导数矩阵;yc(t)为LESO的输出;
为状态变量导数矩阵;yc(t)为LESO的输出;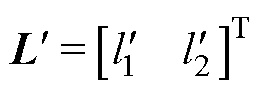 为需要结合被控对象设计的状态观测器增益矩阵。根据极点配置方法[20],对上述LESO做如下配置
为需要结合被控对象设计的状态观测器增益矩阵。根据极点配置方法[20],对上述LESO做如下配置
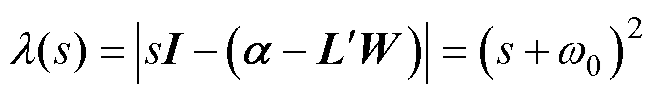 (13)
(13)
式中,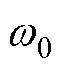 为观测器带宽;I为单位矩阵。经过极点配置过程,算得增益矩阵为
为观测器带宽;I为单位矩阵。经过极点配置过程,算得增益矩阵为
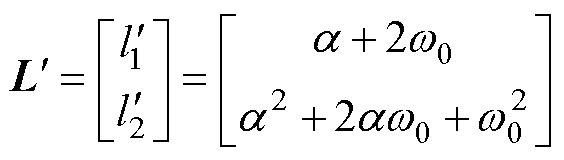 (14)
(14)
针对此二阶LESO,线性状态误差反馈律为比例控制律,则线性状态误差反馈律应为
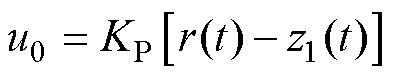 (15)
(15)
式中,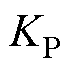 为控制器放大系数。经过参数化,取
为控制器放大系数。经过参数化,取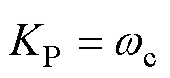 ,
,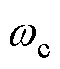 为控制器带宽,与其对应的扰动补偿环节为
为控制器带宽,与其对应的扰动补偿环节为
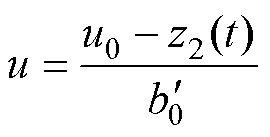 (16)
(16)
通过频域分析,可以得到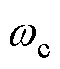 与动态响应之间的关联。将对应关系编辑成期望的模糊逻辑。这样就可利用计算机代替工程师在运行过程中调节参数,实现控制器在运行中的自寻优,具体的对应关系见3.1节。根据式(15)、式(16)并结合模糊逻辑,可以得到本文所设计的FLADRC结构,基于模型信息的FLADRC如图4所示。
与动态响应之间的关联。将对应关系编辑成期望的模糊逻辑。这样就可利用计算机代替工程师在运行过程中调节参数,实现控制器在运行中的自寻优,具体的对应关系见3.1节。根据式(15)、式(16)并结合模糊逻辑,可以得到本文所设计的FLADRC结构,基于模型信息的FLADRC如图4所示。
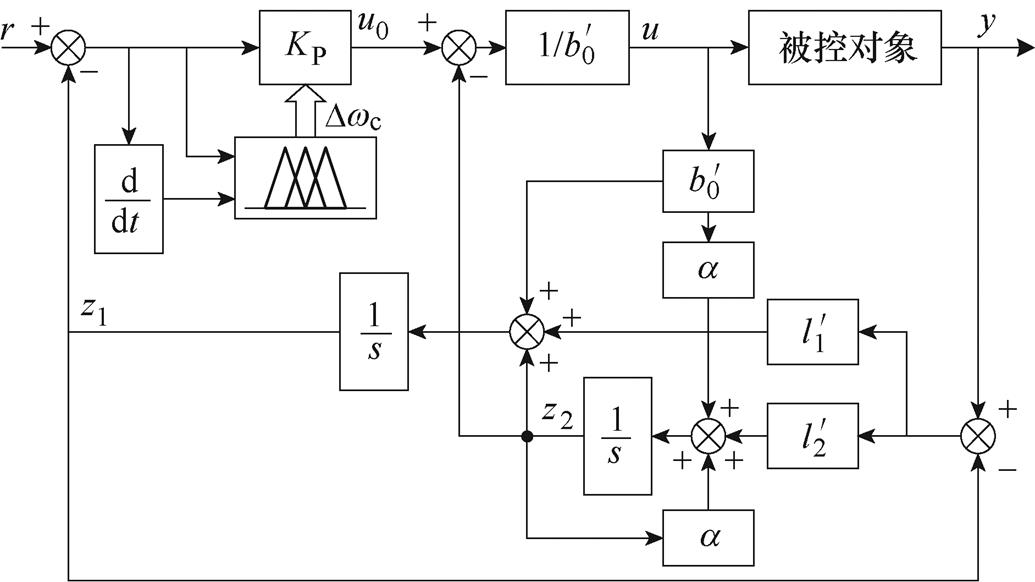
图4 基于模型信息的FLADRC
Fig.4 Detailed structure of FLADRC withmodel
根据式(12)可知,基于模型信息LESO的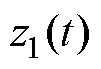 和
和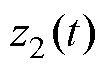 的传递函数分别为
的传递函数分别为
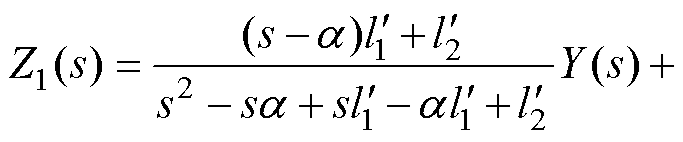
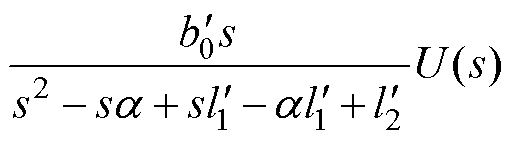 (17)
(17)

 (18)
(18)
由式(12)、式(14)可得
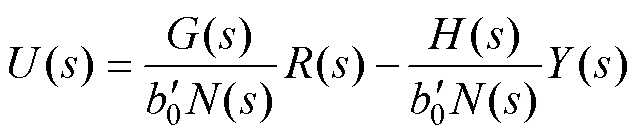 (19)
(19)
其中
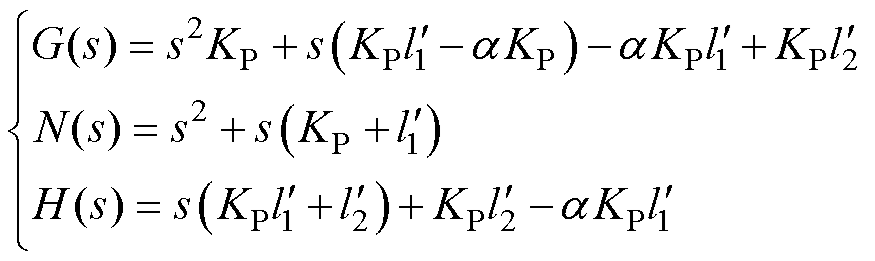
根据式(12),可视被控对象为
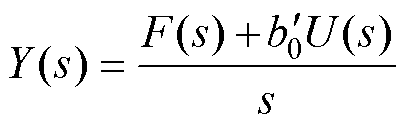 (20)
(20)
结合式(19)、式(20),可将图4所示结构简化为图5结构。进而,可得结合模型信息的FLADRC闭环传递函数为
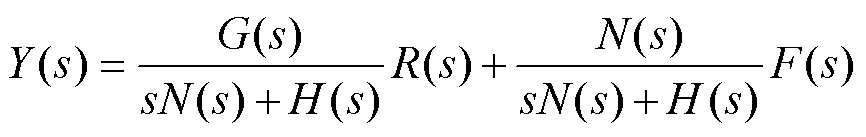
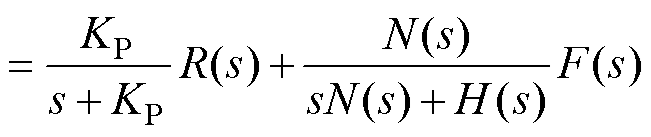 (21)
(21)
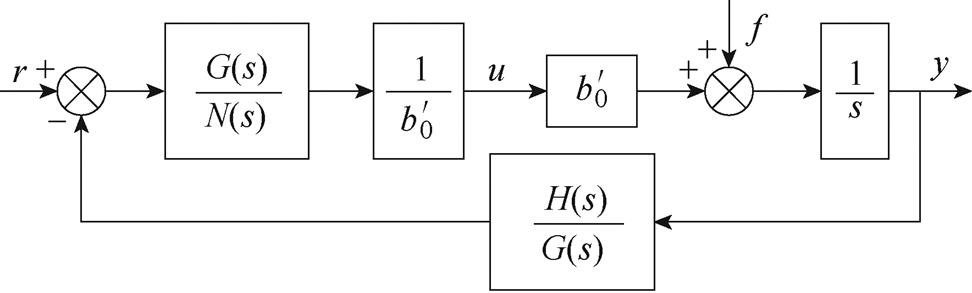
图5 FLADRC简化结构
Fig.5 Simplify the structure of FLADRC
由式(21)可知,变换器的输出由两部分构成,包括输入信号跟踪项和外部干扰项,其中输入信号跟踪项的构成和无模型信息的常规一阶LADRC相同,只和线性误差反馈律参数有关。当忽略扰动项的影响时,通过调整 ,可以改变系统的跟踪性能。wc对LADRC的影响如图6所示。由图6可知,在
,可以改变系统的跟踪性能。wc对LADRC的影响如图6所示。由图6可知,在 较小时,
较小时, 的变化对系统快速性的改变较为明显。在
的变化对系统快速性的改变较为明显。在 增加到一定值后,
增加到一定值后, 变化同样大小的数值对系统的影响较小,即系统跟踪速度对于参数
变化同样大小的数值对系统的影响较小,即系统跟踪速度对于参数 的敏感程度会随着
的敏感程度会随着 的增加而减小。因此,可据此来调整控制器带宽。
的增加而减小。因此,可据此来调整控制器带宽。
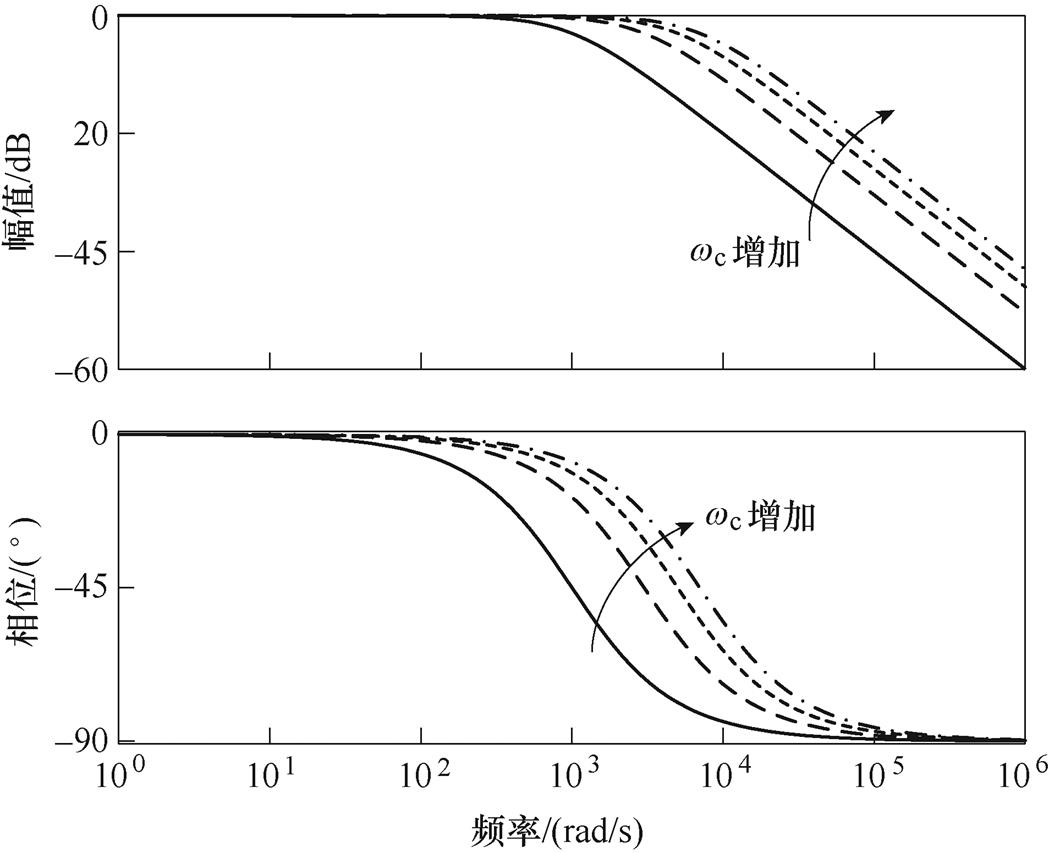
图6 wc对LADRC的影响
Fig.6 Impact of wc on LADRC
根据图6中的频域特性曲线可知,随着 增加,系统的快速性提高,但对噪声的灵敏度也会增加。为此,在对
增加,系统的快速性提高,但对噪声的灵敏度也会增加。为此,在对 参数选择时,要权衡系统快速性和噪声灵敏度两方面因素,即在扰动较大时,
参数选择时,要权衡系统快速性和噪声灵敏度两方面因素,即在扰动较大时, 应较大;而当系统重新进入稳态后,
应较大;而当系统重新进入稳态后, 应较小。以此为调节思想整定模糊逻辑规则,见表1。负载侧电压的偏差
应较小。以此为调节思想整定模糊逻辑规则,见表1。负载侧电压的偏差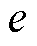 和其导数
和其导数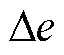 作为模糊逻辑输入,
作为模糊逻辑输入, 的变化量
的变化量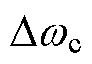 为输出。
为输出。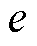 、
、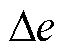 和
和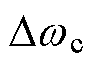 的基本论域均为[-5, 5]。设
的基本论域均为[-5, 5]。设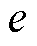 和
和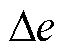 的变化范围为[-5, 5],如果不在此区间,通过线性变换将取值在
的变化范围为[-5, 5],如果不在此区间,通过线性变换将取值在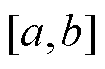 之间的连续量转换到[-5, 5]之间。
之间的连续量转换到[-5, 5]之间。
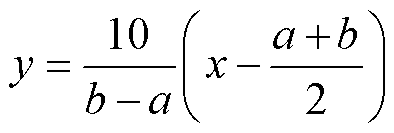 (22)
(22)
表1 模糊逻辑规则
Tab.1 Fuzzy control rule table

De NBNSZOPSPB NBPBPBPSPSZO NSPSPSPSZONS ZOPSPSZONSNS PSPSZONSNSNS PBZONSNSNBNB
根据模糊逻辑规则,其输入、输出如图7所示。根据所选初始数值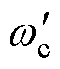 的不同,选取合适的放大系数
的不同,选取合适的放大系数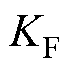 ,可得到最终的比例控制系数为
,可得到最终的比例控制系数为


图7 模糊逻辑的输入与输出信息
Fig.7 Input and output information of fuzzy logic
 (23)
(23)
外部干扰项是影响FLADRC系统性能的重要因素,主要由LESO的动态观测误差组成。图8为结合模型信息FLADRC和无模型FLADRC的频域特性曲线,a=0时表示无模型的FLADRC。可以看出,随着a 等模型信息的引入,FLADRC的扰动抑制能力明显增强。
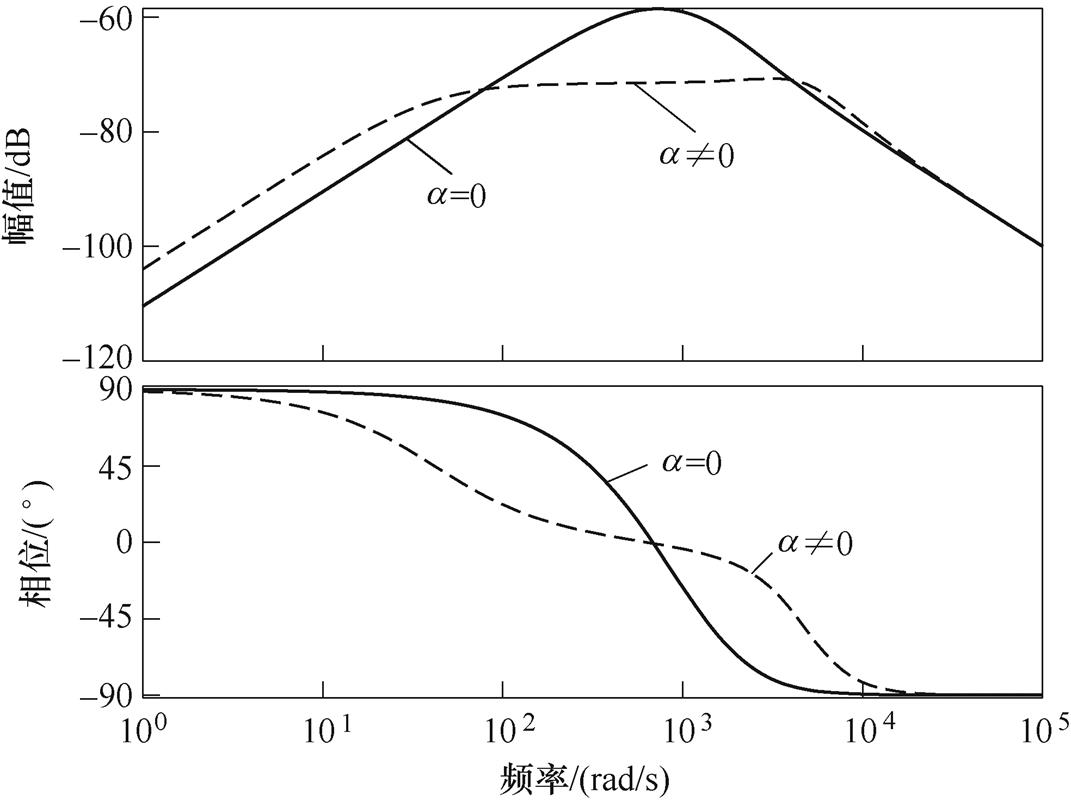
图8 改进前后FLADRC抗扰性能分析
Fig.8 Analysis of FLADRC immunity performance before and after improvement
图9表示不同的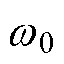 与结合模型信息FLADRC的对应关系。由此可知,在中频段结合模型信息的FLADRC与无模型信息的FLADRC相比,等效输出阻抗幅值明显降低,进而可知抗负载扰动能力更强。在高频段,受限于LESO带宽,两者幅相特性曲线接近。另外,在
与结合模型信息FLADRC的对应关系。由此可知,在中频段结合模型信息的FLADRC与无模型信息的FLADRC相比,等效输出阻抗幅值明显降低,进而可知抗负载扰动能力更强。在高频段,受限于LESO带宽,两者幅相特性曲线接近。另外,在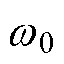 较小时,
较小时,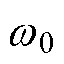 的变化对系统抗扰性的影响比较大,在
的变化对系统抗扰性的影响比较大,在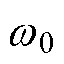 较大时,
较大时,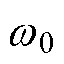 的变化对系统抗扰性的影响比较小。也就是说系统的抗扰性对于参数
的变化对系统抗扰性的影响比较小。也就是说系统的抗扰性对于参数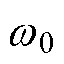 的敏感程度随着
的敏感程度随着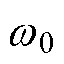 的增加而减小。
的增加而减小。
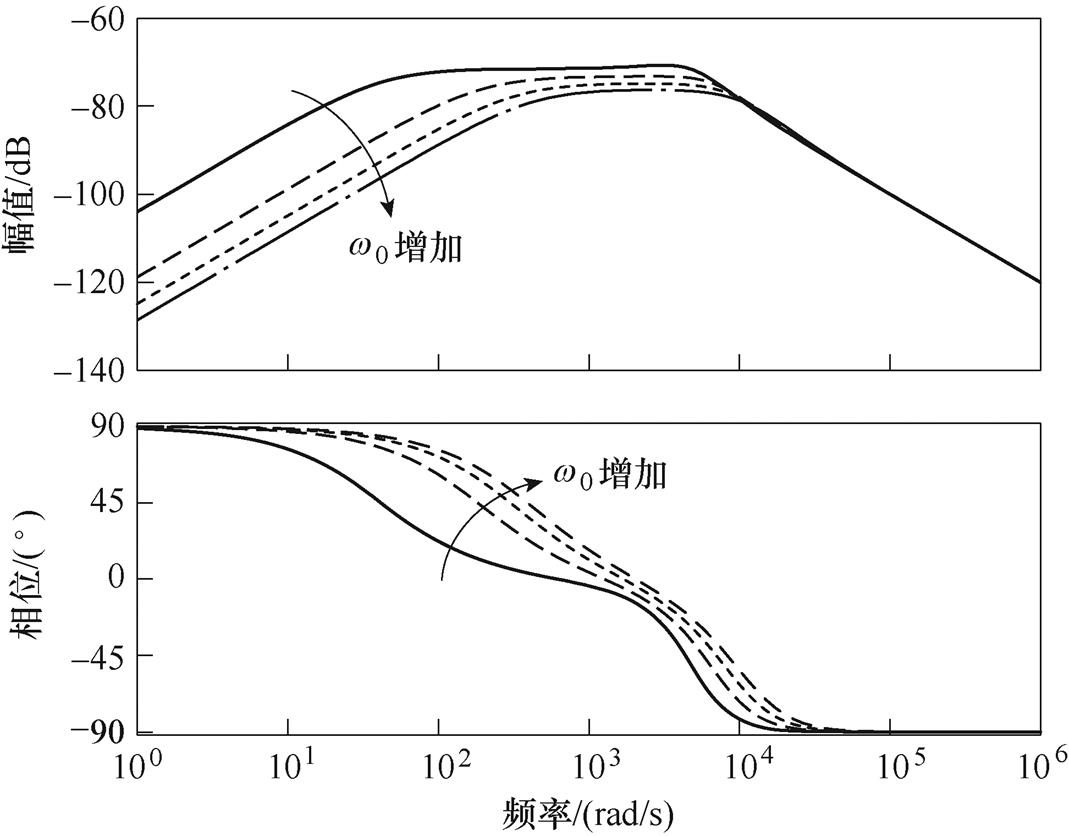
图9 变化带宽对FLADRC的影响
Fig.9 Impact of varying bandwidth on FLADRC
在将模型信息引入LESO的系统矩阵后,其结构发生了一些变化,为了验证收敛性,特对其进行分析。设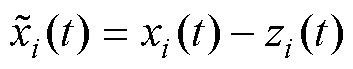 ,
,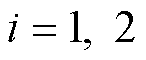 ,由式(12)得LESO的估计误差计算式为
,由式(12)得LESO的估计误差计算式为
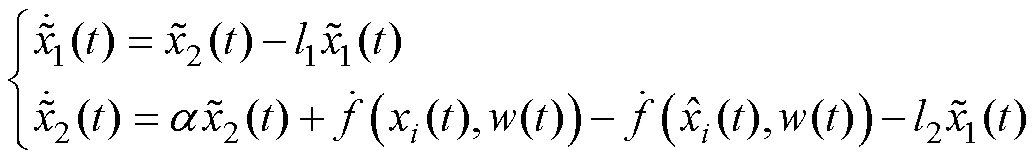 (24)
(24)
设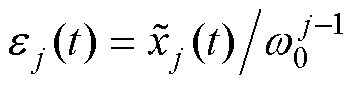 ,
,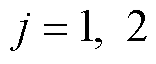 ,则式(24)可改写为
,则式(24)可改写为
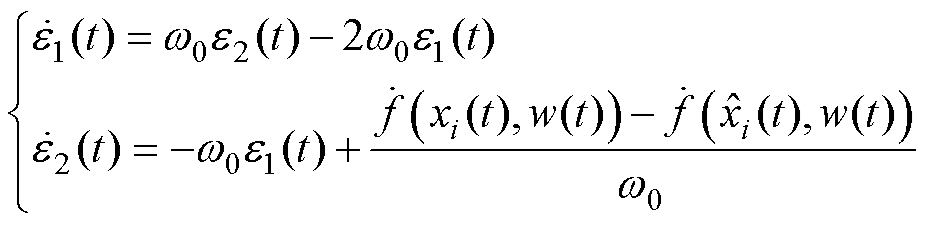 (25)
(25)
即
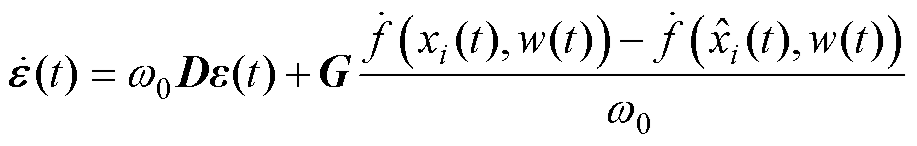 (26)
(26)
其中
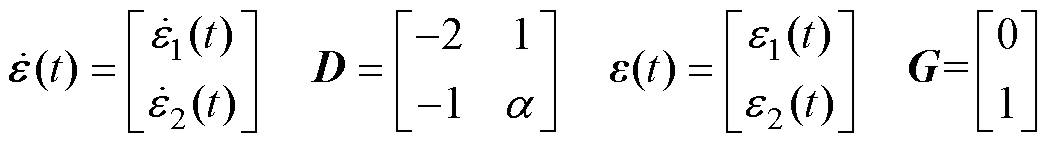
由极点配置法整定的扩张状态观测器增益矩阵可知,LESO的双重极点配置在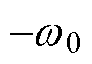 处,
处,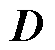 是Hurwitz稳定的。则存在一个正定的Hermitian矩阵
是Hurwitz稳定的。则存在一个正定的Hermitian矩阵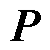 ,使满足
,使满足
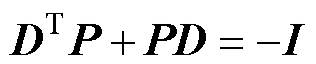 (27)
(27)
其中
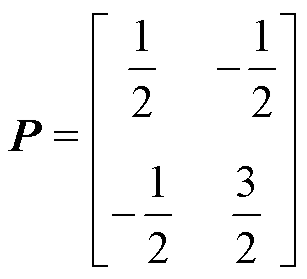
定义Lyapunov函数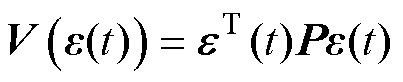 ,则有
,则有
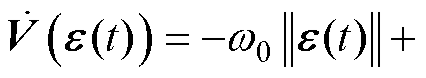
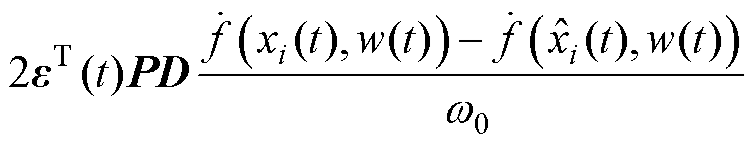 (28)
(28)
由于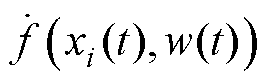 在定义域内满足Lipschitz连续条件,那么存在一个常数
在定义域内满足Lipschitz连续条件,那么存在一个常数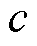 ,使得对于所有的
,使得对于所有的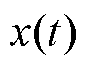 、
、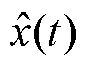 和
和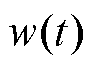 都有
都有
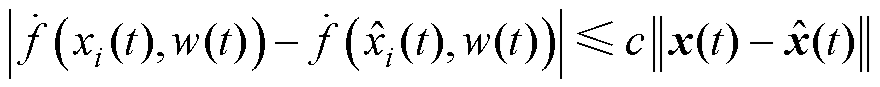 (29)
(29)
成立,则
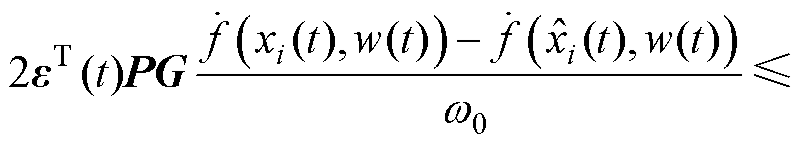
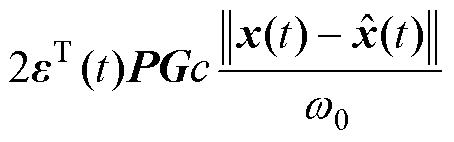 (30)
(30)
当 ,有
,有
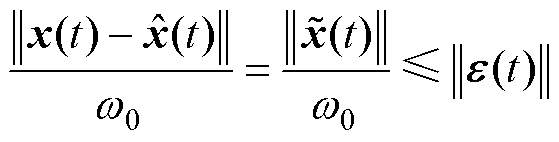 (31)
(31)
同时,又由于 ,故
,故
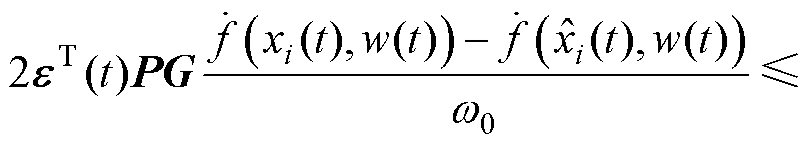
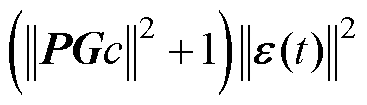 (32)
(32)
由式(28)、式(32)可得
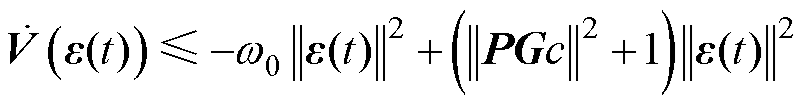 (33)
(33)
当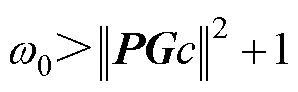 时,
时, 根据Lyapunov渐近稳定的意义为
根据Lyapunov渐近稳定的意义为
 (34)
(34)
成立。根据上述推导并结合式(34)可知,Lyapunov渐近稳定性定理成立。故当时间趋于无穷时,线性扩张状态观测器的估计误差为零,即 ,
,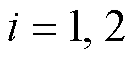 。因此LESO是收敛的。
。因此LESO是收敛的。
交错并联型降压变换器的FLADRC主要包括自抗扰算法与PWM两部分。FLADRC通过LESO和模糊线性误差反馈控制律,将非线性时变系统补偿成积分器串联型。由图4可知,FLADRC是一个含有变换器信息的闭环,因此存在稳定性问题,针对本文所提的模型,证明其稳定性。在控制目标中,假定控制的目标是被控对象的输出跟踪有界输入信号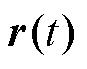 ,为了方便表述,令
,为了方便表述,令
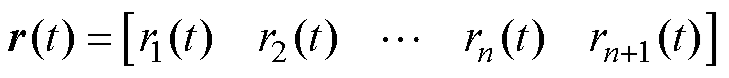
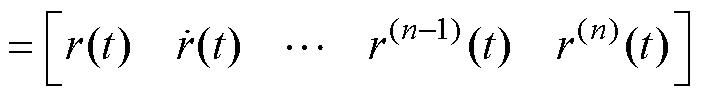 (35)
(35)
在自抗扰控制过程中,由式(16)可知,模糊反馈控制律为
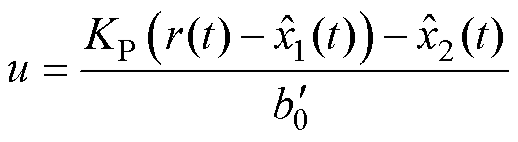 (36)
(36)
设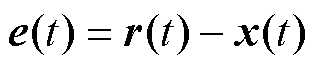 ,由式(36)得
,由式(36)得
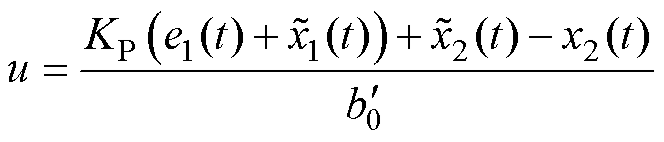 (37)
(37)
 (38)
(38)
此外在LESO精确设计的情况下,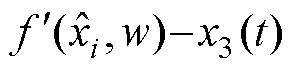 可忽略不计。式(38)又可以写为
可忽略不计。式(38)又可以写为
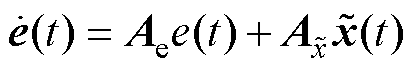 (39)
(39)
其中
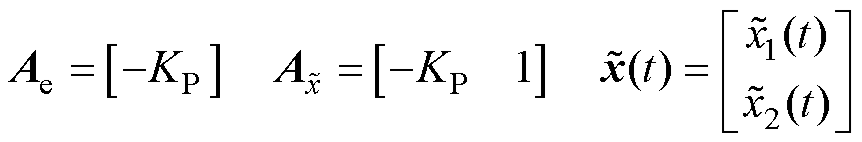
由于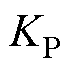 使特征多项式
使特征多项式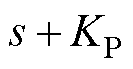 满足Routh判据,故
满足Routh判据,故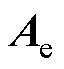 是Hurwitz稳定的。由式(34)可知,
是Hurwitz稳定的。由式(34)可知,
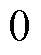 ,所以
,所以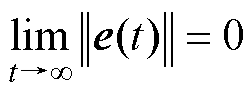 。根据Lyapunov理论可知,LADRC是渐近稳定的,等价于工程意义上的稳定。
。根据Lyapunov理论可知,LADRC是渐近稳定的,等价于工程意义上的稳定。
为了验证微电网负载侧降压接口在不同控制策略下的动态性能,在40kW样机上进行了实验验证。其中,iL为电感电流、Vi为输入电压、Vo为变换器输出电压。实验样机中开关管采用Infineon公司的SiC,IMZ120R045M1。直流母线电压控制器样机如图10所示,其部分参数见表2。

图10 实验样机
Fig.10 Experimental prototype
表2 系统参数
Tab.2 System parameters

参 数数 值 输入电容Ci/mF82 输出电容Cout/mF300 变换器电感L1~L6/mH120 功率Pr/kW40 开关频率fc/kHz100 母线电压/V550 电压环给定值/V450
表3 电气量稳态值
Tab.3 Steady state of electrical volume

电气量输入电压/V输出电压/V输出电流/A 10kW对应的稳态值55045022.5 20kW对应的稳态值55045044.5
为了方便工况的设定,以直流电源代替母线输出功率。接下来,分别对母线处电压突增、突降以及负载侧加、减载4个工况进行测试。为了验证所提FLADRC策略的性能,将PI策略和FLADRC策略分别用作电压外环控制器在不同的工况下进行对比分析,如图11~图14所示。通过最大超调量σ%和恢复时间tv来展示实际运行中的抗扰性。从图11可以观察到,当6路交错并联Buck变换器运行在10kW的功率下,同时在输入侧出现一个电压正向突变时,超调降至89%,恢复时间从300ms缩短至100ms。显然,与经典PI策略相比FLADRC限制了输出电压的波动范围并缩减了输出电压波动的恢复时间。在图12中显示了在输入侧电压骤降和10kW负载运行条件下的输出电压比较波形。当FLADRC应用其中时,可以看出,在电压骤降期间输出电压的波动幅度与PI相同,而速度响应得到了显著的优化,即输出电压恢复时间得以有效缩短,这得益于扩张状态观测器对扰动信号的观测、估计和补偿。可以看出,无论输入侧电压骤升还是骤降,本文提出的FLADRC策略都可以成功地增强抗扰性,这与理论分析的结论一致。图13a、图13b分别为输入电压550V、电压环给定450V且负载增加10kW时,分别采用PI控制器、FLADRC策略的动态响应。可以看出,采用PI策略时,输出电压的波动幅度约为33.75V,恢复时间为260ms,在相同的运行条件下,6路交错并联Buck变换器的电压响应波动和恢复时间明显大于采用FLADRC时的响应。此外,图14a、图14b分别给出了PI和FLADRC在减载工况下的测试结果。可以明显看出,无论是负载投入还是负载切出,通过对负载侧功率的观测和补偿,输出端口的电压值都能很好的跟踪给定。不仅缩短了调节时间也减小了波动范围。
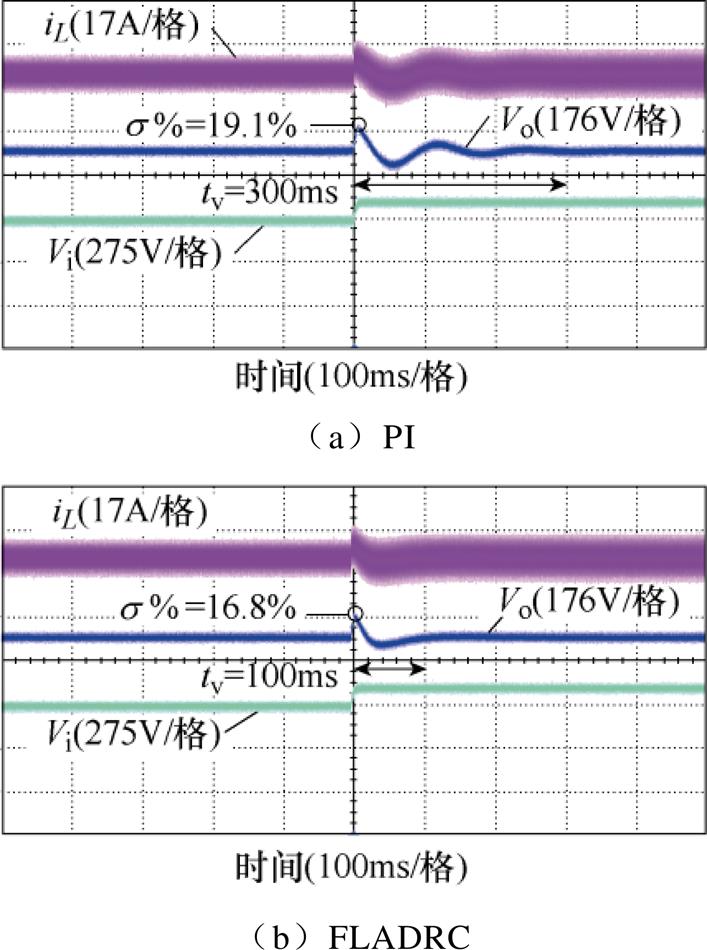
图11 母线电压突增下的动态响应
Fig.11 Dynamic response of bus voltage surge
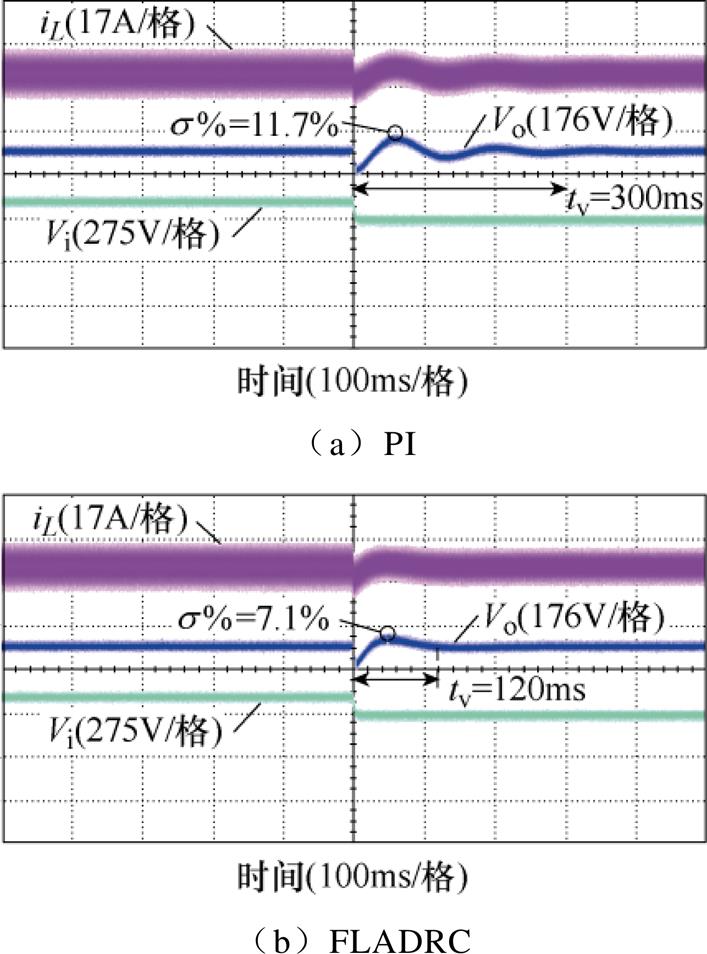
图12 母线电压突降下的动态响应
Fig.12 Dynamic response of bus voltage drop
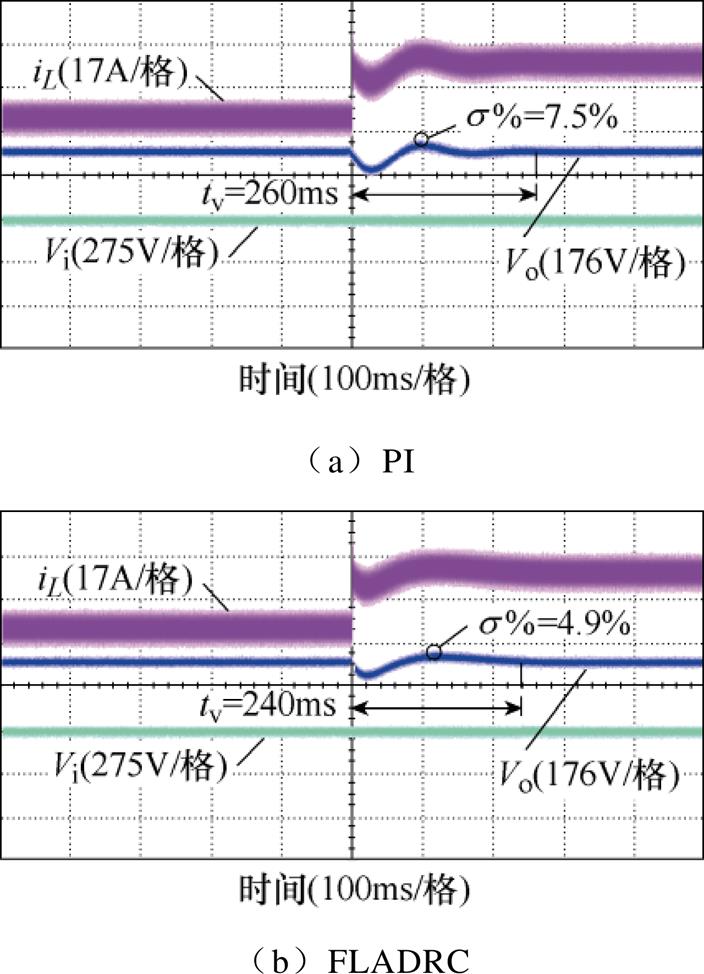
图13 负载增加时的动态响应
Fig.13 Dynamic response as load increases
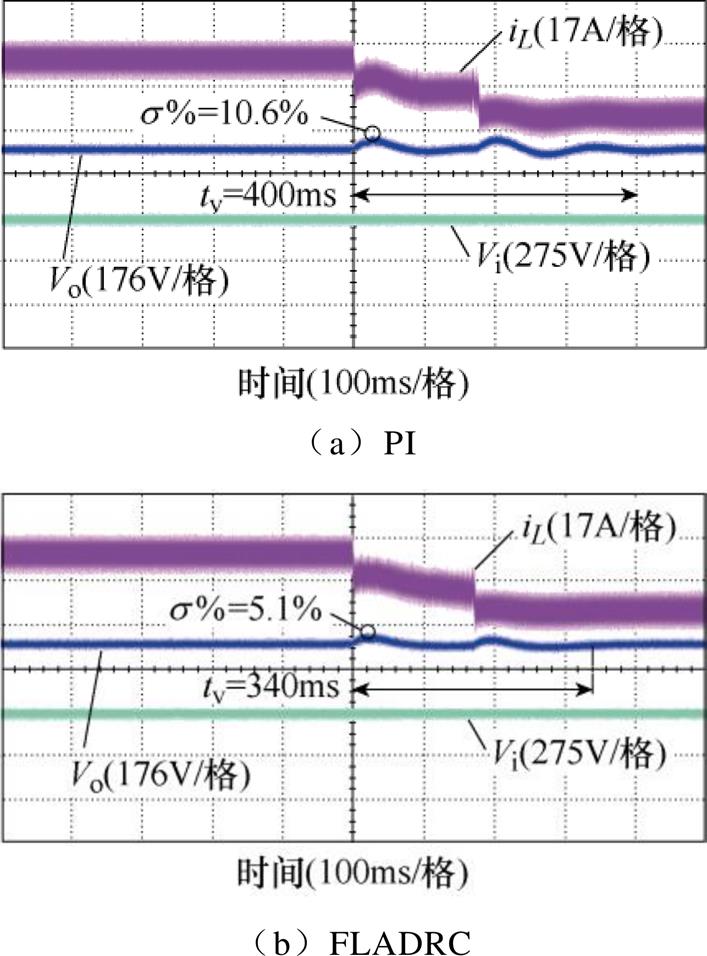
图14 负载减少时的动态响应
Fig.14 Dynamic response to load reduction
根据实验结果的对比可知,采用FLADRC策略时,输出电压的超调较PI有所降低,电感电流的波动也有所减弱。此外,FLADRC的调节速度明显快于PI。FLADRC的暂态过程时间较PI而言得到了明显的缩短。这都表明,FLADRC策略可有效减弱地扰动对系统的冲击。
复杂工况下混合储能微电网的输出侧接口变换器会出现输出电压恶化的情况。为解决这个问题,本文提出了一种结合模糊逻辑的自抗扰控制策略。为改善LESO的观测性能,本文首先依据状态空间平均法对6路交错并联变换器的数学模型进行了分析与化简。并基于此,从系统层面设计了FLADRC的LESO矩阵。此外,在复频域,分析了FLADRC的收敛性与抗扰性,揭示了控制器带宽与跟踪性的关联,并以此作为模糊逻辑的构造依据。再运用Lyapunov稳定性原理,分析证明了在所建立模型情况下设计的FLADRC稳定性。最后,基于40kW的实验平台,在多种工况下对经典PI和FLADRC两种策略进行实验对比,结果显示FLADRC的控制性能明显优于PI控制。这表明模糊逻辑的自动寻优特性有效增强了FLADRC的鲁棒性,解决了微电网在不同工况下输出接口的电压、功率不稳定问题,验证了所提控制策略的正确性、有效性和可行性。希望本文的研究成果能够为自抗扰控制技术在混合储能微电网中的应用提供思路。
参考文献
[1] Che Liang, Shahidehpour M, Alabdulwahab A, et al. Hierarchical coordination of a community microgrid with AC and DC microgrids[J]. IEEE Transactions on Smart Grid, 2015, 6(6): 3042-3051.
[2] Huenteler J, Niebuhr C, Schmidt T S. The effect of local and global learning on the cost of renewable energy in developing countries[J]. Journal of Cleaner Production, 2016, 128: 6-21.
[3] 王宁, 张建忠. 基于开关轨迹优化的SiC MOSFET有源驱动电路研究综述[J]. 电工技术学报, 2022, 37(10): 2523-2537.
Wang Ning, Zhang Jianzhong. Review of active gate driver for SiC MOSFET with switching trajectory optimization[J]. Transactions of China Electro- technical Society, 2022, 37(10): 2523-2537.
[4] 王忠杰, 王议锋, 陈庆, 等. 基于GaN的高频Boost变换器优化设计[J]. 电工技术学报, 2021, 36(12): 2495-2504.
Wang Zhongjie, Wang Yifeng, Chen Qing, et al. Optimal design of high frequency Boost converter based on GaN[J]. Transactions of China Electro- technical Society, 2021, 36(12): 2495-2504.
[5] Fei Chao, Yang Yuchen, Li Qiang, et al. Shielding technique for planar matrix transformers to suppress common-mode EMI noise and improve efficiency[J]. IEEE Transactions on Industrial Electronics, 2018, 65(2): 1263-1272.
[6] 张辉, 梁誉馨, 孙凯, 等. 直流微电网中多端口隔离型DC-DC变换器的改进虚拟电容控制策略[J]. 电工技术学报, 2021, 36(2): 292-304.
Zhang Hui, Liang Yuxin, Sun Kai, et al. Improved virtual capacitor control strategy of multi-port isolated DC-DC converter in DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 292-304.
[7] 李微, 周雪松, 马幼捷, 等. 三端口直流微网母线电压控制器及多目标控制[J]. 电工技术学报, 2019, 34(1): 92-102.
Li Wei, Zhou Xuesong, Ma Youjie, et al. Three-port DC microgrid bus voltage controller and multi- objective control[J]. Transactions of China Electro- technical Society, 2019, 34(1): 92-102.
[8] 佟子昂, 武建文, 马速良, 等. 一种基于主动电压扰动的直流微网负载均流控制策略[J]. 电工技术学报, 2019, 34(24): 5199-5208.
Tong Ziang, Wu Jianwen, Ma Suliang, et al. A load current-sharing control strategy for DC microgrid converters based on active voltage disturbance[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5199-5208.
[9] Zhang Wei, Zhu Huangqiu, Xu Ying, et al. Direct control of bearingless permanent magnet slice motor based on active disturbance rejection control[J]. IEEE Transactions on Applied Superconductivity, 2020, 30(4): 1-5.
[10] 阳同光, 桂卫华. 基于粒子群优化自适应反推光伏并网逆变器控制研究[J]. 中国电机工程学报, 2016, 36(11): 3036-3044.
Yang Tongguang, Gui Weihua. Research on a particle swarm optimization adaptive backstepping control method of grid-connected inverters[J]. Proceedings of the CSEE, 2016, 36(11): 3036-3044.
[11] 周振雄, 石硕. 基于DRNN自整定准PR控制的光伏并网系统研究[J]. 太阳能学报, 2017, 38(11): 2932-2940.
Zhou Zhenxiong, Shi Shuo. Research on quasi-pr control based on DRNN of selftuning for photovoltaic grid-connected system[J]. Acta Energiae Solaris Sinica, 2017, 38(11): 2932-2940.
[12] 韩京清. 自抗扰控制技术: 估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008.
[13] Zhang Chengyong, Chen Yaolong. Tracking control of ball screw drives using ADRC and equivalent- error-model-based feedforward control[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7682-7692.
[14] Xue Wenchao, Bai Wenyan, Yang Sheng, et al. ADRC with adaptive extended state observer and its application to air-fuel ratio control in gasoline engines[J]. IEEE Transactions on Industrial Elec- tronics, 2015, 62(9): 5847-5857.
[15] Zhong Qing, Zhang Ying, Yang Jingan, et al. Non-linear auto-disturbance rejection control of parallel active power filters[J]. IET Control Theory & Applications, 2009, 3(7): 907-916.
[16] Li Shengquan, Cao Mengying, Li Juan, et al. Sensorless-based active disturbance rejection control for a wind energy conversion system with permanent magnet synchronous generator[J]. IEEE Access, 2019, 7: 122663-122674.
[17] Xu Rong, Yu Yong, Yang Rongfeng, et al. A novel control method for transformerless H-bridge cascaded STATCOM with star configuration[J]. IEEE Transa- ctions on Power Electronics, 2015, 30(3): 1189- 1202.
[18] Gao Zhiqiang. Scaling and bandwidth-parameterization based controller tuning[C]//American Control Confer- ence, Denver, CO, 2003: 4989-4996.
[19] 李乔, 吴捷. 自抗扰控制及其在DC-DC变换器中的应用[J]. 电工技术学报, 2005, 20(1): 83-88.
Li Qiao, Wu Jie. auto-disturbance rejection control and its application to DC-DC converter[J]. Transa- ctions of China Electrotechnical Society, 2005, 20(1): 83-88.
Active Disturbance Rejection Control with Automatic Optimization for Low-Voltage Interface Converter in Microgrid
Abstract Hybrid energy storage microgrid can accommodate distributed energy well with flexible switching of parallel and off-grid modes, but the power quality of its step-down interface will be affected under complex working conditions. Therefore, an active disturbance rejection control strategy with parameter optimization (FLADRC) is proposed to transform the outer loop of the traditional double closed loop PI control mode in this paper. Firstly, the converter model is analyzed and simplified according to the requirements, and the model is established by the state space averaging method. Then, the linear extended state observer (LESO) matrix of FLADRC is designed according to the model information contained in the state equation. In the frequency domain analysis part, the system performance of FLADRC is explored, and the tracking, convergence and disturbance immunity of FLADRC are theoretically analyzed. Based on the analysis results, the fuzzy logic rules of parameter optimization are given. In addition, Lyapunov theory is used to prove the stability of the microgrid interface converter when FLADRC is applied. Finally, the dynamic curves of different control strategies under various working conditions were obtained by tests on a 40KW experimental platform, which verifies the feasibility and effectiveness of the proposed FLADRC method.
keywords:Microgrid, state space average method, active disturbance rejection control, fuzzy logic, Lyapunov theory
DOI: 10.19595/j.cnki.1000-6753.tces.211456
中图分类号:TM46
国家自然科学基金资助项目(51977146)。
收稿日期 2021-09-13
改稿日期 2021-10-15
陶 珑 男,1994年生,博士研究生,研究方向为混合储能微电网的能量转换与先进控制策略。E-mail: taolongtl@126.com
王议锋 男,1981年生,副教授,博士生导师,研究方向为新能源发电与电能变换。E-mail: wayif@tju.edu.com(通信作者)
(编辑 陈 诚)