
图1 三电平ANPC整流器拓扑结构
Fig.1 3L-ANPC of rectifier topology structure
摘要 高速磁悬浮列车牵引供电系统采用大功率背靠背三电平有源中点钳位(ANPC)变流器。为在低开关频率下降低网侧电流谐波,基于三相静止坐标系的线性扩张状态观测器(LESO)和比例谐振(PR)控制,提出一种适用于大功率三电平整流器的特定谐波消除脉宽调制(SHEPWM)策略,并设计相应的死区补偿方法。高速磁悬浮列车在运行过程中,定子段换步会造成逆变侧负载剧烈变化,从而引起网侧电流的大幅度改变。考虑到SHEPWM动态性能较差,提出一种在换步阶段对离线计算的开关角进行在线修正的方法,可提高基于SHEPWM整流器闭环控制的动态调节能力。最后,利用背靠背三电平ANPC变流器实验平台进行实验,验证了SHEPWM提高网侧电流质量的优越性以及所提策略提高SHEPWM闭环控制动态性能的有效性。
关键词:高速磁悬浮列车 三电平有源中点钳位整流器 特定谐波消除脉宽调制 线性扩张状态观测器 动态性能
我国自主研制的高速磁悬浮列车牵引供电系统采用大功率背靠背三电平有源中点钳位(Three- Level Active Neutral Point Clamped, 3L-ANPC)变流器,由三电平ANPC整流器、直流环节和逆变器组成,具有可实现四象限运行、输出电能质量高、开关损耗均衡等优点[1-3]。
大功率三电平ANPC整流器连接电网,需降低由调制造成的网侧谐波含量,避免损坏其他用电设备。因开关损耗和散热的限制,开关频率一般低于420Hz[4]。对于大功率整流器,调制策略主要有空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)和基于载波的脉宽调制(Carrier-Based Pulse Width Modulation, CBPWM)[5-6],高速磁悬浮牵引供电系统没有在网侧单独配置滤波器,仅利用输入变压器的漏感进行滤波,无法完全滤除网侧电流中5、7次等较低次数的非3的倍数奇次谐波。为使在低开关频率运行下的整流器消除低次谐波,可采用特定谐波消除脉宽调制(Selective Harmonic Elimination Pulse Width Modulation, SHEPWM)。目前,在宽频率范围、低载波比的牵引逆变器中SHEPWM已有应用[7-8],但在大功率整流器中的研究及应用较少。文献[9]将SHEPWM应用在高速动车组牵引系统的单相两电平PWM整流器中,相比于CBPWM,降低了网侧电流总谐波畸变率(Total Harmonic Distortion, THD)。ABB公司在中压变频器ACS6000的整流器中使用了脉冲数为7的SHEPWM,并加装了消除第23次谐波的滤波器。文献[10]将脉冲数为3的SHEPWM应用在三电平中点钳位(Neutral Point Clamped, NPC)整流器上,只能消除两种次数谐波。
SHEPWM的调制过程基于对离线开关角序列的查询,开关角的选择依赖调制比和调制角度。调制比的波动会导致对开关角序列的选择发生变化,使得功率器件无法在离线计算的开关角处动作,进而相电压波形失去了对称性,网侧谐波消除效果降低,故在目前的大功率变流器中,SHEPWM多用于开环控制[11-12]。在整流器闭环控制系统中,为获得优越的网侧谐波性能,在稳态工况下保证调制比的稳定性至关重要。文献[13]提出了一种网侧电流谐波提取方法,仅控制基波电流,以获得较稳定的调制比,但对谐波的观测需获取准确的网侧电阻和电感。也有学者提出通过降低采样频率来减轻调制比短时间内的波动,这种方式会进一步降低SHEPWM的动态性能,且降低采样频率会导致一个采样周期内跨过多个开关角,造成相电压波形不对称和脉冲数错误。
此外,采用长定子直线同步电机牵引的高速磁悬浮列车存在定子段换步工况,逆变侧负载的变化会引起网侧电流显著变化。基于查询离线开关表的SHEPWM动态调节能力较差,因此换步过程中负载的剧烈变化会导致对网侧电流参考值的跟随性能降低,直流母线电压波动量增大。为适应动态要求较高的磁悬浮列车牵引系统,需提高SHEPWM的动态性能。现有对提高SHEPWM动态性能的方法主要有电枢电流轨迹跟踪策略和定子磁链轨迹跟踪策略[14-16],即设计电流或磁链观测器,观测基波电流或磁链并与实际值比较得到动态调制误差,进而修改离线计算的SHEPWM开关角以达到快速跟踪电流或磁链参考值的目的。该方法观测器设计复杂,且实时修改开关角,消除谐波的能力有限,不适用于大功率整流器中。
为了大功率三电平ANPC整流器在低开关频率下获得优越的网侧谐波性能,本文采用补偿死区效应的SHEPWM策略;针对功率器件的正确动作依赖调制比稳定程度这一问题,提出了对网侧电流采用基于二阶线性扩张状态观测器(Linear Extended State Observer, LESO)的比例谐振(Proportional Resonance, PR)控制策略,补偿了由控制系统内部和低开关频率造成的扰动,可输出稳定、平滑的调制比和调制角度,保证了相电压波形的对称性;针对高速磁悬浮列车由换步造成的网侧电流动态变化剧烈的问题,提出了在换步阶段在线修正SHEPWM开关角策略,降低了由换步造成的直流母线电压波动;最后通过仿真和实验,验证了SHEPWM在大功率三电平整流器中提高网侧电流质量的优越性以及所提策略提高SHEPWM闭环控制动态性能的有效性。
高速磁悬浮列车牵引变流器中三电平ANPC整流器拓扑结构如图1所示。图中,VTx1、VTx2、VTx3、VTx4为上、下桥臂决定输出电平状态的功率器件,VTx5和VTx6为钳位管,VDx1~VDx6为反并联二极管(x=a, b, c)。usa、usb、usc为网侧相电压,ia、ib、ic为网侧电流,R和L分别为网侧等效电阻和变压器漏感,C1和C2分别为整流器上、下直流母线电容。

图1 三电平ANPC整流器拓扑结构
Fig.1 3L-ANPC of rectifier topology structure
与NPC拓扑相比,ANPC的钳位二极管改为全控功率器件,从而新增了OU1、OU2、OL1和OL2四种零电平开关状态,P←→O←→N状态之间的换流方式也更加多样,可以均衡内外功率器件的损耗。三电平ANPC整流器的开关状态见表1[17]。
表1 三电平ANPC整流器开关状态
Tab.1 Switching state of 3L-ANPC rectifier
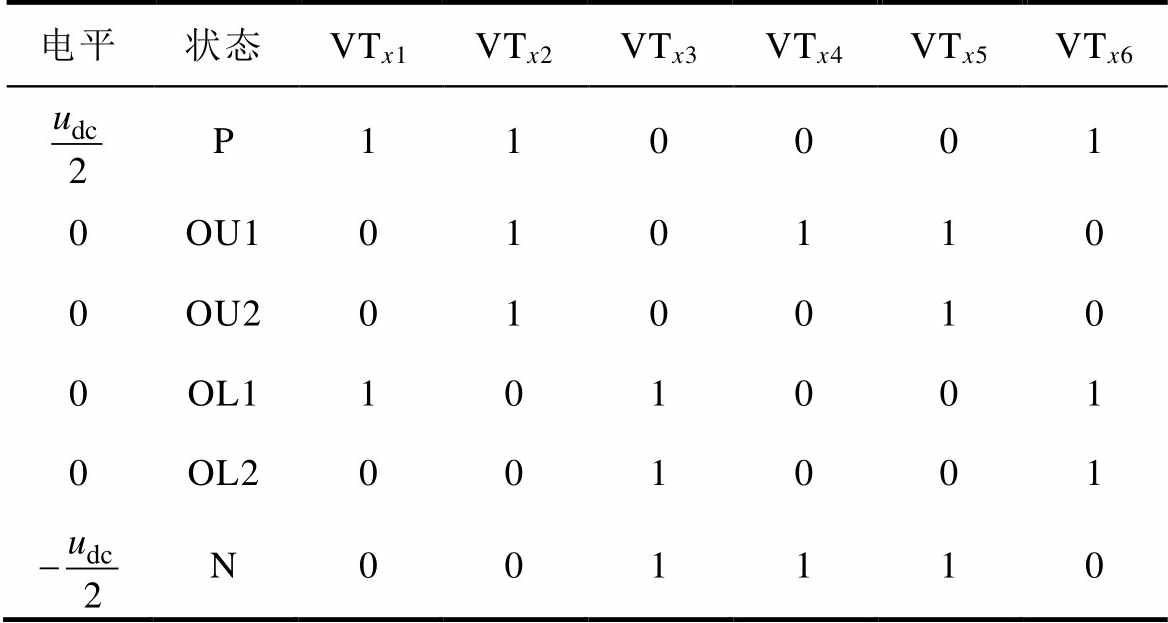
电平状态VTx1VTx2VTx3VTx4VTx5VTx6 P110001 0OU1010110 0OU2010010 0OL1101001 0OL2001001 N001110
在三相静止坐标系下,整流器a相网侧电流为
 (1)
(1)
式中,uan为整流器网侧a相电压,可表示为
 (2)
(2)
式中,uao为整流器a相电压;uon为共模电压。将整流器相电压uao看作是基波分量和开关成分ea的叠加,在控制模型中,基波分量等效为相电压的参考值uao_ref,则有
 (3)
(3)
联立式(1)~式(3)可得,在静止坐标系下网侧三相电流的微分方程为
 (4)
(4)
本文对三电平整流器采用脉冲数P=7的SHEPWM,即正(O←→P)、负(O←→N)脉冲数均为7,相电压uao的正脉冲部分波形如图2所示。

图2 三电平SHEPWM相电压波形
Fig.2 3L-SHEPWM phase voltage waveform
SHEPWM相电压波形满足三相对称,半波奇对称和1/4周期偶对称,则求解a相中0~p/2内的7个开关角a1~a7后,通过对称关系可得到三相基波周期内所有开关角度,且满足上述对称关系的线电压消去了3的倍数次谐波、偶次谐波和奇次谐波的余弦项。P=7的SHEPWM通过在特定角度处开关动作,还可以消除另外六种非3的倍数奇次谐波。对图2中的相电压波形进行傅里叶分解得
 (5)
(5)
忽略直流分量,则a0=0,且根据上述对称关系波形中不含偶次谐波和奇次谐波的余弦项,则式(5)可化为
 (6)
(6)
式中,w 为电压角频率;n为次数,取奇数,n=1时为波形uao(w t)的基波;傅里叶系数bn可表示为
 (7)
(7)
图2中有7个待求开关角度,根据式(7)和uao(w t)中每个积分区间的电平状态可列出7个非线性方程,从而求得相电压的基波分量幅值和满足消除六种谐波的开关角度。本文选择消除23次以内的六种非3的倍数奇次谐波,非线性方程组为
 (8)
(8)
式中,M为调制比,定义为
 (9)
(9)
式中,vref为相电压基波幅值。方程式(8)中直流母线电压udc可以消去,则调制比M是唯一可设定的变量,将M从0以0.01为步长线性增加到1,求得每一调制比下对应的开关角序列。利用SHEPWM开关角多解特性[18],为在调制比小范围变化时整流器相电压脉冲数固定,以每一开关角随调制比的增大而连续变化为前提,另设置约束条件为
 (10)
(10)
由于大功率整流器的相电压需避免最小脉宽,根据式(10)和保证解的连续性情况下,不能满足全调制比区域所有相邻开关角的间隔大于最小脉宽。除此以外,还需避免在一个采样周期Ts内出现跨过多个开关角的情况,即相邻开关角的间隔需大于一个采样周期内相位的增量。综上所述,增加考虑最小脉宽的约束条件为
 (11)
(11)
式中,f为电网电压频率,f =50Hz;Tmin为最小脉宽所对应的时长,由于采样周期Ts约为138ms,故本文设置最小脉宽Tmin=150ms。对部分不满足约束条件的角度,以平移奇数次开关角至最小脉宽为原则,从而使得全调制比范围内相邻开关角的间隔均大于或等于最小脉宽。根据以上约束条件,对非线性方程式(8)进行求解,并且修改调制比0.18以下和0.93以上所对应的部分开关角之后,得到每一开关角的轨迹如图3所示。

图3 P=7的SHEPWM开关角轨迹
Fig.3 Switching angle trajectories of SHEPWM with P=7
根据图3,将相邻开关角度相减可得全调制比范围内脉冲宽度的变化趋势,易得出在相电压波形的正半周期中,第4个正脉冲的宽度随调制比的增大而单调增大。
整流器中驱动信号互补的两个功率器件设置了20ms的死区用来延迟器件开通的时刻,这会造成某些电平的改变滞后一个死区时间,即实际波形的开关角不满足方程式(8),无法消除特定次数谐波。则需要对死区效应进行补偿,实现在有死区的情况下,仍可以消除特定次数谐波。
大功率整流器的相电压电平切换时仅存在逐级切换,即只能以O←→P和O←→N四种方式切换。以a相为例,当从P状态切换为OU1状态时,根据表1,VTa1~VTa6功率器件的开关状态由110001切换为010110(1为开通,0为关断)。先依次断开VTa6和VTa1,经过20ms的死区时间之后,再依次开通VTa5和VTa4,忽略关断的两个器件之间以及开通的两个器件之间的微小时间差,认为二者是同时关断和开通的。规定网侧电流流入整流器的方向为正方向,即ia>0,则根据电流方向的不同,在P到OU1的切换过程中分为两种换流方式,如图4所示。
由P状态切换为OU1状态期间处于死区时,功率器件的开关状态为010000,在一个死区时间内,电流方向可认为是不变的。当ia>0时,电流流经VDa2和VDa1,此时整流器相电压仍维持在P状态,故O电平会被延迟输出,即P到OU1的切换会延迟一个死区时间,切换到OU1状态后,电流流经VDa2和VTa5。当ia<0时,在死区时间内电流流经VDa5和VTa2,此时整流器相电压已经变为O电平,即在这种情况下死区不会造成电平改变的延迟。对于剩余状态的切换,死区效应的分析方法与上述一致。

图4 P→OU1换流过程
Fig.4 Commutation process of P→OU1
P到OU1的切换发生在相电压正半周的偶数次开关角,若此时ia>0,整流器相电压在死区时间内维持P状态,在死区时间之后才输出O电平,这种情况需要对该偶数次开关角进行死区补偿,即让该开关角提前Da 动作,Da 为
 (12)
(12)
式中,Tdt为死区时间,Tdt=20ms。对离线计算的a2k(k=1, 2, 3)开关角左移Da,在Da 内虽然维持在P电平,但实际由P到OU1的状态仍在a2k处切换,从而消除了死区效应,使得相电压按照2.1节中计算到的开关角序列动作。考虑死区时P到OU1的状态切换和死区补偿后的相电压及驱动信号如图5 所示。
采用同样的分析方法可得到其他状态切换时电平延迟情况及死区补偿方式,对于P和N电平与不同开关状态的O电平之间的切换,死区的影响具有一致性。综上所述,是否需要进行死区补偿与当前相电流的方向有关;奇、偶数次开关角电平动作方向不同,需分别考虑。总结三电平ANPC整流器不同状态之间切换的死区影响及其补偿方法见表2。

图5 P→OU1有死区、死区补偿的相电压及驱动信号
Fig.5 Phase voltage with the dead time and dead time compensation of P→OU1 and driving signal
表2 不同电平切换时的死区影响及死区补偿
Tab.2 Dead time effect and compensation during different level switching
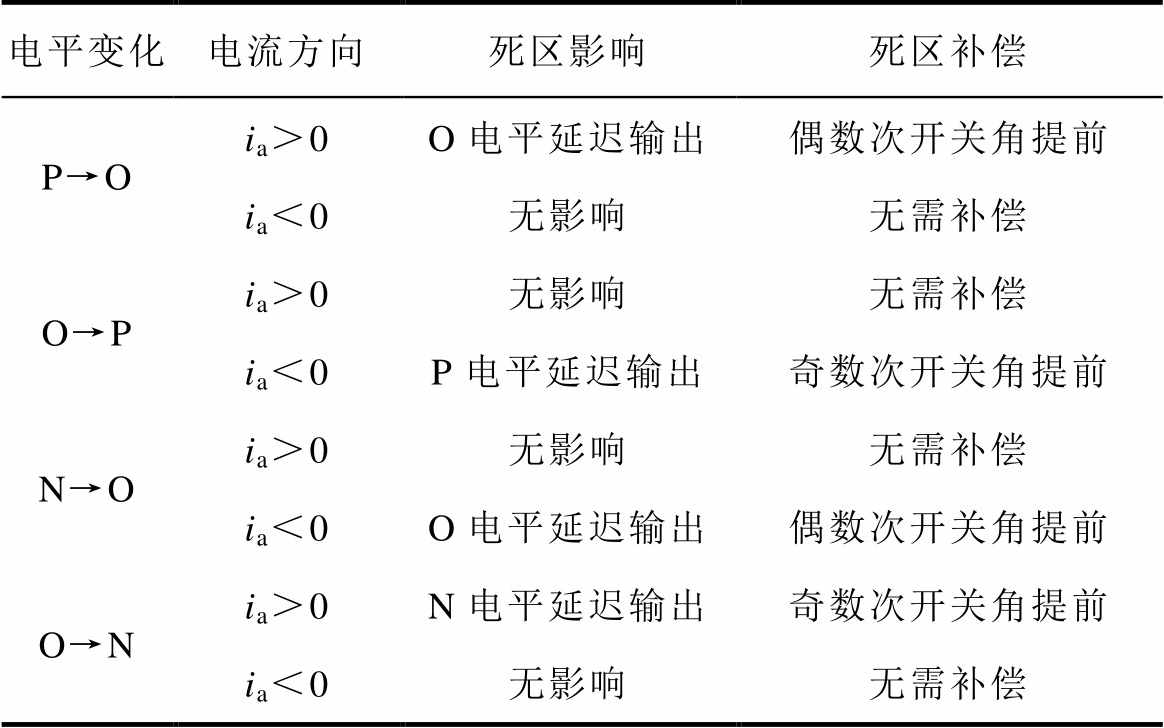
电平变化电流方向死区影响死区补偿 P→Oia>0O电平延迟输出偶数次开关角提前 ia<0无影响无需补偿 O→Pia>0无影响无需补偿 ia<0P电平延迟输出奇数次开关角提前 N→Oia>0无影响无需补偿 ia<0O电平延迟输出偶数次开关角提前 O→Nia>0N电平延迟输出奇数次开关角提前 ia<0无影响无需补偿
当跨越SHEPWM开关角时,检测当前相电流的方向,并且根据电平切换方式判断是否需要进行死区补偿。若需要死区补偿,在离线计算开关角的基础上左移一个补偿角Da 得到新的开关角度,并转化为新的装载值进行开关动作;若不需死区补偿,按照开关角序列中的角度进行动作即可。
对于高性能整流器闭环控制系统,整流器调制比是实时改变的。若当前采样周期调制比为M1,控制器选择M1对应的开关角序列,当下一采样周期的调制比M2相较于M1变化较大时,上一组开关角序列尚未执行完成,就要从M2对应的第一个开关角开始判断是否进行动作。这会造成相电压脉宽和脉冲数目的变化,失去消谐效果,增大直流母线电压的纹波。
由网侧电流微分方程式(4)可看出,网侧电流包含由调制造成的开关成分,这对低开关频率的大功率三电平整流器的影响尤为明显。由开关动作引入的成分和整流器数学模型自身的不确定项均是对网侧电流控制系统的扰动,若能将这种扰动估计出来并补偿到前馈项即可抵消该扰动,从而改善系统的鲁棒性和动态性能[19]。LESO可对总扰动进行实时观测,通过前馈补偿后使得网侧电流仅与整流器相电压的参考值有关,进而得到连续、稳定的调制比和调制角度,可避免相电压波形的紊乱。故本文在控制系统中引入二阶LESO。
首先将式(4)转换为
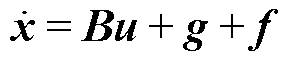 (13)
(13)
其中


式中,x为网侧电流状态变量;f为系统总扰动;u为系统输入。根据式(13)构造二阶LESO为
 (14)
(14)
式中,z1和z2为LESO的两个状态变量,z1为网侧电流观测值;z2为对扰动f的估计;x为网侧电流实际值;e为二者的误差;g为与网侧相电压有关的量;b0为控制增益估计值; 和
和 为观测器系数。
为观测器系数。
直流母线电压采用PI控制,对网侧三相电流采用PR控制和LESO补偿,三电平整流器控制框图如图6所示。

图6 基于LESO的三电平整流器网侧电流PR控制框图
Fig.6 Control block diagram of the grid-side current by PR based on LESO for 3L-rectifier
网侧电流为定频50Hz,在稳态下,谐振控制器在特定频率处增益为无穷大,可实现对网侧电流参考值无静差跟踪。PR控制器的传递函数为
 (15)
(15)
式中,kp为比例系数;kr为谐振系数;qts为考虑数字控制系统的延时补偿角;w1为电网角频率。
离线计算的SHEPWM开关角序列在稳态工况下相电压脉宽是固定的,无法在高速磁悬浮列车的换步等复杂工况下满足高动态响应。故可在定子段换步阶段对离线计算的开关角进行在线修正,以提高网侧电流的动态调节能力。
高速磁悬浮列车在非换步区,整流器相当于带载阶段;在定子段换步过程中的泄流阶段,即逆变电流线性减小为零,相当于整流器在减载,其调制比逐渐减小;在轨道旁开关站切换过程中,逆变电流保持为零,整流器空载,调制比最小;开关站切换完成后,逆变电流逐渐恢复到参考值,即整流器在加载,调制比逐渐增大,至此完成一次换步。整流器a相在磁悬浮列车电动状态下的空载、非换步区、定子段换步时相量如图7所示。

图7 磁悬浮列车在不同工况下整流器交流侧相量
Fig.7 Phasor diagram of rectifier AC-side of maglev train under different working conditions
可见,整流器调制比的动态变化可直接反映逆变侧定子段换步过程。结合2.1节的分析,SHEPWM相电压的第4个正脉冲以及与之半波对称的第4个负脉冲的宽度随调制比的增大而增大。为加快在换步阶段网侧电流的动态响应速度,根据调制比的变化方向在线修正开关角,以拓宽或缩短半波中间脉冲宽度,具体修正规则如下:
(1)在换步阶段若网侧参考电流大于实际电流,说明需要增大调制比,向左平移正半波中O→P的第7个开关角和负半波中O→N的第7个开关角,根据对称关系,对应的P→O和N→O的开关角被向右平移,结果为中间脉冲被拓宽。
(2)在换步阶段若网侧参考电流小于实际电流,说明需要减小调制比,向右平移正半波中O→P的第7个开关角和负半波中O→N的第7个开关角,根据对称关系,对应的P→O和N→O的开关角被向左平移,结果为中间脉冲被缩短。
(3)对开关角的修正并非任意,需考虑被修正的开关角与相邻开关角之间的最小脉宽限制,由于是对特定开关角进行修正,即相位已跨越该开关角,不存在跨越两个开关角的情况,故换步时对最小脉宽的限制可小于采样周期,这里设置为40ms。
对SHEPWM开关角的在线修正只在定子段换步的状态下调用。修正量Dg利用网侧参考直轴电流和经坐标变换并滤波后的实际直轴电流,再通过PI调节器计算输出,限值后作用在特定开关角上。跨越特定开关角时对装载值的计算方式与等效载波的方向有关,等效载波对相位采样的示意图如图8所示,图中给出了整流器调制比需要减小时开关角的修正方法。
SHEPWM在等效载波的峰值点和零点对相位采样。当开关角处于载波的上升沿时,第k个Ts位于载波峰值点,此时跨越了开关角a7,修正后的开关角是 ,即延迟了O→P的动作,实际开关角被向右平移,对应的装载值与开关角的大小呈正相关;当开关角处于载波的下降沿时,第k个Ts位于载波零点,此时装载值与开关角的大小呈负相关。这两种情况修正开关角后得到的装载值CMPA分别为
,即延迟了O→P的动作,实际开关角被向右平移,对应的装载值与开关角的大小呈正相关;当开关角处于载波的下降沿时,第k个Ts位于载波零点,此时装载值与开关角的大小呈负相关。这两种情况修正开关角后得到的装载值CMPA分别为

图8 SHEPWM的对相位的采样示意图
Fig.8 Diagram of sampling phase angle in SHEPWM
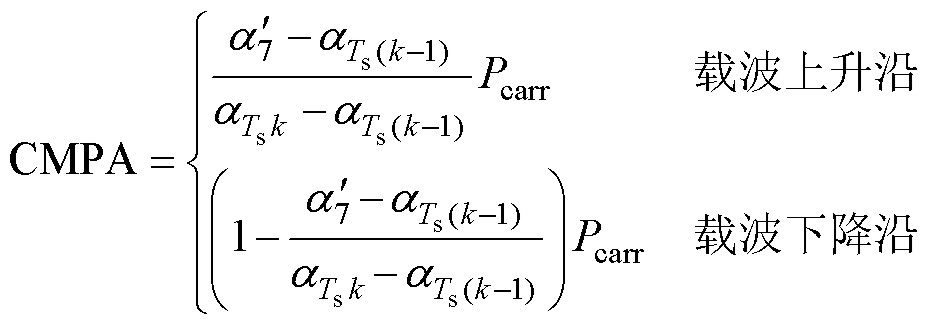 (16)
(16)
式中,Pcarr为等效三角载波峰值。另外当调制比需要增大时,则需要减小特定开关角,装载值的计算方法与上述一致。采用上述开关角在线修正方法后,相电压波形仍满足三相对称、半波对称和1/4周期对称,只是消谐效果会略微降低,但由于换步时间较短,负载变化较大,应首先考虑提高换步阶段SHEPWM的动态性能。
本文所提调制及控制策略面向12MW高速磁悬浮整流器,为验证在大功率工况中的有效性,按照高速磁悬浮牵引供电系统中变流器实际电气参数进行仿真所提的基于SHEPWM的大功率三电平整流器控制策略,搭建一台12MW整流器模型,仿真参数见表3。
表3 三电平ANPC整流器仿真参数
Tab.3 Simulation parameters of 3L-ANPC rectifier

参 数数 值 网侧线电压有效值us/kV3 网侧变压器漏感L/mH0.84 网侧等效电阻R/W0.05 直流侧总电容C/mF20 直流母线目标电压/V5 000 采样周期Ts/ms138
首先对比分析本文计算的SHEPWM开关角在20ms死区影响下和采用所提死区补偿方法时整流器相电压及其谐波分布,如图9所示。

图9 P=7的SHEPWM相电压及其频谱
Fig.9 Phase voltage and spectrum of SHEPWM with P=7
如图9a所示,在死区效应影响下,整流器相电压出现了23次以内的非3的倍数低次谐波,消谐效果变差,基波幅值降低到2 401.25V。采用本文所提对三电平ANPC整流器的SHEPWM死区补偿方法,如图9b所示,23次以内的非3的倍数次谐波被完全消除,基波幅值为2 418.53V。
对网侧电流分别基于dq坐标系下的传统PI控制和本文所提基于LESO的三相静止坐标系下的PR控制进行对比分析,调制策略均采用SHEPWM,仿真结果如图10所示。
在dq坐标系下的网侧电流传统PI控制无法准确补偿由低开关频率和未建模部分造成的扰动,且对相电流不易实现无差跟踪。通过电流闭环输出量计算的调制比和调制角度的抖动造成了相电压脉冲数不固定和波形不对称,这种电压波形紊乱会进一步加剧网侧电流和母线电压的波动。如图10a所示,直流母线电压最大波动达到了120V,相电压脉冲个数不固定为7。图10b为采用所提策略的控制效果,相电压波形对称,母线电压最大波动小于10V。


图10 基于SHEPWM的网侧电流传统控制和所提策略仿真波形
Fig.10 Simulation waveforms of traditional control and proposed strategy of grid-side current based on SHEPWM
仿真12MW整流器半载和满载两种工况,对应直流侧电阻分别4.17W 和2.08W。采用基于LESO的网侧电流PR控制和SHEPWM策略,结果如图11所示。
以上对整流器两种工况的仿真结果显示,均可实现直流母线电压5 000V的闭环控制。随着负载增大,整流器线电压加权总谐波畸变率(Weighted Total Harmonic Distortion, WTHD)和网侧相电流THD均减小,相电流基波幅值逐渐增大,半载时为1 718.45A,对应调制比为0.86;满载时为3 582.97A,对应调制比为0.91,验证了所提控制策略应用在大功率三电平ANPC整流器中的有效性。

图11 不同工况下直流母线电压、整流器线电压及网侧相电流仿真波形
Fig.11 Simulation waveforms of DC-link voltage, line voltage of the rectifier and grid-side phase current under different working conditions
在参数一致的条件下,对比定子段换步过程中不修正开关角和在线修正开关角时控制系统的动态调节性能,如图12所示。

图12 换步时网侧相电流与整流器相电压仿真波形
Fig.12 Simulation waveforms of grid-side phase current and rectifier phase voltage during the changeover
通过分别修正相电压正、负半波的第4个脉冲的前后开关角,使其脉冲宽度按照调制比变化方向缩短或拓宽,从而提高SHEPWM的动态响应能力。如图12a所示,换步时不修正开关角时直流母线电压最大波动为125V。按照3.2节中所述规则在换步时修正开关角,如图12b所示,可见相电流跟随性能提升,直流母线电压最大波动降低到89V;通过相电压局部放大可看出,开关角修正后,波形仍满足三种对称性,不会引入3次谐波和偶次谐波。
利用背靠背三电平ANPC变流器实验平台进一步验证所提策略的有效性。功率器件选用英飞凌公司的FZ800R12KE3,控制系统为基于PowerPC芯片、VxWorks操作系统的机箱,机箱内包含时钟板、AD采样板、PWM输出板、IO控制板等,变流器如图13所示。

图13 三电平ANPC背靠背变流器
Fig.13 3L-ANPC back-to-back converter
变流器负载为高速磁悬浮牵引供电系统模拟实验平台,如图14所示,包含模拟长定子直线同步电机的旋转电机,可模拟高速磁悬浮换步工况。
因实验室设备的限制,实验功率等级较低,为了验证所提策略在高速磁悬浮大功率三电平ANPC整流器中的可行性和有效性,死区时间、采样周期等参数与实际牵引变流系统保持一致。在实验中直流母线电压目标值设为200V,网侧等效电感约为1mH,直流侧总电容为7.8mF。
首先验证SHEPWM在三电平ANPC整流器应用的可行性以及逆变侧换步时的动态调节能力,对网侧电流的控制采用本文所提的基于LESO的PR控制策略,实验结果分别如图15和图16所示。

图14 高速磁悬浮牵引供电系统模拟实验平台
Fig.14 Simulation experiment platform of high-speed maglev traction power supply system

图15 基于SHEPWM的三电平ANPC整流器实验波形
Fig.15 Experimental waveforms of 3L-ANPC rectifier based on SHEPWM

图16 换步时基于SHEPWM的整流器实验波形
Fig.16 Experimental waveforms of the rectifier based on SHEPWM during the changeover
图15给出了整流器在SHEPWM下直流母线电压、网侧相电流、整流器相电压及其频谱,可见母线电压可稳定在目标值200V,网侧电流正弦度较好,相电压满足半波对称和1/4周期对称,所有偶数次谐波和23次以内的所有非3的倍数次谐波被消除。图16给出了换步时逆变电流、直流母线电压波动量和网侧电流波形,网侧电流变化趋势与逆变电流一致,直流侧电压最大波动为30V。以上实验结果验证了SHEPWM在三电平ANPC整流器中应用的可行性。虽然SHEPWM是基于查询离线开关表实现的,但在换步时没有出现网侧电流过电流和直流母线电压失控。
自主研制的12MW高速磁悬浮整流器调制策略为SVPWM和CBPWM,通过实验对比所提策略与现有调制和控制策略的性能。调制比选择0.86和0.91,对应高速磁悬浮整流器半载和满载两种工况;控制策略均采用电压外环PI控制和电流内环PR控制,其中SHEPWM策略在电流环引入二阶LESO。图17和图18分别给出了在这两种调制比下采用三种不同调制策略的整流器相电压、线电压、网侧相电流及线电压谐波分布。根据实验结果,将三电平ANPC整流器在SVPWM、CBPWM和SHEPWM三种调制策略下的平均开关频率以及不同调制比下对应的线电压WTHD和相电流THD汇总见表4。


图17 调制比为0.86时三电平ANPC整流器实验波形
Fig.17 Experimental waveforms of 3L-ANPC rectifier under the modulation ratio of 0.86

图18 调制比为0.91时三电平ANPC整流器实验波形
Fig.18 Experimental waveforms of 3L-ANPC rectifier under the modulation ratio of 0.91
分析图17和图18并结合表4,高速磁悬浮整流器现有调制方式SVPWM和CBPWM均能输出半波对称的相电压波形,可消除网侧电流中的偶次谐波;整流器相电压半波脉冲数为8,平均开关频率为400Hz;通过对比整流器线电压WTHD和网侧相电流THD可看出,CBPWM的谐波特性优于SVPWM。SHEPWM还可以消除特定次数谐波,平均开关频率为350Hz,从而降低了开关损耗。相比于SVPWM和CBPWM,SHEPWM策略可获得更优的电网谐波特性:在调制比为0.86时,线电压WTHD和相电流THD分别降低29.33%和21.72%、9.82%和4.44%;在调制比为0.91时,线电压WTHD和相电流THD分别降低28.65%和20.59%、6.16%和4.84%。说明本文所提SHEPWM策略以及与之相结合的基于LESO的网侧电流PR控制策略在大功率三电平ANPC整流器中具有更优越的电网谐波特性。
表4 三种调制策略下的三电平ANPC整流器实验结果
Tab.4 Experimental results of 3L-ANPC rectifier under three modulation strategies
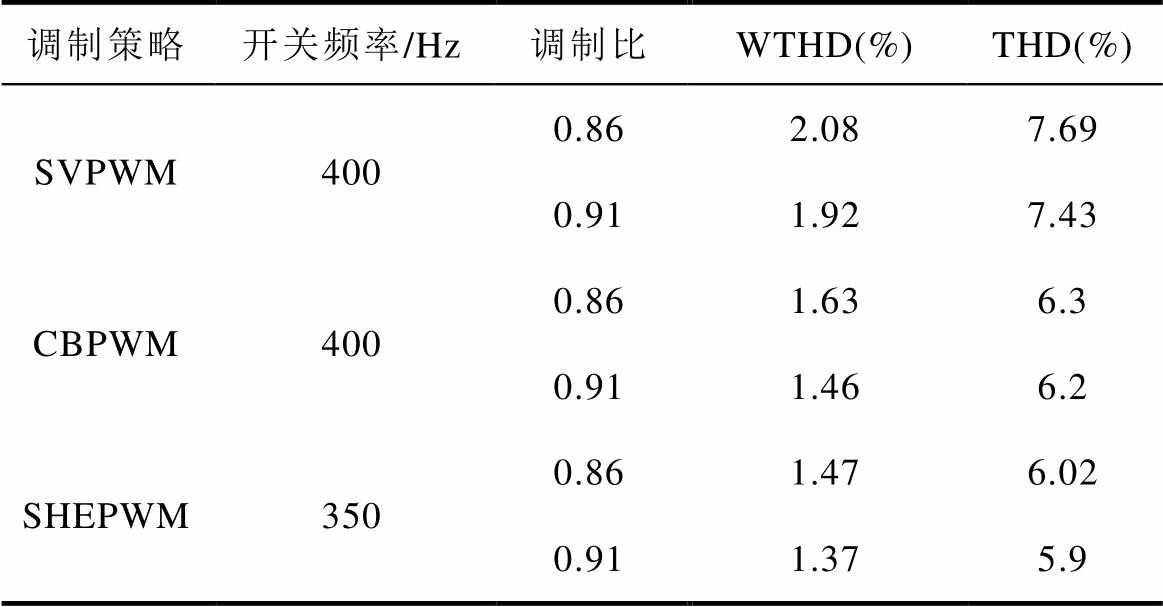
调制策略开关频率/Hz调制比WTHD(%)THD(%) SVPWM4000.862.087.69 0.911.927.43 CBPWM4000.861.636.3 0.911.466.2 SHEPWM3500.861.476.02 0.911.375.9
图19给出了定子段换步时三种不同调制策略的逆变电流、母线电压波动量和网侧电流,其中SHEPWM在定子段换步时在线修正开关角。


图19 不同调制策略下的换步时整流器实验波形
Fig.19 Experimental waveforms of the rectifier during the changeover under different modulation strategies
分析图19,采用SVPWM和CBPWM整流器时,由于二者本质等效,动态性能相同,直流母线电压波动量均为20V。采用本文所提的在换步阶段在线修正SHEPWM开关角策略时,直流母线电压波动量为18V,相比于图16中不修正开关角的情况,波动量降低了40%,动态性能可到达与非离线计算的调制算法SVPWM和CBPWM近似的效果。
本文提出了适用于大功率三电平ANPC整流器的补偿死区效应的SHEPWM策略,对网侧电流的控制采用在三相静止坐标系下基于二阶LESO的PR控制策略。与现有高速磁悬浮整流器调制策略SVPWM、CBPWM以及控制策略相比,通过实验验证了所提策略可降低网侧相电流THD范围是4.44%~9.82%,可降低整流器线电压WTHD范围是20.59%~29.33%,且平均开关频率降低了50Hz,从而整流器的开关损耗得到降低。针对高速磁悬浮定子段换步的特殊工况,提出了在换步阶段根据整流器调制比的变化在线修正SHEPWM开关角策略。通过仿真和实验验证了该策略可提高网侧电流对参考值的跟随性,降低了直流母线电压波动,动态性能可达到与SVPWM和CBPWM基本相同的效果。
参考文献
[1] 孙鹏琨, 葛琼璇, 王晓新, 等. 基于硬件在环实时仿真平台的高速磁悬浮列车牵引控制策略[J]. 电工技术学报, 2020, 35(16): 3426-3435.
Sun Pengkun, Ge Qiongxuan, Wang Xiaoxin, et al. Traction control strategy of high-speed maglev train based on hardware-in-the-loop real-time simulation platform[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3426-3435.
[2] Xu Xiaona, Zheng Zedong, Wang Kui, et al. A com- prehensive study of common mode voltage reduction and neutral point potential balance for a back-to-back three-level NPC converter[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 7910-7920.
[3] 罗龙, 李耀华, 李子欣, 等. 有源中点钳位型三电平逆变器开关器件损耗均衡调制方法[J]. 电工电能新技术, 2021, 40(4): 1-9.
Luo Long, Li Yaohua, Li Zixin, et al. Loss balance modulation method of switching device for active neutral-point-clamped three-level inverter[J]. Advanced Technology of Electrical Engineering and Energy, 2021, 40(4): 1-9.
[4] Gao Zhan, Ge Qiongxuan, Li Yaohua, et al. Hybrid improved carrier-based PWM strategy for three-level neutral-point-clamped inverter with wide frequency range[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 8517-8538.
[5] 高瞻, 李耀华, 葛琼璇, 等. 适用于大功率三电平中点钳位整流器的SVPWM和DPWM策略研究[J]. 电工技术学报, 2020, 35(23): 4864-4876.
Gao Zhan, Li Yaohua, Ge Qiongxuan, et al. Research on SVPWM and DPWM strategies suitable for high power three-level neutral point clamped rectifier[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4864-4876.
[6] Dalessandro L, Round S D, Drofenik U, et al. Dis- continuous space-vector modulation for three-level PWM rectifiers[J]. IEEE Transactions on Power Electronics, 2008, 23(2): 530-542.
[7] Zhao Zhengming, Zhong Yulin, Gao Hongwei, et al. Hybrid selective harmonic elimination PWM for common-mode voltage reduction in three-level neutral- point-clamped inverters for variable speed induction drives[J]. IEEE Transactions on Power Electronics, 2012, 27(3): 1152-1158.
[8] 王堃, 游小杰, 王琛琛, 等. 低开关频率下SHEPWM和SVPWM同步调制策略比较研究[J]. 电工技术学报, 2015, 30(14): 333-341.
Wang Kun, You Xiaojie, Wang Chenchen, et al. Research on the comparison of synchronized modu- lation of SHEPWM and SVPWM under low switching frequency[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 333-341.
[9] 赵鲁, 李耀华, 葛琼璇, 等. 特定谐波消除及优化脉宽调制单相整流器的研究[J]. 电工技术学报, 2014, 29(10): 57-64.
Zhao Lu, Li Yaohua, Ge Qiongxuan, et al. Study of selective harmonic elimination and optimization pulse width modulation single-phase rectifier[J]. Transa- ctions of China Electrotechnical Society, 2014, 29(10): 57-64.
[10] Pontt J A, Rodríguez J R, Liendo A, et al. Network friendly low switching frequency multipulse high- power three-level PWM rectifier[J]. IEEE Transa- ctions on Industrial Electronics, 2009, 56(4): 1254- 1262.
[11] 兰志明, 王成胜, 段巍, 等. 基于IGCT的大功率五电平中点钳位/H桥变流器[J]. 电工技术学报, 2021, 36(20): 4249-4255.
Lan Zhiming, Wang Chengsheng, Duan Wei, et al. Investigation on IGCT-based on large power five- level neutral-point-clamped/H-bridge converter[J]. Transactions of China Electrotechnical Society, 2021, 36(20): 4249-4255.
[12] 韩坤, 宋玉明, 余彬, 等. 牵引逆变器多模式分段同步调制算法FPGA程序设计与实现[J]. 电工技术学报, 2019, 34(20): 4314-4322.
Han Kun, Song Yuming, Yu Bin, et al. Traction inverter multi-section synchronous SVPWM strategy FPGA program design and implementation[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(20): 4314-4322.
[13] Silva C, Oyarz'un J. High dinamic control of a PWM rectifier using harmonic elimination[C]//IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, 2006: 2569-2574.
[14] Holtz J, Bernd B. Fast current trajectory tracking control based on synchronous optimal pulsewidth modulation[J]. IEEE Transactions on Industry Appli- cations, 1995, 31(5): 1110-1120.
[15] Holtz J, Beyer B. The trajectory tracking approach-a new method for minimum distortion PWM in dynamic high-power drives[J]. IEEE Transactions on Industry Applications, 1994, 30(4): 1048-1057.
[16] Holtz J, Qi Xin. Optimal control of medium-voltage drives-an overview[J]. IEEE Transactions on Indu- strial Electronics, 2013, 60(12): 5472-5481.
[17] Brückner T, Bernet S, Güldner H. The active NPC converter and its loss-balancing control[J]. IEEE Transactions on Industrial Electronics, 2005, 52(3): 14.
[18] 张永昌, 赵争鸣, 张颖超. 三电平逆变器SHEPWM多组解特性比较及实验[J]. 电工技术学报, 2007, 22(3): 60-65.
Zhang Yongchang, Zhao Zhengming, Zhang Yingchao. Comparison and experiment of multiple solutions for SHEPWM applied to three-level inverter[J]. Transa- ctions of China Electrotechnical Society, 2007, 22(3): 60-65.
[19] 朱进权, 葛琼璇, 王晓新, 等. 基于自抗扰和负载功率前馈的高速磁悬浮系统PWM整流器控制策略[J]. 电工技术学报, 2021, 36(2): 320-329.
Zhu Jinquan, Ge Qiongxuan, Wang Xiaoxin, et al. Control strategy for PWM rectifier of high-speed maglev based on active disturbance rejection control and load power feed-forward[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 320- 329.
Selective Harmonic Elimination Pulse Width Modulation for High Power Three-Level Rectifier of High-Speed Maglev Traction System
Abstract The traction power supply system of high-speed maglev train adopts high power back-to-back three-level active neutral point clamped (3L-ANPC) converter. In order to reduce the harmonics of grid-side current at low switching frequency, a selective harmonic elimination pulse width modulation (SHEPWM) strategy suitable for high power 3L-rectifiers was proposed based on linear extended state observer (LESO) and proportional resonance (PR) control in the three-phase static coordinate system. The corresponding dead time compensation method was also designed. During the operation of high-speed maglev train, the load on the inverter side would change sharply due to the changeover of the stator segment, resulting in a significant change in the grid-side current. Considering the poor dynamic performance of SHEPWM, an on-line correction method for the off-line calculated switching angle sequence in the changeover stage was proposed, which could improve the dynamic regulation ability of the rectifier closed-loop control based on SHEPWM. Finally, the back-to-back 3L-ANPC experimental platform was utilized to verify the superiority of SHEPWM in improving the grid-side current quality and the effectiveness of the proposed strategy to improve the dynamic performance of SHEPWM closed-loop control.
keywords:High-speed maglev train, three-level active neutral point clamped (3L-ANPC) rectifier, selective harmonic elimination pulse width modulation (SHEPWM), linear extended state observer (LESO), dynamic performance
DOI: 10.19595/j.cnki.1000-6753.tces.211881
中图分类号:TM461
国家重点研发计划高速磁浮交通系统关键技术研究课题(2016YFB1200602-19)和国家自然科学基金(51907188)资助项目。
收稿日期 2021-11-18
改稿日期 2022-01-10
赵牧天 男,1995年生,博士研究生,研究方向为大功率变流器与直线电机牵引控制技术。E-mail: zhaomutian@mail.iee.ac.cn
葛琼璇 女,1967年生,研究员,博士生导师,研究方向为高压大功率变流器控制技术、高性能电机牵引控制技术。E-mail: gqx@mail.iee.ac.cn(通信作者)
(编辑 陈 诚)