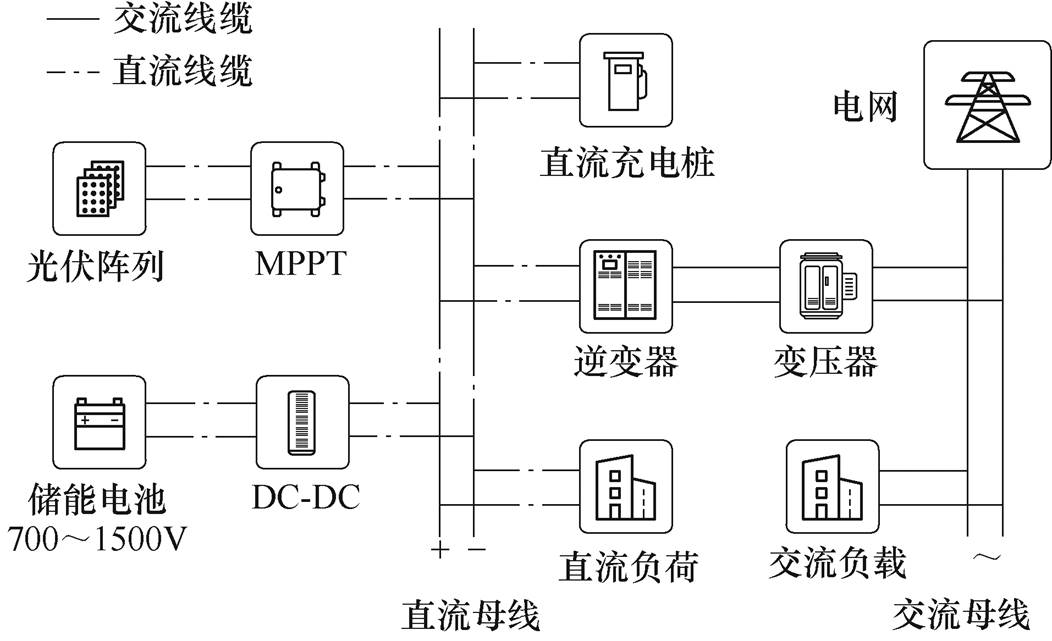
图1 共直流母线的光储系统电网架构
Fig.1 Power grid structure of photovoltaic energy storage system with common DC bus
摘要 光伏系统中直流母线电压受光伏发电端及负载影响变化范围较大，传统储能直流变换器难以适应储能侧及母线侧双端宽电压范围运行。该文提出一种适用于储能系统的飞跨电容三电平双向升降压变换器，该变换器具有对称的拓扑结构，能量向任意方向传递时，均可实现升、降压功率变换，从而解决储能系统在宽母线电压工况下的应用问题。此外，该文提出基于所提变换器的模型预测控制（MPC）策略，该策略通过建立电感电流的预测模型，引入电感电流和输出电压的双闭环控制，实现稳定输出电压的控制目标。同时，建立飞跨电容的独立预测电压闭环，在保证输出稳压的基础上，实现对双侧飞跨电容电压的独立控制。最后，通过搭建小功率实验平台验证了所提变换器及其控制策略的有效性。
关键词：储能系统 飞跨电容三电平双向直流变换器 双向升降压功率变换 模型预测控制
随着新能源技术的快速发展，光伏发电已经成为能源转型的主力之一。然而，光伏间歇发电的特征给电网的安全稳定运行带来了一定挑战。储能技术作为平抑电网功率波动、提升电能质量的有效方式[1]，近年来受到了广泛关注，并应用于新能源发电系统中[2-3]。
如图1所示为共直流母线的光储系统电网架构。储能系统接入直流电网，并以直流母线电压为信息载体控制储能系统运行模式[4]。双向直流变换器作为储能系统能量转换的核心设备，根据网压值调整能量在直流电网与电池设备间的流动，实现稳压目的[5]。但在图1所示的电网架构中，直流网压主要由光伏发电状态及负荷决定，变化范围较大。储能系统接入后，能量在单向传递时，功率变换器既可以工作于降压模式，也能够工作于升压模式，以满足储能单元电压及网压的宽变化范围，从而对储能变换器提出了更高的要求。
图1 共直流母线的光储系统电网架构
Fig.1 Power grid structure of photovoltaic energy storage system with common DC bus
储能功率变流器常采用非隔离拓扑以提升能量转换效率[6]，通常包括两电平拓扑[7]、三电平拓扑[8]和级联多电平拓扑[9]三大类。两电平拓扑常采用半桥结构，结构及控制较为简单，但开关器件的应力较大[10]。文献[7]通过交错并联技术降低了开关器件的电流应力，同时采用约束模型预测控制技术提高了变换器的动态响应性能，然而器件的电压应力没有改变，无法满足高压场合应用。级联多电平拓扑具有模块化的结构，器件应力较低，适用于高压工况[6, 11]，但开关器件数量的增多增大了开关损耗，降低了系统效率[12]。与两电平相比，三电平拓扑将开关器件的电压应力降低了一半，通常包括中点钳位型和飞跨电容型两种类型[13-14]。中点钳位型三电平拓扑由两个半桥拓扑串联构成，文献[15-16]分析了中点钳位型三电平双向直流变换器的工作原理，并提出了闭环控制策略，然而该拓扑由于输入输出端电压不共地，大功率工况下难以实现多机并联运行。飞跨电容型三电平拓扑通过在中间开关管中并联电容的方式，实现了三电平输出。由于变换器的输入与输出端共地，飞跨电容三电平功率变换器易于多机并联运行[17]。相比之下，飞跨电容型拓扑在大功率储能系统中应用具有明显的优势。但是，在当前的储能系统中，受限于拓扑结构，飞跨电容三电平直流变换器只能工作在Buck或Boost状态，当储能侧及母线侧双端电压变化范围较宽时，难以实现稳定的双向功率变换。
此外，飞跨电容拓扑在控制上不仅要实现对输出电压的稳定控制，同时也要时刻保持飞跨电容电压为端电压的一半，来确保开关器件不会因为电压应力过大而损坏[18]。为了实现对飞跨电容电压的稳定控制，文献[19]提出了基于平均状态电路模型的自适应PI控制器，然而PI调节器的线性控制特征导致负载突变时的系统动态响应速度较慢[20-21]。文献[22-24]将模型预测控制（Model Predictive Control, MPC）应用于直流变换器中以提升系统动态性能。MPC技术通过构建各输出变量的约束函数，在有限的控制集内对所有可能出现的未来状态进行评判，选择使约束函数值最小的控制变量作为下一周期的系统输入[25]。其中，MPC对未来状态的评判是建立在变换器数学模型基础上的，所以MPC算法要结合拓扑及实际的工况进行设计[26]。
为解决储能系统双端宽电压变化范围时的双向功率控制问题，本文提出了一种飞跨电容型三电平双向升降压直流变换器。与传统双向直流变换器相比，该变换器向任意方向传递能量时，既可以实现升压变换，也可以实现降压变换，从而解决了在储能电池电压及直流网压宽范围运行工况下，储能系统的双向功率控制问题。此外，针对所提变换器拓扑，文中提出了一种多目标定频寻优模型预测控制策略，该策略在实现双向功率变换的前提下，具备各个飞跨电容的稳压控制能力，同时兼具良好的动态响应性能。最后，通过搭建的实验平台，验证了所提拓扑及控制策略的有效性。
为使变流器在双端宽电压范围变化时具备双向能量变换能力，在传统飞跨电容三电平变换器的输出端增加一组桥臂，构成H桥结构，改进后的变换器拓扑如图2所示。图中，Cf1、Cf2为飞跨电容，u1、u2分别为端电压，L为电感。
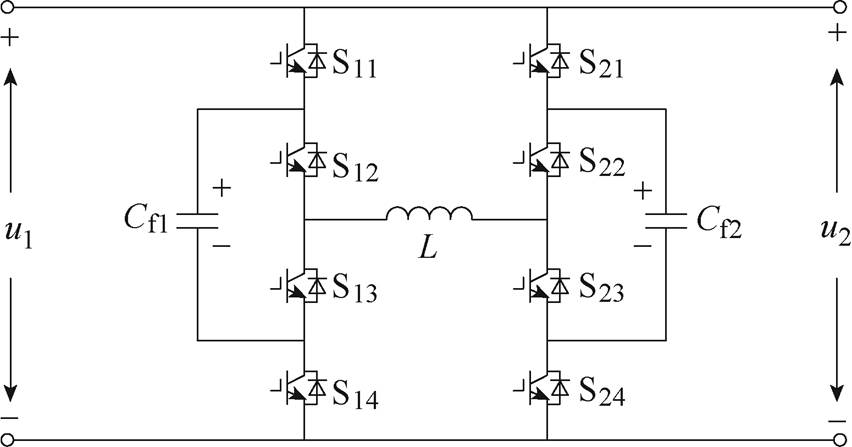
图2 飞跨电容三电平双向Buck-Boost直流变换器拓扑
Fig.2 Topology of flying capacitor three-level bi-directional Buck-Boost DC converter
对称的三电平拓扑结构使得能量由一侧向另一侧传递时变换器的控制更加灵活。为保证变换器按三电平方式工作，S11和S14，S12和S13均互补导通，S11和S12的载波相差180°，S21～S24的驱动方式与之相同。两侧开关虽然驱动方式相同，但是在不同的控制方式下，图2所示变换器将以不同的模式工作。
以能量由左向右流动为例，当S11、S12交替导通，其他开关处于闭合状态时，S13、S14、S21、S22的反并联二极管将给电流提供导通路径，此时变换器将工作于Buck模式，共包含有四种工作模态，如图3所示。
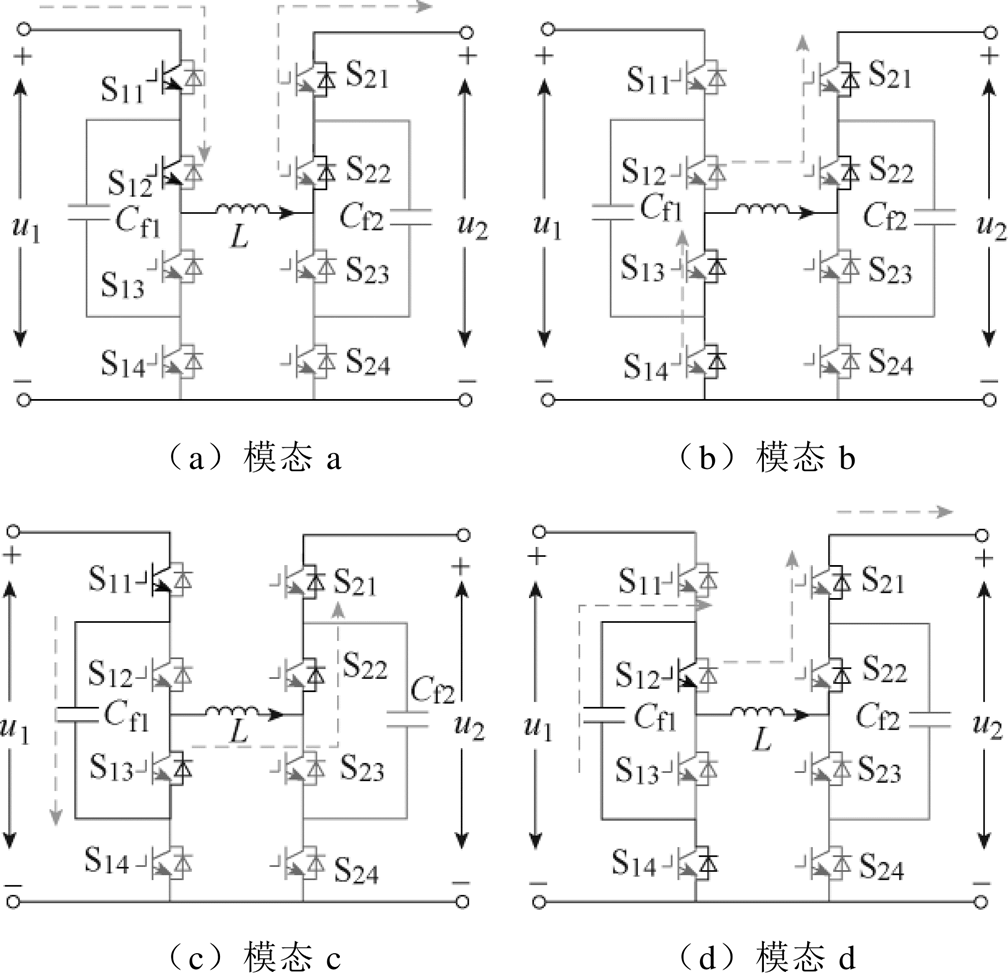
图3 Buck模式下变换器工作模态
Fig.3 Converter operation states under Buck mode
当S11、S12需持续导通，S23与S24交替导通时，变换器将工作于Boost模式，此时变换器仍具有四种工作模态，如图4所示。
图4 Boost模式下变换器工作模态
Fig.4 Converter operation states under Boost mode
当S11和S12，S23和S24交替导通，且S11与S24，S12与S23的驱动信号同相位时，变换器将工作于Buck-Boost模式，此时其工作模态如图5所示。
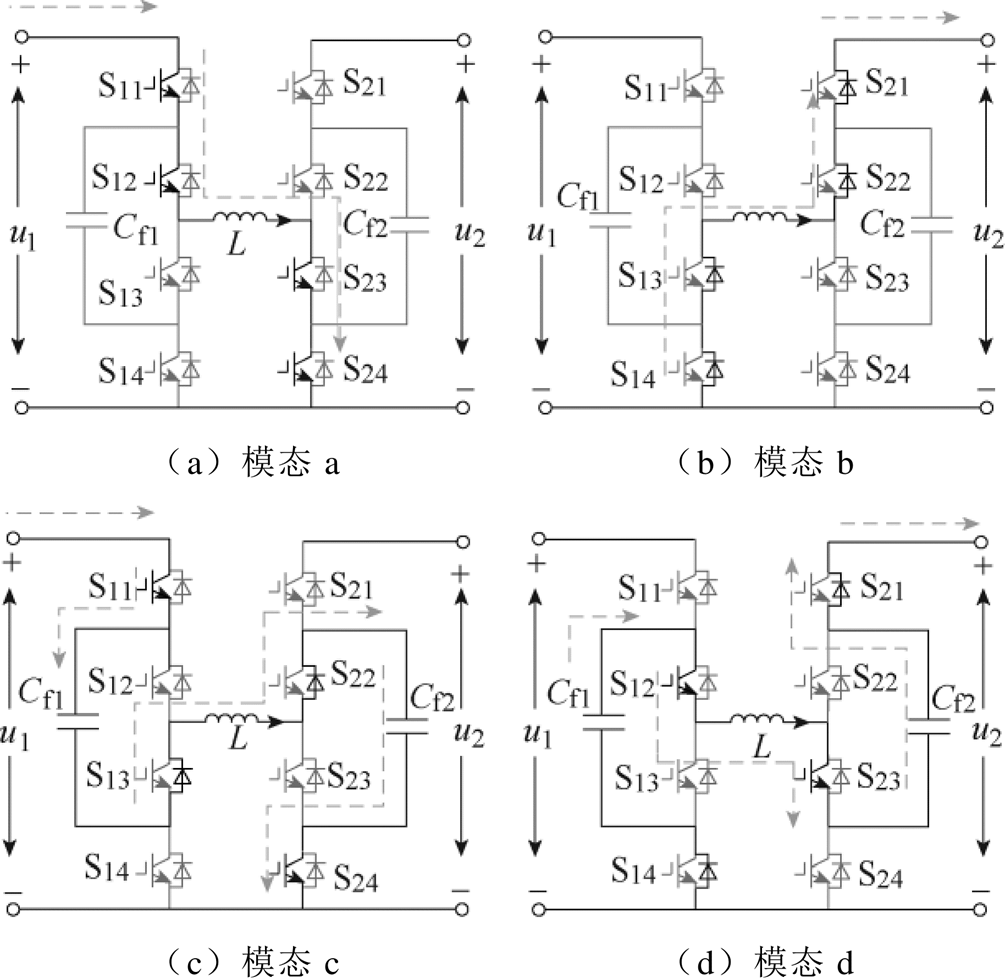
图5 Buck-Boost模式下变换器工作模态
Fig.5 Converter operation states under Buck-Boost mode
变换器在如图3～图5所示的三种模式下，均包含有四种工作模态，切换方式由驱动占空比决定。在移相控制方式下，S11、S12、S23和S24的占空比相同，均为D，当D取不同数值时，变换器工作模态的划分如图6所示。
如图6所示，当占空比D＜0.5时，变换器分别工作于Buck、Boost、Buck-Boost模式下的b、c和d模态；当D＞0.5时，变换器将分别工作于a、c和d模态；当D=0.5时，变换器将工作于临界模态，此时仅包含图3～图5中的c和d两种模态。
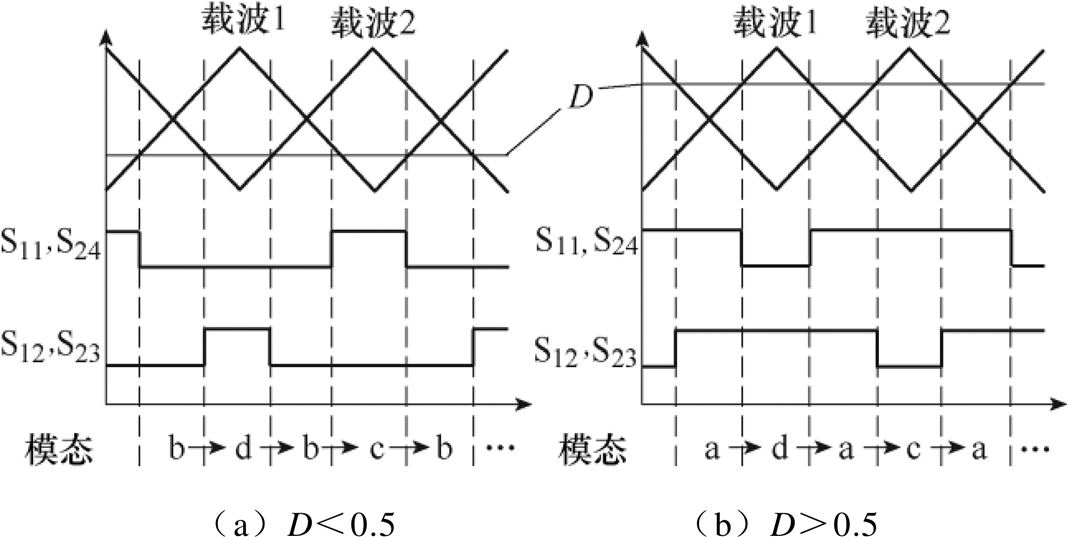
图6 Buck/Boost/Buck-Boost模式下模态切换方式
Fig.6 State switching sequences under Buck/Boost/ Buck-Boost mode
根据图6所示的模态切换方式及图3～图5所示的电路工作模态，可得稳态下的变换器等效状态方程，并由此得到三种工作模式下的变换器输入与输出电压关系为
（1）
飞跨电容三电平双向升降压变换器虽然具有三种模式，但与Buck-Boost模式相比，Buck和Boost模式下变换器仅一侧开关工作于斩波状态，相比之下，变换器的损耗更小，同时当能量由一侧向另一侧传递时，变换器可通过两种模式切换实现单向升降压变换，能够满足使用要求。然而，根据式（1）可得到三种模式下的变换器电压增益曲线如图7所示。
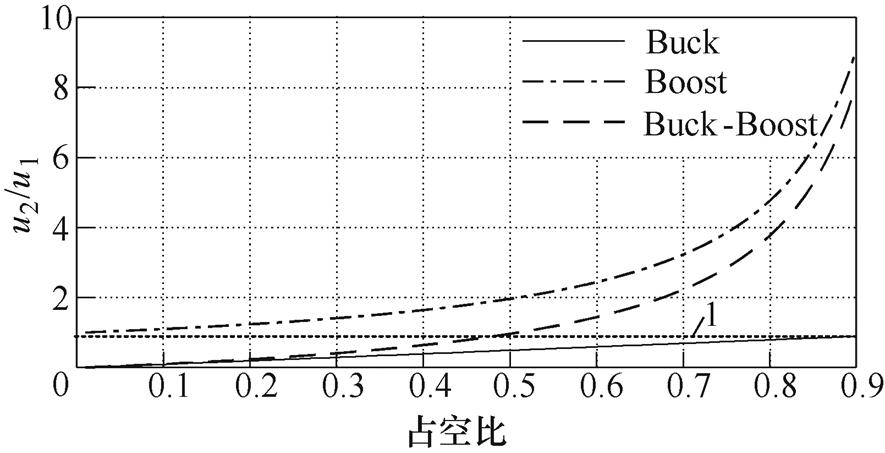
图7 不同工作模式下的变换器电压增益曲线
Fig.7 Converter voltage gain curves under different operation mode
由图7所示电压增益可知，变换器在Buck和Boost模式下的切换不是连续的。当能量转换由Buck模式切换到Boost模式时，为使电流受控，u1＜u2，然而当变换器两侧电压差相近时，结合式（1）和图3、图6可知，此时变换器将主要工作于c、d模态，此时电感压降可以表示为
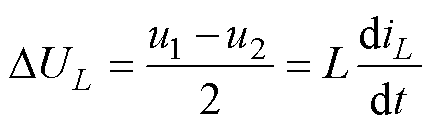（2）
由式（2）不难得知，当u1和u2接近时，系统电流响应势必变慢，进而导致储能系统响应无法满足应用要求。而图7中Buck-Boost模式下的电压增益是连续的，这表明变换器在占空比工作范围内可实现连续输出控制，系统运行将不受两侧压差影响。因此，在双端电压宽变化范围下飞跨电容三电平双向升降压拓扑更适合Buck-Boost模式运行。
当飞跨电容三电平双向升降压变换器应用于储能系统，且工作于Buck-Boost模式时，变换器在控制上需满足以下基本控制目标：①具备双向功率变换功能，能够稳定直流母线电压；②具备双端飞跨电容电压控制能力，使变换器稳定工作于三电平模式；③具备良好的动态响应能力，满足储能系统应用要求。基于上述控制目标，本节将建立适用于所提变换器的MPC策略。
以电感电流iL和飞跨电容电压uf1、uf2为状态变量，可分别建立各模态下的电路状态方程。图5a中，S11、S12、S24和S23同时导通，输入端向电感充电，电感电流上升，飞跨电容Cf1、Cf2无充放电回路，此时电路方程可表示为
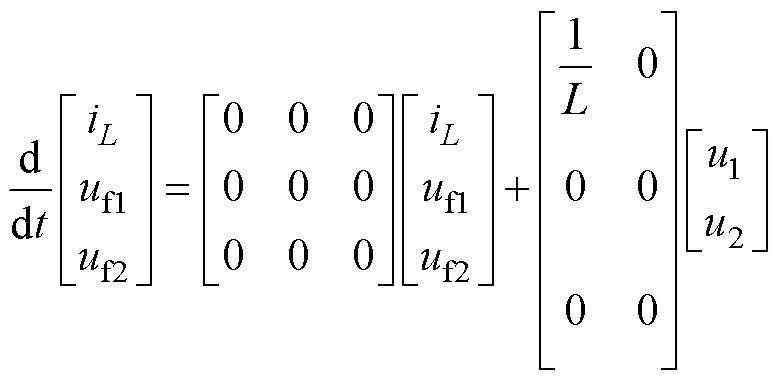（3）
图5b中，S11、S12、S24、S23同时关断，由电感L向负载供电，飞跨电容Cf1、Cf2无充放电回路，电压保持不变，此时电路方程可表示为
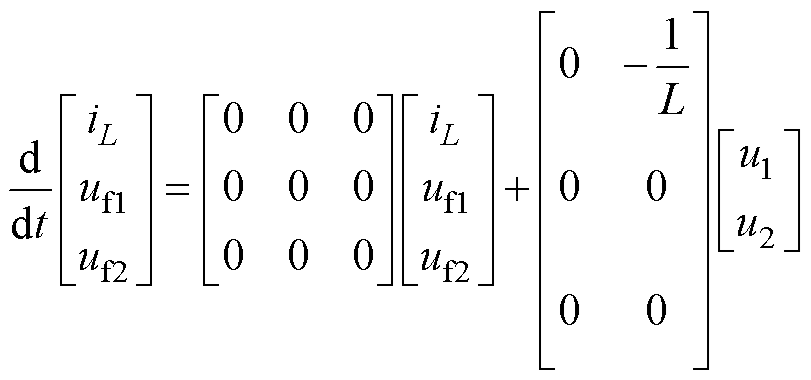（4）
图5c中，S11、S24导通，S12、S23关断，u1侧电源向飞跨电容Cf1、Cf2充电。此时电感L电流由变换器电压增益决定，当增益小于1时，电感电流上升；增益大于1时，电感电流下降。该状态下的电路方程表示为
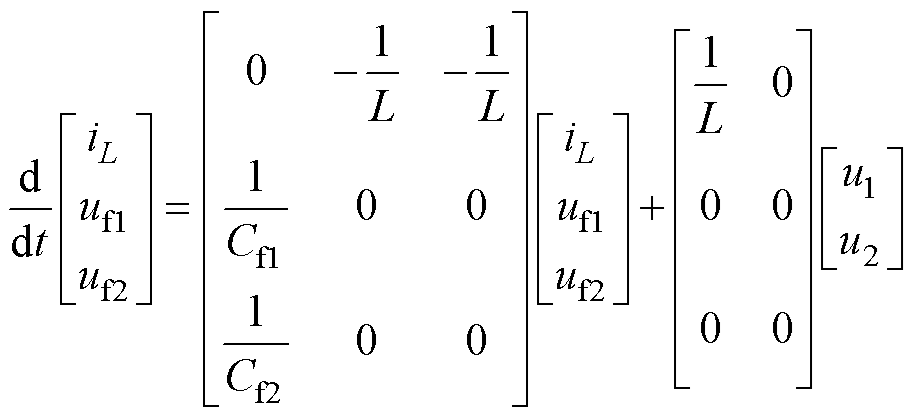（5）
图5d中，S11、S24关断，S12、S23导通。两飞跨电容同时向负载放电，飞跨电容电压下降。此时电感电流仍由变换器增益决定，当变换器电压增益小于1时，电感电流上升；增益大于1时，电感电流下降。该状态下的电路方程表示为
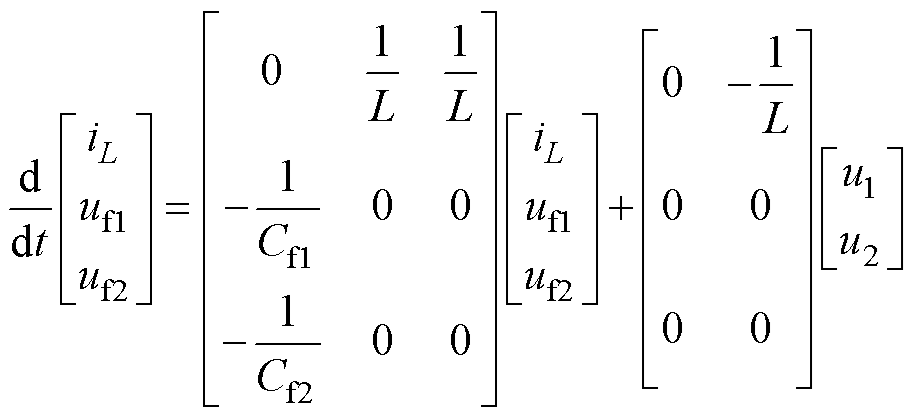（6）
所提变换器工作于三电平模式时，飞跨电容Cf1与Cf2的电压分别为各自侧端电压的一半。因此，理想状态下，飞跨电容电压可以表示为
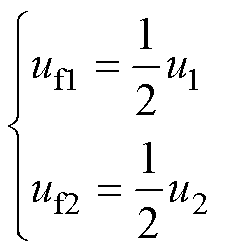（7）
将式（7）分别代入式（5）、式（6）中可得
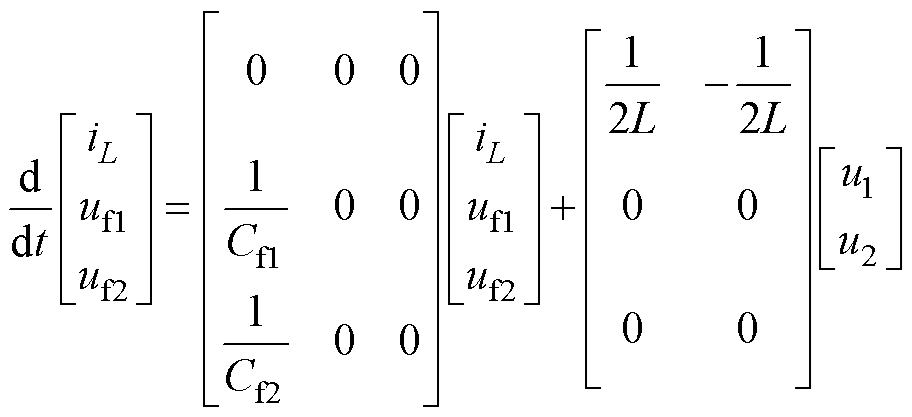（8）
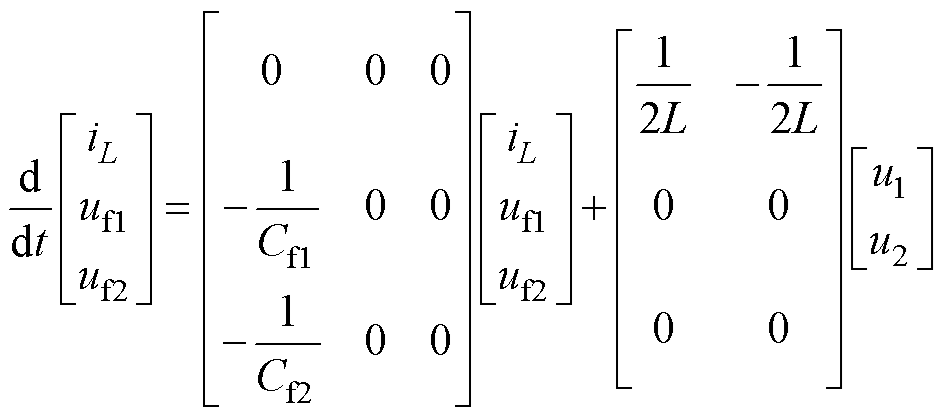（9）
经过式（7）转换后，状态变量iL、uf1和uf2将完全由飞跨电容电压及两侧电压表示，从而简化了状态变量的表达形式。根据式（3）、式（4）、式（8）和式（9）可得周期内变换器的平均状态等效方程为
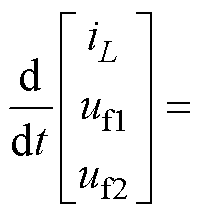
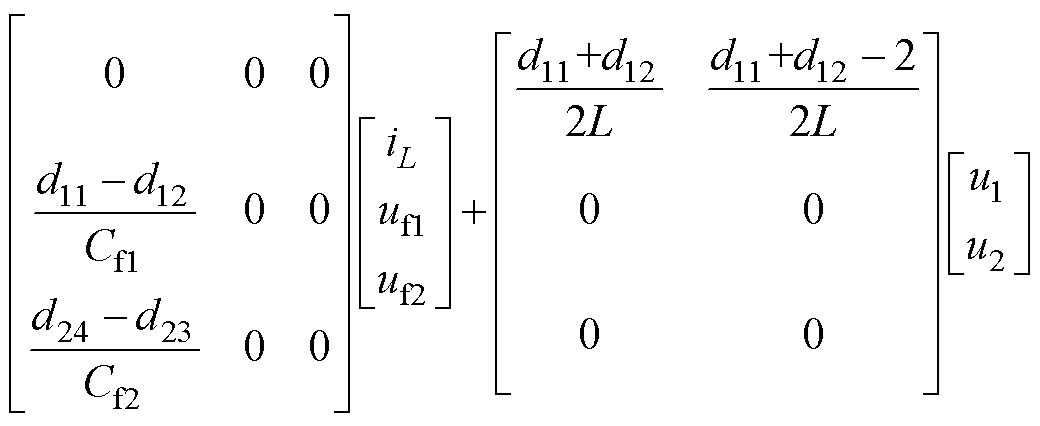（10）
式中，d11、d12、d23、d24分别为开关S11、S12、S23和S24的占空比。
变换器在运行过程中需要控制的变量包括输出电压、电感电流及两侧飞跨电容的电压。将电感电压及飞跨电容电压作为内部控制变量，由式（10）可知，电感电流主要取决于两侧电压差及S11、S12的占空比，而飞跨电容电压则取决于电感电流值和对应侧桥臂上开关的占空比之差。为了稳定母线电压，首先需要严格地控制电感电流，因此，电流受控是变换器运行的前提，而当电流受控时，双侧飞跨电容电压可控。
为了得到电感电流及飞跨电容电压三个变量的预测控制模型，将式（10）进行离散化可得
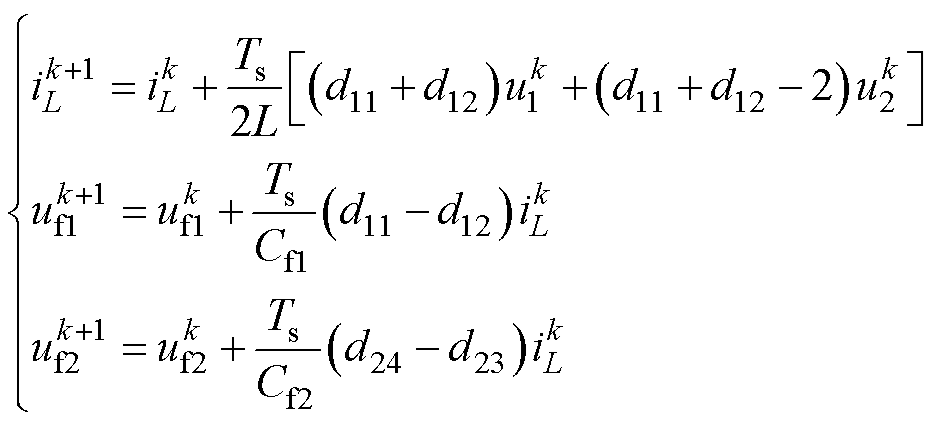（11）
式中，Ts为开关周期；带有上标k的变量表示当前时刻的采样值；上标k+1为下一时刻的预测值。
传统MPC算法根据式（11）可直接建立约束控制函数为
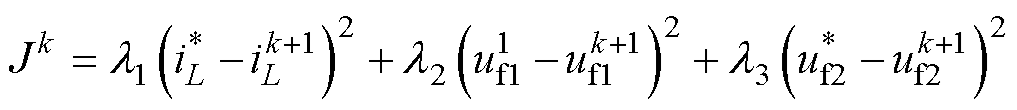（12）
式中，带有上标*的变量表示参考值；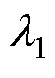
、
、
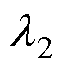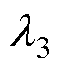分别为电感电流iL、飞跨电容电压uf1、飞跨电容电压uf2的权重系数。
首先，由式（11）可知，在实现对电感电流iL和飞跨电容电压uf1、uf2三个输出变量的控制过程中，传统MPC算法的自变量d11、d12、d24、d23互相耦合，在滚动优化时需要考虑4个自变量的所有组合方式，这将严重影响控制器的计算速度。其次，如式（12）所示，MPC的限制函数需要采用多个权重系数，而目前尚无标准的权重系数校准规则，权重函数设计复杂。此外，MPC算法常采用预测开关状态的方式以获得最优控制效果，但易导致开关工作于变频模式，损耗增加。
针对上述MPC问题，本文将建立基于电感电流和两个飞跨电容电压的独立闭环系统，通过多个限制函数来判断各个输出变量是否达到最佳状态，对多输出系统并行滚动优化。这样不但能够缩小控制集基数，而且省去了对各个输出变量的权重分配过程，进而简化了控制器的设计。为建立独立闭环系统，将式（11）中的占空比做如下变换
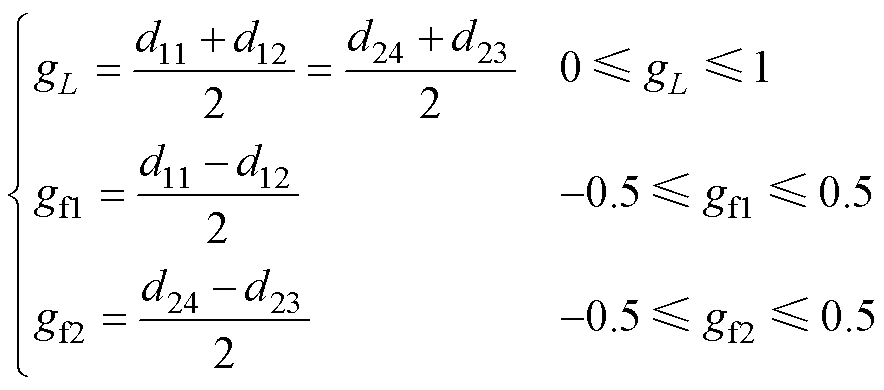（13）
将式（13）代入式（11），可得
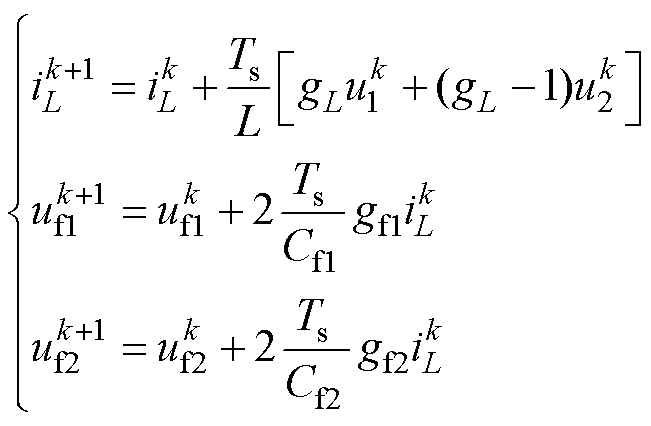（14）
如式（14）所示，占空比经过式（13）的转换后，变换器各输出变量的预测模型将彼此独立，电感电流iL和飞跨电容电压uf1、uf2这三个输出变量将分别由自变量gL、gf1、gf2单独控制，实现解耦。此时若对控制变量建立独立的约束函数，便可消除式（12）中的权重因数，由此改进后的约束函数表示为
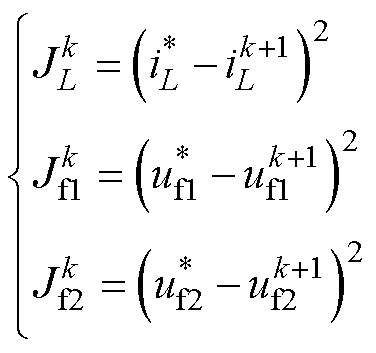（15）
式中，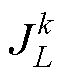
、
、
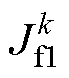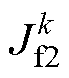分别为电感电流iL、飞跨电容电压uf1及uf2的约束函数。通过建立3个独立的约束函数，可对所提变换器的电感电流、飞跨电容电压预测值分别寻优，各自选取最优控制变量gx（下标x表示L、f1、f2），实现独立闭环系统的建立。
MPC通过选取使约束函数值最小的控制变量gx，来使控制器达到最优控制效果，由式（15）可知，若要使约束函数值最小，需满足的等式关系为
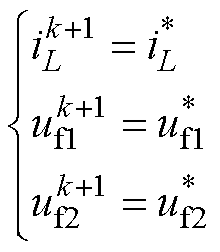（16）
结合式（14）和式（16），可得出计算控制变量gx最优量的显式表达式为
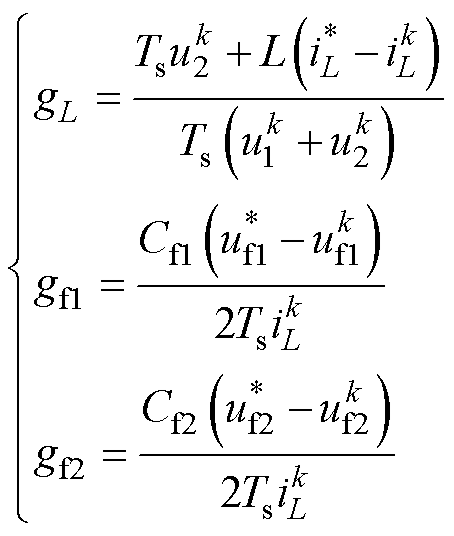（17）
由式（14）可知，各输出变量与对应的控制变量gx分别呈正相关线性关系，据此特性，当式（17）计算出的gx值超出式（13）中的变量区间时，可将其更改为与gx值最接近的区间边界值。此时，gx值需满足的限制条件表示为
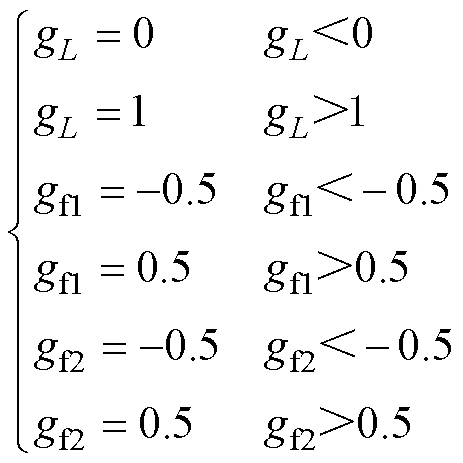（18）
通过对式（17）中gx值显式表达式的求解，并结合式（18）对超出区间范围变量gx的调整，可直接得出控制变量最优值。具体计算寻优次数的数学表达式为
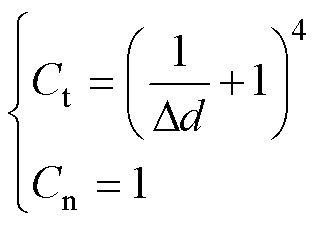（19）
式中，Ct为传统MPC算法按步长寻优次数；Cn为模型解耦合并采用显式表达式求解的MPC算法寻优次数；Dd为占空比搜索步长。由式（19）可知，传统MPC算法寻优次数取决于搜索步长，并且计算量较大。改进后的算法寻优过程仅为1次，而且与搜索步长无关，这样显著地减少了计算时间，同时也提高了计算精度。
此外，由式（13）可得各开关占空比表示为
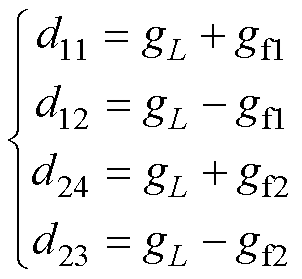（20）
由式（20）可知，本文所提模型预测控制策略将直接求得各开关的最优占空比，从而使变换器工作于定频运行模式。
对于储能变流工况，储能变流器的主要控制目标是直流母线电压。因此，需要在变换器内部电流控制的基础上引入输出电压控制，实现电感电流及母线电压的双闭环控制。根据变换器工作原理，可得电感电流与输出电压的关系式为
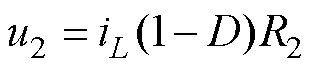（21）
式中，R2为负载阻值。
由式（1）及式（21），得电感电流的参考值为
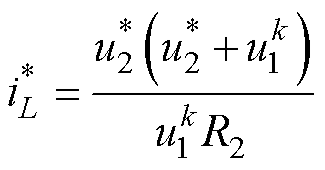（22）
式中，电感电流参考值取决于R2的大小，因此需要引入负载电流采样来估算负载阻值，改进后的电感电流参考值为
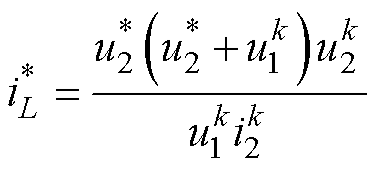（23）
飞跨电容电压的控制目标为对应端电压的一半，据此可知两个飞跨电容电压的参考值为
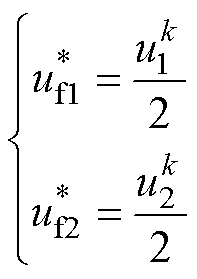（24）
综合式（17）、式（18）、式（20）及式（24），可得MPC策略框图如图8所示。
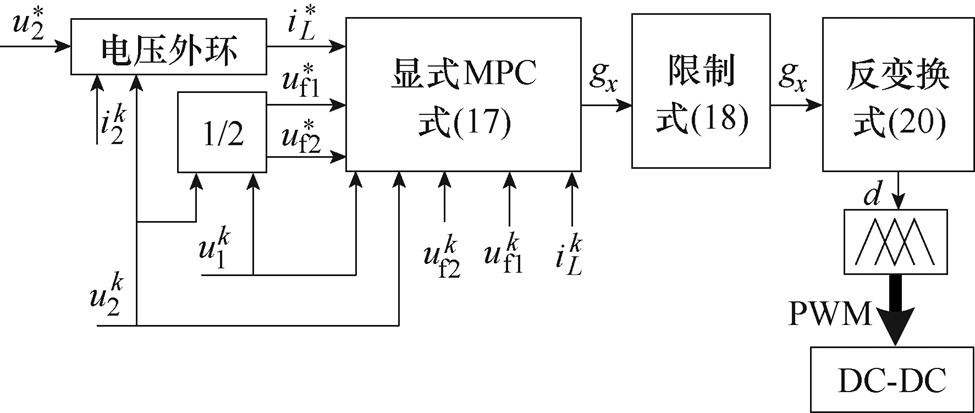
图8 多目标定频寻优MPC策略框图
Fig.8 Block diagram of MPC strategy based on multi-target fixed frequency optimization
图8中，电压外环用于稳定输出电压，同时产生内环电感电流的参考值。MPC根据当前时刻的采样信息、系统参数和输出变量参考值来求解控制变量gx，再对超出区间范围的控制变量进一步优化，便能够在可控区间内求出最优的gx。然后经反变换生成各开关的占空比，再与移相的三角波比较便能得到各开关的驱动信号。其中，MPC算法流程如图9所示。该算法以式（14）建立的模型为基础，通过三个独立的计算过程分别对电感电流和两个飞跨电容电压进行调节。
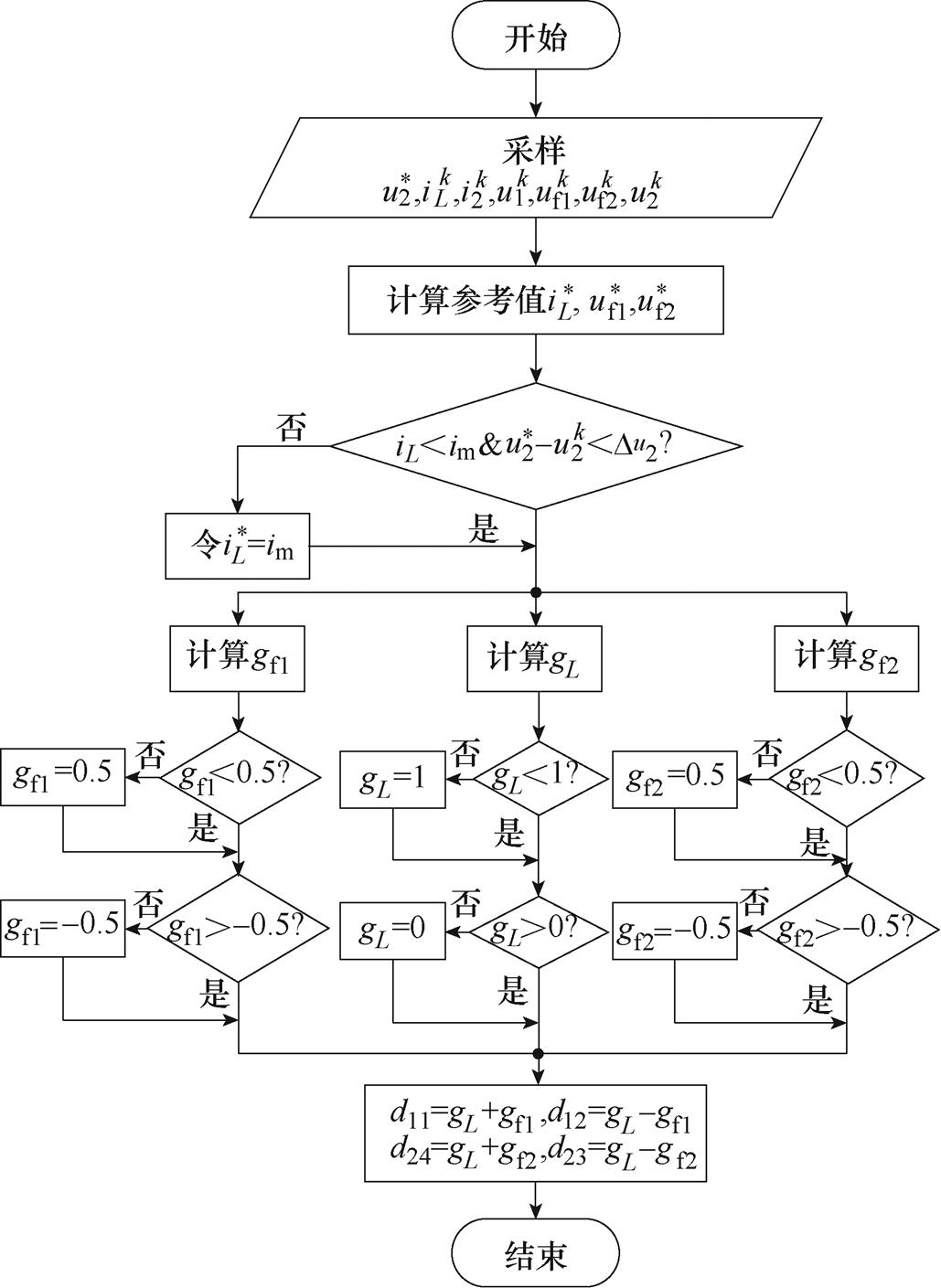
图9 MPC算法流程
Fig.9 Flow chart of MPC algorithm
图9中，im为电感电流限幅值，Du2为输出电压采样值与参考值的误差裕度。当电感电流超出限幅值时，为保证系统不会超出最大运行负荷，将会对电感电流进行限制。此外当输出电压小于参考值过多超出误差裕度时，系统将以最大运行功率工作，令负载母线电压迅速提升至目标值。
为了验证所提出的拓扑及其控制方法的有效性，搭建了以TMS320F28335+XC3S500E为控制器的飞跨电容三电平双向升降压直流储能实验平台，其中，DSP负责采样及数据运算，FPGA负责生成驱动信号及系统保护，实验平台如图10所示。图10中，采用超级电容模组作为储能单元，超级电容单模组容量为9.6F/16V，直流电源用于为储能模组和飞跨电容预充电。由于拓扑为对称结构，双向控制原理相同，实验只需验证能量从储能电池流向直流母线的工况。
图10 实验平台
Fig.10 Experimental platform
根据实验设定，实验前需要将超级电容模组预充至48V，同时需要将输入侧的飞跨电容电压uf1预充至24V，直流母线侧采用功率电阻并联电容模拟负载工况。系统起动阶段，电感电流目标值为限幅值8A，系统以最大功率工作，直至直流侧电压达到目标值，之后系统达到稳态，电感电流下降，跟随输出电流变动，保证母线电压的正常稳定工作。当系统工作于稳态时，通过调整输出电压参考值来模拟实际中的加、减载工况，通过比较输出电压的跟随能力来验证所提拓扑及其控制策略的稳压能力。控制器中算法的控制周期与开关周期相同，具体实验参数见表1。
表1 实验参数
Tab.1 Experiment parameters
参 数数 值 储能侧电压/V48 开关频率/kHz10 电感/mH1.6 飞跨电容/mF220 输出侧滤波电容/mF500 电感电流限幅值/A8
开环模式下驱动及电感电流波形如图11所示。由图中电流纹波可知，所提变换器在不同占空比下纹波频率始终是开关频率的2倍，表明该变换器在此驱动方式下工作于三电平模式。
所提变换器及其控制策略在降压模式下的实验波形如图12所示。图12a为输出侧电压给定由10V突增至30V时的输出电压及电流响应曲线。由于超级电容储能模组侧电压为48V，在此阶跃响应下变换器仍工作于降压模式。从电压u2的响应曲线可知，所提MPC策略在降压模式下具有良好的动态及稳压性能。图12b为两侧飞跨电容电压的响应曲线，由于储能侧电压在短时间没有发生变化，所以uf1电压基本保持在24V，uf2为负载侧飞跨电容电压，其电压值跟随负载电压变化，由5V升至15V，保持为输出侧电压的一半。图12c和图12d所示为负载侧电压由30V突降至10V时的响应曲线。此时负载电压能够严格跟踪电压参考值，同时uf2的电压由15降至5V，uf1电压保持为24V。
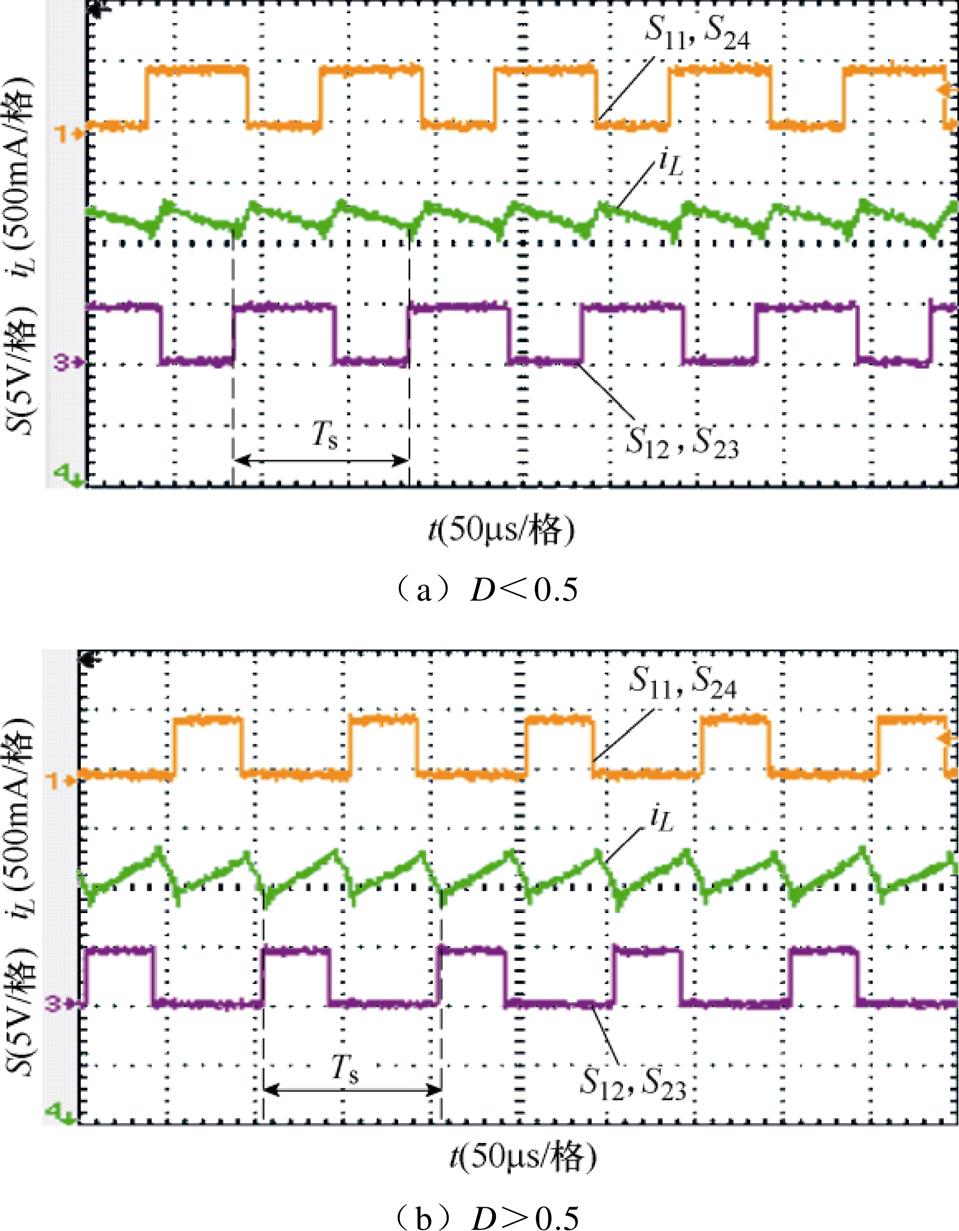
图11 开环模式下的驱动及电感电流波形
Fig.11 The waveforms of drive and inductance current signal in open loop mode
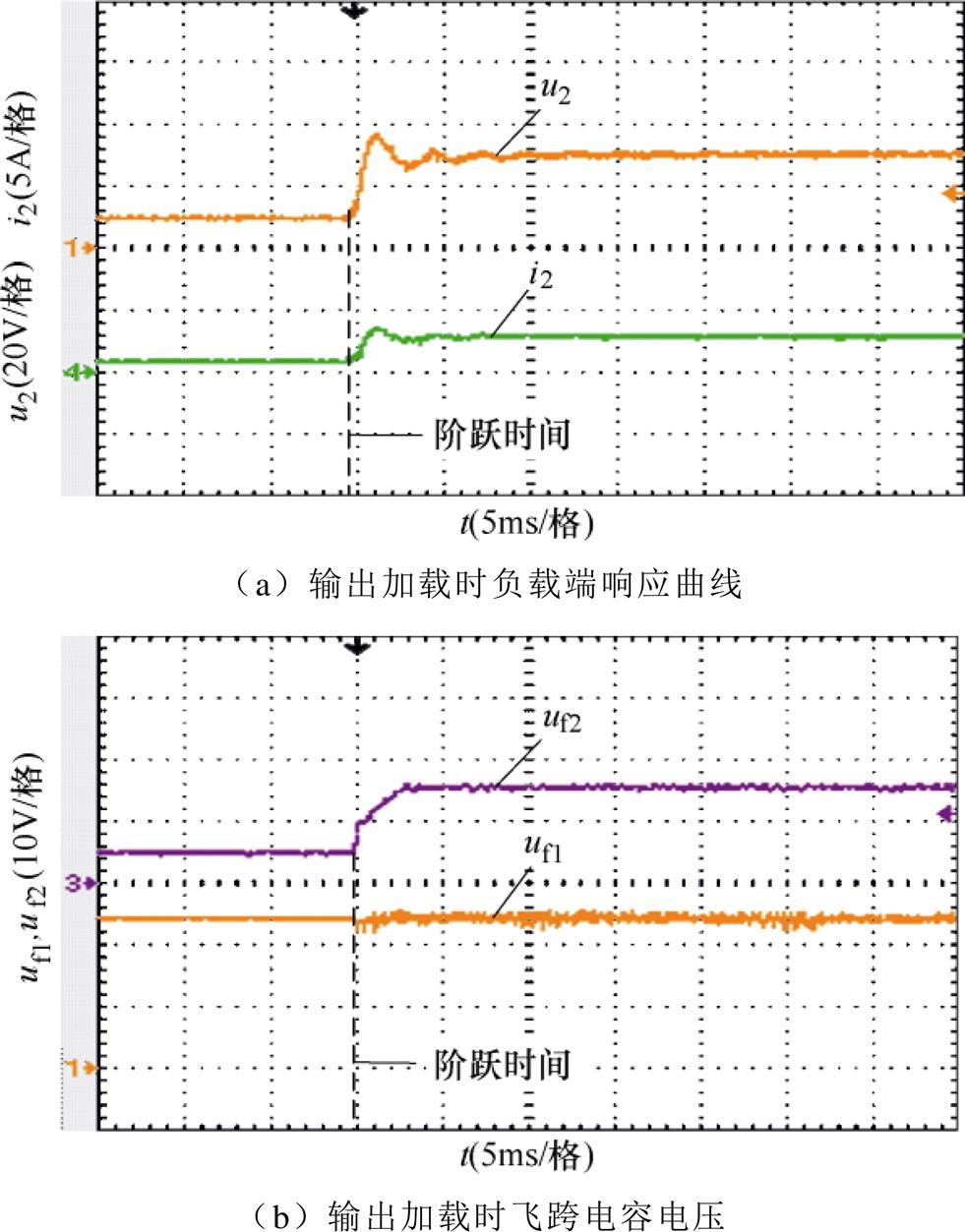
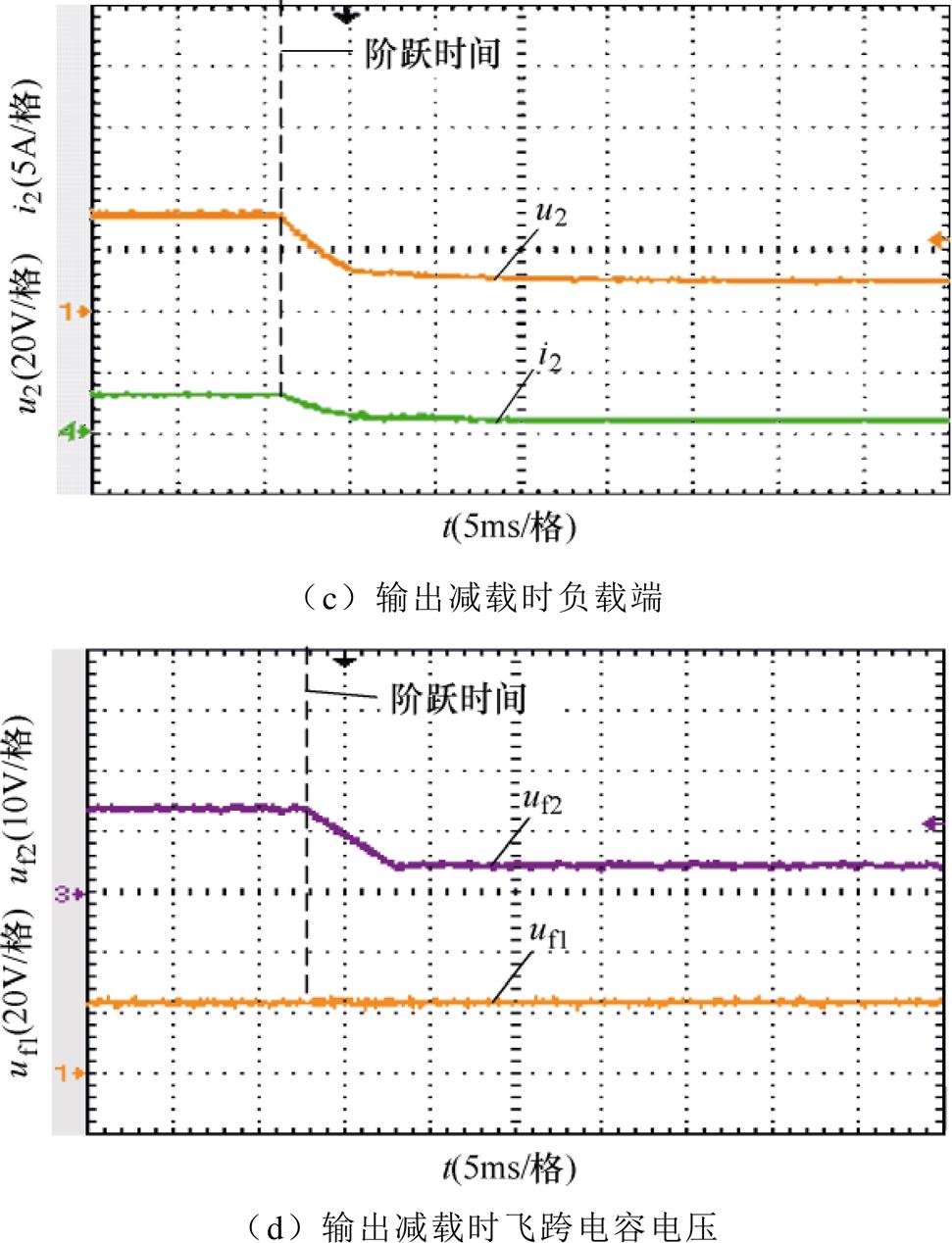
图12 Buck模式下变换器的实验波形
Fig.12 Experimental waveforms of converter in Buck mode
图13所示为变换器输出侧电压参考在30～ 60V变动时变换器的实验波形，变换器在该测试工况下工作于Buck-Boost模式。如图13a所示，变换器可由Buck模式直接转换成Boost模式工作，输出电压由30V跟踪参考给定，最终稳定输出60V，图13c所示为变换器由Boost转换成Buck模式时的响应曲线，输出电压由60V突减至30V，输出电压能严格跟踪电压参考值。由图13a和图13c的响应曲线不难看出，变换器可实现输出电压的连续控制。图13b和图13d为飞跨电容uf1和uf2的响应曲线，在Buck-Boost模式下仍具备良好的飞跨电容电压控制能力。
由于拓扑结构对称，当能量由u2侧向u1侧传递时变换器及其控制策略将具有相同的实验结果，在此不再赘述。通过上述实验结果可知，本文所提变换器能够以三电平方式进行工作，在Buck-Boost模式下可实现连续输出，同时所提MPC策略具备良好的稳压、控流及飞跨电容电压控制能力。
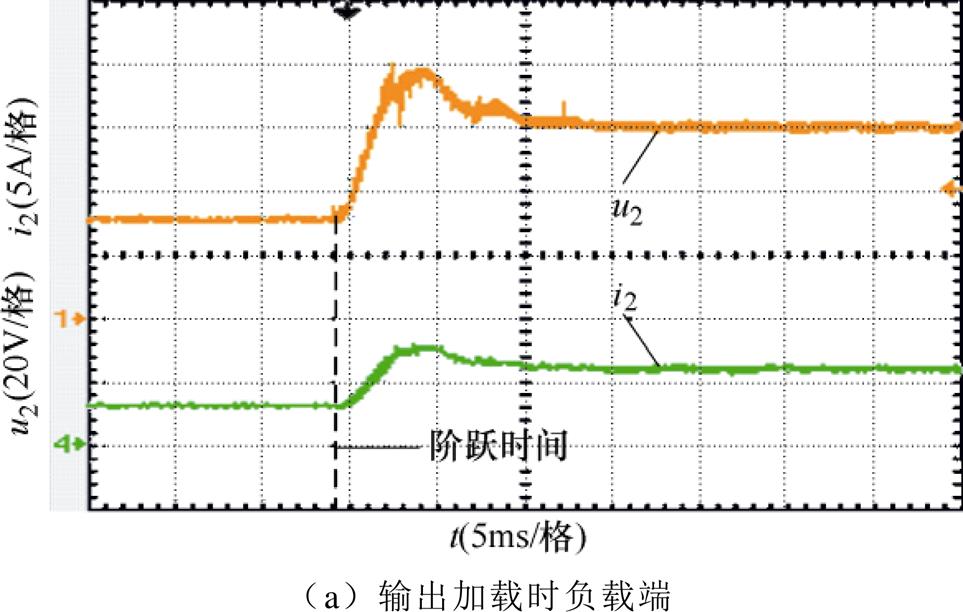
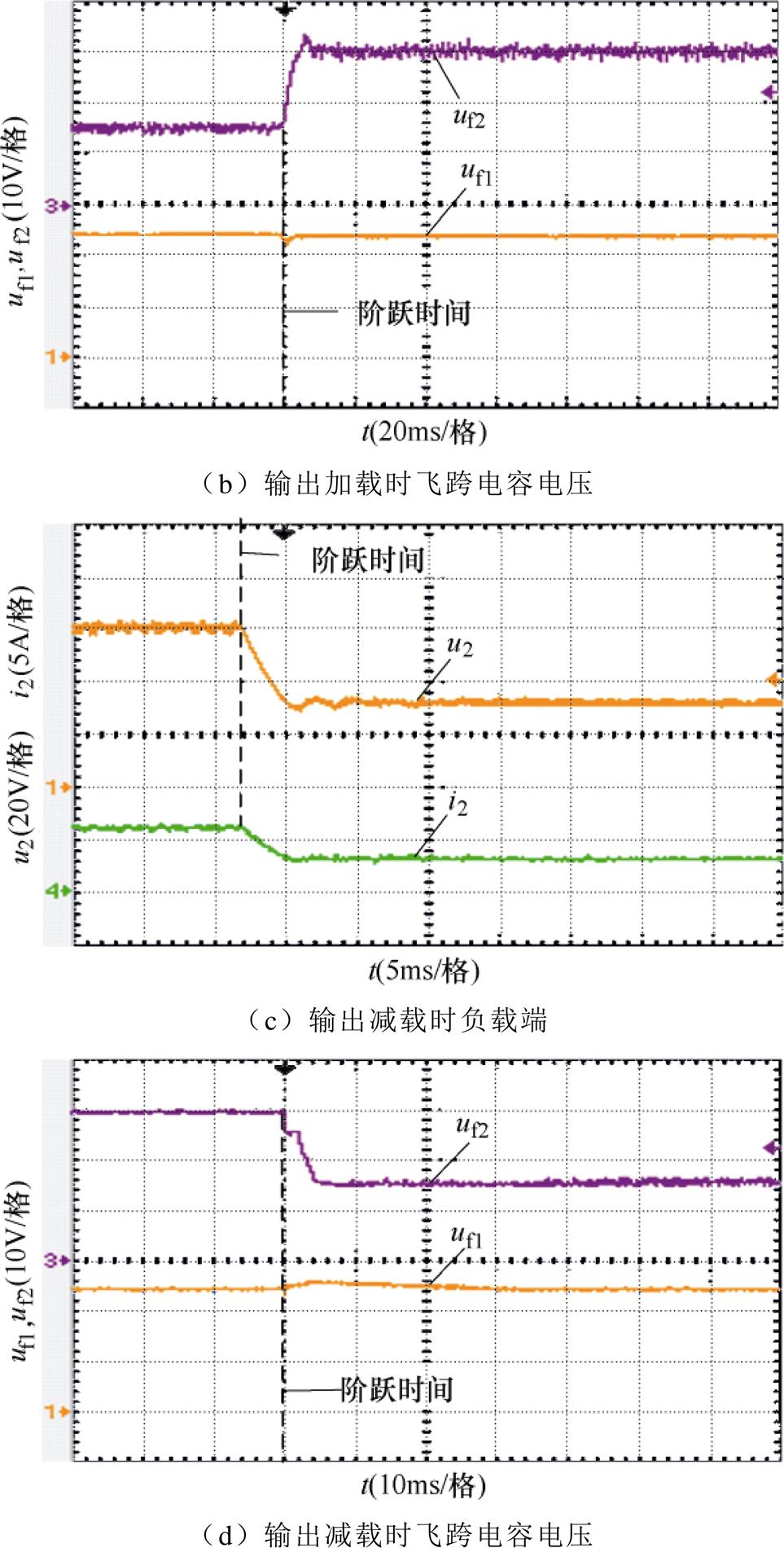
图13 Boost模式下变换器的实验波形
Fig.13 Experimental waveforms of converter in Boost mode
针对共直流母线的储能系统，本文提出一种基于对称拓扑结构的飞跨电容三电平双向升降压变换器，以解决储能侧及直流母线双端电压宽变化范围下的功率变换问题。本文详细分析了变换器的工作原理，建立了Buck-Boost模式下变换器数学模型，并提出了以变换器电感电流及两侧飞跨电容电压为目标的定频寻优模型预测控制策略。通过建立电感电流与两个飞跨电容电压的独立闭环系统，省去了权重分配的环节，实现了三环独立调节，简化了控制器的设计。同时，为了保证输出电压的稳定，引入了电感电流与输出电压双闭环控制，实现了“稳压控流”的功能，因此满足直流储能系统电池与直流母线双端宽电压变化范围的应用需求。最后，通过搭建的小功率储能系统实验平台对所提拓扑及其控制策略进行了有效验证。
参考文献
[1] 吴振威, 蒋小平, 马会萌, 等. 用于混合储能平抑光伏波动的小波包-模糊控制[J]. 中国电机工程学报, 2014, 34(3): 317-324.
Wu Zhenwei, Jiang Xiaoping, Ma Huimeng, et al. Wavelet packet-fuzzy control of hybrid energy storage systems for PV power smoothing[J]. Pro- ceedings of the CSEE, 2014, 34(3): 317-324.
[2] Sun Kai, Zhang Li, Xing Yan, et al. A distributed control strategy based on DC bus signaling for modular photovoltaic generation systems with battery energy storage[J]. IEEE Transactions on Power Electronics, 2011, 26(10): 3032-3045.
[3] Manandha U, Tummuru N R, Kollimalla S K. Validation of faster joint control strategy for battery- and supercapacitor-based energy storage system[J]. IEEE Transactions on Industrial Electronics, 2018, 65(4): 3286-3295.
[4] 张犁, 孙凯, 吴田进, 等. 基于光伏发电的直流微电网能量变换与管理[J]. 电工技术学报, 2013, 28(2): 248-254.
Zhang Li, Sun Kai, Wu Tianjin, et al. Energy conversion and management for DC microgrid based on photovoltaic generation[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 248-254.
[5] Wu Yuen, Ke Yaoting. A novel bidirectional isolated DC-DC converter with high voltage gain and wide input voltage[J]. IEEE Transactions on Power Elec- tronics, 2021, 36(7): 7973-7985.
[6] 李彬彬, 张书鑫, 赵晓东, 等. 基于容性能量转移原理的高压大容量DC/DC 变换器[J]. 中国电机工程学报, 2021, 41(3): 1103-1113.
Li Binbin, Zhang Shuxin, Zhao Xiaodong, et al. Capacitive energy transfer principle based high- voltage high-power DC/DC converters[J]. Proceedings of the CSEE, 2021, 41(3): 1103-1113.
[7] 肖智明, 陈启宏, 张立炎. 电动汽车双向DC-DC变换器约束模型预测控制研究[J]. 电工技术学报, 2018, 33(2): 489-498.
Xiao Zhiming, Chen Qihong, Zhang Liyan. Con- strained model predictive control for bidirectional DC-DC converter of electric vehicles[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 489- 498.
[8] Zhang Xinan, Wang Benfei, Manandhar U, et al. A model predictive current controlled bidirectional three-level DC/DC converter for hybrid energy storage system in DC microgrids[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(5): 4025-4030.
[9] Bi Kaitao, Sun Li, An Quntao, et al. Active SOC balancing control strategy for modular multilevel super capacitor energy storage system[J]. IEEE Transactions on Power Electronics, 2019, 34(5): 4981-4992.
[10] 丁杰, 高双, 赵世伟, 等. 基于拓扑组合的交错并联耦合电感高增益DC-DC 变换器[J]. 中国电机工程学报, 2021, 41(5): 1860-1870.
Ding Jie, Gao Shuang, Zhao Shiwei, et al. A high step-up DC-DC converter with interleaved and coupled inductor based on topology combination[J]. Proceedings of the CSEE, 2021, 41(5): 1860-1870.
[11] Jiang Wei, Huang Lili, Zhang Lei, et al. Control of active power exchange with auxiliary power loop in a single-phase cascaded multilevel converter-based energy storage system[J]. IEEE Transactions on Power Electronics, 2017, 32(2): 1518-1532.
[12] 吴刚, 阮新波, 叶志红. 采用开关电容的非隔离型高升压比直流变换器[J]. 中国电机工程学报, 2015, 35(2): 442-450.
Wu Gang, Ruan Xinbo, Ye Zhihong. Non-isolated high step-up DC-DC converters adopting switched- capacitor cell[J]. Proceedings of the CSEE, 2015, 35(2): 442-450.
[13] Grbovic P J, Delarue P, Moigne P L, et al. A bidirectional three-level DC-DC converter for the ultracapacitor applications[J]. IEEE Transactions on Industrial Electronics, 2010, 57(10): 3415-3430.
[14] Watanabe H, Sakuraba T, Furukawa K, et al. Development of DC to single-phase AC voltage source inverter with active power decoupling based on flying capacitor DC/DC converter[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 4992-5004.
[15] Tan Longcheng, Wu Bin, Rivera S, et al. Com- prehensive DC power balance management in high-power three-level DC-DC converter for electric vehicle fast charging[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 89-100.
[16] Rivera S, Wu Bin, Kouro S, et al. Electric vehicle charging station using a neutral point clamped converter with bipolar DC bus[J]. IEEE Transactions on Industrial Electronics, 2015, 62(4): 1999-2009.
[17] 胡斌, 杨中平, 黄先进, 等. 用于超级电容储能系统的三电平双向直流变换器及其控制[J]. 电工技术学报, 2015, 30(8): 83-89.
Hu Bin, Yang Zhongping, Huang Xianjin, et al. Three-level bi-directional DC-DC converter and its control strategy used for super-capacitor energy storage system[J]. Transactions of China Electro- technical Society, 2015, 30(8): 83-89.
[18] 庄桂元, 张兴, 刘威, 等. 带飞跨电容的三电平拓扑中SiC MOSFET过电压与过电流保护[J]. 电工技术学报, 2021, 36(2): 341-351.
Zhuang Guiyuan, Zhang Xing, Liu Wei, et al. Overvoltage and overcurrent protection of SiC MOSFET in three-level topology with flying capa- citor[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 341-351.
[19] Chen Hungchi, Lu Cheyu, Lien Weihsiang, et al. Active capacitor voltage balancing control for three- level flying capacitor Boost converter based on average-behavior circuit model[J]. IEEE Transactions on Industry Applications, 2019, 55(2): 1628-1638.
[20] Shan Yinghao, Hu Jiefeng, Li Zilin, et al. A model predictive control for renewable energy based AC microgrids without any PID regulators[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9122-9126.
[21] 年珩, 叶余桦. 三端口隔离双向DC-DC变换器模型预测控制技术[J]. 电工技术学报, 2020, 35(16): 3478-3488.
Nian Heng, Ye Yuhua. Model predictive control of three-port isolated bidirectional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3478-3488.
[22] Zhou Ze, Zhang Liyan, Liu Zhitao, et al. Model predictive control for the receiving-side DC-DC converter of dynamic wireless power transfer[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 8985-8997.
[23] 周兵凯, 杨晓峰, 张智, 等. 能量路由器中双有源桥直流变换器多目标优化控制策略[J]. 电工技术学报, 2020, 35(41): 3030-3040.
Zhou Bingkai, Yang Xiaofeng, Zhang Zhi, et al. Multi-objective optimization control strategy of dual- active-bridge DC-DC converter in electric energy router application[J]. Transactions of China Electro- technical Society, 2020, 35(41): 3030-3040.
[24] Wei Qiang, Wu Bin, Xu Dewei, et al. Model predictive control of capacitor voltage balancing for cascaded modular DC-DC converters[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(1): 752-761.
[25] 何志兴, 罗安, 熊桥坡, 等. 模块化多电平变换器模型预测控制[J]. 中国电机工程学报, 2016, 36(5): 1366-1375.
He Zhixing, Luo An, Xiong Qiaopo, et al. Model predictive control of modular multilevel converters[J]. Proceedings of the CSEE, 2016, 36(5): 1366-1375.
[26] 郭磊磊, 金楠, 李琰琰, 等. 并网逆变器无电网电压传感器模型预测控制[J]. 电工技术学报, 2020, 35(12): 2612-2622.
Guo Leilei, Jin Nan, Li Yanyan, et al. Grid voltage sensorless model predictive control for grid- connected inverters[J]. Transactions of China Elec- trotechnical Society, 2020, 35(12): 2612-2622.
Flying Capacitor Three-Level Bi-Directional Buck-Boost Converter and Its Model Predictive Control Strategy for DC Energy Storage System
Abstract The DC bus voltage in the photovoltaic system is affected by the generator and load in a wide range. The traditional energy storage DC-DC converter is difficult to adapt to the wide voltage range operation of both energy storage side and bus side. This paper presents a flying capacitor three-level bi-directional Buck-Boost converter for energy storage system, which has a symmetrical topology. When the energy is transferred to any direction, it can realize the power conversion of Boost and Buck, thus solving the application problem under wide bus voltage condition. In addition, a model predictive control (MPC) strategy based on the this converter is proposed. By establishing the predictive model of the inductor current and introducing the double closed-loop control of the inductor current and output voltage, the control objective of stabilizing the output voltage is achieved. At the same time, the independent predictive voltage closed-loop of the flying capacitor is established. On the basis of ensuring the output voltage stabilization, the independent control of the voltage of the bilateral flying capacitor is realized. Finally, the effectiveness of the proposed converter and its control strategy is verified by building a small power experimental platform.
keywords：Energy storage system, flying capacitor three-level bi-directional DC-DC converter, bi-directional buck-boost power converter, model predictive control
DOI: 10.19595/j.cnki.1000-6753.tces.211127
中图分类号：TM46
国家自然科学基金（51807079）、江苏省自然科学基金（BK20200623）和博士后科学基金（2020M681692）资助项目。
收稿日期 2021-07-23
改稿日期 2021-09-29
樊启高 男，1986年生，博士，副教授，研究方向为新能源发电及机电一体化技术。E-mail: qgfan@jiangnan.edu.cn
毕恺韬 男，1989年生，博士，讲师，研究方向为大功率储能功率变流技术。E-mail: bkt1989@163.com（通信作者）
（编辑 陈 诚）