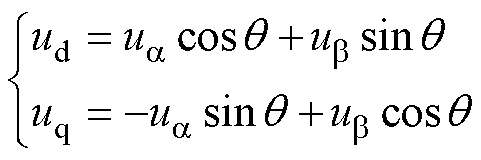 (1)
(1)
摘要 有限集模型预测控制(FCS-MPC)在逆变器控制中具有简单直观、响应快速、易于多目标优化等优点,但无调制器的特点造成逆变器开关频率随工作点、系统参数等多种因素变化。为保留FCS-MPC优点的同时解决开关频率不固定的问题,该文提出一种基于自适应代价函数的开关频率控制方法,通过检测开关频率与参考频率的误差,自动调节开关代价权重系数,实现开关频率对参考值的跟随。通过三相永磁同步电机逆变器驱动实验结果表明,所提出方法可以在全工作范围跟踪参考频率,对系统参数变化具有一定的鲁棒性,同时保留了FCS-MPC的优点。
关键词:有限集模型预测控制 开关频率控制 代价函数 电流控制
有限集模型预测控制(Finite-Control-Set Model Predictive Control, FCS-MPC)[1-3]以其原理简单直观、响应快速、设计灵活、容易实现多目标和非线性等特点,近年来在电力电子和电机驱动领域逐渐成为研究热点。FCS-MPC根据一定的优化目标,在所有可能的开关状态中选出最优的一组作为下一周期的输出,并在整个周期中保持恒定,从而无需调制器。这种直接控制的特点贴合电力半导体开关器件的离散特性,使其比通过调制器间接控制的方式具有更快的响应速度[3]。
然而,由于不使用调制器,FCS-MPC的开关频率并非由采样周期直接决定,而是受到电流、转速、代价函数中权重系数、被控对象参数等多方面因素影响[4],相同采样周期下,开关频率可在几百Hz到几十kHz范围内变化。对于电动汽车电机驱动等工作点变化范围极大的应用场合,则需要确保系统能承受的开关频率大于FCS-MPC所有工作点下的最大开关频率,这提高了对硬件的要求和成本,而且在其他大部分工作点存在开关频率冗余。若通过增大采样周期[5]来限制可能的最大开关频率,则会进一步导致全工作范围控制性能的下降。
无调制器导致FCS-MPC开关频率变化的问题,使一类有调制器的MPC[6-10]得到关注。多矢量MPC[6-8],与FCS-MPC整个周期保持同一个电压矢量的特点不同,在每个周期选取两个[7]或三个[8]矢量,再通过最小拍等优化原则解算占空比。但该类算法一般只以跟踪参考值为目标,较难实现多目标优化。为了保留FCS-MPC多目标优化的优点,文献[9]提出一类调制型MPC,其占空比由各电压矢量对应的代价函数计算,而在代价函数中可实现与FCS-MPC相同的多目标优化。然而其占空比和代价函数之间的比例关系只是一种近似[10],因此最优化性不如多矢量MPC以及传统的FCS-MPC。以上有调制器的方法,开关频率可由采样周期确定进而保持恒定。然而调制器也在一定程度上削弱了FCS- MPC直接开关控制快速性的优点,并且,占空比计算在计算量和模型参数鲁棒性上都不具备优势。
可见,FCS-MPC具备有调制器方法无法完全替代的优点,因此,保留优点的同时对FCS-MPC开关频率进行控制的思路具有一定的吸引力。文献中已有一些关于降低开关频率的研究[11-13]。在代价函数中引入开关代价[11],可以使控制器优先选择开关动作数较少的下一控制输出,该方法无需降低采样频率,通过提高开关代价权重系数即可降低开关频率。另一种方法引入滞环控制的思想[12-13],当预测状态(如电流、磁链)不超出滞环边界时,开关状态保持恒定,超出边界时才改变开关状态,从而通过提高滞环宽度即可降低开关频率。然而,这些方案虽然能从整体上降低开关频率,但开关频率仍随工作点等各种因素变化,未能做到恒频或者跟踪参考频率,因此同样存在频率冗余的问题。
为了能实现恒频FCS-MPC,Zhang Xing等[14]利用FCS-MPC开关频率随模型参数变化的特点,提出了一种通过调节模型电感实现恒开关频率控制的方法,在开关频率偏高时增大预测模型电感,以减小开关频率;反之,则减小电感。但这也导致模型与实际对象不匹配,预测准确度降低,从而造成控制结果非最优。另一类周期控制法[15]通过控制每个开关上升沿到下降沿之间的周期个数从而达到恒频,但实际频率和参考频率之间的误差和权重系数有关,无法做到稳态无差,而权重系数的整定又依赖于试错或工程经验。此外,对模型参数失配带来的影响[16]也没有进行评估。
针对FCS-MPC开关频率随多种因素变化的问题,本文提出一种基于自适应代价函数的开关频率控制方法,使FCS-MPC开关频率可控,可以在全工作范围保持恒定或跟踪参考频率,同时保留FCS- MPC响应快速、多目标优化等优点。
本节以三相两电平电压型逆变器驱动的永磁同步电机(Permanent Magnet Synchronous Machine, PMSM)系统中常见的dq坐标系下电流控制为例,简要介绍FCS-MPC的原理。
首先建立FCS-MPC预测模型,对逆变器每种可能的开关状态作用下的系统状态进行预测。开关状态见表1,逆变器共允许八种不同的开关状态Sabc,其中,1表示对应相上桥臂开关导通,下桥臂开关关断;0表示下桥臂开关导通,上桥臂开关关断。根据表1可查出每种开关状态对应静止ab 坐标系下的电压ua、ub,UDC为母线电压,通过Park变换可计算出dq坐标系下的电压为
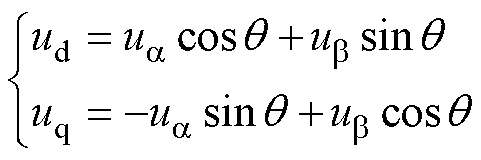 (1)
(1)
式中,q 为转子电角度。ud、uq满足
 (2)
(2)
式中,R为定子电阻;Ld、Lq分别为d、q轴电感;yf为PMSM转子永磁体磁链;id、iq分别为d、q轴定子电流;we为转子电角速度。
由式(2)在第k时刻进行一阶欧拉离散化,得
表1 开关状态
Tab.1 Switching state

Sabc=(SaSbSc)uaub (0 0 0)00 (0 0 1) (0 1 0) (0 1 1)0 (1 0 0)0 (1 0 1) (1 1 0) (1 1 1)00
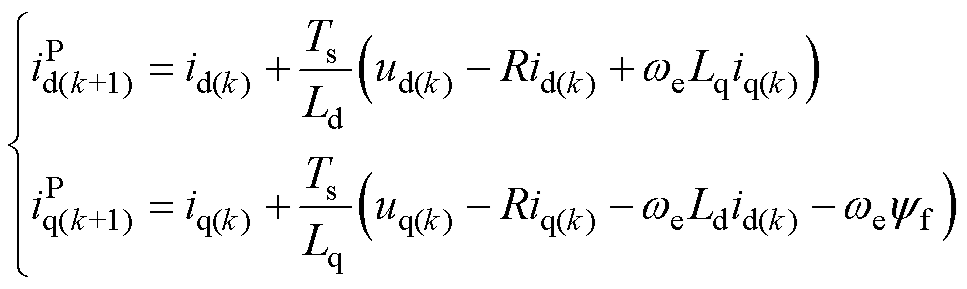 (3)
(3)
即为预测模型,Ts为采样周期,上标“P”表示预测值。根据式(3),可以由k时刻的系统状态和下周期开关状态对应的电压,预测k+1时刻的dq轴电流。实际应用中常用两步法[3]来补偿微控制器执行时间所带来的延时:k时刻根据上周期优化得到的开关状态由式(3)计算出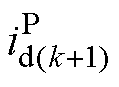 、
、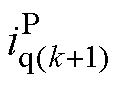 ,代入得
,代入得
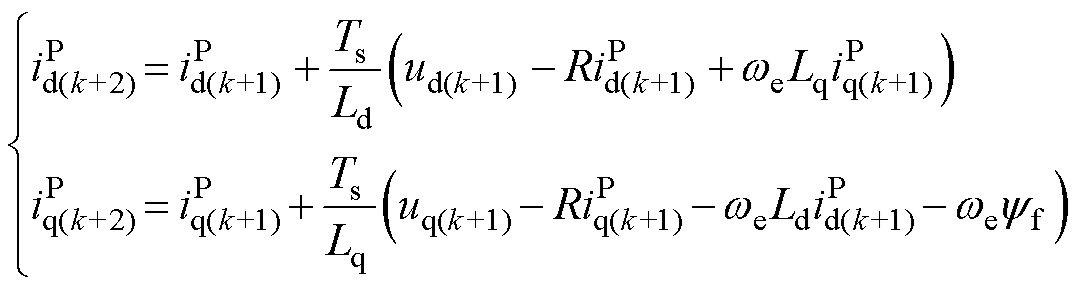 (4)
(4)
可分别预测出八种Sabc作用下k+2时刻的dq轴电流,再代入表征控制目标的代价函数J,即
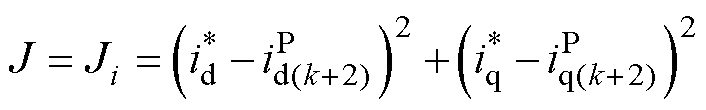 (5)
(5)
式中,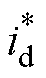 和
和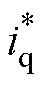 为电流指令;Ji为电流代价,是dq预测电流与参考电流之差的二次方和。评估能使Ji最小的
为电流指令;Ji为电流代价,是dq预测电流与参考电流之差的二次方和。评估能使Ji最小的 、
、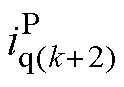 所对应的开关状态Sabc,即为下一周期的最优控制量。
所对应的开关状态Sabc,即为下一周期的最优控制量。
可以看出,FCS-MPC的预测模型式(3)和式(4)直接由对象数学模型离散化得到,采用直观的代价函数评估出能使预测电流误差最小的控制量,而遍历所有开关组合可以确保全局最优性。多目标控制可通过在式(5)中引入n个新的代价项实现,即
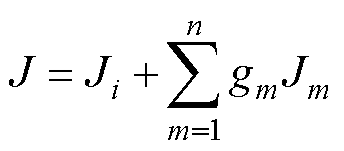 (6)
(6)
式中,Jm为除电流跟踪外的其他控制目标对应的代价项,如过电流限幅、共模电压抑制、指定谐波消去等的代价函数;gm为其权重系数,gm越大则该目标的优先级越高。
第1节所述的FCS-MPC具有很高的响应速度,但从其控制原理容易看出,每个周期开关状态与上周期相比,可以保持不变或者变化1~3个开关状态,因此开关频率取决于代价函数的评估结果,受工作点、系统参数等多方面影响,不像有调制器时那样固定。传统FCS-MPC在不同工作点下的频率特性如图1所示。
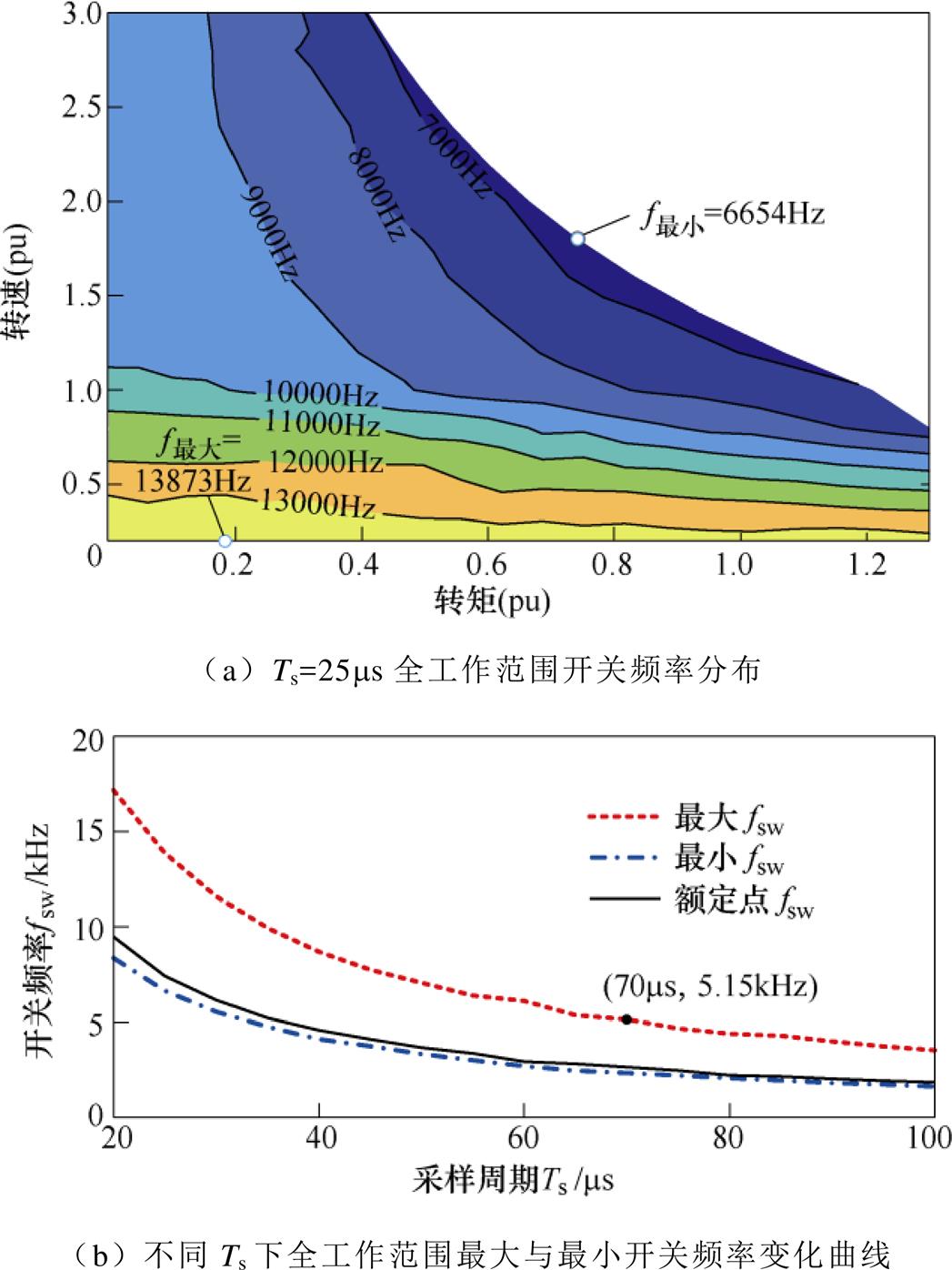
图1 传统FCS-MPC在不同工作点下的频率特性
Fig.1 The switching frequency of the conventional FCS-MPC at different working points
图1a为PMSM不同转速和转矩下FCS-MPC电流控制稳态平均开关频率仿真结果,控制周期Ts= 25ms。可以看出,不同速度、转矩下,FCS-MPC输出开关频率在6.7~13.9kHz之间变化。随着速度和转矩的上升,开关频率有变小的趋势。
图1b为不同Ts下,全工作范围内最大、最小以及额定点开关频率变化曲线。可以看出,控制周期越小,开关频率越大。不同周期下,最大频率均为最小值的2倍左右,而额定点更接近全范围最小频率。假设系统允许开关频率为5kHz,则应选择Ts>70ms,但类似图1a,包括额定点在内的绝大部分工作点开关频率达不到最大值,系统允许开关频率存在冗余,没有达到最佳的控制性能。
利用FCS-MPC容易实现多目标控制的特点,在代价函数中增设开关代价Jsw表示为
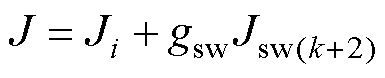 (7)
(7)
式中,gsw为权重系数,其大小影响开关动作惩罚的优先级,gsw越大,控制器越倾向于选择较少的开关动作,而放松对电流跟踪性能的控制;Jsw(k+2)为k+1~k+2周期三相开关动作的总数,用以“惩罚”所需开关动作较多的控制量,使其总代价J较大而不易被选择,其表达式为
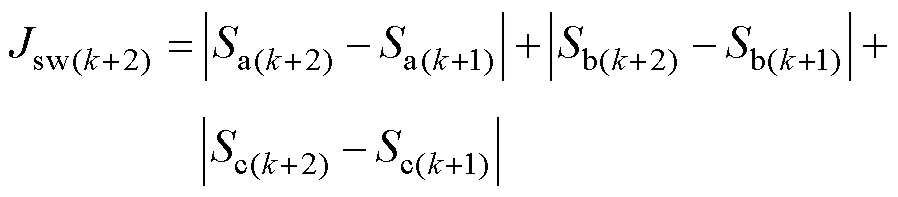 (8)
(8)
选取不同的gsw,在对图1重新仿真,设置Ts= 25ms,开关频率与开关代价权重系数的关系如图2所示。可以看出,利用开关代价能从整体上降低开关频率和开关损耗,相比于图1b,设置gsw=0.002即可将系统所需承受的开关频率从13.9kHz降至5kHz左右,无需降低采样频率。然而也应当观察到,整个工作范围内的开关频率仍非恒定值,系统允许开关频率仍然存在冗余。
因此,本节进一步提出一种开关频率可控(Switching-Frequency-Controlled, SFC)的FCS-MPC,简写为SFC-MPC。SFC-MPC系统框图如图3所示。利用开关代价和开关频率负相关的特点,设计了基于自适应代价函数的开关频率控制器,如图3点划线框内所示,使开关频率能跟随参考值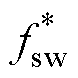 。
。
首先设计频率反馈模块。根据开关频率定义式(9),可以推导出FCS-MPC频率计算式。

图2 开关频率与开关代价权重系数的关系
Fig.2 Relationship between the switching frequency and the weighting factor of the switching cost
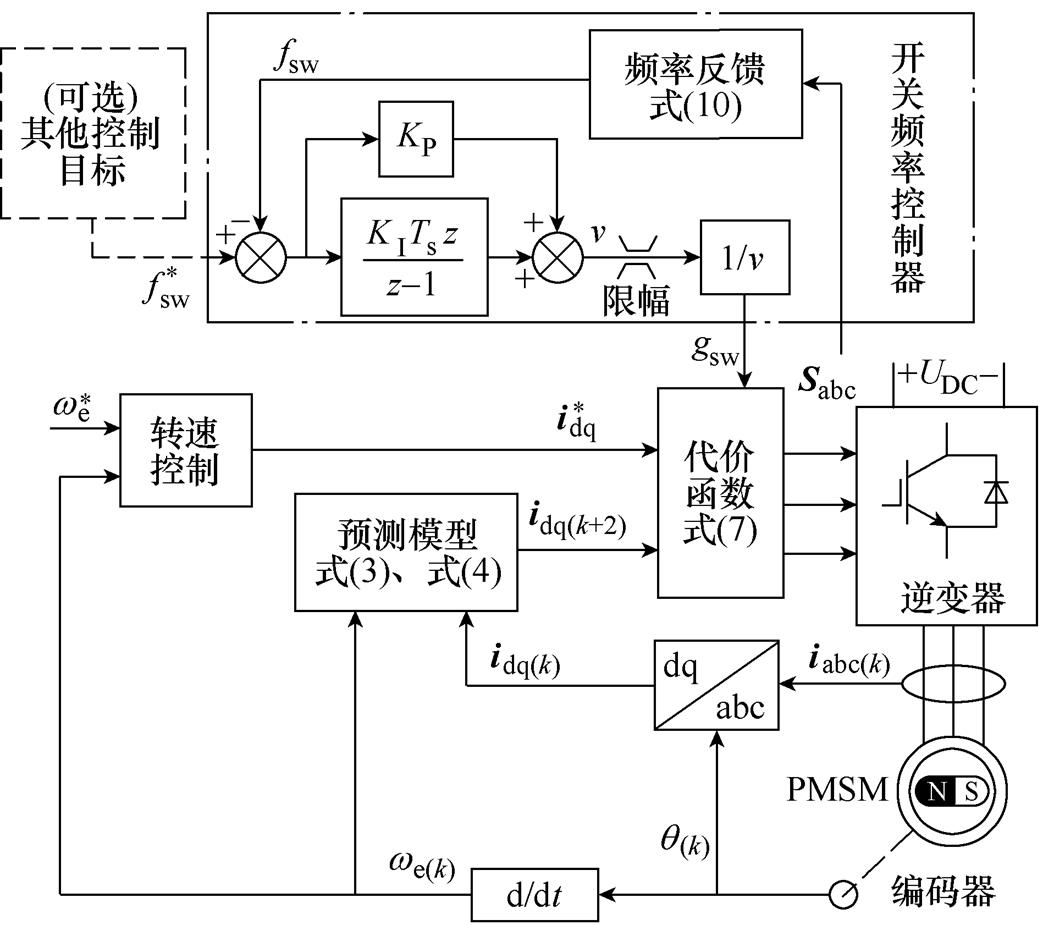
图3 SFC-MPC系统框图
Fig.3 Block diagram of proposed SFC-MPC
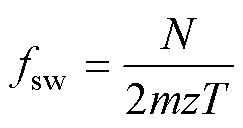 (9)
(9)
式中,T为统计时长;N为T内开关动作总次数;m为相数;z为每相开关器件个数。对三相两电平逆变器有
 (10)
(10)
因此,频率估计器从下一周期即将作用的开关状态Sabc(k+1)和本周期开关状态Sabc(k)比较得到开关次数,进而通过低通滤波计算出频率fsw为
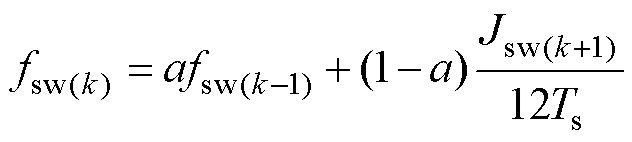 (11)
(11)
式中,a为滤波因子,可由所需截止频率wc计算得
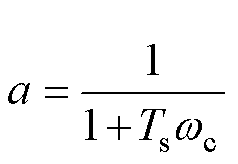 (12)
(12)
由于下一周期开关状态Sabc(k+1)已提前计算得到,故采用该值进行开关频率解算,可部分抵消滤波带来的延时,起到类似超前校正的效果。
应当指出,由于开关动作的离散性,开关频率实际指的是平均开关频率,而不像速度、电压等物理量存在瞬时值。即便是在常见的空间矢量调制中,所谓频率(fsw=1/Ts)恒定,也指的是在一个采样周期Ts内的平均开关频率恒定,即Ts周期内6个开关总动作次数恒为12,由式(10)得fsw=1/Ts。因此,开关频率的控制只能是平均意义上的控制,所以采用低通滤波进行频率反馈,否则单位采样时间内的开关次数为离散值,得到的频率量也为离散值,无法连续调节。低通滤波器截止频率wc可根据具体应用情况来选择:若系统工作点不会频繁变化,如风机、压缩机类负载,则wc可取1~10rad/s等较小值;若频率指令或工作点频繁变化,如伺服系统、电动汽车等应用,则可取几十rad/s。
得到频率反馈值后,根据以下思路设计频率控制器。根据开关代价的定义,其他条件相同时,fsw与gsw呈负相关,如图2a所示。因此,计算出频率fsw后,与参考值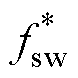 之差经过一定的反馈控制器(如PI控制器)可以实现频率控制。但图2a同时表明,fsw与gsw之间的关系具有很强的非线性,用常规的线性PI控制器难以获得理想的性能。而1/fsw与gsw则有近似线性的关系,如图2b所示。因此,级联1/v函数对PI输入输出关系进行前馈线性化处理,有利于提高频率控制的性能。实际应用中,可将PI输出限幅在v∈[CL,CU],CL、CU均为正常数,此时gsw∈[1/CU,1/CL]。不难看出,gsw=0时,式(7)等效为式(5),SFC-MPC等效为传统FCS-MPC。但此时两个零矢量(0 0 0)和(1 1 1)的代价没有区别,会导致误选非最优零矢量而增加不必要的开关动作,因此传统FCS-MPC一般会通过查表等方式进行区分。而此处限幅保证了gsw>0,从而无需对两个零矢量作专门的区分。此外,由于保留了代价函数,SFC-MPC多目标控制的实现方式与传统FCS-MPC完全一致。
之差经过一定的反馈控制器(如PI控制器)可以实现频率控制。但图2a同时表明,fsw与gsw之间的关系具有很强的非线性,用常规的线性PI控制器难以获得理想的性能。而1/fsw与gsw则有近似线性的关系,如图2b所示。因此,级联1/v函数对PI输入输出关系进行前馈线性化处理,有利于提高频率控制的性能。实际应用中,可将PI输出限幅在v∈[CL,CU],CL、CU均为正常数,此时gsw∈[1/CU,1/CL]。不难看出,gsw=0时,式(7)等效为式(5),SFC-MPC等效为传统FCS-MPC。但此时两个零矢量(0 0 0)和(1 1 1)的代价没有区别,会导致误选非最优零矢量而增加不必要的开关动作,因此传统FCS-MPC一般会通过查表等方式进行区分。而此处限幅保证了gsw>0,从而无需对两个零矢量作专门的区分。此外,由于保留了代价函数,SFC-MPC多目标控制的实现方式与传统FCS-MPC完全一致。
最后,参考频率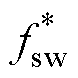 可以根据系统能承受的频率直接设置为恒定值,或者根据需要,引入电流纹波、逆变器温度等与开关频率有关的量作为外环控制对象,控制器输出为参考频率,如图3虚线框部分所示。本文主要讨论频率跟随,故对其他可在外环实现的控制目标不作进一步讨论。
可以根据系统能承受的频率直接设置为恒定值,或者根据需要,引入电流纹波、逆变器温度等与开关频率有关的量作为外环控制对象,控制器输出为参考频率,如图3虚线框部分所示。本文主要讨论频率跟随,故对其他可在外环实现的控制目标不作进一步讨论。
为验证所提出SFC-MPC的有效性,在DSP TMS320F28335中实现SFC-MPC算法,并采用IPM模块FSBB20CH60作为三相两电平逆变器,对一台三相4对极PMSM进行控制实验。电机通过行星齿轮接磁粉制动器作为负载,制动转矩通过励磁电源调节。采用TBC25C04电流传感器进行电流采样。实验装置如图4所示,系统参数见表2。

图4 实验装置
Fig.4 Experimental setup
表2 系统参数
Tab.2 System specification
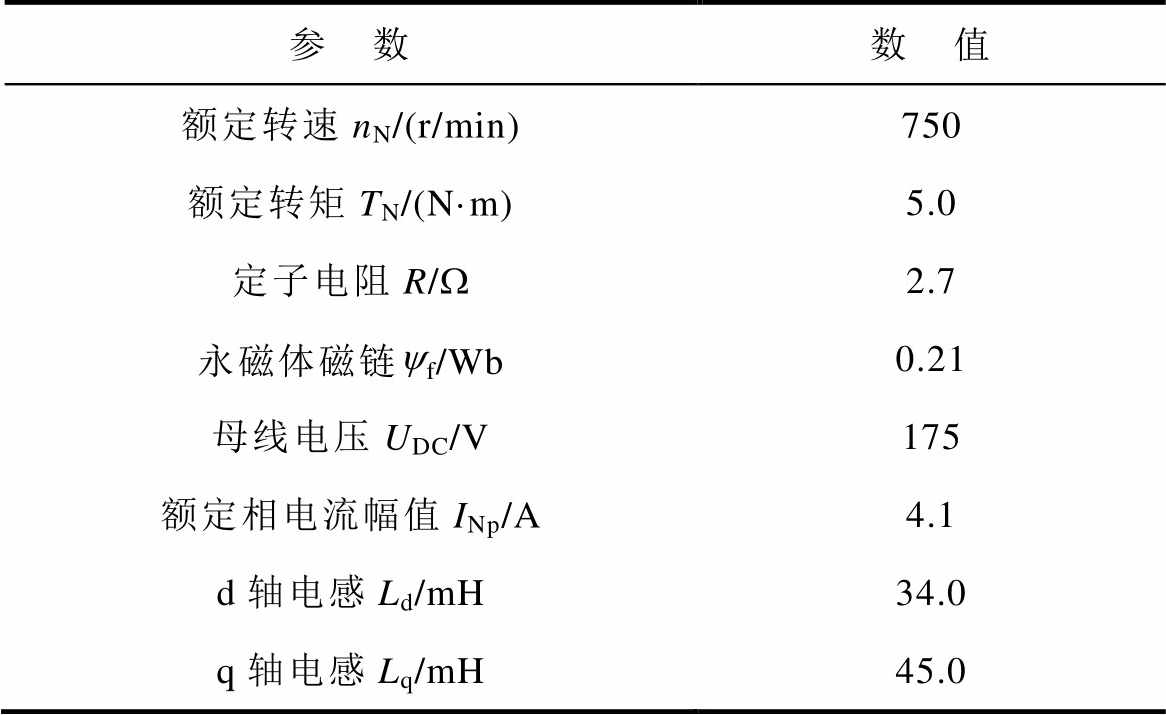
参 数数 值 额定转速nN/(r/min)750 额定转矩TN/(N·m)5.0 定子电阻R/W2.7 永磁体磁链yf/Wb0.21 母线电压UDC/V175 额定相电流幅值INp/A4.1 d轴电感Ld/mH34.0 q轴电感Lq/mH45.0
本节各实验中速度外环完全相同,作为电流内环控制器的各对照组缩写分别如下:
(1)SFC-MPC为本文提出的频率可控FCS-MPC,频率控制器中,KP=1,KI=40,a=0.999。
(2)C-MPC为传统FCS-MPC。
(3)CWF-MPC为常权重系数(Constant WeightingFactor, CWF)开关代价的FCS-MPC,代价函数如式(7)所示,权重系数gsw为恒值。
以上方法采样周期Ts均为25ms,另有说明除外。
图5为额定转矩、额定转速下SFC-MPC开关频率控制实验。参考开关频率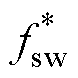 从200Hz起以100Hz/s的速率增大。图中,fsw0为直接由开关频率定义式(10)求取的开关频率,T=50Ts=1.25ms。
从200Hz起以100Hz/s的速率增大。图中,fsw0为直接由开关频率定义式(10)求取的开关频率,T=50Ts=1.25ms。
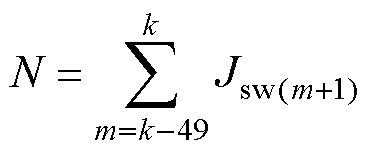 (13)
(13)
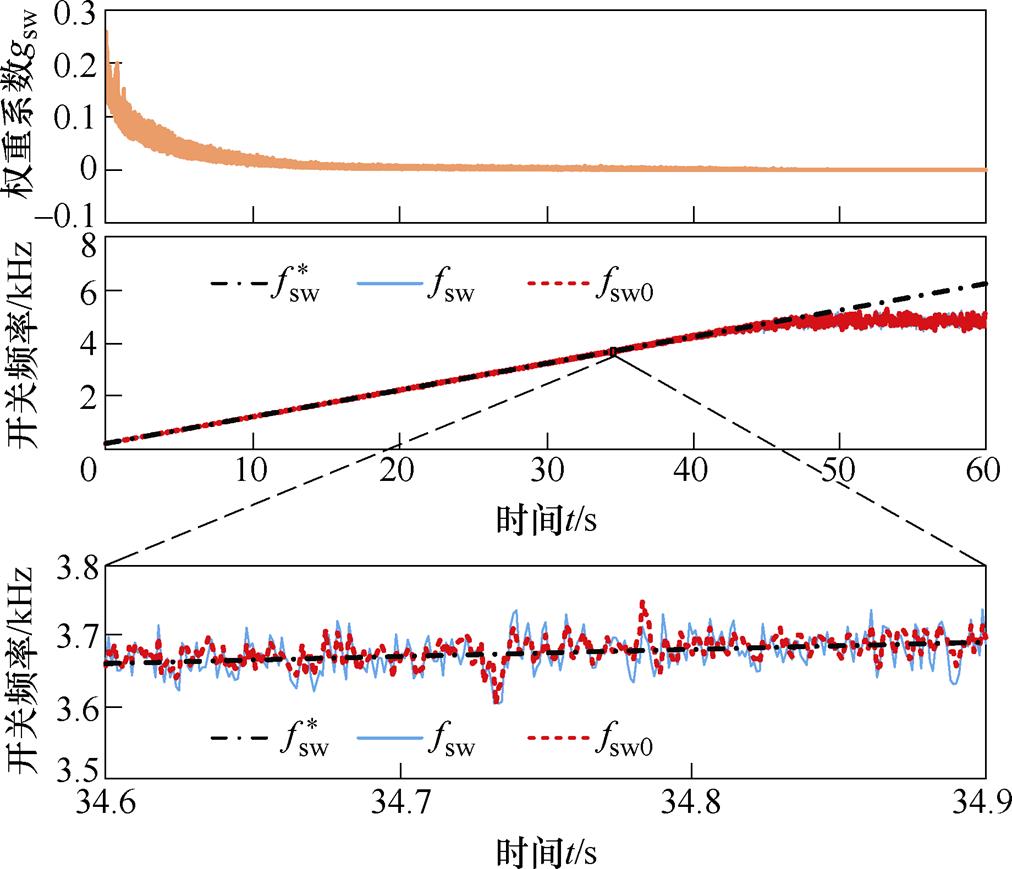
图5 开关频率斜坡给定跟踪测试
Fig.5 Switching frequency ramp reference tracking test
比较fsw和fsw0的波形可知,频率估计器得到的结果与直接由定义式得到的fsw0接近,故证明了频率反馈值的准确性。
同时可看出,SFC-MPC通过调节gsw在一定频率范围内可实现对开关频率指令的准确跟随。当频率指令超过当前工作点在C-MPC下的开关频率(额定点约为4.8kHz)时,gsw达到下限值,SFC-MPC退化为C-MPC。若希望提高该上限频率,则需要提高采样频率。
图6~图8为SFC-MPC在不同转速、转矩下的控制以及与C-MPC、CWF-MPC对比的实验结果。
图6a中,电机在1.2N·m恒负载转矩下,根据SFC-MPC,参考开关频率设为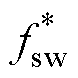 =2kHz,转速n从-1.5kr/min经斜坡变化至1.5kr/min。可以看出,在2倍额定值范围内的不同转速下,SFC-MPC能通过调节gsw使开关频率恒为参考值而不随工作点变化。图中给出的开关计数为从t =0起三相六开关总开关次数的累计,每到96 000次则清零。可以看出,开关次数累加的速率恒为24 000次/s,斜率恒定,通过定义式(10)可知开关频率为2kHz,这进一步验证了频率反馈和频率控制的准确性。
=2kHz,转速n从-1.5kr/min经斜坡变化至1.5kr/min。可以看出,在2倍额定值范围内的不同转速下,SFC-MPC能通过调节gsw使开关频率恒为参考值而不随工作点变化。图中给出的开关计数为从t =0起三相六开关总开关次数的累计,每到96 000次则清零。可以看出,开关次数累加的速率恒为24 000次/s,斜率恒定,通过定义式(10)可知开关频率为2kHz,这进一步验证了频率反馈和频率控制的准确性。
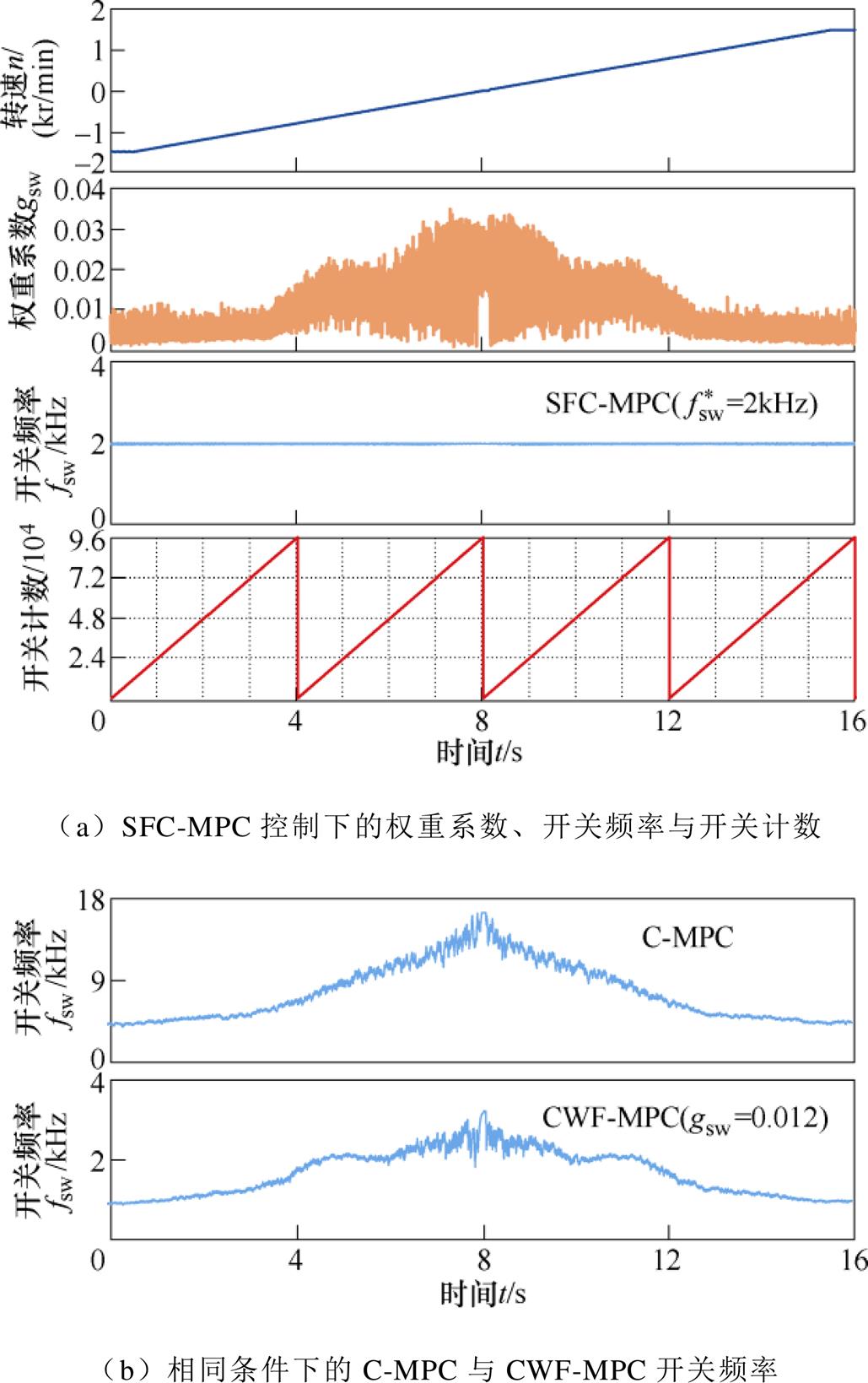
图6 变化速度下的开关频率对比
Fig.6 Comparison of switching frequency under varying speed
作为对比,图6b展示了在同样的恒转矩斜坡变化转速条件下,传统C-MPC以及常权重系数CWF- MPC下的开关频率波形,其中,CWF-MPC选取开关权重gsw=0.012。可以看出,C-MPC在不同转速下,开关频率大范围变化,而CWF-MPC开关频率虽然有所降低,但仍随工作点变化而变化,因此仍存在频率冗余问题,给系统设计带来不便。
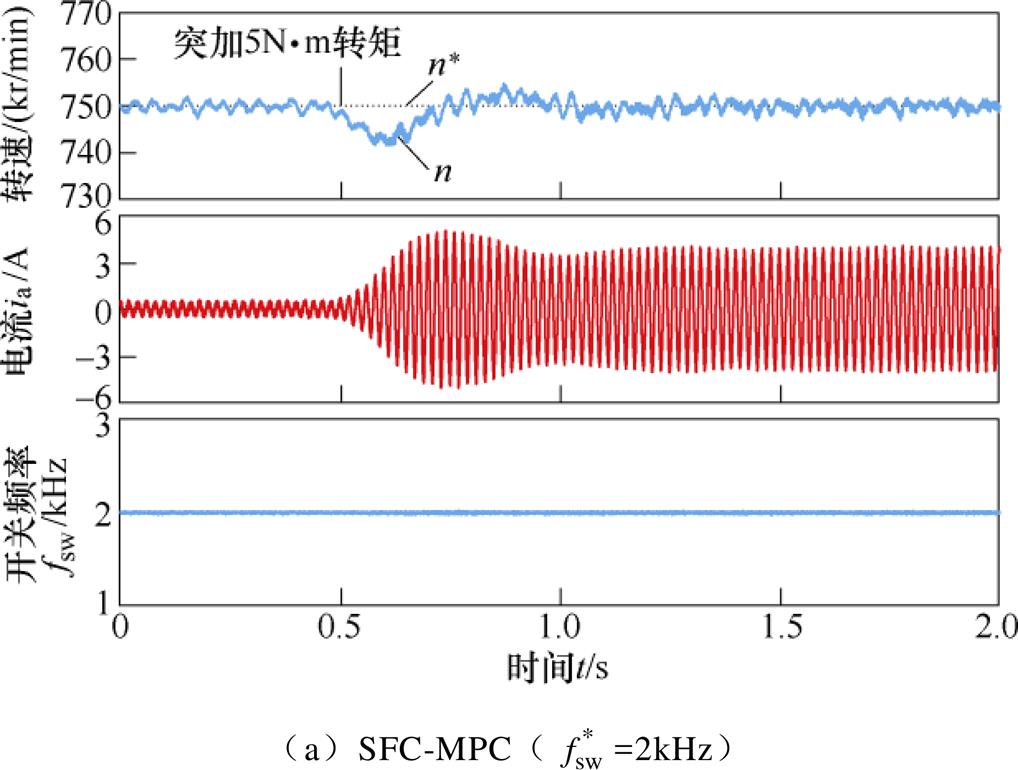
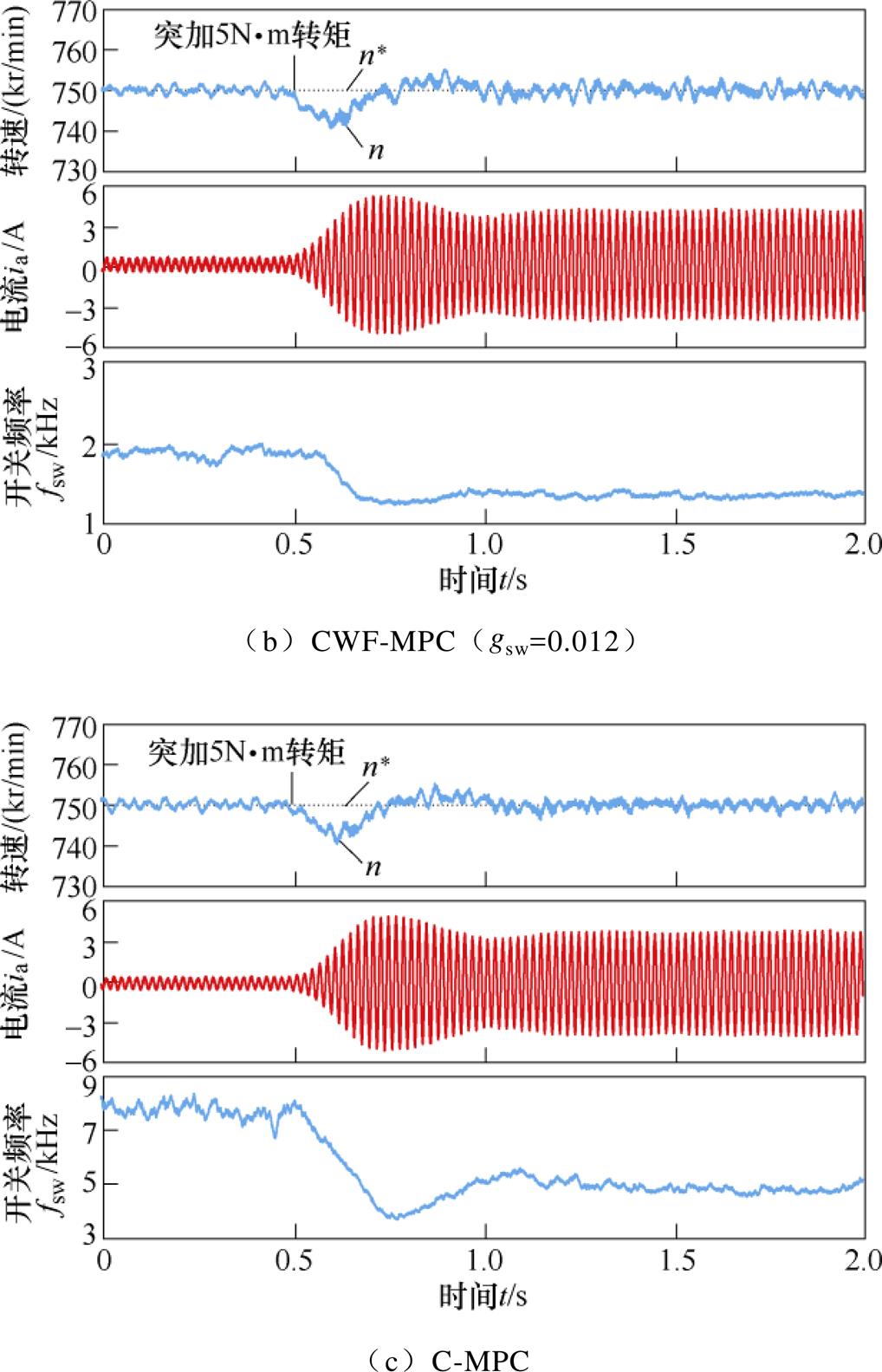
图7 变化转矩下的开关频率
Fig.7 Switching frequency under varying load torque
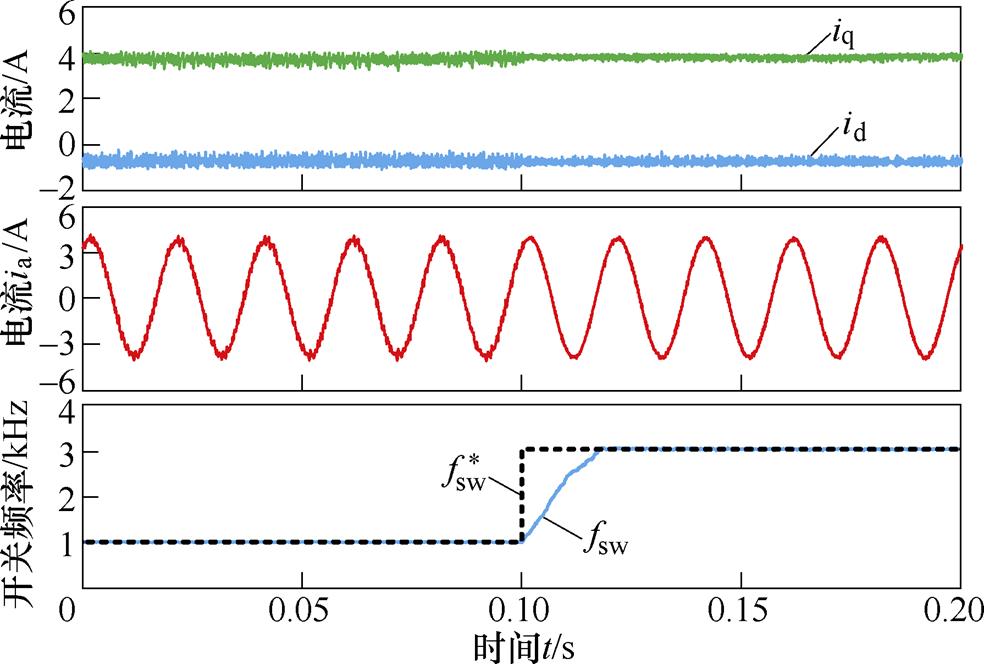
图8 SFC-MPC开关频率指令跟随
Fig.8 Switching frequency reference tracking of SFC-MPC
图7为电机空载运行在额定转速,于0.5s施加5N·m额定转矩的对比实验。三种方法转速响应基本一致,但C-MPC和CWF-MPC开关频率随负载转矩变化而变化,而SFC-MPC则能在不同转矩下维持恒定开关频率。
图8为SFC-MPC开关频率跟随阶跃给定的实验。电机在额定转速和额定转矩下运行,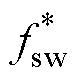 设为1kHz,并在t =0.1s时刻阶跃至3kHz。可以看出,SFC-MPC下,fsw能快速跟随阶跃的
设为1kHz,并在t =0.1s时刻阶跃至3kHz。可以看出,SFC-MPC下,fsw能快速跟随阶跃的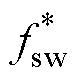 。此外,从dq坐标系下的电流id、iq以及相电流ia波形可知,除电流纹波随开关频率fsw提高而降低外,频率指令
。此外,从dq坐标系下的电流id、iq以及相电流ia波形可知,除电流纹波随开关频率fsw提高而降低外,频率指令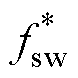 阶跃的瞬态过程对电流控制不造成明显影响。
阶跃的瞬态过程对电流控制不造成明显影响。
电流指令阶跃响应对比如图9所示。图9通过电流指令跟踪实验验证SFC-MPC的动态性能。设置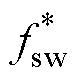 =2kHz,电流指令在t =30ms时由
=2kHz,电流指令在t =30ms时由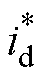 =-1A、
=-1A、 =4A阶跃为
=4A阶跃为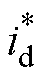 =0A、
=0A、 =1A。可以看出,d、q轴电流能够实现响应快速的解耦控制,不存在传统电流环PI控制时超调和dq轴间耦合的问题。图9b为相同实验条件下C-MPC的dq电流响应波形。可以看出,两者电流响应基本一致,因此可以证明,SFC- MPC在控制开关频率的同时,保留了C-MPC快速响应和多目标协同控制的优点。
=1A。可以看出,d、q轴电流能够实现响应快速的解耦控制,不存在传统电流环PI控制时超调和dq轴间耦合的问题。图9b为相同实验条件下C-MPC的dq电流响应波形。可以看出,两者电流响应基本一致,因此可以证明,SFC- MPC在控制开关频率的同时,保留了C-MPC快速响应和多目标协同控制的优点。
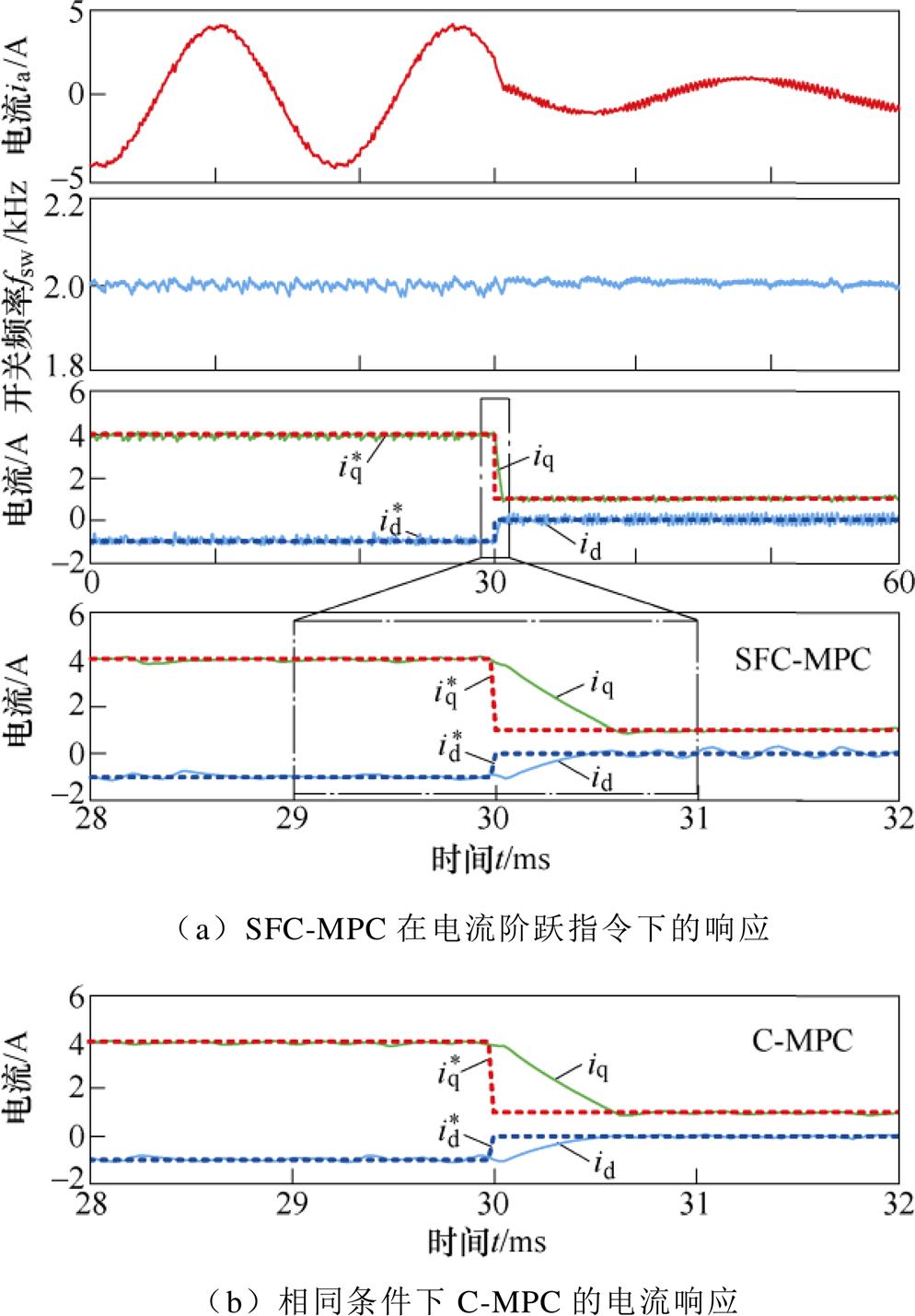
图9 电流指令阶跃响应对比
Fig.9 Comparison of current step reference response
模型参数鲁棒性是FCS-MPC等基于模型的方法不可回避的问题。模型参数与实际参数不匹配情况下得到的预测结果不准确,进而影响控制的最优性。在逆变器控制中,不少研究[17-18]已证明,负载电感是FCS-MPC最敏感的参数。因此,本节比较了模型电感参数在0.1~10倍额定值范围变化下,C-MPC、CWF-MPC、SFC-MPC方案在额定工作点下开关频率和相电流总谐波畸变率(Total Harmonic Distortion, THD)变化情况,模型电感变化时开关频率与电流THD如图10所示。
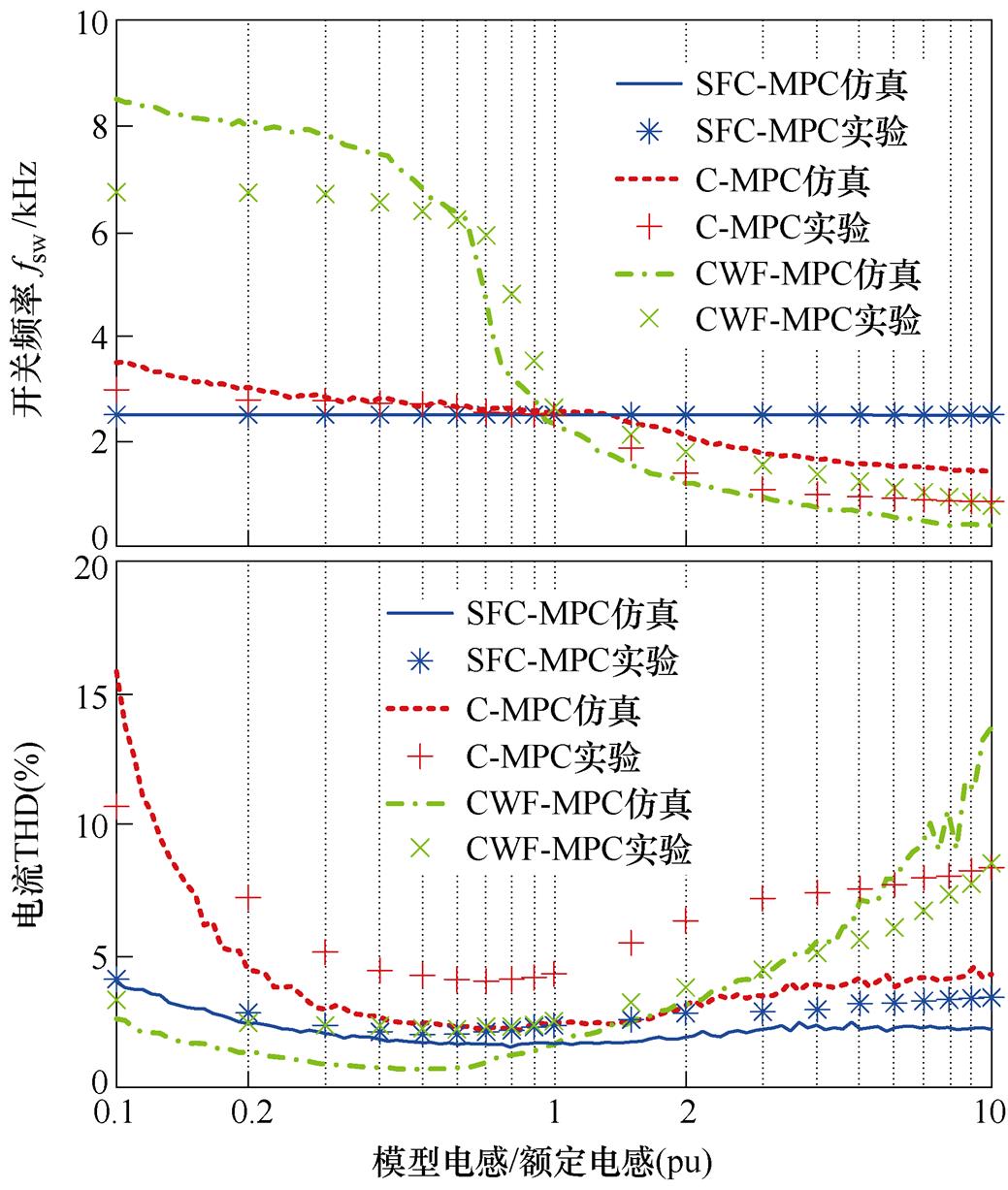
图10 模型电感变化时开关频率与电流THD
Fig.10 Switching frequency and current THD under varying model inductance parameter
图10中,SFC-MPC设置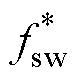 =2.5kHz,Ts=25ms;C-MPC设置Ts=75ms;CWF-MPC设置Ts=25ms,开关权重gsw=0.004。该设置下三种方法在参数匹配时额定点开关频率均在2.5kHz附近。从仿真和实验结果可看出,C-MPC在模型电感偏小时开关频率增大,模型电感偏大时开关频率减小,这与文献[14]结论相同,且电流THD受电感参数影响较大。CWF- MPC在电感参数偏小时,尽管电流THD略小于SFC- MPC,但这有赖于开关频率的增大,因此容易导致开关损耗过大而引起温度过高;在电感参数偏大时,开关频率偏低,造成电流THD增大,控制性能变差。而SFC-MPC在电感参数为0.1~10倍额定值大范围变化时,开关频率被稳定控制在2.5kHz,电流THD在参数不匹配时略有上升,但变化不大。这是由于参数失配引起的频率变化由gsw自适应调节,间接弥补了受频率变化影响的电流控制性能。尽管参数失配仍不可避免地造成电流控制非最优、THD略有上升,但SFC-MPC相比于传统方案仍具有更好的模型参数鲁棒性。
=2.5kHz,Ts=25ms;C-MPC设置Ts=75ms;CWF-MPC设置Ts=25ms,开关权重gsw=0.004。该设置下三种方法在参数匹配时额定点开关频率均在2.5kHz附近。从仿真和实验结果可看出,C-MPC在模型电感偏小时开关频率增大,模型电感偏大时开关频率减小,这与文献[14]结论相同,且电流THD受电感参数影响较大。CWF- MPC在电感参数偏小时,尽管电流THD略小于SFC- MPC,但这有赖于开关频率的增大,因此容易导致开关损耗过大而引起温度过高;在电感参数偏大时,开关频率偏低,造成电流THD增大,控制性能变差。而SFC-MPC在电感参数为0.1~10倍额定值大范围变化时,开关频率被稳定控制在2.5kHz,电流THD在参数不匹配时略有上升,但变化不大。这是由于参数失配引起的频率变化由gsw自适应调节,间接弥补了受频率变化影响的电流控制性能。尽管参数失配仍不可避免地造成电流控制非最优、THD略有上升,但SFC-MPC相比于传统方案仍具有更好的模型参数鲁棒性。
此外,从图10参数匹配时的结果还能看出,调节开关权重gsw而不改变采样周期Ts的SFC-MPC,与通过增大Ts来降低开关频率的传统C-MPC方法相比,在相同开关频率下电流THD更小,即稳态电流控制性能更好。
本文针对FCS-MPC无调制器特点造成的开关频率变化的问题,提出了一种开关频率可控的FCS-MPC(SFC-MPC)。该方法基于权重系数自适应的代价函数实现开关频率对参考值的跟随,可在全工作范围实现恒开关频率,方便系统设计。仿真和实验结果证明,SFC-MPC在变化的转速和转矩下均能使开关频率跟随参考频率,稳态电流THD小于同开关频率的传统FCS-MPC,并且仍具备传统FCS- MPC响应快速、多目标协同控制实现容易等优点,同时,相比于传统FCS-MPC,模型参数具有更好的鲁棒性。
参考文献
[1] Wang Fengxiang, Mei Xuezhu, Rodriguez J, et al. Model predictive control for electrical drive systems- an overview[J]. CES Transactions on Electrical Machines and Systems, 2017, 1(3): 219-230.
[2] 齐昕, 苏涛, 周珂, 等. 交流电机模型预测控制策略发展概述[J]. 中国电机工程学报, 2021, 41(18): 6408-6418.
Qi Xin, Su Tao, Zhou Ke, et al. Development of AC motor model predictive control strategy-an overview[J]. Proceedings of the CSEE, 2021, 41(18): 6408-6418.
[3] Vazquez S, Rodriguez J, Rivera M, et al. Model predictive control for power converters and drives: advances and trends[J]. IEEE Transactions on Indu- strial Electronics, 2017, 64(2): 935-947.
[4] Wang Luocheng, Zhao Tiefu, He Jiangbiao. Investi- gation of variable switching frequency in finite control set model predictive control on grid- connected inverters[J]. IEEE Open Journal of Industry Applications, 2021, 2: 178-193.
[5] Karamanakos P, Geyer T. Guidelines for the design of finite control set model predictive controllers[J]. IEEE Transactions on Power Electronics, 2020, 35(7): 7434-7450.
[6] Zhang Yongchang, Bai Yuning, Yang Haitao. A universal multiple-vector-based model predictive control of induction motor drives[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(8): 6957- 6969.
[7] 郭磊磊, 李国昊, 金楠, 等. 两电平电压源逆变器双矢量调制模型预测控制: 理论分析、实验验证和推广[J]. 电工技术学报, 2021, 36(1): 39-49.
Guo Leilei, Li Guohao, Jin Nan, et al. Two-vector- based modulated model predictive control method for 2-level voltage source inverters: theoretical analysis, experimental verification and extension[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(1): 39-49.
[8] Wang Xiaohe, Sun Dan. Three-vector-based low- complexity model predictive direct power control strategy for doubly fed induction generators[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 773-782.
[9] Tarisciotti P, Zanchetta P, Watson P, et al. Modulated model predictive control for a three-phase active rectifier[J]. IEEE Transactions on Industry Appli- cations, 2015, 51(2): 1610-1620.
[10] Wang Yuchen, Li Hongmei, Liu Rundong, et al. Modulated model-free predictive control with mini- mum switching losses for PMSM drive system[J]. IEEE Access, 2020, 8: 20942-20953.
[11] Rivera M, Kouro S, Rodriguez J, et al. Predictive current control in a current source inverter operating with low switching frequency[C]//4th International Conference on Power Engineering, Energy and Elec- trical Drives, Istanbul, 2013: 334-339.
[12] Geyer T. Model predictive direct torque control: derivation and analysis of the state-feedback control law[J]. IEEE Transactions on Industry Applications, 2013, 49(5): 2146-2157.
[13] 陈琢, 王琛琛, 成前. 基于单一矢量的两电平逆变器快速模型预测控制[J]. 电工技术学报, 2021, 36(增刊2): 654-664.
Chen Zhuo, Wang Chenchen, Cheng Qian. Fast model predictive control of two-level inverter based on single vector[J]. Transactions of China Electro- technical Society, 2021, 36(S2): 654-664.
[14] Zhang Xing, Wang Yangjun, Yu Changzhou, et al. Hysteresis model predictive control for high-power grid-connected inverters with output LCL filter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(1): 246-256.
[15] Aguirre M, Kouro S, Rojas C A, et al. Switching frequency regulation for FCS-MPC based on a period control approach[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5764-5773.
[16] 陈卓易, 屈稳太. 基于PID型代价函数的永磁同步电机模型预测电流控制[J]. 电工技术学报, 2021, 36(14): 2971-2978.
Chen Zhuoyi, Qu Wentai. Model predictive current control for permanent magnet synchronous motors based on PID-type cost function[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2971- 2978.
[17] Young H A, Perez M A, Rodriguez J. Analysis of finite-control-set model predictive current control with model parameter mismatch in a three-phase inverter[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(5): 3100-3107.
[18] Chen Zhuoyi, Qiu Jianqi, Jin Mengjia. Adaptive finite-control-set model predictive current control for IPMSM drives with inductance variation[J]. IET Electric Power Applications, 2017, 11(5): 874-884.
A Switching-Frequency-Controlled Finite-Control-Set Model Predictive Control Method
Abstract The finite-control-set model predictive control (FCS-MPC) for the inverters has the advantages of simplicity, fast responsiveness and easy inclusion of multiple objectives. However, the absence of the modulator makes the switching frequency of the inverter vary with various factors such as the working point and system parameters. To solve the problem of variable switching frequency while retaining the advantages of the FCS-MPC, this paper proposed a switching-frequency-controlled FCS-MPC based on the adaptive cost function. The weighting factor of the switching cost is adjusted according to the error between the reference and the sampled frequency to realize the reference tracking. Experimental results on a 3-phase permanent magnet synchronous motor drive validate that the proposed method can track the reference frequency in the full working range, and has robustness against parameter variation, while retaining the advantages of the FCS-MPC.
keywords:Finite-control-set model predictive control (FCS-MPC), switching frequency control, cost function, current control
DOI: 10.19595/j.cnki.1000-6753.tces.211387
国家自然科学基金资助项目(51907176)。
中图分类号:TM46
收稿日期 2021-09-03
改稿日期 2021-12-24
陈卓易 男,1990年生,讲师,博士,研究方向为永磁电机预测控制与无位置传感器控制。E-mail: chenzhuoyi@nbt.edu.cn
邱建琪 男,1974年生,副教授,博士生导师,研究方向为电机系统及其控制。E-mail: motor@zju.edu.cn(通信作者)
(编辑 陈 诚)