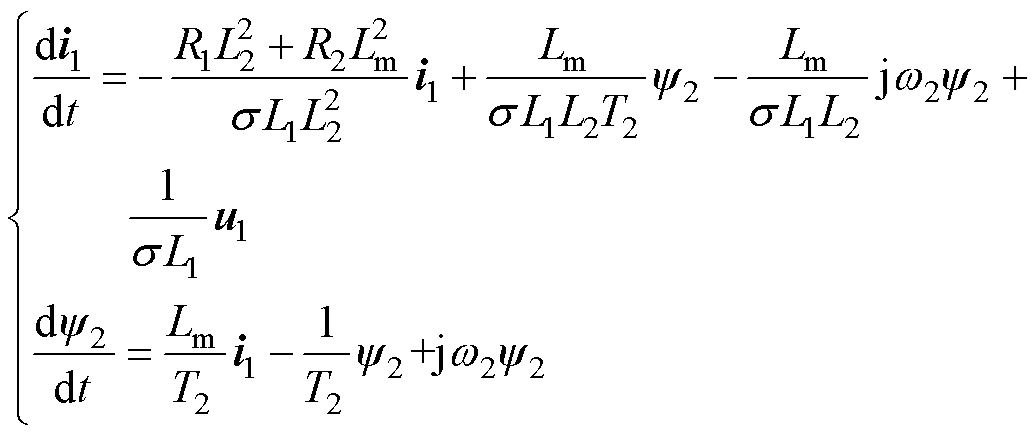 (1)
(1)
摘要 为降低变换器硬件成本及开关损耗,强电流大功率的轨道交通用直线感应电机及驱动系统通常需运行在低开关频率模式下。但是,传统的低开关频率控制方法经常会在引入较为严重的谐波电流和推力波动的同时放大微处理器离散化带来的影响,从而恶化观测器性能。针对该问题,该文提出一种带在线参数辨识的多步长有限集模型预测控制策略,可有效降低低开关频率下的电流谐波,同时利用高精度参数增强系统的可靠性。首先,采用目标函数带开关项的模型预测控制算法,实现了高采样频率下的低开关频率控制,并借助多步长模式成功抑制了因开关频率降低所引起的谐波含量上升等问题。其次,详细对比分析了两种方法控制下的低开关频率模式对观测器性能的影响。基于分析结果,同时考虑到轨道交通用直线感应电机中励磁电感受边端效应影响程度较深,进一步综合分析了该模型预测方法的参数敏感性并引入参数在线辨识算法,实现了低开关频率下的励磁电感的精确估计,提高了模型预测控制算法的预测精度和参数鲁棒性,降低了驱动系统的谐波含量。大量仿真和实验充分表明,所提出的方法可很好地实现低开关频率下直线感应电机励磁电感的准确跟踪,配合多步长模型预测控制算法,可对驱动系统电流谐波进行有效抑制。
关键词:直线感应电机 边端效应 模型预测控制 参数辨识 低开关频率 谐波抑制
近年来,直线感应电机(Linear Induction Motor, LIM)由于其无需中间传动机构便可产生直线运动所带来的优势,逐渐引起工业和研究界的关注[1-6]。相比旋转感应电机,采用直线感应电机的轨道交通驱动系统具备转弯半径小、无需齿轮箱、加减速能力和爬坡能力强等特性,因此拥有巨大的应用潜力。目前,国内外已有40余条直线感应电机驱动的轨道交通商业化线路。然而,直线感应电机所特有的边端效应会对电机等效参数产生较为严重的影响,在大功率时这一影响将更为明显。因此,必须在控制算法中对参数变化加以考虑,以削弱其对控制系统性能的不利影响。
为了定量分析直线感应电机边端效应的影响,文献[7-10]对其等效电路、数学模型以及参数变化规律进行了综合性的研究。目前,诸多直线感应电机控制策略相关文献主要针对等效励磁电感进行了考虑及修正[11-12]。相比旋转感应电机,直线感应电机等效励磁电感具有如下特点:一方面,其数值相比漏感差距不大;另一方面,其关键影响因素从磁饱和变为电机边端效应。当电机速度上升时,由于边端效应的程度加深,入端涡流增强,磁场被进一步削弱,进而使得等效励磁电感明显降低[8]。此外,负载情况变化引起的转差频率变化也将对励磁电感产生影响[7, 9]。通过参数在线辨识算法可以对励磁电感进行在线估计[13-16],以全面考虑多种因素对励磁电感数值的影响。文献[14]给出两种励磁电感在线辨识方案,分别采用基于转子磁链的模型参考自适应方法和基于无功功率的开环计算方法。文献[15]提出一种基于全阶状态观测器的励磁电感参数在线辨识方法,相当于以电机作为参考模型,以定子电流作为误差变量。文献[16]在文献[15]的基础上提出一种基于反电动势的模型参考自适应方案,并采用二阶滑模观测器代替参考模型,同时消除了纯积分和微分环节。通过将辨识参数引入控制策略中,可以增强系统的抗扰能力和参数鲁棒性。但是,传统的励磁电感修正方案主要是围绕磁链幅值控制、定向控制、观测器等环节展开,而忽视了对主控制环路如电流内环的修正。当电机参数发生漂移时,控制器参数需要进行适应性的调整才能保证较优的动静态性能。相关的PI参数自整定方案大多围绕转动惯量进行[17],且经常会面临设计复杂、计算量大、难以达到最优等问题。当采用模型预测电流控制算法时,则可以较为方便地在电流控制中考虑参数变化带来的影响[11],进而保持系统的快响应和高控制精度。在线参数辨识与模型预测控制(Model Predictive Control, MPC)相结合可以很好地解决后者对电机参数的依赖问题[18-19]。
特别地,受到散热等方面的限制,在中大功率的轨道交通驱动系统中变换器通常需要运行在低开关频率下,以降低开关损耗[20-21]。而传统的低开关频率控制方法将导致各种基于观测器的参数辨识方法迭代频率较低,进而影响离散化辨识系统的精度甚至稳定性[22-24]。针对这一问题,可采取一些特殊化的离散方案代替一阶前向欧拉来解决,如双图斯汀离散化方法[22]。文献[23]提出一种对离散模型的状态矩阵进行分解和重组的方法来避免离散解发散。但是这些方法均面临着计算量较大的问题。文献[24]在不同坐标系下对电流以及磁链公式分别进行离散化处理,以此来改变观测器的极点轨迹进而实现离散全阶状态观测器的稳定,并降低了算法的计算量。但是该方法并不具有普遍性且缺乏系统性的理论指导,基于其他形式观测器的系统需要重新进行分析,会造成程序可移植性较差。考虑到模型预测控制方法可以灵活地设计目标函数来实现诸如动态电压、电流限幅等功能[25],文献[26]提出一种带开关项的多步长模型预测控制简化实现方法,可以实现灵活可控的低开关频率控制。
本文在文献[26]的基础上,深入对比分析了该方法所实现的低开关频率与传统方案的本质区别,并定性描述了传统方案下算法失稳的原因。结果表明,各种高性能参数辨识算法可以无需改进直接移植于该控制策略中,实现低开关频率下的离散域稳定和高精度辨识。通过借助多步长的优势,可以一定程度上缓解低开关频率带来的谐波影响。除此之外,本文还对该模型预测控制方法的参数敏感性进行了系统的研究,分析了其受励磁电感误差的影响机理与程度。通过将参数辨识结果馈入模型预测控制算法进行在线修正,可以增强其参数鲁棒性,提升控制器对参数变化的自适应能力,进一步保障谐波的抑制。最后,通过充分的仿真和实验对比分析证明了本文所提方法的有效性。
考虑到直线感应电机结构的特殊性,如磁路开断、大气隙等,文献[7-10]对其数学模型进行了细致的研究。为了便于控制策略的设计,目前诸多直线感应电机控制相关文献[11-12]采用的数学模型为
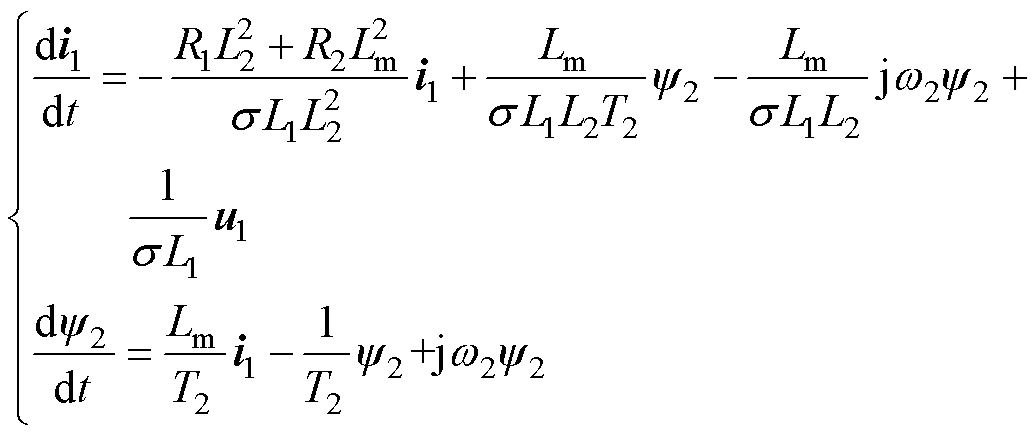 (1)
(1)
式中,下标1和2分别为直线感应电机初、次级变量;i、u、y 分别为电流、电压和磁链矢量;R为电阻;L为等效电感;Lm为等效励磁电感;T2=L2/R2为等效次级时间常数; 为等效漏磁系数,
为等效漏磁系数,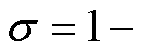
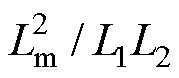 ;w2为等效电角速度,w2=vp/t ,其中,v为直线速度,t 为电机极距。
;w2为等效电角速度,w2=vp/t ,其中,v为直线速度,t 为电机极距。
可以看出,直线感应电机与旋转感应电机的主要区别在于等效励磁电感(后面统一称作“励磁电感”)的影响因素和变化规律不同。除了磁饱和因素外,直线感应电机特有的边端效应也将对励磁电感数值造成不可忽视的影响,具体影响因素有电机速度和转差频率。随着转速上升,励磁电感将呈现出被削弱的趋势,这将在一定程度上造成电机的推力输出能力下降。传统的直线感应电机控制方法通常采用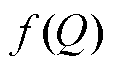 系数[10]对励磁电感进行修正。但是这种修正方式仅考虑了速度的影响,在对参数精度要求较高的部分场合将不能满足性能的需求。因此,有必要对励磁电感进行在线辨识,以综合考虑多种因素对参数的影响,增强系统的参数鲁棒性。
系数[10]对励磁电感进行修正。但是这种修正方式仅考虑了速度的影响,在对参数精度要求较高的部分场合将不能满足性能的需求。因此,有必要对励磁电感进行在线辨识,以综合考虑多种因素对参数的影响,增强系统的参数鲁棒性。
在数字控制器中,为了对电机状态量进行预测,需要对电机数学模型进行离散化处理,通常采用一阶前向欧拉法实现,有
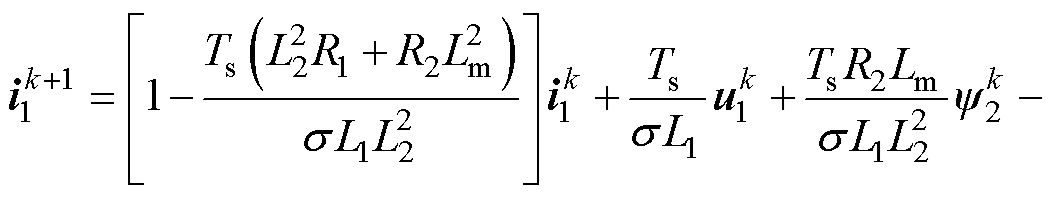
 (2)
(2)
为简化书写,定义系数
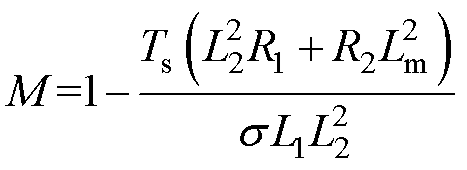
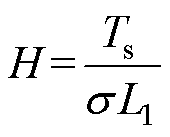
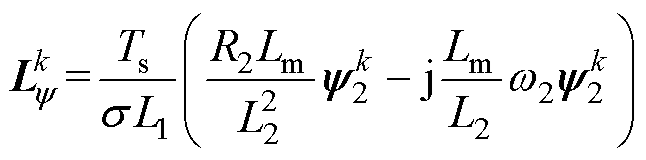
式中,上标k和k+1分别为在k时刻和k+1时刻的变量;Ts为采样周期。
传统模型预测电流控制的目标函数一般仅以电机电流误差作为评价指标,可表示为
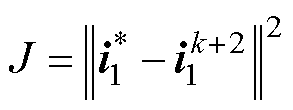 (3)
(3)
式中,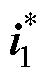 为参考电流;
为参考电流;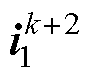 为考虑一拍延迟补偿后由k+1时刻待选电压矢量
为考虑一拍延迟补偿后由k+1时刻待选电压矢量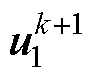 预测的k+2时刻电流,
预测的k+2时刻电流,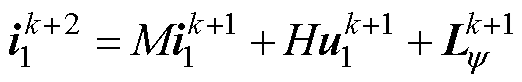 ,而k+1时刻的预测电流
,而k+1时刻的预测电流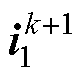 可以由已知的k时刻电压矢量
可以由已知的k时刻电压矢量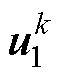 通过式(2)计算得到。结合式(2)、式(3),通过将7个待选电压矢量逐个代入计算,使得目标函数值最小的便是最优电压矢量。
通过式(2)计算得到。结合式(2)、式(3),通过将7个待选电压矢量逐个代入计算,使得目标函数值最小的便是最优电压矢量。
模型预测控制除了具有响应迅速、便于处理参数变化及模型非线性等显著优势外,还可以通过在目标函数中增加合适的控制项来实现一些特殊功能。为了使其具备主动调控开关频率的能力,可以将目标函数改造为
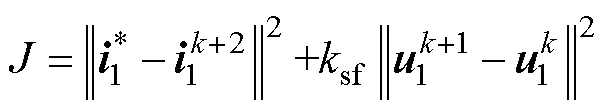 (4)
(4)
式中,ksf为调控开关频率在目标函数中比重的权重系数;矢量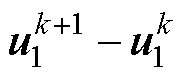 的模长可以反映出开关切换的复杂度。当选择较大的ksf时,就可以使得当前预测更加倾向于选择使开关状态不发生切换或仅部分开关管发生切换的电压矢量,进而降低开关频率。
的模长可以反映出开关切换的复杂度。当选择较大的ksf时,就可以使得当前预测更加倾向于选择使开关状态不发生切换或仅部分开关管发生切换的电压矢量,进而降低开关频率。
为了避免逐个代入电压矢量进行预测评估而导致计算量较大,可以借助参考电压方法对算法进行简化,具体如下。
将式(2)代入式(4)可得
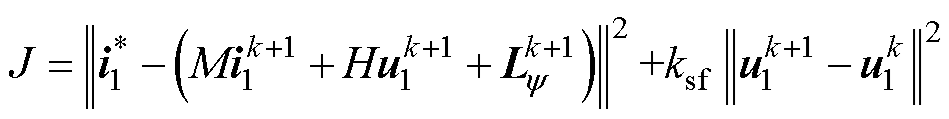
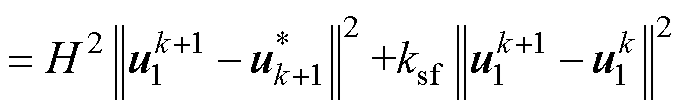 (5)
(5)
式中,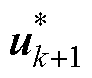 为不考虑开关项时的k+1时刻参考电压矢量。此时选取距离参考电压矢量最近的待选电压矢量即为最优电压矢量,如图1所示,整个电压空间矢量平面被分割为7个区间,图中,u*为参考电压矢量。
为不考虑开关项时的k+1时刻参考电压矢量。此时选取距离参考电压矢量最近的待选电压矢量即为最优电压矢量,如图1所示,整个电压空间矢量平面被分割为7个区间,图中,u*为参考电压矢量。
为了将开关项的评价考虑进参考电压矢量,对式(5)进行进一步的简化得
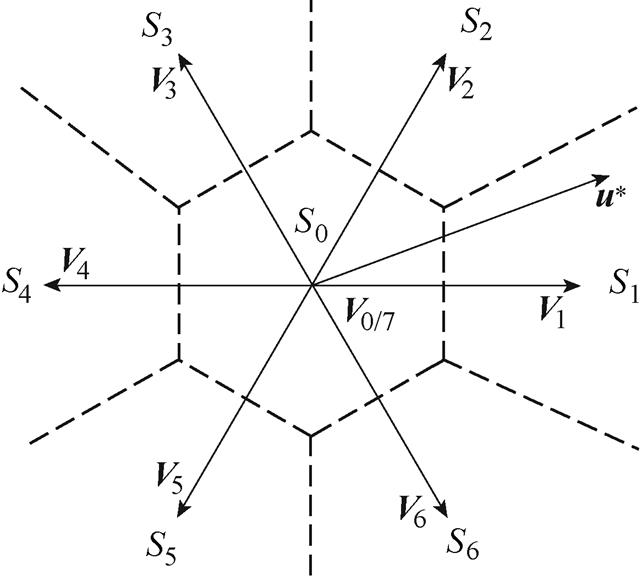
图1 根据参考电压矢量选取待选电压矢量
Fig.1 Selecting candidate voltage vector according to reference voltage vector
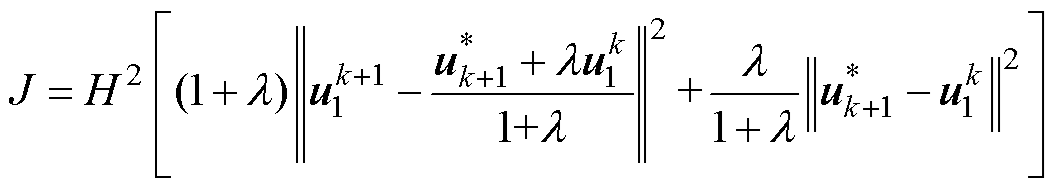 (6)
(6)
式中,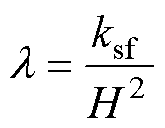 ;
;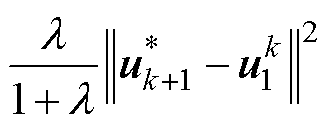 为常数项,考虑开关项后待选电压矢量变为
为常数项,考虑开关项后待选电压矢量变为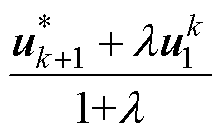 。
。
此时,最优电压矢量选取的扇区划分仍如图1所示。可以看出,无论是否考虑开关项,此时仅需要计算出相应的参考电压矢量,然后根据所在扇区直接判断得到最优电压矢量,从而将评估计算量由7个电压矢量变为1个电压矢量。
虽然得到的带开关项的模型预测控制方法可以主动调控开关频率,但是和传统频率控制方法类似,它将不可避免地以牺牲电流控制质量为代价。通过引入多步长方法可以在降低开关频率的同时尽量提高电流质量,抑制系统谐波。而多步长带来的计算量增加则可以通过类似2.2节参考电压矢量方法进行合理简化[26]。考虑到篇幅的限制,这里仅以两步长为例进行推导和后续仿真实验验证,具体如下。
对于两步长模型预测控制,目标函数变为
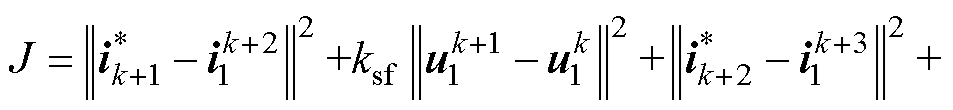
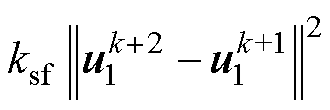 (7)
(7)
考虑到步长的增加将导致计算量呈指数级增加,具体来说,两步长的待选电压矢量序列为7×7条,因此有必要对其进行简化以缩小计算量。为了推导和计算的简便,做出如下假设:在预测步长内,次级磁链、角速度和参考电流几乎不变。可以对目标函数式(7)进行类似式(4)的简化,具体为
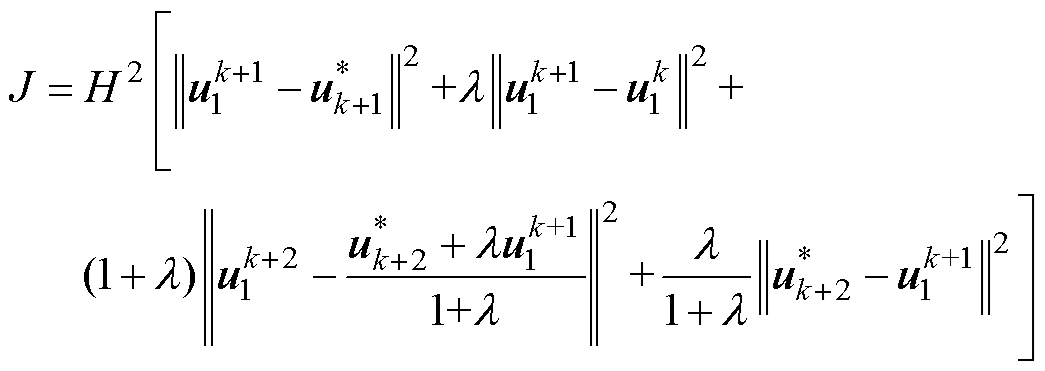 (8)
(8)
其中
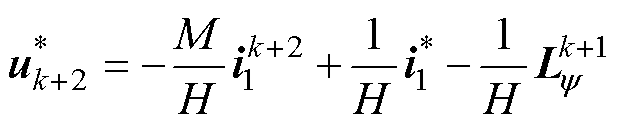
将k+2时刻电流预测方程代入可得
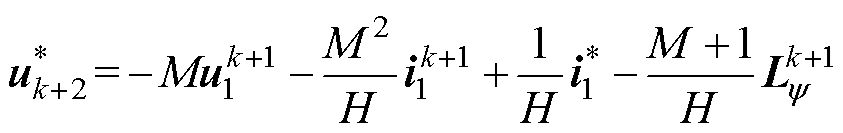 (9)
(9)
此时,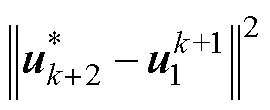 项不能被看作常数,因为其与待选电压矢量
项不能被看作常数,因为其与待选电压矢量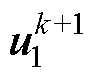 相关,将式(9)代入式(8)可得
相关,将式(9)代入式(8)可得
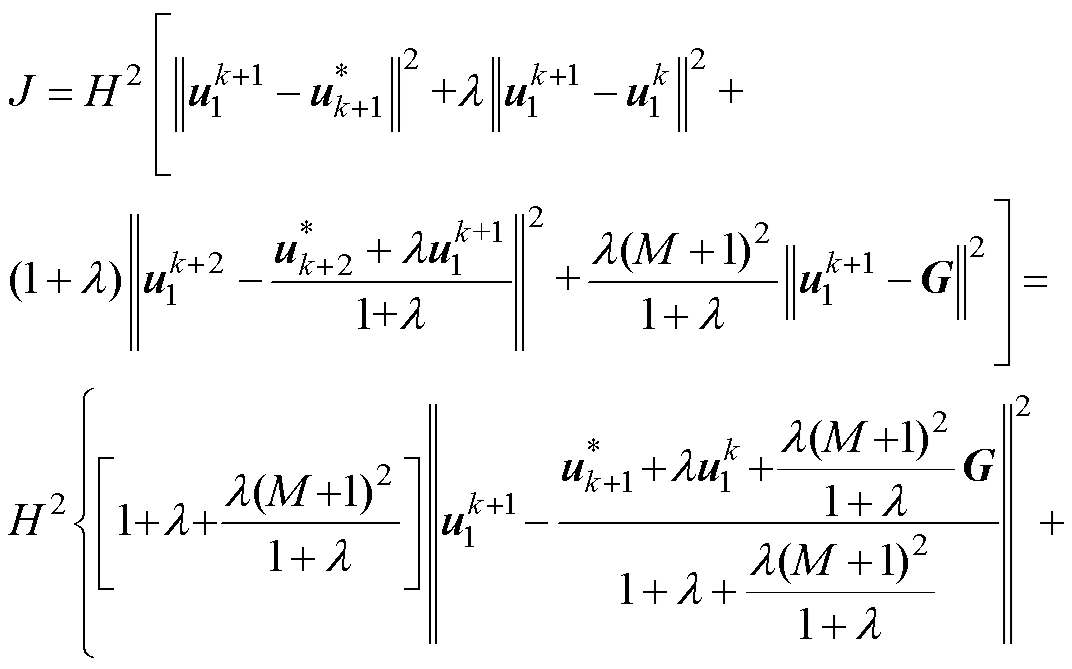
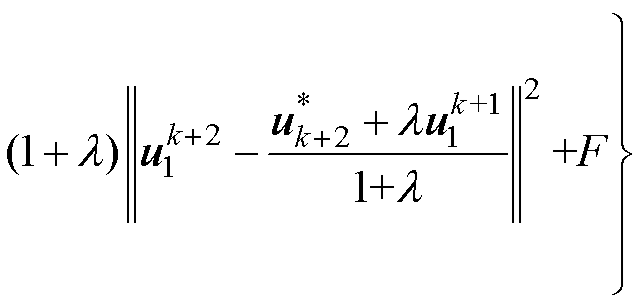 (10)
(10)
式中,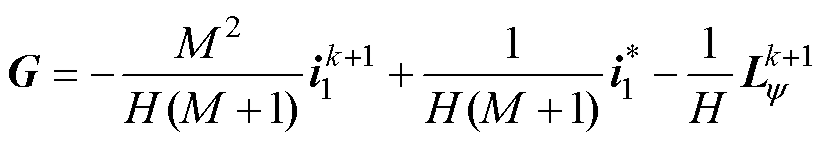 为常数;
为常数;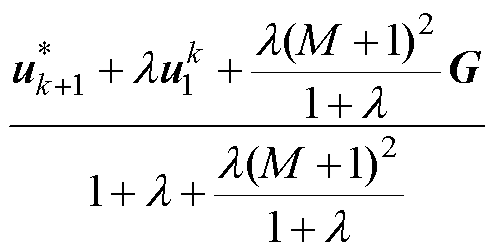 为两步长模型预测控制考虑开关项时的k+1时刻参考电压矢量;
为两步长模型预测控制考虑开关项时的k+1时刻参考电压矢量;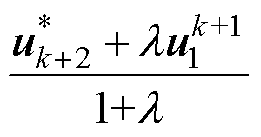 为相应的k+2时刻参考电压矢量;F为常数项,此处其推导结果省略。
为相应的k+2时刻参考电压矢量;F为常数项,此处其推导结果省略。
据此,可以得出如下结论:
(1)k+1时刻参考电压矢量仅与已知量有关,可以直接确定,而k+2时刻参考电压矢量需要用到k+1时刻选择的电压矢量信息。
(2)当开关项不存在时,两步预测的参考电压矢量可以分别简化为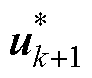 和
和 ,开关项的出现使得参考电压矢量计算趋于复杂化。
,开关项的出现使得参考电压矢量计算趋于复杂化。
(3)相比式(6),步长的增加不仅使得最优电压矢量选定变为最优电压矢量序列选定,还将影响k+1时刻参考电压矢量的计算结果。
(4)k+1时刻的评估结果权重大于k+2时刻,即目标函数将重点考虑k+1时刻的电压矢量选取。
结合上述结论可知,采用多步长时,不能像单步长一样直接确定最优电压矢量,需要逐步进行评估,具体步骤如下。
首先,在第一步预测时,可以通过评估参考电压矢量与待选电压矢量的距离,排除一部分电压矢量,具体逻辑为:根据参考电压矢量所在扇区,选取该扇区对应的两个非零电压矢量和一个零电压矢量作为评估对象,而排除其他过远的电压矢量。多步长的第一步电压矢量选择如图2所示。以图2为例,当参考电压矢量位于第一扇区时,选取V1、V2和V0/7作为待选电压矢量,而距离参考电压矢量较远的如V3则直接排除。此时所需评估的电压矢量序列减少为3×7条。
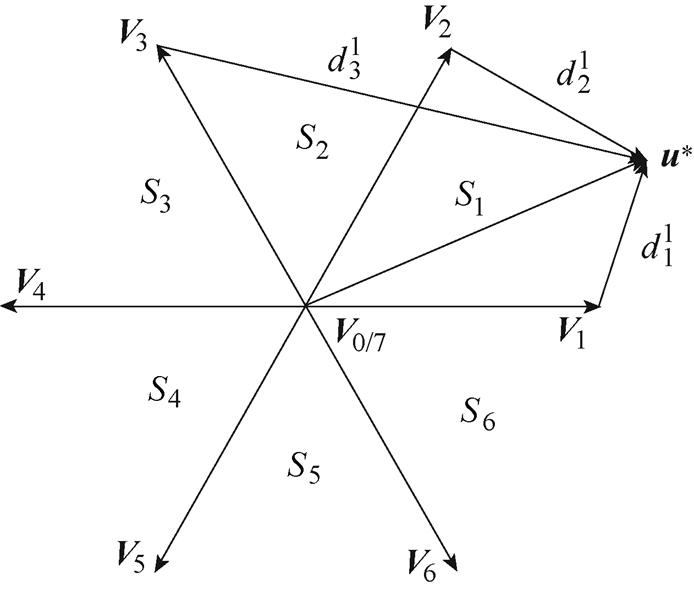
图2 多步长的第一步电压矢量选择
Fig.2 Selecting of first step voltage vector in multistep
然后,在第二步预测时,可以直接按照图1的方式选取距离参考电压矢量最近的基本电压矢量为最优电压矢量。此时所需评估的电压矢量序列进一步减少为3×1条。因此,采用该方法可以大幅度缩减多步长的计算复杂度,降低对处理器运算能力的要求。
传统开关频率控制一般通过改变调制频率来实现,但是会同时改变采样/控制频率。采用该方法除了会带来系统谐波含量上升,还会影响部分控制、观测方法的精度甚至是稳定性。而本文所采取的低开关频率控制方法可以直接从根本上解决问题,维持系统的采样控制频率不变。对于传统低开关频率控制方法下全阶观测器的稳定性问题已在文献[18]进行了详细的理论分析。相应的解决方案主要集中在改进离散化方案及观测辨识方法。这里将对其原因进行直观的分析并与本文采用的方法进行对比,主要从电压和电流两个侧面进行。
(1)从电压角度。传统开关频率控制方法主要是从改变采样控制频率进而改变调制频率入手,以空间矢量脉宽调制(Space Vector Pulse Width Modu- lation, SVPWM)为例,分析如图3所示。可以看出,当前控制周期计算得到的参考电压矢量直到下一个周期才施加到电机上,且实际脉冲宽度调制(Pulse Width Modulation, PWM)波相比参考电压体现出的是一种平均效应。此时,若控制/观测方法中仅对电压进行积分操作,尚可以保证积分周期内的数值相对准确,即
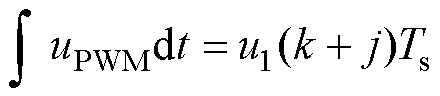 (11)
(11)
式中,uPWM为调制得到的实际PWM电压波形;j为自然数;u1(k+j)为相应的PWM前一控制周期计算得到的参考电压。
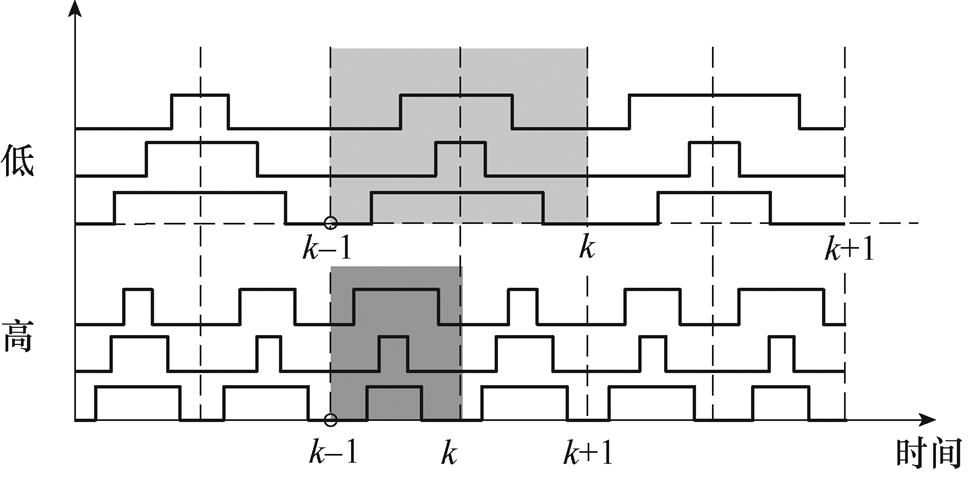
图3 传统方法下开关频率对SVPWM的影响
Fig.3 Impact of switching frequency on SVPWM by the conventional method
在其他低开关频率控制方法中,也均满足式(11)。但是,当涉及具体时刻点数值的直接计算时,如反电动势等,会由于延迟的存在而难以确定某一时刻电压的真实值,如图3中的k-1时刻。此时,若以u1(k-1)代替该时刻电压值,当采样控制频率较高时,该延迟对观测器的影响一般可以忽略或通过一些方式进行较为准确的补偿。然而随着Ts的增大,由于采样及控制周期均变大,误差也会增大,补偿难度将上升且精度难以保证。
反观本文所提出的低开关频率控制方案,其单相PWM电压分布结构如图4所示。此时没有采用调制策略,由模型预测控制直接给出最优基本电压矢量。其开关频率控制通过连续作用相同的电压矢量来实现。此时,虽然整体的开关频率降低,但是采样及控制频率保持不变,另外可以较为准确地确定某一时刻的实际电压值,可表示为
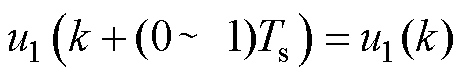 (12)
(12)
式中,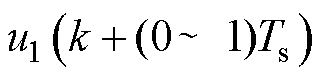 为k~k+1时刻间的电机作用电压。
为k~k+1时刻间的电机作用电压。
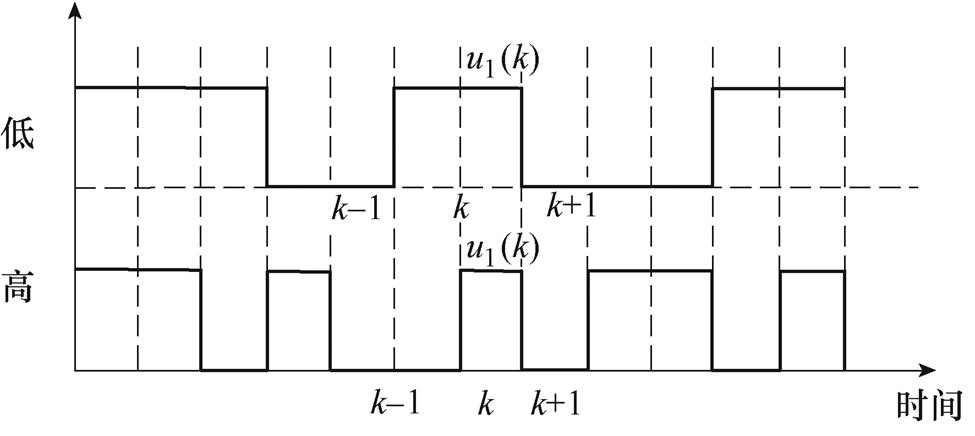
图4 所用方法下开关频率对PWM的影响
Fig.4 Impact of switching frequency on PWM by the adopted method
(2)从电流角度。传统控制方法和本文所采用的控制方法在低开关频率下的电流波形对比如图5所示。可以看出,由于所采用的方法可以在不改变采样频率的基础上实现开关频率的控制,因此电流采样可以始终保持高精度,在进行传统离散化积分、微分和取中间值等操作时均具有显著优势,具体可表示为
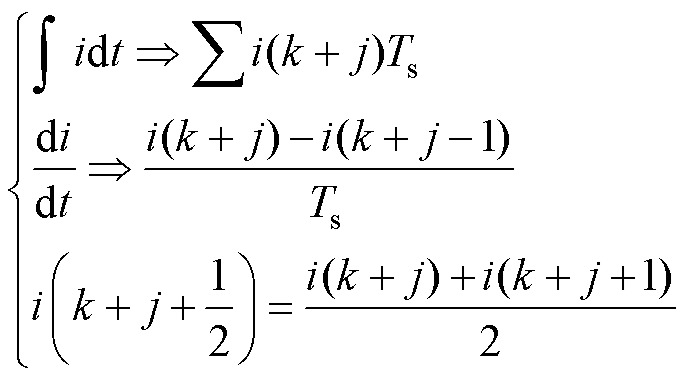 (13)
(13)
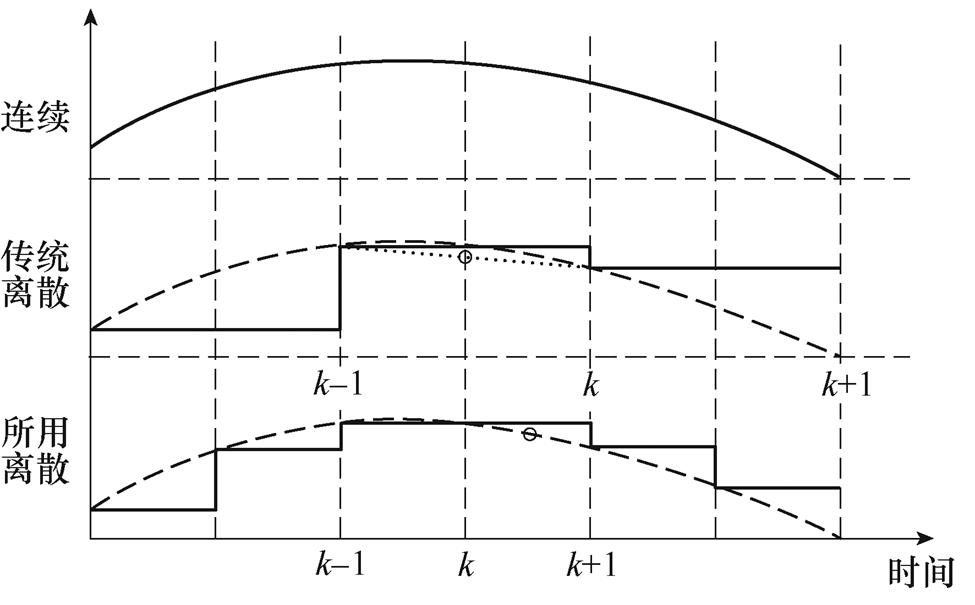
图5 连续和两种离散情况下的对比
Fig.5 Comparison between continuous and two discrete situations
由式(13)可知,Ts的大小将在较大程度上影响离散化的效果,特别是对于常用的简易方法如一阶欧拉法,其离散化精度将难以满足部分应用的需求。
可以看出,本文所采用的低开关频率控制方法的优势主要在于可以在降低开关频率的同时不降低采样控制频率。但是,与之对应的将造成单个采样控制周期内处理器的运算能力受限。另外,该方法所实现的低开关频率是不固定的,会在一定范围内波动,且可能存在短时间开关频率较高的情况。对于以降低开关损耗为目的的应用场合而言,主要关注的是平均开关损耗,因此该影响可以接受。
首先,为了便于研究所采用的带开关项模型预测控制的参数敏感性,选取参考电压矢量的计算结果误差作为评估量,即定义
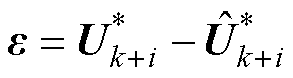 (14)
(14)
式中,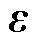 为参考电压矢量计算误差;
为参考电压矢量计算误差;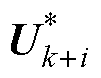 和
和 分别为参数无偏差和出现偏差时的参考电压矢量。
分别为参数无偏差和出现偏差时的参考电压矢量。
当参数误差影响到参考电压矢量计算结果时,可能会使得选取的电压矢量发生变化,进而影响控制效果。另外,考虑到分析计算的简便,将参考电压矢量计算变换到dq坐标系下进行,且主要考虑基于转子磁场定向下的稳态工况,以初步得出参数敏感性规律。而动态下的计算将在仿真和实验中实现。另外,考虑到直线感应电机励磁电感动态变化的特殊性,这里重点研究励磁电感参数的影响。
首先,将式(1)所示的直线感应电机数学模型变换到dq坐标系下,可表示为
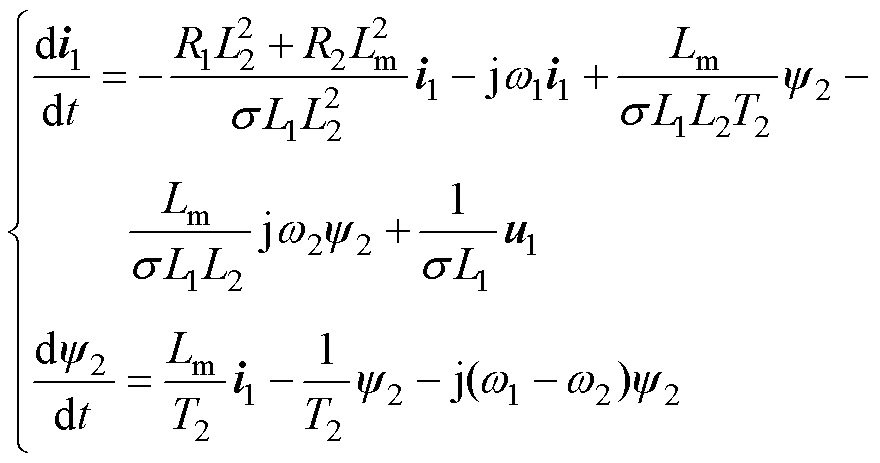 (15)
(15)
对应的离散化电流预测方程为
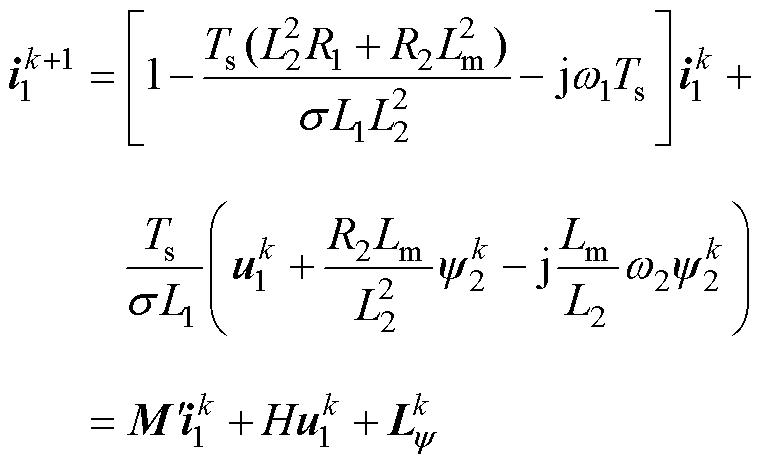 (16)
(16)
其中
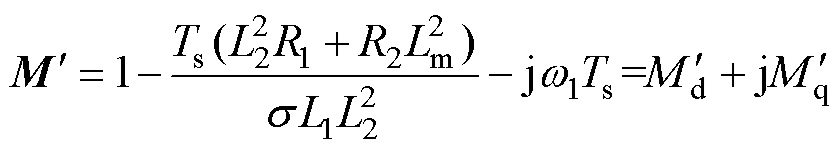
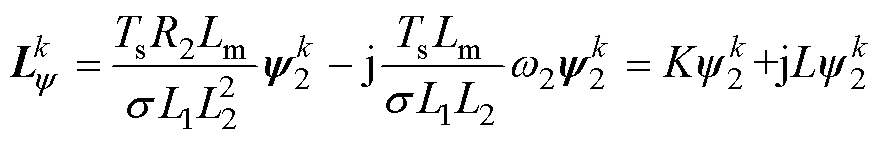
而磁链预测方程也发生了变化,可表示为
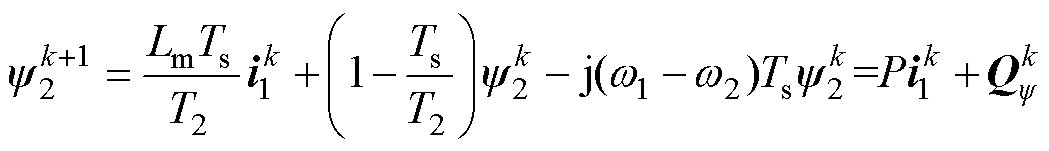 (17)
(17)
其中
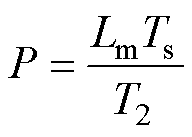
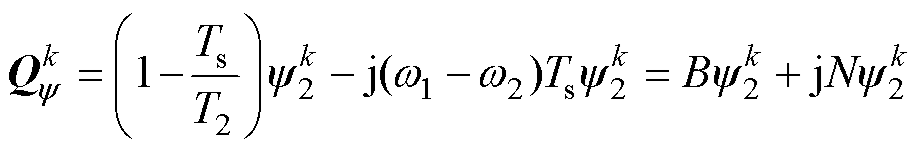
为了推导结果的简便,易于进一步分析,这里仅以单步长为例。考虑到采样频率较高,有理由假设前后两步基本电压矢量dq分量形式几乎不变,因此目标函数形式可以保持不变。基于同步旋转坐标系的参考电压矢量推导与静止坐标系的类似,这里不再重复赘述,根据式(6)将其参考电压计算公式展开为k时刻电压、电流、磁链及参考电流的表达式,有
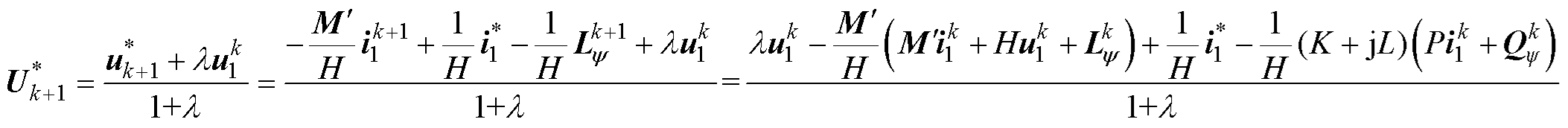
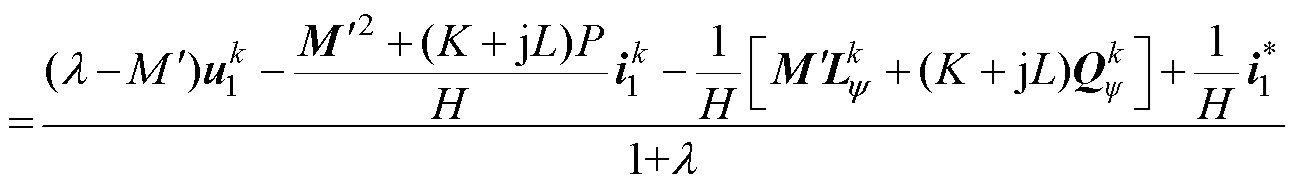 (18)
(18)
至此,参考电压矢量的计算完全由k时刻的电压、电流、磁链及电流参考值决定。其中,电压、电流及其参考值均可以通过采样测量得到。当假设k时刻观测得到的磁链值准确时,便可以根据式(18)计算k+1时刻的参考电压矢量,测试参数不准确的影响。值得一提的是,延迟补偿、磁链预测和一步预测中的参数误差均被考虑了进来。为了便于理论分析,将其进一步展开成dq分量形式并考虑转子磁场定向中转子磁链的d、q分量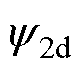 和
和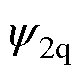 满足:
满足: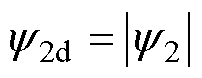 ,
,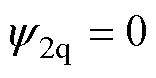 ,可得
,可得
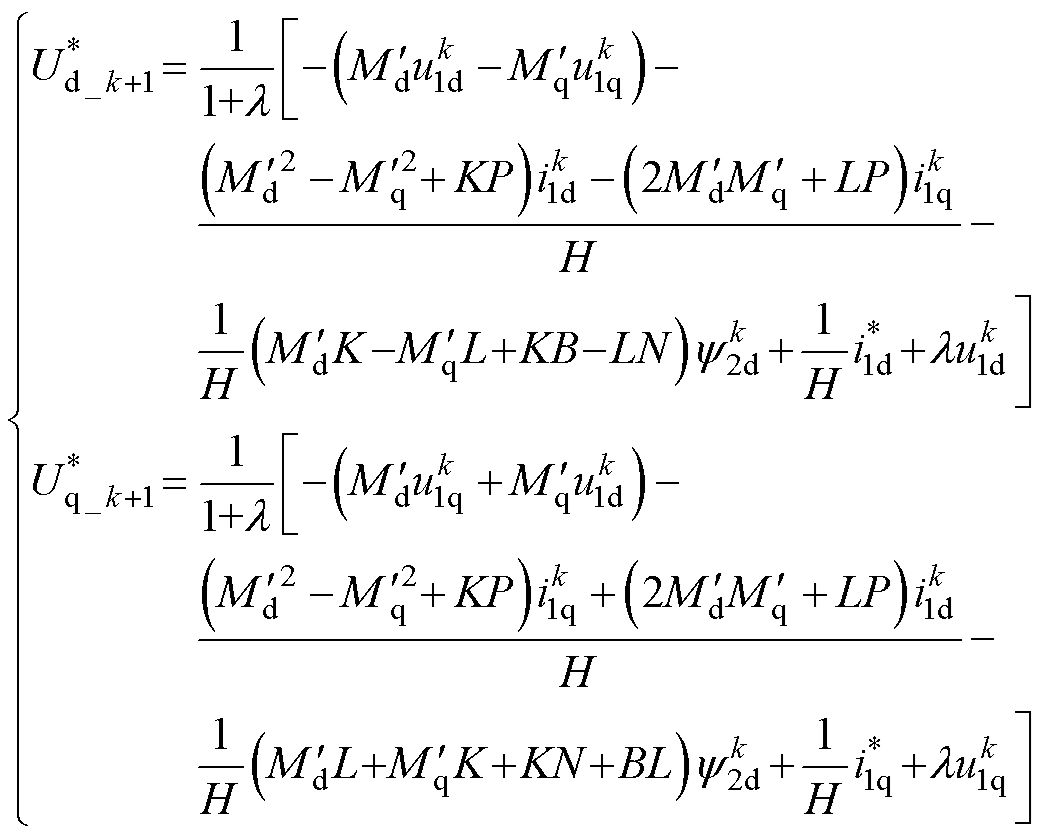 (19)
(19)
稳态工况下,转子磁链与d轴电流满足
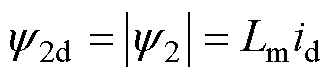 (20)
(20)
将式(20)代入式(19),进一步可得
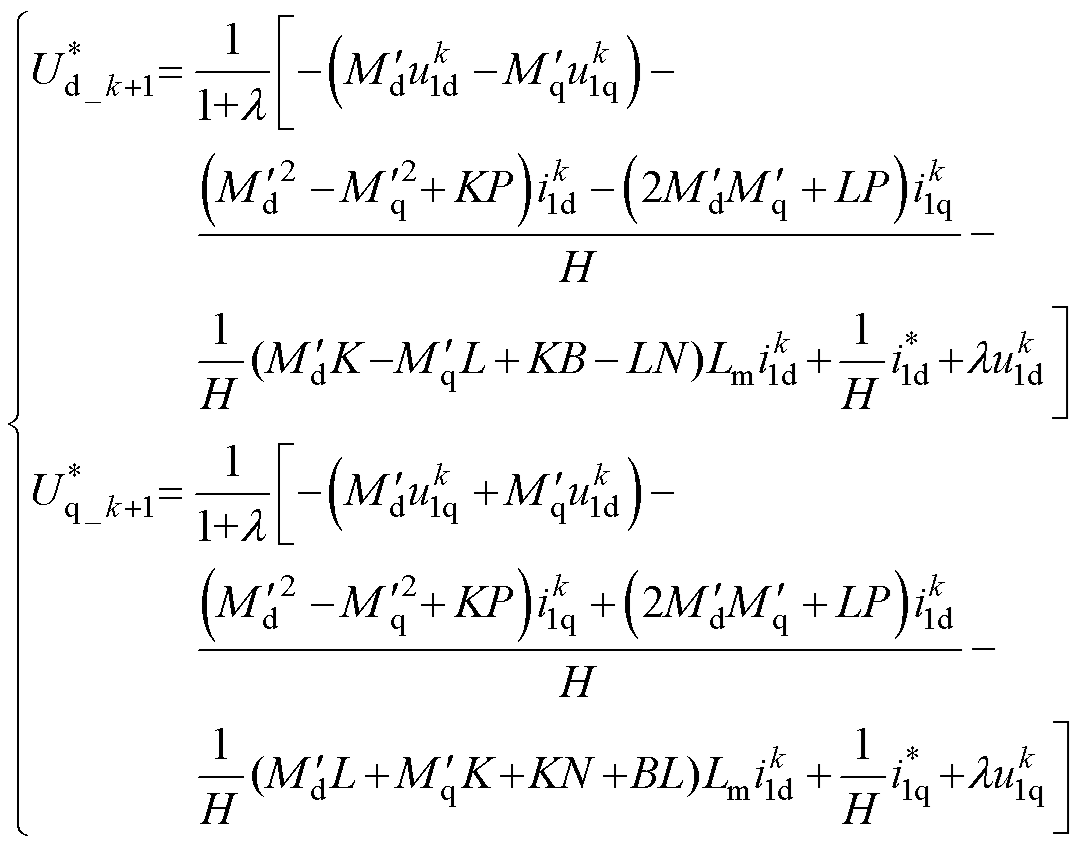 (21)
(21)
从式(21)得知,所有的系数均被变换到电流和电压项下,为后续参数敏感性的理论评估提供了方便。结合本文的轨道交通研究背景,直线感应电机励磁电感相比次级漏感较大,而相对初级漏感较小,因而可简化为
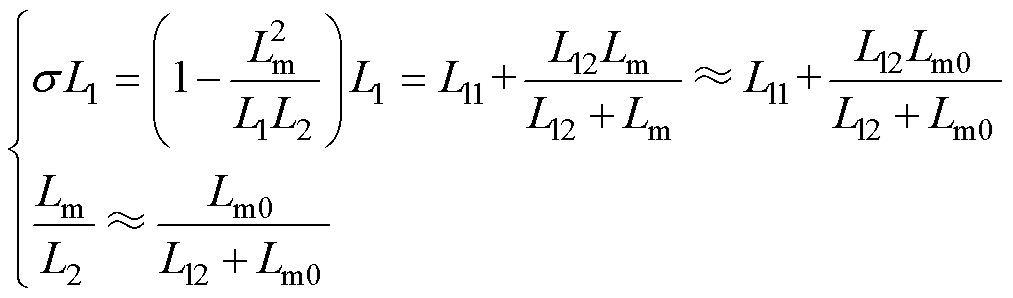 (22)
(22)
式中,Ll1和Ll2分别为初级和次级漏感;Lm0为电机静止时的励磁电感。
因此,电压系数在参数敏感性理论分析中可以考虑近似忽略,以重点关注主要影响因素。但是,需要注意的是,1/H中除了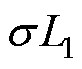 之外,还存在采样时间Ts。而在本方法中采样频率较大且直线感应电机的特殊性导致
之外,还存在采样时间Ts。而在本方法中采样频率较大且直线感应电机的特殊性导致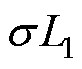 受励磁电感参数影响程度远大于旋转感应电机,因此该项的误差不能忽略。同时,这也将导致其他系数的误差被放大,如
受励磁电感参数影响程度远大于旋转感应电机,因此该项的误差不能忽略。同时,这也将导致其他系数的误差被放大,如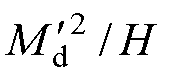 。除此之外,系数L中不仅存在Lm/L2,还存在次级角频率项w2,当电机工作在高速时,同样地,该项的误差也不能被忽略。因此,不能简单地根据式(22)简化原理对参数进行过度简化,这也是本文针对直线感应电机模型预测控制的参数敏感性分析不同于旋转感应电机之处。而对于系数B,尽管其带有参数敏感性较强的1/T2,但是一方面其分子包含Ts,另一方面存在常数1,反而对参数变化不敏感。结合上述分析及式(14)和式(21),可得简化的误差方程为
。除此之外,系数L中不仅存在Lm/L2,还存在次级角频率项w2,当电机工作在高速时,同样地,该项的误差也不能被忽略。因此,不能简单地根据式(22)简化原理对参数进行过度简化,这也是本文针对直线感应电机模型预测控制的参数敏感性分析不同于旋转感应电机之处。而对于系数B,尽管其带有参数敏感性较强的1/T2,但是一方面其分子包含Ts,另一方面存在常数1,反而对参数变化不敏感。结合上述分析及式(14)和式(21),可得简化的误差方程为
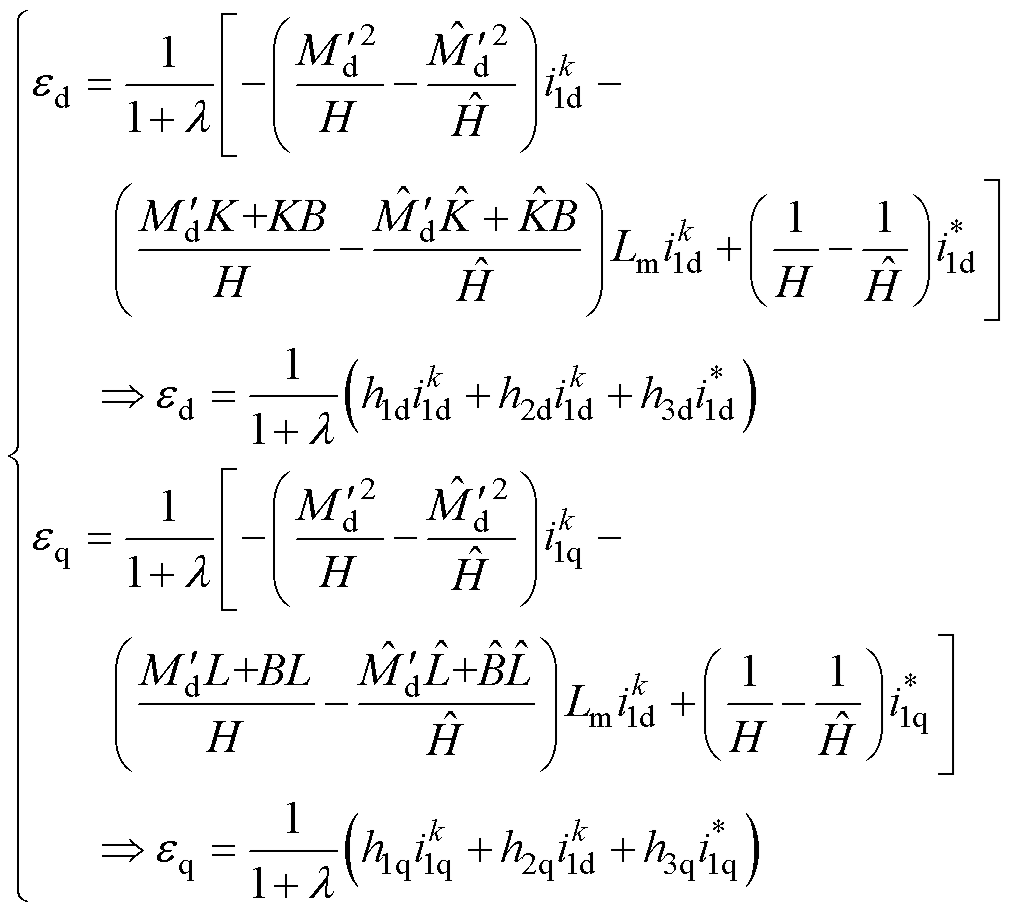 (23)
(23)
式中,上标 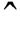 表示参数存在偏差时的各个变量。
表示参数存在偏差时的各个变量。
为定量评估参数变化的影响,本文定义励磁电感的参数误差为
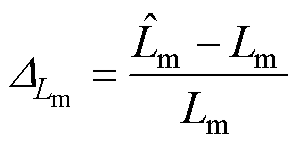 (24)
(24)
结合式(23)和式(24),可绘制出权重系数为0时的6个系数(h1~3dq)随励磁电感误差变化的曲线,具体如图6所示。通过综合分析可得如下结论:
(1)参考电压的计算对励磁电感误差较为敏感,且电压误差的上下限基本不受当前电压值影响,而主要和电流值相关,因此参数误差的影响在参考电压本身较低时影响较大。
(2)d轴参考电压误差主要取决于d轴电流和d轴参考电流,即电机的励磁情况。
(3)q轴参考电压误差和d、q轴电流以及q轴参考电流均有关,即会受到励磁和负载情况的影响。
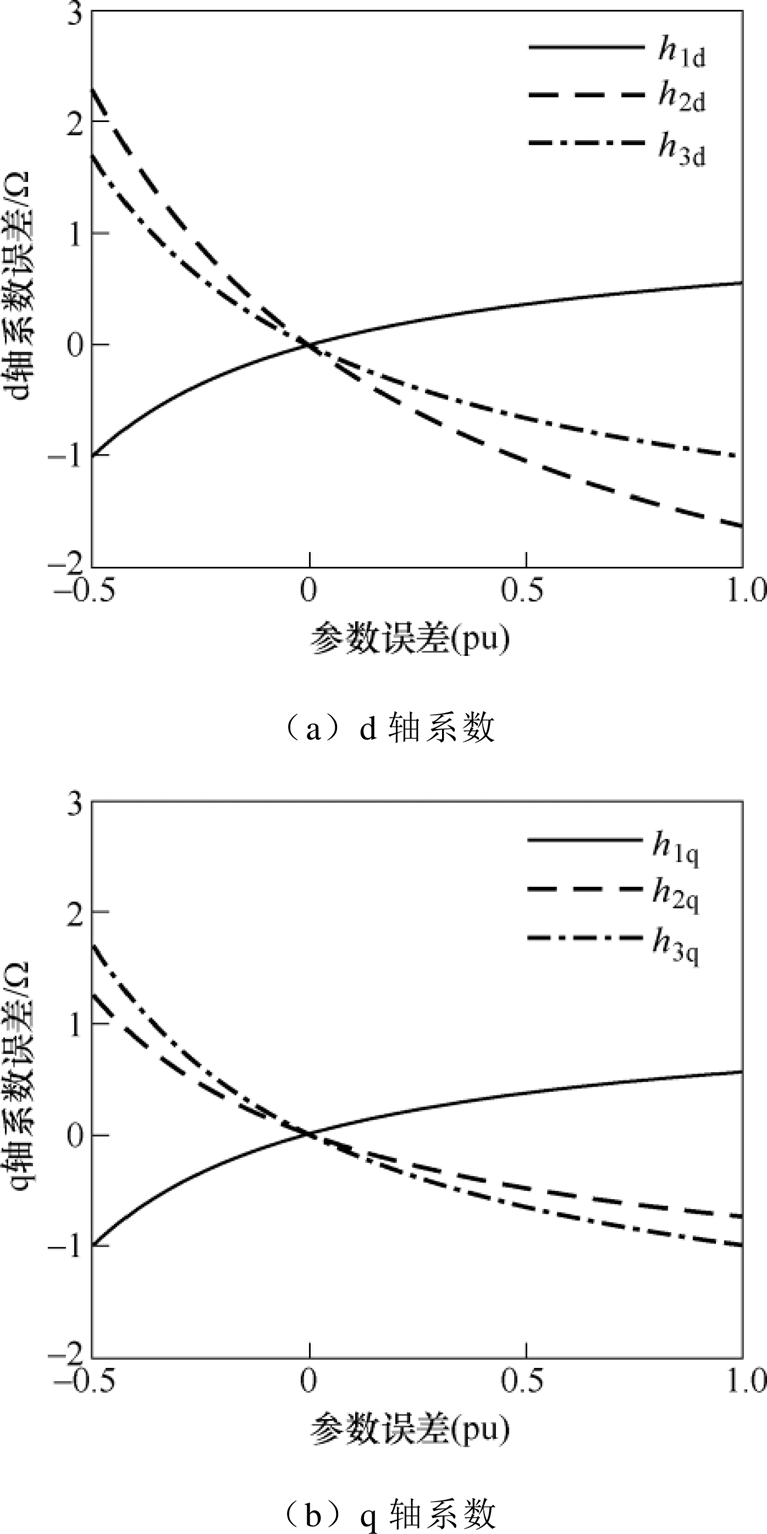
图6 参考电压计算中关键系数变化趋势
Fig.6 Trend of key coefficients of reference voltage calculation
(4)电机运行速度也会对参数敏感性产生影响,其体现在对L参数的敏感性上,转速越高,L受励磁电感的影响程度越深,进而主要导致q轴参考电压误差加大。
(5)权重系数的增加会降低参数敏感性,使得参考电压矢量的计算更加趋近于当前时刻作用的电压矢量而非计算出的电压矢量。
(6)尽管h1dq与参数误差的关系与其他系数相反,但是其系数相对较小,整体d轴误差无论在何种工况均保持符号关系不变,而整体q轴误差取决于励磁情况和负载情况的对比。
结合式(14)、式(18)和式(24),可绘制出预测的参考电压矢量误差(ed和eq)与励磁电感误差之间的关系曲线,如图7所示。由图可知,参考电压在励磁电感误差较大时会出现较大程度偏离,并且偏离值会随着权重系数增大而缩小。另外,通过对比不同负载工况下的偏离程度大小,可进一步验证前面分析的dq轴参考电压误差与负载情况的关系:即d轴误差基本保持不变,q轴误差则会随负载加重而明显增大。
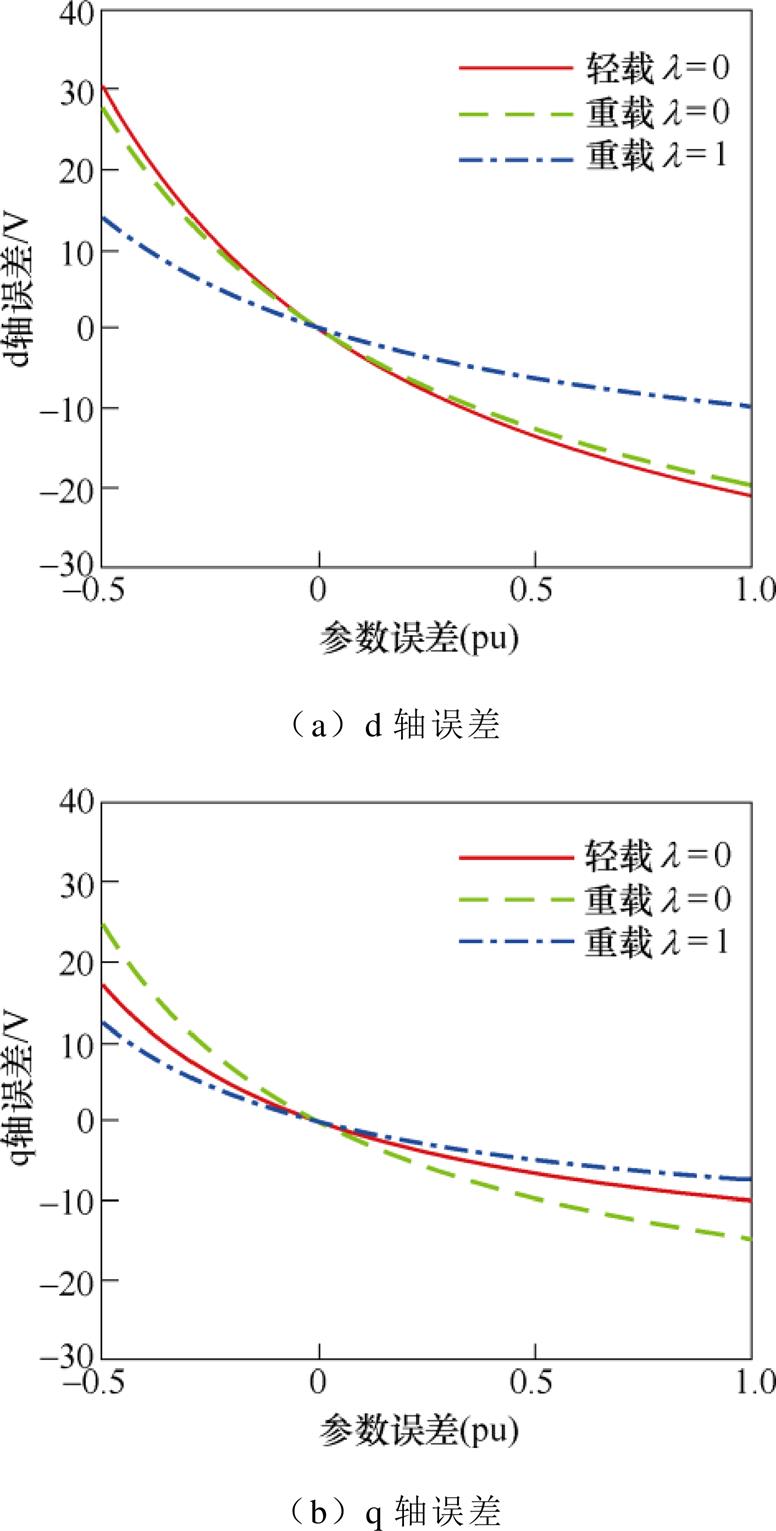
图7 参考电压矢量误差与励磁电感误差之间的关系
Fig.7 Relationship between reference voltage and magnetizing inductance
考虑到直线感应电机的特殊性,有必要对其励磁电感进行在线辨识补偿,以保证模型预测控制的预测精度,进而提升电流控制性能,起到降低系统谐波的目的。这里采用一种基于反电动势的模型参考自适应方法对其励磁电感进行在线辨识[16],以避免纯积分环节的影响。值得一提的是,此处引入该方法只是为了便于后续验证,亦可采用其他参数在线辨识算法。定义反电动势为
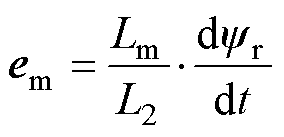 (25)
(25)
由式(25)及式(1)可得以反电动势为观测量的电压、电流模型分别为
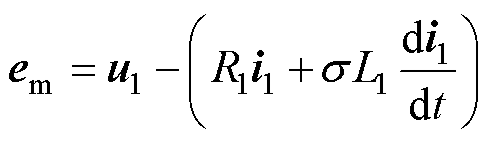 (26)
(26)
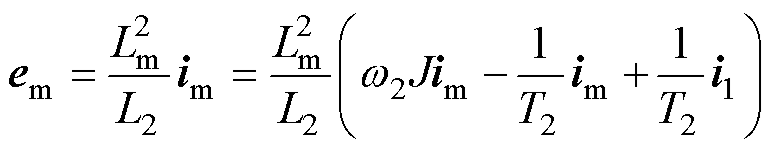 (27)
(27)
式中,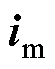 为励磁电流矢量,
为励磁电流矢量,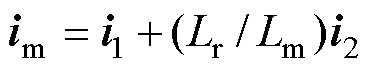 。
。
考虑到直线感应电机励磁电感相比次级漏感较大,而与初级漏感相比差距较小,作出如下简化
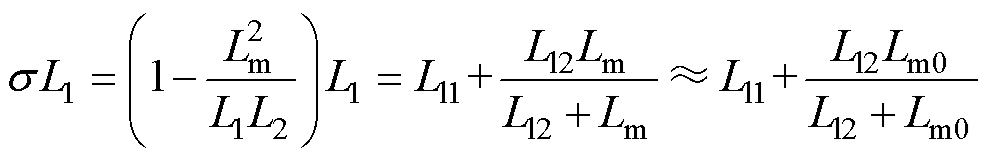 (28)
(28)
综合考虑式(26)~式(28),可以将电压模型式(26)看作参考模型,电流模型式(27)看作可调模型构建模型参考自适应系统。而根据Popov超稳定理论可以得到相应的自适应率为
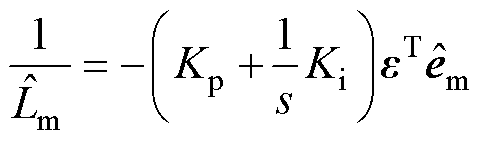 (29)
(29)
式中,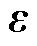 为参考与自适应反电动势的误差,
为参考与自适应反电动势的误差,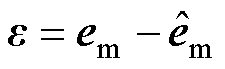 ;Kp和Ki为励磁电感辨识系统PI控制器参数。相应的结构框图如图8所示。
;Kp和Ki为励磁电感辨识系统PI控制器参数。相应的结构框图如图8所示。
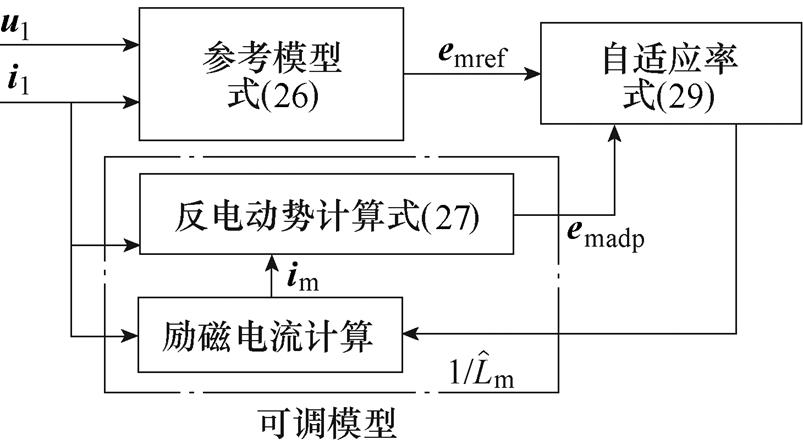
图8 励磁电感在线辨识系统结构框图
Fig.8 Structure of magnetizing inductance identification
结合式(12)可知,电机参数变化将影响参考电压计算,进而可能会改变所选取的最优电压矢量,造成电机的控制失当,影响电流控制性能。除此之外,式(2)得到的一拍延迟补偿电流也对参数较为敏感。因此,有必要对模型预测控制中的相关参数进行在线修正,以避免因参数变化造成系统性能降低。另外,考虑到直线感应电机励磁电感主要受转速等因素影响,假设其在预测步长内基本保持不变,因此在进行在线修正时,各步预测均统一采用当前辨识值进行补偿。
结合上述参数在线辨识算法,可以构建电感参数自适应模型预测控制策略如图9所示。其中,参数辨识系统除了可以用来修正励磁电感参数外,还能够实现磁链的精确估计,省去了原系统中的磁链观测器的同时增强了估计磁链对励磁电感的参数鲁棒性,具体可表示为
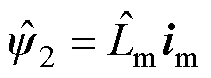 (30)
(30)
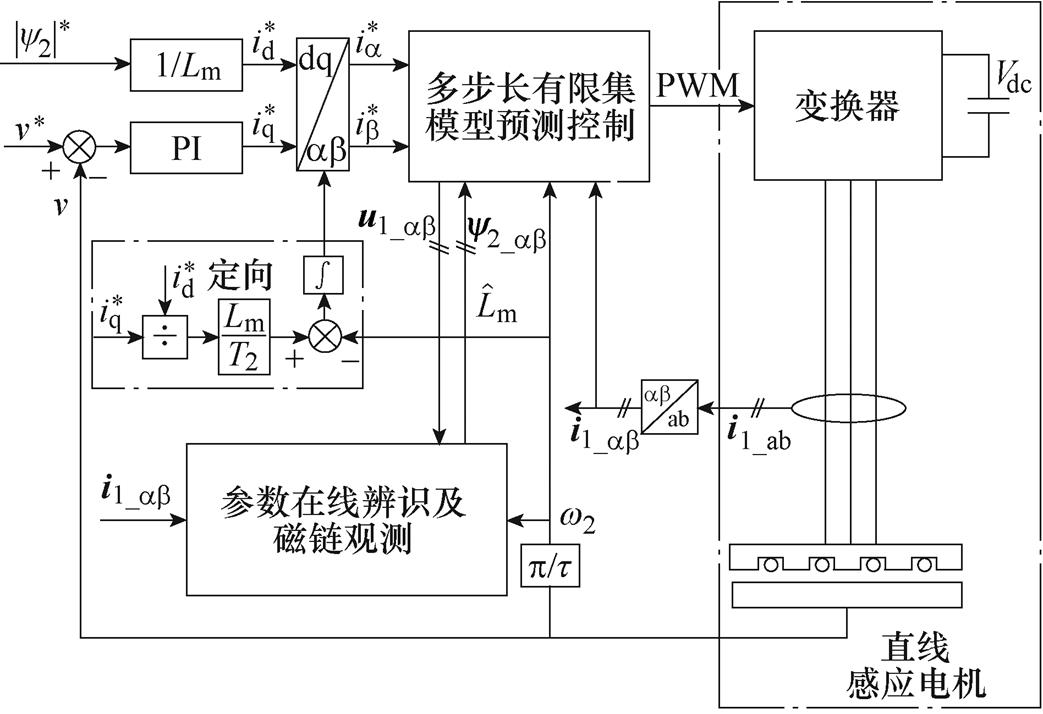
图9 所提出自适应模型预测控制结构框图
Fig.9 Structure of proposed adaptive MPC strategy
值得一提的是,该模型预测控制方法除了可以和本文所采用参数辨识算法相结合外,还可采用其他参数鲁棒性增强策略,如扰动观测器、多参数辨识方法对其进行在线补偿。这里结合励磁电感在线辨识方法,主要出于以下两点考虑:①验证采用该模型预测控制实现的低开关频率几乎不会影响参数辨识精度;②检验励磁电感在线修正对所采用模型预测控制的增强效果,以及对本文所围绕的低采样频率下低谐波控制的提升能力。
因实验场地面积和建设费用限制,本文搭建了大半径弧形感应电机模拟平台,如图10所示。为真实反映边端效应对直线感应电机参数以及运行性能的影响,弧形电机的转子直径需要足够大,进而其弧形运动可以等效为直线运动[27]。通过大量的优化分析,本文弧形电机的转子直径选择为1.23m,机械气隙10mm,额定功率3kW,额定速度40km/h,相关的等效电路参数见表1。外围驱动系统采用IGBT全控型器件变频器,控制芯片为DSP28335。

图10 直线感应电机模拟平台
Fig.10 Simulated platform of linear induction motor
表1 直线感应电机主要参数
Tab.1 Main parameters of prototyped LIMs
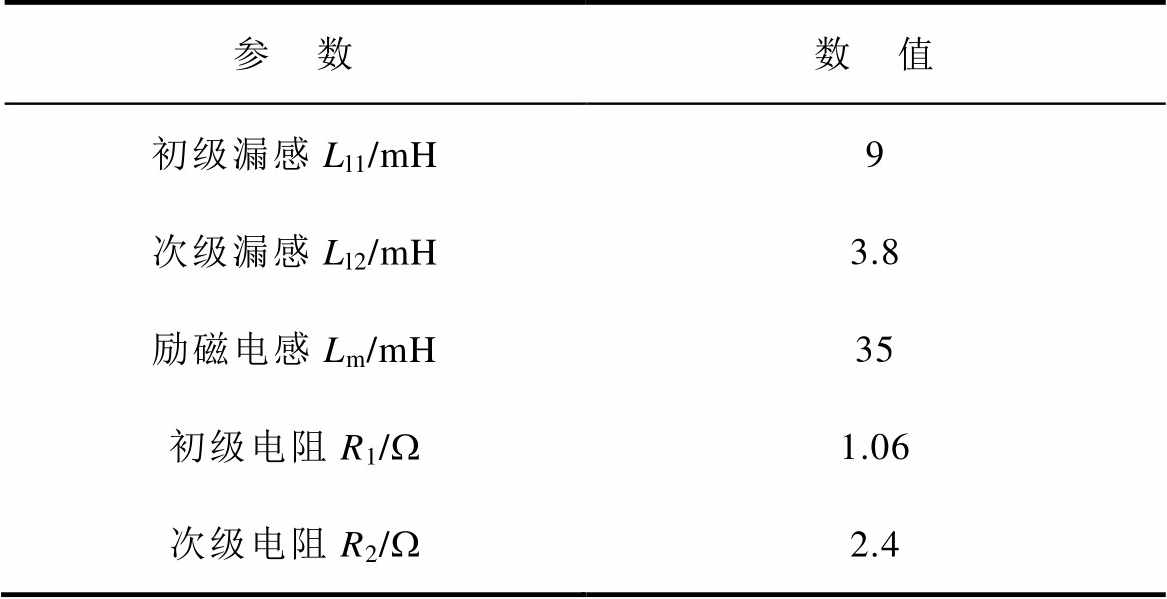
参 数数 值 初级漏感Ll1/mH9 次级漏感Ll2/mH3.8 励磁电感Lm/mH35 初级电阻R1/W1.06 次级电阻R2/W2.4
为了在仿真中充分反映出直线感应电机励磁电感随运行工况变化的特性,采用了广泛接受的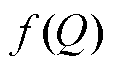 模型[8]对励磁电感进行模拟调整。为了进行对比,这里采用经典间接磁场定向控制作为传统方案,其中调制策略采用SVPWM。通过改变其采样控制频率,可以实现不同的开关频率模式。而对于模型预测控制算法,则始终保持采样频率恒定,通过改变权重系数来灵活调节开关频率。
模型[8]对励磁电感进行模拟调整。为了进行对比,这里采用经典间接磁场定向控制作为传统方案,其中调制策略采用SVPWM。通过改变其采样控制频率,可以实现不同的开关频率模式。而对于模型预测控制算法,则始终保持采样频率恒定,通过改变权重系数来灵活调节开关频率。
4.2.1 低开关频率对参数辨识影响分析
图11及图12分别给出了传统方法与多步长方法实现的500Hz开关频率下的转速、推力及电流波形。为了较为全面地测试电机控制系统的综合性能,仿真设置了起动、加速、减速、加载等环节。可以看出,两种低开关频率实现方法都可实现较为精准迅速的转速控制,但是亦均存在较大的转矩脉动和电流谐波。值得一提的是,采用模型预测控制后,无论是转矩还是电流均具有更加优良的动态响应能力,几乎不存在超调和振荡过程。
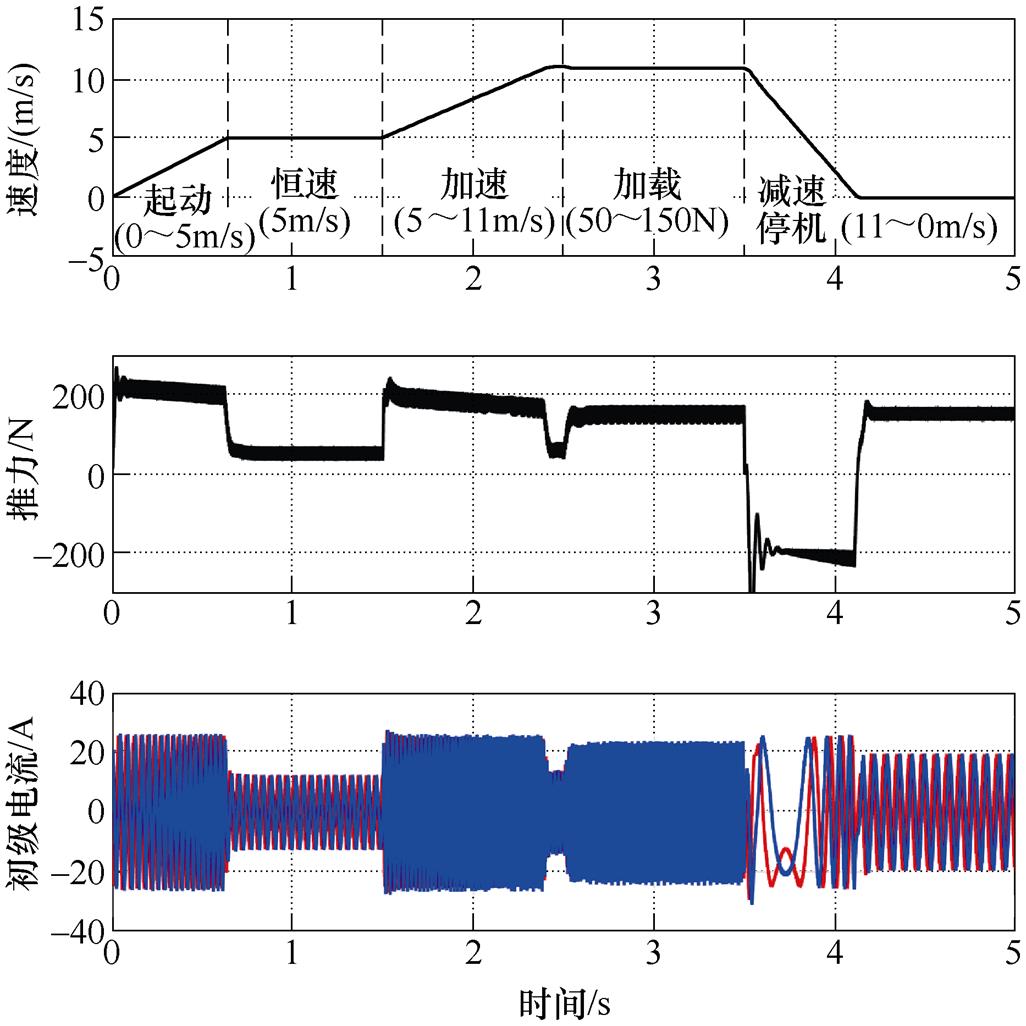
图11 传统方法实现的低开关频率控制效果
Fig.11 Low-frequency control performance of conventional method
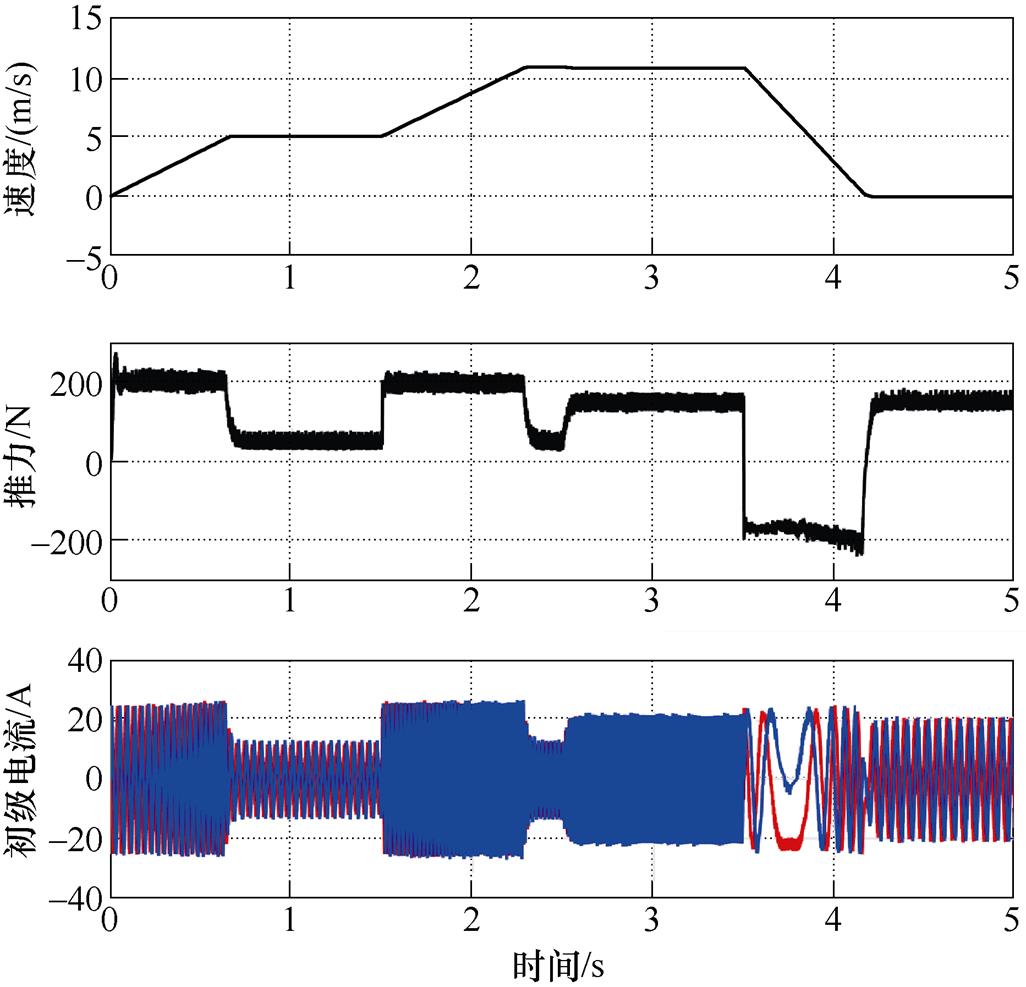
图12 所采用方法实现的低开关频率控制效果
Fig.12 Low-frequency control performance of adopted method
为了验证2.4节分析的两种不同的低开关频率实现方法对观测器的影响差异,图13和图14分别给出了不同开关频率下两种方法的参数辨识结果。可以看出,采用传统控制方法可以在高开关频率下实现较为准确的参数辨识,但是随着开关频率的降低,估计结果的准确性将明显降低,尤其是在高速区,甚至将会出现辨识结果的发散,这也与文献[24]的理论分析结果相符合。除此之外,辨识误差还与负载情况有关。然而对于所采用的控制方案,在不同的开关频率下的各个测试转速、负载工况中均可以保持精准的参数辨识。
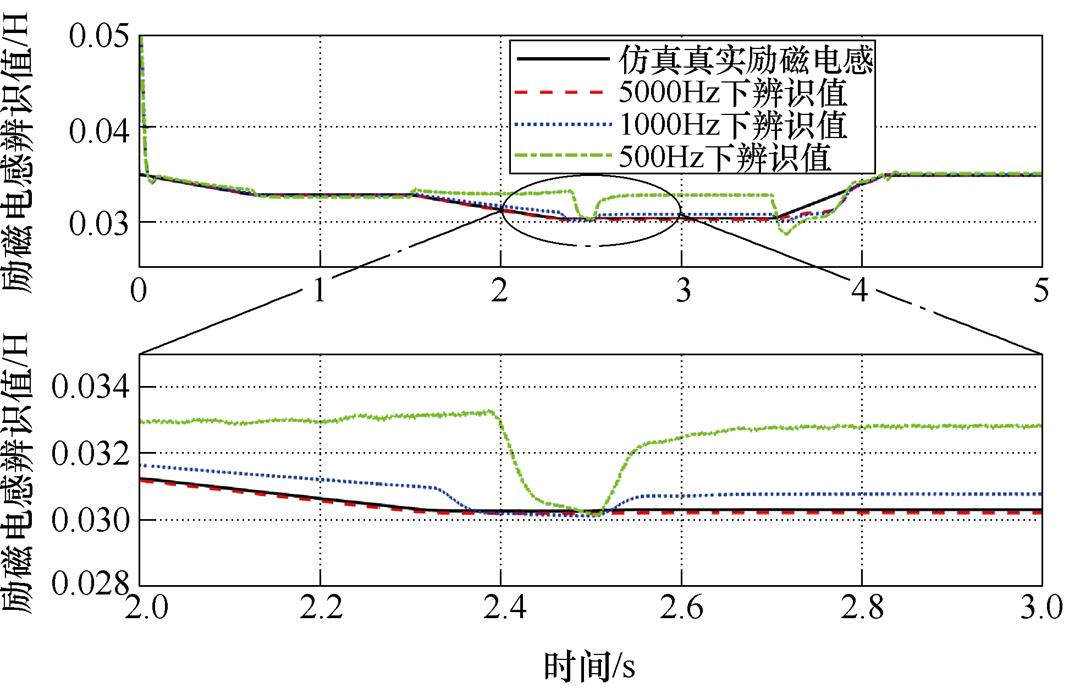
图13 传统方法下励磁电感辨识结果
Fig.13 Identification results of magnetizing inductance under conventional method
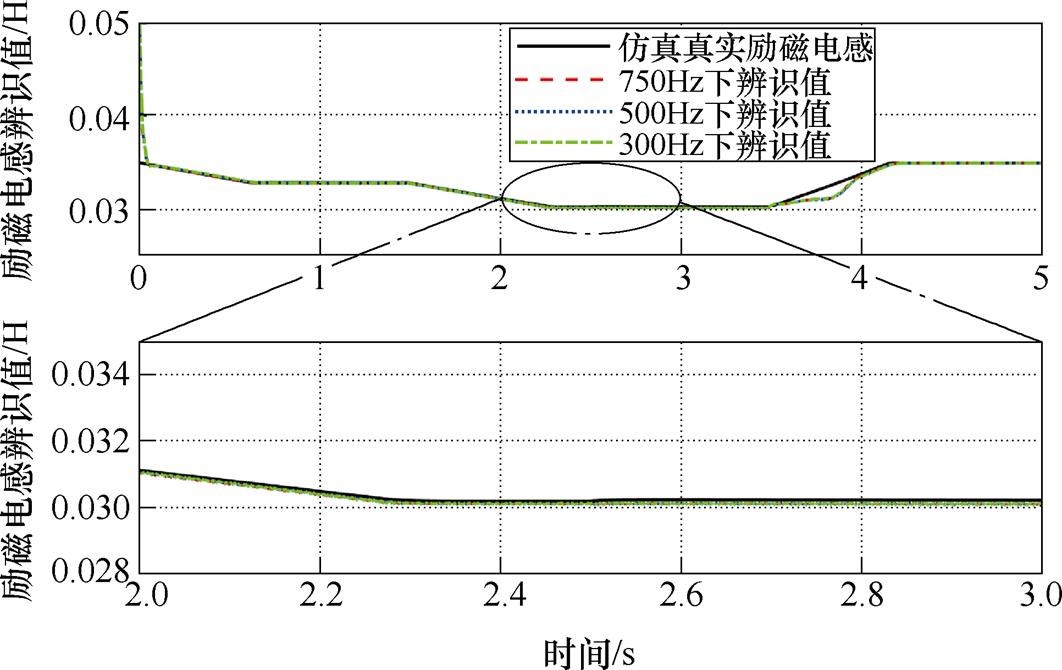
图14 所采用方法下励磁电感辨识结果
Fig.14 Identification results of magnetizing inductance under adopted method
具体而言,以500Hz下的辨识结果为例,此时采用传统方案已无法在额定速度、150N负载工况中对励磁电感进行正确估计;然而对于所采用的模型预测控制方案,此时参数辨识的误差仅为约0.1mH(约占静态励磁电感的0.28%),且无明显波动,动态性能优良。需要注意的是,在减速区域两种方案下的参数辨识均出现短时的偏差,这主要是因为定子频率经历了由正变负的剧烈动态过程,这方面的性能提升需要对参数辨识算法进行改进优化。考虑到这不是本文的研究重点,上述有待提升之处将在后续进一步深入研究。
4.2.2 参数敏感性分析
为了便于和3.1节理论分析结果进行对照验证,首先对单步长的参数敏感性进行仿真分析。图15和图16分别为给出单步长模型预测控制下的d、q轴参考电压的参数敏感性仿真结果。
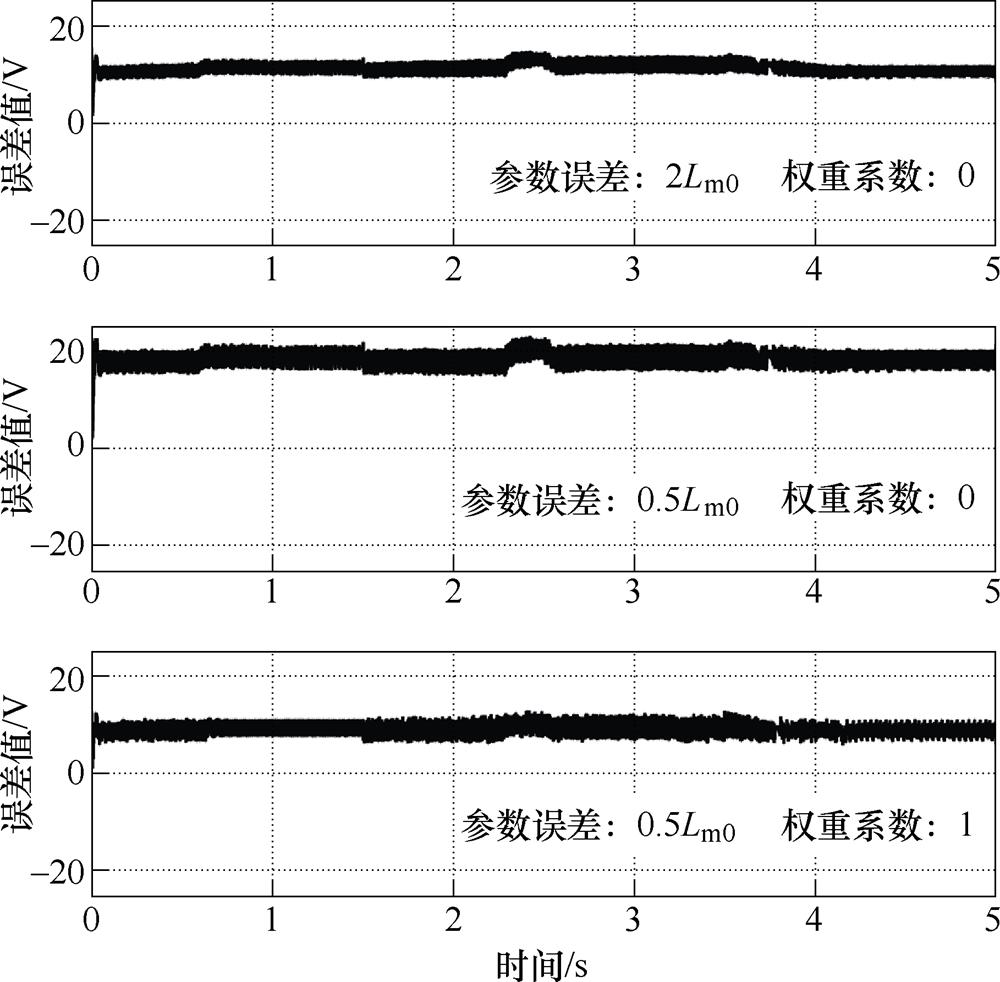
图15 单步长下d轴参考电压计算误差
Fig.15 Calculation error of d-component reference voltage under single-step mode
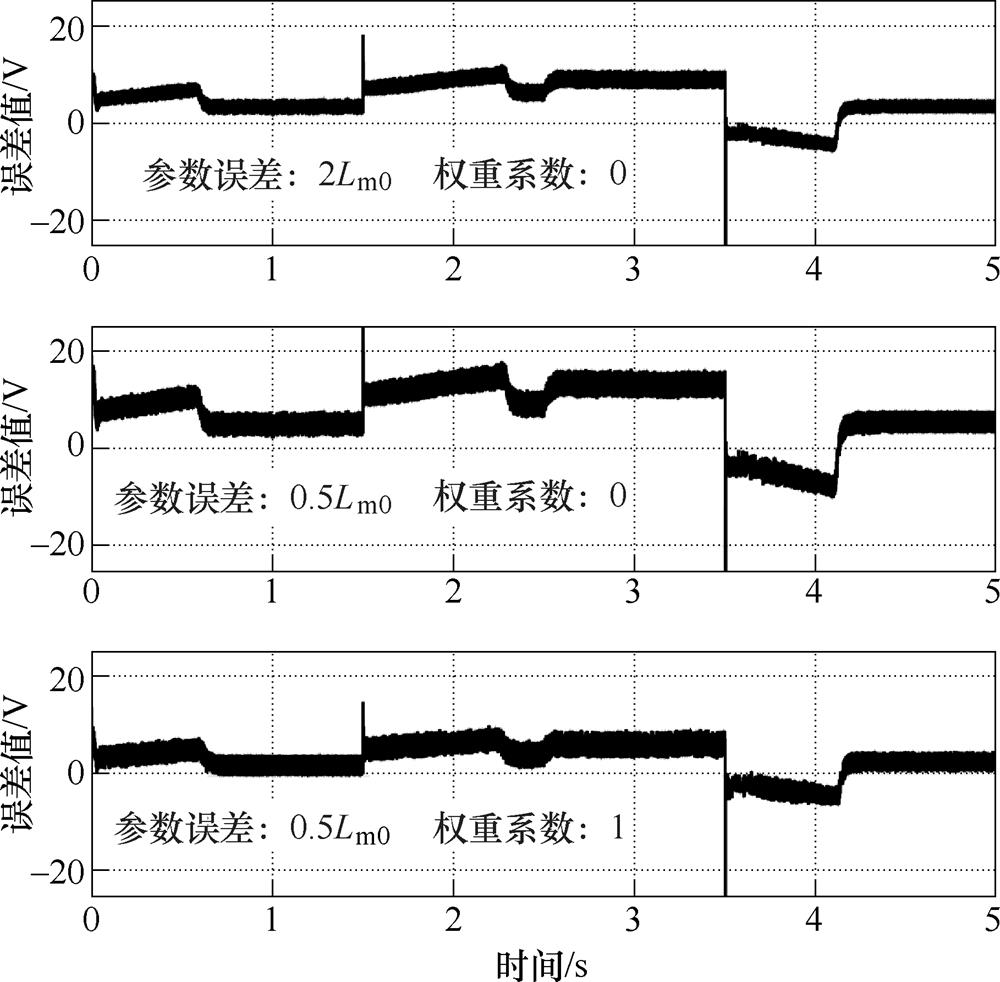
图16 单步长下q轴参考电压计算误差
Fig.16 Calculation error of q-component reference voltage under single-step mode
可以看出,dq轴电压随参数变化的整体规律与3.1节分析结果相符合。具体来说:
(1)励磁电感的d轴误差基本不受负载情况和转速情况影响,而q轴误差恰恰相反,不仅数值大小受负载情况影响,其符号也将随电机运行工况改变而改变,这与3.1节的分析结论相符。
(2)励磁电感变为标准值的一半时的dq轴参考电压计算误差比变为标准值的两倍时的误差要大,且权重系数的增大将削弱该算法的参数敏感性,这与图7的数值计算结果相符。
仿真结果有效地说明了数值分析计算的可靠性,也为其他模型预测控制参数敏感性的分析指明了方向。为了进一步直观说明励磁电感参数变化对控制性能的影响程度,图17给出了不同参数下所采用的两步长模型预测控制性能的对比结果。可以看出,当参数发生偏移时,将会通过参考电压矢量计算偏差进而影响到电流控制性能,导致电流总谐波畸变率(Total Harmonic Distortion, THD)上升。而具体上升程度与参考电压计算偏差相符,即当励磁电感变为标准值的一半时,相比变为标准值的两倍,电流THD上升程度更大,分别约为12.7%和5%。因此,有必要对励磁电感参数进行在线修正以尽量维持电流THD在较低的水平。
4.2.3 THD抑制能力提升分析
考虑到本文的目标是提出一种低开关频率下高参数鲁棒性的低电流THD控制算法,以降低系统损耗的同时减小电机振动和噪声,提升驱动性能。因此需要对电流THD的提升效果进行定量的对比分析。具体的思路为:首先,通过引入带开关项的模型预测控制来实现灵活低开关频率控制;随后,考虑到该方法在降低开关频率的同时将导致电流THD上升,引入多步长模型控制来进行抑制;同时,基于所实现的低开关频率控制的特殊性,可以引入高性能参数辨识算法来提升系统的参数鲁棒性以避免因参数变化而导致的电流THD上升。下面将以500Hz开关频率下的控制性能为例进行分析。
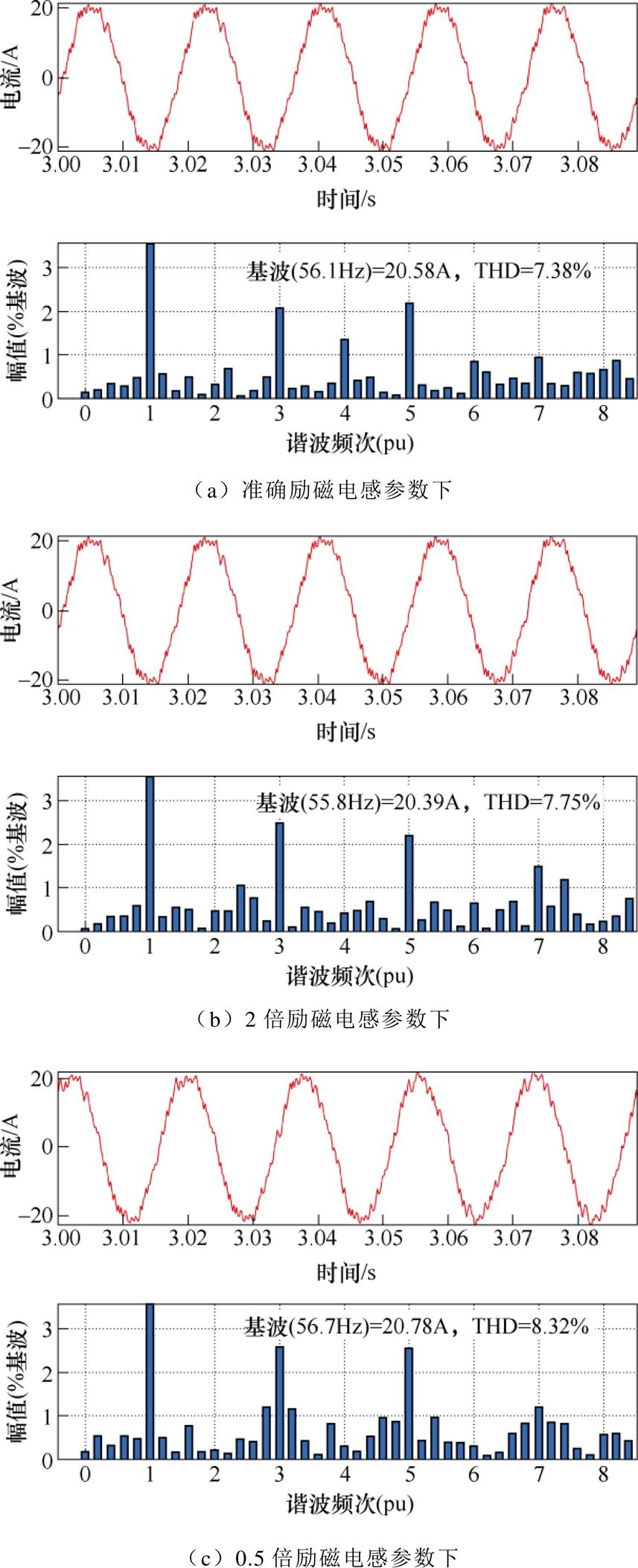
图17 不同励磁电感参数下仿真谐波分析结果
Fig.17 Harmonic analysis results of simulations under different magnetizing inductance parameters
图18和图19分别给出了参数准确时两步长和单步长模型预测控制下,控制开关频率为500Hz时的电流谐波分析结果。可以看出,采取多步长控制可以有效地将电流THD降低为单步长的80.9%。
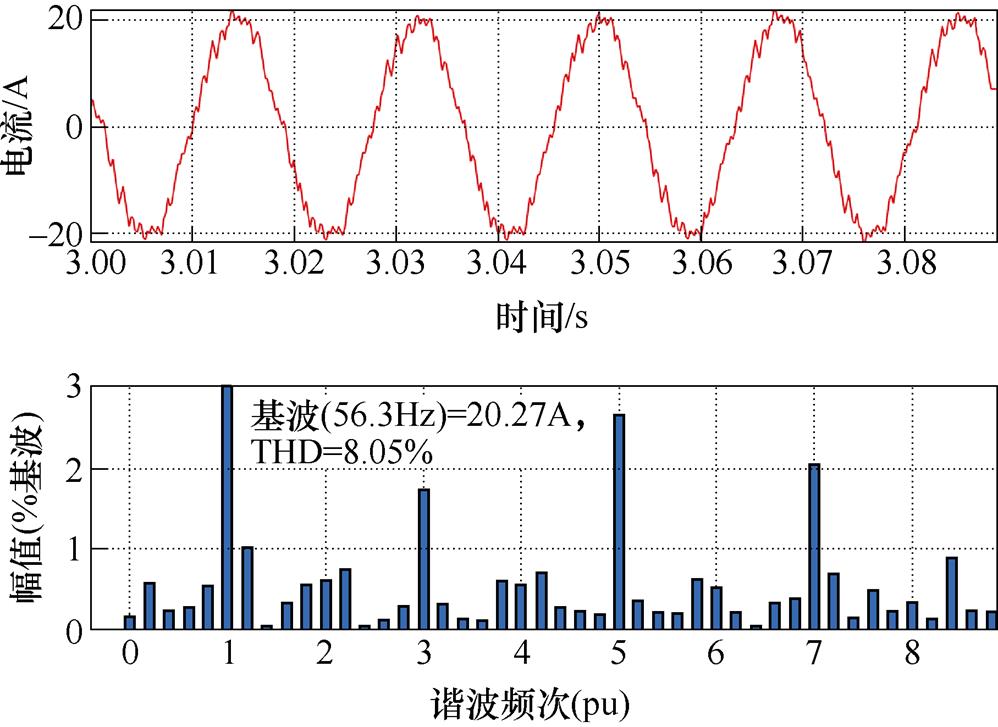
图18 所采用方法下的电流谐波分析结果
Fig.18 Current harmonic analysis result under adopted method
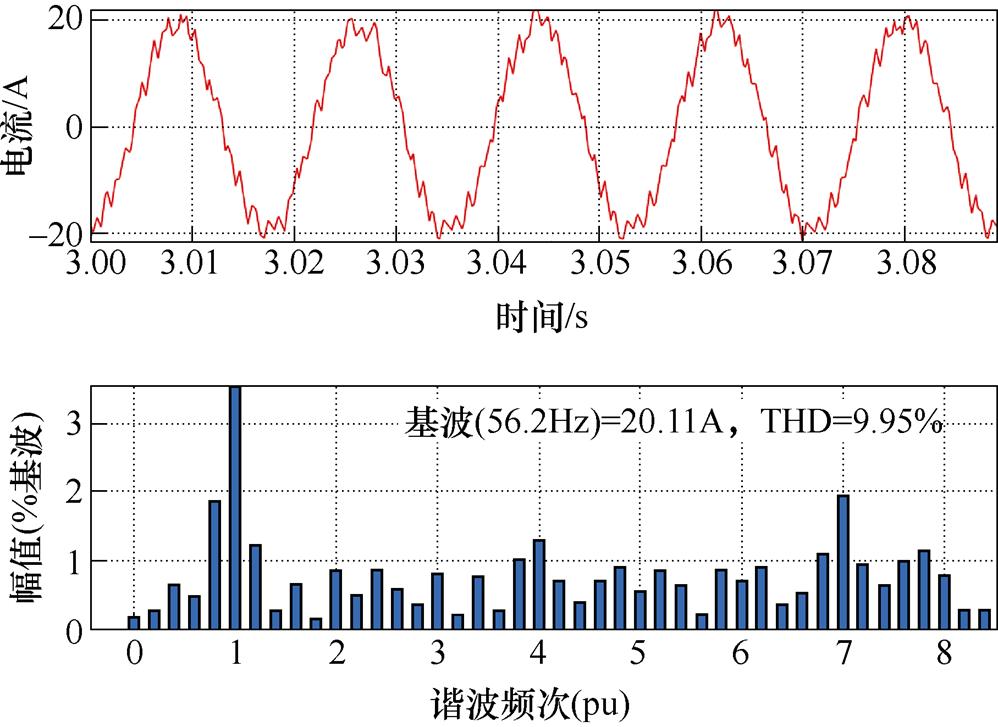
图19 单步长预测下的电流谐波分析结果
Fig.19 Current harmonic analysis result under single step
在两步长预测且权重系数为零时的参数敏感性分析已在图17中给出,可以看出,此时通过对励磁电感进行在线辨识补偿可以较大幅度增强系统参数鲁棒性,避免电流THD出现高达12.7%的恶化。为了验证低开关频率下的改善情况,图20给出500Hz开关频率下励磁电感为标准值一半时的电流THD分析结果。可以看出,当参数出现偏差时,电流THD呈现上升趋势,程度约为4.7%。相比图17c,其上升程度较低,这主要是由于增加了权重系数使得参数敏感性程度下降,这也进一步验证了3.1节理论分析的有效性,且与图15及图16的结果相符。
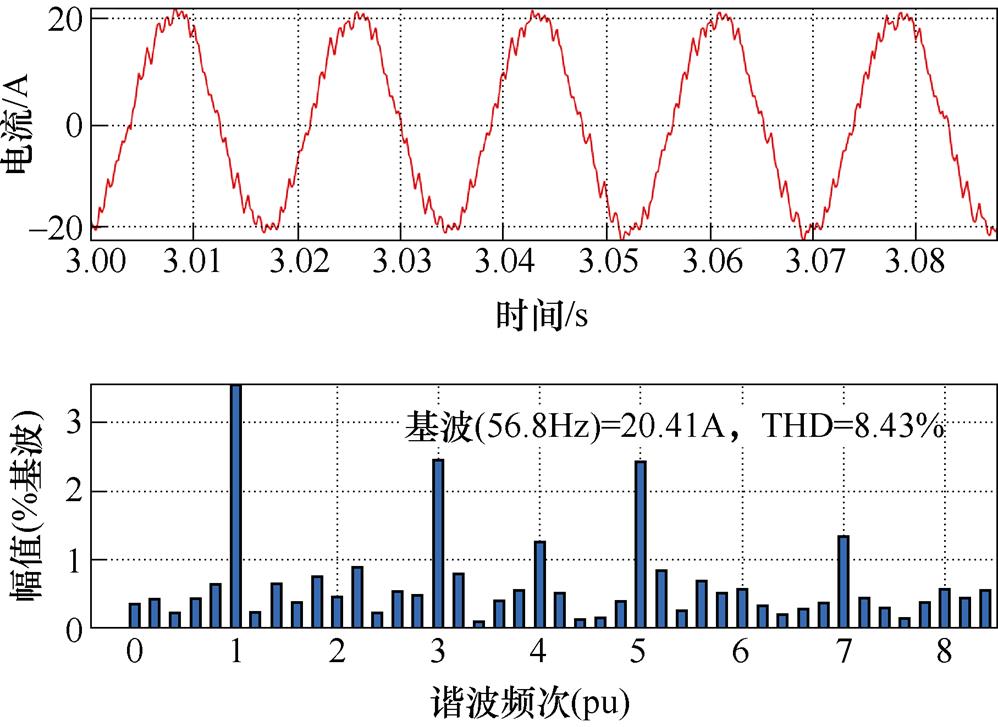
图20 两步长预测下参数偏差时的电流谐波分析结果
Fig.20 Current harmonic analysis result with parameter deviation under dual-step prediction
总的来说,通过采用本文所提出的低开关频率优化控制方案,可以在保证系统开关频率维持较低水平的前提下,以一定程度的计算量增加为代价,有效地提升了电流THD抑制能力,在500Hz下由最初的10.26%逐步下降至8.05%,并维持较高的参数鲁棒性,以避免参数变化对开关频率和电流谐波的影响。
为了验证实际数字控制系统下所采用的方案在参数辨识可靠性、谐波抑制能力等方面提升上的有效性,基于图10所示平台开展了综合性实验。图21给出5 000Hz、1 000Hz、500Hz三种不同开关频率下的励磁电感辨识结果。为了具有一定的参考性,同时绘制出了基于Duncan模型离线计算出的励磁电感变化曲线。可以看出,在5 000Hz采样/开关频率下,励磁电感辨识结果与根据电机参数得到的离线计算结果比较接近,参数辨识较为准确。但是,随着开关频率降低至1 000Hz,辨识结果开始出现一定程度的偏离,这主要受到离散化、延时和谐波等因素的影响,但是辨识值仍然可以在1~11m/s的运行范围内保持稳定,且偏离程度不严重。然而,当开关频率进一步降低至500Hz,在1~10m/s下励磁电感辨识值偏离程度进一步加大,且随着转速上升而越来越明显。相应地,500Hz开关频率下5m/s和10m/s速度时的反电动势波形如图21所示。可以看出,在低采样率下,不仅仅开关频率将会被降低,观测值数据的更新计算频率也将明显降低,在高速下,观测反电动势离散化特征严重,此时谐波含量较大,也一定程度上影响了参数辨识精度。除此之外,由于控制系统的离散化程度同样严重,当转速上升至11m/s时,传统矢量控制系统稳定性受到影响,电流严重畸变,进而导致观测反电动势波形紊乱,辨识结果严重偏离,如图22所示。
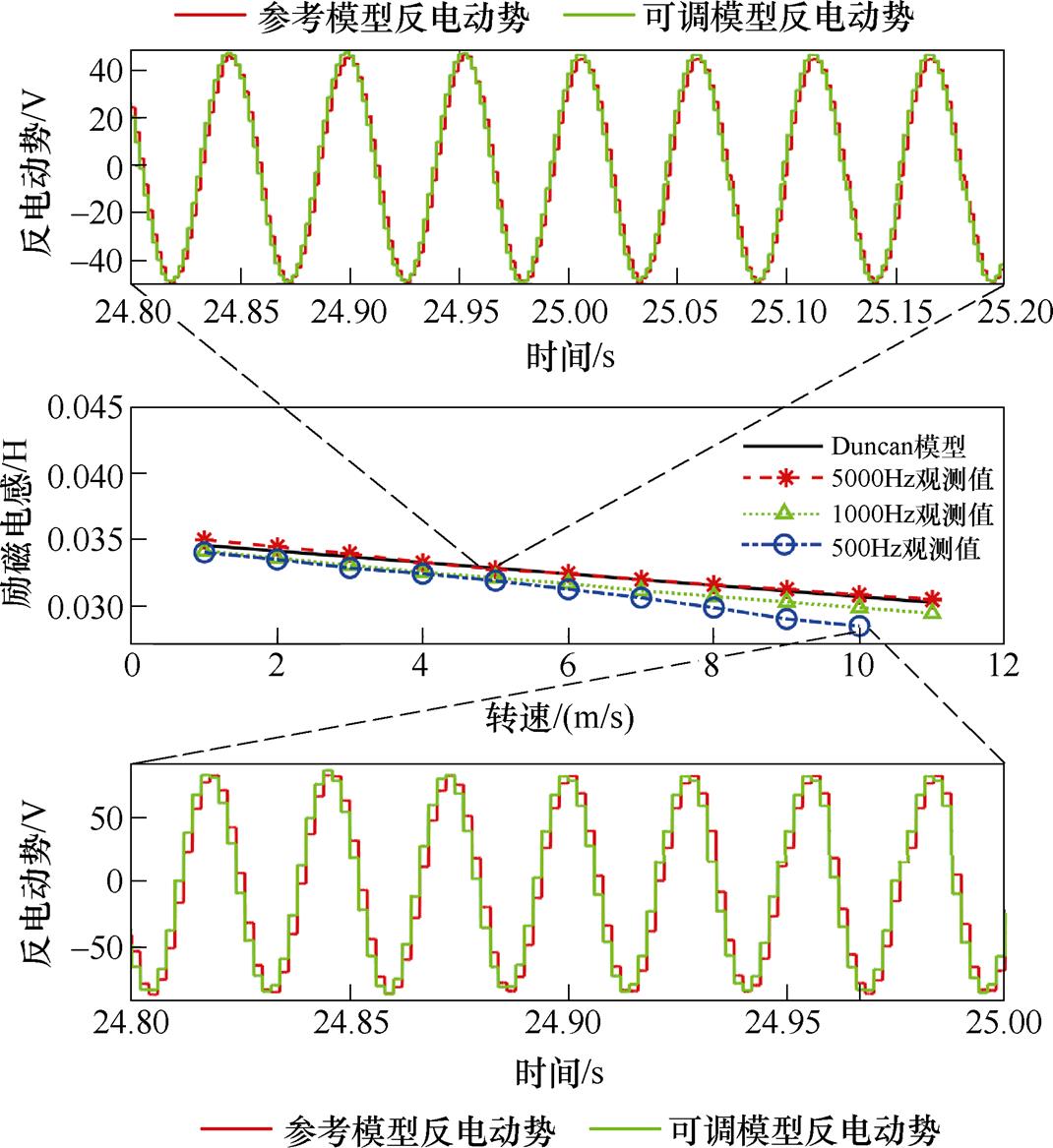
图21 不同开关频率下传统方案励磁电感辨识实验结果
Fig.21 Experimental results of magnetizing inductance identification under different switching frequencies with conventional method
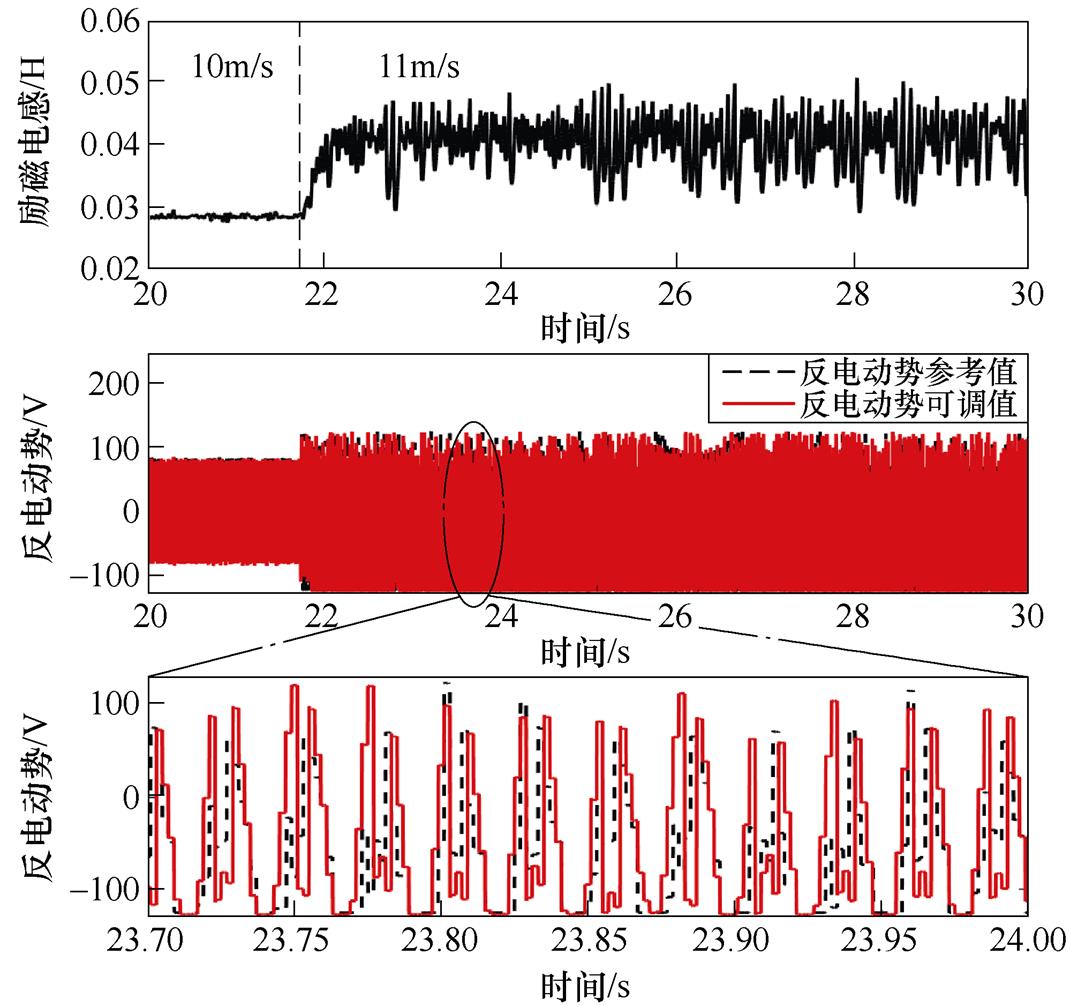
图22 低开关频率下高速时控制性能恶化
Fig.22 Performance deterioration under high speed and low switching frequency
而本文所采用的多步长模型预测控制方法是通过在目标函数中增加开关项来实现对开关频率的控制,无需降低采样频率,且可以便捷地实现开关频率的灵活切换。图23给出单步长和两步长模式中采用开关项调节开关频率时两种典型速度(8m/s和11m/s)下的励磁电感辨识结果。为了增强对比性,此处所采用的参数辨识算法与前面矢量控制系统中的完全一致。可以看出,励磁电感辨识结果整体趋势随着开关频率降低而增大,但是变化范围非常小。以额定速度11m/s下的辨识结果为例,在约650Hz到150Hz的开关频率范围内,励磁电感的辨识结果仅从约29.8mH上升至30.9mH。图24给出所采用的模型预测方法下开关频率切换突变时的励磁电感辨识值和初级电流的实验波形。可以看出,该方法实现的开关频率切换非常平滑,动态过程中电流波形未发生剧烈波动,且励磁电感辨识值也可以迅速平滑进入新的稳态值。
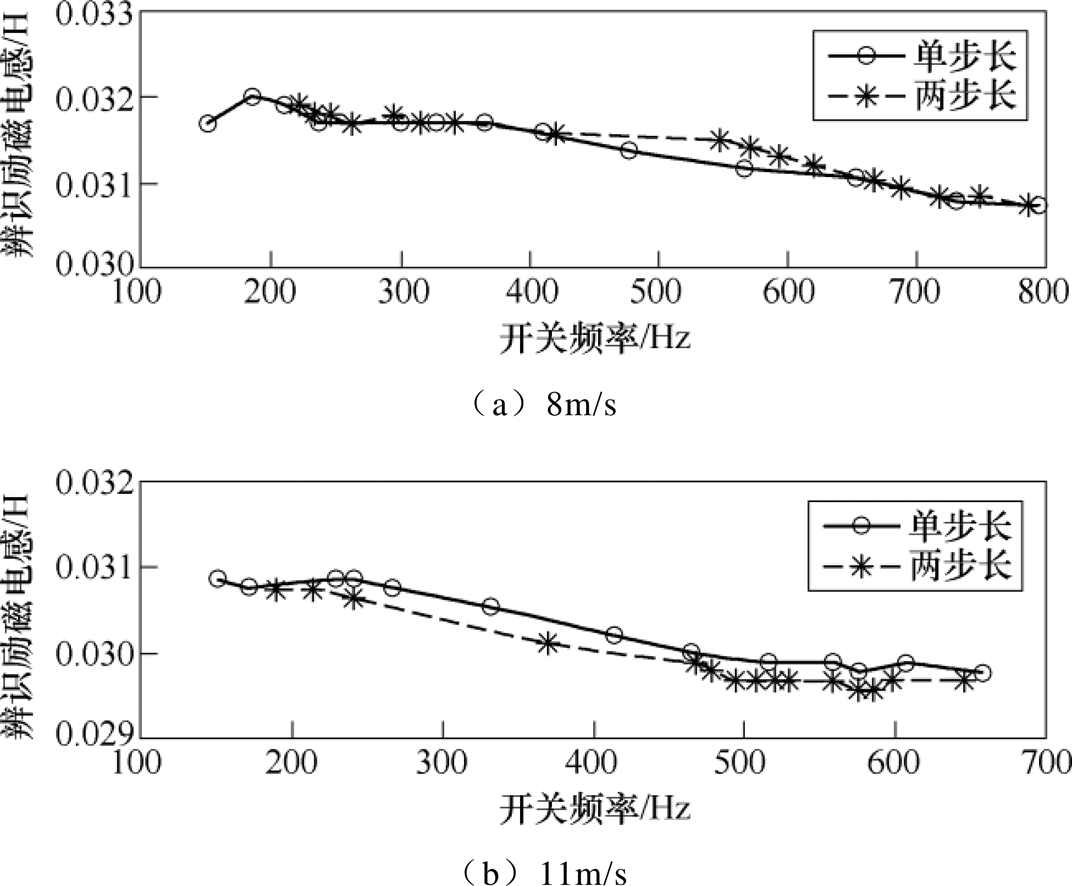
图23 不同开关频率下所采用方案励磁电感辨识实验结果
Fig.23 Experimental results of magnetizing inductance identification under different switching frequencies with adopted method
而由图21可知,在传统矢量控制中,当开关频率从1 000Hz降低至500Hz时,在速度为10m/s下所辨识的励磁电感已经从29.9mH变化至28.5mH。当开关频率进一步降低和速度进一步上升时,其辨识值的变化范围即辨识误差将会进一步扩大。因此,采用带开关项的模型预测控制来实现低开关频率控制时,可较容易地实现直线感应电机励磁电感的准确辨识,进而提高驱动系统在该运行模式下的可靠性。另外,两步长和单步长的辨识结果吻合程度很高,说明此时参数辨识系统对谐波不敏感,抗干扰能力较强。
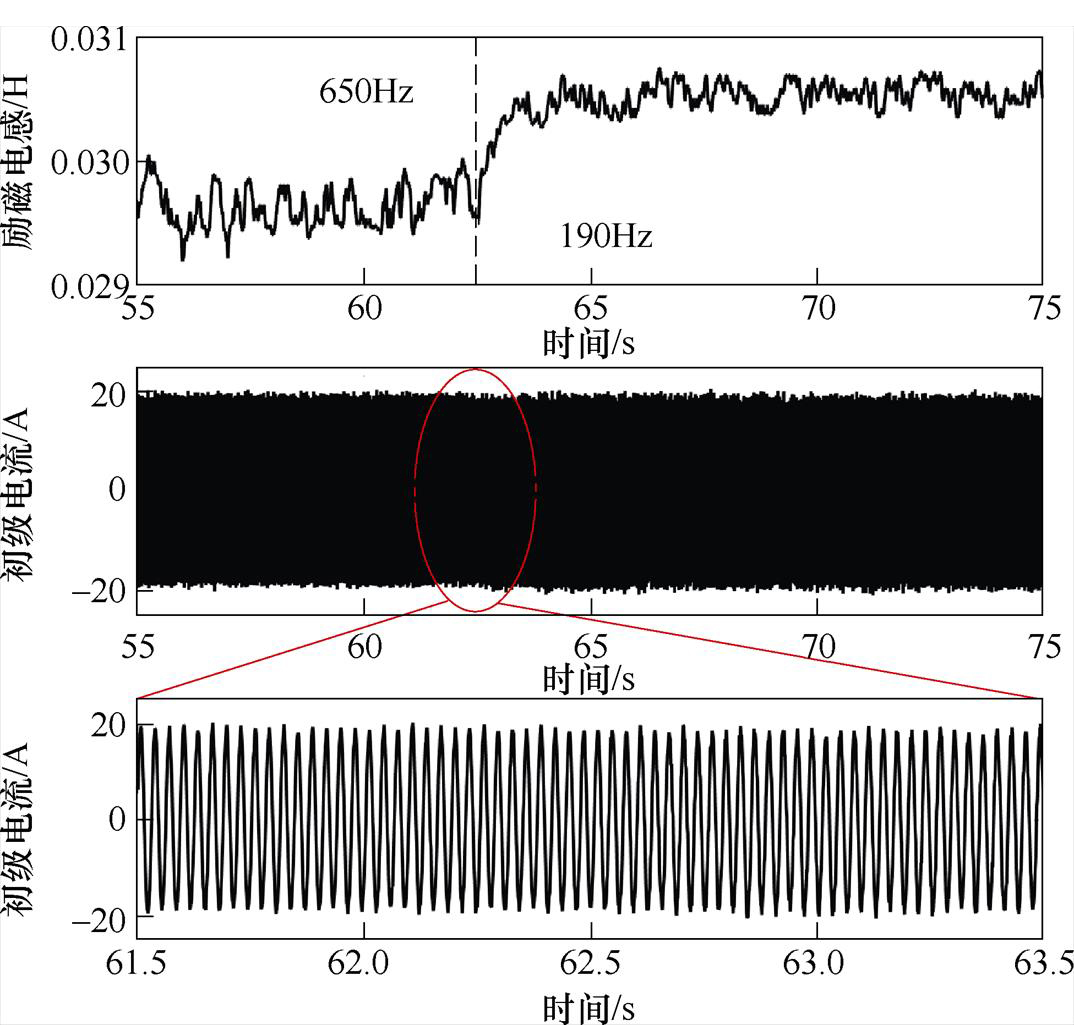
图24 开关频率突变时辨识励磁电感和初级电流波形
Fig.24 Waveforms of identified magnetizing inductance and primary current under sudden change of switching frequency
为了验证采用多步长方法对控制性能提升的作用,表2给出了额定速度时部分典型开关频率下的初级电流谐波分析结果。可以看出,随着开关频率的降低,同一步长下的THD将会一定程度上升;而同一开关频率下,采用两步长的THD低于单步长,且随着开关频率的降低提升幅度变得更加显著。当处理器运算能力较强时,还可以进一步采用更多步长的模型预测控制来得到更为理想的谐波抑制能力。
表2 部分典型开关频率下谐波对比
Tab.2 Harmonic comparison under different typical switching frequencies
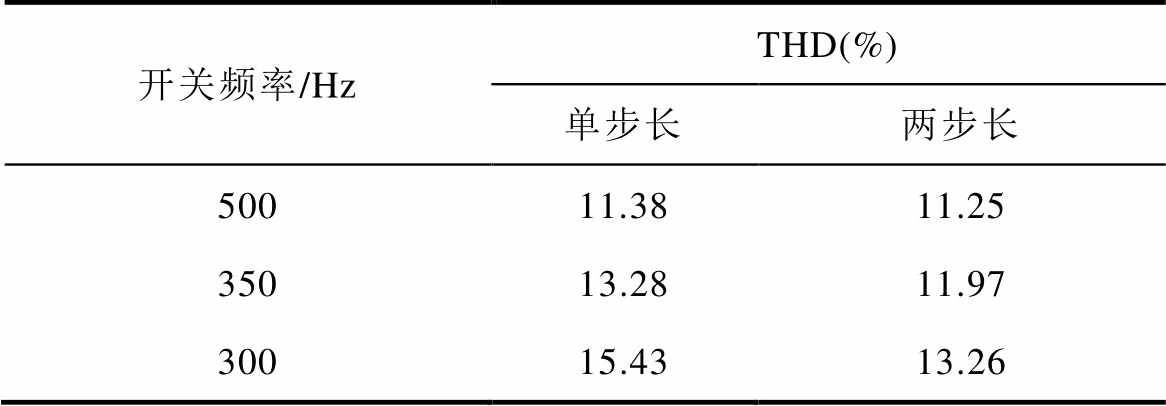
开关频率/HzTHD(%) 单步长两步长 50011.3811.25 35013.2811.97 30015.4313.26
在上述谐波分析的基础上,为了测试所采用的模型预测控制算法对电机参数的依赖性,图25给出500Hz开关频率下单步长控制中不同励磁电感参数下的电流波形和谐波分析结果。可以看出,当励磁电感参数发生变化时,电流THD会不同程度的上升。并且,同3.1节的理论分析结果以及仿真结果类似,当控制系统设定的励磁电感参数变为额定值的1/2时,THD的恶化程度要高于励磁电感参数变为额定值的2倍时的情况,分别为8.6%和12.1%。
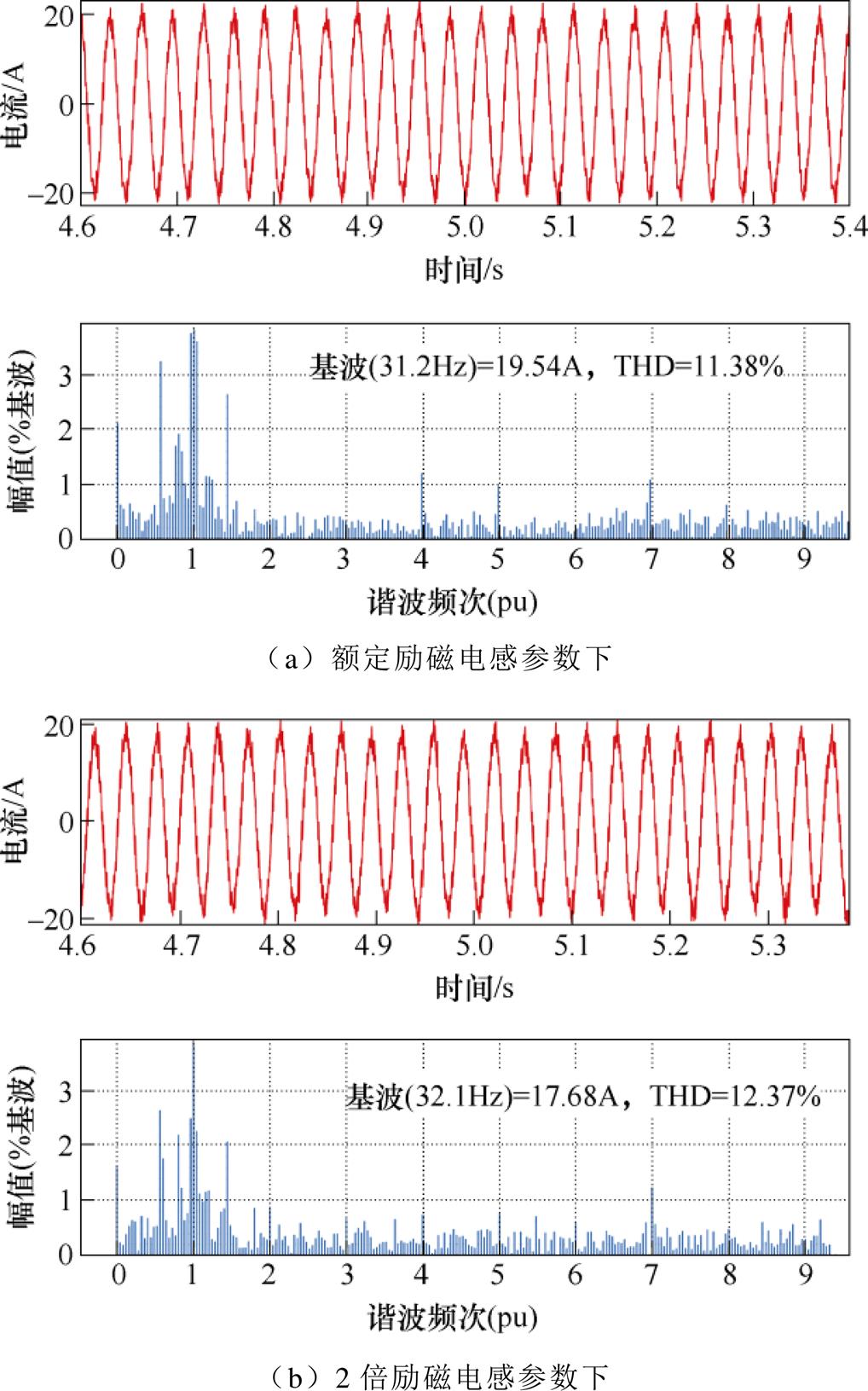
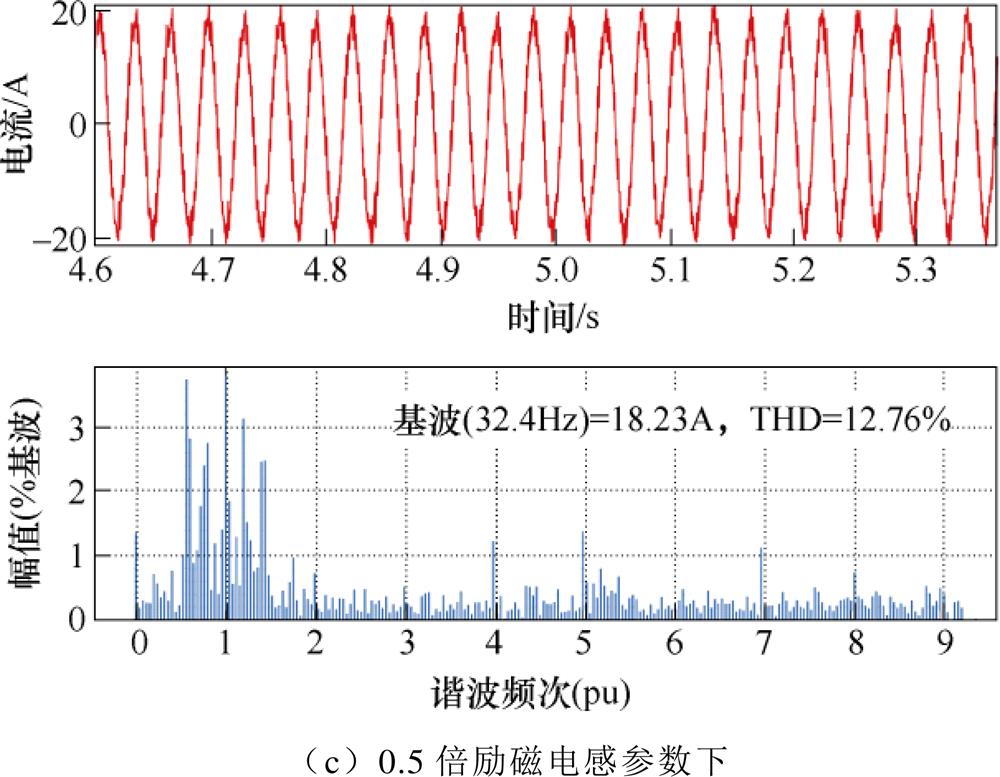
图25 不同励磁电感参数下实验谐波分析结果
Fig.25 Harmonic analysis results of experiments under different magnetizing inductance parameters
针对直线感应电机轨道牵引系统对低开关频率运行的需求,本文对比分析了基于调制和采样控制频率的低开关频率控制方法和一种带开关项的多步长模型预测控制方法。大量理论分析和仿真实验表明:采用前者时参数辨识结果会随着开关频率的降低和速度的上升而出现较大偏离;而采用后者则无需特殊设计参数辨识算法便可较容易地实现低开关频率下的精准参数辨识,比如电机运行在150Hz开关频率下,其参数辨识结果仍然稳定可靠。除此之外,本文还全面分析了该模型预测控制方法对励磁电感的敏感性,相关结果表明:参数不准确将给参考电压矢量的计算引入偏差,进而对控制系统的性能参数(如电流THD)造成一定的负面影响。因此,通过结合参数辨识算法和带开关项的多步长模型预测控制,本文成功地实现了低开关频率、低电流THD、高可靠度的直线感应电机及系统的控制。
参考文献
[1] 徐伟, 肖新宇, 董定昊, 等. 直线感应电机效率优化控制技术综述[J]. 电工技术学报, 2021, 36(5): 902-915, 934.
Xu Wei, Xiao Xinyu, Dong Dinghao, et al. Review on efficiency optimization control strategies of linear induction machines[J]. Transactions of China Electro- technical Society, 2021, 36(5): 902-915, 934.
[2] 叶云岳. 直线电机原理与应用[M]. 北京: 机械工业出版社, 2000.
[3] 龙遐令. 直线感应电动机的理论和电磁设计方法[M]. 北京: 科学出版社, 2006.
[4] 吕刚. 直线电机在轨道交通中的应用与关键技术综述[J]. 中国电机工程学报, 2020, 40(17): 5665- 5674.
Lü Gang. Review of the application and key tech- nology in the linear motor for the rail transit[J]. Proceedings of the CSEE, 2020, 40(17): 5665-5674.
[5] 张千, 刘慧娟, 马杰芳, 等. 考虑后退行波的长初级双边直线感应电机电磁性能计算[J]. 电工技术学报, 2020, 35(7): 1398-1409.
Zhang Qian, Liu Huijuan, Ma Jiefang, et al. Calcu- lation of electromagnetic performance for long primary double sided linear induction motors con- sidering backward traveling wave[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1398- 1409.
[6] 吕刚, 罗志昆. 次级断续时直线感应牵引电机的等效电路[J]. 电工技术学报, 2021, 36(6): 1103-1112.
Lü Gang, Luo Zhikun. An equivalent circuit of linear induction traction motor with discontinuous second- dary[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1103-1112.
[7] Xu Wei, Zhu Jianguo, Guo Youguang, et al. Equiva- lent circuits for single-sided linear induction motors[C]//IEEE Energy Conversion Congress and Exposition, San Jose, USA, 2009: 1288-1295.
[8] Duncan J. Linear induction motor-equivalent-circuit model[J]. IEE Proceedings B Electric Power Appli- cations, 1983, 130(1): 51-57.
[9] Xu Wei, Zhu Jianguo, Zhang Yongchang, et al. An improved equivalent circuit model of a single-sided linear induction motor[J]. IEEE Transactions on Vehicular Technology, 2010, 59(5): 2277-2289.
[10] Pucci M. State space-vector model of linear induction motors[J]. IEEE Transactions on Industry Appli- cations, 2014, 50(1): 195-207.
[11] Zou Jianqiao, Xu Wei, Yu Xinghuo, et al. Multistep model predictive control with current and voltage constraints for linear induction machine based urban transportation[J]. IEEE Transactions on Vehicular Technology, 2017, 66(12): 10817-10829.
[12] Dian Renjun, Xu Wei, Zhu Jianguo, et al. An improved speed sensorless control strategy for linear induction machines based on extended state observer for linear metro drives[J]. IEEE Transactions on Vehicular Technology, 2018, 67(10): 9198-9210.
[13] Levi E, Wang Mingyu. Online identification of the mutual inductance for vector controlled induction motor drives[J]. IEEE Transactions on Energy Con- version, 2003, 18(2): 299-305.
[14] Liu Lu, Guo Yafeng, Wang Jun. Online identification of mutual inductance of induction motor without mag- netizing curve[C]//2018 IEEE Annual American Control Conference (ACC), Milwaukee, WI, USA, 2018: 3293-3297.
[15] Ren Jinqi, Li Yaohua. MRAS based online mag- netizing inductance estimation of linear induction motor[C]//2007 IEEE International Conference on Electrical Machines and Systems (ICEMS), Seoul, Korea (South), 2007: 1580-1583.
[16] Dong Dinghao, Xu Wei, Xiao Xinyu, et al. Online magnetizing inductance identification strategy of linear induction motor based on second-order sliding- mode observer and MRAS[C]//2021 IEEE 13th Inter- national Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 2021: 1-6.
[17] 杨明, 张扬, 曹何金生, 等. 交流伺服系统控制器参数自整定及优化[J]. 电机与控制学报, 2010, 14(12): 29-34.
Yang Ming, Zhang Yang, Cao Hejinsheng, et al. Gain self-tuning of PI controller and parameter optimum for PMSM drives[J]. Electric Machines and Control, 2010, 14(12): 29-34.
[18] Zhang Yongchang, Jiao Jian, Liu Jie. Direct power control of PWM rectifiers with online inductance identification under unbalanced and distorted network conditions[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(12): 12524-12537.
[19] Kwak S, Moon U C, Park J C. Predictive-control- based direct power control with an adaptive parameter identification technique for improved AFE perfor- mance[J]. IEEE Transactions on Power Electronics, 2014, 29(11): 6178-6187.
[20] 周明磊, 游小杰, 王琛琛. 电力机车牵引传动系统矢量控制[J]. 电工技术学报, 2011, 26(9): 110-115, 129.
Zhou Minglei, You Xiaojie, Wang Chenchen. Vector control of driving system of locomotive[J]. Transa- ctions of China Electrotechnical Society, 2011, 26(9): 110-115, 129.
[21] 陈杰, 李军, 邱瑞昌, 等. 轨道交通牵引系统空间矢量脉宽调制同步过调制策略研究[J]. 电工技术学报, 2020, 35(增刊1): 91-100.
Chen Jie, Li Jun, Qiu Ruichang, et al. Research on space vector PWM synchronous overmodulation in rail transit traction system[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 91-100.
[22] Xin Zhen, Loh P C, Wang Xiongfei, et al. Highly accurate derivatives for LCL-filtered grid converter with capacitor voltage active damping[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3612-3625.
[23] Bottura C P, Silvino J L, de Resende P. A flux observer for induction machines based on a time- variant discrete model[J]. IEEE Transactions on Industry Applications, 1993, 29(2): 349-354.
[24] Yin Shaobo, Huang Yingwei, Xue Yaru, et al. Improved full-order adaptive observer for sensorless induction motor control in railway traction systems under low-switching frequency[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(4): 2333-2345.
[25] 贾成禹, 王旭东, 周凯. 基于线性变参数模型预测控制的内置式永磁同步电机转速控制器设计[J]. 电工技术学报, 2020, 35(22): 4666-4677.
Jia Chengyu, Wang Xudong, Zhou Kai. Design of interior permanent magnet synchronous motor speed controller based on linear parameter-varying model predictive control[J]. Transactions of China Electro- technical Society, 2020, 35(22): 4666-4677.
[26] Xu Wei, Dong Dinghao, Zou Jianqiao, et al. Low- complexity multistep model predictive current control for linear induction machines[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 8388-8398.
[27] Majumdar A, Bhattacharya T K. Comparison of force developed in a linear induction machine and an equivalent arc linear induction machine at zero velocity[C]//2018 IEEE International Conference on Power Electronics, Drives and Energy Systems, Chennai, India, 2018: 1-5.
Low Switching Frequency Model Predictive Control Strategy Based on Online Parameter Identification Compensation of Linear Induction Motor for Urban Rail Application
Abstract To reduce the hardware cost of converter and switching loss, the linear induction motor (LIM) and drive system for urban rail application with strong current and high capacity usually need to operate in a low-switching-frequency mode. However, the conventional low-switching-frequency control method often amplify the influence of discretization error in micro-processor while introducing severe harmonic current and thrust fluctuations, thereby deteriorating the observer performance. Therefore, a multistep finite control set model predictive control (FCS-MPC) strategy with online parameter identification is proposed, which can reduce the current harmonic under low-switching- frequencies and enhance the reliability of system by using high precise parameters. Firstly, the MPC algorithm with switching item in cost function is adopted to realize low switching frequency control at high sampling frequency. Furthermore, the multistep mode is used to suppress the increase of harmonic content caused by the reduction of switching frequency. Then, the influence of the two different low-switching-frequency realization methods on performance is compared. Considering that the magnetizing inductance in LIM for urban rail is deeply affected by the end effect, the parameter sensitivity of the MPC method is further analyzed and the parameter identification is introduced, which realizes the accurate estimation of magnetizing inductance at low-switching-frequency, improves the precision of prediction accuracy and parameter robustness of MPC, and reduces the harmonic content in the drive system. Simulation and experimental results show that the proposed method can well realize accurate tracking of the magnetizing inductance in LIM at low-switching frequency, and effectively suppress the current harmonic of the drive system combined with the multistep FCS-MPC algorithm.
keywords:Linear induction motor, end effect, model predictive control, parameter identification, low switching frequency, harmonic suppression
DOI: 10.19595/j.cnki.1000-6753.tces.211816
中图分类号:TM359.4
国家自然科学基金项目(51877093)、国家重点研发计划金砖国际合作重点项目(2018YFE0100200)和湖北省重大科技创新项目(2019AAA026)资助。
收稿日期 2021-11-10
改稿日期 2022-01-02
徐 伟 男,1980年生,教授,博士生导师,研究方向为直线电机设计及控制。E-mail: weixu@hust.edu.com(通信作者)
董定昊 男,1995年生,博士,研究方向为直线感应电机高性能控制算法与参数辨识方法。E-mail: dinghaodongee@foxmail.com
(编辑 崔文静)