图1 不同转子磁场分布下的转子磁链对比
Fig.1 Comparison of rotor flux linkage under different rotor field distribution
摘要 该文提出一种考虑非正弦磁场分布特征的无刷直流电机转子磁场定向矢量控制技术，此技术既在无需换相区检测的前提下抑制了转矩脉动，又解决了由于直轴电枢反应造成的助磁和去磁的问题。为此，首先，通过对比分析不同转子磁场分布下的转子磁链波形，得出在非正弦转子磁场分布下以转子位置角作为旋转角的等功率3s/2r变换不能实现转子磁场定向的结论；其次，通过改变等功率3s/2r变换矩阵中的旋转角，使得变换后转子磁链无q轴分量，从而建立非正弦转子磁场定向坐标系并得出该坐标系下的动态数学模型；最后，理论推导出无直轴电枢反应运行时给定参考转矩下所需的d、q轴电枢电流求解方程，并以此构建出无刷直流电机无直轴电枢反应的转子磁场定向矢量控制系统。所提控制技术通过相应的数字信号处理（DSP）驱动实验验证了其可行性和有效性。
关键词：无刷直流电机 非正弦磁场分布 转子磁场定向 无直轴电枢反应 转矩脉动抑制
无刷直流电机（Brushless DC Motor, BLDCM）具有结构简单、功率密度高、转矩电流比大、调速性能好等优点，在工业控制、电动汽车、家用电器、航空航天等领域被广泛应用[1-3]。但是，120°导通方式作为其主流控制方式，非平滑换相过程不可避免地带来换相转矩脉动问题，限制了其在高精尖场合的应用，因此如何抑制转矩脉动成为国内外学者研究的热点问题[4-5]。
文献[6-11]通过增加逆变器前级拓扑结构使得无刷直流电机在换相期间与非换相期间采用不同的直流母线电压，从而平衡换相期间电流的变化率以抑制换相转矩脉动。其中，文献[6]结合Cuk变换器与中点钳位电路，扩大母线电压范围的同时减小了电流谐波；文献[7]采用由反激变压器、电容及转换电路组成的升压前端电路来提高换相期间的直流母线电压；文献[8]自行设计了无电感升压拓扑并构建了四种开关矢量；文献[9-11]分别使用单端初级电感变换器（Single Ended Primary Inductor Converter, SEPIC）电路、无电感的Boost电路、二极管辅助的Buck-Boost电路作为前级DC-DC电路来调节直流侧母线电压。以上文献虽对转矩脉动抑制有一定效果，但必然使系统控制更为复杂，增加系统成本，也会带来新增拓扑结构损耗的问题。
文献[12-17]改变调制方式以抑制转矩脉动，通过换相区与非换相区采用不同的调制方式实现上升相与下降相电流变化率相等。文献[12-13]在两相静止坐标系下对转矩脉动进行分析并分别对电流矢量与电压矢量进行控制；文献[14-15]通过重叠换相即提前切入开通相或延迟切出关断相来减小非换相相电流的波动；文献[16]提出一种适合于回馈制动的PWM-OFF-PWM方式，通过抑制非导通相续流达到抑制转矩脉动的效果；文献[17]提出双极性H_PWM- L_PWM模式的换向转矩脉动减小策略，以实现稳定的制动控制。但是以上文献控制过程必然面临换相区检测的问题，电流的过零点检测增加了系统复杂度并影响了控制精度。
此外，直接转矩控制方法通过选择电压矢量对转矩进行控制，由零矢量与其他电压矢量相互配合并在换相区与非换相区采用不同的开关管状态选择表来减小转矩脉动。文献[18]提出滞环结合脉冲宽度调制的直接转矩控制方案，在换相和非换相期间设置了不同占空比并完成了四象限运行；文献[19-20]重新定义了不同扇区的零电压矢量并依此改进了电压矢量查询表，通过选择不同的零电压矢量抑制转矩脉动；文献[21]建立了与速度无关的统一开关表。但是由于以上文献非换相区开关状态查询表与换相区并不相同，故此类方法也涉及电流的过零检测问题。
另外，值得关注的是，直轴电枢反应的存在会对转子磁场产生助磁或去磁的作用，其中，助磁易引起磁场饱和，严重时会引起转矩的丢失，降低电机的带负载能力；而去磁会增大电机失磁的风险；并且助磁与去磁均会增加电机的铜耗。文献[22]在d轴电枢反应和电磁转矩不变的前提下，将每相绕组单独变换至两相旋转坐标系下完成控制，虽可实现无助磁和去磁的瞬时恒定转矩控制，但并未给出非正弦转子磁场下的电枢反应模型。此外，目前针对无刷直流电机无直轴电枢反应控制的研究较少。
为了实现抑制转矩脉动的同时便于定量分析交直轴电枢反应，本文提出一种无直轴电枢反应的非正弦转子磁场定向矢量控制技术。该技术建立了非正弦转子磁场定向dq旋转坐标系，理论推导出该坐标系下数学模型及电枢反应模型，结合所需参考转矩与无直轴电枢反应两个条件实时获得d、q轴电流参考值，在无需换相区检测的前提下实现无直轴电枢反应的瞬时转矩控制。所提方法通过相应的数字信号处理（Digital Signal Processing, DSP）驱动实验验证了其可行性和有效性。
图1分别给出了转子磁场不同分布波形及其对应的三相转子磁链和合成转子磁链波形。如图1a所示，若给定转子位置下（图1中以电角度0°与20°为例）转子永磁体产生的磁场沿电枢内表面呈正弦波分布，则在匀速旋转时，其与a、b、c相电枢绕组分别交链的三相转子磁链yra、yrb、yrc随时间以正弦规律变化，并且在相位上互差120°。当以各相绕组轴线作为yra、yrb、yrc的空间矢量方向时，不同时刻该三相磁链的合成空间矢量yr大小始终保持不变，方向qyr与转子磁场位置q 重合。其中，yr的大小为三相转子磁链峰值y3max的1.5倍。
图1 不同转子磁场分布下的转子磁链对比
Fig.1 Comparison of rotor flux linkage under different rotor field distribution
若转子永磁体产生的磁场沿电枢内表面呈非正弦波分布，以无刷直流电机为例，在给定转子位置下（图1中以0°与20°为例），转子永磁体产生的磁场沿电枢内表面的理想分布波形为图1b所示的梯形波。当匀速旋转时，转子磁场与a、b、c相电枢绕组交链的三相转子磁链yra、yrb、yrc随时间的变化规律并非正弦波。同样以各相绕组轴线作为yra、yrb、yrc的空间矢量方向时，则在不同时刻三相磁链的合成空间矢量yr不但大小不会恒定，而且方向也不与转子磁场方向重合。这与正弦波转子磁场分布时有着显著区别。
图2给出了三相静止坐标系与转子磁场定向dq两轴同步旋转坐标系下的永磁电机等效模型。图中，d轴取转子磁场方向，q轴取空间上超前于d轴90°的方向；q 为当前时刻的转子位置角，同时也是转子磁场位置角。由图2可知，在转子磁场定向dq两轴同步旋转坐标系下，永磁电机的等效模型存在转子磁链仅有d轴分量、无q轴分量的特点，使得在瞬时电磁转矩控制中易实现无直轴电枢反应。此外，该特点与转子磁场分布波形是否为正弦波无关。
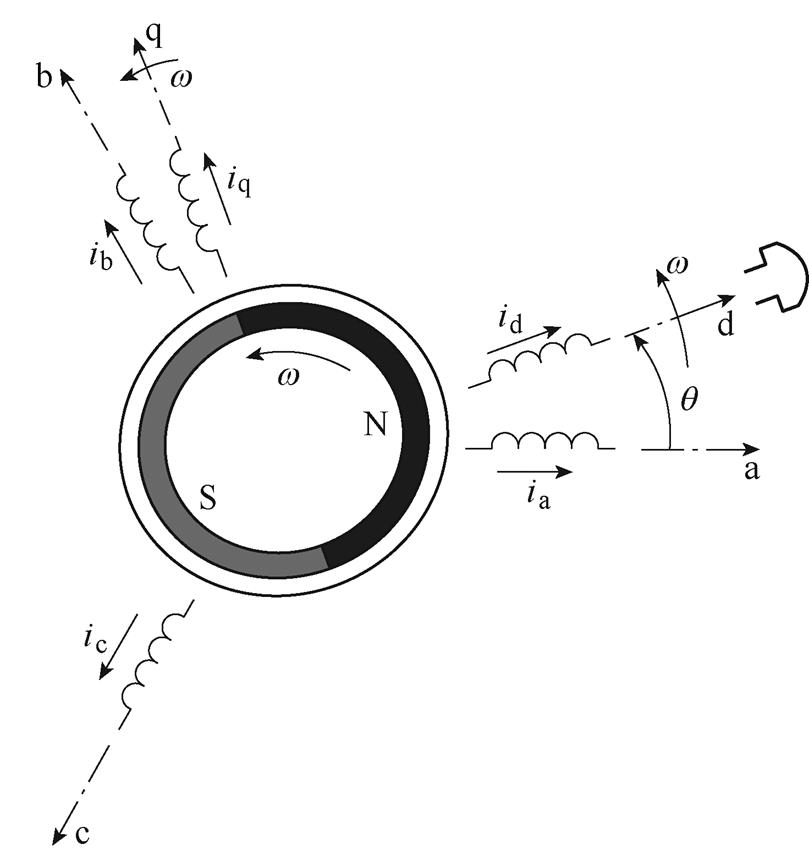
图2 三相静止坐标系与转子磁场定向两轴同步旋转坐标系下的永磁电机等效模型
Fig.2 Equivalent model of permanent magnet motor in three-phase stationary coordinate system and rotor field- oriented two-axis synchronous rotating coordinate system
对于正弦波转子磁场分布的永磁电机而言，如式（1）所示，若对三相电枢绕组进行等功率3s/2r变换得到d、q两轴电枢绕组，则转子磁场与d、q轴绕组交链的转子磁链yrd、yrq分别为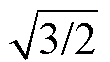
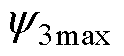和0，这与图2中dq同步旋转坐标系下的特点吻合。
由此可知，正弦波转子磁场分布的永磁电机通过式（1）中的变换矩阵C可得到转子磁场定向dq两轴同步旋转坐标系下的等效模型，即能够实现转子磁场定向。
（1）
其中，变换矩阵C为
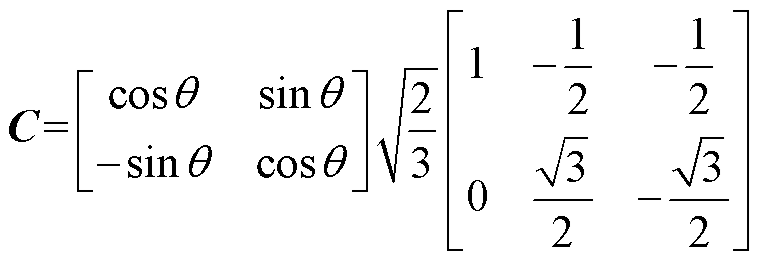
对于无刷直流电机而言，若以式（1）中的变换矩阵C对三相电枢绕组进行坐标变换得到d、q两轴电枢绕组，则转子磁场与d、q轴绕组交链的转子磁链yrd、yrq均随时间发生变化，即在dq同步旋转坐标系下得不到类似正弦波转子磁场分布时的两轴转子磁链为零或常数的结果，这与图2中dq同步旋转坐标系下的特点不一致。由此可知，无刷直流电机通过式（1）中的变换矩阵C未能得到转子磁场定向dq两轴同步旋转坐标系下的等效模型，即未能实现转子磁场定向。
对于无刷直流电机，正是由于其转子磁场分布的非正弦特征，导致不同转子位置下存在三相转子磁链的不对称，使得采用式（1）中变换矩阵C得到的d、q两轴旋转坐标系并非转子磁场定向坐标系。
为实现非正弦转子磁场定向，并得到如图2所示的转子磁场定向dq两轴同步旋转坐标系下的等效模型，需给出非正弦分布转子磁场下能将d、q轴绕组置于转子磁场位置的变换矩阵
。考虑到Clarke与Park变换作为目前理论最成熟的坐标变换，具有逆矩阵的方便求解与变换前后功率守恒的优点，故沿用Clarke与Park变换的矩阵结构，仅将式（1）变换矩阵C中的旋转角度由q 调整为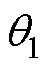
，得到非正弦磁场定向所需变换矩阵为
（2）
式中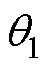，为旋转变换矩阵的旋转角。
采用式（2）给出的变换矩阵对三相转子磁链进行坐标变换可得非正弦转子磁场定向dq旋转坐标系下dq两轴转子磁链为
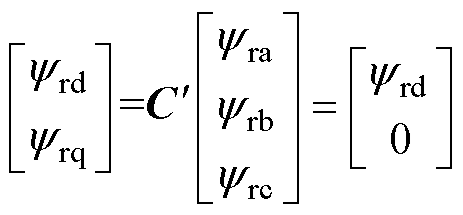（3）
式中，yrd为旋转坐标变换后的d轴转子磁链。
变换矩阵中的旋转角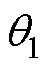可由式（3）计算得出，其瞬时值表达式为
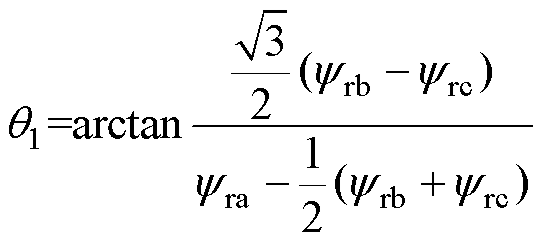（4）
将式（4）代入式（3）中，可以得到经过非正弦转子磁场定向dq旋转坐标变换后d轴转子磁链yrd大小，由于沿用了Clarke变换与Park变换的矩阵形式，因此未能在q轴转子磁链为0的同时做到d轴转子磁链为常数。
无刷直流电机三相静止坐标系下电压方程为
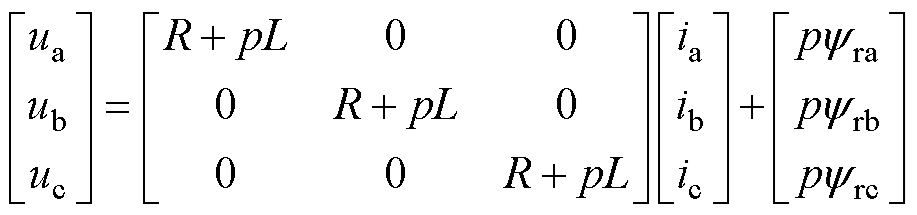（5）
式中，ua、ub、uc分别为a、b、c相相电压；ia、ib、ic分别为a、b、c相相电流；R为相电阻；L为等效相电感；p为微分算子。
采用式（2）给出的变换矩阵对式（5）进行旋转坐标变换，推导出两相旋转坐标系下的电压方程，有
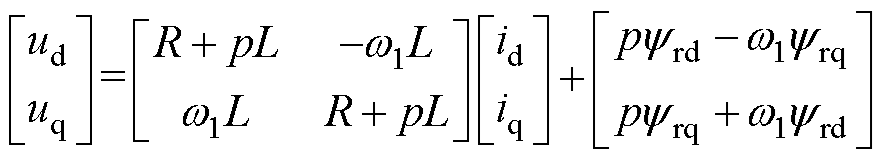（6）
式中，ud、uq分别为旋转变换后d、q轴绕组的电压；id、iq分别为旋转变换后流过d、q轴绕组的电流；w1为旋转角q1对时间的导数。
将式（3）代入式（6）中，得到非正弦转子磁场定向dq旋转坐标系下电压方程，有
（7）
由式（7）可知，坐标变换后d、q轴绕组的电动势为
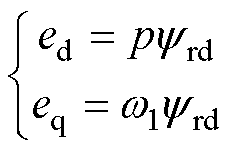（8）
无刷直流电机dq坐标系下的转矩方程为
（9）
式中，np为无刷直流电机的极对数；w 为转子电角速度。
负载运行时，电枢绕组电流产生的电枢反应磁场会对转子磁场产生助磁或去磁的影响，建立非正弦转子磁场下的电枢反应磁场模型，可对其影响进行定量分析。
当无刷直流电机三相电枢绕组通入瞬时值大小分别为ia、ib、ic的电流时，三相电枢绕组皆产生沿电枢圆周表面正弦波分布的磁动势，此时三相电枢绕组产生的磁动势大小为
（10）
式中，Fa、Fb、Fc分别为三相电枢绕组电流产生的磁动势大小；N为每相绕组的有效串联匝数；a 为沿电枢圆周的角度。
对Fa、Fb、Fc进行叠加得到电枢绕组电流产生的合成磁动势，并将其分解到d、q轴，有
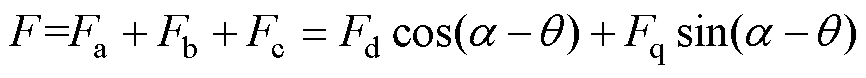（11）
式中，Fd、Fq分别为d、q轴绕组产生的磁动势大小。
将三相电流ia、ib、ic通过变换矩阵的逆矩阵由id、iq表示并与式（10）一起代入式（11）中，求得d、q轴电枢反应磁动势为
（12）
若要实现无直轴电枢反应，则式（12）中的Fd须为零。由此可得d、q轴电枢电流之间的关系式为
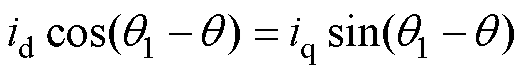（13）
图3给出了无直轴电枢反应下基于非正弦转子磁场定向的无刷直流电机控制系统框图。图中，q -q1数据库根据转子位置q 通过式（4）建立。占空比补偿单元对反电动势相关占空比进行补偿。d、q轴电流给定值可由d、q轴电流给定值计算单元根据式（9）与式（13）联立计算得出。
另外，非正弦转子磁场定向坐标反变换单元以2.2节提出的坐标变换方法为依据，对d、q轴电流给定值进行反变换得出三相电流的给定值。通过对式（2）变换矩阵求逆易得到d、q轴电流到a、b、c三相电流的反变换关系式为
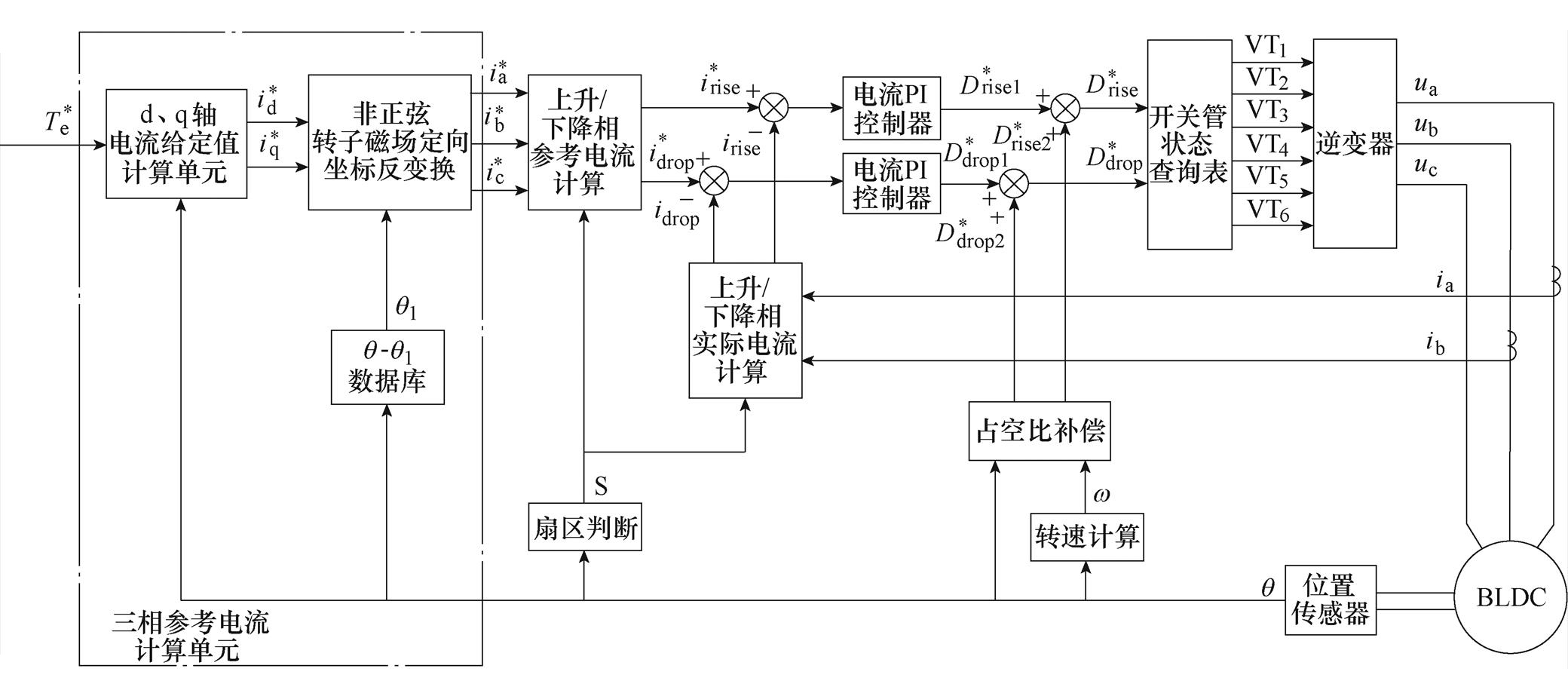
图3 无直轴电枢反应下基于非正弦转子磁场定向的无刷直流电机控制系统框图
Fig.3 Block diagram of BLDCM control system based on non-sinusoidal rotor field orientation without d-axis armature reaction
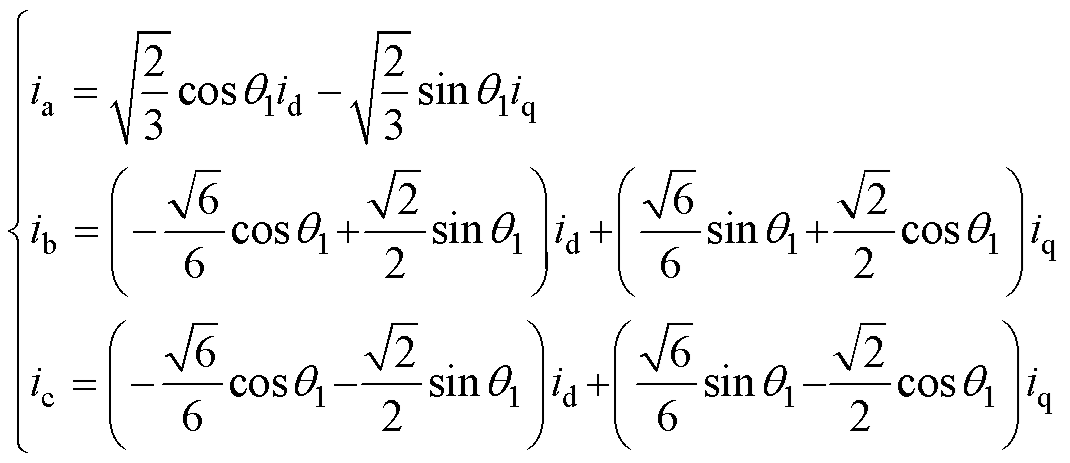（14）
为减轻微处理器的运算负担，可将d、q轴电流给定值计算单元、非正弦转子磁场定向坐标反变换单元、q -q1数据库单元合并为三相参考电流计算单元，由参考转矩
分别和各相参考电流计算系数相乘得到三相电流参考值，各相参考电流计算系数仅与转子位置q 有关，可通过查询事先离线建立的数据库获得。
当转矩一定时，求得三相电流给定值，观察三相电流给定值的特点并对其进行扇区的重新划分，如图4所示。
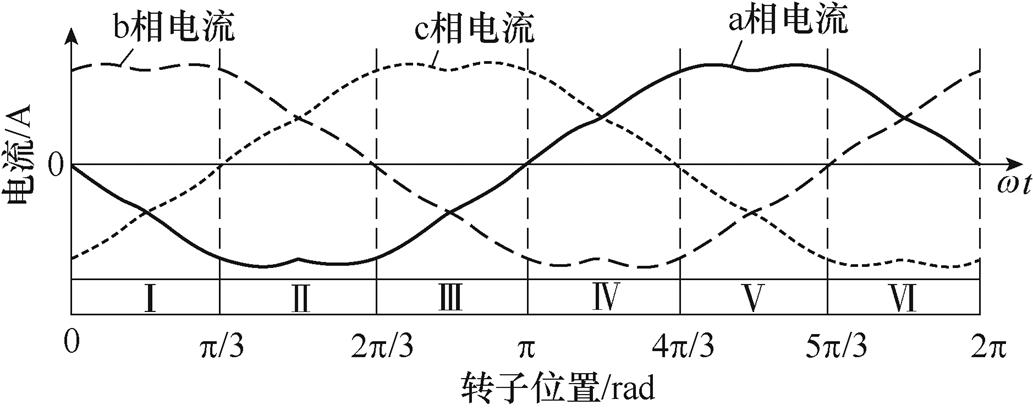
图4 三相电流参考值及扇区划分
Fig.4 Reference three-phase current and sector division
为减小开关损耗，希望任意时刻仅由两个开关管进行脉宽调制，在所划分扇区中，任意扇区中均有一相电流近似不变，此时将其他两相电流分别与不变相电流作差，结合其上升和下降的特点，重新记为上升相和下降相。
表1给出了各扇区对应的开关状态查询表，表中，开关管状态中的六位分别表示a、b、c相上下桥臂开关管的状态；0和1分别表示截止和导通，Drise和Ddrop分别表示该开关管进行占空比为Drise和Ddrop的PWM。
表1 各扇区的开关状态查询表
Tab.1 Switching table for each sector
扇区S开关管状态 Ⅰ0Ddrop100Drise Ⅱ01Ddrop0Drise0 Ⅲ0Drise0Ddrop10 ⅣDrise001Ddrop0 Ⅴ100Drise0Ddrop ⅥDdrop0Drise001
图5给出了实验所用控制系统实验平台，本平台包括单相调压器、无刷直流电机、主电路、控制电路、DSP28335控制器、磁滞测功机及数字示波器等。控制系统的主要参数见表2。
图5 控制系统实验平台
Fig.5 Experiment platform of control system
表2 控制系统参数
Tab.2 Parameters of control system
参 数数值 (型号) 电机92BL430 额定功率/W400 额定电压/V300 额定电流/A1.5 额定转速/(r/min)3 000 额定转矩/(N·m)1.27 极对数5 相电阻/W3.05 相电感/mH17 编码器线数/(P/R)2 048 控制周期/ms50 开关频率/kHz20
由于电机设计及制造等问题，实验样机的实际磁场分布波形并非理想梯形波，故实际三相电流参考值与图4所示理想梯形波磁场分布下三相电流参考值有所区别。图6给出了实验样机转子永磁体产生的磁场沿电枢内表面分布曲线和所提控制方法下实际三相电流参考值的波形。
图7给出了转速分别为570r/min和1 000r/min，参考转矩为额定转矩（1.27N×m）时，方波电流驱动下相关实验结果，该实验以理想方波电流作为电流参考值进行电流PI控制，作为实验结果，分别给出了实际转矩、占空比、a相实际电流、a相电压波形，其中，a相电压是直流母线负极与逆变器a相引出线之间的电压。
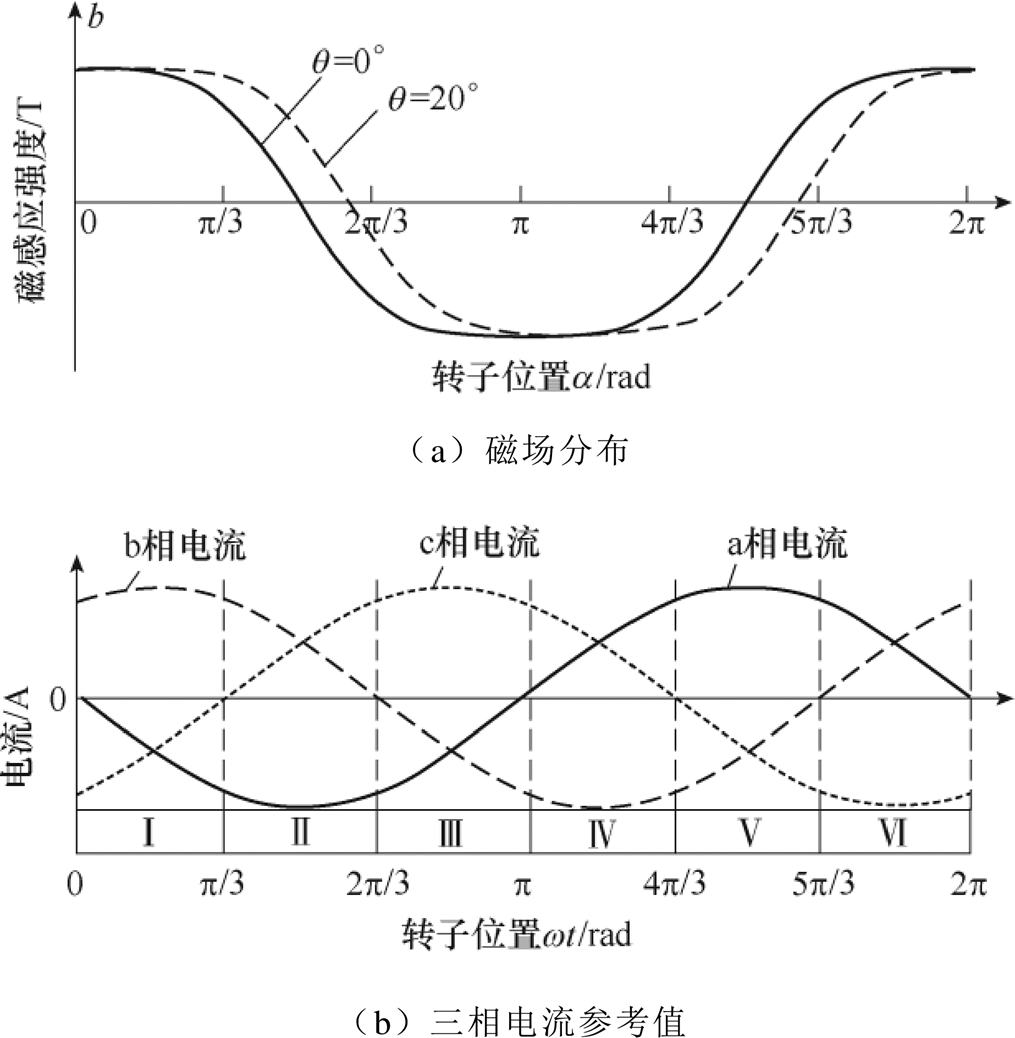
图6 永磁体实际磁场分布及实际三相电流参考值
Fig.6 Actual field distribution and actual reference three-phase current
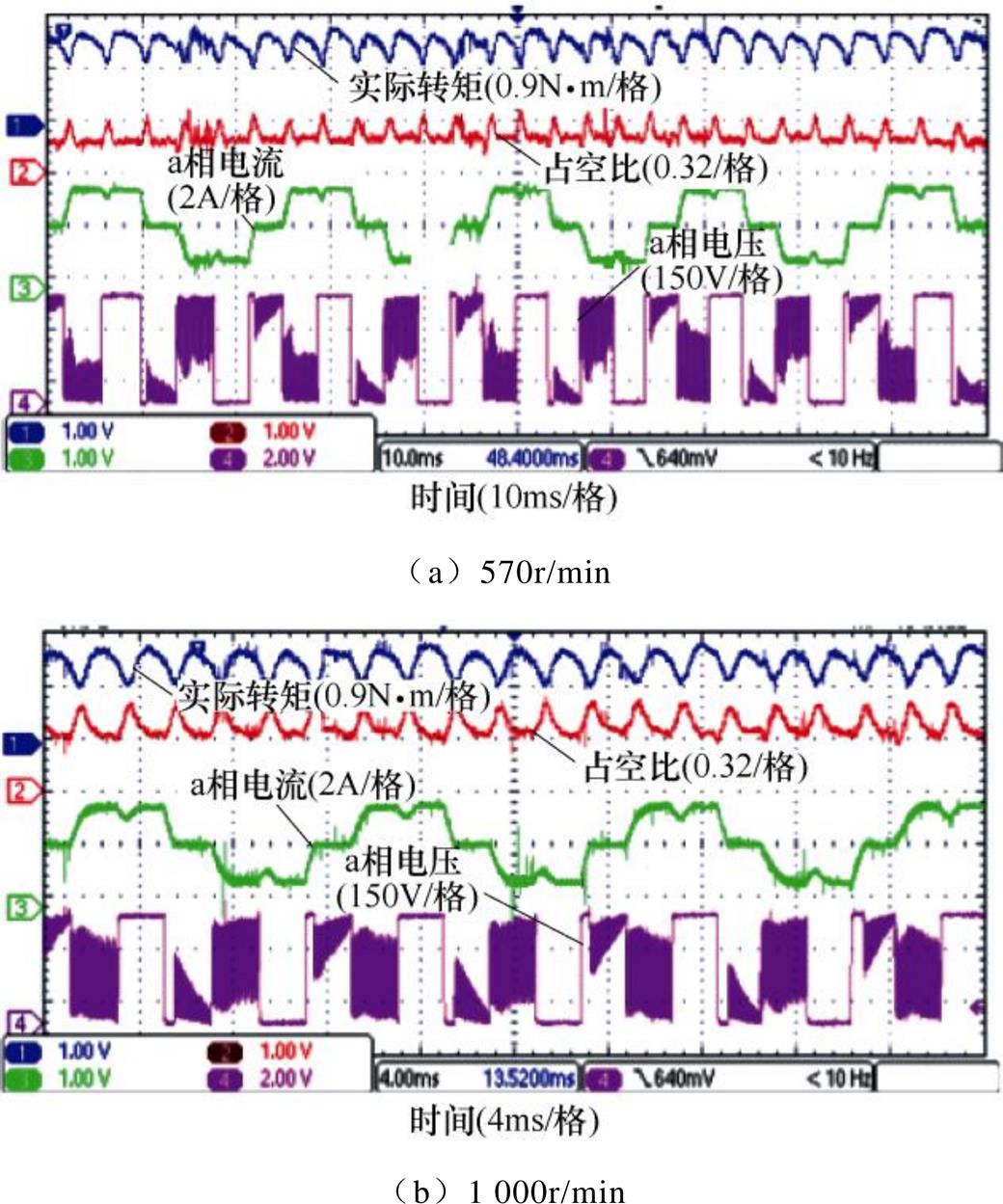
图7 方波电流驱动下的实验结果
Fig.7 Experimental results under square-wave current drive
由图7可知，在方波电流驱动下转矩脉动较大，其中换相转矩脉动尤为明显，这是由于非理想换相过程导致的。此外，方波电流驱动无法实现无直轴电枢反应运行，且其较大的谐波电流会产生较大的噪声与铁耗。
图8给出了转速分别为570r/min和1 200r/min、参考转矩为额定转矩（1.27N×m）时，无直轴电枢反应下非正弦转子磁场定向瞬时转矩控制系统实验结果，该实验所采用的系统框图为图3所示的控制系统框图。电流闭环所用到的上升相及下降相的计算方法在第3节中已经给出。作为实验结果，分别给出了实际转矩、a相参考电流和实际电流波形、a相电压波形，该电压是直流母线负极与逆变器a相引出线之间的电压。
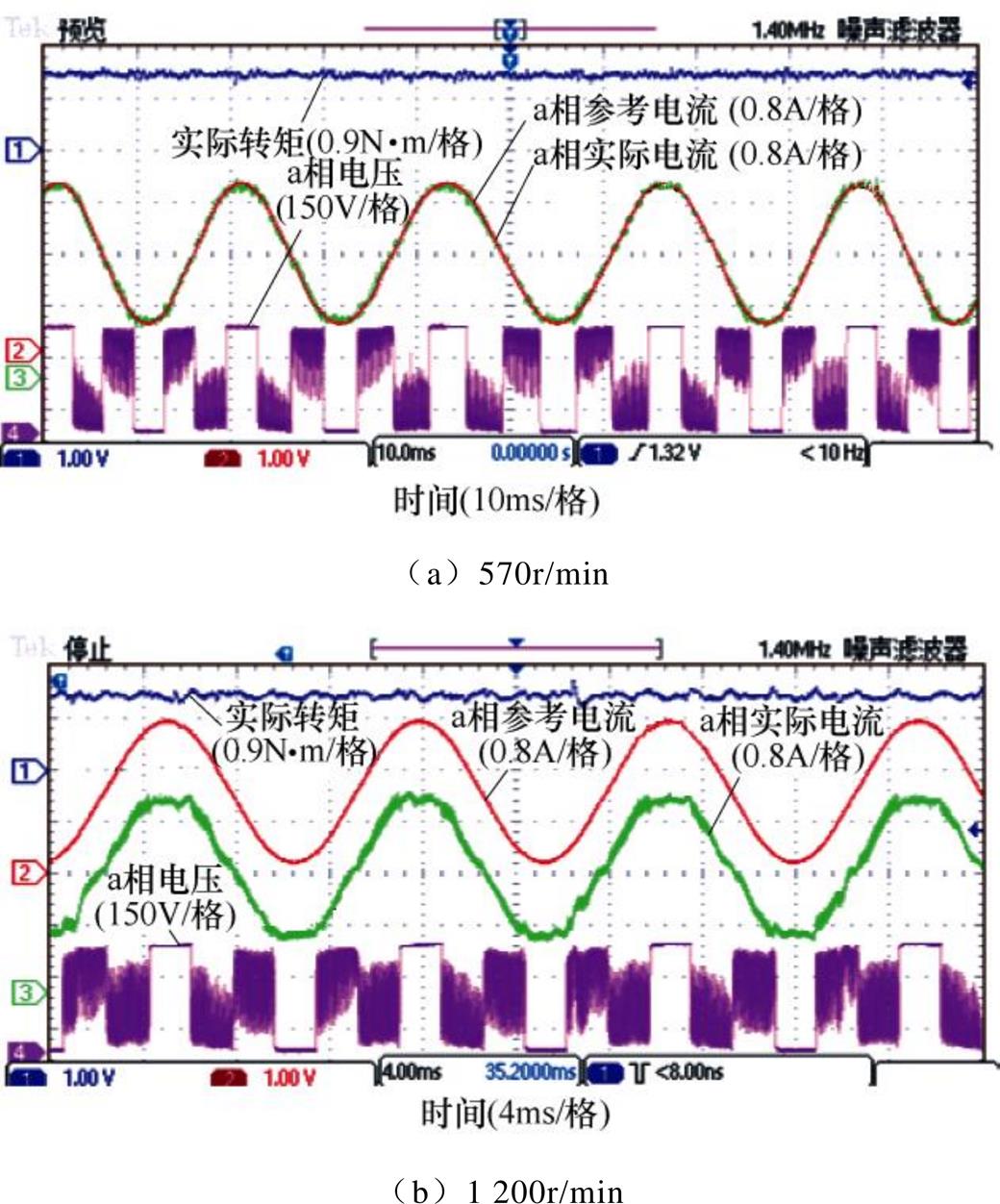
图8 额定参考转矩下的实验结果
Fig.8 Experimental results under rated reference torque
由图8可知，在不同转速下瞬时转矩的控制效果良好，转矩脉动低于10%，并且不存在换相转矩脉动。同时，实际电流能较好地跟踪参考电流。另外可以看出，图8中的电流及电压波形与表1给出的调制方式对应。如图8中在a相电流峰值附近，对照图6可知，转子位置处于第Ⅴ扇区，a、b相电流相减构成上升相，a、c相电流相减构成下降相，根据表1可知，第Ⅴ扇区a相上桥臂开关管恒通，a相电压应为直流母线电压，与图8给出的a相实际电压波形相符。
图9分别给出了转速为570r/min与1 200r/min时，参考转矩由0.2N×m阶跃增加到额定转矩（1.27N×m）再阶跃减小到0.2N×m情况下，无直轴电枢反应的非正弦转子磁场定向瞬时转矩控制系统相关实验结果以及实际转矩局部放大结果。作为实验结果，分别给出了实际转矩、a相参考电流和实际电流波形、a相电压波形，该电压是直流母线负极与逆变器a相引出线之间的电压。作为实际转矩放大结果，给出了实际转矩阶跃变化位置处（图中①③位置）与转矩稳定位置处（图中②位置）的局部放大图。
图9 阶跃参考转矩下的实验结果
Fig.9 Experimental results under step reference torque
由图9可以看出，在不同转速下，随着转矩的突增或突减其跟踪效果良好，控制效果平稳，并且不存在换相转矩脉动。图9b中，当转速为570r/min时，转矩最大最小值之间的偏差为0.16N×m，转矩脉动约为7%；图9d中，当转速为1 200r/min时，转矩最大最小值之间的偏差为0.24N×m，转矩脉动约为10%。
图10分别给出了额定转矩时方波驱动下和本文所提无直轴电枢反应的转子磁场定向驱动方式下定子磁链轨迹的实验结果。其中，定子磁链由转子磁链与电枢反应磁链叠加得到。
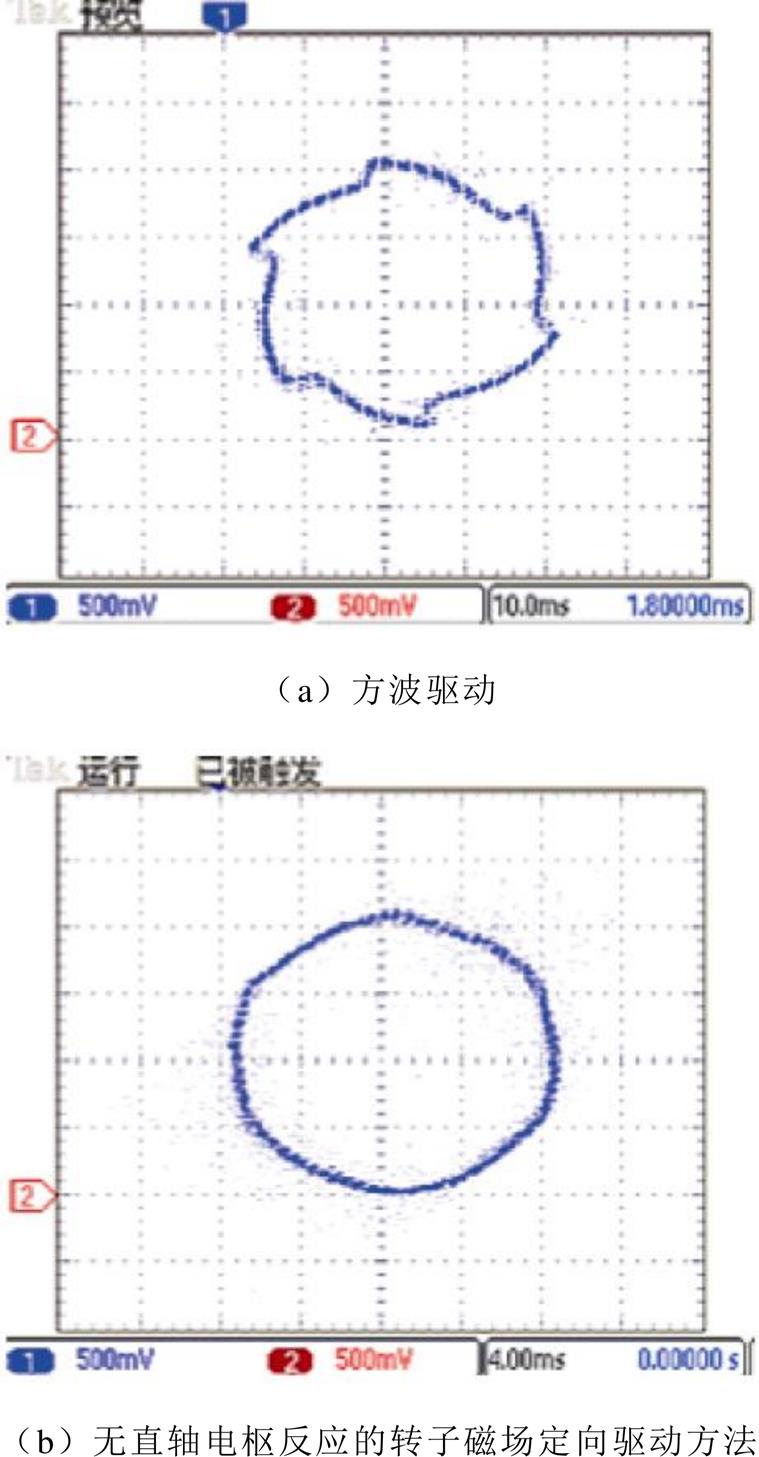
图10 定子磁链轨迹实验结果
Fig.10 Experimental results of stator flux trajectory
由图10可知，定子磁链轨迹由锯齿形变为近似圆形，在瞬时转矩控制的同时实现了无直轴电枢反应运行。
考虑到无刷直流电机的非正弦转子磁场分布特征，本文提出了一种无刷直流电机无直轴电枢反应的非正弦转子磁场定向矢量控制技术，并得出以下结论：
1）对于转子永磁体磁场沿电枢内表面非正弦波分布的电机而言，若以转子所在位置作为旋转角对其三相转子磁链进行等功率3s/2r变换可以得到d、q两相转子磁链，但所得d、q轴转子磁链大小均随时间发生变化，故未能实现转子磁场定向。
2）为了实现转子磁场定向，仅改变等功率3s/2r变换矩阵中的旋转角，做到了d轴磁链为0，建立了非正弦转子磁场定向下的动态数学模型。
3）根据所需参考转矩与无直轴电枢反应两个约束条件可实时获得d、q轴电流参考值，并以此构建了无直轴电枢反应的转子磁场定向矢量控制系统，在抑制转矩脉动的同时实现了无直轴电枢反应运行。
4）所提无直轴电枢反应的矢量控制技术，具有结构简单、无需换相区检测、无需额外硬件、容易实现的特点。
参考文献
[1] 边春元, 邢海洋, 李晓霞, 等. 基于速度变化率的无位置传感器无刷直流电机风力发电系统换相误差补偿策略[J]. 电工技术学报, 2021, 36(11): 2374- 2382.
Bian Chunyuan, Xing Haiyang, Li Xiaoxia, et al. Compensation strategy for commutation error of sensorless brushless DC motor wind power generation system based on speed change rate[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2374- 2382.
[2] 付兴贺, 江政龙, 吕鸿飞, 等. 电励磁同步电机无刷励磁与转矩密度提升技术发展综述[J]. 电工技术学报, 2022, 37(7): 1689-1702.
Fu Xinghe, Jiang Zhenglong, Lü Hongfei, et al. Review of the blushless excitation and torque density improvement in wound field synchronous motors[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1689-1702.
[3] 张文晶, 徐衍亮, 李树才. 新型盘式横向磁通永磁无刷电机的结构原理及设计优化[J]. 电工技术学报, 2021, 36(14): 2979-2988.
Zhang Wenjing, Xu Yanliang, Li Shucai. Structure principle and optimization of a novel disk transverse flux permanent magnet brushless motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(14): 2979-2988.
[4] Xia Changliang, Chen He, Li Xinmin, et al. Direct self-control strategy for brushless DC motor with reduced torque ripple[J]. IET Electric Power Appli- cations, 2018, 12(3): 398-404.
[5] Jiang Weidong, Huang Hui, Wang Jinping, et al. Commutation analysis of brushless DC motor and reducing commutation torque ripple in the two-phase stationary frame[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4675-4682.
[6] 朱俊杰, 刘浩然, 蒋峰, 等. 无刷直流电机转矩脉动抑制系统的新型拓扑研究[J]. 电工技术学报, 2018, 33(17): 4060-4068.
Zhu Junjie, Liu Haoran, Jiang Feng, et al. A new topology research on torque ripple suppression system of brushless motor[J]. Transactions of China Elec- trotechnical Society, 2018, 33(17): 4060-4068.
[7] 姚绪梁, 赵继成, 王景芳, 等. 一种基于辅助升压前端的无刷直流电机换相转矩脉动抑制方法研究[J]. 中国电机工程学报, 2020, 40(9): 3021-3030.
Yao Xuliang, Zhao Jicheng, Wang Jingfang, et al. Research on suppressing commutation torque ripple of brushless DC motor based on an auxiliary step-up front end[J]. Proceedings of the CSEE, 2020, 40(9): 3021-3030.
[8] 曹彦飞, 陆海天, 李新旻, 等. 基于无电感升压拓扑的无刷直流电机电流控制策略[J]. 电工技术学报, 2021, 36(6): 1249-1258.
Cao Yanfei, Lu Haitian, Li Xinmin, et al. Current control strategy of brushless DC motor based on non- inductive Boost topology[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1249-1258.
[9] Shi Tingna, Guo Yuntao, Song Peng, et al. A new approach of minimizing commutation torque ripple for brushless DC motor based on DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2010, 57(10): 3483-3490.
[10] Jiang Guokai, Xia Changliang, Chen Wei, et al. Commutation torque ripple suppression strategy for brushless DC motors with a novel noninductive Boost front end[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 4274-4284.
[11] Cao Yanfei, Shi Tingna, Li Xinmin, et al. A com- mutation torque ripple suppression strategy for brushless DC motor based on diode-assisted Buck- Boost inverter[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(6): 5594-5605.
[12] Yao Xuliang, Lu Guangxu, Zhao Jicheng, et al. Torque ripple minimization in brushless DC motor with optimal current vector control technique[C]// 2018 IEEE Chinese Automation Congress (CAC), Xi'an, China, 2018: 2524-2529.
[13] 陆可, 蔡广瀚, 向南辉, 等. 基于电压矢量注入的无刷直流电机换相转矩脉动抑制方法[J]. 中国电机工程学报, 2021, 41(10): 3592-3601.
Lu Ke, Cai Guanghan, Xiang Nanhui, et al. Method for suppressing commutation torque ripple of brushless DC motor based on voltage vector injection[J]. Pro- ceedings of the CSEE, 2021, 41(10): 3592-3601.
[14] Shi Jian, Li Tiecai. New method to eliminate com- mutation torque ripple of brushless DC motor with minimum commutation time[J]. IEEE Transactions on Industrial Electronics, 2013, 60(6): 2139-2146.
[15] 盛田田, 王晓琳, 顾聪, 等. 一种使用重叠换相法的无刷直流电机平均转矩控制[J]. 中国电机工程学报, 2015, 35(15): 3939-3947.
Sheng Tiantian, Wang Xiaolin, Gu Cong, et al. An average torque control method for brushless DC motors using overlap commutation strategy[J]. Pro- ceedings of the CSEE, 2015, 35(15): 3939-3947.
[16] 边春元, 段鹏飞, 肖鸿权, 等. 一种用于无刷直流电机回馈制动的PWM调制方式[J]. 中国电机工程学报, 2019, 39(17): 5247-5256, 5305.
Bian Chunyuan, Duan Pengfei, Xiao Hongquan, et al. A PWM scheme for regenerative braking of brushless DC motor[J]. Proceedings of the CSEE, 2019, 39(17): 5247-5256, 5305.
[17] Shi Tingna, Niu Xingzhuo, Chen Wei, et al. Com- mutation torque ripple reduction of brushless DC motor in braking operation[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1463-1475.
[18] 李珍国, 章松发, 周生海, 等. 考虑转矩脉动最小化的无刷直流电机直接转矩控制系统[J]. 电工技术学报, 2014, 29(1): 139-146.
Li Zhenguo, Zhang Songfa, Zhou Shenghai, et al. Direct torque control of brushless DC motor con- sidering torque ripple minimization[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 139- 146.
[19] 杨建飞, 曹伟, 李德才, 等. 两相导通无刷直流电机直接转矩控制零电压矢量特性分析[J]. 电工技术学报, 2019, 34(23): 4948-4956.
Yang Jianfei, Cao Wei, Li Decai, et al. Analysis on zero voltage vector in two-phase conduction direct torque control of brushless DC motor[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4948-4956.
[20] 杨建飞, 胡育文, 刘建, 等. 两相导通BLDCM DTC电压空间矢量分析[J]. 电机与控制学报, 2018, 22(3): 95-104.
Yang Jianfei, Hu Yuwen, Liu Jian, et al. Analysis on voltage spacial vector in two-phase conduction direct torque control of brushless DC motor[J]. Electric Machines and Control, 2018, 22(3): 95-104.
[21] Shi Tingna, Cao Yanfei, Jiang Guokai, et al. A torque control strategy for torque ripple reduction of brushless DC motor with nonideal back electromotive force[J]. IEEE Transactions on Industrial Electronics, 2017, 64(6): 4423-4433.
[22] 李珍国, 孙启航, 王鹏磊, 等. 基于转子永磁体磁场定向的无刷直流电机转矩脉动抑制[J]. 电工技术学报, 2020, 35(14): 2987-2996.
Li Zhenguo, Sun Qihang, Wang Penglei, et al. Torque ripple reduction of brushless DC motor based on rotor permanent magnet field orientation[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 2987-2996.
Non-Sinusoidal Rotor Field Oriented Vector Control Technology Without d-Axis Armature Reaction in Brushless DC Motor
Abstract This paper proposes a vector control strategy of brushless DC motor (BLDCM) based on rotor field orientation considering the non-sinusoidal field distribution, which can not only suppress the torque ripple without the detection of commutation zone, but also solve the problems of magnetization and demagnetization caused by d-axis armature reaction. Firstly, through the comparative analysis of the rotor flux waveform under different rotor field distributions, it is concluded that the 3s/2r transformation with the rotor position as rotation angle cannot achieve rotor field orientation when rotor field distribution is non-sinusoidal. Secondly, by changing the rotation angle in the 3s/2r transformation matrix, the rotor flux has no q-axis component after the transformation, thereby establishing a non-sinusoidal rotor field orientation coordinate system and obtaining a dynamic mathematical model under this coordinate system. Finally, the d-axis and q-axis armature currents for a given reference torque without d-axis armature reaction is deduced theoretically, and accordingly the rotor field oriented vector control system without d-axis armature reaction of BLDCM is constructed. The results of DSP experiments show the feasibility and effectiveness of the proposed strategy.
keywords：Brushless DC motor (BLDCM), non-sinusoidal magnetic field distribution, rotor field orientation, without d-axis armature reaction, torque ripple reduction
DOI: 10.19595/j.cnki.1000-6753.tces.210377
中图分类号：TM351
国家自然科学基金（61873226）和河北省自然科学基金（E2017203320）资助项目。
收稿日期 2021-03-19
改稿日期 2021-06-01
李珍国 男，1973年生，博士，副教授，研究方向为电力电子与电力传动。E-mail: lzg@ysu.edu.cn（通信作者）
孙启航 女，1997年生，硕士，研究方向为电力电子与电力传动。E-mail: 1018525294@qq.com
（编辑 崔文静）