
图1 带护套表贴式永磁电机示意图
Fig.1 Schematic diagram of surface-mounted permanent magnet motor with rotor sleeve
摘要 现有二维精确子域法在计算转子涡流损耗时,为了便于系数矩阵求解,通常忽略涡流反作用的影响。对于高速永磁电机,电枢电流中含有大量的时间谐波,涡流反作用对转子损耗影响大,忽略涡流反作用会严重影响计算精度。该文基于精确子域法,通过在有源区域内求解包含时间导数及导体运动速度的扩散方程,建立了一个考虑涡流反作用和各次时空谐波的高速永磁同步电机转子涡流损耗解析模型。为提高计算精度,该模型对槽口建立方程考虑槽口对磁场分布的影响。为提高计算速度,利用电机的周期性,建立周期性边界条件。通过该解析模型研究了不同变频器开关频率及气隙长度下,各次时空谐波在转子上产生的涡流损耗变化规律。通过对一台7.5kW非晶合金高速永磁电机进行损耗分离实验,将解析结果与有限元、实验结果对比,证明了所提出解析模型的正确性。
关键词:高速永磁电机 精确子域模型 涡流反作用 周期性边界条件 损耗分离实验
高速永磁电机具有高效和高功率密度等优点,在飞轮储能、高速磨床、鼓风机和压缩机等方面得到广泛应用[1-2]。然而,变频器供电时引入了大量高频的电流时间谐波,会在转子上造成较大的涡流损耗,且转子的散热条件差,会引起转子温度升高,增大永磁体不可逆失磁风险,影响电机运行的可靠性。因此,在高速永磁电机的设计阶段,快速准确计算转子涡流损耗尤为重要。
转子涡流损耗的计算方法主要采用有限元分析与解析法。有限元分析方法计算转子涡流损耗可以考虑饱和、漏磁、材料非线性等因素的影响[3-4],有着较高的精度,并且三维有限元可以考虑端部效 应[5]。然而,为了获得更高的计算精度,需要设置精细的网格剖分和时间步长,这就意味着需要更多的计算时间[6]。采用解析法可以有效地解决计算速度时间长的问题[7],同时解析方程可以直观地显示各参数对转子涡流损耗的影响。
目前,国内外研究的转子涡流损耗解析模型依据是否考虑电机轴向有限长度分为二维解析模型和三维解析模型。二维转子涡流损耗解析方法的应用较为广泛。在计算定子磁动势引起的永磁电机转子涡流损耗时,为便于计算,解析模型通常将电枢绕组等效为电流片并假设涡流为电阻限制型,从而忽略定子开槽及涡流反作用的影响[8-9],这种方法用于高速电机会造成较大误差。文献[10]分别采用极坐标系在有源区域中对涡流密度建立扩散方程以考虑涡流反作用的影响,但忽略了定子开槽。在考虑定子开槽时,一般采用磁导模型对磁场进行修正[11],而磁导函数只考虑开口槽中心线一点的影响,难以考虑槽口的影响。文献[12]对槽口处的每一点进行保角映射,提出复数形式的磁导函数;文献[13-14]将其引入到永磁同步发电机分析模型中,考虑定子磁动势谐波与磁导谐波间的相互作用,计算两者共同作用下的负载涡流损耗。然而,复平面间的映射点数过多时求解困难、精度低。因此,映射的方法存在一定局限性。
相比于磁导函数法,精确子域法将槽作为一个独立的求解区域,在考虑定子开槽影响时计算精度更高[15]。文献[16-17]基于精确子域法计算了空载及负载时转子涡流损耗的大小,但忽略了涡流反作用及电流时间谐波的影响。然而,高速永磁电机涡流反作用对损耗影响很大,忽略涡流反作用会严重高估涡流损耗,影响计算精度[18]。文献[19]基于精确子域法建立了考虑涡流反作用的空载磁场解析模型,分析齿槽效应对转子涡流损耗的影响,而对于变频器供电的高速电机,定子磁动势谐波是导致转子涡流损耗的主要因素。文献[20]给出了考虑涡流反作用的负载磁场解析模型,但是没有考虑护套及电流时间谐波。此外,上述解析模型少有对电机周期性进行研究。对于忽略转子偏心的精确子域模型,若不考虑电机内磁场分布周期性,将会使得谐波系数求解矩阵维度过大,大大降低计算效率。
为提高解析计算精度,考虑涡流的三维分布,文献[21]提出了一种基于广义图像理论的三维转子涡流损耗解析方法,采用分离变量法导出永磁体中的三维涡流分布。为了方便计算,把永磁体近似等效成矩形,忽略曲率效应且未考虑定子开槽的影响。为了考虑开槽影响,文献[22-23]将该方法与精确子域模型结合,提出了一种改进的三维永磁体涡流损耗解析模型。三维解析模型虽然能有效考虑涡流三维分布,但由于其解析模型过于复杂,解析过程需要较高的数学理论,因此,三维解析模型研究较少,其应用还不成熟。
针对带有护套的高速永磁电机,本文基于二维精确子域法,通过在有源区域内求解包含时间导数及导体运动速度的扩散方程建立了一个考虑各次时空谐波和涡流反作用的转子涡流损耗解析模型。该模型通过建立槽口子域方程考虑槽开口的存在,并引入了周期系数,提高模型计算精度的同时减小了系数矩阵维度,提高计算速度。基于该解析模型研究了PWM开关频率和气隙长度对转子涡流损耗的影响。为了验证解析模型的正确性,对一台7.5kW带有护套的非晶合金高速永磁电机进行损耗分离实验,将PWM供电时转子涡流损耗的实验结果与解析及有限元结果对比,证明了该解析模型具有较高的计算精度。
为计算转子涡流损耗,本文针对带有护套的表贴式永磁电机建立基于二维极坐标系(r, a)的转子涡流损耗解析模型,图1为电机横截面示意图。根据电机结构和材料的不同特性,将电机分为五个区域:槽、槽开口、气隙、护套、永磁体。

图1 带护套表贴式永磁电机示意图
Fig.1 Schematic diagram of surface-mounted permanent magnet motor with rotor sleeve
以图1所示的第一个槽中心为初始位置,则第y个槽及第y个槽开口的中心位置可以表示为
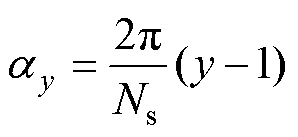 (1)
(1)
式中,y=1, 2, 3,…, Ns,Ns为定子槽数。
为便于推导转子涡流损耗解析解,作如下假设:
(1)高速电机为减小铁耗,通常将定转子磁通密度设计在非饱和区域,因此解析模型中假设定转子铁心的磁导率无穷大。
(2)忽略转子铁心的涡流损耗。
(3)护套和永磁体材料各向同性,磁导率及电导率为常数。
(4)槽内电流密度均匀分布。
(5)采用如图2b所示的简化槽型结构,图2a所示的实际梨形槽简化过程可参考文献[24]。
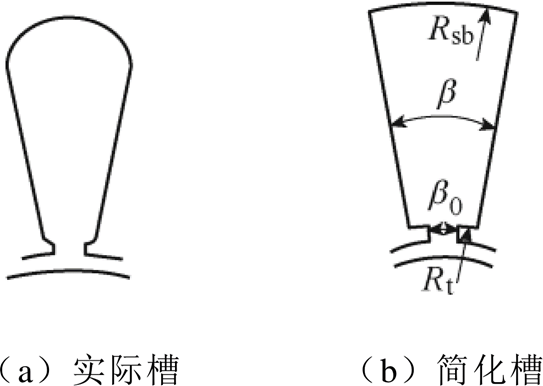
图2 定子槽示意图
Fig.2 Schematic diagram of stator slot
双层绕组排布形式如图3所示。本文对图3所示的上下排布和左右排布的双层绕组建立解析模型,单层绕组视为双层绕组的一种特殊形式,即J1y-1=J1y-2。
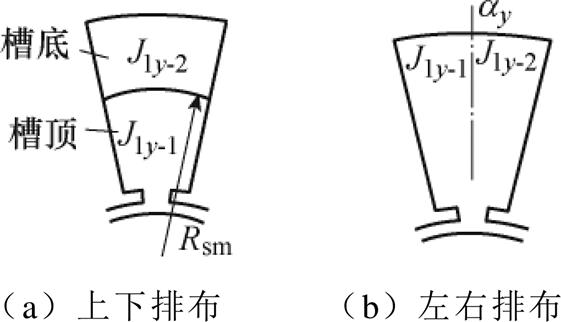
图3 双层绕组排布形式
Fig.3 Arrangement of double-layer windings
为便于求解,本文解析方程采用复数形式的傅里叶级数对方程进行推导。为提高解析模型计算效率,利用电机周期性来降低计算量。对于定、转子同心状态的电机,对称周期数为极对数p和槽数Ns的最大公约数。以下推导中假设c=GCD(Ns, p)[25]。解析模型的计算流程如图4所示。
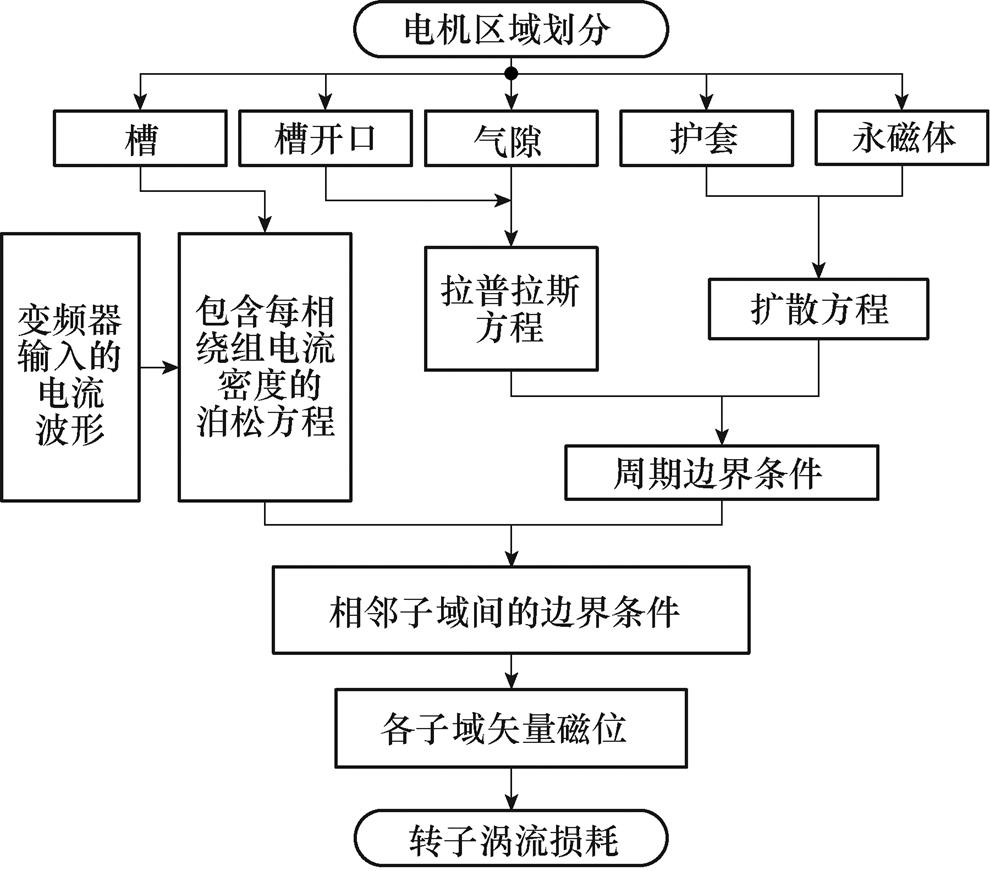
图4 解析模型流程
Fig.4 Flow chart of analytical model
对于电枢绕组,其三相电流表达式为
 (2)
(2)
式中,Il为第l次谐波电流的幅值;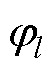 为第l次谐波电流的初始相位;
为第l次谐波电流的初始相位; 为基波电流的电角频率;l为电流谐波次数。
为基波电流的电角频率;l为电流谐波次数。
槽内电流密度均匀分布,因此复数域中各相绕组在槽内的电流密度为
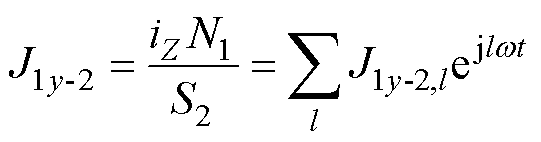 (3)
(3)
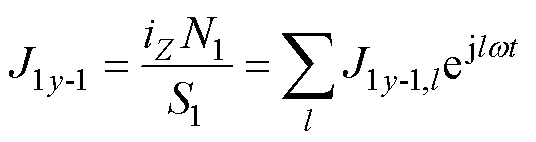 (4)
(4)
式中,N1为每相串联匝数;S1、S2分别为槽内上、下绕组所占的面积,S1=S2;iZ为槽内电流,Z表示绕组的某一相。
槽内电枢绕组中通有电流,因此第y个槽区域满足泊松方程
 (5)
(5)
引入周期系数c,此时,y=1, 2, 3,…, Ns/c;J为槽内的电流密度;A1y为第y个槽区域矢量磁位。
对于图3a所示的绕组形式,在槽底和槽顶区域根据磁矢位连续和切向磁场强度连续的边界条件,求得第y个槽的槽底区域矢量磁位表达式为
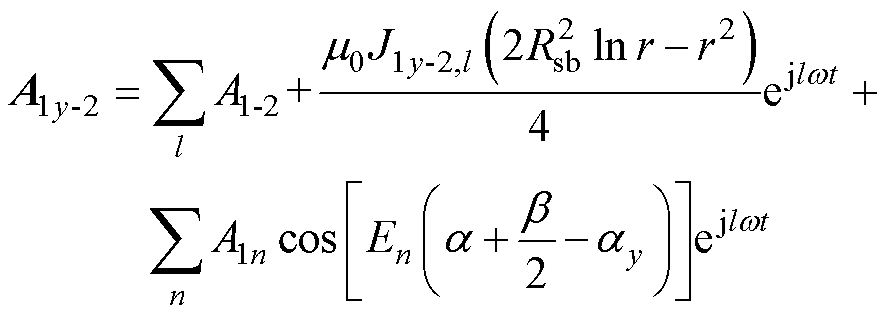 (6)
(6)
其中
 (7)
(7)
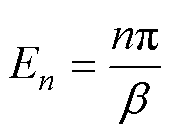 (8)
(8)
式中,m0为真空磁导率;n为槽中的空间谐波;b为槽宽角度;Rsb为槽底半径;Rt为槽开口外半径;J1y-2,l为槽底的电流密度;D1为第y个槽区域未知系数。
槽顶区域矢量磁位表达式为
 (9)
(9)
其中
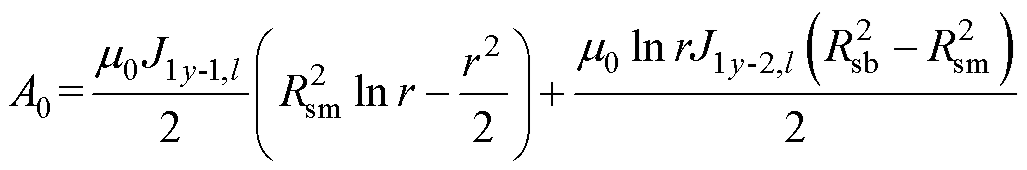 (10)
(10)
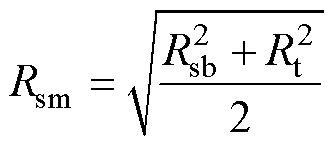 (11)
(11)
式中,A1-1为槽顶区域未知系数;Rsm为上下排布的双层绕组分界处半径;J1y-1,l、J1y-2,l为槽顶、槽底的电流密度。
对于图3b所示的绕组形式,考虑槽底铁磁边界条件得到第y个槽的矢量磁位为
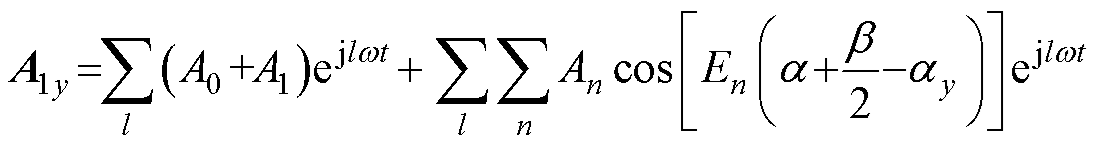 (12)
(12)
其中
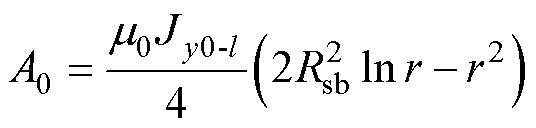 (13)
(13)
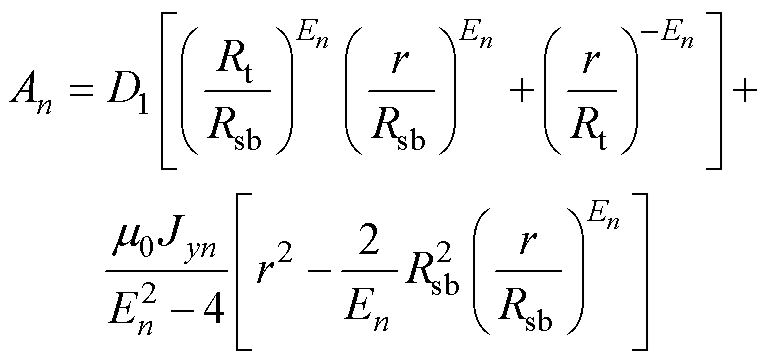 (14)
(14)
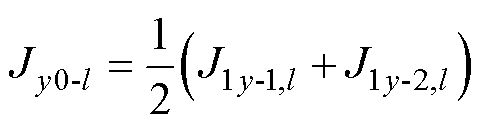 (15)
(15)
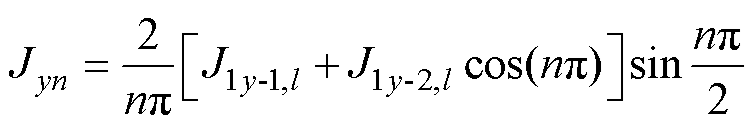 (16)
(16)
第y个槽开口区域满足拉普拉斯方程
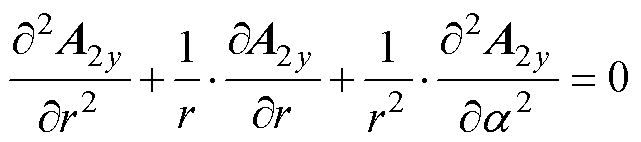 (17)
(17)
考虑电机的对称性,此时,y=1, 2, 3,…, Ns/c;A2y为第y个槽开口区域矢量磁位。
采用分离变量法,同时考虑铁磁边界条件,得到槽开口区域矢量磁位为
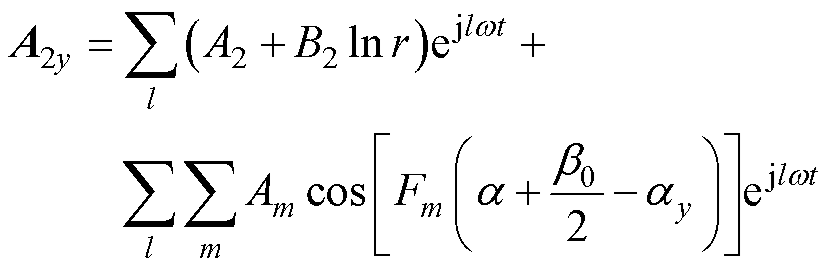 (18)
(18)
其中
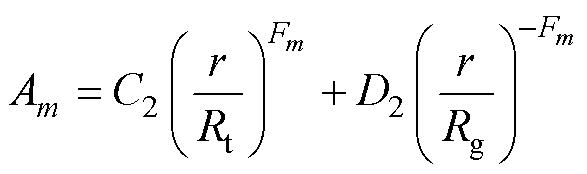 (19)
(19)
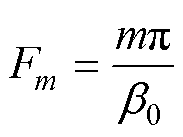 (20)
(20)
式中,m为槽开口区域空间谐波次数;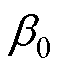 为槽开口角度;Rg为气隙外半径;A2、B2、C2、D2为槽开口区域未知系数。
为槽开口角度;Rg为气隙外半径;A2、B2、C2、D2为槽开口区域未知系数。
对于图1所示的电机模型,电机的对称性仅影响了气隙、护套、永磁体区域方程的通解形式,因此对气隙、护套和永磁体区域方程求解时,需要在原有边界条件基础上附加一个周期边界条件,有
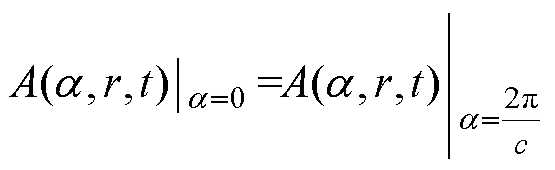 (21)
(21)
为了考虑谐波相对于基波的旋转方向,定义一个符号s,s取值为1或-1,分别代表谐波旋转方向与基波相反或相同[11]。
气隙区域满足拉普拉斯方程为
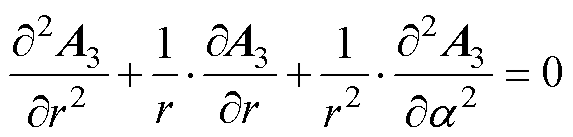 (22)
(22)
式中,A3为气隙区域矢量磁位。
采用分离变量法,得到气隙区域矢量磁位式为
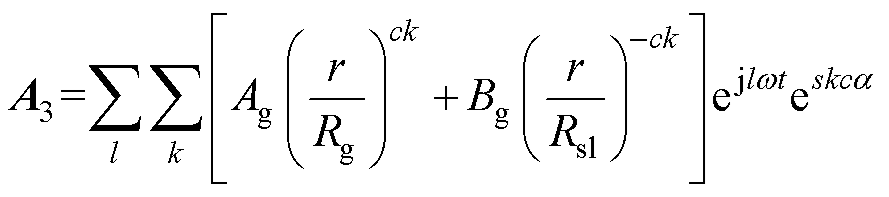 (23)
(23)
式中,k为气隙区域空间谐波次数;Rsl为护套外半径;Ag、Bg为气隙区域未知系数。
对于变频器供电的高速永磁电机,气隙磁场中含有大量的高次谐波,须考虑涡流反作用对转子涡流损耗的影响。对护套区域建立包含时间导数及导体运动速度的扩散方程为
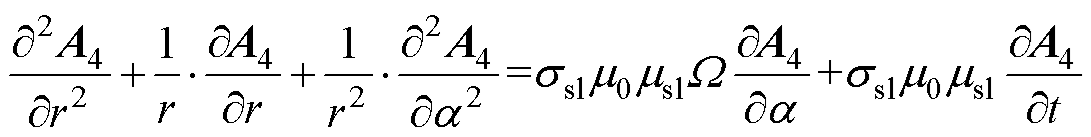 (24)
(24)
式中,A4为护套区域矢量磁位;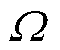 为机械角频率;
为机械角频率; 为护套的相对磁导率;
为护套的相对磁导率;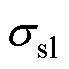 为护套的电导率。
为护套的电导率。
永磁体区域满足的扩散方程为
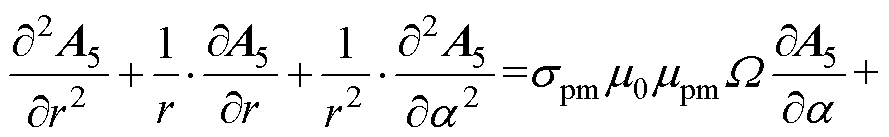
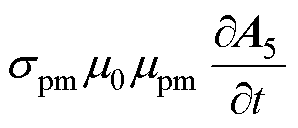 (25)
(25)
式中,A5为永磁体区域矢量磁位; 和
和 分别为永磁体相对磁导率和电导率。
分别为永磁体相对磁导率和电导率。
通过分离变量法对式(24)进行求解,得到护套区域的矢量磁位为

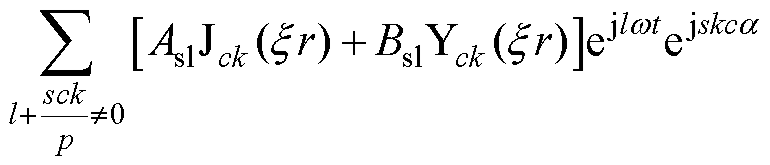 (26)
(26)
其中
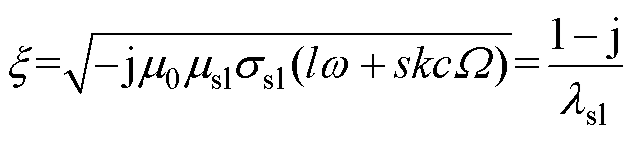 (27)
(27)
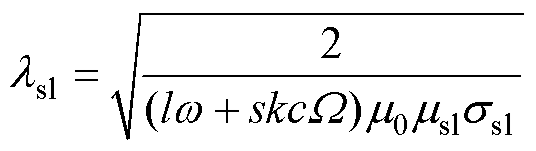 (28)
(28)
式中,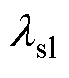 为护套的趋肤深度;Rpm为永磁体外半径;Asl、Bsl为护套区域未知系数。
为护套的趋肤深度;Rpm为永磁体外半径;Asl、Bsl为护套区域未知系数。
同理,永磁体区域的矢量磁位为

 (29)
(29)
其中
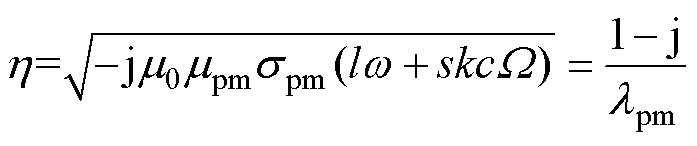 (30)
(30)
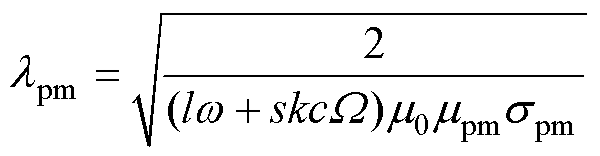 (31)
(31)
式中,Apm、Bpm为永磁体区域未知系数; 为永磁体的趋肤深度;Rr为转子铁心外径;Jck、Yck分别为第一类和第二类贝塞尔函数。
为永磁体的趋肤深度;Rr为转子铁心外径;Jck、Yck分别为第一类和第二类贝塞尔函数。
以相邻区域间的矢量磁位连续和切向磁场强度连续为边界条件,可以联立方程组对方程中的未知系数进行求解,即A1、A1-1、A1-2、D1、A2、B2、C2、D2、Ag、Bg、Asl、Bsl、Apm、Bpm。从而得到各个区域的矢量磁位,进而求解转子涡流损耗,各个系数的求解过程见附录。
由于方程解中包含贝塞尔函数,为此采用坡印廷定理对导体区域内的涡流损耗进行求解。
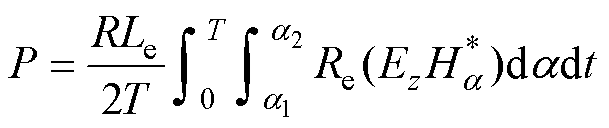 (32)
(32)
式中,R为导体表面半径;a1~a2为导体周向范围;T为一个电周期,T=2p/w;Le为导体区域轴向长度;Ez为电场强度轴向分量;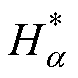 为切向磁场强度的共轭。
为切向磁场强度的共轭。
根据永磁体区域矢量磁位表达式(29),可计算出一个电周期内永磁体的平均涡流损耗解析式为
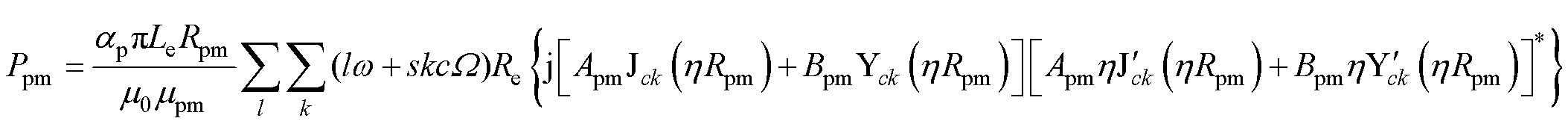 (33)
(33)
式中,ap为永磁体的极弧系数; 、
、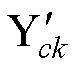 分别为第一类和第二类贝塞尔函数的一阶导数。
分别为第一类和第二类贝塞尔函数的一阶导数。
同理可得护套区域涡流损耗解析式为
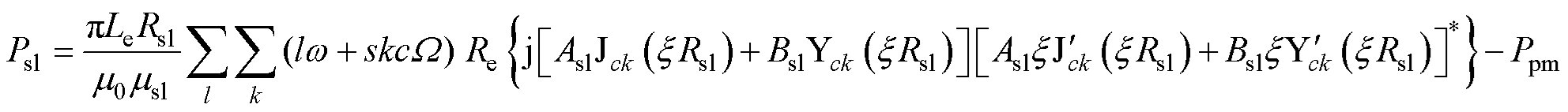 (34)
(34)
本文以一台7.5kW,15 000r/min,4极18槽高速永磁电机为例进行分析,该电机定子铁心材料为非晶合金(2605SA1),永磁材料采用烧结钕铁硼(N38UH),极弧系数为1,同时护套采用材料为钛合金(TC4),其主要参数见表1。图5给出实验测试得到的A相绕组电流波形及其谐波分量。为了验证解析模型的适用性,图6给出电枢气隙磁通密度波形的解析与有限元结果,从气隙磁通密度径向分量与切向分量波形对比可以看出,解析模型与实际槽型结构有限元结果吻合较好。
表1 电机主要参数
Tab.1 Main parameters of motor

参 数数 值 额定功率/kW7.5 额定频率/Hz500 永磁体相对磁导率mpm1.058 42 永磁体电导率/(S/m)694 400 护套相对磁导率msl1.000 05 护套电导率/(S/m)610 000 定子外径/mm130 定子内径/mm60 气隙长度/mm2 永磁体厚度/mm5 护套厚度/mm2 铁心长度/mm70
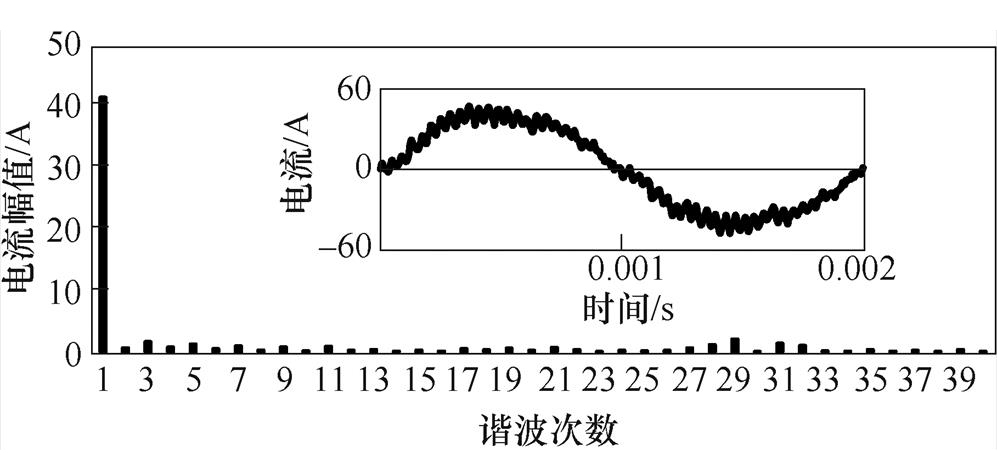
图5 变频器供电电流波形谐波分析
Fig.5 Harmonic analysis of current waveform of inverter
图7给出电机在额定频率下采用实际槽型与简化槽型结构时和转子涡流损耗计算结果。从图中有限元计算的转子损耗结果看,槽型简化对转子涡流损耗影响可忽略不计。对比图中解析法和有限元法的计算结果可知,解析法与有限元的计算误差为3.8%,产生偏差是由于解析模型是基于一些简化假设条件而建立的,这些假设会导致计算结果与实际存在偏差;同时有限元的计算结果受模型处理和网格剖分影响较大,也会与实际值产生一定偏差。未考虑涡流反作用的解析结果与考虑涡流反作用解析结果相差48.8%,与有限元计算相差54.56%,忽略涡流反作用的影响会导致高速永磁电机转子涡流损耗计算结果存在较大误差,因此,高速永磁电机转子涡流损耗计算时有必要考虑涡流反作用的影响。

图6 电枢磁场产生的气隙磁通密度
Fig.6 Air gap flux density generated by armature magnetic field

图7 额定频率时护套及永磁体的涡流损耗
Fig.7 Loss of sleeve and magnet at rated frequency
表2给出有限元仿真与解析模型计算时间对比。可以看出,本文所建立的解析模型通过引入周期系数c,并对Ns/c个槽建立方程,可求得整个电机转子涡流损耗,因此本文所建立的解析模型计算时间约为无周期系数解析模型的1/c。引入周期系数的解析模型计算时间分别为有限元局部模型的14.2%和有限元整体模型的7.1%,相比于有限元,本文所建立的解析模型在计算速度上具有显著优势。
表2 解析法与有限元法计算时间对比
Tab.2 Comparison of calculation time of analytical method and finite element method(单位: s)

模 型计算时间 解析 (周期系数)69 解析 (无周期系数)140 有限元 (1/2模型)485 有限元 (整体模型)960
为进一步验证解析模型的准确性,图8给出护套及永磁体涡流损耗随转速变化时解析结果与有限元计算结果。由结果可知,护套及永磁体涡流损耗均随转速升高而增加,当转速从5 000r/min增加到10 000r/min时,护套涡流损耗增加了48.92%,永磁体涡流损耗增加了35.86%,高频时转子涡流损耗主要集中于护套。当转速从10 000r/min增加到15 000r/min时转子涡流损耗增加了21.9%,可以明显看出,护套涡流损耗增加幅度较大,增加了27.09%,而永磁体涡流损耗变化幅度较小,这主要是由于电机频率的增加导致谐波透入深度减小以及护套对透入永磁体的谐波削弱作用增强。
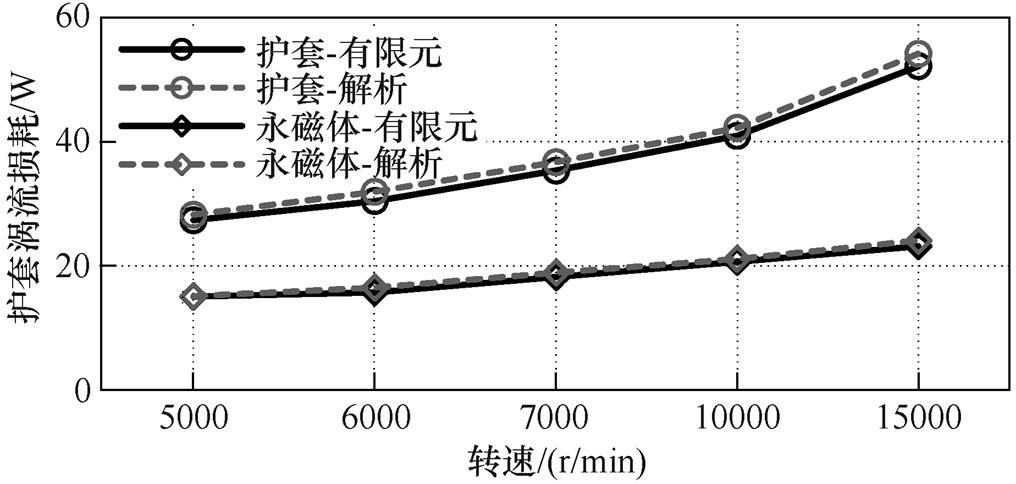
图8 不同转速时护套及永磁体涡流损耗
Fig.8 Loss of sleeve and magnet at different speeds
各次电流时间谐波产生的转子涡流损耗如图9所示。通过解析模型计算了电机额定频率时输入电流波形前60次时间谐波产生的转子涡流损耗,结果显示,变频器供电所引入的高次电流时间谐波是产生涡流损耗的主要原因,高次谐波电流幅值占比较大且谐波频率高,因此,产生的涡流损耗相对较大。
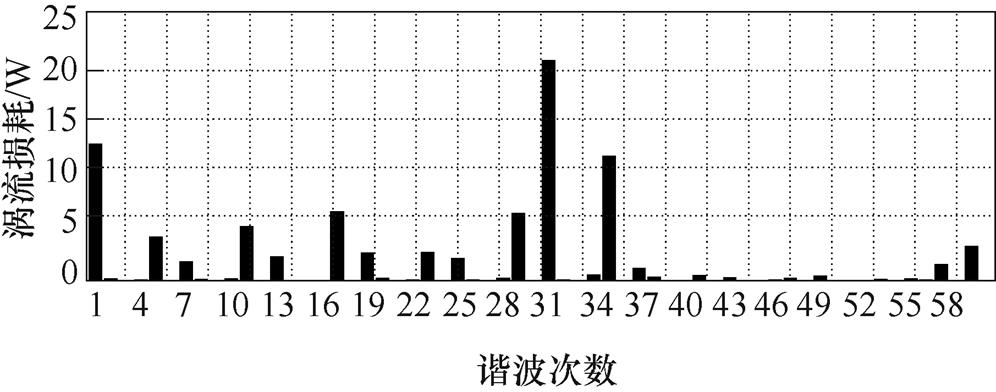
图9 各次电流时间谐波产生的转子涡流损耗
Fig.9 Rotor eddy current loss caused by time harmonics
高速永磁电机转子涡流损耗主要来源于PWM供电引入的电流时间谐波、定子绕组非正弦分布引起的空间谐波和定子开槽导致的磁导谐波。其中,电流时间谐波对高速永磁电机转子涡流损耗的影响尤为显著,而PWM开关频率是影响电流时间谐波的重要因素。气隙长度的改变会影响气隙中谐波含量进而影响转子涡流损耗。这些因素的研究对转子涡流损耗具有重要意义。
由图9可以看出,电流时间谐波是造成转子涡流损耗的主要原因,而载波比是影响电流时间谐波的重要因素。图10给出开关频率为2kHz、4kHz、6kHz、12kHz、14kHz、15kHz、16kHz时转子涡流损耗的解析与有限元结果对比。随PWM开关频率的上升,转子涡流损耗呈现显著的下降趋势,当开关频率达到14kHz时,转子涡流损耗下降趋势减缓。

图10 不同开关频率时转子涡流损耗
Fig.10 Rotor eddy current loss at different switching frequencies
为了进一步分析提高开关频率对转子涡流损耗的影响,图11给出不同开关频率时各次电流谐波幅值(未包含基波电流)和基波与各次电流谐波产生的转子涡流损耗。由图11可知,产生涡流损耗的电流谐波次数主要集中在载波比及其倍数次附近。当开关频率较低时,载波比较小,基波附近的低次谐波所产生的损耗占比较大;随着开关频率的提高,载波比增大,此时高频谐波所产生的损耗占比较大。同时,开关频率的提高使得电流波形畸变率降低,从而引起载波比及其倍数次附近电流谐波幅值大幅减小,使得转子涡流损耗呈下降趋势。

图11 不同开关频率下电流谐波幅值及转子损耗
Fig.11 Amplitude of current harmonic and rotor eddy current loss at different switching frequencies
在保证空载反电动势大小基本不变的情况下,本文分别对1mm、1.25mm、1.5mm、1.75mm、2mm、2.25mm、2.5mm气隙长度下转子涡流损耗进行解析和有限元计算,得到转子涡流损耗随气隙长度的变化规律如图12所示。结果显示,在气隙长度小于1.75mm时,转子涡流损耗随气隙长度增加而显著减小,其中护套涡流损耗的减小起主要作用。当气隙长度大于2mm时,转子涡流损耗变化趋缓。具体结果为:气隙长度从1mm增加到1.5mm时转子涡流损耗减少了23.7%,从2mm增加到2.5mm时涡流损耗减少了5.9%。由此可知,当气隙长度增大到一定程度时,转子涡流损耗随着气隙长度增大而减小趋势逐渐变缓,而增大气隙长度的同时永磁体用量也会增加,从而导致生产成本提高。
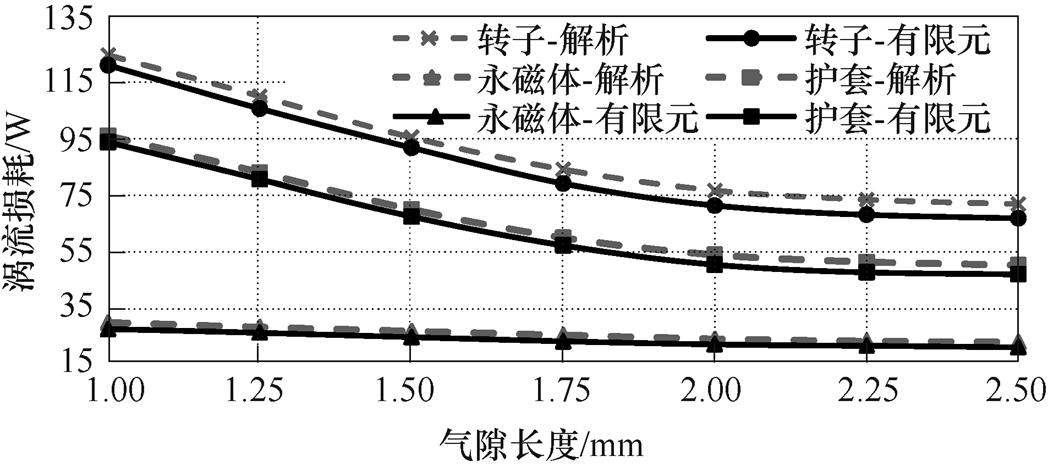
图12 转子涡流损耗随气隙长度的变化
Fig.12 Eddy current loss changes with air gap length
气隙长度的增加主要反映在各次电流时间谐波引起的磁场空间谐波上。以基波电流为例,图13给出不同气隙长度时基波电流引起的各次空间谐波所产生的涡流损耗。从图13中可以看出,第8、10次谐波所产生的涡流损耗最大,而其对应的是一阶齿谐波,由此可以看出,空间谐波中齿谐波对转子涡流损耗影响较大。从图13中还可以看出,气隙长度的增加减小了各次空间谐波所产生的涡流损耗,而且,相比于气隙长度从1mm到1.5mm,从2mm到2.5mm损耗的下降幅度明显变小,因此,各次空间谐波引起的涡流损耗变化导致了图12所示的变化规律。
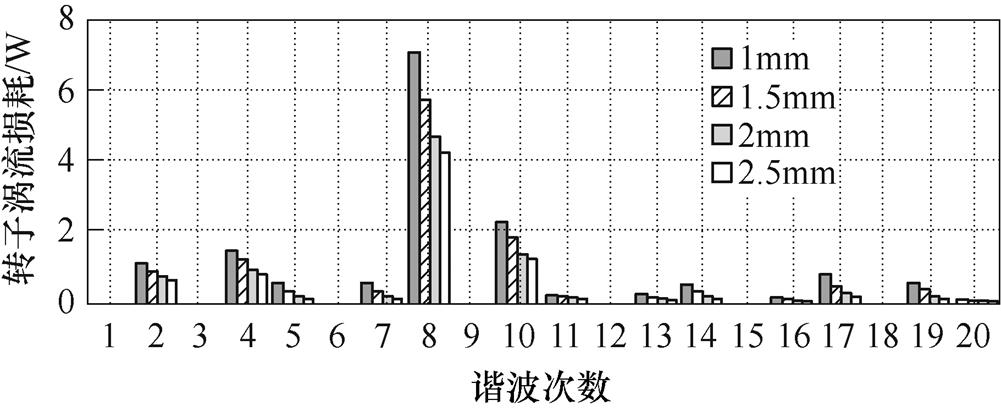
图13 基波电流产生的空间谐波磁场引起的涡流损耗
Fig.13 Rotor eddy current loss induced by space harmonics caused by fundamental current
为了验证解析模型的准确性,本文采用损耗分离的方法获得转子涡流损耗。当电机工作在负载状态,测量电机输入功率和输出功率,从中分离出铜耗、铁耗、机械损耗,进而得到转子总的涡流损耗。该部分损耗分布于护套、永磁体和转子铁心,由于转子铁心距离气隙较远,加之护套的屏蔽作用,因此转子铁心中的损耗很小,可忽略不计(该电机在额定频率下,采用有限元计算得到转子铁心损耗仅为1.75W)。因此,可将损耗分离实验得到的转子涡流损耗近似为护套和永磁体中的涡流损耗。
样机负载实验平台如图14所示。损耗分离实验流程如图15所示。电枢绕组的铜耗包括直流电阻铜耗和由电流趋肤效应与临近效应引起的附加铜耗。根据文献[26]可知,对于多股并绕的圆铜导线绕组,当导线半径小于工作频率对应的导体趋肤深度时,其交流绕组损耗接近于直流绕组损耗,可忽略趋肤效应和邻近效应的影响。本文实验样机额定工作频率为500Hz,基波电流的趋肤深度为2.95mm,而电机采用多股直径为0.56mm的漆包线并绕,其趋肤深度远大于导线的半径,因此,可忽略趋肤效应和邻近效应所引起的附加铜耗。本文通过测量电机热态相电阻和负载电流,计算得到电枢绕组铜耗PCu。

图14 样机负载实验平台
Fig.14 Experimental platform for the load test
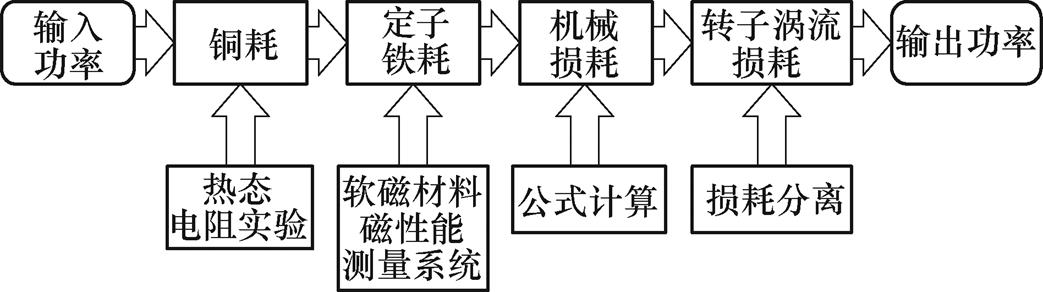
图15 损耗分离实验流程
Fig.15 Flow chart of loss separation experiment
定子铁耗PFe采用文献[27]的计算方法,通过如图16所示的德国MPG 200D AC-DC软磁材料磁性能测量系统测得不同频率、不同磁通密度下非晶合金定子铁心的损耗曲线,通过Matlab工具箱对损耗曲线进行拟合得到非晶合金铁心的损耗系数,将得到的损耗系数输入有限元模型中计算得到定子铁耗,表3为计算时所用到的定子铁心损耗系数。

图16 MPG 200D AC-DC软磁材料磁性能测量平台
Fig.16 MPG 200D AC-DC measurement platform
表3 额定频率非晶合金定子铁心损耗系数
Tab.3 Loss coefficient of amorphous alloy stator core at rated frequencies

参 数数 值 频率/Hz500 磁滞系数0.009 577 涡流系数0.000 040 16 b 系数1.65
机械损耗Pmec包括空气摩擦损耗和轴承摩擦损耗。空气摩擦损耗Pair可参考文献[28-29]公式计算,有
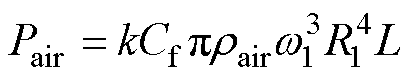 (35)
(35)
其中
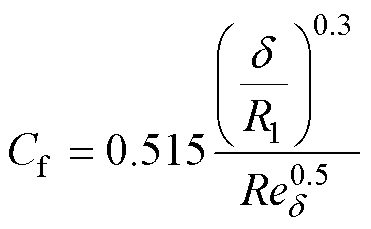 (36)
(36)
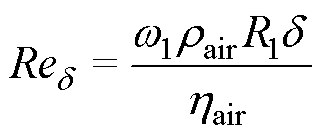 (37)
(37)
式中,k为转子表面粗糙度系数(对于光滑转子表面,k=1);rair为空气密度,rair=1.293kg/m3;R1为转子半径;L为转子轴向长度;w1为转子角速度;Cf为空气摩擦因数;Red为雷诺数;hair为一个大气压下空气的动力粘度,hair=1.8×10-5Pa×s;d 为气隙长度。
轴承摩擦损耗Pbea可以通过文献[30]提出的经验方法从轴承摩擦转矩计算出来,有
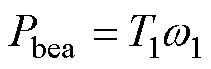 (38)
(38)
式中,T1为总摩擦转矩。总摩擦转矩T1由与负载相关的摩擦转矩TL和粘性摩擦转矩TV组成,有
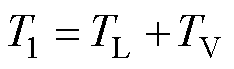 (39)
(39)
与负载相关的摩擦转矩TL的计算公式为
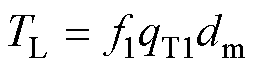 (40)
(40)
其中
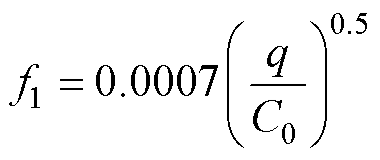 (41)
(41)
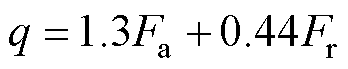 (42)
(42)
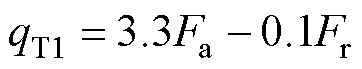 (43)
(43)
式中,dm为轴承内径和外径的平均直径;C0为轴承额定静载荷;Fa为轴承的轴向加载力;Fr为转子重力。
粘性摩擦转矩TV为
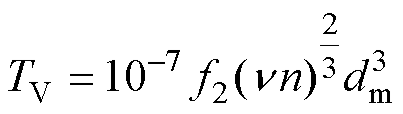 (44)
(44)
式中,f2为润滑系数,f2=1.75; 为润滑剂工作粘度,
为润滑剂工作粘度, =4.5cSt;n为轴承转速。
=4.5cSt;n为轴承转速。
转子涡流损耗Protor为
 (45)
(45)
式中,P1为电机输入功率;P2为电机输出功率。
在电机温升稳定情况下,测量得到额定转速下不同负载的输入和输出功率见表4,同时给出采用损耗分离方法得到的各部分损耗值。图17给出额定转速下不同输出功率时解析、有限元和实验转子涡流损耗的结果对比。
表4 不同负载下电机各部分损耗
Tab.4 Loss of each part of the motor under different load

P1/kWP2/kWPCu/WPmec/WPFe/WProtor/W 5.485.1573.846.93142.1267.15 6.396.0485.947.514769.6 6.756.3895.847.72153.6772.81 7.927.5123.848.43162.6385.14
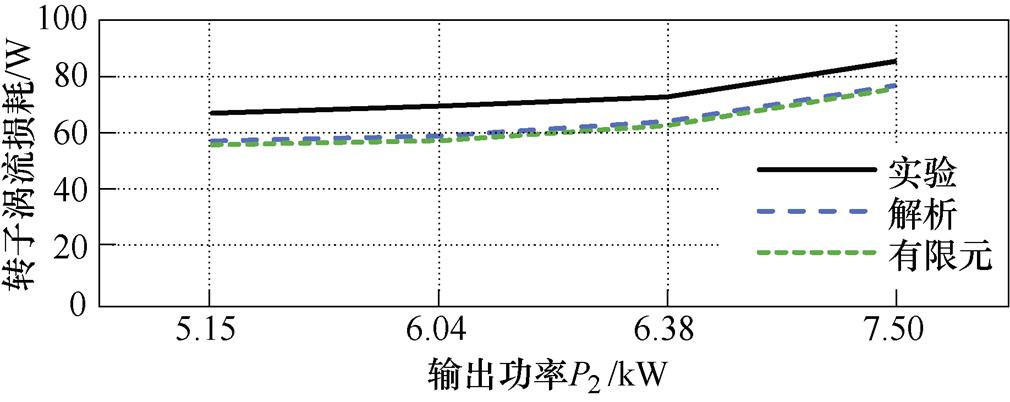
图17 解析、有限元结果与实验结果对比
Fig.17 Comparison of analytical results and finite element results with experimental results
由图17可知,解析模型的计算结果和有限元仿真结果与实验结果相比平均误差分别为12.7%和14.6%。导致解析和有限元的计算结果与实验结果存在误差的原因:一方面是由于有限元和解析模型均为二维模型,未考虑端部效应所引起的涡流损耗;另一方面是损耗分离实验中各部分损耗计算存在误差导致分离出的转子涡流损耗也存在一定误差。
本文基于精确子域法,通过在有源区域内求解包含时间导数及导体运动速度的扩散方程,建立了一个考虑各次时空谐波和涡流反作用的带有护套的高速永磁电机转子涡流损耗解析模型,并给出了详细的计算过程。该模型通过建立槽口子域考虑槽口对磁场影响,提高计算精度,并引入周期系数减小系数矩阵,提高了计算速度。
通过计算PWM供电开关频率和气隙长度对转子涡流损耗的影响,得出随着PWM供电开关频率和气隙长度的增加,转子涡流损耗逐渐减小并趋于平缓。采用损耗分离实验得到转子涡流损耗,将解析、实验和有限元结果对比,验证了解析模型的正确性。
以图3a所示绕组为例,对各个区域系数进行求解。在槽顶与槽开口区域,根据矢量磁位连续可得
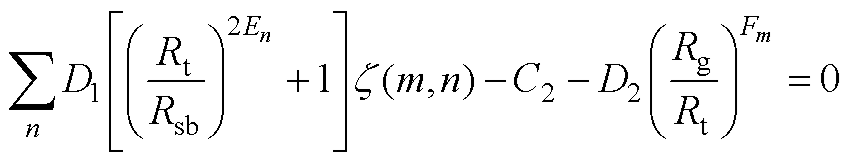 (A1)
(A1)
其中
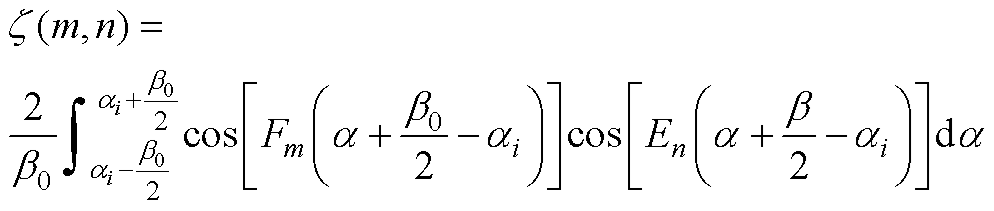 (A2)
(A2)
当Fm=En时
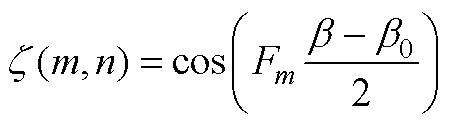 (A3)
(A3)
当Fm¹En时
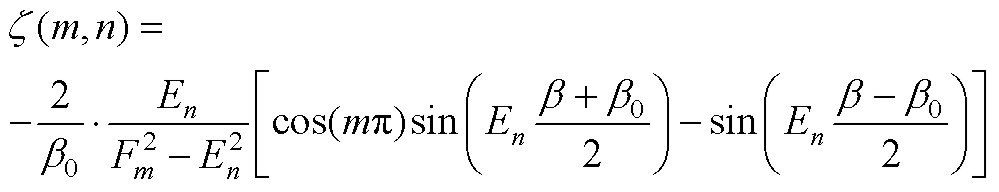 (A4)
(A4)
由切向磁场强度连续得
 (A5)
(A5)
其中
 (A6)
(A6)
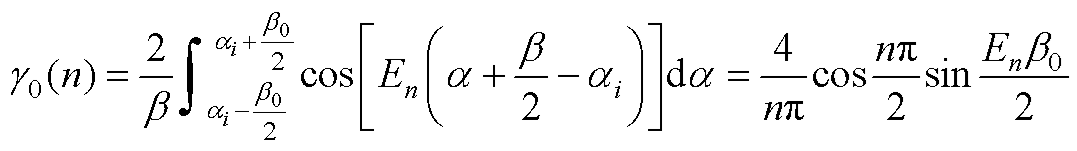 (A7)
(A7)
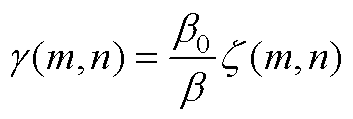 (A8)
(A8)
在槽开口与气隙区域根据矢量磁位连续,可得
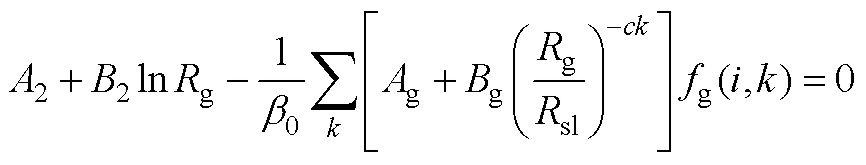 (A9)
(A9)
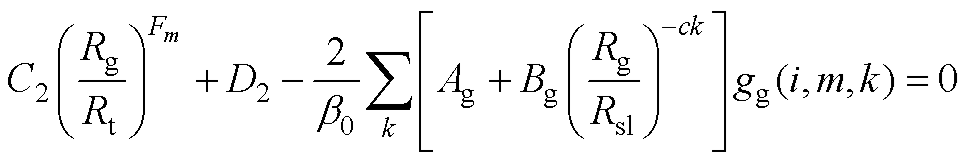 (A10)
(A10)
其中
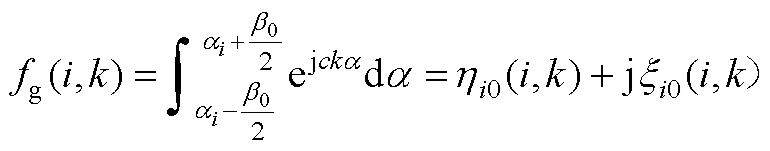 (A11)
(A11)
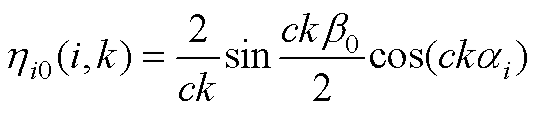 (A12)
(A12)
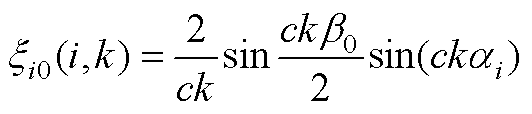 (A13)
(A13)
 (A14)
(A14)
当Fm=k时
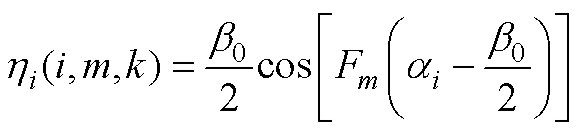 (A15)
(A15)
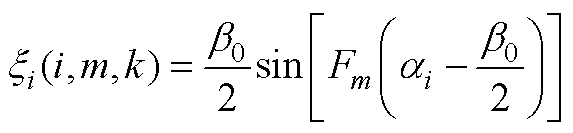 (A16)
(A16)
当Fm¹k时
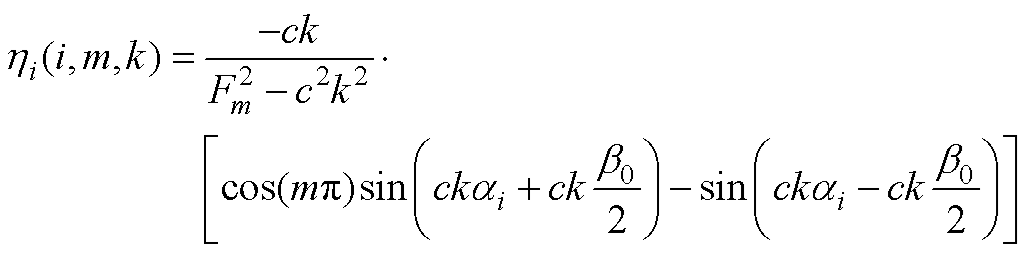 (A17)
(A17)
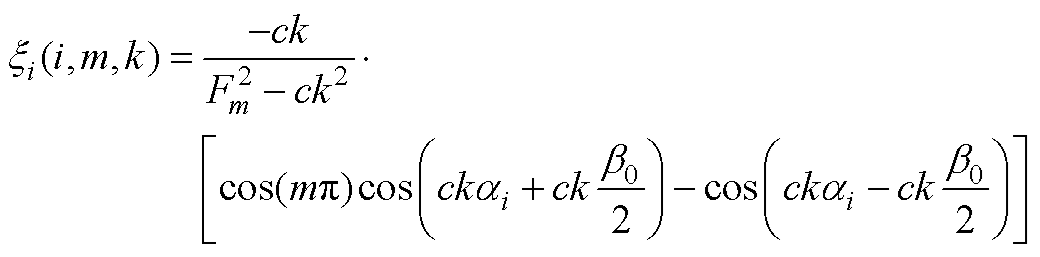 (A18)
(A18)
根据切向磁场强度连续得
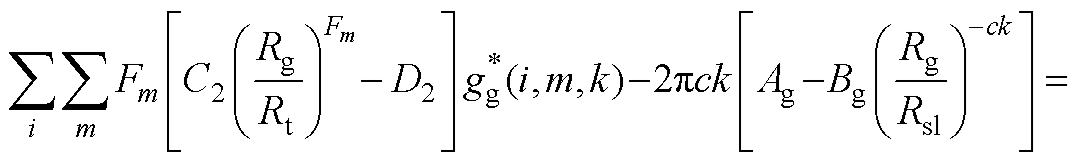
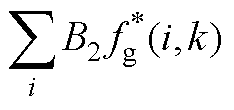 (A19)
(A19)
气隙与护套区域间由矢量磁位连续得
 (A20)
(A20)
由切向磁场强度连续得
 (A21)
(A21)
护套与永磁体区域,由矢量磁位连续得
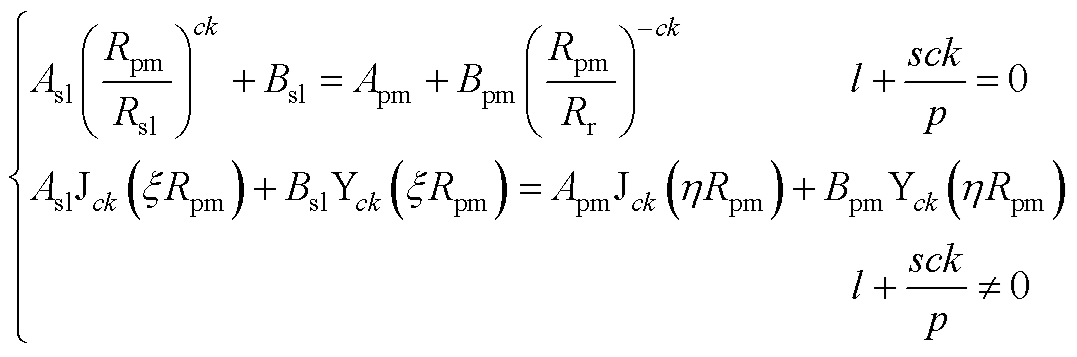 (A22)
(A22)
根据切向磁场强度连续得
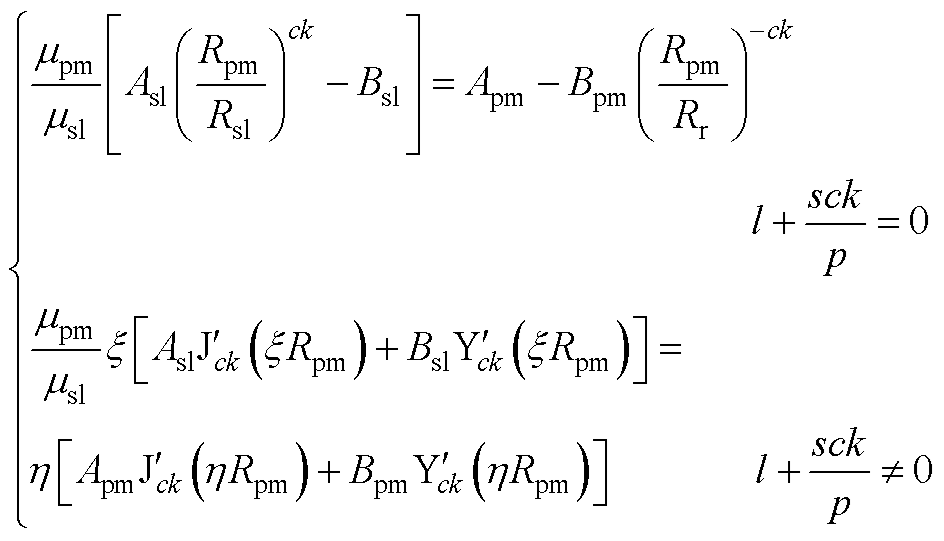 (A23)
(A23)
在永磁体与铁心区域之间,根据切向磁场强度得
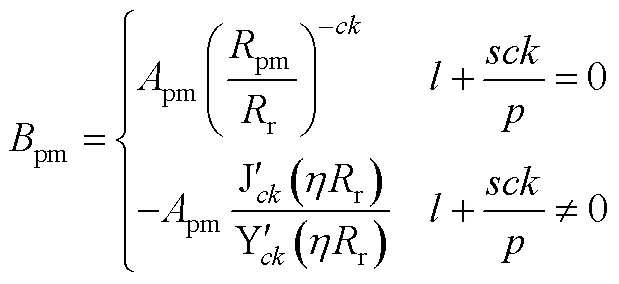 (A24)
(A24)
将式(A1)、式(A5)、式(A9)、式(A10)、式(A19)~式(A24)联立方程组,通过数学软件,取有限阶次,建立矩阵对系数进行求解。
参考文献
[1] 沈建新, 韩婷, 尧磊, 等. 提高永磁体电阻率对降低高速永磁交流电机转子涡流损耗的有效性分析(英文)[J]. 电工技术学报, 2020, 35(9): 2074-2078.
Shen Jianxin, Han Ting, Yao Lei, et al. Is higher resistivity of magnet beneficial to reduce rotor eddy current loss in high-speed permanent magnets AC machines?[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2074-2078.
[2] 张凤阁, 杜光辉, 王天煜, 等. 高速电机发展与设计综述[J]. 电工技术学报, 2016, 31(7): 1-18.
Zhang Fengge, Du Guanghui, Wang Tianyu, et al. Review on development and design of high speed machines[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 1-18.
[3] Ma Jie, Zhu Z Q. Optimal split ratio in small high speed PM machines considering both stator and rotor loss limitations[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(1): 3-11.
[4] Cheng Xin, Xu Wei, Du Guanghui, et al. Novel rotors with low eddy current loss for high speed permanent magnet machines[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(2): 187-194.
[5] Yamazaki K, Fukushima Y, Sato M. Loss analysis of permanent-magnet motors with concentrated windings-variation of magnet eddy-current loss due to stator and rotor shapes[J]. IEEE Transactions on Industry Applications, 2009, 45(4): 1334-1342.
[6] Fu Xinghe, Xu Da, Lin Mingyao, et al. Calculation and analysis of rotor eddy current loss of permanent magnet-inductor hybrid excited synchronous gener- ator[J]. IEEE Transactions on Magnetics, 2013, 49(5): 2389-2392.
[7] 高锋阳, 齐晓东, 李晓峰, 等. 部分分段Halbach永磁同步电机优化设计[J]. 电工技术学报, 2021, 36(4): 787-800.
Gao Fengyang, Qi Xiaodong, Li Xiaofeng, et al. Optimization design of partially-segmented Halbach permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(4): 787-800.
[8] Ishak D, Zhu Z Q, Howe D. Eddy-current loss in the rotor magnets of permanent-magnet brushless machines having a fractional number of slots per pole[J]. IEEE Transactions on Magnetics, 2005, 41(9): 2462-2469.
[9] Wang Jiabin, Atallah K, Chin R, et al. Rotor eddy- current loss in permanent-magnet brushless AC machines[J]. IEEE Transactions on Magnetics, 2010, 46(7): 2701-2707.
[10] Zhu Z Q, Ng K, Schofield N, et al. Improved analytical modelling of rotor eddy current loss in brushless machines equipped with surface-mounted permanent magnets[J]. IEE Proceedings-Electric Power Applications, 2004, 151(6): 641-650.
[11] 唐任远, 陈萍, 佟文明, 等. 考虑涡流反作用的永磁体涡流损耗解析计算[J]. 电工技术学报, 2015, 30(24): 1-10.
Tang Renyuan, Chen Ping, Tong Wenming, et al. Analytical calculation of eddy current loss accounting for eddy current reaction[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 1-10.
[12] Zarko D, Ban D, Lipo T A. Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent-magnet motor using complex relative air-gap permeance[J]. IEEE Transactions on Magnetics, 2006, 42(7): 1828-1837.
[13] Qazalbash A A, Sharkh S M, Irenji N T, et al. Rotor eddy loss in high-speed permanent magnet syn- chronous generators[J]. IET Electric Power Appli- cations, 2015, 9(5): 370-376.
[14] Chiodetto N, Bianchi N, Alberti L. Improved analytical estimation of rotor losses in high-speed surface-mounted PM synchronous machines[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3548-3556.
[15] Zhu Z Q, Wu Lijian, Xia Zhenping. An accurate subdomain model for magnetic field computation in slotted surface-mounted permanent-magnet machines[J]. IEEE Transactions on Magnetics, 2010, 46(4): 1100- 1115.
[16] Wu Lijian, Zhu Z Q, Staton D, et al. Analytical modeling and analysis of open-circuit magnet loss in surface-mounted permanent-magnet machines[J]. IEEE Transactions on Magnetics, 2012, 48(3): 1234-1247.
[17] Wu Lijian, Zhu Z Q, Staton D, et al. Analytical model for predicting magnet loss of surface-mounted per- manent magnet machines accounting for slotting effect and load[J]. IEEE Transactions on Magnetics, 2012, 48(1): 107-117.
[18] Atallah K, Howe D, Mellor P H, et al. Rotor loss in permanent-magnet brushless AC machines[J]. IEEE Transactions on Industry Applications, 2000, 36(6): 1612-1618.
[19] 孙权贵, 邓智泉, 张忠明. 基于齿槽效应的高速永磁电机转子涡流损耗解析计算[J]. 电工技术学报, 2018, 33(9): 1994-2004.
Sun Quangui, Deng Zhiquan, Zhang Zhongming. Analytical calculation of rotor eddy current losses in high speed permanent magnet machines accounting for influence of slot opening[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 1994- 2004.
[20] Pfister P D, Yin Xin, Fang Youtong. Slotted permanent- magnet machines: general analytical model of mag- netic fields, torque, eddy currents, and permanent- magnet power losses including the diffusion effect[J]. IEEE Transactions on Magnetics, 2016, 52(5): 1-13.
[21] Chen Liang, Wang Jiabin, Nair S S. An analytical method for predicting 3-D eddy current loss in permanent magnet machines based on generalized image theory[J]. IEEE Transactions on Magnetics, 2016, 52(6): 1-11.
[22] Nair S S, Wang Jiabin, Chin R, et al. Analytical prediction of 3-D magnet eddy current losses in surface mounted PM machines accounting slotting effect[J]. IEEE Transactions on Energy Conversion, 2017, 32(2): 414-423.
[23] Nair S S, Wang Jiabin, Chen Liang, et al. Prediction of 3-D high-frequency eddy current loss in rotor magnets of SPM machines[J]. IEEE Transactions on Magnetics, 2016, 52(9): 1-10.
[24] Tong Wenming, Li Shiqi, Pan Xuelong, et al. Analytical model for cogging torque calculation in surface-mounted permanent magnet motors with rotor eccentricity and magnet defects[J]. IEEE Transactions on Energy Conversion, 2020, 35(4): 2191-2200.
[25] 张守首, 郭思源. 考虑分段斜极和磁性槽楔的永磁同步电机磁场解析方法[J]. 电工技术学报, 2019, 34(1): 11-22.
Zhang Shoushou, Guo Siyuan. Analytical magnetic field method of permanent magnet synchronous machine considering step-skewed magnets and mag- netic slot wedge[J]. Transactions of China Elec- trotechnical Society, 2019, 34(1): 11-22.
[26] Gonzalez D A, Saban D M. Study of the copper losses in a high-speed permanent-magnet machine with form-wound windings[J]. IEEE Transactions on Industrial Electronics, 2014, 61(6): 3038-3045.
[27] Tong Wenming, Li Shiqi, Sun Ruolan, et al. Modified core loss calculation for high-speed PMSMs with amorphous metal stator cores[J]. IEEE Transactions on Energy Conversion, 2021, 36(1): 560-569.
[28] Sarri J. Thermal analysis of high-speed induction machines[D]. Finland: Helsinki University of Tech- nology, 1998.
[29] Huang Ziyuan, Fang Jiancheng, Liu Xiquan, et al. Loss calculation and thermal analysis of rotors supported by active magnetic bearings for high-speed permanent-magnet electrical machines[J]. IEEE Transa- ctions on Industrial Electronics, 2016, 63(4): 2027- 2035.
[30] Brändlein J. Ball and roller bearings: theory, design, and application[M]. 3rd ed. Chichester: John Wiley, 1999.
Analytical Method of Rotor Eddy Current Loss for High-Speed Surface-Mounted Permanent Magnet Motor with Rotor Retaining Sleeve
Abstract When calculating the rotor eddy current loss (RECL) by the existing two-dimensional accurate subdomain method, in order to facilitate the solution of the coefficient matrix, the influence of the eddy current reaction is usually ignored. For high-speed permanent magnet synchronous motors (HS-PMSM) powered by converters, the armature current contains a large number of time harmonics, and the eddy current reaction has a great influence on the RECL. Ignoring the eddy current reaction seriously affects the calculation accuracy. Based on the accurate subdomain method, an analytical model for RECL analysis in HS-PMSM is established by solving the diffusion equation including time derivative and conductor motion velocity in the active region. An equation is established in the slot opening considering the influence of the slot opening on the magnetic field to improve the calculation accuracy, and periodic boundary conditions are established using the periodicity of the motor to increase the calculation speed. Then, the eddy current loss changes caused by time-space harmonics are analyzed at different inverter switching frequencies and air gap lengths. Through a loss separation experiment of a 7.5kW amorphous alloy HS-PMSM, the comparison of the analytical results, the finite element results and experimental results verifies the analytical model.
keywords:High-speed permanent magnet motor, accurate subdomain model, eddy current reaction, periodic boundary conditions, loss separation experiment
DOI: 10.19595/j.cnki.1000-6753.tces.210424
中图分类号:TM351
国家重点研发计划(2016YFB0300503)、辽宁省“兴辽英才计划”(XLYC2007107)和辽宁省百千万人才工程资助项目。
收稿日期 2021-03-28
改稿日期 2021-05-21
佟文明 男,1984年生,教授,博士生导师,研究方向为高品质永磁电机及其控制。E-mail: twm822@126.com(通信作者)
侯明君 男,1996年生,硕士研究生,研究方向为高速永磁电机转子涡流损耗。E-mail: hmj104107@163.com
(编辑 崔文静)