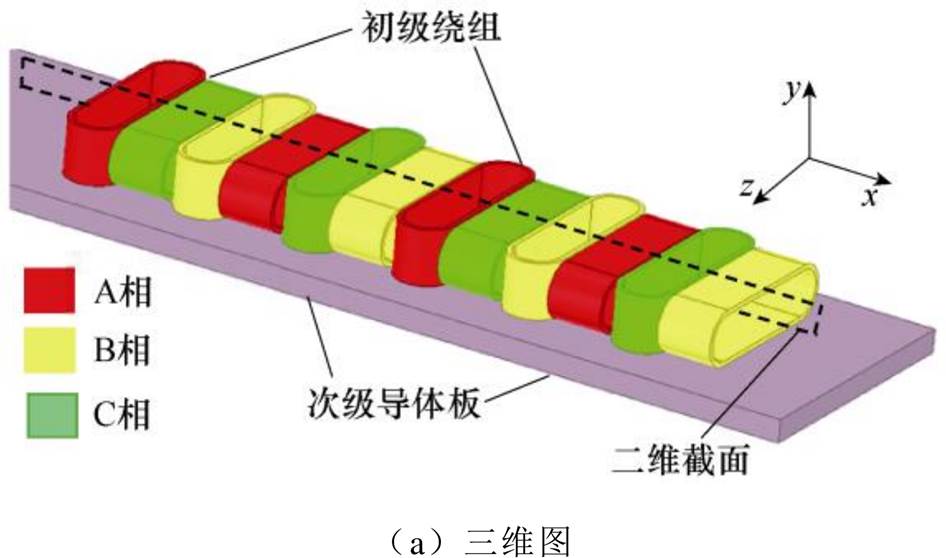
图1 无铁心直线感应悬浮电机拓扑结构
Fig.1 Topology of CLIMM
摘要 该文研究一种适用于低真空管道高速磁悬浮列车的高温超导无铁心直线感应悬浮电机,该电机是一种可以同时提供悬浮力和推进力的一体化电动式磁悬浮系统。首先,介绍该新型直线感应悬浮电机的拓扑结构及其工作原理。其次,采用积分法求解得到电机初级绕组的矢量磁位,以矢量磁位为求解变量,建立该新型直线电机的二维解析模型,得到各子域矢量磁位和磁通密度的数学表达式。在此基础上,研究无铁心初级绕组排列方式、导体板厚度等不同参数对电机性能的影响。最后,通过小型样机实验和有限元仿真计算,来验证解析模型的准确性和合理性。
关键词:低真空管道 磁悬浮 积分法 电磁特性 解析模型
磁悬浮列车具有运行速度高、爬坡能力强、转弯半径小、环保性能好、线路适应性强、安全可靠等诸多优点[1-4],可有效弥补高铁和航空之间的速度空白,助推我国立体交通网络的构建。磁悬浮成为新时代轨道交通创新发展的技术方向[5-7]。电动式磁悬浮(electrodynamic suspension)具有气隙大、稳定性强、能耗低、控制简单等优点[8-11],同时随着列车运行速度的提高,其运行稳定性更好。因此,电动式磁悬浮是高速磁悬浮系统和低真空管道列车的重要发展方向[12]。
现阶段研究的电动式磁悬浮方案主要有超导电动悬浮和永磁电动悬浮[2, 13-15]。超导电动悬浮技术使用两套电磁系统,实现其在三维空间的电磁约束。该电动悬浮方案存在工程造价高、悬浮和导向性能差、抬升速度高及后期维护量大等技术缺陷,阻碍了其在高速磁悬浮系统的应用和发展。
永磁电动悬浮技术轨道采用金属感应板,系统可靠性更高、制造和运营成本更低。根据主磁通磁路的不同,永磁电动悬浮技术可分为直线型[16-17]、径向磁通型[18-20]和轴向磁通型[21-23]。直线型永磁电动悬浮存在运行阻力大、浮阻比小等问题;径向磁通型永磁电动悬浮的磁体有效利用率和有效载荷都较低,且悬浮力与推力无法独立解耦控制;轴向磁通型永磁电动悬浮需要在“不均匀”气隙工况下才可以产生推进和导向力,造成系统推进、导向困难。而且永磁电动悬浮系统内部只存在单一永磁励磁源,气隙磁场调节困难,从而限制了其运行调速范围、高效区拓展以及故障保护的能力。同时,永磁电动悬浮系统本身是临界稳定的,容易受到外界的干扰而引起振动,且由于自身欠阻尼的特性,受到外界干扰后系统将无法收敛,在实际应用中会产生灾难性的后果,阻碍了永磁电动悬浮技术的推广应用。
在总结前人研究的基础上,本文提出了初级无铁心高温超导直线感应悬浮电机方案,该电机是一种可以同时产生悬浮力和推进力的一体化电动式磁悬浮技术。相对于现有的磁悬浮方案,该方案具有如下特点:
(1)该电机可同时产生悬浮与推进力,且轨道只含有非磁性金属导体板(铜或铝),结构简单、可靠高且成本较低,适合长行程应用下全行程范围内铺设。
(2)初级绕组采用无铁心的空芯线圈,不存在铁心磁饱和问题,可通过提高励磁电流获得适用于超高速管道高铁所需的动力,提高了磁悬浮系统的“浮重比”和运载能力。
本文立足于电机初级拓扑结构的设计,提出一种新型电磁Halbach阵列,并研究了阵列结构参数对电机性能的影响。首先,采用积分法求解电磁Halbach线圈阵列的矢量磁位函数,之后对该函数进行了傅里叶级数转换,使初级无铁心绕组的磁场函数具有连续统一的解析表达式。然后,建立考虑纵向边端效应的无铁心直线感应悬浮电机(Coreless Linear Induction Maglev Motor, CLIMM)的全域解析模型。最后,利用矢量磁位和边界条件对电机的电磁关系进行了分析,得到悬浮力、推进力和效率等关键性能指标的解析表达式。通过研究初级绕组结构的排列方式、导体板厚度等不同结构参数对悬浮力、牵引力和效率的影响,给出适用于磁悬浮轨道交通的设计参数,为进一步开展工程化应用提供理论支撑。
该新型磁悬浮电机包括初级和次级两部分。次级只含有非磁性金属导体板(铜或铝),结构简单可靠且成本较低。初级由三相空芯线圈和不导电的非磁性线圈骨架构成,空芯线圈由开口方向垂直于导体板的竖直线圈和开口方向平行于导体板的水平线圈两组线圈组成,两组线圈在空间上有一定的相位差。对称三相线圈依次错开120°电角度,均匀地绕制在非磁性骨架上,无铁心直线感应悬浮电机拓扑结构如图1所示,其中图1b为图1a沿虚线所示的平面将电机切开所得的二维截面图。


图1 无铁心直线感应悬浮电机拓扑结构
Fig.1 Topology of CLIMM
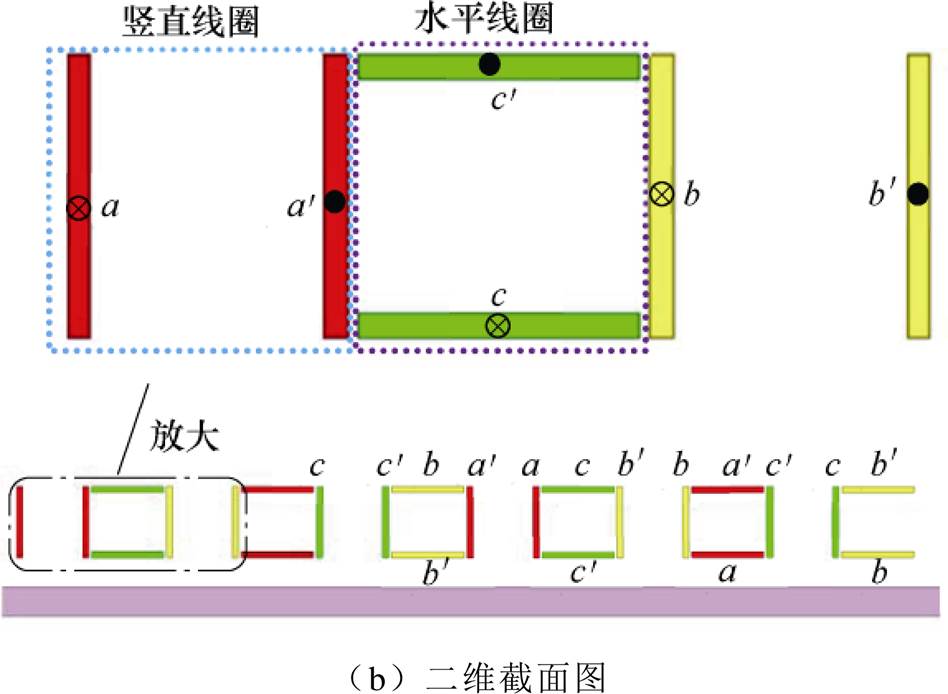
当三相绕组中通入合适的对称三相交变电流时,就会在气隙中产生行波磁场,从而在次级轨道导体板中感应出涡流,涡流磁场与初级源磁场相互作用,即可同时产生悬浮和牵引力,实现车体的悬浮和推进运行。通过合理排列两组线圈的空间位置,可以使得初级绕组其中一侧的磁场得以加强从而提高电机的力能密度,又可以使得另一磁场减弱实现自屏蔽,减小对外辐射,初级绕组的磁场特性如图2所示。
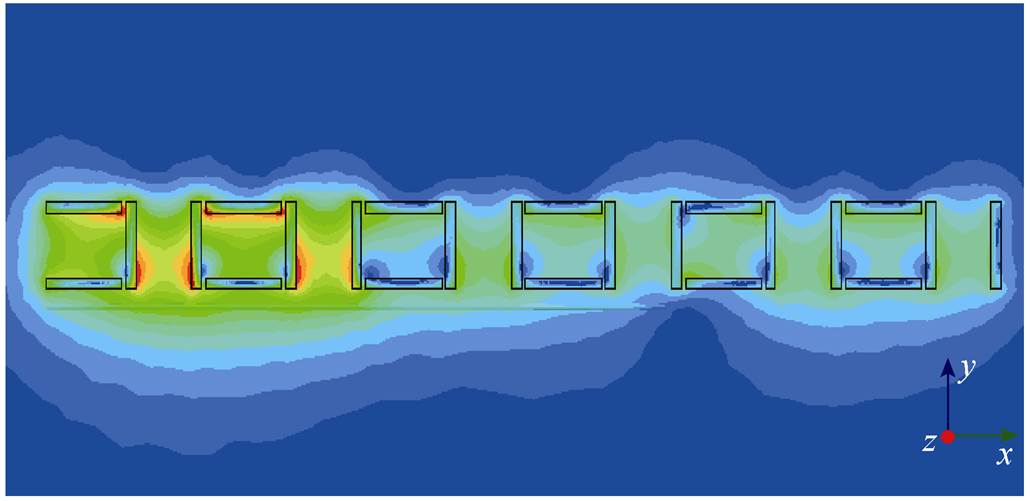
图2 初级绕组的磁场特性
Fig.2 Contour plot of flux density for the primary
为了简化模型,做如下假设:
(1)初级绕组电流沿z方向流动,各电磁参量与z无关。
(2)次级导体板沿x方向无限长。
(3)气隙磁场强度沿z轴是恒定的值。
(4)所有电磁场参量均为x轴和时间t的函数。
为使得初级无铁心绕组实现磁场一侧加强,另一侧减弱,本文提出了电磁Halbach阵列,如图2所示,其线圈结构是竖直线圈和水平线圈交替排列。由于本文提出的电机系统中不含任何铁磁物质,属于线性系统,为便于明确初级绕组的电磁机理,可将电磁Halbach阵列分为独立的竖直线圈阵列和水平线圈阵列分别求解,如图3和图4所示,G 为线圈宽度,L为极距,然后利用叠加定理将两种阵列的空间磁场进行叠加。
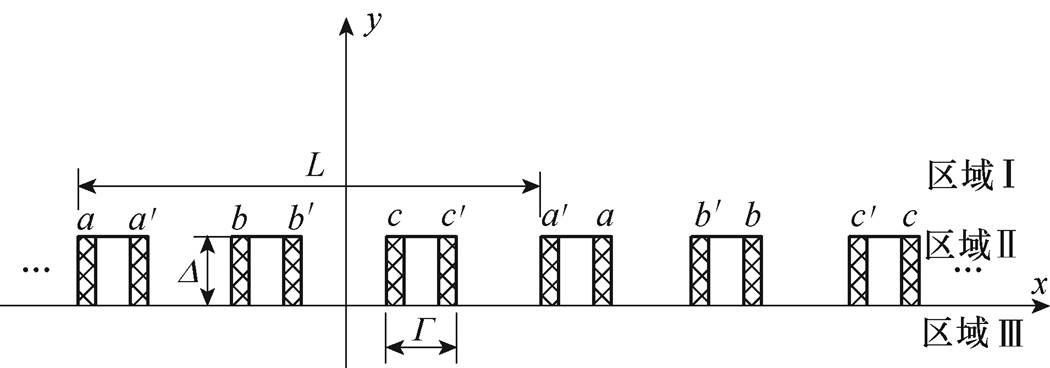
图3 竖直线圈的解析模型
Fig.3 Analytical model for vertical coil
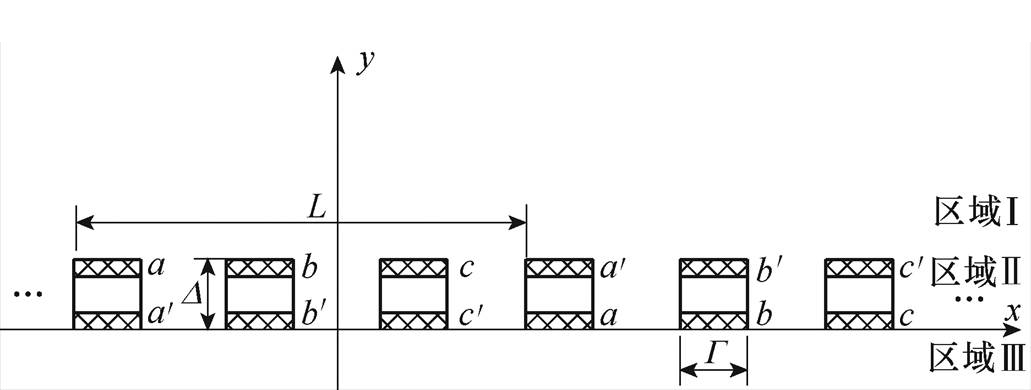
图4 水平线圈的解析模型
Fig.4 Analytical model for horizontal coil
采用积分法求解初级绕组线圈的矢量磁位。一个线圈边可视为矩形截面载流导体,由假设(2)可知,电流密度只有z向分量Jz,通过电流密度的面积分,可得矩形截面载流导体的矢量磁位为
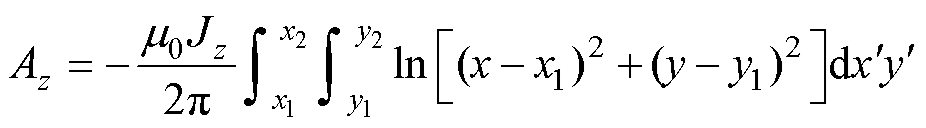 (1)
(1)
式中,m0为真空磁导率;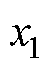 、
、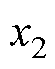 为线圈边在x轴上对应的坐标;
为线圈边在x轴上对应的坐标;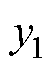 、
、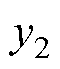 为线圈边在y轴上对应的坐标。该积分过程可以通过Mathematica快速求解。通过叠加定理,将电机初级所有线圈边的矢量磁位相加,即可得到电磁Halbach阵列的总矢量磁位。
为线圈边在y轴上对应的坐标。该积分过程可以通过Mathematica快速求解。通过叠加定理,将电机初级所有线圈边的矢量磁位相加,即可得到电磁Halbach阵列的总矢量磁位。
通过对矢量磁位A求偏导,可得线圈在二维空间的磁感应强度为
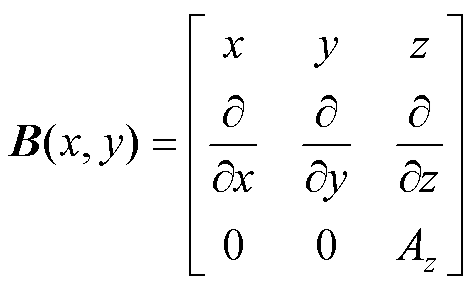 (2)
(2)
计算参数见表1。
表1 计算参数
Tab.1 Parameters of calculation

参 数数 值 竖直线圈截面宽度/mm120 竖直线圈截面高度/mm120 竖直线圈边宽度/mm20 水平线圈截面宽度/mm120 水平线圈截面高度/mm120 水平线圈边宽度/mm20 电流密度/(A/m2)1×108
基于表1数据,计算了水平线圈和竖直线圈在距离其下表面10mm处的法向磁感应强度,结果对比如图5所示。从图中可以看到,水平线圈磁场和竖直线圈磁感应强度在相位上相差90°电角度。因此,水平线圈和竖直线圈在空间位置上相差90°电角度,即可实现电磁Halbach阵列的磁场在一侧得到加强和另外一侧减弱的效果,如图6所示。依据上述电磁Halbach阵列的拓扑规律,提出了改进型电磁Halbach阵列,如图7所示。
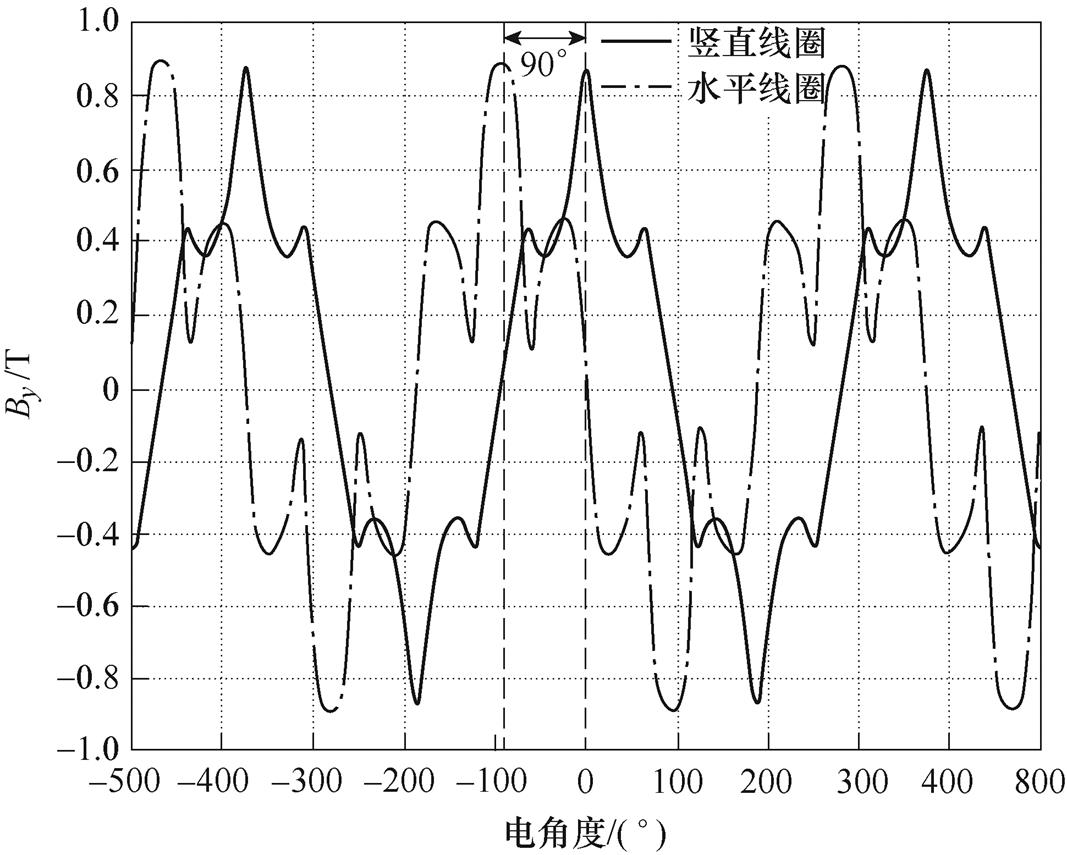
图5 水平和竖直线圈磁感应强度计算结果对比
Fig.5 Field comparison between vertical coils and horizontal coils
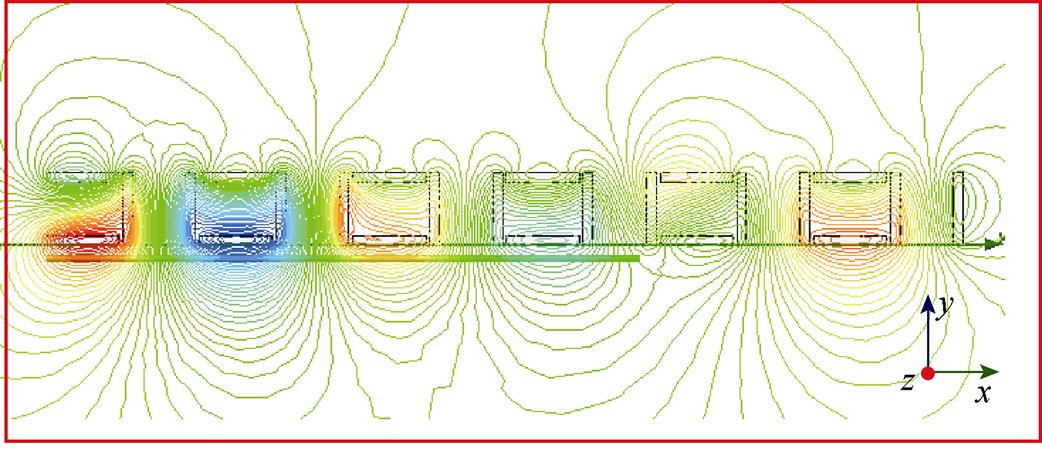
图6 电磁Halbach阵列的磁力线分布(t =0)
Fig.6 The flux line of the electromagnetic Halbach at t =0
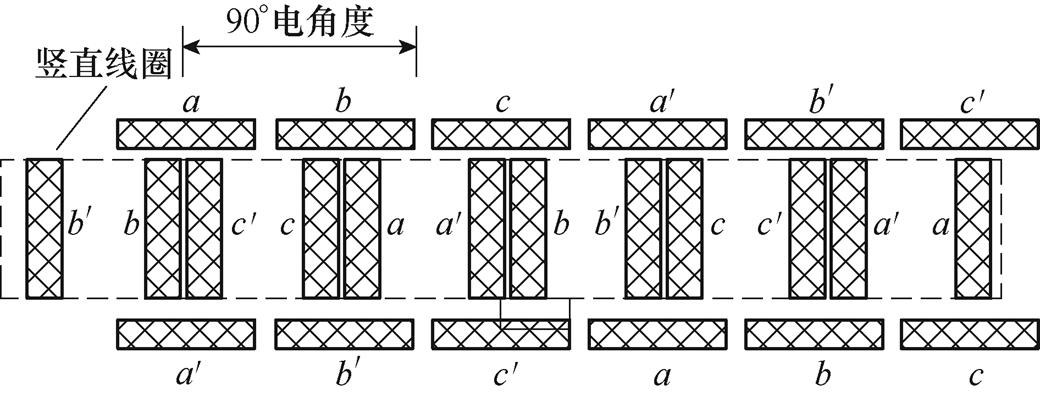
图7 改进型电磁Halbach阵列
Fig.7 The improved traveling magnetic electromagnetic Halbach array
通过积分法,可以计算电磁Halbach阵列的二维空间磁场分布,但是所得结果是离散的数值点。本节通过离散傅里叶变换(Discrete Fourier Transform, DFT)将离散的数值点用傅里叶级数的形式表示,从而使得二维空间磁场具有形式上统一的解析表达式,为计算电机电磁特性奠定基础。
傅里叶级数重构计算模型如图8所示,假设距离电磁Halbach阵列下表面g处,沿x轴方向任一点的y向磁感应强度By可表示为
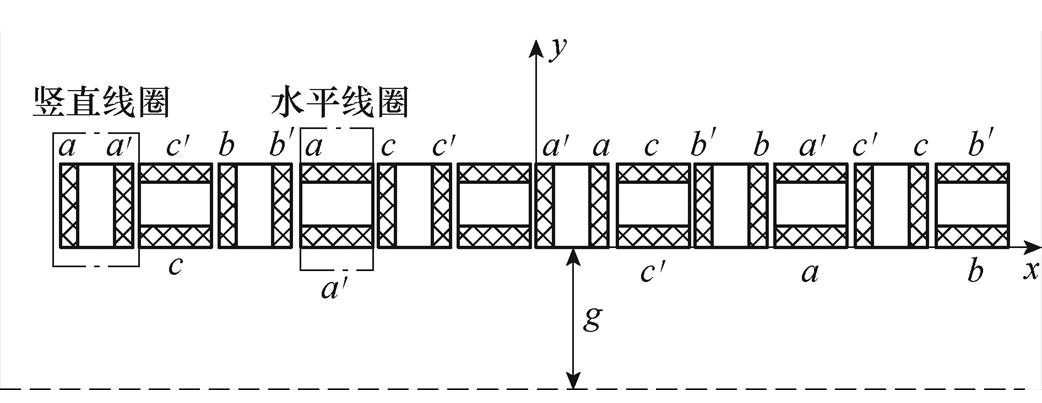
图8 傅里叶级数重构计算模型
Fig.8 Model for Fourier series
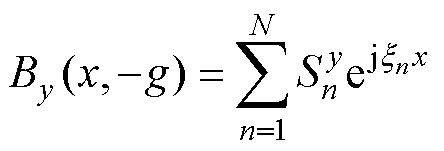 (3)
(3)
其中
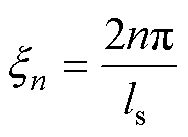
式中,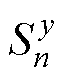 为傅里叶系数;ls为磁场衰减为0的计算长度,通过选取合适的计算长度(一般选取初级长度的1.5~2倍),可将电机初级开断造成的磁场畸变,即入端和出端对气隙磁场的影响考虑在内,如图9中点画线部分,从而得到考虑了基本行波、入端行波和出端行波的气隙磁通密度解析表达式,实现了纵向边端效应的磁场解析建模。
为傅里叶系数;ls为磁场衰减为0的计算长度,通过选取合适的计算长度(一般选取初级长度的1.5~2倍),可将电机初级开断造成的磁场畸变,即入端和出端对气隙磁场的影响考虑在内,如图9中点画线部分,从而得到考虑了基本行波、入端行波和出端行波的气隙磁通密度解析表达式,实现了纵向边端效应的磁场解析建模。
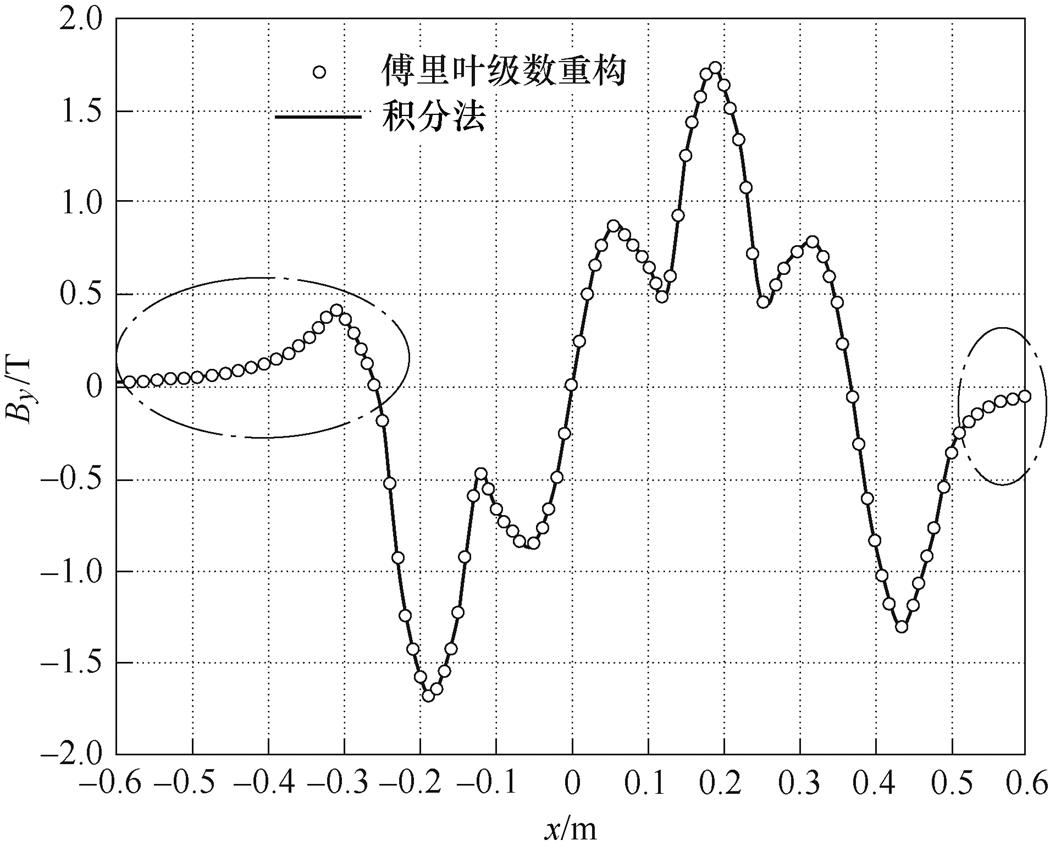
图9 傅里叶级数重构与积分法计算结果对比
Fig.9 Comparison of By by the integral approach and Fourier transform reconstructed
通过傅里叶变换可得
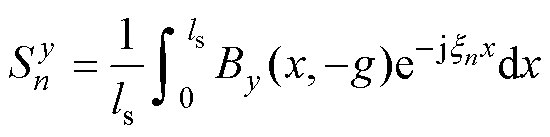 (4)
(4)
通过式(4)可求得傅里叶系数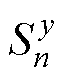 ,即可得到运动磁场的电磁Halbach阵列空间磁场的连续函数表达式。
,即可得到运动磁场的电磁Halbach阵列空间磁场的连续函数表达式。
图9所示是通过积分法和傅里叶级数重构两种方法计算的沿x轴分布的y向磁感应强度,从图中看到,两种方法计算的结果完全一致,证明了傅里叶级数表达式的正确性和有效性。
建立无铁心直线感应悬浮电机的无初级等效解析模型,电机等效计算模型空间划分如图10所示。磁场空间可等效化分为3个区域,气隙区域1、导体板区域2和气隙区域3。以矢量磁位A为求解变量,计算该电机的电磁特性,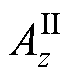 、
、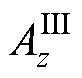 分别为导体板区域和气隙区域3的矢量磁位的z向分量。气隙区域1的矢量磁位A分为:电磁Halbach阵列产生的源磁场
分别为导体板区域和气隙区域3的矢量磁位的z向分量。气隙区域1的矢量磁位A分为:电磁Halbach阵列产生的源磁场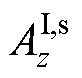 和导体板涡流产生的反射磁场
和导体板涡流产生的反射磁场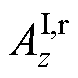 ,可表示为
,可表示为
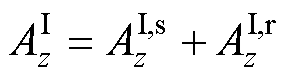 (5)
(5)
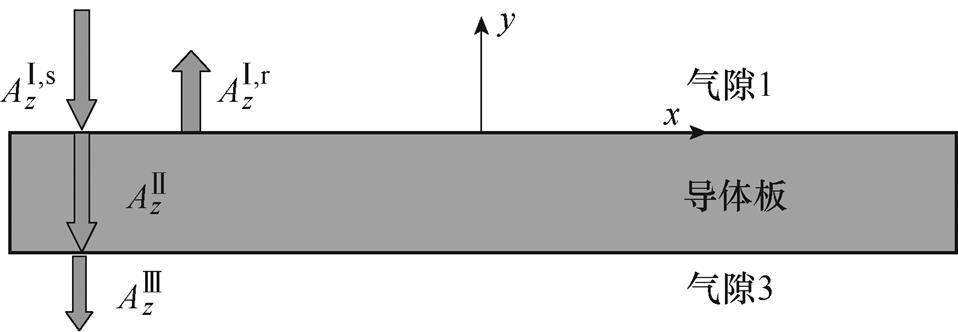
图10 电机等效计算模型空间划分
Fig.10 Sketch of dividing spaces for CLIMM
在直角坐标系下,各区域控制方程分别为
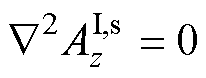 气隙1 (6)
气隙1 (6)
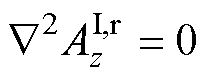 气隙1 (7)
气隙1 (7)
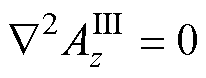 气隙3 (8)
气隙3 (8)
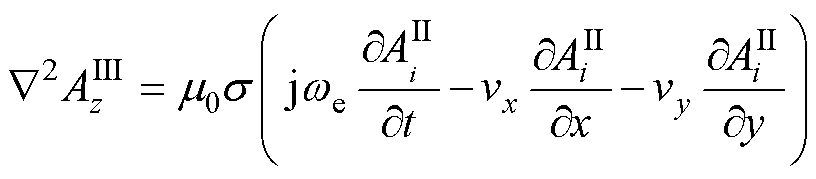 导体板2(9)
导体板2(9)
由分离变量法可得式(6)~式(9)的通解分别为
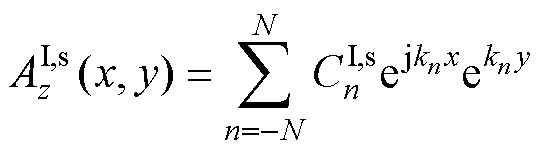 (10)
(10)
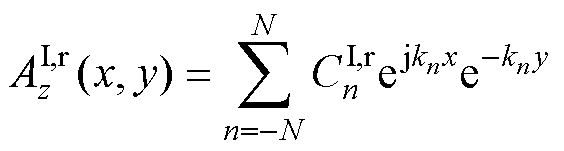 (11)
(11)
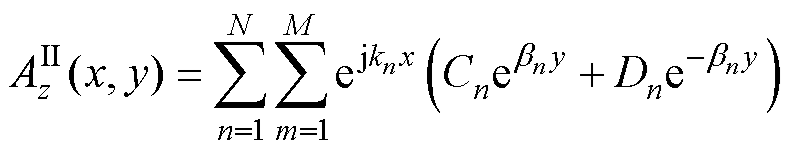 (12)
(12)
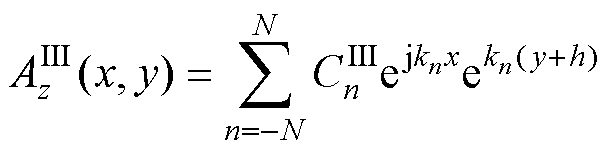 (13)
(13)
其中
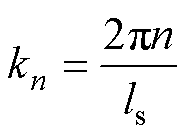

式中,n为谐波次数;vx、vy分别为沿x、y方向的速度; 为次级导体板电导率;
为次级导体板电导率;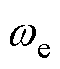 为角速度。式(10)~式(13)中,
为角速度。式(10)~式(13)中,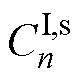 、
、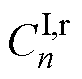 、
、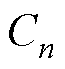 、
、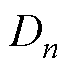 、
、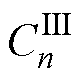 为5个谐波待定系数,根据各区域边界之间的关系,建立满足各边界条件的系数方程,得到矢量磁位的唯一解。
为5个谐波待定系数,根据各区域边界之间的关系,建立满足各边界条件的系数方程,得到矢量磁位的唯一解。
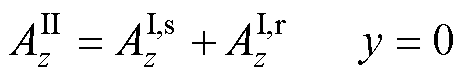 (14)
(14)
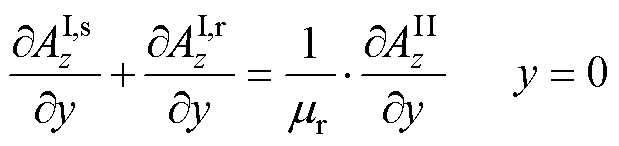 (15)
(15)
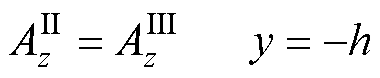 (16)
(16)
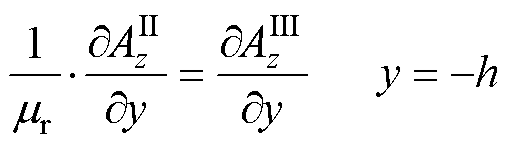 (17)
(17)
对比式(4)和式(10)可得
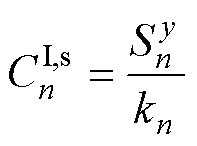 (18)
(18)
综合式(14)~式(18)5个方程,可求得矢量磁位的唯一解。
依据麦克斯韦张量定理求解次级导体板表面的电磁力,可表示为
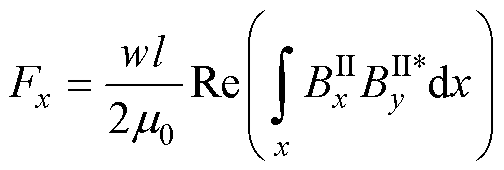 (19)
(19)
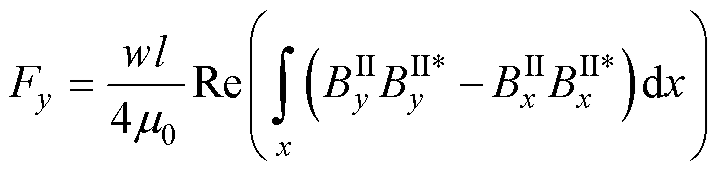 (20)
(20)
式中,Fx为推进力;Fy为悬浮力;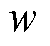 为电机初级宽度;
为电机初级宽度; 为电机初级长度;
为电机初级长度;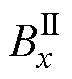 、
、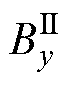 分别为次级导体板表面沿x轴方向和y轴方向的磁感应强度;“
分别为次级导体板表面沿x轴方向和y轴方向的磁感应强度;“ ”表示变量取其共轭。
”表示变量取其共轭。
根据文献[17]可知,无铁心直线感应悬浮电机的储能表达式为
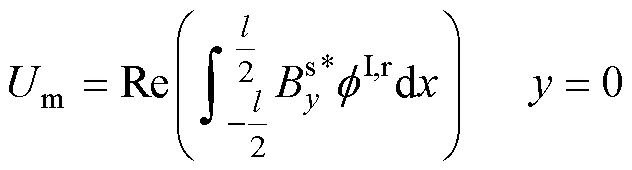 (21)
(21)
式中,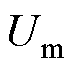 为系统储能;
为系统储能;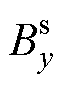 为电磁Halbach阵列在导体板表面产生的法向磁感应强度;
为电磁Halbach阵列在导体板表面产生的法向磁感应强度;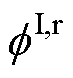 为涡流反射磁场的标量磁位。
为涡流反射磁场的标量磁位。
通过对电机储能求时间的偏导,可得由电机初级传输到次级的电磁功率为
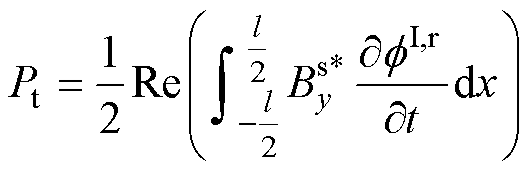 (22)
(22)
假设电机只沿x方向运动,忽略机械损耗,则无铁心直线感应悬浮电机的损耗为
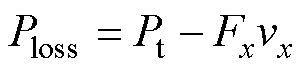 (23)
(23)
无铁心直线感应悬浮电机的效率为
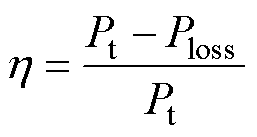 (24)
(24)
为了验证悬浮感应电机解析模型的正确性,建立了改进型的电磁Halbach阵列有限元分析(Finite Element Analysis, FEA)模型,改进型电磁Halbach阵列磁感应强度云图及磁力线分布如图11所示,对电机悬浮力、推力和效率等电机的性能参数进行计算,建模计算参数见表2。由于该电机初级无铁心,不受铁心饱和影响,因此可通过提高励磁电流来增加气隙磁场强度,未来可用超导线圈来构建电磁Halbach阵列,在减少铜线圈电阻损耗的同时充分发挥超导线圈大电流强磁场的特性,因此本文计算过程将电流密度设计为1×108A/m2。
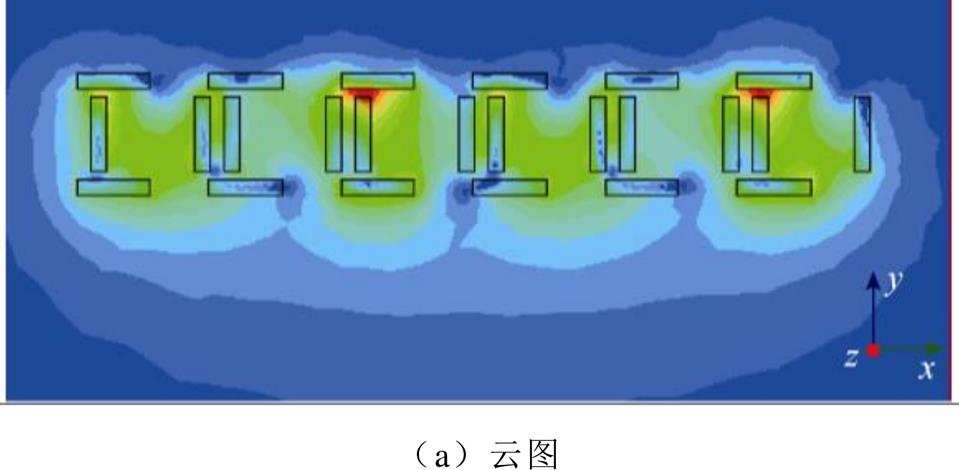
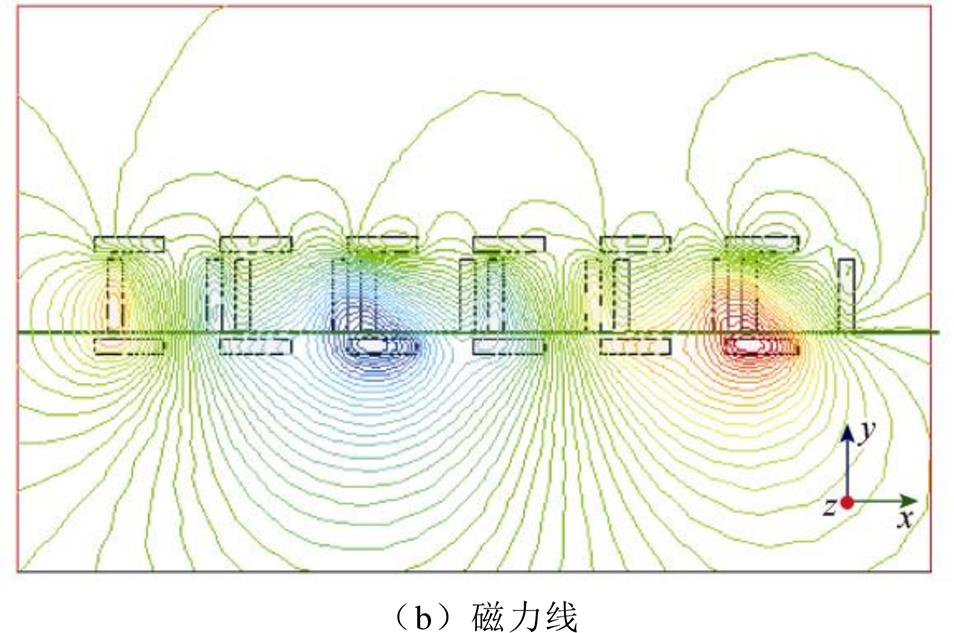
图11 改进型电磁Halbach阵列磁感应强度
Fig.11 The flux density of the improved TMEHA
图12为解析计算和有限元仿真计算的改进型电磁Halbach阵列的加强侧气隙10mm处的磁感应强度,从图中可以看出,本文提出的解析计算结果和二维有限元结果吻合较高,验证了解析计算的正确性。
图13为电机在导体板为10mm、气隙长度为10mm时,电机悬浮力、推力和效率随转差率的变化曲线。从图13中可以看出,悬浮力随着转差率的增加而增加,在转差率为0.6左右时变化趋势趋于平缓。在转差率为0.1~0.4时,随着速度的增加,导体板中感应出的涡流逐渐增大,此时推力随着转差率逐渐变大,但当转差率继续增大即大于0.4后,导体板中的涡流持续增加,此时能量以焦耳热的形式被次级导体板消耗,从而使得对外输出功率降低,推进力随着转差率的增加而减小。从图13中可以看出,电机效率随转差率的变化趋势与推进力随转差的变化趋势相同,因此为保证该悬浮电机有足够的悬浮力和牵引力,电机的额定工作转差率应为0.6左右。
表2 计算参数
Tab.2 Parameters of calculation
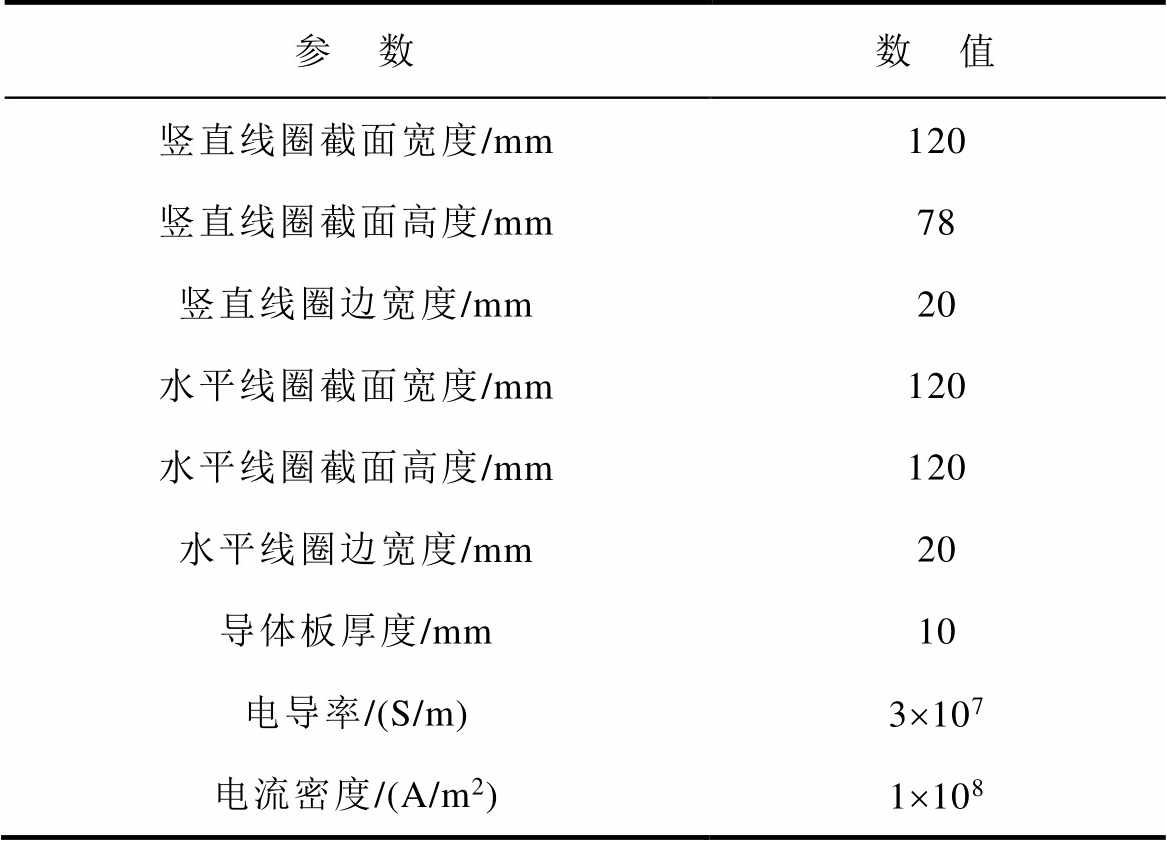
参 数数 值 竖直线圈截面宽度/mm120 竖直线圈截面高度/mm78 竖直线圈边宽度/mm20 水平线圈截面宽度/mm120 水平线圈截面高度/mm120 水平线圈边宽度/mm20 导体板厚度/mm10 电导率/(S/m)3´107 电流密度/(A/m2)1´108
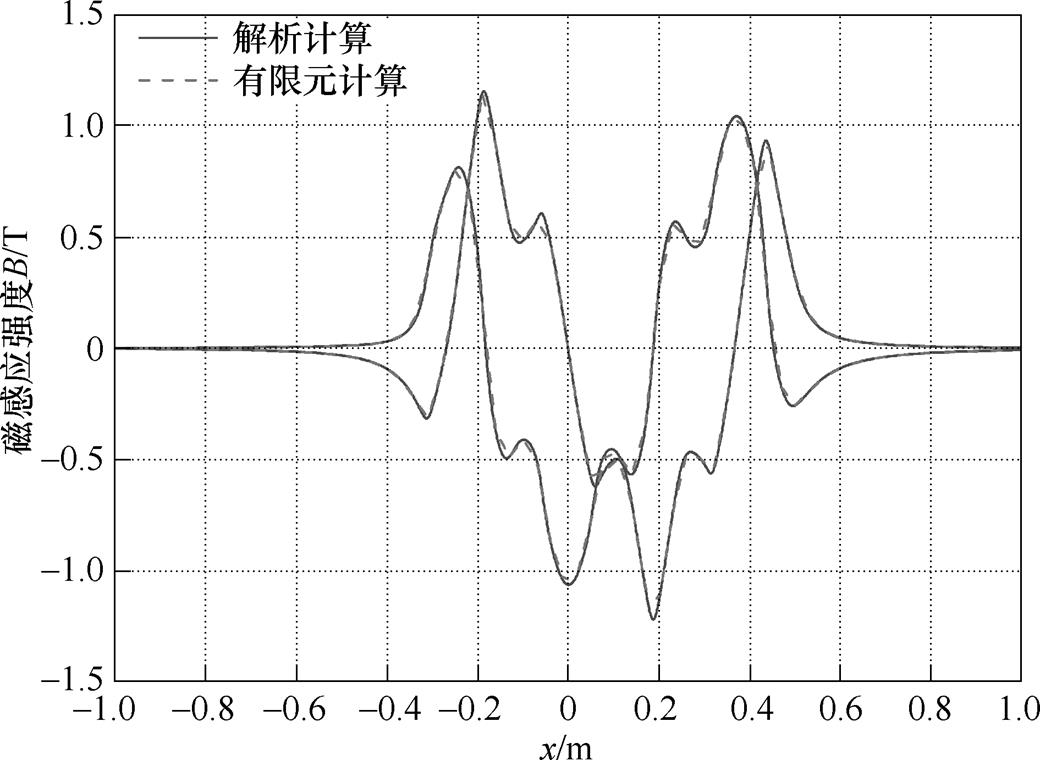
图12 解析计算和有限元计算的对比
Fig.12 Field comparison between the finite element analysis and analytical method
图14为电机在转差率为0.6、气隙长度为10mm时,电机悬浮力、推力和效率随导体板厚度的变化曲线。从图14中可以看出,当导体板为9mm时,电机效率最高,且保持较高的悬浮力和推力输出,因此最优的导体板厚度为9mm。
为了验证解析法和有限元法计算的正确性,加工制作了初级为铜绕组的改进型电磁Halbach阵列样机,通过拉压力传感器对电磁力进行测量,样机参数见表3,实验平台如图15所示。
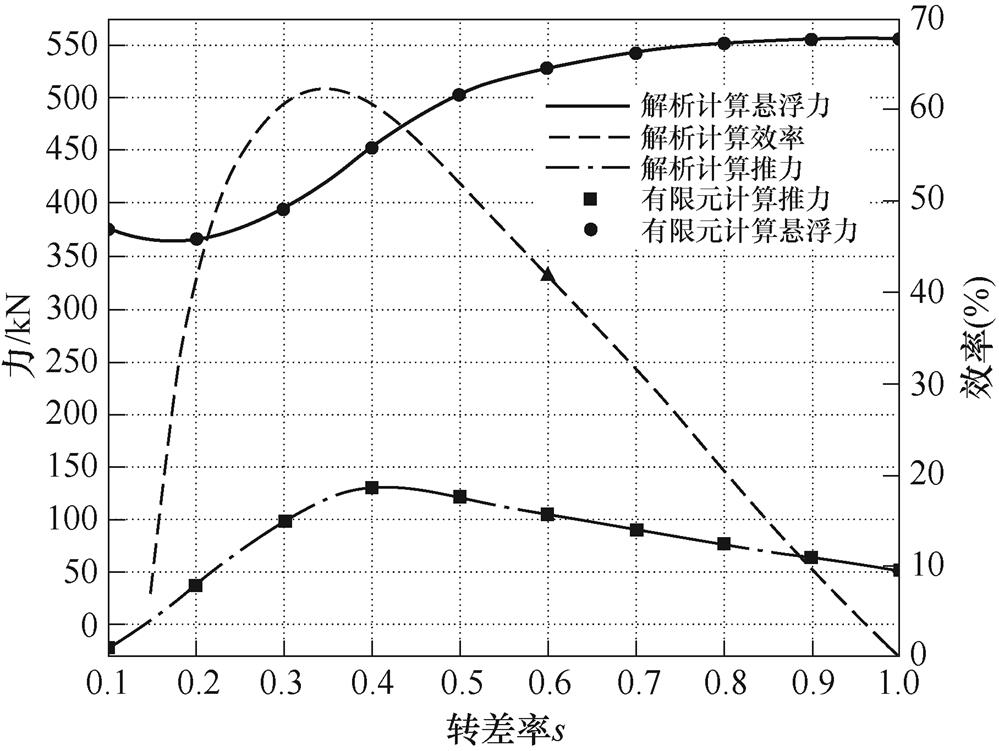
图13 力特性、效率与转差率的关系
Fig.13 Relationship between force, efficiency and the slip speed
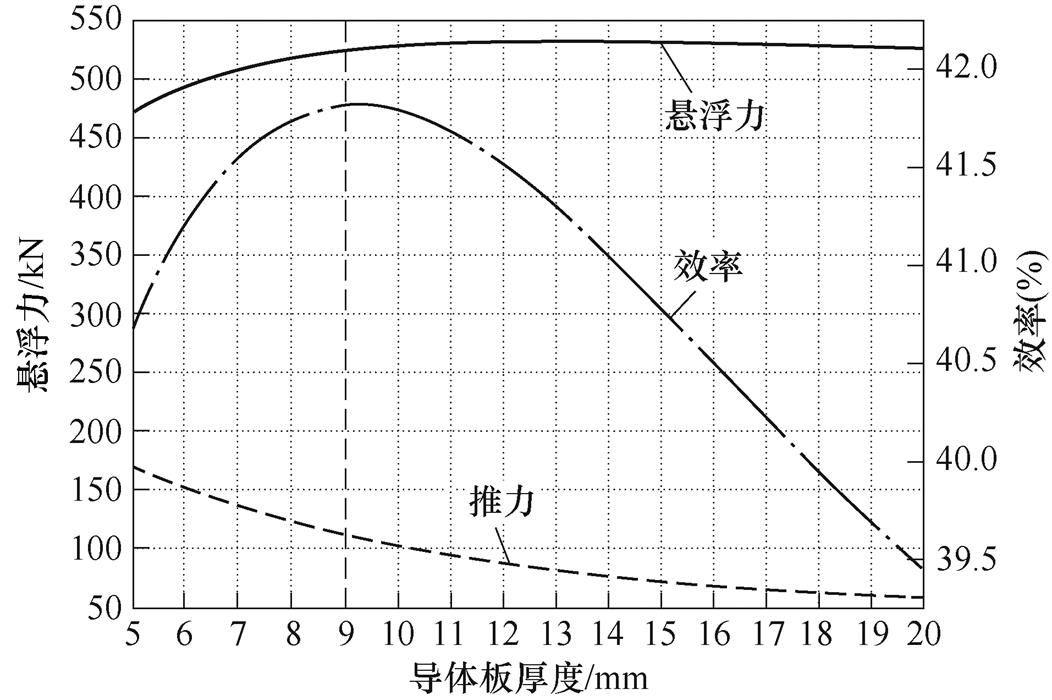
图14 悬浮力、推力和效率与导体板的关系
Fig.14 Relationship among forces, efficiency and the thickness
表3 样机参数
Tab.3 Parameters of prototype
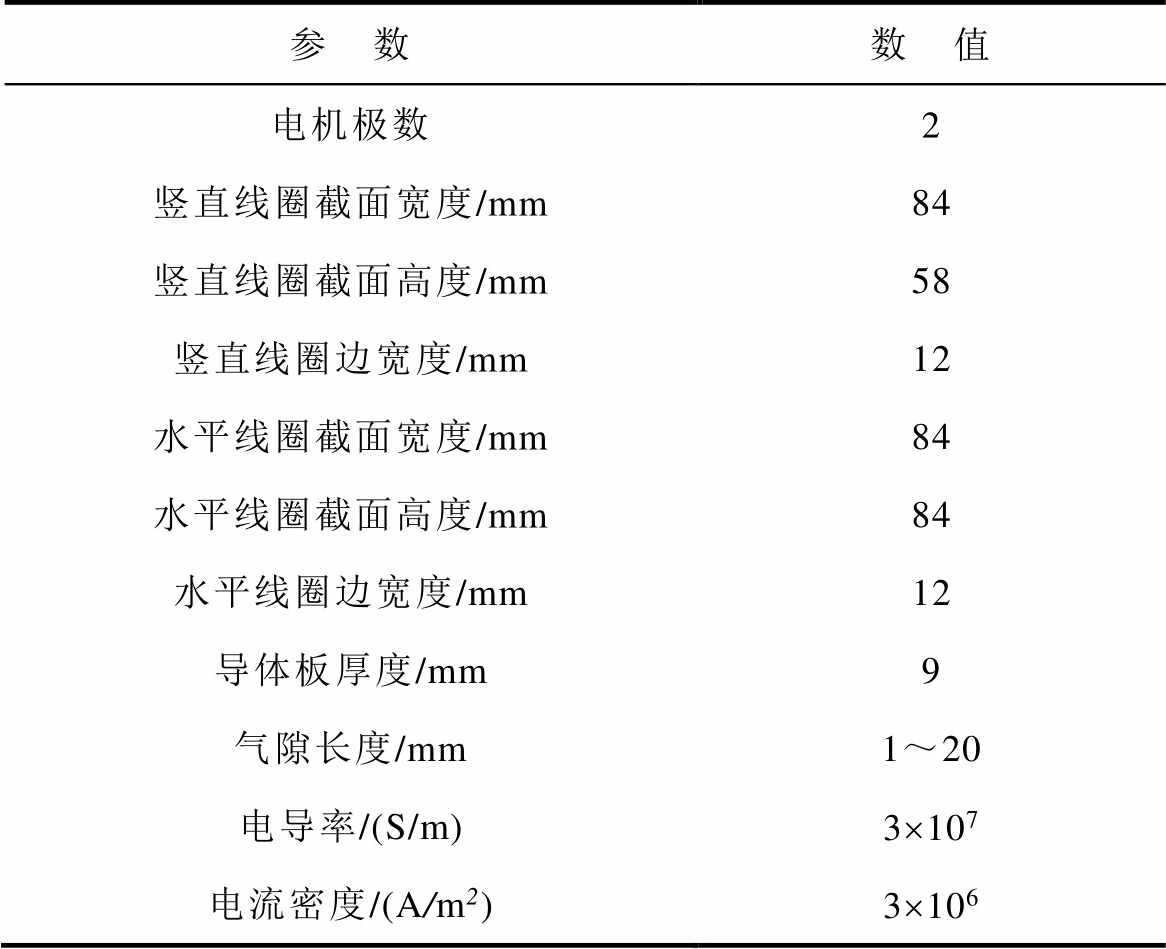
参 数数 值 电机极数2 竖直线圈截面宽度/mm84 竖直线圈截面高度/mm58 竖直线圈边宽度/mm12 水平线圈截面宽度/mm84 水平线圈截面高度/mm84 水平线圈边宽度/mm12 导体板厚度/mm9 气隙长度/mm1~20 电导率/(S/m)3´107 电流密度/(A/m2)3´106

图15 无铁心直线感应悬浮电机铜绕组样机
Fig.15 The prototype of CLIMM with the copper TMEHA
图16给出样机电流密度为3A/mm2、气隙为10mm、导体板厚度为9mm、电流频率为50Hz时,悬浮力随转差率变化的曲线,由图16中可以看出,有限元法、解析计算与实验数据基本吻合,实验、解析计算和有限元计算的误差百分比如图17所示。从图17可以看出,最大误差为3.46%,证明本文提出的基于积分法的磁场求解方法准确有效,对于电机的优化设计具有重要的意义。

图16 实验、解析计算和有限元计算的悬浮力对比
Fig.16 Comparison of the lift force as a function of slip
本文提出了一种悬浮与推进一体化的电动式磁悬浮方案。该电机初级利用无铁心高温超导线圈能够承载大电流强磁场,次级结构简单、可靠性高、造价低,可应用于低真空管(隧)道高速磁悬浮列车系统中。通过解析计算、有限元仿真和实验验证,得到以下结论:

图17 实验、解析计算和有限元计算的误差百分比
Fig.17 Percentage error between finite element analysis, analytic mode and experiment results with slip
1)采用积分法和傅里叶级数法,求解了电磁Halbach阵列的矢量磁位。以矢量磁位为求解变量建立的二维解析模型,考虑了高温超导无铁心直线感应悬浮电机的纵向边端效应,具有更高的计算准确性和通用性。二维解析模型计算结果与二维有限元计算结果和实验测试结果的最大误差分别为1.8%和3.46%,证明了本文所提计算方法的有效性。
2)在解析计算的基础上,研究了不同参数对电机性能的影响,得出了无铁心直线感应悬浮电机的可行设计参数,即电机的额定工作转差率应为0.6左右,次级导体板厚度为9mm,为运动磁场电磁Halbach阵列在高温超导中的应用提供了理论基础。
参考文献
[1] 马卫华, 罗世辉, 张敏, 等. 中低速磁浮车辆研究综述[J]. 交通运输工程学报, 2021, 21(1): 199-216.
Ma Weihua, Luo Shihui, Zhang Min, et al. Research review on medium and low speed maglev vehicle[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 199-216.
[2] 熊嘉阳, 邓自刚. 高速磁悬浮轨道交通研究进展[J]. 交通运输工程学报, 2021, 21(1): 177-198.
Xiong Jiayang, Deng Zigang. Research progress of high-speed maglev rail transit[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 177- 198.
[3] 章九鼎, 卢琴芬. 长定子直线同步电机齿槽效应的计算与影响[J]. 电工技术学报, 2021, 36(5): 964- 972, 1026.
Zhang Jiuding, Lu Qinfen. Calculation and influences of cogging effects in long-stator linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 964-972, 1026.
[4] Xu Wei, Hu Dong, Lei Gang, et al. System-level efficiency optimization of a linear induction motor drive system[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(3): 285-291.
[5] 朱进权, 葛琼璇, 王晓新, 等. 基于自抗扰和负载功率前馈的高速磁悬浮系统PWM整流器控制策略[J]. 电工技术学报, 2021, 36(2): 320-329.
Zhu Jinquan, Ge Qiongxuan, Wang Xiaoxin, et al. Control strategy for PWM rectifier of high-speed maglev based on active disturbance rejection control and load power feed-forward[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 320-329.
[6] 朱进权, 葛琼璇, 孙鹏琨, 等. 高速磁悬浮列车在双端供电模式下的电流控制策略[J]. 电工技术学报, 2021, 36(23): 4937-4947.
Zhu Jinquan, Ge Qiongxuan, Sun Pengkun, et al. Current control strategy for high-speed maglev in the double feeding mode[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4937-4947.
[7] 王一宇, 蔡尧, 宋旭亮, 等. 零磁通式电动悬浮等效模拟系统的特性分析与实验[J]. 电工技术学报, 2021, 36(8): 1628-1635.
Wang Yiyu, Cai Yao, Song Xuliang, et al. Charac- teristic analysis and experiment of the equivalent simulation system for null-flux electrodynamic suspension[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1628-1635.
[8] Sawada K. Outlook of the superconducting maglev[J]. Proceedings of the IEEE, 2009, 97(11): 1881-1885.
[9] Murai M, Tanaka M. Magnetic levitation (maglev) technologies[J]. Japan Railway & Transport Review, 2000, 25: 61-67.
[10] Fujiwara S, Fujimoto T. Characteristics of combined levitation and guidance EDS maglev system[J]. Electrical Engineering in Japan, 1993, 113(3): 123- 134.
[11] Lee H W, Kim K C, Lee Ju. Review of maglev train technologies[J]. IEEE Transactions on Magnetics, 2006, 42(7): 1917-1925.
[12] 冯仲伟, 方兴, 李红梅, 等. 低真空管道高速磁悬浮系统技术发展研究[J]. 中国工程科学, 2018, 20(6): 105-111.
Feng Zhongwei, Fang Xing, Li Hongmei, et al. Technological development of high speed maglev system based on low vacuum pipeline[J]. Engineering Sciences, 2018, 20(6): 105-111.
[13] 刘文旭, 李文龙, 方进. 高温超导磁悬浮技术研究论述[J]. 低温与超导, 2020, 48(2): 44-49.
Liu Wenxu, Li Wenlong, Fang Jin. Review of research on high temperature maglev[J]. Cryogenics & Superconductivity, 2020, 48(2): 44-49.
[14] 邓自刚, 李海涛. 高温超导磁悬浮车研究进展[J]. 中国材料进展, 2017, 36(5): 329-334, 351.
Deng Zigang, Li Haitao. Recent development of high- temperature superconducting maglev[J]. Materials China, 2017, 36(5): 329-334, 351.
[15] 孙鹏琨, 葛琼璇, 王晓新, 等. 磁悬浮列车在双端供电模式下的无速度传感器控制[J]. 电工技术学报, 2018, 33(18): 4249-4256.
Sun Pengkun, Ge Qiongxuan, Wang Xiaoxin, et al. Speed sensorless control of maglev train with double- end power supply[J]. Transactions of China Electro- technical Society, 2018, 33(18): 4249-4256.
[16] Post R F, Ryutov D D. The inductrack: a simpler approach to magnetic levitation[J]. IEEE Transactions on Applied Superconductivity, 2000, 10(1): 901-904.
[17] 巫川, 李冠醇, 王东. 永磁电动悬浮系统三维解析建模与电磁力优化分析[J]. 电工技术学报, 2021, 36(5): 924-934.
Wu Chuan, Li Guanchun, Wang Dong. 3-D analytical modeling and electromagnetic force optimization of permanent magnet electrodynamic suspension system[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 924-934.
[18] Paul S, Bobba D, Paudel N, et al. Source field modeling in air using magnetic charge sheets[J]. IEEE Transactions on Magnetics, 2012, 48(11): 3879-3882.
[19] Paul S, Bird J Z. Improved analytic model for eddy current force considering edge-effect of a conductive plate[C]//2016 IEEE XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 2016: 789-795.
[20] Bird J, Lipo T A. Modeling the 3-D rotational and translational motion of a Halbach rotor above a split- sheet guideway[J]. IEEE Transactions on Magnetics, 2009, 45(9): 3233-3242.
[21] Fujii N, Nonaka S, Hayashi G. Design of magnet wheel integrated own drive[J]. IEEE Transactions on Magnetics, 1999, 35(5): 4013-4015.
[22] Fujii N, Chida M, Ogawa K. Three dimensional force of magnet wheel with revolving permanent mag- nets[J]. IEEE Transactions on Magnetics, 1997, 33(5): 4221-4223.
[23] Fujii N, Naotsuka K, Ogawa K, et al. Basic charac- teristics of magnet wheels with rotating permanent magnets[C]//Proceedings of 1994 IEEE Industry Applications Society Annual Meeting, Denver, CO, USA, 1994: 203-209.
Analyzing and Designing a Novel Coreless Linear Induction Maglev Motor for Low Vacuum Pipeline
Abstract A new kind of coreless linear induction maglev motor (CLIMM), which can be used in ultra-high speed maglev, is studied in this paper. The motor is an electro-dynamic system that can simultaneously create suspension and propulsion forces. The basic structure and principle of the proposed motor is firstly described. Then, an integral approach is proposed for modeling the vector magnetic potential of the primary winding. Taking the vector magnetic potential as the variable, a 2D analytic model of the CLIMM is proposed. Consequently, the magnetic field in the air gap, the lift force, the thrust force and the efficiency are calculated. Finite element analysis results verify the analytical prediction. Finally, the CLIMM with copper coil is designed and established to verify the analytical model.
keywords:Low vacuum pipeline, maglev, integral approach, electromagnetic performance, analytical model
DOI: 10.19595/j.cnki.1000-6753.tces.210413
中图分类号:TM351
中央高校基本科研业务费资助项目(2020JBM066)。
收稿日期 2021-03-26
改稿日期 2021-08-03
秦 伟 男,1986年生,博士,研究方向为直线电机分析与控制。E-mail: weiqin@bjtu.edu.cn(通信作者)
马育华 男,1981年生,高工,研究方向为直线电机及其控制、电机优化设计。E-mail: 214708852@qq.com
(编辑 崔文静)