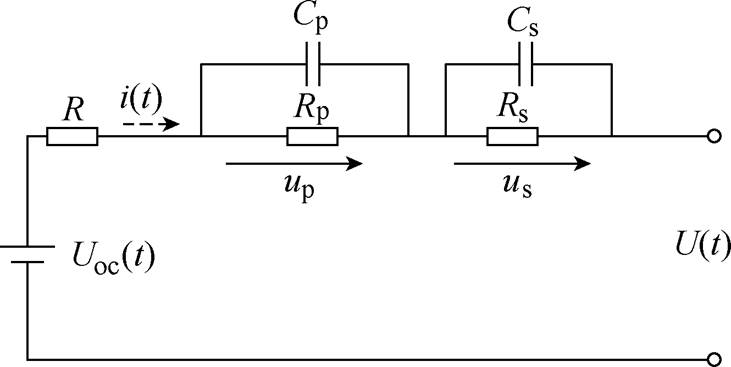
图1 DP等效电路模型
Fig.1 DP equivalent circuit model
摘要 递推最小二乘法（RLS）应用于锂电池这种多时间尺度系统时，会出现模型参数辨识精度低、工况适应性差等问题。为此，以双极化（DP）等效电路模型为研究对象，首先，根据模型参数不同的时变特性，通过分离欧姆电阻的辨识过程，使得RLS需要辨识的参数减少，并降低待辨识参数的相互影响，提高RLS辨识的精度及降低运算量；其次，根据模型参数在线辨识对恒流工况辨识精度低，而离线辨识对恒流工况辨识精度高的特点，提出全工况自适应输出等效电路模型，进一步提高模型精度。基于实际工况的仿真实验表明，全工况自适应等效电路模型相比欧姆电阻已知的R-DP在线模型及DP离线模型具有更高的精度，能够在模型精度和运行速度之间取得更好的平衡。
关键词：锂电池 电池模型 参数辨识 最小二乘法 模型精度 全工况
锂电池凭借其比能量高、循环寿命长等特性，逐渐成为新能源汽车动力电池的首选。电池模型是电池特性的数学表现形式，精确的电池模型不仅能反映出电池特性与众多影响因素间的关系，也为精确的状态估计提供了重要基础，电池模型的研究对提高新能源汽车电池管理水平具有重要意义[1]。
常见的动力电池模型包含电化学模型、等效电路模型和黑箱模型等[2-3]。其中，等效电路模型具有模型方程简单、参数辨识方便等特点，广泛应用于各类动力电池状态估计方法[4-5]。近年来，国内外学者提出了Rint模型、Thevenin模型、新一代汽车合作伙伴计划（Partnership for a New Generation of Vehicles, PNGV）模型、双极化（Dual Polarization, DP）模型以及多阶电阻电容（Resistance Capacitance, RC）模型等多种多样的等效电路模型。理论上，多阶RC模型具有更高的精度，但应用过程中，多阶RC环路需要辨识的参数增多，各参数的误差也更大，其模型精度甚至小于DP模型。上述模型中，DP模型能够在精度和运算量方面取得良好的平衡[6]，应用尤其广泛，本文针对DP模型展开研究。在DP模型参数辨识过程中，目前较多文献都是对其欧姆电阻和两个RC环路参数同时辨识。而实际上，模型各个参数的时变特性不同，其中欧姆电阻在相同温度、相同健康状态条件下，某个确定充放电周期内几乎不变[7]，而为了模拟动力电池对不同倍率的响应特性，其RC环路的参数在某个确定周期内保持时变。参数辨识过程以相同的时变特性对各参数进行辨识是不可取的，容易导致欧姆电阻变化剧烈，且对RC环路的辨识产生不利影响。
针对系统模型参数容易受到应用环境不确定影响而发生较大变化的情况，递推最小二乘法（Recur- sive Least Square, RLS）能周期性地对参数优化和更新，可以克服模型参数的不确定性，从而精确捕捉系统的实时特性[8]。目前，动力电池参数辨识最常见的方法是带遗忘因子的RLS，其具有方法简单易懂、易于工程化应用等特点。但也存在一些问题：根据它的方程特性，其对时变工况辨识效果较好，对时不变的工况辨识效果较差甚至可能发散[9-10]。而实际上，工况的变化具有很强的随机性，新能源汽车在行驶过程中，不仅有快速变化的工况，也有匀速相对稳定的工况，这就导致RLS的应用具有一定的局限性，使其适用于时变工况。而根据不同恒流倍率辨识出的离线模型，在恒流工况相比于在线模型，具有更高的精度。
基于DP等效电路模型各参数时变特性，为减小模型参数辨识过程的相互影响，本文将欧姆电阻和其他两组RC参数分离，对欧姆电阻和RC环路分别采用不同的辨识方法，提出某个确定充放电周期内欧姆电阻已知的R-DP在线模型，不仅可以提高模型精度，还可以减小计算量。在此基础上，针对RLS对不同工况的适应性及离线模型在恒流工况下具有更高的精度，提出基于R-DP在线模型、DP离线模型自适应输出的全工况等效电路模型，进一步提高模型精度。
DP等效电路模型如图1所示，i为电流（设放电时符号为正，充电时符号为负），Uoc为动力电池的开路电压，R为欧姆电阻，Rp、Cp分别为极化电阻和极化电容，Rs、Cs分别为扩散电阻和扩散电容，极化效应由RpCp环路和RsCs环路共同模拟[11]。
图1 DP等效电路模型
Fig.1 DP equivalent circuit model
DP模型离线参数辨识目前已有较多文献[6, 12-14]涉及，本文依据文献[6]进行DP模型的离线参数辨识。R-DP在线模型即某个确定充放电过程欧姆电阻已知的DP在线模型。相比于整个寿命周期，在确定温度条件下，某个充放电过程锂电池欧姆电阻几乎不变[15]，基于此特性，首先，由充放电初始时刻的电压突变求得初始温度条件下的内阻，随着电池的持续工作，温度变化到一定程度时，根据温度对内阻的影响函数，求取当前温度条件下的内阻；其次，利用带遗忘因子RLS在线辨识RC环路4个参数。
可靠的开路电压-荷电状态（Open Circuit Voltage- State of Charge, OCV-SOC）曲线是利用带遗忘因子RLS对RC环路参数辨识的基础。本节首先建立OCV-SOC曲线，其次对RC环路参数辨识进行详细的数学推导。
基于图2所示电池测试系统，参照文献[6]标定OCV-SOC曲线，相同温度及健康状态条件下，不同放电倍率标定结果的多项式拟合曲线如图3所示。
图2 电池测试系统
Fig.2 Battery test system
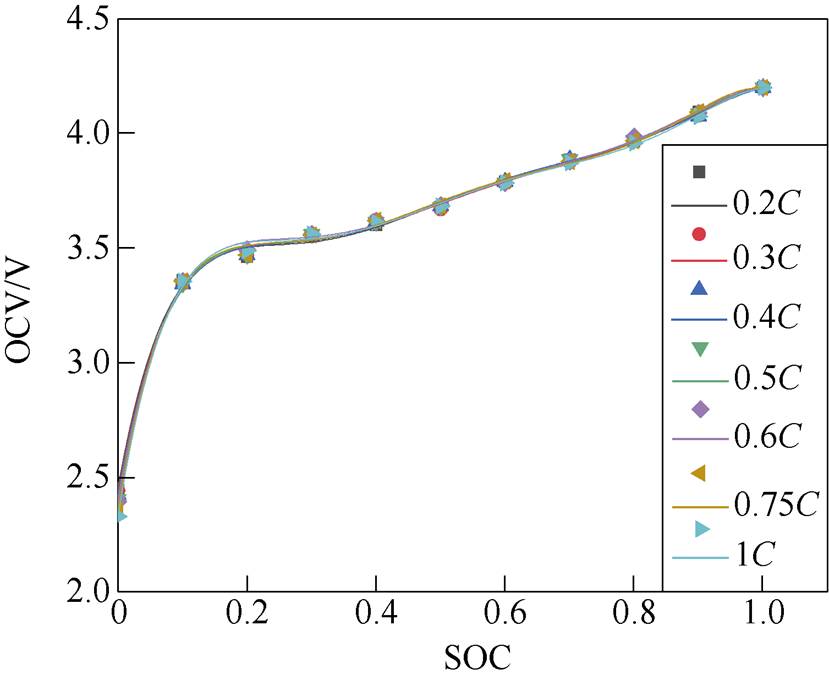
图3 不同倍率OCV-SOC标定曲线
Fig.3 Calibration curves of OCV-SOC at different rates
由图3可知，不同放电倍率的OCV-SOC曲线非常接近，几乎一致，说明在温度、健康状态一致的条件下，不同放电倍率对OCV-SOC曲线影响很小[16-17]。工作电流越小，电流倍率对电池的影响也越小，选取0.2C对应的OCV-SOC曲线作为参考曲线，拟合方程为
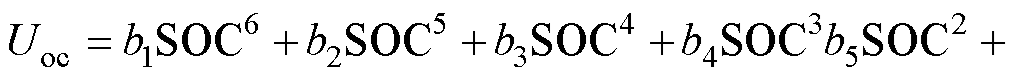
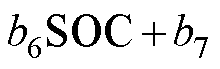（1）
式中，b1～b7为六阶多项式拟合的系数，b1=-5.694 4，b2=23.766，b3=-39.455 7，b4=32.961 2，b5=-14.048 3，b6=3.561，b7=3.111 7。
R-DP在线模型RC环路参数辨识的难点在于把欧姆电阻R从DP模型的传递函数中分离。考虑如下系统
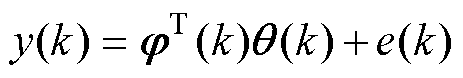（2）
针对DP模型，有
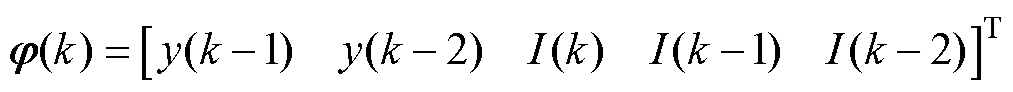（3）
（4）
式中，e(k)为平稳零均值白噪声；y(k)为系统的输出变量；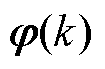
为系统的数据矩阵；I(k)为系统输入；
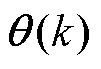为系统的待辨识参数矩阵；
～
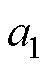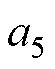为与模型参数相关的系数。
RLS在辨识参数过程中会出现数据饱和，从而不能精准地反映新数据的特性[18-20]。为避免上述情况，引入遗忘因子l，0＜l＜1，l 越小，辨识的跟踪能力越强，但参数估计波动也越大，一般取0.95＜ l＜1[21]，本文仿真模型l =0.98。
为将欧姆电阻的辨识从整个模型的参数辨识分离，对图1所示DP模型，其函数关系可写为
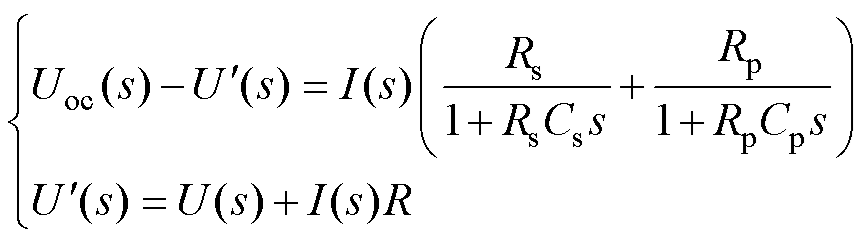（5）
式中，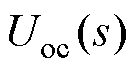
、
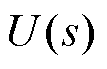分别为电池模型开路电压及端电压。进而传递函数为
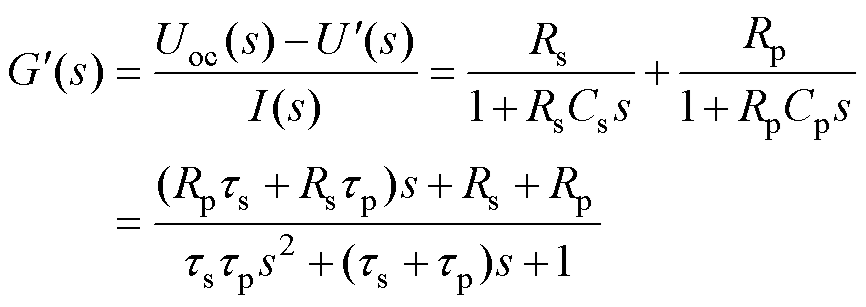（6）
式中，
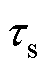和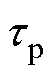
为时间常数。
采用双线性变换[22]将系统从s平面映射到z平面，双线性变换为
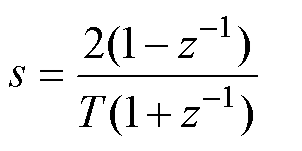（7）
式中，T为系统采样间隔时间。基于z平面的系统方程为
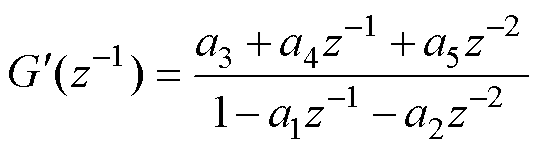（8）
由双线性变换系数对应相等可得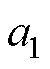
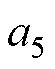～为
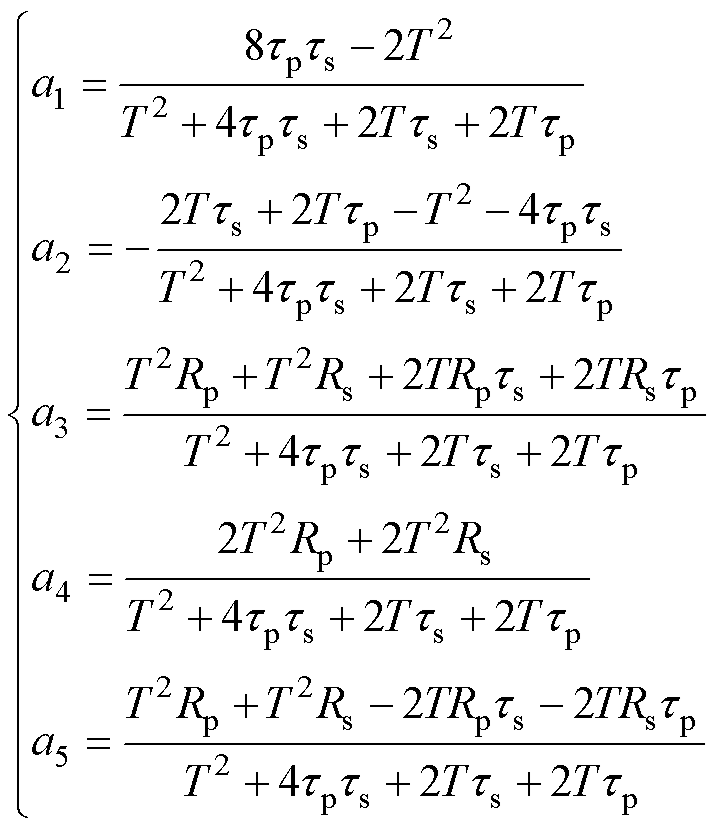（9）
将式（8）转化为差分方程得
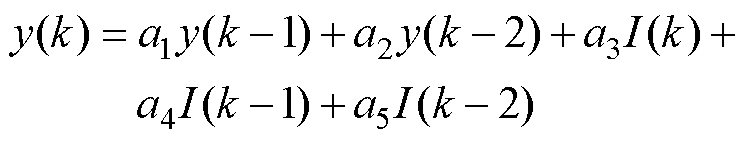（10）
进而有
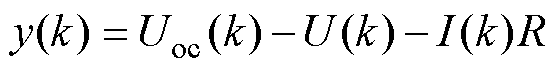（11）
由式（9）可知，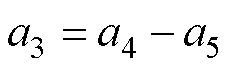
，待辨识参数矩阵可写为
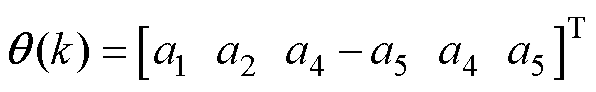（12）
依据式（3）和式（12），式（10）可简写为
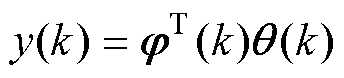（13）
式（13）即可采用带遗忘因子RLS对参数矩阵进行辨识。将式（14）所示双线性逆变换因子代入式（10）可得式（15）。
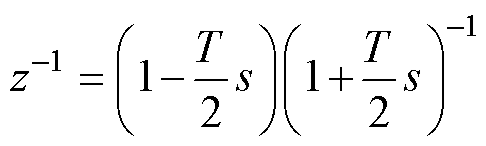（14）
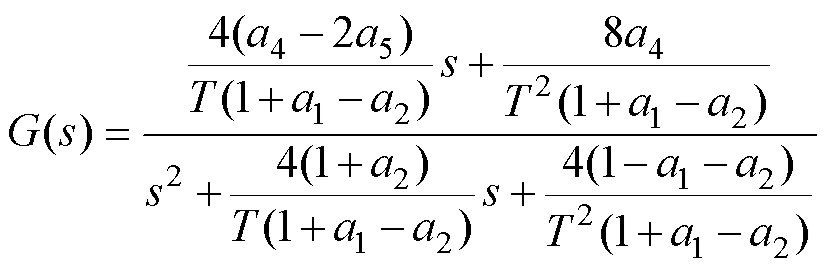（15）
由式（6）和式（15）系数对应相等可得
（16）
至此，基于带遗忘因子RLS及式（16）即可由4个方程求解RC环路的4个参数。上述辨识过程和普通的基于带遗忘因子RLS的辨识过程相比，辨识对象由5个未知数变为4个未知数，理论上不仅提高了辨识精度，也降低了计算量。
根据RLS的推导过程，数据矩阵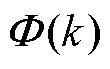
必须满秩才可以进行求逆计算。也就是说每一列的
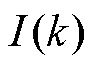必须不相等，这就要求在0～N的时间内，至少存在一个时刻使得
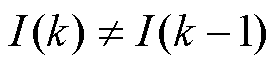，并且RLS的收敛需要一定的时间，电流变化的速度较慢或电流恒定持续的时间较长时往往达不到收敛效果，甚至发散。所以，RLS能够应用到在线参数辨识的前提条件是电池的电流是时变的，对于恒流工况，其辨识精度会受到较大影响。
离线模型是基于不同的恒流倍率对模型参数进行辨识，其针对恒流工况相比在线模型具有更高的精度。离线模型参数应用过程是根据查表法或函数拟合法，这两种方法都是仅仅基于各参数独立的变化过程进行查表或拟合，并未考虑各参数之间的相互关系。而基于RLS的参数辨识，在所有时刻都考虑了各参数之间的数学关系。理论上，针对变电流工况，RLS在线辨识比离线辨识具有更高的精度。
由以上分析可知，不同的参数辨识方法，其对不同工况的辨识精度是有区别的。基于此，建立基于在线模型、离线模型自适应输出的全工况等效电路模型。当工况电流恒定时，输出离线模型辨识结果；当工况电流时变时，输出在线模型辨识结果。考虑到电流采样的精度即采样过程的干扰，工况恒定和时变的电流临界值设为0.05A。全工况自适应输出过程如图4所示。
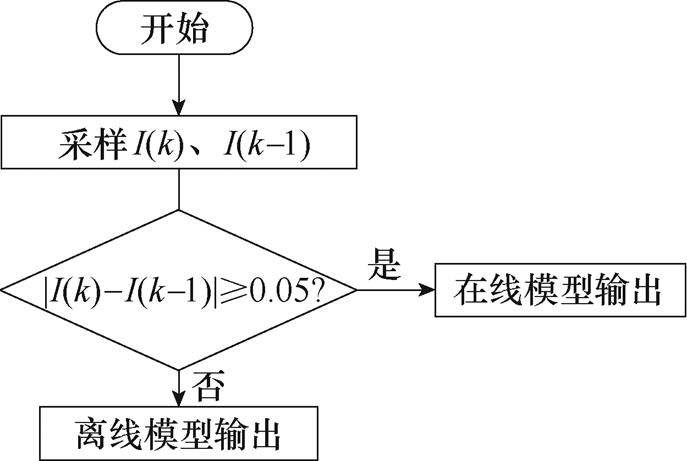
图4 全工况自适应输出
Fig.4 Adaptive output for all working condition
模型验证主要包含两个内容，分别是基于RLS的R-DP在线模型和DP在线模型的精度对比验证，全工况自适应输出模型和基于RLS的R-DP在线模型、DP离线模型精度对比验证。为同时模拟电池恒流、变流充放电过程，模型验证采用两个工况[8, 14]，第一个是自定义工况，如图5a所示，电流大于零表示电池放电，小于零表示充电，这个工况既包含了变流工况也包含了恒流工况，总时长4 200s。图5b所示为依据联合国欧洲经济委员会（Economic Commission for Europe, ECE）汽车法规工况进行适当比例缩小以适合实验对象的工况，文中也称为ECE工况，单个周期200s，模型验证过程仿真时长为10个周期。
图5 模型输入工况
Fig.5 Model input conditions
工况测试实验平台如图6所示，核心设备为新威CT-4008-5V6A程控电池测试仪，其测试精度可达到0.05%，最大电流上升时间为1ms，最高数据记录频率为10Hz。需要说明的是，在利用图6所示实验平台测试电流工况时，电池的温度变化小于1℃，所以仿真过程的内阻设置为固定值，由离线方式辨识获得。
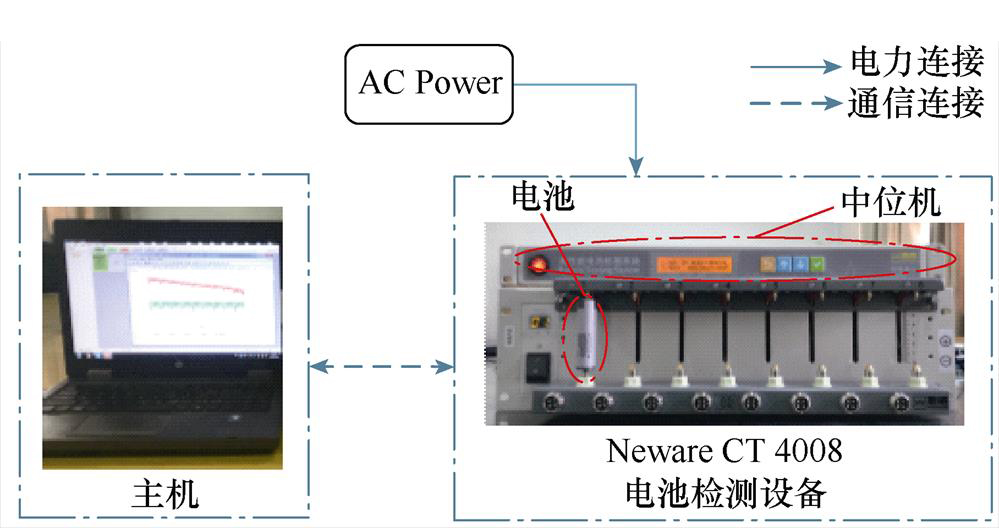
图6 工况测试平台
Fig.6 Working condition test platform
图7和图8所示为基于RLS的R-DP在线模型和DP在线模型的仿真结果。模型平均绝对误差见表1。由图7可以看出，两个模型均能较好地跟踪实测端电压的变化。由图8及表1可知，整体而言，基于R-DP在线模型的输出更接近真实测量值，造成这种结果的原因主要是R-DP在线模型相比于普通DP在线模型，一方面R的辨识结果更接近实际情况，更可靠、更精确；另一方面R-DP模型只需要辨识4个参数，理论上具有更高的辨识精度。
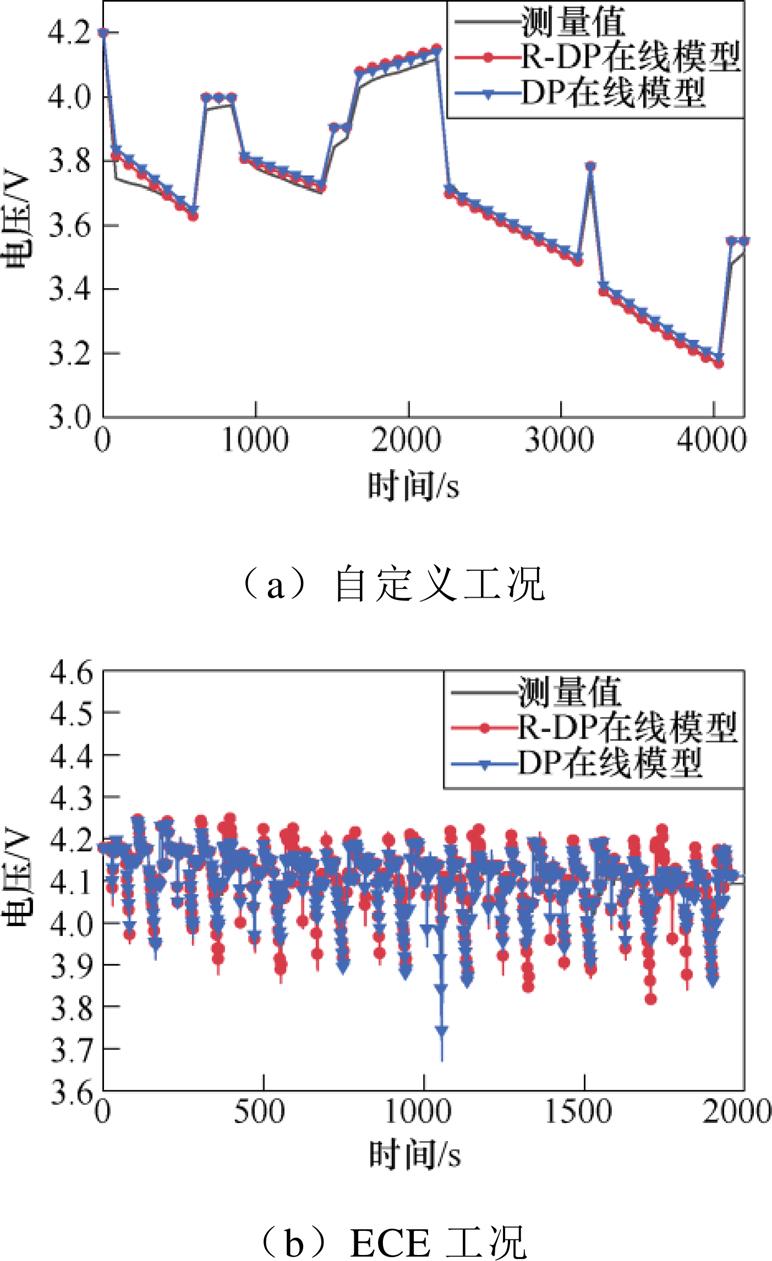
图7 R-DP在线模型和DP在线模型仿真结果
Fig.7 Simulation results of R-DP and DP online model
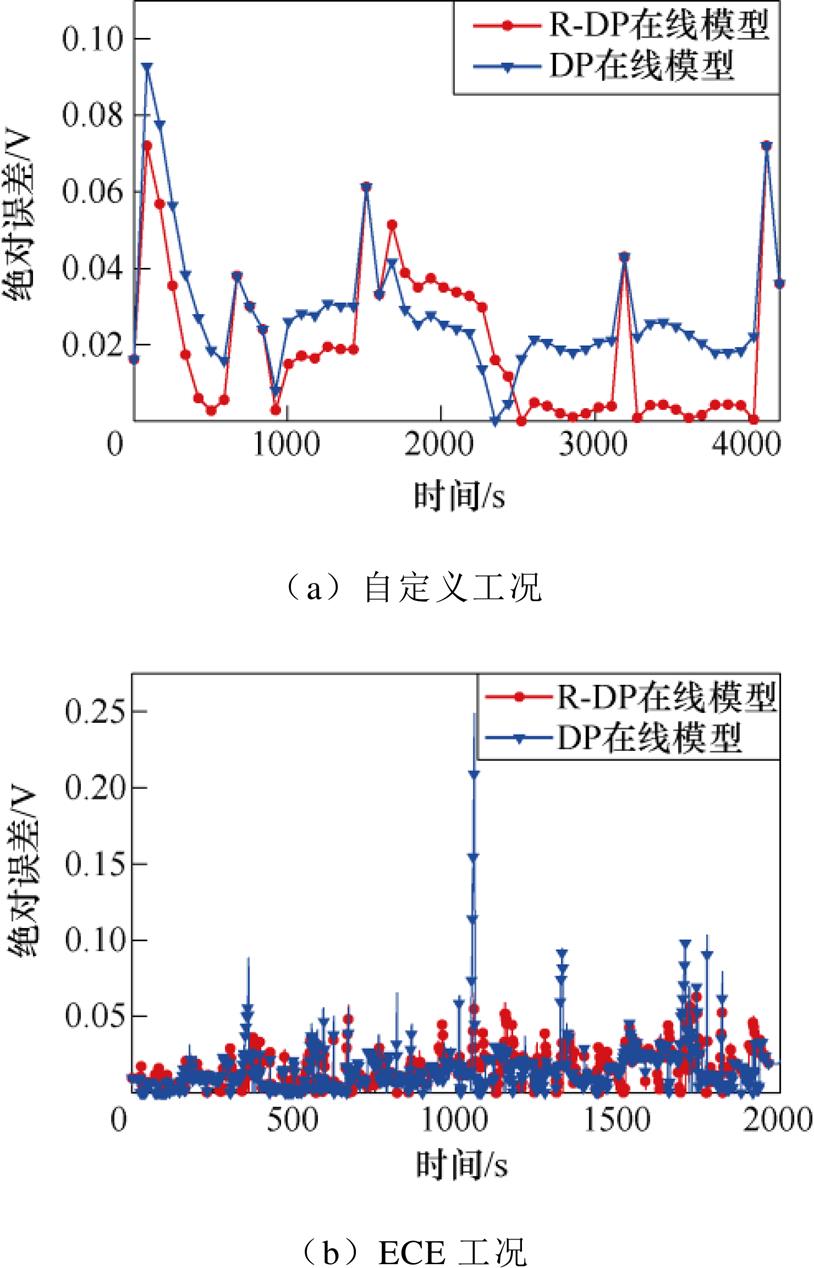
图8 R-DP在线模型和DP在线模型误差比较
Fig.8 Error comparison of R-DP and DP online model
表1 模型平均绝对误差
Tab.1 Average absolute error of each model
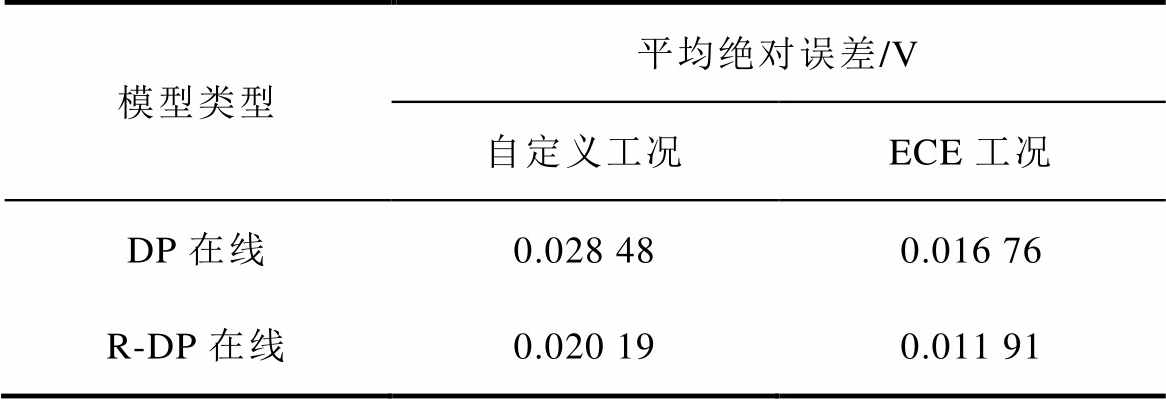
模型类型平均绝对误差/V 自定义工况ECE工况 DP在线0.028 480.016 76 R-DP在线0.020 190.011 91
图9所示为基于RLS的R-DP在线模型和DP离线模型的仿真结果，图10所示为全工况自适应输出模型仿真结果。图11所示为各模型误差曲线，表2为各模型平均绝对误差。
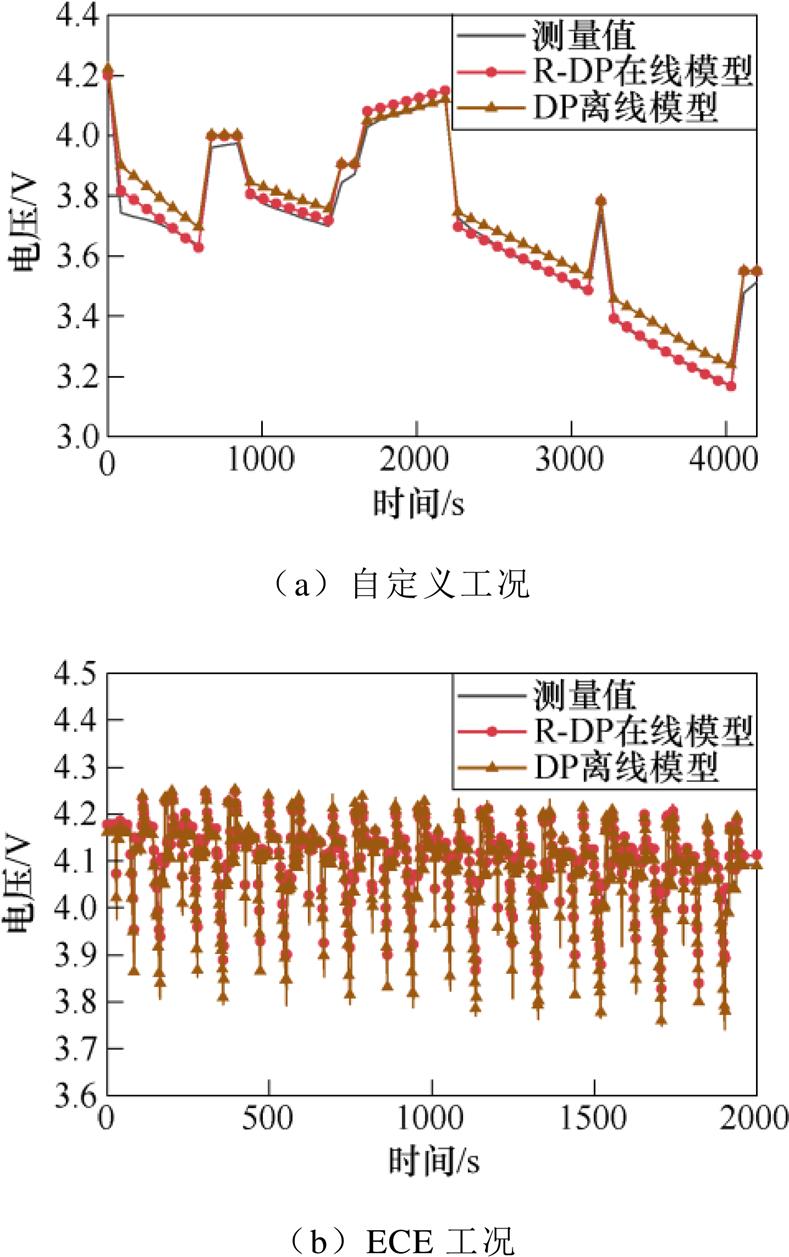
图9 R-DP在线模型和DP离线模型仿真结果
Fig.9 Simulation results of R-DP online and DP offline model
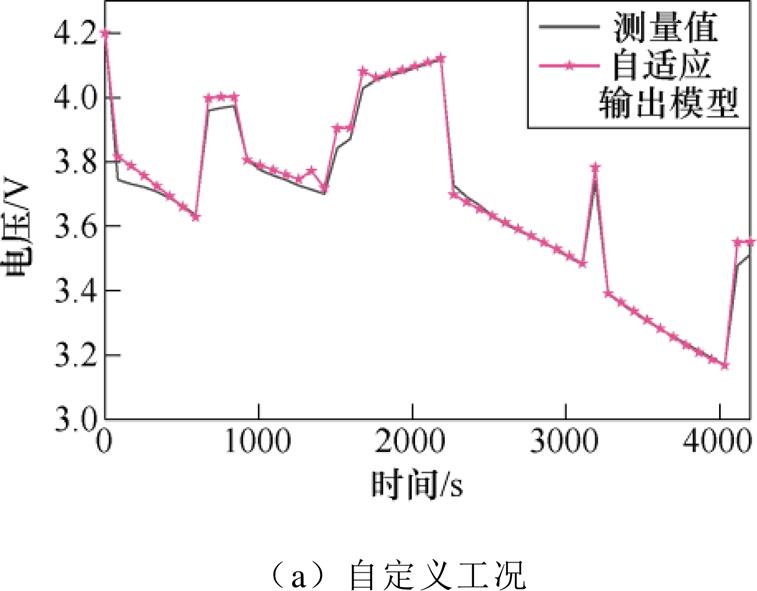
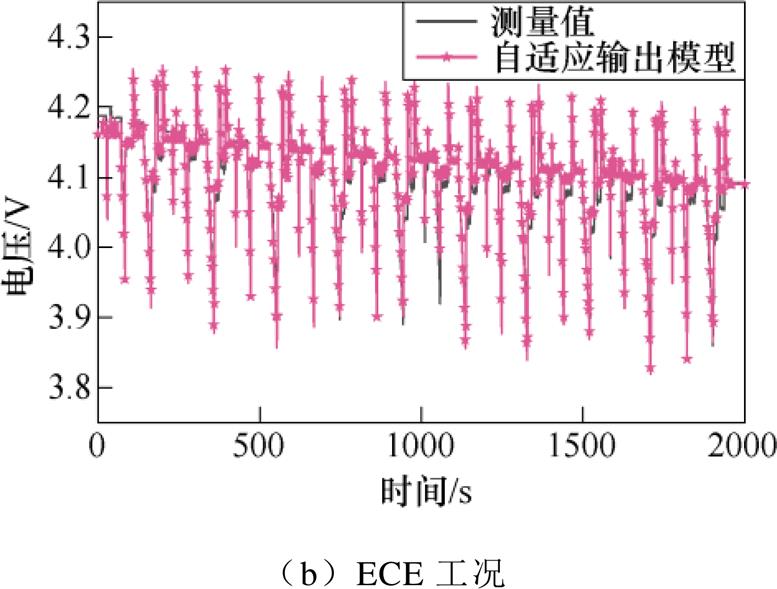
图10 全工况自适应输出模型仿真结果
Fig.10 Simulation results of adaptive output model under full working condition
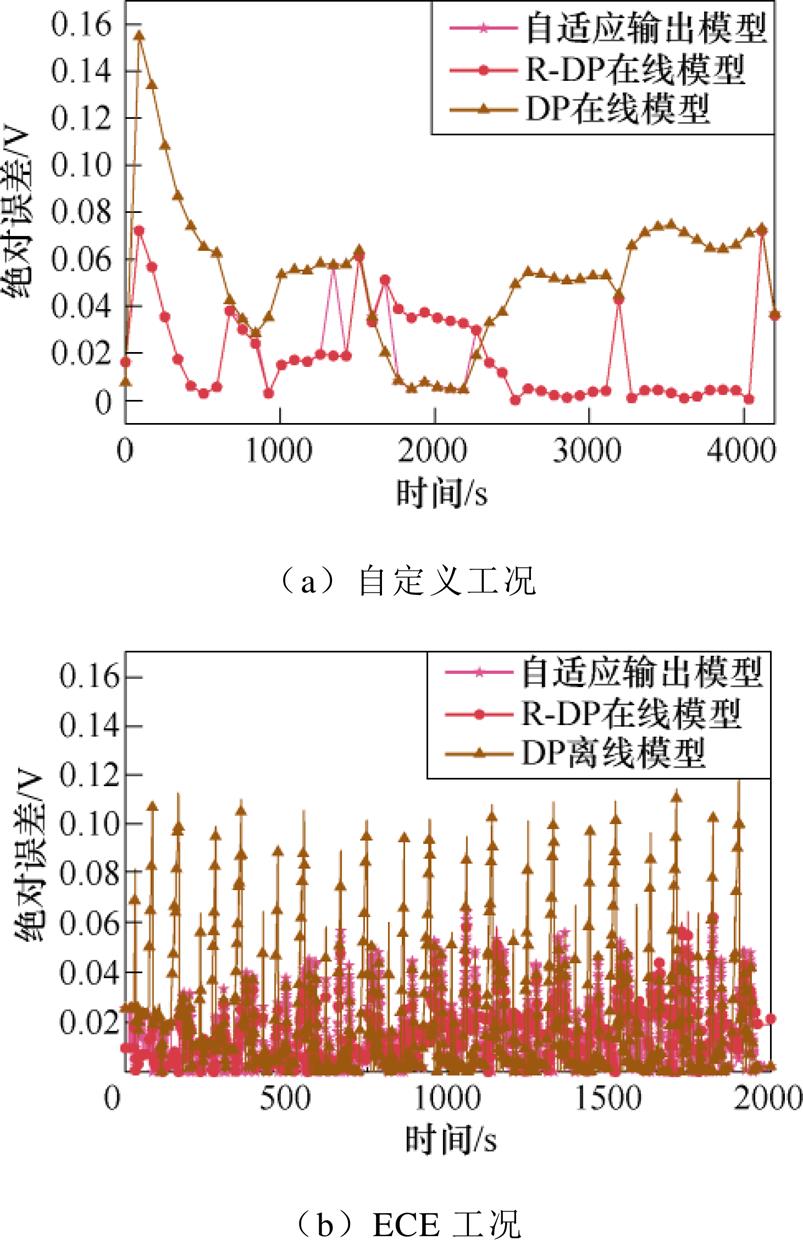
图11 各模型误差曲线
Fig.11 Error curves of each model
表2 各模型平均绝对误差
Tab.2 Average absolute error of each model
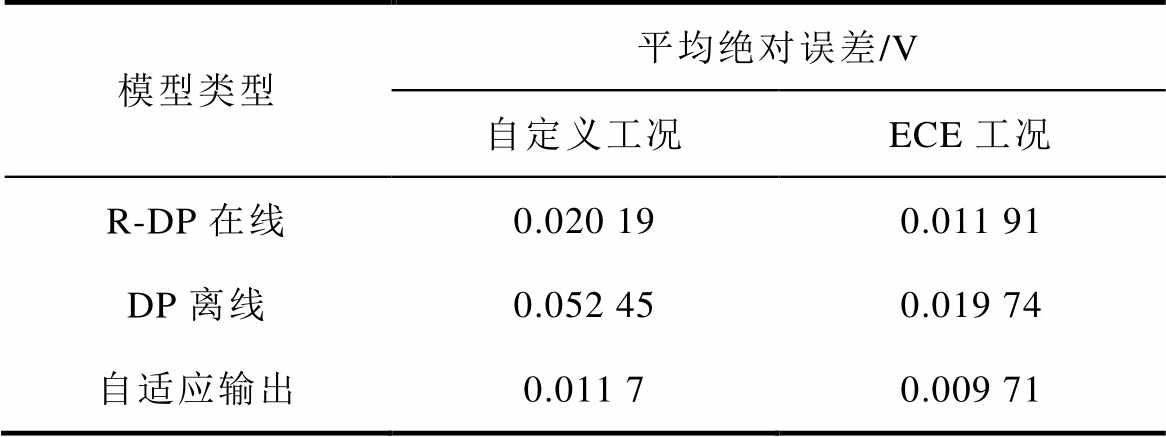
模型类型平均绝对误差/V 自定义工况ECE工况 R-DP在线0.020 190.011 91 DP离线0.052 450.019 74 自适应输出0.011 70.009 71
由表1、表2可知，整体而言离线模型误差最大，达到了50mV左右，影响离线模型精度的主要因素是离线辨识过程实际采样数据的精度及数量。基于RLS的R-DP在线模型相比于普通的DP在线模型，由于欧姆电阻的辨识更可靠，在线辨识过程参数更少，因此具有更高的精度。全工况自适应输出模型结合了R-DP在线模型和DP离线模型的优缺点，相比于R-DP在线模型，具有更小的误差。需要说明的是，模型误差的大小受工况的变化影响较大，换个工况，精度提高的比率可能发生变化，但两种改进模型精度的方法效果是确定的。
综合以上分析，基于RLS的全工况自适应等效电路模型通过对DP模型在线参数辨识过程的改进和在线模型、离线模型相结合的方式提高了DP等效电路模型的精度，进而对提高新能源汽车动力电池状态估计精度具有重要意义。
为验证上述模型运行速度的可靠性，采用5台不同的计算机基于上述模型对两种工况进行仿真，不同模型的平均运行时间见表3。由表3可知，DP离线模型的运行时间最短，这和其计算方程最少吻合；R-DP在线模型比DP在线模型运行时间短，和理论分析过程吻合；自适应输出模型相比于R-DP模型运行时间更长，但总体相差不大。具体而言，对于自定义工况，DP离线模型运行时间最短，DP在线模型运行时间是其1.76倍，R-DP在线模型运行时间是其1.52倍，自适应输出模型是其1.66倍；对于ECE工况，DP在线模型运行时间是其1.55倍，R-DP在线模型运行时间是其1.35倍，自适应输出模型是其1.41倍。
表3 各模型仿真时间
Tab.3 Simulation time of each model
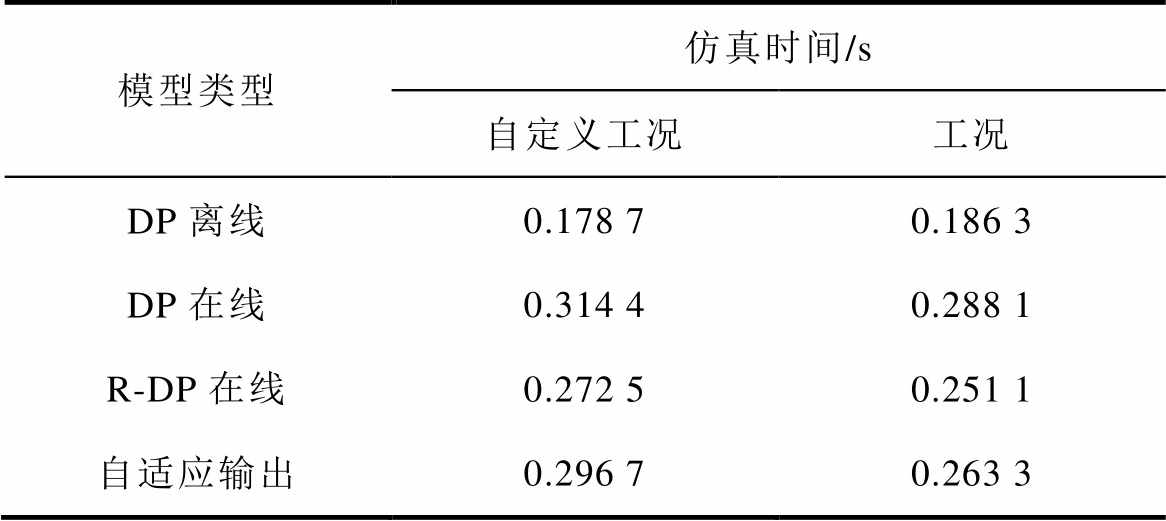
模型类型仿真时间/s 自定义工况工况 DP离线0.178 70.186 3 DP在线0.314 40.288 1 R-DP在线0.272 50.251 1 自适应输出0.296 70.263 3
由模型验证内容可知，DP离线模型、DP在线模型、R-DP在线模型及自适应输出模型等4个模型在精度和速度方面各有优劣。自适应输出模型比其他模型具有更高的精度，而DP离线模型与其他模型相比具有更快的速度。实际应用中，往往需要同时考虑精度和速度，使两者得到一个良好的平衡。基于模型选择过程设定的精度和速度的权重系数定义模型选择因子，有
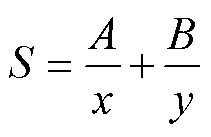（17）
式中，S为各模型的选择因子；A、B分别为主观设定的精度和速度的选择权重系数，A+B=1；x反映的是各模型平均绝对误差相对于自适应输出模型平均绝对误差的倍数；y反映的是各模型平均仿真时间相对于DP离线模型仿真时间的y倍。各模型选择因子越大，说明该模型能够在精度和速度方面取得更好的平衡。当模型精度和速度权重系数相同，均为0.5时，针对前述两种工况，每个模型的选择因子如图12所示。
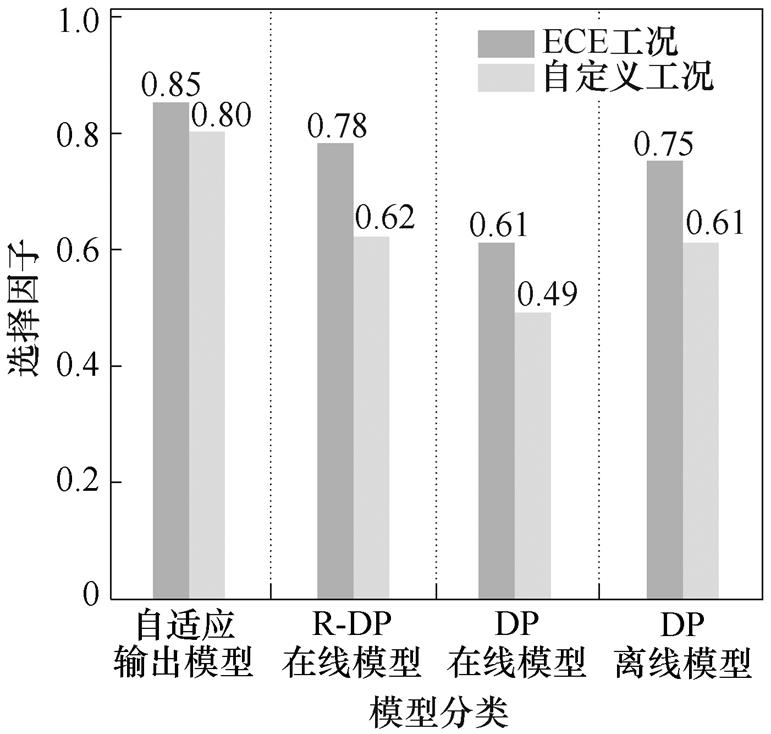
图12 各模型选择因子
Fig.12 Selection factors of each model
由图12可知，自适应输出模型针对自定义工况和ECE工况均具有最大的模型选择因子，说明和其他模型相比，自适应输出模型能够在精度和速度方面取得更好的平衡。综合以上分析，基于RLS的全工况自适应输出等效电路模型通过对DP模型在线参数辨识过程的改进和在线模型、离线模型相结合的方式，在运行速度变化不大的前提下，提高了模型精度，在精度和速度之间取得了更好的平衡。
精确的电池模型对于准确获取电池的工作状态具有重要意义。首先，结合本文模型参数不同的时变特性，将欧姆电阻从在线辨识过程分离，提出了欧姆电阻已知的R-DP在线等效电路模型，使得基于RLS的在线辨识对象由5个参数减少为4个参数，提高了精度，减少了计算量。其次，提出根据不同工况在线模型、离线模型自适应输出的等效电路模型，进一步提高了模型精度。仿真实验结果表明，基于RLS的锂电池全工况自适应等效电路模型相比于欧姆电阻已知的R-DP在线模型及DP离线模型具有更高的精度。最后，建立基于精度与速度的模型评价方法，验证了自适应输出模型相比于其他模型能够在精度和速度方面取得更好的平衡。下一步拟将温度采集模块融入模型，使其更适合于新能源汽车电池管理系统。
参考文献
[1] 庞辉, 郭龙, 武龙星, 等. 考虑环境温度影响的锂离子电池改进双极化模型及其荷电状态估算[J]. 电工技术学报, 2021, 36(10): 2178-2189.
Pang Hui, Guo Long, Wu Longxing, et al. An improved dual polarization model of Li-ion battery and its state of charge estimation considering ambient temperature[J]. Transactions of China Electrotech- nical Society, 2021, 36(10): 2178-2189.
[2] 刘芳, 马杰, 苏卫星, 等. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工技术学报, 2020, 35(4): 698-707.
Liu Fang, Ma Jie, Su Weixing, et al. State of charge estimation method of electric vehicle power battery life cycle based on auto regression extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 698-707.
[3] 刘伟, 杨耕, 孟德越, 等. 计及常用恒流工况的锂离子电池建模方法[J]. 电工技术学报, 2021, 36(24): 5186-5200.
Liu Wei, Yang Geng, Meng Deyue, et al. Modeling method of lithium-ion battery considering commonly used constant current conditions[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5186- 5200.
[4] Berrueta A, Urtasun A, Ursúa A, et al. A com- prehensive model for lithium-ion batteries: from the physical principles to an electrical model[J]. Energy, 2018, 144: 286-300.
[5] 潘海鸿, 张沫, 王惠民, 等. 基于多影响因素建立锂离子电池充电内阻的动态模型[J]. 电工技术学报, 2021, 36(10): 2199-2206.
Pan Haihong, Zhang Mo, Wang Huimin, et al. Establishing a dynamic model of lithium-ion battery charging internal resistance based on multiple factors[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2199-2206.
[6] 郭向伟. 电动汽车电池荷电状态估计及均衡技术研究[D]. 广州: 华南理工大学, 2016.
[7] Tian Huixin, Qin Pengliang, Li Kun, et al. A review of the state of health for lithium-ion batteries: research status and suggestions[J]. Journal of Cleaner Production, 2020, 261: 120813.
[8] 卫志农, 原康康, 成乐祥, 等. 基于多新息最小二乘算法的锂电池参数辨识[J]. 电力系统自动化, 2019, 43(15): 139-145.
Wei Zhinong, Yuan Kangkang, Cheng Lexiang, et al. Parameter identification of lithium-ion battery based on multi-innovation least squares algorithm[J]. Auto- mation of Electric Power Systems, 2019, 43(15): 139-145.
[9] 熊瑞. 动力电池管理系统核心算法[M]. 北京: 机械工业出版社, 2018.
[10] Jarraya I, Masmoudi F, Chabchoub M H, et al. An online state of charge estimation for lithium-ion and supercapacitor in hybrid electric drive vehicle[J]. Journal of Energy Storage, 2019, 26: 100946.
[11] Sun Li, Li Guanru, You Fengqi. Combined internal resistance and state-of-charge estimation of lithium- ion battery based on extended state observer[J]. Renewable and Sustainable Energy Reviews, 2020, 131: 109994.
[12] Yan Chong, Yao Yuxing, Cai Wenlong, et al. The influence of formation temperature on the solid electrolyte interphase of graphite in lithium ion batteries[J]. Journal of Energy Chemistry, 2020, 49: 335-338.
[13] Qaisar S M. Event-driven approach for an efficient coulomb counting based Li-ion battery state of charge estimation[J]. Procedia Computer Science, 2020, 168: 202-209.
[14] 宋轩宇, 黄敬尧, 段俊强. 基于自适应递推最小二乘法与无迹卡尔曼滤波的电池SOC估算[J]. 电力科学与工程, 2019, 35(12): 41-48.
Song Xuanyu, Huang Jingyao, Duan Junqiang. Estimation of state of charge of battery based on adaptive recursive least squares and unscented Kalman filtering[J]. Electric Power Science and Engineering, 2019, 35(12): 41-48.
[15] 李华. 动力锂电池建模与SOC估计策略研究[D]. 太原: 太原科技大学, 2018.
[16] Ji Yingping, Chen Xiaoping, Wang Tao, et al. Coupled effects of charge-discharge cycles and rates on the mechanical behavior of electrodes in lithium- ion batteries[J]. Journal of Energy Storage, 2020, 30: 101577.
[17] 张振宇, 汪光森, 聂世雄, 等. 脉冲大倍率放电条件下磷酸铁锂电池荷电状态估计[J]. 电工技术学报, 2019, 34(8): 1769-1779.
Zhang Zhenyu, Wang Guangsen, Nie Shixiong, et al. State of charge estimation of LiFePO4 battery under the condition of high rate pulsed discharge[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1769-1779.
[18] Lu Yao, Tang Yinggan, Zhang Xuguang, et al. Parameter identification of fractional order systems with nonzero initial conditions based on block pulse functions[J]. Measurement, 2020, 158: 107684.
[19] 朱瑞, 段彬, 温法政, 等. 基于分布式最小二乘法的锂离子电池建模及参数辨识[J]. 机械工程学报, 2019, 55(20): 85-93.
Zhu Rui, Duan Bin, Wen Fazheng, et al. Lithium-ion battery modeling and parameter identification based on decentralized least squares method[J]. Journal of Mechanical Engineering, 2019, 55(20): 85-93.
[20] 刘安迪, 李妍, 谢伟, 等. 基于多源数据多时间断面的配电网线路参数估计方法[J]. 电力系统自动化, 2021, 45(2): 46-54.
Liu Andi, Li Yan, Xie Wei, et al. Estimation method of line parameters in distribution network based on multi-source data and multi-time sections[J]. Auto- mation of Electric Power Systems, 2021, 45(2): 46-54.
[21] 董喜乐. 锂离子电池模型参数和荷电状态联合在线估计方法研究[D]. 北京: 北京交通大学, 2019.
[22] Ding Feng, Chen Tongwen. Performance bounds of forgetting factor least-squares algorithms for time- varying systems with finite measurement data[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2005, 52(3): 555-566.
RLS Adaptive Equivalent Circuit Model of Lithium Battery under Full Working Condition
Abstract When the recursive least square (RLS) method is applied to the multi-time scale system of lithium battery, problems such as low accuracy of model parameter identification and poor adaptability of working conditions will occur. For this reason, the dual polarization (DP) model is taken as the research object. Firstly, according to the different time-varying characteristics of the model parameters, the identification process of ohmic resistance is separated to reduce the number of parameters to be identified by RLS, and the mutual influence of the parameters is reduced, which improves the accuracy of RLS identification and reduces the amount of calculation. Secondly, considering the low accuracy of the model parameter online identification and the high accuracy of offline identification for constant current condition, an adaptive output equivalent circuit model for the full working condition is proposed to further improve the accuracy of the model. Simulations based on the actual operating conditions show that, the full-condition adaptive equivalent circuit model has higher accuracy than the R-DP online model with known ohmic resistance and the DP offline model, the better balance is achieved between model accuracy and running speed.
keywords：Lithium battery, battery model, parameters identification, least square method, model accuracy, full working condition
DOI: 10.19595/j.cnki.1000-6753.tces.210384
中图分类号：TM912.8
国家自然科学基金项目（61703145）、河南省科技攻关项目（202102210093）和河南省高校基本科研业务费专项资金青年探索项目（NSFRF210332）资助。
收稿日期 2021-03-22
改稿日期 2021-09-26
郭向伟 男，1987年生，博士，副教授，研究方向为电力电子及其在电池管理系统中的应用。E-mail: gxw@hpu.edu.cn（通信作者）
邢 程 男，1997年生，硕士研究生，研究方向为电池管理系统。E-mail: xingcheng20210130@.126.com
（编辑 崔文静）