 (1)
(1)
摘要 表面粗糙度直接决定着工件的性能和使用寿命,由于传统的基于光学或三维形貌的表面粗糙度检测方法存在对工件表面清洁状态及操作环境要求较高等问题,因此,该文提出一种基于深度学习的非接触式电磁超声表面粗糙度识别方法。首先通过建立不同表面粗糙度的电磁超声有限元仿真模型,研究了涡流密度和洛仑兹力对激励与接收信号的影响。然后利用所提出的卷积神经网络,对从电磁超声换能器检测得到的A扫描信号的时频系数图进行特征提取,输入至预训练的支持向量机分类器中完成表面粗糙度识别和预测。为了验证所提方法的有效性,对通过立铣工艺加工的表面粗糙度比较样块进行测试。实验结果表明,所提出的超声识别方法平均精度为98.83%,具有较高的预测精度与稳定性,解决了超声信号信噪比较低而导致信号特征识别困难的问题,同时减少了特征提取过程对于人工干预的依赖。
关键词:表面粗糙度 电磁超声换能器 深度学习 卷积神经网络 图像识别
金属管、板材因具有较高的强度和韧性在我国铁路、船舶、航空航天等行业广泛应用。表面粗糙度作为表征金属材料表面质量的指标之一,其数值与工件的抗疲劳、抗摩擦、热传导、使用寿命等性能密切相关[1],同时对评估加工产品质量方面起着重要作用。因此,如何高效地实现金属材料表面粗糙度的检测是研究的热点问题。
传统的材料表面粗糙度检测方法主要分为接触式和非接触式两个大类[2]。接触式测量法主要通过探针在金属材料表面移动来获取表面的特征参数,但其检测效率较低且会对材料表面造成划痕;非接触式检测法包括光干涉法、光散斑法、三维形貌法等方法。Tian Xiaobo等[3]通过非平行光干涉照明显微镜获得材料表面形貌图,经过特征提取后计算材料表面粗糙度。E. Baradit等[4]利用相干光被粗糙表面散射产生的散斑现象对材料表面粗糙度进行检测。以上两种方法均属于光学检测法,能够克服接触式检测法在测量时面临的问题,但因光学检测法易受到外界温度、光照等影响,其检测稳定性较差且无法满足在线检测的要求。通过三维轮廓仪扫描[5]得到材料形貌图对表面粗糙度进行检测的方法稳定性较强,但其扫描速度相对较慢,对被测物表面清洁程度要求较高且检测经济成本相对较高。电磁超声检测技术[6-8]作为一种新兴的非接触式检测方法,具有无需对被测试件表面预处理、可对材料表面及内部缺陷进行精准定位识别、能适用复杂的现场环境等优点,广泛应用于无损检测领域。电磁超声换能器(Electromagnetic Acoustic Transducer, EMAT)检测是通过激励高频信号在材料内部产生超声波信号,并根据回波信号的特征来评估材料表面或内部的缺陷状况。当材料表面粗糙程度不同时,其接收的时频域信号特征将存在差异,因此可以通过对回波信号的时频特征分析来实现对材料表面粗糙度的识别。然而,工件的表面粗糙状况在一定程度上限制了EMAT检测精度的提高。F. Shi等[9]基于基尔霍夫理论计算了超声波在粗糙表面上的反射与传输问题。Wang Zhe等[10-11]首先通过建立等距三角形粗糙表面,研究了其对EMAT测厚过程中激励信号能量的变化,然后利用压电换能器,探究了随机粗糙表面在固液耦合的二维平底孔超声模型检测时的回波信号和噪声幅度变化情况,但并未研究随机粗糙表面对EMAT激励与接收信号过程的影响。
为实现对EMAT回波信号进行解析,国内外学者对此开展了大量研究。常规的超声信号特征提取算法包括统计特征、短时傅里叶变换[12](Short Time Fourier Transformation, STFT)、离散小波变换[13](Discrete Wavelet Transformation, DWT)、连续小波变换(Continuous Wavelet Transform, CWT)[14](约1150000个连续小波变换)等,这些算法对信号的低级特征较为敏感。当检测信号的信噪比较低时,其特征提取效果就会受到极大的影响。随着深度学习在图像处理技术领域的不断发展,极大地促进了信号特征提取的研究[15-16]。侯智等[17]利用BP神经网络对轴承套圈磨削状态参数进行训练和验证,间接实现对轴承套圈沟道磨削粗糙度的识别。肖雄等[18]通过二维卷积神经网络(Convolutional Neural Networks, CNN)对预处理后的轴承故障信号进行诊断,极大地提高了故障预测的准确率。Liu Hongmei等[19]提出了一种基于短时傅里叶变换的深度学习滚动轴承诊断算法,通过实例证明该方法具有优异的泛化能力。A. A. Zakri等[20]通过使用离散傅里叶变换对输电线路中的电流与电压信号进行特征提取后,输入到支持向量机(Support Vector Machines, SVM)中实现了出色的分类结果。
在上述研究基础之上,本文提出了一种基于深度学习的CNN-SVM分类器的超声信号识别方法,用于对EMAT回波信号的时频系数图进行特征提取并分类,最终实现不同表面粗糙度的识别。本文的第一部分分析了EMAT的工作原理,并通过有限元仿真模型研究了随机粗糙表面对电磁超声信号激励与接收的影响;第二部分研究了所提出的CNN-SVM模型对微弱EMAT检测信号的识别方法;第三部分通过实验对所提方法进行验证。
由腐蚀、切加工等形成的粗糙表面轮廓数据的高度相关函数与理论高斯分布相关函数非常吻合。试件表面具有的微小间距和峰谷所组成的微观几何形状误差用表面粗糙度Ra来表示。以一维粗糙面为例,假设随机粗糙面的高度起伏函数为z=f(x),其概率密度分布函数反映了高度起伏的分布情况,用p(h)表示,则p(h)dh表示为相对参考平面高度z~z+dz的概率。粗糙面的方均根高度δ是反映粗糙程度的一个基本量,其值可由高度分布的概率密度函数求出,文献[21]将其定义为
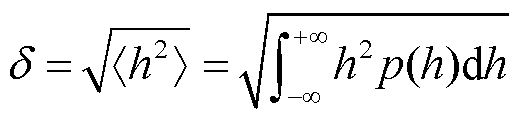 (1)
(1)
式中,<h2>表示粗糙面上所有的点相对于参考平面的平均值,为了简化计算,通常将参考平面设为h(x)=0。此外,因为粗糙表面上任意两点的高度具有相关性,其相关系数定义为
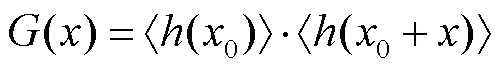 (2)
(2)
当x=0, G(x) =δ2时,符合高斯分布的相关函数表示为
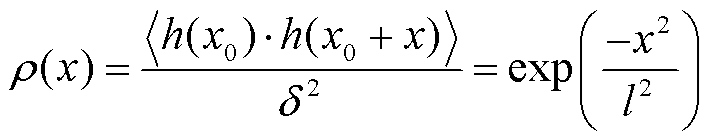 (3)
(3)
式中,l为相关长度,是随机粗糙表面的一个基本物理量,用来描述粗糙面上任意两点高度在统计上的独立性。当表面上两点的水平方向上的相隔距离大于l时,即认定这两个点从统计意义上讲是近似独立的。
为了探究粗糙表面对超声回波信号的影响,本文采用蒙特卡罗法[22]模拟生成随机粗糙表面。通过控制方均根高度δ和相关长度l两个基本参数,结合蒙特卡罗方法,设置仿真采样点个数N=1 280,取样长度L=20mm,模拟生成的高斯随机粗糙面如图1所示。由图1可知,当相关长度l一定时,方均根高度δ值越大,随机粗糙表面的高度起伏就越大;方均根高度δ数值一定时,相关长度l越小,随机粗糙表面的起伏波动越剧烈。下文中的电磁超声有限元模型也是基于以上两个粗糙几何参数展开研究。
本文采用COMSOL Multiphysics有限元仿真软件,建立了具有随机粗糙表面的收发一体式二维电磁超声体波模型,其原理如图2所示。有限元模型由提供静态偏置磁场的钕铁硼永磁体、产生脉冲涡流的线圈和被测金属试件构成。永磁体的磁场强度为1.2T,待测试件材料为45号钢,尺寸为12mm×8mm,其杨氏模量为200GPa、泊松比为0.33、电导率为8.41×106S/m、密度为7 850kg/m3,试件与线圈提离距离为0.2mm。线圈中加载的电流峰值为100A,频率为5MHz。随机粗糙面由几何组件导入至有限元模型中。
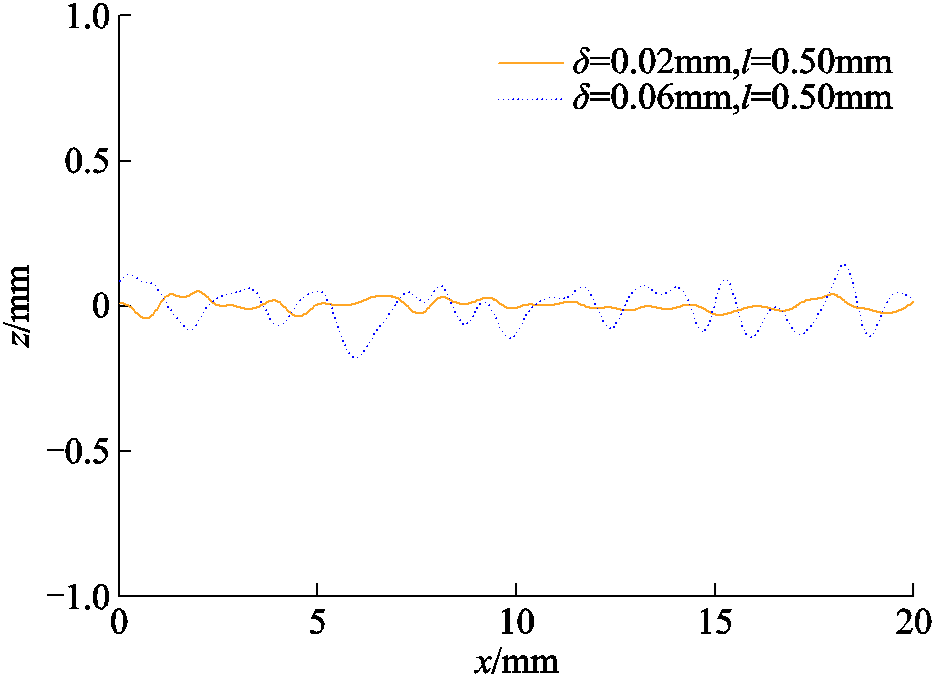
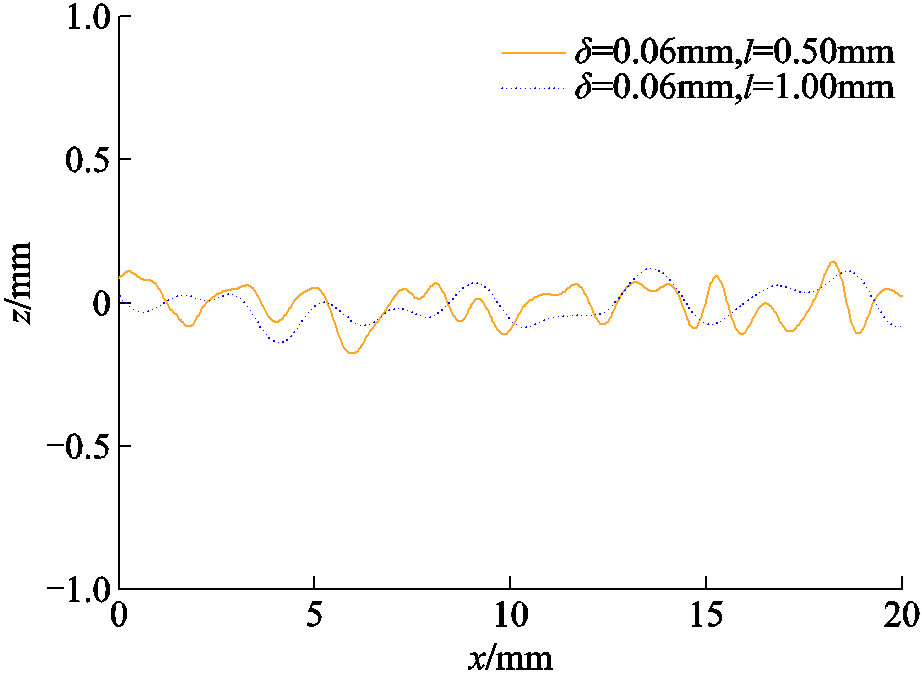
图1 一维高斯随机粗糙面示意图
Fig.1 One-dimensional Gaussian random rough surface diagram
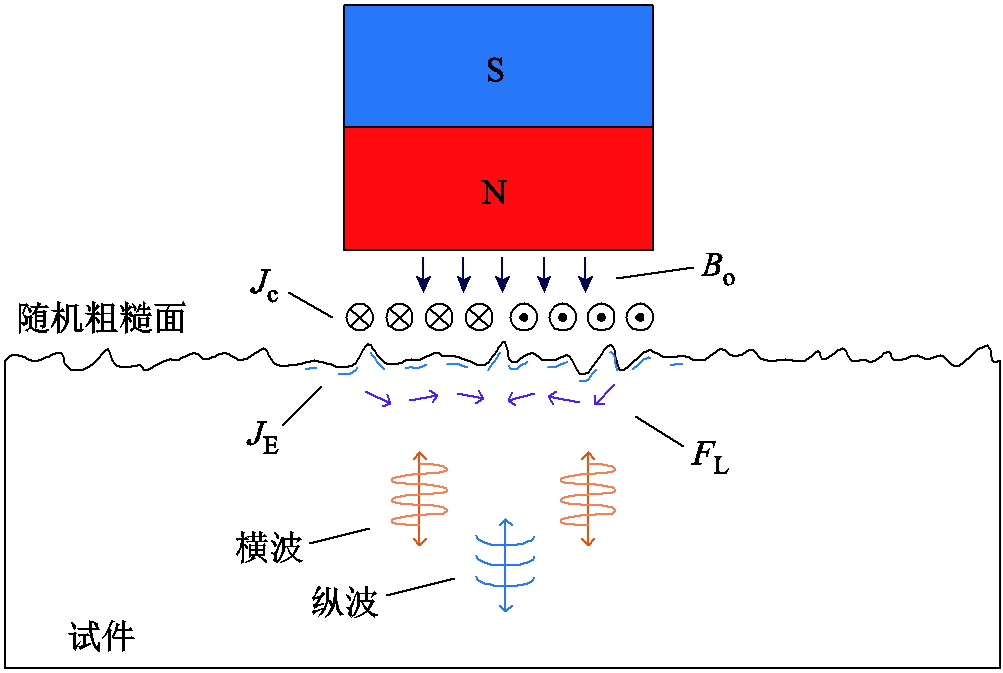
图2 EMAT结构及原理图
Fig.2 Structure and schematic diagram of EMAT
当高频大功率交变电流Jc通入线圈时,会在试件表面趋肤深度内感生出与激励电流方向相反的涡流JE,涡流在外加静态磁场Bo的共同作用下产生洛仑兹力FL。金属试件内的质点在洛仑兹力FL的作用下发生被迫振动产生向下传播的体波。当体波传播到试件底部时将产生声波反射,进而向上传播至试件表面。此时位于试件顶部的EMAT能够感应出电压信号,用于分析粗糙表面对体波的影响。由于本节有限元仿真模型中的永磁体产生的静态磁场以垂直方向为主,所以质点主要受到水平方向的洛仑兹力,产生的声波以横波为主。
当试件上、下底面均为光滑表面时,系统所激发的体波传播示意图如图3a~图3c所示,在试件内部会同时产生垂直向下传播的横波及少量的纵波。为了分析粗糙表面对体波传播的影响,将试件上表面调整为不同粗糙程度的粗糙表面,得到体波传播示意图如图3d~图3f所示。通过对比可以清晰地看出,上表面粗糙的试件内部声波的传播情况与前者具有较大区别。由于其表面起伏高度的影响,导致粗糙表面的感生涡流分布不再具有均匀性,如图4所示,进而导致洛仑兹力将分布在粗糙表面的各个方向上。随之造成体波的传播方向发生一定变化,不再垂直向下传播,而与竖直方向呈现一定的夹角,且声波的入射角度受表面的粗糙程度影响较大,但依然是以产生横波为主。同时,当声波沿粗糙表面逐步扩散时,由于部分声波会在表面来回反射,从而在试件内部产生沿各个方向发散的散射波。

图3 光滑表面与不同粗糙程度表面声波传播示意图
Fig.3 Schematic diagram of acoustic wave propagation between smooth surface and different roughness surface

图4 0.5μs时刻试件表面涡流示意图
Fig.4 Eddy current diagram of specimen surface at 0.5μs
此外,为了分析不同位置粗糙表面对激励与接收回波信号的影响,另设一组对照实验。在这组对照实验中,分别建立三个仿真模型,见表1。
表1 不同位置粗糙表面模型组
Tab.1 Rough surface model groups in different locations

模型上表面下表面 一粗糙光滑 二光滑粗糙 三粗糙粗糙
以上三个模型的粗糙表面参数与图3e仿真的参数保持一致。经过计算后,三者的接收回波时域信号如图5a所示。由图5a可知,模型一的回波信号幅值最大,模型三次之,模型二最低。这是因为试件上表面粗糙时,由于起伏高度的存在,导致线圈与下部的表面提离距离相对减小,此时位于趋肤深度内的质点受到的洛仑兹力相对较大,质点的振动也更加强烈,进而导致激励的声波能量更高。与此同时,当试件下表面为粗糙面时,由于其反射回波能量衰减较大,最终致使接收EMAT中的感应电压信号幅值较低。但由于粗糙表面是随机生成的,即使方均根高度δ和相关长度l保持一致,也会产生具有不同波动程度的随机粗糙面,所以会对信号的激励和接收结果产生一定的影响。
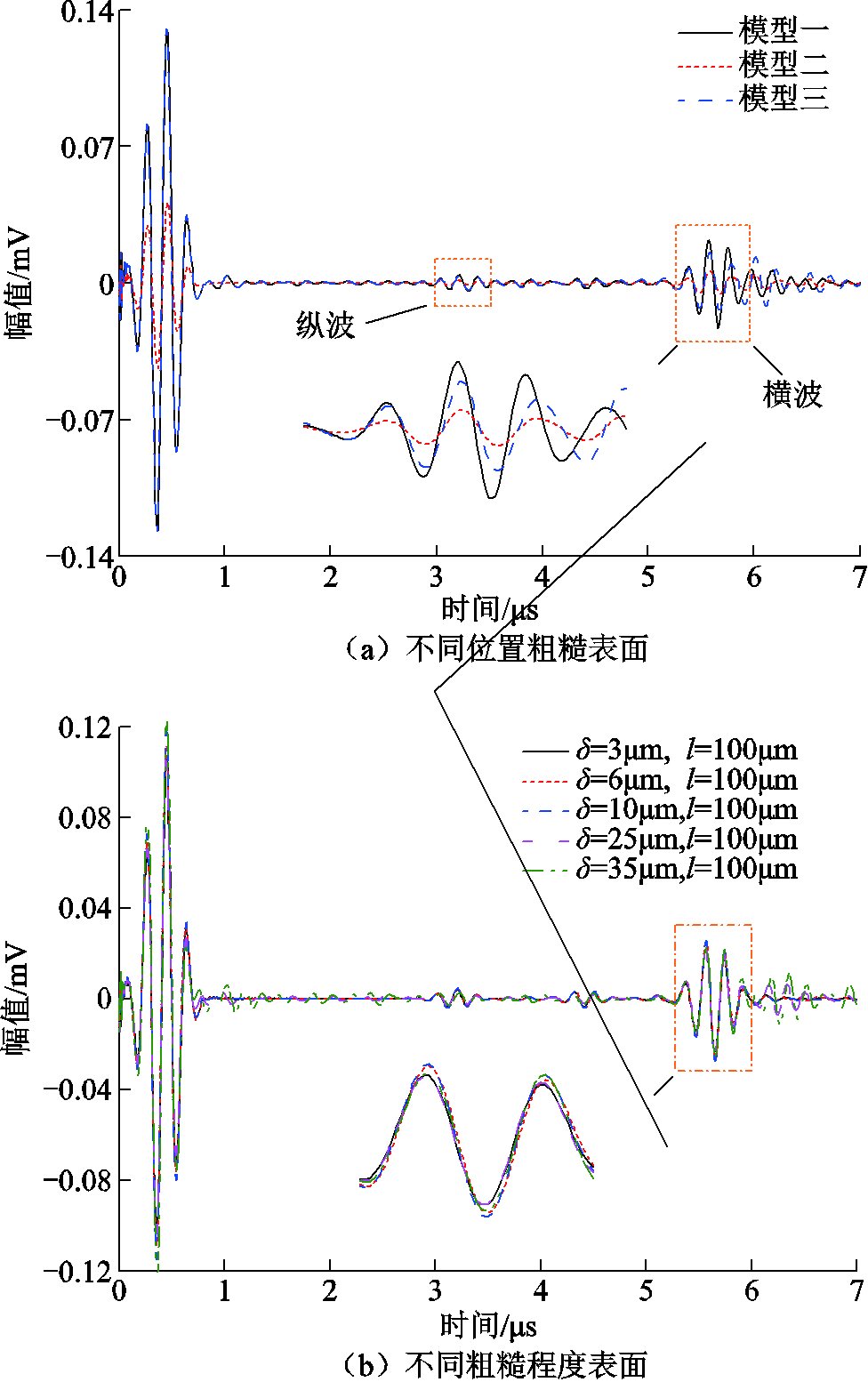
图5 不同位置粗糙表面和不同粗糙程度表面的回波信号
Fig.5 Echo signal graph of rough surface at different positions and with different roughness
为了分析不同方均根高度δ对接收EMAT中回波信号幅值的影响,将试件上表面设置为粗糙表面,下表面保持光滑,然后将相关长度l设置为定值100μm,方均根高度δ依次设置为3μm、6μm、10μm、25μm、35μm,最终计算得到的结果如图5b所示。由局部放大图可知,随着方均根高度δ的增加,时域回波信号的幅值虽有波动但无明显变化趋势,很难仅从宏观角度观测信号之间的差异,无法实现不同表面粗糙度的识别工作,需要对信号做进一步的处理。
CWT作为一种提取信号特征信息的方法,常用于处理和分析非平稳信号问题中,其定义如下:假设一个小波函数y(t)∈L2(R),当其满足容许条件,即有
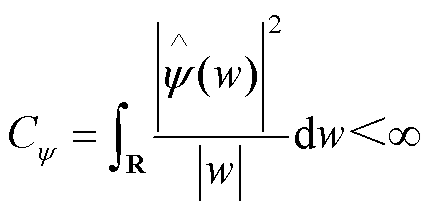 (4)
(4)
时,称其为基小波或母小波。将母小波经过平移与伸缩变换后,可以得到一个小波序列。对于连续的情况,其序列为
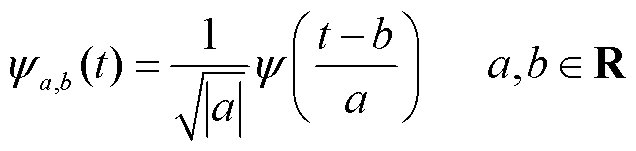 (5)
(5)
式中,a为伸缩因子;b为平移因子。在小波处理的过程中,母小波的选择不是单一的。考虑到 Morlet小波不但拥有非正交性而且还是由Gaussian调节的复值小波,可以得到平滑连顺的小波振幅及时域和频域两种信息。因此本文选用Morlet小波作为CWT的母小波。
通过CWT变换,将图5b中的时域信号转换至时频域进行特征分析,结果如图6所示。由1.2节有限元仿真结论可知,随着表面粗糙程度的增大,EMAT所激励的超声信号在传播过程中产生的散射波的幅值就越大,其接收回波信号的拖尾噪声也越大。最终反映在时频图像中的结果为表面粗糙程度越大,其能量分布就越宽,能量强度就越大,因此可以通过时频特征分析来实现工件表面粗糙度的识别工作。但是,在实际测量过程中,由于环境与设备噪声的存在,会进一步限制测量信号的信噪比,降低时频特征的可区分度,影响最终的测量结果。
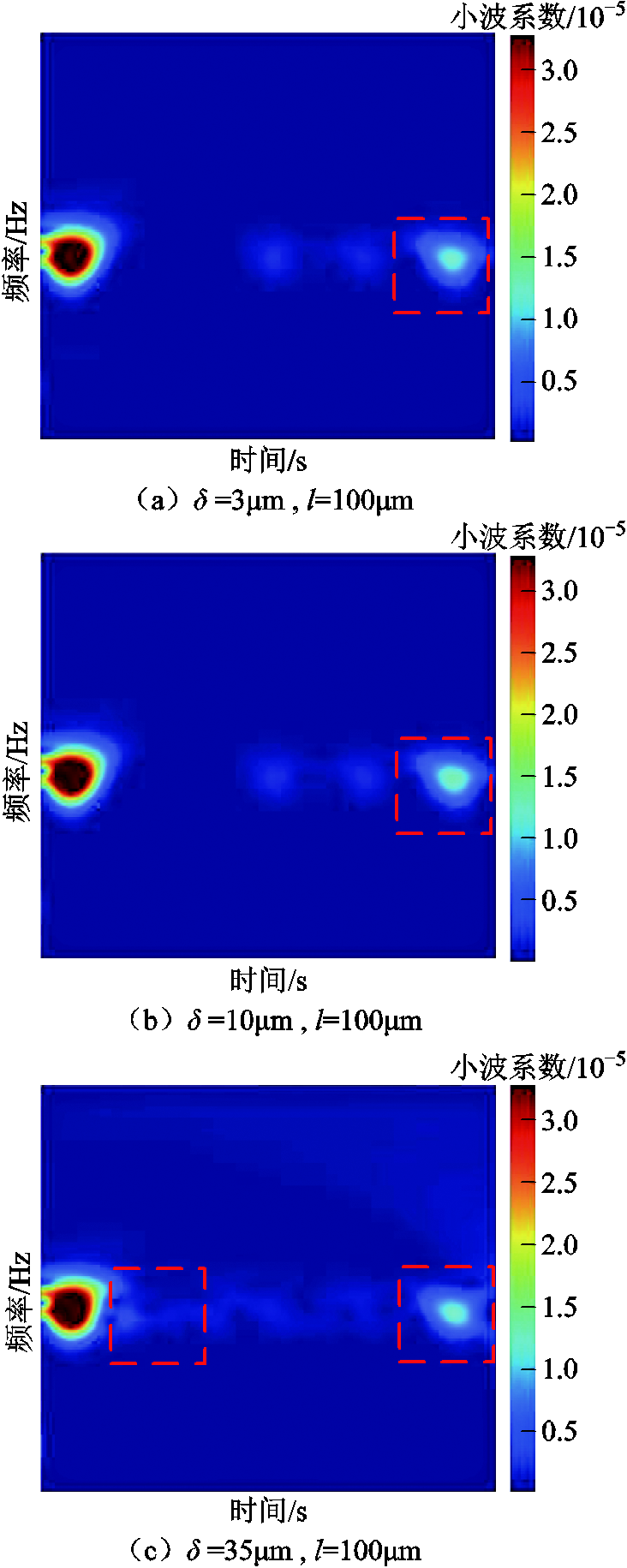
图6 不同粗糙程度的表面回波信号时频特征图
Fig.6 Time-frequency characteristic map of surface echo signals with different roughness
本文提出的超声信号识别方法流程如图7所示。首先利用电磁超声检测设备对金属试件的上粗糙表面进行扫描,获得表面A扫描(A-Scan)信号,进而通过CWT变换将其转换为时频系数图。然后再利用CNN对训练集数据进行训练,提取时频图像的特征矩阵,最终输入至预训练的SVM分类器中完成分类识别工作,并对所提出的识别方法进行评价。
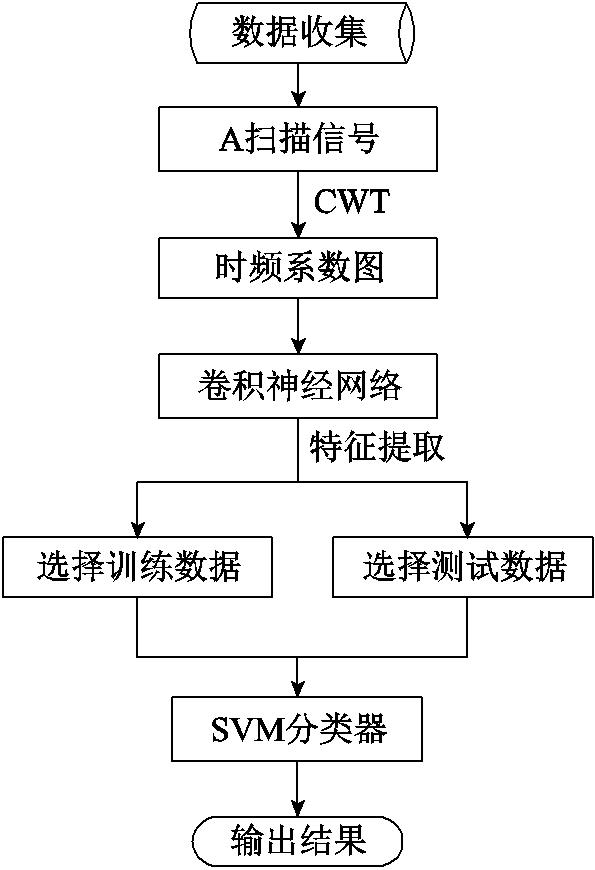
图7 所提出的超声信号识别方法
Fig.7 The proposed ultrasonic signal recognition method
当使用经典的CNN网络对电磁超声时域信号的时频图像进行处理时,首先需要将处理的目标图像输入神经网络中,通过卷积层中的滤波器进行卷积计算,提取图像的局部特征;再经过池化层对提取到的特征图像进行下采样处理;最后将获得的包含最丰富信息的特征图像与全连接层相连接,对图像进行分类处理并输出结果。
基于经典的CNN架构模型,本文在此基础之上对其进行了优化,新的网络结构如图8所示。该网络可划分为三个部分,在第一个部分中,首先将经过CWT处理过的A-Scan图像转化为具有R,G,B
三通道的二维尺度图,然后将其宽度和高度压缩至224×224,作为目标图像输入到CNN网络中进行运算。在第二个部分中,首先选取16个3×3大小的步长为1的卷积核对输入图像进行卷积计算,为了得到与输入图像相同大小的特征图,将Padding值设为1。提取出特征图像后,引入Batch normalization层,对同一维度特征进行归一化处理。经过归一化后再输入激活函数,会使大部分得到的值落入非线性函数的线性区域内,远离导数饱和区,避免了梯度消失,以此来加速整个网络的收敛过程。激活层主要负责对卷积提取到的特征进行激活,本文选用Relu函数作为激活层的激活函数。然后使用Maxpooling函数对特征图像进行下采样处理,降低特征图的维度,在减少网络参数的同时还可以防止过拟合现象,经下采样处理后的图像尺寸被压缩为112×112×16。将以上四层网络设置为一个组块,该模型总计包含7个组块,并且每个组块中的卷积核数量呈倍增关系。经过计算处理后,将前层的所有特征连接到全连接层中,对图像进行分类。在本次实验中,需要对四种粗糙度不同的试件进行分类,所以全连接层的参数设置为4。由于SVM在面对小样本数据、非线性和高维度的问题时具有优异的表现,所以在第三个部分中,为了优化模型的分类识别能力,使用带有RBF核函数的SVM分类器替换原CNN网络中的Softmax层,将从全连接层输出的图像特征输入SVM中进行分类预测,输出最终的识别结果。

图8 所提出的CNN模型结构
Fig.8 Architecture of the proposed CNN
本文选用立铣工艺制造方法制成的上表面粗糙度Ra为0.8μm、1.6μm、3.2μm、6.3μm,下表面均为光滑表面的4个表面粗糙度比较样块,试件材质均为45号优质碳素钢,几何尺寸为22.5mm×20mm× 5mm。为了更好地表征试件表面样貌状态,使用光学3D表面轮廓仪对试件进行非接触式扫描并建立了表面3D图像,如图9所示。由图9可知,在物镜放大倍数为20的条件下,各个试件表面之间有着显著的区别,即粗糙痕迹从左至右逐渐加深,宽度逐渐增加。
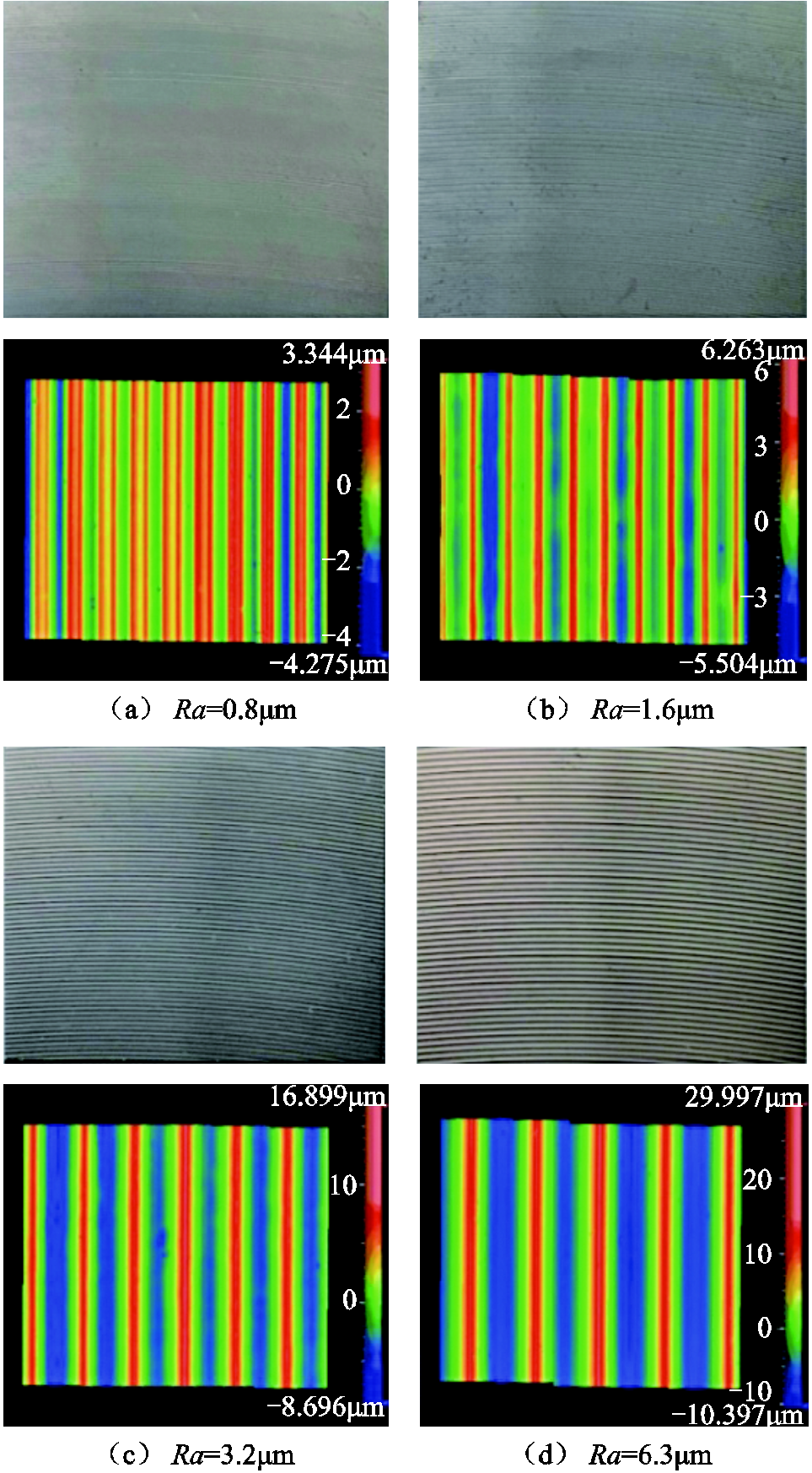
图9 试件表面状态及三维形貌图
Fig.9 The surface state and three-dimensional topography of the specimen
实验所使用的电磁超声检测系统如图10所示,其中包括由螺旋线圈和钕铁硼永磁体组成的EMAT换能器、来自Ritec公司研发的RAM-5000超声检测系统、数字示波器以及用于控制超声系统运行的PC终端。实验采用收发一体式换能器,激发信号的中心频率为6 MHz,脉冲宽度为5个周期。
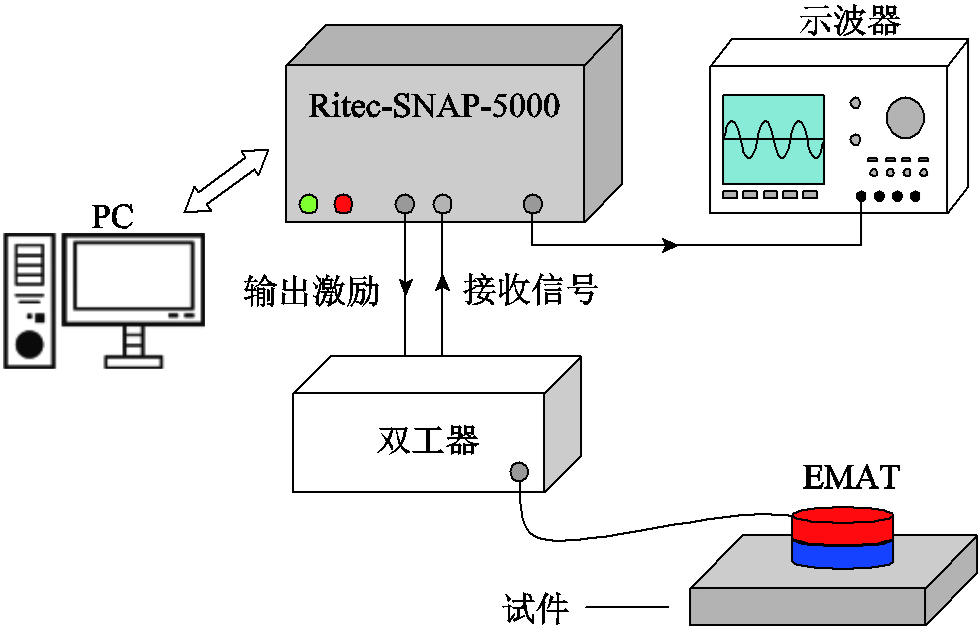
图10 实验平台设备框图
Fig.10 Block diagram of experimental platform equipment
在实验过程中,保持每个试件的信号采集位置均处于试件中心测量点,对每个试件分别进行扫描,其相应的时域回波信号如图11所示。经实际测量结果可知,位于相同位置测量点的时域回波信号的信号强度与声波衰减规律十分相似,很难通过回波信号去分辨其为哪种粗糙表面,与1.2节所做仿真的结果相一致。
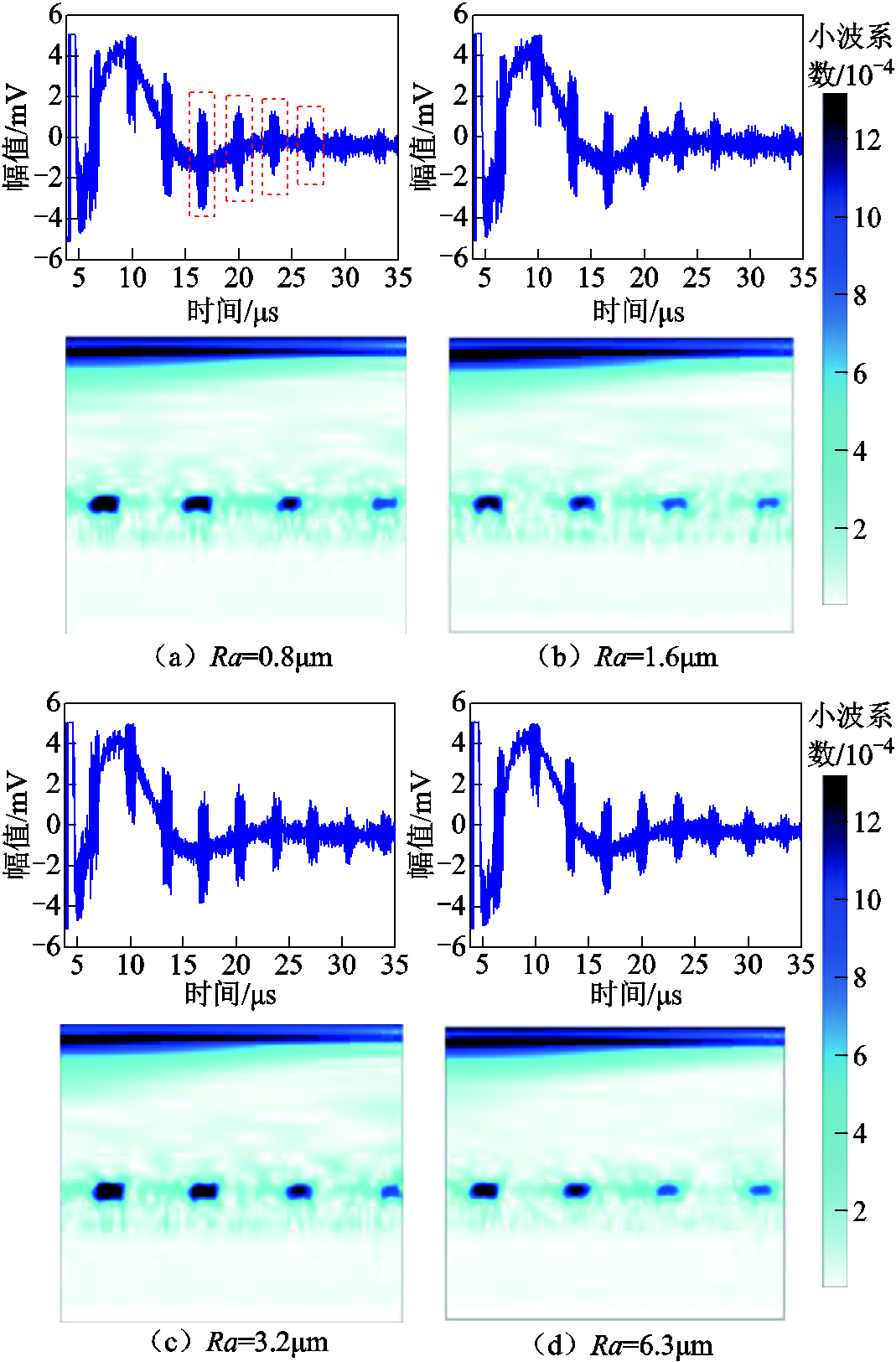
图11 试件中心采集点时频信号对比图
Fig.11 Time-frequency signal comparison diagram of the central collection point of the specimen
随后对四组时域信号进行CWT变换,为了方便数据处理,选取图11a中虚线框中的4个回波信号作为数据分析对象,并分别展示了实验所得的4个时域回波信号的时频图像,图中颜色的深浅表示幅值的大小。由图可知,经过CWT处理后,位于同一数据采集点的各个回波的小波系数绝对值存在明显的差异,即随着试件表面粗糙度的增大,其激励信号强度与散射波强度也会随之增大。进而导致其多次回波信号被淹没在噪声信号中,最终影响时频图中的能量分布和强度,使得不同粗糙度试件之间具备区分度,从而适合输入所提的CNN模型中进行特征提取,完成后续的实验。
基于上述分析结果,对实验样本进行扩充。为了消除检测时人工放置换能器所造成的位移偏差,增加实验测量的精度,在对试件进行扫描时,分别对每个试件选取如图12所示的五个具有代表性的位置作为数据样本采集点,使用体波EMAT沿着每个试件的上粗糙表面进行扫描,每个采集点分别记录50次。当完成全部扫描后,将创建一个含有1 000个A-Scan信号的样本数据库,然后通过CWT将其转换为时频系数图,用于训练和验证所提出的CNN模型及SVM分类器。
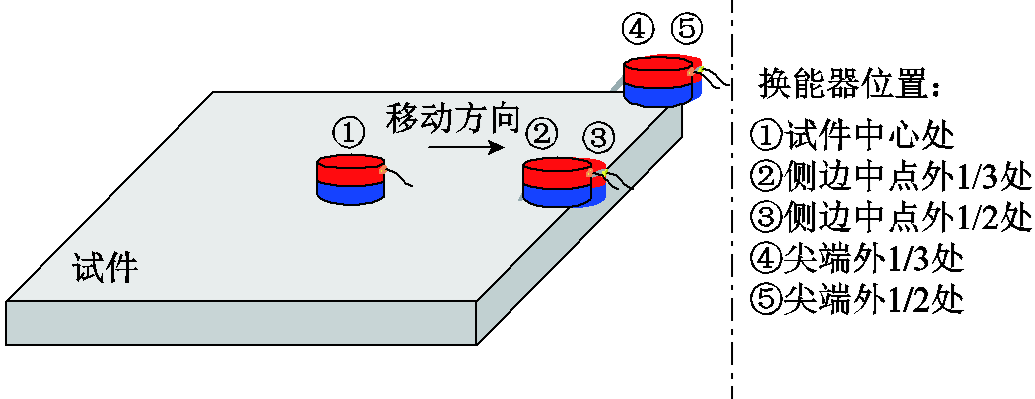
图12 测量数据样本采集点
Fig.12 Sampling point of measurement data
通过使用本文构建的CNN模型对全部图像进行特征提取后,得到了一个1 000行4列的特征矩阵。然后随机选取每个试件的210组数据作为训练样本,其余40组数据作为测试样本,输入到带有RBF核函数的SVM分类器中。而核函数的参数g与惩罚因子c会对结果产生较大影响,为了得到更好的预测结果,本文选用网格搜索加5折交叉验证法来获得最优的参数。图13展示了CNN单独识别时测试数据的混淆矩阵,具体给出了每个类别的识别结果,其总精度为96.9%;而在图14和图15中可以清晰地看出,经过优化后的CNN-SVM模型的识别精度达到了98.75%,有显著的提高,并且交叉验证的精度达到了100%,证明了该方法具有优异的分类识别能力。
同时,为了验证所提方法的稳定性,对实验数据重复测试了10次。表2列出了重复试验中的最高精度、最低精度、平均精度、标准差和平均计算时间。可以看出,所提模型的平均精度为98.83%±0.636%,证明了该方法具有出色的识别稳定性。
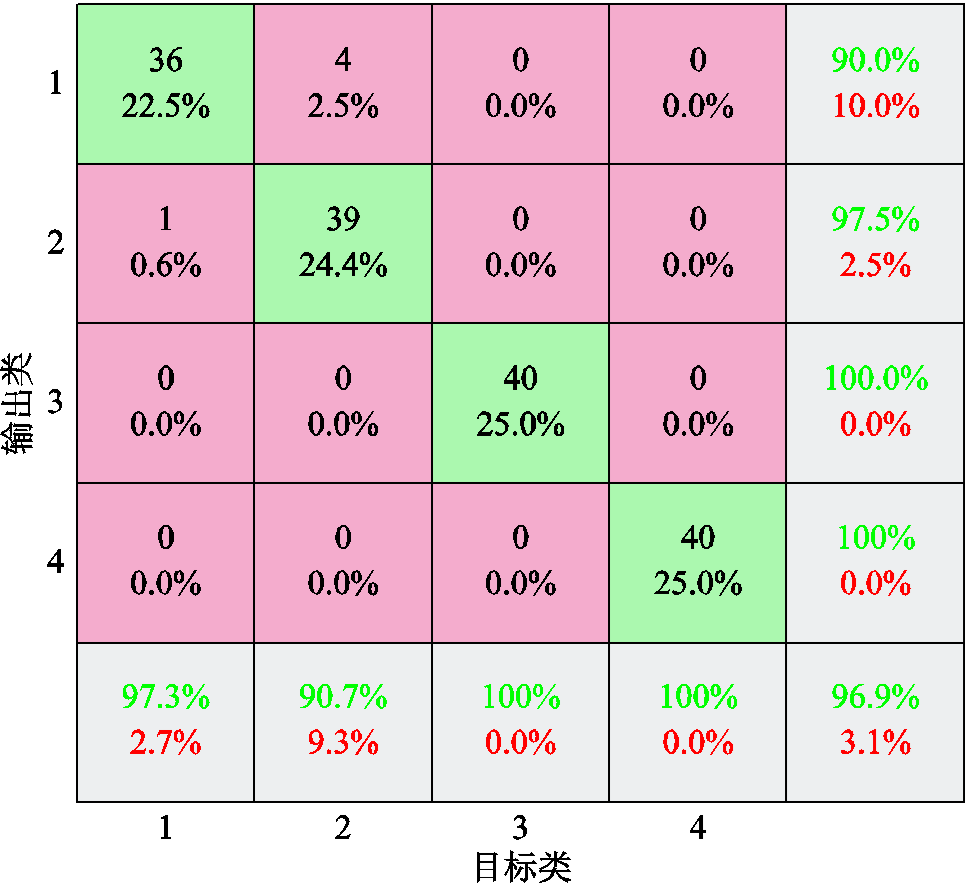
图13 CNN测试样本混淆矩阵
Fig.13 CNN test sample confusion matrix
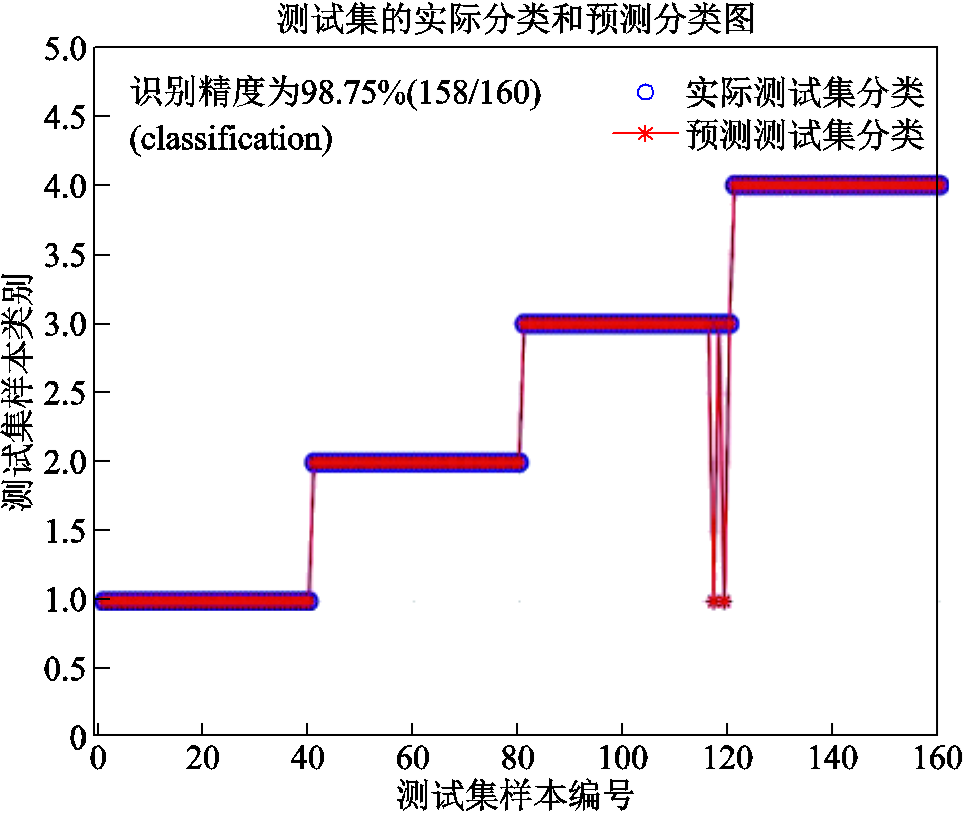
图14 SVM测试集识别结果
Fig.14 SVM test set recognition result
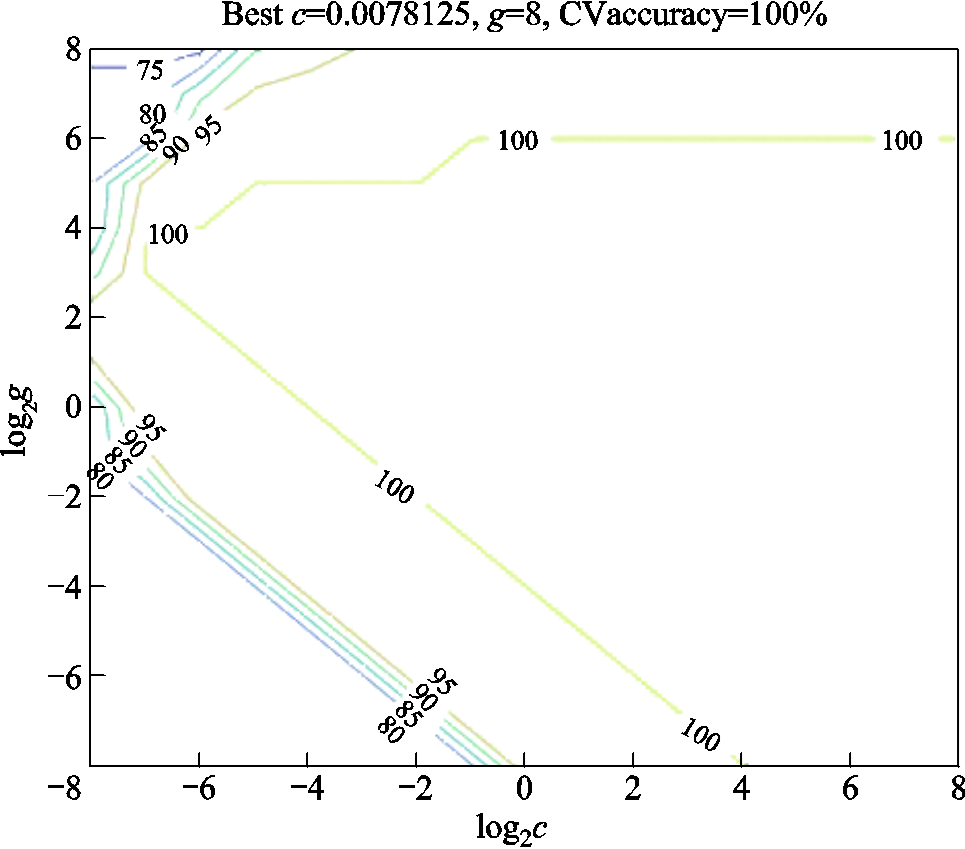
图15 训练集交叉验证结果
Fig.15 Training set cross-validation result
表2 所提出的CNN-SVM模型识别结果
Tab.2 Recognition results of the proposed CNN-SVM model

最高精度(%)最低精度(%)平均精度(%)标准差(%)平均计算时间/s 10097.7598.830.636124s
为了解决金属试件在表面无预处理的状态下,实现表面粗糙度快速识别的问题,本文提出了一种基于深度学习的非接触式电磁超声表面粗糙度识别方法。基于此方法,得出以下结论:
1)粗糙面的存在会影响试件表面涡流与洛仑兹力密度的分布,进而影响激励与接收信号的强度和超声波在试件内部的传播路径。同时,当粗糙面的粗糙程度差异较小时,其回波信号幅值的可区分度非常微弱。
2)相比于单CNN识别模型,本文所提出的CNN-SVM模型的超声信号识别方法在金属试件表面粗糙度识别分类方面具有较高的准确性与稳定性,平均精度达到了98.83%±0.636%。克服了EMAT实际测量时信噪比较低而导致信号特征难以解析的问题,极大地提高了超声信号的特征识别能力。
3)实验测量结果可以反映出,当换能器部分作用于被测试件时,该方法依然能够准确地对其接收信号进行识别。
参考文献
[1] Haghshenas A, Khonsari M M. Damage accumulation and crack initiation detection based on the evolution of surface roughness parameters[J]. International Journal of Fatigue, 2018, 107: 130-144.
[2] 瞿雪元, 顾廷权, 方百友. 带钢表面粗糙度在线检测技术最新进展[J]. 电子测量与仪器学报, 2017, 31(4): 493-500.
Qu Xueyuan, Gu Tingquan, Fang Baiyou. Review of surface roughness online measurement techniques of steel strip[J]. Journal of Electronic Measurement and Instrumentation, 2017, 31(4): 493-500.
[3] Tian Xiaobo, Tu Xingzhou, Zhang Junchao, et al. Snapshot multi-wavelength interference microscope[J]. Optics Express, 2018, 26(14): 18279-18291.
[4] Baradit E, Gatica C, Yáñez M, et al. Surface roughness estimation of wood boards using speckle interferometry[J]. Optics and Lasers in Engineering, 2020, 128: 106009.
[5] Liao H S, Cheng S H, Hwu E T. Development of a resonant scanner to improve the imaging rate of astigmatic optical profilometers[J]. IEEE/ASME Transactions on Mechatronics, 2021, 26(2): 1172-1177.
[6] 刘素贞, 王淑娟, 张闯, 等. 钢板电磁超声表面波的仿真分析及缺陷定量检测[J]. 电工技术学报, 2020, 35(1): 97-105.
Liu Suzhen, Wang Shujuan, Zhang Chuang, et al. Simulation analysis of electromagnetic acoustic surface wave of steel plate and quantitative defect detection[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 97-105.
[7] 张闯, 魏琦, 刘素贞, 等. 小尺寸试件检测用单向单模态电磁超声换能器设计[J]. 电工技术学报, 2019, 34(17): 3563-3571.
Zhang Chuang, Wei Qi, Liu Suzhen, et al. Design of unidirectional single-mode electromagnetic acoustic transducer for small size specimen detection[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3563-3571.
[8] 翟国富, 梁宝, 贾文斌, 等. 横波电磁超声相控阵换能器设计[J]. 电工技术学报, 2019, 34(7): 1441-1448.
Zhai Guofu, Liang Bao, Jia Wenbin, et al. Design of the shear wave electromagnetic ultrasonic phased array transducer[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1441-1448.
[9] Shi F, Lowe M J S, Xi X, et al. Diffuse scattered field of elastic waves from randomly rough surfaces using an analytical Kirchhoff theory[J]. Journal of the Mechanics and Physics of Solids, 2016, 92: 260-277.
[10] Wang Zhe, Cui Ximing, Pu Haiming, et al. Influence of surface roughness on energy change of excitation process in EMAT thickness measurement[J]. International Journal of Applied Electromagnetics and Mechanics, 2019, 59(4): 1479-1486.
[11] Wang Zhe, Cheng Jingwei. Numerical and analytical study for ultrasonic testing of internal delamination defects considering surface roughness[J]. Ultrasonics, 2021, 110: 106290.
[12] Manhertz G, Bereczky A. STFT spectrogram based hybrid evaluation method for rotating machine transient vibration analysis[J]. Mechanical Systems and Signal Processing, 2021, 154: 107583.
[13] Dharitri D. A new steganalysis DWT domain implicit image analysis method[J]. Journal of Social Science and Humanities, 2020, 2(4): 29-32.
[14] Cho H, Yoon H J, Jung J Y. Image-based crack detection using crack width transform (CWT) algorithm[J]. IEEE Access, 2018, 6: 60100-60114.
[15] Ye Jiaxing, Ito S, Toyama N. Computerized ultrasonic imaging inspection: from shallow to deep learning[J]. Sensors (Basel, Switzerland), 2018, 18(11): 3820.
[16] 杨秋玉, 阮江军, 黄道春, 等. 基于振动信号时频图像识别的高压断路器分闸缓冲器状态评估[J]. 电工技术学报, 2019, 34(19): 4048-4057.
Yang Qiuyu, Ruan Jiangjun, Huang Daochun, et al. Opening damper condition evaluation based on vibration time-frequency images for high-voltage circuit breakers[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4048-4057.
[17] 侯智, 曾杰. 基于BP神经网络的轴承套圈沟道磨削粗糙度识别[J]. 机械设计与研究, 2019, 35(3): 119-122.
Hou Zhi, Zeng Jie. Roughness identification of bearing ring groove grinding based on BP neural network[J]. Machine Design & Research, 2019, 35(3): 119-122.
[18] 肖雄, 王健翔, 张勇军, 等. 一种用于轴承故障诊断的二维卷积神经网络优化方法[J]. 中国电机工程学报, 2019, 39(15): 4558-4567.
Xiao Xiong, Wang Jianxiang, Zhang Yongjun, et al. A two-dimensional convolutional neural network optimization method for bearing fault diagnosis[J]. Proceedings of the CSEE, 2019, 39(15): 4558-4567.
[19] Liu Hongmei, Li Lianfeng, Ma Jian. Rolling bearing fault diagnosis based on STFT-deep learning and sound signals[J]. Shock and Vibration, 2016, 2016: 6127479.
[20] Zakri A A, Darmawan S, Usman J, et al. Extract fault signal via DWT and penetration of SVM for fault classification at power system transmission[C]//2018 2nd International Conference on Electrical Engineering and Informatics (ICon EEI), Batam, Indonesia, 2018: 191-196.
[21] Ogilvy J A. Wave scattering from rough surfaces[J]. Reports on Progress in Physics, 1987, 50(12): 1553-1608.
[22] Jiang Yuxiang, Li Zhenhua. Monte Carlo simulation of Mueller matrix of randomly rough surfaces[J]. Optics Communications, 2020, 474: 126113.
A Deep Learning-Based Electromagnetic Ultrasonic Recognition Method for Surface Roughness of Workpeice
Abstract Surface roughness directly determines the performance and service life of the workpiece. As customary surface roughness detection methods based on optical or three-dimensional profilometers have higher requirements on the surface cleaning state and operating environment, a non-contact electromagnetic ultrasonic surface roughness recognition method based on deep learning is proposed under this paper. Firstly, the effects of eddy current density and the Lorentz force on the excitation and reception signals are investigated by establishing the finite element simulation model of electromagnetic ultrasound with different surface roughness. Then, the proposed convolutional neural network is utilized to extract the features of the time-frequency coefficient map of the A-scan signal detected by the electromagnetic ultrasonic transducer, which is input into the pre-trained support vector machine classifier to complete the roughness recognition and prediction. To verify the proposed method, the surface roughness comparison block processed by the end milling process is tested. The experimental results show that the average accuracy of the proposed ultrasonic recognition method is 98.83%, which has high prediction accuracy and stability, solves the problem of the low signal-to-noise ratio of the ultrasonic signal which leads to difficult signal feature recognition, and reduces the dependence of feature extraction process on manual intervention.
Keywords:Surface roughness, electromagnetic acoustic transducer(EMAT), deep learning, convolution neural network, image recognition
DOI:10.19595/j.cnki.1000-6753.tces.210707
中图分类号:TB553; TP183
国家自然科学基金青年基金(51807065)、无损检测技术福建省高校重点实验室(S2-KF2007)和江西省重点研发计划一般项目(20202BBEL53015)资助。
收稿日期 2021-05-15
改稿日期 2021-07-13
蔡智超 男,1989年生,博士,副教授,硕士生导师,研究方向为工程电磁场、无损检测技术。E-mail:zccai@foxmail.com(通信作者)
孙翼虎 男,1998年生,硕士研究生,研究方向为电磁无损检测技术。E-mail:sunyh1619@163.com
(编辑 郭丽军)