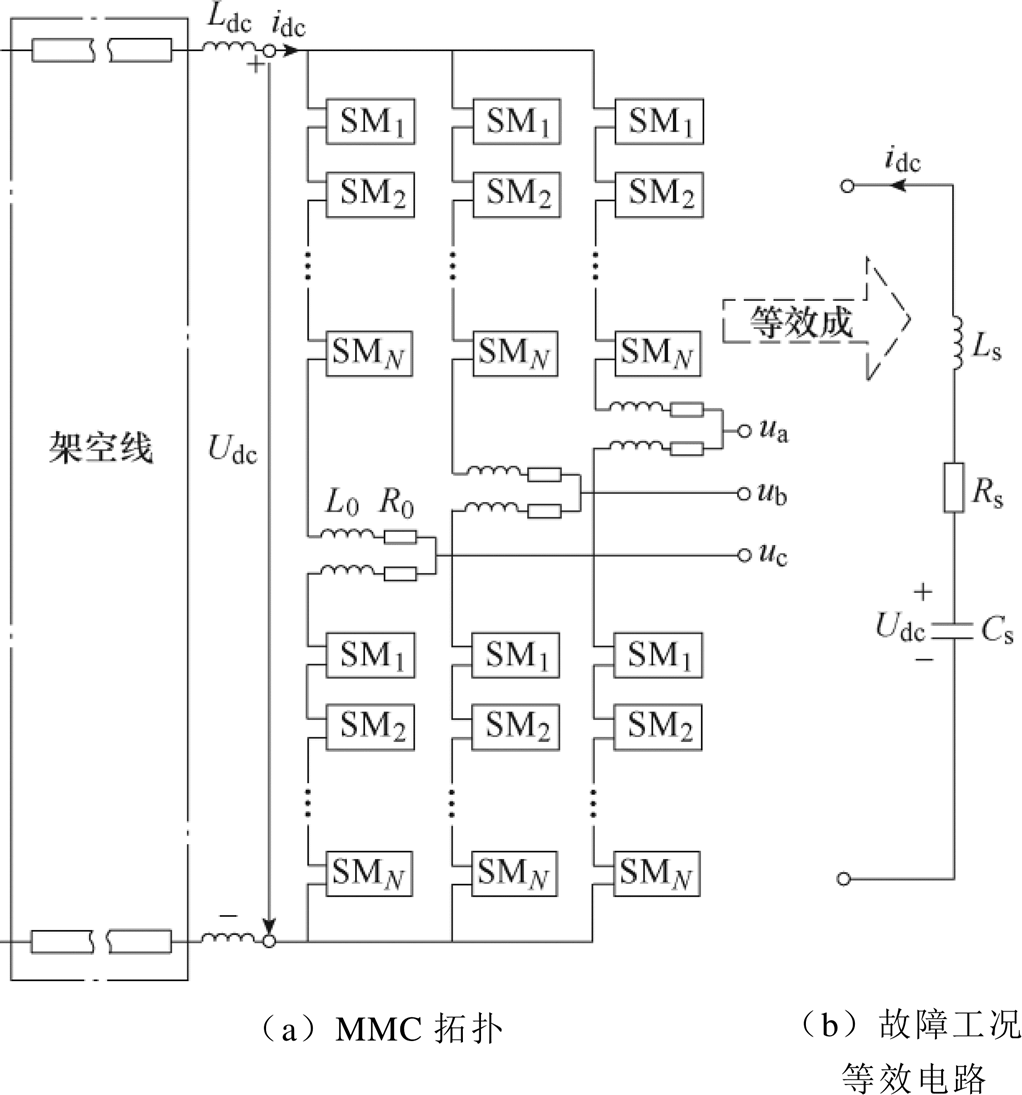
图1 MMC拓扑及故障工况等效电路
Fig.1 Topology of MMC and DC fault equivalent circuit
摘要 通过谐波电流注入方式可有效减小子模块电容容值，进而降低模块化多电平变换器（MMC）的体积和质量，实现MMC的轻型化。该文通过对低容值半桥MMC直流故障工况特性的理论分析，指出在其他参数不变的情况下，低电容容值下的子模块电容存在放电速度快的现象，可导致故障清除过程中子模块低压闭锁问题。从等电荷角度出发，提出一种基于低容值半桥MMC的直流故障辅助清除策略。通过在MMC故障清除过程中根据电容比调整相投入子模块总数，可有效减小MMC子模块电容的放电量并实现系统的快速恢复。基于PSCAD/EMTDC仿真环境下搭建仿真程序，通过仿真和实验验证了低容值MMC故障辅助清除策略的有效性。
关键词：电流注入 低容值半桥MMC 等电荷 快速恢复 直流故障清除策略 实验验证
模块化多电平变换器（Modular Multilevel Converter, MMC）由于其拓扑结构高对称性和强扩展性的优点，自问世以来就受到国内外学者的广泛关注，并推广应用在实际工程[1-3]中。基于MMC的柔性直流输电技术作为风能、光伏等新能源并网的有效手段，可有效助推“碳中和”目标的实现[4-5]。
现有MMC由大量子模块级联而成，导致其体积和占地面积巨大，从而增加了整个换流站的建设成本。因此亟须提高MMC的功率密度，降低MMC子模块的电容容值，以实现MMC的轻型化设计[6-7]。
通过谐波注入调整MMC桥臂内部能量分布来提高子模块电容功率密度，从而降低子模块电容电压纹波和容值是MMC轻型化的有效措施[8-14]。文献[8]针对MMC相间环流问题，首次提出环流抑制控制器（Circulating Current Suppressing Controller, CCSC）的设计方法。文献[9]通过程序遍历寻优来确定使子模块电容电压波动最小的偶数次谐波电流注入量，可有效降低子模块电容电压纹波，但无明显的物理意义。文献[10]基于桥臂瞬时功率不变的原则来确定谐波注入量，具有相应的物理意义。文献[11]通过零序电压的注入来提高MMC阀侧电压幅值，有效降低子模块电容电压纹波。文献[12]在考虑CCSC后进行最优零序电压的注入，在增加MMC阀侧电压幅值的同时，可降低桥臂子模块的使用个数。文献[13-14]基于子模块混合型MMC拓扑，利用双谐波注入法，从不同角度来大幅降低子模块电容电压纹波。此外，系统网压不平衡下也可基于谐波注入来降低子模块电容电压纹波[15-16]。文献[15]指出，在网压不平衡工况下通过谐波电流注入可有效降低子模块电容电压纹波。文献[16]指出，在网压不平衡下基于零序电压注入降低子模块电容电压波动。
以上研究均基于稳态或网压不平衡状态下进行MMC子模块电容纹波的降低，但对于低容值MMC直流故障工况下的理论分析鲜有报道。且目前大多配合直流断路器（Direct Circuit Breaker, DCCB）实现直流故障清除的辅助策略[17]均不涉及低容值MMC。
基于此，本文提出一种基于架空线的低容值半桥MMC的直流故障辅助清除策略。主要对现有研究MMC轻型化谐波注入方法进行总结；并指出低容值MMC直流故障工况研究鲜有报道；之后对低容值MMC故障工况进行分析，得出低容值对MMC直流故障特性的影响，并提出一种故障辅助清除策略；最后进行仿真和实验验证。
MMC拓扑及故障工况等效电路如图1所示。
图1 MMC拓扑及故障工况等效电路
Fig.1 Topology of MMC and DC fault equivalent circuit
图1a为MMC基本拓扑，图中，SM表示桥臂子模块；Udc为直流电压；L0为相桥臂电感；R0为相桥臂电阻；Ldc为直流电抗；uj（j=a, b, c）为MMC交流侧相电压；idc为直流侧电流。图1b为故障工况系统等效电路，Rs为等效电阻；Ls为等效电感；Cs为等效电容。
半桥典型MMC（Typical MMC, T-MMC）、半桥低容值MMC（Low capacitance MMC, L-MMC）均为图1a中的拓扑结构，两者的电容容值不同，具体T-MMC和L-MMC的电容比为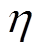
，则T-MMC和L-MMC的子模块电容关系为
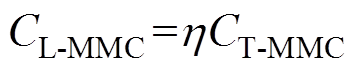（1）
式中，CL-MMC为L-MMC的子模块电容；CT_MMC为T-MMC的子模块电容。
电容值的改变将对整个MMC储存的能量及故障工况下的等效电容均产生影响，下面将分别阐述。
MMC储存的能量W为
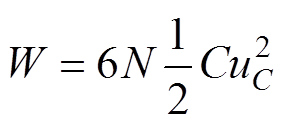（2）
式中，N为MMC桥臂子模块个数；C为子模块电容；uC为子模块电容电压。将式（1）代入式（2），在其他量一致的情况下，可得T-MMC和L-MMC储存能量的关系为
（3）
式中，WL-MMC为L-MMC存储的能量；WT-MMC为T-MMC存储的能量。因此从式（3）可看出，L-MMC储存能量为T-MMC的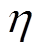倍。
MMC故障工况下直流侧等效电容Cs可计算[18]为
（4）
结合式（1）和式（4）可知，L-MMC和T-MMC故障工况下等效电容的关系为
（5）
式中，CsT-MMC为T-MMC在直流故障下的等效电容；CsL-MMC为L-MMC在直流故障下的等效电容。
综上所述，相对于T-MMC，L-MMC储存能量和故障等效电容容值均与电容比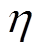成比例，并对L-MMC的故障特性产生影响。
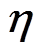对L-MMC故障特性的影响规律本节主要就不同电容比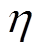对L-MMC故障工况下直流侧故障电流和子模块电容电压放电过程的影响进行分析。
MMC直流侧故障主要关注故障发生后5ms内故障电流的发展情况[19]，因此需要就不同电容比对故障电流的影响进行分析。MMC直流故障下的短路电流表达式[18]为
（6）
式中，C0为MMC子模块电容；Rdc为直流侧电阻；t为时间。其他参数与图1a对应。从式（6）中可看出，不同C0值影响直流侧故障电流。在PSCAD/EMTDC仿真环境下进行不同h 下故障电流的仿真模拟及以式（6）进行不同h 下的故障电流的理论计算，具体不同电容比对故障电流的影响如图2所示。
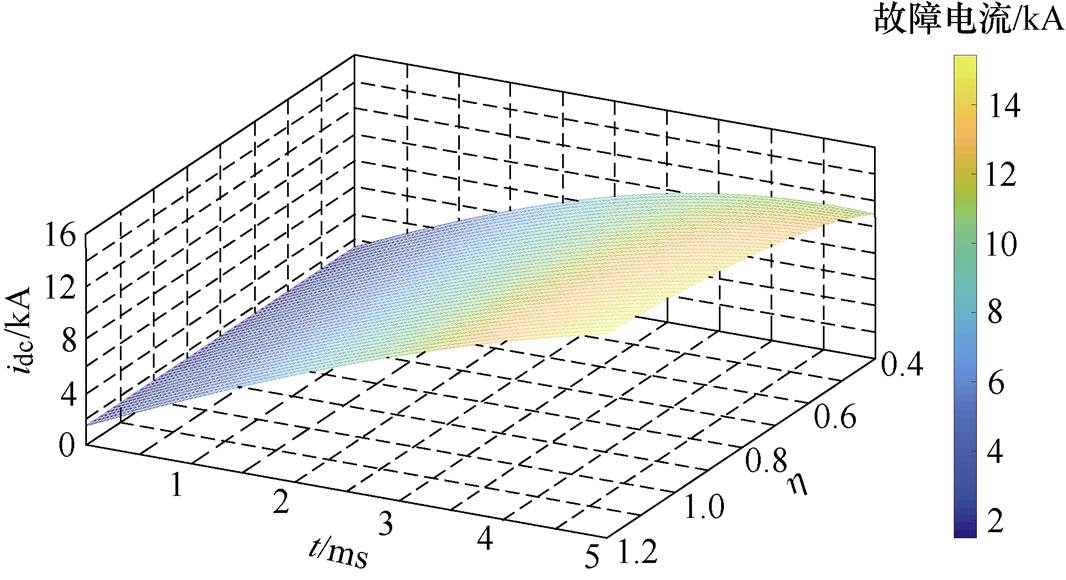
图2 不同电容比对故障电流的影响
Fig.2 Influence of different hon fault current
图2为不同电容比下的故障电流三维图，仿真程序参数为厦门工程整流侧参数。其中，idc为故障电流。从图中可知，随着电容比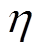的减小，故障电流的峰值逐渐减小，同时故障电流的上升速度也减缓。从图中进一步看出，在电容比取1.2时，直流故障电流峰值最大。
此外，不同电容比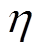对故障工况下子模块电容电压的放电过程亦产生影响。故障工况下的子模块电容放电过程较复杂，无法精确解析模拟。不同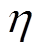下子模块电容电压从额定值放电到其额定值25%的时刻TUL（考虑到子模块IGBT驱动电压的取能需求，这里取额定值的25%）的关系如图3所示。
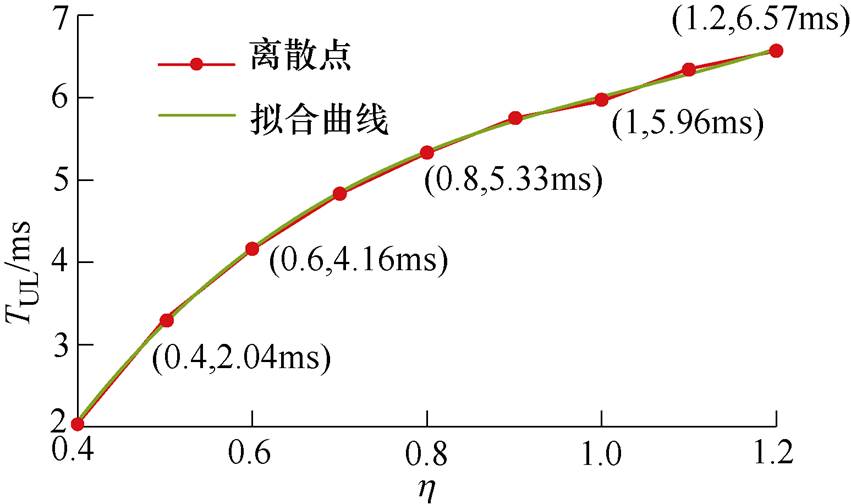
图3 不同h 对子模块电容放电过程的影响
Fig.3 Influence of different h on discharge process of sub module capacitance
在Matlab中通过曲线拟合得到两者关系为
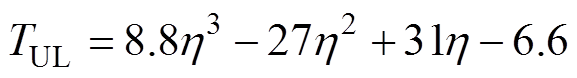（7）
令TUL=5ms（DCCB一般5ms内可清除故障），可得出h =0.73。即以厦门工程整流侧参数为例，子模块电容容值最多降到额定值的0.73，否则就会在故障清除过程中由于子模块电容电压放电过大而导致其低压闭锁，进而加长整个系统的恢复时间，这将极大地限制MMC轻型化运行范围。
参照图1b，则MMC直流故障下任意时刻t储存的能量为
（8）
式中，t0为MMC直流故障发生时刻；W(t)为以时间t为自变量的MMC的能量函数；WLs(t)为等效电抗Ls储存的能量；WRs(t)为等效电阻Rs产生的热损耗。从式（8）中可看出，虽然低容值下MMC的直流故障电流上升速度慢，降低了其转化为磁场能和热损耗的速度，减小了L-MMC能量的快速释放，但由于其本身储存能量少，因此随着时间t的推移，L-MMC中子模块电容的能量相对于T-MMC更易快速逼近于零。
以上分析可看出，低容值不仅会对故障电流的峰值、数值计算公式的精度产生影响，同时会导致子模块电容的快速放电。
由1.1节分析可知，由于L-MMC储存的能量W和故障工况下的等效电容Cs均减小到T-MMC的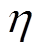倍。故障工况下，MMC等效电容Cs中存储的能量为
（9）
式中，Qs为等效电容Cs储存的电荷。结合式（3）和式（5）可知，L-MMC相对于T-MMC在储存的能量W和故障工况下的等效电容Cs变化的实质为等效电容Cs储存的电荷量Qs减小到T-MMC的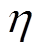倍。
因此，为有效减缓L-MMC的放电速度，令两类MMC的等效电容Cs储存的电荷量相等，即
（10）
式中，QL-MMC为故障工况下L-MMC等效电容CL-MMC储存的电荷量；QT-MMC为故障工况下T-MMC等效电容CT-MMC储存的电荷量。
将式（3）、式（5）、式（9）代入式（10）中，可得
（11）
式（11）可看出，保证L-MMC和T-MMC的储存能量和等效电容乘积相等，即可保证故障工况下等效电容储存的电荷量相等。
两类MMC稳态下电容储存的能量关系固定，将式（3）代入式（11），两类MMC故障工况下的等效电容的关系为
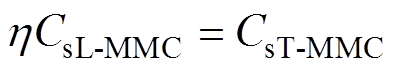（12）
从式（12）看出，需改变CsL-MMC的值以满足式（11）。改写式（4）为
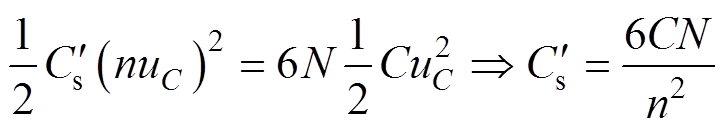（13）
式中，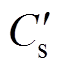
为MMC直流故障下相投入子模块个数为n的等效电容。从式（13）中看出，通过调整L-MMC在故障工况下相投入子模块个数n，可满足式（11），将式（13）代入式（12）并结合式（1）和式（4）可得
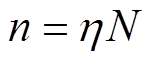（14）
基于式（14）进行控制器的设计，具体含基于等电荷的低容值MMC故障辅助清除策略（Auxiliary Strategy for Fault Clearance, ASFC）的控制器框图如图4所示。
图4 含ASFC的控制器框图
Fig.4 Controller diagram with ASFC strategy
图4中ASFC部分：Udcref为直流电压的参考值；Idcref为直流电流的参考值；KI为一个乘法因子，通过调整KI的数值，可灵活调整系统检测到故障的电流边界条件，进而调整辅助控制器的灵敏度。Idcm为直流电流的测量值；ABS（absolute value）表示绝对值函数，ABS函数的使用可使不同潮流方向的MMC使用一套辅助控制器。Idcm通过ABS后得到VA；Idcref乘以系数KI后通过ABS得到VB；VA与VB比较后得到Ctrl逻辑信号进行控制，当Ctrl=1时，即可根据电容比动态调整相直流电压，进而按式（14）调整相投入子模块总数。整体上看，本文所提ASFC，可在故障工况下根据故障电流的数值自适应投入，无需人为干预。
图4中其他控制器部分：Psref为有功功率的参考值；Ps为有功功率的测量值；Qsref为无功功率的参考值；Qs为无功功率的测量值；vd和vq为MMC主控制器在dq旋转坐标系下的输出值，经Park反变换得到vd和vq在abc时域坐标系下的输出值（以A相Ua为例）。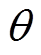
为锁相环（Phase Locked Loop, PLL）输出的角度；PI（proportion integration）为比例积分控制器；ucref为子模块电容电压的设定值，是一个固定的常量，数值不受ASFC的影响；其值为Udcref与MMC桥臂子模块总数N的比值。环流注入控制器（Circulating Current Injecting Controller, CCIC）输入值为三相桥臂重构电流ijc（j=a, b, c）；输出值Ujc（j=a, b, c）为CCIC输出的三相电压。采用最近电平逼近调制（Nearest Level Modulation, NLM）；N/D表示除法运算。上、下桥臂控制通过桥臂电压Uap、Uan与ucref做商得到上、下桥臂实际投入的子模块数Nap、Nan，通过NLM产生触发脉冲。
本节主要分析ASFC对L-MMC故障工况下故障电流和子模块电容放电过程影响。
将2.1节中的式（14）代入式（13）中，得
（15）
结合式（1）、式（4）、式（5）和式（15），可得
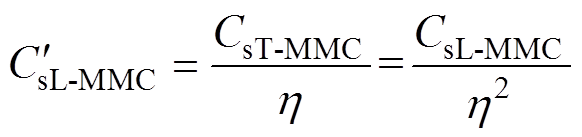（16）
式中，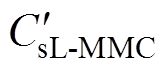
为L-MMC以式（14）进行故障相子模块个数投入后的等效电容。从式（16）看出，当L-MMC故障工况下相子模块总数按式（14）进行时，可使L-MMC的等效电容增大为原来的
倍，使L-MMC和T-MMC的储存能量和等效电容乘积相等，进而使两者的等效电容Cs中储存的电荷相等。
当考虑式（14）时，故障电流的计算需调整为
（17）
式中，带下标1的均为考虑式（14）后的故障电流idc1的相关量。对比式（6）和式（17）可知，ASFC可有效减缓L-MMC故障电流的上升速度，且降低故障电流的幅值。
假设无ASFC下L-MMC的等效电容为Cpeq，ASFC下L-MMC的等效电容为Cpeq1，两者的关系仍满足式（16）。在t0～t1时间段内等效电容下的电容变化量为
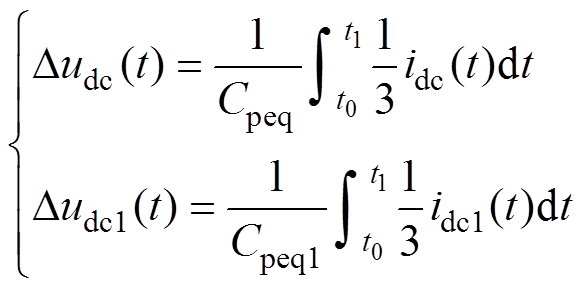（18）
式中，
为无ASFC下等效电容Cpeq的电压变化量；idc(t)为直流故障电流；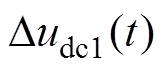
为ASFC下等效电容Cpeq1的电压变化量；idc1(t)为直流故障电流。则相单个子模块电容电压的变化量为
（19）
式中，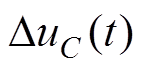
为无ASFC下单个子模块电容电压变化量；
为ASFC下单个子模块电容的电压变化量。
将式（18）代入式（19）中可得
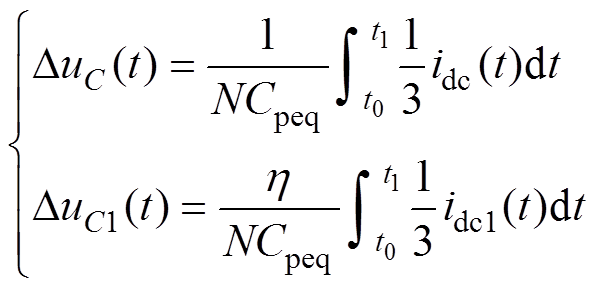（20）
式中，由于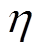＜1，故障发生后所关注的时间段内：idc1＜idc，因此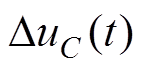＜。同时在推导等效电容时以子模块电容电压不变原则将电容进行等效[18]。因此通过式（20）可有效说明ASFC在减缓放电速度的有效性。
具体ASFC对不同电容比下故障电流峰值和子模块电容放电过程的影响如图5所示。
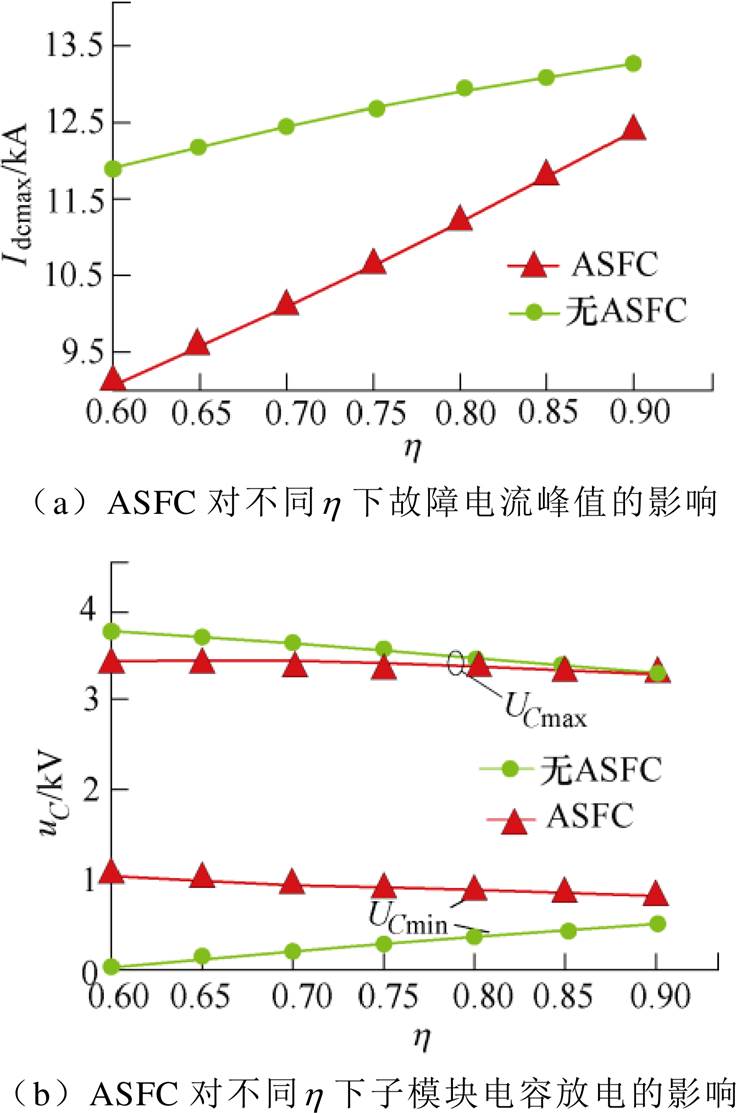
图5 ASFC对不同电容比下关键变量的影响
Fig.5 Effect of ASFC on keyvariables under different h
图5中，UCmax为故障工况下子模块电容电压波动的最大值，UCmin为故障工况下子模块电容电压波动的最小值，h 的变化范围为0.6～0.9，间隔为0.05，图5a为ASFC在直流故障工况中不同h 下对直流故障电流峰值Idcmax的影响。由图中可明显看出，投入ASFC后，Idcmax会显著下降，但随着h 的增大，ASFC对故障电流峰值的影响减弱。图5b为ASFC在直流故障工况中不同h 下对子模块电容放电情况的影响。由图中可看出，ASFC可明显减小故障工况下子模块电容电压的波动范围（减小Ucmax，增大Ucmin），但随着h 的增大，效果会减弱。
为充分验证本文所提ASFC的有效性，本节将所提策略分别应用在点对点MMC工程、四端柔直电网工程中进行仿真证明，并在低功率单端MMC物理样机进行实验验证。
为证明所提ASFC在点对点MMC工程中的有效性，在PSCAD/EMTDC仿真环境下搭建相应仿真程序进行证明，具体仿真程序框图如图6所示。
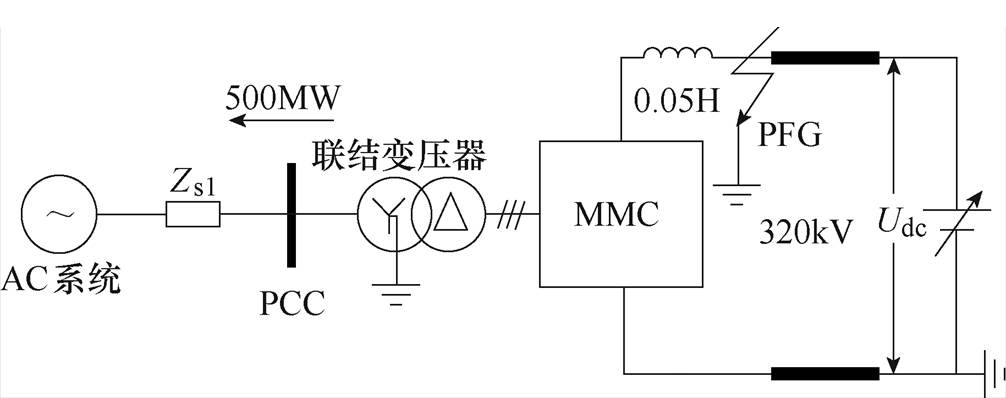
图6 MMC仿真程序框图
Fig.6 Simulation diagram of MMC
图6中，Zs1为AC系统的阻抗；Udc为直流电压；PCC（point of common coupling）为公共连接点。因MMC单极接地，因此极对地故障（Pole Fault to Ground, PFG）即为最严重的故障。
图6中MMC系统参数见表1。
表1 MMC系统参数
Tab.1 Parameter of MMC
参 数数 值 额定直流电压/kV320 额定有功功率/MW-500 电平数201 桥臂电感Larm/H0.06 等效变压器漏抗LT/H0.025 直流侧平抗LDC/H0.05 子模块电容C/mF6
目前，采用提高调制比（三倍频电压注入或增加部分全桥子模块）与谐波电流注入相结合的降容策略，可有效降低子模块电容容值达40%以上[6]。这里仅关注低容值MMC的故障清除过程，因此对稳态降容策略不再描述。以h =0.6，KI=2.5（正常工况下负荷不会过载2.5倍）为例进行说明。低容值MMC在4.5s时发生PFG，5ms后故障清除，则关键测点波形如图7所示。
图7a为PFG工况下（h =0.6）各个桥臂中子模块电容电压uC（取平均值）的波形。从图中可看出，在整个故障清除过程中，MMC子模块电容电压波动范围为0.05～2.01kV，低容值下子模块电容电压值快速跌落，在实际工况中不允许这种状况出现，会直接导致整个换流站闭锁，进而减缓系统的恢复速度。投入本文所提ASFC后，MMC所有桥臂子模块电容电压波动范围为0.63～1.89kV，有效降低故障工况下子模块电容的放电量。图7b为MMC的6个桥臂的电流波形，其电流波动范围为-3.866～3.776kA。投入附加策略后，桥臂电流波动范围为-3.189～3.184kA，附加控制策略未恶化桥臂电流。因此，投入ASFC进行直流故障清除，不管是桥臂电流还是子模块电容电压均不会导致L-MMC在故障清除过程中闭锁，验证了ASFC的有效性。
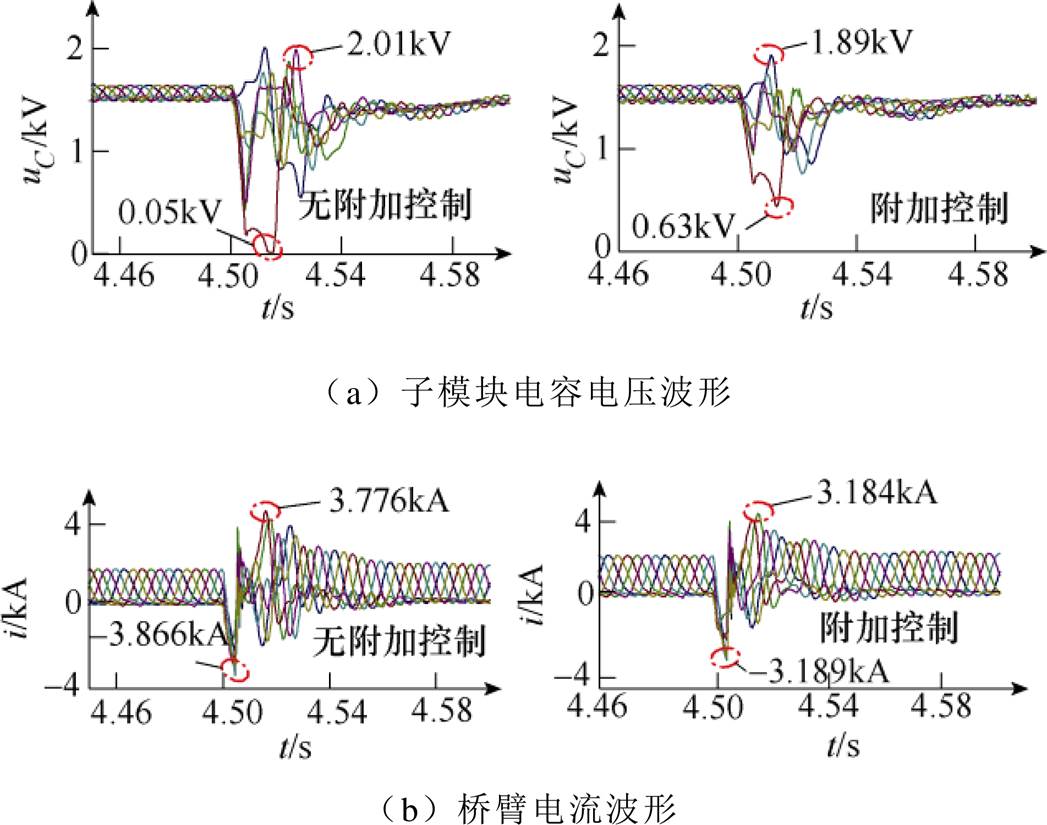
图7 PFG工况MMC关键测点波形
Fig.7 Waveforms of key points in MMC under PFG condition
为更方便进行多类MMC的比对，将T-MMC在PFG下子模块电容电压和桥臂电流波形截取如图8所示。
图8 PFG工况T-MMC关键测点波形
Fig.8 Waveforms of key points in T-MMC under PFG condition
图8a为T-MMC在PFG下各个桥臂子模块电容电压（平均值）波形，从图中可看出，整个故障清除期间，MMC子模块电容电压波动范围为0.65～1.81kV，和L-MMC+ASFC在PFG工况下子模块电容电压波动范围相当。图8b为T-MMC在PFG下的所有桥臂的电流波形，其波动范围为-3.90～3.33kV，对比图7b可知，三类MMC在PFG工况下桥臂电流波动范围相当。
此外，将T-MMC、L-MMC和L-MMC+ASFC三类MMC在PFG工况下的故障电流理论计算值和仿真值进行比对分析，具体以式（17）进行数值计算，故障电流的EMT解和数值解如图9所示。
由图9中可看出，在三类MMC中，L-MMC+ASFC故障电流理论计算值和仿真值吻合时间最长，相对于L-MMC，L-MMC+ASFC的吻合时间增长了3ms，且故障电流的上升速度最缓，侧面也证明式（17）的正确性。T-MMC由于其子模块电容容值较大，因此T-MMC的故障电流峰值在三类MMC中最高，与图2中的结论对应。
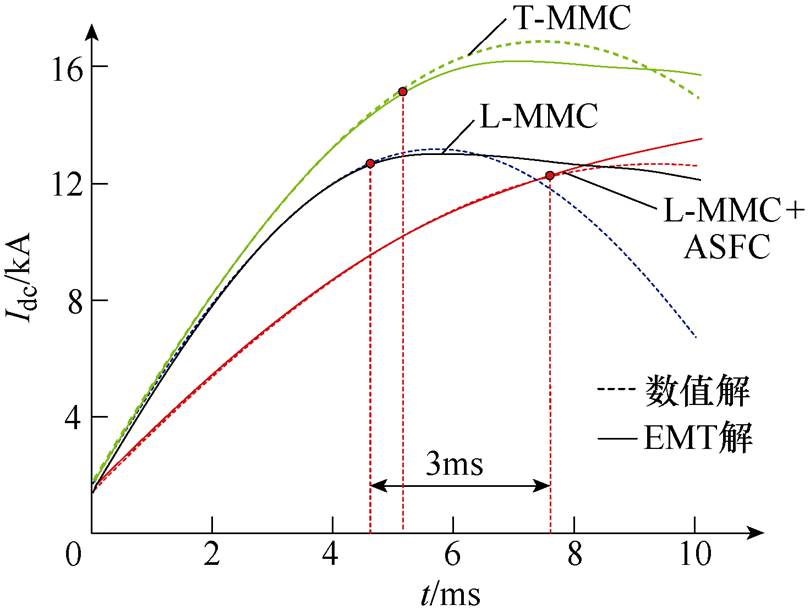
图9 PFG工况下故障电流理论与仿真值对比波形
Fig.9 Comparison waveforms of theoretical and simulation values of fault current under PFG conditions
为对ASFC进行更有效的验证，将所提策略应用在四端直流电网中。四端直流电网的拓扑如图10所示。
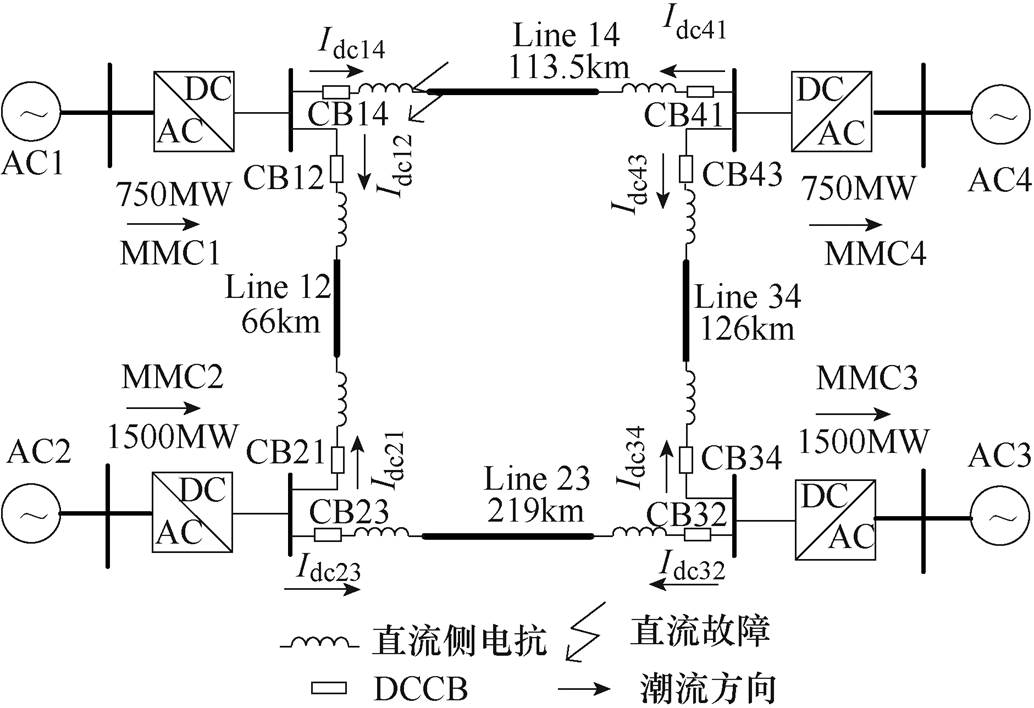
图10 四端直流电网
Fig.10 Four-terminal grid
图10中，Idc为直流电流；DCCB表示直流断路器。Line为线路，具体长度已在图中标出。图中整个直流侧电抗值为0.075H，每个MMC桥臂子模块个数为233。四端直流电网其他参数见表2。
表2 四端直流电网参数
Tab.2 Parameters of the 4 terminal DC grid
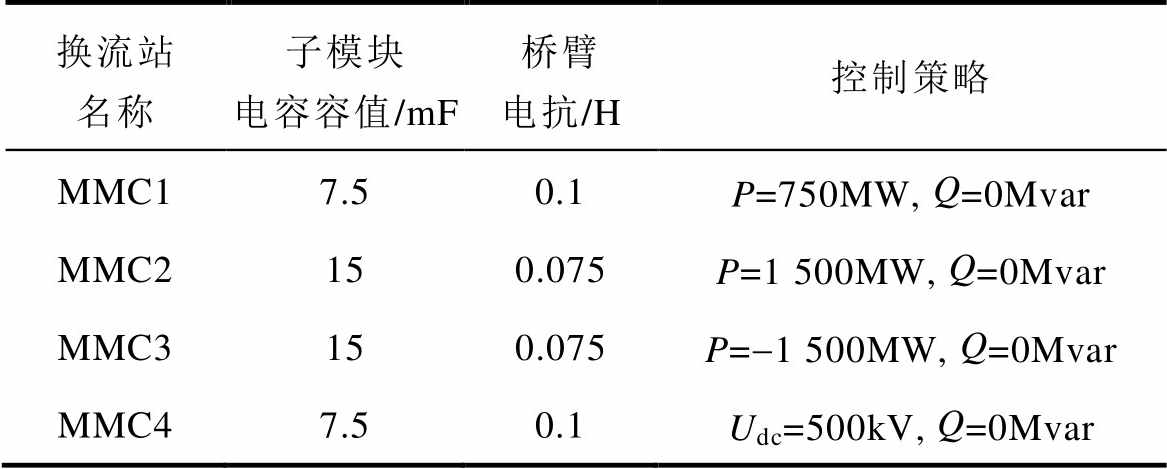
换流站名称子模块电容容值/mF桥臂电抗/H控制策略 MMC17.50.1P=750MW, Q=0Mvar MMC2150.075P=1 500MW, Q=0Mvar MMC3150.075P=-1 500MW, Q=0Mvar MMC47.50.1Udc=500kV, Q=0Mvar
直流电网稳态下的控制策略与h 值均与单端L-MMC一致。以MMC1直流侧电抗附近在1.5s发生直流侧双级短路故障为例，5ms内DCCB清除故障。低容值MMC1在直流故障工况下关键测点波形如图11所示。
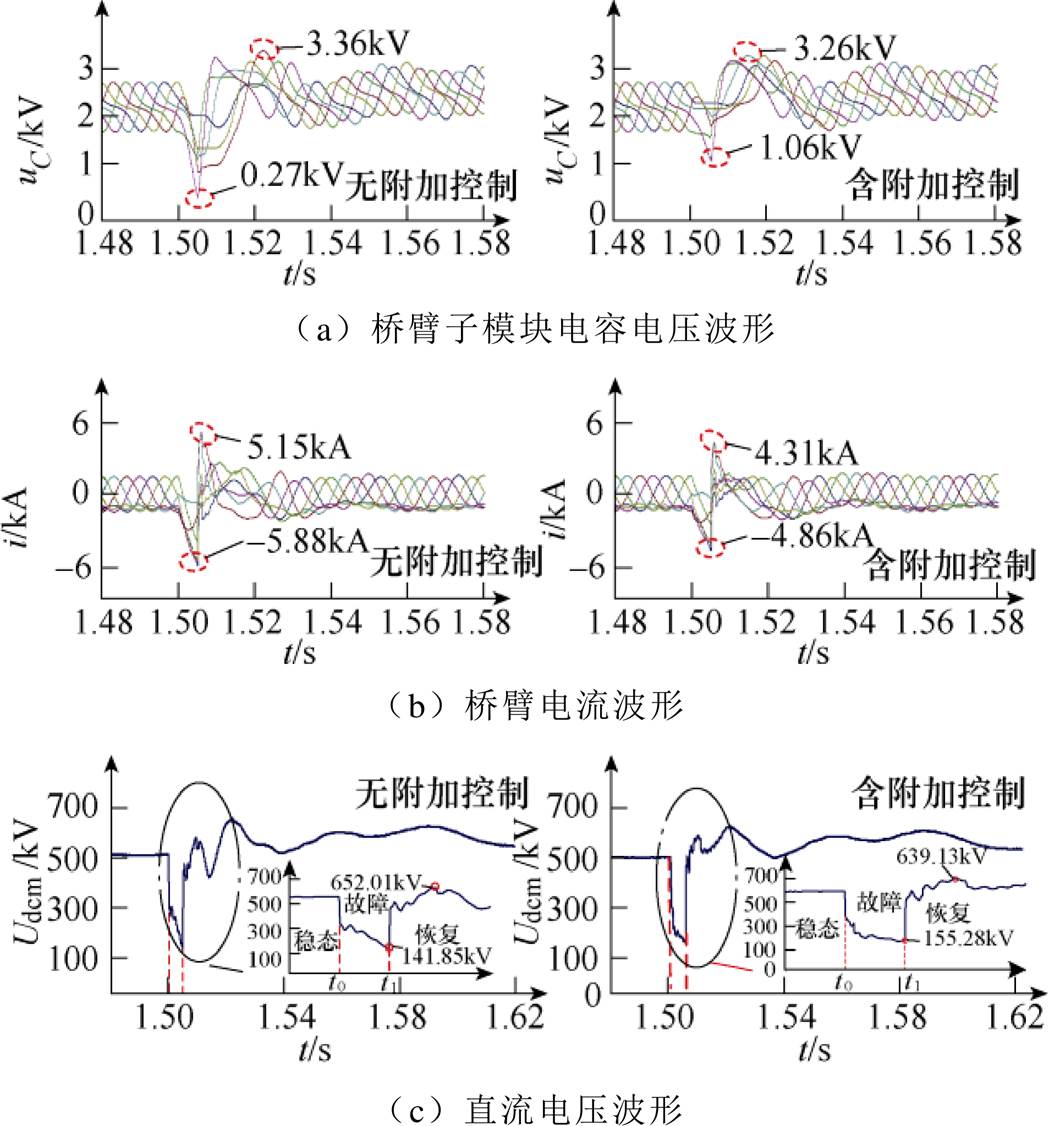
图11 直流故障工况下MMC1关键测点波形
Fig.11 Waveforms of key points of MMC1under DC fault
图11a为MMC1各个桥臂子模块电容电压（平均值）波形，从图中可看出，采用ASFC后，可使子模块电容电压波动从0.27～3.36kV减小为1.06～3.26kV；图11b为MMC1各个桥臂电流波形，图中可看出，桥臂电流从-5.88～5.15kA减小为-4.86～4.31kA，可有效增加直流电网在故障清除过程中器件的安全裕度，避免系统在故障清除过程中发生闭锁操作，增强整个系统的运行稳定性。图11c为MMC1直流电压波形，从图中可看出，采用ASFC后，可使直流故障电压的变化范围从141.85～652.01kV变为155.28～639.13kV，通过对比可看出，ASFC不会恶化直流故障下直流电压的波动范围。以上仿真证明所提ASFC在不同类型柔性直流工程的有效性。
为更有效验证ASFC在MMC直流故障清除发挥的作用。本文在单端低功率MMC物理平台进行了实验验证，实验中，MMC中的电容容值没有变化，仅在直流故障中投入ASFC。具体将图6中的直流电压源Udc变成一个直流电阻Rdc，其余均和图6一致。具体物理平台参数见表3。
MMC物理平台实物如图12所示。
表3 单端MMC物理平台参数
Tab.3 Prototype parameters of single terminal MMC
参 数数 值 额定直流电压/V60 电平数11 桥臂电抗Larm/mH20 子模块电容C/mF6 600 变压器两侧电压/V380/115
图12 MMC物理平台实物
Fig.12 Physics experiment platform of MMC
MMC物理实验平台每个桥臂共有N=12个全桥子模块（有两个子模块为热备用子模块），以故障发生点为零时刻，故障持续时间为6ms。为更方便显示ASFC在直流故障工况下减小子模块电容电压纹波的有效性。在故障发生3ms后投入所提策略，使用泰克混合信号示波器录波（型号为MSO56，带宽为500MHz，采样频率为6.25GS/s）对单端MMC的直流电压Udc、直流电流Idc和桥臂子模块电容电压uC和桥臂电流（以c相下桥臂电流icd为例）进行录波。具体波形如图13所示。
为更方便直观地进行实验数据对比，将图13中的各个关键测点的数据以条形柱状图的形式进行对比，具体如图14所示。
结合图13和图14中可看出，在投入附加控制器后，可使子模块电容电压uC波动范围从5～8.98V变为6.1～8.98V，有效降低故障工况下子模块电容的放电量。同时可使直流电压Udc的峰值从328.88V降为316.27V。故障电流峰值从Idcmax从13.4A降为9.97A，桥臂电流的变化范围从-8.24～2.67A变为-5.97～2.67A，验证了本文所提策略在故障工况下降低子模块电容放电速率的有效性。
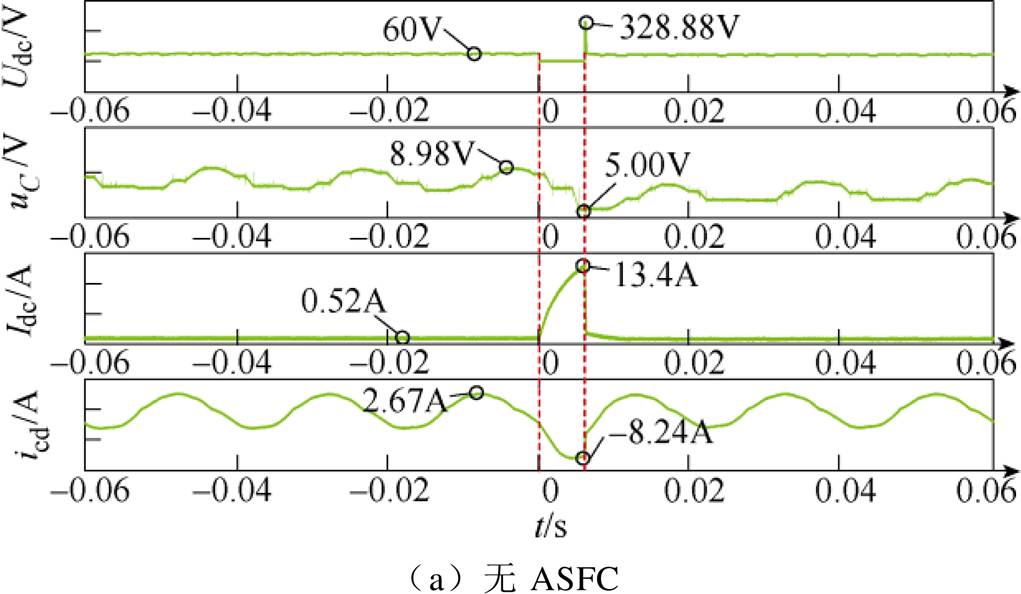
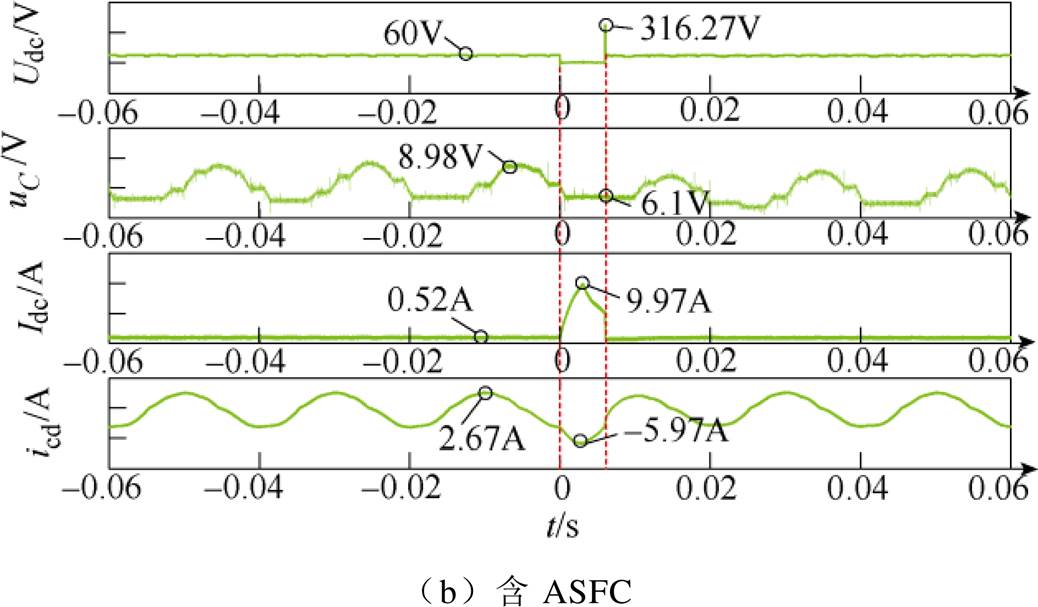
图13 MMC关键测点录波波形（示波器）
Fig.13 Recording waveforms of key points of MMC (oscilloscope)
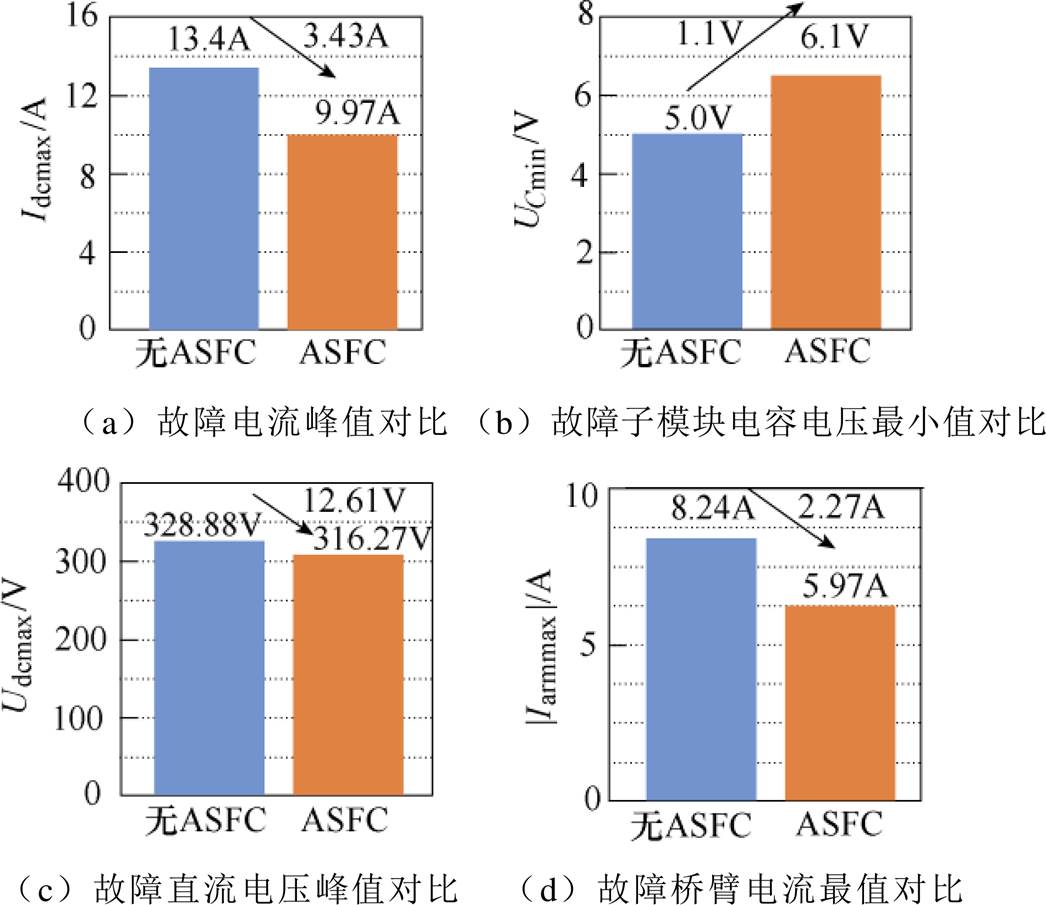
图14 MMC关键测点数据柱状图
Fig.14 Histogram of key points'dates of MMC
为有效降低基于架空线的低容值MMC在直流工况下子模块电容的放电速度，保证直流故障快速可靠的清除。本文提出了一种基于等电荷的故障清除辅助策略，可避免故障清除过程中由于子模块快速放电导致MMC自动闭锁的情况，并可加快系统的重启。具体得到以下结论：
1）不同电容比会对L-MMC故障工况下直流侧故障电流和子模块电容电压放电过程产生直接影响。分析表明，随着电容比的减小，故障电流的峰值在逐渐减小，同时，故障电流的上升速度也减缓。但故障电流的仿真计算值与EMT解析值的吻合度降低。
2）基于等电荷的故障辅助清除策略在故障清除前后无需人为切换，可通过直流故障电流的幅值自动投入，且可通过调节系数KI调节整个附加控制器的灵敏度。
3）仿真和物理实验结果表明，ASFC可有效降低故障工况下子模块电容电压的放电速度，避免MMC在故障清除过程中进行闭锁。
参考文献
[1] Lesnicar A, Marquardt R, An innovative modular multilevel converter topology suitable for a wide power range[C]//2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 2003, DOI: 10.1109/PTC.2003.1304403.
[2] 徐殿国, 刘瑜超, 武健. 多端直流输电系统控制研究综述[J]. 电工技术学报, 2015, 30(17): 1-12.
Xu Dianguo, Liu Yuchao, Wu Jian. Review on control strategies of multi-terminal direct current trans- mission system[J]. Transactions of China Electro- technical Society, 2015, 30(17): 1-12.
[3] 谭翔宇, 任丽, 唐跃进, 等. 饱和铁心型超导限流器在柔直系统中的限流特性研究[J]. 电工技术学报, 2020, 35(增刊2): 556-561.
Tan Xiangyu, Ren Li, Tang Yuejin, et al. Study on the current-limiting characteristics of saturated iron core superconducting fault current limiter in MMC-HVDC system[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 556-561.
[4] 孟沛彧, 王志冰, 迟永宁, 等. 适应多能源基地远距离输送电能的混合四端直流输电系统控制策略研究[J]. 电工技术学报, 2020, 35(增刊2): 523-534.
Meng Peiyu, Wang Zhibing, Chi Yongning, et al. Control strategy of hybrid four-terminal HVDC trans- mission system dedicated for long-distance power delivery from multiple energy bases[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 523-534.
[5] 李英, 胡佳欣. “碳达峰、碳中和”两会精神对我国电力行业发展的影响[J]. 大众用电, 2021, 36(3): 10-11.
Li Ying, Hu Jiaxin. Influence of the two Sessions' spirits of “peak carbon dioxide emissions and carbon neutrality” on power industry development in China[J]. Popular Utilization of Electricity, 2021, 36(3): 10-11.
[6] 许建中, 李钰, 陆锋, 等. 降低MMC子模块电容电压纹波幅值的方法综述[J]. 中国电机工程学报, 2019, 39(2): 571-584, 654.
Xu Jianzhong, Li Yu, Lu Feng, et al. A review of suppression methods for sub-module capacitor voltage ripple amplitudes in modular multilevel converters[J]. Proceedings of the CSEE, 2019, 39(2): 571-584, 654.
[7] 李凯, 赵争鸣, 袁立强, 等. 基于能量平衡的降低模块化多电平变换器子模块电容电压波动控制策略[J]. 电工技术学报, 2017, 32(14): 17-26.
Li Kai, Zhao Zhengming, Yuan Liqiang, et al. Con- trolstrategy based on the energy balance for reducing submodule capacitor voltage fluctuation of modular multilevel converter[J]. Transactions of China Elec- trotechnical Society, 2017, 32(14): 17-26.
[8] 屠卿瑞, 徐政, 管敏渊, 等. 模块化多电平换流器环流抑制控制器设计[J]. 电力系统自动化, 2010, 34(18): 57-61, 83.
Tu Qingrui, Xu Zheng, Guan Minyuan, et al. Design of circulating current suppressing controllers for modular multilevel converter[J]. Automation of Electric Power Systems, 2010, 34(18): 57-61, 83.
[9] Engel S P, De Doncker R W. Control of the modular multi-level converter for minimized cell capacitance[C]// Proceedings of 14th European Conference on Power Electronics and Applications, Birmingham, 2011: 1-10.
[10] Vasiladiotis M, Cherix N, Rufer A. Accurate capacitor voltage ripple estimation and current control considerations for grid-connected modular multilevel converters[J]. IEEE Transactions on Power Elec- tronics, 2014, 29(9): 4568-4579.
[11] Li Rui, Fletcher J E, Williams B W. Influence of third harmonic injection on modular multilevel converter- based high-voltage direct current transmission systems[J]. IET Generation, Transmission & Distri- bution, 2016, 10(11): 2764-2770.
[12] Guo Gaopeng, Song Qiang, Yang Wenbo, et al. Appli- cation of third-order harmonic voltage injection in a modular multilevel converter[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5260- 5271.
[13] 董鹏, 蔡旭, 吕敬. 大幅减小子模块电容容值的MMC优化方法[J]. 中国电机工程学报, 2018, 38(18): 5369-5380.
Dong Peng, Cai Xu, Lü Jing. Optimized method of MMC for greatly reducing the capacitance of the submodules[J]. Proceedings of the CSEE, 2018, 38(18): 5369-5380.
[14] Xu Jianzhong, Deng Weicheng, Gao Chenxiang, et al. Dual harmonic injection for reducing the sub-module capacitor voltage ripples of hybrid MMC[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(3): 3622-3633.
[15] 施恩泽, 吴学智, 荆龙, 等. 网压不平衡下环流注入对模块化多电平换流器的影响分析[J]. 电工技术学报, 2018, 33(16): 3719-3731.
Shi Enze, Wu Xuezhi, Jing Long, et al. Analysis of the impact on modular multilevel converter with circulating current injection under unbalanced grid voltage[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3719-3731.
[16] 李钰, 陆锋, 樊强, 等. 不平衡电网电压下的MMC子模块电压波动抑制方法[J]. 电力系统自动化, 2020, 44(4): 91-100.
Li Yu, Lu Feng, Fan Qiang, et al. Suppression method for voltage fluctuation of sub-module in multilevel modular converter with unbalanced power grid voltage[J]. Automation of Electric Power Systems, 2020, 44(4): 91-100.
[17] Wang Sheng, Li Chuanyue, Adeuyi O D, et al. Coordination of MMCs with hybrid DC circuit breakers for HVDC grid protection[J]. IEEE Transa- ctions on Power Delivery, 2018, 34(1): 11-22.
[18] 徐政. 柔性直流输电系统[M]. 2版. 北京: 机械工业出版社, 2016.
[19] 周光阳, 李妍, 何大瑞, 等. 含限流器的多端柔直系统故障保护策略[J]. 电工技术学报, 2020, 35(7): 1432-1443.
Zhou Guangyang, Li Yan, He Darui, et al. Protection scheme for VSC-MTDC system with fault current limiter[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1432-1443.
Abstract The current injection method can reduce the capacitance value of bridge arm sub modules (SMs), thereby reducing the volume and weight of MMC, and realizing the lightweight of MMC. Based on the theoretical analysis of the characteristics of low capacitance MMC in DC fault conditions, it is pointed out that the discharge speed of SM sunder low capacitance is fast when other parameters remain unchanged, which may lead to low voltage blocking of SMs during the DC fault clearing process. From the perspective of equivalent charge, a DC fault clearing strategy based on low capacitance half bridge MMC is proposed. By adjusting the total number of SMs in each phase according to the capacitance reduction ratio in MMC during the fault clearing process, the discharge capacity of the SM capacitors can be effectively reduced and the system recovery can be accelerated. A simulation program is built in PSCAD/EMTDC simulation environment, and the effectiveness of auxiliary strategy for DC fault clearing in low capacitance MMC is verified.
keywords：Current injection, low capacitance half-bridge MMC, equivalent charge, fast recovery, DC fault clearing strategy, experimental verification
DOI: 10.19595/j.cnki.1000-6753.tces.211233
中图分类号：TM721.1
中国华能集团有限公司总部科技资助项目（HNKJ20-H88）。
收稿日期 2021-08-09
改稿日期 2021-10-09
樊 强 男，1992年生，博士研究生，研究方向为直流输电。E-mail: 13910548020@163.com（通信作者）
俞永杰 男，1995年生，硕士，研究方向为直流输电。E-mail: 18811337377@163.com
（编辑 陈 诚）