图1 牵引变流器拓扑结构
Fig.1 Topology of traction converter
摘要 为解决厂内静调试验中高速动车组牵引变流器模拟牵引工况下，其中间直流环节发生电压大幅振荡的问题，该文针对源侧整流器提出引入补偿环节的虚拟电阻控制方法。在单相PWM整流器dq坐标系数学模型的基础上，建立源侧整流器与二次谐振电路并联的等效输出阻抗模型以及牵引逆变单元和辅助变流器的等效输入阻抗模型，并基于上述模型，结合Bode图和Nyquist曲线分析直流环节电压出现振荡的主要原因，即二次谐振电路与恒功率负载间的交互作用会引发中间直流环节电压振荡。所提振荡抑制方法利用虚拟电阻等效增加了负载侧输入阻抗，使得系统开环增益满足禁区稳定判据，可提升系统的稳定裕度。最后，通过仿真和实验验证了该文分析的正确性和所提控制方法的有效性。
关键词：牵引变流器 级联系统 电压振荡 虚拟电阻控制
近年来，我国轨道交通领域发展迅猛，高速动车组设计产品谱系化发展。牵引变流器作为电力电子装置，是级联系统动车组牵引供电的关键，保证其稳定可靠运行是首要目标。在中车唐山机车车辆有限公司厂内静调工位试验中，CR400BF-A-3096“复兴号”长编动车组曾出现11车升弓后，设备启动过程中，中间直流环节电压异常，引起牵引控制单元（Transmission Control Unit, TCU）误动，造成受电弓“顶网”的不利情况。后经铁科院软件监测，发现中间直流环节电压出现了大幅振荡的情况（实时监测如附图1所示）。中间直流环节电压振荡失稳将对动车组供电系统乃至动车组安全稳定运行造成极大威胁。此外有研究表明，城轨车辆牵引系统直流侧同样存在耦合振荡的情况[1]。
学者们对于提升电力电子变换器直流侧稳定性进行了深入的研究，总结归纳出直流侧电压出现振荡的原因与直流侧滤波装置、网侧电压电流波动、恒功率负载投切以及电力电子装置级联等因素有关。针对以上影响直流侧稳定性的因素，研究人员多在阻抗匹配[2]的角度，依据实际情况选用无源[3]或有源抑制[4]方案。针对负载工作于恒功率工况下引起的中间直流环节失稳问题，文献[5]提出了虚拟电阻控制，利用电流反馈提升系统等效输出阻抗。文献[6]提出了在柔性直流输电（Voltage Source Converter based on High Voltage Direct Current transmission, VSC-HVDC）系统中将虚拟电阻控制改进为虚拟阻感性阻抗控制方法，提升系统控制带宽以增强海岛供电系统稳定性，但并未考虑由控制方式所引起的稳态误差。文献[7]提出了有源阻尼策略可以有效地解决LC滤波器与Buck变换器级联系统谐振问题，但由于其稳定性判据十分保守，会限制改进后系统性能。文献[8]在直流微电网背景下通过改进下垂控制，引入阻尼来抑制电压振荡。文献[9]针对直交型电力机车直流侧电压振荡提出了有源阻抗稳定控制，并引入控制回馈系数对控制效果进行了改善，使改进后系统直流电压更加稳定。文献[10]针对城轨车辆牵引电机与直流侧LC滤波器间可能出现的直流侧电压耦合振荡，提出了针对牵引逆变器的基于前馈电压补偿的稳定性控制方法，此类方法有效地抑制了直流侧电压振荡。虽然文献[9-10]所提方式对于机车、城轨车抑制振荡作用显著，但由于二者被控对象均为牵引逆变器，不符合动车组系统“主辅一体化”的现状，仅针对牵引逆变器不考虑辅助变流器时，可能难以达到预期效果，所以本文考虑将源侧整流器作为被控对象。
由于动车组现多采用“轻量化”的设计思路，所以对于其源侧整流器多以改进控制方法[11]的形式展开。学者们利用自抗扰控制（Active Disturbance Rejection Control, ADRC）等现代控制理论对原有PID控制器进行改进[12-13]，解决了诸如快速性与超调之间的矛盾等[14]，但其参数设计复杂。相较于ADRC等控制方式，双闭环PID控制具有控制结构简单、工程应用成熟等技术优势[15]，对于动车组等进行实际工程应用时，应将安全、稳定、成熟作为重要指标，所以本文选择基于原有双闭环PI控制器进行改进，以抑制直流侧电压大幅振荡。
综上所述，现有研究多对直流微电网[8, 16]、VSC-HVDC[17-18]系统和轨道交通牵引逆变器[9, 19]等领域的直流侧电压振荡以及由于动车组与牵引网耦合交互所导致的低频振荡现象[20]进行细致深入的分析研究，而对由于系统耦合交互而导致的动车组中间直流环节大幅振荡的研究相对较少。在高速动车组设计“主辅一体化”和“轻量化”的背景下，通过研究针对源侧整流器的控制策略来提高牵引变流器中间直流环节稳定性是很有意义的。本文基于以下假设，针对复兴号动车组静调试验环节投入负载时，中间直流环节电压可能出现大幅跌落至正常工作电压值以下以及出现短时大幅振荡的情况，在系统耦合交互层面探究出现振荡的原因并提出改进措施。假设：
（1）建模时忽略了中间直流环节接地故障模块和保护模块等非线性元件，上述元器件对直流电压影响可忽略不计。
（2）网侧电压稳定理想，未计及网侧电压扰动。
（3）两台单相PWM整流器各项参数保持一致，视为完全相同。
本文从阻抗匹配的角度，首先依据牵引变流器拓扑结构，建立了牵引变流系统阻抗模型；其次依据阻抗模型结合禁区稳定判据分析了存在失稳现象的原因；再次提出了引入补偿环节的虚拟电阻控制并对相应参数进行设计；最后通过仿真和实验，验证了所提方案在抑制电压跌落、提升系统稳定裕度上的有效性。
牵引变流器系统拓扑结构如图1所示。us、is分别为交流侧电压、输入电流；Ls为交流侧等效电感；L2、C2分别为直流侧二次滤波电感、电容，两者构成二次谐振电路；Cd为整流器直流侧支撑电容；Cd1为斩波器支撑电容；Cd2为辅助变流器直流侧支撑电容；udc为直流侧电压。负载侧为并联的牵引逆变模块、辅助变流单元以及无火回送装置，其中牵引逆变模块由支撑电容、斩波器、牵引逆变器和牵引电机构成；辅助变流单元包含辅助逆变器和辅助系统。
图1 牵引变流器拓扑结构
Fig.1 Topology of traction converter
当动车组运行在牵引工况时，牵引变流器的主要功能是通过预充电单元（在接通期间）和两个并联四象限变流器（4-Quadrant Converter, 4QC）模块（每个模块为一个半桥）为中间直流环节电压回路供电，进而为四台牵引电机的运行提供三相交流电源。其由集成在牵引变流器箱体内的牵引控制单元控制牵引变流器的工作状态。而由于动车组的主辅一体化设计，辅助变流器没有自身的四象限斩波器，因此牵引变流器为辅助变流器提供中间直流环节电压。中间直流环节电容器作为一个平滑并缓冲中间直流环节线电压的储能电路。每个变流器的中间直流环节电容电池由4个并联的0.75mF电容器构成，共3mF。由L2、C2构成的二次谐振电路，分两次过滤由线频率输入电压能流导致的中间直流环节中的波动。
本文中，4QC模块采用dq电流解耦控制策略[21]，基于二阶广义积分（Second Order Generalized Integrator, SOGI）的dq电流解耦控制系统框图如图2所示，通过SOGI模块结合锁相环（Phase Locked Loop, PLL）可获得交流侧电压us和交流侧输入电流is在两相静止坐标系下的虚拟正交分量，并经2s/2r变换为两相相对静止坐标系下的dq轴分量，电压外环和电流内环均采用PI控制器。图2中，usd和usq分别为us的d轴、q轴分量；isd和isq分别为is的d轴、q轴分量；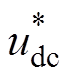
为直流侧给定电压；
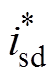和
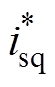分别为d轴、q轴参考电流；ud和uq分别为整流器网侧输入电压的d轴、q轴分量；kvp和kvi分别为直流电压外环PI控制器比例、积分系数；kip和kii分别为电流内环PI控制器比例、积分系数；umod为所生成的电压调制信号；idc为单相PWM整流器输出电流。
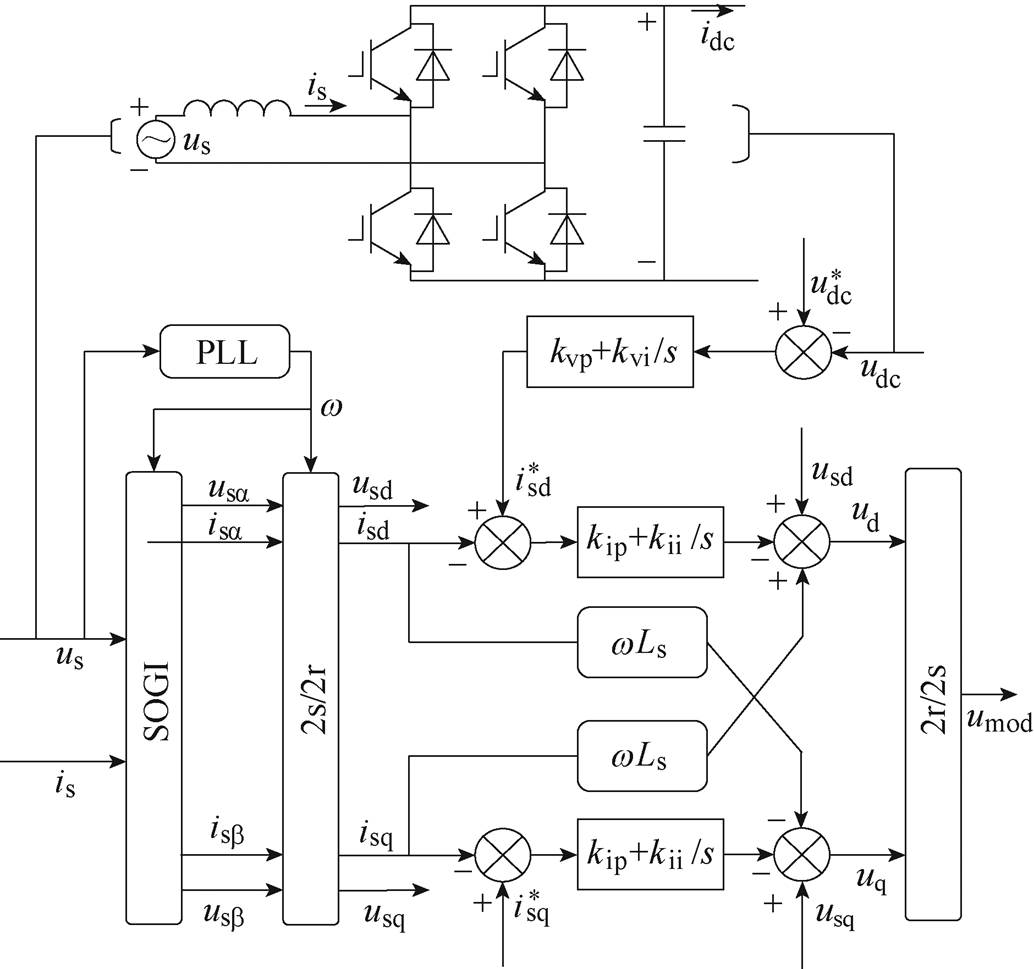
图2 单相PWM整流器dq解耦控制框图
Fig.2 Diagram of dq decoupling control for the single-phase PWM rectifier
本文采用基于阻抗匹配的稳定性分析方法，首先对4QC输出阻抗、中间直流环节和负载侧输入阻抗建模，接着依据禁区稳定性判据[22]对现有系统稳定裕度进行分析，得到现有牵引变流系统存在失稳可能的原因。
“复兴号”动车组采用两个4QC模块并联的方式为中间直流环节电压回路供电，可看作是两个单相电压源整流器在输出侧并联，其中单相整流器电路及控制策略如图2所示，可先求得一个4QC模块的输出阻抗，再通过并联的方式得到4QC系统总的输出阻抗。4QC在dq轴坐标系下的数学表达式为
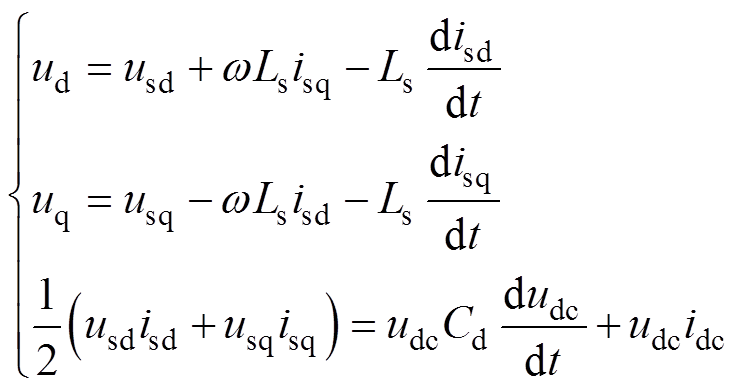（1）
将式（1）中的变量小信号化，得
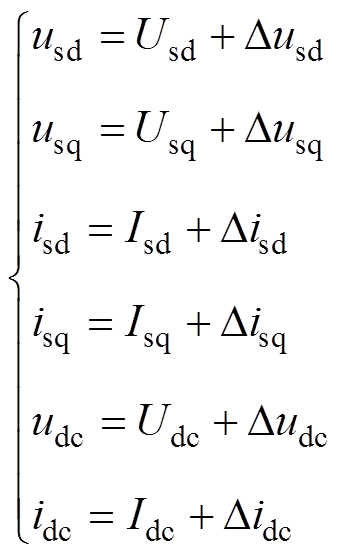（2）
式中，等号右侧大写物理量为其对应物理量的稳态分量；D 为其对应物理量的小扰动分量。由功率平衡整理得
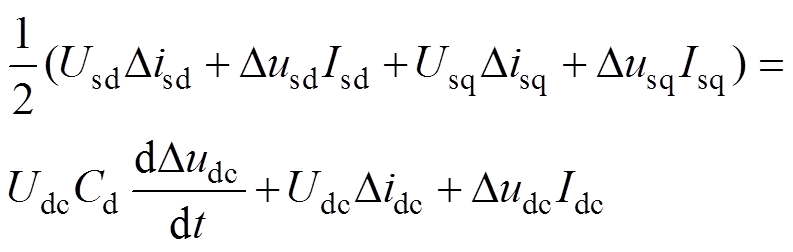（3）
由于整流器近似单位功率因数运行，不向牵引变压器传输无功功率，所以可令Usq=0，Isq=0。经过拉氏变换后，整理得
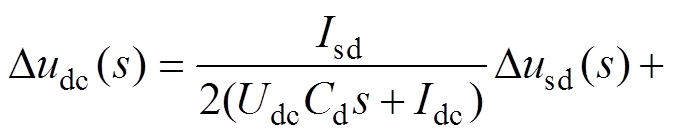
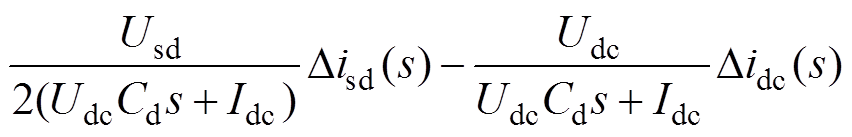（4）
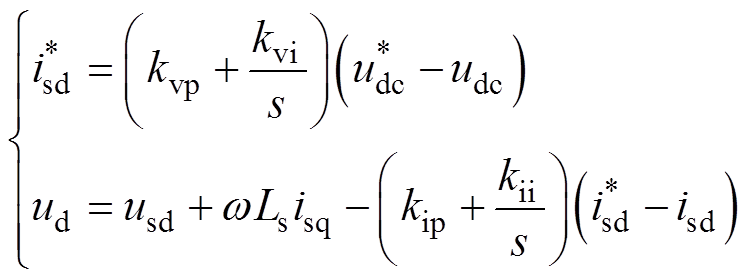（5）
结合双闭环控制表达式（5），可得到单台4QC模块输出导纳（详细推导过程见附录第2节）为
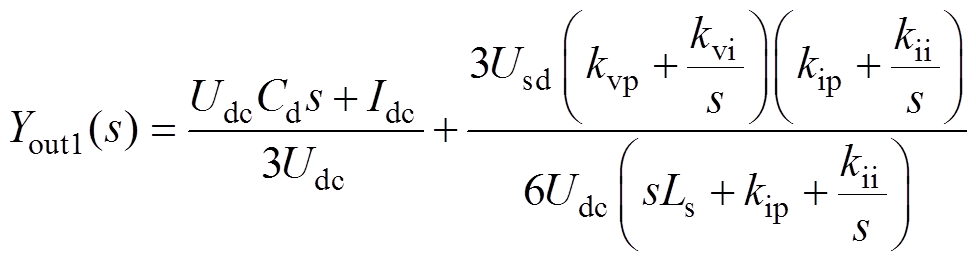（6）
式中，Yout1(s)为单台4QC模块输出导纳。则总的4QC模块输出阻抗Zout(s)为
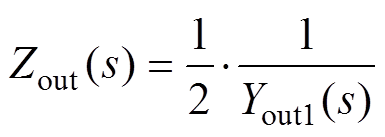（7）
动车组牵引变流器负载主要为牵引逆变单元和辅助变流器，当列车处于牵引工况下，辅助电机处于额定功率运行时，牵引电机也一定满足额定功率运行条件，则此时牵引变流器负载侧可视为恒功率负载[10]。
在列车实际运行时，动车组运行速度超过200km/h时，可视为恒功点，此时牵引逆变单元和辅助变流器均处于额定工作状态，牵引变流系统实际运行状态如图3所示（图中列车升03车、11车受电弓，实色部分表示对应设备正常启动）。
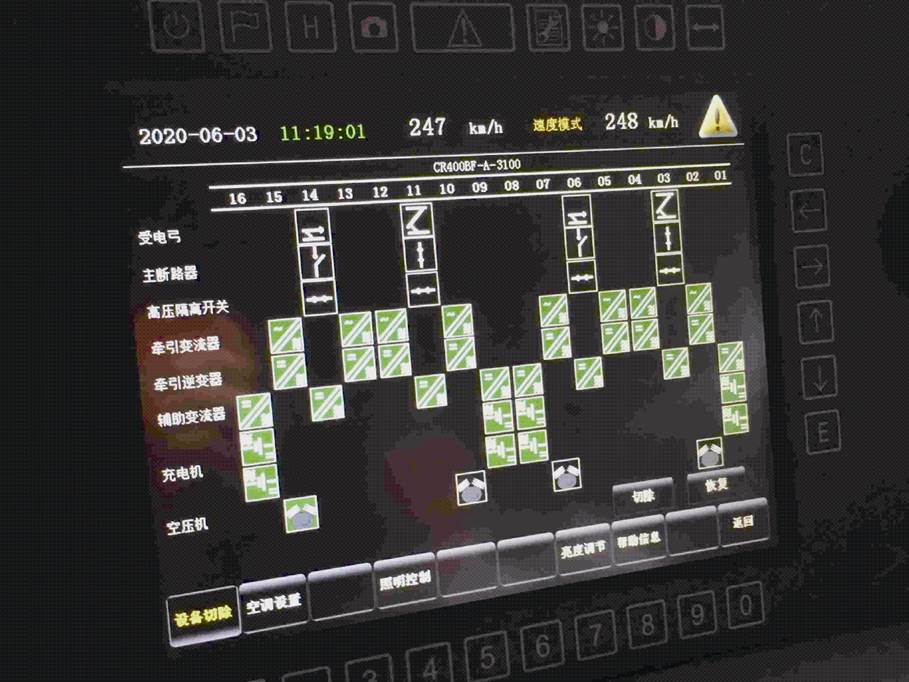
图3 牵引变流系统实际运行状态
Fig.3 Actual running state of traction converter system
对于负载建模时，同样要考虑到负载并联的情况，并联的牵引逆变单元和辅助变流器可等效为一个恒功率负载[23]，其中
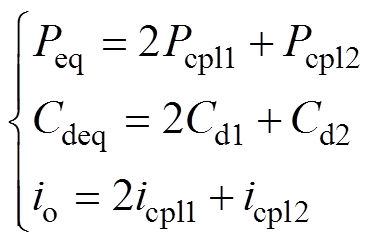（8）
式中，Pcpl1和Pcpl2分别为单台牵引逆变模块、辅助变流器的功率；Cd1、Cd2分别为牵引逆变模块、辅助变流器的直流支撑电容；Cdeq为恒功率负载等效电容；icpl1和icpl2分别为单台牵引逆变模块、辅助变流器的输入电流，且
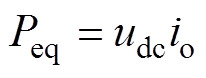（9）
式中，Peq为等效后的恒功率负载的功率；io为等效后的恒功率负载输入电流，结合式（8）、式（9），经过泰勒展开后可得
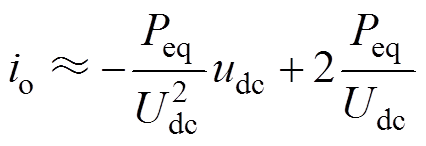（10）
则可定义牵引变流器负载输入阻抗Zin(s)为
（11）
综合2.1节和2.2节所述，牵引变流器阻抗模型如图4所示，从负载侧看向源侧的输出阻抗Zs(s)为
（12）
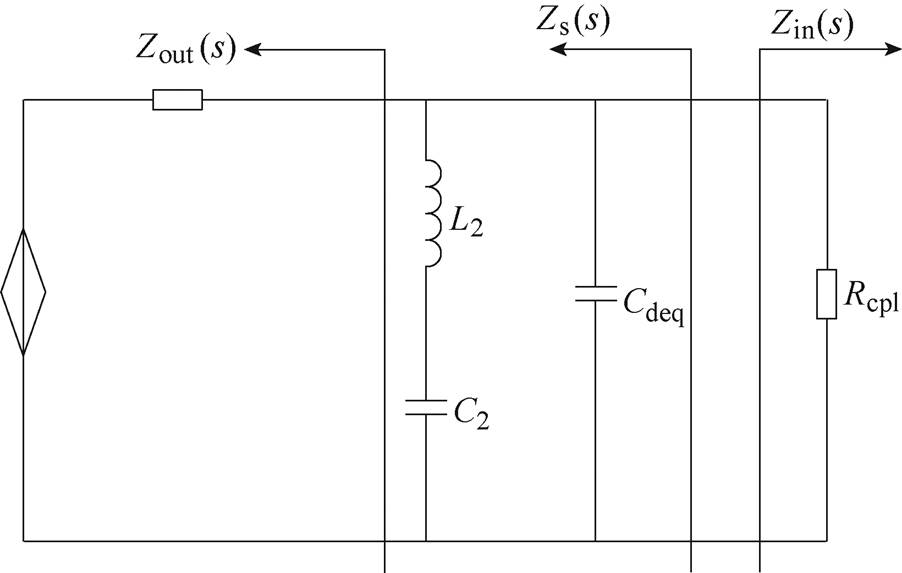
图4 等效RLC电路模型
Fig.4 Equivalent RLC circuit model
基于所建立的输出输入阻抗模型，采用阻抗匹配的方式，结合禁区稳定性判据探索了牵引工况下在设备启动时中间直流环节产生振荡的机理。其中
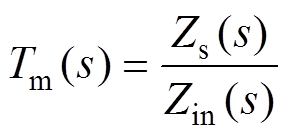（13）
式中，Tm(s)为系统开环增益。可利用Tm(s)的Nyquist曲线判断系统稳定性，涉及的单相PWM整流器系统参数见表1，所绘制的不同负载功率下，Tm(s)的Nyquist曲线如图5所示。
由图5可看出，随着Peq逐渐增大，系统Nyquist曲线逐渐向实部减小方向移动。结合禁区稳定性判据可知，当曲线与图中虚线存在交点时，表明系统存在失稳可能，当系统全功率运行时，稳定裕度较差。图6绘制了当Peq=2 600kW，取不同单相整流器支撑电容值时，Tm(s)的Nyquist曲线。由图可知，支撑电容值的增加有助于提升系统稳定裕度，但影响有限。
表1 单相PWM整流器系统参数
Tab.1 System parameters of the single-phase PWM rectifier
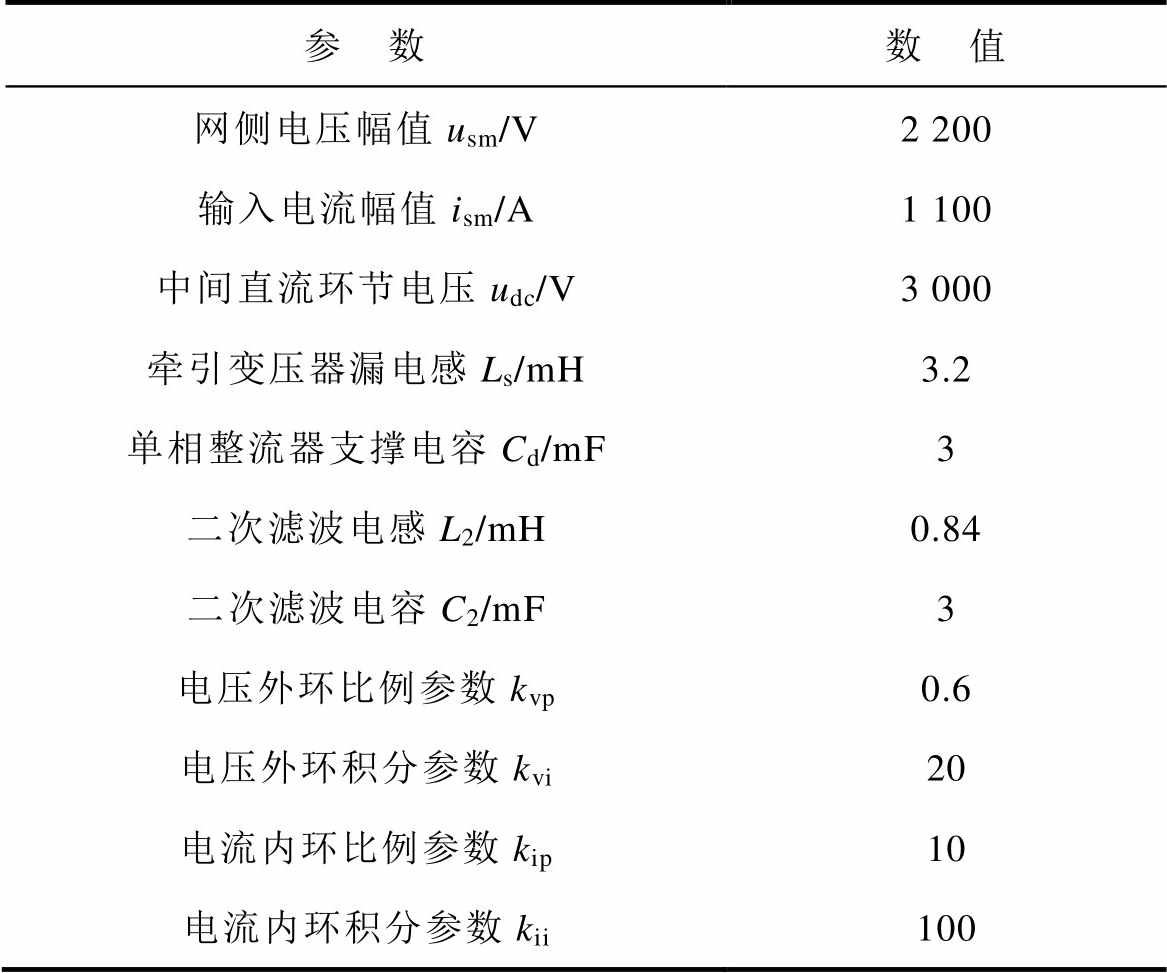
参 数数 值 网侧电压幅值usm/V2 200 输入电流幅值ism/A1 100 中间直流环节电压udc/V3 000 牵引变压器漏电感Ls/mH3.2 单相整流器支撑电容Cd/mF3 二次滤波电感L2/mH0.84 二次滤波电容C2/mF3 电压外环比例参数kvp0.6 电压外环积分参数kvi20 电流内环比例参数kip10 电流内环积分参数kii100
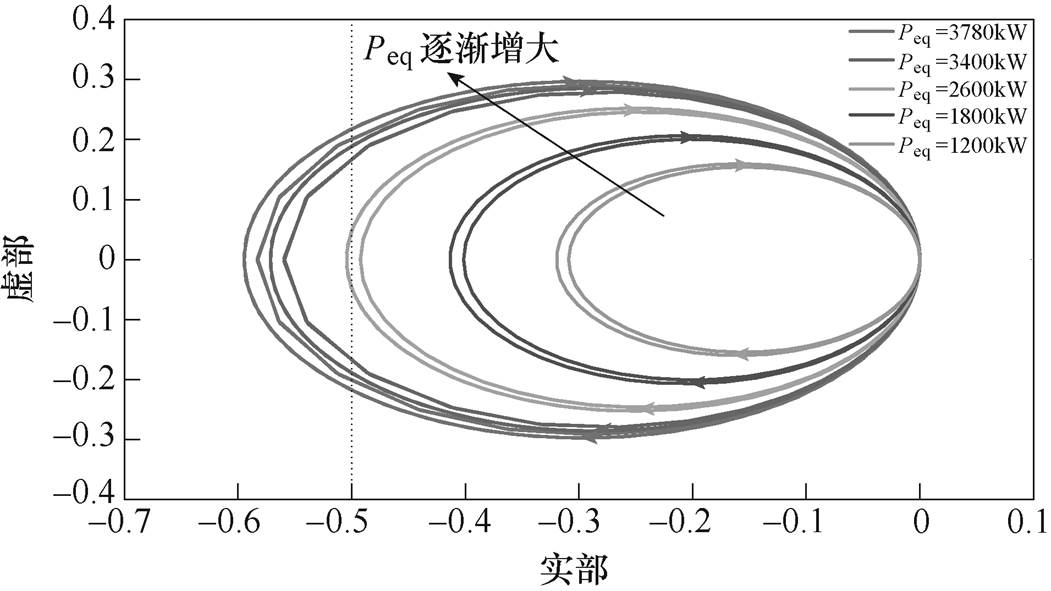
图5 不同Peq下，Tm(s)的Nyquist曲线
Fig.5 Nyquist curves of Tm(s) with different Peq
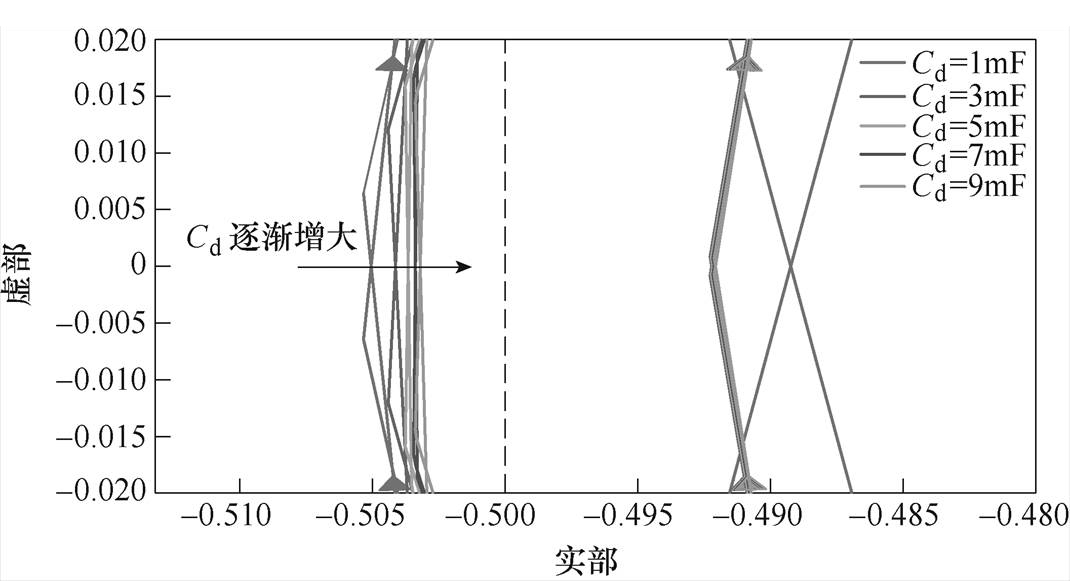
图6 不同Cd时，Tm(s)的Nyquist曲线
Fig.6 Nyquist curves of Tm(s) with different Cd
为进一步探究系统稳定裕度较差的原因，利用Matlab软件绘制了未考虑和考虑二次谐振电路时的系统Bode图，如图7和图8所示。
由于幅频曲线越远离0dB直线，系统稳定性越好，对比以上两个Bode图可知，随着Peq的增大，系统稳定裕度降低。当系统负载功率为3 400kW（此时假定系统全功率运行且系统效率为1）时，在二次谐振电路的谐振尖峰处，系统幅频曲线相较于图7尖峰处，更加靠近0dB直线。且可由图7、图8中局部放大图可知，如以-5dB虚线为界，仅考虑整流器输出阻抗与负载交互时，负载功率为3 400kW时所对应的尖峰未与-5dB虚线相交。而考虑到二次谐振电路时，在相同功率下由二次谐振电路所引入的谐振尖峰会与虚线相交。
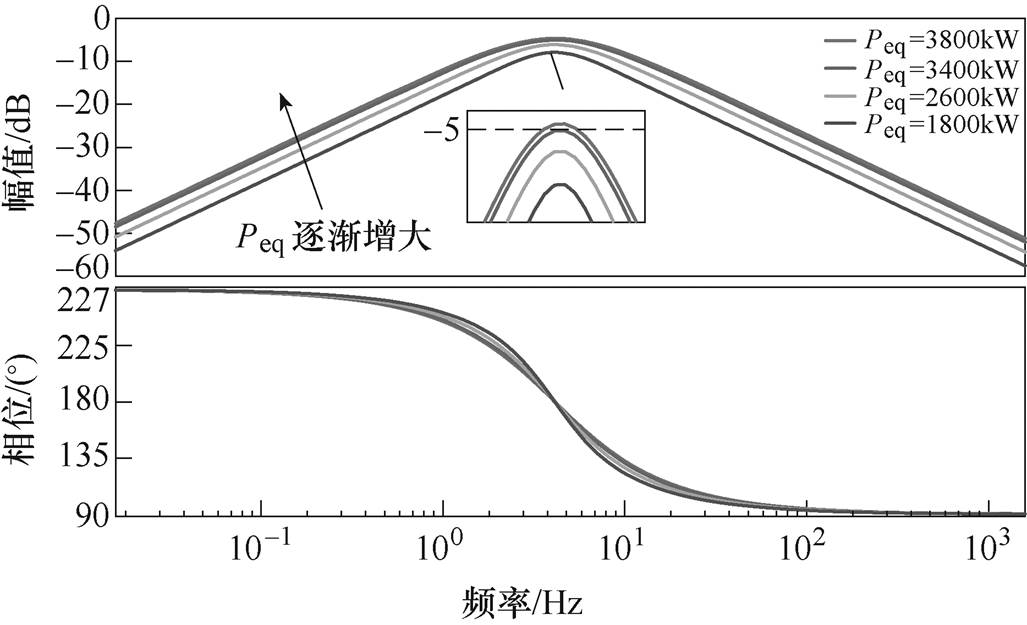
图7 未考虑二次谐振电路时的系统Bode图
Fig.7 Bode diagram of the system without considering the secondary resonant circuit
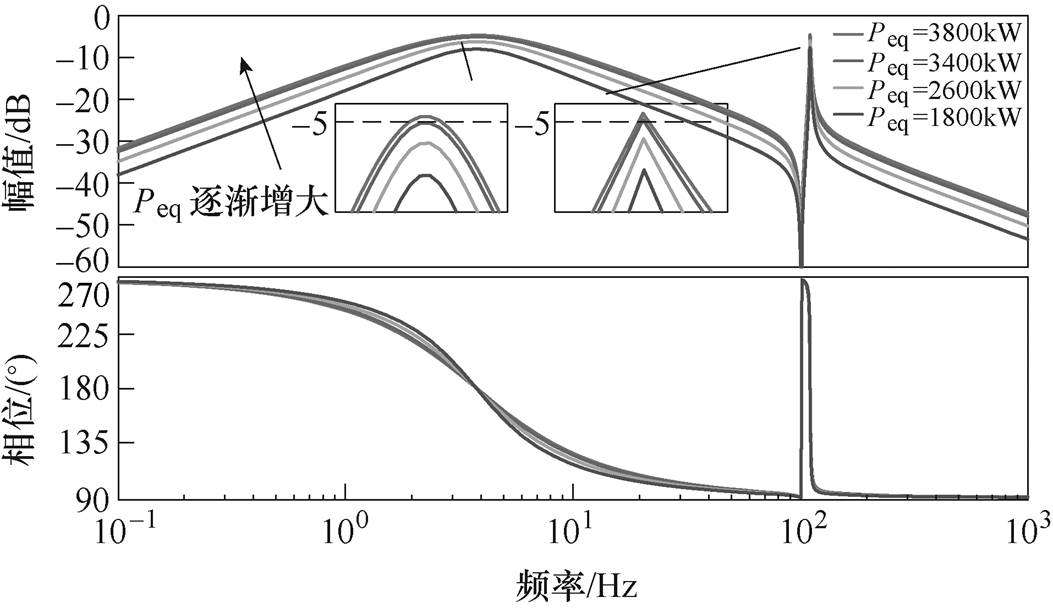
图8 考虑二次谐振电路时的系统Bode图
Fig.8 Bode diagram of the system with considering the secondary resonant circuit
由此可知，整流器输出阻抗和二次谐振电路两者与负载的交互作用会影响系统稳定性，使原系统稳定裕度较差。其中，二次谐振电路和负载之间的交互作用对系统稳定性影响相对较大。
为提升系统稳定裕度，可在直流侧增加并联电容的数量（见图6）或是串接电阻（见图5），考虑到成本、体积及功率损耗要求，现有相关研究多采用虚拟电容及其改进方法[24]对直流侧支撑电容进行控制或是采用将直流电压振荡信号应用于力矩补偿抑制、振荡的方法。对于动车组源侧整流器，如若采用虚拟电容控制提高支撑电容的等效大小，将相应地影响二次谐振电路中电容的取值大小[25]。
故本文提出了针对整流器的虚拟电阻控制，通过在直流侧引入虚拟电阻，等效地增加了负载侧的输入阻抗，以满足禁区稳定判据，提升系统稳定裕度。但由于在双闭环控制中虚拟电阻控制存在局限性[26-28]：阻值越大提升稳定性的效果越好，但相应地会使中间直流母线电压稳态误差增大。于是本文提出了对电压外环给定值进行修正，增加补偿环节，以减小由于引入虚拟电阻而引起的中间直流环节电压稳态误差，进一步增强系统稳定裕度。所提改进控制策略部分框图如图9所示。
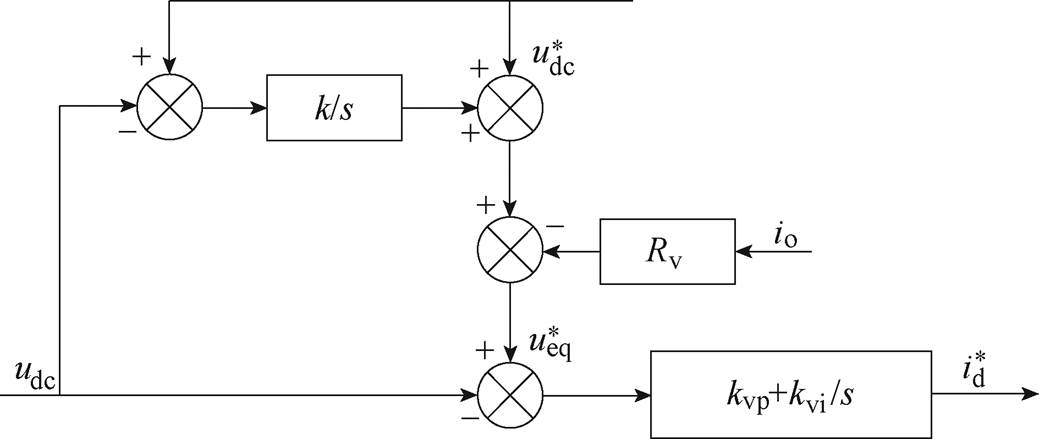
图9 本文所提的4QC控制策略
Fig.9 Proposed control structure of the 4QC
图9中，Rv为虚拟电阻，k为补偿环节参数，引入所提策略后的电压给定值为
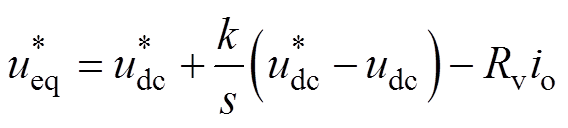（14）
引入的补偿环节增设了原有电压给定值和电压实际值的比较环节，并通过积分环节将比较结果引入到等效后的电压给定中，实现闭环控制，有助于减小稳态误差。
需要说明的是，虽然在直流微电网等领域对直流侧引入虚拟电阻会影响负载动态性能，但对于动车组牵引变流器系统，负载为牵引逆变器和辅助逆变器以及无火回送装置，中间直流环节电压将由TCU自动调节，电压只要大于2 800V且保证最大值小于3 600V，即可满足负载侧的实际需要，且由附图1可知，现有复兴号动车组中间直流环节额定电压为2 800V或略大于2 800V。所以在实际应用时，当额定值设为3 000V时，可通过设计虚拟电阻大小来保证全功率牵引运行时直流侧最低电压仍高于2 800V。但随着动车组“主辅一体化”中牵引变流器负载输出功率的提高，辅助变流器额定输入电压值也将相应提高（跨国互联互通动车组辅助变流器额定输入电压值为3 000～3 600V），所以在本文中引入补偿环节具备必要性。
根据所提控制策略绘制改进后的系统开环传递函数Tm的Nyquist曲线，判断所提控制策略的改善效果并进行相关参数设计。
3.2.1 虚拟电阻值对系统稳定性的影响
相较于原有双闭环控制，所提控制策略引入了Rv和k两个参数。由于k为引入虚拟电阻后的补偿系数，所以应先确定Rv的取值范围，再对k的大小进行设计。
由图5所示，负载功率越大时，系统稳定性越差。为提升系统稳定裕度，选定负载全功率运行且系统效率为90%时（Peq=3 780kW）的负载为实际研究对象。改变虚拟电阻值时，Tm(s)的Nyquist曲线如图10所示。
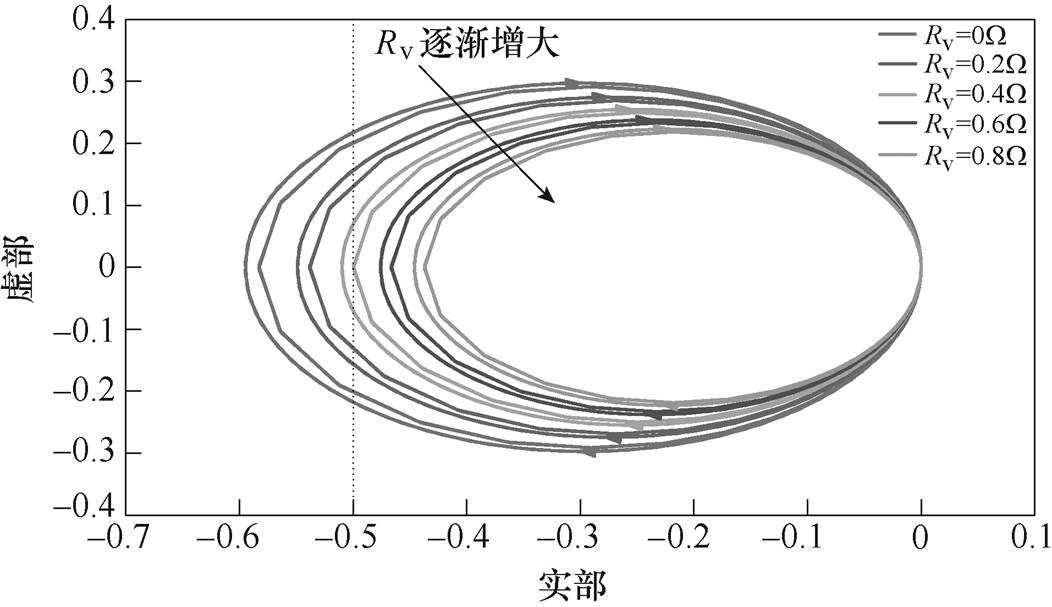
图10 不同Rv下，Tm(s)的Nyquist曲线
Fig.10 Nyquist curves of Tm(s) with different Rv
可见，虚拟阻值越大，系统稳定性越好，但无补偿环节时，虚拟阻值的增大会增大系统稳态误差，所以本文将虚拟阻值选取在[0.4W, 0.6W]。
3.2.2 补偿系数值对系统稳定性的影响
为进一步验证补偿系数k对系统稳定性的影响，选取虚拟阻值为临界值0.4W，利用Matlab绘制不同补偿系数时，Tm(s)的Nyquist曲线，如图11所示。
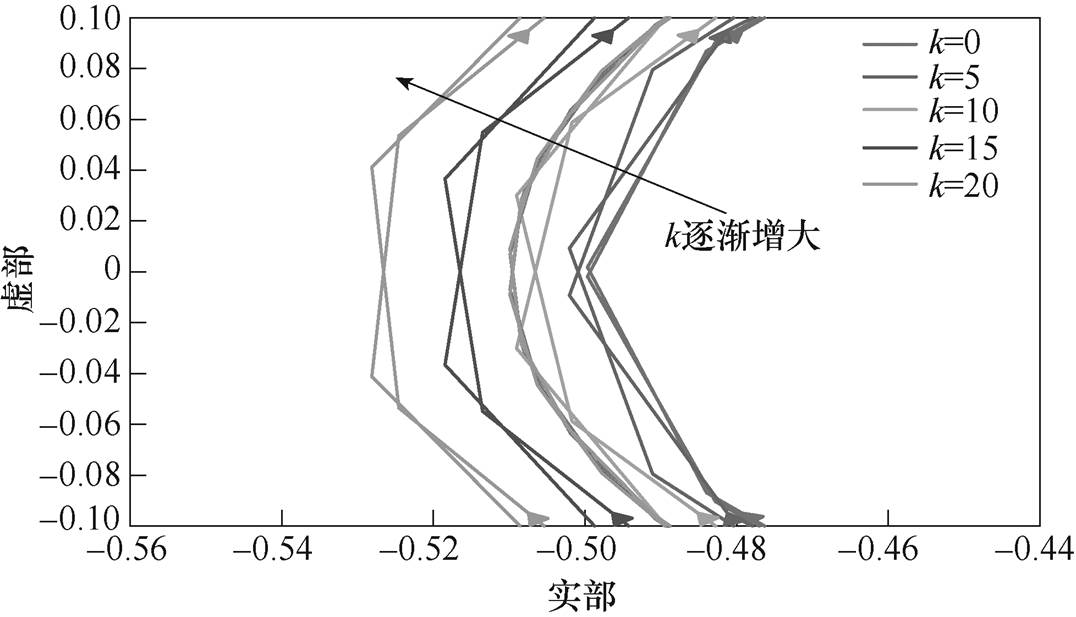
图11 不同k下，Tm(s)的Nyquist曲线
Fig.11 Nyquist curves of Tm(s) with different k
当k值逐渐增大时，系统稳定性变差，且随k值的变大，曲线左移越明显。为在保证系统稳定性的前提下，尽可能减小系统稳态误差，本文对于所提控制策略参数选定为虚拟电阻Rv=0.4W，补偿系数k =5。
为验证所提控制策略对于提升动车组中间直流环节稳定裕度的正确性和有效性，在仿真软件Matlab/Simulink环境中搭建了如图1所示的动车组牵引变流器仿真平台，其中将负载等效为电阻，仿真所用参数见表1。分别在1s，1.5s，2s，2.5s投入负载，投入后其对应运行情况见表2，假定牵引电机额定输出功率为800kW，辅助变流器额定输出功率为200kW。
表2 负载功率随时间变化参数
Tab.2 Parameter of load power variation with time
时间/s负载/kW 11 800 (2×800+200) 1.52 600 (3×800+200) 23 400 (4×800+200) 2.53 780 (3 400÷0.9)
首先，验证了改善后动车组4QC仍能保证近似单位功率运行，稳态情况下交流侧电压、交流侧电流仿真结果如图12所示，依据仿真结果证明了改善后动车组4QC交流侧电压电流仍能满足正常工作需要。
图12 稳态情况下交流侧电压、交流侧电流仿真结果
Fig.12 Simulation results of us、is under steady state operation
接着，对改善前后的负载电压和负载输入电流进行对比分析。图13为引入虚拟电阻控制策略时加入补偿环节前后的中间直流环节直流电压波形对比。图14为引入本文所提控制策略前后的直流母线电压波形（改进前所反映的投入负载后电压波形与附图1中实际系统投入负载后的电压波形变化情况一致，故仿真具备参照意义）。图15为引入本文所提控制策略前后的直流侧输入电流波形。
图13 加入补偿环节前后的直流电压仿真结果
Fig.13 Simulation results of intermediate DC voltage with and without compensation
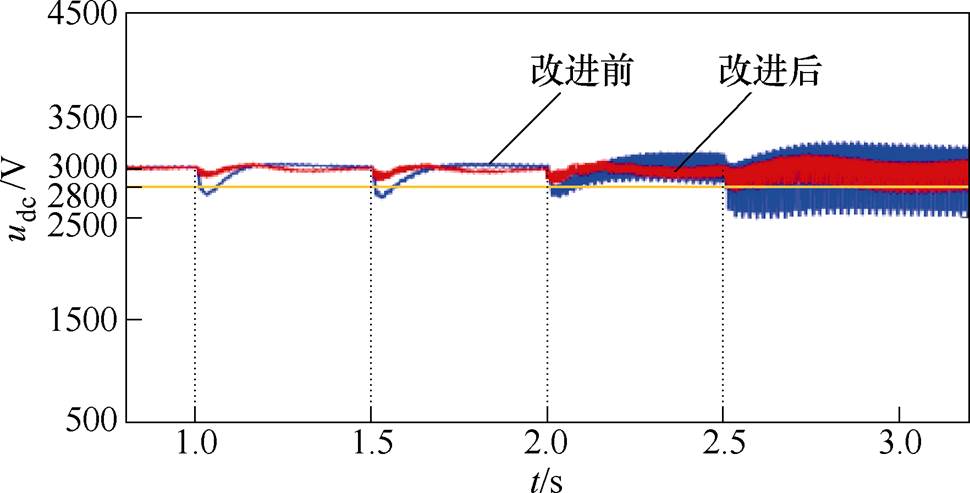
图14 改善前和改善后中间直流电压仿真结果
Fig.14 Simulation results of intermediate DC voltage with and without improvement
图15 改善前和改善后负载输入电流仿真结果
Fig.15 Simulation results of load input current with and without improvement
由图13可知，在模拟动车组整备状态时，即1s前，加入补偿环节前后均可令电压维持在给定值；而模拟投入负载至全功率运行且系统工作效率为理想100%的过程中，未加入补偿时直流电压波形出现明显跌落，并于模拟工作效率为90%时跌落至2 800V以下，无法保证牵引变流器负载侧正常运行；而引入的补偿环节抑制了由于虚拟电阻控制而使稳态误差变大的趋势，系统仍可保证正常运行。仿真验证了加入补偿环节的必要性。
由图14可以看出，改善前系统在前2.5s，即在系统启动至全功率运行过程中，中间直流母线电压最大跌落约250V；在2～2.5s过程中，电压存在振荡情况，但由于其振荡电压仍高于2 800V，满足辅助变流器输入电压要求，且不高于3 600V，系统仍可正常运行。但由于较大电压振荡幅度会使得牵引电机或者辅助电机出现较大的转矩脉动，甚至会影响机车的运行速度和平稳度，所以依据仿真结果证明了现有牵引变流系统需抑制电压大幅振荡、提升系统稳定裕度。此外，在2.5～3s过程中，模拟了负载侧效率为90%时，改善前系统的直流母线电压振荡范围为2 500～3 200V，已不满足辅助变流器输入电压要求，可能对负载侧稳定性造成影响，系统稳定裕度已大为降低。
而改善后，系统在前2.5s直流母线电压波动较小；在2.5～3s，电压振荡范围约为2 800～3 080V，可满足辅助变流器实际需要。将引入改进控制策略前后的电压波形进行总体对比，验证了虚拟电阻控制对于提升牵引变流系统稳定裕度的正确性与有效性，仿真结果与理论分析相符。
由图15可以看出，改善前后负载输入电流曲线变化趋势与直流侧电压波形变化趋势相似，故未做具体分析。
根据加入虚拟电阻控制策略的直流电压波形可看出，虽然在虚拟电阻控制中引入了电压补偿环节，但仍存在一定的电压损耗。此外，由图15可以看出，改善前后在负载投入瞬间，负载输入侧均存在冲击电流。综上，虚拟电阻控制仍有待进一步改进。
为进一步验证所提虚拟电阻控制策略在实际应用中的正确性与有效性，在中车大连电力牵引研发中心有限公司的半实物仿真实验平台上，将引入补偿环节的虚拟电阻控制策略的实验结果与原有dq电流解耦控制策略的实验结果进行对比。
图16给出了半实物实验系统结构，控制芯片为TMS320F28335。实验中，模拟系统维持90%效率时全功率运行，观察示波器波形。改进前后实验波形如图17、图18所示，图中，uo为整流器未经支撑电容的输出电压，udc为中间直流环节电压，icon为斩波电流，io负载输入电流，upwm为牵引电机输入电压，imon为牵引电机输入电流。
通过对比图17和图18中的udc和io波形可知，改进后的中间直流环节电压udc较原有控制方法下的电压波动更小，改进控制策略增强了中间直流环节稳定性。由于此时负载可等效为恒功率负载，当udc波动很小时，也会改善实际负载输入电流io的波形。
图16 半实物实验平台
Fig.16 Hardware-in-the-loop experimental platform
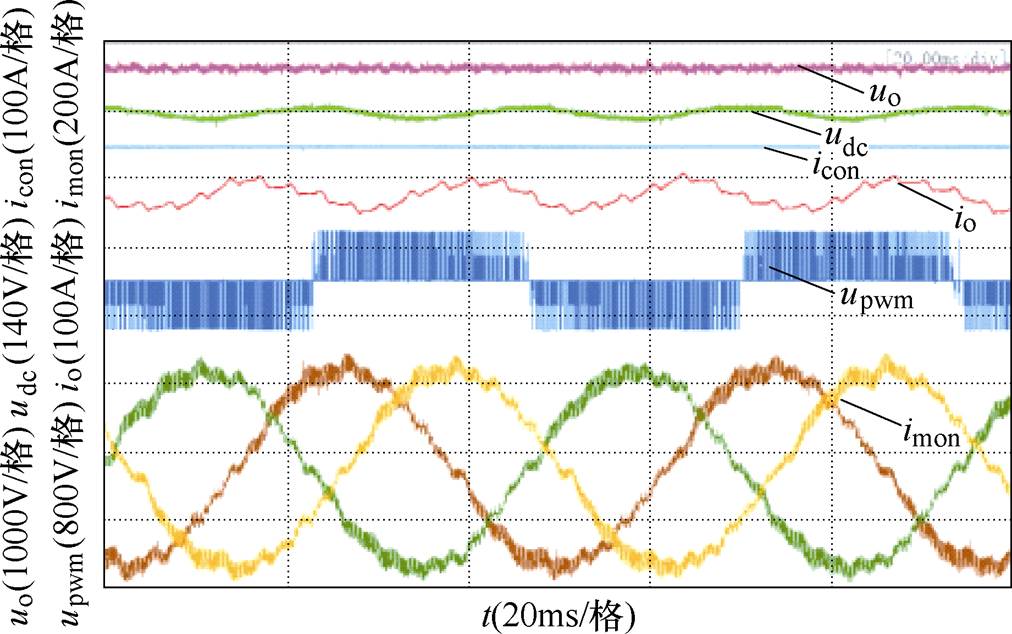
图17 改进前实验中各个参数的实测波形
Fig.17 The measured waveforms of each parameter in the experiment before improvement
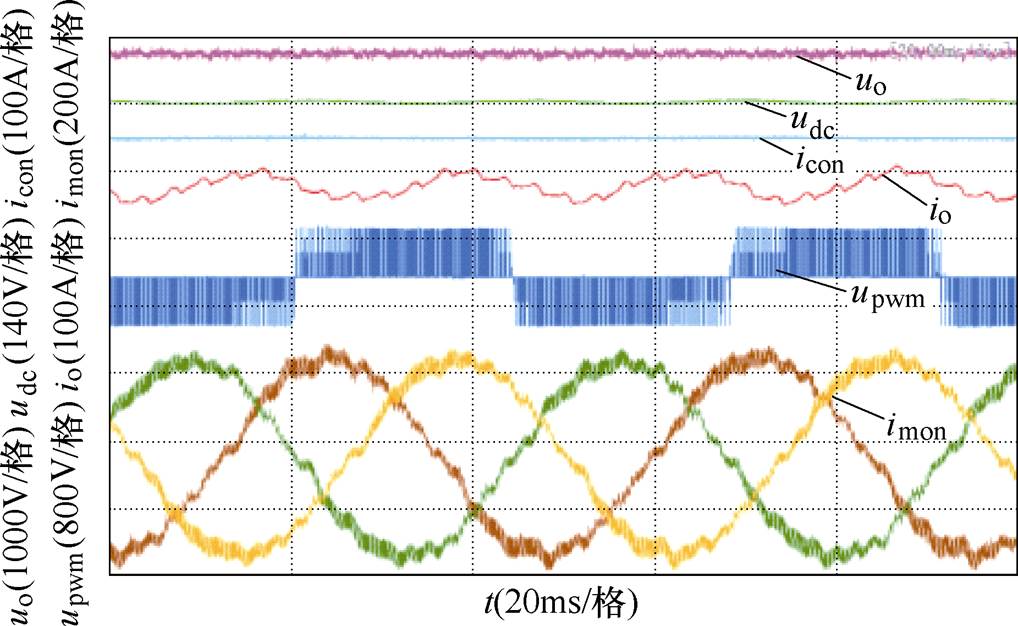
图18 改进后实验中各个参数的实测波形
Fig.18 The measured waveforms of each parameter in the experiment after improvement
对比图17和图18中uo波形，改善前后整流器输出电压未经支撑电容和二次谐振电路滤波时，波形差异不大，可见改进控制策略对源侧整流器影响较小。此外，通过对比两中的upwm和imon波形可知，牵引电机输入电压和输入电流差别不大，可知，增加所提虚拟电阻控制对实际负载运行的影响较小。
综上，仿真和实验结果验证了所提虚拟电阻控制策略能够抑制中间直流环节电压波动，提升系统稳定裕度。
动车组牵引变流器牵引工况下投入负载时，由于中间直流环节的二次谐振电路与牵引逆变模块和辅助变流器的直流侧输入阻抗交互容易产生阻抗不匹配，导致牵引变流系统中间直流环节发生振荡失稳。对此，分析了系统的振荡机理及影响因素，并提出了一种引入电压补偿环节的虚拟电阻控制方法，可提高牵引变流系统的稳定性，得出以下结论：
1）负载电机功率和电压补偿系数的增加都会使得牵引变流系统的稳定性变差。
2）虚拟阻值越大，等效于增大了负载输入阻抗的大小，抑制了中间直流环节电压振荡，使系统开环传函满足禁区稳定判据，提升了系统稳定裕度。
3）虚拟电阻控制会增大系统稳态误差，而电压补偿环节能够减小系统稳态误差，但其补偿效果有限，仍需后续进一步改进。
1. 实时监测波形
铁科纵横监控软件针对故障车4QC交流侧电压、交流侧输入电流和中间直流环节电压的实时监测波形如附图1所示。
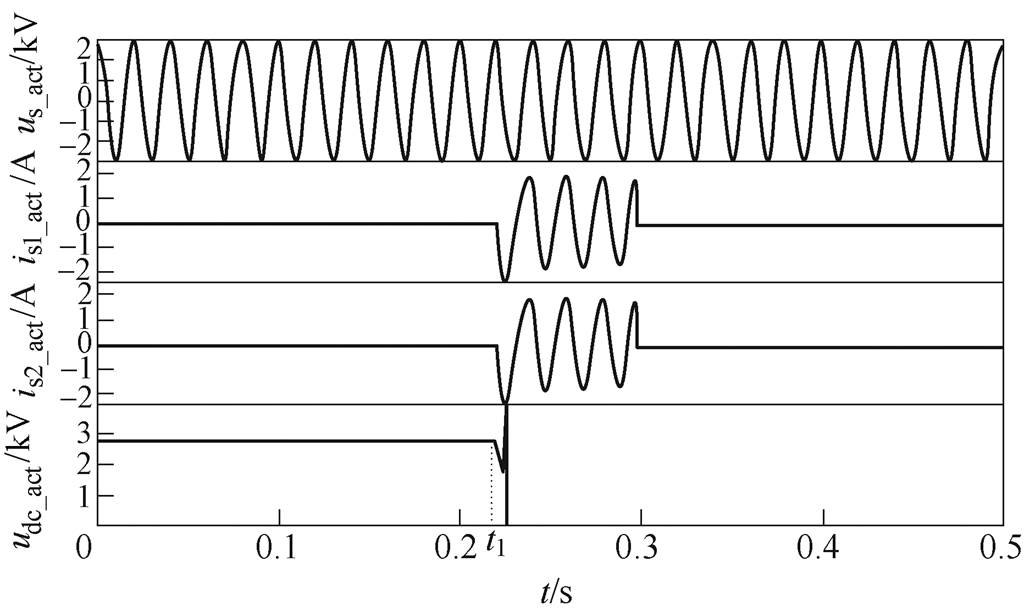
附图1 实时监测波形
App.Fig.1 Real-time monitoring waveforms
由于原有软件监测图仅以拍照形式保存，故根据原有数据拟合出如附图1所示的监测波形。图中依次为交流侧电压、两台整流器交流侧输入电流和中间直流环节电压的波形，并假定在t1时刻开始模拟试验。厂内静调试验中，该车升6车14车弓时，未报故障；而升03车11车弓时，列车HMI显示屏报故障。
通过分析列车22、23功能组牵引系统工作逻辑以及由铁科纵横监测波形判断：在静调试验模拟系统牵引工况下，当设备起动至正常运行过程中，中间直流环节电压逐渐下降至低于正常工作所需电压值并且电压短时大幅振荡（此处涉及故障点，故障代码34C4和34F2），引发了车辆受电弓“顶网”，TCU误动，造成中间直流环节电压被迫大幅升高（此时报故障：中间直流电压超限，故障代码34C5），而引起了中间直流环节被迫启动保护逻辑将直流电压迅速降至0V。该故障过程中，电压幅值大幅振荡，对牵引变流系统乃至整车安全造成了极大威胁。最终，判断为由于运行过程中，中间直流环节电压大幅跌落至正常运行所需电压值以下，且动车组中间直流环节电压大幅振荡变化过快，导致了该故障的发生。
此前类似故障在短编标动静调试验中以及同批次长编标动试验中同样发生过，为避免后续厂内动车组再次出现类似故障，本文从控制方式的角度，提出了针对4QC的虚拟电阻控制加以改进。
2. 单台4QC输出导纳推导过程补充
结合式（1）、式（5）可知
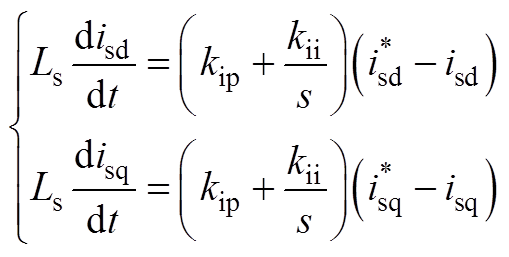（A1）
拉式变换后，忽略采样延时可得电流内环开环传递函数Gi(s)为
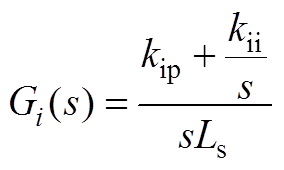（A2）
进而推导出电流内环闭环传函Gii(s)为
（A3）
结合式（A3）推导出idc的小信号分量为输入、udc的小信号分量为输出的闭环系统反馈传函H(s)为
（A4）
结合式（2）将变量小信号化并进行拉氏变换，则单台4QC输出阻抗Zout1(s)为
（A5）
代入化简得单台4QC输出导纳为
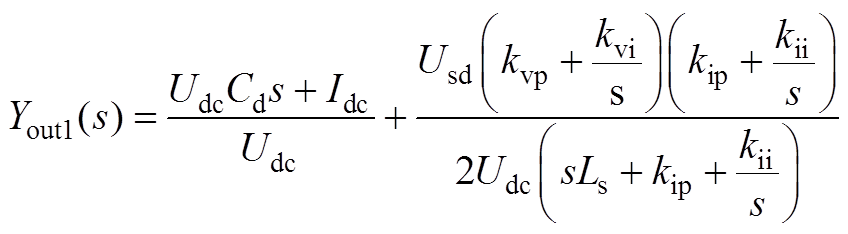（A6）
3. Nyquist图说明
此图5为例，文中Nyquist图表现为“四圈”，而常见奈式图大多为“两圈”，如附图2所示。这是因为本文将计算出的变换器输出阻抗并联了二次谐振电路作为总的输出阻抗所致。
附图2 未考虑谐振电路时，Tm(s)的Nyquist曲线
App.Fig.2 Nyquist curves of Tm(s) without resonant circuit
参考文献
[1] 牟岩. 城轨车辆牵引系统耦合振荡研究[J]. 机车电传动, 2019(3): 111-116, 135.
Mu Yan. Study on coupling oscillation of urban rail vehicle traction system[J]. Electric Drive for Locomo- tives, 2019(3): 111-116, 135.
[2] Francés A, Asensi R, García Ó, et al. Modeling electronic power converters in smart DC microgrids- an overview[J]. IEEE Transactions on Smart Grid, 2018, 9(6): 6274-6287.
[3] Song Wensheng, Jiao Shilei, Li Yunwei, et al. High- frequency harmonic resonance suppression in high- speed railway through single-phase traction converter with LCL filter[J]. IEEE Transactions on Trans- portation Electrification, 2016, 2(3): 347-356.
[4] Dragičević T, Lu Xiaonan, Vasquez J C, et al. DC microgrids-part I: a review of control strategies and stabilization techniques[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4876-4891.
[5] Wu Mingfei, Lu D D C. A novel stabilization method of LC input filter with constant power loads without load performance compromise in DC microgrids[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4552-4562.
[6] Wu Wenhua, Chen Yandong, Zhou Leming, et al. A virtual phase-lead impedance stability control strategy for the maritime VSC-HVDC system[J]. IEEE Transa- ctions on Industrial Informatics, 2018, 14(12): 5475- 5486.
[7] 庄绪州, 张勤进, 刘彦呈, 等. 船舶全电力推进系统恒功率负载有源阻尼控制策略[J]. 电工技术学报, 2020, 35(增刊1): 101-109.
Zhuang Xuzhou, Zhang Qinjin, Liu Yancheng, et al. An active damping control of constant power load for all-electric ships[J]. Transactions of China Electro- technical Society, 2020, 35(S1): 101-109.
[8] Prabhakaran P, Goyal Y, Agarwal V. Novel nonlinear droop control techniques to overcome the load sharing and voltage regulation issues in DC microgrid[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 4477-4487.
[9] 许加柱, 郝铭轩, 王涛, 等. 直交型电力机车直流侧电压稳定控制及改善方法[J]. 电力自动化设备, 2019, 39(7): 64-69, 106.
Xu Jiazhu, Hao Mingxuan, Wang Tao, et al. Stability control and improvement strategy for DC side voltage of DC-AC electric locomotives[J]. Electric Power Automation Equipment, 2019, 39(7): 64-69, 106.
[10] 张颖, 王惠民, 葛兴来. 基于前馈电压补偿的地铁牵引变流器直流侧振荡抑制方法[J]. 中国电机工程学报, 2018, 38(9): 2728-2735, 2842.
Zhang Ying, Wang Huimin, Ge Xinglai. DC-link stabilization method for metro traction converter- motor system based on feedforward voltage com- pensation[J]. Proceedings of the CSEE, 2018, 38(9): 2728-2735, 2842.
[11] 陈杰, 李军, 邱瑞昌, 等. 轨道交通牵引系统空间矢量脉宽调制同步过调制策略研究[J]. 电工技术学报, 2020, 35(增刊1): 91-100.
Chen Jie, Li Jun, Qiu Ruichang, et al. Research on space vector PWM synchronous overmodulation in rail transit traction system[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 91-100.
[12] Zhang Guinan, Liu Zhigang, Yao Shulong, et al. Suppression of low-frequency oscillation in traction network of high-speed railway based on auto- disturbance rejection control[J]. IEEE Transactions on Transportation Electrification, 2016, 2(2): 244-255.
[13] 朱进权, 葛琼璇, 王晓新, 等. 基于自抗扰和负载功率前馈的高速磁悬浮系统PWM整流器控制策略[J]. 电工技术学报, 2021, 36(2): 320-329.
Zhu Jinquan, Ge Qiongxuan, Wang Xiaoxin, et al. Control strategy for PWM rectifier of high-speed maglev based on active disturbance rejection control and load power feed-forward[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 320-329.
[14] 韩京清. 从PID技术到“自抗扰控制”技术[J]. 控制工程, 2002, 9(3): 13-18.
Han Jingqing. From PID technique to active dis- turbances rejection control technique[J]. Control Engineering of China, 2002, 9(3): 13-18.
[15] Ang K H, Chong G, Li Yun. PID control system analysis, design, and technology[J]. IEEE Transa- ctions on Control Systems Technology, 2005, 13(4): 559-576.
[16] Tian Hao, Li Yunwei. Virtual resistor based second- order ripple sharing control for distributed bidirectional DC-DC converters in hybrid AC-DC microgrid[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 2258-2269.
[17] Rodríguez-Cabero A, Roldán-Pérez, Prodanovic M, et al. Coupling of AC grids via VSC-HVDC intercon- nections for oscillation damping based on differential and common power control[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 6548-6558.
[18] Wang Yizhen, Wen Weijie, Wang Chengshan, et al. Adaptive voltage droop method of multiterminal VSC-HVDC systems for DC voltage deviation and power sharing[J]. IEEE Transactions on Power Delivery, 2019, 34(1): 169-176.
[19] 钟志宏, 方晓春, 林飞, 等. MTPA控制下逆变器- IPMSM系统直流侧电压稳定性研究[J]. 电工技术学报, 2017, 32(21): 34-43.
Zhong Zhihong, Fang Xiaochun, Lin Fei, et al. DC voltage stability studies with IPMSM system under the control of MTPA[J]. Transactions of China Elec- trotechnical Society, 2017, 32(21): 34-43.
[20] 王迎晨, 杨少兵, 宋可荐, 等. 基于滑模结构无源控制的车网耦合系统低频振荡抑制方法[J] 电工技术学报, 2020, 35(3): 553-563.
Wang Yingchen, Yang Shaobing, Song Kejian, et al. An approach based on SMS to suppress low-frequency oscillation in the EMUs and traction network coupling system using PBC[J]. Transactions of China Elec- trotechnical Society, 2020, 35(3): 553-563.
[21] 刘龙. 机车单相PWM整流器的研究与实现[D]. 武汉: 华中科技大学, 2016.
[22] Liu Jinjun, Feng Xiaogang, Lee F C, et al. Stability margin monitoring for DC distributed power systems via perturbation approaches[J]. IEEE Transactions on Power Electronics, 2003, 18(6): 1254-1261.
[23] 许加柱, 夏静, 杨雅倩, 等. 抑制直流电压振荡的虚拟阻感超前控制策略[J]. 电力电子技术, 2019, 53(12): 43-47.
Xu Jiazhu, Xia Jing, Yang Yaqian, et al. The virtual inductive-resistive leading control strategy for suppressing DC voltage oscillation[J]. Power Electronics, 2019, 53(12): 43-47.
[24] 汪春江, 孙建军, 宫金武, 等. 并网逆变器与电网阻抗交互失稳机理及阻尼策略[J]. 电工技术学报, 2020, 35(增刊2): 503-511.
Wang Chunjiang, Sun Jianjun, Gong Jinwu, et al. Mechanism and damping strategy of interactive instability between grid-connected inverter and grid impedance[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 503-511.
[25] 陈燕平, 忻力, 李中浩. 单相电压型脉冲整流器中二次谐振电路的研究[J]. 机车电传动, 2010(2): 28-32.
Chen Yanping, Xin Li, Li Zhonghao. Research on the secondary resonant circuit of single-phase voltage- pulse rectifier[J]. Electric Drive for Locomotives, 2010(2): 28-32.
[26] 唐欣, 张凯峰, 许强, 等. 提高VSC-HVDC系统供电无源网络的传输容量的控制方法[J]. 电工技术学报, 2016, 31(5): 44-51.
Tang Xin, Zhang Kaifeng, Xu Qiang, et al. Control strategy for enlarging the transmission capacity of VSC-HVDC systems supplying passive networks[J]. Transactions of China Electrotechnical Society, 2016, 31(5): 44-51.
[27] 陈杰, 章新颖, 闫震宇, 等. 基于虚拟阻抗的逆变器死区补偿及谐波电流抑制分析[J]. 电工技术学报, 2021, 36(8): 1671-1680.
Chen Jie, Zhang Xinying, Yan Zhenyu, et al. Dead- time effect and background grid-voltage harmonic suppression methods for inverters with virtual impedance control[J]. Transactions of China Electro- technical Society, 2021, 36(8): 1671-1680.
[28] 黄远胜, 刘和平, 苗轶如, 等. 基于并联虚拟电阻的级联DC-DC变换器稳定控制方法[J]. 电工技术学报, 2020, 35(18): 3927-3937.
Huang Yuansheng, Liu Heping, Miao Yiru, et al. Cascaded DC-DC converter stability control method based on paralleling virtual resistor[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3927-3937.
Analysis and Suppression of Voltage Oscillation for DC Bus in Static Adjustment Test of EMU
Abstract In the static adjustment test in the factory, the traction converter of the high-speed EMU has a large voltage oscillation in the intermediate DC link under the simulated traction condition. Therefore, a virtual resistance control method with compensation link was proposed for the single-phase rectifier at the source side. Based on the dq coordinate mathematical model of the single-phase PWM rectifier, this paper built the equivalent output impedance model of the source-side rectifier in parallel with the secondary resonant circuit and the equivalent input impedance model of the traction inverter unit and the auxiliary converter. Then, the reason for voltage oscillations in the DC link was revealed by combining Bode diagram and Nyquist curve, that is, the interaction between the secondary resonant circuit and the constant power load will lead to the voltage oscillation in the intermediate DC link. The proposed oscillation suppression method uses virtual resistance to increase the load-side input impedance, so that the system gain can meet the exclusion zone stability criterion, and the stability margin of the system can be improved. Finally, simulation and experimental results verify the effectiveness of the analysis and the proposed control method.
keywords：Traction converter, cascade system, voltage oscillation, virtual resistance control
DOI: 10.19595/j.cnki.1000-6753.tces.211092
中图分类号：TM46
国家自然科学基金面上项目（51877152）和天津市自然科学基金项目（18JCZDJC97300）资助。
收稿日期 2021-07-19
改稿日期 2021-10-11
周雪松 男，1964年生，博士，教授，博士生导师，研究方向为微电网动态谐波交互机理与控制方法。E-mail: zxsmyj@126.com
胡一凡 男，1997年生，硕士研究生，研究方向为高速动车组交直流电能变换系统与新技术。E-mail: huyifan118@126.com（通信作者）
（编辑 陈 诚）