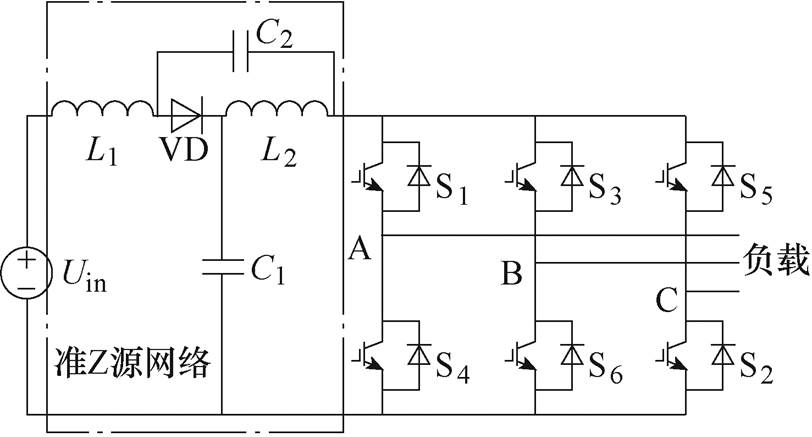
图1 准Z源逆变器的拓扑结构
Fig.1 Quasi Z-source inverter topology
摘要 准Z源逆变器是一种允许桥臂直通的特殊升压变换器,在新能源电动汽车、光伏和风电等分布式发电系统中具有广泛应用前景。准Z源逆变器直流链电压泵升时存在一个潜在问题,若直流侧电感储能不足会使二极管电流断续,从而导致直流链电压发生跌落,严重降低了准Z源逆变器的输出性能和安全可靠性。针对该问题,首先,该文定义电压跌落深度的概念来计算和衡量直流链电压升高和降低的幅值。然后,在综合分析造成二极管电流断续因素的基础上,提出直流链电压跌落判断方法,可根据当前系统参数和状态预判直流链电压是否发生跌落。最后,为了防止准Z源逆变器出现非正常状态,基于系统协调控制的思想提出了直流链电压跌落抑制方法。结果表明,所提出的方法能够准确预测直流链电压跌落的条件,并能够有效防止直流链电压跌落。
关键词:准Z源逆变器 直流链电压 电压跌落深度 二极管电流断续
逆变器作为风能、太阳能、燃料电池等新能源发电系统中的重要组成部分,在能源转换与能量传递过程中发挥着重要作用。在当前大力发展新能源应用技术的背景下,学者们普遍认为,需要研发具有安全可靠性高、成本低、性能高的新型逆变器[1-3]。
准Z源逆变器是彭方正教授提出的一种具有独特升降压方式的新型功率变换拓扑[4-5],它的现实意义在于:在有电磁干扰的环境下,允许桥臂直通的特性一定程度上降低了逆变器损坏的风险,提高了设备的可靠性和安全性[6];脉冲宽度调制(Pulse Width Modulation, PWM)控制信号中无需加入死区时间,解决了死区时间造成交流输出电压畸变的问题[6];实现了直流升降压与交直流变换一体化的设计结构,降低了软硬件成本[7]。交流调速系统、燃料电池供电系统、光伏和风电等分布式发电系统以及微电网系统等具有随负载和环境因素的变化而导致输出电压波动范围很大的共同特点[8-10],因此准Z源逆变器在这些领域中具有广阔应用价值。
准Z源逆变器是通过电感周期性的充放电,实现直流链电压的泵升。然而当准Z源网络的电感储能不足时,二极管电流会发生断续。此时准Z源逆变器会处于一种非正常工作状态[11-12],电感停止放电,直流链电压仅由电容电压决定。这将导致直流链电压发生跌落,严重降低了准Z源逆变器的安全可靠性和输出电能质量[13]。
国内外学者对准Z源逆变器直流链电压跌落的原因进行了大量研究。高奇等首先发现了有效电压矢量作用期间的电压暂降现象会对阻抗源逆变器升压性能造成极大影响[14]。A. K. Chauhan等认为以往文献分析准Z源逆变器电路工作原理时所假设的直流侧电感电流较大、电流连续、纹波较小是一种理想情况[15]。在一些要求电感尺寸和质量较小的应用场合,负载功率因数很低或电感很小,电感电流断续就会发生。因此,其将负载功率因数归为导致二极管电流断续的因素之一。R. Pashaei等基于已有二极管电流断续的研究,提出了一种划分准Z源逆变器工作模式的方法[16-17]。综合分析了连续导通模式、断续导通模式和临界导通模式下逆变器的电压电流波形、功率器件的最大电流和电压应力以及电容器纹波,对直流链电压跌落现象的基础研究做出了进一步的贡献。
解决直流链电压跌落问题主要采用适应负载大范围变动的双向准Z源逆变器拓扑[18]。该拓扑在二极管两端反并联了一个开关器件。当二极管电流即将断续时打开开关器件,逆变器直流侧产生的回馈电流能够避免电流断续。但是,增加的反并联开关器件会提高电路的成本和控制难度;此外,如果在切换直通状态时没有关断反并联开关器件,会使电容和桥臂受到巨大的电流冲击而损坏逆变器[19]。
综上所述,目前关于准Z源逆变器直流链电压跌落的研究还存在三方面的不足:①虽然现有文献已得出准Z源逆变器直流链电压跌落的原因,但分析的角度较为单一,缺乏全面性和深入性;②尚无可预判直流链电压跌落的方法,给准Z源逆变器运行状态带来了不确定性;③解决直流链电压跌落问题的方法非常有限,有待进一步研究。
本文深入研究了准Z源逆变器直流链电压跌落的原因,发现了直流链电压在二极管电流断续时不仅会跌落,还有高于正常幅值的情况,极大地增加了逆变器过电压损坏的风险,该现象也未有文献研究过。针对该问题本文给出了电压跌落深度的定义,可用于计算和衡量直流链电压升高和降低的幅值;然后综合分析了造成二极管电流断续的各方面因素,提出了直流链电压跌落的判断和抑制方法,可以准确计算准Z源逆变器发生直流链电压跌落的条件,以及如何防止电压跌落。本文的研究成果进一步完善了直流链电压跌落的基础理论,为保证准Z源逆变器正常工作提供了新的依据和方法。
本节首先介绍准Z源逆变器的基本工作原理,从非直通状态下电感放电规律引出二极管电流断续的问题;然后根据非正常工作状态下准Z源逆变器拓扑结构的变化,分析直流链电压跌落现象;最后提出了电压跌落深度的定义研究直流链电压幅值的变化及其对电路的影响。
准Z源逆变器的拓扑结构如图1所示,它由直流电源、准Z源网络、逆变器三部分组成。准Z源网络是由两个电感、两个电容和一个二极管构成的阻抗源网络,它位于直流源和逆变器之间。准Z源逆变器既可以工作在直通状态下,又可以工作在非直通状态下。电感和电容在这两种状态下周期性地充放电,从而实现直流链电压的泵升。直流链电压增益是通过改变直通状态的占空比来调整的。

图1 准Z源逆变器的拓扑结构
Fig.1 Quasi Z-source inverter topology
准Z源逆变器在直通状态和非直通状态下的等效电路如图2所示。图2a中,电压源电流经准Z源网络,最终流向负载;电压源、电感L1、电容C1处在一个回路中,该回路的电压方程可表示为
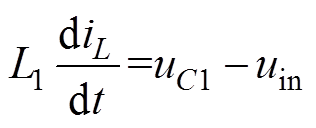 (1)
(1)
式中,iL为流过电感L1的电流;uC1为电容C1两端的电压;uin为电压源电压。
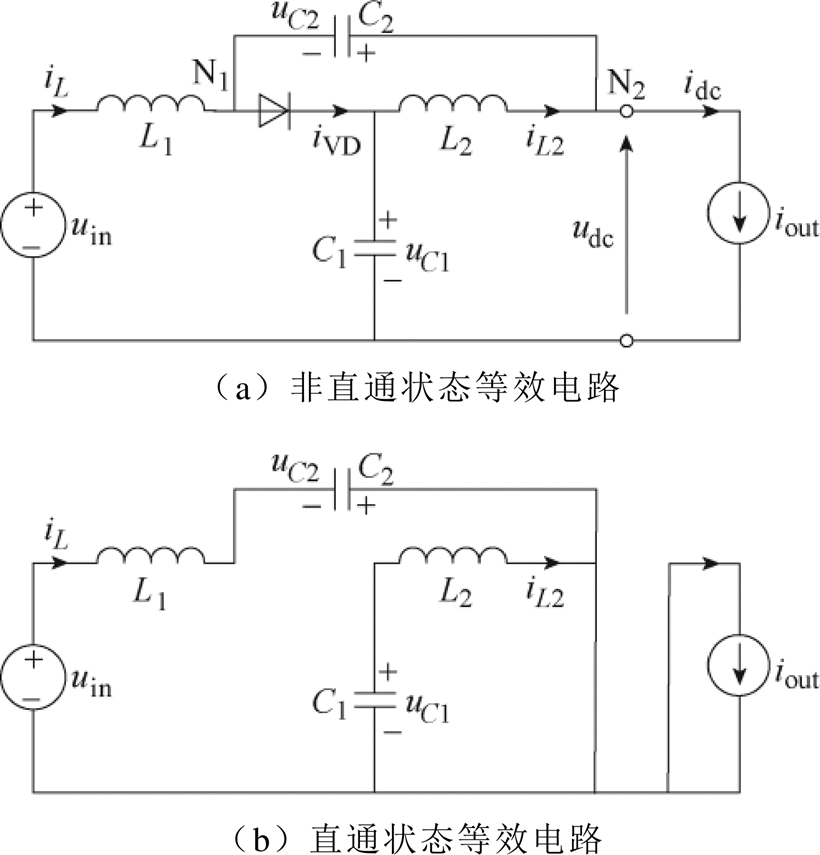
图2 准Z源逆变器的等效电路
Fig.2 Equivalent circuit of quasi Z-source inverter
如图2b所示,当准Z源逆变器处于直通状态时,二极管反向截止,三相逆变器的桥臂被短路。准Z源网络和负载分别通过短路的桥臂形成各自的回路。电容C1所在回路的电压方程可表示为
 (2)
(2)
由于电感L1和L2的取值相同,则流过它们的电流iL和iL2相等,因此式(2)中的iL2可被iL所取代。
根据式(1)和式(2),非直通状态下直流链电压udc为
 (3)
(3)
式中,uL为电感的端电压;dsh为直通占空比。
在准Z源网络中,二极管的电流因电感放电而下降。若电感储能不足,二极管电流会降为0。此时,准Z源逆变器的等效电路发生变化使其工作在非正常状态。
根据式(1),电感电流在非直通状态期间满足
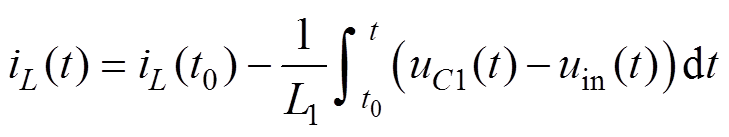 (4)
(4)
式中,iL(t0)为电感电流在非直通状态的初始值。
在图2a中,按照基尔霍夫电流定律,流过节点N1和N2的电流构成两个等式:二极管电流iVD等于流过电感L1和电容C2的电流之和;电感L1的电流等于直流侧电流idc与电容C2的电流之和。由此可以推出二极管电流为
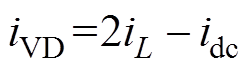 (5)
(5)
式中,idc与逆变器的三相输出电流有关,其周期远大于开关周期。因此,idc在一个开关周期内几乎不变,而二极管电流则会明显减小。将式(4)代入到式(5)得到
 (6)
(6)
式(6)中的二极管电流在整个非直通状态期间必须大于0,否则二极管电流断续将改变准Z源逆变器的等效电路,使其工作在非正常状态。图3给出了准Z源逆变器在非正常状态下的等效电路,它与直通状态的等效电路非常相似,区别在于逆变器的上下桥臂没有直通,所以直流链电压并没有变为零,逆变器的交直流侧依然存在电流回路。根据准Z源逆变器对称性,uL1=uL2=uL, iL1=iL2=iL,图3中的电容C1、电感L2和负载构成了一个新的回路,直流链电压为
 (7)
(7)
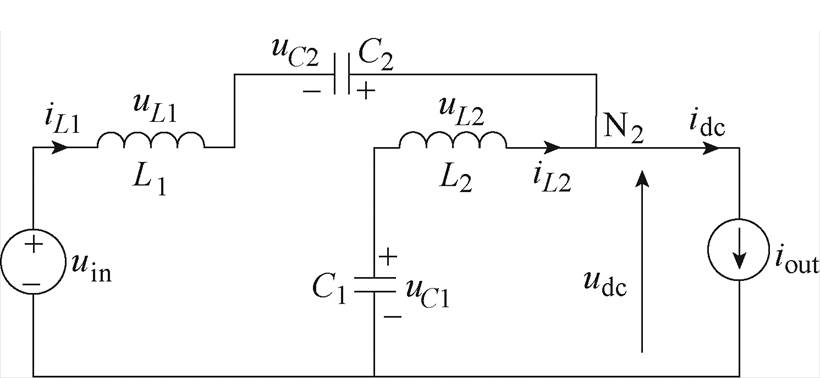
图3 准Z源逆变器在非正常状态下的等效电路
Fig.3 Equivalent circuit of quasi Z-source inverter in abnormal state
直流源、电感L1、电容C2和负载构成了一个回路。电感L1和L2的电流流过节点N2后合并为电流idc,因此idc为
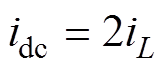 (8)
(8)
准Z源逆变器处于非正常状态时,电感电流在一个开关周期内几乎不变,因此电感电压为零。这将导致直流链电压在二极管电流连续时高于其正常值,而在二极管电流断续时发生跌落。其中,直流链电压高于正常值的现象会增加逆变器过电压损坏的风险。本节引入电压跌落深度地描述二极管电流断续的时间,在此基础上重新定义了直通占空比来计算直流链电压,具体分析如下。
1.3.1 二极管电流连续时的直流链电压
为了便于分析准Z源逆变器在非正常状态下的直流链电压,图4给出了正常工作和发生电压跌落时的二极管电流、直流链电压和电感电流的波形。
图4a中,二极管电流在整个开关周期都是连续的;图4b中,二极管电流在t1~t2和t3~t4期间连续,在t2~t3期间发生断续。首先研究二极管电流在t1~t2和t3~t4期间连续时的直流链电压变化情况。根据式(8),在t2~t3期间,电感电流等于直流侧电流的一半并且不发生变化。因此,电感既不充电也不放电,t2~t3这段时间既不属于直通状态也不属于非直通状态。非直通状态的时间由原来的时长t1~t4减小为t1~t2与t3~t4之和,因此直通占空比将变为

图4 准Z源逆变器的二极管电流、直流链电压和电感电流的波形
Fig.4 Waveforms of diode current, DC-link voltage, and inductor current of quasi Z-source inverter
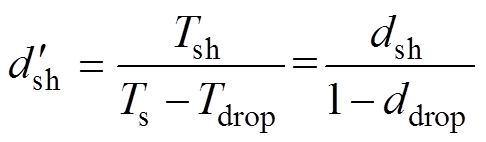 (9)
(9)
式中,Ts为开关周期; 为在非正常状态下的直通占空比;Tdrop和ddrop分别为直流链电压在t2~t3跌落的时间和它在开关周期的占空比。ddrop也称为电压跌落深度,表示了二极管电流断续的时间,用于衡量直流链电压跌落的程度。电压跌落深度越深,直流链电压跌落的程度越严重。由
为在非正常状态下的直通占空比;Tdrop和ddrop分别为直流链电压在t2~t3跌落的时间和它在开关周期的占空比。ddrop也称为电压跌落深度,表示了二极管电流断续的时间,用于衡量直流链电压跌落的程度。电压跌落深度越深,直流链电压跌落的程度越严重。由 可导出二极管电流在t1~t2和t3~t4期间连续时的直流链电压
可导出二极管电流在t1~t2和t3~t4期间连续时的直流链电压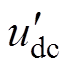 为
为
 (10)
(10)
对比式(3)和式(10)可知,准Z源逆变器处于非正常状态时的直通占空比将增加。因此,图4b中,t1~t2和t3~t4期间的直流链电压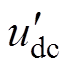 高于图4a中t1~t4期间的直流链电压udc。
高于图4a中t1~t4期间的直流链电压udc。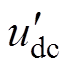 和udc的关系可表示为
和udc的关系可表示为
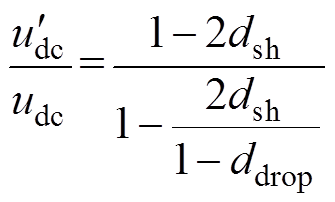 (11)
(11)
利用式(11)可以衡量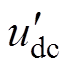 较udc上升的幅度,非正常状态下直流链电压上升的幅度如图5所示。可以看出,随着电压跌落深度ddrop的增加,直流链电压
较udc上升的幅度,非正常状态下直流链电压上升的幅度如图5所示。可以看出,随着电压跌落深度ddrop的增加,直流链电压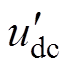 变得越来越大。当ddrop=0.5且dsh=0.2时,
变得越来越大。当ddrop=0.5且dsh=0.2时,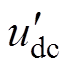 是直流链电压正常值udc的3倍。当ddrop=0.35且dsh=0.3时,
是直流链电压正常值udc的3倍。当ddrop=0.35且dsh=0.3时,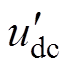 =5udc。这说明,如果准Z源逆变器处于非正常状态,直流链电压的幅值不可控并且远高于其正常值。逆变器过电压易烧毁开关器件,导致逆变器的安全可靠性下降。
=5udc。这说明,如果准Z源逆变器处于非正常状态,直流链电压的幅值不可控并且远高于其正常值。逆变器过电压易烧毁开关器件,导致逆变器的安全可靠性下降。
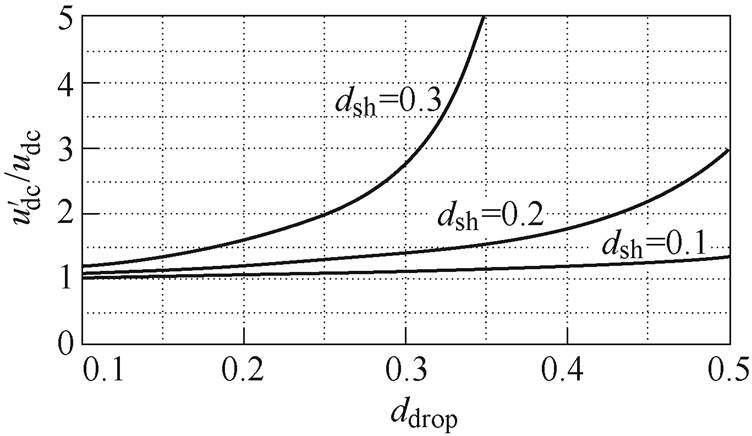
图5 非正常状态下直流链电压上升的幅度
Fig.5 Rising amplitude of DC-link voltage under abnormal state
1.3.2 二极管电流断续时的直流链电压
由于二极管电流断续期间直流侧电流几乎不变,电感电流将保持恒定值。这会导致电感电压降为零,直流链电压发生跌落。如图4b所示,直流链电压不仅在二极管电流连续(t1~t2和t3~t4)时会高于正常值,而且在二极管电流断续(t2~t3)时还发生了跌落。由于t2~t3期间电感电压降为零,直流链电压产生了一个幅值等于电感电压的压降。直流链电压跌落幅值udrop为
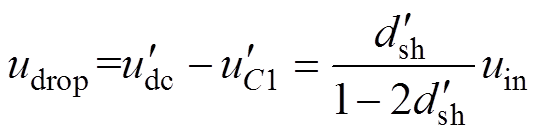 (12)
(12)
式中,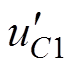 为非正常状态下电容C1的电压。直流链电压跌落的百分比为
为非正常状态下电容C1的电压。直流链电压跌落的百分比为
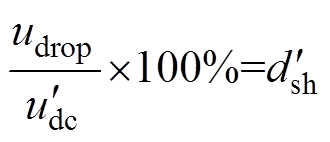 (13)
(13)
根据式(13),可以用图6描述直流链电压跌落的幅度。当直通占空比取0.1、0.2和0.3时,直流链电压分别跌落了11%~21%、22%~40%、33%~60%。
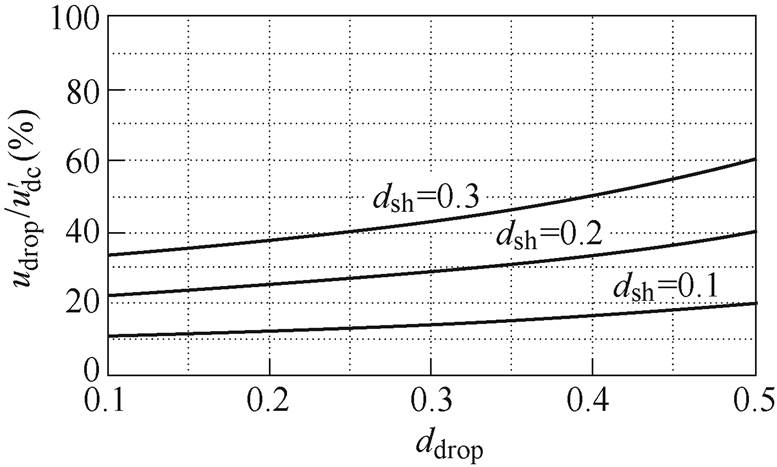
图6 直流链电压跌落的幅度
Fig.6 Amplitude of DC-link voltage sag
通过以上分析可知,二极管电流连续时直流链电压高于正常值,二极管电流断续时直流链电压发生跌落,低于正常值。一方面,过高的直流链电压会给逆变器的安全性带来极大的隐患;另一方面,不恒定的直流链电压导致逆变器的输出电压畸变,影响了负载的正常工作。例如,当准Z源逆变器的负载为交流电机时,直流链电压跌落使逆变器输出电压和频率之比不恒定,产生了较大的转矩脉动和转速波动;当准Z逆变器应用于光伏并网发电系统时,直流链电压跌落将降低最大功率点跟踪控制的性能。
已有文献在分析直流链电压跌落问题时得出一个定性的结论:二极管电流断续是造成直流链电压跌落的原因。然而,二极管电流受到诸多因素的影响,如电路参数、控制方法、逆变器工作状态等。目前,关于这方面的研究还不够深入,仅有少量文献从准Z源网络的电感和负载功率因素两方面分析了它们对二极管电流造成的影响,因此还没有一种能够准确判断直流链电压跌落的方法。本节深入研究了造成二极管电流断续的各个因素,利用综合分析法将它们分类归总,进而提出判断直流链电压跌落的方法。然后,基于系统协调控制的思想提出了直流链电压跌落抑制方法。
由于二极管电流的状态是判断直流链电压是否发生跌落的最直接依据,本文从影响二极管电流的因素出发,从多个视角综合分析了准Z源逆变器的电路参数设计、调制方法及其参数、工作状态在时域的变化情况。从中总结归纳出主要影响因素,提出了一种判断直流链电压跌落的方法。该方法能够快速准确地计算出二极管电流并判断直流链电压处于跌落、临界跌落还是安全区域。
根据式(5)可知,二极管电流等于电感电流和直流侧电流之差。其中,电感电流是周期性变化的直流量,可用电感电流平均值和电感电流脉动表示。因此,式(5)可以进一步表示为
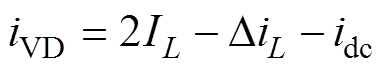 (14)
(14)
式中,IL为电感电流平均值;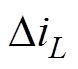 为电感电流脉动。通过分析式(14),进一步细化并系统地归类影响二极管电流的因素,从而找到判断直流链电压跌落的方法。
为电感电流脉动。通过分析式(14),进一步细化并系统地归类影响二极管电流的因素,从而找到判断直流链电压跌落的方法。
2.1.1 平均电感电流
准Z源逆变器的电感L1与电源直接相连,电感电流即为电源输出电流。根据直流源的电压和电感电流可以计算出准Z源逆变器的输入功率,再由逆变器的输入输出功率守恒可导出电感电流平均值IL表达式为
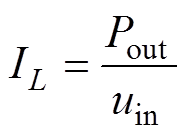 (15)
(15)
式中,Pout为逆变器的输出功率。由式(15)可知,逆变器的输出功率和输入电压是影响电感电流平均值的两个因素。
2.1.2 电感电流脉动
在直通和非直通状态交替作用下,对准Z源网络的电感进行周期性的充放电,产生电感电流脉动。一方面,根据式(1)和式(2)可知,电感电流脉动与电感量有关,电感量越大,电感电流脉动越小;另一方面,采用的调制策略决定了直通矢量和非直通矢量在开关周期的相对位置,进而影响电感电流的充放电规律,造成了不同的电感电流脉动。因此,通过研究调制策略中直通矢量的插入方式,可以计算出电感电流脉动。在表1中列出了常用的调制策略的电感电流脉动。
表1 常用调制策略的电感电流脉动
Tab.1 Inductor current ripples of common modulation strategies

调制策略电感电流脉动 ZSVM6 ZSVM2DiZSVM2=6km ZSVM1DiZSVM1=6k(1+m) ZSVMD6DiZSVMD6= ZSVMD1DiZSVMD1=6k(1-dsh)
本节以常用的调制策略ZSVM1、ZSVM2、ZSVM6、ZSVMD1、ZSVMD6[13]为研究对象,在表1中,k=uindshTs/[12L1(1-2dsh)]。电感电流脉动与调制度m、直通占空比dsh、输入电压uin、开关周期Ts、电感L1直接相关,更重要的是它很大程度取决于调制方法。
2.1.3 直流侧电流
直流侧电流经过逆变器流入三相负载,因此通过分析三相电流的变化规律可得到直流侧电流。以第一扇区的输出电流为例,设ia、ib和ic是三相输出电流。当ib<0且有效矢量V1(开关状态为100101)被应用时,开关S1、S2和S6均开通,idc经S1流入S2和S6,满足idc=ia=ib+ic;当V1切换为V2(开关状态为101001)时,开关S1、S2和S3开通,ib从S1流入B相上桥臂的续流二极管,而idc由S1流入S2,满足idc=ic=ia-ib。随着ib幅值的减小,ib将大于0。此时,当矢量V1作用时,ib从S2流入B相下桥臂的续流二极管,而idc从S1流入S2,满足idc=ia=ic-ib。当矢量V2作用时,idc从S1和S3流入S2,因此idc=ic=ia+ib。以上分析可得出idc为
 (16)
(16)
式中,w t为A相电流的相位。在式(16)中,直流侧电流idc是个分段函数;ia和ic可根据直流链电压和负载计算得到。根据坐标变换可知,ua 与A相电压具有相同的相位q。因为A相电流滞后于A相电压一个功率因数角a,则q 与w t的关系可表示为
 (17)
(17)
将式(17)代入到式(16)中,得
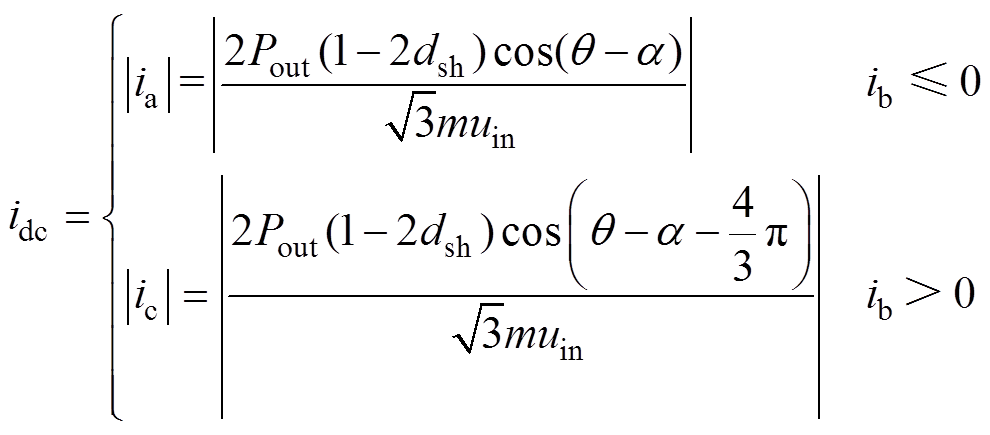 (18)
(18)
式中,与idc直接相关的量分别为调制度m、直通占空比dsh、输入电压uin、输出功率Pout和功率因数角a。
二极管在充放电过程中需要特别关注电流最小值。一方面,只要二极管电流的最小值大于零,直流链电压就不会跌落;另一方面,二极管电流的最小值越大说明了抑制直流链电压的跌落能力越强。由于不同调制方法的二极管电流略有差异,这里以ZSVM1策略为例,提出了判断直流链电压跌落的方法。
将式(15)的电感电流平均值、表1中的ZSVM1电感电流脉动和式(18)的直流侧电流代入到二极管电流的表达式(14)中,可以推导出ZSVM1的二极管电流iVD1为
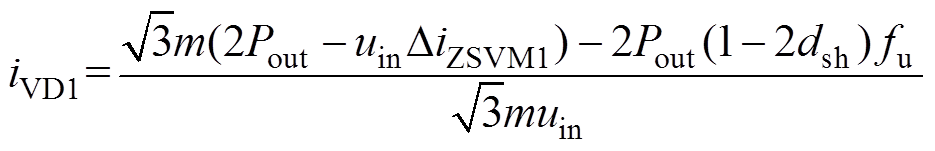 (19)
(19)
其中
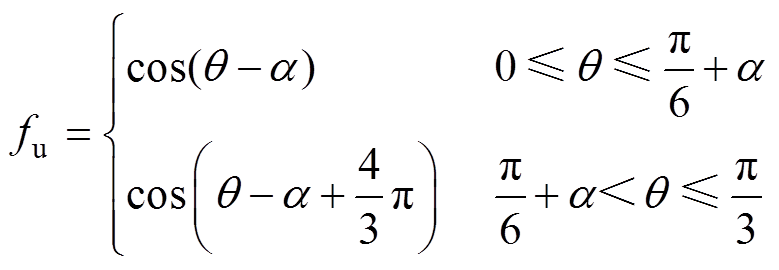
由式(19)可知,二极管电流是一个与电感L1、功率因数角、调制度、直通占空比、输入电压、调制方法、开关周期以及输出功率相关的量,因此可将二极管电流进一步表示为
 (20)
(20)
式中,电感L1为准Z源逆变器的电路参数;调制度m、直通占空比dsh、电感电流脉动DiZSVM1、开关周期Ts属于调制方法的参数;输入电压uin、输出功率Pout、功率因数角a为逆变器的工作条件。将这些参数代入式(19)中,如果二极管电流小于等于零,则证明直流链电压在这组参数下会发生跌落。一般情况下,准Z源逆变器工作时仅有输出功率、调制度、直通占空比会频繁地调节变化。因此,为了更加直观地描述如何判断直流链电压跌落,令式(20)中的a、uin、L1、Ts选取本文的实验参数,调制方法采用ZSVM1,将m、dsh、Pout三个变量对直流链电压跌落的影响绘制于图7中。直流链电压跌落的条件如图7所示。
图7a中,准Z源逆变器直通占空比dsh和调制度m分别取0.1~0.3和0.7~0.9。因为直通矢量会占用非直通矢量的作用时间,所以m和dsh之和不能大于1。在此约束条件下,m和dsh的可行域呈等腰三角形。
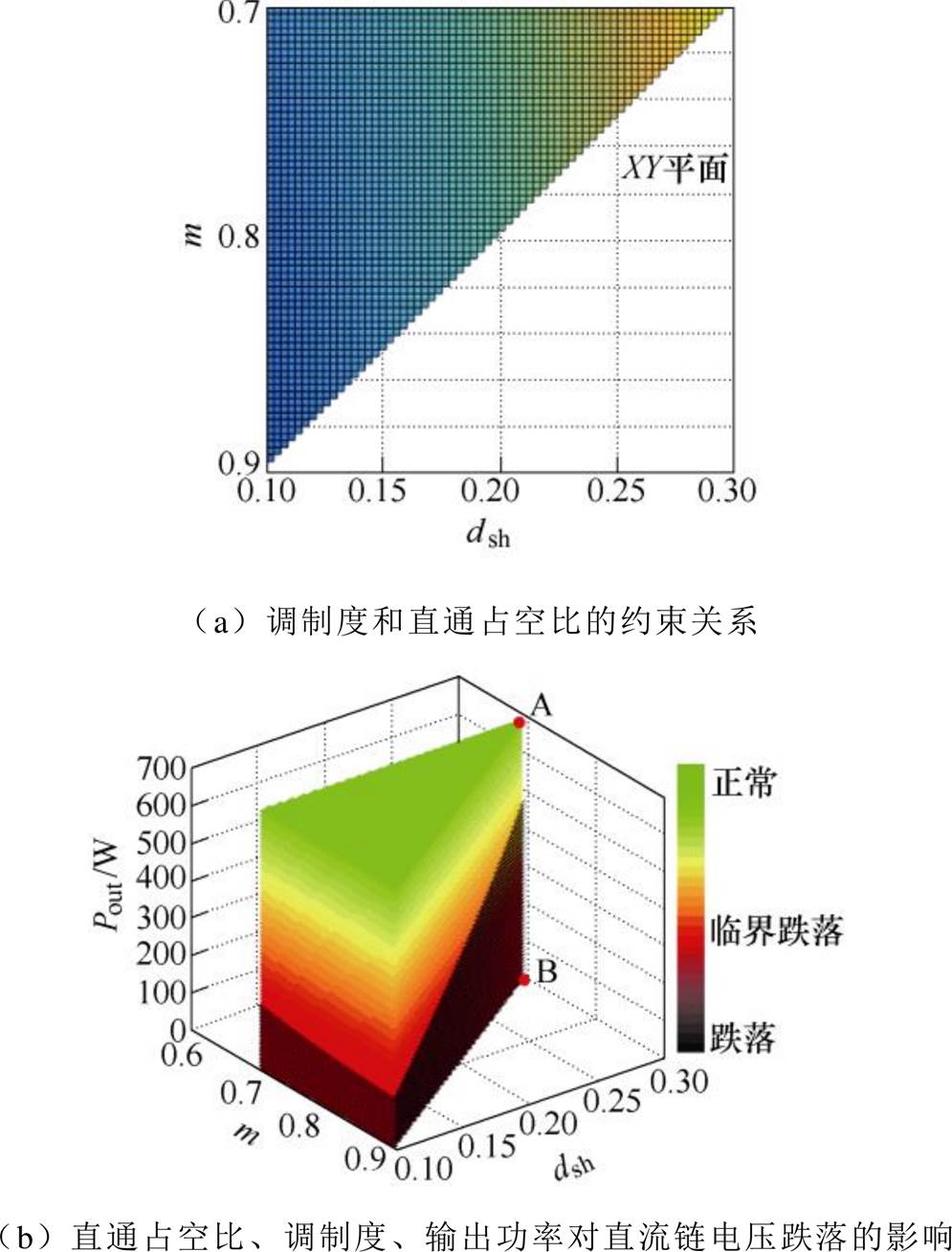
图7 直流链电压跌落的条件
Fig.7 Condition of DC-link voltage sag
图7b中,将m和dsh作为XY平面,Z坐标为输出功率Pout,绘制出了直流链电压跌落的的条件。m、dsh、Pout的取值范围构成了一个三角体,利用式(19)对直流链电压跌落的区域进行划分。从侧面看,沿着黑色部分和红色部分相接的线切割三角体,可以将三角体划分为两个部分。其中,贴近XY平面的黑色部分是直流链电压跌落的区域。如果m、dsh、Pout的取值都落在此区域,直流链电压必然发生跌落。例如,直线AB上的点对应的m=0.7、dsh= 0.3,如果Pout取值小于471W,m、dsh、Pout将落入黑色区域,直流链电压发生跌落。三角体呈红色、黄色、绿色的部分是直流链电压未跌落的区域。红色部分表示临界跌落,即直流链电压有发生跌落的风险;黄色部分是相对安全的区域,直流链电压不易发生跌落;绿色部分是绝对安全区域,表示准Z源逆变器工作正常。
根据图7b对直流链电压跌落区域的划分,得到:①输出功率越低,调制度越低,直通占空比越高,则直流链电压越容易跌落;②直流链电压满足一定条件时就会发生跌落,虽然可以被避免,但无法彻底消除;③准Z源逆变器应工作在功率的下限和上限之间,即无直流链电压跌落的最小输出功率和额定输出功率。
对应于图7,图8给出了输出功率Pout为200W、400W、600W的二极管电流,图中用不同颜色表示二极管电流的大小。在图8a中,当Pout=200W时, m=0.7~0.82和dsh=0.15~0.3所围成的区域表示二极管电流断续区域,如图中黑色曲面。红色和黄色曲面代表了二极管电流连续区域,且二极管的最大电流仅有1.5A左右。图8b给出了Pout=400W的二极管电流,仅在m=0.7且dsh=0.3附近二极管电流有断续。在其他区域的二极管电流处于连续状态,最大值为5.3A。这说明提高输出功率在一定程度上抑制了直流链电压跌落。当Pout=600W时,二极管的电流如图8c所示。可以看出,在m和dsh的整个区域内二极管电流都是连续的,并且二极管电流的最小值为3.7A,证明了该条件下无直流链电压跌落。
文献[12, 15]分别从降低电感电流脉动和改变功率因数的角度抑制直流链电压跌落。但是,从2.2节得到的结论可知,以上文献中的方法只从单一的方面抑制直流链电压跌落,因而不能达到显著的效果。
本文在研究二极管电流断续的问题时,将造成直流链电压跌落的因素归结为三个方面:准Z源逆变器的电路参数、调制方法及其参数和逆变器的工作条件。结合这三方面,本文基于系统协调控制的思想提出了抑制直流链电压跌落的综合方法。换个角度而言,判断直流链电压跌落的方法为抑制直流链电压跌落提供了理论依据。
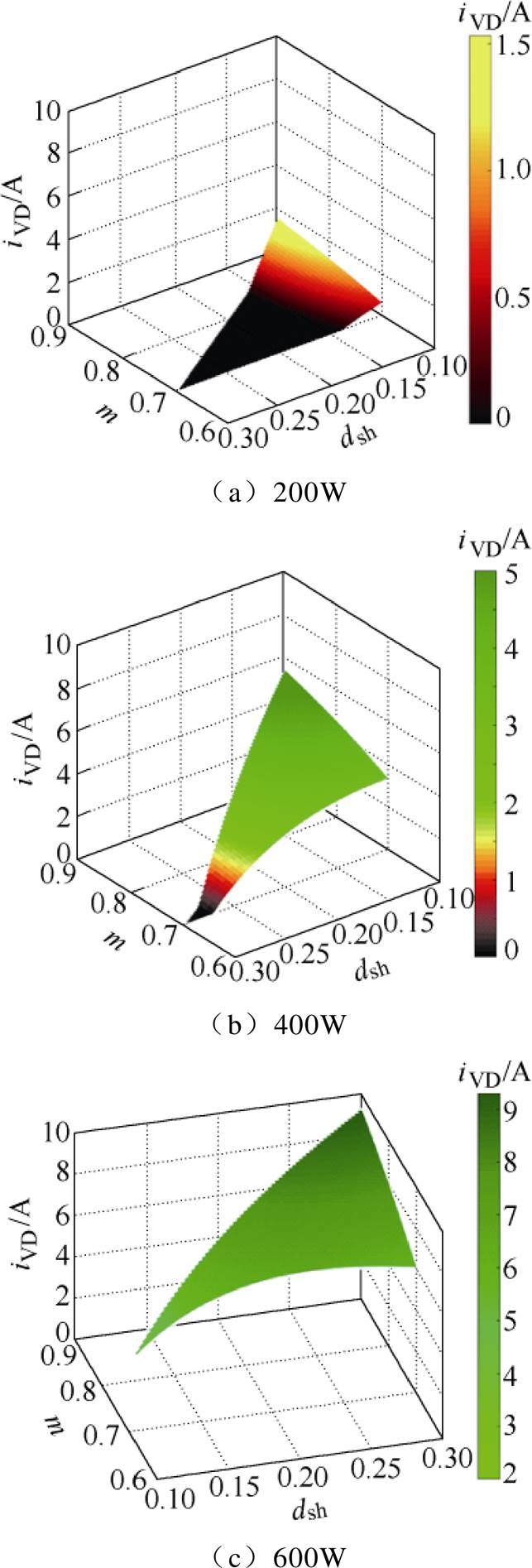
图8 不同输出功率下的二极管电流
Fig.8 Diode current at different output load power
抑制直流链电压跌落综合方法通过合理配置系统参数来有效地增加准Z源网络的二极管电流,从而提高系统抑制直流链电压跌落的能力。该方法可被视为是一种参数优化的方法,其结构框图如图9所示。
(1)根据已知的系统参数及其与直流链电压跌落的关系,列出抑制直流电压跌落的目标函数与约束条件。其中,输出功率P、直流源电压uin、开关周期Ts和功率因数角a 可直接得到。为了使抑制效果最大化,电感电流脉动DiL和电感L1应该取其可行域内的临界值。将这些参数代入式(19)和输出功率的表达式(15)中,得到抑制直流电压跌落的目标函数和约束条件。
(2)由(1)的运算结果可知二极管电流是一个关于调制度m和直通占空比dsh的函数。利用最优化理论能够求出一组具有最佳抑制电压跌落效果的m和dsh。
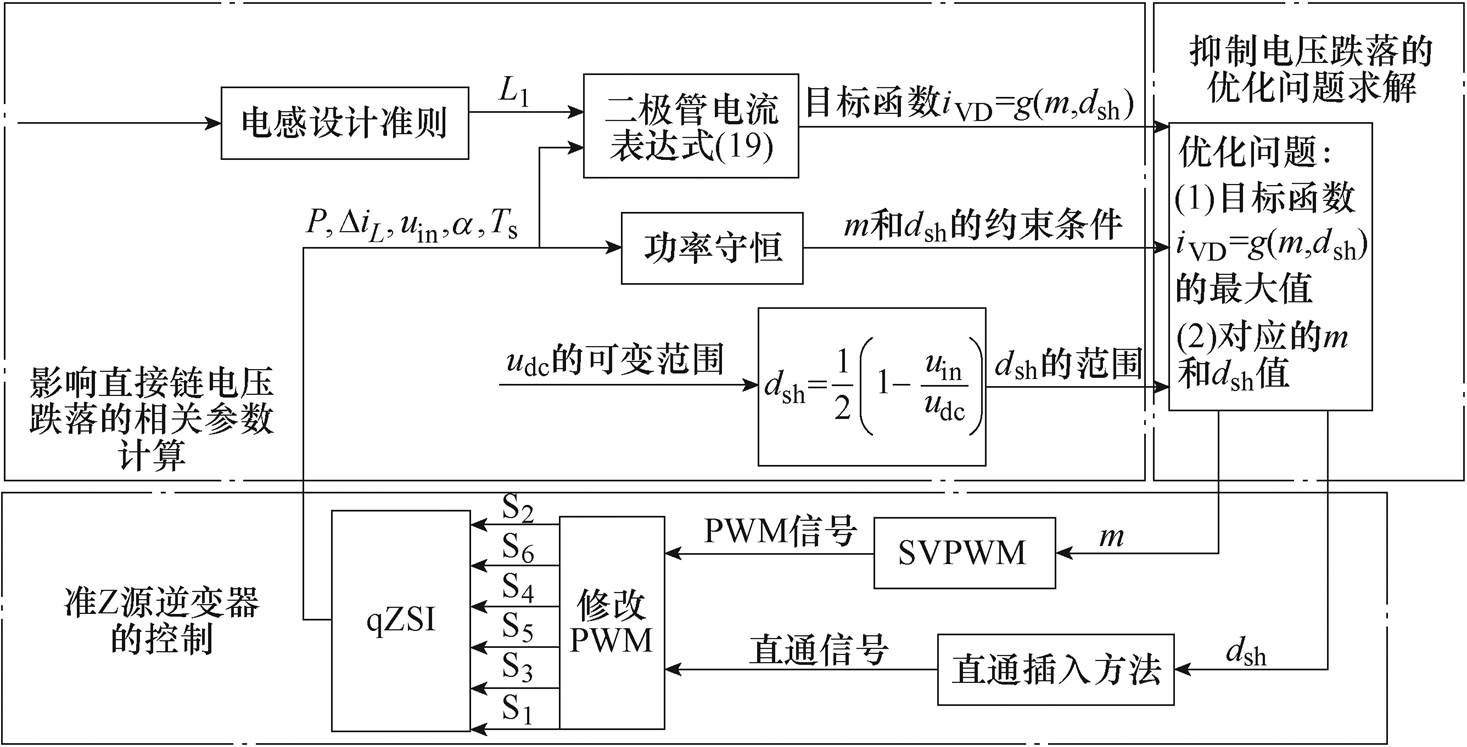
图9 抑制直流链电压跌落综合方法的结构框图
Fig.9 Block diagram of synthesis method for suppressing DC-link voltage sag
(3)根据第(2)步求解出的m和dsh,空间矢量脉冲宽度调制(Space Vector Pulse Width Modulation, SVPWM)算法和直通插入方法分别产生PWM信号和直通信号;然后将直通信号插入到PWM信号中,生成准Z源逆变器的驱动信号。
在满足准Z源逆变器输出性能要求的前提下,本文所提方法可以保证系统具有最强的抑制直流链电压跌落的能力。此外,若需兼顾系统多方面性能,在本文所提方法基础上产生了一种抑制直流链电压跌落的性能均衡方案。抑制直流链电压跌落综合方法的流程如图10所示,根据系统对抑制直流链电压跌落能力的强弱有无要求,可以采用最佳抑制直流链电压跌落方案和系统性能均衡方案。前者的实现流程与图9所对应,后者实现流程则与前者相反,但是各个环节的运算基本相同。在系统性能均衡方案中,根据准Z逆变器输出性能的要求先计算出dsh和m;然后,在二极管电流不小于零的前提下灵活选择电感量和调制方法。该方案为电感的设计和调制方法的选取留出了充分的裕度。例如,当限制准Z源逆变器体积时,直流侧电感L1受限,导致直流链电压跌落抑制效果变差。在这种情况下,采用性能均衡方案来改变调制方法,提高系统抑制电压跌落的能力,从而弥补电感量过小引起的负效应。

图10 抑制直流链电压跌落综合方法的流程
Fig.10 Flow chart of synthesis method for suppressing DC-link voltage sag
为了验证直流链电压跌落判断和抑制方法的正确性,以及利用电压跌落深度计算直流链电压的准确性,搭建了三相电压型准Z源逆变器实验平台进行相关实验研究。在实验中,通过改变调制方法及其参数和逆变器工作条件,观测直流链电压从不跌落到发生跌落的过程。在直流链电压发生跌落以后,根据抑制直流链电压跌落的综合方法来改变调制方法,抑制直流链电压跌落。
由于准Z源逆变器的直流链电压跌落易在低输出功率和低电压时发生,实验中的输出功率范围取85~270W,直流源电压为50V。其余实验参数:L1=L2=500mH、C1=C2=560mF,Ts=200ms,阻感负载的功率因数角a =p/10。三相电压型准Z源逆变器实验平台如图11所示,实验平台主要由隔离变压器、调压器、整流桥、准Z源网络、三相电压型逆变器构成。微控制器采用TI公司的数字信号处理器,型号为TMS320F28335。驱动电路驱动用于驱动主电路的开关器件MOSFET。

图11 三相电压型准Z源逆变器实验平台
Fig.11 Experimental platform of three-phase voltage source quasi Z-source inverter
当直流源电压、电感L1、功率因数角、控制周期确定以后,影响直流链电压跌落的可变因素只有输出功率、调制度、直通占空比、调制方法。本节的实验验证中采用ZSVM1方法。根据判断直流链电压跌落的方法可知:当调制度为0.8、直通占空比为0.2时,直流链电压发生跌落的临界输出功率为261W。这表明当输出功率大于261W时,直流链电压不会跌落。因此,分别取输出功率270W和138W观测准Z源逆变器的工作状态,实验结果如图12和图13所示。
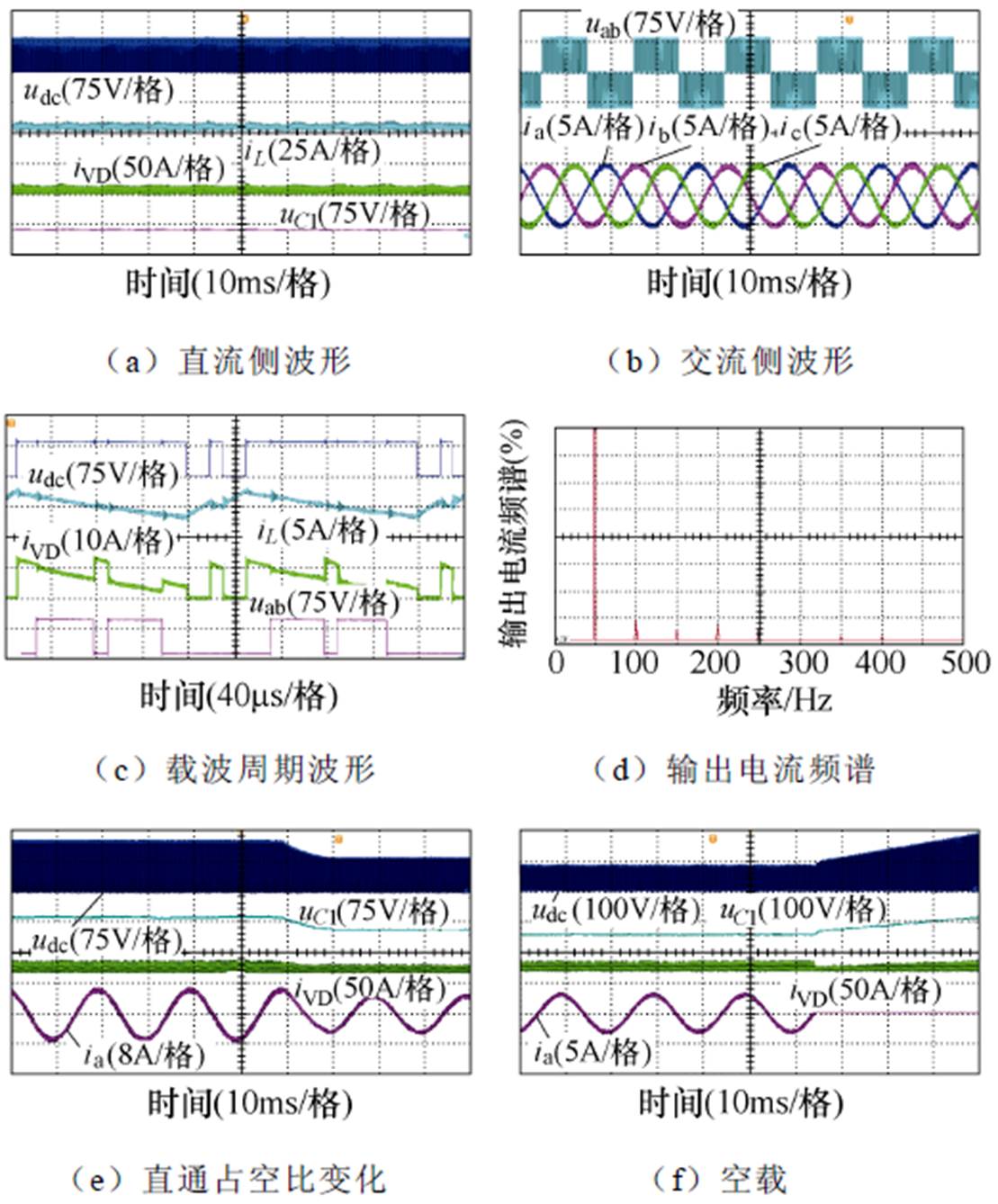
图12 输出功率为270W的实验结果
Fig.12 Experimental results of output power of 270W
在图12a~图12d中,输出功率为270W时的二极管电流一直处于连续状态,直流链电压峰值在直通状态下为0V、非直通状态下为83V,证明了直流链电压没有发生跌落。电容电压、输出电压和输出电流峰值分别为63V、83V和5A,输出电流的各次谐波均小于0.2%,证明了准Z源逆变器的控制性能较好。值得注意的是,二极管电流的最小值仅有1.3A,说明直流链电压有跌落的趋势。

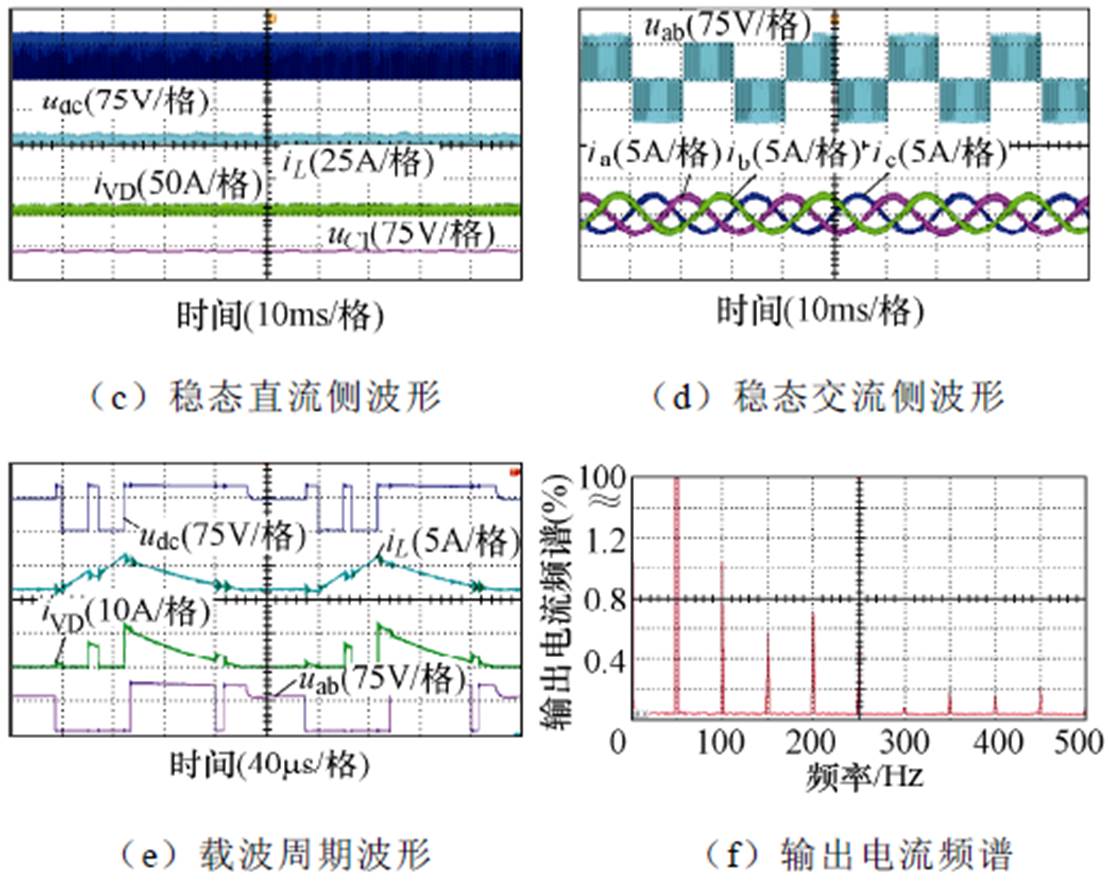
图13 输出功率从270W降为138W的实验结果
Fig.13 Experimental results of output power from 270W to 138W
图12e给出了直通占空比从0.3变为0.2时的动态实验结果。准Z源逆变器经过了12ms完成了过渡过程,直流链电压从125V降为83V,电容电压从88V降为63V,输出电流从6.5A降为5A,整个过程中无电压跌落发生,证明了直流链电压跌落判断方法正确性。图12f给出了空载时的实验结果。由式(19)可知,准Z源逆变器工作空载时必然发生直流链电压跌落,导致直流链电压峰值不断升高,威胁逆变器的安全。因此,本实验中先让准Z源逆变器的输出功率为270W,然后短时间内断开负载,观察准Z源逆变器的状态变化。从图12f中可看出,当负载被断开后,直流链电压和电容电压几乎呈线性规律上升,经过36ms后分别达到了185V和117V,而输出电流则在负载断开后变为零。由于空载会使准Z源逆变器直流链电压跌落程度越来越严重,在实际操作中应当避免空载情况的发生。
图13给出了通过改变负载使输出功率从270W降为138W的动态和稳态实验结果。从图13a和图13b中可看出,输出功率的降低导致直流链电压峰值、输出相电压峰值和电容电压升高,直流链电压和输出相电压峰值均从83V增加到97V,电容电压从63V增加到71V,而输出电流从5A降低3A。
在图13c~图13f中,输出功率为138W时的二极管电流在非直通状态结束之前已经断续,持续时间为45ms。在二极管电流断续期间,直流链电压为97V;而在二极管电流连续期间,直流链电压从97V下降到73V,跌落了24V。直流链电压的暂升和暂降导致准Z源逆变器的输出性能急剧下降。输出电压uab和三相输出电流发生畸变,输出电流的2、3、4和5次谐波分别增加到了1%、0.52%、0.64%和0.44%。这组实验证明了直流链电压跌落判断方法的正确性和预判的准确性。
当直通占空比保持0.2不变,而调制度由0.8降低为0.6时,输出功率将由138W降低为85W,此时根据直流链电压跌落判断方法可预判直流链电压将发生严重的跌落。在此条件下进行实验,实验结果如图14所示。利用电压跌落深度定义推算直流链电压在跌落期间的幅值变化,并与实验结果对比。
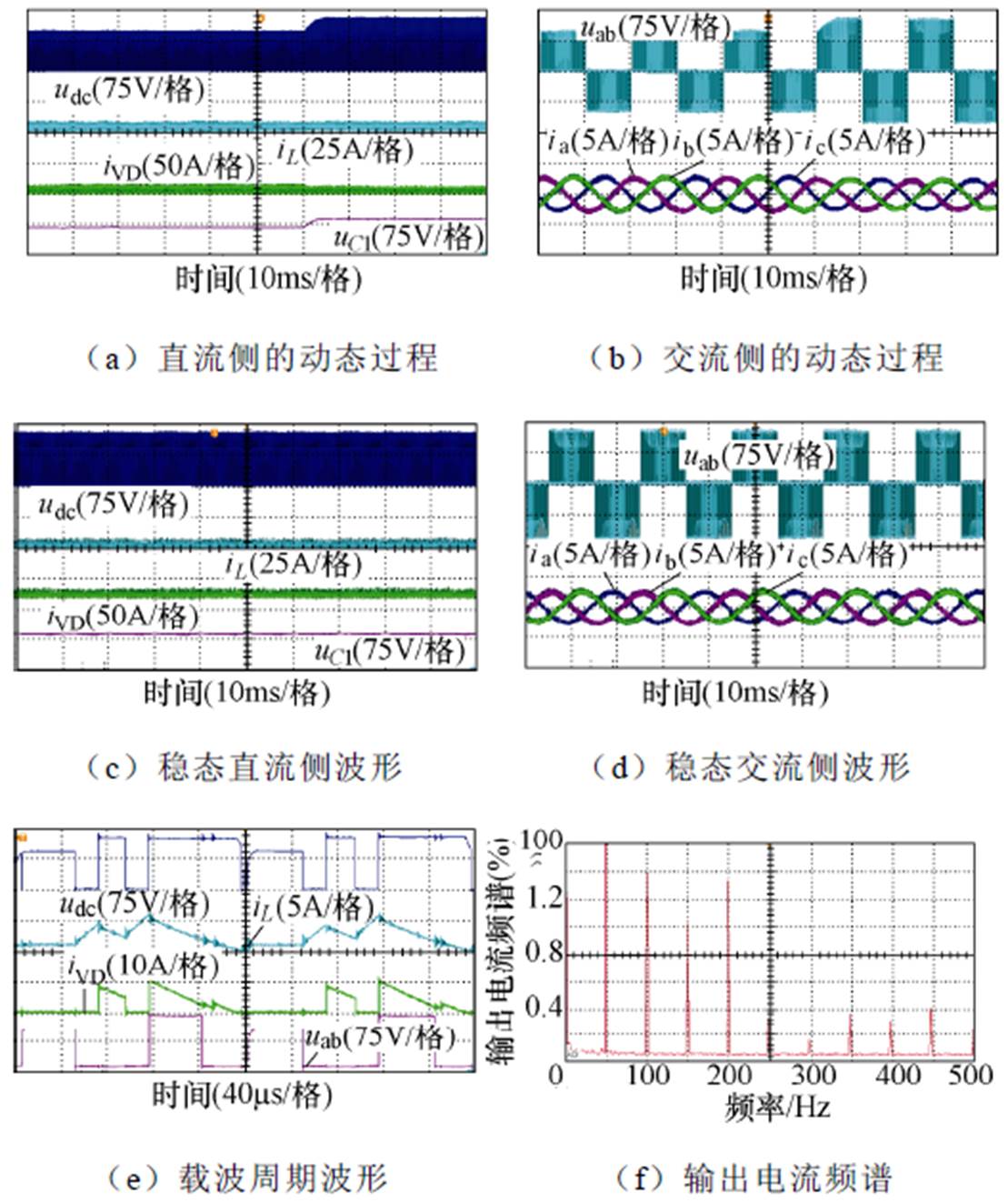
图14 输出功率从138W降为85W的实验结果
Fig.14 Experimental results of output power from 138W to 85W
图14给出了通过改变调制度使输出功率从138W降为85W的实验结果。从图14a和图14b中可看出,输出功率的降低导致直流链电压峰值、输出相电压峰值和电容电压进一步升高,直流链电压和输出相电压峰值均从97V增加到130V,电容电压从71V增加到90V,而输出电流从3A降低2.5A。
在图14c~图14f中,输出功率为85W时的二极管电流断续时间长达75ms,约占非直通状态时间的一半,导致了直流链电压波形畸变严重。在二极管电流断续期间,直流链电压升高到130V;而在二极管电流连续期间,直流链电压从130V下降到89V,跌落了41V。同时,直流链电压跌落导致了输出电压波形畸变,输出电流的2、3、4和5次谐波分别增加到1.52%、1%、1.28%和0.88%。
由二极管电流的断续时间可知,电压跌落深度为0.375。利用式(10)和式(12)计算出的直流链电压峰值为137V,跌落幅值为43V。理论计算与实验结果基本一致,证明了本文提出的电压跌落深度的正确性。
根据直流链电压跌落抑制方法的原理,改变准Z源逆变器的电路参数、调制方法及其参数、逆变器的工作条件可使准Z源逆变器工作在非跌落区域。因此,在3.2节的实验条件下,可将调制方法ZSVM1换为具有更小电感电流脉动的ZSVMD1,提高抑制电压跌落的能力,实验结果如图15所示。
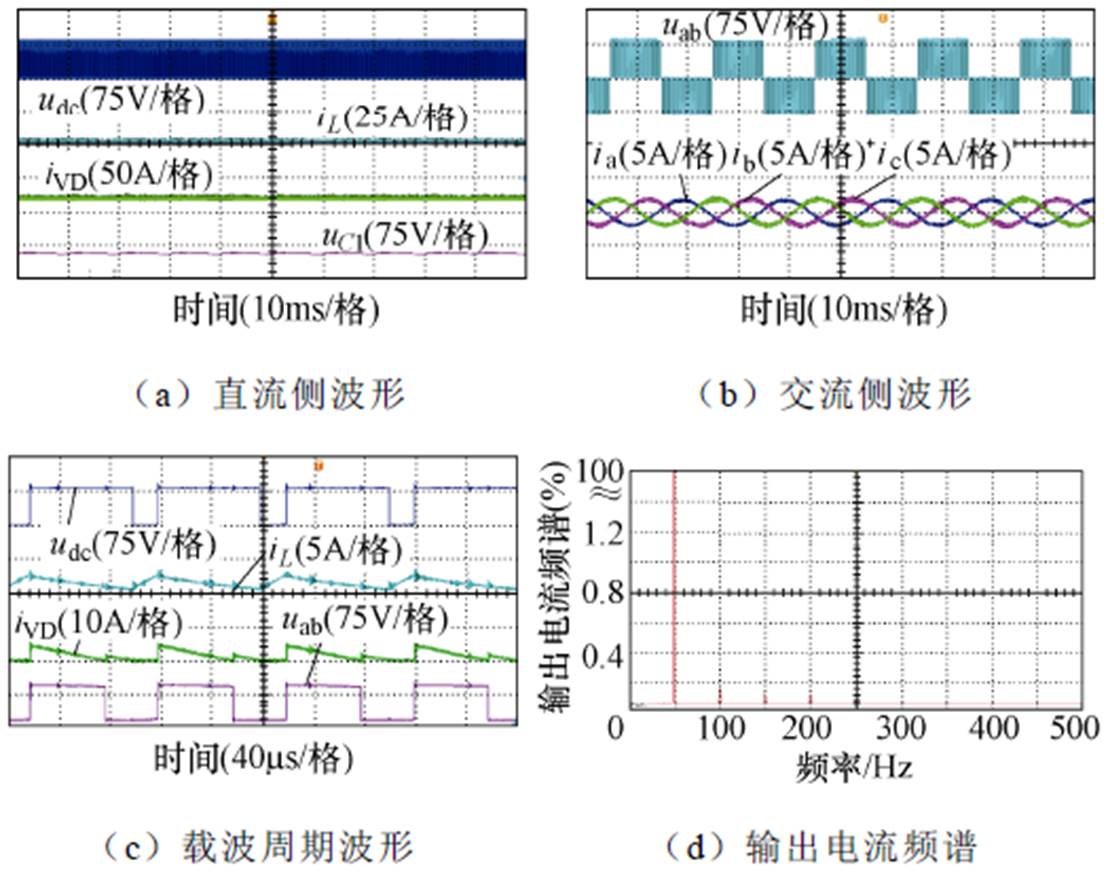
图15 抑制直流链电压跌落的实验结果
Fig.15 Experimental results of suppressing DC-link voltage sag
在图15中,准Z源逆变器的直流链电压、电容电压、输出电压和输出电流峰值分别为83V、63V、83V和2A。虽然二极管电流的最小值接近于0,但是始终是连续的。可以看出,在相同的实验条件下,替换调制方法可实现二极管电流由断续变为连续,有效地抑制了直流链电压跌落,证明了本文提出方法的正确性和有效性。
本文深入研究了准Z源逆变器直流链电压跌落问题及其解决方案,主要工作和结论如下:
1)提出了电压跌落深度的定义,研究了二极管电流连续和断续期间的直流链电压变化规律,分析了直流链电压变化对准Z源逆变器的危害,完善了直流链电压跌落的基础理论。
2)提出了一种直流链电压跌落的判断方法。根据造成二极管电流断续的因素,将准Z源逆变器的系统参数和状态划分为跌落、临界跌落和安全区域。该方法可准确地预测直流链电压发生跌落的条件,为准Z源逆变器工作状态预测和直流链电压跌落预防提供了理论依据。
3)提出了一种直流链电压跌落抑制方法。以二极管电流为控制目标,以电路参数、调制方法及其参数、逆变器工作条件为约束条件,利用系统协调控制的思想调整准Z源逆变器的系统参数和状态,使其进入安全工作区域,避免了直流链电压跌落的发生,提高了准Z源逆变器的安全可靠性。
参考文献
[1] Zhao Nan, Liu Jiangqiang, Ai Yu, et al. Power-linked predictive control strategy for power electronic traction transformer[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 6559-6571.
[2] Elsaharty M A, Luna A, Candela J I, et al. A unified power flow controller using a power electronics integrated transformer[J]. IEEE Transactions on Power Delivery, 2019, 34(3): 828-839.
[3] 李晓华, 赵容健, 田晓彤, 等. 逆变器供电对电动汽车内置式永磁同步电机振动噪声特性影响研究[J]. 电工技术学报, 2020, 35(21): 4455-4464.
Li Xiaohua, Zhao Rongjian, Tian Xiaotong, et al. Study on vibration and noise characteristics of interior permanent magnet synchronous machine for electric vehicles by inverter[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4455-4464.
[4] Ellabban O, Abu-Rub H. Z-source inverter: topology improvements review[J]. IEEE Industrial Electronics Magzine, 2016, 10(1): 6-24.
[5] Ho A V, Chun T, Kim H G. Extended Boost active switched capacitor/switched inductor quasi Z-source inverters[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5681-5690.
[6] 张千帆, 董帅, 周超伟, 等. Z源逆变器直通电流回路及功率开关管电流应力分析[J]. 电工技术学报, 2016, 31(4): 123-128.
Zhang Qianfan, Dong Shuai, Zhou Chaowei, et al. Analysis of circuit path and current stress of power devices under shoot-through mode in Z-source inverter[J]. Transactions of China Electrotechnical Society, 2016, 31(4): 123-128.
[7] Siwakoti Y P, Peng Fangzheng, Blaabjerg, et al. Impedance-source networks for electric power conversion part II: review of control and modulation techniques[J]. IEEE Transactions on Power Electro- nics, 2015, 30(2): 1887-1906.
[8] 程启明, 江畅, 沈磊, 等. 准Z源三电平并网逆变器的无源控制策略[J]. 电工技术学报, 2020, 35(20): 4361-4372.
Cheng Qiming, Jiang Chang, Shen Lei, et al. Passivity based control strategy of quasi Z-source three-level grid-connected inverter[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4361-4372.
[9] 张峰, 谢运祥, 胡炎申, 等. 临界模式混合光伏微型逆变器的特性分析[J]. 电工技术学报, 2020, 35(6): 1290-1302.
Zhang Feng, Xie Yunxiang, Hu Yanshen, et al. Characteristics analysis for a boundary conduction mode hybrid-type photovoltaic micro-inverter[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1290-1302.
[10] 朱泓晖, 屈艾文, 周扬忠. 基于储能型准Z源光伏并网逆变器的改进型自适应粒子群最大功率点跟踪算法研究[J]. 电气技术, 2021, 22(3): 6-13.
Zhu Honghui, Qu Aiwen, Zhou Yangzhong. Research on improved adaptive particle swarm optimization maximum power point tracking algorithm based on energy stored quasi Z-source photovoltaic grid connected inverter[J]. Electrical Engineering, 2021, 22(3): 6-13.
[11] 蔡春伟, 曲延滨, 盛况. 准Z源逆变器的暂态建模与分析[J]. 电机与控制学报, 2011, 15(10): 7-13.
Cai Chunwei, Qu Yanbin, Sheng Kuang. Transient modeling and analysis of quasi Z-source inverter[J]. Electric Machines and Control, 2011, 15(10): 7-13.
[12] 贺昱曜, 张柳明扬, 陈金平. 抑制Z-源逆变器母线电压跌落的空间矢量脉宽调制方法[J]. 电工技术学报, 2017, 32(2): 228-237.
He Yuyao, Zhang Liumingyang, Chen Jinping. Voltage drop suppression of Z-source inverter ssing space vector PWM method[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 228-237.
[13] He Yuyao, Xu Yuhao, Chen Jinping. New space vector modulation strategies to reduce inductor current ripple of Z-source inverter[J]. IEEE Transa- ctions on Power Electronic, 2018, 33(3): 2643- 2654.
[14] 高奇, 钱照明, 顾斌, 等. 阻抗型逆变器的一种非正常工作状态分析[J]. 电工技术学报, 2005, 20(8): 55-58.
Gao Qi, Qian Zhaoming, Gu Bin, et al. An abnormal operating state analysis of Z-source inverter[J]. Transactions of China Electrotechnical Society, 2005, 20(8): 55-58.
[15] Chauhan A K, Raghuram M, Singh S K. Nonzero discontinuous inductor current mode in certain Z-source converters[J]. IEEE Transactions on Power Electronic, 2018, 33(4): 2809-2814.
[16] Pashaei R, Babaei E, Cecati C, et al. Analysis of Z-source based DC/DC converter in CCM, DCM and BCM operations[C]//International Conference on Electrical Engineering/Electronics, Computer, Telecom- munications and Information Technology, ECTI-CON, Phuket, Thailand, 2017: 777-780.
[17] Kayiranga T, Li Hongbo, Lin Xinchun, et al. Abnormal operation State analysis and control of asymmetric impedance network-based quasi Z-source PV inverter[J]. IEEE Transactions on Industrial Electronics, 2016, 31(11): 7642-7650.
[18] 董帅, 张千帆, 王睿, 等. SVPWM控制时双向Z源逆变器电容电压纹波分析[J]. 电工技术学报, 2017, 32(24): 107-114.
Dong Shuai, Zhang Qianfan, Wang Rui, et al. Analysis of capacitor voltage ripple for bi-directional Z-source inverters based on SVPWM[J]. Transactions of China Electrotechnical Society, 2017, 32(24): 107- 114.
[19] 董帅, 张千帆, 王睿, 等. Z源逆变器关键技术发展综述[J]. 电气工程学报, 2016, 11(3): 1-12.
Dong Shuai, Zhang Qianfan, Wang Rui, et al. Development of the Z-source inverters and its key technologies: a review[J]. Journal of Electrical Engineering, 2016, 11(3): 1-12.
Judgment and Suppression Methods for DC-Link Voltage Sag of Quasi Z-Source Inverter
Abstract The quasi Z-source inverter is a special boost converter with ability of short-circuiting the bridge arm in the same phase. It has a wide application prospect in new energy electric vehicles and distributed generation systems, such as photovoltaic and wind power systems. However, there is a potential problem when the DC-link voltage is boosted, i.e., the inductoron the dc-side of inverter with insufficient energy storage will make the diode current discontinuous. This will lead to DC-link voltage sag, a phenomenon that seriously reduces the output performance and safety and reliability of the quasi Z-source inverter. To solve this problem, the definition of voltage sag depth is firstly proposed to calculate and measure the rise and fall amplitude of DC-link voltage. Secondly, based on the comprehensive analysis of the factors causing the diode current interruption, a method for judging DC-link voltage sag is proposed. It can be used to predict whether DC-link voltage drops or not according to the system parameters and state. Thirdly, to prevent the quasi Z-source inverter from operating in the abnormal state, a method for suppressing DC-link voltage sag is proposed based on the idea of system coordinated control. The results indicate that the proposed method can accurately predict the conditions of DC-link voltage sag and effectively avoidDC-link voltage sag.
keywords:Quasi Z-source inverter, DC-link voltage, voltage sag depth, diode current interruption
DOI: 10.19595/j.cnki.1000-6753.tces.211197
中图分类号:TM13
陕西省科技厅项目(2020JM-632)和陕西省教育厅项目(21JX012, 21JK0704)资助。
收稿日期 2021-08-04
改稿日期 2021-09-15
许宇豪 男,1990年生,讲师,研究方向为Z源逆变器和交流电机的控制。E-mail: xyuh7006@126.com(通信作者)
肖海峰 男,1977年生,教授,硕士生导师,研究方向为永磁同步电机的非线性控制。E-mail: xhf_xhdq@xaau.edu.cn
(编辑 陈 诚)