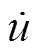和
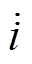分别为逆变器端电压和输出电流；Lf、Cf和Lg分别为滤波电感、滤波电容和线路电感；
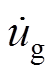为电网电压。摘要 下垂控制型逆变器能够为电网提供电压与频率支撑，其安全稳定运行对电网意义重大。然而，在故障工况下，下垂控制型逆变器面临功角失稳与过电流问题，这严重威胁了下垂控制型逆变器的安全运行。目前的研究往往将功角控制与故障电流控制作为两个独立问题进行解决，鲜有研究兼顾功角控制与故障电流控制对下垂控制型逆变器展开综合调控。基于此，首先，对下垂控制型逆变器暂态特性展开分析，详细阐述电流限幅环节与无功-电压环路对逆变器暂态特性的影响。接着，提出兼顾故障限流与功角稳定性的下垂控制型逆变器暂态控制方法。所提方法综合考虑故障期间电网电压与逆变器端电压的变化，通过对有功-频率环路的优化调控实现功角稳定控制。此外，在功角控制的基础上，改进无功-电压环路控制实现故障电流的有效抑制。最后，通过仿真与实验验证了该文所提方法的有效性。
关键词：下垂控制型逆变器 暂态特性分析 故障限流 暂态控制
随着可再生能源发电的发展，以风电、光伏为代表的分布式电源大量并入电网[1-2]。电力电子变换器作为新能源并网的接口，其安全稳定运行对新能源可靠并网意义重大[3-5]。
现有的逆变器分为电网跟随型[6-7]、电网组建型及电网支撑型[8-11]三大类。下垂控制型逆变器作为一种电网支撑型逆变器，其具备有功-频率与无功-电压下垂特性，能够为系统提供电压频率支撑[12-13]，广泛应用于新能源并网。然而，分布式电源一般分布于故障频发的配电网末端[14-15]或鲁棒性较差的弱电网[16-17]。因此，逆变器的暂、稳态运行稳定性问题成为当前研究热点。
当故障发生时，下垂控制型逆变器的稳定运行受到威胁，主要表现在两个方面：一方面，在故障工况下，下垂控制型逆变器存在与传统同步发电机（Synchronous Generator, SG）类似的暂态同步失稳问题[18-20]；另一方面，下垂控制型逆变器作为一种电力电子装备，其承受大电流能力较差，电网发生故障时，下垂控制型逆变器会出现因过电流而烧毁的问题。然而，随着电力系统中分布式电源渗透率逐渐提升，下垂控制型逆变器被要求具备一定的故障鲁棒性能，在一定情况下可以继续为电网提供必要的电压频率支撑[21]。因此，深入分析下垂控制型逆变器在电网故障下的暂态特性，并研究其在故障下的暂态稳定性能提升方法具有重要意义。
目前，针对下垂控制型逆变器在故障工况下的研究主要包含暂态功角控制与故障电流控制两方面。在暂态功角控制方面，文献[22]对下垂控制型逆变器与SG展开对比分析，结果证明下垂控制型逆变器有功环路的一阶特性使其暂态性能优于SG，但该文在进行暂态分析时忽略了下垂控制型逆变器故障电流的问题。文献[18]以暂态过程存在功率平衡点为控制目标，对下垂控制型逆变器进行调控，实现其在故障过程中的暂态稳定，但在暂态分析过程中忽视了无功环路的影响。文献[23]利用相平面法对四种不同控制类型的电压型逆变器稳定性展开对比分析，为下垂控制型逆变器暂态控制提供指导。在故障电流控制方面，文献[24]采取控制模式切换的方法对逆变器进行控制，在故障期间将逆变器由电压型控制切换为电流型，实现了故障电流的有效调控，但故障过程中逆变器不能为电网提供电压支撑且模式切换时存在过电压问题。文献[25]分析故障限流对逆变器暂态稳定性能的影响，研究发现，某些限流方式会降低逆变器的暂态稳定性能，进而导致暂态失稳现象发生。为进一步分析电流限幅对系统稳定性能的影响，文献[18, 26-27]提出虚拟功角的概念，并基于虚拟功角阐述了限流环节对逆变器暂态功角影响机理。功角稳定与故障电流限制是下垂控制型逆变器稳定运行不可或缺的两个重要因素。此外，不恰当的限流措施会恶化逆变器功角稳定性，因此对下垂控制型逆变器进行暂态控制时，应兼顾功角稳定与故障电流控制。
基于此，首先，本文对下垂控制型逆变器的暂态特性展开研究，分析无功-电压环路与故障限流控制对下垂控制型逆变器暂态稳定性能的影响，为下垂控制型逆变器暂态控制提供指导；其次，本文提出一种兼顾暂态功角稳定与故障电流限制的下垂控制型逆变器暂态控制策略，通过对有功-频率环路与无功-电压环路的优化控制，保证故障期间下垂控制型逆变器的安全稳定运行；最后，结合仿真与实验结果证明所提控制策略的正确性和有效性。
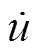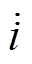下垂控制型逆变器的主电路与控制结构如图1所示。图中，和分别为逆变器端电压和输出电流；Lf、Cf和Lg分别为滤波电感、滤波电容和线路电感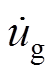；为电网电压。
下垂控制型逆变器的有功-频率、无功-电压控制方程分别为
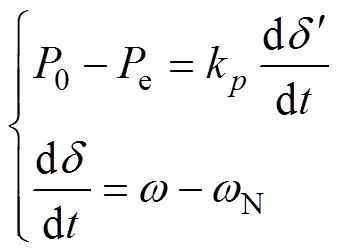（1）
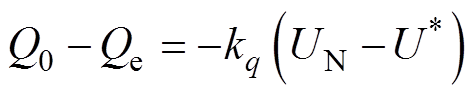（2）
式中，P0、Pe分别为下垂控制型逆变器有功功率指令值与实际输出值；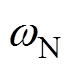
、
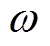分别为虚拟转速额定值与实际值；kp、kq分别为有功-频率与无功-电压下垂系数；
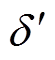为下垂控制型逆变器虚拟功角[18,26-27]；Q0、Qe分别为逆变器无功功率指令值与实际输出值；UN、
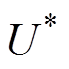分别为逆变器额定电压幅值与电压指令值。
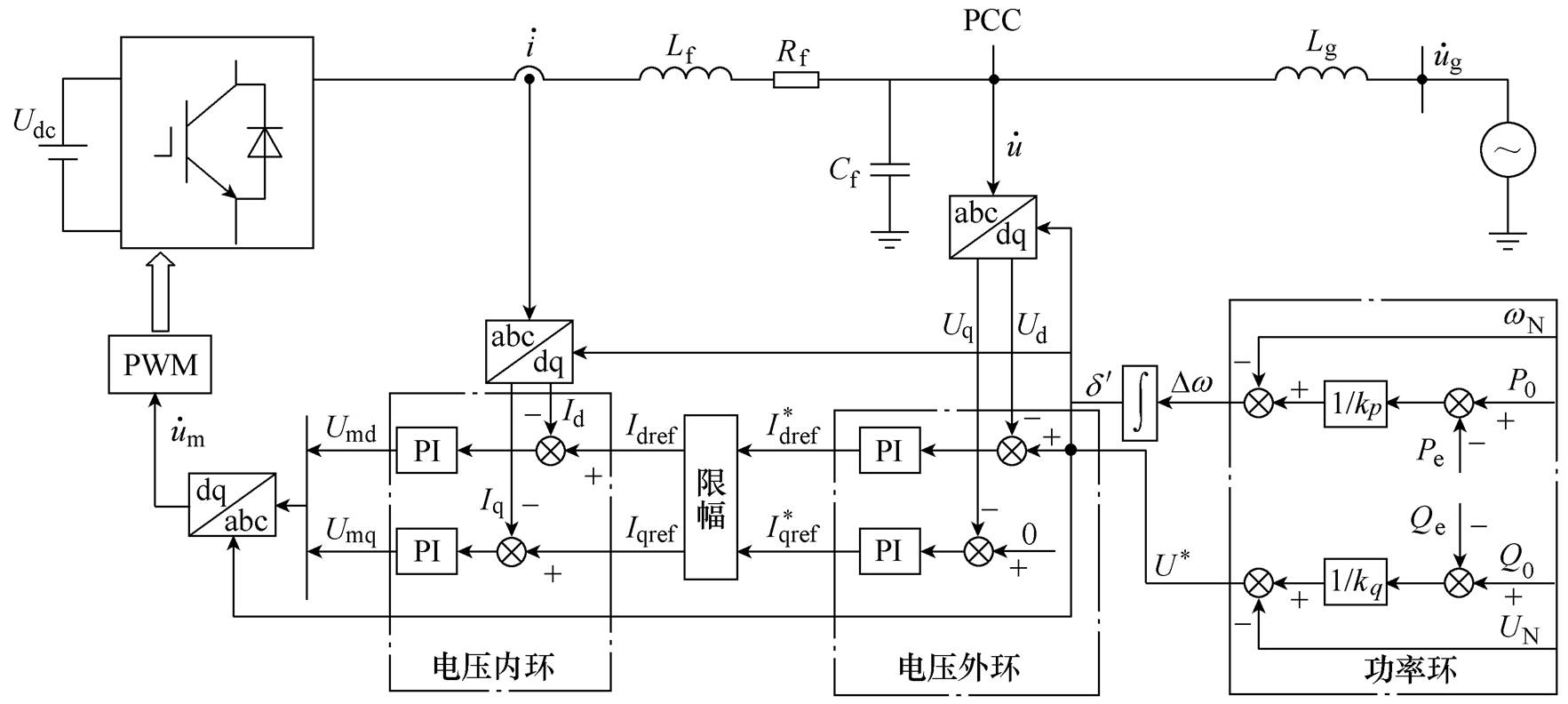
图1 下垂控制型逆变器的主电路和控制结构
Fig.1 Topology and control scheme of a droop-controlled inverter
下垂控制型逆变器向电网输送的有功功率和无功功率分别为
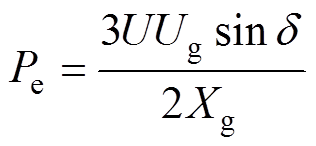（3）
（4）
式中，Xg为线路电抗，Xg=wLg；Ug为电网电压幅值；U为逆变器端电压幅值；d 为系统实际功角，即VSC端电压相位与电网电压相位的差值，电流限幅环节不动作时，
。
现有研究证明，下垂控制型逆变器输出有功功率中含有正弦函数项使其具有非线性特征，一旦故障发生，下垂控制型逆变器会表现出与SG类似的暂态功角特性[20]。但由于下垂控制型逆变器不具有惯性，因而其功角动态特性也与SG存在一定差异。下面对下垂控制型逆变器暂态功角特性展开详细分析。
下垂控制型逆变器有功-频率控制方程呈现一阶特性，其功角变化率与有功功率输入、输出差值直接相关。故障过程中，若存在功率平衡点，此时下垂控制型逆变器输入输出有功功率满足P0-Pe= 0。根据式（1），功率平衡点处功角变化率为0，下垂控制逆变器能够实现功角暂态稳定。不同故障程度下，下垂控制型逆变器功角曲线与
曲线如图2所示。
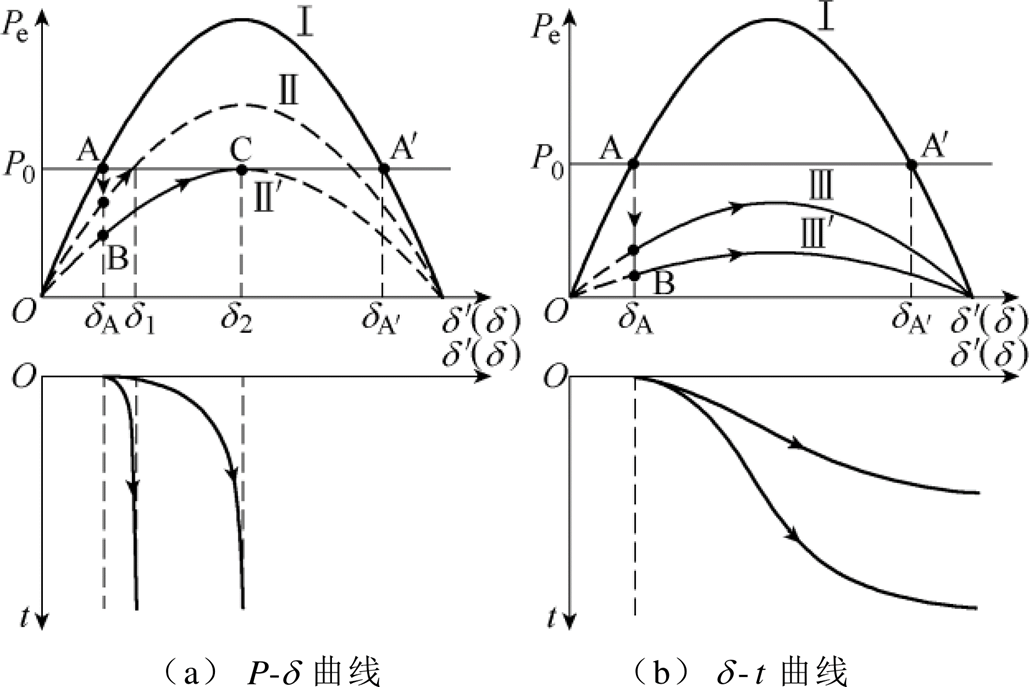
图2 下垂控制型逆变器功角曲线与δ-t曲线
Fig.2 
and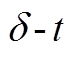 
curves of a droop-controlled inverter
图2中，曲线
为正常工况下的下垂控制型逆变器功角曲线，曲线
、
、
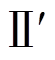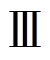及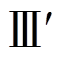
分别为不同故障深度下的下垂控制型逆变器功角曲线。A和
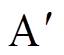为功率平衡点，其中A为稳定平衡点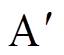，为不稳定平衡点。
图2a为故障过程中存在功率平衡点的情况。以曲线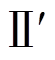表示的情况为例，逆变器首先运行在A点处，故障发生后，运行点跳变为B，之后沿曲线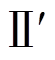运动，直至到达新的功率平衡点C。到达C点后，功角保持稳定值
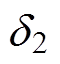不再发生变化，下垂控制型逆变器实现暂态稳定。
图2b为故障过程中不存在故障平衡点。逆变器首先运行在A点，故障发生后，由于不存在功率平衡点，下垂控制型逆变器功角不断增大，最后失稳。
结合式（2）与式（4），可以得到下垂控制型逆变器电压指令值为
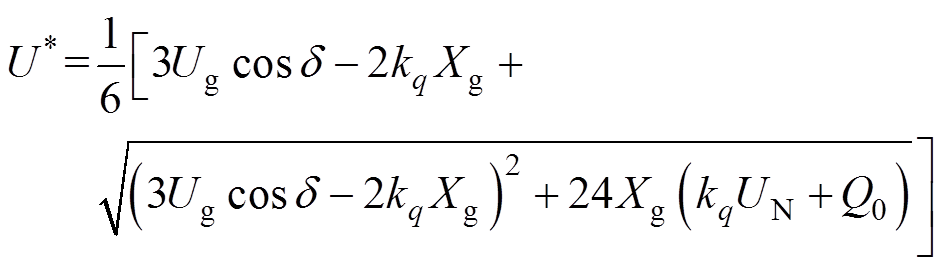（5）
由于功率外环的带宽远小于电压电流双闭环的带宽，其时间尺度约为电压电流双闭环的十数倍。因此，在分析逆变器功角稳定性时可认为U可以对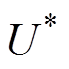实现无差跟踪，即
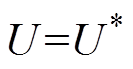（6）
结合式（1）～式（3）以及式（6）可以得到
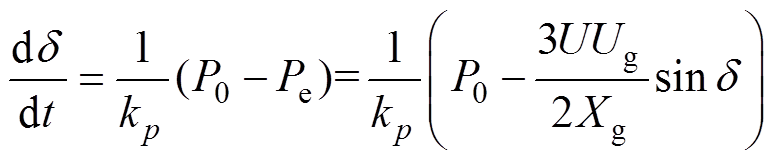（7）
根据式（7）绘制不同kq的下垂控制型逆变器相平面如图3所示。图中，随着kq减小，下垂控制型逆变器由暂态稳定变为暂态失稳。这是由于故障发生后，下垂控制型逆变器端电压与电网电压之间差值增大，导致逆变器输出无功功率增加。根据式（2），由于无功环路下垂特性，逆变器端电压下降。根据式（3），下垂控制型逆变器输出有功功率随逆变器端电压下降而减小，这进一步加剧了逆变器输入输出有功功率不平衡程度，恶化下垂控制型逆变器的暂态稳定性能。kq越小，逆变器的无功-电压下垂特征越显著。因此，随着kq减小，逆变器由暂态稳定变为暂态失稳。基于以上分析可知，暂态控制时必须考虑无功-电压环路的影响。
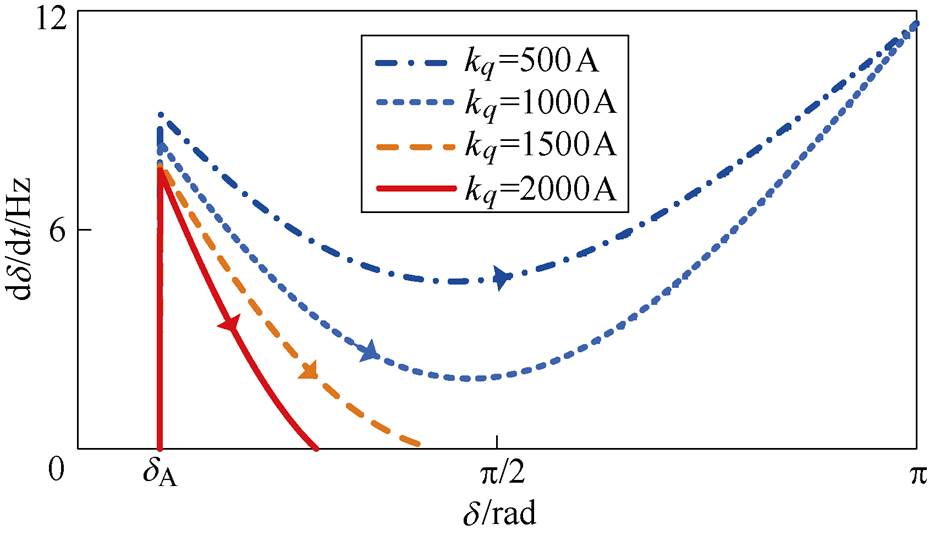
图3 不同kq的下垂控制型逆变器相平面
Fig.3 Phase portraits of a droop-controlled inverter with different kq
电网电压跌落至0.35(pu)时，不同kq的下垂控制型逆变器波形如图4所示。图4a为kq=2 000A时的波形，故障期间逆变器端电压跌落至0.88(pu)，暂态功角增加至4.8(pu)，但下垂控制型逆变器依然可以维持暂态稳定。图4b为kq=500A时的波形，故障期间，下垂控制型逆变器暂态失稳，导致暂态功角及端电压周期振荡。仿真结果与理论分析相吻合，证明kq减小将恶化逆变器暂态性能，无功-电压环路对下垂控制型逆变器功角稳定性的影响不可忽视。
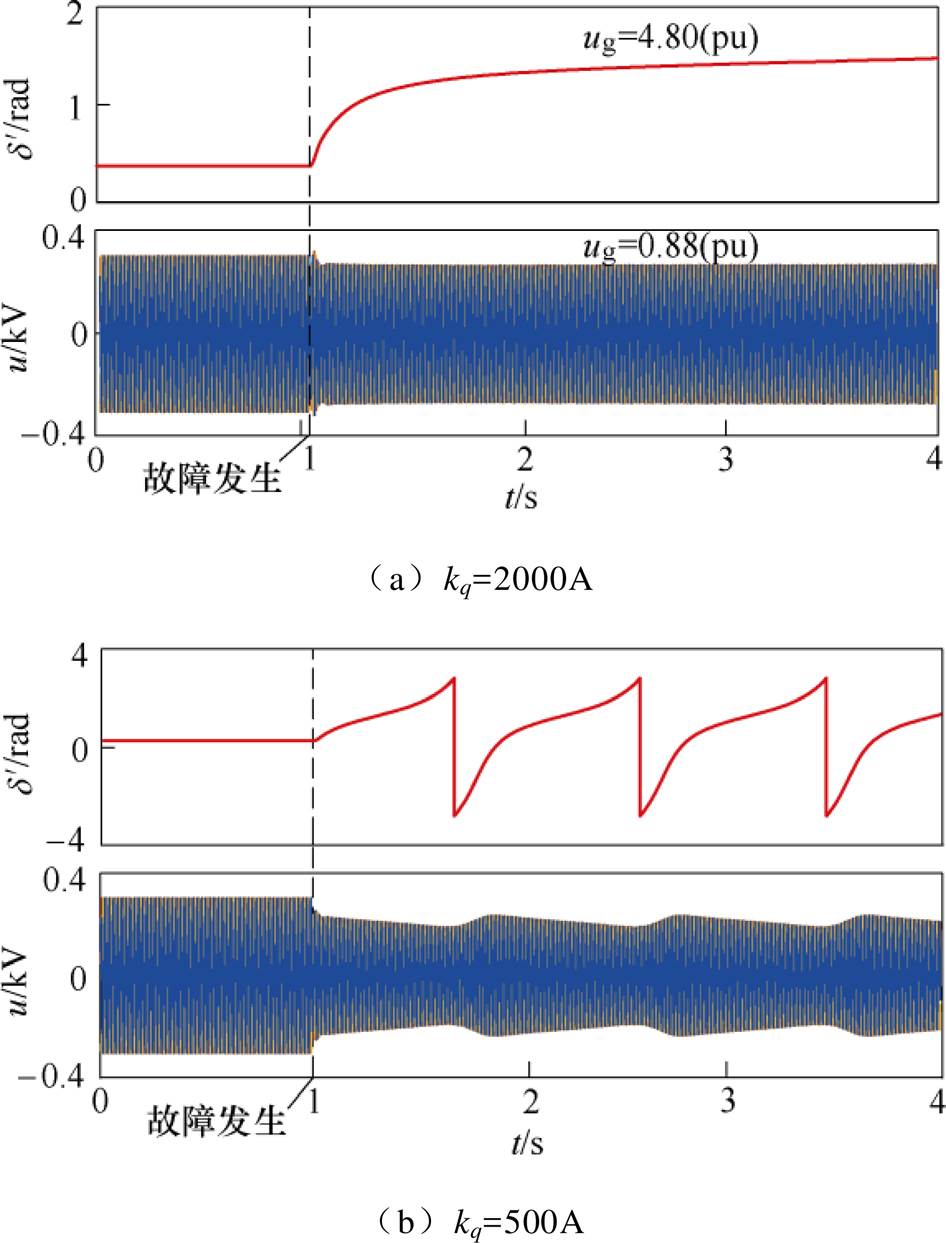
图4 不同kq的下垂控制型逆变器波形
Fig.4 Waveforms of a droop-controlled inverter with different kq
以电网电压相位为基准，则逆变器端电压与电网电压之间的相位差（功角）即逆变器端电压的相位d。下垂控制型逆变器的电压、电流满足电路方程
（8）
式中，
为逆变器端电压与电网电压之间相量差，即线路压降。
由式（8）得到逆变器故障电流为
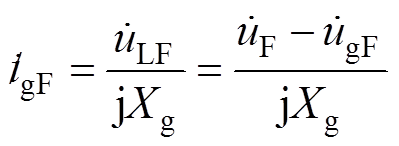（9）
式中，下标F为故障过程中相应变量的值。
下垂控制型逆变器的电压电流相量如图5所示。图中，实线和虚线分别表示正常工况和故障工况。
图5a中的虚线表示故障过程中系统存在功率平衡点的情况。此时，故障电流维持恒定，其幅值大小取决于逆变器与电网之间电压差。图5b中虚线表示故障期间系统不存在功率平衡点的情况。此时，故障电流不断增加，最终失去控制。
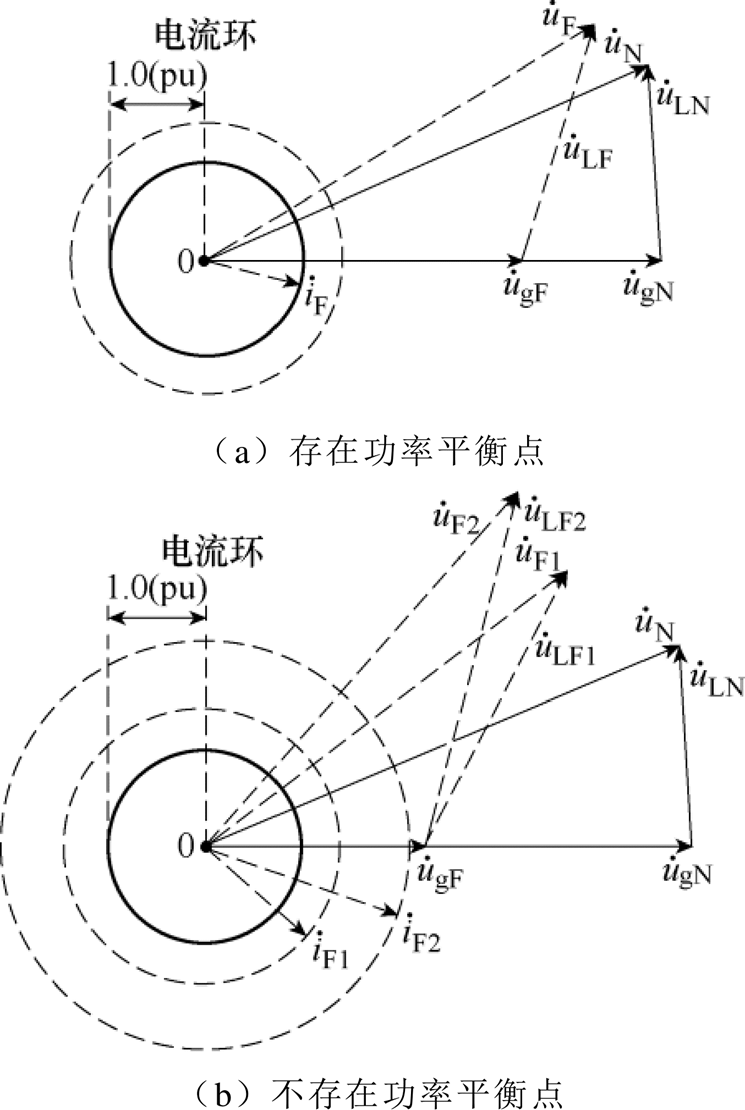
图5 故障前后电压电流相量
Fig.5 Phasor diagram before and after fault
由于逆变器过电流能力较弱，因此需对故障电流进行控制。当逆变器参考电流超过安全阈值时，电流限幅环节作用，此时下垂控制型逆变器输出电流幅值为Ilimit。一般而言，Ilimit=1.5IN。电流限幅前，下垂控制型逆变器的虚拟功角与功角相等；电流限幅后下垂控制型逆变器受限幅环节影响而出现偏离虚拟功角的情况[18, 26-27]。
限幅环节作用后，下垂控制型逆变器输出有功功率为
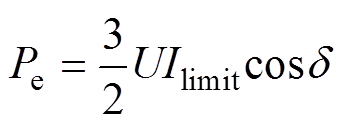（10）
根据式（3）与式（10）得到限流前后下垂控制型逆变器虚拟功角曲线如图6所示。图6a中，由于故障期间存在功率平衡点，下垂控制型逆变器运行点由A跳变为M点后沿功角曲线运行至N后实现暂态稳定。图6b中，考虑电流限幅环节作用，逆变器输出有功功率由于输出电流受限而降低，进而导致故障期间不存在功率平衡点，系统暂态失稳。
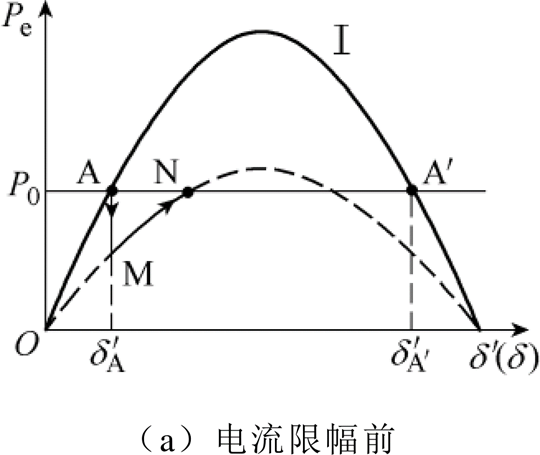
图6 电流限幅前后下垂控制型逆变器虚拟功角曲线
Fig.6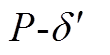 
curves of a droop-controlled inverter before and after fault current limitation
电网电压跌落至0.35(pu)时，故障电流限幅前后下垂控制型逆变器波形如图7所示。图7a为故障电流限幅前的波形，图中故障电流达到2.94(pu)，但逆变器虚拟功角（功角）暂态稳定。图7b为加入电流限幅环节的波形，图中故障电流被限制在1.50(pu)，但虚拟功角稳定性无法保证，下垂控制型逆变器暂态稳定性能受到影响。仿真结果与理论分析相吻合，证明现有电流限幅控制对下垂控制型逆变器暂态稳定性的影响不可忽视。因此，暂态控制时必须同时考虑暂态稳定性能与故障电流控制。
图7 电流限幅前后的下垂控制型逆变器波形
Fig.7 Waveforms of a droop-controlled inverter before and after fault current limitation
下垂控制型逆变器具备有功-频率与无功-电压下垂特性，能够在故障期间为电网提供电压与频率支撑。此外，下垂控制型逆变器有功环路的一阶特性赋予其独特的暂态特征。相较于有功环路为二阶特性的虚拟同步发电机（或者SG），下垂控制型逆变器在故障切除后无需减速面积，只需暂态期间存在功率平衡点即能恢复暂态稳定。因而，从某些方面而言，下垂控制型逆变器故障鲁棒性能优于虚拟同步发电机（或者SG）[22]。因而，有必要对下垂控制型逆变器加以控制，进一步优化其暂态性能。
本文所提故障电流调控方法为主动控制，调控过程中虚拟功角与实际功角相等，因此后文统称为功角。由第2节分析可知：功角暂态失稳与逆变器有功功率输入输出不平衡有关，故障电流大小取决于逆变器与电网之间电压向量差。基于此，本节提出了考虑功角稳定与故障电流限制的下垂控制型逆变器暂态控制方法。通过有功-频率和无功-电压环路的优化设计，实现暂态功角与故障电流有效控制。
由2.1节与2.2节分析可知，电网电压与下垂控制型逆变器端电压的跌落导致逆变器输出有功功率偏离参考值。基于此，本节提出一种综合考虑电网电压与逆变器端电压变化的暂态功角控制方法。
正常工况下，电网电压幅值与下垂控制型逆变器端电压幅值分别为UgN和UN，功角为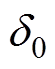
。故障期间，电网电压幅值与下垂控制型逆变器端电压幅值分别为UgF和UF，功角为
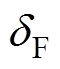。故障前后下垂控制型逆变器输出有功功率比值为
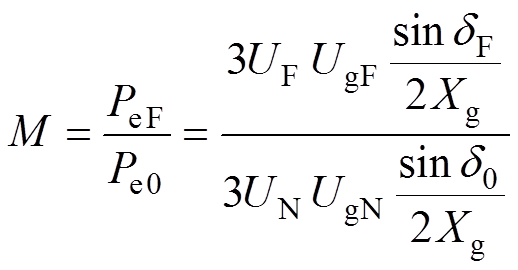（11）
式中，Pe0为故障前下垂控制型逆变器输出有功功率；PeF为故障期间逆变器输出有功功率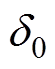；为正常工况下的功角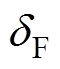；为故障工况下的功角。
为保证下垂控制型逆变器功角暂态稳定，以故障前后功角不发生偏移为控制目标，即保证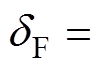
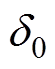。此时，式（11）可以表示为
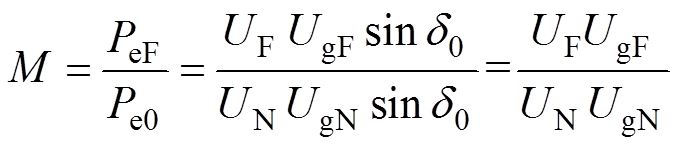（12）
基于以上分析，暂态功角控制可以通过调整有功功率指令值来实现。调整规则如下
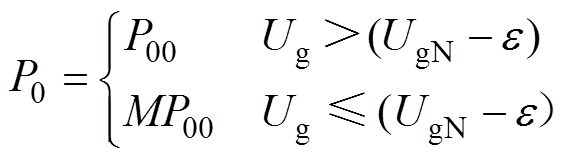（13）
式中，P00为下垂控制型逆变器有功功率指令初始值；M=UFUgF/(UNUgN)为有功功率指令调节系数；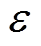
= UgN´10%为电网电压允许的最大波动。
以故障过程中不存在功率平衡点为例，功角控制后的下垂控制型逆变器功角曲线如图8所示。为保证故障过程中功角不偏离初始值，下垂控制型逆变器的有功功率参考值依据逆变器端电压与电网电压的变化进行动态调整。在故障期间，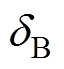
与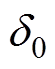无限接近，即下垂控制型逆变器在故障期间功角保持额定值。
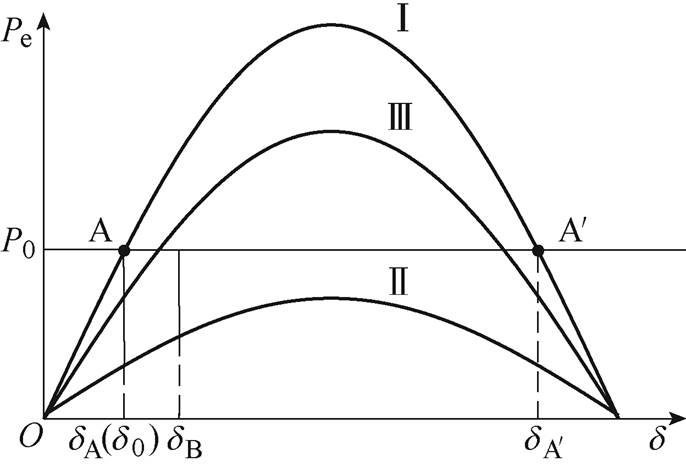
图8 功角控制后下垂控制型逆变器功角曲线
Fig.8 P-d curves of droop-controlled inverter with power angle control
加入功角控制后，系统相量关系如图9所示。实线和虚线分别代表正常和故障情况下的系统变量。图9中，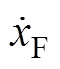
（x=u, i）为传统下垂控制型逆变器输出量，
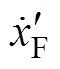为加入功角控制后的下垂控制型逆变器输出量。通过功率角控制，逆变器端电压从
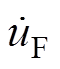调整到
，功角在故障前后保持不变。电网与下垂控制型逆变器之间的电压相量差缩小，故障电流相应减小。
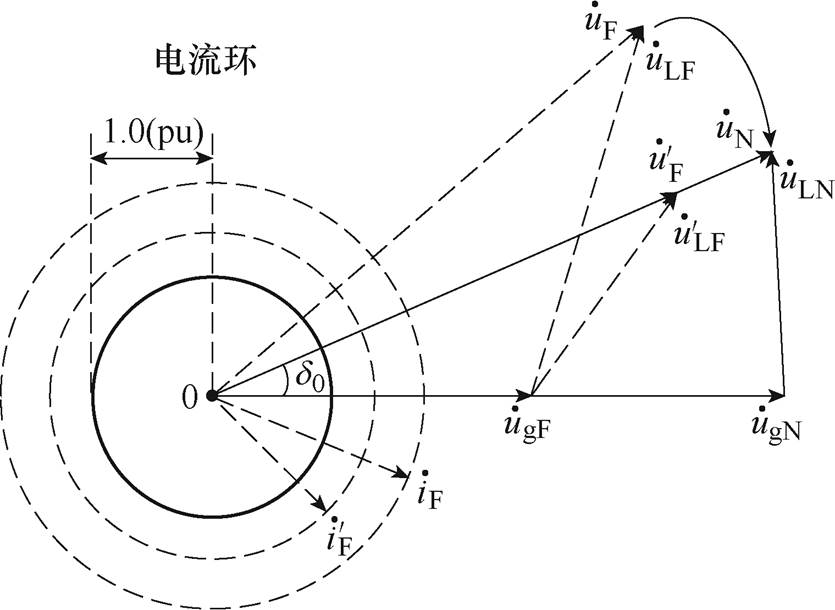
图9 功角控制前后系统相量
Fig.9 Phasor diagram of droop-controlled inverter before and after power angle control
根据3.1节可知，功角控制能够在一定程度上限制故障电流。但当故障比较严重时，仅通过功角控制不能完全保证故障电流满足逆变器安全要求。因此，本节在功角控制的基础上，通过对无功-电压环路的优化调控来实现故障电流的进一步控制。
无功环调整前后电压电流相量如图10所示。从图10中看出，在电网电压幅值与功角一定的情况下，下垂控制型逆变器输出电流由其端电压幅值决定。由于电压-电流内环带宽较大，下垂控制型逆变器端电压能够快速地跟踪电压指令值。因此，通过Q-U功率回路的优化设计，合理控制参考电压，可以实现对故障电流的抑制。
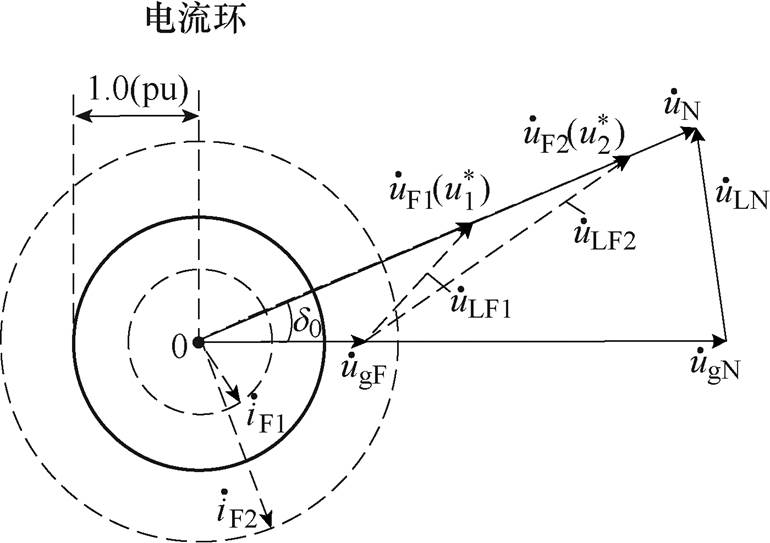
图10 无功环调整前后电压电流相量
Fig.10 Phasor diagram before and after reactive control loop adjustment
根据图10，正常工况时下垂控制型逆变器端电压、输出电流与功角之间满足
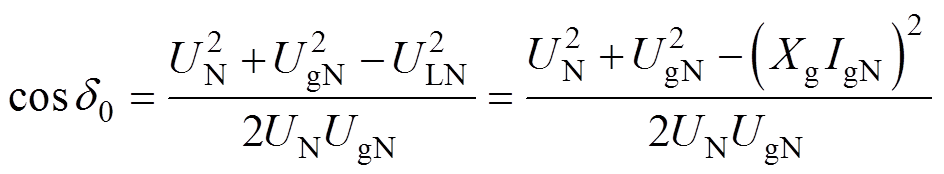（14）
故障发生后，令UF=
，则加入功角控制后，下垂控制型逆变器功角、端电压及故障电流满足
（15）
式中，为故障期间下垂控制型逆变器电压指令值。
综合式（14）与式（15），令UgF=kUgN，得到故障电流与电压指令值满足
（16）
其中
通过调整电压指令值，可将故障电流控制在安全范围内。将IgF=Ilimit=1.5IgN代入式（16），得到
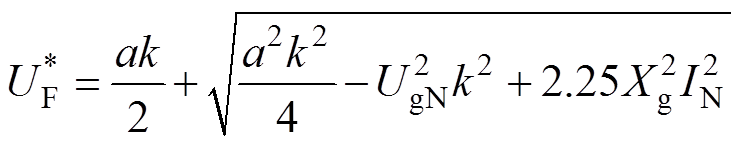（17）
通过无功-电压环路的优化设计，可以实现电压参考值的灵活调控，进一步改变下垂控制型逆变器端电压，实现故障电流的有效控制。为了防止故障冲击电流超过阈值导致限流模块的误差动作，控制模块将Q-U端电压信号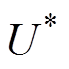
作为判别信号。如果
，则认为需要调整电压基准，以控制下垂控制型逆变器与电网的电压差；如果
，则无需调整电压参考值。根据式（2）与式（4）及以上分析，电压参考值可控制为
（18）
正常情况下，下垂控制型逆变器以单位功率因数运行。由2.2节可知，故障期间下垂控制型逆变器可以根据式（4）自动为电网提供快速的动态无功支持，有利于故障点电压的恢复。故障时设置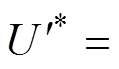
，即冻结Q-U下垂特性。该方法既可以限制故障电流，又可以为电网提供一定的无功功率支持。
暂态控制框图如图11所示。图11a为暂态控制流程。首先，对电网电压与逆变器输出电流进行实时监测。当电网电压波动达到阈值时，暂态控制投入运行，通过有功-频率环路的优化设计保证功角稳定性。同时，当故障电流超过阈值时，通过无功-电压环路的优化设计，实现故障电流的有效控制。
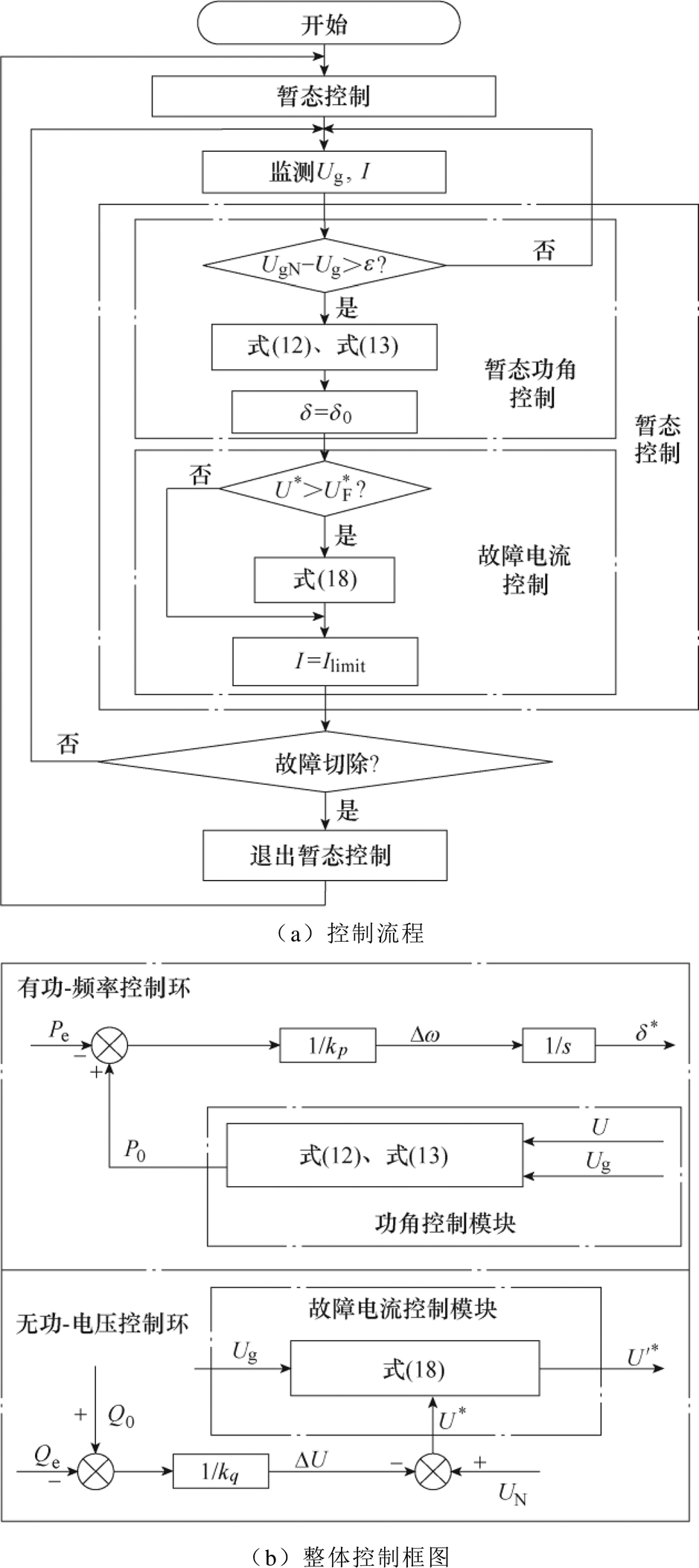
图11 暂态控制框图
Fig.11 Block diagram of the transient control
图11b为暂态控制方案。暂态控制分为暂态功角控制和故障电流限制两部分。功角控制由有功-频率控制环通过式（12）和式（13）实现；故障电流限制由无功-电压控制环通过式（18）实现。通过对下垂控制型逆变器功率控制环的优化调控，保证下垂控制型逆变器功角暂态稳定的同时故障电流不越限，实现故障工况下的安全稳定运行。值得一提的是，传统直接限幅的方法会导致实际功角偏离虚拟功角的情况。而本文中的电流控制策略为主动控制方法，在故障过程中下垂控制型逆变器的实际功角与虚拟功角相等。
为验证本文暂态控制策略的有效性，在Matlab/ Simulink中搭建如图1所示的下垂控制型逆变器并网仿真模型，主要仿真参数见表1。逆变器首先运行在稳定状态，1s时电网发生短路故障，故障持续2s。下面分两种工况电网电压跌落至0.4(pu)与0.2(pu)对不同控制策略下的下垂控制型逆变器进行仿真。
电网电压跌落至0.4(pu)时的下垂控制型逆变器波形如图12所示。图12a为传统下垂逆变波形，图中传统下垂控制型逆变器暂态稳定，故障期间功角维持在2.87(pu)，但故障期间电流增加至2.61(pu)，超过安全范围，不利于逆变器的安全运行；此外，逆变器端电压受无功-电压下垂关系影响降至0.75(pu)。图12b为加入功角控制后的下垂控制型逆变器波形，图中，有功功率参考值在故障期间动态调整，下垂控制型逆变器暂态功角维持在额定值附近，故障电流减小至1.62(pu)，但仍超出安全范围。同时，由于有功功率参考值调整，故障期间逆变器输出有功功率减小。图12c为加入功角与故障电流综合控制后的下垂控制型逆变器波形，图中下垂控制型逆变器暂态功角维持在额定值附近，故障电流被限制在1.5(pu)，满足安全运行条件。此外，下垂控制型逆变器端电压被控制在0.79(pu)，有功功率参考值随电网电压与逆变器端电压的变化动态调整；值得一提的是，故障期间下垂控制型逆变器输出无功功率增加，有利于故障点电压恢复。
表1 仿真参数
Tab.1 Simulation parameters
参 数数 值 直流侧电压Udc/V800 电网电压UgN/V380 滤波电容Cf/mF50 滤波电感Lf/mH3 线路电感Lg/mH4 额定有功功率P0/kW35 额定角速度/(rad/s)314 有功-频率下垂系数kp/[(N·m·s)/rad]3 000 无功-电压下垂系数kq/A1 000
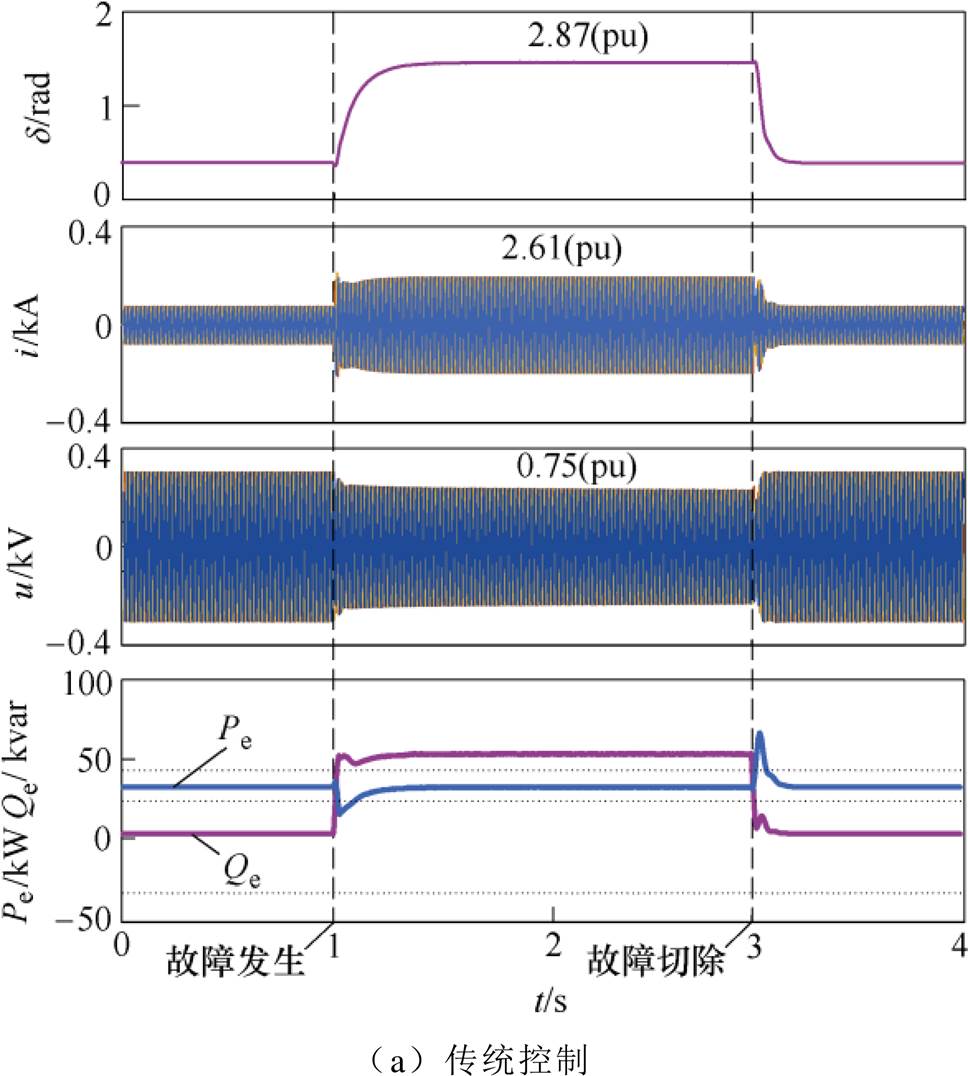
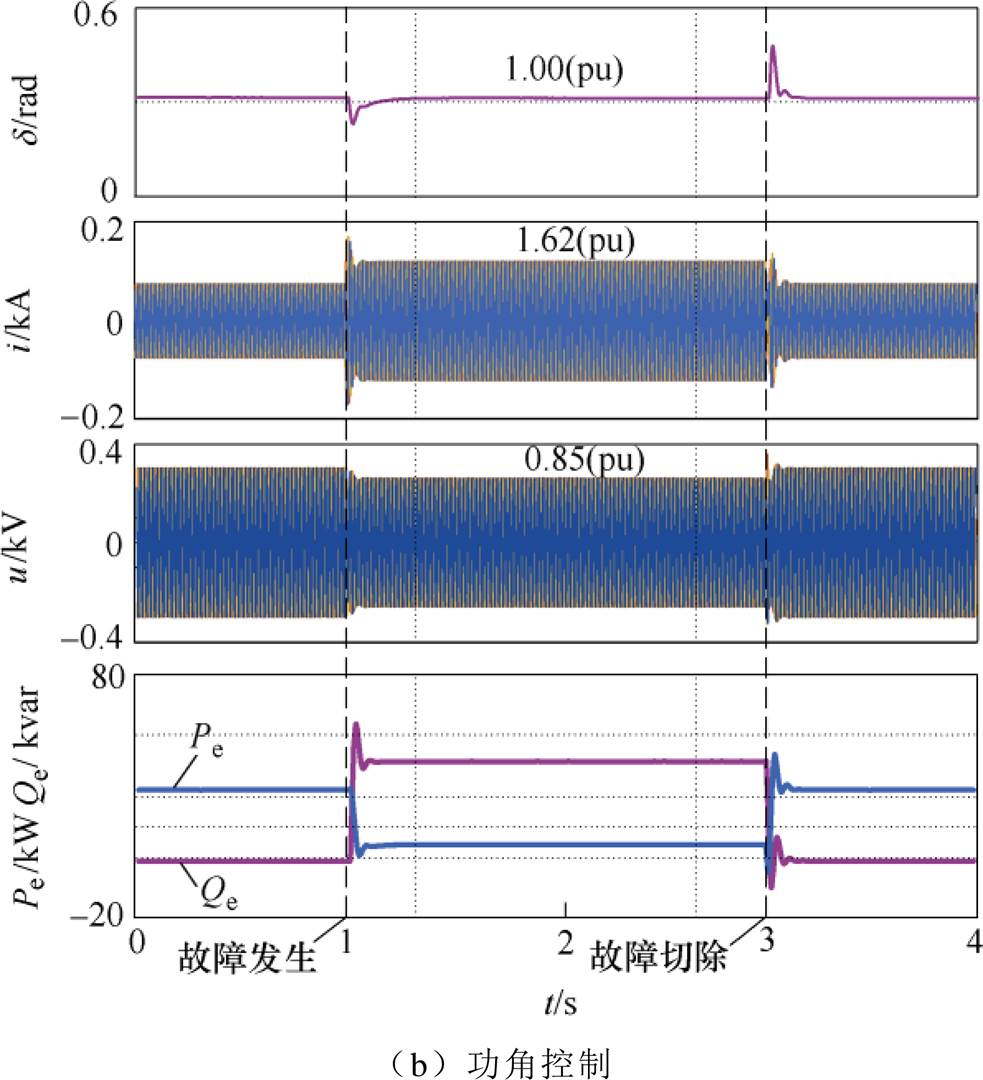
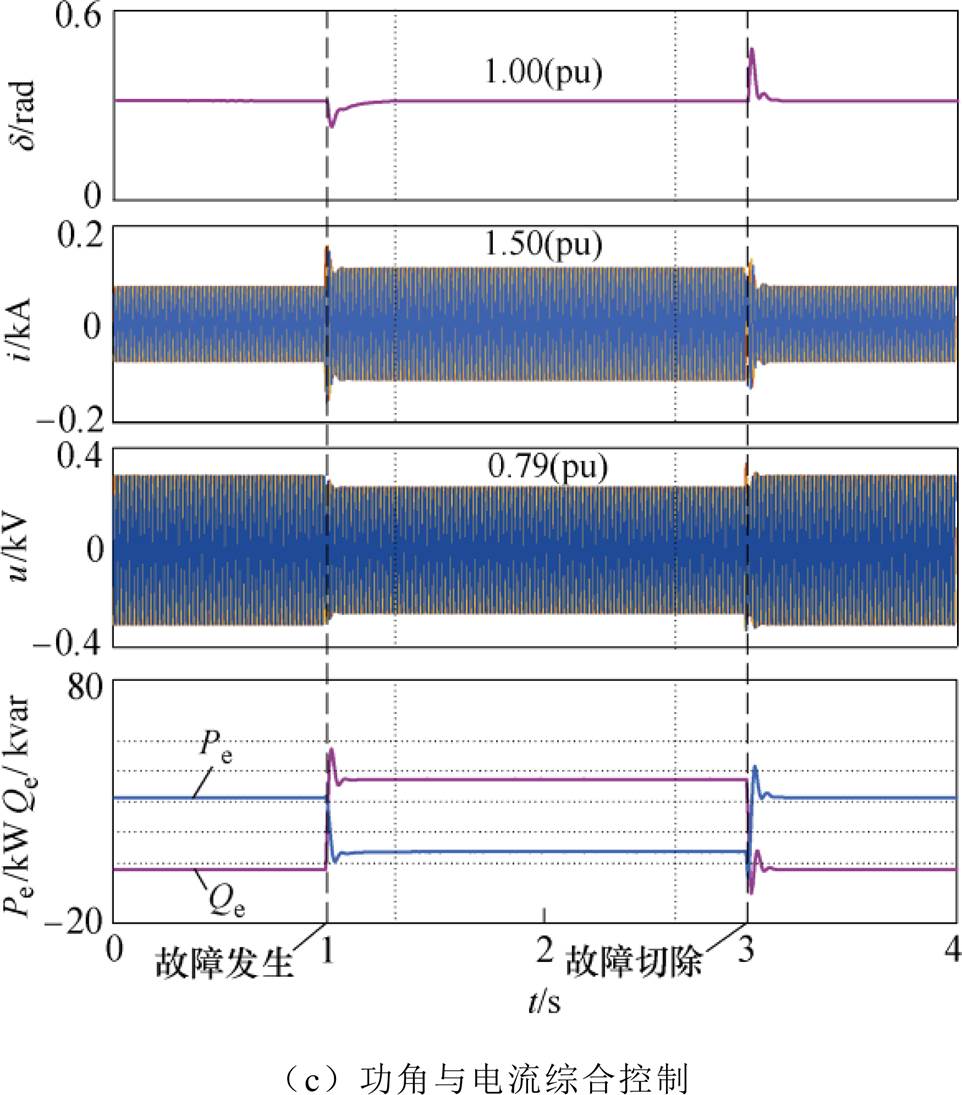
图12 电网电压0.4(pu)的下垂控制型逆变器仿真波形
Fig.12 Simulation waveforms when grid voltage drops to 0.4(pu)
电网电压跌落至0.2(pu)时的下垂控制型逆变器波形如图13所示。图13a为传统下垂逆变波形，图中传统下垂控制型逆变器在故障期间失去稳定性，功角、电流等电气量周期振荡。图13b为加入功角控制后的下垂控制型逆变器波形，图中暂态功角在故障期间维持额定值，下垂控制型逆变器暂态稳定。但故障电流达到2.03(pu)，威胁逆变器的安全运行。图13c为加入功角与故障电流综合控制后下垂控制型逆变器波形，图中下垂控制型逆变器暂态功角维持在额定值附近，故障电流被限制在1.5(pu)，满足安全运行需求。
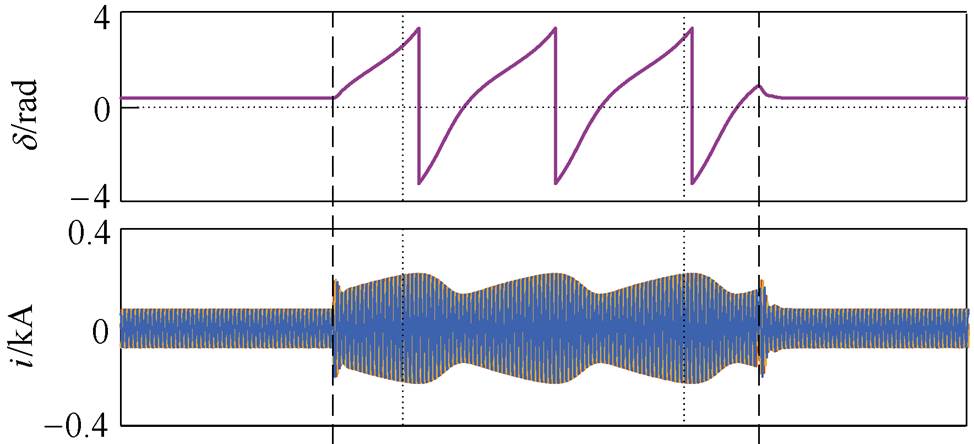
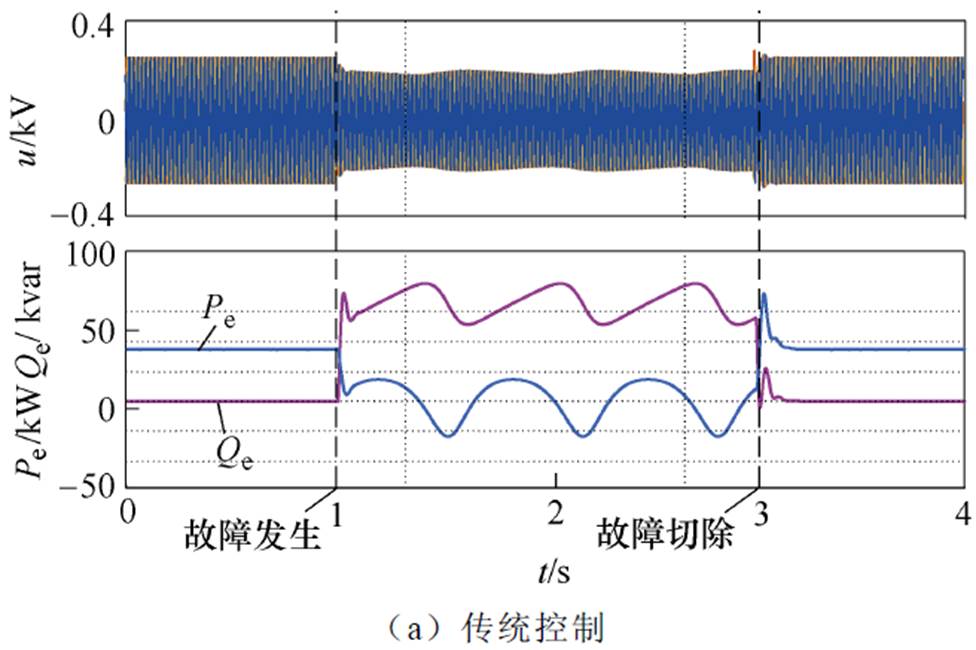
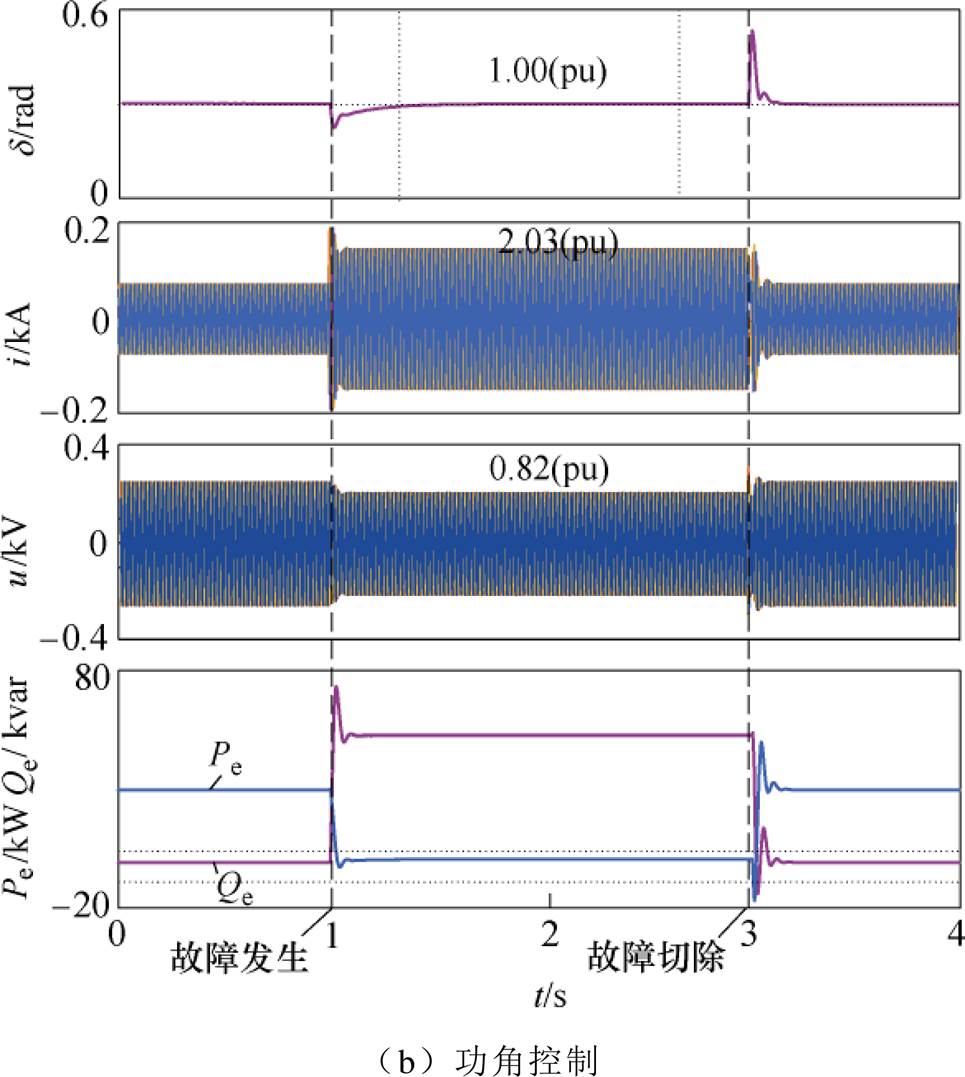
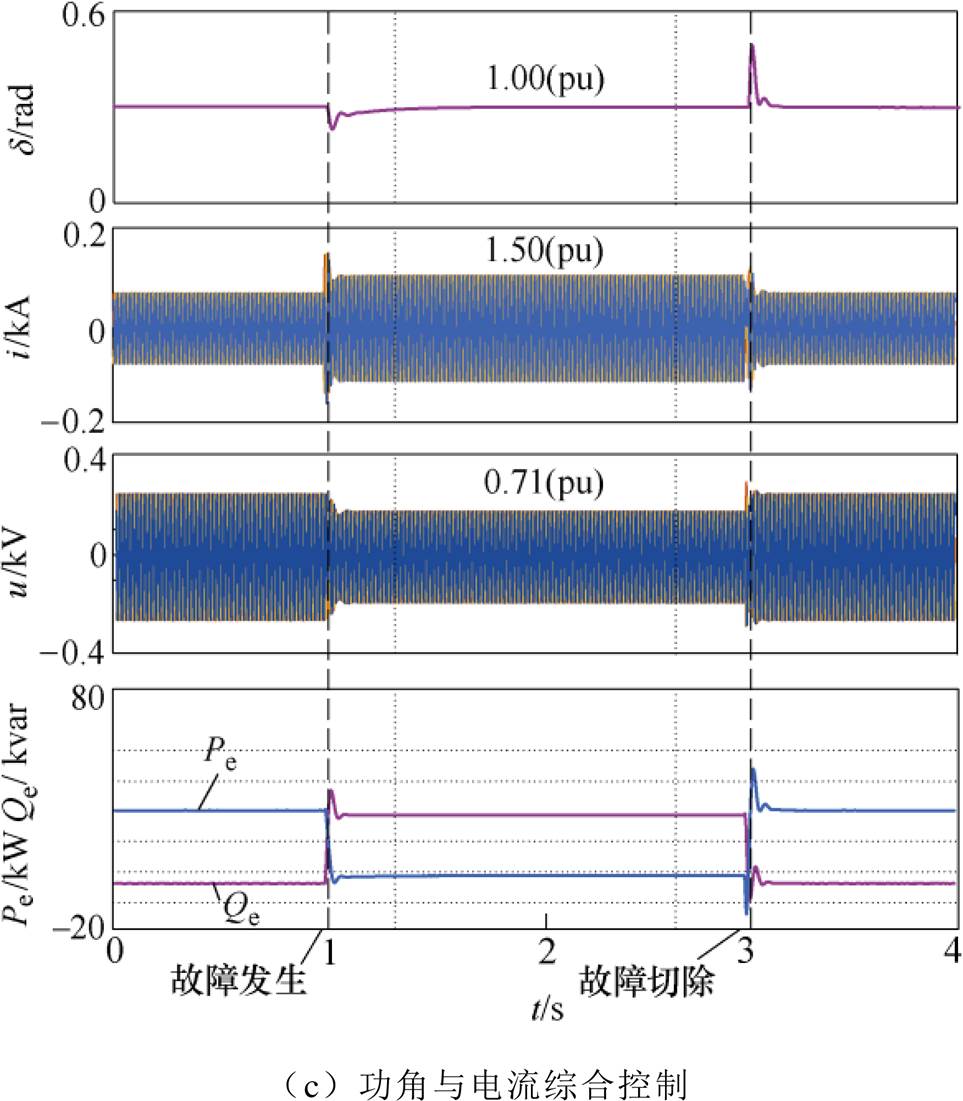
图13 电网电压0.2(pu)的下垂控制型逆变器仿真波形
Fig.13 Simulation waveforms when grid voltage drops to 0.2(pu)
为进一步验证本文所提暂态控制策略的有效性，搭建实验平台进行相应实验。其中，实验工况及控制参数与仿真部分保持一致。
图14为电网电压跌落至0.4(pu)时不同控制策略下的下垂控制型逆变器实验波形。从图中看出，传统下垂控制型逆变器在故障期间虽然能够暂态稳定，但故障电流超过安全阈值，无法保证逆变器安全运行。加入功角与电流综合控制后，逆变器功角与故障电流得到有效抑制。实验结果与仿真及分析结果相吻合，表明本文所提方法具有较好的控制效果。
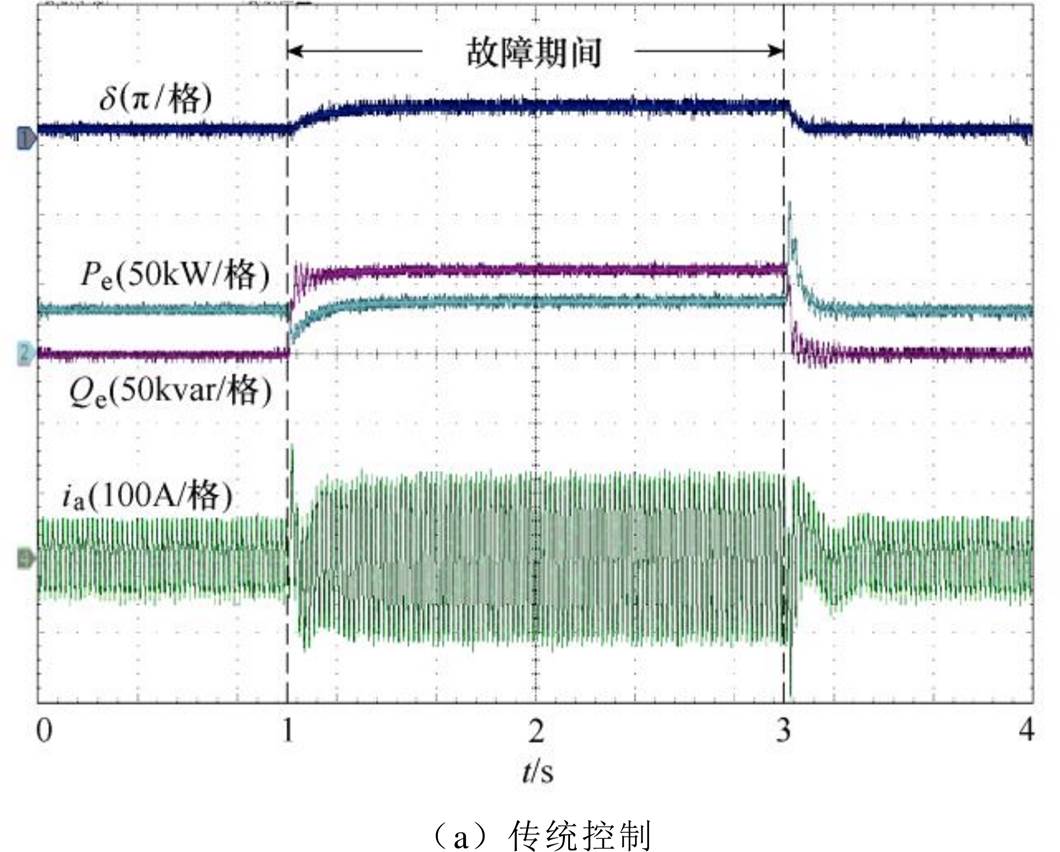
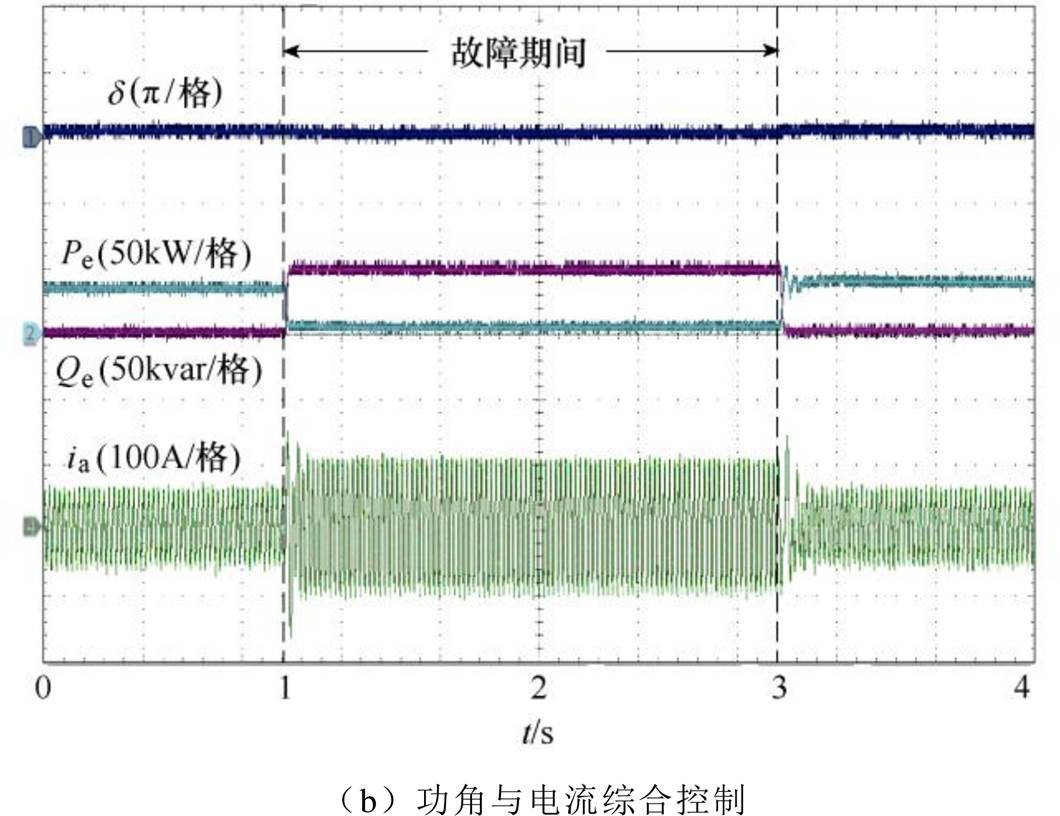
图14 电网电压0.4(pu)的下垂控制型逆变器实验波形
Fig.14 Experimental wavefomrs when grid voltage drops to 0.4(pu)
图15为电网电压跌落至0.2(pu)时不同控制策略下的下垂控制型逆变器实验波形。图中传统下垂控制型逆变器在故障期间暂态失稳。加入功角与电流综合控制后，下垂控制型逆变器能够实现暂态稳定运行，故障电流被控制在1.5(pu)。实验结果与仿真及分析结果相吻合，表明本文所提方法具备较好的控制效果。
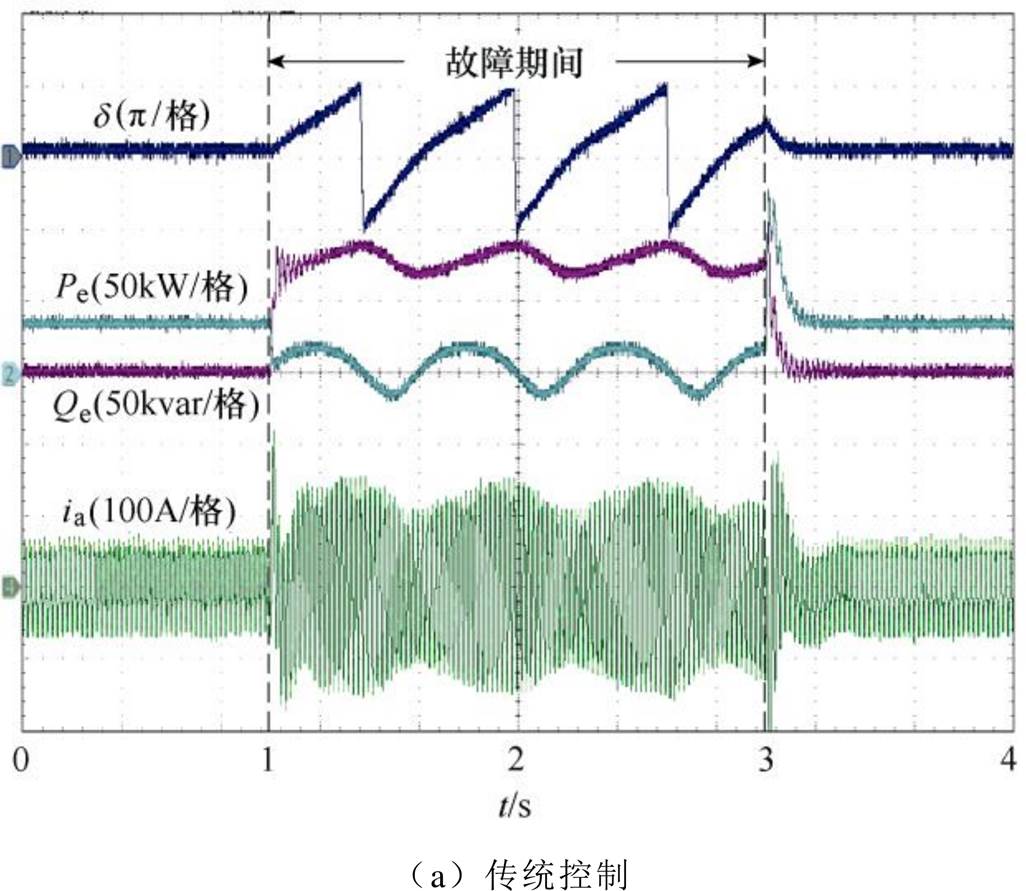
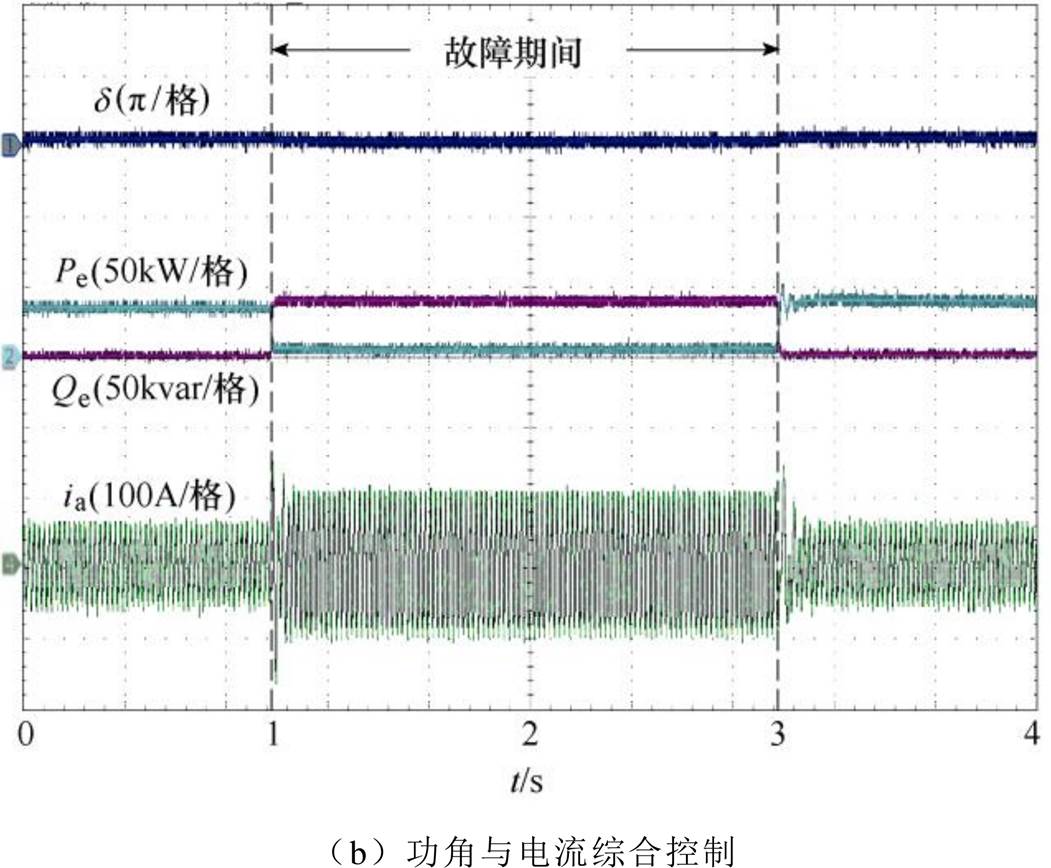
图15 电网电压0.2(pu)的下垂控制型逆变器实验波形
Fig.15 Experimental wavefomrs when grid voltage drops to 0.2(pu)
本文通过对下垂控制型逆变器暂态特性进行分析，提出一种兼顾功角稳定与故障电流控制的暂态调控方法，并通过仿真与实验得出以下结论：
1）故障期间下垂控制型逆变器的暂态功角失稳与有功功率输入输出不平衡有关；故障电流大小与逆变器及电网之间的电压相量差有关。
2）本文所提暂态控制策略同时兼顾暂态功角与故障电流。通过有功-频率环路的优化控制实现暂态功角有效控制。在暂态功角控制的基础上，通过无功-电压环路的优化控制实现故障电流的有效控制。
3）使用本文所提暂态控制策略后，下垂控制型逆变器可以在故障期间向电网注入一定量的无功功率，以支撑电网电压。
参考文献
[1] 陈国平, 李明节, 许涛, 等. 关于新能源发展的技术瓶颈研究[J]. 中国电机工程学报, 2017, 37(1): 20-27.
Chen Guoping, Li Mingjie, Xu Tao, et al. Study on technical bottleneck of new energy development[J]. Proceedings of the CSEE, 2017, 37(1): 20-27.
[2] 钟庆昌, 霍尔尼克. 新能源接入智能电网的逆变控制关键技术[M]. 北京: 机械工业出版社, 2016.
[3] 肖湘宁. 新一代电网中多源多变换复杂交直流系统的基础问题[J]. 电工技术学报, 2015, 30(15): 1-14.
Xiao Xiangning. Basic problems of the new complex AC-DC power grid with multiple energy resources and multiple conversions[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 1-14.
[4] 王成山, 王守相. 分布式发电供能系统若干问题研究[J]. 电力系统自动化, 2008, 32(20): 1-4.
Wang Chengshan, Wang Shouxiang. Study on some key problems related to distributed generation systems[J]. Automation of Electric Power Systems, 2008, 32(20): 1-4.
[5] 曾正, 赵荣祥, 汤胜清, 等. 可再生能源分散接入用先进并网逆变器研究综述[J]. 中国电机工程学报, 2013, 33(24): 1-12.
Zeng Zheng, Zhao Rongxiang, Tang Shengqing, et al. An overview on advanced grid-connected inverters used for decentralized renewable energy resources[J]. Proceedings of the CSEE, 2013, 33(24): 1-12.
[6] Rocabert J, Luna A, Blaabjerg F, et al. Control of power converters in AC microgrids[J]. IEEE Transa- ctions on Power Electronics, 2012, 27(11): 4734- 4749.
[7] Milano F, Dörfler F, Hug G, et al. Foundations and challenges of low-inertia systems[C]//Power Systems Computation Conference, Dublin, 2018, DOI: 10.23919/ PSCC.2018.8450880.
[8] Elkhatib M E, Du W, Lasseter R H. Evaluation of inverter-based grid frequency support using frequency- watt and grid-forming PV inverters[C]//IEEE Power & Energy Society General Meeting, Portland, 2018, DOI: 10.1109/PESGM.2018.8585958.
[9] Markovic U, Stanojev O, Aristidou P, et al. Partial grid forming concept for 100% inverter-based trans- mission systems[C]//IEEE Power Energy Soc. General Meeting, Portland, 2018, DOI: 10.1109/PESGM.2018. 8586114.
[10] 姜静雅, 王玮, 吴学智, 等. 基于自适应无功功率补偿的虚拟同步机功率解耦策略[J]. 电工技术学报, 2020, 35(13): 2747-2756.
Jiang Jingya, Wang Wei, Wu Xuezhi, et al. Power decoupling strategy in virtual synchronous generator based on adaptive reactive power compensation[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2747-2756.
[11] 王晓寰, 张旭东, 郭红强, 等. 基于相位簇扰动的下垂控制并网逆变器孤岛检测[J]. 电工技术学报, 2020, 35(8): 1728-1738.
Wang Xiaohuan, Zhang Xudong, Guo Hongqiang, et al. Islanding detection of droop-controlled grid- connected inverters on phase cluster disturbance[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1728-1738.
[12] Arani M F M, Mohamed Y A I. Analysis and impacts of implementing droop control in DFIG-based wind turbines on microgrid/weak-grid stability[J]. IEEE Trans on Power Systems, 2015, 30(1): 385-396.
[13] Brabandere K D, Bolsens B, Keybus J V D, et al. A voltage and frequency droop control method for parallel inverters[J]. IEEE Transactions on Power Electronics, 2007, 22(4): 1107-1115.
[14] 张健磊, 高湛军, 陈明, 等. 考虑复故障的有源配电网故障定位方法[J]. 电工技术学报, 2021, 36(11): 2265-2276.
Zhang Jianlei, Gao Zhanjun, Chen Ming, et al. Fault location method for active distribution networks considering combination faults[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2265- 2276.
[15] 刘彦超. 含分布式电源配电网的快速故障区段定位[J]. 电气技术, 2017, 18(9): 61-65, 71.
Liu Yanchao. Fast fault section locating for distri- bution network with distributed generations[J]. Electrical Engineering, 2017, 18(9): 61-65, 71.
[16] Geng Hua, Liu Cong, Yang Geng. LVRT capability of DFIG-based WECS under asymmetrical grid fault condition[J]. IEEE Transactions on Industrial Elec- tronics, 2013, 60(6): 2495-2509.
[17] Alam M R, Muttaqi K M, Bouzerdoum A. Characteri- zing voltage sags and swells using three-phase voltage ellipse parameters[J]. IEEE Transactions on Industry Applications, 2015, 51(4): 2780-2790.
[18] 章雷其, 黄林彬, 黄伟, 等. 提高下垂控制逆变器虚拟功角暂态稳定性的控制方法[J]. 电力系统自动化, 2017, 41(12): 56-62, 99.
Zhang Leiqi, Huang Linbin, Huang Wei, et al. Control methods for improving virtual power angle transient stability of droop-controlled inverters[J]. Automation of Electric Power Systems, 2017, 41(12): 56-62, 99.
[19] D'Arco S, Suul J A. Equivalence of virtual syn- chronous machines and frequency-droops for converter- based microgrids[J]. IEEE Transactions on Smart Grid, 2014, 5(1): 394-395.
[20] Simpson-Porco J W, Drfler F, Bullo F. Synchroni- zation and power sharing for droop-controlled inverters in islanded microgrids[J]. Automatica, 2012, 49(9): 2603-2611.
[21] Rodriguez P, Timbus A V, Teodorescu R, et al. Flexible active power control of distributed power generation systems during grid faults[J]. IEEE Transactions on Industrial Electronics, 2007, 54(5): 2583-2592.
[22] Wu Heng, Wang Xiongfei. Design-oriented transient stability analysis of grid-connected converters with power synchronization control[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 6473-6482.
[23] Pan Donghua, Wang Xiongfei, Liu Fangcheng, et al. Transient stability of voltage-source converters with grid-forming control: a design-oriented study[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1019-1033.
[24] Oureilidis K O, Demoulias C S. A fault clearing method in converter-dominated microgrids with conventional protection means[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 4628-4640.
[25] Paquette A D, Divan D M. Virtual impedance current limiting for inverters in microgrids with synchronous generators[J]. IEEE Transactions on Industry Appli- cations, 2014, 51(2): 1630-1638.
[26] 黄林彬, 章雷其, 辛焕海, 等. 下垂控制逆变器的虚拟功角稳定机理分析[J]. 电力系统自动化, 2016, 40(12): 117-123, 150.
Huang Linbin, Zhang Leiqi, Xin Huanhai, et al. Mechanism analysis of virtual power angle stability in droop-controlled inverters[J]. Automation of Electric Power Systems, 2016, 40(12): 117-123, 150.
[27] Huang Linbin, Xin Huanhai, Wang Zhen, et al. Transient stability analysis and control design of droop-controlled voltage source converters con- sidering current limitation[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 578-591.
Transient Control Strategy of Droop-Controlled Inverter Considering Fault Current Limitation
Abstract The droop-controlled inverter can provide voltage and frequency support for the power grid, and its transient stability is important. However, the stability of power angle and fault current affects the safe operation of the droop-controlled inverter under fault conditions. In this paper, the transient characteristics of the droop-controlled inverter are analyzed, and the influence of current limiter and Q-U loop on the transient characteristics of the inverter is described in detail. Accordingly, this paper proposes a transient control method for the droop-controlled inverter which takes into account both fault current limitation and power angle stability. The proposed method considers the variation of the grid voltage and the output voltage of the inverter during the fault period and realizes the power angle stability of the inverter by adjusting the active power reference. In addition, the fault current can be effectively suppressed by the optimal control of the Q-U control loop. Finally, the effectiveness of the proposed method is verified by simulation and experiment.
keywords：Droop-controlled inverter, transient stability analysis, fault current limitation, transient control strategy
DOI: 10.19595/j.cnki.1000-6753.tces.211118
中图分类号：TM464
国家自然科学基金面上项目（52077072）和国家自然科学基金青年项目（51907057）资助。
收稿日期 2021-07-21
改稿日期 2021-11-19
葛平娟 女，1996年生，博士研究生，研究方向为分布式发电与电力电子技术。E-mail: pingjuan_ge@163.com
肖 凡 男，1988年生，副研究员，研究方向为电力电子在电力系统中的应用。E-mail: woliaokk123@126.com（通信作者）
（编辑 陈 诚）