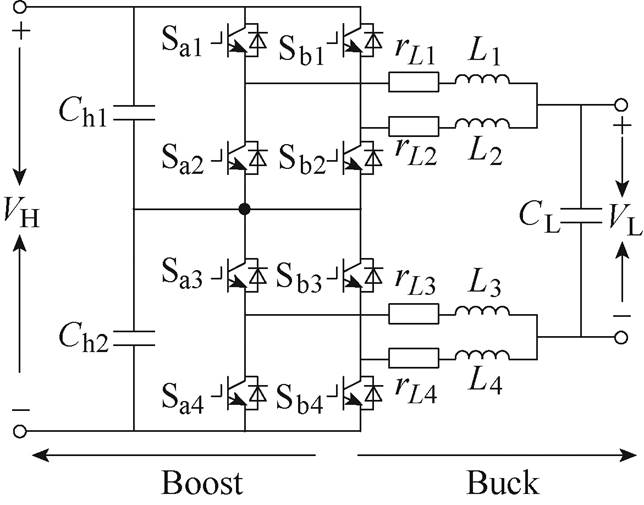
图1 两相交错并联三电平双向DC-DC变换器
Fig.1 Topology of the interleaved two-phase three-level DC-DC converter
摘要 该文提出一种两相交错并联三电平双向DC-DC变换器功率均衡解耦控制策略,并有效地减少了电流传感器的使用。通过对变换器拓扑工作原理的分析,得出两相交错三电平拓扑的等效两电平分析方法。在此基础上,提出基于总电流分时倍频采样功率均衡解耦控制策略,使变换器的电压调节与相间电流均衡控制实现了完全解耦。此外,将常规均衡控制所需的四路电流采样,减少为两路,达到了简化控制结构的目的。建立基于等效拓扑下的小信号模型,利用该模型对所提方案进行理论验证,并给出控制器参数的具体设计方案。最后通过小功率物理仿真实验对所提控制策略进行了有效验证。
关键词:交错并联 三电平双向直流变换器 功率均衡解耦控制 倍频采样策略
在“碳中和”愿景目标下,以光伏、风电为代表的新能源将成为未来主力能源[1]。而要解决新能源稳定并网及其消纳问题,储能则成为了关键技术支撑[2]。储能系统要实现能量在电网和储能设备间的双向流动,双向DC-DC功率变换器是储能系统的核心设备,相关拓扑结构和控制方案已成为近年来的研究热点[2-7]。
储能系统通常采用非隔离型双向DC-DC功率变换器以提升能量转换效率。由于非隔离型三电平双向DC-DC拓扑电路结构简单、效率较高,且开关器件的电压等级较低,所以在储能系统中的应用具有一定优势[8-9]。文献[5]提出了一种基于输入端串联电容分压的三电平功率变换器。该变换器结构简单,在实际工业场合应用较为广泛[10-11]。大功率工况下,通常采用交错并联方式以提升系统容量[12]。但是由于元器件参数的误差以及不同的局部设计结构,交错并联工况下存在相间功率不均衡的问题,不仅导致开关器件电流应力增加,同时也会影响系统的可靠性[13]。
文献[14-15]对交错并联DC-DC拓扑功率均衡控制机理展开了研究,论证了占空比和元器件等效电阻的差异是引起功率不均衡的主要原因。目前,实现各相功率均衡的方法主要分为下垂控制法和有源控制法。下垂控制法需要在每一相的输出增加一个模拟电阻,利用各阶段的负荷调节特性斜率来实现功率均衡[16]。文献[17]提出了一种改进的下垂控制方法,外部电压环采用I-V下垂控制方法,电流内环采用自适应的PI控制方法,该方法在提高动态响应的同时,也保证了良好的稳态性能。虽然下垂方法容易实现,但由于在负载调整率和均衡性能上无法兼顾,导致其只能在小功率场合适用[16]。
有源控制法是在传感器的基础之上,通过检测相电流,实现功率均衡的目的[18]。传统方案在各相电路中均添加了电流传感器,并构建了均衡控制算法,但是系统硬件结构复杂,功率控制存在耦合问题[19-20]。为减少电流传感器数量,近年来单电流传感器技术被广泛应用于直流变换器中。文献[21]提出了基于开关时序测量的单电流传感器检测方案,但需要在各相电路中串联开关,电路结构和控制策略较复杂。此外,有源电流重构,但电流传感器方法也被应用于各种场合中。文献[22]将有源电流重构法运用在多相耦合变换器中,利用数字控制器主动重构相电流,根据重构的电流重新分配各相开关管的占空比,从而起到均衡电流的效果,但是该方法运算较为复杂,对控制器的计算要求较高。文献[23]将有源电流重构的方法应用到了断续电流模式,但是对采样频率要求较高。
此外,一些无传感器的功率均衡方法也在被研究。文献[21, 24-25]分别利用电感等效电阻电压、输出电压纹波和输入电容电压纹波来估算各相电流,并使观测结果参与系统控制,然而功率均衡性能受负载波动影响严重。文献[26-27]采用串接电容的方法,通过修改两相开关的占空比调整串接电容的充放电时间,达到了均流效果。但该方法引入了额外电容,增加了系统的体积和成本。为提高功率均衡性能,文献[28-29]分别提出基于变换器数学模型的多速率数据采样和模型预测均衡控制器,然而这两种方法数据运算量较大,且均衡性能受模型精度影响严重。
为了减少系统的运算量,文献[30]提出了一种可变移相的自动均流控制策略,该策略只要求相邻两相的相移角度j 满足2p (1-D)≤j≤2pD,并且均流条件与变换器的相数无关。但是该均流控制策略在大功率的工况下,开关管的导通损耗较大,效率较低,并且控制器设计较复杂。针对此问题,文献[31]提出了一种将输出电流参考跟踪控制任务与电流平衡控制解耦的方法,控制器参数的整定可以独立进行,简化了控制器的设计。但是该方法的均流效果受到输出电流的跟踪精度影响。
针对两相交错三电平双向DC-DC变换器的功率均衡控制问题,本文提出一种有效降低电流传感器数量的功率均衡控制方案,不仅使电流传感器的数量减少一倍,简化了系统的结构,同时使变换器的主功率控制与均衡功率控制实现解耦,便于系统控制设计。本文首先对变换器的基本原理进行分析,得出了对称等效分析的方法,进而提出功率均衡解耦控制方案,实现了相间功率均衡控制,并设计了基于变换器总电流的倍频采样控制方案,有效地减少了电流传感器的使用。基于对称等效电路,利用小信号模型对所提控制方案进行了全面的分析,并给出了控制器参数设计方法。最后,利用小功率物理仿真实验平台进行了有效的验证。
两相交错三电平双向DC-DC变换器拓扑如图1所示。该拓扑共包含L1~L4 4路电感,rL1~rL4为电感等效电阻,Ch1、Ch2为输入侧支撑电容,CL为输出侧滤波电容。

图1 两相交错并联三电平双向DC-DC变换器
Fig.1 Topology of the interleaved two-phase three-level DC-DC converter
图1所示拓扑在控制上,Sa1与Sa2互补导通,Sa3与Sa4互补导通,Sa1与Sa4的载波相差180°。以a相为例,变换器在Buck或Boost模式下均包含四种工作模态,单相三电平拓扑工作模态如图2所示。
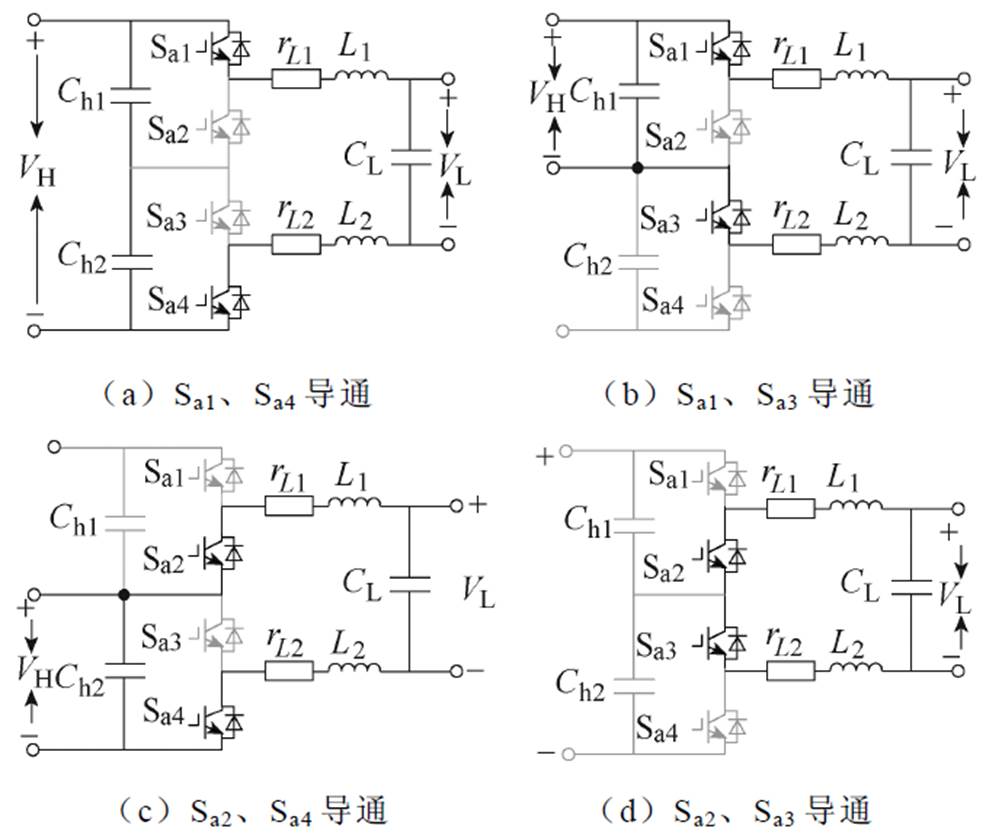
图2 单相三电平拓扑工作模态
Fig.2 Single-phase three level topology operating modes
令Sa1和Sa4的占空比分别为D1和D3,Buck模式下能量由VH向VL流动,Boost模式与之相反,能量由VL向VH流动,表1给出了D1=D3=D变换器的工作模态。
表1 单相三电平拓扑模态
Tab.1 Single-phase three level topological mode

模式占空比D电路模态 Buck>0.5图4a~图4c <0.5图4b~图4d Boost>0.5图4a~图4c <0.5图4b~图4d
Sb1~Sb4的驱动方式与a相相同,但是在相位上相差180°。结合图2所示工作模态,两相交错时,变换器共有16种工作模态,因此以两相并联方式对变换器进行分析将过于复杂。
图1所示的拓扑是由4个半桥组成,且上下对称,每一相是由两个半桥串联而成,将图1中变换器中的下半桥臂进行180°旋转,可以得到如图3所示的等效电路。在理想情况下,电容Ch1和Ch2的电压相等,所以旋转之后Ch1的正负极电位分别为VH和VH/2,Ch2的正负极电位分别为VH/2和0。

图3 三电平拓扑等效电路
Fig.3 Equivalent circuit of three level topology
以Buck工作模式为例,在每一相的1、4开关管导通时,由Ch1和Ch2串联为负载供电,负载两端电压为VH,其余状态下两个电容均可以独立为负载供电。当各相开关管1导通,4关闭时,由电容Ch1通过开关管1和开关管3的反并联二极管向负载供电,负载两端的电压为VH/2;当1、4开关管均关断时,电流通过开关管2、3的反并联二极管构成回路,此时负载两端的电压为0。电容Ch2向负载供电的情况与上述相同,在此不再赘述。因此左、右两组桥臂可独立进行分析。
经图3旋转等效后,任意一侧电路将包含四种工作模态,等效交错两电平电路工作模态如图4 所示。
令D2为Sb1的占空比,G1~G4分别为开关管Sa1、Sb1、Sa2、Sb2的触发脉冲信号,Ts为开关周期。假定D1<D2,此时图4等效电路存在两种工况:①当D1+D2≤1时,如图5a所示,电路工作于图4b~图4d模态;②当D1+D2>1时,如图5b所示,电路工作于图4a~图4c模态;当D1>D2时,D1+D2≤1和D1+D2>1出现的工作模态与D1<D2时相同。
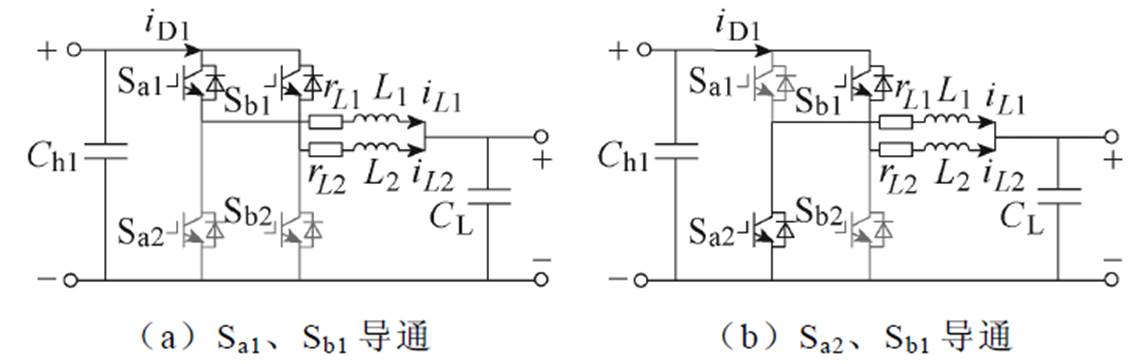
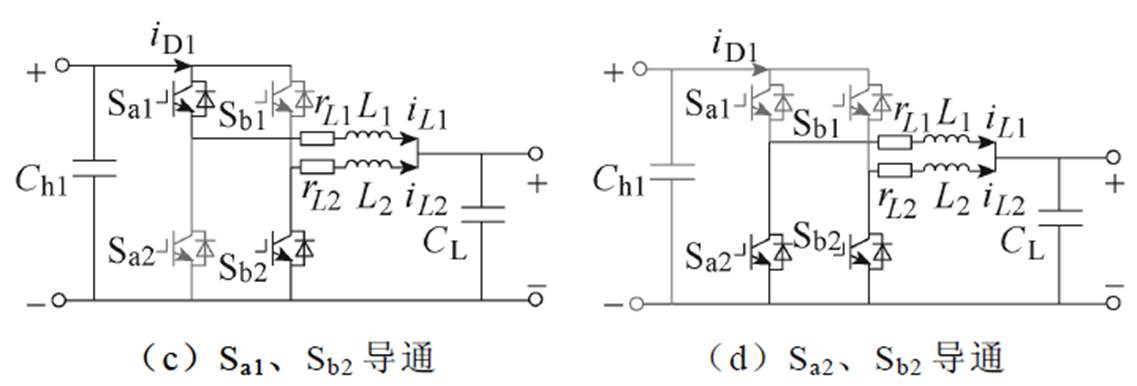
图4 等效交错两电平电路工作模态
Fig.4 Two phase two-level operation mode diagram

图5 开关管驱动示意图
Fig.5 Diagram of switch tube drive
由于等效拓扑结构相同,且彼此独立,三电平双向变换器的分析可通过对单一等效电路的分析获得,这样可将三电平双向变换器工作模态分析的数量进行有效简化,进而便于对变换器进行建模分析。此外,由图1所示电路结构可知,要实现各相电流均衡控制,传统方案需要4路电流传感器,系统成本及硬件结构较为复杂。所以,可以结合等效拓扑探索减少电流传感器的功率均衡控制方案。
为实现两重交错下的功率均衡控制,并减少电流传感器使用,本文提出的功率均衡控制策略框图如图6所示。
该策略以稳压控制为目标,并加入了均衡控制算法,以实现4路电感均流控制。对于输入端两个支撑电容Ch1和Ch2的电压均衡策略,本文采用了文献[32]中前馈控制的方法,以输入电压的1/2为给定电压对其中一个支撑电容进行均压控制。图6中,Gdc(s)为电压闭环调节器,用于控制变换器的总输出电压;Gi1(s)和Gi2(s)为两路均衡调节器,分别控制上、下等效电路的功率均衡;D4为开关Sb4的最终占空比。占空比D1和D2可以表示为

图6 功率均衡控制框图
Fig.6 Power balancing control block diagram
 (1)
(1)
式中,DPI为主占空比,用于实现变换器的稳压控制;DPI,B12为电流均衡控制占空比,用于消除相间电感电流偏差,实现功率均衡。由式(1)可知,当D1=D2时,DPI,B12=0,此时两相的电感电流大小是相等的。D3和D4的表达式与之相同。
事实上,根据文中所提控制方案,DPI与DPI,B12实现了完全解耦,电压控制与均衡控制彼此独立,相关分析将在后文展开。此外,为得到各相电感电流,并减少电流传感器的使用,提出了基于总电流采样的策略,分别采样变换器输入与输出的总电流iD1和iD2,以准确获取各相电流值。
以iD1采样为例,根据等效电路占空比的关系,可得等效电路中各相电流及总电流与占空比的对应关系如图7所示。
图7中,iL1和iL2分别为电感L1和L2的电流。由于Sa1和Sb1相位相差180°,需交错采样。在三角波Vtri1的零点处对iD1进行采样,由于在t2~t3时间段内开关管Sa1开通、Sb1关断,所以总电流iD1和电感电流iL1相等,此时采样的平均电流I1可以表示为
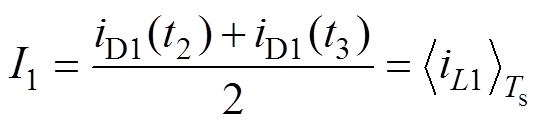 (2)
(2)
式中,Ts为开关周期;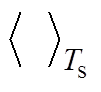 为变量周期平均值。
为变量周期平均值。

图7 采样策略
Fig.7 Sampling strategy
同理,在t4~t5时间段,开关管Sb1开通、Sa1关断,总电流iD1和电感电流iL2相等,那么在三角波Vtri2的零点处采样,获得总电流iD1与iL2是相等的。电流I2可以表示为
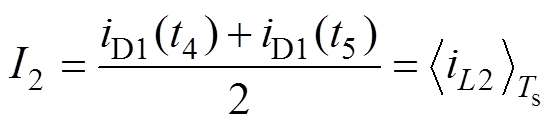 (3)
(3)
由于电路结构对称,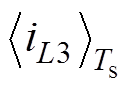 和
和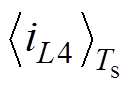 的电流同样可以通过对输出电流iD2进行移相采样获得,分别表示为I3和I4。该采样策略根据三角波的波谷触发控制器进行采样,在移相控制方式下,单周期内包含两个三角波波谷,所以采样频率相比于开关频率的关系为
的电流同样可以通过对输出电流iD2进行移相采样获得,分别表示为I3和I4。该采样策略根据三角波的波谷触发控制器进行采样,在移相控制方式下,单周期内包含两个三角波波谷,所以采样频率相比于开关频率的关系为
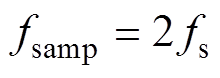 (4)
(4)
式中,fsamp为采样频率。
为了对功率均衡策略进行充分的分析,需要根据图4等效电路进行重新建模。
令Vin为高压侧电压,R为低压侧负载电阻,vout为其端电压。则图4a中,Sa1和Sb1开通、Sa2和Sb2关断,此时总电流iD1=iL1+iL2,电路状态方程为
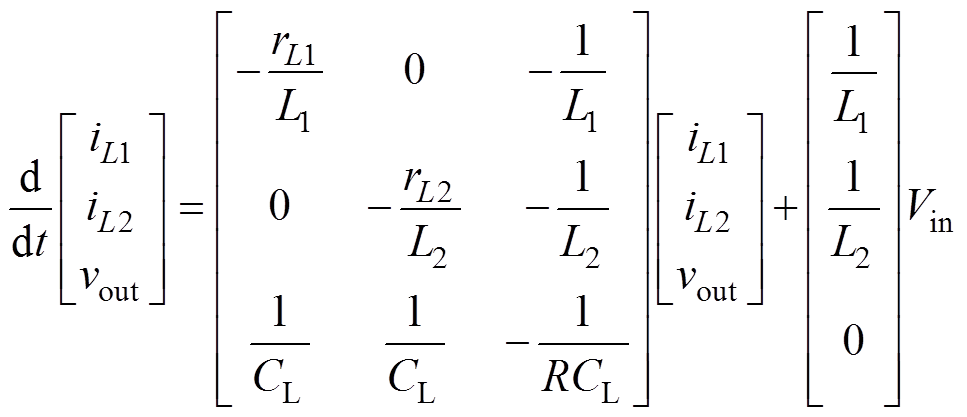 (5)
(5)
图4b中,Sa2和Sb1开通、Sa1和Sb2关断,此时iD1=iL2,电路状态方程为
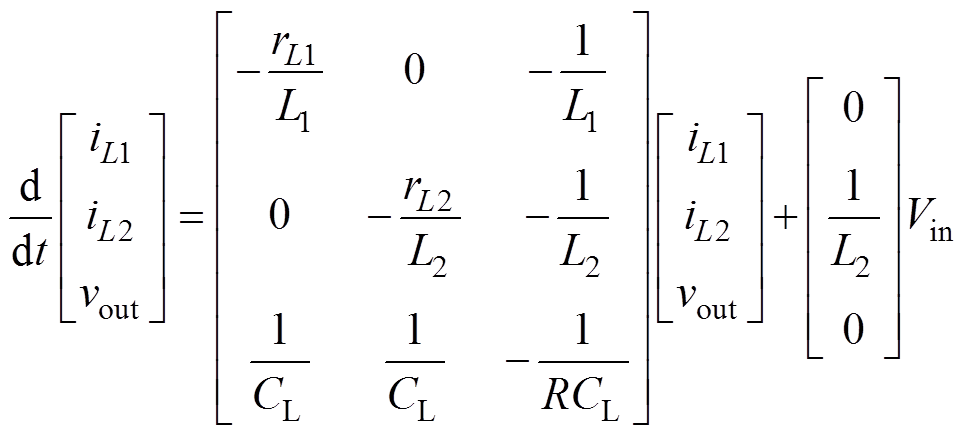 (6)
(6)
图4c中,Sa1和Sb2开通、Sa2和Sb1关断,此时iD1=iL1,电路状态方程为
 (7)
(7)
图4d中,Sa1和Sb1关断、Sa2和Sb2开通,此时总电流iD1=0,电路状态方程为
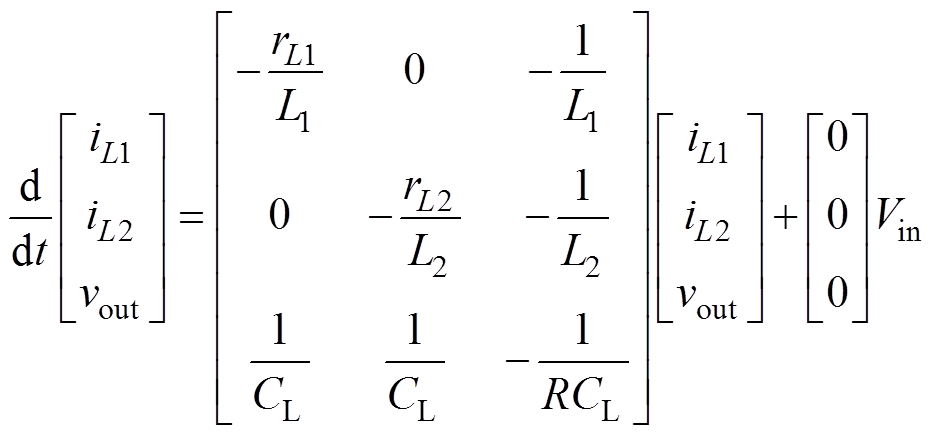 (8)
(8)
令D1+D2<1,如图5a所示,电路b、c、d模态的导通时间分别为D2Ts、D1Ts、(1-D1-D2)Ts;D1+D2>1时,如图5b所示,电路a、b、c模态的导通时间分别为(D1+D2-1)Ts、(1-D1)Ts、(1-D2)Ts。联立式(5)~式(8)及各模态运行时间,可得电路平均状态方程。两工况下电路的平均状态方程相同,表示形式为
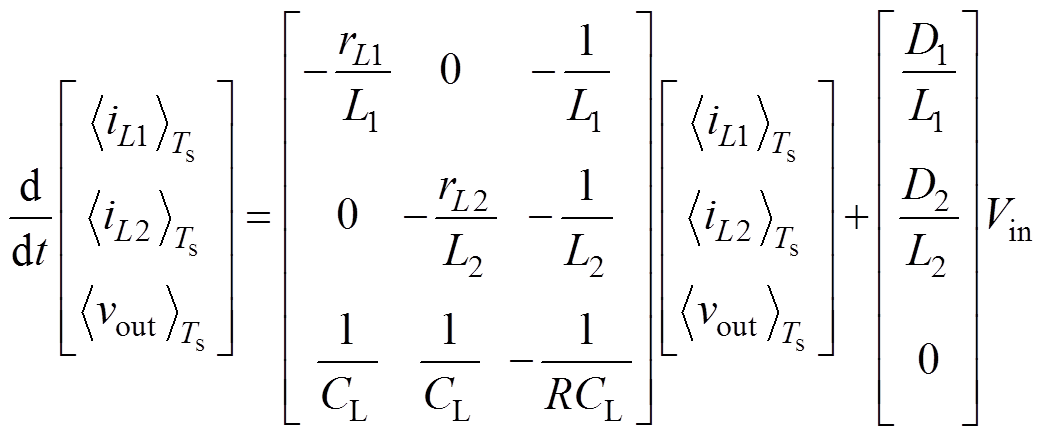 (9)
(9)
选取平均输出电压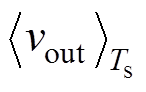 和电感电流差值
和电感电流差值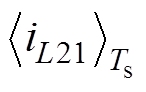 作为系统分析变量,其数学形式表示为
作为系统分析变量,其数学形式表示为
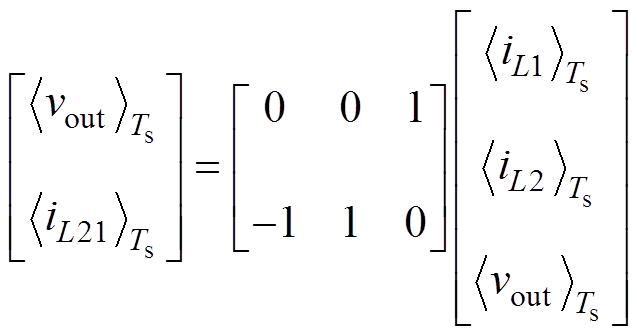 (10)
(10)
由式(1)、式(9)、式(10)可知,系统状态变量包括电感电流、输出电压、占空比及两相电流差值。分别将小信号扰动代入到上述状态变量中,可得各变量的扰动表示形式为
 (11)
(11)
式中,IL1和IL2分别为系统电流的直流分量;Vout为输出电压直流分量;带上标的符号为各自状态量的扰动量。
联立式(9)~式(11)得到频域下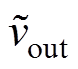 和
和 与占空比
与占空比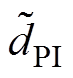 与
与 间的关系如式(12)~式(15)所示。
间的关系如式(12)~式(15)所示。
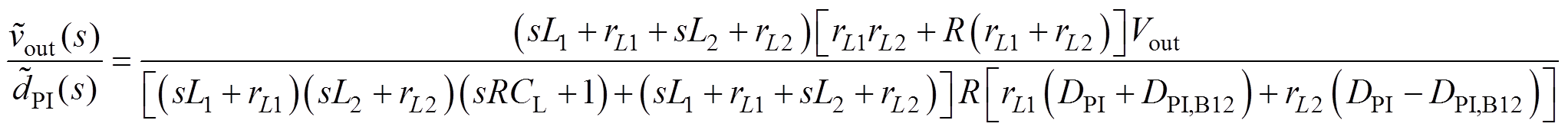 (12)
(12)
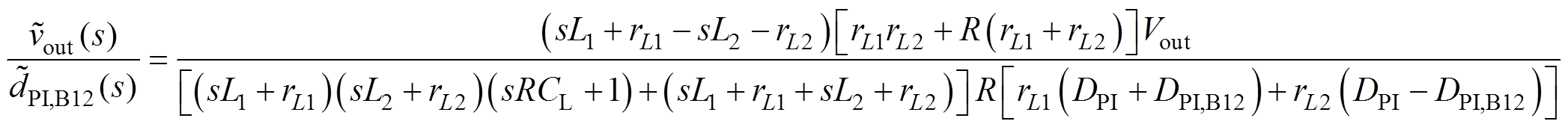 (13)
(13)
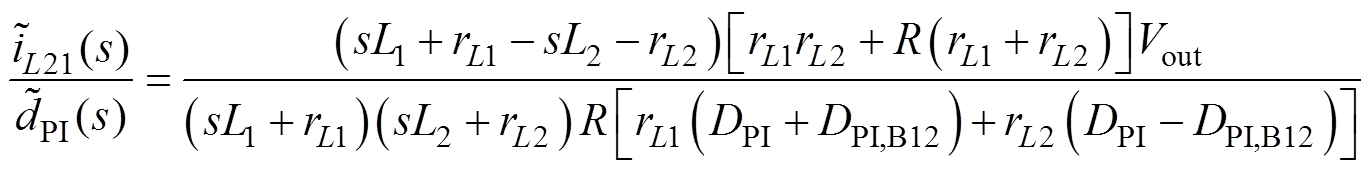 (14)
(14)
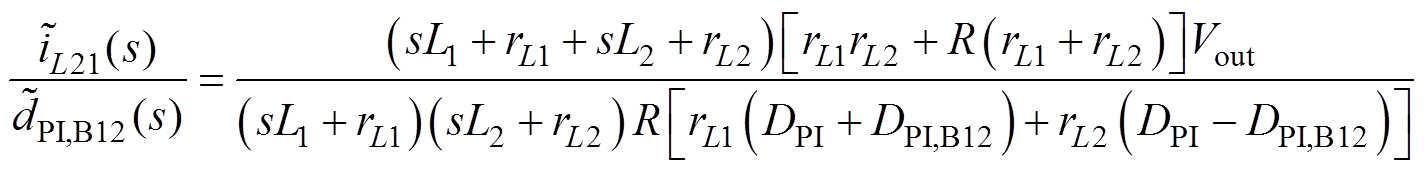 (15)
(15)
理想情况下变换器电感及其等效电阻参数相同,将两相电感及电阻以相同变量进行表示,即
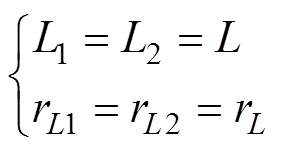 (16)
(16)
当式(16)成立时,两相电流也应该相同,即IL1=IL2=IL。将式(16)分别代入式(12)~式(15),可得
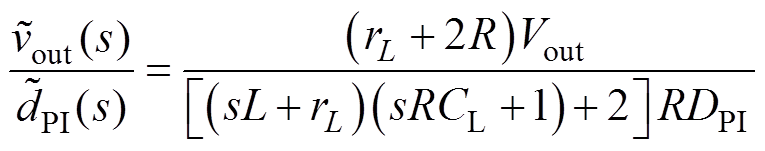 (17)
(17)
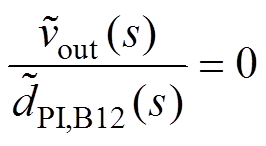 (18)
(18)
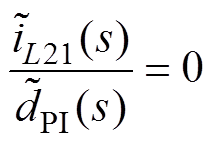 (19)
(19)
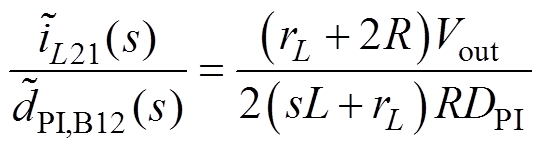 (20)
(20)
由式(18)和式(19)可知,变换器输出电压与两相电流差值不存在控制耦合关系,式(1)中,DPI与DPI,B12的控制彼此独立,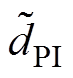 只影响输出电压
只影响输出电压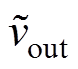 。而均衡占空比
。而均衡占空比 只影响两相电流差值
只影响两相电流差值 。二者是解耦的,因此,各控制闭环可独立设计。
。二者是解耦的,因此,各控制闭环可独立设计。
根据式(17)~式(20)可知,变换器的小信号模型可以看成是以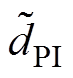 和
和 为输入,
为输入,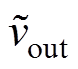 和
和 为输出的双输入双输出系统。因此,再次联立式(9)~式(11),可得输出电压和输入电压关系为
为输出的双输入双输出系统。因此,再次联立式(9)~式(11),可得输出电压和输入电压关系为
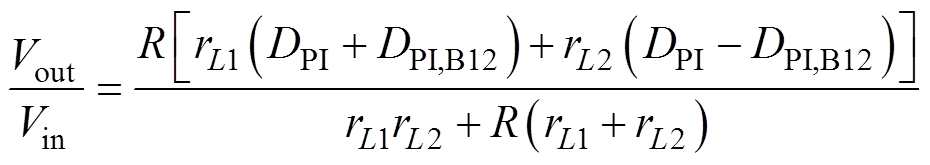 (21)
(21)
由于DPI,B12用于实现电流均衡控制,均衡工况下DPI,B12可忽略,式(21)可简化为
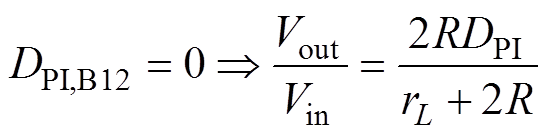 (22)
(22)
理想情况下变换器电感及其等效电阻参数相同,那么忽略电感电阻rL后,式(22)可改写为
 (23)
(23)
系统建模后变换器输入与输出增益与Buck变换器相同,从而验证了式(17)~式(20)小信号模型的准确性,进而从理论推导上证明了本文所提控制策略的正确性。
由于电压闭环与电流均衡控制闭环彼此解耦,根据图6和式(17)可得电压闭环控制框图如图8所示。

图8 电压闭环控制框图
Fig.8 Control block diagram of voltage closed loop
根据控制器的设计原则,中频段对数幅频特性斜率一般为-20dB/dec,并占据充分的带宽,以保证具备合理的相位裕度。电压闭环采用比例积分调节器以满足系统的高频幅值衰减特性,使已校正系统的截止频率下降。根据控制器的设计原则,相位裕度(Phase Margin, PM)大于45°,增益裕度(Gain Margin, GM)为正。其次调节PI控制器的参数,以满足不同的输入电压。最终的参数选择分别为KP= 0.62和KI=9.33。利用表2参数及控制器参数设计值,得到了电压调节控制伯德图,如图9所示。
表2 仿真参数
Tab.2 Simulation parameters

参 数数 值 电感L1, L2/mH1 电感电阻rL1, rL2/mW100 输出电容CL/mF500 负载R/W5 输出电压Vout/V20
在图9中绘制出了输入电压分别是48V和24V时电压调节回路加上比例积分控制器的伯德图,以供比较。
结果表明,得到的GM≈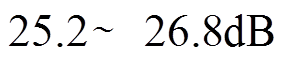 ,PM≈
,PM≈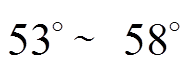 。图中,虚线表示该系统的截止频率。根据伯德图判稳原则,相位裕度大于45°,幅值裕度大于0,所以设计的该电压调节器稳定。
。图中,虚线表示该系统的截止频率。根据伯德图判稳原则,相位裕度大于45°,幅值裕度大于0,所以设计的该电压调节器稳定。
根据式(20)可得均衡控制闭环如图10所示。

图9 电压调节控制的伯德图
Fig.9 Sampling strategy diagram

图10 电流均衡环控制框图
Fig.10 Control block diagram of current balancing closed loop
根据图10可得电流均衡闭环的传递函数为
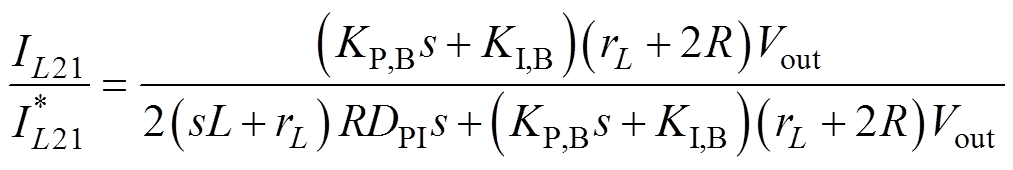 (24)
(24)
令参数比KI,B/KP,B=rL/L后,可以将其化简为一个一阶的低通滤波器,并将其代入式(24)后得
 (25)
(25)
通过选择1kHz的如式(25)所示的低通滤波器,f =KP,BVout/(pL)=1kHz,以此获得电流均衡回路的参数分别为
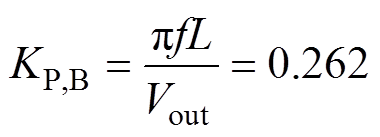 (26)
(26)
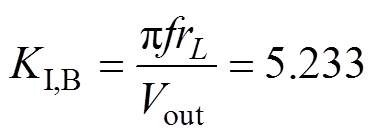 (27)
(27)
为了验证文中提出的基于倍频采样的功率均衡控制策略的有效性,本文搭建了一个小功率物理仿真实验平台如图11所示,元件参数与表2相同。

图11 两相交错并联三电平DC-DC变换器实验平台
Fig.11 The experiment platform for the interleaved two-phase three-level DC-DC converter
Buck模式下的实验波形如图12所示,高压侧电压为48V,负载侧给定电压为24V,系统的动态响应曲线如图12a所示。占空比D1+D2≤1和D1+D2>1时,电感电流iL1、iL2与总电流iD1之间的关系如图12b和图12c所示,采样时刻点已经在图中标出。为了更好地验证均流的性能,在电感L2支路串入了1mH的电感,构造两相参数差异工况。图12d为增加均流环前后,两相电感电流iL1和iL2的波形。如图所示,在未施加均流环时,两相电感电流是不均衡的。在施加均流环5ms后,两相电感电流实现了均衡控制,并稳定运行。Buck模式下突加负载的电感电流响应曲线如图12e所示,在负载突变后,系统经过10ms的调节达到了稳定状态,且具有较快的响应速度。图12f为在采用文献[32]均压策略之后,支撑电容Ch1和Ch2的电压动态变化。
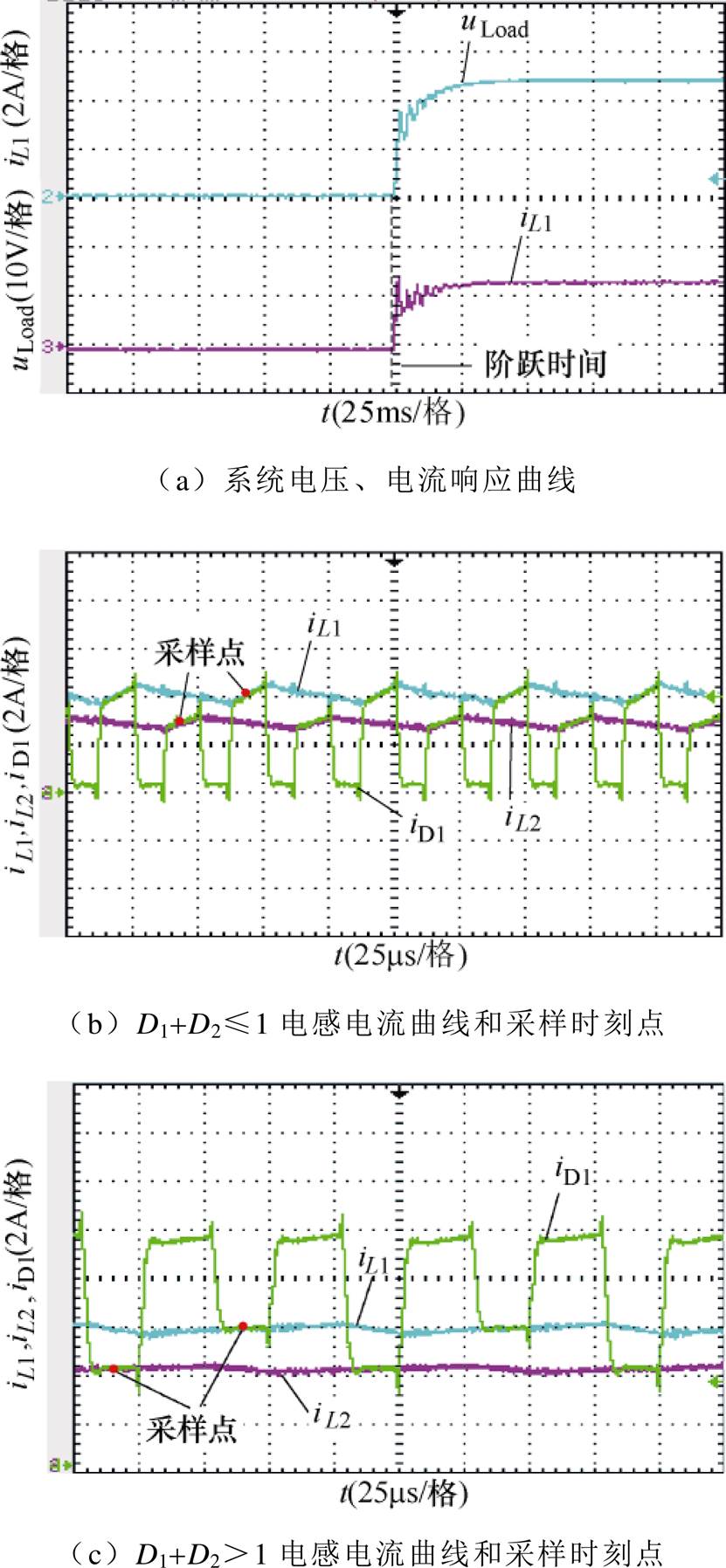

图12 Buck模式实验波形
Fig.12 Buck mode experimental waveforms
Boost模式下的实验波形如图13所示,高压侧负载给定电压为48V,低压侧电源输入为24V,系统的动态响应曲线如图13a所示。由于Boost能量的流动方向与Buck模式相反,所以在占空比D1+D2≤1和D1+D2>1时的电感电流iL1、iL2与总电流iD1之间的关系与Buck模式也相反,如图13b和图13c所示。Boost模式下,在电感L1支路又串入了1mH的电感,均衡效果如图13d所示。在施加均流环5ms后,两相电感电流实现了均衡,并且系统能够稳定运行。Boost模式下突加负载的电感电流响应曲线如图13e所示,与Buck模式相比,Boost模式在负载突变后系统调节时间较长,但经过短暂的波动后系统仍能达到稳定状态。同样图13f表示支撑电容电压的均压效果。
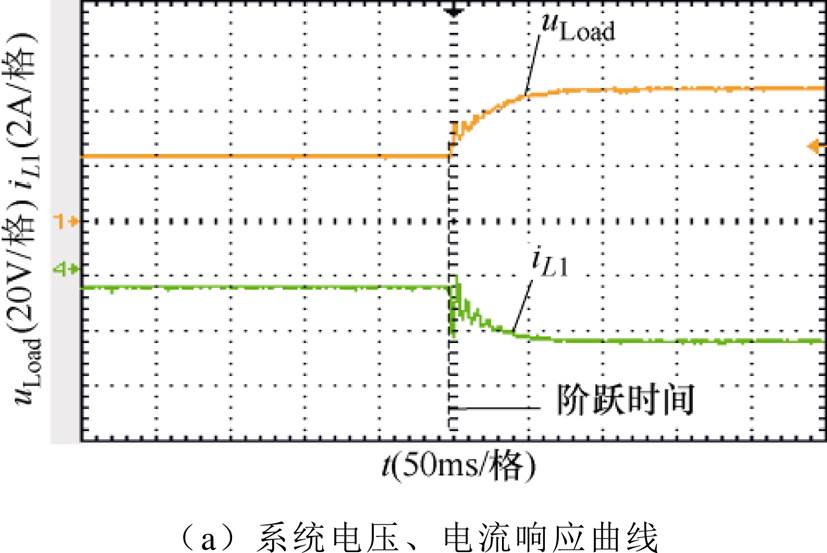
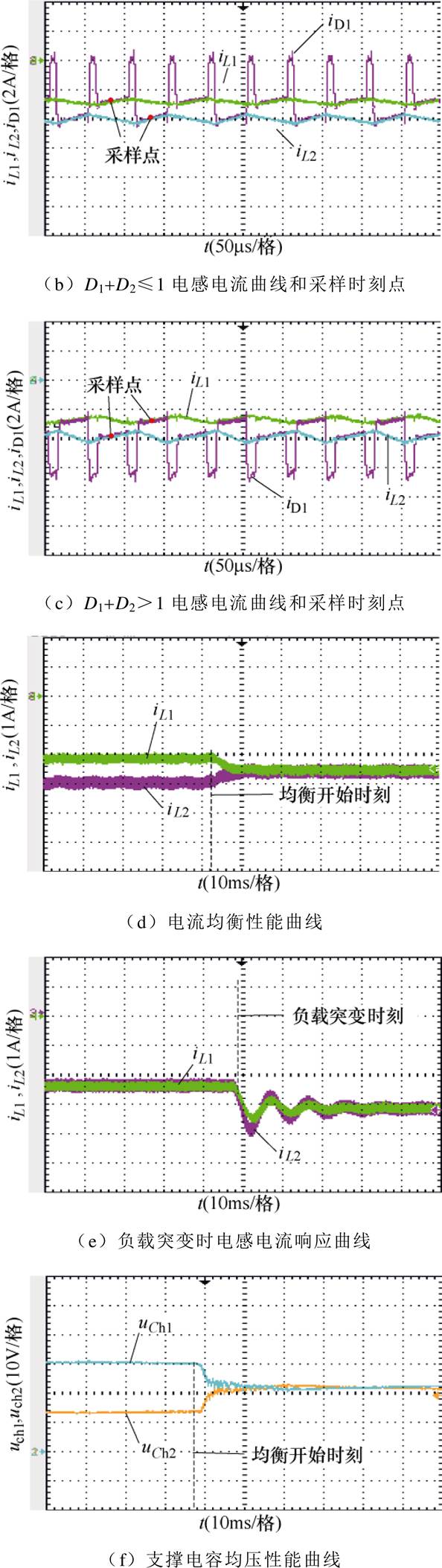
图13 Boost模式实验波形
Fig.13 Boost mode experimental waveforms
通过上述实验的结果可以证明,本文所提出的基于倍频采样的功率均衡解耦控制方法都具有良好的性能。变换器在Buck和Boost模式下不仅能够实现良好的稳压和均流控制,同时在负载突变情况下也具有良好的稳定性。
本文提出了一种两相交错并联三电平双向直流变换器功率均衡解耦控制策略,使变换器的主功率控制与相间功率均衡控制实现了解耦。同时,为减少电流传感器的使用,通过分析变换器输入、输出电流特征,提出总电流分时倍频采样策略,将电流传感器数量较传统方案减少一倍。文中利用等效两电平分析方法建立了变换器的小信号模型,从理论角度对所提控制策略进行了全面的分析、验证,并给出了控制器参数的设计方法。通过小功率储能实验平台的验证结果可知,该策略具备良好的功率均衡能力,且能够有效减少电流传感器的使用。
参考文献
[1] 丁杰, 高双, 赵世伟, 等. 基于耦合电感的对称式交错并联低输入电流纹波高增益DC-DC变换器[J]. 电工技术学报, 2021, 36(7): 1507-1515.
Ding Jie, Gao Shuang, Zhao Shiwei, et al. Sym- metrical interleaved low input current ripple high step-up DC-DC converter based on coupled indu- ctor[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1507-1515.
[2] 孙玉树, 杨敏, 师长立, 等. 储能的应用现状和发展趋势分析[J]. 高电压技术, 2020, 46(1): 80-89.
Sun Yushu, Yang Min, Shi Changli, et al. Analysis of application status and development trend of energy storage[J]. High Voltage Engineering, 2020, 46(1): 80-89.
[3] 金科, 杨孟雄, 阮新波. 三电平双向变换器[J]. 中国电机工程学报, 2006, 26(18): 41-46.
Jin Ke, Yang Mengxiong, Ruan Xinbo. Three-level bidirectional DC-DC converter[J]. Proceedings of the CSEE, 2006, 26(18): 41-46.
[4] Dusmez S, Hasanzadeh A, Khaligh A, et al. Com- parative analysis of bidirectional three-level DC-DC converter for automotive applications[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 3305-3315.
[5] 阮新波, 危健, 薛雅丽. 非隔离三电平变换器中分压电容均压的一种方法[J]. 中国电机工程学报, 2003, 23(10): 27-31.
Ruan Xinbo, Wei Jian, Xue Yali. A method to balance the voltage of the divided capacitors in non-isolated three-level converters[J]. Proceedings of the CSEE, 2003, 23(10): 27-31.
[6] 鲁思兆, 吴雷, 李思奇, 等. 零电压开关N型交错并联三电平双向DC-DC 变换器[J]. 电工技术学报, 2020, 35(2): 461-470.
Lu Sizhao, Wu Lei, Li Siqi, et al. Zero voltage switching N-type interleaved three-level bidire- ctional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 461-470.
[7] 王朝强, 曹太强, 郭筱瑛, 等. 三相交错并联双向DC-DC变换器动态休眠控制策略[J]. 电工技术学报, 2020, 35(15): 3214-3223.
Wang Chaoqiang, Cao Taiqiang, Guo Xiaoying, et al. Dynamic dormancy control strategy of three-phase staggered parallel bidirectional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3214-3223.
[8] 姚志刚, 张煜欣, 刘涛, 等. 三相交错并联三电平DC-DC变换器的ZVS控制[J]. 中国电机工程学报, 2020, 40(13): 4256-4266.
Yao Zhigang, Zhang Yuxin, Liu Tao, et al. ZVS control of an interleaved three-phase three-level DC-DC converter[J]. Proceedings of the CSEE, 2020, 40(13): 4256-4266.
[9] 孙孝峰, 袁野, 王宝诚, 等. 零电压开关三电平Buck-Boost双向变换器[J]. 电工技术学报, 2018, 33(2): 293-300.
Sun Xiaofeng, Yuan Ye, Wang Baocheng, et al. Zero-voltage switching three-level Buck-Boost bidire- ctional converter[J]. Transactions of China Electro- technical Society, 2018, 33(2): 293-300.
[10] Tan Longcheng, Wu Bin, Rivera S, et al. Com- prehensive DC power balance management in high-power three-level DC-DC converter for electric vehicle fast charging[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 89-100.
[11] Lu Sizhao, Mu Mingkai, Jiao Yang, et al. Coupled inductors in interleaved multiphase three-level DC- DC converter for high-power applications[J]. IEEE Transactions on Power Electronics, 2020, 31(1): 120-134.
[12] 苏冰, 王玉斌, 王璠, 等. 基于耦合电感的多相交错并联双向DC-DC变换器及其均流控制[J]. 电工技术学报, 2020, 35(20): 4337-4349.
Su Bing, Wang Yubin, Wang Fan, et al. Multi-phase interleaved bidirectional DC-DC converter with coupled inductors and current sharing control strategy[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4337-4349.
[13] Eirea G, Sanders Seth R. Phase current unbalance estimation in multiphase buck converters[J]. IEEE Transactions on Power Electronics, 2008, 23(1): 137-143.
[14] Gordillo J, Aguilar C. A simple sensorless current sharing technique for multiphase DC-DC buck converters[J]. IEEE Transactions on Power Elec- tronics, 2017, 32(5): 3480-3489.
[15] 李山, 赵瑜, 郭强, 等. 三相交错并联双向直流变换器无电流传感器均流控制[J]. 高电压技术, 2021, 47(3): 894-902.
Li Shan, Zhao Yu, Guo Qiang, et al. Sensorless current sharing control of three-phase interleaved bidirectional DC converter[J]. High Voltage Engin- eering, 2021, 47(3): 894-902.
[16] 张军明, 谢小高, 吴新科, 等. DC/DC模块有源均流技术研究[J]. 中国电机工程学报, 2005, 25(19): 31-36.
Zhang Junming, Xie Xiaogao, Wu Xinke, et al. Research on active current-sharing methods for DC/DC converters[J]. Proceedings of the CSEE, 2005, 25(19): 31-46.
[17] Wang Haojie, Han Minxiao, Han Renke, et al. A decentralized current-sharing controller endows fast transient response to parallel DC-DC converters[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 4362-4372.
[18] Gordillo J, Aguilar C. A simple sensorless current sharing technique for multiphase DC-DC Buck con- verters[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3480-3489.
[19] Lee P W, Lee Y S, Cheng D K W, et al. Steady-state analysis of an interleaved Boost converter with coupled inductors[J]. IEEE Transactions on Industrial Electronics, 2000, 47(4): 787-795.
[20] Chae Y S, Song Y J, Park S K, et al. Digital current sharing method for parallel interleaved DC-DC converters using input ripple voltage[J]. IEEE Transa- ctions on Industrial Informatics, 2012, 8(3): 536-544.
[21] Singh R P, Khambadkone A M. Current sharing and sensing in N-paralleled converters using single current sensor[J]. IEEE Transactions on Industry Applications, 2010, 46(3): 4117-4125.
[22] Cho Y H, Koran A, Miwa H, et al. An active current reconstruction and balancing strategy with DC-link current sensing for a multi-phase coupled-inductor converter[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1697-1705.
[23] Han J H, Song J H. Phase current-balance control using DC-link current sensor for multiphase converters with discontinuous current mode considered[J]. IEEE Transactions on Industry Electronics, 2016, 63(7): 4020-4030.
[24] Liu Guanliang, Wang Mengqi, Zhou Weiyang, et al. A sensorless current balance control method for interleaved Boost converters based on output voltage ripple[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 7138-7149.
[25] Huang W, Qahouq J A A. Input voltage ripple-based sensorless current sharing autotuning controller for multiphase DC-DC converters[J]. IEEE Transactions on Industry Applications, 2016, 52(5): 4117-4125.
[26] Jang Y, Jovanovic M M. Interleaved Boost converter with intrinsic voltage-doubler characteristic for universal-line PFC front end[J]. IEEE Transactions on Power Electronics, 2007, 22(4): 1394-1401.
[27] 赵玲玲, 吴云峰, 陈章勇, 等. 全占空比范围电容串接式交错并联Boost变换器均流策略研究[J]. 中国电机工程学报, 2020, 40(7): 2330-2339.
Zhao Lingling, Wu Yunfeng, Chen Zhangyong, et al. Study on current sharing strategy about series capacitor interleaved Boost converter in full-duty range[J]. Proceedings of the CSEE, 2020, 40(7): 2330-2339.
[28] Villarruel-Parra A, Forsyth A J. Enhanced average- value modeling of interleaved DC-DC converters using sampler decomposition[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2290-2299.
[29] Ho K M, Yeh C A, Lai Y S. Novel digital-controlled transition current-mode control and duty com- pensation techniques for interleaved power factor corrector[J]. IEEE Transactions on Power Electronics, 2010, 25(12): 3085-3094.
[30] 章治国, 徐堂意, 向林朋, 等. 多相交错并联自均流高增益DC/DC变换器及其控制策略[J]. 电机与控制学报, 2021, 25(1): 27-37.
Zhang Zhiguo, Xu Tangyi, Xiang Linpeng, et al. Multi-phase interleaved bidirectional DC-DC con- verter with coupled inductors and current sharing control strategy[J]. Electric Machines and Control, 2021, 25(1): 27-37.
[31] Jovanovic D P, Broadmeadow M A H, Taylor Y Y, et al. Decoupling of current balancing and reference tracking control in parallel interleaved converters[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4286-4295.
[32] Ruan Xinbo, Li Bin, Chen Qianhong, et al. Funda- mental considerations of three-level DC-DC con- verters: topologies, analyses, and control[J]. IEEE Transactions on Circuits and Systems, 2008, 11(55): 1255-1262.
Decoupled Power-Balancing Control Strategy for Two-Phase Interleaved Parallel Bidirectional DC Converter Based on Frequency-Doubling Sampling
Abstract A decoupled power-balancing control strategy for the two-phase interleaved parallel three-level bidirectional DC-DC converter is proposed in this paper, and the use of current sensors is effectively reduced. By analyzing the working principle of topology, an equivalent two-level analysis method under the two-phase interleaved parallel topology is obtained. On this basis, a decoupled power-balancing control strategy based on total current time-sharing and frequency-doubling sampling is proposed to fully decouple the voltage regulation of the converter from the current-balancing control between phases. In addition, the four channels of current sampling required by the conventional balance control are reduced to two channels, which simplifies the control structure. A small signal model based on the equivalent topology is established, and the specific design scheme of the controller parameters is given. Finally, the proposed control strategy is verified by a physical experiment.
keywords:Interleaved parallel, three-level bidirectional DC converter, decoupled power- balancing control, frequency-doubling sampling strategy
DOI: 10.19595/j.cnki.1000-6753.tces.211057
中图分类号:TM46
中国博士后科学基金(2020M681692)和江苏省自然科学基金(BK20200623)资助项目。
收稿日期 2021-07-15
改稿日期 2021-09-23
樊启高 男,1986年生,副教授,硕士生导师,研究方向为新能源发电及机电一体化技术。E-mail: qgfan@jiangnan.edu.cn
毕恺韬 男,1989年生,讲师,研究方向为大功率储能功率变换技术。E-mail: bkt1989@163.com(通信作者)
(编辑 陈 诚)