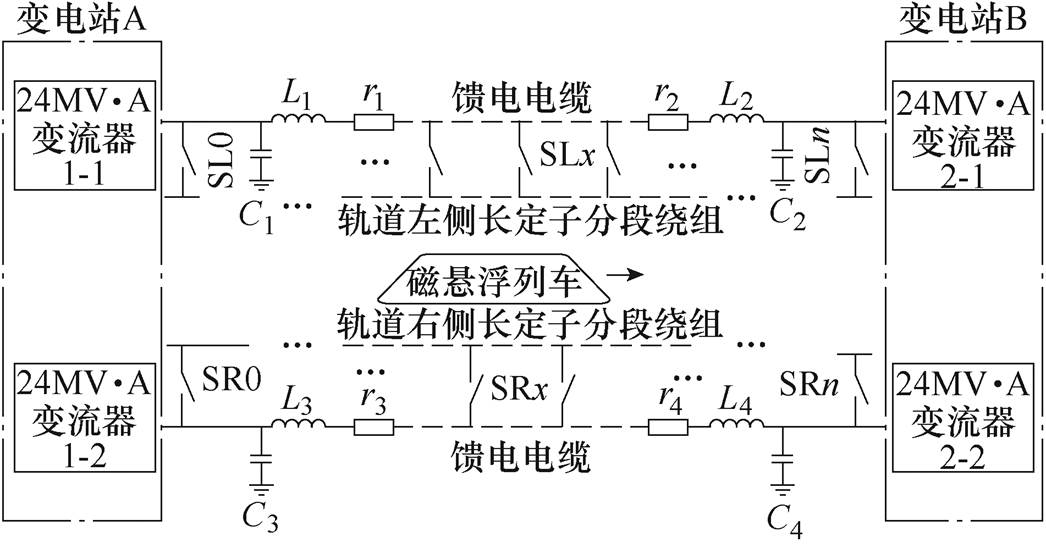
图1 磁悬浮列车的牵引供电系统
Fig.1 Traction power supply system of maglev train
摘要 高速磁悬浮列车用长定子直线同步电机工作在双端供电模式时，是多变量、非线性、强耦合系统。传统的线性控制方法对参数摄动较为敏感，因此该文分析了参数摄动对电流环控制性能的影响并提出一种基于积分滑模的电流控制策略。该策略将状态变量的积分项引入到滑模面中，避免了高频噪声的干扰，并改进了指数趋近律以削弱抖振，使得电流的动态跟随性能和抗参数摄动性能都得到改善。硬件在环实验验证了该策略与传统线性控制策略相比，可提高磁悬浮列车在定子段换步过程中的电流跟随性能，并且对电机参数摄动具有较强的鲁棒性。
关键词：高速磁悬浮列车 双端供电 参数摄动 积分滑模控制
高速磁悬浮列车是目前世界上最快的陆上交通工具，它采用长定子直线同步电机作为牵引系统和悬浮系统[1]，所以，对长定子直线同步电机的高性能控制是高速磁悬浮列车系统的一项核心技术。高速磁悬浮列车的牵引供电系统如图1所示，为了满足高速运行的要求，磁悬浮列车在低速时采用单端供电模式，高速时采用双端供电模式。双端供电模式相当于两端的功率模块并联给定子绕组供电，可以提供足够大的牵引力，并且降低了每台变流器单元的设计容量[2]。
图1 磁悬浮列车的牵引供电系统
Fig.1 Traction power supply system of maglev train
列车在定子段换步时采用了两步法，换步一侧的定子电流会降为零再增加。当磁悬浮列车运行在双端模式时，是多变量、强耦合、非线性系统。在列车高速运行时，电机参数极容易受到列车运行环境的影响。不同的电流、不同的工作温度以及不同的工作频率等变化也会给电机和馈电电缆的电阻、电感造成较大的摄动变化，而系统模型的建立又依赖于这些参数，所以参数摄动必然会影响系统的动静态控制性能，并且带来大量的电流谐波，造成列车牵引力波动[3]。因此，需要对磁悬浮列车用长定子直线同步电机在双端供电模式下的高性能控制策略展开研究。
高速磁悬浮列车是一个大惯量系统，电流内环的控制是电机控制的核心。对于电流环控制，要求其具有较快的响应速度和较高的鲁棒性。传统的比例积分控制虽然具有算法简单、参数易调节等优点，但是在换步时不能满足快速响应的要求，在电机参数摄动时容易产生电流谐波，存在抗扰性能和跟踪性能相矛盾的缺点，所以不能满足高性能电机控制的要求。文献[3]采用基于自抗扰的电流控制策略，提高了系统的鲁棒性和响应速度，但是在实际控制中还存在着算法复杂和参数整定优化困难等问题；文献[4]在PI控制器的基础上采用电压前馈解耦控制（Voltage Feedforward Decoupling Control, VFDC），与传统的PI控制相比，改善了系统的动态性能，但由于前馈项依赖于电机参数，在磁悬浮列车运行过程中，参数摄动对系统动态性能的影响较大；文献[5]采用基于内模的滑模电流解耦控制器，对参数摄动具有较好的鲁棒性，但是电流的动态跟随性能没有明显改善；文献[6]采用模型预测电流控制，获得了较高的动态响应，但是此方法依赖于电机准确的数学模型，需要结合其他算法提高其模型不确定时的鲁棒性。
滑模变结构控制具有对内部参数摄动和外部扰动不敏感、鲁棒性强、动态响应快并且易于实现等优点，故在电机电流控制中有很好的应用前景[7]。滑模变结构控制本身存在抖振的固有问题，因此，在采用滑模变结构控制进行电流环控制时，如何消除抖振也成为了控制策略的关键。文献[7-8]通过改进趋近律以提高趋近速度，同时也削弱了抖振；文献[9]采用基于快速终端滑模永磁同步电机电流鲁棒控制。虽然上述方法能够提高系统的鲁棒性和响应速度，但是设计滑模面时会引入状态量的微分，这一过程会引入高频噪声，从而影响系统的动态性能。文献[10]引入了积分项至滑模面中；文献[11]在永磁同步电机的控制中引入了积分滑模控制（Integral Sliding Mode Control, ISMC）方法并体现了其算法的鲁棒性；文献[12-13]将积分滑模面引入到永磁同步电机的速度外环控制器设计之中，提高了系统的鲁棒性和动态跟随性能；文献[14]针对永磁直线同步电机设计了直接推力的积分滑模控制器；文献[15]将积分滑模控制与负载观测器相结合应用于永磁同步电机，抑制了由负载转矩引起的系统扰动。
本文针对高速磁悬浮列车在双端供电模式下，参数摄动时电流波动大、定子段换步过程中跟踪性能差的问题，提出一种基于积分滑模的牵引控制策略，应用到长定子直线同步电机的电流环控制之中，并对传统的滑模控制策略进行改进，提高了系统鲁棒性和动态响应性能，降低了参数摄动时的电流波动并且削弱了抖振。最后基于RT-Lab的高速磁悬浮半实物系统硬件在环实验，验证了算法的正确性。
磁悬浮列车在高速运行时，需要采用双端并联的供电模式，其等效原理如图2所示。图中，ua、ub、uc和ia、ib、ic分别为长定子直线同步电机的定子绕组端部电压和定子绕组三相电流；ua1、ub1、uc1和ua2、ub2、uc2分别为两台变流器的输出电压；ia1、ib1、ic1和ia2、ib2、ic2分别为两台变流器的输出电流。
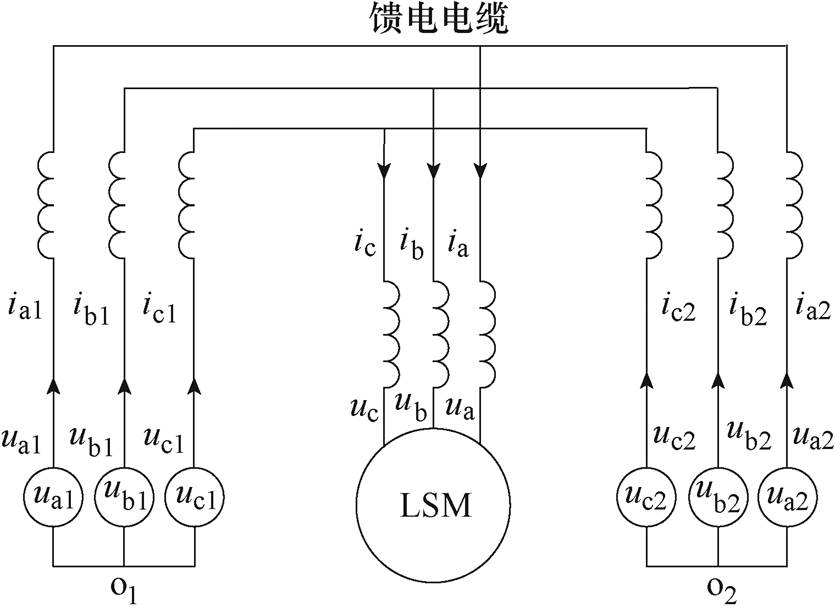
图2 长定子直线同步电机双端并联供电等效电路
Fig.2 Equivalent circuit of dual-terminal parallel power supply for long-stator linear synchronous motor
根据图2并结合参考文献[3]中所推导，对于双端供电下的高速磁悬浮列车系统而言，如果将两台变流器看成一个供电系统，以两台变流器输出的电压之和与电压之差作为输入，以两台变流器共同输出到电机的总电流和环流作为状态变量，可得到此种模式下的状态方程为
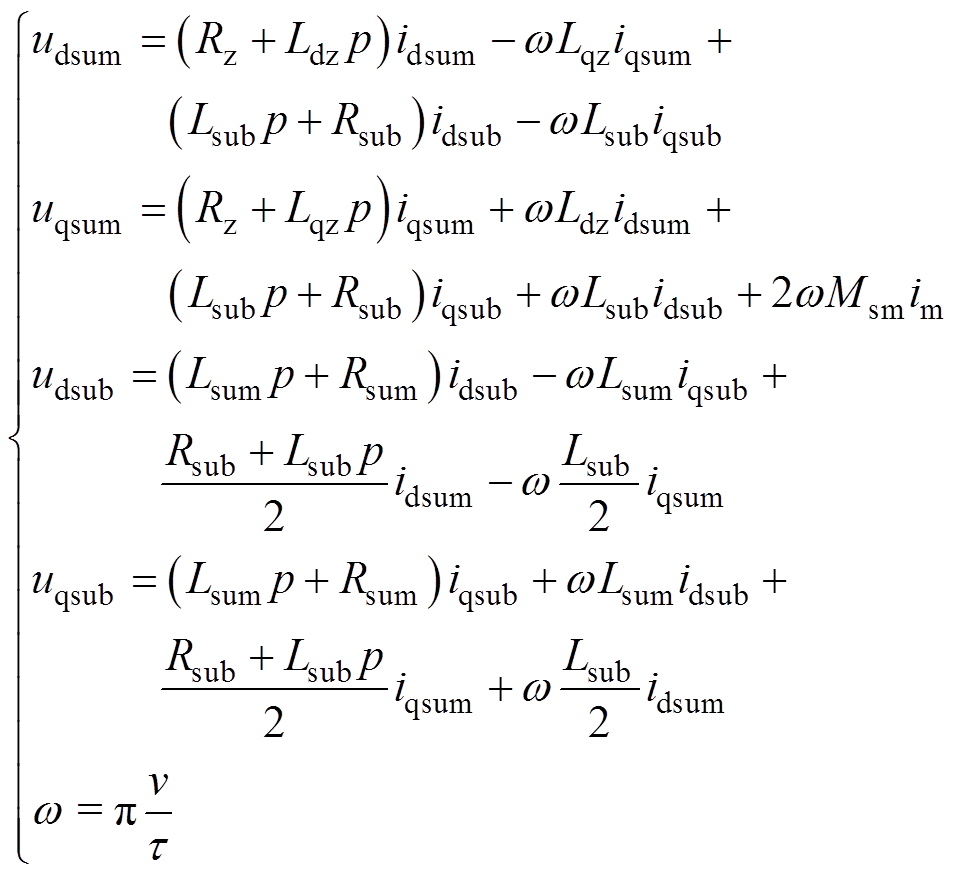（1）
其中
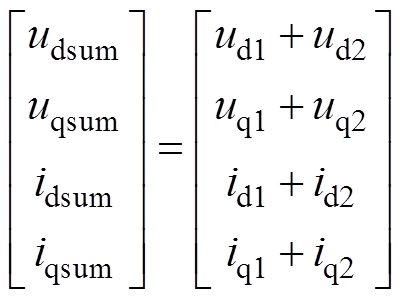
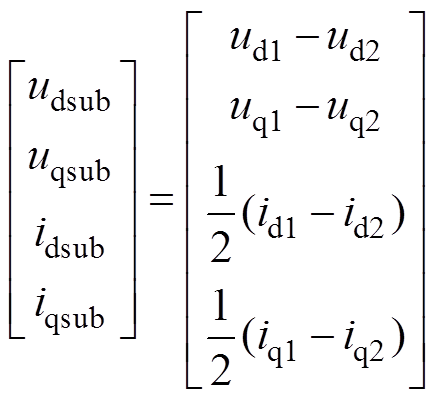
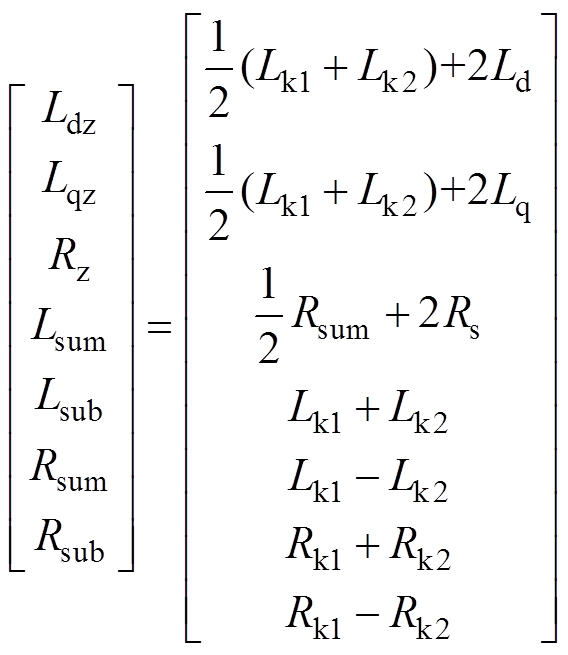
式中，udsum、uqsum、udsub、uqsub为两台变流器输出的电压之和与电压之差在dq坐标系下的分量；idsum、iqsum、idsub、iqsub为两台变流器共同输出到电机的总电流和两台变流器之间的环流在dq坐标系下的分量；Ld、Lq为定子绕组在dq坐标系下的电感；Rk1、Rk2、Lk1、Lk2为两侧馈电电缆的电阻和电感；Rs为定子电阻；Rsum、Lsum分别为两端馈电电缆电阻之和与电感之和；Rsub、Lsub分别为两端馈电电缆电阻之差与电感之差；Rz、Ldz、Lqz分别为式中电阻、电感项的合并项；Msm为定子与转子间的互感；im为励磁电流；ud1、uq1、id1、iq1和ud2、uq2、id2、iq2分别为第一台变流器和第二台变流器的输出电压和输出电流在dq坐标系下的分量；v为列车速度；t 为极距；w 为动子角速度；p为微分算子。
由式（1）可知，直接调节两台变流器输出电压之和与输出电压之差从而控制变流器输出到电机的总电流和环流，使得电机总电流环和环流环的控制器可以独立设计。状态方程中的耦合项也被简化，耦合项分为与电机参数和励磁电流有关的电机内部耦合项和与馈电电缆参数有关的馈电电缆耦合项。
在双端供电模式下磁悬浮列车运行过程中，电机总定子电流较大而环流很小。假设悬浮和励磁系统扰动很小，将系统参数摄动带来的影响归入扰动，并且主要考虑电机总定子电流，系统状态方程式（1）可表示为
（2）
其中
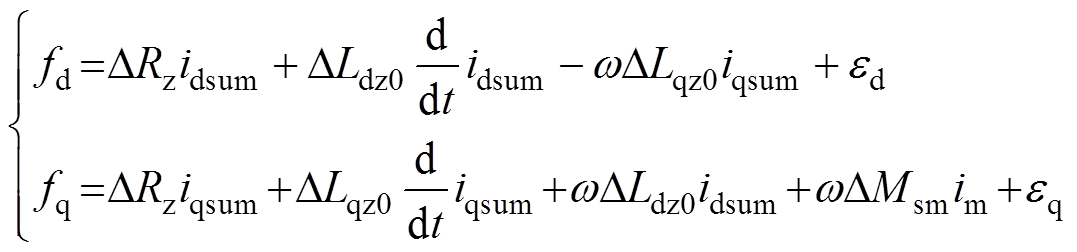
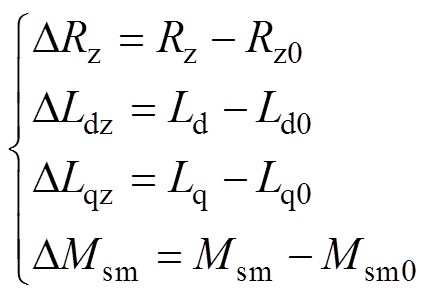
式中，fd、fq分别为d、q轴的总扰动项；下标“0”为对应参数的初始估算值；DRz为电阻参数摄动值；DLdz和DLqz为电感参数摄动值；DMsm为互感参数的摄动值；ed和eq分别为包含了环流项和参数摄动带来的d、q轴不确定项。
结合式（2），可得到如图3所示的双端供电模式下考虑扰动的电机电流内环模型框图。
由图3可知，电机电流内环具有时变、非线性的特点，且存在耦合与扰动。
图3 考虑扰动的电机电流内环模型框图
Fig.3 Block diagram of the inner loop model considering the disturbance of the motor current
由式（2）可知，电流内环扰动与电机参数摄动和电流环状态量有关。
忽略不确定项ed和eq带来的影响，重点分析扰动项fd和fq中参数摄动带来的影响，将式（2）对时间t求微分可得
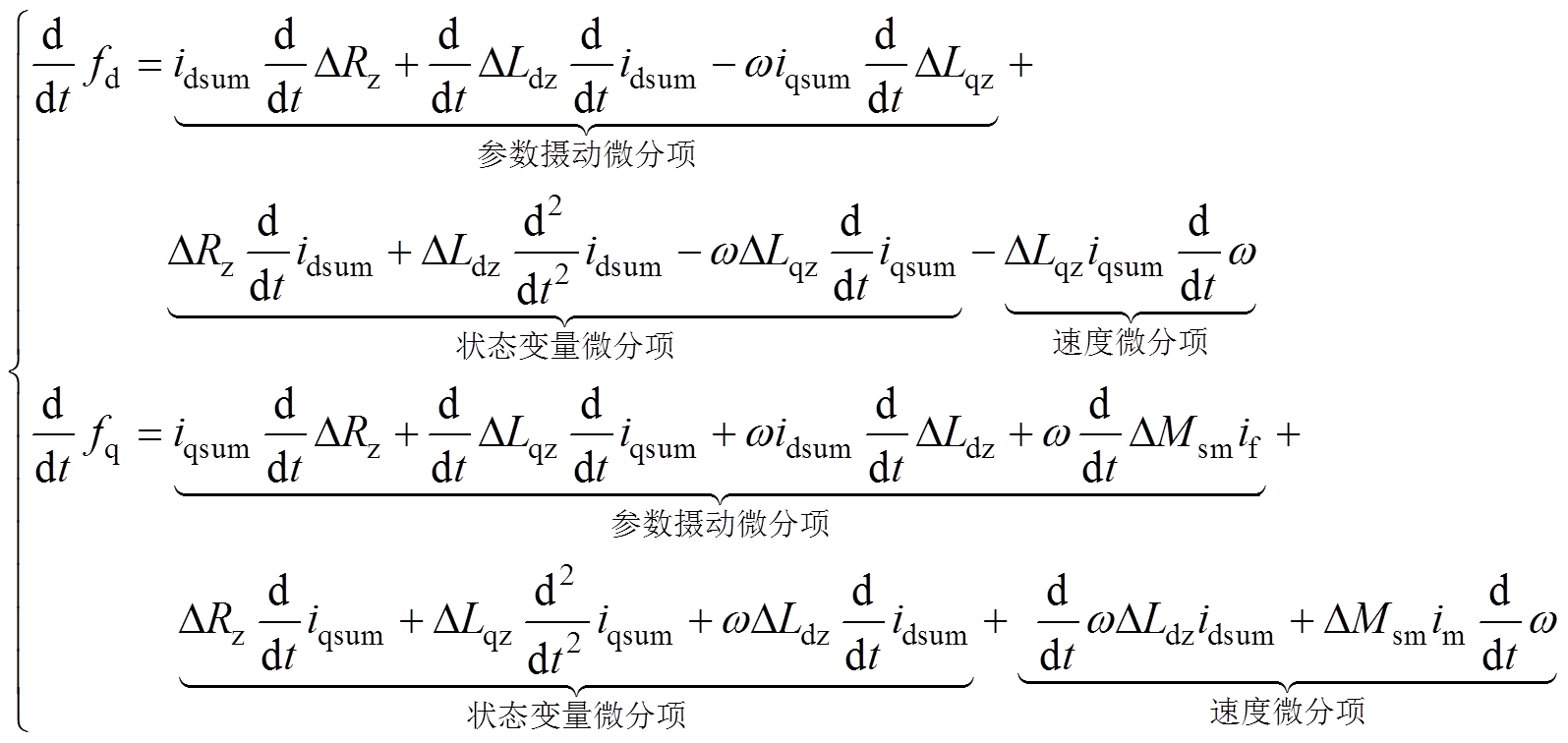（3）
由式（3）分析可知，电流环扰动项fd和fq的变化率主要由参数摄动微分项、状态变量微分项和速度微分项组成。另外，高速磁悬浮列车是一个大惯量系统，速度变化率很小，并且假设d轴电流的值很小，则式（3）可简化为
（4）
由式（4）可知，在电感参数变化时和定子段换步时，d轴电流扰动变化显著；在电感和电阻参数摄动时和定子段换步时，q轴电流扰动变化显著。此外，由于d轴电流扰动变化依赖于速度，所以列车在高速运行中，d轴电流扰动变化将更为剧烈。此时再结合式（3）中q轴的状态变量微分项中idsum的微分项，d轴电流的显著变化将加剧电感摄动对q轴电流的影响，并随着速度上升而加大。同时也可以分析得到，若d轴电流控制得很小，电阻摄动对d轴电流影响也很小。
根据上述分析，参数摄动对电流的影响可以归结为：①列车在定子段换步时，dq轴电流均有扰动变化；②电感参数摄动时，dq轴电流均有扰动变化，且d轴电流扰动随着列车速度上升而更为剧烈；③电阻参数摄动时，q轴电流有扰动变化而d轴电流变化很小；④电感参数摄动比电阻参数摄动对q轴电流的扰动变化更显著。
另外，当上述理想条件的假设不能满足时，扰动的动态变化将更为复杂。
滑模控制是一种用于非线性系统的控制方法，使系统按照预定的滑动模态的状态轨迹进行运动，又称滑模变结构控制。由于滑动模态可以人为设计而与控制对象的参数和扰动无关，这使得该控制策略具有响应速度快、动态性能好、对参数变化和外部扰动不敏感、实现简单等优点[16-18]。
积分滑模面是一种新型滑模面，通过在滑模中引入积分环节，在有限时间内系统状态将迅速地收敛至滑动模态的预定轨迹，从而提高了滑模控制的收敛速度并减小跟踪误差，避免了电流的微分项带来的高频噪声。选取积分滑模面为
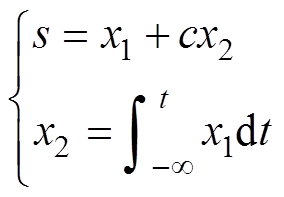（5）
式中，s为滑模面的切换函数；c为积分常数；x1和x2为系统的状态变量。
滑模运动包括趋近运动和滑模运动两个过程，系统从任意初始状态趋向滑模切换面的过程称为趋近运动。其中，指数趋近律能更好地削弱抖振[16]，有
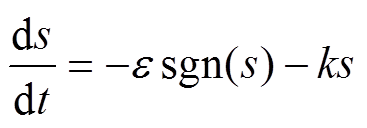（6）
式中，-ks为指数趋近项且k＞0，使趋近过程中趋近速度从一较大值逐步减小至零，从而缩短了趋近时间；-esgn(s)为等速趋近项，e 为符号函数sgn(s)的开关增益且e＞0，使当s接近于零时，趋近速度是e 而不是零，可以保证到达滑动模态的时间是有限的，抖振也来源于此项。
为了保证快速趋近的同时削弱抖振，选择参数时应增大k并且减小e。
式（6）所表示的传统的指数趋近律中，增大e 会在加快收敛速度的同时增强抖振；减小e 会削弱滑动模态的抖振，但是收敛速度变慢。
本文针对上述问题，对传统的指数趋近律进行改进，有
（7）
对比式（6）可知，改进型指数趋近律的等速趋近项中增加了滑模面的绝对值。当系统状态的运动离滑模面较远时，|s|较大，运动点将以更快的速度趋近滑动模态；接近滑模面时，|s|减小，等速趋近项与指数趋近项的共同作用下以更低的速度平滑地进入滑模面，同时运动点的抖振振幅将衰减，最终稳定于原点。
采用饱和函数替代控制率中的符号函数可以进一步削弱抖振，有
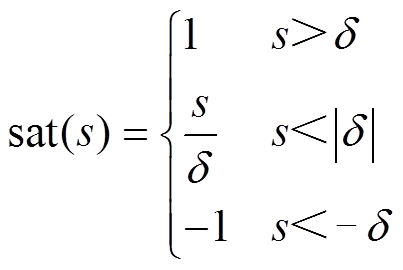（8）
式中，d 为饱和宽度。
最终的改进型指数趋近律为
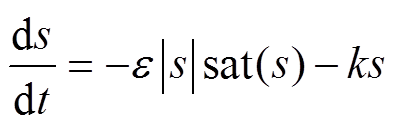（9）
为了证明系统满足滑模到达条件且稳定，给定李雅普诺夫函数为
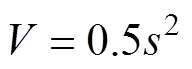（10）
对式（10）求导，由于sat(s)和s的正负同号且考虑到e、k＞0，当s≠0时，可推出
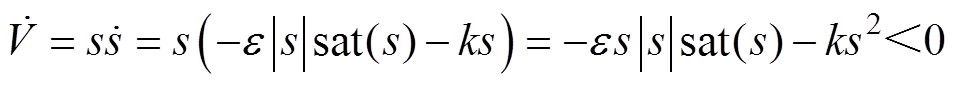（11）
综上所述，即使系统参数摄动、外部干扰或其他噪声等扰动的存在对滑模面的切换函数s(x)的大小产生影响，改进型指数趋近律总是满足滑模控制的可达性条件，保证了系统可以进入滑动模态且稳定，具有强鲁棒性[19]。
根据式（1）所建立的电机总电流的状态方程，取d轴电流环状态变量为
（12）
式中，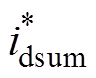
为d轴电流参考值。
结合式（1）、式（2）并忽略环流项，对式（12）求微分，有
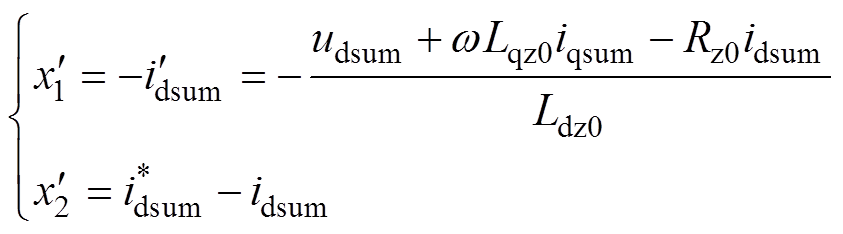（13）
选择d轴电流控制器的滑模面函数为式（5），结合式（13）并对式（5）进行求导，有
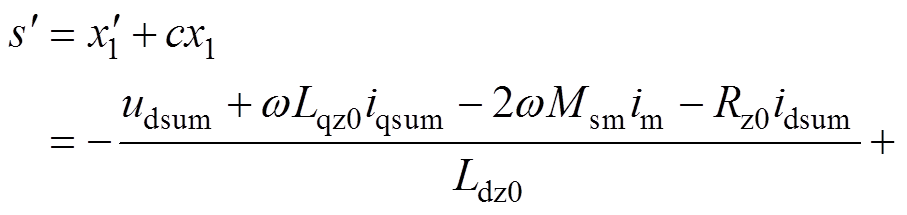
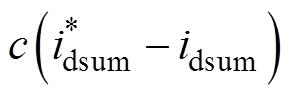（14）
由式（9）、式（14）得d轴电流控制器的控制律为
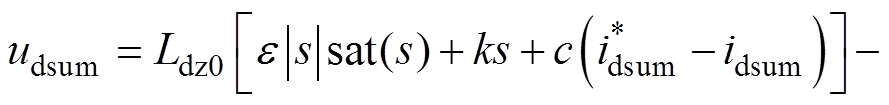
（15）
同理，可推出q轴电流控制器的控制律为
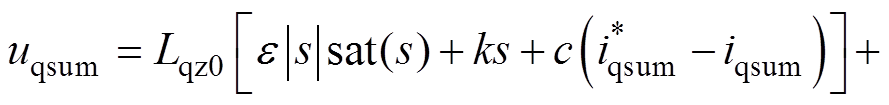
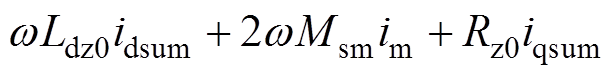（16）
综上所述，基于积分滑模电机总电流控制的速度电流双闭环控制框图如图4所示。
为了验证本文所设计控制器的有效性，在基于RT-Lab的高速磁悬浮半实物系统上进行了硬件在环实验，所用的长定子直线电机参数见表1。
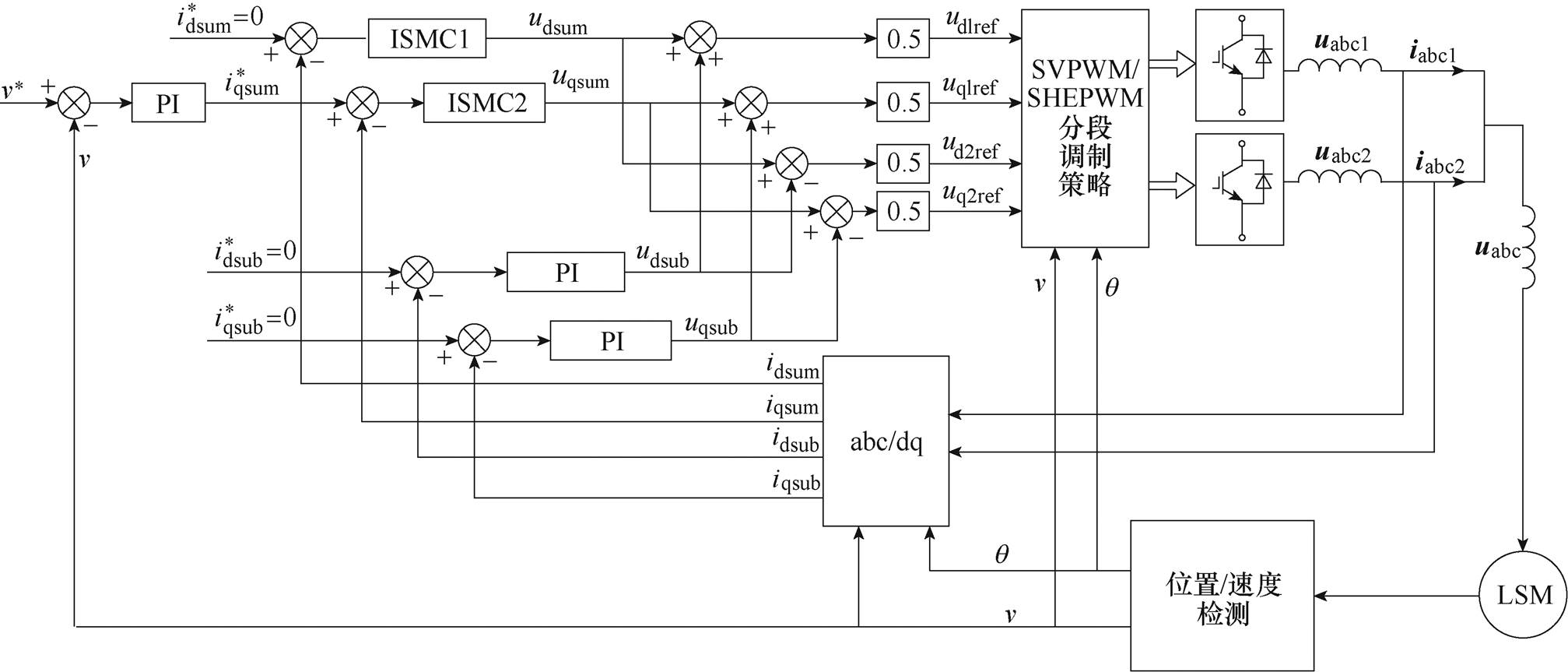
图4 基于积分滑模总电流控制的速度电流双闭环控制框图
Fig.4 Block diagram of speed current double closed loop control based on integral sliding mode total current control
表1 长定子直线电机参数
Tab.1 Long stator linear motor parameters
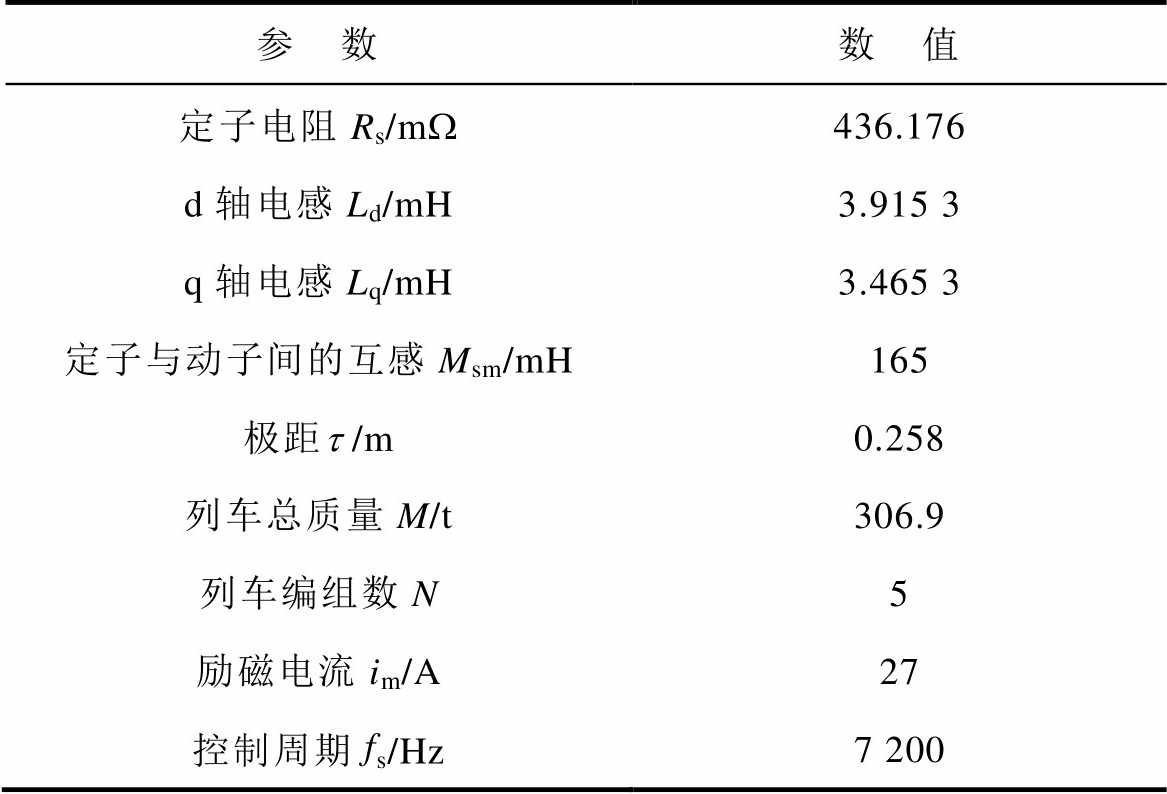
参 数数 值 定子电阻Rs/mW436.176 d轴电感Ld/mH3.915 3 q轴电感Lq/mH3.465 3 定子与动子间的互感Msm/mH165 极距t /m0.258 列车总质量M/t306.9 列车编组数N5 励磁电流im/A27 控制周期fs/Hz7 200
另外，在双端供电模式下的磁悬浮列车在行驶过程中，两端馈电电缆的参数随着列车行驶里程和电流的频率实时变化，馈电电缆的电阻和电感的计算公式[20]分别为
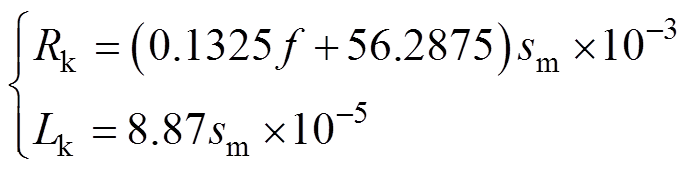（17）
其中
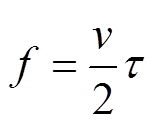
式中，v为磁悬浮列车的运行速度（m/s）；sm为列车与牵引变电站之间的距离（m）；Rk为一侧馈电电缆的电阻（W）；Lk为馈电电缆的电感（H）。
选取PI控制器参数为kp=10，ki=20。积分滑模控制器参数见表2，在基于RT-Lab高速磁悬浮硬件在环半实物实时仿真系统上对所提出的控制策略进行实验验证。仿真平台如图5所示。
高速磁悬浮牵引控制系统采用id=0的转子磁场定向的控制策略，所使用的参数按照表1选取。实验目标是使磁悬浮列车加速至600km/h后减速为0，行驶总里程为56km，实验得到的速度与里程曲线如图6和图7所示。在里程为7.57～7.95km时设置总电感估算参数Lz摄动为初始值的1.5倍；在里程为8.74～9.12km时设置总电阻估算参数Rz摄动为初始值的1.5倍。上述两个里程区间各包含一个定子段换步点，以分析参数摄动对换步过程中电流的控制效果。
表2 积分滑模控制器参数
Tab.2 ISMC parameters
参数ISMC1ISMC2 e100100 k8 0008 000 c1818 d11
图5 高速磁悬浮牵引半实物仿真平台
Fig.5 Semi-physical traction platform of high-speed maglev
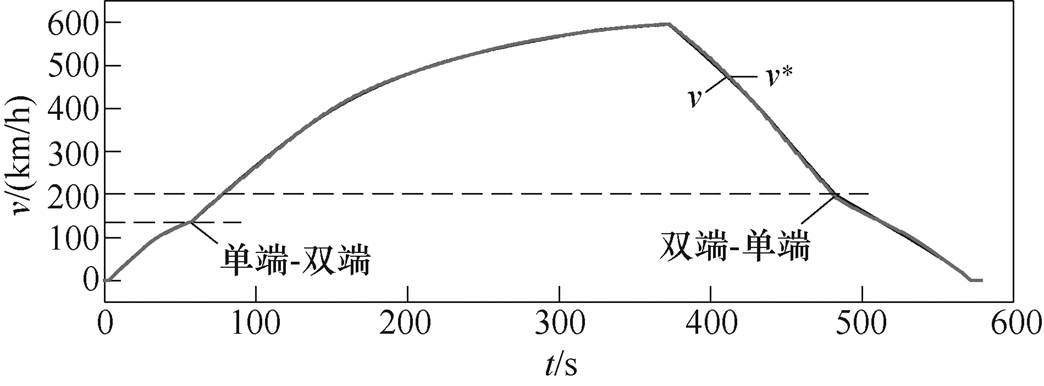
图6 磁悬浮列车速度曲线
Fig.6 The speed curves of high-speed maglev
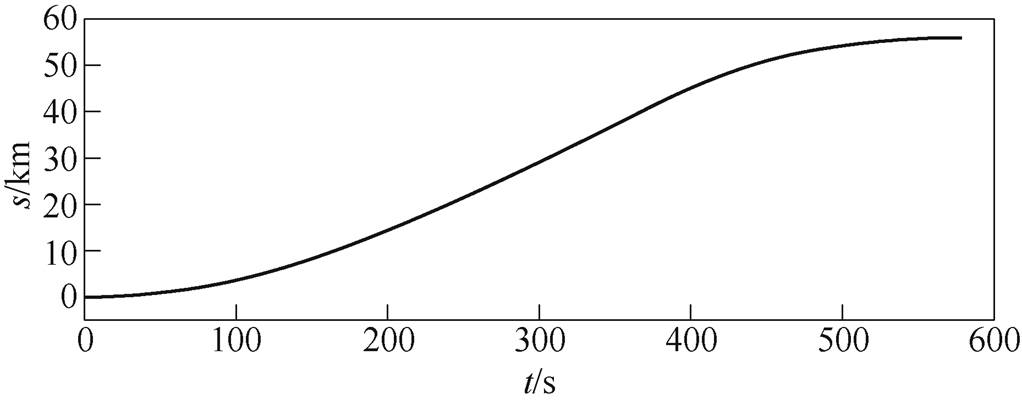
图7 磁悬浮列车里程曲线
Fig.7 The mileage curve of high-speed maglev
在加速阶段，磁悬浮列车在时速135km/h时由单端供电模式切换为双端供电模式；在减速阶段，列车在时速200km/h时由双端供电模式切换为单端供电模式。
实验中的定子段沿轨道分段排布并采用两步法的换步方式。当列车进行定子段换步时，定子电流会先减小为零，换步完成之后定子电流再恢复。由本文分析可知，在电机参数发生摄动时，dq轴定子电流将产生波动，影响列车的稳定运行。
在双端供电模式下采用PI+电压前馈解耦策略（Voltage Feed-Forward Decoupling Control, VFDC）的dq轴电流曲线如图8所示。由图8a可知，随着车速升高，dq轴电流耦合加剧，跟随性能逐渐变差，且在换步过程中，d轴电流波动最大超过了140A；从图8b可知，当无参数摄动时，d轴电流在换步过程中电流波动恢复速度与q轴电流在换步时跟踪速度较慢，约为0.48s；从图8c可知，当存在电感参数摄动时，d轴电流在电感参数摄动的瞬间和换步时都存在幅值超过400A的电流波动，且摄动的瞬间电流恢复速度很慢，约为1.7s，q轴在参数摄动的瞬间电流存在约250A的电流波动，恢复时间约为0.14s，换步过程中也存在较小的电流波动；从图8d可知，当存在电阻参数摄动时，dq轴电流的波动都比较小，其中d轴电流在参数摄动的瞬间和换步过程中波动约为70A和90A，q轴电流在参数摄动瞬间波动约80A，换步时基本无波动。
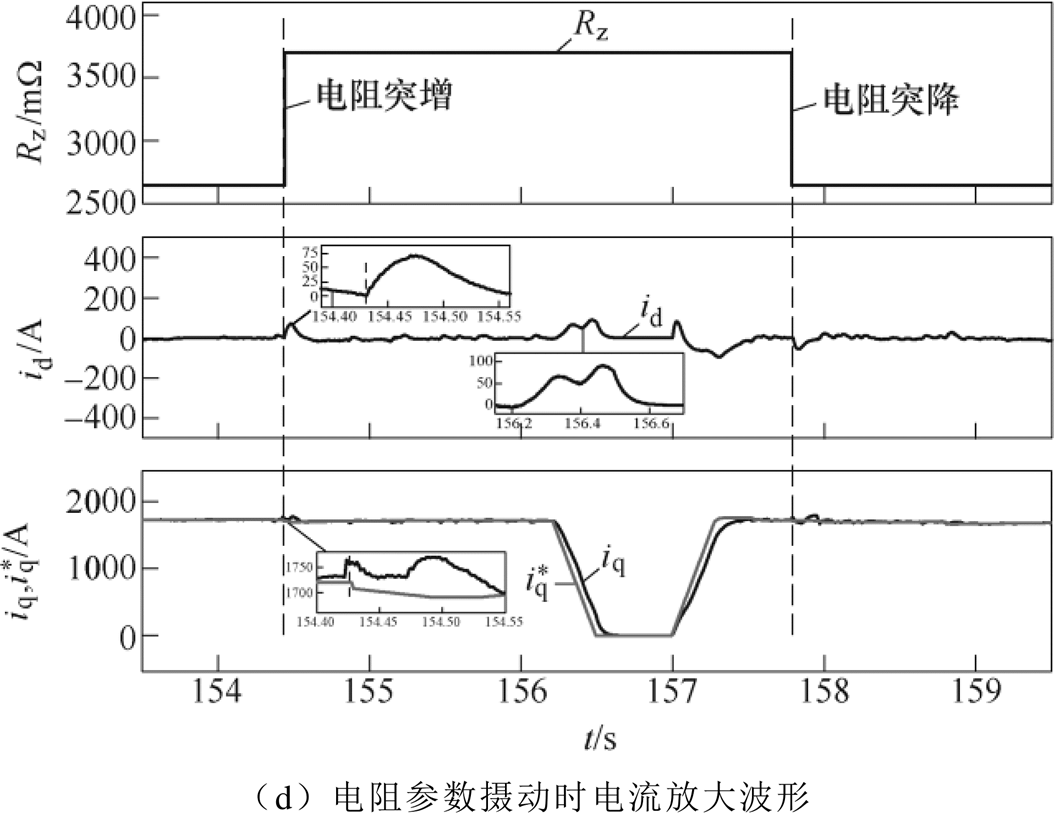
图8 采用PI+VFDC策略时电流响应波形
Fig.8 Current responses waveforms with PI+VFDC
在双端供电模式下采用ISMC策略的dq轴电流响应波形如图9所示。由图9a可知，在换步过程中，d轴电流依然存在波动但是波动幅值最大不超过90A。由图9b可知，当无参数摄动时，在换步时d轴电流波动的恢复时间明显缩短，约为0.32s。同时，q轴电流在换步时跟随性能几乎无滞后；由图9c可知，当存在电感参数摄动时，d轴电流在参数摄动的瞬间存在约80A的电流波动，恢复时间仅为0.14s，换步时存在约34A的电流波动，q轴在参数摄动的瞬间电流存在约100A的电流波动，恢复时间约为0.12s，换步过程中基本无电流波动；由图9d可知，当存在电阻参数摄动时，dq轴电流在参数摄动的瞬间均无明显波动，换步过程中的电流和无扰动时电流波形无明显差异。
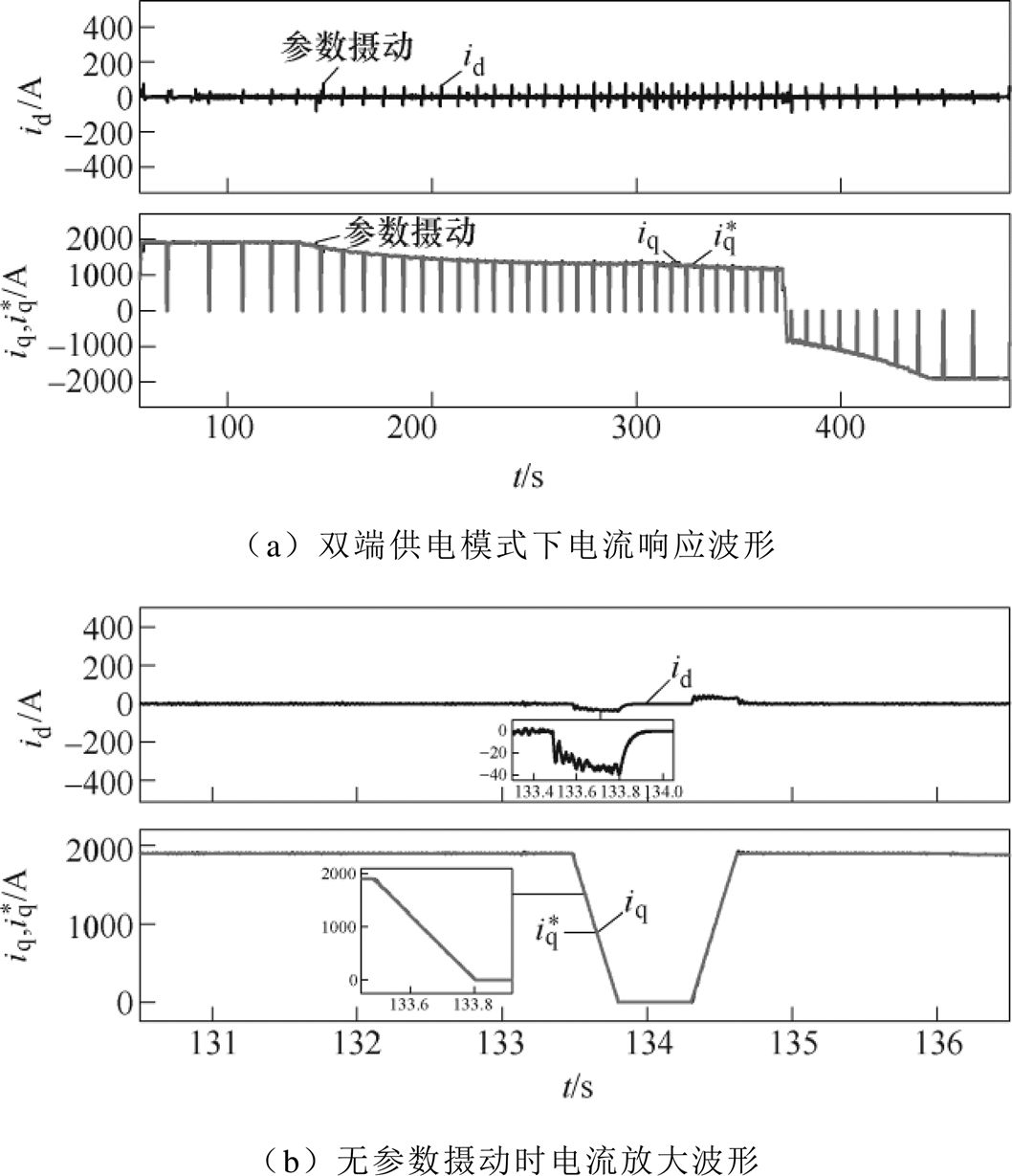
图9 采用ISMC策略时电流响应波形
Fig.9 Current responses waveforms with ISMC
综上所述，当磁悬浮列车运行在双端供电模式下，在电感、电阻参数发生变化时，参数变化的瞬间和定子段换步的过程中，基于PI+VFDC策略的dq轴电流将发生严重的波动，且恢复时间较长；而基于积分滑模的电流控制策略，得益于其强鲁棒性和良好的动态性能，降低了电流波动并且实现了电流在换步过程中的快速跟随。通过实验验证，参数摄动时电流的波动趋势也符合本文对参数摄动影响的分析结论。
高速磁悬浮列车运行在双端供电模式时，电机和馈电电缆的电感、电阻参数的摄动将会造成较为严重的电流波动，影响列车的稳定运行。传统的PI+ VFDC策略依赖于电机的估计参数，因此本文提出了基于积分滑模的电流控制策略，该策略实现简单、动态性能好、对参数摄动具有较强的鲁棒性。本文分析了参数摄动对长定子直线同步电机电流控制的影响，并通过半实物实验平台的硬件在环实验证明了所提方法的有效性，对高速磁悬浮列车的高性能运行具有实际应用意义。
参考文献
[1] 章九鼎, 卢琴芬. 长定子直线同步电机齿槽效应的计算与影响[J]. 电工技术学报, 2021, 36(5): 964-972, 1026.
Zhang Jiuding, Lu Qinfen. Calculation and influences of cogging effects in long-stator linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 964-972, 1026.
[2] 朱进权, 葛琼璇, 孙鹏琨, 等. 高速磁悬浮列车在双端供电模式下的电流控制策略[J]. 电工技术学报, 2021, 36(23): 4937-4947.
Liu Jinxin, Ge Qiongxuan, Sun Pengkun, et al. Current control strategy for high-speed maglev in the double feeding mode[J]. Transactions of China Elec- trotechnical Society, 2021, 36(23): 4937-4947.
[3] 朱进权, 葛琼璇, 孙鹏琨, 等. 基于自抗扰的高速磁浮列车牵引控制策略[J]. 电工技术学报, 2020, 35(5): 1065-1074.
Zhu Jinquan, Ge Qiongxuan, Sun Pengkun, et al. Traction-system research of high-speed maglev based on active disturbance rejection control[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(5): 1065-1074.
[4] 刘金鑫, 葛琼璇, 王晓新, 等. 双端供电模式下高速磁浮列车牵引控制策略研究[J]. 电工电能新技术, 2015, 34(6): 16-21, 44.
Liu Jinxin, Ge Qiongxuan, Wang Xiaoxin, et al. Traction-system research for high-speed maglev based on double-end supply[J]. Advanced Technology of Electrical Engineering and Energy, 2015, 34(6): 16-21, 44.
[5] 周华伟, 温旭辉, 赵峰, 等. 基于内模的永磁同步电机滑模电流解耦控制[J]. 中国电机工程学报, 2012, 32(15): 91-99, 10.
Zhou Huawei, Wen Xuhui, Zhao Feng, et al. Decoupled current control of permanent magnet synchronous motors drives with sliding mode control strategy based on internal model[J]. Proceedings of the CSEE, 2012, 32(15): 91-99, 10.
[6] Hu Yuansheng, Hu Cungang, Zhang Pinjia, et al. A novel hybrid seven-level converter for permanent magnet synchronous motor driving system based on model predictive control[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 389- 396.
[7] 张晓光, 赵克, 孙力, 等. 永磁同步电动机滑模变结构调速系统新型趋近率控制[J]. 中国电机工程学报, 2011, 31(24): 77-82.
Zhang Xiaoguang, Zhao Ke, Sun Li, et al. A PMSM sliding mode control system based on a novel reaching law[J]. Proceedings of the CSEE, 2011, 31(24): 77-82.
[8] 陈闯, 王勃, 于泳, 等. 基于改进指数趋近律的感应电机滑模转速观测器研究[J]. 电工技术学报, 2020, 35(增刊1): 155-163.
Chen Chuang, Wang Bo, Yu Yong, et al. An improved exponential reaching law based-sliding mode observer for speed-sensorless induction motor drives[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(S1): 155-163.
[9] 齐亮. 基于滑模变结构方法的永磁同步电机控制问题研究及应用[D]. 上海: 华东理工大学, 2013.
[10] 张立伟, 魏维, 张超, 等. 基于全局非线性积分滑模的永磁交流伺服系统研究[J]. 电工技术学报, 2018, 33(16): 3917-3924.
Zhang Liwei, Wei Wei, Zhang Chao, et al. Study on permanent magnet synchronous motor servo system based on total sliding mode control approach with nonlinear integrator[J]. Transactions of China Electro- technical Society, 2018, 33(16): 3917-3924.
[11] Baik I C, Kim K H, Youn M J. Robust nonlinear speed control of PM synchronous motor using boundary layer integral sliding mode control tech- nique[J]. IEEE Transactions on Control Systems Technology, 2000, 8(1): 47-54.
[12] 李政, 胡广大, 崔家瑞, 等. 永磁同步电机调速系统的积分型滑模变结构控制[J]. 中国电机工程学报, 2014, 34(3): 431-437.
Li Zheng, Hu Guangda, Cui Jiarui, et al. Sliding-mode variable structure control with integral action for permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2014, 34(3): 431-437.
[13] 王勃, 王天擎, 于泳, 等. 感应电机电流环非线性积分滑模控制策略[J]. 电工技术学报, 2021, 36(10): 2039-2048.
Wang Bo, Wang Tianqing, Yu Yong, et al. Nonlinear integral sliding mode control strategy for current loop of induction motor drives[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2039-2048.
[14] 原浩, 赵希梅. 基于积分滑模的永磁直线同步电动机直接推力控制[J]. 电工技术学报, 2019, 34(3): 483-488.
Yuan Hao, Zhao Ximei. Direct thrust force control based on integral sliding mode for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 483-488.
[15] Song Liye, Wan Yingcai, Li Taochang. Integral sliding mode control for permanent magnet syn- chronous motor based on load observer[C]//IEEE 2017 32nd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Hefei, China, 2017: 770-773.
[16] 魏惠芳, 王丽梅. 永磁直线同步电机自适应模糊神经网络时变滑模控制[J]. 电工技术学报, 2022, 37(4): 861-869.
Wei Huifang, Wang Limei. Adaptive fuzzy neural network time-varying sliding mode control for per- manent magnet linear synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(4): 861-869.
[17] 张康, 王丽梅. 基于反馈线性化的永磁直线同步电机自适应动态滑模控制[J]. 电工技术学报, 2021, 36(19): 4016-4024.
Zhang Kang, Wang Limei. Adaptive dynamic sliding mode control of permanent magnet linear synchronous motor based on feedback linerization[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4016-4024.
[18] 张国荣, 侯立凯, 彭勃, 等. 柔性多状态开关反馈线性化滑模控制[J]. 电力系统自动化, 2020, 44(1): 126-133.
Zhang Guorong, Hou Likai, Peng Bo, et al. Feedback linearization sliding mode control strategy for soft open point[J]. Automation of Electric Power Systems, 2020, 44(1): 126-133.
[19] 武志涛, 李帅, 程万胜. 基于扩展滑模扰动观测器的永磁直线同步电机定结构滑模位置跟踪控制[J]. 电工技术学报, 2022, 37(10): 2503-2512.
Wu Zhitao, Li Shuai, Cheng Wansheng. Fixed structure sliding mode position tracking control for permanent magnet linear synchronous motor based on extended sliding mode disturbance observer[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2503-2512.
[20] 王娟. 磁悬浮列车用长定子直线同步电机特性研究与故障分析[D]. 北京: 中国科学院电工研究所, 2004.
Traction-System Research of High-Speed Maglev Train Based on Integral Sliding Mode Control
Abstract When the long-stator linear synchronous motor for high-speed maglev train works in the double feed mode, it is a multi-variable, nonlinear, and strongly coupled system. The traditional linear control method is more sensitive to parameter perturbation, so this paper analyzes the influence of parameter perturbation on current loop control performance and proposes a current control strategy based on integral sliding mode. This strategy introduces the integral term of the state variables into the sliding mode surface, avoids the interference of high-frequency noise, and improves the exponential reaching law to weaken chattering, so that the current dynamic following performance and parameter perturbation resistance are improved. Hardware-in-the-loop (HIL) experiments verify that compared with the traditional linear control strategy, this strategy can improve the current following performance of the maglev train in the step change process of the stator section and has strong robustness to the perturbation of motor parameters.
keywords：High-speed maglev, double feed mode, parameter perturbation, integral sliding mode control
DOI: 10.19595/j.cnki.1000-6753.tces.210261
中图分类号：TM359.4
国家重点研发计划资助项目（2016YFB1200602-20）。
收稿日期 2021-03-01
改稿日期 2021-06-01
曹学谦 男，1996年生，博士研究生，研究方向为高性能电机牵引控制技术。E-mail: caoxueqian@mail.iee.ac.cn
葛琼璇 女，1967年生，研究员，博士生导师，研究方向为高压大功率变流器控制技术、高性能电机牵引控制技术。E-mail: gqx@mail.iee.ac.cn（通信作者）
（编辑 崔文静）