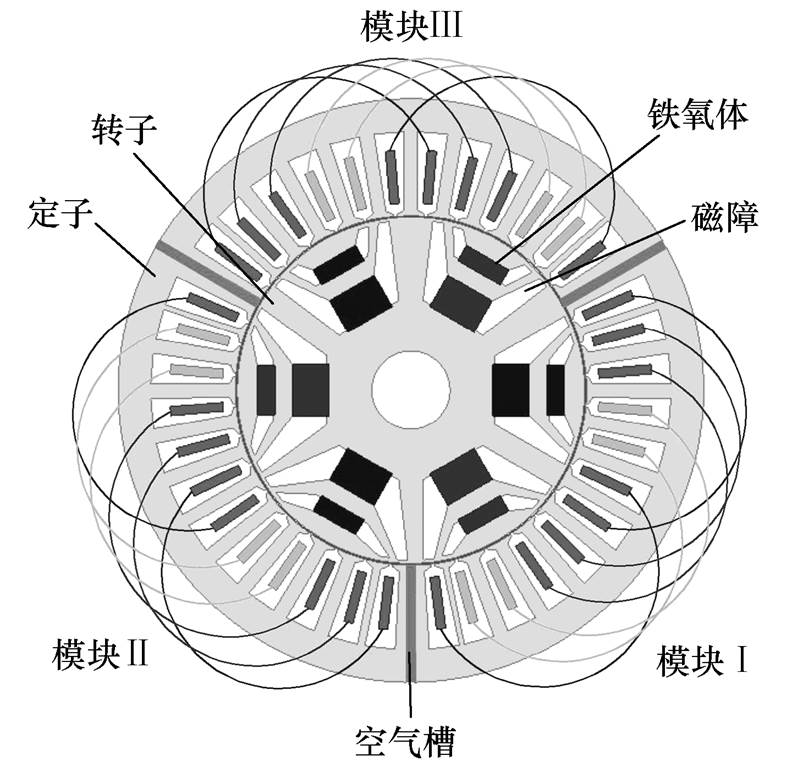
图1 3×3相PMa-SynRM截面
Fig.1 Cross-section of 3×3 phase PMa-SynRM
摘要 单逆变器驱动的3×3相永磁辅助同步磁阻电机系统具有低成本、高可靠性的优点。该文针对此系统的两相开路故障，提出一种各模块转矩重新分配的容错控制策略。当同一模块发生两相开路故障时，将该故障模块完全切除，通过增加非故障模块的电流来实现容错运行。对于不同模块同相位两相开路，通过分析故障后各模块的等效电路，获得两相静止坐标系下电流之间的关系，然后构造拉格朗日函数，以铜耗最小为目标，求解电流幅值的最优解，最终实现转矩的重新分配。当发生不同相位两相开路时，以故障模块输出最大平均转矩以及总的转矩脉动最小为目标，对各模块转矩进行重新分配。该方法通过增加正常模块转矩脉动来部分抵消故障模块产生的脉动，达到抑制输出转矩脉动的目的。实验结果验证了所提容错控制策略能有效降低故障后电机的转矩脉动，提高了控制系统的可靠性。
关键词：3×3相永磁辅助同步磁阻电机 单逆变器 容错控制 开路故障 转矩分配
模块化的多相永磁辅助同步磁阻电机（Permanent Magnet assisted Synchronous Reluctance Motor, PMa-SynRM）因其高功率因数、宽调速范围、低成本、高容错能力等优点，在电动汽车、航空航天、军事装备等领域得到了广泛应用[1-3]。
对于传统的n×3相电机，需要至少n个逆变器桥臂来进行驱动，因此随着电机相数的增加，系统成本也随之增加[4]。为了缩小控制器的体积，提高产品的价格优势，国内外研究学者对单逆变器驱动n×3相电机展开了深入研究[5-6]。
在电机驱动系统中存在开路和短路两种故障类型[7]。在短路故障发生瞬间会产生较大的电流，造成局部热量积聚，严重时会烧毁电机[8-11]。因此，目前多数驱动器增加了短路保护装置，即通过硬件故障隔离的方法将短路故障转换为开路故障。由于机器端子连接器的机械故障、内部绕组破裂等电气故障引起的电机绕组的开路故障占电机故障的27%～31%，并且随着电机绕组的增加，发生故障的概率也会增加[12]。此外，当发生开路故障后，转子上存在转矩波动和磁力的不平衡，从而引起振动，这不仅会影响电机的性能，而且若不及时处理，可能会产生二次故障。因此，多相电机的容错控制已成为相关领域的研究热点[13-14]。模块化电机被设计成多个三相模块，不仅可以利用成熟的三相电机驱动技术，而且可以提高电机的容错能力。
目前，针对多相电机一般基于故障前后磁动势不变原理，以幅值相等或铜耗最小为约束条件，优化故障后的容错电流，消除转矩脉动，实现电机的平稳运行[15-16]。但是，该方法采用电流滞环控制策略，存在开关频率不固定、开关损耗大的问题。为解决上述问题，文献[17]在定子磁动势不变的前提下，根据优化后的容错电流，建立六相电机缺相后的解耦数学模型，实现了故障后磁场定向控制。文献[18]提出了五相电机两相开路故障下基于空间矢量脉宽调制的容错控制，该方法通过构建故障后的降阶矩阵，对参考电压矢量进行重构，改善了故障后电机的运行性能。以上方法均能有效抑制故障后的转矩脉动，但需要采用多个逆变器桥臂来驱动电机，具有一定的应用局限性。此外，n×3相电机无法构建故障后的解耦数学模型，因此上述方法针对模块化电机并不适用。当n×3相电机中某模块发生开路故障后，将该故障模块从系统中切除，从而不会影响健康模块的正常运行[19]。但是，该方法在负载一定的情况下，相电流增加为正常状态下的1.73倍，会导致热量积聚，影响电机可靠性。文献[20-21]针对2×3相电机，充分利用故障模块剩余相电流，跟踪非正弦参考电流，实现故障后的无扰动容错运行。但是该方法只适用于表贴式电机，忽略了磁阻转矩的影响。
本文以3×3相PMa-SynRM为研究对象，提出了单逆变器驱动下两相开路故障的容错控制。与传统方法相比，该方法能把功率分布到剩余的正常相上，使热量得到分散，利于故障下电机的散热和可靠性的提高。在构建PMa-SynRM数学模型的基础上，分析了同一模块两相开路、同相位以及不同相位两相开路的容错策略。当发生同一模块两相开路时，系统能够实现自容错；当发生同相位两相开路时，以铜耗最小为约束条件，平均转矩为目标函数，构造拉格朗日函数，从而求取各模块电流幅值的最优解，实现故障后转矩的重新分配；当发生不同相位两相开路时，以故障模块电流幅值相等、平均转矩最大以及总的输出转矩脉动最小为目标，对转矩进行重新分配。最后搭建3×3相PMa-SynRM控制系统实验平台，实验结果验证了所提容错控制策略的正确性和可行性。
本文研究的3×3相PMa-SynRM截面如图1所示。该电机定子分为3个无磁耦合的模块，模块化的设计实现了各模块之间物理隔离（电、磁、热隔离），降低了故障相绕组对其他模块的影响，提高了电机的容错性能[22]。转子采用双层U型磁障结构设计，每个磁障底部嵌有铁氧体。非对称的转子结构设计有效降低了电机的转矩脉动[23]。电机绕组采用星形联结方式，每个模块存在一个独立的中性点 （n1, n2, n3）。
图1 3×3相PMa-SynRM截面
Fig.1 Cross-section of 3×3 phase PMa-SynRM
三套独立的定子绕组分别为：ABC相、DEF相以及GHI相。每个模块相邻两相定子绕组之间相位相差120°。此外，3个模块对应相之间同相位，各模块电机参数近似相等。由于各模块之间互感很小，因此，该电机可以等效为3个独立的三相电机。
一般情况下，逆变器的桥臂数与电机相数相对应，对于多相电机，这不仅会增加控制器的体积，还会增加整个控制系统的成本。为了解决上述问题，本文采用一个两电平三相逆变器来并联驱动电机的3个模块，拓扑结构如图2所示。
图2 单逆变器驱动3×3相PMa-SynRM
Fig.2 3×3-phase PMa-SynRM driven by mono-inverter
从图2可以看出，逆变器的一个输出端a与定子绕组的A、D和G相相连，因此正常运行时各模块输入电压相同。为了简化分析，假设各模块电机参数相同，则正常状态下各模块相电流是母线电流的1/3。
由于该电机等效为3个参数相同的三相电机，因此在正常状态下以模块Ⅰ为例构建3×3相PMa- SynRM的数学模型。
两相静止坐标系下的电压方程为
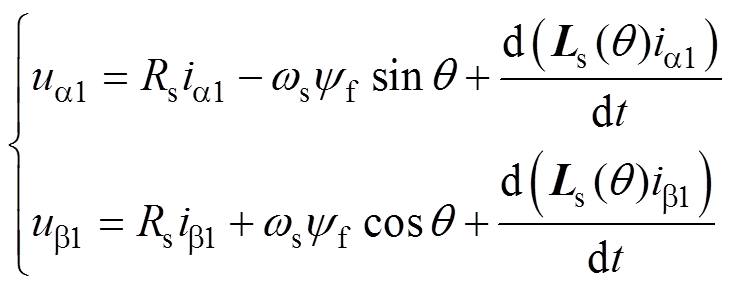（1）
（2）
其中
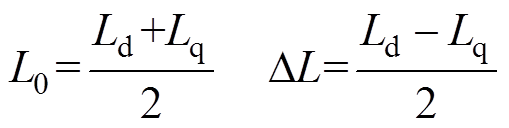
式中，Rs、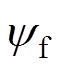
分别为定子绕组和永磁磁链；ua1、ub1以及ia1、ib1分别为模块Ⅰ中a、b 坐标系下电压及电流；q 为电机转子位置角，即d轴与a 轴夹角；ws为电角速度；
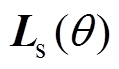为电感矩阵；Ld、Lq分别为d、q轴电感。
假设定子电流是三相对称的正弦波，经过Clarke和Park矩阵变换，可以将相电流变换到dq坐标系下[24]，有
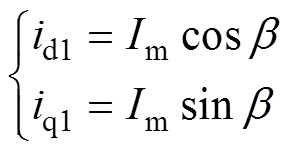（3）
式中，Im为相电流幅值；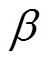
为电流矢量角。
因此，PMa-SynRM的电磁转矩可以表示为
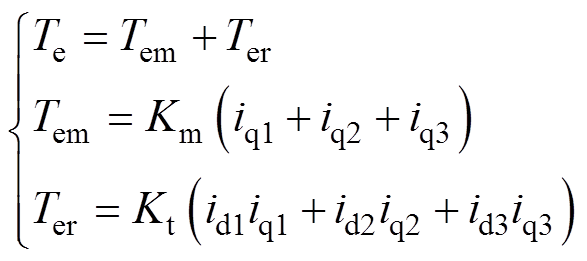（4）
式中，Tem为永磁转矩；Km=1.5p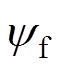为永磁转矩系数，p为电机极对数；Ter为磁阻转矩；Kt=1.5P(Ld-Lq)为磁阻转矩系数；id、iq分别为d、q轴电流；下标1, 2, 3分别表示模块Ⅰ、Ⅱ、Ⅲ。
由于该电机永磁体为铁氧体，且用量较少，因此相较于磁阻转矩，永磁转矩占比较小。此外，磁阻转矩脉动是电磁转矩脉动的主要成分，因此本文忽略永磁转矩脉动的影响。
每个模块的中性点与直流母线电压中点不相连，因此每个模块中的相电流需满足和为零的约束条件。假设模块Ⅰ中A、B两相发生开路故障，则模块Ⅰ中三相电流均为0，这意味着整个模块Ⅰ被从控制系统中剔除。模块化的设计使得电机具有较强的电磁隔离，因此模块Ⅰ的开路故障对模块Ⅱ、Ⅲ影响较小。该故障模式下，无需增加容错控制策略，电机依然能保证平稳运行。正常状态下每个模块提供1/3的输出转矩，而故障后每个模块需提供1/2的输出转矩。因此，在保证输出转矩的前提下，当模块Ⅰ发生两相开路故障后，模块Ⅱ、Ⅲ的电流幅值较正常状态有所增加。
该部分以A、D两相发生开路故障为例，对同相位两相开路故障展开分析研究。此时，模块Ⅰ和Ⅱ中的剩余相电流需满足
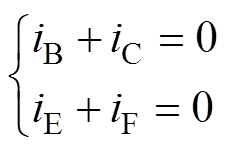（5）
由式（1）可知，电机正常运行时，电压由电阻压降、电感压降以及反电动势组成。当发生开路故障后，将正常和故障模块进行等效，A相开路的等效电路如图3a所示。根据基尔霍夫电压定律，可以得出稳态下模块Ⅰ和模块Ⅲ的相电流表达式分别为
（6）
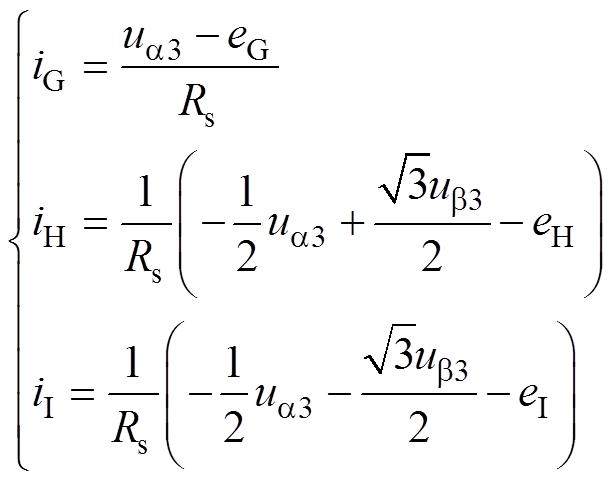（7）
式中，iA、iB、iC、iG、iH、iI分别为A、B、C、G、H、I相电流；eB、eC、eG、eH、eI分别为B、C、G、H、I相反电动势，且满足eB=eH，eC=eI。由于模块Ⅱ与模块Ⅰ故障相相同、运行工况相同，因此只对模块Ⅰ、Ⅲ展开分析。
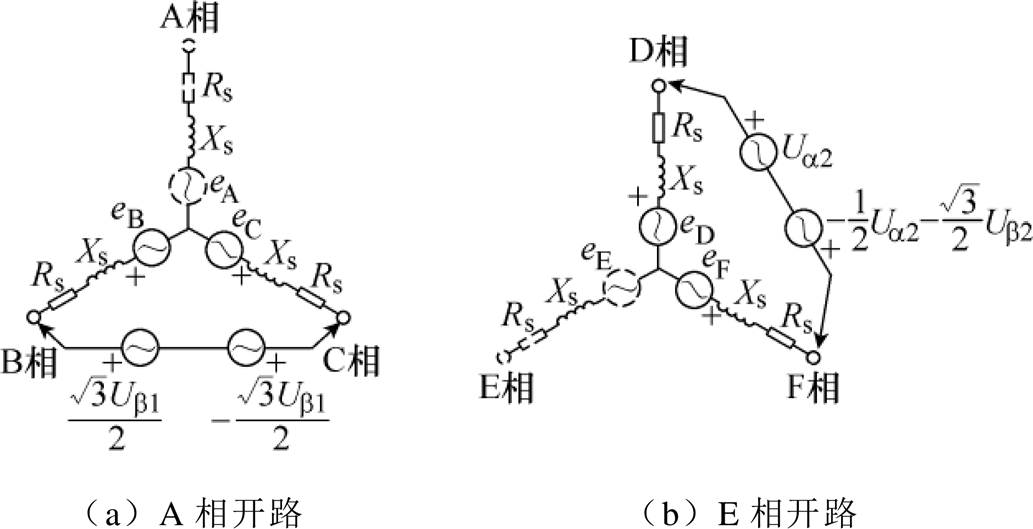
图3 电机等效电路
Fig.3 Equivalent circuit diagram of motor
根据Clarke变换矩阵，相电流式（6）、式（7）可以转换到两相静止坐标系下，有
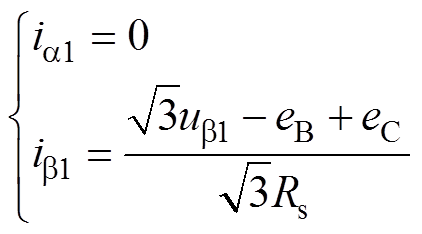（8）
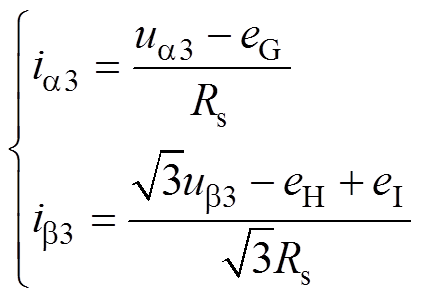（9）
由于电机各模块之间采用并联连接方式，因此ub1=ub3。此外，相同的电机参数使得式（8）、式（9）中两相静止坐标系下的电流满足
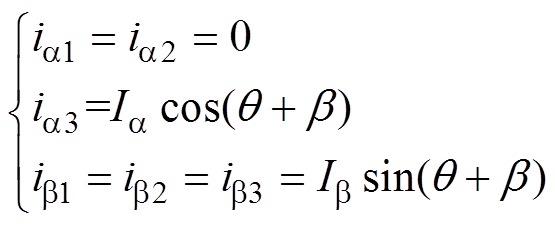（10）
式中，Ia、Ib 分别为a、b 坐标系下电流幅值。
将式（10）经过Park变换后，模块Ⅰ和模块Ⅲ中d、q坐标系下电流可以表示为
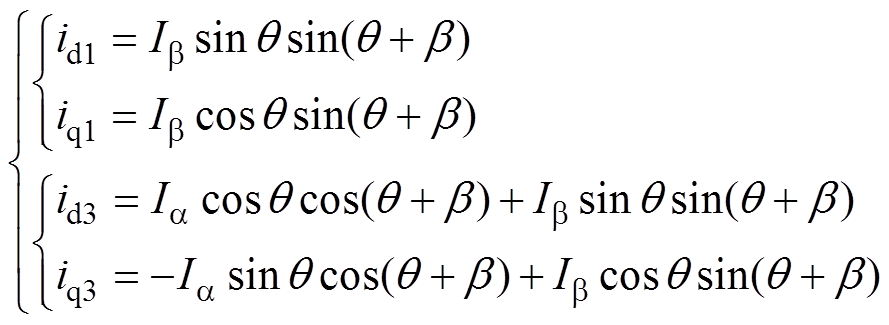（11）
将式（11）代入式（4）中计算故障后的磁阻转矩为
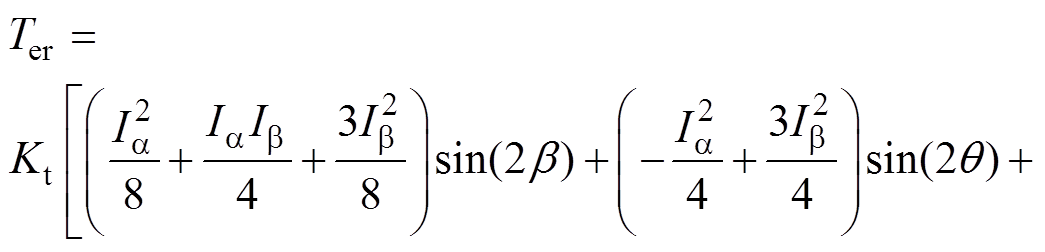
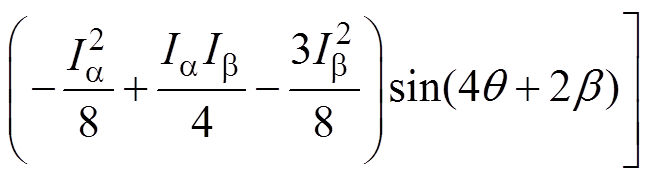（12）
由此可见，故障后的磁阻转矩包括2次、4次脉动分量。分析可知，无法选择Ia、Ib 使得脉动分量约束为0，因此容错转矩脉动存在不为0的最小值。
为了求取式（12）中2个未知参数，采取定子铜耗最小为约束条件，平均转矩为目标函数，定子铜耗可以表示为
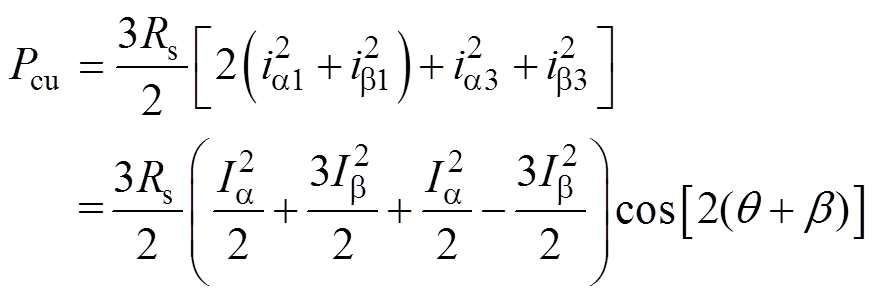（13）
构造的拉格朗日函数可以表示为
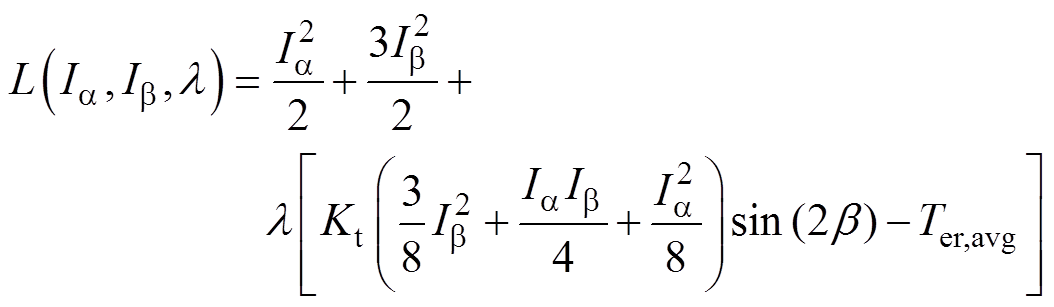（14）
式中，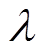
为拉格朗日系数；Ter,avg为磁阻转矩的平均值。因此，Ia、Ib 的最优解就可以转换为两个变量一个约束条件下的求极值问题。
令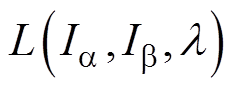
对Ia、Ib 和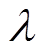的一阶偏导数为0，即
（15）
求得Ia、Ib 之间的最优关系为
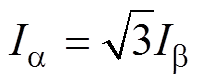（16）
将式（11）、式（16）代入磁阻转矩的计算公式中，可以获得各模块的磁阻转矩表达式为
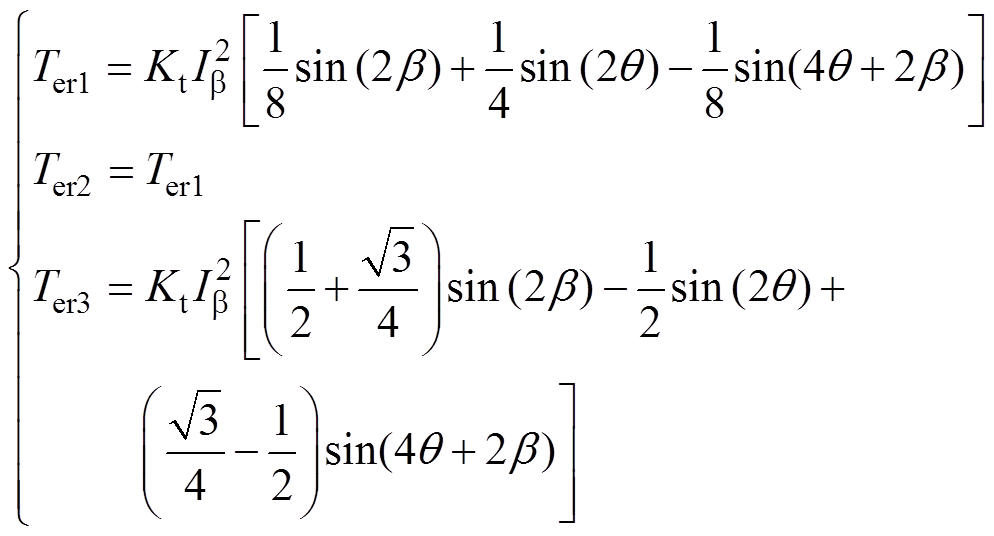（17）
根据式（17）可以得到各模块平均磁阻转矩的分配关系为：Ter1=0.105 7Ter，Ter2=0.105 7Ter，Ter3= 0.788 6Ter。最终可以计算出电流幅值Ib 为
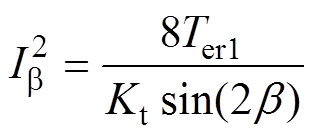（18）
通过式（10）～式（18），可以求出当电机发生A、D两相开路故障时各模块d、q轴电流参考值，并参与电流的闭环控制，实现同相位两相开路故障的容错控制。
上文论述了A、D两相开路故障的容错控制，对于其他同相位的两相开路可以通过旋转坐标系得到。例如，当B、E两相开路时，将旋转坐标系逆时针旋转120°。图4给出B相开路时的坐标定位。当B相开路时，将B相视作A相，记为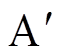
，E相开路同理。
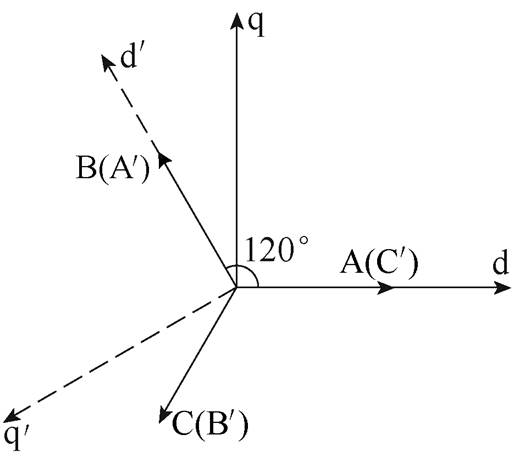
图4 B相开路后的坐标定位
Fig.4 Coordinate of B-phase opened
变换前后相电流及位置角存在关系为
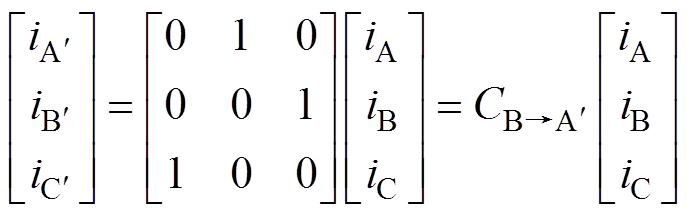（19）
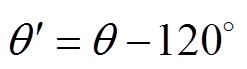（20）
通过该方法，可以实现将A、D两相开路故障的容错控制策略变换到B、E两相开路故障情况。其他同相位两相开路故障均可通过该方法实现，此处不再重复分析。
该部分以A、E两相发生开路故障为例，对不同相位两相开路故障展开分析研究。当A相开路后，B、C两相电流幅值相等，相位相差180°。因此，模块Ⅰ中的电流可以表示为
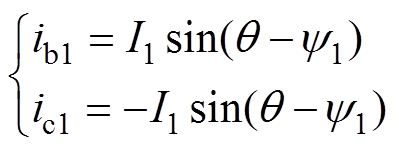（21）
式中，I1、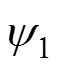
分别为相电流的幅值及相位。
经过Clarke和Park变换，将相电流转换到dq坐标系下，从而可以得到模块Ⅰ磁阻转矩的表达式为
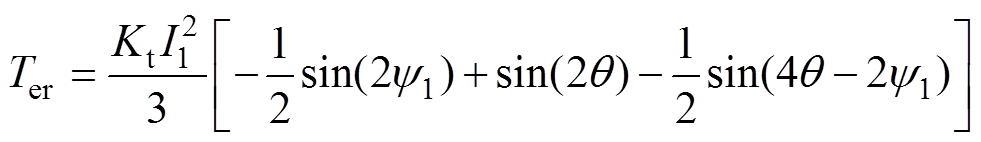（22）
因此，该磁阻转矩由平均转矩和脉动转矩两部分组成。当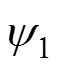=45°时，可以获得最大的平均转矩。同理可得模块Ⅱ中电流的相位为-15°。综上所述，ib1与ib2相位相差60°。
E相开路后模块Ⅱ的等效电路如图3b所示。A、E两相开路与A、D两相开路本质上是相同的，均为不同模块发生单相开路，因此，假设故障模块相电流幅值相同。鉴于此，模块Ⅰ、Ⅱ在两相静止坐标系下的电流需满足
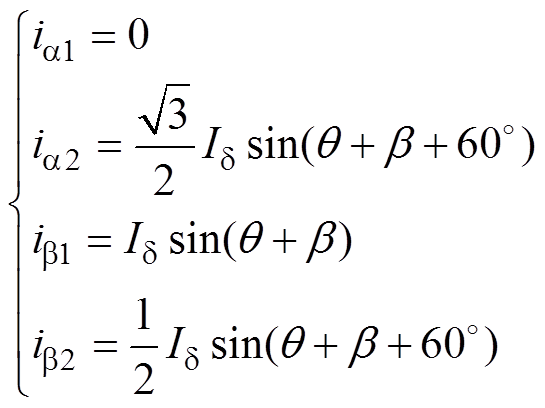（23）
由于故障后模块Ⅰ、Ⅲ仍满足式（8）、式（9），因此ib1=ib3依旧成立，则
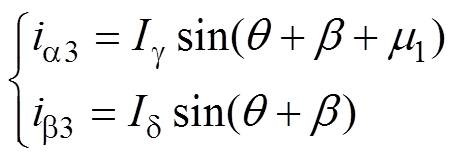（24）
式中，Ig、Id 分别为故障后模块Ⅰ、Ⅱ、Ⅲ在a、b 坐标系下电流幅值；m1为ia3与ib3之间的相位差。
故障后总的磁阻转矩表示为
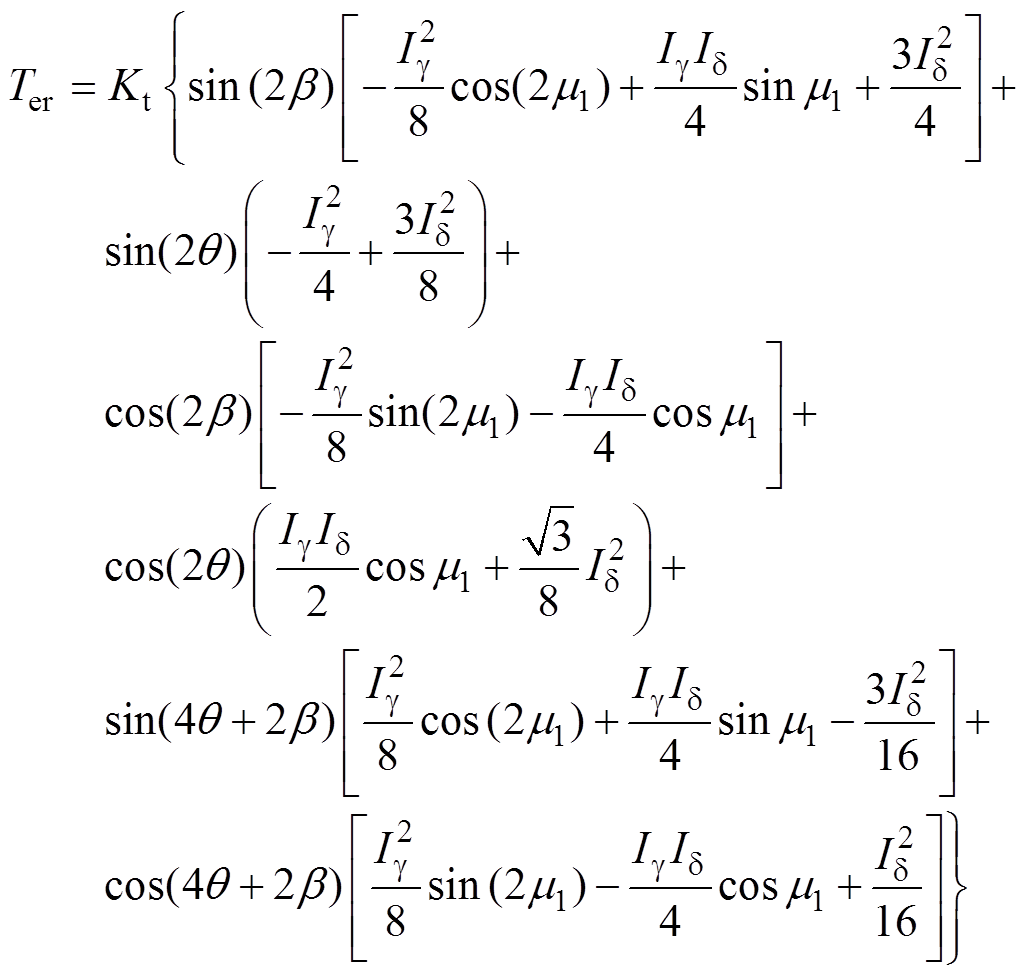（25）
以转矩脉动最小为目标求得
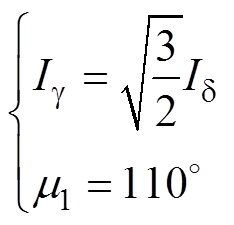（26）
根据式（21）～式（26）以及式（4），得到不同相位两相开路故障下各模块平均磁阻转矩的分配关系为Ter1=0.168Ter, Ter2=0.168Ter, Ter3=0.664Ter。
单逆变器驱动3×3相PMa-SynRM控制系统框图如图5所示。图5a适用于同相位（或不同相位）两相开路故障。转速误差经PI控制器后输出转矩参考值，该参考值参与转矩的分配。正常状态下，各模块转矩平均分配，相电流幅值相等；容错状态下，为抑制转矩脉动，对各模块转矩进行重新分配，各模块电流幅值需满足式（16）（或式（26））的关系。需要强调的是，由于3个模块之间采用并联连接方式，因此电流计算模块采集的电流（ia, ib, ic）是三个模块同相位电流之和。此后，将采集到的三相电流经过Clarke和Park变换后计算出总的d、q轴电流并参与电流的闭环控制。
图5 单逆变器控制系统框图
Fig.5 Block diagram of control system with mono-inverter
当发生B、E两相开路故障时，只需要将图5a中的容错控制模块替换成图5b所示的模块。图中，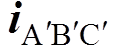
为模块Ⅰ和Ⅱ中发生B、E两相开路时采用A、D两相开路的容错算法得到的容错电流，通过坐标变换将A、D两相开路故障的容错控制算法转换为B、E两相开路情况，从而得到新的容错电流iBCA。无需对该类故障类型进行重新分析，从而降低了系统的复杂度。
为了验证上述两相开路故障容错控制策略的合理性，搭建如图6所示的实验平台，样机参数见表1。在实验过程中，通过在逆变器与电机绕组之间串联开关来模拟电机开路故障。采用高精度转矩传感器（T20WN/20N·m）测量电机的输出转矩波形。
以A、B两相开路为例，对同一模块两相开路进行实验验证。图7为A、B两相开路故障下正常、故障切换的实验结果。Zoom1和Zoom2分别为正常和故障状态下的局部放大图。给定转速100r/min，负载转矩1.3N·m（下同）。图7中的转矩波形是转矩传感器测得的3×3相PMa-SynRM的输出转矩（下同）。从图7中可以看出，故障后模块Ⅰ中三相电流均为0，模块Ⅱ中电流正弦度高，但幅值提升为正常的1.22倍。此外，故障后转矩脉动几乎没有增加。综上所述，当发生同一模块两相开路故障后，无需增加容错控制策略即可实现电机的平稳运行。
图6 实验平台
Fig.6 Experimental setup
表1 样机参数
Tab.1 Parameters of prototype machine
参 数数 值 永磁体极对数3 相电阻/W0.202 d轴电感/mH6.13 q轴电感/mH15.57 额定转速/(r/min)1 600 电流有效值/A10 平均转矩/(N·m)9
图7 A、B两相开路下正常、故障切换转矩和电流波形
Fig.7 Waveforms of torque and current under normal and fault conditions of A- and B-phase open-circuit fault
以A、D两相开路为例，对同相位两相开路进行实验验证。A、D两相开路故障后的转矩及电流波形如图8所示。Zoom1和Zoom2分别为故障和容错状态下的局部放大图。从图8中可以看出，故障后转矩脉动明显增加，A相电流为0，B、C两相电流幅值相等，相位相差180°。在加入本文所提出的容错控制策略后，转矩脉动降低了36.2%。此外，相电流幅值较故障状态下明显降低，有效减少了该模块电机铜耗。电机总的磁阻转矩是各模块产生的磁阻转矩之和，因此，根据式（17）可以发现，仍有一部分转矩脉动无法消除，但此时已是该方法下所能得到的转矩脉动最小的情况。
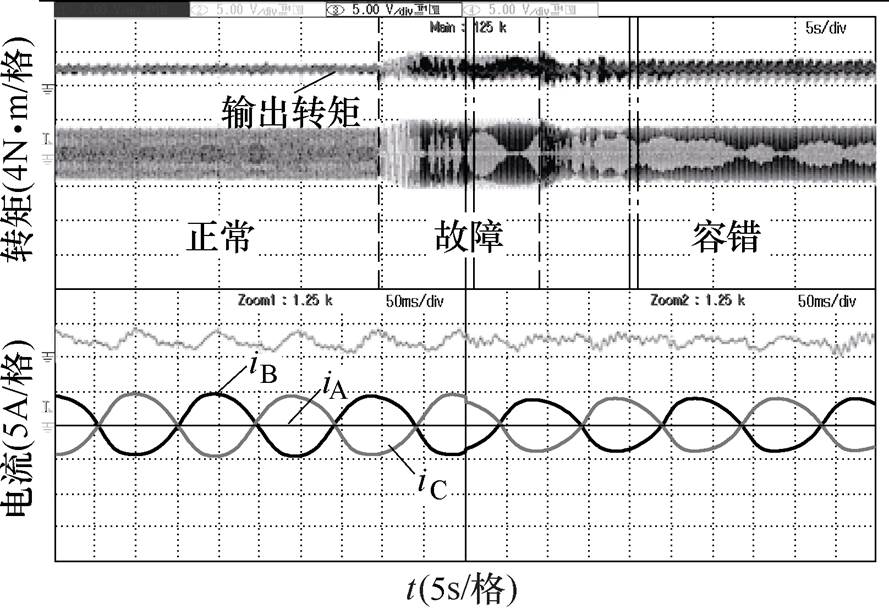
图8 A、D两相开路下正常、故障和容错切换转矩和电流波形
Fig.8 Waveforms of torque and current under normal, fault and fault-tolerant conditions of A- and D-phase open-circuit fault
图9为文献[16]中传统的针对模块化电机的容错控制算法的转矩及电流波形。该方法在A、D两相开路时，将故障模块Ⅰ和Ⅱ均从系统中剔除，只剩下模块Ⅲ工作，因此容错后电流增加为正常状态下的1.73倍，这会导致热量积聚，在影响电机可靠性的同时还会使得系统需降载运行。此外，当发生同相位两相开路以及不同相位两相开路时，容错效果均如图9所示。
图10给出A、D两相开路容错状态下各模块d、q轴电流和磁阻转矩波形。由于磁阻转矩无法采用转矩传感器进行采集，因此该部分磁阻转矩是根据磁阻转矩系数Kt乘以d、q轴电流而得到的。此外，增加电流检测电路分别检测A、B以及G、H相电流，然后根据坐标变换矩阵计算出对应模块的d、q轴电流。需要指出的是，由于模块Ⅱ和模块Ⅰ故障类型相同，因此未对模块Ⅱ进行电流检测。从图10中可以看出，正常和故障模块d、q轴电流相位差近似180°，从而使得总的d、q轴电流脉动降低。此外，模块Ⅰ和模块Ⅲ产生的磁阻转矩Ter1、Ter3波形相位差也近似为180°，而电机总的磁阻转矩是各模块的磁阻转矩之和，因此电机输出转矩的脉动能得到有效的抑制。实验结果与理论分析一致。
图9 不同模块两相开路下正常、容错切换转矩和电流波形
Fig.9 Torque and current waveforms of two-phase open circuit of different modules under normal and fault-tolerant conditions
图10 容错状态下各模块电流、转矩波形
Fig.10 Current and torque waveforms under fault-tolerant condition
经过旋转坐标系逆时针旋转120°，可以将A、D两相开路故障的容错控制策略应用到B、E两相开路下，转矩及电流波形如图11所示。与A、D两相开路故障的容错效果相同，在容错策略加入之后，能有效抑制电机转矩脉动。此时，相较于故障状态，容错后的转矩脉动降低了42.7%。
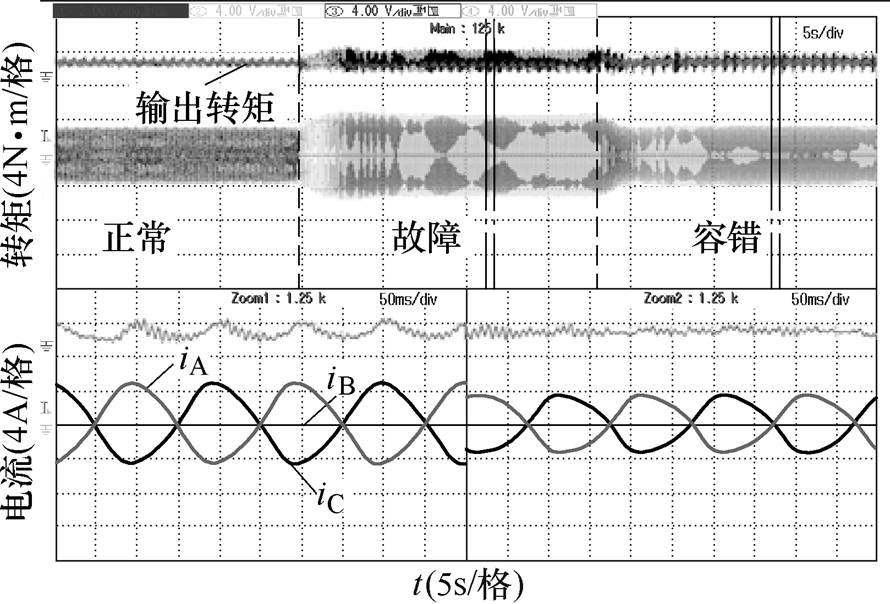
图11 B、E两相开路下正常、故障和容错切换转矩和电流波形
Fig.11 Waveforms of torque and current under normal, fault and fault-tolerant conditions of B- and E-phase open-circuit fault
以A、E两相开路为例，对不同相位两相开路进行实验验证。A、E两相开路故障后的转矩及电流波形如图12所示。当发生故障后，故障相电流为零，转矩脉动明显增加。当加入所提出的容错控制策略之后，转矩脉动降低了44.4%。上述实验结果充分验证了本文所提出的容错控制策略的有效性和可行性。
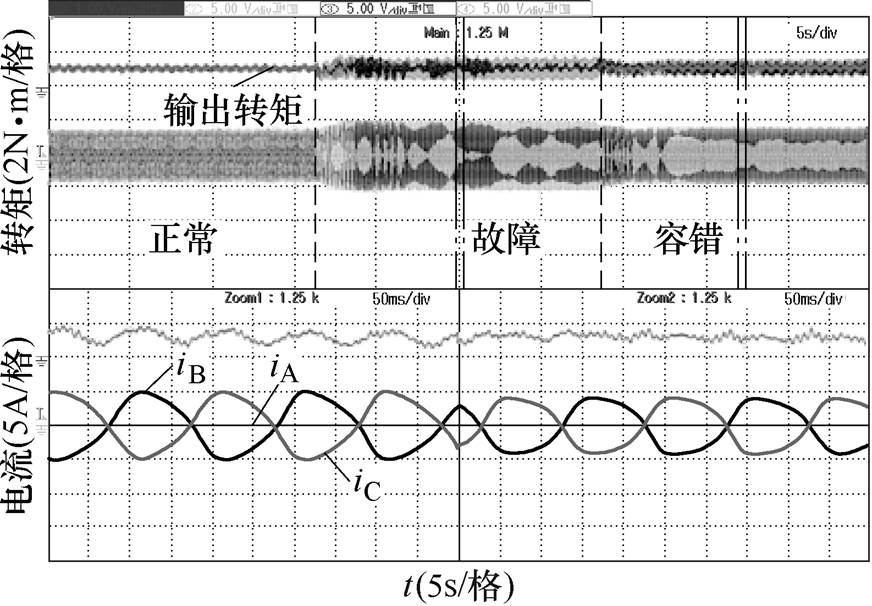
图12 A、E两相开路下正常、故障和容错切换转矩和电流波形
Fig.12 Waveforms of torque and current under normal, fault and fault-tolerant conditions of A- and E-phase open-circuit fault
本文针对3×3相PMa-SynRM两相开路故障，提出了简单有效的容错控制算法。采用单逆变器来实现3个模块的并联驱动，有效降低了控制系统的复杂性。此外，当发生开路故障后，故障模块的正常相依旧参与机电能量转换，提供电机的输出转矩。通过对故障后各模块转矩重新分配，实现抑制转矩脉动的目的。具体结论如下：
当发生同一模块两相开路时，故障模块直接切除，通过增加非故障模块的电流来实现故障后的无扰运行，电流幅值增加为正常状态下的1.22倍。
当发生同相位两相开路时，首先，根据故障后各模块在两相静止坐标系下电流之间的关系，计算出磁阻转矩的脉动分量。然后，构造拉格朗日函数，以铜耗最小为约束条件，平均磁阻转矩为目标函数，求得当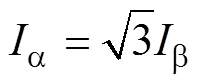
时能有效抑制磁阻转矩脉动。简单而言，该方法通过改变各模块电流幅值，增加正常模块的转矩脉动来抵消一部分由于故障模块产生的转矩脉动。
当发生不同相位两相开路时，通过假设故障模块相电流幅值相同，以故障模块平均转矩最大以及总的输出转矩脉动最小为目标，对各模块转矩进行重新分配，实现抑制转矩脉动的目的。
除此之外，本文还通过旋转两相旋转坐标系，将A、D两相开路故障的容错控制算法拓展到其他故障相的容错控制。实验结果验证了本文所提出的容错控制算法的有效性和可行性。需要指出的是，该连接方式及容错算法同样可以适用于其他n×3相磁阻电机的开路故障。
参考文献
[1] 杨晨, 白保东, 陈德志, 等. 可变磁通永磁辅助同步磁阻电机设计与性能分析[J]. 电工技术学报, 2019, 34(3): 489-496.
Yang Chen, Bai Baodong, Chen Dezhi, et al. Design and analysis of a variable flux permanent magnet assisted synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 489-496.
[2] Arafat K M, Choi S. Active current harmonic suppression for torque ripple minimization at open- phase faults in a five-phase PMa-SynRM[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 922-931.
[3] Tap A, Xheladini L, Yilmaz M, et al. Comprehensive design and analysis of a PMaSynRM for washing machine applications[J]. IET Electric Power Appli- cations, 2018, 12(9): 1311-1319.
[4] Gradev S, Herzog H. Integration of iron-loss resistance into dynamic models of 2×3-phase hybrid-excited synchronous machine[J]. IEEE Transactions on Energy Conversion, 2018, 33(4): 1700-1711.
[5] Janous S, Talla J, Smidl V, et al. Constrained LQR control of dual induction motor single inverter drive[J]. IEEE Transactions on Industrial Electronics, 2021, 68(7): 5548-5558.
[6] Liu Tianyi, Maurice F. An efficiency-optimal control method for mono-inverter dual-PMSM systems[J]. IEEE Transactions on Industry Applications, 2018, 54(2): 1737-1745.
[7] 孙德博, 胡艳芳, 牛峰, 等. 开关磁阻电机调速系统故障诊断和容错控制方法研究现状及展望[J]. 电工技术学报, 2022, 37(9): 2211-2229.
Sun Debo, Hu Yanfang, Niu Feng, et al. Status and prospect of fault diagnosis and tolerant control methods[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2211-2229.
[8] 张业成, 刘国海, 陈前. 基于电流波动特征的永磁同步电机匝间短路与局部退磁故障分类诊断研究[J]. 电工技术学报, 2022, 37(7): 1634-1643, 1653.
Zhang Yecheng, Liu Guohai, Chen Qian. Dis- crimination of interturn short-circuit and local demag- netization in permanent magnet synchronous motor based on current fluctuation characteristics[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1634-1643, 1653.
[9] 谢颖, 胡圣明, 陈鹏, 等. 永磁同步电机匝间短路故障温度场分析[J]. 电工技术学报, 2022, 37(2): 322-331.
Xie Ying, Hu Shengming, Chen Peng, et al. Thermal field analysis on inter-turn short circuit fault of permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(2): 322-331.
[10] 王栋悦, 谷怀广, 魏书荣, 等. 基于机电信号融合的DFIG定子绕组匝间短路故障诊断[J]. 电力系统自动化, 2020, 44(9): 171-178.
Wang Dongyue, Gu Huaiguang, Wei Shurong, et al. Diagnosis of inter-turn short-circuit fault in stator windings of DFIG based on mechanical and electrical signal fusion[J]. Automation of Electric Power System, 2020, 44(9): 171-178.
[11] Zhang Zeliang, Luo Guangzhao, Zhang Zhengbin, et al. A hybrid diagnosis method for inverter open- circuit faults in PMSM drives[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(3): 180-189.
[12] Welchko B A, Jahns T M, Hiti S. IPM synchronous machine drive response to a single-phase open circuit fault[J]. IEEE Transactions on Power Electronics, 2002, 17(5): 764-771.
[13] Cheng Ming, Jun Hang, Zhang Jianzhong. Overview of fault diagnosis theory and method for permanent magnet machine[J]. Chinese Journal of Electrical Engineering, 2015, 1(1): 21-36.
[14] 范舒婷, 孟大伟, 艾萌萌. 不同定子绕组结构五相感应电机开路故障时性能对比分析[J]. 电工技术学报, 2022, 37(7): 1679-1688.
Fan Shuting, Meng Dawei, Ai Mengmeng. Com- parison and analysis of the performance of five-phase induction motors with different stator winding connections under open-circuit conditions[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(7): 1679-1688.
[15] 赵文祥, 张步峰, 吉敬华, 等. 降低铜耗的容错式磁通切换永磁电机容错控制算法[J]. 农业工程学报, 2015, 31(17): 228-234.
Zhao Wenxiang, Zhang Bufeng, Ji Jinghua, et al. Copper loss-minimized remedial control algorithm of fault-tolerant flux-switching permanent-magnet motor[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(17): 228-234.
[16] 吴一丰, 邓智泉, 王宇, 等. 六相永磁容错磁通切换电机及其单相故障的容错控制[J]. 电工技术学报, 2013, 28(3): 71-79, 106.
Wu Yifeng, Deng Zhiquan, Wang Yu, et al. Six-phase fault-tolerant flux switching permanent magnet motor and control strategy for single-phase fault con- dition[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 71-79, 106.
[17] 王永兴, 温旭辉, 赵峰. 六相永磁同步电机缺相容错控制[J]. 电工技术学报, 2015, 30(5): 49-58.
Wang Yongxing, Wen Xuhui, Zhao Feng. The fault- tolerant control for six-phase permanent magnet synchronous machines with one phase failure[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 49-58.
[18] 刘国海, 宋成炎, 徐亮, 等. 基于SVPWM的五相永磁同步电机两相开路故障容错控制策略[J]. 电工技术学报, 2019, 34(1): 23-32.
Liu Guohai, Song Chengyan, Xu Liang, et al. SVPWM- based fault-tolerant control strategy under two-phase open-circuit fault of five-phase permanent-magnet synchronous motor[J]. Proceedings of the CSEE, 2019, 34(1): 23-32.
[19] Wang Bo, Wang Jiabin, Griffo A, et al. Experi- mental assessments of a triple redundant nine-phase fault-tolerant PMA SynRM drive[J]. IEEE Transa- ctions on Industrial Electronics, 2019, 66(1): 772-783.
[20] Shamsi-Nejad M, Nahid-Mobarakeh B, Pierfederici S, et al. Fault tolerant and minimum loss control of double-star synchronous machines under open phase conditions[J]. IEEE Transactions on Industrial Elec- tronics, 2008, 55(5): 1956-1965.
[21] Zheng Wang, Chen Jian, Cheng Ming, et al. Fault- tolerant control of paralleled-voltage-source-inverter- fed PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2015, 62(8): 4749-4760.
[22] 徐媚媚, 刘国海, 陈前, 等. 永磁辅助同步磁阻电机设计及其关键技术发展综述[J]. 中国电机工程学报, 2019, 39(23): 7033-7043, 7116.
Xu Meimei, Liu Guohai, Chen Qian, et al. Design and key technology development of permanent magnet assisted synchronous reluctance motor[J]. Proceedings of the CSEE, 2019, 39(23): 7033-7043, 7116.
[23] Xu Meimei, Liu Guohai, Chen Qian, et al. Design and optimization of a fault tolerant modular PMaSynRM with torque ripple minimization[J]. IEEE Transa- ctions on Industrial Electronics, 2021, 68(9): 8519- 8530.
[24] Gradev S, Reuss J, Herzog H. A general voltage- behind-reactance formulation of a multivoltage n×3- phase hybrid-excited synchronous machine[J]. IEEE Transactions on Energy Conversion, 2016, 31(4): 1452-1461.
Fault-Tolerant Control Strategy for 3×3 Phase Permanent Magnet Assisted Synchronous Reluctance Motor with Two-Phase Failure
Abstract The 3×3-phase permanent magnet assisted synchronous reluctance motor (PMa- SynRM) driven by the mono-inverter has the advantages of low cost and high reliability. Besides, a fault-tolerant control strategy for torque redistribution of each module is proposed for the two-phase open-circuit fault of the control system. When the two-phase open-circuit fault occurs in the same module, the faulty module is completely removed, and the fault-tolerant operation is realized by increasing the current amplitude of the non-fault module. For the phase-aligned two-phase open circuit of different modules, the relationship between the currents in the static coordinate system can be obtained by analyzing the equivalent circuit of each module after the fault. Then, the Lagrange function is constructed to solve the optimal solution of the current amplitude with the minimum copper loss as the objective, and finally the torque redistribution is realized. When two-phase open circuit occurs in different phases, it is necessary to take the maximum average torque output of the faulty module and the minimum output torque pulsation as targets to redistribute the torque of each module. By this method, the torque ripple of the non-fault module will be increased to partially offset the ripple generated by the fault module, so as to suppress the output torque ripple. The experimental results verify that the proposed fault-tolerant control strategy can effectively reduce the torque ripple and improve the reliability of the control system.
keywords：3×3 phase permanent magnet assisted synchronous reluctance motor, mono-inverter, fault-tolerant control, open-circuit fault, torque redistribution
DOI: 10.19595/j.cnki.1000-6753.tces.210166
中图分类号：TM351
国家自然科学基金（51877098, 52077097）和江苏省高校优势学科项目资助。
收稿日期 2021-02-01
改稿日期 2021-04-13
赵美玲 女，1992年生，博士研究生，研究方向为多相电机控制。E-mail: 2111907003@stmail.ujs.edu.cn
刘国海 男，1964年生，教授，博士生导师，研究方向为电动机系统及其控制，包括电气传动自动化、复杂过程的智能控制等。E-mail: ghliu@ujs.edu.cn（通信作者）
（编辑 崔文静）