
图1 四层绕组分数槽表贴式永磁电机子域模型
Fig.1 Subdomain model for fractional slot surface-mounted permanent-magnet machine with four-layer winding
摘要 准确求解分数槽永磁电机电枢磁场下的永磁体涡流损耗解析解,探究谐波涡流损耗随绕组结构的变化规律是改进绕组结构抑制涡流损耗的关键。针对此问题,该文提出四层绕组电流密度建模方法,实现对三相/双三相、双层/四层绕组结构的建模。基于现有的子域模型,将四层绕组结构的槽身区域划分为上层绕组和下层绕组区域,增加上层绕组与下层绕组交界处的边界条件,确定各子域磁场的谐波系数。通过设计瞬态电枢磁场求解程序,建立涡流损耗解析模型。以四台仅绕组结构不同的10极12槽永磁电机为例,利用有限元仿真验证了损耗模型的精确性。基于该损耗模型,探究了谐波涡流损耗随绕组相数和层数的变化规律,并使用磁动势从机理上分析该规律,为改进绕组结构抑制涡流损耗的研究方向提供一些思路。
关键词:分数槽永磁电机 电枢磁场 永磁体涡流损耗 谐波涡流损耗 双三相绕组 四层绕组
分数槽永磁电机具有绕组端部短、槽利用率高、齿槽转矩低、容错能力强等优点,近年来在风力发电与电动汽车等领域受到高度关注[1-2]。然而,分数槽永磁电机的电枢磁场中含有高幅值的空间谐波分量,其旋转速度与转子旋转速度不同。当永磁电机高速运行时,谐波磁场会在永磁体中感应出较大的涡流损耗,使得永磁电机的转子发热、效率降低,严重时甚至会导致永磁体退磁,损坏永磁电机[3-4]。
针对该问题,研究人员提出了多种解决办法,如使用不等匝绕组[5]、在定子轭部设置隔磁桥[6],但这两种方法会使电机的制造工艺变得复杂。除了上述方法,一些文献还通过改进分数槽绕组的相数和层数在抑制谐波磁场上取得了理想的效果。文献[7-8]使用双三相绕组抑制了10极12槽永磁电机电枢磁场中的1次谐波。文献[9-10]提出了一种四层绕组设计方法,且以两台8极9槽和10极12槽永磁电机为例进行有限元仿真和实验,结果表明四层绕组结构可抑制转子涡流损耗。
然而,双三相绕组和四层绕组结构的分数槽永磁电机永磁体涡流损耗的计算多采用有限元法,其仿真结果无法直接反映涡流损耗与电枢磁场谐波分量的映射关系,使改进绕组结构抑制涡流损耗的研究方向面临难题。为此,本文将建立分数槽永磁电机的永磁体谐波涡流损耗解析模型,探究电枢磁场空间谐波造成的谐波涡流损耗随绕组相数和层数的变化规律。
目前,现有文献主要通过推导标量或矢量磁位函数的Laplace/Poisson偏微分方程组求解分数槽永磁电机永磁体涡流损耗解析解[11-18]。根据是否考虑定子开槽因素,该解析方法可大致分为以下两类:第一类方法是不考虑定子开槽影响,如将电枢绕组等效为分布在定子槽口的电流片,利用转子铁心外半径和定子铁心内半径处的边界条件,求解永磁体区域的矢量磁位函数,进而求解永磁体涡流损耗解析解。文献[19-21]分别使用该方法探究了两台42极36槽和10极12槽永磁电机永磁体周向分段数对空间谐波涡流损耗的影响,对比了两台单层和双层绕组结构的10极12槽永磁电机永磁体空间谐波涡流损耗,求解了10极12槽永磁电机永磁体分段时涡流损耗的分布,并用有限元仿真对其进行验证。第一类解析方法虽然建模过程较简单,但是忽略了定子开槽因素,而且需通过定子绕组的绕组因数求解等效电流片的电流密度,不便于比较不同绕组结构电机的永磁体涡流损耗。
第二类方法则是考虑定子开槽影响,该方法将电机整个二维面域划分为不同子域,利用各子域交界处的边界条件,推导出永磁体内的标量或矢量磁位函数,求解永磁体涡流损耗。文献[22]基于标量磁位的子域模型分析了三台不同极、槽组合的分数槽永磁电机空载永磁体涡流损耗。文献[23-24]分别基于矢量磁位的子域模型求解了8极12槽分数槽永磁电机、2极18槽整数槽永磁电机电枢磁场下的永磁体谐波涡流损耗。相比于第一类方法,第二类方法考虑了定子开槽和定子槽之间的相互影响,且便于对比分析不同绕组结构电机的永磁体涡流损耗。然而,现阶段基于子域模型方法求解永磁体涡流损耗的研究仅针对三相绕组和双层绕组结构电机,还未涉及到双三相绕组和四层绕组结构电机。
因此,为了求解双三相绕组和四层绕组结构的分数槽永磁电机电枢磁场下的永磁体涡流损耗,首先,本文提出一种四层绕组电流密度建模方法,将四层绕组的槽身区域划分为上层绕组区域和下层绕组区域,与永磁体、气隙及定子槽口一起构成研究区域。然后,本文建立各子域矢量磁位函数,增加上层绕组与下层绕组交界处的边界条件,确定各子域磁场的谐波系数。接着,本文通过设计瞬态电枢磁场的计算程序,求解永磁体内的涡流密度分布,建立永磁体涡流损耗解析模型。最后,本文利用有限元软件对四台分别采用三相双层、双三相双层、三相四层及双三相四层绕组结构的10极12槽永磁电机进行仿真,通过对比四台电机的涡流损耗解析解和有限元仿真结果验证损耗模型的精确性。基于该损耗模型,本文探究了空间谐波涡流损耗随绕组相数和层数的变化规律,并使用磁动势从机理上分析该规律。
为了实现对四层绕组结构电机的建模,本文将四层绕组的槽身区域划分为上层绕组区域和下层绕组区域,其子域模型如图1所示。

图1 四层绕组分数槽表贴式永磁电机子域模型
Fig.1 Subdomain model for fractional slot surface-mounted permanent-magnet machine with four-layer winding
图1中,区域1为永磁体,区域2为气隙,区域3it和区域3ib分别为第i个槽身的上层绕组和下层绕组,区域4i为第i个槽口;Rr、Rm、Rs分别为转子铁心外半径、永磁体外半径、定子铁心内半径;Rt、Rsb分别为槽身内、外半径;Rsm为上层绕组和下层绕组交界处的半径;abs、abo分别为槽身宽、槽口宽对应的圆心角;ai为第i个槽身的中心位置;Ji1、Ji2和Ji3、Ji4分别为第i个槽身的上层绕组和下层绕组区域的电流密度;wr为转子机械角速度;a0为转子初始位置角,a0=0°记为N磁极中心与水平轴线重合。记电机极对数为p,定子槽数为Q。
为便于分析,本文对该电机模型做如下假设:忽略电机端部效应;忽略绕组趋肤效应和邻近效应;忽略定子铁心和转子铁心饱和,即铁心相对磁导率为无穷大;忽略定子铁心和转子铁心的涡流,即铁心电导率为0;永磁体内的涡流均匀分布。
四层绕组电流密度分布如图1所示。上层绕组和下层绕组区域的电流密度Ji1、Ji2和Ji3、Ji4的分布如图2所示。
上层绕组区域即当Rt≤r<Rsm时,电流密度Jit的表达式为
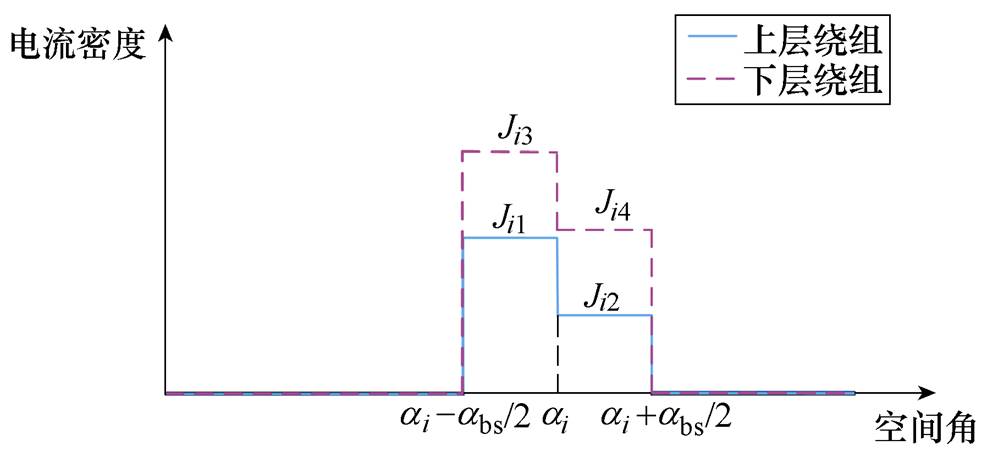
图2 四层绕组电流密度分布
Fig.2 Current density distribution of four-layer winding
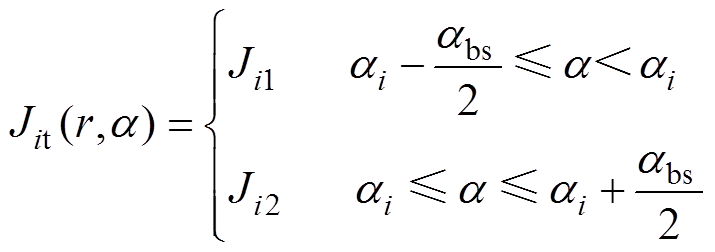 (1)
(1)
下层绕组区域即当Rsm≤r≤Rsb时,电流密度Jib的表达式为
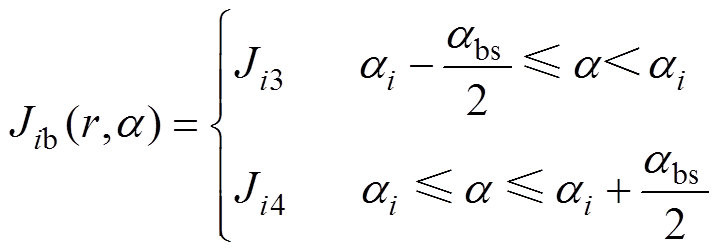 (2)
(2)
电流密度Ji1、Ji2和Ji3、Ji4满足
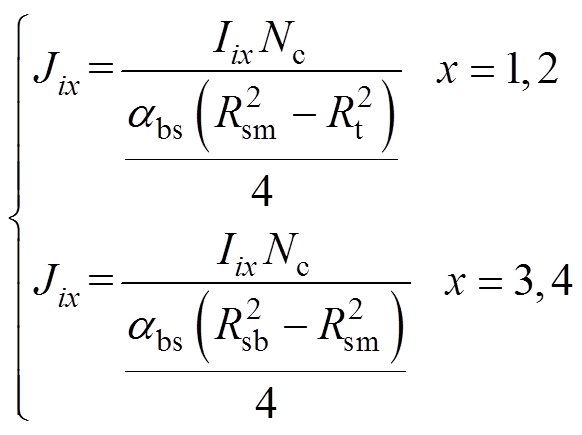 (3)
(3)
式中,Iix为第i个槽内x层线圈的电流;Nc为每层线圈串联匝数。
针对同一极、槽组合的电机,绕组相数和层数的不同主要体现在Ji1、Ji2和Ji3、Ji4分布的不同。Iix为三相电流分布时,可视为三相绕组;Iix为两组相位相差30°的三相电流分布时,可视为双三相绕组。Ji1=Ji3且Ji2=Ji4时,可视为双层绕组;Ji1≠Ji3或Ji2≠Ji4时,可视为四层绕组。
将Jit和Jib展开为傅里叶级数,有
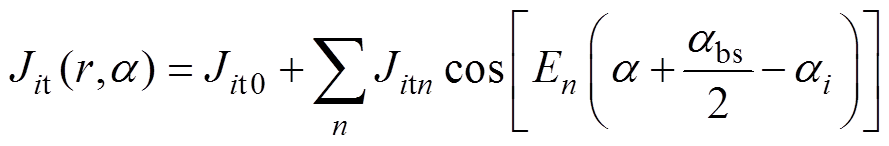 (4)
(4)
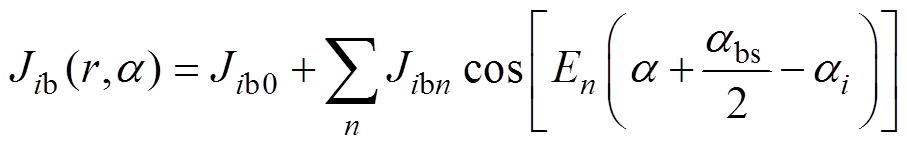 (5)
(5)
其中
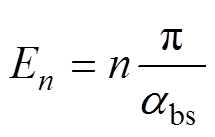 (6)
(6)
式中,n为电流密度分布的空间谐波阶数;Jit0、Jitn和Jib0、Jibn分别为Jit和Jib傅里叶级数中的系数,其表达式见附录式(A1)和式(A2)。
为求解电机电枢磁场下的永磁体涡流损耗,电机内磁场仅由电枢电流建立,不考虑永磁体励磁作用。在二维极坐标系下,矢量磁位A、电流密度J仅有z轴分量。
因此,在永磁体区域内即Rr≤r<Rm、0≤a≤2p,矢量磁位z轴分量Az1[23]满足
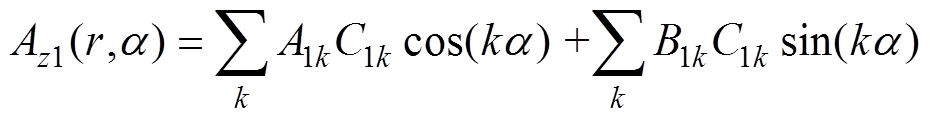 (7)
(7)
其中
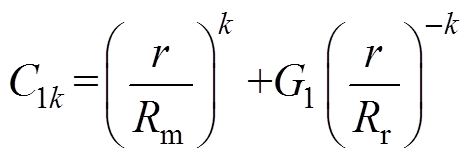 (8)
(8)
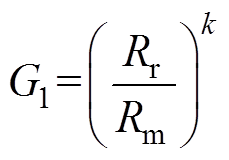 (9)
(9)
式中,k为永磁体磁场的空间谐波阶数;A1k、B1k为磁场的谐波系数。
在气隙区域内即Rm≤r≤Rs、0≤a≤2p,矢量磁位z轴分量Az2满足
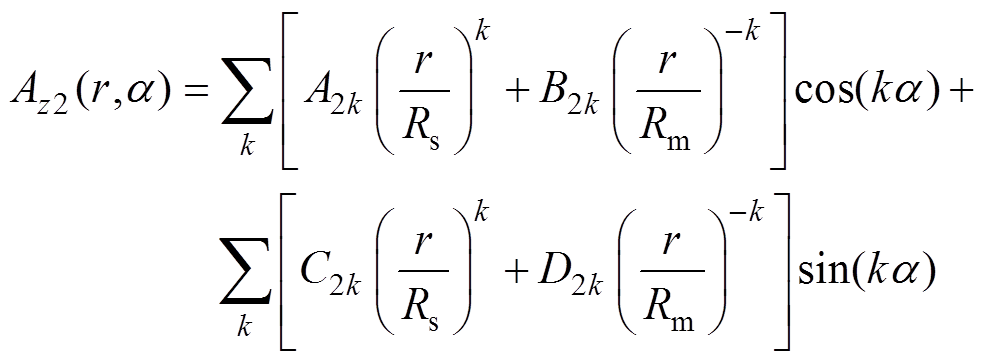 (10)
(10)
式中,A2k、B2k、C2k及D2k为气隙磁场的谐波系数。
在上层绕组区域内即Rt≤r<Rsm、ai-abs/2≤a≤ai+abs/2,矢量磁位z轴分量Az3it满足
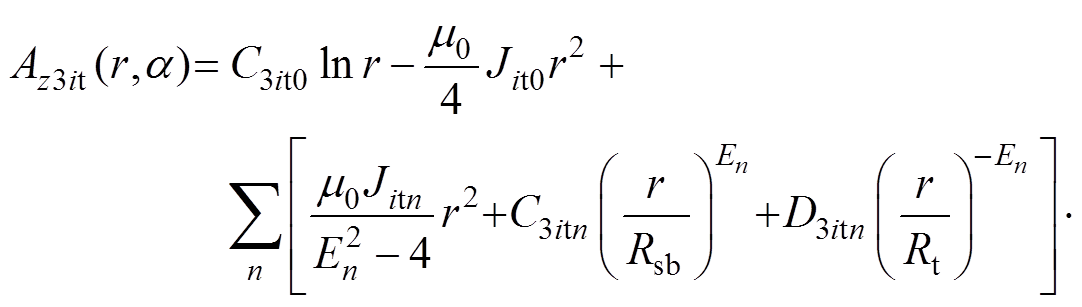
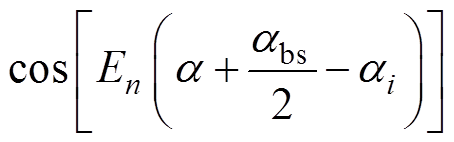 (11)
(11)
式中,C3it0和C3itn、D3itn分别为磁场的常系数、谐波系数。
在下层绕组区域内即Rsm≤r≤Rsb、ai-abs/2≤a≤ai+abs/2,矢量磁位z轴分量Az3ib满足
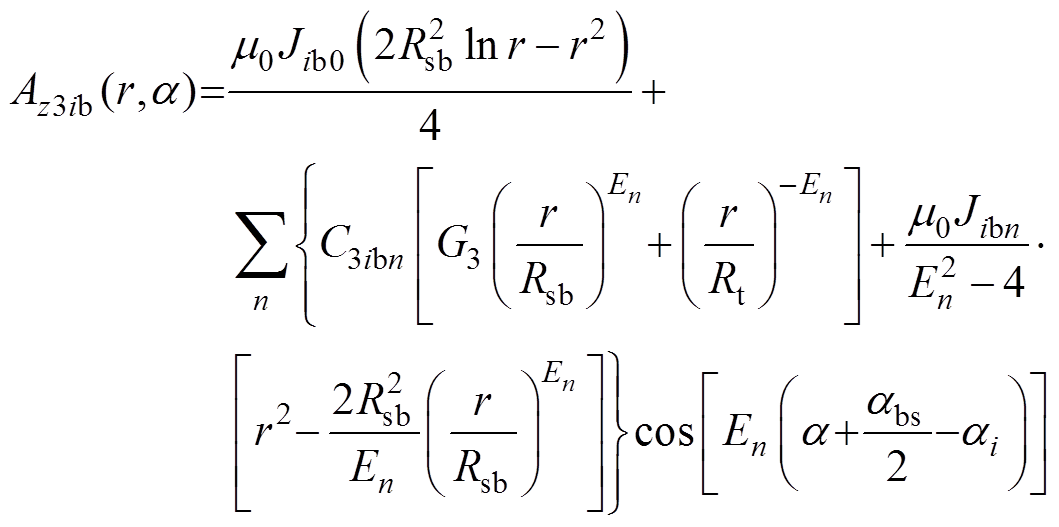 (12)
(12)
其中
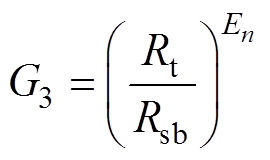 (13)
(13)
式中,C3ibn为下层绕组区域磁场的谐波系数。
在定子槽口区域内即Rs≤r<Rt、ai-abo/2≤a≤ai+abo/2,矢量磁位z轴分量Az4i满足
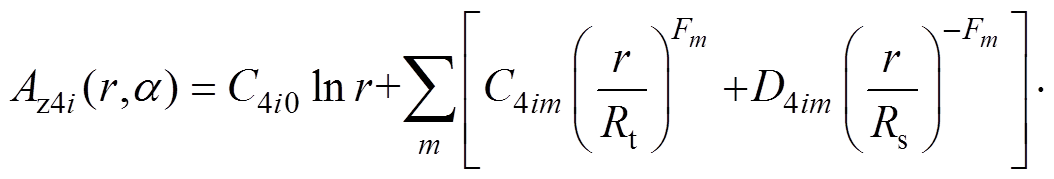
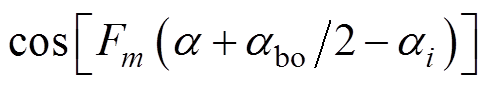 (14)
(14)
其中
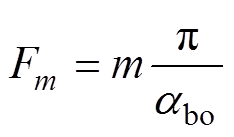 (15)
(15)
式中,m为槽口磁场的空间谐波阶数;C4i0和C4im、D4im为磁场的常系数、谐波系数。
各区域中磁通密度的径向分量Br和切向分量Ba与矢量磁位z轴分量Az满足
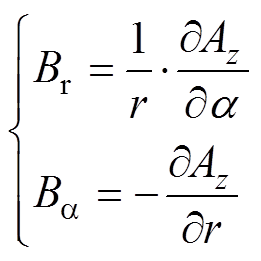 (16)
(16)
为确定式(7)、式(10)~式(12)、式(14)中矢量磁位函数中的谐波系数,施加如下的边界条件。
永磁体与气隙交界面即r=Rm处,满足
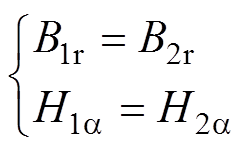 (17)
(17)
上层绕组区域与下层绕组区域交界面即r=Rsm处,满足
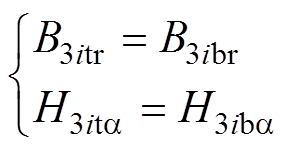
 (18)
(18)
槽口与上层绕组区域交界面即r=Rt处,满足
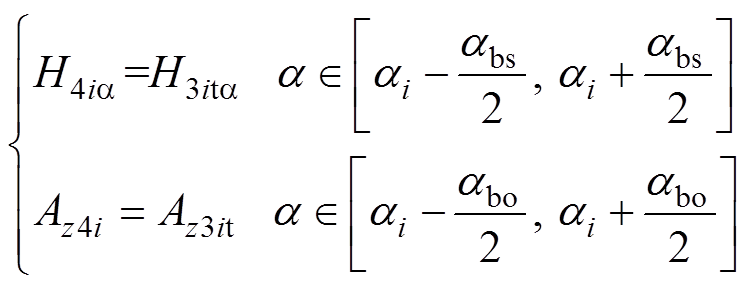 (19)
(19)
槽口与气隙交界面即r=Rs处,满足
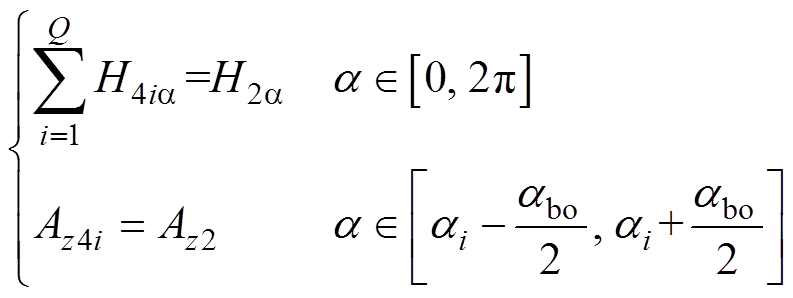 (20)
(20)
式中,Ha 为切向磁场强度,下角标1、2、3it、3ib及4i表示相应的区域。
由式(17)~式(20)可得关于各区域磁场谐波系数的方程组,通过求解该方程组确定各谐波系数,实现电机电枢磁场的求解。具体的求解过程见附录式(A3)~式(A32)。
结合式(10)和式(16),气隙磁通密度中B2r和B2a可计算为
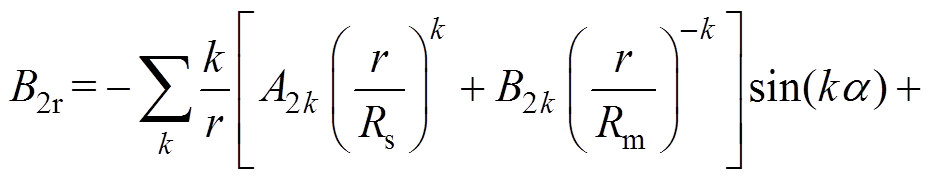
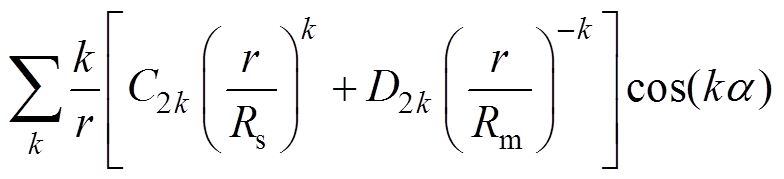 (21)
(21)
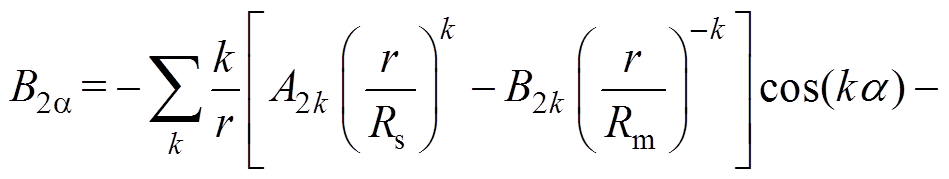
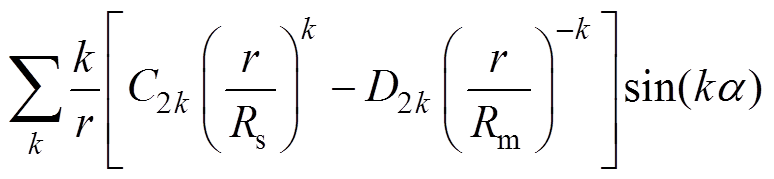 (22)
(22)
式(1)、式(2)中电流密度Jit、Jib与式(7)、式(10)~式(12)、式(14)中矢量磁位z轴分量Az1、Az2、Az3it、Az3ib、Az4i仅是关于半径r和空间角a 的函数,所求得的是某一时刻下电枢电流产生的磁场,即静磁场。然而永磁体涡流损耗是基于瞬态磁场计算的,即瞬时功率经过转子旋转周期T积分后的平均值。因此,本节首先设计瞬态电枢磁场求解程序,其流程如图3所示,图中,Kmax为永磁体磁场的最大空间谐波阶数。
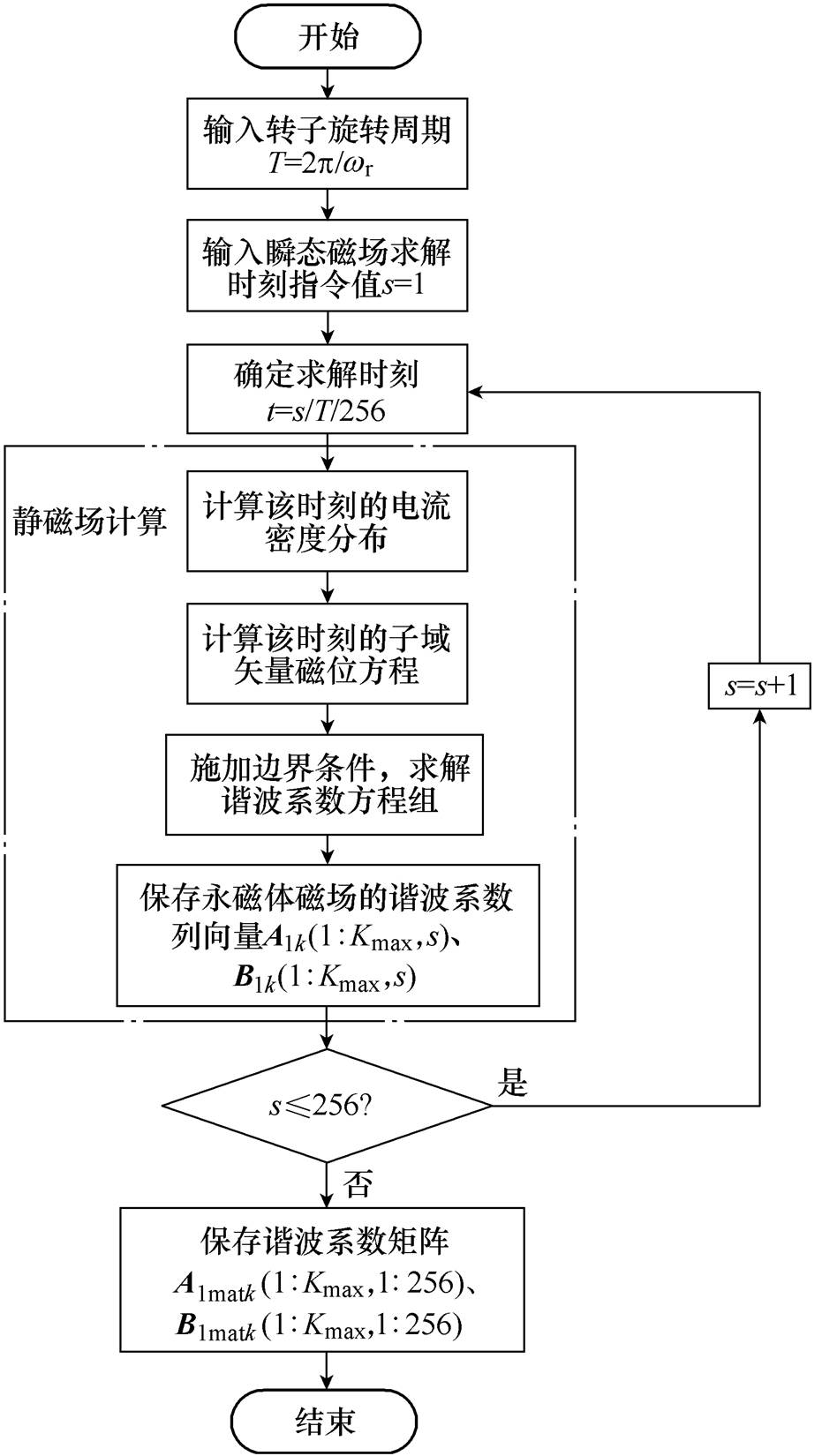
图3 瞬态电枢磁场计算流程
Fig.3 Flow chart of transient armature magnetic field calculation
将永磁体磁场中的谐波系数行向量A1matk(k, 1 256)、B1matk(k, 1
256)、B1matk(k, 1 256)展开为傅里叶级数,有
256)展开为傅里叶级数,有
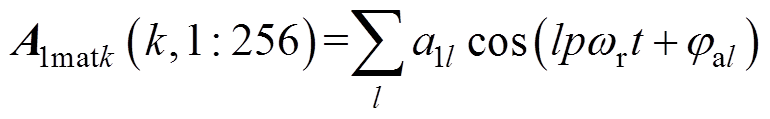 (23)
(23)
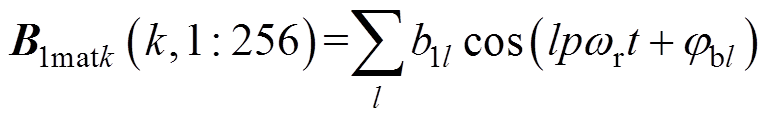 (24)
(24)
式中,l为A1matk(k, 1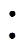 256)、B1matk(k, 1
256)、B1matk(k, 1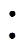 256)的时间谐波阶数;a1l、jal和b1l、jbl分别为A1matk(k, 1
256)的时间谐波阶数;a1l、jal和b1l、jbl分别为A1matk(k, 1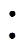 256)和B1matk(k, 1
256)和B1matk(k, 1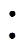 256)的l次谐波的幅值和相位。
256)的l次谐波的幅值和相位。
将式(23)、式(24)代入式(7)中,并利用三角函数积化和差、和差化积公式对其变换,可得永磁体瞬态磁场的表达式为

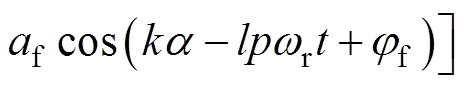 (25)
(25)
其中
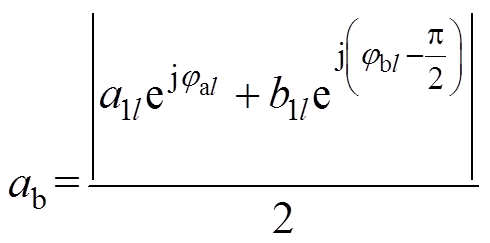 (26)
(26)
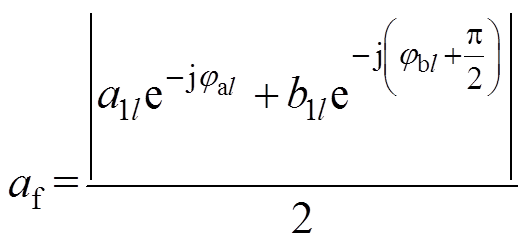 (27)
(27)
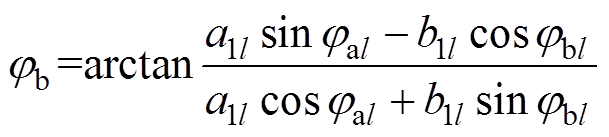 (28)
(28)
 (29)
(29)
式中,j为虚数单位。
又由a=qr+wrt,qr为转子空间角,则永磁体矢量磁位函数在转子坐标系下的表达式为
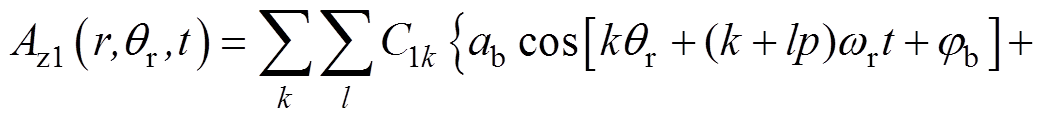
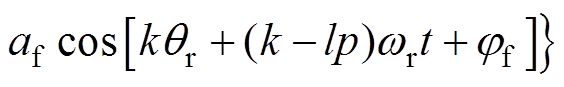 (30)
(30)
永磁体内部涡流密度Je的表达式为
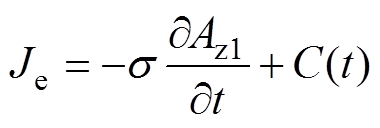 (31)
(31)
由于永磁体表面的绝缘材料,C(t)是为了保证每块永磁体的总电流为0,有
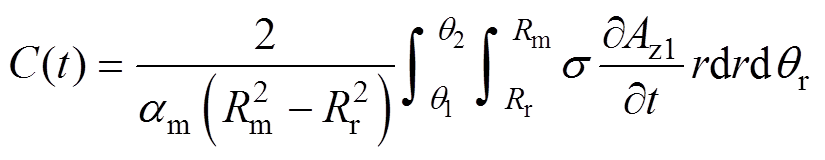 (32)
(32)
式中,s 为永磁体电导率;q1、q2为永磁体两边的周向位置;am为永磁体的极弧,am=q2-q1。
则永磁体在一个转子旋转周期T的平均涡流损耗pave表达式为
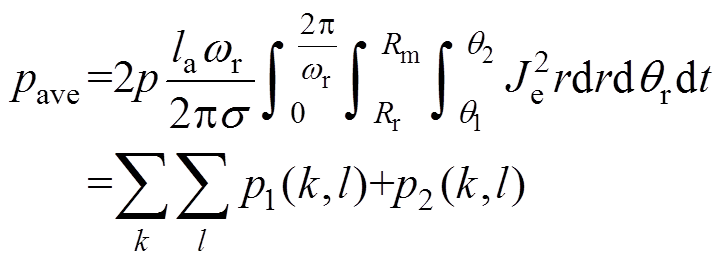 (33)
(33)
其中
 (34)
(34)
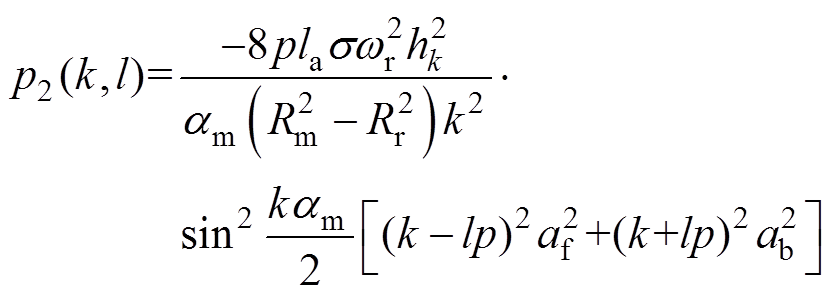 (35)
(35)
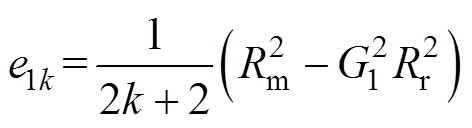 (36)
(36)
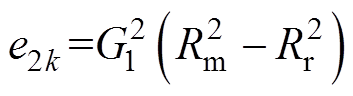 (37)
(37)
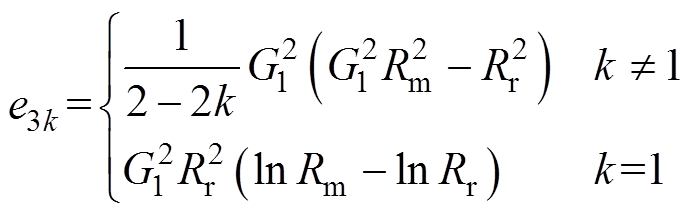 (38)
(38)
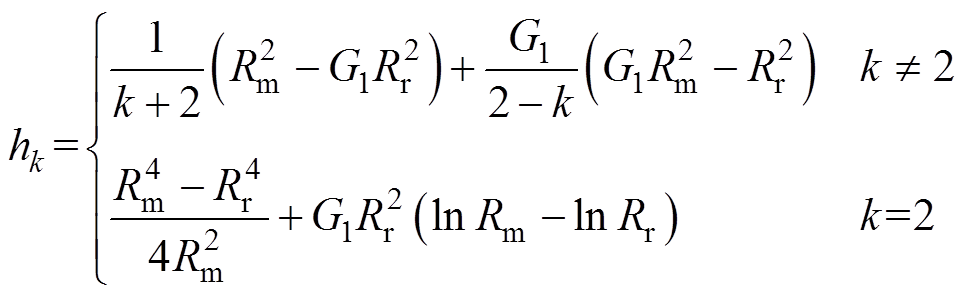 (39)
(39)
式中,la为电机的轴向长度。
电枢磁场k阶空间谐波造成的谐波涡流损耗可计算为
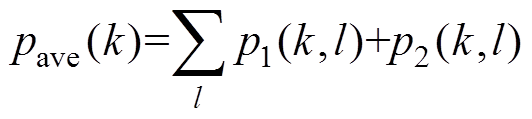 (40)
(40)
为验证永磁体谐波涡流损耗模型的精确性,本节以四台分别采用三相双层、双三相双层、三相四层及双三相四层的10极12槽永磁电机为例,将解析模型计算的永磁体涡流损耗与有限元软件计算结果进行对比。解析模型中,永磁体、气隙磁场的最大空间谐波阶数Kmax设置为60,上层绕组、下层绕组区域磁场的最大空间谐波阶数Mmax设置为25,槽口磁场的最大空间谐波阶数Nmax设置为25。永磁体磁场的最大时间谐波阶数Lmax设置为60。
为便于对比分析,四台电机的定子铁心、转子铁心及永磁体参数全部相同,每槽导体数和槽身面积相同,定子槽内的额定电流密度设计为12.66A/mm2。四台电机的基本参数见表1,绕组参数见表2。为确保四台电机的每槽导体数相同,双层绕组结构中每层导体数为96,四层绕组结构中每层导体数为48。
四台电机的绕组结构分布如图4所示,图中,A~C和X~Z表示绕组相序,符号+、-表示绕组的绕向。双三相绕组结构是将三相绕组结构A相中相邻线圈分为两个独立的、机械角相差30°的A相和X相,B相、C相也是按照相同的规律划分为B相和Y相、C相和Z相,通过两组相位相差30°的三相电流供电。四层绕组结构中,下层绕组通过上层绕组逆时针旋转150°得到。
表1 四台电机的基本参数
Tab.1 Basic parameters of the four machines
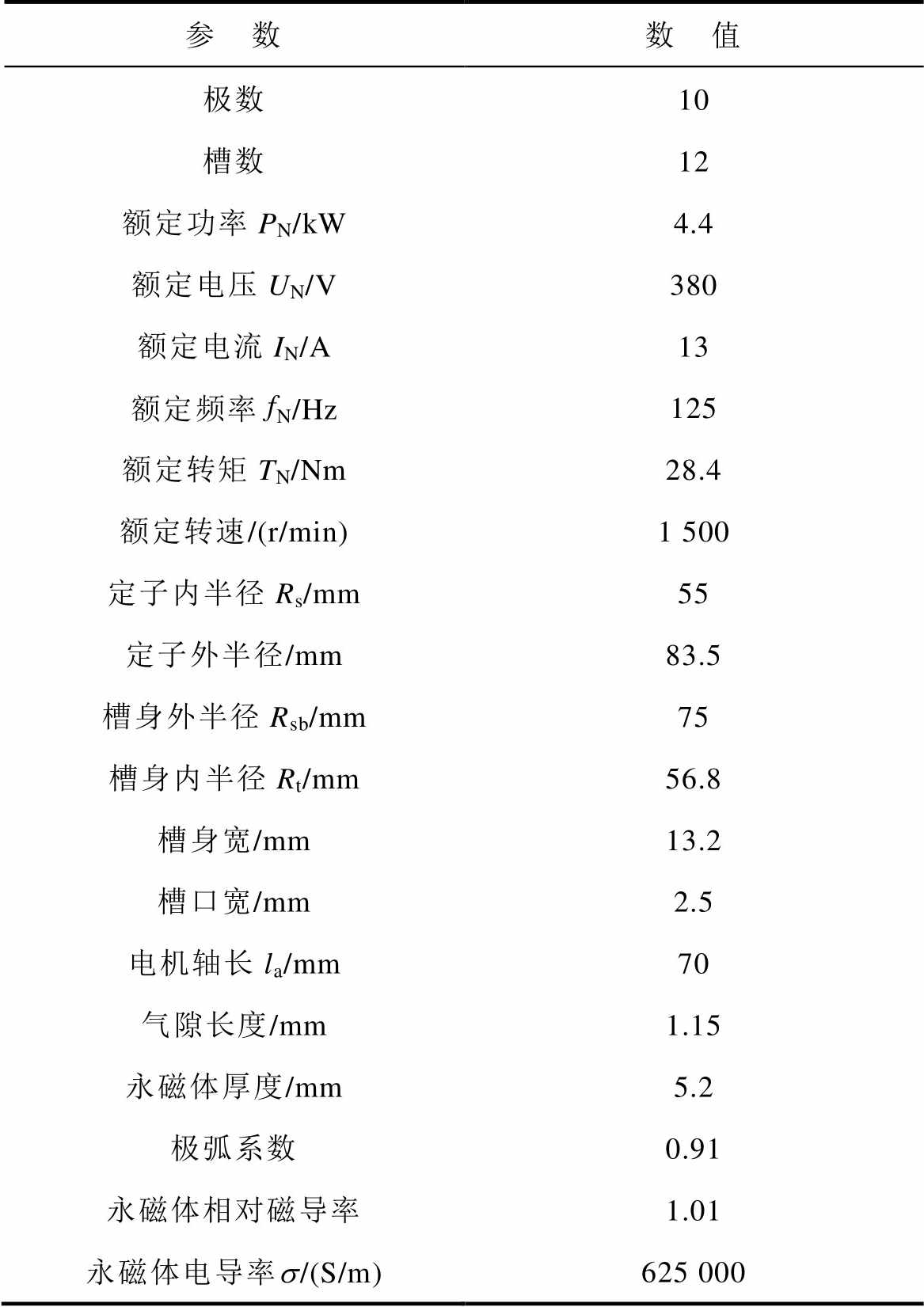
参 数数 值 极数10 槽数12 额定功率PN/kW4.4 额定电压UN/V380 额定电流IN/A13 额定频率fN/Hz125 额定转矩TN/Nm28.4 额定转速/(r/min)1 500 定子内半径Rs/mm55 定子外半径/mm83.5 槽身外半径Rsb/mm75 槽身内半径Rt/mm56.8 槽身宽/mm13.2 槽口宽/mm2.5 电机轴长la/mm70 气隙长度/mm1.15 永磁体厚度/mm5.2 极弧系数0.91 永磁体相对磁导率1.01 永磁体电导率s/(S/m)625 000
表2 四台电机的绕组参数
Tab.2 Winding parameters of the four machines
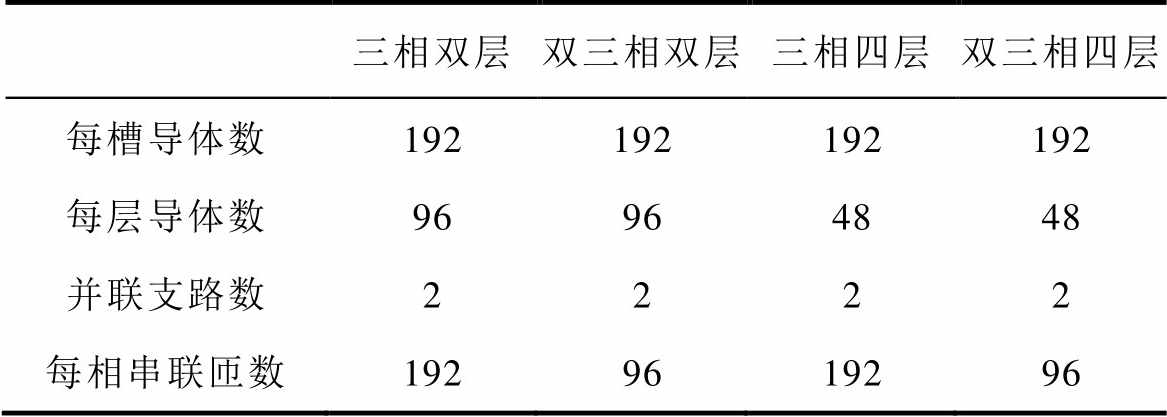
三相双层双三相双层三相四层双三相四层 每槽导体数192192192192 每层导体数96964848 并联支路数2222 每相串联匝数1929619296
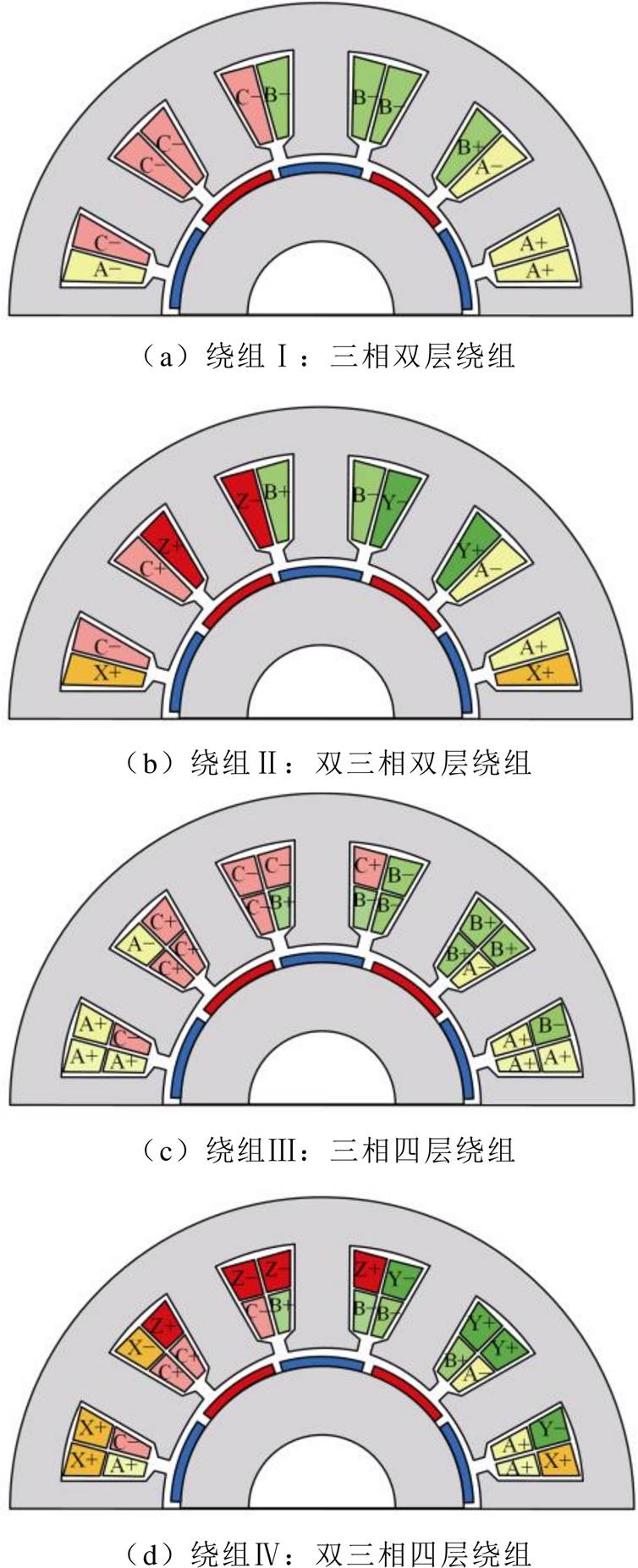
图4 四台电机的绕组结构
Fig.4 Winding configurations of the four machines
由式(3)可知,t=0ms时四台电机的电流密度分布如图5所示。

图5 t =0ms时四台电机的电流密度分布
Fig.5 Current density distribution of the four machines at t =0ms
此时,绕组Ⅱ、绕组Ⅳ的4号和10号槽的电流密度为5.91A/mm2;瞬态电流密度的计算如图3所示,确定求解时刻后,计算该时刻的电流分布,进而计算电流密度分布。
电枢磁场分布由绕组的电流密度分布决定,图6为t =0ms时四台电机的电枢磁场分布。表3为定子轭、定子齿、齿尖及永磁体的电枢磁通密度。
由图6和表3可知,由于四台电机电流密度分布的不同,其电枢磁场分布有所不同,但定子轭、定子齿、齿尖及永磁体的磁通密度一致,表明四台电机定子和永磁体的磁化程度相同;由于齿尖的面积小,磁力线分布密集,出现了轻微的磁饱和现象,但定子轭和定子齿部位的磁力线分布均匀且稀疏,说明忽略铁心饱和是合理的;由于大部分磁力线均是径向穿过永磁体,只有少量磁力线聚集在靠近槽口的永磁体表面,说明假设涡流在永磁体内分布均匀,采用积分法求解涡流损耗是合理的。
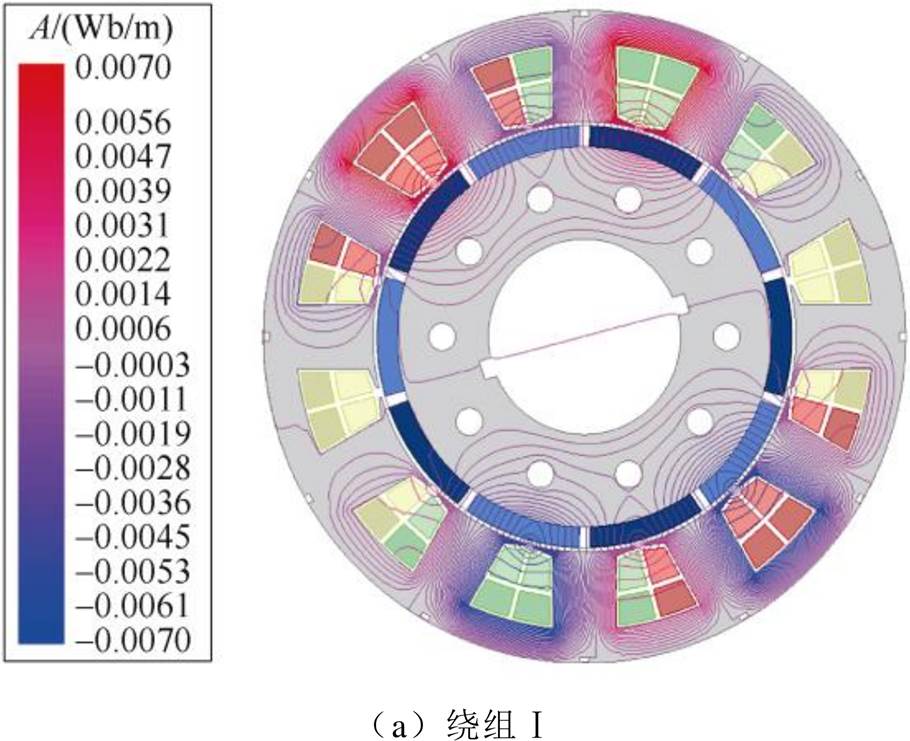

图6 t =0ms时四台电机的电枢磁场分布
Fig.6 Armature magnetic field distribution of the four machines at t =0ms
表3 各部件电枢磁通密度
Tab.3 Armature flux density of the four parts(单位: T)
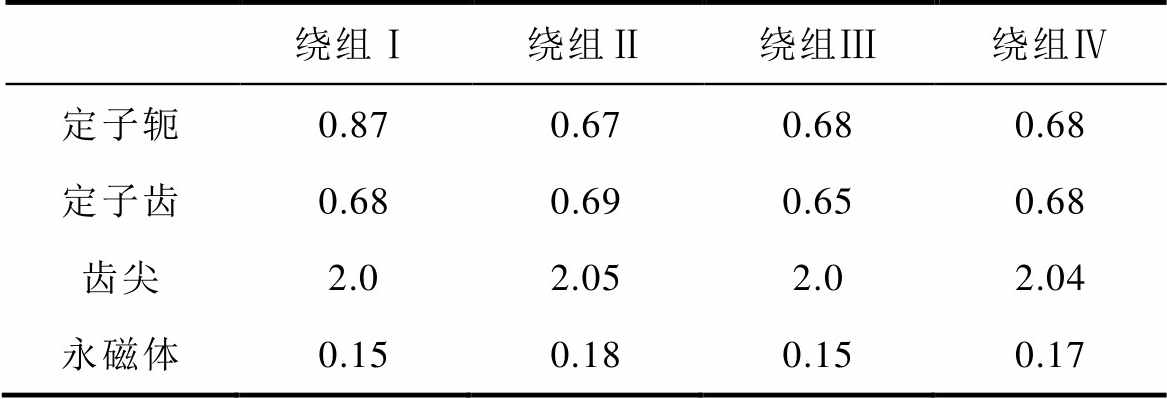
绕组Ⅰ绕组Ⅱ绕组Ⅲ绕组Ⅳ 定子轭0.870.670.680.68 定子齿0.680.690.650.68 齿尖2.02.052.02.04 永磁体0.150.180.150.17
由式(21)和式(22)可知,四台电机在电枢磁场下气隙磁通密度的解析解和有限元计算结果如图7所示。
由图7可知,四台电机气隙磁通密度的解析解均与有限元计算结果一致,验证了磁场计算的准确性。由图6可知,磁力线总是均匀且径向穿过靠近定子齿的气隙,而呈椭圆状穿过靠近槽口的气隙,所以气隙磁通密度的径向分量在定子齿处近似为常值、在槽口处出现尖峰,切向分量在定子齿处近似为0、在槽口处出现尖峰;机械角度0°~180°范围内的气隙共包含6个定子槽,所以气隙磁通密度共存在6处尖峰,体现了该磁场模型能够考虑齿槽效应。
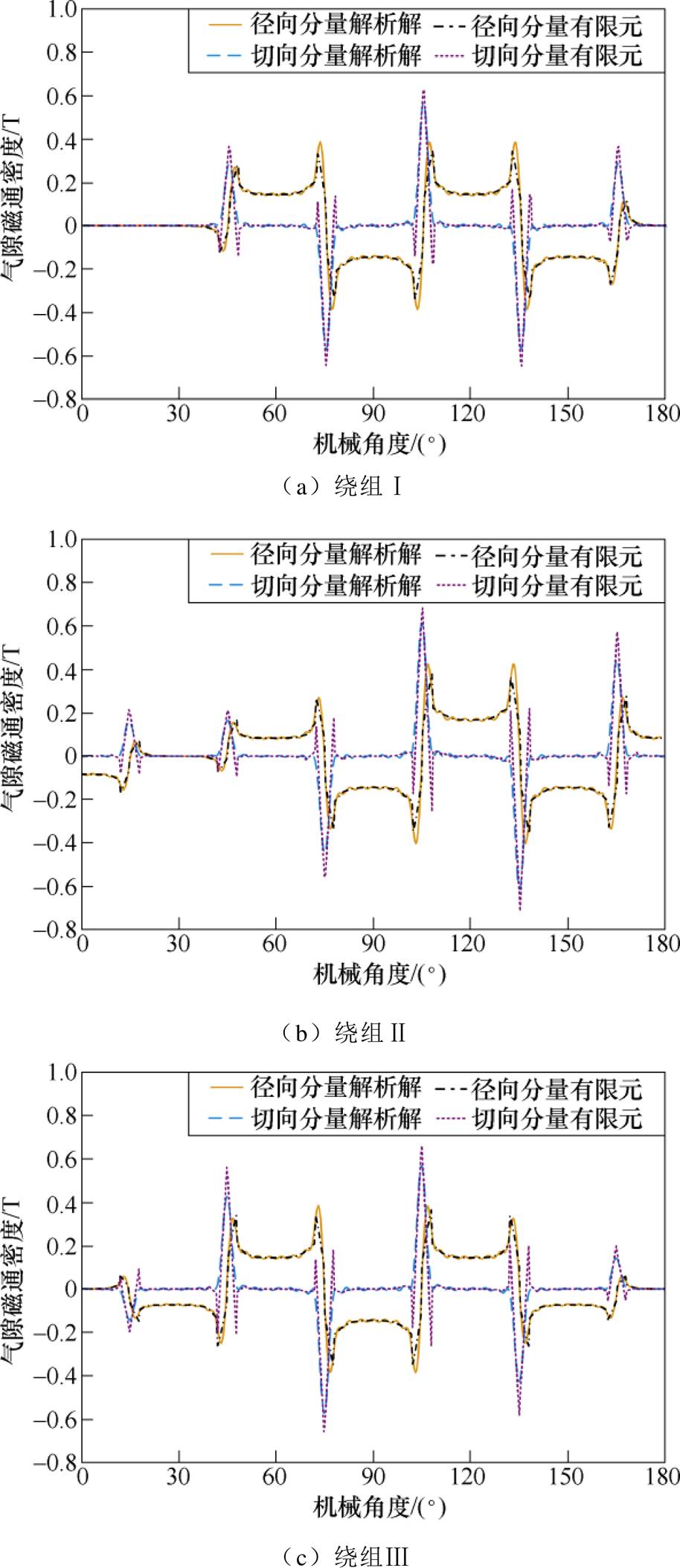
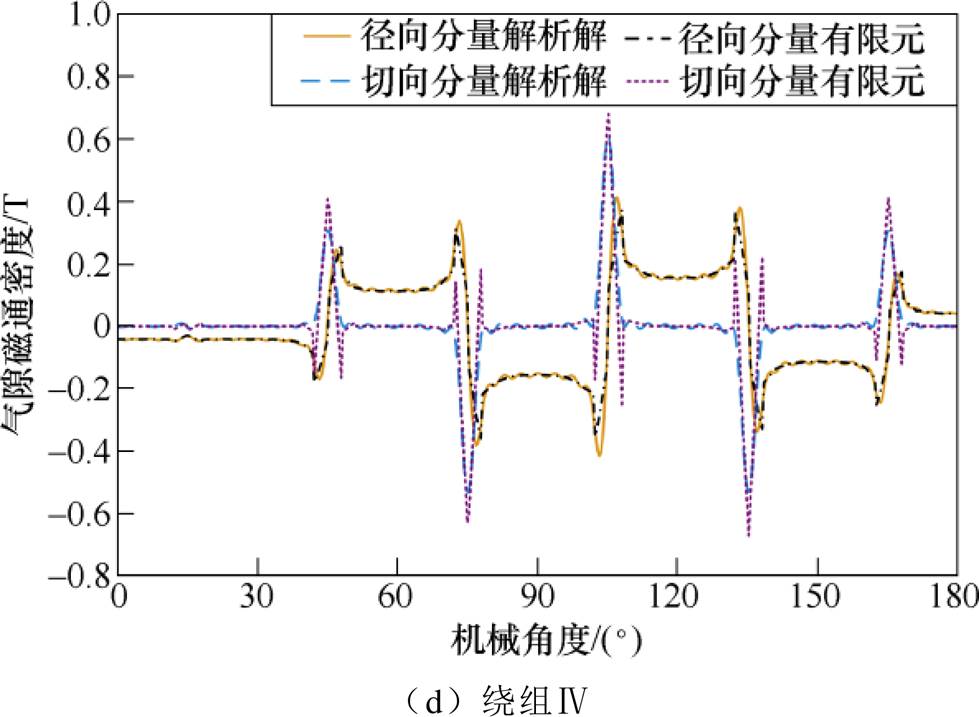
图7 t =0ms时四台电机的气隙磁通密度分布
Fig.7 Air-gap flux density distribution of the four machines at t =0ms
由式(33)可知,当电机由额定电流供电时,四台电机在电枢磁场下的永磁体涡流损耗随转速的变化规律如图8所示。当电机运行在额定转速时,涡流损耗随电枢电流的变化规律如图9所示。
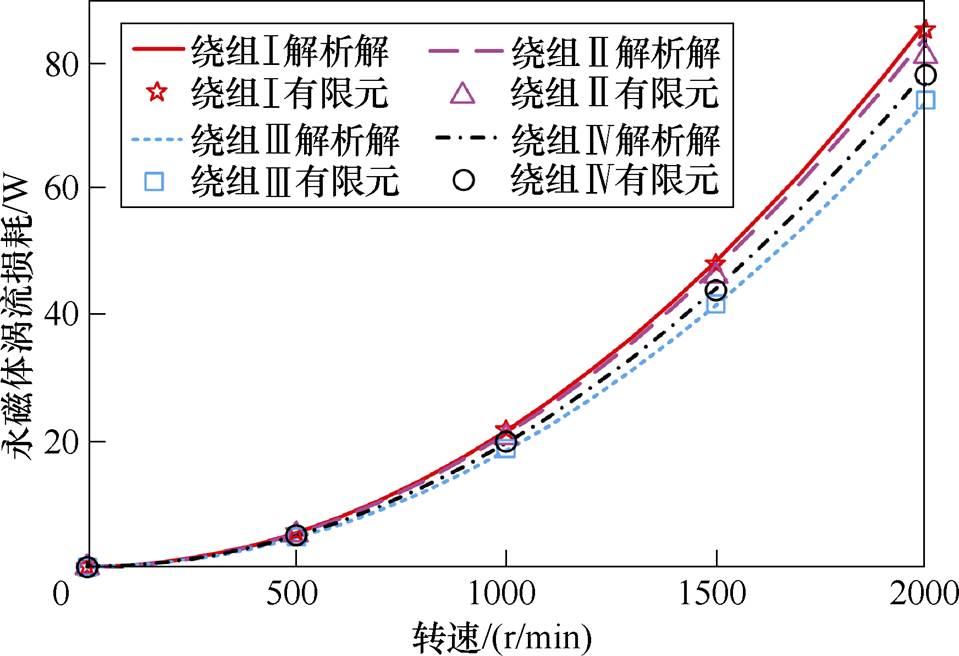
图8 电流为13A时永磁体涡流损耗随转速的变化曲线
Fig.8 Variation of magnet eddy-current losses with rotor speed at 13A
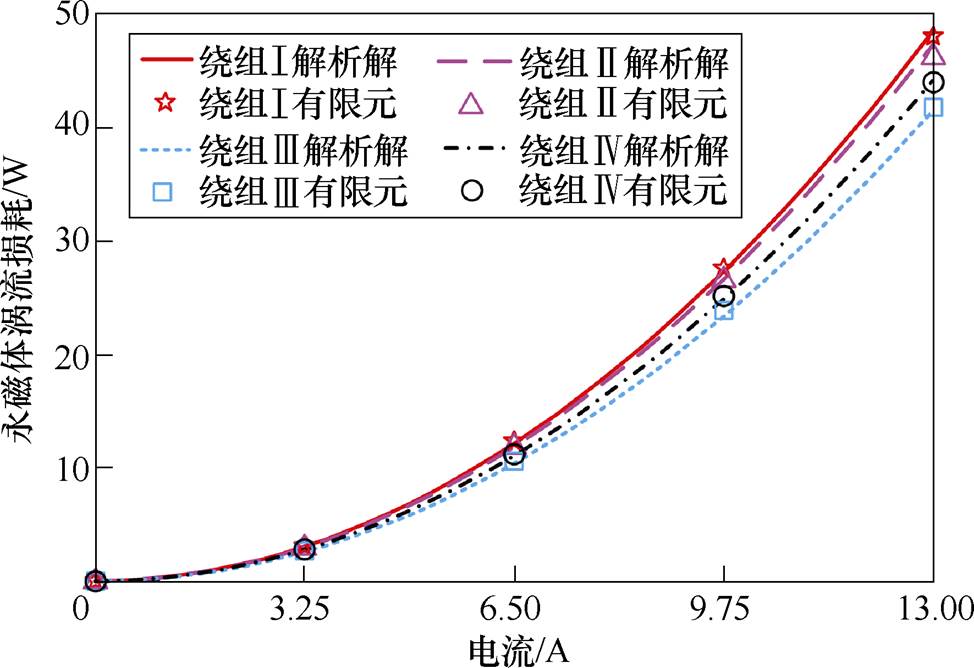
图9 转速为1 500r/min时永磁体涡流损耗随电枢电流的变化曲线
Fig.9 Variation of magnet eddy-current losses with armature current at 1 500r/min
由图8和图9可知,涡流损耗的解析计算结果与有限元计算结果的吻合程度较好,最大误差仅有2.5%,验证了损耗模型的精确性;在四种绕组结构中,三相四层绕组电枢磁场谐波分量造成的涡流损耗最小,三相双层绕组最大。
本文所提出的谐波涡流损耗模型,除了可以得到电机总的涡流损耗,还可以得到各次空间谐波磁场分别产生的涡流损耗大小,如式(40)所示。因而,可深入分析空间谐波涡流损耗随绕组相数和层数的变化规律。表4为四台电机运行在额定转速、额定电流时的空间谐波涡流损耗分布。
由表4可知,对于三相双层10极12槽绕组而言,1次、7次、17次、19次谐波涡流损耗比重大,分别占总损耗的8.8%、79.8%、2.2%、5.7%;偶数与3的整数倍阶次谐波涡流损耗为0。磁动势理论可从机理上解释该分布规律,三相双层10极12槽绕组的k阶谐波磁动势分布如图10所示。图中,FA1k~-FA4k、FB1k~-FB4k、FC1k~-FC4k分别表示A相、B相、C相的线圈磁动势矢量,其正负与线圈的绕向相关。
表4 额定转速、额定电流下空间谐波涡流损耗分布
Tab.4 Space harmonic eddy-current loss distribution at 1 500r/min and 13A
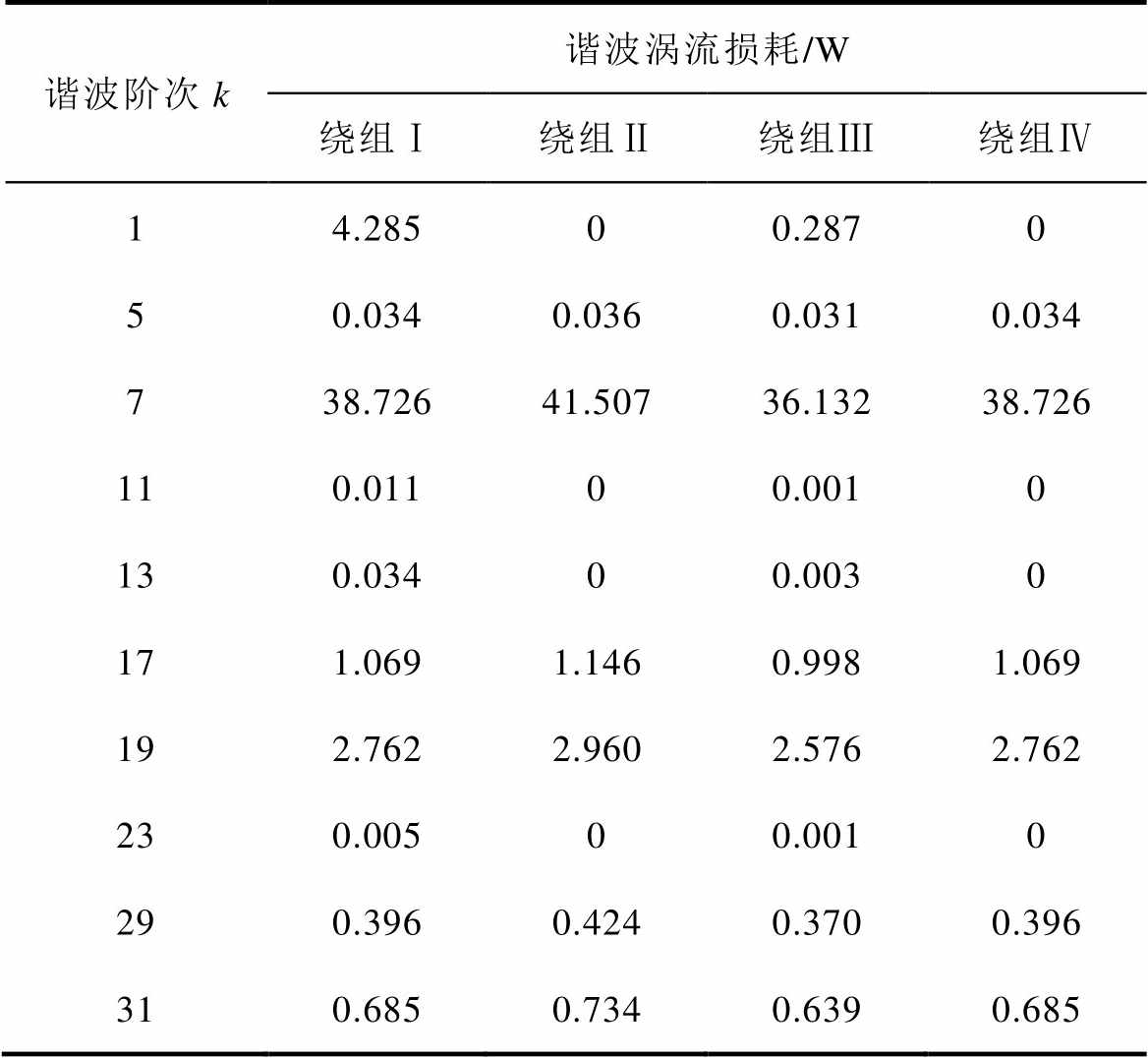
谐波阶次k谐波涡流损耗/W 绕组Ⅰ绕组Ⅱ绕组Ⅲ绕组Ⅳ 14.28500.2870 50.0340.0360.0310.034 738.72641.50736.13238.726 110.01100.0010 130.03400.0030 171.0691.1460.9981.069 192.7622.9602.5762.762 230.00500.0010 290.3960.4240.3700.396 310.6850.7340.6390.685
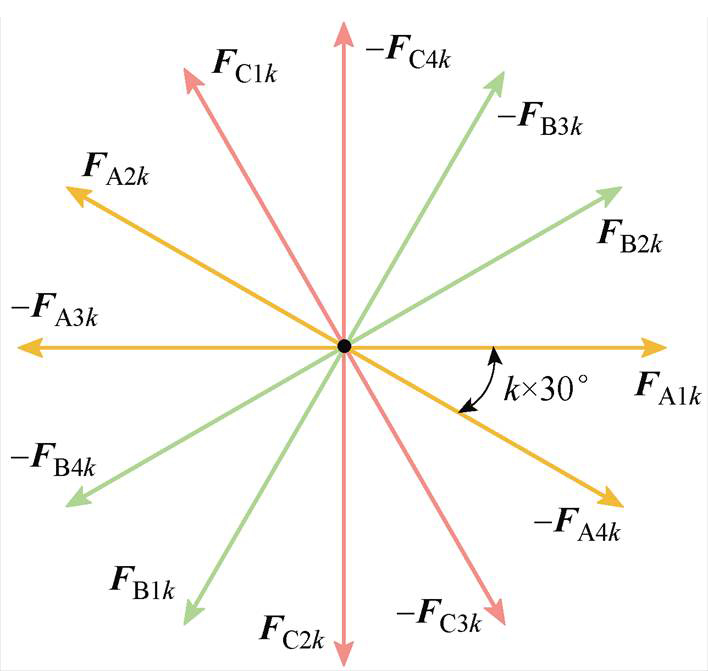
图10 三相双层绕组k阶谐波磁动势分布
Fig.10 The kth harmonic magnetomotive force distribution of three-phase double-layer winding
当k为偶数阶次时,FA1k与-FA3k、FA2k与-FA4k的夹角为0°,A相合成磁动势为0,电枢磁场中不存在偶数阶次空间谐波;当k为3的整数倍阶次时,A、B、C三相合成磁动势为0,电枢磁场中不存在3的整数倍阶次空间谐波。所以偶数与3的整数倍阶次谐波涡流损耗为0。
那么,电枢磁场次谐波(阶次小于转子永磁体极对数)中仅有1次谐波分量,因其阶次低、幅值高,所以1次谐波涡流损耗占比大。电枢磁场超谐波(阶次大于永磁体极对数)中有7, 11,…, 6v±1(v=2, 3, 4,…)次谐波,其中7, 17,…, 12v±5(v= 1, 2, 3,…)次谐波磁动势分布与5次基波相同,其分布系数相同,所以7, 17, 19次谐波幅值高、涡流损耗占比大。
相比于三相双层绕组,双三相双层绕组1, 11, 13, 23次谐波涡流损耗减小为0;7, 17, 19, 29, 31次谐波涡流损耗增大7.2%,谐波涡流损耗的下降幅度高于升高幅度,所以总的涡流损耗减小。相比于三相四层绕组,双三相四层绕组的谐波涡流损耗也呈现出相同的规律。但由于三相四层绕组的1次谐波涡流损耗较低,双三相四层绕组的谐波涡流损耗下降幅度低于升高幅度,所以总的涡流损耗增大。
当绕组相数由三相变为双三相时,A相、X相k阶谐波磁动势分布如图11所示。
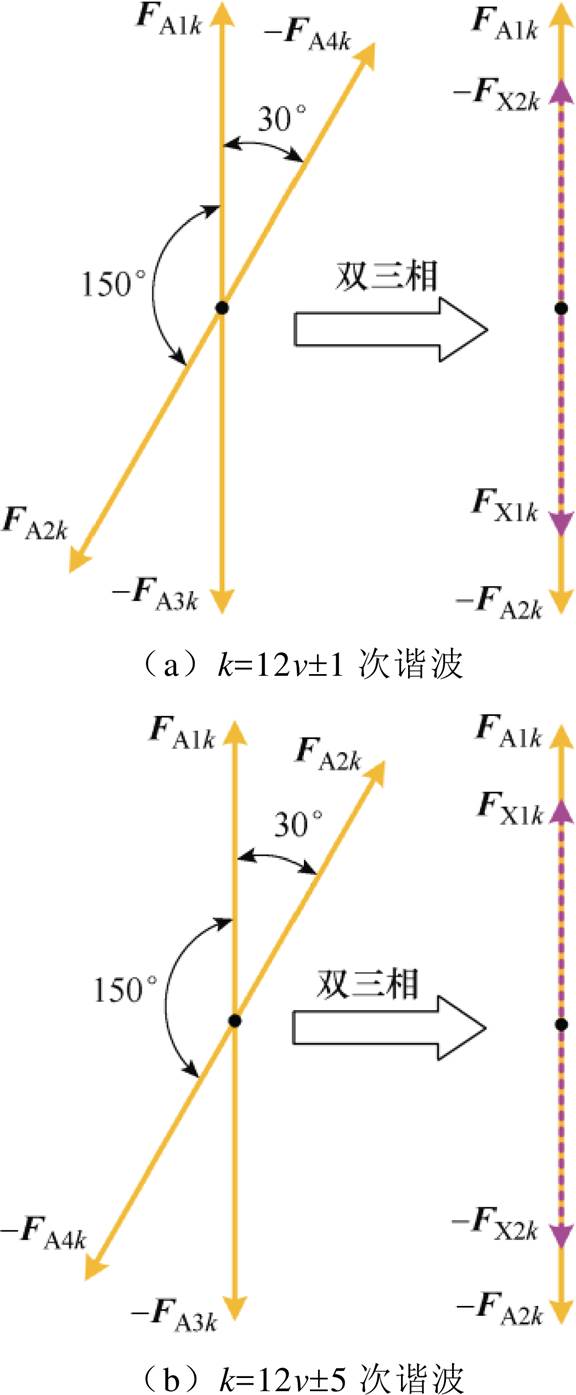
图11 双三相双层绕组A相与X相k阶谐波磁动势分布
Fig.11 The kth harmonic magnetomotive force distribution of phase A and X of dual three-phase double-layer winding
由图11可知,当k为1, 11,…, 12v±1(v=1, 2, 3,…)阶次谐波时,FA1k与FX1k、-FA2k与-FX2k的夹角由150°变为180°、相互抵消,A相与X相合成磁动势为0,所以谐波涡流损耗为0;当k为7, 17,…, 12v±5(v=1, 2, 3,…)阶次谐波时,FA1k与FX1k、-FA2k与-FX2k的夹角由30°变为0°,合成磁动势的分布系数增大3.4%,谐波涡流损耗增大7.2%。
相比于三相双层绕组,三相四层绕组1次谐波涡流损耗减小93.3%,7, 17, 19, 29, 31次谐波涡流损耗减小6.7%,所以总的涡流损耗减小。相比于双三相双层绕组,双三相四层绕组7, 17, 19, 29, 31次谐波涡流损耗同样减小6.7%,总的涡流损耗减小。
当绕组层数由双层变为四层时,A相k阶谐波磁动势分布如图12所示,Ft1k、Ft2k、-Ft3k、-Ft4k表示上层绕组的线圈磁动势矢量,Fb1k、Fb2k、-Fb3k、-Fb4k表示下层绕组的线圈磁动势矢量。需要说明的是,由于磁动势矢量F幅值与线圈匝数呈正相关,四层绕组每层导体数是双层绕组的1/2,所以四层绕组线圈磁动势矢量F的幅值是双层绕组的1/2。
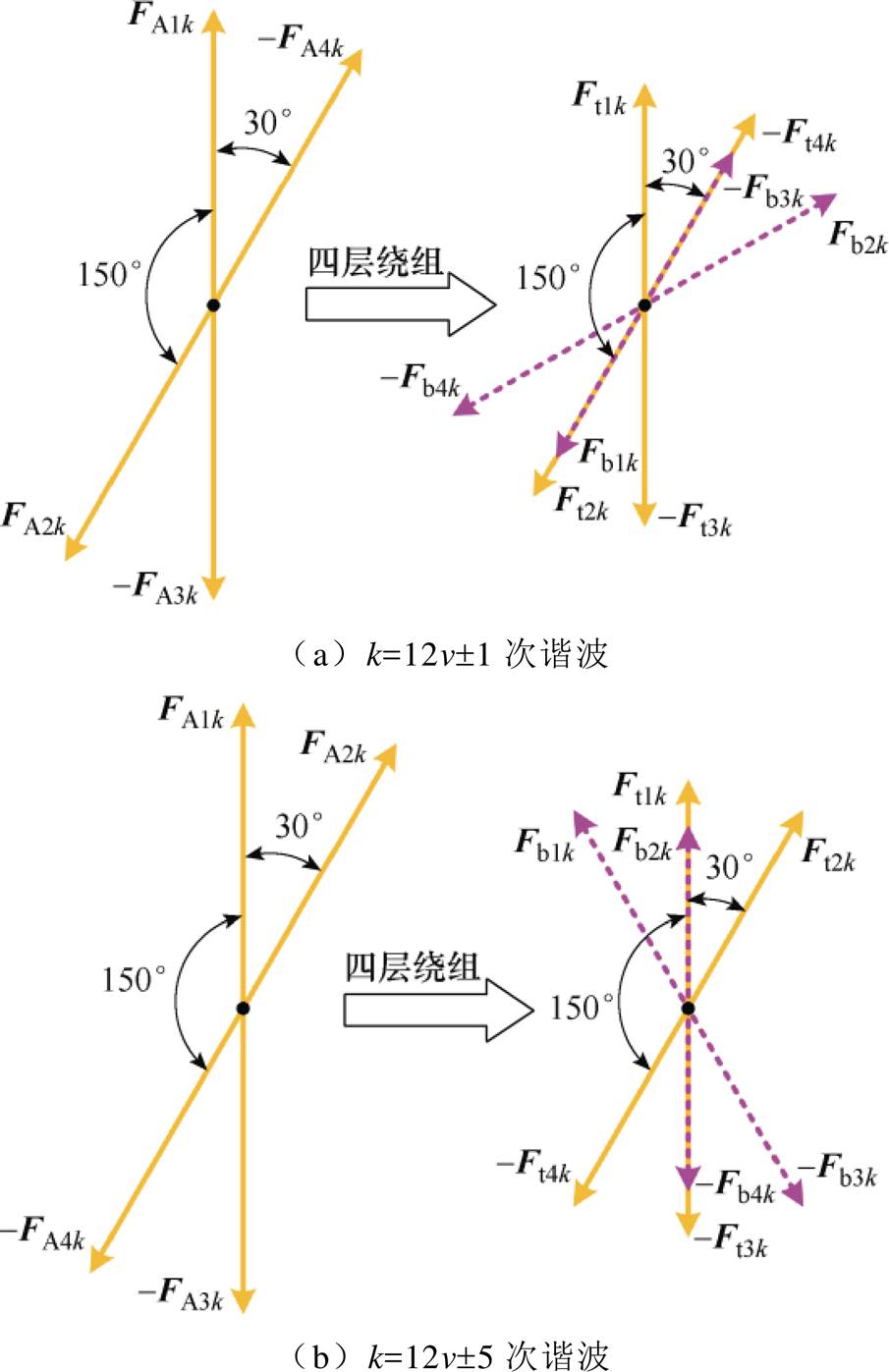
图12 三相四层绕组A相k阶谐波磁动势分布
Fig.12 The kth harmonic magnetomotive force distribution of phase A of three-phase four-layer winding
由图12可知,当k为1, 11,…, 12v±1(v=1, 2, 3,…)次谐波时,三相四层绕组A相合成磁动势的分布系数相比于双层绕组下降74.1%,1次谐波涡流损耗减小93.3%;当k为7, 17,…, 12v±5(v=1, 2, 3,…)次谐波时,A相合成磁动势的分布系数相比于双层绕组下降3.4%,谐波涡流损耗减小6.7%。
相比于三相双层绕组,双三相四层绕组1, 11, 13, 23次谐波涡流损耗下降为0。由于双三相绕组抵消了四层绕组给7, 17,…, 12v±5(v=1, 2, 3,…)次谐波带来的分布系数减小的作用,所以7, 17, 19, 29, 31次谐波涡流损耗没有变化。
本文提出了一种四层绕组分数槽永磁电机电流密度的建模方法,建立了永磁体谐波涡流损耗解析模型,能够用于求解三相/双三相、双层/四层绕组电机电枢磁场下的永磁体涡流损耗。以四台分别采用三相双层、双三相双层、三相四层及双三相四层绕组结构的10极12槽永磁电机为例,进一步探究了谐波涡流损耗随绕组相数和层数的变化规律,并使用绕组的磁动势从机理上分析该规律。研究表明,本文所提出的永磁体谐波涡流损耗模型准确度高,与有限元计算结果的最大误差仅有2.5%。三相双层10极12槽永磁电机的7次谐波涡流损耗占比最大,1次谐波涡流损耗次之。当绕组相数由三相变为双三相时,1, 11,…, 12v±1(v=1, 2, 3,…)阶次谐波涡流损耗减小为0;当绕组层数由双层变为四层时,1次谐波涡流损耗减小93.3%,双三相绕组、四层绕组抑制1次谐波涡流损耗的效果显著。若想取得更为理想的永磁体涡流损耗抑制效果,未来改进绕组的研究应关注电枢磁场7次谐波的抑制。
1. 电枢绕组电流密度傅里叶级数
上层绕组电流密度Jit傅里叶级数中Jit0、Jitn的表达式为
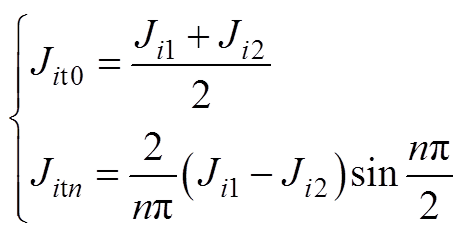 (A1)
(A1)
下层绕组电流密度Jib傅里叶级数中Jib0、Jibn的表达式为
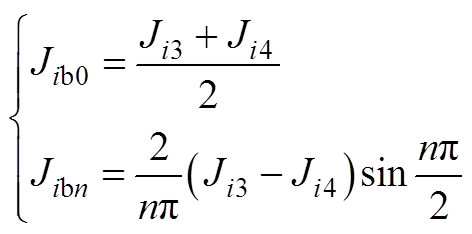 (A2)
(A2)
2. 矢量磁位谐波系数的求解
在永磁体与气隙交界面即r=Rm处,由式(17)中径向磁通密度连续可得
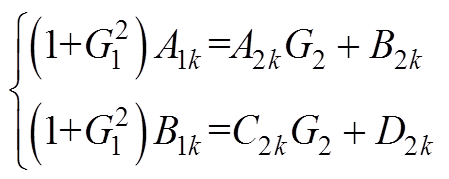 (A3)
(A3)
其中
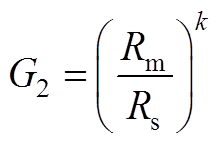 (A4)
(A4)
由式(17)中切向磁场强度连续,可得
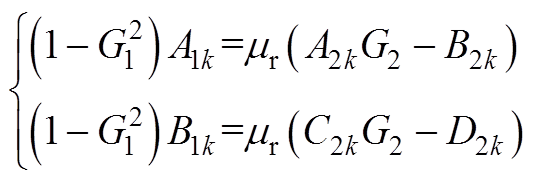 (A5)
(A5)
式中,mr为永磁体相对磁导率。
在上层绕组区域与下层绕组区域交界面即r=Rsm处,由式(18)中径向磁通密度连续可得
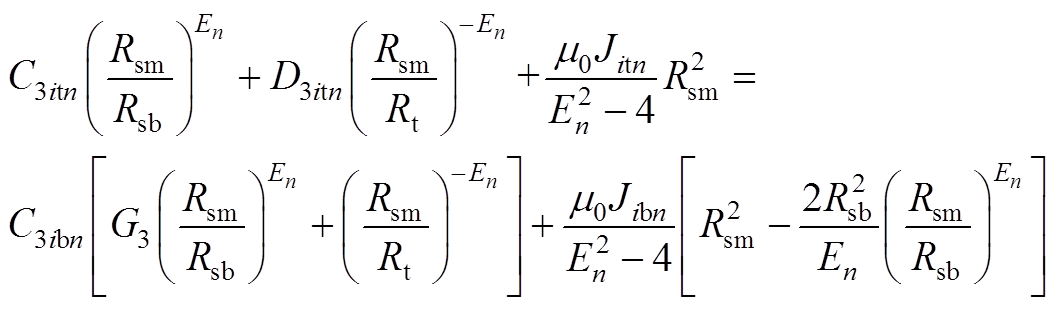 (A6)
(A6)
由式(18)中切向磁场强度连续可得
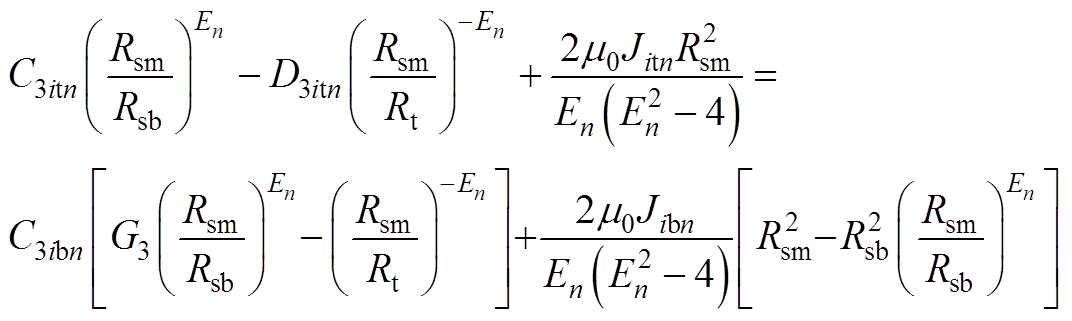 (A7)
(A7)
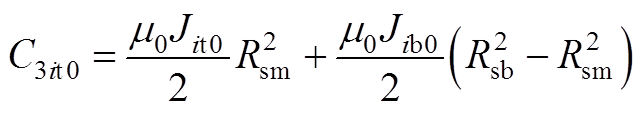 (A8)
(A8)
联立式(A6)、式(A7)可解得C3itn、D3itn的表达式为
 (A9)
(A9)
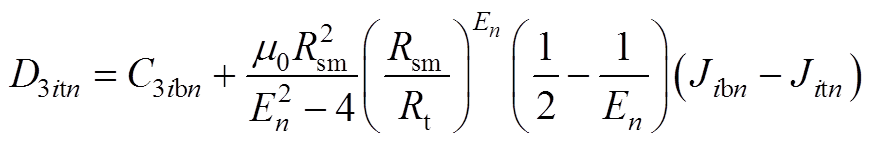 (A10)
(A10)
在槽口与上层绕组区域交界面即r=Rt处,由式(19)中切向磁场强度连续,可得
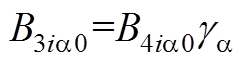 (A11)
(A11)
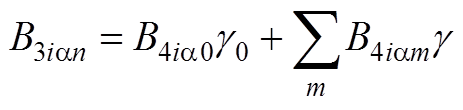 (A12)
(A12)
其中
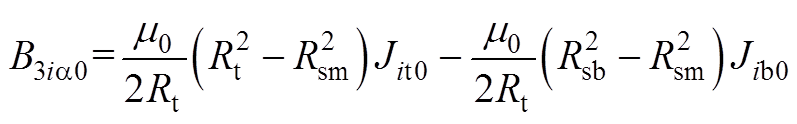 (A13)
(A13)
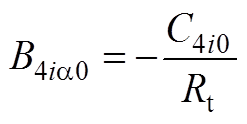 (A14)
(A14)
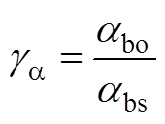 (A15)
(A15)
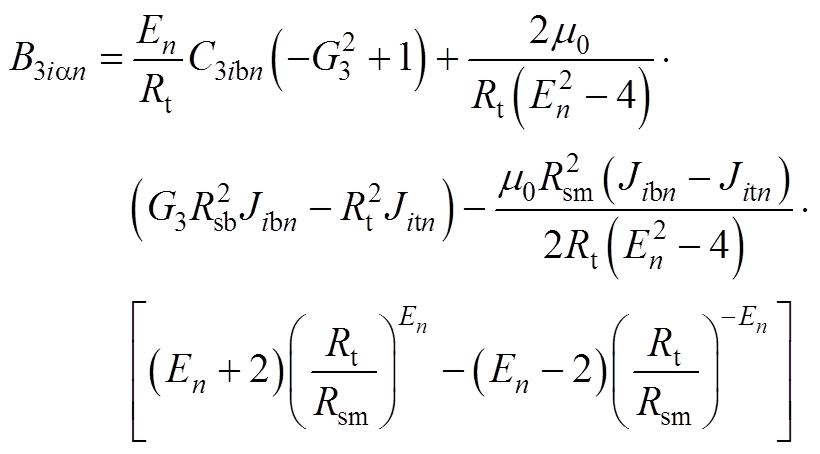 (A16)
(A16)
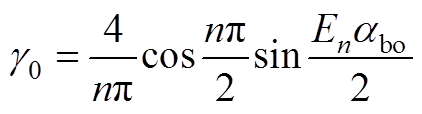 (A17)
(A17)
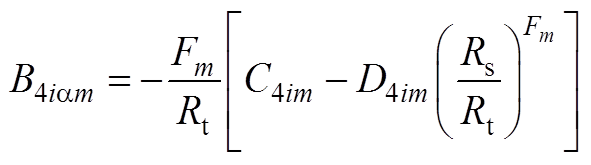 (A18)
(A18)
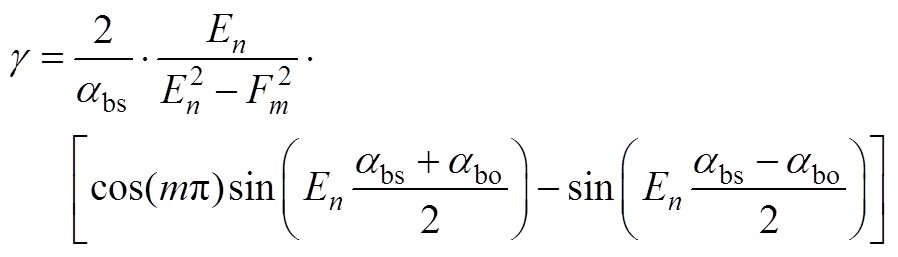 (A19)
(A19)
联立式(A11)、式(A13)~式(A15)可解得
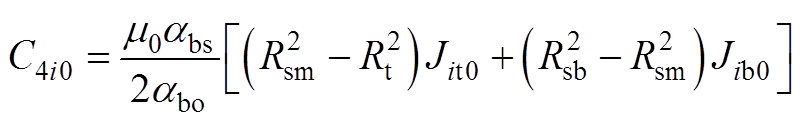 (A20)
(A20)
由式(19)中矢量磁位连续可得
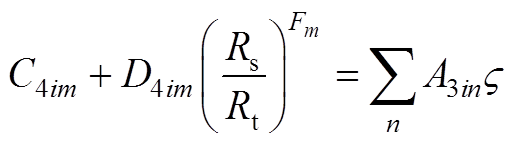 (A21)
(A21)
其中
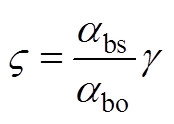 (A22)
(A22)
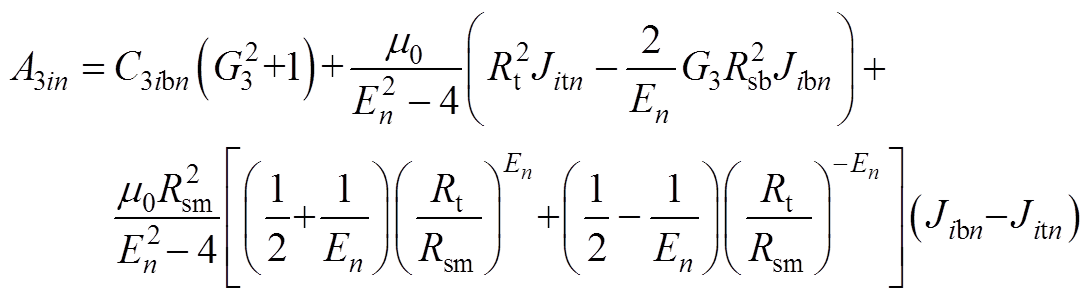 (A23)
(A23)
在槽口与气隙交界面即r=Rs处,由式(20)中切向磁场强度连续可得
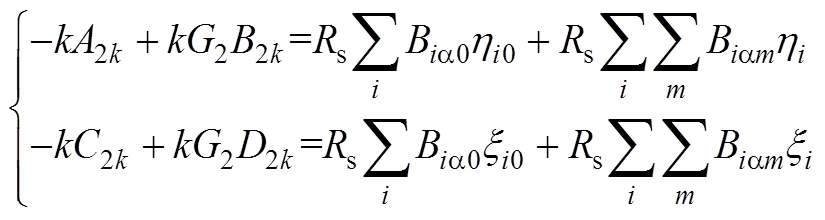 (A24)
(A24)
其中
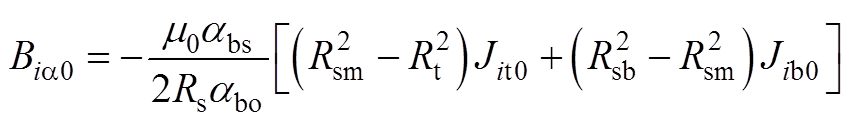 (A25)
(A25)
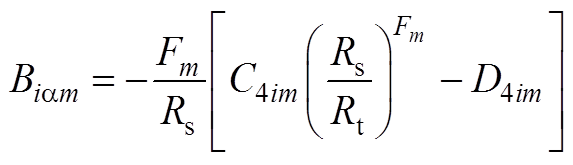 (A26)
(A26)
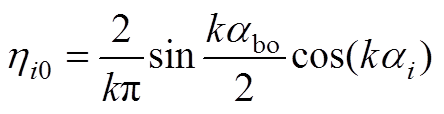 (A27)
(A27)
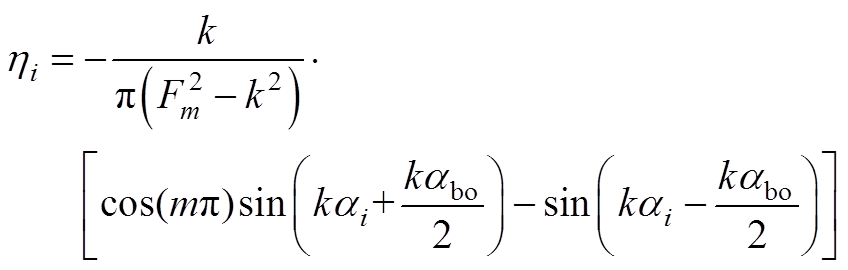 (A28)
(A28)
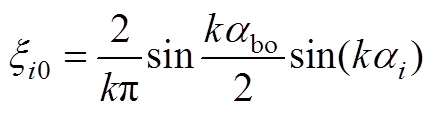 (A29)
(A29)
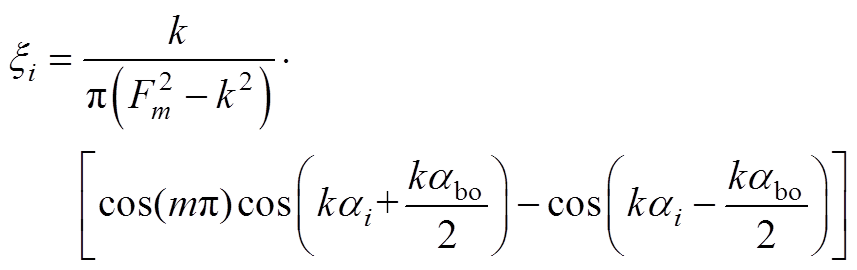 (A30)
(A30)
由式(20)中矢量磁位连续可得
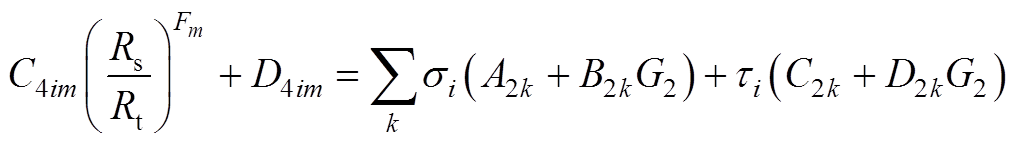 (A31)
(A31)
其中
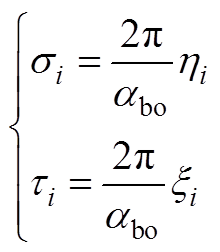 (A32)
(A32)
联立式(A3)、式(A5)、式(A12)、式(A21)、式(A24)及式(A31),可解得永磁体、气隙、上层绕组、下层绕组及槽口区域矢量磁位的谐波系数。
参考文献
[1] 鲍晓华, 刘佶炜, 孙跃, 等. 低速大转矩永磁直驱电机研究综述与展望[J]. 电工技术学报, 2019, 34(6): 1148-1160.
Bao Xiaohua, Liu Jiwei, Sun Yue, et al. Review and prospect of low-speed high-torque permanent magnet machines[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1148-1160.
[2] Li Wei, Cheng Ming. Investigation of influence of winding structure on reliability of permanent magnet machines[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(2): 87-95.
[3] 陈益广, 潘玉玲, 贺鑫. 永磁同步电机分数槽集中绕组磁动势[J]. 电工技术学报, 2010, 25(10): 30-36.
Chen Yiguang, Pan Yuling, He Xin. Magnetomotive force in permanent magnet synchronous machine with concentrated fractional-slot winding[J]. Transactions of China Electrotechnical Society, 2010, 25(10): 30-36.
[4] 沈建新, 李鹏, 郝鹤, 等. 高速永磁无刷电机电磁损耗的研究概况(英文)[J]. 中国电机工程学报, 2013, 33(3): 62-74.
Shen Jianxin, Li Peng, Hao He, et al. Study on electromagnetic losses in high-speed permanent magnet brushless machines-the state of the art[J]. Proceedings of the CSEE, 2013, 33(3): 62-74.
[5] Dajaku G, Gerling D. Eddy current loss minimization in rotor magnets of PM machines using high- efficiency 12-teeth/10-slots winding topology[C]// 2011 International Conference on Electrical Machines and Systems, Beijing, 2011: 1-6.
[6] Dajaku G, Xie Wei, Gerling D. Reduction of low space harmonics for the fractional slot concentrated windings using a novel stator design[J]. IEEE Transa- ctions on Magnetics, 2014, 50(5): 1-12.
[7] Abdel-Khalik A S, Ahmed S, Massoud A M. Low space harmonics cancelation in double-layer fractional slot winding using dual multiphase minding[J]. IEEE Transactions on Magnetics, 2015, 51(5): 1-10.
[8] Abdel-Khalik A S, Ahmed S, Massoud A M. Effect of multilayer windings with different stator winding connections on interior PM machines for EV appli- cations[J]. IEEE Transactions on Magnetics, 2016, 52(2): 1-7.
[9] Alberti L, Bianchi N. Theory and design of fractional- slot multilayer windings[J]. IEEE Transactions on Industry Applications, 2013, 49(2): 841-849.
[10] Chen Qixu, Liang Deliang, Jia Shaofeng, et al. Analysis of multi-phase and multi-layer factional-slot concentrated-winding on PM eddy current loss considering axial segmentation and load operation[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-6.
[11] 唐任远, 陈萍, 佟文明, 等. 考虑涡流反作用的永磁体涡流损耗解析计算[J]. 电工技术学报, 2015, 30(24): 1-10.
Tang Renyuan, Chen Ping, Tong Wenming, et al. Analytical calculation of eddy current loss accounting for eddy current reaction[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 1-10.
[12] 倪有源, 王磊, 王群京. 凸形不等厚磁极永磁电机建模与分析[J]. 电工技术学报, 2020, 35(11): 2406- 2414.
Ni Youyuan, Wang Lei, Wang Qunjing. Modeling and analysis of permanent magnet machines with salient shape unequal thickness magnets[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2406- 2414.
[13] 王明杰, 徐伟, 杨存祥, 等. 基于精确子域模型的永磁直线同步电机空载磁场解析计算[J]. 电工技术学报, 2020, 35(5): 942-953.
Wang Mingjie, Xu Wei, Yang Cunxiang, et al. Analytical calculation of no-load magnetic field in permanent magnet linear synchronous motors based on an accurate subdomain model[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 942-953.
[14] 李岩, 井永腾, 杜建民, 等. 基于混合磁场解析法的磁极偏心型表贴式永磁同步电机空载特性分析[J]. 电工技术学报, 2020, 35(18): 3811-3820.
Li Yan, Jing Yongteng, Du Jianmin, et al. No-load characteristic analysis of surface-mounted permanent magnet synchronous motor with non-concentric pole based on hybrid magnetic field analysis method[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3811-3820.
[15] Zhu Minchen, Wu Lijian, Fang Youtong, et al. Sub- domain model for predicting armature reaction field of dual-stator consequent-pole PM machines accoun- ting for tooth-tips[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(2): 143-150.
[16] 高锋阳, 齐晓东, 李晓峰, 等. 部分分段Halbach永磁同步电机优化设计[J]. 电工技术学报, 2021, 36(4): 787-800.
Gao Fengyang, Qi Xiaodong, Li Xiaofeng, et al. Optimization design of partially-segmented Halbach permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(4): 787-800.
[17] 陈浈斐, 夏长亮, 王慧敏. 考虑齿槽效应的表贴式永磁电机空载磁场建模[J]. 电工技术学报, 2014, 29(5): 9-16.
Chen Zhenfei, Xia Changliang, Wang Huimin, et al. Modeling for open circuit magnetic field prediction in slotted surface-mounted permanent-magnet machine[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 9-16.
[18] 孙权贵, 邓智泉, 张忠明. 基于齿槽效应的高速永磁电机转子涡流损耗解析计算[J]. 电工技术学报, 2018, 33(9): 1994-2004.
Sun Quangui, Deng Zhiquan, Zhang Zhongming. Analytical calculation of rotor eddy current losses in high speed permanent magnet machines accounting for influence of slot opening[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 1994- 2004.
[19] Atallah K, Howe D, Mellor P H, et al. Rotor loss in permanent-magnet brushless AC machines[J]. IEEE Transactions on Industry Applications, 2000, 36(6): 1612-1618.
[20] Ishak D, Zhu Ziqiang, Howe D. Eddy-current loss in the rotor magnets of permanent-magnet brushless machines having a fractional number of slots per pole[J]. IEEE Transactions on Magnetics, 2005, 41(9): 2462-2469.
[21] Wang Jiabin, Atallah K, Chin R, et al. Rotor eddy- current loss in permanent-magnet brushless AC machines[J]. IEEE Transactions on Magnetics, 2010, 46(7): 2701-2707.
[22] Wu Lijian, Zhu Ziqiang, Staton D, et al. Analytical modeling and analysis of open-circuit magnet loss in surface-mounted permanent-magnet machines[J]. IEEE Transactions on Magnetics, 2012, 48(3): 1234-1247.
[23] Wu Lijian, Zhu Ziqiang, Staton D, et al. Analytical model for predicting magnet loss of surface mounted permanent magnet machines accounting for slotting effect and load[J]. IEEE Transactions on Magnetics, 2012, 48(1): 107-117.
[24] Zhang Zhongming, Deng Zhiquan, Sun Quangui, et al. Analytical modeling and experimental validation of rotor harmonic eddy-current loss in high-speed surface-mounted permanent magnet motors[J]. IEEE Transactions on Magnetics, 2019, 55(2): 1-11.
Analytical Modeling and Analysis of Magnet Harmonic Loss in Fractional Slot Permanent-Magnet Machines
Abstract The key to optimize winding layouts and reduce magnet eddy-current loss of fractional slot permanent-magnet machines is to calculate the loss under armature magnetic field and investigate the variation of harmonic loss with winding layouts. To solve this problem, this paper proposes a current density modeling method of four-layer winding to realize the modeling of three- phase/dual-three-phase, double-layer/four-layer windings. Based on the subdomain model, the slot area of four-layer winding is further divided into the top-layer winding part and the bottom-layer winding part, the boundary condition between the two winding parts is added, and the harmonic coefficients of each subdomain are determined. The analytical model of eddy-current loss is established by solving the transient armature magnetic field. Four 10-pole/12-slot machines with different windings are taken as examples to validate the proposed model by finite element simulation. Based on the proposed model, the variation of harmonic eddy-current loss with the number of winding phases and layers is summarized and analyzed by magnetomotive force, which provides some ideas for optimizing the winding configurations to reduce eddy-current loss.
keywords:Fractional slot permanent-magnet machine, armature magnetic field, magnet eddy- current loss, harmonic eddy-current loss, dual three-phase winding, four-layer winding
DOI: 10.19595/j.cnki.1000-6753.tces.210112
中图分类号:TM341
国家自然科学基金项目(51907052)、中国博士后科学基金项目(2017M621606)和江苏省博士后科研项目(2016-416109)资助。
收稿日期 2021-01-21
改稿日期 2021-03-25
陈浈斐 女,1987年生,副教授,硕士生导师,研究方向为永磁电机设计与电磁分析、电力设备故障诊断。E-mail: chenzhenfei@hhu.edu.cn(通信作者)
邢 宁 男,1997年生,硕士研究生,研究方向为永磁电机电磁分析。E-mail: 1292983488@qq.com
(编辑 崔文静)