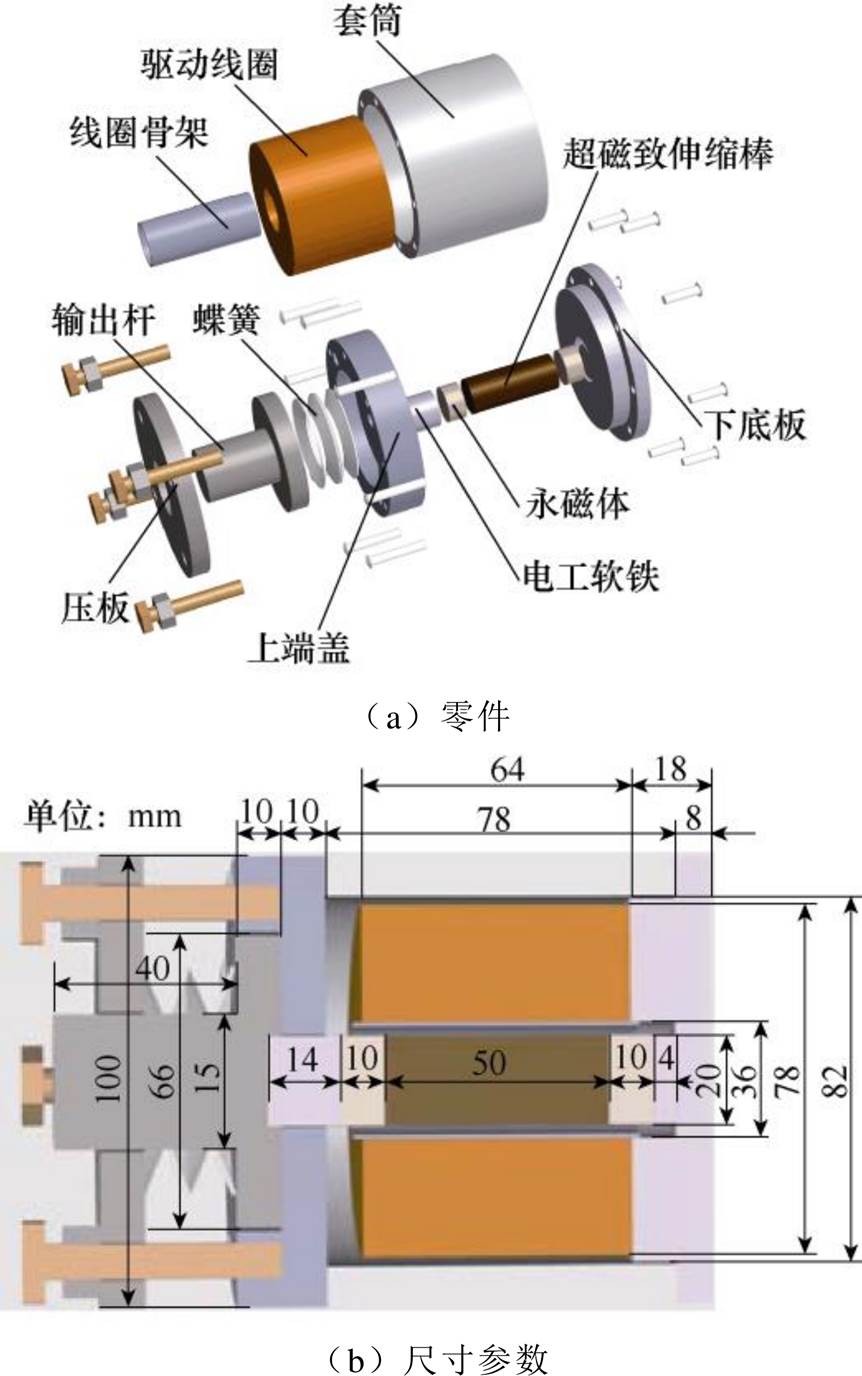
图1 纵振式超磁致伸缩换能器结构示意图
Fig.1 Structural diagram of longitudinal vibration GMT
摘要 超磁致伸缩换能器的工作特性与温度密切相关，快速准确地对换能器温度分布进行分析计算与预测是换能器设计与性能评估的关键。凭借仿真速度快、准确性高等显著优势，热网络建模广泛用于换能器热分析，但多聚焦于稳态建模研究，忽略超磁致伸缩棒由于热导率低所导致的明显的瞬态温度梯度。为此，该文以纵振式超磁致伸缩换能器为研究对象，计及超磁致伸缩棒作为热源的特殊性和对棒材温度空间分布的影响，建立超磁致伸缩换能器瞬态等效热网络模型。首先基于换能器的结构和工作原理，对其进行热分析；然后重点对超磁致伸缩棒进行建模，根据换能器内部传热过程，建立换能器瞬态热网络模型并对模型参数进行计算；最后搭建有限元仿真模型和换能器温升实验平台，从仿真和实验两方面验证了所提热网络模型对换能器温度时空分析的准确性和有效性。
关键词：超磁致伸缩换能器 等效热网络瞬态模型 参数计算 有限元模型 温度分布
稀土超磁致伸缩材料（Terfenol-D）是一种在磁场作用下能够产生大应变的新型功能材料。以此材料为核心元件的超磁致伸缩换能器（Giant Magneto- strictive Transducer, GMT）具有输出功率大、响应速度快、机磁耦合系数高等优点，广泛应用于水下电声换能器、精密加工、超声无损检测等领域[1-2]。
大功率超磁致伸缩换能器在工作过程中输入的电能除了转化为机械能外，还会产生大量的热损耗，导致换能器各部件特别是超磁致伸缩棒温度快速升高[3]。由于超磁致伸缩材料不仅具有较大的热膨胀系数，而且材料参数对外界温度非常敏感，导致换能器的输出特性与温度密切相关[4-5]。文献[6]中A. E. Clark等通过实验绘制出了不同预应力和磁场下，Terfenol-D磁致伸缩系数随温度的变化曲线，从曲线可以看出，当Terfenol-D的温度超过50℃时，材料的磁致伸缩系数开始迅速下降。除了应变系数，N. Nersessian等制备了一种Terfenol-D复合材料，并研究了不同工况下材料杨氏模量、磁导率以及压磁系数随温度的变化关系，验证了材料物理参数对温度的敏感性[7]。
为确保超磁致伸缩换能器在适合的温度范围内稳定工作，需要对换能器各部件的温度进行准确分析和监测。嵌入式温度传感器是常用的温度监测手段，然而在工程应用中存在很多问题。例如，换能器组装灌封后，传感器难以取出[8]；深水工作的电声换能器，无法远距离监测。因此对换能器温度场的准确建模与估计是解决换能器热问题的关键。
对超磁致伸缩换能器温度场的建模方法主要有热网络法和数值分析法[9]。有限元法是最常用的数值分析方法，曾海泉等计算出线圈以及超磁致伸缩棒的损耗热源，用有限元法进行换能器热分析，并加以实验验证，仿真结果与实验较为吻合[10]。K. Uchino等用ATILA有限元仿真软件对一款超磁致伸缩换能器进行热建模，模拟换能器内部温度分布并与实验进行对比，证明了模型的准确性[5]。有限元法的优点在于可以对复杂结构进行热建模，但是模型越复杂，对网格划分和边界条件设置的要求也越高，计算时间越长。等效热网络法则凭借数学形式简单、计算速度快等优势，被广泛应用于热动态分析[11-13]。目前热网络模型在解决电机的热限制问题中发挥着巨大的作用[14-16]，P. H. Mellor首次运用改进的T型等效热模型搭建热网络模拟电机热传递过程[17]。G. Verez等建立了轴向磁通永磁同步电机的三维热网络模型，并利用数值方法对模型进行对比[18]。A. Boglietti等提出了四种复杂度的热网络模型，用于电机定子-绕组短期内的瞬态温度预测，并以全封闭扇冷式感应电机为例进行实验验证，模型误差均控制在1.6%～8.6%内[19]。汪文博对永磁同步电机的各部件建立了详细的热网络模型，并总结了各部件的热阻计算公式，通过实验对提出的热路模型和热路参数进行验证，额定工况下误差能够控在5%以内[20]。20世纪90年代，热网络模型开始应用于换能器热分析，B. Dubus等搭建了双端纵振换能器和Ⅳ型弯张换能器热网络模型，计算换能器的稳态温度[21]。M. Anjanappa等运用热路模型对磁致伸缩微型制动器进行二维稳态热分析，在此基础上修正了磁致伸缩本构方程[22]。并用实验验证了热效应对制动器的显著影响。Zhu Yuchuan等为了研究磁致伸缩棒热变形与制动器参数之间的关系，建立了超磁致伸缩制动器稳态等效热阻模型和热致位移计算模型，得到的结果与实验的热致位移结果基本一致[23]。目前用于电机设计的热网络模型已接近成熟，但是针对换能器的热网络模型普遍只考虑稳态，而忽略了超磁致伸缩棒作为热源的特殊性，以及温升过程中由于棒材导热能力差而存在的明显的温度梯度问题。
针对以上问题，本文以纵振式超磁致伸缩换能器为研究对象，对换能器各部件特别是超磁致伸缩棒进行准确建模，并建立了完整的换能器等效热网络瞬态模型。为了验证模型的准确度，搭建有限元仿真模型和换能器温升实验平台，从仿真和实验两方面验证了所提热网络模型对换能器温度时空分析的准确性和有效性。
纵振式超磁致伸缩换能器结构如图1所示。主要部件包括超磁致伸缩棒、驱动线圈、永磁体、导磁块、上下盖板、套筒、输出杆、压板和蝶簧。驱动线圈和永磁体分别为超磁致伸缩棒提供交变磁场和偏置磁场。导磁块、上下盖板和套筒选用高磁导率的电工软铁DT4，与棒材、永磁体共同组成闭合磁路。输出杆与压板等其他部件选用不导磁的304不锈钢材料，与蝶簧一起为棒材施加稳定预应力。换能器工作时，在驱动线圈中通入交流电，棒材在交变磁场和偏置磁场的共同作用下产生周期性振动，通过输出杆输出相同频率的位移，对外做功。在图1b中对纵振式超磁致伸缩换能器的关键尺寸参数进行了标注，方便后续模型参数的计算。
图1 纵振式超磁致伸缩换能器结构示意图
Fig.1 Structural diagram of longitudinal vibration GMT
超磁致伸缩棒和驱动线圈是换能器两大主要热源。驱动线圈上通过交流电产生焦耳损耗，从而产生大量的热量，线圈通过与内部空气对流换热以及与下盖板接触传热将热量传递到外壳；棒材在交变磁场的作用下产生涡流损耗和磁滞损耗，热量通过与内部空气对流换热以及与永磁体、导磁块之间接触换热向外壳传递；传递到外壳的热量通过与外部空气进行对流换热和辐射换热，向外消散。当产生的热量等于消散的热量时，换能器各部件温度不再变化，换能器内部传热过程如图2所示。
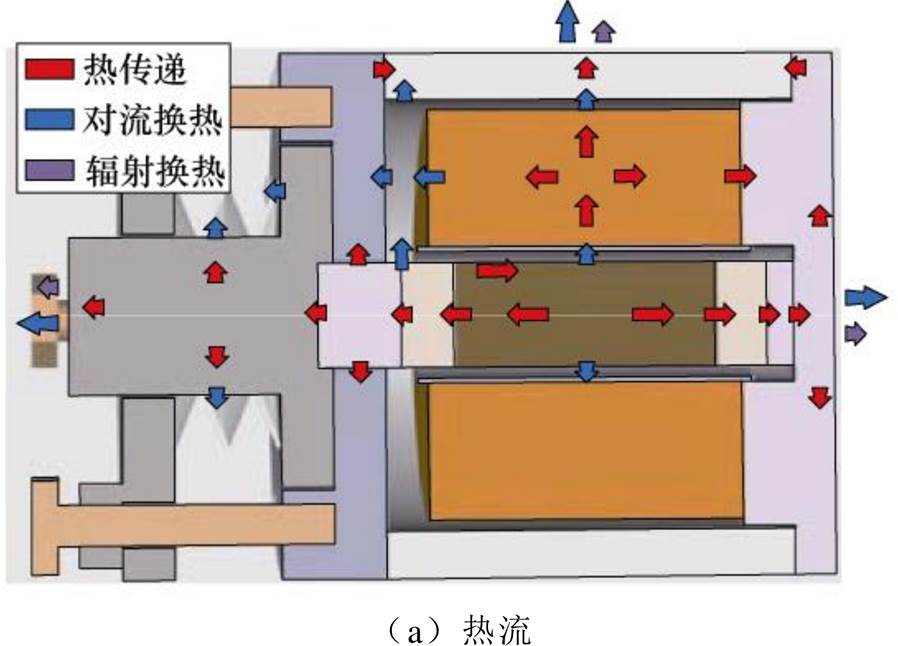
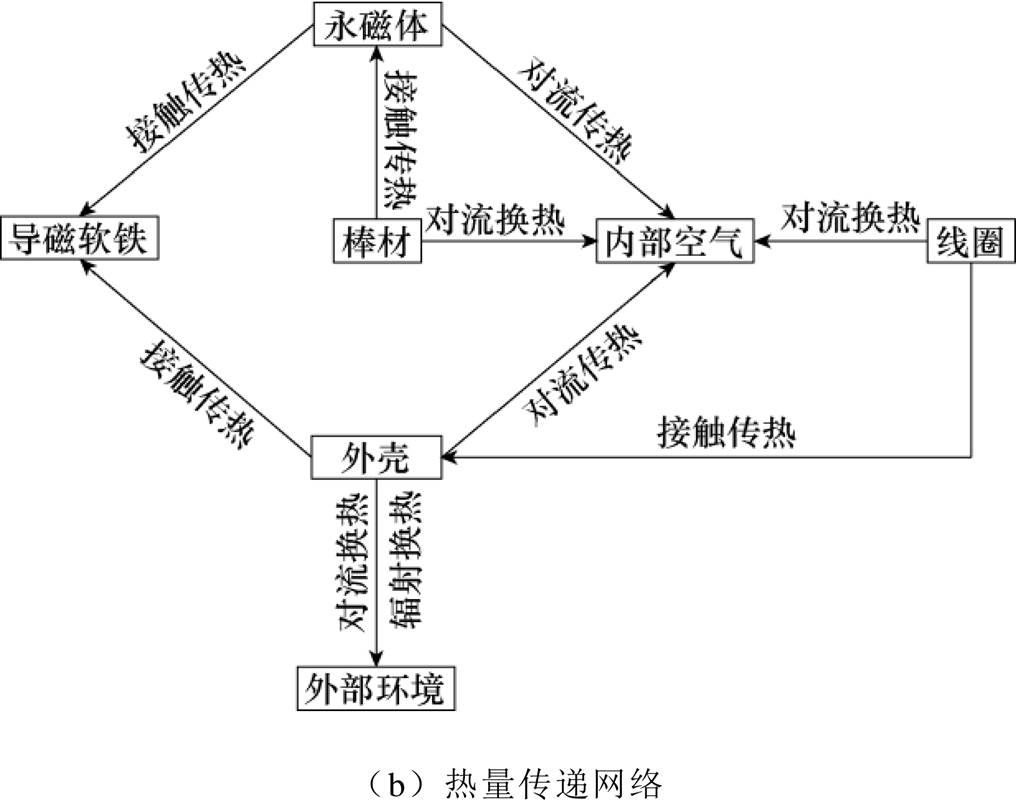
图2 纵振式超磁致伸缩换能器内部传热过程
Fig.2 Heat transfer process in longitudinal vibration GMT
除了线圈和棒材上产生的热量外，磁回路中的其他部件均会因为涡流效应产生损耗，然而这些损耗难以准确的估计。因此对永磁体、导磁块、上下盖板和套筒等部件进行切缝处理，从而减小其他部件产生的损耗对换能器传热过程的影响。
搭建瞬态等效热网络模型对换能器进行热分析的主要步骤为[15]：首先将温度相近的区域用节点表示；然后将存在热传递关系的节点连接起来，中间用对应的传递热阻分开，同时将每个区域对应的热源和热容并联在节点与零电压之间（在电路中用“地”表示）；接着计算模型中各区域的参数，如热阻、热容、热源功率等；最后利用计算机求解热网络模型，得到换能器各区域的温度分布与时域范围内的变化规律。
在换能器热网络模型搭建过程中，为了建模和计算方便，需要对模型进行简化处理。本文提出的热网络模型是在以下假设基础上建立的：
（1）只考虑棒材和线圈的损耗，其他部分的损耗忽略不计。
（2）换能器各部件的热学特性保持稳定，忽略温度变化对其热物理性能参数的影响。
（3）由于外壁温度与室温接近，忽略辐射传热，只考虑传导传热和对流传热。
（4）忽略部件之间的接触热阻。
2.2.1 热源等效热网络模型的建立
热源部件需要用T型等效热网络模型表示[24]。
1）线圈等效热网络模型
驱动线圈是基于图3a所示的圆柱形部件。如图3b所示，线圈的轴向和径向的热传导过程分别用两个独立的三端网络表示，在每个网络中，两个终端温度表示驱动线圈两端表面的平均温度，第三个温度T6表示线圈的温度。线圈产热功率P6和热容C6分别注入线圈的平均温度节点，其中P6的计算方法详见3.1节，C6可以表示为
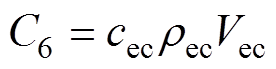（1）
式中，cec、rec和Vec分别为励磁线圈的比热容，密度和体积。
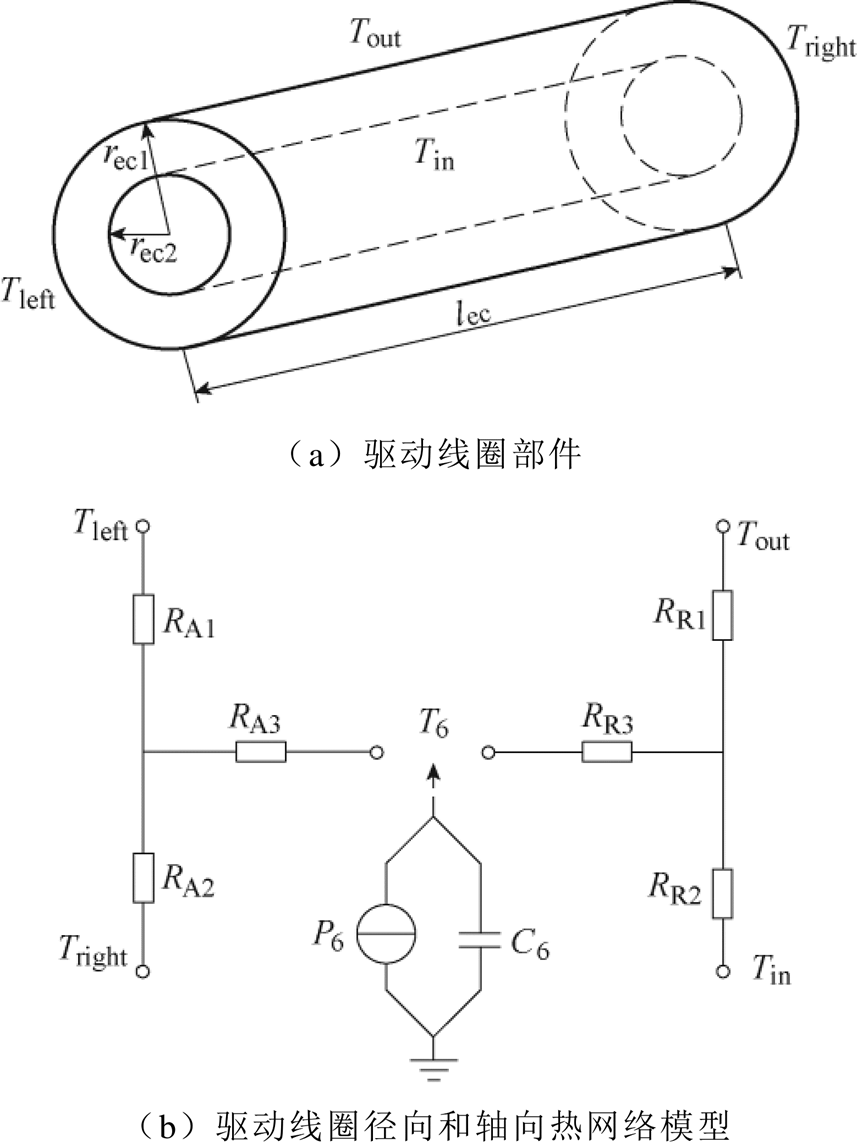
图3 驱动线圈及其T型等效热网络模型
Fig.3 Excitation coil and its T-equivalent thermal circuit
线圈T型等效电路模型中的热阻计算见表1。
表1 线圈T型等效热网络模型相关热阻计算
Tab.1 Thermal resistances for T-equivalent thermal circuit of the excitation coil
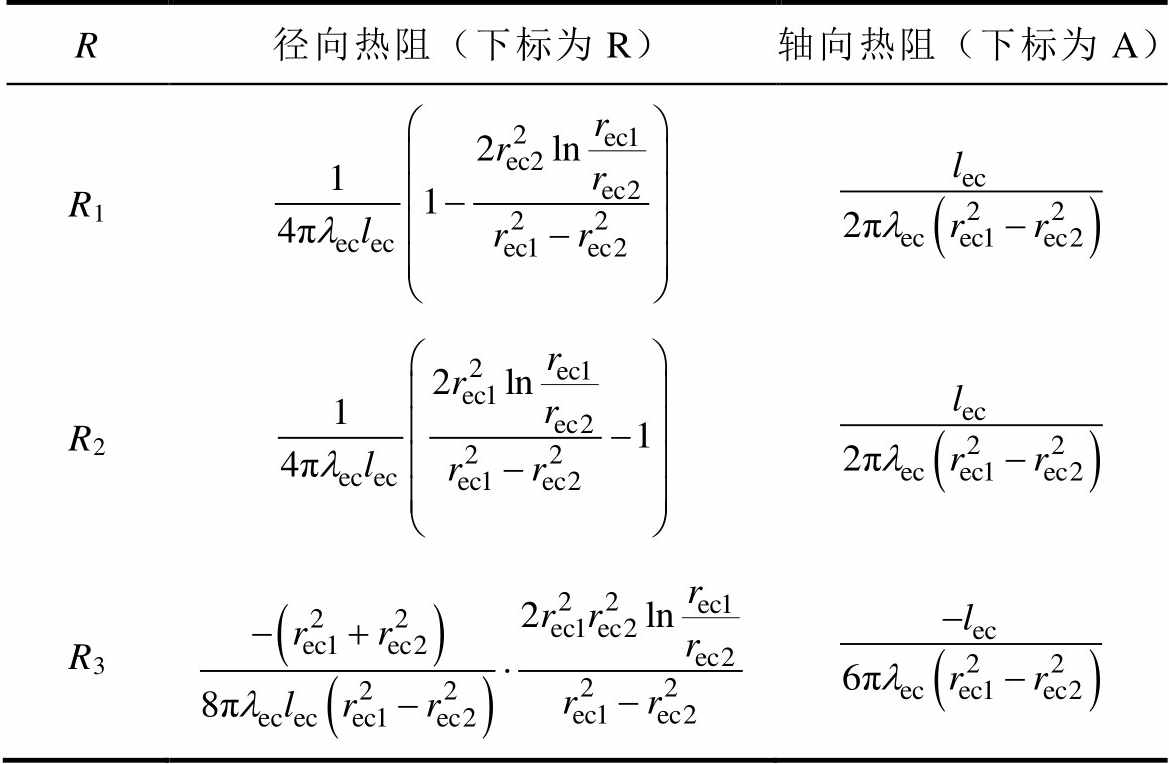
R径向热阻（下标为R）轴向热阻（下标为A） R1 R2 R3
表中，lec为线圈长度，lec为线圈导热系数，rec2和rec1分别为线圈的内、外半径。
2）超磁致伸缩棒等效热网络模型
因为超磁致伸缩棒径向半径远小于轴向长度，所以认为其径向温度分布均匀，只考虑轴向温度分布。因此仅用轴向T型等效热网络模型来表示棒材热传递过程。
作为换能器的主要热源，超磁致伸缩棒是换能器温度最高的部件，同时由于材料热导率低、棒材轴向温度梯度大、单节点无法准确描述棒材温度分布情况，轴向选取节点越多，对棒材温度分布的求解越准确。为了确定棒材轴向选取节点个数，分别搭建不同复杂度的超磁致伸缩换能器热网络模型，并对计算结果进行对比，如图4所示。
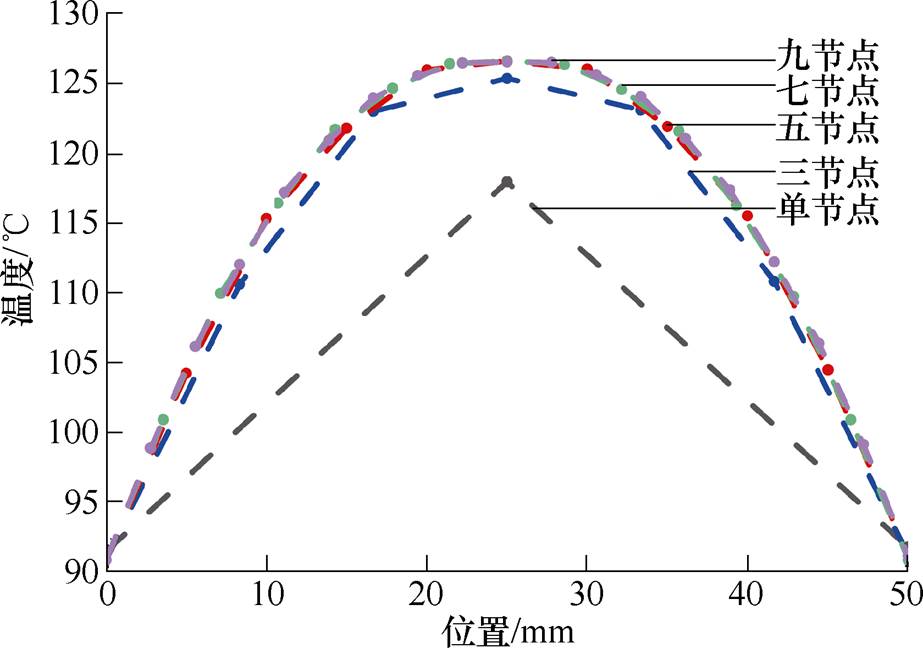
图4 不同复杂度热网络模型中超磁致伸缩棒温度分布
Fig.4 Temperature distribution of the GMM rod in thermal network model with different complexity
从图中可以看出，用单节点和三节点热网络模型无法准确描述超磁致伸缩棒温度分布情况，从五节点开始，计算结果趋于稳定，然而随着模型节点个数的增加，模型的准确度并没有明显的提高。
基于对不同复杂度热网络模型结果对比分析，本文棒材等分为五段，其热网络模型如图5所示。图中，五个节点的温度T1～T5分别为棒材五个区域的平均温度。P1～P5分别为棒材不同区域磁滞损耗和涡流损耗的总热功率，其计算方法详见3.2节。由于棒材位于线圈中心，且线圈长度大于棒材长度，所以认为棒材在轴向的不同位置磁场强度分布均匀，图中损耗功率P1～P5相等。C1～C5为不同区域的热容，即
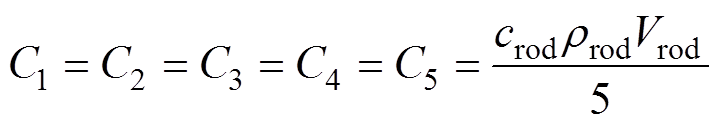（2）
式中，crod、rrod和Vrod分别为棒材的比热容、密度和体积。
与线圈热阻计算方法相同，图5所示棒材热网络模型的相关热阻可以根据T型轴向等效电路热阻计算方法得到，即
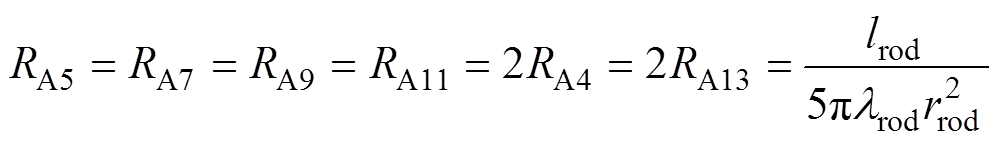（3）
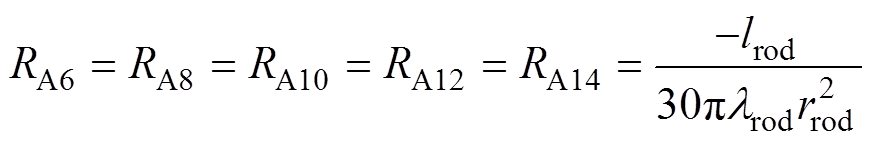（4）
式中，lrod、rrod和lrod分别为棒材的长度、半径和热导率。
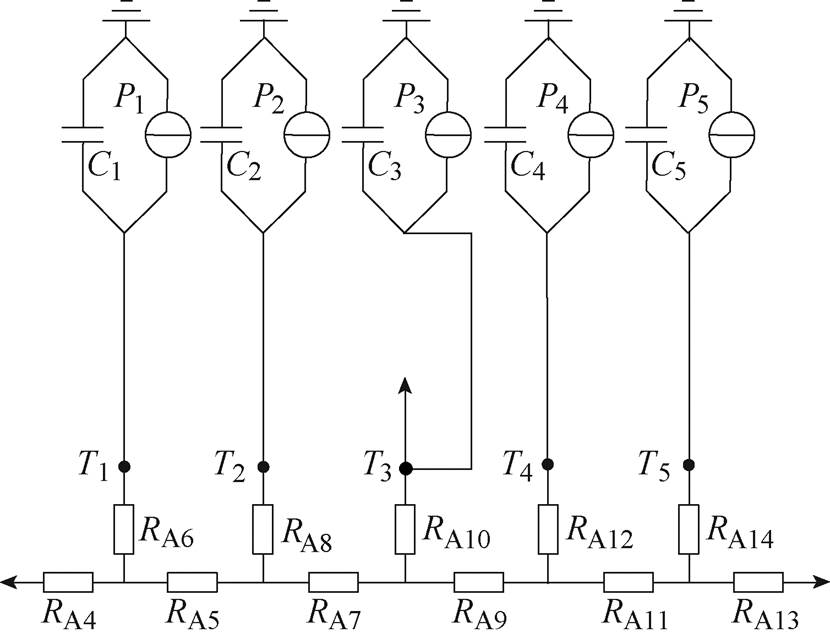
图5 超磁致伸缩棒热网络模型
Fig.5 Equivalent thermal circuit for the GMM rod
2.2.2 其他区域热网络模型的建立
对于本文研究的纵振式超磁致伸缩换能器，其他区域包括换能器除热源外的其他部件以及内部空气。由于这些区域对热传导过程影响小，分别可以用单节点电路表示。其中由于导磁块、永磁体以及输出杆的上半部分径向热阻小，可以忽略不计。除此以外，输出杆靠近导磁块的下半部分沿轴向具有相同的温度，轴向热阻忽略不计。
这些区域均可以当作是由一个或多个圆柱形部件组成。根据傅里叶定律，圆柱形部件的传热热阻分别为
径向热阻
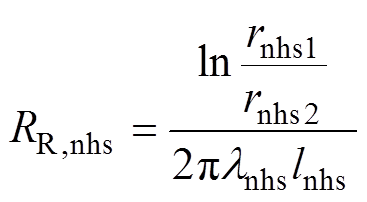（5）
轴向热阻
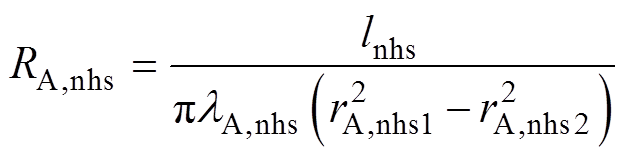（6）
式中，lnhs为传热区域的热导率；lnhs、rnhs2和rnhs1分别为传热部件的轴向长度和内、外半径。
式（5）用于计算图6中的径向热阻RR4～RR12，式（6）被用来计算图6中的轴向热阻RA15～RA33。
上述区域的热容在图6中分别用C7～C15表示，可以用式（7）计算得到。
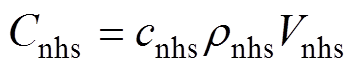（7）
式中，rnhs、cnhs和Vnhs分别为区域的密度、比热容和体积。
2.2.3 对流热阻计算
纵振式超磁致伸缩换能器对流热传递过程包括各部件与内部空气之间的对流换热以及外壳与环境之间的对流换热，均可对对流热阻计算公式进行建模，即
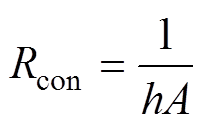（8）
式中，A为接触面的面积；h为表面对流传热系数。文献[25]列举了热系统中使用的经典对流传热系数值。根据空气自然对流系数范围，本文选取25W/(m2·K)作为外壳与环境对流热阻（见图6中的RH4～RH6和RH1～RH14）的传热系数，选取10W/(m2·K)作为换能器部件与内部空气对流热阻（见图6中的RH1～RH13和RH7～RH9）的传热系数。
2.2.4 纵振式超磁致伸缩换能器完整热网络模型
根据图2所示换能器内部传热过程，建立换能器完整热网络模型如图6所示。图中换能器热网络模型共有16个节点，其中T0为环境温度，T1～T5为棒材上的五个区域的平均温度，T6为线圈温度，T7、T8为上、下永磁体的温度，T9、T10为上、下导磁块的温度，T11～T13为外壳的温度，T14为内部空气温度，T15为输出杆温度。棒材每个区域的总电磁损耗功率分别用P1～P5表示，P6为电流通过线圈所产生的焦耳损耗功率；C1～C15分别为棒材、上下永磁体、导磁块、外壳、内部空气、线圈以及输出杆的热容；另外用59个热阻分别表示相邻节点之间的传导热阻和对流热阻。图中热容和热阻的计算表达式在2.2.1～2.2.3节中被详细描述。
为了方便计算模型中各部件的参数值，表2中给出了换能器所用材料的重要热特性参数。
超磁致伸缩换能器主要的发热损耗包括棒材的涡流损耗和磁滞损耗、线圈的电阻损耗、机械损耗以及附加损耗等。其中附加损耗与机械损耗占比较小，可以忽略[26]。
图6 纵振式超磁致伸缩换能器完整热网络模型
Fig.6 Equivalent thermal network model of the longitudinal vibration GMT
表2 超磁致伸缩换能器各部件物理性能参数
Tab.2 Thermophysical properties of the main materials in longitudinal vibration GMT
部件导热系数/ [W/(m·K)]比热容/ [J/(kg·K)]密度/ (kg/m3)备注 棒材13.53509 250Terfenol-D 线圈4014868 933铜 永磁体8.9514.867 400SmCo 外壳及导磁块54.75747 870DT4 输出杆17.25008 000304不锈钢
线圈的交流电阻包括直流电阻Rdc和由于趋肤效应引起的电阻Rs两部分。给线圈通入有效值为I的正弦交流电，则线圈的产热功率P6[27]为
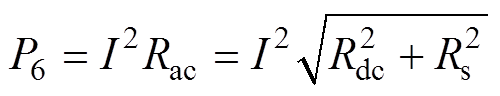（9）
式中，直流电阻Rdc可以表示为
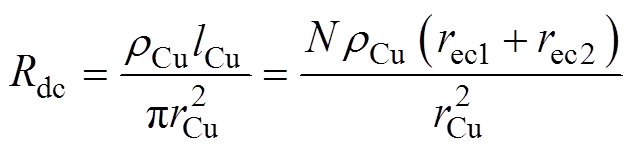（10）
由趋肤效应引起的电阻Rs可以表示为
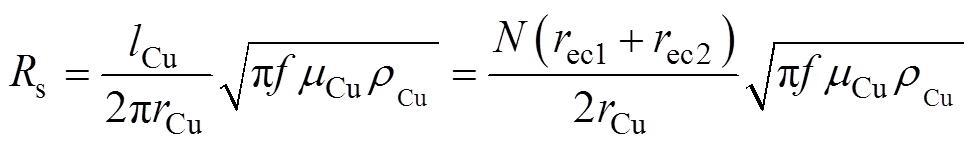（11）
式中，lCu为线圈的漆包线总长度；rCu为漆包线除去绝缘层的有效半径；rCu为铜线的电阻率；N为线圈总匝数，本文为340匝；f为驱动电流的驱动频率；mCu为铜线的磁导率。
超磁致伸缩棒的发热功率主要是由涡流损耗功率Peddy和磁滞损耗功率Ph组成，即
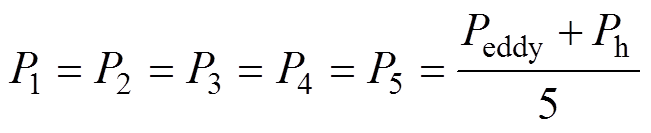（12）
3.2.1 涡流损耗
如附录所示，超磁致伸缩棒单位时间内产生的涡流损耗[28]为
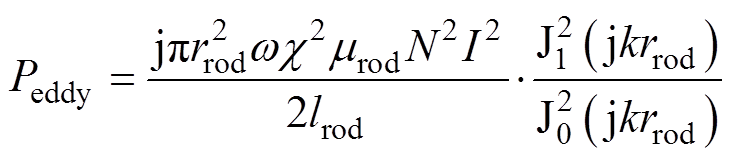（13）
式中，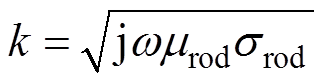
，srod为棒材的电导率，mrod为磁导率，w 为角频率；H为磁场强度；J0为0阶第一类贝塞尔函数；J1为1阶第一类贝塞尔函数；c为漏磁系数，用来对磁场分布函数进行修正，本文取值为0.72。
为了更准确地反映工作时的涡流损耗，磁导率mrod用换能器工作时动态等效磁导率meq代替[29]，即
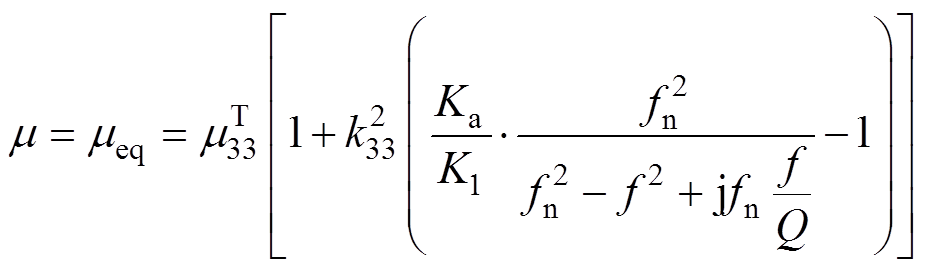（14）
式中，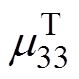
为棒材恒预应力下的磁导率；上标“T”为预应力，表示恒定不变的；k33为磁机耦合系数；Ka和Kl分别为恒定磁场下的棒材刚度和换能器等效刚度；fn为换能器一阶谐振频率；Q为品质因数。
3.2.2 磁滞损耗
超磁致伸缩棒的磁滞损耗功率Ph与闭合磁滞回线面积成正比[30]，且满足
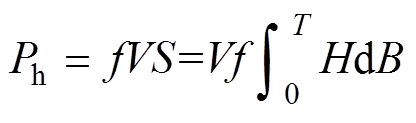（15）
式中，V为棒材的体积；S为闭合磁滞回线所围成的面积。
通过附录的推导，超磁致伸缩棒的磁滞损耗功率Ph[31]为
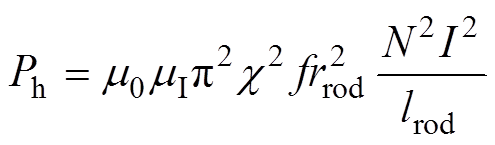（16）
式中，m0为真空磁导率；mI为棒材相对磁导率的虚部，本文取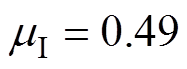
[32]。
通过式（9）、式（13）和式（16）计算出驱动电流为2A，驱动频率为500Hz、750Hz、1 000Hz和1 250Hz时换能器线圈以及棒材损耗大小如图7所示。
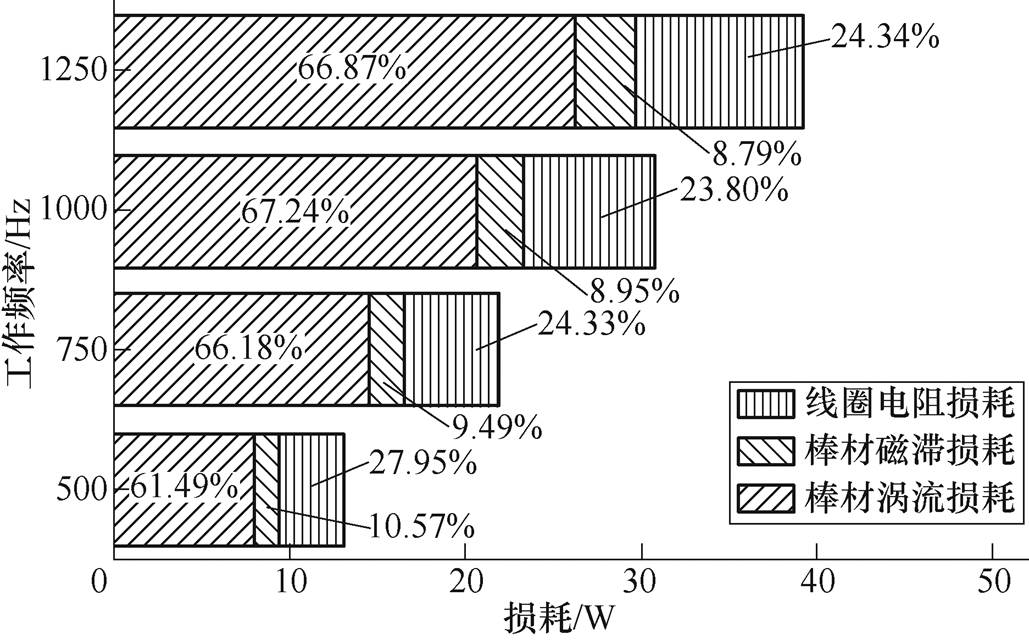
图7 纵振式超磁致伸缩换能器损耗及其占比
Fig.7 Ratio of loss of the longitudinal vibration GMT
从图中可以看出，换能器在500～1 250Hz频段内工作时，棒材的涡流损耗占比最大，且随着驱动频率增加，涡流损耗不断增大。因此作为换能器的核心元件，棒材的准确建模和热分析是换能器温度场建模的关键环节。
由于本文所研究的换能器内部空间有限，难以通过实验对所有节点的准确性进行验证，因此首先用Comsol Multiphysics软件搭建了纵振式超磁致伸缩换能器的有限元模型，与热网络模型仿真结果进行对比，验证本文所搭建模型中不同节点温升特性的准确性。
因为纵振式超磁致伸缩换能器对称分布，为简化计算，只对换能器一半进行建模如图8所示。
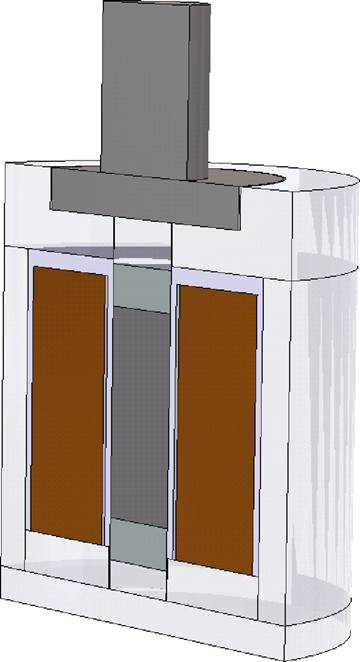
图8 纵振式超磁致伸缩换能器有限元模型
Fig.8 Finite element model of longitudinal vibration giant magnetostrictive transducer
根据传热微分方程对有限元模型的边界条件进行设置如下：
（1）由于结构对称性，模型对称面设置为绝热边界条件；其他边界设置为对流换热边界条件。
（2）将图7所示棒材和线圈热损耗功率作为热源代入有限元模型中。
（3）假定换能器各部分均紧密接触，忽略相粘接部件间的接触热阻。
（4）模型所有部件的初始温度均为室温，且环境温度在瞬态计算过程中保持不变，为实验时测得的室温25℃。
纵振式超磁致伸缩换能器有限元模型进行网格划分时，对部件采用传统的自由四面体网格划分方法，共划分单元数87 106个，边界单元数16 817个。本节以驱动电流有效值2A，驱动频率1 250Hz为例，用有限元模型对热网络模型中各节点温升特性进行验证，对比结果如图9所示。
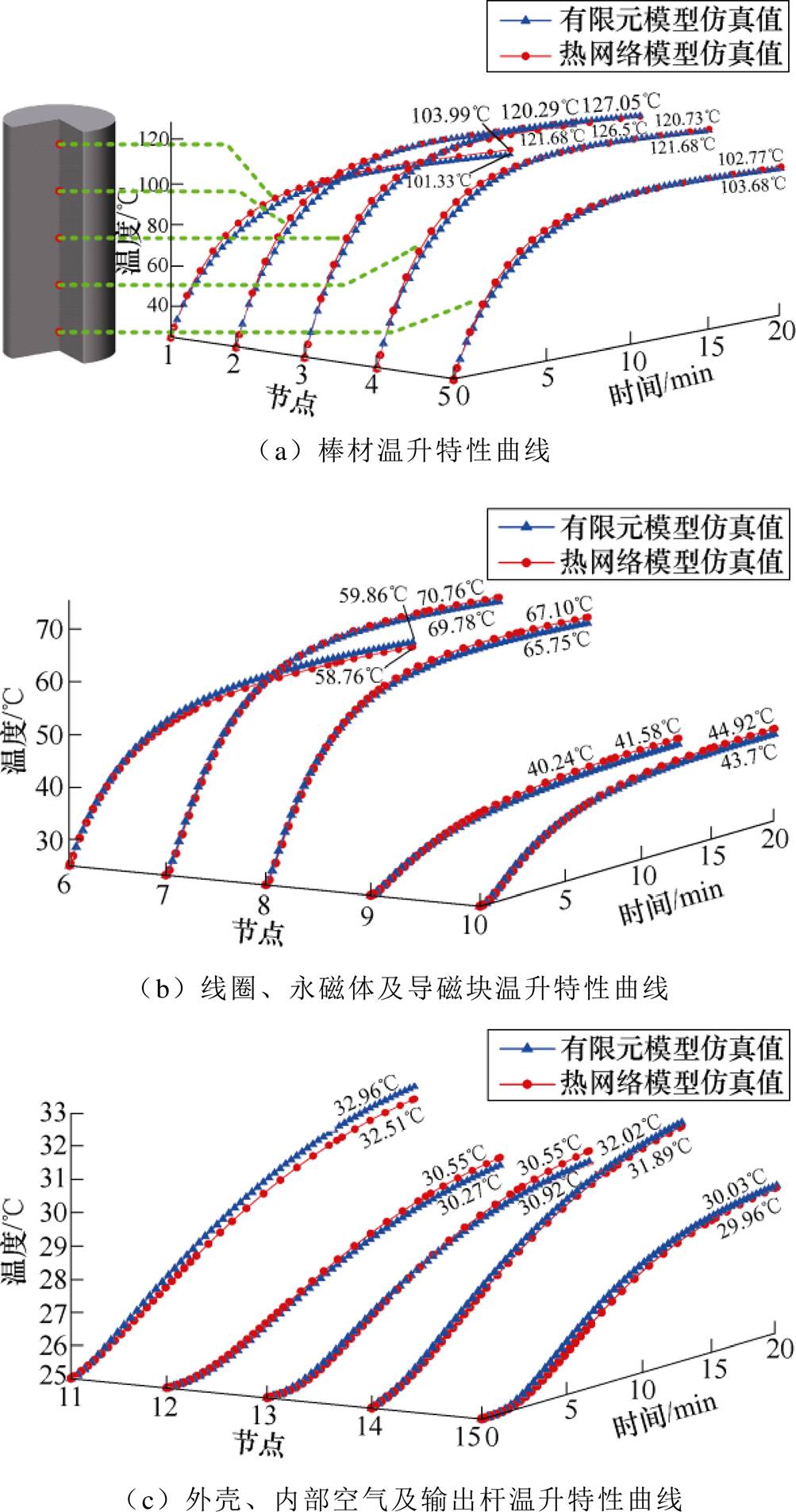
图9 热网络模型和有限元模型仿真值对比
Fig.9 Comparison of thermal network model and finite element simulation values
从图中可以看出，热网络模型与有限元模型结果基本吻合，验证了热网络模型各节点温升特性的准确性，热网络模型具有建模简单、快速计算等优点，对换能器热建模研究更加方便。特别需要注意的是，从图9a可以看出，超磁致伸缩棒作为换能器内的主要热源，热导率低、中心的温度难以散出，出现明显的温度梯度现象；中心温度最高，两端温度最低，温差约26℃，验证了对超磁致伸缩棒材进行温度梯度建模的必要性。
4.2.1 纵振式超磁致伸缩换能器温升实验平台
在有限元法验证换能器等效热网络模型准确性的基础上，搭建换能器温升实验平台进行实验验证，如图10所示。平台主要包括三个模块：供电模块、负载模块和测试模块。供电模块选用Chroma61 512可编程交流电源为换能器提供不同频率和幅值的交流电流。负载模块即为纵振式超磁致伸缩换能器，通过对换能器施加不同的工况来验证热网络模型的适用性。测试模块包括K型温度传感器、泰克MDO34混合域示波器和日置MR8 875-30温度储存记录仪，负责测量和记录换能器不同工况下的实时温度情况，最后用PC对储存的数据进行统一处理和分析。
图10 纵振式超磁致伸缩换能器温升试验测量平台
Fig.10 Giant magnetostrictive longitudinal vibration transducer temperature rise test and measurement platform
实验前分别在棒材中心表面、线圈内壁以及外壳内壁上固定温度传感器，并与温度存储记录仪连接。通过可编程电流电源向换能器负载供电，并用示波器采集输出的电流和电压数据。实验结束后，将采集的热电偶温度数据以及电压电流数据上传到PC进行后处理。
由于超磁致伸缩材料特性参数对温度非常敏感，且超磁致伸缩材料居里温度低、升温快，长时间工作会导致材料特性明显变化，甚至可能使其失去磁致伸缩特性而不能继续工作，所以根据实际换能器工作时间，设定温升时间为20min，采集换能器在该过程中实验数据，并与热网络模型和有限元模型进行对比分析。
4.2.2 实验分析
保持驱动电流有效值2A不变，改变不同的驱动频率（500Hz、750Hz、1 000Hz、1 250Hz），记录不同工况下示波器的波形与换能器温升数据，与热网络模型，有限元模型仿真结果进行对比，换能器不同位置的温升曲线如图11所示。
通过三者对比曲线可以看出，热网络模型瞬态分析结果与有限元仿真结果和实验测试结果均有较好的吻合度，验证了热网络模型及其计算结果的有效性。但是仿真与实验结果依然存在一定的误差：工作频率越高，损耗越大，棒材仿真结果与实验结果相差也越大；在温升过程中，线圈仿真结果与实验结果基本吻合，但是稳态温度存在一定误差；外壳由于温度比较低，仿真结果与实验温度相差不大，但是温升趋势有明显的不同。误差分析如下：①模型中没有考虑损耗分布对温度的影响；②损耗模型都是基于理想情况下推导得到的，没有结合实际工况进行建模[33]；③线圈建模没有考虑实际制作过程中导体的随机分布问题；④没有考虑外壳对外辐射散热过程。通过进一步对超磁致伸缩换能器热网络模型和参数计算的修正和优化，可是使得仿真结果更加准确。
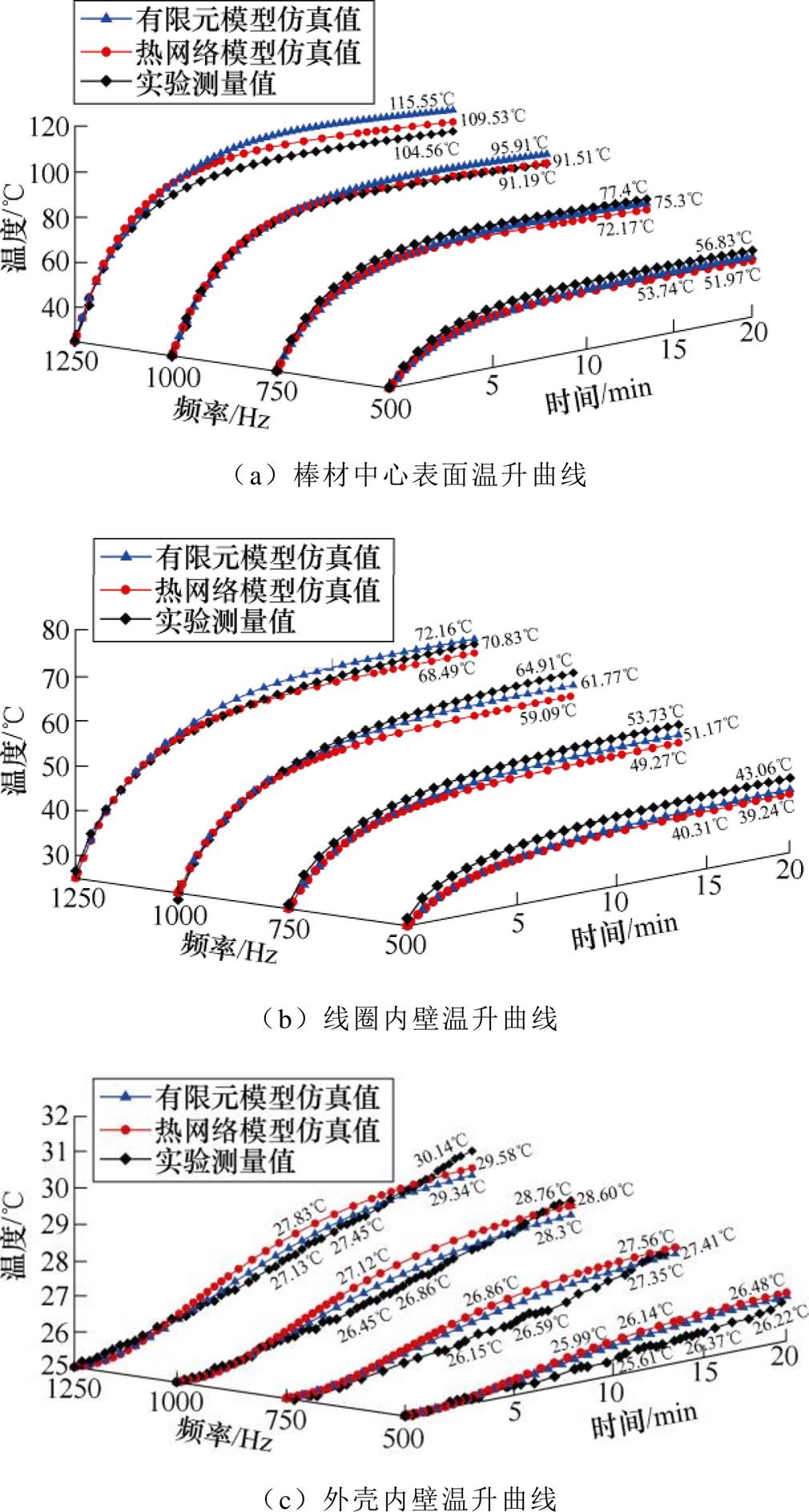
图11 模型计算换能器不同位置温升与实验数据对比
Fig.11 The model calculated the temperature rise at different positions of the transducer and compared with the experimental data
本文以纵振式超磁致伸缩换能器为研究对象，计及超磁致伸缩棒作为热源的特殊性和棒材温度空间分布的影响，创建了超磁致伸缩换能器等效热网络瞬态模型，并用有限元模型和实验验证了模型的准确性。首先基于纵振式超磁致伸缩换能器结构和工作原理，对换能器进行了热分析；然后根据换能器内部传热过程，建立了完整的换能器瞬态热网络模型，并对模型参数进行计算；最后搭建有限元仿真模型和换能器温升实验平台，从仿真和实验两方面验证了所提热网络模型对换能器温度时空分析的准确性和有效性。同时也提出了热网络模型中存在的问题，如没有考虑损耗分布、没有利用实验数据对换能器损耗进行准确建模等，进一步还需要对热网络模型进行修正和优化，使仿真结果更加准确。
1. 超磁致伸缩棒涡流损耗计算
假设棒材内部磁场沿着轴向分布均匀，则棒材径向磁场分布的偏微分方程为
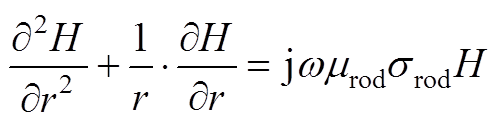（A1）
式中，srod为棒材的电导率；mrod为磁导率；w 为角频率；H为磁场强度。
磁场强度幅值为
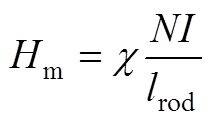（A2）
式中，N为线圈匝数；I为线圈通入正弦交流电的有效值；lrod为棒材长度；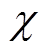
为漏磁系数。
联立边界条件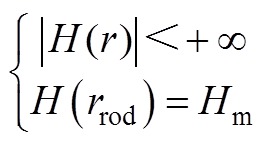
，求得超磁致伸缩棒磁场分布函数关系式为
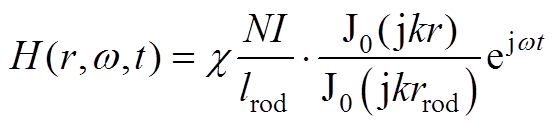（A3）
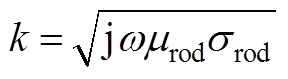（A4）
式中，rrod为超磁致伸缩棒外半径；J0为0阶第一类贝塞尔函数。
在棒材半径为r区域内磁通量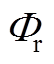
为
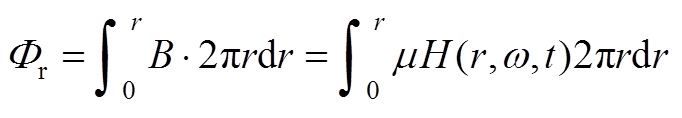（A5）
超磁致伸缩棒内部产生的感应电动势e为
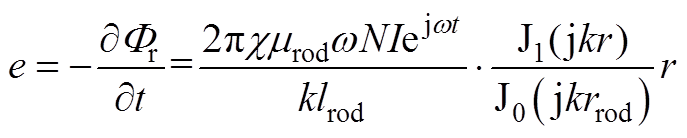（A6）
式中，J1为1阶第一类贝塞尔函数。
单位时间内棒材上对应的涡流损耗为
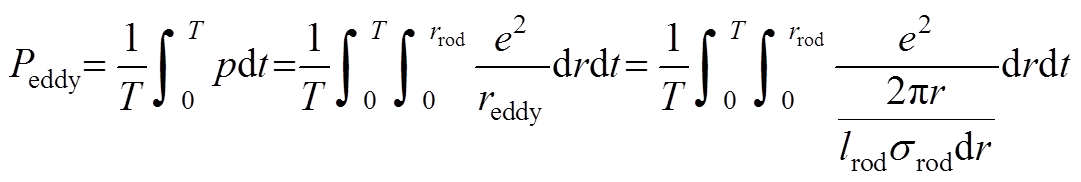（A7）
式中，reddy为棒材内部半径r处圆环对应电阻。
忽略棒材径向磁场的不均匀性，将式（A6）代入式（A7）中可以得到棒材单位时间的涡流损耗为
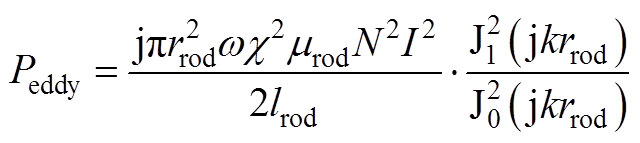（A8）
2. 超磁致伸缩棒磁滞损耗计算
假设激励磁场为
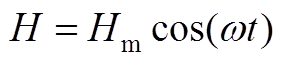（A9）
则由于磁滞效应，磁感应强度B比外加磁场H落后一个相位，即为损耗角b。
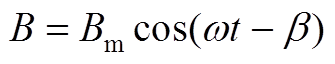（A10）
交变磁场下超磁致伸缩棒复数相对磁导率为
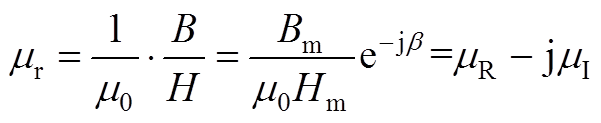（A11）
式中，m0为真空磁导率，超磁致伸缩棒相对磁导率实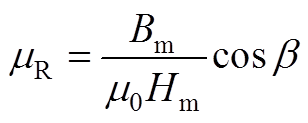部
，虚部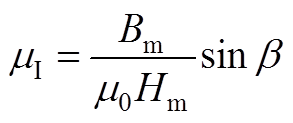
。
将式（A9）和式（A10）代入式（15）中可得
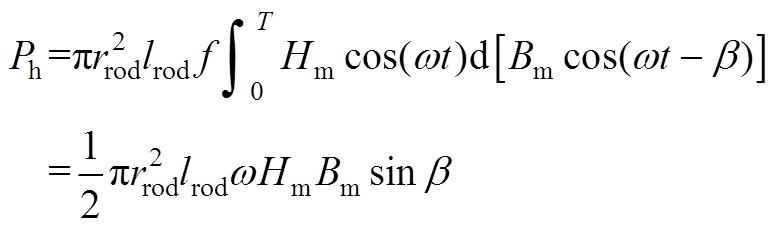（A12）
将超磁致伸缩相对磁导率的虚部表达式以及交变磁场的幅值表达式（A2）代入式（A12）中，可以得到超磁致伸缩棒磁滞损耗为
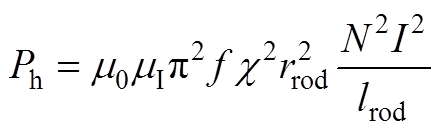（A13）
参考文献
[1] 黄文美, 薛胤龙, 王莉, 等. 考虑动态损耗的超磁致伸缩换能器的多场耦合模型[J]. 电工技术学报, 2016, 31(7): 173-178.
Huang Wenmei, Xue Yinlong, Wang Li, et al. Multi- field coupling model considering dynamic losses for giant magnetostrictive transducers[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 173-178.
[2] 翁玲, 常振, 孙英, 等. 不同磁致伸缩材料的高频磁能损耗分析与实验研究[J]. 电工技术学报, 2020, 35(10): 2079-2087.
Weng Ling, Chang Zhen, Sun Ying, et al. Analysis and experimental study on high frequency magneto- strictive energy loss of different magnetostrictive materials[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2079-2087.
[3] 刘楚辉. 相变温控及其在超磁致伸缩致动器中的应用[J]. 组合机床与自动化加工技术, 2006(10): 50-52.
Liu Chuhui. Application of phase change temperature control to GMA[J]. Modular Machine Tool & Auto- matic Manufacturing Technique, 2006(10): 50-52.
[4] Blottman J, Butler S C, Gittings K D, et al. Thermal design of high-power active transducers with the Atila finite element code[J]. Proceedings of the Institute of Acoustics, 2005, 27(1): 87-91.
[5] Uchino K, Debus J C. Applications of ATILA FEM software to smart materials: case studies in designing devices[M]. Philadelphia, USA: Woodhead Publishing Ltd, 2012.
[6] Clark A E, Crowder D H. High temperature magneto- striction of TbFe2 and Tb0.27Dy0.73Fe2[J]. IEEE Transactions on Magnetics, 1985, 21(5): 1945-1947.
[7] Nersessian N, Or S W, Carman G P. Magneto-thermo- mechanical characterization of 1-3 type polymer- bonded Terfenol-D composites[J]. Journal of Magnet- ism and Magnetic Materials, 2003, 263(1/2): 101-112.
[8] Wallscheid O, Böcker J. Global identification of a low-order lumped-parameter thermal network for per- manent magnet synchronous motors[J]. IEEE Transa- ctions on Energy Conversion, 2016, 31(1): 354-365.
[9] Dubus B, Bigotte P, Boucher D. Thermal limit analysis of low-frequency high power sonar pro- jectors[C]//1st European Conference on Underwater Acoustics, New York, USA, 1992: 623-626.
[10] 曾海泉, 曾庚鑫, 曾建斌, 等. 超磁致伸缩功率超声换能器热分析[J]. 中国电机工程学报, 2011, 31(6): 116-120.
Zeng Haiquan, Zeng Gengxin, Zeng Jianbin, et al. Thermal analysis of giant magnetostrictive high power ultrasonic transducer[J]. Proceedings of the CSEE, 2011, 31(6): 116-120.
[11] 吴亮, 彭辉, 关向雨, 等. 考虑触头结构的气体绝缘母线热网络模型[J]. 电工技术学报, 2020, 35(18): 3838-3847.
Wu Liang, Peng Hui, Guan Xiangyu, et al. Gas insulated bus thermal network model considering contact structure[J]. Transactions of China Electro- technical Society, 2020, 35(18): 3838-3847.
[12] 胡剑, 熊小伏, 王建. 基于热网络模型的架空输电线路径向和周向温度计算方法[J]. 电工技术学报, 2019, 34(1): 139-152.
Hu Jian, Xiong Xiaofu, Wang Jian. Radial and cir- cumferential temperature calculation method of over- head transmission lines based on thermal network model[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 139-152.
[13] 姜鑫, 应展烽, 万萌, 等. 计及环境对流随机性的功率器件结-环境热网络模型[J]. 电工技术学报, 2021, 36(14): 3090-3100.
Jiang Xin, Ying Zhanfeng, Wan Meng, et al. Junction- to-ambient thermal network model of power devices considering randomness of thermal convective environ- ment[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 3090-3100.
[14] 王红宇, 李和明, 罗应立. 计及轴向周向热传导的耦合网络模型和有限元模型的比较研究[J]. 电工技术学报, 2008, 23(7): 1-8.
Wang Hongyu, Li Heming, Luo Yingli. Comparison between thermal-liquid coupled network model with the axial-/circle-heat transfer and FEM model[J]. Transactions of China Electrotechnical Society, 2008, 23(7): 1-8.
[15] Kral C, Haumer A, Lee Sangbin. A practical thermal model for the estimation of permanent magnet and stator winding temperatures[J]. IEEE Transactions on Power Electronics, 2014, 29(1): 455-464.
[16] Wallscheid O, Böcker J. Global identification of a low-order lumped-parameter thermal network for Permanent magnet synchronous motors[J]. IEEE Transactions on Energy Conversion, 2016, 31(1): 354-365.
[17] Mellor P H, Roberts D, Turner D R. Lumped parameter thermal model for electrical machines of TEFC design[J]. IEE Proceedings B (Electric Power Applications). IET Digital Library, 1991, 138(5): 205-218.
[18] Verez G, Tiegna H, Barakat G, et al. Analytical thermal modelling of axial flux permanent magnet synchronous machines[C]//2012 20th International Conference on Electrical Machines, Marseille, France, 2012: 2799-2805.
[19] Boglietti A, Cavagnino A, Staton D. Determination of critical parameters in electrical machine thermal models[J]. IEEE transactions on Industry Applica- tions, 2008, 44(4): 1150-1159.
[20] 汪文博. 永磁同步电机的热路模型研究[D]. 杭州:浙江大学, 2014.
[21] Dubus B, Boucher D. An analytical evaluation of the heating of low-frequency sonar projectors[J]. The Journal of the Acoustical Society of America, 1994, 95(4): 1983-1990.
[22] Anjanappa M, Bi J. A theoretical and experimental study of magnetostrictive mini-actuators[J]. Smart Materials and Structures, 1994, 3(2): 83-91.
[23] Zhu Yuchuan, Ji Liang. Theoretical and experimental investigations of the temperature and thermal defor- mation of a giant magnetostrictive actuator[J]. Sensors and Actuators A: Physical, 2014, 218: 167- 178.
[24] Nerg J, Rilla M, Pyrhonen J. Thermal analysis of radial-flux electrical machines with a high power density[J]. IEEE Transactions on industrial electro- nics, 2008, 55(10): 3543-3554.
[25] Bahman A S, Ma Ke, Blaabjerg F. A lumped thermal model including thermal coupling and thermal boundary conditions for high-power IGBT modules[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2518-2530.
[26] 管海滨. 超磁致伸缩换能器的损耗和温升特性分析[D]. 天津: 河北工业大学, 2014.
[27] Angara R. High frequency high amplitude magnetic field driving system for magnetostrictive actuators[D]. Baltimore County: University of Maryland, 2009.
[28] 纪良. 超磁致伸缩电静液作动器温度场分布与热位移特性研究[D]. 南京: 南京航空航天大学, 2016.
[29] Hall D L. Dynamics and vibrations of magneto- strictive transducers[D]. Iowa State University, 1994.
[30] Du Ruoyang, Robertson P. Modelling of dynamic magnetic hysteresis loops and power losses in laminated steel[C]//2015 17th UKSim-AMSS International Con- ference on Modelling and Simulation (UKSim), Cambridge, UKL, 2015: 432-437.
[31] 高嘉纬. 超磁致伸缩换能器的高频损耗和温升特性研究[D]. 天津: 河北工业大学, 2016.
[32] Greenough R D, Reed J, O'Connor K. Characteri- sation of magnetostrictive or piezoelectric materials and transducers[C]//IEEE Colloquium on Innovative Actuators for Mechatronic Systems, London, UK, 1995.
[33] Guo Pingping, Huang Wenmei, Xia Zhiyu, et al. Variable coefficient magnetic energy loss calculating model for magnetostrictive materials considering compressive stress[J]. AIP Advances, 2021, 11(3): 035227.
Research on Equivalent Thermal Network Modeling for Rare-Earth Giant Magnetostrictive Transducer
Abstract The working characteristics of giant magnetostrictive transducers (GMT) are closely related to temperature. Fast and accurate calculation and prediction of transducer temperature distribution is the key to transducer design. With the advantages of low calculation cost and high accuracy, thermal network modeling has been developed for GMT thermal analysis. However, most studies focus on steady-state modeling, ignoring the obvious temperature gradient of giant magnetostrictive rod caused by the poor thermal conductivity in the thermal transient. Therefore, this paper established a transient equivalent thermal network model of the GMT, considering the distinctiveness of the giant magnetostrictive rod as a heat source and the influence of the spatial distribution of the rod temperature. Firstly, based on the structure and working principle of the transducer, the thermal analysis was carried out. Then, the giant magnetostrictive rod was modeled. According to the internal heat transfer process of the GMT, a complete transient thermal network model was established and the model parameters were calculated. Finally, the finite element simulation model and the experimental platform of a GMT were built, and the effectiveness and accuracy of the proposed model were verified.
keywords：Giant magnetostrictive transducer, equivalent thermal network model, parameter calculation, finite element model, temperature distribution
DOI: 10.19595/j.cnki.1000-6753.tces.211326
中图分类号：TN712+.2
收稿日期 2021-08-23
改稿日期 2021-12-20
张智贺 男，1999年生，博士研究生，研究方向为电声变换技术与装备研究。E-mail: zhangzhihe@hnu.edu.cn
杨 鑫 男，1987年生，教授、博士生导师，研究方向为电力电子技术、功率半导体器件、电声换能系统。E-mail: xyang@hnu.edu.cn（通信作者）
（编辑 陈 诚）