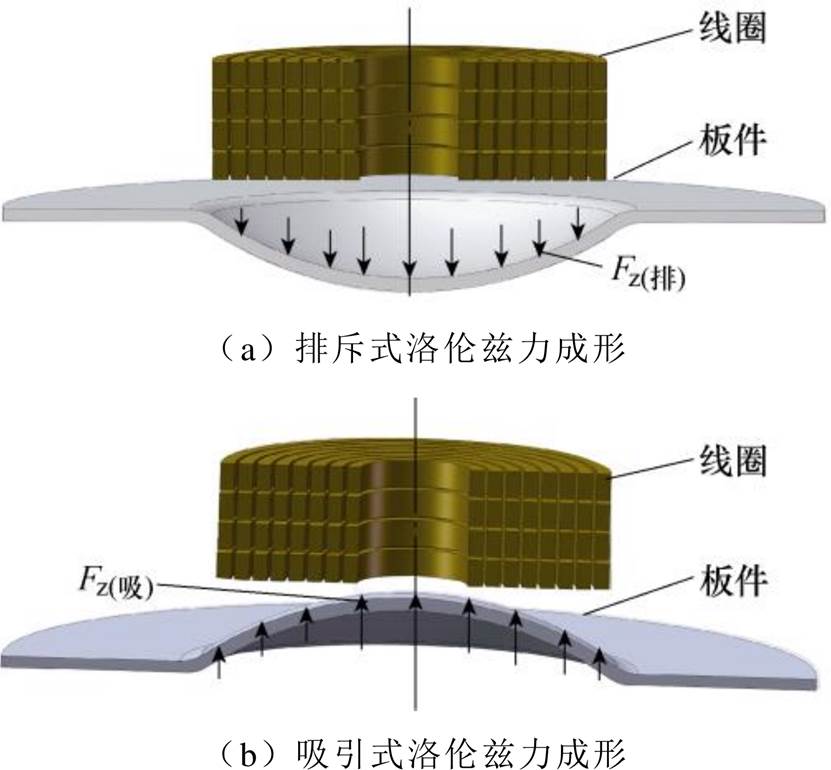
图1 电磁成形示意图
Fig.1 Schematic diagram of electromagnetic forming
摘要 电磁成形技术是一种利用洛伦兹力驱动金属材料发生高速变形的先进制造技术。与传统静态成形工艺相比,电磁成形因其极高的应变速率能显著地改善轻质合金材料的成形性能。同时,相比传统机械力或液压力,电磁成形所利用的洛伦兹力能够在时间和空间上灵活调控,因而具备更丰富的工艺潜能。然而,现有研究多将重点放在金属工件的成形方式及效果上,对其最主要部分——洛伦兹力,在电磁成形过程中随时间的变化过程及复杂的竞争关系并未系统分析。因此,该文针对典型的单脉冲电磁成形过程,细化电磁成形过程中各个物理量之间的动态变化关系,研究了成形过程中随时间变化洛伦兹力在铝合金板件上的竞争关系及对成形效果的影响,阐明了随时间变化的洛伦兹力的竞争关系,对所呈现成形效果的影响及原因进行了分析,更加深刻全面地理解电磁成形技术过程。
关键词:电磁成形 单脉冲 板件 力的竞争 成形效果
电磁成形(Electromagnetic Forming, EMF)是一种利用脉冲电磁力实现轻质合金加工的高速成形技术。在电磁成形的过程中,通常采用电容器组对驱动线圈放电产生脉冲强电流,脉冲强电流产生脉冲磁场进而在金属工件中产生感应涡流,涡流与磁场共同作用产生洛伦兹力驱动金属工件,最终实现加工成形。相对于传统成形技术,其具有以下显著优势[1-2]:①可明显提升材料成形极限,有效减少零件回弹、起皱等[2]问题,成形精度高。②非接触施力,避免了与材料直接接触,可减少变形过程中的摩擦,有利于提高成形件的表面质量。③洛伦兹力的方向及大小可通过仅改变驱动电路参数进行调控,灵活性远胜于传统机械力。因此,EMF尤其适合铝、钛等轻质合金的成形加工,被认为是制造轻质合金具有前途的技术[3]之一。
近年来,电磁成形工艺发展较为迅速,成形方案复杂多变。如:改善洛伦兹力分布的电磁成形技术[4-5](板件匀压力成形[6-7]、板件局部电磁力成形[8]等)、改善洛伦兹力施加方式的电磁成形技术(轴-径双向加载管件电磁翻边[9-10]、管件成形均匀度优化[11-12]等),但在这些现有的研究中,研究重点多放在成形工艺及成形效果讨论上,对变形的主导因素洛伦兹力,在成形过程中随时间推移产生的复杂的动态过程及关系,并未仔细探究。其实无论是探究成形工艺还是成形效果(如吸引式[13-14]、排斥式成形[15-16]),都是通过洛伦兹力随时间的竞争关系最终呈现在工件的成形上,如具代表性的单脉冲电磁成形。
电磁成形工艺初期,使用单脉冲的电磁成形技术占据主流。由于在单脉冲电源条件下,工件上多以排斥式洛伦兹力主导,因此研究主要以排斥力成形为主。如熊奇[17]利用单脉冲电源对铝合金大板件进行有限元模拟与成形实验,完善了铝合金大板件的排斥力成形;Cao Quanliang等[18]利用在外电路中增加续流回路,在基本不改变成形效果的情况下,降低线圈温升[19],优化了单脉冲铝合金板件的排斥力成形;而近期Ouyang Shaowei等[20]提出了采用单脉冲低频放电的吸引力成形方案,并验证了方案的可行性,实现了单脉冲板件的吸引力成形,指出了前期的排斥力成形阶段可能有助于板件后期的吸引力成形,且吸引力小于排斥力。
同样是使用单脉冲电源进行放电,最终的成形效果却完全不同。而现有研究并未对其动态过程进行系统分析,洛伦兹力的变化更未完全呈现。而在电磁成形的过程中,影响洛伦兹力变化的各个参数随时间的动态变化关系复杂,导致洛伦兹力在成形过程中,随时间变化在板件上的竞争关系剧烈,最终导致板件在成形效果上呈现巨大差异。
因此,为了系统研究单脉冲电磁成形过程中,洛伦兹力随时间的竞争关系,由于电磁成形实验极其快速且过程中的数据变化通过实验无法得到,本文通过建立已有实验验证的单脉冲方案下板件电磁成形仿真模型,对典型的单脉冲电磁成形进行分析,细化动态过程,通过调节外电路的参数着重分析:影响洛伦兹力变化的因素、成形过程中随时间变化的洛伦兹力在铝合金板件上的竞争关系,以及洛伦兹力的竞争对于成形效果的影响。
在电磁成形方案中,将使工件远离线圈变形的洛伦兹力称作排斥式洛伦兹力,变形称作排斥力形变,如图1a所示;使工件靠近线圈变形的洛伦兹力称作吸引式洛伦兹力,变形称为吸引力形变,如图1b所示。

图1 电磁成形示意图
Fig.1 Schematic diagram of electromagnetic forming
现阶段电磁成形最常用的是以电容器为电源的RLC放电电路,其等效电路如图2所示。传统的放电电路产生的都是脉冲衰减的放电电流波形,而对于电磁成形技术而言,仅需放电电流的第一个半波,后续的电流波形会对电磁成形过程产生影响,因此,采用在放电电路中并联一个续流回路的方法,以保证放电电流不振荡。

图2 放电电路等效电路
Fig.2 Equivalent schematic diagram of discharge circuit
含续流回路的放电电流方程为
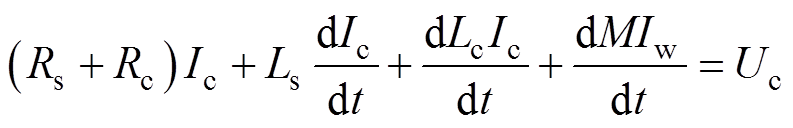 (1)
(1)
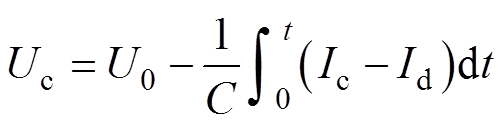 (2)
(2)
其中,续流回路中电流满足
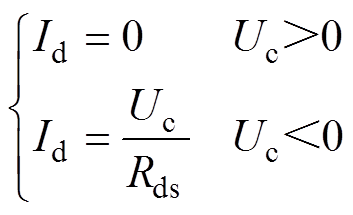 (3)
(3)
式中,Rs、Ls分别为线圈电阻与电感;Rc、Lc分别为成形线圈的等效电阻与等效电感;Rw、Lw分别为工件的等效电阻与等效电感;Ic为流过成形线圈的放电电流;Iw为工件中的感应电流;U0为电容初始电压;Uc为放电电压;C为电容;M为成形线圈与板件之间的互感系数(M是个连续变化的量);Id为流过续流回路的电流;Rds为续流电阻。
首先,通过充电系统对电容器组Cs进行充电,将电能储存在电容器组中,闭合开关,放电电路产生的放电电流流入成形线圈中,产生一个瞬态变化的脉冲强磁场,磁场在工件内感应一个抵抗磁场变化的涡流[21],电磁场方程由麦克斯韦方程组表示为
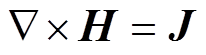 (4)
(4)
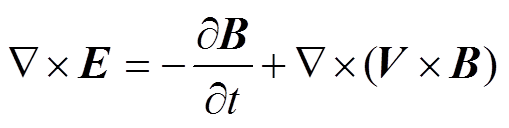 (5)
(5)
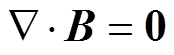 (6)
(6)
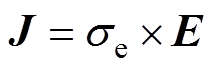 (7)
(7)
式中,H为磁场强度;J为感应涡流密度;B为磁通密度;E为电场强度;V为介质的运动速度;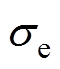 为电导率。式(5)右边附加了动生电动势,考虑了在电磁成形过程中由于工件变形对磁场的影响。
为电导率。式(5)右边附加了动生电动势,考虑了在电磁成形过程中由于工件变形对磁场的影响。
工件上的感应涡流与磁场共同作用,瞬间产生强大的洛伦兹力,促使工件发生形变。作用在板件上的洛伦兹力密度可以表示为
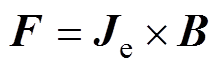 (8)
(8)
式中,Je为板件上感应涡流密度。由于在电磁成形方案中所使用的线圈基本为螺线管线圈,在忽略螺线管线圈的渐近线影响时,螺线管线圈可以视作若干个轴向分布的同轴闭合圆环。故由于其结构影响,涡流密度Je只有环向分量Jephi。因此,根据洛伦兹力公式,洛伦兹力F可以表示为
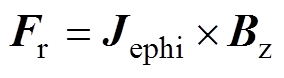 (9)
(9)
 (10)
(10)
式中,Bz和Br分别为磁通密度B的轴向分量和径向分量;Fr和Fz分别为板件所受到的洛伦兹力径向分量和轴向分量;负号表示该力为排斥力。而对于板件而言,变形主要取决于洛伦兹力的轴向分量Fz。由式(10)可知,Jephi和Br共同影响着Fz的大小。
电流影响板件所受洛伦兹力变化趋势如图3所示。电流曲线斜率为电流变化率,影响着工件上|Jephi|的大小。由图3可知,0~t1时间段,电流处于上升沿,将此时涡流密度方向定为正向,则Jephi为正值,洛伦兹力亦如图3所示,此时板件上主要受到方向向下的排斥式洛伦兹力。在此时间段内,|F|值先增大后减小,由于0~ta内电流变化率较大,故|Jephi|较大,当ta时刻斜率到达最大时,出现排斥力最大值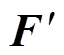 ;ta~t1内,电流变化率较小,故|Jephi|较小,虽径向磁通密度Br持续增大,但|Jephi|减小占主导趋势,故|F|减小。t1~tn时间段,电流进入下降沿,径向磁通密度Br随之减小,此时电流变化率为负,Jephi发生反向,此时板件上主要受到方向向上的吸引式洛伦兹力。由于续流回路的接入,电流下降沿阶段放电回路中相当于仅存在等效电感和等效电阻;电路处于一阶零输入状态,故在该时段内,电流处于快速下降阶段,此时反向Jephi模值相对较大,虽径向磁通密度Br减小,但|Jephi|增大为主导趋势,故在t1~tb时间段中会有一个吸引力的增加过程。
;ta~t1内,电流变化率较小,故|Jephi|较小,虽径向磁通密度Br持续增大,但|Jephi|减小占主导趋势,故|F|减小。t1~tn时间段,电流进入下降沿,径向磁通密度Br随之减小,此时电流变化率为负,Jephi发生反向,此时板件上主要受到方向向上的吸引式洛伦兹力。由于续流回路的接入,电流下降沿阶段放电回路中相当于仅存在等效电感和等效电阻;电路处于一阶零输入状态,故在该时段内,电流处于快速下降阶段,此时反向Jephi模值相对较大,虽径向磁通密度Br减小,但|Jephi|增大为主导趋势,故在t1~tb时间段中会有一个吸引力的增加过程。
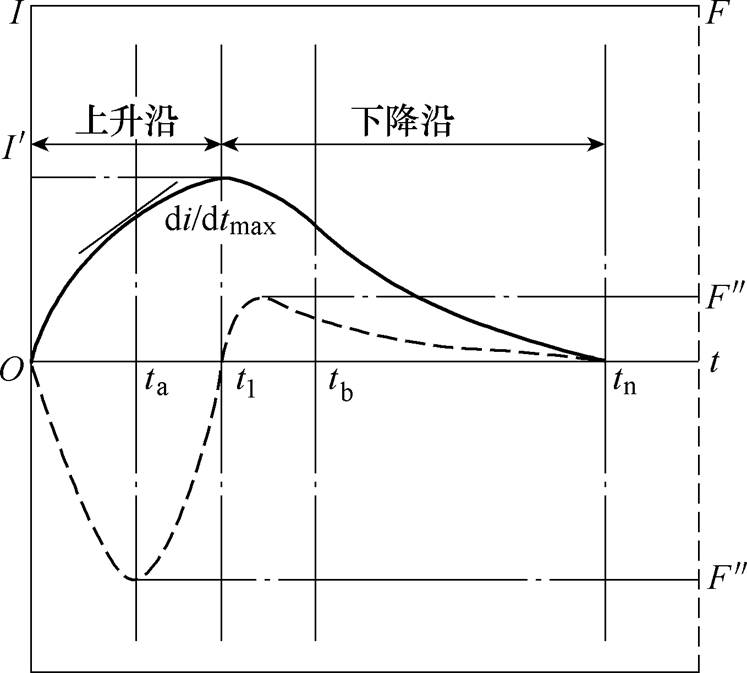
图3 脉冲电流与洛伦兹力在时间上的变化关系
Fig.3 The relationship between pulse current and Lorentz force in time
然而,影响洛伦兹力的关键因素Jephi和Br是由外电路中电流脉宽与幅值共同决定的。而RLC电路中的放电电流频率取决于电路中电阻、电感和电容值,实际上频率可以近似地用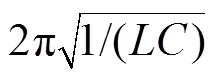 表示,对于给定的线圈和工件,可以通过改变电容器组的电容来控制电流频率。由频率公式可知,在不改变其他参数情况下,电容值越大,电流幅值越大(峰值时刻延后),电流频率越小(当C1<C2,则I1<I2,t1<t2,tn1<tn2
表示,对于给定的线圈和工件,可以通过改变电容器组的电容来控制电流频率。由频率公式可知,在不改变其他参数情况下,电容值越大,电流幅值越大(峰值时刻延后),电流频率越小(当C1<C2,则I1<I2,t1<t2,tn1<tn2 。
。
因此,电容值不同时,对应的电流变化关系如图4a所示,电流I曲线与磁通密度B呈正相关,如图4b所示(其中t1<t2,B1<B2 。对应的洛伦兹力动态变化过程也有所不同,如图4c所示,不同脉宽下的大小关系见表1。
。对应的洛伦兹力动态变化过程也有所不同,如图4c所示,不同脉宽下的大小关系见表1。
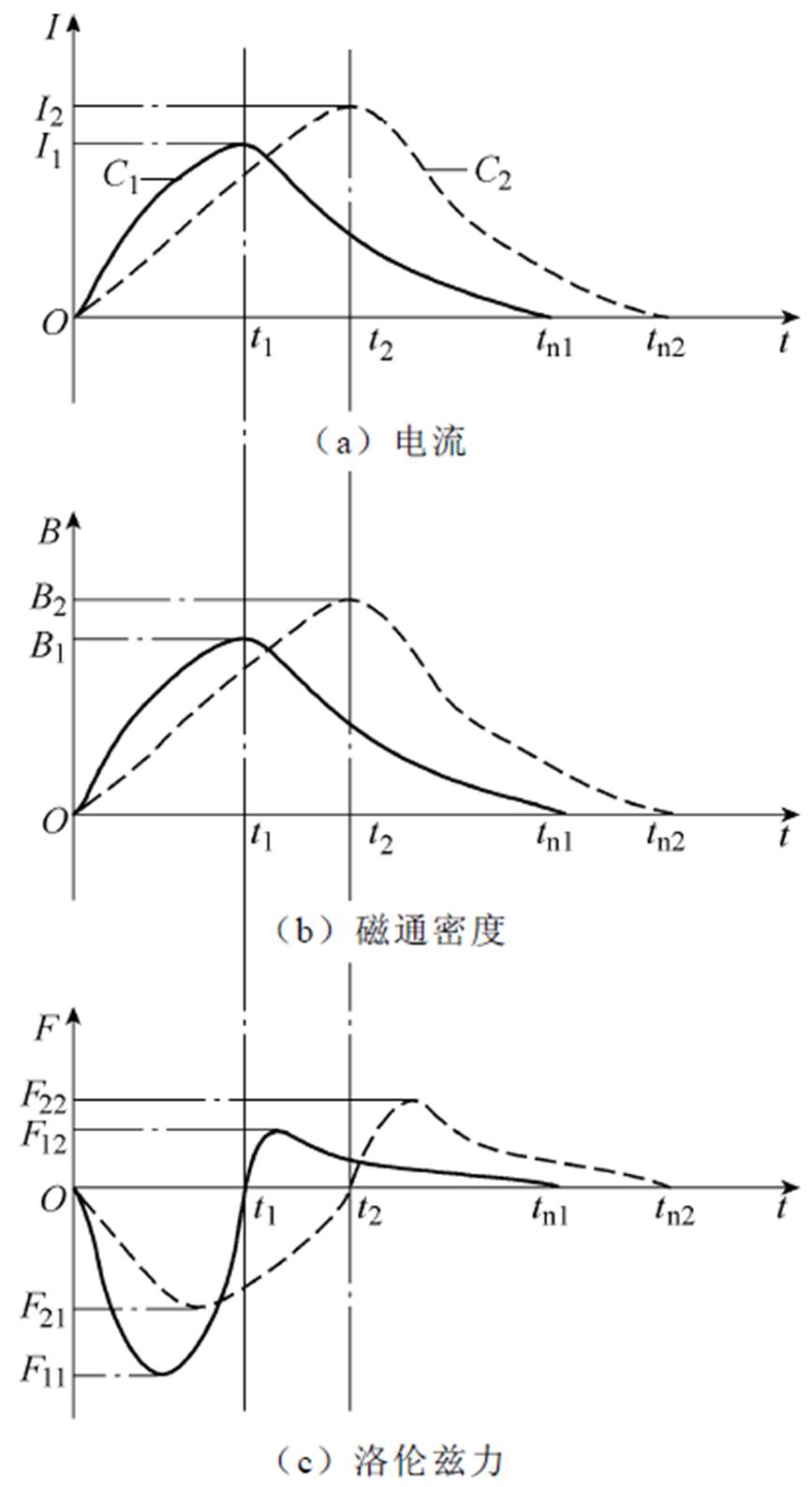
图4 不同电容下的电流、磁通密度、洛伦兹力波形
Fig.4 Waveforms diagram of current and magnetic induction intensity under different capacitances
表1 不同脉宽下对应关系
Tab.1 Correspondence under different pulse width

电流脉宽C1<C2C1>C2 排斥式洛伦兹力(max)F11>F21F11<F21 作用时间t1<t2t1>t2 吸引式洛伦兹力(max)F12<F22F12>F22 作用时间tn1<tn2tn1>tn2
在以往成形方案中,单脉冲通常用来实现工件的排斥力成形,由Ouyang Shaowei等[20]提出了单脉冲吸引力成形方案,方案所产生的吸引式洛伦兹力是小于排斥式洛伦兹力的。由此可知,在单脉冲电磁成形的情况下,洛伦兹力并非数值越大越能占据主导。
在单脉冲电磁成形过程中,若排斥式洛伦兹力远大于吸引式洛伦兹力,且作用时间极短,那么在排斥力作用阶段,将会使板件变形较大;而吸引式洛伦兹力较小,无法使板件产生吸引式形变。此时,在竞争关系中,排斥力占据主导。
而在脉宽逐渐变大的过程中,电流上升沿变缓,排斥力减小,导致板件的形变量较小或基本无形变,竞争关系中吸引力占据主导两种不同情况,如图5所示。图中,Fa1、Fa2、Fb1、Fb2为洛伦兹力最值。此时的两种情况为:①在排斥力成形后的弹塑性阶段,排斥式洛伦兹力虽大于吸引式洛伦兹力,但吸引式洛伦兹力占据主导(Fa1>Fa2);②吸引式洛伦兹力大于排斥洛伦兹力的情况下,吸引力占据主导(Fb1<Fb2)。
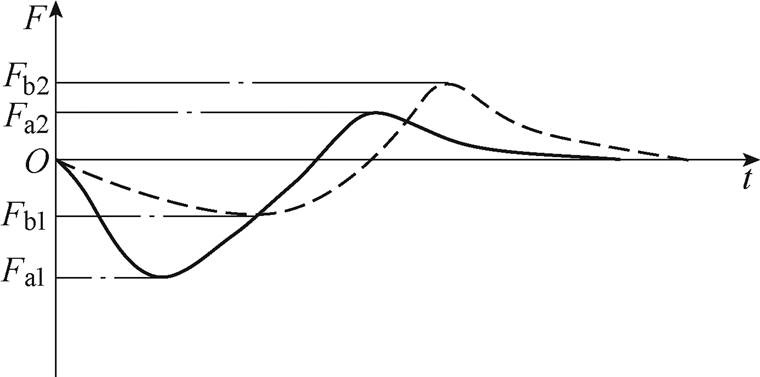
图5 竞争关系中吸引力占据主导两种不同情况
Fig.5 In the competitive relationship, attractiveness dominates in two different situations
从板件受到洛伦兹力开始直至变形,其中经过速度V、加速度a在时间分布上的动态变化,这些物理量不仅受洛伦兹力的影响,同时也会影响电路及变形,因此讨论是有必要的。
由于竞争关系的不同,故分为排斥力占主导和吸引力占主导两种情况讨论。速度V在成形过程中的变化趋势如图6所示。
(1)当排斥力占据主导时。起初板件是无速度的,主要由于起初的排斥式洛伦兹力未能到达板件初始屈服应力Fd,待排斥式洛伦兹力到达初始屈服应力点后,板件形变,速度随之变化。起初由于排斥力增加较为迅速,故速度随之变化较快,而在排斥力到达峰值前,速度变化减缓,因此ta时刻前的速度变化如图6a所示。ta时刻排斥力到达峰值,而速度在ta时刻后的tx到达峰值,ta~t1时间段,排斥力逐渐减小,速度随排斥力的减小而减小,当排斥力减小到Fd 后,已不足以使板件继续发生形变,而电磁成形过程中板件会存在一定回弹,故速度会有所波动直至为0。t1时刻后,板件上所受洛伦兹力由排斥式转变为吸引式,由于此时的吸引力远小于排斥力,不足使板件发生形变,故速度保持为0。

图6 不同竞争情况下的洛伦兹力及速度曲线
Fig.6 Lorentz force & speed curves under different competition situations
(2)当吸引力占据主导时。板件先经过排斥力成形阶段,此时洛伦兹力到达Fd 的时间较长,故速度在0值维持时间较长。两种情况下0~t1时间段,速度曲线变化趋势相同,分析同图6a。在t1时间后,吸引力增加,由于此时吸引力较大,速度在一段时间后开始反向增加,在吸引力峰值之后的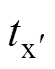 时刻达到最大,而后随吸引力的减小而减小,当吸引力减小到某一时刻不足以再使板件上吸,此时速度减小直至再次为0。
时刻达到最大,而后随吸引力的减小而减小,当吸引力减小到某一时刻不足以再使板件上吸,此时速度减小直至再次为0。
而加速度a在成形过程中随速度的变化而变化,在不同竞争情况下加速度的变化如图7所示。
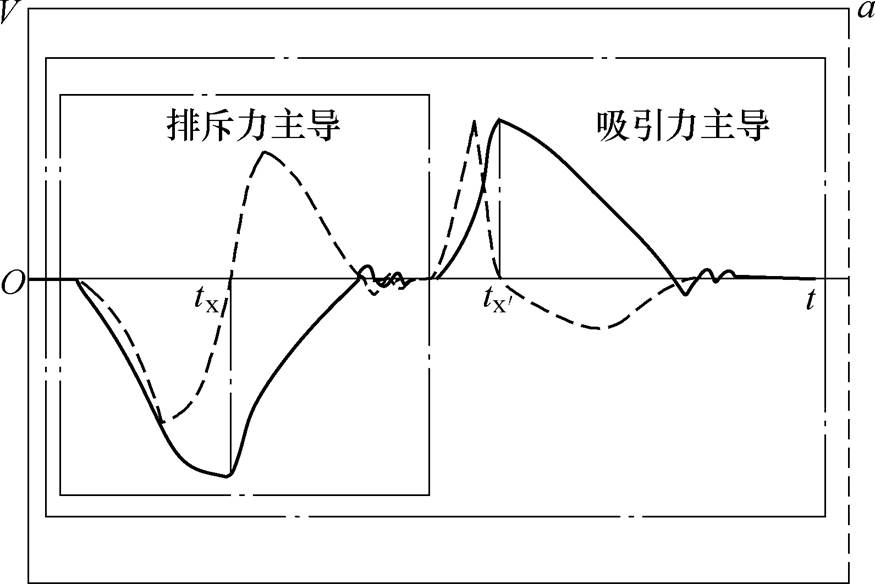
图7 不同竞争情况下的速度及加速度曲线
Fig.7 Speed & speed graphs under different competition situations
不同洛伦兹力主导的情况下,排斥力在时间轴上的变化趋势相同(但大小不同),由图7可知,排斥力主导的情况下,在0~tx时刻内,速度变化分为三个阶段。第一阶段,当洛伦兹力还未达到工件初始屈服应力时,工件无速度(速度为0),此时加速度也为0;当洛伦兹力达到工件初始屈服应力后进入第二阶段,第二阶段速度极快,此时加速度快速增加;当洛伦兹力接近峰值时进入第三阶段,第三阶段速度增长缓慢,加速度随之减小,在tx时刻速度最大时加速度降为0。tx时刻后,速度有一段快速降低的过程,故加速度迅速增大,直至某一时刻速度缓慢减小,加速度随之减小直至为0。
而在吸引力主导的情况下,排斥力阶段加速度变化趋势相同,而在吸引力阶段由于吸引力较大,使板件重新开始运动,速度增加,在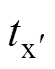 时刻加速度降为0,
时刻加速度降为0,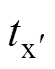 时刻后速度减小,故加速度反向先增大后减小,而后经历惯性振荡阶段,直至稳定。
时刻后速度减小,故加速度反向先增大后减小,而后经历惯性振荡阶段,直至稳定。
洛伦兹力在时间上的竞争关系不同,其对最终成形效果的影响也存在较大差异。由于电磁成形过程极快且十分复杂,其中涉及单脉冲电磁成形过程中机理层面的动态变化关系,实验不能得到详细数据随时间的变化趋势,因此必须借助仿真详细探究单脉冲成形过程中,洛伦兹力在时间上的双向竞争关系及其对成形效果的影响。因此,采用文献[18-20]中均采用的有限元法分析电磁成形的物理过程。
通过改变外电路参数进行探究。为了证明仿真结果的可靠性,本文选用文献[18]中的仿真参数,结合其实验效果利用有限元软件还原其考虑板件位移和形变速率影响的全耦合仿真部分。采用型号为AA5083-O的铝合金板件作为研究对象,该板件半径为90mm,厚度为2mm,并采用电导率为0的柴龙纤维材料对板件进行压边及固定。板件电磁成形方案示意图如图8所示。
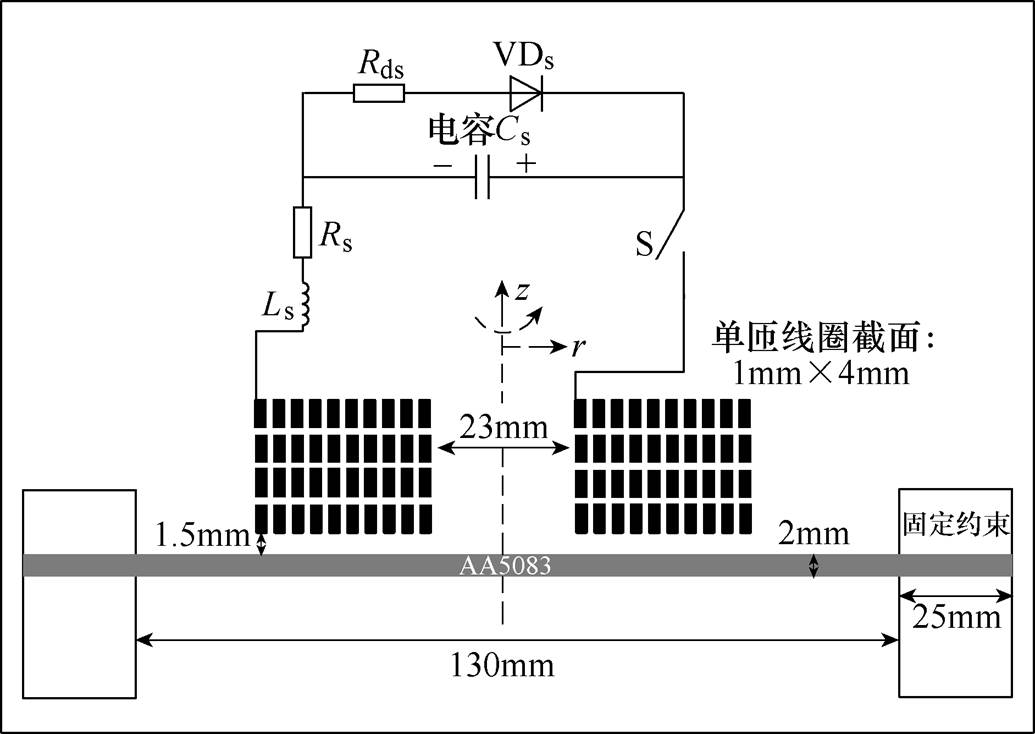
图8 板件电磁成形方案示意图
Fig.8 Schematic diagram of plate electromagnetic forming scheme
单脉宽电流系统外电路放电参数见表2,其中续流电阻选用具体实验方案中的0.3W。
表2 外电路放电参数
Tab.2 External circuit discharge parameters

参 数数 值 电容Cs/mF320 放电电压Us/kV8 线路电阻Rs/mW25 线路电感Ls/mH6.5 续流电阻Rds/W0.3
主要分析不同脉宽下的洛伦兹力在时间上的竞争关系及对最终板件成形效果的影响。由于仅改变电容值不仅会造成洛伦兹力作用时间的改变,也会造成幅值的改变。因此,在此模型下,通过同时改变电容Cs与放电电压Us的方式分别分析。在此模型下,进行:
(1)调整外电路参数(主要是电容Cs与放电电压Us),由于改变的电容值相差较大,基本不能做到电流幅值相同,故在保证能量相同的情况下,使洛伦兹力作用时间t为变量。
(2)在保证电容Cs不变的情况下,调整放电电压Us,使电流幅值不同,但作用时间t相同。
本文对文献[18]中的实验方案进行了仿真验证,板件最终变形位移结果与仿真对比如图9a所示,其电流及洛伦兹力竞争如图9b所示。
具体实验下的单脉冲板件排斥力最大变形位移为23.2mm,仿真结果为24mm,由于实验与仿真本就存在一定误差,且板件本身较厚,故0.8mm的误差可忽略不计。此时C=320mF,U=8kV,电流幅值为16.15kA,电流基本在0.3ms内就完成了主要变化,所得排斥式洛伦兹力最大值为73.04kN,吸引式洛伦兹力为0.25kN。此时的排斥式洛伦兹力远远大于吸引式洛伦兹力且作用时间极短,在竞争关系稳稳占据主导,故最终所呈现在板件上也为排斥力成形。
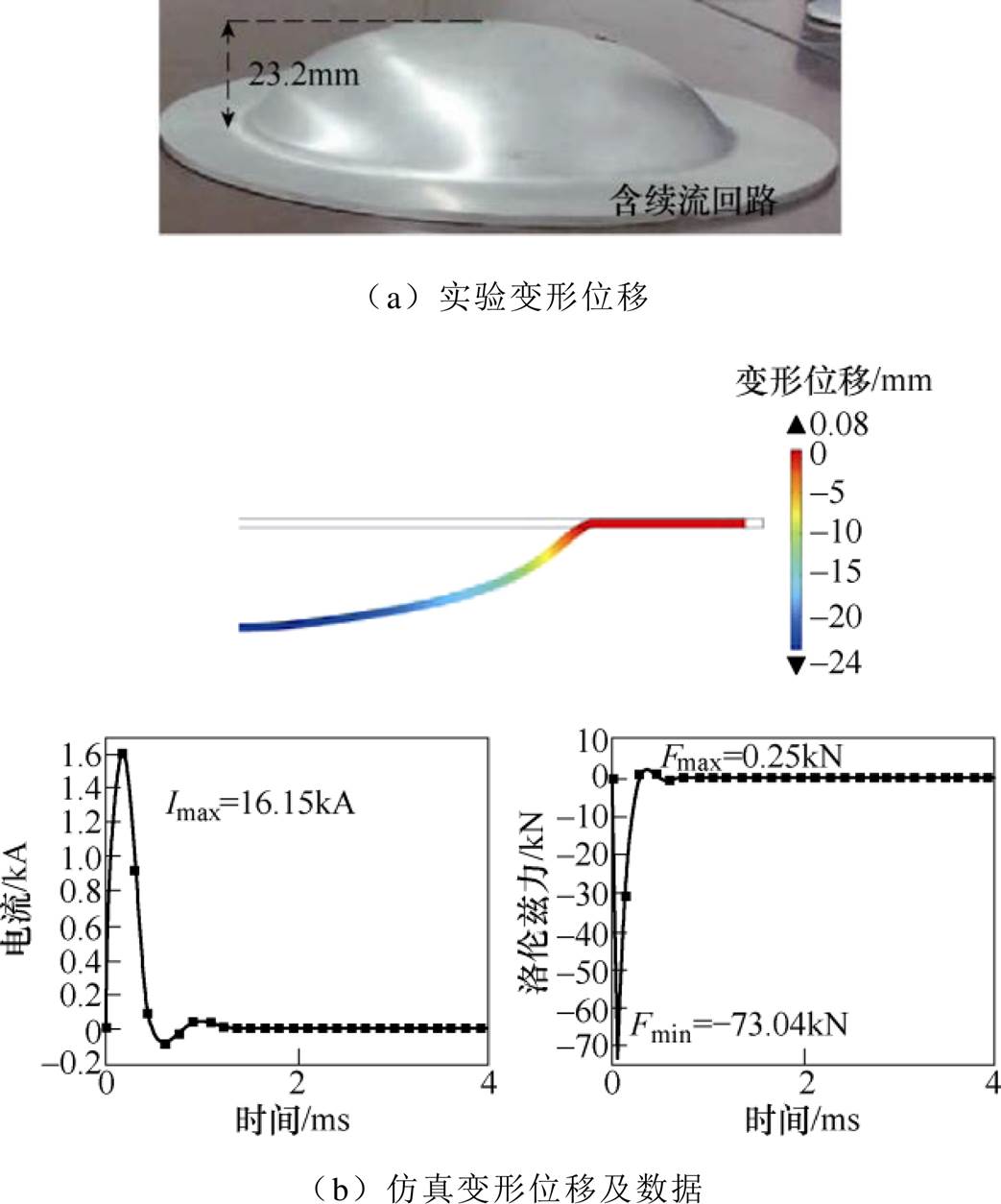
图9 变形位移
Fig.9 Displacement deformation map
改变电容Cs与放电电压Us,保证能量Ws相同。三种情况下的参数见表3,电流数据如图10所示。在板件的建模过程中,由于此方案下的板件半径较长,为了更好地对主要受力部分的洛伦兹力进行分析,将板件分为0~10mm、10~40mm、40~50mm三段建模。电容值分别为1 400mF、2 000mF、2 600mF的三种情况下放电能量相同,但所得电流脉宽不同,如图10所示。由图10可知,各种情况下电流上升沿与下降沿的变化率不同,故洛伦兹力在各种情况下的竞争关系不同。三种情况下电流到达峰值的时间分别为1.26ms、2.12ms、2.78ms,电流最大值已在图中标注。且其电流脉宽、幅值均符合第1节原理部分分析。在洛伦兹力的变化过程中存在一些小抖动的现象,主要是由于在电容与电压变化的过程中的外电路参数不匹配导致的。
表3 放电能量相等的三种情况
Tab.3 Three cases of equal discharging energy

情况Cs/mFUs/kVWs/kJ 11 4004.60015.0 22 0003.87315.0 32 6003.39715.0
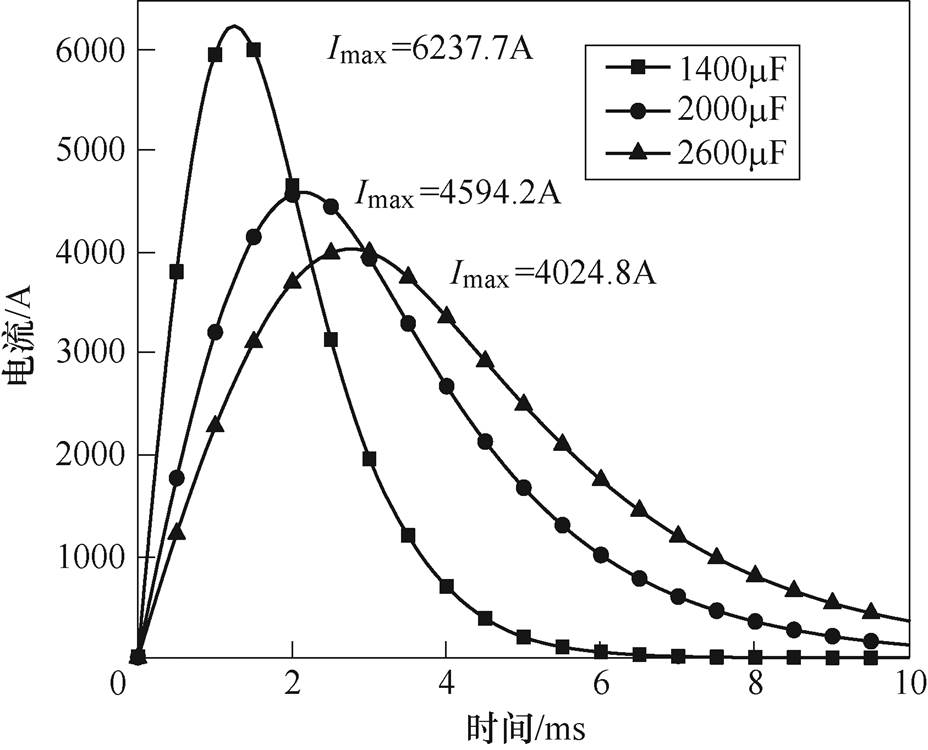
图10 不同电容值下的电流波形
Fig.10 Current waveforms under different capacitance values
不同电容值下的洛伦兹力竞争如图11所示,不同电容值下板件成形示意图如图12所示。
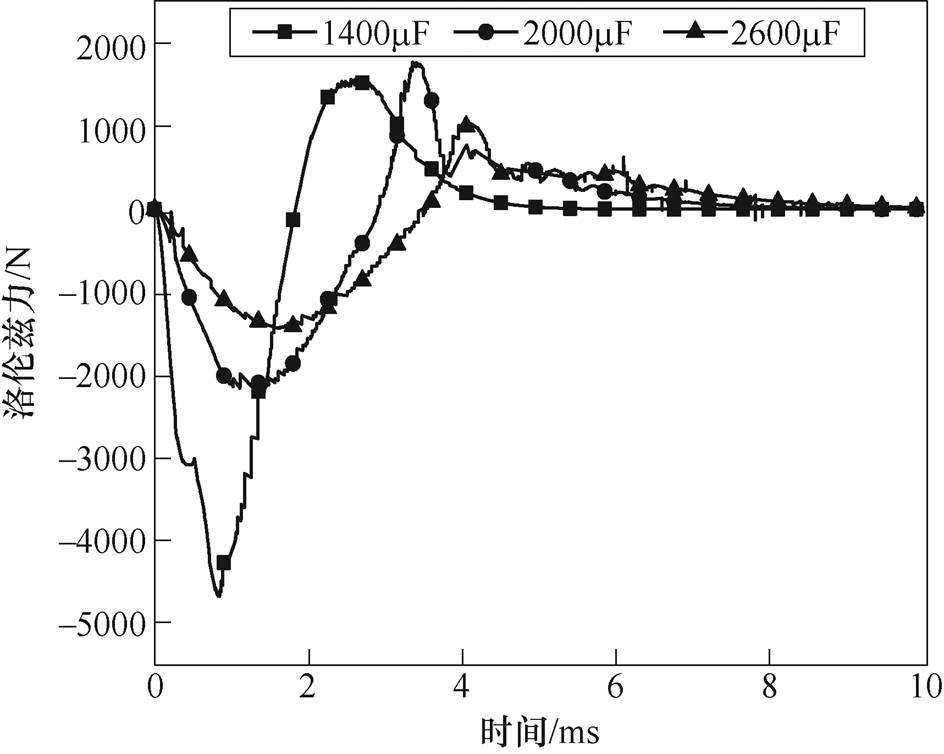
图11 不同电容值下的洛伦兹力竞争
Fig.11 Lorentz force competition graph under different capacitance values
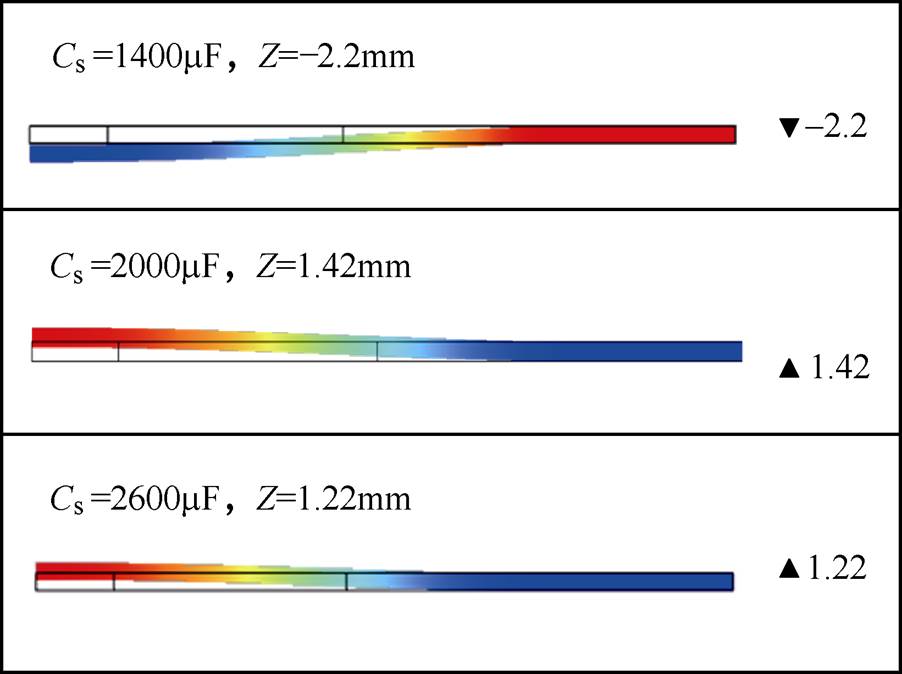
图12 不同电容值下板件成形示意图
Fig.12 Schematic diagram of plate forming under different capacitance values
(1)1 400mF的电流在1.26ms时就达到峰值6 237.7A,电流变化极快,感应涡流较大,排斥式洛伦兹力在0.887ms时达到最大值4 538.9N,排斥力作用时间为1.82ms,在电流下降沿产生的吸引式洛伦兹力最大值仅为1 543.1N。由于吸引力的主要作用部分基本就在第一个波峰处,整个过程计算时间较长,在这里就不讨论吸引力的作用时间了。在此竞争过程中,虽不像文献[17]中的吸引力与排斥力不在一个数量级上,但此情况下排斥式洛伦兹力还是远大于吸引式洛伦兹力的(相差大约3 000N)。因此,在此竞争情况下,依旧是排斥力占据主导,体现在最终的板件成形上为排斥力成形,变形位移为2.2mm。
(2)2 000mF的电流在幅值上与1 400mF具有较大差异,此时的电流在2.12ms达到最大,最大值为4 594.2A。由于电容值变大,电流上升沿波形变缓,产生的排斥式洛伦兹力最大值为2 092.5N,作用时间为2.90ms。特别是此时的吸引力为1 770.9N,大于1 400mF时所产生的吸引式洛伦兹力,此时排斥力虽大于吸引力,但相差不大,并且前半段的排斥力作用时间长,数值变化较缓慢,而吸引力的主要作用部分时间短,数值变化较快。由于两种洛伦兹力数值不相上下而吸引式洛伦兹力变化较快,故此时吸引力占据主导,且体现在最终的板件成形上为吸引力成形,变形位移为1.42mm。
(3)2 600mF的情况下,电流变化更加缓慢,且电流幅值更小。此时的电流在2.78ms时达到最大,最大值为4 024.8A。由于电流上升沿更缓,此时的排斥式洛伦兹力最大值为1 386.3N,吸引式洛伦兹力最大值为1 035.3N。在排斥力与吸引力不相上下的情况下,吸引力主要部分变化更快、作用时间更短暂,因此吸引式洛伦兹力在此竞争中占据主导。体现在最终的板件成形上为吸引力成形,最大变形位移为1.22mm。
电流脉宽的大小(电容值的大小)是能否使吸引式洛伦兹力在竞争关系中占据主导的关键。脉宽大小的变化影响前半段排斥式洛伦兹力的变化率以及与吸引式洛伦兹力的差值情况。在排斥力与吸引力差值较大的情况下,差值是影响竞争关系的关键,而在排斥力与吸引力不相上下的情况下,洛伦兹力波峰与波谷的尖锐度成为竞争关系中重要的一环。
选用2 000mF电容值,分析分别在3kV、4kV、5kV情况下的洛伦兹力竞争关系及成形情况。相同电容值、不同电压下的电流波形如图13所示。由图13可知,在电容值不变的情况下,电压越大,电流幅值越大:3kV电压时的放电电流最大值为3 546.7A、4kV电压时的放电电流最大值为4 741.5A、5kV电压时的放电电流最大值为5 910.2A,且其电流到达峰值的时间相同。但由于电流的变化率不同,故其产生的洛伦兹力大小自然不同。
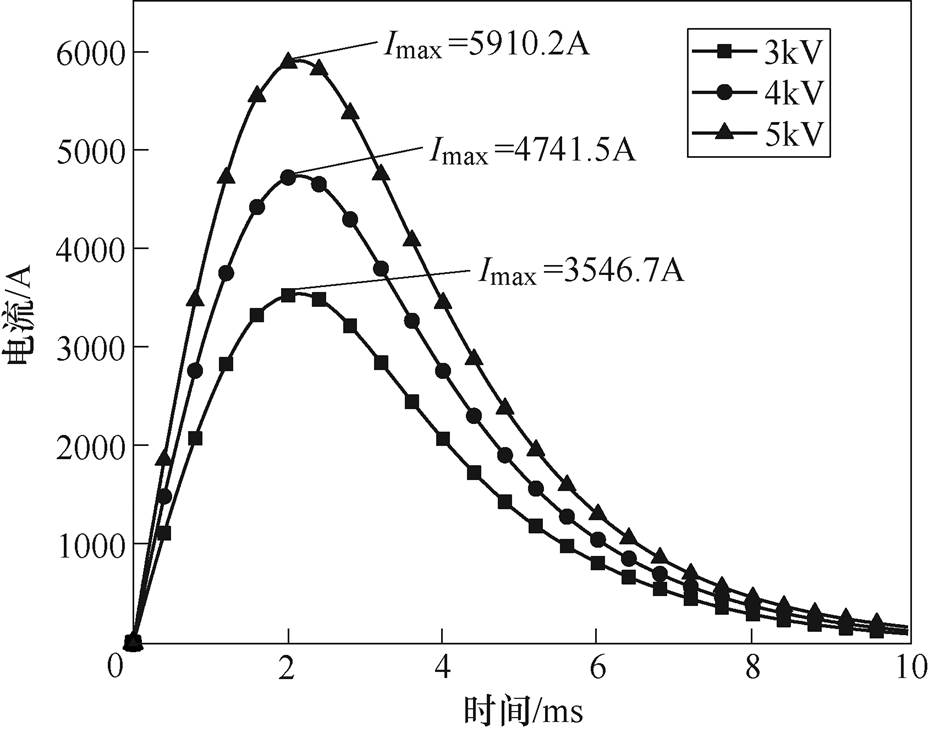
图13 相同电容值、不同电压下的电流波形
Fig.13 Schematic diagram of plate forming under different capacitance values
三种情况下的排斥式洛伦兹力最大值分别为1 421.5N、2 241.3N、3 370.3N;吸引式洛伦兹力分别为723.35N、1 510.5N、2 242.4N。在电容值不变的情况下,电压值越大,产生的洛伦兹力越大。2 000mF、不同电压下的洛伦兹力竞争如图14所示。由图14可知,电容值相同的条件下,三种情况到达排斥式洛伦兹力最大值的时间与到达吸引式洛伦兹力的时间均有部分差异,主要是由于电压值越大,电流幅值越大,上升沿与下降沿电流变化率不同,自然变化率最大值所处位置不同。在第4.2节中已经分析了此种结构参数下2 000mF的洛伦兹力竞争关系为吸引力占据主导,由于电容值并未发生变化,且排斥式与吸引式洛伦兹力相差并不大,故所得皆是吸引力成形,变形位移为0.84mm、1.5mm、1.88mm。2 000mF、不同电压下板件成形示意图如图15所示。
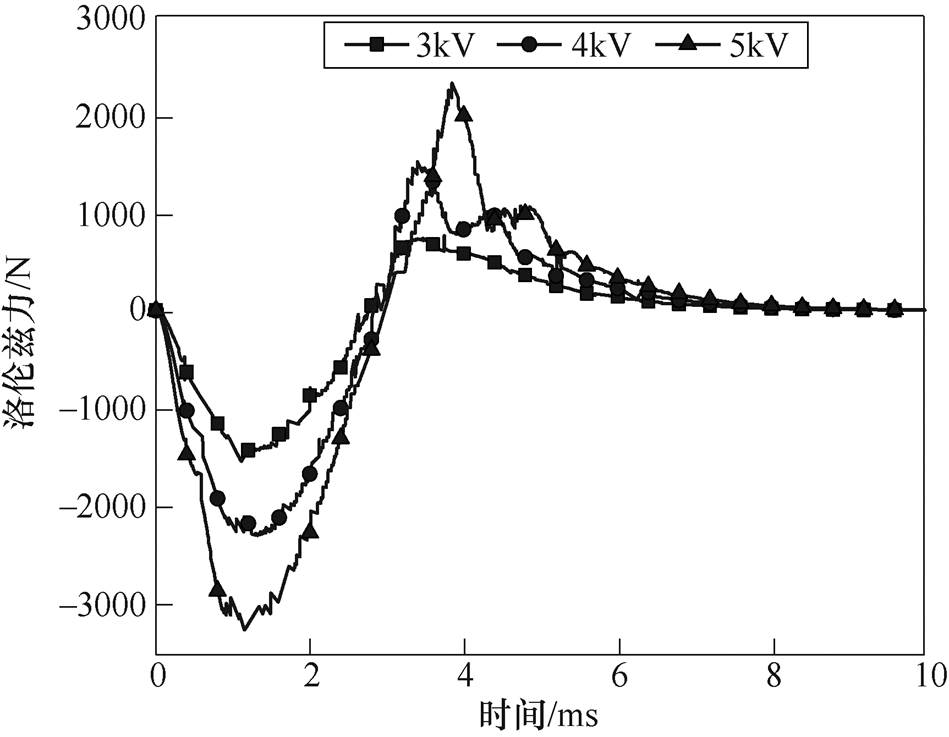
图14 2 000mF、不同电压下的洛伦兹力竞争
Fig.14 Lorentz force competition graph under 2 000mF and different voltages

图15 2 000mF、不同电压下板件成形示意图
Fig.15 Schematic diagram of sheet metal forming under 2 000mF and different voltages
在2 000mF的容值,三种电压情况下,洛伦兹力大小相差最大在1 100N,并且均为吸引力占据主导,呈现出吸引力形变。且由图15可知,在之前分析中已知2 000mF的容值可以使吸引式洛伦兹力占据主导的的情况下,增大电压,吸引式洛伦兹力增大,且图形越尖锐,形变也越大。
此时还存在一种可能发生的情况:由于排斥式与吸引式洛伦兹力相差并不大,在同一电容值下电压一直增加过程中,排斥式与吸引式洛伦兹力相差慢慢变大,还能否实现吸引力成形?因此,在2 000mF的电容频率下,给出了电压为8kV的情况下的洛伦兹力竞争及成形,结果如图16所示。
在此情况下,排斥式洛伦兹力远比吸引式洛伦兹力大,相差大约3 000N,且从作用时间上看,排斥式洛伦兹力变化快,作用时间短,吸引式洛伦兹力变化缓慢,且主要部分作用时间长,尖锐度明显减小,最终板件成形情况为排斥力成形,也充分证明了此种竞争情况下,依旧是排斥式洛伦兹力占据主导。虽电容值未改变,但在洛伦兹力相差太大的情况下,竞争关系依旧会发生改变。且在同一容值下的洛伦兹力的竞争及成形并非电压越大,就一定能够实现吸引力成形,力的差值还是竞争关系的关键。
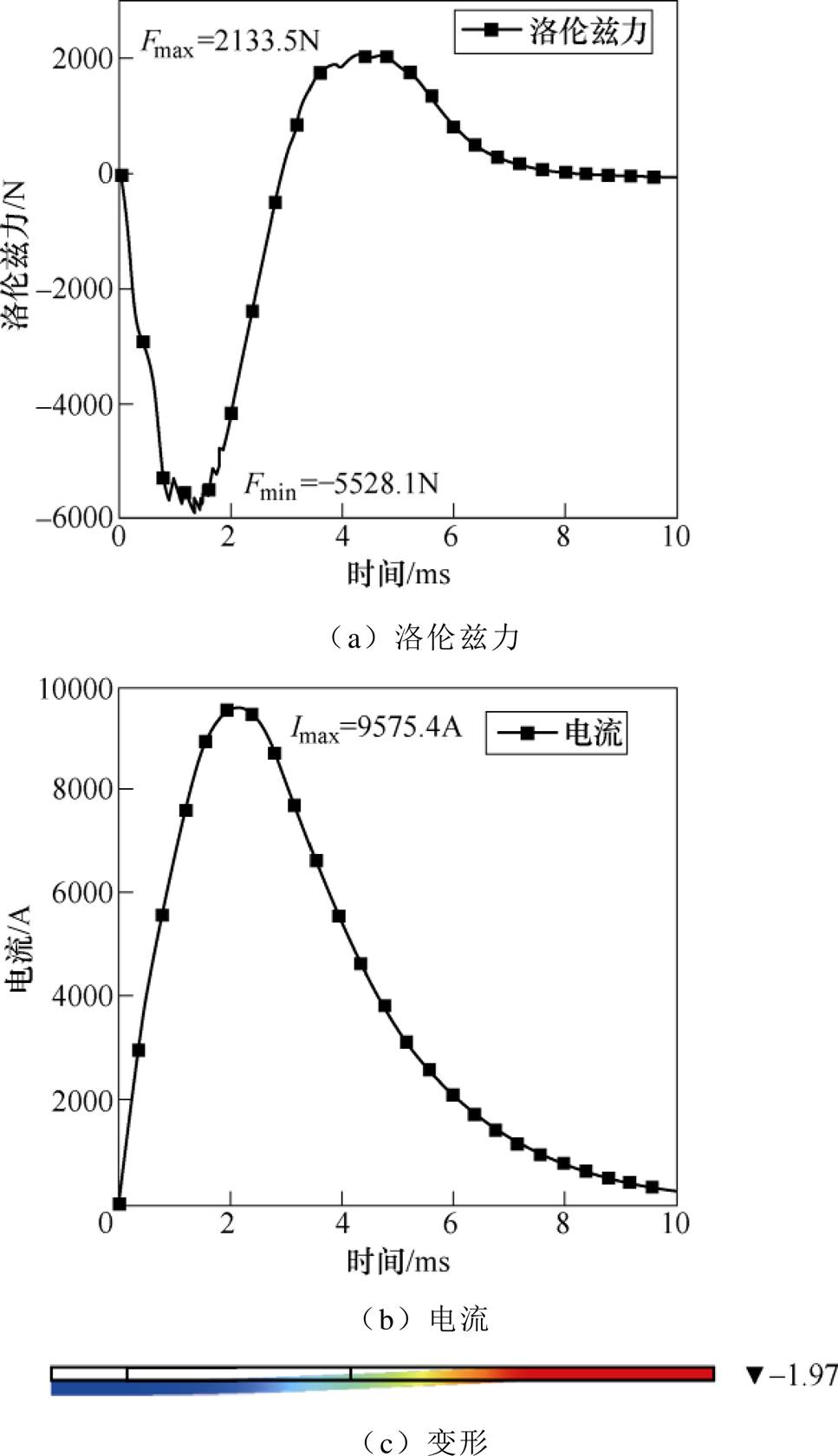
图16 2 000mF、8kV下仿真结果示意图
Fig.16 Schematic diagram of simulation results at 2 000mF and 8kV
在单脉冲电磁成形的过程中,洛伦兹力的双向竞争关系决定工件最终的成形效果。而据上述分析可知,影响竞争关系的因素主要有以下两点:
1)电流脉宽(力的差值)。在电容值很小的情况下,电流在上升沿阶段变化极快,产生的排斥式与吸引式洛伦兹力相差一个或数个量级,排斥力在竞争关系中占绝对主导的地位。而在电容值慢慢变大的过程中,产生的洛伦兹力才具有可比性。在满足吸引力成形的脉宽下,也并非电压越大,变形越大,主要是在电压变化的过程中,由于力的差值在变化,竞争关系也是会发生变化的,最终还是要观察力的差值。
2)洛伦兹力波峰与波谷的尖锐度。在排斥力与吸引力相差较小的情况下,洛伦兹力波峰与波谷的尖锐度作为竞争关系中重要的因素,排斥力虽大于吸引力,但作用时波谷处变化缓慢;吸引力虽略小于排斥力,但波峰处变化较快,一般为吸引力占据主导,并最终呈现出吸引力形变。
参考文献
[1] Kiliclar Y, Demir O K, Engelhardt M, et al. Experi- mental and numerical investigation of increased formability in combined quasi-static and high-speed forming processes[J]. Journal of Materials Processing Technology, 2016, 237: 254-269.
[2] 熊奇, 唐红涛, 王沐雪, 等. 2011年以来电磁成形研究进展[J]. 高电压技术, 2019, 45(4): 1171-1181.
Xiong Qi, Tang Hongtao, Wang Muxue, et al. Research progress of electromagnetic forming technique since 2011[J]. High Voltage Engineering, 2019, 45(4): 1171-1181.
[3] Psyk V, Risch D, Kinsey B L, et al. Electromagnetic forming-a review[J]. Journal of Materials Processing Technology, 2011, 211(5): 787-829.
[4] 邱立, 李彦涛, 苏攀, 等. 电磁成形中电磁技术问题研究进展[J]. 电工技术学报, 2019, 34(11): 2247- 2259.
Qiu Li, Li Yantao, Su Pan, et al. Research on elec- tromagnetic problems in electromagnetic forming process[J]. Transactions on China Electrotechnical Society, 2019, 34(11): 2247-2259.
[5] Xiong Qi, Tang Hongtao, Deng Changzheng, et al. Electromagnetic attraction-based bulge forming in small tubes: fundamentals and simulations[J]. IEEE Transactions on Applied Superconductivity, 2017, 28(3): 1-5.
[6] Kamal M, Daehn G S. A uniform pressure electro- magnetic actuator for forming flat sheets[J]. Journal of Manufacturing Science and Engineering, 2007, 129(2): 369-379.
[7] Wu Zelin, Cao Quanliang, Fu Junyu, et al. An inner- field uniform pressure actuator with high performance and its application to titanium bipolar plate for- ming[J]. International Journal of Machine Tools and Manufacture, 2020, 155: 103570.
[8] Qiu Li, Yu Yijie, Yang Yuqi, et al. Analysis of electromagnetic force and experiments in electro- magnetic forming with local loading[J]. International Journal of Applied Electromagnetics & Mechanics, 2018, 57(1): 29-37.
[9] 张望, 王于東, 李彦涛, 等. 基于双向电磁力加载的管件电磁翻边理论与实验[J]. 电工技术学报, 2021, 36(14): 2904-2911.
Zhang Wang, Wang Yudong, Li Yantao, et al. Theory and experiment of tube electromagnetic flanging based on bidirectional electromagnetic force loading[J]. Transactions on China Electrotechnical Society, 2021, 36(14): 2904-2911.
[10] Xiong Qi, Huang Hao, Xia Liangyu, et al. A research based on advance dual-coil electromagnetic forming method on flanging of small-size tubes[J]. Inter- national Journal of Advanced Manufacturing Tech- nology, 2019, 102(9): 4087-4094.
[11] Xiong Qi, Zhao Xiang, Zhou Hang, et al. A triple-coil electromagnetic two-step forming method for tube fitting[J]. The International Journal of Advanced Manu-facturing Technology, 2021, 116(11): 3905- 3915.
[12] 邱立, 余一杰, 聂小鹏, 等. 管件电磁胀形过程中的材料变形性能问题与电磁力加载方案[J]. 电工技术学报, 2019, 34(2): 212-218.
Qiu Li, Yu Yijie, Nie Xiaopeng, et al. Study on material deformation performance and electro- magnetic force loading in electromagnetic tube expansion process[J]. Transactions on China Elec- trotechnical Society, 2019, 34(2): 212-218.
[13] 熊奇, 杨猛, 周丽君, 等. 双线圈吸引式板件电磁成形过程中的涡流竞争问题[J]. 电工技术学报, 2021, 36(10): 2007-2017.
Xiong Qi, Yang Meng, Zhou Lijun, et al. The problem of eddy current competition in the electromagnetic forming process of double-coil attracted sheet metal[J]. Transactions on China Electrotechnical Society, 2021, 36(10): 2007-2017.
[14] Xiong Qi, Tang Hongtao, Wang Muxue, et al. Design and implementation of tube bulging by an attractive electromagnetic force[J]. Journal of Materials Pro- cessing Technology, 2019, 273: 116240.
[15] Ouyang Shaowei, Cao Quanliang, Li Liang, et al. Improving the uniformity and controllability of tube deformation via a three-coil forming system[J]. The International Journal of Advanced Manufacturing Technology, 2021, 291: 117001.
[16] 李成祥, 杜建, 周言, 等. 电磁脉冲板件焊接设备研制及镁/铝合金板焊接实验研究[J]. 电工技术学报, 2021, 36(10): 2018-2027.
Li Chengxiang, Du Jian, Zhou Yan, et al. Develop- ment of electromagnetic pulse welding equipment for plates and experimental research on magnesium/ aluminum alloy welding[J]. Transactions on China Electrotechnical Society, 2021, 36(10): 2018-2027.
[17] 熊奇. 大尺寸铝合金板件电磁成形设计与实现[D].武汉: 华中科技大学, 2016.
[18] Cao Quanliang, Han Xiaotao, Lai Zhipeng, et al. Analysis and reduction of coil temperature rise in electromagnetic forming[J]. Journal of Materials Pro- cessing Technology, 2015, 225: 185-194.
[19] 王紫叶, 杨猛, 熊奇. 电磁成形过程中线圈温升及结构优化[J]. 电工技术学报, 2021, 36(18): 3891- 3901.
Wang Ziye, Yang Meng, Xiong Qi. Coil temperature rise and structure optimization in electromagnetic forming[J]. Transactions on China Electrotechnical Society, 2021, 36(18): 3891-3901.
[20] Ouyang Shaowei, Li Changxing, Du Limeng, et al. Electromagnetic forming of aluminum alloy sheet metal utilizing a low-frequency discharge: a new method for attractive forming[J]. Journal of Materials Processing Technology, 2020, 291: 117001.
[21] 段志荣, 解社娟, 李丽娟, 等. 基于磁力传动式阵列涡流探头的管道缺陷检测[J]. 电工技术学报, 2020, 35(22): 4627-4635.
Duan Zhirong, Xie Shejuan, Li Lijuan, et al. Dete- ction of defects in pipeline structures based on magnetic transmission eddy current array probe[J]. Transactions on China Electrotechnical Society, 2020, 35(22): 4627-4635.
The Two-Way Competitive Relationship of Lorentz Force in Time in Single Pulse Electromagnetic Forming and Its Influence on Forming Effect
Abstract Electromagnetic forming technology is an advanced manufacturing technology that uses Lorentz force to drive high-speed deformation of metal materials. Compared with the traditional static forming process, electromagnetic forming can significantly improve the forming performance of light alloy materials due to its extremely high strain rate. At the same time, compared with the traditional mechanical force or hydraulic pressure, the Lorentz force used in electromagnetic forming can be flexibly adjusted in time and space, so it has richer process potential. However, the existing research mostly focuses on the forming method and effect of metal workpieces, and the most important part, the Lorentz force and the complex competitive relationship have not been systematically analyzed. Therefore, this paper focuses on the typical single-pulse electromagnetic forming process, refines the dynamic relationship between the various physical quantities in the electromagnetic forming process, and studies the competitive relationship of the time-varying Lorentz force on the aluminum alloy plate during the forming process and its influence on the forming process. The competitive relationship of the Lorentz force that changes with time is clarified, the influence on the forming effect is analyzed, and the electromagnetic forming technology process can be comprehensively understood.
keywords:Electromagnetic forming, single pulse power supply, sheet metals, force competition, forming effect
DOI: 10.19595/j.cnki.1000-6753.tces.210289
中图分类号:TM154
国家自然科学基金(51707104)和武汉强磁场学科交叉基金(WHMFC202121)资助项目。
收稿日期 2021-03-05
改稿日期 2021-07-06
熊 奇 男,1990年生,博士,副教授,博士生导师,IEEE Senior Member,研究方向为电磁场工业应用。E-mail: pandaqi0218@gmail.com(通信作者)
周丽君 女,1997年生,硕士研究生,研究方向为电磁场分析及应用。E-mail: 754914487@qq.com
(编辑 崔文静)