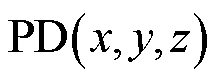 ,第
,第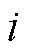 个天线的坐标为
个天线的坐标为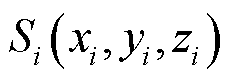 ,其中,
,其中,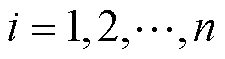 。如图1所示。
。如图1所示。摘要 针对复杂环境中特高频信号达时差误差较大,引起非线性方程求解不准确的问题,提出一种基于截断奇异值分解(TSVD)与K-Medians的局部放电(PD)源定位方法。首先,通过超高频天线获取PD信号,利用能量积累提取时差信息。其次,针对线性方程求解困难且不准确的难题,提出随机组合线性变换方法。将非线性定位方程组进行线性转化,同时利用预处理技术消除坐标系选取对定位方程的影响。然后,采用TSVD正则化算法求解线性方程,引入K-Medians聚类算法对TSVD正则化算法进行优化改进,进而实现了变电站场景下PD源的坐标定位。最后,通过理论验证与现场实验两种途径对所提出的方法进行分析。实验结果验证了所提定位方法的可行性与准确性。
关键词:局部放电源 定位 线性变换 预处理 截断奇异值分解(TSVD) K-Medians
局部放电(Partial Discharge, PD)是导致电力设备局部故障的重要原因[1-2]。绝缘老化程度与放电量以及放电位置密切相关[3]。准确检测局部放电是保证电气设备可靠性的关键。电气设备局部放电的准确定位可以有效避免停电造成的经济损失[4]。因此,对电气设备进行绝缘监测具有重要意义。
局部放电的定位方法通常包括基于声光的气体检测法、超声波测量技术以及特高频(Ultrahigh Frequency, UHF)定位方法[5]。与其他定位方法相比,基于UHF的定位方法具有较高的灵敏度和稳定的传播速度[6]。因此,UHF技术近年来被广泛用于局部放电源的定位。通常,UHF的定位方法可以通过时域反射法[7]、到达时差法(Time Difference of Arrival,TDOA)等技术方法实现[8]。TDOA定位方法利用多个UHF天线建立非线性方程组[9],再通过求解定位方程达到对局部放电源定位的目的。
非线性方程组的求解一般利用牛顿迭代算法计算[10]。文献[10]分析了时间差对定位计算的影响,并在复数域内利用牛顿迭代法对非线性方程进行求解,结合网格搜索方法实现了PD源的定位求解。为了避免求解复杂的非线性方程,文献[11]提出了一种基于L形阵列天线的定位方法。该定位方法利用旋转不变技术寻找波达方向,同时采用高阶累积量抑制超高频信号的噪声[11]。为了降低非线性定位方程对时间差的依赖性,文献[12]提出了一种PD源逐次逼近的定位方法。该方法利用粒子群算法寻优目标函数逐次递归寻优逼近PD源的空间位置[12]。文献[13]提出了一种基于深度神经网络的变电站局部放电数据驱动定位方法[13]。虽然该方法中的深度神经网络方法大大加快了非线性定位方程的求解速度,但该算法需要先验知识来训练神经网络,定位精度对训练数据的依赖性较强。
因此,在利用时差理论进行PD源定位的方法中,如何准确求解非线性方程至关重要。由于实际测量环境复杂多变。背景噪声和测量误差不可避免,导致非线性定位方程的病态性问题。对于病态非线性方程组,利用传统的迭代法和导数算法难以准确求解[10,14]。当时间误差信息存在一定的误差时,会导致定位方程的多解或无解。如果定位方程没有解,则精确定位无法实现。如果得到多个解,则无法确定局部放电源的空间位置。
基于以上分析,本文提出了一种基于截断奇异值分解(Truncated Singular Value Decomposition, TSVD正则化与K-Medians聚类优化的局部放电源定位方法。首先,在变电站空间区域布置超高频传感器获取PD源信号,采用能量积累法计算局部放电源的时差信息。其次,为了避免非线性方程求解的不确定性,采用随机组合线性变换方法将非线性定位方程进行线性变换。然后,利用中心化技术对定位方程进行优化预处理,避免了坐标系的选取对求解的影响。为了找到方程的稳定近似解,引入截断奇异值分解正则化方法求解优化后的线性方程组。通过交叉验证(Generalized Cross-Validation, GCV)方法确定TSVD正则化参数。最后,引入K-Medians聚类算法对正则化解进行优化。本文进行了理论仿真和场景验证。实验结果表明,该算法可行有效。
当电气设备出现绝缘缺陷时,带电运行的电气设备可能发生PD,同时伴随特高频信号发射。特高频信号在不同介质中传播,利用UHF传感器可以接收特高频信号并转换成电信号。对采集的电信号进行预处理等运算过程,可以得到发生PD电气设备的具体位置。
利用UHF天线阵列在三维空间中确定PD的具体位置,至少需要4个及以上天线同时检测信号源。通过测量特高频信号到达各天线的时间差,组建与之对应的双曲面方程组,曲面的焦点即为PD源的空间位置。假设PD源的空间位置为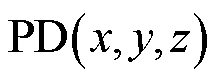 ,第
,第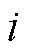 个天线的坐标为
个天线的坐标为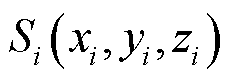 ,其中,
,其中,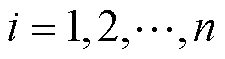 。如图1所示。
。如图1所示。
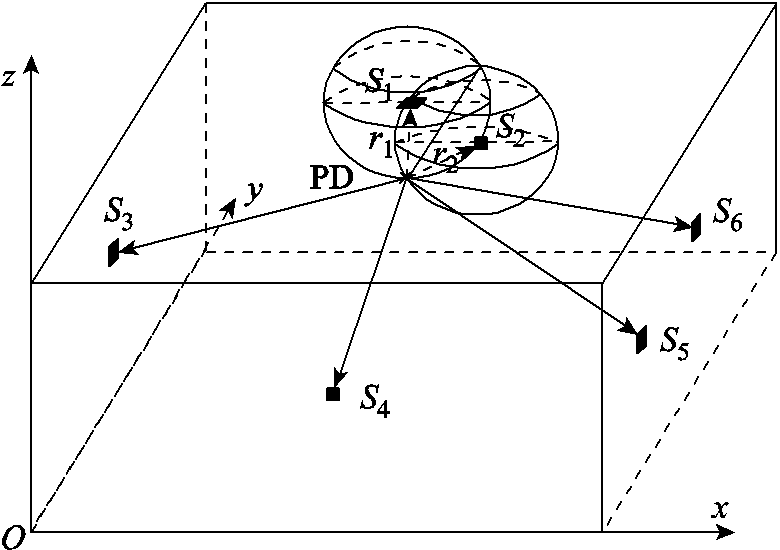
图1 基于多传感器的局部放电源定位原理图
Fig.1 The diagram of PD location based on multi-sensor
特高频信号由PD源到第一个天线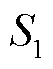 的时间为
的时间为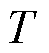 ,UHF信号从PD源到达第
,UHF信号从PD源到达第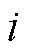
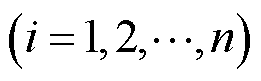 个天线的时间差为
个天线的时间差为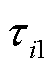 。
。
基于TDOA定位原理,可以建立基于UHF阵列信号的定位方程组
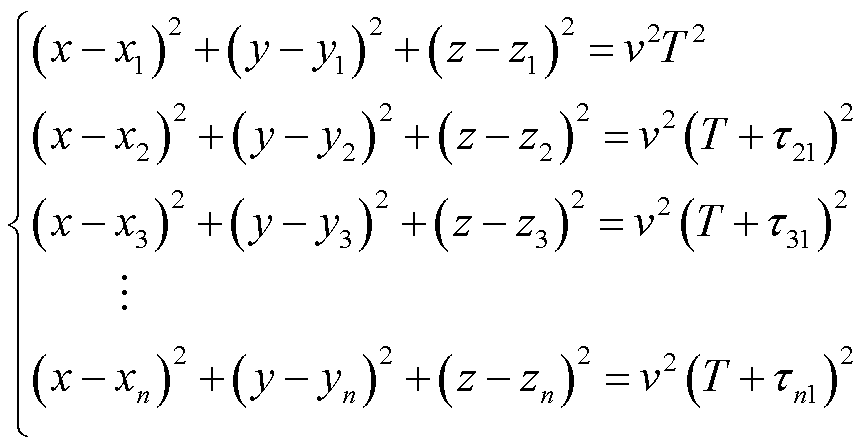 (1)
(1)
通过求解UHF阵列的非线性定位方程组(1)可以获取电气设备PD源坐标。
一般的方法是直接用迭代法求解局部化定位方程(1)[10,15]。然而,迭代算法的计算比较复杂,由于测量过程与计算过程均存在误差。很可能导致非线性方程组存在多解或无解,进而引起定位结果不准。针对非线性方程组模型的缺陷,本文提出了球面模型随机组合线性变换方法。当天线数设为6时,由式(1)可得
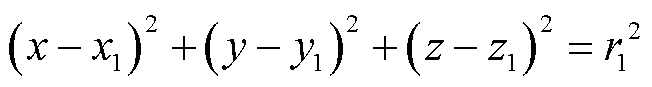 (2)
(2)
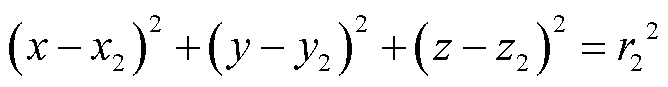 (3)
(3)
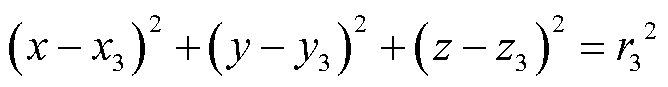 (4)
(4)
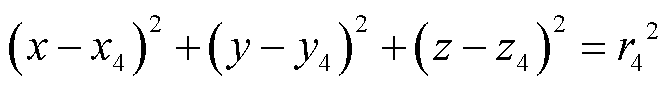 (5)
(5)
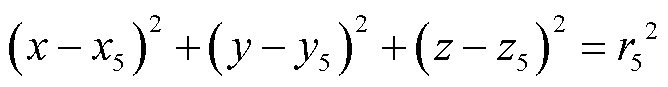 (6)
(6)
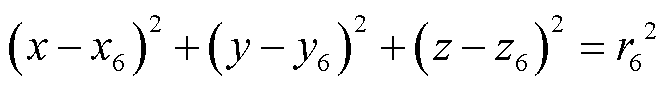 (7)
(7)
式中,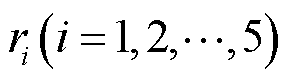 为PD源到第
为PD源到第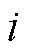 个传感器的距离。式(2)~式(7)为球面方程,传感器位于球面的中心,任意两个球面相交与一个圆面,PD源位于这些圆面上。
个传感器的距离。式(2)~式(7)为球面方程,传感器位于球面的中心,任意两个球面相交与一个圆面,PD源位于这些圆面上。
从六个球面方程中随机选取五个,由五个球面方程得到圆曲面方程组。如:选择式(2)~式(6),组成球面方程组。再用式(3)减去式(2),可以得到圆面方程为
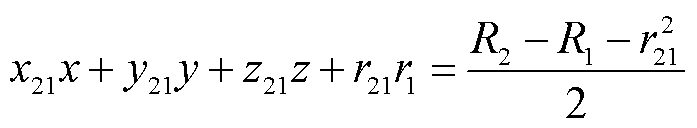 (8)
(8)
式中,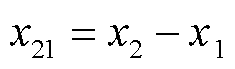 ,
,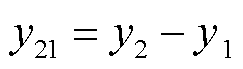 ,
,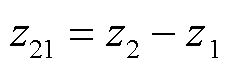 ,
,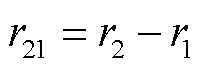 ,
,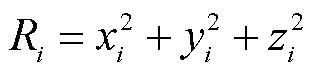 。
。
同理,将球面(式(2))与球面(式(4)~式(6))结合,可以得到相应的圆面方程。相应的方程式可以表示为
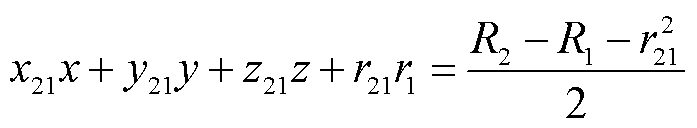 (9)
(9)
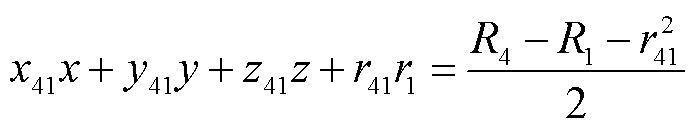 (10)
(10)
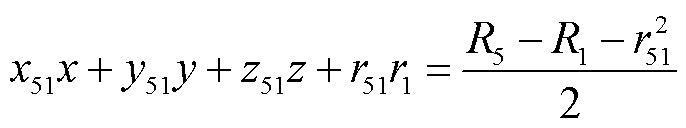 (11)
(11)
将方程式(8)~式(11)组合,可得到线性方程,可以重写为
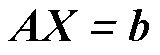 (12)
(12)
其中
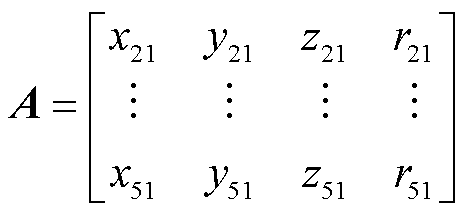
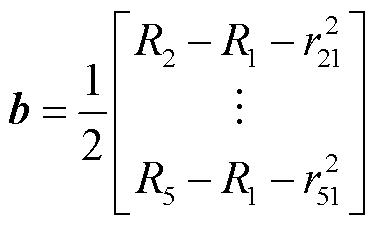
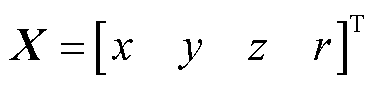
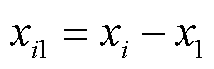
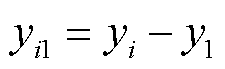
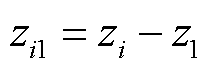
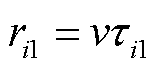
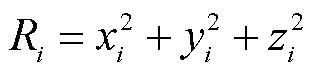
可通过直接求解线性方程组(12)来定位PD源坐标。由于方程(12)是由六个球面方程随机选择五个来获得的,因此存在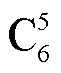 种组合。
种组合。
在变电站中,当开放式电气设备发生局部放电时,则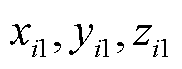 与
与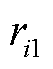 的空间坐标是确定的。这些值的大小不取决于天线之间的空间位置关系。因此,
的空间坐标是确定的。这些值的大小不取决于天线之间的空间位置关系。因此, 是确定的。方程式(12)右端的矩阵
是确定的。方程式(12)右端的矩阵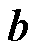 可表示为
可表示为
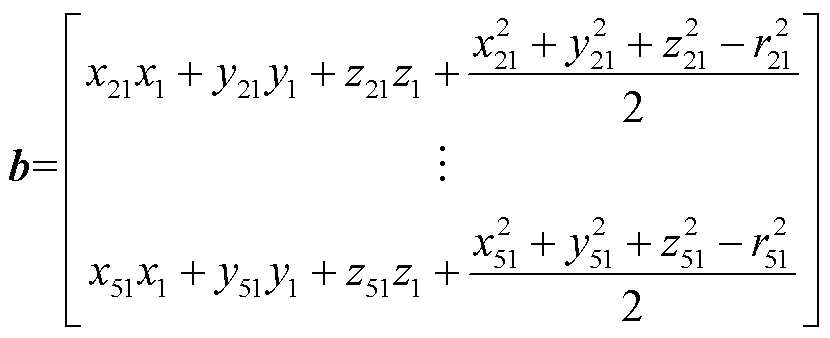 (13)
(13)
从式(13)可以看出,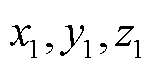 的选择对矩阵
的选择对矩阵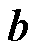 有直接影响。为了使矩阵
有直接影响。为了使矩阵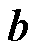 不受坐标系选择的影响,可以采用中心化预处理法对矩阵进行变换,即
不受坐标系选择的影响,可以采用中心化预处理法对矩阵进行变换,即
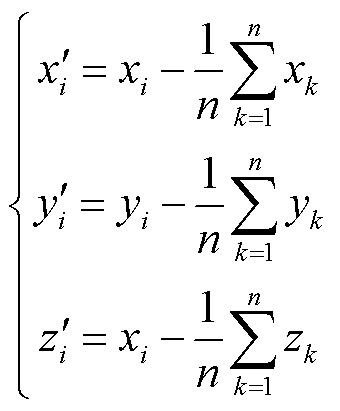 (14)
(14)
式中,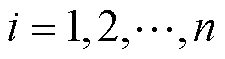 。然后将相应的
。然后将相应的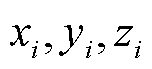 替换为
替换为 。同时,将其代入线性定位方程式(12)的右矩阵
。同时,将其代入线性定位方程式(12)的右矩阵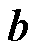 中。因此,经过中心化预处理后矩阵
中。因此,经过中心化预处理后矩阵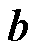 不再受坐标系选取的影响。
不再受坐标系选取的影响。
经过预处理,线性定位方程(12)病态程度有所降低,但是经过特高频天线测量的矩阵 和
和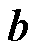 ,会带来一定的扰动误差
,会带来一定的扰动误差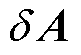 和误差
和误差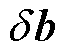 。这种扰动误差会引起方程组解的变化。假设
。这种扰动误差会引起方程组解的变化。假设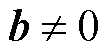 ,扰动方程可以表示为
,扰动方程可以表示为
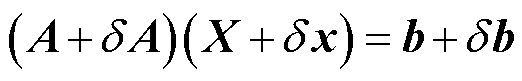 (15)
(15)
式中,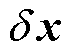 的大小直接影响解的可靠性。
的大小直接影响解的可靠性。
当矩阵 或矩阵
或矩阵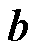 的微弱波动会引起方程组(12)的解出现较大波动时,则系数矩阵
的微弱波动会引起方程组(12)的解出现较大波动时,则系数矩阵 称为病态矩阵,方程组(12)称为病态系统[16]。如果线性方程有解,则
称为病态矩阵,方程组(12)称为病态系统[16]。如果线性方程有解,则 的条件数
的条件数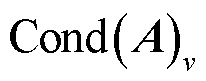 定义为
定义为
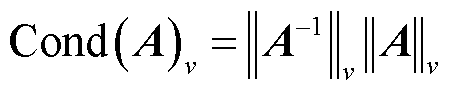 (16)
(16)
当矩阵 与矩阵
与矩阵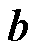 存在一定的扰动时,解的相对误差不超过
存在一定的扰动时,解的相对误差不超过 与
与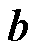 相对误差的倍数
相对误差的倍数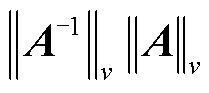 [17]。因此,条件数模型能很好地反映方程组(12)的病态程度。
[17]。因此,条件数模型能很好地反映方程组(12)的病态程度。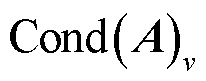 能够很好地反映线性方程组(12)对原始PD数据误差的敏感性。
能够很好地反映线性方程组(12)对原始PD数据误差的敏感性。
如果方程组的条件数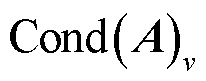 相对较小,则称为良态系统。当
相对较小,则称为良态系统。当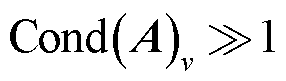 ,矩阵
,矩阵 是病态矩阵,则方程(12)称为病态方程。而且,条件数的数值越大,线性方程组的病态程度越严重。在这种情况下,一般的算法会造成解的较大偏差。为了保证近似解的稳定性,本文引入了TSVD正则化求解方法。
是病态矩阵,则方程(12)称为病态方程。而且,条件数的数值越大,线性方程组的病态程度越严重。在这种情况下,一般的算法会造成解的较大偏差。为了保证近似解的稳定性,本文引入了TSVD正则化求解方法。
在线性方程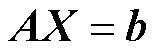 中,预处理后矩阵
中,预处理后矩阵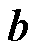 误差较小,为了使近似解稳定,需要用正则化方法使不适定的线性方程组适定化。在众多正则化方法中,TSVD正则化方法是最典型、最有效的一种[18]。与其他方法相比,它可以消除奇异值对方程(12)解的影响,从而消除方程(12)的不适定问题。最终通过一个与原问题等价的解逐次逼近真实解。
误差较小,为了使近似解稳定,需要用正则化方法使不适定的线性方程组适定化。在众多正则化方法中,TSVD正则化方法是最典型、最有效的一种[18]。与其他方法相比,它可以消除奇异值对方程(12)解的影响,从而消除方程(12)的不适定问题。最终通过一个与原问题等价的解逐次逼近真实解。
本文所提出的TSVD正则化方法是在反演目标函数中加入约束函数,将原不适定问题转化为适定问题。矩阵 可以通过式(17)分解为奇异值。
可以通过式(17)分解为奇异值。
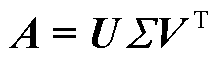 (17)
(17)
其中
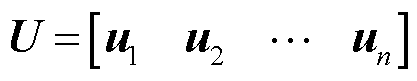
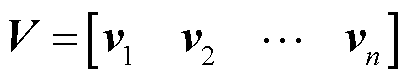
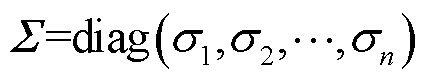
式中,U和V分别为正交矩阵,这两个矩阵分别为矩阵 的左右奇异向量;
的左右奇异向量;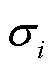 称为矩阵
称为矩阵 的奇异值。
的奇异值。
矩阵 的奇异值的最小值趋近于无限小,意味着矩阵
的奇异值的最小值趋近于无限小,意味着矩阵 没有边际。极小的奇异值
没有边际。极小的奇异值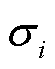 对应的
对应的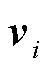 向量是矩阵
向量是矩阵 相关的数值零向量。因此,可以得出离散不适定问题的矩阵总是高度病态的结论。
相关的数值零向量。因此,可以得出离散不适定问题的矩阵总是高度病态的结论。
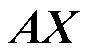 为向量
为向量
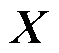 的映射,可以通过奇异值分解(SVD)得到
的映射,可以通过奇异值分解(SVD)得到
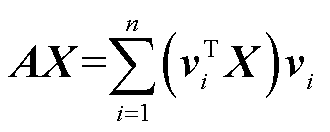 (18)
(18)
这清楚地表明,由于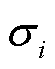 在SVD中被放大,高频分量比低频分量更受抑制。通过
在SVD中被放大,高频分量比低频分量更受抑制。通过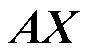 求解
求解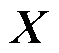 ,必然产生相反的效果。该过程放大了
,必然产生相反的效果。该过程放大了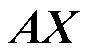 中
中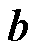 的高频分量。
的高频分量。
针对这种病态方程组,本文引入TSVD正则化方法进行求解。TSVD正则化的本质是在观测的基础上进行求解以下问题:
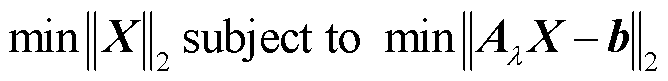 (19)
(19)
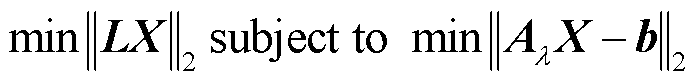 (20)
(20)
式中,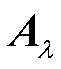 为式(18)中秩为
为式(18)中秩为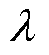 的矩阵,
的矩阵,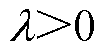 定义为正则化参数;
定义为正则化参数;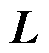 为正则化矩阵。
为正则化矩阵。
式(19)与式(20)问题的解可通过式(21)与式(22)表示。
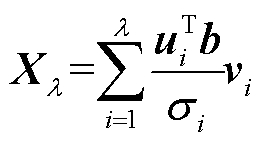 (21)
(21)
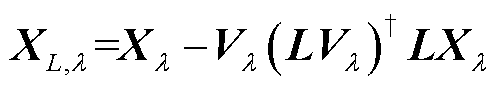 (22)
(22)
式中,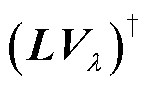 是
是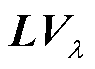 的伪逆,
的伪逆,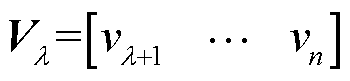 。换句话说,式(22)中的修正是对式(23)问题的求解。
。换句话说,式(22)中的修正是对式(23)问题的求解。
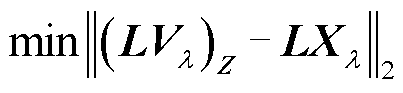 (23)
(23)
同时,注意到TSVD的解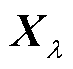 是一个正则解,矩阵
是一个正则解,矩阵 在数值零空间中没有分量。
在数值零空间中没有分量。
正则化参数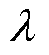 是TSVD正则化方法求解反问题关键。为了保证
是TSVD正则化方法求解反问题关键。为了保证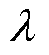 为最优正则化参数,本文引入了GCV正则化参数求解方法[19]。基于GCV的PD定位方程正则化参数求解方法,其基本原理是:在
为最优正则化参数,本文引入了GCV正则化参数求解方法[19]。基于GCV的PD定位方程正则化参数求解方法,其基本原理是:在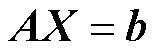 中,
中,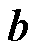 的任意一个局部化项
的任意一个局部化项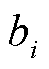 被移除时,所选择的正则化参数可以预测被移除项所引起的变化。通过GCV函数优化确定正则化参数
被移除时,所选择的正则化参数可以预测被移除项所引起的变化。通过GCV函数优化确定正则化参数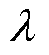 。最优的正则化参数是在GCV函数的最小值处取得。GCV函数的定义为
。最优的正则化参数是在GCV函数的最小值处取得。GCV函数的定义为
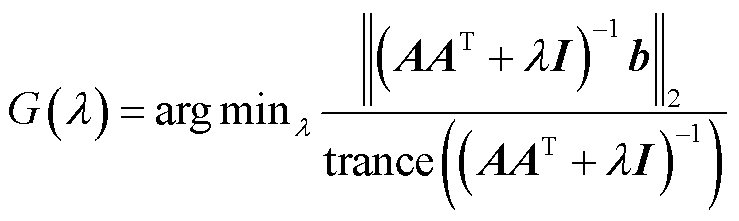 (24)
(24)
式中,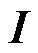 为单位矩阵;
为单位矩阵;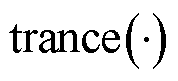 表示迹的运算;
表示迹的运算;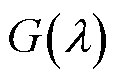 为包含正则化参数
为包含正则化参数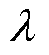 的目标函数。
的目标函数。
图2给出了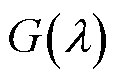 函数曲线,当
函数曲线,当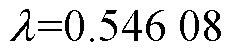 时,取得最小值100.17。
时,取得最小值100.17。
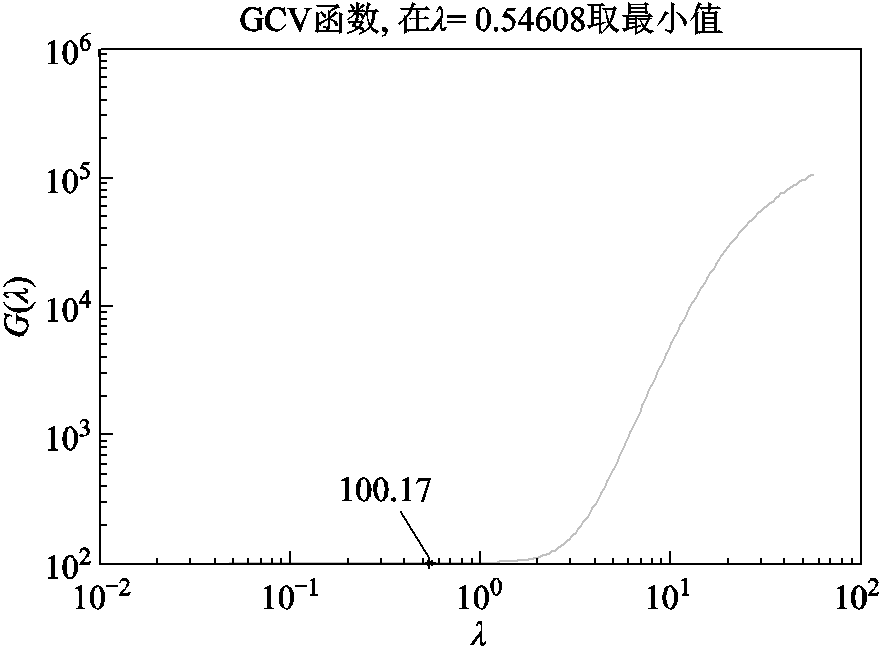
图2 GCV函数曲线
Fig.2 Curve of the GCV function
通过随机组合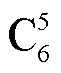 法获得式(12)后,利用TSVD法求解线性方程式(12),求得的解有六种可能性。随机组合方法可以提高定位的可靠性,但是由于求解过程本身是近似求解,基于不同传感器的组合求解的结果必然分布于真实定位点附近。利用定位点分布特性,在TSVD解的基础上结合K-Medians聚类算法进一步提高定位精度。
法获得式(12)后,利用TSVD法求解线性方程式(12),求得的解有六种可能性。随机组合方法可以提高定位的可靠性,但是由于求解过程本身是近似求解,基于不同传感器的组合求解的结果必然分布于真实定位点附近。利用定位点分布特性,在TSVD解的基础上结合K-Medians聚类算法进一步提高定位精度。
K-Medians是K-均值的一种变种,利用数据集的中位数计算聚类中心点。这种方法的好处在于可以避免异常点的影响,使得定位点进一步收敛。因此,利用K-Medians对TSVD求解的结果进一步聚类优化,可以进一步提升定位效果。
K-Medians的权重矩阵元素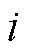 和
和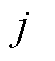 之间的权重为
之间的权重为
 (25)
(25)
由权值矩阵拓扑矩阵构造普拉斯变换矩阵为
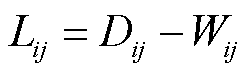 (26)
(26)
式中,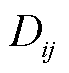 为K-Medians的度量矩阵元素,它依赖加权拓扑矩阵元素
为K-Medians的度量矩阵元素,它依赖加权拓扑矩阵元素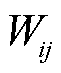 。
。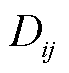 可以表示为
可以表示为
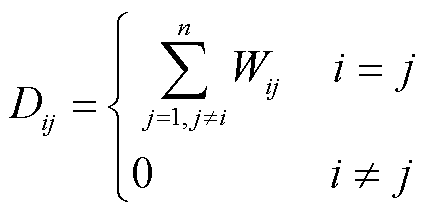 (27)
(27)
通过计算拉普拉斯矩阵的特征值和特征向量,得到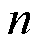 个非零最小特征值
个非零最小特征值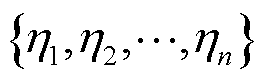 ,依据求得的这组特征值构造低维特征矩阵
,依据求得的这组特征值构造低维特征矩阵
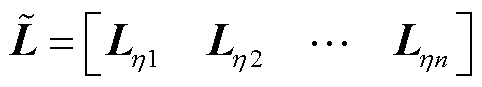 (28)
(28)
式中,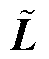 为降维后的拉普拉斯矩阵;Lhi为特征值
为降维后的拉普拉斯矩阵;Lhi为特征值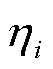 所对应的特征向量。在正则解的基础上引入K-Medians来消除具有较大定位误差的点。削弱了离群点对局部放电整体定位的影响,使得定位点进一步收敛,进一步提高了定位精度。
所对应的特征向量。在正则解的基础上引入K-Medians来消除具有较大定位误差的点。削弱了离群点对局部放电整体定位的影响,使得定位点进一步收敛,进一步提高了定位精度。
为了清楚地说明本文定位方法,给出了本文所提的变电站局部放电定位方法的详细步骤如下。
(1)通过不同的特高频天线获取局部放电源信号,利用能量累积法获取时间差信息。
(2)利用时间差信息与天线坐标信息建立球面方程组。
(3)通过随机组合线性变换方法获取线性方程组AX=b。
(4)对线性方程进行中心化预处理。
(5)利用GCV计算TSVD正则化参数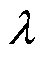 。
。
(6)利用TSVD正则化方法求解线性方程,实现局部放电源的定位。
(7)应用K-Medians 聚类算法对步骤(6)中定位结果进行优化,得到聚类中心点坐标。
为了更清楚地说明本文所提出的定位方法的系统结构,图3给出了本文定位方法的系统架构。该定位方法系统主要分为两部分:一部分为硬件支持;另一部分为软件分析。其中硬件部分主要由特高频天线、运算放大器、示波器以及电源组成。软件分析在计算机上实现完成,具体环节如图3所示。
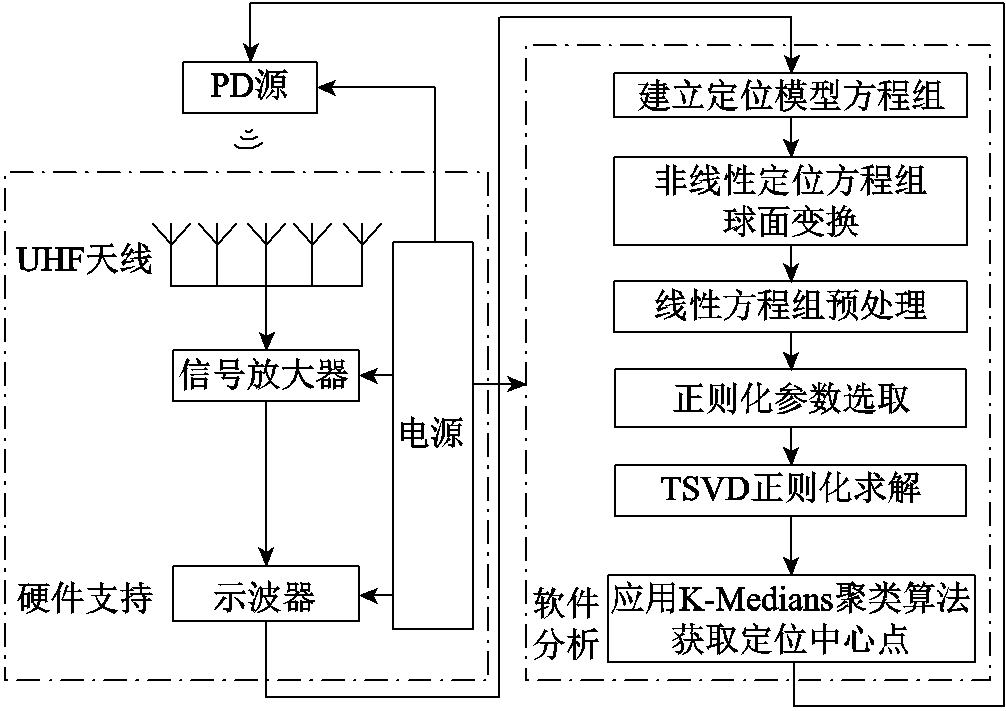
图3 基于TSVD正则化与K-Medians的PD定位方法架构
Fig.3 Architecture of the PD location method based on TSVD regularization and K-medians
为了验证本文所提出定位方法的准确性,本节对变电站PD源进行了定位仿真。假设在变电站环境中设置一组天线。天线的空间坐标如下:S1 (23m, 20m, 0.8m),S2 (0m, 0m, 1.2m) m,S3 (50m, 0m, 1.2m),S4 (50m, 20m, 1.2m),S5 (50m, 40m, 1.2m),S6 (0m, 40m, 1.2m)。设置两个PD源的坐标分别为: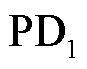 (13m, 28m, 0.9m),
(13m, 28m, 0.9m),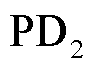 (30m,7m,1.1m)。
(30m,7m,1.1m)。
为了更加逼真地测试算法在实际变电站场景中的性能,本文在到达时差的基础上增加了一定范围的时间误差。到达时间误差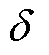 定义为
定义为
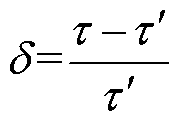 (29)
(29)
式中,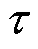 为理论到达时差;
为理论到达时差;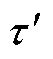 为延迟到达时差。
为延迟到达时差。
在理论时差的基础上增加了5个不同的随机时差。具体为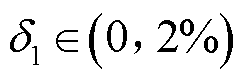 、
、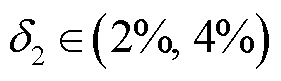 、
、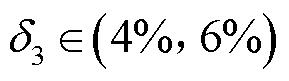 、
、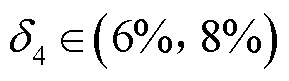 、
、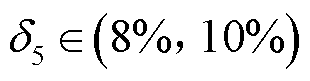 。表1给出了随机选择S1~S5建立球面方程后,
。表1给出了随机选择S1~S5建立球面方程后,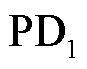 到不同UHF天线的到达时间差。
到不同UHF天线的到达时间差。
表1 特高频天线时间差数据
Tab.1 Time difference data of UHF antenna (单位:ns)
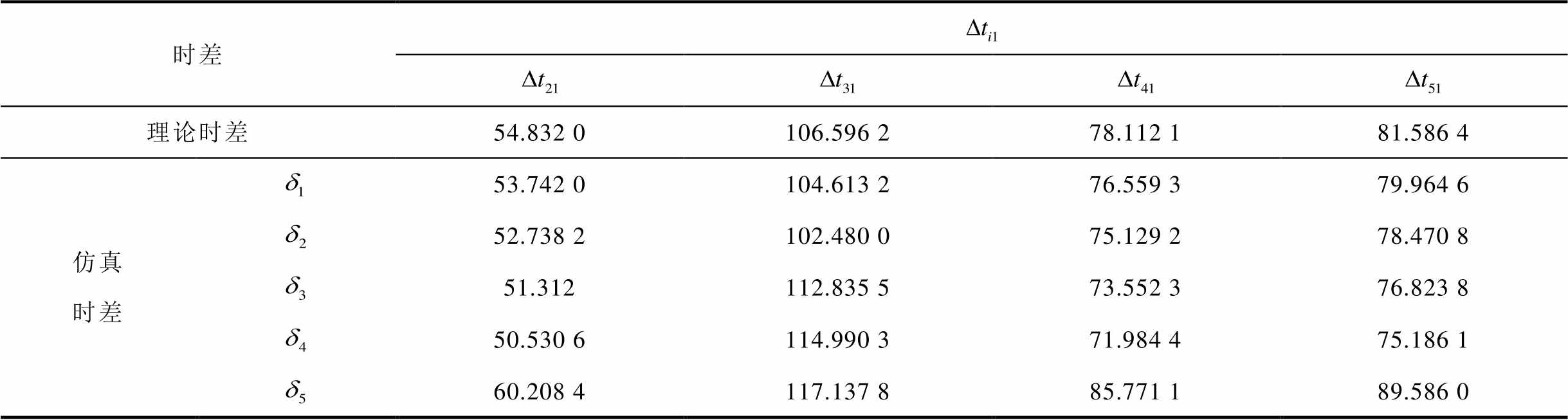
时差 理论时差54.832 0106.596 278.112 181.586 4 仿真时差53.742 0104.613 276.559 379.964 6 52.738 2102.480 075.129 278.470 8 51.312 112.835 573.552 376.823 8 50.530 6114.990 371.984 475.186 1 60.208 4117.137 885.771 189.586 0
本节将对本文提出的定位方法进行验证。首先,验证了TSVD在求解线性方程组(12)时的正确性。其次,验证了K-Medians算法对TSVD求解聚类中心点的有效性。然后通过对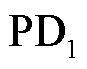 的定位实验,将几种典型定位方法的效果进行了比较。为了对本文定位方法的效果进行综合评价,本文还进一步地做了蒙特卡罗实验。图4显示了该方法在时间误差为
的定位实验,将几种典型定位方法的效果进行了比较。为了对本文定位方法的效果进行综合评价,本文还进一步地做了蒙特卡罗实验。图4显示了该方法在时间误差为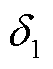 时的定位结果。
时的定位结果。
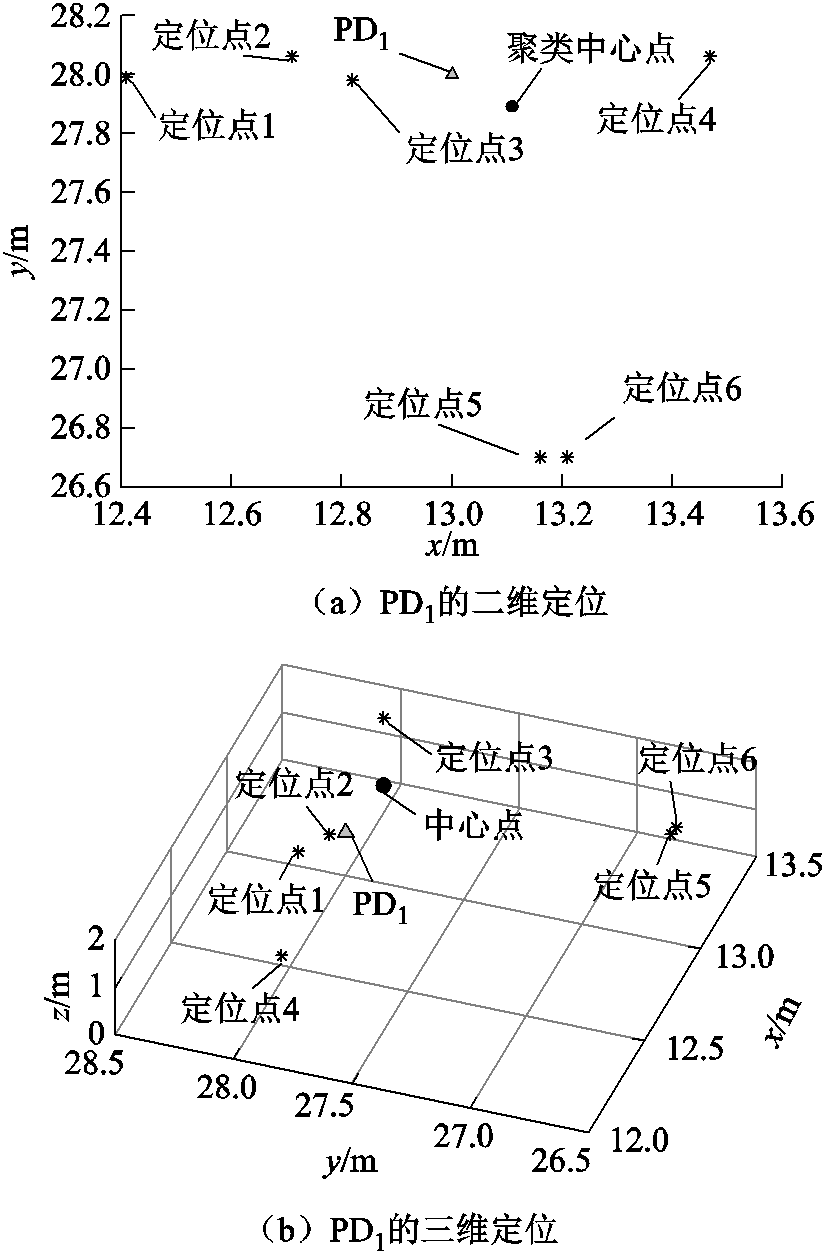
图4 时间误差为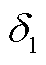 时本文定位方法的定位结果
时本文定位方法的定位结果
Fig.4 The location results of this method are compared when the time error is 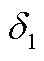
图4中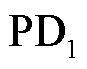 表示真实发生PD的位置。通过TSVD方法得到2D和3D定位坐标。点1~6表示直接利用TSVD求解的线性方程组的解。聚类中心点是采用K-Medians聚类算法对多个TSVD方法定位结果进行聚类的结果。从图4可以看出,通过TSVD定位方法获得的定位点位于真实PD点附近。证明了TSVD定位方法的有效性。采用K-Medians聚类算法对多个点进行聚类后,聚类中心更接近实际放电点。结果表明,K-Medians聚类提高了TSVD的定位效果。
表示真实发生PD的位置。通过TSVD方法得到2D和3D定位坐标。点1~6表示直接利用TSVD求解的线性方程组的解。聚类中心点是采用K-Medians聚类算法对多个TSVD方法定位结果进行聚类的结果。从图4可以看出,通过TSVD定位方法获得的定位点位于真实PD点附近。证明了TSVD定位方法的有效性。采用K-Medians聚类算法对多个点进行聚类后,聚类中心更接近实际放电点。结果表明,K-Medians聚类提高了TSVD的定位效果。
因此,本文提出的定位方法在理论上得到验证。为了更好地说明本文方法定位的精确性,本文将该方法与三种不同的定位算法进行比较。其中,方法1是传统的高斯消元法,高斯消元法是经典算法的代表。方法2是选择较为先进的Tikhonov正则化方法,Tikhonov正则化方法为正则化求解线性方程组的典型。方法3是直接TSVD正则化方法。方法4是本文提出的定位方法。
在保持时间差和UHF天线坐标相同的情况下,将相应的数据代入等式(12)。然后,使用四种不同的方法来求解方程(12)。不同方法对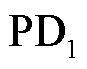 的定位结果及2D和3D的定位误差见表2。
的定位结果及2D和3D的定位误差见表2。
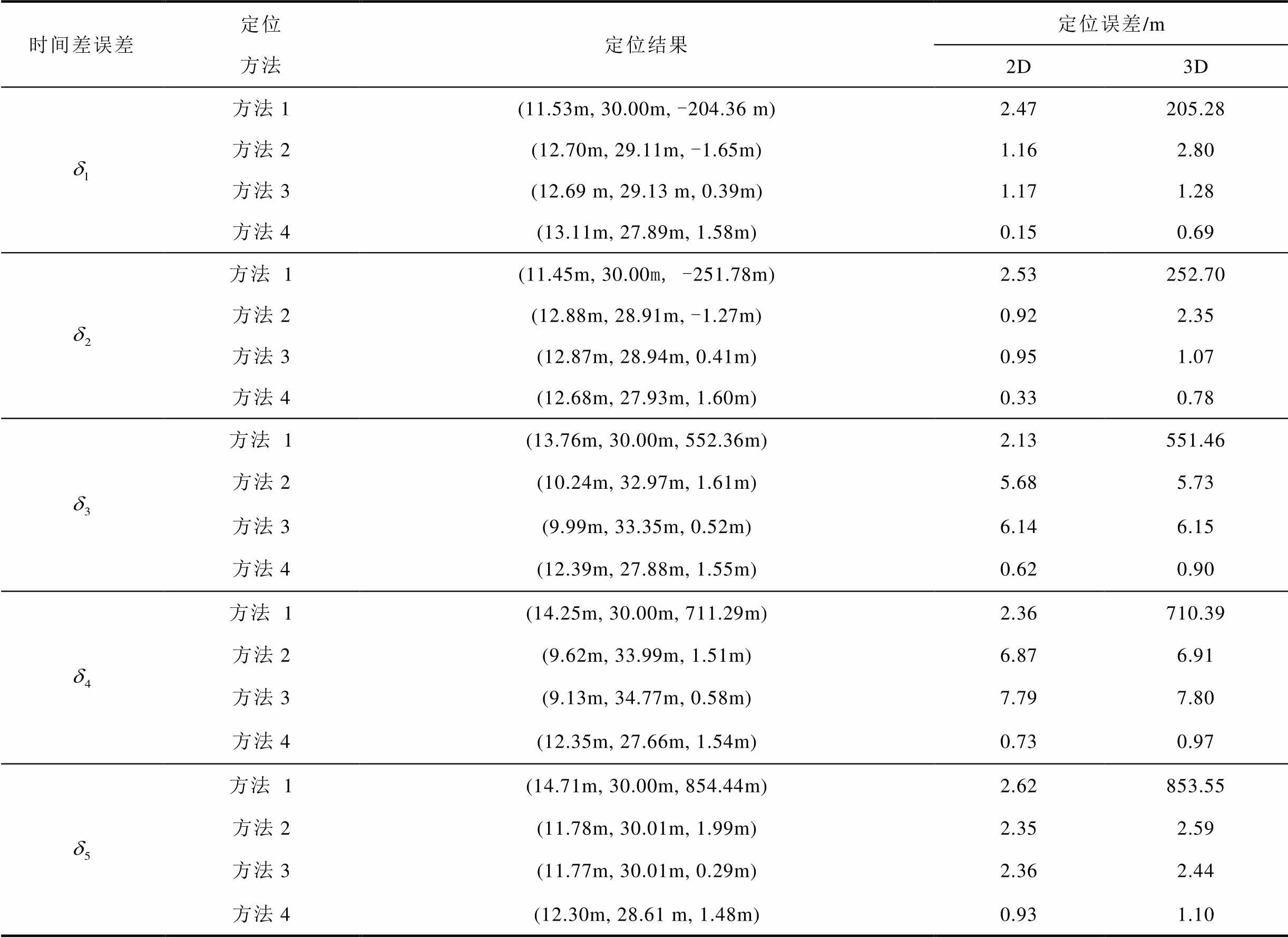
表2 不同方法对相同PD1源的定位结果及误差
Tab.2 The location results and errors of different methods for the same PD source
时间差误差定位方法定位结果定位误差/m 2D3D 方法1(11.53m, 30.00m, -204.36 m)2.47205.28 方法2(12.70m, 29.11m, -1.65m)1.162.80 方法3(12.69 m, 29.13 m, 0.39m)1.171.28 方法4(13.11m, 27.89m, 1.58m)0.150.69 方法 1(11.45m, 30.00m, -251.78m)2.53252.70 方法2(12.88m, 28.91m, -1.27m)0.922.35 方法3(12.87m, 28.94m, 0.41m)0.951.07 方法4(12.68m, 27.93m, 1.60m)0.330.78 方法 1(13.76m, 30.00m, 552.36m)2.13551.46 方法2(10.24m, 32.97m, 1.61m)5.685.73 方法3(9.99m, 33.35m, 0.52m)6.146.15 方法4(12.39m, 27.88m, 1.55m)0.620.90 方法 1(14.25m, 30.00m, 711.29m)2.36710.39 方法2(9.62m, 33.99m, 1.51m)6.876.91 方法3(9.13m, 34.77m, 0.58m)7.797.80 方法4(12.35m, 27.66m, 1.54m)0.730.97 方法 1(14.71m, 30.00m, 854.44m)2.62853.55 方法2(11.78m, 30.01m, 1.99m)2.352.59 方法3(11.77m, 30.01m, 0.29m)2.362.44 方法4(12.30m, 28.61 m, 1.48m)0.931.10
如表2所示,以时间误差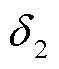 为例进行分析。方法1的定位结果为(11.45m, 30.00m, -251.78m),方法1的2D和3D定位误差分别为2.53m和252.70m。实验结果表明,方法1在三维空间中定位已经失效。方法2的定位结果为(12.88m, 28.91m, -1.27m),2D和3D的定位误差分别为0.92m和2.35m。与方法1相比,方法2的定位性能有了很大的提高,3D定位效果更好。此时方法3的定位结果为(12.87m, 28.94m, 0.41m),与方法2相比更接近于真实的局部放电点坐标(13m, 28m, 0.9m)。第四种方法的结果为(12.68m, 27.93m, 1.60m),2D和3D的定位误差分别为0.33 m和0.78m。因此,方法4的定位误差最小。所以本文所提出的PD定位方法最为准确。为了更直观地比较不同方法的定位效果,图5给出了几种方法对
为例进行分析。方法1的定位结果为(11.45m, 30.00m, -251.78m),方法1的2D和3D定位误差分别为2.53m和252.70m。实验结果表明,方法1在三维空间中定位已经失效。方法2的定位结果为(12.88m, 28.91m, -1.27m),2D和3D的定位误差分别为0.92m和2.35m。与方法1相比,方法2的定位性能有了很大的提高,3D定位效果更好。此时方法3的定位结果为(12.87m, 28.94m, 0.41m),与方法2相比更接近于真实的局部放电点坐标(13m, 28m, 0.9m)。第四种方法的结果为(12.68m, 27.93m, 1.60m),2D和3D的定位误差分别为0.33 m和0.78m。因此,方法4的定位误差最小。所以本文所提出的PD定位方法最为准确。为了更直观地比较不同方法的定位效果,图5给出了几种方法对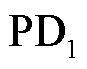 的定位误差。
的定位误差。
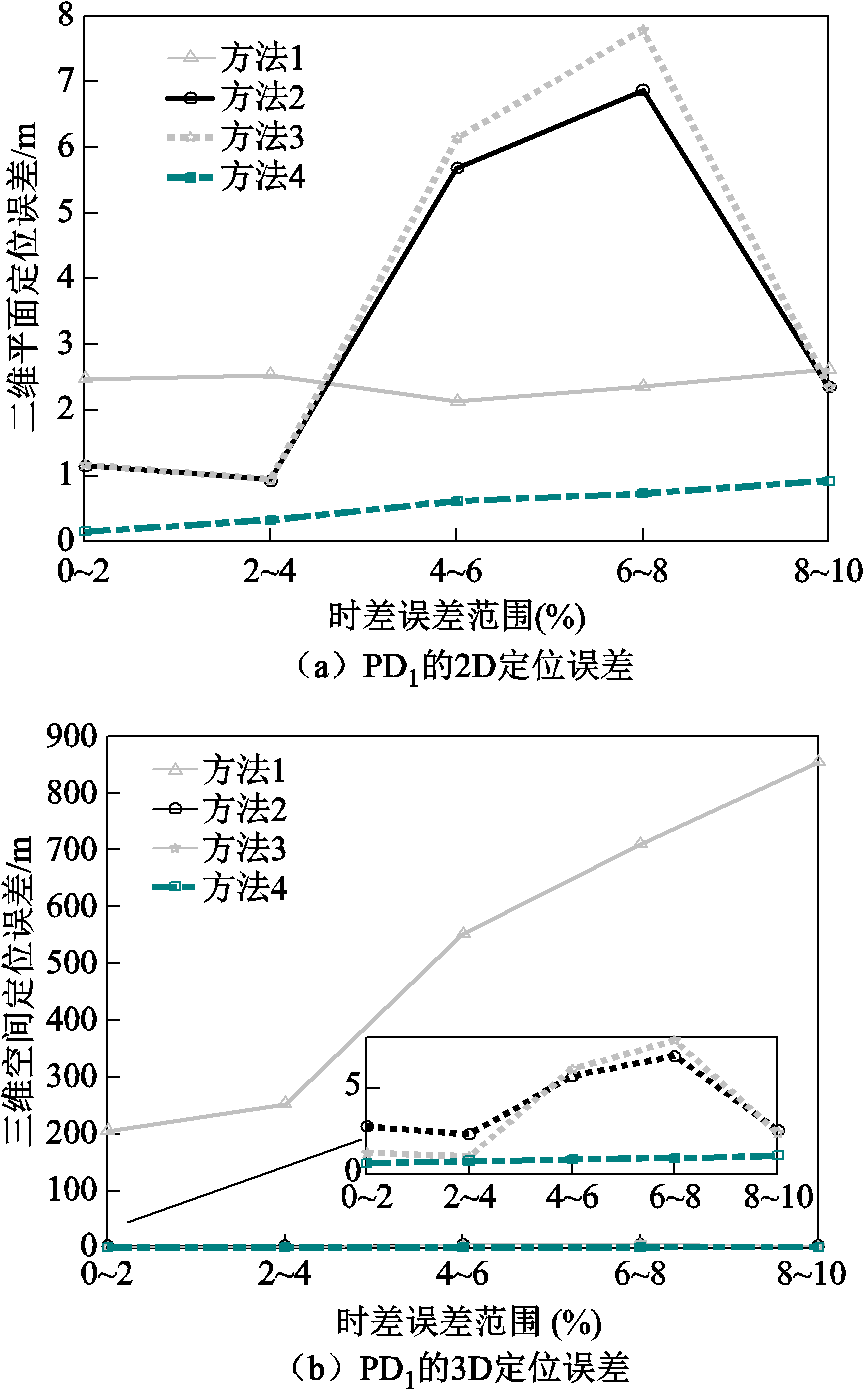
图5 不同方法对PD1定位误差
Fig.5 The location errorss of different methods forPD1
从图5a可以看出,当时间误差较小时,方法1在2D中的定位误差最大。方法2和方法3的定位效果相当。方法4的定位误差最小。当时间误差大于4%时,方法2和方法3的定位误差波动较大,方法4的定位误差仍然最小。如图5b所示,方法1不再适用于三维空间定位,方法2和方法3的定位效果仍然相当。随着时间误差的增大,方法4的定位误差逐渐增大。但是从二维和三维定位结果可以看出,方法4定位误差与其他方法相比依然最小,且较为稳定。因此,方法4具有良好的鲁棒性。
为了进一步验证本文所提定位算法的通用性和准确性,还对两个局部放电源进行了蒙特卡罗实验。在理论时间的基础上,加入不同的时间误差,对每个误差范围进行50次重复实验。简而言之,实验是对PD1与PD2进行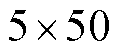 次实验。对应实验的2D和3D散点图如图6所示。
次实验。对应实验的2D和3D散点图如图6所示。
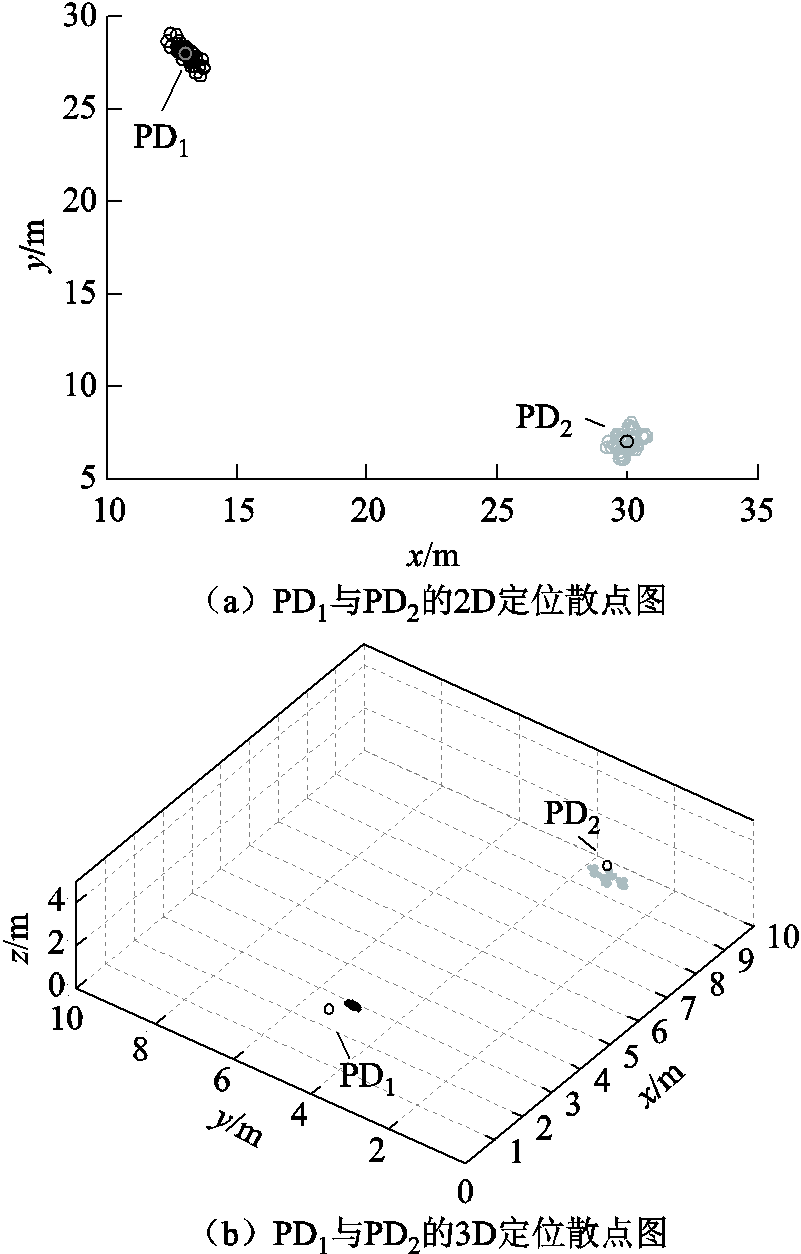
图6 时间误差为0%~10%时,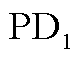 与
与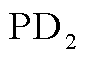 蒙特卡罗定位实验结果散点图
蒙特卡罗定位实验结果散点图
Fig.6 Scatter plot of experimental results of PD1 and PD2 based on Monte Carlo localization when the time error is 0%~10%
从图6可以看出,在二维平面上,局部化散射点集中在两个局部放电源附近。在二维平面上,该方法定位误差小,表明该方法是准确的。三维定位散点依然集中在放电源附近,定位效果仍然良好。通过此部分的蒙特卡罗实验,本文进一步验证了所提定位方法的准确性。针对不同PD源的定位效果显著,说明本文方法具有普遍适用性。为了更直观地阐述蒙特卡罗定位结果的准确性,图7给出了蒙特卡罗实验中不同局部放电源的定位误差。
由图7的实验结果可以看出,本文所提方法在蒙特卡罗实验中定位误差较小,PD1和PD2的2D最大误差保持在1 m以内,PD源的3D定位误差略大于2D,总体实验结果保持了较高的定位精度。蒙特卡罗实验表明,该方法具有很强的鲁棒性。
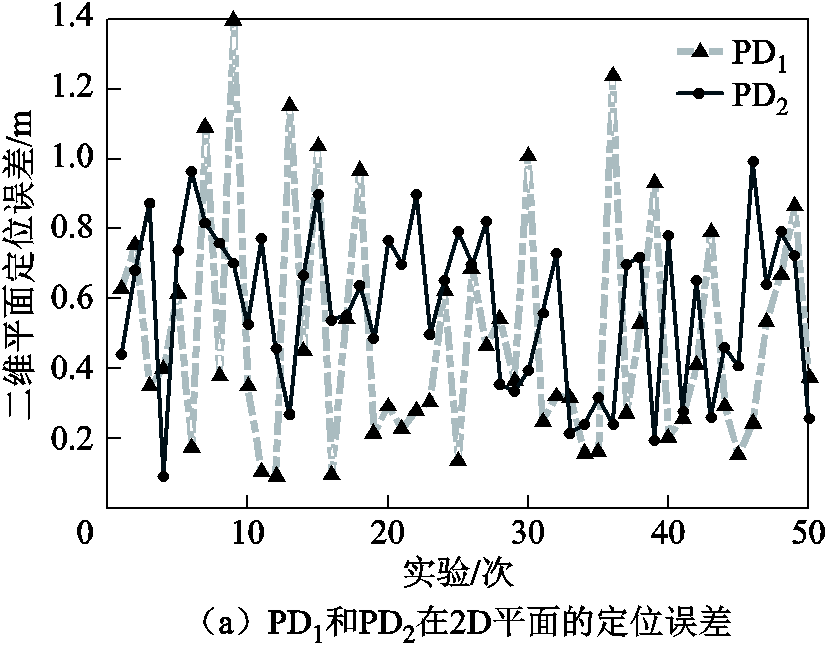
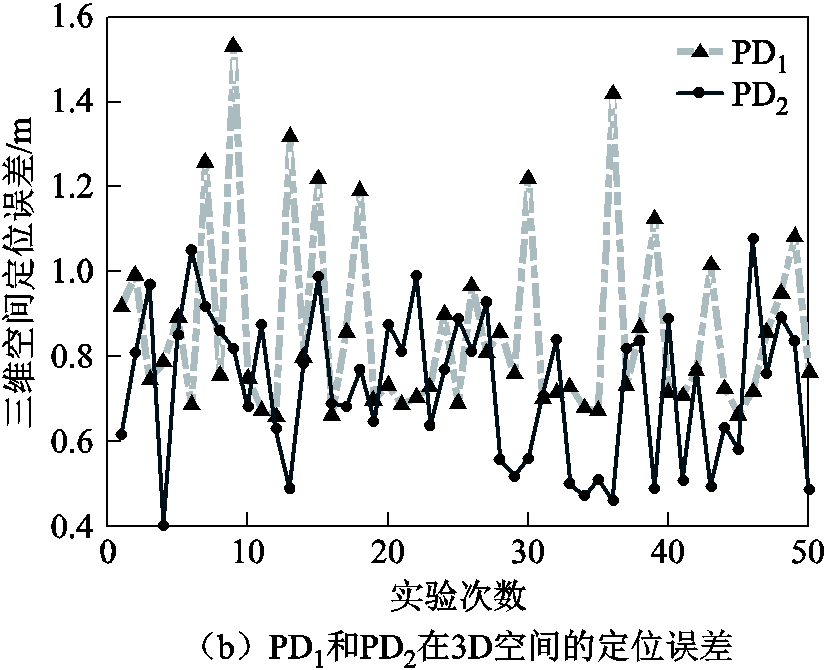
图7 50次蒙特卡罗实验中,PD1和PD2的定位误差
Fig.7 The location errors of PD1 and PD2 in 50 Monte Carlo experiments
为了验证该方法在现场环境中的定位效果,本文在变电站环境中进行了现场环境测试。六个超高频天线的空间分布如图8所示。它们的空间坐标如下:S1(23m, 12m, 0.8m),S2(0m, 24m, 1.2 m),S3(0m, 0m, 1.2m),S4(23m, 0m, 1.2m),S5(46m, 0m, 1.2m),S6(46m, 24m, 1.2m)。两个局部放电源的空间位置分别位于PD1(12m, 20m, 1.6m)和PD2(26m, 5m, 2m)。超高频存储示波器用于记录超高频天线的高频信号。

图8 220 kV变电站中的局部放电的定位实验
Fig.8 Partial discharge location experiment in 220kV substation
为了验证本文定位方法的现场定位效果,使用放电枪模拟生成这两种不同的局部放电信号。其中PD1是由金属突起缺陷引起的局部电晕放电,PD2是绝缘体表面金属污染造成的缺陷放电。金属突出物缺陷是一种典型的电晕放电,该放电类型是尖端放电的典型。绝缘体表面金属污染造成的缺陷是由导电污染物附着于绝缘子表面引起的放电类型。这两种放电类型较为典型且放电的机理不同。因此,使用放电枪模拟生成这两种不同的局部放电信号,并进行单次验证性实验。
通过6根UHF天线从局部放电源同步采集并存储UHF信号。信号采集系统采用具有存储功能的示波器,现场试验中,采样频率为2.5GHz,采样点数为1 250。采集的时域波形如图9所示。
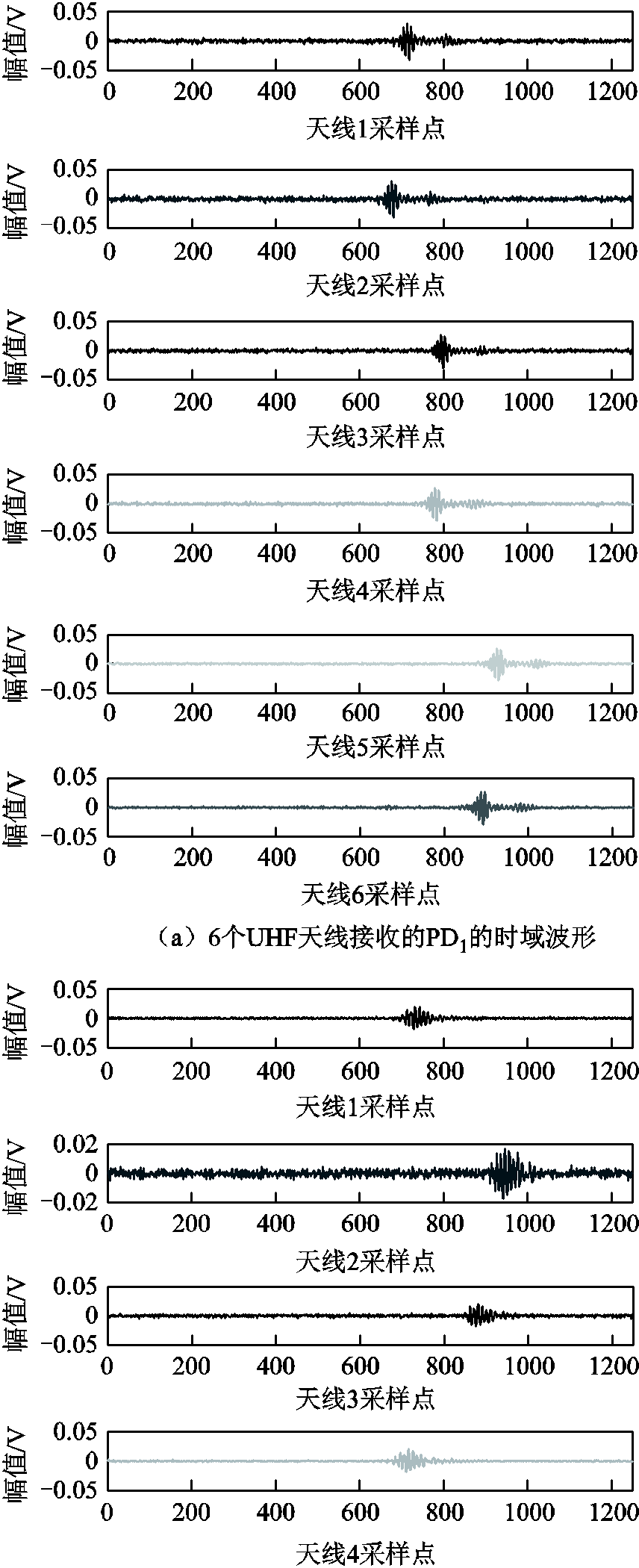
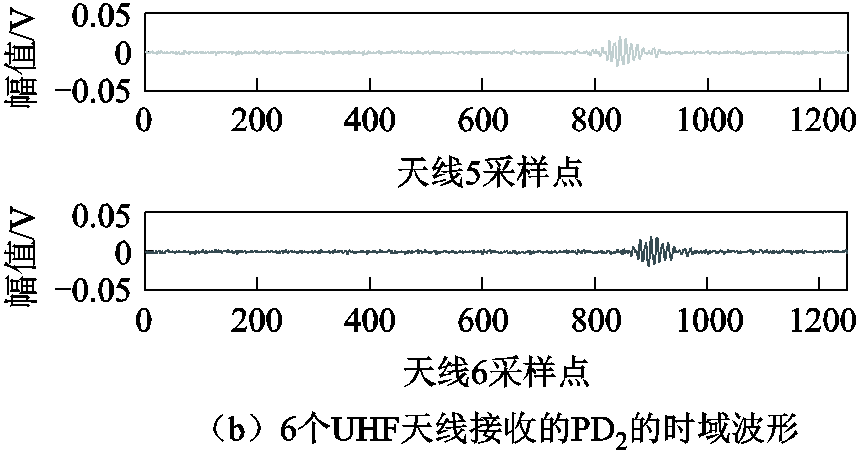
图9 变电站环境中接收到的局部放电信号的时域波形
Fig.9 Time domain waveform of partial discharge signal received in substation environment
本文采用能量积累法计算到达时间。图10给出了不同天线的局部放电源的能量累积曲线。
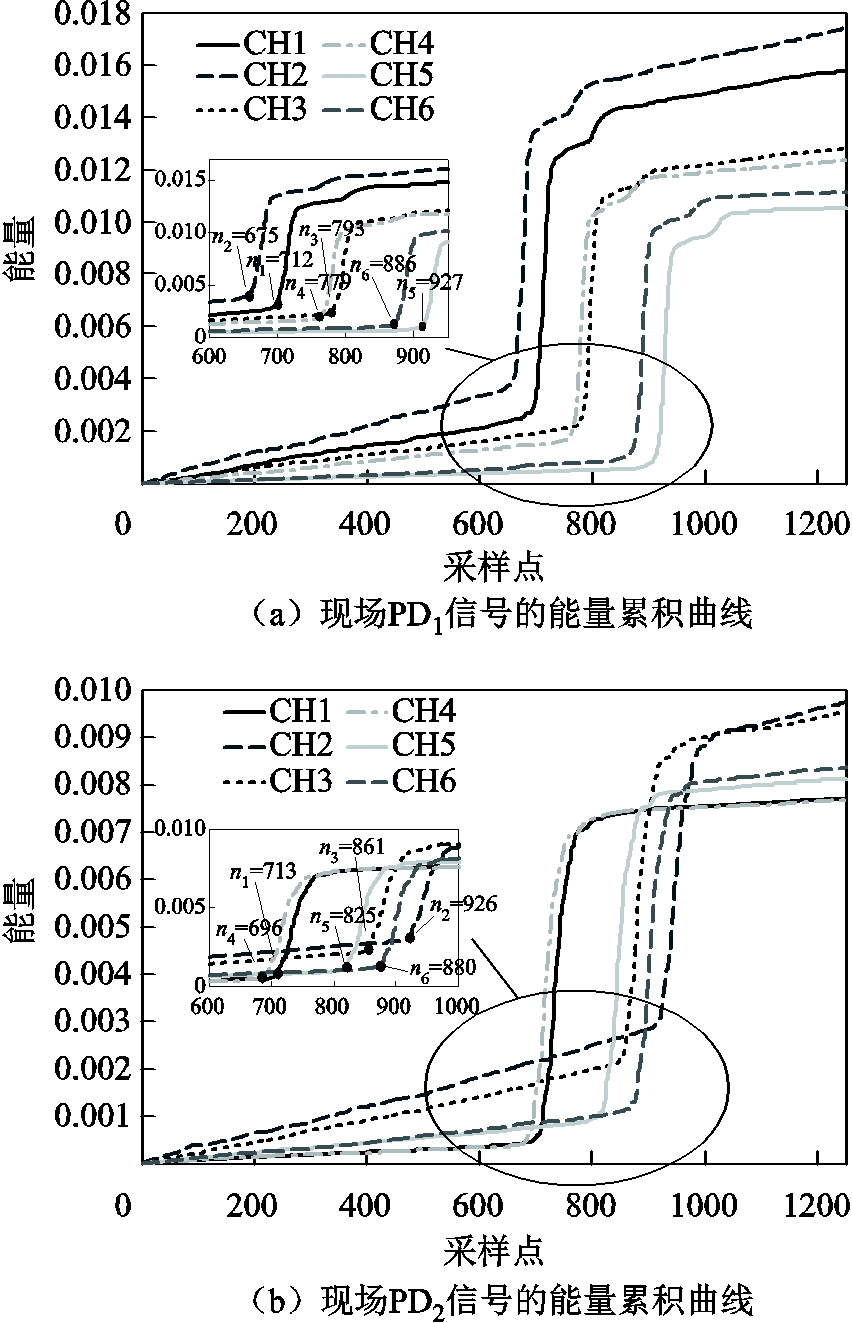
图10 不同PD源的能量积累曲线
Fig.10 Energy accumulation curves of different PD sources
不同放电源到不同UHF天线的时差数据见表3。应用不同的实验方法对现场测试数据进行验证,相应的测试结果见表4。
表3 变电站特高频天线阵时差数据
Tab.3 Time difference data of UHF antenna array in substation (单位:ns)
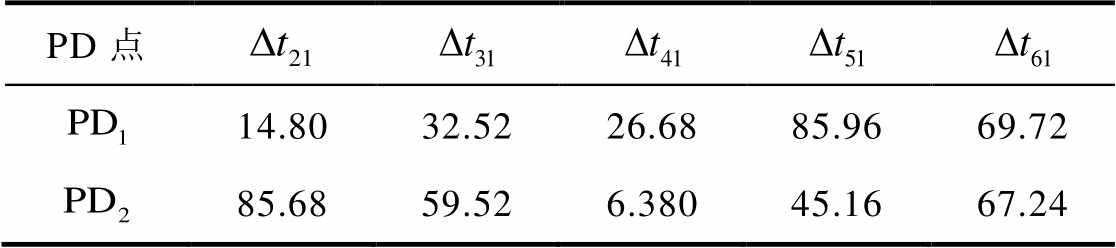
PD点 14.8032.5226.6885.9669.72 85.6859.526.38045.1667.24
表4 变电站中PD1与PD2的定位坐标及误差
Tab.4 Location coordinates and errors of PD1 and PD2 in substation
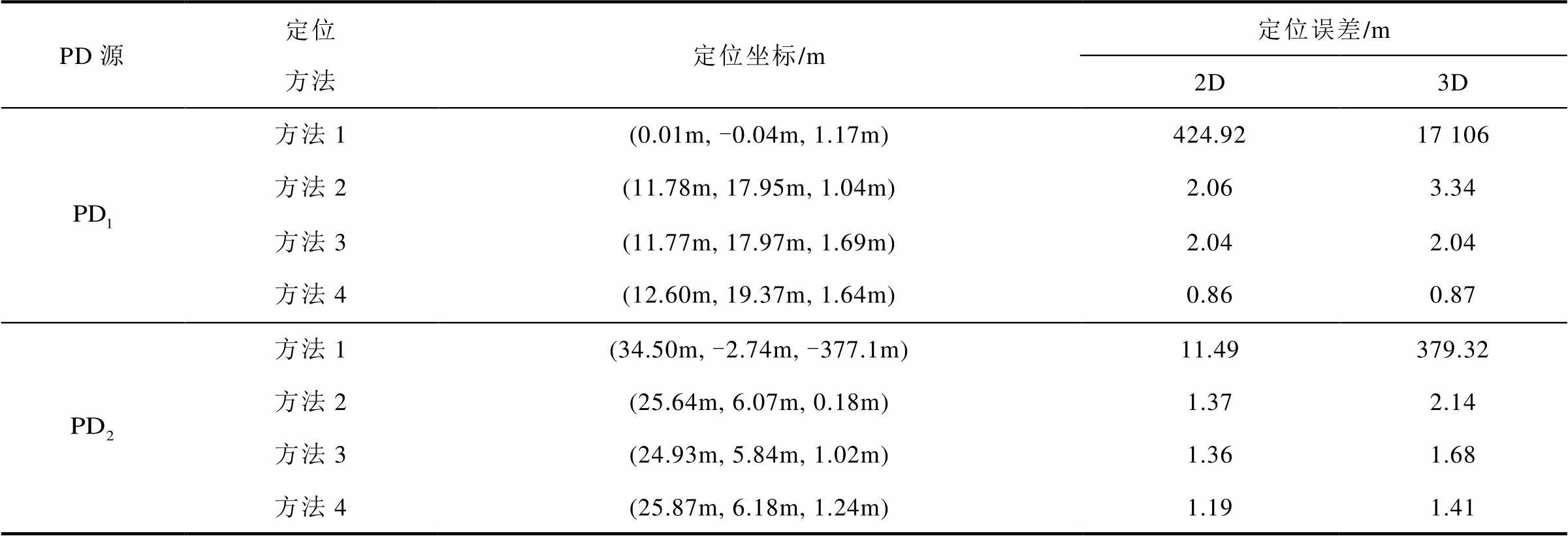
PD源定位方法定位坐标/m定位误差/m 2D3D 方法1(0.01m, -0.04m, 1.17m)424.9217 106 方法2(11.78m, 17.95m, 1.04m)2.063.34 方法3(11.77m, 17.97m, 1.69m)2.042.04 方法4(12.60m, 19.37m, 1.64m)0.860.87 方法1(34.50m, -2.74m, -377.1m)11.49379.32 方法2(25.64m, 6.07m, 0.18m)1.372.14 方法3(24.93m, 5.84m, 1.02m)1.361.68 方法4(25.87m, 6.18m, 1.24m)1.191.41
从表4可以看出,本文的定位方法在2D平面和3D空间的误差分别在1.19m和1.41m以内。现场实验结果表明,本文定位方法能准确定位变电站环境中的局部放电源。
为了进一步验证本文方法的优越性与先进性,查阅了相关文献以及实验定位结果,将不同方法定位的结果进行了统计与对比。其中,文献[6]代表的是牛顿迭代网格搜索算法,文献[20]表示L形天线阵列方法,文献[21]则阐述了基于概率统计算法的定位方法。不同定位方法的定位结果见表5。
表5 不同定位方法的定位结果对比
Tab.5 Comparison of positioning results of different localization methods

文献定位方法天线尺寸范围/m2定位误差/m误差率(%) [6]牛顿迭代网格搜索法3´4<0.21.67 [20]L形天线阵列方法3´4<0.32.50 [21]基于概率定位算法1.16´1.58<0.361.50 本文TSVD+K-Medians24´46<1.141.03
给出定位误差率公式:误差率=误差/天线尺寸覆盖范围的面积。通过表5的统计结果可知,本文定位误差率为1.03%,定位精度明显优于其他几种定位算法。
本文提出了一种变电站局部放电源定位的新方法。首先,利用特高频天线获取局部放电信号,通过能量积累法获得时差信息。其次,通过时差与UHF坐标信息得到非线性方程,并利用球面模型变换法将非线性定位方程转化为线性定位方程。再次,利用集中化预处理方法避免了坐标系选取对系数矩阵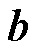 的影响。然后,采用TSVD正则化方法求解线性方程组,实现了局部放电源定位的目的。最后,为了提高局部放电定位的精度,采用K-Medians聚类算法对TSVD正则化进行优化。仿真结果表明,当时差误差范围为8%~10%时,该方法的最大定位误差为1.10m。在现场实验中,采用广义S变换对PD源信号进行滤波处理,目的在于滤除噪声信号。最终现场实验结果表明,在变电站场景中,最大定位误差为1.41m。
的影响。然后,采用TSVD正则化方法求解线性方程组,实现了局部放电源定位的目的。最后,为了提高局部放电定位的精度,采用K-Medians聚类算法对TSVD正则化进行优化。仿真结果表明,当时差误差范围为8%~10%时,该方法的最大定位误差为1.10m。在现场实验中,采用广义S变换对PD源信号进行滤波处理,目的在于滤除噪声信号。最终现场实验结果表明,在变电站场景中,最大定位误差为1.41m。
参考文献
[1] 刘青, 常丁戈, 邓军波. 用于变电站站域局部放电特高频测向的空间谱估计算法优化选择[J]. 电工技术学报, 2020, 35(16): 3551-3560.
Liu Qing, Chang Dingge, Deng Junbo. Optimal selection on spatial spectrum estimation algorithms for UHF direction finding of partial discharge in substation [J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3551-3560.
[2] 宋思蒙, 钱勇, 王辉, 等. 基于方向梯度直方图属性空间的局部放电模式识别改进算法[J]. 电工技术学报, 2021, 36(10): 2153-2160.
Song Simeng, Qian Yong, Wang Hui, et al. Improved algorithm for partial discharge pattern recognition based on histogram of oriented gradient attribute space[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2153-2160.
[3] 李元, 张冠军, 梁钰, 等. 不同热老化程度下油纸绝缘沿面放电发展特性[J]. 高电压技术, 2017, 43(3): 923-930.
Li Yuan, Zhang Guanjun, Liang Yu, et al. Envolutionary characteristics of surface discharge within oil-paper insulation under different thermally aged conditions[J]. High Voltage Engineering, 2017, 43(3): 923-930.
[4] 王永强, 仲钊, 谢军, 等. 温度对不同老化程度的绝缘纸板沿面放电的影响[J]. 高电压技术, 2017, 43(8): 2724-2732.
Wang Yongqiang, Zhong Zhao, Xie Jun, et al. Influence of temperature on the surface discharge of insulating paperboard with different aging degree[J]. High Voltage Engineering, 2017, 43(8): 2724-2732.
[5] 邹阳, 周求宽, 刘明军, 等. 局部放电特高频检测装置抗电磁干扰性能的量化评估方法研究[J]. 电工技术学报, 2020, 35(10): 2275-2282.
Zou Yang, Zhou Qiukuan, Liu Mingjun, et al. Research on quantitative evaluation on anti-electromagnetic interference capability of ultra high frequency partial discharge detection instrument [J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2275-2282.
[6] 侯慧娟, 盛戈皞, 苗培青, 等. 基于超高频电磁波的变电站局部放电空间定位[J]. 高电压技术, 2012, 38(6):1334-1340.
Hou Huijuan, Sheng Gehao, Miao Peiqing, et al. Partial discharge location based on radio frequency antenna array in substation[J]. High Voltage Engineering, 2012, 38(6):1334-1340.
[7] Hou Zhe, Li Hongjie, Sun Zhenquan, et al. A novel sinusoidal damped oscillating voltage generator for the detection of partial discharge in MV distribution power cables[J]. IEEE Transactions on Power Delivery, 2016, 31(1): 410-411.
[8] 陈金祥. 基于介质窗口和UHF传感器的变压器局部放电检测与定位方法[J]. 电网技术, 2014, 38(6): 1676-1680.
Chen Jinxiang. Detection and location of partial discharge in power transformers based on dielectric window and UHF sensors[J]. Power System Technology, 2014, 38(6): 1676-1680.
[9] 胡岳, 王红斌, 汤林, 等. 基于UHF天线阵列的变电站局部放电全站监测研究与实践[J]. 电工技术学报, 2014, 29(增刊1): 502-509.
Hu Yue, Wang Hongbin, Tang Lin, et al. Research and practice of partial discharge online monitoring and locating for substation using UHF sensor array[J]. Transactions of China Electrotechnical Society, 2014, 29(S1): 502-509.
[10] 郑书生, 李成榕, 何梦. 变压器局部放电复数域牛顿迭代网格搜索定位方法[J]. 中国电机工程学报, 2013, 33(9):155-161.
Zheng Shusheng, Li Chengrong, He Meng, et al. A novel method of Newton iteration in complex field and Lattice search for locating partial discharges in transformers[J]. Proceedings of the CSEE, 2013, 33(9):155-161.
[11] Hou Huijuan, Sheng Gehao, Jiang Xiucheng. Localization algorithm for the PD source in substation based on L-shaped antenna array signal processing[J]. IEEE Transactions on Power Delivery, 2015, 30(1): 472-479.
[12] 唐炬, 黄亮, 曾福平, 等. 一种多样本信息的局部放电源逐次逼近定位方法[J]. 电工技术学报, 2016, 31(10):119-126.
Tang Ju, Huang Liang, Zeng Fuping, et al. A positioning approach based on successive approximation of multi-samples for partial discharge source[J]. Transactions of China Electrotechnical Society, 2016, 31(10):119-126.
[13] Liu Jiangting, Hu Yue, Peng Hui, et al. A data-driven method using DNN for PD location in substations[J]. IET Science Measurement Technology, 2020, 14(3): 314-321.
[14] Weng Yang, Xiao Wendong, Xie Lihua, et al. Total least squares method for robust source localization in sensor networks using TDOA measurements[J]. International Journal of Distributed Sensor Networks, 2011, 7(1): 1063-1067.
[15] Mountassir O E, Stewart B G, McMeekin S G, et al. Evaluation of an iterative method used for partial discharge RF location techniques[C]//2011 10th International Conference on Environment and Electrical Engineering, Rome, Italy, 2011: 1-4.
[16] Kim H J, Choi K, Lee H B, A new algorithm for solving ill conditioned linear systems[J]. IEEE Transactions on Magnetics, 1996, 32(3):1373-1376.
[17] 朱晓临. 数值分析[M]. 2版. 合肥: 中国科学技术大学出版社, 2014.
[18] Abe M, Sakakibara K, Fujikawa T, et al. Static magnetic field shimming calculation using TSVD regularization with constraints of iron piece placements[J]. IEEE Transactions on Applied Superconductivity, 2017, 27(7): 1-12.
[19] Ramani S, Liu Zhihao, Rosen J, et al. Regularization parameter selection for nonlinear iterative image restoration and MRI reconstruction using GCV and SURE-based methods[J]. IEEE Transactions on Image Processing, 2012, 21(8): 3659-3672.
[20] Hou Huijuan, Sheng Gehao, Jiang Xiuchen. Localization algorithm for the PD source in substation based on L-shaped antenna array signal processing[J]. IEEE Transactions on Power Delivery,2015, 30(1): 472-479.
[21] Zhu Mingxiao, Wang Yanbo, Liu Qing, et al. Localization of multiple partial discharge sources in air-insulated substation using probability-based algorithm[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(1): 157-166.
A Location Method of Partial Discharge Based on Truncated Singular Value Decomposition and K-Medians
Abstract Aiming at the problem that the time difference of arrival (TDOA) error of UHF signal is large in a complex environment, which leads to the inaccurate solution of nonlinear equation, a PD source location method is proposed which based on truncated singular value decomposition (TSVD) and K-Medians. First, PD signal is obtained via UHF antenna, and TDOA information is extracted by energy accumulation. Second, as for the difficulty and inaccuracy of solving linear equations, the random combination linear transformation method is proposed. The nonlinear localization equations are transformed into linear equations, and the influence of coordinate system selection on the location equation is eliminated via pretreatment technology. Then, the TSVD regularization algorithm is used to solve the linear equation, and the K-Medians clustering algorithm is introduced to optimize the TSVD regularization algorithm. The PD source coordinate location is realized in the substation. Finally, the proposed method is analyzed through theoretical verification and field experiments. The experimental results verify the feasibility and accuracy of the proposed method.
keywords:Partial discharge (PD) source, location, linear transformation, pretreatment, truncated singular value decomposition (TSVD), K-Medians
DOI:10.19595/j.cnki.1000-6753.tces.210623
中图分类号:TM835
国家自然科学基金(51977153, 51977161, 51577046)、国家重点研发计划“重大科学仪器设备开发”项目(2016YFF0102200)、国家自然科学基金重点项目(51637004)和装备预先研究重点项目(41402040301)资助。
收稿日期 2021-04-28
改稿日期 2021-05-24
宁暑光 男,1992年生,博士研究生,研究方向为局部放电检测,电力设备局部放电定位及故障诊断。E-mail:18726386659@163.com
何怡刚 男,1966年生,教授,博士生导师,研究方向为模拟和混合信号电路的测试和故障诊断、智能电网、自动测试与诊断装备、射频识别技术和智能信号处理等。E-mail: 18655136887@ 163.com(通信作者)
(编辑 郭丽军)