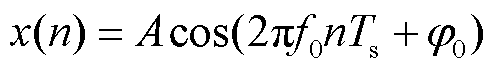 (1)
(1)
摘要 非线性负载、电力电子设备等给电力系统引入了大量的谐波、间谐波,对电力系统的安全稳定运行造成威胁。离散傅里叶变换(DFT)技术频率分辨率较低,当间谐波与基波或者谐波之间的频率间隔较小时,无法对邻近频率分量进行准确分辨;矩阵束法等频率分辨率较高的算法通常运算量较大,只能进行谐波、间谐波的离线分析。该文结合全相位傅里叶变换(ApFFT)和泰勒傅里叶多频模型,提出一种频率分辨率高、计算量小的谐波、间谐波分析模型,其频率分辨率远大于传统DFT技术,运算速度约是矩阵束法的39倍。该文对该模型的噪声鲁棒性、频率分辨率、运算速度进行了仿真分析和实验验证。仿真和实验结果表明,所提出的模型具有良好的噪声鲁棒性,频率分辨率可以达到12Hz,进行谐波、间谐波分析时的频率误差小于0.01Hz,幅值误差小于5%,可以实现谐波、间谐波的快速检测。
关键词:间谐波分析 泰勒-傅里叶 频率分辨率 噪声鲁棒性
谐波、间谐波检测对电能质量评估与治理、电能计量等具有重要的意义[1-4]。谐波频率为基波频率的整数倍,其频率分布比较固定,相对来说比较容易检测,检测方法丰富多样[5-8];间谐波频率分布具有不确定性,且与其他分量之间的频率间隔较小,较难检测。目前,谐波、间谐波分析方法主要有离散傅里叶变换(Discrete Fourier Transform, DFT)、希尔伯特-黄变换(Hilbert-Huang Transform, HHT)、矩阵束法(Matrix Pencil Method, MPM)和泰勒傅里叶变换(Taylor Fourier Transform, TFT)等。
DFT在非同步采样时存在严重的频谱泄漏和栅栏效应,使得分析结果误差较大,有学者提出了同步化采样[9]等技术,在一定程度上降低了频谱泄漏和栅栏效应引入的误差。卿柏元等[10]提出了频谱泄漏抑制性能优良的窗函数,实现了改进的DFT谱分析方法,进一步提高了DFT分析的准确度。He Wen等[11-13]提出多种针对DFT的插值校正方法,即使在非整周期截断和非同步采样条件下,也能够对幅值、频率和初相位的分析结果进行插值校正,得到更为精确的分析结果。王兆华等[14]提出了具有相位不变特性的全相位快速傅里叶变换(All phase Fast Fourier Transformation, ApFFT),并对其插值校正方法进行了研究,实现了具有更强频谱泄漏抑制能力的ApFFT插值校正技术。此外,学者们还提出了很多参数化模型及其他动态信号分析方法。F. F. Costa等将滤波算法加入到经典Prony算法中,提出一种改进的谐波、间谐波分析算法[15],增强了Prony算法分析精度和抗噪性能,但是运算量也相应增加。K. Sheshyekani等[16]和L. Bernard等[17]基于矩阵束法提出了各自的谐波、间谐波分析方法,MPM和Prony模型求解精度高,但运算量较大,难以实现快速分析。A. Bracale等通过对多重信号分类(Multiple Signal Classification, MUSIC)[18]、旋转不变技术信号参数估计(Estimation of Signal Parameters via Rotational Invariance Techniques, ESPRIT)[19]等研究和改进,提出了相应的谐波、间谐波分析算法,该类型分析算法由于计算量巨大,多用于离线分析计算场合。除了上面提到的方法外,还有如稀疏分解法[20]和改进TFT法[21]等,TFT技术具有良好的动态信号分析能力,但使用TFT进行间谐波分析需要预先知道各分量的频率信息。M. Bertocco等对TFT技术进行扩展,结合压缩感知(Compressed Sensing, CS)技术提出考虑间谐波分量的泰勒傅里叶多频(Taylor Fourier Multifrequency, TFM)模型,实现了一种能够用于同步相量测量的CSTFM模型,并对模型的运算速度在一定程度上进行了优化,但频率分辨率依然较低[22-23]。
本文提出一种频率分辨率高、计算量小的谐波、间谐波分析模型ApTFM,并对ApTFM模型的噪声鲁棒性、频率分辨能力进行了仿真分析和实验验证。
ApFFT具有相位不变性。以单一频率信号对ApFFT插值校正过程进行介绍,令输入信号x(n)为单一频率信号,即
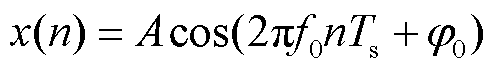 (1)
(1)
式中,A为信号幅值;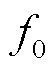 为信号频率;
为信号频率;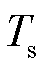 为采样周期;
为采样周期;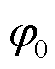 为初相位;N为采样点数;
为初相位;N为采样点数;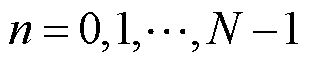 。
。
将采样点数扩展为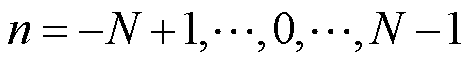 ,对长度为2N-1的采样数据进行ApFFT计算,采用双汉宁窗对上述输入信号x(n)进行加窗FFT变换,得到频点f0附近的离散频谱函数为
,对长度为2N-1的采样数据进行ApFFT计算,采用双汉宁窗对上述输入信号x(n)进行加窗FFT变换,得到频点f0附近的离散频谱函数为
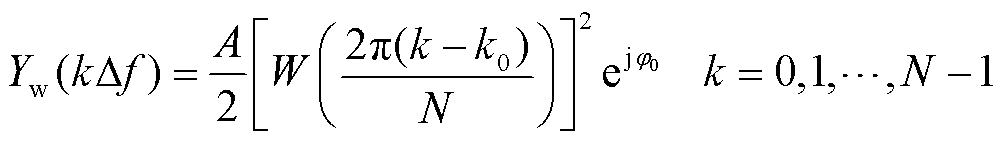 (2)
(2)
式中, Df为该窗口对应的频率分辨率, ;
; 为
为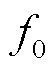 对应的k值。从式(2)可以看出,ApFFT得到的离散频谱的初相位始终为
对应的k值。从式(2)可以看出,ApFFT得到的离散频谱的初相位始终为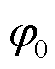 ,不随k值变化,说明ApFFT具有相位不变性。加窗操作在一定程度上降低了ApFFT的频谱泄漏和栅栏效应。借鉴双谱线插值校正算法可以对ApFFT的分析结果进行校正[12]。非整周期采样导致ApFFT的谱峰频点f0=k0Δf通常并不刚好处于离散频点上,也就是说k0通常不是整数。设谱峰频点f0=k0Δf左右两侧的谱线分别为k1和k2,则有k1<k0<k2= k1+1,它们对应的两条谱线幅值分别为
,不随k值变化,说明ApFFT具有相位不变性。加窗操作在一定程度上降低了ApFFT的频谱泄漏和栅栏效应。借鉴双谱线插值校正算法可以对ApFFT的分析结果进行校正[12]。非整周期采样导致ApFFT的谱峰频点f0=k0Δf通常并不刚好处于离散频点上,也就是说k0通常不是整数。设谱峰频点f0=k0Δf左右两侧的谱线分别为k1和k2,则有k1<k0<k2= k1+1,它们对应的两条谱线幅值分别为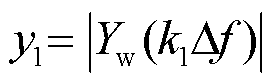 和
和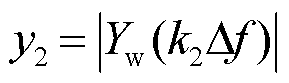 ,令
,令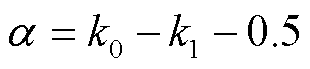 ,则
,则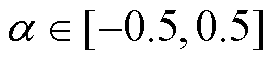 。令
。令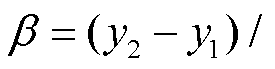
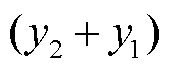 ,由式(2)得
,由式(2)得
 (3)
(3)
进而得到频率校正公式为
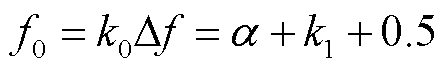 (4)
(4)
幅值校正公式为
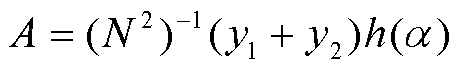 (5)
(5)
式中,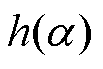 为与窗函数相关的函数,可以通过多项式拟合得到。
为与窗函数相关的函数,可以通过多项式拟合得到。
本文采用的窗函数为汉宁窗,其表达式为
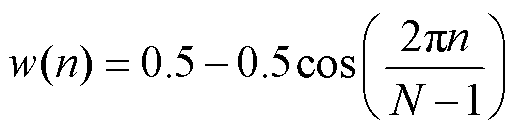 (6)
(6)
根据上述分析得到双汉宁窗ApFFT的校正参数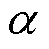 为
为
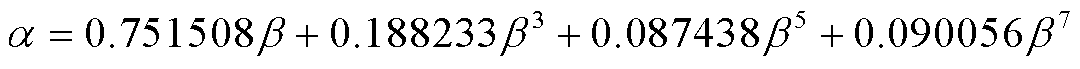 (7)
(7)
幅值校正函数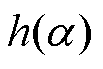 为
为
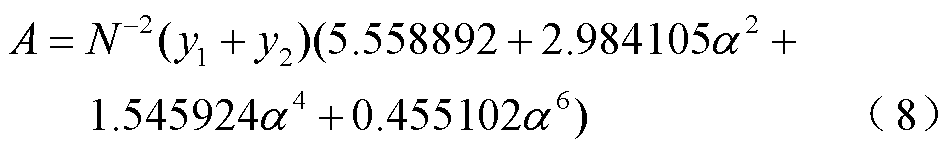
由于ApFFT具有相位不变性,因此不需要进行相位校正。上述推导采用单一频率信号作为输入信号,根据信号的叠加性可知,上述推导及结论同样适用于包含复杂谐波、间谐波的输入信号。
实际电力系统中的电信号x(n)由系统基波、谐波和间谐波构成,其离散化数学模型可以表示为
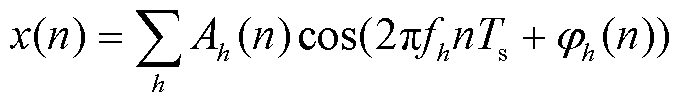 (9)
(9)
式中,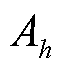 和
和 分别为h次谐波的幅值和初相位;
分别为h次谐波的幅值和初相位;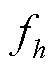 为h次谐波的频率。这里的h可以是非整数,表示间谐波分量。
为h次谐波的频率。这里的h可以是非整数,表示间谐波分量。
输入信号x(n)的TFM模型可以表示为[23]
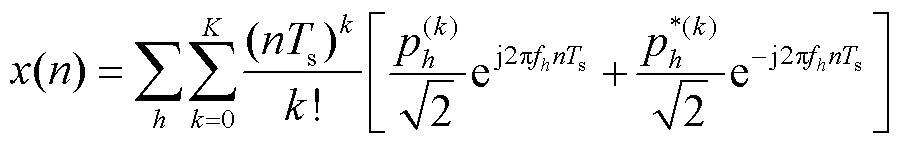 (10)
(10)
式中,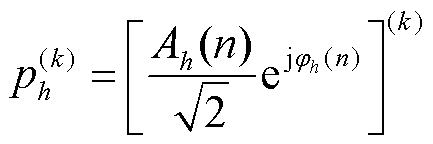 为频率
为频率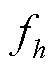 对应分量相量的k阶导数;*表示共轭。不同于传统FFT技术,TFM模型中
对应分量相量的k阶导数;*表示共轭。不同于传统FFT技术,TFM模型中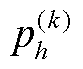 包含的信号幅值
包含的信号幅值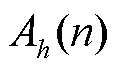 和初相位
和初相位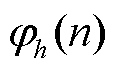 并非常数,而是随时间变化的量,也就是说TFM模型具有动态分析性能。
并非常数,而是随时间变化的量,也就是说TFM模型具有动态分析性能。
设输入信号x(n)中包含的频率分量总数为M,泰勒展开式的阶数为K,窗口长度为奇数Nw,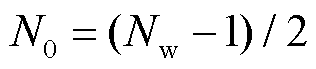 ,则可以将式(10)改写成矩阵形式,即
,则可以将式(10)改写成矩阵形式,即
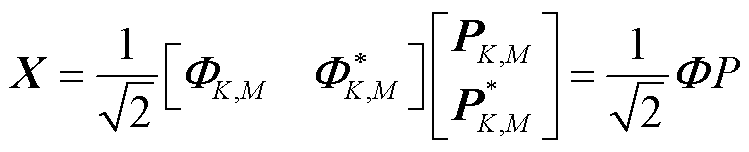 (11)
(11)
式中, X为输入信号的Nw个采样点构成的列向量,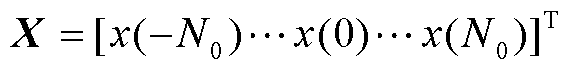 ;FK,M为由
;FK,M为由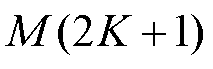 个列向量构成的矩阵,
个列向量构成的矩阵,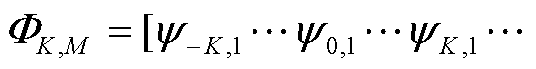
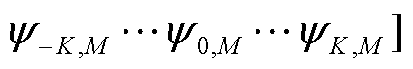 ,每一个列向量由
,每一个列向量由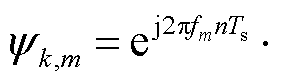
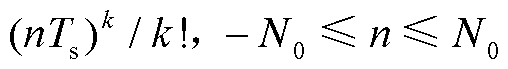 构成;
构成;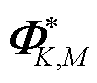 为
为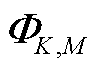 的共轭矩阵;PK,M为与动态同步相量有关的列向量,
的共轭矩阵;PK,M为与动态同步相量有关的列向量,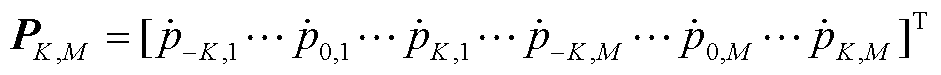 ;
;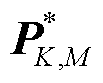 为
为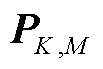 的共轭矩阵。
的共轭矩阵。
由最小方差法得到列向量P为
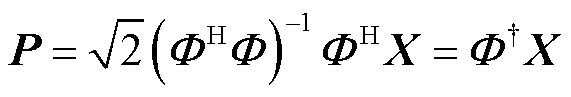 (12)
(12)
式中,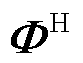 和
和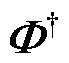 分别为
分别为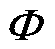 的共轭转置矩阵和伪逆矩阵。
的共轭转置矩阵和伪逆矩阵。
可以看出,对于待分析输入信号x(n),只需要知道各分量的频率值,就可以根据泰勒-傅里叶多频模型求得各分量相量的k阶导数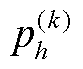 ,进而可以得到输入信号中各分量的幅值、相位。TFM多用于谐波分析,进行间谐波分析时,由于间谐波频率未知,需要结合ApFFT进行频率检测。
,进而可以得到输入信号中各分量的幅值、相位。TFM多用于谐波分析,进行间谐波分析时,由于间谐波频率未知,需要结合ApFFT进行频率检测。
进一步可以求得各分量的频率和频率变化率为
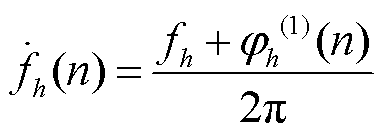 (13)
(13)
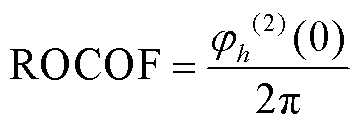 (14)
(14)
TFM模型用于间谐波分析时具有良好的动态性能,但需要预先求得所有分量的频率估计值。ApFFT相对于传统FFT分析精度更高,因此本文采用ApFFT求取各频率分量。分析时先采用ApFFT求出谐波分量,将其从原信号中减去,再进行间谐波频率计算,以降低各分量之间的相互干扰,提高频率分辨率。最后根据ApFFT得到的各分量频率,结合TFM模型求解各分量精确参数。本文所提出的ApTFM模型实现流程如图1所示。
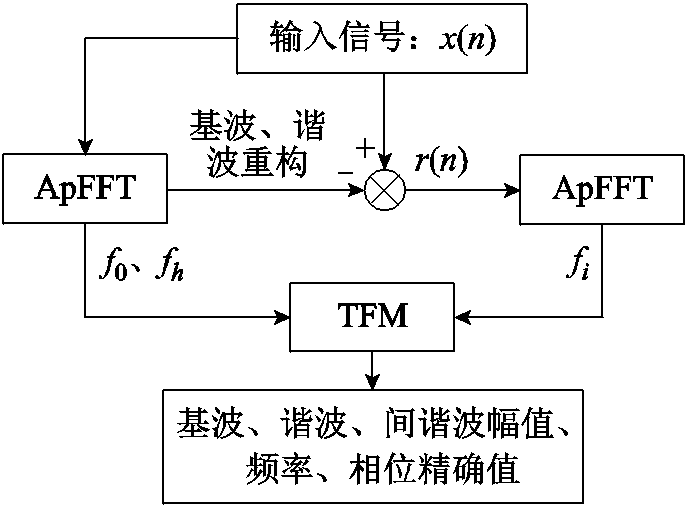
图1 ApTFM模型实现流程
Fig.1 Implementation flowchart of the ApTFM model
详细实现流程可以分为以下五步:
(1)利用加窗、插值校正ApFFT对采样序列x(n)进行分析,得到基波和谐波的幅值、频率fh和初相位参数,并根据计算出的参数值重构出基波、谐波分量。
(2)从原数据x(n)中减去基波、谐波分量,得到剩余分量r(n)。
(3)利用加窗、插值校正ApFFT对剩余分量r(n)进行分析,得到间谐波频率fi。
(4)根据步骤(1)、步骤(3)计算得到的基波、谐波频率f0、fh和间谐波频率fi生成相应的TFM系数矩阵FK,M。
(5)通过TFM模型得到基波、谐波、间谐波的参数值。
使用ApTFM模型进行计算时,主要的运算量来自于加窗、插值ApFFT和TFM矩阵运算两部分。窗口长度为N时,ApFFT加窗过程需要2N-1次实数乘法、N-1次实数加法运算;N点的FFT变换需要 次实数乘法、
次实数乘法、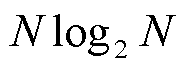 次实数加法运算;插值校正过程主要运算量来源于式(3)、式(4)、式(7)、式(8),总共需要31(N-1)次实数乘法、11(N-1)次实数加法运算。当包含的频率分量数为M时,令R=M(2K+1)。TFM模型涉及复数运算,一次复数运算相当于两次实数运算。实现流程步骤(4)生成系数矩阵FK,M需要6NR次实数乘法运算;矩阵求逆采用LU分解法,TFM通过F 矩阵求解P向量的主要运算量来源于式(12),需要
次实数加法运算;插值校正过程主要运算量来源于式(3)、式(4)、式(7)、式(8),总共需要31(N-1)次实数乘法、11(N-1)次实数加法运算。当包含的频率分量数为M时,令R=M(2K+1)。TFM模型涉及复数运算,一次复数运算相当于两次实数运算。实现流程步骤(4)生成系数矩阵FK,M需要6NR次实数乘法运算;矩阵求逆采用LU分解法,TFM通过F 矩阵求解P向量的主要运算量来源于式(12),需要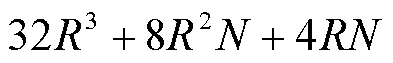 次实数乘法、
次实数乘法、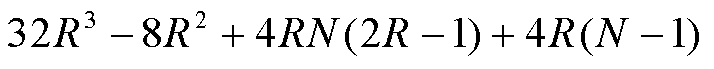 次实数加法运算。根据以上统计,ApTFM模型总共需要的实数乘法、实数加法运算量分别为
次实数加法运算。根据以上统计,ApTFM模型总共需要的实数乘法、实数加法运算量分别为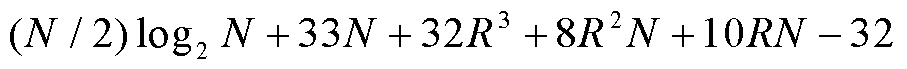 次、
次、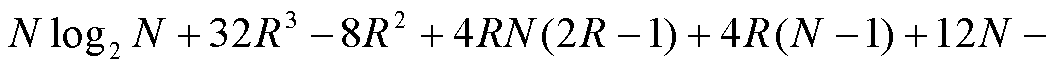
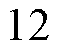 次。
次。
取采样频率为10kHz,M=20,N=2 001,K=2,窗口长度为10个基波周期0.2s。ApTFM模型总共需要194 159 373次实数乘法、192 045 544次实数加法运算,总计需要386 204 917次浮点运算。以TI公司的TMS320C6712D芯片为例,它的时钟频率为150MHz,运算速度达到900MFLOPS。如果采用该系列处理器进行计算,总计算时间约0.43s。为了进一步对比ApTFM和MPM模型的运算速度,采用ApTFM和MPM模型对长度为20s的采样数据进行分析。使用Intel(R) Core(TM) i5-10400F CPU @ 2.9GHz双核处理器,在64位Matlab R2017a上进行测试,测得ApTFM、MPM模型每个窗口的平均计算时间分别为17.5ms、687.5ms,ApTFM模型的运算速度大约为MPM的39倍。
仿真中,在每种实验条件下进行1 000次仿真,每次仿真中各分量的初相位取0~360°之间的随机数,用1 000次仿真得到的平均相对误差(MRE)代表幅值误差,平均绝对误差(MAE)代表频率、相位误差。ApTFM模型进行谐波、间谐波分析时,窗口长度设置为10个基波周期,采样频率设置为10kHz,待分析频率分量设置为20个。
本文进行噪声鲁棒性测试的信号中包含了谐波和间谐波,其数学表达式为

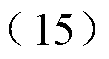
式中,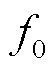 为系统频率;
为系统频率;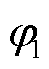 、
、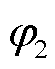 和
和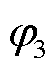 分别为基波、70Hz间谐波和3次谐波的初相位,测试中取0~360°之间的随机数;e为加入的噪声。
分别为基波、70Hz间谐波和3次谐波的初相位,测试中取0~360°之间的随机数;e为加入的噪声。
测试时加入白噪声,使信号信噪比(Signal Noise Ratio, SNR)从40dB以10dB为步长逐步增加到100dB。ApTFM模型在不同信噪比下对基波、谐波和间谐波的分析误差如图2所示。图例中,“50Hz”、“70Hz”、“150Hz”分别表示基波、间谐波和谐波的误差。
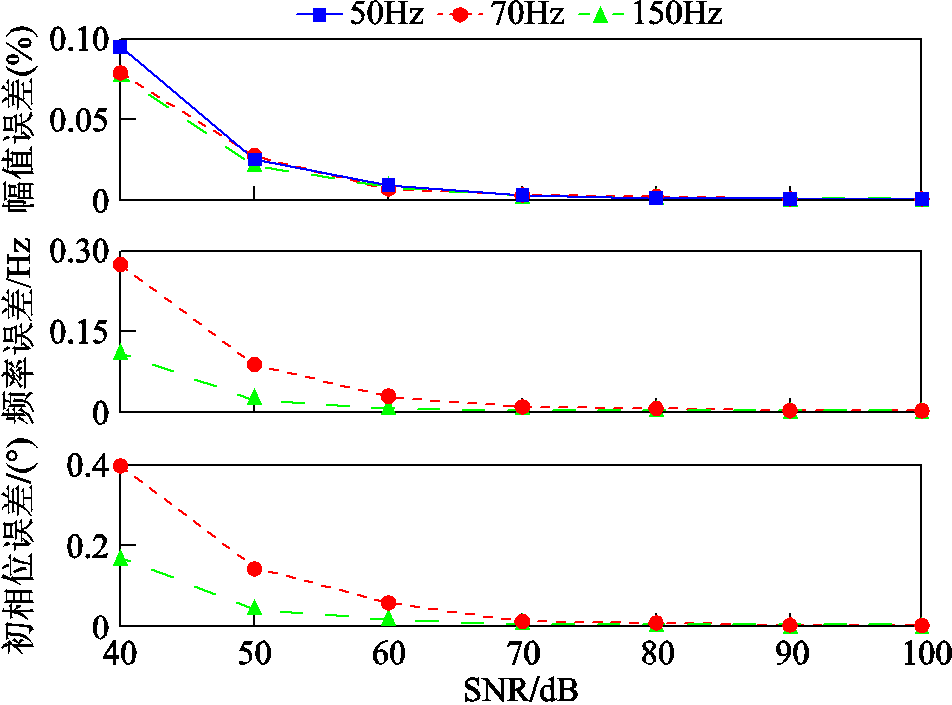
图2 不同信噪比下各分量幅值、频率、初相位分析误差
Fig.2 Analysis errors of the amplitude, frequency and initial phase of each component of different SNR
研究结果表明,SNR=60dB时,ApTFM模型得到各分量的幅值、频率、初相位误差分别小于0.01%、0.04Hz、0.56°,基波分量的幅值误差、频率误差、初相位误差分别小于0.01%、0.32mHz、0.005°。在电力系统精确测量中,通常采用16位甚至更高的数据采集系统,其信噪比可以达到90dB以上,即便采用12位采集系统,其信噪比也能达到70dB。ApTFM模型在SNR=60dB时,测量结果已经能够满足谐波、间谐波分析需求。
在谐波、间谐波检测中,间谐波的频率可能会比较接近基波或者谐波,给谐波、间谐波的检测带来困难。下面对ApTFM、IpDFT和MPM的频率分辨率进行对比,研究中采用的信号表达式为
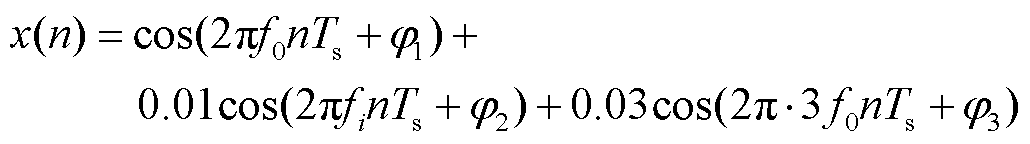 (16)
(16)
式中,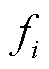 为间谐波频率;
为间谐波频率;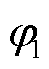 、
、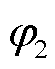 和
和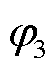 分别为基波、间谐波和三次谐波的初相位,测试中取0~360°之间的随机数。测试中加入白噪声,使得SNR=70dB。
分别为基波、间谐波和三次谐波的初相位,测试中取0~360°之间的随机数。测试中加入白噪声,使得SNR=70dB。
保持基波频率不变,当间谐波频率从65Hz以2Hz为步长减小到55Hz时,基波与间谐波之间的频率间隔从15Hz减小到5Hz。研究结果表明,IpDFT在间谐波与基波之间的频率间隔为13Hz时,基波分析的幅值、频率、初相位误差分别为0.77%、0.25Hz、9.09°,频率间隔减小后基波分析误差进一步增大;间谐波测量结果基本失去意义,仿真结果不再给出。MPM和ApTFM模型得到的仿真结果如图3所示,图中MPM-f0、ApTFM-f0和MPM-fi、ApTFM-fi分别表示两种模型对基波、间谐波进行分析的结果。ApTFM模型在间谐波与基波之间的频率间隔为9Hz时,基波分析的幅值、频率、初相位误差分别0.00%、0.00Hz、0.02°,间谐波分析对应的幅值、频率、初相位误差分别0.04%、0.06Hz、0.62°。频率间隔为11Hz时,基波分析的幅值、频率、初相位误差在保留两位小数时接近于0;间谐波的幅值、频率、初相位误差分别0.0%、0.01Hz、0.23°。MPM模型的分析误差最小,ApTFM分析精度接近于MPM模型,但是运算量更小,两种算法各有优劣。

图3 间谐波靠近基波时MPM和ApTFM的分析误差
Fig.3 Analysis errors of MPM and ApTFM when the interharmonic frequency is close to the fundamental wave
调整间谐波与3次谐波之间的频率间隔,使间谐波频率从135Hz以2Hz为步长增大到145Hz,间谐波与三次谐波之间的频率间隔从15Hz减小到5Hz。IpDFT在间谐波与基波之间的频率间隔为13Hz时,3次谐波分析的幅值、频率、初相位误差分别为0.41%、3.97Hz、122.71°,间谐波分析的幅值、频率、初相位误差分别为0.41%、7.03Hz、116.9°,频率间隔减小后基波分析误差进一步增大,分析结果失去实际意义,仿真结果不再给出。MPM和ApTFM模型得到的仿真结果如图4所示,图中MPM-f3、ApTFM-f3和MPM-fi、ApTFM-fi分别表示三次谐波、间谐波的分析结果。
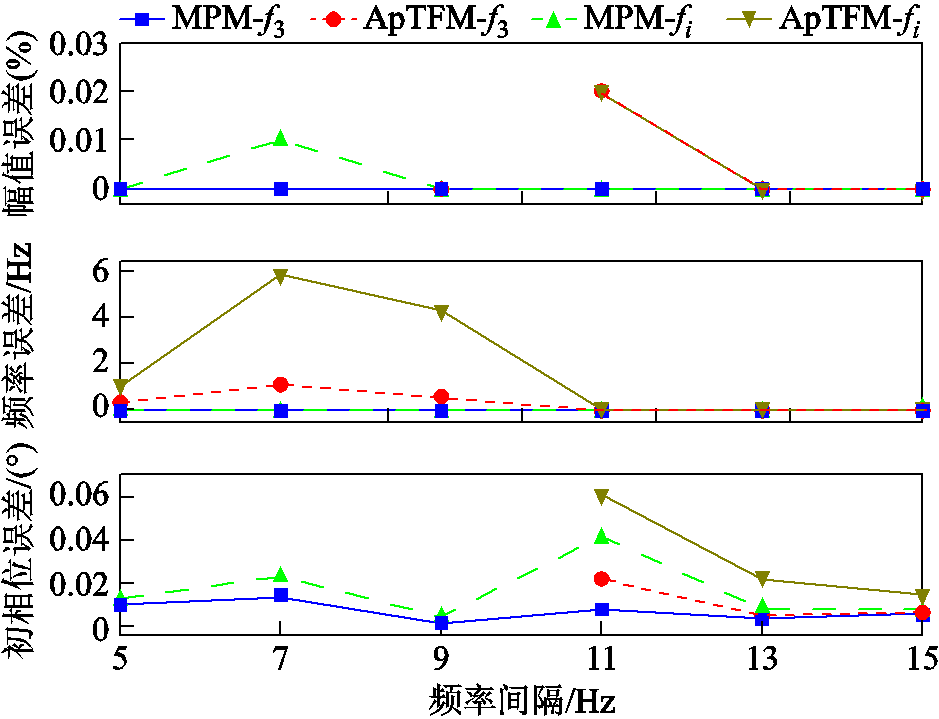
图4 间谐波靠近3次谐波时MPM和ApTFM的分析误差
Fig.4 Analysis errors of MPM and ApTFM when the interharmonic frequency is close to the 3rd harmonic
对于ApTFM模型,当间谐波与3次谐波之间的频率间隔为9Hz时,对间谐波和3次谐波的分析误差较大,图中不再给出。当频率间隔为11Hz时,3次谐波分量的幅值、频率、初相位误差分别0.02%、0.02Hz、0.22°,间谐波分量的幅值、频率、初相位误差分别0.02%、0.07Hz、0.62°,此时ApTFM能够较准确的提出各分量的参数。MPM模型的分析误差最小,当频率间隔大于11Hz时,ApTFM分析精度接近于MPM模型,说明ApTFM模型可以分辨频率间隔为11Hz的分量。
综上所述,ApTFM模型频率分辨率远大于传统IpDFT技术,达到11Hz;MPM模型频率分辨率比ApTFM更高,但是运算量较大。相比之下,ApTFM模型运算量小、频率分辨率尚可,具有自身的优势。
为了分析ApTFM模型的谐波、间谐波检测能力,本文搭建了相关的实验平台,实验平台如图5所示。通过实验平台生成包含基波、谐波、间谐波的电流,通过电流传感器测得谐波电流。实验平台主要包括1台程控交流源、1台信号发生器、1台音频功率放大器、1个耦合器、高精度宽带电流传感器、导线等。程控交流源的型号为安捷伦AC6804A,额定交流输出功率为4 000V·A,最大稳态输出电流为40A,输出频率范围为40~500Hz,在该实验中用于产生基波、谐波电流。音频功率放大器用来对信号发生器产生的特定频率电压信号进行功率放大,生成特定频率的间谐波电流。耦合器的作用是利用变压器原理,使二次绕组的输出电流为两个一次绕组电流的叠加,实现不同频率电流的叠加。通过16位采集卡进行采样,再采用谐波、间谐波分析模型对采集到的电流数据进行谐波、间谐波分析,评估ApTFM模型频率分辨率等性能。
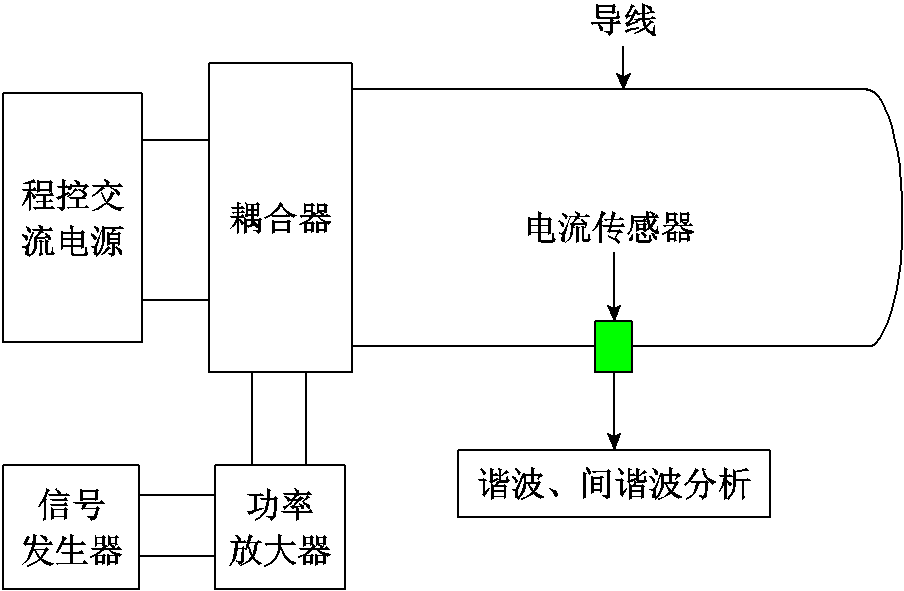
图5 实验平台示意图
Fig.5 Schematic diagram of experimental platform
实验中待测电流的幅值真值未知,MPM模型虽然耗时巨大,但是其结果很精确,本文在实验中采用MPM、ApTFM模型对实测电流波形进行分析,并以MPM模型的分析结果作为参照,对ApTFM模型的性能进行评价。实验时保持基波频率为51Hz,即基波频率存在1Hz的频率偏移。实验分为间谐波频率靠近基波频率、3次谐波频率(153Hz)两种情况进行。通过实验平台产生实验电流,采用电流传感器对其进行测量,使用IpDFT、APTFM、MPM模型对电流测量数据进行分析、对比。
加入的间谐波频率为61Hz时,间谐波与基波之间的频率间隔为10Hz,IpDFT不能分辨间谐波分量,且分析得到的基波误差较大。ApTFM模型得到的间谐波频率为60.78Hz,误差为0.22Hz。ApTFM和MPM得到的61Hz间谐波幅值分别为1.04A、0.96A,以MPM的结果作为参照,ApTFM模型在频率间隔为10Hz时间谐波分析结果误差较大。
当间谐波频率为63Hz时,间谐波与基波之间的频率间隔为12Hz,实验得到各分量的幅值、频率见表1。IpDFT整体分析误差较大,且分辨不出间谐波分量。ApTFM得到63Hz间谐波的频率、频率误差分别为63.03Hz、0.03Hz,ApTFM与MPM得到的各分量幅值、频率基本一致,以MPM模型的分析结果作为参照,得到ApTFM的分析误差见表1。可以看出,ApTFM模型的基波幅值误差约为0,频率误差约为0Hz;间谐波的幅值误差约为3.03%,频率误差约为0.01Hz;其他谐波的最大幅值误差低于3%,相关标准对谐波、间谐波测量的幅值误差要求低于5%,ApTFM模型满足要求。
表1 间谐波与基波频率间隔为12Hz时实验结果
Tab.1 Experimental results when the frequency interval between the interharmonic and fundamental is 12Hz
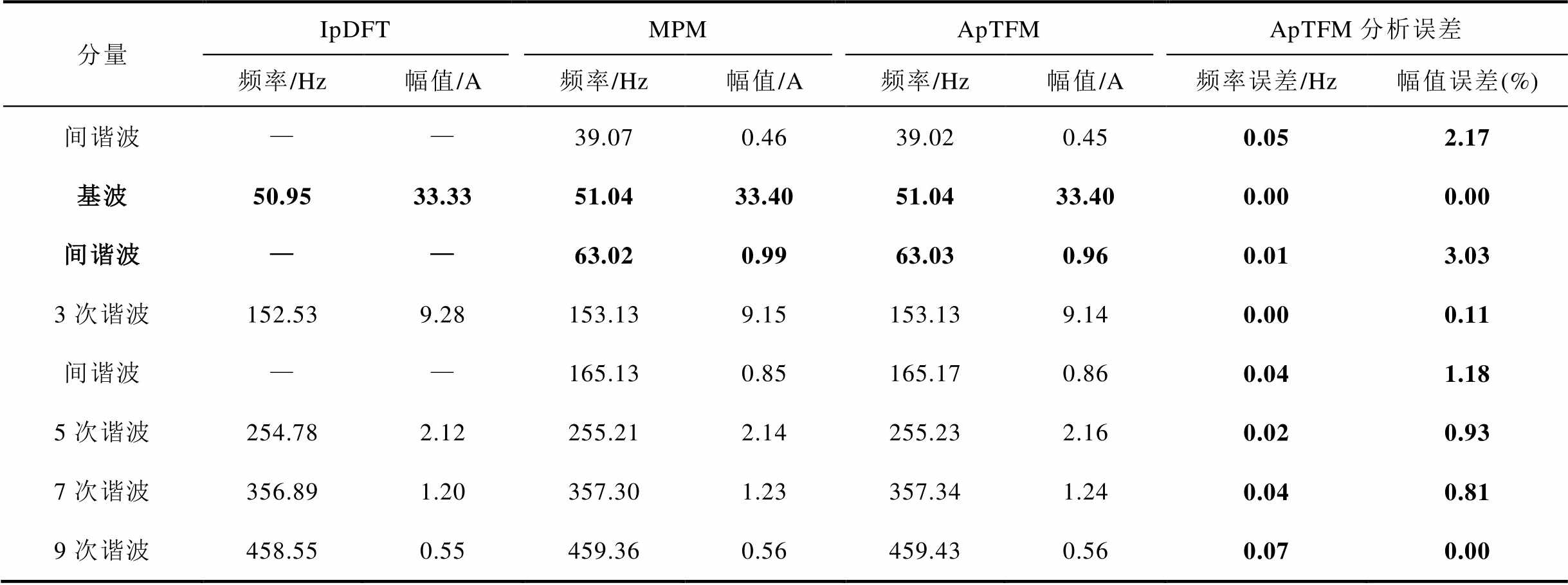
分量IpDFTMPMApTFMApTFM分析误差 频率/Hz幅值/A频率/Hz幅值/A频率/Hz幅值/A频率误差/Hz幅值误差(%) 间谐波——39.07 0.46 39.02 0.45 0.05 2.17 基波50.95 33.33 51.04 33.40 51.04 33.40 0.00 0.00 间谐波——63.02 0.99 63.03 0.96 0.01 3.03 3次谐波152.53 9.28 153.13 9.15 153.13 9.14 0.00 0.11 间谐波——165.13 0.85 165.17 0.86 0.04 1.18 5次谐波254.78 2.12 255.21 2.14 255.23 2.16 0.02 0.93 7次谐波356.89 1.20 357.30 1.23 357.34 1.24 0.04 0.81 9次谐波458.55 0.55 459.36 0.56 459.43 0.56 0.07 0.00
当间谐波频率为143Hz时,间谐波与3次谐波之间的频率间隔分别为10Hz,IpDFT分析误差较大,且不能分辨间谐波分量。MPM得到的间谐波频率为143.13Hz,频率误差为0.13Hz;ApTFM得到的间谐波频率为145.78Hz,频率误差达到2.78Hz,说明频率间隔为10Hz时,ApTFM模型分析误差较大。
当间谐波频率为141Hz时,间谐波与3次谐波之间的频率间隔分别为12Hz,实验得到各分量幅值、频率见表2。
表2 间谐波与3次谐波频率间隔为12Hz时实验结果
Tab.2 Experimental results when the frequency interval between the interharmonic and 3rd harmonic is 12Hz

分量IpDFTMPMApTFMApTFM分析误差 频率/Hz幅值/A频率/Hz幅值/A频率/Hz幅值/A频率误差/Hz幅值误差(%) 间谐波——39.02 0.42 39.11 0.43 0.09 2.38 基波51.03 33.71 51.04 33.69 51.04 33.72 0.00 0.09 间谐波——141.14 1.26 141.13 1.27 0.01 0.79 3次谐波153.15 9.51 153.13 9.53 153.13 9.50 0.00 0.31 间谐波——243.24 0.63 243.20 0.60 0.04 4.76 5次谐波255.502.18 255.20 2.25 255.20 2.22 0.00 1.33 7次谐波357.521.29 357.29 1.32 357.28 1.33 0.01 0.76 9次谐波459.740.58 459.38 0.61 459.35 0.62 0.03 1.64
IpDFT分析误差较大,且不能分辨间谐波分量。ApTFM得到的间谐波频率为141.13Hz,频率误差为0.13Hz。ApTFM与MPM得到的各分量幅值、频率结果非常接近,以频率分辨率更高的MPM模型的分析结果作为参照,得到ApTFM的分析误差见表2。可以看出,ApTFM模型分析得到的3次谐波幅值误差约为0.31%,频率误差约为0Hz;间谐波的幅值误差约为0.79%,频率误差约为0.01Hz;其他谐波的最大幅值误差低于5%,GBT 14549—1993、GBT 24337—2009、IEC 61000-4-7—2009等标准对谐波、间谐波测量的幅值误差要求低于5%,ApTFM模型满足要求。
综上所述,所提出的ApTFM模型频率分辨率可以达到12Hz,即当间谐波与基波、谐波之间的频率间隔大于12Hz时,ApTFM模型能够对间谐波分量进行精确分辨,对基波、谐波、间谐波的频率分析精度较高,对各分量幅值分析的误差低于5%,达到了GBT 14549—1993、GBT 24337—2009、IEC 61000-4-7—2009对谐波、间谐波分析的要求。
本文提出一种频率分辨率高、运算速度快的谐波、间谐波分析模型ApTFM,并对其运算速度、噪声鲁棒性、频率分辨率进行了仿真分析和实验验证。仿真和实验结果表明,ApTFM模型的运算速度约为MPM模型的39倍,频率分辨率达到12Hz,对各分量进行分析的频率误差小于0.01Hz,幅值误差小于5%,满足GBT 14549—1993、GBT 24337—2009、IEC 61000-4-7—2009对谐波、间谐波分析的要求。ApTFM模型的综合性能能够满足谐波、间谐波分析与电能计量等应用场合的基本要求,但对频率间隔小于12Hz的密集频率分量无法进行准确检测。
参考文献
[1] Manikandan M S, Samantaray S R, Kamwa I. Detection and classification of power quality disturbances using sparse signal decomposition on hybrid dictionaries[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(1): 27-38.
[2] 孟令辉, 舒泽亮, 闫晗, 等. 基于特征次谐波补偿的单相统一电能质量调节器并联变换器控制策略[J]. 电工技术学报, 2020, 35(24): 5125-5133.
Meng Linghui, Shu Zeliang, Yan Han, et al. Control strategy for single-phase unified power quality conditioner of parallel converter based on specific order harmonics compensation[J]. Transactions of China Electrotechnical Society, 2020, 35(24): 5125-5133.
[3] 严静, 邵振国. 电能质量谐波监测与评估综述[J]. 电气技术, 2020, 21(7): 1-7.
Yan Jing, Shao Zhenguo. Summary of harmonic monitoring and evaluation[J]. Electrical Engineering, 2020, 21(7): 1-7.
[4] Arenas L D, Melo G D E, Canesin C A. A methodology for power quantities calculation applied to an FPGA-based smart-energy meter[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70.
[5] Nie Xiaohua. Detection of grid voltage fundamental and harmonic components using kalman filter based on dynamic tracking model[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 1191-1200.
[6] Platas-Garza M A, De La O Serna J A. Dynamic harmonic analysis through Taylor–Fourier transform[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(3): 804-813.
[7] 辛国庆, 董唯光, 高锋阳, 等. 感应电能供电技术下含间谐波的谐波信号重构[J]. 电工技术学报, 2020, 35(21): 4544-4552.
Xin Guoqing, Dong Weiguang, Gao Fengyang, et al. Reconstruction of harmonic signal with inter-harmonics under inductive power supply technology[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4544-4552.
[8] 王鹤, 李石强, 于华楠, 等. 基于分布式压缩感知和边缘计算的配电网电能质量数据压缩存储方法[J]. 电工技术学报, 2020, 35(21): 4553-4564.
Wang He, Li Shiqiang, Yu Huanan. Compression acquisition method for power quality data of distribution network based on distributed compressed sensing and edge computing[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4553-4564.
[9] Chen C I, Chen Y C. Comparative study of harmonic and interharmonic estimation methods for stationary and time-varying signals[J]. IEEE Transactions on Industrial Electronics, 2014, 61(1): 397-404.
[10] 曾博, 唐求, 卿柏元, 等. 基于Nuttall自卷积窗的改进FFT谱分析方法[J]. 电工技术学报, 2014, 29(7): 59-65.
Zeng Bo, Tang Qiu, Qing Baiyuan, et al. Spectral analysis method based on improved FFT by Nuttall self-convolution window[J]. Transactions of China Electrotechnical Society, 2014, 29(7): 59-65.
[11] Wen He, Li Chengcheng, Yao Wenxuan. Power system frequency estimation of Sine-wave corrupted with noise by windowed three-point interpolated DFT[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 5163-5172.
[12] Wang Kai, Wen He, Tai Wensi, et al. Estimation of damping factor and signal frequency for damped sinusoidal signal by three points interpolated DFT[J]. IEEE Signal Processing Letters, 2019, 26(12): 1927-1930.
[13] 杨超, 张淮清, 王耀, 等. 计及全泄漏影响的多点插值离散傅里叶变换校正方法[J]. 电工技术学报, 2020, 35(16): 3385-3395.
Yang Chao, Zhang Huaiqing, Wang Yao, et al. Multipoint interpolated discrete Fourier transform correction method considering total leakage effect[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3385-3395.
[14] 黄翔东, 王兆华. 基于全相位频谱分析的相位差频谱校正法[J]. 电子与信息学报, 2008(2): 293-297.
Huang Xiangdong, Wang Zhaohua. Phase difference correcting spectrum method based on all-phase spectrum analysis[J]. Journal of Electronics and Information Technology, 2008(2): 293-297.
[15] Costa F F, Cardoso A J M. Harmonic and interharmonic identification based on improved prony's method[C]//IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 2006: 4963.
[16] Sheshyekani K, Fallahi G, Hamzeh M, et al. A general noise-resilient technique based on the matrix pencil method for the assessment of harmonics and interharmonics in power systems[J]. IEEE Transactions on Power Delivery, 2017, 32(5): 2179-2188.
[17] Bernard L, Goondram S, Bahrani B, et al. Harmonic and interharmonic phasor estimation using matrix pencil method for phasor measurement units[J]. IEEE Sensors Journal, 2021, 21(2): 945-954.
[18] Bracale A, Caramia P, Carpinelli G. Optimal evaluation of waveform distortion indices with prony and root music methods[J]. International Journal of Power and Energy Systems, 2007, 27(4): 371-379.
[19] Jain S K, Singh S N. Exact model order ESPRIT technique for harmonics and interharmonics estimation[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(7): 1915-1923.
[20] De Almeida Prado T, Macario Barros A, Guarneri G A. An algorithm based on sparse decomposition for estimating harmonic and interharmonic components of stationary signals in power systems[J]. IEEE Access, 2019, 7: 163958-163968.
[21] Chen Lei, Zhao Wei, Wang Fuping, et al. An interharmonic phasor and frequency estimator for subsynchronous oscillation identification and monitoring[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(6): 1714-1723.
[22] Bertocco M, Frigo G, Narduzzi C, et al. Compressive sensing of a Taylor-Fourier multifrequency model for synchrophasor estimation[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(12): 3274-3283.
[23] Narduzzi C, Bertocco M, Frigo G, et al. Fast-TFM—multifrequency phasor measurement for distribution networks[J]. IEEE Transactions on Instrumentation and Measurement, 2018, 67(8): 1825-1835.
A High Frequency Resolution Harmonic and Interharmonic Analysis Model
Abstract The nonlinear loads and power electronic equipment have introduced a large number of harmonics and inter-harmonics into the power system, posing a threat to the safe and stable operation of the power system. The existing DFT technology has a low frequency resolution. When the frequency interval between the interharmonic and the fundamental or harmonic is small, the adjacent frequency components cannot be accurately distinguished. Algorithms with higher frequency resolution, such as Matrix Pencil Method, usually require a lot of calculations and can only perform offline analysis of harmonics and inter-harmonics. Combining ApFFT and Taylor Fourier multi-frequency model, this paper proposes a harmonic and interharmonic analysis model with high frequency resolution and small calculation amount, and its frequency resolution is much greater than that of traditional DFT technology, and its operation speed is about 39 times that of the Matrix Pencil Method. The noise robustness, frequency resolution, calculation speed of it have been simulated and verified by experiments in this paper. The simulation and experimental results show that the proposed model has good noise robustness and needs small amount of calculation, the frequency resolution can reach 12Hz. The frequency error and amplitude error during harmonic and inter-harmonic analysis is less than 0.01Hz and 5% respectively, and it can realize rapid detection of harmonics and inter-harmonics.
keywords:Inter-harmonic analysis, Taylor-Fourier, frequency resolution, noise robustness
DOI:10.19595/j.cnki.1000-6753.tces.210983
中图分类号:TM93
李文番 男,1989年生,博士研究生,研究方向为电流测量、谐波分析、同步相量检测等。E-mail:18109314169@163.com
张国钢 男,1976年生,教授,博士生导师,研究方向为智能电器理论与工程、储能与新能源电力系统以及电弧等离子体与电接触等。E-mail:ggzhang@mail. xjtu.edu.cn(通信作者)
收稿日期 2021-07-05
改稿日期 2021-08-16
国家重点研发计划(2016YFF0201205)和电力设备电气绝缘国家重点实验室开放课题(EIPE20211)资助项目。
(编辑 赫蕾)