Stackelberg博弈在电力市场中的应用研究综述
张 衡1 张沈习1 程浩忠1 张希鹏2 谷青发3
(1. 电力传输与功率变换控制教育部重点实验室(上海交通大学) 上海 200240 2. 国网上海市电力公司市北供电公司 上海 200070 3. 国网河南省电力公司电力科学研究院 郑州 450052)
摘要 可再生能源并网常态化、储能投资商业化、需求侧管理多样化、多能互补成熟化等在电力系统源、网、荷侧引入的利益主体不断增多,而受自身规模、所处市场地位不同造成了决策次序的差异性。针对电力市场环境下电力系统投资、交易等环节中普遍存在的次序决策问题,该文以具有主从递阶结构的Stackelberg博弈理论为切入点,综述了其在电力市场中的应用情况。首先,阐述了Stackelberg博弈理论的数学结构,并根据主/从问题中博弈者的数量进行了分类;然后,梳理了Stackelberg博弈在电力市场中的典型应用,总结了模型对等转换技巧,归纳了各类求解方法及其优缺点;最后,提炼了Stackelberg博弈理论在电力市场应用中仍然存在的关键问题。该文为处于不同决策位置的利益主体参与电力市场竞争提供了参考。
关键词:博弈论 Stackelberg博弈 主从博弈 电力市场 电力系统优化
0 引言
《中共中央国务院关于进一步深化电力体制改革的若干意见》的下发,拉开了我国新一轮电改序幕。借助人工智能、区块链、大数据等新技术提供的支撑平台,电力市场准入门槛进一步降低。除了传统燃料电厂和电网公司外,可再生能源发电商、储能设备运营商、负荷聚合商、需求侧管理资源供应商、增量配电网投资商等大量参与者也逐渐进入市场[1-3],不同利益主体的市场行为可以用博弈论来描述。随着“源-网-荷”侧市场参与者的种类和数量大幅增加,电力市场由传统寡头垄断逐渐向充分竞争过渡,参与者面临的决策问题越发复杂,除面临同类产品竞争外,还要考虑决策次序带来的影响。
参与者受自身规模、市场地位等制约,在决策次序上具有显著差异性,体现在两个方面:①市场地位不同,如发电商以自身利益最大进行报价,独立调度机构(Independent System Operator, ISO)以最大化社会效益进行市场出清,发电商优先决策,ISO在观察到发电商策略后再做决策;②处于同一地位的参与者由于生产规模不同引起决策的次序问题,如大型发电集团参与竞价,而小规模发电商只能被动接受电价做出决策。从上述分析可以看出,次序决策在电力市场中普遍存在。此类问题可以采用具有主从递阶结构的Stackelberg博弈进行描述,该理论最初由德国经济学家H. Von Stackelberg在1934年出版的《Market Structure and Equilibrium》一书中提出,并用于研究处于不同市场地位的两寡头竞争问题。
Stackelberg博弈虽起源于国外,但在国内也引起了众多学者关注,研究和应用范围包括市场交易、攻防安全、供应链规划、计算机科学等。具体到电力市场方向,其早期被用于研究市场力[4]。此后,文献[5]对Stackelberg博弈在智能电网中的应用进行了系统性概括,并应用于零售市场定价与调度,同时期文献[6]将其用于零售商实时定价中。近些年,电力市场逐步开放,Stackelberg博弈研究与应用的深度和广度均得到了加强,包括电力投资[7-16]、市场竞价[17-27]、需求侧管理资源交易[28-40]、综合能源服务[41-47]等。而随着能源互联网发展,市场参与者进一步增多,次序决策问题越发复杂。通过总结现有研究成果,明确未来亟需解决的关键问题和挑战,能够为处于不同决策次序的利益主体参与电力市场竞争提供理论依据和方法指导,具有重要的科学价值和实际意义。
本文介绍了Stackelberg博弈的理论框架,综述了其在电力市场方面的应用,并总结了博弈模型对等转换技巧及求解方法。最后,结合当前电网发展趋势,从未来高比例可再生能源电力系统市场出清、非市场主要参与者的收益、收益与风险的衡量、综合能源投资/竞价交易、含不确定因素的Stackelberg博弈问题建模与求解五个方面总结了仍然存在的关键问题。
1 Stackelberg博弈框架
Stackelberg博弈基本元素、均衡解等概念与其他博弈方法一致,关于此方面描述可参考文献[48]。该方法最初应用于“一主一从”的双寡头博弈,各方在行动上存在先后顺序,过程具有主从递阶结构特征,属于完全信息动态非合作博弈。在整个博弈问题中处于主导地位的参与者称为领导者(Leader),处于被领导地位的参与者称为跟随者(Follower)。随着问题复杂程度不断增加,Stackelberg 博弈不再局限于两寡头竞争范畴,市场参与者数量逐渐增加,衍生出了新的博弈形式。根据领导者和跟随者数量可以进行更详细的区分,具体分类见表1。
表1 Stackelberg博弈模型分类
Tab.1 Classification of Stackelberg game approaches

i = 1i>1 j = 1单一领导者与单一跟随者(One Leader One Follower, OLOF)多领导者与单一跟随者(Multi Leaders One Follower, MLOF) j>1单一领导者与多跟随者(One Leader Multi Followers, OLMF)多领导者与多跟随者(Multi Leaders Multi Followers, MLMF)
对于扩展后的Stackelberg博弈问题,其上、下层之间仍然属于非合作博弈,但同层之间可能形成合作或非合作博弈。同层构建合作博弈模型后,实际上可以简化Stackelberg博弈问题。例如,如果领导者之间实现合作,则可以避免形成含均衡约束的均衡问题(Equilibrium Problem with Equilibrium Constraints, EPEC)结构,问题复杂度会降低。但合作博弈需要面临利益分配的问题[49],不仅需要考虑联盟成员收益不低于单独经营所得,还需要利用VIKOR(vlse kriterijumska optimizacija i kompromisnoresenje)算法[50]、Shapley值[51]、多目标Pareto均衡[52]等方法对合作剩余进行分配,而电力信息由于保密等因素,同层竞争者之间有时难以形成合作联盟。当前Stackelberg博弈问题中同层间考虑合作方式的研究比较少,文献[22]在含多智能的微电网分布式发电商竞价Stackelberg博弈中,分别考虑了作为跟随者的分布式发电商非合作/合作两种情况,研究结果表明,清算价格在合作博弈时更低。文献[26]考虑碳税政策,基于Stackelberg博弈研究了政府与常规机组和微电网群之间的博弈问题。其中,政府作为碳税率制定者属于领导者,而常规机组和微电网群则属于跟随者。结果表明,通过合理的碳税率和收益分配策略,可以保证参与者的积极性和收益,同时也能够有效降低碳排放。本文后续重点关注同层间为非合作博弈的情况。由于Stackelberg博弈结构具有很多新的特点,为了与现有研究保持一致性,本文沿用文献[5]的框架,将含次序决策的问题均归结为Stackelberg博弈,其结构可由优化问题表示为
s.t. 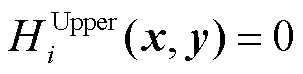 (2)
(2)
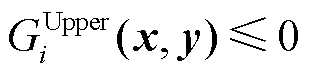 (3)
(3)
s.t. 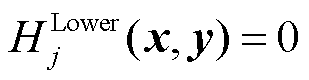 (5)
(5)
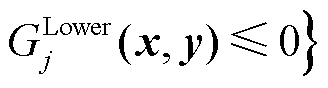 (6)
(6)
式中,x和y为决策变量,y由下层问题式(4)~式(6)决定;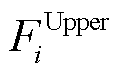 、
、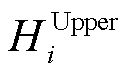 和
和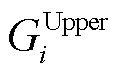 分别为上层优化问题的目标函数、等式约束和不等式约束;
分别为上层优化问题的目标函数、等式约束和不等式约束;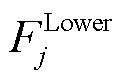 、
、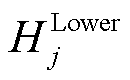 和
和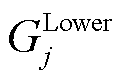 分别为下层优化问题的目标函数、等式约束和不等式约束;i和j分别为领导者和跟随者的数量。
分别为下层优化问题的目标函数、等式约束和不等式约束;i和j分别为领导者和跟随者的数量。
从上述模型结构可以看出,由于博弈各方所处市场地位不对等,造成了博弈各方是不同质的。领导者的策略是下层问题的参数,会影响跟随者的最优策略和收益;而跟随者问题是上层模型的约束条件。即领导者能够掌握跟随者的效用函数等信息,其在进行决策时能够将跟随者的反应考虑在内,做出利于自身的决策。而跟随者只能在观察到领导者决策后,做出使自身收益最大的反应[5]。特别地,如果领导者不能掌握跟随者的博弈信息,则此时Stackelberg博弈退化为Nash博弈。
2 Stackelberg博弈在电力市场中的典型应用
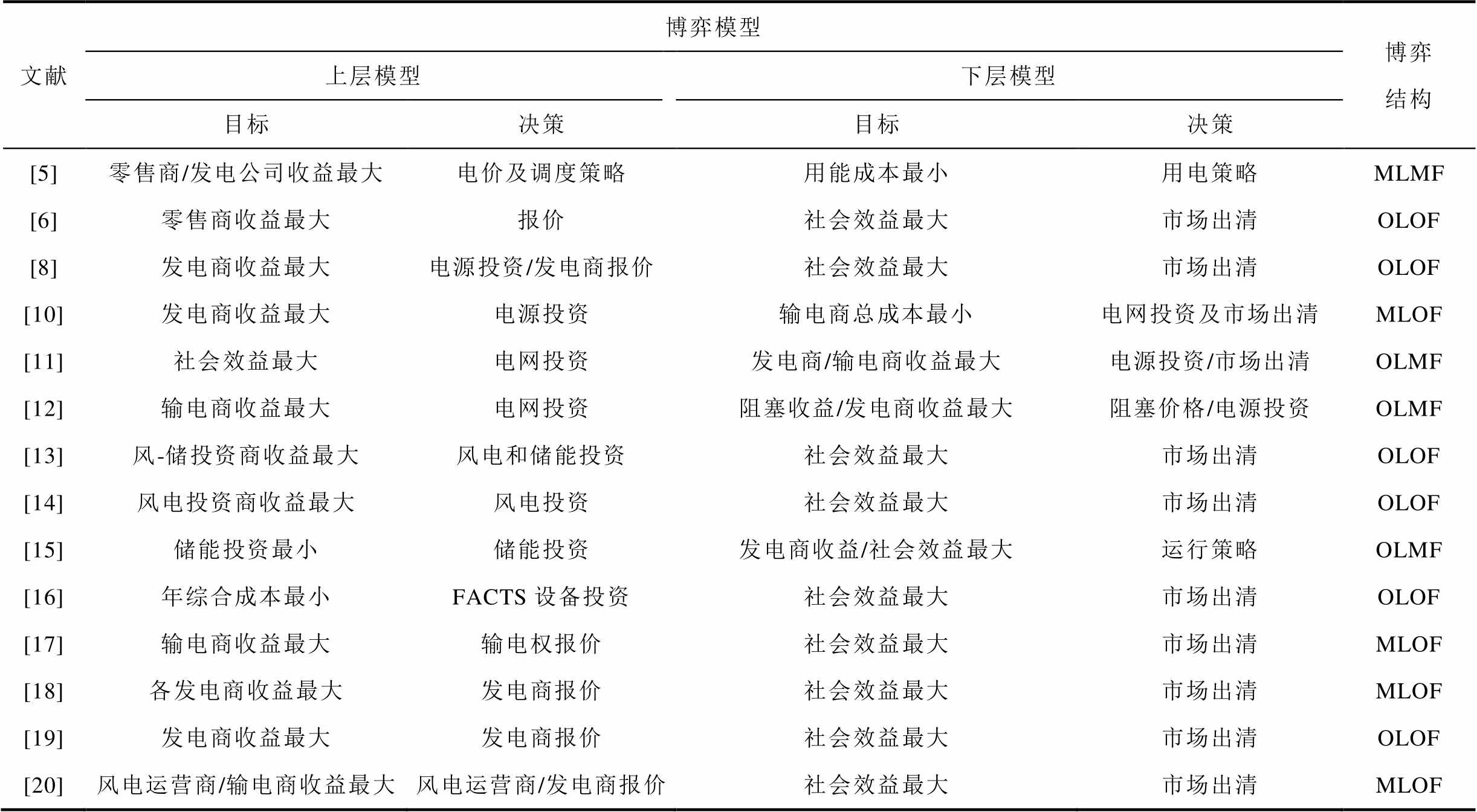
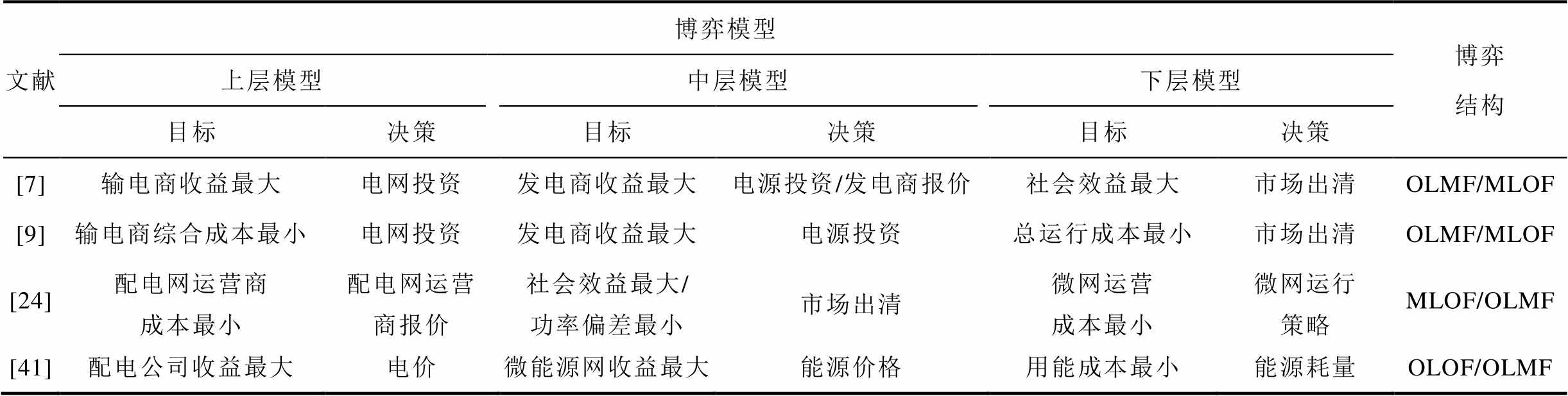
当前Stackelberg博弈在电力市场中的典型应用包括电力设备投资、电力市场定价、需求侧管理资源交易、综合能源服务交易等。针对文献分类及博弈特点,附表1和附表2进行了总结。本节将关注Stackelberg博弈在上述领域的研究内容及成果。
2.1 电力市场环境下的设备投资
在源网投资方面,发电商以最大化收益进行投资。而输电网由于具有天然的垄断特性,其归属问题分为两类:①私人投资,属于输电商范畴,实现自身收益最大化;②国家投资并持有,实现社会效益最大化。但是,无论上述何种类型,发/输电商及ISO会将形成Stackelberg博弈。其中,发/输电商作为领导者进行投资决策、报价等。ISO则在观察到规划方案等策略后,以社会效益最大化进行市场出清,得到节点边际电价以供发电商等测算收益。文献[8]在电源投资和报价中利用场景表征竞争对手策略,结果显示Stackelberg博弈模型能够有效地模拟电源投资的市场结构。文献[9]建立了具有主从递阶结构的三层源网博弈规划模型,上层电网投资与中层电源投资形成OLMF结构,电源投资与下层市场出清形成MLOF结构,算例结果验证了所提方法能够有效地适用于大型电力系统的网源协调规划。文献[10]分别研究了主动和被动源网博弈规划方法,结果表明电源和输电网投资次序会影响投资者收益。文献[11]和文献[12]分别研究了输电网与传统电源、风电场投资的博弈问题。
在可再生能源投资方面,文献[13]研究了风电场和储能设备的投资问题,结果表明受担保合约的激励,投资者会倾向于增加风-储系统,以提高自身收益。文献[14]考虑电力市场环境下风电场的投资问题,结果显示通过控制网络的拓扑结构能有效促进风电消纳,降低弃能。
在其他投资方面,针对可再生能源并网比例提高时电价剧烈波动的问题,文献[15]提出了用于平抑节点边际电价波动的储能投资方法,结果显示调节性储能比策略性储能在平抑电价波动方面更有优势。文献[16]研究了市场环境下柔性交流传输设备(Flexible Alternative Current Transmission System, FACTS)的投资与可再生能源消纳问题。
2.2 电力市场定价
在市场定价方面,不同发电商会考虑自身利益,相互之间形成竞争关系。而由于发电商自身规模与占据的市场地位不同,会存在处于领导者地位的发电商和作为跟随者的发电商。此外,考虑输电商收取过网费、ISO机构在市场出清时对社会效益的追求与发电商竞价之间的矛盾等问题,也会构成电力市场定价的Stackelberg博弈问题。
在电力批发市场定价方面,文献[17]研究了金融输电权定价博弈问题,结果显示故障约束对某些参与者有利。文献[18-19]分别研究了单时段和多时段的竞价问题,并且在多时段竞价中考虑了旋转备用等约束。文献[20]提出了日前和实时寡头市场中风力发电商在交易中的竞价方法,文中使用了机组组合对市场进行出清,通过对比风电运营商是否参与市场定价,得到了风电自身具备市场力,能够影响日前和实时市场电价的结论。文献[21]研究了水力发电商竞价策略问题,上层各发电公司以自身利益最大化为目标进行报价,下层则由ISO统一出清,决定成交价格。
在零售市场定价方面,文献[23]研究了虚拟电厂间的竞价博弈问题。文献[24]考虑零售公司作为连接发电商、用户及微电网群的纽带,建立了多层竞价框架,既包括输电网层面的发电商与零售商竞价问题,又包括配电网层面零售商与微电网群之间的博弈竞争,结果显示微电网可以为输电系统的实时电力平衡提供辅助服务并实现互利互惠。针对主动配电网中微电网群参与市场竞争的问题,文献[25]建立了多微电网群竞价策略的优化问题。
在无功辅助服务定价方面,文献[27]将Stackelberg博弈用于研究无功辅助服务的市场机制问题,结果表明所提方法能够有效保证系统电压幅值不出现大范围波动,在电力系统故障时仍然能够保证无功需求得到有效满足并且不会造成无功价格的剧烈波动。
2.3 需求侧管理资源交易
分布式电源、电动汽车、可中断负荷等灵活性资源作为实现需求侧管理的重要手段,使得电力市场的参与者甚至下沉到了个体层面,传统的电力消费者开始扮演既能提供产品又能消纳电力的产消者角色。当前研究的典型结构中,上层领导者包括配电零售商、需求侧管理聚合商、虚拟电厂、微电网等,将实时电价、需求侧管理资源价目表、调度运行策略等传递给下层。跟随者包括配电网运营商(Distributed System Operator, DSO)、灵活性资源聚合商/个体、分布式电源供应商等,其依据领导者的策略做出响应,提供边际出清价格、资源交易规模等。
在基于实时电价的经济政策激励型需求侧管理资源交易方面,文献[6]针对电力零售商采用实时电价制定需求侧响应策略的问题,提出将零售商分为领头型和尾随型,分别作为领导者和跟随者,结果表明Stackelberg博弈方法更符合智能电网对需求侧管理实时和持续能量平衡的要求。文献[28]将Stackelberg博弈应用于配电网需求侧响应资源定价问题中,配电零售商为需求侧管理聚合商制定电力交易量和实时价格,下层为需求侧管理聚合商依据交易价格制定用电策略。
在虚拟电厂需求侧管理资源交易方面,文献[29]研究了虚拟电厂与灵活性负荷之间的博弈问题。文献[30]研究了Stackelberg博弈在虚拟电厂日前能量调度管理中的应用,其中拥有热电机组和可中断负荷的产消者作为上层领导者,制定内部交易价格及高级产消者聚合商的运行策略,而下层拥有可再生能源和可平移负荷的产消者聚合商则根据上层价格信号制定可再生能源出力调度策略,结果显示所提方法能够实现虚拟电厂中产消者的共赢。
在配电网及微电网需求侧管理资源交易方面,文献[31]考虑各零售商的综合运行成本及配电网运营商组织的市场出清,针对含有分布式电源和可中断负荷参与零售市场交易的问题进行了研究,结果表明配电公司可以利用分布式电源和可中断负荷有效地降低运行费用和损耗。文献[32]考虑智能电网中需求侧管理的问题,其中零售商制定电力资源交易价目表,各需求侧管理个体(产消者)根据交易价目表决定各自的充放电策略、可控负荷运行策略等,结果表明所提Stackelberg博弈模型转换为二次型约束的二次规划问题同样具有很好的求解效率。现有需求侧管理的双层报价策略模型中,通常假设零售商已知批发市场电价,文献[33]指出该假设并不符合实际,进而提出了基于Stackelberg博弈的需求侧管理资源报价策略,结果表明通过促使零售商在批发市场低电价时刻购买更多电量,减少高电价时刻的购电量,会降低零售商的购电总成本。文献[34]将微电网视为产消者,研究了其在日前-日内能量管理中与配电网的灵活互动问题,结果显示基于Stackelberg博弈的日前-日内能量管理策略能够充分发挥柔性多状态开关对潮流的灵活调节作用,降低系统网损和电压偏差。文献[35]研究了微电网群通过优化自身灵活性资源运行策略来获得收益的问题,结果表明所提Stackelberg博弈方法能有效降低微电网群运行成本,提升分布式电源利用效率。
在社区住宅及电动汽车需求侧管理资源交易方面,文献[36]利用Stackelberg博弈研究了住宅侧电力需求响应的问题。文献[37]将Stackelberg博弈应用于社区级电网的能量管理。其中,上层为供应商根据产消者的需求制定交易价目表,下层为产消者考虑最坏净负荷场景制定运行策略,结果显示,竞价机制有助于促进产消者参与需求侧响应,提高整个系统综合效益。文献[38-40]研究了电动汽车作为灵活性移动储能在电力交易中的收益问题及对能量管理的影响。
2.4 综合能源服务交易
综合能源系统涉及电、热、冷、气等多种用能形式,利益主体更加多元化,占据的市场地位差别较大,并且不同能源的市场结构具有差异性。不同种类的能源供应商作为上层领导者提交报价及交易量,以决策各类能源价格、设备运行策略等为目的市场出清作为下层跟随者,构成Stackelberg博弈问题。
在用户级综合能源交易方面,文献[41]考虑了“供电公司-微能源网-用户”之间的能源交易,提出了微能源网能量管理优化方法,结果表明Stackelberg博弈模型不仅能够优化微能源网的能量管理,同时也兼顾了用户的主动性和用能体验。文献[42]针对中小工业园区系统能量失衡及盈利模式单一的问题,提出了三阶段博弈框架下的氢储能优化配置方法,结果表明,氢储能的配置能够有效提升运营商收益。文献[43]研究了短期市场中“电-热-水”在Energy Hub中的优化调度问题,结果表明系统阻塞能够为生产者提供更高的收益,但是阻塞线路对收益的影响与其连接的具体母线相关。文献[44]研究了电力零售商与商业楼宇用能之间的博弈,零售商提供电价,楼宇用户观察到零售电价后调整用电策略,结果表明对含有较低比例需求侧响应资源的楼宇,增加对电价灵敏度较高的暖通空调比向系统售电的收益更高。文献[45]研究了在开放市场环境下的社区综合能源系统协同优化运行方法,结果表明所提模型能提高参与者收益。
在区域级综合能源交易方面,文献[46]基于常数替代弹性效用函数,提出了热电交易的博弈框架,热力和电力供应商相互竞争并由交易中心决定出清价格,而消费者受预算制约,考虑出清中电与热力价格,决策购电/热规模,结果表明消费者的决策行为与效用函数紧密相关,且差异较大。
在跨区级综合能源交易方面,文献[47]考虑电力和天然气系统的优化运行,在电力系统最优经济调度中考虑电转气设备,作为下层天然气系统的气源,而天然气系统在优化运行时考虑上层燃气机组的用气需求,作为电力系统燃料来源,结果显示加入电转气设备能够有效提高风电的消纳水平。
3 Stackelberg博弈模型的转换与求解
3.1 Stackelberg博弈模型转换
Stackelberg博弈问题的求解可以利用模型转换将下层问题以约束集的形式添加到上层优化中,从而避免问题嵌套。常用转换方法有三类。
1)构造KKT条件
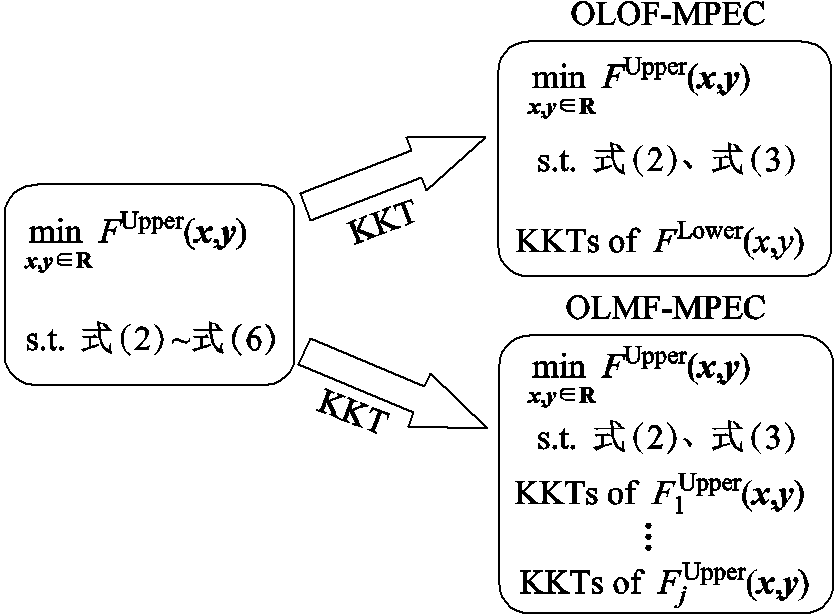
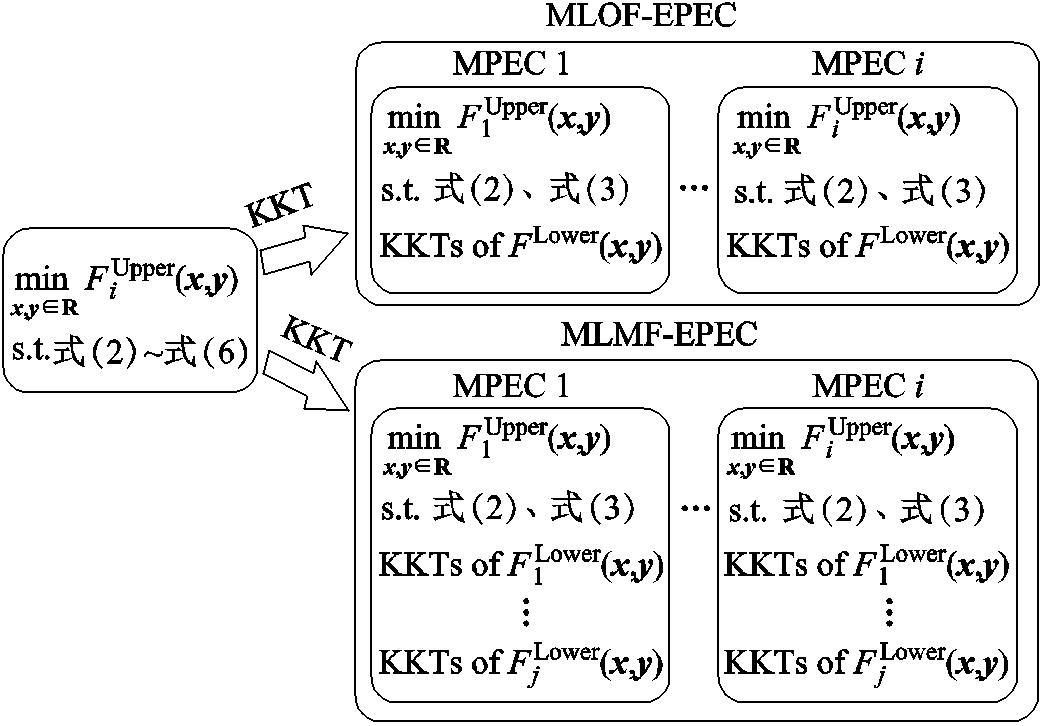
现有Stackelberg博弈在电力市场应用中,下层跟随者问题通常是具有含参的凸优化结构,可以利用KKT(Karush-Kuhn-Tucker)条件替代。由于构造KKT条件时会形成互补约束,因此,Stackelberg博弈模型经过其转换后又被称为含均衡约束的数学优化(Mathematical Programming with Equilibrium Constraints, MPEC)或者EPEC,转换后的结构关系分别如图1和图2所示。其中,OLOF和OLMF结构的Stackelberg博弈会形成MPEC问题,而MLOF和MLMF结构的Stackelberg博弈则会形成EPEC问题。
问题转换后,为了提高求解效率,通常使用大M法对互补约束进行松弛,此时会涉及M取值问题。由于拉格朗日乘子的取值难以预估,故当M取值不合适时,可能会得到局部均衡点,甚至造成问题无可行解。为确定合适数值,常用方法有分析法和试错法[10]。其中分析法对于小规模系统效果较好,但大规模系统难以找到M取值的有效边界;试错法虽然可用于大系统,但文献[53]通过算例指出,该方法容易得到较差的均衡解。因此,利用KKT条件转换时,M取值范围的选取仍然是一个值得深入研究的问题。
2)对偶转换
当下层问题满足强对偶性质时,可以利用对偶理论将其转换为上层问题的约束条件。例如,文献[54]通过对偶转换将下层问题以约束形式添加到各上层优化问题中,形成EPEC结构。但是该方法可能会使转换后的问题出现双线性项,模型呈现非凸特性,需要进一步线性化等操作。文献[55]在考虑输电网投资的双层Stackelberg博弈问题中,将下层市场出清问题以对偶约束和强对偶条件表征为上层问题的约束集,进而转换为单层优化问题。
3)枚举法
在某些投资博弈问题中,由于下层问题中存在0-1变量,或者下层转换到上层时新引入了0-1变量,无法使用KKT或者对偶理论。部分文献为了方便对模型转换和求解,通过枚举部分0-1量,构造混合整数线性约束(Mixed Integer Linear Constraints, MILCs),将原优化问题转换为约束条件,通过同时求解所有问题的MILCs,得到最终的Stackelberg均衡解。文献[10]枚举了参与者的投资策略,将其收益问题转换为MILCs约束集形式,通过构造新的优化问题进行求解。文献[16,19]则由于下层问题本身含有0-1变量,通过枚举将其转换为线性约束,利用KKT构造了MPEC问题进行求解。通过枚举构造约束的方法,仅当变量较少时有效,当变量增多时,无法枚举所有可能的组合,限制了该方法的进一步应用。
3.2 Stackelberg博弈模型求解
Stackelberg博弈模型常用的求解方法包括对角化法、驻点法和人工智能方法。其中,对角化和人工智能方法通常不需要对模型进行转换,而驻点法用于求解经转换后形成的MPEC或者EPEC结构问题。
1)对角化法
对角化方法,又称为不动点迭代法。不同利益主体交替做出决策,每次决策后会公布结果,其他参与者以此为依据做出决策,问题最终收敛于均衡点。该方法不需要对原模型进行转换,其求解过程与Stackelberg博弈的物理含义相对应,便于对博弈过程的理解。文献[17,20]利用对角化方法分别对金融输电权和发电商多时段竞价问题进行求解。文献[56]提出双层源网动态博弈规划模型,上层包含发电商、输电商等多个领导者,构造了EPEC结构,使用对角化方法进行迭代求解。由于该方法属于迭代求解,目前收敛性难以保证,且求解速度慢,当参与者较多时,如存在多个领导者或者跟随者时,求解效率十分低下,但其可以作为后校验方法或其他方法的参照,判断结果是否为最优均衡点。
2)驻点法
驻点法是通过构造原问题的KKT条件进行求解。对于仅含单个领导者的问题,可以将下层问题用KKT代替,作为上层问题的约束条件,从而得到MPEC问题进行求解。如文献[5]针对零售市场定价与调度的Stackelberg博弈问题,采用驻点法进行求解。对于含多个领导者的问题,由于EPEC可以看成同时考虑多个MPEC的问题。那么,一个简单的思路就是收集所有问题的KKT条件,这种将所有MPEC问题同时取KKT的求解方法又称为ALL KKT驻点法[5]。由于ALL KKT驻点法最终会形成约束集,为得到适应不同目标的均衡解,文献[57]分别以生产者利益之和最大和总社会效益最大为目标,构造了新的优化问题进行求解。
驻点法不需要迭代,通过对模型转换,能够一次求得博弈问题的所有均衡解,但需要求取问题的KKT最优性条件或进行对偶转换。即便对于凸优化结构的问题,仍然可能存在均衡解不唯一的情况;若转换后为非凸问题,则无法保证得到最优均衡解,且同样可能存在多解的问题。因此,驻点法存在求得的最终解是否为Stackelberg最优均衡点、局部最优均衡点或者鞍点的问题。在求得最终结果后,通常需要利用对角化方法进行后校验。
3)人工智能法
近些年,人工智能技术得到了发展。其中,启发式智能算法和强化学习算法具有很强的通用性,并且不需要对原问题进行转换。文献[58]利用改进粒子群算法对天然气与电力联合系统的双层Stackelberg投资博弈问题进行了求解。文献[59]利用深度迁移强化学习算法对实时供需互动的Stackelberg博弈问题进行了求解,同时也对比了遗传、粒子群等智能算法的效果。这类算法存在迭代次数多,收敛性及解的质量无法保证等缺点,尤其当问题规模增大时,求解效率大幅下降。但是这类算法可以快速得到可行解,为数学优化方法提供高质量初始解。
对上述三类求解方法的对比见表2。总体来看,对角化法和人工智能法在求解Stackelberg博弈问题中各项特征比较接近,但现有人工智能方法在求解加速策略方面更具优势。而驻点法只能在跟随者问题不含整型变量时使用,限制了其应用范围。对角化法在三种求解方法中效率最低,但由于可能存在多个均衡解的情况,驻点法和人工智能法需要借鉴对角化法的思路,对求得的均衡解进行后校验。但当Stackelberg博弈中领导者和跟随者数量增多时,上述算法的性能都会大打折扣,未来在更高效的加速策略(如分布式)等方面仍然有较大的改进空间。
表2 Stackelberg博弈求解方法对比
Tab.2 Comparison of solution methods of Stackelberg game

对角化法驻点法人工智能法 对等转换不需要需要不需要 加速策略无有有 适用范围无特殊要求跟随者问题不含整型变量无特殊要求 收敛问题存在不存在存在
4 仍然面临的关键问题
4.1 面向高比例可再生能源系统的市场出清
市场出清是电力市场中的基础环节,也是Stackelberg博弈中各利益主体测算自身收益的基础。现有市场出清理论以化石燃料发电机运行成本最小化为目标,或考虑非间歇性可再生能源机组和电力用户申报的电力电量及价格,以最小化生产者剩余为目标,构造市场出清问题。而未来面向高比例可再生能源系统,电网供电主体将不再是传统燃料电厂,考虑可再生能源自身出力特性,现有节点边际电价理论能否继续指导含高比例可再生能源电力系统的市场出清,将会有很大疑问。因此,基于随机/鲁棒优化理论提出适应高比例可再生能源电力系统的节点边际电价算法,对促进市场公平,提高整体社会效益具有重要作用。
4.2 市场非主要参与者的收益
以储能等为代表的的市场非主要参与者逐渐增多,其具有体量小、种类繁多的特点,不具有参与市场定价的能力,被动接受市场出清价格,这些市场参与者在考虑收益时,必须将本地发电商的竞价等问题考虑在内,进而采取使自身利益最大化的投资和运行策略。以储能为例,可以从以下两个角度考虑自身收益问题:①储能投资商能获得发电商投资、报价信息,则储能投资商、发电商、ISO/DSO之间形成Stackelberg博弈结构,发电商为领导者,储能投资商为跟随者;②储能投资商无法获得发电商信息,则储能投资商与发电商形成Nash博弈,进而与ISO/DSO形成Stackelberg博弈。因此,不具备市场定价能力的参与者可以根据上述两种情况,选择合适的模型评估自身收益,实现利益最大化。
4.3 投资收益与风险衡量
电力市场化改革逐步推进,可再生能源占比不断提高,除了源、荷的随机性、间歇性、波动性带来的弃能和切负荷等运行风险外,市场参与者投资计划、报价方式、生产策略等主观因素使得电力系统面临更加复杂的投资收益风险。如何在Stackelberg博弈模型中考虑领导者与跟随者所面临的风险因素,并对其量化建模,提出计及投资者收益风险的Stackelberg博弈模型,通过协调不同利益主体的投资、运行策略,以达到提高投资效益,降低潜在风险损失,促进可再生能源消纳的目的。
4.4 综合能源投资/竞价交易
综合能源系统包含电、冷、热、气,不同能源之间的转换使得综合能源系统中利益主体更加复杂。在横向对比上,不同能源公司形成了Nash博弈,在纵向上,同一类型能源公司又面临投资收益与市场出清形成的Stackelberg博弈以及各自市场中处于不同地位的公司之间形成的博弈问题。综合能源系统涉及多市场出清问题,属于典型的MLMF结构。虽然当前综合能源得到了广泛认可,发展步伐加快,但对应的综合能源市场建设却远远落后其发展,导致商业模式不清晰,收益难以预测。亟需结合Stackelberg博弈提出多市场联合出清等方法用以研究综合能源投资/竞价交易的问题。
4.5 含不确定因素的Stackelberg博弈建模与求解
从问题结构来看,鲁棒优化与OLOF形式的Stackelberg博弈在结构上具有相同特点,决策都是依次完成。跟随者能观察到领导者策略且两者之间决策会相互影响。实际上,文献[5]已经指出,鲁棒调度属于电力系统中典型的主从博弈问题。未来高比例风电、太阳能等间歇性可再生能源接入,电动汽车等灵活性负荷规模增大,使得电力系统不确定性大大增加。虽然现有文献将随机优化引入Stackelberg博弈模型中处理不确定因素,但是否可以引入鲁棒优化以得到更加鲁棒的博弈策略,仍值得深入研究。而引入鲁棒不确定集合后,原有的确定性市场出清将会变成双层优化问题,最下层已经是一个Bilevel结构了,原有两层Stackelberg博弈模型OLOF或OLMF将会呈现出混合整数双层规划的特点。原有MLOF和MLMF结构可能无法直接求解,只能通过对角化方法进行迭代,大大增加了问题的求解难度。因此,如何结合鲁棒优化,以及如何对含鲁棒不确定集合的Stackelberg博弈模型进行转换,并从分布式优化等角度提出高效求解方法,值得研究。
5 结论
随着电力市场改革的逐步加深以及现代信息技术的快速发展,市场参与者的规模差异性大且数量急剧增加,典型如发电商、分布式能源电站投资商、负荷聚合商,甚至电动汽车、商业楼宇等都可作为利益主体参与到需求侧管理、系统调峰等市场中。然而,基于市场参与者的体量和规模特征,并不是所有参与者都拥有同样的市场地位和决策能力,有些参与者是直接影响市场出清,而有些则是被动接受市场出清。因此,基于上述市场特征,利用具有主从递阶结构的Stackelberg博弈研究电力市场环境下的规划、竞价、优化运行等具有先天优势,且符合电力市场结构与运行机理。本文系统地阐述了Stackelberg博弈的基本理论及在电力系统中的典型应用,结合实际电力市场的复杂性及其发展趋势,总结了未来亟需解决的几个关键问题。希望本文工作能为复杂环境下具有不同市场地位的各方利益主体构建博弈策略提供参考。
附录 Stackelberg博弈模型对比
附表1 双层Stackelberg博弈在电力市场中的模型结构
App.Tab.1 Mathematical structure of bilevel Stackelberg game in power market
(续)

文献博弈模型博弈结构 上层模型下层模型 目标决策目标决策 [21]水利发电商收益最大水力发电商报价社会效益最大市场出清MLOF [22]分布式发电商收益最大竞标电价/电量购电成本最小市场出清MLOF [23]虚拟电厂运营成本最小分布式电源/负荷电价各参与商效益最大竞标电量OLMF [25]配电网运营商收益最大配电网运营商竞标社会效益最大市场出清MLOF [26]碳排放量最小碳排放税率总发电成本最小机组运行策略OLOF [27]无功购入成本最小市场出清发电商收益最大无功生产策略OLMF [28]配电零售商收益最大需求侧资源价格需求侧资源聚合商收益最大需求侧资源响应策略OLMF [29]虚拟电厂收益最大灵活性负荷响应价目表灵活性负荷收益最大灵活性负荷运行策略OLOF [30]高级产消者收益最大灵活性资源买/售价格产消者聚合商运行成本最小运行策略OLMF [31]零售商成本最小灵活性资源购买策略社会效益最大市场出清MLOF [32]零售商收益最大电价需求侧资源供应个体收益最大运行策略OLMF [33]零售商收益最大电价个体收益最大/社会效益最大运行策略OLMF [34]配网运行成本最小购/售电价微电网收益最大购/售电量OLMF [35]微电网群运营商收益最大购/售电价微电网运营商收益最大购/售电量OLMF [36]需求侧响应聚合商收益最大需求侧响应资源价格需求侧资源供应商用能成本最小需求侧资源响应策略OLMF [37]零售商收益最大电价产消者收益最大产消者运行策略OLMF [38]电动汽车代理商收益最大电价电动汽车收益最大充/放电策略OLOF [39]快充电站收益最大充电价格电动汽车收益最大充电和备用策略OLMF [40]各充电站收益最大充电电价各电动汽车收益最大充电策略MLMF [42]能源系统运营商收益最大购能价格能源/储能服务商收益最大用户聚合商成本最小能量交互策略OLMF [43]能源供应商收益最大能源价格社会效益最大市场出清OLOF [44]零售商收益最大电价购电成本最小用能策略OLOF [45]综合能源供应商收益最大能源/需求响应价格综合能源供应商/负荷聚合商收益最大可中断负荷供应量OLMF [46]电力/热力成本最小电/热价格消费者效益最大电/热消费量MLOF [47]社会效益最大电转气供应量天然气系统购气成本最小天然气供应量OLOF [54]输电商收益最大检修计划/报价社会效益最大市场出清MLOF
附表2 多层Stackelberg博弈在电力市场中的模型结构
App.Tab.2 Mathematical structure of multi-level Stackelberg game in power market
参考文献
[1] 李力行, 苗世洪, 孙丹丹, 等. 多利益主体参与下主动配电网完全信息动态博弈行为[J]. 电工技术学报, 2018, 33(15): 3499-3509.
Li Lixing, Miao Shihong, Sun Dandan, et al. Dynamic games of complete information in active distribution network with multi-stakeholder participation[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3499-3509.
[2] 刘念, 余星火, 王剑辉, 等. 泛在物联的配用电优化运行:信息物理社会系统的视角[J]. 电力系统自动化, 2020, 44(1): 1-12.
Liu Nian, Yu Xinghuo, Wang Jianhui, et al. Optimal operation of power distribution and consumption system based on ubiquitous internet of things: a cyber-physical-social system perspective[J]. Automation of Electric Power Systems, 2020, 44(1): 1-12.
[3] 郭通, 李永刚, 徐姗姗, 等. 考虑多主体博弈的火电机组灵活性改造规划[J]. 电工技术学报, 2020, 35(11): 170-181.
Guo Tong, Li Yonggang, Xu Shanshan, et al. Planning of flexibility retrofits of thermal power units considering multi-agent game[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 170-181.
[4] 宋依群, 侯志俭, 文福拴, 等. 电力市场三种寡头竞争模型的市场力分析比较[J]. 电网技术, 2003, 27(8): 10-15.
Song Yiqun, Hou Zhijian, Wen Fushuan, et al. Comparison of market power in three oligopoly models of elecetricity market[J]. Power System Technology, 2003, 27(8): 10-15.
[5] 梅生伟, 魏韡. 智能电网环境下主从博弈模型及应用实例[J]. 系统科学与数学, 2014, 34(11): 1331-1344.
Mei Shengwei, Wei Wei. Hierarchal game and its applications in the smart grid[J]. Journal of Systems Science and Mathematical Sciences, 2014, 34(11): 1331-1344.
[6] 代业明, 高岩. 基于智能电网需求侧管理的多零售商实时定价策略[J]. 中国电机工程学报, 2014, 34(25): 4244-4249.
Dai Yeming, Gao Yan. Real-time pricing strategy with multi-retailers based on demand-side management for the smart grid[J]. Proceedings of the CSEE, 2014, 34(25): 4244-4249.
[7] Taheri S, Kazempour J, Seyedshenava S. Transmission expansion in an oligopoly considering generation investment equilibrium[J]. Energy Economics, 2017, 64: 55-62.
[8] Kazempour J, Conejo A, Ruiz C. Strategic generation investment using a complementarity approach[J]. IEEE Transactions on Power Systems, 2011, 26(2): 940-948.
[9] David P, Enzo E, Contreras J. A three-level static MILP model for generation and transmission expansion planning[J]. IEEE Transactions on Power Systems, 2013, 28(1): 202-210.
[10] Yaser T, Mohammad R, Francois R. Sequential coordination of transmission expansion planning with strategic generation investments[J]. IEEE Transactions on Power Systems, 2017, 32(4): 2521-2534.
[11] Isaac-Camilo G, Sonja W, Tomas G. Proactive transmission expansion planning with storage considerations[J]. Energy Strategy Reviews, 2019, 24: 154-165.
[12] Lajos M, Trine K, Afzal S. Transmission and wind investment in a deregulated electricity industry[J]. IEEE Transactions on Power Systems, 2015, 30(3): 1633-1643.
[13] Rafiei S, Mohammadi A. Bi-level model for generation expansion planning with contract pricing of renewable energy in the presence of energy storage[J]. IET Renewable Power Generation, 2019, 13(9): 1544-1553.
[14] Wang Yifan, Liu Shixin, Wang Jianhui, et al. Capacity expansion of wind power in a market environment with topology control[J]. IEEE Transactions on Sustainable Energy, 2019, 10(4): 1834-1843.
[15] Masoumzadeh A, Nekouei E, Alpcan T, et al. Impact of optimal storage allocation on price volatility in energy-only electricity markets[J]. IEEE Transactions on Power Systems, 2018. 33(2): 1903-1914.
[16] Zhang Xiaohu, Shi Di, Wang Zhiwei, et al. Optimal allocation of series facts devices under high penetration of wind power within a market environment[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6206-6217.
[17] Li Tao, Shahidehpour M. Risk-constrained FTR bidding strategy in transmission markets[J]. IEEE Transactions on Power Systems, 2005, 20(2): 1014-1021.
[18] Haghighat H, Seifi H, Kian A. Gaming analysis in joint energy and spinning reserve markets[J]. IEEE Transactions on Power Systems, 2007, 22(4): 2074-2085.
[19] Fampa M, Barroso L, Candal D, et al. Bilevel optimization applied to strategic pricing in competitive electricity markets[J]. Computational Optimization and Applications, 2008, 39(2): 121-142.
[20] Shafie-Khah M, Heydarian-Forushani E, Golshan M, et al. Strategic offering for a price-maker wind power producer in oligopoly markets considering demand response exchange[J]. IEEE Transactions on Industrial Informatics, 2015, 11(6): 1542-1553.
[21] Cruz M, Finardi E, Matos V, et al. Strategic bidding for price-maker producers in predominantly hydroelectric systems[J]. Electric Power Systems Research, 2016, 140: 435-444.
[22] 窦春霞, 贾星蓓, 李恒. 基于多智能体的微电网中分布式发电的市场博弈竞标发电[J]. 电网技术, 2016, 40(2): 579-586.
Dou Chunxia, Jia Xingbei, Li Heng. Multi-agent-system-based market bidding strategy for distributed generation in microgrid[J]. Power System Technology, 2016, 40(2): 579-586.
[23] 方燕琼, 甘霖, 艾芊, 等. 基于主从博弈的虚拟电厂双层竞标策略[J]. 电力系统自动化, 2017, 41(14): 61-69.
Fang Yanqiong, Gan Lin, Ai Qian, et al. Stackelberg game based bi-level bidding strategy for virtual power plant[J]. Automation of Electric Power Systems, 2017, 41(14): 61-69.
[24] Du Yan, Li Fangxing. A hierarchical real-time balancing market considering multi-microgrids with distributed sustainable resources[J]. IEEE Transactions on Sustainable Energy, 2020, 11(1): 72-83.
[25] Naebi A, SeyedShenava S, Contreras J, et al. EPEC approach for finding optimal day-ahead bidding strategy equilibria of multi-microgrids in active distribution networks[J]. International Journal of Electrical Power & Energy Systems, 2020, 117: 105702.
[26] 徐意婷, 艾芊. 考虑碳税策略的微网与常规机组协同运行[J]. 电力系统自动化, 2016, 40(14): 25-32.
Xu Yiting, Ai Qian. Coordinated operation of microgrid and conventional generators considering carbon tax strategy[J]. Automation of Electric Power Systems, 2016, 40(14): 25-32.
[27] Jay D, Swarup S. Game theoretical approach to novel reactive power ancillary service market mechanism[J]. IEEE Transactions on Power Systems, 2021, 36(2): 1298-1308.
[28] Feng Changsen, Li Zhiyi, Shahidehpour M, et al. Stackelberg game based transactive pricing for optimal demand response in power distribution systems[J]. International Journal of Electrical Power & Energy Systems, 2020, 118: 105764.
[29] Wu Hongbin, Liu Xin, Ye Bin, et al. Optimal dispatch and bidding strategy of a virtual power plant based on a Stackelberg game[J]. IET Generation, Transmission & Distribution, 2020, 14(4): 552-563.
[30] Yin Shuangrui, Ai Qian, Li Zhouyu, et al. Energy management for aggregate prosumers in a virtual power plant: a robust Stackelberg game approach[J]. International Journal of Electrical Power & Energy Systems, 2020, 117: 105605.
[31] Haghighat H, Kennedy S. A bilevel approach to operational decision making of a distribution company in competitive environments[J]. IEEE Transactions on Power Systems, 2012, 27(4): 1797-1807.
[32] Kovács A. Bilevel programming approach to demand response management with day-ahead tariff[J]. Journal of Modern Power Systems and Clean Energy, 2019, 7(6): 1632-1643.
[33] Qiu Dawei, Papadaskalopoulos D, Ye Yujian, et al. Investigating the effects of demand flexibility on electricity retailers’ business through a tri-level optimisation model[J]. IET Generation, Transmission & Distribution, 2020, 14(9): 1739-1750.
[34] 孙峰洲, 马骏超, 于淼, 等. 含多端柔性多状态开关的主动配电网日前–日内协调能量管理方法[J]. 中国电机工程学报, 2020, 40(3): 778-790.
Sun Fengzhou, Ma Junchao, Yu Miao, et al. A day-ahead and intraday coordinated energy management method for active distribution networks based on multi-terminal flexible distribution switch[J]. Proceedings of the CSEE, 2020, 40(3): 778-790.
[35] 芮涛, 李国丽, 胡存刚, 等. 考虑电价机制的微电网群主从博弈优化方法[J]. 中国电机工程学报, 2020, 40(8): 2535-2545.
Rui Tao, Li Guoli, Hu Cungang, et al. Stackelberg game optimization method for microgrid cluster considering electricity price mechanism[J]. Proceedings of the CSEE, 2020, 40(8): 2535-2545.
[36] Bruninx K, Pandzic H, Cadre L, et al. On the interaction between aggregators, electricity markets and residential demand response providers[J]. IEEE Transactions on Power Systems, 2020, 35(2): 840-853.
[37] Qiu Haifeng, Gu Wei, Wang Lu, et al. Trilayer stackelberg game approach for robustly power management in community grids[J/OL]. IEEE Transactions on Industrial Informatics: 1-10[2021-1-23]. https://ieeexplore. ieee. org/stamp/stamp. jsp?tp= &arnumber=9165150.
[38] 杨健维, 黄宇, 王湘, 等. 基于动态概率潮流的住宅区电动汽车代理商定价策略[J]. 中国电机工程学报, 2016, 36(21): 5822-5830.
Yang Jianwei, Huang Yu, Wang Xiang, et al. A pricing strategy for electric vehicle aggregator in residential area based on dynamic probability power flow[J]. Proceedings of the CSEE, 2016, 36(21): 5822-5830.
[39] Zhao Tianyang, Li Yuanzheng, Pan Xuewei, et al. Real-time optimal energy and reserve management of electric vehicle fast charging station: hierarchical game approach[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 5357-5370.
[40] 刘洪, 阎峻, 葛少云, 等. 考虑多车交互影响的电动汽车与快充站动态响应[J]. 中国电机工程学报, 2020, 40(20): 6455-6468.
Liu Hong, Yan Jun, Ge Shaoyun, et al. Dynamic response of electric vehicle and fast charging stations considering multi-vehicle interaction[J]. Proceedings of the CSEE, 2020, 40(20): 6455-6468.
[41] 林凯骏, 吴俊勇, 刘迪, 等. 基于双层Stackelberg博弈的微能源网能量管理优化[J]. 电网技术, 2019, 43(3): 973-983.
Lin Kaijun, Wu Junyong, Liu Di, et al. Energy management optimization of micro energy grid based on hierarchical Stackelberg game theory[J]. Power System Technology, 2019, 43(3): 973-983.
[42] 熊宇峰, 司杨, 郑天文, 等. 基于主从博弈的工业园区综合能源系统氢储能优化配置[J]. 电工技术学报, 2021, 36(3): 507-516.
Xiong Yufeng, Si Yang, Zheng Tianwen, et al. Optimal configuration of hydrogen storage in industrial park integrated energy system based on stackelberg game[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 507-516.
[43] Kavousi-Fard A, Su Wencong, Jin Tao, et al. Two-stage stochastic operation framework for optimal management of the water–energy–hub[J]. IET Generation, Transmission & Distribution, 2019, 13(22): 5218-5228.
[44] Yoon A, Kim Y, Moon S. Optimal retail pricing for demand response of HVAC systems in commercial buildings considering distribution network voltages[J]. IEEE Transactions on Smart Grid, 2019, 10(5): 5492-5505.
[45] 王海洋, 李珂, 张承慧, 等. 基于主从博弈的社区综合能源系统分布式协同优化运行策略[J]. 中国电机工程学报, 2020, 17(5): 5435-5444.
Wang Haiyang, Li Ke, Zhang Chenghui, et al. Distributed coordinative optimal operation of community integrated energy system based on Stackelberg game[J]. Proceedings of the CSEE, 2020, 17(5): 5435-5444.
[46] 陈玥, 魏韡, 刘锋, 等. 基于CES型效用函数的热-电市场消费者最优决策[J]. 电力系统自动化, 2018, 42(13): 118-126.
Chen Yue, Wei Wei, Liu Feng, et al. CES utility function based consumer optimal decision making in heat-power market[J]. Automation of Electric Power Systems, 2018, 42(13): 118-126.
[47] Li Guoqing, Zhang Rufeng, Jiang Tao, et al. Security-constrained bi-level economic dispatch model for integrated natural gas and electricity systems considering wind power and power-to-gas process[J]. Applied Energy, 2017, 194: 696-704.
[48] 卢强, 陈来军, 梅生伟. 博弈论在电力系统中典型应用及若干展望[J]. 中国电机工程学报, 2014, 34(29): 5009-5017.
Lu Qiang, Chen Laijun, Mei Shengwei. Typical applications and prospects of game theory in power system[J]. Proceedings of the CSEE, 2014, 34(29): 5009-5017.
[49] 唐博文, 孙元章, 徐箭, 等. 售电公司参与下的工业园区局域电网建设项目新模式探讨[J]. 电力系统自动化, 2020, 44(19): 185-193.
Tang Bowen, Sun Yuanzhang, Xu Jian, et al. Discussion on new mode of construction project for regional power grid in industrial park with participation of electricity retailers[J]. Transactions of China Electrotechnical Society, 2020, 44(19): 185-193.
[50] 杨丽君, 曹玉洁, 张子振. 基于博弈思想的主动配电网故障灵活分层恢复策略[J]. 电工技术学报, 2018, 33(6): 1410-1421.
Yang Lijun, Cao Yujie, Zhang Zizhen. A flexible layered service restoration strategy for active distribution network based on game theory[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1410-1421.
[51] 刘念, 赵璟, 王杰, 等. 基于合作博弈论的光伏微电网群交易模型[J]. 电工技术学报, 2018, 33(8): 1903-1910.
Liu Nian, Zhao Jing, Wang Jie, et al. A trading model of PV microgrid cluster based on cooperative game theory[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1903-1910.
[52] 叶畅, 苗世洪, 刘昊, 等. 联盟链框架下主动配电网电力交易主体合作演化策略[J]. 电工技术学报, 2020, 35(8): 141-155.
Ye Chang, Miao Shihong, Liu Hao, et al. Cooperative evolutionary game strategy for electricity trading stakeholders in active distribution network under consortium blockchain framework[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 141-155.
[53] Salvador P, Morales J. Solving linear bilevel problems using Big-Ms: not all that glitters is gold[J]. IEEE Transactions on Power Systems, 2019, 34(3): 2469-2471.
[54] Pandzic H, Conejo A, Kuzle I. An EPEC approach to the yearly maintenance scheduling of generating units[J]. IEEE Transactions on Power Systems, 2013, 28(2): 922-930.
[55] Garces L, Conejo A, Garcia-Bertrand R, et al. A bilevel approach to transmission expansion planning within a market environment[J]. IEEE Transactions on Power Systems, 2009, 24(3): 1513-1522.
[56] Tohid A, Saeed Z, Ehsan P, et al. Coordinated planning of generation capacity and transmission network expansion: a game approach with multi-leader-follower[J]. International Transaction on Electrical Energy Systems, 2017, 27: e2339.
[57] Ruiz C, Conejo A, Yves S. Equilibria in an oligopolistic electricity pool with stepwise offer curves[J]. IEEE Transactions on Power Systems, 2012, 27(2): 752-761.
[58] Zeng Qing, Zhang Baohua, Chen Zhe, et al. A bi-level programming for multistage co-expansion planning of the integrated gas and electricity system[J]. Applied Energy, 2017, 200: 192-203.
[59] 包涛, 张孝顺, 余涛, 等. 反映实时供需互动的Stackelberg博弈模型及其强化学习求解[J]. 中国电机工程学报, 2018, 38(10): 2947-2955.
Bao Tao, Zhang Xiaoshun, Yu Tao, et al. A Stackelberg game model of real-time supply-demand interaction and the solving method via reinforcement learning[J]. Proceedings of the CSEE, 2018, 38(10): 2947-2955.
A State-of-the-Art Review on Stackelberg Game and Its Applications in Power Market
Zhang Heng1 Zhang Shenxi1 Cheng Haozhong1 Zhang Xipeng2 Gu Qingfa3
(1. Key Laboratory of Control of Power Transmission and Conversion of Ministry of Education Shanghai Jiao Tong University Shanghai 200240 China 2. Shanghai Electric Power Company Shibei Power Supply Company Shanghai 200070 China 3. Electric Power Research Institute of State Grid Henan Electric Power Company Zhengzhou 450052 China)
Abstract With increasing penetration of renewables to the electricity grid, commercialization of energy storage technology, diversification of demand side management resources type, and maturity of multi-energy complementation, more and more stakeholders are being progressively introduced into source-grid-load of power systems. However, due to trading volume and market position, the decision-makers have different priorities. The application of Stackelberg game theory, which has master-slave hierarchical structure, was investigated in this manuscript to solve sequential decision-making problems in investment and energy trading under the deregulated environment. Firstly, the mathematical structure of Stackelberg game was described, and it was classified according to the number of players in the master/slave problems; then, the application of Stackelberg game in power market was sorted out, and equivalent transformation skills, the advantages and disadvantages of various solving methods were summarized; finally, the key scientific problems still existing in the application of Stackelberg game in power market were refined. It is hoped that the work can provide a method reference for those stakeholders who participate in sequential decision-making in power market.
Keywords: Game theory, Stackelberg game, sequential game, power market, power system optimization
DOI:10.19595/j.cnki.1000-6753.tces.210663
中图分类号:TM73
作者简介
张 衡 男,1991年生,博士,助理研究员,研究方向为博弈论在电力系统优化规划及经济运行中的应用。E-mail:zhangheng_sjtu@sjtu. edu. cn(通信作者)
张沈习 男,1988年生,博士,副研究员,研究方向为电力系统规划。E-mail:willzsx@sjtu. edu. Cn
上海市青年科技英才扬帆计划资助项目(20YF1418900)。
收稿日期 2021-05-11
改稿日期 2021-08-19
(编辑 赫蕾)

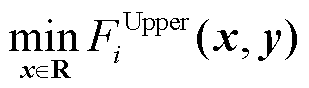 (1)
(1)
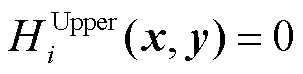 (2)
(2)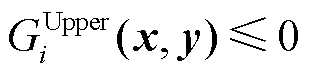 (3)
(3)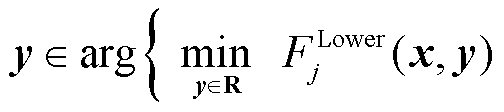 (4)
(4)
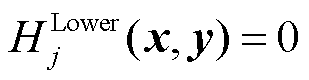 (5)
(5)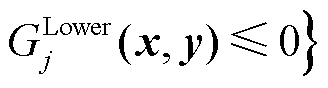 (6)
(6)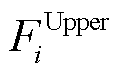 、
、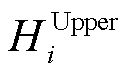 和
和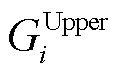 分别为上层优化问题的目标函数、等式约束和不等式约束;
分别为上层优化问题的目标函数、等式约束和不等式约束;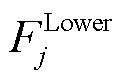 、
、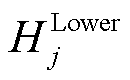 和
和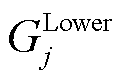 分别为下层优化问题的目标函数、等式约束和不等式约束;i和j分别为领导者和跟随者的数量。
分别为下层优化问题的目标函数、等式约束和不等式约束;i和j分别为领导者和跟随者的数量。