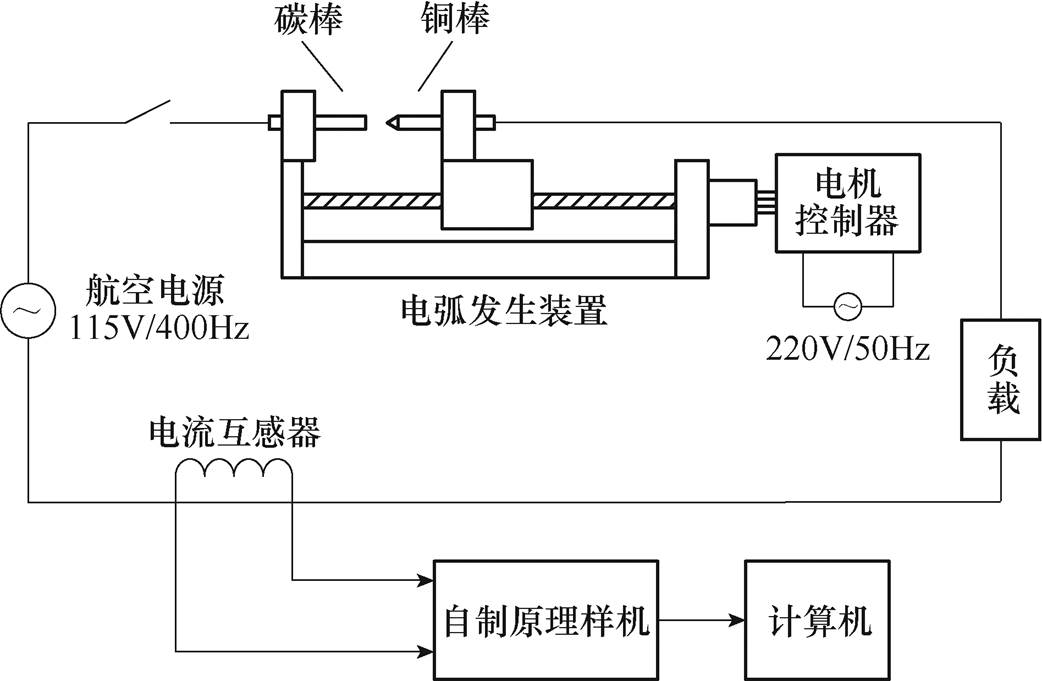
图1 点接触试验电路
Fig.1 Schematic diagram of contact test circuit
摘要 针对时频域分析方法经验模态分解(EMD)在处理电弧信号上存在模态混叠现象,提出一种基于改进经验小波变换(IEWT)多特征融合与极限学习机(ELM)的电弧故障检测方法。该方法首先将电弧电流信号进行IEWT变换,自适应分解为5个经验模态分量(EMFs),提取EMFs的权重能量熵、EMF4的样本熵及EMF1的方均根值作为特征量。在进行数据标准化后,将3个电弧故障特征融合并形成多维特征矩阵,最后通过ELM进行故障识别。在分析中对IEWT和EMD分解进行比较,结果表明,IEWT方法要优于EMD对信号的处理,并且在多特征提取下也避免了单一特征造成的误判,再结合ELM可以准确识别出电弧故障,经试验验证平均准确率为97.85%。
关键词:航空电弧故障 经验小波变换 多特征融合 极限学习机 经验模态分解 时频分析
随着多电/全电飞机的出现,电缆数增多,飞机配电系统更加复杂,线路故障发生的概率也将增加。加上航空电缆大多都是在高温、高振动和高辐射的环境下运行,很容易出现线缆接线松动以及绝缘损坏,这都是极易发生电弧故障的部位。在高温环境下,电弧连续放电产生的高温,即便是燃点很高的绝缘物质也容易被引燃,进而导致火灾甚至爆炸危险发生[1]。由于串联电弧电流值小于正常电流,传统的过电流保护装置不能有效检测,需要额外增加电弧故障检测装置,因此进行航空系统串联电弧故障检测技术研究有着重要意义。
现如今针对串联型电弧故障的检测方法主要分为两大类:一类是根据电弧产生时伴随的弧光、弧声、电磁辐射等物理量进行检测,该方法由于其检测效果与传感器位置有关,不便于配置在线路中,因此常用于开关柜中[2-4];另一类是根据电弧产生时电压电流波形的畸变,通过提取电弧电压电流的时域、频域及时频域特征来进行检测,目前此类方法为国内外学者研究电弧检测的热点方法[5-17]。文献[5]将电流相邻周期相减,结合小波阈值去噪和归一化,提取差信号的幅值进行电弧故障判定。文献[6]通过电压信号相邻峰值和之间的过零点将其分为左右两窗,分别计算窗内的二次方和,设定多个阈值条件来判断电弧故障的产生。时域方法简单易理解,但容易受到外界干扰。为了更深层次地分析电弧的电流电压波形,部分学者在频域方面提取电弧的特征量。文献[7]通过对电流信号进行快速傅里叶变换,提取频谱上1~15kHz范围内幅值和的平均值作为判断电弧故障的依据。文献[8]采用线性调频Z变换分析电流信号低频频谱,并结合多种指标对电弧故障检测。但频域方法是将信号的全部时域信息描述为一个整体,很难确定干扰在时域中的具体位置,这对于分析非线性负载是不利的,提取时频域特征有效克服了这一点。
目前,电弧故障检测的时频域分析方法主要有小波变换[9-10]和经验模态分解(Empirical Mode Decomposition, EMD)[11-13]。文献[9]对电流信号进行小波变换,提取前5层细节系数能量比作为特征量输入到BP神经网络进行故障检测。文献[10]采用差分法对电流信号预处理,利用小波包技术分解重构后转化为灰度图像,并通过灰度-梯度共生矩阵提取特征,最后通过支持向量机进行识别。但小波变换的分解尺度无法随信号本身特点而自适应变化,因此部分学者使用EMD来对信号自适应分解。文献[11]对电弧电流信号进行EMD分解,结合相关性理论提取故障信号的多种无量纲指标并形成多变量判据,使用概率神经网络进行诊断。文献[12-13]都是先对电弧电流信号进行EMD分解,分别选取一个或多个故障特征明显的固有模态函数(Intrinsic Mode Function, IMF)分量,并进行希尔伯特三维时频谱分析。然而,EMD也会出现模态混叠、计算效率低、缺乏完备理论基础等缺点。为此,有部分学者通过加入白噪声进行改进引入集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)[14],EEMD一定程度上缓解了模态混叠问题,但该方法想要得到分解的一致性,需要多次加入白噪声进行分解后取均值,从而又增加了计算量。
针对以上方法的不足,Gilles在2013年提出了一种新的时频域分析方法,即经验小波变换(Empirical Wavelet Transform, EWT),该方法结合了小波的理论框架以及EMD的自适性,在对频谱进行自适应划分后,建立一组正交的小波滤波器组,从而将信号分解为一系列具有紧支撑的经验模态分量(Empirical Mode Functions, EMFs),不但解决了模态混叠问题,而且具有计算量小、分解模态个数少等优点。这种方法目前已被应用于机械故障诊断中[15]。不过传统的EWT频带划分比较粗糙,易于受到噪声污染干扰,本文结合电弧信号特征在EWT基础上进行频带划分改进。为了更加可靠地检测电弧故障,防止单一变量受电弧信号的不稳定性以及随机性影响,提取故障信息的多种特征量作为故障诊断判据已被学者们广泛应用[11, 13, 16]。
本文针对EMD方法易出现模态混叠等问题,采用改进经验小波变换(Improve Empirical Wavelet Transform, IEWT)对电弧信号进行分解处理,分解后又从三个角度对电弧故障特征进行了提取,最后,将提取的融合多特征集输入到极限学习机(Extreme Learning Machine, ELM)中进行识别,试验结果表明,IEWT能有效克服EMD的诸多缺点,并且在多特征融合下故障检测准确率更高,检测方法具有更强的鲁棒性。
参照美国出版的UL 1699标准[18],搭建串联型点接触试验平台,根据美国航空标准SAE AS5692[19]搭建振动试验平台,试验原理及实物如图1~图4所示。点接触试验电弧发生装置由固定的碳棒和可移动的铜棒组成,铜棒置于绝缘木块中,由步进电机控制其前后移动,使铜棒匀速移动,与接触的碳棒分离,这一过程实现电路的通断,从而模拟了电弧故障的产生。振动试验电弧发生装置模拟了飞机在振动环境下,出现线缆接线柱松动而接触不良引发的串联电弧故障。

图1 点接触试验电路
Fig.1 Schematic diagram of contact test circuit
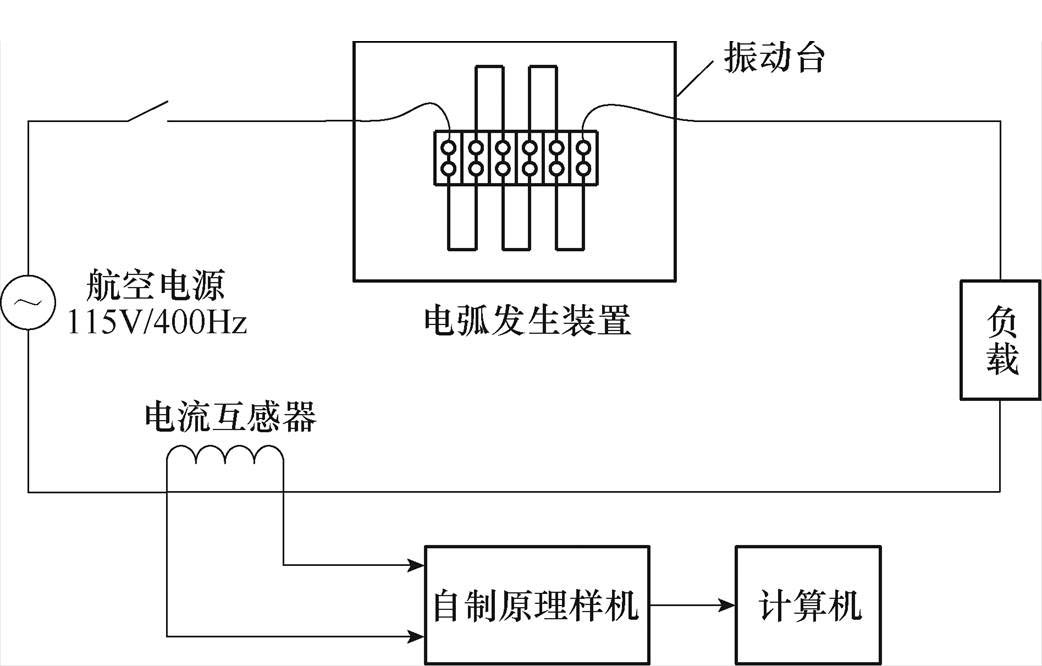
图2 振动试验电路
Fig.2 Schematic diagram of vibration test circuit
试验中选用115V/400Hz航空静变电源作为试验电源,由自制原理样机进行控制,通过ADS8568模块进行数据采集,采样频率为409.6kHz,为了消除部分噪声干扰,采样前设有100kHz的低通滤波器MAX274AENG,使用莱姆公司生产的LA25-NP型电流传感器,传感器副边输出电流最大有效值为25mA,原边输入电流最大有效值量程可以设置为5/6/8/12/25A。

图3 点接触电弧试验平台
Fig.3 Point contact arc test platform

图4 振动电弧试验平台
Fig.4 Vibration arc test platform
进行多次点接触试验和振动试验,获取大量正常工作到电弧故障的电流波形,点接触试验以线性负载纯阻(57.5W)、阻感(57.5W+5mH)、阻容(57.5W+47mF),非线性负载以自耦变压器带负载(1.6W)和自耦变压整流器(Auto Transformer Rectifier Units, ATRU)为例,振动试验以纯阻(115W)和阻感(11.5W+5mH)为例。截取电弧发生时刻的前后各10个周期分别对应图5a~图5e以及图6a、图6b。
从图5、图6可以观察到,发生串联电弧故障时各负载电流波形的幅值均稍有降低。在点接触实验中,纯阻负载和阻容负载的回路电流过零处出现明显的平肩部,而阻感性负载和非线性负载自耦变压器的平肩部并不明显,这是因为其中的感性元件存在储能,从而使电压恢复得快。对于非线性负载ATRU,其内部晶闸管的开断,使波形成阶梯状,正常运行状态下的波形与电弧故障的波形类似,也存在平肩现象,非线性负载波形的特殊性也使得单独通过时域或者频域信息进行电弧检测变得困难。振动试验中,在发生故障时电流波形畸变更为严重,会出现明显的平肩部以及半波缺失情况,但由于会出现完全接通状态,因此也会夹杂着正常周期。
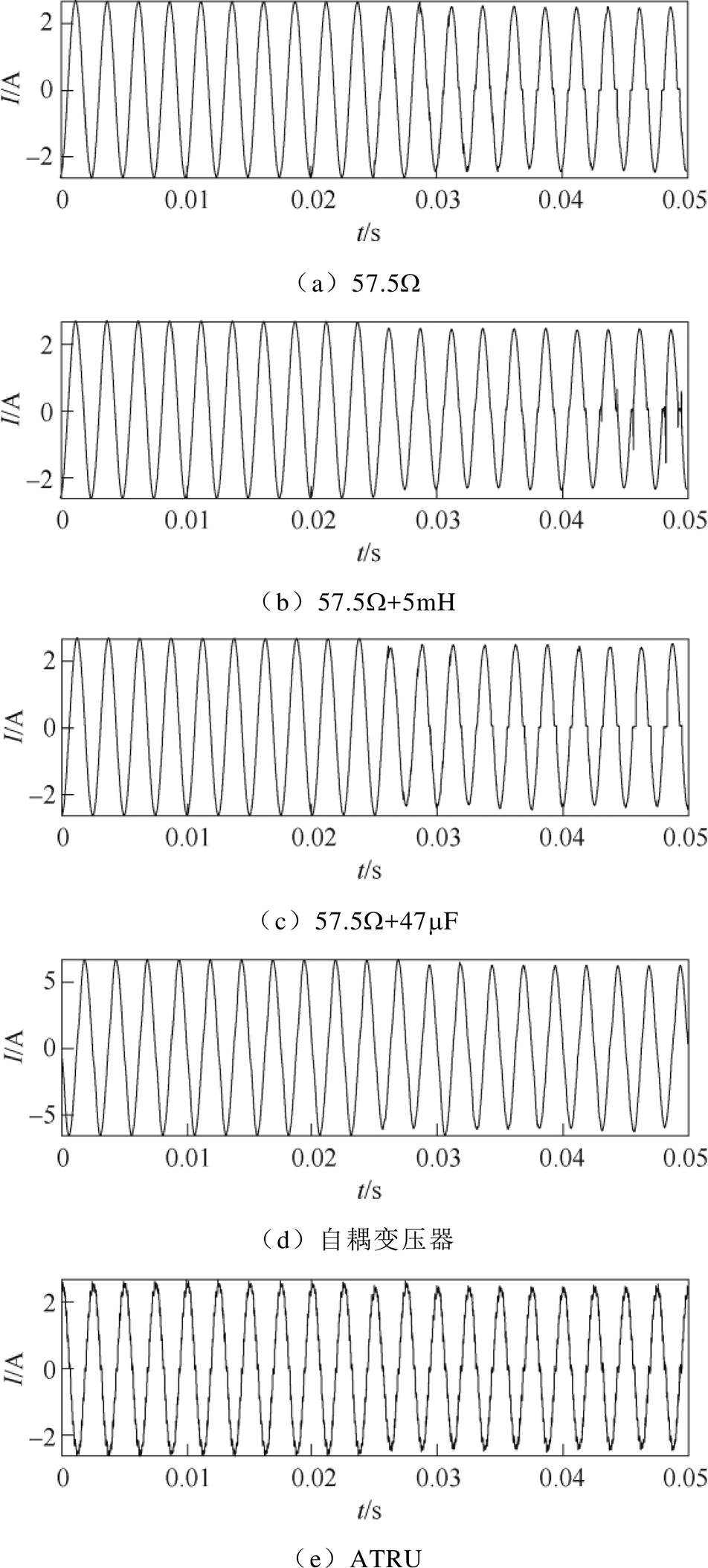
图5 点接触试验电流波形
Fig.5 Current waveforms of point contact test
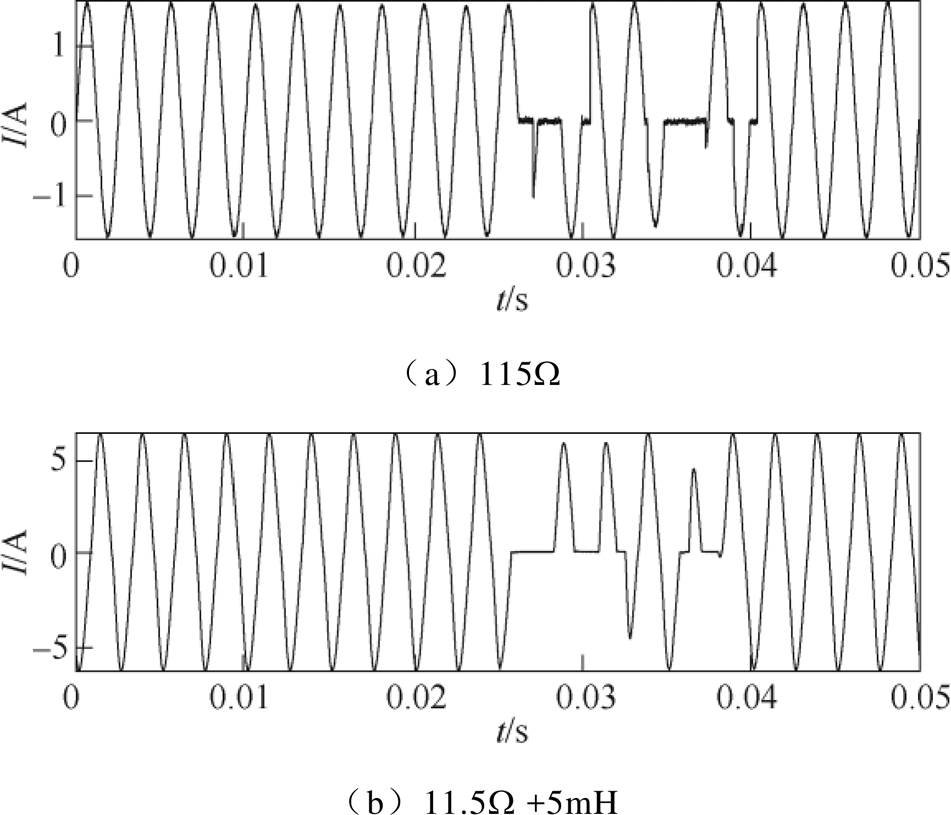
图6 振动试验电流波形
Fig.6 Current waveforms of vibration test
EMD是将信号f(t)分解为N个固有模态函数ck和残差Rn之和,即
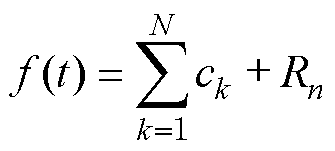 (1)
(1)
EWT与EMD稍有不同,将信号f(t)分解成N+1个经验模态函数fk(t)之和,即
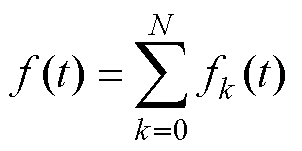 (2)
(2)
EWT的实质是先将原始信号进行傅里叶变换,然后根据频谱特点进行自适应划分来构建一组合适的正交小波滤波器,从而提取出原始信号的不同调幅-调频成分。EWT的主要步骤如下。
首先进行小波滤波器组的构建,假设划分的区间段数为M,依据香农准则,将信号的Fourier频谱范围映射至[0, p]。通过检测信号频谱上前M个最大局部极大值,求得其两两相邻之间的最小值[20],即为信号区间的边界wn(n=1, 2,…, M-1),并且w0=0,wM =p。从而将Fourier频谱分割成M个连续的区间,则每个区间可以表示为
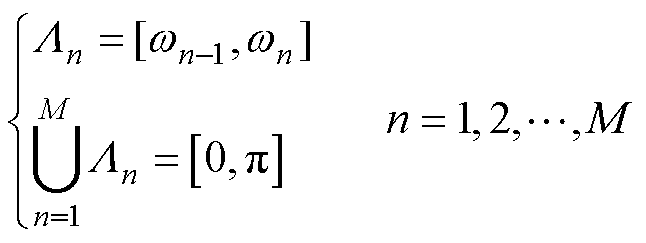 (3)
(3)
以每个wn为中心,定义了宽度为Tn=2tn的过渡段,如图7的阴影区所示。
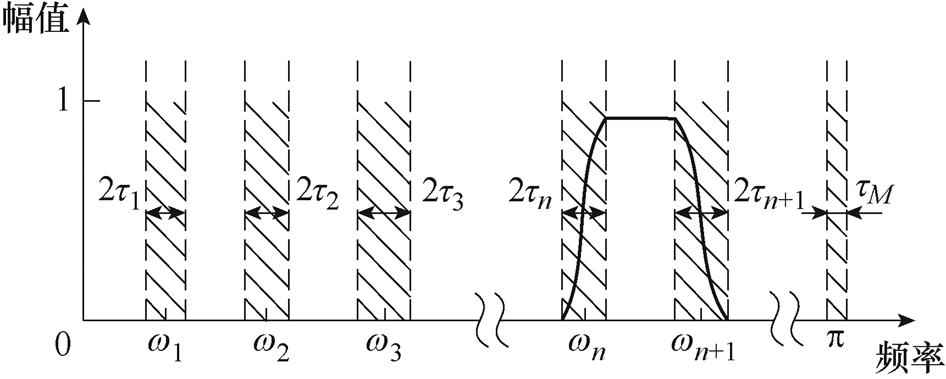
图7 Fourier轴的分割
Fig.7 Partitioning of the Fourier axis
进行区间划分后,通过经验小波为每个区间wn设定相应的带通滤波器。根据Meyer小波构造方法,尺度函数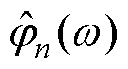 和经验小波函数
和经验小波函数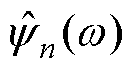 分别[21]为
分别[21]为
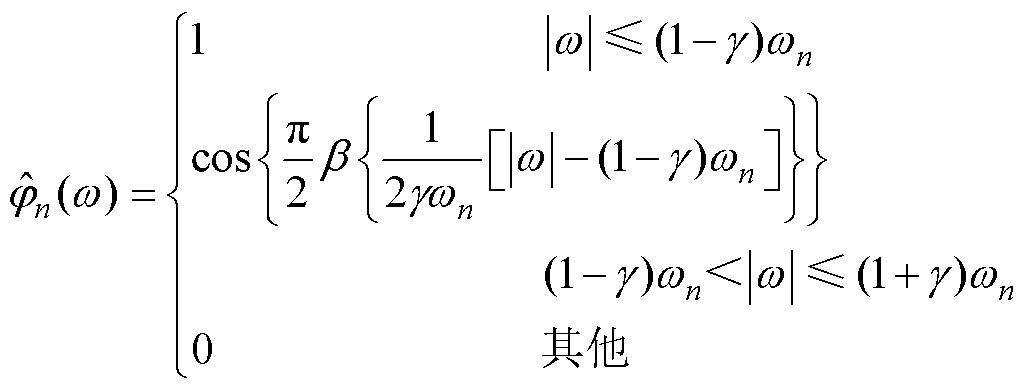 (4)
(4)
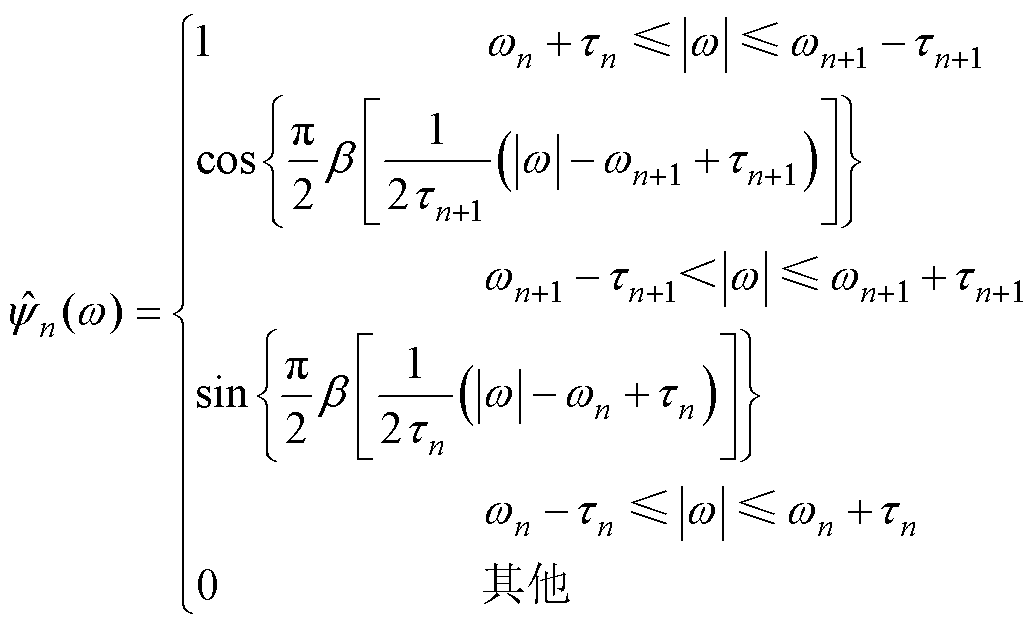 (5)
(5)
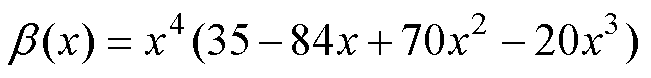 (6)
(6)
式中,b(x)为任意的Ck([0, 1])函数;g 为伸缩因子;tn为滤波带半带宽。
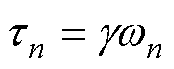 (7)
(7)
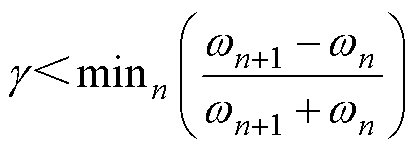 (8)
(8)
利用式(4)~式(5)对信号进行EWT变换,然后原始信号可被重构为
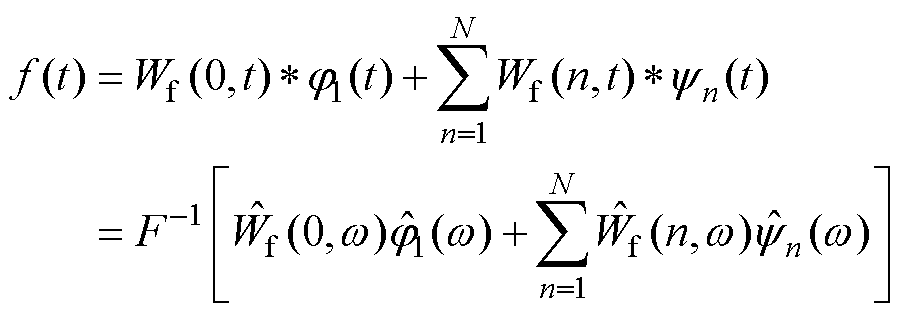 (9)
(9)
式中,Wf(0, t)为尺度函数与信号内积的近似系数;Wf(n, t)为经验小波函数与信号内积的细节系数;*为卷积运算符;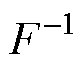 为进行Fourier反变换;
为进行Fourier反变换;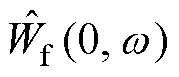 、
、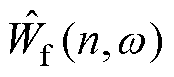 、
、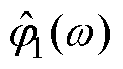 、
、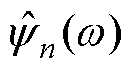 分别为Wf(0, t)、Wf(n, t)、
分别为Wf(0, t)、Wf(n, t)、 、
、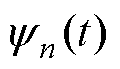 的Fourier变换。
的Fourier变换。
经验模态函数fk(t)定义为
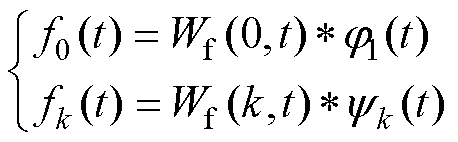 (10)
(10)
针对传统的EWT频带划分会出现如图8所示的“过分割”情况,这是由于频谱泄露及噪声污染干扰所导致的[22]。为了更好地提取出电弧信号在各频带的特征信息,结合电弧信号特征对EWT的频谱分割进行改进。
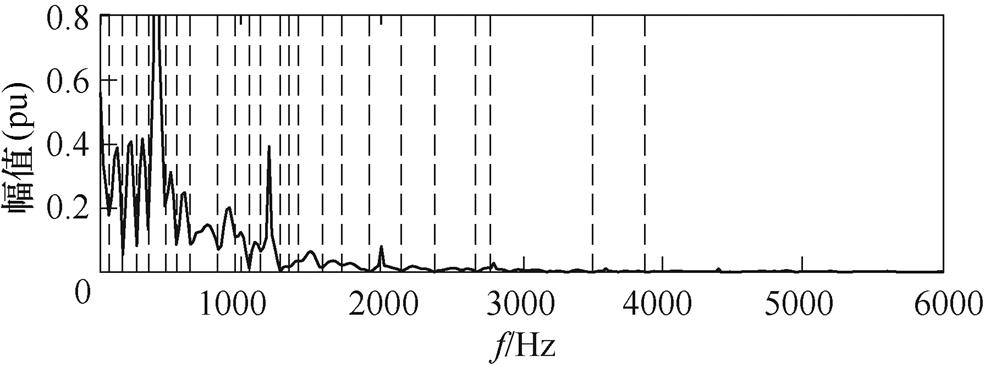
图8 EWT频谱分割
Fig.8 Spectrum segmentation of EWT
EWT的频谱分割方式LocalMaxMin以及LocalMax均选用局部极大值作为划分的参照点,极大值对应的频段是该分量中的主要能量[20]。而电弧信号的主要能量除了基频分量,通常在奇偶次谐波上[23],通过极大值的选取将蕴含主要能量的谐波分量单独分离出来以反映电弧故障信息。因此,可以在EWT的基础上通过等间距稀疏频谱来抑制频谱泄露及噪声对电弧信号的干扰。为了能更好地针对于电弧信号的高频信号特征,从基频的5倍及以上频段选取极大值。沿用LocalMaxMin的分割方式并加以改进,主要步骤如下。
(1)做出信号f(t)的单边傅里叶频谱F(w),并根据频谱最大幅值求得近似基频数值。
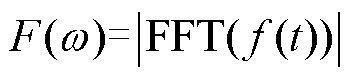 (11)
(11)
(2)将F(w)分成u段,使每段区间范围为1/2基频的区间段,依次提取每段中的最大幅值与对应的横坐标记为节点Aj(j=1, 2, 3,…, u)。
(3)按横坐标顺序排列Aj,在横坐标大于等于基频5倍频所对应的幅值中选取M-1个最大局部极大值,并在原Fourier频谱中找到这M-1个点,加上基频所对应的点,将这M个点作为参照点,求得两两相邻之间的最小值作为频谱划分的边界点。
(4)通过尺度函数和经验小波函数求得各EMFs。
改进后的频谱划分如图9所示,可以看到,改进后的EWT不再出现“过分割”情况。
选择发生电弧故障时刻的前后共20个周期,分别进行IEWT和EMD变换。IEWT可以设置分解层数,经过反复试验,从各负载均能有效分解出多个高频电弧故障信息、分解层数越少计算量越小两方面考虑,最终确定分解层数M=5。而EMD需要不断地对原始信号进行分解,来获取符合一定条件的 IMF分量,其分解层数具有不确定性。由于篇幅有限,本文主要对各负载进行了IEWT分解,IEWT分解结果如图10~图16所示,对EMD选取具有代表性的负载进行分解,如图5d与图6b所示,并比较出EMD存在的问题,EMD分解结果如图17、图18所示。
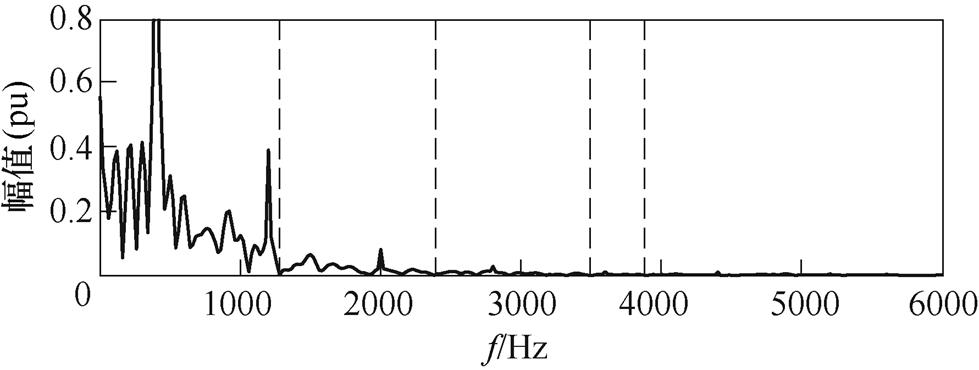
图9 IEWT频谱分割
Fig.9 Spectrum segmentation of IEWT
如图10~图16所示,经IEWT变换后,原始信号被分解为5个经验模态分量EMF1~EMF5,各模态频率依次增加。EMF1为低频趋势分量,EMF2~EMF5分别为相应的中高频分量。可以看出,在未产生电弧故障时,IEWT分解出的各模态波形稳定且周期一致,在产生电弧故障后EMF1幅值降低,而中高频模态会出现周期性尖峰的情况,这是电弧发生时,伴随产生多种谐波的结果。还可以发现,线性负载的中高频分量变化程度较非线性负载要明显,主要原因是非线性负载比线性负载的频谱更加复杂,其本身蕴含多种谐波,这也使得非线性负载比线性负载更难提取其故障信息。综合图10~图16中各个经验模态分量表明,在多种线性负载、非线性负载下,使用IEWT算法得到的经验模态分量,在多个频段直观地表征出了电弧的故障信息。
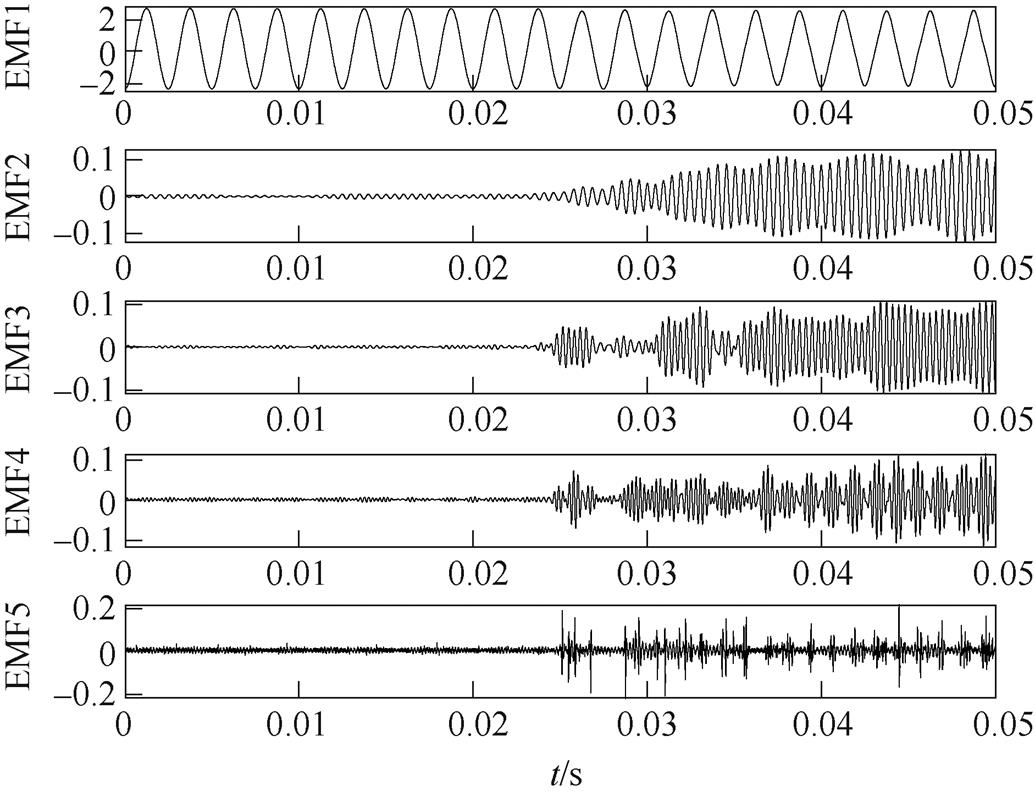
图10 纯阻(57.5W)的IEWT分解
Fig.10 IEWT results of pure resistance (57.5W)
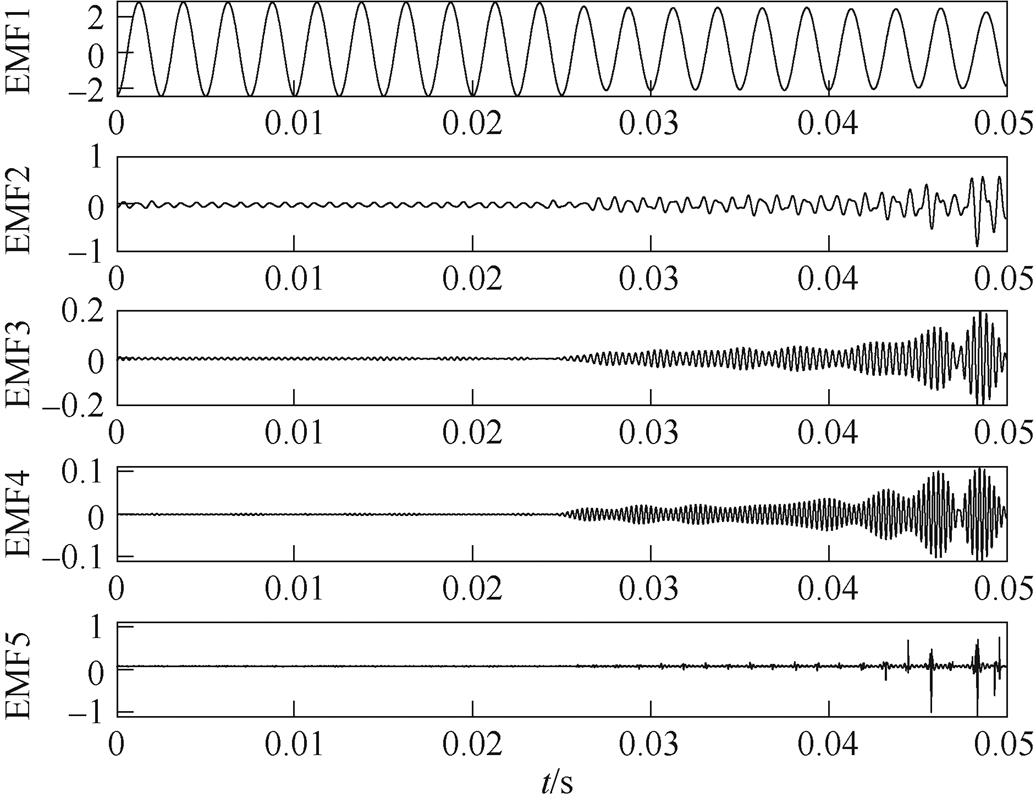
图11 阻感(57.5W+5mH)的IEWT分解
Fig.11 IEWT results of RL (57.5W+5mH)
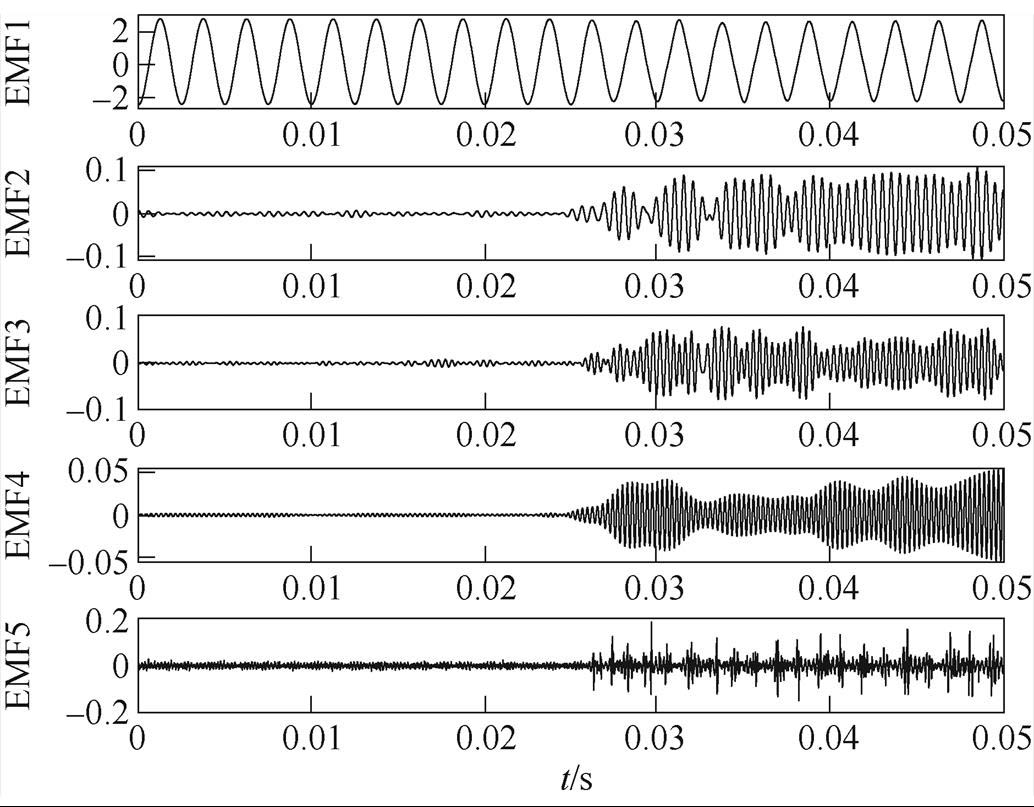
图12 阻容(57.5W+47mF)的IEWT分解
Fig.12 IEWT results of RC (57.5W+47mF)

图13 自耦变压器的IEWT分解
Fig.13 IEWT results of autotransformer
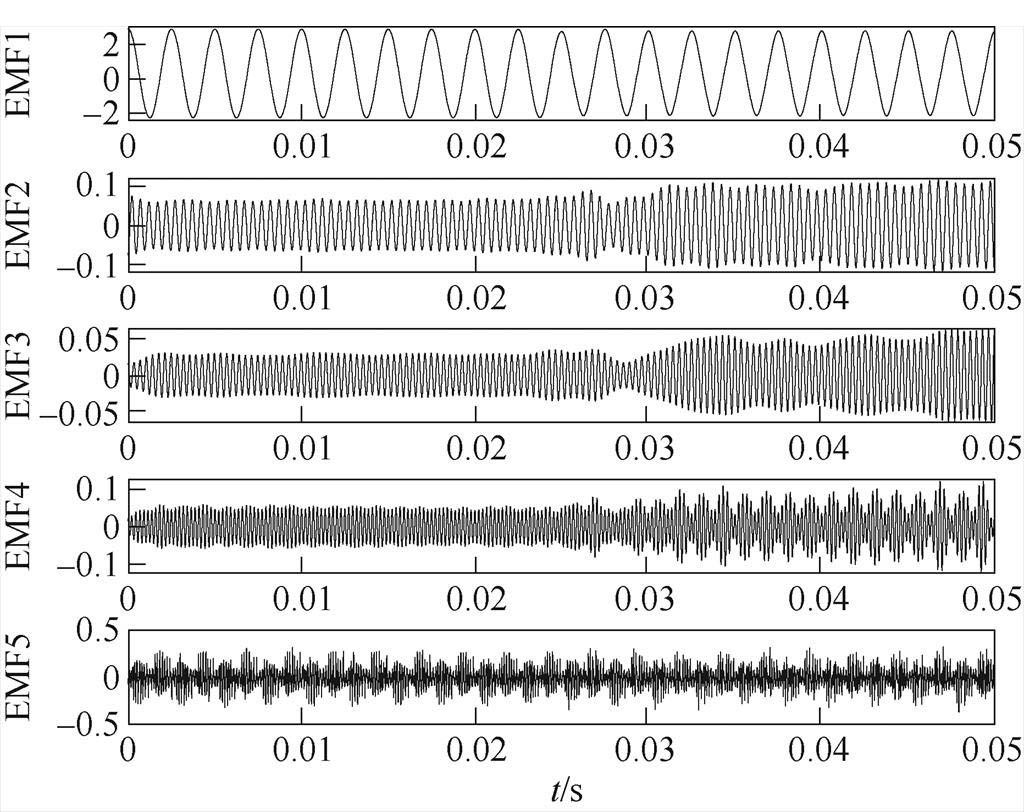
图14 ATRU的IEWT分解
Fig.14 IEWT results of ATRU
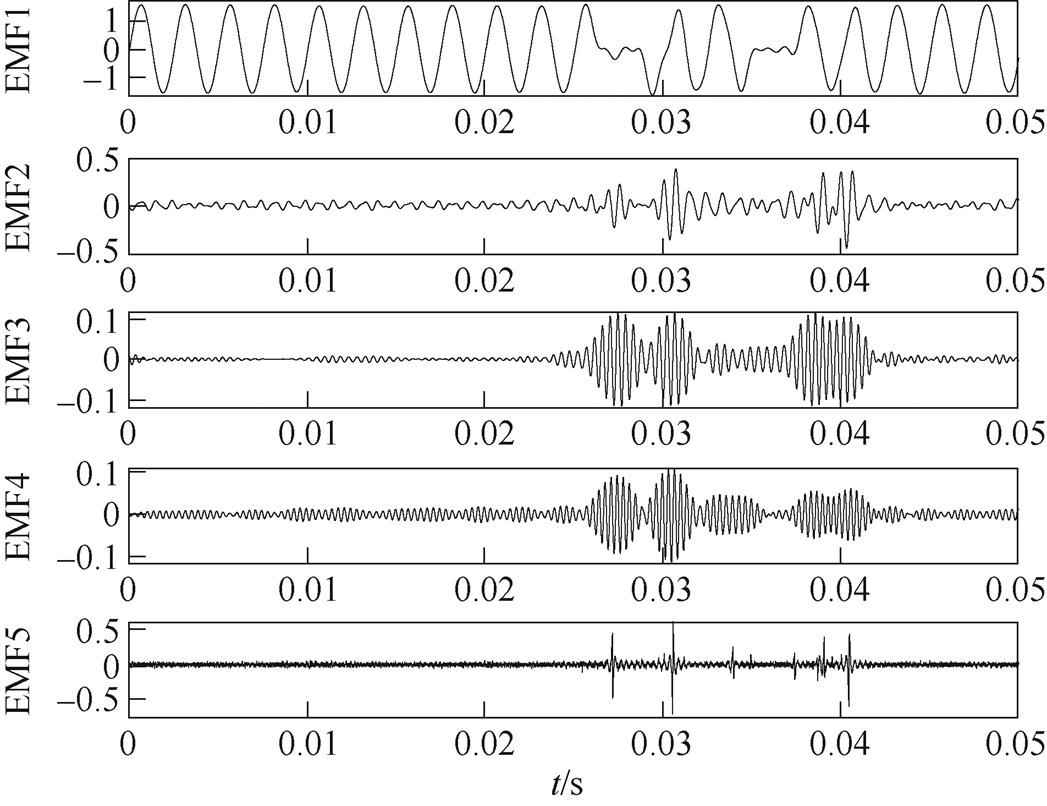
图15 振动试验纯阻(115W)的IEWT分解
Fig.15 IEWT results of vibration test pure resistance (115W)

图16 振动试验阻感(11.5W+5mH)的IEWT分解
Fig.16 IEWT results of vibration test RL (11.5W+5mH)
如图17、图18所示,经EMD分解后,可以看出EMD分解的模态数多且不同。与IEWT分解出的信号频率顺序相反,从上到下,各IMF分量频率依次减小。在EMD分解出的低频分量中,各负载均出现了模态混叠现象的两种情况,即相近的特征时间尺度被分布在不同的IMF分量中,或者一个IMF分量中包含差异极大的特征时间尺度的情况,如图17中的IMF4~IMF9,图18中的IMF6~IMF10。在EMD分解出的各高频分量中,虽然能够看到电弧故障发生前后的变化,却很难找到一个共同而有效的IMF进行特征提取。

图17 自耦变压器的EMD分解
Fig.17 EMD results of autotransformer
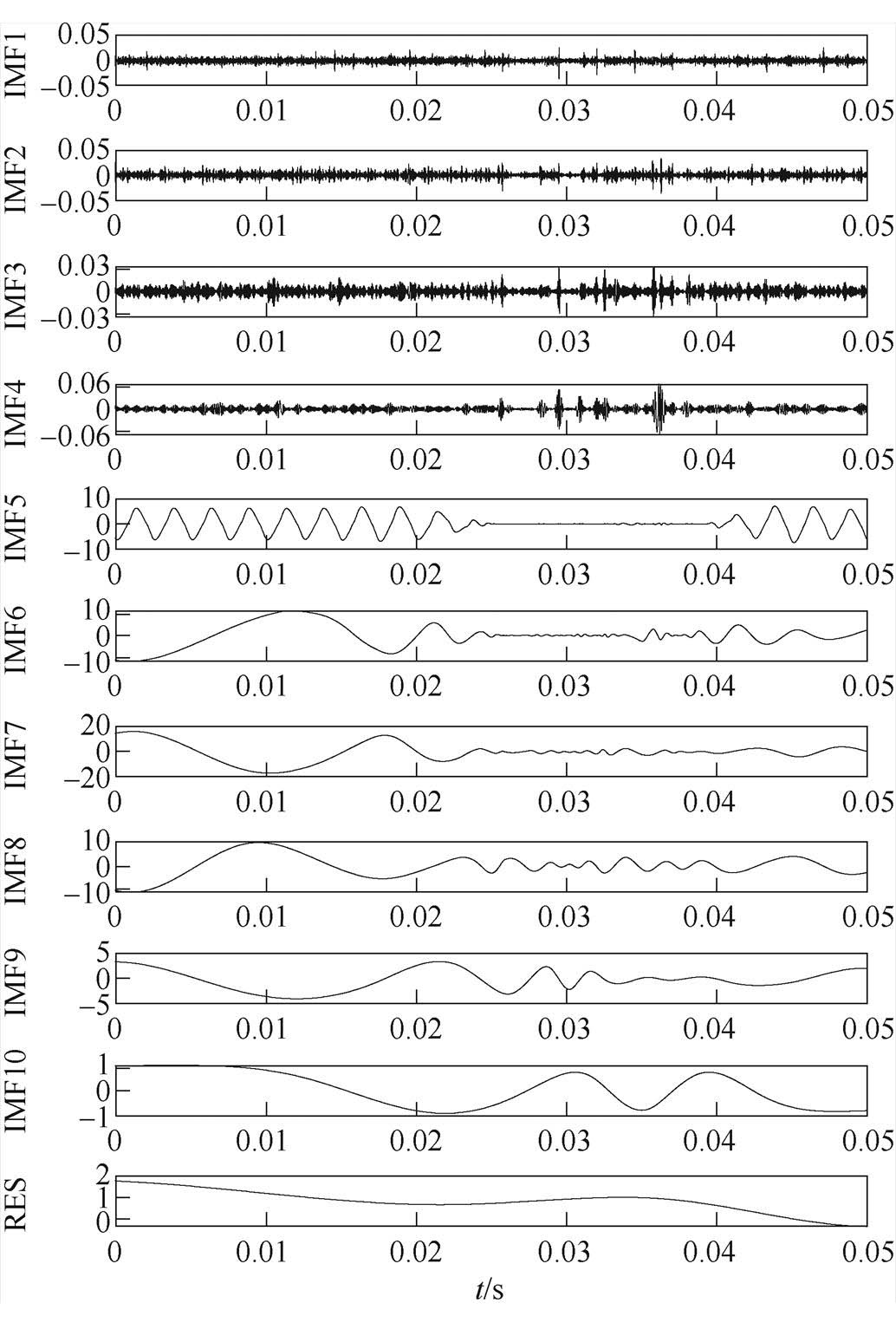
图18 振动试验阻感(11.5W+5mH)的EMD分解
Fig.18 EMD results of vibration test RL (11.5W+5mH)
由于EMD存在的模态混叠导致分解出过多的模态,故障特征少且在非线性负载下不明显,不利于电弧故障信息的提取。相比之下,IEWT对每种负载均有着良好的分解,能分解出多个有效反映电弧信息的EMFs分量,所以本文只对IEWT分解出的模态分量进行特征提取。根据不同频段模态分量的特征,提取可以反映所有模态分布情况的能量熵,能很好地表征高频模态复杂程度变化的样本熵,以及可以很好描述低频趋势变化的方均根值。
当发生电弧故障时,信号会产生多种高次谐波,这使得电流信号中频率分布会发生改变,同时其能量分布也将会发生相应的改变。为了有效获取这一变化信息,在IEWT变换的基础上,计算每个EMF的能量分布。为了更好地反映出电弧电流信号的能量分布情况,应用能量权重及能量熵的概念[24]。由EWT原理可知,EWT按照信号不同特征时间尺度自适应地将信号分解为M个经验模态EMFs,得到一组频率由低到高排列的平稳序列。能量权重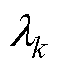 的本质就是其中的每个EMF模态的能量与原始电流信号I(t)能量的比值,即
的本质就是其中的每个EMF模态的能量与原始电流信号I(t)能量的比值,即
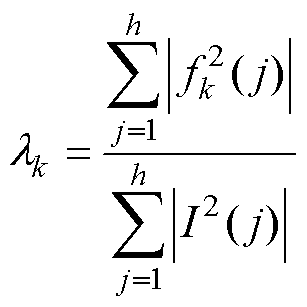 (12)
(12)
式中,h为每周期数据点数;k为第几个模态。
能量熵定义为
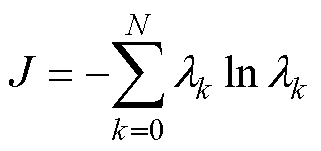 (13)
(13)
熵反映了信息的不确定度,权重能量熵则反映着电流信号在各模态下能量的分布情况,能量熵越大,说明信号谐波成分越复杂。按照上述方法,计算的各试验负载下能量熵曲线如图19、图20所示。

图19 点接触试验能量熵曲线
Fig.19 Energy entropy curves of point contact test
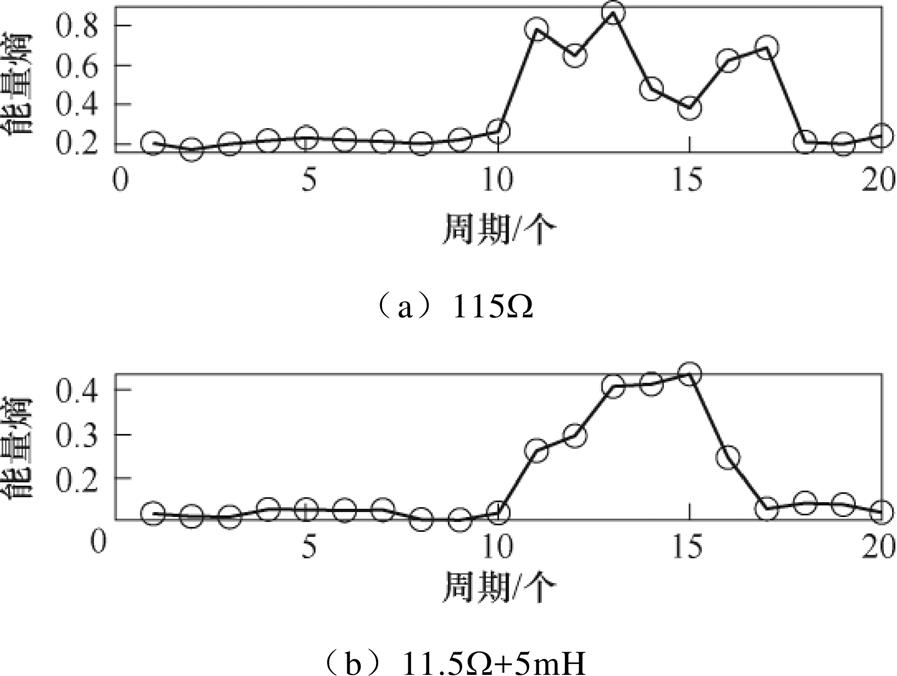
图20 振动试验能量熵曲线
Fig.20 Energy entropy curves of vibration test
由图19、图20能量熵曲线可知,正常周期能量熵值稳定为一条直线,而发生电弧故障后,能量熵变大。点接触试验中,随着电弧的剧烈燃烧,增加幅度逐渐加大;振动试验中,会在出现电弧故障的周期里表现出熵值增大的情况。能量熵在线性负载中能很好地表征故障信息,在非线性负载ATRU下,由于信号本身包含丰富的谐波,使得临近起弧时特征区分度较小。
样本熵是在近似熵理论基础上提出的一种描述时间序列复杂程度的改进方法。其原理是通过度量信号中产生新模式的概率大小来衡量时间序列的复杂性,产生新模式的概率越大,序列的复杂性越大,样本熵也就越大。根据样本熵的特点,对IEWT分解后的敏感信号进行样本熵分析,能更加有效地反映出电弧故障情况。
样本熵计算步骤如下。
(1)通过数据样本{p(i), i=1, 2,…, N},构建m维向量,有
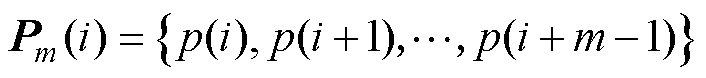 1≤i≤N-m+1(14)
1≤i≤N-m+1(14)
(2)定义向量Pm(i)与Pm( j)两者对应元素中最大差值的绝对值为距离d,表示为
 (15)
(15)
(3)统计向量Pm(i)与Pm( j)之间距离小于或等于r的个数记为Bi。对于1≤i≤N-m,有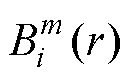 定义为
定义为
 (16)
(16)
(4)定义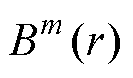 为
为
 (17)
(17)
(5)令m=m+1,重复步骤(1)~步骤(4),计算得到Bm+1(r)。
这样,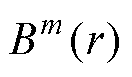 为两个序列在相似容限r下匹配m个点的概率,而Bm+1(r)为两个序列匹配m+1个点的概率。样本熵定义为
为两个序列在相似容限r下匹配m个点的概率,而Bm+1(r)为两个序列匹配m+1个点的概率。样本熵定义为
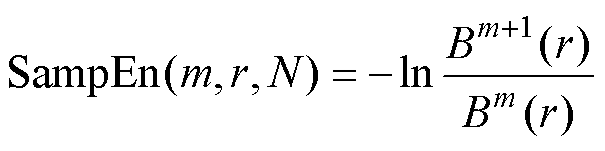 (18)
(18)
样本熵的大小主要与维数m、r有关,根据文献[25]研究成果,当m取1或2,r取0.1~0.25Std(Std为数据序列的标准差)时,有较合理的统计特征。本文选取m=2,r=0.2Std为计算样本熵的参数。
电流信号经IEWT分解后,可以观察到,在发生电弧故障后的中高频模态,谐波分量的增加使得波形的复杂度与正常时有所不同。经过多次试验,在各负载的高频分量EMF4下均能很好反映电弧故障的信息,为了有效提取这一特征,计算其每周期样本熵,各试验负载样本熵曲线如图21、图22所示。
分析图21和图22,与能量熵类似,在发生电弧故障时,样本熵的熵值一般会大于正常周期的熵值。在各负载下样本熵很好地描述了电弧信号经IEWT分解后的高频故障信息。但在振动试验的阻感负载下出现了正常周期数据波动较大的情况,为了更全面地分析串联电弧的特征信息,以对比高频分量的特征,在IEWT分解出的低频分量同样进行了特征提取。
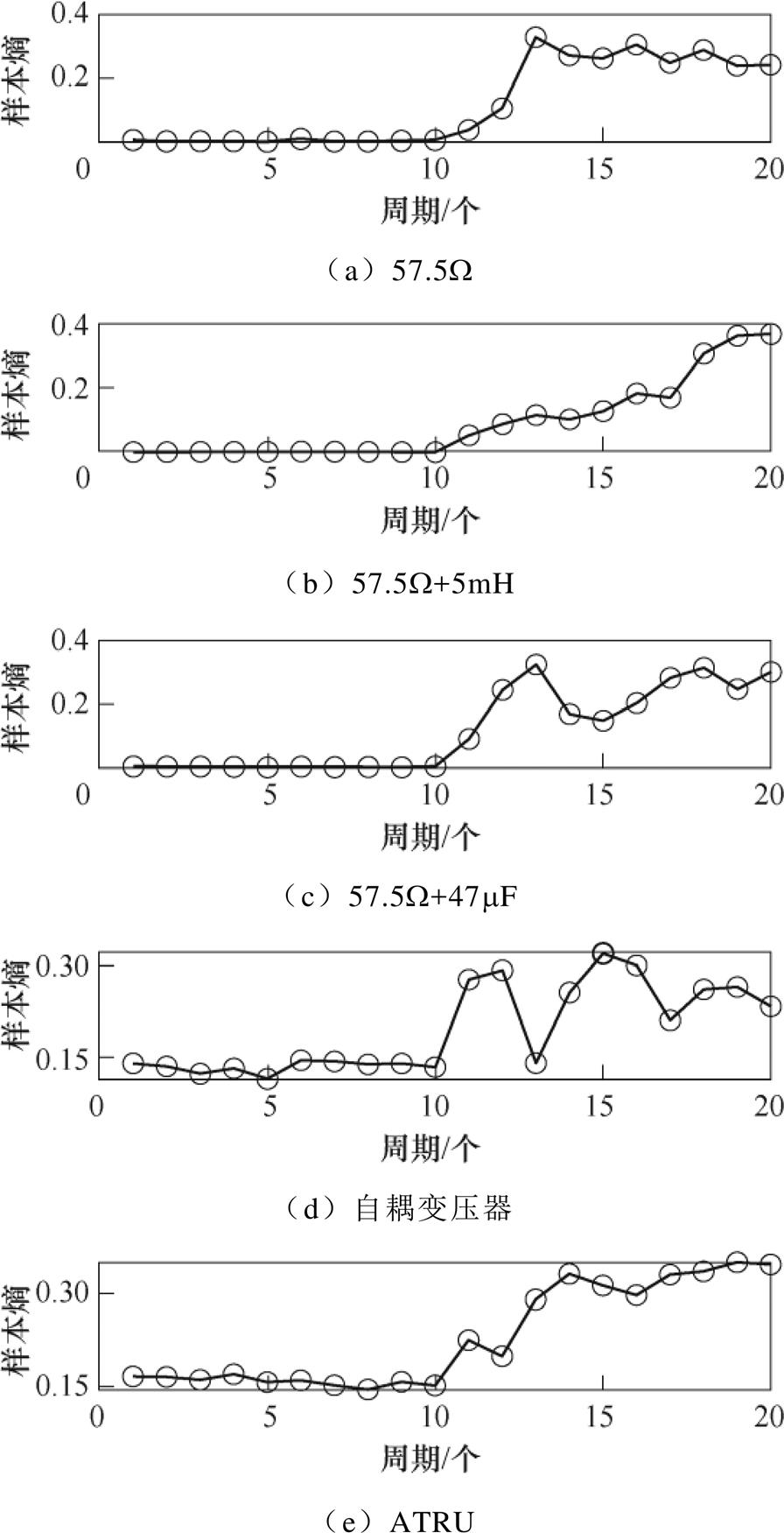
图21 点接触试验样本熵曲线
Fig.21 Sample entropy curves of point contact test
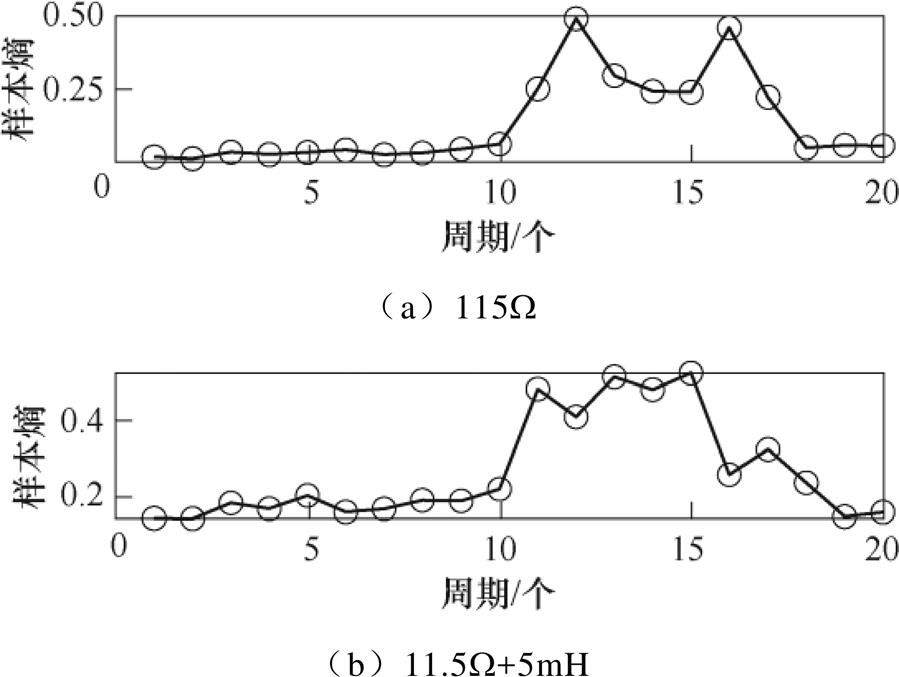
图22 振动试验样本熵曲线
Fig.22 Sample entropy curves of vibration test
经IEWT分解后的低频分量EMF1很好地保留着串联电弧幅值减小趋势,相比原始信号有着更好的稳定性和抗噪声干扰能力。为了能获得这一低频信息,求取每周期方均根值,各试验负载方均根值结果如图23、图24所示。
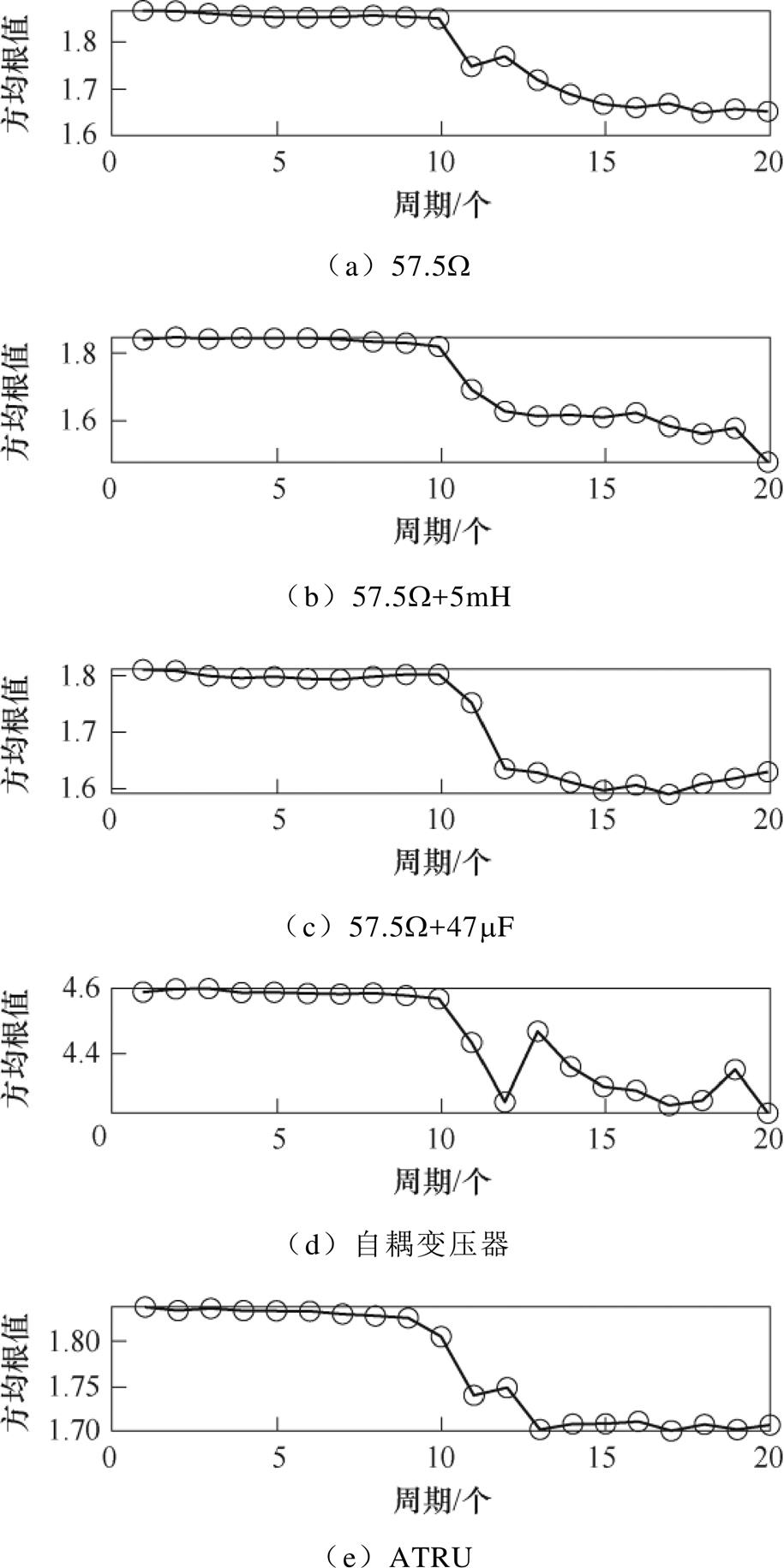
图23 点接触试验方均根值曲线
Fig.23 Root mean square value curves of point contact test
从图23、图24可以看出,在产生电弧时,各试验负载下的EMF1方均根值减小,很好地表征了串联电弧的低频信息,由于该特征与电流等级大小有关,需要进行标准化以统一各负载这一特性。
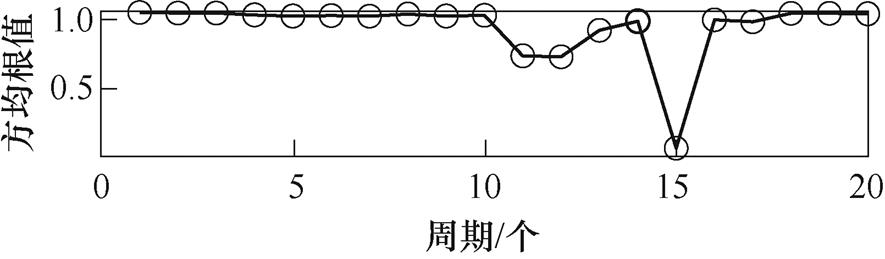
(a)115W
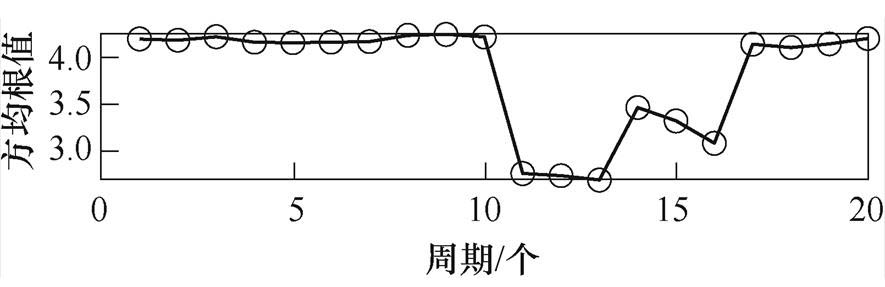
(b)11.5W+5mH
图24 振动试验方均根值曲线
Fig.24 Root mean square value curves of vibration test
为了更好地统一各负载之间特征值差异,以便后文进行数据分类,需要进行标准化,Z-score标准化公式为
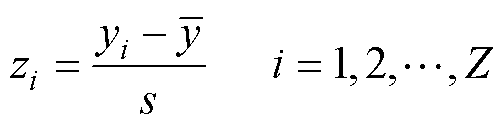 (19)
(19)
式中,yi为某种特征量的Z个数据;zi为标准化结果,主要是为了解决故障前后特征数据比较问题;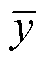 与s分别为该组数据的前4个周期特征量的平均值和标准差,即为正常周期特征量下计算的数值。因为电弧故障检测是一个从正常到故障的过程,所以可以通过控制IEWT变换的周期选取方式来确保前4个周期数据中含有正常周期数据。IEWT周期信号框选示意图如图25所示。
与s分别为该组数据的前4个周期特征量的平均值和标准差,即为正常周期特征量下计算的数值。因为电弧故障检测是一个从正常到故障的过程,所以可以通过控制IEWT变换的周期选取方式来确保前4个周期数据中含有正常周期数据。IEWT周期信号框选示意图如图25所示。
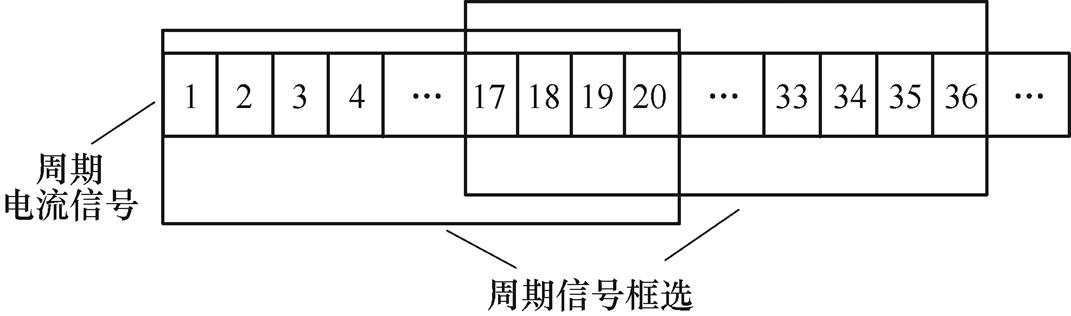
图25 周期信号框选示意图
Fig.25 Schematic diagram of periodic signal box selection
ELM是一种单隐含层前馈神经网络,与传统的神经网络训练算法不同,输入层权值和隐含层阈值都是随机产生,且无需再次调整,只需要设置隐含层神经元个数,便可获得唯一的最优解[26]。所以,ELM具有训练参数少、学习速度快、泛化能力强的优点。电弧检测是一个需要快速实时检测的项目,因此ELM能很好地适用于电弧故障的诊断。
设有Q个样本(xi, ti),ELM数学模型为
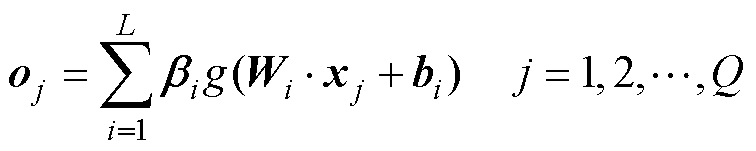 (20)
(20)
式中,Wi为输入权值;bi为隐含层节点的阈值;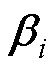 为输出权值;g(x)为激活函数;xi为n维输入向量;ti为m维输出向量;L为隐含层个数。ELM网络训练模型如图26所示。
为输出权值;g(x)为激活函数;xi为n维输入向量;ti为m维输出向量;L为隐含层个数。ELM网络训练模型如图26所示。
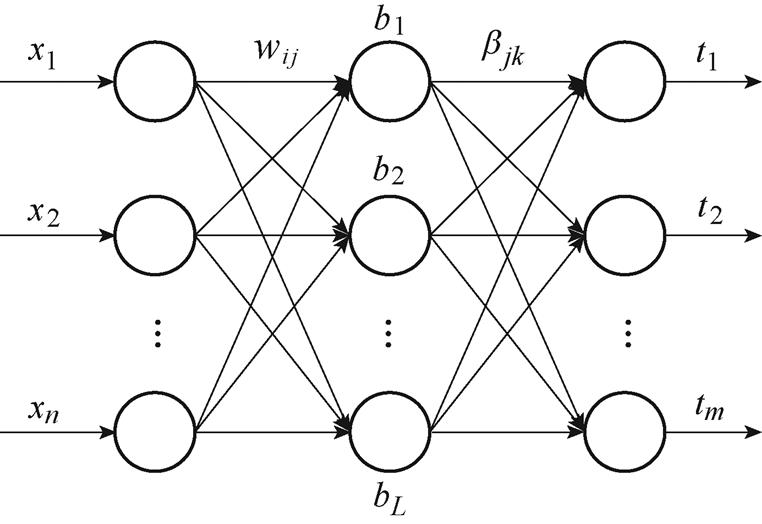
图26 ELM网络训练模型
Fig.26 ELM network training model
极限学习机的学习目标是为了使输出误差最小,即
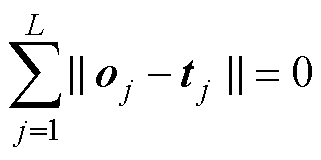 (21)
(21)
ELM算法步骤为:
(1)随机产生输入权值Wi以及阈值bi。
(2)计算输出矩阵H。
(3)求解隐含层与输出层之间的输出权值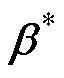 =
=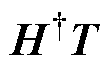 。其中,
。其中,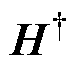 为矩阵H的Moore-Penrose广义逆;
为矩阵H的Moore-Penrose广义逆;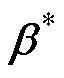 为极小范数最小二乘解。
为极小范数最小二乘解。
用IEWT方法进行信号时频域分析,在此基础上提取能量熵、样本熵和方均根值三种特征量,并进行融合,最后采用ELM方法进行电弧故障的鉴别。整个鉴别过程的流程如图27所示。
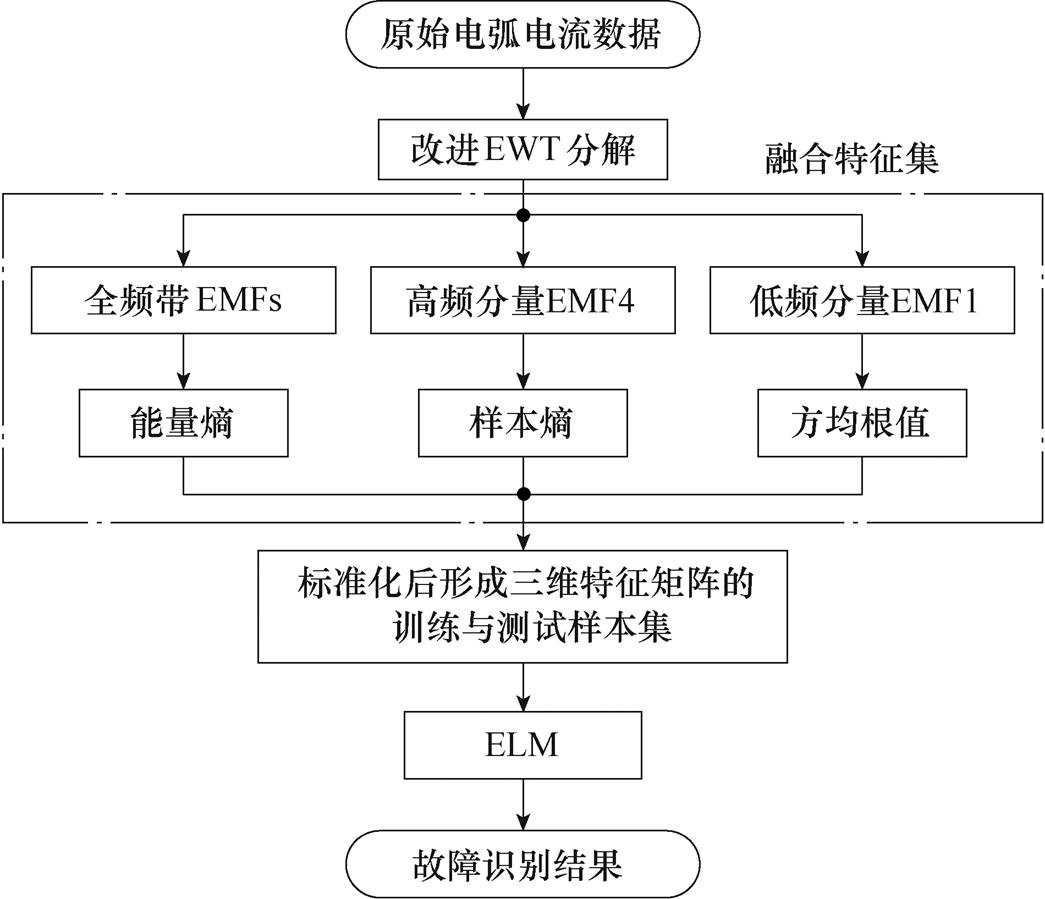
图27 故障诊断流程
Fig.27 Fault diagnosis flow chart
为了验证该方法的有效性,对文中点接触试验五种负载数据以及振动试验两种负载数据,使用上述方法计算出的特征量作为ELM的输入。将200组数据作为训练样本,由正常情况与电弧故障各100次组成,测试样本160组由正常情况与电弧故障各80次组成。激活函数选用Sigmoid函数,ELM隐含层神经元个数依次设置为5~60,以平均正确率达到最大值且不再改变为寻优结果,ELM-融合特征集下确定神经元个数为36,如图28所示。将正常、电弧故障两种状态对应的输出分别设置为1和2,ELM分类结果如图29所示。
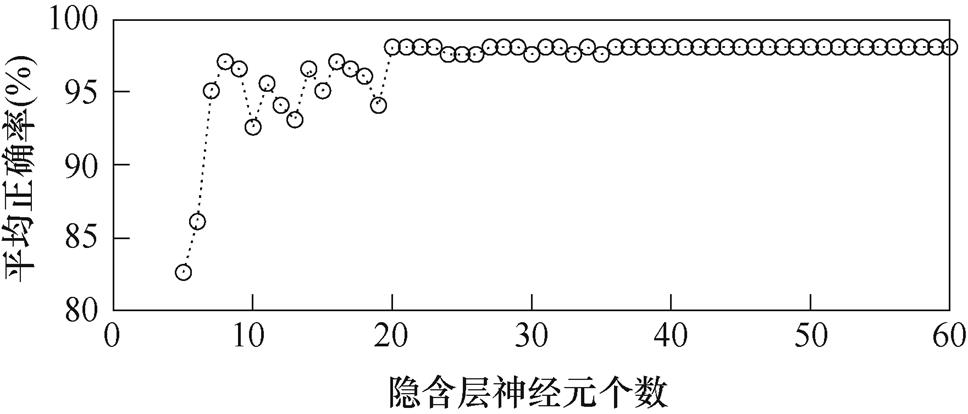
图28 不同神经元个数对应的平均正确率
Fig.28 Average accuracy of different number of neurons
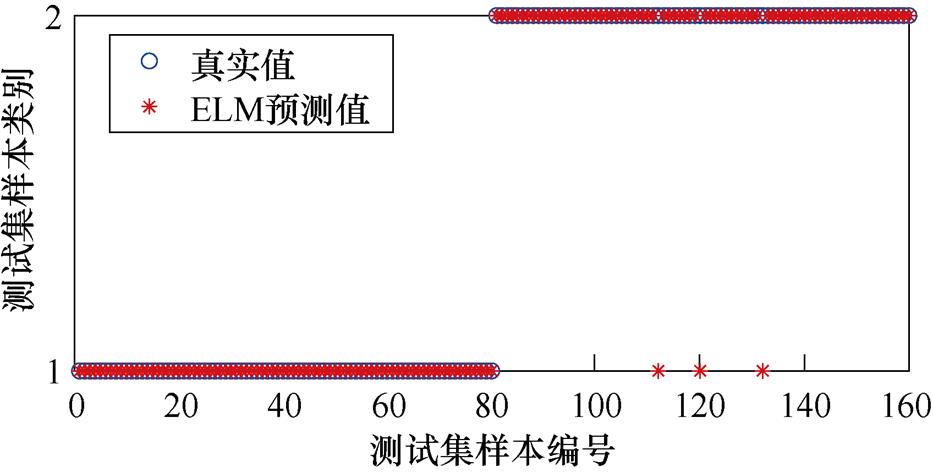
图29 ELM融合特征集分类结果
Fig.29 ELM fusion feature set classification results
如图29所示,仅有3次分类结果与实际不同,此时分类准确率为98.12%。同时为了对比单一特征与融合特征集的识别效果,又将每个角度特征量分别单独输入到ELM中,使用同样激活函数、参数优化以及训练方法,结果见表1。
表1 各特征量识别准确率
Tab.1 Recognition accuracy of each feature

特征量隐含层神经元个数识别准确率(%) 能量熵1492.5 样本熵2095 方均根值2593.75 融合特征集3698.12
对比表1可以看出,ELM-融合特征集使用的隐含层神经元个数虽多,但故障诊断准确率要明显高于单一角度特征量的故障识别准确率。
模拟未知负载及未知串联电弧故障,对方法的有效性进行检验。将训练好的ELM-融合特征集模型分别对点接触试验以及振动试验各负载进行单独识别,测试集为80组,正常与电弧故障各40次,其结果见表2,所有负载下准确率均在95%以上,平均准确率达到了97.85%。因此,该方法能可靠地识别出航空系统的电弧故障。
表2 各测试负载识别结果
Tab.2 Identification results for each load

试验类型负载类型识别准确率(%) 点接触试验57.5W100 57.5W+5mH98.75 57.5W+47mF98.75 自耦变压器95 ATRU96.25 振动试验115W98.75 11.5W+5mH97.5
1)IEWT在线性负载以及非线性负载下均能有效分解出电弧信号的故障信息,该方法分解的模态少,不存在难以解释的虚假模态;而EMD分解出现模态混叠,非线性负载下的特征不明显,难以找到共同而有效的IMF等问题。
2)EMFs的能量熵、EMF4的样本熵和EMF1的方均根值均能有效提取出经IEWT分解后的航空电弧故障特征,并且在融合后具有更高的电弧鉴别准确率。
3)本文针对航空串联型电弧故障,对EWT频带划分进行改进后,使用IEWT对电流信号分解并进行多角度特征提取,结合ELM进行故障诊断,能可靠地识别出电弧故障。
参考文献
[1] 张栋善, 陈沛树. 航空电气系统中故障电弧的分析[J]. 电子制作, 2017(22): 27-28.
Zhang Dongshan, Chen Peishu. Analysis of fault arc in aviation electrical system[J]. Practical Electronics, 2017(22): 27-28.
[2] Zhao Long, Zhou Yuhao, Chen Kunlong, et al. Using spectrum of the light for high speed arcing fault detection[C]//2018 IEEE IAS Electrical Safety Work- shop (ESW), Fort Worth, TX, USA, 2018: 1-8.
[3] 刘柱揆, 丁心志, 陈福明, 等. 开关柜电弧故障及其测量方法研究[J]. 电网技术, 2017, 41(4): 1345- 1349.
Liu Zhukui, Ding Xinzhi, Chen Fuming, et al. Research on switchgear arc discharge fault and its measurement[J]. Power System Technology, 2017, 41(4): 1345-1349.
[4] 王尧, 张彦风, 牛峰, 等. 光伏直流电弧电磁辐射特性分析与测量方法[J]. 电工技术学报, 2019, 34(14): 2913-2921.
Wang Yao, Zhang Yanfeng, Niu Feng, et al. Characteri- zation and measurement method of DC arc electro- magnetic radiation for photovoltaic systems[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2913-2921.
[5] 张冠英, 张晓亮, 刘华, 等. 低压系统串联故障电弧在线检测方法[J]. 电工技术学报, 2016, 31(8): 109-115.
Zhang Guanying, Zhang Xiaoliang, Liu Hua, et al. Online detection method for series arcing fault in low voltage system[J]. Transactions of China Electro- technical Society, 2016, 31(8): 109-115.
[6] Kim J C, Neacşu D O, Lehman B, et al. Series AC arc fault detection using only voltage waveforms[C]// 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 2019: 2385-2389.
[7] Syafi'i M A, Prasetyono E, Khafidli M K, et al. Real time series DC arc fault detection based on fast fourier transform[C]//2018 International Electronics Symposium on Engineering Technology and Appli- cations, (IES-ETA), Bali, Indonesia, 2018: 25-30.
[8] Artale G, Cataliotti A, Cosentino V, et al. Arc fault detection method based on CZT low-frequency harmonic current analysis[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(5): 888- 896.
[9] 张士文, 张峰, 王子骏, 等. 一种基于小波变换能量与神经网络结合的串联型故障电弧辨识方法[J]. 电工技术学报, 2014, 29(6): 290-295, 302.
Zhang Shiwen, Zhang Feng, Wang Zijun, et al. Series arc fault identification method based on energy produced by wavelet transformation and neural network[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 290-295, 302.
[10] 郭凤仪, 邓勇, 王智勇, 等. 基于灰度-梯度共生矩阵的串联故障电弧特征[J]. 电工技术学报, 2018, 33(1): 71-81.
Guo Fengyi, Deng Yong, Wang Zhiyong, et al. Arc fault characteristics based on gray level-gradient co- occurrence matrix[J]. Transactions of China Electro- technical Society, 2018, 33(1): 71-81.
[11] 苏晶晶, 许志红. 基于EMD和PNN的故障电弧多变量判据诊断方法[J]. 电力自动化设备, 2019, 39(4): 106-113.
Su Jingjing, Xu Zhihong. Diagnosis method of multi- variable criterion based on EMD and PNN for arc fault diagnosis[J]. Electric Power Automation Equipment, 2019, 39(4): 106-113.
[12] Chen Changken, Guo Fengyi, Liu Yanli, et al. Recognition of series arc fault based on the Hilbert Huang transform[C]//2015 IEEE 61st Holm Con- ference on Electrical Contacts, San Diego, CA, USA, 2015: 324-330.
[13] 张瑶佳, 王莉, 尹振东, 等. 基于HHT的航空直流串行电弧特征提取方法[J]. 航空学报, 2019, 40(1): 522404.
Zhang Yaojia, Wang Li, Yin Zhendong, et al. Research on characteristics extraction method of aviation DC serial arc fault based on HHT[J]. Acta Aeronautica ET Astronautica Sinica, 2019, 40(1): 522404.
[14] 高飞, 董伟, 桂美景, 等. 基于集合经验模态分解的交流航空故障电弧识别[J]. 电工电能新技术, 2020, 39(4): 73-80.
Gao Fei, Dong Wei, Gui Meijing, et al. Aviation AC arc fault detection based on ensemble empirical mode decomposition[J]. Advanced Technology of Electrical Engineering and Energy, 2020, 39(4): 73-80.
[15] 李志农, 朱明, 褚福磊, 等. 基于经验小波变换的机械故障诊断方法研究[J]. 仪器仪表学报, 2014, 35(11): 2423-2432.
Li Zhinong, Zhu Ming, Chu Fulei, et al. Mechanical fault diagnosis method based on empirical wavelet transform[J]. Chinese Journal of Scientific Instrument, 2014, 35(11): 2423-2432.
[16] 崔芮华, 李泽, 佟德栓. 基于三维熵距和熵空间的航空电弧故障检测与分类技术[J]. 电工技术学报, 2021, 36(4): 869-880.
Cui Ruihua, Li Ze, Tong Deshuan. Arc fault detection and classification based on three-dimensional entropy distance and entropy space in aviation power system[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 869-880.
[17] 郑昕, 单潇洁. 低压交流电弧电流零区电压波形特征分析与应用[J]. 电工技术学报, 2020, 35(22): 4717-4725.
Zheng Xin, Shan Xiaojie. Characteristic analysis and application research of low voltage AC arc voltage waveform at the current zero[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4717- 4725.
[18] UL 1699-2006. Standard for arc-fault circuit- interrupters[S]. USA: Underwriters Laboratories, 2006.
[19] SAE AS 5692-2009 Arc fault circuit breaker (AFCB), aircraft, trip-free single phase and three phase 115V AC, 400Hz-constant frequency[S]. USA: Society of Automotive Engineers, 2009.
[20] Gilles J, Heal K. A parameterless scale-space approach to find meaningful modes in histograms application to image and spectrum segmentation[J]. International Journal of Wavelets Multiresolution and Information Processing, 2014, 12(6): 1450044.
[21] Gilles J. Empirical wavelet transform[J]. IEEE Transa- ctions on Signal Processing, 2013, 61(16): 3999- 4010.
[22] 吴建章, 梅飞, 潘益, 等. 基于改进经验小波变换的电能质量扰动检测新方法[J]. 电力自动化设备, 2020, 40(6): 142-151.
Wu Jianzhang, Mei Fei, Pan Yi, et al. Novel detection method of power quality disturbance based on IEWT[J]. Electric Power Automation Equipment, 2020, 40(6): 142-151.
[23] 刘艳丽, 郭凤仪, 李磊, 等. 一种串联型故障电弧数学模型[J]. 电工技术学报, 2019, 34(14): 2901- 2912.
Liu Yanli, Guo Fengyi, Li Lei, et al. A kind of series fault arc mathematical model[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2901-2912.
[24] 陈琳, 陈静, 王惠民, 等. 基于小波包能量熵的电池剩余寿命预测[J]. 电工技术学报, 2020, 35(8): 1827-1835.
Chen Lin, Chen Jing, Wang Huimin, et al. Prediction of battery remaining useful life based on wavelet packet energy entropy[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1827-1835.
[25] 何海, 胡姝博, 张建华, 等. 基于样本熵的新能源电力系统净负荷分时段调度[J]. 电力系统自动化, 2019, 43(24): 77-86.
He Hai, Hu Shubo, Zhang Jianhua, et al. Sample entropy based divided-period dispatch of net load in new energy power system[J]. Automation of Electric Power Systems, 2019, 43(24): 77-86.
[26] 张血琴, 张玉翠, 郭裕钧, 等. 基于高光谱技术的复合绝缘子表面老化程度评估[J]. 电工技术学报, 2021, 36(2): 388-396.
Zhang Xueqin, Zhang Yucui, Guo Yujun, et al. Aging degree evaluation of composite insulator based on hyperspectral technology[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 388-396.
Aviation AC Series Arc Fault Detection Based on Improve Empirical Wavelet Transform Multi-Feature Fusion
Abstract An arc fault detection method based on improved empirical wavelet transform (IEWT) multi-feature fusion and extreme learning machine (ELM) was proposed to deal with the mode mixing phenomenon of the time-frequency domain analysis method (EMD). Firstly, the arc current signal was decomposed into five empirical mode components (EMFs) by IEWT, and the weight energy entropy of EMFs, sample entropy of EMF4, and root mean square value of EMF1 were extracted as characteristic variables. After data standardization, the three arc fault features were fused to form a multi-dimensional feature matrix, and finally the fault was identified by ELM. Comparing the IEWT and EMD decomposition, the results show that the IEWT method is superior to the signal processing of EMD, and it also avoids the misjudgment caused by a single feature under the multi-feature extraction. Combined with ELM, arc faults can be accurately identified, and the average accuracy is 97.85%.
keywords:Aviation arc fault, empirical wavelet transform, multi-feature fusion, extreme learning machine, empirical mode decomposition, time-frequency analysis
DOI: 10.19595/j.cnki.1000-6753.tces.201706
中图分类号:TM501
河北省自然科学基金资助项目(E2016202106)。
收稿日期 2020-12-29
改稿日期 2021-02-18
崔芮华 女,1962年生,博士,教授,研究方向为电弧电接触。E-mail: 710667045@qq.com
张 振 男,1997年生,硕士研究生,研究方向为电工装备可靠性理论及应用。E-mail: 953327937@qq.com(通信作者)
(编辑 崔文静)