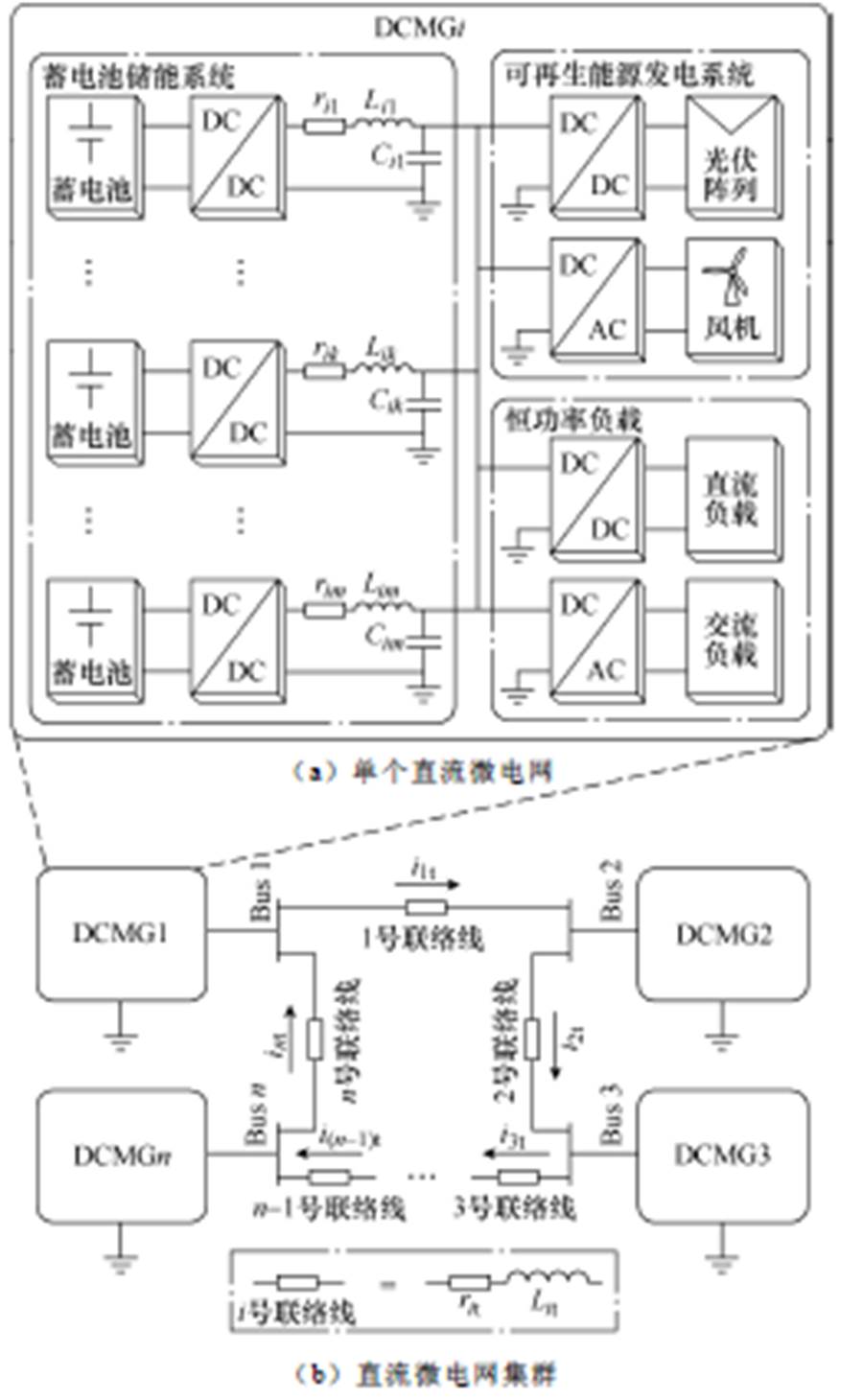
图1 直流微电网集群拓扑结构
Fig.1 Topology of the DCMGC
摘要 直流微电网集群通常由多个直流微电网互联而成,通过灵活的功率流动控制实现区域能源共享和优化利用,以充分发挥直流分布式发电系统的优势。然而,小规模直流微电网具有低惯性和高阻抗的“弱电网”特性,“弱-弱”互联会降低集群系统的阻尼,甚至出现振荡或系统崩溃等严重后果。同时,直流微电网集群的高阶、强耦合以及非线性动态特性也对其稳定性分析带来了巨大挑战。为此,基于Brayton-Moser混合势理论,提出针对直流微电网集群的大信号稳定性分析方法。建立集群的大信号降阶模型,详细推导用于系统大信号稳定性判据的混合势函数,并分析关键参数对稳定区间的影响,最后通过实时仿真结果验证了该分析的正确性。
关键词:直流微电网集群 大信号稳定性 恒功率负载 Brayton-Moser混合势理论
随着直流功率变换技术的发展,基于直流技术的电力应用得到了复苏,尤其是在分布式发电领 域[1]。在此背景下,直流微电网(DC Microgrids, DCMGs)作为整合可再生能源的有效解决方案应运而生。与交流微电网相比,直流微电网因具有高效率、低成本、控制设计简单等诸多优点而受到越来越多的关注[2-3]。为进一步发挥分布式发电系统的优势,地理上毗邻的多个直流微电网可互联构成直流微电网集群(DCMG Clusters, DCMGC),通过网间灵活的功率流动控制实现电源系统高弹性、高可靠性、经济性以及最优负载响应等目标[4-6]。
然而,由于直流微电网通常由分布式可再生能源(如光伏和风电)、储能系统(如蓄电池和超级电容)以及各类负载等异构单元通过电力电子接口连接至母线,其功率等级为kW级的小规模电源系统,导致系统等效惯量较小、网络阻抗较大,易受各类暂态扰动(如新能源的间歇性、负载投切、工作模式的切换及短路故障等)的影响,为典型的弱电网特性[7-11]。从这个意义上讲,直流微电网集群可看作为多个直流微电网的“弱-弱”互联,系统阻尼将因此进一步降低,可能导致振荡或系统崩溃,严重威胁系统的安全稳定运行。同时,直流微电网集群的动态分析涉及众多状态变量及多种非线性因素,如开关行为和恒功率负载(Constant Power Load, CPL)等,其高阶动态非线性特性也对集群系统的稳定性分析带来了巨大挑战。
一方面,目前对于直流微电网集群的关注不够,仅有少量文献研究其稳定性,且重点针对小信号扰动,将系统的非线性问题简化为线性时不变系统。文献[12]中,基于直流微电网集群的多输入多输出线性状态空间模型,推导出了局部Lyapunov函数,保证了系统的渐近稳定性。文献[13]中,通过简化各直流微电网的传递函数建立了直流微电网集群的小信号模型,通过根轨迹可以观察到联络线的电感和CPL等参数对系统小信号稳定性的影响。相同的方法也被应用于交流微电网集群的小信号稳定性评估与参数优化设计[14]。然而,小信号分析只能预测平衡点附近一个小区域内的系统动态行为,不适于大扰动分析。另一方面,与直流微电网及其系统相关的大信号稳定性研究尚集中于单个直流微电网,对于集群层面的大信号研究不足[15]。文献[16]针对含有CPL的分布式电力系统的大信号稳定性进行了分析,并在Lyapunov稳定性背景下,讨论了混合势理论稳定性判据。此后,CPL引起的大信号稳定性问题在复杂电力电子系统中得到了广泛的关注和研究[17]。文献[18]运用混合势函数、Takagi-Sugeno(T-S)模糊模型与逆轨迹等方法对比分析了含有CPL的直流微电网的大信号稳定性。在文献[7, 19-20]中,对直流微电网的大信号稳定性分析中重点考虑了下垂控制的影响。文献[20]同时运用分岔图辅助分析了直流微电网下垂控制在平衡点处的稳定性。考虑到CPL的不确定性,文献[21]研究了直流微电网在公共耦合点的大信号稳定问题,并对电网阻抗进行估计。文献[22]中,以并网电压源换流器为主电源的直流微电网为研究对象,建立了混合势函数模型,并分别分析了恒阻抗、恒电流及恒功率负载所对应的稳定性判据。
这些研究工作促进了单个直流微电网大信号稳定性的研究,但目前尚欠缺对于由多个直流微电网互联形成的集群系统的建模和分析。仅有文献[23]提出了基于T-S多模型法分析直流微电网集群的渐进稳定性区域(Region of Asymptotic Stability, RAS),但由于集群网络的复杂性,对于系统大信号稳定判定条件不易得到其全解析解,而采取部分解析、部分数值的混合分析方式。
为进一步简化直流微电网集群的大信号稳定性解析,本文提出基于Brayton-Moser混合势理论的分析方法。首先,针对直流微电网集群系统,将其等效成降阶模型,借助混合势理论,直接构造直流微电网集群系统等效降阶模型的能量泛函,在Lyapunov理论框架下进行系统的大信号稳定性评估,为直流微电网集群的大信号稳定性解析提供简便且有效的理论工具。本文将详细推导用于系统大信号稳定性判据的混合势函数,分析关键参数对稳定区间的影响,并给出实时仿真验证结果。
根据具体需求,直流微电网集群的组网可存在多种形式。例如,在直流配电网环境下,可采用串联、并联以及混联等结构[24]。文献[25]进一步指出,并联结构也分为直接并联、并联接入母线以及分段母线并联等方式。本文考虑集群中各直流微电网为同一电压等级,即采用直接互联的方式组网。
图1给出了研究对象的拓扑结构。图1a所示为单个低压直流微电网的电路拓扑,由可再生能源发电系统、蓄电池储能系统和恒功率负载构成,各异构单元均需通过DC-DC或DC-AC电力电子接口连接至直流母线。图1b为采用多个直流微电网通过联络线互联形成且具有环形拓扑结构的直流微电网集群,而环形拓扑集群能够实现高可靠性和高灵活性的供电目标。图中,rik、Lik和Cik分别为蓄电池储能单元线路电阻、蓄电池储能单元滤波器电感和滤波器电容;rit和Lit分别为第i条网间联络线的等效电阻和等效电感,iit为第i条网间联络线上的电流。

图1 直流微电网集群拓扑结构
Fig.1 Topology of the DCMGC
分层控制策略广泛应用于公共大电网和交流微电网[26],随着直流微电网技术的发展[27-28],直流微电网集群系统也逐渐引入分层控制策略以实现电压电流的调节及网间的能量管理[29-32]。使得直流微电网集群系统能够在不同的时间尺度上实现设备级控制与系统级解耦控制,保证了灵活的电压电流调节和功率均衡,实现集群内各直流微电网间区域能源共享和优化利用。下面针对本文所研究的直流微电网集群系统,以光伏-蓄电池储能型(Photovoltaic- Battery Energy Storage System, PV-BESS)直流微电网为研究对象,首先说明单个微电网内各单元的主电路拓扑及其控制结构。
蓄电池储能系统(BESS)及其接口为组网(Grid- Forming, GF)单元,主要起到控制母线电压的目的,其主电路拓扑及其控制策略如图2所示。图2a给出了储能单元的主电路为双向Buck-Boost变换器和LC滤波器串联的结构。图中,vbatik、voik、iBLik和ioik分别为第i个DCMGi内第k个蓄电池储能单元变换器的输入电压、输出电压、电感电流和输出电流;rBik、LBik、CBik和vbusi分别为蓄电池储能单元变换器的电感寄生电阻、电感、输出电容和第i个DCMGi的直流母线电压。图2b为储能单元的分层控制结构框图。一次控制采用下垂控制,通过虚拟电阻来改变变换器的输出特性,以实现各变换器间的功率分配;二次控制主要目的是补偿由下垂控制所带来的电压跌落,一般通过一致性算法来实现;而各直流微电网间的功率流动通常由三次控制所决定,以实现功率均衡和应力分担等目标。图中,ioi和ioj分别为本网内各储能单元输出总电流和除本网外其他网内各储能单元输出总电流;vavg-i和vavg-j分别为由一致性算法求出的本单元和相邻单元的平均输出电压;Rdik、voref和dvm分别为下垂电阻、参考电压和参考电压调整量。

(a)蓄电池储能单元主电路拓扑
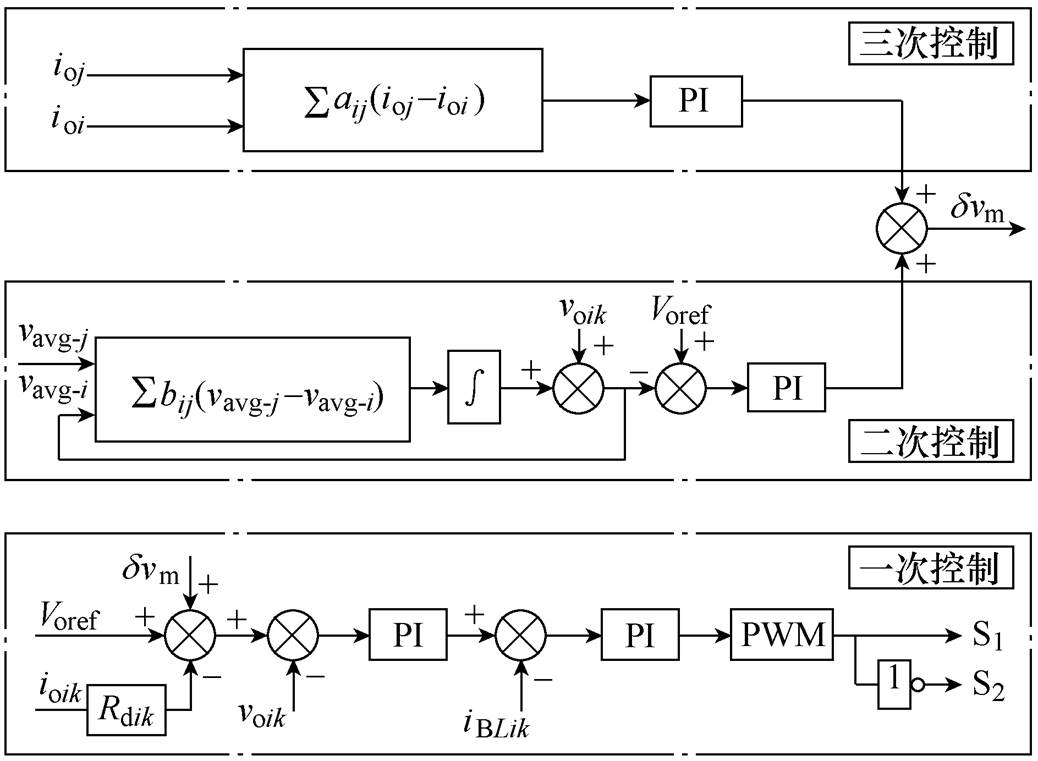
(b)分层控制策略
图2 蓄电池储能系统主电路拓扑及其分层控制策略
Fig.2 Topology and hierarchical control strategy of the BESS
光伏发电单元的主电路拓扑及其控制框图如图3所示,主电路为Boost变换器。为了提高发电效率,光伏发电单元通常工作在最大功率点追踪(Maximum Power Point Tracking, MPPT)模式。当光伏发电单元工作在MPPT模式时,从直流母线侧看,整个光伏发电单元可以等效成一个恒功率源(Constant Power Source, CPS),其功率值对应光伏阵列最大功率点功率。图中,vpvi和ipvi分别为第i个DCMGi内光伏阵列的输出电压和输出电流;rPi、LPi和CPi分别为光伏单元变换器的电感寄生电阻、电感和输出电容。

图3 光伏单元主电路拓扑及其控制框图
Fig.3 Topology and control block diagram of the PV unit
在实际应用中,直流微电网的负载通常由一个严格控制的DC-DC或DC-AC变换器加上直流或者交流负载[15]。本文所考虑的恒功率负载主电路及其控制框图如图4所示,主电路为单向Buck变换器加电阻性负载,控制环路为传统电压电流双闭环比例积分(Proportional Integral, PI)控制。图中,iCPLi、iLLi和vLi分别为第i个DCMGi内CPL的输入电流、电感电流和输出电压;rLi、LLi、CLi和RLi分别为CPL变换器的电感寄生电阻、电感、输出电容和负载电阻。在一定的电压、电流范围内,输入端口可以被看成是一个恒功率负载(Constant Power Load, CPL)。换言之,从直流母线侧看,CPL又可被等效成一个受直流母线电压控制的电流源,CPL输入电流iCPL与直流母线电压vbus呈非线性关系,可表示为
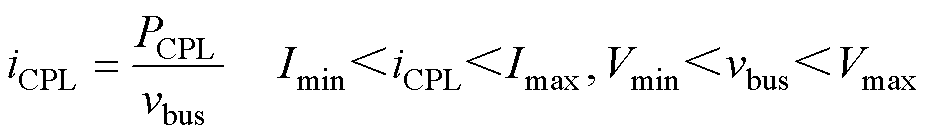 (1)
(1)
式中,PCPL为恒功率负载的功率;Imin、Imax和Vmin、Vmax分别为CPL输入电流和电压的最小、最大值。
图5给出了恒功率负载的特性曲线,对于曲线上任意一点 (
( ),电流和电压分别为
),电流和电压分别为 (
( )和
)和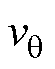 (
(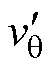 ),该点处的斜率1/Req为负,因此CPL的等效阻抗Req也为负。由于具有负阻抗特性,当CPL输入电压增大(从q 点到
),该点处的斜率1/Req为负,因此CPL的等效阻抗Req也为负。由于具有负阻抗特性,当CPL输入电压增大(从q 点到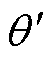 点)时,流经它的电流反而会减小;同理,当CPL输入电压减小(
点)时,流经它的电流反而会减小;同理,当CPL输入电压减小(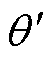 点到
点到 点)时,流经它的电流则会增大。这对与之相连的系统产生不稳定的影响,降低系统阻尼并会放大响应振荡[33]。进而,当CPL发生大幅度扰动时,在其非线性和负阻抗特性的共同作用下,可能导致直流母线电压振荡甚至崩溃等显著失稳现象[8, 22]。因此,在直流电源系统大信号稳定性研究中,CPL通常被认为是主要的不稳定因素。
点)时,流经它的电流则会增大。这对与之相连的系统产生不稳定的影响,降低系统阻尼并会放大响应振荡[33]。进而,当CPL发生大幅度扰动时,在其非线性和负阻抗特性的共同作用下,可能导致直流母线电压振荡甚至崩溃等显著失稳现象[8, 22]。因此,在直流电源系统大信号稳定性研究中,CPL通常被认为是主要的不稳定因素。

图4 恒功率负载主电路拓扑及其控制框图
Fig.4 Topology and control block diagram of the CPL
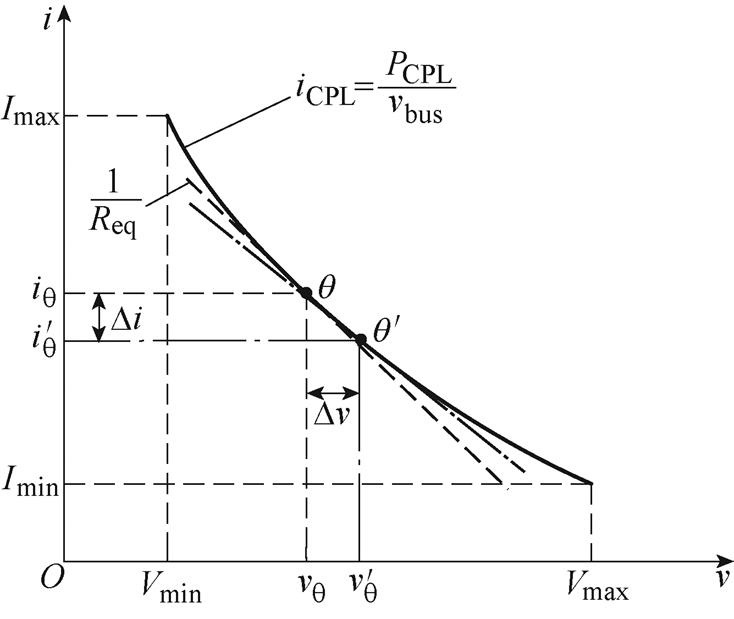
图5 恒功率负载特性曲线
Fig.5 Characteristic curves of the CPL
通过图1可知,由于单个直流微电网内存在多个电力电子接口电路,且考虑了连接线路阻抗、恒功率负载等多种因素,因此整体集群系统为典型的高阶、非线性复杂电路网络,对系统的大信号建模与分析带来了挑战。
然而,通过研究发现,在直流微电网的分层控制中,直流微电网集群的功率流动通常由系统的三次控制层所决定。相对于一次和二次控制,三次控制环路具有更低截止频率的低通滤波特性,因此系统的高频动态特性可以被忽略。这为通过低频降阶模型研究直流微电网集群的动态特性奠定了基础,能够从一定程度上简化分析。
考虑直流微电网内BESS由并联的多个蓄电池储能单元构成,一般通过一次和二次控制来维持母线电压的稳定;而三次控制动态调整电压参考值以实现网间功率流动,且电压偏差被控制在一定的范围内,其输出特性保持一致。因此,可将BESS等效为一个受控电压源。
另一方面,由光伏发电单元的输出特性及恒功率负载的输入特性可知,导出其等效大信号模型如图6所示。光伏单元作为CPS与CPL可以看成一个新的等效恒功率负载(Equivalent Constant Power Load, ECPL),其等效功率PECPLi可表示为
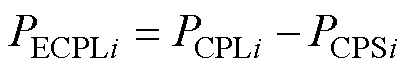 (2)
(2)
式中,PCPLi为恒功率负载功率之和;PCPSi为光伏单元在MPPT模式下作为CPS所提供的功率之和。
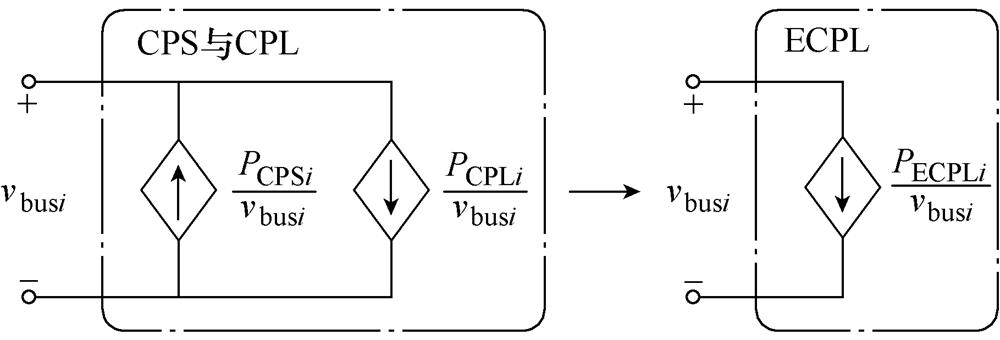
图6 等效恒功率负载大信号模型
Fig.6 Large signal model of the ECPL
对于单个直流微电网,目前已有多篇文献采用二阶简化电路模型对系统稳定性进行了分析[7, 21, 23]。基于上述等效分析,图7给出了本文所考虑的直流微电网等效降阶电路模型,单个直流微电网被简化为RLC电路网络。如第i个DCMGi由等效受控电压源Vi、线路电阻ri、线路电感Li、母线电容Ci和等效恒功率负载PECPLi组成。

图7 直流微电网等效降阶电路模型
Fig.7 Equivalent reduced-order circuit model of DCMG
根据电路参数取值区间,考虑设计条件
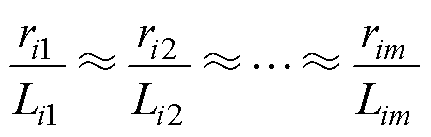 (3)
(3)
式中,等效线路电阻ri可推导为
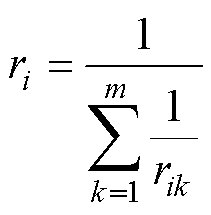 (4)
(4)
等效线路电感Li为
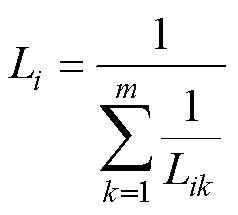 (5)
(5)
等效母线电容Ci为
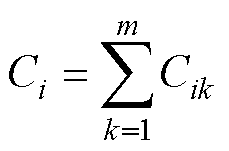 (6)
(6)
根据图7所示直流微电网的等效电路模型,可导出集群网络的动态模型,其状态方程可描述为
 (7)
(7)
式中,ii为DCMGi内输出总电流。
观察式(7)发现:①等效电路模型为3×n阶动态系统;②由式(7)中直流母线电压的微分方程可知,系统的非线性因素重点表现为各直流微电网内等效恒功率负载的特性。运用通用Lyapunov稳定性理论分析非线性系统稳定性,关键在于构造一个合适的Lyapunov函数。由于非线性系统的复杂性,目前尚无构造Lyapunov函数的统一方法,通常采用克拉索夫斯基法(Krasovsky Method, KM)和变量梯度法(Variable Gradient Method, VGM)构造Lyapunov函数。对于直流微电网集群这样一个高阶非线性系统,通过现有方法构造Lyapunov函数对其进行大信号稳定性分析会带来庞大的计算量;随着集群微电网个数的增加,计算量将呈指数增长,维数灾难将最终导致函数无法求解的问题。
在基于Lyapunov函数的非线性系统稳定性分析中,一般有两种途径可达到简化分析的目的: ①得到有效的简化模型以便于Lyapunov函数的构造;②提出简化的Lyapunov函数构造形式。本文提出基于Brayton-Moser混合势理论的直流微电网集群大信号稳定性分析方法属于两者结合,首先对直流微电网集群系统进行模型降阶,而后基于降阶模型利用混合势理论对系统进行大信号稳定性分析。混合势理论就是一种简化的Lyapunov类型函数构造方法,通过建立一个特殊形式的能量函数(势函数),为非线性RLC电路网络的动态特性分析提供了有效的解决途径,近年来也被应用于各类电力电子系统的稳定性分析[17-19, 22, 34]。
根据Brayton-Moser混合势理论的定义,混合势函数可以在特定的条件下构造Lyapunov型函数以分析和证明非线性电路网络的稳定性[35]。其中,“势函数”代表函数项包含电压和电流的乘积,“混合势函数”进一步表明其构造直接来源于电感、电容和电阻等多个相关混合变量势函数的叠加。同时,混合势理论也特别适于包含负阻抗元件的非线性电路网络的稳定性分析。
假设对一个非线性电路网络,其动态特性可表述为
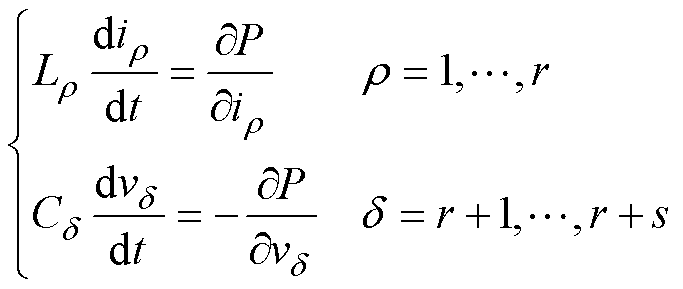 (8)
(8)
式中,Lr 为电路中电感元件;Cd 为电路中电容元件。
那么对于这个非线性电路网络,其混合势函数P可构造为
 (9)
(9)
式中,i=i1,…, ir为流经电感的电流;v=vr+1,…, vr+s为电容支路的电压,其用于非线性电路网络稳定性分析标量函数的一般形式可改写为
 (10)
(10)
式中,A(i)为电路中非储能元件的电流势函数;B(v)为电路中非储能元件的电压势函数;(i, Dv)为电路中电容的能量以及部分非储能元件的能量,它由电路的拓扑结构决定,D为常数矩阵。
混合势函数稳定性定理[35]:对于稳定性分析,可以构造函数为
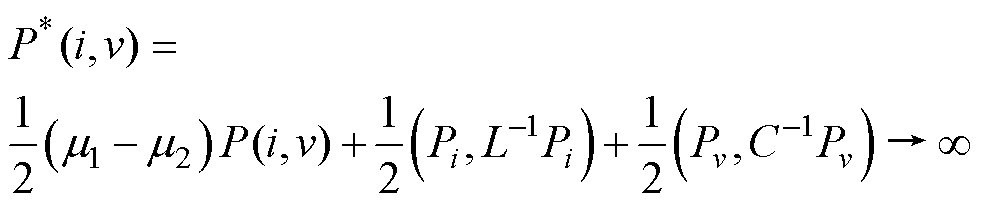 (11)
(11)
其中
 (12)
(12)
式中,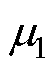 为
为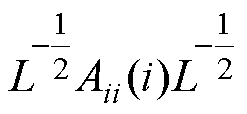 的最小特征值;
的最小特征值;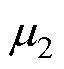 为
为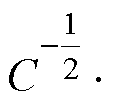
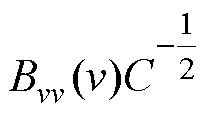 的最小特征值。
的最小特征值。
如果对于电路中所有i、v,满足条件
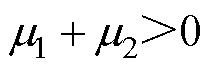 (13)
(13)
且当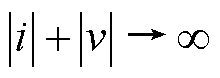 时,得到
时,得到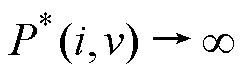 ;当
;当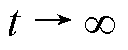 时,非线性系统的所有解在平衡点大范围内渐进稳定。
时,非线性系统的所有解在平衡点大范围内渐进稳定。
根据1.3节建立的直流微电网集群等效降阶电路模型,对其构造混合势函数,可依据电路元件分为以下几部分:
(1)等效电压源Vi的电流势为
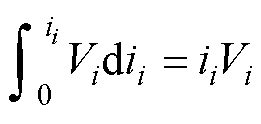 (14)
(14)
(2)网内线路电阻ri的电流势为
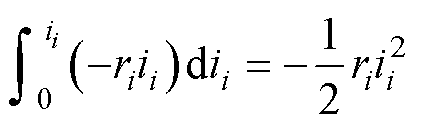 (15)
(15)
(3)网间联络线电阻rit的电流势为
 (16)
(16)
(4)等效恒功率负载PECPLi的电流势为
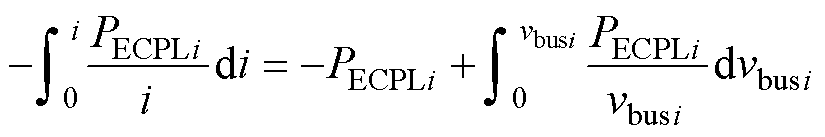 (17)
(17)
(5)网内母线电容Ci的能量为
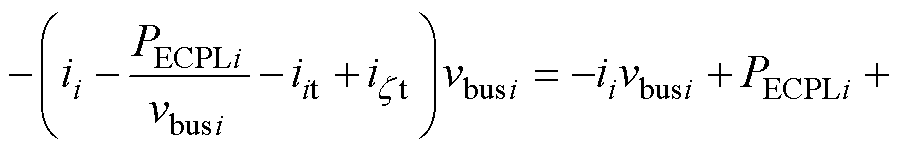
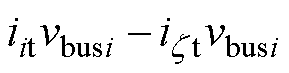 (18)
(18)
式中,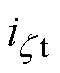 的下标
的下标 ,当1<i≤n时,
,当1<i≤n时, =i-1;当i=1时,
=i-1;当i=1时, =n。
=n。
综合直流微电网集群等效降阶模型的各部分电流势和能量函数,整体集群系统的混合势函数可表示为
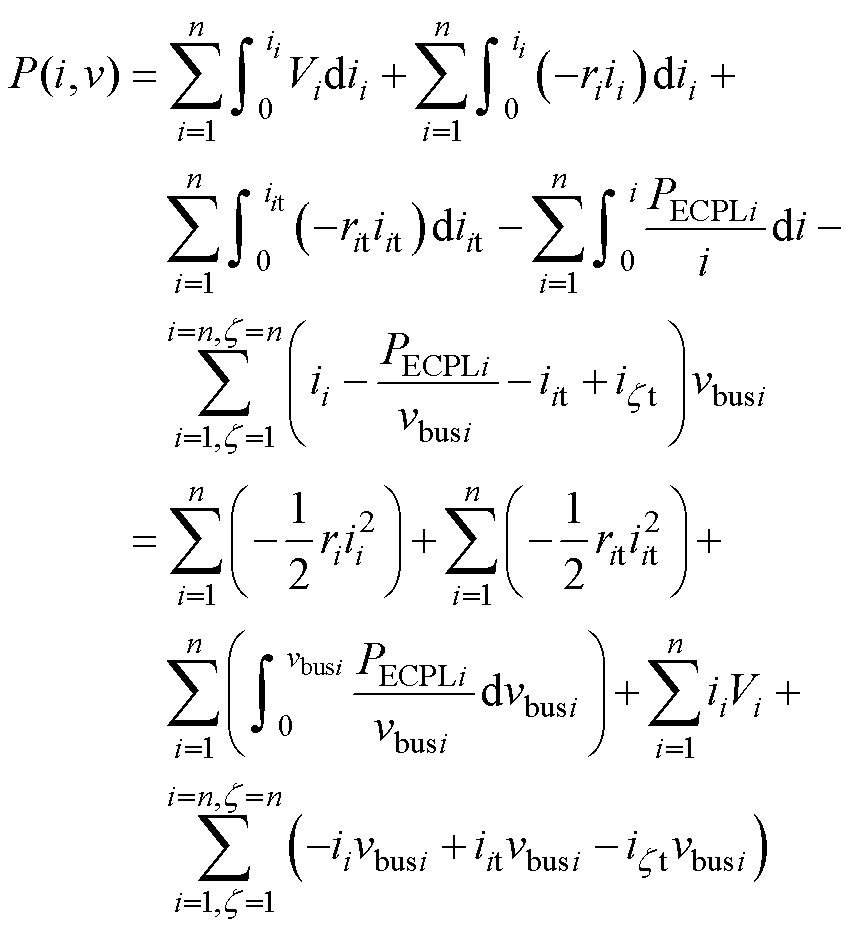 (19)
(19)
根据式(19)对系统各状态变量求偏导可得
 (20)
(20)
通过对比可知,式(20)满足式(8),说明系统混合势函数模型建立正确。
由式(19),根据2.1节所介绍的Brayton-Moser混合势理论可导出
 (21)
(21)
式中,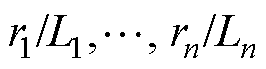 为网内线路参数;
为网内线路参数;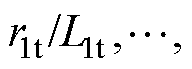
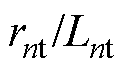 为网间线路参数;
为网间线路参数;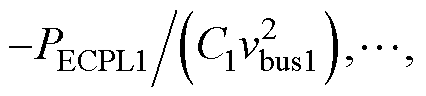
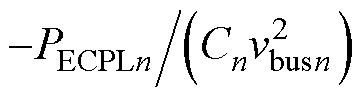 为等效恒功率负载支路参数。
为等效恒功率负载支路参数。
进而,由稳定性定理导出确保系统大信号稳定的充分条件为
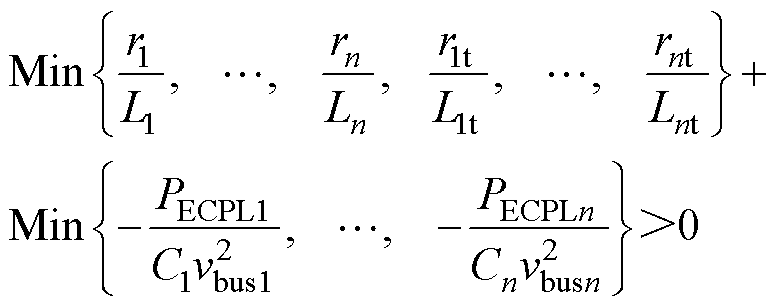 (22)
(22)
式中,函数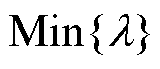 表示取最小元素(特征值)。
表示取最小元素(特征值)。
本文以4个直流微电网通过联络线互联形成具有环形拓扑结构的集群为具体研究对象,其结构如图1所示,其中每个直流微电网由一个光伏发电单元、一个蓄电池储能系统(包含2个储能单元)以及一个恒功率负载构成,则n=4, m=2。
因此,基于混合势理论的稳定性定理,得到确保系统大信号稳定的充分条件为
 (23)
(23)
为便于分析,假设集群内各微电网的参数保持一致,本文中主要变量参数的单位分别为电压单位为V、电阻单位为W、电感单位为mH、电容单位为mF、功率单位为kW;光伏发电单元、蓄电池储能单元和恒功率负载的主电路及控制环路参数分别见表1~表3,其中光伏发电单元采用增量电导法(Incre- mental Conductance Method, ICM)实现MPPT控制,在标准工况下(辐照强度Ir=1kW/m2,温度T=25℃),输出最大功率约为1kW(即PCPSi=1kW)。
根据1.3节建立直流微电网集群系统等效降阶电路模型的方法,针对上述具体研究对象,可以得出整个直流微电网集群系统等效降阶模型和联络线阻抗的参数见表4。
表1 光伏发电单元主电路及控制环路参数
Tab.1 Circuit and control loop parameters of the photovoltaic power generation unit

参 数数 值 变换器输入电压vpvi/V35~45 变换器电感LPi/mH1 变换器电感寄生电阻rPi/W0.02 变换器输出电容CPi/mF0.8 PI参数Kp1 Ki10 开关频率fsP/kHz10
表2 蓄电池储能系统单元主电路及控制环路参数
Tab.2 Parameters of the power circuit and the control loop of the BESS unit

参 数数 值 变换器额定输入电压vbatik/V100 变换器输出电压参考值Voref/V48 变换器电感LBik/mH1 变换器电感寄生电阻rBik/W0.02 变换器输出电容CBik/mF5 线路电阻rik/W0.2 LC滤波器电感Lik/mH0.4 LC滤波器电容Cik/mF0.4 三次控制环路系数aij1 三次控制环路PI参数Kp30.1 Ki310 二次控制环路系数bij1 二次控制环路PI参数Kp20.2 Ki220 下垂系数Rdik0.1 一次控制电压环PI参数Kvp10.5 Kvi120 一次控制电流环PI参数Kip10.1 Kii140 开关频率fsB/kHz10
表3 恒功率负载主电路及控制环路参数
Tab.3 Circuit and control loop parameters of the CPL

参 数数 值 变换器额定输入电压vbusi/V48 变换器输出电压参考值VLref/V24 变换器电感LLi/mH0.8 变换器电感寄生电阻rLi/W0.015 变换器输出电容CLi/mF1 负载电阻RLi根据功率需求改变 电压环PI参数Kvp0.4 Kvi50 电流环PI参数Kip0.4 Kii10 开关频率fsL/kHz10
表4 直流微电网集群等效降阶模型参数
Tab.4 Equivalent reduced-order model parameters of the DCMG cluster

参 数数 值 直流母线电压等级vbusi/V48 等效线路电阻ri/W0.1 等效线路电感Li/mH0.2 等效母线电容Ci/mF0.8 网间联络线电阻rit/W0.2 网间联络线电感Lit/mH0.1
由图1给出的环形集群拓扑可知,若因网络故障其中一条网间联络线发生断路的情况,仍能够保持各直流微电网互联,集群拓扑则由环形演变为链形,但此种拓扑的变化对系统大信号稳定性的影响尚未可知。
针对本文具体研究对象,假设4号联络线断路,系统动态从阶数而言由12阶变为11阶系统。此时,根据混合势理论导出满足系统大信号稳定性的充分条件为
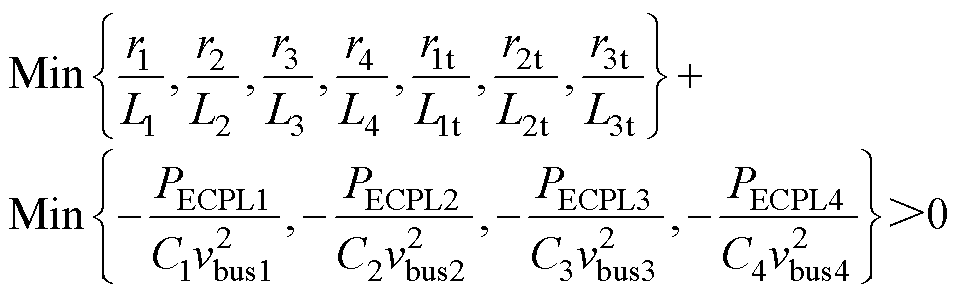 (24)
(24)
假设在集群内各直流微电网参数及各网间联络线保持一致的情况下,对比式(23)与式(24)发现,环形拓扑和链形拓扑的大信号稳定性条件保持一致,均为
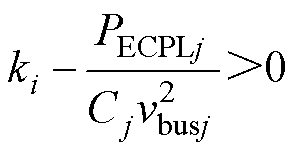 (25)
(25)
式中,当rit/Lit>ri/Li时,则ki=ri/Li,此时ri/Li为最小特征值;当rit/Lit<ri/Li时,则ki=rit/Lit,此时rit/Lit为最小特征值,可分别考虑i=j或i≠j的情况。
将各参数代入式(25)中的稳定性判据可得
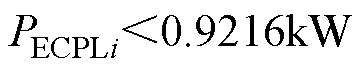 (26)
(26)
需要指出,尽管基于混合势函数得到的稳定性条件为充分非必要条件,但仍旧为直流微电网集群的大信号稳定性判定与分析提供了可供参考的依据,同时有效降低了分析计算量。
根据稳定性判据式(23)、式(24)可知,只需取稳定性判据中两部分最小值的和即可得到最终判据,所以分析不同电路参数对系统稳定性的影响时,需区分两种情况:①rit/Lit>ri/Li;②rit/Lit<ri/Li。
针对第①种情况,考虑rit/Lit>ri/Li时,只需考虑网内线路参数的影响,根据大信号稳定性判据 ,假设ECPL功率为PECPLi=0.8kW,研究某两个或三个参数的影响时,代入其他确定参数(见表4)可得如图8所示网内等效线路电阻ri、线路电感Li、母线电容Ci与ECPL功率PECPLi相对于母线电压vbusi的稳定边界。由图8可知,根据实际情况,在一定的直流母线电压允许变化范围(一般为±5%~±10%额定值),提升网内等效电阻等同于提高网络阻尼,有助于扩大系统稳定区域,提高稳定性。但随着网内线路电阻的提升会使得母线电压跌落及系统损耗的增加,因此改变电阻应综合考虑稳定性、母线电压偏差和系统效率等多方面因素。提高网内线路电感将会降低稳定裕度,增加母线电容能够增加稳定裕度,而增加ECPL功率则会减小稳定区域。为进一步确定ECPL导致系统稳定区间的变化趋势,图9给出了四种情况下的三维稳定空间。由图可知,ECPL的稳定工作区间随着直流母线电压和网内线路电阻的提高而增加,随着网内线路电感的减小和母线电压的提高而增加,随着母线电容和电压的提高而增加;同时也随着网内线路电感的减小和母线电容的提高而增加。
,假设ECPL功率为PECPLi=0.8kW,研究某两个或三个参数的影响时,代入其他确定参数(见表4)可得如图8所示网内等效线路电阻ri、线路电感Li、母线电容Ci与ECPL功率PECPLi相对于母线电压vbusi的稳定边界。由图8可知,根据实际情况,在一定的直流母线电压允许变化范围(一般为±5%~±10%额定值),提升网内等效电阻等同于提高网络阻尼,有助于扩大系统稳定区域,提高稳定性。但随着网内线路电阻的提升会使得母线电压跌落及系统损耗的增加,因此改变电阻应综合考虑稳定性、母线电压偏差和系统效率等多方面因素。提高网内线路电感将会降低稳定裕度,增加母线电容能够增加稳定裕度,而增加ECPL功率则会减小稳定区域。为进一步确定ECPL导致系统稳定区间的变化趋势,图9给出了四种情况下的三维稳定空间。由图可知,ECPL的稳定工作区间随着直流母线电压和网内线路电阻的提高而增加,随着网内线路电感的减小和母线电压的提高而增加,随着母线电容和电压的提高而增加;同时也随着网内线路电感的减小和母线电容的提高而增加。
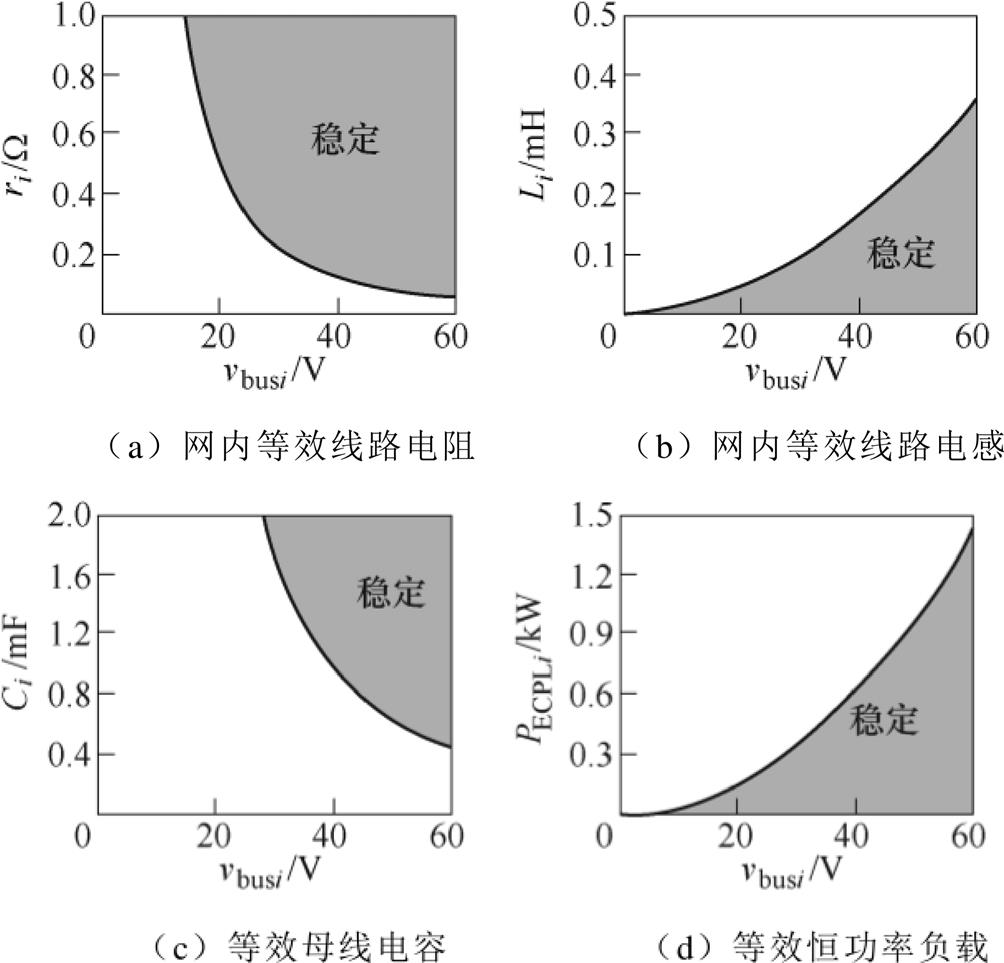
图8 当rit/Lit>ri/Li时的参数稳定性边界
Fig.8 Stability boundaries for circuit parameters with rit/Lit>ri/Li
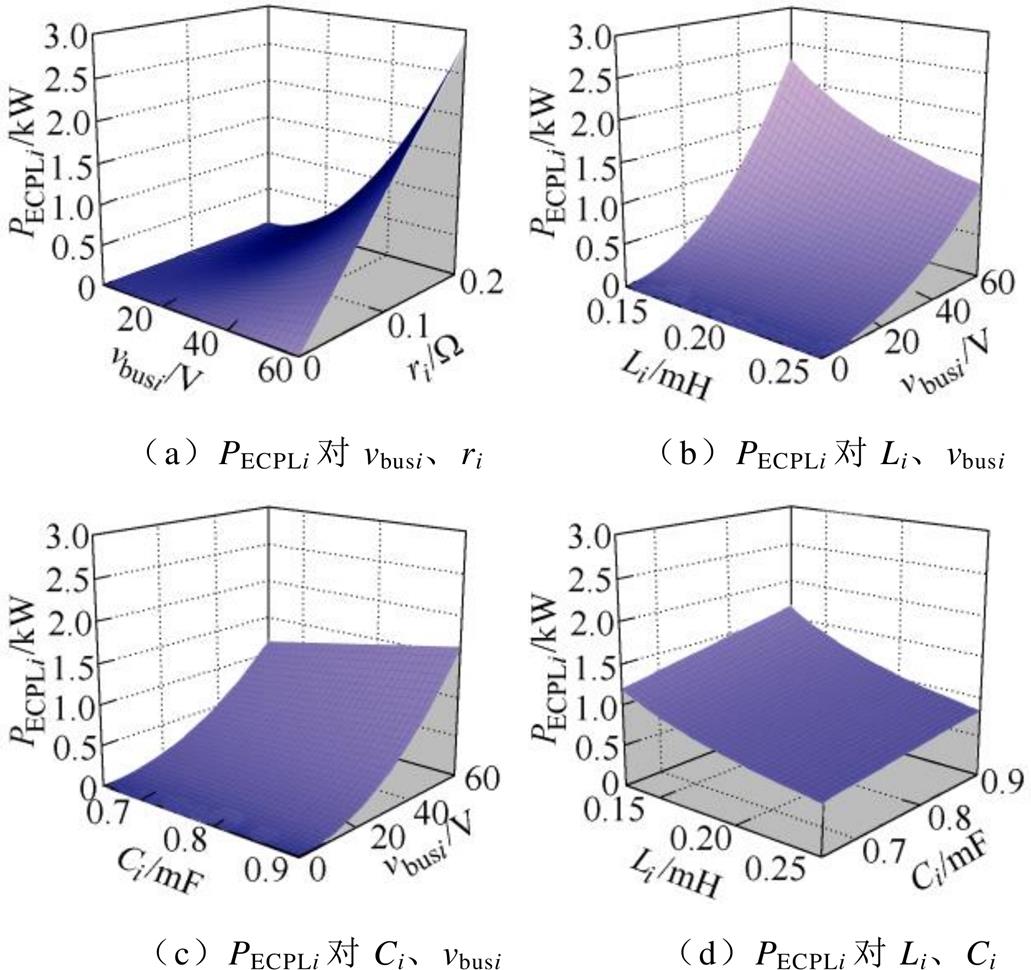
图9 当rit/Lit>ri/Li时的三维稳定空间
Fig.9 3-D stability space with rit/Lit>ri/Li
针对第②种情况,考虑rit/Lit<ri/Li时,此时只需考虑网间线路参数的影响,根据大信号稳定性判据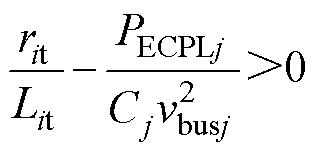 ,假设Lit=0.5mH,同理代入参数可得图10和图11所示的参数稳定区间和三维稳定空间。通过图10可发现,在一定范围内提高网间联络线电阻能够扩大稳定区域,而提高网间联络线电感将会降低稳定区域;同时,增加母线电容和ECPL功率会分别提高和降低集群系统的稳定裕度。通过图11可知,稳定工作区间随着母线电压和网间线路电阻的提高而增加,随着网间联络线电感的减小和母线电压的提高而增加,随着母线电容和电压的提高而增加;同时也随着网间联络线电感的减小和母线电容的提高而增加。与第①种情况不同的是,网间联络线电阻介于直流母线之间,由于各直流母线电压主要受各网内组网单元控制,因此联络线电阻对各母线电压的影响较小;同时联络线电阻的提升也应考虑线路损耗的要求。
,假设Lit=0.5mH,同理代入参数可得图10和图11所示的参数稳定区间和三维稳定空间。通过图10可发现,在一定范围内提高网间联络线电阻能够扩大稳定区域,而提高网间联络线电感将会降低稳定区域;同时,增加母线电容和ECPL功率会分别提高和降低集群系统的稳定裕度。通过图11可知,稳定工作区间随着母线电压和网间线路电阻的提高而增加,随着网间联络线电感的减小和母线电压的提高而增加,随着母线电容和电压的提高而增加;同时也随着网间联络线电感的减小和母线电容的提高而增加。与第①种情况不同的是,网间联络线电阻介于直流母线之间,由于各直流母线电压主要受各网内组网单元控制,因此联络线电阻对各母线电压的影响较小;同时联络线电阻的提升也应考虑线路损耗的要求。
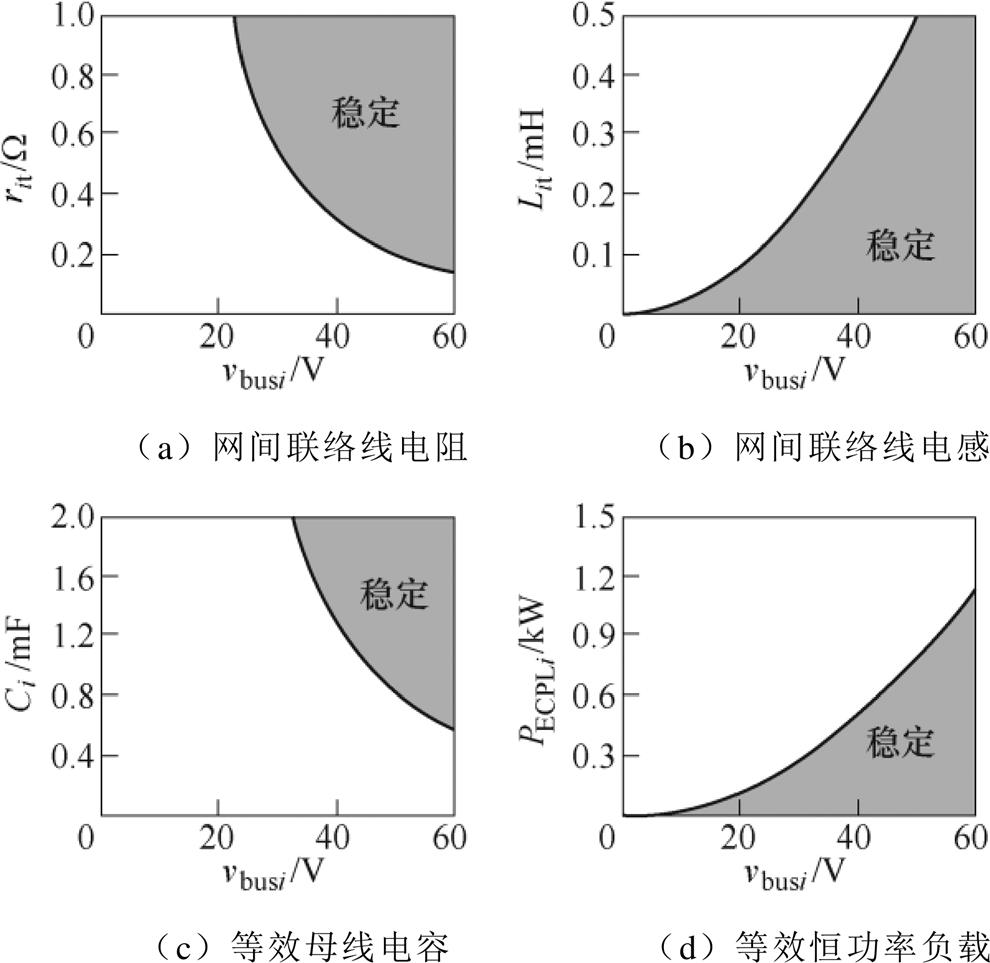
图10 当rit/Lit<ri/Li时的参数稳定性边界
Fig.10 Stability boundaries for circuit parameters with rit/Lit<ri/Li
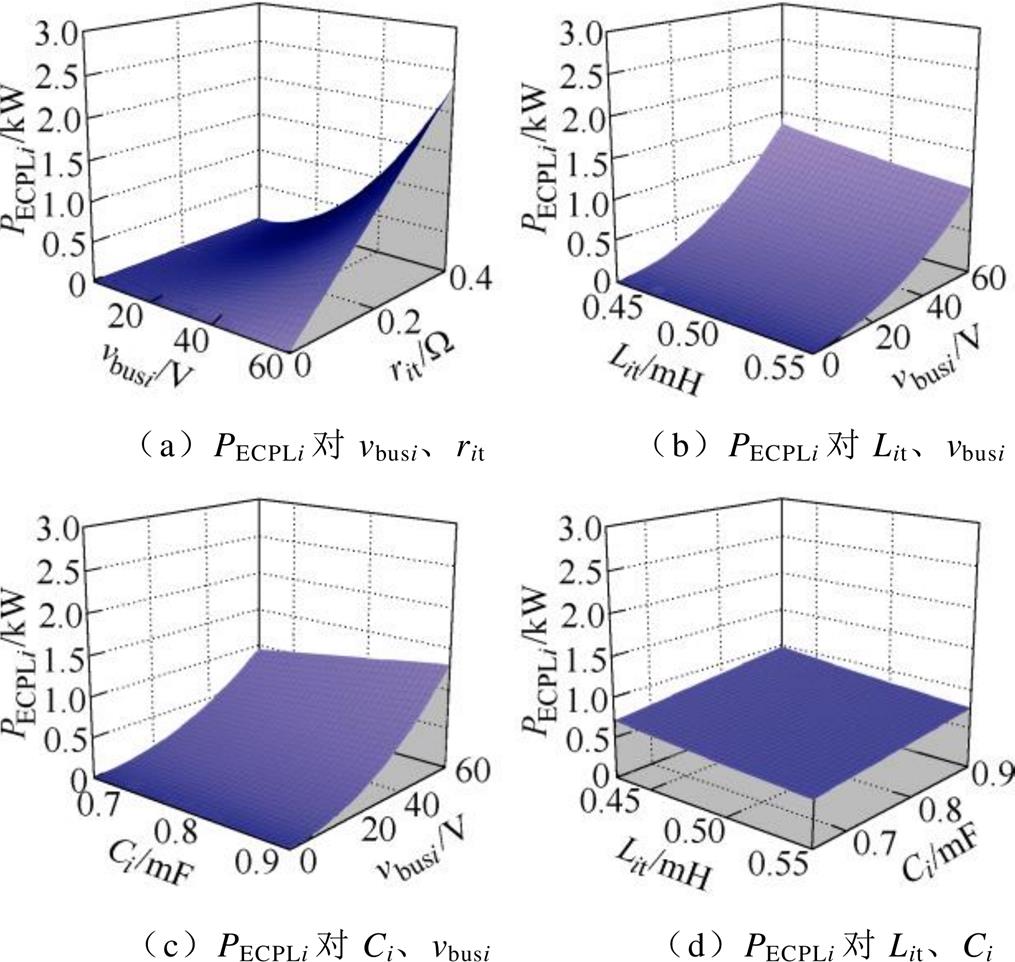
图11 当rit/Lit<ri/Li时的三维稳定空间
Fig.11 3-D stability space with rit/Lit<ri/Li
综合上述,根据稳定性判据分别讨论了两种情况下系统参数对稳定性的影响,图8、图9对应第①种情况: (只需考虑网内线路参数),图10、图11对应第②种情况:
(只需考虑网内线路参数),图10、图11对应第②种情况: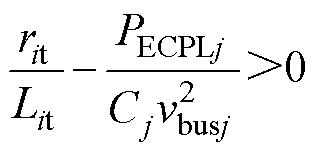 (只需考虑网间线路参数)。进而对比分析上述两种情况可发现,虽然上述两种情况的稳定性对于参数的变化趋势基本一致,但参数对稳定性影响的敏感程度有所不同。例如,对比图9b与图11b以及图9d与图11d可知,当rit/Lit>ri/Li时,无需考虑网间联络线的影响,此时系统大信号稳定性对网内线路电感的敏感度较高;当rit/Lit<ri/Li时,无需考虑网内线路影响,系统大信号稳定性对网间联络线电感的敏感度较低。因此,在满足稳定性判据的前提下,相对于网内线路电感,网间联络线电感的变化对系统大信号稳定域影响较小。另外,在实际情况中,各网间联络线上电感参数远小于由LC滤波器等效的网内线路上的电感参数。因此,根据稳定性判据可知,可暂时不考虑网间联络线参数的影响。
(只需考虑网间线路参数)。进而对比分析上述两种情况可发现,虽然上述两种情况的稳定性对于参数的变化趋势基本一致,但参数对稳定性影响的敏感程度有所不同。例如,对比图9b与图11b以及图9d与图11d可知,当rit/Lit>ri/Li时,无需考虑网间联络线的影响,此时系统大信号稳定性对网内线路电感的敏感度较高;当rit/Lit<ri/Li时,无需考虑网内线路影响,系统大信号稳定性对网间联络线电感的敏感度较低。因此,在满足稳定性判据的前提下,相对于网内线路电感,网间联络线电感的变化对系统大信号稳定域影响较小。另外,在实际情况中,各网间联络线上电感参数远小于由LC滤波器等效的网内线路上的电感参数。因此,根据稳定性判据可知,可暂时不考虑网间联络线参数的影响。
为了验证上述直流微电网集群大信号稳定性分析的正确性,搭建了实时仿真平台,仿真模型参数与表1~表4所列一致。图12给出了实时仿真测试平台及实时仿真过程。如图12所示,实时仿真过程主要包括三个步骤:①在Matlab/Simulink环境中搭建所研究直流微电网集群系统的仿真模型并初步进行数值仿真证明;②将仿真模型编译成代码文件,然后通过上位机(dSPACE Control Desk)下载到dSPACE(DS1202)MicroLabBox硬件平台上;③进行实时仿真证明。
图12 实时仿真测试平台
Fig.12 Platform of the real-time simulation test
本节重点对直流微电网集群分层控制策略的有效性进行验证。根据3.2节的稳定性判据求出系统大信号稳定的充分条件为PECPLi<0.921 6kW,由于光伏发电单元在MPPT模式下输出最大功率为PCPSi=1kW,因此,假设在光伏单元输出功率不变的情况下,可得出恒功率负载的稳定范围为PCPLi<1.921 6kW。图13给出了集群系统各网内恒功率负载超过功率界限后系统不稳定运行又跳变回稳定界限内的系统响应波形。由图13可知,系统首先运行在初始工况:各网内恒功率负载均为PCPLi=1.2kW、光伏在MPPT模式下输出最大功率PCPSi=1kW;而后各网内恒功率负载跳变至PCPLi=2.3kW,超出稳定界限,系统处于不稳定运行状态;最后,各网内恒功率负载分别跳变至PCPL1=1.2kW、PCPL2=1.4kW、PCPL3=1.6kW和PCPL4=1.8kW,此时各网内负荷均不相同,而系统在分层控制的作用下实现了网间的功率均衡,由图13b可知,各直流微电网内蓄电池储能系统的出力保持一致。由此可知,系统在超过稳定界限后再次跳变回稳定界限内依然能够稳定地实现分层控制策略。因此,系统在满足大信号稳定性判据的情况,且直流微电网集群在分层控制的作用下,有效地保证了灵活的电压电流调节和功率流动控制,实现了区域能源共享和优化利用。

图13 系统在分层控制策略下功率均衡响应
Fig.13 Power balance responses of the system under the hierarchical control strategy
由4.1节分析结果可知,恒功率负载的稳定范围为PCPLi<1.921 6kW。图14所示为系统在环形拓扑下直流母线电压随CPL跳变的响应波形,图14分别为4个CPL功率(PCPLi, i=1, 2, 3, 4)同时从1.2kW跳变到2.1kW、2.2kW和2.3kW直流母线电压响应波形。图15所示为系统在链形拓扑下直流母线电压随CPL跳变的响应波形,图15同样分别为4个CPL功率(PCPLi, i=1, 2, 3, 4)同时从1.2kW跳变到2.1kW、2.2kW和2.3kW直流母线电压响应波形。由图14a、图15a可知,当CPL功率从1.2kW跳变到2.1kW时,虽然已超出稳定边界,但系统依旧能够维持母线电压稳定运行。由图14b和图15b可知,当CPL功率从1.2kW跳变到2.2kW时,直流母线电压开始小幅振荡,系统运行开始趋于不稳定。如图14c和图15c所示,当CPL功率从1.2kW跳变到2.3kW时,直流母线电压开始大幅振荡,系统不稳定运行。
另外,综合比较图14和图15可知,直流微电网集群在环形拓扑和链形拓扑下的大信号稳定性基本一致,这与前文大信号稳定性理论分析结果相吻合。结合大信号稳定性判据及实时仿真结果可知,基于混合势函数得到的大信号稳定性判据虽为充分非必要条件,预测具有一定的保守性,但分析偏差仍在可接受范围。
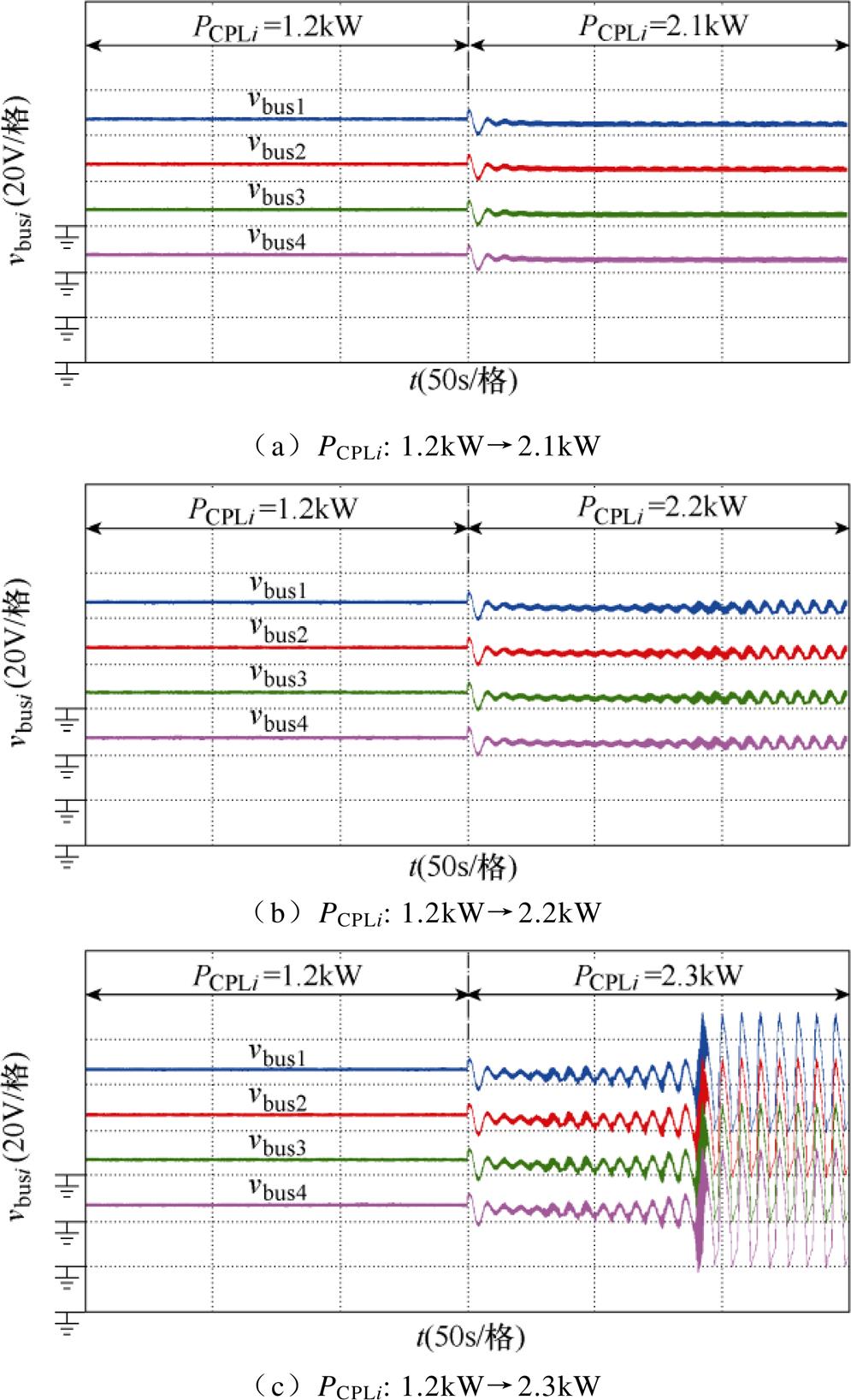
图14 环形拓扑下直流母线电压随CPL跳变的响应
Fig.14 Responses of DC bus voltage with CPL step change in the ring topology

图15 链形拓扑下直流母线电压随CPL跳变的响应
Fig.15 Responses of DC bus voltage with CPL step change in the chain topology
根据1.3节等效恒功率负载建模可知,当光伏单元工作于MPPT模式,由于光照、温度等因素而导致输出功率发生变化时,等效恒功率负载的功率也随之变化。为此,本节主要验证系统随光伏发电单元输出功率变化的响应情况。图16所示为系统随光伏发电单元输出功率变化的响应,集群系统首先运行在初始工况:各网内恒功率负载均为PCPLi= 1.2kW、光伏在MPPT模式下输出最大功率PCPSi= 1kW;然后,各网内恒功率负载跳变为PCPLi=1.9kW,由于满足大信号稳定性条件,系统还能够稳定运行;假设辐照强度从Ir=1kW/m2减弱到原来的一半Ir= 0.5kW/m2,此时各光伏单元出力约为0.46kW,各直流母线电压开始剧烈振荡,系统不稳定运行。根据3.2节的稳定性判据求出系统大信号稳定的充分条件PECPLi<0.9216kW,在网内各恒功率负载功率为1.9kW的情况下可得光伏出力的稳定性边界为PCPSi>0.978 4kW。由上述条件可知,在辐照强度减半后,光伏单元出力减弱,不满足系统大信号稳定性条件,因此无法保证系统稳定。
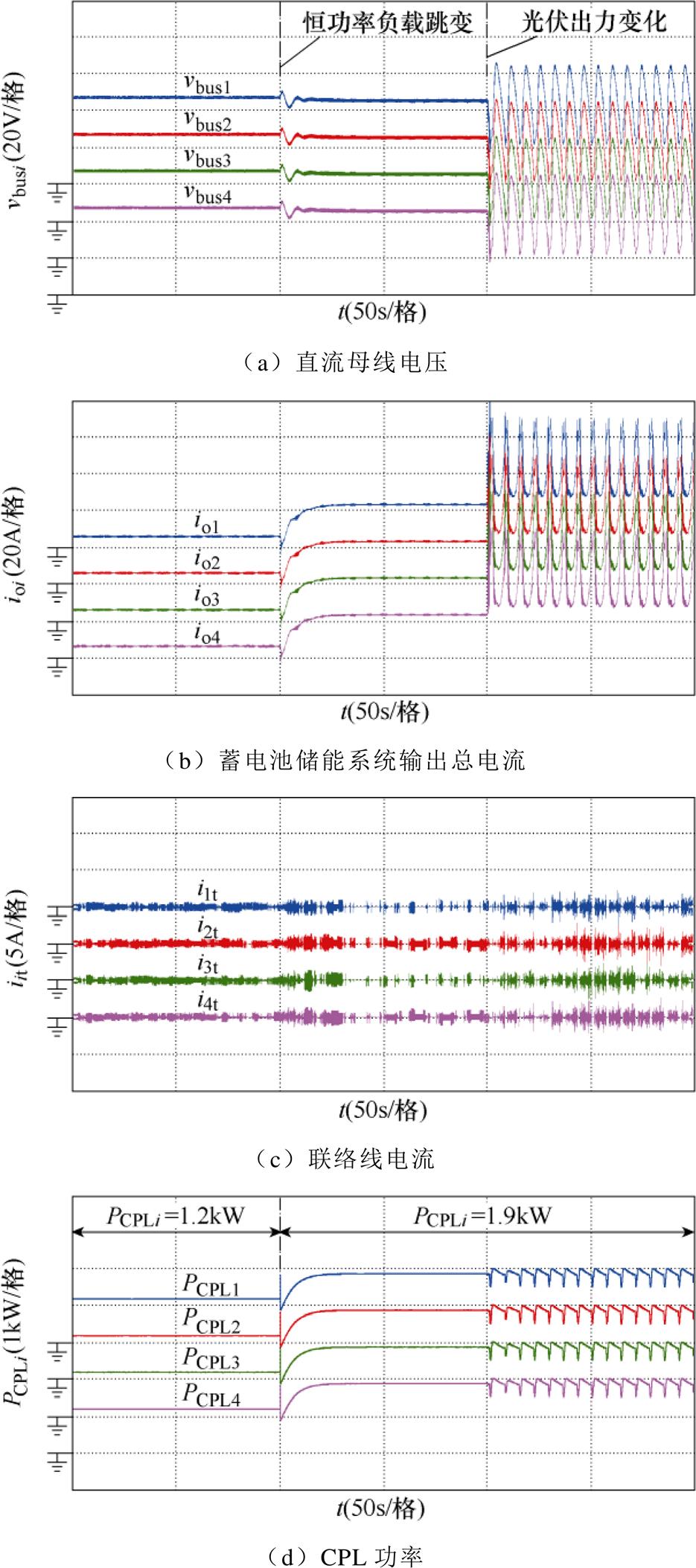
图16 系统随光伏发电单元输出功率变化的响应
Fig.16 Responses of the system with the output power change of PV units
基于第3.2节的理论分析可知,直流微电网集群在环形拓扑和链形拓扑结构下稳定性判据保持一致。因此,可推论得到,环形拓扑和链形拓扑结构间的变化对系统稳定性无本质影响。另外,根据4.1节验证结果,当各直流微电网内负荷相同时,则各网间无功率流动,即网间联络线上电流为零,此时网间联络线是否连接则对系统运行无影响。
为了得到有效的验证分析结果,本节采用了各网内负荷均不相同的情况(PCPL1=1.2kW、PCPL2= 1.4kW、PCPL3=1.6kW和PCPL4=1.8kW)对拓扑变化进行了验证。图17给出了直流微电网集群在环形拓扑切换到链形拓扑后再切换回环形拓扑的系统响应波形。由图可知,当4号联络线断路时,系统从环形拓扑变化为链形拓扑,此时网间联络线上的电流进行了重新分配。而当4号联络线恢复时,系统又从链形拓扑切换回环形拓扑,经过短暂调整,系统又稳定运行在环形拓扑下。同时,各微电网的直流母线电压和蓄电池储能系统的出力做了微调以适应拓扑结构的变化,从而达到新的功率均衡状态。因此可知,只要系统满足大信号稳定判据,环形拓扑与链形拓扑的切换能够保证直流微电网集群的稳定运行。
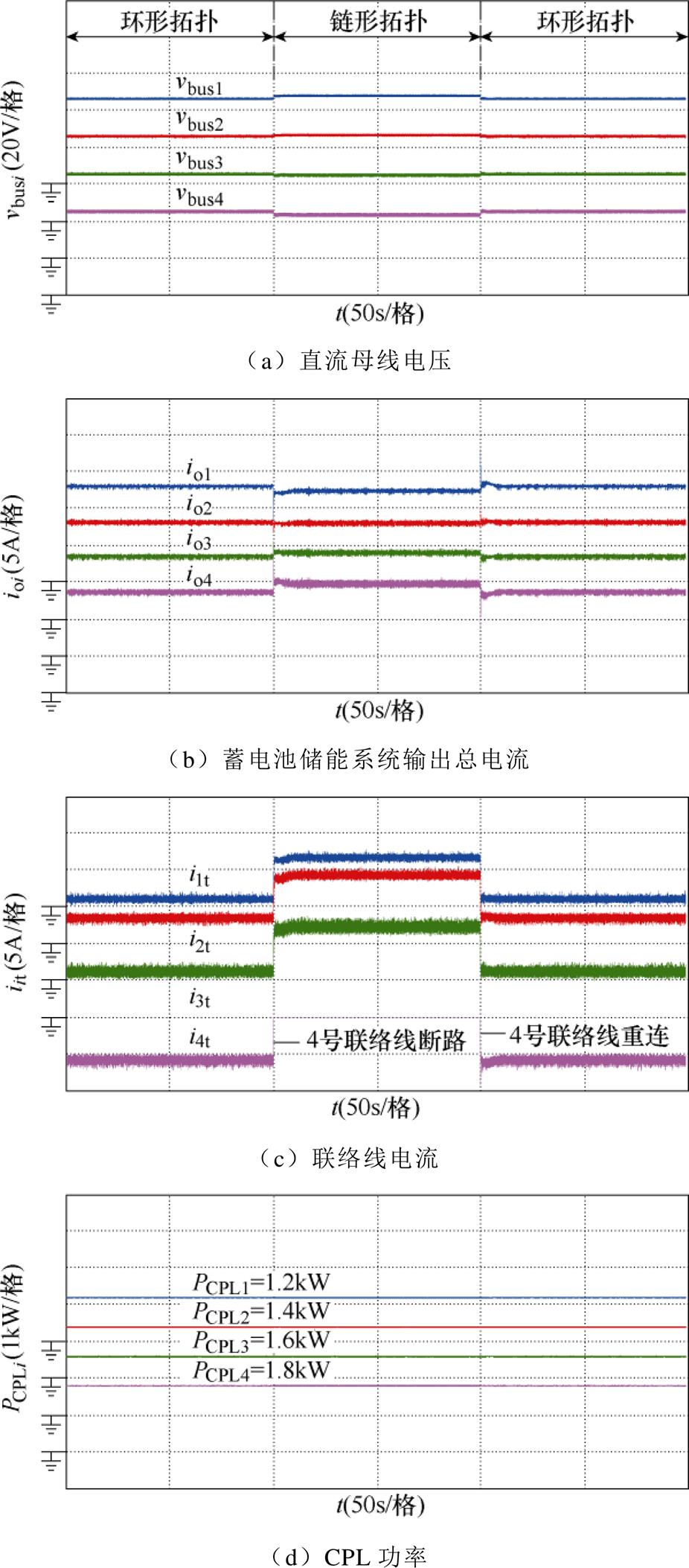
图17 拓扑结构变化下的系统响应
Fig.17 Responses of the system with topology change
针对直流微电网集群,本文提出了基于混合势理论的大信号稳定性分析方法,通过分析与验证可得如下结论:
1)混合势理论适用于直流微电网集群系统,为通过构造能量函数分析此类复杂网络的大信号稳定性提供了简便且有效的依据。
2)导出的稳定性判据能够有效预测系统的大信号稳定区间,其保守性在可接受范围之内。
3)恒功率负载为影响集群系统稳定性的主要因素;系统大信号稳定性对联络线电感的敏感度相对较低,稳定区域对联络线电感的相对变化量并不显著。
4)环形与链形拓扑切换并未对系统的大信号稳定性产生本质影响,链形拓扑能够保证系统大信号稳定运行;但从组网结构而言,环形拓扑比链形拓扑多一条潮流通道,因此环形拓扑具有更好的冗余性和更高的可靠性。
后续研究将重点针对直流微电网集群系统的实证,同时考虑分布式通信网络对系统稳定性的影响,进一步深入评估与验证大信号稳定性的分析结果,形成有效的系统控制与设计方法。
参考文献
[1] Dragičević T, Lu Xiaonan, Vasquez J C, et al. DC microgrids-part I: a review of control strategies and stabilization techniques[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4876-4891.
[2] Lasseter R H. Microgrids[C]//2002 IEEE Power Engineering Society Winter Meeting, New York, NY, USA, 2002: 305-308.
[3] Ito Y, Yang Zhongqing, Akagi H. DC microgrid based distribution power generation system[C]//the 4th International Power Electronics and Motion Control Conference, Xi’an, China, 2004: 1740-1745.
[4] Li Xialin, Guo Li, Li Yunwei, et al. Flexible interlinking and coordinated power control of multiple DC microgrids clusters[J]. IEEE Transa- ctions on Sustainable Energy, 2018, 9(2): 904-915.
[5] Meng Lexuan, Shafiee Q, Trecate G F, et al. Review on control of DC microgrids and multiple microgrid clusters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(3): 928-948.
[6] 张伟亮, 张辉, 支娜, 等. 考虑网络损耗的基于模型预测直流微电网群能量优化策略[J]. 电力系统自动化, 2021, 45(13): 49-56.
Zhang Weiliang, Zhang Hui, Zhi Na, et al. Model prediction based energy optimization strategy for DC microgrid groups considering network loss[J]. Auto- mation of Electric Power Systems, 2021, 45(13): 49-56.
[7] Xie Wenqiang, Han Minxiao, Cao Wenyuan, et al. System-level large-signal stability analysis of droop- controlled DC microgrids[J]. IEEE Transactions on Power Electronics, 2021, 36(4): 4224-4236.
[8] Liu Sucheng, Zheng Jiazhu, Li Run, et al. Multiple Lyapunov function-based large signal stability analysis of DC microgrid with coordinated control[C]// 2019 22nd International Conference on Electrical Machines and Systems, Harbin, China, 2019: 1-6.
[9] 朱晓荣, 李铮, 孟凡奇. 基于不同网架结构的直流微电网稳定性分析[J]. 电工技术学报, 2021, 36(1): 166-178.
Zhu Xiaorong, Li Zheng, Meng Fanqi. Stability analysis of DC microgrid based on different grid structures[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 166-178.
[10] 施静容, 李勇, 贺悝, 等. 一种提升交直流混合微电网动态特性的综合惯量控制方法[J]. 电工技术学报, 2020, 35(2): 337-345.
Shi Jingrong, Li Yong, He Li, et al. A comprehensive inertia control method for improving the dynamic characteristics of hybrid AC-DC microgrid[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(2): 337-345.
[11] 张伟亮, 张辉, 支娜, 等. 环形直流微电网故障分析与保护[J]. 电力系统自动化, 2020, 44(24): 105- 110.
Zhang Weiliang, Zhang Hui, Zhi Na, et al. Fault analysis and protection of ring DC microgrid[J]. Automation of Electric Power Systems, 2020, 44(24): 105-110.
[12] Han Renke, Tucci M, Martinelli A, et al. Stability analysis of primary plug-and-play and secondary leader-based controllers for DC microgrid clusters[J]. IEEE Transactions on Power Systems, 2019, 34(3): 1780-1800.
[13] Shafiee Q, Dragicevic T, Vasquez J C, et al. Modeling, stability analysis and active stabilization of multiple DC-microgrid clusters[C]//2014 IEEE international energy conference, Cavtat, Croatia, 2014: 1284-1290.
[14] He Jinghan, Wu Xiaoyu, Wu Xiangyu, et al. Small- signal stability analysis and optimal parameters design of microgrid clusters[J]. IEEE Access, 2019, 7: 36896-36909.
[15] Marx D, Magne P, Nahid-Mobarakeh B, et al. Large signal stability analysis tools in DC power systems with constant power loads and variable power loads-a review[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1773-1787.
[16] Belkhayat M, Cooley R, Witulski A. Large signal stability criteria for distributed systems with constant power loads[C]//Proceedings of PESC'95-Power Elec- tronics Specialist Conference, Atlanta, GA, USA, 1995: 1333-1338.
[17] Jiang Jianbo, Liu Fei, Pan Shangzhi, et al. A conservatism-free large signal stability analysis method for DC microgrid based on mixed potential theory[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 11342-11351.
[18] 滕昌鹏, 王玉斌, 周博恺, 等. 含恒功率负载的直流微网大信号稳定性分析[J]. 电工技术学报, 2019, 34(5): 973-982.
Teng Changpeng, Wang Yubin, Zhou Bokai, et al. Large-signal stability analysis of DC microgrid with constant power loads[J]. Transactions of China Elec- trotechnical Society, 2019, 34(5): 973-982.
[19] Li Zekun, Pei Wei, Ye Hua, et al. Large signal stability analysis for DC microgrid under droop control based on mixed potential theory[J]. The Journal of Engineering, 2019, 2019(16): 1189-1193.
[20] Liu Haiyuan, Guo Wenzhong, Cheng Dong, et al. Stability and bifurcation analysis of DC microgrid with multiple droop control sources and loads[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 2361-2372.
[21] Sanchez S, Molinas M. Large signal stability analysis at the common coupling point of a DC microgrid: a grid impedance estimation approach based on a recursive method[J]. IEEE Transactions on energy conversion, 2015, 30(1): 122-131.
[22] 厉泽坤, 孔力, 裴玮. 直流微电网大扰动稳定判据及关键因素分析[J]. 高电压技术, 2019, 45(12): 3993-4002.
Li Zekun, Kong Li, Pei Wei. Analyses of stability criterion and key factors of DC microgrid under large disturbance[J]. High Voltage Engineering, 2019, 45(12): 3993-4002.
[23] Liu Sucheng, Li Xiang, Xia Mengyu, et al. Takagi- Sugeno multimodeling-based large signal stability analysis of DC microgrid clusters[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(11): 12670- 12684.
[24] 刘海涛, 熊雄, 季宇, 等. 直流配电下多微网系统集群控制研究[J]. 中国电机工程学报, 2019, 39(24): 7159-7167, 7489.
Liu Haitao, Xiong Xiong, Ji Yu, et al. Cluster control research of multi-microgrids system under DC distribution system[J]. Proceedings of the CSEE, 2019, 39(24): 7159-7167, 7489.
[25] 顾后生, 李霞林, 郭力, 等. 多直流微电网群柔性互联与控制[J]. 电力系统及其自动化学报, 2020, 32(4): 1-8.
Gu Housheng, Li Xialin, Guo Li, et al. Flexible interconnection and control of multiple DC microgrid clusters[J]. Proceedings of the CSU-EPSA, 2020, 32(4): 1-8.
[26] Tan D. Structured microgrids (SμGs) and flexible electronic large power transformers (FeLPTs)[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 255-263.
[27] 胡长斌, 王慧圣, 罗珊娜, 等. 计及直流微电网扰动抑制的残差动态分散补偿控制策略[J]. 电工技术学报, 2021, 36(21): 4493-4507, 4543.
Hu Changbin, Wang Huisheng, Luo Shanna, et al. Sesidual dynamic decentralized compensation control strategy considering disturbance suppression[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4493-4507, 4543.
[28] 喻礼礼, 张兆云, 刘艺涛. 基于改进自适应下垂的直流微电网稳定分析与研究[J]. 电气技术, 2020, 21(5): 28-32.
Yu Lili, Zhang Zhaoyun, Liu Yitao. Stability analysis and research of DC microgrid based on improved adaptive drooping[J]. Electrical Engineering, 2020, 21(5): 28-32.
[29] Shafiee Q, Dragičević T, Vasquez J C, et al. Hierarchical control for multiple DC-microgrids clusters[J]. IEEE Transactions on Energy Conversion, 2014, 29(4): 922-933.
[30] Liu Sucheng, Liu Rui, Zheng Jiazhu, et al. Predictive function control in tertiary level for power flow management of DC microgrid clusters[J]. Electronics Letters, 2020, 56(13): 675-676.
[31] 李忠文, 程志平, 张书源, 等. 考虑经济调度及电压恢复的直流微电网分布式二次控制[J]. 电工技术学报, 2021, 36(21): 4482-4492.
Li Zhongwen, Cheng Zhiping, Zhang Shuyuan, et al. Distributed secondary control for economic dispatch and voltage restoration of DC microgrid[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(21): 4482-4492.
[32] 杨美辉, 周念成, 王强钢, 等. 基于分布式协同的双极直流微电网不平衡电压控制策略[J]. 电工技术学报, 2021, 36(3): 634-645.
Yang Meihui, Zhou Niancheng, Wang Qianggang, et al. Unbalanced voltage control strategy of bipolar DC microgrid based on distributed cooperation[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 634-645.
[33] Emadi A, Khaligh A, Rivetta C H, et al. Constant power loads and negative impedance instability in automotive systems: definition, modeling, stability, and control of power electronic converters and motor drives[J]. IEEE Transactions on Vehicular Tech- nology, 2006, 55(4): 1112-1125.
[34] Peng Dongdong, Huang Meng, Li Jinhua, et al. Large-signal stability criterion for parallel-connected DC-DC converters with current source equivalence[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2019, 66(12): 2037-2041.
[35] Brayton R K, Moser J K. A theory of nonlinear networks. I[J]. Quarterly of Applied Mathematics, 1964, 22(1): 1-33.
Large Signal Stability Analysis for DC Microgrid Clusters
Abstract DC microgrid (DCMG) clusters are in general formed by interconnecting multiple DCMGs to achieve zonal energy sharing and optimized utilization through flexible power flow control, and thus the advantages of DC-based distributed generation systems can be fully exploited. However, small-scale DCMGs are weak grids of low inertia and high impedance, and hence the weak-weak interconnection will reduce the damping of DCMG clusters, and even lead to severe consequences like oscillation and system collapse. In the meantime, the dynamic characteristics of higher-order, strong coupling, and nonlinearity bring great challenges to the stability analysis of DCMG clusters. To address this issue, a method for large signal stability analysis of DCMG clusters was proposed based on Brayton-Moser mixed potential theory. The large signal reduced-order model of the DCMG cluster was built, and the mixed potential function that facilitates large signal stability criterion was derived in detail, and the influence of the critical parameters on the stability region was analyzed. The correctness of the analysis is verified by real-time simulation results.
keywords:DC microgrid (DCMG) cluster, large signal stability, constant power load (CPL), Brayton-Moser mixed potential theory
DOI: 10.19595/j.cnki.1000-6753.tces.210977
中图分类号:TM46; TM712
国家自然科学基金资助项目(51407003)。
收稿日期 2021-07-05
改稿日期 2021-08-04
刘宿城 男,1981年生,博士,副教授,研究方向为电力电子系统建模与控制、直流微电网。E-mail: liusucheng@126.com(通信作者)
李 响 男,1996年生,硕士研究生,研究方向为直流微电网。E-mail: lixiang960120@gmail.com
(编辑 陈 诚)