图1 直流配电系统
Fig.1 DC distribution system
摘要 区别于交流配电网,直流配电网中电源具有低惯性特性,当配电网负载突变时,直流母线电压波动较大,母线电压质量面临巨大挑战。在解决直流配电网惯性低的问题上,可采用超级电容增加物理惯性或者采用虚拟电容(需要变流器配置冗余容量提供)增加虚拟惯性,配置的电容越大,供电质量越高,但成本也会越高。然而,目前关于电容对电压跌落幅度抑制作用的研究以定性分析为主,缺乏定量计算。为此,该文对辐射型直流配电网中直流母线电压在负载突增下的暂态响应进行分析,求得母线电压跌落峰值与联络变流器直流侧电容值之间的数学关系,为系统惯性参数设计提供理论支持。由于获得的数学关系式比较复杂,为方便工程应用,设计简化方法,得到近似的代数关系。最后,利用仿真和实验对电压跌落峰值计算方法进行了验证,仿真与实验结果验证该文所提计算方法的正确性。
关键词:直流配电网 低惯性特性 电压跌落 抑制电压跌落峰值计算
相比于交流配电网,直流配电网具有建设成本低、电能损耗小、供电可靠性高、环保等优点,在快速独立地控制有功和无功、减少电能变换环节、改善用户侧电能质量等方面具有独特优势,是未来智能配电系统中的重要组成部分[1-4]。虽然直流配电网不存在功角稳定、频率稳定等问题,但由于电源的惯性较小,负载的投切会引起直流母线电压剧烈波动,对直流母线暂态电压质量造成冲击甚至影响到直流配电网的安全稳定运行[5-6]。
在解决直流配电网电压质量问题上,一种方法采取在直流母线上并联超级电容(Super Capacitor, SC)等措施增加直流配电网的物理惯性[7-11]。文献[7]对直流母线电压波动范围进行等级划分,提出不同等级应采取不同的控制方案,但只是划定了大致的范围,并未给出超级电容与电压波动峰值之间的定量关系。文献[8]提出超级电容的加入对系统惯量阻尼特性的提升有显著效果,并指出系统等效的惯量阻尼特性受稳态工作点、结构参数以及控制器参数等的共同影响,但也只是定性分析不同参数对电压波动抑制效果的影响。文献[9]优化了超级电容的控制方法,可有效治理直流母线电压暂降,但并未分析电压降落的最小值与超级电容值之间的关系,只是在假定电压已经降落到最小值的基础上定性地分析超级电容的控制策略对电压恢复的影响。文献[10-11]虽然在设计直流电容时计算了负载突变产生电压跌落的峰值,但均未考虑控制的作用,计算过于粗略。
另一种方法是通过改进联络变流器的控制策略来增加直流配电网的虚拟惯性。有学者通过类比交流电网中的虚拟同步发电机(Virtual Synchronous Generator, VSG)控制[12-15],提出了直流配电网中的虚拟电容(Virtual Capacitor, VC)控制[16-22]。文献[16]融合VSG控制与下垂控制,提出一种适用于双向并网变换器的虚拟电容控制策略,平抑了直流母线电压波动。文献[17]提出了一种适用于多端口隔离型DC-DC变换器的改进VSG控制策略,并给出相应参数整定设计的方法,可推广至其他DC-DC变换器。文献[18]提出一种AVSG控制策略来增强直流微电网的惯性和阻尼,其启动特性及动静态特性俱佳,且该文在抑制电压振荡的基础上,通过根轨迹法分析了控制策略对系统稳定性的影响。文献[19-20]提出了灵活虚拟惯性控制策略,对虚拟电容参数自适应进行了研究。文献[21]通过对主要控制参数进行灵敏度分析,研究了参数对直流母线电压波动影响的规律。文献[22]提出了一种基于VSG的灵活虚拟电容控制策略,并利用李雅普诺夫稳定性判据确定了控制参数的稳定运行边界。上述虚拟电容控制策略虽然有效减缓了负荷突变时直流母线电压的波动,但只针对稳定边界判定、灵敏度分析等方面进行了定量分析,而针对虚拟电容对电压波动的抑制作用也只是进行了定性分析。
配置的电容越大,供电质量越高,但成本也会越高。然而,无论是考虑增加物理惯性还是虚拟惯性,目前关于超级电容或虚拟电容(需要变流器配置冗余容量提供)对直流母线电压波动抑制的理论分析与实验都停留在定性分析。因此,有必要研究直流母线电压跌落峰值的理论计算方法,为联络变流器直流侧电容的合理配置提供理论依据。为此,本文对联络变流器等效控制模型进行近似处理与化简,推导出直流母线电压在负荷扰动下的闭环传递函数,通过暂态特性分析以及线性化处理得到简明且相对保守的代数关系,最终得到电压跌落峰值的定量计算公式,获得保证最大冲击负载下电能质量的最小电容配置值。
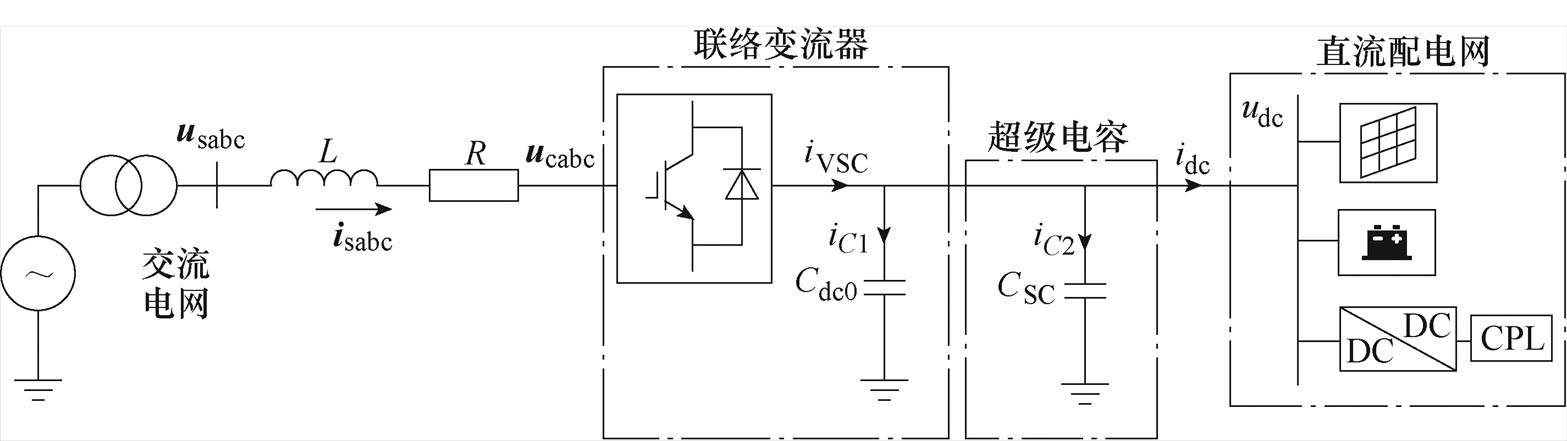
本文以安徽金梧桐直流配电系统示范工程为研究对象,该系统接入了交直流联络变流器、光伏电池、储能电池、超级电容和充电桩等设备,控制方式为主从控制[23-25],联络变流器采用定直流母线电压控制来平衡系统功率。图1给出了直流配电系统的结构示意图,图中,L和R分别为联络变流器网侧滤波电感和等效电阻;usabc为变压器二次电压;isabc为流过滤波电感的电流;ucabc为联络变流器交流侧电压;udc和iVSC分别为联络变流器直流侧电压(直流母线电压)和直流侧电流;Cdc0为联络变流器直流侧支撑电容;CSC为连接在直流母线上的超级电容;iC1为流过联络变流器支撑电容的电流;iC2为流过超级电容的电流;idc为直流母线流入直流配电网的电流。

图1 直流配电系统
Fig.1 DC distribution system
联络变流器采用双闭环前馈解耦控制,外环采用定直流母线电压控制方式,内环采用电流矢量控制方式,控制策略如图2所示。图中,w 为交流电网基波角频率;usd和usq分别为usabc的d轴和q轴分量;isd和isq分别为isabc的d轴和q轴分量;ucd和ucq分别为ucabc的d轴和q轴分量;Gi(s)=kpi+kii/s为电流调节器,kpi、kii分别为电流环比例和积分系数;Gu(s)=kpu+kiu/s为电压调节器,kpu、kiu分别为电压环比例和积分系数。文中大写表示对应变量的稳态值,上标*表示对应变量的指令值,后面不再重复说明。

图2 联络变流器前馈解耦控制策略
Fig.2 Feedforward decoupling control strategy for tie converter
图3所示为联络变流器等效控制模型[26]。图中,GC(s)=1/(sCdc)为直流侧等效电容传递函数,其中Cdc=Cdc0+CSC为直流侧等效电容;iC=iC1+iC2为流过Cdc的等效电流;Wci(s)为电流内环等效传递函数;m为PWM的调制比;q0为稳态时开关函数基波 相位。
稳态时,忽略R,根据功率平衡方程,有
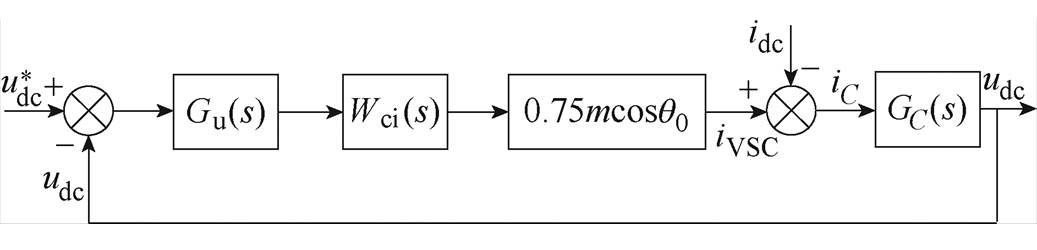
图3 联络变流器等效控制模型
Fig.3 Equivalent control model of tie converter
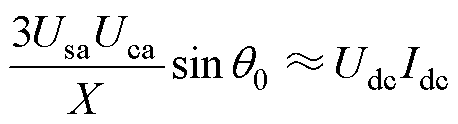 (1)
(1)
式中,X=wL为变流器滤波电感的电抗值。
又有
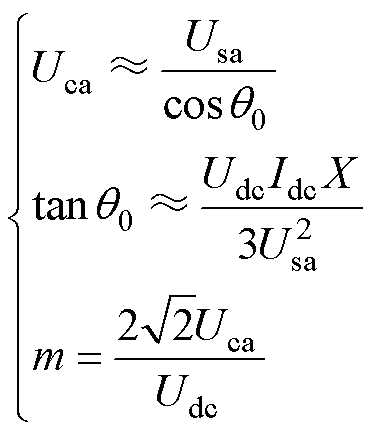 (2)
(2)
将式(2)合并化简后有
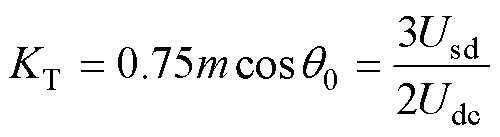 (3)
(3)
式中,KT为转换系数。
由于电流内环的带宽远大于电压外环,因此闭环传递函数Wci(s)可近似为1,图3所示的结构可简化为如图4所示。
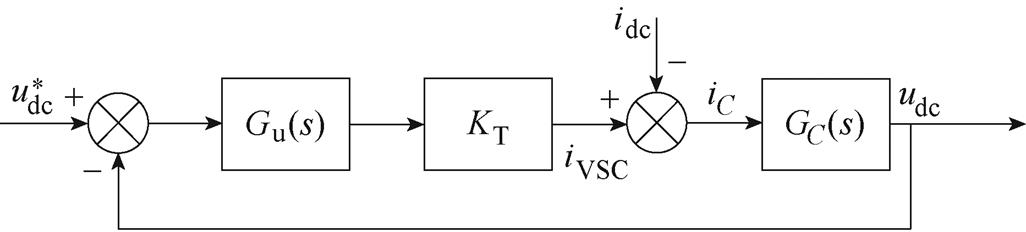
图4 变流器控制简化结构
Fig.4 Simplified structure diagram of converter control
由图4可得变流器控制传递函数表达式为
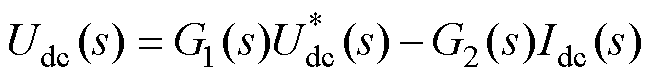 (4)
(4)
其中
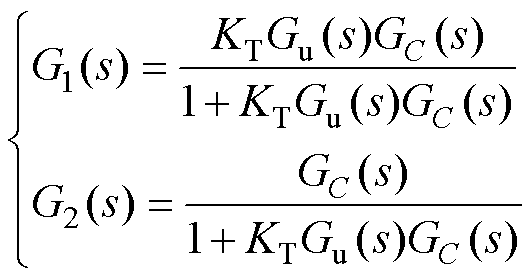 (5)
(5)
由式(5)可知,若稳定运行时负荷突增,则有
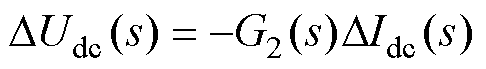 (6)
(6)
将G2(s)展开后,可得
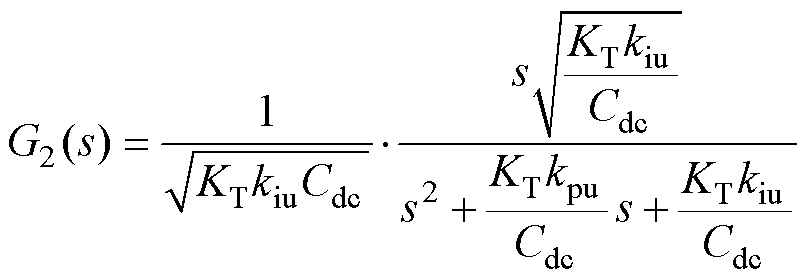 (7)
(7)
根据终值定理,由式(7)可知,直流母线电压对负荷扰动的稳态响应为0,因此可以通过计算系统响应的超调量来计算电压跌落峰值。
将负荷扰动下的闭环传递函数转换为包含微分环节和常系数的二阶模型,即
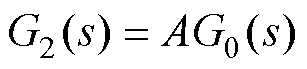 (8)
(8)
其中
 (9)
(9)
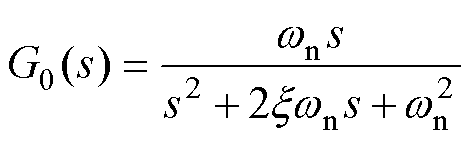 (10)
(10)
式中,自然角频率wn和阻尼比x 分别为
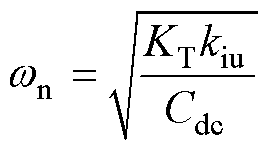 (11)
(11)
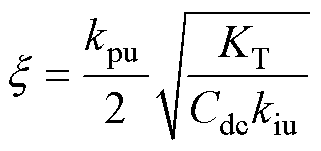 (12)
(12)
对于G0(s),其单位阶跃响应为
 (13)
(13)
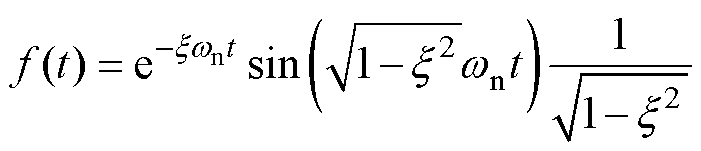 (14)
(14)
令
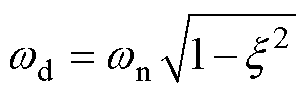 (15)
(15)
则有
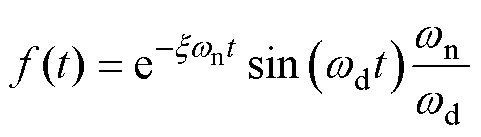 (16)
(16)
为求f(t)的极值,对f(t)求导得
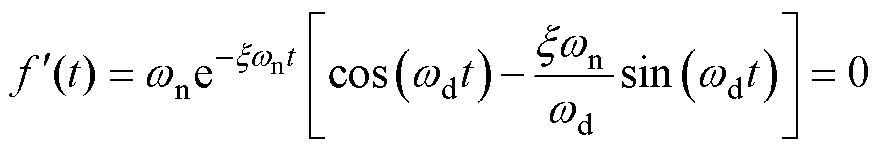 (17)
(17)
整理得
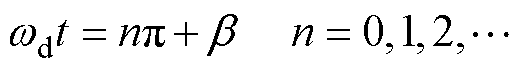 (18)
(18)
其中
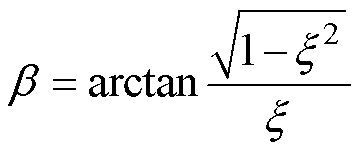
系统稳定前提下,响应的第一个峰值时间达到最大超调量,取n=1,有第一个峰值时间为
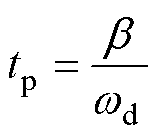 (19)
(19)
将峰值时间tp代入式(16),得最大峰值为
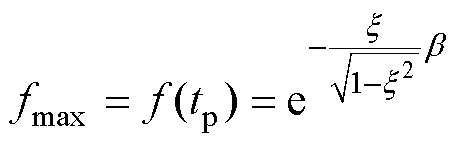 (20)
(20)
结合式(8)、式(20),可得到电压跌落峰值与电容之间的关系,但关系式太复杂,不便于工程应用。为此,将式(20)线性化,简化电压跌落峰值与电容之间的关系式(为保证式(23)的简明且可反解出Cdc,未采用高次拟合)。由式(20)画fmax关于x的曲线如图5所示,设x 在0~x0(对应Cdc为+∞~Cdc0)范围内变化,则可用直线近似这段曲线。取描述这段直线的函数为
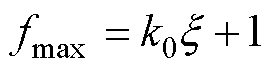 (21)
(21)
式中,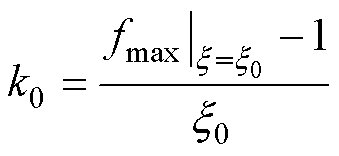 为线性化后的直线斜率。
为线性化后的直线斜率。
因此,负荷突增后的电压跌落峰值近似为
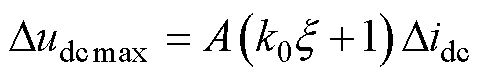 (22)
(22)
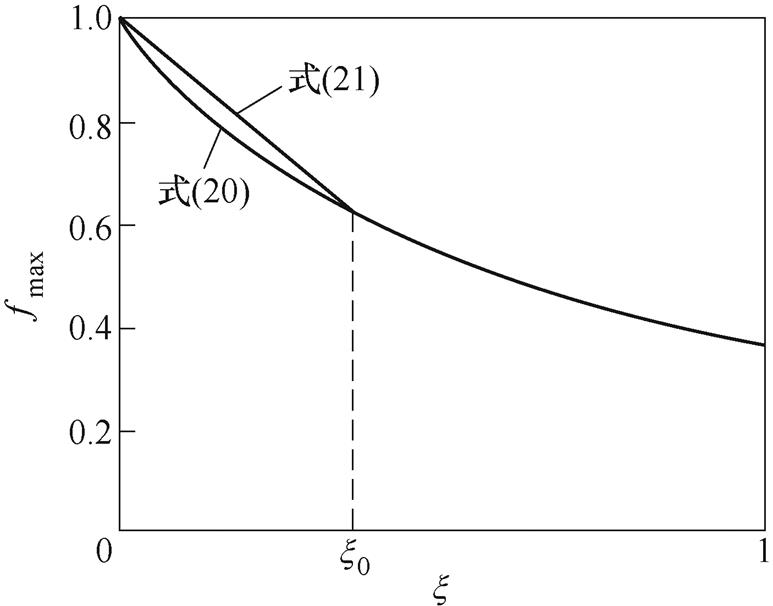
图5 x 与fmax的关系曲线
Fig.5 The relation curves between x and fmax
展开式(22),有
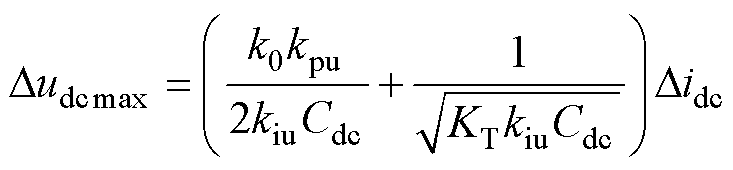 (23)
(23)
由式(23)可知,随着电容的增加,在相同负荷扰动下,电压波动的幅值减小。由于图5中直线位于曲线上方,式(23)近似计算得到电压跌落峰值更大,说明近似计算值更为保守。
式(23)给出了Dudcmax对于电容Cdc的表达式,将其反解,可得电容Cdc对于Dudcmax的表达式为
 (24)
(24)
其中
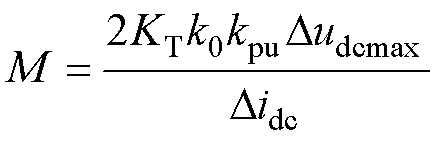
式(23)、式(24)反映了电容与暂态电压跌落峰值之间的关系,为满足母线暂态电压质量要求下电容值的选取提供了理论依据。可通过最大冲击负载确定Didc的取值,根据电能质量的要求确定Dudcmax的取值,从而求得最小惯性电容Cdc的配置值。
由式(23)可得负荷突增后直流母线电压最小值udcmin为
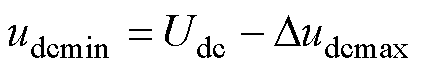 (25)
(25)
从式(23)中还可以看出,联络变流器的控制参数也对电压跌落幅度有影响:①kiu与Cdc处于式(23)相同位置,因此变化规律近似相同,增大kiu后Dudcmax减小;②由于线性化后k0为负,增大kpu后Dudcmax减小。
为了验证本文计算方法的正确性,本文利用Matlab/Simulink仿真软件和实验平台进行证明,仿真和实验系统如图1所示,系统主要参数见表1。由于光伏电池、储能电池以及复杂结构的负荷可能对直流电压质量有积极的影响,而超级电容的配置需要考虑系统在极端工况下的正常运行,因此在仿真和实验时停运光伏电池、储能电池等设备且负载侧采用恒功率负载。
表1 直流配电系统主要参数
Tab.1 Main parameters of DC distribution system

参 数数 值 变压器二次侧相电压Usabc/V132 交流电网频率f/Hz50 直流母线电压Udc/V450 联络变流器网侧滤波电感L/mH2 联络变流器网侧等效电阻R/W0.01 联络变流器直流侧支撑电容Cdc0/mF2 040 联络变流器额定功率PVSC/kW7.5 恒功率负载额定功率PL/kW2.7×3 光伏发电单元额定功率Ppv/kW7.5 储能电池额定功率Pbat/kW6 联络变流器电压外环PI参数kpu0.1 kiu5 联络变流器电流内环PI参数kpi6.67 kii33.33
3.1.1 工况1:负载突增
图6所示为不同超级电容下负荷突增时,直流母线电压跌落的仿真波形,仿真中,在1s时负载突增2.7kW。图中,CSC取0~8mF间不同值(间隔为1mF),从图中可知,CSC越大,对电压跌落抑制作用越强。
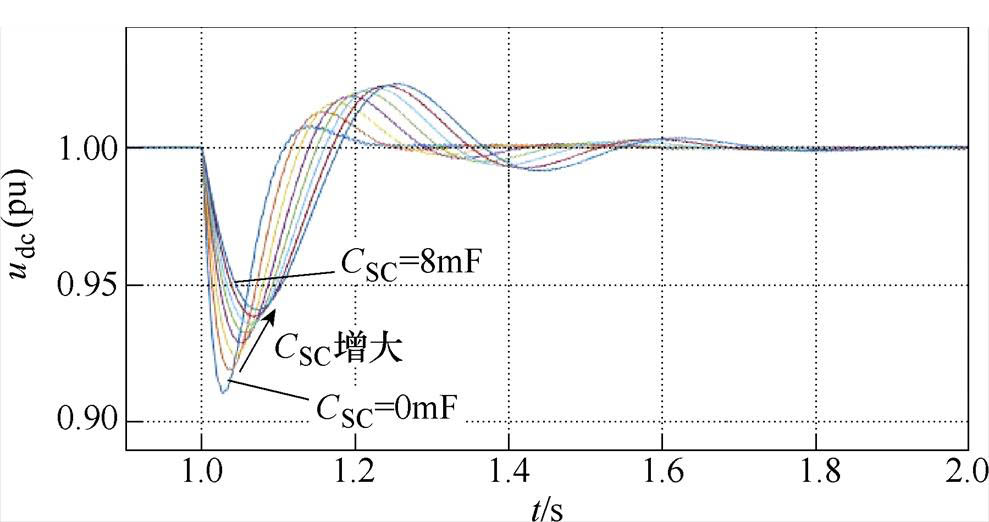
图6 工况1下,不同超级电容值时直流母线电压跌落仿真波形
Fig.6 Simulation waveforms of DC bus voltage sag with different super capacitance values under Condition 1
测出图6中不同超级电容下负荷突增后直流母线电压最小值udcmin,然后与式(25)计算出的udcmin进行比较,比较结果如图7所示。从图中可知,udcmin(pu)的计算值与仿真值之差小于2%,验证了计算方法的正确性。
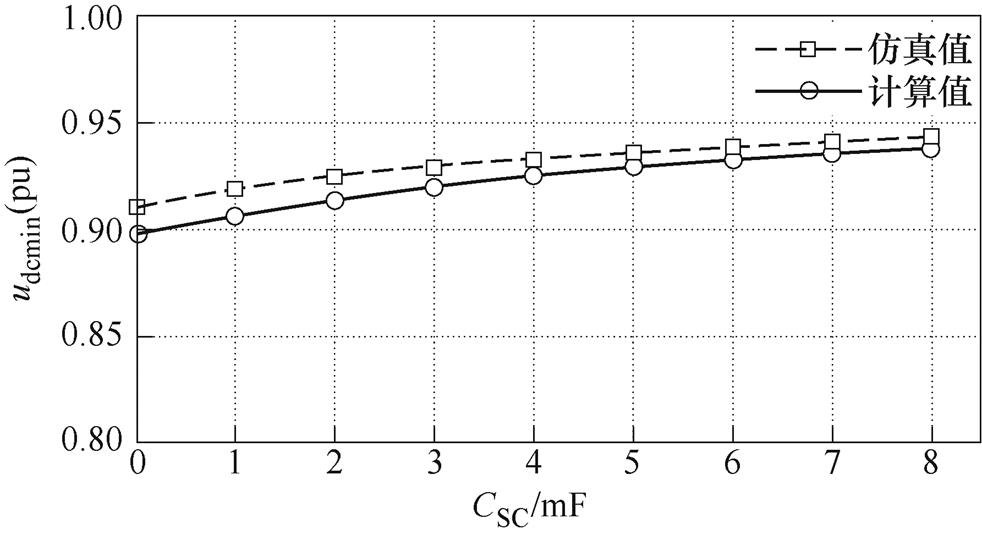
图7 工况1下,不同超级电容值时udcmin仿真值与计算值的对比
Fig.7 Comparison of simulation value and calculation value of udcmin with different super capacitance values under Condition 1
3.1.2 工况2:与工况1不同控制参数时负载突增
为考察本文方法对不同工况的适用性,改变电压外环的PI参数(kpu=0.2,kiu=10),且负载突增量变成5.4kW。图8所示为改变参数后负载突增时,直流母线电压跌落的仿真波形,仿真中,在1s时负载突增5.4kW。图中CSC分别为0~8mF(间隔为1mF),从图中可知,CSC越大,对电压跌落抑制作用越强。
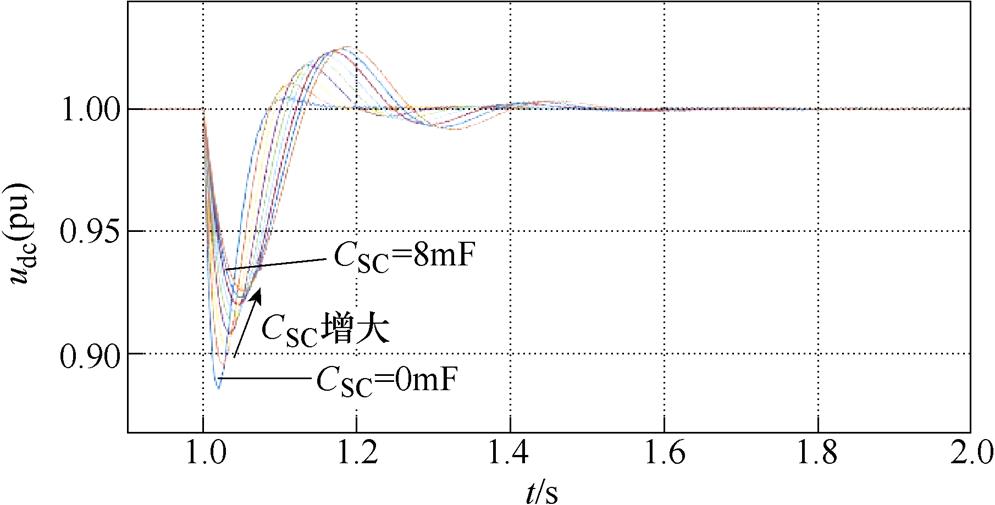
图8 工况2下,不同超级电容值时直流母线电压跌落仿真波形
Fig.8 Simulation waveforms of DC bus voltage sag with different super capacitance values under Condition 2
测出图8中不同超级电容下负荷突增后直流母线电压最小值udcmin,然后与式(25)计算出的udcmin进行比较,比较结果如图9所示。从图中可知,udcmin(pu)的计算值与仿真值之差小于2%,再次验证了计算方法的正确性。
3.1.3 工况3:负载突减
虽然理论部分是基于负载突增时电压跌落情况下的定量计算,但从式(23)的推导过程可知,式(23)同样适用于负载突减时直流母线电压骤升峰值的定量计算(此时式(23)中电流为负)。工况3给出保持表1参数不变(与工况1同参数)的情况下,负载突减时的仿真结果。
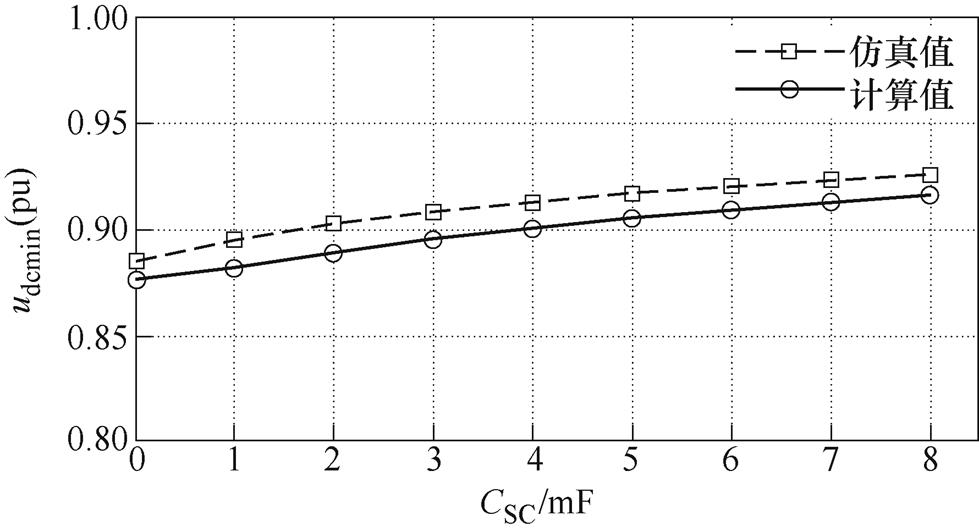
图9 工况2下,不同超级电容值时udcmin仿真值与计算值的对比
Fig.9 Comparison of simulation value and calculation value of udcmin with different super capacitance values under Condition 2
图10所示为不同超级电容值下负荷突减时,直流母线电压骤升的仿真波形,仿真中,在1s时负载突减2.7kW。图中CSC取0~8mF间的值(间隔为1mF)。测出图10中不同超级电容值下负载突减后直流母线电压最大值udcmax,然后与udcmax的计算值进行比较,比较结果如图11所示。从图中可知,式(23)同样适用于负载突减工况下的定量计算。
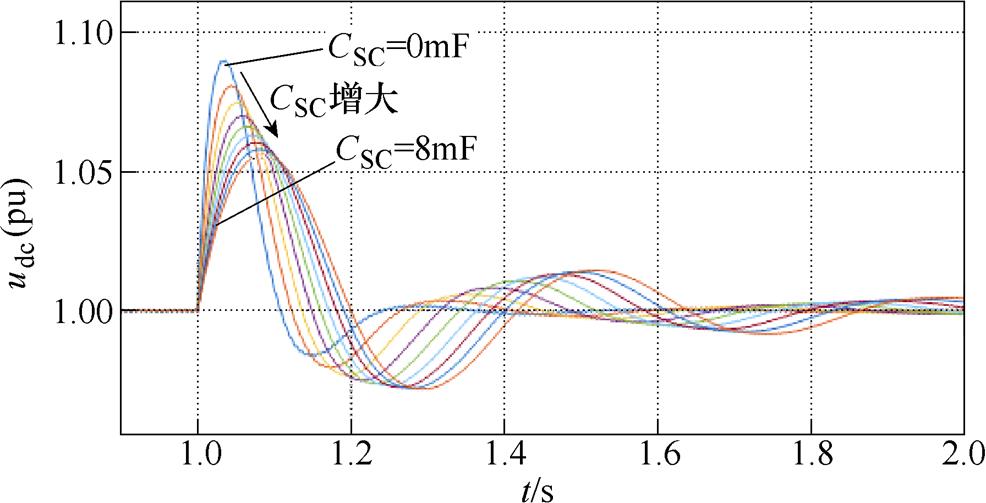
图10 工况3下,不同超级电容值时直流母线电压骤升仿真波形
Fig.10 Simulation waveforms of DC bus voltage surge with different super capacitance values under Condition 3
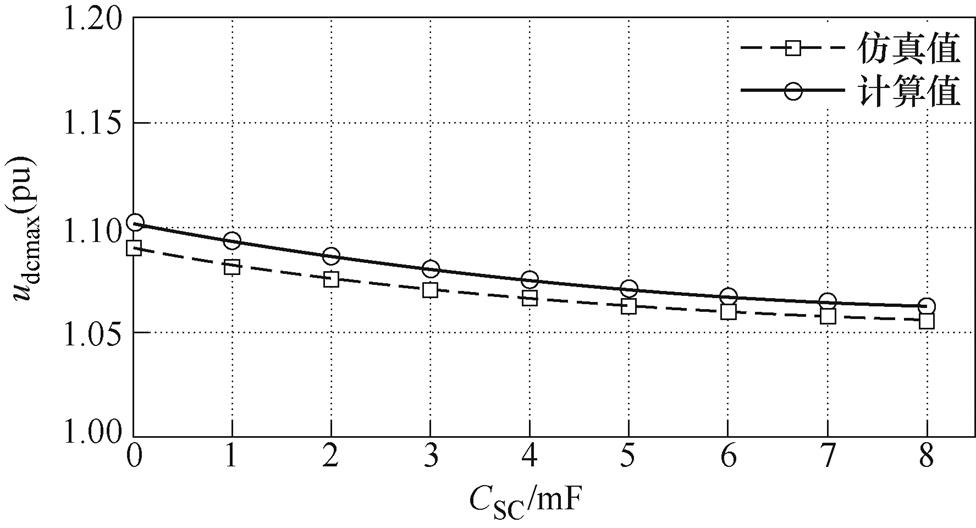
图11 工况3下,不同超级电容值时udcmax仿真值与计算值的对比
Fig.11 Comparison of simulation value and calculation value of udcmax with different super capacitance values under Condition 3
为了进一步验证本文计算方法的正确性,在直流配电网平台进行了实验验证,考虑到实验设备的安全性及对现有设备的充分利用,负载突增量取2.7kW。图12为实验平台实物。

图12 实验平台实物
Fig.12 Physical diagram of experimental platform
图13所示为未加入超级电容,等效电容Cdc= Cdc0=2 040mF时,直流母线电压跌落的实验波形。从图中可知,负载突增2.7kW后,直流母线电压最小值udcmin=403.78V。由式(25)计算得到udcmin= 404.14V,计算值与实验值之差小于额定值的0.1%,证明本文计算方法的正确性。
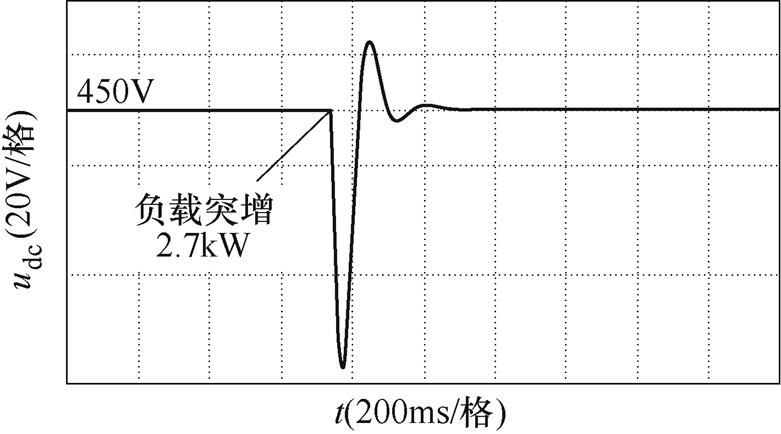
图13 未加入超级电容时,直流母线电压跌落实验波形
Fig.13 Experimental waveforms of DC bus voltage sag without super capacitor
图14所示为加入超级电容后,CSC=8mF时,直流母线电压跌落的实验波形。从图中可知,负载突增2.7kW后,直流母线电压最小值udcmin=425.66V。因此,加入超级电容后,直流母线电压跌落得到了显著抑制。
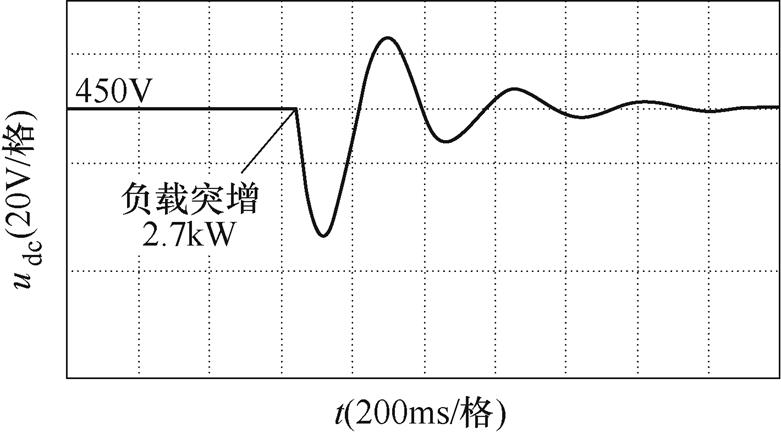
图14 加入超级电容后,直流母线电压跌落实验波形
Fig.14 Experimental waveforms of DC bus voltage sag with super capacitor
图15所示为加入超级电容后,CSC分别取0~8mF(间隔为1mF)时,udcmin实验值与计算值的对比。实验中,负载突增2.7kW,而计算值同仿真验证时所述一致。从图中可知,udcmin(pu)的计算值与实验值之差小于2%,再次从实验的角度验证了计算方法的正确性。

图15 不同超级电容值下udcmin实验值与计算值的对比
Fig.15 Comparison of experimental value and calculated value of udcmin with different super capacitance values
由于直流配电网中电源的低惯性特性容易产生电压质量问题。系统中配置惯性电容越大,供电质量越高,但成本也会越高。为合理配置系统的电容,本文以辐射型主从控制的直流配电网为对象,研究了直流母线电压跌落的峰值定量计算及抑制方法,得出如下结论:
1)直流配电网母线电压质量与联络变流器直流侧等效电容大小强相关,但不是线性关系,等效电容越大,电压波动越小。可以通过分析系统对扰动的暂态响应,求得联络变流器直流侧电压跌落峰值与其直流侧等效电容值之间的数学关系,为惯性电容配置提供理论依据。
2)式(23)同样适用于切负荷时电压突增的情况。本文为了论述的简洁性,仅针对电压跌落时的暂态过程进行分析。
3)为简化计算,式(3)中参数Udc取为直流电压稳态值,造成了电压跌落峰值的计算值同仿真与实验值存在一定误差。
参考文献
[1] 李海波, 赵宇明, 刘国伟, 等. 基于时序仿真的商业楼宇交流与直流配电系统能效对比[J]. 电工技术学报, 2020, 35(19): 4194-4206.
Li Haibo, Zhao Yuming, Liu Guowei, et al. The time sequential simulation based energy efficiency com- parison of AC and DC distribution power system in commercial buildings[J]. Transactions of China Elec- trotechnical Society, 2020, 35(19): 4194-4206.
[2] 梁永亮, 吴跃斌, 马钊, 等. 新一代低压直流供用电系统在“新基建”中的应用技术分析及发展展望[J]. 中国电机工程学报, 2021, 41(1): 13-24.
Liang Yongliang, Wu Yuebin, Ma Zhao, et al. Appli- cation and development prospect of new generation of LVDC supply and utilization system in “new infrastructure”[J]. Proceedings of the CSEE, 2021, 41(1): 13-24.
[3] 金国彬, 潘狄, 陈庆, 等. 考虑源荷不确定性的直流配电网模糊随机日前优化调度[J]. 电工技术学报, 2021, 36(21): 4517-4528.
Jin Guobin, Pan Di, Chen Qing, et al. Fuzzy random day-ahead optimal dispatch of DC distribution network considering the uncertainty of source-load[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4517-4528.
[4] Shamsoddini M, Vahidi B, Razani R, et al. A novel protection scheme for low voltage DC microgrid using inductance estimation[J]. International Journal of Electrical Power & Energy Systems, 2020, 120: 105992.
[5] Dragičević T, Guerrero J M, Vasquez J C, et al. Supervisory control of an adaptive-droop regulated DC microgrid with battery management capability[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 695-706.
[6] Wu T F, Chang C H, Lin L C, et al. DC-bus voltage control with a three-phase bidirectional inverter for DC distribution systems[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1890-1899.
[7] 张继红, 赵锐, 高雷, 等. 直流微网母线电压稳定控制策略[J/OL]. 电网技术, 2021, http://kns.cnki. net/kcms/detail/11.2410.TM.20210101.1431.002.html.
Zhang Jihong, Zhao Rui, Gao Lei, et al. DC bus voltage stability control strategy for DC micro- grid[J/OL]. Power System Technology, 2021, http:// kns.cnki.net/kcms/detail/11.2410.TM.20210101.1431.002.html.
[8] 农仁飚, 杨晓峰, 周兵凯, 等. 基于低压直流母线系统的惯量阻尼特性研究[J]. 电网技术, 2021, 45(11): 4512-4522.
Nong Renbiao, Yang Xiaofeng, Zhou Bingkai, et al. Inertia and damping characteristics of LVDC system[J]. Power System Technology, 2021, 45(11): 4512-4522.
[9] 马智远, 栾乐, 许中, 等. 一种基于超级电容的变频器电压暂降治理装置[J]. 电力电子技术, 2020, 54(12): 60-63.
Ma Zhiyuan, Luan Le, Xu Zhong, et al. A voltage sag mitigation device for adjustable speed drives based on super capacitor[J]. Power Electronics, 2020, 54(12): 60-63.
[10] 王久和, 李华德, 王立明. 电压型PWM整流器直接功率控制系统[J]. 中国电机工程学报, 2006, 26(18): 54-60.
Wang Jiuhe, Li Huade, Wang Liming. Direct power control system of three phase Boost type PWM rectifiers[J]. Proceedings of the CSEE, 2006, 26(18): 54-60.
[11] 史伟伟, 蒋全, 胡敏强, 等. 三相电压型PWM整流器的数学模型和主电路设计[J]. 东南大学学报(自然科学版), 2002, 32(1): 50-55.
Shi Weiwei, Jiang Quan, Hu Minqiang, et al. Mathematical model and main circuit design of three- phase voltage-source PWM rectifier[J]. Journal of Southeast University (Science and Technology), 2002, 32(1): 50-55.
[12] Zhong Qingchang, Nguyen P L, Ma Zhenyu, et al. Self-synchronized synchronverters: inverters without a dedicated synchronization unit[J]. IEEE Transa- ctions on Power Electronics, 2014, 29(2): 617-630.
[13] 石荣亮, 张兴, 徐海珍, 等. 光储柴独立微电网中的虚拟同步发电机控制策略[J]. 电工技术学报, 2017, 32(23): 127-139.
Shi Rongliang, Zhang Xing, Xu Haizhen, et al. A control strategy for islanded photovoltaic-battery- diesel microgrid based on virtual synchronous generator[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 127-139.
[14] 伍文华, 陈燕东, 周乐明, 等. 虚拟同步发电机接入弱电网的序阻抗建模与稳定性分析[J]. 中国电机工程学报, 2019, 39(6): 1560-1571, 1853.
Wu Wenhua, Chen Yandong, Zhou Leming, et al. Sequence impedance modeling and stability analysis for virtual synchronous generator connected to the weak grid[J]. Proceedings of the CSEE, 2019, 39(6): 1560-1571, 1853.
[15] 于鸿儒, 苏建徽, 徐华电, 等. 并网逆变器虚拟惯性与阻尼的等效及辨识[J]. 中国电机工程学报, 2019, 39(20): 6034-6043, 6184.
Yu Hongru, Su Jianhui, Xu Huadian, et al. Equivalent and identification of virtual inertia and damping of grid-connected inverter[J]. Proceedings of the CSEE, 2019, 39(20): 6034-6043, 6184.
[16] 伍文华, 陈燕东, 罗安, 等. 一种直流微网双向并网变换器虚拟惯性控制策略[J]. 中国电机工程学报, 2017, 37(2): 360-371.
Wu Wenhua, Chen Yandong, Luo An, et al. A virtual inertia control strategy for bidirectional grid-connected converters in DC micro-grids[J]. Proceedings of the CSEE, 2017, 37(2): 360-371.
[17] 张辉, 梁誉馨, 孙凯, 等. 直流微电网中多端口隔离型DC-DC变换器的改进虚拟电容控制策略[J]. 电工技术学报, 2021, 36(2): 292-304.
Zhang Hui, Liang Yuxin, Sun Kai, et al. Improved virtual capacitor control strategy of multi-port isolated DC-DC converter in DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 292- 304.
[18] 朱晓荣, 孟凡奇, 谢志云. 基于虚拟同步发电机的直流微网DC-DC变换器控制策略[J]. 电力系统自动化, 2019, 43(21): 132-140.
Zhu Xiaorong, Meng Fanqi, Xie Zhiyun. Control strategy of DC-DC converter in DC microgrid based on virtual synchronous generator[J]. Automation of Electric Power Systems, 2019, 43(21): 132-140.
[19] 邹培根, 孟建辉, 王毅, 等. 一种直流微电网的灵活虚拟惯性控制策略[J]. 电力建设, 2018, 39(6): 56-62.
Zou Peigen, Meng Jianhui, Wang Yi, et al. A flexible virtual inertia control strategy for DC microgrid[J]. Electric Power Construction, 2018, 39(6): 56-62.
[20] Wang Chen, Meng Jianhui, Wang Yi, et al. Adaptive virtual inertia control for DC microgrid with variable droop coefficient[C]//International Conference on Electrical Machines and Systems, Sydney, Australia, 2017: 1-5.
[21] 孟建辉, 邹培根, 王毅, 等. 基于灵活虚拟惯性控制的直流微网小信号建模及参数分析[J]. 电工技术学报, 2019, 34(12): 2615-2626.
Meng Jianhui, Zou Peigen, Wang Yi, et al. Small- signal modeling and parameter analysis of the DC microgrid based on flexible virtual inertia control[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2615-2626.
[22] 孟建辉, 宋美琪, 王毅, 等. 虚拟电容控制下并网型直流微网VSC多约束稳定运行边界[J]. 电力系统自动化, 2019, 43(15): 172-179, 199.
Meng Jianhui, Song Meiqi, Wang Yi, et al. Multi- constraint stable operation boundary of grid- connected voltage source converter of DC microgrid with virtual capacitance control[J]. Automation of Electric Power Systems, 2019, 43(15): 172-179, 199.
[23] 汤广福. 基于电压源换流器的高压直流输电技术[M]. 北京: 中国电力出版社, 2010.
[24] 季一润, 袁志昌, 赵剑锋, 等. 一种适用于柔性直流配电网的电压控制策略[J]. 中国电机工程学报, 2016, 36(2): 335-341.
Ji Yirun, Yuan Zhichang, Zhao Jianfeng, et al. A suitable voltage control strategy for DC distribution power network[J]. Proceedings of the CSEE, 2016, 36(2): 335-341.
[25] 曹文远, 韩民晓, 谢文强, 等. 交直流配电网逆变器并联控制技术研究现状分析[J]. 电工技术学报, 2019, 34(20): 4226-4241.
Cao Wenyuan, Han Minxiao, Xie Wenqiang, et al. Analysis on research status of parallel inverters control technologies for AC/DC distribution net- work[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4226-4241.
[26] 张兴, 张崇巍. PWM 整流器及其控制[M]. 北京: 机械工业出版社, 2012.
Quantitative Calculation Method of Bus Voltage Sag Peak Value in Radial DC Distribution Network
Abstract Different from AC distribution network, DC distribution network has low inertia characteristics. When the load of distribution network changes suddenly, DC bus voltage fluctuates greatly, and the quality of bus voltage faces great challenges. In order to solve the problem of low inertia of DC distribution network, super capacitor can be used to increase physical inertia or virtual capacitor (which needs to be provided by redundant capacity of converter configuration) to increase virtual inertia. The larger the capacitance, the higher the quality of power supply, but the higher the cost. However, the research on the suppression effect of capacitor on voltage sag is mainly qualitative analysis and lacks quantitative calculation. Therefore, the transient response of DC bus voltage under sudden load increase in radial DC distribution network is analyzed, and the mathematical relationship between the peak value of bus voltage sag and the DC side capacitance value of tie converter is obtained, which provides theoretical support for the design of system inertia parameters. Due to the complexity of the mathematical relation, a simplified method is designed to obtain the approximate algebraic relation for the convenience of engineering application. Finally, the calculation method of voltage sag peak value is verified by simulation and experiment.
keywords:DC distribution network, low inertia characteristics, voltage sag suppression, calculation of voltage sag peak value
DOI: 10.19595/j.cnki.1000-6753.tces.210846
中图分类号:TM721.1
唐 欣 男,1975年生,教授,博士生导师,研究方向为电力电子在电力系统中的应用。E-mail: tangxin_csu@163.com
蔡明君 男,1993年生,硕士研究生,研究方向为电力电子在电力系统中的应用。E-mail: 656632880@qq.com(通信作者)
国家自然科学基金资助项目(51977013)。
收稿日期 2021-06-14
改稿日期 2022-04-27
(编辑 陈 诚)