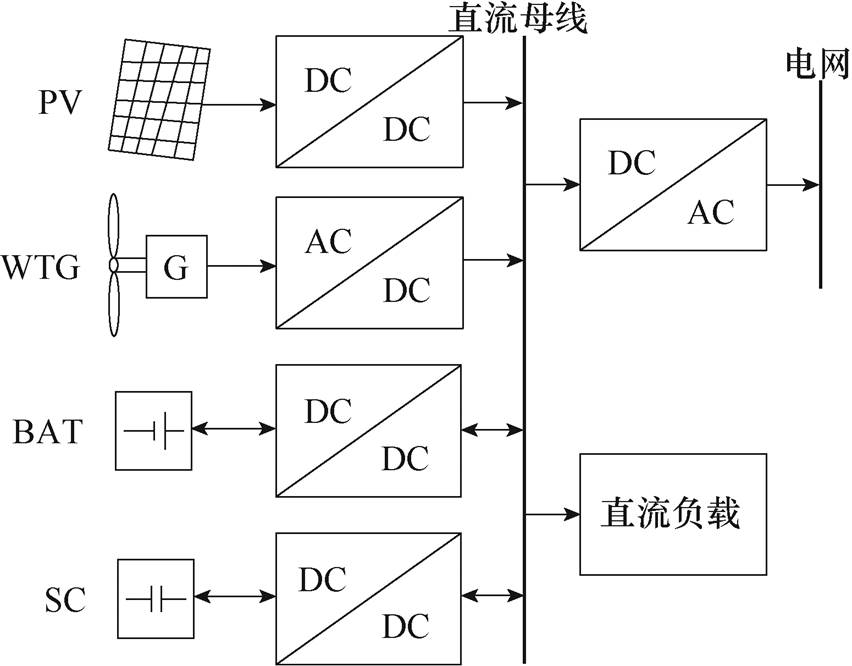
图1 基于可再生能源的微电网系统
Fig.1 Micro grid system based on renewable energy
摘要 针对微电网系统中双向直流变换器需同时具有良好的稳态特性和动态响应这一问题,该文提出一种结合电流应力优化的双有源全桥(DAB)DC-DC变换器自抗扰控制方案,并对DAB变换器在扩展移相调制下的传输功率和电流应力数学模型、电流应力优化与自抗扰控制相结合等关键技术展开分析研究。在扩展移相调制基础上,利用条件极值法求解不同工作模式的电流应力最优解。同时构建自抗扰闭环,通过扩张状态观测器对系统状态进行实时估算,将输入电压突变、负载投切、电流应力优化策略导致传输功率波动等视作系统扰动并进行补偿。最后设计并研制一套200W实验样机,对比不同控制方案的性能,样机动稳态实验结果验证了所提出控制方案的可行性和先进性。
关键词:自抗扰控制 动态性能 电流应力优化 双有源全桥DC-DC变换器 扩展移相调制
随着环境污染、能源短缺等问题的日益严重,可再生能源引起了广泛关注,基于可再生能源的微电网系统得到了快速发展[1-3]。这类微电网系统通常采用如图1所示的电路架构,太阳能(Photovoltaic, PV)、风能(Wind Turbine Generator, WTG)等可再生能源输出最大功率,蓄电池(Battery, BAT)、超级电容(Super Capacitor, SC)等储能元件用以平抑输入输出的功率波动。由于太阳能、风能的间歇性与随机性强,直流母线功率波动大,则连接在储能元件与直流母线之间的双向直流变换器需要具有良好的稳态特性和动态响应性能[4]。

图1 基于可再生能源的微电网系统
Fig.1 Micro grid system based on renewable energy
双有源全桥(Dual Active Bridge, DAB)DC-DC变换器因其具有功率密度高、电气隔离易实现模块化串并联、软开关等优点,逐渐成为双向直流变换器的研究热点[5]。传统单移相(Single-Phase-Shift, SPS)调制策略具有控制简单、易实现软开关等优点,但存在电流应力大、回流功率多等问题。为了解决这类问题,文献[6]提出了基于双重移相(Dual- Phase-Shift, DPS)的回流功率优化策略,该策略优化回流功率的同时能够降低电感电流应力,但并非全局最优解。文献[7]基于DPS调制,进一步推导DPS所有移相模式电流应力最小的条件以及实现方案,显著降低电感电流应力。文献[8-9]在SPS的基础上,加入变压器一次侧H桥内移相角,即扩展移相(Extended-Phase-Shift, EPS),提出一种EPS调制下DAB变换器移相角优化选取方案,但并不能保证变换器性能最优。文献[10-11]采用三重移相(Triple-Phase-Shift, TPS)调制,取得了较好的电流应力优化效果,然而由于存在3个控制自由度,建模分析与控制实现较为复杂。
文献[12-13]分别在EPS与TPS调制下,分析实现完全零电压开通(Zero Voltage Switching, ZVS)条件,而完全ZVS是通过回流功率实现的,这会导致电流应力与回流功率大幅增加[14]。此种情况下,变换器的开通损耗虽然降为零,但是导通损耗、磁性损耗等都将增加。尤其当DAB变换器电压比k较大时,失去ZVS约束,损耗将进一步增加。对于DAB变换器而言,电流应力与电流有效值具有一致性[15],降低电流应力的同时电流有效值也将减小,进而降低导通损耗。并且,相比于电流有效值繁琐的优化推导过程,电流应力优化更加简洁明了。因此,研究如何降低电流应力具有重要意义。
此外,上述文献均只针对变换器稳态性能进行优化,未论述变换器的动态性能。输出电压值仅通过单一PI控制器跟踪,这使得变换器动态性能较差。为了提升DAB变换器的动态性能,文献[16]采用负载电流前馈控制,该算法在面对负载波动时具有较好的动态性能,然而单一的负载电流前馈控制使系统在面对其他扰动如硬件参数变化时效果不明显,因此前馈控制一般需与其他控制策略结合使用。文献[17]将输入电压前馈与直接功率控制结合,该策略在输入电压及负载波动时均有良好控制效果。文献[18]通过模型预测控制算法提高变换器动态响应速度,但建模与分析较为复杂。且上述控制策略均采用SPS调制,在保证变换器动态性能的同时,难以兼顾稳态性能的优化。为使DAB变换器具有较高的动态与稳态性能,文献[19]提出一种电压模型预测控制与梯度下降算法优化回流功率的混合控制算法,实现对回流功率与动态性能的同时优化,但该算法所需系统参数众多,导致鲁棒性降低、算法可移植性差。文献[20]在EPS调制基础上采用直接功率控制,提高变换器动态性能的同时优化电流应力,但仅考虑EPS中的一种工作模式,因此求出的电流应力优化解并非是全局最优解。文献[21]提出一种基于模型前馈的电流应力优化算法,由于需要电感电容等参数参与实时计算,导致算法易受参数影响。文献[22]求解EPS调制下电流应力优化表达式并构建功率环给定内外移相角,提升变换器动态响应速度,但引入电容电流及效率参数降低了控制灵活性。
对此,考虑EPS调制电流优化效果与DPS、TPS相仿,同时仅增加变压器一次侧H桥内移相角,控制实现简单。本文基于EPS调制,提出了一种结合电流应力优化的自抗扰控制(Active Disturbance Rejection Control, ADRC)策略,实现了DAB变换器电流应力全局最优,同时结合自抗扰闭环控 制[23],提升了系统的动态性能及鲁棒性。首先,推导了EPS调制下三种工作模式的功率及电流应力的数学模型;其次,对比分析了EPS调制下三种工作模式的电流应力并采用条件极值法求解变换器电流应力全局最优解;构建自抗扰反馈闭环,将电流应力优化策略导致的功率波动、输入电压突变、负载投切等视作总扰动,通过扩张状态观测器(Extended State Observer, ESO)进行实时估算并补偿,实现对系统动态性能的优化;最后,通过实验验证了该方案的可行性与先进性。
DAB DC-DC变换器的电路拓扑如图2所示。为简化分析,以功率正向传输为例。图中,Uin、Uo分别为变压器一次、二次侧直流电压;C1、C2分别为一次、二次侧滤波电容;L等效为串联辅助电感以及变压器漏感之和;iL、Io分别为电感电流、输出电流;R为二次侧H桥等效负载;变压器电压比为n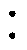 1。
1。
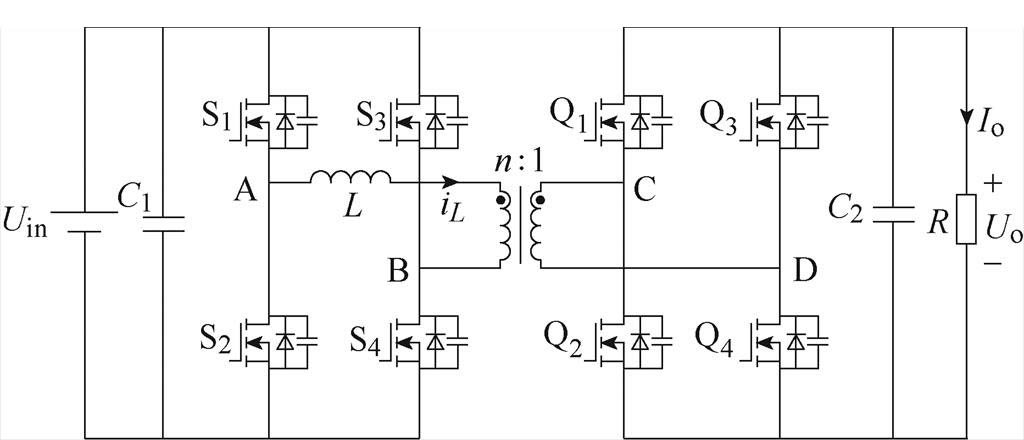
图2 双有源全桥DC-DC变换器电路拓扑
Fig.2 The topology of DAB DC-DC converter
根据移相角D1、D2大小的不同,DAB变换器在扩展移相调制下存在三种模式:D1/2<D2<D1<1、0<D1<D2<1、0<D1<1<D2<1+D1/2,其主要波形如图3所示。图3中,D1、D2分别为一次侧H桥内移相量和一次、二次侧H桥间外移相量;Ts为开关周期;UAB、UCD分别为一次侧A、B两点间的电压和二次侧C、D两点折算到一次侧的电压。S1、S4为一次侧对角功率管,Q1、Q4为二次侧对角功率管,并且同一桥臂任意时刻互补导通。
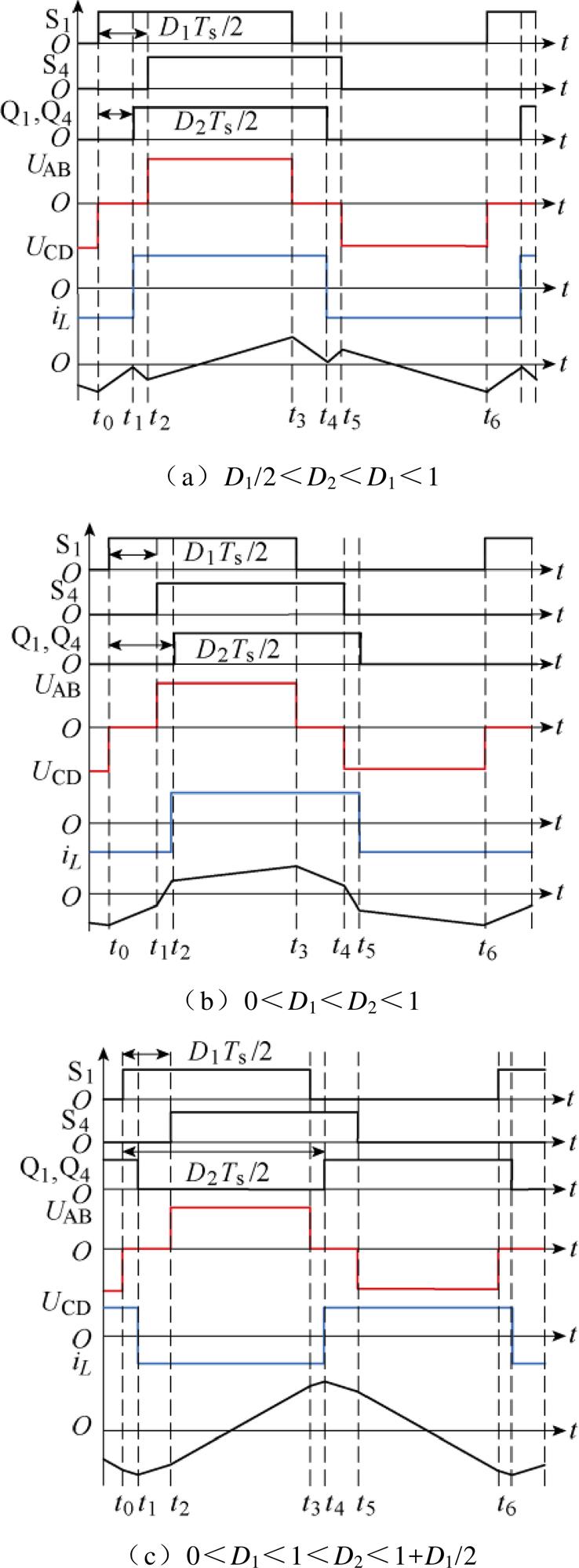
图3 DAB 变换器在EPS 调制下的波形
Fig.3 Waveforms of DAB converter based on EPS modulation
由于电感电流iL半开关周期对称,可得DAB变换器在EPS调制下,三种工作模式a、b、c半开关周期电感电流表达式分别为
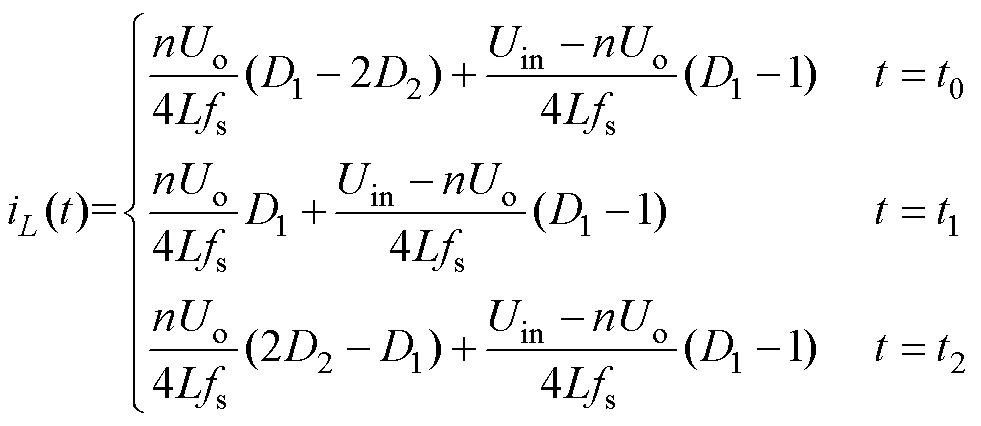 (1)
(1)
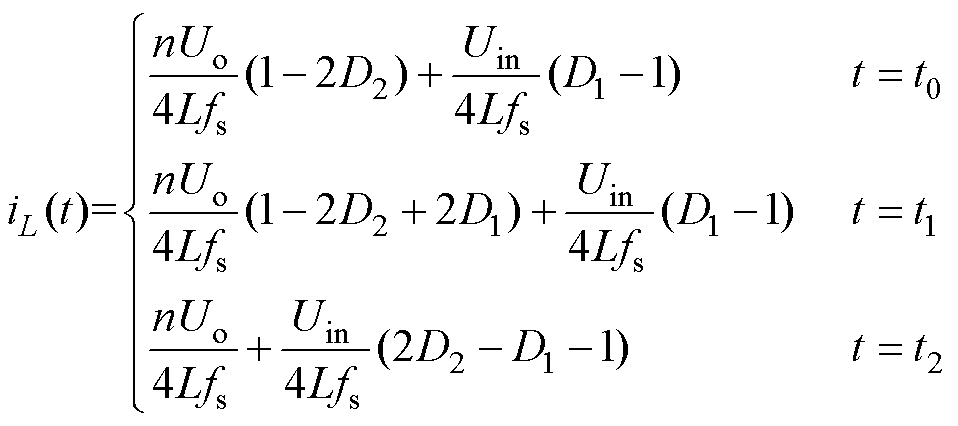 (2)
(2)
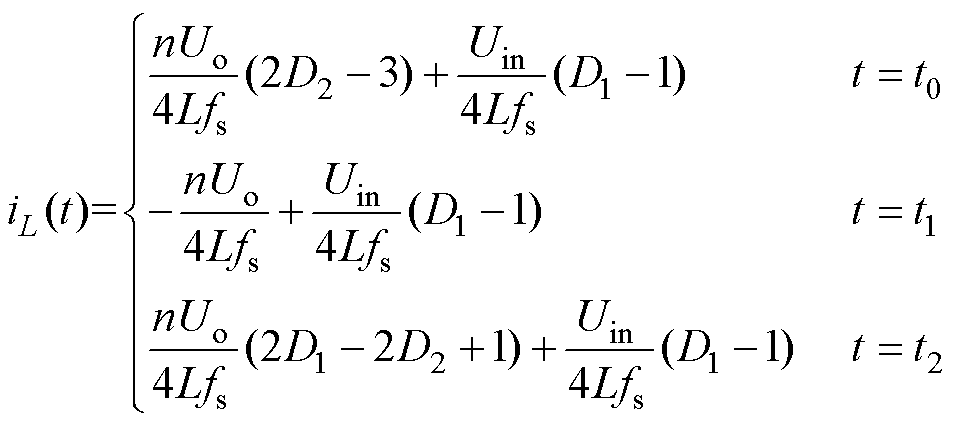 (3)
(3)
DAB变换器平均传输功率P和电流应力iP可表示为

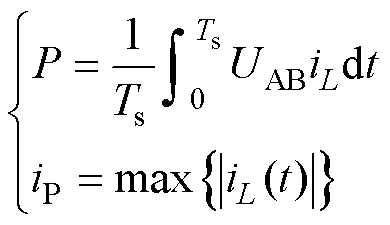 (4)
(4)
定义变换器的电压转换比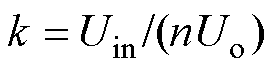 ,以Buck模式为例,规定k≥1,则DAB变换器在EPS调制下三种工作模式的平均传输功率和电流应力标幺值分别为
,以Buck模式为例,规定k≥1,则DAB变换器在EPS调制下三种工作模式的平均传输功率和电流应力标幺值分别为
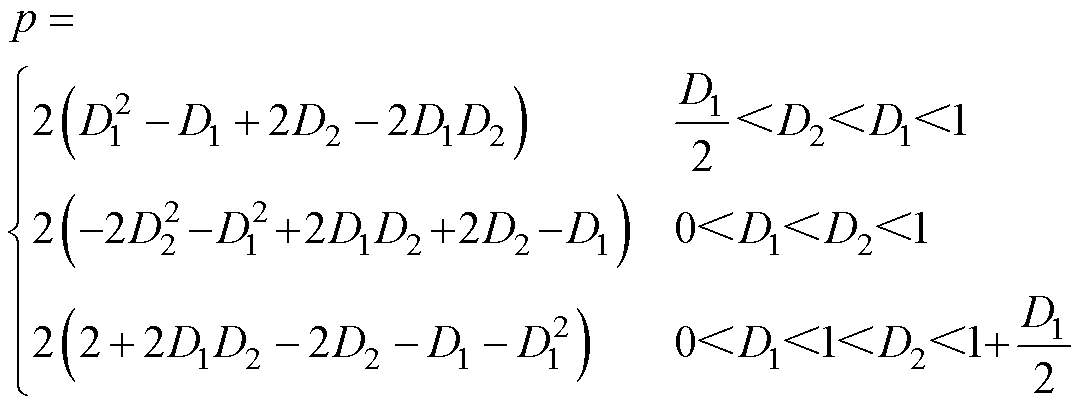 (5)
(5)
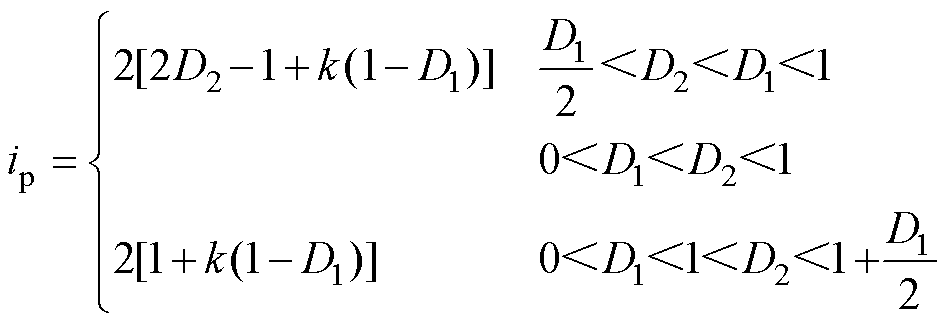 (6)
(6)
DAB变换器电感电流基准值和平均传输功率基准值分别为
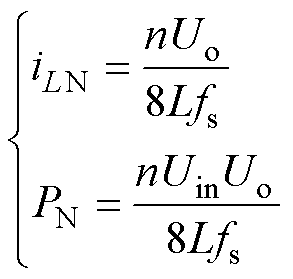 (7)
(7)
分别对式(5)中D1、D2求偏导,将所得驻点[D1, D2]与边界限制条件分别代入式(5)可求得各模式下平均传输功率取值范围,见表1。
表1 扩展移相下各模式传输功率范围
Tab.1 Power range of modes in EPS scheme

扩展移相模式平均传输功率范围 a0≤p≤0.5 b0≤p≤1 c0≤p≤0.5
相比于SPS调制,EPS调制由于加入了内移相角D1,在传输相同功率时,移相角[D1, D2]有无数种组合,故必存在一种组合[D1, D2]使得电流应力最小,需分别对EPS三种移相工作模式进行求解。
DAB变换器工作在模式a时,设给定传输功率pa=p,由式(5)可得
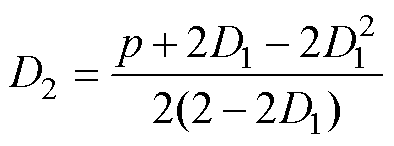 (8)
(8)
代入式(4)可得模式a下电流应力为
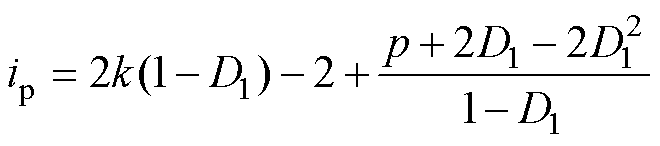 (9)
(9)
以电流应力最小为目标求取移相角组合[D1, D2],对式(9)求导有
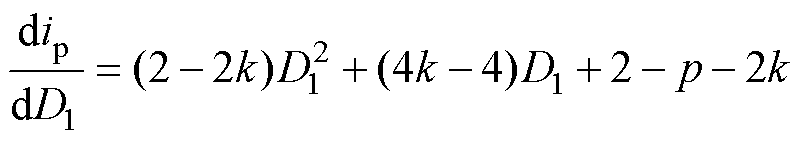 (10)
(10)
令dip/dD1=0,并代入式(8)可得
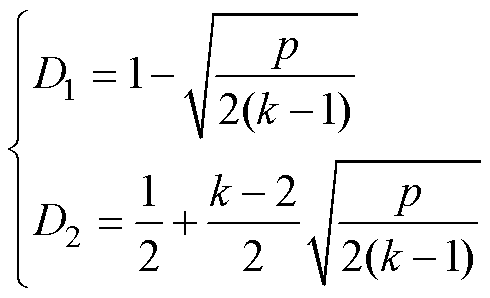 (11)
(11)
由此模式a电流应力最小值为
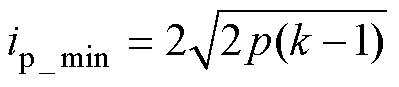 (12)
(12)
为了满足D1/2<D2<D1<1的限制条件,将式(11)代入限制条件可得传输功率标幺值p与电压比k之间的关系式为
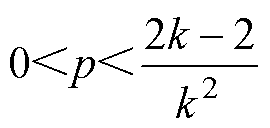 (13)
(13)
同理,当DAB变换器工作在模式b时,令pb=p,由式(5)可得
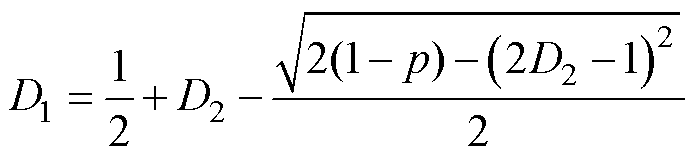 (14)
(14)
将式(14)代入式(6),可得模式b下电流应力表达式为
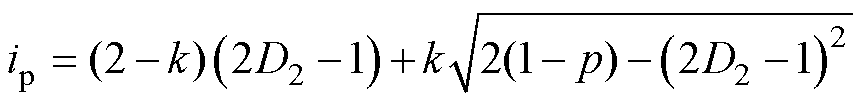 (15)
(15)
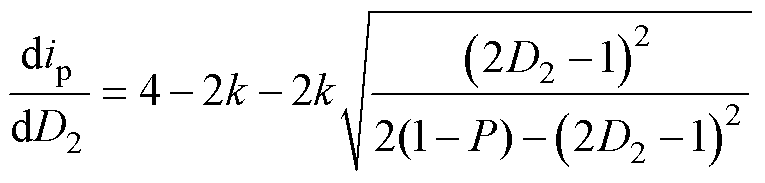 (16)
(16)
由式(14)、式(16)可得
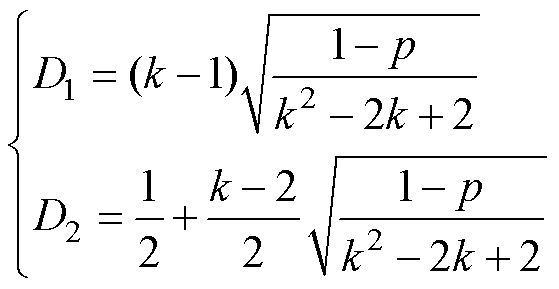 (17)
(17)
由此可知模式b下电流应力最小表达式为
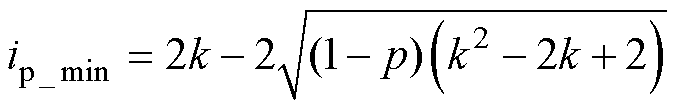 (18)
(18)
代入限制条件0<D1<D2<1有
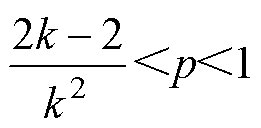 (19)
(19)
由图3模式c波形可知,UAB与UCD的乘积恒小于或等于零,即输入源Uin先向电感存储能量,再由电感向输出源Uo传输功率,不存在Uin直接向Uo传输功率的工作模态。因此,对于给定的传输功率pa=pb=pc,模式c的电流应力必定大于模式a和模式b。对于式(6)模式c可知,电流应力与内移相角D1呈负相关,即求取满足给定传输功率的内移相角D1最大值,令pc=p,可求出电流应力最小值表达式以及移相角组合[D1, D2]分别为
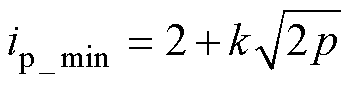 (20)
(20)
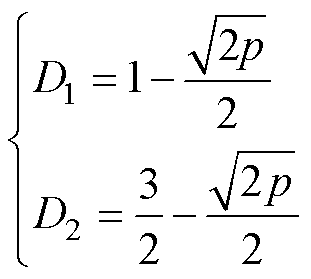 (21)
(21)
图4给出了变换器在EPS调制a、b、c三种工作模式下,传输相同功率时的电流应力最小值对比。由于模式a、模式c传输功率范围为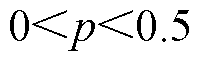 ,只需比较该范围下电流应力大小。由图4可知,传输相同功率时,模式c电流应力大于模式a与模式b组合(其工作模式切换点p=2(k-1)/k2),因此在EPS调制时,DAB变换器应避免工作在模式c。
,只需比较该范围下电流应力大小。由图4可知,传输相同功率时,模式c电流应力大于模式a与模式b组合(其工作模式切换点p=2(k-1)/k2),因此在EPS调制时,DAB变换器应避免工作在模式c。
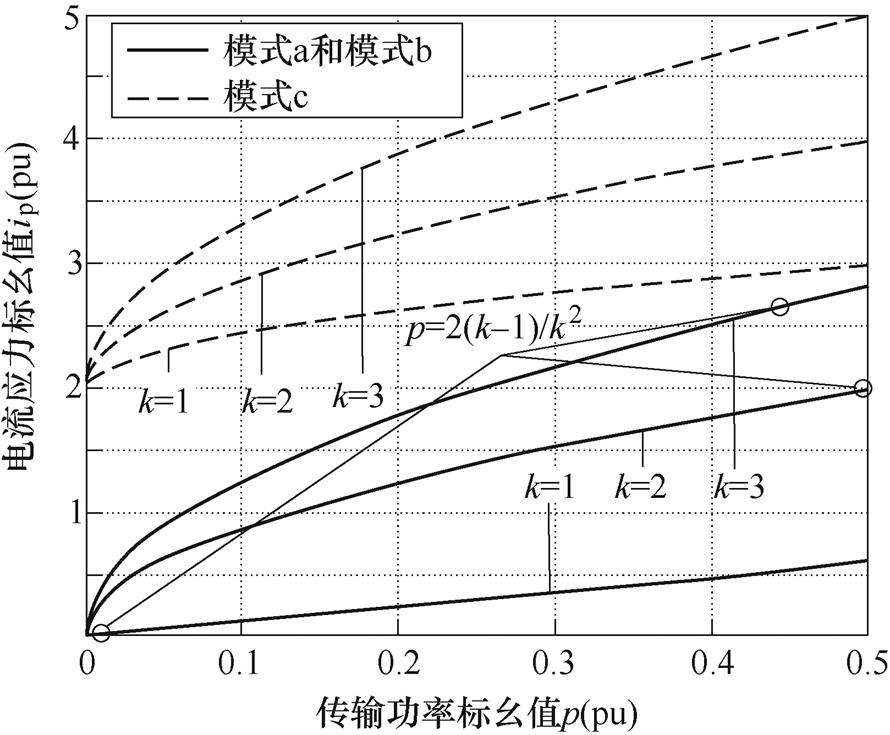
图4 EPS调制方法下的各模式电流应力曲线
Fig.4 Current stress curves in EPS modulation schemes
结合式(11)、式(12)、式(17)、式(18)可得,DAB变换器在EPS调制下的电流应力最优解移相角组合[D1, D2],以及电流应力最小值ip_min,如式(22)、式(23)所示。其中,传输功率标幺值p满足0<p<2(k-1)/k2,对应工作模式a,即D1/2<D2<D1<1;满足2(k-1)/k2<p<1,对应工作模式b,即0<D1<D2<1。
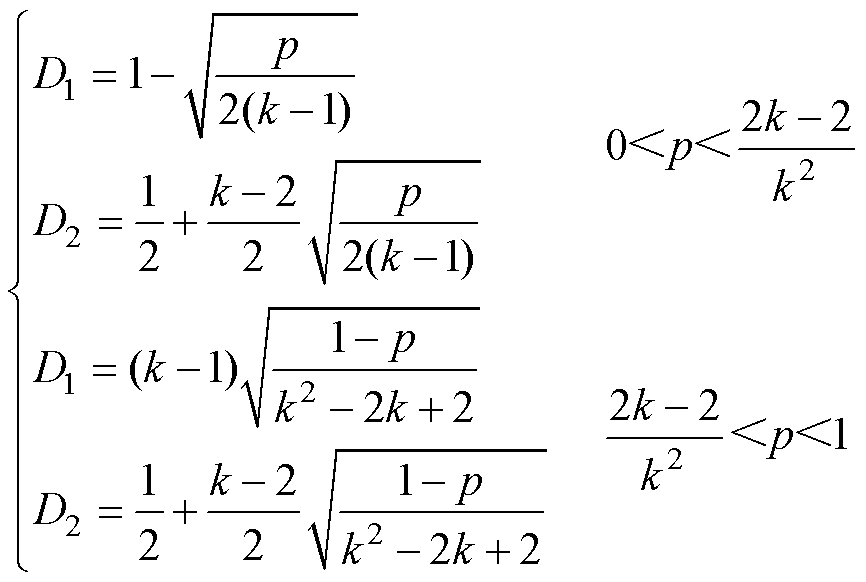 (22)
(22)
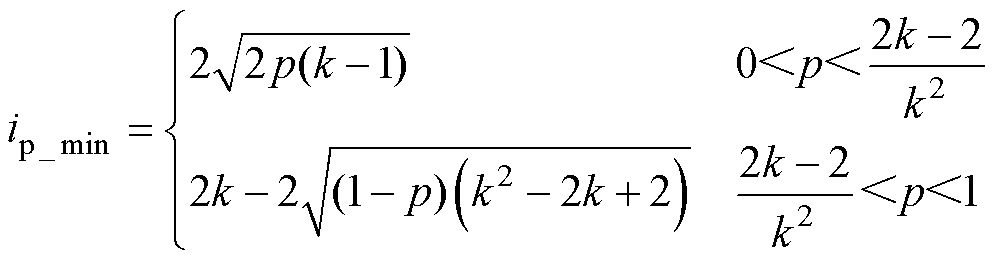 (23)
(23)
DAB变换器分别工作在SPS调制、EPS调制方案非最优[20](EPS)以及最优(OP-EPS)电流应力标幺值曲线,如图5所示。当一次、二次电压转换比k较大时,采用SPS调制,电流应力将急剧增大;相比于SPS调制,文献[20]所提出的EPS电流应力优化调制能够降低电流应力,然而由于仅考虑了0<D1<D2<1一种移相模式,因此并非EPS调制下电流应力全局最优解。本文考虑EPS调制所有工作模式,尤其当DAB变换器处于低传输功率标幺值段时,能够进一步降低电流应力,从而提升变换器效率,同时也降低了开关器件损坏风险,避免过大的电流导致电感以及变压器磁心失磁,提升变换器的安全性与可靠性。
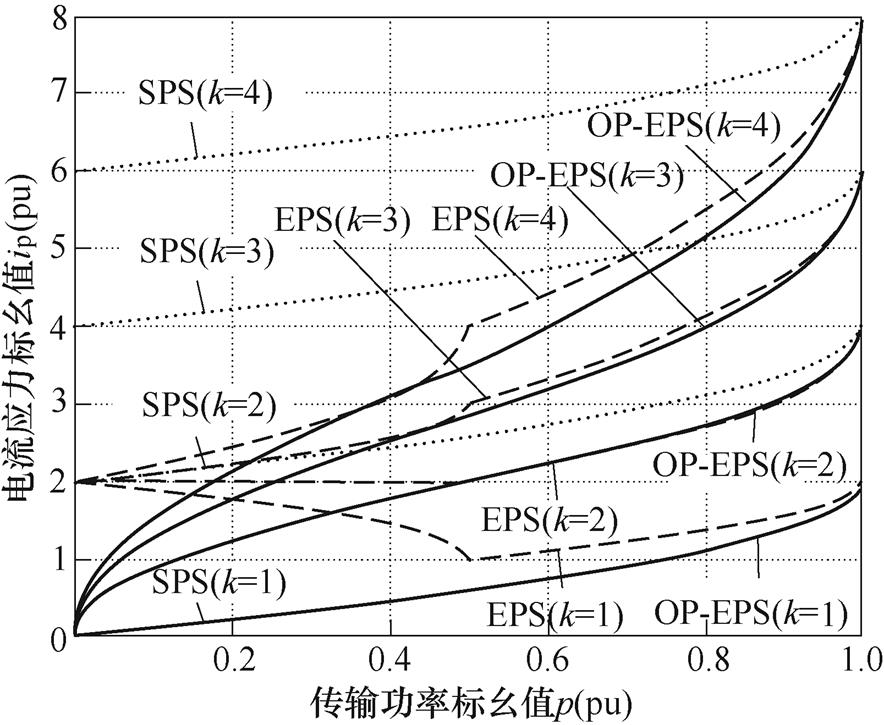
图5 SPS与EPS调制下电流应力曲线
Fig.5 Current stress curves in SPS and EPS modulation
传统的扩展移相电流应力优化算法控制框图如图6所示。该电流应力优化控制策略通过PI控制器输出桥间移相角D2以实现输出电压稳定,通过所求解的电流优化模型,输出一次侧H桥内移相角D1来实现电流应力优化。在上述算法执行中,由传输功率表达式(5)可知,传输功率标幺值p与D1、D2均有关联,故通过电流应力优化公式改变移相角D1的同时也会使得传输功率发生变化,影响输出电压稳定,系统的动态响应性能较差。
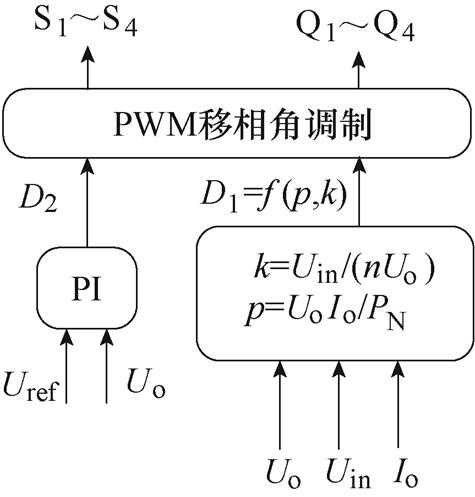
图6 扩展移相电流应力优化算法控制框图
Fig.6 Control block diagram of current stress optimizationin EPS modulation scheme
为了在减小变换器电流应力的同时提高其动态响应速度,本文引入自抗扰控制,通过观测器对输出电压进行实时估算,将D1变化视作系统扰动,并利用其前馈补偿性质,提出了一种结合电流应力优化的DAB变换器自抗扰控制方法。因ADRC仅与外移相角D2相关,故变换器仍可按SPS调制时分析,从而简化分析过程。
DAB变换器在SPS调制下的平均传输功率表达式为
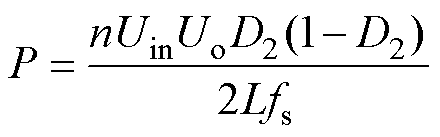 (24)
(24)
通过式(24)可求得二次侧平均输出电流,进一步求偏导即可得二次侧输出电流的小信号值为
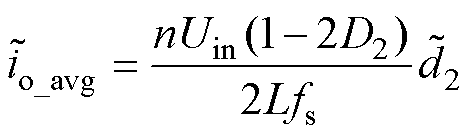 (25)
(25)
式中,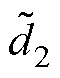 为桥间移相角D2的小信号值。对应的DAB变换器的小信号模型如图7所示。
为桥间移相角D2的小信号值。对应的DAB变换器的小信号模型如图7所示。
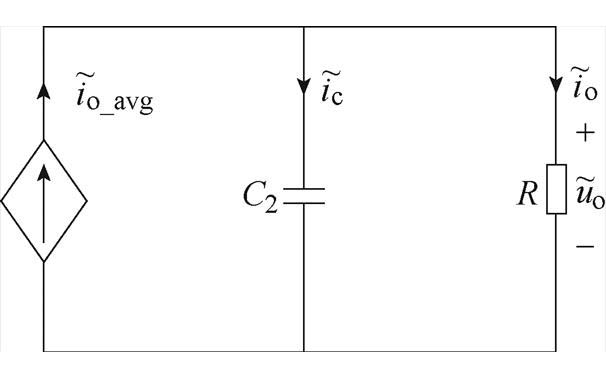
图7 DAB变换器小信号模型
Fig.7 Small-signal model of DAB converter
应用基尔霍夫电流定律即可得输出电压的动态特性微分方程为
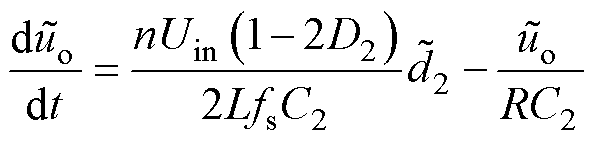 (26)
(26)
式中,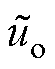 为输出电压的小信号值,可简化为
为输出电压的小信号值,可简化为
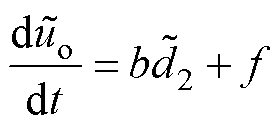 (27)
(27)
所提出的结合电流应力优化的ADRC算法控制框图,如图8所示。该控制策略通过扩张状态观测器实时观测系统内部及外部扰动,将其集总为扰动z2,并在反馈控制中补偿扰动造成的影响。将电流应力优化内移相角D1而导致的传输功率波动部分视为系统内部扰动N2,利用ADRC进行补偿,从而提升系统动态响应速度。图8中,z1、z2分别为输出电压Uo的实时估计值、扰动f的实时估计值;Kp、b0为可调参数;N1为负载、输入电压突变等系统外部扰动;N2为内移相量D1变化、系统硬件参数变化等系统内部扰动。
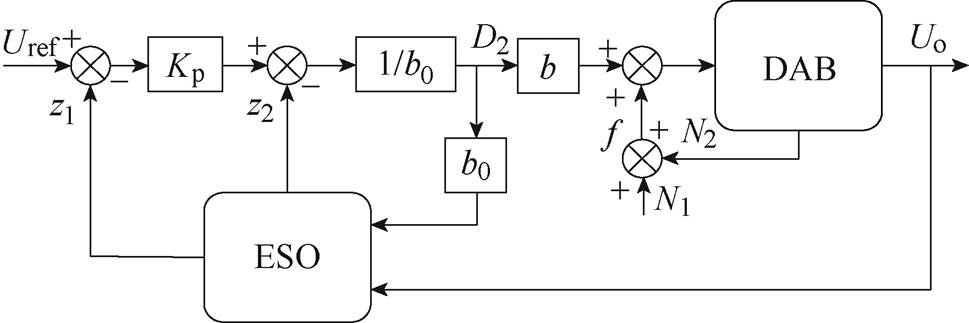
图8 EPS调制下的ADRC算法控制框图
Fig.8 Block diagram of active disturbance rejection control in EPS modulation
当b0=b时,自抗扰控制器能够获得最佳的控制效果。然而通过式(26)可知,参数b与输入电压Uin等参数相关。对此,以接近b的固定常数作为b0,尽管这增加了观测器对模型不确定性扰动的估计负担,但能够减少控制器对于参数的依赖。
由此,集总扰动f为
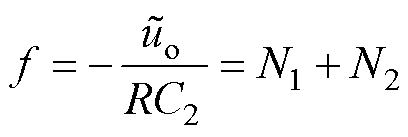 (28)
(28)
以DAB变换器为控制对象,构建观测器为
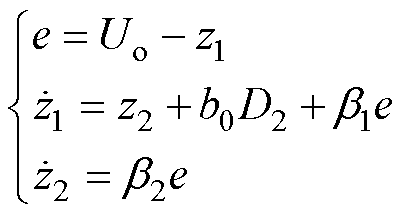 (29)
(29)
式中, 、
、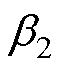 为ESO增益;e为ESO的观测误差。
为ESO增益;e为ESO的观测误差。
定义 ,
,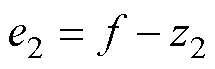 ,代入式(29)可得
,代入式(29)可得
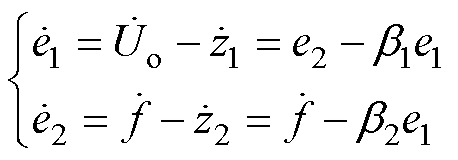 (30)
(30)
式(30)可重写为矩阵形式,即
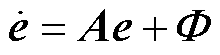 (31)
(31)
其中
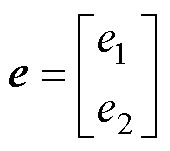
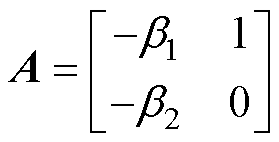
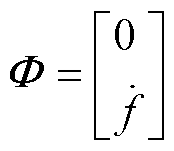
此时,如果 和
和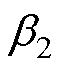 大于零,则
大于零,则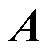 的特征多项式的根都存在于s平面的左半部,这种情况下
的特征多项式的根都存在于s平面的左半部,这种情况下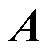 将是赫尔维兹稳定的,并且ESO的估计误差将指数收敛到0,即ESO能够准确估计输出电压Uo以及集总扰动f。
将是赫尔维兹稳定的,并且ESO的估计误差将指数收敛到0,即ESO能够准确估计输出电压Uo以及集总扰动f。
为满足数字控制的需要,利用前向欧拉公式将ESO离散化得
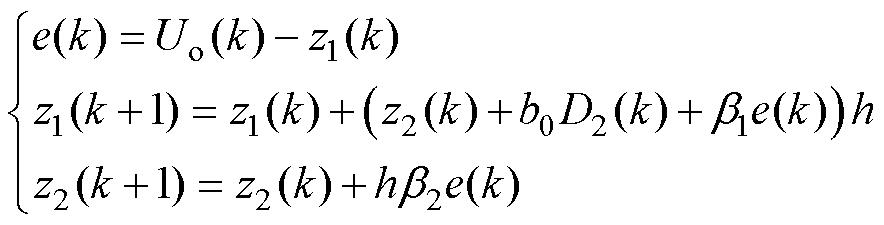 (32)
(32)
式中,h为控制器控制周期,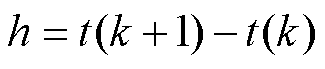 。
。
由式(32)可知,观测器性能与增益 、
、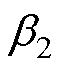 的选取相关,不同的
的选取相关,不同的 、
、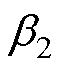 将带来不同的ESO跟踪性能与稳定性。令
将带来不同的ESO跟踪性能与稳定性。令
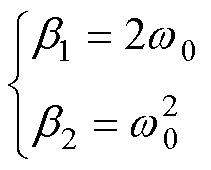 (33)
(33)
对于观测器来说,其输入信号为输出电压Uo及外移相角D2,输出信号为输出电压的估计值z1及集总扰动的估计值z2,将式(33)代入式(29),令d2=0,并做拉氏变换有
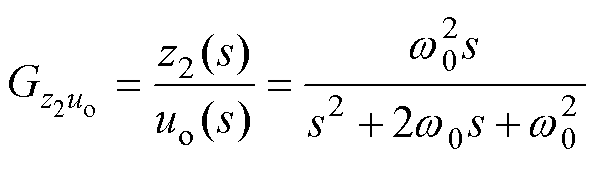 (34)
(34)
由式(27)与式(34)可得,扰动估计值z2与集总扰动f之间的传递函数为
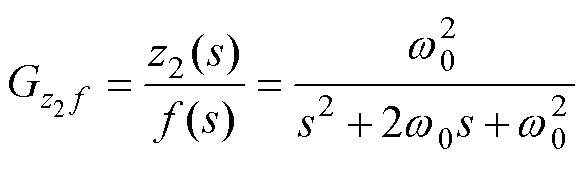 (35)
(35)
图9为ESO在不同带宽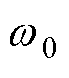 下的传递函数H(s)伯德图。由图可知,当带宽
下的传递函数H(s)伯德图。由图可知,当带宽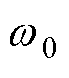 越大时,ESO的跟踪性能越好。然而,由于抗噪性与抗扰性两者之间不可避免的矛盾,
越大时,ESO的跟踪性能越好。然而,由于抗噪性与抗扰性两者之间不可避免的矛盾,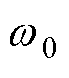 越大时,ESO的抗噪性能将减弱。因此,
越大时,ESO的抗噪性能将减弱。因此,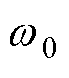 的选取应当在抗扰性与抗噪性之间权衡。本文选取
的选取应当在抗扰性与抗噪性之间权衡。本文选取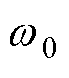 =700rad/s。
=700rad/s。
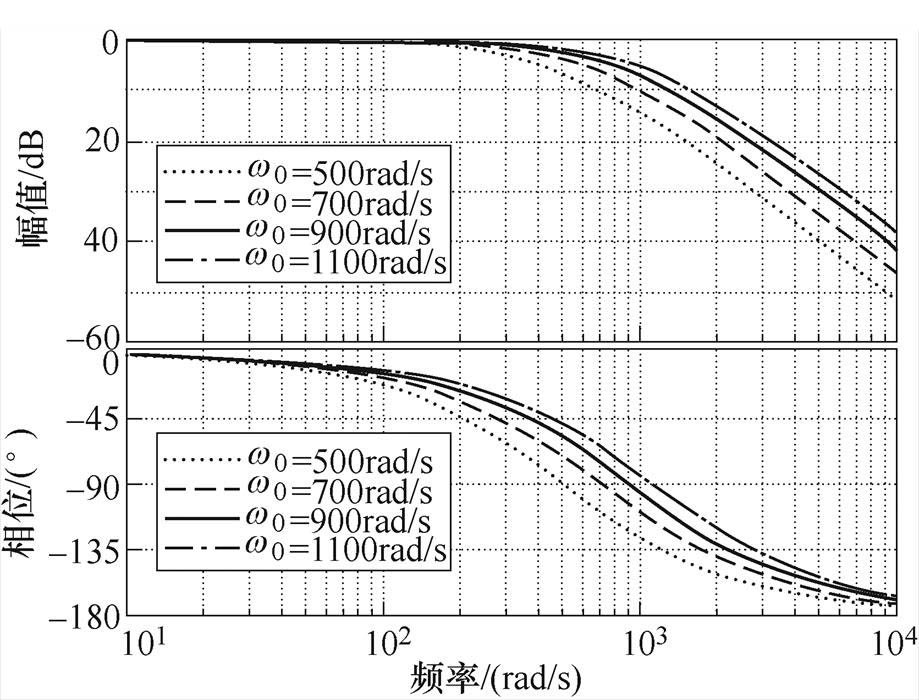
图9 传递函数H(s)的伯德图
Fig.9 Bode diagram of transfer function H(s)
ADRC控制输出桥间移相角D2为
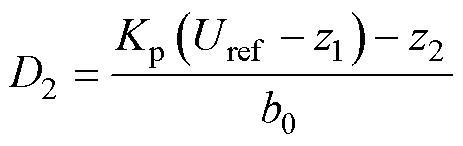 (36)
(36)
式中,Kp(Uref -z1)/b0为反馈控制分量;-z2/b0为扰动补偿分量。当ESO观测准确时,有z1=Uo、z2=f,且b0异于b部分由z2补偿,则D2为
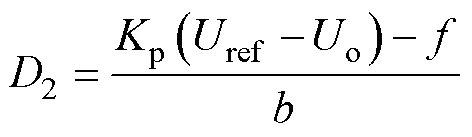 (37)
(37)
此时即可通过观测器和补偿环节将系统补偿成串级积分器系统,即无扰理想系统,增强控制器的抗扰能力,因此,仅需比例控制就能获得良好的控制效果,从而提升系统的动态性能。
结合电流应力优化的自抗扰控制算法如图10所示。采样输入电压Uin、输出电压Uo、输出电流Io,从而计算电压转换比k与传输功率标幺值p,根据p与k的大小,判断变换器工作在移相模式a或模式b,进而通过式(11)、式(17)给定内移相角D1。采样输出电压Uo,改变D1而产生功率波动、输入电压突变、负载投切等均被集总为扰动,由ESO实时估计并以前馈的方式补偿。通过式(31)给定桥间移相角D2跟踪输出电压期望值Uref,实现对电流应力及动态性能的同时优化。
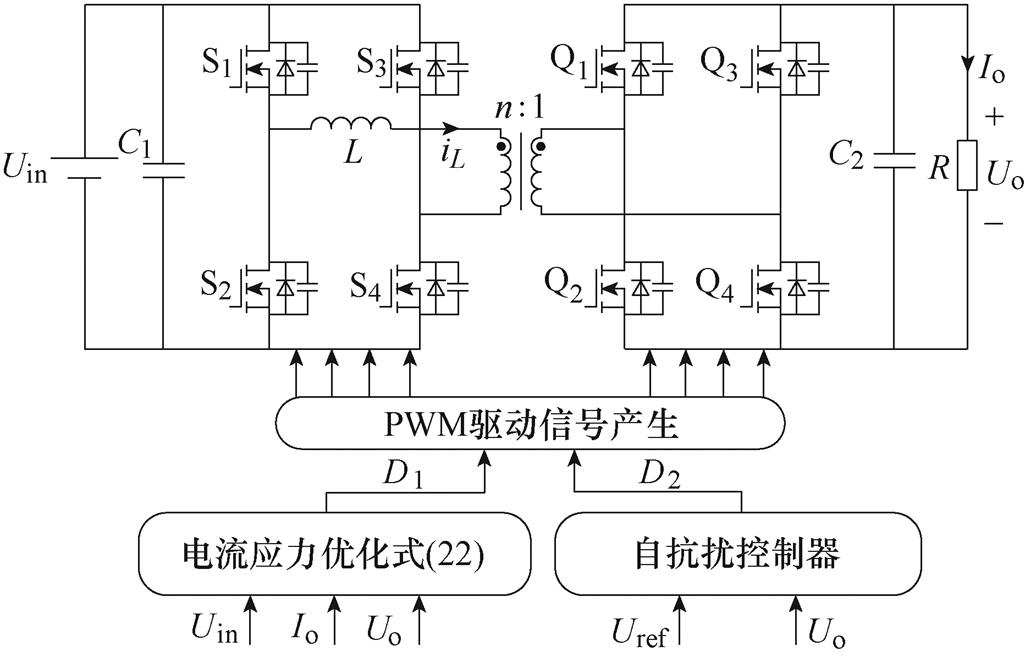
图10 结合电流应力优化的自抗扰控制算法
Fig.10 Algorithm of active disturbance rejection control combined with current stress optimization
为验证本文所提出的结合电流应力优化的自抗扰控制方法(Expanded Phase Shift-Active Distur- bance Rejection Control, EPS-ADRC)的有效性和先进性,搭建以TMS320F28069为控制核心的小功率实验样机,具体实验平台参数见表2。并与单重移相传统电压环(Single Phase Shift-Traditional Voltage Loop, SPS-TVL)、扩展移相直接功率控制(EPS- Direct Power Control, EPS-DPC)[20]以及扩展移相下采用本文电流应力优化策略,提高动态性能的固定前馈加抗饱和积分PI控制(EPS-Anti Windup PI, EPS-AWPI)作为对比。
表2 实验平台参数
Tab.2 Parameters of the experiment platform
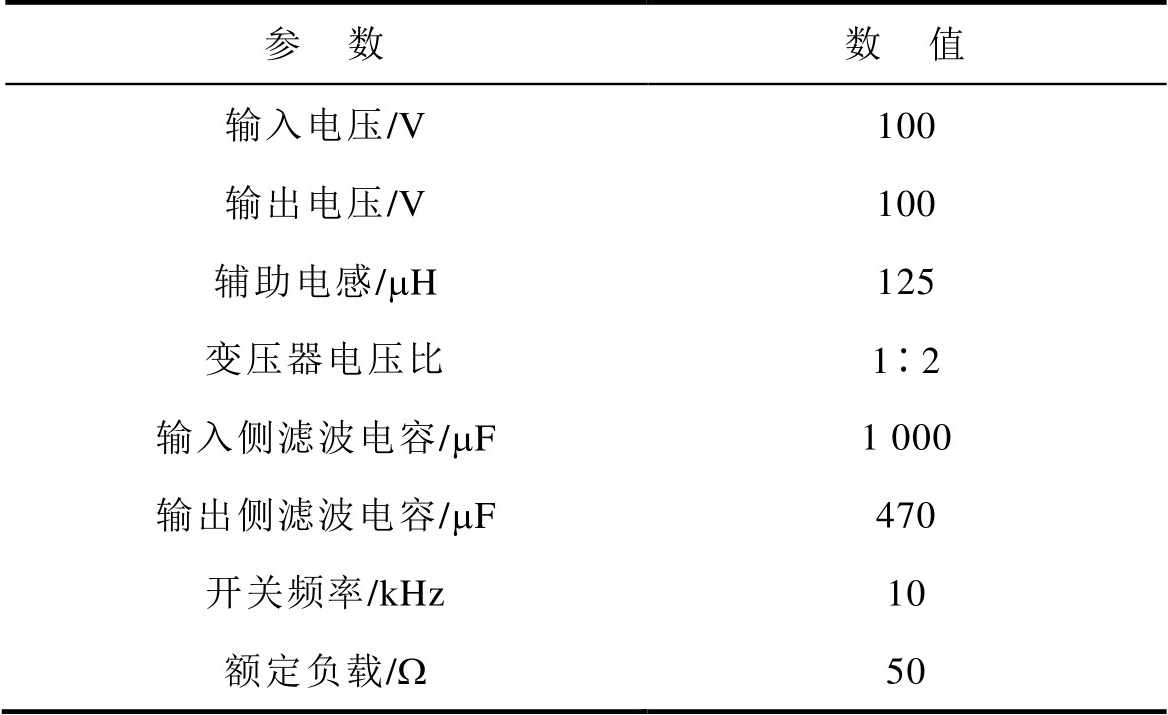
参 数数 值 输入电压/V100 输出电压/V100 辅助电感/mH125 变压器电压比12 输入侧滤波电容/mF1 000 输出侧滤波电容/mF470 开关频率/kHz10 额定负载/W50
以响应进入稳态值2%内所需要的时间作为调节时间ts。当输入电压Uin=100V、输出电压Uo=100V、负载R=50W、k=2、p=0.4(pu)时,四种不同方案的DAB变换器系统在启动过程中的输入电压、输出电压和电感电流的实验波形,如图11所示。图中,SPS- TVL方案的启动时间为85ms、超调量为12V;EPS- DPC方案的启动时间为55ms、超调量为4V;EPS- AWPI方案的启动时间为70ms、超调量为7V;相比于上述三个方案,所提出的EPS-ADRC方案的启动时间为50ms、超调量0V,因此,EPS-ADRC方案相比于其他三种方案具有更快的启动响应。
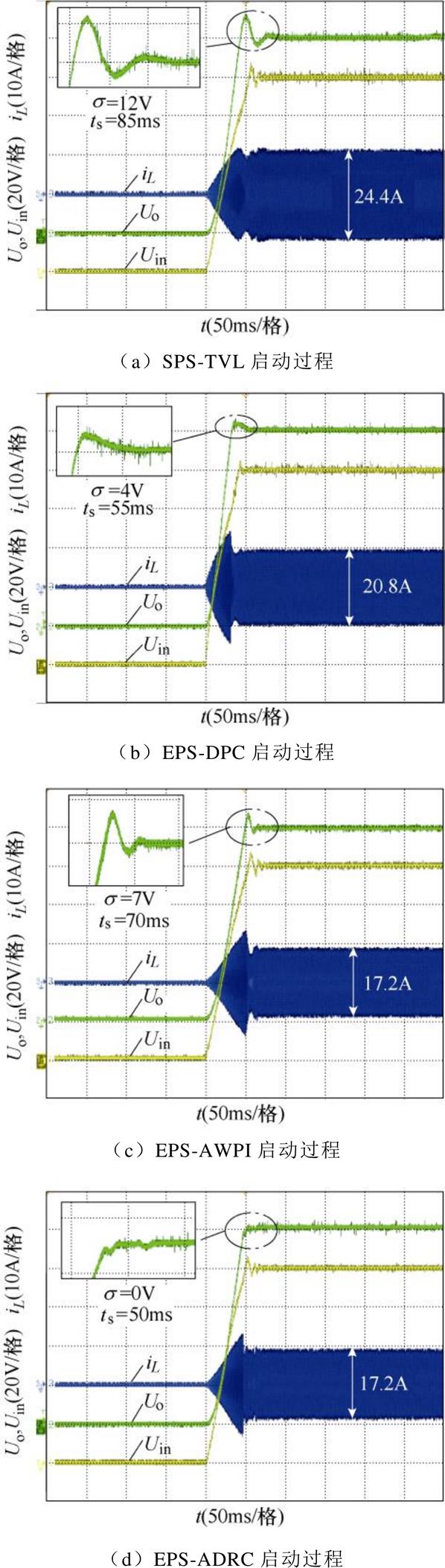
图11 四种不同方法的启动响应
Fig.11 Startup response of SPS-TVL, EPS-DPC, EPS-AWPI and EPS-ADRC control schems
四种不同方案的DAB变换器在负载50W →100W突变时的输入电压、输出电压和电感电流的实验波形,如图12所示。图中,SPS-TVL、EPS-DPC、EPS-AWPI方案的输出电压调节时间分别为32ms、20ms、15ms,输出电压波动分为6V、6V、3V;而EPS-ADRC方案输出调节时间为3ms,电压波动仅为2V。
四种不同方案的DAB变换器在负载100W →50W突变时的输入电压、输出电压和电感电流的实验波形,如图13所示。图中,SPS-TVL、EPS-DPC、EPS- AWPI方案的输出电压调节时间分别为30ms、20ms、15ms,输出电压波动分为6.5V、6V、3.5V;而所提出的EPS-ADRC方案的输出调节时间为2ms,电压波动约为2V。
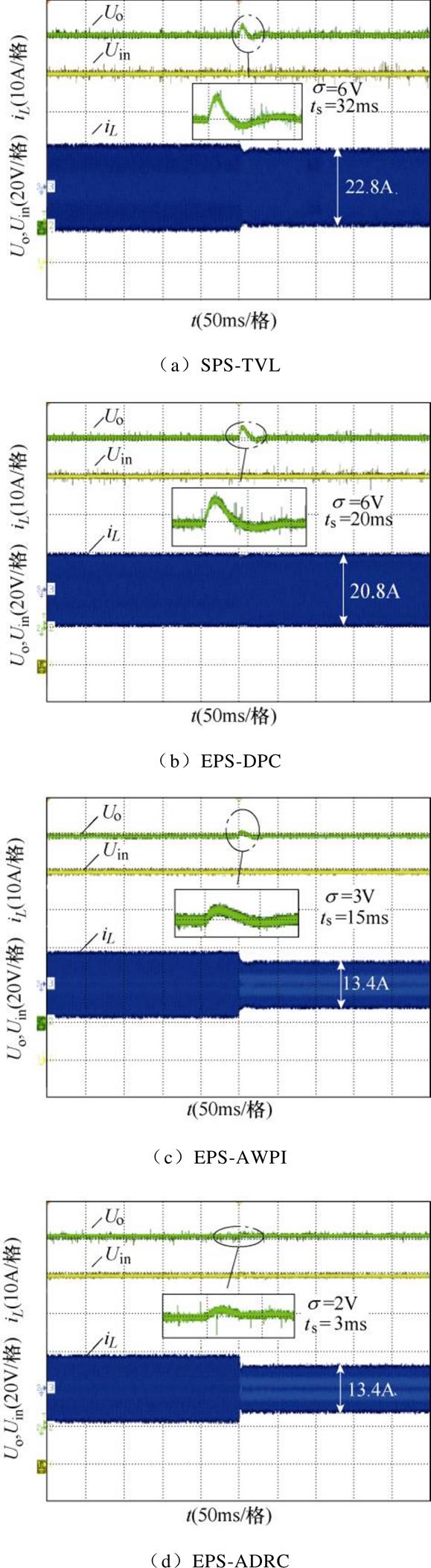
图12 四种不同方法的半载切满载响应(50W 切100W)
Fig.12 50W to 100W response of SPS-TVL, EPS-DPC, EPS-AWPI and EPS-ADRC control schems
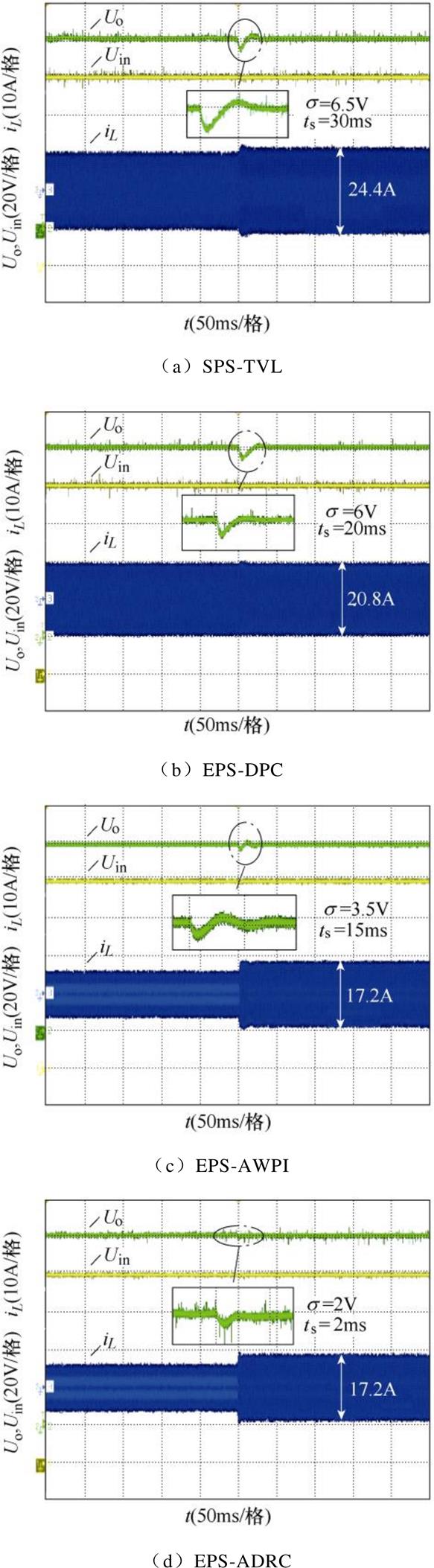
图13 四种不同方法的半载切满载响应(100W 切50W)
Fig.13 100W to 50W response of SPS-TVL, EPS-DPC, EPS-AWPI and EPS-ADRC control schems
因此,本文所提方案具有良好的抗负载扰动能力。此外,采用本文电流应力优化策略的EPS-AWPI与EPS-ADRC方案具有最小的电流应力,尤其当负载R=100W 时,EPS-ADRC采用D1/2<D2<D1<1移相工作模式,优化效果最为明显。
当输出电压Uo=100V、负载R=50W、输入电压由100V→70V变化时,四种不同方案的输入电压、输出电压和电感电流的实验波形,如图14所示。在输入电压突变时,SPS-TVL、EPS-DPC、EPS-AWPI方案的输出电压调节时间分别为50ms、20ms、30ms,输出电压波动分为4.5V、3V、4.5V;而本文方案调节时间为19ms、电压波动约为2V。可看出EPS-DPC与本文方案在输入电压突变时动态响应均较好。
此外,表3还给出了本文所提控制策略与输入电压前馈的虚拟功率控制[17]、模型预测控制策略[19]的性能对比。其中,采用输入电压前馈的虚拟功率控制在负载突增、突减时的输出电压波动为6V、5V,调节时间为60ms、58ms;采用模型预测控制在负载突减时输出电压波动为2.6V、调节时间26ms,负载突增并未给出相关数据;本文所提出的方案在负载突增、突减时输出电压波动分别为2V、2V,调节时间为3ms、2ms。在输入电压突变时,模型预测控制的动态响应为2.1V、34ms,本文所提出的方案为2V、19ms,同时,在启动过程中,本文方案的动态响应也仅为0V、50ms。因此,本文方案在启动过程、负载突变、输入电压突变时均具有良好的动态性能。
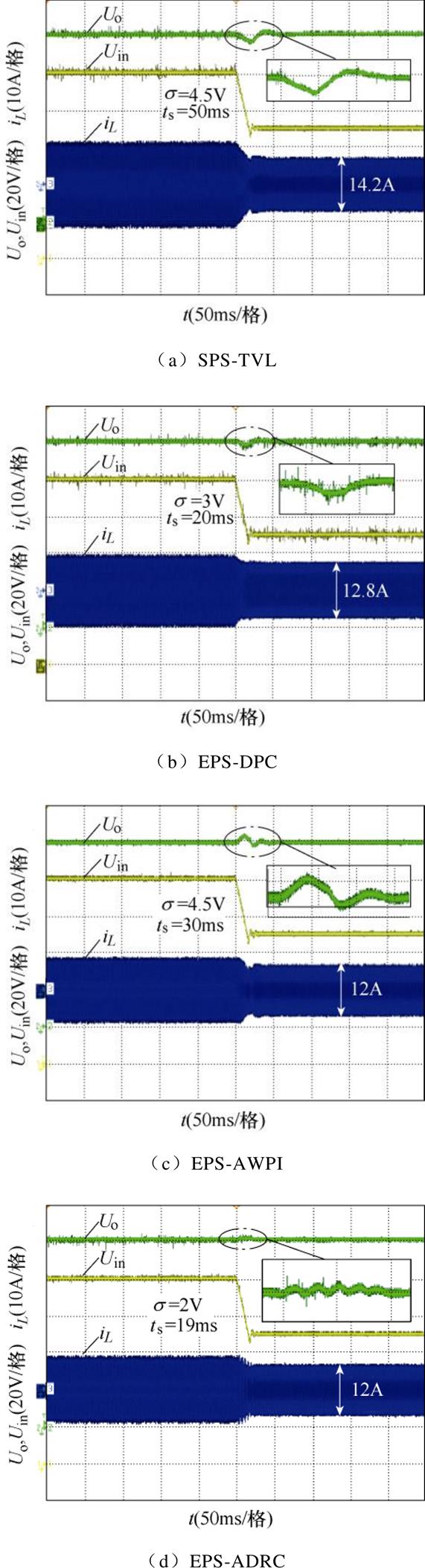
图14 四种不同方案的输入电压突变响应
Fig.14 Input voltage step change response of SPS-TVL, EPS-DPC, EPS-AWPI and EPS-ADRC control schems
表3 不同文献的控制策略对比
Tab.3 Comparison of different literature control strategies
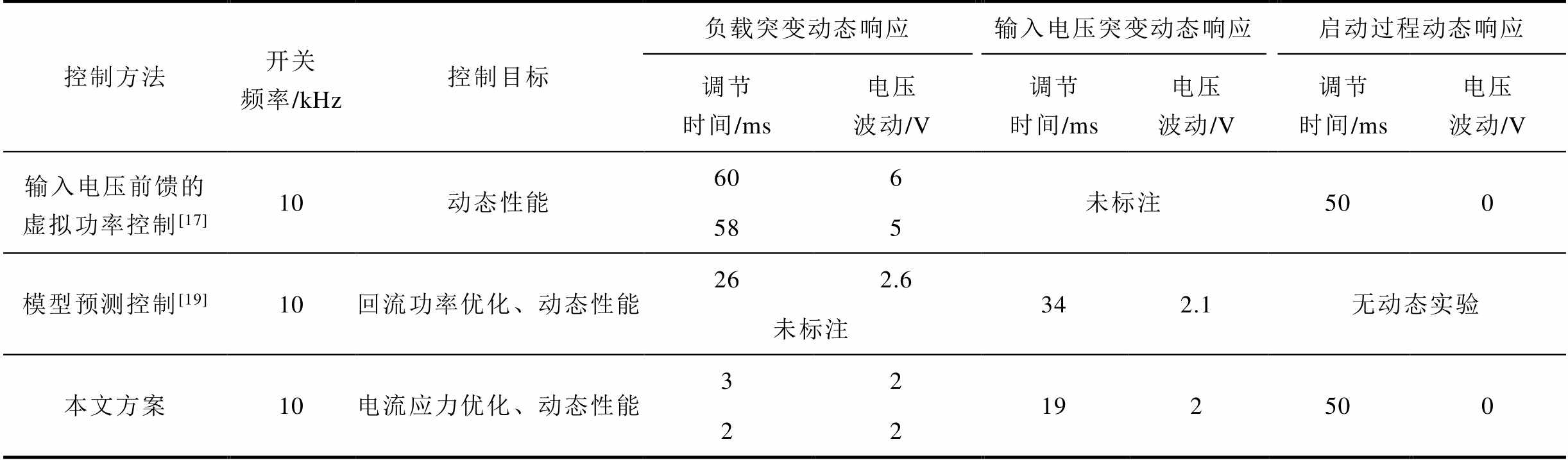
控制方法开关频率/kHz控制目标负载突变动态响应输入电压突变动态响应启动过程动态响应 调节时间/ms电压波动/V调节时间/ms电压波动/V调节时间/ms电压波动/V 输入电压前馈的虚拟功率控制[17]10动态性能606未标注500 585 模型预测控制[19]10回流功率优化、动态性能262.6342.1无动态实验 未标注 本文方案10电流应力优化、动态性能32192500 22
当输入电压Uin=100V、输出电压Uo=100V、负载R=100W,即k=2,p=0.2(pu)时的三种控制方案下辅助电感两端交流输出电压UAB、UCD以及电感电流iL的实验波形,如图15所示。在SPS-TVL、EPS-DPC、EPS-ADRC方案下,变换器电流应力分别为11.4A、10.4A、6.7A,本文所提出的电流应力优化方法有效地降低了电流应力。
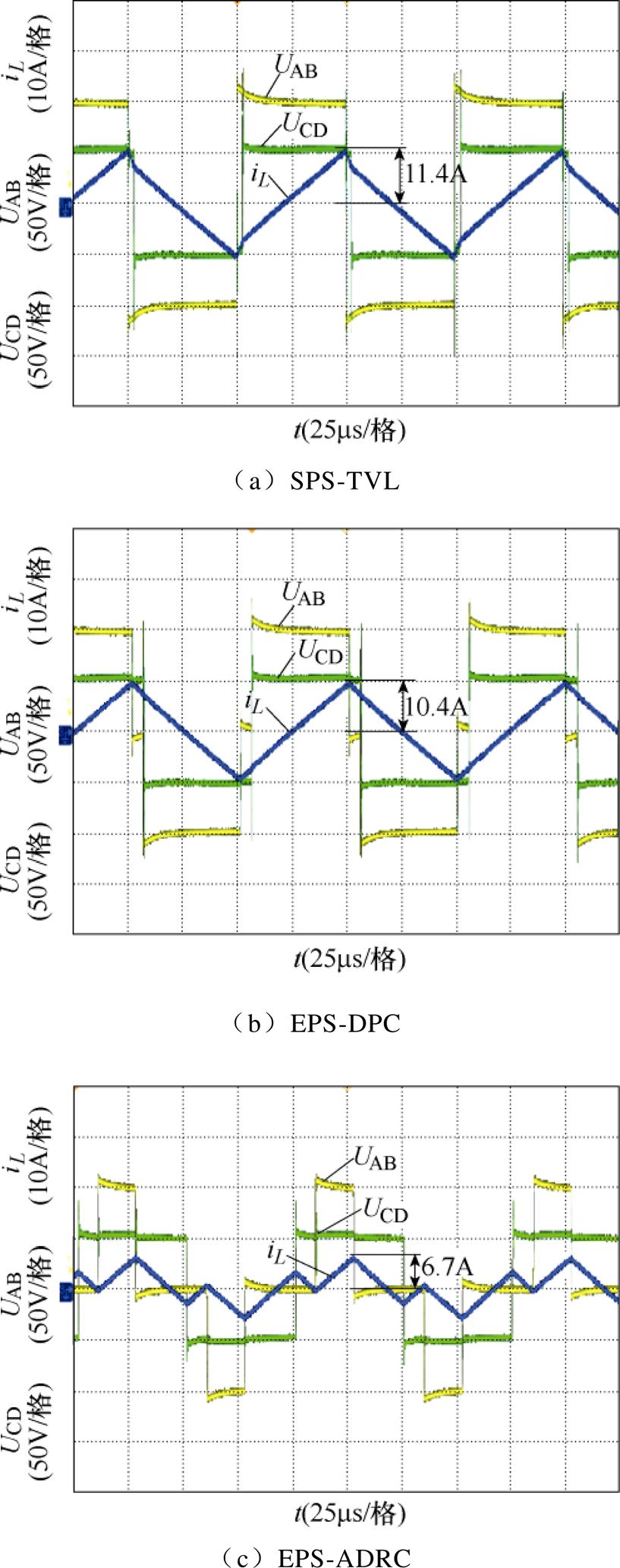
图15 k=2, p=0.2(pu)时电压电流波形
Fig.15 Voltage and current waveforms when k=2, p=0.2(pu)
当Uin=125V、Uo=100V、R=80W,即k=2.5, p= 0.2(pu)时三种方案下的电电压电流实验波形,如图16所示。在SPS-TVL、EPS-DPC、EPS-ADRC方案下,变换器电流应力分别为15.8A、10.2A、8.4A,验证了本文方案在不同电压比k下仍具有更小的电流应力。
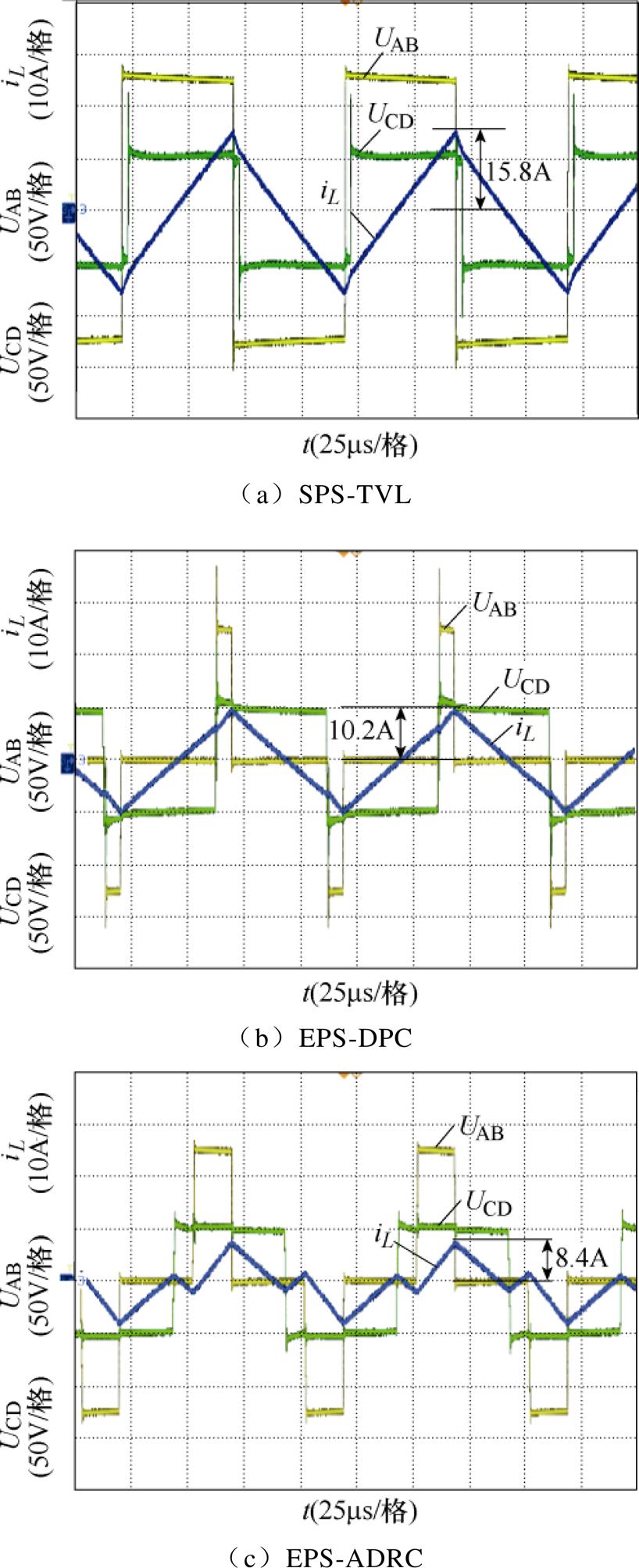
图16 k=2.5, p=0.2(pu)时电压电流波形
Fig.16 Voltage and current waveforms when k=2.5, p=0.2(pu)
当Uo=100V、R=50W、输入电压逐渐从70V递增至120V时,电压比k逐渐从1.4递增至2.4。图17给出了输入电压与电流应力、传输效率之间的关系。可知本文方案电流应力始终最低、传输效率始终最高,且随着输入电压递增,电流应力优化效果愈显著,变换器效率最高可达到96.2%。
当Uo=100V、Uin=100V时,图18为传输功率递增时,三种方案的效率关系曲线。SPS-TVL、EPS-DPC、EPS-ADRC三种方案传输效率逐渐递增,可知在任意传输功率标幺值段,本文方案电流应力优化效果始终最好。

图17 输入电压递增时的电流应力以及效率曲线
Fig.17 Current stress and efficiency curves with increasing input voltage

图18 传输功率递增时的效率曲线
Fig.18 Efficiency curves with increasing transmission power
本文对双有源全桥DC-DC变换器在扩展移相调制时的功率及电流应力进行了分析建模,求解了不同工作模式下的最优电流应力组合;提出了结合电流应力优化的自抗扰控制,通过扩张状态观测器对输出电压等扰动进行实时观测估算并补偿,提升变换器的动态性能。最后,通过与单重移相传统电压环控制、扩展移相直接功率控制对比实验验证,理论和实验一致性高,结果表明:
1)相比于单重移相调制,扩展移相调制在传输相同功率的同时,能够对稳态目标进行优化。且变换器应避免工作在0<D1<1<D2<1+D1/2移相模式下(即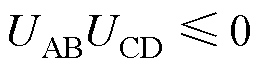 恒成立),该结论可推广至双重移相与三重移相调制。
恒成立),该结论可推广至双重移相与三重移相调制。
2)本文所提出的基于扩展移相调制的电流应力优化算法具有最小的电流应力,降低了对开关器件的耐流值要求,提高了变换器的安全性与可靠性,同时有效地提高了变换器效率。
3)所提出的结合电流应力优化的自抗扰方案在启动过程、输入电压突变、负载突变时,均具有良好的动态响应。构建的自抗扰控制器无需对象精确模型,仅需采样输出电压信息,具有控制简单、鲁棒性与适用性强等优点。
参考文献
[1] Sandler S, Williams E, Hittinger E, et al. The non- linear shift to renewable microgrids: phase transitions in electricity systems[J]. International Journal of Energy Research, 2021, 45(2): 3016-3030.
[2] 李涛, 胡维昊, 李坚, 等. 基于深度强化学习算法的光伏-抽蓄互补系统智能调度[J]. 电工技术学报, 2020, 35(13): 2757-2768.
Li Tao, Hu Weihao, Li Jian, et al. Intelligent economic dispatch for PV-PHS integrated system: a deep reinforcement learning-based approach[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2757-2768.
[3] Xing Zhang, Wang Mingda, Zhao Tao, et al. Topolo- gical comparison and analysis of medium-voltage and high-power direct-linked PV inverter[J]. CES Transa- ctions on Electrical Machines and Systems, 2019, 3(4): 327-334.
[4] Jiang Jiahui, Zhang Tao, Chen Daolian. Analysis, design and implementation of a differential power processing DMPPT with multiple Buck-Boost choppers for photovoltaic module[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(9): 10214- 10223.
[5] Hou Nie, Li Yunwei. Overview and comparison of modulation and control strategies for non-resonant single-phase dual-active-bridge DC-DC converter[J]. IEEE Transactions on Power Electronics, 2019, 35(3): 3148-3172.
[6] 张勋, 王广柱, 商秀娟, 等. 双向全桥DC-DC变换器回流功率优化的双重移相控制[J]. 中国电机工程学报, 2016, 36(4): 1090-1097.
Zhang Xun, Wang Guangzhu, Shang Xiujuan, et al. An optimized strategy based on backflow power of bi-directional dual-active-bridge DC-DC converters with dual-phase-shifting control[J]. Proceedings of the CSEE, 2016, 36(4): 1090-1097.
[7] 曾进辉, 孙志峰, 雷敏, 等. 双重移相控制的双主动全桥变换器全局电流应力分析及优化控制策略[J]. 电工技术学报, 2019, 34(12): 2507-2518.
Zeng Jinhui, Sun Zhifeng, Lei Min, et al. Global current stress analysis and optimal control strategy of dual-active full bridge converter based on dual phase shift control[J]. Transactions of China Electro- technical Society, 2019, 34(12): 2507-2518.
[8] 涂春鸣, 管亮, 肖凡, 等. 基于扩展移相控制下双有源桥移相角优化选取与分析[J]. 电工技术学报, 2020, 35(4): 850-861.
Tu Chunming, Guan Liang, Xiao Fan, et al. Parameter optimization selection and analysis of dual active bridge based on extended phase shift control[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 850-861.
[9] 张勋, 王广柱, 王婷. 双向全桥 DC-DC变换器基于电感电流应力的双重移相优化控制[J]. 电工技术学报, 2016, 31(22): 100-106.
Zhang Xun, Wang Guangzhu, Wang Ting. Optimized control based on current-stress of bi-directional full- bridge DC-DC converters with dual phase shifting control[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 100-106.
[10] Huang Jun, Wang Yue, Li Zhuoqiang, et al. Unified triple-phase-shift control to minimize current stress and achieve full soft-switching of isolated bidire- ctional DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4169-4179.
[11] Hou Nie, Song Wensheng, Wu Mingyi. Minimum- current-ctress scheme of dual active bridge DC-DC converter with unified-phase-shift control[J]. IEEE Transactions on Power Electronics, 2016, 31(12): 8552-8561.
[12] Xu Guo, Li Liting, Chen Xiaoying, et al. Optimized EPS control to achieve full load range ZVS with seamless transition for dual active bridge con- verters[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(9): 8379-8390.
[13] Tong Anping, Hang Lijun, Li Guojie, et al. Modeling and analysis of a dual-active-bridge-isolated bidire- ctional DC/DC converter to minimize RMS current with whole operating range[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5302-5316.
[14] 胡燕, 张宇, 张天晖, 等. 考虑不同软开关模式的双有源桥变换器电流应力优化方法[J]. 电力系统自动化, 2019, 43(23): 58-68.
Hu Yan, Zhang Yu, Zhang Tianhui, et al. Optimi- zation method of current stress for dual active bridge converter considering different soft switching modes[J]. Automation of Electric Power Systems, 2019, 43(23): 58-68.
[15] 胡燕, 张天晖, 杨立新, 等. 双重移相DAB变换器回流功率优化与电流应力优化的对比研究[J]. 中国电机工程学报, 2020, 40(增刊1): 243-253.
Hu Yan, Zhang Tianhui, Yang Lixin, et al. Com- parative study of reactive power optimization and current stress optimization of DAB converter with dual phase shift control[J]. Proceedings of the CSEE, 2020, 40(S1): 243-253.
[16] 侯聂, 宋文胜, 武明义. 双向全桥DC-DC变换器的负载电流前馈控制方法[J]. 中国电机工程学报, 2016, 36(9): 2478-2485.
Hou Nie, Song Wensheng, Wu Mingyi. A load current feedforward control scheme of dual active bridge DC/DC converters[J]. Proceedings of the CSEE, 2016, 36(9): 2478-2485.
[17] 宋文胜, 杨柯欣, 安峰, 等. 基于输入电压前馈的双向有源桥式 DC-DC变换器虚拟功率控制方法[J]. 中国电机工程学报, 2018, 38(22): 6491-6502.
Song Wensheng, Yang Kexin, An Feng, et al. Virtual power control scheme of dual active bridge DC-DC converters based on input voltage feedforward[J]. Proceedings of the CSEE, 2018, 38(22): 6491-6502.
[18] Chen Linglin, Gao Fei, Shen Ke, et al. Predictive control based DC microgrid stabilization with the dual active bridge converter[J]. IEEE Transactions on Industrial Electronics, 2020, 67(10): 8944-8956.
[19] 周兵凯, 杨晓峰, 张智, 等. 能量路由器中双有源桥直流变换器多目标优化控制策略[J]. 电工技术学报, 2020, 35(14): 3030-3040.
Zhou Bingkai, Yang Xiaofeng, Zhang Zhi, et al. Multi-objective optimization control strategy of dual- active-bridge DC-DC converter in electric energy router application[J]. Transactions of China Electro- technical Society, 2020, 35(14): 3030-3040.
[20] Hou Nie, Song Wensheng, Zhu Yutong, et al. Dynamic and static performance optimization of dual active bridge DC-DC converters[J]. Journal of Modern Power Systems and Clean Energy, 2018, 6(3): 607-618.
[21] 安峰, 杨柯欣, 王嵩, 等. 基于模型前馈的双有源全桥DC-DC变换器电流应力优化方法[J]. 电工技术学报, 2019, 34(14): 2946-2956.
An Feng, Yang Kexin, Wang Song, et al. Current stress optimized scheme with model-based feedfor- ward for dual-active-bridge DC-DC converters[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2946-2956.
[22] 郭华越, 张兴, 赵文广, 等. 扩展移相控制的双有源桥DC-DC变换器的优化控制策略[J]. 中国电机工程学报, 2019, 39(13): 3889-3898.
Guo Huayue, Zhang Xing, Zhao Wenguang, et al. Optimal control strategy of dual active bridge DC-DC converters with extended-phase-shift control[J]. Pro- ceedings of the CSEE, 2019, 39(13): 3889-3898.
[23] Han Jingqing. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.
Active Disturbance Rejection Control of Dual-Active-Bridge DC-DC Converter with Current Stress Optimization
Abstract Aiming at bi-directional DC-DC converter in microgrid system needs to have excellent steady-state characteristics and dynamic response at the same time, this paper proposes an active disturbance rejection control scheme of dual active bridge (DAB) DC-DC converter combined with current stress optimization. And the key technologies, such as the mathematical model of transmission power and current stress, the combination of current stress optimization and active disturbance rejection control, are analyzed. On the basis of extended phase-shift modulation, the optimal solution of current stress in different working modes is solved by the conditional extreme value method. The extended state observer is used to estimate the system state in real-time. The input voltage mutation, load switching, transmission power fluctuation caused by current stress optimization strategy are regarded as system disturbances and compensated. Finally, a set of 200W prototype is designed and developed. The experimental results verify the feasibility and advancement of the proposed control scheme.
keywords:Active disturbance rejection control, dynamic response, current stress optimization, dual-active-bridge DC-DC converters, extended-phase-shift modulation
DOI: 10.19595/j.cnki.1000-6753.tces.210809
中图分类号:TM46
山东省自然科学基金项目(ZR2019QEE004)和福州市科技计划项目(2019-G-44)资助。
收稿日期 2021-06-07
改稿日期 2021-08-14
王 武 男,1973年生,教授,硕士生导师,研究方向为电力电子建模。E-mail: wangwu@fzu.edu.com
蔡逢煌 男,1976年生,教授,硕士生导师,研究方向为电力电子变换技术。E-mail: caifenghuang@fzu.edu.cn(通信作者)
(编辑 陈 诚)